prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
```
# Putting the initialisation at the top now!
import veneer
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
v = veneer.Veneer(port=9876)
```
# Session 6 - Model Setup and Reconfiguration
This session covers functionality in Veneer and veneer-py for making larger changes to model setup, including structural changes.
Using this functionality, it is possible to:
* Create (and remove) nodes and links
* Change model algorithms, such as changing links from Straight Through Routing to Storage Routing
* Assign input time series to model variables
* Query and modify parameters across similar nodes/links/catchments/functional-units
## Overview
- (This is a Big topic)
- Strengths and limitations of configuring from outside
- +ve repeatability
- +ve clarity around common elements - e.g. do one thing everywhere, parameterised by spatial data
- -ve feedback - need to query the system to find out what you need to do vs a GUI that displays it
- Obvious and compelling use cases
- Catchments: Applying a constituent model everywhere and assigning parameters using spatial data
- Catchments: Climate data
- How it works:
- The Python <-> IronPython bridge
- What’s happening under the hood
- Layers of helper functions
- How to discover parameters
- Harder examples (not fully worked)
- Creating and configuring a storage from scratch
- Extending the system
## Which Model?
**Note:** This session uses `ExampleProject/RiverModel2.rsproj`. You are welcome to work with your own model instead, however you will need to change the notebook text at certain points to reflect the names of nodes, links and functions in your model file.
## Warning: Big Topic
This is a big topic and the material in this session will only touch on some of the possibilities.
Furthermore, its an evolving area - so while there is general purpose functionality that is quite stable, making the functionality easy to use for particular tasks is a case by case basis that has been tackled on an as-needed basis. **There are lots of gaps!**
## Motivations, Strengths and Limitations of Scripting configuration
There are various motivations for the type of automation of Source model setup described here. Some of these motivations are more practical to achieve than others!
### Automatically build a model from scratch, using an executable 'recipe'
Could you build a complete Source model from scratch using a script?
In theory, yes you could. However it is not practical at this point in time using Veneer. (Though the idea of building a catchments-style model is more foreseeable than building a complex river model).
For some people, building a model from script would be desirable as it would have some similarities to configuring models in text files as was done with the previous generation of river models. A script would be more powerful though, because it has the ability to bring in adhoc data sources (GIS layers, CSV files, etc) to define the model structure. The scripting approach presented here wouldn't be the most convenient way to describe a model node-by-node, link-by-link - it would be quite cumbersome. However it would be possible to build a domain-specific language for describing models that makes use of the Python scripting.
### Automate bulk changes to a model
Most of the practical examples to date have involved applying some change across a model (whether that model is a catchments-style geographic model or a schematic style network). Examples include:
* **Apply a new constituent generation model:** A new generation model was being tested and needed to be applied to every catchment in the model. Some of the parameters would subsequently be calibrated (using PEST), but others needed to be derived from spatial data.
* **Add and configure nodes for point source inputs:** A series of point sources needed to be represented in the models. This involved adding inflow nodes for each point source, connecting those inflows to the most appropriate (and available) downstream node and computing and configuring time series inputs for the inflows.
* **Bulk rename nodes and links based on a CSV file:** A complex model needed a large number of nodes and links renamed to introduce naming conventions that would allow automatic post-processing and visualisation. A CSV was created with old node/link names (extracted from Source using veneer-py). A second column in the CSV was then populated (by hand) with new node/link names. This CSV file was read into Python and used to apply new names to affected nodes/links.
### Change multiple models in a consistent way
* **Testing a plugin in multiple catchments:** A new plugin model was being tested across multiple catchments models, including calibration. A notebook was written to apply the plugin to a running Source model, parameterise the plugin and configure PEST. This notebook was then applied to each distinct Source model in turn.
### Change a model without making the changes permanent
There are several reasons for making changes to the Source model without wanting the changes to be permanently saved in the model.
1. Testing an alternative setup, such as a different set of routing parameters. Automating the application of new parameters means you can test, and then re-test at a later date, without needing manual rework.
2. Maintaining a single point-of-truth for a core model that needs to support different purposes and users.
3. Persistence not available. In the earlier examples of testing new plugin models, the automated application of model setup allowed sophisticated testing, including calibration by PEST, to take place before the plugin was stable enough to be persisted using the Source data management system.
## Example - Switching routing methods and configuring
This example uses the earlier `RiverModel.rsproj` example file although it will work with other models.
Here, we will convert all links to use Storage Routing except for links that lead to a water user.
**Note:** To work through this example (and the others that follow), you will need to ensure the 'Allow Scripts' option is enabled in the Web Server Monitoring window.
### The `v.model` namepsace
Most of our work in this session will involve the `v.model` namespace. This namespace contains functionality that provides query and modification of the model structure. Everything in `v.model` relies on the 'Allow Scripts' option.
As with other parts of veneer-py (and Python packages in general), you can use `<tab>` completion to explore the available functions and the `help()` function (or the `?` suffix) to get help.
### Finding the current routing type
We can use `v.model.link.routing.get_models()` to find the routing models used on each link
```
existing_models = v.model.link.routing.get_models()
existing_models
```
**Note:**
* The `get_models()` functions is available in various places through the `v.model` namespace. For example, `v.model.catchments.runoff.get_models()` queries the rainfall runoff models in subcatchments (actually in functional units). There are other such methods, available in multiple places, including:
* `set_models`
* `get_param_values`
* `set_param_values`
* These functions are all *bulk* functions - that is they operate across *all* matching elements (all nodes, all links, etc).
* Each of these functions accept parameters to restrict the search, such as only including links with certain names. These query parameters differ in different contexts (ie between runoff models and routing models), but they are consistent between the functions in a given context. Confused?
* For example, in link routing you can look for links of certain names and you can do this with the different methods:
```python
v.model.link.routing.get_models(links='Default Link #3')
v.model.link.routing.set_models('RiverSystem.Flow.LaggedFlowRoutingWrapper',links='Default Link #3')
```
Whereas, with runoff models, you can restrict by catchment or by fus:
```python
v.model.catchment.runoff.get_models(fus='Grazing')
v.model.catchment.runoff.set_models('MyFancyRunoffModel',fus='Grazing')
```
* You can find out what query parameters are available by looking at the help, one level up:
```python
help(v.model.link.routing)
```
* The call to `get_models()` return a list of model names. Two observations about this:
1. The model name is the fully qualified class name as used internally in Source. This is a common pattern through the `v.model` namespace - it uses the terminology within Source. There are, however, help functions for finding what you need. For example:
```python
v.model.find_model_type('gr4')
v.model.find_parameters('RiverSystem.Flow.LaggedFlowRoutingWrapper')
```
2. Returning a list doesn't tell you which link has which model - so how are you going to determine which ones should be Storage Routing and which should stay as Straight Through? In general the `get_` functions return lists (although there is a `by_name` option being implemented) and the `set_` functions accept lists (unless you provide a single value in which case it is applied uniformly). It is up to you to interpret the lists returned by `get_*` and to provide `set_*` with a list in the right order. The way to get it right is to separately query for the _names_ of the relevant elements (nodes/links/catchments) and order accordingly. This will be demonstrated!
### Identifying which link should stay as StraightThroughRouting
We can ask for the names of each link in order to establish which ones should be Storage Routing and which should stay as Straight Through
```
link_names_order = v.model.link.routing.names()
link_names_order
```
OK - that gives us the names - but it doesn't help directly. We could look at the model in Source to
work out which one is connected to the Water User - but that's cheating!
More generally, we can ask Veneer for the network and perform a topological query
```
network = v.network()
```
Now that we've got the network, we want all the water users.
Now, the information we've been returned regarding the network is in GeoJSON format and is intended for use in visualisation. It doesn't explicitly say 'this is a water user' at any point, but it does tell us indirectly tell us this by telling us about the icon in use:
```
network['features']._unique_values('icon')
```
So, we can find all the water users in the network, by finding all the network features with `'/resources/WaterUserNodeModel'` as their icon!
```
water_users = network['features'].find_by_icon('/resources/WaterUserNodeModel')
water_users
```
Now, we can query the network for links upstream of each water user.
We'll loop over the `water_users` list (just one in the sample model)
```
links_upstream_of_water_users=[]
for water_user in water_users:
links_upstream_of_water_users += network.upstream_links(water_user)
links_upstream_of_water_users
```
Just one link (to be expected) in the sample model. Its the name we care about though:
```
names_of_water_user_links = [link['properties']['name'] for link in links_upstream_of_water_users]
names_of_water_user_links
```
To recap, we now have:
* `existing_models` - A list of routing models used on links
* `link_names_order` - The name of each link, in the same order as for `existing_models`
* `names_of_water_user_links` - The names of links immediately upstream of water users. These links need to stay as Straight Through Routing
We're ultimately going to call
```python
v.model.link.routing.set_models(new_models,fromList=True)
```
so we need to construct `new_models`, which will be a list of model names to assign to links, with the right mix and order of storage routing and straight through. We'll want `new_models` to be the same length as `existing_models` so there is one entry per link. (There are cases where you my use `set_models` or `set_param_values` with shorter lists. You'll get R-style 'recycling' of values, but its more useful in catchments where you're iterating over catchments AND functional units)
The entries in `new_models` need to be strings - those long, fully qualified class names from the Source world. We can find them using `v.model.find_model_type`
```
v.model.find_model_type('StorageRo')
v.model.find_model_type('StraightThrough')
```
We can construct our list using a list comprehension, this time with a bit of extra conditional logic thrown in
```
new_models = ['RiverSystem.Flow.StraightThroughRouting' if link_name in names_of_water_user_links
else 'RiverSystem.Flow.StorageRouting'
for link_name in link_names_order]
new_models
```
This is a more complex list comprehension than we've used before. It goes like this, reading from the end:
* Iterate over all the link names. This will be the right number of elements - and it tells us which link we're dealling with
```python
for link_name in link_names_order]
```
* If the current `link_name` is present in the list of links upstream of water users, use straight through routing
```python
['RiverSystem.Flow.StraightThroughRouting' if link_name in names_of_water_user_links
```
* Otherwise use storage routing
```python
else 'RiverSystem.Flow.StorageRouting'
```
All that's left is to apply this to the model
```
v.model.link.routing.set_models(new_models,fromList=True)
```
**Notes:**
* The Source Applications draws links with different line styles based on their routing types - but it might not redraw until you prompt it - eg by resizing the window
* The `fromList` parameter tells the `set_models` function that you want the list to be applied one element at a time.
Now that you have Storage Routing used in most links, you can start to parameterise the links from the script.
To do so, you could use an input set, as per the previous session. To change parameters via input sets, you would first need to know the wording to use in the input set commands - and at this stage you need to find that wording in the Source user interface.
Alternatively, you can set the parameters directly using `v.model.link.routing.set_param_values`, which expects the variable name as used internally by Source. You can query for the parameter names for a particular model, using `v.model.find_parameters(model_type)` and, if that doesn't work `v.model.find_properties(model_type)`.
We'll start by using `find_parameters`:
```
v.model.find_parameters('RiverSystem.Flow.StorageRouting')
```
The function `v.model.find_parameters`, accepts a model type (actually, you can give it a list of model types) and it returns a list of parameters.
This list is determined by the internal code of Source - a parameter will only be returned if it has a `[Parameter]` tag in the C\# code.
From the list above, we see some parameters that we expect to see, but not all of the parameters for a Storage Routing reach. For example, the list of parameters doesn't seem to say how we'd switch from Generic to Piecewise routing mode. This is because the model property in question (`IsGeneric`) doesn't have a `[Property]` attribute.
We can find a list of all fields and properties of the model using `v.model.find_properties`. It's a lot more information, but it can be helpful:
```
v.model.find_properties('RiverSystem.Flow.StorageRouting')
```
Lets apply an initial parameter set to every Storage Routing link by setting:
* `RoutingConstant` to 86400, and
* `RoutingPower` to 1
We will call `set_param_values`
```
help(v.model.link.routing.set_param_values)
v.model.link.routing.set_param_values('RoutingConstant',86400.0)
v.model.link.routing.set_param_values('RoutingPower',1.0)
```
You can check in the Source user interface to see that the parameters have been applied
### Setting parameters as a function of other values
Often, you will want to calculate model parameters based on some other information, either within the model or from some external data source.
The `set_param_values` can accept a list of values, where each item in the list is applied, in turn, to the corresponding models - in much the same way that we used the known link order to set the routing type.
The list of values can be computed in your Python script based on any available information. A common use case is to compute catchment or functional unit parameters based on spatial data.
We will demonstrate the list functionality here with a contrived example!
We will set a different value of `RoutingPower` for each link. We will compute a different value of `RoutingPower` from 1.0 down to >0, based on the number of storage routing links
```
number_of_links = len(new_models) - len(names_of_water_user_links)
power_vals = np.arange(1.0,0.0,-1.0/number_of_links)
power_vals
v.model.link.routing.set_param_values('RoutingPower',power_vals,fromList=True)
```
If you open the Feature Table for storage routing, you'll now see these values propagated.
The `fromList` option has another characteristic that can be useful - particularly for catchments models with multiple functional units: value recycling.
If you provide a list with few values than are required, the system will start again from the start of the list.
So, for example, the following code will assign the three values: `[0.5,0.75,1.0]`
```
v.model.link.routing.set_param_values('RoutingPower',[0.5,0.75,1.0],fromList=True)
```
Check the Feature Table to see the effect.
**Note:** You can run these scripts with the Feature Table open and the model will be updated - but the feature table won't reflect the new values until you Cancel the feature table and reopen it.
## How it Works
As mentioned, everything under `v.model` works by sending an IronPython script to Source to be run within the Source software itself.
IronPython is a native, .NET, version of Python and hence can access all the classes and objects that make up Source.
When you call a function witnin `v.model`, veneer-py is *generating* an IronPython script for Source.
To this point, we haven't seen what these IronPython scripts look like - they are hidden from view. We can see the scripts that get sent to Source by setting the option `veneer.general.PRINT_SCRIPTS=True`
```
veneer.general.PRINT_SCRIPTS=True
v.model.link.routing.get_models(links=['Default Link #3','Default Link #4'])
veneer.general.PRINT_SCRIPTS=False
```
*Writing these IronPython scripts from scratch requires an understanding of the internal data structures of Source. The functions under `v.model` are designed to shield you from these details.*
That said, if you have an idea of the data structures, you may wish to try writing IronPython scripts, OR, try working with some of the lower-level functionality offered in `v.model`.
Most of the `v.model` functions that we've used, are ultimately based upon two, low level thems:
* `v.model.get` and
* `v.model.set`
Both `get` and `set` expect a query to perform on a Source scenario object. Structuring this query is where an understanding of Source data structures comes in.
For example, the following query will return the number of nodes in the network. (We'll use the PRINT_SCRIPTS option to show how the query translates to a script):
```
veneer.general.PRINT_SCRIPTS=True
num_nodes = v.model.get('scenario.Network.Nodes.Count()')
num_nodes
```
The follow example returns the names of each node in the network. The `.*` notation tells veneer-py to generate a loop over every element in a collection
```
node_names = v.model.get('scenario.Network.Nodes.*Name')
node_names
```
You can see from the script output that veneer-py has generated a Python for loop to iterate over the nodes:
```python
for i_0 in scenario.Network.Nodes:
```
There are other characteristics in there, such as ignoring exceptions - this is a common default used in `v.model` to silently skip nodes/links/catchments/etc that don't have a particular property.
The same query approach can work for `set`, which can set a particular property (on one or more objects) to a particular value (which can be the same value everywhere, or drawn from a list)
```
# Generate a new name for each node (based on num_nodes)
names = ['New Name %d'%i for i in range(num_nodes)]
names
v.model.set('scenario.Network.Nodes.*Name',names,fromList=True,literal=True)
```
If you look at the Source model now (you may need to trigger a redraw by resizing the window), all the nodes have been renamed.
(Lets reset the names - note how we saved `node_names` earlier on!)
```
v.model.set('scenario.Network.Nodes.*Name',node_names,fromList=True,literal=True)
```
**Note:** The `literal=True` option is currently necessary setting text properties using `v.model.set`. This tells the IronPython generator to wrap the strings in quotes in the final script. Otherwise, IronPython would be looking for symbols (eg classes) with the same names
The examples of `v.model.get` and `v.model.set` illustrate some of the low level functionality for manipulating the source model.
The earlier, high-level, functions (eg `v.model.link.routing.set_param_values`) take care of computing the query string for you, including context dependent code such as searching for links of a particular name, or nodes of a particular type. They then call the lower level functions, which takes care of generating the actual IronPython script.
The `v.model` namespace is gradually expanding with new capabilities and functions - but at their essence, most new functions provide a high level wrapper, around `v.model.get` and `v.model.set` for some new area of the Source data structures. So, for example, you could envisage a `v.model.resource_assessment` which provides high level wrappers around resource assessment functionality.
### Exploring the system
Writing the high level wrappers (as with writing the query strings for `v.model.get/set`) requires an understanding of the internal data structures of Source. You can get this from the C# code for Source, or, to a degree, from a help function `v.model.sourceHelp`.
Lets say you want to discover how to change the description of the scenario (say, to automatically add a note about the changes made by your script)
Start, by asking for help on `'scenario'` and explore from there
```
veneer.general.PRINT_SCRIPTS=False
v.model.sourceHelp('scenario')
```
This tells you everything that is available on a Source scenario. It's a lot, but `Description` looks promising:
```
existing_description = v.model.get('scenario.Description')
existing_description
```
OK. It looks like there is no description in the existing scenario. Lets set one
```
v.model.set('scenario.Description','Model modified by script',literal=True)
```
## Harder examples
Lets look at a simple model building example.
We will test out different routing parameters, by setting up a scenario with several parallel networks. Each network will consist of an Inflow Node and a Gauge Node, joined by a Storage Routing link.
The inflows will all use the same time series of flows, so the only difference will be the routing parameters.
To proceed,
1. Start a new copy of Source (in the following code, I've assumed that you're leaving the existing copy open)
2. Create a new schematic model - but don't add any nodes or links
3. Open Tools|Web Server Monitoring
4. Once Veneer has started, make a note of what port number it is using - it will probably be 9877 if you've left the other copy of Source open.
5. Make sure you tick the 'Allow Scripts' option
Now, create a new veneer client (creatively called `v2` here)
```
v2 = veneer.Veneer(port=9877)
```
And check that the network has nothing in it at the moment
```
v2.network()
```
We can create nodes with `v.model.node.create`
```
help(v2.model.node.create)
```
There are also functions to create different node types:
```
help(v2.model.node.new_gauge)
```
First, we'll do a bit of a test run. Ultimately, we'll want to create a number of such networks - and the nodes will definitely need unique names then
```
loc = [10,10]
v2.model.node.new_inflow('The Inflow',schematic_location=loc,location=loc)
loc = [20,10]
v2.model.node.new_gauge('The Gauge',schematic_location=loc,location=loc)
```
**Note:** At this stage (and after some frustration) we can't set the location of the node on the schematic. We can set the 'geographic' location - which doesn't have to be true geographic coordinates, so that's what we'll do here.
Creating a link can be done with `v2.model.link.create`
```
help(v2.model.link.create)
v2.model.link.create('The Inflow','The Gauge','The Link')
```
Now, lets look at the information from `v2.network()` to see that it's all there. (We should also see the model in the geographic view)
```
v2.network().as_dataframe()
```
Now, after all that, we'll delete everything we've created and then recreate it all in a loop to give us parallel networks
```
v2.model.node.remove('The Inflow')
v2.model.node.remove('The Gauge')
```
So, now we can create (and delete) nodes and links, lets create multiple parallel networks, to test out our flow routing parameters. We'll create 20, because we can!
```
num_networks=20
for i in range(1,num_networks+1): # Loop from 1 to 20
veneer.log('Creating network %d'%i)
x = i
loc_inflow = [i,10]
loc_gauge = [i,0]
name_inflow = 'Inflow %d'%i
name_gauge = 'Gauge %d'%i
v2.model.node.new_inflow(name_inflow,location=loc_inflow,schematic_location=loc_inflow)
v2.model.node.new_gauge(name_gauge,location=loc_gauge,schematic_location=loc_gauge)
# Create the link
name_link = 'Link %d'%i
v2.model.link.create(name_inflow,name_gauge,name_link)
# Set the routing type to storage routing (we *could* do this at the end, outside the loop)
v2.model.link.routing.set_models('RiverSystem.Flow.StorageRouting',links=name_link)
```
We'll use one of the flow files from the earlier model to drive each of our inflow nodes. We need to know where that data is. Here, I'm assuming its in the `ExampleProject` directory within the same directory as this notebook. We'll need the absolute path for Source, and the Python `os` package helps with this type of filesystem operation
```
import os
os.path.exists('ExampleProject/Fish_G_flow.csv')
absolute_path = os.path.abspath('ExampleProject/Fish_G_flow.csv')
absolute_path
```
We can use `v.model.node.assign_time_series` to attach a time series of inflows to the inflow node. We could have done this in the for loop, one node at a time, but, like `set_param_values` we can assign time series to multiple nodes at once.
One thing that we do need to know is the parameter that we're assigning the time series to (because, after all, this could be any type of node - veneer-py doesn't know at this stage). We can find the model type, then check `v.model.find_parameters` and, if that doesn't work, `v.model.find_inputs`:
```
v2.model.node.get_models(nodes='Inflow 1')
v2.model.find_parameters('RiverSystem.Nodes.Inflow.InjectedFlow')
v2.model.find_inputs('RiverSystem.Nodes.Inflow.InjectedFlow')
```
So `'Flow'` it is!
```
v2.model.node.assign_time_series('Flow',absolute_path,'Inflows')
```
Almost there.
Now, lets set a range of storage routing parameters (much like we did before)
```
power_vals = np.arange(1.0,0.0,-1.0/num_networks)
power_vals
```
And assign those to the links
```
v2.model.link.routing.set_param_values('RoutingConstant',86400.0)
v2.model.link.routing.set_param_values('RoutingPower',power_vals,fromList=True)
```
Now, configure recording
```
v2.configure_recording(disable=[{}],enable=[{'RecordingVariable':'Downstream Flow Volume'}])
```
And one last thing - work out the time period for the run from the inflow time series
```
inflow_ts = pd.read_csv(absolute_path,index_col=0)
start,end=inflow_ts.index[[0,-1]]
start,end
```
That looks a bit much. Lets run for a year
```
v2.run_model(start='01/01/1999',end='31/12/1999')
```
Now, we can retrieve some results. Because we used a naming convention for all the nodes, its possible to grab relevant results using those conventions
```
upstream = v2.retrieve_multiple_time_series(criteria={'RecordingVariable':'Downstream Flow Volume','NetworkElement':'Inflow.*'})
downstream = v2.retrieve_multiple_time_series(criteria={'RecordingVariable':'Downstream Flow Volume','NetworkElement':'Gauge.*'})
downstream[['Gauge 1:Downstream Flow Volume','Gauge 20:Downstream Flow Volume']].plot(figsize=(10,10))
```
If you'd like to change and rerun this example, the following code block can be used to delete all the existing nodes. (Or, just start a new project in Source)
```
#nodes = v2.network()['features'].find_by_feature_type('node')._all_values('name')
#for n in nodes:
# v2.model.node.remove(n)
```
## Conclusion
This session has looked at structural modifications of Source using Veneer, veneer-py and the use of IronPython scripts that run within Source.
Writing IronPython scripts requires a knowledge of internal Source data structures, but there is a growing collection of helper functions, under the `v.model` namespace to assist.
| true |
code
| 0.696346 | null | null | null | null |
|
# [Hashformers](https://github.com/ruanchaves/hashformers)
Hashformers is a framework for hashtag segmentation with transformers. For more information, please check the [GitHub repository](https://github.com/ruanchaves/hashformers).
# Installation
The steps below will install the hashformers framework on Google Colab.
Make sure you are on GPU mode.
```
!nvidia-smi
```
Here we install `mxnet-cu110`, which is compatible with Google Colab.
If installing in another environment, replace it by the mxnet package compatible with your CUDA version.
```
%%capture
!pip install mxnet-cu110
!pip install hashformers
```
# Segmenting hashtags
Visit the [HuggingFace Model Hub](https://huggingface.co/models) and choose any GPT-2 and a BERT models for the WordSegmenter class.
The GPT-2 model should be informed as `segmenter_model_name_or_path` and the BERT model as `reranker_model_name_or_path`.
Here we choose `distilgpt2` and `distilbert-base-uncased`.
```
%%capture
from hashformers import TransformerWordSegmenter as WordSegmenter
ws = WordSegmenter(
segmenter_model_name_or_path="distilgpt2",
reranker_model_name_or_path="distilbert-base-uncased"
)
```
Now we can simply segment lists of hashtags with the default settings and look at the segmentations.
```
hashtag_list = [
"#myoldphonesucks",
"#latinosinthedeepsouth",
"#weneedanationalpark"
]
segmentations = ws.segment(hashtag_list)
print(*segmentations, sep='\n')
```
Remember that any pair of BERT and GPT-2 models will work. This means you can use **hashformers** to segment hashtags in any language, not just English.
```
%%capture
from hashformers import TransformerWordSegmenter as WordSegmenter
portuguese_ws = WordSegmenter(
segmenter_model_name_or_path="pierreguillou/gpt2-small-portuguese",
reranker_model_name_or_path="neuralmind/bert-base-portuguese-cased"
)
hashtag_list = [
"#benficamemes",
"#mouraria",
"#CristianoRonaldo"
]
segmentations = portuguese_ws.segment(hashtag_list)
print(*segmentations, sep='\n')
```
# Advanced usage
## Speeding up
If you want to investigate the speed-accuracy trade-off, here are a few things that can be done to improve the speed of the segmentations:
* Turn off the reranker model by passing `use_reranker = False` to the `ws.segment` method.
* Adjust the `segmenter_gpu_batch_size` (default: `1` ) and the `reranker_gpu_batch_size` (default: `2000`) parameters in the `WordSegmenter` initialization.
* Decrease the beamsearch parameters `topk` (default: `20`) and `steps` (default: `13`) when calling the `ws.segment` method.
```
%%capture
from hashformers import TransformerWordSegmenter as WordSegmenter
ws = WordSegmenter(
segmenter_model_name_or_path="distilgpt2",
reranker_model_name_or_path="distilbert-base-uncased",
segmenter_gpu_batch_size=1,
reranker_gpu_batch_size=2000
)
%%timeit
hashtag_list = [
"#myoldphonesucks",
"#latinosinthedeepsouth",
"#weneedanationalpark"
]
segmentations = ws.segment(hashtag_list)
%%timeit
hashtag_list = [
"#myoldphonesucks",
"#latinosinthedeepsouth",
"#weneedanationalpark"
]
segmentations = ws.segment(
hashtag_list,
topk=5,
steps=5,
use_reranker=False
)
```
## Getting the ranks
If you pass `return_ranks == True` to the `ws.segment` method, you will receive a dictionary with the ranks generated by the segmenter and the reranker, the dataframe utilized by the ensemble and the final segmentations. A segmentation will rank higher if its score value is **lower** than the other segmentation scores.
Rank outputs are useful if you want to combine the segmenter rank and the reranker rank in ways which are more sophisticated than what is done by the basic ensembler that comes by default with **hashformers**.
For instance, you may want to take two or more ranks ( also called "runs" ), convert them to the trec format and combine them through a rank fusion technique on the [trectools library](https://github.com/joaopalotti/trectools).
```
hashtag_list = [
"#myoldphonesucks",
"#latinosinthedeepsouth",
"#weneedanationalpark"
]
ranks = ws.segment(
hashtag_list,
use_reranker=True,
return_ranks=True
)
# Segmenter rank
ranks.segmenter_rank
# Reranker rank
ranks.reranker_rank
```
## Evaluation
The `evaluate_df` function can evaluate the accuracy, precision and recall of our segmentations. It uses exactly the same evaluation method as previous authors in the field of hashtag segmentation ( Çelebi et al., [BOUN Hashtag Segmentor](https://tabilab.cmpe.boun.edu.tr/projects/hashtag_segmentation/) ).
We have to pass a dataframe with fields for the gold segmentations ( a `gold_field` ) and your candidate segmentations ( a `segmentation_field` ).
The relationship between gold and candidate segmentations does not have to be one-to-one. If we pass more than one candidate segmentation for a single hashtag, `evaluate_df` will measure what is the upper boundary that can be achieved on our ranks ( e.g. Acc@10, Recall@10 ).
### Minimal example
```
# Let's measure the actual performance of the segmenter:
# we will evaluate only the top-1.
import pandas as pd
from hashformers.experiments.evaluation import evaluate_df
gold_segmentations = {
"myoldphonesucks" : "my old phone sucks",
"latinosinthedeepsouth": "latinos in the deep south",
"weneedanationalpark": "we need a national park"
}
gold_df = pd.DataFrame(gold_segmentations.items(),
columns=["characters", "gold"])
segmenter_top_1 = ranks.segmenter_rank.groupby('characters').head(1)
eval_df = pd.merge(gold_df, segmenter_top_1, on="characters")
eval_df
evaluate_df(
eval_df,
gold_field="gold",
segmentation_field="segmentation"
)
```
### Benchmarking
Here we evaluate a `distilgpt2` model on 1000 hashtags.
We collect our hashtags from 10 word segmentation datasets by taking the first 100 hashtags from each dataset.
```
%%capture
!pip install datasets
%%capture
from hashformers.experiments.evaluation import evaluate_df
import pandas as pd
from hashformers import TransformerWordSegmenter
from datasets import load_dataset
user = "ruanchaves"
dataset_names = [
"boun",
"stan_small",
"stan_large",
"dev_stanford",
"test_stanford",
"snap",
"hashset_distant",
"hashset_manual",
"hashset_distant_sampled",
"nru_hse"
]
dataset_names = [ f"{user}/{dataset}" for dataset in dataset_names ]
ws = TransformerWordSegmenter(
segmenter_model_name_or_path="distilgpt2",
reranker_model_name_or_path=None
)
def generate_experiments(datasets, splits, samples=100):
for dataset_name in datasets:
for split in splits:
try:
dataset = load_dataset(dataset_name, split=f"{split}[0:{samples}]")
yield {
"dataset": dataset,
"split": split,
"name": dataset_name
}
except:
continue
benchmark = []
for experiment in generate_experiments(dataset_names, ["train", "validation", "test"], samples=100):
hashtags = experiment['dataset']['hashtag']
annotations = experiment['dataset']['segmentation']
segmentations = ws.segment(hashtags, use_reranker=False, return_ranks=False)
eval_df = [{
"gold": gold,
"hashtags": hashtag,
"segmentation": segmentation
} for gold, hashtag, segmentation in zip(annotations, hashtags, segmentations)]
eval_df = pd.DataFrame(eval_df)
eval_results = evaluate_df(
eval_df,
gold_field="gold",
segmentation_field="segmentation"
)
eval_results.update({
"name": experiment["name"],
"split": experiment["split"]
})
benchmark.append(eval_results)
benchmark_df = pd.DataFrame(benchmark)
benchmark_df["name"] = benchmark_df["name"].apply(lambda x: x[(len(user) + 1):])
benchmark_df = benchmark_df.set_index(["name", "split"])
benchmark_df = benchmark_df.round(3)
benchmark_df
benchmark_df.agg(['mean', 'std']).round(3)
```
| true |
code
| 0.518973 | null | null | null | null |
|
A quick look at GAMA bulge and disk colours in multi-band GALAPAGOS fits versus single-band GALAPAGOS and SIGMA fits.
Pretty plots at the bottom.
```
%matplotlib inline
from matplotlib import pyplot as plt
# better-looking plots
plt.rcParams['font.family'] = 'serif'
plt.rcParams['figure.figsize'] = (10.0*1.3, 8*1.3)
plt.rcParams['font.size'] = 18*1.3
import pandas
#from galapagos_to_pandas import galapagos_to_pandas
## convert the GALAPAGOS data
#galapagos_to_pandas()
## convert the SIGMA data
#galapagos_to_pandas('/home/ppzsb1/projects/gama/qc/raw/StructureCat_SersicExp.fits',
# '/home/ppzsb1/quickdata/StructureCat_SersicExp.h5')
## read in GALAPAGOS data
## no attempt has been made to select only reliable bulges and discs
store = pandas.HDFStore('/home/ppzsb1/quickdata/GAMA_9_all_combined_gama_only_bd6.h5')
data = store['data'].set_index('CATAID')
print len(data)
## read in SIGMA data - this is the raw sersic+exponential catalogue
## no attempt has been made here to select true two-component systems
store = pandas.HDFStore('/home/ppzsb1/quickdata/StructureCat_SersicExp.h5')
sigma = store['data'].set_index('CATAID')
print len(sigma)
## get overlap between the catalogue objects
data = data.join(sigma, how='inner', rsuffix='_SIGMA')
len(data)
## restrict to bright objects
data = data[data['MAG_GALFIT'] < 18.0]
len(data)
## band information
allbands = list('ugrizYJHK')
#band_wl = pandas.Series([3543,4770,6231,7625,9134,10395,12483,16313,22010], index=allbands)
normband = 'K'
bands = list('ugrizYJH')
band_labels = ['${}$'.format(i) for i in bands]
band_wl = pandas.Series([3543,4770,6231,7625,9134,10395,12483,16313], index=bands)
#normband = 'Z'
#bands = list('ugriYJHK')
#band_wl = numpy.array([3543,4770,6231,7625,10395,12483,16313,22010])
## extract magnitudes and use consistent column labels
mags_b = data[['MAG_GALFIT_BAND_B_{}'.format(b.upper()) for b in allbands]]
mags_d = data[['MAG_GALFIT_BAND_D_{}'.format(b.upper()) for b in allbands]]
mags_b_single = data[['SINGLE_MAG_GALFIT_B_{}'.format(b.upper()) for b in allbands]]
mags_d_single = data[['SINGLE_MAG_GALFIT_D_{}'.format(b.upper()) for b in allbands]]
mags_b_sigma = data[['GALMAG_01_{}'.format(b) for b in allbands]]
mags_d_sigma = data[['GALMAG_02_{}'.format(b) for b in allbands]]
mags_b.columns = mags_d.columns = allbands
mags_b_single.columns = mags_d_single.columns = allbands
mags_b_sigma.columns = mags_d_sigma.columns = allbands
## normalise SEDs and select only objects for which all magnitudes are sensible
def get_normsed(mags, bands, normband):
normsed = mags[bands]
normsed = normsed.sub(mags[normband], axis='index')
good = ((normsed > -50) & (normsed < 50)).T.all()
good &= ((mags[normband] > -50) & (mags[normband] < 50))
return normsed, good
## get normalised SEDs
normsed_b, good_b = get_normsed(mags_b, bands, normband)
normsed_b_single, good_b_single = get_normsed(mags_b_single, bands, normband)
normsed_b_sigma, good_b_sigma = get_normsed(mags_b_sigma, bands, normband)
normsed_d, good_d = get_normsed(mags_d, bands, normband)
normsed_d_single, good_d_single = get_normsed(mags_d_single, bands, normband)
normsed_d_sigma, good_d_sigma = get_normsed(mags_d_sigma, bands, normband)
print len(normsed_d)
## restrict sample to set of object that are good in all three catalogues
good_b &= good_b_single & good_b_sigma
good_d &= good_d_single & good_d_sigma
normsed_b_single = normsed_b_single[good_b]
normsed_d_single = normsed_d_single[good_d]
normsed_b_sigma = normsed_b_sigma[good_b]
normsed_d_sigma = normsed_d_sigma[good_d]
normsed_b = normsed_b[good_b]
normsed_d = normsed_d[good_d]
print len(normsed_d)
## overlay all SEDS
def plot_labels(i, label):
if i == 1:
plt.title('bulges')
if i == 2:
plt.title('discs')
if i == 3:
plt.ylabel('mag offset from $K$-band')
if i % 2 == 0:
plt.ylabel(label)
fig = plt.figure(figsize=(12,8))
def plot(d, label):
if not hasattr(plot, "plotnum"):
plot.plotnum = 0
plot.plotnum += 1
ax = plt.subplot(3, 2, plot.plotnum)
d.T.plot(ax=ax, x=band_wl, ylim=(5,-2), legend=False, color='r', alpha=0.2)
ax.xaxis.set_ticks(band_wl)
ax.xaxis.set_ticklabels(bands)
plot_labels(plot.plotnum, label)
plt.axis(ymin=8, ymax=-5)
plot(normsed_b, 'GALA multi')
plot(normsed_d, 'GALA multi')
plot(normsed_b_single, 'GALA single')
plot(normsed_d_single, 'GALA single')
plot(normsed_b_sigma, 'SIGMA')
plot(normsed_d_sigma, 'SIGMA')
plt.subplots_adjust(wspace=0.25, hspace=0.25)
## produce boxplots
fig = plt.figure(figsize=(12,8))
def boxplot(d, label):
if not hasattr(boxplot, "plotnum"):
boxplot.plotnum = 0
boxplot.plotnum += 1
plt.subplot(3, 2, boxplot.plotnum)
d.boxplot(sym='b.')
plot_labels(boxplot.plotnum, label)
plt.axis(ymin=8, ymax=-5)
boxplot(normsed_b, 'GALA multi')
boxplot(normsed_d, 'GALA multi')
boxplot(normsed_b_single, 'GALA single')
boxplot(normsed_d_single, 'GALA single')
boxplot(normsed_b_sigma, 'SIGMA')
boxplot(normsed_d_sigma, 'SIGMA')
plt.subplots_adjust(wspace=0.25, hspace=0.25)
## functions to produce nice asymmetric violin plots
## clip tails of the distributions to produce neater violins
from scipy.stats import scoreatpercentile
def clip(x, p=1):
y = []
for xi in x:
p_lo = scoreatpercentile(xi, p)
p_hi = scoreatpercentile(xi, 100-p)
y.append(xi.clip(p_lo, p_hi))
return y
## fancy legend text, which mimics the appearance of the violin plots
import matplotlib.patheffects as PathEffects
def outlined_text(x, y, text, color='k', rotation=0):
## \u2009 is a hairspace
## DejaVu Serif is specified as the default serif fonts on my system don't have this character
plt.text(x, y, u'\u2009'.join(text), color='white', alpha=0.5,
fontname='DejaVu Serif', rotation=rotation,
path_effects=[PathEffects.withStroke(linewidth=2.5, foreground=color, alpha=1.0)])
## produce asymmetric violin plots
from statsmodels.graphics.boxplots import violinplot
def bdviolinplot(bm, bs, dm, ds, mtext='', stext=''):
wl = np.log10(band_wl)*10
vw = 0.5
vlw = 1.5
p = violinplot(clip(bm.T.values), labels=band_labels, positions=wl,
side='left', show_boxplot=False,
plot_opts={'violin_width':vw, 'violin_fc':'red',
'violin_ec':'darkred', 'violin_lw':vlw})
p = violinplot(clip(bs.T.values), ax=plt.gca(), labels=band_labels,
positions=wl, side='right', show_boxplot=False,
plot_opts={'violin_width':vw, 'violin_fc':'red',
'violin_ec':'darkred', 'violin_lw':vlw})
p = violinplot(clip(dm.T.values), ax=plt.gca(), labels=band_labels,
positions=wl, side='left', show_boxplot=False,
plot_opts={'violin_width':vw, 'violin_fc':'blue',
'violin_ec':'darkblue', 'violin_lw':vlw})
p = violinplot(clip(ds.T.values), ax=plt.gca(), labels=band_labels,
positions=wl, side='right', show_boxplot=False,
plot_opts={'violin_width':vw, 'violin_fc':'blue',
'violin_ec':'darkblue', 'violin_lw':vlw})
## overlay median trends
plt.plot(wl, bm.median(), color='r', lw=2)
plt.plot(wl, bs.median(), color='r', ls='--', lw=2)
plt.plot(wl, dm.median(), color='b', lw=2)
plt.plot(wl, ds.median(), color='b', ls='--', lw=2)
## tidy up
plt.axis(ymin=8, ymax=-5)
plt.ylabel('mag offset from $K$-band')
plt.text(38.5, 7.3, '{} galaxies'.format(len(bm)))
## legend
x, y = (41.0, 6.9)
outlined_text(x, y, 'discs', 'darkblue')
outlined_text(x, y+0.75, 'bulges', 'darkred')
x, y = (x-0.35, 2.2)
outlined_text(x, y, 'multi-band', '0.1', rotation=90)
outlined_text(x+0.4, y, 'single-band', '0.1', rotation=90)
outlined_text(x-0.3, y, mtext, '0.3', rotation=90)
outlined_text(x+0.7, y, stext, '0.3', rotation=90)
bdviolinplot(normsed_b, normsed_b_single, normsed_d, normsed_d_single,
'GALAPAGOS', 'GALAPAGOS')
```
The figure is an asymmetric violin plot, which compares the distribution of disc and bulge SEDs with one another and between multi- and single-band fitting approaches. For the multi-band fits, all the images were fit simultaneously, constrained to the same structural parameters, but with magnitude free to vary. For the single-band fits, each image was fit completely independently. All the fits were performed with GALAPAGOS and GALFITM, which allows a simple, fair comparison. However, as SIGMA contains logic to retry fits which do not meet physical expectations, it is likely to perform somewhat differently. The same sample used is ~400 galaxies with r < 18 mag and 0.025 < redshift < 0.06 for which none of the fits crashed (more sophisticated cleaning could certainly be done). The SEDs are normalised to the K-band magnitude.
The disc data are shown in blue, while the bulge data are shown in red. The shape of each side of a violin represents the distribution of magnitude offset for that band. The left-side of each violin presents the multi-band fit results, while the right-sides present the single-band results. The medians of each distribution are also plotted in their corresponding colour, with solid lines for multi-band and dashed lines for single-band results.
The single-band results do not distinguish very much between the SEDs of bulge and disc components, as can be seen from the coincidence between the dashed lines and the fact that the right-sides of the red and blue violins mostly overlap.
In constrast, the multi-band results show a significant difference in the SEDs of bulges and discs, in terms of both medians, and overall distributions. Note that there is no colour difference between the components in the initial parameters. The colour difference simply arises from the improved decomposition afforded by the multi-band approach.
```
bdviolinplot(normsed_b, normsed_b_sigma, normsed_d, normsed_d_sigma,
'GALAPAGOS', 'SIGMA')
```
The figure is the same as above, but now compares the GALAPAGOS multi-band fit results to single-band fits using SIGMA. The SIGMA results show less scatter the the GALAPAGS single-band fits, but there is still very little differentiation between the SEDs of bulges and discs.
| true |
code
| 0.577734 | null | null | null | null |
|
# Creating your own dataset from Google Images
*by: Francisco Ingham and Jeremy Howard. Inspired by [Adrian Rosebrock](https://www.pyimagesearch.com/2017/12/04/how-to-create-a-deep-learning-dataset-using-google-images/)*
In this tutorial we will see how to easily create an image dataset through Google Images. **Note**: You will have to repeat these steps for any new category you want to Google (e.g once for dogs and once for cats).
```
from fastai.vision.all import *
from nbdev.showdoc import *
```
## Get a list of URLs
### Search and scroll
Go to [Google Images](http://images.google.com) and search for the images you are interested in. The more specific you are in your Google Search, the better the results and the less manual pruning you will have to do.
Scroll down until you've seen all the images you want to download, or until you see a button that says 'Show more results'. All the images you scrolled past are now available to download. To get more, click on the button, and continue scrolling. The maximum number of images Google Images shows is 700.
It is a good idea to put things you want to exclude into the search query, for instance if you are searching for the Eurasian wolf, "canis lupus lupus", it might be a good idea to exclude other variants:
"canis lupus lupus" -dog -arctos -familiaris -baileyi -occidentalis
You can also limit your results to show only photos by clicking on Tools and selecting Photos from the Type dropdown.
### Download into file
Now you must run some Javascript code in your browser which will save the URLs of all the images you want for you dataset.
Press <kbd>Ctrl</kbd><kbd>Shift</kbd><kbd>J</kbd> in Windows/Linux and <kbd>Cmd</kbd><kbd>Opt</kbd><kbd>J</kbd> in Mac, and a small window the javascript 'Console' will appear. That is where you will paste the JavaScript commands.
You will need to get the urls of each of the images. Before running the following commands, you may want to disable ad blocking extensions (uBlock, AdBlockPlus etc.) in Chrome. Otherwise the window.open() command doesn't work. Then you can run the following commands:
```javascript
urls = Array.from(document.querySelectorAll('.rg_di .rg_meta')).map(el=>JSON.parse(el.textContent).ou);
window.open('data:text/csv;charset=utf-8,' + escape(urls.join('\n')));
```
### Create directory and upload urls file into your server
Choose an appropriate name for your labeled images. You can run these steps multiple times to create different labels.
```
path = Config().data/'bears'
path.mkdir(parents=True, exist_ok=True)
path.ls()
```
Finally, upload your urls file. You just need to press 'Upload' in your working directory and select your file, then click 'Upload' for each of the displayed files.
## Download images
Now you will need to download your images from their respective urls.
fast.ai has a function that allows you to do just that. You just have to specify the urls filename as well as the destination folder and this function will download and save all images that can be opened. If they have some problem in being opened, they will not be saved.
Let's download our images! Notice you can choose a maximum number of images to be downloaded. In this case we will not download all the urls.
```
classes = ['teddy','grizzly','black']
for c in classes:
print(c)
file = f'urls_{c}.csv'
download_images(path/c, path/file, max_pics=200)
# If you have problems download, try with `max_workers=0` to see exceptions:
#download_images(path/file, dest, max_pics=20, max_workers=0)
```
Then we can remove any images that can't be opened:
```
for c in classes:
print(c)
verify_images(path/c, delete=True, max_size=500)
```
## View data
```
np.random.seed(42)
dls = ImageDataLoaders.from_folder(path, train=".", valid_pct=0.2, item_tfms=RandomResizedCrop(460, min_scale=0.75),
bs=64, batch_tfms=[*aug_transforms(size=224, max_warp=0), Normalize.from_stats(*imagenet_stats)])
# If you already cleaned your data, run this cell instead of the one before
# np.random.seed(42)
# dls = ImageDataLoaders.from_csv(path, folder=".", valid_pct=0.2, csv_labels='cleaned.csv',
# item_tfms=RandomResizedCrop(460, min_scale=0.75), bs=64,
# batch_tfms=[*aug_transforms(size=224, max_warp=0), Normalize.from_stats(*imagenet_stats)])
```
Good! Let's take a look at some of our pictures then.
```
dls.vocab
dls.show_batch(rows=3, figsize=(7,8))
dls.vocab, dls.c, len(dls.train_ds), len(dls.valid_ds)
```
## Train model
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fit_one_cycle(4)
learn.save('stage-1')
learn.unfreeze()
```
If the plot is not showing try to give a start and end learning rate:
`learn.lr_find(start_lr=1e-5, end_lr=1e-1)`
```
learn.lr_find()
learn.load('stage-1')
learn.fit_one_cycle(2, lr_max=slice(3e-5,3e-4))
learn.save('stage-2')
```
## Interpretation
```
learn.load('stage-2');
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix()
```
## Putting your model in production
First thing first, let's export the content of our `Learner` object for production:
```
learn.export()
```
This will create a file named 'export.pkl' in the directory where we were working that contains everything we need to deploy our model (the model, the weights but also some metadata like the classes or the transforms/normalization used).
You probably want to use CPU for inference, except at massive scale (and you almost certainly don't need to train in real-time). If you don't have a GPU that happens automatically. You can test your model on CPU like so:
```
defaults.device = torch.device('cpu')
img = Image.open(path/'black'/'00000021.jpg')
img
```
We create our `Learner` in production environment like this, just make sure that `path` contains the file 'export.pkl' from before.
```
learn = torch.load(path/'export.pkl')
pred_class,pred_idx,outputs = learn.predict(path/'black'/'00000021.jpg')
pred_class
```
So you might create a route something like this ([thanks](https://github.com/simonw/cougar-or-not) to Simon Willison for the structure of this code):
```python
@app.route("/classify-url", methods=["GET"])
async def classify_url(request):
bytes = await get_bytes(request.query_params["url"])
img = PILImage.create(bytes)
_,_,probs = learner.predict(img)
return JSONResponse({
"predictions": sorted(
zip(cat_learner.dls.vocab, map(float, probs)),
key=lambda p: p[1],
reverse=True
)
})
```
(This example is for the [Starlette](https://www.starlette.io/) web app toolkit.)
## Things that can go wrong
- Most of the time things will train fine with the defaults
- There's not much you really need to tune (despite what you've heard!)
- Most likely are
- Learning rate
- Number of epochs
### Learning rate (LR) too high
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fit_one_cycle(1, lr_max=0.5)
```
### Learning rate (LR) too low
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
```
Previously we had this result:
```
Total time: 00:57
epoch train_loss valid_loss error_rate
1 1.030236 0.179226 0.028369 (00:14)
2 0.561508 0.055464 0.014184 (00:13)
3 0.396103 0.053801 0.014184 (00:13)
4 0.316883 0.050197 0.021277 (00:15)
```
```
learn.fit_one_cycle(5, lr_max=1e-5)
learn.recorder.plot_loss()
```
As well as taking a really long time, it's getting too many looks at each image, so may overfit.
### Too few epochs
```
learn = cnn_learner(dls, resnet34, metrics=error_rate, pretrained=False)
learn.fit_one_cycle(1)
```
### Too many epochs
```
from fastai.basics import *
from fastai.callback.all import *
from fastai.vision.all import *
from nbdev.showdoc import *
path = Config().data/'bears'
np.random.seed(42)
dls = ImageDataLoaders.from_folder(path, train=".", valid_pct=0.8, item_tfms=RandomResizedCrop(460, min_scale=0.75),
bs=32, batch_tfms=[AffineCoordTfm(size=224), Normalize.from_stats(*imagenet_stats)])
learn = cnn_learner(dls, resnet50, metrics=error_rate, config=cnn_config(ps=0))
learn.unfreeze()
learn.fit_one_cycle(40, slice(1e-6,1e-4), wd=0)
```
| true |
code
| 0.522202 | null | null | null | null |
|
# NLP Feature Engineering
## Feature Creation
```
# Read in the text data
import pandas as pd
data = pd.read_csv("./data/SMSSpamCollection.tsv", sep='\t')
data.columns = ['label', 'body_text']
```
### Create feature for text message length
```
data['body_len'] = data['body_text'].apply(lambda x: len(x) - x.count(" "))
data.head()
```
### Create feature for % of text that is punctuation
```
import string
# Create a function to count punctuation
def count_punct(text):
count = sum([1 for char in text if char in string.punctuation])
return round(count/(len(text) - text.count(" ")), 3)*100
# Create a column for the % of punctuation in each body text
data['punct%'] = data['body_text'].apply(lambda x: count_punct(x))
data.head()
```
## Evaluate Created Features
```
# Import the dependencies
from matplotlib import pyplot
import numpy as np
%matplotlib inline
# Create a plot that demonstrates the length of the message for 'ham' and 'spam'
bins = np.linspace(0, 200, 40)
pyplot.hist(data[data['label']=='spam']['body_len'], bins, alpha=0.5, normed=True, label='spam')
pyplot.hist(data[data['label']=='ham']['body_len'], bins, alpha=0.5, normed=True, label='ham')
pyplot.legend(loc='upper left')
pyplot.show()
# Create a plot that demonstrates the punctuation % for 'ham' and 'spam'
bins = np.linspace(0, 50, 40)
pyplot.hist(data[data['label']=='spam']['punct%'], bins, alpha=0.5, normed=True, label='spam')
pyplot.hist(data[data['label']=='ham']['punct%'], bins, alpha=0.5, normed=True, label='ham')
pyplot.legend(loc='upper right')
pyplot.show()
```
## Transformation
### Plot the two new features
```
bins = np.linspace(0, 200, 40)
pyplot.hist(data['body_len'], bins)
pyplot.title("Body Length Distribution")
pyplot.show()
bins = np.linspace(0, 50, 40)
pyplot.hist(data['punct%'], bins)
pyplot.title("Punctuation % Distribution")
pyplot.show()
```
### Transform the punctuation % feature
### Box-Cox Power Transformation
**Base Form**: $$ y^x $$
| X | Base Form | Transformation |
|------|--------------------------|--------------------------|
| -2 | $$ y ^ {-2} $$ | $$ \frac{1}{y^2} $$ |
| -1 | $$ y ^ {-1} $$ | $$ \frac{1}{y} $$ |
| -0.5 | $$ y ^ {\frac{-1}{2}} $$ | $$ \frac{1}{\sqrt{y}} $$ |
| 0 | $$ y^{0} $$ | $$ log(y) $$ |
| 0.5 | $$ y ^ {\frac{1}{2}} $$ | $$ \sqrt{y} $$ |
| 1 | $$ y^{1} $$ | $$ y $$ |
| 2 | $$ y^{2} $$ | $$ y^2 $$ |
**Process**
1. Determine what range of exponents to test
2. Apply each transformation to each value of your chosen feature
3. Use some criteria to determine which of the transformations yield the best distribution
| true |
code
| 0.473049 | null | null | null | null |
|
# Stochastic Gradient Descent
- 上节梯度下降法如图所示
[](https://imgchr.com/i/8mATJK)
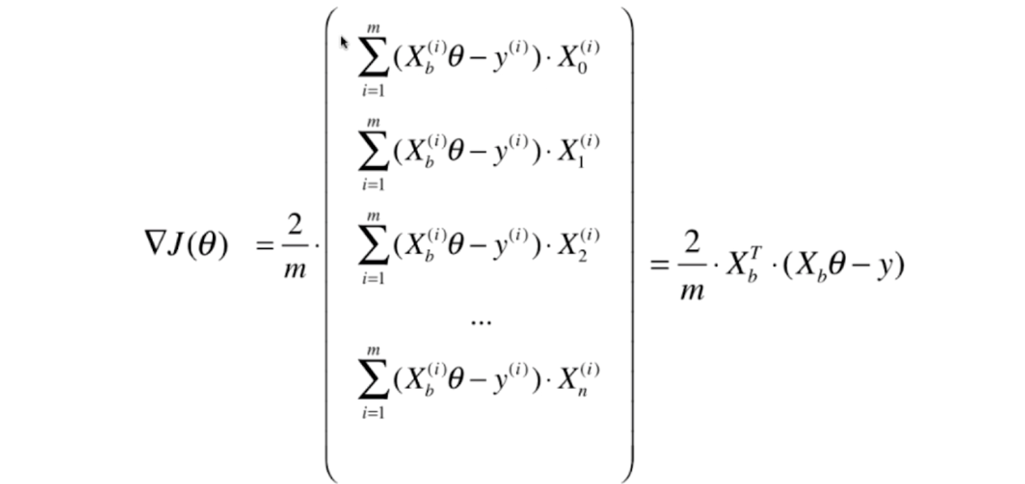
- 我们每次都把所有的梯度算出来,称为**批量梯度下降法**
- 但是这样在样本容量很大时,也是比较耗时的,解决方法是**随机梯度下降法**
[](https://imgchr.com/i/8mALsH)
- 我们随机的取一个 $i$ ,然后用这个 $i$ 得到一个向量,然后向这个方向搜索迭代
[](https://imgchr.com/i/8mAHzD)
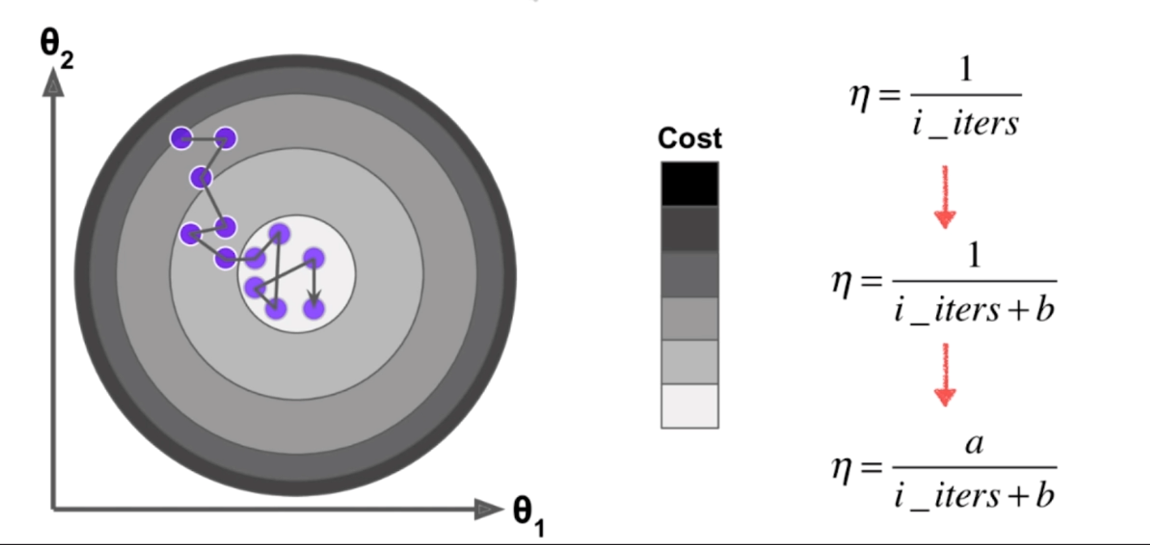
- 在随机梯度下降法中,我们不能保证寻找的方向就是损失函数减小的方向
- 更不能保证时减小的最快的方向
- 我们希望 $\eta$ 随着迭代次数增大越来越小,于是 $\eta$ 就有右边表示形式
- 其中 a 和 b 是两个超参数
### 1. 批量梯度下降算法
```
import numpy as np
import matplotlib.pyplot as plt
m = 100000
x = np.random.normal(size = m)
X = x.reshape(-1, 1)
y = 4. * x + 3. + np.random.normal(0, 3, size=m)
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta))**2) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
theta = initial_theta
i_iter = 0
while i_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if np.abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon:
break
i_iter += 1
return theta
X_b = np.hstack([np.ones([len(X), 1]), X])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
theta = gradient_descent(X_b, y, initial_theta, eta)
theta
```
### 2. 随机梯度下降法
```
# 传入具体的某一行
def dJ(theta, X_b_i, y_i):
return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2.
def sgd(X_b, y, initial_theta, n_iters):
t0 = 5
t1 = 50
def learning_rate(cur_iter):
return t0 / (cur_iter + t1)
theta = initial_theta
for cur_iter in range(n_iters):
# 随机取一个 i
rand_i = np.random.randint(len(X_b))
gradient = dJ(theta, X_b[rand_i], y[rand_i])
# 迭代 theta
theta = theta - learning_rate(cur_iter) * gradient
return theta
X_b = np.hstack([np.ones([len(X), 1]), X])
initial_theta = np.zeros(X_b.shape[1])
theta = sgd(X_b, y, initial_theta, n_iters=len(X_b)//3)
# 可以看出,我们只使用了三分之一的样本,就达到了很好的效果
theta
# theta 值和批量梯度下降算法几乎一致
```
### 3. 使用我们自己的SGD
```
from LR.LinearRegression import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit_sgd(X, y, n_iters=2)
lin_reg.coef_
lin_reg.intercept_
```
#### 使用真实数据
```
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
from LR.model_selection import train_test_split
# 数据集分割
X_train, X_test, y_train, y_test = train_test_split(X, y, seed=333)
# 归一化处理
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
lin_reg2 = LinearRegression()
%time lin_reg2.fit_sgd(X_train_standard, y_train)
lin_reg2.score(X_test_standard, y_test)
```
### 4. scikit-learn中的SGD
```
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor()
%time sgd_reg.fit(X_train_standard, y_train)
sgd_reg.score(X_test_standard, y_test)
SGDRegressor?
sgd_reg = SGDRegressor(n_iter=100)
%time sgd_reg.fit(X_train_standard, y_train)
sgd_reg.score(X_test_standard, y_test)
```
| true |
code
| 0.53522 | null | null | null | null |
|
# Siamese Convolutional Neural Network
```
from model import siamese_CNN
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import pickle
import numpy as np
from pandas import DataFrame
import tensorflow as tf
import keras.backend as K
# model imports
from keras.models import Sequential, Model, Input
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense
from keras.layers import Dropout, BatchNormalization
from keras.layers import Lambda, concatenate
from keras.initializers import RandomNormal
from tensorflow.keras.regularizers import l2
from keras.optimizers import Adam, RMSprop
from keras.callbacks import EarlyStopping
# plotting
from tensorflow.keras.utils import plot_model
import pydotplus as pydot
import matplotlib.pyplot as plt
%matplotlib inline
```
## Setting up datasets
```
def load_pickle(file):
with open(file, 'rb') as f:
return pickle.load(f)
def load_dataset(i):
print("\nLoading dataset...", end="")
data = load_pickle(PATHS[i][0]) # training data
pairs = load_pickle(PATHS[i][1]) # pairs of data
pairs = [pairs[0], pairs[1]]
targets = load_pickle(PATHS[i][2]) # targets of the data
print("dataset {0} loaded successfully!\n".format(PATHS.index(PATHS[i])))
return data, pairs, targets
def data_shapes():
print("\nNumber of classes : ", data.shape[0])
print("Original signatures : ", len(data[0][0]))
print("Forged signatures : ", len(data[0][1]))
print("Image shape : ", data[0][0][0].shape)
print("Total number of pairs : ", pairs[0].shape[0])
print("Number of pairs for each class : ", pairs[0].shape[0]//data.shape[0])
print("Targets shape : ", targets.shape)
print()
def plot_13(id1, id2, id3):
fig, ax = plt.subplots(1, 3, sharex=True, sharey=True, figsize=(8,8))
ax[0].imshow(pairs[0][id1])
ax[1].imshow(pairs[1][id2])
ax[2].imshow(pairs[1][id3])
# subplot titles
ax[0].set_title('Anchor image of class {0}'.format(id1//42))
ax[1].set_title('Target: {0}'.format(targets[id2]))
ax[2].set_title('Target: {0}'.format(targets[id3]))
fig.tight_layout()
```
## Setting up models
```
def contrastive_loss(y_true, y_pred):
"""Contrastive loss.
if y = true and d = pred,
d(y,d) = mean(y * d^2 + (1-y) * (max(margin-d, 0))^2)
Args:
y_true : true values.
y_pred : predicted values.
Returns:
contrastive loss
"""
margin = 1
return K.mean(y_true * K.square(y_pred) + (1 - y_true) * K.square(K.maximum(margin - y_pred, 0)))
def model_setup(verbose=False):
rms = RMSprop(lr=1e-4, rho=0.9, epsilon=1e-08)
model = siamese_CNN((224, 224, 1))
model.compile(optimizer=rms, loss=contrastive_loss)
if verbose:
model.summary()
tf.keras.utils.plot_model(
model,
show_shapes=True,
show_layer_names=True,
to_file="resources\\model_plot.png"
)
return model
```
## Training
```
def model_training(model, weights_name):
print("\nStarting training!\n")
# hyperparameters
EPOCHS = 100 # number of epochs
BS = 32 # batch size
# callbacks
callbacks = [EarlyStopping(monitor='val_loss', patience=3, verbose=1,)]
history = model.fit(
pairs, targets,
batch_size=BS,
epochs=EPOCHS,
verbose=1,
callbacks=callbacks,
validation_split=0.25,
)
ALL_HISTORY.append(history)
print("\nSaving weight for model...", end="")
siamese_net.save_weights('weights\\{0}.h5'.format(weights_name))
print("saved successfully!")
```
## Evaluation
```
def compute_accuracy_roc(predictions, labels):
"""Compute ROC accuracyand threshold.
Also, plot FAR-FRR curves and P-R curves for input data.
Args:
predictions -- np.array : array of predictions.
labels -- np.array : true labels (0 or 1).
plot_far_frr -- bool : plots curves of True.
Returns:
max_acc -- float : maximum accuracy of model.
best_thresh --float : best threshold for the model.
"""
dmax = np.max(predictions)
dmin = np.min(predictions)
nsame = np.sum(labels == 1) #similar
ndiff = np.sum(labels == 0) #different
step = 0.01
max_acc = 0
best_thresh = -1
frr_plot = []
far_plot = []
pr_plot = []
re_plot = []
ds = []
for d in np.arange(dmin, dmax+step, step):
idx1 = predictions.ravel() <= d # guessed genuine
idx2 = predictions.ravel() > d # guessed forged
tp = float(np.sum(labels[idx1] == 1))
tn = float(np.sum(labels[idx2] == 0))
fp = float(np.sum(labels[idx1] == 0))
fn = float(np.sum(labels[idx2] == 1))
tpr = float(np.sum(labels[idx1] == 1)) / nsame
tnr = float(np.sum(labels[idx2] == 0)) / ndiff
acc = 0.5 * (tpr + tnr)
pr = tp / (tp + fp)
re = tp / (tp + fn)
if (acc > max_acc):
max_acc, best_thresh = acc, d
far = fp / (fp + tn)
frr = fn / (fn + tp)
frr_plot.append(frr)
pr_plot.append(pr)
re_plot.append(re)
far_plot.append(far)
ds.append(d)
plot_metrics = [ds, far_plot, frr_plot, pr_plot, re_plot]
return max_acc, best_thresh, plot_metrics
def model_evaluation(model):
print("\nEvaluating model...", end="")
pred = model.predict(pairs)
acc, thresh, plot_metrics = compute_accuracy_roc(pred, targets)
print("evaluation finished!\n")
ACCURACIES.append(acc)
THRESHOLDS.append(thresh)
PLOTS.append(plot_metrics)
```
## Visualizing models
```
def visualize_history():
losses = ['loss', 'val_loss']
accs = ['accuracy', 'val_accuracy']
fig, ax = plt.subplots(3, 2, sharex=True, sharey=True, figsize=(8,8))
for i in range(3):
for x, y in zip(losses, accs):
ax[i,0].plot(ALL_HISTORY[i].history[x])
ax[i,0].set_title('Losses')
ax[i,1].plot(ALL_HISTORY[i].history[y])
ax[i,1].set_title('Accuracies')
ax[i,0].legend(losses)
ax[i,1].legend(accs)
plt.grid(True)
plt.tight_layout()
def evaluation_plots(metrics):
ds = metrics[0]
far_plot = metrics[1]
frr_plot = metrics[2]
pr_plot = metrics[3]
re_plot = metrics[4]
fig = plt.figure(figsize=(15,6))
# error rate
ax = fig.add_subplot(121)
ax.plot(ds, far_plot, color='red')
ax.plot(ds, frr_plot, color='blue')
ax.set_title('Error rate')
ax.legend(['FAR', 'FRR'])
ax.set(xlabel = 'Thresholds', ylabel='Error rate')
# precision-recall curve
ax1 = fig.add_subplot(122)
ax1.plot(ds, pr_plot, color='green')
ax1.plot(ds, re_plot, color='magenta')
ax1.set_title('P-R curve')
ax1.legend(['Precision', 'Recall'])
ax.set(xlabel = 'Thresholds', ylabel='Error rate')
plt.show()
```
## Everything put together
```
# paths to datasets
PATHS = [
[
'data\\pickle-files\\cedar_pairs1_train.pickle',
'data\\pickle-files\\cedar_pairs1_pairs.pickle',
'data\\pickle-files\\cedar_pairs1_targets.pickle'
],
[
"data\\pickle-files\\bengali_pairs1_pairs.pickle"
'data\\pickle-files\\bengali_pairs1_train.pickle',
'data\\pickle-files\\bengali_pairs1_targets.pickle'
],
[
'data\\pickle-files\\hindi_pairs1_train.pickle',
'data\\pickle-files\\hindi_pairs1_pairs.pickle',
'data\\pickle-files\\hindi_pairs1_targets.pickle'
]
]
# for kaggle
# PATHS = [
# [
# '../usr/lib/preprocess/cedar_pairs1_train.pickle',
# '../usr/lib/preprocess/cedar_pairs1_pairs.pickle',
# '../usr/lib/preprocess/cedar_pairs1_targets.pickle'
# ],
# [
# '../usr/lib/preprocess/bengali_pairs1_train.pickle',
# '../usr/lib/preprocess/bengali_pairs1_pairs.pickle',
# '../usr/lib/preprocess/bengali_pairs1_targets.pickle'
# ],
# [
# '../usr/lib/preprocess/hindi_pairs1_train.pickle',
# '../usr/lib/preprocess/hindi_pairs1_pairs.pickle',
# '../usr/lib/preprocess/hindi_pairs1_targets.pickle'
# ]
# ]
# evaluation
ALL_HISTORY = []
ACCURACIES = []
THRESHOLDS = []
PLOTS = []
for i in range(3):
data, pairs, targets = load_dataset(i)
data_shapes()
for bs in range(0, 3*42, 42):
plot_13(0+bs, 20+bs, 41+bs)
print()
if i == 0:
siamese_net = model_setup(True)
model_training(siamese_net, 'siamese_cedar')
elif i == 1:
siamese_net = model_setup()
model_training(siamese_net, 'siamese_bengali')
elif i == 2:
siamese_net = model_setup()
model_training(siamese_net, 'siamese_hindi')
model_evaluation(siamese_net)
del data
del pairs
del targets
visualize_history()
df = DataFrame.from_dict({'Accuracies': ACCURACIES,
'Thresholds': THRESHOLDS})
df.index = ['Cedar', 'BhSig260 Bengali', 'BhSig260 Hindi']
df
for met in PLOTS:
evaluation_plots(met)
```
| true |
code
| 0.740479 | null | null | null | null |
|
# Example 10 A: Inverted Pendulum with Wall
```
import numpy as np
import scipy.linalg as spa
import pypolycontain as pp
import pydrake.solvers.mathematicalprogram as MP
import pydrake.solvers.gurobi as Gurobi_drake
# use Gurobi solver
global gurobi_solver, license
gurobi_solver=Gurobi_drake.GurobiSolver()
license = gurobi_solver.AcquireLicense()
import pypolycontain as pp
import pypolycontain.pwa_control as pwa
import matplotlib.pyplot as plt
```
## Dynamcis and matrices
The system is constrained to $|\theta| \le 0.12$, $|\dot{\theta}| \le 1$, $|u| \le 4$, and the wall is situated at $\theta=0.1$. The problem is to identify a set of states $\mathcal{X} \in \mathbb{R}^2$ and the associated control law $\mu: [-0.12,0.12] \times [-1,1] \rightarrow [-4,4]$ such that all states in $\mathcal{X}$ are steered toward origin in finite time, while respecting the constraints. It is desired that $\mathcal{X}$ is as large as possible. The dynamical system is described as a hybrid system with two modes associated with ``contact-free" and ``contact". The piecewise affine dynamics is given as:
\begin{equation*}
A_1=
\left(
\begin{array}{cc}
1 & 0.01 \\
0.1 & 1
\end{array}
\right),
A_2=
\left(
\begin{array}{cc}
1 & 0.01 \\
-9.9 & 1
\end{array}
\right),
\end{equation*}
\begin{equation*}
B_1=B_2=
\left(
\begin{array}{c}
0 \\ 0.01
\end{array}
\right),
c_1=
\left(
\begin{array}{c}
0 \\ 0
\end{array}
\right) ,
c_2=
\left(
\begin{array}{c}
0 \\ 1
\end{array}
\right),
\end{equation*}
where mode 1 and 2 correspond to contact-free $\theta \le 0.1$ and contact dynamics $\theta >0.1$, respectively.
```
A=np.array([[1,0.01],[0.1,1]])
B=np.array([0,0.01]).reshape(2,1)
c=np.array([0,0]).reshape(2,1)
C=pp.unitbox(N=3).H_polytope
C.h=np.array([0.1,1,4,0.1,1,4]).reshape(6,1)
S1=pwa.affine_system(A,B,c,name='free',XU=C)
# X=pp.zonotope(G=np.array([[0.1,0],[0,1]]))
# U=pp.zonotope(G=np.ones((1,1))*4)
# W=pp.zonotope(G=np.array([[0.1,0],[0,1]]))
# Omega=rci_old(A, B, X, U , W, q=5,eta=0.001)
import pickle
(H,h)=pickle.load(open('example_inverted_pendulum_H.pkl','rb'))
Omega=pp.H_polytope(H, h)
A=np.array([[1,0.01],[-9.9,1]])
B=np.array([0,0.01]).reshape(2,1)
c=np.array([0,1]).reshape(2,1)
C=pp.unitbox(N=3).H_polytope
C.h=np.array([0.12,1,4,-0.1,1,4]).reshape(6,1)
S2=pwa.affine_system(A,B,c,name='contact',XU=C)
myS=pwa.pwa_system()
myS.add_mode(S1)
myS.add_mode(S2)
```
## A Polytopic Trajectory
```
T=50
goal=0.0001*pp.unitbox(2).H_polytope
x0=np.array([0,0.75]).reshape(2,1)
F,FH,_,_,_=pwa.extend(myS,x0,T,[goal],H_rep=False,color='blue')
fig,ax=plt.subplots()
pp.visualize(F,fig=fig,ax=ax,a=0.01,alpha=0.9)
ax.set_xlabel(r'$\theta$',FontSize=30)
ax.set_ylabel(r'$\dot{\theta}$',FontSize=30)
ax.set_title('A Polytopic Trajectory (Blue)',FontSize=30)
ax.axvline(x=0.1,LineWidth=1,linestyle=':',color='black')
```
## My first branch: connect polytopic trajectories
```
T=18
x0=np.array([0.075,0]).reshape(2,1)
F2,_,_,_,_=pwa.extend(myS,x0,T,F,H_rep=False,color='red')
fig,ax=plt.subplots()
pp.visualize(F+F2,fig=fig,ax=ax,a=0.01,alpha=0.9)
ax.set_xlabel(r'$\theta$',FontSize=30)
ax.set_ylabel(r'$\dot{\theta}$',FontSize=30)
ax.set_title('A Branch Added (red)',FontSize=30)
ax.axvline(x=0.1,LineWidth=1,linestyle=':',color='black')
```
## Building A Tree
```
def sampler():
L=np.array([0.12,1])
return np.random.uniform(-L,L).reshape(2,1)
T=10
list_of_H_polytopes=[Omega]
list_of_nodes=[Omega]
stop_sampling=False
sample=lambda :sampler()
branch=0
trajectory={}
i=0
while branch<30 and i<500:
i+=1
print("i:",i, "branch:", branch)
while not stop_sampling:
x0=sample()
flag=pwa.in_the_tree(x0,list_of_H_polytopes)
stop_sampling=not flag
try:
print("sample:",x0.T)
x,u,mu=pwa.point_trajectory(myS,x0,T=60,goal=Omega,Q=np.eye(2)*1)
Y,YY,xx,mumu,G=pwa.extend(myS,x0,T,list_of_nodes)
trajectory[branch]=(x,u,mu,xx,mumu,G)
# Y,YY=extend(x0,T,[Omega])
list_of_nodes.extend(Y)
list_of_H_polytopes.extend(YY)
branch+=1
except:
print('failed to extend')
stop_sampling=False
```
## Visualization
```
fig,ax=plt.subplots()
pp.visualize([Omega]+list_of_nodes,fig=fig,ax=ax,a=0.01,alpha=0.9)
ax.set_xlabel(r'$\theta$',FontSize=30)
ax.set_ylabel(r'$\dot{\theta}$',FontSize=30)
ax.set_title('%d Branches %d AH-polytopes'%(branch,len(list_of_nodes)),FontSize=30)
ax.axvline(x=0.1,LineWidth=1,linestyle=':',color='black')
```
### Studying Coverage
We generate random points and see
```
Trials=200
covered=0
false_positive=0
feasible=0
feasible_but_not_covered_by_N_10=0
for N in range(Trials):
x0=sample()
print(N)
try:
_,_,_=pwa.point_trajectory(myS,x0,T=50,goal=Omega,Q=np.eye(2)*100)
feasible+=1
covered+=pwa.in_the_tree(x0,list_of_H_polytopes)
try:
_,_,_=pwa.point_trajectory(myS,x0,T=10,goal=Omega,Q=np.eye(2)*100)
except:
feasible_but_not_covered_by_N_10+=1
except:
false_positive+=pwa.in_the_tree(x0,list_of_H_polytopes)
print("feasible: %d covered: %d"%(feasible,covered))
print("covered by N=10: %d"%(feasible - feasible_but_not_covered_by_N_10))
print("infeasible: %d false positive because of H-rep over-approximation: %d"%(Trials-feasible,false_positive))
```
| true |
code
| 0.254254 | null | null | null | null |
|
# End-to-end demo of the ``stadv`` package
We use a small CNN pre-trained on MNIST and try and fool the network using *Spatially Transformed Adversarial Examples* (stAdv).
### Import the relevant libraries
```
%matplotlib inline
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import sys
import os
import numpy as np
import tensorflow as tf
import stadv
# dependencies specific to this demo notebook
import matplotlib.pyplot as plt
import idx2numpy
```
### Load MNIST data
The test data for the MNIST dataset should be downloaded from http://yann.lecun.com/exdb/mnist/,
decompressed, and put in a directory ``mnist_data_dir``.
This can be done in command line with:
```
wget http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz && gunzip -f t10k-images-idx3-ubyte.gz
wget http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz && gunzip -f t10k-labels-idx1-ubyte.gz
```
```
mnist_data_dir = '.'
mnist_images = idx2numpy.convert_from_file(os.path.join(mnist_data_dir, 't10k-images-idx3-ubyte'))
mnist_labels = idx2numpy.convert_from_file(os.path.join(mnist_data_dir, 't10k-labels-idx1-ubyte'))
mnist_images = np.expand_dims(mnist_images, -1)
print("Shape of images:", mnist_images.shape)
print("Range of values: from {} to {}".format(np.min(mnist_images), np.max(mnist_images)))
print("Shape of labels:", mnist_labels.shape)
print("Range of values: from {} to {}".format(np.min(mnist_labels), np.max(mnist_labels)))
```
### Definition of the graph
The CNN we consider is using the `layers` module of TensorFlow. It was heavily inspired by this tutorial: https://www.tensorflow.org/tutorials/layers
```
# definition of the inputs to the network
images = tf.placeholder(tf.float32, shape=[None, 28, 28, 1], name='images')
flows = tf.placeholder(tf.float32, [None, 2, 28, 28], name='flows')
targets = tf.placeholder(tf.int64, shape=[None], name='targets')
tau = tf.placeholder_with_default(
tf.constant(0., dtype=tf.float32),
shape=[], name='tau'
)
# flow-based spatial transformation layer
perturbed_images = stadv.layers.flow_st(images, flows, 'NHWC')
# definition of the CNN in itself
conv1 = tf.layers.conv2d(
inputs=perturbed_images,
filters=32,
kernel_size=[5, 5],
padding="same",
activation=tf.nn.relu
)
pool1 = tf.layers.max_pooling2d(inputs=conv1, pool_size=[2, 2], strides=2)
conv2 = tf.layers.conv2d(
inputs=pool1,
filters=64,
kernel_size=[5, 5],
padding="same",
activation=tf.nn.relu
)
pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2)
pool2_flat = tf.reshape(pool2, [-1, 7 * 7 * 64])
logits = tf.layers.dense(inputs=pool2_flat, units=10)
# definition of the losses pertinent to our study
L_adv = stadv.losses.adv_loss(logits, targets)
L_flow = stadv.losses.flow_loss(flows, padding_mode='CONSTANT')
L_final = L_adv + tau * L_flow
grad_op = tf.gradients(L_final, flows, name='loss_gradient')[0]
```
### Import the learned weights
The network has been trained independently and its learned weights are shipped with the demo. The final error on the test set is of 1.3%.
```
init = tf.global_variables_initializer()
saver = tf.train.Saver()
sess = tf.Session()
sess.run(init)
saver.restore(sess, os.path.join('saved_models', 'simple_mnist'))
```
### Test the model on a single image
The test image is randomly picked from the test set of MNIST. Its target label is also selected randomly.
```
i_random_image = np.random.randint(0, len(mnist_images))
test_image = mnist_images[i_random_image]
test_label = mnist_labels[i_random_image]
random_target = np.random.choice([num for num in range(10) if num != test_label])
print("Considering image #", i_random_image, "from the test set of MNIST")
print("Ground truth label:", test_label)
print("Randomly selected target label:", random_target)
# reshape so as to have a first dimension (batch size) of 1
test_image = np.expand_dims(test_image, 0)
test_label = np.expand_dims(test_label, 0)
random_target = np.expand_dims(random_target, 0)
# with no flow the flow_st is the identity
null_flows = np.zeros((1, 2, 28, 28))
pred_label = np.argmax(sess.run(
[logits],
feed_dict={images: test_image, flows: null_flows}
))
print("Predicted label (no perturbation):", pred_label)
```
### Where the magic takes place
Optimization of the flow so as to minimize the loss using an L-BFGS-B optimizer.
```
results = stadv.optimization.lbfgs(
L_final,
flows,
# random initial guess for the flow
flows_x0=np.random.random_sample((1, 2, 28, 28)),
feed_dict={images: test_image, targets: random_target, tau: 0.05},
grad_op=grad_op,
sess=sess
)
print("Final loss:", results['loss'])
print("Optimization info:", results['info'])
test_logits_perturbed, test_image_perturbed = sess.run(
[logits, perturbed_images],
feed_dict={images: test_image, flows: results['flows']}
)
pred_label_perturbed = np.argmax(test_logits_perturbed)
print("Predicted label after perturbation:", pred_label_perturbed)
```
### Show the results
```
image_before = test_image[0, :, :, 0]
image_after = test_image_perturbed[0, :, :, 0]
difference = image_after - image_before
max_diff = abs(difference).max()
plt.rcParams['figure.figsize'] = [10, 10]
f, (ax1, ax2, ax3) = plt.subplots(1, 3)
ax1.imshow(image_before)
ax1.set_title("True: {} - Pred: {} - Target: {}".format(test_label[0], pred_label, random_target[0]))
ax1.axis('off')
ax2.imshow(image_after)
ax2.set_title("Pred: {} - Loss: {}".format(pred_label_perturbed, round(results['loss'], 2)))
ax2.axis('off')
ax3.imshow(difference)
ax3.set_title("Max Difference: {}".format(round(max_diff, 2)))
ax3.axis('off')
plt.show()
```
| true |
code
| 0.715697 | null | null | null | null |
|
```
# default_exp utils
```
# utils
> Provides different util functions
```
#export
import json
from copy import deepcopy
import numpy as np
from PIL import Image
from icevision.core.mask import EncodedRLEs, MaskArray
from pycocotools import mask as mask_utils
```
## Test data setup
```
import icedata
from icevision.data.data_splitter import SingleSplitSplitter
test_data_path_instance_segmentation = icedata.pennfudan.load_data()
test_instance_segmentation_parser = icedata.pennfudan.parser(data_dir=test_data_path_instance_segmentation)
test_instance_segmentation_records = test_instance_segmentation_parser.parse(SingleSplitSplitter())[0]
test_instance_segmentation_class_map = test_instance_segmentation_records[0].detection.class_map
```
## Instance segmentation
```
#export
def erles_to_string(erles):
erles_copy = deepcopy(erles)
erles_copy["counts"] = erles_copy["counts"].decode("utf-8")
return json.dumps(erles_copy)
#hide
test_erles = test_instance_segmentation_records[0].as_dict()["detection"]["masks"][0].to_erles(None, None).erles
test_string_erles = erles_to_string(test_erles[0])
assert test_string_erles == '{"size": [536, 559], "counts": "ecc22g`00O2O0O1O100O1O00100O001O10O01O1O0010OO2N2M2O2M2O2M2O2M2O2N1N3N1N3N1N3N0O01O01O00000O1000000O2O001`NbNfC^1Z<dNcC^1\\\\<eNaC[1_<gN_CZ1`<iN\\\\CX1e<iNXCY1h<iNUCX1o9cNhG6VNX1l9mNjGLXNX1n9oNhGHXNZ1Q:ROcGDZN\\\\1R:SObGBZN[1U:UO_G@ZN]1W:TO_G^OYN^1Y:UO]G]OXN`1[:UO[G[OXNa1^:UOYG[OWNa1`:VOXGXOVNc1c:VOVGWOUNd1g:UOSGWOTNf1j:SOQGWOTNf1m:SOoF[1S9dNhF`1Z9`NVFo1k9QNhEZ2Z:iMVEb2l:d11N2N2O1N3M3N2M3M3N2M2O200YKbDS4R<01O1O10O4L3N3L3M4M2M4ZE\\\\Ko8d4PG^Ko8b4PG^KR9`4nF`KS9_4lFbKU9]4kFcKX9Z4hFeK]9W4cFiKb9V4ZFjKj9V4QFkKT:T4gEmK]:h1jD6d0SNh:a1hD<:UNX;T1bDh01UNf;i0^DR1GVNU<>WD]1_OVNc<3SDU2W<`MmC]2Y=N3M2N3M2N3M2N3M2N3M3M3M3M3M3M2N3L4M3M3M3M6J5K6J6J^SV4"}'
#export
def erles_to_counts_to_utf8(erles):
erles_copy = deepcopy(erles)
for entry in erles_copy:
entry["counts"] = entry["counts"].decode("utf-8")
return erles_copy
#hide
test_erles_with_utf_8_counts = erles_to_counts_to_utf8(test_erles)
for erles in test_erles_with_utf_8_counts:
assert isinstance(erles["counts"], str)
#export
def string_to_erles(erles_string):
erles = json.loads(erles_string)
erles["counts"] = erles["counts"].encode()
return erles
#hide
erles_string = json.dumps(erles_to_counts_to_utf8(test_erles)[0])
test_erles_from_string = string_to_erles(erles_string)
assert isinstance(test_erles_from_string["counts"], bytes)
#export
def correct_mask(mask_array, pad_x, pad_y, width, height):
# correct mask
corrected_mask_array = mask_array.transpose(2, 0, 1)
if round(pad_x/2) > 0:
corrected_mask_array=corrected_mask_array[:,:,round(pad_x/2):round(-pad_x/2)]
if round(pad_y/2) > 0:
corrected_mask_array=corrected_mask_array[:,round(pad_y/2):round(-pad_y/2),:]
corrected_mask_array = np.array(Image.fromarray(corrected_mask_array[0,:,:]).resize([width, height], Image.NEAREST))
corrected_mask_array = np.expand_dims(corrected_mask_array, 0)
# convert mask array to mask and get erles (only one erles exist!)
corrected_mask = MaskArray(corrected_mask_array)
return corrected_mask
#hide
test_mask = np.zeros([1, 30, 30])
test_mask_corrected = correct_mask(test_mask, 10, 0, 30, 20)
assert test_mask_corrected.data.shape == (1, 20, 30)
#export
def decorrect_mask(mask_array, pad_x, pad_y, width, height):
corrected_mask_array = mask_array.transpose(2, 0, 1)
# resize
corrected_mask_array = np.array(Image.fromarray(corrected_mask_array[0,:,:]).resize([width, height], Image.NEAREST))
corrected_mask_array = np.expand_dims(corrected_mask_array, 0)
# pad
corrected_mask_array = np.pad(corrected_mask_array, [[0,0], [pad_y, pad_y], [pad_x, pad_x],])
corrected_mask = MaskArray(corrected_mask_array)
return corrected_mask
test_mask = np.ones([1, 10,10])
test_mask_decorrected = decorrect_mask(test_mask, 1, 2, 5, 5)
assert test_mask_decorrected.shape == (1,9,7)
```
| true |
code
| 0.446857 | null | null | null | null |
|
<hr style="height:2px;">
# Demo: Neural network training for joint denoising and surface projection of *Drosophila melanogaster* wing
This notebook demonstrates training a CARE model for a 3D → 2D denoising+projection task, assuming that training data was already generated via [1_datagen.ipynb](1_datagen.ipynb) and has been saved to disk to the file ``data/my_training_data.npz``.
Note that training a neural network for actual use should be done on more (representative) data and with more training time.
More documentation is available at http://csbdeep.bioimagecomputing.com/doc/.
```
from __future__ import print_function, unicode_literals, absolute_import, division
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
from tifffile import imread
from csbdeep.utils import axes_dict, plot_some, plot_history
from csbdeep.utils.tf import limit_gpu_memory
from csbdeep.io import load_training_data
from csbdeep.models import Config, ProjectionCARE
```
The TensorFlow backend uses all available GPU memory by default, hence it can be useful to limit it:
```
# limit_gpu_memory(fraction=1/2)
```
<hr style="height:2px;">
# Training data
Load training data generated via [1_datagen.ipynb](1_datagen.ipynb), use 10% as validation data.
```
(X,Y), (X_val,Y_val), axes = load_training_data('data/my_training_data.npz', validation_split=0.1, verbose=True)
c = axes_dict(axes)['C']
n_channel_in, n_channel_out = X.shape[c], Y.shape[c]
plt.figure(figsize=(12,5))
plot_some(X_val[:5],Y_val[:5])
plt.suptitle('5 example validation patches (top row: source, bottom row: target)');
```
<hr style="height:2px;">
# CARE model
Before we construct the actual CARE model, we have to define its configuration via a `Config` object, which includes
* parameters of the underlying neural network,
* the learning rate,
* the number of parameter updates per epoch,
* the loss function, and
* whether the model is probabilistic or not.
The defaults should be sensible in many cases, so a change should only be necessary if the training process fails.
---
<span style="color:red;font-weight:bold;">Important</span>: Note that for this notebook we use a very small number of update steps per epoch for immediate feedback, whereas this number should be increased considerably (e.g. `train_steps_per_epoch=400`) to obtain a well-trained model.
```
config = Config(axes, n_channel_in, n_channel_out, unet_n_depth=3, train_batch_size=8, train_steps_per_epoch=20)
print(config)
vars(config)
```
We now create a CARE model with the chosen configuration:
```
model = ProjectionCARE(config, 'my_model', basedir='models')
```
Note that there are additional parameters for the projection part of the CARE model. If you need to change them, you can do so by specifying them with the prefix `proj_` when creating the `Config` above. For example, use `proj_n_filt = 16` to change the parameter `n_filt` of the `ProjectionParameters` shown below.
```
model.proj_params
```
<hr style="height:2px;">
# Training
Training the model will likely take some time. We recommend to monitor the progress with [TensorBoard](https://www.tensorflow.org/programmers_guide/summaries_and_tensorboard) (example below), which allows you to inspect the losses during training.
Furthermore, you can look at the predictions for some of the validation images, which can be helpful to recognize problems early on.
You can start TensorBoard from the current working directory with `tensorboard --logdir=.`
Then connect to [http://localhost:6006/](http://localhost:6006/) with your browser.

```
history = model.train(X,Y, validation_data=(X_val,Y_val))
```
Plot final training history (available in TensorBoard during training):
```
print(sorted(list(history.history.keys())))
plt.figure(figsize=(16,5))
plot_history(history,['loss','val_loss'],['mse','val_mse','mae','val_mae']);
```
<hr style="height:2px;">
# Evaluation
Example results for validation images.
```
plt.figure(figsize=(12,7))
_P = model.keras_model.predict(X_val[:5])
if config.probabilistic:
_P = _P[...,:(_P.shape[-1]//2)]
plot_some(X_val[:5],Y_val[:5],_P,pmax=99.5)
plt.suptitle('5 example validation patches\n'
'top row: input (source), '
'middle row: target (ground truth), '
'bottom row: predicted from source');
```
<hr style="height:2px;">
# Export model to be used with CSBDeep **Fiji** plugins and **KNIME** workflows
See https://github.com/CSBDeep/CSBDeep_website/wiki/Your-Model-in-Fiji for details.
```
model.export_TF()
```
| true |
code
| 0.736871 | null | null | null | null |
|
###### Reference:
https://finthon.com/learn-cnn-two-tfrecord-read-data/
https://finthon.com/learn-cnn-three-resnet-prediction/
# 匯入圖片資料並輸出成tfrecord檔案
```
import os
from PIL import Image
import tensorflow as tf
'''
設置路徑
# 將需分類之圖片目錄放置Working Directory於之下,Folder以Int作為命名
'''
# 图片路径,两组标签都在该目录下
cwd = r"./OM/"
# tfrecord文件保存路径
file_path = r"./"
# 每个tfrecord存放图片个数
bestnum = 10000
# 第几个图片
num = 0
# 第几个TFRecord文件
recordfilenum = 0
# 将labels放入到classes中
classes = []
for i in os.listdir(cwd):
classes.append(i)
# tfrecords格式文件名
ftrecordfilename = ("traindata_63.tfrecords-%.3d" % recordfilenum)
writer = tf.python_io.TFRecordWriter(os.path.join(file_path, ftrecordfilename))
'''
tfrecord 製造函數
'''
for index, name in enumerate(classes):
class_path = os.path.join(cwd, name)
for img_name in os.listdir(class_path):
num = num + 1
if num > bestnum:
num = 1
recordfilenum += 1
ftrecordfilename = ("traindata_63.tfrecords-%.3d" % recordfilenum)
writer = tf.python_io.TFRecordWriter(os.path.join(file_path, ftrecordfilename))
img_path = os.path.join(class_path, img_name) # 每一个图片的地址
img = Image.open(img_path, 'r')
img_raw = img.tobytes() # 将图片转化为二进制格式
example = tf.train.Example(
features=tf.train.Features(feature={
'label': tf.train.Feature(int64_list=tf.train.Int64List(value=[index])),
'img_raw': tf.train.Feature(bytes_list=tf.train.BytesList(value=[img_raw])),
}))
writer.write(example.SerializeToString()) # 序列化为字符串
writer.close()
```
# 自tfrecord輸入資料集
```
'''
tfrecord 輸入函數
'''
import tensorflow as tf
def read_and_decode_tfrecord(filename):
filename_deque = tf.train.string_input_producer(filename)
reader = tf.TFRecordReader()
_, serialized_example = reader.read(filename_deque)
features = tf.parse_single_example(serialized_example, features={
'label': tf.FixedLenFeature([], tf.int64),
'img_raw': tf.FixedLenFeature([], tf.string)})
label = tf.cast(features['label'], tf.int32)
img = tf.decode_raw(features['img_raw'], tf.uint8)
img = tf.reshape(img, [640, 480, 3])
img = tf.cast(img, tf.float32) / 255.0
return img, label
```
# 訓練CNN模型
```
import tensorflow as tf
import tensorflow.contrib.slim.nets as nets
'''
定义模型保存地址,batch_sizes设置的小一点训练效果更好,将当前目录下的tfrecord文件放入列表中:
# tf.train.shuffle_batch: 随机打乱队列里面的数据顺序
# num_threads: 表示线程数
# capacity" 表示队列的容量,在这里设置成10000
# min_after_dequeue: 队列里保留的最小数据量,并且控制着随机的程度,
设置成9900的意思是,当队列中的数据出列100个,剩下9900个的时候,就要重新补充100个数据进来并打乱顺序。
如果你要按顺序导入队列,改成tf.train.batch函数,并删除min_after_dequeue参数。
这些参数都要根据自己的电脑配置进行相应的设置。
接下来将label值进行onehot编码,直接调用tf.one_hot函数。因为我们这里有2类,depth设置成2:
'''
save_dir = r"./train_image_63.model" # 模型保存路径
batch_size_ = 2
lr = tf.Variable(0.0001, dtype=tf.float32) # 学习速率
x = tf.placeholder(tf.float32, [None, 640, 480, 3]) # 图片大小为224*224*3
y_ = tf.placeholder(tf.float32, [None])
'''
train_list = ['traindata_63.tfrecords-000', 'traindata_63.tfrecords-001', 'traindata_63.tfrecords-002',
'traindata_63.tfrecords-003', 'traindata_63.tfrecords-004', 'traindata_63.tfrecords-005',
'traindata_63.tfrecords-006', 'traindata_63.tfrecords-007', 'traindata_63.tfrecords-008',
'traindata_63.tfrecords-009', 'traindata_63.tfrecords-010', 'traindata_63.tfrecords-011',
'traindata_63.tfrecords-012', 'traindata_63.tfrecords-013', 'traindata_63.tfrecords-014',
'traindata_63.tfrecords-015', 'traindata_63.tfrecords-016', 'traindata_63.tfrecords-017',
'traindata_63.tfrecords-018', 'traindata_63.tfrecords-019', 'traindata_63.tfrecords-020',
'traindata_63.tfrecords-021'] #制作成的所有tfrecord数据,每个最多包含1000个图片数据
'''
train_list = ['traindata_63.tfrecords-000']
# 随机打乱顺序
img, label = read_and_decode_tfrecord(train_list)
img_batch, label_batch = tf.train.shuffle_batch([img, label], num_threads=2, batch_size=batch_size_, capacity=10000,
min_after_dequeue=9900)
'''
接下来将label值进行onehot编码,直接调用tf.one_hot函数。因为我们这里有100类,depth设置成100:
'''
# 将label值进行onehot编码
one_hot_labels = tf.one_hot(indices=tf.cast(y_, tf.int32), depth=2)
pred, end_points = nets.resnet_v2.resnet_v2_50(x, num_classes=2, is_training=True)
pred = tf.reshape(pred, shape=[-1, 2])
'''
# nets.resnet_v2.resnet_v2_50: 直接调用ResNet_50网络
# num_classes等于类别总数
# is_training表示我们是否要训练网络里面固定层的参数,True表示所有参数都重新训练,False表示只训练后面几层的参数。
网络搭好后,我们继续定义损失函数和优化器,损失函数选择sigmoid交叉熵,优化器选择Adam:
'''
# 定义损失函数和优化器
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=pred, labels=one_hot_labels))
optimizer = tf.train.AdamOptimizer(learning_rate=lr).minimize(loss)
# 准确度
a = tf.argmax(pred, 1)
b = tf.argmax(one_hot_labels, 1)
correct_pred = tf.equal(a, b)
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
saver = tf.train.Saver()
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
# 创建一个协调器,管理线程
coord = tf.train.Coordinator()
# 启动QueueRunner,此时文件名队列已经进队
threads = tf.train.start_queue_runners(sess=sess, coord=coord)
i = 0
while True:
i += 1
b_image, b_label = sess.run([img_batch, label_batch])
_, loss_, y_t, y_p, a_, b_ = sess.run([optimizer, loss, one_hot_labels, pred, a, b], feed_dict={x: b_image,
y_: b_label})
print('step: {}, train_loss: {}'.format(i, loss_))
if i % 20 == 0:
_loss, acc_train = sess.run([loss, accuracy], feed_dict={x: b_image, y_: b_label})
print('--------------------------------------------------------')
print('step: {} train_acc: {} loss: {}'.format(i, acc_train, _loss))
print('--------------------------------------------------------')
if i == 200:
saver.save(sess, save_dir, global_step=i)
#elif i == 300000:
# saver.save(sess, save_dir, global_step=i)
#elif i == 400000:
# saver.save(sess, save_dir, global_step=i)
break
coord.request_stop()
# 其他所有线程关闭之后,这一函数才能返回
coord.join(threads)
```
# 使用模型進行預測
```
import tensorflow as tf
import tensorflow.contrib.slim.nets as nets
from PIL import Image
import os
test_dir = r'./test' # 原始的test文件夹,含带预测的图片
model_dir = r'./train_image_63.model-300000' # 模型地址
test_txt_dir = r'./test.txt' # 原始的test.txt文件
result_dir = r'./result.txt' # 生成输出结果
x = tf.placeholder(tf.float32, [None, 640, 480, 3])
'''
classes = ['1', '10', '100', '11', '12', '13', '14', '15', '16', '17', '18', '19', '2', '20', '21', '22', '23', '24',
'25', '26', '27', '28', '29', '3', '30', '31', '32', '33', '34', '35', '36', '37', '38', '39', '4', '40',
'41', '42', '43', '44', '45', '46', '47', '48', '49', '5', '50', '51', '52', '53', '54', '55', '56', '57',
'58', '59', '6', '60', '61', '62', '63', '64', '65', '66', '67', '68', '69', '7', '70', '71', '72', '73',
'74', '75', '76', '77', '78', '79', '8', '80', '81', '82', '83', '84', '85', '86', '87', '88', '89', '9',
'90', '91', '92', '93', '94', '95', '96', '97', '98', '99'] # 标签顺序
'''
classes = ['0', '1'] # 标签顺序
pred, end_points = nets.resnet_v2.resnet_v2_50(x, num_classes=2, is_training=True)
pred = tf.reshape(pred, shape=[-1, 2])
a = tf.argmax(pred, 1)
saver = tf.train.Saver()
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
saver.restore(sess, model_dir)
with open(test_txt_dir, 'r') as f:
data = f.readlines()
for i in data:
test_name = i.split()[0]
for pic in os.listdir(test_dir):
if pic == test_name:
img_path = os.path.join(test_dir, pic)
img = Image.open(img_path)
img = img.resize((640, 480))
img = tf.reshape(img, [1, 640, 480, 3])
img1 = tf.reshape(img, [1, 640, 480, 3])
img = tf.cast(img, tf.float32) / 255.0
b_image, b_image_raw = sess.run([img, img1])
t_label = sess.run(a, feed_dict={x: b_image})
index_ = t_label[0]
predict = classes[index_]
with open(result_dir, 'a') as f1:
print(test_name, predict, file=f1)
break
```
| true |
code
| 0.434581 | null | null | null | null |
|
Zipline Beginner Tutorial
=========================
Basics
------
Zipline is an open-source algorithmic trading simulator written in Python.
The source can be found at: https://github.com/quantopian/zipline
Some benefits include:
* Realistic: slippage, transaction costs, order delays.
* Stream-based: Process each event individually, avoids look-ahead bias.
* Batteries included: Common transforms (moving average) as well as common risk calculations (Sharpe).
* Developed and continuously updated by [Quantopian](https://www.quantopian.com) which provides an easy-to-use web-interface to Zipline, 10 years of minute-resolution historical US stock data, and live-trading capabilities. This tutorial is directed at users wishing to use Zipline without using Quantopian. If you instead want to get started on Quantopian, see [here](https://www.quantopian.com/faq#get-started).
This tutorial assumes that you have zipline correctly installed, see the [installation instructions](https://github.com/quantopian/zipline#installation) if you haven't set up zipline yet.
Every `zipline` algorithm consists of two functions you have to define:
* `initialize(context)`
* `handle_data(context, data)`
Before the start of the algorithm, `zipline` calls the `initialize()` function and passes in a `context` variable. `context` is a persistent namespace for you to store variables you need to access from one algorithm iteration to the next.
After the algorithm has been initialized, `zipline` calls the `handle_data()` function once for each event. At every call, it passes the same `context` variable and an event-frame called `data` containing the current trading bar with open, high, low, and close (OHLC) prices as well as volume for each stock in your universe. For more information on these functions, see the [relevant part of the Quantopian docs](https://www.quantopian.com/help#api-toplevel).
My first algorithm
----------------------
Lets take a look at a very simple algorithm from the `examples` directory, `buyapple.py`:
```
# assuming you're running this notebook in zipline/docs/notebooks
import os
if os.name == 'nt':
# windows doesn't have the cat command, but uses 'type' similarly
! type "..\..\zipline\examples\buyapple.py"
else:
! cat ../../zipline/examples/buyapple.py
```
As you can see, we first have to import some functions we would like to use. All functions commonly used in your algorithm can be found in `zipline.api`. Here we are using `order()` which takes two arguments -- a security object, and a number specifying how many stocks you would like to order (if negative, `order()` will sell/short stocks). In this case we want to order 10 shares of Apple at each iteration. For more documentation on `order()`, see the [Quantopian docs](https://www.quantopian.com/help#api-order).
Finally, the `record()` function allows you to save the value of a variable at each iteration. You provide it with a name for the variable together with the variable itself: `varname=var`. After the algorithm finished running you will have access to each variable value you tracked with `record()` under the name you provided (we will see this further below). You also see how we can access the current price data of the AAPL stock in the `data` event frame (for more information see [here](https://www.quantopian.com/help#api-event-properties)).
## Ingesting data for your algorithm
Before we can run the algorithm, we'll need some historical data for our algorithm to ingest, which we can get through a data bundle. A data bundle is a collection of pricing data, adjustment data, and an asset database. Bundles allow us to preload all of the data we will need to run backtests and store the data for future runs. Quantopian provides a default bundle called `quandl` which uses the [Quandl WIKI Dataset](https://www.quandl.com/data/WIKI-Wiki-EOD-Stock-Prices). You'll need a [Quandl API Key](https://docs.quandl.com/docs#section-authentication), and then you can ingest that data by running:
```
! QUANDL_API_KEY=<yourkey> zipline ingest -b quandl
```
For more information on data bundles, such as building custom data bundles, you can look at the [zipline docs](http://www.zipline.io/bundles.html).
## Running the algorithm
To now test this algorithm on financial data, `zipline` provides two interfaces. A command-line interface and an `IPython Notebook` interface.
### Command line interface
After you installed zipline you should be able to execute the following from your command line (e.g. `cmd.exe` on Windows, or the Terminal app on OSX):
```
!zipline run --help
```
Note that you have to omit the preceding '!' when you call `run_algo.py`, this is only required by the IPython Notebook in which this tutorial was written.
As you can see there are a couple of flags that specify where to find your algorithm (`-f`) as well as the time-range (`--start` and `--end`). Finally, you'll want to save the performance metrics of your algorithm so that you can analyze how it performed. This is done via the `--output` flag and will cause it to write the performance `DataFrame` in the pickle Python file format.
Thus, to execute our algorithm from above and save the results to `buyapple_out.pickle` we would call `run_algo.py` as follows:
```
!zipline run -f ../../zipline/examples/buyapple.py --start 2016-1-1 --end 2018-1-1 -o buyapple_out.pickle
```
`run_algo.py` first outputs the algorithm contents. It then uses historical price and volume data of Apple from the `quantopian-quandl` bundle in the desired time range, calls the `initialize()` function, and then streams the historical stock price day-by-day through `handle_data()`. After each call to `handle_data()` we instruct `zipline` to order 10 stocks of AAPL. After the call of the `order()` function, `zipline` enters the ordered stock and amount in the order book. After the `handle_data()` function has finished, `zipline` looks for any open orders and tries to fill them. If the trading volume is high enough for this stock, the order is executed after adding the commission and applying the slippage model which models the influence of your order on the stock price, so your algorithm will be charged more than just the stock price * 10. (Note, that you can also change the commission and slippage model that `zipline` uses, see the [Quantopian docs](https://www.quantopian.com/help#ide-slippage) for more information).
Note that there is also an `analyze()` function printed. `run_algo.py` will try and look for a file with the ending with `_analyze.py` and the same name of the algorithm (so `buyapple_analyze.py`) or an `analyze()` function directly in the script. If an `analyze()` function is found it will be called *after* the simulation has finished and passed in the performance `DataFrame`. (The reason for allowing specification of an `analyze()` function in a separate file is that this way `buyapple.py` remains a valid Quantopian algorithm that you can copy&paste to the platform).
Lets take a quick look at the performance `DataFrame`. For this, we use `pandas` from inside the IPython Notebook and print the first ten rows. Note that `zipline` makes heavy usage of `pandas`, especially for data input and outputting so it's worth spending some time to learn it.
```
import pandas as pd
perf = pd.read_pickle('buyapple_out.pickle') # read in perf DataFrame
perf.head()
```
As you can see, there is a row for each trading day, starting on the first business day of 2016. In the columns you can find various information about the state of your algorithm. The very first column `AAPL` was placed there by the `record()` function mentioned earlier and allows us to plot the price of apple. For example, we could easily examine now how our portfolio value changed over time compared to the AAPL stock price.
```
%pylab inline
figsize(12, 12)
import matplotlib.pyplot as plt
ax1 = plt.subplot(211)
perf.portfolio_value.plot(ax=ax1)
ax1.set_ylabel('Portfolio Value')
ax2 = plt.subplot(212, sharex=ax1)
perf.AAPL.plot(ax=ax2)
ax2.set_ylabel('AAPL Stock Price')
```
As you can see, our algorithm performance as assessed by the `portfolio_value` closely matches that of the AAPL stock price. This is not surprising as our algorithm only bought AAPL every chance it got.
### IPython Notebook
The [IPython Notebook](http://ipython.org/notebook.html) is a very powerful browser-based interface to a Python interpreter (this tutorial was written in it). As it is already the de-facto interface for most quantitative researchers `zipline` provides an easy way to run your algorithm inside the Notebook without requiring you to use the CLI.
To use it you have to write your algorithm in a cell and let `zipline` know that it is supposed to run this algorithm. This is done via the `%%zipline` IPython magic command that is available after you run `%load_ext zipline` in a separate cell. This magic takes the same arguments as the command line interface described above.
```
%load_ext zipline
%%zipline --start 2016-1-1 --end 2018-1-1 -o perf_ipython.pickle
from zipline.api import symbol, order, record
def initialize(context):
context.asset = symbol('AAPL')
def handle_data(context, data):
order(context.asset, 10)
record(AAPL=data.current(context.asset, 'price'))
```
Note that we did not have to specify an input file as above since the magic will use the contents of the cell and look for your algorithm functions there.
```
pd.read_pickle('perf_ipython.pickle').head()
```
## Access to previous prices using `data.history()`
### Working example: Dual Moving Average Cross-Over
The Dual Moving Average (DMA) is a classic momentum strategy. It's probably not used by any serious trader anymore but is still very instructive. The basic idea is that we compute two rolling or moving averages (mavg) -- one with a longer window that is supposed to capture long-term trends and one shorter window that is supposed to capture short-term trends. Once the short-mavg crosses the long-mavg from below we assume that the stock price has upwards momentum and long the stock. If the short-mavg crosses from above we exit the positions as we assume the stock to go down further.
As we need to have access to previous prices to implement this strategy we need a new concept: History
`data.history()` is a convenience function that keeps a rolling window of data for you. The first argument is the asset or iterable of assets you're using, the second argument is the field you're looking for i.e. price, open, volume, the third argument is the number of bars, and the fourth argument is your frequency (either `'1d'` for `'1m'` but note that you need to have minute-level data for using `1m`).
For a more detailed description of `data.history()`'s features, see the [Quantopian docs](https://www.quantopian.com/help#ide-history). Let's look at the strategy which should make this clear:
```
%pylab inline
figsize(12, 12)
%%zipline --start 2014-1-1 --end 2018-1-1 -o perf_dma.pickle
from zipline.api import order_target, record, symbol
import numpy as np
import matplotlib.pyplot as plt
def initialize(context):
context.i = 0
context.asset = symbol('AAPL')
def handle_data(context, data):
# Skip first 300 days to get full windows
context.i += 1
if context.i < 300:
return
# Compute averages
# data.history() has to be called with the same params
# from above and returns a pandas dataframe.
short_mavg = data.history(context.asset, 'price', bar_count=100, frequency="1d").mean()
long_mavg = data.history(context.asset, 'price', bar_count=300, frequency="1d").mean()
# Trading logic
if short_mavg > long_mavg:
# order_target orders as many shares as needed to
# achieve the desired number of shares.
order_target(context.asset, 100)
elif short_mavg < long_mavg:
order_target(context.asset, 0)
# Save values for later inspection
record(AAPL=data.current(context.asset, 'price'),
short_mavg=short_mavg,
long_mavg=long_mavg)
def analyze(context, perf):
ax1 = plt.subplot(211)
perf.portfolio_value.plot(ax=ax1)
ax1.set_ylabel('portfolio value in $')
ax1.set_xlabel('time in years')
ax2 = plt.subplot(212, sharex=ax1)
perf['AAPL'].plot(ax=ax2)
perf[['short_mavg', 'long_mavg']].plot(ax=ax2)
perf_trans = perf.ix[[t != [] for t in perf.transactions]]
buys = perf_trans.ix[[t[0]['amount'] > 0 for t in perf_trans.transactions]]
sells = perf_trans.ix[[t[0]['amount'] < 0 for t in perf_trans.transactions]]
ax2.plot(buys.index, perf.short_mavg.ix[buys.index], '^', markersize=10, color='m')
ax2.plot(sells.index, perf.short_mavg.ix[sells.index],'v', markersize=10, color='k')
ax2.set_ylabel('price in $')
ax2.set_xlabel('time in years')
plt.legend(loc=0)
plt.show()
```
Here we are explicitly defining an `analyze()` function that gets automatically called once the backtest is done (this is not possible on Quantopian currently).
Although it might not be directly apparent, the power of `history` (pun intended) can not be under-estimated as most algorithms make use of prior market developments in one form or another. You could easily devise a strategy that trains a classifier with [`scikit-learn`](http://scikit-learn.org/stable/) which tries to predict future market movements based on past prices (note, that most of the `scikit-learn` functions require `numpy.ndarray`s rather than `pandas.DataFrame`s, so you can simply pass the underlying `ndarray` of a `DataFrame` via `.values`).
We also used the `order_target()` function above. This and other functions like it can make order management and portfolio rebalancing much easier. See the [Quantopian documentation on order functions](https://www.quantopian.com/help#api-order-methods) fore more details.
# Conclusions
We hope that this tutorial gave you a little insight into the architecture, API, and features of `zipline`. For next steps, check out some of the [examples](https://github.com/quantopian/zipline/tree/master/zipline/examples).
Feel free to ask questions on [our mailing list](https://groups.google.com/forum/#!forum/zipline), report problems on our [GitHub issue tracker](https://github.com/quantopian/zipline/issues?state=open), [get involved](https://github.com/quantopian/zipline/wiki/Contribution-Requests), and [checkout Quantopian](https://quantopian.com).
| true |
code
| 0.566918 | null | null | null | null |
|
# Derived Fields and Profiles
One of the most powerful features in yt is the ability to create derived fields that act and look exactly like fields that exist on disk. This means that they will be generated on demand and can be used anywhere a field that exists on disk would be used. Additionally, you can create them by just writing python functions.
```
%matplotlib inline
import yt
import numpy as np
from yt import derived_field
from matplotlib import pylab
```
## Derived Fields
This is an example of the simplest possible way to create a derived field. All derived fields are defined by a function and some metadata; that metadata can include units, LaTeX-friendly names, conversion factors, and so on. Fields can be defined in the way in the next cell. What this does is create a function which accepts two arguments and then provide the units for that field. In this case, our field is `dinosaurs` and our units are `K*cm/s`. The function itself can access any fields that are in the simulation, and it does so by requesting data from the object called `data`.
```
@derived_field(name="dinosaurs", units="K * cm/s", sampling_type="cell")
def _dinos(field, data):
return data["temperature"] * data["velocity_magnitude"]
```
One important thing to note is that derived fields must be defined *before* any datasets are loaded. Let's load up our data and take a look at some quantities.
```
ds = yt.load_sample("IsolatedGalaxy")
dd = ds.all_data()
print (list(dd.quantities.keys()))
```
One interesting question is, what are the minimum and maximum values of dinosaur production rates in our isolated galaxy? We can do that by examining the `extrema` quantity -- the exact same way that we would for density, temperature, and so on.
```
print (dd.quantities.extrema("dinosaurs"))
```
We can do the same for the average quantities as well.
```
print (dd.quantities.weighted_average_quantity("dinosaurs", weight="temperature"))
```
## A Few Other Quantities
We can ask other quantities of our data, as well. For instance, this sequence of operations will find the most dense point, center a sphere on it, calculate the bulk velocity of that sphere, calculate the baryonic angular momentum vector, and then the density extrema. All of this is done in a memory conservative way: if you have an absolutely enormous dataset, yt will split that dataset into pieces, apply intermediate reductions and then a final reduction to calculate your quantity.
```
sp = ds.sphere("max", (10.0, 'kpc'))
bv = sp.quantities.bulk_velocity()
L = sp.quantities.angular_momentum_vector()
rho_min, rho_max = sp.quantities.extrema("density")
print (bv)
print (L)
print (rho_min, rho_max)
```
## Profiles
yt provides the ability to bin in 1, 2 and 3 dimensions. This means discretizing in one or more dimensions of phase space (density, temperature, etc) and then calculating either the total value of a field in each bin or the average value of a field in each bin.
We do this using the objects `Profile1D`, `Profile2D`, and `Profile3D`. The first two are the most common since they are the easiest to visualize.
This first set of commands manually creates a profile object the sphere we created earlier, binned in 32 bins according to density between `rho_min` and `rho_max`, and then takes the density-weighted average of the fields `temperature` and (previously-defined) `dinosaurs`. We then plot it in a loglog plot.
```
prof = yt.Profile1D(sp, "density", 32, rho_min, rho_max, True, weight_field="mass")
prof.add_fields(["temperature","dinosaurs"])
pylab.loglog(np.array(prof.x), np.array(prof["temperature"]), "-x")
pylab.xlabel('Density $(g/cm^3)$')
pylab.ylabel('Temperature $(K)$')
```
Now we plot the `dinosaurs` field.
```
pylab.loglog(np.array(prof.x), np.array(prof["dinosaurs"]), '-x')
pylab.xlabel('Density $(g/cm^3)$')
pylab.ylabel('Dinosaurs $(K cm / s)$')
```
If we want to see the total mass in every bin, we profile the `mass` field with no weight. Specifying `weight=None` will simply take the total value in every bin and add that up.
```
prof = yt.Profile1D(sp, "density", 32, rho_min, rho_max, True, weight_field=None)
prof.add_fields(["mass"])
pylab.loglog(np.array(prof.x), np.array(prof["mass"].in_units("Msun")), '-x')
pylab.xlabel('Density $(g/cm^3)$')
pylab.ylabel('Cell mass $(M_\odot)$')
```
In addition to the low-level `ProfileND` interface, it's also quite straightforward to quickly create plots of profiles using the `ProfilePlot` class. Let's redo the last plot using `ProfilePlot`
```
prof = yt.ProfilePlot(sp, 'density', 'mass', weight_field=None)
prof.set_unit('mass', 'Msun')
prof.show()
```
## Field Parameters
Field parameters are a method of passing information to derived fields. For instance, you might pass in information about a vector you want to use as a basis for a coordinate transformation. yt often uses things like `bulk_velocity` to identify velocities that should be subtracted off. Here we show how that works:
```
sp_small = ds.sphere("max", (50.0, 'kpc'))
bv = sp_small.quantities.bulk_velocity()
sp = ds.sphere("max", (0.1, 'Mpc'))
rv1 = sp.quantities.extrema("radial_velocity")
sp.clear_data()
sp.set_field_parameter("bulk_velocity", bv)
rv2 = sp.quantities.extrema("radial_velocity")
print (bv)
print (rv1)
print (rv2)
```
| true |
code
| 0.524882 | null | null | null | null |
|
# One time pad
In the previous lesson we performed an attack over the Monoalphabetic cipher where the attacker (Charlie) only knew that Alice and Bob were communicating in english and that they were using this concrete cipher. Therefore the ciphertext is leaking information. Can we find a cipher whose ciphertext doesn't leak any information on the original message?. We are going to answer this question using the Vigenere cipher.
# Table of contents:
* [Vigenere revisited](#vigenere-revisited)
* [Gathering plain english data](#nineteen-eighty-four)
* [Counting letter frequencies](#counting-frequencies)
* [Frequencies with short key](#counting-frequencies-2)
* [Frequencies with large key](#counting-frequencies3)
* [The One Time Pad](#onetimepad)
* [Why is the one time pad impractical?](#impractical-onetimepad)
Author: [Sebastià Agramunt Puig](https://github.com/sebastiaagramunt) for [OpenMined](https://www.openmined.org/) Privacy ML Series course.
## Vigenère cipher revisited <a class="anchor" id="vigenere-revisited"></a>
First, lets copy paste the code for the Vingenère cipher already coded in the first notebook
```
from copy import deepcopy
from random import randrange
import string
def vigenere_key_generator(secret_key_size: int) -> str:
n = len(string.ascii_lowercase)
secret_key = ''
while len(secret_key) < secret_key_size:
secret_key += string.ascii_lowercase[randrange(n)]
return secret_key
def shift_letter(letter: str, shiftby: str, forward: bool=True) -> str:
n = len(string.ascii_lowercase)
letter_int = ord(letter) - 97
shiftby_int = ord(shiftby) - 97
if forward:
return string.ascii_lowercase[(letter_int+shiftby_int)%n]
else:
return string.ascii_lowercase[(letter_int-shiftby_int)%n]
def vigenere_encrypt_decrypt(message: str, secret_key: str, encrypt:bool = True) -> str:
key_len = len(secret_key)
encoded = ''
for i, letter in enumerate(message):
if letter != " ":
encoded += shift_letter(letter, secret_key[i%key_len], forward=encrypt)
else:
encoded += letter
return encoded
```
## Downloading data from the book Nineteen Eighty Four <a class="anchor" id="nineteen-eighty-four"></a>
```
from utils import download_data, process_load_textfile
import string
import os
url = 'http://gutenberg.net.au/ebooks01/0100021.txt'
filename = 'Nineteen-eighty-four_Orwell.txt'
download_path = '/'.join(os.getcwd().split('/')[:-1]) + '/data/'
#download data to specified path
download_data(url, filename, download_path)
#load data and process
data = process_load_textfile(filename, download_path)
```
Have a look at the data
```
data[10000:11000]
```
## Counting letter frequencies <a class="anchor" id="counting-frequencies"></a>
First we write a function to count the frequency of the letters for a given text and outputs a sorted tuple with the letter and the counts of that letter
```
from typing import List, Tuple
from collections import Counter
def letter_count(text: str) -> List[Tuple[str, int]]:
text2 = text.replace(" ", "")
letters = [c for c in text2]
return Counter(letters).most_common()
```
And calculate the frequency for the book nineteen eighty four
```
freq = letter_count(data)
freq
```
And let's write a function that gives a bar plot for the frequencies:
```
import matplotlib.pyplot as plt
def freq_plotter(text: str, title: str) -> plt.figure:
plt.clf()
freq = letter_count(text)
names = [x[0] for x in freq]
values = [x[1] for x in freq]
fig = plt.figure(figsize=(16,7))
plt.bar(names, values)
plt.title(title)
return fig
fig = freq_plotter(data, "Frequencies of letters for Nineteen Eighty Four")
```
And finally let's code another nice utility, a function that randomly draws a random portion of the text
```
from random import randrange, seed
def draw_sample(text: str, size: int) -> str:
n = len(text)
i_init = randrange(n)
i_final = i_init + size
c = ''
for i in range(i_init, i_final):
c += text[i%n]
return c
seed(3)
draw_sample(data, 100)
```
## Counting frequencies with short key <a class="anchor" id="counting-frequencies-2"></a>
Now let's count the frequency in the ciphertext for a randomly sampled text from the book. Let's begin with the shift cipher (i.e. Vigenere with key size 1)
```
seed(10)
message_size = len(data)//4
secret_key_size = 1
print(f"message_size = {message_size}\nsecret_key_size = {secret_key_size}")
# generating random message
message = draw_sample(data, message_size)
# generating secret key
secret_key = vigenere_key_generator(secret_key_size)
# calculating ciphertext that Alice sends to Bob
ciphertext = vigenere_encrypt_decrypt(message, secret_key, encrypt=True)
# just to make sure Vigenere is well coded
assert message==vigenere_encrypt_decrypt(ciphertext, secret_key, encrypt=False), "something went wrong"
fig = freq_plotter(ciphertext, f"Frequencies for ciphertext size {message_size} and key size {secret_key_size}")
```
We observe that the frequencies of the letters are not the same, and therefore if the attacker knows Alice and Bob communicate in english he will probably be able to say that the shift is 1, i.e. the secret key is "b" because the most frequent letter in english is "e" and that corresponds to the peak in "f", therefore the shift is of one position. Here we can extract information from the ciphertext.
## Counting frequencies with large key <a class="anchor" id="counting-frequencies3"></a>
Instead of having a short key, let's take a super long key, actually the size of our message:
```
seed(10)
message_size = len(data)//4
secret_key_size = message_size
print(f"message_size = {message_size}\nsecret_key_size = {secret_key_size}")
# generating random message
message = draw_sample(data, message_size)
# generating secret key
secret_key = vigenere_key_generator(secret_key_size)
# calculating ciphertext that Alice sends to Bob
ciphertext = vigenere_encrypt_decrypt(message, secret_key, encrypt=True)
# just to make sure Vigenere is well coded
assert message==vigenere_encrypt_decrypt(ciphertext, secret_key, encrypt=False), "something went wrong"
fig = freq_plotter(ciphertext, f"Frequencies for ciphertext size {message_size} and key size {secret_key_size}")
```
Great!. The attacker computes the frequency of the letters in the ciphertext and determines that the probability for each letter to appear is almost the same. In this context we can say that the ciphertext does not contain any information from the original message.
## The one time pad <a class="anchor" id="onetimepad"></a>
Let's have a deeper look on what we've done in the previous section. First let's see what is the frequency for each letter when randomly generating the key
```
rdm_secret_keys = [vigenere_key_generator(secret_key_size=1) for _ in range(15000)]
count = Counter(rdm_secret_keys)
count.most_common()
```
These are very similar, this means that the probability for generating any letter is almost the same, around 1/26. Then when we encrypt what we do is to "shift" or "pad" our character by the key number. This means that the character in the ciphertext has probability 1/26 independent on what the character of the message was. We can formalise this using Bayesian statistics:
A cryptosystem has perfect secrecy if for all possible messages and for all possible ciphertext the probability of finding a message is independent of the ciphertext
$$P(m|c) = P(m)$$
where $P(m)$ is the probability of message $m$ from the corpus of all possible messages $M$ and $P(m|c)$ is the conditional probability for $m$ having observed the ciphertext $c$ belonging to the corpus of all possible ciphertexts $C$.
Equivalently we can write
$$P(m|c) = P(m|c^\prime)$$
for any two arbitrary ciphertext $c$ and $c^\prime$. This means that the probability for the message $m$ is independent of the ciphertext.
## One time pad is impractical because... <a class="anchor" id="impractical-onetimepad"></a>
* The key has to be at least as long as the message one wants to transmit
* For perfect secrecy one has to use a new key every time.
* Alice and Bob have to make sure that they are the only ones that know the key. They cannot stablish a common key communicating through an insecure channel
| true |
code
| 0.556038 | null | null | null | null |
|
# Anna KaRNNa
In this notebook, I'll build a character-wise RNN trained on Anna Karenina, one of my all-time favorite books. It'll be able to generate new text based on the text from the book.
This network is based off of Andrej Karpathy's [post on RNNs](http://karpathy.github.io/2015/05/21/rnn-effectiveness/) and [implementation in Torch](https://github.com/karpathy/char-rnn). Also, some information [here at r2rt](http://r2rt.com/recurrent-neural-networks-in-tensorflow-ii.html) and from [Sherjil Ozair](https://github.com/sherjilozair/char-rnn-tensorflow) on GitHub. Below is the general architecture of the character-wise RNN.
<img src="assets/charseq.jpeg" width="500">
```
import time
from collections import namedtuple
import numpy as np
import tensorflow as tf
```
First we'll load the text file and convert it into integers for our network to use. Here I'm creating a couple dictionaries to convert the characters to and from integers. Encoding the characters as integers makes it easier to use as input in the network.
```
with open('anna.txt', 'r') as f:
text=f.read()
vocab = sorted(set(text))
vocab_to_int = {c: i for i, c in enumerate(vocab)}
int_to_vocab = dict(enumerate(vocab))
encoded = np.array([vocab_to_int[c] for c in text], dtype=np.int32)
```
Let's check out the first 100 characters, make sure everything is peachy. According to the [American Book Review](http://americanbookreview.org/100bestlines.asp), this is the 6th best first line of a book ever.
```
text[:100]
```
And we can see the characters encoded as integers.
```
encoded[:100]
```
Since the network is working with individual characters, it's similar to a classification problem in which we are trying to predict the next character from the previous text. Here's how many 'classes' our network has to pick from.
```
len(vocab)
```
## Making training mini-batches
Here is where we'll make our mini-batches for training. Remember that we want our batches to be multiple sequences of some desired number of sequence steps. Considering a simple example, our batches would look like this:
<img src="assets/sequence_batching@1x.png" width=500px>
<br>
We have our text encoded as integers as one long array in `encoded`. Let's create a function that will give us an iterator for our batches. I like using [generator functions](https://jeffknupp.com/blog/2013/04/07/improve-your-python-yield-and-generators-explained/) to do this. Then we can pass `encoded` into this function and get our batch generator.
The first thing we need to do is discard some of the text so we only have completely full batches. Each batch contains $N \times M$ characters, where $N$ is the batch size (the number of sequences) and $M$ is the number of steps. Then, to get the number of batches we can make from some array `arr`, you divide the length of `arr` by the batch size. Once you know the number of batches and the batch size, you can get the total number of characters to keep.
After that, we need to split `arr` into $N$ sequences. You can do this using `arr.reshape(size)` where `size` is a tuple containing the dimensions sizes of the reshaped array. We know we want $N$ sequences (`n_seqs` below), let's make that the size of the first dimension. For the second dimension, you can use `-1` as a placeholder in the size, it'll fill up the array with the appropriate data for you. After this, you should have an array that is $N \times (M * K)$ where $K$ is the number of batches.
Now that we have this array, we can iterate through it to get our batches. The idea is each batch is a $N \times M$ window on the array. For each subsequent batch, the window moves over by `n_steps`. We also want to create both the input and target arrays. Remember that the targets are the inputs shifted over one character. You'll usually see the first input character used as the last target character, so something like this:
```python
y[:, :-1], y[:, -1] = x[:, 1:], x[:, 0]
```
where `x` is the input batch and `y` is the target batch.
The way I like to do this window is use `range` to take steps of size `n_steps` from $0$ to `arr.shape[1]`, the total number of steps in each sequence. That way, the integers you get from `range` always point to the start of a batch, and each window is `n_steps` wide.
```
def get_batches(arr, n_seqs, n_steps):
'''Create a generator that returns batches of size
n_seqs x n_steps from arr.
Arguments
---------
arr: Array you want to make batches from
n_seqs: Batch size, the number of sequences per batch
n_steps: Number of sequence steps per batch
'''
# Get the number of characters per batch and number of batches we can make
characters_per_batch = n_seqs * n_steps
n_batches = len(arr)//characters_per_batch
# Keep only enough characters to make full batches
arr = arr[:n_batches * characters_per_batch]
# Reshape into n_seqs rows
arr = arr.reshape((n_seqs, -1))
for n in range(0, arr.shape[1], n_steps):
# The features
x = arr[:, n:n+n_steps]
# The targets, shifted by one
y = np.zeros_like(x)
y[:, :-1], y[:, -1] = x[:, 1:], x[:, 0]
yield x, y
```
Now I'll make my data sets and we can check out what's going on here. Here I'm going to use a batch size of 10 and 50 sequence steps.
```
batches = get_batches(encoded, 10, 50)
x, y = next(batches)
print('x\n', x[:10, :10])
print('\ny\n', y[:10, :10])
```
If you implemented `get_batches` correctly, the above output should look something like
```
x
[[55 63 69 22 6 76 45 5 16 35]
[ 5 69 1 5 12 52 6 5 56 52]
[48 29 12 61 35 35 8 64 76 78]
[12 5 24 39 45 29 12 56 5 63]
[ 5 29 6 5 29 78 28 5 78 29]
[ 5 13 6 5 36 69 78 35 52 12]
[63 76 12 5 18 52 1 76 5 58]
[34 5 73 39 6 5 12 52 36 5]
[ 6 5 29 78 12 79 6 61 5 59]
[ 5 78 69 29 24 5 6 52 5 63]]
y
[[63 69 22 6 76 45 5 16 35 35]
[69 1 5 12 52 6 5 56 52 29]
[29 12 61 35 35 8 64 76 78 28]
[ 5 24 39 45 29 12 56 5 63 29]
[29 6 5 29 78 28 5 78 29 45]
[13 6 5 36 69 78 35 52 12 43]
[76 12 5 18 52 1 76 5 58 52]
[ 5 73 39 6 5 12 52 36 5 78]
[ 5 29 78 12 79 6 61 5 59 63]
[78 69 29 24 5 6 52 5 63 76]]
```
although the exact numbers will be different. Check to make sure the data is shifted over one step for `y`.
## Building the model
Below is where you'll build the network. We'll break it up into parts so it's easier to reason about each bit. Then we can connect them up into the whole network.
<img src="assets/charRNN.png" width=500px>
### Inputs
First off we'll create our input placeholders. As usual we need placeholders for the training data and the targets. We'll also create a placeholder for dropout layers called `keep_prob`.
```
def build_inputs(batch_size, num_steps):
''' Define placeholders for inputs, targets, and dropout
Arguments
---------
batch_size: Batch size, number of sequences per batch
num_steps: Number of sequence steps in a batch
'''
# Declare placeholders we'll feed into the graph
inputs = tf.placeholder(tf.int32, [batch_size, num_steps], name='inputs')
targets = tf.placeholder(tf.int32, [batch_size, num_steps], name='targets')
# Keep probability placeholder for drop out layers
keep_prob = tf.placeholder(tf.float32, name='keep_prob')
return inputs, targets, keep_prob
```
### LSTM Cell
Here we will create the LSTM cell we'll use in the hidden layer. We'll use this cell as a building block for the RNN. So we aren't actually defining the RNN here, just the type of cell we'll use in the hidden layer.
We first create a basic LSTM cell with
```python
lstm = tf.contrib.rnn.BasicLSTMCell(num_units)
```
where `num_units` is the number of units in the hidden layers in the cell. Then we can add dropout by wrapping it with
```python
tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
```
You pass in a cell and it will automatically add dropout to the inputs or outputs. Finally, we can stack up the LSTM cells into layers with [`tf.contrib.rnn.MultiRNNCell`](https://www.tensorflow.org/versions/r1.0/api_docs/python/tf/contrib/rnn/MultiRNNCell). With this, you pass in a list of cells and it will send the output of one cell into the next cell. Previously with TensorFlow 1.0, you could do this
```python
tf.contrib.rnn.MultiRNNCell([cell]*num_layers)
```
This might look a little weird if you know Python well because this will create a list of the same `cell` object. However, TensorFlow 1.0 will create different weight matrices for all `cell` objects. But, starting with TensorFlow 1.1 you actually need to create new cell objects in the list. To get it to work in TensorFlow 1.1, it should look like
```python
def build_cell(num_units, keep_prob):
lstm = tf.contrib.rnn.BasicLSTMCell(num_units)
drop = tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
return drop
tf.contrib.rnn.MultiRNNCell([build_cell(num_units, keep_prob) for _ in range(num_layers)])
```
Even though this is actually multiple LSTM cells stacked on each other, you can treat the multiple layers as one cell.
We also need to create an initial cell state of all zeros. This can be done like so
```python
initial_state = cell.zero_state(batch_size, tf.float32)
```
Below, we implement the `build_lstm` function to create these LSTM cells and the initial state.
```
def build_lstm(lstm_size, num_layers, batch_size, keep_prob):
''' Build LSTM cell.
Arguments
---------
keep_prob: Scalar tensor (tf.placeholder) for the dropout keep probability
lstm_size: Size of the hidden layers in the LSTM cells
num_layers: Number of LSTM layers
batch_size: Batch size
'''
### Build the LSTM Cell
def build_cell(lstm_size, keep_prob):
# Use a basic LSTM cell
lstm = tf.contrib.rnn.BasicLSTMCell(lstm_size)
# Add dropout to the cell
drop = tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
return drop
# Stack up multiple LSTM layers, for deep learning
cell = tf.contrib.rnn.MultiRNNCell([build_cell(lstm_size, keep_prob) for _ in range(num_layers)])
initial_state = cell.zero_state(batch_size, tf.float32)
return cell, initial_state
```
### RNN Output
Here we'll create the output layer. We need to connect the output of the RNN cells to a full connected layer with a softmax output. The softmax output gives us a probability distribution we can use to predict the next character.
If our input has batch size $N$, number of steps $M$, and the hidden layer has $L$ hidden units, then the output is a 3D tensor with size $N \times M \times L$. The output of each LSTM cell has size $L$, we have $M$ of them, one for each sequence step, and we have $N$ sequences. So the total size is $N \times M \times L$.
We are using the same fully connected layer, the same weights, for each of the outputs. Then, to make things easier, we should reshape the outputs into a 2D tensor with shape $(M * N) \times L$. That is, one row for each sequence and step, where the values of each row are the output from the LSTM cells.
One we have the outputs reshaped, we can do the matrix multiplication with the weights. We need to wrap the weight and bias variables in a variable scope with `tf.variable_scope(scope_name)` because there are weights being created in the LSTM cells. TensorFlow will throw an error if the weights created here have the same names as the weights created in the LSTM cells, which they will be default. To avoid this, we wrap the variables in a variable scope so we can give them unique names.
```
def build_output(lstm_output, in_size, out_size):
''' Build a softmax layer, return the softmax output and logits.
Arguments
---------
x: Input tensor
in_size: Size of the input tensor, for example, size of the LSTM cells
out_size: Size of this softmax layer
2
'''
# Reshape output so it's a bunch of rows, one row for each step for each sequence.
# That is, the shape should be batch_size*num_steps rows by lstm_size columns
seq_output = tf.concat(lstm_output, axis=1)
x = tf.reshape(seq_output, [-1, in_size])
# Connect the RNN outputs to a softmax layer
with tf.variable_scope('softmax'):
softmax_w = tf.Variable(tf.truncated_normal((in_size, out_size), stddev=0.1))
softmax_b = tf.Variable(tf.zeros(out_size))
# Since output is a bunch of rows of RNN cell outputs, logits will be a bunch
# of rows of logit outputs, one for each step and sequence
logits = tf.matmul(x, softmax_w) + softmax_b
# Use softmax to get the probabilities for predicted characters
out = tf.nn.softmax(logits, name='predictions')
return out, logits
```
### Training loss
Next up is the training loss. We get the logits and targets and calculate the softmax cross-entropy loss. First we need to one-hot encode the targets, we're getting them as encoded characters. Then, reshape the one-hot targets so it's a 2D tensor with size $(M*N) \times C$ where $C$ is the number of classes/characters we have. Remember that we reshaped the LSTM outputs and ran them through a fully connected layer with $C$ units. So our logits will also have size $(M*N) \times C$.
Then we run the logits and targets through `tf.nn.softmax_cross_entropy_with_logits` and find the mean to get the loss.
```
def build_loss(logits, targets, lstm_size, num_classes):
''' Calculate the loss from the logits and the targets.
Arguments
---------
logits: Logits from final fully connected layer
targets: Targets for supervised learning
lstm_size: Number of LSTM hidden units
num_classes: Number of classes in targets
'''
# One-hot encode targets and reshape to match logits, one row per batch_size per step
y_one_hot = tf.one_hot(targets, num_classes)
y_reshaped = tf.reshape(y_one_hot, logits.get_shape())
# Softmax cross entropy loss
loss = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y_reshaped)
loss = tf.reduce_mean(loss)
return loss
```
### Optimizer
Here we build the optimizer. Normal RNNs have have issues gradients exploding and disappearing. LSTMs fix the disappearance problem, but the gradients can still grow without bound. To fix this, we can clip the gradients above some threshold. That is, if a gradient is larger than that threshold, we set it to the threshold. This will ensure the gradients never grow overly large. Then we use an AdamOptimizer for the learning step.
```
def build_optimizer(loss, learning_rate, grad_clip):
''' Build optmizer for training, using gradient clipping.
Arguments:
loss: Network loss
learning_rate: Learning rate for optimizer
'''
# Optimizer for training, using gradient clipping to control exploding gradients
tvars = tf.trainable_variables()
grads, _ = tf.clip_by_global_norm(tf.gradients(loss, tvars), grad_clip)
train_op = tf.train.AdamOptimizer(learning_rate)
optimizer = train_op.apply_gradients(zip(grads, tvars))
return optimizer
```
### Build the network
Now we can put all the pieces together and build a class for the network. To actually run data through the LSTM cells, we will use [`tf.nn.dynamic_rnn`](https://www.tensorflow.org/versions/r1.0/api_docs/python/tf/nn/dynamic_rnn). This function will pass the hidden and cell states across LSTM cells appropriately for us. It returns the outputs for each LSTM cell at each step for each sequence in the mini-batch. It also gives us the final LSTM state. We want to save this state as `final_state` so we can pass it to the first LSTM cell in the the next mini-batch run. For `tf.nn.dynamic_rnn`, we pass in the cell and initial state we get from `build_lstm`, as well as our input sequences. Also, we need to one-hot encode the inputs before going into the RNN.
```
class CharRNN:
def __init__(self, num_classes, batch_size=64, num_steps=50,
lstm_size=128, num_layers=2, learning_rate=0.001,
grad_clip=5, sampling=False):
# When we're using this network for sampling later, we'll be passing in
# one character at a time, so providing an option for that
if sampling == True:
batch_size, num_steps = 1, 1
else:
batch_size, num_steps = batch_size, num_steps
tf.reset_default_graph()
# Build the input placeholder tensors
self.inputs, self.targets, self.keep_prob = build_inputs(batch_size, num_steps)
# Build the LSTM cell
cell, self.initial_state = build_lstm(lstm_size, num_layers, batch_size, self.keep_prob)
### Run the data through the RNN layers
# First, one-hot encode the input tokens
x_one_hot = tf.one_hot(self.inputs, num_classes)
# Run each sequence step through the RNN and collect the outputs
outputs, state = tf.nn.dynamic_rnn(cell, x_one_hot, initial_state=self.initial_state)
self.final_state = state
# self.seq_output = tf.concat(outputs, axis=1)
# self.xval = tf.reshape(self.seq_output, [-1, lstm_size])
self.x2 = tf.concat(outputs, axis=0)
# Get softmax predictions and logits
self.prediction, self.logits = build_output(outputs, lstm_size, num_classes)
# Loss and optimizer (with gradient clipping)
self.loss = build_loss(self.logits, self.targets, lstm_size, num_classes)
self.optimizer = build_optimizer(self.loss, learning_rate, grad_clip)
```
## Hyperparameters
Here I'm defining the hyperparameters for the network.
* `batch_size` - Number of sequences running through the network in one pass.
* `num_steps` - Number of characters in the sequence the network is trained on. Larger is better typically, the network will learn more long range dependencies. But it takes longer to train. 100 is typically a good number here.
* `lstm_size` - The number of units in the hidden layers.
* `num_layers` - Number of hidden LSTM layers to use
* `learning_rate` - Learning rate for training
* `keep_prob` - The dropout keep probability when training. If you're network is overfitting, try decreasing this.
Here's some good advice from Andrej Karpathy on training the network. I'm going to copy it in here for your benefit, but also link to [where it originally came from](https://github.com/karpathy/char-rnn#tips-and-tricks).
> ## Tips and Tricks
>### Monitoring Validation Loss vs. Training Loss
>If you're somewhat new to Machine Learning or Neural Networks it can take a bit of expertise to get good models. The most important quantity to keep track of is the difference between your training loss (printed during training) and the validation loss (printed once in a while when the RNN is run on the validation data (by default every 1000 iterations)). In particular:
> - If your training loss is much lower than validation loss then this means the network might be **overfitting**. Solutions to this are to decrease your network size, or to increase dropout. For example you could try dropout of 0.5 and so on.
> - If your training/validation loss are about equal then your model is **underfitting**. Increase the size of your model (either number of layers or the raw number of neurons per layer)
> ### Approximate number of parameters
> The two most important parameters that control the model are `lstm_size` and `num_layers`. I would advise that you always use `num_layers` of either 2/3. The `lstm_size` can be adjusted based on how much data you have. The two important quantities to keep track of here are:
> - The number of parameters in your model. This is printed when you start training.
> - The size of your dataset. 1MB file is approximately 1 million characters.
>These two should be about the same order of magnitude. It's a little tricky to tell. Here are some examples:
> - I have a 100MB dataset and I'm using the default parameter settings (which currently print 150K parameters). My data size is significantly larger (100 mil >> 0.15 mil), so I expect to heavily underfit. I am thinking I can comfortably afford to make `lstm_size` larger.
> - I have a 10MB dataset and running a 10 million parameter model. I'm slightly nervous and I'm carefully monitoring my validation loss. If it's larger than my training loss then I may want to try to increase dropout a bit and see if that helps the validation loss.
> ### Best models strategy
>The winning strategy to obtaining very good models (if you have the compute time) is to always err on making the network larger (as large as you're willing to wait for it to compute) and then try different dropout values (between 0,1). Whatever model has the best validation performance (the loss, written in the checkpoint filename, low is good) is the one you should use in the end.
>It is very common in deep learning to run many different models with many different hyperparameter settings, and in the end take whatever checkpoint gave the best validation performance.
>By the way, the size of your training and validation splits are also parameters. Make sure you have a decent amount of data in your validation set or otherwise the validation performance will be noisy and not very informative.
```
batch_size = 100 # Sequences per batch
num_steps = 100 # Number of sequence steps per batch
lstm_size = 512 # Size of hidden layers in LSTMs
num_layers = 2 # Number of LSTM layers
learning_rate = 0.001 # Learning rate
keep_prob = 0.5 # Dropout keep probability
```
## Time for training
This is typical training code, passing inputs and targets into the network, then running the optimizer. Here we also get back the final LSTM state for the mini-batch. Then, we pass that state back into the network so the next batch can continue the state from the previous batch. And every so often (set by `save_every_n`) I save a checkpoint.
Here I'm saving checkpoints with the format
`i{iteration number}_l{# hidden layer units}.ckpt`
```
epochs = 20
# Save every N iterations
save_every_n = 200
model = CharRNN(len(vocab), batch_size=batch_size, num_steps=num_steps,
lstm_size=lstm_size, num_layers=num_layers,
learning_rate=learning_rate)
saver = tf.train.Saver(max_to_keep=100)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
# Use the line below to load a checkpoint and resume training
#saver.restore(sess, 'checkpoints/______.ckpt')
counter = 0
for e in range(epochs):
# Train network
new_state = sess.run(model.initial_state)
loss = 0
for x, y in get_batches(encoded, batch_size, num_steps):
counter += 1
start = time.time()
feed = {model.inputs: x,
model.targets: y,
model.keep_prob: keep_prob,
model.initial_state: new_state}
# sess.run(model.xval)
batch_loss, new_state, _ = sess.run([model.loss,
model.final_state,
model.optimizer],
feed_dict=feed)
sess.run(model.x2)
sess.run(model.x2.eval())
end = time.time()
print('Epoch: {}/{}... '.format(e+1, epochs),
'Training Step: {}... '.format(counter),
'Training loss: {:.4f}... '.format(batch_loss),
'{:.4f} sec/batch'.format((end-start)))
if (counter % save_every_n == 0):
saver.save(sess, "checkpoints/i{}_l{}.ckpt".format(counter, lstm_size))
saver.save(sess, "checkpoints/i{}_l{}.ckpt".format(counter, lstm_size))
```
#### Saved checkpoints
Read up on saving and loading checkpoints here: https://www.tensorflow.org/programmers_guide/variables
```
tf.train.get_checkpoint_state('checkpoints')
```
## Sampling
Now that the network is trained, we'll can use it to generate new text. The idea is that we pass in a character, then the network will predict the next character. We can use the new one, to predict the next one. And we keep doing this to generate all new text. I also included some functionality to prime the network with some text by passing in a string and building up a state from that.
The network gives us predictions for each character. To reduce noise and make things a little less random, I'm going to only choose a new character from the top N most likely characters.
```
def pick_top_n(preds, vocab_size, top_n=5):
p = np.squeeze(preds)
p[np.argsort(p)[:-top_n]] = 0
p = p / np.sum(p)
c = np.random.choice(vocab_size, 1, p=p)[0]
return c
def sample(checkpoint, n_samples, lstm_size, vocab_size, prime="The "):
samples = [c for c in prime]
model = CharRNN(len(vocab), lstm_size=lstm_size, sampling=True)
saver = tf.train.Saver()
with tf.Session() as sess:
saver.restore(sess, checkpoint)
new_state = sess.run(model.initial_state)
for c in prime:
x = np.zeros((1, 1))
x[0,0] = vocab_to_int[c]
feed = {model.inputs: x,
model.keep_prob: 1.,
model.initial_state: new_state}
preds, new_state = sess.run([model.prediction, model.final_state],
feed_dict=feed)
c = pick_top_n(preds, len(vocab))
samples.append(int_to_vocab[c])
for i in range(n_samples):
x[0,0] = c
feed = {model.inputs: x,
model.keep_prob: 1.,
model.initial_state: new_state}
preds, new_state = sess.run([model.prediction, model.final_state],
feed_dict=feed)
c = pick_top_n(preds, len(vocab))
samples.append(int_to_vocab[c])
return ''.join(samples)
```
Here, pass in the path to a checkpoint and sample from the network.
```
tf.train.latest_checkpoint('checkpoints')
checkpoint = tf.train.latest_checkpoint('checkpoints')
samp = sample(checkpoint, 2000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i200_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i600_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i1200_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
```
| true |
code
| 0.660993 | null | null | null | null |
|
# Circuit Translation
In this notebook we will introduce a tool of `sqwalk` that is useful to decompose (or translate) an unitary transormation (in our case the one generated by the walker's Hamiltonian) into a series of gates that can be simulated or even run on quantum hardware. The decomposition method is based on `qiskit` thus we will need it as a dependency, in addition to our usual `SQWalker` class and some QuTiP objects.
Before jumping to the tutorial, it is useful to note here that this decomposition, for the sake of being general, it is not optimized. Indeed, while it supports any kind of quantum computer and every kind of quantum walker it usually takes up a lot of gates to implement the decomposition. To optimize the number of gate one must resort to some specific techniques in the literature that leverage the symmetries and characteristics of some particular graphs and are not general.
```
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import scipy
from sqwalk import SQWalker
from sqwalk import gate_decomposition
from qiskit import Aer
from qiskit.visualization import *
```
First we create the walker as we have seen in the previous notebooks and we run it for a certain time to have a reference result. In this case we have picked a time of 1000.
```
#Create and run the walker
graph = nx.path_graph(8)
adj = nx.adj_matrix(graph).todense()
walker = SQWalker(np.array(adj))
time_samples = 1000
initial_node = 0
result = walker.run_walker(initial_node, time_samples)
new_state = result.final_state
nodelist = [i for i in range(adj.shape[0])]
plt.bar(nodelist, new_state.diag())
plt.show()
```
Our decomposition, albeit being devised as a tool to decompose walkers, can be used with any Unitary or Hamiltonian.
Note that since we will use a system of $n$ qubits, our Hamiltonian has to be $2^n$ dimensional, if the problem has the wrong dimensionality one can zero-pad it to make it work.
The time we used above in `time_samples` has to be rescaled of a factor of $100$ since the timestep of the master equation in run_walker is $10^{-2}$.
```
#Estract the Hamiltonian from the walker
hamiltonian = walker.quantum_hamiltonian.full()
#Set the time one wants to simulate
time_rescaled = 10
#Compute the respective unitary
unitary = scipy.linalg.expm(-1j*time_rescaled*hamiltonian)
```
Now it is all set up to decompose our walker using the `gate_decomposition` function from `sqwalk`. To decompose it, it is suffiicent to pass our unitary to the function that, leveraging qiskit transpiling, will give us back the quantum circuit.
The `gate_decomposition` function also accepts two more arguments:
- topology: a list of connections between qubits specifying the topology of the particular hardware we want to decompose on, default topology is fully connected.
- gates: a list of allowed gates that can be used to create the decomposition, defaults to single qubit rotations and CNOT.
The resulting decomposition is a qiskit circuit object that can be exported into QASM instructions ot be executed on virtually every device.
```
#Decompose into gates
circuit_decomp = gate_decomposition(unitary)
circuit_decomp.qasm() # port it to whatever hardware
#circuit_decomp.draw()
```
As an example we take a simulator backend from `qiskit` itself (it could be a real device instead of a simulator), we execute the decomposed circuit and plot the result.
```
backend=Aer.get_backend('aer_simulator')
circuit_decomp.measure_all()
result=backend.run(circuit_decomp).result()
counts = result.get_counts(circuit_decomp)
plot_histogram(counts)
```
We can see that the decomposition is perfectly consistent with the quantum walker we have simulated above with SQWalk!
```
```
| true |
code
| 0.629319 | null | null | null | null |
|
# Boston Housing Prices Dataset
## Contents
0. [Introduction](#intro)
1. [Pre-processing and Splitting Data](#split)
2. [Models for median price predictions](#model)
3. [Stacked model](#stack)
## Introduction <a class="anchor" id="intro"></a>
This notebook illustrates the use of the `Stacker` to conveniently stack models over folds to perform predictions. In this example, the Boston Housing dataset (included in scikit-learn) is used. Two linear models (Ridge Regression and LASSO) are stacked. The single stacker is a Ridge Regression model.
```
import warnings
import numpy as np
import pandas as pd
from scipy import stats
from sklearn.model_selection import train_test_split, StratifiedKFold, RepeatedKFold, KFold, ParameterGrid, GridSearchCV
from sklearn.linear_model import Ridge, RidgeCV, Lasso, LassoCV
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR, LinearSVR
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import RobustScaler
# Stacking
from Pancake.Stacker import *
# Data
from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
warnings.filterwarnings('ignore')
# Random seed
seed=123
```
## Data Loading and Pre-processing <a class="anchor" id="split"></a>
```
# Get data
boston=load_boston()
X = boston['data']
y = boston['target']
print(boston['DESCR'])
```
Features and target variables:
```
feats = boston["feature_names"]
df_boston = pd.DataFrame(X, columns=feats)
df_boston['MEDV'] = y
# Unique values for each feature
df_boston.apply(lambda x: len(set(x)))
```
The following features benefit from a log transform:
* `CRIM`, `DIS`, `LSTAT`
```
fig, (ax1,ax2,ax3) = plt.subplots(1,3,figsize=(18,6))
sns.distplot(df_boston['CRIM'],ax=ax1)
sns.distplot(df_boston['DIS'], ax=ax2)
sns.distplot(df_boston['LSTAT'],ax=ax3)
plt.suptitle('Original Features')
plt.show()
fig, (ax1,ax2,ax3) = plt.subplots(1,3,figsize=(18,6))
sns.distplot(df_boston['CRIM'].apply(lambda x: np.log10(x)),ax=ax1)
sns.distplot(df_boston['DIS'].apply(lambda x: np.log10(x)), ax=ax2)
sns.distplot(df_boston['LSTAT'].apply(lambda x: np.log10(x)),ax=ax3)
plt.suptitle('Log transformed features')
plt.show()
```
To split the data into train/test sets, we can stratify using `MEDV` percentiles. This helps in a more balanced distribution between train and test sets
```
def quantileClasses(y, percs=[25,50,75]):
quantiles = np.percentile(y, percs)
yq = np.zeros_like(y,dtype=int)
# Categorical yq based on quantiles
yq[(y>quantiles[0]) & (y < quantiles[1])] = 1
yq[(y>quantiles[1]) & (y < quantiles[2])] = 2
yq[(y>quantiles[2])] = 3
return yq
yq = quantileClasses(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=yq, test_size=0.25, random_state=seed)
```
Let's pre-process and use robust scaler to re-scale:
```
feats_toLog = ['CRIM','DIS','LSTAT']
df_train = pd.DataFrame(X_train, columns=feats)
df_test = pd.DataFrame(X_test, columns=feats)
for f in feats_toLog:
df_train[f] = np.log10(df_train[f])
df_test[f] = np.log10(df_test[f])
```
Let's also rescale the features (except the categorical `CHAS`):
```
feats_to_normalize = [f for f in feats if f != 'CHAS']
X_ = df_train[feats_to_normalize].values
# Scale training data
scaler = RobustScaler()
X_rscl = scaler.fit_transform(X_)
center_, scale_ = scaler.center_, scaler.scale_
```
Training and test sets:
```
# Train
df_train_new = pd.DataFrame(X_rscl, columns=feats_to_normalize)
df_train_new['CHAS'] = df_train['CHAS']
# Test
X_ = df_test[feats_to_normalize].values
X_ = (X_ - center_) / scale_
df_test_new = pd.DataFrame(X_, columns=feats_to_normalize)
df_test_new['CHAS'] = df_test['CHAS']
```
## Modeling <a class="anchor" id="model"></a>
As a simple case, let's use Ridge Regression and LASSO as in-layer models. We will train both models separately in all training data, as well as on folds for the stacked model
```
X_train = df_train_new[feats].values
X_test = df_test_new[feats].values
```
#### Ridge Regression
```
skf = RepeatedKFold(n_repeats=10,n_splits=5,random_state=seed)
regMod_1 = RidgeCV(alphas=np.logspace(-2,2,100), scoring='neg_mean_squared_error', cv=skf)
regMod_1.fit(X_train, y_train)
print("Best hyper-parameter: alpha = {:.4f}".format(regMod_1.alpha_))
# Predict on train/test sets
y_pred_tr = regMod_1.predict(X_train)
mse_tr = mean_squared_error(y_train, y_pred_tr)
y_pred_ts = regMod_1.predict(X_test)
mse_ts = mean_squared_error(y_test, y_pred_ts)
# Performance
print("Training RMSE = {:.4f}".format(np.sqrt(mse_tr)))
print("Test RMSE = {:.4f}".format(np.sqrt(mse_ts)))
```
#### Lasso
```
skf = RepeatedKFold(n_repeats=10,n_splits=5,random_state=seed)
regMod_2 = LassoCV(n_alphas=100, cv=skf)
regMod_2.fit(X_train, y_train)
print("Best hyper-parameter: alpha = {:.4f}".format(regMod_2.alpha_))
# Train/test predictions
y_pred_tr = regMod_2.predict(X_train)
mse_tr = mean_squared_error(y_train, y_pred_tr)
y_pred_ts = regMod_2.predict(X_test)
mse_ts = mean_squared_error(y_test, y_pred_ts)
# Performance
print("Training RMSE = {:.4f}".format(np.sqrt(mse_tr)))
print("Test RMSE = {:.4f}".format(np.sqrt(mse_ts)))
```
## Stacking <a class="anchor" id="stack"></a>
We can now stack predictions from the above models. We choose to re-train the in-layer models over the folds since it leads to better performance
```
# Metric to maximize (negative RMSE)
def nrmse(y,y_pred):
return -np.sqrt(mean_squared_error(y,y_pred))
# Folds
splt = KFold(n_splits=5,random_state=seed)
# Initiate stacker
stacker = Stacker(X_train, y_train, splitter=splt, evalMetric=nrmse, family="regression")
# Hyper-parameters
hypers = {'alpha':np.logspace(-2,2,100)}
# Add one in-layer model
stacker.addModelIn(Ridge(), trainable = True, hyperParameters = hypers)
stacker.addModelIn(Lasso(), trainable = True, hyperParameters = hypers)
# Add one out-layer model
stacker.addModelOut(Ridge(), hypers)
# Train
predsTrain = stacker.stackTrain()
# Test
predsTest = stacker.stackTest(X_test)
# Train/Test set predictions and performance
mse_tr = mean_squared_error(y_train, predsTrain[0])
rmse_tr = np.sqrt(mse_tr)
print("Ridge Regression RMSE (train) = {:.4f}".format(rmse_tr))
mse_ts = mean_squared_error(y_test, predsTest[0])
rmse_ts = np.sqrt(mse_ts)
print("Ridge Regression RMSE (test) = {:.4f}".format(rmse_ts))
```
This result is better than single models trained on all data. Also, the difference between the training and test set performance is lower.
Let's now use the summary method of the stacker to get some more information:
```
stacker.summary()
```
| true |
code
| 0.595787 | null | null | null | null |
|
## Model - Infinite DPM - Chinese Restaurant Mixture Model (CRPMM)
#### Dirichlet mixture model where number of clusters is learned.
ref = reference sequence
$N$ = number of reads
$K$ = number of clusters/components
$L$ = genome length (number of positions)
alphabet = {A, C, G, T, -}
no-mutation rate: $\gamma \sim Beta(a,b)$
no-error rate: $\theta \sim Beta(c,d)$
Cluster weights ($K$-dim): $\pi | \alpha \sim Dir(\alpha)$
Cluster assignments ($N$-dim): $z|\pi \sim Categorical(\pi)$
Cluster centers/haplotypes ($K$x$L$-dim): $h | ref, \gamma \sim Categorical(W) $
with $W(l,i)=
\begin{cases}
\gamma, \text{ if }i = ref[l] \\
\frac{1-\gamma}{4}, \text{ else. }
\end{cases}$ for $l \in {1, ..., L}$ and $i\in {1,..., |alphabet|}$
Likelihood of the reads ($N$-dim): $r | z, h, \theta \sim Categorical(E)$
with $E(n,l,i)=
\begin{cases}
\theta, \text{ if }i = h_{z_n}[l] \\
\frac{1-\theta}{4}, \text{ else. }
\end{cases}$ for $n \in {1, ..., N}$, $l \in {1, ..., L}$ and $i\in {1,..., |alphabet|}$
```
import numpyro
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS, DiscreteHMCGibbs, Predictive
from jax import random
import jax
import jax.numpy as jnp
import arviz as az
import matplotlib.pyplot as plt
# Minimal example
reference = jnp.array([0])
reads = jnp.array([[0], [1], [1], [1], [0], [1], [0], [1]])
alphabet ='01'
cluster_num = 5
input_data = reference, reads, len(alphabet)
# Use the following as inspiration
# https://forum.pyro.ai/t/variational-inference-for-dirichlet-process-clustering/98/2
def model_infiniteCRPMM(input_data):
reference, read_data, alphabet_length = input_data
# parameters
read_count = read_data.shape[0]
genome_length = read_data.shape[1]
alphabet_length = alphabet_length
alpha0 = 0.1
haplotypes = {} # sample this lazily
crp_counts = []
# define rates
mutation_rate = numpyro.sample('mutation_rate', dist.Beta(1, 1))
error_rate = numpyro.sample('error_rate', dist.Beta(1, 1))
# create matrix of rates
mutation_rate_matrix = jnp.full((genome_length, alphabet_length), (1 - mutation_rate) / (alphabet_length - 1))
mutation_rate_matrix = custom_put_along_axis(mutation_rate_matrix, reference.reshape(genome_length, 1), mutation_rate, axis=1)
#loc, scale = jnp.zeros(1), jnp.ones(1)*2
#alpha = numpyro.sample("alpha", dist.LogNormal(loc,scale)) # alpha must be more than zero
for n in range(read_count):
print('----')
print('read number ', n)
print('crp_counts ', crp_counts)
# sample from a CRP
weights = jnp.array(crp_counts + [alpha0])
weights /= weights.sum()
print('weights ', weights)
cluster_assignments = numpyro.sample("cluster_assignments"+str(n), dist.Categorical(weights))
print('cluster_assignments', cluster_assignments)
if cluster_assignments >= len(crp_counts):
# new cluster
crp_counts.append(1)
else:
# cluster already exists
crp_counts[cluster_assignments] += 1
# sample haplotypes
# lazily sample cluster mean
if int(cluster_assignments) not in haplotypes.keys():
haplotypes[int(cluster_assignments)] = numpyro.sample("haplotypes"+str(cluster_assignments), dist.Categorical(mutation_rate_matrix))
print('shape haplotypes[int(cluster_assignments)] ', haplotypes[int(cluster_assignments)].shape)
error_rate_matrix = jnp.full((genome_length, alphabet_length), (1 - error_rate) / (alphabet_length - 1))
print('error_rate ', error_rate)
print('shape error_rate_matrix', error_rate_matrix.shape)
print('before ' , type(error_rate_matrix))
print('haplotypes[int(cluster_assignments)] ',haplotypes[int(cluster_assignments)])
error_rate_matrix = custom_put_along_axis(error_rate_matrix, haplotypes[int(cluster_assignments)].reshape(genome_length, 1), error_rate, axis=1)
print('after ',type(error_rate_matrix))
obs = numpyro.sample("obs"+str(n), dist.Categorical(error_rate_matrix), obs=read_data[n])
rng_key = jax.random.PRNGKey(0)
num_warmup, num_samples = 2000, 20000
model = model_infiniteCRPMM
# Run NUTS. How many chains?
kernel = NUTS(model)
mcmc = MCMC(
DiscreteHMCGibbs(kernel),
num_warmup=num_warmup,
num_samples=num_samples,
num_chains=2
)
mcmc.run(rng_key, input_data)
```
| true |
code
| 0.381767 | null | null | null | null |
|
# Nonstationary Temporal Matrix Factorization
Taking into account both seasonal differencing and first-order differencing.
```
import numpy as np
def compute_mape(var, var_hat):
return np.sum(np.abs(var - var_hat) / var) / var.shape[0]
def compute_rmse(var, var_hat):
return np.sqrt(np.sum((var - var_hat) ** 2) / var.shape[0])
def generate_Psi(T, d, season):
Psi = []
for k in range(0, d + 1):
if k == 0:
Psi.append(np.append(np.zeros((T - d - season, d)),
np.append(-1 * np.eye(T - d - season), np.zeros((T - d - season, season)), axis = 1)
+ np.append(np.zeros((T - d - season, season)), np.eye(T - d - season), axis = 1), axis = 1))
else:
Psi.append(np.append(np.append(np.zeros((T - d - season, d - k)),
np.append(-1 * np.eye(T - d - season), np.zeros((T - d - season, season)), axis = 1)
+ np.append(np.zeros((T - d - season, season)), np.eye(T - d - season), axis = 1), axis = 1),
np.zeros((T - d - season, k)), axis = 1))
return Psi
def update_cg(var, r, q, Aq, rold):
alpha = rold / np.inner(q, Aq)
var = var + alpha * q
r = r - alpha * Aq
rnew = np.inner(r, r)
q = r + (rnew / rold) * q
return var, r, q, rnew
def ell_w(ind, W, X, rho):
return X @ ((W.T @ X) * ind).T + rho * W
def conj_grad_w(sparse_mat, ind, W, X, rho, maxiter = 5):
rank, dim1 = W.shape
w = np.reshape(W, -1, order = 'F')
r = np.reshape(X @ sparse_mat.T - ell_w(ind, W, X, rho), -1, order = 'F')
q = r.copy()
rold = np.inner(r, r)
for it in range(maxiter):
Q = np.reshape(q, (rank, dim1), order = 'F')
Aq = np.reshape(ell_w(ind, Q, X, rho), -1, order = 'F')
w, r, q, rold = update_cg(w, r, q, Aq, rold)
return np.reshape(w, (rank, dim1), order = 'F')
def ell_x(ind, W, X, A, Psi, d, lambda0, rho):
rank, dim2 = X.shape
temp = np.zeros((d * rank, Psi[0].shape[0]))
for k in range(1, d + 1):
temp[(k - 1) * rank : k * rank, :] = X @ Psi[k].T
temp1 = X @ Psi[0].T - A @ temp
temp2 = np.zeros((rank, dim2))
for k in range(d):
temp2 += A[:, k * rank : (k + 1) * rank].T @ temp1 @ Psi[k + 1]
return W @ ((W.T @ X) * ind) + rho * X + lambda0 * (temp1 @ Psi[0] - temp2)
def conj_grad_x(sparse_mat, ind, W, X, A, Psi, d, lambda0, rho, maxiter = 5):
rank, dim2 = X.shape
x = np.reshape(X, -1, order = 'F')
r = np.reshape(W @ sparse_mat - ell_x(ind, W, X, A, Psi, d, lambda0, rho), -1, order = 'F')
q = r.copy()
rold = np.inner(r, r)
for it in range(maxiter):
Q = np.reshape(q, (rank, dim2), order = 'F')
Aq = np.reshape(ell_x(ind, W, Q, A, Psi, d, lambda0, rho), -1, order = 'F')
x, r, q, rold = update_cg(x, r, q, Aq, rold)
return np.reshape(x, (rank, dim2), order = 'F')
def notmf(dense_mat, sparse_mat, rank, d, lambda0, rho, season, maxiter):
dim1, dim2 = sparse_mat.shape
W = 0.01 * np.random.randn(rank, dim1)
X = 0.01 * np.random.randn(rank, dim2)
A = 0.01 * np.random.randn(rank, d * rank)
if np.isnan(sparse_mat).any() == False:
ind = sparse_mat != 0
pos_test = np.where((dense_mat != 0) & (sparse_mat == 0))
elif np.isnan(sparse_mat).any() == True:
pos_test = np.where((dense_mat != 0) & (np.isnan(sparse_mat)))
ind = ~np.isnan(sparse_mat)
sparse_mat[np.isnan(sparse_mat)] = 0
dense_test = dense_mat[pos_test]
del dense_mat
Psi = generate_Psi(dim2, d, season)
Phi = (np.append(np.zeros((dim2 - d - 1 - season, 1)), np.eye(dim2 - d - 1 - season), axis = 1)
- np.append(np.eye(dim2 - d - 1 - season), np.zeros((dim2 - d - 1 - season, 1)), axis = 1))
for k in range(d + 1):
Psi[k] = Phi @ Psi[k]
show_iter = 100
temp = np.zeros((d * rank, dim2 - d - season - 1))
for it in range(maxiter):
W = conj_grad_w(sparse_mat, ind, W, X, rho)
X = conj_grad_x(sparse_mat, ind, W, X, A, Psi, d, lambda0, rho)
for k in range(1, d + 1):
temp[(k - 1) * rank : k * rank, :] = X @ Psi[k].T
A = X @ Psi[0].T @ np.linalg.pinv(temp)
mat_hat = W.T @ X
if (it + 1) % show_iter == 0:
temp_hat = mat_hat[pos_test]
print('Iter: {}'.format(it + 1))
print('MAPE: {:.6}'.format(compute_mape(dense_test, temp_hat)))
print('RMSE: {:.6}'.format(compute_rmse(dense_test, temp_hat)))
print()
return mat_hat, W, X, A
def notmf_dic(obs, W, X, A, d, lambda0, rho, season):
dim1, dim2 = obs.shape
rank = X.shape[0]
if np.isnan(obs).any() == False:
ind = obs != 0
elif np.isnan(obs).any() == True:
ind = ~np.isnan(obs)
obs[np.isnan(obs)] = 0
Psi = generate_Psi(dim2, d, season)
Phi = (np.append(np.zeros((dim2 - d - 1 - season, 1)), np.eye(dim2 - d - 1 - season), axis = 1)
- np.append(np.eye(dim2 - d - 1 - season), np.zeros((dim2 - d - 1 - season, 1)), axis = 1))
for k in range(d + 1):
Psi[k] = Phi @ Psi[k]
X = conj_grad_x(obs, ind, W, X, A, Psi, d, lambda0, rho)
temp = np.zeros((d * rank, dim2 - d - season - 1))
for k in range(1, d + 1):
temp[(k - 1) * rank : k * rank, :] = X @ Psi[k].T
A = X @ Psi[0].T @ np.linalg.pinv(temp)
return X, A
def var4cast(X, A, d, delta, season):
dim1, dim2 = X.shape
X_hat = np.append((X[:, season + 1 : dim2] - X[:, 1 : dim2 - season]
- X[:, season : dim2 - 1] + X[:, 0 : dim2 - season - 1]),
np.zeros((dim1, delta)), axis = 1)
for t in range(delta):
X_hat[:, dim2 - season - 1 + t] = A @ X_hat[:, dim2 - season - 1 + t - np.arange(1, d + 1)].T.reshape(dim1 * d)
X = np.append(X, np.zeros((dim1, delta)), axis = 1)
for t in range(delta):
X[:, dim2 + t] = (X[:, dim2 - season + t] + X[:, dim2 - 1 + t]
- X[:, dim2 - season - 1 + t] + X_hat[:, dim2 - season - 1 + t])
return X
from ipywidgets import IntProgress
from IPython.display import display
def rolling4cast(dense_mat, sparse_mat, pred_step, delta, rank, d, lambda0, rho, season, maxiter):
dim1, T = sparse_mat.shape
start_time = T - pred_step
max_count = int(np.ceil(pred_step / delta))
mat_hat = np.zeros((dim1, max_count * delta))
f = IntProgress(min = 0, max = max_count) # instantiate the bar
display(f) # display the bar
for t in range(max_count):
if t == 0:
_, W, X, A = notmf(dense_mat[:, : start_time], sparse_mat[:, : start_time],
rank, d, lambda0, rho, season, maxiter)
else:
X, A = notmf_dic(sparse_mat[:, : start_time + t * delta], W, X_new, A, d, lambda0, rho, season)
X_new = var4cast(X, A, d, delta, season)
mat_hat[:, t * delta : (t + 1) * delta] = W.T @ X_new[:, - delta :]
f.value = t
small_dense_mat = dense_mat[:, start_time : T]
pos = np.where((small_dense_mat != 0) & (np.invert(np.isnan(small_dense_mat))))
mape = compute_mape(small_dense_mat[pos], mat_hat[pos])
rmse = compute_rmse(small_dense_mat[pos], mat_hat[pos])
print('Prediction MAPE: {:.6}'.format(mape))
print('Prediction RMSE: {:.6}'.format(rmse))
print()
return mat_hat, W, X, A
import numpy as np
dense_mat = np.load('../datasets/NYC-movement-data-set/hourly_speed_mat_2019_1.npz')['arr_0']
for month in range(2, 4):
dense_mat = np.append(dense_mat, np.load('../datasets/NYC-movement-data-set/hourly_speed_mat_2019_{}.npz'.format(month))['arr_0'], axis = 1)
import time
for rank in [10]:
for delta in [1, 2, 3, 6]:
for d in [1, 2, 3, 6]:
start = time.time()
dim1, dim2 = dense_mat.shape
pred_step = 7 * 24
lambda0 = 1
rho = 5
season = 7 * 24
maxiter = 50
mat_hat, W, X, A = rolling4cast(dense_mat[:, : 24 * 7 * 10], dense_mat[:, : 24 * 7 * 10],
pred_step, delta, rank, d, lambda0, rho, season, maxiter)
print('delta = {}'.format(delta))
print('rank R = {}'.format(rank))
print('Order d = {}'.format(d))
end = time.time()
print('Running time: %d seconds'%(end - start))
```
### License
<div class="alert alert-block alert-danger">
<b>This work is released under the MIT license.</b>
</div>
| true |
code
| 0.270492 | null | null | null | null |
|
# ---------------------------------------------------------------
# python best courses https://courses.tanpham.org/
# ---------------------------------------------------------------
# 100 numpy exercises
This is a collection of exercises that have been collected in the numpy mailing list, on stack overflow and in the numpy documentation. The goal of this collection is to offer a quick reference for both old and new users but also to provide a set of exercices for those who teach.
#### 1. Import the numpy package under the name `np` (★☆☆)
```
import numpy as np
a=np.array([1,2,3])
b=np.array([4,5,6])
print(np.vstack((a,b)))
```
#### 2. Print the numpy version and the configuration (★☆☆)
```
print(np.__version__)
np.show_config()
```
#### 3. Create a null vector of size 10 (★☆☆)
```
Z = np.zeros(10)
print(Z)
```
#### 4. How to find the memory size of any array (★☆☆)
```
Z = np.zeros((10,10))
print("%d bytes" % (Z.size * Z.itemsize))
```
#### 5. How to get the documentation of the numpy add function from the command line? (★☆☆)
```
%run `python -c "import numpy; numpy.info(numpy.add)"`
```
#### 6. Create a null vector of size 10 but the fifth value which is 1 (★☆☆)
```
Z = np.zeros(10)
Z[4] = 1
print(Z)
```
#### 7. Create a vector with values ranging from 10 to 49 (★☆☆)
```
Z = np.arange(10,50)
print(Z)
```
#### 8. Reverse a vector (first element becomes last) (★☆☆)
```
Z = np.arange(50)
Z = Z[::-1]
print(Z)
```
#### 9. Create a 3x3 matrix with values ranging from 0 to 8 (★☆☆)
```
Z = np.arange(9).reshape(3,3)
print(Z)
```
#### 10. Find indices of non-zero elements from \[1,2,0,0,4,0\] (★☆☆)
```
nz = np.nonzero([1,2,0,0,4,0])
print(nz)
```
#### 11. Create a 3x3 identity matrix (★☆☆)
```
Z = np.eye(3)
print(Z)
```
#### 12. Create a 3x3x3 array with random values (★☆☆)
```
Z = np.random.random((3,3,3))
print(Z)
```
#### 13. Create a 10x10 array with random values and find the minimum and maximum values (★☆☆)
```
Z = np.random.random((10,10))
Zmin, Zmax = Z.min(), Z.max()
print(Zmin, Zmax)
```
#### 14. Create a random vector of size 30 and find the mean value (★☆☆)
```
Z = np.random.random(30)
m = Z.mean()
print(Z)
print(m)
```
#### 15. Create a 2d array with 1 on the border and 0 inside (★☆☆)
```
Z = np.ones((10,10))
Z[1:-1,1:-1] = 0
print(Z)
```
#### 16. How to add a border (filled with 0's) around an existing array? (★☆☆)
```
Z = np.ones((5,5))
Z = np.pad(Z, pad_width=1, mode='constant', constant_values=0)
print(Z)
```
#### 17. What is the result of the following expression? (★☆☆)
```
print(0 * np.nan)
print(np.nan == np.nan)
print(np.inf > np.nan)
print(np.nan - np.nan)
print(0.3 == 3 * 0.1)
```
#### 18. Create a 5x5 matrix with values 1,2,3,4 just below the diagonal (★☆☆)
```
Z = np.diag(1+np.arange(4),k=-1)
print(Z)
```
#### 19. Create a 8x8 matrix and fill it with a checkerboard pattern (★☆☆)
```
Z = np.zeros((8,8),dtype=int)
Z[1::2,::2] = 1
Z[::2,1::2] = 2
print(Z)
```
#### 20. Consider a (6,7,8) shape array, what is the index (x,y,z) of the 100th element?
```
print(np.unravel_index(100,(6,7,8)))
```
#### 21. Create a checkerboard 8x8 matrix using the tile function (★☆☆)
```
Z = np.tile( np.array([[0,1],[1,0]]), (4,4))
print(Z)
```
#### 22. Normalize a 5x5 random matrix (★☆☆)
```
Z = np.random.random((5,5))
Zmax, Zmin = Z.max(), Z.min()
Z = (Z - Zmin)/(Zmax - Zmin)
print(Z)
```
#### 23. Create a custom dtype that describes a color as four unsigned bytes (RGBA) (★☆☆)
```
color = np.dtype([("r", np.ubyte, 1),
("g", np.ubyte, 1),
("b", np.ubyte, 1),
("a", np.ubyte, 1)])
```
#### 24. Multiply a 5x3 matrix by a 3x2 matrix (real matrix product) (★☆☆)
```
Z = np.dot(np.ones((5,3)), np.ones((3,2)))
print(Z)
# Alternative solution, in Python 3.5 and above
#Z = np.ones((5,3)) @ np.ones((3,2))
```
#### 25. Given a 1D array, negate all elements which are between 3 and 8, in place. (★☆☆)
```
# Author: Evgeni Burovski
Z = np.arange(11)
Z[(3 < Z) & (Z <= 8)] *= -1
print(Z)
```
#### 26. What is the output of the following script? (★☆☆)
```
# Author: Jake VanderPlas
print(sum(range(5),-1))
from numpy import *
print(sum(range(5),-1))
```
#### 27. Consider an integer vector Z, which of these expressions are legal? (★☆☆)
```
Z**Z
2 << Z >> 2
Z <- Z
1j*Z
Z/1/1
Z<Z>Z
```
#### 28. What are the result of the following expressions?
```
print(np.array(0) / np.array(0))
print(np.array(0) // np.array(0))
print(np.array([np.nan]).astype(int).astype(float))
```
#### 29. How to round away from zero a float array ? (★☆☆)
```
# Author: Charles R Harris
Z = np.random.uniform(-10,+10,10)
print (np.copysign(np.ceil(np.abs(Z)), Z))
```
#### 30. How to find common values between two arrays? (★☆☆)
```
Z1 = np.random.randint(0,10,10)
Z2 = np.random.randint(0,10,10)
print(np.intersect1d(Z1,Z2))
```
#### 31. How to ignore all numpy warnings (not recommended)? (★☆☆)
```
# Suicide mode on
defaults = np.seterr(all="ignore")
Z = np.ones(1) / 0
# Back to sanity
_ = np.seterr(**defaults)
An equivalent way, with a context manager:
with np.errstate(divide='ignore'):
Z = np.ones(1) / 0
```
#### 32. Is the following expressions true? (★☆☆)
```
np.sqrt(-1) == np.emath.sqrt(-1)
```
#### 33. How to get the dates of yesterday, today and tomorrow? (★☆☆)
```
yesterday = np.datetime64('today', 'D') - np.timedelta64(1, 'D')
today = np.datetime64('today', 'D')
tomorrow = np.datetime64('today', 'D') + np.timedelta64(1, 'D')
```
#### 34. How to get all the dates corresponding to the month of July 2016? (★★☆)
```
Z = np.arange('2016-07', '2016-08', dtype='datetime64[D]')
print(Z)
```
#### 35. How to compute ((A+B)\*(-A/2)) in place (without copy)? (★★☆)
```
A = np.ones(3)*1
B = np.ones(3)*2
C = np.ones(3)*3
np.add(A,B,out=B)
np.divide(A,2,out=A)
np.negative(A,out=A)
np.multiply(A,B,out=A)
```
#### 36. Extract the integer part of a random array using 5 different methods (★★☆)
```
Z = np.random.uniform(0,10,10)
print (Z - Z%1)
print (np.floor(Z))
print (np.ceil(Z)-1)
print (Z.astype(int))
print (np.trunc(Z))
```
#### 37. Create a 5x5 matrix with row values ranging from 0 to 4 (★★☆)
```
Z = np.zeros((5,5))
Z += np.arange(5)
print(Z)
```
#### 38. Consider a generator function that generates 10 integers and use it to build an array (★☆☆)
```
def generate():
for x in range(10):
yield x
Z = np.fromiter(generate(),dtype=float,count=-1)
print(Z)
```
#### 39. Create a vector of size 10 with values ranging from 0 to 1, both excluded (★★☆)
```
Z = np.linspace(0,1,11,endpoint=False)[1:]
print(Z)
```
#### 40. Create a random vector of size 10 and sort it (★★☆)
```
Z = np.random.random(10)
Z.sort()
print(Z)
```
#### 41. How to sum a small array faster than np.sum? (★★☆)
```
# Author: Evgeni Burovski
Z = np.arange(10)
np.add.reduce(Z)
```
#### 42. Consider two random array A and B, check if they are equal (★★☆)
```
A = np.random.randint(0,2,5)
B = np.random.randint(0,2,5)
# Assuming identical shape of the arrays and a tolerance for the comparison of values
equal = np.allclose(A,B)
print(equal)
# Checking both the shape and the element values, no tolerance (values have to be exactly equal)
equal = np.array_equal(A,B)
print(equal)
```
#### 43. Make an array immutable (read-only) (★★☆)
```
Z = np.zeros(10)
Z.flags.writeable = False
Z[0] = 1
```
#### 44. Consider a random 10x2 matrix representing cartesian coordinates, convert them to polar coordinates (★★☆)
```
Z = np.random.random((10,2))
X,Y = Z[:,0], Z[:,1]
R = np.sqrt(X**2+Y**2)
T = np.arctan2(Y,X)
print(R)
print(T)
```
#### 45. Create random vector of size 10 and replace the maximum value by 0 (★★☆)
```
Z = np.random.random(10)
Z[Z.argmax()] = 0
print(Z)
```
#### 46. Create a structured array with `x` and `y` coordinates covering the \[0,1\]x\[0,1\] area (★★☆)
```
Z = np.zeros((5,5), [('x',float),('y',float)])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0,1,5),
np.linspace(0,1,5))
print(Z)
```
#### 47. Given two arrays, X and Y, construct the Cauchy matrix C (Cij =1/(xi - yj))
```
# Author: Evgeni Burovski
X = np.arange(8)
Y = X + 0.5
C = 1.0 / np.subtract.outer(X, Y)
print(np.linalg.det(C))
```
#### 48. Print the minimum and maximum representable value for each numpy scalar type (★★☆)
```
for dtype in [np.int8, np.int32, np.int64]:
print(np.iinfo(dtype).min)
print(np.iinfo(dtype).max)
for dtype in [np.float32, np.float64]:
print(np.finfo(dtype).min)
print(np.finfo(dtype).max)
print(np.finfo(dtype).eps)
```
#### 49. How to print all the values of an array? (★★☆)
```
np.set_printoptions(threshold=np.nan)
Z = np.zeros((16,16))
print(Z)
```
#### 50. How to find the closest value (to a given scalar) in a vector? (★★☆)
```
Z = np.arange(100)
v = np.random.uniform(0,100)
index = (np.abs(Z-v)).argmin()
print(Z[index])
```
#### 51. Create a structured array representing a position (x,y) and a color (r,g,b) (★★☆)
```
Z = np.zeros(10, [ ('position', [ ('x', float, 1),
('y', float, 1)]),
('color', [ ('r', float, 1),
('g', float, 1),
('b', float, 1)])])
print(Z)
```
#### 52. Consider a random vector with shape (100,2) representing coordinates, find point by point distances (★★☆)
```
Z = np.random.random((10,2))
X,Y = np.atleast_2d(Z[:,0], Z[:,1])
D = np.sqrt( (X-X.T)**2 + (Y-Y.T)**2)
print(D)
# Much faster with scipy
import scipy
# Thanks Gavin Heverly-Coulson (#issue 1)
import scipy.spatial
Z = np.random.random((10,2))
D = scipy.spatial.distance.cdist(Z,Z)
print(D)
```
#### 53. How to convert a float (32 bits) array into an integer (32 bits) in place?
```
Z = np.arange(10, dtype=np.int32)
Z = Z.astype(np.float32, copy=False)
print(Z)
```
#### 54. How to read the following file? (★★☆)
```
from io import StringIO
# Fake file
s = StringIO("""1, 2, 3, 4, 5\n
6, , , 7, 8\n
, , 9,10,11\n""")
Z = np.genfromtxt(s, delimiter=",", dtype=np.int)
print(Z)
```
#### 55. What is the equivalent of enumerate for numpy arrays? (★★☆)
```
Z = np.arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index])
```
#### 56. Generate a generic 2D Gaussian-like array (★★☆)
```
X, Y = np.meshgrid(np.linspace(-1,1,10), np.linspace(-1,1,10))
D = np.sqrt(X*X+Y*Y)
sigma, mu = 1.0, 0.0
G = np.exp(-( (D-mu)**2 / ( 2.0 * sigma**2 ) ) )
print(G)
```
#### 57. How to randomly place p elements in a 2D array? (★★☆)
```
# Author: Divakar
n = 10
p = 3
Z = np.zeros((n,n))
np.put(Z, np.random.choice(range(n*n), p, replace=False),1)
print(Z)
```
#### 58. Subtract the mean of each row of a matrix (★★☆)
```
# Author: Warren Weckesser
X = np.random.rand(5, 10)
# Recent versions of numpy
Y = X - X.mean(axis=1, keepdims=True)
# Older versions of numpy
Y = X - X.mean(axis=1).reshape(-1, 1)
print(Y)
```
#### 59. How to sort an array by the nth column? (★★☆)
```
# Author: Steve Tjoa
Z = np.random.randint(0,10,(3,3))
print(Z)
print(Z[Z[:,1].argsort()])
```
#### 60. How to tell if a given 2D array has null columns? (★★☆)
```
# Author: Warren Weckesser
Z = np.random.randint(0,3,(3,10))
print((~Z.any(axis=0)).any())
```
#### 61. Find the nearest value from a given value in an array (★★☆)
```
Z = np.random.uniform(0,1,10)
z = 0.5
m = Z.flat[np.abs(Z - z).argmin()]
print(m)
```
#### 62. Considering two arrays with shape (1,3) and (3,1), how to compute their sum using an iterator? (★★☆)
```
A = np.arange(3).reshape(3,1)
B = np.arange(3).reshape(1,3)
it = np.nditer([A,B,None])
for x,y,z in it: z[...] = x + y
print(it.operands[2])
```
#### 63. Create an array class that has a name attribute (★★☆)
```
class NamedArray(np.ndarray):
def __new__(cls, array, name="no name"):
obj = np.asarray(array).view(cls)
obj.name = name
return obj
def __array_finalize__(self, obj):
if obj is None: return
self.info = getattr(obj, 'name', "no name")
Z = NamedArray(np.arange(10), "range_10")
print (Z.name)
```
#### 64. Consider a given vector, how to add 1 to each element indexed by a second vector (be careful with repeated indices)? (★★★)
```
# Author: Brett Olsen
Z = np.ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z)
# Another solution
# Author: Bartosz Telenczuk
np.add.at(Z, I, 1)
print(Z)
```
#### 65. How to accumulate elements of a vector (X) to an array (F) based on an index list (I)? (★★★)
```
# Author: Alan G Isaac
X = [1,2,3,4,5,6]
I = [1,3,9,3,4,1]
F = np.bincount(I,X)
print(F)
```
#### 66. Considering a (w,h,3) image of (dtype=ubyte), compute the number of unique colors (★★★)
```
# Author: Nadav Horesh
w,h = 16,16
I = np.random.randint(0,2,(h,w,3)).astype(np.ubyte)
#Note that we should compute 256*256 first.
#Otherwise numpy will only promote F.dtype to 'uint16' and overfolw will occur
F = I[...,0]*(256*256) + I[...,1]*256 +I[...,2]
n = len(np.unique(F))
print(n)
```
#### 67. Considering a four dimensions array, how to get sum over the last two axis at once? (★★★)
```
A = np.random.randint(0,10,(3,4,3,4))
# solution by passing a tuple of axes (introduced in numpy 1.7.0)
sum = A.sum(axis=(-2,-1))
print(sum)
# solution by flattening the last two dimensions into one
# (useful for functions that don't accept tuples for axis argument)
sum = A.reshape(A.shape[:-2] + (-1,)).sum(axis=-1)
print(sum)
```
#### 68. Considering a one-dimensional vector D, how to compute means of subsets of D using a vector S of same size describing subset indices? (★★★)
```
# Author: Jaime Fernández del Río
D = np.random.uniform(0,1,100)
S = np.random.randint(0,10,100)
D_sums = np.bincount(S, weights=D)
D_counts = np.bincount(S)
D_means = D_sums / D_counts
print(D_means)
# Pandas solution as a reference due to more intuitive code
import pandas as pd
print(pd.Series(D).groupby(S).mean())
```
#### 69. How to get the diagonal of a dot product? (★★★)
```
# Author: Mathieu Blondel
A = np.random.uniform(0,1,(5,5))
B = np.random.uniform(0,1,(5,5))
# Slow version
np.diag(np.dot(A, B))
# Fast version
np.sum(A * B.T, axis=1)
# Faster version
np.einsum("ij,ji->i", A, B)
```
#### 70. Consider the vector \[1, 2, 3, 4, 5\], how to build a new vector with 3 consecutive zeros interleaved between each value? (★★★)
```
# Author: Warren Weckesser
Z = np.array([1,2,3,4,5])
nz = 3
Z0 = np.zeros(len(Z) + (len(Z)-1)*(nz))
Z0[::nz+1] = Z
print(Z0)
```
#### 71. Consider an array of dimension (5,5,3), how to mulitply it by an array with dimensions (5,5)? (★★★)
```
A = np.ones((5,5,3))
B = 2*np.ones((5,5))
print(A * B[:,:,None])
```
#### 72. How to swap two rows of an array? (★★★)
```
# Author: Eelco Hoogendoorn
A = np.arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A)
```
#### 73. Consider a set of 10 triplets describing 10 triangles (with shared vertices), find the set of unique line segments composing all the triangles (★★★)
```
# Author: Nicolas P. Rougier
faces = np.random.randint(0,100,(10,3))
F = np.roll(faces.repeat(2,axis=1),-1,axis=1)
F = F.reshape(len(F)*3,2)
F = np.sort(F,axis=1)
G = F.view( dtype=[('p0',F.dtype),('p1',F.dtype)] )
G = np.unique(G)
print(G)
```
#### 74. Given an array C that is a bincount, how to produce an array A such that np.bincount(A) == C? (★★★)
```
# Author: Jaime Fernández del Río
C = np.bincount([1,1,2,3,4,4,6])
A = np.repeat(np.arange(len(C)), C)
print(A)
```
#### 75. How to compute averages using a sliding window over an array? (★★★)
```
# Author: Jaime Fernández del Río
def moving_average(a, n=3) :
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
Z = np.arange(20)
print(moving_average(Z, n=3))
```
#### 76. Consider a one-dimensional array Z, build a two-dimensional array whose first row is (Z\[0\],Z\[1\],Z\[2\]) and each subsequent row is shifted by 1 (last row should be (Z\[-3\],Z\[-2\],Z\[-1\]) (★★★)
```
# Author: Joe Kington / Erik Rigtorp
from numpy.lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)
```
#### 77. How to negate a boolean, or to change the sign of a float inplace? (★★★)
```
# Author: Nathaniel J. Smith
Z = np.random.randint(0,2,100)
np.logical_not(Z, out=Z)
Z = np.random.uniform(-1.0,1.0,100)
np.negative(Z, out=Z)
```
#### 78. Consider 2 sets of points P0,P1 describing lines (2d) and a point p, how to compute distance from p to each line i (P0\[i\],P1\[i\])? (★★★)
```
def distance(P0, P1, p):
T = P1 - P0
L = (T**2).sum(axis=1)
U = -((P0[:,0]-p[...,0])*T[:,0] + (P0[:,1]-p[...,1])*T[:,1]) / L
U = U.reshape(len(U),1)
D = P0 + U*T - p
return np.sqrt((D**2).sum(axis=1))
P0 = np.random.uniform(-10,10,(10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10,10,( 1,2))
print(distance(P0, P1, p))
```
#### 79. Consider 2 sets of points P0,P1 describing lines (2d) and a set of points P, how to compute distance from each point j (P\[j\]) to each line i (P0\[i\],P1\[i\])? (★★★)
```
# Author: Italmassov Kuanysh
# based on distance function from previous question
P0 = np.random.uniform(-10, 10, (10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10, 10, (10,2))
print(np.array([distance(P0,P1,p_i) for p_i in p]))
```
#### 80. Consider an arbitrary array, write a function that extract a subpart with a fixed shape and centered on a given element (pad with a `fill` value when necessary) (★★★)
```
# Author: Nicolas Rougier
Z = np.random.randint(0,10,(10,10))
shape = (5,5)
fill = 0
position = (1,1)
R = np.ones(shape, dtype=Z.dtype)*fill
P = np.array(list(position)).astype(int)
Rs = np.array(list(R.shape)).astype(int)
Zs = np.array(list(Z.shape)).astype(int)
R_start = np.zeros((len(shape),)).astype(int)
R_stop = np.array(list(shape)).astype(int)
Z_start = (P-Rs//2)
Z_stop = (P+Rs//2)+Rs%2
R_start = (R_start - np.minimum(Z_start,0)).tolist()
Z_start = (np.maximum(Z_start,0)).tolist()
R_stop = np.maximum(R_start, (R_stop - np.maximum(Z_stop-Zs,0))).tolist()
Z_stop = (np.minimum(Z_stop,Zs)).tolist()
r = [slice(start,stop) for start,stop in zip(R_start,R_stop)]
z = [slice(start,stop) for start,stop in zip(Z_start,Z_stop)]
R[r] = Z[z]
print(Z)
print(R)
```
#### 81. Consider an array Z = \[1,2,3,4,5,6,7,8,9,10,11,12,13,14\], how to generate an array R = \[\[1,2,3,4\], \[2,3,4,5\], \[3,4,5,6\], ..., \[11,12,13,14\]\]? (★★★)
```
# Author: Stefan van der Walt
Z = np.arange(1,15,dtype=np.uint32)
R = stride_tricks.as_strided(Z,(11,4),(4,4))
print(R)
```
#### 82. Compute a matrix rank (★★★)
```
# Author: Stefan van der Walt
Z = np.random.uniform(0,1,(10,10))
U, S, V = np.linalg.svd(Z) # Singular Value Decomposition
rank = np.sum(S > 1e-10)
print(rank)
```
#### 83. How to find the most frequent value in an array?
```
Z = np.random.randint(0,10,50)
print(np.bincount(Z).argmax())
```
#### 84. Extract all the contiguous 3x3 blocks from a random 10x10 matrix (★★★)
```
# Author: Chris Barker
Z = np.random.randint(0,5,(10,10))
n = 3
i = 1 + (Z.shape[0]-3)
j = 1 + (Z.shape[1]-3)
C = stride_tricks.as_strided(Z, shape=(i, j, n, n), strides=Z.strides + Z.strides)
print(C)
```
#### 85. Create a 2D array subclass such that Z\[i,j\] == Z\[j,i\] (★★★)
```
# Author: Eric O. Lebigot
# Note: only works for 2d array and value setting using indices
class Symetric(np.ndarray):
def __setitem__(self, index, value):
i,j = index
super(Symetric, self).__setitem__((i,j), value)
super(Symetric, self).__setitem__((j,i), value)
def symetric(Z):
return np.asarray(Z + Z.T - np.diag(Z.diagonal())).view(Symetric)
S = symetric(np.random.randint(0,10,(5,5)))
S[2,3] = 42
print(S)
```
#### 86. Consider a set of p matrices wich shape (n,n) and a set of p vectors with shape (n,1). How to compute the sum of of the p matrix products at once? (result has shape (n,1)) (★★★)
```
# Author: Stefan van der Walt
p, n = 10, 20
M = np.ones((p,n,n))
V = np.ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector.
```
#### 87. Consider a 16x16 array, how to get the block-sum (block size is 4x4)? (★★★)
```
# Author: Robert Kern
Z = np.ones((16,16))
k = 4
S = np.add.reduceat(np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
np.arange(0, Z.shape[1], k), axis=1)
print(S)
```
#### 88. How to implement the Game of Life using numpy arrays? (★★★)
```
# Author: Nicolas Rougier
def iterate(Z):
# Count neighbours
N = (Z[0:-2,0:-2] + Z[0:-2,1:-1] + Z[0:-2,2:] +
Z[1:-1,0:-2] + Z[1:-1,2:] +
Z[2: ,0:-2] + Z[2: ,1:-1] + Z[2: ,2:])
# Apply rules
birth = (N==3) & (Z[1:-1,1:-1]==0)
survive = ((N==2) | (N==3)) & (Z[1:-1,1:-1]==1)
Z[...] = 0
Z[1:-1,1:-1][birth | survive] = 1
return Z
Z = np.random.randint(0,2,(50,50))
for i in range(100): Z = iterate(Z)
print(Z)
```
#### 89. How to get the n largest values of an array (★★★)
```
Z = np.arange(10000)
np.random.shuffle(Z)
n = 5
# Slow
print (Z[np.argsort(Z)[-n:]])
# Fast
print (Z[np.argpartition(-Z,n)[:n]])
```
#### 90. Given an arbitrary number of vectors, build the cartesian product (every combinations of every item) (★★★)
```
# Author: Stefan Van der Walt
def cartesian(arrays):
arrays = [np.asarray(a) for a in arrays]
shape = (len(x) for x in arrays)
ix = np.indices(shape, dtype=int)
ix = ix.reshape(len(arrays), -1).T
for n, arr in enumerate(arrays):
ix[:, n] = arrays[n][ix[:, n]]
return ix
print (cartesian(([1, 2, 3], [4, 5], [6, 7])))
```
#### 91. How to create a record array from a regular array? (★★★)
```
Z = np.array([("Hello", 2.5, 3),
("World", 3.6, 2)])
R = np.core.records.fromarrays(Z.T,
names='col1, col2, col3',
formats = 'S8, f8, i8')
print(R)
```
#### 92. Consider a large vector Z, compute Z to the power of 3 using 3 different methods (★★★)
```
# Author: Ryan G.
x = np.random.rand(5e7)
%timeit np.power(x,3)
%timeit x*x*x
%timeit np.einsum('i,i,i->i',x,x,x)
```
#### 93. Consider two arrays A and B of shape (8,3) and (2,2). How to find rows of A that contain elements of each row of B regardless of the order of the elements in B? (★★★)
```
# Author: Gabe Schwartz
A = np.random.randint(0,5,(8,3))
B = np.random.randint(0,5,(2,2))
C = (A[..., np.newaxis, np.newaxis] == B)
rows = np.where(C.any((3,1)).all(1))[0]
print(rows)
```
#### 94. Considering a 10x3 matrix, extract rows with unequal values (e.g. \[2,2,3\]) (★★★)
```
# Author: Robert Kern
Z = np.random.randint(0,5,(10,3))
print(Z)
# solution for arrays of all dtypes (including string arrays and record arrays)
E = np.all(Z[:,1:] == Z[:,:-1], axis=1)
U = Z[~E]
print(U)
# soluiton for numerical arrays only, will work for any number of columns in Z
U = Z[Z.max(axis=1) != Z.min(axis=1),:]
print(U)
```
#### 95. Convert a vector of ints into a matrix binary representation (★★★)
```
# Author: Warren Weckesser
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128])
B = ((I.reshape(-1,1) & (2**np.arange(8))) != 0).astype(int)
print(B[:,::-1])
# Author: Daniel T. McDonald
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))
```
#### 96. Given a two dimensional array, how to extract unique rows? (★★★)
```
# Author: Jaime Fernández del Río
Z = np.random.randint(0,2,(6,3))
T = np.ascontiguousarray(Z).view(np.dtype((np.void, Z.dtype.itemsize * Z.shape[1])))
_, idx = np.unique(T, return_index=True)
uZ = Z[idx]
print(uZ)
```
#### 97. Considering 2 vectors A & B, write the einsum equivalent of inner, outer, sum, and mul function (★★★)
```
A = np.random.uniform(0,1,10)
B = np.random.uniform(0,1,10)
np.einsum('i->', A) # np.sum(A)
np.einsum('i,i->i', A, B) # A * B
np.einsum('i,i', A, B) # np.inner(A, B)
np.einsum('i,j->ij', A, B) # np.outer(A, B)
```
#### 98. Considering a path described by two vectors (X,Y), how to sample it using equidistant samples (★★★)?
```
# Author: Bas Swinckels
phi = np.arange(0, 10*np.pi, 0.1)
a = 1
x = a*phi*np.cos(phi)
y = a*phi*np.sin(phi)
dr = (np.diff(x)**2 + np.diff(y)**2)**.5 # segment lengths
r = np.zeros_like(x)
r[1:] = np.cumsum(dr) # integrate path
r_int = np.linspace(0, r.max(), 200) # regular spaced path
x_int = np.interp(r_int, r, x) # integrate path
y_int = np.interp(r_int, r, y)
```
#### 99. Given an integer n and a 2D array X, select from X the rows which can be interpreted as draws from a multinomial distribution with n degrees, i.e., the rows which only contain integers and which sum to n. (★★★)
```
# Author: Evgeni Burovski
X = np.asarray([[1.0, 0.0, 3.0, 8.0],
[2.0, 0.0, 1.0, 1.0],
[1.5, 2.5, 1.0, 0.0]])
n = 4
M = np.logical_and.reduce(np.mod(X, 1) == 0, axis=-1)
M &= (X.sum(axis=-1) == n)
print(X[M])
```
#### 100. Compute bootstrapped 95% confidence intervals for the mean of a 1D array X (i.e., resample the elements of an array with replacement N times, compute the mean of each sample, and then compute percentiles over the means). (★★★)
```
# Author: Jessica B. Hamrick
X = np.random.randn(100) # random 1D array
N = 1000 # number of bootstrap samples
idx = np.random.randint(0, X.size, (N, X.size))
means = X[idx].mean(axis=1)
confint = np.percentile(means, [2.5, 97.5])
print(confint)
```
| true |
code
| 0.226655 | null | null | null | null |
|
```
# default_exp image.color_palette
# hide
from nbdev.showdoc import *
# hide
%reload_ext autoreload
%autoreload 2
```
# Color Palettes
> Tools for generating color palettes of various data-sets.
```
# export
def pascal_voc_palette(num_cls=None):
"""
Generates the PASCAL Visual Object Classes (PASCAL VOC) data-set color palette.
Data-Set URL:
http://host.robots.ox.ac.uk/pascal/VOC/ .
Original source taken from:
https://gluon-cv.mxnet.io/_modules/gluoncv/utils/viz/segmentation.html .
`num_cls`: the number of colors to generate
return: the generated color palette
"""
# by default generate 256 colors
if num_cls is None:
num_cls = 256
palette = [0] * (num_cls * 3)
for j in range(0, num_cls):
lab = j
palette[j*3+0] = 0
palette[j*3+1] = 0
palette[j*3+2] = 0
i = 0
while lab > 0:
palette[j*3+0] |= (((lab >> 0) & 1) << (7-i))
palette[j*3+1] |= (((lab >> 1) & 1) << (7-i))
palette[j*3+2] |= (((lab >> 2) & 1) << (7-i))
i = i + 1
lab >>= 3
return palette
# export
def ade20k_palette(num_cls=None):
"""
Generates the ADE20K data-set color palette.
Data-Set URL:
http://host.robots.ox.ac.uk/pascal/VOC/
Color palette definition:
https://docs.google.com/spreadsheets/d/1se8YEtb2detS7OuPE86fXGyD269pMycAWe2mtKUj2W8/edit#gid=0 .
Original source taken from:
https://gluon-cv.mxnet.io/_modules/gluoncv/utils/viz/segmentation.html .
`num_cls`: the number of colors to generate
return: the generated color palette
"""
palette = [
0, 0, 0, 120, 120, 120, 180, 120, 120, 6, 230, 230, 80, 50, 50, 4, 200, 3, 120, 120, 80, 140, 140, 140, 204,
5, 255, 230, 230, 230, 4, 250, 7, 224, 5, 255, 235, 255, 7, 150, 5, 61, 120, 120, 70, 8, 255, 51, 255, 6, 82,
143, 255, 140, 204, 255, 4, 255, 51, 7, 204, 70, 3, 0, 102, 200, 61, 230, 250, 255, 6, 51, 11, 102, 255, 255,
7, 71, 255, 9, 224, 9, 7, 230, 220, 220, 220, 255, 9, 92, 112, 9, 255, 8, 255, 214, 7, 255, 224, 255, 184, 6,
10, 255, 71, 255, 41, 10, 7, 255, 255, 224, 255, 8, 102, 8, 255, 255, 61, 6, 255, 194, 7, 255, 122, 8, 0, 255,
20, 255, 8, 41, 255, 5, 153, 6, 51, 255, 235, 12, 255, 160, 150, 20, 0, 163, 255, 140, 140, 140, 250, 10, 15,
20, 255, 0, 31, 255, 0, 255, 31, 0, 255, 224, 0, 153, 255, 0, 0, 0, 255, 255, 71, 0, 0, 235, 255, 0, 173, 255,
31, 0, 255, 11, 200, 200, 255, 82, 0, 0, 255, 245, 0, 61, 255, 0, 255, 112, 0, 255, 133, 255, 0, 0, 255, 163,
0, 255, 102, 0, 194, 255, 0, 0, 143, 255, 51, 255, 0, 0, 82, 255, 0, 255, 41, 0, 255, 173, 10, 0, 255, 173, 255,
0, 0, 255, 153, 255, 92, 0, 255, 0, 255, 255, 0, 245, 255, 0, 102, 255, 173, 0, 255, 0, 20, 255, 184, 184, 0,
31, 255, 0, 255, 61, 0, 71, 255, 255, 0, 204, 0, 255, 194, 0, 255, 82, 0, 10, 255, 0, 112, 255, 51, 0, 255, 0,
194, 255, 0, 122, 255, 0, 255, 163, 255, 153, 0, 0, 255, 10, 255, 112, 0, 143, 255, 0, 82, 0, 255, 163, 255,
0, 255, 235, 0, 8, 184, 170, 133, 0, 255, 0, 255, 92, 184, 0, 255, 255, 0, 31, 0, 184, 255, 0, 214, 255, 255,
0, 112, 92, 255, 0, 0, 224, 255, 112, 224, 255, 70, 184, 160, 163, 0, 255, 153, 0, 255, 71, 255, 0, 255, 0,
163, 255, 204, 0, 255, 0, 143, 0, 255, 235, 133, 255, 0, 255, 0, 235, 245, 0, 255, 255, 0, 122, 255, 245, 0,
10, 190, 212, 214, 255, 0, 0, 204, 255, 20, 0, 255, 255, 255, 0, 0, 153, 255, 0, 41, 255, 0, 255, 204, 41, 0,
255, 41, 255, 0, 173, 0, 255, 0, 245, 255, 71, 0, 255, 122, 0, 255, 0, 255, 184, 0, 92, 255, 184, 255, 0, 0,
133, 255, 255, 214, 0, 25, 194, 194, 102, 255, 0, 92, 0, 255]
if num_cls is not None:
if num_cls >= len(palette):
raise Exception("Palette Color Definition exceeded.")
palette = palette[:num_cls*3]
return palette
# export
def cityscapes_palette(num_cls=None):
"""
Generates the Cityscapes data-set color palette.
Data-Set URL:
https://www.cityscapes-dataset.com/
Color palette definition:
https://github.com/mcordts/cityscapesScripts/blob/master/cityscapesscripts/helpers/labels.py
Original source taken from:
https://gluon-cv.mxnet.io/_modules/gluoncv/utils/viz/segmentation.html .
`num_cls`: the number of colors to generate
return: the generated color palette
"""
palette = [
128, 64, 128,
244, 35, 232,
70, 70, 70,
102, 102, 156,
190, 153, 153,
153, 153, 153,
250, 170, 30,
220, 220, 0,
107, 142, 35,
152, 251, 152,
0, 130, 180,
220, 20, 60,
255, 0, 0,
0, 0, 142,
0, 0, 70,
0, 60, 100,
0, 80, 100,
0, 0, 230,
119, 11, 32,
]
if num_cls is not None:
if num_cls >= len(palette):
raise Exception("Palette Color Definition exceeded.")
palette = palette[:num_cls*3]
return palette
# export
def mhp_palette_v1(num_cls=None):
"""
Generates the Multi-Human Parsing (MHP) v1.0 data-set color palette.
Data-Set URL:
https://lv-mhp.github.io/
Color palette definition:
https://lv-mhp.github.io/human_parsing_task
Original source taken from:
https://gluon-cv.mxnet.io/_modules/gluoncv/utils/viz/segmentation.html .
`num_cls`: the number of colors to generate
return: the generated color palette
"""
palette = [
255, 255, 255,
165, 42, 42,
255, 0, 0,
0, 128, 0,
165, 42, 42,
255, 69, 0,
255, 20, 147,
30, 144, 255,
85, 107, 47,
0, 128, 128,
139, 69, 19,
70, 130, 180,
50, 205, 50,
0, 0, 205,
0, 191, 255,
0, 255, 255,
0, 250, 154,
173, 255, 47,
255, 255, 0,
]
if num_cls is not None:
if num_cls >= len(palette):
raise Exception("Palette Color Definition exceeded.")
palette = palette[:num_cls*3]
return palette
# hide
# for generating scripts from notebook directly
from nbdev.export import notebook2script
notebook2script()
```
| true |
code
| 0.673514 | null | null | null | null |
|
# Edafa on ImageNet dataset
This notebook shows an example on how to use Edafa to obtain better results on **classification task**. We use [ImageNet](http://www.image-net.org/) dataset which has **1000 classes**. We use *pytorch* and pretrained weights of AlexNet. At the end we compare results of the same model with and without augmentations.
#### Import dependencies
```
%load_ext autoreload
%autoreload 2
# add our package directory to the path
import sys
sys.path.append('../../')
import torchvision.models as models
import torchvision.transforms as transforms
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
#### Constants
```
# Filename to use for comparison (4 sample files are given in 'data' folder)
FILE = '000559'
# Input size of the model
IN_SIZE = 224
```
#### get labels
```
# Let's get our class labels.
labels = []
with open('labels.txt') as f:
for line in f:
labels.append(line.split(': ')[-1][1:-3])
```
#### Now we build our model (using pretrained weights)
```
model = models.alexnet(pretrained=True)
```
#### Read and preprocess image
```
img_path = '../data/images/%s.jpg'%FILE
img = plt.imread(img_path)
plt.imshow(img)
transform_pipeline = transforms.Compose([ transforms.ToPILImage(),
transforms.Resize((IN_SIZE,IN_SIZE)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])])
x = transform_pipeline(img)
x = x.unsqueeze(0)
x = Variable(x)
```
### Exp1: Predict image without augmentation
```
pred = model(x)
pred_without = pred.data.numpy()
```
### Exp2: Using same model with Edafa
#### step 1: import base class `ClassPredictor`
```
from edafa import ClassPredictor
```
#### step 2: inherit `ClassPredictor` and implement the main virtual functions: predict_patches()
```
class myPredictor(ClassPredictor):
def __init__(self,vgg16,pipeline,*args,**kwargs):
super().__init__(*args,**kwargs)
self.model = vgg16
self.pipe = pipeline
def predict_patches(self,patches):
preds = []
for i in range(patches.shape[0]):
processed = self.pipe(patches[i])
processed = processed.unsqueeze(0)
processed = Variable(processed)
pred = self.model(processed)
preds.append(pred.data.numpy())
return np.array(preds)
```
#### step 3: make an instance of your class with the correct parameters
```
p = myPredictor(model,transform_pipeline,"../../conf/imagenet.json")
```
#### step 4: call predict_images()
```
preds_with = p.predict_images([img])
```
### Compare results of Exp1 and Exp2
```
print('Predicted without augmentation: ', labels[pred_without.argmax()])
print('Predicted with augmentation:', labels[preds_with.argmax()])
```
We can clearly see from the object image that it's a desktop computer.
With *no augmentation* the top prediction is **Polaroid camera, Polaroid Land camera**.
With *augmentation* the top prediction is **desktop computer**
### Conclusion
Results showed that with the exact same model and by applying Edafa we can obtain better results!
| true |
code
| 0.5835 | null | null | null | null |
|
**Chapter 16 – Natural Language Processing with RNNs and Attention**
_This notebook contains all the sample code in chapter 16._
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/ageron/handson-ml2/blob/master/16_nlp_with_rnns_and_attention.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
</table>
# Setup
First, let's import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20 and TensorFlow ≥2.0.
```
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
!pip install -q -U tensorflow-addons
IS_COLAB = True
except Exception:
IS_COLAB = False
# TensorFlow ≥2.0 is required
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.0"
if not tf.config.list_physical_devices('GPU'):
print("No GPU was detected. LSTMs and CNNs can be very slow without a GPU.")
if IS_COLAB:
print("Go to Runtime > Change runtime and select a GPU hardware accelerator.")
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
tf.random.set_seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "nlp"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
```
# Char-RNN
## Splitting a sequence into batches of shuffled windows
For example, let's split the sequence 0 to 14 into windows of length 5, each shifted by 2 (e.g.,`[0, 1, 2, 3, 4]`, `[2, 3, 4, 5, 6]`, etc.), then shuffle them, and split them into inputs (the first 4 steps) and targets (the last 4 steps) (e.g., `[2, 3, 4, 5, 6]` would be split into `[[2, 3, 4, 5], [3, 4, 5, 6]]`), then create batches of 3 such input/target pairs:
```
np.random.seed(42)
tf.random.set_seed(42)
n_steps = 5
dataset = tf.data.Dataset.from_tensor_slices(tf.range(15))
dataset = dataset.window(n_steps, shift=2, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(n_steps))
dataset = dataset.shuffle(10).map(lambda window: (window[:-1], window[1:]))
dataset = dataset.batch(3).prefetch(1)
for index, (X_batch, Y_batch) in enumerate(dataset):
print("_" * 20, "Batch", index, "\nX_batch")
print(X_batch.numpy())
print("=" * 5, "\nY_batch")
print(Y_batch.numpy())
```
## Loading the Data and Preparing the Dataset
```
shakespeare_url = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt"
filepath = keras.utils.get_file("shakespeare.txt", shakespeare_url)
with open(filepath) as f:
shakespeare_text = f.read()
print(shakespeare_text[:148])
"".join(sorted(set(shakespeare_text.lower())))
tokenizer = keras.preprocessing.text.Tokenizer(char_level=True)
tokenizer.fit_on_texts(shakespeare_text)
tokenizer.texts_to_sequences(["First"])
tokenizer.sequences_to_texts([[20, 6, 9, 8, 3]])
max_id = len(tokenizer.word_index) # number of distinct characters
dataset_size = tokenizer.document_count # total number of characters
[encoded] = np.array(tokenizer.texts_to_sequences([shakespeare_text])) - 1
train_size = dataset_size * 90 // 100
dataset = tf.data.Dataset.from_tensor_slices(encoded[:train_size])
n_steps = 100
window_length = n_steps + 1 # target = input shifted 1 character ahead
dataset = dataset.repeat().window(window_length, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_length))
np.random.seed(42)
tf.random.set_seed(42)
batch_size = 32
dataset = dataset.shuffle(10000).batch(batch_size)
dataset = dataset.map(lambda windows: (windows[:, :-1], windows[:, 1:]))
dataset = dataset.map(
lambda X_batch, Y_batch: (tf.one_hot(X_batch, depth=max_id), Y_batch))
dataset = dataset.prefetch(1)
for X_batch, Y_batch in dataset.take(1):
print(X_batch.shape, Y_batch.shape)
```
## Creating and Training the Model
```
model = keras.models.Sequential([
keras.layers.GRU(128, return_sequences=True, input_shape=[None, max_id],
dropout=0.2, recurrent_dropout=0.2),
keras.layers.GRU(128, return_sequences=True,
dropout=0.2, recurrent_dropout=0.2),
keras.layers.TimeDistributed(keras.layers.Dense(max_id,
activation="softmax"))
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="adam")
history = model.fit(dataset, steps_per_epoch=train_size // batch_size,
epochs=10)
```
## Using the Model to Generate Text
```
def preprocess(texts):
X = np.array(tokenizer.texts_to_sequences(texts)) - 1
return tf.one_hot(X, max_id)
X_new = preprocess(["How are yo"])
Y_pred = model.predict_classes(X_new)
tokenizer.sequences_to_texts(Y_pred + 1)[0][-1] # 1st sentence, last char
tf.random.set_seed(42)
tf.random.categorical([[np.log(0.5), np.log(0.4), np.log(0.1)]], num_samples=40).numpy()
def next_char(text, temperature=1):
X_new = preprocess([text])
y_proba = model.predict(X_new)[0, -1:, :]
rescaled_logits = tf.math.log(y_proba) / temperature
char_id = tf.random.categorical(rescaled_logits, num_samples=1) + 1
return tokenizer.sequences_to_texts(char_id.numpy())[0]
tf.random.set_seed(42)
next_char("How are yo", temperature=1)
def complete_text(text, n_chars=50, temperature=1):
for _ in range(n_chars):
text += next_char(text, temperature)
return text
tf.random.set_seed(42)
print(complete_text("t", temperature=0.2))
print(complete_text("t", temperature=1))
print(complete_text("t", temperature=2))
```
## Stateful RNN
```
tf.random.set_seed(42)
dataset = tf.data.Dataset.from_tensor_slices(encoded[:train_size])
dataset = dataset.window(window_length, shift=n_steps, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_length))
dataset = dataset.repeat().batch(1)
dataset = dataset.map(lambda windows: (windows[:, :-1], windows[:, 1:]))
dataset = dataset.map(
lambda X_batch, Y_batch: (tf.one_hot(X_batch, depth=max_id), Y_batch))
dataset = dataset.prefetch(1)
batch_size = 32
encoded_parts = np.array_split(encoded[:train_size], batch_size)
datasets = []
for encoded_part in encoded_parts:
dataset = tf.data.Dataset.from_tensor_slices(encoded_part)
dataset = dataset.window(window_length, shift=n_steps, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_length))
datasets.append(dataset)
dataset = tf.data.Dataset.zip(tuple(datasets)).map(lambda *windows: tf.stack(windows))
dataset = dataset.repeat().map(lambda windows: (windows[:, :-1], windows[:, 1:]))
dataset = dataset.map(
lambda X_batch, Y_batch: (tf.one_hot(X_batch, depth=max_id), Y_batch))
dataset = dataset.prefetch(1)
model = keras.models.Sequential([
keras.layers.GRU(128, return_sequences=True, stateful=True,
dropout=0.2, recurrent_dropout=0.2,
batch_input_shape=[batch_size, None, max_id]),
keras.layers.GRU(128, return_sequences=True, stateful=True,
dropout=0.2, recurrent_dropout=0.2),
keras.layers.TimeDistributed(keras.layers.Dense(max_id,
activation="softmax"))
])
class ResetStatesCallback(keras.callbacks.Callback):
def on_epoch_begin(self, epoch, logs):
self.model.reset_states()
model.compile(loss="sparse_categorical_crossentropy", optimizer="adam")
steps_per_epoch = train_size // batch_size // n_steps
history = model.fit(dataset, steps_per_epoch=steps_per_epoch, epochs=50,
callbacks=[ResetStatesCallback()])
```
To use the model with different batch sizes, we need to create a stateless copy. We can get rid of dropout since it is only used during training:
```
stateless_model = keras.models.Sequential([
keras.layers.GRU(128, return_sequences=True, input_shape=[None, max_id]),
keras.layers.GRU(128, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(max_id,
activation="softmax"))
])
```
To set the weights, we first need to build the model (so the weights get created):
```
stateless_model.build(tf.TensorShape([None, None, max_id]))
stateless_model.set_weights(model.get_weights())
model = stateless_model
tf.random.set_seed(42)
print(complete_text("t"))
```
# Sentiment Analysis
```
tf.random.set_seed(42)
```
You can load the IMDB dataset easily:
```
(X_train, y_test), (X_valid, y_test) = keras.datasets.imdb.load_data()
X_train[0][:10]
word_index = keras.datasets.imdb.get_word_index()
id_to_word = {id_ + 3: word for word, id_ in word_index.items()}
for id_, token in enumerate(("<pad>", "<sos>", "<unk>")):
id_to_word[id_] = token
" ".join([id_to_word[id_] for id_ in X_train[0][:10]])
import tensorflow_datasets as tfds
datasets, info = tfds.load("imdb_reviews", as_supervised=True, with_info=True)
datasets.keys()
train_size = info.splits["train"].num_examples
test_size = info.splits["test"].num_examples
train_size, test_size
for X_batch, y_batch in datasets["train"].batch(2).take(1):
for review, label in zip(X_batch.numpy(), y_batch.numpy()):
print("Review:", review.decode("utf-8")[:200], "...")
print("Label:", label, "= Positive" if label else "= Negative")
print()
def preprocess(X_batch, y_batch):
X_batch = tf.strings.substr(X_batch, 0, 300)
X_batch = tf.strings.regex_replace(X_batch, rb"<br\s*/?>", b" ")
X_batch = tf.strings.regex_replace(X_batch, b"[^a-zA-Z']", b" ")
X_batch = tf.strings.split(X_batch)
return X_batch.to_tensor(default_value=b"<pad>"), y_batch
preprocess(X_batch, y_batch)
from collections import Counter
vocabulary = Counter()
for X_batch, y_batch in datasets["train"].batch(32).map(preprocess):
for review in X_batch:
vocabulary.update(list(review.numpy()))
vocabulary.most_common()[:3]
len(vocabulary)
vocab_size = 10000
truncated_vocabulary = [
word for word, count in vocabulary.most_common()[:vocab_size]]
word_to_id = {word: index for index, word in enumerate(truncated_vocabulary)}
for word in b"This movie was faaaaaantastic".split():
print(word_to_id.get(word) or vocab_size)
words = tf.constant(truncated_vocabulary)
word_ids = tf.range(len(truncated_vocabulary), dtype=tf.int64)
vocab_init = tf.lookup.KeyValueTensorInitializer(words, word_ids)
num_oov_buckets = 1000
table = tf.lookup.StaticVocabularyTable(vocab_init, num_oov_buckets)
table.lookup(tf.constant([b"This movie was faaaaaantastic".split()]))
def encode_words(X_batch, y_batch):
return table.lookup(X_batch), y_batch
train_set = datasets["train"].repeat().batch(32).map(preprocess)
train_set = train_set.map(encode_words).prefetch(1)
for X_batch, y_batch in train_set.take(1):
print(X_batch)
print(y_batch)
embed_size = 128
model = keras.models.Sequential([
keras.layers.Embedding(vocab_size + num_oov_buckets, embed_size,
mask_zero=True, # not shown in the book
input_shape=[None]),
keras.layers.GRU(128, return_sequences=True),
keras.layers.GRU(128),
keras.layers.Dense(1, activation="sigmoid")
])
model.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
history = model.fit(train_set, steps_per_epoch=train_size // 32, epochs=5)
```
Or using manual masking:
```
K = keras.backend
embed_size = 128
inputs = keras.layers.Input(shape=[None])
mask = keras.layers.Lambda(lambda inputs: K.not_equal(inputs, 0))(inputs)
z = keras.layers.Embedding(vocab_size + num_oov_buckets, embed_size)(inputs)
z = keras.layers.GRU(128, return_sequences=True)(z, mask=mask)
z = keras.layers.GRU(128)(z, mask=mask)
outputs = keras.layers.Dense(1, activation="sigmoid")(z)
model = keras.models.Model(inputs=[inputs], outputs=[outputs])
model.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
history = model.fit(train_set, steps_per_epoch=train_size // 32, epochs=5)
```
## Reusing Pretrained Embeddings
```
tf.random.set_seed(42)
TFHUB_CACHE_DIR = os.path.join(os.curdir, "my_tfhub_cache")
os.environ["TFHUB_CACHE_DIR"] = TFHUB_CACHE_DIR
import tensorflow_hub as hub
model = keras.Sequential([
hub.KerasLayer("https://tfhub.dev/google/tf2-preview/nnlm-en-dim50/1",
dtype=tf.string, input_shape=[], output_shape=[50]),
keras.layers.Dense(128, activation="relu"),
keras.layers.Dense(1, activation="sigmoid")
])
model.compile(loss="binary_crossentropy", optimizer="adam",
metrics=["accuracy"])
for dirpath, dirnames, filenames in os.walk(TFHUB_CACHE_DIR):
for filename in filenames:
print(os.path.join(dirpath, filename))
import tensorflow_datasets as tfds
datasets, info = tfds.load("imdb_reviews", as_supervised=True, with_info=True)
train_size = info.splits["train"].num_examples
batch_size = 32
train_set = datasets["train"].repeat().batch(batch_size).prefetch(1)
history = model.fit(train_set, steps_per_epoch=train_size // batch_size, epochs=5)
```
## Automatic Translation
```
tf.random.set_seed(42)
vocab_size = 100
embed_size = 10
import tensorflow_addons as tfa
encoder_inputs = keras.layers.Input(shape=[None], dtype=np.int32)
decoder_inputs = keras.layers.Input(shape=[None], dtype=np.int32)
sequence_lengths = keras.layers.Input(shape=[], dtype=np.int32)
embeddings = keras.layers.Embedding(vocab_size, embed_size)
encoder_embeddings = embeddings(encoder_inputs)
decoder_embeddings = embeddings(decoder_inputs)
encoder = keras.layers.LSTM(512, return_state=True)
encoder_outputs, state_h, state_c = encoder(encoder_embeddings)
encoder_state = [state_h, state_c]
sampler = tfa.seq2seq.sampler.TrainingSampler()
decoder_cell = keras.layers.LSTMCell(512)
output_layer = keras.layers.Dense(vocab_size)
decoder = tfa.seq2seq.basic_decoder.BasicDecoder(decoder_cell, sampler,
output_layer=output_layer)
final_outputs, final_state, final_sequence_lengths = decoder(
decoder_embeddings, initial_state=encoder_state,
sequence_length=sequence_lengths)
Y_proba = tf.nn.softmax(final_outputs.rnn_output)
model = keras.models.Model(
inputs=[encoder_inputs, decoder_inputs, sequence_lengths],
outputs=[Y_proba])
model.compile(loss="sparse_categorical_crossentropy", optimizer="adam")
X = np.random.randint(100, size=10*1000).reshape(1000, 10)
Y = np.random.randint(100, size=15*1000).reshape(1000, 15)
X_decoder = np.c_[np.zeros((1000, 1)), Y[:, :-1]]
seq_lengths = np.full([1000], 15)
history = model.fit([X, X_decoder, seq_lengths], Y, epochs=2)
```
### Bidirectional Recurrent Layers
```
model = keras.models.Sequential([
keras.layers.GRU(10, return_sequences=True, input_shape=[None, 10]),
keras.layers.Bidirectional(keras.layers.GRU(10, return_sequences=True))
])
model.summary()
```
### Positional Encoding
```
class PositionalEncoding(keras.layers.Layer):
def __init__(self, max_steps, max_dims, dtype=tf.float32, **kwargs):
super().__init__(dtype=dtype, **kwargs)
if max_dims % 2 == 1: max_dims += 1 # max_dims must be even
p, i = np.meshgrid(np.arange(max_steps), np.arange(max_dims // 2))
pos_emb = np.empty((1, max_steps, max_dims))
pos_emb[0, :, ::2] = np.sin(p / 10000**(2 * i / max_dims)).T
pos_emb[0, :, 1::2] = np.cos(p / 10000**(2 * i / max_dims)).T
self.positional_embedding = tf.constant(pos_emb.astype(self.dtype))
def call(self, inputs):
shape = tf.shape(inputs)
return inputs + self.positional_embedding[:, :shape[-2], :shape[-1]]
max_steps = 201
max_dims = 512
pos_emb = PositionalEncoding(max_steps, max_dims)
PE = pos_emb(np.zeros((1, max_steps, max_dims), np.float32))[0].numpy()
i1, i2, crop_i = 100, 101, 150
p1, p2, p3 = 22, 60, 35
fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1, sharex=True, figsize=(9, 5))
ax1.plot([p1, p1], [-1, 1], "k--", label="$p = {}$".format(p1))
ax1.plot([p2, p2], [-1, 1], "k--", label="$p = {}$".format(p2), alpha=0.5)
ax1.plot(p3, PE[p3, i1], "bx", label="$p = {}$".format(p3))
ax1.plot(PE[:,i1], "b-", label="$i = {}$".format(i1))
ax1.plot(PE[:,i2], "r-", label="$i = {}$".format(i2))
ax1.plot([p1, p2], [PE[p1, i1], PE[p2, i1]], "bo")
ax1.plot([p1, p2], [PE[p1, i2], PE[p2, i2]], "ro")
ax1.legend(loc="center right", fontsize=14, framealpha=0.95)
ax1.set_ylabel("$P_{(p,i)}$", rotation=0, fontsize=16)
ax1.grid(True, alpha=0.3)
ax1.hlines(0, 0, max_steps - 1, color="k", linewidth=1, alpha=0.3)
ax1.axis([0, max_steps - 1, -1, 1])
ax2.imshow(PE.T[:crop_i], cmap="gray", interpolation="bilinear", aspect="auto")
ax2.hlines(i1, 0, max_steps - 1, color="b")
cheat = 2 # need to raise the red line a bit, or else it hides the blue one
ax2.hlines(i2+cheat, 0, max_steps - 1, color="r")
ax2.plot([p1, p1], [0, crop_i], "k--")
ax2.plot([p2, p2], [0, crop_i], "k--", alpha=0.5)
ax2.plot([p1, p2], [i2+cheat, i2+cheat], "ro")
ax2.plot([p1, p2], [i1, i1], "bo")
ax2.axis([0, max_steps - 1, 0, crop_i])
ax2.set_xlabel("$p$", fontsize=16)
ax2.set_ylabel("$i$", rotation=0, fontsize=16)
plt.savefig("positional_embedding_plot")
plt.show()
embed_size = 512; max_steps = 500; vocab_size = 10000
encoder_inputs = keras.layers.Input(shape=[None], dtype=np.int32)
decoder_inputs = keras.layers.Input(shape=[None], dtype=np.int32)
embeddings = keras.layers.Embedding(vocab_size, embed_size)
encoder_embeddings = embeddings(encoder_inputs)
decoder_embeddings = embeddings(decoder_inputs)
positional_encoding = PositionalEncoding(max_steps, max_dims=embed_size)
encoder_in = positional_encoding(encoder_embeddings)
decoder_in = positional_encoding(decoder_embeddings)
```
Here is a (very) simplified Transformer (the actual architecture has skip connections, layer norm, dense nets, and most importantly it uses Multi-Head Attention instead of regular Attention):
```
Z = encoder_in
for N in range(6):
Z = keras.layers.Attention(use_scale=True)([Z, Z])
encoder_outputs = Z
Z = decoder_in
for N in range(6):
Z = keras.layers.Attention(use_scale=True, causal=True)([Z, Z])
Z = keras.layers.Attention(use_scale=True)([Z, encoder_outputs])
outputs = keras.layers.TimeDistributed(
keras.layers.Dense(vocab_size, activation="softmax"))(Z)
```
Here's a basic implementation of the `MultiHeadAttention` layer. One will likely be added to `keras.layers` in the near future. Note that `Conv1D` layers with `kernel_size=1` (and the default `padding="valid"` and `strides=1`) is equivalent to a `TimeDistributed(Dense(...))` layer.
```
K = keras.backend
class MultiHeadAttention(keras.layers.Layer):
def __init__(self, n_heads, causal=False, use_scale=False, **kwargs):
self.n_heads = n_heads
self.causal = causal
self.use_scale = use_scale
super().__init__(**kwargs)
def build(self, batch_input_shape):
self.dims = batch_input_shape[0][-1]
self.q_dims, self.v_dims, self.k_dims = [self.dims // self.n_heads] * 3 # could be hyperparameters instead
self.q_linear = keras.layers.Conv1D(self.n_heads * self.q_dims, kernel_size=1, use_bias=False)
self.v_linear = keras.layers.Conv1D(self.n_heads * self.v_dims, kernel_size=1, use_bias=False)
self.k_linear = keras.layers.Conv1D(self.n_heads * self.k_dims, kernel_size=1, use_bias=False)
self.attention = keras.layers.Attention(causal=self.causal, use_scale=self.use_scale)
self.out_linear = keras.layers.Conv1D(self.dims, kernel_size=1, use_bias=False)
super().build(batch_input_shape)
def _multi_head_linear(self, inputs, linear):
shape = K.concatenate([K.shape(inputs)[:-1], [self.n_heads, -1]])
projected = K.reshape(linear(inputs), shape)
perm = K.permute_dimensions(projected, [0, 2, 1, 3])
return K.reshape(perm, [shape[0] * self.n_heads, shape[1], -1])
def call(self, inputs):
q = inputs[0]
v = inputs[1]
k = inputs[2] if len(inputs) > 2 else v
shape = K.shape(q)
q_proj = self._multi_head_linear(q, self.q_linear)
v_proj = self._multi_head_linear(v, self.v_linear)
k_proj = self._multi_head_linear(k, self.k_linear)
multi_attended = self.attention([q_proj, v_proj, k_proj])
shape_attended = K.shape(multi_attended)
reshaped_attended = K.reshape(multi_attended, [shape[0], self.n_heads, shape_attended[1], shape_attended[2]])
perm = K.permute_dimensions(reshaped_attended, [0, 2, 1, 3])
concat = K.reshape(perm, [shape[0], shape_attended[1], -1])
return self.out_linear(concat)
Q = np.random.rand(2, 50, 512)
V = np.random.rand(2, 80, 512)
multi_attn = MultiHeadAttention(8)
multi_attn([Q, V]).shape
```
# Exercise solutions
## 1. to 7.
See Appendix A.
## 8.
_Exercise:_ Embedded Reber grammars _were used by Hochreiter and Schmidhuber in [their paper](https://homl.info/93) about LSTMs. They are artificial grammars that produce strings such as "BPBTSXXVPSEPE." Check out Jenny Orr's [nice introduction](https://homl.info/108) to this topic. Choose a particular embedded Reber grammar (such as the one represented on Jenny Orr's page), then train an RNN to identify whether a string respects that grammar or not. You will first need to write a function capable of generating a training batch containing about 50% strings that respect the grammar, and 50% that don't._
First we need to build a function that generates strings based on a grammar. The grammar will be represented as a list of possible transitions for each state. A transition specifies the string to output (or a grammar to generate it) and the next state.
```
default_reber_grammar = [
[("B", 1)], # (state 0) =B=>(state 1)
[("T", 2), ("P", 3)], # (state 1) =T=>(state 2) or =P=>(state 3)
[("S", 2), ("X", 4)], # (state 2) =S=>(state 2) or =X=>(state 4)
[("T", 3), ("V", 5)], # and so on...
[("X", 3), ("S", 6)],
[("P", 4), ("V", 6)],
[("E", None)]] # (state 6) =E=>(terminal state)
embedded_reber_grammar = [
[("B", 1)],
[("T", 2), ("P", 3)],
[(default_reber_grammar, 4)],
[(default_reber_grammar, 5)],
[("T", 6)],
[("P", 6)],
[("E", None)]]
def generate_string(grammar):
state = 0
output = []
while state is not None:
index = np.random.randint(len(grammar[state]))
production, state = grammar[state][index]
if isinstance(production, list):
production = generate_string(grammar=production)
output.append(production)
return "".join(output)
```
Let's generate a few strings based on the default Reber grammar:
```
np.random.seed(42)
for _ in range(25):
print(generate_string(default_reber_grammar), end=" ")
```
Looks good. Now let's generate a few strings based on the embedded Reber grammar:
```
np.random.seed(42)
for _ in range(25):
print(generate_string(embedded_reber_grammar), end=" ")
```
Okay, now we need a function to generate strings that do not respect the grammar. We could generate a random string, but the task would be a bit too easy, so instead we will generate a string that respects the grammar, and we will corrupt it by changing just one character:
```
POSSIBLE_CHARS = "BEPSTVX"
def generate_corrupted_string(grammar, chars=POSSIBLE_CHARS):
good_string = generate_string(grammar)
index = np.random.randint(len(good_string))
good_char = good_string[index]
bad_char = np.random.choice(sorted(set(chars) - set(good_char)))
return good_string[:index] + bad_char + good_string[index + 1:]
```
Let's look at a few corrupted strings:
```
np.random.seed(42)
for _ in range(25):
print(generate_corrupted_string(embedded_reber_grammar), end=" ")
```
We cannot feed strings directly to an RNN, so we need to encode them somehow. One option would be to one-hot encode each character. Another option is to use embeddings. Let's go for the second option (but since there are just a handful of characters, one-hot encoding would probably be a good option as well). For embeddings to work, we need to convert each string into a sequence of character IDs. Let's write a function for that, using each character's index in the string of possible characters "BEPSTVX":
```
def string_to_ids(s, chars=POSSIBLE_CHARS):
return [POSSIBLE_CHARS.index(c) for c in s]
string_to_ids("BTTTXXVVETE")
```
We can now generate the dataset, with 50% good strings, and 50% bad strings:
```
def generate_dataset(size):
good_strings = [string_to_ids(generate_string(embedded_reber_grammar))
for _ in range(size // 2)]
bad_strings = [string_to_ids(generate_corrupted_string(embedded_reber_grammar))
for _ in range(size - size // 2)]
all_strings = good_strings + bad_strings
X = tf.ragged.constant(all_strings, ragged_rank=1)
y = np.array([[1.] for _ in range(len(good_strings))] +
[[0.] for _ in range(len(bad_strings))])
return X, y
np.random.seed(42)
X_train, y_train = generate_dataset(10000)
X_valid, y_valid = generate_dataset(2000)
```
Let's take a look at the first training sequence:
```
X_train[0]
```
What classes does it belong to?
```
y_train[0]
```
Perfect! We are ready to create the RNN to identify good strings. We build a simple sequence binary classifier:
```
np.random.seed(42)
tf.random.set_seed(42)
embedding_size = 5
model = keras.models.Sequential([
keras.layers.InputLayer(input_shape=[None], dtype=tf.int32, ragged=True),
keras.layers.Embedding(input_dim=len(POSSIBLE_CHARS), output_dim=embedding_size),
keras.layers.GRU(30),
keras.layers.Dense(1, activation="sigmoid")
])
optimizer = keras.optimizers.SGD(lr=0.02, momentum = 0.95, nesterov=True)
model.compile(loss="binary_crossentropy", optimizer=optimizer, metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))
```
Now let's test our RNN on two tricky strings: the first one is bad while the second one is good. They only differ by the second to last character. If the RNN gets this right, it shows that it managed to notice the pattern that the second letter should always be equal to the second to last letter. That requires a fairly long short-term memory (which is the reason why we used a GRU cell).
```
test_strings = ["BPBTSSSSSSSXXTTVPXVPXTTTTTVVETE",
"BPBTSSSSSSSXXTTVPXVPXTTTTTVVEPE"]
X_test = tf.ragged.constant([string_to_ids(s) for s in test_strings], ragged_rank=1)
y_proba = model.predict(X_test)
print()
print("Estimated probability that these are Reber strings:")
for index, string in enumerate(test_strings):
print("{}: {:.2f}%".format(string, 100 * y_proba[index][0]))
```
Ta-da! It worked fine. The RNN found the correct answers with very high confidence. :)
## 9.
_Exercise: Train an Encoder–Decoder model that can convert a date string from one format to another (e.g., from "April 22, 2019" to "2019-04-22")._
Let's start by creating the dataset. We will use random days between 1000-01-01 and 9999-12-31:
```
from datetime import date
# cannot use strftime()'s %B format since it depends on the locale
MONTHS = ["January", "February", "March", "April", "May", "June",
"July", "August", "September", "October", "November", "December"]
def random_dates(n_dates):
min_date = date(1000, 1, 1).toordinal()
max_date = date(9999, 12, 31).toordinal()
ordinals = np.random.randint(max_date - min_date, size=n_dates) + min_date
dates = [date.fromordinal(ordinal) for ordinal in ordinals]
x = [MONTHS[dt.month - 1] + " " + dt.strftime("%d, %Y") for dt in dates]
y = [dt.isoformat() for dt in dates]
return x, y
```
Here are a few random dates, displayed in both the input format and the target format:
```
np.random.seed(42)
n_dates = 3
x_example, y_example = random_dates(n_dates)
print("{:25s}{:25s}".format("Input", "Target"))
print("-" * 50)
for idx in range(n_dates):
print("{:25s}{:25s}".format(x_example[idx], y_example[idx]))
```
Let's get the list of all possible characters in the inputs:
```
INPUT_CHARS = "".join(sorted(set("".join(MONTHS)))) + "01234567890, "
INPUT_CHARS
```
And here's the list of possible characters in the outputs:
```
OUTPUT_CHARS = "0123456789-"
```
Let's write a function to convert a string to a list of character IDs, as we did in the previous exercise:
```
def date_str_to_ids(date_str, chars=INPUT_CHARS):
return [chars.index(c) for c in date_str]
date_str_to_ids(x_example[0], INPUT_CHARS)
date_str_to_ids(y_example[0], OUTPUT_CHARS)
def prepare_date_strs(date_strs, chars=INPUT_CHARS):
X_ids = [date_str_to_ids(dt, chars) for dt in date_strs]
X = tf.ragged.constant(X_ids, ragged_rank=1)
return (X + 1).to_tensor() # using 0 as the padding token ID
def create_dataset(n_dates):
x, y = random_dates(n_dates)
return prepare_date_strs(x, INPUT_CHARS), prepare_date_strs(y, OUTPUT_CHARS)
np.random.seed(42)
X_train, Y_train = create_dataset(10000)
X_valid, Y_valid = create_dataset(2000)
X_test, Y_test = create_dataset(2000)
Y_train[0]
```
### First version: a very basic seq2seq model
Let's first try the simplest possible model: we feed in the input sequence, which first goes through the encoder (an embedding layer followed by a single LSTM layer), which outputs a vector, then it goes through a decoder (a single LSTM layer, followed by a dense output layer), which outputs a sequence of vectors, each representing the estimated probabilities for all possible output character.
Since the decoder expects a sequence as input, we repeat the vector (which is output by the decoder) as many times as the longest possible output sequence.
```
embedding_size = 32
max_output_length = Y_train.shape[1]
np.random.seed(42)
tf.random.set_seed(42)
encoder = keras.models.Sequential([
keras.layers.Embedding(input_dim=len(INPUT_CHARS) + 1,
output_dim=embedding_size,
input_shape=[None]),
keras.layers.LSTM(128)
])
decoder = keras.models.Sequential([
keras.layers.LSTM(128, return_sequences=True),
keras.layers.Dense(len(OUTPUT_CHARS) + 1, activation="softmax")
])
model = keras.models.Sequential([
encoder,
keras.layers.RepeatVector(max_output_length),
decoder
])
optimizer = keras.optimizers.Nadam()
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit(X_train, Y_train, epochs=20,
validation_data=(X_valid, Y_valid))
```
Looks great, we reach 100% validation accuracy! Let's use the model to make some predictions. We will need to be able to convert a sequence of character IDs to a readable string:
```
def ids_to_date_strs(ids, chars=OUTPUT_CHARS):
return ["".join([("?" + chars)[index] for index in sequence])
for sequence in ids]
```
Now we can use the model to convert some dates
```
X_new = prepare_date_strs(["September 17, 2009", "July 14, 1789"])
ids = model.predict_classes(X_new)
for date_str in ids_to_date_strs(ids):
print(date_str)
```
Perfect! :)
However, since the model was only trained on input strings of length 18 (which is the length of the longest date), it does not perform well if we try to use it to make predictions on shorter sequences:
```
X_new = prepare_date_strs(["May 02, 2020", "July 14, 1789"])
ids = model.predict_classes(X_new)
for date_str in ids_to_date_strs(ids):
print(date_str)
```
Oops! We need to ensure that we always pass sequences of the same length as during training, using padding if necessary. Let's write a little helper function for that:
```
max_input_length = X_train.shape[1]
def prepare_date_strs_padded(date_strs):
X = prepare_date_strs(date_strs)
if X.shape[1] < max_input_length:
X = tf.pad(X, [[0, 0], [0, max_input_length - X.shape[1]]])
return X
def convert_date_strs(date_strs):
X = prepare_date_strs_padded(date_strs)
ids = model.predict_classes(X)
return ids_to_date_strs(ids)
convert_date_strs(["May 02, 2020", "July 14, 1789"])
```
Cool! Granted, there are certainly much easier ways to write a date conversion tool (e.g., using regular expressions or even basic string manipulation), but you have to admit that using neural networks is way cooler. ;-)
However, real-life sequence-to-sequence problems will usually be harder, so for the sake of completeness, let's build a more powerful model.
### Second version: feeding the shifted targets to the decoder (teacher forcing)
Instead of feeding the decoder a simple repetition of the encoder's output vector, we can feed it the target sequence, shifted by one time step to the right. This way, at each time step the decoder will know what the previous target character was. This should help is tackle more complex sequence-to-sequence problems.
Since the first output character of each target sequence has no previous character, we will need a new token to represent the start-of-sequence (sos).
During inference, we won't know the target, so what will we feed the decoder? We can just predict one character at a time, starting with an sos token, then feeding the decoder all the characters that were predicted so far (we will look at this in more details later in this notebook).
But if the decoder's LSTM expects to get the previous target as input at each step, how shall we pass it it the vector output by the encoder? Well, one option is to ignore the output vector, and instead use the encoder's LSTM state as the initial state of the decoder's LSTM (which requires that encoder's LSTM must have the same number of units as the decoder's LSTM).
Now let's create the decoder's inputs (for training, validation and testing). The sos token will be represented using the last possible output character's ID + 1.
```
sos_id = len(OUTPUT_CHARS) + 1
def shifted_output_sequences(Y):
sos_tokens = tf.fill(dims=(len(Y), 1), value=sos_id)
return tf.concat([sos_tokens, Y[:, :-1]], axis=1)
X_train_decoder = shifted_output_sequences(Y_train)
X_valid_decoder = shifted_output_sequences(Y_valid)
X_test_decoder = shifted_output_sequences(Y_test)
```
Let's take a look at the decoder's training inputs:
```
X_train_decoder
```
Now let's build the model. It's not a simple sequential model anymore, so let's use the functional API:
```
encoder_embedding_size = 32
decoder_embedding_size = 32
lstm_units = 128
np.random.seed(42)
tf.random.set_seed(42)
encoder_input = keras.layers.Input(shape=[None], dtype=tf.int32)
encoder_embedding = keras.layers.Embedding(
input_dim=len(INPUT_CHARS) + 1,
output_dim=encoder_embedding_size)(encoder_input)
_, encoder_state_h, encoder_state_c = keras.layers.LSTM(
lstm_units, return_state=True)(encoder_embedding)
encoder_state = [encoder_state_h, encoder_state_c]
decoder_input = keras.layers.Input(shape=[None], dtype=tf.int32)
decoder_embedding = keras.layers.Embedding(
input_dim=len(OUTPUT_CHARS) + 2,
output_dim=decoder_embedding_size)(decoder_input)
decoder_lstm_output = keras.layers.LSTM(lstm_units, return_sequences=True)(
decoder_embedding, initial_state=encoder_state)
decoder_output = keras.layers.Dense(len(OUTPUT_CHARS) + 1,
activation="softmax")(decoder_lstm_output)
model = keras.models.Model(inputs=[encoder_input, decoder_input],
outputs=[decoder_output])
optimizer = keras.optimizers.Nadam()
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit([X_train, X_train_decoder], Y_train, epochs=10,
validation_data=([X_valid, X_valid_decoder], Y_valid))
```
This model also reaches 100% validation accuracy, but it does so even faster.
Let's once again use the model to make some predictions. This time we need to predict characters one by one.
```
sos_id = len(OUTPUT_CHARS) + 1
def predict_date_strs(date_strs):
X = prepare_date_strs_padded(date_strs)
Y_pred = tf.fill(dims=(len(X), 1), value=sos_id)
for index in range(max_output_length):
pad_size = max_output_length - Y_pred.shape[1]
X_decoder = tf.pad(Y_pred, [[0, 0], [0, pad_size]])
Y_probas_next = model.predict([X, X_decoder])[:, index:index+1]
Y_pred_next = tf.argmax(Y_probas_next, axis=-1, output_type=tf.int32)
Y_pred = tf.concat([Y_pred, Y_pred_next], axis=1)
return ids_to_date_strs(Y_pred[:, 1:])
predict_date_strs(["July 14, 1789", "May 01, 2020"])
```
Works fine! :)
### Third version: using TF-Addons's seq2seq implementation
Let's build exactly the same model, but using TF-Addon's seq2seq API. The implementation below is almost very similar to the TFA example higher in this notebook, except without the model input to specify the output sequence length, for simplicity (but you can easily add it back in if you need it for your projects, when the output sequences have very different lengths).
```
import tensorflow_addons as tfa
np.random.seed(42)
tf.random.set_seed(42)
encoder_embedding_size = 32
decoder_embedding_size = 32
units = 128
encoder_inputs = keras.layers.Input(shape=[None], dtype=np.int32)
decoder_inputs = keras.layers.Input(shape=[None], dtype=np.int32)
sequence_lengths = keras.layers.Input(shape=[], dtype=np.int32)
encoder_embeddings = keras.layers.Embedding(
len(INPUT_CHARS) + 1, encoder_embedding_size)(encoder_inputs)
decoder_embedding_layer = keras.layers.Embedding(
len(INPUT_CHARS) + 2, decoder_embedding_size)
decoder_embeddings = decoder_embedding_layer(decoder_inputs)
encoder = keras.layers.LSTM(units, return_state=True)
encoder_outputs, state_h, state_c = encoder(encoder_embeddings)
encoder_state = [state_h, state_c]
sampler = tfa.seq2seq.sampler.TrainingSampler()
decoder_cell = keras.layers.LSTMCell(units)
output_layer = keras.layers.Dense(len(OUTPUT_CHARS) + 1)
decoder = tfa.seq2seq.basic_decoder.BasicDecoder(decoder_cell,
sampler,
output_layer=output_layer)
final_outputs, final_state, final_sequence_lengths = decoder(
decoder_embeddings,
initial_state=encoder_state)
Y_proba = keras.layers.Activation("softmax")(final_outputs.rnn_output)
model = keras.models.Model(inputs=[encoder_inputs, decoder_inputs],
outputs=[Y_proba])
optimizer = keras.optimizers.Nadam()
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit([X_train, X_train_decoder], Y_train, epochs=15,
validation_data=([X_valid, X_valid_decoder], Y_valid))
```
And once again, 100% validation accuracy! To use the model, we can just reuse the `predict_date_strs()` function:
```
predict_date_strs(["July 14, 1789", "May 01, 2020"])
```
However, there's a much more efficient way to perform inference. Until now, during inference, we've run the model once for each new character. Instead, we can create a new decoder, based on the previously trained layers, but using a `GreedyEmbeddingSampler` instead of a `TrainingSampler`.
At each time step, the `GreedyEmbeddingSampler` will compute the argmax of the decoder's outputs, and run the resulting token IDs through the decoder's embedding layer. Then it will feed the resulting embeddings to the decoder's LSTM cell at the next time step. This way, we only need to run the decoder once to get the full prediction.
```
inference_sampler = tfa.seq2seq.sampler.GreedyEmbeddingSampler(
embedding_fn=decoder_embedding_layer)
inference_decoder = tfa.seq2seq.basic_decoder.BasicDecoder(
decoder_cell, inference_sampler, output_layer=output_layer,
maximum_iterations=max_output_length)
batch_size = tf.shape(encoder_inputs)[:1]
start_tokens = tf.fill(dims=batch_size, value=sos_id)
final_outputs, final_state, final_sequence_lengths = inference_decoder(
start_tokens,
initial_state=encoder_state,
start_tokens=start_tokens,
end_token=0)
inference_model = keras.models.Model(inputs=[encoder_inputs],
outputs=[final_outputs.sample_id])
```
A few notes:
* The `GreedyEmbeddingSampler` needs the `start_tokens` (a vector containing the start-of-sequence ID for each decoder sequence), and the `end_token` (the decoder will stop decoding a sequence once the model outputs this token).
* We must set `maximum_iterations` when creating the `BasicDecoder`, or else it may run into an infinite loop (if the model never outputs the end token for at least one of the sequences). This would force you would to restart the Jupyter kernel.
* The decoder inputs are not needed anymore, since all the decoder inputs are generated dynamically based on the outputs from the previous time step.
* The model's outputs are `final_outputs.sample_id` instead of the softmax of `final_outputs.rnn_outputs`. This allows us to directly get the argmax of the model's outputs. If you prefer to have access to the logits, you can replace `final_outputs.sample_id` with `final_outputs.rnn_outputs`.
Now we can write a simple function that uses the model to perform the date format conversion:
```
def fast_predict_date_strs(date_strs):
X = prepare_date_strs_padded(date_strs)
Y_pred = inference_model.predict(X)
return ids_to_date_strs(Y_pred)
fast_predict_date_strs(["July 14, 1789", "May 01, 2020"])
```
Let's check that it really is faster:
```
%timeit predict_date_strs(["July 14, 1789", "May 01, 2020"])
%timeit fast_predict_date_strs(["July 14, 1789", "May 01, 2020"])
```
That's more than a 10x speedup! And it would be even more if we were handling longer sequences.
### Fourth version: using TF-Addons's seq2seq implementation with a scheduled sampler
**Warning**: due to a TF bug, this version only works using TensorFlow 2.2.
When we trained the previous model, at each time step _t_ we gave the model the target token for time step _t_ - 1. However, at inference time, the model did not get the previous target at each time step. Instead, it got the previous prediction. So there is a discrepancy between training and inference, which may lead to disappointing performance. To alleviate this, we can gradually replace the targets with the predictions, during training. For this, we just need to replace the `TrainingSampler` with a `ScheduledEmbeddingTrainingSampler`, and use a Keras callback to gradually increase the `sampling_probability` (i.e., the probability that the decoder will use the prediction from the previous time step rather than the target for the previous time step).
```
import tensorflow_addons as tfa
np.random.seed(42)
tf.random.set_seed(42)
n_epochs = 20
encoder_embedding_size = 32
decoder_embedding_size = 32
units = 128
encoder_inputs = keras.layers.Input(shape=[None], dtype=np.int32)
decoder_inputs = keras.layers.Input(shape=[None], dtype=np.int32)
sequence_lengths = keras.layers.Input(shape=[], dtype=np.int32)
encoder_embeddings = keras.layers.Embedding(
len(INPUT_CHARS) + 1, encoder_embedding_size)(encoder_inputs)
decoder_embedding_layer = keras.layers.Embedding(
len(INPUT_CHARS) + 2, decoder_embedding_size)
decoder_embeddings = decoder_embedding_layer(decoder_inputs)
encoder = keras.layers.LSTM(units, return_state=True)
encoder_outputs, state_h, state_c = encoder(encoder_embeddings)
encoder_state = [state_h, state_c]
sampler = tfa.seq2seq.sampler.ScheduledEmbeddingTrainingSampler(
sampling_probability=0.,
embedding_fn=decoder_embedding_layer)
# we must set the sampling_probability after creating the sampler
# (see https://github.com/tensorflow/addons/pull/1714)
sampler.sampling_probability = tf.Variable(0.)
decoder_cell = keras.layers.LSTMCell(units)
output_layer = keras.layers.Dense(len(OUTPUT_CHARS) + 1)
decoder = tfa.seq2seq.basic_decoder.BasicDecoder(decoder_cell,
sampler,
output_layer=output_layer)
final_outputs, final_state, final_sequence_lengths = decoder(
decoder_embeddings,
initial_state=encoder_state)
Y_proba = keras.layers.Activation("softmax")(final_outputs.rnn_output)
model = keras.models.Model(inputs=[encoder_inputs, decoder_inputs],
outputs=[Y_proba])
optimizer = keras.optimizers.Nadam()
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
def update_sampling_probability(epoch, logs):
proba = min(1.0, epoch / (n_epochs - 10))
sampler.sampling_probability.assign(proba)
sampling_probability_cb = keras.callbacks.LambdaCallback(
on_epoch_begin=update_sampling_probability)
history = model.fit([X_train, X_train_decoder], Y_train, epochs=n_epochs,
validation_data=([X_valid, X_valid_decoder], Y_valid),
callbacks=[sampling_probability_cb])
```
Not quite 100% validation accuracy, but close enough!
For inference, we could do the exact same thing as earlier, using a `GreedyEmbeddingSampler`. However, just for the sake of completeness, let's use a `SampleEmbeddingSampler` instead. It's almost the same thing, except that instead of using the argmax of the model's output to find the token ID, it treats the outputs as logits and uses them to sample a token ID randomly. This can be useful when you want to generate text. The `softmax_temperature` argument serves the
same purpose as when we generated Shakespeare-like text (the higher this argument, the more random the generated text will be).
```
softmax_temperature = tf.Variable(1.)
inference_sampler = tfa.seq2seq.sampler.SampleEmbeddingSampler(
embedding_fn=decoder_embedding_layer,
softmax_temperature=softmax_temperature)
inference_decoder = tfa.seq2seq.basic_decoder.BasicDecoder(
decoder_cell, inference_sampler, output_layer=output_layer,
maximum_iterations=max_output_length)
batch_size = tf.shape(encoder_inputs)[:1]
start_tokens = tf.fill(dims=batch_size, value=sos_id)
final_outputs, final_state, final_sequence_lengths = inference_decoder(
start_tokens,
initial_state=encoder_state,
start_tokens=start_tokens,
end_token=0)
inference_model = keras.models.Model(inputs=[encoder_inputs],
outputs=[final_outputs.sample_id])
def creative_predict_date_strs(date_strs, temperature=1.0):
softmax_temperature.assign(temperature)
X = prepare_date_strs_padded(date_strs)
Y_pred = inference_model.predict(X)
return ids_to_date_strs(Y_pred)
tf.random.set_seed(42)
creative_predict_date_strs(["July 14, 1789", "May 01, 2020"])
```
Dates look good at room temperature. Now let's heat things up a bit:
```
tf.random.set_seed(42)
creative_predict_date_strs(["July 14, 1789", "May 01, 2020"],
temperature=5.)
```
Oops, the dates are overcooked, now. Let's call them "creative" dates.
### Fifth version: using TFA seq2seq, the Keras subclassing API and attention mechanisms
The sequences in this problem are pretty short, but if we wanted to tackle longer sequences, we would probably have to use attention mechanisms. While it's possible to code our own implementation, it's simpler and more efficient to use TF-Addons's implementation instead. Let's do that now, this time using Keras' subclassing API.
**Warning**: due to a TensorFlow bug (see [this issue](https://github.com/tensorflow/addons/issues/1153) for details), the `get_initial_state()` method fails in eager mode, so for now we have to use the subclassing API, as Keras automatically calls `tf.function()` on the `call()` method (so it runs in graph mode).
In this implementation, we've reverted back to using the `TrainingSampler`, for simplicity (but you can easily tweak it to use a `ScheduledEmbeddingTrainingSampler` instead). We also use a `GreedyEmbeddingSampler` during inference, so this class is pretty easy to use:
```
class DateTranslation(keras.models.Model):
def __init__(self, units=128, encoder_embedding_size=32,
decoder_embedding_size=32, **kwargs):
super().__init__(**kwargs)
self.encoder_embedding = keras.layers.Embedding(
input_dim=len(INPUT_CHARS) + 1,
output_dim=encoder_embedding_size)
self.encoder = keras.layers.LSTM(units,
return_sequences=True,
return_state=True)
self.decoder_embedding = keras.layers.Embedding(
input_dim=len(OUTPUT_CHARS) + 2,
output_dim=decoder_embedding_size)
self.attention = tfa.seq2seq.LuongAttention(units)
decoder_inner_cell = keras.layers.LSTMCell(units)
self.decoder_cell = tfa.seq2seq.AttentionWrapper(
cell=decoder_inner_cell,
attention_mechanism=self.attention)
output_layer = keras.layers.Dense(len(OUTPUT_CHARS) + 1)
self.decoder = tfa.seq2seq.BasicDecoder(
cell=self.decoder_cell,
sampler=tfa.seq2seq.sampler.TrainingSampler(),
output_layer=output_layer)
self.inference_decoder = tfa.seq2seq.BasicDecoder(
cell=self.decoder_cell,
sampler=tfa.seq2seq.sampler.GreedyEmbeddingSampler(
embedding_fn=self.decoder_embedding),
output_layer=output_layer,
maximum_iterations=max_output_length)
def call(self, inputs, training=None):
encoder_input, decoder_input = inputs
encoder_embeddings = self.encoder_embedding(encoder_input)
encoder_outputs, encoder_state_h, encoder_state_c = self.encoder(
encoder_embeddings,
training=training)
encoder_state = [encoder_state_h, encoder_state_c]
self.attention(encoder_outputs,
setup_memory=True)
decoder_embeddings = self.decoder_embedding(decoder_input)
decoder_initial_state = self.decoder_cell.get_initial_state(
decoder_embeddings)
decoder_initial_state = decoder_initial_state.clone(
cell_state=encoder_state)
if training:
decoder_outputs, _, _ = self.decoder(
decoder_embeddings,
initial_state=decoder_initial_state,
training=training)
else:
start_tokens = tf.zeros_like(encoder_input[:, 0]) + sos_id
decoder_outputs, _, _ = self.inference_decoder(
decoder_embeddings,
initial_state=decoder_initial_state,
start_tokens=start_tokens,
end_token=0)
return tf.nn.softmax(decoder_outputs.rnn_output)
np.random.seed(42)
tf.random.set_seed(42)
model = DateTranslation()
optimizer = keras.optimizers.Nadam()
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit([X_train, X_train_decoder], Y_train, epochs=25,
validation_data=([X_valid, X_valid_decoder], Y_valid))
```
Not quite 100% validation accuracy, but close. It took a bit longer to converge this time, but there were also more parameters and more computations per iteration. And we did not use a scheduled sampler.
To use the model, we can write yet another little function:
```
def fast_predict_date_strs_v2(date_strs):
X = prepare_date_strs_padded(date_strs)
X_decoder = tf.zeros(shape=(len(X), max_output_length), dtype=tf.int32)
Y_probas = model.predict([X, X_decoder])
Y_pred = tf.argmax(Y_probas, axis=-1)
return ids_to_date_strs(Y_pred)
fast_predict_date_strs_v2(["July 14, 1789", "May 01, 2020"])
```
There are still a few interesting features from TF-Addons that you may want to look at:
* Using a `BeamSearchDecoder` rather than a `BasicDecoder` for inference. Instead of outputing the character with the highest probability, this decoder keeps track of the several candidates, and keeps only the most likely sequences of candidates (see chapter 16 in the book for more details).
* Setting masks or specifying `sequence_length` if the input or target sequences may have very different lengths.
* Using a `ScheduledOutputTrainingSampler`, which gives you more flexibility than the `ScheduledEmbeddingTrainingSampler` to decide how to feed the output at time _t_ to the cell at time _t_+1. By default it feeds the outputs directly to cell, without computing the argmax ID and passing it through an embedding layer. Alternatively, you specify a `next_inputs_fn` function that will be used to convert the cell outputs to inputs at the next step.
## 10.
_Exercise: Go through TensorFlow's [Neural Machine Translation with Attention tutorial](https://homl.info/nmttuto)._
Simply open the Colab and follow its instructions. Alternatively, if you want a simpler example of using TF-Addons's seq2seq implementation for Neural Machine Translation (NMT), look at the solution to the previous question. The last model implementation will give you a simpler example of using TF-Addons to build an NMT model using attention mechanisms.
## 11.
_Exercise: Use one of the recent language models (e.g., GPT) to generate more convincing Shakespearean text._
The simplest way to use recent language models is to use the excellent [transformers library](https://huggingface.co/transformers/), open sourced by Hugging Face. It provides many modern neural net architectures (including BERT, GPT-2, RoBERTa, XLM, DistilBert, XLNet and more) for Natural Language Processing (NLP), including many pretrained models. It relies on either TensorFlow or PyTorch. Best of all: it's amazingly simple to use.
First, let's load a pretrained model. In this example, we will use OpenAI's GPT model, with an additional Language Model on top (just a linear layer with weights tied to the input embeddings). Let's import it and load the pretrained weights (this will download about 445MB of data to `~/.cache/torch/transformers`):
```
from transformers import TFOpenAIGPTLMHeadModel
model = TFOpenAIGPTLMHeadModel.from_pretrained("openai-gpt")
```
Next we will need a specialized tokenizer for this model. This one will try to use the [spaCy](https://spacy.io/) and [ftfy](https://pypi.org/project/ftfy/) libraries if they are installed, or else it will fall back to BERT's `BasicTokenizer` followed by Byte-Pair Encoding (which should be fine for most use cases).
```
from transformers import OpenAIGPTTokenizer
tokenizer = OpenAIGPTTokenizer.from_pretrained("openai-gpt")
```
Now let's use the tokenizer to tokenize and encode the prompt text:
```
prompt_text = "This royal throne of kings, this sceptred isle"
encoded_prompt = tokenizer.encode(prompt_text,
add_special_tokens=False,
return_tensors="tf")
encoded_prompt
```
Easy! Next, let's use the model to generate text after the prompt. We will generate 5 different sentences, each starting with the prompt text, followed by 40 additional tokens. For an explanation of what all the hyperparameters do, make sure to check out this great [blog post](https://huggingface.co/blog/how-to-generate) by Patrick von Platen (from Hugging Face). You can play around with the hyperparameters to try to obtain better results.
```
num_sequences = 5
length = 40
generated_sequences = model.generate(
input_ids=encoded_prompt,
do_sample=True,
max_length=length + len(encoded_prompt[0]),
temperature=1.0,
top_k=0,
top_p=0.9,
repetition_penalty=1.0,
num_return_sequences=num_sequences,
)
generated_sequences
```
Now let's decode the generated sequences and print them:
```
for sequence in generated_sequences:
text = tokenizer.decode(sequence, clean_up_tokenization_spaces=True)
print(text)
print("-" * 80)
```
You can try more recent (and larger) models, such as GPT-2, CTRL, Transformer-XL or XLNet, which are all available as pretrained models in the transformers library, including variants with Language Models on top. The preprocessing steps vary slightly between models, so make sure to check out this [generation example](https://github.com/huggingface/transformers/blob/master/examples/run_generation.py) from the transformers documentation (this example uses PyTorch, but it will work with very little tweaks, such as adding `TF` at the beginning of the model class name, removing the `.to()` method calls, and using `return_tensors="tf"` instead of `"pt"`.
Hope you enjoyed this chapter! :)
| true |
code
| 0.670824 | null | null | null | null |
|
## The Psychology of Growth
The field of positive psychology studies what are the human behaviours that lead to a great life. You can think of it as the intersection between self help books with the academic rigor of statistics. One of the famous findings of positive psychology is the **Growth Mindset**. The idea is that people can have a fixed or a growth mindset. If you have a fixed mindset, you believe that abilities are given at birth or in early childhood. As such, intelligence is fixed and can't change throughout life. If you don't have it by now, you can't acquire it. The corollary of this though is that you should not waste time on areas where you don't excel, since you will never learn how to handle them. On the other hand, if you have a growth mindset, you believe that intelligence can be developed. The direct consequence of this is you see failure not as lack of intelligence, put as part of a learning process.
I don't want to debate which of these mindsets is the correct one (its probably somewhere in the middle). For our purpose, it doesn't matter much. What does matter is that psychologists found out that people who have a growth mindset tend to do better in life. They are more likely to achieve what they've set to.
As versed as we are with causal inference, we've learned to see those statements with skepticism. Is it that a growth mindset causes people to achieve more? Or is simply the case that people who achieve more are prone to develop a growth mindset as a result of their success? Who came first, the egg or the chicken? In potential outcome notation, we have reasons to believe that there is bias in these statements. \\(Y_0|T=1\\) is probably larger than \\(Y_0|T=0\\), which means that those with a growth mindset would have achieved more even if they had a fixed mindset.
To settle things, researches designed the [The National Study of Learning Mindsets](https://mindsetscholarsnetwork.org/about-the-network/current-initatives/national-mindset-study/#). It is a randomised study conducted in U.S. public high schools which aims at finding the impact of a growth mindset. The way it works is that students receive from the school a seminary to instil in them a growth mindset. Then, they follow up the students in their college years to measure how well they've performed academically. This measurement was compiled into an achievement score and standardised. The real data on this study is not publicly available in order to preserve students' privacy. However, we have a simulated dataset with the same statistical properties provided by [Athey and Wager](https://arxiv.org/pdf/1902.07409.pdf), so we will use that instead.
```
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf
import graphviz as gr
%matplotlib inline
style.use("fivethirtyeight")
pd.set_option("display.max_columns", 6)
```
Besides the treated and outcome variables, the study also recorded some other features:
* schoolid: identifier of the student's school;
* success_expect: self-reported expectations for success in the future, a proxy for prior achievement, measured prior to random assignment;
* ethnicity: categorical variable for student race/ethnicity;
* gender: categorical variable for student identified gender;
* frst_in_family: categorical variable for student first-generation status, i.e. first in family to go to college;
* school_urbanicity: school-level categorical variable for urbanicity of the school, i.e. rural, suburban, etc;
* school_mindset: school-level mean of students’ fixed mindsets, reported prior to random assignment, standardised;
* school_achievement: school achievement level, as measured by test scores and college preparation for the previous 4 cohorts of students, standardised;
* school_ethnic_minority: school racial/ethnic minority composition, i.e., percentage of student body that is Black, Latino, or Native American, standardised;
* school_poverty: school poverty concentration, i.e., percentage of students who are from families whose incomes fall below the federal poverty line, standardised;
* school_size: total number of students in all four grade levels in the school, standardised.
```
data = pd.read_csv("./data/learning_mindset.csv")
data.sample(5, random_state=5)
```
Although the study was randomised, it doesn't seem to be the case that this data is free from confounding. If we look at the additional features, we will notice that they vary systematically between treatment and control. One possible reason for this is that the treatment variable is measured by the student's receipt of the seminar. So, although the opportunity to participate was random, participation itself is not. We are here dealing with a case of non-compliance here. One evidence of this is how the student's success expectation is correlated with the participation in the seminar. Students with higher self-reported participation are more likely to have joined the growth mindset seminar.
```
data.groupby("success_expect")["intervention"].mean()
```
Still, let's see what the difference in means \\(E[Y|T=1] - E[Y|T=0]\\) looks like. This will be a useful baseline to compare against.
```
smf.ols("achievement_score ~ intervention", data=data).fit().summary().tables[1]
```
Simply comparing those with and without the intervention, we can see that the treated have an achievement score that is, on average, 0.3185 (0.4723 - 0.1538) higher than the untreated. But is this big or small? I know that interpreting standardised outcomes can be challenging, but bear with me for a moment. I think it is worth going through this because it won't be the last time you will encounter standardized scores.
The outcome variable being standardised means that it is measured in standard deviations. So, the treated are 0.3185 deviations above the untreated. That is what this means. As for if this is small or big, let's remember some stuff about the normal distribution. We know that 95% of its mass is between 2 standard deviations, leaving 2.5% on one tail and 2.5% on another. This also means that if someone is 2 standard deviations above the mean, 97.5% (95% plus the left 2.5% tail) of all the individuals are below that person. By looking at the normal CDF, we also know that about 0.85% of its mass is below 1 standard deviation and that 70% of its mass is below 0.5 standard deviations. So, this means that the average of the treated is above 70% of the individual achievements. The untreated mean, on the other hand, have only 44% of the individuals below.
Here is what this looks like in a picture.
```
plt.hist(data["achievement_score"], bins=20, alpha=0.3, label="All")
plt.hist(data.query("intervention==0")["achievement_score"], bins=20, alpha=0.3, color="C2")
plt.hist(data.query("intervention==1")["achievement_score"], bins=20, alpha=0.3, color="C3")
plt.vlines(-0.1538, 0, 300, label="Untreated", color="C2")
plt.vlines(-0.1538+0.4723, 0, 300, label="Treated", color="C3")
plt.legend();
```
Of course, we still think this result is biased. The difference between treated and untreated is probably smaller than this, because we think the bias is positive. We've already seen that more ambitious people are more willing to go to the seminar, so they probably would have achieved more even if they had attended it. To control for this bias, we could use regression or matching, but it's time to learn about a new technique.
## Propensity Score
Propensity score comes from the realisation that you don't need to directly control for confounders X to achieve conditional independence \\((Y_1, Y_0) \perp T | X\\). Instead, it is sufficient to control for a balancing score \\(E[T|X]\\). This balancing score is often the conditional probability of the treatment, \\(P(T|X)\\), also called the propensity score \\(P(x)\\). The propensity score makes it so that you don't have to condition on the entirety of X to achieve independence of the potential outcomes on the treatment. It is sufficient to condition on this single variable with is the propensity score:
$
(Y_1, Y_0) \perp T | P(x)
$
There is a formal proof for why this is, but we can forget it for now and approach the matter in a more intuitive way. The propensity score is the conditional probability of receiving the treatment right? So we can think of it as some sort of function that converts X into the treatment T. The propensity score makes this middle ground between the variable X and the treatment T. If we show this in a causal graph, this is what it would look like.
```
g = gr.Digraph()
g.edge("T", "Y")
g.edge("X", "Y")
g.edge("X", "P(x)")
g.edge("P(x)", "T")
g
```
If I know what P(x) is, X alone tells me nothing more that can help me learn what T would be. Which means that controlling for P(x) acts the same way as controlling for X directly. Think of it in terms of our mindset program. Treated and non treated are initially not comparable because the more ambitious are both more likely to take the treatment and of achieving more in life. However, if I take 2 individuals, one from the treated and one from the control, but with the same probability of receiving the treatment, they are comparable. Think about it. If they have the exact same probability of receiving the treatment, the only reason one of them received it and the other did not is pure chance. Holding the propensity score constant acts in a way of making the data look as good as randomly assigned.
Now that we got the intuition, let's look at the mathematical proof. We want to show that \\((Y_1, Y_0) \perp T | P(x)\\) is equivalent to saying that
$
E[T|P(x), X] = E[T|P(x)]
$
This simply says that once I condition on P(x), X can give me no extra information about T. The proof of this is quite weird. We will show that the equation above is true by converting it to a trivial statement. First take a look at the left hand side \\(E[T|P(x), X]\\).
$
E[T|P(x), X] = E[T|X] = P(x)
$
We use the fact that P(x) is just a function of X, so conditioning on it gives no further information after we've conditioned on X itself. Then, we use the definition of the propensity score \\(E[T|X]\\). For the right hand side, we will use the law of iterated expectations \\(E[A] = E[E[A|B]]\\) This law says that we can compute the expected value of A by looking at the value of A broken down by B and then averaging that.
$
E[T|P(x)] = E[E[T|P(x),X]|P(x)] = E[P(x)|P(x)] = P(x)
$
The first equality comes from the law of iterated expectations. The second comes from what we've figured out when dealing with the left hand side. Since both the left and right hand side equals, \\(P(x)\\), this equation is trivially true.
## Propensity Weighting

OK, we got the propensity score. Now what? Like I've said, all we need to do is condition on it. For example, we could run a linear regression that conditions only on the propensity score, instead of all the Xs. For now, let's look at a technique that just uses the propensity score and nothing else. The idea is to write the conditional difference in means with the propensity score
$
E[Y|X,T=1]−E[Y|X,T=0] = E\bigg[\dfrac{Y}{P(x)}|X,T=1\bigg]P(x) - E\bigg[\dfrac{Y}{(1-P(x))}|X,T=0\bigg](1-P(x))
$
We can simplify this further, but let's take a look at it like this because it gives us some nice intuition of what the propensity score is doing. The first term is estimating \\(Y_1\\). It is taking all those that are treated and scaling them by the inverse probability of treatment. What this does is makes those with very low probability of treatment have a high weight. This makes sense right? If someone has a low probability of treatment, that individual looks like the untreated. However, that same individual was treated. This must be interesting. We have a treatment that looks like the untreated, so we will give that entity a high weight. What this does is create a population with the same size as the original, but where everyone is treated. By the same reasoning, the other term looks at the untreated and gives a high weight to those that look like the treated. This estimator is called the Inverse Probability of Treatment Weighting, since it scales each unit by the probability of receiving some treatment other than the one it received.
In a picture, here is what this weightin does.

The upper left plot shows the original data. The blue dots are the untreated and the red dots are the treated. The bottom plot shows the propensity score P(x). Notice how it is between 0 and 1 and it grows as X increases. Finally, the upper right plot is the data after weighting. Notice how the red (treated) that are more to the left (lower propensity score) have a higher weight. Similarly, the blue plots that are to the right have also a higher weight.
Not that we got the intuition, we can simplify the terms above to
$
E\bigg[Y \dfrac{T-P(x)}{P(x)(1-P(x))}\bigg|X\bigg]
$
which if we integrate over X becomes our propensity score weighting estimator.
$
E\bigg[Y \dfrac{T-P(x)}{P(x)(1-P(x))}\bigg]
$
Notice that this estimator requires that neither \\(P(x)\\) nor \\(1-P(x)\\) be strictly positive. In words, this means that everyone needs to have at least some chance of receiving the treatment and of not receiving it. Another way of stating this is that the treated and untreated distributions overlap. This is the **positivity assumption** of causal inference. It also makes intuitive sense. If treated and untreated don't overlap, it means they are very different and I won't be able to extrapolate the effect of one group to the other. This extrapolation is not impossible (regression does it), but it is very dangerous. It is like testing a new drug in an experiment where only men receive the treatment and then assume women will respond to it equally well.
## Propensity Score Estimation
In an ideal world, we would have the true propensity score \\(P(x)\\). However, in practice, the mechanism that assigns the treatment is unknown and we need to replace the true propensity score by an estimation of it \\(\hat{P}(x)\\). One common way of doing so is using logistic regression but other machine learning methods, like gradient boosting, can be used as well (although it requires some additional steps to avoid overfitting).
Here, I'll stick to logistic regression. This means that I'll have to convert the categorical features in the dataset to dummies.
```
categ = ["ethnicity", "gender", "school_urbanicity"]
cont = ["school_mindset", "school_achievement", "school_ethnic_minority", "school_poverty", "school_size"]
data_with_categ = pd.concat([
data.drop(columns=categ), # dataset without the categorical features
pd.get_dummies(data[categ], columns=categ, drop_first=False)# dataset without categorical converted to dummies
], axis=1)
print(data_with_categ.shape)
```
Now, let's estimate the propensity score using logistic regression.
```
from sklearn.linear_model import LogisticRegression
T = 'intervention'
Y = 'achievement_score'
X = data_with_categ.columns.drop(['schoolid', T, Y])
ps_model = LogisticRegression(C=1e6).fit(data_with_categ[X], data_with_categ[T])
data_ps = data.assign(propensity_score=ps_model.predict_proba(data_with_categ[X])[:, 1])
data_ps[["intervention", "achievement_score", "propensity_score"]].head()
```
First, we can make sure that the propensity score weight indeed reconstructs a population where everyone is treated. By producing weights \\(1/P(x)\\), it creates the population where everyone is treated and by providing the weights \\(1/(1-P(x))\\) it creates the population where everyone is untreated.
```
weight_t = 1/data_ps.query("intervention==1")["propensity_score"]
weight_nt = 1/(1-data_ps.query("intervention==0")["propensity_score"])
print("Original Sample Size", data.shape[0])
print("Treated Population Sample Size", sum(weight_t))
print("Untreated Population Sample Size", sum(weight_nt))
```
We can also use the propensity score to find evidence of confounding. If a segmentation of the population has a higher propensity score than another, it means that something that is not random is causing the treatment. If that same thing is also causing the outcome, we have confounding. In our case, we can see that students that reported to be more ambitious also have a higher probability of attending the growth mindset seminar.
```
sns.boxplot(x="success_expect", y="propensity_score", data=data_ps)
plt.title("Confounding Evidence");
```
We also have to check that there is overlap between the treated and untreated population. To do so, we can see the empirical distribution of the propensity score on the untreated and on the treated. Looking at the image below, we can see that no one has a propensity score of zero and that even in lower regions of the propensity score we can find both treated and untreated individuals. This is what we called a nicely balanced treated and untreated population.
```
sns.distplot(data_ps.query("intervention==0")["propensity_score"], kde=False, label="Non Treated")
sns.distplot(data_ps.query("intervention==1")["propensity_score"], kde=False, label="Treated")
plt.title("Positivity Check")
plt.legend();
```
Finally, we can use our propensity score weighting estimator to estimate the average treatment effect.
```
weight = ((data_ps["intervention"]-data_ps["propensity_score"]) /
(data_ps["propensity_score"]*(1-data_ps["propensity_score"])))
y1 = sum(data_ps.query("intervention==1")["achievement_score"]*weight_t) / len(data)
y0 = sum(data_ps.query("intervention==0")["achievement_score"]*weight_nt) / len(data)
ate = np.mean(weight * data_ps["achievement_score"])
print("Y1:", y1)
print("Y0:", y0)
print("ATE", np.mean(weight * data_ps["achievement_score"]))
```
Propensity score weighting is saying that we should expect treated individuals to be 0.38 standard deviations above their untreated fellows, in terms of achievements. We can also see that if no one got the treatment, we should expect the general level of achievements to be 0.12 standard deviation lower than what it is now. By the same reasoning, we should expect the general level of achievement to be 0.25 standards deviation higher if we've given everyone the seminar. Compare this to the 0.47 ATE estimate we've got by simply comparing treated and untreated. This is evidence that the bias we have is indeed positive and that controlling for X gives us a more modest estimate of the impact of the growth mindset.
## Standard Error

To compute the standard error for the IPTW estimator, we can use the formula of the variance of a weighted average.
$
\sigma^2_w = \dfrac{\sum_{i=1}^{n}w_i(y_i-\hat{\mu})^2}{\sum_{i=1}^{n}w_i}
$
However, we can only use this if we have the true propensity score. If we are using the estimated version of it, \\(\hat{P}(x)\\), we need to account for the errors in the estimation process. The easiest way of doing this is by bootstrapping the whole procedure. This is achieved by sampling with replacement from the original data and computing the ATE like we did above. We then repeat this many times to get the distribution of the ATE estimate.
```
from joblib import Parallel, delayed # for parallel processing
# define function that computes the IPTW estimator
def run_ps(df, X, T, y):
# estimate the propensity score
ps = LogisticRegression(C=1e6).fit(df[X], df[T]).predict_proba(df[X])[:, 1]
weight = (df[T]-ps) / (ps*(1-ps)) # define the weights
return np.mean(weight * df[y]) # compute the ATE
np.random.seed(88)
# run 1000 bootstrap samples
bootstrap_sample = 1000
ates = Parallel(n_jobs=4)(delayed(run_ps)(data_with_categ.sample(frac=1, replace=True), X, T, Y)
for _ in range(bootstrap_sample))
ates = np.array(ates)
```
The ATE is then the mean of the bootstrap samples and the standard error is the standard deviation of these samples.
```
print(f"ATE 95% CI: {ates.mean()} +- {1.96*ates.std()}")
```
We can also have a visual on what the bootstrap samples look like, along with the confidence intervals.
```
sns.distplot(ates, kde=False)
plt.vlines(ates.mean()-1.96*ates.std(), 0, 20, linestyles="dotted")
plt.vlines(ates.mean()+1.96*ates.std(), 0, 20, linestyles="dotted", label="95% CI")
plt.title("ATE Bootstrap Distribution")
plt.legend();
```
## Common Issues with Propensity Score
As a data scientist, I know it can be tempting to use all the power of the machine learning toolkit to make propensity score estimation as precise as possible. You can quickly get taken away by the all AUC optimisation, cross validation and bayesian hyper-parameter tuning. Now, I'm not saying you shouldn't do that. In fact, all of the theory about propensity score and machine learning is very recent, so there are lots we don't know yet. But it pays to understand something first.
The first thing is that the predictive quality of the propensity score does not translate into its balancing properties. Coming from the field of machine learning, one of the most challenging aspects of getting acquainted with causal inference is letting go of treating everything as a prediction problem. In fact, maximising the prediction power of the propensity score can even hurt the causal inference goal. **Propensity score doesn't need to predict the treatment very well. It just needs to include all the confounding variables**. If we include variables that are very good in predicting the treatment but have no bearing on the outcome this will actually increase the variance of the propensity score estimator. This is similar to the problem linear regression faces when we include variables correlated with the treatment but not with the outcome.

To see this, consider the following example (adapted from Hernán's Book). You have 2 schools, one of them apply the growth mindset seminar to 99% of its students and the other to 1%. Suppose that the schools have no impact on the treatment effect (except through the treatment), so it's not necessary to control for it. If you add the school variable to the propensity score model, it's going to have a very high predictive power. However, by chance, we could end up with a sample where everyone in school A got the treatment, leading to a propensity score of 1 for that school, which would lead to an infinite variance. This is an extreme example, but let's see how it would work with simulated data.
```
np.random.seed(42)
school_a = pd.DataFrame(dict(T=np.random.binomial(1, .99, 400), school=0, intercept=1))
school_b = pd.DataFrame(dict(T=np.random.binomial(1, .01, 400), school=1, intercept=1))
ex_data = pd.concat([school_a, school_b]).assign(y = lambda d: np.random.normal(1 + 0.1 * d["T"]))
ex_data.head()
```
Having simulated this data, we run bootstrap with the Propensity Score algorithm twice. The first including school as a feature to the propensity score model. The second time, we don't include school in the model.
```
ate_w_f = np.array([run_ps(ex_data.sample(frac=1, replace=True), ["school"], "T", "y") for _ in range(500)])
ate_wo_f = np.array([run_ps(ex_data.sample(frac=1, replace=True), ["intercept"], "T", "y") for _ in range(500)])
sns.distplot(ate_w_f, kde=False, label="PS W School")
sns.distplot(ate_wo_f, kde=False, label="PS W/O School")
plt.legend();
```
As you can see, the propensity score estimator that adds the feature school has a humongous variance, while the one without it is much more well behaved. Also, since school is not a confounder, the model without it is also not biased.
As I've said, simply predicting the treatment is not what this is about. We actually need to construct the prediction in a way that controls for confounding, not in a way to predict the treatment. This leads to another problem often encountered in propensity score methods. In our mindset case, the data turned out to be very balanced. But this is not always the case. In some situations, the treated have a much higher probability of treatment than the untreated and the propensity score distribution doesn't overlap much.
```
sns.distplot(np.random.beta(4,1,500), kde=False, label="Non Treated")
sns.distplot(np.random.beta(1,3,500), kde=False, label="Treated")
plt.title("Positivity Check")
plt.legend();
```
If this happens, it means that positivity is not very strong. If a treated has a propensity score of, say, 0.9 and the maximum propensity score of the untreated is 0.7, we won't have any untreated to compare to the individual with the 0.9 propensity score. This lack of balancing can generate some bias, because we will have to extrapolate the treatment effect to unknown regions. Not only that, entities with very high or very low propensity scores have a very high weight, which increases variance. As a general rule of thumb, you are in trouble if any weight is higher than 20 (which happens with an untreated propensity score of 0.95 or a treated with a propensity score of 0.05).
An alternative is clipping the weight to be at a maximum size of 20. This will decrease the variance, but it will actually generate more bias. To be honest, although this is a common practice to reduce variance, I don't really like it. You will never know if the bias you are inducing with clipping is too much. Also, if the distributions don't overlap, your data is probably not enough to make a causal conclusion anyway. To gain some further intuition about this, we can look at a technique that combines propensity score and matching
## Propensity Score Matching
As I've said before, you don't need to control for X when you have the propensity score. It suffices to control it. As such, you can think of the propensity score as performing a kind of dimensionality reduction on the feature space. It condenses all the features in X into a single treatment assignment dimension. For this reason, we can treat the propensity score as an input feature for other models. Take a regression, model for instance.
```
smf.ols("achievement_score ~ intervention + propensity_score", data=data_ps).fit().summary().tables[1]
```
If we control for the propensity score, we now estimate a ATE of 0.39, which is lower than the 0.47 we did previously with a regression model without controlling for the propensity score. We can also use matching on the propensity score. This time, instead of trying to find matches that are similar in all the X features, we can find matches that just have the same propensity score.
This is a huge improvement on top of the matching estimator, since it deals with the curse of dimensionality. Also, if a feature is unimportant for the treatment assignment, the propensity score model will learn that and give low importance to it when fitting the treatment mechanism. Matching on the features, on the other hand, would still try to find matches where individuals are similar on this unimportant feature.
```
from causalinference import CausalModel
cm = CausalModel(
Y=data_ps["achievement_score"].values,
D=data_ps["intervention"].values,
X=data_ps[["propensity_score"]].values
)
cm.est_via_matching(matches=1, bias_adj=True)
print(cm.estimates)
```
As we can see, we also get an ATE of 0.38, which is more in line with what we've seen before with propensity score weighting. Matching on the propensity score also give us some intuition about why is dangerous to have a small overlap in the propensity score between treated and untreated. If this happens, the matching on the propensity score discrepancy will be large, which will lead to bias.
One final word of caution here is that the above standard errors are wrong, as they don't account for the uncertainty in the estimation of the propensity score. Unfortunately, [bootstrap doesn't work with matching](https://economics.mit.edu/files/11862). Also, the theory above is so recent that there are no Python implementations of propensity score methods with the correct standard errors. For this reason, we don't see a lot of propensity score matching in Python.
## Key Ideas
Here, we've learned that the probability of getting the treatment is called the propensity score and that we can use this as a balancing score. What this means is that, if we have the propensity score, we don't need to control for the confounders directly. It is sufficient to control for the propensity score in order to identify the causal effect. We saw how the propensity scores acts as a dimensionality reduction on the confounder space.
These proprieties allowed us to derive a weighting estimator for causal inference. Not only that, we saw how the propensity score can be used along other methods to control for confounding bias.
Finally, we looked at some extrapolation problems that we might run into if we are unable to have a good overlap between the treated and untreated propensity score distribution.
## References
I like to think of this entire series is a tribute to Joshua Angrist, Alberto Abadie and Christopher Walters for their amazing Econometrics class. Most of the ideas here are taken from their classes at the American Economic Association. Watching them is what is keeping me sane during this tough year of 2020.
* [Cross-Section Econometrics](https://www.aeaweb.org/conference/cont-ed/2017-webcasts)
* [Mastering Mostly Harmless Econometrics](https://www.aeaweb.org/conference/cont-ed/2020-webcasts)
I'll also like to reference the amazing books from Angrist. They have shown me that Econometrics, or 'Metrics as they call it, is not only extremely useful but also profoundly fun.
* [Mostly Harmless Econometrics](https://www.mostlyharmlesseconometrics.com/)
* [Mastering 'Metrics](https://www.masteringmetrics.com/)
My final reference is Miguel Hernan and Jamie Robins' book. It has been my trustworthy companion in the most thorny causal questions I had to answer.
* [Causal Inference Book](https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/)
The data that we used was taken from the article [Estimating Treatment Effects with Causal Forests: An Application](https://arxiv.org/pdf/1902.07409.pdf), by Susan Athey and Stefan Wager.
| true |
code
| 0.624923 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/satyajitghana/TSAI-DeepVision-EVA4.0/blob/master/05_CodingDrill/EVA4S5F3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Import Libraries
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
```
## Data Transformations
We first start with defining our data transformations. We need to think what our data is and how can we augment it to correct represent images which it might not see otherwise.
```
# Train Phase transformations
train_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
# Test Phase transformations
test_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
```
# Dataset and Creating Train/Test Split
```
train = datasets.MNIST('./data', train=True, download=True, transform=train_transforms)
test = datasets.MNIST('./data', train=False, download=True, transform=test_transforms)
```
# Dataloader Arguments & Test/Train Dataloaders
```
SEED = 1
# CUDA?
cuda = torch.cuda.is_available()
print("CUDA Available?", cuda)
# For reproducibility
torch.manual_seed(SEED)
if cuda:
torch.cuda.manual_seed(SEED)
# dataloader arguments - something you'll fetch these from cmdprmt
dataloader_args = dict(shuffle=True, batch_size=128, num_workers=4, pin_memory=True) if cuda else dict(shuffle=True, batch_size=64)
# train dataloader
train_loader = torch.utils.data.DataLoader(train, **dataloader_args)
# test dataloader
test_loader = torch.utils.data.DataLoader(test, **dataloader_args)
```
# Data Statistics
It is important to know your data very well. Let's check some of the statistics around our data and how it actually looks like
```
# We'd need to convert it into Numpy! Remember above we have converted it into tensors already
train_data = train.train_data
train_data = train.transform(train_data.numpy())
print('[Train]')
print(' - Numpy Shape:', train.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', train.train_data.size())
print(' - min:', torch.min(train_data))
print(' - max:', torch.max(train_data))
print(' - mean:', torch.mean(train_data))
print(' - std:', torch.std(train_data))
print(' - var:', torch.var(train_data))
dataiter = iter(train_loader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
# Let's visualize some of the images
%matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(images[0].numpy().squeeze(), cmap='gray_r')
```
## MORE
It is important that we view as many images as possible. This is required to get some idea on image augmentation later on
```
figure = plt.figure()
num_of_images = 60
for index in range(1, num_of_images + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(images[index].numpy().squeeze(), cmap='gray_r')
```
# The model
Let's start with the model we first saw
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# Input Block
self.convblock1 = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=10, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU()
) # output_size = 26
# CONVOLUTION BLOCK 1
self.convblock2 = nn.Sequential(
nn.Conv2d(in_channels=10, out_channels=10, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU()
) # output_size = 24
self.convblock3 = nn.Sequential(
nn.Conv2d(in_channels=10, out_channels=20, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU()
) # output_size = 22
# TRANSITION BLOCK 1
self.pool1 = nn.MaxPool2d(2, 2) # output_size = 11
self.convblock4 = nn.Sequential(
nn.Conv2d(in_channels=20, out_channels=10, kernel_size=(1, 1), padding=0, bias=False),
nn.ReLU()
) # output_size = 11
# CONVOLUTION BLOCK 2
self.convblock5 = nn.Sequential(
nn.Conv2d(in_channels=10, out_channels=10, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU()
) # output_size = 9
self.convblock6 = nn.Sequential(
nn.Conv2d(in_channels=10, out_channels=20, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU()
) # output_size = 7
# OUTPUT BLOCK
self.convblock7 = nn.Sequential(
nn.Conv2d(in_channels=20, out_channels=10, kernel_size=(1, 1), padding=0, bias=False),
nn.ReLU()
) # output_size = 7
self.convblock8 = nn.Sequential(
nn.Conv2d(in_channels=10, out_channels=10, kernel_size=(7, 7), padding=0, bias=False),
# nn.BatchNorm2d(10), NEVER
# nn.ReLU() NEVER!
) # output_size = 1
def forward(self, x):
x = self.convblock1(x)
x = self.convblock2(x)
x = self.convblock3(x)
x = self.pool1(x)
x = self.convblock4(x)
x = self.convblock5(x)
x = self.convblock6(x)
x = self.convblock7(x)
x = self.convblock8(x)
x = x.view(-1, 10)
return F.log_softmax(x, dim=-1)
```
# Model Params
Can't emphasize on how important viewing Model Summary is.
Unfortunately, there is no in-built model visualizer, so we have to take external help
```
!pip install torchsummary
from torchsummary import summary
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
print(device)
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
```
# Training and Testing
Looking at logs can be boring, so we'll introduce **tqdm** progressbar to get cooler logs.
Let's write train and test functions
```
from tqdm import tqdm
train_losses = []
test_losses = []
train_acc = []
test_acc = []
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
correct = 0
processed = 0
for batch_idx, (data, target) in enumerate(pbar):
# get samples
data, target = data.to(device), target.to(device)
# Init
optimizer.zero_grad()
# In PyTorch, we need to set the gradients to zero before starting to do backpropragation because PyTorch accumulates the gradients on subsequent backward passes.
# Because of this, when you start your training loop, ideally you should zero out the gradients so that you do the parameter update correctly.
# Predict
y_pred = model(data)
# Calculate loss
loss = F.nll_loss(y_pred, target)
train_losses.append(loss)
# Backpropagation
loss.backward()
optimizer.step()
# Update pbar-tqdm
pred = y_pred.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
processed += len(data)
pbar.set_description(desc= f'Loss={loss.item()} Batch_id={batch_idx} Accuracy={100*correct/processed:0.2f}')
train_acc.append(100*correct/processed)
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
test_acc.append(100. * correct / len(test_loader.dataset))
```
# Let's Train and test our model
```
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
EPOCHS = 20
for epoch in range(EPOCHS):
print("EPOCH:", epoch)
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
fig, axs = plt.subplots(2,2,figsize=(15,10))
axs[0, 0].plot(train_losses)
axs[0, 0].set_title("Training Loss")
axs[1, 0].plot(train_acc)
axs[1, 0].set_title("Training Accuracy")
axs[0, 1].plot(test_losses)
axs[0, 1].set_title("Test Loss")
axs[1, 1].plot(test_acc)
axs[1, 1].set_title("Test Accuracy")
```
| true |
code
| 0.910823 | null | null | null | null |
|
# Autoencoder
```
from keras.layers import Input, Dense
from keras.models import Model
import matplotlib.pyplot as plt
import matplotlib.colors as mcol
from matplotlib import cm
def graph_colors(nx_graph):
#cm1 = mcol.LinearSegmentedColormap.from_list("MyCmapName",["blue","red"])
#cm1 = mcol.Colormap('viridis')
cnorm = mcol.Normalize(vmin=0,vmax=9)
cpick = cm.ScalarMappable(norm=cnorm,cmap='Set1')
cpick.set_array([])
val_map = {}
for k,v in nx.get_node_attributes(nx_graph,'attr').items():
#print(v)
val_map[k]=cpick.to_rgba(v)
#print(val_map)
colors=[]
for node in nx_graph.nodes():
#print(node,val_map.get(str(node), 'black'))
colors.append(val_map[node])
return colors
```
##### 1 Write a function that builds a simple autoencoder
The autoencoder must have a simple Dense layer with relu activation. The number of node of the dense layer is a parameter of the function
The function must return the entire autoencoder model as well as the encoder and the decoder
##### Load the mnist dataset
##### 2. Buil the autoencoder with a embedding size of 32 and print the number of parameters of the model. What do they relate to ?
##### 3. Fit the autoencoder using 32 epochs with a batch size of 256
##### 4. Using the history module of the autoencoder write a function that plots the learning curves with respect to the epochs on the train and test set. What can you say about these learning curves ? Give also the last loss on the test set
##### 5. Write a function that plots a fix number of example of the original images on the test as weel as their reconstruction
### Nearest neighbours graphs
The goal of this part is to visualize the neighbours graph in the embedding. It corresponds the the graph of the k-nearest neighbours using the euclidean distance of points the element in the embedding
```
from sklearn.neighbors import kneighbors_graph
import networkx as nx
def plot_nearest_neighbour_graph(encoder,x_test,y_test,ntest=100,p=3): #to explain
X=encoder.predict(x_test[1:ntest])
y=y_test[1:ntest]
A = kneighbors_graph(X, p, mode='connectivity', include_self=True)
G=nx.from_numpy_array(A.toarray())
nx.set_node_attributes(G,dict(zip(range(ntest),y)),'attr')
fig, ax = plt.subplots(figsize=(10,10))
pos=nx.layout.kamada_kawai_layout(G)
nx.draw(G,pos=pos
,with_labels=True
,labels=nx.get_node_attributes(G,'attr')
,node_color=graph_colors(G))
plt.tight_layout()
plt.title('Nearest Neighbours Graph',fontsize=15)
plt.show()
```
### Reduce the dimension of the embedding
##### 6. Rerun the previous example using an embedding dimension of 16
## Adding sparsity
##### 7. In this part we will add sparisity over the weights on the embedding layer. Write a function that build such a autoencoder (using a l1 regularization with a configurable regularization parameter and using the same autoencoder architecture that before)
# Deep autoencoder
# Convolutionnal autoencoder
# Application to denoising
| true |
code
| 0.671444 | null | null | null | null |
|
# Module 2 Tutorial 1
There are numerous open-source libraries, collections of functions, that have been developed in Python that we will make use of in this course.
The first one is called NumPy and you can find the documentation [here](https://numpy.org/). It is one of the most widely-used libraries for scientific computating in python. The second library we will use will be a module from Scipy, called scipy.stats ([scipy.stats documentation](https://docs.scipy.org/doc/scipy/reference/stats.html)), and the third is a library for handling database-like structures called Pandas for which you can find the documentation at this link: [Pandas documentation](https://pandas.pydata.org/docs/user_guide/index.html).
We import the libraries with the following statement:
```
import numpy
from scipy import stats
import pandas
```
Now we will start building our toolbox with some simple tools to describe our data:
## Confidence Intervals and Descriptive Statistics
In this module of the course one of the first things that is covered is confidence intervals. As we only have access to samples of data we assume that neither the population mean or the population standard deviation are known and we work with point estimates, sample mean, and sample standard deviation (also called standard error).
To build a confidence interval we must specify a confidence level and provide the sample of our data.
Below is a simple function to obtain the confidence interval of your sample.
```
def get_confidence_interval(data, confidence=0.95):
""" Determines the confidence interval for a given set of data,
assuming the population standard deviation is not known.
Args: # 'arguments', or inputs to the function
data (single-column or list): The data
confidence (float): The confidence level on which to produce the interval.
Returns:
c_interval (tuple): The confidence interval on the given data (lower, upper).
"""
n = len(data) # determines the sample size
m = numpy.mean(data) # obtains mean of the sample
se = stats.sem(data) # obtains standard error of the sample
c_interval = stats.t.interval(confidence, n-1, m, se) # determines the confidence interval
return c_interval # which is of the form (lower bound, upper bound)
```
We can walk through the function above:
The name of the function is *get_confidence_interval* and the function takes two arguments, the first is the sample that you are interested in calculating the confidence interval for, and the second is the desired confidence level. The second argument is optional and will default to 95% if not specified. 95% is a very typical confidence level used in most applications.
Inside the function we first obtain *n*, the sample size. Then we calculate the sample mean using the numpy.mean function ([numpy.mean documentation](https://numpy.org/doc/stable/reference/generated/numpy.mean.html)), and the sample standard error with the scipy.stats.sem function ([scipy.stats.mean documentation](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.sem.html)).
Finally, we calculate the confidence interval using the scipy.stats.t.interval function ([scipy.stats.t documentation](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.t.html)), this function needs the desired confidence level, the degrees of freedom, the sample mean, and the standard error, in order to calculate the upper and lower bounds of the confidence interval.
Let us illustrate this function with Example 12.6 from the course book: in this example both $\mu$ and $\sigma$, the population parameters are unknown. The sample data is given as {1, 0, 5} and the question asks for the 99% confidence interval for $\mu$ assuming a normally distributed population.
This is easily calculated using the function we defined above:
```
sample_data = [1, 0, 5]
get_confidence_interval(sample_data, confidence=0.99)
```
Another tool that could be useful in order to help us understand our data is provided by the pandas library. The .describe() function produces a statistical description of our sample. In order to call this function however our data needs to be in a pandas.Series or pandas.DataFrame object, and we need a column for each group we want to describe.
Let's say we have some data stored in two columns labeled "Day" and "Temperature", which contains the temperature readings at 6 set times over the course of two different days:
```
sample_dataframe = pandas.DataFrame(
{
"Day": ["Day 1"]*6 + ["Day 2"]*6,
"Temperature": [15, 17, 19, 19, 18, 16, 14, 15, 18, 19, 21, 18]
}
)
```
The DataFrame looks like this:
```
sample_dataframe
```
Now, because we created the DataFrame we know what is in it. But if we didn't, we could ask what the columns are:
```
column_names = sample_dataframe.columns
column_names
```
We can assign these column names as either independent or dependent to help us keep track of what we're doing:
```
independent_col = column_names[0]
dependent_col = column_names[1]
```
And we can also see how many values our independent variable takes and what they are by using the pandas.unique function:
```
independent_variable_values = pandas.unique(sample_dataframe[independent_col])
independent_variable_values
```
Now, we want to separate the samples corresponding to each independent variable and obtain a statistical description of them.
We do this as follows:
```
dependent_variable_data = pandas.DataFrame(columns=[day for day in independent_variable_values])
```
This is equivalent to pandas.DataFrame(columns=["Day 1", "Day 2"]), but the code in the block above would automatically create an additional column for any more days added to the dataset.
Right now the DataFrame looks like this:
```
dependent_variable_data
```
Let's put the correct data into it now.
It looks complicated, but don't worry too much.
If we unpack the lines below:
1. sample_dataframe[dependent_col] selects the data in the dependent variable column.
2. [sample_dataframe[independent_col]==independent_variable_values[0]] selects all the data where independent_col (Day) is equal to a specific value, independent_variable_values[0], ('Day 1').
3. The final .reset_index(drop) ensures that the selected data does not retain a label showing its index in the original file.
```
dependent_variable_data["Day 1"] = sample_dataframe[dependent_col][sample_dataframe[independent_col]==independent_variable_values[0]].reset_index(drop=True)
dependent_variable_data["Day 2"] = sample_dataframe[dependent_col][sample_dataframe[independent_col]==independent_variable_values[1]].reset_index(drop=True)
```
Just to be clear, the following is equivalent, but less general:
```
dependent_variable_data["Day 1"] = sample_dataframe["Temperature"][sample_dataframe["Day"]=="Day 1"].reset_index(drop=True)
dependent_variable_data["Day 2"] = sample_dataframe["Temperature"][sample_dataframe["Day"]=="Day 2"].reset_index(drop=True)
```
The data now looks like this:
```
dependent_variable_data
```
We can now request a statistical description of each column from our dataset:
```
sample_statistics = dependent_variable_data.describe()
sample_statistics
```
And what we see returned is the sample size, the mean of our sample, the standard deviation (which is not of great use, can you explain why?), the minumum, maximum, and different percentiles. We can access the different information from each column by name or by index:
```
print(sample_statistics["Day 1"]["mean"])
print(sample_statistics["Day 1"][1])
```
We can now move on to the next part of module 1.
## Hypothesis Testing
We have already constructed a set of sample data to test our functions with, we have one indepedendent variable (Day) which takes on two different values (Day 1 and Day 2), and we have the temperature on those days as our dependent variables.
The question we could ask now is, is the mean temperature of the two days statistically different? We can write this as a hypothesis test:
$H_0 : \mu_1 - \mu_2 = 0$\
$H_1 : \mu_1 - \mu_2 \neq 0$
The independent sample t-test can be used to test this hypothesis. But, an underlying assumption of the independent samples t-test is that the two populations being compared have equal variances.
The test for equal variance can be written as another hypothesis test and is commonly called the Levene test:
$H_0 : \sigma^2_1 - \sigma^2_2 = 0$\
$H_1 : \sigma^2_1 - \sigma^2_2 \neq 0$
So let's add to our toolbox again.
This time we are not writing our own function immediately, but first using a function from the stats library. This library includes the function stats.levene which performs the levene test.
The Levene test function takes the data from each group and returns an $F$ and $p$ value. Depending on the desired significance level, we can then accept or reject the Levene test.
```
stats.levene(dependent_variable_data["Day 1"], dependent_variable_data["Day 2"])
```
If our significance level, $\alpha$, is 0.05 (a common value), we can observe that in this case the $p$ value is larger than $\alpha$ and so we fail to reject the null hypothesis: we cannot statistically discount the possibility that the two samples have equal variance at this level of significance.
We now want to adress the question of equal means. Let's add the t-test to our toolbox:
```
def t_test(data_group1, data_group2, confidence=0.95):
alpha = 1-confidence
if stats.levene(data_group1, data_group2)[1]>alpha:
equal_variance = True
else:
equal_variance = False
t, p = stats.ttest_ind(data_group1, data_group2, equal_var = equal_variance)
reject_H0 = "True"
if p > alpha:
reject_H0 = "False"
return({'t': t, "p": p, "Reject H0": reject_H0})
```
Our function to perform the $t$-test is called "t-test" and it takes three possible inputs:
1. The data of the first column (or group) that would correspond to $\mu_1$ in the hypothesis test,
2. The data of the second column (or group) that would correspond to $\mu_2$ in the hypothesis test, and finally,
3. The desired confidence level, this will default to 95% if not specified.
Inside the function, the confidence level is used to determine the $\alpha$ value which is the significance level for the $t$-test.\
Then, the Levene test (which we discussed previously) is run to determine if the two groups have equal variance or not. This is done because the function that performs the $t$-test, [stats.ttest_ind](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html), needs this as an input; it modifies the calculations based on whether or not the two groups have equal variance.
So, after the Levene test we calculate the $t$ value and $p$ value of the $t$-test. The inputs to "stats.ttest_ind" are the data for the first group, the data for the second group, and the results of the Levene test.
Finally, we check if $p$ is larger than our desired significance level.
Let us illustrate this for our previous temperature dataset:
```
t_test(dependent_variable_data["Day 1"], dependent_variable_data["Day 2"], confidence=0.95)
```
The outputs from our function are the $t$ value, the $p$ value, and whether or not we accept the null hypothesis.
We see that because the $p$ value is larger than our confidence level, we fail to reject the null hypothesis.
| true |
code
| 0.804348 | null | null | null | null |
|
Want, the ability to generate various tensors and measure their properties.
Pretty much, want to do unsupervised learning of matrices and tensors.
Properties are defined not by their values but by how they can be composed, transformed, ... Not sure how to make this happen, but !!!.
What are we generating based on?
- Structure/symmetry?
- How it transforms a space?
- Topology of a TN?
- ?
Is it possible to construct a toeplitz matrix with a tensor-network?
***
Toeplitz (can be used to encode convolutions), circulant (?) and hankel (can be used to encode automata!?).
Orthogonal, stochastic, orthonormal,
Block, block-diagonal (used to encode independent systems?), ?
Hermitian,
https://en.wikipedia.org/wiki/List_of_matrices
## Approaches to TN contraction
* Boundary conditions!?!?
* Algebraically contractible tensor networks
*
https://en.wikipedia.org/wiki/Multigraph
https://en.wikipedia.org/wiki/Hypergraph
> As far as hypergraphs are concerned, a hypergraph is equivalent to a bi-partite graph, with two different set of nodes. One represents the regular nodes, the other a set of edges
http://20bits.com/article/graph-theory-part-ii-linear-algebra
http://www.math.utah.edu/~gustafso/s2017/2270/projects-2017/dylanJohnson/Dylan%20Johnson%20Graph%20Theory%20and%20Linear%20Algebra.pdf
```
import numpy as np
import numpy.random as rnd
import networkx as nx
class TreeTN():
# https://arxiv.org/pdf/1710.04833.pdf
def construct():
pass
# cool. I can construct one. But how can I make a fast kernel for calculating it...
# that is what i need tensor-comprehension and/or xla and/or hand-written c/cuda.
# need to define matrix vector ops (and others) that can take advantage of the structure.
m = rnd.randint(0, 2, (10,10))
m
np.sum(m, axis=0)
np.sum(m, axis=1)
g = nx.from_numpy_matrix(m)
g = nx.convert_node_labels_to_integers(g)
nx.draw(g, pos=nx.spring_layout(g))
import scipy.linalg as lin
m = lin.circulant([0,1,0,0,0,0,1,1])
print(m)
g = nx.from_numpy_matrix(m)
g = nx.convert_node_labels_to_integers(g)
nx.draw(g, pos=nx.spring_layout(g))
m = lin.toeplitz([0,1,0,0,0,0,0,1], [0,1,0,1,1,1,0,1])
print(m)
g = nx.from_numpy_matrix(m)
g = nx.convert_node_labels_to_integers(g)
nx.draw(g, pos=nx.spring_layout(g))
m = lin.hankel([0,1,0,0,0,0,0,1], [0,1,0,1,1,0,0,1])
print(m)
g = nx.from_numpy_matrix(m)
g = nx.convert_node_labels_to_integers(g)
nx.draw(g, pos=nx.spring_layout(g))
m = np.kron(lin.circulant([0,1,0,1]), np.ones((2,2)), )
print(m)
g = nx.from_numpy_matrix(m)
g = nx.convert_node_labels_to_integers(g)
nx.draw(g, pos=nx.spring_layout(g))
def construct_cores(m, k=2): # assume all connections are of the same dimension
d = np.sum(m ,axis=0)
return [rnd.random([2]*int(i)) for i in d]
cores = construct_cores(m)
print([c.shape for c in cores])
G = nx.MultiGraph()
G.add_node(1)
G.add_nodes_from([2,3])
G.add_edge(2,3) #G.add_edge(1,2)
G.add_edge(2,3)
nx.draw(G, pos=nx.spring_layout(G))
```
| true |
code
| 0.365046 | null | null | null | null |
|
# Introducing CartPole
Cartpole is a classic control problem from OpenAI.
https://gym.openai.com/envs/CartPole-v0/
A pole is attached by an un-actuated joint to a cart, which moves along a frictionless track. The system is controlled by applying a force of +1 or -1 to the cart. The pendulum starts upright, and the goal is to prevent it from falling over. A reward of +1 is provided for every timestep that the pole remains upright. The episode ends when the pole is more than 15 degrees from vertical, or the cart moves more than 2.4 units from the center.
## Load libraries
```
import gym
import matplotlib.pyplot as plt
import numpy as np
import random
# Turn warnings off to keep notebook tidy
import warnings
warnings.filterwarnings("ignore")
# Set whether enviornment will be rendered
RENDER = True
```
## Random choice
Our first baseline is random action of pushing the cart left or right.
Note: The CartPole visualisation of this demo may not work on remote servers. If this does not work set `RENDER = False` in cell above to run rest of Notebook with visualisation (re-run the cell after changing the setting).
```
def random_choice(obs):
"""
Random choice.
`obs` is passed to function to make use consistent with other methods.
"""
return random.randint(0,1)
# Set up environemnt
env = gym.make("CartPole-v1")
totals = []
for episode in range(10):
episode_reward = 0
obs = env.reset()
for step in range(200):
if RENDER:
env.render()
action = random_choice(obs)
obs, reward, done, info = env.step(action)
episode_reward += reward
# Pole has fallen over if done is True
if done:
break
totals.append(episode_reward)
env.close()
print ("Average: {0:.1f}".format(np.mean(totals)))
print ("Stdev: {0:.1f}".format(np.std(totals)))
print ("Minumum: {0:.0f}".format(np.min(totals)))
print ("Maximum: {0:.0f}".format(np.max(totals)))
```
## A simple policy
Here we use a simple policy that accelerates left when the pole is leaning to the right, and accelerates right when the pole is leaning to the left.
```
def basic_policy(obs):
"""
A Simple policy that accelerates left when the pole is leaning to the right,
and accelerates right when the pole is leaning to the left
Cartpole observations:
X position (0 = centre)
velocity (+ve = right)
angle (0 = upright)
angular velocity (+ve = clockwise)
"""
angle = obs[2]
return 0 if angle < 0 else 1
# Set up environemnt
env = gym.make("CartPole-v1")
totals = []
for episode in range(10):
episode_reward = 0
obs = env.reset()
for step in range(200):
if RENDER:
env.render()
action = basic_policy(obs)
obs, reward, done, info = env.step(action)
episode_reward += reward
# Pole has fallen over if done is True
if done:
break
totals.append(episode_reward)
env.close()
print ("Average: {0:.1f}".format(np.mean(totals)))
print ("Stdev: {0:.1f}".format(np.std(totals)))
print ("Minumum: {0:.0f}".format(np.min(totals)))
print ("Maximum: {0:.0f}".format(np.max(totals)))
```
The next notebook will use a Deep Q Network (Double DQN) to see if we can improve on the simple policy.
| true |
code
| 0.357497 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import h5py
import heapq
import matplotlib.colors
import PIL
import datetime
```
# Algorithm
Custom adaptation of astar algorithm for 3D array with forced forward
```
def heuristic_function(a, b):
return (b[0] - a[0]) ** 2 + (b[1] - a[1]) ** 2
def astar_3D(space, origin_xy, destination_xy):
# make origin 3D with timeslice 0
origin = origin_xy[0], origin_xy[1], 0
# logs the path
came_from = {}
# holds the legal next moves in order of priority
frontier = []
# define legal moves:
# up, down, left, right, stay in place.
# no diagonals and always move forward one time step (z)
neighbours = [(0,0,1),(0,1,1),(0,-1,1),(1,0,1),(-1,0,1)]
cost_so_far = {origin: 0}
priority = {origin: heuristic_function(origin_xy, destination_xy)}
heapq.heappush(frontier, (priority[origin], origin))
# While there is still options to explore
while frontier:
current = heapq.heappop(frontier)[1]
# if current position is destination,
# break the loop and find the path that lead here
if (current[0], current[1]) == destination_xy:
data = []
while current in came_from:
data.append(current)
current = came_from[current]
return data
for i, j, k in neighbours:
move = current[0] + i, current[1] + j, current[2] + k
# check that move is legal
if ((0 <= move[0] < space.shape[0]) &
(0 <= move[1] < space.shape[1]) &
(0 <= move[2] < space.shape[2])):
if space[move[0], move[1], move[2]] != 1:
new_cost = 1
new_total = cost_so_far[current] + new_cost
if move not in cost_so_far:
cost_so_far[move] = new_total
# calculate total cost
priority[move] = new_total + heuristic_function(move, destination_xy)
# update frontier
heapq.heappush(frontier, (priority[move], move))
# log this move
came_from[move] = current
return 'no solution found :('
def convert_forecast(data_cube):
# take mean of forecasts
arr_world = np.min(data_cube, axis=2)
# binarize to storm (1) or safe (0)
arr_world = arr_world >= 15
# from boolean to binary
arr_world = arr_world.astype(int)
# swap axes so x=0, y=1, z=2, day=3
arr_world = np.swapaxes(arr_world,0,2)
arr_world = np.swapaxes(arr_world,1,3)
arr_world = np.swapaxes(arr_world,2,3)
return(arr_world)
def plot_timeslice(timeslice, cities, solution):
plt.figure(figsize=(5,5))
# black for storm
plt.imshow(timeslice[:,:].T, aspect='equal', cmap=plt.get_cmap('binary'))
for c,x,y in zip(cities.cid, cities.xid, cities.yid):
if c == 0:
plt.scatter([x-1], [y-1], c='red')
else:
plt.scatter([x-1], [y-1], c='blue')
#x, y, z = zip(*solution)
x = solution.x
y = solution.y
z = solution.z
plt.plot(list(x), list(y), linestyle='-', color='r')
plt.show()
def plot_series(world, cities, solution):
timesteps = list(range(0, 540, 30))
for t in timesteps:
print(t)
timeslice = world[:,:,t]
solution_subset = [i for i in solution if t <= i[2] <= t + 30]
if len(solution_subset) > 0:
plot_timeslice(timeslice, cities, solution_subset)
def plot_solution(world, cities, solution, day):
timesteps = list(range(0, 540, 30))
solution = solution.loc[solution.day == day,:]
# colour map for cities
cmap = plt.cm.cool
norm = matplotlib.colors.Normalize(vmin=1, vmax=10)
# colour map for weather
cm = matplotlib.colors.LinearSegmentedColormap.from_list('grid', [(1, 1, 1), (0.5, 0.5, 0.5)], N=2)
for t in timesteps:
timeslice = world[:,:,t]
moves_sofar = solution.loc[solution.z <= t,:]
moves_new = solution.loc[(t <= solution.z) & (solution.z <= t + 30),:]
if len(solution_subset) > 0:
plt.figure(figsize=(5,5))
plt.imshow(timeslice[:,:].T, aspect='equal', cmap = cm)
# plot old moves
for city in moves_sofar.city.unique():
moves_sofar_city = moves_sofar.loc[moves_sofar.city == city,:]
x = moves_sofar_city.x
y = moves_sofar_city.y
z = moves_sofar_city.z
plt.plot(list(x), list(y), linestyle='-', color='black')
# plot new moves
for city in moves_new.city.unique():
moves_new_city = moves_new.loc[moves_new.city == city,:]
x = moves_new_city.x
y = moves_new_city.y
z = moves_new_city.z
plt.plot(list(x), list(y), linestyle='-', color=cmap(norm(city)))
# plot cities
for city,x,y in zip(cities.cid, cities.xid, cities.yid):
if city == 0:
plt.scatter([x-1], [y-1], c='black')
else:
# balloon still en-route?
if city in moves_new.city.unique():
plt.scatter([x-1], [y-1], c=cmap(norm(city)))
else:
plt.scatter([x-1], [y-1], c='black')
# save and display
plt.savefig('img_day' + str(day) + '_timestep_' + str(t) + '.png')
plt.show()
# Toy data
world = np.ones((10,10,100))
world = world >= 15
world = world.astype(int)
origin = (0,0,0)
destinations = [(9,9, timeslice) for timeslice in range(0,100)]
print(world.shape)
```
# Data
Generate map of the world as binary 3D numpy array to find path in
```
# read h5 format back to numpy array
# h5f = h5py.File('../data/METdata.h5', 'r')
# train = h5f['train'][:]
# test = h5f['test'][:]
# h5f.close()
%pwd
data_cube = np.load('../data/5D_test.npy')
# convert forecast to world array
arr_world = convert_forecast(data_cube)
print(data_cube.shape)
print(arr_world.shape)
# repeat time slices x30
arr_world_big = np.repeat(arr_world, repeats=30, axis=2)
print(arr_world_big.shape)
```
# Run
```
#x = astar_3D(space=arr_world_big[:,:,:,0],
# origin_xy=origin,
# destination_xy=destination)
solution = pd.DataFrame([], columns=['x','y','z','day','city'])
origin = cities.loc[cities.cid == 0, ['xid', 'yid']]
origin = (origin.iloc[0,0], origin.iloc[0,1])
# iterate over days
for i in range(arr_world.shape[3]):
# get data for specific day
arr_day = arr_world_big[:,:,:,i]
# iterate over destinations
for j in range(cities.shape[0] - 1):
print('calculating day: '+str(i+1)+', city: '+str(j+1))
# find coordinates of target city
destination = cities.loc[cities.cid == j+1, ['xid', 'yid']]
destination = (destination.iloc[0,0], destination.iloc[0,1])
x = astar_3D(space=arr_day,
origin_xy=origin,
destination_xy=destination)
# check if solution was found
if type(x) == str:
out = pd.DataFrame(
np.array([[i]*540,[j]*540,[origin[0]]*540,[origin[1]]*540,range(540)]).T,
columns=['day','city','x','y','z'])
else:
out = (pd.DataFrame(zip(*x))
.transpose()
.rename(index=str, columns={0:'x', 1:'y', 2:'z'})
.append(pd.DataFrame({'x':origin[0],'y':origin[1],'z':[0]}))
.sort_values(by=['z'])
.assign(day=i+1,
city=j+1))
solution = solution.append(out, ignore_index=True)
solution.to_csv('solution.csv')
solution = pd.read_csv('solution.csv', index_col=0)
# convert time slices to timestamps
solution['time'] = solution['z'].apply(lambda x: ':'.join(str(datetime.timedelta(seconds=x * 2 + 180)).split(':')[1:]))
# re-adjust day number
solution['day'] = solution.day + 5
solution.head()
out = solution[['city','day','time','x','y']]
out.head()
out.to_csv('out.csv', index=False, header=False)
x2 = solution.loc[solution.day == 11,['x','y','z','city']]
x2.head()
plot_solution(arr_world_big[:,:,:,0], cities, solution, 15)
```
| true |
code
| 0.551996 | null | null | null | null |
|
# Fully Convolutional Networks for Change Detection
Example code for training the network presented in the paper:
```
Daudt, R.C., Le Saux, B. and Boulch, A., 2018, October. Fully convolutional siamese networks for change detection. In 2018 25th IEEE International Conference on Image Processing (ICIP) (pp. 4063-4067). IEEE.
```
Code uses the OSCD dataset:
```
Daudt, R.C., Le Saux, B., Boulch, A. and Gousseau, Y., 2018, July. Urban change detection for multispectral earth observation using convolutional neural networks. In IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium (pp. 2115-2118). IEEE.
```
FresUNet architecture from paper:
```
Daudt, R.C., Le Saux, B., Boulch, A. and Gousseau, Y., 2019. Multitask learning for large-scale semantic change detection. Computer Vision and Image Understanding, 187, p.102783.
```
Please consider all relevant papers if you use this code.
```
# Rodrigo Daudt
# rcdaudt.github.io
# rodrigo.daudt@onera.fr
%%bash
hostname
# Imports
# PyTorch
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
from torch.autograd import Variable
import torchvision.transforms as tr
# Models imported for .py files in local directory. Hashed out here - models just put in a cell.
#from unet import Unet
#from siamunet_conc import SiamUnet_conc
#from siamunet_diff import SiamUnet_diff
#from fresunet import FresUNet
#from smallunet import SmallUnet
#from smallunet_attempt import Unet
# Other
import os
import numpy as np
import random
from skimage import io
from scipy.ndimage import zoom
import matplotlib.pyplot as plt
%matplotlib inline
from tqdm import tqdm as tqdm
from pandas import read_csv
from math import floor, ceil, sqrt, exp
from IPython import display
import time
from itertools import chain
import warnings
from pprint import pprint
print('IMPORTS OK')
from google.colab import drive
drive.mount('/content/drive')
# Global Variables' Definitions
PATH_TO_DATASET = '/content/drive/MyDrive/onera/'
IS_PROTOTYPE = False
FP_MODIFIER = 1 # Tuning parameter, use 1 if unsure
BATCH_SIZE = 32
PATCH_SIDE = 96
N_EPOCHS = 50
NORMALISE_IMGS = True
TRAIN_STRIDE = int(PATCH_SIDE/2) - 1
TYPE = 1 # 0-RGB | 1-RGBIr | 2-All bands s.t. resulution <= 20m | 3-All bands
LOAD_TRAINED = False
DATA_AUG = True
print('DEFINITIONS OK')
### This cell defines a load of functions that we will need to train the network e.g. data augmentation functions,
### functions that call the different bands of the sentinel data, etc.
# Functions
def adjust_shape(I, s):
"""Adjust shape of grayscale image I to s."""
# crop if necesary
I = I[:s[0],:s[1]]
si = I.shape
# pad if necessary
p0 = max(0,s[0] - si[0])
p1 = max(0,s[1] - si[1])
return np.pad(I,((0,p0),(0,p1)),'edge')
def read_sentinel_img(path):
"""Read cropped Sentinel-2 image: RGB bands."""
im_name = os.listdir(path)[0][:-7]
r = io.imread(path + im_name + "B04.tif")
g = io.imread(path + im_name + "B03.tif")
b = io.imread(path + im_name + "B02.tif")
I = np.stack((r,g,b),axis=2).astype('float')
if NORMALISE_IMGS:
I = (I - I.mean()) / I.std()
return I
def read_sentinel_img_4(path):
"""Read cropped Sentinel-2 image: RGB and NIR bands."""
im_name = os.listdir(path)[0][:-7]
r = io.imread(path + im_name + "B04.tif")
g = io.imread(path + im_name + "B03.tif")
b = io.imread(path + im_name + "B02.tif")
nir = io.imread(path + im_name + "B08.tif")
I = np.stack((r,g,b,nir),axis=2).astype('float')
if NORMALISE_IMGS:
I = (I - I.mean()) / I.std()
return I
def read_sentinel_img_leq20(path):
"""Read cropped Sentinel-2 image: bands with resolution less than or equals to 20m."""
im_name = os.listdir(path)[0][:-7]
r = io.imread(path + im_name + "B04.tif")
s = r.shape
g = io.imread(path + im_name + "B03.tif")
b = io.imread(path + im_name + "B02.tif")
nir = io.imread(path + im_name + "B08.tif")
ir1 = adjust_shape(zoom(io.imread(path + im_name + "B05.tif"),2),s)
ir2 = adjust_shape(zoom(io.imread(path + im_name + "B06.tif"),2),s)
ir3 = adjust_shape(zoom(io.imread(path + im_name + "B07.tif"),2),s)
nir2 = adjust_shape(zoom(io.imread(path + im_name + "B8A.tif"),2),s)
swir2 = adjust_shape(zoom(io.imread(path + im_name + "B11.tif"),2),s)
swir3 = adjust_shape(zoom(io.imread(path + im_name + "B12.tif"),2),s)
I = np.stack((r,g,b,nir,ir1,ir2,ir3,nir2,swir2,swir3),axis=2).astype('float')
if NORMALISE_IMGS:
I = (I - I.mean()) / I.std()
return I
def read_sentinel_img_leq60(path):
"""Read cropped Sentinel-2 image: all bands."""
im_name = os.listdir(path)[0][:-7]
r = io.imread(path + im_name + "B04.tif")
s = r.shape
g = io.imread(path + im_name + "B03.tif")
b = io.imread(path + im_name + "B02.tif")
nir = io.imread(path + im_name + "B08.tif")
ir1 = adjust_shape(zoom(io.imread(path + im_name + "B05.tif"),2),s)
ir2 = adjust_shape(zoom(io.imread(path + im_name + "B06.tif"),2),s)
ir3 = adjust_shape(zoom(io.imread(path + im_name + "B07.tif"),2),s)
nir2 = adjust_shape(zoom(io.imread(path + im_name + "B8A.tif"),2),s)
swir2 = adjust_shape(zoom(io.imread(path + im_name + "B11.tif"),2),s)
swir3 = adjust_shape(zoom(io.imread(path + im_name + "B12.tif"),2),s)
uv = adjust_shape(zoom(io.imread(path + im_name + "B01.tif"),6),s)
wv = adjust_shape(zoom(io.imread(path + im_name + "B09.tif"),6),s)
swirc = adjust_shape(zoom(io.imread(path + im_name + "B10.tif"),6),s)
I = np.stack((r,g,b,nir,ir1,ir2,ir3,nir2,swir2,swir3,uv,wv,swirc),axis=2).astype('float')
if NORMALISE_IMGS:
I = (I - I.mean()) / I.std()
return I
def read_sentinel_img_trio(path):
"""Read cropped Sentinel-2 image pair and change map."""
# read images
if TYPE == 0:
I1 = read_sentinel_img(path + '/imgs_1/')
I2 = read_sentinel_img(path + '/imgs_2/')
elif TYPE == 1:
I1 = read_sentinel_img_4(path + '/imgs_1/')
I2 = read_sentinel_img_4(path + '/imgs_2/')
elif TYPE == 2:
I1 = read_sentinel_img_leq20(path + '/imgs_1/')
I2 = read_sentinel_img_leq20(path + '/imgs_2/')
elif TYPE == 3:
I1 = read_sentinel_img_leq60(path + '/imgs_1/')
I2 = read_sentinel_img_leq60(path + '/imgs_2/')
cm = io.imread(path + '/cm/cm.png', as_gray=True) != 0
# crop if necessary
s1 = I1.shape
s2 = I2.shape
I2 = np.pad(I2,((0, s1[0] - s2[0]), (0, s1[1] - s2[1]), (0,0)),'edge')
return I1, I2, cm
def reshape_for_torch(I):
"""Transpose image for PyTorch coordinates."""
# out = np.swapaxes(I,1,2)
# out = np.swapaxes(out,0,1)
# out = out[np.newaxis,:]
out = I.transpose((2, 0, 1))
return torch.from_numpy(out)
class ChangeDetectionDataset(Dataset):
"""Change Detection dataset class, used for both training and test data."""
def __init__(self, path, train = True, patch_side = 96, stride = None, use_all_bands = False, transform=None):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
# basics
self.transform = transform
self.path = path
self.patch_side = patch_side
if not stride:
self.stride = 1
else:
self.stride = stride
if train:
fname = 'train.txt'
else:
fname = 'test.txt'
# print(path + fname)
self.names = read_csv(path + fname).columns
self.n_imgs = self.names.shape[0]
n_pix = 0
true_pix = 0
# load images
self.imgs_1 = {}
self.imgs_2 = {}
self.change_maps = {}
self.n_patches_per_image = {}
self.n_patches = 0
self.patch_coords = []
for im_name in tqdm(self.names):
# load and store each image
I1, I2, cm = read_sentinel_img_trio(self.path + im_name)
self.imgs_1[im_name] = reshape_for_torch(I1)
self.imgs_2[im_name] = reshape_for_torch(I2)
self.change_maps[im_name] = cm
s = cm.shape
n_pix += np.prod(s)
true_pix += cm.sum()
# calculate the number of patches
s = self.imgs_1[im_name].shape
n1 = ceil((s[1] - self.patch_side + 1) / self.stride)
n2 = ceil((s[2] - self.patch_side + 1) / self.stride)
n_patches_i = n1 * n2
self.n_patches_per_image[im_name] = n_patches_i
self.n_patches += n_patches_i
# generate path coordinates
for i in range(n1):
for j in range(n2):
# coordinates in (x1, x2, y1, y2)
current_patch_coords = (im_name,
[self.stride*i, self.stride*i + self.patch_side, self.stride*j, self.stride*j + self.patch_side],
[self.stride*(i + 1), self.stride*(j + 1)])
self.patch_coords.append(current_patch_coords)
self.weights = [ FP_MODIFIER * 2 * true_pix / n_pix, 2 * (n_pix - true_pix) / n_pix]
def get_img(self, im_name):
return self.imgs_1[im_name], self.imgs_2[im_name], self.change_maps[im_name]
def __len__(self):
return self.n_patches
def __getitem__(self, idx):
current_patch_coords = self.patch_coords[idx]
im_name = current_patch_coords[0]
limits = current_patch_coords[1]
centre = current_patch_coords[2]
I1 = self.imgs_1[im_name][:, limits[0]:limits[1], limits[2]:limits[3]]
I2 = self.imgs_2[im_name][:, limits[0]:limits[1], limits[2]:limits[3]]
label = self.change_maps[im_name][limits[0]:limits[1], limits[2]:limits[3]]
label = torch.from_numpy(1*np.array(label)).float()
sample = {'I1': I1, 'I2': I2, 'label': label}
if self.transform:
sample = self.transform(sample)
return sample
class RandomFlip(object):
"""Flip randomly the images in a sample."""
# def __init__(self):
# return
def __call__(self, sample):
I1, I2, label = sample['I1'], sample['I2'], sample['label']
if random.random() > 0.5:
I1 = I1.numpy()[:,:,::-1].copy()
I1 = torch.from_numpy(I1)
I2 = I2.numpy()[:,:,::-1].copy()
I2 = torch.from_numpy(I2)
label = label.numpy()[:,::-1].copy()
label = torch.from_numpy(label)
return {'I1': I1, 'I2': I2, 'label': label}
class RandomRot(object):
"""Rotate randomly the images in a sample."""
# def __init__(self):
# return
def __call__(self, sample):
I1, I2, label = sample['I1'], sample['I2'], sample['label']
n = random.randint(0, 3)
if n:
I1 = sample['I1'].numpy()
I1 = np.rot90(I1, n, axes=(1, 2)).copy()
I1 = torch.from_numpy(I1)
I2 = sample['I2'].numpy()
I2 = np.rot90(I2, n, axes=(1, 2)).copy()
I2 = torch.from_numpy(I2)
label = sample['label'].numpy()
label = np.rot90(label, n, axes=(0, 1)).copy()
label = torch.from_numpy(label)
return {'I1': I1, 'I2': I2, 'label': label}
print('UTILS OK')
### Simple UNet implementation
#import torch
#import torch.nn as nn
#import torch.nn.functional as F
#from torch.nn.modules.padding import ReplicationPad2d
class Unet(nn.Module):
"""EF segmentation network."""
def __init__(self, input_nbr, label_nbr):
super(Unet, self).__init__()
self.input_nbr = input_nbr
self.conv11 = nn.Conv2d(input_nbr, 16, kernel_size=3, padding=1)
self.bn11 = nn.BatchNorm2d(16)
self.do11 = nn.Dropout2d(p=0.2)
self.conv12 = nn.Conv2d(16, 16, kernel_size=3, padding=1)
self.bn12 = nn.BatchNorm2d(16)
self.do12 = nn.Dropout2d(p=0.2)
self.conv21 = nn.Conv2d(16, 32, kernel_size=3, padding=1)
self.bn21 = nn.BatchNorm2d(32)
self.do21 = nn.Dropout2d(p=0.2)
self.conv22 = nn.Conv2d(32, 32, kernel_size=3, padding=1)
self.bn22 = nn.BatchNorm2d(32)
self.do22 = nn.Dropout2d(p=0.2)
self.conv31 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
self.bn31 = nn.BatchNorm2d(64)
self.do31 = nn.Dropout2d(p=0.2)
self.conv32 = nn.Conv2d(64, 64, kernel_size=3, padding=1)
self.bn32 = nn.BatchNorm2d(64)
self.do32 = nn.Dropout2d(p=0.2)
self.conv33 = nn.Conv2d(64, 64, kernel_size=3, padding=1)
self.bn33 = nn.BatchNorm2d(64)
self.do33 = nn.Dropout2d(p=0.2)
self.conv41 = nn.Conv2d(64, 128, kernel_size=3, padding=1)
self.bn41 = nn.BatchNorm2d(128)
self.do41 = nn.Dropout2d(p=0.2)
self.conv42 = nn.Conv2d(128, 128, kernel_size=3, padding=1)
self.bn42 = nn.BatchNorm2d(128)
self.do42 = nn.Dropout2d(p=0.2)
self.conv43 = nn.Conv2d(128, 128, kernel_size=3, padding=1)
self.bn43 = nn.BatchNorm2d(128)
self.do43 = nn.Dropout2d(p=0.2)
self.upconv4 = nn.ConvTranspose2d(128, 128, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv43d = nn.ConvTranspose2d(256, 128, kernel_size=3, padding=1)
self.bn43d = nn.BatchNorm2d(128)
self.do43d = nn.Dropout2d(p=0.2)
self.conv42d = nn.ConvTranspose2d(128, 128, kernel_size=3, padding=1)
self.bn42d = nn.BatchNorm2d(128)
self.do42d = nn.Dropout2d(p=0.2)
self.conv41d = nn.ConvTranspose2d(128, 64, kernel_size=3, padding=1)
self.bn41d = nn.BatchNorm2d(64)
self.do41d = nn.Dropout2d(p=0.2)
self.upconv3 = nn.ConvTranspose2d(64, 64, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv33d = nn.ConvTranspose2d(128, 64, kernel_size=3, padding=1)
self.bn33d = nn.BatchNorm2d(64)
self.do33d = nn.Dropout2d(p=0.2)
self.conv32d = nn.ConvTranspose2d(64, 64, kernel_size=3, padding=1)
self.bn32d = nn.BatchNorm2d(64)
self.do32d = nn.Dropout2d(p=0.2)
self.conv31d = nn.ConvTranspose2d(64, 32, kernel_size=3, padding=1)
self.bn31d = nn.BatchNorm2d(32)
self.do31d = nn.Dropout2d(p=0.2)
self.upconv2 = nn.ConvTranspose2d(32, 32, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv22d = nn.ConvTranspose2d(64, 32, kernel_size=3, padding=1)
self.bn22d = nn.BatchNorm2d(32)
self.do22d = nn.Dropout2d(p=0.2)
self.conv21d = nn.ConvTranspose2d(32, 16, kernel_size=3, padding=1)
self.bn21d = nn.BatchNorm2d(16)
self.do21d = nn.Dropout2d(p=0.2)
self.upconv1 = nn.ConvTranspose2d(16, 16, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv12d = nn.ConvTranspose2d(32, 16, kernel_size=3, padding=1)
self.bn12d = nn.BatchNorm2d(16)
self.do12d = nn.Dropout2d(p=0.2)
self.conv11d = nn.ConvTranspose2d(16, label_nbr, kernel_size=3, padding=1)
self.sm = nn.LogSoftmax(dim=1)
def forward(self, x1, x2):
x = torch.cat((x1, x2), 1)
"""Forward method."""
# Stage 1
x11 = self.do11(F.relu(self.bn11(self.conv11(x))))
x12 = self.do12(F.relu(self.bn12(self.conv12(x11))))
x1p = F.max_pool2d(x12, kernel_size=2, stride=2)
# Stage 2
x21 = self.do21(F.relu(self.bn21(self.conv21(x1p))))
x22 = self.do22(F.relu(self.bn22(self.conv22(x21))))
x2p = F.max_pool2d(x22, kernel_size=2, stride=2)
# Stage 3
x31 = self.do31(F.relu(self.bn31(self.conv31(x2p))))
x32 = self.do32(F.relu(self.bn32(self.conv32(x31))))
x33 = self.do33(F.relu(self.bn33(self.conv33(x32))))
x3p = F.max_pool2d(x33, kernel_size=2, stride=2)
# Stage 4
x41 = self.do41(F.relu(self.bn41(self.conv41(x3p))))
x42 = self.do42(F.relu(self.bn42(self.conv42(x41))))
x43 = self.do43(F.relu(self.bn43(self.conv43(x42))))
x4p = F.max_pool2d(x43, kernel_size=2, stride=2)
# Stage 4d
x4d = self.upconv4(x4p)
pad4 = ReplicationPad2d((0, x43.size(3) - x4d.size(3), 0, x43.size(2) - x4d.size(2)))
x4d = torch.cat((pad4(x4d), x43), 1)
x43d = self.do43d(F.relu(self.bn43d(self.conv43d(x4d))))
x42d = self.do42d(F.relu(self.bn42d(self.conv42d(x43d))))
x41d = self.do41d(F.relu(self.bn41d(self.conv41d(x42d))))
# Stage 3d
x3d = self.upconv3(x41d)
pad3 = ReplicationPad2d((0, x33.size(3) - x3d.size(3), 0, x33.size(2) - x3d.size(2)))
x3d = torch.cat((pad3(x3d), x33), 1)
x33d = self.do33d(F.relu(self.bn33d(self.conv33d(x3d))))
x32d = self.do32d(F.relu(self.bn32d(self.conv32d(x33d))))
x31d = self.do31d(F.relu(self.bn31d(self.conv31d(x32d))))
# Stage 2d
x2d = self.upconv2(x31d)
pad2 = ReplicationPad2d((0, x22.size(3) - x2d.size(3), 0, x22.size(2) - x2d.size(2)))
x2d = torch.cat((pad2(x2d), x22), 1)
x22d = self.do22d(F.relu(self.bn22d(self.conv22d(x2d))))
x21d = self.do21d(F.relu(self.bn21d(self.conv21d(x22d))))
# Stage 1d
x1d = self.upconv1(x21d)
pad1 = ReplicationPad2d((0, x12.size(3) - x1d.size(3), 0, x12.size(2) - x1d.size(2)))
x1d = torch.cat((pad1(x1d), x12), 1)
x12d = self.do12d(F.relu(self.bn12d(self.conv12d(x1d))))
x11d = self.conv11d(x12d)
return self.sm(x11d)
# Rodrigo Caye Daudt
# https://rcdaudt.github.io/
# Daudt, R. C., Le Saux, B., & Boulch, A. "Fully convolutional siamese networks for change detection". In 2018 25th IEEE International Conference on Image Processing (ICIP) (pp. 4063-4067). IEEE.
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.padding import ReplicationPad2d
class SiamUnet_diff(nn.Module):
"""SiamUnet_diff segmentation network."""
def __init__(self, input_nbr, label_nbr):
super(SiamUnet_diff, self).__init__()
self.input_nbr = input_nbr
self.conv11 = nn.Conv2d(input_nbr, 16, kernel_size=3, padding=1)
self.bn11 = nn.BatchNorm2d(16)
self.do11 = nn.Dropout2d(p=0.2)
self.conv12 = nn.Conv2d(16, 16, kernel_size=3, padding=1)
self.bn12 = nn.BatchNorm2d(16)
self.do12 = nn.Dropout2d(p=0.2)
self.conv21 = nn.Conv2d(16, 32, kernel_size=3, padding=1)
self.bn21 = nn.BatchNorm2d(32)
self.do21 = nn.Dropout2d(p=0.2)
self.conv22 = nn.Conv2d(32, 32, kernel_size=3, padding=1)
self.bn22 = nn.BatchNorm2d(32)
self.do22 = nn.Dropout2d(p=0.2)
self.conv31 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
self.bn31 = nn.BatchNorm2d(64)
self.do31 = nn.Dropout2d(p=0.2)
self.conv32 = nn.Conv2d(64, 64, kernel_size=3, padding=1)
self.bn32 = nn.BatchNorm2d(64)
self.do32 = nn.Dropout2d(p=0.2)
self.conv33 = nn.Conv2d(64, 64, kernel_size=3, padding=1)
self.bn33 = nn.BatchNorm2d(64)
self.do33 = nn.Dropout2d(p=0.2)
self.conv41 = nn.Conv2d(64, 128, kernel_size=3, padding=1)
self.bn41 = nn.BatchNorm2d(128)
self.do41 = nn.Dropout2d(p=0.2)
self.conv42 = nn.Conv2d(128, 128, kernel_size=3, padding=1)
self.bn42 = nn.BatchNorm2d(128)
self.do42 = nn.Dropout2d(p=0.2)
self.conv43 = nn.Conv2d(128, 128, kernel_size=3, padding=1)
self.bn43 = nn.BatchNorm2d(128)
self.do43 = nn.Dropout2d(p=0.2)
self.upconv4 = nn.ConvTranspose2d(128, 128, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv43d = nn.ConvTranspose2d(256, 128, kernel_size=3, padding=1)
self.bn43d = nn.BatchNorm2d(128)
self.do43d = nn.Dropout2d(p=0.2)
self.conv42d = nn.ConvTranspose2d(128, 128, kernel_size=3, padding=1)
self.bn42d = nn.BatchNorm2d(128)
self.do42d = nn.Dropout2d(p=0.2)
self.conv41d = nn.ConvTranspose2d(128, 64, kernel_size=3, padding=1)
self.bn41d = nn.BatchNorm2d(64)
self.do41d = nn.Dropout2d(p=0.2)
self.upconv3 = nn.ConvTranspose2d(64, 64, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv33d = nn.ConvTranspose2d(128, 64, kernel_size=3, padding=1)
self.bn33d = nn.BatchNorm2d(64)
self.do33d = nn.Dropout2d(p=0.2)
self.conv32d = nn.ConvTranspose2d(64, 64, kernel_size=3, padding=1)
self.bn32d = nn.BatchNorm2d(64)
self.do32d = nn.Dropout2d(p=0.2)
self.conv31d = nn.ConvTranspose2d(64, 32, kernel_size=3, padding=1)
self.bn31d = nn.BatchNorm2d(32)
self.do31d = nn.Dropout2d(p=0.2)
self.upconv2 = nn.ConvTranspose2d(32, 32, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv22d = nn.ConvTranspose2d(64, 32, kernel_size=3, padding=1)
self.bn22d = nn.BatchNorm2d(32)
self.do22d = nn.Dropout2d(p=0.2)
self.conv21d = nn.ConvTranspose2d(32, 16, kernel_size=3, padding=1)
self.bn21d = nn.BatchNorm2d(16)
self.do21d = nn.Dropout2d(p=0.2)
self.upconv1 = nn.ConvTranspose2d(16, 16, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv12d = nn.ConvTranspose2d(32, 16, kernel_size=3, padding=1)
self.bn12d = nn.BatchNorm2d(16)
self.do12d = nn.Dropout2d(p=0.2)
self.conv11d = nn.ConvTranspose2d(16, label_nbr, kernel_size=3, padding=1)
self.sm = nn.LogSoftmax(dim=1)
def forward(self, x1, x2):
"""Forward method."""
# Stage 1
x11 = self.do11(F.relu(self.bn11(self.conv11(x1))))
x12_1 = self.do12(F.relu(self.bn12(self.conv12(x11))))
x1p = F.max_pool2d(x12_1, kernel_size=2, stride=2)
# Stage 2
x21 = self.do21(F.relu(self.bn21(self.conv21(x1p))))
x22_1 = self.do22(F.relu(self.bn22(self.conv22(x21))))
x2p = F.max_pool2d(x22_1, kernel_size=2, stride=2)
# Stage 3
x31 = self.do31(F.relu(self.bn31(self.conv31(x2p))))
x32 = self.do32(F.relu(self.bn32(self.conv32(x31))))
x33_1 = self.do33(F.relu(self.bn33(self.conv33(x32))))
x3p = F.max_pool2d(x33_1, kernel_size=2, stride=2)
# Stage 4
x41 = self.do41(F.relu(self.bn41(self.conv41(x3p))))
x42 = self.do42(F.relu(self.bn42(self.conv42(x41))))
x43_1 = self.do43(F.relu(self.bn43(self.conv43(x42))))
x4p = F.max_pool2d(x43_1, kernel_size=2, stride=2)
####################################################
# Stage 1
x11 = self.do11(F.relu(self.bn11(self.conv11(x2))))
x12_2 = self.do12(F.relu(self.bn12(self.conv12(x11))))
x1p = F.max_pool2d(x12_2, kernel_size=2, stride=2)
# Stage 2
x21 = self.do21(F.relu(self.bn21(self.conv21(x1p))))
x22_2 = self.do22(F.relu(self.bn22(self.conv22(x21))))
x2p = F.max_pool2d(x22_2, kernel_size=2, stride=2)
# Stage 3
x31 = self.do31(F.relu(self.bn31(self.conv31(x2p))))
x32 = self.do32(F.relu(self.bn32(self.conv32(x31))))
x33_2 = self.do33(F.relu(self.bn33(self.conv33(x32))))
x3p = F.max_pool2d(x33_2, kernel_size=2, stride=2)
# Stage 4
x41 = self.do41(F.relu(self.bn41(self.conv41(x3p))))
x42 = self.do42(F.relu(self.bn42(self.conv42(x41))))
x43_2 = self.do43(F.relu(self.bn43(self.conv43(x42))))
x4p = F.max_pool2d(x43_2, kernel_size=2, stride=2)
# Stage 4d
x4d = self.upconv4(x4p)
pad4 = ReplicationPad2d((0, x43_1.size(3) - x4d.size(3), 0, x43_1.size(2) - x4d.size(2)))
x4d = torch.cat((pad4(x4d), torch.abs(x43_1 - x43_2)), 1)
x43d = self.do43d(F.relu(self.bn43d(self.conv43d(x4d))))
x42d = self.do42d(F.relu(self.bn42d(self.conv42d(x43d))))
x41d = self.do41d(F.relu(self.bn41d(self.conv41d(x42d))))
# Stage 3d
x3d = self.upconv3(x41d)
pad3 = ReplicationPad2d((0, x33_1.size(3) - x3d.size(3), 0, x33_1.size(2) - x3d.size(2)))
x3d = torch.cat((pad3(x3d), torch.abs(x33_1 - x33_2)), 1)
x33d = self.do33d(F.relu(self.bn33d(self.conv33d(x3d))))
x32d = self.do32d(F.relu(self.bn32d(self.conv32d(x33d))))
x31d = self.do31d(F.relu(self.bn31d(self.conv31d(x32d))))
# Stage 2d
x2d = self.upconv2(x31d)
pad2 = ReplicationPad2d((0, x22_1.size(3) - x2d.size(3), 0, x22_1.size(2) - x2d.size(2)))
x2d = torch.cat((pad2(x2d), torch.abs(x22_1 - x22_2)), 1)
x22d = self.do22d(F.relu(self.bn22d(self.conv22d(x2d))))
x21d = self.do21d(F.relu(self.bn21d(self.conv21d(x22d))))
# Stage 1d
x1d = self.upconv1(x21d)
pad1 = ReplicationPad2d((0, x12_1.size(3) - x1d.size(3), 0, x12_1.size(2) - x1d.size(2)))
x1d = torch.cat((pad1(x1d), torch.abs(x12_1 - x12_2)), 1)
x12d = self.do12d(F.relu(self.bn12d(self.conv12d(x1d))))
x11d = self.conv11d(x12d)
return self.sm(x11d)
# Daudt, R. C., Le Saux, B., & Boulch, A. "Fully convolutional siamese networks for change detection". In 2018 25th IEEE International Conference on Image Processing (ICIP) (pp. 4063-4067). IEEE.
### SiamUNet_conc network. Improvement on simple UNet, as outlined in the paper above. Siamese architectures are pretty nifty.
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.padding import ReplicationPad2d
class SiamUnet_conc(nn.Module):
"""SiamUnet_conc segmentation network."""
def __init__(self, input_nbr, label_nbr):
super(SiamUnet_conc, self).__init__()
self.input_nbr = input_nbr
self.conv11 = nn.Conv2d(input_nbr, 16, kernel_size=3, padding=1)
self.bn11 = nn.BatchNorm2d(16)
self.do11 = nn.Dropout2d(p=0.2)
self.conv12 = nn.Conv2d(16, 16, kernel_size=3, padding=1)
self.bn12 = nn.BatchNorm2d(16)
self.do12 = nn.Dropout2d(p=0.2)
self.conv21 = nn.Conv2d(16, 32, kernel_size=3, padding=1)
self.bn21 = nn.BatchNorm2d(32)
self.do21 = nn.Dropout2d(p=0.2)
self.conv22 = nn.Conv2d(32, 32, kernel_size=3, padding=1)
self.bn22 = nn.BatchNorm2d(32)
self.do22 = nn.Dropout2d(p=0.2)
self.conv31 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
self.bn31 = nn.BatchNorm2d(64)
self.do31 = nn.Dropout2d(p=0.2)
self.conv32 = nn.Conv2d(64, 64, kernel_size=3, padding=1)
self.bn32 = nn.BatchNorm2d(64)
self.do32 = nn.Dropout2d(p=0.2)
self.conv33 = nn.Conv2d(64, 64, kernel_size=3, padding=1)
self.bn33 = nn.BatchNorm2d(64)
self.do33 = nn.Dropout2d(p=0.2)
self.conv41 = nn.Conv2d(64, 128, kernel_size=3, padding=1)
self.bn41 = nn.BatchNorm2d(128)
self.do41 = nn.Dropout2d(p=0.2)
self.conv42 = nn.Conv2d(128, 128, kernel_size=3, padding=1)
self.bn42 = nn.BatchNorm2d(128)
self.do42 = nn.Dropout2d(p=0.2)
self.conv43 = nn.Conv2d(128, 128, kernel_size=3, padding=1)
self.bn43 = nn.BatchNorm2d(128)
self.do43 = nn.Dropout2d(p=0.2)
self.upconv4 = nn.ConvTranspose2d(128, 128, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv43d = nn.ConvTranspose2d(384, 128, kernel_size=3, padding=1)
self.bn43d = nn.BatchNorm2d(128)
self.do43d = nn.Dropout2d(p=0.2)
self.conv42d = nn.ConvTranspose2d(128, 128, kernel_size=3, padding=1)
self.bn42d = nn.BatchNorm2d(128)
self.do42d = nn.Dropout2d(p=0.2)
self.conv41d = nn.ConvTranspose2d(128, 64, kernel_size=3, padding=1)
self.bn41d = nn.BatchNorm2d(64)
self.do41d = nn.Dropout2d(p=0.2)
self.upconv3 = nn.ConvTranspose2d(64, 64, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv33d = nn.ConvTranspose2d(192, 64, kernel_size=3, padding=1)
self.bn33d = nn.BatchNorm2d(64)
self.do33d = nn.Dropout2d(p=0.2)
self.conv32d = nn.ConvTranspose2d(64, 64, kernel_size=3, padding=1)
self.bn32d = nn.BatchNorm2d(64)
self.do32d = nn.Dropout2d(p=0.2)
self.conv31d = nn.ConvTranspose2d(64, 32, kernel_size=3, padding=1)
self.bn31d = nn.BatchNorm2d(32)
self.do31d = nn.Dropout2d(p=0.2)
self.upconv2 = nn.ConvTranspose2d(32, 32, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv22d = nn.ConvTranspose2d(96, 32, kernel_size=3, padding=1)
self.bn22d = nn.BatchNorm2d(32)
self.do22d = nn.Dropout2d(p=0.2)
self.conv21d = nn.ConvTranspose2d(32, 16, kernel_size=3, padding=1)
self.bn21d = nn.BatchNorm2d(16)
self.do21d = nn.Dropout2d(p=0.2)
self.upconv1 = nn.ConvTranspose2d(16, 16, kernel_size=3, padding=1, stride=2, output_padding=1)
self.conv12d = nn.ConvTranspose2d(48, 16, kernel_size=3, padding=1)
self.bn12d = nn.BatchNorm2d(16)
self.do12d = nn.Dropout2d(p=0.2)
self.conv11d = nn.ConvTranspose2d(16, label_nbr, kernel_size=3, padding=1)
self.sm = nn.LogSoftmax(dim=1)
def forward(self, x1, x2):
"""Forward method."""
# Stage 1
x11 = self.do11(F.relu(self.bn11(self.conv11(x1))))
x12_1 = self.do12(F.relu(self.bn12(self.conv12(x11))))
x1p = F.max_pool2d(x12_1, kernel_size=2, stride=2)
# Stage 2
x21 = self.do21(F.relu(self.bn21(self.conv21(x1p))))
x22_1 = self.do22(F.relu(self.bn22(self.conv22(x21))))
x2p = F.max_pool2d(x22_1, kernel_size=2, stride=2)
# Stage 3
x31 = self.do31(F.relu(self.bn31(self.conv31(x2p))))
x32 = self.do32(F.relu(self.bn32(self.conv32(x31))))
x33_1 = self.do33(F.relu(self.bn33(self.conv33(x32))))
x3p = F.max_pool2d(x33_1, kernel_size=2, stride=2)
# Stage 4
x41 = self.do41(F.relu(self.bn41(self.conv41(x3p))))
x42 = self.do42(F.relu(self.bn42(self.conv42(x41))))
x43_1 = self.do43(F.relu(self.bn43(self.conv43(x42))))
x4p = F.max_pool2d(x43_1, kernel_size=2, stride=2)
####################################################
# Stage 1
x11 = self.do11(F.relu(self.bn11(self.conv11(x2))))
x12_2 = self.do12(F.relu(self.bn12(self.conv12(x11))))
x1p = F.max_pool2d(x12_2, kernel_size=2, stride=2)
# Stage 2
x21 = self.do21(F.relu(self.bn21(self.conv21(x1p))))
x22_2 = self.do22(F.relu(self.bn22(self.conv22(x21))))
x2p = F.max_pool2d(x22_2, kernel_size=2, stride=2)
# Stage 3
x31 = self.do31(F.relu(self.bn31(self.conv31(x2p))))
x32 = self.do32(F.relu(self.bn32(self.conv32(x31))))
x33_2 = self.do33(F.relu(self.bn33(self.conv33(x32))))
x3p = F.max_pool2d(x33_2, kernel_size=2, stride=2)
# Stage 4
x41 = self.do41(F.relu(self.bn41(self.conv41(x3p))))
x42 = self.do42(F.relu(self.bn42(self.conv42(x41))))
x43_2 = self.do43(F.relu(self.bn43(self.conv43(x42))))
x4p = F.max_pool2d(x43_2, kernel_size=2, stride=2)
####################################################
# Stage 4d
x4d = self.upconv4(x4p)
pad4 = ReplicationPad2d((0, x43_1.size(3) - x4d.size(3), 0, x43_1.size(2) - x4d.size(2)))
x4d = torch.cat((pad4(x4d), x43_1, x43_2), 1)
x43d = self.do43d(F.relu(self.bn43d(self.conv43d(x4d))))
x42d = self.do42d(F.relu(self.bn42d(self.conv42d(x43d))))
x41d = self.do41d(F.relu(self.bn41d(self.conv41d(x42d))))
# Stage 3d
x3d = self.upconv3(x41d)
pad3 = ReplicationPad2d((0, x33_1.size(3) - x3d.size(3), 0, x33_1.size(2) - x3d.size(2)))
x3d = torch.cat((pad3(x3d), x33_1, x33_2), 1)
x33d = self.do33d(F.relu(self.bn33d(self.conv33d(x3d))))
x32d = self.do32d(F.relu(self.bn32d(self.conv32d(x33d))))
x31d = self.do31d(F.relu(self.bn31d(self.conv31d(x32d))))
# Stage 2d
x2d = self.upconv2(x31d)
pad2 = ReplicationPad2d((0, x22_1.size(3) - x2d.size(3), 0, x22_1.size(2) - x2d.size(2)))
x2d = torch.cat((pad2(x2d), x22_1, x22_2), 1)
x22d = self.do22d(F.relu(self.bn22d(self.conv22d(x2d))))
x21d = self.do21d(F.relu(self.bn21d(self.conv21d(x22d))))
# Stage 1d
x1d = self.upconv1(x21d)
pad1 = ReplicationPad2d((0, x12_1.size(3) - x1d.size(3), 0, x12_1.size(2) - x1d.size(2)))
x1d = torch.cat((pad1(x1d), x12_1, x12_2), 1)
x12d = self.do12d(F.relu(self.bn12d(self.conv12d(x1d))))
x11d = self.conv11d(x12d)
return self.sm(x11d)
# Daudt, R.C., Le Saux, B., Boulch, A. and Gousseau, Y., 2019. Multitask learning for large-scale semantic change detection. Computer Vision and Image Understanding, 187, p.102783.
# FresUNet - comes from the above paper. Still not sure how it improves on UNet tbh. Will find out soon.
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.padding import ReplicationPad2d
def conv3x3(in_planes, out_planes, stride=1):
"3x3 convolution with padding"
return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride, padding=1)
class BasicBlock_ss(nn.Module):
def __init__(self, inplanes, planes = None, subsamp=1):
super(BasicBlock_ss, self).__init__()
if planes == None:
planes = inplanes * subsamp
self.conv1 = conv3x3(inplanes, planes)
self.bn1 = nn.BatchNorm2d(planes)
self.relu = nn.ReLU(inplace=True)
self.conv2 = conv3x3(planes, planes)
self.bn2 = nn.BatchNorm2d(planes)
self.subsamp = subsamp
self.doit = planes != inplanes
if self.doit:
self.couple = nn.Conv2d(inplanes, planes, kernel_size=1)
self.bnc = nn.BatchNorm2d(planes)
def forward(self, x):
if self.doit:
residual = self.couple(x)
residual = self.bnc(residual)
else:
residual = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
if self.subsamp > 1:
out = F.max_pool2d(out, kernel_size=self.subsamp, stride=self.subsamp)
residual = F.max_pool2d(residual, kernel_size=self.subsamp, stride=self.subsamp)
out = self.conv2(out)
out = self.bn2(out)
out += residual
out = self.relu(out)
return out
class BasicBlock_us(nn.Module):
def __init__(self, inplanes, upsamp=1):
super(BasicBlock_us, self).__init__()
planes = int(inplanes / upsamp) # assumes integer result, fix later
self.conv1 = nn.ConvTranspose2d(inplanes, planes, kernel_size=3, padding=1, stride=upsamp, output_padding=1)
self.bn1 = nn.BatchNorm2d(planes)
self.relu = nn.ReLU(inplace=True)
self.conv2 = conv3x3(planes, planes)
self.bn2 = nn.BatchNorm2d(planes)
self.upsamp = upsamp
self.couple = nn.ConvTranspose2d(inplanes, planes, kernel_size=3, padding=1, stride=upsamp, output_padding=1)
self.bnc = nn.BatchNorm2d(planes)
def forward(self, x):
residual = self.couple(x)
residual = self.bnc(residual)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out += residual
out = self.relu(out)
return out
class FresUNet(nn.Module):
"""FresUNet segmentation network."""
def __init__(self, input_nbr, label_nbr):
"""Init FresUNet fields."""
super(FresUNet, self).__init__()
self.input_nbr = input_nbr
cur_depth = input_nbr
base_depth = 8
# Encoding stage 1
self.encres1_1 = BasicBlock_ss(cur_depth, planes = base_depth)
cur_depth = base_depth
d1 = base_depth
self.encres1_2 = BasicBlock_ss(cur_depth, subsamp=2)
cur_depth *= 2
# Encoding stage 2
self.encres2_1 = BasicBlock_ss(cur_depth)
d2 = cur_depth
self.encres2_2 = BasicBlock_ss(cur_depth, subsamp=2)
cur_depth *= 2
# Encoding stage 3
self.encres3_1 = BasicBlock_ss(cur_depth)
d3 = cur_depth
self.encres3_2 = BasicBlock_ss(cur_depth, subsamp=2)
cur_depth *= 2
# Encoding stage 4
self.encres4_1 = BasicBlock_ss(cur_depth)
d4 = cur_depth
self.encres4_2 = BasicBlock_ss(cur_depth, subsamp=2)
cur_depth *= 2
# Decoding stage 4
self.decres4_1 = BasicBlock_ss(cur_depth)
self.decres4_2 = BasicBlock_us(cur_depth, upsamp=2)
cur_depth = int(cur_depth/2)
# Decoding stage 3
self.decres3_1 = BasicBlock_ss(cur_depth + d4, planes = cur_depth)
self.decres3_2 = BasicBlock_us(cur_depth, upsamp=2)
cur_depth = int(cur_depth/2)
# Decoding stage 2
self.decres2_1 = BasicBlock_ss(cur_depth + d3, planes = cur_depth)
self.decres2_2 = BasicBlock_us(cur_depth, upsamp=2)
cur_depth = int(cur_depth/2)
# Decoding stage 1
self.decres1_1 = BasicBlock_ss(cur_depth + d2, planes = cur_depth)
self.decres1_2 = BasicBlock_us(cur_depth, upsamp=2)
cur_depth = int(cur_depth/2)
# Output
self.coupling = nn.Conv2d(cur_depth + d1, label_nbr, kernel_size=1)
self.sm = nn.LogSoftmax(dim=1)
def forward(self, x1, x2):
x = torch.cat((x1, x2), 1)
# pad5 = ReplicationPad2d((0, x53.size(3) - x5d.size(3), 0, x53.size(2) - x5d.size(2)))
s1_1 = x.size()
x1 = self.encres1_1(x)
x = self.encres1_2(x1)
s2_1 = x.size()
x2 = self.encres2_1(x)
x = self.encres2_2(x2)
s3_1 = x.size()
x3 = self.encres3_1(x)
x = self.encres3_2(x3)
s4_1 = x.size()
x4 = self.encres4_1(x)
x = self.encres4_2(x4)
x = self.decres4_1(x)
x = self.decres4_2(x)
s4_2 = x.size()
pad4 = ReplicationPad2d((0, s4_1[3] - s4_2[3], 0, s4_1[2] - s4_2[2]))
x = pad4(x)
# x = self.decres3_1(x)
x = self.decres3_1(torch.cat((x, x4), 1))
x = self.decres3_2(x)
s3_2 = x.size()
pad3 = ReplicationPad2d((0, s3_1[3] - s3_2[3], 0, s3_1[2] - s3_2[2]))
x = pad3(x)
x = self.decres2_1(torch.cat((x, x3), 1))
x = self.decres2_2(x)
s2_2 = x.size()
pad2 = ReplicationPad2d((0, s2_1[3] - s2_2[3], 0, s2_1[2] - s2_2[2]))
x = pad2(x)
x = self.decres1_1(torch.cat((x, x2), 1))
x = self.decres1_2(x)
s1_2 = x.size()
pad1 = ReplicationPad2d((0, s1_1[3] - s1_2[3], 0, s1_1[2] - s1_2[2]))
x = pad1(x)
x = self.coupling(torch.cat((x, x1), 1))
x = self.sm(x)
return x
# Dataset
if DATA_AUG:
data_transform = tr.Compose([RandomFlip(), RandomRot()])
else:
data_transform = None
train_dataset = ChangeDetectionDataset(PATH_TO_DATASET, train = True, stride = TRAIN_STRIDE, transform=data_transform)
#weights = torch.FloatTensor(train_dataset.weights)
weights = torch.FloatTensor(train_dataset.weights).cuda()
print(weights)
train_loader = DataLoader(train_dataset, batch_size = BATCH_SIZE, shuffle = True, num_workers = 4)
test_dataset = ChangeDetectionDataset(PATH_TO_DATASET, train = False, stride = TRAIN_STRIDE)
test_loader = DataLoader(test_dataset, batch_size = BATCH_SIZE, shuffle = True, num_workers = 4)
print('DATASETS OK')
# print(weights)
# 0-RGB | 1-RGBIr | 2-All bands s.t. resulution <= 20m | 3-All bands
if TYPE == 0:
# net, net_name = Unet(2*3, 2), 'FC-EF'
net, net_name = SiamUnet_conc(3, 2), 'FC-Siam-conc'
# net, net_name = SiamUnet_diff(3, 2), 'FC-Siam-diff'
# net, net_name = FresUNet(2*3, 2), 'FresUNet'
elif TYPE == 1:
# net, net_name = Unet(2*4, 2), 'FC-EF'
net, net_name = SiamUnet_conc(4, 2), 'FC-Siam-conc'
# net, net_name = SiamUnet_diff(4, 2), 'FC-Siam-diff'
# net, net_name = FresUNet(2*4, 2), 'FresUNet'
elif TYPE == 2:
# net, net_name = Unet(2*10, 2), 'FC-EF'
net, net_name = SiamUnet_conc(10, 2), 'FC-Siam-conc'
# net, net_name = SiamUnet_diff(10, 2), 'FC-Siam-diff'
# net, net_name = FresUNet(2*10, 2), 'FresUNet'
elif TYPE == 3:
# net, net_name = Unet(2*13, 2), 'FC-EF'
net, net_name = SiamUnet_conc(13, 2), 'FC-Siam-conc'
# net, net_name = SiamUnet_diff(13, 2), 'FC-Siam-diff'
# net, net_name = FresUNet(2*13, 2), 'FresUNet'
net.cuda()
criterion = nn.NLLLoss(weight=weights) # to be used with logsoftmax output - need to think about tweaking this too.
print('NETWORK OK')
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
print('Number of trainable parameters:', count_parameters(net))
### This cell gives the procedure to train the model on the training dataset, and output
### graphs that show the progress of the training through the epochs e.g. loss, recall etc.
### Uses the Adam optimiser.
### There are lots of things we could tweak here - optimiser, learning rate, weight decay (regularisation),
### no. of epochs, as well as tweaking the fundamental structure of the ConvNet models used.
# net.load_state_dict(torch.load('net-best_epoch-1_fm-0.7394933126157746.pth.tar'))
def train(n_epochs = N_EPOCHS, save = True):
t = np.linspace(1, n_epochs, n_epochs)
epoch_train_loss = 0 * t
epoch_train_accuracy = 0 * t
epoch_train_change_accuracy = 0 * t
epoch_train_nochange_accuracy = 0 * t
epoch_train_precision = 0 * t
epoch_train_recall = 0 * t
epoch_train_Fmeasure = 0 * t
epoch_test_loss = 0 * t
epoch_test_accuracy = 0 * t
epoch_test_change_accuracy = 0 * t
epoch_test_nochange_accuracy = 0 * t
epoch_test_precision = 0 * t
epoch_test_recall = 0 * t
epoch_test_Fmeasure = 0 * t
# mean_acc = 0
# best_mean_acc = 0
fm = 0
best_fm = 0
lss = 1000
best_lss = 1000
plt.figure(num=1)
plt.figure(num=2)
plt.figure(num=3)
optimizer = torch.optim.Adam(net.parameters(), weight_decay=1e-4)
# optimizer = torch.optim.Adam(net.parameters(), lr=0.0005)
scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, 0.95)
for epoch_index in tqdm(range(n_epochs)):
net.train()
print('Epoch: ' + str(epoch_index + 1) + ' of ' + str(N_EPOCHS))
tot_count = 0
tot_loss = 0
tot_accurate = 0
class_correct = list(0. for i in range(2))
class_total = list(0. for i in range(2))
# for batch_index, batch in enumerate(tqdm(data_loader)):
for batch in train_loader:
I1 = Variable(batch['I1'].float().cuda())
I2 = Variable(batch['I2'].float().cuda())
label = torch.squeeze(Variable(batch['label'].cuda()))
#I1 = Variable(batch['I1'].float())
#I2 = Variable(batch['I2'].float())
#label = torch.squeeze(Variable(batch['label']))
optimizer.zero_grad()
output = net(I1, I2)
loss = criterion(output, label.long())
loss.backward()
optimizer.step()
scheduler.step()
epoch_train_loss[epoch_index], epoch_train_accuracy[epoch_index], cl_acc, pr_rec = test(train_dataset)
epoch_train_nochange_accuracy[epoch_index] = cl_acc[0]
epoch_train_change_accuracy[epoch_index] = cl_acc[1]
epoch_train_precision[epoch_index] = pr_rec[0]
epoch_train_recall[epoch_index] = pr_rec[1]
epoch_train_Fmeasure[epoch_index] = pr_rec[2]
# epoch_test_loss[epoch_index], epoch_test_accuracy[epoch_index], cl_acc, pr_rec = test(test_dataset)
epoch_test_loss[epoch_index], epoch_test_accuracy[epoch_index], cl_acc, pr_rec = test(test_dataset)
epoch_test_nochange_accuracy[epoch_index] = cl_acc[0]
epoch_test_change_accuracy[epoch_index] = cl_acc[1]
epoch_test_precision[epoch_index] = pr_rec[0]
epoch_test_recall[epoch_index] = pr_rec[1]
epoch_test_Fmeasure[epoch_index] = pr_rec[2]
plt.figure(num=1)
plt.clf()
l1_1, = plt.plot(t[:epoch_index + 1], epoch_train_loss[:epoch_index + 1], label='Train loss')
l1_2, = plt.plot(t[:epoch_index + 1], epoch_test_loss[:epoch_index + 1], label='Test loss')
plt.legend(handles=[l1_1, l1_2])
plt.grid()
# plt.gcf().gca().set_ylim(bottom = 0)
plt.gcf().gca().set_xlim(left = 0)
plt.title('Loss')
display.clear_output(wait=True)
display.display(plt.gcf())
plt.figure(num=2)
plt.clf()
l2_1, = plt.plot(t[:epoch_index + 1], epoch_train_accuracy[:epoch_index + 1], label='Train accuracy')
l2_2, = plt.plot(t[:epoch_index + 1], epoch_test_accuracy[:epoch_index + 1], label='Test accuracy')
plt.legend(handles=[l2_1, l2_2])
plt.grid()
plt.gcf().gca().set_ylim(0, 100)
# plt.gcf().gca().set_ylim(bottom = 0)
# plt.gcf().gca().set_xlim(left = 0)
plt.title('Accuracy')
display.clear_output(wait=True)
display.display(plt.gcf())
plt.figure(num=3)
plt.clf()
l3_1, = plt.plot(t[:epoch_index + 1], epoch_train_nochange_accuracy[:epoch_index + 1], label='Train accuracy: no change')
l3_2, = plt.plot(t[:epoch_index + 1], epoch_train_change_accuracy[:epoch_index + 1], label='Train accuracy: change')
l3_3, = plt.plot(t[:epoch_index + 1], epoch_test_nochange_accuracy[:epoch_index + 1], label='Test accuracy: no change')
l3_4, = plt.plot(t[:epoch_index + 1], epoch_test_change_accuracy[:epoch_index + 1], label='Test accuracy: change')
plt.legend(handles=[l3_1, l3_2, l3_3, l3_4])
plt.grid()
plt.gcf().gca().set_ylim(0, 100)
# plt.gcf().gca().set_ylim(bottom = 0)
# plt.gcf().gca().set_xlim(left = 0)
plt.title('Accuracy per class')
display.clear_output(wait=True)
display.display(plt.gcf())
plt.figure(num=4)
plt.clf()
l4_1, = plt.plot(t[:epoch_index + 1], epoch_train_precision[:epoch_index + 1], label='Train precision')
l4_2, = plt.plot(t[:epoch_index + 1], epoch_train_recall[:epoch_index + 1], label='Train recall')
l4_3, = plt.plot(t[:epoch_index + 1], epoch_train_Fmeasure[:epoch_index + 1], label='Train Dice/F1')
l4_4, = plt.plot(t[:epoch_index + 1], epoch_test_precision[:epoch_index + 1], label='Test precision')
l4_5, = plt.plot(t[:epoch_index + 1], epoch_test_recall[:epoch_index + 1], label='Test recall')
l4_6, = plt.plot(t[:epoch_index + 1], epoch_test_Fmeasure[:epoch_index + 1], label='Test Dice/F1')
plt.legend(handles=[l4_1, l4_2, l4_3, l4_4, l4_5, l4_6])
plt.grid()
plt.gcf().gca().set_ylim(0, 1)
# plt.gcf().gca().set_ylim(bottom = 0)
# plt.gcf().gca().set_xlim(left = 0)
plt.title('Precision, Recall and F-measure')
display.clear_output(wait=True)
display.display(plt.gcf())
# mean_acc = (epoch_test_nochange_accuracy[epoch_index] + epoch_test_change_accuracy[epoch_index])/2
# if mean_acc > best_mean_acc:
# best_mean_acc = mean_acc
# save_str = 'net-best_epoch-' + str(epoch_index + 1) + '_acc-' + str(mean_acc) + '.pth.tar'
# torch.save(net.state_dict(), save_str)
# fm = pr_rec[2]
fm = epoch_train_Fmeasure[epoch_index]
if fm > best_fm:
best_fm = fm
save_str = 'net-best_epoch-' + str(epoch_index + 1) + '_fm-' + str(fm) + '.pth.tar'
torch.save(net.state_dict(), save_str)
lss = epoch_train_loss[epoch_index]
if lss < best_lss:
best_lss = lss
save_str = 'net-best_epoch-' + str(epoch_index + 1) + '_loss-' + str(lss) + '.pth.tar'
torch.save(net.state_dict(), save_str)
# print('Epoch loss: ' + str(tot_loss/tot_count))
if save:
im_format = 'png'
# im_format = 'eps'
plt.figure(num=1)
plt.savefig(net_name + '-01-loss.' + im_format)
plt.figure(num=2)
plt.savefig(net_name + '-02-accuracy.' + im_format)
plt.figure(num=3)
plt.savefig(net_name + '-03-accuracy-per-class.' + im_format)
plt.figure(num=4)
plt.savefig(net_name + '-04-prec-rec-fmeas.' + im_format)
out = {'train_loss': epoch_train_loss[-1],
'train_accuracy': epoch_train_accuracy[-1],
'train_nochange_accuracy': epoch_train_nochange_accuracy[-1],
'train_change_accuracy': epoch_train_change_accuracy[-1],
'test_loss': epoch_test_loss[-1],
'test_accuracy': epoch_test_accuracy[-1],
'test_nochange_accuracy': epoch_test_nochange_accuracy[-1],
'test_change_accuracy': epoch_test_change_accuracy[-1]}
print('pr_c, rec_c, f_meas, pr_nc, rec_nc')
print(pr_rec)
return out
L = 1024
N = 2
def test(dset):
net.eval()
tot_loss = 0
tot_count = 0
tot_accurate = 0
n = 2
class_correct = list(0. for i in range(n))
class_total = list(0. for i in range(n))
class_accuracy = list(0. for i in range(n))
tp = 0
tn = 0
fp = 0
fn = 0
for img_index in dset.names:
I1_full, I2_full, cm_full = dset.get_img(img_index)
s = cm_full.shape
steps0 = np.arange(0,s[0],ceil(s[0]/N))
steps1 = np.arange(0,s[1],ceil(s[1]/N))
for ii in range(N):
for jj in range(N):
xmin = steps0[ii]
if ii == N-1:
xmax = s[0]
else:
xmax = steps0[ii+1]
ymin = jj
if jj == N-1:
ymax = s[1]
else:
ymax = steps1[jj+1]
I1 = I1_full[:, xmin:xmax, ymin:ymax]
I2 = I2_full[:, xmin:xmax, ymin:ymax]
cm = cm_full[xmin:xmax, ymin:ymax]
I1 = Variable(torch.unsqueeze(I1, 0).float()).cuda()
I2 = Variable(torch.unsqueeze(I2, 0).float()).cuda()
cm = Variable(torch.unsqueeze(torch.from_numpy(1.0*cm),0).float()).cuda()
output = net(I1, I2)
loss = criterion(output, cm.long())
# print(loss)
tot_loss += loss.data * np.prod(cm.size())
tot_count += np.prod(cm.size())
_, predicted = torch.max(output.data, 1)
c = (predicted.int() == cm.data.int())
for i in range(c.size(1)):
for j in range(c.size(2)):
l = int(cm.data[0, i, j])
class_correct[l] += c[0, i, j]
class_total[l] += 1
pr = (predicted.int() > 0).cpu().numpy()
gt = (cm.data.int() > 0).cpu().numpy()
tp += np.logical_and(pr, gt).sum()
tn += np.logical_and(np.logical_not(pr), np.logical_not(gt)).sum()
fp += np.logical_and(pr, np.logical_not(gt)).sum()
fn += np.logical_and(np.logical_not(pr), gt).sum()
net_loss = tot_loss/tot_count
net_accuracy = 100 * (tp + tn)/tot_count
for i in range(n):
class_accuracy[i] = 100 * class_correct[i] / max(class_total[i],0.00001)
prec = tp / (tp + fp)
rec = tp / (tp + fn)
f_meas = 2 * prec * rec / (prec + rec)
prec_nc = tn / (tn + fn)
rec_nc = tn / (tn + fp)
pr_rec = [prec, rec, f_meas, prec_nc, rec_nc]
return net_loss, net_accuracy, class_accuracy, pr_rec
### This cell either loads trained weights, or it begins the training process of a network by calling train().
if LOAD_TRAINED:
net.load_state_dict(torch.load('net_final.pth.tar'))
print('LOAD OK')
else:
t_start = time.time()
out_dic = train()
t_end = time.time()
print(out_dic)
print('Elapsed time:')
print(t_end - t_start)
### This cell saves the weights of the trained network for future use.
if not LOAD_TRAINED:
torch.save(net.state_dict(), 'siamunet_conc_net_final.pth.tar')
print('SAVE OK')
### This cell outputs the results of the trained network when applied to the test set.
### Results come in the form of png files showing the network's predictions of change.
def save_test_results(dset):
for name in tqdm(dset.names):
with warnings.catch_warnings():
I1, I2, cm = dset.get_img(name)
I1 = Variable(torch.unsqueeze(I1, 0).float()).cuda()
I2 = Variable(torch.unsqueeze(I2, 0).float()).cuda()
out = net(I1, I2)
_, predicted = torch.max(out.data, 1)
I = np.stack((255*cm,255*np.squeeze(predicted.cpu().numpy()),255*cm),2)
io.imsave(f'{net_name}-{name}.png',I)
t_start = time.time()
# save_test_results(train_dataset)
save_test_results(test_dataset)
t_end = time.time()
print('Elapsed time: {}'.format(t_end - t_start))
### This cell returns various metrics that relate to the performance of the network.
### It does this by testing the trained network on the test set (called by test) and then
### computing the various metrics e.g. accuracy, precision, recall.
L = 1024
def kappa(tp, tn, fp, fn):
N = tp + tn + fp + fn
p0 = (tp + tn) / N
pe = ((tp+fp)*(tp+fn) + (tn+fp)*(tn+fn)) / (N * N)
return (p0 - pe) / (1 - pe)
def test(dset):
net.eval()
tot_loss = 0
tot_count = 0
tot_accurate = 0
n = 2
class_correct = list(0. for i in range(n))
class_total = list(0. for i in range(n))
class_accuracy = list(0. for i in range(n))
tp = 0
tn = 0
fp = 0
fn = 0
for img_index in tqdm(dset.names):
I1_full, I2_full, cm_full = dset.get_img(img_index)
s = cm_full.shape
for ii in range(ceil(s[0]/L)):
for jj in range(ceil(s[1]/L)):
xmin = L*ii
xmax = min(L*(ii+1),s[1])
ymin = L*jj
ymax = min(L*(jj+1),s[1])
I1 = I1_full[:, xmin:xmax, ymin:ymax]
I2 = I2_full[:, xmin:xmax, ymin:ymax]
cm = cm_full[xmin:xmax, ymin:ymax]
I1 = Variable(torch.unsqueeze(I1, 0).float()).cuda()
I2 = Variable(torch.unsqueeze(I2, 0).float()).cuda()
cm = Variable(torch.unsqueeze(torch.from_numpy(1.0*cm),0).float()).cuda()
output = net(I1, I2)
loss = criterion(output, cm.long())
tot_loss += loss.data * np.prod(cm.size())
tot_count += np.prod(cm.size())
_, predicted = torch.max(output.data, 1)
c = (predicted.int() == cm.data.int())
for i in range(c.size(1)):
for j in range(c.size(2)):
l = int(cm.data[0, i, j])
class_correct[l] += c[0, i, j]
class_total[l] += 1
pr = (predicted.int() > 0).cpu().numpy()
gt = (cm.data.int() > 0).cpu().numpy()
tp += np.logical_and(pr, gt).sum()
tn += np.logical_and(np.logical_not(pr), np.logical_not(gt)).sum()
fp += np.logical_and(pr, np.logical_not(gt)).sum()
fn += np.logical_and(np.logical_not(pr), gt).sum()
net_loss = tot_loss/tot_count
net_loss = float(net_loss.cpu().numpy())
net_accuracy = 100 * (tp + tn)/tot_count
for i in range(n):
class_accuracy[i] = 100 * class_correct[i] / max(class_total[i],0.00001)
class_accuracy[i] = float(class_accuracy[i].cpu().numpy())
prec = tp / (tp + fp)
rec = tp / (tp + fn)
dice = 2 * prec * rec / (prec + rec)
prec_nc = tn / (tn + fn)
rec_nc = tn / (tn + fp)
pr_rec = [prec, rec, dice, prec_nc, rec_nc]
k = kappa(tp, tn, fp, fn)
return {'net_loss': net_loss,
'net_accuracy': net_accuracy,
'class_accuracy': class_accuracy,
'precision': prec,
'recall': rec,
'dice': dice,
'kappa': k}
results = test(test_dataset)
pprint(results)
```
| true |
code
| 0.695674 | null | null | null | null |
|
# `Probability Distributions`
```
%matplotlib inline
# for inline plots in jupyter
import matplotlib.pyplot as plt# import matplotlib
import seaborn as sns
import warnings
warnings.simplefilter("ignore")
from ipywidgets import interact
styles = ['seaborn-notebook', 'seaborn', 'seaborn-darkgrid', 'classic',
'_classic_test', 'seaborn-poster', 'tableau-colorblind10', 'grayscale',
'fivethirtyeight', 'seaborn-ticks', 'seaborn-dark',
'dark_background', 'seaborn-pastel',
'fast', 'Solarize_Light2', 'seaborn-colorblind', 'seaborn-white',
'seaborn-dark-palette',
'bmh', 'seaborn-talk', 'seaborn-paper', 'seaborn-deep', 'seaborn-bright',
'seaborn-muted',
'seaborn-whitegrid', 'ggplot']
```
## `5. Poisson Distribution`
1. The Poisson distribution is used to model the number of events occurring within a given time interval.

```
# import poisson module from scipy.stats to generate poisson random variables.
from scipy.stats import poisson
# Poisson random variable is typically used to model the number of times an event
# happened in a time interval. For example, number of users visited your website in an interval
# can be thought of a Poisson process. Poisson distribution is described in terms of the rate (mu) at which
# the events happen. We can generate Poisson random variables in Python using poisson.rvs.
poisson = poisson.rvs(mu=3, size=10000)
# Let us generate 10000 random numbers from Poisson random variable with mu = 0.3 and plot them.
ax = sns.distplot(poisson,
kde=False,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Poisson', ylabel='Frequency')
def PoissonDistribution(palette="dark",kde = False,style = "ggplot"):
plt.figure(figsize=(13,10))
plt.style.use(style)
sns.set_palette(palette)
ax = sns.distplot(poisson,
kde=kde,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Poisson', ylabel='Frequency')
plt.show()
interact(PoissonDistribution,palette = ["deep", "muted", "pastel", "bright",
"dark", "colorblind","Set3","Set2"],kde = [True,False],style = styles);
```
## `6. Beta Distribution`
1. We can understand Beta distribution as a distribution for probabilities. Beta distribution is a continuous distribution taking values from 0 to 1. It is defined by two parameters alpha and beta, depending on the values of alpha and beta they can assume very different distributions.
```
# Let us generate 10000, random numbers from Beta distribution
# with alpha = 1 and beta = 1. The histogram of Beta(1,1) is a uniform distribution.
from scipy.stats import beta
beta = beta.rvs(1, 1, size=10000)
ax = sns.distplot(beta,
kde=False,
bins=100,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta(1,1)', ylabel='Frequency')
# Let us generate 10000, random numbers from Beta distribution with alpha = 10 and beta = 1.
# The histogram of Beta(10,1) is skewed towards right.
from scipy.stats import beta
beta_right = beta.rvs(10, 1, size=10000)
sns.distplot(beta_right,
kde=False,
bins=50,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta(10,1)', ylabel='Frequency')
# Let us generate 10000, random numbers from Beta distribution with alpha = 1 and beta = 10.
# The histogram of Beta(1,10) is skewed towards left.
beta_left = beta.rvs(1, 10, size=10000)
ax = sns.distplot(beta_left,
kde=False,
bins=100,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta(1,10)', ylabel='Frequency')
# Let us generate 10000, random numbers from Beta distribution with alpha = 10 and beta = 10.
# The histogram of Beta(10,10) is symmetric and looks like a normal distribution
beta_symmetric = beta.rvs(10, 10, size=10000)
ax = sns.distplot(beta_symmetric,
kde=False,
bins=100,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta(10,10)', ylabel='Frequency')
def BetaDistribution(palette="dark",kde = False,style = "ggplot",kind = "left"):
plt.figure(figsize=(13,10))
plt.style.use(style)
sns.set_palette(palette)
if kind == "left":
ax = sns.distplot(beta_left,
kde=kde,
bins=100,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta(1,10)', ylabel='Frequency')
elif kind == "right":
ax = sns.distplot(beta_right,
kde=kde,
bins=50,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta(10,1)', ylabel='Frequency')
elif kind == "symmetric":
ax = sns.distplot(beta_symmetric,
kde=kde,
bins=100,
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta(10,10)', ylabel='Frequency')
plt.show()
interact(BetaDistribution,palette = ["deep", "muted", "pastel", "bright",
"dark", "colorblind","Set3","Set2"],kde = [True,False],style = styles,
kind = ["left","right","symmetric"]);
```
| true |
code
| 0.585694 | null | null | null | null |
|
# 4️⃣ Zero-Shot Cross-Lingual Transfer using Adapters
Beyond AdapterFusion, which we trained in [the previous notebook](https://github.com/Adapter-Hub/adapter-transformers/blob/master/notebooks/04_Cross_Lingual_Transfer.ipynb), we can compose adapters for zero-shot cross-lingual transfer between tasks. We will use the stacked adapter setup presented in **MAD-X** ([Pfeiffer et al., 2020](https://arxiv.org/pdf/2005.00052.pdf)) for this purpose.
In this example, the base model is a pre-trained multilingual **XLM-R** (`xlm-roberta-base`) ([Conneau et al., 2019](https://arxiv.org/pdf/1911.02116.pdf)) model. Additionally, two types of adapters, language adapters and task adapters, are used. Here's how the MAD-X process works in detail:
1. Train language adapters for the source and target language on a language modeling task. In this notebook, we won't train them ourselves but use [pre-trained language adapters from the Hub](https://adapterhub.ml/explore/text_lang/).
2. Train a task adapter on the target task dataset. This task adapter is **stacked** upon the previously trained language adapter. During this step, only the weights of the task adapter are updated.
3. Perform zero-shot cross-lingual transfer. In this last step, we simply replace the source language adapter with the target language adapter while keeping the stacked task adapter.
Now to our concrete example: we select **XCOPA** ([Ponti et al., 2020](https://ducdauge.github.io/files/xcopa.pdf)), a multilingual extension of the **COPA** commonsence reasoning dataset ([Roemmele et al., 2011](https://people.ict.usc.edu/~gordon/publications/AAAI-SPRING11A.PDF)) as our target task. The setup is trained on the original **English** dataset and then transferred to **Chinese**.
## Installation
Besides `adapter-transformers`, we use HuggingFace's `datasets` library for loading the data. So let's install both first:
```
!pip install -U adapter-transformers
!pip install -U datasets
```
## Dataset Preprocessing
We need the English COPA dataset for training our task adapter. It is part of the SuperGLUE benchmark and can be loaded via `datasets` using one line of code:
```
from datasets import load_dataset
from transformers.adapters.composition import Stack
dataset_en = load_dataset("super_glue", "copa")
dataset_en.num_rows
```
Every dataset sample has a premise, a question and two possible answer choices:
```
dataset_en['train'].features
```
In this example, we model COPA as a multiple-choice task with two choices. Thus, we encode the premise and question as well as both choices as one input to our `xlm-roberta-base` model. Using `dataset.map()`, we can pass the full dataset through the tokenizer in batches:
```
from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained("xlm-roberta-base")
def encode_batch(examples):
"""Encodes a batch of input data using the model tokenizer."""
all_encoded = {"input_ids": [], "attention_mask": []}
# Iterate through all examples in this batch
for premise, question, choice1, choice2 in zip(examples["premise"], examples["question"], examples["choice1"], examples["choice2"]):
sentences_a = [premise + " " + question for _ in range(2)]
# Both answer choices are passed in an array according to the format needed for the multiple-choice prediction head
sentences_b = [choice1, choice2]
encoded = tokenizer(
sentences_a,
sentences_b,
max_length=60,
truncation=True,
padding="max_length",
)
all_encoded["input_ids"].append(encoded["input_ids"])
all_encoded["attention_mask"].append(encoded["attention_mask"])
return all_encoded
def preprocess_dataset(dataset):
# Encode the input data
dataset = dataset.map(encode_batch, batched=True)
# The transformers model expects the target class column to be named "labels"
dataset.rename_column_("label", "labels")
# Transform to pytorch tensors and only output the required columns
dataset.set_format(columns=["input_ids", "attention_mask", "labels"])
return dataset
dataset_en = preprocess_dataset(dataset_en)
```
## Task Adapter Training
In this section, we will train the task adapter on the English COPA dataset. We use a pre-trained XLM-R model from HuggingFace and instantiate our model using `AutoModelWithHeads`.
```
from transformers import AutoConfig, AutoModelWithHeads
config = AutoConfig.from_pretrained(
"xlm-roberta-base",
)
model = AutoModelWithHeads.from_pretrained(
"xlm-roberta-base",
config=config,
)
```
Now we only need to set up the adapters. As described, we need two language adapters (which are assumed to be pre-trained in this example) and a task adapter (which will be trained in a few moments).
First, we load both the language adapters for our source language English (`"en"`) and our target language Chinese (`"zh"`) from the Hub. Then we add a new task adapter (`"copa"`) for our target task.
Finally, we add a multiple-choice head with the same name as our task adapter on top.
```
from transformers import AdapterConfig
# Load the language adapters
lang_adapter_config = AdapterConfig.load("pfeiffer", reduction_factor=2)
model.load_adapter("en/wiki@ukp", config=lang_adapter_config)
model.load_adapter("zh/wiki@ukp", config=lang_adapter_config)
# Add a new task adapter
model.add_adapter("copa")
# Add a classification head for our target task
model.add_multiple_choice_head("copa", num_choices=2)
```
We want the task adapter to be stacked on top of the language adapter, so we have to tell our model to use this setup via the `active_adapters` property.
A stack of adapters is represented by the `Stack` class, which takes the names of the adapters to be stacked as arguments.
Of course, there are various other possibilities to compose adapters beyonde stacking. Learn more about those [in our documentation](https://docs.adapterhub.ml/adapter_composition.html).
```
# Unfreeze and activate stack setup
model.active_adapters = Stack("en", "copa")
```
Great! Now, the input will be passed through the English language adapter first and the COPA task adapter second in every forward pass.
Just one final step to make: Using `train_adapter()`, we tell our model to only train the task adapter in the following. This call will freeze the weights of the pre-trained model and the weights of the language adapters to prevent them from further finetuning.
```
model.train_adapter(["copa"])
```
For training, we make use of the `Trainer` class built-in into `transformers`. We configure the training process using a `TrainingArguments` object.
As the dataset splits of English COPA in the SuperGLUE are slightly different, we train on both the train and validation split of the dataset. Later, we will evaluate on the test split of XCOPA.
```
from transformers import TrainingArguments, Trainer
from datasets import concatenate_datasets
training_args = TrainingArguments(
learning_rate=1e-4,
num_train_epochs=8,
per_device_train_batch_size=32,
per_device_eval_batch_size=32,
logging_steps=100,
output_dir="./training_output",
overwrite_output_dir=True,
# The next line is important to ensure the dataset labels are properly passed to the model
remove_unused_columns=False,
)
train_dataset = concatenate_datasets([dataset_en["train"], dataset_en["validation"]])
trainer = Trainer(
model=model,
args=training_args,
train_dataset=train_dataset,
)
```
Start the training 🚀 (this will take a while)
```
trainer.train()
```
## Cross-lingual transfer
With the model and all adapters trained and ready, we can come to the cross-lingual transfer step here. We will evaluate our setup on the Chinese split of the XCOPA dataset.
Therefore, we'll first download the data and preprocess it using the same method as the English dataset:
```
dataset_zh = load_dataset("xcopa", "zh", ignore_verifications=True)
dataset_zh = preprocess_dataset(dataset_zh)
print(dataset_zh["test"][0])
```
Next, let's adapt our setup to the new language. We simply replace the English language adapter with the Chinese language adapter we already loaded previously. The task adapter we just trained is kept. Again, we set this architecture using `active_adapters`:
```
model.active_adapters = Stack("zh", "copa")
```
Finally, let's see how well our adapter setup performs on the new language. We measure the zero-shot accuracy on the test split of the target language dataset. Evaluation is also performed using the built-in `Trainer` class.
```
import numpy as np
from transformers import EvalPrediction
def compute_accuracy(p: EvalPrediction):
preds = np.argmax(p.predictions, axis=1)
return {"acc": (preds == p.label_ids).mean()}
eval_trainer = Trainer(
model=model,
args=TrainingArguments(output_dir="./eval_output", remove_unused_columns=False,),
eval_dataset=dataset_zh["test"],
compute_metrics=compute_accuracy,
)
eval_trainer.evaluate()
```
You should get an overall accuracy of about 56 which is on-par with full finetuning on COPA only but below the state-of-the-art which is sequentially finetuned on an additional dataset before finetuning on COPA.
For results on different languages and a sequential finetuning setup which yields better results, make sure to check out [the MAD-X paper](https://arxiv.org/pdf/2005.00052.pdf).
| true |
code
| 0.824144 | null | null | null | null |
|
# Day 19 - regular expressions
* https://adventofcode.com/2020/day/19
The problem description amounts to a [regular expression](https://www.regular-expressions.info/); by traversing the graph of rules you can combine the string literals into a regex pattern that the Python [`re` module](https://docs.python.org/3/library/re.html) can compile into a pattern. Using the [`Pattern.fullmatch()` method](https://docs.python.org/3/library/re.html#re.Pattern.fullmatch) you can then check each message for validity.
Having just used the `tokenize` module the [day before](./Day%2018.ipynb), I found it very helpful to parse the rules, as well.
```
import re
from collections import deque
from collections.abc import Iterable, Mapping, MutableMapping
from io import StringIO
from itertools import islice
from tokenize import generate_tokens, NUMBER, STRING, TokenInfo
from typing import Callable, Dict, Tuple
def parse_rules(lines: Iterable[str], make_regex: Callable[[str], re.Pattern[str]]) -> re.Pattern[str]:
def rule_to_tokens(rule: str) -> Tuple[str, Iterable[TokenInfo]]:
tokens = generate_tokens(StringIO(rule).readline)
# tokens are NUMBER, COLON, (...)+, we skip the COLON.
return next(tokens).string, list(islice(tokens, 1, None))
unprocessed = dict(map(rule_to_tokens, lines))
rules: MutableMapping[str, str] = {}
dispatch: Mapping[int, Callable[[str], str]] = {NUMBER: rules.__getitem__, STRING: lambda s: s[1:-1]}
stack = deque(['0'])
while stack:
tokens = unprocessed[stack[-1]]
if missing := {t.string for t in tokens if t.type == NUMBER and t.string not in rules}:
stack += missing
continue
rule = "".join([dispatch.get(t.type, str)(t.string) for t in tokens])
rules[stack.pop()] = f"(?:{rule})"
return make_regex(rules["0"])
def validate_messages(data: str, make_regex: Callable[[str], re.Pattern[str]] = re.compile) -> int:
rule_data, messages = data.split("\n\n")
rule_regex = parse_rules(rule_data.splitlines(), make_regex)
return sum(bool(rule_regex.fullmatch(msg)) for msg in messages.splitlines())
assert validate_messages("""\
0: 4 1 5
1: 2 3 | 3 2
2: 4 4 | 5 5
3: 4 5 | 5 4
4: "a"
5: "b"
ababbb
bababa
abbbab
aaabbb
aaaabbb
""") == 2
import aocd
data = aocd.get_data(day=19, year=2020)
print("Part 1:", validate_messages(data))
```
## Part 2 - recursive regex
Part two introduces _recursion_; patterns `8` and `11` add self-references.
For rule 8, that just means that the contained rule `42` just matches 1 or more times (`"42 | 42 8"` will match `"42"`, `"42 42"`, `"42 42 42"`, etc), so can be simplified using the [`+` repetition operator](https://www.regular-expressions.info/repeat.html), to `"8: 42 +"` which my tokenizer-based parser will happily assemble.
But the change for rule 11, `"42 31 | 42 11 31"` is not so easily simplified. The rule matches for any number of repetitions of `"42"` and `"31"` **provided they repeat an equal number of times**. To check for such patterns using regular expressions, you need a regex engine that supports either [balancing groups](https://www.regular-expressions.info/balancing.html) or [recursion](https://www.regular-expressions.info/recurse.html). .NET's regex engine would let you use balancing groups (the pattern, with spaces around the pattern IDs, would be `(?'g42' 42 )+ (?'-g42' 31 )+ (?(g42)(?!))`), and Perl, Ruby and any regex engine based on PCRE would let you use recursion.
Lucky for me, the [`regex` package](https://pypi.org/project/regex/) _does_ support recursion. The package may one day be ready to replace the standard-library `re` module, but that day has not yet arrived. In the meantime, if you have advanced regex needs, do keep the existence of that package in mind! As for the recursion syntax: given a named group `(?P<groupname>...)`, the expression `(?&groupname)` will match everything within the named pattern, and `(?&groupname)?` will do so 0 or more times. So, we can replace `"42 31 | 42 11 31"` with `"(?P<rule_11> 42 (?&rule_11)? 31 )"` to get the desired regex validation pattern.
```
import regex
def validate_corrected_rules(data: str) -> int:
return validate_messages(
data
# 42 | 42 8, repeating 42 one or more times.
.replace("8: 42\n", "8: 42 +\n")
# 42 31 | 42 11 31, recursive self-reference
.replace("11: 42 31\n", "11: (?P<rule_11> 42 (?&rule_11)? 31 )\n"),
regex.compile
)
assert validate_corrected_rules("""\
42: 9 14 | 10 1
9: 14 27 | 1 26
10: 23 14 | 28 1
1: "a"
11: 42 31
5: 1 14 | 15 1
19: 14 1 | 14 14
12: 24 14 | 19 1
16: 15 1 | 14 14
31: 14 17 | 1 13
6: 14 14 | 1 14
2: 1 24 | 14 4
0: 8 11
13: 14 3 | 1 12
15: 1 | 14
17: 14 2 | 1 7
23: 25 1 | 22 14
28: 16 1
4: 1 1
20: 14 14 | 1 15
3: 5 14 | 16 1
27: 1 6 | 14 18
14: "b"
21: 14 1 | 1 14
25: 1 1 | 1 14
22: 14 14
8: 42
26: 14 22 | 1 20
18: 15 15
7: 14 5 | 1 21
24: 14 1
abbbbbabbbaaaababbaabbbbabababbbabbbbbbabaaaa
bbabbbbaabaabba
babbbbaabbbbbabbbbbbaabaaabaaa
aaabbbbbbaaaabaababaabababbabaaabbababababaaa
bbbbbbbaaaabbbbaaabbabaaa
bbbababbbbaaaaaaaabbababaaababaabab
ababaaaaaabaaab
ababaaaaabbbaba
baabbaaaabbaaaababbaababb
abbbbabbbbaaaababbbbbbaaaababb
aaaaabbaabaaaaababaa
aaaabbaaaabbaaa
aaaabbaabbaaaaaaabbbabbbaaabbaabaaa
babaaabbbaaabaababbaabababaaab
aabbbbbaabbbaaaaaabbbbbababaaaaabbaaabba
""") == 12
print("Part 2:", validate_corrected_rules(data))
```
| true |
code
| 0.560854 | null | null | null | null |
|
# Kriging Example1
- Author: Mohit S. Chauhan
- Date: Jan 08, 2019
In this example, Kriging is used to generate a surrogate model for a given data. In this data, sample points are generated using STS class and functional value at sample points are estimated using a model defined in python script ('python_model_function.py).
Import the necessary libraries. Here we import standard libraries such as numpy and matplotlib, but also need to import the STS, RunModel and Krig class from UQpy.
```
from UQpy.Surrogates import Kriging
from UQpy.SampleMethods import RectangularStrata, RectangularSTS
from UQpy.RunModel import RunModel
from UQpy.Distributions import Gamma
import numpy as np
import matplotlib.pyplot as plt
```
Create a distribution object.
```
marginals = [Gamma(a= 2., loc=1., scale=3.)]
```
Create a strata object.
```
strata = RectangularStrata(nstrata=[20])
```
Run stratified sampling
```
x = RectangularSTS(dist_object=marginals, strata_object=strata, nsamples_per_stratum=1, random_state=2)
```
RunModel is used to evaluate function values at sample points. Model is defined as a function in python file 'python_model_function.py'.
```
rmodel = RunModel(model_script='python_model_1Dfunction.py', delete_files=True)
rmodel.run(samples=x.samples)
K = Kriging(reg_model='Linear', corr_model='Gaussian', nopt=20, corr_model_params=[1], random_state=2)
K.fit(samples=x.samples, values=rmodel.qoi_list)
print(K.corr_model_params)
```
Kriging surrogate is used to compute the response surface and its gradient.
```
num = 1000
x1 = np.linspace(min(x.samples), max(x.samples), num)
y, y_sd = K.predict(x1.reshape([num, 1]), return_std=True)
y_grad = K.jacobian(x1.reshape([num, 1]))
```
Actual model is evaluated at all points to compare it with kriging surrogate.
```
rmodel.run(samples=x1, append_samples=False)
```
This plot shows the input data as blue dot, blue curve is actual function and orange curve represents response curve. This plot also shows the gradient and 95% confidence interval of the kriging surrogate.
```
fig = plt.figure()
ax = plt.subplot(111)
plt.plot(x1, rmodel.qoi_list, label='Sine')
plt.plot(x1, y, label='Surrogate')
plt.plot(x1, y_grad, label='Gradient')
plt.scatter(K.samples, K.values, label='Data')
plt.fill(np.concatenate([x1, x1[::-1]]), np.concatenate([y - 1.9600 * y_sd,
(y + 1.9600 * y_sd)[::-1]]),
alpha=.5, fc='y', ec='None', label='95% CI')
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
# Put a legend to the right of the current axis
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.show()
```
| true |
code
| 0.779731 | null | null | null | null |
|
# sbpy.activity: dust
[sbpy.activity](https://sbpy.readthedocs.io/en/latest/sbpy/activity.html) has classes and functions for models of cometary dust comae. Comet brightness can be estimated for observations of scattered light or themral emission.
## Light scattered by dust via Afρ
Light scattered by coma dust can be estimated via the cometary parameter Afρ. For a circular aperture, the Αfρ quantity is the product of albedo, filling factor of dust in the aperture, and aperture radius. It has units of length, is aperture-size independent for an idealized coma, and is proportional to mass loss rate under certain assumptions (see [A'Hearn et al. 1984 for details](https://ui.adsabs.harvard.edu/#abs/1984AJ.....89..579A/abstract)):
$$ Af\rho = \frac{(2 r_h \Delta)^2}{\rho}\frac{F_\lambda}{S_\lambda} $$
where $r_h$ is the heliocentric distance in au, $\Delta$ is the observer-comet distance in the same units as $\rho$, $F_\lambda$ is the flux desnity of the comet continuum, and $S_\lambda$ is the flux desnity of sunlight at 1 au in the same units as $F_\lambda$.
`sbpy` has a class that represents this parameter: `Afrho`. With this quantity, we can estimate the brightness of a comet, under the assumptions of the Afρ model (isotropic coma in free expansion).
### Afρ is a quantity
`Afrho` is an `astropy` `Quantity` that has units of length.
```
import astropy.units as u
from sbpy.activity import Afrho
afrho = Afrho(100 * u.cm)
afrho = Afrho('100 cm') # alternate initialization
afrho = Afrho(100, unit='cm') # alternate initialization
print(afrho)
# Arithmetic works as usual:
print(afrho * 2)
# unit conversion, too
print(afrho.to('m'))
```
### Afρ from observed continuum flux density
`Afrho` can also be initialized from continuum flux densities. Let's work with some photometry of comet 46P/Wirtanen by [Farnham & Schleicher (1998)](https://ui.adsabs.harvard.edu/#abs/1998A&A...335L..50F/abstract). The following observations were taken through the IHW blue continuum filter (λ=4845 Å).
```
import numpy as np
# comet ephemeris as a dictionary:
eph = {
'rh': [1.12, 1.14, 1.07, 1.49, 1.72] * u.au,
'delta': [1.41, 1.60, 1.54, 1.96, 2.31] * u.au,
'phase': [45, 38, 40, 31, 24] * u.deg
}
# observational data:
wave = 4845 * u.AA
rho = 10**np.array((4.29, 4.64, 4.49, 5.03, 4.96)) * u.km
fluxd = 10**np.array((-13.74, -13.84, -13.48, -14.11, -14.30)) * u.erg / (u.cm**2 * u.s * u.AA)
afrho = Afrho.from_fluxd(wave, fluxd, rho, eph)
print(afrho)
```
Compare with the Farnham et al. values:
```
f98 = 10**np.array((2.05, 1.71, 2.14, 1.47, 1.61)) * u.cm
print('Mean percent difference: {:.1%}'.format(np.mean(np.abs(afrho - f98) / f98)))
```
### Afρ and sbpy's solar spectrum
The few percent difference is due to the assumed solar flux density. We asked for the conversion at a specific wavelength, but the observation was through a filter with a specific width. With the `spectroscopy` module we can show the solar flux density used:
```
from sbpy.spectroscopy.sun import default_sun
sun = default_sun.get()
print(sun(wave, unit=fluxd.unit))
```
But rather than having `sbpy` compute the solar flux density at 1 au, we can pass the precomputed value for this filter from [A'Hearn et al. 1995](https://ui.adsabs.harvard.edu/#abs/1995Icar..118..223A/abstract):
```
S = 189.7 * u.erg / (u.cm**2 * u.s * u.AA)
afrho = Afrho.from_fluxd(None, fluxd, rho, eph, S=S)
print('Mean percent difference: {:.1%}'.format(np.mean(np.abs(afrho - f98) / f98)))
```
In the future, we will be able to provide the filter transmission and have `sbpy` automatically compute the mean solar flux density in the filter.
## Dust thermal emission via εfρ
Dust can also be modeled with εfρ, a thermal emission corollary to Afρ ([Kelley et al. 2013](https://ui.adsabs.harvard.edu/#abs/2013Icar..225..475K/abstract)). Albedo is replaced with emissivity, and the solar spectrum with the Planck function. It is an approximation to the thermal emission from a comet that can be useful for observation planning and making comet-to-comet comparisions:
$$ \epsilon f \rho = \frac{F_\lambda}{\pi \rho B_\lambda(T_c)} $$
where $B_\lambda(T_c)$ is the Planck function evaluated at the apparent continuum temperature $T_c$. The parameter is has units of length and is included in sbpy as the `Efrho` class.
The continuum temperature is parameterized with respect to the temperature of an isothermal blackbody sphere in LTE:
$$ T_{scale} = \frac{T_c}{278\,r_h^{-0.5}} $$
Plot a model spectrum of comet 46P/Wirtanen in December 2018 from 0.3 to 30 μm, varying the contintuum temperature:
```
import numpy as np
import matplotlib.pyplot as plt
import astropy.units as u
from sbpy.activity import Afrho, Efrho
from sbpy.spectroscopy.sun import default_sun
%matplotlib notebook
afrho = Afrho(100 * u.cm)
efrho = Efrho(afrho * 3.5)
# comet 46P/Wirtanen on 13 Dec 2018 as observed by Earth
eph = {
'rh': 1.055 * u.au,
'delta': 0.080 * u.au,
'phase': 27 * u.deg
}
wave = np.logspace(-0.5, 1.5, 1000) * u.um
rho = 1 * u.arcsec
fsca = afrho.fluxd(wave, rho, eph)
fth = efrho.fluxd(wave, rho, eph, Tscale=1.1)
ftot = fsca + fth
fig = plt.figure(1)
fig.clear()
ax = fig.add_subplot(111)
for Tscale in [1.0, 1.1, 1.2]:
fth = efrho.fluxd(wave, rho, eph, Tscale=Tscale)
T = Tscale * 278 * u.K / np.sqrt(eph['rh'] / u.au)
ax.plot(wave, wave * fth, label="{:.0f}".format(T))
ax.plot(wave, wave * fsca)
ax.plot(wave, wave * ftot, color='k')
plt.setp(ax, xlabel='Wavelength (μm)', xscale='log',
ylabel='$\lambda F_\lambda$ (W/m$^2$)', ylim=[1e-15, 1e-12], yscale='log')
ax.legend()
plt.tight_layout()
```
| true |
code
| 0.665872 | null | null | null | null |
|
# Retroceso de Fase (Phase Kickback)
En esta página, cubriremos un comportamiento de compuertas cuánticas controladas conocido como "retroceso de fase" (phase kickback). Este interesante efecto cuántico es un bloque de construcción en muchos algoritmos cuánticos famosos, incluido el algoritmo de factorización de Shor y el algoritmo de búsqueda de Grover.
## Vectores propios
Ya deberías estar familiarizado con los vectores propios y los valores propios, pero si no, puedes leer una buena introducción [aquí](https://www.khanacademy.org/math/linear-algebra/alternate-bases/eigen-everything/v/linear-algebra-introduction-to-eigenvalues-and-eigenvectors) . Si *estás* familiarizado, entonces deberías reconocer la ecuación de vector propio:
$$ \class{_matrix-A}{A}\class{_eig-vec-A}{|x\rangle} = \class{_eig-val-A}{\lambda}\class{_eig-vec-A}{|x\rangle} $$
Esto es aún más simple en la computación cuántica. Dado que todos nuestros vectores de estado tienen una magnitud de 1, nuestros valores propios también deben tener una magnitud de 1, es decir, $\lambda = e^{2\pi i \theta}$. Entonces, para una compuerta cuántica $U$ y su estado propio $|x\rangle$, tenemos:
$$ \class{_matrix-U}{U}\class{_eig-vec-U}{|x\rangle} = \class{_eig-val-U}{e^{2\pi i \theta}}\class{_eig-vec-U}{|x\rangle} $$
Para resumir: si una compuerta gira (y solo gira) todas las amplitudes de un vector de estado en la misma cantidad, entonces ese estado es un *estado* propio de esa compuerta.
<!-- ::: q-block -->
### Explorando los vectores propios
Usa el widget a continuación para ver cómo una compuerta de un solo qubit transforma un estado de un solo qubit. ¿Puedes averiguar qué estados son propios y de qué compuertas?
```
q-eigenvector-widget
```
<!-- ::: -->
## Compuertas controladas y estados propios
Una vez que te sientas cómodo con el concepto de estados propios, podemos comenzar a pensar en lo que sucede cuando controlamos estos circuitos en el estado de otro qubit. Por ejemplo, sabemos que la compuerta Z que actúa sobre el estado $|1\rangle$ introduce una fase global negativa ($\theta = 0.5$), averigüemos qué sucede cuando controlamos esta operación.
<!-- ::: q-block.tabs -->
### La compuerta Z controlada
<!-- ::: tab -->
### |10〉
<!-- ::: column(width=200) -->
Si el qubit de control es $|0\rangle$, entonces el comportamiento es trivial, no pasa nada.
<!-- ::: column(width=400) -->

<!-- ::: -->
<!-- ::: tab -->
### |11〉
<!-- ::: column(width=200) -->
Si el qubit de control es $|1\rangle$, la compuerta introduce una fase global (observa el signo menos en la imagen de la derecha), pero los estados del qubit no cambian.
<!-- ::: column(width=400) -->

<!-- ::: -->
<!-- ::: tab -->
### |1+〉
<!-- ::: column(width=200) -->
La compuerta Z controlada no hace nada cuando el control es $|0\rangle$, e introduce una fase negativa cuando el control es $|1\rangle$. Cuando el qubit de control está en superposición, la compuerta cambia la fase *relativa* entre los estados $|0\rangle$ y $|1\rangle$ del qubit de control.
<!-- ::: column(width=400) -->

<!-- ::: -->
<!-- ::: -->
<!-- ::: -->
Cuando el control es $|{+}\rangle$, y el objetivo es $|1\rangle$, la compuerta Z controlada cambia el estado del qubit de *control* , pero deja el qubit objetivo sin cambios. Este efecto se denomina "retroceso de fase" (phase kickback), ya que el valor propio regresa al estado del qubit de control.
En términos más generales, si tenemos una compuerta cuántica $U$ y su estado propio $|x\rangle$, entonces $U$ actuando sobre $|x\rangle$ agregará una fase global $\theta$ como vimos anteriormente.
$$ \class{_matrix-U}{U}\class{_eig-vec-U}{|x\rangle} = \class{_eig-val-U}{e^{2\pi i \theta}}\class{_eig-vec-U}{|x\rangle} $$
Si controlamos la operación $U|x\rangle$ por otro qubit en una superposición de $|0\rangle$ y $|1\rangle$, entonces esto tendrá el efecto de rotar el qubit de control alrededor del eje Z por un ángulo $\theta$. Es decir:
$$ \class{_matrix-CU}{CU}\class{_eig-vec-U}{|x\rangle}\class{_control-qubit-pre}{(\alpha|0\rangle + \beta|1\rangle)} = \class{_eig-vec-U}{|x\rangle}\class{_control-qubit-post}{(\alpha|0\rangle + \beta e^{2\pi i \theta}|1\rangle)} $$
En el ejemplo anterior, vemos que el 'control' de la compuerta Z controlada en realidad está haciendo una rotación en Z; algo que solo debería haber estado observando el qubit que ha cambiado. Por esta razón, a menudo verás la compuerta Z controlada dibujada como dos controles.
```
from qiskit import QuantumCircuit
qc = QuantumCircuit(2)
qc.cz(0,1)
qc.draw()
```
## La Compuerta CNOT
Veamos el efecto de retroceso de fase con una compuerta diferente de dos qubits. Dado que el estado $|{-}\rangle$ es un estado propio de la compuerta X, con valor propio $-1$, obtenemos:
$$ \class{_matrix-CX}{CX}\class{_eig-vec-X}{|{-}\rangle}\class{_control-qubit-pre}{(\alpha|0\rangle + \beta|1\rangle)} = \class{_eig-vec-X}{|{-}\rangle}\class{_control-qubit-post}{(\alpha|0\rangle - \beta |1\rangle)} $$

Nuevamente, en este caso el cambio de fase es $\theta = 0.5$, por lo que nuestro qubit de control se voltea alrededor del eje Z.
<!-- ::: q-block -->
### Ejemplo resuelto
<details>
<summary>Retroceso con la compuerta CNOT (haz clic para expander)</summary>
q-carousel
div.md
<img src="images/kickback/carousel/cnot/carousel-img-0.svg"><br>Por definición, la compuerta X controlada (CNOT) cambia el estado del qubit objetivo (en nuestro ejemplo, el bit más a la derecha es el objetivo) si el qubit de control es $|1\rangle$. En la imagen de arriba, mostramos la compuerta CNOT transformando un vector de estado a otro.
div.md
<img src="images/kickback/carousel/cnot/carousel-img-1.svg"><br>Por ejemplo, si el qubit de control está en el estado $|0\rangle$, siempre obtenemos exactamente el mismo vector de estado. En la imagen de arriba, las amplitudes de los estados donde el control es $|1\rangle$ son cero, por lo que no vemos ningún efecto cuando los intercambiamos.
div.md
<img src="images/kickback/carousel/cnot/carousel-img-2.svg"><br>Otro ejemplo: si el qubit de control está en el estado $|1\rangle$, entonces usamos una compuerta X en el qubit objetivo. En este caso, el qubit objetivo está en un estado propio de la compuerta X, por lo que obtenemos el mismo vector de estado, hasta la fase global. Este cambio es una fase global, ya que la fase relativa entre las amplitudes $|0\rangle$ y $|1\rangle$ del qubit objetivo permaneció igual.
div.md
<img src="images/kickback/carousel/cnot/carousel-img-3.svg"><br>Veamos el vector de estado cuando el control está en el estado $|{+}\rangle$ (es decir, $\tfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$), y el objetivo en el estado $|{-}\rangle$ (es decir, $\tfrac{1}{\sqrt{2}}(|0\rangle - |1\rangle)$). Podemos ver que estos dos qubits son separables, ya que medir uno no afecta el estado del otro.
div.md
<img src="images/kickback/carousel/cnot/carousel-img-4.svg"><br> Por ejemplo, independientemente de si medimos el qubit de control como $|0\rangle$ o $|1\rangle$, las amplitudes para medir el objetivo como $|0\rangle$ o $|1\rangle$ permanecen iguales.
div.md
<img src="images/kickback/carousel/cnot/carousel-img-5.svg"><br>Con todo esto en mente, veamos qué sucede cuando aplicamos el CNOT a este estado $|{+}{-}\rangle$.
div.md
<img src="images/kickback/carousel/cnot/carousel-img-6.svg"><br>Después del CNOT, estos qubits siguen siendo separables, ya que el estado de uno no cambia cuando medimos el otro. Sin embargo, la fase relativa entre las amplitudes $|0\rangle$ y $|1\rangle$ del qubit de control ha cambiado.
</details>
<!-- ::: -->
Cuando recordamos que la compuerta H hace la transformación $|0\rangle \rightarrow |{+}\rangle$ y $|1\rangle \rightarrow |{-}\rangle$ (y viceversa), obtenemos lo siguiente identidad:

## El problema de Deutsch
Acabamos de ver que condicionar una acción en el estado de un qubit en realidad puede cambiar el estado del qubit de control. Este es un efecto 'cuántico', es decir, algo que no vemos que suceda con los bits clásicos.
En la computación cuántica, queremos crear algoritmos que las computadoras clásicas *no puedan* ejecutar, por lo que un buen lugar para comenzar es tratar de replantear este efecto como un problema a resolver. De esta manera, podemos probar que las computadoras cuánticas son al menos un poco mejores en algo que las computadoras clásicas.
El problema de Deutsch hace exactamente esto. Este es un problema de 'caja negra'; un problema artificial en el que se nos permite aplicar una función a nuestros bits, pero no podemos ver cómo opera la función. El desafío es descubrir algunas propiedades de la caja probando diferentes entradas y salidas.
El problema de Deutsch es el siguiente: tenemos una función reversible clásica (a la que llamaremos $f$ de forma abreviada), que actúa sobre dos bits, $ a $ y $ b $. La función dejará el bit $ a $ solo, pero puede o no cambiar el bit $ b $. El problema de Deutsch nos pide que averigüemos si $f$ se comporta de manera diferente dependiendo del valor de $ a $ (lo llamaremos comportamiento "balanceado"), o si ignora a $ a $ y siempre hace lo mismo con $ b $ (comportamiento "constante"). El desafío es hacer esto aplicando $f$ la menor cantidad de veces posible.

El mejor algoritmo clásico para este problema aplica $f$ dos veces con diferentes valores de $ a $, luego observa si $f$ se comportó de manera diferente.
## Algoritmo de Deutsch
Como habrás adivinado, podemos usar el retroceso de fase (phase kickback) para crear un algoritmo cuántico que funciona incluso mejor que el algoritmo clásico. Si ponemos el qubit $ a $ en el estado $|{+}\rangle$ y el qubit $ b $ en el estado $|{-}\rangle$, entonces cualquier cambio condicionado a $ a $ devolverá una fase negativa relativa, volteando al qubit $ a $ de $|{+}\rangle$ a $|{-}\rangle$. Luego podemos aplicar una compuerta H a $ a $ para ver si se produjo un retroceso de fase o no.

<!-- ::: q-block.reminder -->
### Más información
<details><summary>Dentro de la caja negra (haz clic para ampliar)</summary> Si esto todavía parece mágico, puede ayudar pensar en todas las posibles funciones de Deutsch y los circuitos cuánticos que las implementan. Hay cuatro posibles funciones de Deutsch: dos constantes y dos balanceadas.</details>
Si es constante, la función puede no hacer nada o voltear el qubit $ b $. Si está balanceada, la función puede voltear a $ b $ solo cuando $ a $ es $|1\rangle$, o voltear a $ b $ solo cuando $ a $ es $|0\rangle$. Puedes ver los cuatro escenarios en la imagen a continuación.
<img src="images/kickback/deutsch-oracles.svg">
Con ambas funciones constantes, el qubit superior permanecerá sin cambios (ya que no le estamos haciendo nada), y con las funciones equilibradas, el efecto de retroceso cambia el qubit superior de $|{+}\rangle$ a $|{- }\rangle$.
<!-- ::: -->
Este no es el ejemplo más impresionante de aceleración cuántica; es muy específico y no encontramos problemas de caja negra en la naturaleza. En cambio, el problema de Deutsch nos da un resultado alentador y algunos efectos interesantes para ser explorados. En el resto de este curso, ampliaremos este sencillo experimento para resolver problemas aún más impresionantes, incluida la factorización.
<!-- ::: q-block.exercise -->
### Ejercicio
Haz una función, `deutsch()` que tome una función Deutsch como `QuantumCircuit` y use el algoritmo Deutsch para resolverlo en un simulador cuántico. Tu función debe devolver `True` si la función Deutsch está balanceada y `False` si es constante.
Puedes usar la función `deutsch_problem()` para crear un `QuantumCircuit` que puedes usar como entrada para tu función `deutsch()`.
<!-- ::: -->
```
from qiskit import QuantumCircuit
import numpy as np
def deutsch_problem(seed=None):
"""Devuelve un circuito que realiza la función del
problema de Deutsch.
Args:
seed (int): Si se establece, el circuito devuelto
siempre será el mismo para la misma semilla.
Returns: QuantumCircuit
"""
np.random.seed(seed)
problem = QuantumCircuit(2)
if np.random.randint(2):
print("La función es balanceada.")
problem.cx(0, 1)
else:
print("La función es constante.")
if np.random.randint(2):
problem.x(1)
return problem
def deutsch(function):
"""Implementa el algoritmo de Deutsch.
Args:
function (QuantumCircuit): Función Deutsch a ser resuelta.
Debe ser un circuito de 2 qubits ya sea balanceado
o constante.
Returns:
bool: True si el circuito está balanceado,
de lo contrario False.
"""
# tu código aquí
```
## Resumen
En esta página revisamos:
- recapitulación del concepto de valores y vectores propios
- exploración del efecto de retroceso de fase (phase kickback) y revisión de algunos ejemplos específicos
- se introdujo el problema de Deutsch como un escenario donde las computadoras cuánticas tienen una ventaja sobre las computadoras clásicas
Si olvidas todo lo demás de esta página, lo más importante que debes recordar y sentirte cómodo es este resumen de retroceso de fase a continuación:
<!-- ::: q-block.reminder -->
### Recordatorio: Retroceso de fase (Phase kickback)
Si tenemos una compuerta cuántica $U$ y su estado propio $|x\rangle$, entonces $U$ actuando sobre $|x\rangle$ agregará una fase global $\theta$. Es decir:
$$ \class{_matrix-U}{U}\class{_eig-vec-U}{|x\rangle} = \class{_eig-val-U}{e^{2\pi i \theta}}\class{_eig-vec-U}{|x\rangle} $$
Si controlamos la operación $U|x\rangle$ por otro qubit en una superposición de $|0\rangle$ y $|1\rangle$, entonces esto tendrá el efecto de rotar el qubit de control alrededor del eje Z por un ángulo $\theta$. Es decir:
$$ \class{_matrix-CU}{CU}\class{_eig-vec-U}{|x\rangle}\class{_control-qubit-pre}{(\alpha|0\rangle + \beta|1\rangle)} = \class{_eig-vec-U}{|x\rangle}\class{_control-qubit-post}{(\alpha|0\rangle + \beta e^{2\pi i \theta}|1\rangle)} $$
<!-- ::: -->
| true |
code
| 0.643105 | null | null | null | null |
|
# Plotting and Visualization
```
from __future__ import division
from numpy.random import randn
import numpy as np
import os
import matplotlib.pyplot as plt
np.random.seed(12345)
plt.rc('figure', figsize=(10, 6))
from pandas import Series, DataFrame
import pandas as pd
np.set_printoptions(precision=4)
%matplotlib inline
%pwd
```
## A brief matplotlib API primer
### Figures and Subplots
```
fig = plt.figure()
ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
fig
from numpy.random import randn
ax3.plot(randn(50).cumsum(), 'k--')
'''sort of random walk'''
_ = ax1.hist(randn(100), bins=20, color='k', alpha=0.3)
ax2.scatter(np.arange(30), np.arange(30) + 3 * randn(30))
fig
plt.close('all')
fig, axes = plt.subplots(2, 3)
axes
```
#### Adjusting the spacing around subplots
```
plt.subplots_adjust(left=None, bottom=None, right=None, top=None,
wspace=None, hspace=None)
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True)
for i in range(2):
for j in range(2):
axes[i, j].hist(randn(500), bins=50, color='k', alpha=0.5)
plt.subplots_adjust(wspace=0, hspace=0)
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True)
for i in range(2):
for j in range(2):
#two for loop are designed for plot four figures secsussionally
axes[i, j].hist(randn(500), bins=50, color='k', alpha=0.5)
plt.subplots_adjust(wspace=0, hspace=0)
```
### Colors, markers, and line styles
```
plt.plot(randn(30).cumsum(), 'ko--')
#this is so-called random walking
data = randn(30).cumsum()
plt.plot(data, 'k--', label='Default')
plt.plot(data, 'k-', drawstyle='steps-post', label='steps-post')
plt.legend(loc='best')
```
### Ticks, labels, and legends
#### Setting the title, axis labels, ticks, and ticklabels
```
fig = plt.figure(); ax = fig.add_subplot(1, 1, 1)
ax.plot(randn(1000).cumsum())
ticks = ax.set_xticks([0, 250, 500, 750, 1000])
labels = ax.set_xticklabels(['one', 'two', 'three', 'four', 'five'],
rotation=30, fontsize='small')
ax.set_title('My first matplotlib plot')
ax.set_xlabel('Stages')
```
#### Adding legends
```
#Random Walk for 3 times
fig = plt.figure(); ax = fig.add_subplot(1, 1, 1)
ax.plot(randn(1000).cumsum(), 'k', label='one')
ax.plot(randn(1000).cumsum(), 'k--', label='two')
ax.plot(randn(1000).cumsum(), 'k.', label='three')
ax.legend(loc='best') # choose the best location for the legend location
```
### Annotations and drawing on a subplot
```
'''for the error, it is because that the lack of local data file'''
from datetime import datetime
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
data = pd.read_csv('ch08/spx.csv', index_col=0, parse_dates=True)
spx = data['SPX']
spx.plot(ax=ax, style='k-')
crisis_data = [
(datetime(2007, 10, 11), 'Peak of bull market'),
(datetime(2008, 3, 12), 'Bear Stearns Fails'),
(datetime(2008, 9, 15), 'Lehman Bankruptcy')
]
for date, label in crisis_data:
ax.annotate(label, xy=(date, spx.asof(date) + 50),
xytext=(date, spx.asof(date) + 200),
arrowprops=dict(facecolor='black'),
horizontalalignment='left', verticalalignment='top')
# Zoom in on 2007-2010
ax.set_xlim(['1/1/2007', '1/1/2011'])
ax.set_ylim([600, 1800])
ax.set_title('Important dates in 2008-2009 financial crisis')
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
rect = plt.Rectangle((0.2, 0.75), 0.4, 0.15, color='k', alpha=0.3)
circ = plt.Circle((0.7, 0.2), 0.15, color='b', alpha=0.3)
pgon = plt.Polygon([[0.15, 0.15], [0.35, 0.4], [0.2, 0.6]],
color='g', alpha=0.5)
ax.add_patch(rect)
ax.add_patch(circ)
ax.add_patch(pgon)
```
### Saving plots to file
```
from io import BytesIO
buffer = BytesIO()
plt.savefig(buffer)
plot_data = buffer.getvalue()
```
### matplotlib configuration
```
plt.rc('figure', figsize=(10, 10))
```
## Plotting functions in pandas
### Line plots
```
plt.close('all')
s = Series(np.random.randn(10).cumsum(), index=np.arange(0, 100, 10))
s.plot()
df = DataFrame(np.random.randn(10, 4).cumsum(0),
columns=['A', 'B', 'C', 'D'],
index=np.arange(0, 100, 10))
df.plot()
```
### Bar plots
```
fig, axes = plt.subplots(2, 1)
data = Series(np.random.rand(16), index=list('abcdefghijklmnop'))
data.plot(kind='bar', ax=axes[0], color='k', alpha=0.7)
data.plot(kind='barh', ax=axes[1], color='k', alpha=0.7)
df = DataFrame(np.random.rand(6, 4),
index=['one', 'two', 'three', 'four', 'five', 'six'],
columns=pd.Index(['A', 'B', 'C', 'D'], name='Genus'))
df
df.plot(kind='bar')
#try a different plot kind, and with stacked
df.plot(kind='barh', stacked=True, alpha=0.5)
```
### Histograms and density plots
```
comp1 = np.random.normal(0, 1, size=200) # N(0, 1)
comp2 = np.random.normal(10, 2, size=200) # N(10, 4)
values = Series(np.concatenate([comp1, comp2]))
values.hist(bins=100, alpha=0.3, color='k', normed=True)
values.plot(kind='kde', style='k--')
```
## Plotting Maps: Visualizing Haiti Earthquake Crisis data
```
def to_cat_list(catstr):
stripped = (x.strip() for x in catstr.split(','))
return [x for x in stripped if x]
def get_all_categories(cat_series):
cat_sets = (set(to_cat_list(x)) for x in cat_series)
return sorted(set.union(*cat_sets))
def get_english(cat):
code, names = cat.split('.')
if '|' in names:
names = names.split(' | ')[1]
return code, names.strip()
get_english('2. Urgences logistiques | Vital Lines')
```
**The rest part of codes I leaved blank here, because it is required to load local data files, but the basic idea is similiar with previous part**
| true |
code
| 0.648299 | null | null | null | null |
|
```
#Importing openCV
import cv2
#Displaying image
image = cv2.imread('test_image.jpg')
cv2.imshow('input_image', image)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
### Converting the image to grayscale
```
import cv2
import numpy as np
image = cv2.imread('test_image.jpg')
lanelines_image = np.copy(image)
gray_conversion= cv2.cvtColor(lanelines_image, cv2.COLOR_RGB2GRAY)
#Displaying grayscale image
cv2.imshow('input_image', gray_conversion)
cv2.waitKey(0)
cv2.destroyAllWindows()
#Smoothing the image
import cv2
import numpy as np
image = cv2.imread('test_image.jpg')
lanelines_image = np.copy(image)
gray_conversion= cv2.cvtColor(lanelines_image, cv2.COLOR_RGB2GRAY)
blur_conversion = cv2.GaussianBlur(gray_conversion, (5,5),0)
cv2.imshow('input_image', blur_conversion)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
### Canny edge detection
```
import cv2
import numpy as np
image = cv2.imread('test_image.jpg')
lanelines_image = np.copy(image)
gray_conversion= cv2.cvtColor(lanelines_image, cv2.COLOR_RGB2GRAY)
blur_conversion = cv2.GaussianBlur(gray_conversion, (5,5),0)
canny_conversion = cv2.Canny(blur_conversion, 50,155)
cv2.imshow('input_image', canny_conversion)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
### Masking the region of interest
```
import cv2
import numpy as np
import matplotlib.pyplot as plt
def canny_edge(image):
gray_conversion= cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
blur_conversion = cv2.GaussianBlur(gray_conversion, (5,5),0)
canny_conversion = cv2.Canny(blur_conversion, 50,150)
return canny_conversion
def reg_of_interest(image):
Image_height = image.shape[0]
polygons = np.array([[(200, Image_height), (1100, Image_height), (550, 250)]])
image_mask = np.zeros_like(image)
cv2.fillPoly(image_mask, polygons, 255)
return image_mask
image = cv2.imread('test_image.jpg')
lanelines_image = np.copy(image)
canny_conversion = canny_edge(lanelines_image)
cv2.imshow('result', reg_of_interest(canny_conversion))
cv2.waitKey(0)
cv2.destroyAllWindows()
# Applying bitwise_and
import cv2
import numpy as np
import matplotlib.pyplot as plt
def canny_edge(image):
gray_conversion= cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
blur_conversion = cv2.GaussianBlur(gray_conversion, (5,5),0)
canny_conversion = cv2.Canny(blur_conversion, 50,150)
return canny_conversion
def reg_of_interest(image):
image_height = image.shape[0]
polygons = np.array([[(200, image_height), (1100, image_height), (551, 250)]])
image_mask = np.zeros_like(image)
cv2.fillPoly(image_mask, polygons, 255)
masking_image = cv2.bitwise_and(image,image_mask)
return masking_image
image = cv2.imread('test_image.jpg')
lanelines_image = np.copy(image)
canny_conversion = canny_edge(lanelines_image)
cropped_image = reg_of_interest(canny_conversion)
cv2.imshow('result', cropped_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
#Applying the Hough transform
import cv2
import numpy as np
import matplotlib.pyplot as plt
def canny_egde(image):
gray_conversion= cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
blur_conversion = cv2.GaussianBlur(gray_conversion, (5,5),0)
canny_conversion = cv2.Canny(blur_conversion, 50,150)
return canny_conversion
def reg_of_interest(image):
image_height = image.shape[0]
polygons = np.array([[(200, image_height), (1100, image_height), (551, 250)]])
image_mask = np.zeros_like(image)
cv2.fillPoly(image_mask, polygons, 255)
masking_image = cv2.bitwise_and(image,image_mask)
return masking_image
def show_lines(image, lines):
lines_image = np.zeros_like(image)
if lines is not None:
for line in lines:
X1, Y1, X2, Y2 = line.reshape(4)
cv2.line(lines_image, (X1, Y1), (X2, Y2), (255,0,0), 10)
return lines_image
image = cv2.imread('test_image.jpg')
lanelines_image = np.copy(image)
canny_conv = canny_edge(lanelines_image)
cropped_image = reg_of_interest(canny_conv)
lane_lines = cv2.HoughLinesP(cropped_image, 2, np.pi/180, 100, np.array([]), minLineLength= 40, maxLineGap=5)
linelines_image = show_lines(lanelines_image, lane_lines)
cv2.imshow('result', linelines_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
#Combining with actual image
image = cv2.imread('test_image.jpg')
lane_image = np.copy(image)
canny = canny_edge(lane_image)
cropped_image = reg_of_interest(canny)
lines = cv2.HoughLinesP(cropped_image, 2, np.pi/180, 100, np.array([]), minLineLength= 40, maxLineGap=5)
line_image = show_lines(lane_image, lines)
combine_image = cv2.addWeighted(lane_image, 0.8, line_image, 1, 1)
cv2.imshow('result', combine_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
### Detect road marking in images
```
#Optimization the detected road markings
import cv2
import numpy as np
import matplotlib.pyplot as plt
def make_coordinates(image, line_parameters):
slope, intercept = line_parameters
y1 = image.shape[0]
y2 = int(y1*(3/5))
x1 = int((y1- intercept)/slope)
x2 = int((y2 - intercept)/slope)
return np.array([x1, y1, x2, y2])
def average_slope_intercept(image, lines):
left_fit = []
right_fit = []
for line in lines:
x1, y1, x2, y2 = line.reshape(4)
parameter = np.polyfit((x1, x2), (y1, y2), 1)
slope = parameter[0]
intercept = parameter[1]
if slope < 0:
left_fit.append((slope, intercept))
else:
right_fit.append((slope, intercept))
left_fit_average =np.average(left_fit, axis=0)
right_fit_average = np.average(right_fit, axis =0)
left_line =make_coordinates(image, left_fit_average)
right_line = make_coordinates(image, right_fit_average)
return np.array([left_line, right_line])
def canny_edge(image):
gray_coversion= cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
blur_conversion = cv2.GaussianBlur(gray_conversion, (5,5),0)
canny_conversion = cv2.Canny(blur_conversion, 50,150)
return canny_conversion
def show_lines(image, lines):
lanelines_image = np.zeros_like(image)
if lines is not None:
for line in lines:
X1, Y1, X2, Y2 = line.reshape(4)
cv2.line(lanelines_image, (X1, Y1), (X2, Y2), (255,0,0), 10)
return lanelines_image
def reg_of_interest(image):
image_height = image.shape[0]
polygons = np.array([[(200, image_height), (1100, image_height), (551, 250)]])
image_mask = np.zeros_like(image)
cv2.fillPoly(image_mask, polygons, 255)
masking_image = cv2.bitwise_and(image,image_mask)
return masking_image
image = cv2.imread('test_image.jpg')
lanelines_image = np.copy(image)
canny_image = canny_edge(lanelines_image)
cropped_image = reg_of_interest(canny_image)
lines = cv2.HoughLinesP(cropped_image, 2, np.pi/180, 100, np.array([]), minLineLength= 40, maxLineGap=5)
averaged_lines = average_slope_intercept(lanelines_image, lines)
line_image = show_lines(lanelines_image, averaged_lines)
combine_image = cv2.addWeighted(lanelines_image, 0.8, line_image, 1, 1)
cv2.imshow('result', combine_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
### Detecting road markings in video
```
#Detecting road markings in video
import cv2
import numpy as np
import matplotlib.pyplot as plt
def make_coordinates(image, line_parameters):
try:
slope, intercept = line_parameters
except TypeError:
slope, intercept = 0.001,0
#slope, intercept = line_parameters
y1 = image.shape[0]
y2 = int(y1*(3/5))
x1 = int((y1- intercept)/slope)
x2 = int((y2 - intercept)/slope)
return np.array([x1, y1, x2, y2])
def average_slope_intercept(image, lines):
left_fit = []
right_fit = []
for line in lines:
x1, y1, x2, y2 = line.reshape(4)
parameter = np.polyfit((x1, x2), (y1, y2), 1)
slope = parameter[0]
intercept = parameter[1]
if slope < 0:
left_fit.append((slope, intercept))
else:
right_fit.append((slope, intercept))
left_fit_average =np.average(left_fit, axis=0)
right_fit_average = np.average(right_fit, axis =0)
left_line =make_coordinates(image, left_fit_average)
right_line = make_coordinates(image, right_fit_average)
return np.array([left_line, right_line])
def canny_edge(image):
gray_conversion= cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
blur_conversion = cv2.GaussianBlur(gray_conversion, (5,5),0)
canny_conversion = cv2.Canny(blur_conversion, 50,150)
return canny_conversion
def show_lines(image, lines):
line_image = np.zeros_like(image)
if lines is not None:
for line in lines:
x1, y1, x2, y2 = line.reshape(4)
cv2.line(line_image, (x1, y1), (x2, y2), (255,0,0), 10)
return line_image
def reg_of_interest(image):
image_height = image.shape[0]
polygons = np.array([[(200, image_height), (1100, image_height), (550, 250)]])
image_mask = np.zeros_like(image)
cv2.fillPoly(image_mask, polygons, 255)
masking_image = cv2.bitwise_and(image,image_mask)
return masking_image
cap = cv2.VideoCapture("test2.mp4")
while(cap.isOpened()):
_, frame = cap.read()
canny_image = canny_edge(frame)
cropped_canny = reg_of_interest(canny_image)
lines = cv2.HoughLinesP(cropped_canny, 2, np.pi/180, 100, np.array([]), minLineLength=40,maxLineGap=5)
averaged_lines = average_slope_intercept(frame, lines)
line_image = show_lines(frame, averaged_lines)
combo_image = cv2.addWeighted(frame, 0.8, line_image, 1, 1)
cv2.imshow("result", combo_image)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cap.release()
cv2.waitKey(0)
cv2.destroyAllWindows()
```
| true |
code
| 0.364834 | null | null | null | null |
|
# _MiSTree Tutorial 2_ - Minimum Spanning Trees
## (1) _Basic Usage_
To construct the minimum spanning tree (MST) from a data set we will usually
interact with the ``get_mst`` class. Unless you need to do something more sophisticated
with the MST you will not need to use the internal functions that are used by the class.
To initiate the class we will run:
```
from __future__ import print_function
import numpy as np
import matplotlib.pylab as plt
import mistree as mist
```
### (1.1) _Initialising_
#### _In 2D_
```
x = np.random.random_sample(1000)
y = np.random.random_sample(1000)
mst = mist.GetMST(x=x, y=y)
```
#### _In 3D_
```
x = np.random.random_sample(1000)
y = np.random.random_sample(1000)
z = np.random.random_sample(1000)
mst = mist.GetMST(x=x, y=y, z=z)
```
#### _In Tomographic Coordinates_
We generate a uniform random distribution on the sphere.
```
phi = 360.*np.random.random_sample(1000)
theta = np.rad2deg(np.arccos(1.-2.*np.random.random_sample(1000)))
mst = mist.GetMST(phi=phi, theta=theta)
```
#### _In Tomographic Celestial Coordinates_
Once again using a uniform random distribution on the sphere.
```
ra = 360.*np.random.random_sample(1000)
dec = np.rad2deg(np.arccos(1.-2.*np.random.random_sample(1000))) - 90.
mst = mist.GetMST(ra=ra, dec=dec)
```
#### _In Spherical Polar Coordinates_
This generates a uniform distribution of points with a sphere of radius 10.
```
phi = 360.*np.random.random_sample(1000)
theta = np.rad2deg(np.arccos(1.-2.*np.random.random_sample(1000)))
r = 10.*(np.random.random_sample(1000))**(1./3.)
mst = mist.GetMST(phi=phi, theta=theta, r=r)
```
#### _In Spherical Celestial Coordinates_
This generates a uniform distribution of points with a sphere of radius 10.
```
ra = 360.*np.random.random_sample(1000)
dec = np.rad2deg(np.arccos(1.-2.*np.random.random_sample(1000))) - 90.
r = 10.*np.random.random_sample(1000)**(1./3.)
mst = mist.GetMST(ra=ra, dec=dec, r=r)
```
### (1.2) _Measure MST statistics_
And to construct the MST and output the MST statistics: degree (d), edge length (l),
branch length (b) and branch shape (s):
```
x = np.random.random_sample(1000)
y = np.random.random_sample(1000)
mst = mist.GetMST(x=x, y=y)
d, l, b, s = mst.get_stats()
```
If you would also like the edge (``l_index``) and branch index (``b_index``),
this can be done in two ways:
```
d, l, b, s, l_index, b_index = mst.get_stats(include_index=True)
# alternatively:
d, l, b, s = mst.get_stats()
l_index = mst.edge_index
b_index = mst.branch_index
```
The edge index (``l_index``) is a 2 dimensional array, indicating the pair of nodes
that make up each edge. The branch index are list of the member edges in each branches.
### (1.3) _Plotting the MST_
#### _Plotting Edges_
To plot the MST, i.e. the nodes and edges you can use the following piece of python code
where we plot a set of 2D random points:
```
x = np.random.random_sample(100)
y = np.random.random_sample(100)
mst = mist.GetMST(x=x, y=y)
d, l, b, s, l_index, b_index = mst.get_stats(include_index=True)
plt.figure(figsize=(7., 7.))
# plotting nodes:
plt.scatter(x, y, s=10, color='r')
# plotting MST edges:
plt.plot([x[l_index[0]], x[l_index[1]]],
[y[l_index[0]], y[l_index[1]]],
color='k')
plt.xlim(0., 1.)
plt.ylim(0., 1.)
plt.xlabel(r'$X$', size=16)
plt.ylabel(r'$Y$', size=16)
plt.tight_layout()
plt.show()
```
#### _Plotting Branches_
If you would also like to plot branches then you can use the following piece of python code:
```
plt.figure(figsize=(7., 7.))
# plotting nodes:
plt.scatter(x, y, s=10, color='r')
# plotting branches:
for i in range(0, len(b_index)):
plt.plot([x[l_index[0][b_index[i][0]]], x[l_index[1][b_index[i][0]]]],
[y[l_index[0][b_index[i][0]]], y[l_index[1][b_index[i][0]]]],
color='C0', linestyle=':')
plt.plot([x[l_index[0][b_index[i][1:-1]]], x[l_index[1][b_index[i][1:-1]]]],
[y[l_index[0][b_index[i][1:-1]]], y[l_index[1][b_index[i][1:-1]]]],
color='C0')
plt.plot([x[l_index[0][b_index[i][-1]]], x[l_index[1][b_index[i][-1]]]],
[y[l_index[0][b_index[i][-1]]], y[l_index[1][b_index[i][-1]]]],
color='C0', linestyle=':')
# ploting MST edges:
plt.plot([x[l_index[0]], x[l_index[1]]],
[y[l_index[0]], y[l_index[1]]],
color='grey', linewidth=2, alpha=0.25)
plt.plot([], [], color='C0', label=r'$Branch$ $Mid$')
plt.plot([], [], color='C0', label=r'$Branch$ $End$', linestyle=':')
plt.plot([], [], color='grey', alpha=0.25, label=r'$MST$ $Edges$')
plt.xlim(0., 1.)
plt.ylim(0., 1.)
plt.xlabel(r'$X$', size=16)
plt.ylabel(r'$Y$', size=16)
plt.legend(loc='best')
plt.tight_layout()
plt.show()
```
## (2) _Binning and Plotting_
### (2.1) _Quick Bin and Plot_
A very simple plot of the MST summary statistics can be generated using:
```
x = np.random.random_sample(1000)
y = np.random.random_sample(1000)
z = np.random.random_sample(1000)
mst = mist.GetMST(x=x, y=y, z=z)
d, l, b, s = mst.get_stats()
# begins by binning the data and storing this in a dictionary.
hmst = mist.HistMST()
hmst.setup()
mst_dict = hmst.get_hist(d, l, b, s)
# plotting which takes as input the dictionary created before.
pmst = mist.PlotHistMST()
pmst.read_mst(mst_dict)
pmst.plot()
```
The first ``HistMST`` class bins the data and stores it as a dictionary and the
``PlotHistMST`` class is used make the plot.
### (2.1) _Binning_
Once we have created the data set we need to bin the data. This is done by first
initialising the ``HistMST`` class and then setting it up. The most simple case
(using the default settings) is shown below.
```
hmst = mist.HistMST()
hmst.setup()
```
We can make the following changes:
```
# to bin in log_10(l) and log_10(b) rather than just l and b:
hmst.setup(uselog=True)
# to bin using s rather than sqrt(1-s)
hmst.setup(use_sqrt_s=False)
# to output the unnormalised histograms (i.e. just counts)
hmst.setup(usenorm=False)
# to change the range of the binning, the number of bins, etc:
# for the degree, although this is rarely necessary, please ensure the minimum
# and maximum are half integers and the number of bins is equal to maximum-minimum.
hmst.setup(d_min=0.5, d_max=6.5, num_d_bins=6) # these are the default values.
# for edge lengths, note the default values are l_min=0., l_max=1.05*l.max()
# and ``num_l_bins=100``.
hmst.setup(l_min=0., l_max=10., num_l_bins=100)
# for edge lengths, note the default value are b_min=0. and b_max=1.05*b.max()
# and ``num_b_bins=100``.
hmst.setup(b_min=0., b_max=10., num_b_bins=100)
# for branch shape in either projections the range can be altered by changing the following,
# however it will rarely be necessary to change from the default values of s_min=0 and s_max=1.,
# but you may want to alter the binning (default is 50).
hmst.setup(s_min=0., s_max=1., num_s_bins=50)
# if you are instead using $log_{10}l$ and $log_{10}b$ then you would specify the range
# by using the following but note the binning still uses num_l_bins and num_b_bins.
hmst.setup(logl_min=-2., logl_max=4., logb_min=-1, logb_max=5.)
```
Once this is done we can actually pass the MST statistics to the class and create a dictionary
of the binned statistics:
```
hmst = mist.HistMST()
hmst.setup(uselog=True)
mst_dict = hmst.get_hist(d, l, b, s)
```
The dictionary created is stored with the following entries:
```
print(mst_dict.keys())
```
- ``uselog`` : stores whether the bins for l and b are in logs.
- ``use_sqrt_s`` : stores whether the the bins for s are in s or sqrt(1-s)
- ``usenorm`` : stores whether the histograms are normalised.
- ``isgroup`` : stores whether the histogram come from a group of histograms (discussed later)
- ``x_d`` : bin centres for degree
- ``y_d`` : bin heights for degree
- ``x_l`` : bin centres for edge length
- ``y_l`` : bin heights for edge length
- ``x_b`` : bin centres for branch length
- ``y_b`` : bin heights for branch length
- ``x_s`` : bin centres for branch shape
- ``y_s`` : bin heights for branch shape
Finally, if we want to instead store the ensemble mean and standard deviation of a group of MSTs we would
add the individual MST to ``HistMST`` class in the following way:
```
hmst = mist.HistMST()
hmst.setup(uselog=True)
hmst.start_group() # this tells HistMST to store the individual binned MST statistics
for i in range(0, 10):
# Read or measure MST statistics, we will use the default levy flight distribution here
x, y, z = mist.get_levy_flight(50000)
mst = mist.GetMST(x=x, y=y, z=z)
d, l, b, s = mst.get_stats()
# we use it just as we did before, where the outputted dictionary is for that single
# realisation
mst_dict = hmst.get_hist(d, l, b, s)
print(i+1, '/ 10')
# to output the mean and standard deviation of the ensemble histograms.
mst_dict_group = hmst.end_group()
# you must use hmst.start_group() to start collecting MST statistics from another group
# otherwise this will continue collecting histograms for the current group
```
Similarly to before the dictionary contains many of the same elements with some additional ones.
```
print(mst_dict_group.keys())
```
- ``y_d_std`` : standard deviation for the bin heights for degree
- ``y_l_std`` : standard deviation for the bin heights for edge length
- ``y_b_std`` : standard deviation for the bin heights for branch length
- ``y_s_std`` : standard deviation for the bin heights for branch shape
This makes the assumption that the counts follow a Gaussian distribution, since these
are counts this actually follows a discrete Poisson distribution but for large values
a Gaussian is an appropriate approximation (usually greater than 50 should be okay).
This is important to consider if you use these summary statistics in regions where
the counts are small.
### (2.2) _Plotting_
You can choose to use this as well or use the default matplotlib fonts.
Once we have the binned MST dictionary we can plot it very simply using ``PlotHistMST`` class:
```
pmst = mist.PlotHistMST()
pmst.read_mst(mst_dict)
pmst.plot()
```
To alter how the plot looks we can alter the following:
```
pmst = mist.PlotHistMST()
pmst.read_mst(mst_dict, color='Dodgerblue', linewidth=2., linestyle='--', alpha=0.8,
label='Levy Flight')
pmst.plot()
```
To change from the default box binned plots to smooth lines (excluding degree):
```
pmst = mist.PlotHistMST()
pmst.read_mst(mst_dict)
pmst.plot(usebox=False)
```
Comparing randoms points, a Levy-Flight distribution and adjusted Levy-Flight distribution:
```
# We first create a random distribution
x_r = 75.*np.random.random_sample(50000)
y_r = 75.*np.random.random_sample(50000)
z_r = 75.*np.random.random_sample(50000)
# a levy flight distribution
x_lf, y_lf, z_lf = mist.get_levy_flight(50000)
# an adjusted levy flight distribution
x_alf, y_alf, z_alf = mist.get_adjusted_levy_flight(50000)
# then construct and measure the MST for each distribution
mst = mist.GetMST(x=x_r, y=y_r, z=z_r)
d_r, l_r, b_r, s_r = mst.get_stats()
mst = mist.GetMST(x=x_lf, y=y_lf, z=z_lf)
d_lf, l_lf, b_lf, s_lf = mst.get_stats()
mst = mist.GetMST(x=x_alf, y=y_alf, z=z_alf)
d_alf, l_alf, b_alf, s_alf = mst.get_stats()
# bin the MST statistics
hmst = mist.HistMST()
hmst.setup(uselog=True)
hist_alf = hmst.get_hist(d_alf, l_alf, b_alf, s_alf)
hist_lf = hmst.get_hist(d_lf, l_lf, b_lf, s_lf)
hist_r = hmst.get_hist(d_r, l_r, b_r, s_r)
# and plot it
pmst = mist.PlotHistMST()
pmst.read_mst(hist_r, label='Randoms')
pmst.read_mst(hist_lf, label='Levy Flight')
pmst.read_mst(hist_alf, label='Adjusted Levy Flight')
pmst.plot()
```
We can plot difference subplots:
```
pmst = mist.PlotHistMST()
pmst.read_mst(hist_lf, label='Levy Flight')
pmst.read_mst(hist_alf, label='Adjusted Levy Flight')
pmst.plot(usecomp=True)
```
Finally plotting the histogram for a group works in the very same way except we
pass the dictionary of a group. The final plot has 1 sigma error bars.
```
hmst = mist.HistMST()
hmst.setup(uselog=True)
hist_lf = hmst.get_hist(d_lf, l_lf, b_lf, s_lf)
hmst.start_group()
for i in range(0, 10):
x_alf, y_alf, z_alf = mist.get_adjusted_levy_flight(50000)
mst = mist.GetMST(x=x_alf, y=y_alf, z=z_alf)
d_alf, l_alf, b_alf, s_alf = mst.get_stats()
_hist_alf = hmst.get_hist(d_alf, l_alf, b_alf, s_alf)
print(i+1, '/ 10')
hist_alf_group = hmst.end_group()
pmst = mist.PlotHistMST()
pmst.read_mst(hist_lf, label='Levy Flight')
pmst.read_mst(hist_alf_group, label='Adjusted Levy Flight')
pmst.plot(usecomp=True)
```
## (3) _Advanced Usage_
### (3.1) _k Nearest Neighbours_
The k-nearest neighbour graph is a spanning graph which is passed on to the
``scipy`` kruskal algorithm. The actual graph is constructed using the ``scikit-learn``
``kneighbors_graph`` and by default will include the nearest 20 neighbours to
each node. We can specify the number of nearest neighbours (we will set this to 30)
in the following way:
```
x = np.random.random_sample(1000)
y = np.random.random_sample(1000)
mst = mist.GetMST(x=x, y=y) # Assuming our input data set is 2D.
mst.define_k_neighbours(30)
d, l, b, s = mst.get_stats()
# or directly:
mst = mist.GetMST(x=x, y=y) # Assuming our input data set is 2D.
d, l, b, s = mst.get_stats(k_neighbours=30)
```
Note: changing ``k`` to larger values will result in longer computation time to construct
the MST.
### (3.2) _Scale Cuts_
In cosmological data sets we often need to remove small scales due to numerical
simulation or observational limitations. To remove this we carry out
the following:
```
x = np.random.random_sample(100000)
y = np.random.random_sample(100000)
mst = mist.GetMST(x=x, y=y)
mst.scale_cut(0.002)
d, l, b, s = mst.get_stats()
# or directly:
mst = mist.GetMST(x=x, y=y)
d, l, b, s = mst.get_stats(scale_cut_length=0.002)
```
| true |
code
| 0.630799 | null | null | null | null |
|
# Quantizing RNN Models
In this example, we show how to quantize recurrent models.
Using a pretrained model `model.RNNModel`, we convert the built-in pytorch implementation of LSTM to our own, modular implementation.
The pretrained model was generated with:
```time python3 main.py --cuda --emsize 1500 --nhid 1500 --dropout 0.65 --tied --wd=1e-6```
The reason we replace the LSTM that is because the inner operations in the pytorch implementation are not accessible to us, but we still want to quantize these operations. <br />
Afterwards we can try different techniques to quantize the whole model.
_NOTE_: We use `tqdm` to plot progress bars, since it's not in `requirements.txt` you should install it using
`pip install tqdm`.
```
from model import DistillerRNNModel, RNNModel
from data import Corpus
import torch
from torch import nn
import distiller
from distiller.modules import DistillerLSTM as LSTM
from tqdm import tqdm # for pretty progress bar
import numpy as np
from copy import deepcopy
```
### Preprocess the data
```
corpus = Corpus('./data/wikitext-2/')
def batchify(data, bsz):
# Work out how cleanly we can divide the dataset into bsz parts.
nbatch = data.size(0) // bsz
# Trim off any extra elements that wouldn't cleanly fit (remainders).
data = data.narrow(0, 0, nbatch * bsz)
# Evenly divide the data across the bsz batches.
data = data.view(bsz, -1).t().contiguous()
return data.to(device)
device = 'cuda:0'
batch_size = 20
eval_batch_size = 10
train_data = batchify(corpus.train, batch_size)
val_data = batchify(corpus.valid, eval_batch_size)
test_data = batchify(corpus.test, eval_batch_size)
```
### Loading the model and converting to our own implementation
```
rnn_model = torch.load('./checkpoint.pth.tar.best')
rnn_model = rnn_model.to(device)
rnn_model
```
Here we convert the pytorch LSTM implementation to our own, by calling `LSTM.from_pytorch_impl`:
```
def manual_model(pytorch_model_: RNNModel):
nlayers, ninp, nhid, ntoken, tie_weights = \
pytorch_model_.nlayers, \
pytorch_model_.ninp, \
pytorch_model_.nhid, \
pytorch_model_.ntoken, \
pytorch_model_.tie_weights
model = DistillerRNNModel(nlayers=nlayers, ninp=ninp, nhid=nhid, ntoken=ntoken, tie_weights=tie_weights).to(device)
model.eval()
model.encoder.weight = nn.Parameter(pytorch_model_.encoder.weight.clone().detach())
model.decoder.weight = nn.Parameter(pytorch_model_.decoder.weight.clone().detach())
model.decoder.bias = nn.Parameter(pytorch_model_.decoder.bias.clone().detach())
model.rnn = LSTM.from_pytorch_impl(pytorch_model_.rnn)
return model
man_model = manual_model(rnn_model)
torch.save(man_model, 'manual.checkpoint.pth.tar')
man_model
```
### Batching the data for evaluation
```
sequence_len = 35
def get_batch(source, i):
seq_len = min(sequence_len, len(source) - 1 - i)
data = source[i:i+seq_len]
target = source[i+1:i+1+seq_len].view(-1)
return data, target
hidden = rnn_model.init_hidden(eval_batch_size)
data, targets = get_batch(test_data, 0)
```
### Check that the convertion has succeeded
```
rnn_model.eval()
man_model.eval()
y_t, h_t = rnn_model(data, hidden)
y_p, h_p = man_model(data, hidden)
print("Max error in y: %f" % (y_t-y_p).abs().max().item())
```
### Defining the evaluation
```
criterion = nn.CrossEntropyLoss()
def repackage_hidden(h):
"""Wraps hidden states in new Tensors, to detach them from their history."""
if isinstance(h, torch.Tensor):
return h.detach()
else:
return tuple(repackage_hidden(v) for v in h)
def evaluate(model, data_source):
# Turn on evaluation mode which disables dropout.
model.eval()
total_loss = 0.
ntokens = len(corpus.dictionary)
hidden = model.init_hidden(eval_batch_size)
with torch.no_grad():
with tqdm(range(0, data_source.size(0), sequence_len)) as t:
# The line below was fixed as per: https://github.com/pytorch/examples/issues/214
for i in t:
data, targets = get_batch(data_source, i)
output, hidden = model(data, hidden)
output_flat = output.view(-1, ntokens)
total_loss += len(data) * criterion(output_flat, targets).item()
hidden = repackage_hidden(hidden)
avg_loss = total_loss / (i + 1)
t.set_postfix((('val_loss', avg_loss), ('ppl', np.exp(avg_loss))))
return total_loss / len(data_source)
```
# Quantizing the Model
## Collect activation statistics
The model uses activation statistics to determine how big the quantization range is. The bigger the range - the larger the round off error after quantization which leads to accuracy drop.
Our goal is to minimize the range s.t. it contains the absolute most of our data.
After that, we divide the range into chunks of equal size, according to the number of bits, and transform the data according to this scale factor.
Read more on scale factor calculation [in our docs](https://nervanasystems.github.io/distiller/algo_quantization.html).
The class `QuantCalibrationStatsCollector` collects the statistics for defining the range $r = max - min$.
Each forward pass, the collector records the values of inputs and outputs, for each layer:
- absolute over all batches min, max (stored in `min`, `max`)
- average over batches, per batch min, max (stored in `avg_min`, `avg_max`)
- mean
- std
- shape of output tensor
All these values can be used to define the range of quantization, e.g. we can use the absolute `min`, `max` to define the range.
```
import os
from distiller.data_loggers import QuantCalibrationStatsCollector, collector_context
man_model = torch.load('./manual.checkpoint.pth.tar')
distiller.utils.assign_layer_fq_names(man_model)
collector = QuantCalibrationStatsCollector(man_model)
if not os.path.isfile('manual_lstm_pretrained_stats.yaml'):
with collector_context(collector) as collector:
val_loss = evaluate(man_model, val_data)
collector.save('manual_lstm_pretrained_stats.yaml')
```
## Prepare the Model For Quantization
We quantize the model after the training has completed.
Here we check the baseline model perplexity, to have an idea how good the quantization is.
```
from distiller.quantization import PostTrainLinearQuantizer, LinearQuantMode
from copy import deepcopy
# Load and evaluate the baseline model.
man_model = torch.load('./manual.checkpoint.pth.tar')
val_loss = evaluate(man_model, val_data)
print('val_loss:%8.2f\t|\t ppl:%8.2f' % (val_loss, np.exp(val_loss)))
```
Now we do our magic - __Preparing the model for quantization__.
The quantizer replaces the layers in out model with their quantized versions.
```
# Define the quantizer
quantizer = PostTrainLinearQuantizer(
deepcopy(man_model),
model_activation_stats='./manual_lstm_pretrained_stats.yaml')
# Quantizer magic
stats_before_prepare = deepcopy(quantizer.model_activation_stats)
dummy_input = (torch.zeros(1,1).to(dtype=torch.long), man_model.init_hidden(1))
quantizer.prepare_model(dummy_input)
```
### Net-Aware Quantization
Note that we passes a dummy input to `prepare_model`. This is required for the quantizer to be able to create a graph representation of the model, and to infer the connectivity between the modules.
Understanding the connectivity of the model is required to enable **"Net-aware quantization"**. This term (coined in [\[1\]](#references), section 3.2.2), means we can achieve better quantization by considering sequences of operations.
In the case of LSTM, we have an element-wise add operation whose output is split into 4 and fed into either Tanh or Sigmoid activations. Both of these ops saturate at relatively small input values - tanh at approximately $|4|$, and sigmoid saturates at approximately $|6|$. This means we can safely clip the output of the element-wise add operation between $[-6,6]$. `PostTrainLinearQuantizer` detects this patterm and modifies the statistics accordingly.
```
import pprint
pp = pprint.PrettyPrinter(indent=1)
print('Stats BEFORE prepare_model:')
pp.pprint(stats_before_prepare['rnn.cell_0.eltwiseadd_gate']['output'])
print('\nStats AFTER to prepare_model:')
pp.pprint(quantizer.model_activation_stats['rnn.cell_0.eltwiseadd_gate']['output'])
```
Note the value for `avg_max` did not change, since it was already below the clipping value of $6.0$.
### Inspecting the Quantized Model
Let's see how the model has after being prepared for quantization:
```
quantizer.model
```
Note how `encoder` and `decoder` have been replaced with wrapper layers (for the relevant module type), which handle the quantization. The same holds for the internal layers of the `DistillerLSTM` module, which we don't print for brevity sake. To "peek" inside the `DistillerLSTM` module, we need to access it directly. As an example, let's take a look at a couple of the internal layers:
```
print(quantizer.model.rnn.cell_0.fc_gate_x)
print(quantizer.model.rnn.cell_0.eltwiseadd_gate)
```
## Running the Quantized Model
### Try 1: Initial settings - simple symmetric quantization
Finally, let's go ahead and evaluate the quantized model:
```
val_loss = evaluate(quantizer.model.to(device), val_data)
print('val_loss:%8.2f\t|\t ppl:%8.2f' % (val_loss, np.exp(val_loss)))
```
As we can see here, the perplexity has increased much - meaning our quantization has damaged the accuracy of our model.
### Try 2: Assymetric, per-channel
Let's try quantizing each channel separately, and making the range of the quantization asymmetric.
```
quantizer = PostTrainLinearQuantizer(
deepcopy(man_model),
model_activation_stats='./manual_lstm_pretrained_stats.yaml',
mode=LinearQuantMode.ASYMMETRIC_SIGNED,
per_channel_wts=True
)
quantizer.prepare_model(dummy_input)
quantizer.model
val_loss = evaluate(quantizer.model.to(device), val_data)
print('val_loss:%8.2f\t|\t ppl:%8.2f' % (val_loss, np.exp(val_loss)))
```
A tiny bit better, but still no good.
### Try 3: Mixed FP16 and INT8
Let us try the half precision (aka FP16) version of the model:
```
model_fp16 = deepcopy(man_model).half()
val_loss = evaluate(model_fp16, val_data)
print('val_loss: %8.6f\t|\t ppl:%8.2f' % (val_loss, np.exp(val_loss)))
```
The result is very close to our original model! That means that the roundoff when quantizing linearly to 8-bit integers is what hurts our accuracy.
Luckily, `PostTrainLinearQuantizer` supports quantizing some/all layers to FP16 using the `fp16` parameter. In light of what we just saw, and as stated in [\[2\]](#References), let's try keeping element-wise operations at FP16, and quantize everything else to 8-bit using the same settings as in try 2.
```
overrides_yaml = """
.*eltwise.*:
fp16: true
encoder:
fp16: true
decoder:
fp16: true
"""
overrides = distiller.utils.yaml_ordered_load(overrides_yaml)
quantizer = PostTrainLinearQuantizer(
deepcopy(man_model),
model_activation_stats='./manual_lstm_pretrained_stats.yaml',
mode=LinearQuantMode.ASYMMETRIC_SIGNED,
overrides=overrides,
per_channel_wts=True
)
quantizer.prepare_model(dummy_input)
quantizer.model
val_loss = evaluate(quantizer.model.to(device), val_data)
print('val_loss:%8.6f\t|\t ppl:%8.2f' % (val_loss, np.exp(val_loss)))
```
The accuracy is still holding up very well, even though we quantized the inner linear layers!
### Try 4: Clipping Activations
Now, lets try to choose different boundaries for `min`, `max`.
Instead of using absolute ones, we take the average of all batches (`avg_min`, `avg_max`), which is an indication of where usually most of the boundaries lie. This is done by specifying the `clip_acts` parameter to `ClipMode.AVG` or `"AVG"` in the quantizer ctor:
```
overrides_yaml = """
encoder:
fp16: true
decoder:
fp16: true
"""
overrides = distiller.utils.yaml_ordered_load(overrides_yaml)
quantizer = PostTrainLinearQuantizer(
deepcopy(man_model),
model_activation_stats='./manual_lstm_pretrained_stats.yaml',
mode=LinearQuantMode.ASYMMETRIC_SIGNED,
overrides=overrides,
per_channel_wts=True,
clip_acts="AVG"
)
quantizer.prepare_model(dummy_input)
val_loss = evaluate(quantizer.model.to(device), val_data)
print('val_loss:%8.6f\t|\t ppl:%8.2f' % (val_loss, np.exp(val_loss)))
```
Great! Even though we quantized all of the layers except the embedding and the decoder - we got almost no accuracy penalty. Lets try quantizing them as well:
```
quantizer = PostTrainLinearQuantizer(
deepcopy(man_model),
model_activation_stats='./manual_lstm_pretrained_stats.yaml',
mode=LinearQuantMode.ASYMMETRIC_SIGNED,
per_channel_wts=True,
clip_acts="AVG"
)
quantizer.prepare_model(dummy_input)
val_loss = evaluate(quantizer.model.to(device), val_data)
print('val_loss:%8.6f\t|\t ppl:%8.2f' % (val_loss, np.exp(val_loss)))
quantizer.model
```
Here we see that sometimes quantizing with the right boundaries gives better results than actually using floating point operations (even though they are half precision).
## Conclusion
Choosing the right boundaries for quantization was crucial for achieving almost no degradation in accrucay of LSTM.
Here we showed how to use the Distiller quantization API to quantize an RNN model, by converting the PyTorch implementation into a modular one and then quantizing each layer separately.
## References
1. **Jongsoo Park, Maxim Naumov, Protonu Basu, Summer Deng, Aravind Kalaiah, Daya Khudia, James Law, Parth Malani, Andrey Malevich, Satish Nadathur, Juan Miguel Pino, Martin Schatz, Alexander Sidorov, Viswanath Sivakumar, Andrew Tulloch, Xiaodong Wang, Yiming Wu, Hector Yuen, Utku Diril, Dmytro Dzhulgakov, Kim Hazelwood, Bill Jia, Yangqing Jia, Lin Qiao, Vijay Rao, Nadav Rotem, Sungjoo Yoo, Mikhail Smelyanskiy**. Deep Learning Inference in Facebook Data Centers: Characterization, Performance Optimizations and Hardware Implications. [arxiv:1811.09886](https://arxiv.org/abs/1811.09886)
2. **Qinyao He, He Wen, Shuchang Zhou, Yuxin Wu, Cong Yao, Xinyu Zhou, Yuheng Zou**. Effective Quantization Methods for Recurrent Neural Networks. [arxiv:1611.10176](https://arxiv.org/abs/1611.10176)
| true |
code
| 0.839487 | null | null | null | null |
|
```
"""
3D forward modeling of total-field magnetic anomaly using triaxial
ellipsoids (model with isotropic and anisotropic susceptibilities)
"""
# insert the figures in the notebook
%matplotlib inline
import numpy as np
from fatiando import utils, gridder
import triaxial_ellipsoid
from mesher import TriaxialEllipsoid
import plot_functions as pf
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
from matplotlib.ticker import MaxNLocator
from matplotlib.colors import BoundaryNorm
# The regional field
F, inc, dec = 23500., 30, -15
# Create a model formed by two ellipsoids
# The first ellipsoid does not have remanent magnetization and
# has an anisotropic susceptibility (different principal susceptibilities
# k1 = 0.3, k2 = 0.2, k3 = 0.1).
# The second has a remanent magnetization of 2 A/m
# and an isotropic susceptibility of (all principal susceptibilities
# equal to 0.01)
model = [TriaxialEllipsoid(-2500., -2500., 1000., 900., 600., 300., 45., -10., 34.,
{'principal susceptibilities': [0.3, 0.2, 0.1],
'susceptibility angles': [-20., 20., 9.]}),
TriaxialEllipsoid(2500., 2500., 1000., 950., 640., 600., 45., 62., -7.,
{'remanent magnetization': [1.2, 90, 0.],
'principal susceptibilities': [0.01, 0.01, 0.01],
'susceptibility angles': [13, 50, 7]})]
# Create a regular grid at 0m height
shape = (200, 200)
area = [-5000, 5000, -5000, 5000]
xp, yp, zp = gridder.regular(area, shape, z = 0)
# Time execution of the function triaxial_ellipsoid.tf
%timeit triaxial_ellipsoid.tf(xp, yp, zp, model, F, inc, dec)
# Calculate the total-field anomaly
tf = triaxial_ellipsoid.tf(xp, yp, zp, model, F, inc, dec)
# Plot the results
plt.close('all')
plt.figure()
plt.axis('scaled')
ranges = np.max(np.abs([np.min(tf), np.max(tf)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('RdBu_r')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=True)
plt.contourf(0.001*yp.reshape(shape), 0.001*xp.reshape(shape),
tf.reshape(shape), levels=levels,
cmap = cmap, norm=norm)
plt.ylabel('x (km)')
plt.xlabel('y (km)')
plt.xlim(0.001*np.min(yp), 0.001*np.max(yp))
plt.ylim(0.001*np.min(xp), 0.001*np.max(xp))
cbar = plt.colorbar()
plt.tight_layout()
plt.show()
plt.close('all')
fig = plt.figure(figsize=(8,6))
ax = fig.gca(projection='3d')
ranges = np.max(np.abs([np.min(tf), np.max(tf)]))
levels = MaxNLocator(nbins=20).tick_values(-ranges, ranges)
cmap = plt.get_cmap('seismic')
norm = BoundaryNorm(levels, ncolors=cmap.N, clip=False)
cs = ax.contour(xp.reshape(shape), yp.reshape(shape), tf.reshape(shape),
zdir='z', offset=0, cmap=cmap, norm=norm, levels=levels,
linewidths=2)
#cbar = fig.colorbar(cs)
for m in model:
pf.draw_ellipsoid(ax, m, body_color=(1,1,0), body_alpha=0.3)
ax.set_xlabel('x (m)')
ax.set_ylabel('y (m)')
ax.set_zlabel('z (m)')
ax.view_init(215, 20)
plt.tight_layout(True)
plt.show()
```
| true |
code
| 0.895637 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/PGM-Lab/probai-2021-pyro/blob/main/Day2/notebooks/solutions_bayesian_regression_VI.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<span style="color:red">This notebook is an adapted version from </span> http://pyro.ai/examples/bayesian_regression.html
## Setup
Let's begin by installing and importing the modules we'll need.
```
!pip install -q --upgrade torch
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import torch
import torch.nn as nn
# ignore future warnings
from warnings import simplefilter
simplefilter(action='ignore', category=FutureWarning)
```
# Dataset
The following example is taken from \[1\]. We would like to explore the relationship between topographic heterogeneity of a nation as measured by the Terrain Ruggedness Index (variable *rugged* in the dataset) and its GDP per capita. In particular, it was noted by the authors in \[1\] that terrain ruggedness or bad geography is related to poorer economic performance outside of Africa, but rugged terrains have had a reverse effect on income for African nations. Let us look at the data \[2\] and investigate this relationship. We will be focusing on three features from the dataset:
- `rugged`: quantifies the Terrain Ruggedness Index
- `cont_africa`: whether the given nation is in Africa
- `rgdppc_2000`: Real GDP per capita for the year 2000
We will take the logarithm for the response variable GDP as it tends to vary exponentially. We also use a new variable `african_rugged`, defined as the product between the variables `rugged` and `cont_africa`, to capture the correlation between ruggedness and whether a country is in Africa.
```
DATA_URL = "https://raw.githubusercontent.com/PGM-Lab/probai-2021-pyro/main/Day1/rugged_data.csv"
data = pd.read_csv(DATA_URL, encoding="ISO-8859-1")
df = data[["cont_africa", "rugged", "rgdppc_2000"]]
df = df[np.isfinite(df.rgdppc_2000)]
df["rgdppc_2000"] = np.log(df["rgdppc_2000"])
df["african_rugged"] = data["cont_africa"] * data["rugged"]
df = df[["cont_africa", "rugged", "african_rugged", "rgdppc_2000"]]
# Divide the data into predictors and response and store the data in numpy arrays
data_array = np.array(df)
x_data = data_array[:, :-1]
y_data = data_array[:, -1]
# Display first 10 entries
display(df[0:10])
```
# 1. Linear Regression
Regression is one of the most common and basic supervised learning tasks in machine learning. Suppose we're given a dataset $\mathcal{D}$ of the form
$$ \mathcal{D} = \{ (X_i, y_i) \} \qquad \text{for}\qquad i=1,2,...,N$$
The goal of linear regression is to fit a function to the data of the form:
$$ y = w X + b + \epsilon $$
where $w$ and $b$ are learnable parameters and $\epsilon$ represents observation noise. Specifically $w$ is a matrix of weights and $b$ is a bias vector.
Let's first implement linear regression in PyTorch and learn point estimates for the parameters $w$ and $b$. Then we'll see how to incorporate uncertainty into our estimates by using Pyro to implement Bayesian regression.
```
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
african_nations = data[data["cont_africa"] == 1]
non_african_nations = data[data["cont_africa"] == 0]
sns.scatterplot(non_african_nations["rugged"],
np.log(non_african_nations["rgdppc_2000"]),
ax=ax[0])
ax[0].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="Non African Nations")
sns.scatterplot(african_nations["rugged"],
np.log(african_nations["rgdppc_2000"]),
ax=ax[1])
ax[1].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="African Nations")
```
## 1.1 Model
We would like to predict log GDP per capita of a nation as a function of three features from the dataset - whether the nation is in Africa, its Terrain Ruggedness Index, and the interaction between these two. Let's define our regression model. We'll define an specific object encapsulating this linear regression model. Our input `x_data` is a tensor of size $N \times 3$ and our output `y_data` is a tensor of size $N \times 1$. The method `predict(self,x_data)` defines a linear transformation of the form $Xw + b$ where $w$ is the weight matrix and $b$ is the additive bias.
The parameters of the model are defined using ``torch.nn.Parameter``, and will be learned during training.
```
class RegressionModel():
def __init__(self):
self.w = torch.nn.Parameter(torch.zeros(1, 3))
self.b = torch.nn.Parameter(torch.zeros(1, 1))
def params(self):
return {"b":self.b, "w": self.w}
def predict(self, x_data):
return (self.b + torch.mm(self.w, torch.t(x_data))).squeeze(0)
regression_model = RegressionModel()
```
## 1.2 Training
We will use the mean squared error (MSE) as our loss and Adam as our optimizer. We would like to optimize the parameters of the `regression_model` neural net above. We will use a somewhat large learning rate of `0.05` and run for 1000 iterations.
```
loss_fn = torch.nn.MSELoss(reduction='sum')
optim = torch.optim.Adam(regression_model.params().values(), lr=0.05)
num_iterations = 5000
data_array = torch.tensor(df.values, dtype=torch.float)
x_data, y_data = data_array[:, :-1], data_array[:, -1]
def main():
x_data = data_array[:, :-1]
y_data = data_array[:, -1]
for j in range(num_iterations):
# run the model forward on the data
y_pred = regression_model.predict(x_data)
# calculate the mse loss
loss = loss_fn(y_pred, y_data)
# initialize gradients to zero
optim.zero_grad()
# backpropagate
loss.backward()
# take a gradient step
optim.step()
if (j + 1) % 500 == 0:
print("[iteration %04d] loss: %.4f" % (j + 1, loss.item()))
# Inspect learned parameters
print("Learned parameters:")
for name, param in regression_model.params().items():
print(name, param.data.numpy())
main()
```
## 1.3 Evaluating the model
We now plot the regression line learned for african and non-african nations relating the rugeedness index with the GDP of the country.
```
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
fig.suptitle("Regression line ", fontsize=16)
ax[0].scatter(x_data[x_data[:,0]==0,1].detach().numpy(), y_data[x_data[:,0]==0].detach().numpy())
ax[1].scatter(x_data[x_data[:,0]==1,1].detach().numpy(), y_data[x_data[:,0]==1].detach().numpy())
for i in range(10):
ax[0].plot(x_data[x_data[:,0]==0,1].detach().numpy(),regression_model.predict(x_data[x_data[:,0]==0,:]).detach().numpy(), color='r')
ax[1].plot(x_data[x_data[:,0]==1,1].detach().numpy(),regression_model.predict(x_data[x_data[:,0]==1,:]).detach().numpy(), color='r')
ax[0].set(xlabel="Terrain Ruggedness Index",ylabel="log GDP (2000)",title="Non African Nations")
ax[1].set(xlabel="Terrain Ruggedness Index",ylabel="log GDP (2000)",title="African Nations")
plt.show()
```
## 1.4 The relationship between ruggedness and log GPD
Using this analysis, we can estimate the relationship between ruggedness and log GPD. As can be seen, this relationship is positive for African nations, but negative for Non African Nations.
```
slope_within_africa = regression_model.params()['w'][0,1] + regression_model.params()['w'][0,2]
slope_outside_africa = regression_model.params()['w'][0,1]
print(slope_within_africa.detach().numpy())
print(slope_outside_africa.detach().numpy())
```
# 2. Bayesian Linear Regression
[Bayesian modeling](http://mlg.eng.cam.ac.uk/zoubin/papers/NatureReprint15.pdf) offers a systematic framework for reasoning about model uncertainty. Instead of just learning point estimates, we're going to learn a _distribution_ over variables that is consistent with the observed data.
In order to make our linear regression Bayesian, we need to put priors on the parameters $w$ and $b$. These are distributions that represent our prior belief about reasonable values for $w$ and $b$ (before observing any data).
## 2.1 Model
We now have all the ingredients needed to specify our model. First we define priors over weights and bias. Note the priors that we are using for the different latent variables in the model.
The following figures shows a graphical description of the model:
<img src="https://github.com/PGM-Lab/probai-2021-pyro/raw/main/Day2/Figures/BayesianLinearRegressionModel.png" alt="Drawing" width=800 >
## 2.2 Full mean field
First we consider a full mean filed approach, where the variational approximation factorizes as
$$
q({\bf w}, b) = q(b)\prod _{i=1}^Mq(w_i)
$$
### Helper-routine: Calculate ELBO
```
def calculate_ELBO(x_data, y_data, gamma_w, gamma_b, theta, q_w_mean, q_w_prec, q_b_mean, q_b_prec):
"""
Helper routine: Calculate ELBO. Data is the sampled x and y values, gamma is the prior precision over the
weights and theta is the prior precision associated with y. Everything prefixed a 'q' relates to the
variational posterior.
Note: This function obviously only works for this particular model and is not a general solution.
:param x_data: The predictors
:param y_data: The response variable
:param gamma_w: prior precision for the weights
:param gamma_b: prior precision for the intercept
:param theta: prior precision for y
:param q_w_mean: VB posterior mean for the distribution of the weights w
:param q_w_prec: VB posterior precision for the distribution of the weights w
:param q_b_mean: VB posterior mean for the intercept b
:param q_b_prec: VB posterior precision for the intercept b
:return: the ELBO
"""
# We calculate the ELBO as E_q log p(y,x,w,b) - E_q log q(w,b), where
# log p(y,x,w) = sum_i log p(y|x,w,b) + log p(w) + log p(b)
# log q(w,b) = log q(w) + log q(b)
M = x_data.shape[1]
# E_q log p(w)
E_log_p = -0.5 * M * np.log(2 * np.pi) + 0.5 * M * gamma_w - 0.5 * gamma_w * np.sum(np.diagonal(np.linalg.inv(q_w_prec))
+ (q_w_mean*q_w_mean).flatten())
# E_q log p(b)
E_log_p += -0.5 * np.log(2 * np.pi) + 0.5 * np.log(gamma_b) - 0.5 * gamma_b * (1/q_b_prec + q_b_mean**2)
# sum_i E_q log p(y|x,w,b)
E_w_w = np.linalg.inv(q_w_prec) + q_w_mean @ q_w_mean.transpose()
E_b_b = 1/q_b_prec + q_b_mean**2
for i in range(x_data.shape[0]):
E_x_ww_x = np.matmul(x_data[i, :].transpose(), np.matmul(E_w_w, x_data[i, :]))
E_log_p += -0.5 * np.log(2 * np.pi) + 0.5 * np.log(theta) \
- 0.5 * theta * (y_data[i]**2 + E_x_ww_x + E_b_b
+ 2 * q_b_mean * np.matmul(q_w_mean.transpose(), x_data[i, :])
- 2 * y_data[i] * np.matmul(q_w_mean.transpose(), x_data[i,:])
- 2 * y_data[i] * q_b_mean)
# Entropy of q_b
ent = 0.5 * np.log(1 * np.pi * np.exp(1) / q_b_prec)
ent += 0.5 * np.log(np.linalg.det(2 * np.pi * np.exp(1) * np.linalg.inv(q_w_prec)))
return E_log_p - ent
```
### <span style="color:red">Exercise 1: Introduce the variational updating rules</span>
* Introduce variational updating rules for $q(w_i)$, which is normally distributed.
- Updating equation for **precision** of $q(w_i)$:
$$
\tau \leftarrow (\gamma_w+\theta\sum_{i=1}^N(x_{ij}^2))
$$
- Updating equation for **mean** of $q(w_i)$:
$$\mu \leftarrow \tau^{-1}\theta\sum_{i=1}^Nx_{ij}(y_i - (\sum_{k\neq j}x_{ik}\mathbb{E}(W_k)+\mathbb{E}(B)))
$$
* Introduce variational updating rules for $q(b)$, which is normally distributed.
- Updating equation for **precision** of $q(b)$:
$$
\tau \leftarrow (\gamma_b+\theta N)
$$
- Updating equation for **mean** of $q(b)$:
$$
\mu \leftarrow \tau^{-1} \theta\sum_{i=1}^N(y_i -
\mathbb{E}(\mathbf{W}^T)\mathbf{x}_i)
$$
```
# The variational updating rule for weight component 'comp'
def update_w_comp(x_data, y_data, gamma_w, theta, q_w_mean, q_w_prec, q_b_mean, comp):
# Lenght of weight vector
M = x_data.shape[1]
# The precision (a scalar)
Q = gamma_w
# The mean (a scalar)
mu = 0.0
for i in range(x_data.shape[0]):
Q += theta * x_data[i, comp]**2
mu += (y_data[i] - q_b_mean - (np.sum(x_data[i, :] @ q_w_mean) - x_data[i, comp]*q_w_mean[comp])) \
* x_data[i, comp]
mu = theta * 1/Q * mu
# Update the appropriate entries in the mean vector and precision matrix
q_w_prec[comp, comp] = Q
q_w_mean[comp] = mu.item()
return q_w_prec, q_w_mean
# The variational updating rule for the intercept
def update_b(x_data, y_data, gamma_b, theta, q_w_mean):
# The precision (a scalar)
tau = (gamma_b + theta * x_data.shape[0])
# The mean (a scalar)
mu = 0
for i in range(x_data.shape[0]):
mu += (y_data[i] - q_w_mean.transpose() @ x_data[i, :])
mu = 1/tau * theta * mu
return tau, mu
```
## 2.3 Inference
To do inference we'll use coordinate ascent, which is implemented by the above updating rules. Just like in the non-Bayesian linear regression, each iteration of our training objective will be optimzed, with the difference that in this case, we'll use the ELBO objective instead of the MSE loss.
```
# Initialize the variational distributions
data_array = np.array(df)
x_data = data_array[:, :-1]
y_data = data_array[:, -1]
M = x_data.shape[1]
gamma_w = 1
gamma_b = 1
theta = 1
q_w_mean = np.random.normal(0, 1, (3, 1))
q_w_prec = np.diag((1, 1, 1))
q_b_mean = np.random.normal(0, 1)
q_b_prec = 1
elbos = []
# Calculate ELBO
this_lb = calculate_ELBO(x_data, y_data, gamma_w, gamma_b, theta, q_w_mean, q_w_prec, q_b_mean, q_b_prec)
elbos.append(this_lb)
previous_lb = -np.inf
# Start iterating
print("\n" + 100 * "=" + "\n VB iterations:\n" + 100 * "=")
for iteration in range(100):
# Update the variational distributions
for i in range(M):
q_w_prec, q_w_mean = update_w_comp(x_data, y_data, gamma_w, theta, q_w_mean, q_w_prec, q_b_mean, i)
q_b_prec, q_b_mean = update_b(x_data, y_data, gamma_b, theta, q_w_mean)
this_lb = calculate_ELBO(x_data, y_data, gamma_w, gamma_b, theta, q_w_mean, q_w_prec, q_b_mean, q_b_prec)
elbos.append(this_lb)
print(f"Iteration {iteration:2d}. ELBO: {this_lb.item():13.7f}")
if this_lb < previous_lb:
raise ValueError("ELBO is decreasing. Something is wrong! Goodbye...")
if iteration > 0 and np.abs((this_lb - previous_lb) / previous_lb) < 1E-8:
# Very little improvement. We are done.
break
# If we didn't break we need to run again. Update the value for "previous"
previous_lb = this_lb
print("\n" + 100 * "=" + "\n")
# Store the results
w_mean_mf = q_w_mean
w_prec_mf = q_w_prec
b_mean_mf = q_b_mean
b_prec_mf = q_b_prec
plt.plot(range(len(elbos)), elbos)
plt.xlabel('NUmber of iterations')
plt.ylabel('ELBO')
```
Now, we have a Gaussian posterior for $q(b)$ and $q(w)$ with means and precisions:
```
print("Mean q(b):", b_mean_mf)
print("Precision q(b):", b_prec_mf)
print("Mean q(w):", w_mean_mf)
print("Precision q(w):", w_prec_mf)
```
Note that instead of just point estimates, we now have uncertainty estimates for our learned parameters.
## 2.4 Model's Uncertainty
We can now sample different regression lines from the variational posteriors, thus reflecting the model uncertainty.
```
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
fig.suptitle("Uncertainty in Regression line ", fontsize=16)
num_samples = 20
ax[0].scatter(x_data[x_data[:,0]==0,1], y_data[x_data[:,0]==0])
for _ in range(num_samples):
b_sample = np.random.normal(loc=q_b_mean, scale=1/np.sqrt(q_b_prec))
w_sample = np.random.multivariate_normal(mean=q_w_mean.flatten(), cov=np.linalg.inv(q_w_prec))
ax[0].plot(x_data[x_data[:,0]==0,1], (x_data[x_data[:,0]==0,:] @ w_sample)+b_sample, 'r-')
ax[0].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="Non African Nations")
ax[1].scatter(x_data[x_data[:,0]==1,1], y_data[x_data[:,0]==1])
for _ in range(num_samples):
b_sample = np.random.normal(loc=q_b_mean, scale=1/np.sqrt(q_b_prec))
w_sample = np.random.multivariate_normal(mean=q_w_mean.flatten(), cov=np.linalg.inv(q_w_prec))
ax[1].plot(x_data[x_data[:,0]==1,1], (x_data[x_data[:,0]==1,:] @ w_sample)+b_sample, 'r-')
ax[1].set(xlabel="Terrain Ruggedness Index",
ylabel="log GDP (2000)",
title="African Nations")
plt.show()
```
The above figure shows the uncertainty in our estimate of the regression line. Note that for lower values of ruggedness there are many more data points, and as such, the regression lines are less uncertainty than in high ruggness values, where there is much more uncertainty, specially in the case of African nations.
## 2.5 The relationship between ruggedness and log GPD
Finally, we go back to the previous analysis about the relationship between ruggedness and log GPD. Now, we can compute uncertainties over this relationship. As can be seen, this relationship is negative for Non African Nations with high probability, and positive for African nations in most of the cases. But there is non-negligible probability that this is relationship is also negative. This is the consequence of the low number of samples in the case of African nations.
```
weight = np.random.multivariate_normal(mean=q_w_mean.flatten(), cov=np.linalg.inv(q_w_prec),size=1000)
gamma_within_africa = weight[:,1] + weight[:,2]
gamma_outside_africa = weight[:,1]
fig = plt.figure(figsize=(10, 6))
sns.distplot(gamma_within_africa, kde_kws={"label": "African nations"},)
sns.distplot(gamma_outside_africa, kde_kws={"label": "Non-African nations"})
fig.suptitle("Density of Slope : log(GDP) vs. Terrain Ruggedness", fontsize=16)
plt.legend()
plt.show()
```
### References
1. McElreath, D., *Statistical Rethinking, Chapter 7*, 2016
2. Nunn, N. & Puga, D., *[Ruggedness: The blessing of bad geography in Africa"](https://diegopuga.org/papers/rugged.pdf)*, Review of Economics and Statistics 94(1), Feb. 2012
```
```
| true |
code
| 0.732047 | null | null | null | null |
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plotly.com/python/getting-started/) by downloading the client and [reading the primer](https://plotly.com/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plotly.com/python/getting-started/#initialization-for-online-plotting) or [offline](https://plotly.com/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plotly.com/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Version Check
Plotly's Python API is updated frequently. Run `pip install plotly --upgrade` to update your Plotly version.
```
import plotly
plotly.__version__
```
#### Simple Candlestick with Pandas
```
import plotly.plotly as py
import plotly.graph_objs as go
import pandas as pd
from datetime import datetime
df = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/finance-charts-apple.csv')
trace = go.Candlestick(x=df['Date'],
open=df['AAPL.Open'],
high=df['AAPL.High'],
low=df['AAPL.Low'],
close=df['AAPL.Close'])
data = [trace]
py.iplot(data, filename='simple_candlestick')
```
#### Candlestick without Rangeslider
```
import plotly.plotly as py
import plotly.graph_objs as go
import pandas as pd
from datetime import datetime
df = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/finance-charts-apple.csv')
trace = go.Candlestick(x=df['Date'],
open=df['AAPL.Open'],
high=df['AAPL.High'],
low=df['AAPL.Low'],
close=df['AAPL.Close'])
layout = go.Layout(
xaxis = dict(
rangeslider = dict(
visible = False
)
)
)
data = [trace]
fig = go.Figure(data=data,layout=layout)
py.iplot(fig, filename='simple_candlestick_without_range_slider')
```
#### Adding Customized Text and Annotations
```
import plotly.plotly as py
import plotly.graph_objs as go
import pandas as pd
from datetime import datetime
df = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/finance-charts-apple.csv')
trace = go.Candlestick(x=df['Date'],
open=df['AAPL.Open'],
high=df['AAPL.High'],
low=df['AAPL.Low'],
close=df['AAPL.Close'])
data = [trace]
layout = {
'title': 'The Great Recession',
'yaxis': {'title': 'AAPL Stock'},
'shapes': [{
'x0': '2016-12-09', 'x1': '2016-12-09',
'y0': 0, 'y1': 1, 'xref': 'x', 'yref': 'paper',
'line': {'color': 'rgb(30,30,30)', 'width': 1}
}],
'annotations': [{
'x': '2016-12-09', 'y': 0.05, 'xref': 'x', 'yref': 'paper',
'showarrow': False, 'xanchor': 'left',
'text': 'Increase Period Begins'
}]
}
fig = dict(data=data, layout=layout)
py.iplot(fig, filename='aapl-recession-candlestick')
```
#### Custom Candlestick Colors
```
import plotly.plotly as py
import plotly.graph_objs as go
import pandas as pd
from datetime import datetime
df = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/finance-charts-apple.csv')
trace = go.Candlestick(
x=df['Date'],
open=df['AAPL.Open'],
high=df['AAPL.High'],
low=df['AAPL.Low'],
close=df['AAPL.Close'],
increasing=dict(line=dict(color= '#17BECF')),
decreasing=dict(line=dict(color= '#7F7F7F'))
)
data = [trace]
py.iplot(data, filename='styled_candlestick')
```
#### Simple Example with `datetime` Objects
```
import plotly.plotly as py
import plotly.graph_objs as go
from datetime import datetime
open_data = [33.0, 33.3, 33.5, 33.0, 34.1]
high_data = [33.1, 33.3, 33.6, 33.2, 34.8]
low_data = [32.7, 32.7, 32.8, 32.6, 32.8]
close_data = [33.0, 32.9, 33.3, 33.1, 33.1]
dates = [datetime(year=2013, month=10, day=10),
datetime(year=2013, month=11, day=10),
datetime(year=2013, month=12, day=10),
datetime(year=2014, month=1, day=10),
datetime(year=2014, month=2, day=10)]
trace = go.Candlestick(x=dates,
open=open_data,
high=high_data,
low=low_data,
close=close_data)
data = [trace]
py.iplot(data, filename='candlestick_datetime')
```
### Dash Example
[Dash](https://plotly.com/products/dash/) is an Open Source Python library which can help you convert plotly figures into a reactive, web-based application. Below is a simple example of a dashboard created using Dash. Its [source code](https://github.com/plotly/simple-example-chart-apps/tree/master/dash-candlestickplot) can easily be deployed to a PaaS.
```
from IPython.display import IFrame
IFrame(src= "https://dash-simple-apps.plotly.host/dash-candlestickplot/", width="100%", height="750px", frameBorder="0")
from IPython.display import IFrame
IFrame(src= "https://dash-simple-apps.plotly.host/dash-candlestickplot/code", width="100%", height=500, frameBorder="0")
```
#### Reference
For more information on candlestick attributes, see: https://plotly.com/python/reference/#candlestick
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
!pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'candlestick-charts.ipynb', 'python/candlestick-charts/', 'Candlestick Charts',
'How to make interactive candlestick charts in Python with Plotly. '
'Six examples of candlestick charts with Pandas, time series, and yahoo finance data.',
title = 'Python Candlestick Charts | plotly',
thumbnail='thumbnail/candlestick.jpg', language='python',
page_type='example_index', has_thumbnail='true', display_as='financial', order=2,
ipynb= '~notebook_demo/275')
```
| true |
code
| 0.608856 | null | null | null | null |
|
# Keep Calm and Parquet
In this workshop we will be leveraging a number of analytics tools to show the diversity of the AWS platform. We will walk through querying unoptimized csv files and converting them to Parquet to improve performance. We also want to show how you can access data in your data lake with Redshift, Athena, and EMR giving you freedom of choice to choose the right tool for the job keeping a single source of truth of your data in S3.

```
import boto3
import botocore
import json
import time
import os
import getpass
import project_path # path to helper methods
from lib import workshop
from pandas import read_sql
glue = boto3.client('glue')
s3 = boto3.resource('s3')
s3_client = boto3.client('s3')
cfn = boto3.client('cloudformation')
redshift_client = boto3.client('redshift')
ec2_client = boto3.client('ec2')
session = boto3.session.Session()
region = session.region_name
account_id = boto3.client('sts').get_caller_identity().get('Account')
database_name = 'taxi' # AWS Glue Data Catalog Database Name
redshift_database_name = 'taxidb'
environment_name = 'taxi-workshop'
table_name = 'yellow'
redshift_node_type = 'ds2.xlarge'
redshift_port=5439
use_existing = True
```
### [Create S3 Bucket](https://docs.aws.amazon.com/AmazonS3/latest/gsg/CreatingABucket.html)
We will create an S3 bucket that will be used throughout the workshop for storing our data.
[s3.create_bucket](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/s3.html#S3.Client.create_bucket) boto3 documentation
```
bucket = workshop.create_bucket_name('taxi-')
session.resource('s3').create_bucket(Bucket=bucket, CreateBucketConfiguration={'LocationConstraint': region})
print(bucket)
```
### [Copy Sample Data to S3 bucket](https://boto3.amazonaws.com/v1/documentation/api/latest/guide/s3-example-download-file.html)
We will download some files from New York City Taxi and Limousine Commission (TLC) Trip Record Data dataset available on the [AWS Open Data Registry](https://registry.opendata.aws/nyc-tlc-trip-records-pds/).
```
!aws s3 cp s3://nyc-tlc/trip\ data/yellow_tripdata_2017-01.csv s3://$bucket/datalake/yellow/
!aws s3 cp s3://nyc-tlc/trip\ data/yellow_tripdata_2017-02.csv s3://$bucket/datalake/yellow/
```
### [Upload to S3](https://docs.aws.amazon.com/AmazonS3/latest/dev/Welcome.html)
Next, we will upload the json file created above to S3 to be used later in the workshop.
[s3.upload_file](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/s3.html#S3.Client.upload_file) boto3 documentation
```
file_name = 'paymenttype.csv'
session.resource('s3').Bucket(bucket).Object(os.path.join('datalake', 'paymenttype', file_name)).upload_file(file_name)
file_name = 'ratecode.csv'
session.resource('s3').Bucket(bucket).Object(os.path.join('datalake', 'ratecode', file_name)).upload_file(file_name)
file_name = 'taxi_zone_lookup.csv'
session.resource('s3').Bucket(bucket).Object(os.path.join('datalake', 'taxi_zone_lookup', file_name)).upload_file(file_name)
```
### [Create VPC](https://docs.aws.amazon.com/vpc/index.html)
We need a VPC for some of the resources in this workshop. You have the option to create a brand new VPC or use the VPC flaged as the default.
```
if use_existing:
vpc_filter = [{'Name':'isDefault', 'Values':['true']}]
default_vpc = ec2_client.describe_vpcs(Filters=vpc_filter)
vpc_id = default_vpc['Vpcs'][0]['VpcId']
subnet_filter = [{'Name':'vpc-id', 'Values':[vpc_id]}]
subnets = ec2_client.describe_subnets(Filters=subnet_filter)
subnet1_id = subnets['Subnets'][0]['SubnetId']
subnet2_id = subnets['Subnets'][1]['SubnetId']
else:
vpc, subnet1, subnet2 = workshop.create_and_configure_vpc()
vpc_id = vpc.id
subnet1_id = subnet1.id
subnet2_id = subnet2.id
print(vpc_id)
print(subnet1_id)
print(subnet2_id)
```
### Upload [CloudFormation](https://docs.aws.amazon.com/AWSCloudFormation/latest/UserGuide/GettingStarted.html) template
In the interest of time we will leverage CloudFormation to launch EMR and Redshift instances to leverage on the analytics side after we have cataloged and transformed the data.
```
redshift_file = 'redshift.yaml'
session.resource('s3').Bucket(bucket).Object(os.path.join('cfn', redshift_file)).upload_file(redshift_file)
emr_file = 'emr.yaml'
session.resource('s3').Bucket(bucket).Object(os.path.join('cfn', emr_file)).upload_file(emr_file)
```
### Enter the user name used for the Redshift Cluster
```
admin_user = getpass.getpass()
```
### Enter the password used in creating the Redshift Cluster
```
#Password must be 8 characters long alphanumeric only 1 Upper, 1 Lower
admin_password = getpass.getpass()
import re
pattern = re.compile(r"^(?=.*[a-z])(?=.*[A-Z])(?=.*\d)[a-zA-Z\d]{8,}$")
result = pattern.match(admin_password)
if result:
print('Valid')
else:
print('Invalid, Password must be 8 characters long alphanumeric only 1 Upper, 1 Lower')
```
### Execute CloudFormation Stack to generate Redshift Data Warehouse
Later in the workshop we will be using this [Redshift](https://aws.amazon.com/redshift/) cluster to run queries over data populated in our data lake with [Redshift Spectrum](https://aws.amazon.com/blogs/big-data/amazon-redshift-spectrum-extends-data-warehousing-out-to-exabytes-no-loading-required/).
```
cfn_template = 'https://s3-{0}.amazonaws.com/{1}/cfn/{2}'.format(region, bucket, redshift_file)
print(cfn_template)
redshift_stack_name = 'RedshiftTaxiStack'
response = cfn.create_stack(
StackName=redshift_stack_name,
TemplateURL=cfn_template,
Capabilities = ["CAPABILITY_NAMED_IAM"],
Parameters=[
{
'ParameterKey': 'EnvironmentName',
'ParameterValue': environment_name
},
{
'ParameterKey': 'AdministratorUser',
'ParameterValue': admin_user
},
{
'ParameterKey': 'AdministratorPassword',
'ParameterValue': admin_password
},
{
'ParameterKey': 'DatabaseName',
'ParameterValue': redshift_database_name
},
{
'ParameterKey': 'NodeType',
'ParameterValue': redshift_node_type
},
{
'ParameterKey': 'S3Bucket',
'ParameterValue': bucket
}
]
)
print(response)
```
### Execute CloudFormation Stack to generate EMR Cluster
We will also be querying data in the Data Lake from [EMR](https://aws.amazon.com/emr/) as well through the use of an [EMR Notebook](https://docs.aws.amazon.com/emr/latest/ManagementGuide/emr-managed-notebooks.html).
```
cfn_template = 'https://s3-{0}.amazonaws.com/{1}/cfn/{2}'.format(region, bucket, emr_file)
print(cfn_template)
emr_stack_name = 'EMRTaxiStack'
response = cfn.create_stack(
StackName=emr_stack_name,
TemplateURL=cfn_template,
Capabilities = ["CAPABILITY_NAMED_IAM"],
Parameters=[
{
'ParameterKey': 'EnvironmentName',
'ParameterValue': environment_name
},
{
'ParameterKey': 'VPC',
'ParameterValue': vpc_id
},
{
'ParameterKey': 'PublicSubnet',
'ParameterValue': subnet1_id
},
{
'ParameterKey': 'OutputS3Bucket',
'ParameterValue': bucket
}
]
)
print(response)
```
### Discover the data in your Data Lake
In this next section we will be using [AWS Glue](https://aws.amazon.com/glue/) to discover, catalog, and transform your data. Glue currently only supports `Python 2.7`, hence we'll write the script in `Python 2.7`.
### Permission setup for invoking AWS Glue from this Notebook
In order to enable this Notebook to run AWS Glue jobs, we need to add one additional permission to the default execution role of this notebook. We will be using SageMaker Python SDK to retrieve the default execution role and then you have to go to [IAM Dashboard](https://console.aws.amazon.com/iam/home) to edit the Role to add AWS Glue specific permission.
### Finding out the current execution role of the Notebook
We are using SageMaker Python SDK to retrieve the current role for this Notebook which needs to be enhanced to support the functionality in AWS Glue.
```
# Import SageMaker Python SDK to get the Session and execution_role
import sagemaker
from sagemaker import get_execution_role
sess = sagemaker.Session()
role = get_execution_role()
role_name = role[role.rfind('/') + 1:]
print(role_name)
```
### Adding AWS Glue as an additional trusted entity to this role
This step is needed if you want to pass the execution role of this Notebook while calling Glue APIs as well without creating an additional **Role**. If you have not used AWS Glue before, then this step is mandatory.
If you have used AWS Glue previously, then you should have an already existing role that can be used to invoke Glue APIs. In that case, you can pass that role while calling Glue (later in this notebook) and skip this next step.
On the IAM dashboard, please click on **Roles** on the left sidenav and search for this Role. Once the Role appears, click on the Role to go to its **Summary** page. Click on the **Trust relationships** tab on the **Summary** page to add AWS Glue as an additional trusted entity.
Click on **Edit trust relationship** and replace the JSON with this JSON.
```
{
"Version": "2012-10-17",
"Statement": [
{
"Effect": "Allow",
"Principal": {
"Service": [
"sagemaker.amazonaws.com",
"glue.amazonaws.com"
]
},
"Action": "sts:AssumeRole"
}
]
}
```
Once this is complete, click on **Update Trust Policy** and you are done.

```
print("https://console.aws.amazon.com/iam/home?region={0}#/roles/{1}".format(region, role_name))
```
### Create the [AWS Glue Catalog Database](https://docs.aws.amazon.com/glue/latest/dg/define-database.html)
When you define a table in the AWS Glue Data Catalog, you add it to a database. A database is used to organize tables in AWS Glue. You can organize your tables using a crawler or using the AWS Glue console. A table can be in only one database at a time.
There is a central Glue Catalog for each AWS account. When creating the database you will use your account id declared above as `account_id`
[glue.create_database](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/glue.html#Glue.Client.create_database)
```
def create_db(glue_client, account_id, database_name, description):
"""Create the specified Glue database if it does not exist"""
try:
glue_client.get_database(
CatalogId=account_id,
Name=database_name
)
except glue_client.exceptions.EntityNotFoundException:
print("Creating database: %s" % database_name)
glue_client.create_database(
CatalogId=account_id,
DatabaseInput={
'Name': database_name,
'Description': description
}
)
create_db(glue, account_id, database_name, 'New York City Taxi and Limousine Commission (TLC) Trip Record Data')
```
### Use a [Glue Crawler](https://docs.aws.amazon.com/glue/latest/dg/add-crawler.html) to Discover the transformed data
You can use a crawler to populate the AWS Glue Data Catalog with tables. This is the primary method used by most AWS Glue users. You add a crawler within your Data Catalog to traverse your data stores. The output of the crawler consists of one or more metadata tables that are defined in your Data Catalog. Extract, transform, and load (ETL) jobs that you define in AWS Glue use these metadata tables as sources and targets.
A crawler can crawl both file-based and table-based data stores. Crawlers can crawl the following data stores:
* Amazon Simple Storage Service (Amazon S3)
* [Built-in Classifiers](https://docs.aws.amazon.com/glue/latest/dg/add-classifier.html#classifier-built-in)
* [Custom Classifiers](https://docs.aws.amazon.com/glue/latest/dg/custom-classifier.html)
* Amazon Redshift
* Amazon Relational Database Service (Amazon RDS)
* Amazon Aurora
* MariaDB
* Microsoft SQL Server
* MySQL
* Oracle
* PostgreSQL
* Amazon DynamoDB
* Publicly accessible databases [Blog](https://aws.amazon.com/blogs/big-data/how-to-access-and-analyze-on-premises-data-stores-using-aws-glue/)
* Aurora
* MariaDB
* SQL Server
* MySQL
* Oracle
* PostgreSQL
[glue.create_crawler](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/glue.html#Glue.Client.create_crawler)
```
crawler_name = 'NY-Taxi-Crawler'
crawler_path = 's3://'+bucket+'/datalake/'
response = glue.create_crawler(
Name=crawler_name,
Role=role,
DatabaseName=database_name,
Description='Crawler for NY Taxi Data',
Targets={
'S3Targets': [
{
'Path': crawler_path
}
]
},
SchemaChangePolicy={
'UpdateBehavior': 'UPDATE_IN_DATABASE',
'DeleteBehavior': 'DEPRECATE_IN_DATABASE'
}
)
```
### Start the Glue Crawler
You can use a crawler to populate the AWS Glue Data Catalog with tables. This is the primary method used by most AWS Glue users. You add a crawler within your Data Catalog to traverse your data stores. The output of the crawler consists of one or more metadata tables that are defined in your Data Catalog. Extract, transform, and load (ETL) jobs that you define in AWS Glue use these metadata tables as sources and targets.
[glue.start_crawler](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/glue.html#Glue.Client.start_crawler)
```
response = glue.start_crawler(
Name=crawler_name
)
print ("Crawler: https://{0}.console.aws.amazon.com/glue/home?region={0}#crawler:name={1}".format(region, crawler_name))
```
### Checking Glue crawler status
We will now monitor the crawler status waiting for it to get back into the `READY` state meaning the crawler completed it's crawl. You can also look at the [CloudWatch logs](https://docs.aws.amazon.com/glue/latest/dg/console-crawlers.html#console-crawlers-details) for the crawler for more details.
```
crawler_status = glue.get_crawler(Name=crawler_name)['Crawler']['State']
while crawler_status not in ('READY'):
crawler_status = glue.get_crawler(Name=crawler_name)['Crawler']['State']
print(crawler_status)
time.sleep(30)
```
### View Crawler Results
Now that we have crawled the raw data available, we want to look at the results of the crawl to see the tables that were created. You will click on the link `Tables in taxi` to view the tables the crawler found. It will look like the image below:

```
print('https://{0}.console.aws.amazon.com/glue/home?region={0}#database:name={1}'.format(region, database_name))
```
### Create Parquet version of the yellow CSV table
From [Wikipedia](https://en.wikipedia.org/wiki/Apache_Parquet), "Apache Parquet is a free and open-source column-oriented data storage format of the Apache Hadoop ecosystem. It is similar to the other columnar-storage file formats available in Hadoop namely RCFile and ORC. It is compatible with most of the data processing frameworks in the Hadoop environment. It provides efficient data compression and encoding schemes with enhanced performance to handle complex data in bulk."
The key points in this code is how easy it is to get access to the AWS Glue Data Catalog leveraging the [Glue libraries](https://github.com/awslabs/aws-glue-libs). Some of the key concepts are below:
* [`glueContext.create_dynamic_frame.from_catalog`](https://docs.aws.amazon.com/glue/latest/dg/aws-glue-api-crawler-pyspark-extensions-glue-context.html#aws-glue-api-crawler-pyspark-extensions-glue-context-create_dynamic_frame_from_catalog) - Read table metadata from the Glue Data Catalog using Glue libs to load tables into the pyspark job.
* Writing back S3 [`glueContext.write_dynamic_frame.from_options`](https://docs.aws.amazon.com/glue/latest/dg/aws-glue-api-crawler-pyspark-extensions-glue-context.html#aws-glue-api-crawler-pyspark-extensions-glue-context-write_dynamic_frame_from_catalog) with options:
* Convert data to different format `format="parquet"`. This format is [columnar](https://docs.aws.amazon.com/athena/latest/ug/columnar-storage.html) and provides [Snappy](https://en.wikipedia.org/wiki/Snappy_(compression)) compression by default.
You can find more best practices for Glue and Athena [here](https://docs.aws.amazon.com/athena/latest/ug/glue-best-practices.html)
```
%%writefile yellow_parquet_etl.py
import sys
import os
from awsglue.transforms import *
from awsglue.utils import getResolvedOptions
from pyspark.context import SparkContext
from awsglue.context import GlueContext
from awsglue.job import Job
## @params: [JOB_NAME]
args = getResolvedOptions(sys.argv, ['JOB_NAME', 'S3_OUTPUT_BUCKET', 'S3_OUTPUT_KEY_PREFIX', 'DATABASE_NAME', 'TABLE_NAME', 'REGION'])
sc = SparkContext()
glueContext = GlueContext(sc)
spark = glueContext.spark_session
job = Job(glueContext)
job.init(args['JOB_NAME'], args)
## @type: DataSource
## @args: [database = "taxi", table_name = "yellow", transformation_ctx = "datasource0"]
## @return: datasource0
## @inputs: []
datasource0 = glueContext.create_dynamic_frame.from_catalog(database=args['DATABASE_NAME'], table_name=args['TABLE_NAME'], transformation_ctx = "datasource0")
## @type: ResolveChoice
## @args: [choice = "make_struct", transformation_ctx = "resolvechoice1"]
## @return: resolvechoice1
## @inputs: [frame = datasource0]
resolvechoice1 = ResolveChoice.apply(frame = datasource0, choice = "make_struct", transformation_ctx = "resolvechoice1")
## @type: DropNullFields
## @args: [transformation_ctx = "dropnullfields2"]
## @return: dropnullfields2
## @inputs: [frame = resolvechoice1]
dropnullfields2 = DropNullFields.apply(frame = resolvechoice1, transformation_ctx = "dropnullfields2")
parquet_output_path = 's3://' + os.path.join(args['S3_OUTPUT_BUCKET'], args['S3_OUTPUT_KEY_PREFIX'])
print(parquet_output_path)
## @type: DataSink
## @args: [connection_type = "s3", connection_options = {"path": ""}, format = "parquet", transformation_ctx = "datasink3"]
## @return: datasink3
## @inputs: [frame = dropnullfields2]
datasink3 = glueContext.write_dynamic_frame.from_options(frame = dropnullfields2, connection_type = "s3", connection_options = {"path": parquet_output_path}, format = "parquet", transformation_ctx = "datasink4")
job.commit()
```
### Upload the ETL script to S3
We will be uploading the `yellow_parquet_etl` script to S3 so Glue can use it to run the PySpark job. You can replace it with your own script if needed. If your code has multiple files, you need to zip those files and upload to S3 instead of uploading a single file like it's being done here.
```
script_location = sess.upload_data(path='yellow_parquet_etl.py', bucket=bucket, key_prefix='codes')
# Output location of the data.
s3_output_key_prefix = 'datalake/yellow_parquet/'
```
### [Authoring jobs with AWS Glue](https://docs.aws.amazon.com/glue/latest/dg/author-job.html)
Next we'll be creating Glue client via Boto so that we can invoke the `create_job` API of Glue. `create_job` API will create a job definition which can be used to execute your jobs in Glue. The job definition created here is mutable. While creating the job, we are also passing the code location as well as the dependencies location to Glue.
`AllocatedCapacity` parameter controls the hardware resources that Glue will use to execute this job. It is measures in units of `DPU`. For more information on `DPU`, please see [here](https://docs.aws.amazon.com/glue/latest/dg/add-job.html).
[glue.create_job](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/glue.html#Glue.Client.create_job)
```
from time import gmtime, strftime
import time
timestamp_prefix = strftime("%Y-%m-%d-%H-%M-%S", gmtime())
job_name = 'ny-yellow-parquet-' + timestamp_prefix
response = glue.create_job(
Name=job_name,
Description='PySpark job to convert yellow taxi csv data to parquet',
Role=role, # you can pass your existing AWS Glue role here if you have used Glue before
ExecutionProperty={
'MaxConcurrentRuns': 1
},
Command={
'Name': 'glueetl',
'ScriptLocation': script_location
},
DefaultArguments={
'--job-language': 'python',
'--job-bookmark-option': 'job-bookmark-disable'
},
AllocatedCapacity=5,
Timeout=60,
)
glue_job_name = response['Name']
print(glue_job_name)
```
The aforementioned job will be executed now by calling `start_job_run` API. This API creates an immutable run/execution corresponding to the job definition created above. We will require the `job_run_id` for the particular job execution to check for status. We'll pass the data and model locations as part of the job execution parameters.
[glue.start_job_run](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/glue.html#Glue.Client.start_job_run)
```
job_run_id = glue.start_job_run(JobName=job_name,
Arguments = {
'--S3_OUTPUT_BUCKET': bucket,
'--S3_OUTPUT_KEY_PREFIX': s3_output_key_prefix,
'--DATABASE_NAME': database_name,
'--TABLE_NAME': table_name,
'--REGION': region
})['JobRunId']
print(job_run_id)
```
### Checking Glue Job Status
Now we will check for the job status to see if it has `SUCCEEDED`, `FAILED` or `STOPPED`. Once the job is succeeded, we have the transformed data into S3 in Parquet format which we will use to query with Athena and visualize with QuickSight. If the job fails, you can go to AWS Glue console, click on **Jobs** tab on the left, and from the page, click on this particular job and you will be able to find the CloudWatch logs (the link under **Logs**) link for these jobs which can help you to see what exactly went wrong in the job execution.
[glue.get_job_run](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/glue.html#Glue.Client.get_job_run)
```
job_run_status = glue.get_job_run(JobName=job_name,RunId=job_run_id)['JobRun']['JobRunState']
while job_run_status not in ('FAILED', 'SUCCEEDED', 'STOPPED'):
job_run_status = glue.get_job_run(JobName=job_name,RunId=job_run_id)['JobRun']['JobRunState']
print (job_run_status)
time.sleep(60)
print(job_run_status)
```
### Create Crawler to populate Parquet formated table in Glue Data Catalog
We will create another crawler for the curated dataset we created converting the CSV files into Parquet formatted data.
```
parq_crawler_name = 'NY-Curated-Crawler'
parq_crawler_path = 's3://'+bucket+'/datalake/yellow_parquet/'
response = glue.create_crawler(
Name=parq_crawler_name,
Role=role,
DatabaseName=database_name,
Description='Crawler for the Parquet transformed yellow taxi data',
Targets={
'S3Targets': [
{
'Path': parq_crawler_path
}
]
},
SchemaChangePolicy={
'UpdateBehavior': 'UPDATE_IN_DATABASE',
'DeleteBehavior': 'DEPRECATE_IN_DATABASE'
}
)
```
### Start Crawler
Much like we did with the raw data crcawler we will start the curated crawler pointing to the new data set created from the Glue job.
```
response = glue.start_crawler(
Name=parq_crawler_name
)
print ("Crawler: https://{0}.console.aws.amazon.com/glue/home?region={0}#crawler:name={1}".format(region, parq_crawler_name))
```
### Monitor the status of the Parquet crawler
```
crawler_status = glue.get_crawler(Name=parq_crawler_name)['Crawler']['State']
while crawler_status not in ('READY'):
crawler_status = glue.get_crawler(Name=parq_crawler_name)['Crawler']['State']
print(crawler_status)
time.sleep(30)
print('https://{0}.console.aws.amazon.com/glue/home?region={0}#database:name={1}'.format(region, database_name))
```
### [Query the Data Lake with Athena](https://aws.amazon.com/athena/)
For the self-serve end users that need the ability to create ad-hoc queries against the data Athena is a great choice the utilizes Presto and ANSI SQL to query a number of file formats on S3.
To query the tables created by the crawler we will be installing a python library for querying the data in the Glue Data Catalog with Athena. For more information jump to [PyAthena](https://pypi.org/project/PyAthena/). You can also use the AWS console by browsing to the Athena service and run queries through the browser. Alternatively, you can also use the [JDBC/ODBC](https://docs.aws.amazon.com/athena/latest/ug/athena-bi-tools-jdbc-odbc.html) drivers available.
```
!pip install PyAthena
```
### Simple Select Query
In this first query we will create a simple query to show the ability of Athena to query the raw CSV data.
```
%%time
from pyathena import connect
from pyathena.util import as_pandas
cursor = connect(region_name=region, s3_staging_dir='s3://'+bucket+'/athena/temp').cursor()
cursor.execute('select * from ' + database_name + '.yellow limit 10')
df = as_pandas(cursor)
df.head(5)
```
### Complex Join Query
Now we will get more complex and create a query that utilizes multiple joins using Athena.
```
%%time
cursor.execute('''SELECT * FROM ''' + database_name + '''.yellow
JOIN ''' + database_name + '''.paymenttype ON yellow.payment_type = paymenttype.id
JOIN ''' + database_name + '''.ratecode ON yellow.ratecodeid = ratecode.id
JOIN ''' + database_name + '''.taxi_zone_lookup AS pu_taxizone ON yellow.pulocationid = pu_taxizone.locationid
JOIN ''' + database_name + '''.taxi_zone_lookup AS do_taxizone ON yellow.dolocationid = do_taxizone.locationid
limit 10;''')
df = as_pandas(cursor)
df.head(5)
```
### Complex Join Query With Where Clause
Taking it a step further, we will now utilize the query with multiple joins and aggregate the number of entries by vendor looking at just the data found in the first 10 days of Jan. 2017.
In our Glue job we could have taken it a step further to optimze queries like this using data partitioning by date.
#### What is data partitioning?
A partition is a division of a logical database or its constituent elements into distinct independent parts. Database partitioning is normally done for manageability, performance or availability reasons, or for load balancing.
Examples in S3 would utilize prefixes in the bucket for the partitions in key=value pairs.
* s3://datalake/taxi/yellow/year=2018/month=1/<objects>
* s3://datalake/taxi/yellow/year=2018/month=1/day=1/<objects>
**Optional Exercise**
If you would like to try this for yourself you can change the Glue Job above when writing the data to S3 you select how to partition the data.
#### Glue context writing patitions
* Extract `year`, `month`, and `day` from the `tpep_pickup_datetime`. Look at [Pyspark documentation](http://spark.apache.org/docs/2.1.0/api/python/pyspark.sql.html#pyspark.sql.DataFrame.withColumn) for help.
* Writing back S3 [`glueContext.write_dynamic_frame.from_options`](https://docs.aws.amazon.com/glue/latest/dg/aws-glue-api-crawler-pyspark-extensions-glue-context.html#aws-glue-api-crawler-pyspark-extensions-glue-context-write_dynamic_frame_from_catalog) with options:
* [Partition](https://docs.aws.amazon.com/athena/latest/ug/partitions.html) the data based on columns `connection_options = {"path": parquet_output_path, "partitionKeys": ["year, month, day"]}`
* Convert data to a [columnar format](https://docs.aws.amazon.com/athena/latest/ug/columnar-storage.html) `format="parquet"`
```
%%time
cursor.execute('''WITH yellow AS (SELECT date_parse(yellow.tpep_pickup_datetime,'%Y-%m-%d %H:%i:%s') AS pu_datetime, yellow.* FROM ''' + database_name + '''.yellow )
SELECT count(yellow.vendorid) as cnt FROM yellow
JOIN ''' + database_name + '''.paymenttype ON yellow.payment_type = paymenttype.id
JOIN ''' + database_name + '''.ratecode ON yellow.ratecodeid = ratecode.id
JOIN ''' + database_name + '''.taxi_zone_lookup AS pu_taxizone ON yellow.pulocationid = pu_taxizone.locationid
JOIN ''' + database_name + '''.taxi_zone_lookup AS do_taxizone ON yellow.dolocationid = do_taxizone.locationid
WHERE year(pu_datetime) = 2017
AND month(pu_datetime) = 1
AND day(pu_datetime) BETWEEN 1 AND 10''')
df = as_pandas(cursor)
df.head(1)
```
### Optimized queries using the Parquet yellow taxi data
We will run the same queries again but this time we will use the dataset utilizing the parquet format to show the performance gains you get when converting.
```
%%time
cursor.execute('select * from ' + database_name + '.yellow_parquet limit 10')
df = as_pandas(cursor)
df.head(5)
```
Same complex queries using the `yellow_parquet` table instead.
```
%%time
cursor.execute('''
WITH yellow AS (SELECT date_parse(yellow.tpep_pickup_datetime,'%Y-%m-%d %H:%i:%s') AS pu_datetime, yellow.* FROM ''' + database_name + '''.yellow_parquet as yellow )
select count( yellow.vendorid)
FROM yellow
Inner JOIN ''' + database_name + '''.paymenttype ON yellow.payment_type = paymenttype.id
Inner JOIN ''' + database_name + '''.ratecode ON yellow.ratecodeid = ratecode.id
Inner JOIN ''' + database_name + '''.taxi_zone_lookup AS pu_taxizone ON yellow.pulocationid = pu_taxizone.locationid
Inner JOIN ''' + database_name + '''.taxi_zone_lookup AS do_taxizone ON yellow.dolocationid = do_taxizone.locationid
WHERE year(pu_datetime) = 2017
AND month(pu_datetime) = 1
AND day(pu_datetime) BETWEEN 1 AND 10''')
df = as_pandas(cursor)
df.head(5)
```
### Check status Redshift Cloudformation Stacks
Let's check in on the status of the EMR and Redshift CloudFormation stacks. Now that we showed how you can leverage Athena for querying the raw and curated data we want to dive into using other analytics engines to show the capability of keeping all your data in your data lake and leverage the right tools for the job.
Separating your storage from your compute allows you to scale each component independently. This gives you the flexibility needed when making tool selection as well providing agility in upgrading to new tools and services as they come out helping future proof your data lake solution.
```
response = cfn.describe_stacks(
StackName=redshift_stack_name
)
if response['Stacks'][0]['StackStatus'] == 'CREATE_COMPLETE':
for output in response['Stacks'][0]['Outputs']:
if (output['OutputKey'] == 'RedshiftAddress'):
redshift_cluster_name = output['OutputValue'].split('.')[0]
print(redshift_cluster_name)
else:
print('Not yet complete.')
response = redshift_client.describe_clusters(
ClusterIdentifier=redshift_cluster_name
)
status = response['Clusters'][0]['ClusterStatus']
if status == 'available':
redshift_address = response['Clusters'][0]['Endpoint']['Address']
print(redshift_address)
jdbc_url = 'jdbc:redshift://' + redshift_address + ':' + str(redshift_port) + '/' + redshift_database_name
print(jdbc_url)
iam_role = response['Clusters'][0]['IamRoles'][0]['IamRoleArn']
print(iam_role)
else:
print('Not yet available. Current status is {}'.format(status))
```
### Install the psycopg2 library to connect to Redshift
Psycopg is the most popular PostgreSQL database adapter for the Python programming language. Its main features are the complete implementation of the Python DB API 2.0 specification and the thread safety.
[psycopg2](http://initd.org/psycopg/)
```
!pip install psycopg2
```
### Create connection attributes
```
conn_string = { 'dbname': redshift_database_name,
'user': admin_user,
'pwd':admin_password,
'host': redshift_address,
'port':redshift_port
}
import psycopg2
def create_conn(config):
try:
# get a connection, if a connect cannot be made an exception will be raised here
con=psycopg2.connect(dbname=config['dbname'], host=config['host'],
port=config['port'], user=config['user'],
password=config['pwd'])
return con
except Exception as err:
print(err)
con = create_conn(config=conn_string)
print("Connected to Redshift!\n")
```
### Create Redshift Spectrum external table
```
statement = '''create external schema spectrum
from data catalog
database \'''' + database_name + '''\'
iam_role \'''' + iam_role + '''\'
create external database if not exists;'''
print(statement)
# con.cursor will return a cursor object, you can use this cursor to perform queries
cur = con.cursor()
cur.execute(statement)
con.commit()
Get the count by vendor for Jan 1st - 10th on 2017 using the CSV formatted data.
%%time
## Unoptimized
statement = '''select count(yellow.vendorid)
from spectrum.yellow
Inner JOIN spectrum.paymenttype ON yellow.payment_type = paymenttype.id
Inner JOIN spectrum.ratecode ON yellow.ratecodeid = ratecode.id
Inner JOIN spectrum.taxi_zone_lookup AS pu_taxizone ON yellow.pulocationid =
pu_taxizone.locationid
Inner JOIN spectrum.taxi_zone_lookup AS do_taxizone ON yellow.dolocationid =
do_taxizone.locationid
where extract(month from cast(tpep_pickup_datetime as date)) = 1 and
extract(year from cast(tpep_pickup_datetime as date)) = 2017 and
extract(day from cast(tpep_pickup_datetime as date)) between 1 and 10;'''
df = read_sql(statement, con=con)
```
### View results
```
df
```
Get the count by vendor for Jan 1st - 10th on 2017 using the Parquet formatted data.
```
%%time
## Optimized
statement = '''select count(yellow.vendorid)
from spectrum.yellow_parquet as yellow
Inner JOIN spectrum.paymenttype ON yellow.payment_type = paymenttype.id
Inner JOIN spectrum.ratecode ON yellow.ratecodeid = ratecode.id
Inner JOIN spectrum.taxi_zone_lookup AS pu_taxizone ON yellow.pulocationid =
pu_taxizone.locationid
Inner JOIN spectrum.taxi_zone_lookup AS do_taxizone ON yellow.dolocationid =
do_taxizone.locationid
where extract(month from cast(tpep_pickup_datetime as date)) = 1 and
extract(year from cast(tpep_pickup_datetime as date)) = 2017 and
extract(day from cast(tpep_pickup_datetime as date)) between 1 and 10;'''
df = read_sql(statement, con=con)
df
```
### Check status EMR Cloudformation Stacks
Let's check in on the status of the EMR cluster. If it's not yet finished please wait until it's ready.
```
response = cfn.describe_stacks(
StackName=emr_stack_name
)
if response['Stacks'][0]['StackStatus'] == 'CREATE_COMPLETE':
for output in response['Stacks'][0]['Outputs']:
if (output['OutputKey'] == 'EMRClusterId'):
cluster_id = output['OutputValue']
print(cluster_id)
else:
print('Not yet complete.')
notebook_prefix = 's3://{0}/notebooks/'.format(bucket)
emr_notebooks_file = 'TaxiEMRNotebook.ipynb'
print('Notebook Name: {}'.format(emr_notebooks_file.split('.')[0]))
print('Notebook Location: {}'.format(notebook_prefix))
print('Notebook Cluster: {}'.format(cluster_id))
```
### Create an EMR Notebook
Create a notebook in EMR to run Spark queries in based on the attributes above.
```
print('https://{0}.console.aws.amazon.com/elasticmapreduce/home?region={0}#create-notebook:'.format(region))
```
### Find Notebook id and import TaxiEMRNotebook into EMR Notebook
There is a notebook `TaxiEMRNotebook.ipynb` that you will want to download and import into the EMR notebook you just created and walk through the cells comparing the optimized vs. unoptimized schema format.
```
#Get Notebook Id
notebook_id = '{{notebook_id}}'
session.resource('s3').Bucket(bucket).Object(os.path.join('notebooks', notebook_id, emr_notebooks_file)).upload_file(emr_notebooks_file)
```
### Open EMR Notebook and execute queries
```
print('https://{0}.console.aws.amazon.com/elasticmapreduce/home?region={0}#notebooks-list:'.format(region))
```
**Congratulations!!!!** You have completed the workshops showing the capabilities of leveraging a Data Lake on AWS and the flexibility of choice when using analytics tools in AWS. Before you run the cleanup please delete the EMR Notebook you created above by selecting the notebook and clicking `Delete` in the toolbar on the EMR Notebook console.
### Cleanup
```
response = cfn.delete_stack(StackName=redshift_stack_name)
response = cfn.delete_stack(StackName=emr_stack_name)
response = glue.delete_crawler(Name=parq_crawler_name)
response = glue.delete_crawler(Name=crawler_name)
response = glue.delete_job(JobName=glue_job_name)
response = glue.delete_database(
CatalogId = account_id,
Name = database_name
)
!aws s3 rb s3://$bucket --force
waiter = cfn.get_waiter('stack_delete_complete')
waiter.wait(
StackName=emr_stack_name
)
print('The wait is over for {0}'.format(emr_stack_name))
waiter = cfn.get_waiter('stack_delete_complete')
waiter.wait(
StackName=redshift_stack_name
)
print('The wait is over for {0}'.format(redshift_stack_name))
if not use_existing:
workshop.vpc_cleanup(vpc_id)
```
| true |
code
| 0.274011 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/aayushkumar20/ML-based-projects./blob/main/Lane%20Detection/Lane%20Detection.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!import os
!import numpy as np
!import tkinter as tk
!import cv2
#Importing all the required modules on the local python environment.
#Please make sure that you have installed all the modules properly.
#Missing these all modules or a part of modules cam create some error.
from tkinter import *
from PIL import Image, ImageTk
#Importing the required part from the insatlled modules.
#type or copy it correctly.
global last_frame1 #global variable to store the last frame
last_frame1 = np.zeros((480,640,3), np.uint8)
global last_frame2 #global variable to store the last frame
last_frame2 = np.zeros((480,640,3), np.uint8)
global cap1 #global variable to store the video capture object
global cap2 #global variable to store the video capture object
cap1=cv2.VideoCapture("./videos/video1.mp4") #Change the path to your video file
cap2=cv2.VideoCapture("./videos/video2.mp4") #Change the path to your video file
#In case you are using a linux machine or a unix based machine
#Please specify the camera module location or the port associated with the camera module.
#Defining the first camera module for video capture and the properties related to the camera module.
def show_vid():
if not cap1.isOpened():
print("Error opening video stream or file")
flag1, frame1 = cap1.read()
frame1=cv2.resize(frame1,(640,480))
if flag1 is None:
print("No frame read")
elif flag1:
global last_frame1
last_frame1=frame1.copy()
pic=cv2.cvtColor(frame1,cv2.COLOR_BGR2RGB)
img=Image.fromarray(pic)
imgtk=ImageTk.PhotoImage(image=img)
lmain1.imgtk=imgtk #Shows frame for first video
lmain1.configure(image=imgtk)
lmain1.after(10,show_vid)
#Defining the second camera modules for video capture and the properties related to the second modules.
def show_vid2():
if not cap2.isOpened():
print("Error opening video stream or file")
flag2, frame2 = cap2.read()
frame2=cv2.resize(frame2,(640,480))
if flag2 is None:
print("No frame read")
elif flag2:
global last_frame2
last_frame2=frame2.copy()
pic=cv2.cvtColor(frame2,cv2.COLOR_BGR2RGB)
img=Image.fromarray(pic)
imgtk=ImageTk.PhotoImage(image=img)
lmain2.imgtk=imgtk #Shows frame for second video
lmain2.configure(image=imgtk)
lmain2.after(10,show_vid2)
if __name__ == '__main__':
root=tk.Tk()
img=ImageTk.PhotoImage(Image.open("logo.png"))
heading=Label(root,image=img,bg="black",text="Video Comparison",fg="white",font=("Helvetica",20))
#heading.pack(background="black",fill=BOTH)
heading.pack()
heading2=Label(root,pady=20,text="Video 1",font=("Helvetica",20))
heading2.configure(background="black",fg="white")
heading2.pack()
lmain1=tk.Label(master=root)
lmain2=tk.Label(master=root)
lmain1.pack(side=LEFT)
lmain2.pack(side=RIGHT)
root.title("Lanne Detector")
root.geometry("1280x720")
exitbutton=Button(root,text="Exit",command=root.destroy,font=("Helvetica",20),fg="red").pack(side=BOTTOM)
show_vid()
show_vid2()
root.mainloop()
cap1.release()
```
| true |
code
| 0.220301 | null | null | null | null |
|
作业五 相似度计算
任务描述:采用word2vec方法,进行句子相似度计算训练。
给出一个有关句子相似度的二分类数据集msr_paraphrase(包含train、test、README三个文件),其中第一列数字1代表相似,0代表不相似。
选择文件train中的string1&2部分作为训练语料,选择文件test计算句子相似度,然后与标注结果比较,输出你认为合适的分类阈值,以及该阈值下的准确率Accuracy,精确率Precision,召回率Recall和F1值(精确到小数点后两位)。
句向量相似度计算方式:
首先对句子分词,获取每个词的词向量,然后将所有的词向量相加求平均,得到句子向量,最后计算两个句子向量的余弦值(余弦相似度)。
Word2vec部分,使用Gensim的Word2Vec训练模型,自行调整合适的参数。
注意可能会出现word xx not in vocabulary的情况,这是由于训练时默认参数min_count=5,会过滤掉低频词。可以手动设定min_count=1,或者在计算句向量时,遇到低频词则忽略。自行选择其一,并注释。
gensim镜像安装方式
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple gensim
导入方式from gensim.models import word2vec
**1.读取文本并对句子分词**
```
import pandas as pd
import nltk.tokenize as tk
import re
data = pd.read_csv('msr_train.csv',keep_default_na=False) # 读取train文件,设置忽略NAN,否则后期会出问题
num_row, num_col = (data.shape) # 记录train中的行列值
sentences= [] # 记录train中读到的句子
pattern = re.compile("[^a-zA-Z0-9\n ]")# 定义去标点用的模式
def formating(words): # 定义一个格式化函数(对传入列表匹配英文单词并全部转小写)
new_words = []
for i in words:
pattern = re.compile("[^a-zA-Z\n ]")
word = re.sub(pattern, "", i).lower()
if(word!=''):
new_words.append(re.sub(pattern, "", i).lower())
return new_words
for i in range(num_row): # 分词
words_1 = tk.word_tokenize(data['#1 String'].loc[i])
words_2 = tk.word_tokenize(data['#2 String'].loc[i])
sentences.append(formating(words_1))
sentences.append(formating(words_2))
print(sentences[:5]) # 随便输出几个
```
**2.用Word2vec训练出每个词的词向量**
```
from gensim.models import word2vec
model = word2vec.Word2Vec(sentences, size=200, min_count=1) # 训练skip-gram模型; 默认window=5
print(model['who'][:5]) # 输出某个词词向量的一部分,以确认模型生成好了. 由于方法快过时了,所以会有红色的警告
```
**3.将所有的词向量相加求平均,得到句子向量,最后计算两个句子向量的余弦值(余弦相似度)。**
```
import numpy as np
def sentence_vector(s): #计算句子向量
vec = np.zeros(200)
for word in s:
vec += model[word]
vec /= len(s)
return vec
def sentence_similarity(s1, s2): #计算两个句子向量的余弦值(用numpy可以写的很优雅)
v1, v2 = sentence_vector(s1), sentence_vector(s2)
return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))
for i in range(0, 6, 2): #测试几个句子的相似值
print(sentence_similarity(sentences[i],sentences[i + 1]))
```
**4.输出你认为合适的分类阈值**
```
import csv
# 寻找最好的分类阈值理论上可以用多种方法来做,比如决策树等人工智能方法
# 由于时间有限我选择通过平均值选取
# 把相似度和标签写入到csv里面
csv_file = open("msr_classify.csv","w",newline = "")
classify_data = csv.writer(csv_file)
for i in range (num_row):
sentence_1 = formating(tk.word_tokenize(data['#1 String'].loc[i]))
sentence_2 = formating(tk.word_tokenize(data['#2 String'].loc[i]))
classify_data.writerow([data['Quality'].loc[i], sentence_similarity(sentence_1,sentence_2)])
csv_file.close()
```
由msr_classify.csv得到:

**正数据的平均相似度**

**负数据的平均相似度**
**将阈值取值为:0.998663876**
**5.该阈值下的准确率Accuracy,精确率Precision,召回率Recall和F1值(精确到小数点后两位)**
$$Accuracy = \frac{TP+TN}{TP+TN+FP+FN}$$
$$Precision = \frac{TP}{TP+FP}$$
$$Recall = \frac{TP}{TP+FN}$$
$$F_1 = \frac{2TP}{2TP+FP+FN}$$
```
Accuracy_image = []
Precision_image = []
Recall_image = []
F1_image = []
# 定义TP、FP、TN、FN
def find_num(number):
csv_file = csv.reader(open("msr_classify.csv", 'r'))
true_pos, false_pos, true_neg, false_neg = 0, 0, 0, 0
for i in csv_file:
if float(i[1]) > number:
tag = '1'
else:
tag = '0'
if(tag == i[0]): # True类
if(i[0]=='0'):
true_neg+=1 # TN
else:
true_pos+=1 # TP
else:
if(i[0]=='0'):
false_pos+=1 # FP
else:
false_neg+=1 # FN
#print(true_pos, false_pos, true_neg, false_neg)
Accuracy = (true_pos + true_neg)/(true_pos + false_pos + true_neg + false_neg)
Precision = true_pos / (true_pos + false_pos)
Recall = true_pos / (true_pos + false_neg)
F1 = 2*true_pos / (2*true_pos + false_pos + false_neg)
Accuracy_image.append(Accuracy)
Precision_image.append(Precision)
Recall_image.append(Recall)
F1_image.append(F1)
#print("%.2f"%Accuracy)
#print("%.2f"%Precision)
#print("%.2f"%Recall)
#print("%.2f"%F1)
# 阈值选的不太成功(lll¬ω¬)
import matplotlib.pyplot as plt
indexs = []
for i in range(100):
find_num(0.99+0.0001*i)
indexs.append(0.99+0.0001*i)
plt.plot(indexs,Accuracy_image,color='red')
plt.plot(indexs,Precision_image,color='blue')
plt.plot(indexs,Recall_image,color='green')
plt.plot(indexs,F1_image,color='yellow')
plt.show()
```
| true |
code
| 0.217795 | null | null | null | null |
|
```
import pandas as pd
import numpy as np
import seaborn as sns
import folium
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest
%matplotlib inline
data = pd.read_csv("../data/StockX-Data-Consolidated.csv")
data.info(verbose=True)
```
# 1. EDA on Target Value
```
y = pd.DataFrame(data[['Pct_change']])
x = data.loc[:, ~data.columns.isin(['Pct_change'])]
plt.hist(y['Pct_change'], color = 'blue', edgecolor = 'black',
bins = 50)
plt.show()
plt.hist(x['Sale Price'], color = 'blue', edgecolor = 'black',
bins = 50)
plt.show()
```
## 1.1 target value voilin plot and box plot
```
sns.set(style="whitegrid")
ax = sns.violinplot(x=y['Pct_change'])
```
## 1.2 Anomaly Dectection: Train an Isolation Forest on log(Y)
```
model=IsolationForest(n_estimators=100, max_samples='auto', contamination= 0.05 ,max_features=1.0)
model.fit(y[['Pct_change']])
y['scores']=model.decision_function(y[['Pct_change']])
y['anomaly']=model.predict(y[['Pct_change']])
```
#### Print Anomoly Datapoints
```
anomaly=y.loc[y['anomaly']==-1]
anomaly_index=list(anomaly.index)
anomaly[0:19]
mean = np.array([[np.mean(y['Pct_change']),np.mean(y.loc[y['anomaly']==1]['Pct_change']),np.mean(anomaly['Pct_change'])]])
median = np.array([[np.median(y['Pct_change']),np.median(y.loc[y['anomaly']==1]['Pct_change']),np.median(anomaly['Pct_change'])]])
comp = pd.DataFrame(index = ['mean','median'],columns= ['whole','normal','anamaly'])
comp.iloc[0] = mean
comp.iloc[1] = median
comp
y['scores']=model.decision_function(y[['Pct_change']])
y['anomaly']=model.predict(y[['Pct_change']])
sns.set(style="whitegrid")
ax = sns.violinplot(x=anomaly["Pct_change"])
```
## 1.3 Compare group and the anomaly
```
plt.hist(y['Pct_change'], bins = 50, label = 'whole group', alpha = 0.5)
plt.hist(anomaly['Pct_change'], bins = 50, label = 'anomaly', alpha = 0.5)
plt.legend(loc = "best")
plt.show()
```
## 1.4 Explore Anomaly Points
```
anomaly_data = data[data.index.isin(anomaly_index)]
## Get brand, region and color count in the dataset
def get_brand(row):
for brand in data.columns[4:14]:
if row[brand] == 1:
return brand
def get_region(row):
for region in data.columns[14:20]:
if row[region] == 1:
return region
def get_col(row):
for color in data.columns[21:32]:
if row[color] == 1:
return color
anomaly_data['brand'] = anomaly_data.apply(get_brand, axis=1)
anomaly_data['region'] = anomaly_data.apply(get_region, axis=1)
anomaly_data['color'] = anomaly_data.apply(get_col, axis=1)
anomaly_data.brand.value_counts().plot(kind = 'bar',color = sns.color_palette("YlGnBu"))
anomaly_data.color.value_counts().plot(kind = 'bar',color = sns.color_palette("YlGnBu"))
anomaly_data.region.value_counts().plot(kind = 'bar',color = sns.color_palette("YlGnBu"))
```
# 2. EDA on feature variables
### EDA on Timing features
```
## group brand, region and color variables
data['week_since_release'] = (data['Days Since Release']/7).round(1)
data['brand'] = data.apply(get_brand, axis=1)
data['region'] = data.apply(get_region, axis=1)
data['color'] = data.apply(get_col, axis=1)
# create a new dataframe on grouped input features
timing = data[['Days Since Release',"week_since_release",'region', "brand",'color','Pct_change']]
timing = timing.rename(columns = {'Days Since Release':"days_since_release"})
# explore price premium change throughout weeks
np.random.seed(19680801)
N = 99956
#colors = np.random.rand(N)
cmap1 = sns.color_palette("YlGnBu")
plt.scatter(timing['week_since_release'],timing['Pct_change'], c = cmap1[0],alpha=0.5)
plt.title('Price premium on Weeks since release')
plt.xlabel('weeks since release')
plt.ylabel('price premium')
plt.show()
# Price Premium on different states over time
fig, ax = plt.subplots(figsize = (8,5))
sc = ax.scatter(timing.region,timing.week_since_release, c=timing.Pct_change,linewidths = 1.5, cmap="YlGnBu")
fig.colorbar(sc, ax=ax)
plt.ylabel('Week Since Release')
plt.title('Price Premium on different states over time', fontsize = 'large')
plt.show()
## Price Premium on different styles over time
fig, ax = plt.subplots(figsize = (11,5))
sc = ax.scatter(timing.brand,timing.week_since_release, c=timing.Pct_change, cmap="YlGnBu")
fig.colorbar(sc, ax=ax)
plt.ylabel('Week Since Release')
plt.title('Price Premium on different styles over time', fontsize = 'large')
plt.show()
# explore those heavy weighted features in anomaly points
#first group data by their brands
offwhite= timing.loc[timing['brand'] != 'yeezy']
#since white is heavily weighted, we explore color effect by first
#excluding white color
ow_nowhite = offwhite.loc[offwhite['color'] != 'White']
ow_white = offwhite.loc[offwhite['color'] == 'White']
ow_color = ow_nowhite.groupby(['color'])
img = plt.imread('../data/media/nike.jpg')
# Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-80, 800, 0, 8), zorder=-1,alpha = 0.5)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap2[-1],cmap1[7],cmap1[4],'brown']
for i, (name, group) in enumerate(ow_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.2)
# ax.spines['bottom'].set_color('white')
# ax.xaxis.label.set_color('white')
# ax.tick_params(axis='x', colors='white')
# ax.spines['left'].set_color('white')
# ax.yaxis.label.set_color('white')
# ax.tick_params(axis='y', colors='white')
#ax.patch.set_visible(False)
plt.title('Nike: Off-White(without white)', fontsize = 'large')
plt.xlabel('Days Since Release', )
plt.ylabel('Price Premium')
plt.legend()
plt.show()
offwhite['brand'].value_counts(sort=True, ascending=False, bins=None, dropna=True)
```
### Explore Top 3 Most-Selling Nike Sneakers
```
## Nike Off white
aj = offwhite.loc[offwhite['brand'] == 'airjordan']
aj_color = aj.groupby(['color'])
presto = offwhite.loc[offwhite['brand'] == 'presto']
presto_color = presto.groupby(['color'])
zoom = offwhite.loc[offwhite['brand'] == 'zoom']
zoom_color = zoom.groupby(['color'])
blazer = offwhite.loc[offwhite['brand'] == 'blazer']
blazer_color = blazer.groupby(['color'])
af = offwhite.loc[offwhite['brand'] == 'airforce']
af_color = af.groupby(['color'])
# Explore airjordan subbrand in Nike
# AJ Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-20, 500, -2, 8), zorder=-1,alpha = 0.4)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[0],cmap2[-1],cmap1[7],cmap1[4],'brown']
for i, (name, group) in enumerate(aj_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.4)
plt.title('Nike: Off-White Air Jordan', fontsize = 'large')
plt.xlabel('Days Since Release')
plt.ylabel('Price Premium')
plt.legend()
plt.show()
# Presto Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-20, 500, 0, 8), zorder=-1,alpha = 0.4)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap1[0],cmap1[7],cmap1[4],'brown']
for i, (name, group) in enumerate(presto_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.3)
plt.title('Nike: Off-White Presto', fontsize = 'large')
plt.xlabel('Days Since Release')
plt.ylabel('Price Premium')
plt.legend()
plt.show()
# Zoom Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-20, 500, -2, 8), zorder=-1,alpha = 0.4)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap1[7],cmap1[4],cmap1[0]]
for i, (name, group) in enumerate(zoom_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.3)
plt.title('Nike: Off-White Zoom', fontsize = 'large')
plt.xlabel('Days Since Release')
plt.ylabel('Price Premium')
plt.legend()
plt.show()
```
### Explore Yeezy Sneakers
```
yeezy= timing.loc[timing['brand'] == 'yeezy']
img2 = plt.imread('../data/media/yeezy.jpg')
yeezy_color = yeezy.groupby(['color'])
# Plot
fig, ax = plt.subplots()
ax.imshow(img2, aspect='auto', extent=(-5, 1500, -2, 12), zorder=-1,alpha = 0.5)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap2[-1],cmap1[-1],cmap1[4],cmap1[0]]
for i, (name, group) in enumerate(yeezy_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.3)
plt.title('Adidas: Yeezy', fontsize = 'large')
plt.xlabel('Days Since Release')
plt.ylabel('Price Premium')
plt.legend()
plt.show()
plt.scatter(x = yeezy['week_since_release'], y = yeezy['Pct_change'], c=sns.color_palette("YlGnBu")[1], alpha=0.5)
plt.title('Yeezy: Price premium on Weeks since release')
plt.xlabel('weeks since release')
plt.ylabel('price premium')
plt.show()
```
| true |
code
| 0.614799 | null | null | null | null |
|
<div align="center">
<h1><img width="30" src="https://madewithml.com/static/images/rounded_logo.png"> <a href="https://madewithml.com/">Made With ML</a></h1>
Applied ML · MLOps · Production
<br>
Join 30K+ developers in learning how to responsibly <a href="https://madewithml.com/about/">deliver value</a> with ML.
<br>
</div>
<br>
<div align="center">
<a target="_blank" href="https://newsletter.madewithml.com"><img src="https://img.shields.io/badge/Subscribe-30K-brightgreen"></a>
<a target="_blank" href="https://github.com/GokuMohandas/MadeWithML"><img src="https://img.shields.io/github/stars/GokuMohandas/MadeWithML.svg?style=social&label=Star"></a>
<a target="_blank" href="https://www.linkedin.com/in/goku"><img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a target="_blank" href="https://twitter.com/GokuMohandas"><img src="https://img.shields.io/twitter/follow/GokuMohandas.svg?label=Follow&style=social"></a>
<br>
🔥 Among the <a href="https://github.com/topics/deep-learning" target="_blank">top ML</a> repositories on GitHub
</div>
<br>
<hr>
# Convolutional Neural Networks (CNN)
In this lesson we will explore the basics of Convolutional Neural Networks (CNNs) applied to text for natural language processing (NLP) tasks.
<div align="left">
<a target="_blank" href="https://madewithml.com/courses/foundations/convolutional-neural-networks/"><img src="https://img.shields.io/badge/📖 Read-blog post-9cf"></a>
<a href="https://github.com/GokuMohandas/MadeWithML/blob/main/notebooks/11_Convolutional_Neural_Networks.ipynb" role="button"><img src="https://img.shields.io/static/v1?label=&message=View%20On%20GitHub&color=586069&logo=github&labelColor=2f363d"></a>
<a href="https://colab.research.google.com/github/GokuMohandas/MadeWithML/blob/main/notebooks/11_Convolutional_Neural_Networks.ipynb"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"></a>
</div>
# Overview
At the core of CNNs are filters (aka weights, kernels, etc.) which convolve (slide) across our input to extract relevant features. The filters are initialized randomly but learn to act as feature extractors via parameter sharing.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/cnn/convolution.gif" width="500">
</div>
* **Objective:** Extract meaningful spatial substructure from encoded data.
* **Advantages:**
* Small number of weights (shared)
* Parallelizable
* Detects spatial substrcutures (feature extractors)
* [Interpretability](https://arxiv.org/abs/1312.6034) via filters
* Can be used for processing in images, text, time-series, etc.
* **Disadvantages:**
* Many hyperparameters (kernel size, strides, etc.) to tune.
* **Miscellaneous:**
* Lot's of deep CNN architectures constantly updated for SOTA performance.
* Very popular feature extractor that's usually prepended onto other architectures.
# Set up
```
import numpy as np
import pandas as pd
import random
import torch
import torch.nn as nn
SEED = 1234
def set_seeds(seed=1234):
"""Set seeds for reproducibility."""
np.random.seed(seed)
random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed) # multi-GPU
# Set seeds for reproducibility
set_seeds(seed=SEED)
# Set device
cuda = True
device = torch.device('cuda' if (
torch.cuda.is_available() and cuda) else 'cpu')
torch.set_default_tensor_type('torch.FloatTensor')
if device.type == 'cuda':
torch.set_default_tensor_type('torch.cuda.FloatTensor')
print (device)
```
## Load data
We will download the [AG News dataset](http://www.di.unipi.it/~gulli/AG_corpus_of_news_articles.html), which consists of 120K text samples from 4 unique classes (`Business`, `Sci/Tech`, `Sports`, `World`)
```
# Load data
url = "https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/datasets/news.csv"
df = pd.read_csv(url, header=0) # load
df = df.sample(frac=1).reset_index(drop=True) # shuffle
df.head()
```
## Preprocessing
We're going to clean up our input data first by doing operations such as lower text, removing stop (filler) words, filters using regular expressions, etc.
```
import nltk
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
import re
nltk.download('stopwords')
STOPWORDS = stopwords.words('english')
print (STOPWORDS[:5])
porter = PorterStemmer()
def preprocess(text, stopwords=STOPWORDS):
"""Conditional preprocessing on our text unique to our task."""
# Lower
text = text.lower()
# Remove stopwords
pattern = re.compile(r'\b(' + r'|'.join(stopwords) + r')\b\s*')
text = pattern.sub('', text)
# Remove words in paranthesis
text = re.sub(r'\([^)]*\)', '', text)
# Spacing and filters
text = re.sub(r"([-;;.,!?<=>])", r" \1 ", text)
text = re.sub('[^A-Za-z0-9]+', ' ', text) # remove non alphanumeric chars
text = re.sub(' +', ' ', text) # remove multiple spaces
text = text.strip()
return text
# Sample
text = "Great week for the NYSE!"
preprocess(text=text)
# Apply to dataframe
preprocessed_df = df.copy()
preprocessed_df.title = preprocessed_df.title.apply(preprocess)
print (f"{df.title.values[0]}\n\n{preprocessed_df.title.values[0]}")
```
> If you have preprocessing steps like standardization, etc. that are calculated, you need to separate the training and test set first before applying those operations. This is because we cannot apply any knowledge gained from the test set accidentally (data leak) during preprocessing/training. However for global preprocessing steps like the function above where we aren't learning anything from the data itself, we can perform before splitting the data.
## Split data
```
import collections
from sklearn.model_selection import train_test_split
TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15
def train_val_test_split(X, y, train_size):
"""Split dataset into data splits."""
X_train, X_, y_train, y_ = train_test_split(X, y, train_size=TRAIN_SIZE, stratify=y)
X_val, X_test, y_val, y_test = train_test_split(X_, y_, train_size=0.5, stratify=y_)
return X_train, X_val, X_test, y_train, y_val, y_test
# Data
X = preprocessed_df["title"].values
y = preprocessed_df["category"].values
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, train_size=TRAIN_SIZE)
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"Sample point: {X_train[0]} → {y_train[0]}")
```
## LabelEncoder
Next we'll define a `LabelEncoder` to encode our text labels into unique indices
```
import itertools
class LabelEncoder(object):
"""Label encoder for tag labels."""
def __init__(self, class_to_index={}):
self.class_to_index = class_to_index
self.index_to_class = {v: k for k, v in self.class_to_index.items()}
self.classes = list(self.class_to_index.keys())
def __len__(self):
return len(self.class_to_index)
def __str__(self):
return f"<LabelEncoder(num_classes={len(self)})>"
def fit(self, y):
classes = np.unique(y)
for i, class_ in enumerate(classes):
self.class_to_index[class_] = i
self.index_to_class = {v: k for k, v in self.class_to_index.items()}
self.classes = list(self.class_to_index.keys())
return self
def encode(self, y):
encoded = np.zeros((len(y)), dtype=int)
for i, item in enumerate(y):
encoded[i] = self.class_to_index[item]
return encoded
def decode(self, y):
classes = []
for i, item in enumerate(y):
classes.append(self.index_to_class[item])
return classes
def save(self, fp):
with open(fp, 'w') as fp:
contents = {'class_to_index': self.class_to_index}
json.dump(contents, fp, indent=4, sort_keys=False)
@classmethod
def load(cls, fp):
with open(fp, 'r') as fp:
kwargs = json.load(fp=fp)
return cls(**kwargs)
# Encode
label_encoder = LabelEncoder()
label_encoder.fit(y_train)
NUM_CLASSES = len(label_encoder)
label_encoder.class_to_index
# Convert labels to tokens
print (f"y_train[0]: {y_train[0]}")
y_train = label_encoder.encode(y_train)
y_val = label_encoder.encode(y_val)
y_test = label_encoder.encode(y_test)
print (f"y_train[0]: {y_train[0]}")
# Class weights
counts = np.bincount(y_train)
class_weights = {i: 1.0/count for i, count in enumerate(counts)}
print (f"counts: {counts}\nweights: {class_weights}")
```
# Tokenizer
Our input data is text and we can't feed it directly to our models. So, we'll define a `Tokenizer` to convert our text input data into token indices. This means that every token (we can decide what a token is char, word, sub-word, etc.) is mapped to a unique index which allows us to represent our text as an array of indices.
```
import json
from collections import Counter
from more_itertools import take
class Tokenizer(object):
def __init__(self, char_level, num_tokens=None,
pad_token='<PAD>', oov_token='<UNK>',
token_to_index=None):
self.char_level = char_level
self.separator = '' if self.char_level else ' '
if num_tokens: num_tokens -= 2 # pad + unk tokens
self.num_tokens = num_tokens
self.pad_token = pad_token
self.oov_token = oov_token
if not token_to_index:
token_to_index = {pad_token: 0, oov_token: 1}
self.token_to_index = token_to_index
self.index_to_token = {v: k for k, v in self.token_to_index.items()}
def __len__(self):
return len(self.token_to_index)
def __str__(self):
return f"<Tokenizer(num_tokens={len(self)})>"
def fit_on_texts(self, texts):
if not self.char_level:
texts = [text.split(" ") for text in texts]
all_tokens = [token for text in texts for token in text]
counts = Counter(all_tokens).most_common(self.num_tokens)
self.min_token_freq = counts[-1][1]
for token, count in counts:
index = len(self)
self.token_to_index[token] = index
self.index_to_token[index] = token
return self
def texts_to_sequences(self, texts):
sequences = []
for text in texts:
if not self.char_level:
text = text.split(' ')
sequence = []
for token in text:
sequence.append(self.token_to_index.get(
token, self.token_to_index[self.oov_token]))
sequences.append(np.asarray(sequence))
return sequences
def sequences_to_texts(self, sequences):
texts = []
for sequence in sequences:
text = []
for index in sequence:
text.append(self.index_to_token.get(index, self.oov_token))
texts.append(self.separator.join([token for token in text]))
return texts
def save(self, fp):
with open(fp, 'w') as fp:
contents = {
'char_level': self.char_level,
'oov_token': self.oov_token,
'token_to_index': self.token_to_index
}
json.dump(contents, fp, indent=4, sort_keys=False)
@classmethod
def load(cls, fp):
with open(fp, 'r') as fp:
kwargs = json.load(fp=fp)
return cls(**kwargs)
```
We're going to restrict the number of tokens in our `Tokenizer` to the top 500 most frequent tokens (stop words already removed) because the full vocabulary size (~30K) is too large to run on Google Colab notebooks.
> It's important that we only fit using our train data split because during inference, our model will not always know every token so it's important to replicate that scenario with our validation and test splits as well.
```
# Tokenize
tokenizer = Tokenizer(char_level=False, num_tokens=500)
tokenizer.fit_on_texts(texts=X_train)
VOCAB_SIZE = len(tokenizer)
print (tokenizer)
# Sample of tokens
print (take(5, tokenizer.token_to_index.items()))
print (f"least freq token's freq: {tokenizer.min_token_freq}") # use this to adjust num_tokens
# Convert texts to sequences of indices
X_train = tokenizer.texts_to_sequences(X_train)
X_val = tokenizer.texts_to_sequences(X_val)
X_test = tokenizer.texts_to_sequences(X_test)
preprocessed_text = tokenizer.sequences_to_texts([X_train[0]])[0]
print ("Text to indices:\n"
f" (preprocessed) → {preprocessed_text}\n"
f" (tokenized) → {X_train[0]}")
```
# One-hot encoding
One-hot encoding creates a binary column for each unique value for the feature we're trying to map. All of the values in each token's array will be 0 except at the index that this specific token is represented by.
There are 5 words in the vocabulary:
```json
{
"a": 0,
"e": 1,
"i": 2,
"o": 3,
"u": 4
}
```
Then the text `aou` would be represented by:
```python
[[1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]]
```
One-hot encoding allows us to represent our data in a way that our models can process the data and isn't biased by the actual value of the token (ex. if your labels were actual numbers).
> We have already applied one-hot encoding in the previous lessons when we encoded our labels. Each label was represented by a unique index but when determining loss, we effectively use it's one hot representation and compared it to the predicted probability distribution. We never explicitly wrote this out since all of our previous tasks were multi-class which means every input had just one output class, so the 0s didn't affect the loss (though it did matter during back propagation).
```
def to_categorical(seq, num_classes):
"""One-hot encode a sequence of tokens."""
one_hot = np.zeros((len(seq), num_classes))
for i, item in enumerate(seq):
one_hot[i, item] = 1.
return one_hot
# One-hot encoding
print (X_train[0])
print (len(X_train[0]))
cat = to_categorical(seq=X_train[0], num_classes=len(tokenizer))
print (cat)
print (cat.shape)
# Convert tokens to one-hot
vocab_size = len(tokenizer)
X_train = [to_categorical(seq, num_classes=vocab_size) for seq in X_train]
X_val = [to_categorical(seq, num_classes=vocab_size) for seq in X_val]
X_test = [to_categorical(seq, num_classes=vocab_size) for seq in X_test]
```
# Padding
Our inputs are all of varying length but we need each batch to be uniformly shaped. Therefore, we will use padding to make all the inputs in the batch the same length. Our padding index will be 0 (note that this is consistent with the `<PAD>` token defined in our `Tokenizer`).
> One-hot encoding creates a batch of shape (`N`, `max_seq_len`, `vocab_size`) so we'll need to be able to pad 3D sequences.
```
def pad_sequences(sequences, max_seq_len=0):
"""Pad sequences to max length in sequence."""
max_seq_len = max(max_seq_len, max(len(sequence) for sequence in sequences))
num_classes = sequences[0].shape[-1]
padded_sequences = np.zeros((len(sequences), max_seq_len, num_classes))
for i, sequence in enumerate(sequences):
padded_sequences[i][:len(sequence)] = sequence
return padded_sequences
# 3D sequences
print (X_train[0].shape, X_train[1].shape, X_train[2].shape)
padded = pad_sequences(X_train[0:3])
print (padded.shape)
```
# Dataset
We're going to place our data into a [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) and use a [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) to efficiently create batches for training and evaluation.
```
FILTER_SIZE = 1 # unigram
class Dataset(torch.utils.data.Dataset):
def __init__(self, X, y, max_filter_size):
self.X = X
self.y = y
self.max_filter_size = max_filter_size
def __len__(self):
return len(self.y)
def __str__(self):
return f"<Dataset(N={len(self)})>"
def __getitem__(self, index):
X = self.X[index]
y = self.y[index]
return [X, y]
def collate_fn(self, batch):
"""Processing on a batch."""
# Get inputs
batch = np.array(batch, dtype=object)
X = batch[:, 0]
y = np.stack(batch[:, 1], axis=0)
# Pad sequences
X = pad_sequences(X, max_seq_len=self.max_filter_size)
# Cast
X = torch.FloatTensor(X.astype(np.int32))
y = torch.LongTensor(y.astype(np.int32))
return X, y
def create_dataloader(self, batch_size, shuffle=False, drop_last=False):
return torch.utils.data.DataLoader(
dataset=self, batch_size=batch_size, collate_fn=self.collate_fn,
shuffle=shuffle, drop_last=drop_last, pin_memory=True)
# Create datasets for embedding
train_dataset = Dataset(X=X_train, y=y_train, max_filter_size=FILTER_SIZE)
val_dataset = Dataset(X=X_val, y=y_val, max_filter_size=FILTER_SIZE)
test_dataset = Dataset(X=X_test, y=y_test, max_filter_size=FILTER_SIZE)
print ("Datasets:\n"
f" Train dataset:{train_dataset.__str__()}\n"
f" Val dataset: {val_dataset.__str__()}\n"
f" Test dataset: {test_dataset.__str__()}\n"
"Sample point:\n"
f" X: {test_dataset[0][0]}\n"
f" y: {test_dataset[0][1]}")
# Create dataloaders
batch_size = 64
train_dataloader = train_dataset.create_dataloader(batch_size=batch_size)
val_dataloader = val_dataset.create_dataloader(batch_size=batch_size)
test_dataloader = test_dataset.create_dataloader(batch_size=batch_size)
batch_X, batch_y = next(iter(test_dataloader))
print ("Sample batch:\n"
f" X: {list(batch_X.size())}\n"
f" y: {list(batch_y.size())}\n"
"Sample point:\n"
f" X: {batch_X[0]}\n"
f" y: {batch_y[0]}")
```
# CNN
## Inputs
We're going to learn about CNNs by applying them on 1D text data. In the dummy example below, our inputs are composed of character tokens that are one-hot encoded. We have a batch of N samples, where each sample has 8 characters and each character is represented by an array of 10 values (`vocab size=10`). This gives our inputs the size `(N, 8, 10)`.
> With PyTorch, when dealing with convolution, our inputs (X) need to have the channels as the second dimension, so our inputs will be `(N, 10, 8)`.
```
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
# Assume all our inputs are padded to have the same # of words
batch_size = 64
max_seq_len = 8 # words per input
vocab_size = 10 # one hot size
x = torch.randn(batch_size, max_seq_len, vocab_size)
print(f"X: {x.shape}")
x = x.transpose(1, 2)
print(f"X: {x.shape}")
```
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/cnn/inputs.png" width="500">
</div>
This diagram above is for char-level tokens but extends to any level of tokenization (word-level in our case).
## Filters
At the core of CNNs are filters (aka weights, kernels, etc.) which convolve (slide) across our input to extract relevant features. The filters are initialized randomly but learn to pick up meaningful features from the input that aid in optimizing for the objective. The intuition here is that each filter represents a feature and we will use this filter on other inputs to capture the same feature (feature extraction via parameter sharing).
We can see convolution in the diagram below where we simplified the filters and inputs to be 2D for ease of visualization. Also note that the values are 0/1s but in reality they can be any floating point value.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/cnn/convolution.gif" width="500">
</div>
Now let's return to our actual inputs `x`, which is of shape (8, 10) [`max_seq_len`, `vocab_size`] and we want to convolve on this input using filters. We will use 50 filters that are of size (1, 3) and has the same depth as the number of channels (`num_channels` = `vocab_size` = `one_hot_size` = 10). This gives our filter a shape of (3, 10, 50) [`kernel_size`, `vocab_size`, `num_filters`]
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/cnn/filters.png" width="500">
</div>
* **stride**: amount the filters move from one convolution operation to the next.
* **padding**: values (typically zero) padded to the input, typically to create a volume with whole number dimensions.
So far we've used a `stride` of 1 and `VALID` padding (no padding) but let's look at an example with a higher stride and difference between different padding approaches.
Padding types:
* **VALID**: no padding, the filters only use the "valid" values in the input. If the filter cannot reach all the input values (filters go left to right), the extra values on the right are dropped.
* **SAME**: adds padding evenly to the right (preferred) and left sides of the input so that all values in the input are processed.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/cnn/padding.png" width="500">
</div>
We're going to use the [Conv1d](https://pytorch.org/docs/stable/generated/torch.nn.Conv1d.html#torch.nn.Conv1d) layer to process our inputs.
```
# Convolutional filters (VALID padding)
vocab_size = 10 # one hot size
num_filters = 50 # num filters
filter_size = 3 # filters are 3X3
stride = 1
padding = 0 # valid padding (no padding)
conv1 = nn.Conv1d(in_channels=vocab_size, out_channels=num_filters,
kernel_size=filter_size, stride=stride,
padding=padding, padding_mode='zeros')
print("conv: {}".format(conv1.weight.shape))
# Forward pass
z = conv1(x)
print (f"z: {z.shape}")
```
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/cnn/conv.png" width="700">
</div>
When we apply these filter on our inputs, we receive an output of shape (N, 6, 50). We get 50 for the output channel dim because we used 50 filters and 6 for the conv outputs because:
$W_1 = \frac{W_2 - F + 2P}{S} + 1 = \frac{8 - 3 + 2(0)}{1} + 1 = 6$
$H_1 = \frac{H_2 - F + 2P}{S} + 1 = \frac{1 - 1 + 2(0)}{1} + 1 = 1$
$D_2 = D_1 $
where:
* `W`: width of each input = 8
* `H`: height of each input = 1
* `D`: depth (# channels)
* `F`: filter size = 3
* `P`: padding = 0
* `S`: stride = 1
Now we'll add padding so that the convolutional outputs are the same shape as our inputs. The amount of padding for the `SAME` padding can be determined using the same equation. We want out output to have the same width as our input, so we solve for P:
$ \frac{W-F+2P}{S} + 1 = W $
$ P = \frac{S(W-1) - W + F}{2} $
If $P$ is not a whole number, we round up (using `math.ceil`) and place the extra padding on the right side.
```
# Convolutional filters (SAME padding)
vocab_size = 10 # one hot size
num_filters = 50 # num filters
filter_size = 3 # filters are 3X3
stride = 1
conv = nn.Conv1d(in_channels=vocab_size, out_channels=num_filters,
kernel_size=filter_size, stride=stride)
print("conv: {}".format(conv.weight.shape))
# `SAME` padding
padding_left = int((conv.stride[0]*(max_seq_len-1) - max_seq_len + filter_size)/2)
padding_right = int(math.ceil((conv.stride[0]*(max_seq_len-1) - max_seq_len + filter_size)/2))
print (f"padding: {(padding_left, padding_right)}")
# Forward pass
z = conv(F.pad(x, (padding_left, padding_right)))
print (f"z: {z.shape}")
```
> We will explore larger dimensional convolution layers in subsequent lessons. For example, [Conv2D](https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html#torch.nn.Conv2d) is used with 3D inputs (images, char-level text, etc.) and [Conv3D](https://pytorch.org/docs/stable/generated/torch.nn.Conv3d.html#torch.nn.Conv3d) is used for 4D inputs (videos, time-series, etc.).
## Pooling
The result of convolving filters on an input is a feature map. Due to the nature of convolution and overlaps, our feature map will have lots of redundant information. Pooling is a way to summarize a high-dimensional feature map into a lower dimensional one for simplified downstream computation. The pooling operation can be the max value, average, etc. in a certain receptive field. Below is an example of pooling where the outputs from a conv layer are `4X4` and we're going to apply max pool filters of size `2X2`.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/cnn/pooling.png" width="500">
</div>
$W_2 = \frac{W_1 - F}{S} + 1 = \frac{4 - 2}{2} + 1 = 2$
$H_2 = \frac{H_1 - F}{S} + 1 = \frac{4 - 2}{2} + 1 = 2$
$ D_2 = D_1 $
where:
* `W`: width of each input = 4
* `H`: height of each input = 4
* `D`: depth (# channels)
* `F`: filter size = 2
* `S`: stride = 2
In our use case, we want to just take the one max value so we will use the [MaxPool1D](https://pytorch.org/docs/stable/generated/torch.nn.MaxPool1d.html#torch.nn.MaxPool1d) layer, so our max-pool filter size will be max_seq_len.
```
# Max pooling
pool_output = F.max_pool1d(z, z.size(2))
print("Size: {}".format(pool_output.shape))
```
## Batch Normalization
The last topic we'll cover before constructing our model is [batch normalization](https://arxiv.org/abs/1502.03167). It's an operation that will standardize (mean=0, std=1) the activations from the previous layer. Recall that we used to standardize our inputs in previous notebooks so our model can optimize quickly with larger learning rates. It's the same concept here but we continue to maintain standardized values throughout the forward pass to further aid optimization.
```
# Batch normalization
batch_norm = nn.BatchNorm1d(num_features=num_filters)
z = batch_norm(conv(x)) # applied to activations (after conv layer & before pooling)
print (f"z: {z.shape}")
# Mean and std before batchnorm
print (f"mean: {torch.mean(conv1(x)):.2f}, std: {torch.std(conv(x)):.2f}")
# Mean and std after batchnorm
print (f"mean: {torch.mean(z):.2f}, std: {torch.std(z):.2f}")
```
# Modeling
## Model
Let's visualize the model's forward pass.
1. We'll first tokenize our inputs (`batch_size`, `max_seq_len`).
2. Then we'll one-hot encode our tokenized inputs (`batch_size`, `max_seq_len`, `vocab_size`).
3. We'll apply convolution via filters (`filter_size`, `vocab_size`, `num_filters`) followed by batch normalization. Our filters act as character level n-gram detectors.
4. We'll apply 1D global max pooling which will extract the most relevant information from the feature maps for making the decision.
5. We feed the pool outputs to a fully-connected (FC) layer (with dropout).
6. We use one more FC layer with softmax to derive class probabilities.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/foundations/cnn/model.png" width="1000">
</div>
```
NUM_FILTERS = 50
HIDDEN_DIM = 100
DROPOUT_P = 0.1
class CNN(nn.Module):
def __init__(self, vocab_size, num_filters, filter_size,
hidden_dim, dropout_p, num_classes):
super(CNN, self).__init__()
# Convolutional filters
self.filter_size = filter_size
self.conv = nn.Conv1d(
in_channels=vocab_size, out_channels=num_filters,
kernel_size=filter_size, stride=1, padding=0, padding_mode='zeros')
self.batch_norm = nn.BatchNorm1d(num_features=num_filters)
# FC layers
self.fc1 = nn.Linear(num_filters, hidden_dim)
self.dropout = nn.Dropout(dropout_p)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, inputs, channel_first=False):
# Rearrange input so num_channels is in dim 1 (N, C, L)
x_in, = inputs
if not channel_first:
x_in = x_in.transpose(1, 2)
# Padding for `SAME` padding
max_seq_len = x_in.shape[2]
padding_left = int((self.conv.stride[0]*(max_seq_len-1) - max_seq_len + self.filter_size)/2)
padding_right = int(math.ceil((self.conv.stride[0]*(max_seq_len-1) - max_seq_len + self.filter_size)/2))
# Conv outputs
z = self.conv(F.pad(x_in, (padding_left, padding_right)))
z = F.max_pool1d(z, z.size(2)).squeeze(2)
# FC layer
z = self.fc1(z)
z = self.dropout(z)
z = self.fc2(z)
return z
# Initialize model
model = CNN(vocab_size=VOCAB_SIZE, num_filters=NUM_FILTERS, filter_size=FILTER_SIZE,
hidden_dim=HIDDEN_DIM, dropout_p=DROPOUT_P, num_classes=NUM_CLASSES)
model = model.to(device) # set device
print (model.named_parameters)
```
> We used `SAME` padding (w/ stride=1) which means that the conv outputs will have the same width (`max_seq_len`) as our inputs. The amount of padding differs for each batch based on the `max_seq_len` but you can calculate it by solving for P in the equation below.
$ \frac{W_1 - F + 2P}{S} + 1 = W_2 $
$ \frac{\text{max_seq_len } - \text{ filter_size } + 2P}{\text{stride}} + 1 = \text{max_seq_len} $
$ P = \frac{\text{stride}(\text{max_seq_len}-1) - \text{max_seq_len} + \text{filter_size}}{2} $
If $P$ is not a whole number, we round up (using `math.ceil`) and place the extra padding on the right side.
## Training
Let's create the `Trainer` class that we'll use to facilitate training for our experiments. Notice that we're now moving the `train` function inside this class.
```
from torch.optim import Adam
LEARNING_RATE = 1e-3
PATIENCE = 5
NUM_EPOCHS = 10
class Trainer(object):
def __init__(self, model, device, loss_fn=None, optimizer=None, scheduler=None):
# Set params
self.model = model
self.device = device
self.loss_fn = loss_fn
self.optimizer = optimizer
self.scheduler = scheduler
def train_step(self, dataloader):
"""Train step."""
# Set model to train mode
self.model.train()
loss = 0.0
# Iterate over train batches
for i, batch in enumerate(dataloader):
# Step
batch = [item.to(self.device) for item in batch] # Set device
inputs, targets = batch[:-1], batch[-1]
self.optimizer.zero_grad() # Reset gradients
z = self.model(inputs) # Forward pass
J = self.loss_fn(z, targets) # Define loss
J.backward() # Backward pass
self.optimizer.step() # Update weights
# Cumulative Metrics
loss += (J.detach().item() - loss) / (i + 1)
return loss
def eval_step(self, dataloader):
"""Validation or test step."""
# Set model to eval mode
self.model.eval()
loss = 0.0
y_trues, y_probs = [], []
# Iterate over val batches
with torch.inference_mode():
for i, batch in enumerate(dataloader):
# Step
batch = [item.to(self.device) for item in batch] # Set device
inputs, y_true = batch[:-1], batch[-1]
z = self.model(inputs) # Forward pass
J = self.loss_fn(z, y_true).item()
# Cumulative Metrics
loss += (J - loss) / (i + 1)
# Store outputs
y_prob = F.softmax(z).cpu().numpy()
y_probs.extend(y_prob)
y_trues.extend(y_true.cpu().numpy())
return loss, np.vstack(y_trues), np.vstack(y_probs)
def predict_step(self, dataloader):
"""Prediction step."""
# Set model to eval mode
self.model.eval()
y_probs = []
# Iterate over val batches
with torch.inference_mode():
for i, batch in enumerate(dataloader):
# Forward pass w/ inputs
inputs, targets = batch[:-1], batch[-1]
z = self.model(inputs)
# Store outputs
y_prob = F.softmax(z).cpu().numpy()
y_probs.extend(y_prob)
return np.vstack(y_probs)
def train(self, num_epochs, patience, train_dataloader, val_dataloader):
best_val_loss = np.inf
for epoch in range(num_epochs):
# Steps
train_loss = self.train_step(dataloader=train_dataloader)
val_loss, _, _ = self.eval_step(dataloader=val_dataloader)
self.scheduler.step(val_loss)
# Early stopping
if val_loss < best_val_loss:
best_val_loss = val_loss
best_model = self.model
_patience = patience # reset _patience
else:
_patience -= 1
if not _patience: # 0
print("Stopping early!")
break
# Logging
print(
f"Epoch: {epoch+1} | "
f"train_loss: {train_loss:.5f}, "
f"val_loss: {val_loss:.5f}, "
f"lr: {self.optimizer.param_groups[0]['lr']:.2E}, "
f"_patience: {_patience}"
)
return best_model
# Define Loss
class_weights_tensor = torch.Tensor(list(class_weights.values())).to(device)
loss_fn = nn.CrossEntropyLoss(weight=class_weights_tensor)
# Define optimizer & scheduler
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(
optimizer, mode='min', factor=0.1, patience=3)
# Trainer module
trainer = Trainer(
model=model, device=device, loss_fn=loss_fn,
optimizer=optimizer, scheduler=scheduler)
# Train
best_model = trainer.train(
NUM_EPOCHS, PATIENCE, train_dataloader, val_dataloader)
```
## Evaluation
```
import json
from pathlib import Path
from sklearn.metrics import precision_recall_fscore_support
def get_performance(y_true, y_pred, classes):
"""Per-class performance metrics."""
# Performance
performance = {"overall": {}, "class": {}}
# Overall performance
metrics = precision_recall_fscore_support(y_true, y_pred, average="weighted")
performance["overall"]["precision"] = metrics[0]
performance["overall"]["recall"] = metrics[1]
performance["overall"]["f1"] = metrics[2]
performance["overall"]["num_samples"] = np.float64(len(y_true))
# Per-class performance
metrics = precision_recall_fscore_support(y_true, y_pred, average=None)
for i in range(len(classes)):
performance["class"][classes[i]] = {
"precision": metrics[0][i],
"recall": metrics[1][i],
"f1": metrics[2][i],
"num_samples": np.float64(metrics[3][i]),
}
return performance
# Get predictions
test_loss, y_true, y_prob = trainer.eval_step(dataloader=test_dataloader)
y_pred = np.argmax(y_prob, axis=1)
# Determine performance
performance = get_performance(
y_true=y_test, y_pred=y_pred, classes=label_encoder.classes)
print (json.dumps(performance['overall'], indent=2))
# Save artifacts
dir = Path("cnn")
dir.mkdir(parents=True, exist_ok=True)
label_encoder.save(fp=Path(dir, 'label_encoder.json'))
tokenizer.save(fp=Path(dir, 'tokenizer.json'))
torch.save(best_model.state_dict(), Path(dir, 'model.pt'))
with open(Path(dir, 'performance.json'), "w") as fp:
json.dump(performance, indent=2, sort_keys=False, fp=fp)
```
## Inference
```
def get_probability_distribution(y_prob, classes):
"""Create a dict of class probabilities from an array."""
results = {}
for i, class_ in enumerate(classes):
results[class_] = np.float64(y_prob[i])
sorted_results = {k: v for k, v in sorted(
results.items(), key=lambda item: item[1], reverse=True)}
return sorted_results
# Load artifacts
device = torch.device("cpu")
label_encoder = LabelEncoder.load(fp=Path(dir, 'label_encoder.json'))
tokenizer = Tokenizer.load(fp=Path(dir, 'tokenizer.json'))
model = CNN(
vocab_size=VOCAB_SIZE, num_filters=NUM_FILTERS, filter_size=FILTER_SIZE,
hidden_dim=HIDDEN_DIM, dropout_p=DROPOUT_P, num_classes=NUM_CLASSES)
model.load_state_dict(torch.load(Path(dir, 'model.pt'), map_location=device))
model.to(device)
# Initialize trainer
trainer = Trainer(model=model, device=device)
# Dataloader
text = "What a day for the new york stock market to go bust!"
sequences = tokenizer.texts_to_sequences([preprocess(text)])
print (tokenizer.sequences_to_texts(sequences))
X = [to_categorical(seq, num_classes=len(tokenizer)) for seq in sequences]
y_filler = label_encoder.encode([label_encoder.classes[0]]*len(X))
dataset = Dataset(X=X, y=y_filler, max_filter_size=FILTER_SIZE)
dataloader = dataset.create_dataloader(batch_size=batch_size)
# Inference
y_prob = trainer.predict_step(dataloader)
y_pred = np.argmax(y_prob, axis=1)
label_encoder.decode(y_pred)
# Class distributions
prob_dist = get_probability_distribution(y_prob=y_prob[0], classes=label_encoder.classes)
print (json.dumps(prob_dist, indent=2))
```
# Interpretability
We went through all the trouble of padding our inputs before convolution to result is outputs of the same shape as our inputs so we can try to get some interpretability. Since every token is mapped to a convolutional output on whcih we apply max pooling, we can see which token's output was most influential towards the prediction. We first need to get the conv outputs from our model:
```
import collections
import seaborn as sns
class InterpretableCNN(nn.Module):
def __init__(self, vocab_size, num_filters, filter_size,
hidden_dim, dropout_p, num_classes):
super(InterpretableCNN, self).__init__()
# Convolutional filters
self.filter_size = filter_size
self.conv = nn.Conv1d(
in_channels=vocab_size, out_channels=num_filters,
kernel_size=filter_size, stride=1, padding=0, padding_mode='zeros')
self.batch_norm = nn.BatchNorm1d(num_features=num_filters)
# FC layers
self.fc1 = nn.Linear(num_filters, hidden_dim)
self.dropout = nn.Dropout(dropout_p)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, inputs, channel_first=False):
# Rearrange input so num_channels is in dim 1 (N, C, L)
x_in, = inputs
if not channel_first:
x_in = x_in.transpose(1, 2)
# Padding for `SAME` padding
max_seq_len = x_in.shape[2]
padding_left = int((self.conv.stride[0]*(max_seq_len-1) - max_seq_len + self.filter_size)/2)
padding_right = int(math.ceil((self.conv.stride[0]*(max_seq_len-1) - max_seq_len + self.filter_size)/2))
# Conv outputs
z = self.conv(F.pad(x_in, (padding_left, padding_right)))
return z
# Initialize
interpretable_model = InterpretableCNN(
vocab_size=len(tokenizer), num_filters=NUM_FILTERS, filter_size=FILTER_SIZE,
hidden_dim=HIDDEN_DIM, dropout_p=DROPOUT_P, num_classes=NUM_CLASSES)
# Load weights (same architecture)
interpretable_model.load_state_dict(torch.load(Path(dir, 'model.pt'), map_location=device))
interpretable_model.to(device)
# Initialize trainer
interpretable_trainer = Trainer(model=interpretable_model, device=device)
# Get conv outputs
conv_outputs = interpretable_trainer.predict_step(dataloader)
print (conv_outputs.shape) # (num_filters, max_seq_len)
# Visualize a bi-gram filter's outputs
tokens = tokenizer.sequences_to_texts(sequences)[0].split(' ')
sns.heatmap(conv_outputs, xticklabels=tokens)
```
The filters have high values for the words `stock` and `market` which influenced the `Business` category classification.
> This is a crude technique (maxpool doesn't strictly behave this way on a batch) loosely based off of more elaborate [interpretability](https://arxiv.org/abs/1312.6034) methods.
| true |
code
| 0.633098 | null | null | null | null |
|
# Monte Carlo Methods: Lab 1
Take a look at Chapter 10 of Newman's *Computational Physics with Python* where much of this material is drawn from.
```
from IPython.core.display import HTML
css_file = 'https://raw.githubusercontent.com/ngcm/training-public/master/ipython_notebook_styles/ngcmstyle.css'
HTML(url=css_file)
```
## Integration
If we have an ugly function, say
$$
\begin{equation}
f(x) = \sin^2 \left(\frac{1}{x (2-x)}\right),
\end{equation}
$$
then it can be very difficult to integrate. To see this, just do a quick plot.
```
%matplotlib inline
import numpy
from matplotlib import pyplot
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 16
rcParams['figure.figsize'] = (12,6)
from __future__ import division
def f(x):
return numpy.sin(1.0/(x*(2.0-x)))**2
x = numpy.linspace(0.0, 2.0, 10000)
pyplot.plot(x, f(x))
pyplot.xlabel(r"$x$")
pyplot.ylabel(r"$\sin^2([x(x-2)]^{-1})$");
```
We see that as the function oscillates *infinitely often*, integrating this with standard methods is going to be very inaccurate.
However, we note that the function is bounded, so the integral (given by the shaded area below) must itself be bounded - less than the total area in the plot, which is $2$ in this case.
```
pyplot.fill_between(x, f(x))
pyplot.xlabel(r"$x$")
pyplot.ylabel(r"$\sin^2([x(x-2)]^{-1})$");
```
So if we scattered (using a *uniform* random distribution) a large number of points within this box, the fraction of them falling *below* the curve is approximately the integral we want to compute, divided by the area of the box:
$$
\begin{equation}
I = \int_a^b f(x) \, dx \quad \implies \quad I \simeq \frac{k A}{N}
\end{equation}
$$
where $N$ is the total number of points considered, $k$ is the number falling below the curve, and $A$ is the area of the box. We can choose the box, but we need $y \in [\min_{x \in [a, b]} (f(x)), \max_{x \in [a, b]} (f(x))] = [c, d]$, giving $A = (d-c)(b-a)$.
So let's apply this technique to the function above, where the box in $y$ is $[0,1]$.
```
def mc_integrate(f, domain_x, domain_y, N = 10000):
"""
Monte Carlo integration function: to be completed. Result, for the given f, should be around 1.46.
"""
import numpy.random
return I
```
### Accuracy
To check the accuracy of the method, let's apply this to calculate $\pi$.
The area of a circle of radius $2$ is $4\pi$, so the area of the *quarter* circle in $x, y \in [0, 2]$ is just $\pi$:
$$
\begin{equation}
\pi = \int_0^2 \sqrt{4 - x^2} \, dx.
\end{equation}
$$
Check the convergence of the Monte Carlo integration with $N$. (I suggest using $N = 100 \times 2^i$ for $i = 0, \dots, 19$; you should find the error scales roughly as $N^{-1/2}$)
## Mean Value Method
Monte Carlo integration is pretty inaccurate, as seen above: it converges slowly, and has poor accuracy at all $N$. An alternative is the *mean value* method, where we note that *by definition* the average value of $f$ over the interval $[a, b]$ is precisely the integral multiplied by the width of the interval.
Hence we can just choose our $N$ random points in $x$ as above, but now just compute
$$
\begin{equation}
I \simeq \frac{b-a}{N} \sum_{i=1}^N f(x_i).
\end{equation}
$$
```
def mv_integrate(f, domain_x, N = 10000):
"""
Mean value Monte Carlo integration: to be completed
"""
import numpy.random
return I
```
Let's look at the accuracy of this method again applied to computing $\pi$.
The convergence *rate* is the same (only roughly, typically), but the Mean Value method is *expected* to be better in terms of its absolute error.
### Dimensionality
Compared to standard integration methods (Gauss quadrature, Simpson's rule, etc) the convergence rate for Monte Carlo methods is very slow. However, there is one crucial advantage: as you change dimension, the amount of calculation required is *unchanged*, whereas for standard methods it grows geometrically with the dimension.
Try to compute the volume of an $n$-dimensional unit *hypersphere*, which is the object in $\mathbb{R}^n$ such that
$$
\begin{equation}
\sum_{i=1}^n x_i^2 \le 1.
\end{equation}
$$
The volume of the hypersphere [can be found in closed form](http://en.wikipedia.org/wiki/Volume_of_an_n-ball#The_volume), but can rapidly be computed using the Monte Carlo method above, by counting the $k$ points that randomly fall within the hypersphere and using the standard formula $I \simeq V k / N$.
```
def mc_integrate_multid(f, domain, N = 10000):
"""
Monte Carlo integration in arbitrary dimensions (read from the size of the domain): to be completed
"""
return I
from scipy import special
def volume_hypersphere(ndim=3):
return numpy.pi**(float(ndim)/2.0) / special.gamma(float(ndim)/2.0 + 1.0)
```
Now let us repeat this across multiple dimensions.
The errors clearly vary over a range, but the convergence remains roughly as $N^{-1/2}$ independent of the dimension; using other techniques such as Gauss quadrature would see the points required scaling geometrically with the dimension.
## Importance sampling
Consider the integral (which arises, for example, in the theory of Fermi gases)
$$
\begin{equation}
I = \int_0^1 \frac{x^{-1/2}}{e^x + 1} \, dx.
\end{equation}
$$
This has a finite value, but the integrand diverges as $x \to 0$. This *may* cause a problem for Monte Carlo integration when a single value may give a spuriously large contribution to the sum.
We can get around this by changing the points at which the integrand is sampled. Choose a *weighting* function $w(x)$. Then a weighted average of any function $g(x)$ can be
$$
\begin{equation}
<g>_w = \frac{\int_a^b w(x) g(x) \, dx}{\int_a^b w(x) \, dx}.
\end{equation}
$$
As our integral is
$$
\begin{equation}
I = \int_a^b f(x) \, dx
\end{equation}
$$
we can, by setting $g(x) = f(x) / w(x)$ get
$$
\begin{equation}
I = \int_a^b f(x) \, dx = \left< \frac{f(x)}{w(x)} \right>_w \int_a^b w(x) \, dx.
\end{equation}
$$
This gives
$$
\begin{equation}
I \simeq \frac{1}{N} \sum_{i=1}^N \frac{f(x_i)}{w(x_i)} \int_a^b w(x) \, dx,
\end{equation}
$$
where the points $x_i$ are now chosen from a *non-uniform* probability distribution with pdf
$$
\begin{equation}
p(x) = \frac{w(x)}{\int_a^b w(x) \, dx}.
\end{equation}
$$
This is a generalization of the mean value method - we clearly recover the mean value method when the weighting function $w(x) \equiv 1$. A careful choice of the weighting function can mitigate problematic regions of the integrand; e.g., in the example above we could choose $w(x) = x^{-1/2}$, giving $p(x) = x^{-1/2}/2$. In general, the hard part of the algorithm is going to be generating the samples from this non-uniform distribution. Here we have the advantage that $p$ is given by the `numpy.random.power` distribution.
So, let's try to solve the integral above. We need $\int_0^1 w(x) = 2$. The expected solution is around 0.84.So, let's try to solve the integral above. The expected solution is around 0.84.
In the general case, how do we generate the samples from the non-uniform probability distribution $p$?
What really matters here is not the function $p$ from which we draw the random numbers `x`. What really matters is that the random numbers appear to follow the behaviour, the distribution $p$, that we want. This may seem like stating the same thing, but it's not. We can use a technique called *rejection sampling* to construct a set of numbers that follows a certain (cumulative) distribution without having to construct the pdf that it actually follows at all.
To do this, we need to know the distribution we want (here $p(x) = 1/(2 \sqrt{x})$) and another distribution $q(x)$ that we can easily compute with a constant $K$ such that $p(x) \le K q(x)$. What we're doing here is just for illustration, as the *power* distribution $p(x) = a x^{a-1}$ is provided by `numpy.random.power` and perfectly matches the distribution we want for $a=1/2$. Here we're going to need some distribution that diverges faster than $p$ for small $x$, so we can choose the power distribution with $a=1/3$, provided, for example, $K = 1.6$:
```
x = numpy.linspace(0.01,1,2000)
p = 1/(2*numpy.sqrt(x))
q = 1/(3*x**(2/3))
K = 1.6
pyplot.semilogy(x, p, lw=2, label=r"$p(x)$")
pyplot.semilogy(x, K * q, lw=2, label=r"$K q(x)$")
pyplot.xlabel(r"$x$")
pyplot.legend()
pyplot.show()
```
Rejection sampling works by drawing random samples from the easy-to-compute distribution $q$. We then keep the samples drawn from $q$ with a certain probability: if $p(x) / (K q(x)) < U$, where $U$ is drawn from the uniform distribution, then we keep the sample. As we're calculating $p$, not drawing samples from it, this shouldn't be a problem.
Let's check this working:
So now we can write an importance sampling algorithm without having to integrate the weighting function first, by using rejection sampling to find a set of samples from the resulting pdf without actually having to sample it.
We won't do that here, but it's a key conceptual step for MCMC algorithms such as Metropolis Hastings.
| true |
code
| 0.70854 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc" style="margin-top: 1em;"><ul class="toc-item"><li><span><a href="#はじめに" data-toc-modified-id="はじめに-1"><span class="toc-item-num">1 </span>はじめに</a></span><ul class="toc-item"><li><span><a href="#研究の目的" data-toc-modified-id="研究の目的-1.1"><span class="toc-item-num">1.1 </span>研究の目的</a></span></li><li><span><a href="#研究の動機" data-toc-modified-id="研究の動機-1.2"><span class="toc-item-num">1.2 </span>研究の動機</a></span></li></ul></li><li><span><a href="#基本的事項" data-toc-modified-id="基本的事項-2"><span class="toc-item-num">2 </span>基本的事項</a></span><ul class="toc-item"><li><span><a href="#Emacs" data-toc-modified-id="Emacs-2.1"><span class="toc-item-num">2.1 </span>Emacs</a></span></li><li><span><a href="#Ruby" data-toc-modified-id="Ruby-2.2"><span class="toc-item-num">2.2 </span>Ruby</a></span></li><li><span><a href="#RubyGems" data-toc-modified-id="RubyGems-2.3"><span class="toc-item-num">2.3 </span>RubyGems</a></span></li><li><span><a href="#Keybind" data-toc-modified-id="Keybind-2.4"><span class="toc-item-num">2.4 </span>Keybind</a></span></li><li><span><a href="#CUI(Character-User-Interface)" data-toc-modified-id="CUI(Character-User-Interface)-2.5"><span class="toc-item-num">2.5 </span>CUI(Character User Interface)</a></span></li><li><span><a href="#使用したgemファイル" data-toc-modified-id="使用したgemファイル-2.6"><span class="toc-item-num">2.6 </span>使用したgemファイル</a></span><ul class="toc-item"><li><span><a href="#diff-lcs" data-toc-modified-id="diff-lcs-2.6.1"><span class="toc-item-num">2.6.1 </span>diff-lcs</a></span></li><li><span><a href="#Thor" data-toc-modified-id="Thor-2.6.2"><span class="toc-item-num">2.6.2 </span>Thor</a></span></li><li><span><a href="#Minitest" data-toc-modified-id="Minitest-2.6.3"><span class="toc-item-num">2.6.3 </span>Minitest</a></span></li><li><span><a href="#FileUtils" data-toc-modified-id="FileUtils-2.6.4"><span class="toc-item-num">2.6.4 </span>FileUtils</a></span></li><li><span><a href="#open3" data-toc-modified-id="open3-2.6.5"><span class="toc-item-num">2.6.5 </span>open3</a></span></li><li><span><a href="#Bundler" data-toc-modified-id="Bundler-2.6.6"><span class="toc-item-num">2.6.6 </span>Bundler</a></span></li><li><span><a href="#Rubocop" data-toc-modified-id="Rubocop-2.6.7"><span class="toc-item-num">2.6.7 </span>Rubocop</a></span></li></ul></li></ul></li><li><span><a href="#editor_learnerの概要" data-toc-modified-id="editor_learnerの概要-3"><span class="toc-item-num">3 </span>editor_learnerの概要</a></span><ul class="toc-item"><li><span><a href="#Installation" data-toc-modified-id="Installation-3.1"><span class="toc-item-num">3.1 </span>Installation</a></span><ul class="toc-item"><li><span><a href="#githubによるinstall" data-toc-modified-id="githubによるinstall-3.1.1"><span class="toc-item-num">3.1.1 </span>githubによるinstall</a></span></li><li><span><a href="#gemによるinstall" data-toc-modified-id="gemによるinstall-3.1.2"><span class="toc-item-num">3.1.2 </span>gemによるinstall</a></span></li></ul></li><li><span><a href="#uninstall" data-toc-modified-id="uninstall-3.2"><span class="toc-item-num">3.2 </span>uninstall</a></span><ul class="toc-item"><li><span><a href="#githubからinstallした場合のuninstall方法" data-toc-modified-id="githubからinstallした場合のuninstall方法-3.2.1"><span class="toc-item-num">3.2.1 </span>githubからinstallした場合のuninstall方法</a></span></li><li><span><a href="#gemからinstallした場合のuninstall方法" data-toc-modified-id="gemからinstallした場合のuninstall方法-3.2.2"><span class="toc-item-num">3.2.2 </span>gemからinstallした場合のuninstall方法</a></span></li></ul></li><li><span><a href="#動作環境" data-toc-modified-id="動作環境-3.3"><span class="toc-item-num">3.3 </span>動作環境</a></span><ul class="toc-item"><li><span><a href="#error時の対処法" data-toc-modified-id="error時の対処法-3.3.1"><span class="toc-item-num">3.3.1 </span>error時の対処法</a></span></li></ul></li><li><span><a href="#初期設定" data-toc-modified-id="初期設定-3.4"><span class="toc-item-num">3.4 </span>初期設定</a></span></li><li><span><a href="#delete" data-toc-modified-id="delete-3.5"><span class="toc-item-num">3.5 </span>delete</a></span></li><li><span><a href="#random_h.rbとsequential_h.rb" data-toc-modified-id="random_h.rbとsequential_h.rb-3.6"><span class="toc-item-num">3.6 </span>random_h.rbとsequential_h.rb</a></span></li><li><span><a href="#random_checkの動作" data-toc-modified-id="random_checkの動作-3.7"><span class="toc-item-num">3.7 </span>random_checkの動作</a></span></li><li><span><a href="#sequential_checkの動作" data-toc-modified-id="sequential_checkの動作-3.8"><span class="toc-item-num">3.8 </span>sequential_checkの動作</a></span></li></ul></li><li><span><a href="#実装コードの解説" data-toc-modified-id="実装コードの解説-4"><span class="toc-item-num">4 </span>実装コードの解説</a></span><ul class="toc-item"><li><span><a href="#起動時に毎回動作するプログラム" data-toc-modified-id="起動時に毎回動作するプログラム-4.1"><span class="toc-item-num">4.1 </span>起動時に毎回動作するプログラム</a></span><ul class="toc-item"><li><span><a href="#プログラム内のインスタンス変数の概要" data-toc-modified-id="プログラム内のインスタンス変数の概要-4.1.1"><span class="toc-item-num">4.1.1 </span>プログラム内のインスタンス変数の概要</a></span></li><li><span><a href="#Fileの作成" data-toc-modified-id="Fileの作成-4.1.2"><span class="toc-item-num">4.1.2 </span>Fileの作成</a></span></li></ul></li><li><span><a href="#ファイル削除処理delete" data-toc-modified-id="ファイル削除処理delete-4.2"><span class="toc-item-num">4.2 </span>ファイル削除処理delete</a></span></li><li><span><a href="#random_check" data-toc-modified-id="random_check-4.3"><span class="toc-item-num">4.3 </span>random_check</a></span></li><li><span><a href="#sequential_check" data-toc-modified-id="sequential_check-4.4"><span class="toc-item-num">4.4 </span>sequential_check</a></span><ul class="toc-item"><li><span><a href="#インスタンス定数に格納されたパス" data-toc-modified-id="インスタンス定数に格納されたパス-4.4.1"><span class="toc-item-num">4.4.1 </span>インスタンス定数に格納されたパス</a></span></li><li><span><a href="#動作部分" data-toc-modified-id="動作部分-4.4.2"><span class="toc-item-num">4.4.2 </span>動作部分</a></span></li></ul></li><li><span><a href="#新しいターミナルを開くopen_terminal" data-toc-modified-id="新しいターミナルを開くopen_terminal-4.5"><span class="toc-item-num">4.5 </span>新しいターミナルを開くopen_terminal</a></span></li></ul></li><li><span><a href="#他のソフトとの比較" data-toc-modified-id="他のソフトとの比較-5"><span class="toc-item-num">5 </span>他のソフトとの比較</a></span><ul class="toc-item"><li><span><a href="#PTYPING" data-toc-modified-id="PTYPING-5.1"><span class="toc-item-num">5.1 </span>PTYPING</a></span></li><li><span><a href="#e-typing" data-toc-modified-id="e-typing-5.2"><span class="toc-item-num">5.2 </span>e-typing</a></span></li><li><span><a href="#寿司打" data-toc-modified-id="寿司打-5.3"><span class="toc-item-num">5.3 </span>寿司打</a></span></li><li><span><a href="#考察" data-toc-modified-id="考察-5.4"><span class="toc-item-num">5.4 </span>考察</a></span></li></ul></li><li><span><a href="#総括" data-toc-modified-id="総括-6"><span class="toc-item-num">6 </span>総括</a></span></li><li><span><a href="#謝辞" data-toc-modified-id="謝辞-7"><span class="toc-item-num">7 </span>謝辞</a></span></li><li><span><a href="#付録" data-toc-modified-id="付録-8"><span class="toc-item-num">8 </span>付録</a></span></li><li><span><a href="#参考文献" data-toc-modified-id="参考文献-9"><span class="toc-item-num">9 </span>参考文献</a></span></li></ul></div>
# はじめに
## 研究の目的
editor_learnerの開発の大きな目的はeditor(Emacs)操作,CUI操作(キーバインドなど),Ruby言語の習熟とタイピング速度の向上である.editor上で動かすためファイルの開閉,保存,画面分割といった基本操作を習熟することができ,Ruby言語のプログラムを写経することでRuby言語の習熟へと繋げる.更にコードを打つことで正しい運指を身につけタイピング速度の向上も図っている.コードを打つ際にキーバインドを利用することでGUIではなくCUI操作にも適応していく.これら全てはプログラマにとって作業を効率化させるだけでなく,プログラマとしての質の向上につながる.
## 研究の動機
初めはタッチタイピングを習得した経験を活かして,西谷によって開発されたshunkuntype(ターミナル上で実行するタイピングソフト)の再開発をテーマにしていたが,これ以上タイピングに特化したソフトを開発しても同じようなものがWeb上に大量に転がっており,そのようなものをいくつも開発しても意味がないと考えた.そこで西谷研究室ではタイピング,Ruby言語,Emacsによるeditor操作,CUI操作の習熟が作業効率に非常に大きな影響を与えるので習熟を勧めている.そこで西谷研究室で使用されているeditorであるEmacs操作,Ruby言語の学習,タイピング速度,正確性の向上,CUI操作.これらの習熟を目的としたソフトを開発しようと考えた.
# 基本的事項
## Emacs
本研究において使用するeditorはEmacsである.ツールはプログラマ自身の手の延長である.これは他のどのようなソフトウェアツールよりもEditorに対して当てはまる.テキストはプログラミングにおける最も基本的な生素材なので,できる限り簡単に操作できる必要があります.
そこで西谷研究室で勧められているEmacsの機能については以下の通りである,
1. 設定可能である. フォント,色,ウィンドウサイズ,キーバインドを含めた全ての外見が好みに応じて設定できるようになっていること.通常の操作がキーストロークだけで行えると,手をキーボードから離す必要がなくなり,結果的にマウスやメニュー駆動型のコマンドよりも効率的に操作できるようになります
1. 拡張性がある. 新しいプログラミング言語が出てきただけで,使い物にならなくなるようなエディタではなく,どんな新しい言語やテキスト形式が出てきたとしても,その言語の意味合いを「教え込む」ことが可能です
1. プログラム可能であること. 込み入った複数の手順を実行できるよう,Editorはプログラム可能であることが必須である.
これらの機能は本来エディタが持つべき基本的な機能である.これらに加えてEmacsは,
1. 構文のハイライト Rubyの構文にハイライトを入れたい場合はファイル名の後に.rbと入れることでRubyモードに切り替わり構文にハイライトを入れることが可能になる.
1. 自動インデント. テキストを編集する際,改行時に自動的にスペースやタブなどを入力しインデント調整を行ってくれる.
などのプログラミング言語に特化した特徴を備えています.強力なeditorを習熟することは生産性を高めることに他ならない.カーソルの移動にしても,1回のキー入力で単語単位,行単位,ブロック単位,関数単位でカーソルを移動させることができれば,一文字ずつ,あるいは一行ずつ繰り返してキー入力を行う場合とは効率が大きく変わってきます.Emacsはこれらの全ての機能を孕んでいてeditorとして非常に優秀である.よって本研究はEmacsをベースとして研究を進める.
## Ruby
Rubyの基本的な説明は以下の通り,Rubyはまつもとゆきひろにより開発されたオブジェクト指向スクリプト言語であり,スクリプト言語が用いられてきた領域でのオブジェクト指向プログラミングを実現する言語である.
本研究はRuby言語を使用しています.大きな理由としては
* 構文の自由度が高く,記述量が少なくて済む.
* 強力な標準ライブラリが備えられている.
Rubyは変数の型付けがないため,記述量を少なく済ませることができ,"gem"という形式で公開されているライブラリが豊富かつ強力なので本研究はRuby言語を使用しました.
## RubyGems
Rubygemの基本的な説明は以下の通り,RubyGemsは,Ruby言語用のパッケージ管理システムであり,Rubyのプログラムと("gem"と呼ばれる)ライブラリの配布用標準フォーマットを提供している.gemを容易に管理でき,gemを配布するサーバの機能も持つ.
本研究ではRubyGemsのgemを利用してファイル操作やパスの受け取りなどを行い,本研究で開発したソフトもgemに公開してある.
## Keybind
Keybindの基本的な説明は以下の通り,押下するキー(単独キーまたは複数キーの組み合わせ)と,実行される機能との対応関係のことである.また,キーを押下したときに実行させる機能を割り当てる行為のことである.
以下controlを押しながらをc-と記述する.本研究におけるKeybindの習熟はCUI操作の習熟に酷似している.カーソル移動においてもGUIベースでマウスを使い行の先頭をクリックするより,CUIによりc-aを押すことで即座に行の先頭にカーソルを持っていくことができる.習熟するのであれば,どちらの方が早いかは一目瞭然である.本研究はKeybindの習熟によるCUI操作の適応で作業の効率化,高速化に重点を置いている.
## CUI(Character User Interface)
CUIは,キーボード等からの文字列を入力とし,文字列が表示されるウィンドウや古くはラインプリンタで印字される文字などを出力とする,ユーザインタフェースの様式で,GUI(Graphical User Interface)の対義語として使われる.
CUIとGUIにはそれぞれ大きな違いがある.GUIの利点は以下の通り,
* 文字だけでなくアイコンなどの絵も表示できる.
* 対象物が明確な点や,マウスで比較的簡単に操作できる.
* 即座に操作結果が反映される.
CUIの利点は以下の通り,
* コマンドを憶えていれば複雑な処理が簡単に行える.
* キーボードから手を離すことなく作業の高速化が行える.
今回GUIではなくCUI操作の習熟を目的にした理由は,
* コマンドを憶えることで作業効率が上がる.
* editor操作の習熟も孕んでいるから.
カーソル移動においてもGUIではなくCUI操作により,ワンコマンドで動かした方が効率的である.上記の理由から,GUIではなくCUI操作の習熟を目的としている.
## 使用したgemファイル
### diff-lcs
diff-lcsは,二つのファイルの差分を求めて出力してくれる.テキストの差分を取得するメソッドは,Diff::LCS.sdiff と Diff::LCS.diff の2つがある.複数行の文字列を比較した場合の2つのメソッドの違いは以下のとおり.
1. Diff::LCS.sdiff
1. 比較結果を1文字ずつ表示する
1. Diff::LCS.diff
1. 比較した結果,違いがあった行について,違いがあった箇所のみ表示する.
今回使用したのは後者(Diff:LCS.diff)である.理由は間違った部分だけを表示した方が見やすいと考えたからである.
### Thor
Thorは,コマンドラインツールの作成を支援するライブラリです.gitやbundlerのようなサブコマンドツールを簡単に作成することができます.
Thorの使用でサブコマンドを自然言語に近い形で覚えることができる.
### Minitest
Minitestはテストを自動化するためのテスト用のフレームワークである.Rubyにはいくつかのテスティングフレームワークがありますが,Minitestというフレームワークを利用した理由は以下の通りです.
1. Rubyをインストールすると一緒にインストールされるため,特別なセットアップが不要.
1. 学習コストが比較的低い.
1. Railsのデフォルトのテスティングフレームワークなので,Railsを開発するときにも知識を活かしやすい.
上記の理由から,sequential_checkではminitestを採用しております.
### FileUtils
再帰的な削除などの基本的なファイル操作を行うためのライブラリ
### open3
プログラムを実行し,そのプロセスの標準出力,標準入力,標準エラー出力にパイプをつなぐためのものである.
### Bundler
Bundlerはアプリケーション谷で依存するgemパッケージを管理するためのツールです.1つのシステム上で複数のアプリケーションを開発する場合や,デプロイ時にアプリケーションに紐付けてgemパッケージを管理したい場合に利用される.
### Rubocop
RubocopはRubyのソースコード解析ツールである.Rubyスタイルガイドや他のスタイルガイドに準拠しているかどうかを自動チェックしてくれるソフトウェアです.自分が打ち込んだ問題文となるソースコードのチェックに使用しました.
# editor_learnerの概要
## Installation
### githubによるinstall
githubによるインストール方法は以下の通りである.
1. "https://github.com/souki1103/editor_learner" へアクセス
1. Clone or downloadを押下,SSHのURLをコピー
1. コマンドラインにてgit clone(コピーしたURL)を行う
上記の手順で開発したファイルがそのまま自分のディレクトリにインストールされる.
### gemによるinstall
gemによるインストール方法は以下の通りである.
1. コマンドラインにてgem install editor_learnerと入力,実行
1. ファイルがホームディレクトの.rbenv/versions/2.4.0/lib/ruby/gems/2.4.0/gemsにeditor_learnerが収納される
これでeditor_learnerとコマンドラインで入力することで実行可能となる.
## uninstall
### githubからinstallした場合のuninstall方法
gituhubからinstallした場合のuninstall方法は以下の通りである.
1. ホームディレクトで
1. rm -rf editor_learnerを入力
1. ホームディレクトリからeditor_learnerが削除されていることを確認する.
以上がuninstall方法である.
### gemからinstallした場合のuninstall方法
gemからinstallした場合のuninstall方法は以下の通りである.
1. ターミナル上のコマンドラインで
1. gem uninstall editor_learnerを入力
1. ホームディレクトの.rbenv/versions/2.4.0/lib/ruby/gems/2.4.0/gemsにeditor_learnerが削除されていることを確認する.
以上がuninstall方法である.
## 動作環境
Rubyのversionが2.4.0以上でなければ動かない.理由としては,gemに格納されているパスを正しいく受け渡しできないからである.2.4.0以下で動作させるためにはeditor_learnerの最新versionのみを入れることによって動作することが確認できている.
### error時の対処法
errorが出た場合は以下の方法を試してください
1. rm -rf editor_learnerをコマンドラインで入力
これによりファイル生成によるバグを解消できる.もう一つの方法は
1. gem uninstall editor_learnerをコマンドラインで入力
1. 全てのversionをuninstallする.
1. 再度gem install editor_learnerで最新versionのみをinstallする.
上記の手順によりRubyのversionによるバグが解消されることが確認できている.現在起こるであろうと予想されるバグの解消法は上記の2つである.Rubyのversionが2.4.0以上であればなんの不具合もなく動作することが確認できている.
## 初期設定
特別な初期設定はほとんどないが起動方法は以下の通りである,
1. コマンドライン上にてeditor_learnerを入力する.
2. editor_learnerを起動することでホームディレクトリにeditor_learner/workshopと呼ばれるファイルが作成される.workshopは作業場という意味である.
2. workshopの中にquestion.rbとanswer.rb,random_h.rbとruby_1~ruby_6が作成され,ruby_1~ruby_6の中に1.rb~3.rbが作成されていることを確認する.

1. 起動すると以下のようなサブコマンドの書かれた画面が表示されることを確認する.
```
Commands:
editor_lerner delete [number~number]
editor_learner help [COMMAND]
editor_learner random_check
editor_leraner sequential_check [lesson_number] [1~3numbers]
```
1. editor_learnerの後にサブコマンドと必要に応じた引数を入力すると動作する.それぞれのサブコマンドの更に詳しい説明は以下の通りである.
## delete
editor_learnerを起動することで初期設定で述べたようにホームディレクトリにeditor_learner/workshopが作成される.deleteはworkshopに作成されたruby_1~ruby_6を削除するために作成されたものである.sequential_checkで1度プログラムを作成してしまうと再度実行するとIt have been finished!と表示されてしまうので,削除するコマンドを作成しました.コマンド例は以下の通りである.
コマンド例
1. editor_learner delete 1 3
上記のように入力することで1〜3までのファイルが削除される.サブコマンドの後の引数は2つの数字(char型)であり,削除するファイルの範囲を入力する.
## random_h.rbとsequential_h.rb
random_h.rbとsequential_h.rbが初期設定で作成され,editor_learnerを起動することで自動的に作成され,random_checkとsequential_checkを行う際に最初に開くファイルとなる.random_check用とsequential_check用に二つのファイルがある.random_check用のファイルは以下の通りである.
random_h.rb

上から順に説明すると,
1. question.rbを開くためにc-x 2で画面を2分割にする.
1. c-x c-fでquestion.rbを探して開く.
1. 次にanswer.rbを開くために画面を3分割する
1. 同様にc-x c-fでanswer.rbを探して開く.
1. c-x oでanswer.rbを編集するためにポインタを移動させる.
1. question.rbに書かれているコードをanswer.rbに写す.
これらの手順がrandom_h.rbに記述されている.全ての手順を終えたターミナルの状態は以下の通り,

上記の画像では,右上に問題であるquestion.rbが表示され,それを左上にあるanswer.rbに写す形となる.
次にsequential_h.rb

書かれている内容自体はrandom_h.rbとほとんど差異がないが,開くファイルの名前が違うため別のファイルとして作成された.この手順に沿って作業することになる.下に書かれているのは主要キーバインドであり,必要に応じて見て,使用する形となっている.上記の手順を行なったターミナル画面の状態はrandom_h.rbの最終形態を同じである.
## random_checkの動作
random_checkの動作開始から終了は以下の通りである.
1. コマンドライン上にてeditor_learne random_checkを入力
1. 新しいターミナル(ホームディレクトリ/editor_learner/workshopから始まる)が開かれる.
1. random_h.rbを開いてrandom_h.rbに沿ってquestion.rbに書かれているコードをanswer.rbに写す.
1. 前のターミナルに戻り,コマンドラインに"check"と入力することで正誤判定を行ってくれる.
1. 間違っていればdiff-lcsにより間違った箇所が表示される.
1. 正しければ新しいターミナルが開かれてから終了までの時間とIt have been finished!が表示され終了となる.
更に次回random_check起動時には前に書いたコードがanswer.rbに格納されたままなので全て削除するのではなく,前のコードの必要な部分は残すことができる.
random_checkの大きな目的はtyping速度,正確性の向上,editor操作やRuby言語の習熟に重点を置いている.いかに早く終わらせるかのポイントがtyping速度,正確性とeditor操作である.
## sequential_checkの動作
sequential_checkの動作開始から終了は以下の通りである.
1. コマンドライン上でeditor_learner sequential_check(1~6の数字) (1~3の数字)を入力
1. 新しいターミナル(ホームディレクトリ/editor_learner/workshop/ruby_(1~6の数字))が開かれる.
1. sequential_h.rbを開いてsequential_h.rbに沿ってq.rbに書かれている内容を第2引数の数字.rbに写す.
1. 前のターミナルに戻り,コマンドラインに"check"と入力することで正誤判定を行う.
1. 間違っていれば間違った箇所が表示される.再度q.rbと第2引数の数字.rbを開いて間違った箇所を修正する.
1. 正しければruby_1/1.rb is done!のように表示される.
sequential_checkは1~3の順に1.rbがリファクタリングや追加され2.rbになり,完成形が3.rbになるといった形式である.連続的なプログラムの完成までを写経するのでsequential_checkと名付けられた.
sequential_checkの大きな目的はリファクタリングによるRuby言語の学習とCUI操作によるキーバインドの習熟,タイピング速度,正確性の向上に重点を置いている.コードがリファクタリングされる様を写経することで自分自身でRubyのコードを書くときに他の人が見やすくなるようなコードが書けるようになる.
# 実装コードの解説
本章では,今回作成したプログラムをライブラリ化し継続的な発展が可能なようにそれぞれの処理の解説を記述する.
## 起動時に毎回動作するプログラム
editor_learnerを起動したときに自動に動く部分である.コードは以下の通りである.
```
def initialize(*args)
super
@prac_dir="#{ENV['HOME']}/editor_learner/workshop"
@lib_location = Open3.capture3("gem environment gemdir")
@versions = Open3.capture3("gem list editor_learner")
p @latest_version = @versions[0].chomp.gsub(' (', '-').gsub(')','')
@inject = File.join(@lib_location[0].chomp, "/gems/#{@latest_version}/lib")
if File.exist?(@prac_dir) != true then
FileUtils.mkdir_p(@prac_dir)
FileUtils.touch("#{@prac_dir}/question.rb")
FileUtils.touch("#{@prac_dir}/answer.rb")
FileUtils.touch("#{@prac_dir}/random_h.rb")
if File.exist?("#{@inject}/random_h.rb") == true then
FileUtils.cp("#{@inject}/random_h.rb", "#{@prac_dir}/random_h.rb")
elsif
FileUtils.cp("#{ENV['HOME']}/editor_learner/lib/random_h.rb", "#{@prac_dir}/random_h.rb")
end
end
range = 1..6
range_ruby = 1..3
range.each do|num|
if File.exist?("#{@prac_dir}/ruby_#{num}") != true then
FileUtils.mkdir("#{@prac_dir}/ruby_#{num}")
FileUtils.touch("#{@prac_dir}/ruby_#{num}/q.rb")
FileUtils.touch("#{@prac_dir}/ruby_#{num}/sequential_h.rb")
if File.exist?("#{@inject}/sequential_h.rb") == true then
FileUtils.cp("#{@inject}/sequential_h.rb", "#{@prac_dir}/ruby_#{num}/sequential_h.rb")
else
FileUtils.cp("#{ENV['HOME']}/editor_learner/lib/sequential_h.rb", "#{@prac_dir}/ruby_#{num}/sequential_h.rb")
end
range_ruby.each do|n|
FileUtils.touch("#{@prac_dir}/ruby_#{num}/#{n}.rb")
end
end
end
end
```
この部分は基本的にディレクトリやファイルの作成が主である.上から順に説明すると,@prac_dirはホームディレクトリ/editor_learner/workshopを指しており,ファイルを作る際のパスとして作成されたインスタンス定数である.その後の3つのインスタンス定数(@lib_location,@versions,@latest_version)はgemでinstallされた場合ファイルの場所がホームディレクトリ/.rbenv/versions/2.4.0/lib/ruby/gems/2.4.0/gemsのeditor_learnerに格納されているためgemでinstallした人とgithubでinstallした人とではパスが変わってしまうためこれらの3つのインスタンス定数を用意した.実際の振る舞いとしては,File.existによりprac_dirがなければディレクトリを作成しさらにその中にquestion.rbとanswer.rbを作成する.gemにリリースしていることからgemでinstallした人とgithubでinstallした人のパスの違いをif文で条件分岐させている.これによりrandom_h.rbを正常にコピーすることができた.
### プログラム内のインスタンス変数の概要
インスタンス変数は,'@'で始まる変数はインスタンス変数であり,特定のオブジェクトに所属しています.インスタンス変数はそのクラスまたはサブクラスのメソッドから参照できます.初期化されない孫スタンス変数を参照した時の値はnillです.
このメソッドで使用されているインスタンス変数は5つである.prac_dirはホームディレクトリ/editor_learner/workshopを指しており,必要なファイルをここに作るのでパスとして受け渡すインスタンス変数となっている.その後の4つのインスタンス変数はgemからinstallした場合における,editor_learnerが格納されているパスを受け渡すためのインスタンス変数である.一つずつの説明は以下の通り,
* lib_locationはターミナル上で"gem environment gemdir"を入力した場合に出力されるパスを格納している.(自分のターミナル場で実行すると/Users/souki/.rbenv/versions/2.4.0/lib/ruby/gems/2.4.0)
* versionsはgemでinstallされたeditor_learnerのversionを受け取るためのパスを格納したインスタンス変数である.
* latest_versionははversionsで受け取ったeditor_learnerのversionの最新部分のパスを格納したインスタンス変数である.
* injectは実際にこれらのパスをつなぎ合わせてできるgemでinstallされたeditor_learnerが格納されているパスが格納されているインスタン変数である.(自分の場合は/Users/souki/.rbenv/versions/2.4.0/lib/ruby/gems/2.4.0/gems/editor_learner-1.1.2となる)
### Fileの作成
全てのパスの準備が整ったら実際に作業する場所に必要なファイル(question.rbやanswer.rb)などの作成が行われる.本研究のコードではeditor_learner/workshopがホームディレクトリになければ作成する.さらに,その中にrandom_checkに必要なファイル(question.rb,answer.rb,random_h.rb)が作成される.random_h.rbはgemでinstallした場合はeditor_learnerの格納されている部分からコピーを行なっている.
次に,sequential_checkに必要なファイルを作成する.editor_learner/workshopにruby_1~ruby6がなければ作成し,その中に1.rb~3.rbとq.rb(問題をコピーするためのファイル)とsequential_h.rbが作成される.sequential_h.rbはrandom_h.rbと同じでgemからinstallした場合はeditor_learnerの格納されている部分からコピーを行なっている.このメソッドの大きな役割はファイル作成である.
## ファイル削除処理delete
sequential_checkで終了したchapterをもう一度したい場合に一度ファイルを削除しなければいけないので,deleteメソッドの大きな役割はsequential_checkで終了したファイルの削除である.
```
desc 'delete [number~number]', 'delete the ruby_file choose number to delet\
e file'
def delete(n, m)
range = n..m
range.each{|num|
if File.exist?("#{@prac_dir}/ruby_#{num}") == true then
system "rm -rf #{@prac_dir}/ruby_#{num}"
end
}
end
```
コード自体はいたってシンプルで引数を2つ受け取ることでその間の範囲のFileを削除するようなコードとなっている.systemの"rm -rf ファイル名"がファイルを削除するコマンドなのでそこで受け取った引数の範囲でファイルの削除を行っている.
## random_check
random_checkのコードは以下の通り,
```
desc 'random_check', 'ramdom check your typing and edit skill.'
def random_check(*argv)
random = rand(1..15)
p random
s = "#{random}.rb"
puts "check starting ..."
puts "type following commands on the terminal"
puts "> emacs question.rb answer.rb"
src_dir = File.expand_path('../..', __FILE__) # "Users/souki/editor_learner"
if File.exist?("#{@inject}/random_check_question/#{s}") == true then
FileUtils.cp("#{@inject}/random_check_question/#{s}", "#{@prac_dir}/question.rb")
elsif
FileUtils.cp(File.join(src_dir, "lib/random_check_question/#{s}"), "#{@prac_dir}/question.rb")
end
open_terminal
start_time = Time.now
loop do
a = STDIN.gets.chomp
if a == "check" && FileUtils.compare_file("#{@prac_dir}/question.rb", "#{@prac_dir}/answer.rb") == true then
puts "It have been finished!"
break
elsif FileUtils.compare_file("#{@prac_dir}/question.rb", "#{@prac_dir}/answer.rb") != true then
@inputdata = File.open("#{@prac_dir}/answer.rb").readlines
@checkdata = File.open("#{@prac_dir}/question.rb").readlines
diffs = Diff::LCS.diff("#{@inputdata}", "#{@checkdata}")
diffs.each do |diff|
p diff
end
end
end
end_time = Time.now
time = end_time - start_time - 1
puts "#{time} sec"
end
```
random_checkの概要を簡単に説明すると15個あるRubyのコードから1~15の乱数を取得し,選ばれた数字のファイルが問題としてコピーされて,それをanswer.rbに入力することで正解していたら新しいターミナルが開かれてから終了までの時間を評価する仕組みとなっている.
上から解説を行うと,1から15のrandomな乱数を取得,起動と同時にどのファイルがコピーされたか表示される.そして,src_dirでホームディレクトリ/editor_learnerのパスが代入される.そして,gemでinstallした人とgithubからcloneした場合によるファイルコピーのパスの違いをifで条件分岐.そして,1から15の乱数のファイルがquestion.rbにコピーされる.コピーされた後に新しいターミナルが開かれ,時間計測が開始される.そして,checkを前の画面に入力できるようにgetsを使った.初めにgetsだけを使用した時改行が入ってしまいうまく入力できなかった.しかし,chompを入れることで改行をなくすことに成功.しかし,argvとgetsを両方入れることが不可能なことが判明した.そこでgetsの前にSTDINを入れることでargvとの併用が可能なことがわかり,STDIN.gets.chompと入力することでキーボードからの入力を受け取ることができた.そして,checkが入力されてかつFileUtils.compareでファイルの比較で正しければ時間計測を終了し,表示する.間違っていた場合はインスタンス定数であるinputとoutputにquestion.rbとanswer.rbの中身が格納されてDiff::LCSのdiffによって間違っている箇所だけを表示する.一連のコード解説は以上である.
## sequential_check
sequential_checkの場合はリファクタリングにあたりたくさんのインスタンス定数を作った.コードは以下の通り,
```
desc 'sequential_check [lesson_number] [1~3number] ','sequential check your typing skill and edit skill choose number'
def sequential_check(*argv, n, m)
l = m.to_i - 1
@seq_dir = "lib/sequential_check_question"
q_rb = "ruby_#{n}/#{m}.rb"
@seqnm_dir = File.join(@seq_dir,q_rb)
@pracnm_dir = "#{ENV['HOME']}/editor_learner/workshop/ruby_#{n}/#{m}.rb"
@seqnq_dir = "lib/sequential_check_question/ruby_#{n}/q.rb"
@pracnq_dir = "#{ENV['HOME']}/editor_learner/workshop/ruby_#{n}/q.rb"
@seqnl_dir = "lib/sequential_check_question/ruby_#{n}/#{l}.rb"
@pracnl_dir = "#{ENV['HOME']}/editor_learner/workshop/ruby_#{n}/#{l}.rb"
puts "check starting ..."
puts "type following commands on the terminal"
src_dir = File.expand_path('../..', __FILE__)
if File.exist?("#{@inject}/sequential_check_question/ruby_#{n}/#{m}.rb") == true then
FileUtils.cp("#{@inject}/sequential_check_question/ruby_#{n}/#{m}.rb", "#{@pracnq_dir}")
elsif
FileUtils.cp(File.join(src_dir, "#{@seqnm_dir}"), "#{@pracnq_dir}")
end
if l != 0 && FileUtils.compare_file("#{@pracnm_dir}", "#{@pracnq_dir}") != true
FileUtils.compare_file("#{@pracnl_dir}", (File.join(src_dir, "#{@seqnl_dir}"))) == true
FileUtils.cp("#{@pracnl_dir}", "#{@pracnm_dir}")
end
if FileUtils.compare_file(@pracnm_dir, @pracnq_dir) != true then
system "osascript -e 'tell application \"Terminal\" to do script \"cd #{@prac_dir}/ruby_#{n} \" '"
loop do
a = STDIN.gets.chomp
if a == "check" && FileUtils.compare_file("#{@pracnm_dir}", "#{@pracnq_dir}") == true then
puts "ruby_#{n}/#{m}.rb is done!"
break
elsif FileUtils.compare_file("#{@pracnm_dir}", "#{@pracnq_dir}") != true then
@inputdata = File.open("#{@pracnm_dir}").readlines
@checkdata = File.open("#{@pracnq_dir}").readlines
diffs = Diff::LCS.diff("#{@inputdata}", "#{@checkdata}")
diffs.each do |diff|
p diff
end
end
end
else
p "ruby_#{n}/#{m}.rb is finished!"
end
end
```
### インスタンス定数に格納されたパス
インスタンス定数に格納されているパスについての説明は上から順に以下の通り,
1. seq_dirはgithubでcloneした人が問題をコピーするときに使うパスである.
1. seqnm_dirはその名の通りseq_dirに引数であるnとmを代入したパスである.例として引数に1と1が代入された時は以下の通り,
1. editor_learner/sequential_check_question/ruby_1/1.rbとなる.
1. pracnm_dirはprac_dirに二つの引数nとmを代入したものである.実際に作業するところのパスとして使用する.例として引数として1と1が代入された時は以下の通り,
1. ホームディレクトリ/editor_learner/workshop/ruby_1/1.rbが格納される.
1. 同様にseqとpracの後についている文字はその後のruby_(数字)/(数字).rbの数字に入る文字を後につけている.
### 動作部分
まずgemでinstallした場合とgithubでinstallした場合による違いを条件分岐によりパスを変えている.さらに1.rbが終了していた場合2.rbに1.rbをコピーした状態から始まるように処理が行われている.その後は"check"が入力された時かつFileUtils.compareで正解していれば終了.間違っていればDiff::LCSで間違っている箇所を表示.もう一度修正し,"check"を入力,正解していれば終了.以上が一連のコードの解説である.
## 新しいターミナルを開くopen_terminal
新しいターミナルを開くメソッドである.コードは以下の通りである.
```
def open_terminal
pwd = Dir.pwd
system "osascript -e 'tell application \"Terminal\" to do script \"cd #{@prac_dir} \" '"
end
```
新しく開かれたターミナルはprac_dir(editor_learner/workshop)のディレクトリからスタートするように設定されている.random_checkではeditor_learner/workshopでターミナルが開かれ,sequential_checkではeditor_learner/workshop/第1引数で入力されたファイルの場所が開かれるようになっている.
# 他のソフトとの比較
他のタイピングソフトとの比較を行った表が以下の通りである.

上記のタイピングソフトは自分もよく使っていたタイピングソフトであり,評価も高いソフトである.それぞれの特徴は以下の通り,
## PTYPING
PTYPINGは豊富なプログラム言語が入力可能である.しかし,コードを打つのではなく,コードに使われるintなどよく使われる単語が60秒の間にどれだけ打てるかというソフトです.
## e-typing
e-typingはインターネットで無料提供されているソフトである.ローマ字入力を基本として,単語,短文,長文の3部構成となっておりタイピングの資格取得の練習もできる.
## 寿司打
自分が一番利用したサイト,GUIベースによりローマ字入力を基本とし,打てば打つほど秒数が伸びていきどれだけ入力できるかをランキング形式で表示される.
## 考察
これら全てのソフトを利用した結果,editor_learnerはローマ字入力ができない点では他のソフトに遅れをとるが,実際にプログラムを書くようになってからコードを写経することで{}や()などといったローマ字入力ではあまり入力しないような記号の入力が非常に早くなった.さらに,editor_learnerは現段階ではRubyの学習のみだが,引数を変えて元となるプログラムを作成することで全てのプログラム言語を学ぶことができる.さらに,実際にコードを入力することができるソフトはたくさんあるが,実行可能なものは少ない(Webで行うものが大半を占めているから.)実際に西谷研究室でeditor_learnerで学習を行っていない学生と行った自分のrandom_check平均秒数は前者は200秒程なのに対して,自分は60秒程である.これらの結果からeditor_learnerによる学習により,Ruby言語の学習にもなり,タイピング速度,正確性の向上,CUI操作の適応による差が出たと考えた.
# 総括
実際に今までたくさんのタイピングソフトやプログラムコードの打てるタイピングソフトを数多く利用してきたが,editor操作の習熟が可能なソフトは見たことも聞いたこともなかった.実際にタイピングだけが早い学生はたくさんいるがeditor操作やキーバインドも使いこなせる学生は少なかった.本研究で開発したeditor_learnerによりそれらの技術も上達し,作業効率などの向上が見込める結果となった.
# 謝辞
本研究を行うにあたり,終始多大なるご指導,御鞭撻をいただいた西谷滋人教授に対し,深く御礼申し上げます.また,本研究の進行に伴い,様々な助力,知識の供給をいただきました西谷研究室の同輩,先輩方に心から感謝の意を示します.本当にありがとうございました.
# 付録
```
require 'fileutils'
require 'colorize'
require 'thor'
require "editor_learner/version"
require 'diff-lcs'
require "open3"
module EditorLearner
class CLI < Thor
def initialize(*args)
super
@prac_dir="#{ENV['HOME']}/editor_learner/workshop"
@lib_location = Open3.capture3("gem environment gemdir")
@versions = Open3.capture3("gem list editor_learner")
p @latest_version = @versions[0].chomp.gsub(' (', '-').gsub(')','')
@inject = File.join(@lib_location[0].chomp, "/gems/#{@latest_version}/lib")
if File.exist?(@prac_dir) != true then
FileUtils.mkdir_p(@prac_dir)
FileUtils.touch("#{@prac_dir}/question.rb")
FileUtils.touch("#{@prac_dir}/answer.rb")
FileUtils.touch("#{@prac_dir}/random_h.rb")
if File.exist?("#{@inject}/random_h.rb") == true then
FileUtils.cp("#{@inject}/random_h.rb", "#{@prac_dir}/random_h.rb")
elsif
FileUtils.cp("#{ENV['HOME']}/editor_learner/lib/random_h.rb", "#{@prac_dir}/random_h.rb")
end
end
range = 1..6
range_ruby = 1..3
range.each do|num|
if File.exist?("#{@prac_dir}/ruby_#{num}") != true then
FileUtils.mkdir("#{@prac_dir}/ruby_#{num}")
FileUtils.touch("#{@prac_dir}/ruby_#{num}/q.rb")
FileUtils.touch("#{@prac_dir}/ruby_#{num}/sequential_h.rb")
if File.exist?("#{@inject}/sequential_h.rb") == true then
FileUtils.cp("#{@inject}/sequential_h.rb", "#{@prac_dir}/ruby_#{num}/sequential_h.rb")
else
FileUtils.cp("#{ENV['HOME']}/editor_learner/lib/sequential_h.rb", "#{@prac_dir}/ruby_#{num}/sequential_h.rb")
end
range_ruby.each do|n|
FileUtils.touch("#{@prac_dir}/ruby_#{num}/#{n}.rb")
end
end
end
end
desc 'delete [number~number]', 'delete the ruby_file choose number to delete file'
def delete(n, m)
range = n..m
range.each{|num|
if File.exist?("#{@prac_dir}/ruby_#{num}") == true then
system "rm -rf #{@prac_dir}/ruby_#{num}"
end
}
end
desc 'sequential_check [lesson_number] [1~3number] ','sequential check your typing skill and edit skill choose number'
def sequential_check(*argv, n, m)
l = m.to_i - 1
@seq_dir = "lib/sequential_check_question"
q_rb = "ruby_#{n}/#{m}.rb"
@seqnm_dir = File.join(@seq_dir,q_rb)
@pracnm_dir = "#{ENV['HOME']}/editor_learner/workshop/ruby_#{n}/#{m}.rb"
@seqnq_dir = "lib/sequential_check_question/ruby_#{n}/q.rb"
@pracnq_dir = "#{ENV['HOME']}/editor_learner/workshop/ruby_#{n}/q.rb"
@seqnl_dir = "lib/sequential_check_question/ruby_#{n}/#{l}.rb"
@pracnl_dir = "#{ENV['HOME']}/editor_learner/workshop/ruby_#{n}/#{l}.rb"
puts "check starting ..."
puts "type following commands on the terminal"
src_dir = File.expand_path('../..', __FILE__)
if File.exist?("#{@inject}/sequential_check_question/ruby_#{n}/#{m}.rb") == true then
FileUtils.cp("#{@inject}/sequential_check_question/ruby_#{n}/#{m}.rb", "#{@pracnq_dir}")
elsif
FileUtils.cp(File.join(src_dir, "#{@seqnm_dir}"), "#{@pracnq_dir}")
end
if l != 0 && FileUtils.compare_file("#{@pracnm_dir}", "#{@pracnq_dir}") != true
FileUtils.compare_file("#{@pracnl_dir}", (File.join(src_dir, "#{@seqnl_dir}"))) == true
FileUtils.cp("#{@pracnl_dir}", "#{@pracnm_dir}")
end
if FileUtils.compare_file(@pracnm_dir, @pracnq_dir) != true then
system "osascript -e 'tell application \"Terminal\" to do script \"cd #{@prac_dir}/ruby_#{n} \" '"
loop do
a = STDIN.gets.chomp
if a == "check" && FileUtils.compare_file("#{@pracnm_dir}", "#{@pracnq_dir}") == true then
puts "ruby_#{n}/#{m}.rb is done!"
break
elsif FileUtils.compare_file("#{@pracnm_dir}", "#{@pracnq_dir}") != true then
@inputdata = File.open("#{@pracnm_dir}").readlines
@checkdata = File.open("#{@pracnq_dir}").readlines
diffs = Diff::LCS.diff("#{@inputdata}", "#{@checkdata}")
diffs.each do |diff|
p diff
end
end
end
else
p "ruby_#{n}/#{m}.rb is finished!"
end
end
desc 'random_check', 'ramdom check your typing and edit skill.'
def random_check(*argv)
random = rand(1..15)
p random
s = "#{random}.rb"
puts "check starting ..."
puts "type following commands on the terminal"
puts "> emacs question.rb answer.rb"
src_dir = File.expand_path('../..', __FILE__) # "Users/souki/editor_learner"
if File.exist?("#{@inject}/random_check_question/#{s}") == true then
FileUtils.cp("#{@inject}/random_check_question/#{s}", "#{@prac_dir}/question.rb")
else
FileUtils.cp(File.join(src_dir, "lib/random_check_question/#{s}"), "#{@prac_dir}/question.rb")
end
open_terminal
start_time = Time.now
loop do
a = STDIN.gets.chomp
if a == "check" && FileUtils.compare_file("#{@prac_dir}/question.rb", "#{@prac_dir}/answer.rb") == true then
puts "It have been finished!"
break
elsif FileUtils.compare_file("#{@prac_dir}/question.rb", "#{@prac_dir}/answer.rb") != true then
@inputdata = File.open("#{@prac_dir}/answer.rb").readlines
@checkdata = File.open("#{@prac_dir}/question.rb").readlines
diffs = Diff::LCS.diff("#{@inputdata}", "#{@checkdata}")
diffs.each do |diff|
p diff
end
end
end
end_time = Time.now
time = end_time - start_time - 1
puts "#{time} sec"
end
no_commands do
def open_terminal
pwd = Dir.pwd
system "osascript -e 'tell application \"Terminal\" to do script \"cd #{@prac_dir} \" '"
end
end
end
end
```
# 参考文献
Andrew Hunt著,「達人プログラマー」 (オーム社出版,2016).
| true |
code
| 0.207135 | null | null | null | null |
|
# Named Entity Recognition in Mandarin on a Weibo Social Media Dataset
---
[Github](https://github.com/eugenesiow/practical-ml/blob/master/notebooks/Named_Entity_Recognition_Mandarin_Weibo.ipynb) | More Notebooks @ [eugenesiow/practical-ml](https://github.com/eugenesiow/practical-ml)
---
Notebook to train a [flair](https://github.com/flairNLP/flair) model in mandarin using stacked embeddings (with word and BERT embeddings) to perform named entity recognition (NER).
The [dataset](https://github.com/hltcoe/golden-horse) used contains 1,890 Sina Weibo messages annotated with four entity types (person, organization, location and geo-political entity), including named and nominal mentions from the paper [Peng et al. (2015)](https://www.aclweb.org/anthology/D15-1064/) and with revised annotated data from [He et al. (2016)](https://arxiv.org/abs/1611.04234).
The current state-of-the-art model on this dataset is from [Peng et al. (2016)](https://www.aclweb.org/anthology/P16-2025/) with an average F1-score of **47.0%** (Table 1) and from [Peng et al. (2015)](https://www.aclweb.org/anthology/D15-1064.pdf) with an F1-score of **44.1%** (Table 2). The authors say that the poor results on the test set show the "difficulty of this task" - which is true a sense because the dataset is really quite small for the NER task with 4 classes (x2 as they differentiate nominal and named entities) with a test set of only 270 sentences.
Our flair model is able to improve the state-of-the-art with an F1-score of **67.5%**, which is a cool 20+ absolute percentage points better than the current state-of-the-art performance.
The notebook is structured as follows:
* Setting up the GPU Environment
* Getting Data
* Training and Testing the Model
* Using the Model (Running Inference)
## Task Description
> Named entity recognition (NER) is the task of tagging entities in text with their corresponding type. Approaches typically use BIO notation, which differentiates the beginning (B) and the inside (I) of entities. O is used for non-entity tokens.
# Setting up the GPU Environment
#### Ensure we have a GPU runtime
If you're running this notebook in Google Colab, select `Runtime` > `Change Runtime Type` from the menubar. Ensure that `GPU` is selected as the `Hardware accelerator`. This will allow us to use the GPU to train the model subsequently.
#### Install Dependencies
```
pip install -q flair
```
# Getting Data
The dataset, including the train, test and dev sets, has just been included in the `0.7 release` of flair, hence, we just use the `flair.datasets` loader to load the `WEIBO_NER` dataset into the flair `Corpus`. The [raw datasets](https://github.com/87302380/WEIBO_NER) are also available on Github.
```
import flair.datasets
from flair.data import Corpus
corpus = flair.datasets.WEIBO_NER()
print(corpus)
```
We can see that the total 1,890 sentences have already been split into train (1,350), dev (270) and test (270) sets in a 5:1:1 ratio.
# Training and Testing the Model
#### Train the Model
To train the flair `SequenceTagger`, we use the `ModelTrainer` object with the corpus and the tagger to be trained. We use flair's sensible default options in the `.train()` method, while specifying the output folder for the `SequenceTagger` model to be `/content/model/`. We also set the `embeddings_storage_mode` to be `gpu` to utilise the GPU to store the embeddings for more speed. Note that if you run this with a larger dataset you might run out of GPU memory, so be sure to set this option to `cpu` - it will still use the GPU to train but the embeddings will not be stored in the CPU and there will be a transfer to the GPU each epoch.
Be prepared to allow the training to run for about 0.5 to 1 hour. We set the `max_epochs` to 50 so the the training will complete faster, for higher F1-score you can increase this number to 100 or 150.
```
import flair
from typing import List
from flair.trainers import ModelTrainer
from flair.models import SequenceTagger
from flair.embeddings import TokenEmbeddings, WordEmbeddings, StackedEmbeddings, BertEmbeddings, BytePairEmbeddings
tag_type = 'ner'
tag_dictionary = corpus.make_tag_dictionary(tag_type=tag_type)
# For an even faster training time, you can comment out the BytePairEmbeddings
# Note: there will be a small drop in performance if you do so.
embedding_types: List[TokenEmbeddings] = [
WordEmbeddings('zh-crawl'),
BytePairEmbeddings('zh'),
BertEmbeddings('bert-base-chinese'),
]
embeddings: StackedEmbeddings = StackedEmbeddings(embeddings=embedding_types)
tagger: SequenceTagger = SequenceTagger(hidden_size=256,
embeddings=embeddings,
tag_dictionary=tag_dictionary,
tag_type=tag_type,
use_crf=True)
trainer: ModelTrainer = ModelTrainer(tagger, corpus)
trainer.train('/content/model/',
learning_rate=0.1,
mini_batch_size=32,
max_epochs=50,
embeddings_storage_mode='gpu')
```
We see that the output accuracy (F1-score) for our new model is **67.5%** (F1-score (micro) 0.6748). We use micro F1-score (rather than macro F1-score) as there are multiple entity classes in this setup with [class imbalance](https://datascience.stackexchange.com/questions/15989/micro-average-vs-macro-average-performance-in-a-multiclass-classification-settin).
> We have a new SOTA NER model in mandarin, over 20 percentage points (absolute) better than the previous SOTA for this Weibo dataset!
## Using the Model (Running Inference)
Running the model to do some predictions/inference is as simple as calling `tagger.predict(sentence)`. Do note that for mandarin each character needs to be split with spaces between each character (e.g. `一 节 课 的 时 间`) so that the tokenizer will work properly to split them to tokens (if you're processing them for input into the model when building an app). For more information on this, check out the [flair tutorial on tokenization](https://github.com/flairNLP/flair/blob/master/resources/docs/TUTORIAL_1_BASICS.md#tokenization).
```
from flair.data import Sentence
from flair.models import SequenceTagger
from flair.data import Corpus
# Load the model that we trained, you can comment this out if you already have
# the model loaded (e.g. if you just ran the training)
tagger: SequenceTagger = SequenceTagger.load("/content/model/final-model.pt")
# Load the WEIBO corpus and use the first 5 sentences from the test set
corpus = flair.datasets.WEIBO_NER()
for idx in range(0, 5):
sentence = corpus.test[idx]
tagger.predict(sentence)
print(sentence.to_tagged_string())
```
We can connect to Google Drive with the following code to save any files you want to persist. You can also click the `Files` icon on the left panel and click `Mount Drive` to mount your Google Drive.
The root of your Google Drive will be mounted to `/content/drive/My Drive/`. If you have problems mounting the drive, you can check out this [tutorial](https://towardsdatascience.com/downloading-datasets-into-google-drive-via-google-colab-bcb1b30b0166).
```
from google.colab import drive
drive.mount('/content/drive/')
```
You can move the model files from our local directory to your Google Drive.
```
import shutil
shutil.move('/content/model/', "/content/drive/My Drive/model/")
```
More Notebooks @ [eugenesiow/practical-ml](https://github.com/eugenesiow/practical-ml) and do drop us some feedback on how to improve the notebooks on the [Github repo](https://github.com/eugenesiow/practical-ml/).
| true |
code
| 0.701956 | null | null | null | null |
|
```
%matplotlib inline
```
`파이토치(PyTorch) 기본 익히기 <intro.html>`_ ||
`빠른 시작 <quickstart_tutorial.html>`_ ||
`텐서(Tensor) <tensorqs_tutorial.html>`_ ||
`Dataset과 Dataloader <data_tutorial.html>`_ ||
`변형(Transform) <transforms_tutorial.html>`_ ||
`신경망 모델 구성하기 <buildmodel_tutorial.html>`_ ||
`Autograd <autogradqs_tutorial.html>`_ ||
**최적화(Optimization)** ||
`모델 저장하고 불러오기 <saveloadrun_tutorial.html>`_
모델 매개변수 최적화하기
==========================================================================
이제 모델과 데이터가 준비되었으니, 데이터에 매개변수를 최적화하여 모델을 학습하고, 검증하고, 테스트할 차례입니다.
모델을 학습하는 과정은 반복적인 과정을 거칩니다; (*에폭(epoch)*\ 이라고 부르는) 각 반복 단계에서 모델은 출력을 추측하고,
추측과 정답 사이의 오류(\ *손실(loss)*\ )를 계산하고, (`이전 장 <autograd_tutorial.html>`_\ 에서 본 것처럼)
매개변수에 대한 오류의 도함수(derivative)를 수집한 뒤, 경사하강법을 사용하여 이 파라매터들을 **최적화(optimize)**\ 합니다.
이 과정에 대한 자세한 설명은 `3Blue1Brown의 역전파 <https://www.youtube.com/watch?v=tIeHLnjs5U8>`__ 영상을 참고하세요.
기본(Pre-requisite) 코드
------------------------------------------------------------------------------------------
이전 장인 `Dataset과 DataLoader <data_tutorial.html>`_\ 와 `신경망 모델 구성하기 <buildmodel_tutorial.html>`_\ 에서
코드를 기져왔습니다.
```
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor, Lambda
training_data = datasets.FashionMNIST(
root="data",
train=True,
download=True,
transform=ToTensor()
)
test_data = datasets.FashionMNIST(
root="data",
train=False,
download=True,
transform=ToTensor()
)
train_dataloader = DataLoader(training_data, batch_size=64)
test_dataloader = DataLoader(test_data, batch_size=64)
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(28*28, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 10),
nn.ReLU()
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = NeuralNetwork()
```
하이퍼파라매터(Hyperparameter)
------------------------------------------------------------------------------------------
하이퍼파라매터(Hyperparameter)는 모델 최적화 과정을 제어할 수 있는 조절 가능한 매개변수입니다.
서로 다른 하이퍼파라매터 값은 모델 학습과 수렴율(convergence rate)에 영향을 미칠 수 있습니다.
(하이퍼파라매터 튜닝(tuning)에 대해 `더 알아보기 <https://tutorials.pytorch.kr/beginner/hyperparameter_tuning_tutorial.html>`__)
학습 시에는 다음과 같은 하이퍼파라매터를 정의합니다:
- **에폭(epoch) 수** - 데이터셋을 반복하는 횟수
- **배치 크기(batch size)** - 매개변수가 갱신되기 전 신경망을 통해 전파된 데이터 샘플의 수
- **학습률(learning rate)** - 각 배치/에폭에서 모델의 매개변수를 조절하는 비율. 값이 작을수록 학습 속도가 느려지고, 값이 크면 학습 중 예측할 수 없는 동작이 발생할 수 있습니다.
```
learning_rate = 1e-3
batch_size = 64
epochs = 5
```
최적화 단계(Optimization Loop)
------------------------------------------------------------------------------------------
하이퍼파라매터를 설정한 뒤에는 최적화 단계를 통해 모델을 학습하고 최적화할 수 있습니다.
최적화 단계의 각 반복(iteration)을 **에폭**\ 이라고 부릅니다.
하나의 에폭은 다음 두 부분으로 구성됩니다:
- **학습 단계(train loop)** - 학습용 데이터셋을 반복(iterate)하고 최적의 매개변수로 수렴합니다.
- **검증/테스트 단계(validation/test loop)** - 모델 성능이 개선되고 있는지를 확인하기 위해 테스트 데이터셋을 반복(iterate)합니다.
학습 단계(training loop)에서 일어나는 몇 가지 개념들을 간략히 살펴보겠습니다. 최적화 단계(optimization loop)를 보려면
`full-impl-label` 부분으로 건너뛰시면 됩니다.
손실 함수(loss function)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
학습용 데이터를 제공하면, 학습되지 않은 신경망은 정답을 제공하지 않을 확률이 높습니다. **손실 함수(loss function)**\ 는
획득한 결과와 실제 값 사이의 틀린 정도(degree of dissimilarity)를 측정하며, 학습 중에 이 값을 최소화하려고 합니다.
주어진 데이터 샘플을 입력으로 계산한 예측과 정답(label)을 비교하여 손실(loss)을 계산합니다.
일반적인 손실함수에는 회귀 문제(regression task)에 사용하는 `nn.MSELoss <https://pytorch.org/docs/stable/generated/torch.nn.MSELoss.html#torch.nn.MSELoss>`_\ (평균 제곱 오차(MSE; Mean Square Error))나
분류(classification)에 사용하는 `nn.NLLLoss <https://pytorch.org/docs/stable/generated/torch.nn.NLLLoss.html#torch.nn.NLLLoss>`_ (음의 로그 우도(Negative Log Likelihood)),
그리고 ``nn.LogSoftmax``\ 와 ``nn.NLLLoss``\ 를 합친 `nn.CrossEntropyLoss <https://pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html#torch.nn.CrossEntropyLoss>`_
등이 있습니다.
모델의 출력 로짓(logit)을 ``nn.CrossEntropyLoss``\ 에 전달하여 로짓(logit)을 정규화하고 예측 오류를 계산합니다.
```
# 손실 함수를 초기화합니다.
loss_fn = nn.CrossEntropyLoss()
```
옵티마이저(Optimizer)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
최적화는 각 학습 단계에서 모델의 오류를 줄이기 위해 모델 매개변수를 조정하는 과정입니다. **최적화 알고리즘**\ 은 이 과정이 수행되는 방식(여기에서는 확률적 경사하강법(SGD; Stochastic Gradient Descent))을 정의합니다.
모든 최적화 절차(logic)는 ``optimizer`` 객체에 캡슐화(encapsulate)됩니다. 여기서는 SGD 옵티마이저를 사용하고 있으며, PyTorch에는 ADAM이나 RMSProp과 같은 다른 종류의 모델과 데이터에서 더 잘 동작하는
`다양한 옵티마이저 <https://pytorch.org/docs/stable/optim.html>`_\ 가 있습니다.
학습하려는 모델의 매개변수와 학습률(learning rate) 하이퍼파라매터를 등록하여 옵티마이저를 초기화합니다.
```
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
```
학습 단계(loop)에서 최적화는 세단계로 이뤄집니다:
* ``optimizer.zero_grad()``\ 를 호출하여 모델 매개변수의 변화도를 재설정합니다. 기본적으로 변화도는 더해지기(add up) 때문에 중복 계산을 막기 위해 반복할 때마다 명시적으로 0으로 설정합니다.
* ``loss.backward()``\ 를 호출하여 예측 손실(prediction loss)을 역전파합니다. PyTorch는 각 매개변수에 대한 손실의 변화도를 저장합니다.
* 변화도를 계산한 뒤에는 ``optimizer.step()``\ 을 호출하여 역전파 단계에서 수집된 변화도로 매개변수를 조정합니다.
전체 구현
------------------------------------------------------------------------------------------
최적화 코드를 반복하여 수행하는 ``train_loop``\ 와 테스트 데이터로 모델의 성능을 측정하는 ``test_loop``\ 를 정의하였습니다.
```
def train_loop(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
for batch, (X, y) in enumerate(dataloader):
# 예측(prediction)과 손실(loss) 계산
pred = model(X)
loss = loss_fn(pred, y)
# 역전파
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch % 100 == 0:
loss, current = loss.item(), batch * len(X)
print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
def test_loop(dataloader, model, loss_fn):
size = len(dataloader.dataset)
num_batches = len(dataloader)
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
pred = model(X)
test_loss += loss_fn(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
```
손실 함수와 옵티마이저를 초기화하고 ``train_loop``\ 와 ``test_loop``\ 에 전달합니다.
모델의 성능 향상을 알아보기 위해 자유롭게 에폭(epoch) 수를 증가시켜 볼 수 있습니다.
```
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
epochs = 10
for t in range(epochs):
print(f"Epoch {t+1}\n-------------------------------")
train_loop(train_dataloader, model, loss_fn, optimizer)
test_loop(test_dataloader, model, loss_fn)
print("Done!")
```
더 읽어보기
------------------------------------------------------------------------------------------
- `Loss Functions <https://pytorch.org/docs/stable/nn.html#loss-functions>`_
- `torch.optim <https://pytorch.org/docs/stable/optim.html>`_
- `Warmstart Training a Model <https://tutorials.pytorch.kr/recipes/recipes/warmstarting_model_using_parameters_from_a_different_model.html>`_
| true |
code
| 0.854521 | null | null | null | null |
|
```
%matplotlib inline
```
Learning Hybrid Frontend Syntax Through Example
===============================================
**Author:** `Nathan Inkawhich <https://github.com/inkawhich>`_
This document is meant to highlight the syntax of the Hybrid Frontend
through a non-code intensive example. The Hybrid Frontend is one of the
new shiny features of Pytorch 1.0 and provides an avenue for developers
to transition their models from **eager** to **graph** mode. PyTorch
users are very familiar with eager mode as it provides the ease-of-use
and flexibility that we all enjoy as researchers. Caffe2 users are more
aquainted with graph mode which has the benefits of speed, optimization
opportunities, and functionality in C++ runtime environments. The hybrid
frontend bridges the gap between the the two modes by allowing
researchers to develop and refine their models in eager mode (i.e.
PyTorch), then gradually transition the proven model to graph mode for
production, when speed and resouce consumption become critical.
Hybrid Frontend Information
---------------------------
The process for transitioning a model to graph mode is as follows.
First, the developer constructs, trains, and tests the model in eager
mode. Then they incrementally **trace** and **script** each
function/module of the model with the Just-In-Time (JIT) compiler, at
each step verifying that the output is correct. Finally, when each of
the components of the top-level model have been traced and scripted, the
model itself is traced. At which point the model has been transitioned
to graph mode, and has a complete python-free representation. With this
representation, the model runtime can take advantage of high-performance
Caffe2 operators and graph based optimizations.
Before we continue, it is important to understand the idea of tracing
and scripting, and why they are separate. The goal of **trace** and
**script** is the same, and that is to create a graph representation of
the operations taking place in a given function. The discrepency comes
from the flexibility of eager mode that allows for **data-dependent
control flows** within the model architecture. When a function does NOT
have a data-dependent control flow, it may be *traced* with
``torch.jit.trace``. However, when the function *has* a data-dependent
control flow it must be *scripted* with ``torch.jit.script``. We will
leave the details of the interworkings of the hybrid frontend for
another document, but the code example below will show the syntax of how
to trace and script different pure python functions and torch Modules.
Hopefully, you will find that using the hybrid frontend is non-intrusive
as it mostly involves adding decorators to the existing function and
class definitions.
Motivating Example
------------------
In this example we will implement a strange math function that may be
logically broken up into four parts that do, and do not contain
data-dependent control flows. The purpose here is to show a non-code
intensive example where the use of the JIT is highlighted. This example
is a stand-in representation of a useful model, whose implementation has
been divided into various pure python functions and modules.
The function we seek to implement, $Y(x)$, is defined for
$x \epsilon \mathbb{N}$ as
\begin{align}z(x) = \Biggl \lfloor \frac{\sqrt{\prod_{i=1}^{|2 x|}i}}{5} \Biggr \rfloor\end{align}
\begin{align}Y(x) = \begin{cases}
\frac{z(x)}{2} & \text{if } z(x)\%2 == 0, \\
z(x) & \text{otherwise}
\end{cases}\end{align}
\begin{align}\begin{array}{| r | r |} \hline
x &1 &2 &3 &4 &5 &6 &7 \\ \hline
Y(x) &0 &0 &-5 &20 &190 &-4377 &-59051 \\ \hline
\end{array}\end{align}
As mentioned, the computation is split into four parts. Part one is the
simple tensor calculation of $|2x|$, which can be traced. Part two
is the iterative product calculation that represents a data dependent
control flow to be scripted (the number of loop iteration depends on the
input at runtime). Part three is a trace-able
$\lfloor \sqrt{a/5} \rfloor$ calculation. Finally, part 4 handles
the output cases depending on the value of $z(x)$ and must be
scripted due to the data dependency. Now, let's see how this looks in
code.
Part 1 - Tracing a pure python function
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We can implement part one as a pure python function as below. Notice, to
trace this function we call ``torch.jit.trace`` and pass in the function
to be traced. Since the trace requires a dummy input of the expected
runtime type and shape, we also include the ``torch.rand`` to generate a
single valued torch tensor.
```
import torch
def fn(x):
return torch.abs(2*x)
# This is how you define a traced function
# Pass in both the function to be traced and an example input to ``torch.jit.trace``
traced_fn = torch.jit.trace(fn, torch.rand(()))
```
Part 2 - Scripting a pure python function
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We can also implement part 2 as a pure python function where we
iteratively compute the product. Since the number of iterations depends
on the value of the input, we have a data dependent control flow, so the
function must be scripted. We can script python functions simply with
the ``@torch.jit.script`` decorator.
```
# This is how you define a script function
# Apply this decorator directly to the function
@torch.jit.script
def script_fn(x):
z = torch.ones([1], dtype=torch.int64)
for i in range(int(x)):
z = z * (i + 1)
return z
```
Part 3 - Tracing a nn.Module
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Next, we will implement part 3 of the computation within the forward
function of a ``torch.nn.Module``. This module may be traced, but rather
than adding a decorator here, we will handle the tracing where the
Module is constructed. Thus, the class definition is not changed at all.
```
# This is a normal module that can be traced.
class TracedModule(torch.nn.Module):
def forward(self, x):
x = x.type(torch.float32)
return torch.floor(torch.sqrt(x) / 5.)
```
Part 4 - Scripting a nn.Module
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the final part of the computation we have a ``torch.nn.Module`` that
must be scripted. To accomodate this, we inherit from
``torch.jit.ScriptModule`` and add the ``@torch.jit.script_method``
decorator to the forward function.
```
# This is how you define a scripted module.
# The module should inherit from ScriptModule and the forward should have the
# script_method decorator applied to it.
class ScriptModule(torch.jit.ScriptModule):
@torch.jit.script_method
def forward(self, x):
r = -x
if int(torch.fmod(x, 2.0)) == 0.0:
r = x / 2.0
return r
```
Top-Level Module
~~~~~~~~~~~~~~~~
Now we will put together the pieces of the computation via a top level
module called ``Net``. In the constructor, we will instantiate the
``TracedModule`` and ``ScriptModule`` as attributes. This must be done
because we ultimately want to trace/script the top level module, and
having the traced/scripted modules as attributes allows the Net to
inherit the required submodules' parameters. Notice, this is where we
actually trace the ``TracedModule`` by calling ``torch.jit.trace()`` and
providing the necessary dummy input. Also notice that the
``ScriptModule`` is constructed as normal because we handled the
scripting in the class definition.
Here we can also print the graphs created for each individual part of
the computation. The printed graphs allows us to see how the JIT
ultimately interpreted the functions as graph computations.
Finally, we define the ``forward`` function for the Net module where we
run the input data ``x`` through the four parts of the computation.
There is no strange syntax here and we call the traced and scripted
modules and functions as expected.
```
# This is a demonstration net that calls all of the different types of
# methods and functions
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
# Modules must be attributes on the Module because if you want to trace
# or script this Module, we must be able to inherit the submodules'
# params.
self.traced_module = torch.jit.trace(TracedModule(), torch.rand(()))
self.script_module = ScriptModule()
print('traced_fn graph', traced_fn.graph)
print('script_fn graph', script_fn.graph)
print('TracedModule graph', self.traced_module.__getattr__('forward').graph)
print('ScriptModule graph', self.script_module.__getattr__('forward').graph)
def forward(self, x):
# Call a traced function
x = traced_fn(x)
# Call a script function
x = script_fn(x)
# Call a traced submodule
x = self.traced_module(x)
# Call a scripted submodule
x = self.script_module(x)
return x
```
Running the Model
~~~~~~~~~~~~~~~~~
All that's left to do is construct the Net and compute the output
through the forward function. Here, we use $x=5$ as the test input
value and expect $Y(x)=190.$ Also, check out the graphs that were
printed during the construction of the Net.
```
# Instantiate this net and run it
n = Net()
print(n(torch.tensor([5]))) # 190.
```
Tracing the Top-Level Model
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The last part of the example is to trace the top-level module, ``Net``.
As mentioned previously, since the traced/scripted modules are
attributes of Net, we are able to trace ``Net`` as it inherits the
parameters of the traced/scripted submodules. Note, the syntax for
tracing Net is identical to the syntax for tracing ``TracedModule``.
Also, check out the graph that is created.
```
n_traced = torch.jit.trace(n, torch.tensor([5]))
print(n_traced(torch.tensor([5])))
print('n_traced graph', n_traced.graph)
```
Hopefully, this document can serve as an introduction to the hybrid
frontend as well as a syntax reference guide for more experienced users.
Also, there are a few things to keep in mind when using the hybrid
frontend. There is a constraint that traced/scripted methods must be
written in a restricted subset of python, as features like generators,
defs, and Python data structures are not supported. As a workaround, the
scripting model *is* designed to work with both traced and non-traced
code which means you can call non-traced code from traced functions.
However, such a model may not be exported to ONNX.
| true |
code
| 0.766938 | null | null | null | null |
|
The **beta-binomial** can be written as
$$
y_i \sim Bin(\theta_i, n_i)
$$
$$
\theta_i \sim Beta(\alpha, \beta)
$$
The **posterior distribution** is approximately equivalent to
$$
p(\theta, \alpha, \beta|y) \propto p(\alpha, \beta) \times p(\theta | \alpha, \beta) \times p( y| \theta, \alpha, \beta)
$$
The **beta distribution** has the form
$$
p(\theta) = \frac{\Gamma(\alpha + \beta}{\Gamma(\alpha)\times \Gamma(\beta)}\theta^{\alpha -1}(1 - \theta)^{\beta - 1}
$$
The second half of the joint posterior distribution, $ p(y|\theta, \alpha, \beta)$, is a binomial distribution. We can ignore the **binomial coefficient** here since we are only approximating the posterior distribution, and it is a constant value.
In general, for a hierarchical Bayesian model with observed values $y$, distribution parameters $\theta$, and hyperparameters $\phi$, the posterior distribution of $\phi$ is
$$
p(\phi | y) = \int p(\theta, \phi|y) d\theta
$$
This is equivalent to
$$
p(\phi | y) = \frac{p(\theta, \phi | y)}{p(\theta| \phi, y)}
$$
We can compute the log-likelihood of N total observed experiments, each with $n$ trials and $y$ successes, and parameters $\alpha$ and $\beta$:
$$
p(\alpha, \beta|y) \propto p(\alpha, \beta) \prod_{i}^{N}
\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \times \Gamma(\beta)}
\frac{\Gamma(\alpha + y_i)\Gamma(\beta + n_i - y_i)}{\Gamma(\alpha + \beta + n_j)}
$$
This can be converted into a log-likelihood so that we sum the individual experiment likelihoods, instead of multiplying:
$$
p(\alpha, \beta|y) \propto p(\alpha, \beta) \times \sum_{i}^{N}{log\Gamma(\alpha + \beta) - log\Gamma(\alpha) - log\Gamma(\beta) + log\Gamma(\alpha + y_i) + log\Gamma(\beta + n_i - y_i) - log\Gamma(\alpha + \beta + n_i)}
$$
```
from typing import List
from scipy.special import gammaln
def log_likelihood(α: float, β: float, y:List[int], n: List[int])-> float:
LL = 0
for Y, N in zip(y, n):
LL += (gammaln(α + β) - gammaln(α) - gammaln(β) + gammaln(α + Y) +
gammaln(β + N - Y) - gammaln(α + β + N))
return LL
y = [1,5,10]
n = [10, 51, 120]
α = 1
β = 1
# we intuitively expect that θ should be somewhere around ~ 0.10, so our
# likelihood should be relatively low
log_likelihood(α, β, y, n)
α = 2
β = 10
# should be a much better model
log_likelihood(α, β, y, n)
import numpy as np
X, Z = np.meshgrid(np.arange(1,20), np.arange(1,20))
param_space = np.c_[X.ravel(), Z.ravel()]
surface = np.zeros(X.shape)
best_parameters = {
"α": 1,
"β": 1,
"LL": -9e12
}
for parameters in param_space:
α = parameters[0]
β = parameters[1]
LL = log_likelihood(α, β, y, n)
if LL > best_parameters["LL"]:
best_parameters["α"] = α
best_parameters["β"] = β
best_parameters["LL"] = LL
surface[α - 1, β - 1] = LL
print(best_parameters)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize = (5,5))
CS = ax.contourf(X,Z, surface,cmap=plt.cm.bone)
cbar = plt.colorbar(CS)
cbar.ax.set_ylabel('Log Likelihood')
# Add the contour line levels to the colorbar
plt.xlabel("β")
plt.ylabel("α")
plt.show()
```
| true |
code
| 0.793356 | null | null | null | null |
|
<div style="text-align: right">NEU Skunkworks AI workshop at Northeastern with EM Lyon Business School</div>
## Predicting Ad Lift with a Neural Network
### What is lift?
When one serves ads one has a choice of various channels to place ads. For an individual that choice might be to place ads on facebook, Twitter, Instagram, etc. For large ad companies they place ads with large Digital Service Providers (DSPs) such as Google’s Walled Garden, Open Web, and others which allow for an ad to be placed across many thousands of digital properties.
The effectiveness of an ad is usually measured through a metric called "lift." As different digital properties have different measures of effectiveness such as views, clicks, likes, shares, etc. and these measures are combined into a single metric, _lift_, which can be used to estimate the increase in sales over no advertising.
_Suprevised prediction of lift_
We use historical lift data to predict the lift that occured in the past. When what we want to predict is known this is called _supervised learning_. Supervised learning is the machine learning task of learning a function that maps an input to an output based on example input-output pairs. It infers a function from labeled training data consisting of a set of training examples. The idea is to create a function that can predict known data well under that assumption it well continue tp predict accurately with new unkown data.
### Neural networks
[Artificial neural networks](https://en.wikipedia.org/wiki/Artificial_neural_network) (**ANNs**) or **[connectionist] systems** are computing systems inspired by the biological neural networks that constitute animal brains. Such systems learn (progressively improve
performance) to do tasks by considering examples, generally without task-specific programming. For example, in image recognition, they might learn to identify images that contain cats by analyzing example images that have been manually labeled as “cat” or “no cat” and using the
analytic results to identify cats in other images. They have found most use in applications difficult to express in a traditional computer algorithm using rule-based programming.
An ANN is based on a collection of connected units called artificial neurons, (analogous to axons in a biological brain). Each connection synapse) between neurons can transmit a signal to another neuron. The receiving (postsynaptic) neuron can process the signal(s) and then signal downstream neurons connected to it. Neurons may have state, generally represented by [real numbers], typically between 0 and 1.
Neurons and synapses may also have a weight that varies as learning proceeds, which can increase or decrease the strength of the signal that it sends downstream. Further, they may have a threshold such that only if the aggregate signal is below (or above) that level is the downstream signal sent.
Typically, neurons are organized in layers. Different layers may perform different kinds of transformations on their inputs. Signals travel from the first (input), to the last (output) layer, possibly after traversing the layers multiple times.
_Multiclass perceptron (MLP)_
We will be using a Multiclass perceptron (MLP) to predict lift.
Like most other techniques for training classifiers, the perceptron generalizes naturally to multiclass classification. Here, the input $x$ and the output $y$ are drawn from arbitrary sets. A feature representation function $f(x,y)$ maps each possible input/output pair to a finite-dimensional real-valued feature vector. As before, the feature vector is multiplied by a weight vector $w$, but now the resulting score is used to choose among many possible outputs:
$$\hat y = \operatorname{argmax}_y f(x,y) \cdot w.$$ ≈ Learning again iterates over the examples, predicting an output for each, leaving the weights unchanged when the predicted output matches the target, and changing them when it does not. The update becomes:
$$w_{t+1} = w_t + f(x, y) - f(x,\hat y).$$
This multiclass feedback formulation reduces to the original perceptron when $x$ is a real-valued vector, $y$ is chosen from $\{0,1\}$, and $f(x,y) = y x$.
For certain problems, input/output representations and features can be chosen so that $\mathrm{argmax}_y f(x,y) \cdot w$ can be found efficiently even though $y$ is chosen from a very large or even infinite set.
### Backpropagation Algorithm
**Backpropagation** is a method used in artificial neural networks to calculate a gradient that is needed in the calculation of the weights to be used in the network. It is commonly used to train deep neural networks, a term referring to neural networks with more than one hidden layer.
Backpropagation is a special case of an older and more general technique called automatic differentiation. In the context of learning, backpropagation is commonly used by the gradient descent optimization algorithm to adjust the weight of neurons by calculating the gradient
of the loss function. This technique is also sometimes called **backward propagation of errors**, because the error is calculated at the output and distributed back through the network layers.
These videos are great for learning more about backpropagation:
* [What is backpropagation really doing?](https://youtu.be/Ilg3gGewQ5U)
* [Gradient descent, how neural networks learn?](https://youtu.be/IHZwWFHWa-w)
* [Backpropagation calculus](https://youtu.be/tIeHLnjs5U8)
**Loss function**
Sometimes referred to as the **cost function** or **error function**, the loss function
is a function that maps values of one or more variables onto a real number intuitively representing some \"cost\" associated with those values. For backpropagation, the loss function calculates the difference between the network output and its expected output, after a case propagates through the network.
The cost function will the root-mean-square error (RMSE). The **root-mean-square deviation (RMSD)** or **root-mean-square error (RMSE)** (or sometimes **root-mean-square*d* error**) is a frequently used measure of the differences between values (sample or population
values) predicted by a model or an estimator and the values observed.
The RMSD represents the square root of the second sample moment of the differences between predicted values and observed values or the quadratic mean of these differences. These deviations are called *residuals* when the calculations are performed over the data sample
that was used for estimation and are called *errors* (or prediction errors) when computed out-of-sample. The RMSD serves to aggregate the magnitudes of the errors in predictions for various times into a single measure of predictive power. RMSD is a measure of accuracy, to compare forecasting errors of different models for a particular dataset and not
between datasets, as it is scale-dependent.
RMSD is always non-negative, and a value of 0 (almost never achieved in practice) would indicate a perfect fit to the data. In general, a lower RMSD is better than a higher one. However, comparisons across different types of data would be invalid because the measure is dependent on the scale of the numbers used.
_Formula_
The RMSD of an estimator $\hat{\theta}$ with respect to an estimated parameter $\theta$ is defined as the square root of the mean square error:
$$\operatorname{RMSD}(\hat{\theta}) = \sqrt{\operatorname{MSE}(\hat{\theta})} = \sqrt{\operatorname{E}((\hat{\theta}-\theta)^2)}.$$
For an unbiased estimator, the RMSD is the square root of the variance, known as the standard deviation. The RMSD of predicted values $\hat y_t$ for times *t* of a regression\'s dependent variable $y_t,$ with variables observed over *T* times, is computed for *T* different predictions as the square root of the mean of the squares of the deviations:
$$\operatorname{RMSD}=\sqrt{\frac{\sum_{t=1}^T (\hat y_t - y_t)^2}{T}}.$$
(For regressions on cross-sectional data, the subscript *t* is replaced by *i* and *T* is replaced by *n*.)
In some disciplines, the RMSD is used to compare differences between two things that may vary, neither of which is accepted as the \"standard\". For example, when measuring the average difference between two time series $x_{1,t}$ and $x_{2,t}$, the formula becomes
$$\operatorname{RMSD}= \sqrt{\frac{\sum_{t=1}^T (x_{1,t} - x_{2,t})^2}{T}}.$$
_Example loss function_
Let $y,y'$ be vectors in $\mathbb{R}^n$.
Select an error function $E(y,y')$ measuring the difference between two
outputs.
The standard choice is $E(y,y') = \tfrac{1}{2} \lVert y-y'\rVert^2$,
the square of the Euclidean distance between the vectors $y$ and $y'$.
The factor of $\tfrac{1}{2}$ conveniently cancels the exponent when the
error function is subsequently differentiated.
The error function over $n$ training examples can be written as an average $$E=\frac{1}{2n}\sum_x\lVert (y(x)-y'(x)) \rVert^2$$And the partial derivative with respect to the
outputs $$\frac{\partial E}{\partial y'} = y'-y$$
_Cross entropy_
In our case we are doing a regression on the value of lift so RSME makes sense. If we were measuring the differnce between two probability distributions we may choose a loss function like cross entropy or KL-divergence. In information theory, the cross entropy (https://en.wikipedia.org/wiki/Cross_entropy) between two probability distributions $p$ and $q$ over the same underlying set of events measures the average number of bits needed to identify an event drawn from the set, if a coding scheme is used that is optimized for an
“unnatural” probability distribution $q$, rather than the “true” distribution $p$.
The cross entropy for the distributions $p$ and $q$ over a given set is
defined as follows:
$$H(p, q) = \operatorname{E}_p[-\log q] = H(p) + D_{\mathrm{KL}}(p \| q),\!$$
where $H(p)$ is the entropy of $p$, and $D_{\mathrm{KL}}(p \| q)$ is
the [Kullback–Leibler divergence](https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence) of $q$ from $p$ (also known as the *relative entropy* of *p* with respect to *q* — note the reversal of
emphasis).
For discrete $p$ and $q$ this means
$$H(p, q) = -\sum_x p(x)\, \log q(x). \!$$
The situation for continuous distributions is analogous. We have to
assume that $p$ and $q$ are absolutely continuous with respect to some
reference measure $r$ (usually $r$ is a Lebesgue measure on a
Borel σ-algebra). Let $P$ and $Q$ be probability density functions
of $p$ and $q$ with respect to $r$. Then
$$-\int_X P(x)\, \log Q(x)\, dr(x) = \operatorname{E}_p[-\log Q]. \!$$
NB: The notation $H(p,q)$ is also used for a different concept, the joint entropy of $p$ and $q$.
### Assumptions
Two assumptions must be made about the form of the error function. The first is that it can be written as an average $E=\frac{1}{n}\sum_xE_x$ over error functions $E_x$, for $n$ individual
training examples, $x$. The reason for this assumption is that the backpropagation algorithm calculates the gradient of the error function for a single training example, which needs to be generalized to the overall error function. The second assumption is that it can be written
as a function of the outputs from the neural network.
**Algorithm**
Let $N$ be a neural network with $e$ connections, $m$ inputs, and $n$
outputs.
Below, $x_1,x_2,\dots$ will denote vectors in $\mathbb{R}^m$, $y_1,y_2,\dots$ vectors in $\mathbb{R}^n$, and $w_0, w_1, w_2, \ldots$ vectors in $\mathbb{R}^e$. These are called *inputs*, *outputs* and *weights* respectively.
The neural network corresponds to a function $y = f_N(w, x)$ which, given a weight $w$, maps an input $x$ to an output $y$.
The optimization takes as input a sequence of *training examples* $(x_1,y_1), \dots, (x_p, y_p)$ and produces a sequence of weights $w_0, w_1, \dots, w_p$ starting from some initial weight $w_0$, usually chosen at random.
These weights are computed in turn: first compute $w_i$ using only $(x_i, y_i, w_{i-1})$ for $i = 1, \dots, p$. The output of the algorithm is then $w_p$, giving us a new function $x \mapsto f_N(w_p, x)$. The computation is the same in each step, hence only the case $i = 1$ is
described.
Calculating $w_1$ from $(x_1, y_1, w_0)$ is done by considering a variable weight $w$ and applying gradient descent to the function $w\mapsto E(f_N(w, x_1), y_1)$ to find a local minimum, starting at $w = w_0$.
This makes $w_1$ the minimizing weight found by gradient descent.
**Algorithm in code**
To implement the algorithm above, explicit formulas are required for the gradient of the function $w \mapsto E(f_N(w, x), y)$ where the function is $E(y,y')= |y-y'|^2$.
The learning algorithm can be divided into two phases: propagation and weight update.
### Phase 1: propagation
Each propagation involves the following steps:
1. Propagation forward through the network to generate the output
value(s)
2. Calculation of the cost (error term)
3. Propagation of the output activations back through the network using
the training pattern target in order to generate the deltas (the
difference between the targeted and actual output values) of all
output and hidden neurons.
### Phase 2: weight update
For each weight, the following steps must be followed:
1. The weight\'s output delta and input activation are multiplied to
find the gradient of the weight.
2. A ratio (percentage) of the weight\'s gradient is subtracted from
the weight.
This ratio (percentage) influences the speed and quality of learning; it is called the *learning rate*. The greater the ratio, the faster the neuron trains, but the lower the ratio, the more accurate the training is. The sign of the gradient of a weight indicates whether the error varies directly with, or inversely to, the weight. Therefore, the weight
must be updated in the opposite direction, \"descending\" the gradient.
Learning is repeated (on new batches) until the network performs adequately.
### Pseudocode
The following is pseudocode for a stochastic gradient descent
algorithm for training a three-layer network (only one hidden layer):
```python
initialize network weights (often small random values)\
**do**\
**forEach** training example named ex\
prediction = _neural-net-output_(network, ex) *// forward pass*\
actual = _teacher-output_(ex)\
compute error (prediction - actual) at the output units\
*// backward pass*\
*// backward pass continued*\
update network weights *// input layer not modified by error estimate*\
**until** all examples classified correctly or another stopping criterion satisfied\
**return** the network
```
The lines labeled \"backward pass\" can be implemented using the backpropagation algorithm, which calculates the gradient of the error of the network regarding the network\'s modifiable weights.
To learn more about MLPS and neural networks:
```
# import necessary libraries
# Use pip install or conda install if missing a library
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import random
import warnings
random.seed(5)
warnings.filterwarnings('ignore')
%matplotlib inline
```
## Load Lift Data
Let's load the lift data plot it and look at desriptive statistics.
```
df = pd.read_csv("data/Ad_Lift_Channels.csv",na_values=['null'],index_col='timestamp',parse_dates=True,infer_datetime_format=True)
# Visually check the data to make sure it loaded properly
df.head(5)
# Make a copy of the data called df_ma to add some moving average features
# It is a good idea to play with copies of the data until you are sure of an analysis
df_ma = df
df_ma.head(5)
df_ma.tail(5)
# Let's plot the data at indices 0,2,4,6 lift a through D
df_ma.iloc[:,[0,2,4,6]].plot()
df_ma.loc[:,['lift_A']].plot()
```
### What supervised learning algorithms to choose?
This simulated lift data looks like stock data, trending up and down based on many complex external factors that end up being reflected in a single price. If the data looked closer to a we might use some form of linear regression to predict it. Linear regression predicts the response variable $y$ assuming it has a linear relationship with predictor variable(s) $x$ or $x_1, x_2, ,,, x_n$.
$$y = \beta_0 + \beta_1 x + \varepsilon .$$
**Note: Linear regression IS NOT our first choice as the data does not look linear.**
We could also use traditional time series models such as an Autoregressive integrated moving average (ARIMA). An [autoregressive integrated moving average (ARIMA or ARMA)](https://en.wikipedia.org/wiki/Autoregressive_integrated_moving_average) model is a generalization of an autoregressive moving average (ARMA) model. These models are fitted to time series data either to better understand the data or to predict future points in the series (forecasting). They are applied in some cases where data show evidence of non-stationarity, where an initial differencing step (corresponding to the "integrated" part of the model) can be applied to reduce the non-stationarity.
Non-seasonal ARIMA models are generally denoted $ARIMA(p, d, q)$ where parameters $p, d, \quad and \quad q$ are non-negative integers, $p$ is the order of the Autoregressive model, $d$ is the degree of differencing, and $q$ is the order of the Moving-average model. The he number of differences $d$ is determined using repeated statistical tests. The values of $p$ and $q$ are then chosen by minimizing the AIC after differencing the data $d$ times.
* AR: Autoregression. A dependent relationship between an observation and some number of lagged observations.
* I: Integrated. The use of differencing of raw observations in order to make the time series stationary.
* MA: Moving Average. A model that uses the dependency between an observation and a residual error from a moving average model applied to lagged observations.
A non-seasonal ARIMA model can be (almost) completely summarized by three numbers:
* $p$ = the number of autoregressive terms. he number of lag observations included in the model.
* $d$ = the number of nonseasonal differences. The number of times that the raw observations are differenced, also called the degree of differencing.
* $q$ = the number of moving-average terms. The size of the moving average window, also called the order of moving average.
When a value of 0 is used as a parameter, it means that parameter is not used the model.
The ARIMA model uses an iterative three-stage modeling approach:
Model identification and model selection: making sure that the variables are stationary, identifying seasonality in the dependent series (seasonally differencing it if necessary), and using plots of the autocorrelation and partial autocorrelation functions of the dependent time series to decide which (if any) autoregressive or moving average component should be used in the model.
Parameter estimation using computation algorithms to arrive at coefficients that best fit the selected ARIMA model. The most common methods use maximum likelihood estimation or non-linear least-squares estimation.
Model checking by testing whether the estimated model conforms to the specifications of a stationary univariate process. In particular, the residuals should be independent of each other and constant in mean and variance over time. (Plotting the mean and variance of residuals over time and performing a Ljung-Box test or plotting autocorrelation and partial autocorrelation of the residuals are helpful to identify misspecification.) If the estimation is inadequate, we have to return to step one and attempt to build a better model.
**Note: ARIMA IS NOT our first choice, in spite of the data being time-series data, as eventually we would like to incorporate features other than previous mmeasures of lift that are specific to an adverister, their campaign, their target demographic. The mathematics of ARIMA make customization and personlazation to advertisers, campaigns and consumers**
A neural network can fit data like this simulated lift data, unlike linear regression, and unlike the ARIMA, it can take any number of input varibles called independent variables. If we start with a simple model and get a pretty good fit we can iteratiively improve the model by finding and feeding it more and more data relevant to making a good prediction of lift.
### Create lift indicators (Feature Engineering)
Note that we only has lift and volume and we are trying to predict lift. The is called feature engineering. We will start by creating the following features:
* The momentum difference between the 2-day moving volume average and 5-day volume moving average
* The momentum difference between the 2-day moving lift average and 5-day moving lift average
* 3-day moving lift average
* 7-day moving lift average
* 15-day moving lift average
* Average lift standard deviation within 15
_Naive & Simple Averaging_
The idea is to use past neasures of lift to predict future lift. Naive or "simple" averaging is just the mean (or median) of past data. Of course, the "simple" average or mean of all past observations is only a useful estimate for forecasting when there are no trends. Note that we can detrend these data but that is beyond the scope of this workshop.
For example, if we have prices are $p_M, p_{M-1},\dots,p_{M-(n-1)}$ then the formula is
$$
\textit{SMA} = { p_M + p_{M-1} + \cdots + p_{M-(n-1)} \over n }
$$
_Moving Averages_
A moving average (rolling average or running average) is an average that is updated for a window or history of n events. This is sometimes called the arithmetic moving average the most recent n data values. For an an equally weighted average of the sequence of n values $x_1. \ldots, x_n$ up to the current time:
$$
\textit{MA}_n = {{x_1 + \cdots + x_n} \over n}\,.
$$
There are other kinds of averaging such as weighted moving averages, exponential moving average (also called Single Exponential Smoothing). and many others that won't be discussed.
**What about dates and time?**
We also have a timestamp of the form _6/1/2019 4:00:00 AM_. We could easily add features like the month, the season, the year, the hour, morning or night, etc.. In fact, this will be a suggested excercise for the lab. This is simulated lift data but in real lift data, the prefered use of various digital properties on the weekend, versus weekday, and day or night shows strong association with various demogrpahic groups.
_One hot encoding_
While it is easy to extract the month as the numbers 1 though 12, when we keep them in that form it tells a mathematical model that December (12) is somehow 12 times that of January (1). This doesn't really make sense. But we can always use a boolean yes/no December. This is called one hot encoding. In machine learning, one-hot is a group of bits among which the legal combinations of values are only those with a single high (1) bit and all the others low (0).
```bash
Binary Gray code One-hot
-------- ----------- ----------
000 000 00000001
001 001 00000010
010 011 00000100
011 010 00001000
100 110 00010000
101 111 00100000
110 101 01000000
111 100 10000000
```
It is a suggsted excercise that you feature extract some time information from the timestamp field and check how it effects the model. Do a google search something like "How To Convert Timestamp To Date and Time in Python" to learn how extract something like "Summer" from a string like _6/1/2019 4:00:00 AM_.
```
# Extract some Naive & Simple Averaging features
df_ma['volume_A_Momentum'] = df_ma['volume_A'].shift(1).rolling(window = 2).mean() - df_ma['volume_A'].shift(1).rolling(window = 5).mean()
df_ma['lift_A_Momentum'] = df_ma['lift_A'].shift(1).rolling(window = 2).mean() - df_ma['lift_A'].shift(1).rolling(window = 5).mean()
df_ma['3step_MA_lift_A'] = df_ma['lift_A'].shift(1).rolling(window = 3).mean()
df_ma['7step_MA_lift_A'] = df_ma['lift_A'].shift(1).rolling(window = 7).mean()
df_ma['15step_MA_lift_A'] = df_ma['lift_A'].shift(1).rolling(window = 15).mean()
df_ma['Std_Dev_lift_A']= df_ma['lift_A'].rolling(15).std()
df_ma['volume_B_Momentum'] = df_ma['volume_B'].shift(1).rolling(window = 2).mean() - df_ma['volume_B'].shift(1).rolling(window = 5).mean()
df_ma['lift_B_Momentum'] = df_ma['lift_B'].shift(1).rolling(window = 2).mean() - df_ma['lift_B'].shift(1).rolling(window = 5).mean()
df_ma['3step_MA_lift_B'] = df_ma['lift_B'].shift(1).rolling(window = 3).mean()
df_ma['7step_MA_lift_B'] = df_ma['lift_B'].shift(1).rolling(window = 7).mean()
df_ma['15step_MA_lift_B'] = df_ma['lift_B'].shift(1).rolling(window = 15).mean()
df_ma['Std_Dev_lift_B']= df_ma['lift_B'].rolling(15).std()
df_ma['volume_C_Momentum'] = df_ma['volume_C'].shift(1).rolling(window = 2).mean() - df_ma['volume_C'].shift(1).rolling(window = 5).mean()
df_ma['lift_C_Momentum'] = df_ma['lift_C'].shift(1).rolling(window = 2).mean() - df_ma['lift_C'].shift(1).rolling(window = 5).mean()
df_ma['3step_MA_lift_C'] = df_ma['lift_C'].shift(1).rolling(window = 3).mean()
df_ma['7step_MA_lift_C'] = df_ma['lift_C'].shift(1).rolling(window = 7).mean()
df_ma['15step_MA_lift_C'] = df_ma['lift_C'].shift(1).rolling(window = 15).mean()
df_ma['Std_Dev_lift_C']= df_ma['lift_C'].rolling(15).std()
df_ma['volume_D_Momentum'] = df_ma['volume_D'].shift(1).rolling(window = 2).mean() - df_ma['volume_D'].shift(1).rolling(window = 5).mean()
df_ma['lift_D_Momentum'] = df_ma['lift_D'].shift(1).rolling(window = 2).mean() - df_ma['lift_D'].shift(1).rolling(window = 5).mean()
df_ma['3step_MA_lift_D'] = df_ma['lift_D'].shift(1).rolling(window = 3).mean()
df_ma['7step_MA_lift_D'] = df_ma['lift_D'].shift(1).rolling(window = 7).mean()
df_ma['15step_MA_lift_D'] = df_ma['lift_D'].shift(1).rolling(window = 15).mean()
df_ma['Std_Dev_lift_D']= df_ma['lift_D'].rolling(15).std()
# Check the size
df_ma.shape
# Check the transformed data
df_ma.head()
```
### The moving average created NaNs
Note that we can't create a 15-step moving average until we have 15 time steps. The simplest way to deal with this is to drop the first 15 rows of transformed data.
```
df_ma.tail()
```
## Drop all NaN
```
# Drop early rows
df_ma = df_ma.dropna()
df_ma.shape
df_ma.head()
# Let's save the transformed data for the other analysis
df_ma.to_csv("data/Ad_Lift_Channels_MA.csv")
```
## Deep Learning Model
We will be using a Multiclass perceptron (MLP) to predict lift. An MLP is a very simple neural network. There are a few things we must decide before running the model. These are called hyperparameters. In machine learning, a hyperparameter is a parameter whose value is set before the learning process begins. By contrast, the values of other parameters are derived via training.
### Hyperparameters
The input and output are defined for us.
X is the inputs. The data indicators we calculated before. There will be one neuron for each feature/independent variable. One great strength of these models is the we can have many, many neurons in our input layer, each representing a feature.
y is output the lift. We are predicting a single value which is typical of regression. If we wanted to predict several classes then we might have a neuron in the output layer for each class that we wanted to represent.
_Network Architecture_
For an MLP, our choice relates to the "hidden layers." We will make the arbirary choice of 128x64x64 nodes for our hidden layers. This choice is a starting point based on that the data doesn't seem that complex. To prevent overfitting and for speed one may reduce to network to as small as possible to create a great fit, but the first step is to determine whether a great fit is possible.
_Cost function_
For our cost function RSME is a common one used for regression. Mean residual deviance, MSE, MAE, RMSLE and Coefficient of Determination (R Squared) are common choices for regression. To understand the difference please read [Metrics to Understand Regression Models in Plain English](https://towardsdatascience.com/metrics-to-understand-regression-models-in-plain-english-part-1-c902b2f4156f).
_Activation function_
RELU is a very common activation function used in teaching neural networks so we will use it. However leaky RELU and others are probably better (for reason beyond the focus of this workshop). You are encouraged in the lab to try other activation functions and look at their effect on the model.
## Activation functions
In computational networks, the [activation function](https://en.wikipedia.org/wiki/Activation_function) of a node defines the output of that node given an input or set of inputs. A standard computer chip circuit can be seen as a digital network of activation functions that can be “ON” (1) or “OFF” (0), depending on input. This is similar to the behavior of the linear perceptron in neural networks. However, only *nonlinear* activation functions allow such networks to compute nontrivial problems using only a small number of nodes. In artificial neural networks this function is also called the **transfer function**.
_Functions_
In biologically inspired neural networks, the activation function is usually an abstraction representing the rate of action potential firing in the cell. In its simplest form, this function is binary—that is, either the neuron is firing or not. The function looks like
$\phi(v_i)=U(v_i)$, where $U$ is the Heaviside step function. In this case many neurons must be used in computation beyond linear separation of categories.
A line of positive slope may be used to reflect the increase in firing rate that occurs as input current increases. Such a function would be of the form $\phi(v_i)=\mu v_i$, where $\mu$ is the slope. This activation function is linear, and therefore has the same problems as the binary function. In addition, networks constructed using this model have unstable convergence because neuron inputs along favored paths tend to increase without bound, as this function is not normalizable.
All problems mentioned above can be handled by using a normalizable sigmoid activation function. One realistic model stays at zero until input current is received, at which point the firing frequency increases quickly at first, but gradually approaches an asymptote at 100% firing rate. Mathematically, this looks like $\phi(v_i)=U(v_i)\tanh(v_i)$, where the hyperbolic tangent function can be replaced by any sigmoid function. This behavior is realistically reflected in the neuron, as neurons cannot physically fire faster than a certain rate. This model runs into problems, however, in computational networks as it is not differentiable, a requirement to calculate backpropagation.
The final model, then, that is used in multilayer perceptrons is a sigmoidal activation function in the form of a hyperbolic tangent. Two forms of this function are commonly used: $\phi(v_i)=\tanh(v_i)$ whose range is normalized from -1 to 1, and $\phi(v_i) = (1+\exp(-v_i))^{-1}$ is vertically translated to normalize from 0 to 1. The latter model is often considered more biologically realistic, but it runs into theoretical and experimental difficulties with certain types.
## Comparison of activation functions
Some desirable properties in an activation function include:
- Nonlinear – When the activation function is non-linear, then a
two-layer neural network can be proven to be a universal function
approximator. The identity activation function does not satisfy
this property. When multiple layers use the identity activation
function, the entire network is equivalent to a single-layer model.
- Continuously differentiable – This property is necessary for
enabling gradient-based optimization methods. The binary step
activation function is not differentiable at 0, and it
differentiates to 0 for all other values, so gradient-based methods
can make no progress with it.
- Range – When the range of the activation function is finite,
gradient-based training methods tend to be more stable, because
pattern presentations significantly affect only limited weights.
When the range is infinite, training is generally more efficient
because pattern presentations significantly affect most of the
weights. In the latter case, smaller learning rates are typically
necessary.
- Monotonic – When the activation function is monotonic, the error
surface associated with a single-layer model is guaranteed to be
convex.
- Smooth Functions with a Monotonic derivative – These have been shown
to generalize better in some cases. The argument for these
properties suggests that such activation functions are more
consistent with Occam's razor.
- Approximates identity near the origin – When activation functions
have this property, the neural network will learn efficiently when
its weights are initialized with small random values. When the
activation function does not approximate identity near the origin,
special care must be used when initializing the weights.
_Rectified linear unit (ReLU) transfer function_
Rectified linear unit (ReLU)
Activation identity
$f(x)=x$
$f'(x)=1$
$(-\infty,\infty)$
$C^\infty$

Logistic (a.k.a. Soft step)
$f(x)=\frac{1}{1+e^{-x}}$
$f'(x)=f(x)(1-f(x))$
$(0,1)$
$C^\infty$

TanH
$f(x)=\tanh(x)=\frac{2}{1+e^{-2x}}-1$
$f'(x)=1-f(x)^2$
$(-1,1)$
$C^\infty$

Rectified linear unit (ReLU)
$f(x) = \begin{cases}
0 & \text{for } x < 0\\
x & \text{for } x \ge 0\end{cases}$
$f'(x) = \begin{cases}
0 & \text{for } x < 0\\
1 & \text{for } x \ge 0\end{cases}$
$[0,\infty)$
$C^0$
```
df_ma.columns
# Specifiy our features and target
X=['volume_A','volume_A_Momentum','lift_A_Momentum','3step_MA_lift_A','7step_MA_lift_A','15step_MA_lift_A','Std_Dev_lift_A']
y ='lift_A'
print(X)
print(y)
# Subset out data for only the desired features
X = df_ma.loc[:,X]
y = df_ma.iloc[:,0]
X.head()
y.head()
```
### Split dataset we used
Part of dataset wiil be used in training(80%). Others will be used in testing(20%).
The model uses the training data set to obtain weights, and the test data set to see how well the model performs on new data
Note that this split IS NOT random. We are using older data to train and more recent data to test. This kind of test-training split is common when we are forecasting as we are using the past to predict the future.
```
split = int(len(df_ma)*0.8)
X_train, X_test, y_train, y_test = X[:split], X[split:], y[:split], y[split:]
```
### Feature scaling
Another important step in preprocessing the data is to normalize the data set. This step will average all input features to 0 and convert their variance to 1. This can ensure that the model will not be biased due to different input features when training the model. If this step is not handled properly, the model may be confused and give higher weight to those input features with higher averages. This is particularly important in neural networks as on neuron maps to one feature in the input layer and the should learn their importance from training and not to to implicit bias due to different feature scale.
```
# Normalize our training and test data
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
```
### Build the Simple MLP
You will need tensorflow library in your environment first. Created by the Google Brain team, TensorFlow is an open source library for numerical computation and large-scale machine learning. TensorFlow bundles together a slew of machine learning and deep learning (aka neural networking) models and algorithms. It is very commonly used to build neural network models.
_Really Awesome TensorFlow Tutorials_
TensorFlow 101 (Really Awesome Intro Into TensorFlow) [https://youtu.be/arl8O22aa6I](https://youtu.be/arl8O22aa6I)
Getting Started with TensorFlow and Deep Learning | SciPy 2018 Tutorial ... [https://youtu.be/tYYVSEHq-io](https://youtu.be/tYYVSEHq-io)
Hands-on TensorBoard (TensorFlow Dev Summit 2017) [https://youtu.be/eBbEDRsCmv4](https://youtu.be/eBbEDRsCmv4)
```
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
DLmodel = Sequential()
```
_Input Layer_
* Units: It defines the number of nodes or neurons in a layer. We set the value here to 128, which means that there will be 128 neurons in our hidden layer.
* Kernel_initializer: It defines the starting values of different neuron weights in the hidden layer. We define it here as "uniform", which means that the weight is initialized with evenly distributed values.
* Activation: It is the activation function of neurons in the hidden layer. Here we define the activation function as a modified linear unit function called RELU.
* Input_dim: It defines the number of inputs to the hidden layer. We define the value of the number of inputs as equal to the number of columns in the input feature data frame. However, this argument is no longer needed in subsequent layers because the model knows how much output was generated in the previous layer.
```
DLmodel.add(
Dense(
units = 128,
kernel_initializer = 'uniform',
activation = 'relu',
input_dim = X.shape[1]))
```
_Hidden Layer_
```
DLmodel.add(
Dense(
units = 64,
kernel_initializer = 'uniform',
activation = 'relu'))
DLmodel.add(
Dense(
units = 64,
kernel_initializer = 'uniform',
activation = 'relu'))
```
_Output Layer_
```
DLmodel.add(
Dense(
units = 1,
kernel_initializer = 'uniform',
activation = 'relu'))
```
Add an output layer
```
DLmodel.compile(optimizer = 'adam', loss = 'mean_squared_error', metrics = ['accuracy'])
```
Finally, the following arguments are passed to compile the DLmodel:
* Optimizer: Choose optimizer as "Adam", which is an extended form of the stochastic gradient descent algorithm.
* Loss: It will define the loss that needs to be optimized during the training process. We define loss as the mean square error.
* Metrics: It defines a matrix that the model evaluates during training and testing. We choose an evaluation matrix whose accuracy is the model.
### Train the network
The model is trained for a number of runs called epochs. We usually visualize the training runs using a tool called TensorBoard and well as tell it stop when to doesn't improve, called early stopping. We will show early stopping in the third notebook. It is recommeded that you look at the TensorBoard tutorial below to understand how to visualize the networks learning.
Hands-on TensorBoard (TensorFlow Dev Summit 2017) [https://youtu.be/eBbEDRsCmv4](https://youtu.be/eBbEDRsCmv4)
```
DLmodel.fit(X_train, y_train, batch_size = 11, epochs = 55)
```
### Make Prediction
```
# Generate some predictions from our test data
y_pred = DLmodel.predict(X_test)
(y_pred,y_test.tolist())
# Calculate the accuracy
from sklearn import metrics
accuracy=np.sqrt(metrics.mean_squared_error(y_test.tolist(), y_pred))
print(accuracy)
```
## Create a Null Model
Another way to predict the value of lift is just the take the average value of lift and use this as a prediction. This gives one a base model for comparison.
If one can get as good or better prediction from taking the mean value than with an MLP than the MLP isn't very useful.
```
y_train_mean=np.mean(y_train.tolist())
print(y_train_mean)
y_null = np.zeros_like(y_test.tolist(), dtype=float)
y_null.fill(y_train_mean)
y_null[0:5]
null_accuracy=np.sqrt(metrics.mean_squared_error(y_test.tolist(),y_null))
print(null_accuracy)
```
## Visualize the differnce
The null model gives an RSME of around 0.092 and our MLP gives an RSME of around 0.017 so it seems much better than the null model.
```
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.plot(y_pred, color='r', label='Predicted lift Channel A')
plt.plot(y_test.tolist(), color='g', label='Actual lift Channel A')
plt.plot(y_null, color='k', label='Null model lift Channel A')
plt.legend()
plt.show()
df_ma.iloc[:,[1]].plot()
```
## Weird spikes?
There are some weird spikes in our MLP prediction. Can we get rid of those and further improve our model. The volume feature also has some large spikes. Is it possible that including extra features is actually hurting our model.
In machine learning, models that we will discuss in the second notebook will automatically downweight the importance of features and weight poorly predictive features to close to zero.
MLPs don't do this so let's remove the volume features as predictors and see if that helps?
```
# Rerun model without volume features
X=['lift_A_Momentum','3step_MA_lift_A','7step_MA_lift_A','15step_MA_lift_A','Std_Dev_lift_A']
X = df_ma.loc[:,X]
X.head()
X_train, X_test = X[:split], X[split:]
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
DLmodel2 = Sequential()
DLmodel2.add(
Dense(
units = 128,
kernel_initializer = 'uniform',
activation = 'relu',
input_dim = X.shape[1]))
DLmodel2.add(
Dense(
units = 64,
kernel_initializer = 'uniform',
activation = 'relu'))
DLmodel2.add(
Dense(
units = 64,
kernel_initializer = 'uniform',
activation = 'relu'))
DLmodel2.add(
Dense(
units = 1,
kernel_initializer = 'uniform',
activation = 'relu'))
DLmodel2.compile(optimizer = 'adam', loss = 'mean_squared_error', metrics = ['accuracy'])
DLmodel2.fit(X_train, y_train, batch_size = 11, epochs = 55)
# Generate some predictions from our test data
y_pred = DLmodel2.predict(X_test)
(y_pred,y_test.tolist())
accuracy=np.sqrt(metrics.mean_squared_error(y_test.tolist(), y_pred))
print(accuracy)
y_pred = DLmodel2.predict(X_test)
plt.figure(figsize=(10,5))
plt.plot(y_pred, color='r', label='Predicted lift Channel A')
plt.plot(y_test.tolist(), color='g', label='Actual lift Channel A')
plt.plot(y_null, color='k', label='Null model lift Channel A')
plt.legend()
plt.show()
```
## Removing a feature improved the model
Removing a feature improved the model from a RSME of 0.017 to 0.010 and we can see the weird spikes are gone.
## Todo
The above code should provide you with a starting framework for incorporating more complex features into a model. Here are a few things you can try out:
- Try the analysis on different channels.
- Experiment with different network architectures, cost functions, activation functions.
- Use more realistic features such as buying seasons, weekend versus weekday
<div style="text-align: right">NEU Skunkworks AI workshop at Northeastern with EM Lyon Business School</div>
<div style="text-align: right">Contributors</div>
<div style="text-align: right">Srijoni Biswas, Zixiao Wang, Abhishek Dabas, Kailash Dhondoo Nadkar,Abhi Patodi
</div>
<div style="text-align: right"> 3 December 2019</div>
Copyright 2019 NEU AI Skunkworks
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
| true |
code
| 0.625038 | null | null | null | null |
|
# PCA for Algorithmic Trading: Eigen Portfolios
## Imports & Settings
```
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA
from sklearn.preprocessing import scale
sns.set_style('white')
np.random.seed(42)
```
## Eigenportfolios
Another application of PCA involves the covariance matrix of the normalized returns. The principal components of the correlation matrix capture most of the covariation among assets in descending order and are mutually uncorrelated. Moreover, we can use standardized the principal components as portfolio weights.
Let’s use the 30 largest stocks with data for the 2010-2018 period to facilitate the exposition:
### Data Preparation
```
idx = pd.IndexSlice
with pd.HDFStore('../../data/assets.h5') as store:
stocks = store['us_equities/stocks'].marketcap.nlargest(30)
returns = (store['quandl/wiki/prices']
.loc[idx['2010': '2018', stocks.index], 'adj_close']
.unstack('ticker')
.pct_change())
```
We again winsorize and also normalize the returns:
```
normed_returns = scale(returns
.clip(lower=returns.quantile(q=.025),
upper=returns.quantile(q=.975),
axis=1)
.apply(lambda x: x.sub(x.mean()).div(x.std())))
returns = returns.dropna(thresh=int(returns.shape[0] * .95), axis=1)
returns = returns.dropna(thresh=int(returns.shape[1] * .95))
returns.info()
cov = returns.cov()
sns.clustermap(cov);
```
### Run PCA
After dropping assets and trading days as in the previous example, we are left with 23 assets and over 2,000 trading days. We estimate all principal components and find that the two largest explain 57.6% and 12.4% of the covariation, respectively:
```
pca = PCA()
pca.fit(cov)
pd.Series(pca.explained_variance_ratio_).to_frame('Explained Variance').head().style.format('{:,.2%}'.format)
```
### Create PF weights from principal components
Next, we select and normalize the four largest components so that they sum to 1 and we can use them as weights for portfolios that we can compare to an equal-weighted portfolio formed from all stocks::
```
top4 = pd.DataFrame(pca.components_[:4], columns=cov.columns)
eigen_portfolios = top4.div(top4.sum(1), axis=0)
eigen_portfolios.index = [f'Portfolio {i}' for i in range(1, 5)]
```
### Eigenportfolio Weights
The weights show distinct emphasis, e.g., portfolio 3 puts large weights on Mastercard and Visa, the two payment processors in the sampel whereas potfolio 2 has more exposure to some technology companies:
```
axes = eigen_portfolios.T.plot.bar(subplots=True,
layout=(2, 2),
figsize=(14, 8),
legend=False)
for ax in axes.flatten():
ax.set_ylabel('Portfolio Weight')
ax.set_xlabel('')
sns.despine()
plt.tight_layout()
```
### Eigenportfolio Performance
When comparing the performance of each portfolio over the sample period to ‘the market’ consisting of our small sample, we find that portfolio 1 performs very similarly, whereas the other portfolios capture different return patterns.
```
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(14, 6), sharex=True)
axes = axes.flatten()
returns.mean(1).add(1).cumprod().sub(1).plot(title='The Market', ax=axes[0])
for i in range(3):
rc = returns.mul(eigen_portfolios.iloc[i]).sum(1).add(1).cumprod().sub(1)
rc.plot(title=f'Portfolio {i+1}', ax=axes[i+1], lw=1, rot=0)
for i in range(4):
axes[i].set_xlabel('')
sns.despine()
fig.tight_layout()
```
| true |
code
| 0.651881 | null | null | null | null |
|
# Build and train your first deep learning model
This notebook describes how to build a basic neural network with CNTK. We'll train a model on [the iris data set](https://archive.ics.uci.edu/ml/datasets/iris) to classify iris flowers. This dataset contains 4 features that describe an iris flower belonging to one of three possible species contained in the dataset.
# Step 1: Building the network structure
We're setting the random seed for this notebook to a fixed value. This ensures that you get the same results each time you run the sample code.
```
import cntk
cntk.cntk_py.set_fixed_random_seed(1337)
```
## Define the layers
This step defines the layer structure for the neural network. We're using a default `relu` activation function for each of the neurons in the hidden layers. The output layer gets a `log_softmax` activation function.
```
from cntk import default_options, input_variable
from cntk.layers import Dense, Sequential
from cntk.ops import log_softmax, sigmoid
model = Sequential([
Dense(4, activation=sigmoid),
Dense(3, activation=log_softmax)
])
```
## Define the input for the neural network
The input for the model is a vector with four features:
- Sepal length
- Sepal width
- Petal length
- Petal width
In order for the model to work we need to define its input as an `input_variable`. This variable should have the same size as the number of features that we want to use for making a prediction. In this case it should be 4, because we have 4 different features in our dataset.
```
features = input_variable(4)
```
## Finalize the neural network structure
The last step is to finalize the neural network structure. We define a new variable `z` and invoke the model function with the input variable to bind it as the input for our model.
```
z = model(features)
```
# Train the model
After we've defined the model we need to setup the training logic. This is done in three steps:
1. Load the dataset and prepare it for use
2. Define the loss for the model.
3. Set up the trainer and learner for the model.
3. Use the trainer to train the model with the loaded data.
## Loading the data
Before we can actually train the model, we need to load the data from disk. We will use pandas for this.
Pandas is widely used python library for working with data. It contains functions to load and process data
as well as a large amount functions to perform statistical operations.
```
import pandas as pd
df_source = pd.read_csv('iris.csv',
names=['sepal_length', 'sepal_width','petal_length','petal_width', 'species'],
index_col=False)
df_source.info()
df_source.describe()
```
We split the dataset into features `X` and labels `y`. We need to feed these separately to the trainer later on to train the model. We convert the features and labels to numpy arrays as this is what CNTK expects as input.
```
import numpy as np
X = df_source.iloc[:, :4].values
y = df_source['species'].values
```
Our model doesn't take strings as values. It needs floating point values to do its job. So we need to encode the strings into a floating point representation. We can do this using a standard label encoder which is available in the `scikit-learn` python package.
```
def one_hot(x, length):
result = np.zeros(length)
result[x] = 1
return result
label_mapping = {
'Iris-setosa': 0,
'Iris-versicolor': 1,
'Iris-virginica': 2
}
y = np.array([one_hot(label_mapping[v], 3) for v in y])
```
CNTK is configured to use 32-bit floats by default. Right the features are stored as 64-bit floats and the labels are stored as integers. In order to help CNTK make sense of this, we will have to convert our data to 32-bit floats.
```
X = X.astype(np.float32)
y = y.astype(np.float32)
```
One of the challenges with machine learning is the fact that your model will try to memorize every bit of data it saw. This is called overfitting and bad for your model as it is no longer able to correctly predict outcome correctly for samples it didn't see before. We want our model to learn a set of rules that predict the correct class of flower.
In order for us to detect overfitting we need to split the dataset into a training and test set. This is done using a utility function found in the scikit-learn python package which is included with your standard anaconda installation.
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, stratify=y)
```
## Defining the target and loss
Let's define a target for our model and a loss function. The loss function measures the distance between the actual and predicted value. The loss is later used by the learner to optimize the parameters in the model.
```
from cntk.losses import cross_entropy_with_softmax
from cntk.metrics import classification_error
label = input_variable(3)
loss = cross_entropy_with_softmax(z, label)
error_rate = classification_error(z, label)
```
## Setting up the learner and trainer
When we have a model and loss we can setup the learner and trainer to train the model.
We first define the learner, which is going to use the loss function and target to optimize the model.
```
from cntk.learners import sgd
from cntk.train.trainer import Trainer
learner = sgd(z.parameters, 0.001)
trainer = Trainer(z, (loss, error_rate), [learner])
```
# Train the model
To train the model you can use different methods on the trainer. The `train_minibatch` method can be used to manually feed data into the model as minibatches. You typically use this method when you have a dataset that you've loaded manually using Pandas or numpy.
We're going to train our model by running our dataset 10 times through the trainer. Each time we perform a full pass over the dataset we perform one training epoch.
At the end of the training process we have a fully trained model that we can use to make predictions.
```
for _ in range(5):
trainer.train_minibatch({ features: X_train, label: y_train })
print('Loss: {}, Acc: {}'.format(
trainer.previous_minibatch_loss_average,
trainer.previous_minibatch_evaluation_average))
```
# Evaluate the model
After we've trained the model using the training set we can measure the models performance using a call to the test_minibatch method on the trainer instance we used earlier. This outputs a value between 0 and 1. A value closer to 1 indicates a perfectly working classifier.
Please note that at this point the model performance may be a little underwhelming. You can try running all the cells in the notebook again and it will most likely improve. This happens because the weights are initialized using a random number which changes every time you rerun all the cells in this notebook. You may get lucky!
```
trainer.test_minibatch( {features: X_test, label: y_test })
```
# Make a prediction with the trained model
Once trained we can make predictions with our model by simply invoking the model. This produces a vector with the activation values of the output layer of our model. We can then use the `argmax` function from numpy to determine the neuron with the highest activation, which is the species the flower was classified as.
```
sample_index = np.random.choice(X_test.shape[0])
sample = X_test[sample_index]
inverted_mapping = {
0: 'Iris-setosa',
1: 'Iris-versicolor',
2: 'Iris-virginica'
}
prediction = z(sample)
predicted_label = inverted_mapping[np.argmax(prediction)]
print(predicted_label)
```
| true |
code
| 0.563198 | null | null | null | null |
|
# Use Your Own Inference Code with Amazon SageMaker XGBoost Algorithm
_**Customized inference for computing SHAP values with Amazon SageMaker XGBoost script mode**_
---
## Contents
1. [Introduction](#Introduction)
2. [Setup](#Setup)
3. [Training the XGBoost model](#Training-the-XGBoost-model)
4. [Deploying the XGBoost endpoint](#Deploying-the-XGBoost-endpoint)
---
## Introduction
This notebook shows how you can configure the SageMaker XGBoost model server by defining the following three functions in the Python source file you pass to the XGBoost constructor in the SageMaker Python SDK:
- `input_fn`: Takes request data and deserializes the data into an object for prediction,
- `predict_fn`: Takes the deserialized request object and performs inference against the loaded model, and
- `output_fn`: Takes the result of prediction and serializes this according to the response content type.
We will write a customized inference script that is designed to illustrate how [SHAP](https://github.com/slundberg/shap) values enable the interpretion of XGBoost models.
We use the [Abalone data](https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/regression.html), originally from the [UCI data repository](https://archive.ics.uci.edu/ml/datasets/abalone). More details about the original dataset can be found [here](https://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.names). In this libsvm converted version, the nominal feature (Male/Female/Infant) has been converted into a real valued feature as required by XGBoost. Age of abalone is to be predicted from eight physical measurements.
This notebook uses the Abalone dataset to deploy a model server that returns SHAP values, which enable us to create model explanation such as the following plots that show each features contributing to push the model output from the base value.
<table><tr>
<td> <img src="images/shap_young_abalone.png" alt="Drawing"/> </td>
<td> <img src="images/shap_old_abalone.png" alt="Drawing"/> </td>
</tr></table>
---
## Setup
This notebook was tested in Amazon SageMaker Studio on a ml.t3.medium instance with Python 3 (Data Science) kernel.
Let's start by specifying:
1. The S3 bucket and prefix that you want to use for training and model data. This should be within the same region as the Notebook Instance, training, and hosting.
2. The IAM role arn used to give training and hosting access to your data. See the documentation for how to create these. Note, if more than one role is required for notebook instances, training, and/or hosting, please replace the boto regex with a the appropriate full IAM role arn string(s).
```
%%time
import io
import os
import boto3
import sagemaker
import time
role = sagemaker.get_execution_role()
region = boto3.Session().region_name
# S3 bucket for saving code and model artifacts.
# Feel free to specify a different bucket here if you wish.
bucket = sagemaker.Session().default_bucket()
prefix = "sagemaker/DEMO-xgboost-inference-script-mode"
```
### Fetching the dataset
The following methods download the Abalone dataset and upload files to S3.
```
%%time
s3 = boto3.client("s3")
# Load the dataset
FILE_DATA = "abalone"
s3.download_file(
"sagemaker-sample-files", f"datasets/tabular/uci_abalone/abalone.libsvm", FILE_DATA
)
sagemaker.Session().upload_data(FILE_DATA, bucket=bucket, key_prefix=prefix + "/train")
```
## Training the XGBoost model
SageMaker can now run an XGboost script using the XGBoost estimator. A typical training script loads data from the input channels, configures training with hyperparameters, trains a model, and saves a model to `model_dir` so that it can be hosted later. In this notebook, we use the same training script [abalone.py](https://github.com/awslabs/amazon-sagemaker-examples/blob/master/introduction_to_amazon_algorithms/xgboost_abalone/abalone.py) from [Regression with Amazon SageMaker XGBoost algorithm](https://github.com/awslabs/amazon-sagemaker-examples/blob/master/introduction_to_amazon_algorithms/xgboost_abalone/xgboost_abalone_dist_script_mode.ipynb). Refer to [Regression with Amazon SageMaker XGBoost algorithm](https://github.com/awslabs/amazon-sagemaker-examples/blob/master/introduction_to_amazon_algorithms/xgboost_abalone/xgboost_abalone_dist_script_mode.ipynb) for details on the training script.
After setting training parameters, we kick off training, and poll for status until training is completed, which in this example, takes between few minutes.
To run our training script on SageMaker, we construct a `sagemaker.xgboost.estimator.XGBoost` estimator, which accepts several constructor arguments:
* __entry_point__: The path to the Python script SageMaker runs for training and prediction.
* __role__: Role ARN
* __framework_version__: SageMaker XGBoost version you want to use for executing your model training code, e.g., `0.90-1`, `0.90-2`, `1.0-1`, or `1.2-1`.
* __train_instance_type__ *(optional)*: The type of SageMaker instances for training. __Note__: Because Scikit-learn does not natively support GPU training, Sagemaker Scikit-learn does not currently support training on GPU instance types.
* __sagemaker_session__ *(optional)*: The session used to train on Sagemaker.
* __hyperparameters__ *(optional)*: A dictionary passed to the train function as hyperparameters.
```
from sagemaker.inputs import TrainingInput
from sagemaker.xgboost.estimator import XGBoost
job_name = "DEMO-xgboost-inference-script-mode-" + time.strftime("%Y-%m-%d-%H-%M-%S", time.gmtime())
print("Training job", job_name)
hyperparameters = {
"max_depth": "5",
"eta": "0.2",
"gamma": "4",
"min_child_weight": "6",
"subsample": "0.7",
"objective": "reg:squarederror",
"num_round": "50",
"verbosity": "2",
}
instance_type = "ml.c5.xlarge"
xgb_script_mode_estimator = XGBoost(
entry_point="abalone.py",
hyperparameters=hyperparameters,
role=role,
instance_count=1,
instance_type=instance_type,
framework_version="1.2-1",
output_path="s3://{}/{}/{}/output".format(bucket, prefix, job_name),
)
content_type = "text/libsvm"
train_input = TrainingInput(
"s3://{}/{}/{}/".format(bucket, prefix, "train"), content_type=content_type
)
```
### Train XGBoost Estimator on Abalone Data
Training is as simple as calling `fit` on the Estimator. This will start a SageMaker Training job that will download the data, invoke the entry point code (in the provided script file), and save any model artifacts that the script creates. In this case, the script requires a `train` and a `validation` channel. Since we only created a `train` channel, we re-use it for validation.
```
xgb_script_mode_estimator.fit({"train": train_input, "validation": train_input}, job_name=job_name)
```
## Deploying the XGBoost endpoint
After training, we can host the newly created model in SageMaker, and create an Amazon SageMaker endpoint – a hosted and managed prediction service that we can use to perform inference. If you call `deploy` after you call `fit` on an XGBoost estimator, it will create a SageMaker endpoint using the training script (i.e., `entry_point`). You can also optionally specify other functions to customize the behavior of deserialization of the input request (`input_fn()`), serialization of the predictions (`output_fn()`), and how predictions are made (`predict_fn()`). If any of these functions are not specified, the endpoint will use the default functions in the SageMaker XGBoost container. See the [SageMaker Python SDK documentation](https://sagemaker.readthedocs.io/en/stable/frameworks/xgboost/using_xgboost.html#sagemaker-xgboost-model-server) for details.
In this notebook, we will run a separate inference script and customize the endpoint to return [SHAP](https://github.com/slundberg/shap) values in addition to predictions. The inference script that we will run in this notebook is provided as the accompanying file (`inference.py`) and also shown below:
```python
import json
import os
import pickle as pkl
import numpy as np
import sagemaker_xgboost_container.encoder as xgb_encoders
def model_fn(model_dir):
"""
Deserialize and return fitted model.
"""
model_file = "xgboost-model"
booster = pkl.load(open(os.path.join(model_dir, model_file), "rb"))
return booster
def input_fn(request_body, request_content_type):
"""
The SageMaker XGBoost model server receives the request data body and the content type,
and invokes the `input_fn`.
Return a DMatrix (an object that can be passed to predict_fn).
"""
if request_content_type == "text/libsvm":
return xgb_encoders.libsvm_to_dmatrix(request_body)
else:
raise ValueError(
"Content type {} is not supported.".format(request_content_type)
)
def predict_fn(input_data, model):
"""
SageMaker XGBoost model server invokes `predict_fn` on the return value of `input_fn`.
Return a two-dimensional NumPy array where the first columns are predictions
and the remaining columns are the feature contributions (SHAP values) for that prediction.
"""
prediction = model.predict(input_data)
feature_contribs = model.predict(input_data, pred_contribs=True, validate_features=False)
output = np.hstack((prediction[:, np.newaxis], feature_contribs))
return output
def output_fn(predictions, content_type):
"""
After invoking predict_fn, the model server invokes `output_fn`.
"""
if content_type == "text/csv":
return ','.join(str(x) for x in predictions[0])
else:
raise ValueError("Content type {} is not supported.".format(content_type))
```
### transform_fn
If you would rather not structure your code around the three methods described above, you can instead define your own `transform_fn` to handle inference requests. An error is thrown if a `transform_fn` is present in conjunction with any `input_fn`, `predict_fn`, and/or `output_fn`. In our case, the `transform_fn` would look as follows:
```python
def transform_fn(model, request_body, content_type, accept_type):
dmatrix = xgb_encoders.libsvm_to_dmatrix(request_body)
prediction = model.predict(dmatrix)
feature_contribs = model.predict(dmatrix, pred_contribs=True, validate_features=False)
output = np.hstack((prediction[:, np.newaxis], feature_contribs))
return ','.join(str(x) for x in predictions[0])
```
where `model` is the model object loaded by `model_fn`, `request_body` is the data from the inference request, `content_type` is the content type of the request, and `accept_type` is the request content type for the response.
### Deploy to an endpoint
Since the inference script is separate from the training script, here we use `XGBoostModel` to create a model from s3 artifacts and specify `inference.py` as the `entry_point`.
```
from sagemaker.xgboost.model import XGBoostModel
model_data = xgb_script_mode_estimator.model_data
print(model_data)
xgb_inference_model = XGBoostModel(
model_data=model_data,
role=role,
entry_point="inference.py",
framework_version="1.2-1",
)
predictor = xgb_inference_model.deploy(
initial_instance_count=1,
instance_type="ml.c5.xlarge",
)
```
### Explain the model's predictions on each data point
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
def plot_feature_contributions(prediction):
attribute_names = [
"Sex", # nominal / -- / M, F, and I (infant)
"Length", # continuous / mm / Longest shell measurement
"Diameter", # continuous / mm / perpendicular to length
"Height", # continuous / mm / with meat in shell
"Whole weight", # continuous / grams / whole abalone
"Shucked weight", # continuous / grams / weight of meat
"Viscera weight", # continuous / grams / gut weight (after bleeding)
"Shell weight", # continuous / grams / after being dried
]
prediction, _, *shap_values, bias = prediction
if len(shap_values) != len(attribute_names):
raise ValueError("Length mismatch between shap values and attribute names.")
df = pd.DataFrame(data=[shap_values], index=["SHAP"], columns=attribute_names).T
df.sort_values(by="SHAP", inplace=True)
df["bar_start"] = bias + df.SHAP.cumsum().shift().fillna(0.0)
df["bar_end"] = df.bar_start + df.SHAP
df[["bar_start", "bar_end"]] = np.sort(df[["bar_start", "bar_end"]].values)
df["hue"] = df.SHAP.apply(lambda x: 0 if x > 0 else 1)
sns.set(style="white")
ax1 = sns.barplot(x=df.bar_end, y=df.index, data=df, orient="h", palette="vlag")
for idx, patch in enumerate(ax1.patches):
x_val = patch.get_x() + patch.get_width() + 0.8
y_val = patch.get_y() + patch.get_height() / 2
shap_value = df.SHAP.values[idx]
value = "{0}{1:.2f}".format("+" if shap_value > 0 else "-", shap_value)
ax1.annotate(value, (x_val, y_val), ha="right", va="center")
ax2 = sns.barplot(x=df.bar_start, y=df.index, data=df, orient="h", color="#FFFFFF")
ax2.set_xlim(
df[["bar_start", "bar_end"]].values.min() - 1, df[["bar_start", "bar_end"]].values.max() + 1
)
ax2.axvline(x=bias, color="#000000", alpha=0.2, linestyle="--", linewidth=1)
ax2.set_title("base value: {0:.1f} → model output: {1:.1f}".format(bias, prediction))
ax2.set_xlabel("Abalone age")
sns.despine(left=True, bottom=True)
plt.tight_layout()
plt.show()
def predict_and_plot(predictor, libsvm_str):
label, *features = libsvm_str.strip().split()
predictions = predictor.predict(" ".join(["-99"] + features)) # use dummy label -99
np_array = np.array([float(x) for x in predictions[0]])
plot_feature_contributions(np_array)
```
The below figure shows features each contributing to push the model output from the base value (9.9 rings) to the model output (6.9 rings). The primary indicator for a young abalone according to the model is low shell weight, which decreases the prediction by 3.0 rings from the base value of 9.9 rings. Whole weight and shucked weight are also powerful indicators. The whole weight pushes the prediction lower by 0.84 rings, while shucked weight pushes the prediction higher by 1.6 rings.
```
a_young_abalone = "6 1:3 2:0.37 3:0.29 4:0.095 5:0.249 6:0.1045 7:0.058 8:0.067"
predict_and_plot(predictor, a_young_abalone)
```
The second example shows feature contributions for another sample, an old abalone. We again see that the primary indicator for the age of abalone according to the model is shell weight, which increases the model prediction by 2.36 rings. Whole weight and shucked weight also contribute significantly, and they both push the model's prediction higher.
```
an_old_abalone = "15 1:1 2:0.655 3:0.53 4:0.175 5:1.2635 6:0.486 7:0.2635 8:0.415"
predict_and_plot(predictor, an_old_abalone)
```
### (Optional) Delete the Endpoint
If you're done with this exercise, please run the `delete_endpoint` line in the cell below. This will remove the hosted endpoint and avoid any charges from a stray instance being left on.
```
predictor.delete_endpoint()
```
| true |
code
| 0.603319 | null | null | null | null |
|
### Our Mission
In this lesson you gained some insight into a number of techniques used to understand how well our model is performing. This notebook is aimed at giving you some practice with the metrics specifically related to classification problems. With that in mind, we will again be looking at the spam dataset from the earlier lessons.
First, run the cell below to prepare the data and instantiate a number of different models.
```
# Import our libraries
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier, AdaBoostClassifier
from sklearn.svm import SVC
import tests as t
# Read in our dataset
df = pd.read_table('smsspamcollection/SMSSpamCollection',
sep='\t',
header=None,
names=['label', 'sms_message'])
# Fix our response value
df['label'] = df.label.map({'ham':0, 'spam':1})
# Split our dataset into training and testing data
X_train, X_test, y_train, y_test = train_test_split(df['sms_message'],
df['label'],
random_state=1)
# Instantiate the CountVectorizer method
count_vector = CountVectorizer()
# Fit the training data and then return the matrix
training_data = count_vector.fit_transform(X_train)
# Transform testing data and return the matrix. Note we are not fitting the testing data into the CountVectorizer()
testing_data = count_vector.transform(X_test)
# Instantiate a number of our models
naive_bayes = MultinomialNB()
bag_mod = BaggingClassifier(n_estimators=200)
rf_mod = RandomForestClassifier(n_estimators=200)
ada_mod = AdaBoostClassifier(n_estimators=300, learning_rate=0.2)
svm_mod = SVC()
```
> **Step 1**: Now, fit each of the above models to the appropriate data. Answer the following question to assure that you fit the models correctly.
```
# Fit each of the 4 models
# This might take some time to run
naive_bayes.fit(training_data, y_train)
bag_mod.fit(training_data, y_train)
rf_mod.fit(training_data, y_train)
ada_mod.fit(training_data, y_train)
svm_mod.fit(training_data, y_train)
# The models you fit above were fit on which data?
a = 'X_train'
b = 'X_test'
c = 'y_train'
d = 'y_test'
e = 'training_data'
f = 'testing_data'
# Change models_fit_on to only contain the correct string names
# of values that you oassed to the above models
models_fit_on = {e, c} # update this to only contain correct letters
# Checks your solution - don't change this
t.test_one(models_fit_on)
```
> **Step 2**: Now make predictions for each of your models on the data that will allow you to understand how well our model will extend to new data. Then correctly add the strings to the set in the following cell.
```
# Make predictions using each of your models
preds_nb = naive_bayes.predict(testing_data)
preds_bag = bag_mod.predict(testing_data)
preds_rf = rf_mod.predict(testing_data)
preds_ada = ada_mod.predict(testing_data)
preds_svm = svm_mod.predict(testing_data)
# Which data was used in the predict method to see how well your
# model would work on new data?
a = 'X_train'
b = 'X_test'
c = 'y_train'
d = 'y_test'
e = 'training_data'
f = 'testing_data'
# Change models_predict_on to only contain the correct string names
# of values that you oassed to the above models
models_predict_on = {f} # update this to only contain correct letters
# Checks your solution - don't change this
t.test_two(models_predict_on)
```
Now that you have set up all your predictions, let's get to topics addressed in this lesson - measuring how well each of your models performed. First, we will focus on how each metric was calculated for a single model, and then in the final part of this notebook, you will choose models that are best based on a particular metric.
You will be writing functions to calculate a number of metrics and then comparing the values to what you get from sklearn. This will help you build intuition for how each metric is calculated.
> **Step 3**: As an example of how this will work for the upcoming questions, run the cell below. Fill in the below function to calculate accuracy, and then compare your answer to the built in to assure you are correct.
```
# accuracy is the total correct divided by the total to predict
def accuracy(actual, preds):
'''
INPUT
preds - predictions as a numpy array or pandas series
actual - actual values as a numpy array or pandas series
OUTPUT:
returns the accuracy as a float
'''
return np.sum(preds == actual)/len(actual)
print(accuracy(y_test, preds_nb))
print(accuracy_score(y_test, preds_nb))
print("Since these match, we correctly calculated our metric!")
```
> **Step 4**: Fill in the below function to calculate precision, and then compare your answer to the built in to assure you are correct.
```
# precision is the true positives over the predicted positive values
def precision(actual, preds):
'''
INPUT
(assumes positive = 1 and negative = 0)
preds - predictions as a numpy array or pandas series
actual - actual values as a numpy array or pandas series
OUTPUT:
returns the precision as a float
'''
tp = len(np.intersect1d(np.where(preds==1), np.where(actual==1)))
pred_pos = (preds==1).sum()
return tp/(pred_pos) # calculate precision here
print(precision(y_test, preds_nb))
print(precision_score(y_test, preds_nb))
print("If the above match, you got it!")
```
> **Step 5**: Fill in the below function to calculate recall, and then compare your answer to the built in to assure you are correct.
```
# recall is true positives over all actual positive values
def recall(actual, preds):
'''
INPUT
preds - predictions as a numpy array or pandas series
actual - actual values as a numpy array or pandas series
OUTPUT:
returns the recall as a float
'''
tp = len(np.intersect1d(np.where(preds==1), np.where(actual==1)))
act_pos = (actual==1).sum()
return tp/act_pos # calculate recall here
print(recall(y_test, preds_nb))
print(recall_score(y_test, preds_nb))
print("If the above match, you got it!")
```
> **Step 6**: Fill in the below function to calculate f1-score, and then compare your answer to the built in to assure you are correct.
```
# f1_score is 2*(precision*recall)/(precision+recall))
def f1(actual, preds):
'''
INPUT
preds - predictions as a numpy array or pandas series
actual - actual values as a numpy array or pandas series
OUTPUT:
returns the f1score as a float
'''
tp = len(np.intersect1d(np.where(preds==1), np.where(actual==1)))
pred_pos = (preds==1).sum()
prec = tp/(pred_pos)
act_pos = (actual==1).sum()
recall = tp/act_pos
return 2*(prec*recall)/(prec+recall) # calculate f1-score here
print(f1(y_test, preds_nb))
print(f1_score(y_test, preds_nb))
print("If the above match, you got it!")
```
> **Step 7:** Now that you have calculated a number of different metrics, let's tie that to when we might use one versus another. Use the dictionary below to match a metric to each statement that identifies when you would want to use that metric.
```
# add the letter of the most appropriate metric to each statement
# in the dictionary
a = "recall"
b = "precision"
c = "accuracy"
d = 'f1-score'
seven_sol = {
'We have imbalanced classes, which metric do we definitely not want to use?': c, # letter here
'We really want to make sure the positive cases are all caught even if that means we identify some negatives as positives': a, # letter here
'When we identify something as positive, we want to be sure it is truly positive': b, # letter here
'We care equally about identifying positive and negative cases': d # letter here
}
t.sol_seven(seven_sol)
```
> **Step 8:** Given what you know about the metrics now, use this information to correctly match the appropriate model to when it would be best to use each in the dictionary below.
```
# use the answers you found to the previous questiona, then match the model that did best for each metric
a = "naive-bayes"
b = "bagging"
c = "random-forest"
d = 'ada-boost'
e = "svm"
eight_sol = {
'We have imbalanced classes, which metric do we definitely not want to use?': a, # letter here
'We really want to make sure the positive cases are all caught even if that means we identify some negatives as positives': a, # letter here
'When we identify something as positive, we want to be sure it is truly positive': c, # letter here
'We care equally about identifying positive and negative cases': a # letter here
}
t.sol_eight(eight_sol)
# cells for work
# If you get stuck, also notice there is a solution available by hitting the orange button in the top left
def print_metrics(y_true, preds, model_name=None):
'''
INPUT:
y_true - the y values that are actually true in the dataset (numpy array or pandas series)
preds - the predictions for those values from some model (numpy array or pandas series)
model_name - (str - optional) a name associated with the model if you would like to add it to the print statements
OUTPUT:
None - prints the accuracy, precision, recall, and F1 score
'''
if model_name == None:
print('Accuracy score: ', format(accuracy_score(y_true, preds)))
print('Precision score: ', format(precision_score(y_true, preds)))
print('Recall score: ', format(recall_score(y_true, preds)))
print('F1 score: ', format(f1_score(y_true, preds)))
print('\n\n')
else:
print('Accuracy score for ' + model_name + ' :' , format(accuracy_score(y_true, preds)))
print('Precision score ' + model_name + ' :', format(precision_score(y_true, preds)))
print('Recall score ' + model_name + ' :', format(recall_score(y_true, preds)))
print('F1 score ' + model_name + ' :', format(f1_score(y_true, preds)))
print('\n\n')
# Print Bagging scores
print_metrics(y_test, preds_bag, 'bagging')
# Print Random Forest scores
print_metrics(y_test, preds_rf, 'random forest')
# Print AdaBoost scores
print_metrics(y_test, preds_ada, 'adaboost')
# Naive Bayes Classifier scores
print_metrics(y_test, preds_nb, 'naive bayes')
# SVM Classifier scores
print_metrics(y_test, preds_svm, 'svm')
```
As a final step in this workbook, let's take a look at the last three metrics you saw, f-beta scores, ROC curves, and AUC.
**For f-beta scores:** If you decide that you care more about precision, you should move beta closer to 0. If you decide you care more about recall, you should move beta towards infinity.
> **Step 9:** Using the fbeta_score works similar to most of the other metrics in sklearn, but you also need to set beta as your weighting between precision and recall. Use the space below to show that you can use [fbeta in sklearn](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.fbeta_score.html) to replicate your f1-score from above. If in the future you want to use a different weighting, [this article](http://mlwiki.org/index.php/Precision_and_Recall) does an amazing job of explaining how you might adjust beta for different situations.
```
# import fbeta_score
from sklearn.metrics import fbeta_score
# Show that you can produce the same f1_score results using fbeta_score
print(fbeta_score(y_test, preds_bag, beta=1))
print(f1_score(y_test, preds_bag))
```
> **Step 10:** Building ROC curves in python is a pretty involved process on your own. I wrote the function below to assist with the process and make it easier for you to do so in the future as well. Try it out using one of the other classifiers you created above to see how it compares to the random forest model below.
Run the cell below to build a ROC curve, and retrieve the AUC for the random forest model.
```
# Function for calculating auc and roc
def build_roc_auc(model, X_train, X_test, y_train, y_test):
'''
INPUT:
model - an sklearn instantiated model
X_train - the training data
y_train - the training response values (must be categorical)
X_test - the test data
y_test - the test response values (must be categorical)
OUTPUT:
auc - returns auc as a float
prints the roc curve
'''
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn.metrics import roc_curve, auc, roc_auc_score
from scipy import interp
y_preds = model.fit(X_train, y_train).predict_proba(X_test)
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(len(y_test)):
fpr[i], tpr[i], _ = roc_curve(y_test, y_preds[:, 1])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_preds[:, 1].ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
plt.plot(fpr[2], tpr[2], color='darkorange',
lw=2, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.show()
return roc_auc_score(y_test, np.round(y_preds[:, 1]))
# Finding roc and auc for the random forest model
build_roc_auc(rf_mod, training_data, testing_data, y_train, y_test)
# Your turn here - choose another classifier to see how it compares
build_roc_auc(naive_bayes, training_data, testing_data, y_train, y_test)
build_roc_auc(bag_mod, training_data, testing_data, y_train, y_test)
build_roc_auc(ada_mod, training_data, testing_data, y_train, y_test)
```
| true |
code
| 0.625667 | null | null | null | null |
|
# Week 6 - An introduction to machine learning (Part II) - Exercise and Solution
We'll apply some of the material from the previous lectures to recreating the analysis from a [nature machine intelligence](https://www.nature.com/natmachintell/) paper, ["An interpretable mortality prediction model for COVID-19 patients"](https://www.nature.com/articles/s42256-020-0180-7).
## 0. Setup
You will need to install the [xlrd] (https://xlrd.readthedocs.io/en/latest/) package to complete the Exercise.
To install this packages, launch the "Anaconda Prompt (Anaconda3)" program and run:
`conda install -c anaconda xlrd `
<img src="../img/az_conda_prompt.png">
### Training data
The original training datasets for the paper are linked as [Supplementary data](https://static-content.springer.com/esm/art%3A10.1038%2Fs42256-020-0180-7/MediaObjects/42256_2020_180_MOESM3_ESM.zip). You don't have to download this since we have included the single Excel file we need for this example as `data/time_series_375_preprocess_en.xlsx` in this project. Below we provide code to read the Excel data into a Pandas DataFrame.
```
import datetime
import pandas as pd
TRAIN_PATH = '../data/time_series_375_preprocess_en.xlsx'
RANDOM_SEED=42
def load_training_data(path):
""" Load Excel sheet of measurements from patients (timepandas.DataFrame with MultiIndex ['PATIENT_ID', 'RE_DATE'] (the unique patient identifier and patient sample date, corresponding to columns [0,1] respectively of the loaded worksheet), then retain the last set of measurements made per patient, drop 'Admission time', 'Discharge time', 'gender' and 'age' features, and replace NaNs with -1.
"""
# Specify explicitly what columns we want to load and what their data types are expected to be.
DTYPES = {
'PATIENT_ID': int,
'RE_DATE': str,
'age': int,
'gender': int,
'Admission time': str,
'Discharge time': str,
'outcome': float,
'Hypersensitive cardiac troponinI': float,
'hemoglobin': float,
'Serum chloride': float,
'Prothrombin time': float,
'procalcitonin': float,
'eosinophils(%)': float,
'Interleukin 2 receptor': float,
'Alkaline phosphatase': float,
'albumin': float,
'basophil(%)': float,
'Interleukin 10': float,
'Total bilirubin': float,
'Platelet count': float,
'monocytes(%)': float,
'antithrombin': float,
'Interleukin 8': float,
'indirect bilirubin': float,
'Red blood cell distribution width': float,
'neutrophils(%)': float,
'total protein': float,
'Quantification of Treponema pallidum antibodies': float,
'Prothrombin activity': float,
'HBsAg': float,
'mean corpuscular volume': float,
'hematocrit': float,
'White blood cell count': float,
'Tumor necrosis factorα': float,
'mean corpuscular hemoglobin concentration': float,
'fibrinogen': float,
'Interleukin 1β': float,
'Urea': float,
'lymphocyte count': float,
'PH value': float,
'Red blood cell count': float,
'Eosinophil count': float,
'Corrected calcium': float,
'Serum potassium': float,
'glucose': float,
'neutrophils count': float,
'Direct bilirubin': float,
'Mean platelet volume': float,
'ferritin': float,
'RBC distribution width SD': float,
'Thrombin time': float,
'(%)lymphocyte': float,
'HCV antibody quantification': float,
'D-D dimer': float,
'Total cholesterol': float,
'aspartate aminotransferase': float,
'Uric acid': float,
'HCO3-': float,
'calcium': float,
'Amino-terminal brain natriuretic peptide precursor(NT-proBNP)': float,
'Lactate dehydrogenase': float,
'platelet large cell ratio ': float,
'Interleukin 6': float,
'Fibrin degradation products': float,
'monocytes count': float,
'PLT distribution width': float,
'globulin': float,
'γ-glutamyl transpeptidase': float,
'International standard ratio': float,
'basophil count(#)': float,
'2019-nCoV nucleic acid detection': float,
'mean corpuscular hemoglobin': float,
'Activation of partial thromboplastin time': float,
'High sensitivity C-reactive protein': float,
'HIV antibody quantification': float,
'serum sodium': float,
'thrombocytocrit': float,
'ESR': float,
'glutamic-pyruvic transaminase': float,
'eGFR': float,
'creatinine': float
}
# Specify which string columns should be interpreted as datetimes.
DATETIME_COLUMNS = ['RE_DATE', 'Admission time', 'Discharge time']
return (
pd.read_excel(path, index_col=[0,1], dtype=DTYPES, parse_dates=DATETIME_COLUMNS)
.sort_index()
.groupby('PATIENT_ID').last()
.drop(['Admission time', 'Discharge time'], axis=1)
.drop(['age', 'gender'], axis=1) # removed in later preprocessing step in original paper
)
def remove_columns_with_missing_data(df, threshold=0.2):
""" Remove all columns from DataFrame df where the proportion of missing records is greater than threshold.
"""
return df.dropna(axis=1, thresh=(1.0-threshold)*len(df))
data = load_training_data(path=TRAIN_PATH)
print(data.shape)
data.head()
```
To set things up, as done in the paper, we'll remove all the columns with more than 20% missing data, and separate out our predictors ('X') and response ('y') variables.
```
data = remove_columns_with_missing_data(data).fillna(-1)
X = data.drop('outcome', axis=1)
y = data.outcome.astype(int)
```
## Exercises
### 1. Split data into training and test sets.
### 2. Fit a RandomForestClassifier on the training set.
### 3. Evaluate the classifier performance by calculating the confusion matrix and the [F1 score](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.f1_score.html) on the test set.
### 4. Plot the feature importances of the fitted classifier (this is basically the main finding of the Nature paper).
### 5. Try running a different type of classifier and/or see how well you can do on the test set by tuning hyperparameters using cross-validation, grid search or otherwise.
| true |
code
| 0.618521 | null | null | null | null |
|
Deep Learning
=============
Assignment 2
------------
Previously in `1_notmnist.ipynb`, we created a pickle with formatted datasets for training, development and testing on the [notMNIST dataset](http://yaroslavvb.blogspot.com/2011/09/notmnist-dataset.html).
The goal of this assignment is to progressively train deeper and more accurate models using TensorFlow.
```
# These are all the modules we'll be using later. Make sure you can import them
# before proceeding further.
from __future__ import print_function
import numpy as np
import tensorflow as tf
from six.moves import cPickle as pickle
from six.moves import range
```
First reload the data we generated in `1_notmnist.ipynb`.
```
pickle_file = 'notMNIST.pickle'
with open(pickle_file, 'rb') as f:
save = pickle.load(f)
train_dataset = save['train_dataset']
train_labels = save['train_labels']
valid_dataset = save['valid_dataset']
valid_labels = save['valid_labels']
test_dataset = save['test_dataset']
test_labels = save['test_labels']
del save # hint to help gc free up memory
print('Training set', train_dataset.shape, train_labels.shape)
print('Validation set', valid_dataset.shape, valid_labels.shape)
print('Test set', test_dataset.shape, test_labels.shape)
```
Reformat into a shape that's more adapted to the models we're going to train:
- data as a flat matrix,
- labels as float 1-hot encodings.
```
image_size = 28
num_labels = 10
def reformat(dataset, labels):
dataset = dataset.reshape((-1, image_size * image_size)).astype(np.float32)
# Map 0 to [1.0, 0.0, 0.0 ...], 1 to [0.0, 1.0, 0.0 ...]
labels = (np.arange(num_labels) == labels[:,None]).astype(np.float32)
return dataset, labels
train_dataset, train_labels = reformat(train_dataset, train_labels)
valid_dataset, valid_labels = reformat(valid_dataset, valid_labels)
test_dataset, test_labels = reformat(test_dataset, test_labels)
print('Training set', train_dataset.shape, train_labels.shape)
print('Validation set', valid_dataset.shape, valid_labels.shape)
print('Test set', test_dataset.shape, test_labels.shape)
```
We're first going to train a multinomial logistic regression using simple gradient descent.
TensorFlow works like this:
* First you describe the computation that you want to see performed: what the inputs, the variables, and the operations look like. These get created as nodes over a computation graph. This description is all contained within the block below:
with graph.as_default():
...
* Then you can run the operations on this graph as many times as you want by calling `session.run()`, providing it outputs to fetch from the graph that get returned. This runtime operation is all contained in the block below:
with tf.Session(graph=graph) as session:
...
Let's load all the data into TensorFlow and build the computation graph corresponding to our training:
```
# With gradient descent training, even this much data is prohibitive.
# Subset the training data for faster turnaround.
train_subset = 10000
graph = tf.Graph()
with graph.as_default():
# Input data.
# Load the training, validation and test data into constants that are
# attached to the graph.
tf_train_dataset = tf.constant(train_dataset[:train_subset, :])
tf_train_labels = tf.constant(train_labels[:train_subset])
tf_valid_dataset = tf.constant(valid_dataset)
tf_test_dataset = tf.constant(test_dataset)
# Variables.
# These are the parameters that we are going to be training. The weight
# matrix will be initialized using random values following a (truncated)
# normal distribution. The biases get initialized to zero.
weights = tf.Variable(
tf.truncated_normal([image_size * image_size, num_labels]))
biases = tf.Variable(tf.zeros([num_labels]))
# Training computation.
# We multiply the inputs with the weight matrix, and add biases. We compute
# the softmax and cross-entropy (it's one operation in TensorFlow, because
# it's very common, and it can be optimized). We take the average of this
# cross-entropy across all training examples: that's our loss.
logits = tf.matmul(tf_train_dataset, weights) + biases
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=tf_train_labels, logits=logits))
# Optimizer.
# We are going to find the minimum of this loss using gradient descent.
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
# Predictions for the training, validation, and test data.
# These are not part of training, but merely here so that we can report
# accuracy figures as we train.
train_prediction = tf.nn.softmax(logits)
valid_prediction = tf.nn.softmax(
tf.matmul(tf_valid_dataset, weights) + biases)
test_prediction = tf.nn.softmax(tf.matmul(tf_test_dataset, weights) + biases)
```
Let's run this computation and iterate:
```
num_steps = 801
def accuracy(predictions, labels):
return (100.0 * np.sum(np.argmax(predictions, 1) == np.argmax(labels, 1))
/ predictions.shape[0])
with tf.Session(graph=graph) as session:
# This is a one-time operation which ensures the parameters get initialized as
# we described in the graph: random weights for the matrix, zeros for the
# biases.
tf.global_variables_initializer().run()
print('Initialized')
for step in range(num_steps):
# Run the computations. We tell .run() that we want to run the optimizer,
# and get the loss value and the training predictions returned as numpy
# arrays.
_, l, predictions = session.run([optimizer, loss, train_prediction])
if (step % 100 == 0):
print('Loss at step %d: %f' % (step, l))
print('Training accuracy: %.1f%%' % accuracy(
predictions, train_labels[:train_subset, :]))
# Calling .eval() on valid_prediction is basically like calling run(), but
# just to get that one numpy array. Note that it recomputes all its graph
# dependencies.
print('Validation accuracy: %.1f%%' % accuracy(
valid_prediction.eval(), valid_labels))
print('Test accuracy: %.1f%%' % accuracy(test_prediction.eval(), test_labels))
```
Let's now switch to stochastic gradient descent training instead, which is much faster.
The graph will be similar, except that instead of holding all the training data into a constant node, we create a `Placeholder` node which will be fed actual data at every call of `session.run()`.
```
batch_size = 128
graph = tf.Graph()
with graph.as_default():
# Input data. For the training data, we use a placeholder that will be fed
# at run time with a training minibatch.
tf_train_dataset = tf.placeholder(tf.float32,
shape=(batch_size, image_size * image_size))
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels))
tf_valid_dataset = tf.constant(valid_dataset)
tf_test_dataset = tf.constant(test_dataset)
# Variables.
weights = tf.Variable(
tf.truncated_normal([image_size * image_size, num_labels]))
biases = tf.Variable(tf.zeros([num_labels]))
# Training computation.
logits = tf.matmul(tf_train_dataset, weights) + biases
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=tf_train_labels, logits=logits))
# Optimizer.
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
# Predictions for the training, validation, and test data.
train_prediction = tf.nn.softmax(logits)
valid_prediction = tf.nn.softmax(
tf.matmul(tf_valid_dataset, weights) + biases)
test_prediction = tf.nn.softmax(tf.matmul(tf_test_dataset, weights) + biases)
```
Let's run it:
```
num_steps = 3001
with tf.Session(graph=graph) as session:
tf.global_variables_initializer().run()
print("Initialized")
for step in range(num_steps):
# Pick an offset within the training data, which has been randomized.
# Note: we could use better randomization across epochs.
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
# Generate a minibatch.
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
# Prepare a dictionary telling the session where to feed the minibatch.
# The key of the dictionary is the placeholder node of the graph to be fed,
# and the value is the numpy array to feed to it.
feed_dict = {tf_train_dataset : batch_data, tf_train_labels : batch_labels}
_, l, predictions = session.run(
[optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 500 == 0):
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(
valid_prediction.eval(), valid_labels))
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
```
---
Problem
-------
Turn the logistic regression example with SGD into a 1-hidden layer neural network with rectified linear units [nn.relu()](https://www.tensorflow.org/versions/r0.7/api_docs/python/nn.html#relu) and 1024 hidden nodes. This model should improve your validation / test accuracy.
---
```
batch_size = 128
graph = tf.Graph()
with graph.as_default():
# Input data. For the training data, we use a placeholder that will be fed
# at run time with a training minibatch.
tf_train_dataset = tf.placeholder(tf.float32,
shape=(batch_size, image_size * image_size))
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels))
tf_valid_dataset = tf.constant(valid_dataset)
tf_test_dataset = tf.constant(test_dataset)
# Variables.
hidden_layer_size = 1024
weights1 = tf.Variable(
tf.truncated_normal([image_size * image_size, hidden_layer_size]))
biases1 = tf.Variable(tf.zeros([hidden_layer_size]))
hidden = tf.nn.relu(tf.matmul(tf_train_dataset, weights1) + biases1)
weights2 = tf.Variable(
tf.truncated_normal([hidden_layer_size, num_labels]))
biases2 = tf.Variable(tf.zeros([num_labels]))
# Training computation.
logits = tf.matmul(hidden, weights2) + biases2
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=tf_train_labels))
# Optimizer.
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
# Predictions for the training, validation, and test data.
train_prediction = tf.nn.softmax(logits)
print("train_prediction", train_prediction.get_shape())
valid_prediction = tf.nn.softmax(
tf.matmul(tf.nn.relu(tf.matmul(tf_train_dataset, weights1) + biases1), weights2) + biases2
)
print("valid_prediction.get_shape()", valid_prediction.get_shape())
test_prediction = tf.nn.softmax(
tf.matmul(tf.nn.relu(tf.matmul(tf_test_dataset, weights1) + biases1), weights2) + biases2
)
num_steps = 3001
with tf.Session(graph=graph) as session:
tf.global_variables_initializer().run()
print("Initialized")
for step in range(num_steps):
# Pick an offset within the training data, which has been randomized.
# Note: we could use better randomization across epochs.
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
# Generate a minibatch.
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
# Prepare a dictionary telling the session where to feed the minibatch.
# The key of the dictionary is the placeholder node of the graph to be fed,
# and the value is the numpy array to feed to it.
feed_dict = {tf_train_dataset : batch_data, tf_train_labels : batch_labels}
_, l, predictions = session.run(
[optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 500 == 0):
print("Minibatch loss at step", step, ":", l)
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
```
| true |
code
| 0.698072 | null | null | null | null |
|
# Lecture 7: Load/save and structure data
[Download on GitHub](https://github.com/NumEconCopenhagen/lectures-2020)
[<img src="https://mybinder.org/badge_logo.svg">](https://mybinder.org/v2/gh/NumEconCopenhagen/lectures-2020/master?urlpath=lab/tree/07/Load_save_and_structure_data.ipynb)
1. [Pandas dataframes](#Pandas-dataframes)
2. [Reading and writing data](#Reading-and-writing-data)
3. [Summary](#Summary)
You will learn to **load and save data** both to and from offline sources (e.g. CSV or Excel). You will learn about **pandas series and dataframes**, and how to clean, rename, structure and index your data.
**Links:**
1. Official [tutorials](https://pandas.pydata.org/pandas-docs/stable/getting_started/tutorials.html)
2. DataCamp's [pandas' cheat sheet](https://www.datacamp.com/community/blog/python-pandas-cheat-sheet)
```
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('seaborn')
```
<a id="Pandas-dataframes"></a>
# 1. Pandas dataframes
In Pandas, the fundamental object of interest is a pandas dataframe. For example:
```
X = pd.DataFrame(data = [[1,11.7,'Vitus'],[2,13.9,'Maximilian'],[3,14.6,'Bo-Bob']], columns=['id','inc','name'])
X
```
A dataframe is essentially a matrix.
* rows = observations
* columns = variables
```
X.info() # general information
```
**Note:** Show in the middle of some code.
```
from IPython.display import display
print('before\n')
display(X.head()) # first rows in dataset
print('\n\nafter')
```
## 1.1 Indexing ("subsetting")
Choosing a subset of the rows and/or columns of a dataframe is known as "indexing". All pandas dataframes are born with the method `.loc[]`.
* `df.loc[:, ['year']]` selects all rows (indicated by `:`) but only the column (variable) `year`.
* `df.loc[df['year'] == 2002, :]` selects the rows where the variable `year` is equal to 2002 and all columns (indicated by `:`)
* `df.loc[df['year'] == 2002, ['name']]` selects the variable `name` and shows the rows where `year` is equal to 2002.
In general, the syntax is `df.loc[CONDITION, [VARLIST]]`, where `CONDITION` is a vector of logical statements with the same length as the number of rows in the dataframe.
```
X.loc[X['id'] > 1, ['name']]
X.loc[X['id'] > 1] # all variables
```
**Alternatives:**
```
I = X['id'] > 1 # boolean series
X.loc[I, ['name']]
X.loc[X.id > 1, ['name']] # .VAR notation
```
## 1.2 Adding a variable
Variables are added with `df['newvar'] = SOMETHING`.
```
X['year'] = [2003, 2005, 2010]
X
```
**Note:** You cannot write `df.newvar = SOMETHING`. Some of you will forget. I promise.
The *something* can be an expression based on other variables.
```
X['inc_adj'] = X['inc'] / 1.02**(X['year']-2005)
X
```
## 1.3 Assignments to a subset of rows
Use a logical statement to select a subset of rows. Your RHS must then either be:
* a single value (all rows are set to this)
* a list of values with same length as the number of selected rows
```
X
Y = X.copy()
Y.loc[Y['id'] > 1, ['name']] = 'test'
Y
Y = X.copy()
Y.loc[(Y['name'] == 'Vitus') | (Y['year'] == 2005), ['name']] = ['Bib', 'Peter']
Y
Y = X.copy()
J = (Y['name'] == 'Maximilian') | (Y['year'] == 2010)
Y.loc[J, ['name']] = Y.loc[I, ['name']].values*2 # .values is required
Y
```
## 1.4 Copies vs. views
The `.loc[]` method returns a **copy**. Therefore the following cell does not work:.
```
Y = X.copy()
Z = Y.loc[Y['id'] > 1,['name']] # returns a copy
Z = 'test'
Y
```
**Looking** at the data it is natural to do:
```
Y['name']
Y.name
Y[['id','name']]
Y[Y['id'] > 1]
```
Importantly, this **does not work with assignment**:
```
Y = X.copy()
I = Y['id'] > 1
Z = Y['name'] # returns a view (same with Y.name)
Z[I] = 'test'
Y
Y = X.copy()
I = Y['id'] > 1
Z = Y[['id','name']] # returns a copy
Z.loc[I,['name']] = 'test'
Y
Y = X.copy()
I = Y['id'] > 1
Z = Y[I] # returns a copy
Z['name'] = 'test'
Y
```
## 1.5 The index
The first column in the dataset is referred to as the `index` of the dataframe. If you haven't done anything, it is just `[0, 1, 2, ....]`.
```
X.loc[0]
```
You can use many other things as indexes. For example the name:
```
Y = X.set_index('name') # returns a copy
Y # notice name is now below the other variables
Y.loc['Vitus']
```
## 1.6 Series and numpy arrays
When you select an individual variable, it has the data type `series`. Some functions work on a pandas series (e.g. most numpy functions), but it is sometimes nice to extract the underlying numpy objects:
* `df`: pandas dataframe
* `df['variable']`: pandas series
* `df['variabe'].values` (or `.to_numpy()`): Numpy array
```
type(X)
type(X[['year','inc_adj']]) # returns a copy
type(X['year']) # returns a view
type(X['year'].values) # returns a view
```
## 1.7 Calling functions
```
Y = X.copy()
Y
```
Row-by-row:
```
def adj_row_by_row(X):
return X['inc'] / 1.02**(X['year']-2005)
Y['inc_adj_alt1'] = Y.apply(adj_row_by_row,axis=1)
```
Function for numpy arrays:
```
def all_at_once(inc,year):
return inc / 1.02**(year-2005)
Y['inc_adj_alt2'] = all_at_once(Y['inc'].values,Y['year'].values)
```
Funcion for numpy arrays with inplace changes (i.e. a function without any return statement):
```
def all_at_once_inplace(inc,year):
inc[:] = all_at_once(inc,year)
Y['inc_adj_alt3'] = Y['inc']
all_at_once_inplace(Y['inc_adj_alt3'].values,Y['year'].values)
Y # all inc_adj* gives the same result
```
<a id="Reading-and-writing-data"></a>
# 2. Reading and writing data
To make sure that we have the "data" subfolder and that it has the datasets we need, we print its contents:
```
import os
os.listdir('data/')
```
## 2.1 Reading in data
Pandas offers a lot of facilities for reading and writing to different formats. The functions have logical names:
* CSV: `pd.read_csv()`
* SAS: `pd.read_sas()`
* Excel: `pd.read_excel()`
* Stata: `pd.read_stata()`
Whenever we look at larger dataframes, we will be using `df.head(10)` to inspect the first 10 rows, or `df.sample(10)` to look at 10 random rows (when the first 10 are special, for example).
```
# example: raw download from DST
# note: the file must be in a sub folder "data" to the folder where jupyter was launched
filename = 'data/RAS200.xlsx'
pd.read_excel(filename).head(10)
```
### Getting the right columns and rows
**Skipping rows:** Clearly, we should skip the first three rows and the first four columns
```
empl = pd.read_excel(filename, skiprows=2)
empl.head(10)
```
**Dropping columns:** The first couple of columns are not needed and contain only missing values (denoted by `NaN` (Not a Number)), so we will drop those.
```
drop_these = ['Unnamed: 0', 'Unnamed: 1', 'Unnamed: 2', 'Unnamed: 3']
empl.drop(drop_these, axis=1, inplace=True) # axis = 1 -> columns, inplace=True -> changed, no copy made
empl.head(5)
```
> **Alternative:** Use `del empl['Unnamed: 0']`.
### Renaming variables
Let's rename the first variable, which is now called `Unnamed: 4`. This is done using `df.rename(columns=dict)`, where dict must be a Python *dictionary*.
```
empl.rename(columns = {'Unnamed: 4':'municipality'}, inplace=True)
```
We also see that the employment rate in 2008 has been named `2008`. Having a variable that is named a number can cause problems with some functions (and many other programming languages do not even allow it), so let us change their names. To do so, we need to create a dictionary that maps each of the years {2008, ..., 2016} to {e2008, ..., e2016}.
```
myDict = {}
for i in range(2008, 2017): # range goes from 2008 to but not including 2017
myDict[str(i)] = f'e{i}'
myDict
empl.rename(columns = myDict, inplace=True)
empl.head(10)
```
Now we can find the employment rate in the municipality where Anders grew up:
```
empl.loc[empl.municipality == 'Lejre']
```
### Dropping observations that are not actually municipalities
The dataset contains observations like "Region Hovedstaden", which is not a municipality so we want to drop such rows. To do this, we can use the `df['var'].str` functionalities, in particular `df['var'].str.contains('PATTERN')`.
```
I = empl.municipality.str.contains('Region')
empl.loc[I, :]
```
Delete these rows.
```
for val in ['Region', 'Province', 'All Denmark']:
I = empl.municipality.str.contains(val)
empl = empl.loc[I == False] # keep everything else
```
### Summary statistics
To get an overview of employments across municipalities we can use the function `df.describe()`. Note that each observation (municipality) is weighted equally.
```
empl.describe()
```
We can also just get the mean for each year:
```
empl.mean()
```
## 2.2 Long vs. wide datasets: `pd.wide_to_long()`
Often in economic applications, it can be useful to switch between *wide* vs. *long* formats (long is sometimes referred to as *tall*, e.g. in Stata).
This is done by the commands `pd.wide_to_long()` (and `pd.long_to_wide()`).
Many types of analyses are easier to do in one format than in another so it is extremely useful to be able to switch comfortably between formats.
**Common:** Think of a dataset as having an "ID" and a "PERIOD" variable. In our dataset `empl`, the ID variable is `municipality`, and the period variable is `year`.
**Wide dataset:** The default from Statistics Denmark: each row corresponds to an ID and there is a variable for each PERIOD.
**Tall dataset:** There is one row for each combination of (ID, PERIOD).
In general, Pandas will assume that the variables in the *wide* format have a particular structure: namely they are of the form XPERIOD, where X is called the "stub". In our case, the variable names are e.g. `e2011`, so the stub is `e` and the period (for that variable) is `2011`.
```
empl_tall = pd.wide_to_long(empl, stubnames='e', i='municipality', j='year')
empl_tall.head(10)
```
**Note:** The variables `municipality` and `year` are now in the index!! We see that because they are "below" `e` in the `head` overview.
We can **select a specific municipality** using ``.xs``:
```
empl_tall.xs('Lejre',level='municipality')
```
Or ``.loc[]`` in a special way:
```
empl_tall.loc[empl_tall.index.get_level_values('municipality') == 'Lejre', :]
```
We can, alternatively, reset the index, and use `.loc` as normal:
```
empl_tall = empl_tall.reset_index()
empl_tall.loc[empl_tall.municipality == 'Lejre', :]
```
**Teaser:** As a quick teaser for what's to come, here's a cute little plot using the builtin pandas plot function.
```
empl_tall.loc[empl_tall['municipality'] == 'Lejre', :].plot(x='year',y='e');
```
We can even do it interactively:
```
import ipywidgets as widgets
def plot_e(dataframe, municipality):
I = dataframe['municipality'] == municipality
ax=dataframe.loc[I,:].plot(x='year', y='e', style='-o', legend='False')
widgets.interact(plot_e,
dataframe = widgets.fixed(empl_tall),
municipality = widgets.Dropdown(description='Municipality', options=empl_tall.municipality.unique(), value='Lejre')
);
```
## 2.3 Income
Next, we will read in the avg. disposable income for highly educated in each municipality. Here we do the cleaning, renaming and structuring in a few condensed lines.
```
# a. load
inc = pd.read_excel('data/INDKP107.xlsx', skiprows=2)
# b. clean and rename
inc.drop([f'Unnamed: {i}' for i in range(4)], axis=1, inplace=True)
inc.rename(columns = {'Unnamed: 4':'municipality'}, inplace=True) # using list comprehension
inc.rename(columns = {str(i): f'inc{i}' for i in range(2004,2018)}, inplace=True) # usinc dictionary comprehension
# c. drop rows with missing
inc.dropna(inplace=True)
# d. remove non-municipalities
for val in ['Region','Province', 'All Denmark']:
I = inc.municipality.str.contains(val)
inc.drop(inc[I].index, inplace=True) # .index -> get the indexes of the series
inc.head(5)
```
Convert wide -> tall:
```
inc_tall = pd.wide_to_long(df=inc, stubnames='inc', i='municipality', j='year')
inc_tall.reset_index(inplace=True)
inc_tall.head(5)
```
## 2.4 Municipal area
Finally, let's read in a dataset on municipality areas in km$^2$.
```
# a. load
area = pd.read_excel('data/areal.xlsx', skiprows=2)
# b. clean and rename
area.rename(columns = {'Unnamed: 0':'municipality','2019':'km2'}, inplace=True)
# c. drop rows with missing
area.dropna(inplace=True)
# d. remove non-municipalities
for val in ['Region','Province', 'All Denmark']:
I = area.municipality.str.contains(val)
area.drop(area[I].index, inplace=True)
area.head(5)
```
## 2.5 Writing data
As with reading in data, we have the corresponding functions:
* df.to_csv()
* df.to_excel()
* df.to_stata()
* df.to_sas()
* df.to_parquet()
Let's save our dataset to CSV form. We will set `index=False` to avoid saving the index (which does not mean anything here but can in other contexts be an annoying thing).
```
empl_tall.to_csv('data/RAS200_tall.csv', index=False)
inc_tall.to_csv('data/INDKP107_tall.csv', index=False)
area.to_csv('data/area.csv', index=False)
```
<a id="Summary"></a>
# 3. Summary
**This lecture**: We have discussed
1. The generel pandas framework (indexing, assigment, copies vs. views, functions)
2. Loading and saving data
3. Basic data cleaning (renaming, droping etc.)
4. Wide $\leftrightarrow$ long transformations
**Next lecture:** Basic data analysis.
| true |
code
| 0.291434 | null | null | null | null |
|
# Bayesian Linear Regression part 4: Plots

Now I have [priors on the weights](2018-01-03-bayesian-linreg.ipynb) and [observations](2018-01-08-bayesian-linreg-sample.ipynb), and I used this to come up with [the mean and variance of the posterior on the weights](2018-01-09-bayesian-linreg-posterior.ipynb). In this post, I'll show some cool plots.
```
# imports!
import numpy as np
import matplotlib.pyplot as plt
# helper functions you can skip over :D
SAVE = True
def maybe_save_plot(filename):
if SAVE:
plt.tight_layout()
plt.savefig('images/' + filename, bbox_inches="tight")
```
## Set up
You can skip to "sampling from the posterior"! This computes `V_n` again using the code from [the last post](2018-01-09-bayesian-linreg-posterior.ipynb).
```
# Set up the prior
mu_w = 0
mu_b = 0
sigma_w = 0.2
sigma_b = 0.2
w_0 = np.hstack([mu_b, mu_w])[:, None]
V_0 = np.diag([sigma_b, sigma_w])**2
# Get observations
true_sigma_y = 0.1
true_w = np.array([[2, 0.3]]).T
X_in = 2 * np.random.rand(11, 1) - 1
Phi_X_in = np.hstack((
np.ones((X_in.shape[0], 1)), # pad with 1s for the bias term
X_in
))
true_sigma_y = 0.05
noise = true_sigma_y * np.random.randn(X_in.shape[0], 1)
y = Phi_X_in @ true_w + noise
# Compute the posterior
sigma_y = true_sigma_y # I'm going to guess the noise correctly
V0_inv = np.linalg.inv(V_0)
V_n = sigma_y**2 * np.linalg.inv(sigma_y**2 * V0_inv + (Phi_X_in.T @ Phi_X_in))
w_n = V_n @ V0_inv @ w_0 + 1 / (sigma_y**2) * V_n @ Phi_X_in.T @ y
```
#### Quick aside
Above I plot a 2D array to plot multiple lines, which makes matplotlib create a lot of duplicate labels. I'm not sure if plotting matrix is a bad idea to start with, but I did it anyway and used a helper function to deduplicate labels.
```
# hrm, plotting the matrix made for `N` duplicate labels.
# https://stackoverflow.com/questions/26337493/pyplot-combine-multiple-line-labels-in-legend
def get_dedup_labels(plt):
handles, labels = plt.gca().get_legend_handles_labels()
new_handles = []
new_labels = []
for handle, label in zip(handles, labels):
if label not in new_labels:
new_handles.append(handle)
new_labels.append(label)
return new_handles, new_labels
```
## Sampling from the posterior
Much like how I [sampled from the prior]({% post_url 2018-01-03-bayesian-linreg %}), I can sample weights from the posterior.
```
grid_size = 0.01
x_grid = np.arange(-1, 1, grid_size)[:, None]
N = 100
Phi_X = np.hstack((
np.ones((x_grid.shape[0], 1)), # pad with 1s for the bias term
x_grid
))
w = np.random.randn(N, 2) @ np.linalg.cholesky(V_n) + w_n.T
plt.clf()
plt.figure(figsize=(8, 6))
plt.plot(x_grid, Phi_X @ w.T, '-m', alpha=.2, label='weights sampled from posterior')
plt.plot(X_in, y, 'xk', label='observations')
plt.legend(*get_dedup_labels(plt))
maybe_save_plot('2018-01-10-samples') # Graph showing x's for observations, a line from the mean Bayesian prediction, and shaded area of uncertainty.
plt.show()
```
## Prediction with uncertainty
I can also use `V_n` to compute the uncertainty of predictions. The prediction is the true function with some added noise:
$$y = f(\textbf x) + v$$
where \\(v \sim \mathcal N(0, \sigma_y^2)\\). With a little math, I can compute the mean and variance of the prediction posterior's Gaussian distribution. It's [also given in the course notes](http://www.inf.ed.ac.uk/teaching/courses/mlpr/2017/notes/w7a_bayesian_inference_prediction.html#predictions-for-bayesian-linear-regression).
Then I can take the square root of that to get the standard deviation and plot [2 standard deviations](https://en.wikipedia.org/wiki/68–95–99.7_rule) from the mean. In code:
```
grid_size = 0.01
x_grid = np.arange(-1, 1, grid_size)[:, None]
Phi_X = np.hstack((
np.ones((x_grid.shape[0], 1)), # pad with 1s for the bias term
x_grid
))
stdev_pred = np.sqrt(np.sum(np.dot(Phi_X, V_n) * Phi_X, 1)[:, None] + sigma_y**2)
upper_bound = Phi_X @ w_n + 2 * stdev_pred
lower_bound = Phi_X @ w_n - 2 * stdev_pred
plt.clf()
plt.figure(figsize=(8, 6))
plt.plot(X_in, y, 'xk', label='observations')
# I think fill_between wants 1D arrays
plt.fill_between(x_grid[:, 0], lower_bound[:, 0], upper_bound[:, 0], alpha=0.2, label='two standard deviations')
plt.plot(x_grid, Phi_X @ w_n, label='mean prediction')
plt.legend()
maybe_save_plot('2018-01-10-uncertainty') # Graph showing x's for observations, a line from the mean Bayesian prediction, and shaded area of uncertainty.
plt.show()
```
Neat!
If I zoom out like I do below, it's clearer that the shaded area is squeezed around the observations. That's saying there is less uncertainty around where the observations are. That's intuitive; I should be more certain of my prediction around observations.

### Comparison
The difference between these two plots confused me at first but sorting it out was instructive.
In the first plot, I'm sampling from the distribution of the *weights*. I hear sampling from the weights' distribution is not always easy to do. It turns out to be easy when doing Bayesian linear regression using Gaussians for everything.
The second plot shows the distribution of the *prediction*. This is related to the distribution of the weights (equation from [the course notes](http://www.inf.ed.ac.uk/teaching/courses/mlpr/2017/notes/w7a_bayesian_inference_prediction.html#predictions-for-bayesian-linear-regression)):
$$p(y|\mathbf x, \mathcal D) = \int p(y | \mathbf x, \mathbf w) p(\mathbf w|\mathcal D) \, d \mathbf w$$
If I look at a single weight sampled from the weight's posterior, I can plot
\\( p(y|\mathbf x, \mathbf w) \\)
which for each \\(\mathbf x\\) is \\(\mathcal N(y; \mathbf w^{\top} \mathbf x, \sigma_y^2)\\). If I plot it, I get:
```
w = np.random.randn(1, 2) @ np.linalg.cholesky(V_n) + w_n.T
mean_pred = Phi_X @ w.T
plt.clf()
plt.figure(figsize=(8, 6))
upper_bound = mean_pred[:, 0] + 2 * sigma_y
lower_bound = mean_pred[:, 0] - 2 * sigma_y
plt.plot(x_grid, mean_pred[:, 0], '-m', label='weight sampled from posterior')
plt.fill_between(x_grid[:, 0], lower_bound, upper_bound, color='m', alpha=0.2, label='two standard deviations')
plt.plot(X_in, y, 'xk', label='observations')
maybe_save_plot('2018-01-10-sample-with-error') # Graph showing x's for observations, a line for one sample of the weights, and shaded area for uncertainty.
plt.show()
```
To get the prediction, I use the integral, which does a weighted sum (or [expectation](https://en.wikipedia.org/wiki/Expected_value)!) over a bunch (all) of these. Then I get:

### Bonus: basis functions
With linear regression, I can also use basis functions to match even cooler functions.
For fun, I tried polynomials by using a different \\(\Phi \\). The true function was a quadratic. This shows
trying to fit a 5 degree polynomial to it:
model_params = 6 # highest degree + 1
Phi_X_in = np.hstack(X_in**i for i in range(model_params))
Sampling priors gave me lots of squiggles. (It also reminds me of my hair a few years ago!)

I can plot the uncertainty.

I also can add a few more points from the underlying function and see how it changes.

## See Also
- Still thanks to [MLPR](http://www.inf.ed.ac.uk/teaching/courses/mlpr/2017/notes/)!
- I originally posted the bonus [here](https://gist.github.com/jessstringham/827d8582eb4e3e0c26e9b16f6105621a).
| true |
code
| 0.730422 | null | null | null | null |
|
We build a multi-layer perceptron with its hidden layers batch normalized, and contrast it with the version without
batch normalization.
We train and evaluate both versions of the multi-layer perceptron on MNIST dataset.
```
import os
import gzip
import numpy as np
import matplotlib.pyplot as plt
import autodiff as ad
from autodiff import initializers
from autodiff import optimizers
random_state = np.random.RandomState(0)
def read_mnist_labels(fn):
with gzip.open(fn, 'rb') as f:
content = f.read()
num_images = int.from_bytes(content[4:8], byteorder='big')
labels = np.zeros((num_images, 10), dtype=np.float32)
indices = np.fromstring(content[8:], dtype=np.uint8)
labels[range(num_images), indices] += 1
return labels
def read_mnist_images(fn):
with gzip.open(fn, 'rb') as f:
content = f.read()
num_images = int.from_bytes(content[4:8], byteorder='big')
height = int.from_bytes(content[8:12], byteorder='big')
width = int.from_bytes(content[12:16], byteorder='big')
images = np.fromstring(content[16:], dtype=np.uint8).reshape((num_images, height, width))
images = images.astype(np.float32) / 255.
return images
```
Make sure you have the downloaded the following 4 files, and place them under the current directory.
```
train_images = read_mnist_images('train-images-idx3-ubyte.gz')
train_labels = read_mnist_labels('train-labels-idx1-ubyte.gz')
test_images = read_mnist_images('t10k-images-idx3-ubyte.gz')
test_labels = read_mnist_labels('t10k-labels-idx1-ubyte.gz')
tni = initializers.TruncatedNormalInitializer(mean=0.0, stddev=0.01, seed=0)
zi = initializers.ZerosInitializer()
oi = initializers.OnesInitializer()
```
Build the version of MLP with batch norm. Note the function `fused_batch_norm` takes the moving statistics as input. They will be updated in training mode, and treated as estimates of population statistics in test mode.
```
def build_batch_norm(is_training=True, epsilon=1e-3, decay=0.997):
inputs = ad.placeholder((None, 784))
labels = ad.placeholder((None, 10))
weight1 = ad.variable((784, 100), tni)
offset1 = ad.variable((100,), zi)
scale1 = ad.variable((100,), oi)
moving_mean1 = ad.variable((100,), zi, trainable=False)
moving_variance1 = ad.variable((100,), oi, trainable=False)
weight2 = ad.variable((100, 100), tni)
offset2 = ad.variable((100,), zi)
scale2 = ad.variable((100,), oi)
moving_mean2 = ad.variable((100,), zi, trainable=False)
moving_variance2 = ad.variable((100,), oi, trainable=False)
weight3 = ad.variable((100, 10), tni)
bias3 = ad.variable((10,), zi)
hidden1 = ad.matmul(inputs, weight1)
hidden1 = ad.fused_batch_norm(
hidden1, scale1, offset1, moving_mean1, moving_variance1,
epsilon=epsilon, decay=decay, is_training=is_training)
hidden1 = ad.sigmoid(hidden1)
hidden2 = ad.matmul(hidden1, weight2)
hidden2 = ad.fused_batch_norm(
hidden2, scale2, offset2, moving_mean2, moving_variance2,
epsilon=epsilon, decay=decay, is_training=is_training)
hidden2 = ad.sigmoid(hidden2)
logits = ad.matmul(hidden2, weight3) + bias3
loss = ad.softmax_cross_entropy_loss(labels, logits)
return inputs, labels, logits, loss
```
Build the version of MLP without batch norm.
```
def build_mlp():
inputs = ad.placeholder((None, 784))
labels = ad.placeholder((None, 10))
weight1 = ad.variable((784, 100), tni)
bias1 = ad.variable((100,), zi)
weight2 = ad.variable((100, 100), tni)
bias2 = ad.variable((100,), zi)
weight3 = ad.variable((100, 10), tni)
bias3 = ad.variable((10,), zi)
hidden1 = ad.matmul(inputs, weight1) + bias1
hidden1 = ad.sigmoid(hidden1)
hidden2 = ad.matmul(hidden1, weight2) + bias2
hidden2 = ad.sigmoid(hidden2)
logits = ad.matmul(hidden2, weight3) + bias3
loss = ad.softmax_cross_entropy_loss(labels, logits)
return inputs, labels, logits, loss
```
We create three separate graphs, which hold the MLP w/ BN in training mode, MLP w/ BN in test mode, and the regular MLP w/o BN.
```
graph_bn = ad.Graph()
with graph_bn.as_default_graph():
(inputs_bn, labels_bn, logits_bn, loss_bn,
) = build_batch_norm(is_training=True)
graph_bn_test = ad.Graph()
with graph_bn_test.as_default_graph():
(inputs_bn_test, labels_bn_test, logits_bn_test, loss_bn_test,
) = build_batch_norm(is_training=False)
graph = ad.Graph()
with graph.as_default_graph():
inputs, labels, logits, loss = build_mlp()
```
Create three `RunTime` instances, so the three graphs can be run separately.
```
# MLP w/ BN in training mode
graph_bn.initialize_variables()
runtime_bn = ad.RunTime()
graph_bn.set_runtime(runtime_bn)
# MLP w/ BN in test mode
graph_bn_test.initialize_variables()
runtime_bn_test = ad.RunTime()
graph_bn_test.set_runtime(runtime_bn_test)
# MLP w/o BN
graph.initialize_variables()
runtime = ad.RunTime()
graph.set_runtime(runtime)
# For BN, get the references to the variable nodes for training and test graph
# so we can assign variable's value in training graph to test graph
weights_bn = graph_bn.get_variables(False)
weights_bn_test = graph_bn_test.get_variables(False)
gd = optimizers.GradientDescentOptimizer(alpha=0.01)
```
As we train both MLPs, we compute the accuracy on test set every 50 mini-batches.
```
iterations = 30000
batch = 50
accuracies_bn = []
accuracies = []
for i in range(iterations):
which = random_state.choice(train_images.shape[0], batch, False)
inputs_val = train_images[which].reshape((-1, 784))
labels_val = train_labels[which]
feed_dict_bn = {inputs_bn: inputs_val, labels_bn: labels_val}
feed_dict = {inputs: inputs_val, labels: labels_val}
with runtime_bn.forward_backward_cycle():
gd.optimize(loss_bn, feed_dict_bn)
with runtime.forward_backward_cycle():
gd.optimize(loss, feed_dict)
# compute test accuracy every 50 mini batches
if i % 50 == 0:
inputs_val = test_images.reshape((-1, 784))
labels_val = test_labels
feed_dict_bn_test = {inputs_bn_test: inputs_val}
feed_dict = {inputs: inputs_val}
# assgin variable's value in training graph to test graph
for w_bn_test, w_bn in zip(weights_bn_test, weights_bn):
w_bn_test.set_val(w_bn.val)
with runtime_bn_test.forward_backward_cycle():
logits_bn_test_val = logits_bn_test.forward(feed_dict_bn_test)
with runtime.forward_backward_cycle():
logits_val = logits.forward(feed_dict)
acc_bn = np.mean(np.argmax(logits_bn_test_val, axis=1) == np.argmax(labels_val, axis=1))
acc = np.mean(np.argmax(logits_val, axis=1) == np.argmax(labels_val, axis=1))
accuracies_bn.append((i, acc_bn))
accuracies.append((i, acc))
accuracies_bn = np.array(accuracies_bn)
accuracies = np.array(accuracies)
```
Test accuracy is plot as a function of training iterations.
**The MLP w/ BN clearly converges faster, and generalizes better the version w/o BN.**
```
plt.plot(accuracies_bn[:, 0], accuracies_bn[:, 1], color='r')
plt.plot(accuracies[:, 0], accuracies[:, 1], color='b')
plt.ylim([0.8, 1.])
plt.legend(['w/ batch norm', 'w/o batch norm'])
plt.xlabel('iterations')
plt.ylabel('test accuracy')
fig = plt.gcf()
fig.set_size_inches(12, 6)
plt.show()
```
| true |
code
| 0.612715 | null | null | null | null |
|
(nm_ill_conditioning_roundoff_errors)=
# Ill-conditioning and roundoff errors
## Ill-conditioned matrices
The conditioning (or lack of, i.e. the ill-conditioning) of matrices we are trying to invert is incredibly important for the success of any algorithm.
As long as the matrix is non-singular, i.e. \\(\det(A)\ne 0\\), then an inverse exists, and a linear system with that \\(A\\) has a unique solution. What happens when we consider a matrix that is nearly singular, i.e. \\(\det(A)\\) is very small?
```{index} Matrix norm
```
Well smallness is a relative term and so we need to ask the question of how large or small $\det(A)$ is compared to something. That something is the **norm** of the matrix.
```{margin} Note
Norms are always in absolute terms, therefore, they are always positive. We will use \\(||||\\) to symbolise a norm of a matrix.
```
Matrices come in all shape and sizes, and their determinants come in all kinds of values. We know that a ill conditioned matrix has a determinant that is small in absolute terms, but the size of determinants is a relative thing, and we need some kind of comparison to determine what is "small" and what is "large". Thus, we can create such a reference calculating the norms of the matrix. In this notebook, we will explore how to find the norm and how does the norm relate to the ill conditioning of the matrix.
## Vector norms
```{index} Vector norms
```
Just as for vectors \\(\pmb{v}\\) (assumed as a \\(n\times 1\\) column vector) where we have multiple possible norms to help us decide quantify the magnitude of a vector:
$$
||\pmb{v}||_2 = \sqrt{v_1^2 + v_2^2 + \ldots + v_n^2} = \left(\sum_{i=1}^n v_i^2 \right)^{1/2}, \quad{\textrm{the two-norm or Euclidean norm}}\\\\\\
||\pmb{v}||_1 = |v_1| + |v_2| + \ldots + |v_n| = \sum_{i=1}^n |v_i|, \quad{\textrm{the one-norm or taxi-cab norm}}\\\\\\
||\pmb{v}||_{\infty} = \max\{|v_1|,|v_2|, \ldots, |v_n| = \max_{i=1}^n |v_i|,\quad{\textrm{the max-norm or infinity norm}}
$$
## Matrix norms
```{index} Matrix norms
```
We can define measures of the size of matrices, e.g. for \\(A\\) which for complete generality we will assume is of shape \\(m\times n\\):
$$
||A||_F = \left(\sum_{i=1}^m \sum_{j=1}^n A_{ij}^2 \right)^{1/2}, \quad{\textrm{the matrix Euclidean or Frobenius norm}}\\\\\\
||A||_{\infty} = \max_{i=1}^m \sum_{j=1}^n|A_{i,j}|, \quad{\textrm{the maximum absolute row-sum norm}}\\\\\\
$$
Note that while these norms give different results (in both the vector and matrix cases), they are consistent or equivalent in that they are always within a constant factor of one another (a result that is true for finite-dimensional or discrete problems as here). This means we don't really need to worry too much about which norm we're using.
Let's evaluate some examples.
```
import numpy as np
import scipy.linalg as sl
A = np.array([[10., 2., 1.],
[6., 5., 4.],
[1., 4., 7.]])
print("A =", A)
# The Frobenius norm (default)
# equivalent to sl.norm(A)
print("SciPy norm = ", sl.norm(A, 'fro'))
# The maximum absolute row-sum
print("Maximum absolute row-sum = ", sl.norm(A,np.inf))
# The maximum absolute column-sum
print("Maximum absolute column-sum", sl.norm(A,1))
# The two-norm - note not the same as the Frobenius norm
# also termed the spectral norm
print("SciPy spectral norm =", sl.norm(A,2))
# Spectral norm definition
print("Spectral norm by hand =", np.sqrt(np.real((np.max(sl.eigvals( A.T @ A))))))
```
## Norm implementation
We will write some code to explicitly compute the two matrix norms defined mathematically above (i.e. the Frobenius and the maximum absolute row-sum norms) and compare against the values found above using in-built scipy functions.
```
def frob(A):
m, n = A.shape
squsum = 0.
for i in range(m):
for j in range(n):
squsum += A[i,j]**2
return np.sqrt(squsum)
def mars(A):
m, n = A.shape
maxarsum = 0.
for i in range(m):
arsum = np.sum(np.abs(A[i]))
maxarsum = arsum if arsum > maxarsum else maxarsum
return maxarsum
A = np.array([[10., 2., 1.],
[6., 5., 4.],
[1., 4., 7.]])
print("A =", A)
print("Are our norms the same as SciPy?",
frob(A) == sl.norm(A,'fro') and mars(A) == sl.norm(A,np.inf))
```
## Matrix conditioning
The (ill-)conditioning of a matrix is measured with the matrix condition number:
\\[\textrm{cond}(A) = \|A\|\|A^{-1}\|.\\]
If this is close to one then \\(A\\) is termed well-conditioned; the value increases with the degree of ill-conditioning, reaching infinity for a singular matrix.
Let's evaluate the condition number for the matrix above.
```
A = np.array([[10., 2., 1.],[6., 5., 4.],[1., 4., 7.]])
print("A =", A)
print("SciPy cond(A) =", np.linalg.cond(A))
print("Default condition number uses matrix two-norm =", sl.norm(A,2)*sl.norm(sl.inv(A),2))
print("sl.norm(A,2)*sl.norm(sl.inv(A),2) =", sl.norm(A,2)*sl.norm(sl.inv(A),2))
print("SciPy Frobenius cond(A) = ", np.linalg.cond(A,'fro'))
print("sl.norm(A,'fro')*sl.norm(sl.inv(A),'fro') =", sl.norm(A,'fro')*sl.norm(sl.inv(A),'fro'))
```
The condition number is expensive to compute, and so in practice the relative size of the determinant of the matrix can be gauged based on the magnitude of the entries of the matrix.
### Example
We know that a singular matrix does not result in a unique solution to its corresponding linear matrix system. But what are the consequences of near-singularity (ill-conditioning)?
Consider the following example
\\[
\left(
\begin{array}{cc}
2 & 1 \\\\\\
2 & 1 + \epsilon \\\\\\
\end{array}
\right)\left(
\begin{array}{c}
x \\\\\\
y \\\\\\
\end{array}
\right) = \left(
\begin{array}{c}
3 \\\\\\
0 \\\\\\
\end{array}
\right)
\\]
When \\(\epsilon=0\\) the two columns/rows are not linear independent, and hence the determinant of this matrix is zero, the condition number is infinite, and the linear system does not have a solution (as the two equations would be telling us the contradictory information that \\(2x+y\\) is equal to 3 and is also equal to 0).
Let's consider a range of values \\(\epsilon\\) and calculate matrix deteterminant and condition number:
```
A = np.array([[2.,1.],
[2.,1.]])
b = np.array([3.,0.])
print("Matrix is singular, det(A) = ", sl.det(A))
for i in range(3):
A[1,1] += 0.001
epsilon = A[1,1]-1.0
print("Epsilon = %g, det(A) = %g, cond(A) = %g." % (epsilon, sl.det(A), np.linalg.cond(A)),
"inv(A)*b =", sl.inv(A) @ b)
```
We find for \\(\epsilon=0.001\\) that \\(\det(A)=0.002\\) (i.e. quite a lot smaller than the other coefficients in the matrix) and \\(\textrm{cond}(A)\approx 5000\\).
Change to \\(\epsilon=0.002\\) causes 100% change in both components of the solution. This is the consequence of the matrix being ill-conditioned - we should not trust the numerical solution to ill-conditioned problems.
A way to see this is to recognise that computers do not perform arithmetic exactly - they necessarily have to [truncate numbers](http://www.mathwords.com/t/truncating_a_number.htm) at a certain number of significant figures, performing multiple operations with these truncated numbers can lead to an erosion of accuracy. Often this is not a problem, but these so-called [roundoff](http://mathworld.wolfram.com/RoundoffError.html) errors in algorithms generating \\(A\\), or operating on \\(A\\) as in Gaussian elimination, will lead to small inaccuracies in the coefficients of the matrix. Hence, in the case of ill-conditioned problems, will fall foul of the issue seen above where a very small error in an input to the algorithm led to a far larger error in an output.
## Roundoff errors
```{index} Roundoff errors
```
```{margin} Note
For some examples of catastrophic failures due to round off errors see [Prof. Kees Vuik](https://profs.info.uaic.ro/~ancai/CN/bibliografie/CN_disasters.htm).
```
As an example, consider the mathematical formula
\\[f(x)=(1-x)^{10}.\\]
We can relatively easily expand this out by hand
\\[f(x)=1- 10x + 45x^2 - 120x^3 + 210x^4 - 252x^5 + 210x^6 - 120x^7 + 45x^8 - 10x^9 + x^{10}.\\]
Mathematically these two expressions for \\(f(x)\\) are identical; when evaluated by a computer different operations will be performed, which should give the same answer. For numbers \\(x\\) away from \\(1\\) these two expressions do return (pretty much) the same answer.
However, for \\(x\\) close to 1 the second expression adds and subtracts individual terms of increasing size which should largely cancel out, but they don't to sufficient accuracy due to round off errors; these errors accumulate with more and more operations, leading a [loss of significance](https://en.wikipedia.org/wiki/Loss_of_significance).
```
import matplotlib.pyplot as plt
def f1(x):
return (1. - x)**10
def f2(x):
return (1. - 10.*x + 45.*x**2 - 120.*x**3 +
210.*x**4 - 252.*x**5 + 210.*x**6 -
120.*x**7 + 45.*x**8 - 10.*x**9 + x**10)
xi = np.linspace(0, 2, 1000)
fig, axes = plt.subplots(1, 3, figsize=(14, 3))
ax1 = axes[0]
ax2 = axes[1]
ax3 = axes[2]
ax1.plot(xi, f1(xi), label = "unexpanded")
ax1.plot(xi, f2(xi), label = "expanded")
ax1.legend(loc="best")
ax1.set_ylabel("$f(x)$", fontsize=14)
ax2.plot(xi, 1.-f1(xi)/f2(xi) * 100, label="Relative\ndifference\nin %")
ax2.legend(loc="best")
ax2.set_xlabel("x", fontsize=14)
ax2.set_ylabel(r"$1-\frac{unexpanded}{expanded}$", fontsize=14)
ax3.set_xlim(0.75, 1.25)
ax3.plot(xi, 1.-f1(xi)/f2(xi) * 100, label="Relative\ndifference\nin %")
ax3.legend(loc="best")
ax3.set_ylabel(r"$1-\frac{unexpanded}{expanded}$", fontsize=14)
plt.suptitle("Comparison of $(1-x)^{10}$ expansion", fontsize=14)
plt.subplots_adjust(wspace=0.4)
plt.show()
```
As we can see on the graph, for most of the domain, i.e. far away from 1.0, the expansion is almost the same as the unexpanded version. Near \\(x=1\\), the expansion creates huge errors in terms of relative difference.
### Algorithm stability
The susceptibility for a numerical algorithm to dampen (inevitable) errors, rather than to magnify them as we have seen in examples above, is termed stability. This is a concern for numerical linear algebra as considered here, as well as for the numerical solution of differential equations. In that case you don't want small errors to grow and accumulate as you propagate the solution to an ODE or PDE forward in time say. If your algorithm is not inherently stable, or has other limitation, you need to understand and appreciate this, as it can cause catastrophic failures!
| true |
code
| 0.791237 | null | null | null | null |
|
```
import logging
import sys
logging.basicConfig(stream=sys.stdout, level=logging.INFO)
logging.getLogger("exchangelib").setLevel(logging.WARNING)
```
# Connecting melusine to an Outlook Exchange mailbox
The main use-case for Melusine is **email routing**. Melusine mostly focuses on the Machine Learning aspects of email routing, however, in order to make routing effective, ML models need to be connected to a mailbox.
To connect Melusine to a mailbox and process emails, possible options are:
**Option 1: (Online processing) - Exposing the ML models through an API**
With this option, Melusine is used solely to predict target folders, the action of moving emails from a folder to another (or from a mailbox to another) is taken care of by an email processing system. The email processing system is typically run by the company's IT department.
> Example: An email processing system sends a request to the Melusine API. The request contains the email content and associated metadata while the API response contains the predicted target folder for the email. Based on the API response, the email processing system is responsible for effectively moving the email in the right folder.
**Option 2: (Batch processing) - Connecting Melusine to a mailbox using a python email client**
With this option, a script is scheduled to regularly collect the emails in the inbox, predict the target folders and move the emails to the predicted folders. In this scenario, the emails are moved to the right folders directly from the python code, it is not necessary to interact with an email processing system.
> Everyday at 8 a.m, a script is run. The script uses the `ExchangeConnector` to load the emails in an Exchange mailbox, then the Melusine ML functionalities are used to run prediction on each email and finally the `ExchangeConnector` is used again to move the emails to their predicted target folder.
This tutorial demonstrates how the Melusine `ExchangeConnector` can help you with end-to-end email routing. The ExchangeConnector uses the `exchangelib` package behind the scene.
```
>>> pip install exchangelib
```
# Routing process
The process imagined for email routing using Melusine is the following:
* Emails are received on the mailbox mymailbox@maif.fr
* Melusine is used to predict the target folder for the incoming emails
* The `ExchangeConnector` is used to move the emails to the predicted target folders
Since ML models are not perfect, some emails might be misclassified. When that happens, consumers of the mailbox are encouraged to move the emails to the appropriate "correction folder".
The emails in the correction folders will constitute training data for future model trainings and thus improve the model.
# The ExchangeConnector
The Melusine `ExchangeConnector` is instanciated with the following arguments:
* `mailbox_address`: Email address of the mailbox (ex: mymailbox@maif.fr). By default, the login address is used
* `credentials`: ExchangeLib credentials
* `config`: ExchangeLib configuration
* `routing_folder_path`: Path to the folder that contains the routed emails
* `correction_folder_path`: Path to the folder that contains the corrected emails
* `done_folder_path`: Path to the folder that contains "Done" emails (emails that have already been processed)
* `target_column`: When routing, name of the DataFrame column containing target folders"target" (Default: target)
* `account_args`: Extra arguments to instantiate an ExchangeLib Account object
* `sender_address`: Email address to be used to send emails
## Exchange authentification
Authentification methods may differ depending on the user context.
This tutorial uses a **Basic Authentification** which works for most personal Outlook Exchange Accounts.
Other types of authentification methods are shown below but if it doesn't work for you,
you should investigate the `exchangelib` [documentation](https://ecederstrand.github.io/exchangelib/#setup-and-connecting).
```
from exchangelib import Credentials, Configuration, FaultTolerance
from melusine.connectors import ExchangeConnector
authentification_method = "basic"
```
### Basic Authentification
Connect to an outlook mailbox using a login and a password
```
if authentification_method == "basic":
# Parameters
my_mailbox_address = "mymailbox@maif.fr"
my_sender_address = my_mailbox_address
my_password = "melusineisawesome"
max_wait = 60
# Exchangelib configurations
credentials = Credentials(my_mailbox_address, my_password)
config = Configuration(
retry_policy=FaultTolerance(max_wait=max_wait),
credentials=credentials,
)
# Instantiate connector
connector = ExchangeConnector(
credentials=credentials,
config=config,
mailbox_address=my_mailbox_address,
sender_address=my_sender_address,
)
```
### Basic Authentification by Delegation
```
from exchangelib import DELEGATE, NTLM
if authentification_method == "delegate":
# Parameters
my_mailbox_address = "mymailbox@maif.fr"
my_sender_address = my_mailbox_address
my_password = "melusineisawesome"
max_wait = 60
account_args = {
autodiscover=False,
access_type=DELEGATE,
}
# Exchangelib configurations
credentials = Credentials(my_mailbox_address, my_password)
config = Configuration(
retry_policy=FaultTolerance(max_wait=max_wait),
credentials=credentials,
server=my_server,
auth_type=NTLM,
)
# Instantiate connector
connector = ExchangeConnector(
credentials=credentials,
config=config,
mailbox_address=my_mailbox_address,
sender_address=my_sender_address,
account_args=account_args
)
```
### OAuth2 Authentification
```
from exchangelib import OAUTH2, OAuth2Credentials
if authentification_method == "oauth2":
# Parameters
my_mailbox_address = "mymailbox@maif.fr"
my_sender_address = my_mailbox_address
my_client_id = "my_client_id"
my_client_secret = "my_client_secret"
my_tenant_id = "my_tenant_id"
max_wait = 60
account_args = {
autodiscover=False,
access_type=DELEGATE,
}
# Exchangelib configurations
credentials = OAuth2Credentials(
client_id=my_client_id, client_secret=my_client_secret, tenant_id=my_tenant_id
)
config = Configuration(
retry_policy=FaultTolerance(max_wait=max_wait),
credentials=credentials,
auth_type=OAUTH2,
)
# Instantiate connector
connector = ExchangeConnector(
credentials=credentials,
config=config,
mailbox_address=my_mailbox_address,
sender_address=my_sender_address,
)
```
# Send fake emails
In this section a set of fake emails are sent to the mailbox. The fake emails have _"[Melusine Test]"_ as a header to make sure they are not confused with your real emails.
In the following sections, Melusine and the `ExchangeConnector` will be used to route these emails.
## Send emails
The `send_email` method is used to send emails.
```
fake_emails = [
{
"header": "[Melusine Test]",
"body": "This should go to folder Test1"
},
{
"header": "[Melusine Test]",
"body": "This should go to folder Test2"
},
{
"header": "[Melusine Test]",
"body": "This should go to folder Test3"
}
]
for email_dict in fake_emails:
connector.send_email(
to=[my_mailbox_address],
header=email_dict["header"],
body=email_dict["body"],
attachments=None
)
```
**Expected output:**
You should receive 3 emails in your mailbox
# Create folders
In the email routing scenario considered, the following folders are needed:
**Target folders**
These are the folders where the routed emails will be stored.
* `Inbox / ROUTING / Test1`
* `Inbox / ROUTING / Test2`
* `Inbox / ROUTING / Test3`
**Correction folders**
When an email is erroneously routed to a target folder, mailbox consumers can move the email to the appropriate "Correction folder".
* `Inbox / CORRECTION / Test1`
* `Inbox / CORRECTION / Test2`
* `Inbox / CORRECTION / Test3`
**Done folder**
Once the emails in the correction folders have been processed (ex: for model re-training), the correction folders can be flushed by moving all the emails in the Done folder.
* `Inbox / DONE`
## Setup ROUTING folder structure
```
# Print path to the default routing folder (We will update it later)
f"Default ROUTING folder path : '{connector.routing_folder_path}'"
# Create the base routing folder
connector.create_folders(["ROUTING"], base_folder_path=None)
# Create the routing subfolders
connector.create_folders(["Test1", "Test2", "Test3"], base_folder_path="ROUTING")
# Setup the routing folder path
connector.routing_folder_path = "ROUTING"
f"Updated ROUTING folder path :'{connector.routing_folder_path}'"
# Print folder structure
print(connector.routing_folder.tree())
```
**Expected output:**
<pre>
ROUTING
├── Test1
├── Test2
└── Test3
</pre>
## Setup the CORRECTION folder structure
```
f"Default CORRECTION folder path :'{connector.correction_folder_path}'"
# Create the base CORRECTION folder at the inbox root
connector.create_folders(["CORRECTION"], base_folder_path=None)
# Create the correction subfolders
connector.create_folders(["Test1", "Test2", "Test3"], base_folder_path="CORRECTION")
# Setup the correction folder path
connector.correction_folder_path = "CORRECTION"
f"Updated CORRECTION folder path :'{connector.correction_folder_path}'"
# Print folder structure
print(connector.correction_folder.tree())
```
**Expected output:**
<pre>
CORRECTION
├── Test1
├── Test2
└── Test3
</pre>
## Setup the DONE folder
```
# Create the DONE folder at the inbox root
connector.create_folders(["DONE"], base_folder_path=None)
# Setup the done folder path
connector.done_folder_path = "DONE"
f"Updated DONE folder path :'{connector.done_folder_path}'"
# Print folder structure
print(connector.mailbox_account.inbox.tree())
```
**Expected output:**
<pre>
Boîte de réception
├── ROUTING
│ ├── Test1
│ ├── Test2
│ └── Test3
├── CORRECTION
│ ├── Test1
│ ├── Test2
│ └── Test3
└── DONE
</pre>
# Load emails
Before emails can be routed, we need to load the content of new emails.
The `get_emails` method loads the content of a mailbox folder (by default: the inbox folder).
```
df_emails = connector.get_emails(max_emails=50, ascending=False)
# Pick only test emails
mask = df_emails["header"] == "[Melusine Test]"
df_emails = df_emails[mask].copy()
# reverse order
df_emails = df_emails.reindex(index=df_emails.index[::-1])
df_emails.drop(["message_id"], axis=1)
```
**Expected output:**
| | message_id | body | header | date | from | to | attachment |
|---:|:--------------------------------------------------------------------------------|:---------|:----------------|:--------------------------|:-----------------------------|:---------------------------------|:-------------|
| 61 | <1> | This should go to folder Test1 | [Melusine Test] | 2021-05-04T19:07:56+00:00 | mymailbox@maif.fr | ['mymailbox@maif.fr'] | |
| 62 | <2> | This should go to folder Test2 | [Melusine Test] | 2021-05-04T19:07:55+00:00 | mymailbox@maif.fr | ['mymailbox@maif.fr'] | |
| 63 | <3> | This should go to folder Test3 | [Melusine Test] | 2021-05-04T19:07:56+00:00 | mymailbox@maif.fr | ['mymailbox@maif.fr'] | |
# Predict target folders
Melusine offers a variety of models (CNN, RNN, Transformers, etc) to predict the destination folder of an email. However, this tutorial focuses on the exchange connector so the ML model prediction part is mocked. Feel free to check out the `tutorial08_full_pipeline_detailed.ipynb` to see how to use Melusine for ML predictions.
```
import re
def mock_predictions(emails):
# Use a regex to find the target folder
emails["target"] = "Test" + emails["body"].str.extract(r"Test(\d)")
# Introduce a missclassification
emails.loc[0, "target"] = "Test2"
return emails
df_emails = mock_predictions(df_emails)
df_emails[["header", "body", "target"]]
```
**Expected output:**
| | header | body | target |
|---:|:----------------|:-------------------------------|:---------|
| 76 | [Melusine Test] | This should go to folder Test1 | Test1 |
| 77 | [Melusine Test] | This should go to folder Test2 | Test2 |
| 78 | [Melusine Test] | This should go to folder Test3 | Test2 |
As you can see, there is a prediction error, an email was incorrectly classified as Test2
# Route emails
Now that we have predicted the target folders for each email, we use the `ExchangeConnector` to move the emails in the mailbox.
The `route_emails` does exactly that. Its argument are:
classified_emails,
on_error="warning",
id_column="message_id",
target_column="target",
* `classified_emails`: The DataFrame containing the emails and their predicted target folder
* `raise_missing_folder_error`: If activated, an error is raised when the target folder does not exist in the mailbox. Otherwise, a warning is printed and the emails are left in the inbox.
* `id_column`: Name of the DataFrame column containing the message ID
* `target_column`: Name of the DataFrame column containing the target folder
```
connector.route_emails(df_emails)
connector.get_emails(base_folder_path="ROUTING/Test2")[["header", "body"]]
```
**Expected output:**
| | message_id | body | header | date | from | to | attachment |
|---:|:--------------------------------------------------------------------------------|:---------|:----------------|:--------------------------|:-----------------------------|:---------------------------------|:-------------|
| 61 | <1> | This should go to folder Test1 | [Melusine Test] | 2021-05-04T19:07:56+00:00 | mymailbox@maif.fr | ['mymailbox@maif.fr'] | |
| 62 | <2> | This should go to folder Test2 | [Melusine Test] | 2021-05-04T19:07:55+00:00 | mymailbox@maif.fr | ['mymailbox@maif.fr'] | |
Two emails have been routed to the folder `Test2` !
# Make corrections
## Move emails to correction folders
Corrections should be made by the mailbox consumers directly in the mailbox.
Go to your mailbox and move the emails that says:
**"This should go to folder Test1"**
(currently in the Test2 folder)
To the correction folder `CORRECTION/Test1`
## Load corrected data
```
df_corrections = connector.get_corrections()
df_corrections
```
**Expected output:**
| | message_id | body | header | date | from | to | attachment |
|---:|:--------------------------------------------------------------------------------|:---------|:----------------|:--------------------------|:-----------------------------|:---------------------------------|:-------------|
| 61 | <1> | This should go to folder Test1 | [Melusine Test] | 2021-05-04T19:07:56+00:00 | mymailbox@maif.fr | ['mymailbox@maif.fr'] | |
The emails loaded from the correction folder can now be used to train a new ML model !
# Move corrected emails to the "Done" folder
```
connector.move_to_done(df_corrections["message_id"])
```
# Conclusion
With the `ExchangeConnector` you should be able to easily implement email routing for your mailbox using Melusine !
**Hint :** If you like Melusine, don't forget to add a star on [GitHub](https://github.com/MAIF/melusine)
| true |
code
| 0.407363 | null | null | null | null |
|
# Xopt class, TNK test function
This is the class method for running Xopt.
TNK function
$n=2$ variables:
$x_i \in [0, \pi], i=1,2$
Objectives:
- $f_i(x) = x_i$
Constraints:
- $g_1(x) = -x_1^2 -x_2^2 + 1 + 0.1 \cos\left(16 \arctan \frac{x_1}{x_2}\right) \le 0$
- $g_2(x) = (x_1 - 1/2)^2 + (x_2-1/2)^2 \le 0.5$
```
from xopt import Xopt
import matplotlib.pyplot as plt
from botorch.utils.multi_objective.pareto import is_non_dominated
%matplotlib inline
import os
SMOKE_TEST = os.environ.get('SMOKE_TEST')
# To see log messages
from xopt import output_notebook
output_notebook()
```
The `Xopt` object can be instantiated from a JSON or YAML file, or a dict, with the proper structure.
Here we will make one
```
import yaml
# Make a proper input file.
YAML="""
xopt: {output_path: null}
algorithm:
name: mobo
options:
ref: [1.4, 1.4]
n_initial_samples: 5
n_steps: 10
generator_options:
batch_size: 4
simulation:
name: test_TNK
evaluate: xopt.tests.evaluators.TNK.evaluate_TNK
vocs:
name: TNK_test
description: null
simulation: test_TNK
templates: null
variables:
x1: [0, 3.14159]
x2: [0, 3.14159]
objectives: {y1: MINIMIZE, y2: MINIMIZE}
constraints:
c1: [GREATER_THAN, 0]
c2: ['LESS_THAN', 0.5]
linked_variables: {}
constants: {a: dummy_constant}
"""
config = yaml.safe_load(YAML)
# Optional: Connect the function directly
#from xopt.evaluators.test_TNK import evaluate_TNK
#config['simulation']['evaluate'] = evaluate_TNK
if SMOKE_TEST:
config['algorithm']['options']['n_steps'] = 3
config['algorithm']['options']['generator_options']['num_restarts'] = 2
config['algorithm']['options']['generator_options']['raw_samples'] = 2
X = Xopt(config)
X
```
# Run MOBO
MOBO is designed to run in serial or parallel
```
# Pick one of these
from concurrent.futures import ThreadPoolExecutor as PoolExecutor
#from concurrent.futures import ProcessPoolExecutor as PoolExecutor
executor = PoolExecutor()
# This will also work.
#executor=None
%%time
X.run(executor=executor)
```
# Plot
```
fig, ax = plt.subplots()
# get results and get valid observations
results = X.results
train_y = results['objectives']
valid_y = train_y[results['feasibility'].flatten()]
# plot results
ax.plot(train_y[:, 0], train_y[:, 1], '.')
ax.set_ylabel('$f_2$')
ax.set_xlabel('$f_1$')
# highlight Pareto front, ONLY using valid observations (note botorch assumes maximization when determing dominant points)
non_dom = is_non_dominated(-valid_y)
ax.plot(valid_y[:,0][non_dom],valid_y[:,1][non_dom],'C1o')
plt.show()
# Cleanup
!rm results.json
```
| true |
code
| 0.744279 | null | null | null | null |
|
# Introduction to Deep Learning with PyTorch
In this notebook, you'll get introduced to [PyTorch](http://pytorch.org/), a framework for building and training neural networks. PyTorch in a lot of ways behaves like the arrays you love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with Python and the Numpy/Scipy stack compared to TensorFlow and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
## ===========================================================
## Calculate the output of this network using the weights and bias tensors
Using dot product, summation, and the sigmoid function to generate output for a single neural network
```
features
weights
bias
output1 = activation(torch.sum(features * weights) + bias)
```
#### -----------------------------------------------------------------------------
```
output1
```
#### ------------------------------------------------------------------------
## ===========================================================
You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second column. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), and [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
## Calculate the output of this network using matrix multiplication
```
## ===========================================================
## Calculate the output of network using matrix multiplication
```
features
weights
reshaped_weights = weights.view(5,1)
reshaped_weights
matmul_features_weights = torch.mm(features, reshaped_weights)
matmul_features_weights
```
#### ------------------------------------------------------------------------
```
output2 = activation(matmul_features_weights + bias)
output2
```
#### ------------------------------------------------------------------------
checking for equality of outputs using inner product and matrix multiplication
```
bool(output1==output2)
```
## ===========================================================
### Stack them up!
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
# ======================================================
> # **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
features
W1
W2
B1
B2
hidden_layer = activation(torch.mm(features, W1) + B1)
output = activation(torch.mm(hidden_layer, W2) + B2)
```
### --------------------------------------------------------
```
output
```
### --------------------------------------------------------
# ======================================================
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
a = np.random.rand(4,3)
a
b = torch.from_numpy(a)
b
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
```
| true |
code
| 0.629803 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/agemagician/CodeTrans/blob/main/prediction/single%20task/api%20generation/small_model.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Install the library and download the pretrained models
```
print("Installing dependencies...")
%tensorflow_version 2.x
!pip install -q t5==0.6.4
import functools
import os
import time
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
import tensorflow.compat.v1 as tf
import tensorflow_datasets as tfds
import t5
!wget "https://www.dropbox.com/sh/kjoqdpj7e16dny9/AADdvjWVFckCgNQN-AqMKhiDa?dl=1" -O vocabulary.zip
!unzip vocabulary.zip
!rm vocabulary.zip
!wget "https://www.dropbox.com/sh/8dxden58rkczqg9/AADkgZtA6d-RAI2wKL9pavyFa?dl=1" -O api_gen.zip
!unzip api_gen.zip
!rm api_gen.zip
```
## Set sentencepiece model
```
from t5.data.sentencepiece_vocabulary import SentencePieceVocabulary
vocab_model_path = 'code_spm_unigram_40M.model'
vocab = SentencePieceVocabulary(vocab_model_path, extra_ids=100)
print("Vocab has a size of %d\n" % vocab.vocab_size)
```
## Set the preprocessors and the task registry for the t5 model
```
def api_gen_dataset_fn(split, shuffle_files=False):
del shuffle_files
ds = tf.data.TextLineDataset(api_gen_path[split])
ds = ds.map(
functools.partial(tf.io.decode_csv, record_defaults=["", ""], field_delim="\t", use_quote_delim=False),
num_parallel_calls=tf.data.experimental.AUTOTUNE
)
ds = ds.map(lambda *ex: dict(zip(["code", "docstring"], ex)))
return ds
def api_gen_preprocessor(ds):
def normalize_text(text):
return text
def to_inputs_and_targets(ex):
return {
"inputs": tf.strings.join(["description for api: ", normalize_text(ex["code"])]),
"targets": normalize_text(ex["docstring"])
}
return ds.map(to_inputs_and_targets, num_parallel_calls=tf.data.experimental.AUTOTUNE)
t5.data.TaskRegistry.remove('api_gen')
t5.data.TaskRegistry.add(
"api_gen",
dataset_fn=api_gen_dataset_fn,
output_features={
"inputs": t5.data.utils.Feature(vocabulary=vocab),
"targets": t5.data.utils.Feature(vocabulary=vocab),
},
splits=["train", "validation"],
text_preprocessor=[api_gen_preprocessor],
postprocess_fn=t5.data.postprocessors.lower_text,
metric_fns=[t5.evaluation.metrics.bleu, t5.evaluation.metrics.accuracy, t5.evaluation.metrics.rouge],
)
```
## Set t5 small model
```
MODEL_DIR = "small"
model_parallelism = 1
train_batch_size = 256
tf.io.gfile.makedirs(MODEL_DIR)
model = t5.models.MtfModel(
model_dir=MODEL_DIR,
tpu=None,
tpu_topology=None,
model_parallelism=model_parallelism,
batch_size=train_batch_size,
sequence_length={"inputs": 512, "targets": 512},
mesh_shape="model:1,batch:1",
mesh_devices=["GPU:0"],
learning_rate_schedule=0.003,
save_checkpoints_steps=5000,
keep_checkpoint_max=None,
iterations_per_loop=100,
)
```
## Api Generation
### Give the description for api
```
description = "parse the uses licence node of this package, if any, and returns the license definition if theres" #@param {type:"raw"}
```
### Parsing and Tokenization
```
import nltk
nltk.download('punkt')
from nltk.tokenize import word_tokenize
def englishTokenizer(sentence):
result = []
tokens = word_tokenize(sentence)
for t in tokens:
if( not len(t)>50):
result.append(t)
return ' '.join(result)
tokenized_description = englishTokenizer(description)
print("tokenized description: " + tokenized_description)
```
### Record the description with the prefix to a txt file
```
descriptions = [tokenized_description]
inputs_path = 'input.txt'
with tf.io.gfile.GFile(inputs_path, "w") as f:
for c in descriptions:
f.write("description for api: %s\n" % c)
predict_outputs_path = 'MtfModel-output.txt'
```
### Running the model with the best checkpoint to generating api for the given description
```
model.batch_size = 8 # Min size for small model on v2-8 with parallelism 1.
model.predict(
input_file="input.txt",
output_file=predict_outputs_path,
checkpoint_steps=840000,
beam_size=4,
vocabulary=vocab,
# Select the most probable output token at each step.
temperature=0,
)
```
### Api Generation Result
```
prediction_file = "MtfModel-output.txt-840000"
print("\nPredictions using checkpoint 840000:\n" )
with tf.io.gfile.GFile(prediction_file) as f:
for c, d in zip(descriptions, f):
if c:
print("Description: " + c + '\n')
print("Generated api: " + d)
```
| true |
code
| 0.536616 | null | null | null | null |
|
# Coverage of MultiPLIER LV using _P. aeruginosa_ data
The goal of this notebook is to examine why genes were found to be generic. Specifically, this notebook is trying to answer the question: Are generic genes found in more multiplier latent variables compared to specific genes?
The PLIER model performs a matrix factorization of gene expression data to get two matrices: loadings (Z) and latent matrix (B). The loadings (Z) are constrained to aligned with curated pathways and gene sets specified by prior knowledge [Figure 1B of Taroni et. al.](https://www.cell.com/cell-systems/pdfExtended/S2405-4712(19)30119-X). This ensure that some but not all latent variables capture known biology. The way PLIER does this is by applying a penalty such that the individual latent variables represent a few gene sets in order to make the latent variables more interpretable. Ideally there would be one latent variable associated with one gene set unambiguously.
While the PLIER model was trained on specific datasets, MultiPLIER extended this approach to all of recount2, where the latent variables should correspond to specific pathways or gene sets of interest. Therefore, we will look at the coverage of generic genes versus other genes across these MultiPLIER latent variables, which represent biological patterns.
**Definitions:**
* Generic genes: Are genes that are consistently differentially expressed across multiple simulated experiments.
* Other genes: These are all other non-generic genes. These genes include those that are not consistently differentially expressed across simulated experiments - i.e. the genes are specifically changed in an experiment. It could also indicate genes that are consistently unchanged (i.e. housekeeping genes)
Note: This notebook is perfoming the same analysis found in [1_get_multiplier_LV_coverage.ipynb](1_get_multiplier_LV_coverage.ipynb), which used human data. Here we're using _P. aeruginosa_ data.
```
%load_ext autoreload
%autoreload 2
import os
import random
import textwrap
import scipy
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
import rpy2.robjects as ro
from rpy2.robjects import pandas2ri
from rpy2.robjects.conversion import localconverter
from ponyo import utils
from generic_expression_patterns_modules import lv
# Get data directory containing gene summary data
base_dir = os.path.abspath(os.path.join(os.getcwd(), "../"))
data_dir = os.path.join(base_dir, "pseudomonas_analysis")
# Read in config variables
config_filename = os.path.abspath(
os.path.join(base_dir, "configs", "config_pseudomonas_33245.tsv")
)
params = utils.read_config(config_filename)
local_dir = params["local_dir"]
project_id = params["project_id"]
quantile_threshold = 0.97
# Output file
nonzero_figure_filename = "nonzero_LV_coverage_multiPLIER_pa.svg"
highweight_figure_filename = "highweight_LV_coverage_multiPLIER_pa.svg"
```
## Load data
```
# Get gene summary file
summary_data_filename = os.path.join(
data_dir, f"generic_gene_summary_{project_id}_cbrB_v_WT.tsv"
)
# Load gene summary data
data = pd.read_csv(summary_data_filename, sep="\t", index_col=0, header=0)
# Check that genes are unique since we will be using them as dictionary keys below
assert data.shape[0] == len(data["Gene ID"].unique())
# Load multiplier models
# Converted formatted pickle files (loaded using phenoplier environment) from
# https://github.com/greenelab/phenoplier/blob/master/nbs/01_preprocessing/005-multiplier_recount2_models.ipynb
# into .tsv files
multiplier_model_z = pd.read_csv(
"multiplier_Pa_model_z.tsv", sep="\t", index_col=0, header=0
)
# Get a rough sense for how many genes contribute to a given LV
# (i.e. how many genes have a value != 0 for a given LV)
# Notice that multiPLIER is a sparse model
(multiplier_model_z != 0).sum().sort_values(ascending=True)
```
## Get gene data
Define generic genes based on simulated gene ranking. Refer to [figure](https://github.com/greenelab/generic-expression-patterns/blob/master/pseudomonas_analysis/gene_ranking_logFC.svg) as a guide.
**Definitions:**
* Generic genes: `Percentile (simulated) >= 80`
(Having a high rank indicates that these genes are consistently changed across simulated experiments.)
* Other genes: `Percentile (simulated) < 80`
(Having a lower rank indicates that these genes are not consistently changed across simulated experiments - i.e. the genes are specifically changed in an experiment. It could also indicate genes that are consistently unchanged.)
```
generic_threshold = 80
dict_genes = lv.get_generic_specific_genes(data, generic_threshold)
# Check overlap between multiplier genes and our genes
multiplier_genes = list(multiplier_model_z.index)
our_genes = list(data.index)
shared_genes = set(our_genes).intersection(multiplier_genes)
print(len(our_genes))
print(len(shared_genes))
# Drop gene ids not used in multiplier analysis
processed_dict_genes = lv.process_generic_specific_gene_lists(
dict_genes, multiplier_model_z
)
# Check numbers add up
assert len(shared_genes) == len(processed_dict_genes["generic"]) + len(
processed_dict_genes["other"]
)
```
## Get coverage of LVs
For each gene (generic or other) we want to find:
1. The number of LVs that gene is present
2. The number of LVs that the gene contributes a lot to (i.e. the gene is highly weighted within that LV)
### Nonzero LV coverage
```
dict_nonzero_coverage = lv.get_nonzero_LV_coverage(
processed_dict_genes, multiplier_model_z
)
# Check genes mapped correctly
assert processed_dict_genes["generic"][0] in dict_nonzero_coverage["generic"].index
assert len(dict_nonzero_coverage["generic"]) == len(processed_dict_genes["generic"])
assert len(dict_nonzero_coverage["other"]) == len(processed_dict_genes["other"])
```
### High weight LV coverage
```
# Quick look at the distribution of gene weights per LV
sns.distplot(multiplier_model_z["LV3"], kde=False)
plt.yscale("log")
dict_highweight_coverage = lv.get_highweight_LV_coverage(
processed_dict_genes, multiplier_model_z, quantile_threshold
)
# Check genes mapped correctly
assert processed_dict_genes["generic"][0] in dict_highweight_coverage["generic"].index
assert len(dict_highweight_coverage["generic"]) == len(processed_dict_genes["generic"])
assert len(dict_highweight_coverage["other"]) == len(processed_dict_genes["other"])
```
### Assemble LV coverage and plot
```
all_coverage = []
for gene_label in dict_genes.keys():
merged_df = pd.DataFrame(
dict_nonzero_coverage[gene_label], columns=["nonzero LV coverage"]
).merge(
pd.DataFrame(
dict_highweight_coverage[gene_label], columns=["highweight LV coverage"]
),
left_index=True,
right_index=True,
)
merged_df["gene type"] = gene_label
all_coverage.append(merged_df)
all_coverage_df = pd.concat(all_coverage)
all_coverage_df = lv.assemble_coverage_df(
processed_dict_genes, dict_nonzero_coverage, dict_highweight_coverage
)
all_coverage_df.head()
# Plot coverage distribution given list of generic coverage, specific coverage
nonzero_fig = sns.boxplot(
data=all_coverage_df,
x="gene type",
y="nonzero LV coverage",
notch=True,
palette=["#2c7fb8", "lightgrey"],
)
nonzero_fig.set_xlabel(None)
nonzero_fig.set_xticklabels(
["generic genes", "other genes"], fontsize=14, fontname="Verdana"
)
nonzero_fig.set_ylabel(
textwrap.fill("Number of LVs", width=30), fontsize=14, fontname="Verdana"
)
nonzero_fig.tick_params(labelsize=14)
nonzero_fig.set_title(
"Number of LVs genes are present in", fontsize=16, fontname="Verdana"
)
# Plot coverage distribution given list of generic coverage, specific coverage
highweight_fig = sns.boxplot(
data=all_coverage_df,
x="gene type",
y="highweight LV coverage",
notch=True,
palette=["#2c7fb8", "lightgrey"],
)
highweight_fig.set_xlabel(None)
highweight_fig.set_xticklabels(
["generic genes", "other genes"], fontsize=14, fontname="Verdana"
)
highweight_fig.set_ylabel(
textwrap.fill("Number of LVs", width=30), fontsize=14, fontname="Verdana"
)
highweight_fig.tick_params(labelsize=14)
highweight_fig.set_title(
"Number of LVs genes contribute highly to", fontsize=16, fontname="Verdana"
)
```
## Calculate statistics
* Is the reduction in generic coverage significant?
* Is the difference between generic versus other genes signficant?
```
# Test: mean number of LVs generic genes present in vs mean number of LVs that generic gene is high weight in
# (compare two blue boxes between plots)
generic_nonzero = all_coverage_df[all_coverage_df["gene type"] == "generic"][
"nonzero LV coverage"
].values
generic_highweight = all_coverage_df[all_coverage_df["gene type"] == "generic"][
"highweight LV coverage"
].values
(stats, pvalue) = scipy.stats.ttest_ind(generic_nonzero, generic_highweight)
print(pvalue)
# Test: mean number of LVs generic genes present in vs mean number of LVs other genes high weight in
# (compare blue and grey boxes in high weight plot)
other_highweight = all_coverage_df[all_coverage_df["gene type"] == "other"][
"highweight LV coverage"
].values
generic_highweight = all_coverage_df[all_coverage_df["gene type"] == "generic"][
"highweight LV coverage"
].values
(stats, pvalue) = scipy.stats.ttest_ind(other_highweight, generic_highweight)
print(pvalue)
# Check that coverage of other and generic genes across all LVs is NOT signficantly different
# (compare blue and grey boxes in nonzero weight plot)
other_nonzero = all_coverage_df[all_coverage_df["gene type"] == "other"][
"nonzero LV coverage"
].values
generic_nonzero = all_coverage_df[all_coverage_df["gene type"] == "generic"][
"nonzero LV coverage"
].values
(stats, pvalue) = scipy.stats.ttest_ind(other_nonzero, generic_nonzero)
print(pvalue)
```
## Get LVs that generic genes are highly weighted in
Since we are using quantiles to get high weight genes per LV, each LV has the same number of high weight genes. For each set of high weight genes, we will get the proportion of generic vs other genes. We will select the LVs that have a high proportion of generic genes to examine.
```
# Get proportion of generic genes per LV
prop_highweight_generic_dict = lv.get_prop_highweight_generic_genes(
processed_dict_genes, multiplier_model_z, quantile_threshold
)
# Return selected rows from summary matrix
multiplier_model_summary = pd.read_csv(
"multiplier_Pa_model_summary.tsv", sep="\t", index_col=0, header=0
)
lv.create_LV_df(
prop_highweight_generic_dict,
multiplier_model_summary,
0.5,
"Generic_LV_summary_table_Pa.tsv",
)
# Plot distribution of weights for these nodes
node = "LV30"
lv.plot_dist_weights(
node,
multiplier_model_z,
shared_genes,
20,
all_coverage_df,
f"weight_dist_{node}.svg",
)
```
## Save
```
# Save plot
nonzero_fig.figure.savefig(
nonzero_figure_filename,
format="svg",
bbox_inches="tight",
transparent=True,
pad_inches=0,
dpi=300,
)
# Save plot
highweight_fig.figure.savefig(
highweight_figure_filename,
format="svg",
bbox_inches="tight",
transparent=True,
pad_inches=0,
dpi=300,
)
```
**Takeaway:**
* In the first nonzero boxplot, generic and other genes are present in a similar number of LVs. This isn't surprising since the number of genes that contribute to each LV is <1000.
* In the second highweight boxplot, other genes and generic genes are highly weighted in a similar number of LVs, but overall generic genes contribute a lot to very few LVs. Despite the t-test returning a significant p-value for the difference, the distribution looks very similar.
* The only associated LV is related to type IV secretion system, which is a complex responsible for a broad range of functions: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3070162/
Compared to the trend found using [human data](1_get_multiplier_LV_coverage.ipynb), perhaps this indicates that generic genes have similar behavior/roles across organisms.
| true |
code
| 0.610105 | null | null | null | null |
|
# Multi-Class Single-Label classification
The natural extension of binary classification is a multi-class classification task.
We first approach multi-class single-label classification, which makes the assumption that each example is assigned to one and only one label.
We use the *Iris flower* data set, which consists of a classification into three mutually-exclusive classes; call these $A$, $B$ and $C$.
While one could train three unary predicates $A(x)$, $B(x)$ and $C(x)$, it turns out to be more effective if this problem is modelled by a single binary predicate $P(x,l)$, where $l$ is a variable denoting a multi-class label, in this case classes $A$, $B$ or $C$.
- This syntax allows one to write statements quantifying over the classes, e.g. $\forall x ( \exists l ( P(x,l)))$.
- Since the classes are mutually-exclusive in this case, the output layer of the $\mathtt{MLP}$ representing $P(x,l)$ will be a $\mathtt{softmax}$ layer, instead of a $\mathtt{sigmoid}$ function, to learn the probability of $A$, $B$ and $C$. This avoids writing additional constraints $\lnot (A(x) \land B(x))$, $\lnot (A(x) \land C(x))$, ...
```
import logging; logging.basicConfig(level=logging.INFO)
import tensorflow as tf
import pandas as pd
import logictensornetworks as ltn
```
# Data
Load the iris dataset: 50 samples from each of three species of iris flowers (setosa, virginica, versicolor), measured with four features.
```
df_train = pd.read_csv("iris_training.csv")
df_test = pd.read_csv("iris_test.csv")
print(df_train.head(5))
labels_train = df_train.pop("species")
labels_test = df_test.pop("species")
batch_size = 64
ds_train = tf.data.Dataset.from_tensor_slices((df_train,labels_train)).batch(batch_size)
ds_test = tf.data.Dataset.from_tensor_slices((df_test,labels_test)).batch(batch_size)
```
# LTN
Predicate with softmax `P(x,class)`
```
class MLP(tf.keras.Model):
"""Model that returns logits."""
def __init__(self, n_classes, hidden_layer_sizes=(16,16,8)):
super(MLP, self).__init__()
self.denses = [tf.keras.layers.Dense(s, activation="elu") for s in hidden_layer_sizes]
self.dense_class = tf.keras.layers.Dense(n_classes)
self.dropout = tf.keras.layers.Dropout(0.2)
def call(self, inputs, training=False):
x = inputs
for dense in self.denses:
x = dense(x)
x = self.dropout(x, training=training)
return self.dense_class(x)
logits_model = MLP(4)
p = ltn.Predicate(ltn.utils.LogitsToPredicateModel(logits_model,single_label=True))
```
Constants to index/iterate on the classes
```
class_A = ltn.Constant(0, trainable=False)
class_B = ltn.Constant(1, trainable=False)
class_C = ltn.Constant(2, trainable=False)
```
Operators and axioms
```
Not = ltn.Wrapper_Connective(ltn.fuzzy_ops.Not_Std())
And = ltn.Wrapper_Connective(ltn.fuzzy_ops.And_Prod())
Or = ltn.Wrapper_Connective(ltn.fuzzy_ops.Or_ProbSum())
Implies = ltn.Wrapper_Connective(ltn.fuzzy_ops.Implies_Reichenbach())
Forall = ltn.Wrapper_Quantifier(ltn.fuzzy_ops.Aggreg_pMeanError(p=2),semantics="forall")
formula_aggregator = ltn.Wrapper_Formula_Aggregator(ltn.fuzzy_ops.Aggreg_pMeanError(p=2))
@tf.function
def axioms(features, labels, training=False):
x_A = ltn.Variable("x_A",features[labels==0])
x_B = ltn.Variable("x_B",features[labels==1])
x_C = ltn.Variable("x_C",features[labels==2])
axioms = [
Forall(x_A,p([x_A,class_A],training=training)),
Forall(x_B,p([x_B,class_B],training=training)),
Forall(x_C,p([x_C,class_C],training=training))
]
sat_level = formula_aggregator(axioms).tensor
return sat_level
```
Initialize all layers and the static graph
```
for features, labels in ds_test:
print("Initial sat level %.5f"%axioms(features,labels))
break
```
# Training
Define the metrics. While training, we measure:
1. The level of satisfiability of the Knowledge Base of the training data.
1. The level of satisfiability of the Knowledge Base of the test data.
3. The training accuracy.
4. The test accuracy.
```
metrics_dict = {
'train_sat_kb': tf.keras.metrics.Mean(name='train_sat_kb'),
'test_sat_kb': tf.keras.metrics.Mean(name='test_sat_kb'),
'train_accuracy': tf.keras.metrics.CategoricalAccuracy(name="train_accuracy"),
'test_accuracy': tf.keras.metrics.CategoricalAccuracy(name="test_accuracy")
}
```
Define the training and test step
```
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
@tf.function
def train_step(features, labels):
# sat and update
with tf.GradientTape() as tape:
sat = axioms(features, labels, training=True)
loss = 1.-sat
gradients = tape.gradient(loss, p.trainable_variables)
optimizer.apply_gradients(zip(gradients, p.trainable_variables))
sat = axioms(features, labels) # compute sat without dropout
metrics_dict['train_sat_kb'](sat)
# accuracy
predictions = logits_model(features)
metrics_dict['train_accuracy'](tf.one_hot(labels,3),predictions)
@tf.function
def test_step(features, labels):
# sat
sat = axioms(features, labels)
metrics_dict['test_sat_kb'](sat)
# accuracy
predictions = logits_model(features)
metrics_dict['test_accuracy'](tf.one_hot(labels,3),predictions)
```
Train
```
import commons
EPOCHS = 500
commons.train(
EPOCHS,
metrics_dict,
ds_train,
ds_test,
train_step,
test_step,
csv_path="iris_results.csv",
track_metrics=20
)
```
| true |
code
| 0.6961 | null | null | null | null |
|
# Tensor Creation
```
from __future__ import print_function
import torch
import numpy as np
import matplotlib
%matplotlib inline
import matplotlib.pyplot as plt
from datetime import date
date.today()
author = "kyubyong. https://github.com/Kyubyong/pytorch_exercises"
torch.__version__
np.__version__
```
NOTE on notation
_x, _y, _z, ...: NumPy 0-d or 1-d arrays
_X, _Y, _Z, ...: NumPy 2-d or higer dimensional arrays
x, y, z, ...: 0-d or 1-d tensors
X, Y, Z, ...: 2-d or higher dimensional tensors
## From Python list
Q1. Convert a python list `a` into an int32 tensor.
```
a = [[1, 2, 3], [4, 5, 6]]
X = torch.IntTensor(a)
print(X)
```
Q2. Create a float32 tensor of shape (3, 2), filled with 10.
```
X = torch.FloatTensor(3, 2).fill_(10)
print(X)
```
## From Numpy Array
Q3. Convert a NumPy array _x into a tensor.
```
_x = np.array([1, 2, 3])
x = torch.from_numpy(_x)
print(x)
```
## Ones and zeros
Q4. Create a 3-by-3 2-D tensor with ones on the diagonal and zeros elsewhere.
```
X = torch.eye(3)
print(X)
assert np.array_equal(X.numpy(), np.eye(3))
```
Q5. Create a tensor with shape of (3, 2) filled with 1's.
```
X = torch.ones(3, 2)
print(X)
assert np.array_equal(X.numpy(), np.ones([3, 2]))
```
Q6. Create a tensor with shape of (3, 2) filled with 0's.
```
X = torch.zeros(3, 2)
print(X)
assert np.array_equal(X.numpy(), np.zeros([3, 2]))
```
## Numerical ranges
Q7. Create a 1D tensor which looks like 2, 4, 6, 8, ..., 100.
```
x = torch.arange(2, 101, 2) # Unlike numpy api, torch arange function requires the start argument.
print(x)
assert np.array_equal(x.numpy(), np.arange(2, 101, 2))
```
Q8. Create a 1D tensor of 50 evenly spaced elements between 3. and 10., inclusive.
```
x = torch.linspace(3, 10, 50)
print(x)
assert np.allclose(x.numpy(), np.linspace(3., 10, 50))
```
Q9. Create a 1-D tensor of 50 element spaced evenly on a log scale between 3. and 10.
```
x = torch.logspace(3, 10, 50)
assert np.allclose(x.numpy(), np.logspace(3., 10., 50))
plt.figure()
plt.scatter(range(len(_x)), _x)
plt.show()
```
## Matrix
Q10. Get the diagonal of X.
```
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = X.diag()
print(y)
assert np.array_equal(y.numpy(), np.diag(X.numpy()))
```
Q11. Get the 1th diagonal of X.
```
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = X.diag(1)
print(y)
assert np.array_equal(y.numpy(), np.diag(X.numpy(), 1))
```
Q12. Get the sum of the elements of the diagonal of X.
```
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = X.trace()
print(y)
assert np.array_equal(y, np.trace(X.numpy()))
```
Q13. Return the lower triangular part of X, the other elements are set to 0.
```
X = torch.Tensor([[1,2,3], [4,5,6], [7,8,9]])
Y = X.tril()
print(Y)
assert np.array_equal(Y.numpy(), np.tril(X.numpy()))
```
Q14. Return the upper triangular part of X, the other elements are set to 0.
```
X = torch.Tensor([[1,2,3], [4,5,6], [7,8,9]])
Y = X.triu()
print(Y)
assert np.array_equal(Y.numpy(), np.triu(X.numpy()))
```
## Save and Load
Q15. Save X to `temp.pt`.
```
X = torch.randn(1, 10)
torch.save(X, 'temp.pt')
```
Q16. Load the `temp.pt` you just saved.
```
X2 = torch.load('temp.pt')
print(X2)
```
Q17. Print X2 such that all elements are displayed with precision=1 (without actually changing the values of X2).
```
torch.set_printoptions(precision=1)
print(X2)
```
| true |
code
| 0.715126 | null | null | null | null |
|
# Census Notebook
**Authorship**<br />
Original Author: Taurean Dyer<br />
Last Edit: Taurean Dyer, 9/26/2019<br />
**Test System Specs**<br />
Test System Hardware: GV100<br />
Test System Software: Ubuntu 18.04<br />
RAPIDS Version: 0.10.0a - Docker Install<br />
Driver: 410.79<br />
CUDA: 10.0<br />
**Known Working Systems**<br />
RAPIDS Versions:0.8, 0.9, 0.10
# Intro
Held every 10 years, the US census gives a detailed snapshot in time about the makeup of the country. The last census in 2010 surveyed nearly 309 million people. IPUMS.org provides researchers an open source data set with 1% to 10% of the census data set. In this notebook, we want to see how education affects total income earned in the US based on data from each census from the 1970 to 2010 and see if we can predict some results if the census was held today, according to the national average. We will go through the ETL, training the model, and then testing the prediction. We'll make every effort to get as balanced of a dataset as we can. We'll also pull some extra variables to allow for further self-exploration of gender based education and income breakdowns. On a single Titan RTX, you can run the whole notebook workflow on the 4GB dataset of 14 million rows by 44 columns in less than 3 minutes.
**Let's begin!**
## Imports
```
import pandas as pd
import numpy as np
import cuml
import cudf
import dask_cudf
import sys
import os
from pprint import pprint
import warnings
warnings.filterwarnings('ignore')
```
## Get your data!
```
import urllib.request
import time
from dask.distributed import Client, wait
from dask_cuda import LocalCUDACluster
cluster = LocalCUDACluster()
client = Client(cluster)
client
```
The ipums dataset is in our S3 bucket and zipped.
1. We'll need to create a folder for our data in the `/data` folder
1. Download the zipped data into that folder from S3
1. Load the zipped data quickly into cudf using it's read_csv() parameters
```
data_dir = '../data/census/'
if not os.path.exists(data_dir):
print('creating census data directory')
os.system('mkdir ../data/census/')
# download the IPUMS dataset
base_url = 'https://rapidsai-data.s3.us-east-2.amazonaws.com/datasets/'
fn = 'ipums_education2income_1970-2010.csv.gz'
if not os.path.isfile(data_dir+fn):
print(f'Downloading {base_url+fn} to {data_dir+fn}')
urllib.request.urlretrieve(base_url+fn, data_dir+fn)
def load_data(cached = data_dir+fn):
if os.path.exists(cached):
print('use ipums data')
X = cudf.read_csv(cached, compression='infer')
else:
print("No data found! Please check your that your data directory is ../../data/census/ and that you downloaded the data. If you did, please delete the `../../../data/census/` directory and try the above 2 cells again")
X = null
return X
df = load_data(data_dir+fn)
# limit
df = df[0:100]
print('data',df.shape)
print(df.head(5).to_pandas())
df.dtypes
original_counts = df.YEAR.value_counts()
print(original_counts) ### Remember these numbers!
```
## ETL
### Cleaning Income data
First, let's focus on cleaning out the bad values for Total Income `INCTOT`. First, let's see if there are an `N/A` values, as when we did `head()`, we saw some in other columns, like CBSERIAL
```
df['INCTOT_NA'] = df['INCTOT'].isna()
print(df.INCTOT_NA.value_counts())
```
Okay, great, there are no `N/A`s...or are there? Let's drop `INCTOT_NA` and see what our value counts look like
```
df=df.drop('INCTOT_NA', axis=1)
print(df.INCTOT.value_counts().to_pandas()) ### Wow, look how many people in America make $10,000,000! Wait a minutes...
```
Not that many people make $10M a year. Checking https://usa.ipums.org/usa-action/variables/INCTOT#codes_section, `9999999`is INCTOT's code for `N/A`. That was why when we ran `isna`, RAPIDS won't find any. Let's first create a new dataframe that is only NA values, then let's pull those encoded `N/A`s out of our working dataframe!
```
print('data',df.shape)
tdf = df.query('INCTOT == 9999999')
df = df.query('INCTOT != 9999999')
print('working data',df.shape)
print('junk count data',tdf.shape)
```
We're down by nearly 1/4 of our original dataset size. For the curious, now we should be able to get accurate Total Income data, by year, not taking into account inflation
```
print(df.groupby('YEAR')['INCTOT'].mean()) # without that cleanup, the average would have bene in the millions....
```
#### Normalize Income for inflation
Now that we have reduced our dataframe to a baseline clean data to answer our question, we should normalize the amounts for inflation. `CPI99`is the value that IPUMS uses to contian the inflation factor. All we have to do is multipy by year. Let's see how that changes the Total Income values from just above!
```
print(df.groupby('YEAR')['CPI99'].mean()) ## it just returns the CPI99
df['INCTOT'] = df['INCTOT'] * df['CPI99']
print(df.groupby('YEAR')['INCTOT'].mean()) ## let's see what we got!
```
### Cleaning Education Data
Okay, great! Now we have income cleaned up, it should also have cleaned much of our next sets of values of interes, namely Education and Education Detailed. However, there are still some `N/A`s in key variables to worry about, which can cause problmes later. Let's create a list of them...
```
suspect = ['CBSERIAL','EDUC', 'EDUCD', 'EDUC_HEAD', 'EDUC_POP', 'EDUC_MOM','EDUCD_MOM2','EDUCD_POP2', 'INCTOT_MOM','INCTOT_POP','INCTOT_MOM2','INCTOT_POP2', 'INCTOT_HEAD']
for i in range(0, len(suspect)):
df[suspect[i]] = df[suspect[i]].fillna(-1)
print(suspect[i], df[suspect[i]].value_counts())
```
Let's get drop any rows of any `-1`s in Education and Education Detailed.
```
totincome = ['EDUC','EDUCD']
for i in range(0, len(totincome)):
query = totincome[i] + ' != -1'
df = df.query(query)
print(totincome[i])
print(df.shape)
df.head().to_pandas().head()
```
Well, the good news is that we lost no further rows, start to normalize the data so when we do our OLS, one year doesn't unfairly dominate the data
## Normalize the Data
The in the last step, need to keep our data at about the same ratio as we when started (1% of the population), with the exception of 1980, which was a 5% and needs to be reduced. This is why we kept the temp dataframe `tdf` - to get the counts per year. we will find out just how many have to realize
```
print('Working data: \n', df.YEAR.value_counts())
print('junk count data: \n', tdf.YEAR.value_counts())
```
And now, so that we can do MSE, let's make all the dtypes the same.
```
df.dtypes
keep_cols = ['YEAR', 'DATANUM', 'SERIAL', 'CBSERIAL', 'HHWT', 'GQ', 'PERNUM', 'SEX', 'AGE', 'INCTOT', 'EDUC', 'EDUCD', 'EDUC_HEAD', 'EDUC_POP', 'EDUC_MOM','EDUCD_MOM2','EDUCD_POP2', 'INCTOT_MOM','INCTOT_POP','INCTOT_MOM2','INCTOT_POP2', 'INCTOT_HEAD', 'SEX_HEAD']
df = df.loc[:, keep_cols]
#df = df.drop(col for col in df.columns if col not in keep_cols)
for i in range(0, len(keep_cols)):
df[keep_cols[i]] = df[keep_cols[i]].fillna(-1)
print(keep_cols[i], df[keep_cols[i]].value_counts())
df[keep_cols[i]]= df[keep_cols[i]].astype('float64')
## I WANTED TO REDUCE THE 1980 SAMPLE HERE, BUT .SAMPLE() IS NEEDED AND NOT WORKING, UNLESS THERE IS A WORK AROUND...
```
With the important data now clean and normalized, let's start doing the regression
## Ridge Regression
We have 44 variables. The other variables may provide important predictive information. The Ridge Regression technique with cross validation to identify the best hyperparamters may be the best way to get the most accurate model. We'll have to
* define our performance metrics
* split our data into train and test sets
* train and test our model
Let's begin and see what we get!
```
# As our performance metrics we'll use a basic mean squared error and coefficient of determination implementation
def mse(y_test, y_pred):
return ((y_test.reset_index(drop=True) - y_pred.reset_index(drop=True)) ** 2).mean()
def cod(y_test, y_pred):
y_bar = y_test.mean()
total = ((y_test - y_bar) ** 2).sum()
residuals = ((y_test.reset_index(drop=True) - y_pred.reset_index(drop=True)) ** 2).sum()
return 1 - (residuals / total)
from cuml.preprocessing.model_selection import train_test_split
trainsize = .9
yCol = "EDUC"
from cuml.preprocessing.model_selection import train_test_split
from cuml.linear_model.ridge import Ridge
def train_and_score(data, clf, train_frac=0.8, n_runs=20):
mse_scores, cod_scores = [], []
for _ in range(n_runs):
X_train, X_test, y_train, y_test = cuml.preprocessing.model_selection.train_test_split(df, yCol, train_size=.9)
y_pred = clf.fit(X_train, y_train).predict(X_test)
mse_scores.append(mse(y_test, y_pred))
cod_scores.append(cod(y_test, y_pred))
return mse_scores, cod_scores
```
## Results
**Moment of truth! Let's see how our regression training does!**
```
import numpy as np
n_runs = 20
clf = Ridge()
mse_scores, cod_scores = train_and_score(df, clf, n_runs=n_runs)
print(f"median MSE ({n_runs} runs): {np.median(mse_scores)}")
print(f"median COD ({n_runs} runs): {np.median(cod_scores)}")
```
**Fun fact:** if you made INCTOT the y axis, your prediction results would not be so pretty! It just shows that your education level can be an indicator for your income, but your income is NOT a great predictor for your education level. You have better odds flipping a coin!
* median MSE (50 runs): 518189521.07548225
* median COD (50 runs): 0.425769113846303
## Next Steps/Self Study
* You can pickle the model and use it in another workflow
* You can redo the workflow with based on head of household using `EDUC`, `SEX`, and `INCTOT` for X in `X`_HEAD
* You can see the growing role of education with women in their changing role in the workforce and income with "EDUC_MOM" and "EDUC_POP
| true |
code
| 0.389779 | null | null | null | null |
|
# 采用机器翻译实现Seq2Seq
```
import sys
sys.path.append('../')
import collections
import d2l
import zipfile
from d2l.data.base import Vocab
import time
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils import data
from torch import optim
```
## Seq2Seq的结构
# Sequence to Sequence模型
### 模型:
训练

预测

### 具体结构:

### Seq2SeqEncoder实现
```
class Seq2SeqEncoder(d2l.Encoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqEncoder, self).__init__(**kwargs)
self.num_hiddens=num_hiddens
self.num_layers=num_layers
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.LSTM(embed_size,num_hiddens, num_layers, dropout=dropout)
def begin_state(self, batch_size, device):
return [torch.zeros(size=(self.num_layers, batch_size, self.num_hiddens), device=device),
torch.zeros(size=(self.num_layers, batch_size, self.num_hiddens), device=device)]
def forward(self, X, *args):
X = self.embedding(X) # X shape: (batch_size, seq_len, embed_size)
X = X.transpose(0, 1) # RNN needs first axes to be time
# state = self.begin_state(X.shape[1], device=X.device)
out, state = self.rnn(X)
# The shape of out is (seq_len, batch_size, num_hiddens).
# state contains the hidden state and the memory cell
# of the last time step, the shape is (num_layers, batch_size, num_hiddens)
return out, state
encoder = Seq2SeqEncoder(vocab_size=10, embed_size=8,num_hiddens=16, num_layers=2)
X = torch.zeros((4, 7),dtype=torch.long)
output, state = encoder(X)
output.shape, len(state), state[0].shape, state[1].shape
```
### Seq2SeqDecoder实现
```
class Seq2SeqDecoder(d2l.Decoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqDecoder, self).__init__(**kwargs)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.LSTM(embed_size,num_hiddens, num_layers, dropout=dropout)
self.dense = nn.Linear(num_hiddens,vocab_size)
def init_state(self, enc_outputs, *args):
return enc_outputs[1]
def forward(self, X, state):
X = self.embedding(X).transpose(0, 1)
out, state = self.rnn(X, state)
# Make the batch to be the first dimension to simplify loss computation.
out = self.dense(out).transpose(0, 1)
return out, state
decoder = Seq2SeqDecoder(vocab_size=10, embed_size=8,num_hiddens=16, num_layers=2)
state = decoder.init_state(encoder(X))
out, state = decoder(X, state)
out.shape, len(state), state[0].shape, state[1].shape
```
### 训练
```
with open('../data/fra.txt', 'r', encoding='utf-8') as f:
raw_text = f.read()
print(raw_text[0:1000])
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.0
batch_size, num_examples, max_len = 64, 1e3, 10
lr, num_epochs, ctx = 0.005, 300, d2l.try_gpu()
src_vocab, tgt_vocab, train_iter = d2l.load_data_nmt(batch_size, max_len,num_examples)
encoder = Seq2SeqEncoder(
len(src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqDecoder(
len(tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
model = d2l.EncoderDecoder(encoder, decoder)
d2l.train_ch7(model, train_iter, lr, num_epochs, ctx)
```
## 测试
```
for sentence in ['Go .', 'Wow !', "I'm OK .", 'I won !']:
print(sentence + ' => ' + d2l.translate_ch7(
model, sentence, src_vocab, tgt_vocab, max_len, ctx))
```
| true |
code
| 0.726492 | null | null | null | null |
|
# Black Scholes Model
In this notebook we illustrate the basic properties of the Black Scholes model.
The notebook is structured as follows:
1. Black-Scholes model code
2. Analysis of value function
3. Analysis of Greeks, i.e. sensitivities to model parameters
## Black-Scholes Model Code
We use a couple of standard Python modules.
```
import numpy as np
from scipy.stats import norm
from scipy.optimize import brentq
import plotly.express as px
import plotly.graph_objects as go
```
As a basic building block we implement the Black formula.
$$
\begin{aligned}
\text{Black}\left(F,K,\nu,\phi\right) &=\phi\,\left[F\,\Phi\left(\phi d_{1}\right)-K\,\Phi\left(\phi d_{2}\right)\right],\\
d_{1,2}&=\frac{\log\left(F/K\right)}{\nu}\pm\frac{\nu}{2}.
\end{aligned}
$$
```
def BlackOverK(moneyness, nu, callOrPut):
d1 = np.log(moneyness) / nu + nu / 2.0
d2 = d1 - nu
return callOrPut * (moneyness*norm.cdf(callOrPut*d1)-norm.cdf(callOrPut*d2))
def Black(forward, strike, nu, callOrPut):
if nu<1.0e-12: # assume zero
return np.maximum(callOrPut*(forward-strike),0.0) # intrinsic value
return strike * BlackOverK(forward/strike,nu,callOrPut)
def BlackImpliedVol(price, strike, forward, T, callOrPut):
def objective(nu):
return Black(forward, strike, nu, callOrPut) - price
return brentq(objective,0.01*np.sqrt(T), 1.00*np.sqrt(T), xtol=1.0e-8) / np.sqrt(T)
def BlackVega(strike, forward, sigma, T):
stdDev = sigma*np.sqrt(T)
d1 = np.log(forward/strike) / stdDev + stdDev / 2.0
return forward * norm.pdf(d1) * np.sqrt(T)
```
## Analysis of Value Function
$$
v(s,T) = e^{-rT}\,\text{Black}\left(s\,e^{rT},K,\sigma\sqrt{T},\phi\right),
$$
```
def BlackScholesPrice(underlying, strike, rate, sigma, T, callOrPut):
df = np.exp(-rate*T)
nu = sigma*np.sqrt(T)
return df * Black(underlying/df, strike, nu, callOrPut)
```
We need to specify some sensible model and product parameters.
```
r = 0.01 # 1% risk-free rate is a sensible choice in current low-interest rate market environment
sigma = 0.15 # typical values for annualised equity volatility is between 10% - 25%
K = 1.0 # the strike should be in the order of the underlying asset; we will assume S~O(1)
phi = 1.0 # call or put
```
We want to see the value function for a grid of maturities $[0,T_{end}]$ and underlying risky asset prices $(0, S_{max}]$.
```
T = np.linspace(0.0, 2.0, 201)
S = np.linspace(0.01, 2.0, 200)
```
Now, we can calculate the call option prices.
```
v = lambda s, t : BlackScholesPrice(s, K, r, sigma, t, phi)
v_sT = np.array([ v(S,t) for t in T ]).transpose()
print(v_sT.shape)
fig = go.Figure(data=[go.Surface(x=T, y=S, z=v_sT)])
fig.update_layout(
title='Black-Scholes Value Function',
scene = dict(
xaxis = dict(
title = 'T',
),
yaxis = dict(
title = 's',
),
zaxis = dict(
title = 'v',
),
),
width=1200, height=800, autosize=False,
margin=dict(l=65, r=50, b=65, t=90),
)
fig.show()
```
## Analysis of Greeks
Greeks represent sensitivities of the value function with respect to changes in the model parameters.
### Delta
$$
\Delta_{BS}(s,T)=\frac{d}{ds}v(s,T) = \phi\,\Phi\left(\phi d_{1}\right).
$$
```
def BlackScholesDelta(underlying, strike, rate, sigma, T, callOrPut):
moneyness = np.exp(rate*T) * underlying / strike
nu = sigma * np.sqrt(T)
d1 = np.log(moneyness) / nu + nu / 2.0
return callOrPut * norm.cdf(callOrPut * d1)
```
We calculate the Delta for a range of underlyings and times.
```
T = np.linspace(0.01, 2.0, 200)
S = np.linspace(0.01, 2.0, 200)
Delta = lambda s, t : BlackScholesDelta(s, K, r, sigma, t, phi)
dv_ds = np.array([ Delta(S,t) for t in T ]).transpose()
print(dv_ds.shape)
# Check Delta via finite differences
eps = 1.0e-4
Delta_FD = lambda s, t : (BlackScholesPrice(s+eps, K, r, sigma, t, phi) - BlackScholesPrice(s-eps, K, r, sigma, t, phi))/2/eps
dv_ds_FD = np.array([ Delta_FD(S,t) for t in T ]).transpose()
print(np.max(np.abs(dv_ds-dv_ds_FD)))
```
And we plot the resulting sensitivity.
```
fig = go.Figure(data=[go.Surface(x=T, y=S, z=dv_ds)])
fig.update_layout(
title='Black-Scholes Delta',
scene = dict(
xaxis = dict(
title = 'T',
),
yaxis = dict(
title = 's',
),
zaxis = dict(
title = 'Delta',
),
),
width=1200, height=800, autosize=False,
margin=dict(l=65, r=50, b=65, t=90),
)
fig.show()
```
### Gamma
$$
\Gamma_{BS} = \frac{d}{ds}\Delta_{BS}(s,T)=\frac{d^{2}}{ds^{2}}v(s,T) = \frac{\Phi'\left(d_{1}\right)}{s\,\sigma\sqrt{T}}.
$$
```
def BlackScholesGamma(underlying, strike, rate, sigma, T, callOrPut):
moneyness = np.exp(rate*T) * underlying / strike
nu = sigma * np.sqrt(T)
d1 = np.log(moneyness) / nu + nu / 2.0
return norm.pdf(d1) / underlying / nu
```
We calculate the Gamma for a range of underlyings and times.
```
T = np.linspace(0.1, 2.0, 200)
S = np.linspace(0.01, 2.0, 200)
Gamma = lambda s, t : BlackScholesGamma(s, K, r, sigma, t, phi)
d2v_ds2 = np.array([ Gamma(S,t) for t in T ]).transpose()
print(d2v_ds2.shape)
# Check Gamma via finite differences
eps = 1.0e-4
Gamma_FD = lambda s, t : (BlackScholesPrice(s+eps, K, r, sigma, t, phi) - 2 * BlackScholesPrice(s, K, r, sigma, t, phi) + BlackScholesPrice(s-eps, K, r, sigma, t, phi))/eps**2
d2v_ds2_FD = np.array([ Gamma_FD(S,t) for t in T ]).transpose()
print(np.max(np.abs(d2v_ds2 - d2v_ds2_FD)))
fig = go.Figure(data=[go.Surface(x=T, y=S, z=d2v_ds2)])
fig.update_layout(
title='Black-Scholes Gamma',
scene = dict(
xaxis = dict(
title = 'T',
),
yaxis = dict(
title = 's',
),
zaxis = dict(
title = 'Gamma',
),
),
width=1200, height=800, autosize=False,
margin=dict(l=65, r=50, b=65, t=90),
)
fig.show()
```
### Theta
$$
\Theta_{BS}(s,T)=\frac{d}{dT}v(s,T) = \frac{s\,\Phi'\left(d_{1}\right)\,\sigma}{2\,\sqrt{T}}+\phi\,r\,K\,e^{-rT}\,\Phi\left(\phi d_{2}\right)
$$
```
def BlackScholesTheta(underlying, strike, rate, sigma, T, callOrPut):
moneyness = np.exp(rate*T) * underlying / strike
nu = sigma * np.sqrt(T)
d1 = np.log(moneyness) / nu + nu / 2.0
d2 = d1 - nu
return underlying * norm.pdf(d1) * sigma / 2 / np.sqrt(T) + \
callOrPut * rate * strike * np.exp(-rate*T) * norm.cdf(callOrPut * d2)
```
We calculate the Theta for a range of underlyings and times.
```
T = np.linspace(0.1, 2.0, 200)
S = np.linspace(0.01, 2.0, 200)
Theta = lambda s, t : BlackScholesTheta(s, K, r, sigma, t, phi)
dv_dT = np.array([ Theta(S,t) for t in T ]).transpose()
print(dv_dT.shape)
# Check Theta via finite differences
eps = 1.0e-4
Theta_FD = lambda s, t : (BlackScholesPrice(s, K, r, sigma, t+eps, phi) - BlackScholesPrice(s, K, r, sigma, t-eps, phi))/2/eps
dv_dT_FD = np.array([ Theta_FD(S,t) for t in T ]).transpose()
print(np.max(np.abs(dv_dT - dv_dT_FD)))
fig = go.Figure(data=[go.Surface(x=T, y=S, z=dv_dT)])
fig.update_layout(
title='Black-Scholes Theta',
scene = dict(
xaxis = dict(
title = 'T',
),
yaxis = dict(
title = 's',
),
zaxis = dict(
title = 'Theta',
),
),
width=1200, height=800, autosize=False,
margin=dict(l=65, r=50, b=65, t=90),
)
fig.show()
```
### Black-Scholes PDE
We calculate the linear operator
$$
{\cal L}\left[v\right]=-\frac{dv}{dT}+r\,s\,\frac{dv}{ds}+\frac{1}{2}\,\sigma^{2}\,s^{2}\,\frac{d^{2}v}{ds^{2}}-r\,v.
$$
And verify that ${\cal L}\left[v\right]=0$.
```
T = np.linspace(0.1, 2.0, 200)
S = np.linspace(0.01, 2.0, 200)
L_v = lambda s, T : -Theta(s,T) + r * s * Delta(s,T) + 0.5 * sigma**2 * s**2 * Gamma(s,T) - r * v(s,T)
L_v_sT = np.array([ L_v(S,t) for t in T ]).transpose()
print(L_v_sT.shape)
fig = go.Figure(data=[go.Surface(x=T, y=S, z=L_v_sT)])
fig.update_layout(
title='Black-Scholes Operator',
scene = dict(
xaxis = dict(
title = 'T',
),
yaxis = dict(
title = 's',
),
zaxis = dict(
title = 'L[v]',
),
),
width=1200, height=800, autosize=False,
margin=dict(l=65, r=50, b=65, t=90),
)
fig.show()
```
### Rho
$$
\varrho_{BS}(s,T)=\frac{d}{dr}v(s,T) = \phi\,K\,T\,e^{-rT}\,\Phi\left(\phi d_{2}\right).
$$
```
def BlackScholesRho(underlying, strike, rate, sigma, T, callOrPut):
moneyness = np.exp(rate*T) * underlying / strike
nu = sigma * np.sqrt(T)
d1 = np.log(moneyness) / nu + nu / 2.0
d2 = d1 - nu
return callOrPut * strike * T * np.exp(-rate*T) * norm.cdf(callOrPut * d2)
```
We calculate the Theta for a range of underlyings and times.
```
T = np.linspace(0.01, 2.0, 200)
S = np.linspace(0.01, 2.0, 200)
Rho = lambda s, t : BlackScholesRho(s, K, r, sigma, t, phi)
dv_dr = np.array([ Rho(S,t) for t in T ]).transpose()
print(dv_dr.shape)
# Check Rho via finite differences
eps = 1.0e-6
Rho_FD = lambda s, t : (BlackScholesPrice(s, K, r+eps, sigma, t, phi) - BlackScholesPrice(s, K, r-eps, sigma, t, phi))/2/eps
dv_dr_FD = np.array([ Rho_FD(S,t) for t in T ]).transpose()
print(np.max(np.abs(dv_dr - dv_dr_FD)))
fig = go.Figure(data=[go.Surface(x=T, y=S, z=dv_dr)])
fig.update_layout(
title='Black-Scholes Rho',
scene = dict(
xaxis = dict(
title = 'T',
),
yaxis = dict(
title = 's',
),
zaxis = dict(
title = 'Rho',
),
),
width=1200, height=800, autosize=False,
margin=dict(l=65, r=50, b=65, t=90),
)
fig.show()
```
### Vega
$$
\text{Vega}_{BS}(s,T)=\frac{d}{d\sigma}v(s,T) = s\,\Phi'\left(d_{1}\right)\sqrt{T}
$$
```
def BlackScholesVega(underlying, strike, rate, sigma, T, callOrPut):
moneyness = np.exp(rate*T) * underlying / strike
nu = sigma * np.sqrt(T)
d1 = np.log(moneyness) / nu + nu / 2.0
return underlying * norm.pdf(d1) * np.sqrt(T)
```
We calculate the Theta for a range of underlyings and times.
```
T = np.linspace(0.01, 2.0, 200)
S = np.linspace(0.01, 2.0, 200)
Vega = lambda s, t : BlackScholesVega(s, K, r, sigma, t, phi)
dv_dsigma = np.array([ Vega(S,t) for t in T ]).transpose()
print(dv_dr.shape)
# Check Vega via finite differences
eps = 1.0e-6
Vega_FD = lambda s, t : (BlackScholesPrice(s, K, r, sigma+eps, t, phi) - BlackScholesPrice(s, K, r, sigma-eps, t, phi))/2/eps
dv_dsigma_FD = np.array([ Vega_FD(S,t) for t in T ]).transpose()
print(np.max(np.abs(dv_dsigma - dv_dsigma_FD)))
fig = go.Figure(data=[go.Surface(x=T, y=S, z=dv_dsigma)])
fig.update_layout(
title='Black-Scholes Vega',
scene = dict(
xaxis = dict(
title = 'T',
),
yaxis = dict(
title = 's',
),
zaxis = dict(
title = 'Vega',
),
),
width=1200, height=800, autosize=False,
margin=dict(l=65, r=50, b=65, t=90),
)
fig.show()
```
# Implied Volatility Analysis
We add an analysis of market-implied volatilities.
```
S0 = 1.0 # initial asset price
T = 1.4
putStrikes = [ 0.60, 0.70, 0.80, 0.90, 1.00 ]
putPrices = [ 0.0642, 0.0943, 0.1310, 0.1761, 0.2286 ]
callStrikes = [ 1.00, 1.10, 1.20, 1.30, 1.40 ]
callPrices = [ 0.2204, 0.1788, 0.1444, 0.1157, 0.0929 ]
```
We can use strike $K=1$ and put-call parity to calculate the implied risk-free rate $r$,
$$
r = -\frac{\log\left(1+\pi_{BS}\left(C^{put}\right)-\pi_{BS}\left(C^{call}\right)\right)}{T}
$$
```
r = - np.log(1 + putPrices[-1] - callPrices[0])/T
r
```
Next, we can calculate implied volatilities for puts and calls.
```
F = np.exp(r*T) * S0
putFwdPrices = [ np.exp(r*T)*p for p in putPrices ]
callFwdPrices = [ np.exp(r*T)*p for p in callPrices ]
putVols = [ BlackImpliedVol(p,K,F,T,-1) for p, K in zip(putFwdPrices, putStrikes) ]
callVols = [ BlackImpliedVol(p,K,F,T,+1) for p, K in zip(callFwdPrices,callStrikes) ]
print(putVols[-1])
print(callVols[0])
sigma = 0.5 * (putVols[-1] + callVols[0])
```
We calculate the corresponding Black-Scholes model prices.
```
bsPut = [ BlackScholesPrice(S0,K,r,sigma,T,-1) for K in putStrikes ]
bsCall = [ BlackScholesPrice(S0,K,r,sigma,T,+1) for K in callStrikes ]
print('Puts:')
for K, P in zip(putStrikes,bsPut):
print(' %4.2f %6.4f' % (K,P))
print('Calls:')
for K, P in zip(callStrikes,bsCall):
print(' %4.2f %6.4f' % (K,P))
```
Also, we plot the resulting impled volatility smile
```
fig = go.Figure()
fig.add_trace(go.Scatter(x=putStrikes, y=putVols, name='put' ))
fig.add_trace(go.Scatter(x=callStrikes, y=callVols, name='call'))
fig.update_layout(
title='Implied Black-Scholes Volatility, T=%.2f' % T,
xaxis_title="Strike K",
yaxis_title="Implied Volatility",
width=1200, height=800, autosize=False,
margin=dict(l=65, r=50, b=65, t=90),
)
fig.show()
```
| true |
code
| 0.645399 | null | null | null | null |
|
#### Fancy indexing and index tricks
NumPy offers more indexing facilities than regular Python sequences. In addition to indexing by integers and slices, as we saw before, arrays can be indexed by arrays of integers and arrays of booleans.
##### Indexing with Arrays of Indices¶
```
import numpy as np
a = np.arange(12)**2 # the first 12 square numbers
i = np.array( [ 1,1,3,8,5,6 ] ) # an array of indices
print(a[i] ,"# the elements of a at the positions i")
j = np.array( [ [ 3, 4], [ 9, 7 ] ] ) # a bidimensional array of indices
a[j] # the same shape as j
```
When the indexed array a is multidimensional, a single array of indices refers to the first dimension of a. The following example shows this behavior by converting an image of labels into a color image using a palette.
```
palette = np.array( [ [0,0,0], # black
[255,0,0], # red
[0,255,0], # green
[0,0,255], # blue
[255,255,255] ] ) # white
palette
import matplotlib.pyplot as plt
plt.imshow(palette)
image = np.array( [ [ 0, 6, 2, 8 ], # each value corresponds to a color in the palette
... [ 5, 3, 4, 0 ] ] )
print(image)
import matplotlib.pyplot as plt
plt.imshow(image)
palette[image] # the (2,4,3) color image
```
We can also give indexes for more than one dimension. The arrays of indices for each dimension must have the same shape.
```
a = np.arange(12).reshape(3,4);a
i = np.array( [ [0,1], # indices for the first dim of a
... [1,2] ] )
i
j = np.array( [ [2,1], # indices for the second dim
... [3,3] ] )
j
a[i,j] # i and j must have equal shape
a[i,2]
a[:,j] # i.e., a[ : , j]
```
Naturally, we can put i and j in a sequence (say a list) and then do the indexing with the list.
```
l = [i,j]
l
a[l]
time = np.linspace(20, 145, 5) # time scale
data = np.sin(np.arange(20)).reshape(5,4) # 4 time-dependent series
ind = data.argmax(axis=0) # index of the maxima for each series
ind
time_max = time[ind] # times corresponding to the maxima
time_max
a = np.arange(5)
print(a)
a[[1,3,4]] = 0
print(a)
```
### Indexing with Boolean Arrays
When we index arrays with arrays of (integer) indices we are providing the list of indices to pick. With boolean indices the approach is different; we explicitly choose which items in the array we want and which ones we don’t.
The most natural way one can think of for boolean indexing is to use boolean arrays that have the same shape as the original array:
```
a = np.arange(12).reshape(3,4)
b = a > 4
b
a[b] # 1d array with the selected elements
```
#### The ix_() function
The ix_ function can be used to combine different vectors so as to obtain the result for each n-uplet. For example, if you want to compute all the a+b*c for all the triplets taken from each of the vectors a, b and c:
```
a = np.array([2,3,4,5])
b = np.array([8,5,4])
c = np.array([5,4,6,8,3])
ax,bx,cx = np.ix_(a,b,c)
print(ax)
cx
bx
ax.shape, bx.shape, cx.shape
result = ax+bx*cx
result
result[3,2,4]
a[3]+b[2]*c[4]
```
You could also implement the reduce as follows:
```
def ufunc_reduce(ufct, *vectors):
... vs = np.ix_(*vectors)
... r = ufct.identity
... for v in vs:
... r = ufct(r,v)
... return r
ufunc_reduce(np.add,a,b,c)
```
| true |
code
| 0.505127 | null | null | null | null |
|
```
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from matplotlib.ticker import ScalarFormatter
import math
```
This notebook assumes you have completed the notebook [Introduction of sine waves](TDS_Introduction-sine_waves.ipynb). This notebook follows the same pattern of time domain waveform generation: instantaneous frequency -> angle step -> total angle -> time domain waveform.
Our goal is to track features of different acoustic impedance in material using a low power time domain waveform. Time delay spectrometry (TDS) is one implementation of this goal. To understand TDS we need to understand the waveform which is used by TDS called a chirp. A chirp is a sinusoid that is constantly varying in frequency. The chirp is generated by integrating a varying angle step which is derived from an instantaneous frequency profile. We will generate a chirp in this notebook. An overview of this technique is given [here](https://www.youtube.com/watch?v=RQplkt0bw_c).
The angle of the chirp can be found by integrating the instantaneous frequency:
\begin{equation}
f(t)=\frac{f_{end}-f_{start}}{T_c}t + f_{start}
\end{equation}
\begin{equation}
\Delta\phi(t) = 2\pi f(t)\Delta t
\end{equation}
\begin{equation}
\phi (t)=\int_{}^{} \Delta\phi(t) = \int_{}^{} 2\pi f(t) dt = \int_{}^{}\frac{f_{end}-f_{start}}{T_c}tdt + \int_{}^{}f_{start}dt
\end{equation}
\begin{equation}
\phi (t)= \frac{f_{end}-f_{start}}{T_c}\int_{}^{}tdt + f_{start}\int_{}^{}dt
\end{equation}
\begin{equation}
\phi (t)= \frac{f_{end}-f_{start}}{T_c}\frac{t^2}{2} + f_{start}t
\end{equation}
This gives the time series value of
\begin{equation}
x(t) = e^{j\phi (t)} = e^{j(\frac{f_{end}-f_{start}}{T_c}\frac{t^2}{2} + f_{start}t)}
\end{equation}
But the formula for angle requires squaring time which will cause numeric errors as the time increases. Another approach is to implement the formula for angle as a cummulative summation.
\begin{equation}
\phi_{sum} (N)=\sum_{k=1}^{N} \Delta\phi(k) = \sum_{k=1}^{N} 2\pi f(k) t_s = \sum_{k=1}^{N}(\frac{f_{end}-f_{start}}{T_c}k + f_{start})t_s
\end{equation}
This allow for the angle always stay between 0 and two pi by subtracting two phi whenever the angle exceeds the value. We will work with the cummlative sum of angle, but then compare it to the integral to determine how accurate the cummulative sum is.
```
#max free 8 points per sample
#Tc is the max depth we are interested in
Tc_sec=0.00003
f_start_Hz=3e5
#talk about difference and similarity of sine wave example, answer why not 32 samples
f_stop_Hz=16e5
#We choose 8 samples per cycle at the maximum frequency to not require steep pulse shaping filter profiles on the output of the
#digital to analog converter
samplesPerCycle=8
fs=f_stop_Hz*samplesPerCycle
ts=1/fs
total_samples= math.ceil(fs*Tc_sec)
n = np.arange(0,total_samples, step=1, dtype=np.float64)
t_sec=n*ts
t_usec = t_sec *1e6
#This is the frequency of the chirp over time. We assume linear change in frequency
chirp_freq_slope_HzPerSec=(f_stop_Hz-f_start_Hz)/Tc_sec
#Compute the instantaneous frequency which is a linear function
chirp_instantaneous_freq_Hz=chirp_freq_slope_HzPerSec*t_sec+f_start_Hz
chirp_instantaneous_angular_freq_radPerSec=2*np.pi*chirp_instantaneous_freq_Hz
#Since frequency is a change in phase the we can plot it as a phase step
chirp_phase_step_rad=chirp_instantaneous_angular_freq_radPerSec*ts
#The phase step can be summed (or integrated) to produce the total phase which is the phase value
#for each point in time for the chirp function
chirp_phase_rad=np.cumsum(chirp_phase_step_rad)
#The time domain chirp function
chirp = np.exp(1j*chirp_phase_rad)
#We can see, unlike the complex exponential, the chirp's instantaneous frequency is linearly increasing.
#This corresponds with the linearly increasing phase step.
fig, ax = plt.subplots(2, 1, sharex=True,figsize = [8, 8])
lns1=ax[0].plot(t_usec,chirp_instantaneous_freq_Hz,linewidth=4, label='instantanous frequency');
ax[0].set_title('Comparing the instantaneous frequency and phase step')
ax[0].set_ylabel('instantaneous frequency (Hz)')
axt = ax[0].twinx()
lns2=axt.plot(t_usec,chirp_phase_step_rad,linewidth=2,color='black', linestyle=':', label='phase step');
axt.set_ylabel('phase step (rad)')
#ref: https://stackoverflow.com/questions/5484922/secondary-axis-with-twinx-how-to-add-to-legend
lns = lns1+lns2
labs = [l.get_label() for l in lns]
ax[0].legend(lns, labs, loc=0)
#We see that summing or integrating the linearly increasing phase step gives a quadratic function of total phase.
ax[1].plot(t_usec,chirp_phase_rad,linewidth=4,label='chirp');
ax[1].plot([t_usec[0], t_usec[-1]],[chirp_phase_rad[0], chirp_phase_rad[-1]],linewidth=1, linestyle=':',label='linear (x=y)');
ax[1].set_title('Cumulative quandratic phase function of chirp')
ax[1].set_xlabel('time ($\mu$sec)')
ax[1].set_ylabel('total phase (rad)')
ax[1].legend();
#The complex exponential of each phase value gives us the time domain chirp signal.
#We have highlighted the beginning and end of the chirp where it starts at a low frequency and linearly increases to a high frequency
samplesToShowSlow=np.arange(5*samplesPerCycle,dtype=np.int32)
samplesToShowFast=np.flip(np.ceil(t_sec.shape[0]).astype(np.int32) - np.arange(5*samplesPerCycle,dtype=np.int32))-1
fig2 = plt.figure(constrained_layout=True,figsize = [8, 6])
gs = fig2.add_gridspec(2, 3)
f2_ax1 = fig2.add_subplot(gs[0, :])
f2_ax2 = fig2.add_subplot(gs[1, :])
f2_ax1.plot(t_usec,chirp_phase_rad, color='#27A4A3', label='chirp');
f2_ax1.plot(t_usec[samplesToShowSlow],chirp_phase_rad[samplesToShowSlow],color=(1,0,0),linewidth=4, label='slow');
f2_ax1.plot(t_usec[samplesToShowFast],chirp_phase_rad[samplesToShowFast],color=(0,0,1),linewidth=4, label='fast');
f2_ax1.set_title('Cumulative quandratic phase function of chirp')
f2_ax1.set_xlabel('time ($\mu$sec)')
f2_ax1.set_ylabel('total phase (rad)')
f2_ax1.legend();
f2_ax2.plot(t_usec,np.real(chirp),color='#27A4A3', label='real');
f2_ax2.plot(t_usec,np.imag(chirp),color='#27A4A3', linestyle=':', label='imag');
f2_ax2.plot(t_usec[samplesToShowSlow],np.real(chirp[samplesToShowSlow]),color=(1,0,0));
f2_ax2.plot(t_usec[samplesToShowSlow],np.imag(chirp[samplesToShowSlow]),color=(1,0,0), linestyle=':');
f2_ax2.plot(t_usec[samplesToShowFast],np.real(chirp[samplesToShowFast]),color=(0,0,1));
f2_ax2.plot(t_usec[samplesToShowFast],np.imag(chirp[samplesToShowFast]),color=(0,0,1), linestyle=':');
f2_ax2.set_title('Time domain chirp')
f2_ax2.set_xlabel('time ($\mu$sec)')
f2_ax2.set_ylabel('amplitude')
f2_ax2.get_xaxis().get_major_formatter().set_useOffset(False)
f2_ax2.legend();
#With perfect integration we have
#This is the frequency of the chirp over time. We assume linear change in frequency
chirp_freq_slope_HzPerSec=(f_stop_Hz-f_start_Hz)/Tc_sec
#Compute the instantaneous frequency which is a linear function
chirp_phase_continous_time_rad=2*np.pi*(chirp_freq_slope_HzPerSec/2*np.power(t_sec,2)+f_start_Hz*t_sec)
chirp = np.exp(1j*chirp_phase_continous_time_rad)
#The complex exponential of each phase value gives us the time domain chirp signal.
#We have highlighted the beginning and end of the chirp where it starts at a low frequency and linearly increases to a high frequency
fig2 = plt.figure(constrained_layout=True,figsize = [8, 6])
gs = fig2.add_gridspec(2, 3)
f2_ax1 = fig2.add_subplot(gs[0, :])
f2_ax2 = fig2.add_subplot(gs[1, :])
f2_ax1.plot(t_usec,chirp_phase_rad, color='#27A4A3', label='chirp');
f2_ax1.plot(t_usec,chirp_phase_continous_time_rad,color=(1,0,0),linewidth=4, linestyle=':', label='chirp continuous');
f2_ax1.set_title('Cumulative quandratic phase function of chirp')
f2_ax1.set_xlabel('time ($\mu$sec)')
f2_ax1.set_ylabel('total phase (rad)')
f2_ax1.legend();
f2_ax2.plot(t_usec,chirp_phase_rad-chirp_phase_continous_time_rad, color='#27A4A3', label='chirp');
f2_ax2.set_title('Cumulative quandratic phase function of chirp')
f2_ax2.set_xlabel('time ($\mu$sec)')
f2_ax2.set_ylabel('total phase (rad)')
f2_ax2.legend();
```
We examine the error
\begin{equation}
\phi_{sum} (N)=\sum_{k=1}^{N} \Delta\phi(k) = \sum_{k=1}^{N} 2\pi f(k) t_s = \sum_{k=1}^{N}\left(\frac{f_{end}-f_{start}}{T_c}k + f_{start}\right)t_s
\end{equation}
To analyze the error we collect the phase terms into A and
\begin{equation}
A = \left(\frac{f_{end}-f_{start}}{T_c}\right) t_s
\end{equation}
\begin{equation}
B = f_{start} t_s
\end{equation}
This gives a summation of
\begin{equation}
\phi_{sum} (N)= \sum_{k=1}^{N} 2\pi f(k) t_s = \sum_{k=1}^{N}\left(Ak + B\right)
\end{equation}
Which allows us to write
\begin{equation}
\phi_{sum} (N)= \sum_{k=1}^{N}\left(Ak\right) + \sum_{k=1}^{N}\left(B\right) = A\sum_{k=1}^{N}k + BN
\end{equation}
We solve the below summation by recognizing it is half the area of a rectangle with sides N and N+1 so
\begin{equation}
\sum_{k=1}^{N}k = \frac{(N+1)N}{2}
\end{equation}
This formula can be visually illustrated by the graphic
<img src="img/sum_proof.png" width="260" height="260" />
So collecting the terms we eliminate the sum with
\begin{equation}
\phi_{sum} (N)= A\frac{(N+1)N}{2} + BN =\frac{A}{2}N^2 + \frac{A+2B}{2}N
\end{equation}
Using the same A and B we can write the integral of instantaneous frequency as
\begin{equation}
\phi (t)= \frac{f_{end}-f_{start}}{T_c}\frac{t^2}{2} + f_{start}t =\frac{A}{2t_s}t^2 + \frac{B}{t_s}t
\end{equation}
We can also relate N and t by t = Nt_s which lets us rewrite $$ \phi (t) $$ as
\begin{equation}
\phi (N)= \frac{A}{2t_s}\left(Nt_s\right)^2 + \frac{B}{t_s}(Nt_s)= \frac{At_s}{2}N^2 + BN
\end{equation}
Now we can compute the error which is:
\begin{equation}
\phi (N) - \phi_{sum} (N)= \left(\frac{At_s}{2}N^2 + BN\right) - \left(\frac{A}{2}N^2 + \frac{A+2B}{2}N\right)
\end{equation}
This simplifies to
\begin{equation}
\phi (N) - \phi_{sum} (N)= \left(\frac{At_s}{2}N^2 + BN\right) - \left(\frac{A}{2}N^2 + \frac{A+2B}{2}N\right)
\end{equation}
| true |
code
| 0.720319 | null | null | null | null |
|
# ResNet-50 Inference with FINN on Alveo
This notebook demonstrates the functionality of a FINN-based, full dataflow ResNet-50 implemented in Alveo U250. The characteristics of the network are the following:
- residual blocks at 1-bit weights, 2/4-bit activations
- first convolution and last (fully connected) layer use 8-bit weights
- all parameters stored on-chip in BRAM/LUTRAM/URAM
- single DDR controller (DDR0) utilized for input and output
We validate the network against ImageNet. We use the PYNQ APIs for retrieving and recording power information which is then displayed in real-time.
## Set up Accelerator with PYNQ
We load the Alveo accelerator and print its memory-mapped registers:
```
import pynq
ol=pynq.Overlay("resnet50.xclbin")
accelerator=ol.resnet50_1
print(accelerator.register_map)
```
Next we create a data buffer in the Alveo PLRAM memory to hold the weights of the Fully Connected Layer:
```
import numpy as np
#allocate a buffer for FC weights, targeting the Alveo PLRAM
fcbuf = pynq.allocate((1000,2048), dtype=np.int8, target=ol.PLRAM0)
```
Load the weight from a CSV file and push them to the accelerator buffer:
```
#load Weights from file into the PYNQ buffer
fcweights = np.genfromtxt("fcweights.csv", delimiter=',', dtype=np.int8)
#csv reader erroneously adds one extra element to the end, so remove, then reshape
fcweights = fcweights[:-1].reshape(1000,2048)
fcbuf[:] = fcweights
#Move the data to the Alveo DDR
fcbuf.sync_to_device()
```
## Single Image Inference
In this example we perform inference on each of the images in a `pictures` folder and display the top predicted class overlaid onto the image. The code assumes the existence of this `pictures` folder, where you should put the images you want to classificate. There is no restriction on the images that you can use.
```
import shutil
import wget
import os
import glob
from itertools import chain
import cv2
import matplotlib.pyplot as plt
image_list = list(chain.from_iterable([glob.glob('pictures/*.%s' % ext) for ext in ["jpg","gif","png","tga"]]))
#get imagenet classes from file
import pickle
classes = pickle.load(open("labels.pkl",'rb'))
def infer_once(filename):
inbuf = pynq.allocate((224,224,3), dtype=np.int8, target=ol.bank0)
outbuf = pynq.allocate((5,), dtype=np.uint32, target=ol.bank0)
#preprocess image
img = cv2.resize(cv2.imread(filename), (224,224))
#transfer to accelerator
inbuf[:] = img
inbuf.sync_to_device()
#do inference
accelerator.call(inbuf, outbuf, fcbuf, 1)
#get results
outbuf.sync_from_device()
results = np.copy(outbuf)
return results
inf_results = []
for img in image_list:
inf_output = infer_once(img)
inf_result = [classes[i] for i in inf_output]
inf_results.append(inf_result)
plt.figure(figsize=(20,10))
columns = 3
for i, image in enumerate(image_list):
plt.subplot(len(image_list) / columns + 1, columns, i + 1)
top_class = inf_results[i][0].split(',', 1)[0]
display_image = cv2.cvtColor(cv2.resize(cv2.imread(image),(224,224)), cv2.COLOR_BGR2RGB)
plt.imshow(cv2.putText(display_image, top_class, (10,20), cv2.FONT_HERSHEY_TRIPLEX, 0.7, (255,255,255)))
```
## Plot Accelerator Board Power with PYNQ
We first set up data acquisition using PYNQ's PMBus API
```
import plotly
import plotly.graph_objs as go
import pandas as pd
from pynq import pmbus
import time
rails = pmbus.get_xrt_sysfs_rails(pynq.pl_server.Device.active_device)
#We create a recorder monitoring the three rails that have power measurement on Alveo.
#Total board power is obtained by summing together the PCI Express and Auxilliary 12V rails.
#While some current is also drawn over the PCIe 5V rail this is negligible compared to the 12V rails and isn't recorded.
#We also measure the VCC_INT power which is the primary supply to the FPGA.
recorder = pmbus.DataRecorder(rails["12v_aux"].power,
rails["12v_pex"].power,
rails["vccint"].power)
f = recorder.frame
powers = pd.DataFrame(index=f.index)
powers['board_power'] = f['12v_aux_power'] + f['12v_pex_power']
powers['fpga_power'] = f['vccint_power']
#Now we need to specify the layout for the graph. In this case it will be a simple Line/Scatter plot,
#autoranging on both axes with the Y axis having 0 at the bottom.
layout = {
'xaxis': {
'title': 'Time (s)'
},
'yaxis': {
'title': 'Power (W)',
'rangemode': 'tozero',
'autorange': True
}
}
#Plotly expects data in a specific format, namely an array of plotting objects.
#This helper function will update the data in a plot based.
#Th e `DataRecorder` stores the recording in a Pandas dataframe object with a time-based index.
#This makes it easy to pull out the results for a certain time range and compute a moving average.
#In this case we are going to give a 5-second moving average of the results as well as the raw input.
def update_data(frame, start, end, plot):
ranged = frame[start:end]
average_ranged = frame[start-pd.tseries.offsets.Second(5):end]
rolling = (average_ranged['12v_aux_power'] + average_ranged['12v_pex_power']).rolling(
pd.tseries.offsets.Second(5)
).mean()[ranged.index]
powers = pd.DataFrame(index=ranged.index)
powers['board_power'] = ranged['12v_aux_power'] + ranged['12v_pex_power']
powers['rolling'] = rolling
data = [
go.Scatter(x=powers.index, y=powers['board_power'], name="Board Power"),
go.Scatter(x=powers.index, y=powers['rolling'], name="5 Second Avg")
]
plot.update(data=data)
#Next we create an show the plot object, initially there will be no data to display but this plot will be updated after we start the recording.
#Once the plot is running it is possible to right click on it to pop out the graph into a separate window.
plot = go.FigureWidget(layout=layout)
plot
```
Next we create a dynamically-updating power graph:
```
recorder.record(0.1)
#In order to continue updating the graph we need a thread running in the background.
#The following thread will call our update function twice a second to display the most recently collected minute of data.
do_update = True
def thread_func():
while do_update:
now = pd.Timestamp.fromtimestamp(time.time())
past = now - pd.tseries.offsets.Second(60)
update_data(recorder.frame, past, now, plot)
time.sleep(0.5)
from threading import Thread
t = Thread(target=thread_func)
t.start()
```
To manually stop the power graph:
```
do_update = False
recorder.stop()
```
## Synthetic Throughput Test
We execute inference of a configurable-size batch of images, without data movement. We measure the latency and throughput.
```
import ipywidgets as widgets
from IPython.display import clear_output
bs = widgets.IntSlider(
value=128,
min=1,
max=1000,
step=1,
description='Batch Size:',
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='d'
)
fps = widgets.IntProgress(min=0, max=2500, description='FPS: ')
latency = widgets.FloatProgress(min=0, max=0.1, description='Latency (ms): ')
button = widgets.Button(description='Stop')
stop_running = False
def on_button_clicked(_):
global stop_running
stop_running = True
# linking button and function together using a button's method
button.on_click(on_button_clicked)
out_fps = widgets.Text()
out_latency = widgets.Text()
ui_top = widgets.HBox([button, bs])
ui_bottom = widgets.HBox([fps, out_fps, latency, out_latency])
ui = widgets.VBox([ui_top, ui_bottom])
display(ui)
import time
import threading
def benchmark_synthetic():
import pynq
ibuf = pynq.allocate((1000,3,224,224), dtype=np.int8, target=ol.bank0)
obuf = pynq.allocate((1000,5), dtype=np.uint32, target=ol.bank0)
while True:
if stop_running:
print("Stopping")
return
duration = time.monotonic()
accelerator.call(ibuf, obuf, fcbuf, bs.value)
duration = time.monotonic() - duration
fps.value = int(bs.value/duration)
latency.value = duration
out_fps.value = str(fps.value)
out_latency.value = '%.2f' % (duration * 1000)
t = threading.Thread(target=benchmark_synthetic)
t.start()
```
| true |
code
| 0.520314 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/ashikshafi08/Learning_Tensorflow/blob/main/Experiments/Generator_to_Dataset.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
For this experiment, we'll use a dataset from AI Crowd competition (live now) https://www.aicrowd.com/challenges/ai-blitz-8/problems/f1-team-classification
This is just for experiment purposes learning how to use `tf.data.Dataset.from_generators()` and this dataset was a suitable one to experiment with.
# Creating a Dataset object from ImageDataGenerator
Since I am new to tensorflow and the `tf.data` api I wasn't sure how to construct complex pipelines. It was easy using `ImageDataGenerator` (high-level api) especially with directory and dataframe to load in images.
I came over this handy method `tf.data.Dataset.from_generator()` which help us createa a dataset object from the generator object itself. How cool?
Try to wrap the `Dataset` class around this data generators.
We will be looking into `.flow_from_dataframe()` method.
### Things we'll be doing
- Use transfer learning fine tuning to train our model
- Use mixed_precision
- Use prefetch
```
# Checking the GPU
!nvidia-smi
# Getting some helper functions from Daniels' TensorFlow Course
!wget https://raw.githubusercontent.com/mrdbourke/tensorflow-deep-learning/main/extras/helper_functions.py
# Importing the needed functions for our use
from helper_functions import plot_loss_curves , compare_historys
# Using AI Crowd APi to download our data
!pip install aicrowd-cli
API_KEY = '#########'
!aicrowd login --api-key $API_KEY
# Downloading the dataset
!aicrowd dataset download --challenge f1-team-classification -j 3
!rm -rf data
!mkdir data
!unzip train.zip -d data/train
!unzip val.zip -d data/val
!unzip test.zip -d data/test
!mv train.csv data/train.csv
!mv val.csv data/val.csv
!mv sample_submission.csv data/sample_submission.csv
# Let's create a variable for our data paths
train_dir = 'data/train/'
test_dir = 'data/test/'
val_dir = 'data/val/'
# Our ImageID and label dataframes
import pandas as pd
import numpy as np
df_train = pd.read_csv('data/train.csv')
df_val = pd.read_csv('data/val.csv')
# Looking into our train dataframe
df_train.head()
```
## Becoming one with the data
Alright now we've got our data and it's time to visualize it and see how they look.
```
# Are the labels are well balanced?
df_train['label'].value_counts()
# How many images are there in the training directory?
df_train['ImageID'].shape
# Defining some parameters
import tensorflow as tf
BATCH_SIZE = 64
IMG_SIZE = (224 , 224)
# Creating our ImageDataGenerators for train and valid
train_datagen = tf.keras.preprocessing.image.ImageDataGenerator(rescale = 1/255.)
valid_datagen = tf.keras.preprocessing.image.ImageDataGenerator(rescale = 1/255.)
# How does our filenames looks like?
import os
print(os.listdir(train_dir)[:10])
# Adding the jpg extension to our ImageID in our train and valid dataframe
def append_ext(fn):
return f'{fn}.jpg'
# Now applying our function
df_train['ImageID'] = df_train['ImageID'].apply(append_ext)
df_val['ImageID'] = df_val['ImageID'].apply(append_ext)
# Looking into our ImageID column
df_train['ImageID'][:5]
# Now it's time to import our data into the generator
train_data_all = train_datagen.flow_from_dataframe(dataframe= df_train ,
directory = train_dir ,
x_col = 'ImageID' ,
y_col = 'label' ,
target_size = IMG_SIZE ,
class_mode = 'binary' ,
batch_size = 32 ,
shuffle = True)
val_data_all = valid_datagen.flow_from_dataframe(dataframe = df_val ,
directory = val_dir ,
x_col = 'ImageID' ,
y_col = 'label' ,
target_size = IMG_SIZE ,
class_mode = 'binary',
batch_size = 32 ,
shuffle = True)
# Without any transformations (batch_size , imgsize etc..)
train_data_none = train_datagen.flow_from_dataframe(dataframe= df_train ,
directory = train_dir ,
x_col = 'ImageID' ,
y_col = 'label' ,
batch_size = 32 ,
class_mode = 'binary' )
val_data_none = valid_datagen.flow_from_dataframe(dataframe = df_val ,
directory = val_dir ,
x_col = 'ImageID' ,
y_col = 'label' ,
batch_size = 32,
class_mode = 'binary')
# Checking the image , label shape and dtype (with transforms)
images, labels = next(train_data_all)
# Checking their shapes and dtypes
images.shape , labels.shape , images.dtype , labels.dtype
# Checking the image , label shapes an dtypes (without any transforms)
images_none , labels_none = next(train_data_none)
# Checking their shapes and dtypes
images_none.shape , labels_none.shape , images_none.dtype , labels_none.dtype
# Getting the class indices
train_data_all.class_indices
```
### Creating a dataset using `tf.data.Dataset.from_generators()`
Now we're going to convert the generator into Dataset object using the `tf.data.Dataset.from_generator()`
Things to be noted:
- In the place of `lambda` use your datagenerator object.
- The **output_shapes** is really important because our dataset object will returns the exact shape we mention inside the `output_shapes`.
This was the reason we examined our data types and shape above as soon as we built our generator.
#### Creating a dataset with the transforms here (just for experimentation)
```
train_dataset_all = tf.data.Dataset.from_generator(
lambda: train_data_all ,
output_types = (tf.float32 , tf.float32) ,
output_shapes = ([32 , 224 , 224 , 3] , [32 , ])
)
valid_dataset_all = tf.data.Dataset.from_generator(
lambda: val_data_all ,
output_types = (tf.float32 , tf.float32),
output_shapes = ([32 , 224 , 224 , 3] , [32 , ])
)
train_dataset_all , valid_dataset_all
```
#### Creating a dataset without any transforms (just for experimentations)
```
train_dataset_none = tf.data.Dataset.from_generator(
lambda: train_data_none ,
output_types = (tf.float32 , tf.float32) ,
output_shapes = ([32 , 256 , 256 , 3] , [32 , ])
)
valid_dataset_none = tf.data.Dataset.from_generator(
lambda: val_data_all ,
output_types = (tf.float32 , tf.float32),
output_shapes = ([32 , 256 , 256 , 3] , [32 , ])
)
train_dataset_none , valid_dataset_none
```
### **Note**
Since we're derived our from dataset object from a generator we won't be able to use `len()` function to know the number of samples in our dataset.
We can use cardinality to get the number of samples in our dataset. It's because in our case after the conversion the length is unknown and infinite.
`tf.data.experimental.cardinality` --> returns cardinality of the **dataset**
This will return -2 for now.

It should return **40000** (for train) because that was the number of samples (images) in our train directory.

But don't worry we can even fix this by using a similar function, since our length is unknown and it's the common case when you convert from generator to a dataset object.
We can explicitly enter our number of samples and even better we can use the `len()` function now on our dataset using,
`tf.data.experimental.assert_cardinality()` --> Asserts the cardinality of the dataset. Now will apply this to our dataset.
```
# Using assert_cardinality to add the number of samples (input)
train_dataset_all = train_dataset_all.apply(tf.data.experimental.assert_cardinality(40000))
valid_dataset_all = valid_dataset_all.apply(tf.data.experimental.assert_cardinality(4000))
# Same for our without transformations dataset
train_dataset_none = train_dataset_none.apply(tf.data.experimental.assert_cardinality(40000))
valid_dataset_none = valid_dataset_none.apply(tf.data.experimental.assert_cardinality(4000))
train_dataset_all , valid_dataset_all
# Now checkin the len
len(train_dataset_all) , len(valid_dataset_all)
# Setting up mixed precision
from tensorflow.keras import mixed_precision
mixed_precision.set_global_policy(policy = 'mixed_float16')
mixed_precision.global_policy() # should output "mixed_float16"
# How many classes are there?
train_data_all.class_indices
# Visualizing our images
import matplotlib.pyplot as plt
x , y = train_data.next()
for i in range(0, 4):
image = x[i]
label = y[i]
plt.axis(False)
# print(label) --> for checking whether it's plotting right ones
if label == 1.0:
label = 'redbull'
else:
label = 'mercedes'
plt.title(label)
plt.imshow(image)
plt.show()
# Getting our class names in a list
class_names = list(train_data_all.class_indices.keys())
len(class_names)
```
## Modelling
```
from tensorflow.keras import layers
from tensorflow.keras.layers.experimental import preprocessing
# Create base model
input_shape = (224, 224, 3)
base_model = tf.keras.applications.EfficientNetB0(include_top=False)
base_model.trainable = False # freeze base model layers
# Create Functional model
inputs = layers.Input(shape=input_shape, name="input_layer")
# Note: EfficientNetBX models have rescaling built-in but if your model didn't you could have a layer like below
# x = preprocessing.Rescaling(1./255)(x)
x = base_model(inputs, training=False) # set base_model to inference mode only
x = layers.GlobalAveragePooling2D(name="pooling_layer")(x)
x = layers.Dense(1)(x) # want one output neuron per class
# Separate activation of output layer so we can output float32 activations
outputs = layers.Activation("sigmoid", dtype=tf.float32, name="softmax_float32")(x)
model_1 = tf.keras.Model(inputs, outputs)
# Checking whether our layers are using mixed precision
for layer in model_1.layers:
print(layer.name , layer.trainable , layer.dtype , layer.dtype_policy)
# Tensorflow addons for f1-score
!pip install tensorflow_addons
import tensorflow_addons as tfa
f1_score = tfa.metrics.F1Score(average='macro' , num_classes= 1)
# Compile the model
model_1.compile(loss = tf.keras.losses.BinaryCrossentropy() ,
optimizer = tf.keras.optimizers.Adam() ,
metrics = ['accuracy' , f1_score])
```
Let's train the model again
> **Note**: Before using `len(train_data)` in the `steps_per_epoch` we should divide it by our **batch_size**.
```
# To get the actual steps for epochs for our train data
len(train_dataset_all) // 64
# Training a feature extraction model
history_feature_model_1 = model_1.fit(train_dataset_all ,
steps_per_epoch = len(train_dataset_all) // 32,
epochs = 3 ,
validation_data = valid_dataset_all,
validation_steps = int(0.15 * (len(valid_dataset_all))) )
# Gotta unfreeze all the layers
base_model.trainable = True
# Refreeze all layers except last 5
for layer in base_model.layers[:-3]:
layer.trainable = False
# Compiling the model again making the change
model_1.compile(loss = tf.keras.losses.BinaryCrossentropy() ,
optimizer = tf.keras.optimizers.Adam(lr = 0.0001) ,
metrics = ['accuracy' , f1_score])
# Creating learning rate reduction callback
reduce_lr = tf.keras.callbacks.ReduceLROnPlateau(monitor="val_loss",
factor=0.2, # multiply the learning rate by 0.2 (reduce by 5x)
patience=2,
verbose=1, # print out when learning rate goes down
min_lr=1e-7)
# Re-fit to fine tune the model
initial_epochs = 5
fine_tune_epochs = initial_epochs + 25
history_fine_model_1 = model_1.fit(train_dataset_all ,
steps_per_epoch = len(train_dataset_all) // 32 ,
epochs = fine_tune_epochs ,
initial_epoch = history_feature_model_1.epoch[-1] ,
validation_data = valid_dataset_all ,
validation_steps = int(0.15 * (len(valid_dataset_all))) ,
callbacks = [reduce_lr])
```
### Log (should be improved)
Epoch 3/30
1250/1250 [==============================] - 151s 118ms/step - loss: 0.6951 - accuracy: 0.5050 - f1_score: 0.6656 - val_loss: 0.6951 - val_accuracy: 0.4953 - val_f1_score: 0.6624
Epoch 4/30
1250/1250 [==============================] - 145s 116ms/step - loss: 0.6944 - accuracy: 0.5048 - f1_score: 0.6677 - val_loss: 0.6932 - val_accuracy: 0.5073 - val_f1_score: 0.6602
Epoch 5/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6947 - accuracy: 0.4983 - f1_score: 0.6681 - val_loss: 0.6939 - val_accuracy: 0.4971 - val_f1_score: 0.6641
Epoch 6/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6943 - accuracy: 0.5001 - f1_score: 0.6683 - val_loss: 0.6930 - val_accuracy: 0.5061 - val_f1_score: 0.6612
Epoch 7/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6941 - accuracy: 0.5010 - f1_score: 0.6701 - val_loss: 0.6933 - val_accuracy: 0.4938 - val_f1_score: 0.6611
Epoch 8/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6941 - accuracy: 0.4985 - f1_score: 0.6630 - val_loss: 0.6931 - val_accuracy: 0.5199 - val_f1_score: 0.6628
Epoch 00008: ReduceLROnPlateau reducing learning rate to 1.9999999494757503e-05.
Epoch 9/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6933 - accuracy: 0.4955 - f1_score: 0.6656 - val_loss: 0.6931 - val_accuracy: 0.5056 - val_f1_score: 0.6616
Epoch 10/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6932 - accuracy: 0.5005 - f1_score: 0.6648 - val_loss: 0.6932 - val_accuracy: 0.4961 - val_f1_score: 0.6632
Epoch 00010: ReduceLROnPlateau reducing learning rate to 3.999999898951501e-06.
Epoch 11/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5013 - f1_score: 0.6666 - val_loss: 0.6932 - val_accuracy: 0.4939 - val_f1_score: 0.6612
Epoch 12/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5037 - f1_score: 0.6677 - val_loss: 0.6930 - val_accuracy: 0.5054 - val_f1_score: 0.6619
Epoch 00012: ReduceLROnPlateau reducing learning rate to 7.999999979801942e-07.
Epoch 13/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6932 - accuracy: 0.4973 - f1_score: 0.6691 - val_loss: 0.6930 - val_accuracy: 0.5052 - val_f1_score: 0.6620
Epoch 14/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6932 - accuracy: 0.4954 - f1_score: 0.6728 - val_loss: 0.6931 - val_accuracy: 0.5091 - val_f1_score: 0.6610
Epoch 00014: ReduceLROnPlateau reducing learning rate to 1.600000018697756e-07.
Epoch 15/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5219 - f1_score: 0.6698 - val_loss: 0.6931 - val_accuracy: 0.4970 - val_f1_score: 0.6626
Epoch 16/30
1250/1250 [==============================] - 145s 116ms/step - loss: 0.6931 - accuracy: 0.5025 - f1_score: 0.6658 - val_loss: 0.6931 - val_accuracy: 0.5027 - val_f1_score: 0.6623
Epoch 00016: ReduceLROnPlateau reducing learning rate to 1e-07.
Epoch 17/30
1250/1250 [==============================] - 145s 116ms/step - loss: 0.6931 - accuracy: 0.5117 - f1_score: 0.6680 - val_loss: 0.6931 - val_accuracy: 0.4972 - val_f1_score: 0.6609
Epoch 18/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5091 - f1_score: 0.6684 - val_loss: 0.6931 - val_accuracy: 0.4991 - val_f1_score: 0.6626
Epoch 00018: ReduceLROnPlateau reducing learning rate to 1e-07.
Epoch 19/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5043 - f1_score: 0.6677 - val_loss: 0.6931 - val_accuracy: 0.4999 - val_f1_score: 0.6629
Epoch 20/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5048 - f1_score: 0.6670 - val_loss: 0.6931 - val_accuracy: 0.4975 - val_f1_score: 0.6609
Epoch 00020: ReduceLROnPlateau reducing learning rate to 1e-07.
Epoch 21/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5094 - f1_score: 0.6707 - val_loss: 0.6931 - val_accuracy: 0.4972 - val_f1_score: 0.6626
Epoch 22/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5023 - f1_score: 0.6662 - val_loss: 0.6931 - val_accuracy: 0.5002 - val_f1_score: 0.6630
Epoch 00022: ReduceLROnPlateau reducing learning rate to 1e-07.
Epoch 23/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5080 - f1_score: 0.6700 - val_loss: 0.6931 - val_accuracy: 0.4959 - val_f1_score: 0.6616
Epoch 24/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5017 - f1_score: 0.6656 - val_loss: 0.6931 - val_accuracy: 0.4978 - val_f1_score: 0.6614
Epoch 00024: ReduceLROnPlateau reducing learning rate to 1e-07.
Epoch 25/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5032 - f1_score: 0.6659 - val_loss: 0.6931 - val_accuracy: 0.4993 - val_f1_score: 0.6627
Epoch 26/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5052 - f1_score: 0.6682 - val_loss: 0.6931 - val_accuracy: 0.4979 - val_f1_score: 0.6613
Epoch 00026: ReduceLROnPlateau reducing learning rate to 1e-07.
Epoch 27/30
1250/1250 [==============================] - 147s 117ms/step - loss: 0.6931 - accuracy: 0.5065 - f1_score: 0.6702 - val_loss: 0.6931 - val_accuracy: 0.4976 - val_f1_score: 0.6628
Epoch 28/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5035 - f1_score: 0.6687 - val_loss: 0.6931 - val_accuracy: 0.4983 - val_f1_score: 0.6608
Epoch 00028: ReduceLROnPlateau reducing learning rate to 1e-07.
Epoch 29/30
1250/1250 [==============================] - 147s 118ms/step - loss: 0.6931 - accuracy: 0.5078 - f1_score: 0.6692 - val_loss: 0.6931 - val_accuracy: 0.4980 - val_f1_score: 0.6615
Epoch 30/30
1250/1250 [==============================] - 146s 117ms/step - loss: 0.6931 - accuracy: 0.5074 - f1_score: 0.6713 - val_loss: 0.6931 - val_accuracy: 0.5005 - val_f1_score: 0.6632
Epoch 00030: ReduceLROnPlateau reducing learning rate to 1e-07.
```
d
```
| true |
code
| 0.563378 | null | null | null | null |
|
# Machine Translation with Transformer
Tutorial from:
https://www.tensorflow.org/tutorials/text/transformer
```
import tensorflow_datasets as tfds
import tensorflow as tf
import time
import numpy as np
import matplotlib.pyplot as plt
examples, metadata = tfds.load('ted_hrlr_translate/pt_to_en', with_info=True,
as_supervised=True)
train_examples, val_examples = examples['train'], examples['validation']
tokenizer_en = tfds.features.text.SubwordTextEncoder.build_from_corpus(
(en.numpy() for pt, en in train_examples), target_vocab_size=2**13)
tokenizer_pt = tfds.features.text.SubwordTextEncoder.build_from_corpus(
(pt.numpy() for pt, en in train_examples), target_vocab_size=2**13)
BUFFER_SIZE = 20000
BATCH_SIZE = 64
```
## Add start and end tokens to the input and target
```
def encode(lang1, lang2):
lang1 = [tokenizer_pt.vocab_size] + tokenizer_pt.encode(
lang1.numpy()) + [tokenizer_pt.vocab_size+1]
lang2 = [tokenizer_en.vocab_size] + tokenizer_en.encode(
lang2.numpy()) + [tokenizer_en.vocab_size+1]
return lang1, lang2
# Wrap the previous function in a tf.py_function.
def tf_encode(pt, en):
result_pt, result_en = tf.py_function(encode, [pt, en], [tf.int64, tf.int64])
result_pt.set_shape([None])
result_pt.set_shape([None])
return result_pt, result_en
MAX_LENGTH = 40
def filter_max_length(x, y, max_length=MAX_LENGTH):
return tf.logical_and(tf.size(x) <= max_length,
tf.size(y) <= max_length)
train_preprocessed = (
train_examples
.map(tf_encode)
.filter(filter_max_length)
# cache the dataset to memory to get a speedup while reading from it.
.cache()
.shuffle(BUFFER_SIZE))
val_preprocessed = (
val_examples
.map(tf_encode)
.filter(filter_max_length))
```
## Pad and batch examples
```
train_dataset = (train_preprocessed
.padded_batch(BATCH_SIZE, padded_shapes=([None], [None]))
.prefetch(tf.data.experimental.AUTOTUNE))
val_dataset = (val_preprocessed
.padded_batch(BATCH_SIZE, padded_shapes=([None], [None])))
```
## Get a batch from the validation set
```
pt_batch, en_batch = next(iter(val_dataset))
pt_batch, en_batch
```
## Positional encoding
```
def get_angles(pos, i, d_model):
angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
return pos * angle_rates
def positional_encoding(position, d_model):
angle_rads = get_angles(np.arange(position)[:, np.newaxis],
np.arange(d_model)[np.newaxis, :],
d_model)
# apply sin to even indices in the array; 2i
angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
# apply cos to odd indices in the array; 2i+1
angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
pos_encoding = angle_rads[np.newaxis, ...]
return tf.cast(pos_encoding, dtype=tf.float32)
pos_encoding = positional_encoding(50, 512)
print (pos_encoding.shape)
plt.pcolormesh(pos_encoding[0], cmap='RdBu')
plt.xlabel('Depth')
plt.xlim((0, 512))
plt.ylabel('Position')
plt.colorbar()
plt.show()
```
## Masking
Indicate where the pad value "0" is present. Output is "1" for these locations and "0" otherwise.
```
def create_padding_mask(seq):
seq = tf.cast(tf.math.equal(seq, 0), tf.float32)
# Add extra dimensions to add the padding to the
# attention logits.
return seq[:, tf.newaxis, tf.newaxis, :] # (batchSize, 1, 1, seqLen)
x = tf.constant([[7, 6, 0, 0, 1], [1, 2, 3, 0, 0], [0, 0, 0, 4, 5]])
create_padding_mask(x)
def create_look_ahead_mask(size):
mask = 1 - tf.linalg.band_part(tf.ones((size, size)), -1, 0)
return mask # (seq_len, seq_len)
```
## Scaled dot product attention.
```
def scaled_dot_product_attention(q, k, v, mask):
"""Calculate the attention weights.
q, k, v must have matching leading dimensions.
k, v must have matching penultimate dimension, i.e.: seq_len_k = seq_len_v.
The mask has different shapes depending on its type(padding or look ahead)
but it must be broadcastable for addition.
Args:
q: query shape == (..., seq_len_q, depth)
k: key shape == (..., seq_len_k, depth)
v: value shape == (..., seq_len_v, depth_v)
mask: Float tensor with shape broadcastable
to (..., seq_len_q, seq_len_k). Defaults to None.
Returns:
output, attention_weights
"""
matmul_qk = tf.matmul(q, k, transpose_b=True) # (..., seq_len_q, seq_len_k)
# scale matmul_qk
dk = tf.cast(tf.shape(k)[-1], tf.float32)
scaled_attention_logits = matmul_qk / tf.math.sqrt(dk)
# add the mask to the scaled tensor.
if mask is not None:
scaled_attention_logits += (mask * -1e9)
# softmax is normalized on the last axis (seq_len_k) so that the scores
# add up to 1.
attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1) # (..., seq_len_q, seq_len_k)
output = tf.matmul(attention_weights, v) # (..., seq_len_q, depth_v)
return output, attention_weights
def print_out(q, k, v):
temp_out, temp_attn = scaled_dot_product_attention(
q, k, v, None)
print ('Attention weights are:')
print (temp_attn)
print ('Output is:')
print (temp_out)
np.set_printoptions(suppress=True)
temp_k = tf.constant([[10,0,0],
[0,10,0],
[0,0,10],
[0,0,10]], dtype=tf.float32) # (4, 3)
temp_v = tf.constant([[ 1,0],
[ 10,0],
[ 100,5],
[1000,6]], dtype=tf.float32) # (4, 2)
# This `query` aligns with the second `key`,
# so the second `value` is returned.
temp_q = tf.constant([[0, 10, 0]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
# This query aligns with a repeated key (third and fourth),
# so all associated values get averaged.
temp_q = tf.constant([[0, 0, 10]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
# This query aligns equally with the first and second key,
# so their values get averaged.
temp_q = tf.constant([[10, 10, 0]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
# Pass all queries together.
temp_q = tf.constant([[0, 0, 10], [0, 10, 0], [10, 10, 0]], dtype=tf.float32) # (3, 3)
print_out(temp_q, temp_k, temp_v)
```
## Multi-head attention
```
class MultiHeadAttention(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads
self.d_model = d_model
assert d_model % self.num_heads == 0
self.depth = d_model // self.num_heads
self.wq = tf.keras.layers.Dense(d_model)
self.wk = tf.keras.layers.Dense(d_model)
self.wv = tf.keras.layers.Dense(d_model)
self.dense = tf.keras.layers.Dense(d_model)
def split_heads(self, x, batch_size):
"""Split the last dimension into (num_heads, depth).
Transpose the result such that the shape is (batch_size, num_heads, seq_len, depth)
"""
x = tf.reshape(x, (batch_size, -1, self.num_heads, self.depth))
return tf.transpose(x, perm=[0, 2, 1, 3])
def call(self, v, k, q, mask):
batch_size = tf.shape(q)[0]
q = self.wq(q) # (batch_size, seq_len, d_model)
k = self.wk(k) # (batch_size, seq_len, d_model)
v = self.wv(v) # (batch_size, seq_len, d_model)
q = self.split_heads(q, batch_size) # (batch_size, num_heads, seq_len_q, depth)
k = self.split_heads(k, batch_size) # (batch_size, num_heads, seq_len_k, depth)
v = self.split_heads(v, batch_size) # (batch_size, num_heads, seq_len_v, depth)
# scaled_attention.shape == (batch_size, num_heads, seq_len_q, depth)
# attention_weights.shape == (batch_size, num_heads, seq_len_q, seq_len_k)
scaled_attention, attention_weights = scaled_dot_product_attention(
q, k, v, mask)
scaled_attention = tf.transpose(scaled_attention, perm=[0, 2, 1, 3]) # (batch_size, seq_len_q, num_heads, depth)
concat_attention = tf.reshape(scaled_attention,
(batch_size, -1, self.d_model)) # (batch_size, seq_len_q, d_model)
output = self.dense(concat_attention) # (batch_size, seq_len_q, d_model)
return output, attention_weights
# Try the MultiHeadAttention class.
temp_mha = MultiHeadAttention(d_model=512, num_heads=8)
y = tf.random.uniform((1, 60, 512)) # (batch_size, encoder_sequence, d_model)
out, attn = temp_mha(y, k=y, q=y, mask=None)
out.shape, attn.shape
```
## Point wise feed forward network
```
def point_wise_feed_forward_network(d_model, dff):
return tf.keras.Sequential([
tf.keras.layers.Dense(dff, activation='relu'), # (batch_size, seq_len, dff)
tf.keras.layers.Dense(d_model) # (batch_size, seq_len, d_model)
])
sample_ffn = point_wise_feed_forward_network(512, 2048)
sample_ffn(tf.random.uniform((64, 50, 512))).shape
```
## Encoder layer
```
class EncoderLayer(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, dff, rate=0.1):
super(EncoderLayer, self).__init__()
self.mha = MultiHeadAttention(d_model, num_heads)
self.ffn = point_wise_feed_forward_network(d_model, dff)
self.layernorm1 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = tf.keras.layers.Dropout(rate)
self.dropout2 = tf.keras.layers.Dropout(rate)
def call(self, x, training, mask):
attn_output, _ = self.mha(x, x, x, mask) # (batch_size, input_seq_len, d_model)
attn_output = self.dropout1(attn_output, training=training)
out1 = self.layernorm1(x + attn_output) # (batch_size, input_seq_len, d_model)
ffn_output = self.ffn(out1) # (batch_size, input_seq_len, d_model)
ffn_output = self.dropout2(ffn_output, training=training)
out2 = self.layernorm2(out1 + ffn_output) # (batch_size, input_seq_len, d_model)
return out2
```
## Decoder Layer
```
class DecoderLayer(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, dff, rate=0.1):
super(DecoderLayer, self).__init__()
self.mha1 = MultiHeadAttention(d_model, num_heads)
self.mha2 = MultiHeadAttention(d_model, num_heads)
self.ffn = point_wise_feed_forward_network(d_model, dff)
self.layernorm1 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm3 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = tf.keras.layers.Dropout(rate)
self.dropout2 = tf.keras.layers.Dropout(rate)
self.dropout3 = tf.keras.layers.Dropout(rate)
def call(self, x, enc_output, training,
look_ahead_mask, padding_mask):
# enc_output.shape == (batch_size, input_seq_len, d_model)
attn1, attn_weights_block1 = self.mha1(x, x, x, look_ahead_mask) # (batch_size, target_seq_len, d_model)
attn1 = self.dropout1(attn1, training=training)
out1 = self.layernorm1(attn1 + x)
attn2, attn_weights_block2 = self.mha2(
enc_output, enc_output, out1, padding_mask) # (batch_size, target_seq_len, d_model)
attn2 = self.dropout2(attn2, training=training)
out2 = self.layernorm2(attn2 + out1) # (batch_size, target_seq_len, d_model)
ffn_output = self.ffn(out2) # (batch_size, target_seq_len, d_model)
ffn_output = self.dropout3(ffn_output, training=training)
out3 = self.layernorm3(ffn_output + out2) # (batch_size, target_seq_len, d_model)
return out3, attn_weights_block1, attn_weights_block2
```
## Encoder
```
class Encoder(tf.keras.layers.Layer):
def __init__(self, num_layers, d_model, num_heads, dff, input_vocab_size,
maximum_position_encoding, rate=0.1):
super(Encoder, self).__init__()
self.d_model = d_model
self.num_layers = num_layers
self.embedding = tf.keras.layers.Embedding(input_vocab_size, d_model)
self.pos_encoding = positional_encoding(maximum_position_encoding,
self.d_model)
self.enc_layers = [EncoderLayer(d_model, num_heads, dff, rate)
for _ in range(num_layers)]
self.dropout = tf.keras.layers.Dropout(rate)
def call(self, x, training, mask):
seq_len = tf.shape(x)[1]
# adding embedding and position encoding.
x = self.embedding(x) # (batch_size, input_seq_len, d_model)
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32))
x += self.pos_encoding[:, :seq_len, :]
x = self.dropout(x, training=training)
for i in range(self.num_layers):
x = self.enc_layers[i](x, training, mask)
return x # (batch_size, input_seq_len, d_model)
```
## Decoder
```
class Decoder(tf.keras.layers.Layer):
def __init__(self, num_layers, d_model, num_heads, dff, target_vocab_size,
maximum_position_encoding, rate=0.1):
super(Decoder, self).__init__()
self.d_model = d_model
self.num_layers = num_layers
self.embedding = tf.keras.layers.Embedding(target_vocab_size, d_model)
self.pos_encoding = positional_encoding(maximum_position_encoding, d_model)
self.dec_layers = [DecoderLayer(d_model, num_heads, dff, rate)
for _ in range(num_layers)]
self.dropout = tf.keras.layers.Dropout(rate)
def call(self, x, enc_output, training,
look_ahead_mask, padding_mask):
seq_len = tf.shape(x)[1]
attention_weights = {}
x = self.embedding(x) # (batch_size, target_seq_len, d_model)
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32))
x += self.pos_encoding[:, :seq_len, :]
x = self.dropout(x, training=training)
for i in range(self.num_layers):
x, block1, block2 = self.dec_layers[i](x, enc_output, training,
look_ahead_mask, padding_mask)
attention_weights['decoder_layer{}_block1'.format(i+1)] = block1
attention_weights['decoder_layer{}_block2'.format(i+1)] = block2
# x.shape == (batch_size, target_seq_len, d_model)
return x, attention_weights
```
## Create the Transformer
```
class Transformer(tf.keras.Model):
def __init__(self, num_layers, d_model, num_heads, dff, input_vocab_size,
target_vocab_size, pe_input, pe_target, rate=0.1):
super(Transformer, self).__init__()
self.encoder = Encoder(num_layers, d_model, num_heads, dff,
input_vocab_size, pe_input, rate)
self.decoder = Decoder(num_layers, d_model, num_heads, dff,
target_vocab_size, pe_target, rate)
self.final_layer = tf.keras.layers.Dense(target_vocab_size)
def call(self, inp, tar, training, enc_padding_mask,
look_ahead_mask, dec_padding_mask):
enc_output = self.encoder(inp, training, enc_padding_mask) # (batch_size, inp_seq_len, d_model)
# dec_output.shape == (batch_size, tar_seq_len, d_model)
dec_output, attention_weights = self.decoder(
tar, enc_output, training, look_ahead_mask, dec_padding_mask)
final_output = self.final_layer(dec_output) # (batch_size, tar_seq_len, target_vocab_size)
return final_output, attention_weights
```
## Set Hyperparameters
```
num_layers = 4
d_model = 128
dff = 512
num_heads = 8
input_vocab_size = tokenizer_pt.vocab_size + 2
target_vocab_size = tokenizer_en.vocab_size + 2
dropout_rate = 0.1
```
## Optimizer
Adam optimizer with custom learning rate scheduler.
```
class CustomSchedule(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, d_model, warmup_steps=4000):
super(CustomSchedule, self).__init__()
self.d_model = d_model
self.d_model = tf.cast(self.d_model, tf.float32)
self.warmup_steps = warmup_steps
def __call__(self, step):
arg1 = tf.math.rsqrt(step)
arg2 = step * (self.warmup_steps ** -1.5)
return tf.math.rsqrt(self.d_model) * tf.math.minimum(arg1, arg2)
learning_rate = CustomSchedule(d_model)
optimizer = tf.keras.optimizers.Adam(learning_rate, beta_1=0.9, beta_2=0.98,
epsilon=1e-9)
```
## Loss and metrics
```
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')
def loss_function(real, pred):
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_sum(loss_)/tf.reduce_sum(mask)
train_loss = tf.keras.metrics.Mean(name='train_loss')
train_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(
name='train_accuracy')
```
## Training and checkpointing
```
transformer = Transformer(num_layers, d_model, num_heads, dff,
input_vocab_size, target_vocab_size,
pe_input=input_vocab_size,
pe_target=target_vocab_size,
rate=dropout_rate)
def create_masks(inp, tar):
# Encoder padding mask
enc_padding_mask = create_padding_mask(inp)
# Used in the 2nd attention block in the decoder.
# This padding mask is used to mask the encoder outputs.
dec_padding_mask = create_padding_mask(inp)
# Used in the 1st attention block in the decoder.
# It is used to pad and mask future tokens in the input received by
# the decoder.
look_ahead_mask = create_look_ahead_mask(tf.shape(tar)[1])
dec_target_padding_mask = create_padding_mask(tar)
combined_mask = tf.maximum(dec_target_padding_mask, look_ahead_mask)
return enc_padding_mask, combined_mask, dec_padding_mask
checkpoint_path = "./checkpoints/train"
ckpt = tf.train.Checkpoint(transformer=transformer,
optimizer=optimizer)
ckpt_manager = tf.train.CheckpointManager(ckpt, checkpoint_path, max_to_keep=5)
# if a checkpoint exists, restore the latest checkpoint.
if ckpt_manager.latest_checkpoint:
ckpt.restore(ckpt_manager.latest_checkpoint)
print ('Latest checkpoint restored!!')
EPOCHS = 20
# The @tf.function trace-compiles train_step into a TF graph for faster
# execution. The function specializes to the precise shape of the argument
# tensors. To avoid re-tracing due to the variable sequence lengths or variable
# batch sizes (the last batch is smaller), use input_signature to specify
# more generic shapes.
train_step_signature = [
tf.TensorSpec(shape=(None, None), dtype=tf.int64),
tf.TensorSpec(shape=(None, None), dtype=tf.int64),
]
@tf.function(input_signature=train_step_signature)
def train_step(inp, tar):
tar_inp = tar[:, :-1]
tar_real = tar[:, 1:]
enc_padding_mask, combined_mask, dec_padding_mask = create_masks(inp, tar_inp)
with tf.GradientTape() as tape:
predictions, _ = transformer(inp, tar_inp,
True,
enc_padding_mask,
combined_mask,
dec_padding_mask)
loss = loss_function(tar_real, predictions)
gradients = tape.gradient(loss, transformer.trainable_variables)
optimizer.apply_gradients(zip(gradients, transformer.trainable_variables))
train_loss(loss)
train_accuracy(tar_real, predictions)
for epoch in range(EPOCHS):
start = time.time()
train_loss.reset_states()
train_accuracy.reset_states()
# inp -> portuguese, tar -> english
for (batch, (inp, tar)) in enumerate(train_dataset):
train_step(inp, tar)
if batch % 50 == 0:
print ('Epoch {} Batch {} Loss {:.4f} Accuracy {:.4f}'.format(
epoch + 1, batch, train_loss.result(), train_accuracy.result()))
if (epoch + 1) % 5 == 0:
ckpt_save_path = ckpt_manager.save()
print ('Saving checkpoint for epoch {} at {}'.format(epoch+1,
ckpt_save_path))
print ('Epoch {} Loss {:.4f} Accuracy {:.4f}'.format(epoch + 1,
train_loss.result(),
train_accuracy.result()))
print ('Time taken for 1 epoch: {} secs\n'.format(time.time() - start))
```
## Evaluate
```
def evaluate(inp_sentence):
start_token = [tokenizer_pt.vocab_size]
end_token = [tokenizer_pt.vocab_size + 1]
# inp sentence is portuguese, hence adding the start and end token
inp_sentence = start_token + tokenizer_pt.encode(inp_sentence) + end_token
encoder_input = tf.expand_dims(inp_sentence, 0)
# as the target is english, the first word to the transformer should be the
# english start token.
decoder_input = [tokenizer_en.vocab_size]
output = tf.expand_dims(decoder_input, 0)
for i in range(MAX_LENGTH):
enc_padding_mask, combined_mask, dec_padding_mask = create_masks(
encoder_input, output)
# predictions.shape == (batch_size, seq_len, vocab_size)
predictions, attention_weights = transformer(encoder_input,
output,
False,
enc_padding_mask,
combined_mask,
dec_padding_mask)
# select the last word from the seq_len dimension
predictions = predictions[: ,-1:, :] # (batch_size, 1, vocab_size)
predicted_id = tf.cast(tf.argmax(predictions, axis=-1), tf.int32)
# return the result if the predicted_id is equal to the end token
if predicted_id == tokenizer_en.vocab_size+1:
return tf.squeeze(output, axis=0), attention_weights
# concatentate the predicted_id to the output which is given to the decoder
# as its input.
output = tf.concat([output, predicted_id], axis=-1)
return tf.squeeze(output, axis=0), attention_weights
def plot_attention_weights(attention, sentence, result, layer):
fig = plt.figure(figsize=(16, 8))
sentence = tokenizer_pt.encode(sentence)
attention = tf.squeeze(attention[layer], axis=0)
for head in range(attention.shape[0]):
ax = fig.add_subplot(2, 4, head+1)
# plot the attention weights
ax.matshow(attention[head][:-1, :], cmap='viridis')
fontdict = {'fontsize': 10}
ax.set_xticks(range(len(sentence)+2))
ax.set_yticks(range(len(result)))
ax.set_ylim(len(result)-1.5, -0.5)
ax.set_xticklabels(
['<start>']+[tokenizer_pt.decode([i]) for i in sentence]+['<end>'],
fontdict=fontdict, rotation=90)
ax.set_yticklabels([tokenizer_en.decode([i]) for i in result
if i < tokenizer_en.vocab_size],
fontdict=fontdict)
ax.set_xlabel('Head {}'.format(head+1))
plt.tight_layout()
plt.show()
def translate(sentence, plot=''):
result, attention_weights = evaluate(sentence)
predicted_sentence = tokenizer_en.decode([i for i in result
if i < tokenizer_en.vocab_size])
print('Input: {}'.format(sentence))
print('Predicted translation: {}'.format(predicted_sentence))
if plot:
plot_attention_weights(attention_weights, sentence, result, plot)
translate("este é um problema que temos que resolver.")
print ("Real translation: this is a problem we have to solve .")
translate("os meus vizinhos ouviram sobre esta ideia.")
print ("Real translation: and my neighboring homes heard about this idea .")
```
| true |
code
| 0.71307 | null | null | null | null |
|
# Searching
Try running it in a live notebook for animation!
* peakSearch
* bracketSearch
* binarySearch
```
# Reload modules every time code is called. Set autoreload 0 to disable
%load_ext autoreload
%autoreload 2
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(0)
from lightlab.util.search import peakSearch, binarySearch, SearchRangeError
livePlots = False
```
## You want to find a peak? Sweeping is not good enough
```
center = .82
amp = .7
fwhm = .2
defaultNoise = amp * 5e-3
noise = defaultNoise
assertionTolerance = .2
def myPeakedFun(x):
y = amp / (1 + (2 * (x - center) / fwhm) ** 2) + noise * np.random.randn()
return y
xq = np.linspace(0,3, 10)
plt.plot(xq, myPeakedFun(xq))
plt.title('Poor, low-res sampling of underlying peak')
```
## Peak search
This demonstrates noise tolerance when `nSwarm` is greater than 3
```
for noi, nSwarm in zip([defaultNoise, 5e-2], [3, 7]):
noise = noi
xPeak, yPeak = peakSearch(evalPointFun=myPeakedFun, startBounds=[0,3],
nSwarm=nSwarm, xTol=assertionTolerance/4, livePlot=livePlots)
assert abs(xPeak - center) < assertionTolerance
assert abs(yPeak - amp) < assertionTolerance
noise = defaultNoise
```
## Interactive peak descent through binary search
```
binSearchOpts = dict(evalPointFun=myPeakedFun, xTol=.005, livePlot=livePlots)
```
### This is easy, well bounded
```
rightBounds = [xPeak, 3]
leftBounds = [0, xPeak]
hwhmKwargs = dict(targetY=0.5*yPeak, **binSearchOpts)
xRightHalf = binarySearch(startBounds=rightBounds, **hwhmKwargs)
xLeftHalf = binarySearch(startBounds=leftBounds, **hwhmKwargs)
assert abs(xLeftHalf - (center - fwhm/2)) < assertionTolerance
assert abs(xRightHalf - (center + fwhm/2)) < assertionTolerance
```
### Non-monotonic but still well defined
There is only one value in the domain that satisfies. It starts off bracketed
No test for when there is a peak in the middle and it starts *not* bracketed,
i.e. if rightStart fwhm was 0.75
To handle this, bracketSearch would have to report that it bracketed on both sides
```
rightStart = center + fwhm*.4
for leftStart in [0, center - fwhm, center - 0.6 * fwhm]:
xLeftHalf = binarySearch(startBounds=[leftStart, rightStart], **hwhmKwargs)
assert abs(xLeftHalf - (center - fwhm/2)) < assertionTolerance
```
### Bad bound conditioning saved by `bracketSearch`
```
noise = defaultNoise / 10 # turn down noise a little bit
# Bad domain that totally misses peak
xLeftHalf = binarySearch(startBounds=[0, xPeak/2], **hwhmKwargs)
assert abs(xLeftHalf - (center - fwhm/2)) < assertionTolerance
# Target very close to peak
for trialAgainstNoise in range(5):
try:
xRightOnPeak = binarySearch(startBounds=[0, xPeak/4], targetY=0.99*amp, **binSearchOpts)
break
except RangeError as err:
if 'probably noise' in err.args[0]:
continue
else:
raise err
else:
raise Exception('We tried multiple times but noise killed this one')
assert abs(xRightOnPeak - center) < assertionTolerance
noise = defaultNoise
```
### Graceful failures
```
# Targeting something too high, with peak within startBounds
goodAsItGets = binarySearch(startBounds=[0, center + .5 * fwhm], targetY=2, **binSearchOpts)
assert abs(goodAsItGets - center) < assertionTolerance
# Peak starts outside of startBounds
goodAsItGets = binarySearch(startBounds=[center + .5 * fwhm, 3], targetY=2, **binSearchOpts)
assert abs(goodAsItGets - center) < assertionTolerance
```
### These should generate errors
```
# Targeting outside of hard constrain domain
try:
binarySearch(startBounds=[xPeak, xPeak+.1], targetY=0, hardConstrain=True, **binSearchOpts)
assert False
except SearchRangeError as err:
assert err.args[1] == 'low'
```
| true |
code
| 0.604574 | null | null | null | null |
|
# Use a custom parser
While many of the parsers included within this libary may be useful, we do not have parsers for **every** dataset out there. If you are interested in adding your own parser (and hopefully contributing that parser to the main repo 😊 ), check out this walkthrough of how to build one!
## What is a Parser?
Basically, a parser collects information from two main sources:
* The file string
* The dataset itself
This means there are two main steps:
* Parsing out the file string, separating based on some symbol
* Opening the file, and extracting variables and their attributes, or even global attributes
The result from a "parser" is a dictionary of fields to add to the catalog, stored in a `pandas.DataFrame`
It would probably be **more helpful** to walk through a concrete example of this...
## Example of Building a Parser
Let's say we have a list of files which we wanted to parse! In this example, we are using a set of observational data on NCAR HPC resources. A full blog post detailing this dataset and comparison is [included here](https://ncar.github.io/esds/posts/2021/intake-obs-cesm2le-comparison/)
### Imports
```
import glob
import pathlib
import traceback
from datetime import datetime
import xarray as xr
from ecgtools import Builder
from ecgtools.builder import INVALID_ASSET, TRACEBACK
files = sorted(glob.glob('/glade/p/cesm/amwg/amwg_diagnostics/obs_data/*'))
files[::20]
```
Observational datasetsets in this directory follow the convention `source_(month/season/annual)_climo.nc.`
Let’s open up one of those datasets
```
ds = xr.open_dataset('/glade/p/cesm/amwg/amwg_diagnostics/obs_data/CERES-EBAF_01_climo.nc')
ds
```
We see that this dataset is gridded on a global 0.5° grid, with several variables related to solar fluxes (ex. `TOA net shortwave`)
### Parsing the Filepath
As mentioned before, the first step is parsing out information from the filepath. Here, we use [pathlib](https://docs.python.org/3/library/pathlib.html) which can be helpful when working with filepaths generically
```
path = pathlib.Path(files[0])
path.stem
```
This path can be split using `.split('_')`, separates the path into the following:
* Observational dataset source
* Month Number, Season, or Annual
* “climo”
```
path.stem.split('_')
```
### Open the File for More Information
We can also gather useful insight by opening the file!
```
ds = xr.open_dataset(files[0])
ds
```
Let’s look at the variable “Temperature” (`T`)
```
ds.T
```
In this case, we want to include the list of variables available from this single file, such that each entry in our catalog represents a single file. We can search for variables in this dataset using the following:
```
variable_list = [var for var in ds if 'long_name' in ds[var].attrs]
variable_list
```
### Assembling These Parts into a Function
Now that we have methods of extracting the relevant information, we can assemble this into a function which returns a dictionary. You'll notice the addition of the exception handling, which will add the unparsable file to a `pandas.DataFrame` with the unparsable file, and the associated traceback error.
```
def parse_amwg_obs(file):
"""Atmospheric observational data stored in"""
file = pathlib.Path(file)
info = {}
try:
stem = file.stem
split = stem.split('_')
source = split[0]
temporal = split[-2]
if len(temporal) == 2:
month_number = int(temporal)
time_period = 'monthly'
temporal = datetime(2020, month_number, 1).strftime('%b').upper()
elif temporal == 'ANN':
time_period = 'annual'
else:
time_period = 'seasonal'
with xr.open_dataset(file, chunks={}, decode_times=False) as ds:
variable_list = [var for var in ds if 'long_name' in ds[var].attrs]
info = {
'source': source,
'temporal': temporal,
'time_period': time_period,
'variable': variable_list,
'path': str(file),
}
return info
except Exception:
return {INVALID_ASSET: file, TRACEBACK: traceback.format_exc()}
```
### Test this Parser on Some Files
We can try this parser on a single file, to make sure that it returns a dictionary
```
parse_amwg_obs(files[0])
```
Now that we made sure that it works, we can implement in `ecgtools`!
First, we setup the `Builder` object
```
b = Builder('/glade/p/cesm/amwg/amwg_diagnostics/obs_data')
```
Next, we build the catalog using our newly created parser!
```
b.build(parse_amwg_obs)
```
Let's take a look at our resultant catalog...
```
b.df
```
| true |
code
| 0.453201 | null | null | null | null |
|
# Source reconstruction with lens mass fitting
Runs MCMC over lens model parameters, using SLIT to reconstruct the source at each iteration.
```
import os
import sys
import copy
import time
import numpy as np
import matplotlib.pyplot as plt
import astropy.io.fits as pf
import pysap
import corner
import pickle as pkl
from lenstronomy.Data.psf import PSF
from lenstronomy.Data.imaging_data import ImageData
from lenstronomy.ImSim.image_model import ImageModel
from lenstronomy.LensModel.lens_model import LensModel
from lenstronomy.LightModel.light_model import LightModel
from lenstronomy.Util import class_creator
from lenstronomy.Workflow.fitting_sequence import FittingSequence
from lenstronomy.Plots.model_plot import ModelPlot
from lenstronomy.Plots import chain_plot
from lenstronomy.Util import kernel_util
import lenstronomy.Util.simulation_util as sim_util
import lenstronomy.Util.image_util as image_util
import lenstronomy.Util.util as lenstro_util
from lenstronomy.LightModel.Profiles.starlets import Starlets
from slitronomy.Util.plot_util import nice_colorbar, log_cmap
from TDLMCpipeline.Util.plots import plot_convergence_by_walker
from TDLMCpipeline.Util.params import model_from_mcmc_sample
%matplotlib inline
subgrid_res_source = 2
use_threshold_mask = False
start_wayoff = False
n_burn = 0
n_run = 100
walker_ratio = 10
num_threads = 8
# uncomment parameters to fix those to truth
mass_fixed_list = [
#'gamma',
#'theta_E',
#'e1', 'e2',
#'center_x', 'center_y'
]
lin_scale = lambda x: x
log_scale = lambda x: np.log10(x)
sqrt_scale = lambda x: np.sqrt(x)
# data specifics
num_pix = 99 # cutout pixel size
delta_pix = 0.08 # pixel size in arcsec (area per pixel = deltaPix**2)
#background_rms = 0.05 # background noise per pixel
#exp_time = 0 # exposure time (arbitrary units, flux per pixel is in units #photons/exp_time unit)
psf_fwhm = 0.2 # full width half max of PSF, in delta_pix units
psf_num_pix = 15
# data specification (coordinates, etc.)
_, _, ra_at_xy_0, dec_at_xy_0, _, _, Mpix2coord, _ \
= lenstro_util.make_grid_with_coordtransform(numPix=num_pix, deltapix=delta_pix, subgrid_res=1,
inverse=False, left_lower=False)
kwargs_data = {
#'background_rms': background_rms,
#'exposure_time': np.ones((num_pix, num_pix)) * exp_time, # individual exposure time/weight per pixel
'ra_at_xy_0': ra_at_xy_0, 'dec_at_xy_0': dec_at_xy_0,
'transform_pix2angle': Mpix2coord,
'image_data': np.zeros((num_pix, num_pix))
}
data_class = ImageData(**kwargs_data)
# PSF specification
no_convolution = False
if no_convolution:
kwargs_psf = {'psf_type': 'NONE'}
else:
psf_kernel = kernel_util.kernel_gaussian(psf_num_pix, delta_pix, psf_fwhm)
print(psf_kernel.shape)
kwargs_psf = {'psf_type': 'PIXEL', 'kernel_point_source': psf_kernel}
#kwargs_psf = {'psf_type': 'GAUSSIAN', 'fwhm': psf_fwhm, 'pixel_size': delta_pix, 'truncation': 11}
psf_class = PSF(**kwargs_psf)
plt.title("PSF kernel")
im = plt.imshow(psf_class.kernel_point_source, origin='lower')
nice_colorbar(im)
plt.show()
lens_model_list = ['SPEMD']
kwargs_spemd = {'theta_E': 1.8, 'gamma': 2, 'center_x': 0, 'center_y': 0, 'e1': 0.1, 'e2': -0.2}
kwargs_lens = [kwargs_spemd]
lens_model_class = LensModel(lens_model_list=lens_model_list)
# list of source light profiles from Galsim (COSMOS galaxy)
galsim_index = 1
snr = 500
galsim_data_path = ('data/ring_sims/sims_SNR{}/simring_galsim{}_all.pkl'.format(snr, galsim_index))
[data, truth, lens_model] = pkl.load(open(galsim_data_path, 'rb'))
galsim_source_highres = truth['source_galsim_3']
background_rms = data['background_rms']
galsim_num_pix = data['num_pix']
galsim_delta_pix = data['delta_pix']
source_model_list = ['INTERPOL']
kwargs_interpol_source = {'image': galsim_source_highres, 'amp': 3000, 'center_x': +0.3, 'center_y': -0.1, 'phi_G': 0,
'scale': galsim_delta_pix/3}
kwargs_source = [kwargs_interpol_source]
source_model_class = LightModel(light_model_list=source_model_list)
kwargs_truth = {
'kwargs_lens': kwargs_lens,
'kwargs_source': kwargs_source,
'kwargs_special': {'delta_x_source_grid': 0, 'delta_y_source_grid': 0},
}
kwargs_numerics_sim = {'supersampling_factor': 3, 'supersampling_convolution': False}
# get the simalated lens image (i.e. image plane)
imageModel = ImageModel(data_class, psf_class, lens_model_class, source_model_class,
kwargs_numerics=kwargs_numerics_sim)
image_sim_no_noise = imageModel.image(kwargs_lens, kwargs_source)
bkg = image_util.add_background(image_sim_no_noise, sigma_bkd=background_rms)
#poisson = image_util.add_poisson(image_sim_no_noise, exp_time=exp_time)
noise = bkg # + poisson
image_sim = image_sim_no_noise + noise
image_sim_1d = lenstro_util.image2array(image_sim)
kwargs_data['image_data'] = image_sim
kwargs_data['background_rms'] = background_rms
kwargs_data['noise_map'] = background_rms * np.ones_like(image_sim)
data_class.update_data(image_sim)
# get the coordinates arrays of source plane (those are 'thetas' but in source plane !)
x_grid_src_1d, y_grid_src_1d = lenstro_util.make_grid(numPix=num_pix, deltapix=delta_pix,
subgrid_res=subgrid_res_source)
# get the light distribution in source plane on high resolution grid
source_sim_1d_hd = source_model_class.surface_brightness(x_grid_src_1d, y_grid_src_1d, kwargs_source)
source_sim_hd = lenstro_util.array2image(source_sim_1d_hd)
# get the light distribution in source plane at the image plane resolution
source_sim = imageModel.source_surface_brightness(kwargs_source, unconvolved=True, de_lensed=True)
source_sim_1d = lenstro_util.image2array(source_sim)
# get an automatic mask that includes the lensed source light
threshold_noise = 5
image_mask_1d = np.zeros_like(image_sim_1d)
mask_indices = np.where(image_sim_1d > threshold_noise * background_rms)
image_mask_1d[mask_indices] = 1
image_mask = lenstro_util.array2image(image_mask_1d)
fig = plt.figure(figsize=(20, 4))
ax = plt.subplot2grid((1, 3), (0, 0), fig=fig)
ax.set_title("image plane, convolved")
im = ax.imshow(lin_scale(image_sim), origin='lower', cmap='cubehelix')
nice_colorbar(im)
ax = plt.subplot2grid((1, 3), (0, 1))
ax.set_title("source plane, unconvolved")
im = ax.imshow(lin_scale(source_sim), origin='lower', cmap=log_cmap('cubehelix', 0.03, 1))
nice_colorbar(im)
ax = plt.subplot2grid((1, 3), (0, 2))
ax.set_title("mask from threshold {}$\sigma$".format(threshold_noise))
im = ax.imshow(image_mask*image_sim, origin='lower', cmap='gray_r')
nice_colorbar(im)
#ax = plt.subplot2grid((1, 4), (0, 2))
#ax.set_title(r"$\alpha_x$")
#im = ax.imshow(alpha_x, origin='lower', cmap='seismic')
#nice_colorbar(im)
#ax = plt.subplot2grid((1, 4), (0, 3))
#ax.set_title(r"$\alpha_y$")
#im = ax.imshow(alpha_y, origin='lower', cmap='seismic')
#nice_colorbar(im)
plt.show()
fig.savefig("last_mock.png")
```
## Refinement step using starlets (pixel-based)
```
kwargs_numerics = {'supersampling_factor': 1, 'supersampling_convolution': False}
kwargs_data_joint = {
'multi_band_list': [[kwargs_data, kwargs_psf, kwargs_numerics]],
'multi_band_type': 'single-band-sparse',
}
kwargs_model = {
'lens_model_list': lens_model_list,
'source_light_model_list': ['STARLETS'],
}
kwargs_lens_wayoff = [{'theta_E': 1.65, 'gamma': 1.8, 'center_x': 0, 'center_y': 0, 'e1': 0, 'e2': 0}]
if start_wayoff:
kwargs_lens_init = kwargs_lens_wayoff
else:
kwargs_lens_init = kwargs_truth['kwargs_lens']
kwargs_lens_sigma = [{'theta_E': 0.1, 'gamma': 0.05, 'center_x': 0.05, 'center_y': 0.05, 'e1': 0.05, 'e2': 0.05}]
kwargs_lens_lower = [{'theta_E': 1.6, 'gamma': 1.7, 'center_x': -0.5, 'center_y': -0.5, 'e1': -0.5, 'e2': -0.5}]
kwargs_lens_upper = [{'theta_E': 2, 'gamma': 2.2, 'center_x': 0.5, 'center_y': 0.5, 'e1': 0.5, 'e2': 0.5}]
kwargs_lens_fixed = [{}]
for i in range(len(kwargs_lens)):
for fixed_name in mass_fixed_list:
kwargs_lens_fixed[i][fixed_name] = kwargs_lens[i][fixed_name]
if len(kwargs_lens_fixed[0]) == len(kwargs_lens[0]) and len(kwargs_lens_fixed[1]) == len(kwargs_lens[1]):
print("All parameters are fixed !")
raise
kwargs_source_init = [{'coeffs': 1}] # starlet coeffs that are optimized for
kwargs_source_sigma = [{}]
kwargs_source_lower = [{}]
kwargs_source_upper = [{}]
kwargs_source_fixed = [
{
'n_scales': 6, 'n_pixels': num_pix**2 * subgrid_res_source**2,
'scale': 1, 'center_x': 0, 'center_y': 0,
}
]
kwargs_special_init = {'delta_x_source_grid': 0, 'delta_y_source_grid': 0}
kwargs_special_sigma = {'delta_x_source_grid': delta_pix/4., 'delta_y_source_grid': delta_pix/4.}
kwargs_special_lower = {'delta_x_source_grid': -1, 'delta_y_source_grid': -1}
kwargs_special_upper = {'delta_x_source_grid': 1, 'delta_y_source_grid': 1}
kwargs_special_fixed = {}
kwargs_params = {
'lens_model': [kwargs_lens_init, kwargs_lens_sigma, kwargs_lens_fixed, kwargs_lens_lower, kwargs_lens_upper],
'source_model': [kwargs_source_init, kwargs_source_sigma, kwargs_source_fixed, kwargs_source_lower, kwargs_source_upper],
'special': [kwargs_special_init, kwargs_special_sigma, kwargs_special_fixed, kwargs_special_lower, kwargs_special_upper]
}
kwargs_init = {
'kwargs_lens': kwargs_lens_init,
'kwargs_source': kwargs_source_init,
'kwargs_special': kwargs_special_init,
}
kwargs_constraints = {
'solver_type': 'NONE',
'image_plane_source_list': [False],
'source_grid_offset': False, # sample over offset of source plane grid
}
kwargs_sparse_solver = {
'source_interpolation': 'bilinear',
'include_regridding_error': True,
'subgrid_res_source': subgrid_res_source,
'minimal_source_plane': True,
'fix_minimal_source_plane': True, # if False, update source plane grid size when mass model changes (!)
'min_num_pix_source': 130,
'min_threshold': 3,
'threshold_decrease_type': 'exponential',
'num_iter_source': 15,
'num_iter_weights': 3,
'verbose': False,
'show_steps': False,
'thread_count': 1,
}
kwargs_likelihood = {
'image_likelihood': True,
'check_bounds': True,
'kwargs_sparse_solver': kwargs_sparse_solver,
}
if use_threshold_mask:
kwargs_likelihood['image_likelihood_mask_list'] = [image_mask.astype(bool)]
fitting_seq = FittingSequence(kwargs_data_joint, kwargs_model, kwargs_constraints,
kwargs_likelihood, kwargs_params, verbose=True)
fitting_seq.param_class.print_setting()
fitting_list = [
['MCMC', {'n_burn': n_burn, 'n_run': n_run, 'walkerRatio': walker_ratio, 'sampler_type': 'EMCEE',
'sigma_scale': 1, 'threadCount': num_threads}],
]
chain_list = fitting_seq.fit_sequence(fitting_list)
# get MCMC chains
sampler_type, samples_mcmc, param_mcmc, dist_mcmc = chain_list[-1]
print("(num samples, num params) :", samples_mcmc.shape)
walker_ratio = fitting_list[0][1]['walkerRatio']
num_param_nonlinear = len(param_mcmc)
plt.plot(dist_mcmc)
plt.show()
for i in range(len(chain_list)):
chain_plot.plot_chain_list(chain_list, i, num_average=walker_ratio*num_param_nonlinear)
plt.show()
# best fit from MCMC
kwargs_result = fitting_seq.best_fit()
print(kwargs_result)
def corner_add_values_indic(fig, values, color='green', linewidth=1):
# Extract the axes
ndim = len(values)
axes = np.array(fig.axes).reshape((ndim, ndim))
# Loop over the diagonal
for i in range(ndim):
ax = axes[i, i]
ax.axvline(values[i], color=color, linewidth=linewidth)
# Loop over the histograms
for yi in range(ndim):
for xi in range(yi):
ax = axes[yi, xi]
ax.axvline(values[xi], color=color, linewidth=linewidth)
ax.axhline(values[yi], color=color, linewidth=linewidth)
ax.plot(values[xi], values[yi], color=color, marker='s')
# get init/best/true parameter values as list
init_params = fitting_seq.param_class.kwargs2args(**kwargs_init)
print("initial", init_params)
bestlogL_params = fitting_seq.param_class.kwargs2args(**kwargs_result)
print("best logL", bestlogL_params)
truth_params = fitting_seq.param_class.kwargs2args(**kwargs_truth)
print("truth", truth_params)
fig = corner.corner(samples_mcmc, labels=param_mcmc, show_titles=True, quantiles=[0.5], smooth=0.6, smooth1d=0.6)
corner_add_values_indic(fig, truth_params, color='green', linewidth=2)
corner_add_values_indic(fig, bestlogL_params, color='red', linewidth=1)
corner_add_values_indic(fig, init_params, color='gray', linewidth=1)
plt.show()
fig.savefig("last_corner.png")
# convergence by walkers
[fig] = plot_convergence_by_walker(samples_mcmc, param_mcmc, walker_ratio, verbose=True)
plt.show()
fig.savefig("last_mcmc_conv.png")
```
### Update Starlets parameters from best fit
```
multi_band_list = kwargs_data_joint['multi_band_list']
multi_band_type = kwargs_data_joint['multi_band_type']
likelihood_mask_list = kwargs_likelihood.get('image_likelihood_mask_list', None)
kwargs_sparse_solver = kwargs_likelihood['kwargs_sparse_solver']
im_sim = class_creator.create_im_sim(multi_band_list, multi_band_type, kwargs_model,
likelihood_mask_list=likelihood_mask_list,
kwargs_sparse_solver=kwargs_sparse_solver)
# compute starlets "sparse" parameters and update corresponding kwargs
model, model_error, _, _ = im_sim.image_linear_solve(**kwargs_result)
print(kwargs_result, kwargs_result['kwargs_source'][0]['amp'].shape)
reduced_residuals = im_sim.reduced_residuals(model)
source = im_sim.source_surface_brightness(kwargs_result['kwargs_source'], kwargs_lens=None,
unconvolved=True, de_lensed=True)
kwargs_source_result = kwargs_result['kwargs_source'][0]
starlets_class = Starlets(second_gen=False)
x_grid_hd, y_grid_hd = lenstro_util.make_grid(numPix=np.sqrt(kwargs_source_result['n_pixels']),
deltapix=kwargs_source_result['scale'])
source_hd = lenstro_util.array2image(starlets_class.function(x_grid_hd, y_grid_hd,
**kwargs_source_result))
fig, axes = plt.subplots(1, 4, figsize=(20, 4))
ax = axes[0]
im = ax.imshow(source, origin='lower', cmap=log_cmap('cubehelix', 0.03, 1))
nice_colorbar(im)
ax = axes[1]
im = ax.imshow(source_sim, origin='lower', cmap=log_cmap('cubehelix', 0.03, 1))
nice_colorbar(im)
ax = axes[2]
im = ax.imshow(model, origin='lower', cmap='cubehelix')
nice_colorbar(im)
ax = axes[3]
im = ax.imshow(reduced_residuals, origin='lower', cmap='bwr', vmin=-6, vmax=6)
nice_colorbar(im)
#plt.show()
fig.savefig("last_starlets_recon.png")
```
| true |
code
| 0.581125 | null | null | null | null |
|
# Discrete Fourier Transform in Python
This notebook is a quick refresher on how to perform FFT in python/scipy.
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft
```
We define:
- $N$: number of samples
- $f_s$: sampling frequency/rate in samples/second
```
N = 1000
f_s = 100
```
Period between samples $T_s$:
```
T_s = 1/f_s
print(T_s, "seconds")
print(T_s*1000, "ms")
```
Create time vector, each element corresponds to a measurement
```
t = np.linspace(0, T_s*N, N)
```
The signal which we are sampling:
\begin{align}
s(t) = 0.1 sin(2\pi 5t) + sin(2\pi 3t - 0.25\pi)
\end{align}
```
x_t = 0.1*np.sin(2*np.pi*5*t) + np.sin(2*np.pi*3*t-np.pi/4)
plt.figure(figsize=(15,5))
plt.plot(t, x_t)
plt.plot(t, x_t, "k+")
plt.xlabel("time [s]")
plt.xlim([0, 2])
plt.grid()
plt.title("Visualizing samples")
```
Note that we can describe the **period** of each sinus component in number of samples:
- $0.1 sin(2\pi 5t)$: **20** samples ($f=5Hz$ leads to $T=1/5Hz=200ms$ with $T_s = 10ms$, $T/T_s = 20$)
- $sin(2\pi 3t - 0.25\pi)$ : **33** samples
Alternatively we can express the frequency in the reciprocal:
- $0.1 sin(2\pi 5t)$: **1/20 = 0.05**
- $sin(2\pi 3t - 0.25\pi)$ : **1/33 = 0.0303**
Alternatively we can express the frequency relative to the number of samples $N=1000$:
- $0.1 sin(2\pi 5t)$: **1000/20 = 50**
- $sin(2\pi 3t - 0.25\pi)$ : **1000/33 = 30.30**
You can think of the last representation as a reference of the highest $T_s$ (or lowest $f_s$) we can extract from FFT. I.e. the FFT method cannot extract frequency information lower than $\frac{f_s}{2}$ (ignore the $\frac{1}{2}$ for now).
## FFT
We perform the FFT on the sample array, note that the time vector ${t}$ is not used in the `fft` call:
```
a_f = fft(x_t)
a_f.dtype
```
FFT returns a symmetric shape with positive frequencies on the right side and negative on the left:
```
plt.figure(figsize=(10,5))
plt.plot(np.abs(a_f)) # we take abs in order to get the magnitude of a complex number
plt.axvline(N//2, color="red", label="left: positive frequencies | right: negative, from high to low")
plt.xlabel("index k")
plt.legend();
```
The index $k$ represents a frequency component.
Because we are interested in positive frequencies for now we cut the returned array in half:
```
a_f_positive = a_f[:N//2]
a_f_positive.shape
```
Each element in `a_f` represents the real and imaginary part (amplitude $A_i$ and phase $\phi_i$) for a specific frequency $f_i$.
The "frequency" after the FFT is defined as $\frac{N}{s_i}$ in the period of specific sinus component. The period $s_i$ is expressed in number of samples.
I.e. a sinus component with a frequency of $5 Hz$ or period of $\frac{1}{5Hz} = 0.2s$ is $\frac{0.2s}{T_s} = \frac{0.2s}{0.01s} = 20$ samples long. Thus its magnitude peak should appear at $\frac{N}{s_i} = \frac{1000}{20} = 50$.
- $0.1 sin(2\pi 5t)$: low peak (because of $0.1$) at $k=50$
- $sin(2\pi 3t - 0.25\pi)$: greater peak at $k= 30.303 \approx 30$
```
plt.figure(figsize=(10,5))
plt.plot(np.abs(a_f_positive))
plt.xlim([0, 100])
plt.xticks(range(0, 101, 10))
plt.grid()
plt.xlabel("frequency in $k = N/s_i$")
```
In order to relate the sample-frequencies (as $N/1$) into time domain we need to convert the $k$ into frequencies as $1/s$.
\begin{align}
k = \frac{N}{s_i} = \frac{N}{T_i/T_s} = \frac{N f_i}{1/T_s} = \frac{N f_i}{f_s}
\end{align}
Our translation formula from $k$ to frequency is the following
\begin{align}
\Rightarrow f_i =& f_s\frac{k}{N}
\end{align}
```
f_i = np.arange(0, N//2)*f_s/N
plt.figure(figsize=(10,5))
plt.plot(f_i, np.abs(a_f_positive))
plt.grid()
plt.xlabel("frequency in $1/s$")
plt.xticks(range(0, f_s//2, 1));
plt.xlim([0, 10]);
```
We need to normalize the magnitude of the peaks by the factor of $\frac{2}{N}$:
```
plt.figure(figsize=(10,5))
plt.plot(f_i, 2/N*np.abs(a_f_positive))
plt.grid()
plt.xlabel("frequency in $1/s$ (Hz)")
plt.ylabel("amplitude [1]")
plt.xticks(range(0, f_s//2, 1));
plt.xlim([0, 10]);
plt.ylim([-0.2, 1.2]);
plt.title("Final DFT result.")
plt.text(3, 1.02, "$sin(2\pi 3t - 0.25\pi)$", fontdict={"size": 15})
plt.text(5, 0.12, "$0.1 sin(2\pi 5t)$", fontdict={"size": 15});
```
As you can see we found both sinus components.
## Phase
We could find the magnitudes and the frequencies of both signals but not the $45^\circ$ phase of the slower $3Hz$ signal.
In the previous section we saw that the result of the FFT algorithm is a complex array. Let's plot the real and imaginary parts relative to frequency.
```
plt.figure(figsize=(15, 5))
plt.subplot(2, 1, 1)
plt.title("real")
plt.plot(f_i, 2/N*np.real(a_f_positive))
plt.grid()
plt.xlim([0, 10])
plt.subplot(2, 1, 2)
plt.title("imag")
plt.plot(f_i, 2/N*np.imag(a_f_positive))
plt.grid()
plt.xlim([0, 10])
```
Lets calculate the angle of the complex number:
\begin{align}
\alpha = \text{arctan} \frac{imag}{real}
\end{align}
There is a handy function: `np.angle` which does it for us.
```
angle = np.angle(a_f_positive, deg=True)
# OR manually
# angle = np.arctan2(2/N*np.imag(a_f_positive),(2/N*np.real(a_f_positive)))*grad_to_degree_factor
```
and plot it again
```
plt.figure(figsize=(15, 10))
plt.subplot(3, 1, 1)
plt.ylabel("real-component [1]")
plt.plot(f_i, 2/N*np.real(a_f_positive))
plt.grid()
plt.xlim([0, 10])
plt.subplot(3, 1, 2)
plt.ylabel("imag component [1]")
plt.plot(f_i, 2/N*np.imag(a_f_positive))
plt.grid()
plt.xlim([0, 10])
plt.subplot(3, 1, 3)
plt.plot(f_i, angle)
plt.grid()
plt.ylabel("phase [°]")
plt.xlabel("frequency [Hz]")
plt.xlim([0, 10])
plt.scatter(f_i[[30, 50]], angle[[30, 50]], color="k")
plt.text(f_i[30] + 0.1 , angle[30], "%d°" % int(angle[30]))
plt.text(f_i[50] + 0.1 , angle[50], "%d°" % int(angle[50]))
plt.ylim([-150, 100])
```
The $5Hz$ sinus wave with zero phase has an $\alpha \approx -90^\circ$, since a sine wave is a $90^\circ$-shifted cos wave.
The $3Hz$ sinus component with $45^\circ$ phase has an $\alpha \approx -90^\circ-45^\circ = -135^\circ$
## FFT on complex numbers
Because within the multi-chirp FMCW algorithm we do a FFT on a series of complex numbers we want to make a simple example here.
Our example function of interest will be:
\begin{align}
f(t) = 0.25\text{sin}(2\pi 5 t + \phi) \\
\phi = \phi(t) = -\frac{\pi}{8}t = vt
\end{align}
The phase shift is time dependent in this example.
**Goal**: find parameter $v$ via FFT.
```
def f(t, phi=0):
return 0.25*np.sin(2*np.pi*5*t + phi)
```
Let's visualize how the sinus wave develops over time ...
```
t = np.linspace(0, 10, 10000)
plt.figure(figsize=(15,5))
plt.plot(t, f(t), label="$\phi=0$")
plt.plot(t, f(t, -np.pi/8*t), label="$\phi=-\pi/8 \cdot t$")
plt.xlim([0, 4])
plt.xlabel("$t$ [s]")
plt.grid()
plt.legend();
```
For the sake of our example we will run the FFT each $T_{cycle}$ seconds.
```
T_cycle = 2 # seconds
n_cycles = 200
f_cycle = 1/T_cycle
```
Per cycle FFT config
```
f_s = 100
T_s = 1/f_s
N = int(T_cycle/T_s)
print("Sample frequency:", f_s, "Hz")
print("Sample period:", T_s, "sec")
print("Number samples:", N)
```
We run FFT in each cycle and save the results in a list.
```
fft_cycle_results = list() # result list
# for each cycle
for c in range(n_cycles):
# determine start and end of a cycle
t_start = c*T_cycle
t_end = (c+1)*T_cycle
# sample the signal at according timesteps
t_sample = np.arange(t_start, t_end, T_s)
f_sample = f(t_sample, -np.pi/8*t_sample)
# run FFT and append results
fft_res = fft(f_sample)
fft_cycle_results.append(fft_res)
```
We cut the positive frequency range and normalize the amplitudes (see introdcutory example above).
```
fft_cycle_results = [2/N*r[:N//2] for r in fft_cycle_results]
freq = np.arange(0, N//2)*f_s/N
freq
```
**Note**: The FFT frequency resolution is at 1Hz. That's important because the frequency shift by $-\frac{1}{8}Hz$ introduced by $\phi(t)$ is not visible in the FFT!
The FFT will show a peak at 5Hz with a different phase each time.
Because the frequency is almost the same in each cycle, we expect the same behaviour in each result:
```
n_cycles_to_display = 4
fft_res_display = fft_cycle_results[:n_cycles_to_display]
fig, ax = plt.subplots(ncols=len(fft_res_display), figsize=(15, 3), sharex=True, sharey=True)
for i, ax, res in zip(range(n_cycles_to_display), ax, fft_res_display):
res_abs = np.abs(res)
ax.plot(freq, res_abs)
ax.grid(True)
ax.set_xlim([0, 10])
ax.set_xlabel("frequency [Hz]")
k = np.argmax(res_abs)
magn_max = res_abs[k]
freq_max = freq[k]
ax.set_title("Cycle %d:\n%.2f at %.2f Hz" % (i, magn_max, freq_max))
```
Looks fine for the first 4 cycles ... Let's look at all cycles by picking the frequency with max. magnitude from each cycle:
```
freq_list = list()
for res in fft_cycle_results:
res_abs = np.abs(res)
k = np.argmax(res_abs)
freq_list.append(freq[k])
plt.figure(figsize=(15,3))
plt.plot(freq_list)
plt.xlabel("cycle nr.")
plt.ylabel("frequency [Hz]")
plt.title("Frequency with max. peak in FFT domain vs. cycle");
```
It seems that the position (frequency) of the peaks remains **eqal**, despite the changing real and imaginary components.
Let's collect the max. frequency component from each cycle
```
cycle_max_list = list()
for res in fft_cycle_results:
# calc. the magnitude
res_abs = np.abs(res)
# find frequency index
k = np.argmax(res_abs)
cycle_max_list.append(res[k])
```
... and visualize the complex numbers:
```
n_cycles_to_display = 4
cycle_max_list_display = cycle_max_list[:n_cycles_to_display]
fig, ax = plt.subplots(ncols=len(cycle_max_list_display), figsize=(15, 30),
subplot_kw={'projection': "polar"}, sharey=True)
for i, ax, res in zip(range(n_cycles_to_display), ax, cycle_max_list_display):
ax.plot([0, np.angle(res)], [0, np.abs(res)], marker="o")
ax.text(np.angle(res)+0.1, np.abs(res), "%d°" % int(np.angle(res, deg=True)))
ax.set_ylim([0, 0.4])
ax.set_title("Cycle %d:\n" % (i, ))
```
We can observe that the angle moves in negative direction with $-45^\circ = T_{cycle}v = 2\frac{\pi}{8} = \pi/4$ per cycle.
### Solution via phase differences
Now we could calculate ange velocity by taking differences between cycles and put them relative to cycle duration:
```
angle_diff = np.diff(np.angle(cycle_max_list, deg=True))
angle_vel = angle_diff/T_cycle
print(angle_vel[:10])
```
Let's look at the parameter $v = -\frac{\pi}{8}$
```
v = -np.pi/8*360/(2*np.pi)
print(v)
```
Let's calculate the differences right (to remove the $157^\circ-(-157^\circ)$ effect).
```
angle_vel[angle_vel>0] -= 180
print("Angle velocities:", angle_vel[:10])
plt.figure(figsize=(15,3))
plt.plot(angle_vel)
plt.xlabel("cycle nr.")
plt.ylabel("°/s")
plt.title("angular velocity derived by cycle FFT phase differences")
plt.ylim([-40, 0]);
```
As you can see, the phases of the FFT output from each cycle give a hint over the phase velocity $v$ of the signal in time domain.
**Summary**: We found $v$!
### Solution via second FFT
The core idea of this alternative approach is to extract the periodic change of phase $\phi(t)$.
We can find the phase velocity via a **second FFT over the cycle results**, too. Consider the first FFT result as a measurement/sample for the second FFT.
Remember, those are our results (FFT-magnitude from the $5Hz$-component):
```
cycle_max_list[:5]
# here, we take only the positive side of fft
second_fft_res = fft(cycle_max_list)[:n_cycles//2]
second_fft_res[:5]
```
Like in the introductory example, each element of `second_fft_res` represents a frequency component.
```
freq_second = np.arange(0, n_cycles//2)*f_cycle/n_cycles
omega_second = 360*freq_second # same as 2*np.pi*
omega_second
plt.figure(figsize=(10,5))
plt.plot(omega_second, np.abs(second_fft_res))
plt.grid()
plt.xlabel("angle velocity $\omega$ [°/s]")
plt.xticks(range(0, 90, 5));
```
As you could see we could detect the phase change $v=22.5^{\circ}$ with a second FFT on the results of the first FFT.
| true |
code
| 0.558568 | null | null | null | null |
|
# COVID-19 Exploratory Data Analysis
> (Almost) Everything You Want To Know About COVID-19.
- author: Devakumar kp
- comments: true
- categories: [EDA]
- permalink: /corona-eda/
- toc: true
- image: images/copied_from_nb/covid-eda-2-1.png
These visualizations were made by [Devakumar kp](https://twitter.com/imdevskp). Original notebook is [here](https://www.kaggle.com/imdevskp/covid-19-analysis-viz-prediction-comparisons).
```
#hide
# essential libraries
import json
import random
from urllib.request import urlopen
# storing and anaysis
import numpy as np
import pandas as pd
# visualization
import matplotlib.pyplot as plt
import seaborn as sns
import plotly.express as px
import plotly.graph_objs as go
import plotly.figure_factory as ff
import folium
# color pallette
cnf = '#393e46' # confirmed - grey
dth = '#ff2e63' # death - red
rec = '#21bf73' # recovered - cyan
act = '#fe9801' # active case - yellow
# converter
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
# hide warnings
import warnings
warnings.filterwarnings('ignore')
# html embedding
from IPython.display import Javascript
from IPython.core.display import display, HTML
#hide
# importing datasets
url = 'https://raw.githubusercontent.com/imdevskp/covid_19_jhu_data_web_scrap_and_cleaning/master/covid_19_clean_complete.csv'
full_table = pd.read_csv(url,
parse_dates=['Date'])
full_table.head()
#hide
# cases
cases = ['Confirmed', 'Deaths', 'Recovered', 'Active']
# Active Case = confirmed - deaths - recovered
full_table['Active'] = full_table['Confirmed'] - full_table['Deaths'] - full_table['Recovered']
# replacing Mainland china with just China
full_table['Country/Region'] = full_table['Country/Region'].replace('Mainland China', 'China')
# filling missing values
full_table[['Province/State']] = full_table[['Province/State']].fillna('')
full_table[cases] = full_table[cases].fillna(0)
#hide
# cases in the ships
ship = full_table[full_table['Province/State'].str.contains('Grand Princess')|full_table['Province/State'].str.contains('Diamond Princess cruise ship')]
# china and the row
china = full_table[full_table['Country/Region']=='China']
row = full_table[full_table['Country/Region']!='China']
# latest
full_latest = full_table[full_table['Date'] == max(full_table['Date'])].reset_index()
china_latest = full_latest[full_latest['Country/Region']=='China']
row_latest = full_latest[full_latest['Country/Region']!='China']
# latest condensed
full_latest_grouped = full_latest.groupby('Country/Region')['Confirmed', 'Deaths', 'Recovered', 'Active'].sum().reset_index()
china_latest_grouped = china_latest.groupby('Province/State')['Confirmed', 'Deaths', 'Recovered', 'Active'].sum().reset_index()
row_latest_grouped = row_latest.groupby('Country/Region')['Confirmed', 'Deaths', 'Recovered', 'Active'].sum().reset_index()
```
# World-Wide Totals
```
#hide
temp = full_table.groupby(['Country/Region', 'Province/State'])['Confirmed', 'Deaths', 'Recovered', 'Active'].max()
# temp.style.background_gradient(cmap='Reds')
#hide_input
temp = full_table.groupby('Date')['Confirmed', 'Deaths', 'Recovered', 'Active'].sum().reset_index()
temp = temp[temp['Date']==max(temp['Date'])].reset_index(drop=True)
temp.style.background_gradient(cmap='Pastel1')
```
# Progression of Virus Over Time
```
#hide_input
# https://app.flourish.studio/visualisation/1571387/edit
HTML('''<div class="flourish-embed flourish-bar-chart-race" data-src="visualisation/1571387"><script src="https://public.flourish.studio/resources/embed.js"></script></div>''')
```
## Cumalitive Outcomes
```
#hide
temp = full_table.groupby('Date')['Recovered', 'Deaths', 'Active'].sum().reset_index()
temp = temp.melt(id_vars="Date", value_vars=['Recovered', 'Deaths', 'Active'],
var_name='Case', value_name='Count')
temp.head()
fig = px.area(temp, x="Date", y="Count", color='Case',
title='Cases over time', color_discrete_sequence = [rec, dth, act])
fig.write_image('covid-eda-2-1.png')
```

## Recovery and Mortality Rate
```
#hide
temp = full_table.groupby('Date').sum().reset_index()
# adding two more columns
temp['No. of Deaths to 100 Confirmed Cases'] = round(temp['Deaths']/temp['Confirmed'], 3)*100
temp['No. of Recovered to 100 Confirmed Cases'] = round(temp['Recovered']/temp['Confirmed'], 3)*100
# temp['No. of Recovered to 1 Death Case'] = round(temp['Recovered']/temp['Deaths'], 3)
temp = temp.melt(id_vars='Date', value_vars=['No. of Deaths to 100 Confirmed Cases', 'No. of Recovered to 100 Confirmed Cases'],
var_name='Ratio', value_name='Value')
fig = px.line(temp, x="Date", y="Value", color='Ratio', log_y=True,
title='Recovery and Mortality Rate Over The Time', color_discrete_sequence=[dth, rec])
fig.write_image('covid-eda-2-2.png')
```

## No. of Places To Which COVID-19 spread
```
#hide
c_spread = china[china['Confirmed']!=0].groupby('Date')['Province/State'].unique().apply(len)
c_spread = pd.DataFrame(c_spread).reset_index()
fig = px.line(c_spread, x='Date', y='Province/State', text='Province/State',
title='Number of Provinces/States/Regions of China to which COVID-19 spread over the time',
color_discrete_sequence=[cnf,dth, rec])
fig.update_traces(textposition='top center')
fig.write_image('covid-eda-3-1.png')
# ------------------------------------------------------------------------------------------
spread = full_table[full_table['Confirmed']!=0].groupby('Date')['Country/Region'].unique().apply(len)
spread = pd.DataFrame(spread).reset_index()
fig = px.line(spread, x='Date', y='Country/Region', text='Country/Region',
title='Number of Countries/Regions to which COVID-19 spread over the time',
color_discrete_sequence=[cnf,dth, rec])
fig.update_traces(textposition='top center')
fig.write_image('covid-eda-3-2.png')
```


# Maps
```
#hide
# Confirmed
fig = px.choropleth(full_latest_grouped, locations="Country/Region",
locationmode='country names', color="Confirmed",
hover_name="Country/Region", range_color=[1,7000],
color_continuous_scale="aggrnyl",
title='Countries with Confirmed Cases')
fig.update(layout_coloraxis_showscale=False)
fig.write_image('covid-eda-1-1.png')
#hide
# Deaths
fig = px.choropleth(full_latest_grouped[full_latest_grouped['Deaths']>0],
locations="Country/Region", locationmode='country names',
color="Deaths", hover_name="Country/Region",
range_color=[1,50], color_continuous_scale="agsunset",
title='Countries with Deaths Reported')
fig.update(layout_coloraxis_showscale=False)
fig.write_image('covid-eda-1-2.png')
```


# Top 20 Countries
```
#hide
flg = full_latest_grouped
flg.head()
#hide
fig = px.bar(flg.sort_values('Confirmed', ascending=False).head(20).sort_values('Confirmed', ascending=True),
x="Confirmed", y="Country/Region", title='Confirmed Cases', text='Confirmed', orientation='h',
width=700, height=700, range_x = [0, max(flg['Confirmed'])+10000])
fig.update_traces(marker_color=cnf, opacity=0.6, textposition='outside')
fig.write_image('covid-eda-4-1.png')
#hide
fig = px.bar(flg.sort_values('Deaths', ascending=False).head(20).sort_values('Deaths', ascending=True),
x="Deaths", y="Country/Region", title='Deaths', text='Deaths', orientation='h',
width=700, height=700, range_x = [0, max(flg['Deaths'])+500])
fig.update_traces(marker_color=dth, opacity=0.6, textposition='outside')
fig.write_image('covid-eda-4-2.png')
#hide
fig = px.bar(flg.sort_values('Recovered', ascending=False).head(20).sort_values('Recovered', ascending=True),
x="Recovered", y="Country/Region", title='Recovered', text='Recovered', orientation='h',
width=700, height=700, range_x = [0, max(flg['Recovered'])+10000])
fig.update_traces(marker_color=rec, opacity=0.6, textposition='outside')
fig.write_image('covid-eda-4-3.png')
#hide
fig = px.bar(flg.sort_values('Active', ascending=False).head(20).sort_values('Active', ascending=True),
x="Active", y="Country/Region", title='Active', text='Active', orientation='h',
width=700, height=700, range_x = [0, max(flg['Active'])+3000])
fig.update_traces(marker_color=act, opacity=0.6, textposition='outside')
fig.write_image('covid-eda-4-4.png')
#hide
# (Only countries with more than 100 case are considered)
flg['Mortality Rate'] = round((flg['Deaths']/flg['Confirmed'])*100, 2)
temp = flg[flg['Confirmed']>100]
temp = temp.sort_values('Mortality Rate', ascending=False)
fig = px.bar(temp.sort_values('Mortality Rate', ascending=False).head(15).sort_values('Mortality Rate', ascending=True),
x="Mortality Rate", y="Country/Region", text='Mortality Rate', orientation='h',
width=700, height=600, range_x = [0, 8], title='No. of Deaths Per 100 Confirmed Case')
fig.update_traces(marker_color=act, opacity=0.6, textposition='outside')
fig.write_image('covid-eda-4-5.png')
```





# Composition of Cases
```
#hide_input
fig = px.treemap(full_latest.sort_values(by='Confirmed', ascending=False).reset_index(drop=True),
path=["Country/Region", "Province/State"], values="Confirmed", height=700,
title='Number of Confirmed Cases',
color_discrete_sequence = px.colors.qualitative.Prism)
fig.data[0].textinfo = 'label+text+value'
fig.write_image('covid-eda-8-1.png')
fig = px.treemap(full_latest.sort_values(by='Deaths', ascending=False).reset_index(drop=True),
path=["Country/Region", "Province/State"], values="Deaths", height=700,
title='Number of Deaths reported',
color_discrete_sequence = px.colors.qualitative.Prism)
fig.data[0].textinfo = 'label+text+value'
fig.write_image('covid-eda-8-2.png')
```


# Epidemic Span
Note : In the graph, last day is shown as one day after the last time a new confirmed cases reported in the Country / Region
```
#hide_input
# first date
# ----------
first_date = full_table[full_table['Confirmed']>0]
first_date = first_date.groupby('Country/Region')['Date'].agg(['min']).reset_index()
# first_date.head()
from datetime import timedelta
# last date
# ---------
last_date = full_table.groupby(['Country/Region', 'Date', ])['Confirmed', 'Deaths', 'Recovered']
last_date = last_date.sum().diff().reset_index()
mask = last_date['Country/Region'] != last_date['Country/Region'].shift(1)
last_date.loc[mask, 'Confirmed'] = np.nan
last_date.loc[mask, 'Deaths'] = np.nan
last_date.loc[mask, 'Recovered'] = np.nan
last_date = last_date[last_date['Confirmed']>0]
last_date = last_date.groupby('Country/Region')['Date'].agg(['max']).reset_index()
# last_date.head()
# first_last
# ----------
first_last = pd.concat([first_date, last_date[['max']]], axis=1)
# added 1 more day, which will show the next day as the day on which last case appeared
first_last['max'] = first_last['max'] + timedelta(days=1)
# no. of days
first_last['Days'] = first_last['max'] - first_last['min']
# task column as country
first_last['Task'] = first_last['Country/Region']
# rename columns
first_last.columns = ['Country/Region', 'Start', 'Finish', 'Days', 'Task']
# sort by no. of days
first_last = first_last.sort_values('Days')
# first_last.head()
# visualization
# --------------
# produce random colors
clr = ["#"+''.join([random.choice('0123456789ABC') for j in range(6)]) for i in range(len(first_last))]
#plot
fig = ff.create_gantt(first_last, index_col='Country/Region', colors=clr, show_colorbar=False,
bar_width=0.2, showgrid_x=True, showgrid_y=True, height=1600,
title=('Gantt Chart'))
fig.write_image('covid-eda-9-1.png')
```

# China vs. Not China
```
#hide
# In China
temp = china.groupby('Date')['Confirmed', 'Deaths', 'Recovered'].sum().diff()
temp = temp.reset_index()
temp = temp.melt(id_vars="Date",
value_vars=['Confirmed', 'Deaths', 'Recovered'])
fig = px.bar(temp, x="Date", y="value", color='variable',
title='In China',
color_discrete_sequence=[cnf, dth, rec])
fig.update_layout(barmode='group')
fig.write_image('covid-eda-10-1.png')
#-----------------------------------------------------------------------------
# ROW
temp = row.groupby('Date')['Confirmed', 'Deaths', 'Recovered'].sum().diff()
temp = temp.reset_index()
temp = temp.melt(id_vars="Date",
value_vars=['Confirmed', 'Deaths', 'Recovered'])
fig = px.bar(temp, x="Date", y="value", color='variable',
title='Outside China',
color_discrete_sequence=[cnf, dth, rec])
fig.update_layout(barmode='group')
fig.write_image('covid-eda-10-2.png')
#hide
def from_china_or_not(row):
if row['Country/Region']=='China':
return 'From China'
else:
return 'Outside China'
temp = full_table.copy()
temp['Region'] = temp.apply(from_china_or_not, axis=1)
temp = temp.groupby(['Region', 'Date'])['Confirmed', 'Deaths', 'Recovered']
temp = temp.sum().diff().reset_index()
mask = temp['Region'] != temp['Region'].shift(1)
temp.loc[mask, 'Confirmed'] = np.nan
temp.loc[mask, 'Deaths'] = np.nan
temp.loc[mask, 'Recovered'] = np.nan
fig = px.bar(temp, x='Date', y='Confirmed', color='Region', barmode='group',
text='Confirmed', title='Confirmed', color_discrete_sequence= [cnf, dth, rec])
fig.update_traces(textposition='outside')
fig.write_image('covid-eda-10-3.png')
fig = px.bar(temp, x='Date', y='Deaths', color='Region', barmode='group',
text='Confirmed', title='Deaths', color_discrete_sequence= [cnf, dth, rec])
fig.update_traces(textposition='outside')
fig.update_traces(textangle=-90)
fig.write_image('covid-eda-10-4.png')
#hide
gdf = full_table.groupby(['Date', 'Country/Region'])['Confirmed', 'Deaths', 'Recovered'].max()
gdf = gdf.reset_index()
temp = gdf[gdf['Country/Region']=='China'].reset_index()
temp = temp.melt(id_vars='Date', value_vars=['Confirmed', 'Deaths', 'Recovered'],
var_name='Case', value_name='Count')
fig = px.bar(temp, x="Date", y="Count", color='Case', facet_col="Case",
title='China', color_discrete_sequence=[cnf, dth, rec])
fig.write_image('covid-eda-10-5.png')
temp = gdf[gdf['Country/Region']!='China'].groupby('Date').sum().reset_index()
temp = temp.melt(id_vars='Date', value_vars=['Confirmed', 'Deaths', 'Recovered'],
var_name='Case', value_name='Count')
fig = px.bar(temp, x="Date", y="Count", color='Case', facet_col="Case",
title='ROW', color_discrete_sequence=[cnf, dth, rec])
fig.write_image('covid-eda-10-6.png')
```





# Data By Country
### Top 50 Countries By Confirmed Cases
```
#hide_input
temp_f = full_latest_grouped.sort_values(by='Confirmed', ascending=False).head(50)
temp_f = temp_f.reset_index(drop=True)
temp_f.style.background_gradient(cmap='Reds')
```
### Top 25 Countries By Deaths Reported
```
#hide_input
temp_flg = temp_f[temp_f['Deaths']>0][['Country/Region', 'Deaths']].head(25)
temp_flg.sort_values('Deaths', ascending=False).reset_index(drop=True).style.background_gradient(cmap='Reds')
```
## Top 25 Chinese Provinces By Confirmed Cases
```
#hide_input
temp_f = china_latest_grouped[['Province/State', 'Confirmed', 'Deaths', 'Recovered']]
temp_f = temp_f.sort_values(by='Confirmed', ascending=False)
temp_f = temp_f.reset_index(drop=True)
temp_f.style.background_gradient(cmap='Pastel1_r')
```
# Related Work
1. https://www.kaggle.com/imdevskp/mers-outbreak-analysis
2. https://www.kaggle.com/imdevskp/sars-2003-outbreak-analysis
3. https://www.kaggle.com/imdevskp/western-africa-ebola-outbreak-analysis
| true |
code
| 0.417242 | null | null | null | null |
|
```
from __future__ import print_function # to use Python 3 features in Python 2
%matplotlib inline
import matplotlib as mpl
from matplotlib import pyplot as plt
import numpy as np
from astropy import constants as const
```
# Line Plot
```
def gaussian(x, sigma=2):
y = (2*np.pi*sigma**2)**-0.5 * np.exp(- x**2 / (2 * sigma**2))
return y
x = np.linspace(-10,10)
y = gaussian(x)
plt.plot(x, y, label="Gaussian")
plt.title("Sample Plot #1")
plt.xlabel("x [arbitrary units]")
plt.ylabel("y [arbitrary units]")
plt.legend(loc="best")
plt.yscale("log")
```
# Scatter Plot
```
import sys
sys.path.insert(0, "../day2") # to access exoplanets.py
import exoplanets
exoplanets.download_data()
data = exoplanets.parse_data()
data.dtype.names
# pull up `plt.errorbar` documentation
plt.errorbar?
planet_distances = data["pl_orbsmax"]
planet_distances_err = np.array([data["pl_orbsmaxerr1"],
data["pl_orbsmaxerr2"] * -1])
planet_masses = data["pl_bmassj"] *(const.M_jup / const.M_earth)
planet_masses_err = np.array([data["pl_bmassjerr1"],
data["pl_bmassjerr2"] *-1])*(const.M_jup / const.M_earth)
plt.errorbar(planet_distances,
planet_masses,
fmt=".",
xerr = planet_distances_err,
yerr = planet_masses_err)
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Distance to the star (AU)")
plt.ylabel("Planet mass ($M_E$)")
plt.xlim(10**-2, 10**4)
plt.ylim(10**-2, 10**4)
```
# Subplots
```
N_samples = 1000
lambda_1 = 1.5
lambda_2 = 5.0
poisson_samples_1 = np.random.poisson(lam=lambda_1, size=N_samples)
poisson_samples_2 = np.random.poisson(lam=lambda_2, size=N_samples)
bin_edges = np.arange(-.5, 11.5)
f, (ax1, ax2) = plt.subplots(1,2)
ax1.hist(poisson_samples_1, bins = bin_edges)
ax2.hist(poisson_samples_2, bins = bin_edges)
ax1.set_xlim(bin_edges.min(), bin_edges.max())
ax2.set_xlim(bin_edges.min(), bin_edges.max())
ax1.set_title("mean = " + str(lambda_1))
ax2.set_title("mean = " + str(lambda_2))
```
### Seaborn distribution plotting:
```
rc_orig = mpl.rcParams.copy()
import seaborn as sns
sns.set_style(rc = rc_orig) # keep matplotlib default aesthetics
sns.distplot?
# creates a histogram, along with a "KDE" curve,
# which estimates the shape of the distribution
f, (ax1, ax2) = plt.subplots(1,2)
sns.distplot(poisson_samples_1,
bins=bin_edges,
kde_kws={"bw":1}, # set smoothing width of KDE
ax=ax1)
sns.distplot(poisson_samples_2,
bins=bin_edges,
kde_kws={"bw":1}, # set smoothing width of KDE
ax=ax2)
ax1.set_xlim(bin_edges.min(), bin_edges.max())
ax2.set_xlim(bin_edges.min(), bin_edges.max())
ax1.set_title("mean = " + str(lambda_1))
ax2.set_title("mean = " + str(lambda_2))
```
# 2D hist
```
means = [1,2]
covariances = [[5,1],[1,1]]
data1 = np.random.multivariate_normal(mean=means, cov=covariances, size=100000)
means = [6.75, 4.5]
data2 = np.random.multivariate_normal(mean=means, cov=covariances, size=100000)
data = np.append(data1, data2, axis=0)
data = data.T
plt.scatter(data[0], data[1])
plt.hist2d(data[0], data[1], bins=100, normed=True)
plt.colorbar(label="density of points")
```
| true |
code
| 0.783129 | null | null | null | null |
|
## Importação de Bibliotecas
```
import numpy as np
import pandas as pd
import seaborn as sns
import missingno as msno
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
```
## Visualizando os dados
Importação dos Datasets obtidos no site da Policia Rodoviaria Federal
https://antigo.prf.gov.br/dados-abertos-acidentes
```
df_17 = pd.read_excel('acidentes2017.xlsx')
df_18 = pd.read_excel('acidentes2018.xlsx')
df_19 = pd.read_excel('acidentes2019.xlsx')
df_20 = pd.read_excel('acidentes2020.xlsx')
```
Verificação dos datasets que iremos utilizar
```
df_17.info()
df_18.info()
df_19.info()
df_20.info()
```
Criação de uma Coluna em cada Dataset contendo o Ano da ocorrência
```
df_17['ano']=2017
df_18['ano']=2018
df_19['ano']=2019
df_20['ano']=2020
```
Criação de um único Dataset
```
df_17_20 = pd.concat([df_17,df_18,df_19,df_20])
```
Exportação do Dataset unificado com o nome **df_17_20.csv**
```
df_17_20.to_csv('df_17_20.csv',index=False)
```
# Corrigindo o Latilon
A correção do latilon foi feita através do notebook: Crrecao_Latilon devido ao tamanho do código;
Como saíde do Correcao Latilon = 'df_17_20_v02.csv' que iremos resgatar
'df_17_20' é um backup quando nao foi considerado a utilização do latilon
## Analisando dados
Verificando as informações do Dataset
```
df_17_20_indv = pd.read_csv('df_17_20_v02.csv')
df_17_20_indv.info()
```
Verificando Colunas
```
df_17_20_indv.columns
```
Criando uma nova variável com as colunas que iremos utilizar, e recebendo o nome de **df_17_20_indv_cut**
```
df_17_20_indv_cut = df_17_20_indv[['id','data_inversa', 'dia_semana', 'horario', 'uf', 'causa_acidente', 'tipo_acidente',
'classificacao_acidente', 'fase_dia',
'condicao_metereologica', 'tipo_pista', 'tracado_via', 'uso_solo',
'tipo_veiculo', 'ano_fabricacao_veiculo',
'tipo_envolvido', 'idade', 'sexo', 'ilesos',
'mortos', 'latitude', 'longitude', 'ano']].copy()
```
Na nova variável, decidimos agrupar a coluna de feridos leves e feridos graves em uma única coluna, onde a mesma recebe o nome de *feridos_cal*
```
df_17_20_indv_cut['feridos_cal'] = df_17_20_indv['feridos_leves'] + df_17_20_indv['feridos_graves']
```
Como instrução presente no relatorio da Policia Rodoviaria Federal, quando o trecho possui asfalto, o mesmo recebe Sim, e quando não possui Asfalto, recebe o nome Não. Devido a este fator, decidimos substituir os valores escritos como *Sim* por *'Urbano'* e os com o valor igual a *Não* por *'Rural'*
```
df_17_20_indv_cut.loc[df_17_20_indv_cut['uso_solo']=='Sim','uso_solo']='Urbano'
df_17_20_indv_cut.loc[df_17_20_indv_cut['uso_solo']=='Não','uso_solo']='Rural'
df_17_20_indv_cut.sample(9)
```
Verificação de valores únicos
```
df_17_20_indv_cut.nunique()
```
Verificação dos Dados mais presentes nas Colunas
```
df_17_20_indv_cut['causa_acidente'].value_counts()
df_17_20_indv_cut['tipo_acidente'].value_counts()
df_17_20_indv_cut['classificacao_acidente'].value_counts()
df_17_20_indv_cut['fase_dia'].value_counts()
df_17_20_indv_cut['condicao_metereologica'].value_counts()
```
Como possuimos valores "*Ignorado"*, decidimos substitui-los por Nulo
```
df_17_20_indv_cut['condicao_metereologica'].replace('Ignorado',np.nan,inplace=True)
df_17_20_indv_cut['tipo_pista'].value_counts()
df_17_20_indv_cut['tracado_via'].value_counts()
```
Como possuimos valores "Não Informado", decidimos substitui-los por Nulo
```
df_17_20_indv_cut['tracado_via'].replace('Não Informado',np.nan,inplace=True)
df_17_20_indv_cut['uso_solo'].value_counts()
df_17_20_indv_cut['tipo_veiculo'].value_counts()
```
Como possuimos valores "Não Informado" e "Outros", decidimos substitui-los por Nulo
```
df_17_20_indv_cut['tipo_veiculo'].replace('Não Informado',np.nan,inplace=True)
df_17_20_indv_cut['tipo_veiculo'].replace('Outros',np.nan,inplace=True)
df_17_20_indv_cut['ano_fabricacao_veiculo'].value_counts()
```
Verificação dos dados dos Anos de Frabricação com a ajuda do Box Plot
```
sns.boxplot(df_17_20_indv_cut['ano_fabricacao_veiculo'])
df_17_20_indv_cut['tipo_envolvido'].value_counts()
```
Como a pergunta do nosso projeto se refere ao acidente, não vimos motivos deixar os dados da Testemunha no conjunto de dados, pois a mesma não participa ou influencia na ação. Outro ponto, como possuimos apenas 4 dados "Não Informado", decidimos retira-los.
```
df_17_20_indv_cut.drop(df_17_20_indv_cut.index[df_17_20_indv_cut['tipo_envolvido'] == 'Testemunha'], inplace = True)
df_17_20_indv_cut.drop(df_17_20_indv_cut.index[df_17_20_indv_cut['tipo_envolvido'] == 'Não Informado'], inplace = True)
df_17_20_indv_cut['tipo_envolvido'].value_counts()
df_17_20_indv_cut['idade'].value_counts()
```
Verificação da 'idade' com auxilio da ferramenta Box Plot
```
sns.boxplot(df_17_20_indv_cut['idade'])
```
Como podemos ver, possuimos valores errados, onde é possivel perceber dados mostrando idades superiores a 500.
Assim, utilizamos a idade da pessoa mais velha do mundo (117 anos) para ser nossa idade de corte
```
df_17_20_indv_cut.loc[df_17_20_indv_cut.idade>117,'idade'] = np.nan # Considerando outliers como faltantes...
df_17_20_indv_cut.loc[df_17_20_indv_cut.idade<0,'idade'] = np.nan # Considerando outliers como faltantes...
df_17_20_indv_cut['sexo'].value_counts()
```
Como possuimos valores iguais a "Não Informado" e "Ignorado", ambos foram substituido por valores Nulos
```
df_17_20_indv_cut['sexo'].replace('Não Informado',np.nan,inplace=True)
df_17_20_indv_cut['sexo'].replace('Ignorado',np.nan,inplace=True)
df_17_20_indv_cut['sexo'].value_counts()
df_17_20_indv_cut['ilesos'].value_counts()
df_17_20_indv_cut['mortos'].value_counts()
df_17_20_indv_cut['ano'].value_counts()
df_17_20_indv_cut['feridos_cal'].value_counts()
```
## Substituindo os Valores Nulos
**Variaveis Numéricas **
Como possuimos valores nulos na coluna "ano_fabricacao_veiculo", decidimos preencher esses dados com a média do ano presente no coluna.
Coluna *ano_fabricacao_veiculo*
```
df_17_20_indv_cut['ano_fabricacao_veiculo'].fillna(df_17_20_indv_cut['ano_fabricacao_veiculo'].mean(),inplace=True)
df_17_20_indv_cut['ano_fabricacao_veiculo'].isnull().sum()
```
Coluna *idade*
```
sns.boxplot(df_17_20_indv_cut['idade'])
df_17_20_indv_cut['idade'].isnull().sum()
```
Preenchendo os dados faltantes da coluna, com a média de valores presentes na coluna 'idade'.
```
df_17_20_indv_cut['idade'].fillna(df_17_20_indv_cut['idade'].mean(),inplace=True)
df_17_20_indv_cut['idade'].isnull().sum()
df_17_20_indv_cut.isnull().sum()
```
Com isso, podemos perceber que grande parte dos valores nulos/faltantes foram corrigidos, porém possuimos variaveis nominais que estão faltando no nosso dataset.
```
df_17_20_indv_cut.to_csv('df_ind.csv',index=False)
'''Agrupamento de dados e seleção de principais colunas a serem analisadas (2017-2020).
id 0 - Não Alterado
dia_semana 0 - Não Alterado
horario 0 - Não Alterado
uf 0 - Não Alterado
causa_acidente 0 - Não Alterado
tipo_acidente 0 - Não Alterado
classificacao_acidente 0 - Não Alterado
fase_dia 0 - Não Alterado
condicao_metereologica 8597 - Ignorados -> np.nan
tipo_pista 0 - Não Alterado
tracado_via 66609 - Não Informado - np.nan
uso_solo 0 - Sim-> Urbano Não-> Rural
tipo_veiculo 2645 - Outros e Não Informados -> np.nan
ano_fabricacao_veiculo 0 - np.nan - > médias dos anos de fabricação
tipo_envolvido 0 - Não informado e Testemunha -> drop do dataframe
idade 0 - 0 < idade < 117 | outliers -> np.nan -> média de idades
sexo 28618 - Não informado e Ignorados -> np.nan
ilesos 0 - Não Alterado
mortos 0 - Não Alterado
ano 0 - Criado para rastreamento
feridos_cal 0 - feridos_cal = feridos_leves + feridos_graves (criado)
'''
msno.matrix(df_17_20_indv_cut)
```
**Variaveis Nominais **
```
df_ind = pd.read_csv('df_ind.csv')
df_ind.info()
def cat_plot(dataframe):
import matplotlib.pyplot as plt
import seaborn as sns
for i in dataframe.columns:
plt.figure(figsize=(10,10))
sns.barplot(x=dataframe[i].value_counts().index ,y = dataframe[i].value_counts())
plt.xticks(rotation=90);
'''Melhoria de colocar subplot em um grid por exemplo 2 colunas e 10 linhas'''
# fig, axes = plt.subplots(10, 2, figsize=(25,100), sharey=True)
#
# sns.barplot(ax=axes[0,0],x=df_17_20['dia_semana'].value_counts().index ,y = df_17_20['dia_semana'].value_counts())
# plt.xticks(rotation=90);
#
# sns.barplot(ax=axes[0,1],x=df_17_20['tipo_pista'].value_counts().index ,y = df_17_20['tipo_pista'].value_counts())
# plt.xticks(rotation=90);
```
Como é possivel observar no gráfico abaixo, possuimos diversas variáveis nulas. Poderiamos, para solucionar esse problema, apenas dropar os valores, porém o gráfico nos mostra que grande parte dos dados faltantes não possuem relação com a falta de outras colunas, o que iria gerar uma perda grande de dados no nosso dataset. Assim sendo, optamos por tratar esses dados.
```
# https://github.com/ResidentMario/missingno
msno.matrix(df_ind)
msno.bar(df_ind)
msno.heatmap(df_ind)
```
Verificando as colunas que estão com dados faltantes.
```
df_ind.isnull().sum()
```
Com auxílio do grafico de barras, decidimos plotar os grafícos com as variaveis presentes no dataset, tanto para *condicao_metereologica* quanto *veiculos*.
```
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
plt.setp( ax1.xaxis.get_majorticklabels(),rotation=90)
plt.setp( ax2.xaxis.get_majorticklabels(),rotation=90)
sns.barplot(ax=ax1,x=df_ind['condicao_metereologica'].value_counts().index ,y = df_ind['condicao_metereologica'].value_counts())
sns.barplot(ax=ax2,x=df_ind['tipo_veiculo'].value_counts().index ,y = df_ind['tipo_veiculo'].value_counts())
```
Após análise dos graficos, é possivel avaliar alguns pontos:
Na Coluna condicao_metereologica:
1. Possuimos 8597 dados faltantes
Isso gera um valor menor que 1,5 % do nosso dataset (8597 / 623089). Sendo assim, decidos dropa-los já que sua margem de dados faltantes ser baixa.
Na Coluna veiculo:
2. Possuimos 2645 dados faltantes
Isso gera um valor menor que 0,42 % do nosso dataset (2645 / 623089). Sendo assim, decidos também dropa-los já que sua margem de dados faltantes ser baixa.
No final, iremos ter retirado 1,8 % do nosso dataset, sendo que os dados retirados estão distribuidos entre os anos.
623089 -> 611956
```
df_ind.dropna(subset=['condicao_metereologica','tipo_veiculo'],inplace=True)
df_ind.isnull().sum()
```
Em relação as colunas tracado_via quanto sexo, possuimos uma quantidade de dados relevantes, e os mesmos serão tratados. Assim, chegamos na conclusão de substituir os dados faltantes de forma igualitária, onde os dados faltantes irão receber proporcionalmente valores conforme os já preenchidos corretamente (não nulos).
Coluna *tracado_via*
```
sns.barplot(x=df_ind['classificacao_acidente'].value_counts().index ,y = df_ind['classificacao_acidente'].value_counts())
plt.xticks(rotation=90);
sns.barplot(x=df_ind['tracado_via'].value_counts().index ,y = df_ind['tracado_via'].value_counts())
plt.xticks(rotation=90);
# tracado_via 11 % subistituir proporcionalmente ?
```
Proporção de dados presentes no dataset:
```
round(df_ind['tracado_via'].value_counts()/df_ind['tracado_via'].count()*100)
```
Sabendo a proporção de dados presentes no dataset, precisamos saber qual será o valor necéssario em cada variável para continuar com a mesma proporção. Sabendo que teremos 65676 dados para serem substituidos.
```
round(df_ind['tracado_via'].value_counts()/df_ind['tracado_via'].count()*65435)
```
Criamos um nova variavel, para receber as mudanças, que receberá o nome temp.
```
temp = df_ind.copy()
temp.isnull().sum()
sns.barplot(x=temp['tracado_via'].value_counts().index ,y = temp['tracado_via'].value_counts())
plt.xticks(rotation=90);
```
Então, para resolver o problema, foi desenvolvido uma função com a intenção de substituir os valores de forma aleatória no nosso dataset, para assim, não ser gerado nenhum viés durante a reposição de dados
```
def replace_randomly_nan(df_to_replace,column,new_value,size_to_replace):
df_sample_na = df_to_replace.loc[df_to_replace[column].isnull(),column].sample(size_to_replace).copy()
for i in df_sample_na.index:
#print(i)
df_to_replace.loc[df_to_replace.index == i,column] = new_value
replace_randomly_nan(temp,'tracado_via','Reta',45261)
```
Teste da função para verificar se a função preencheu os 45261 dados de forma correta.
```
temp.isnull().sum()
```
Como nossa função obteve sucesso, a mesma foi utilizada para as outras variáveis. Onde era preciso substituir:
* Curva 11320.0
* Interseção de vias 3571.0
* Desvio Temporário 2089.0
* Rotatória 1381.0
* Retorno Regulamentado 835.0
* Viaduto 495.0
* Ponte 411.0
* Túnel 70.0 4 71.0
```
replace_randomly_nan(temp,'tracado_via','Curva',11320)
replace_randomly_nan(temp,'tracado_via','Interseção de vias',3571)
replace_randomly_nan(temp,'tracado_via','Desvio Temporário',2089)
replace_randomly_nan(temp,'tracado_via','Rotatória',1381)
replace_randomly_nan(temp,'tracado_via','Retorno Regulamentado',835)
replace_randomly_nan(temp,'tracado_via','Viaduto',495)
replace_randomly_nan(temp,'tracado_via','Ponte',411)
replace_randomly_nan(temp,'tracado_via','Túnel',72)
```
Verificação da proporção de dados.
```
df_ind['tracado_via'].value_counts()/df_ind['tracado_via'].count()*100
```
Como é possivel ver, continuamos com a mesma proporção de dados.
```
fig, (ax3, ax4) = plt.subplots(1, 2, figsize=(12, 5))
plt.setp( ax3.xaxis.get_majorticklabels(),rotation=90)
plt.setp( ax4.xaxis.get_majorticklabels(),rotation=90)
sns.barplot(ax = ax3,x=temp['tracado_via'].value_counts().index ,y = temp['tracado_via'].value_counts())
sns.barplot(ax = ax4,x=df_ind['sexo'].value_counts().index ,y = df_ind['sexo'].value_counts())
sns.barplot(x=temp['tracado_via'].value_counts().index ,y = temp['tracado_via'].value_counts())
plt.xticks(rotation=90);
```
Assim, a coluna *tracado_via* foi corrigida.
```
temp.isnull().sum()
```
Coluna *sexo*
```
sns.barplot(x=df_ind['sexo'].value_counts().index ,y = df_ind['sexo'].value_counts())
plt.xticks(rotation=90);
```
Proporção de dados presentes no dataset:
```
round(df_ind['sexo'].value_counts()/df_ind['sexo'].count()*100)
```
Sabendo a proporção de dados presentes no dataset, precisamos saber qual será o valor necessário em cada variável para continuar com a mesma proporção. Sabendo que teremos 26259 dados para serem substituidos.
```
round(df_ind['sexo'].value_counts()/df_ind['sexo'].count()*26089)
```
Como a função informada acima, precisamos só substituir os valores calculados anteriormente para ocorrer os reparo.
```
replace_randomly_nan(temp,'sexo','Masculino',19929)
replace_randomly_nan(temp,'sexo','Feminino',6160)
```
Verificação da proporção dos dados.
```
round(df_ind['sexo'].value_counts()/df_ind['sexo'].count()*100)
```
Com isso, finalizamos a correção dessa coluna.
```
sns.barplot(x=temp['sexo'].value_counts().index ,y = temp['sexo'].value_counts())
plt.xticks(rotation=90);
```
Assim, concluimos a limpeza dos nosso dados, e também a correção dos dados que apresentaram algum tipo de problema.
```
temp.isnull().sum()
msno.matrix(temp)
```
Exportação, do dataset limpo, com o nome **'df_acidentes.csv'**
```
temp.to_csv('df_acidentes.csv',index=False)
'''
Parte 2
Correção e Limpeza dos dados (EDA e ETL)
id 0 - Não Alterado
data_inversa 0 - Não Alterado
dia_semana 0 - Não Alterado
horario 0 - Não Alterado
uf 0 - Não Alterado
causa_acidente 0 - Não Alterado
tipo_acidente 0 - Não Alterado
classificacao_acidente 0 - Não Alterado
fase_dia 0 - Não Alterado
condicao_metereologica 0 - np.nan -> dropna
tipo_pista 0 - Não Alterado
tracado_via 0 - np.nan - > replace_randomly_nan() - preenchimento proporcional
uso_solo 0 - Não Alterado
tipo_veiculo 0 - np.nan -> dropna
ano_fabricacao_veiculo 0 - Não Alterado
tipo_envolvido 0 - Não Alterado
idade 0 - Não Alterado
sexo 0 - np.nan - > replace_randomly_nan() - preenchimento proporcional
ilesos 0 - Não Alterado
mortos 0 - Não Alterado
ano 0 - Não Alterado
feridos_cal 0 - Não Alterado
==========================================================================================================================
--------------------------------------------------------------------------------------------------------------------------
==========================================================================================================================
Parte 1
Agrupamento de dados e seleção de principais colunas a serem analisadas (2017-2020).
id 0 - Não Alterado
data_inversa 0 - Não Alterado
dia_semana 0 - Não Alterado
horario 0 - Não Alterado
uf 0 - Não Alterado
causa_acidente 0 - Não Alterado
tipo_acidente 0 - Não Alterado
classificacao_acidente 0 - Não Alterado
fase_dia 0 - Não Alterado
condicao_metereologica 8597 - Ignorados -> np.nan
tipo_pista 0 - Não Alterado
tracado_via 66609 - Não Informado - np.nan
uso_solo 0 - Sim-> Urbano Não-> Rural
tipo_veiculo 2645 - Outros e Não Informados -> np.nan
ano_fabricacao_veiculo 0 - np.nan - > médias dos anos de fabricação
tipo_envolvido 0 - Não informado e Testemunha -> drop do dataframe
idade 0 - 0 < idade < 117 | outliers -> np.nan -> média de idades
sexo 28618 - Não informado e Ignorados -> np.nan
ilesos 0 - Não Alterado
mortos 0 - Não Alterado
ano 0 - Criado para rastreamento
feridos_cal 0 - feridos_cal = feridos_leves + feridos_graves (criado)
==========================================================================================================================
--------------------------------------------------------------------------------------------------------------------------
==========================================================================================================================
Parte 0
id 0
pesid 4
data_inversa 0
dia_semana 0
horario 0
uf 0
br 1083
km 1083
municipio 0
causa_acidente 0
tipo_acidente 0
classificacao_acidente 0
fase_dia 0
sentido_via 0
condicao_metereologica 0
tipo_pista 0
tracado_via 0
uso_solo 0
id_veiculo 4
tipo_veiculo 0
marca 30885
ano_fabricacao_veiculo 36269
tipo_envolvido 0
estado_fisico 0
idade 58641
sexo 0
ilesos 0
feridos_leves 0
feridos_graves 0
mortos 0
latitude 0 - > tratados e corrigidos, valores inconsistentes removidos
longitude 0 - > tratados e corrigidos, valores inconsistentes removidos
regional 0
delegacia 0
uop 27830
ano 0
'''
temp[['classificacao_acidente','ilesos','feridos_cal','mortos']].sample(5)
```
| true |
code
| 0.235856 | null | null | null | null |
|
# Running ProjectQ code on AWS Braket service provided devices
## Compiling code for AWS Braket Service
In this tutorial we will see how to run code on some of the devices provided by the Amazon AWS Braket service. The AWS Braket devices supported are: the State Vector Simulator 'SV1', the Rigetti device 'Aspen-8' and the IonQ device 'IonQ'
You need to have a valid AWS account, created a pair of access key/secret key, and have activated the braket service. As part of the activation of the service, a specific S3 bucket and folder associated to the service should be configured.
First we need to do the required imports. That includes the mail compiler engine (MainEngine), the backend (AWSBraketBackend in this case) and the operations to be used in the cicuit
```
from projectq import MainEngine
from projectq.backends import AWSBraketBackend
from projectq.ops import Measure, H, C, X, All
```
Prior to the instantiation of the backend we need to configure the credentials, the S3 storage folder and the device to be used (in the example the State Vector Simulator SV1)
```
creds = {
'AWS_ACCESS_KEY_ID': 'aws_access_key_id',
'AWS_SECRET_KEY': 'aws_secret_key',
} # replace with your Access key and Secret key
s3_folder = ['S3Bucket', 'S3Directory'] # replace with your S3 bucket and directory
device = 'SV1' # replace by the device you want to use
```
Next we instantiate the engine with the AWSBraketBackend including the credentials and S3 configuration. By setting the 'use_hardware' parameter to False we indicate the use of the Simulator. In addition we set the number of times we want to run the circuit and the interval in secons to ask for the results. For a complete list of parameters and descriptions, please check the documentation.
```
eng = MainEngine(AWSBraketBackend(use_hardware=False,
credentials=creds,
s3_folder=s3_folder,
num_runs=10,
interval=10))
```
We can now allocate the required qubits and create the circuit to be run. With the last instruction we ask the backend to run the circuit.
```
# Allocate the required qubits
qureg = eng.allocate_qureg(3)
# Create the circuit. In this example a quantum teleportation algorithms that teleports the first qubit to the third one.
H | qureg[0]
H | qureg[1]
C(X) | (qureg[1], qureg[2])
C(X) | (qureg[0], qureg[1])
H | qureg[0]
C(X) | (qureg[1], qureg[2])
# At the end we measure the qubits to get the results; should be all-0 or all-1
All(Measure) | qureg
# And run the circuit
eng.flush()
```
The backend will automatically create the task and generate a unique identifier (the task Arn) that can be used to recover the status of the task and results later on.
Once the circuit is executed the indicated number of times, the results are stored in the S3 folder configured previously and can be recovered to obtain the probabilities of each of the states.
```
# Obtain and print the probabilies of the states
prob_dict = eng.backend.get_probabilities(qureg)
print("Probabilites for each of the results: ", prob_dict)
```
## Retrieve results form a previous execution
We can retrieve the result later on (of this job or a previously executed one) using the task Arn provided when it was run. In addition, you have to remember the amount of qubits involved in the job and the order you used. The latter is required since we need to set up a mapping for the qubits when retrieving results of a previously executed job.
To retrieve the results we need to configure the backend including the parameter 'retrieve_execution' set to the Task Arn of the job. To be able to get the probabilities of each state we need to configure the qubits and ask the backend to get the results.
```
# Set the Task Arn of the job to be retrieved and instantiate the engine with the AWSBraketBackend
task_arn = 'your_task_arn' # replace with the actual TaskArn you want to use
eng1 = MainEngine(AWSBraketBackend(retrieve_execution=task_arn, credentials=creds, num_retries=2, verbose=True))
# Configure the qubits to get the states probabilies
qureg1 = eng1.allocate_qureg(3)
# Ask the backend to retrieve the results
eng1.flush()
# Obtain and print the probabilities of the states
prob_dict1 = eng1.backend.get_probabilities(qureg1)
print("Probabilities ", prob_dict1)
```
We can plot an histogram with the probabilities as well.
```
import matplotlib.pyplot as plt
%matplotlib inline
from projectq.libs.hist import histogram
histogram(eng1.backend, qureg1)
plt.show()
```
| true |
code
| 0.729995 | null | null | null | null |
|
# 深度概率编程CVAE
## 概述
本例采用MindSpore的深度概率编程方法应用于条件变分自编码器(CVAE)模型训练。
整体流程如下:
1. 数据集准备
2. 定义条件变分自编码器网络;
3. 定义损失函数和优化器;
4. 训练生成模型。
5. 生成新样本或重构输入样本。
> 本例适用于GPU和Ascend环境。
## 数据准备
### 下载数据集
本例使用MNIST_Data数据集,执行如下命令进行下载并解压到对应位置:
```
!wget -N https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/datasets/MNIST_Data.zip
!unzip -o MNIST_Data.zip -d ./datasets
!tree ./datasets/MNIST_Data/
```
### 数据增强
将数据集增强为适应CVAE网络训练要求的数据,本例主要是将原始图片像素大小由$28\times28$增强为$32\times32$,同时将多张图片组成1个`batch`来加速训练。
```
import mindspore.common.dtype as mstype
import mindspore.dataset as ds
import mindspore.dataset.vision.c_transforms as CV
def create_dataset(data_path, batch_size=32, repeat_size=1,
num_parallel_workers=1):
"""
create dataset for train or test
"""
# define dataset
mnist_ds = ds.MnistDataset(data_path)
resize_height, resize_width = 32, 32
rescale = 1.0 / 255.0
shift = 0.0
# define map operations
resize_op = CV.Resize((resize_height, resize_width)) # Bilinear mode
rescale_op = CV.Rescale(rescale, shift)
hwc2chw_op = CV.HWC2CHW()
# apply map operations on images
mnist_ds = mnist_ds.map(operations=resize_op, input_columns="image", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=rescale_op, input_columns="image", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=hwc2chw_op, input_columns="image", num_parallel_workers=num_parallel_workers)
# apply DatasetOps
mnist_ds = mnist_ds.batch(batch_size)
mnist_ds = mnist_ds.repeat(repeat_size)
return mnist_ds
```
## 定义条件变分自编码器网络
变分自编码器的构成主要分为三个部分,编码器,解码器和隐空间。
其中:
编码器(Encoder)主要作用是将训练数据进行降维,压缩,提取特征,形成特征向量,存储在隐空间中。
解码器(Decoder)主要作用是将训练数据因空间分布的参数进行解码,还原生成出新的图像。
隐空间主要作用是将模型的特征按照某种分布特性进行存储,属于编码器和解码器中间的桥梁。
本例中条件变分自编码器(CVAE)是在变分自编码器的基础上增添标签训练,在后续随机采样生成图片的过程中,可以施加标签指定生成该条件的图片。
```
import os
import mindspore.nn as nn
from mindspore import context, Tensor
import mindspore.ops as ops
context.set_context(mode=context.GRAPH_MODE,device_target="GPU")
IMAGE_SHAPE=(-1,1,32,32)
image_path = os.path.join("./datasets/MNIST_Data","train")
class Encoder(nn.Cell):
def __init__(self, num_classes):
super(Encoder, self).__init__()
self.fc1 = nn.Dense(1024 + num_classes, 400)
self.relu = nn.ReLU()
self.flatten = nn.Flatten()
self.concat = ops.Concat(axis=1)
self.one_hot = nn.OneHot(depth=num_classes)
def construct(self, x, y):
x = self.flatten(x)
y = self.one_hot(y)
input_x = self.concat((x, y))
input_x = self.fc1(input_x)
input_x = self.relu(input_x)
return input_x
class Decoder(nn.Cell):
def __init__(self):
super(Decoder, self).__init__()
self.fc2 = nn.Dense(400, 1024)
self.sigmoid = nn.Sigmoid()
self.reshape = ops.Reshape()
def construct(self, z):
z = self.fc2(z)
z = self.reshape(z, IMAGE_SHAPE)
z = self.sigmoid(z)
return z
```
## 定义优化器和损失函数
定义条件变分自编码器的损失函数,将图像与label关联。
损失函数采用ELBO函数,此函数用于计算解码图像和原图像的差值,并通过对比两个图像的差值,以及图像分布的均值之差来计算两图的损失情况。
优化器采用`nn.Adam`来最小化损失值。
```
from mindspore.nn.probability.dpn import ConditionalVAE
from mindspore.nn.probability.infer import ELBO, SVI
class CVAEWithLossCell(nn.WithLossCell):
"""
Rewrite WithLossCell for CVAE
"""
def construct(self, data, label):
out = self._backbone(data, label)
return self._loss_fn(out, label)
# define the encoder and decoder
encoder = Encoder(num_classes=10)
decoder = Decoder()
# define the vae model
cvae = ConditionalVAE(encoder, decoder, hidden_size=400, latent_size=20,num_classes=10)
# define the loss function
net_loss = ELBO(latent_prior='Normal', output_prior='Normal')
# define the optimizer
optimizer = nn.Adam(params=cvae.trainable_params(), learning_rate=0.001)
net_with_loss = CVAEWithLossCell(cvae,net_loss)
vi = SVI(net_with_loss=net_with_loss,optimizer=optimizer)
```
参数解释:
- num_classes:类别数量,本例中为0-9个数字,共计10个种类。
- ConditionalVAE:条件自编码器模型,将编码器,解码器,压缩大小,隐空间维度和类别数量等变分自编码器网络初始化。
- `encoder`:编码器网络。
- `decoder`:解码器网络。
- `hiddend_size`:数据压缩后的大小,本例为400。
- `latent_size`:隐空间的向量维度,向量维度越大,分别的特征维度越多,图像特征越清晰,本例中可调节维度大小为20。
- `num_classes`:类别数量。
- ELBO:变分自编码器的损失函数。
- `latent_prior`:隐空间初始化分布,本例中隐空间的参数遵循正态分布。
- `output_prior`:输出权重的初始化分布,本例中其权重参数初始化分布遵循正态分布。
- nn.Adam:优化器。
- CVAEWithLossCell:本例重建了`nn.WithlossCell`函数,使得生成的数据,附带标签(label)。
- SVI:模型函数,类似MindSpore中的Model,此函数为变分自编码器专用模型函数。
## 训练生成模型
生成训练数据,将调用上述代码中`vi`的训练模式,对模型进行训练,训练完成后打印出模型的loss值。
```
# define the training dataset
ds_train = create_dataset(image_path, 32, 1)
# run the vi to return the trained network.
cvae = vi.run(train_dataset=ds_train, epochs=5)
# get the trained loss
trained_loss = vi.get_train_loss()
print(trained_loss)
```
### 样本重建
先定义可视化绘图函数`plot_image`,用于样本重建和条件采样生成数据的可视化。
使用训练好的模型,查看重建数据的能力如何,这里取一组原始数据进行重建,执行如下代码:
```
import matplotlib.pyplot as plt
import numpy as np
def plot_image(sample_data,col_num=4,row_num=8,count=0):
for i in sample_data:
plt.subplot(col_num,row_num,count+1)
plt.imshow(np.squeeze(i.asnumpy()))
plt.axis("off")
count += 1
plt.show()
sample = next(ds_train.create_dict_iterator(output_numpy=True, num_epochs=1))
sample_x = Tensor(sample['image'], dtype=mstype.float32)
sample_y = Tensor(sample['label'], dtype=mstype.int32)
reconstructed_sample = cvae.reconstruct_sample(sample_x, sample_y)
print('The shape of the reconstructed sample is ', reconstructed_sample.shape)
print("\n=============The Original Images=============")
plot_image(sample_x)
print("\n============The Reconstruct Images=============")
plot_image(reconstructed_sample)
```
对比原图片,CVAE生成的图片能明显对应上原始图片,但还稍显模糊。说明训练效果已经达到但还有提升空间。
### 条件样本采样
在隐空间中进行条件采样,本例使用条件为`(0,1)`,对应生成`(0,1)`的图像数据,同时将采样生成的数据进行可视化。
```
# test function: generate_sample
sample_label = Tensor([i for i in range(0,2)]*16, dtype=mstype.int32)
# test function: generate_sample
generated_sample = cvae.generate_sample(sample_label, 32, IMAGE_SHAPE)
# test function: reconstruct_sample
print('The shape of the generated sample is ', generated_sample.shape)
plot_image(generated_sample,4,8)
```
在条件为`(0,1)`特征采样中,生成的图片有的看起来像其他的数字,说明图像在特征分布中,其他数字的部分特征与`(0,1)`的特征出现了交叉,而随机采样正好采样到了这些交叉特征,导致`(0,1)`图片出现了其他数字的特征。
| true |
code
| 0.785607 | null | null | null | null |
|
<img src="../_static/pymt-logo-header-text.png">
## Coastline Evolution Model + Waves
* Link to this notebook: https://github.com/csdms/pymt/blob/master/notebooks/cem_and_waves.ipynb
* Install command: `$ conda install notebook pymt_cem`
This example explores how to use a BMI implementation to couple the Waves component with the Coastline Evolution Model component.
### Links
* [CEM source code](https://github.com/csdms/cem-old): Look at the files that have *deltas* in their name.
* [CEM description on CSDMS](http://csdms.colorado.edu/wiki/Model_help:CEM): Detailed information on the CEM model.
### Interacting with the Coastline Evolution Model BMI using Python
Some magic that allows us to view images within the notebook.
```
%matplotlib inline
import numpy as np
```
Import the `Cem` class, and instantiate it. In Python, a model with a BMI will have no arguments for its constructor. Note that although the class has been instantiated, it's not yet ready to be run. We'll get to that later!
```
from pymt import models
cem, waves = models.Cem(), models.Waves()
```
Even though we can't run our waves model yet, we can still get some information about it. *Just don't try to run it.* Some things we can do with our model are get the names of the input variables.
```
waves.get_output_var_names()
cem.get_input_var_names()
```
We can also get information about specific variables. Here we'll look at some info about wave direction. This is the main input of the Cem model. Notice that BMI components always use [CSDMS standard names](http://csdms.colorado.edu/wiki/CSDMS_Standard_Names). The CSDMS Standard Name for wave angle is,
"sea_surface_water_wave__azimuth_angle_of_opposite_of_phase_velocity"
Quite a mouthful, I know. With that name we can get information about that variable and the grid that it is on (it's actually not a one).
OK. We're finally ready to run the model. Well not quite. First we initialize the model with the BMI **initialize** method. Normally we would pass it a string that represents the name of an input file. For this example we'll pass **None**, which tells Cem to use some defaults.
```
args = cem.setup(number_of_rows=100, number_of_cols=200, grid_spacing=200.)
cem.initialize(*args)
args = waves.setup()
waves.initialize(*args)
```
Here I define a convenience function for plotting the water depth and making it look pretty. You don't need to worry too much about it's internals for this tutorial. It just saves us some typing later on.
```
def plot_coast(spacing, z):
import matplotlib.pyplot as plt
xmin, xmax = 0., z.shape[1] * spacing[1] * 1e-3
ymin, ymax = 0., z.shape[0] * spacing[0] * 1e-3
plt.imshow(z, extent=[xmin, xmax, ymin, ymax], origin='lower', cmap='ocean')
plt.colorbar().ax.set_ylabel('Water Depth (m)')
plt.xlabel('Along shore (km)')
plt.ylabel('Cross shore (km)')
```
It generates plots that look like this. We begin with a flat delta (green) and a linear coastline (y = 3 km). The bathymetry drops off linearly to the top of the domain.
```
grid_id = cem.get_var_grid('sea_water__depth')
spacing = cem.get_grid_spacing(grid_id)
shape = cem.get_grid_shape(grid_id)
z = np.empty(shape)
cem.get_value('sea_water__depth', out=z)
plot_coast(spacing, z)
```
Allocate memory for the sediment discharge array and set the discharge at the coastal cell to some value.
```
qs = np.zeros_like(z)
qs[0, 100] = 750
```
The CSDMS Standard Name for this variable is:
"land_surface_water_sediment~bedload__mass_flow_rate"
You can get an idea of the units based on the quantity part of the name. "mass_flow_rate" indicates mass per time. You can double-check this with the BMI method function **get_var_units**.
```
cem.get_var_units('land_surface_water_sediment~bedload__mass_flow_rate')
waves.set_value('sea_shoreline_wave~incoming~deepwater__ashton_et_al_approach_angle_asymmetry_parameter', .3)
waves.set_value('sea_shoreline_wave~incoming~deepwater__ashton_et_al_approach_angle_highness_parameter', .7)
cem.set_value("sea_surface_water_wave__height", 2.)
cem.set_value("sea_surface_water_wave__period", 7.)
```
Set the bedload flux and run the model.
```
for time in range(3000):
waves.update()
angle = waves.get_value('sea_surface_water_wave__azimuth_angle_of_opposite_of_phase_velocity')
cem.set_value('sea_surface_water_wave__azimuth_angle_of_opposite_of_phase_velocity', angle)
cem.set_value('land_surface_water_sediment~bedload__mass_flow_rate', qs)
cem.update()
cem.get_value('sea_water__depth', out=z)
plot_coast(spacing, z)
```
Let's add another sediment source with a different flux and update the model.
```
qs[0, 150] = 500
for time in range(3750):
waves.update()
angle = waves.get_value('sea_surface_water_wave__azimuth_angle_of_opposite_of_phase_velocity')
cem.set_value('sea_surface_water_wave__azimuth_angle_of_opposite_of_phase_velocity', angle)
cem.set_value('land_surface_water_sediment~bedload__mass_flow_rate', qs)
cem.update()
cem.get_value('sea_water__depth', out=z)
plot_coast(spacing, z)
```
Here we shut off the sediment supply completely.
```
qs.fill(0.)
for time in range(4000):
waves.update()
angle = waves.get_value('sea_surface_water_wave__azimuth_angle_of_opposite_of_phase_velocity')
cem.set_value('sea_surface_water_wave__azimuth_angle_of_opposite_of_phase_velocity', angle)
cem.set_value('land_surface_water_sediment~bedload__mass_flow_rate', qs)
cem.update()
cem.get_value('sea_water__depth', out=z)
plot_coast(spacing, z)
```
| true |
code
| 0.618262 | null | null | null | null |
|
This application demonstrates how to build a simple neural network using the Graph mark.
Interactions can be enabled by adding event handlers (click, hover etc) on the nodes of the network.
See the [Mark Interactions notebook](../Interactions/Mark Interactions.ipynb) and the [Scatter Notebook](../Marks/Scatter.ipynb) for details.
```
from itertools import chain, product
import numpy as np
from bqplot import *
class NeuralNet(Figure):
def __init__(self, **kwargs):
self.height = kwargs.get('height', 600)
self.width = kwargs.get('width', 960)
self.directed_links = kwargs.get('directed_links', False)
self.num_inputs = kwargs['num_inputs']
self.num_hidden_layers = kwargs['num_hidden_layers']
self.nodes_output_layer = kwargs['num_outputs']
self.layer_colors = kwargs.get('layer_colors',
['Orange'] * (len(self.num_hidden_layers) + 2))
self.build_net()
super(NeuralNet, self).__init__(**kwargs)
def build_net(self):
# create nodes
self.layer_nodes = []
self.layer_nodes.append(['x' + str(i+1) for i in range(self.num_inputs)])
for i, h in enumerate(self.num_hidden_layers):
self.layer_nodes.append(['h' + str(i+1) + ',' + str(j+1) for j in range(h)])
self.layer_nodes.append(['y' + str(i+1) for i in range(self.nodes_output_layer)])
self.flattened_layer_nodes = list(chain(*self.layer_nodes))
# build link matrix
i = 0
node_indices = {}
for layer in self.layer_nodes:
for node in layer:
node_indices[node] = i
i += 1
n = len(self.flattened_layer_nodes)
self.link_matrix = np.empty((n,n))
self.link_matrix[:] = np.nan
for i in range(len(self.layer_nodes) - 1):
curr_layer_nodes_indices = [node_indices[d] for d in self.layer_nodes[i]]
next_layer_nodes = [node_indices[d] for d in self.layer_nodes[i+1]]
for s, t in product(curr_layer_nodes_indices, next_layer_nodes):
self.link_matrix[s, t] = 1
# set node x locations
self.nodes_x = np.repeat(np.linspace(0, 100,
len(self.layer_nodes) + 1,
endpoint=False)[1:],
[len(n) for n in self.layer_nodes])
# set node y locations
self.nodes_y = np.array([])
for layer in self.layer_nodes:
n = len(layer)
ys = np.linspace(0, 100, n+1, endpoint=False)[1:]
self.nodes_y = np.append(self.nodes_y, ys[::-1])
# set node colors
n_layers = len(self.layer_nodes)
self.node_colors = np.repeat(np.array(self.layer_colors[:n_layers]),
[len(layer) for layer in self.layer_nodes]).tolist()
xs = LinearScale(min=0, max=100)
ys = LinearScale(min=0, max=100)
self.graph = Graph(node_data=[{'label': d,
'label_display': 'none'} for d in self.flattened_layer_nodes],
link_matrix=self.link_matrix,
link_type='line',
colors=self.node_colors,
directed=self.directed_links,
scales={'x': xs, 'y': ys},
x=self.nodes_x,
y=self.nodes_y,
# color=2 * np.random.rand(len(self.flattened_layer_nodes)) - 1
)
self.graph.hovered_style = {'stroke': '1.5'}
self.graph.unhovered_style = {'opacity': '0.4'}
self.graph.selected_style = {'opacity': '1',
'stroke': 'red',
'stroke-width': '2.5'}
self.marks = [self.graph]
self.title = 'Neural Network'
self.layout.width = str(self.width) + 'px'
self.layout.height = str(self.height) + 'px'
NeuralNet(num_inputs=3, num_hidden_layers=[10, 10, 8, 5], num_outputs=1)
```
| true |
code
| 0.573021 | null | null | null | null |
|
<h3>Problem: As a PM, I write lots of blogs. How do I know if they will be received well by readers?</h3>
<table>
<tr>
<td><img src="https://jayclouse.com/wp-content/uploads/2019/06/hacker_news.webp" height=300 width=300></img></td>
<td><img src="https://miro.medium.com/max/852/1*wJ18DgYgtsscG63Sn56Oyw.png" height=300 width=300></img></td>
</tr>
</table>
<h1>Background on Spark ML</h1>
DataFrame: This ML API uses DataFrame from Spark SQL as an ML dataset, which can hold a variety of data types. E.g., a DataFrame could have different columns storing text, feature vectors, true labels, and predictions.
Transformer: A Transformer is an algorithm which can transform one DataFrame into another DataFrame. E.g., an ML model is a Transformer which transforms a DataFrame with features into a DataFrame with predictions.
Estimator: An Estimator is an algorithm which can be fit on a DataFrame to produce a Transformer. E.g., a learning algorithm is an Estimator which trains on a DataFrame and produces a model.
Pipeline: A Pipeline chains multiple Transformers and Estimators together to specify an ML workflow.
Parameter: All Transformers and Estimators now share a common API for specifying parameters.
```
from IPython.display import Image
Image(url='https://spark.apache.org/docs/3.0.0-preview/img/ml-Pipeline.png')
```
<h2>Loading Hackernews Text From BigQuery</h2>
```
from pyspark.sql import SparkSession
spark = SparkSession.builder.getOrCreate()
scala_minor_version = str(spark.sparkContext._jvm.scala.util.Properties.versionString().replace("version ","").split('.')[1])
spark = SparkSession.builder.config("spark.jars.packages", "com.google.cloud.spark:spark-bigquery-with-dependencies_2." + scala_minor_version + ":0.18.0") \
.enableHiveSupport() \
.getOrCreate()
df = spark.read \
.format("bigquery") \
.load("google.com:crosbie-test-project.demos.hackernewssample")
df.describe().show()
```
<h2>Prepare the data using Spark SQL<h2>
<h4>Create a random ID to distribute between test and training sets</h4>
<h4>Make the score a binary variable so we can run a logicistic regression model on it</h4>
```
df.registerTempTable("df")
from pyspark.sql import functions as F
df_full = spark.sql("select cast(round(rand() * 100) as int) as id, text, case when score > 10 THEN 1.0 else 0.0 end as label from df")
df_full.groupby('id').count().sort('count', ascending=False).show()
```
<h4>Create our training and test sets</h4>
```
#use the above table to identify ~10% holdback for test
holdback = "(22,39,25,55,23,47,38,71,5,98)"
#create test set by dropping label
df_test = df_full.where("id in {}".format(holdback))
df_test = df_test.drop("label")
rdd_test = df_test.rdd
test = rdd_test.map(tuple)
testing = spark.createDataFrame(test,["id", "text"])
#training data - Spark ML is expecting tuples so convert to RDD to map back to tuples (may not be required)
df_train = df_full.where("id not in {}".format(holdback))
rdd_train = df_train.rdd
train = rdd_train.map(tuple)
training = spark.createDataFrame(train,["id", "text", "label"])
#a little less than 10% of the trainig data is positively reviewed. Should be okay.
training.where("label > 0").count()
```
<h2>Build our ML Pipeline</h2>
<h3>Configure an ML pipeline, which consists of three stages: tokenizer, hashingTF, and lr.</h3>
```
from pyspark.ml import Pipeline
from pyspark.ml.classification import LogisticRegression
from pyspark.ml.feature import HashingTF, Tokenizer
tokenizer = Tokenizer(inputCol="text", outputCol="words")
hashingTF = HashingTF(inputCol=tokenizer.getOutputCol(), outputCol="features")
lr = LogisticRegression(maxIter=10, regParam=0.001)
pipeline = Pipeline(stages=[tokenizer, hashingTF, lr])
# Fit the pipeline to hacker news articles
model = pipeline.fit(training)
```
<h3>Review model based on test set</h3>
```
# Make predictions on test documents and print columns of interest.
prediction = model.transform(testing)
selected = prediction.select("id", "text", "probability", "prediction").where("prediction > 0")
for row in selected.collect():
rid, text, prob, prediction = row
print("(%d, %s) --> prob=%s, prediction=%f" % (rid, text, str(prob), prediction))
```
<h2>Use the model to decide which PM blog to use</h2>
```
my_blog = """
The life of a data scientist can be challenging. If you’re in this role, your job may involve anything from understanding the day-to-day business behind the data to keeping up with the latest machine learning academic research. With all that a data scientist must do to be effective, you shouldn’t have to worry about migrating data environments or dealing with processing limitations associated with working with raw data.
Google Cloud’s Dataproc lets you run cloud-native Apache Spark and Hadoop clusters easily. This is especially helpful as data growth relocates data scientists and machine learning researchers from personal servers and laptops into distributed cluster environments like Apache Spark, which offers Python and R interfaces for data of any size. You can run open source data processing on Google Cloud, making Dataproc one of the fastest ways to extend your existing data analysis to cloud-sized datasets.
We’re announcing the general availability of several new Dataproc features that will let you apply the open source tools, algorithms, and programming languages that you use today to large datasets. This can be done without having to manage clusters and computers. These new GA features make it possible for data scientists and analysts to build production systems based on personalized development environments.
"""
pmm_blog = """
Dataproc makes open source data and analytics processing fast, easy, and more secure in the cloud.
New customers get $300 in free credits to spend on Dataproc or other Google Cloud products during the first 90 days.
Go to console
Spin up an autoscaling cluster in 90 seconds on custom machines
Build fully managed Apache Spark, Apache Hadoop, Presto, and other OSS clusters
Only pay for the resources you use and lower the total cost of ownership of OSS
Encryption and unified security built into every cluster
Accelerate data science with purpose-built clusters
"""
boss_blog = """
In 2014, we made a decision to build our core data platform on Google Cloud Platform and one of the products which was critical for the decision was Google BigQuery. The scale at which it enabled us to perform analysis we knew would be critical in long run for our business. Today we have more than 200 unique users performing analysis on a monthly basis.
Once we started using Google BiqQuery at scale we soon realized our analysts needed better tooling around it. The key requests we started getting were
Ability to schedule jobs: Analysts needed to have ability to run queries at regular intervals to generate data and metrics.
Define workflow of queries: Basically analysts wanted to run multiple queries in a sequence and share data across them through temp tables.
Simplified data sharing: Finally it became clear teams needed to share this data generated with other systems. For example download it to leverage in R programs or send it to another system to process through Kafka.
"""
pm_blog_off = spark.createDataFrame([
('me', my_blog),
('pmm', pmm_blog),
('sudhir', boss_blog)
], ["id", "text"])
blog_prediction = model.transform(pm_blog_off)
blog_prediction.select("id","prediction").show()
```
<h2>Save our trained model to GCS</h2>
```
model.save("gs://crosbie-dev/blog-validation-model")
```
| true |
code
| 0.651189 | null | null | null | null |
|
# Speed and Quality of Katz-Eigen Community Detection vs Louvain
```
import zen
import pandas as pd
import numpy as np
from clusteringAlgo import lineClustering
import matplotlib.pyplot as plt
```
#### Compare the speed of the Katz-eigen plot method of community detection with that of Louvain community detection, using the 328-node Amazon product network.
```
def katz(G,tol=0.01,max_iter=1000,alpha=0.001,beta=1):
iteration = 0
centrality = np.zeros(G.num_nodes)
while iteration < max_iter:
iteration += 1 # increment iteration count
centrality_old = centrality.copy()
for node in G.nodes_():
Ax = 0
for neighbor in G.neighbors_(node):
weight = G.weight_(G.edge_idx_(neighbor,node))
Ax += np.multiply(centrality[neighbor],weight)
#Ax += centrality[neighbor] #exclude weight due to overflow in multiplication
centrality[node] = np.multiply(alpha,Ax)+beta
if np.sum(np.abs(np.subtract(centrality,centrality_old))) < tol:
return centrality
def modular_graph(Size1, Size2, edges1, edges2, common, katz_alpha=0.001):
g1 = zen.generating.barabasi_albert(Size1,edges1)
avgDeg1 = (2.0 * g1.num_edges)/g1.num_nodes
lcc1 = np.mean(zen.algorithms.clustering.lcc_(g1))
g2 = zen.generating.barabasi_albert(Size2,edges2)
avgDeg2 = (2.0 * g2.num_edges)/g2.num_nodes
lcc2 = np.mean(zen.algorithms.clustering.lcc_(g2))
Size = Size1 + Size2
G = zen.Graph()
for i in range(Size):
G.add_node(i)
for edge in g1.edges_iter():
u = edge[0]
v = edge[1]
G.add_edge(u,v)
for edge in g2.edges_iter():
u = edge[0]+Size1
v = edge[1]+Size1
G.add_edge(u,v)
# Select random pairs of nodes to connect the subgraphs
join_nodes = np.empty((common,2),dtype=np.int64)
nodes1 = np.random.randint(0,Size1,size=common)
nodes2 = np.random.randint(Size1,Size,size=common)
join_nodes[:,0] = nodes1
join_nodes[:,1] = nodes2
for edge in join_nodes:
if not G.has_edge(edge[0],edge[1]):
G.add_edge(edge[0],edge[1])
return G
def modularity(G,classDict,classList):
Q = zen.algorithms.modularity(G,classDict)
# Maximum Modularity
count=0.0
for e in G.edges():
n1 = G.node_idx(e[0])
n2 = G.node_idx(e[1])
if classList[n1] == classList[n2]:
count += 1
same = count / G.num_edges
rand = same - Q
qmax = 1 - rand
return Q, qmax
from zen.algorithms.community import spectral_modularity as spm
def spectral_community_detection(G,ke_plot=False):
cset = spm(G)
if ke_plot:
evc = zen.algorithms.eigenvector_centrality_(G)
kc = katz(G,alpha=1e-4)
#scale
evc = evc - np.min(evc)
evc = evc / np.max(evc)
kc = kc - np.min(kc)
kc = kc / np.max(kc)
comm_dict = {}
comm_list = np.zeros(G.num_nodes)
for i,community in enumerate(cset.communities()):
comm_dict[i] = community.nodes()
comm_list[community.nodes_()] = i
if ke_plot:
plt.scatter(evc[community.nodes_()],kc[community.nodes_()],s=3,label='cluster %d'%i)
if ke_plot:
plt.xlabel('Eigenvector Centrality (normalized)')
plt.xlabel('Katz Centrality (normalized)')
plt.legend()
plt.show()
q,qmax = modularity(G,comm_dict,comm_list)
print '%d communities found.'%(i+1)
print 'Q: %.3f'%q
print 'Normalized Q: %.3f'%(q/qmax)
def ke_community_detection(G,dtheta=0.01,dx=0.5,window=10,plot=False,ke_plot=False):
evc = zen.algorithms.eigenvector_centrality_(G)
kc = katz(G,alpha=1e-4)
#scale
evc = evc - np.min(evc)
evc = evc / np.max(evc)
kc = kc - np.min(kc)
kc = kc / np.max(kc)
clusters = lineClustering(evc,kc,dtheta=dtheta,dx=dx,window=window,plot=plot)
ClassDict = {}
ClassList = np.zeros(G.num_nodes)
for i,c in enumerate(clusters):
ClassDict[i] = [G.node_object(x) for x in c]
ClassList[c]=i
if ke_plot:
plt.scatter(evc[c],kc[c],s=3,label='cluster %d'%i)
if ke_plot:
plt.xlabel('Eigenvector Centrality (normalized)')
plt.xlabel('Katz Centrality (normalized)')
plt.legend()
plt.show()
q,qmax = modularity(G,ClassDict,ClassList)
print '%d communities found.'%(i+1)
print 'Q: %.3f'%q
print 'Normalized Q: %.3f'%(q/qmax)
from zen.algorithms.community import louvain
def louvain_community_detection(G,ke_plot=False):
cset = louvain(G)
if ke_plot:
evc = zen.algorithms.eigenvector_centrality_(G)
kc = katz(G,alpha=1e-4)
#scale
evc = evc - np.min(evc)
evc = evc / np.max(evc)
kc = kc - np.min(kc)
kc = kc / np.max(kc)
comm_dict = {}
comm_list = np.zeros(G.num_nodes)
for i,community in enumerate(cset.communities()):
comm_dict[i] = community.nodes()
comm_list[community.nodes_()] = i
if ke_plot:
plt.scatter(evc[c],kc[c],s=3,label='cluster %d'%i)
if ke_plot:
plt.xlabel('Eigenvector Centrality (normalized)')
plt.xlabel('Katz Centrality (normalized)')
plt.legend()
plt.show()
q,qmax = modularity(G,comm_dict,comm_list)
print '%d communities found.'%(i+1)
print 'Q: %.3f'%q
print 'Normalized Q: %.3f'%(q/qmax)
```
### Test on Amazon Product Graph
```
G = zen.io.gml.read('amazon_product.gml',weight_fxn=lambda x: x['weight'])
%%time
ke_community_detection(G)
%%time
louvain_community_detection(G)
%%time
spectral_community_detection(G)
```
## Test on Amazon Beauty Graph
```
G = zen.io.gml.read('amazon_reviews_beauty.gml',weight_fxn=lambda x: x['weight'])
G_ = zen.io.gml.read('amazon_reviews_beauty.gml',weight_fxn=lambda x: 1.0)
print G.num_nodes
print G.num_edges
%%time
ke_community_detection(G,dx=0.3)
%%time
spectral_community_detection(G_)
```
### Test on Amazon Health Graph
```
G = zen.io.gml.read('amazon_reviews_health.gml',weight_fxn=lambda x: x['weight'])
G_ = zen.io.gml.read('amazon_reviews_health.gml',weight_fxn=lambda x: 1.0)
print G.num_nodes
print G.num_edges
%%time
ke_community_detection(G,dx=0.3)
%%time
spectral_community_detection(G_)
```
## Test on DBLP Graph
```
#G = zen.io.edgelist.read('com-dblp.ungraph.txt')
G = zen.io.gml.read('dblp_top_2_weighted.gml',weight_fxn=lambda x:x['weight'])
G_ = zen.io.gml.read('dblp_top_2_weighted.gml',weight_fxn=lambda x: 1.0)
print G.num_nodes
print G.num_edges
%%time
ke_community_detection(G,dx=0.07)
%%time
louvain_community_detection(G)
%%time
spectral_community_detection(G_)
```
## Test on synthetic graphs
```
G_synth = modular_graph(500,500,15,20,100,katz_alpha=1e-4)
print "Nodes: %d"%G_synth.num_nodes
print "Edges: %d"%G_synth.num_edges
%%time
ke_community_detection(G_synth)
%%time
louvain_community_detection(G_synth)
%%time
spectral_community_detection(G_synth)
G_synth = modular_graph(1000,1000,4,7,100,katz_alpha=1e-4)
print "Nodes: %d"%G_synth.num_nodes
print "Edges: %d"%G_synth.num_edges
%%time
ke_community_detection(G_synth)
%%time
louvain_community_detection(G_synth)
%%time
spectral_community_detection(G_synth)
G_synth = modular_graph(5000,5000,5,14,300,katz_alpha=1e-4)
print "Nodes: %d"%G_synth.num_nodes
print "Edges: %d"%G_synth.num_edges
%%time
ke_community_detection(G_synth)
%%time
louvain_community_detection(G_synth)
%%time
spectral_community_detection(G_synth)
```
| true |
code
| 0.534552 | null | null | null | null |
|
# Recommender Systems using Affinity Analysis
<hr>
Here we will look at affinity analysis that determines when objects occur
frequently together. This is also called market basket analysis, after one of
the use cases of determining when items are purchased together frequently.
In this example, we wish to work out when
two movies are recommended by the same reviewers.
### Affinity analysis
Affinity analysis is the task of determining when objects are used in similar
ways. The data for affinity analysis is often described in the form of a
transaction. Intuitively, this comes from a transaction at a store—determining
when objects are purchased together.
The classic algorithm for affinity analysis is called the Apriori algorithm. It addresses
the exponential problem of creating sets of items that occur frequently within a
database, called frequent itemsets. Once these frequent itemsets are discovered,
creating association rules is straightforward.
#### Apriori algorithm
First, we ensure that a rule
has sufficient support within the dataset. Defining a minimum support level is the
key parameter for Apriori. To build a frequent itemset, for an itemset (A, B) to have a
support of at least 30, both A and B must occur at least 30 times in the database. This
property extends to larger sets as well. For an itemset (A, B, C, D) to be considered
frequent, the set (A, B, C) must also be frequent (as must D).
These frequent itemsets can be built up and possible itemsets that are not frequent
(of which there are many) will never be tested. This saves significant time in testing
new rules.
Other example algorithms for affinity analysis include the Eclat and FP-growth
algorithms. There are many improvements to these algorithms in the data mining
literature that further improve the efficiency of the method. In this chapter, we will
focus on the basic Apriori algorithm.
#### Choosing parameters
To perform association rule mining for affinity analysis, we first use the Apriori
to generate frequent itemsets. Next, we create association rules (for example, if a
person recommended movie X, they would also recommend movie Y) by testing
combinations of premises and conclusions within those frequent itemsets.
For the first stage, the Apriori algorithm needs a value for the minimum support
that an itemset needs to be considered frequent. Any itemsets with less support will
not be considered. Setting this minimum support too low will cause Apriori to test a
larger number of itemsets, slowing the algorithm down. Setting it too high will result
in fewer itemsets being considered frequent.
In the second stage, after the frequent itemsets have been discovered, association
rules are tested based on their confidence. We could choose a minimum confidence
level, a number of rules to return, or simply return all of them and let the user decide
what to do with them.
Here, we will return only rules above a given confidence level. Therefore,
we need to set our minimum confidence level. Setting this too low will result in rules
that have a high support, but are not very accurate. Setting this higher will result in
only more accurate rules being returned, but with fewer rules being discovered.
### The movie recommendation problem
Product recommendation is big business. Online stores use it to up-sell to
customers by recommending other products that they could buy. Making better
recommendations leads to better sales. When online shopping is selling to millions
of customers every year, there is a lot of potential money to be made by selling more
items to these customers.
Product recommendations have been researched for many years; however, the field
gained a significant boost when Netflix ran their Netflix Prize between 2007 and
2009. This competition aimed to determine if anyone can predict a user's rating of a
film better than Netflix was currently doing. The prize went to a team that was just
over 10 percent better than the current solution. While this may not seem like a large
improvement, such an improvement would net millions to Netflix in revenue from
better movie recommendations.
### Obtaining the dataset
Since the inception of the Netflix Prize, Grouplens, a research group at the University
of Minnesota, has released several datasets that are often used for testing algorithms
in this area. They have released several versions of a movie rating dataset, which
have different sizes. There is a version with 100,000 reviews, one with 1 million
reviews and one with 10 million reviews.
The datasets are available from http://grouplens.org/datasets/movielens/
and the dataset we are going to use in this chapter is the MovieLens 1 million
dataset. Download this dataset and unzip it in your data folder. We then load the dataset using Pandas. The MovieLens dataset is in a good shape; however, there are some changes from the
default options in pandas.read_csv that we need to make. To start with, the data is
separated by tabs, not commas. Next, there is no heading line. This means the first
line in the file is actually data and we need to manually set the column names. When loading the file, we set the delimiter parameter to the tab character, tell pandas
not to read the first row as the header (with header=None), and set the column
names.
```
ratings_filename = "data/ml-100k/u.data"
import pandas as pd
all_ratings = pd.read_csv(ratings_filename, delimiter="\t", header=None, names = ["UserID", "MovieID", "Rating", "Datetime"])
all_ratings["Datetime"] = pd.to_datetime(all_ratings['Datetime'],unit='s')
all_ratings[:5]
```
Sparse data formats:
This dataset is in a sparse format. Each row can be thought of as a cell in a large
feature matrix of the type used in previous chapters, where rows are users and
columns are individual movies. The first column would be each user's review
of the first movie, the second column would be each user's review of the second
movie, and so on.
There are 1,000 users and 1,700 movies in this dataset, which means that the full
matrix would be quite large. We may run into issues storing the whole matrix in
memory and computing on it would be troublesome. However, this matrix has the
property that most cells are empty, that is, there is no review for most movies for
most users. There is no review of movie #675 for user #213 though, and not for most
other combinations of user and movie.
```
# As you can see, there are no review for most movies, such as #213
all_ratings[all_ratings["UserID"] == 675].sort("MovieID")
```
The format given here represents the full matrix, but in a more compact way.
The first row indicates that user #196 reviewed movie #242, giving it a ranking
of 3 (out of five) on the December 4, 1997.
Any combination of user and movie that isn't in this database is assumed to not exist.
This saves significant space, as opposed to storing a bunch of zeroes in memory. This
type of format is called a sparse matrix format. As a rule of thumb, if you expect
about 60 percent or more of your dataset to be empty or zero, a sparse format will
take less space to store.
When computing on sparse matrices, the focus isn't usually on the data we don't
have—comparing all of the zeroes. We usually focus on the data we have and
compare those.
### The Apriori implementation
The goal of this chapter is to produce rules of the following form: if a person
recommends these movies, they will also recommend this movie. We will also discuss
extensions where a person recommends a set of movies is likely to recommend
another particular movie.
To do this, we first need to determine if a person recommends a movie. We can
do this by creating a new feature Favorable, which is True if the person gave a
favorable review to a movie:
```
# Not all reviews are favourable! Our goal is "other recommended books", so we only want favourable reviews
all_ratings["Favorable"] = all_ratings["Rating"] > 3
all_ratings[10:15]
all_ratings[all_ratings["UserID"] == 1][:5]
```
We will sample our dataset to form a training dataset. This also helps reduce
the size of the dataset that will be searched, making the Apriori algorithm run faster.
We obtain all reviews from the first 200 users:
```
# Sample the dataset. You can try increasing the size of the sample, but the run time will be considerably longer
ratings = all_ratings[all_ratings['UserID'].isin(range(200))] # & ratings["UserID"].isin(range(100))]
```
Next, we can create a dataset of only the favorable reviews in our sample:
```
# We start by creating a dataset of each user's favourable reviews
favorable_ratings = ratings[ratings["Favorable"]]
favorable_ratings[:5]
```
We will be searching the user's favorable reviews for our itemsets. So, the next thing
we need is the movies which each user has given a favorable. We can compute this
by grouping the dataset by the User ID and iterating over the movies in each group:
```
# We are only interested in the reviewers who have more than one review
favorable_reviews_by_users = dict((k, frozenset(v.values)) for k, v in favorable_ratings.groupby("UserID")["MovieID"])
len(favorable_reviews_by_users)
```
In the preceding code, we stored the values as a frozenset, allowing us to quickly
check if a movie has been rated by a user. Sets are much faster than lists for this type
of operation, and we will use them in a later code.
Finally, we can create a DataFrame that tells us how frequently each movie has been
given a favorable review:
```
# Find out how many movies have favourable ratings
num_favorable_by_movie = ratings[["MovieID", "Favorable"]].groupby("MovieID").sum()
num_favorable_by_movie.sort("Favorable", ascending=False)[:5]
```
### The Apriori algorithm revisited
The Apriori algorithm is part of our affinity analysis and deals specifically with
finding frequent itemsets within the data. The basic procedure of Apriori builds
up new candidate itemsets from previously discovered frequent itemsets. These
candidates are tested to see if they are frequent, and then the algorithm iterates as
explained here:
1. Create initial frequent itemsets by placing each item in its own itemset. Only items with at least the minimum support are used in this step.
2. New candidate itemsets are created from the most recently discovered frequent itemsets by finding supersets of the existing frequent itemsets.
3. All candidate itemsets are tested to see if they are frequent. If a candidate is not frequent then it is discarded. If there are no new frequent itemsets from this step, go to the last step.
4. Store the newly discovered frequent itemsets and go to the second step.
5. Return all of the discovered frequent itemsets.
#### Implementation
On the first iteration of Apriori, the newly discovered itemsets will have a length
of 2, as they will be supersets of the initial itemsets created in the first step. On the
second iteration (after applying the fourth step), the newly discovered itemsets will
have a length of 3. This allows us to quickly identify the newly discovered itemsets,
as needed in second step.
We can store our discovered frequent itemsets in a dictionary, where the key is the
length of the itemsets. This allows us to quickly access the itemsets of a given length,
and therefore the most recently discovered frequent itemsets, with the help of the
following code:
```
frequent_itemsets = {} # itemsets are sorted by length
```
We also need to define the minimum support needed for an itemset to be considered frequent. This value is chosen based on the dataset but feel free to try different
values. I recommend only changing it by 10 percent at a time though, as the time the
algorithm takes to run will be significantly different! Let's apply minimum support:
```
min_support = 50
```
To implement the first step of the Apriori algorithm, we create an itemset with each
movie individually and test if the itemset is frequent. We use frozenset, as they
allow us to perform set operations later on, and they can also be used as keys in our
counting dictionary (normal sets cannot).
```
# k=1 candidates are the isbns with more than min_support favourable reviews
frequent_itemsets[1] = dict((frozenset((movie_id,)), row["Favorable"])
for movie_id, row in num_favorable_by_movie.iterrows()
if row["Favorable"] > min_support)
```
We implement the second and third steps together for efficiency by creating a
function that takes the newly discovered frequent itemsets, creates the supersets,
and then tests if they are frequent. First, we set up the function and the counting
dictionary. In keeping with our rule of thumb of reading through the data as little as possible,
we iterate over the dataset once per call to this function. While this doesn't matter too
much in this implementation (our dataset is relatively small), it is a good practice to
get into for larger applications. We iterate over all of the users and their reviews. Next, we go through each of the previously discovered itemsets and see if it is a
subset of the current set of reviews. If it is, this means that the user has reviewed
each movie in the itemset. We can then go through each individual movie that the user has reviewed that isn't
in the itemset, create a superset from it, and record in our counting dictionary that
we saw this particular itemset. We end our function by testing which of the candidate itemsets have enough support
to be considered frequent and return only those :
```
from collections import defaultdict
def find_frequent_itemsets(favorable_reviews_by_users, k_1_itemsets, min_support):
counts = defaultdict(int)
for user, reviews in favorable_reviews_by_users.items():
for itemset in k_1_itemsets:
if itemset.issubset(reviews):
for other_reviewed_movie in reviews - itemset:
current_superset = itemset | frozenset((other_reviewed_movie,))
counts[current_superset] += 1
return dict([(itemset, frequency) for itemset, frequency in counts.items() if frequency >= min_support])
```
To run our code, we create a loop that iterates over the steps of the Apriori
algorithm, storing the new itemsets as we go. In this loop, k represents the length
of the soon-to-be discovered frequent itemsets, allowing us to access the previously
most discovered ones by looking in our frequent_itemsets dictionary using the
key k - 1. We create the frequent itemsets and store them in our dictionary by their
length. We want to break out the preceding loop if we didn't find any new frequent itemsets
(and also to print a message to let us know what is going on). If we do find frequent itemsets, we print out a message to let us know the loop will
be running again. This algorithm can take a while to run, so it is helpful to know that
the code is still running while you wait for it to complete! Finally, after the end of the loop, we are no longer interested in the first set of
itemsets anymore—these are itemsets of length one, which won't help us create
association rules – we need at least two items to create association rules. Let's
delete them :
```
import sys
print("There are {} movies with more than {} favorable reviews".format(len(frequent_itemsets[1]), min_support))
sys.stdout.flush()
for k in range(2, 20):
# Generate candidates of length k, using the frequent itemsets of length k-1
# Only store the frequent itemsets
cur_frequent_itemsets = find_frequent_itemsets(favorable_reviews_by_users, frequent_itemsets[k-1],
min_support)
if len(cur_frequent_itemsets) == 0:
print("Did not find any frequent itemsets of length {}".format(k))
sys.stdout.flush()
break
else:
print("I found {} frequent itemsets of length {}".format(len(cur_frequent_itemsets), k))
#print(cur_frequent_itemsets)
sys.stdout.flush()
frequent_itemsets[k] = cur_frequent_itemsets
# We aren't interested in the itemsets of length 1, so remove those
del frequent_itemsets[1]
```
This code may take a few minutes to run.
```
print("Found a total of {0} frequent itemsets".format(sum(len(itemsets) for itemsets in frequent_itemsets.values())))
```
As we can see it returns 2968 frequent itemsets of varying lengths. You'll notice
that the number of itemsets grows as the length increases before it shrinks. It grows
because of the increasing number of possible rules. After a while, the large number
of combinations no longer has the support necessary to be considered frequent.
This results in the number shrinking. This shrinking is the benefit of the Apriori
algorithm. If we search all possible itemsets (not just the supersets of frequent ones),
we would be searching thousands of times more itemsets to see if they are frequent.
### Extracting association rules
After the Apriori algorithm has completed, we have a list of frequent itemsets.
These aren't exactly association rules, but they are similar to it. A frequent itemset
is a set of items with a minimum support, while an association rule has a premise
and a conclusion.
We can make an association rule from a frequent itemset by taking one of the movies
in the itemset and denoting it as the conclusion. The other movies in the itemset will
be the premise. This will form rules of the following form: if a reviewer recommends all
of the movies in the premise, they will also recommend the conclusion.
For each itemset, we can generate a number of association rules by setting each
movie to be the conclusion and the remaining movies as the premise.
In code, we first generate a list of all of the rules from each of the frequent itemsets,
by iterating over each of the discovered frequent itemsets of each length. We then iterate over every movie in this itemset, using it as our conclusion.
The remaining movies in the itemset are the premise. We save the premise and
conclusion as our candidate rule. This returns a very large number of candidate rules. We can see some by printing
out the first few rules in the list.
```
# Now we create the association rules. First, they are candidates until the confidence has been tested
candidate_rules = []
for itemset_length, itemset_counts in frequent_itemsets.items():
for itemset in itemset_counts.keys():
for conclusion in itemset:
premise = itemset - set((conclusion,))
candidate_rules.append((premise, conclusion))
print("There are {} candidate rules".format(len(candidate_rules)))
print(candidate_rules[:5])
```
These rules were returned as the resulting output.
In these rules, the first part (the frozenset) is the list of movies in the premise,
while the number after it is the conclusion. In the first case, if a reviewer
recommends movie 50, they are also likely to recommend movie 64.
Next, we compute the confidence of each of these rules. The process starts by creating dictionaries to store how many times we see the
premise leading to the conclusion (a correct example of the rule) and how many
times it doesn't (an incorrect example). We iterate over all of the users, their favorable reviews, and over each candidate
association rule. We then test to see if the premise is applicable to this user. In other words, did the
user favorably review all of the movies in the premise? If the premise applies, we see if the conclusion movie was also rated favorably.
If so, the rule is correct in this instance. If not, it is incorrect. We then compute the confidence for each rule by dividing the correct count by the
total number of times the rule was seen.
```
# Now, we compute the confidence of each of these rules. This is very similar to what we did in chapter 1
correct_counts = defaultdict(int)
incorrect_counts = defaultdict(int)
for user, reviews in favorable_reviews_by_users.items():
for candidate_rule in candidate_rules:
premise, conclusion = candidate_rule
if premise.issubset(reviews):
if conclusion in reviews:
correct_counts[candidate_rule] += 1
else:
incorrect_counts[candidate_rule] += 1
rule_confidence = {candidate_rule:
correct_counts[candidate_rule] / float(correct_counts[candidate_rule] + incorrect_counts[candidate_rule])
for candidate_rule in candidate_rules}
# Choose only rules above a minimum confidence level
min_confidence = 0.9
# Filter out the rules with poor confidence
rule_confidence = {rule: confidence for rule, confidence in rule_confidence.items() if confidence > min_confidence}
print(len(rule_confidence))
```
Now we can print the top five rules by sorting this confidence dictionary and
printing the results:
```
from operator import itemgetter
sorted_confidence = sorted(rule_confidence.items(), key=itemgetter(1), reverse=True)
for index in range(5):
print("Rule #{0}".format(index + 1))
(premise, conclusion) = sorted_confidence[index][0]
print("Rule: If a person recommends {0} they will also recommend {1}".format(premise, conclusion))
print(" - Confidence: {0:.3f}".format(rule_confidence[(premise, conclusion)]))
print("")
```
The resulting printout shows only the movie IDs, which isn't very helpful without
the names of the movies also. The dataset came with a file called u.items, which
stores the movie names and their corresponding MovieID (as well as other
information, such as the genre).
We can load the titles from this file using pandas. Additional information about
the file and categories is available in the README that came with the dataset.
The data in the files is in CSV format, but with data separated by the | symbol;
it has no header and the encoding is important to set. The column names were
found in the README file
```
# Even better, we can get the movie titles themselves from the dataset
movie_name_filename = 'data/ml-100k/u.item'
movie_name_data = pd.read_csv(movie_name_filename, delimiter="|", header=None, encoding = "mac-roman")
movie_name_data.columns = ["MovieID", "Title", "Release Date", "Video Release", "IMDB", "<UNK>", "Action", "Adventure",
"Animation", "Children's", "Comedy", "Crime", "Documentary", "Drama", "Fantasy", "Film-Noir",
"Horror", "Musical", "Mystery", "Romance", "Sci-Fi", "Thriller", "War", "Western"]
```
Getting the movie title is important, so we will create a function that will return a
movie's title from its MovieID, saving us the trouble of looking it up each time. We look up the movie_name_data DataFrame for the given MovieID and return only
the title column. We use the values parameter to get the actual value (and not the pandas Series
object that is currently stored in title_object). We are only interested in the first
value—there should only be one title for a given MovieID anyway! We end the function by returning the title as needed.
```
def get_movie_name(movie_id):
title_object = movie_name_data[movie_name_data["MovieID"] == movie_id]["Title"]
title = title_object.values[0]
return title
get_movie_name(4)
```
We adjust our previous code for printing out the top
rules to also include the titles
```
for index in range(5):
print("Rule #{0}".format(index + 1))
(premise, conclusion) = sorted_confidence[index][0]
premise_names = ", ".join(get_movie_name(idx) for idx in premise)
conclusion_name = get_movie_name(conclusion)
print("Rule: If a person recommends {0} they will also recommend {1}".format(premise_names, conclusion_name))
print(" - Confidence: {0:.3f}".format(rule_confidence[(premise, conclusion)]))
print("")
```
The result is much more readable (there are still some issues, but we can ignore them
for now.)
### Evaluation
In a broad sense, we can evaluate the association rules using the same concept as for
classification. We use a test set of data that was not used for training, and evaluate
our discovered rules based on their performance in this test set.
To do this, we will compute the test set confidence, that is, the confidence of each
rule on the testing set.
We won't apply a formal evaluation metric in this case; we simply examine the rules
and look for good examples.
First, we extract the test dataset, which is all of the records we didn't use in the
training set. We used the first 200 users (by ID value) for the training set, and we will
use all of the rest for the testing dataset. As with the training set, we will also get the
favorable reviews for each of the users in this dataset as well.
```
# Evaluation using test data
test_dataset = all_ratings[~all_ratings['UserID'].isin(range(200))]
test_favorable = test_dataset[test_dataset["Favorable"]]
#test_not_favourable = test_dataset[~test_dataset["Favourable"]]
test_favorable_by_users = dict((k, frozenset(v.values)) for k, v in test_favorable.groupby("UserID")["MovieID"])
#test_not_favourable_by_users = dict((k, frozenset(v.values)) for k, v in test_not_favourable.groupby("UserID")["MovieID"])
#test_users = test_dataset["UserID"].unique()
test_dataset[:5]
```
We then count the correct instances where the premise leads to the conclusion, in the
same way we did before. The only change here is the use of the test data instead of
the training data.
```
correct_counts = defaultdict(int)
incorrect_counts = defaultdict(int)
for user, reviews in test_favorable_by_users.items():
for candidate_rule in candidate_rules:
premise, conclusion = candidate_rule
if premise.issubset(reviews):
if conclusion in reviews:
correct_counts[candidate_rule] += 1
else:
incorrect_counts[candidate_rule] += 1
```
Next, we compute the confidence of each rule from the correct counts.
```
test_confidence = {candidate_rule: correct_counts[candidate_rule] / float(correct_counts[candidate_rule] + incorrect_counts[candidate_rule])
for candidate_rule in rule_confidence}
print(len(test_confidence))
sorted_test_confidence = sorted(test_confidence.items(), key=itemgetter(1), reverse=True)
print(sorted_test_confidence[:5])
```
Finally, we print out the best association rules with the titles instead of the
movie IDs.
```
for index in range(10):
print("Rule #{0}".format(index + 1))
(premise, conclusion) = sorted_confidence[index][0]
premise_names = ", ".join(get_movie_name(idx) for idx in premise)
conclusion_name = get_movie_name(conclusion)
print("Rule: If a person recommends {0} they will also recommend {1}".format(premise_names, conclusion_name))
print(" - Train Confidence: {0:.3f}".format(rule_confidence.get((premise, conclusion), -1)))
print(" - Test Confidence: {0:.3f}".format(test_confidence.get((premise, conclusion), -1)))
print("")
```
The fifth rule, for instance, has a perfect confidence in the training data (1.000), but it
is only accurate in 60 percent of cases for the test data (0.609). Many of the other rules in
the top 10 have high confidences in test data though, making them good rules for
making recommendations.
### Summary
In this example, we performed affinity analysis in order to recommend movies based
on a large set of reviewers. We did this in two stages. First, we found frequent
itemsets in the data using the Apriori algorithm. Then, we created association rules
from those itemsets.
The use of the Apriori algorithm was necessary due to the size of the dataset.
We performed training on a subset of our data in order to find the association rules,
and then tested those rules on the rest of the data—a testing set. From what we
discussed in the previous chapters, we could extend this concept to use cross-fold
validation to better evaluate the rules. This would lead to a more robust evaluation
of the quality of each rule
___
| true |
code
| 0.280951 | null | null | null | null |
|
# Gaussian Process Fitting
by Sarah Blunt
### Prerequisites
This tutorial assumes knowledge of the basic `radvel` API for $\chi^2$ likelihood fitting. As such, please complete the following before beginning this tutorial:
- radvel/docs/tutorials/164922_Fitting+MCMC.ipynb
- radvel/docs/tutorials/K2-24_Fitting+MCMC.ipynb
This tutorial also assumes knowledge of Gaussian Processes (GPs) as applied to radial velocity (RV) timeseries modeling. Grunblatt et al. (2015) and Rajpaul et al. (2015) contain excellent introductions to this topic. Also check out "Gaussian Processes for Machine Learning," by Rasmussen & Williams, a free online textbook hosted at gaussianprocesses.org.
### Objectives
Using the K2-131 (EPIC-228732031) dataset published in Dai et al. (2017), I will show how to:
- perform a maximum a posteriori (MAP) fit using a quasi-periodic kernel GP regression to model stellar activity (with data from multiple telescopes)
- do an MCMC exploration of the corresponding parameter space (with data from multiple telescopes)
### Tutorial
Do some preliminary imports:
```
import numpy as np
import pandas as pd
import os
import radvel
import radvel.likelihood
from radvel.plot import orbit_plots, mcmc_plots
from scipy import optimize
%matplotlib inline
```
Read in RV data from Dai et al. (2017):
```
data = pd.read_csv(os.path.join(radvel.DATADIR,'k2-131.txt'), sep=' ')
t = np.array(data.time)
vel = np.array(data.mnvel)
errvel = np.array(data.errvel)
tel = np.array(data.tel)
telgrps = data.groupby('tel').groups
instnames = telgrps.keys()
```
We'll use a quasi-periodic covariance kernel in this fit. An element in the covariance matrix, $C_{ij}$ is defined as follows:
$$
C_{ij} = \eta_1^2 exp[-\frac{|t_i-t_j|^2}{\eta_2^2} -\frac{sin^2(\pi|t_i-t_j|/\eta_3)}{2\eta_4^2}]
$$
Several other kernels are implemented in `radvel`. The code for all kernels lives in radvel/gp.py. Check out that file if you'd like to implement a new kernel.
Side Note: to see a list of all implemented kernels and examples of possible names for their associated hyperparameters...
```
print(radvel.gp.KERNELS)
```
Define the GP hyperparameters we will use in our fit:
```
hnames = [
'gp_amp', # eta_1; GP variability amplitude
'gp_explength', # eta_2; GP non-periodic characteristic length
'gp_per', # eta_3; GP variability period
'gp_perlength', # eta_4; GP periodic characteristic length
]
```
Define some numbers (derived from photometry) that we will use in our priors on the GP hyperparameters:
```
gp_explength_mean = 9.5*np.sqrt(2.) # sqrt(2)*tau in Dai+ 2017 [days]
gp_explength_unc = 1.0*np.sqrt(2.)
gp_perlength_mean = np.sqrt(1./(2.*3.32)) # sqrt(1/(2*gamma)) in Dai+ 2017
gp_perlength_unc = 0.019
gp_per_mean = 9.64 # T_bar in Dai+ 2017 [days]
gp_per_unc = 0.12
Porb = 0.3693038 # orbital period [days]
Porb_unc = 0.0000091
Tc = 2457582.9360 # [BJD]
Tc_unc = 0.0011
```
Dai et al. (2017) derive the above from photometry (see sect 7.2.1). I'm currently working on implementing joint modeling of RVs & photometry and RVs & activity indicators in `radvel`, so stay tuned if you'd like to use those features!
Initialize `radvel.Parameters` object:
```
nplanets=1
params = radvel.Parameters(nplanets,basis='per tc secosw sesinw k')
```
Set initial guesses for each fitting parameter:
```
params['per1'] = radvel.Parameter(value=Porb)
params['tc1'] = radvel.Parameter(value=Tc)
params['sesinw1'] = radvel.Parameter(value=0.,vary=False) # fix eccentricity = 0
params['secosw1'] = radvel.Parameter(value=0.,vary=False)
params['k1'] = radvel.Parameter(value=6.55)
params['dvdt'] = radvel.Parameter(value=0.,vary=False)
params['curv'] = radvel.Parameter(value=0.,vary=False)
```
Set initial guesses for GP hyperparameters:
```
params['gp_amp'] = radvel.Parameter(value=25.0)
params['gp_explength'] = radvel.Parameter(value=gp_explength_mean)
params['gp_per'] = radvel.Parameter(value=gp_per_mean)
params['gp_perlength'] = radvel.Parameter(value=gp_perlength_mean)
```
Instantiate a `radvel.model.RVmodel` object, with `radvel.Parameters` object as attribute:
```
gpmodel = radvel.model.RVModel(params)
```
Initialize `radvel.likelihood.GPLikelihood` objects (one for each telescope):
```
jit_guesses = {'harps-n':0.5, 'pfs':5.0}
likes = []
def initialize(tel_suffix):
# Instantiate a separate likelihood object for each instrument.
# Each likelihood must use the same radvel.RVModel object.
indices = telgrps[tel_suffix]
like = radvel.likelihood.GPLikelihood(gpmodel, t[indices], vel[indices],
errvel[indices], hnames, suffix='_'+tel_suffix,
kernel_name="QuasiPer"
)
# Add in instrument parameters
like.params['gamma_'+tel_suffix] = radvel.Parameter(value=np.mean(vel[indices]), vary=False, linear=True)
like.params['jit_'+tel_suffix] = radvel.Parameter(value=jit_guesses[tel_suffix], vary=True)
likes.append(like)
for tel in instnames:
initialize(tel)
```
Instantiate a `radvel.likelihood.CompositeLikelihood` object that has both GP likelihoods as attributes:
```
gplike = radvel.likelihood.CompositeLikelihood(likes)
```
Instantiate a `radvel.Posterior` object:
```
gppost = radvel.posterior.Posterior(gplike)
```
Add in priors (see Dai et al. 2017 section 7.2):
```
gppost.priors += [radvel.prior.Gaussian('per1', Porb, Porb_unc)]
gppost.priors += [radvel.prior.Gaussian('tc1', Tc, Tc_unc)]
gppost.priors += [radvel.prior.Jeffreys('k1', 0.01, 10.)] # min and max for Jeffrey's priors estimated by Sarah
gppost.priors += [radvel.prior.Jeffreys('gp_amp', 0.01, 100.)]
gppost.priors += [radvel.prior.Jeffreys('jit_pfs', 0.01, 10.)]
gppost.priors += [radvel.prior.Jeffreys('jit_harps-n', 0.01,10.)]
gppost.priors += [radvel.prior.Gaussian('gp_explength', gp_explength_mean, gp_explength_unc)]
gppost.priors += [radvel.prior.Gaussian('gp_per', gp_per_mean, gp_per_unc)]
gppost.priors += [radvel.prior.Gaussian('gp_perlength', gp_perlength_mean, gp_perlength_unc)]
```
Note: our prior on `'gp_perlength'` isn't equivalent to the one Dai et al. (2017) use because our formulations of the quasi-periodic kernel are slightly different. The results aren't really affected.
Do a MAP fit:
```
res = optimize.minimize(
gppost.neglogprob_array, gppost.get_vary_params(), method='Nelder-Mead',
options=dict(maxiter=200, maxfev=100000, xatol=1e-8)
)
print(gppost)
```
Explore the parameter space with MCMC:
```
chains = radvel.mcmc(gppost,nrun=100,ensembles=3,savename='rawchains.h5')
```
Note: for reliable results, run MCMC until the chains have converged. For this example, nrun=10000 should do the trick, but that would take a minute or two, and I won't presume to take up that much of your time with this tutorial.
Make some nice plots:
```
# try switching some of these (optional) keywords to "True" to see what they do!
GPPlot = orbit_plots.GPMultipanelPlot(
gppost,
subtract_gp_mean_model=False,
plot_likelihoods_separately=False,
subtract_orbit_model=False
)
GPPlot.plot_multipanel()
Corner = mcmc_plots.CornerPlot(gppost, chains) # posterior distributions
Corner.plot()
quants = chains.quantile([0.159, 0.5, 0.841]) # median & 1sigma limits of posterior distributions
for par in gppost.params.keys():
if gppost.params[par].vary:
med = quants[par][0.5]
high = quants[par][0.841] - med
low = med - quants[par][0.159]
err = np.mean([high,low])
err = radvel.utils.round_sig(err)
med, err, errhigh = radvel.utils.sigfig(med, err)
print('{} : {} +/- {}'.format(par, med, err))
```
Compare posterior characteristics with those of Dai et al. (2017):
per1 : 0.3693038 +/- 9.1e-06
tc1 : 2457582.936 +/- 0.0011
k1 : 6.6 +/- 1.5
gp_amp : 26.0 +/- 6.2
gp_explength : 11.6 +/- 2.3
gp_per : 9.68 +/- 0.15
gp_perlength : 0.35 +/- 0.02
gamma_harps-n : -6695 +/- 11
jit_harps-n : 2.0 +/- 1.5
gamma_pfs : -1 +/- 11
jit_pfs : 5.3 +/- 1.4
Thanks for going through this tutorial! As always, if you have any questions, feature requests, or problems, please file an issue on the `radvel` GitHub repo (github.com/California-Planet-Search/radvel).
| true |
code
| 0.510924 | null | null | null | null |
|
This notebook was prepared by [Donne Martin](https://github.com/donnemartin). Source and license info is on [GitHub](https://github.com/donnemartin/interactive-coding-challenges).
# Solution Notebook
## Problem: Implement Fizz Buzz.
* [Constraints](#Constraints)
* [Test Cases](#Test-Cases)
* [Algorithm](#Algorithm)
* [Code](#Code)
* [Unit Test](#Unit-Test)
## Constraints
* What is fizz buzz?
* Return the string representation of numbers from 1 to n
* Multiples of 3 -> 'Fizz'
* Multiples of 5 -> 'Buzz'
* Multiples of 3 and 5 -> 'FizzBuzz'
* Can we assume the inputs are valid?
* No
* Can we assume this fits memory?
* Yes
## Test Cases
<pre>
* None -> Exception
* < 1 -> Exception
* 15 ->
[
'1',
'2',
'Fizz',
'4',
'Buzz',
'Fizz',
'7',
'8',
'Fizz',
'Buzz',
'11',
'Fizz',
'13',
'14',
'FizzBuzz'
]
</pre>
## Algorithm
There is no fancy algorithm to solve fizz buzz.
* Iterate from 1 through n
* Use the mod operator to determine if the current iteration is divisible by:
* 3 and 5 -> 'FizzBuzz'
* 3 -> 'Fizz'
* 5 -> 'Buzz'
* else -> string of current iteration
* return the results
Complexity:
* Time: O(n)
* Space: O(n)
## Code
```
class Solution(object):
def fizz_buzz(self, num):
if num is None:
raise TypeError('num cannot be None')
if num < 1:
raise ValueError('num cannot be less than one')
results = []
for i in range(1, num + 1):
if i % 3 == 0 and i % 5 == 0:
results.append('FizzBuzz')
elif i % 3 == 0:
results.append('Fizz')
elif i % 5 == 0:
results.append('Buzz')
else:
results.append(str(i))
return results
```
## Unit Test
```
%%writefile test_fizz_buzz.py
from nose.tools import assert_equal, assert_raises
class TestFizzBuzz(object):
def test_fizz_buzz(self):
solution = Solution()
assert_raises(TypeError, solution.fizz_buzz, None)
assert_raises(ValueError, solution.fizz_buzz, 0)
expected = [
'1',
'2',
'Fizz',
'4',
'Buzz',
'Fizz',
'7',
'8',
'Fizz',
'Buzz',
'11',
'Fizz',
'13',
'14',
'FizzBuzz'
]
assert_equal(solution.fizz_buzz(15), expected)
print('Success: test_fizz_buzz')
def main():
test = TestFizzBuzz()
test.test_fizz_buzz()
if __name__ == '__main__':
main()
%run -i test_fizz_buzz.py
```
| true |
code
| 0.538862 | null | null | null | null |
|
# Warsztat 4 - funkcje<a id=top></a>
<font size=2>Przed pracą z notatnikiem polecam wykonać kod w ostatniej komórce (zawiera html i css), dzięki czemu całość będzie bardziej estetyczna :)</font>
<a href='#Warsztat-4---funkcje'>Warsztat 4</a>
<ul>
<li><a href='#Składnia'><span>Składnia</span></a></li>
<li><a href='#Instrukcja-return'><span>Instrukcja return</span></a></li>
<li><a href='#Argumenty-nie-wprost'><span>Argumenty nie-wprost</span></a></li>
<li><a href='#Dowolna-ilość-argumentów'><span>Dowolna ilość argumentów</span></a></li>
<li><a href='#Funkcje-Lambda'><span>Funkcje Lambda</span></a></li>
</ul>
Większość programów będzie wymagała wielokrotnego uruchamiania tych samych (albo podobnych) sekwencji komend i przekształceń. Wpisywanie ich ręcznie w całości, za każdym razem kiedy będziemy potrzebowali danego zestawu operacji, jest bardzo nieekonomiczne - zarówno pod względem czasu, wykorzystanej pamięci oraz czytelności kodu.<br>
Zamiast tego wystarczy użyć <b>funkcji</b>.
Funkcja to wydzielony fragment kodu o określonej nazwie, której wywołanie wykona wszystkie operacje w nim zawarte.<br>
Podstawowa składnia do tworzenia funkcji wygląda następująco:
```python
def nazwa_funkcji (argument1, argument2,...,argumentN):
<kod do wykonania>
<kod do wykonania>
<kod do wykonania>
return zwracana_zmienna```
Wewnątrz funkcji może znajdować się dowolny kod, który jest możliwy do stworzenia w pythonie. Spróbujmy zatem wygenerować prostą funkcję do witania się z użytkownikami.
```
def powitanie():
print ("Witaj, użytkowniku!")
powitanie()
powitanie()
```
Powyższy kod zawiera dwa wystąpienia naszej funkcji. Pierwsze wystąpienie zawsze jest <b>deklaracją</b> (definicją) funkcji, czyli "przepisem" na wykonanie określonego zbioru operacji (w tym wypadku wypisania powitania na konsoli). Deklaracja musi pojawić się przed pierwszym użyciem wywołaniem funkcji. Najczęściej umieszcza się je wszystkie, zbiorczo, na początku skryptu a dopiero po wszystkich deklarowanych elementach - kod wykonawczy programu.
Drugie użycie fukncji to <b>wywołanie</b>, podczas którego wykonywany jest kod zawarty wewnątrz funkcji. Wystarczy zatem przywołać nazwę funkcji aby zaaplikować cały kod, co oszczędzi nam mnóstwo czasu i ustrzeże od błędów przy przepisywaniu tego samego kodu w innym miejscu - wystarczy ponownie wywołać daną funkcję.<br>
Istotnym elementem działania funkcji jest także możliwość wkładania do nich danych. Przyjrzyjmy się kolejnemu przykładowi:
```
def powitanie(imie):
print ("Witaj, użytkowniku %s!" % (imie))
zmienna = input("Jak masz na imie? ")
powitanie(zmienna)
```
Dzięki uwzględnieniu zmiennej imię w nawiasie deklaracji funkcji powitanie możemy przekazać jej zmienną, która zostanie użyta w trakcie wykonywania kodu wewnątrz funkcji. 'imię' jest tzw. <b>zmienną lokalną</b>, co oznacza, że widoczna jest wyłącznie dla elementów wewnątrz funkcji - poza nią nie będzie można jej użyć.
```
def powitanie(imie2):
print ("Witaj, użytkowniku %s!" % (imie2))
powitanie("Marcin")
print (imie2)
```
Ten podział na zmienne <b>lokalne</b> oraz <b>globalne</b> jest bardzo przydatny - pozwala zachować porządek w kodzie (przy długich programach minimalizuje szansę na powtórzenie przypadkiem nazwy zmiennej) oraz używanie tej samej nazwy dla zmiennych wewnątrz różnych funkcji (przez co nie trzeba tworzyć np. imie1, nowe_imie, imie_imie etc.), co ułatwia zrozumienie kodu.
Funkcje mogą być wywołane w dowolnym momencie programu - także wewnątrz innych funkcji. Zobaczmy, jak możemy stworzyć drugą funkcję, która zautomatyzuje nam proces pobierania imienia od użytkownika.
```
def powitanie(imie):
print ("Witaj, użytkowniku %s!" % (imie))
def wez_imie():
zmienna = input("Jak masz na imie? ")
powitanie(zmienna)
wez_imie()
```
<a href='#top' style='float: right; font-size: 13px;'>Do początku</a>
### Instrukcja return
Jak mogliśmy zobaczyć na samym początku, na końcu funkcji może pojawić się instrukcja <b>return</b>. Służy ona do deklarowania, jaką wartość ma zostać przez funkcję zwrócona, tzn. dostępna dla innych funkcji i możliwa do przypisania np. do zmiennej globalnej.<br>
Zobaczymy to na przykładzie poniższej funkcji artymetycznej:
```
def dodaj (pierwsza, druga):
return pierwsza+druga
zmienna = dodaj(2,2)
print (dodaj(2,3))
```
Funkcja może zwrócić dowolny obiekt - tekst, liczbę, listę czy słownik. Może też zwracać więcej niż jeden element - należy je wtedy rozdzielić przecinkiem. Jeśli przypiszemy wieloelementowy zwrot do jednej zmiennej, całość zostana przechowana w formie krotki (ang. tuple). Można jednak podać dwie zmienne (oddzielone przecinkiem), dzięki czemu każdy eleme
```
def arytmetyka (pierwsza, druga):
'''Opis funkcji
Funkcja zwraca wyniki działań w kolejności: dodaj, odejmij, mnóż, dziel
'''
dodaj = pierwsza+druga
odejmij = pierwsza-druga
mnoz = pierwsza*druga
dziel = pierwsza/druga
return [dodaj, odejmij, mnoz, dziel], dodaj+odejmij+mnoz+dziel
zmienna = arytmetyka(2,2)
print (zmienna)
print (type(zmienna), "\n")
lista, suma = arytmetyka(2,4)
print (lista)
print (suma)
help(arytmetyka)
```
<a href='#top' style='float: right; font-size: 13px;'>Do początku</a>
### Argumenty nie-wprost
Oprócz argumentów, które użytkownik musi podać podczas każdorazowego użycia funkcji, możemy również zadeklarować argumenty, które będą posiadały standardową wartość. Dzięki temu nie będzie potrzeby ich wprowadzania, ale będzie to możliwe, jeśli tylko tego zażyczy sobie użytkownik.
```
def mnoznik(liczba, druga=5):
return liczba*druga
print (mnoznik(5))
print (mnoznik(5,10))
```
Widzimy, że podczas podania tylko jednego argumentu, drugi jest brany w swojej podstawowej wartości. Podanie drugiego argumentu podczas wywołania funkcji nadpisuje standardową wersję.
### Dowolna ilość argumentów
Mogą się zdarzyć sytuacje, w których nie będziemy chcieli ograniczać ilości argumentów, jakie użytkownik może wprowadzić do danej funkcji. Nieznaną ilość argumentów można zastąpić specjalnym wyrażeniem <b>*args</b>, dzięki czemu interpreter pythona pozwoli na wprowadzenie dowolnej ich ilości.
```
def dodawanie(*args):
suma = 0
for i in args:
suma+=i
return suma
print (dodawanie(*[1,2,3,4,5,6,7,8,9,10,11,12,13,14]))
```
W powyższym przykładzie istotny jest znak " \* ", słowo "args" to tylko element konwencji - może być dowolone. Gwiazdka sugeruje, że otrzymane argumenty należy przekazać w formie listy i zmusza interpreter do rozłożenia tej listy na pojedyncze argumenty.
```
def dodawanie(*args):
return args
print (dodawanie(1,2,3,4,5,6,7,8,9,10))
print (dodawanie([1,2,3,4,5,6,7,8,9,10]))
print (dodawanie(*[1,2,3,4,5,6,7,8,9,10]))
def dodawanie(args):
suma = 0
for i in args:
suma+=i
return suma
print (dodawanie([1,2,3,4,5,6,7,8,9,10]))
```
Oprócz tego istnieje również konstrukcja <b>**kwargs</b>, która interpretuje nadchodzące argumenty jako elementy słownika.
```
def dodawanie(**kwargs):
return kwargs
print (dodawanie(arg1=1,arg2=2,arg3=3))
slownik={'arg1': 1,'arg2': 2,'arg3': 3}
print (dodawanie(**slownik))
print (dodawanie(slownik))
```
Mogliśmy zobaczyć dwie strategie:<br>
1. podanie gwiazdki (dwóch) wyłącznie w deklaracji funkcji - interpreter będzie oczekiwał, że kolejne argumenty będą tworzyć konkretną strukturę, uporządkowaną listę albo słownik.
2. podanie gwiazdki (dwóch) podczas wywoływania funkcji - interpreter weźmie wskazany jeden element i zinterpretuje go jako listę/słownik.
Przy prostych funkcjach tego typu zabiegi zazwyczaj nie są konieczne, ale warto zauważyć, że takie przekazywanie argumentów może np. pozwalać na wstawianie zestawów "ustawień" do wskazanej funkcji, bez konieczności listowania wszystkich elementów w każdym wywołaniu.
```
def dodawanie(**kwargs):
return sum(kwargs.values())
slownik={'arg1': 1,'arg2': 2,'arg3': 3}
print (dodawanie(**slownik))
```
<a href='#top' style='float: right; font-size: 13px;'>Do początku</a>
### Funkcje Lambda
Możliwe jest również tworzenie funkcji bez przypisanej nazwy i o uproszczonej składni - wykonywane jest wyłącznie jedno wyrażenie. Są one szczególne przydatne w pracy z listami (patrz: list comprehensions).
```
zet = lambda x: x*x+4
print (zet(5))
zet = lambda x, y: x*y+4
print (zet(5,7))
```
### Ćwiczenia z funkcji
Stwórz funkcję fibbonacci, która będzie przyjmować jeden argument (liczba całkowita) natomiast efektem jego pracy będzie ciąg Fibbonacciego o wskazanej przez argument ilości elementów.<br>
Wzór na n-ty element ciągu: $fib_n=fib_{n-2}+fib_{n-1}$
```
def fibbonacci(liczba):
fibbonacci(10)
```
```
from IPython.core.display import HTML
from urllib.request import urlopen
HTML(urlopen("https://raw.githubusercontent.com/mkoculak/Warsztat-programowania/master/ipython.css").read().decode("utf-8"))
```
| true |
code
| 0.267473 | null | null | null | null |
|
# Exploration of one customer
Analysis of:
* global stats
* daily pattern
Also, found a week of interest (early 2011-12) for futher work ([Solar home control bench](https://github.com/pierre-haessig/solarhome-control-bench) and SGE 2018 paper)
* daily pattern the month before this week
To be done: [clustering of daily trajectories](#Clustering-of-daily-trajectories)
PH December 23, 2017
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
```
## Load customer data
```
import solarhome as sh
df_raw = sh.read_csv('2011-2012')
df, missing_rec = sh.reshape(df_raw)
```
Choice: customer 12:
* no controlled load (CL channel)
* no oddities consumption and production during 2011-2012
```
n_cust = 12
d = df[n_cust]
d.to_csv('customer/12/data_2011-2012.csv')
d.head()
```
### Customer global stats (over the year)
Statistics close to the [dataset average](Solar%20home%20exploration.ipynb#Global-statistics-of-PV-generation):
* Consumption: avg 0.7 kW, max 4.0 kW. Yearly total of 5 900 kWh/yr
* PV max 0.9 kW (1.04 kW capacity). Yield of 1250 kWh/yr/kWc
```
d.describe([])
```
#### Histograms
```
prod = d.GG
cons = d.GC
cons.hist(bins=30, label='Consumption')
(prod[prod>=0.01]).hist(label='PV prod (>0)', alpha=0.8)
plt.legend();
```
PV yearly production (kWh)
```
dt = 0.5 # hours
E_pv = prod.sum() * dt
E_pv
d_cust_cap = df_raw[['Customer', 'Generator Capacity']]
gen_cap = d_cust_cap.groupby('Customer')['Generator Capacity'].max()
gen_cap = gen_cap[n_cust]
gen_cap
```
PV yield (kWh/kWc/yr)
```
E_pv/gen_cap
```
Yearly consumption
```
E_cons = cons.sum() * dt
E_cons
```
### Time plot
```
%matplotlib inline
fig, (ax1, ax2) = plt.subplots(2,1, sharex=True)
#sl = slice('2011-10-12','2011-10-18') # 3 semi-cloudy, 1 very cloudy, 3 sunny days
sl = slice('2011-11-29','2011-12-05')
#sl=slice(0, -1)
cons[sl].plot(ax=ax1, label='Consumption')
prod[sl].plot(ax=ax2, color='tab:orange', label='PV production')
ax1.legend(loc='upper right')
ax2.legend(loc='upper right')
ax1.set(
title='Customer %d data: 7 days extract' % n_cust,
ylabel='Power (kW)'
)
ax2.set(
ylabel='Power (kW)'
);
fig.tight_layout()
fig.savefig('customer/12/data_week_%s.png' % sl.start, dpi=200, bbox_inches='tight')
```
## Daily pattern
i.e. stats as a function of the hour of the day
```
def hod(tstamp):
'hour of the day (fractional))'
return tstamp.hour + tstamp.minute/60
d_dm = d.groupby(by=hod).mean()
d_d05 = d.groupby(by=hod).quantile(.05)
d_d25 = d.groupby(by=hod).quantile(.25)
d_d75 = d.groupby(by=hod).quantile(.75)
d_d95 = d.groupby(by=hod).quantile(.95)
fig, (ax1, ax2) = plt.subplots(2,1, sharex=True)
c = 'tab:blue'
d_dm.GC.plot(ax=ax1, color=c, label='Consumption')
ax1.fill_between(d_dm.index, d_d05.GC, d_d95.GC, alpha=0.3, color=c, lw=0)
ax1.fill_between(d_dm.index, d_d25.GC, d_d75.GC, alpha=0.3, color=c, lw=0)
ax1.set_ylim(ymin=0)
ax1.legend(loc='upper left')
c = 'tab:orange'
d_dm.GG.plot(ax=ax2, color=c, label='PV production')
ax2.fill_between(d_dm.index, d_d05.GG, d_d95.GG, alpha=0.3, color=c, lw=0)
ax2.fill_between(d_dm.index, d_d25.GG, d_d75.GG, alpha=0.3, color=c, lw=0)
ax2.legend(loc='upper left')
ax1.set(
title='Customer %d daily pattern' % n_cust,
ylabel='Power (kW)'
);
ax2.set(
xlabel='hour of the day',
ylabel='Power (kW)'
);
fig.tight_layout()
fig.savefig('customer/12/daily_pattern_2011-2012.png', dpi=200, bbox_inches='tight')
```
#### Compute all quantiles, to save the pattern for later reuse
```
quantiles = np.linspace(0.05, 0.95, 19)
quantiles
def daily_pattern(ts):
'''compute statistics for each hour of the day (min, max, mean and quantiles)
of the time series `ts`
returns DataFrame with columns 'mean','min', 'qXX'..., 'max'
and rows being the hours of the day between 0. and 24.
'''
dstats = pd.DataFrame({
'q{:02.0f}'.format(q*100) : ts.groupby(by=hod).quantile(q)
for q in quantiles
})
dstats.insert(0, 'min', ts.groupby(by=hod).min())
dstats.insert(0, 'mean', ts.groupby(by=hod).mean())
dstats['max'] = ts.groupby(by=hod).max()
return dstats
prod_dstats = daily_pattern(d.GG)
prod_dstats.to_csv('customer/12/daily_pattern_prod_2011-2012.csv')
cons_dstats = daily_pattern(d.GC)
cons_dstats.to_csv('customer/12/daily_pattern_cons_2011-2012.csv')
def plot_daily_pattern(dstats, title):
fig, ax = plt.subplots(1,1)
q_names = [c for c in dstats.columns if c.startswith('q')]
dstats[q_names[:9]].plot(ax=ax, color='tab:blue', lw=0.5)
dstats['q50'].plot(ax=ax, color='k')
dstats[q_names[11:]].plot(ax=ax, color='tab:red', lw=0.5)
dstats['min'].plot(ax=ax, color='tab:blue', label='min')
dstats['max'].plot(ax=ax, color='tab:red')
dstats['mean'].plot(ax=ax, color='k', lw=6, alpha=0.5)
plt.legend(ax.lines[-3:], ['min', 'max', 'mean']);
ax.set(
xlabel='hour of the day',
ylabel='Power (kW)',
title=title)
fig.tight_layout()
return fig, ax
fig, ax = plot_daily_pattern(cons_dstats,
title='Customer %d daily consumption pattern' % n_cust)
fig.savefig('customer/12/daily_pattern_cons_2011-2012.png', dpi=200)
fig, ax = plot_daily_pattern(prod_dstats,
title='Customer %d daily production pattern' % n_cust)
fig.savefig('customer/12/daily_pattern_prod_2011-2012.png', dpi=200)
```
### The month before 2011-11-29
i.e. before the week extract above
#### Compute all quantiles
```
sl = slice('2011-10-29','2011-11-28')
#sl = '2011-10'
daily_pattern(cons[sl]).to_csv('customer/12/daily_pattern_cons_M-1-%s.csv' % sl.stop)
daily_pattern(prod[sl]).to_csv('customer/12/daily_pattern_prod_M-1-%s.csv' % sl.stop)
fig, ax = plot_daily_pattern(daily_pattern(cons[sl]),
title='Customer %d consumption pattern \nthe month before %s' % (n_cust, sl.stop))
ax.set_ylim(ymax=3)
fig.savefig('customer/12/daily_pattern_cons_M-1-%s.png' % sl.stop, dpi=200)
fig, ax = plot_daily_pattern(daily_pattern(prod[sl]),
title='Customer %d production pattern \nthe month before %s' % (n_cust, sl.stop))
fig.savefig('customer/12/daily_pattern_prod_M-1-%s.png' % sl.stop, dpi=200)
```
#### Spaghetti plots, to compare with quantiles
code inspired from the analysis of daily patterns in [Pattern_daily_consumption.ipynb]( [Pattern_daily_consumption.ipynb#A-look-at-individual-customer])
```
def daily_spaghetti(df, title):
fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True, figsize=(5.5,4.5))
hod_lin = np.arange(48)/2
GC_day_m = df.GC.groupby(by=hod).mean()
GG_day_m = df.GG.groupby(by=hod).mean()
GC_day_traj = df.GC.values.reshape((-1, 48)).T
GG_day_traj = df.GG.values.reshape((-1, 48)).T
ax1.plot(hod_lin, GC_day_traj, 'k', lw=0.5, alpha=0.15);
ax1.plot(hod_lin, GC_day_m, color='tab:blue', lw=3, alpha=0.7)
ax2.plot(hod_lin, GG_day_traj, 'k', lw=0.5, alpha=0.15);
ax2.plot(hod_lin, GG_day_m, color='tab:orange', lw=3, alpha=0.7)
ax1.legend(ax1.lines[-2:], ['each day', 'mean'], loc='upper left')
ax2.legend(ax2.lines[-2:], ['each day', 'mean'], loc='upper left')
ax1.set(
title=title,
ylabel='Consumption (kW)'
)
ax2.set(
xlim=(0, 23.5),
xticks=range(0,24,3),
xlabel='hour of the day',
ylabel='PV production (kW)'
)
fig.tight_layout()
return fig, (ax1, ax2)
fig, (ax1, ax2) = daily_spaghetti(d[sl],
title='Customer %d the month before %s' % (n_cust, sl.stop))
ax1.set_ylim(ymax=3);
fig.savefig('customer/12/daily_traj_M-1-%s.png' % sl.stop, dpi=200)
```
Variation: plot data with solar panel upscaled to 4 kWp
```
d4k = d.copy()
d4k.GG *= 4/1.04
fig, (ax1, ax2) = daily_spaghetti(d4k[sl],
title='')
ax1.set_ylim(ymax=3);
fig.savefig('customer/12/daily_traj_M-1-%s_PV4kWp.png' % sl.stop, dpi=200)
fig.savefig('customer/12/daily_traj_M-1-%s_PV4kWp.pdf' % sl.stop, bbox_inches='tight')
```
### Clustering of daily trajectories
to be done.
## Day ahead forecast
model: autoregression on the previous half-hour, the previous day, with effect of the hour of the day.
$$ y_k = f(y_{k-1}, y_{k-48}, h) $$
More precisely, linear autogression, with coefficient being dependant of the hod:
$$ y_k = a_0(h) + a_1(h).y_{k-1} + a_2(h).y_{k-48} $$
In addition, the series of coefficients $a_0(h)$, $a_1(h)$, $a_2(h)$,... may require some smoothing, that is a penalization of their variations. Either absolute variation around average time-indepent coefficients or variation along the day.
→ pivoted data is saved for further processing in Julia: [Forecast.ipynb](Forecast.ipynb)
### Data preparation: group by day (pivoting)
pivot data: one day per row, one hour per column
```
d1 = d.copy()
d1['date'] = pd.DatetimeIndex(d1.index.date)
d1['hod'] = hod(d1.index)
d1.head()
prod_dpivot = d1.pivot('date', 'hod', 'GG')
cons_dpivot = d1.pivot('date', 'hod', 'GC')
cons_dpivot.head(3)
prod_dpivot[12.0].plot(label='prod @ 12:00')
prod_dpivot[18.0].plot(label='prod @ 18:00')
plt.legend();
```
Save as CSV for further use
```
prod_dpivot.to_csv('customer/12/daily_pivot_prod_2011-2012.csv')
cons_dpivot.to_csv('customer/12/daily_pivot_cons_2011-2012.csv')
```
### PV Production heatmap
Notice the effect of **daylight saving** between days ~92 (Oct 1st) and ~274 (March 31st).
→ this is a *problem for forecasting*
```
prod_dpivot.index[92], prod_dpivot.index[274]
fig = plt.figure(figsize=(7,4))
plt.imshow(prod_dpivot.values.T, aspect='auto',
origin='lower', extent=[0, 365, 0, 24], cmap='inferno');
plt.ylim([4, 20])
cbar = plt.colorbar()
cbar.set_label('Power (kW)')
cbar.locator
ax = plt.gca()
ax.set(
title='Customer %d production 2011-2012' % n_cust,
xlabel='day',
ylabel='hour of day',
yticks=[0, 6, 12, 18, 24]
)
fig.tight_layout()
fig.savefig('customer/12/daily_pivot_prod_2011-2012.png', dpi=200, bbox_inches='tight')
```
### Consumption heatmap
Notice: vmax set to 2 kW (→ saturation) otherwise the plot is dominated by the few spikes between 2.5 and 4 kW
Obs:
* start of the day at 6 am. Not influenced by daylight saving
```
fig = plt.figure(figsize=(7,4))
plt.imshow(cons_dpivot.values.T, aspect='auto',
vmax=2,
origin='lower', extent=[0, 365, 0, 24]);
#plt.ylim([4, 20])
cbar = plt.colorbar()
cbar.set_label('Power (kW) [saturated]')
fig.tight_layout()
ax = plt.gca()
ax.set(
title='Customer %d consumption 2011-2012' % n_cust,
xlabel='day',
ylabel='hour of day',
yticks=[0, 6, 12, 18, 24]
)
fig.tight_layout()
fig.savefig('customer/12/daily_pivot_cons_2011-2012.png', dpi=200, bbox_inches='tight')
```
Same plot, without saturation, but using a compression of high values:
$$ v \to \sqrt{v/v_{max}}$$
```
v = cons_dpivot.values.T
v = v/v.max()
v = v**(0.5)
fig = plt.figure(figsize=(7,4))
plt.imshow(v, aspect='auto',
origin='lower', extent=[0, 365, 0, 24]);
#plt.ylim([4, 20])
cbar = plt.colorbar()
cbar.set_label('normed sqrt(Power)')
ax = plt.gca()
ax.set(
title='Customer %d consumption 2011-2012' % n_cust,
xlabel='day',
ylabel='hour of day',
yticks=[0, 6, 12, 18, 24]
)
fig.tight_layout()
```
| true |
code
| 0.633467 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.