prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Pedersen N07 neutral case with heat flux
## Nalu-Wind with K-SGS model
Comparison between Nalu-wind and Pedersen (2014)
**Note**: To convert this notebook to PDF, use the command
```bash
$ jupyter nbconvert --TagRemovePreprocessor.remove_input_tags='{"hide_input"}' --to pdf postpro_n07.ipynb
```
```
%%capture
# Important header information
naluhelperdir = '../../utilities/'
# Import libraries
import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.insert(1, naluhelperdir)
import plotABLstats
import yaml as yaml
from IPython.display import Image
from matplotlib.lines import Line2D
import matplotlib.image as mpimg
%matplotlib inline
# Nalu-wind parameters
rundir = '/ascldap/users/lcheung/GPFS1/2020/amrcodes/testruns/neutral_n07_ksgs'
statsfile = 'abl_statistics.nc.run2'
avgtimes = [82800,86400]
# Load nalu-wind data
data = plotABLstats.ABLStatsFileClass(stats_file=rundir+'/'+statsfile);
Vprof, vheader = plotABLstats.plotvelocityprofile(data, None, tlims=avgtimes, exportdata=True)
Tprof, theader = plotABLstats.plottemperatureprofile(data, None, tlims=avgtimes, exportdata=True)
# Pedersen parameters
datadir = '../pedersen2014_data'
ped_umag = np.loadtxt(datadir+'/Pedersen2014_N07_velocity.csv', delimiter=',')
ped_T = np.loadtxt(datadir+'/Pedersen2014_N07_temperature.csv', delimiter=',')
h = 757
# Plot the velocity profile comparisons
plt.figure(figsize=(10,8));
plt.rc('font', size=14)
plt.plot(Vprof[:,4], Vprof[:,0]/h, 'b', label='Nalu-wind (k-sgs)')
plt.plot(ped_umag[:,0], ped_umag[:,1], 'r', label='Pedersen(2014)')
# Construct a legend
plt.legend()
plt.ylim([0, 1.5]);
plt.xlim([0, 12])
plt.xlabel('Velocity [m/s]')
plt.ylabel('Z/h')
#plt.grid()
plt.title('N07 Wind speed')
# Plot the temperature profile comparisons
plt.figure(figsize=(10,8));
plt.rc('font', size=14)
plt.plot(Tprof[:,1], Tprof[:,0], 'b', label='Nalu-wind (k-sgs)')
plt.plot(ped_T[:,0], ped_T[:,1], 'r', label='Pedersen(2014)')
# Construct a legend
plt.legend()
plt.ylim([0, 1500]);
#plt.xlim([0, 12])
plt.xlabel('Temperature [K]')
plt.ylabel('Z [m]')
#plt.grid()
plt.title('N07 Temperature')
# Extract TKE and Reynolds stresses
REstresses, REheader = plotABLstats.plottkeprofile(data, None, tlims=avgtimes, exportdata=True)
# Extract the fluxes
tfluxes, tfluxheader = plotABLstats.plottfluxprofile(data, None, tlims=avgtimes, exportdata=True)
# Extract the fluxes
sfstfluxes, sfstfluxheader= plotABLstats.plottfluxsfsprofile(data, None, tlims=[avgtimes[-1]-1, avgtimes[-1]], exportdata=True)
# Extract Utau
avgutau = plotABLstats.avgutau(data, None, tlims=avgtimes)
print('Avg Utau = %f'%avgutau)
# Calculate the inversion height
zi, utauz = plotABLstats.calcInversionHeight(data, [750.0], tlims=avgtimes)
print('zi = %f'%zi)
# Export the Nalu-Wind data for other people to compare
np.savetxt('NaluWind_N07_velocity.dat', Vprof, header=vheader)
np.savetxt('NaluWind_N07_temperature.dat', Tprof, header=theader)
np.savetxt('NaluWind_N07_reynoldsstresses.dat', REstresses, header=REheader)
np.savetxt('NaluWind_N07_temperaturefluxes.dat', tfluxes, header=tfluxheader)
np.savetxt('NaluWind_N07_sfstemperaturefluxes.dat', sfstfluxes, header=sfstfluxheader)
# Write the YAML file with integrated quantities
import yaml
savedict={'zi':float(zi), 'ustar':float(avgutau)}
f=open('istats.yaml','w')
f.write('# Averaged quantities from %f to %f\n'%(avgtimes[0], avgtimes[1]))
f.write(yaml.dump(savedict, default_flow_style=False))
f.close()
```
| true |
code
| 0.625896 | null | null | null | null |
|
# Обучение нейросетей — оптимизация и регуляризация
**Разработчик: Артем Бабенко**
На это семинаре будет необходимо (1) реализовать Dropout-слой и проследить его влияние на обобщающую способность сети (2) реализовать BatchNormalization-слой и пронаблюдать его влияние на скорость сходимости обучения.
## Dropout (0.6 балла)
Как всегда будем экспериментировать на датасете MNIST. MNIST является стандартным бенчмарк-датасетом, и его можно подгрузить средствами pytorch.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import torch.optim as optim
from torch.utils.data.sampler import SubsetRandomSampler
input_size = 784
num_classes = 10
batch_size = 128
train_dataset = dsets.MNIST(root='./MNIST/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = dsets.MNIST(root='./MNIST/',
train=False,
transform=transforms.ToTensor())
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=False)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
```
Определим ряд стандартных функций с прошлых семинаров
```
def train_epoch(model, optimizer, batchsize=32):
loss_log, acc_log = [], []
model.train()
for batch_num, (x_batch, y_batch) in enumerate(train_loader):
data = Variable(x_batch)
target = Variable(y_batch)
optimizer.zero_grad()
output = model(data)
pred = torch.max(output, 1)[1].data.numpy()
acc = np.mean(pred == y_batch)
acc_log.append(acc)
loss = F.nll_loss(output, target).cpu()
loss.backward()
optimizer.step()
loss = loss.data[0]
loss_log.append(loss)
return loss_log, acc_log
def test(model):
loss_log, acc_log = [], []
model.eval()
for batch_num, (x_batch, y_batch) in enumerate(test_loader):
data = Variable(x_batch)
target = Variable(y_batch)
output = model(data)
loss = F.nll_loss(output, target).cpu()
pred = torch.max(output, 1)[1].data.numpy()
acc = np.mean(pred == y_batch)
acc_log.append(acc)
loss = loss.data[0]
loss_log.append(loss)
return loss_log, acc_log
def plot_history(train_history, val_history, title='loss'):
plt.figure()
plt.title('{}'.format(title))
plt.plot(train_history, label='train', zorder=1)
points = np.array(val_history)
plt.scatter(points[:, 0], points[:, 1], marker='+', s=180, c='orange', label='val', zorder=2)
plt.xlabel('train steps')
plt.legend(loc='best')
plt.grid()
plt.show()
def train(model, opt, n_epochs):
train_log, train_acc_log = [], []
val_log, val_acc_log = [], []
for epoch in range(n_epochs):
train_loss, train_acc = train_epoch(model, opt, batchsize=batch_size)
val_loss, val_acc = test(model)
train_log.extend(train_loss)
train_acc_log.extend(train_acc)
steps = train_dataset.train_labels.shape[0] / batch_size
val_log.append((steps * (epoch + 1), np.mean(val_loss)))
val_acc_log.append((steps * (epoch + 1), np.mean(val_acc)))
clear_output()
plot_history(train_log, val_log)
plot_history(train_acc_log, val_acc_log, title='accuracy')
```
Создайте простейшую однослойную модель - однослойную полносвязную сеть и обучите ее с параметрами оптимизации, заданными ниже.
```
class Flatten(nn.Module):
def forward(self, x):
return x.view(x.size()[0], -1)
model = nn.Sequential(
#<your code>
)
opt = torch.optim.Adam(model.parameters(), lr=0.0005)
train(model, opt, 20)
```
Параметром обученной нейросети является матрица весов, в которой каждому классу соответствует один из 784-мерных столбцов. Визуализируйте обученные векторы для каждого из классов, сделав их двумерными изображениями 28-28. Для визуализации можно воспользоваться кодом для визуализации MNIST-картинок с предыдущих семинаров.
```
weights = #<your code>
plt.figure(figsize=[10, 10])
for i in range(10):
plt.subplot(5, 5, i + 1)
plt.title("Label: %i" % i)
plt.imshow(weights[i].reshape([28, 28]), cmap='gray');
```
Реализуйте Dropout-слой для полносвязной сети. Помните, что этот слой ведет себя по-разному во время обучения и во время применения.
```
class DropoutLayer(nn.Module):
def __init__(self, p):
super().__init__()
#<your code>
def forward(self, input):
if self.training:
#<your code>
else:
#<your code>
```
Добавьте Dropout-слой в архитектуру сети, проведите оптимизацию с параметрами, заданными ранее, визуализируйте обученные веса. Есть ли разница между весами, обученными с Dropout и без него? Параметр Dropout возьмите равным 0.7
```
modelDp = nn.Sequential(
#<your code>
)
opt = torch.optim.Adam(modelDp.parameters(), lr=0.0005)
train(modelDp, opt, 20)
weights = #<your code>
plt.figure(figsize=[10, 10])
for i in range(10):
plt.subplot(5, 5, i + 1)
plt.title("Label: %i" % i)
plt.imshow(weights[i].reshape([28, 28]), cmap='gray');
```
Обучите еще одну модель, в которой вместо Dropout-регуляризации используется L2-регуляризация с коэффициентом 0.05. (Параметр weight_decay в оптимизаторе). Визуализируйте веса и сравните с двумя предыдущими подходами.
```
model = nn.Sequential(
Flatten(),
nn.Linear(input_size,num_classes),
nn.LogSoftmax(dim=-1)
)
opt = torch.optim.Adam(model.parameters(), lr=0.0005, weight_decay=0.05)
train(model, opt, 20)
weights = #<your code>
plt.figure(figsize=[10, 10])
for i in range(10):
plt.subplot(5, 5, i + 1)
plt.title("Label: %i" % i)
plt.imshow(weights[i].reshape([28, 28]), cmap='gray');
```
## Batch normalization (0.4 балла)
Реализуйте BatchNormalization слой для полносвязной сети. В реализации достаточно только центрировать и разделить на корень из дисперсии, аффинную поправку (гамма и бета) в этом задании можно не реализовывать.
```
class BnLayer(nn.Module):
def __init__(self, num_features):
super().__init__()
#<your code>
def forward(self, input):
if self.training:
#<your code>
else:
#<your code>
return #<your code>
```
Обучите трехслойную полносвязную сеть (размер скрытого слоя возьмите 100) с сигмоидами в качестве функций активации.
```
model = nn.Sequential(
#<your code>
)
opt = torch.optim.RMSprop(model.parameters(), lr=0.01)
train(model, opt, 3)
```
Повторите обучение с теми же параметрами для сети с той же архитектурой, но с добавлением BatchNorm слоя (для всех трех скрытых слоев).
```
modelBN = nn.Sequential(
#<your code>
)
opt = torch.optim.RMSprop(modelBN.parameters(), lr=0.01)
train(modelBN, opt, 3)
```
Сравните кривые обучения и сделайте вывод о влиянии BatchNorm на ход обучения.
| true |
code
| 0.743762 | null | null | null | null |
|
## Model-Agnostic Meta-Learning
Based on the paper: <i>Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks</i>. Data from this [notebook](https://github.com/hereismari/tensorflow-maml/blob/master/maml.ipynb): sinusoid dataset of sine waves with different amplitude and phase, representing different "tasks". These are shuffled prior to batching, representing the task sampling step.
```
import numpy as np
import tensorflow as tf
import tensorflow_hub as hub
import matplotlib.pyplot as plt
from tensorflow.keras import backend as K
from tensorflow.keras.layers import Input,Dense,Dropout,Activation
from tensorflow.keras.models import Model,Sequential
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.losses import BinaryCrossentropy,MeanSquaredError
from sklearn.model_selection import train_test_split
from sklearn.metrics import balanced_accuracy_score,mean_squared_error
from sklearn.utils import shuffle
```
### Gather data
```
sin_x = np.load("../data/other/sin_x.npy")
sin_y = np.load("../data/other/sin_y.npy")
sin_x_test = np.load("../data/other/sin_x_test.npy")
sin_y_test = np.load("../data/other/sin_y_test.npy")
train_x,test_x = sin_x[:10000],sin_x[10000:]
train_y,test_y = sin_y[:10000],sin_y[10000:]
train_x,train_y = shuffle(train_x,train_y)
test_x,test_y = shuffle(test_x,test_y)
print(train_x.shape,train_y.shape)
print(sin_x_test.shape,sin_y_test.shape)
plt.scatter(train_x[:1000],train_y[:1000])
plt.show()
```
### Modeling
```
def get_model():
""" Model instantiation
"""
x = Input(shape=(1))
h = Dense(50,activation="relu")(x)
h = Dense(50,activation="relu")(h)
o = Dense(1,activation=None)(h)
model = Model(inputs=x,outputs=o)
return model
n_epochs = 100
batch_size = 25
meta_optimizer = Adam(0.01)
meta_model = get_model()
for epoch_i in range(n_epochs):
losses = []
for i in range(0,len(train_x[0]),batch_size):
task_train_x,task_train_y = train_x[i:i+batch_size],train_y[i:i+batch_size]
task_test_x,task_test_y = train_x[i:i+batch_size],train_y[i:i+batch_size]
with tf.GradientTape() as meta_tape: # optimization step
with tf.GradientTape() as tape:
task_train_pred = meta_model(task_train_x) # this cannot be done with model_copy
task_train_loss = MeanSquaredError()(task_train_y,task_train_pred)
gradients = tape.gradient(task_train_loss, meta_model.trainable_variables)
model_copy = get_model()
model_copy.set_weights(meta_model.get_weights())
k=0 # gradient descent this way does not break gradient flow from model_copy -> meta_model
for i in range(1,len(model_copy.layers)): # first layer is input
model_copy.layers[i].kernel = meta_model.layers[i].kernel-0.01*gradients[k]
model_copy.layers[i].bias = meta_model.layers[i].bias-0.01*gradients[k+1]
k+=2
task_test_pred = model_copy(task_test_x)
task_test_loss = MeanSquaredError()(task_test_y,task_test_pred)
gradients = meta_tape.gradient(task_test_loss,meta_model.trainable_variables)
meta_optimizer.apply_gradients(zip(gradients,meta_model.trainable_variables))
losses.append(float(task_test_loss))
if (epoch_i+1)%10==0 or epoch_i==0:
print("Epoch {}: {}".format(epoch_i+1,sum(losses)/len(losses)))
```
| true |
code
| 0.623807 | null | null | null | null |
|
# Hierarchical Clustering
### Validation with Dendogram and Heatmap
Created by Andres Segura-Tinoco
Created on Apr 20, 2021
```
# Import libraries
import numpy as np
from sklearn import datasets
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage
import scipy.cluster.hierarchy as sch
# Plot libraries
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from mpl_toolkits.axes_grid1 import make_axes_locatable
```
## <span>1. Load Iris data</span>
```
# Load the IRIS dataset
iris = datasets.load_iris()
# Preprocessing data
X = iris.data
y = iris.target
n_data = len(X)
delta = 0.3
x_min, x_max = X[:, 0].min() - delta, X[:, 0].max() + delta
y_min, y_max = X[:, 1].min() - delta, X[:, 1].max() + delta
# Plot the training points
fig, ax = plt.subplots(figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1, s=20)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title("IRIS Sepal Data", fontsize=16)
op1 = mpatches.Patch(color='#E41A1C', label='Setosa')
op2 = mpatches.Patch(color='#FF8000', label='Versicolor')
op3 = mpatches.Patch(color='#979797', label='Virginica')
plt.legend(handles=[op1, op2, op3], loc='best')
ax.grid()
plt.show()
```
## <span>2. Hierarchical Agglomerative Clustering</span>
Hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters <a href="https://en.wikipedia.org/wiki/Hierarchical_clustering" target="_blank">[wikipedia]</a>.
### 2.1. Dendogram to Select Optimal Clusters
```
# Calculate average linkage
linkage_method = 'average'
linked = linkage(X, linkage_method)
labelList = range(1, n_data+1)
# Plot Dendogram
plt.figure(figsize=(16, 8))
dendrogram(linked, orientation='top', labels=labelList, distance_sort='descending', show_leaf_counts=True)
plt.title("Dendogram with " + linkage_method.title() + " Linkage", fontsize=16)
plt.show()
```
Clearly, with Hierarchical Clustering with average linkage, the optimal number of clusters is 2.
### 2.2. Hierarchical Clustering with Optimal k
```
# Optimal number of clusters
k = 2
# Apply Hierarchical Agglomerative Clustering
hac = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage=linkage_method)
cluster = hac.fit_predict(X)
cluster
# Plotting clustering
fig, ax = plt.subplots(figsize=(8, 8))
colormap = np.array(["#d62728", "#2ca02c"])
plt.scatter(X[:, 0], X[:, 1], c=colormap[cluster], s=20)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title("Hierarchical Clustering", fontsize=16)
op1 = mpatches.Patch(color=colormap[1], label='Cluster 1')
op2 = mpatches.Patch(color=colormap[0], label='Cluster 2')
plt.legend(handles=[op1, op2], loc='best')
ax.grid()
plt.show()
```
### 2.3. Hierarchical Clustering Heatmap
```
# Calculate distance matrix with Euclidean distance
D = np.zeros([n_data, n_data])
for i in range(n_data):
for j in range(n_data):
D[i, j] = np.linalg.norm(X[i] - X[j])
# Dendrogram that comes to the left
fig = plt.figure(figsize=(14, 14))
# Add left axes with hierarchical cluster
ax1 = fig.add_axes([0.09, 0.1, 0.2, 0.6])
Y = sch.linkage(X, method='single')
Z1 = sch.dendrogram(Y, orientation='left')
ax1.set_xticks([])
ax1.set_yticks([])
# Add top axes with hierarchical cluster
ax2 = fig.add_axes([0.3, 0.71, 0.58, 0.2])
Y = sch.linkage(X, method=linkage_method)
Z2 = sch.dendrogram(Y)
ax2.set_xticks([])
ax2.set_yticks([])
# Main heat-map
axmatrix = fig.add_axes([0.3, 0.1, 0.6, 0.6])
idx1 = Z1['leaves']
idx2 = Z2['leaves']
D = D[idx1, :]
D = D[:, idx2]
# The actual heat-map
im = axmatrix.matshow(D, aspect='auto', origin='lower', cmap="PuBuGn")
divider = make_axes_locatable(axmatrix)
cax = divider.append_axes("right", size="3%", pad=0.05)
plt.colorbar(im, cax=cax)
axmatrix.set_xticks([])
axmatrix.set_yticks([])
plt.show()
```
<hr>
You can contact me on <a href="https://twitter.com/SeguraAndres7" target="_blank">Twitter</a> | <a href="https://github.com/ansegura7/" target="_blank">GitHub</a> | <a href="https://www.linkedin.com/in/andres-segura-tinoco/" target="_blank">LinkedIn</a>
| true |
code
| 0.709177 | null | null | null | null |
|
# Train Eval Baseline for CelebA Dataset
---
## Import Libraries
```
import sys
sys.path.append("..")
import matplotlib.pyplot as plt
%load_ext autoreload
%autoreload 2
%matplotlib inline
import torch
import numpy as np
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision.utils import make_grid
from disenn.datasets.celeba_dataset import CelebA
from disenn.models.conceptizers import VaeConceptizer
from disenn.models.parameterizers import ConvParameterizer
from disenn.models.aggregators import SumAggregator
from disenn.models.disenn import DiSENN
from disenn.models.losses import celeba_robustness_loss
from disenn.models.losses import bvae_loss
from disenn.utils.initialization import init_parameters
```
## Hardware & Seed
```
np.random.seed(42)
torch.manual_seed(42)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
## Sample dataset for baseline
```
SAMPLE_SIZE = 1
celeba_dataset = CelebA(split='train', data_path='data/celeba')
sample_idxs = np.random.permutation(len(celeba_dataset))[:SAMPLE_SIZE]
sample_celeba_dataset = [celeba_dataset[idx] for idx in sample_idxs]
sample_images = [x for x,_ in sample_celeba_dataset]
sample_labels = [y for _,y in sample_celeba_dataset]
print(f"Male: {sum(sample_labels)}")
sample_images_grid = make_grid(sample_images)
fig, ax = plt.subplots(figsize=(20,10))
ax.imshow(sample_images_grid.numpy().transpose(1,2,0))
ax.set_xticks([])
ax.set_yticks([])
fig.tight_layout()
sample_dl = DataLoader(sample_celeba_dataset, batch_size=2, shuffle=True)
x,y = next(iter(sample_dl))
```
# $\beta$-VAE Conceptizer
## Forward Pass
```
conceptizer = VaeConceptizer(num_concepts=10)
concept_mean, concept_logvar, x_reconstruct = conceptizer(x)
x.shape
concept_mean.shape, concept_logvar.shape
x_reconstruct.shape
plt.imshow(x[0].numpy().transpose(1,2,0))
plt.matshow(concept_mean.detach().numpy())
plt.matshow(concept_logvar.detach().numpy())
plt.imshow(x_reconstruct[0].detach().numpy().transpose(1,2,0))
```
## Sanity Check: Initial Loss
```
conceptizer = VaeConceptizer(num_concepts=10)
# concept_mean, concept_logvar, x_reconstruct = conceptizer(x)
# recon_loss, kl_div = BVAE_loss(x, x_reconstruct, concept_mean, concept_logvar)
# loss = recon_loss + kl_div
# loss.backward()
_, _, x_reconstruct = conceptizer(x)
loss = F.binary_cross_entropy(x_reconstruct, x, reduction="mean")
loss.backward()
loss
x_mean = x[0].mean().item()
x_recon_mean = x_reconstruct.mean().item()
0.5 * np.log(0.5) + (1-0.5) * np.log(1-0.5)
x_mean * np.log(x_recon_mean) + (1-x_mean) * np.log(1 - x_recon_mean)
```
## Initialize Parameters
```
conceptizer.apply(init_parameters);
```
## Backward Gradients
```
print(conceptizer.decoder.tconv_block[-1].weight.grad.mean())
print(conceptizer.decoder.tconv_block[-1].weight.grad.std())
print(conceptizer.decoder.tconv_block[-3].weight.grad.mean())
print(conceptizer.decoder.tconv_block[-3].weight.grad.std())
print(conceptizer.encoder.logvar_layer.weight.grad.mean())
print(conceptizer.encoder.mu_layer.weight.grad.std())
```
## Training
```
conceptizer = VaeConceptizer(num_concepts=10).to(device)
# conceptizer.apply(init_parameters);
train_dl = DataLoader(celeba_dataset, batch_size=128, shuffle=True)
optimizer = optim.Adam(conceptizer.parameters())
conceptizer.train();
recorder = []
EPOCHS = 1000
BETA = 1
PRINT_FREQ = 10
for epoch in range(EPOCHS):
for i, (x, _) in enumerate(sample_dl):
x = x.to(device)
optimizer.zero_grad()
concept_mean, concept_logvar, x_reconstruct = conceptizer(x)
recon_loss, kl_div = BVAE_loss(x, x_reconstruct, concept_mean, concept_logvar)
loss = recon_loss + BETA * kl_div
loss.backward()
optimizer.step()
recorder.append([loss.item(), recon_loss.item(), kl_div.item()])
steps = list(range(len(recorder)))
recorder = np.array(recorder)
fig, ax = plt.subplots(figsize=(15,5))
ax.plot(steps, recorder[:,0], label="Concept loss")
ax.plot(steps, recorder[:,1], label="Reconstruction loss")
ax.plot(steps, recorder[:,2], label="KL Div loss")
ax.set_xlabel("Steps")
ax.set_ylabel("Metrics")
ax.legend()
fig.tight_layout()
recorder[-1][0]
conceptizer.eval();
concept_mean, concept_logvar, x_reconstruct = conceptizer(x)
# x_reconstruct, _, _ = conceptizer(x)
plt.imshow(x[0].cpu().numpy().transpose(1,2,0))
plt.matshow(concept_mean.detach().cpu().numpy())
plt.colorbar()
plt.matshow(concept_logvar.detach().cpu().numpy())
plt.colorbar()
plt.imshow(x_reconstruct[0].detach().cpu().numpy().transpose(1,2,0))
```
**Observations**:
* KL Divergence affects the reconstruction loss such that all images tend to look similar
* Reducing beta to 0 drastically improves reconstruction loss
* Increasing the number of epochs do not help
* Will increasing data size help? No.
* The initial reconstruction loss should be 0.69 which is verified
* With 100 epochs and 10 images, loss reaches 0.65 which results in hazy reconstructions
* With 1000 epochs and 1 image, loss reaches 0.62 which results in almost perfect reconstruction
* Loss of 0.62 is our goal (although 0.69 to 0.62 is a pretty close bound)
* Initialization does not help reconstruction even with 1000 epochs
# DiSENN
## Forward Pass
```
NUM_CONCEPTS = 5
NUM_CLASS = 2
conceptizer = VaeConceptizer(NUM_CONCEPTS)
parameterizer = ConvParameterizer(NUM_CONCEPTS, NUM_CLASS)
aggregator = SumAggregator(NUM_CLASS)
disenn = DiSENN(conceptizer, parameterizer, aggregator).to(device)
y_pred, explanation, x_construct = disenn(x)
disenn.explain(x[0], 1, show=True, num_prototypes=20)
```
## Training
```
EPOCHS = 1000
BETA = 1
ROBUST_REG = 1e-4
opt = optim.Adam(disenn.parameters())
disenn.train();
recorder = []
for epoch in range(EPOCHS):
for i, (x, labels) in enumerate(sample_dl):
x = x.to(device)
labels = labels.long().to(device)
opt.zero_grad()
x.requires_grad_(True)
y_pred, (concepts_dist, relevances), x_reconstruct = disenn(x)
concept_mean, concept_logvar = concepts_dist
concepts = concept_mean
pred_loss = F.nll_loss(y_pred.squeeze(-1), labels)
robustness_loss = celeba_robustness_loss(x, y_pred, concepts, relevances)
recon_loss, kl_div = BVAE_loss(x, x_reconstruct, concept_mean, concept_logvar)
concept_loss = recon_loss + BETA * kl_div
total_loss = pred_loss + concept_loss + (ROBUST_REG * robustness_loss)
total_loss.backward()
opt.step()
recorder.append([total_loss.item(), pred_loss.item(), robustness_loss.item(),
concept_loss.item(), recon_loss.item(), kl_div.item()])
steps = list(range(len(recorder)))
recorder = np.array(recorder)
fig, ax = plt.subplots(figsize=(15,5))
ax.plot(steps, recorder[:,0], label="Total loss")
ax.plot(steps, recorder[:,1], label="Prediction loss")
ax.plot(steps, recorder[:,2], label="Robustness loss")
ax.plot(steps, recorder[:,3], label="Concept loss")
ax.plot(steps, recorder[:,4], label="Reconstruction loss")
ax.plot(steps, recorder[:,5], label="KL Div loss")
ax.set_xlabel("Steps")
ax.set_ylabel("Metrics")
ax.legend()
fig.tight_layout()
y[0].item()
recorder[-1]
disenn.explain(x[0].detach(), 1, show=True, num_prototypes=20)
disenn.eval()
y_pred, explanations, x_reconstruct = disenn(x[0].unsqueeze(0))
plt.imshow(x_reconstruct[0].detach().cpu().numpy().transpose(1,2,0))
```
**Observations**:
* With 1000 epochs and 1 image, we reach the best possible loss: 0.623
* Conceptizer reconstruction is almost perfect
| true |
code
| 0.63751 | null | null | null | null |
|
```
# Erasmus+ ICCT project (2018-1-SI01-KA203-047081)
# Toggle cell visibility
from IPython.display import HTML
tag = HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide()
} else {
$('div.input').show()
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
Promijeni vidljivost <a href="javascript:code_toggle()">ovdje</a>.''')
display(tag)
# Hide the code completely
# from IPython.display import HTML
# tag = HTML('''<style>
# div.input {
# display:none;
# }
# </style>''')
# display(tag)
```
## Modalna analiza lunarnog prizemljivača
Matrica dinamike $A$ koja reprezentira dinamiku lunarnog prizemljivača opisanog u prethodnoj interaktivnoj lekciji je:
$$
A=\begin{bmatrix}0&1&0&0 \\ 0&0&F/m&0 \\ 0&0&0&1 \\ 0&0&0&0\end{bmatrix},
$$
gdje je $F$ sila potiska, a $m$ masa prizemljivača. Stanje sustava je $x=[z,\dot{z},\theta,\dot{\theta}]^T$, gdje je $z$ lateralna pozicija (bočni položaj), $\dot{z}$ vremenska promjena bočnog položaja, $\theta$ kut prizemljivača s obzirom na vertikalnu os, a $\dot{\theta}$ njegova promjena/varijacija u vremenu.
Matrica dinamike u ovom obliku prikazuje četiri svojstvene vrijednosti, sve jednake 0. Svojstvene vrijednosti 0 često se nazivaju integratorima (podsjetimo se Laplaceove transformacije integrala signala: što je korijen nazivnika odgovarajućeg izraza?), pa kažemo da ovaj sustav ima 4 integratora. Uz $F\neq0$ ($m\neq0$) sustav predstavlja strukturu koja je slična $4\times4$ Jordanovom bloku, tako da svojstvena vrijednost 0, u ovom slučaju, ima geometrijsku množnost jednaku 1. Uz $F=0$ svojstvena vrijednost ostaje ista s istom algebarskom množnošću, ali s geometrijskom množnošću jednakoj 2.
Dolje je predstavljen primjer s $F\neq0$.
### Kako koristiti ovaj interaktivni primjer?
- Pokušajte postaviti $F=0$ i pokušajte objasniti što fizički podrazumijeva ovaj slučaj za lunarni prizemljivač, posebno za dinamiku $z$ i $\theta$ i njihov odnos.
```
#Preparatory Cell
import control
import numpy
from IPython.display import display, Markdown
import ipywidgets as widgets
import matplotlib.pyplot as plt
%matplotlib inline
#matrixWidget is a matrix looking widget built with a VBox of HBox(es) that returns a numPy array as value !
class matrixWidget(widgets.VBox):
def updateM(self,change):
for irow in range(0,self.n):
for icol in range(0,self.m):
self.M_[irow,icol] = self.children[irow].children[icol].value
#print(self.M_[irow,icol])
self.value = self.M_
def dummychangecallback(self,change):
pass
def __init__(self,n,m):
self.n = n
self.m = m
self.M_ = numpy.matrix(numpy.zeros((self.n,self.m)))
self.value = self.M_
widgets.VBox.__init__(self,
children = [
widgets.HBox(children =
[widgets.FloatText(value=0.0, layout=widgets.Layout(width='90px')) for i in range(m)]
)
for j in range(n)
])
#fill in widgets and tell interact to call updateM each time a children changes value
for irow in range(0,self.n):
for icol in range(0,self.m):
self.children[irow].children[icol].value = self.M_[irow,icol]
self.children[irow].children[icol].observe(self.updateM, names='value')
#value = Unicode('example@example.com', help="The email value.").tag(sync=True)
self.observe(self.updateM, names='value', type= 'All')
def setM(self, newM):
#disable callbacks, change values, and reenable
self.unobserve(self.updateM, names='value', type= 'All')
for irow in range(0,self.n):
for icol in range(0,self.m):
self.children[irow].children[icol].unobserve(self.updateM, names='value')
self.M_ = newM
self.value = self.M_
for irow in range(0,self.n):
for icol in range(0,self.m):
self.children[irow].children[icol].value = self.M_[irow,icol]
for irow in range(0,self.n):
for icol in range(0,self.m):
self.children[irow].children[icol].observe(self.updateM, names='value')
self.observe(self.updateM, names='value', type= 'All')
#self.children[irow].children[icol].observe(self.updateM, names='value')
#overlaod class for state space systems that DO NOT remove "useless" states (what "professor" of automatic control would do this?)
class sss(control.StateSpace):
def __init__(self,*args):
#call base class init constructor
control.StateSpace.__init__(self,*args)
#disable function below in base class
def _remove_useless_states(self):
pass
#define the sliders for m, k and c
m = widgets.FloatSlider(
value=1000,
min=400,
max=2000,
step=1,
description='$m$ [kg]:',
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.1f',
)
F = widgets.FloatSlider(
value=1500,
min=0,
max=5000,
step=10,
description='$F$ [N]:',
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.1f',
)
#function that make all the computations
def main_callback(m, F):
eig1 = 0
eig2 = 0
eig3 = 0
eig4 = 0
if numpy.real([eig1,eig2,eig3,eig4])[0] == 0 and numpy.real([eig1,eig2,eig3,eig4])[1] == 0:
T = numpy.linspace(0,20,1000)
else:
if min(numpy.abs(numpy.real([eig1,eig2,eig3,eig4]))) != 0:
T = numpy.linspace(0,7*1/min(numpy.abs(numpy.real([eig1,eig2,eig3,eig4]))),1000)
else:
T = numpy.linspace(0,7*1/max(numpy.abs(numpy.real([eig1,eig2,eig3,eig4]))),1000)
if F==0:
mode1 = numpy.exp(eig1*T)
mode2 = T*mode1
mode3 = mode1
mode4 = mode2
else:
mode1 = numpy.exp(eig1*T)
mode2 = T*mode1
mode3 = T*mode2
mode4 = T*mode3
fig = plt.figure(figsize=[16, 10])
fig.set_label('Modovi')
g1 = fig.add_subplot(221)
g2 = fig.add_subplot(222)
g3 = fig.add_subplot(223)
g4 = fig.add_subplot(224)
g1.plot(T,mode1)
g1.grid()
g1.set_xlabel('Vrijeme [s]')
g1.set_ylabel('Prvi mod')
g2.plot(T,mode2)
g2.grid()
g2.set_xlabel('Vrijeme [s]')
g2.set_ylabel('Drugi mod')
g3.plot(T,mode3)
g3.grid()
g3.set_xlabel('Vrijeme [s]')
g3.set_ylabel('Treći mod')
g4.plot(T,mode4)
g4.grid()
g4.set_xlabel('Vrijeme [s]')
g4.set_ylabel('Četvrti mod')
modesString = r'Svojstvena vrijednost je jednaka 0 s algebarskom množnošću 4. '
if F==0:
modesString = modesString + r'Odgovarajući modovi su $k$ and $t$.'
else:
modesString = modesString + r'Odgovarajući modovi su $k$, $t$, $\frac{t^2}{2}$ i $\frac{t^3}{6}$.'
display(Markdown(modesString))
out = widgets.interactive_output(main_callback,{'m':m,'F':F})
sliders = widgets.HBox([m,F])
display(out,sliders)
```
| true |
code
| 0.468426 | null | null | null | null |
|
# Summary:
This notebook contains the soft smoothing figures for Amherst (Figure 2(c)).
## load libraries
```
from __future__ import division
import networkx as nx
import numpy as np
import os
from sklearn import metrics
from sklearn.preprocessing import label_binarize
from sklearn.metrics import confusion_matrix
from sklearn.metrics import f1_score
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import StratifiedShuffleSplit
import matplotlib.pyplot as plt
## function to create + save dictionary of features
def create_dict(key, obj):
return(dict([(key[i], obj[i]) for i in range(len(key))]))
```
## load helper functions and datasets
```
# set the working directory and import helper functions
#get the current working directory and then redirect into the functions under code
cwd = os.getcwd()
# parents working directory of the current directory: which is the code folder
parent_cwd = os.path.dirname(cwd)
# get into the functions folder
functions_cwd = parent_cwd + '/functions'
# change the working directory to be .../functions
os.chdir(functions_cwd)
# import all helper functions
exec(open('parsing.py').read())
exec(open('ZGL.py').read())
exec(open('create_graph.py').read())
exec(open('ZGL_softing_new_new.py').read())
# import the data from the data folder
data_cwd = os.path.dirname(parent_cwd)+ '/data'
# change the working directory and import the fb dataset
fb100_file = data_cwd +'/Amherst41'
A, metadata = parse_fb100_mat_file(fb100_file)
# change A(scipy csc matrix) into a numpy matrix
adj_matrix_tmp = A.todense()
#get the gender for each node(1/2,0 for missing)
gender_y_tmp = metadata[:,1]
# get the corresponding gender for each node in a disctionary form
gender_dict = create_dict(range(len(gender_y_tmp)), gender_y_tmp)
#exec(open("/Users/yatong_chen/Google Drive/research/DSG_empirical/code/functions/create_graph.py").read())
(graph, gender_y) = create_graph(adj_matrix_tmp,gender_dict,'gender',0,None,'yes')
```
## Setup
```
adj_matrix_gender = np.array(nx.adjacency_matrix(graph).todense())
percent_initially_unlabelled = [0.99,0.95,0.9,0.8,0.7,0.6,0.5,0.4,0.3,0.2,0.1,0.05]
percent_initially_labelled = np.subtract(1, percent_initially_unlabelled)
n_iter = 10
cv_setup = 'stratified'
w = [0.1,1,10,100,1000,10000]
```
## Hard Smoothing (ZGL method)
```
# run ZGL part
adj_matrix_tmp_ZGL = adj_matrix_tmp
(mean_accuracy_zgl_amherst, se_accuracy_zgl_amherst,
mean_micro_auc_zgl_amherst,se_micro_auc_zgl_amherst,
mean_wt_auc_zgl_amherst,se_wt_auc_zgl_amherst) =ZGL(np.array(adj_matrix_gender),
np.array(gender_y),percent_initially_unlabelled,
n_iter,cv_setup)
```
## Soft smoothing (with different parameters w)
```
# NEW NEW ZGL without original training node
(graph, gender_y) = create_graph(adj_matrix_tmp,gender_dict,'gender',0,None,'yes')
(mean_accuracy_zgl_softing_new_new_amherst01, se_accuracy_zgl_softing_new_new_amherst01,
mean_micro_auc_zgl_softing_new_new_amherst01,se_micro_auc_zgl_softing_new_new_amherst01,
mean_wt_auc_zgl_softing_new_new_amherst01,se_wt_auc_zgl_softing_new_new_amherst01) = ZGL_softing_new_new(w[0], adj_matrix_tmp,
gender_dict,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_amherst1, se_accuracy_zgl_softing_new_new_amherst1,
mean_micro_auc_zgl_softing_new_new_amherst1,se_micro_auc_zgl_softing_new_new_amherst1,
mean_wt_auc_zgl_softing_new_new_amherst1,se_wt_auc_zgl_softing_new_new_amherst1) = ZGL_softing_new_new(w[1], adj_matrix_tmp,
gender_dict,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_amherst10, se_accuracy_zgl_softing_new_new_amherst10,
mean_micro_auc_zgl_softing_new_new_amherst10,se_micro_auc_zgl_softing_new_new_amherst10,
mean_wt_auc_zgl_softing_new_new_amherst10,se_wt_auc_zgl_softing_new_new_amherst10) = ZGL_softing_new_new(w[2], adj_matrix_tmp,
gender_dict,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_amherst100, se_accuracy_zgl_softing_new_new_amherst100,
mean_micro_auc_zgl_softing_new_new_amherst100,se_micro_auc_zgl_softing_new_new_amherst100,
mean_wt_auc_zgl_softing_new_new_amherst100,se_wt_auc_zgl_softing_new_new_amherst100) = ZGL_softing_new_new(w[3], adj_matrix_tmp,
gender_dict,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_amherst1000, se_accuracy_zgl_softing_new_new_amherst1000,
mean_micro_auc_zgl_softing_new_new_amherst1000,se_micro_auc_zgl_softing_new_new_amherst1000,
mean_wt_auc_zgl_softing_new_new_amherst1000,se_wt_auc_zgl_softing_new_new_amherst1000) = ZGL_softing_new_new(w[4], adj_matrix_tmp,
gender_dict,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_amherst10000, se_accuracy_zgl_softing_new_new_amherst10000,
mean_micro_auc_zgl_softing_new_new_amherst10000,se_micro_auc_zgl_softing_new_new_amherst10000,
mean_wt_auc_zgl_softing_new_new_amherst10000,se_wt_auc_zgl_softing_new_new_amherst10000) = ZGL_softing_new_new(w[5], adj_matrix_tmp,
gender_dict,'gender', percent_initially_unlabelled, n_iter,cv_setup)
```
## Plot:
AUC against Initial unlabled node precentage
```
%matplotlib inline
from matplotlib.ticker import FixedLocator,LinearLocator,MultipleLocator, FormatStrFormatter
fig = plt.figure()
#seaborn.set_style(style='white')
from mpl_toolkits.axes_grid1 import Grid
grid = Grid(fig, rect=111, nrows_ncols=(1,1),
axes_pad=0.1, label_mode='L')
for i in range(4):
if i == 0:
# set the x and y axis
grid[i].xaxis.set_major_locator(FixedLocator([0,25,50,75,100]))
grid[i].yaxis.set_major_locator(FixedLocator([0.4, 0.5,0.6,0.7,0.8,0.9,1]))
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_amherst,
yerr=se_wt_auc_zgl_amherst, fmt='--o', capthick=2,
alpha=1, elinewidth=8, color='black')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_amherst01,
yerr=se_wt_auc_zgl_softing_new_new_amherst01, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='gold')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_amherst1,
yerr=se_wt_auc_zgl_softing_new_new_amherst1, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='darkorange')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_amherst10,
yerr=se_wt_auc_zgl_softing_new_new_amherst10, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='crimson')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_amherst100,
yerr=se_wt_auc_zgl_softing_new_new_amherst100, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='red')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_amherst1000,
yerr=se_wt_auc_zgl_softing_new_new_amherst1000, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='maroon')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_amherst10000,
yerr=se_wt_auc_zgl_softing_new_new_amherst10000, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='darkred')
grid[i].set_ylim(0.45,1)
grid[i].set_xlim(0,101)
grid[i].annotate('soft: a = 0.001', xy=(3, 0.96),
color='gold', alpha=1, size=12)
grid[i].annotate('soft: a = 1', xy=(3, 0.92),
color='darkorange', alpha=1, size=12)
grid[i].annotate('soft: a = 10', xy=(3, 0.88),
color='red', alpha=1, size=12)
grid[i].annotate('soft: a = 100', xy=(3, 0.84),
color='crimson', alpha=1, size=12)
grid[i].annotate('soft: a = 1000', xy=(3, 0.80),
color='maroon', alpha=1, size=12)
grid[i].annotate('soft: a = 1000000', xy=(3, 0.76),
color='darkred', alpha=1, size=12)
grid[i].annotate('hard smoothing', xy=(3, 0.72),
color='black', alpha=1, size=12)
grid[i].set_ylim(0.4,0.8)
grid[i].set_xlim(0,100)
grid[i].spines['right'].set_visible(False)
grid[i].spines['top'].set_visible(False)
grid[i].tick_params(axis='both', which='major', labelsize=13)
grid[i].tick_params(axis='both', which='minor', labelsize=13)
grid[i].set_xlabel('Percent of Nodes Initially Labeled').set_fontsize(15)
grid[i].set_ylabel('AUC').set_fontsize(15)
grid[0].set_xticks([0,25, 50, 75, 100])
grid[0].set_yticks([0.4,0.6,0.8,1])
grid[0].minorticks_on()
grid[0].tick_params('both', length=4, width=1, which='major', left=1, bottom=1, top=0, right=0)
```
| true |
code
| 0.48121 | null | null | null | null |
|
# Training a DeepSpeech LSTM Model using the LibriSpeech Data
At the end of Chapter 16 and into Chapter 17 in the book it is suggested try and build an automatic speech recognition system using the LibriVox corpus and long short term memory (LSTM) models just learned in the Recurrent Neural Network (RNN) chapter. This particular excercise turned out to be quite difficult mostly from the perspective again of simply gathering and formatting the data, combined with the work to understand the LSTM was doing. As it turns out, in doing this assignment I taught myself about MFCCs (mel frequency cepstral coefficient) which are simply what is going on in the Bregman Toolkit example earlier in the book. It's a process to convert audio into *num_cepstrals* coefficients using an FFT, and to use those coeffiicents as amplitudes and convert from the frequency into the time domain. LSTMs need time series data and a number of audio files converted using MFCCs into frequency amplitudes corresponding to utterances that you have transcript data for and you are in business!
The other major lesson was finding [RNN-Tutorial](https://github.com/mrubash1/RNN-Tutoria) an existing GitHub repository that implements a simplified version of the [deepspeech model](https://github.com/mozilla/DeepSpeech) from Mozilla which is a TensorFlow implementation of the Baidu model from the [seminal paper](https://arxiv.org/abs/1412.5567) in 2014.
I had to figure out along the way how to tweak hyperparameters including epochs, batch size, and training data. But overall this is a great architecture and example of how to use validation/dev sets during training for looking at validation loss compared to train loss and then overall to measure test accuracy.
### Data Preprocessing Steps:
1. Grab all text files which start out as the full speech from all subsequent \*.flac files
2. Each line in the text file contains:
```
filename(without .txt at end) the speech present in the file, e.g., words separated by spaces
filename N ... words ....
```
3. Then convert all \*.flac files to \*.wav files, using `flac2wav`
4. Remove all the flac files and remove the \*.trans.txt files
5. Run this code in the notebook below to generate the associated \*.txt file to go along with each \*.wav file.
6. Move all the \*.wav and \*.txt files into a single folder, e.g., `LibriSpeech/train-clean-all`
7. Repeat for test and dev
Once complete, you have a dataset to run through [RNN-Tutorial](https://github.com/mrubash1/RNN-Tutorial.git)
### References
1. [PyDub](https://github.com/jiaaro/pydub) - PyDub library
2. [A short reminder of how CTC works](https://towardsdatascience.com/beam-search-decoding-in-ctc-trained-neural-networks-5a889a3d85a7)
3. [OpenSLR - LibriSpeech corpus](http://www.openslr.org/12)
4. [Hamsa's Deep Speech notebook](https://github.com/cosmoshsv/Deep-Speech/blob/master/DeepSpeech_RNN_Training.ipynb)
5. [LSTM's by example using TensorFlow](https://towardsdatascience.com/lstm-by-example-using-tensorflow-feb0c1968537)
6. [How to read an audio file using TensorFlow APIs](https://github.com/tensorflow/tensorflow/issues/28237)
7. [Audio spectrograms in TensorFlow](https://mauri870.github.io/blog/posts/audio-spectrograms-in-tensorflow/)
8. [Reading audio files using TensorFlow](https://github.com/tensorflow/tensorflow/issues/32382)
9. [TensorFlow's decode_wav API](https://www.tensorflow.org/api_docs/python/tf/audio/decode_wav)
10. [Speech Recognition](https://towardsdatascience.com/speech-recognition-analysis-f03ff9ce78e9)
11. [Using TensorFlow's audio ops](https://stackoverflow.com/questions/48660391/using-tensorflow-contrib-framework-python-ops-audio-ops-audio-spectrogram-to-gen)
12. [LSTM by Example - Towards Data Science](https://towardsdatascience.com/lstm-by-example-using-tensorflow-feb0c1968537)
13. [Training your Own Model - DeepSpeech](https://deepspeech.readthedocs.io/en/v0.7.3/TRAINING.html)
14. [Understanding LSTMs](http://colah.github.io/posts/2015-08-Understanding-LSTMs/)
15. [Implementing LSTMs](https://apaszke.github.io/lstm-explained.html)
16. [Mel Frequency Cepstral Coefficient](http://practicalcryptography.com/miscellaneous/machine-learning/guide-mel-frequency-cepstral-coefficients-mfccs/)
17. [TensorFlow - Extract Every Other Element](https://stackoverflow.com/questions/46721407/tensorflow-extract-every-other-element)
18. [Plotting MFCCs in TensorFlow](https://stackoverflow.com/questions/47056432/is-it-possible-to-get-exactly-the-same-results-from-tensorflow-mfcc-and-librosa)
19. [MFCCs in TensorFlow](https://kite.com/python/docs/tensorflow.contrib.slim.rev_block_lib.contrib_framework_ops.audio_ops.mfcc)
20. [How to train Baidu's Deep Speech Model with Kur](https://blog.deepgram.com/how-to-train-baidus-deepspeech-model-with-kur/)
21. [Silicon Valley Data Science SVDS - RNN Tutorial](https://www.svds.com/tensorflow-rnn-tutorial/)
22. [Streaming RNNs with TensorFlow](https://hacks.mozilla.org/2018/09/speech-recognition-deepspeech/)
```
import sys
sys.path.append("../libs/basic_units/")
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.audio import decode_wav
from tensorflow.raw_ops import Mfcc, AudioSpectrogram
from tqdm.notebook import tqdm
from basic_units import cm, inch
import glob
from scipy import signal
import soundfile as sf
import os
import time
import csv
speech_data_path = "../data/LibriSpeech"
train_path = speech_data_path + "/train-clean-100"
dev_path = speech_data_path + "/dev-clean"
test_path = speech_data_path + "/test-clean"
train_transcripts = [file for file in glob.glob(train_path + "/*/*/*.txt")]
dev_transcripts = [file for file in glob.glob(dev_path + "/*/*/*.txt")]
test_transcripts = [file for file in glob.glob(test_path + "/*/*/*.txt")]
train_audio_wav = [file for file in glob.glob(train_path + "/*/*/*.wav")]
dev_audio_wav = [file for file in glob.glob(dev_path + "/*/*/*.wav")]
test_audio_wav = [file for file in glob.glob(test_path + "/*/*/*.wav")]
sys.path.append("../libs/RNN-Tutorial/src")
numcep=26
numcontext=9
filename = '../data/LibriSpeech/train-clean-100/3486/166424/3486-166424-0004.wav'
raw_audio = tf.io.read_file(filename)
audio, fs = decode_wav(raw_audio)
print(np.shape(audio.numpy()))
print(fs.numpy())
# Get mfcc coefficients
spectrogram = AudioSpectrogram(
input=audio, window_size=1024,stride=64)
orig_inputs = Mfcc(spectrogram=spectrogram, sample_rate=fs, dct_coefficient_count=numcep)
audio_mfcc = orig_inputs.numpy()
print(audio_mfcc)
print(np.shape(audio_mfcc))
hist_audio = np.histogram(audio_mfcc, bins=range(9 + 1))
plt.hist(hist_audio)
plt.show()
labels=[]
for i in np.arange(26):
labels.append("P"+str(i+1))
fig, ax = plt.subplots()
ind = np.arange(len(labels))
width = 0.15
colors = ['r', 'g', 'y', 'b', 'black']
plots = []
for i in range(0, 5):
Xs = np.asarray(np.abs(audio_mfcc[0][i])).reshape(-1)
p = ax.bar(ind + i*width, Xs, width, color=colors[i])
plots.append(p[0])
xticks = ind + width / (audio_mfcc.shape[0])
print(xticks)
ax.legend(tuple(plots), ('S1', 'S2', 'S3', 'S4', 'S5'))
ax.yaxis.set_units(inch)
ax.autoscale_view()
ax.set_xticks(xticks)
ax.set_xticklabels(labels)
ax.set_ylabel('Normalized freq coumt')
ax.set_xlabel('Pitch')
ax.set_title('Normalized frequency counts for Various Sounds')
plt.show()
filename = '../data/LibriSpeech/train-clean-100/3486/166424/3486-166424-0004.wav'
raw_audio = tf.io.read_file(filename)
audio, fs = decode_wav(raw_audio)
wsize = 16384 #1024
stride = 448 #64
# Get mfcc coefficients
spectrogram = AudioSpectrogram(
input=audio, window_size=wsize,stride=stride)
numcep=26
numcontext=9
orig_inputs = Mfcc(spectrogram=spectrogram, sample_rate=fs, dct_coefficient_count=numcep)
orig_inputs = orig_inputs[:,::2]
audio_mfcc = orig_inputs.numpy()
print(audio_mfcc)
print(np.shape(audio_mfcc))
train_inputs = np.array([], np.float32)
train_inputs.resize((audio_mfcc.shape[1], numcep + 2 * numcep * numcontext))
# Prepare pre-fix post fix context
empty_mfcc = np.array([])
empty_mfcc.resize((numcep))
empty_mfcc = tf.convert_to_tensor(empty_mfcc, dtype=tf.float32)
empty_mfcc_ev = empty_mfcc.numpy()
# Prepare train_inputs with past and future contexts
# This code always takes 9 time steps previous and 9 time steps in the future along with the current time step
time_slices = range(train_inputs.shape[0])
context_past_min = time_slices[0] + numcontext #starting min point for past content, has to be at least 9 ts
context_future_max = time_slices[-1] - numcontext #ending point max for future content, size time slices - 9ts
for time_slice in tqdm(time_slices):
#print('time slice %d ' % (time_slice))
# Reminder: array[start:stop:step]
# slices from indice |start| up to |stop| (not included), every |step|
# Add empty context data of the correct size to the start and end
# of the MFCC feature matrix
# Pick up to numcontext time slices in the past, and complete with empty
# mfcc features
need_empty_past = max(0, (context_past_min - time_slice))
empty_source_past = np.asarray([empty_mfcc_ev for empty_slots in range(need_empty_past)])
data_source_past = orig_inputs[0][max(0, time_slice - numcontext):time_slice]
assert(len(empty_source_past) + data_source_past.numpy().shape[0] == numcontext)
# Pick up to numcontext time slices in the future, and complete with empty
# mfcc features
need_empty_future = max(0, (time_slice - context_future_max))
empty_source_future = np.asarray([empty_mfcc_ev for empty_slots in range(need_empty_future)])
data_source_future = orig_inputs[0][time_slice + 1:time_slice + numcontext + 1]
assert(len(empty_source_future) + data_source_future.numpy().shape[0] == numcontext)
# pad if needed for the past or future, or else simply take past and future
if need_empty_past:
past = tf.concat([tf.cast(empty_source_past, tf.float32), tf.cast(data_source_past, tf.float32)], 0)
else:
past = data_source_past
if need_empty_future:
future = tf.concat([tf.cast(data_source_future, tf.float32), tf.cast(empty_source_future, tf.float32)], 0)
else:
future = data_source_future
past = tf.reshape(past, [numcontext*numcep])
now = orig_inputs[0][time_slice]
future = tf.reshape(future, [numcontext*numcep])
train_inputs[time_slice] = np.concatenate((past.numpy(), now.numpy(), future.numpy()))
assert(train_inputs[time_slice].shape[0] == numcep + 2*numcep*numcontext)
train_inputs = (train_inputs - np.mean(train_inputs)) / np.std(train_inputs)
print('Train inputs shape %s ' % str(np.shape(train_inputs)))
print('Train inputs '+str(train_inputs))
preprocessing = {
'data_dir': train_path,
'cache_dir' : '../data/cache/LibriSpeech',
'window_size': 20,
'step_size': 10
}
model = {
'verbose': 1,
'conv_channels': [100],
'conv_filters': [5],
'conv_strides': [2],
'rnn_units': [64],
'bidirectional_rnn': True,
'future_context': 2,
'use_bn': True,
'learning_rate': 0.001
}
training = {
'tensorboard': False,
'log_dir': './logs',
'batch_size': 5,
'epochs': 5,
'validation_size': 0.2,
'max_train' : 100
}
if not os.path.exists(preprocessing['cache_dir']):
os.makedirs(preprocessing['cache_dir'])
def clipped_relu(x):
return tf.keras.activations.relu(x, max_value=20)
def ctc_lambda_func(args):
y_pred, labels, input_length, label_length = args
return tf.keras.backend.ctc_batch_cost(labels, y_pred, input_length, label_length)
def ctc(y_true, y_pred):
return y_pred
class SpeechModel(object):
def __init__(self, hparams):
input_data = tf.keras.layers.Input(name='inputs', shape=[hparams['max_input_length'], 161])
x = input_data
if hparams['use_bn']:
x = tf.keras.layers.BatchNormalization()(x)
x = tf.keras.layers.ZeroPadding1D(padding=(0, hparams['max_input_length']))(x)
for i in range(len(hparams['conv_channels'])):
x = tf.keras.layers.Conv1D(hparams['conv_channels'][i], hparams['conv_filters'][i],
strides=hparams['conv_strides'][i], activation='relu', padding='same')(x)
if hparams['use_bn']:
x = tf.keras.layers.BatchNormalization()(x)
for h_units in hparams['rnn_units']:
if hparams['bidirectional_rnn']:
h_units = int(h_units / 2)
gru = tf.keras.layers.GRU(h_units, activation='relu', return_sequences=True)
if hparams['bidirectional_rnn']:
gru = tf.keras.layers.Bidirectional(gru, merge_mode='sum')
x = gru(x)
if hparams['use_bn']:
x = tf.keras.layers.BatchNormalization()(x)
if hparams['future_context'] > 0:
if hparams['future_context'] > 1:
x = tf.keras.layers.ZeroPadding1D(padding=(0, hparams['future_context'] - 1))(x)
x = tf.keras.layers.Conv1D(100, hparams['future_context'], activation='relu')(x)
y_pred = tf.keras.layers.TimeDistributed(tf.keras.layers.Dense(hparams['vocab_size'] + 1,
activation='sigmoid'))(x)
labels = tf.keras.layers.Input(name='labels', shape=[None], dtype='int32')
input_length = tf.keras.layers.Input(name='input_lengths', shape=[1], dtype='int32')
label_length = tf.keras.layers.Input(name='label_lengths', shape=[1], dtype='int32')
loss_out = tf.keras.layers.Lambda(ctc_lambda_func, output_shape=(1,), name='ctc')([y_pred,
labels,
input_length,
label_length])
self.model = tf.keras.Model(inputs=[input_data, labels, input_length, label_length], outputs=[loss_out])
if hparams['verbose']:
print(self.model.summary())
optimizer = tf.keras.optimizers.Adam(lr=hparams['learning_rate'], beta_1=0.9, beta_2=0.999,
epsilon=1e-8, clipnorm=5)
self.model.compile(optimizer=optimizer, loss=ctc)
def train_generator(self, generator, train_params):
callbacks = []
if train_params['tensorboard']:
callbacks.append(tf.keras.callbacks.TensorBoard(train_params['log_dir'], write_images=True))
self.model.fit(generator, epochs=train_params['epochs'],
steps_per_epoch=train_params['steps_per_epoch'],
callbacks=callbacks)
def create_character_mapping():
character_map = {' ': 0}
for i in range(97, 123):
character_map[chr(i)] = len(character_map)
return character_map
def get_data_details(filename):
result = {
'max_input_length': 0,
'max_label_length': 0,
'num_samples': 0
}
# Get max lengths
with open(filename, 'r') as metadata:
metadata_reader = csv.DictReader(metadata, fieldnames=['filename', 'spec_length', 'labels_length', 'labels'])
next(metadata_reader)
for row in metadata_reader:
if int(row['spec_length']) > result['max_input_length']:
result['max_input_length'] = int(row['spec_length'])
if int(row['labels_length']) > result['max_label_length']:
result['max_label_length'] = int(row['labels_length'])
result['num_samples'] += 1
return result
def create_data_generator(directory, max_input_length, max_label_length, batch_size=64, num_epochs=5):
x, y, input_lengths, label_lengths = [], [], [], []
epochs = 0
while epochs < num_epochs:
with open(os.path.join(directory, 'LibriSpeech-metadata.csv'), 'r') as metadata:
metadata_reader = csv.DictReader(metadata, fieldnames=['filename', 'spec_length', 'labels_length', 'labels'])
next(metadata_reader)
for row in metadata_reader:
audio = np.load(os.path.join(directory, row['filename'] + '.npy'))
x.append(audio)
y.append([int(i) for i in row['labels'].split(' ')])
input_lengths.append(row['spec_length'])
label_lengths.append(row['labels_length'])
if len(x) == batch_size:
yield {
'inputs': tf.keras.preprocessing.sequence.pad_sequences(x, maxlen=max_input_length, padding='post'),
'labels': tf.keras.preprocessing.sequence.pad_sequences(y, maxlen=max_label_length, padding='post'),
'input_lengths': np.asarray(input_lengths, dtype=np.int32),
'label_lengths': np.asarray(label_lengths, dtype=np.int32)
}, {
'ctc': np.zeros([batch_size])
}
x, y, input_lengths, label_lengths = [], [], [], []
epochs = epochs + 1
def log_linear_specgram(audio, sample_rate, window_size=20,
step_size=10, eps=1e-10):
nperseg = int(round(window_size * sample_rate / 1e3))
noverlap = int(round(step_size * sample_rate / 1e3))
_, _, spec = signal.spectrogram(audio, fs=sample_rate,
window='hann', nperseg=nperseg, noverlap=noverlap,
detrend=False)
return np.log(spec.T.astype(np.float32) + eps)
def preprocess_librispeech(directory):
print("Pre-processing LibriSpeech corpus")
start_time = time.time()
character_mapping = create_character_mapping()
if not os.path.exists(preprocessing['data_dir']):
os.makedirs(preprocessing['data_dir'])
dir_walk = list(os.walk(directory))
num_hours = 0
num_train = 0
with open(os.path.join(preprocessing['cache_dir'] + '/LibriSpeech-metadata.csv'), 'w', newline='') as metadata:
metadata_writer = csv.DictWriter(metadata, fieldnames=['filename', 'spec_length', 'labels_length', 'labels'])
metadata_writer.writeheader()
for root, dirs, files in tqdm(dir_walk):
for file in files:
if file[-4:] == '.txt' and num_train < training['max_train']:
filename = os.path.join(root, file)
with open(filename, 'r') as f:
txt = f.read().split(' ')
filename_base_no_path = os.path.splitext(file)[0]
filename_base = os.path.splitext(filename)[0]
filename_wav = filename_base + '.wav'
audio, sr = sf.read(filename_wav)
num_hours += (len(audio) / sr) / 3600
spec = log_linear_specgram(audio, sr, window_size=preprocessing['window_size'],
step_size=preprocessing['step_size'])
np.save(os.path.join(preprocessing['cache_dir'], filename_base_no_path) + '.npy', spec)
ids = [character_mapping[c] for c in ' '.join(txt).lower()
if c in character_mapping]
metadata_writer.writerow({
'filename': filename_base_no_path,
'spec_length': spec.shape[0],
'labels_length': len(ids),
'labels': ' '.join([str(i) for i in ids])
})
if num_train + 1 <= training['max_train']:
num_train = num_train + 1
if num_train >= training['max_train']:
print('Processed {} files: max train {} reached...'.format(num_train, training['max_train']))
break
print("Done!")
print("Hours pre-processed: " + str(num_hours))
print("Time: " + str(time.time() - start_time))
preprocess_librispeech(preprocessing['data_dir'])
character_mapping = create_character_mapping()
data_details = get_data_details(filename=os.path.join(preprocessing['cache_dir'], 'LibriSpeech-metadata.csv'))
print(data_details)
training['steps_per_epoch'] = int(data_details['num_samples'] / training['batch_size'])
model['max_input_length'] = data_details['max_input_length']
model['max_label_length'] = data_details['max_label_length']
model['vocab_size'] = len(character_mapping)
data_generator = create_data_generator(directory=preprocessing['cache_dir'],
max_input_length=model['max_input_length'],
max_label_length=model['max_label_length'],
batch_size=training['batch_size'],
num_epochs=training['epochs'])
speech_model = SpeechModel(hparams=model)
speech_model.train_generator(data_generator, training)
tst_gen = create_data_generator(directory=preprocessing['cache_dir'],
max_input_length=model['max_input_length'],
max_label_length=model['max_label_length'],
batch_size=training['batch_size'],
num_epochs=1)
for i in tst_gen:
print(speech_model.model.predict(i[0]))
```
| true |
code
| 0.736667 | null | null | null | null |
|
# Approximate q-learning
In this notebook you will teach a __tensorflow__ neural network to do Q-learning.
__Frameworks__ - we'll accept this homework in any deep learning framework. This particular notebook was designed for tensorflow, but you will find it easy to adapt it to almost any python-based deep learning framework.
```
#XVFB will be launched if you run on a server
import os
if os.environ.get("DISPLAY") is not str or len(os.environ.get("DISPLAY"))==0:
!bash ../xvfb start
%env DISPLAY=:1
import gym
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
env = gym.make("CartPole-v0").env
env.reset()
n_actions = env.action_space.n
state_dim = env.observation_space.shape
plt.imshow(env.render("rgb_array"))
```
# Approximate (deep) Q-learning: building the network
To train a neural network policy one must have a neural network policy. Let's build it.
Since we're working with a pre-extracted features (cart positions, angles and velocities), we don't need a complicated network yet. In fact, let's build something like this for starters:

For your first run, please only use linear layers (L.Dense) and activations. Stuff like batch normalization or dropout may ruin everything if used haphazardly.
Also please avoid using nonlinearities like sigmoid & tanh: agent's observations are not normalized so sigmoids may become saturated from init.
Ideally you should start small with maybe 1-2 hidden layers with < 200 neurons and then increase network size if agent doesn't beat the target score.
```
import tensorflow as tf
import keras
import keras.layers as L
tf.reset_default_graph()
sess = tf.InteractiveSession()
keras.backend.set_session(sess)
network = keras.models.Sequential()
network.add(L.InputLayer(state_dim))
# let's create a network for approximate q-learning following guidelines above
<YOUR CODE: stack more layers!!!1 >
def get_action(state, epsilon=0):
"""
sample actions with epsilon-greedy policy
recap: with p = epsilon pick random action, else pick action with highest Q(s,a)
"""
q_values = network.predict(state[None])[0]
###YOUR CODE
return <epsilon-greedily selected action>
assert network.output_shape == (None, n_actions), "please make sure your model maps state s -> [Q(s,a0), ..., Q(s, a_last)]"
assert network.layers[-1].activation == keras.activations.linear, "please make sure you predict q-values without nonlinearity"
# test epsilon-greedy exploration
s = env.reset()
assert np.shape(get_action(s)) == (), "please return just one action (integer)"
for eps in [0., 0.1, 0.5, 1.0]:
state_frequencies = np.bincount([get_action(s, epsilon=eps) for i in range(10000)], minlength=n_actions)
best_action = state_frequencies.argmax()
assert abs(state_frequencies[best_action] - 10000 * (1 - eps + eps / n_actions)) < 200
for other_action in range(n_actions):
if other_action != best_action:
assert abs(state_frequencies[other_action] - 10000 * (eps / n_actions)) < 200
print('e=%.1f tests passed'%eps)
```
### Q-learning via gradient descent
We shall now train our agent's Q-function by minimizing the TD loss:
$$ L = { 1 \over N} \sum_i (Q_{\theta}(s,a) - [r(s,a) + \gamma \cdot max_{a'} Q_{-}(s', a')]) ^2 $$
Where
* $s, a, r, s'$ are current state, action, reward and next state respectively
* $\gamma$ is a discount factor defined two cells above.
The tricky part is with $Q_{-}(s',a')$. From an engineering standpoint, it's the same as $Q_{\theta}$ - the output of your neural network policy. However, when doing gradient descent, __we won't propagate gradients through it__ to make training more stable (see lectures).
To do so, we shall use `tf.stop_gradient` function which basically says "consider this thing constant when doingbackprop".
```
# Create placeholders for the <s, a, r, s'> tuple and a special indicator for game end (is_done = True)
states_ph = keras.backend.placeholder(dtype='float32', shape=(None,) + state_dim)
actions_ph = keras.backend.placeholder(dtype='int32', shape=[None])
rewards_ph = keras.backend.placeholder(dtype='float32', shape=[None])
next_states_ph = keras.backend.placeholder(dtype='float32', shape=(None,) + state_dim)
is_done_ph = keras.backend.placeholder(dtype='bool', shape=[None])
#get q-values for all actions in current states
predicted_qvalues = network(states_ph)
#select q-values for chosen actions
predicted_qvalues_for_actions = tf.reduce_sum(predicted_qvalues * tf.one_hot(actions_ph, n_actions), axis=1)
gamma = 0.99
# compute q-values for all actions in next states
predicted_next_qvalues = <YOUR CODE - apply network to get q-values for next_states_ph>
# compute V*(next_states) using predicted next q-values
next_state_values = <YOUR CODE>
# compute "target q-values" for loss - it's what's inside square parentheses in the above formula.
target_qvalues_for_actions = <YOUR CODE>
# at the last state we shall use simplified formula: Q(s,a) = r(s,a) since s' doesn't exist
target_qvalues_for_actions = tf.where(is_done_ph, rewards_ph, target_qvalues_for_actions)
#mean squared error loss to minimize
loss = (predicted_qvalues_for_actions - tf.stop_gradient(target_qvalues_for_actions)) ** 2
loss = tf.reduce_mean(loss)
# training function that resembles agent.update(state, action, reward, next_state) from tabular agent
train_step = tf.train.AdamOptimizer(1e-4).minimize(loss)
assert tf.gradients(loss, [predicted_qvalues_for_actions])[0] is not None, "make sure you update q-values for chosen actions and not just all actions"
assert tf.gradients(loss, [predicted_next_qvalues])[0] is None, "make sure you don't propagate gradient w.r.t. Q_(s',a')"
assert predicted_next_qvalues.shape.ndims == 2, "make sure you predicted q-values for all actions in next state"
assert next_state_values.shape.ndims == 1, "make sure you computed V(s') as maximum over just the actions axis and not all axes"
assert target_qvalues_for_actions.shape.ndims == 1, "there's something wrong with target q-values, they must be a vector"
```
### Playing the game
```
def generate_session(t_max=1000, epsilon=0, train=False):
"""play env with approximate q-learning agent and train it at the same time"""
total_reward = 0
s = env.reset()
for t in range(t_max):
a = get_action(s, epsilon=epsilon)
next_s, r, done, _ = env.step(a)
if train:
sess.run(train_step,{
states_ph: [s], actions_ph: [a], rewards_ph: [r],
next_states_ph: [next_s], is_done_ph: [done]
})
total_reward += r
s = next_s
if done: break
return total_reward
epsilon = 0.5
for i in range(1000):
session_rewards = [generate_session(epsilon=epsilon, train=True) for _ in range(100)]
print("epoch #{}\tmean reward = {:.3f}\tepsilon = {:.3f}".format(i, np.mean(session_rewards), epsilon))
epsilon *= 0.99
assert epsilon >= 1e-4, "Make sure epsilon is always nonzero during training"
if np.mean(session_rewards) > 300:
print ("You Win!")
break
```
### How to interpret results
Welcome to the f.. world of deep f...n reinforcement learning. Don't expect agent's reward to smoothly go up. Hope for it to go increase eventually. If it deems you worthy.
Seriously though,
* __ mean reward__ is the average reward per game. For a correct implementation it may stay low for some 10 epochs, then start growing while oscilating insanely and converges by ~50-100 steps depending on the network architecture.
* If it never reaches target score by the end of for loop, try increasing the number of hidden neurons or look at the epsilon.
* __ epsilon__ - agent's willingness to explore. If you see that agent's already at < 0.01 epsilon before it's is at least 200, just reset it back to 0.1 - 0.5.
### Record videos
As usual, we now use `gym.wrappers.Monitor` to record a video of our agent playing the game. Unlike our previous attempts with state binarization, this time we expect our agent to act ~~(or fail)~~ more smoothly since there's no more binarization error at play.
As you already did with tabular q-learning, we set epsilon=0 for final evaluation to prevent agent from exploring himself to death.
```
#record sessions
import gym.wrappers
env = gym.wrappers.Monitor(gym.make("CartPole-v0"),directory="videos",force=True)
sessions = [generate_session(epsilon=0, train=False) for _ in range(100)]
env.close()
#show video
from IPython.display import HTML
import os
video_names = list(filter(lambda s:s.endswith(".mp4"),os.listdir("./videos/")))
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format("./videos/"+video_names[-1])) #this may or may not be _last_ video. Try other indices
```
---
### Submit to coursera
```
from submit import submit_cartpole
submit_cartpole(generate_session, <EMAIL>, <TOKEN>)
```
| true |
code
| 0.577555 | null | null | null | null |
|
# Shape segmentation
The notebooks in this folder replicate the experiments as performed for [CNNs on Surfaces using Rotation-Equivariant Features](https://doi.org/10.1145/3386569.3392437).
The current notebook replicates the shape segmentation experiments from section `5.2 Comparisons`.
## Imports
We start by importing dependencies.
```
# File reading and progressbar
import os.path as osp
import progressbar
# PyTorch and PyTorch Geometric dependencies
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch_geometric.transforms as T
from torch_geometric.data import DataLoader
from torch_geometric.nn.inits import zeros
# Harmonic Surface Networks components
# Layers
from nn import (HarmonicConv, HarmonicResNetBlock,
ParallelTransportPool, ParallelTransportUnpool,
ComplexLin, ComplexNonLin)
# Utility functions
from utils.harmonic import magnitudes
# Rotated MNIST dataset
from datasets import ShapeSeg
# Transforms
from transforms import (HarmonicPrecomp, VectorHeat, MultiscaleRadiusGraph,
ScaleMask, FilterNeighbours, NormalizeArea, NormalizeAxes, Subsample)
```
## Settings
Next, we set a few parameters for our network. You can change these settings to experiment with different configurations of the network. Right now, the settings are set to the ones used in the paper.
```
# Maximum rotation order for streams
max_order = 1
# Number of rings in the radial profile
n_rings = 6
# Number of filters per block
nf = [16, 32]
# Ratios used for pooling
ratios=[1, 0.25]
# Radius of convolution for each scale
radii = [0.2, 0.4]
# Number of datasets per batch
batch_size = 1
# Number of classes for segmentation
n_classes = 8
```
## Dataset
To get our dataset ready for training, we need to perform the following steps:
1. Provide a path to load and store the dataset.
2. Define transformations to be performed on the dataset:
- A transformation that computes a multi-scale radius graph and precomputes the logarithmic map.
- A transformation that masks the edges and vertices per scale and precomputes convolution components.
3. Assign and load the datasets.
```
# 1. Provide a path to load and store the dataset.
# Make sure that you have created a folder 'data' somewhere
# and that you have downloaded and moved the raw datasets there
path = osp.join('data', 'ShapeSeg')
# 2. Define transformations to be performed on the dataset:
# Transformation that computes a multi-scale radius graph and precomputes the logarithmic map.
pre_transform = T.Compose((
NormalizeArea(),
MultiscaleRadiusGraph(ratios, radii, loop=True, flow='target_to_source', sample_n=1024),
VectorHeat(),
Subsample(),
NormalizeAxes()
))
# Apply a random scale and random rotation to each shape
transform = T.Compose((
T.RandomScale((0.85, 1.15)),
T.RandomRotate(45, axis=0),
T.RandomRotate(45, axis=1),
T.RandomRotate(45, axis=2))
)
# Transformations that masks the edges and vertices per scale and precomputes convolution components.
scale0_transform = T.Compose((
ScaleMask(0),
FilterNeighbours(radii[0]),
HarmonicPrecomp(n_rings, max_order, max_r=radii[0]))
)
scale1_transform = T.Compose((
ScaleMask(1),
FilterNeighbours(radii[1]),
HarmonicPrecomp(n_rings, max_order, max_r=radii[1]))
)
# 3. Assign and load the datasets.
test_dataset = ShapeSeg(path, False, pre_transform=pre_transform)
test_loader = DataLoader(test_dataset, batch_size=batch_size)
train_dataset = ShapeSeg(path, True, pre_transform=pre_transform, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
```
## Network architecture
Now, we create the network architecture by creating a new `nn.Module`, `Net`. We first setup each layer in the `__init__` method of the `Net` class and define the steps to perform for each batch in the `forward` method. The following figure shows a schematic of the architecture we will be implementing:
<img src="img/resnet_architecture.png" width="800px" />
Let's get started!
```
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.lin0 = nn.Linear(3, nf[0])
# Stack 1
self.resnet_block11 = HarmonicResNetBlock(nf[0], nf[0], max_order, n_rings, prev_order=0)
self.resnet_block12 = HarmonicResNetBlock(nf[0], nf[0], max_order, n_rings)
# Pool
self.pool = ParallelTransportPool(1, scale1_transform)
# Stack 2
self.resnet_block21 = HarmonicResNetBlock(nf[0], nf[1], max_order, n_rings)
self.resnet_block22 = HarmonicResNetBlock(nf[1], nf[1], max_order, n_rings)
# Stack 3
self.resnet_block31 = HarmonicResNetBlock(nf[1], nf[1], max_order, n_rings)
self.resnet_block32 = HarmonicResNetBlock(nf[1], nf[1], max_order, n_rings)
# Unpool
self.unpool = ParallelTransportUnpool(from_lvl=1)
# Stack 4
self.resnet_block41 = HarmonicResNetBlock(nf[1] + nf[0], nf[0], max_order, n_rings)
self.resnet_block42 = HarmonicResNetBlock(nf[0], nf[0], max_order, n_rings)
# Final Harmonic Convolution
# We set offset to False,
# because we will only use the radial component of the features after this
self.conv_final = HarmonicConv(nf[0], n_classes, max_order, n_rings, offset=False)
self.bias = nn.Parameter(torch.Tensor(n_classes))
zeros(self.bias)
def forward(self, data):
x = data.pos
# Linear transformation from input positions to nf[0] features
x = F.relu(self.lin0(x))
# Convert input features into complex numbers
x = torch.stack((x, torch.zeros_like(x)), dim=-1).unsqueeze(1)
# Stack 1
# Select only the edges and precomputed components of the first scale
data_scale0 = scale0_transform(data)
attributes = (data_scale0.edge_index, data_scale0.precomp, data_scale0.connection)
x = self.resnet_block11(x, *attributes)
x_prepool = self.resnet_block12(x, *attributes)
# Pooling
# Apply parallel transport pooling
x, data, data_pooled = self.pool(x_prepool, data)
# Stack 2
# Store edge_index and precomputed components of the second scale
attributes_pooled = (data_pooled.edge_index, data_pooled.precomp, data_pooled.connection)
x = self.resnet_block21(x, *attributes_pooled)
x = self.resnet_block22(x, *attributes_pooled)
# Stack 3
x = self.resnet_block31(x, *attributes_pooled)
x = self.resnet_block32(x, *attributes_pooled)
# Unpooling
x = self.unpool(x, data)
# Concatenate pre-pooling x with post-pooling x
x = torch.cat((x, x_prepool), dim=2)
# Stack 3
x = self.resnet_block41(x, *attributes)
x = self.resnet_block42(x, *attributes)
x = self.conv_final(x, *attributes)
# Take radial component from features and sum streams
x = magnitudes(x, keepdim=False)
x = x.sum(dim=1)
x = x + self.bias
return F.log_softmax(x, dim=1)
```
## Training
Phew, we're through the hard part. Now, let's get to training. First, move the network to the GPU and setup an optimizer.
```
# We want to train on a GPU. It'll take a long time on a CPU
device = torch.device('cuda')
# Move the network to the GPU
model = Net().to(device)
# Set up the ADAM optimizer with learning rate of 0.0076 (as used in H-Nets)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
```
Next, define a training and test function.
```
def train(epoch):
# Set model to 'train' mode
model.train()
if epoch > 20:
for param_group in optimizer.param_groups:
param_group['lr'] = 0.001
for data in progressbar.progressbar(train_loader):
# Move training data to the GPU and optimize parameters
optimizer.zero_grad()
F.nll_loss(model(data.to(device)), data.y).backward()
optimizer.step()
def test():
# Set model to 'evaluation' mode
model.eval()
correct = 0
total_num = 0
for i, data in enumerate(test_loader):
pred = model(data.to(device)).max(1)[1]
correct += pred.eq(data.y).sum().item()
total_num += data.y.size(0)
return correct / total_num
```
Train for 50 epochs.
```
print('Start training, may take a while...')
# Try with fewer epochs if you're in a timecrunch
for epoch in range(50):
train(epoch)
test_acc = test()
print("Epoch {} - Test: {:06.4f}".format(epoch, test_acc))
```
| true |
code
| 0.766534 | null | null | null | null |
|
# Linear Regression
We will follow the example given by [scikit-learn](https://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html), and use the [diabetes](https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html) dataset to train and test a linear regressor. We begin by loading the dataset (using only two features for this example) and splitting it into training and testing samples (an 80/20 split).
```
from sklearn.model_selection import train_test_split
from sklearn import datasets
dataset = datasets.load_diabetes()
X_train, X_test, y_train, y_test = train_test_split(dataset.data[:, :2], dataset.target, test_size=0.2)
print("Train examples: %d, Test examples: %d" % (X_train.shape[0], X_test.shape[0]))
```
# Non-private baseline
We now use scikit-learn's native LinearRegression function to establish a non-private baseline for our experiments. We will use the [r-squared score](https://en.wikipedia.org/wiki/Coefficient_of_determination) to evaluate the goodness-of-fit of the model, which is built into LinearRegression.
```
from sklearn.linear_model import LinearRegression as sk_LinearRegression
regr = sk_LinearRegression()
regr.fit(X_train, y_train)
baseline = regr.score(X_test, y_test)
print("Non-private baseline R2 score: %.2f" % baseline)
```
# Differentially private Linear Regression
Let's now train a differentially private linear regressor, where the trained model is differentially private with respect to the training data. We will pass additional hyperparameters to the regressor later to suppress the `PrivacyLeakWarning`.
```
from diffprivlib.models import LinearRegression
regr = LinearRegression()
regr.fit(X_train, y_train)
print("R2 score for epsilon=%.2f: %.2f" % (regr.epsilon, regr.score(X_test, y_test)))
```
# Plotting r-squared versus epsilon
We want to evaluate the tradeoff between goodness-of-fit and privacy budget (epsilon), and plot the result using `matplotlib`. For this example, we evaluate the score for epsilon between 1e-2 and 1e2. To ensure no privacy leakage from the hyperparameters of the model, `data_norm`, `range_X` and `range_y` should all be set independently of the data, i.e. using domain knowledge.
```
import numpy as np
epsilons = np.logspace(-1, 2, 100)
accuracy = []
for epsilon in epsilons:
regr = LinearRegression(epsilon=epsilon, bounds_X=(-0.138, 0.2), bounds_y=(25, 346))
regr.fit(X_train, y_train)
accuracy.append(regr.score(X_test, y_test))
```
And then plot the result in a semi-log plot.
```
import matplotlib.pyplot as plt
plt.semilogx(epsilons, accuracy, label="Differentially private linear regression", zorder=10)
plt.semilogx(epsilons, baseline * np.ones_like(epsilons), dashes=[2,2], label="Non-private baseline", zorder=5)
plt.xlabel("epsilon")
plt.ylabel("r-squared score")
plt.ylim(-5, 1.5)
plt.xlim(epsilons[0], epsilons[-1])
plt.legend(loc=2)
```
| true |
code
| 0.785483 | null | null | null | null |
|
# Stochastic optimization landscape of a minimal MLP
In this notebook, we will try to better understand how stochastic gradient works. We fit a very simple non-convex model to data generated from a linear ground truth model.
We will also observe how the (stochastic) loss landscape changes when selecting different samples.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
from torch.nn import Parameter
from torch.nn.functional import mse_loss
from torch.autograd import Variable
from torch.nn.functional import relu
```
Data is generated from a simple model:
$$y= 2x + \epsilon$$
where:
- $\epsilon \sim \mathcal{N}(0, 3)$
- $x \sim \mathcal{U}(-1, 1)$
```
def sample_from_ground_truth(n_samples=100, std=0.1):
x = torch.FloatTensor(n_samples, 1).uniform_(-1, 1)
epsilon = torch.FloatTensor(n_samples, 1).normal_(0, std)
y = 2 * x + epsilon
return x, y
n_samples = 100
std = 3
x, y = sample_from_ground_truth(n_samples=100, std=std)
```
We propose a minimal single hidden layer perceptron model with a single hidden unit and no bias. The model has two tunable parameters $w_1$, and $w_2$, such that:
$$f(x) = w_1 \cdot \sigma(w_2 \cdot x)$$
where $\sigma$ is the ReLU function.
```
class SimpleMLP(nn.Module):
def __init__(self, w=None):
super(SimpleMLP, self).__init__()
self.w1 = Parameter(torch.FloatTensor((1,)))
self.w2 = Parameter(torch.FloatTensor((1,)))
if w is None:
self.reset_parameters()
else:
self.set_parameters(w)
def reset_parameters(self):
self.w1.uniform_(-.1, .1)
self.w2.uniform_(-.1, .1)
def set_parameters(self, w):
with torch.no_grad():
self.w1[0] = w[0]
self.w2[0] = w[1]
def forward(self, x):
return self.w1 * relu(self.w2 * x)
```
As in the previous notebook, we define a function to sample from and plot loss landscapes.
```
from math import fabs
def make_grids(x, y, model_constructor, expected_risk_func, grid_size=100):
n_samples = len(x)
assert len(x) == len(y)
# Grid logic
x_max, y_max, x_min, y_min = 5, 5, -5, -5
w1 = np.linspace(x_min, x_max, grid_size, dtype=np.float32)
w2 = np.linspace(y_min, y_max, grid_size, dtype=np.float32)
W1, W2 = np.meshgrid(w1, w2)
W = np.concatenate((W1[:, :, None], W2[:, :, None]), axis=2)
W = torch.from_numpy(W)
# We will store the results in this tensor
risks = torch.FloatTensor(n_samples, grid_size, grid_size)
expected_risk = torch.FloatTensor(grid_size, grid_size)
with torch.no_grad():
for i in range(grid_size):
for j in range(grid_size):
model = model_constructor(W[i, j])
pred = model(x)
loss = mse_loss(pred, y, reduce=False)
risks[:, i, j] = loss.view(-1)
expected_risk[i, j] = expected_risk_func(W[i, j, 0], W[i, j, 1])
empirical_risk = torch.mean(risks, dim=0)
return W1, W2, risks.numpy(), empirical_risk.numpy(), expected_risk.numpy()
def expected_risk_simple_mlp(w1, w2):
"""Question: Can you derive this your-self?"""
return .5 * (8 / 3 - (4 / 3) * w1 * w2 + 1 / 3 * w1 ** 2 * w2 ** 2) + std ** 2
```
- `risks[k, i, j]` holds loss value $\ell(f(w_1^{(i)} , w_2^{(j)}, x_k), y_k)$ for a single data point $(x_k, y_k)$;
- `empirical_risk[i, j]` corresponds to the empirical risk averaged over the training data points:
$$ \frac{1}{n} \sum_{k=1}^{n} \ell(f(w_1^{(i)}, w_2^{(j)}, x_k), y_k)$$
```
W1, W2, risks, empirical_risk, expected_risk = make_grids(
x, y, SimpleMLP, expected_risk_func=expected_risk_simple_mlp)
```
Let's define our train loop and train our model:
```
from torch.optim import SGD
def train(model, x, y, lr=.1, n_epochs=1):
optimizer = SGD(model.parameters(), lr=lr)
iterate_rec = []
grad_rec = []
for epoch in range(n_epochs):
# Iterate over the dataset one sample at a time:
# batch_size=1
for this_x, this_y in zip(x, y):
this_x = this_x[None, :]
this_y = this_y[None, :]
optimizer.zero_grad()
pred = model(this_x)
loss = mse_loss(pred, this_y)
loss.backward()
with torch.no_grad():
iterate_rec.append([model.w1.clone()[0], model.w2.clone()[0]])
grad_rec.append([model.w1.grad.clone()[0], model.w2.grad.clone()[0]])
optimizer.step()
return np.array(iterate_rec), np.array(grad_rec)
init = torch.FloatTensor([3, -4])
model = SimpleMLP(init)
iterate_rec, grad_rec = train(model, x, y, lr=.01)
print(iterate_rec[-1])
```
We now plot:
- the point-wise risk at iteration $k$ on the left plot
- the total empirical risk on the center plot
- the expected risk on the right plot
Observe how empirical and expected risk differ, and how empirical risk minimization is not totally equivalent to expected risk minimization.
```
import matplotlib.colors as colors
class LevelsNormalize(colors.Normalize):
def __init__(self, levels, clip=False):
self.levels = levels
vmin, vmax = levels[0], levels[-1]
colors.Normalize.__init__(self, vmin, vmax, clip)
def __call__(self, value, clip=None):
quantiles = np.linspace(0, 1, len(self.levels))
return np.ma.masked_array(np.interp(value, self.levels, quantiles))
def plot_map(W1, W2, risks, emp_risk, exp_risk, sample, iter_):
all_risks = np.concatenate((emp_risk.ravel(), exp_risk.ravel()))
x_center, y_center = emp_risk.shape[0] // 2, emp_risk.shape[1] // 2
risk_at_center = exp_risk[x_center, y_center]
low_levels = np.percentile(all_risks[all_risks <= risk_at_center],
q=np.linspace(0, 100, 11))
high_levels = np.percentile(all_risks[all_risks > risk_at_center],
q=np.linspace(10, 100, 10))
levels = np.concatenate((low_levels, high_levels))
norm = LevelsNormalize(levels=levels)
cmap = plt.get_cmap('RdBu_r')
fig, (ax1, ax2, ax3) = plt.subplots(ncols=3, figsize=(12, 4))
risk_levels = levels.copy()
risk_levels[0] = min(risks[sample].min(), risk_levels[0])
risk_levels[-1] = max(risks[sample].max(), risk_levels[-1])
ax1.contourf(W1, W2, risks[sample], levels=risk_levels,
norm=norm, cmap=cmap)
ax1.scatter(iterate_rec[iter_, 0], iterate_rec[iter_, 1],
color='orange')
if any(grad_rec[iter_] != 0):
ax1.arrow(iterate_rec[iter_, 0], iterate_rec[iter_, 1],
-0.1 * grad_rec[iter_, 0], -0.1 * grad_rec[iter_, 1],
head_width=0.3, head_length=0.5, fc='orange', ec='orange')
ax1.set_title('Pointwise risk')
ax2.contourf(W1, W2, emp_risk, levels=levels, norm=norm, cmap=cmap)
ax2.plot(iterate_rec[:iter_ + 1, 0], iterate_rec[:iter_ + 1, 1],
linestyle='-', marker='o', markersize=6,
color='orange', linewidth=2, label='SGD trajectory')
ax2.legend()
ax2.set_title('Empirical risk')
cf = ax3.contourf(W1, W2, exp_risk, levels=levels, norm=norm, cmap=cmap)
ax3.scatter(iterate_rec[iter_, 0], iterate_rec[iter_, 1],
color='orange', label='Current sample')
ax3.set_title('Expected risk (ground truth)')
plt.colorbar(cf, ax=ax3)
ax3.legend()
fig.suptitle('Iter %i, sample % i' % (iter_, sample))
plt.show()
for sample in range(0, 100, 10):
plot_map(W1, W2, risks, empirical_risk, expected_risk, sample, sample)
```
Observe and comment.
### Exercices:
- Change the model to a completely linear one and reproduce the plots. What change do you observe regarding the plot of the stochastic loss landscape?
- Try changing the optimizer. Is it useful in this case?
- Try to initialize the model with pathological weights, e.g., symmetric ones. What do you observe?
- You may increase the number of epochs to observe slow convergence phenomena
- Try augmenting the noise in the dataset. What do you observe?
```
# %load solutions/linear_mlp.py
```
## Utilities to generate the slides figures
```
# from matplotlib.animation import FuncAnimation
# from IPython.display import HTML
# fig, ax = plt.subplots(figsize=(8, 8))
# all_risks = np.concatenate((empirical_risk.ravel(),
# expected_risk.ravel()))
# x_center, y_center = empirical_risk.shape[0] // 2, empirical_risk.shape[1] // 2
# risk_at_center = expected_risk[x_center, y_center]
# low_levels = np.percentile(all_risks[all_risks <= risk_at_center],
# q=np.linspace(0, 100, 11))
# high_levels = np.percentile(all_risks[all_risks > risk_at_center],
# q=np.linspace(10, 100, 10))
# levels = np.concatenate((low_levels, high_levels))
# norm = LevelsNormalize(levels=levels)
# cmap = plt.get_cmap('RdBu_r')
# ax.set_title('Pointwise risk')
# def animate(i):
# for c in ax.collections:
# c.remove()
# for l in ax.lines:
# l.remove()
# for p in ax.patches:
# p.remove()
# risk_levels = levels.copy()
# risk_levels[0] = min(risks[i].min(), risk_levels[0])
# risk_levels[-1] = max(risks[i].max(), risk_levels[-1])
# ax.contourf(W1, W2, risks[i], levels=risk_levels,
# norm=norm, cmap=cmap)
# ax.plot(iterate_rec[:i + 1, 0], iterate_rec[:i + 1, 1],
# linestyle='-', marker='o', markersize=6,
# color='orange', linewidth=2, label='SGD trajectory')
# return []
# anim = FuncAnimation(fig, animate,# init_func=init,
# frames=100, interval=300, blit=True)
# anim.save("stochastic_landscape_minimal_mlp.mp4")
# plt.close(fig)
# HTML(anim.to_html5_video())
# fig, ax = plt.subplots(figsize=(8, 7))
# cf = ax.contourf(W1, W2, empirical_risk, levels=levels, norm=norm, cmap=cmap)
# ax.plot(iterate_rec[:100 + 1, 0], iterate_rec[:100 + 1, 1],
# linestyle='-', marker='o', markersize=6,
# color='orange', linewidth=2, label='SGD trajectory')
# ax.legend()
# plt.colorbar(cf, ax=ax)
# ax.set_title('Empirical risk')
# fig.savefig('empirical_loss_landscape_minimal_mlp.png')
```
| true |
code
| 0.817593 | null | null | null | null |
|
## Day 1: Of Numerical Integration and Python
Welcome to Day 1! Today, we start with our discussion of what Numerical Integration is.
### What is Numerical Integration?
From the point of view of a theoretician, the ideal form of the solution to a differential equation given the initial conditions, i.e. an initial value problem (IVP), would be a formula for the solution function. But sometimes obtaining a formulaic solution is not always easy, and in many cases is absolutely impossible. So, what do we do when faced with a differential equation that we cannot solve? If you are only looking for long term behavior of a solution you can always sketch a direction field. This can be done without too much difficulty for some fairly complex differential equations that we can’t solve to get exact solutions. But, what if we need to determine how a specific solution behaves, including some values that the solution will take? In that case, we have to rely on numerical methods for solving the IVP such as euler's method or the Runge-Kutta Methods.
#### Euler's Method for Numerical Integration
We use Euler's Method to generate a numerical solution to an initial value problem of the form:
$$\frac{dx}{dt} = f(x, t)$$
$$x(t_o) = x_o$$
Firstly, we decide the interval over which we desire to find the solution, starting at the initial condition. We break this interval into small subdivisions of a fixed length $\epsilon$. Then, using the initial condition as our starting point, we generate the rest of the solution by using the iterative formulas:
$$t_{n+1} = t_n + \epsilon$$
$$x_{n+1} = x_n + \epsilon f(x_n, t_n)$$
to find the coordinates of the points in our numerical solution. We end this process once we have reached the end of the desired interval.
The best way to understand how it works is from the following diagram:
<img src="euler.png" alt="euler.png" width="400"/>
#### Euler's Method in Python
Let $\frac{dx}{dt}=f(x,t)$, we want to find $x(t)$ over $t\in[0,2)$, given that $x(0)=1$ and $f(x,t) = 5x$. The exact solution of this equation would be $x(t) = e^{5t}$.
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def f(x,t): # define the function f(x,t)
return 5*x
epsilon = 0.01 # define timestep
t = np.arange(0,2,epsilon) # define an array for t
x = np.zeros(t.shape) # define an array for x
x[0]= 1 # set initial condition
for i in range(1,t.shape[0]):
x[i] = epsilon*f(x[i-1],t[i-1])+x[i-1] # Euler Integration Step
ax = plt.subplot(111)
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
plt.plot(t[::5],x[::5],".",label="Eulers Solution")
plt.plot(t,np.exp(5*t),label="Exact Solution")
plt.xlabel("t")
plt.ylabel("x")
plt.legend()
plt.show()
```
#### Euler and Vectors
Euler's Method also applies to vectors and can solve simultaneous differential equations.
The Initial Value problem now becomes:
$$\frac{d\vec{X}}{dt} = \vec{f}(\vec{X}, t)$$
$$\vec{X}(t_o) = \vec{X_o}$$
where $\vec{X}=[X_1,X_2...]$ and $\vec{f}(\vec{X}, t)=[f_1(\vec{X}, t),f_2(\vec{X}, t)...]$.
The Euler's Method becomes:
$$t_{n+1} = t_n + \epsilon$$
$$\vec{X_{n+1}} = \vec{X_n} + \epsilon \vec{f}(\vec{X_n}, t_n)$$
Let $\frac{d\vec{X}}{dt}=f(\vec{X},t)$, we want to find $\vec{X}(t)$ over $t\in[0,2)$, given that $\vec{X}(t)=[x,y]$, $\vec{X}(0)=[1,0]$ and $f(\vec{X},t) = [x-y,y-x]$.
```
def f(X,t): # define the function f(x,t)
x,y = X
return np.array([x-y,y-x])
epsilon = 0.01 # define timestep
t = np.arange(0,2,epsilon) # define an array for t
X = np.zeros((2,t.shape[0])) # define an array for x
X[:,0]= [1,0] # set initial condition
for i in range(1,t.shape[0]):
X[:,i] = epsilon*f(X[:,i-1],t[i-1])+X[:,i-1] # Euler Integration Step
plt.plot(t[::5],X[0,::5],".",label="Eulers Solution for x")
plt.plot(t[::5],X[1,::5],".",label="Eulers Solution for y")
plt.xlabel("t")
plt.ylabel("x")
plt.legend()
plt.show()
```
#### A Generalized function for Euler Integration
Now, we create a generalized function that takes in 3 inputs ie. the function $\vec{f}(\vec{y},t)$ when $\frac{d\vec{y}}{dt}=f(\vec{y},t)$, the time array, and initial vector $\vec{y_0}$.
##### Algorithm
- Get the required inputs: function $\vec{f}(\vec{y},t)$, initial condition vector $\vec{y_0}$ and time series $t$. Entering a time series $t$ allows for greater control over $\epsilon$ as it can now vary for each timestep. The only difference in the Euler's Method is now : $\epsilon\rightarrow\epsilon(t_n)$.
- Check if the input is of the correct datatype ie. floating point decimal.
- Create a zero matrix to hold the output.
- For each timestep, perform the euler method updation with variable $\epsilon$ and store it in the output matrix.
- Return the output timeseries matrix.
```
def check_type(y,t): # Ensure Input is Correct
return y.dtype == np.floating and t.dtype == np.floating
class _Integrator():
def integrate(self,func,y0,t):
time_delta_grid = t[1:] - t[:-1]
y = np.zeros((y0.shape[0],t.shape[0]))
y[:,0] = y0
for i in range(time_delta_grid.shape[0]):
y[:,i+1]= time_delta_grid[i]*func(y[:,i],t[i])+y[:,i]
return y
def odeint_euler(func,y0,t):
y0 = np.array(y0)
t = np.array(t)
if check_type(y0,t):
return _Integrator().integrate(func,y0,t)
else:
print("error encountered")
solution = odeint_euler(f,[1.,0.],t)
plt.plot(t[::5],solution[0,::5],".",label="Eulers Solution for x")
plt.plot(t[::5],solution[1,::5],".",label="Eulers Solution for y")
plt.xlabel("t")
plt.ylabel("X")
plt.legend()
plt.show()
```
#### Runge-Kutta Methods for Numerical Integration
The formula for the Euler method is $x_{n+1}=x_n + \epsilon f(x_n,t_n)$ which takes a solution from $t_n$ to $t_{n+1}=t_n+\epsilon$. One might notice there is an inherent assymetry in the formula. It advances the solution through an interval $\epsilon$, but uses the derivative information at only the start of the interval. This results in an error in the order of $O(\epsilon^2)$. But, what if we take a trial step and evaluate the derivative at the midpoint of the update interval to evaluate the value of $y_{n+1}$? Take the equations:
$$k_1=\epsilon f(x_n,t_n)$$
$$k_2=\epsilon f(x_n+\frac{k_1}{2},t_n+\frac{\epsilon}{2})$$
$$y_{n+1}=y_n+k_2+O(\epsilon^3)$$
The symmetrization removes the O($\epsilon^2$) error term and now the method is second order and called the second order Runge-Kutta method or the midpoint method. You can look at this method graphically as follows:
<img src="rk2.png" alt="rk2.png" width="400"/>
But we do not have to stop here. By further rewriting the equation, we can cancel higher order error terms and reach the most commonly used fourth-order Runge-Kutta Methods or RK4 method, which is described below:
$$k_1=f(x_n,t_n)$$
$$k_2=f(x_n+\epsilon\frac{k_1}{2},t_n+\frac{\epsilon}{2})$$
$$k_3=f(x_n+\epsilon\frac{k_2}{2},t_n+\frac{\epsilon}{2})$$
$$k_4=f(x_n+\epsilon k_3,t_n+\epsilon)$$
$$y_{n+1}=y_n+\frac{\epsilon}{6}(k_1+2 k_2+2 k_3+k_4)+O(\epsilon^5)$$
Note that this numerical method is again easily converted to a vector algorithm by simply replacing $x_i$ by the vector $\vec{X_i}$.
This method is what we will use to simulate our networks.
#### Generalized RK4 Method in Python
Just like we had created a function for Euler Integration in Python, we create a generalized function for RK4 that takes in 3 inputs ie. the function $f(\vec{y},t)$ when $\frac{d\vec{y}}{dt}=f(\vec{y},t)$, the time array, and initial vector $\vec{y_0}$. We then perform the exact same integration that we had done with Euler's Method. Everything remains the same except we replace the Euler's method updation rule with the RK4 update rule.
```
def check_type(y,t): # Ensure Input is Correct
return y.dtype == np.floating and t.dtype == np.floating
class _Integrator():
def integrate(self,func,y0,t):
time_delta_grid = t[1:] - t[:-1]
y = np.zeros((y0.shape[0],t.shape[0]))
y[:,0] = y0
for i in range(time_delta_grid.shape[0]):
k1 = func(y[:,i], t[i]) # RK4 Integration Steps
half_step = t[i] + time_delta_grid[i] / 2
k2 = func(y[:,i] + time_delta_grid[i] * k1 / 2, half_step)
k3 = func(y[:,i] + time_delta_grid[i] * k2 / 2, half_step)
k4 = func(y[:,i] + time_delta_grid[i] * k3, t + time_delta_grid[i])
y[:,i+1]= (k1 + 2 * k2 + 2 * k3 + k4) * (time_delta_grid[i] / 6) + y[:,i]
return y
def odeint_rk4(func,y0,t):
y0 = np.array(y0)
t = np.array(t)
if check_type(y0,t):
return _Integrator().integrate(func,y0,t)
else:
print("error encountered")
solution = odeint_rk4(f,[1.,0.],t)
plt.plot(t[::5],solution[0,::5],".",label="RK4 Solution for x")
plt.plot(t[::5],solution[1,::5],".",label="RK4 Solution for y")
plt.xlabel("t")
plt.ylabel("X")
plt.legend()
plt.show()
```
As an **Exercise**, try to solve the equation of a simple pendulum and observe its dynamics using Euler Method and RK4 methods. The equation of motion of a simple pendulum is given by: $$\frac{d^2s}{dt^2}=L\frac{d^2\theta}{dt^2}=-g\sin{\theta}$$ where $L$ = Length of String and $\theta$ = angle made with vertical. To solve this second order differential equation you may use a dummy variable $\omega$ representing angular velocity such that:
$$\frac{d\theta}{dt}=\omega$$
$$\frac{d\omega}{dt}=-\frac{g}{L}\sin{\theta}$$
| true |
code
| 0.593433 | null | null | null | null |
|
```
import optuna as op
import pandas as pd
import numpy as np
from scipy.spatial.transform import Rotation
import seaborn as sns
import matplotlib.pyplot as plt
sns.set()
```
This is a slightly lower tech process that attempts to align the datasets via procrustes transformations. Each embedding is performed independently of the other embeddings. We then attempt to find rotations of the data that minimises the procrustes distance between datasets.
Suppose we have two sets of data, $X = {x_1, ..., x_n}$ and $Y = {y_1, ..., y_n}$ that are comparable, such that $x_i$ and $y_i$ are related.
Define the Procrustes distance: $D_p(X, Y) = \sum ||x_i - y_i||_2$
We seek to find a rotation and shift, $Y' = RY + C$ that minimises $D_p(X,Y')$. C is columnwise constant.
```
p2 = pd.read_csv('Data/TTI_Pillar2/SymptomsUMAP_loose_clusteringOrigin P2.csv', index_col=0)
sgss = pd.read_csv('Data/TTI_SGSS/SymptomsUMAP_loose_clusteringOrigin SGSS.csv', index_col=0)
css = pd.read_csv('Data/CovidSymptomStudy/UMAPLooseWide.csv', index_col=0)
cis = pd.read_csv('Data/CommunityInfectionSurvey/SymptomsUMAP_loose_clustering.csv', index_col=0)
class ProcrustesAlignment:
def __init__(self, X: np.array, Y: np.array, X_mapping_idx: list[int], Y_mapping_idx: list[int]) -> None:
self.X = X
self.Y = Y
self.X_mapping_idx = X_mapping_idx
self.Y_mapping_idx = Y_mapping_idx
self.optimized = False
def compute_procrustes_distance(self, X: np.array, Y_dash: np.array) -> float:
return np.sum(np.sqrt( ((X.T[self.X_mapping_idx,:] - Y_dash.T[self.Y_mapping_idx,:])**2).sum(axis = 1) ) )
def get_rotation_matrix(self, theta) -> np.array:
theta = np.radians(theta)
c, s = np.cos(theta), np.sin(theta)
return np.array(((c, -s), (s, c)))
def transform_Y(self, theta: float, x_shift: float, y_shift: float) -> np.array:
return np.matmul(self.get_rotation_matrix(theta), self.Y) + np.array([[x_shift], [y_shift]])
def eval_transformation(self, theta: float, x_shift: float, y_shift: float) -> float:
return self.compute_procrustes_distance(self.X, self.transform_Y(theta, x_shift, y_shift))
def optimize(self, n_trials: int) -> np.array:
self.study = op.create_study()
self.study.optimize(self.objective, n_trials)
self.optimized = True
self.best_params = self.study.best_params
def objective(self, trial):
theta = trial.suggest_float('theta', 0, 360)
x_shift = trial.suggest_float('x_shift', -10, 10)
y_shift = trial.suggest_float('y_shift', -10, 10)
return self.eval_transformation(theta, x_shift, y_shift)
def get_optimal_rotation(self):
if not self.optimized:
print('Optimisation has not yet been performed.')
else:
return self.transform_Y(self.best_params['theta'], self.best_params['x_shift'], self.best_params['y_shift'])
```
We can only align symptoms that are shared across datasets, so we need to find the mapping from one dataset to the other.
```
# load the lookup into memory
symptom_name_category_lookup = pd.read_csv('Data/Lookups/SymptomNameCategoryLookup.csv')
# subset the lookup for each dataset
ctas_lookup = symptom_name_category_lookup[symptom_name_category_lookup.dataset == 'CTAS']
css_lookup = symptom_name_category_lookup[symptom_name_category_lookup.dataset == 'Zoe']
cis_lookup = symptom_name_category_lookup[symptom_name_category_lookup.dataset == 'ONS']
# create tables that contain only the raw symptom variable names in the dataset
p2_symptoms = pd.DataFrame(p2.columns, columns=['symptom'])
sgss_symptoms = pd.DataFrame(sgss.columns, columns=['symptom'])
css_symptoms = pd.DataFrame(css.columns, columns=['symptom'])
cis_symptoms = pd.DataFrame(cis.columns, columns=['symptom'])
# join to the lookup table, this allows us to map the symptoms between datasets
p2_symptoms = pd.merge(left = p2_symptoms, right = ctas_lookup, left_on = 'symptom', right_on='symptom_name_raw')[['symptom', 'symptom_id', 'symptom_name_formatted', 'category']]
sgss_symptoms = pd.merge(left = sgss_symptoms, right = ctas_lookup, left_on = 'symptom', right_on='symptom_name_raw')[['symptom', 'symptom_id', 'symptom_name_formatted', 'category']]
css_symptoms = pd.merge(left = css_symptoms, right = css_lookup, left_on = 'symptom', right_on='symptom_name_raw')[['symptom', 'symptom_id', 'symptom_name_formatted', 'category']]
cis_symptoms = pd.merge(left = cis_symptoms, right = cis_lookup, left_on = 'symptom', right_on='symptom_name_raw')[['symptom', 'symptom_id', 'symptom_name_formatted', 'category']]
# work out which ids are common across all datasets
symptom_ids = [
p2_symptoms.symptom_id.values,
sgss_symptoms.symptom_id.values,
css_symptoms.symptom_id.values,
cis_symptoms.symptom_id.values
]
shared_ids = symptom_ids[0]
for id_set in symptom_ids:
shared_ids = np.intersect1d(shared_ids, id_set)
# convenience function for mapping symptoms in one data to the other
# need to provide a list of the symptoms that are common across all datasets
def get_mapping_indices(symptoms_from, symptoms_to, common_symptom_ids):
from_index = []
to_index = []
for num_from, symptom_id_from in enumerate(symptoms_from.symptom_id.values):
if symptom_id_from in common_symptom_ids:
for num_to, symptom_id_to in enumerate(symptoms_to.symptom_id.values):
if symptom_id_to == symptom_id_from:
from_index.append(num_from)
to_index.append(num_to)
return from_index, to_index
from_idx, to_idx = get_mapping_indices(p2_symptoms, css_symptoms, common_symptom_ids=shared_ids)
def align(dataset, dataset_symptoms):
from_idx, to_idx = get_mapping_indices(p2_symptoms, dataset_symptoms, shared_ids)
aligner = ProcrustesAlignment(X = p2.values, Y = dataset.values, X_mapping_idx=from_idx, Y_mapping_idx=to_idx)
aligner.optimize(n_trials=500)
aligned_embedding = aligner.get_optimal_rotation()
return pd.DataFrame(data=aligned_embedding, columns = dataset.columns)
# we align all the datasets relative to the pillar 2 output. It shouldn't make a difference
sgss = align(sgss, sgss_symptoms)
css = align(css, css_symptoms)
cis = align(cis, cis_symptoms)
p2.to_csv('Data/Alignments/ProcrustesAlignments/p2_loose.csv')
sgss.to_csv('Data/Alignments/ProcrustesAlignments/sgss_loose.csv')
css.to_csv('Data/Alignments/ProcrustesAlignments/css_loose.csv')
cis.to_csv('Data/Alignments/ProcrustesAlignments/cis_loose.csv')
```
| true |
code
| 0.554591 | null | null | null | null |
|
## Neral Networks In Pytorch
* We're just going to use data from Pytorch's "torchvision." Pytorch has a relatively handy inclusion of a bunch of different datasets, including many for vision tasks, which is what torchvision is for.
> Let's visualise the datatets that we can find in `torchvision`
## Imports
```
import torch
import torchvision
from torchvision import datasets, transforms
from matplotlib import pyplot as plt
import numpy as np
```
> The datasets `dir`
```
print(dir(datasets)), len(dir(datasets))
```
> We have `75` items that we can work with in the torchvision dataset.
### The MNIST dataset
The goal is to classify hand-written digits that comes from the `mnist` dataset as our `hello-world-neural-network`. This dataset contains images of handwritten digits from `0` to `9`
### Loading the data
```
train = datasets.MNIST('', train=True, download=True,
transform = transforms.Compose({
transforms.ToTensor()
}))
test = datasets.MNIST('', train=False, download=True,
transform = transforms.Compose({
transforms.ToTensor()
}))
```
> From the above cell we are just downloading the datasets and then transform or preprocess it.
> Now, we need to handle for how we're going to iterate over that dataset:
```
trainset = torch.utils.data.DataLoader(train, batch_size=10, shuffle=True)
testset = torch.utils.data.DataLoader(test, batch_size=10, shuffle=False)
```
> **That was so brutal!! What is happening here?**
**shuffle** - in ML normally we shuffle the data to mix it up so that the data will not have labels of the same type following each other.
**batch_size** - this split our data in batches in our case a batch of `10`
```
for data in trainset:
print(data[0][:2], data[1][:2])
plt.imshow(data[0][0].view(28, 28), cmap="gray")
plt.show()
break
```
### Creating a NN
* Now we have our trainset and testset let's start creating a Neural Network.
```
import torch.nn as nn
import torch.nn.functional as F
```
> The `torch.nn` import gives us access to some helpful neural network things, such as various neural network layer types like:
**regular fully-connected layers**, **convolutional layers** ..etc
> The `torch.nn.functional` area specifically gives us access to some handy functions that we might not want to write ourselves. We will be using the **`relu`** or "rectified linear unit" activation function for our neurons.
```
class Net(nn.Module):
def __init__(self):
super().__init__()
net = Net()
print(net)
```
> We have created a `Net` class which is inheriting from the `nn.Module` class.
```
class Net(nn.Module):
def __init__(self):
super().__init__()
self.FC1 = nn.Linear(28*28, 64)
self.FC2 = nn.Linear(64, 64 )
self.FC3 = nn.Linear(64, 64)
self.FC4 = nn.Linear(64, 10)
net = Net()
print(net)
```
> Each of our `nn.Linear` layers expects the first parameter to be the input size, and the 2nd parameter is the output size. Note that the basic `Nural Network` expect a flattened array not a `28x28`. So at some point we must pass the flattened array.
> The last layer **accepts 64 in_features and outputs 10** which is in our case the total number of unique labels.`
> Let's define a new method called `forward`
```
class Net(nn.Module):
def __init__(self):
super().__init__();
self.FC1 = nn.Linear(28 * 28, 64)
self.FC2 = nn.Linear(64, 64)
self.FC3 = nn.Linear(64, 64)
self.FC4 = nn.Linear(64, 10)
def forward(self, X):
X = self.FC1(X)
X = self.FC2(X)
X = self.FC3(X)
X = self.FC4(X)
return X
Net()
```
> So `X` in this case is our input data, we will pass this to the first `FC1` and the output will be passed down to the `FC2` up to the `FC4` **And also remember that our `X` is a flattened array.**
**Wait** Our layers are missing activation functions. In this case we are going to use `relu` as our activation function for other layers and `log_softmax` for the output layer.
```
class Net(nn.Module):
def __init__(self):
super().__init__()
self.FC1 = nn.Linear(28 * 28, 64)
self.FC2 = nn.Linear(64, 64)
self.FC3 = nn.Linear(64, 64)
self.FC4 = nn.Linear(64, 10)
def forward(self, X):
X = F.relu(self.FC1(X))
X = F.relu(self.FC2(X))
X = F.relu(self.FC3(X))
X = F.log_softmax(self.FC4(X), dim=1)
return X
X = torch.randn((28,28))
X = X.view(-1, 28*28)
net = Net()
np.argmax(net(X).detach().numpy())
```
### Training Our NN
```
net.parameters()
from torch import optim
optimizer = optim.Adam(net.parameters(), lr=1e-3)
```
**loss** - this function calcualetes how far are our classifiaction from reality.
**For one hot vectors** - `mean_square_error` is better to use.
**For scalar classifictaion** - `cross_entropy` is better to use.
> [Loss Functions](https://pytorch.org/docs/stable/nn.html#loss-functions)
**optimizer** - this is what adjust the model's adjustable parameters like weights. The one that is popular is `Adam` (**Adaptive Momentum**) which takes a `lr` which has a default value of `0.001 or 1e-3`. The learning rate dictates the magnitude of changes that the optimizer can make at a time
> Now we can iterate over the data and see more about the **loss** we are going to define our `EPOCHS`
too many epochs can result in the model `over-fitting` and too few epochs may result in the model `under-learning` the data.
```
EPOCHS = 3
for epoch in range(EPOCHS):
print(f"EPOCHS {epoch+1}/{EPOCHS }")
for data in trainset:
X, y = data # a batch of 10 features and 10 labels
net.zero_grad() # sets gradients to 0 before loss calulated
output = net(X.view(-1,784)) ## pass the flattened image
## calculate the loss value
loss = F.nll_loss(output, y)
# apply this loss backwards thru the network's parameters
loss.backward()
# attempt to optimize weights to account for loss/gradients
optimizer.step()
print(loss)
```
The `net.zero_grad()` is a very important step, otherwise these gradients will add up for every pass, and then we'll be re-optimizing for previous gradients that we already optimized for.
### Calculating accuracy
```
correct = 0
total = 0
with torch.no_grad():
for data in testset:
X, y = data
output = net(X.view(-1, 784))
for i, j in enumerate(output):
if torch.argmax(j) == y[i]:
correct +=1
total += 1
print("Accuracy: ", correct/total)
```
> Our model is `97%` accurate on the `testset`
```
correct = 0
total = 0
with torch.no_grad():
for data in trainset:
X, y = data
output = net(X.view(-1, 784))
for i, j in enumerate(output):
if torch.argmax(j) == y[i]:
correct +=1
total += 1
print("Accuracy: ", correct/total)
```
> Our model is `98%` accurate on the trainset. Which is closer to `97%` which means we are not overfitting or underfitting the model. Our model is learning fine with `3` epochs.
### Making Predictions
```
for X in trainset:
X, y = X
break
plt.imshow(X[0].view(28,28), cmap="gray"), y[0]
predictions = net(X[0].view(-1, 28*28))
torch.argmax(predictions).detach().numpy()
```
> The model is cool in predicting the digit `3`.
| true |
code
| 0.85022 | null | null | null | null |
|
# OpenVaccine: COVID-19 mRNA Vaccine Degradation Prediction
In this [Kaggle competition](https://www.kaggle.com/c/stanford-covid-vaccine/overview) we try to develop models and design rules for RNA degradation. As the overview of the competition states:
>mRNA vaccines have taken the lead as the fastest vaccine candidates for COVID-19, but currently, they face key potential limitations. One of the biggest challenges right now is how to design super stable messenger RNA molecules (mRNA). Conventional vaccines (like your seasonal flu shots) are packaged in disposable syringes and shipped under refrigeration around the world, but that is not currently possible for mRNA vaccines.
>
>Researchers have observed that RNA molecules have the tendency to spontaneously degrade. This is a serious limitation--a single cut can render the mRNA vaccine useless. Currently, little is known on the details of where in the backbone of a given RNA is most prone to being affected. Without this knowledge, current mRNA vaccines against COVID-19 must be prepared and shipped under intense refrigeration, and are unlikely to reach more than a tiny fraction of human beings on the planet unless they can be stabilized.
<img src="images/banner.png" width="1000" style="margin-left: auto; margin-right: auto;">
The model should predict likely degradation rates at each base of an RNA molecule. The training data set is comprised of over 3000 RNA molecules and their degradation rates at each position.
# Install necessary packages
We can install the necessary package by either running `pip install --user <package_name>` or include everything in a `requirements.txt` file and run `pip install --user -r requirements.txt`. We have put the dependencies in a `requirements.txt` file so we will use the former method.
> NOTE: Do not forget to use the `--user` argument. It is necessary if you want to use Kale to transform this notebook into a Kubeflow pipeline
```
!pip install --user -r requirements.txt
```
# Imports
In this section we import the packages we need for this example. Make it a habit to gather your imports in a single place. It will make your life easier if you are going to transform this notebook into a Kubeflow pipeline using Kale.
```
import json
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.preprocessing.text import Tokenizer
```
# Project hyper-parameters
In this cell, we define the different hyper-parameters. Defining them in one place makes it easier to experiment with their values and also facilitates the execution of HP Tuning experiments using Kale and Katib.
```
# Hyper-parameters
LR = 1e-3
EPOCHS = 10
BATCH_SIZE = 64
EMBED_DIM = 100
HIDDEN_DIM = 128
DROPOUT = .5
SP_DROPOUT = .3
TRAIN_SEQUENCE_LENGTH = 107
```
Set random seed for reproducibility and ignore warning messages.
```
tf.random.set_seed(42)
np.random.seed(42)
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.INFO)
```
# Load and preprocess data
In this section, we load and process the dataset to get it in a ready-to-use form by the model. First, let us load and analyze the data.
## Load data
The data are in `json` format, thus, we use the handy `read_json` pandas method. There is one train data set and two test sets (one public and one private).
```
train_df = pd.read_json("data/train.json", lines=True)
test_df = pd.read_json("data/test.json", lines=True)
```
We also load the `sample_submission.csv` file, which will prove handy when we will be creating our submission to the competition.
```
sample_submission_df = pd.read_csv("data/sample_submission.csv")
```
Let us now explore the data, their dimensions and what each column mean. To this end, we use the pandas `head` method to visualize a small sample (five rows by default) of our data set.
```
train_df.head()
```
We see a lot of strange entries, so, let us try to see what they are:
* `sequence`: An 107 characters long string in Train and Public Test (130 in Private Test), which describes the RNA sequence, a combination of A, G, U, and C for each sample.
* `structure`: An 107 characters long string in Train and Public Test (130 in Private Test), which is a combination of `(`, `)`, and `.` characters that describe whether a base is estimated to be paired or unpaired. Paired bases are denoted by opening and closing parentheses (e.g. (....) means that base 0 is paired to base 5, and bases 1-4 are unpaired).
* `predicted_loop_type`: An 107 characters long string, which describes the structural context (also referred to as 'loop type') of each character in sequence. Loop types assigned by bpRNA from Vienna RNAfold 2 structure. From the bpRNA_documentation: `S`: paired "Stem" `M`: Multiloop `I`: Internal loop `B`: Bulge `H`: Hairpin loop `E`: dangling End `X`: eXternal loop.
Then, we have `signal_to_noise`, which is quality control feature. It records the measurements relative to their errors; the higher value the more confident measurements are.
The `*_error_*` columns calculate the errors in experimental values obtained in corresponding `reactivity` and `deg_*` columns.
The last five columns (i.e., `recreativity` and `deg_*`) are out depended variables, our targets. Thus, for every base in the molecule we should predict five different values.
These are the main columns we care about. For more details, visit the competition [info](https://www.kaggle.com/c/stanford-covid-vaccine/data).
## Preprocess data
We are now ready to preprocess the data set. First, we define the symbols that encode certain features (e.g. the base symbol or the structure), the features and the target variables.
```
symbols = "().ACGUBEHIMSX"
feat_cols = ["sequence", "structure", "predicted_loop_type"]
target_cols = ["reactivity", "deg_Mg_pH10", "deg_Mg_50C", "deg_pH10", "deg_50C"]
error_cols = ["reactivity_error", "deg_error_Mg_pH10", "deg_error_Mg_50C", "deg_error_pH10", "deg_error_50C"]
```
In order to encode values like strings or characters and feed them to the neural network, we need to tokenize them. The `Tokenizer` class will assign a number to each character.
```
tokenizer = Tokenizer(char_level=True, filters="")
tokenizer.fit_on_texts(symbols)
```
Moreover, the tokenizer keeps a dictionary, `word_index`, from which we can get the number of elements in our vocabulary. In this case, we only have a few elements, but if our dataset was a whole book, that function would be handy.
> NOTE: We should add `1` to the length of the `word_index` dictionary to get the correct number of elements.
```
# get the number of elements in the vocabulary
vocab_size = len(tokenizer.word_index) + 1
```
We are now ready to process our features. First, we transform each character sequence (i.e., `sequence`, `structure`, `predicted_loop_type`) into number sequences and concatenate them together. The resulting shape should be `(num_examples, 107, 3)`.
> Now, we should do this in a way that would permit us to use this processing function with KFServing. Thus, since Numpy arrays are not JSON serializable, this function should accept and return pure Python lists.
```
def process_features(example):
sequence_sentences = example[0]
structure_sentences = example[1]
loop_sentences = example[2]
# transform character sequences into number sequences
sequence_tokens = np.array(
tokenizer.texts_to_sequences(sequence_sentences)
)
structure_tokens = np.array(
tokenizer.texts_to_sequences(structure_sentences)
)
loop_tokens = np.array(
tokenizer.texts_to_sequences(loop_sentences)
)
# concatenate the tokenized sequences
sequences = np.stack(
(sequence_tokens, structure_tokens, loop_tokens),
axis=1
)
sequences = np.transpose(sequences, (2, 0, 1))
prepared = sequences.tolist()
return prepared[0]
```
In the same way we process the labels. We should just extract them and transform them into the correct shape. The resulting shape should be `(num_examples, 68, 5)`.
```
def process_labels(df):
df = df.copy()
labels = np.array(df[target_cols].values.tolist())
labels = np.transpose(labels, (0, 2, 1))
return labels
public_test_df = test_df.query("seq_length == 107")
private_test_df = test_df.query("seq_length == 130")
```
We are now ready to process the data set and make the features ready to be consumed by the model.
```
x_train = [process_features(row.tolist()) for _, row in train_df[feat_cols].iterrows()]
y_train = process_labels(train_df)
unprocessed_x_public_test = [row.tolist() for _, row in public_test_df[feat_cols].iterrows()]
unprocessed_x_private_test = [row.tolist() for _, row in private_test_df[feat_cols].iterrows()]
```
# Define and train the model
We are now ready to define our model. We have to do with sequences, thus, it makes sense to use RNNs. More specifically, we will use bidirectional Gated Recurrent Units (GRUs) and Long Short Term Memory cells (LSTM). The output layer shoud produce 5 numbers, so we can see this as a regression problem.
First let us define two helper functions for GRUs and LSTMs and then, define the body of the full model.
```
def gru_layer(hidden_dim, dropout):
return tf.keras.layers.Bidirectional(
tf.keras.layers.GRU(hidden_dim, dropout=dropout, return_sequences=True, kernel_initializer = 'orthogonal')
)
def lstm_layer(hidden_dim, dropout):
return tf.keras.layers.Bidirectional(
tf.keras.layers.LSTM(hidden_dim, dropout=dropout, return_sequences=True, kernel_initializer = 'orthogonal')
)
```
The model has an embedding layer. The embedding layer projects the tokenized categorical input into a high-dimensional latent space. For this example we treat the dimensionality of the embedding space as a hyper-parameter that we can use to fine-tune the model.
```
def build_model(vocab_size, seq_length=int(TRAIN_SEQUENCE_LENGTH), pred_len=68,
embed_dim=int(EMBED_DIM),
hidden_dim=int(HIDDEN_DIM), dropout=float(DROPOUT), sp_dropout=float(SP_DROPOUT)):
inputs = tf.keras.layers.Input(shape=(seq_length, 3))
embed = tf.keras.layers.Embedding(input_dim=vocab_size, output_dim=embed_dim)(inputs)
reshaped = tf.reshape(
embed, shape=(-1, embed.shape[1], embed.shape[2] * embed.shape[3])
)
hidden = tf.keras.layers.SpatialDropout1D(sp_dropout)(reshaped)
hidden = gru_layer(hidden_dim, dropout)(hidden)
hidden = lstm_layer(hidden_dim, dropout)(hidden)
truncated = hidden[:, :pred_len]
out = tf.keras.layers.Dense(5, activation="linear")(truncated)
model = tf.keras.Model(inputs=inputs, outputs=out)
return model
model = build_model(vocab_size)
model.summary()
```
Submissions are scored using MCRMSE (mean columnwise root mean squared error):
<img src="images/mcrmse.png" width="250" style="margin-left: auto; margin-right: auto;">
Thus, we should code this metric and use it as our objective (loss) function.
```
class MeanColumnwiseRMSE(tf.keras.losses.Loss):
def __init__(self, name='MeanColumnwiseRMSE'):
super().__init__(name=name)
def call(self, y_true, y_pred):
colwise_mse = tf.reduce_mean(tf.square(y_true - y_pred), axis=1)
return tf.reduce_mean(tf.sqrt(colwise_mse), axis=1)
```
We are now ready to compile and fit the model.
```
model.compile(tf.optimizers.Adam(learning_rate=float(LR)), loss=MeanColumnwiseRMSE())
history = model.fit(np.array(x_train), np.array(y_train),
validation_split=.1, batch_size=int(BATCH_SIZE), epochs=int(EPOCHS))
validation_loss = history.history.get("val_loss")[0]
```
## Evaluate the model
Finally, we are ready to evaluate the model using the two test sets.
```
model_public = build_model(vocab_size, seq_length=107, pred_len=107)
model_private = build_model(vocab_size, seq_length=130, pred_len=130)
model_public.set_weights(model.get_weights())
model_private.set_weights(model.get_weights())
public_preds = model_public.predict(np.array([process_features(x) for x in unprocessed_x_public_test]))
private_preds = model_private.predict(np.array([process_features(x) for x in unprocessed_x_private_test]))
```
# Submission
Last but note least, we create our submission to the Kaggle competition. The submission is just a `csv` file with the specified columns.
```
preds_ls = []
for df, preds in [(public_test_df, public_preds), (private_test_df, private_preds)]:
for i, uid in enumerate(df.id):
single_pred = preds[i]
single_df = pd.DataFrame(single_pred, columns=target_cols)
single_df['id_seqpos'] = [f'{uid}_{x}' for x in range(single_df.shape[0])]
preds_ls.append(single_df)
preds_df = pd.concat(preds_ls)
preds_df.head()
submission = sample_submission_df[['id_seqpos']].merge(preds_df, on=['id_seqpos'])
submission.to_csv('submission.csv', index=False)
```
| true |
code
| 0.680587 | null | null | null | null |
|
```
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
```
<h2><font color="darkblue">Support Vector Machine</font></h2>
<hr/>
### Preliminaries
- Linearly separable
> Let $ S_0 $ and $ S_1 $ be two sets of points in an $ n $-dimensional Euclidean space. We say $ S_0 $ and $ S_1 $ are linearly separable if $ \quad \exists w_1, w_2, \cdots, w_n, k \quad $ such that $ \qquad \forall x \in S_0 $, $ \displaystyle \sum_{i=1}^{n} w_i x_i > k \quad $ and $ \quad \forall x \in S_1 $, $ \displaystyle \sum_{i=1}^{n} w_i x_i < k \quad $ where $ x_i $ is the $ i $-th component of $ x $.
- Example: Linearly separable
<img src="http://i.imgur.com/aLZlG.png" width=200 >
- Example: Not linearly separable
<img src="http://i.imgur.com/gWdPX.png" width=200 >
<p style="text-align:center">(Picture from https://www.reddit.com/r/MachineLearning/comments/15zrpp/please_explain_support_vector_machines_svm_like_i/)</p>
### Support Vector Machine (Hard-margin)
- Intuition: Find an optimal hyperplane that could maximize margin between different classes
<img src="https://upload.wikimedia.org/wikipedia/commons/b/b5/Svm_separating_hyperplanes_%28SVG%29.svg" width=300 align=center>
<p style="text-align:center">(Picture from https://en.wikipedia.org/wiki/Support_vector_machine)</p>
- Data
> $ \displaystyle \{(\mathbf{x}_i, y_i) \}_{i=1}^{n} \qquad $ where $ \displaystyle \qquad \mathbf{x}_i \in \mathbb{R}^d, \ y_i \in \{-1, 1 \} $
- Linearly separable if
> $ \displaystyle \exists (\mathbf{w}, b) \quad $ such that $ \displaystyle \quad y_i = \text{sign} \left(\langle \mathbf{w}, \mathbf{x}_i \rangle + b \right) \quad \forall i $
>
> $ \displaystyle \exists (\mathbf{w}, b) \quad $ such that $ \displaystyle \quad y_i \left(\langle \mathbf{w}, \mathbf{x}_i \rangle + b \right) > 0 \quad \forall i $
- Margin
> The margin of a hyperplane w.r.t training data is the minimal distance between a point in the training data and the hyperplane.
>
> In this sense, if a hyperplane has a large margin, then it still could separate the training data even if we slightly perturb each data point.
- Recall
> The distance between a point $ \mathbf{x} $ and the hyperplane defined by $ \quad (\mathbf{w}, b) \quad $ where $ \quad \lvert\lvert \mathbf{w} \rvert\rvert = 1 \quad $ is $ \quad \lvert \langle \mathbf{w}, \mathbf{x} \rangle + b \rvert $
- **Hard-SVM**: Fit a hyperplane that separates the training data with the largest possible margin
> $ \displaystyle \max_{\mathbf{w}, b: \lvert\lvert \mathbf{w} \rvert\rvert = 1} \min\limits_{i \in [n]} \lvert \langle \mathbf{w}, \mathbf{x}_i \rangle + b \rvert \quad $ such that $ \displaystyle \quad y_i(\langle \mathbf{w}, \mathbf{x}_i \rangle + b) > 0 \quad \forall i $
- Example
```
from sklearn import svm
import numpy as np
# Generate 100 separable points
x, y = datasets.make_blobs(n_samples=100, centers=2, random_state=3)
plt.scatter(x[:,0], x[:,1], c=y);
# Fit SVM
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(x, y)
# Create grid to evaluate model
xx = np.linspace(x[:,0].min()-0.5, x[:,0].max()+0.5, 30)
yy = np.linspace(x[:,1].min()-0.5, x[:,1].max()+0.5, 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
# Plot decision boundary and margins
plt.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']);
plt.scatter(x[:,0], x[:,1], c=y);
```
### Support Vector Machine (Soft-margin)
- **Hard-SVM**: Fit a hyperplane that separates the training data with the largest possible margin
> $ \displaystyle \min_{\mathbf{w}, b} \ \lvert\lvert \mathbf{w} \rvert\rvert^2 \quad $ such that $ \displaystyle \quad y_i(\langle \mathbf{w}, \mathbf{x}_i \rangle + b) > 1 \quad \forall i $
- **Soft-SVM**: Relax the condition
> $ \displaystyle \min_{\mathbf{w}, b, \zeta} \lambda \lvert\lvert \mathbf{w} \rvert\rvert^2 + \frac{1}{n} \sum_{i=1}^{n} \zeta_i \qquad $ such that $ \displaystyle \quad y_i(\langle \mathbf{w}, \mathbf{x}_i \rangle + b) \ge 1 - \zeta_i \quad $ where $ \displaystyle \quad \lambda > 0, \ \zeta_i \ge 0 $
- Kernel trick
> Map the original space into feature space (possibly of higher dimension) where data could be linearly separable.
>
> The kernel function transform the data into a higher dimensional feature space to make it possible to perform the linear separation.
<img src="http://i.imgur.com/WuxyO.png" width=300 align=center>
<p style="text-align:center">(Picture from https://www.reddit.com/r/MachineLearning/comments/15zrpp/please_explain_support_vector_machines_svm_like_i/)</p>
<img src="https://cdn-images-1.medium.com/max/1600/1*C3j5m3E3KviEApHKleILZQ.png" width=300 align=center>
We can just project this by mapping kernel using $x^2+y^2=z$
<img src="https://cdn-images-1.medium.com/max/1600/1*FLolUnVUjqV0EGm3CYBPLw.png" width=300 align=center>
```
# Toy Example: not linearly separable in original space (dimension=1)
x = np.arange(-10, 11)
y = np.repeat(-1, x.size)
y[np.abs(x) > 3] = 1
plt.scatter(x, np.repeat(0, x.size), c=y);
```
> $ \displaystyle \phi: \mathbb{R} \rightarrow \mathbb{R}^2 $
>
> $ \displaystyle \phi(x) = (x, x^2) $
```
# Kernel trick: linearly separable in feature space (dimension=2)
plt.scatter(x, x**2, c=y);
plt.axhline(y=12.5);
```
- Some kernels
> Polynomial kernel: $ \displaystyle \qquad K(x, x^\prime) = \left(1 + \langle x, x^\prime \rangle \right)^d $
>
> (Gaussian) radial basis function kernel (RBF): $ \displaystyle \qquad K(x, x^\prime) = \exp \left(- \frac{\lvert\lvert x - x^\prime \rvert\rvert^2}{2 \sigma^2} \right) = \exp (- \gamma \lvert\lvert x - x^\prime \rvert\rvert^2) \qquad $ where $ \displaystyle \qquad \gamma = \frac{1}{2 \sigma^2} $
>
>
- Choice of kernel
```
from sklearn.model_selection import cross_val_score
x, y = datasets.make_circles(n_samples=1000, factor=0.3, noise=0.1, random_state=2018)
plt.subplot(111, aspect='equal');
plt.scatter(x[:,0], x[:,1], c=y);
# Create grid to evaluate model
xx = np.linspace(x[:,0].min()-0.5, x[:,0].max()+0.5, 30)
yy = np.linspace(x[:,1].min()-0.5, x[:,1].max()+0.5, 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
# Linear kernel
clf = svm.SVC(kernel='linear')
clf.fit(x,y)
Z = clf.decision_function(xy).reshape(XX.shape)
# Plot decision boundary and margins
plt.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']);
plt.scatter(x[:,0], x[:,1], c=y);
print('10-fold cv scores with Linear kernel: ', np.mean(cross_val_score(clf, x, y, cv=10)))
# Polynomial kernel
clf = svm.SVC(kernel='poly', gamma='auto')
clf.fit(x,y)
Z = clf.decision_function(xy).reshape(XX.shape)
# Plot decision boundary and margins
plt.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']);
plt.scatter(x[:,0], x[:,1], c=y);
print('10-fold cv scores with Polynomial kernel: ', np.mean(cross_val_score(clf, x, y, cv=10)))
# RBF kernel
clf = svm.SVC(kernel='rbf', gamma='auto')
clf.fit(x,y)
Z = clf.decision_function(xy).reshape(XX.shape)
# Plot decision boundary and margins
plt.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']);
plt.scatter(x[:,0], x[:,1], c=y);
print('10-fold cv scores with RBF kernel: ', np.mean(cross_val_score(clf, x, y, cv=10)))
```
<br/>
- **Note:** For `SVC` in scikit-learn, it tries to solve the following problem:
$ \displaystyle \min_{w, b, \zeta} \frac{1}{2} w^\top w + C \sum_{i=1}^{n} \zeta_i \qquad $ subject to $ \displaystyle \qquad y_i \left(w^\top \phi(x_i) + b \right) \ge 1 - \zeta_i \qquad $ where $ \displaystyle \qquad \zeta_i \ge 0, i = 1, 2, \cdots, n $
[References](http://scikit-learn.org/stable/modules/svm.html#svm-mathematical-formulation)
<br/>
**References**
- Friedman, J., Hastie, T., & Tibshirani, R. (2001). The elements of statistical learning. Springer series in statistics.
- Shalev-Shwartz, S., & Ben-David, S. (2014). Understanding machine learning: From theory to algorithms. Cambridge university press.
## SVM Excercise - Wisconsin Breast Cancer Dataset
> Features are computed from a digitized image of a fine needle aspirate (FNA) of a breast mass. They describe characteristics of the cell nuclei present in the image. n the 3-dimensional space is that described in: [K. P. Bennett and O.L. Mangasarian: "Robust Linear Programming Discrimination of Two Linearly Inseperable Sets", Optimization Methods and Software 1, 1992, 22-34].
## Questions - Can we find some hyperplane separating our samples such that we predict whether they are cancerous?
```
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
# load the breast cancer dataset
d = load_breast_cancer()
x = d['data']
y = d['target']
# reduce dimensionality
pca = PCA(n_components=2)
x = pca.fit_transform(x)
# fit a SVM
clf = svm.SVC(kernel='linear')
clf.fit(x,y)
# Create grid to evaluate model
xx = np.linspace(x[:,0].min()-0.5, x[:,0].max()+0.5, 30)
yy = np.linspace(x[:,1].min()-0.5, x[:,1].max()+0.5, 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
# Plot decision boundary and margins
plt.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']);
plt.scatter(x[:,0], x[:,1], c=y);
print('10-fold cv scores with linear kernel: ', np.mean(cross_val_score(clf, x, y, cv=10)))
```
| true |
code
| 0.670662 | null | null | null | null |
|
# Finetuning of ImageNet pretrained EfficientNet-B0 on CIFAR-100
In 2019, new ConvNets architectures have been proposed in ["EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks"](https://arxiv.org/pdf/1905.11946.pdf) paper. According to the paper, model's compound scaling starting from a 'good' baseline provides an network that achieves state-of-the-art on ImageNet, while being 8.4x smaller and 6.1x faster on inference than the best existing ConvNet.

Following the paper, EfficientNet-B0 model pretrained on ImageNet and finetuned on CIFAR100 dataset gives 88% test accuracy. Let's reproduce this result with Ignite. [Official implementation](https://github.com/tensorflow/tpu/tree/master/models/official/efficientnet) of EfficientNet uses Tensorflow,
for our case we will borrow the code from [katsura-jp/efficientnet-pytorch](https://github.com/katsura-jp/efficientnet-pytorch),
[rwightman/pytorch-image-models](https://github.com/rwightman/pytorch-image-models) and [lukemelas/EfficientNet-PyTorch](https://github.com/lukemelas/EfficientNet-PyTorch/) repositories (kudos to authors!). We will download pretrained weights from [lukemelas/EfficientNet-PyTorch](https://github.com/lukemelas/EfficientNet-PyTorch/) repository.
## Network architecture review
The architecture of EfficientNet-B0 is the following:
```
1 - Stem - Conv3x3|BN|Swish
2 - Blocks - MBConv1, k3x3
- MBConv6, k3x3 repeated 2 times
- MBConv6, k5x5 repeated 2 times
- MBConv6, k3x3 repeated 3 times
- MBConv6, k5x5 repeated 3 times
- MBConv6, k5x5 repeated 4 times
- MBConv6, k3x3
totally 16 blocks
3 - Head - Conv1x1|BN|Swish
- Pooling
- Dropout
- FC
```
where
```
Swish(x) = x * sigmoid(x)
```
and `MBConvX` stands for mobile inverted bottleneck convolution, X - denotes expansion ratio:
```
MBConv1 :
-> DepthwiseConv|BN|Swish -> SqueezeExcitation -> Conv|BN
MBConv6 :
-> Conv|BN|Swish -> DepthwiseConv|BN|Swish -> SqueezeExcitation -> Conv|BN
MBConv6+IdentitySkip :
-.-> Conv|BN|Swish -> DepthwiseConv|BN|Swish -> SqueezeExcitation -> Conv|BN-(+)->
\___________________________________________________________________________/
```
## Installations
1) Torchvision
Please install torchvision in order to get CIFAR100 dataset:
```
conda install -y torchvision -c pytorch
```
2) Let's install Nvidia/Apex package:
We will train with automatic mixed precision using [nvidia/apex](https://github.com/NVIDIA/apex) pacakge
```
# Install Apex:
# If torch cuda version and nvcc version match:
!pip install --upgrade --no-cache-dir --global-option="--cpp_ext" --global-option="--cuda_ext" git+https://github.com/NVIDIA/apex/
# if above command is failing, please install apex without c++/cuda extensions:
# !pip install --upgrade --no-cache-dir git+https://github.com/NVIDIA/apex/
```
3) Install tensorboardX and `pytorch-ignite`
```
!pip install pytorch-ignite tensorboardX
import random
import torch
import ignite
seed = 17
random.seed(seed)
_ = torch.manual_seed(seed)
torch.__version__, ignite.__version__
```
## Model
Let's define some helpful modules:
- Flatten
- Swish
The reason why Swish is not implemented in `torch.nn` can be found [here](https://github.com/pytorch/pytorch/pull/3182).
```
import torch
import torch.nn as nn
class Swish(nn.Module):
def forward(self, x):
return x * torch.sigmoid(x)
class Flatten(nn.Module):
def forward(self, x):
return x.reshape(x.shape[0], -1)
```
Let's visualize Swish transform vs ReLU:
```
import matplotlib.pylab as plt
%matplotlib inline
d = torch.linspace(-10.0, 10.0)
s = Swish()
res = s(d)
res2 = torch.relu(d)
plt.title("Swish transformation")
plt.plot(d.numpy(), res.numpy(), label='Swish')
plt.plot(d.numpy(), res2.numpy(), label='ReLU')
plt.legend()
```
Now let's define `SqueezeExcitation` module
```
class SqueezeExcitation(nn.Module):
def __init__(self, inplanes, se_planes):
super(SqueezeExcitation, self).__init__()
self.reduce_expand = nn.Sequential(
nn.Conv2d(inplanes, se_planes,
kernel_size=1, stride=1, padding=0, bias=True),
Swish(),
nn.Conv2d(se_planes, inplanes,
kernel_size=1, stride=1, padding=0, bias=True),
nn.Sigmoid()
)
def forward(self, x):
x_se = torch.mean(x, dim=(-2, -1), keepdim=True)
x_se = self.reduce_expand(x_se)
return x_se * x
```
Next, we can define `MBConv`.
**Note on implementation**: in Tensorflow (and PyTorch ports) convolutions use `SAME` padding option which in PyTorch requires
a specific padding computation and additional operation to apply. We will use built-in padding argument of the convolution.
```
from torch.nn import functional as F
class MBConv(nn.Module):
def __init__(self, inplanes, planes, kernel_size, stride,
expand_rate=1.0, se_rate=0.25,
drop_connect_rate=0.2):
super(MBConv, self).__init__()
expand_planes = int(inplanes * expand_rate)
se_planes = max(1, int(inplanes * se_rate))
self.expansion_conv = None
if expand_rate > 1.0:
self.expansion_conv = nn.Sequential(
nn.Conv2d(inplanes, expand_planes,
kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(expand_planes, momentum=0.01, eps=1e-3),
Swish()
)
inplanes = expand_planes
self.depthwise_conv = nn.Sequential(
nn.Conv2d(inplanes, expand_planes,
kernel_size=kernel_size, stride=stride,
padding=kernel_size // 2, groups=expand_planes,
bias=False),
nn.BatchNorm2d(expand_planes, momentum=0.01, eps=1e-3),
Swish()
)
self.squeeze_excitation = SqueezeExcitation(expand_planes, se_planes)
self.project_conv = nn.Sequential(
nn.Conv2d(expand_planes, planes,
kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(planes, momentum=0.01, eps=1e-3),
)
self.with_skip = stride == 1
self.drop_connect_rate = drop_connect_rate
def _drop_connect(self, x):
keep_prob = 1.0 - self.drop_connect_rate
drop_mask = torch.rand(x.shape[0], 1, 1, 1) + keep_prob
drop_mask = drop_mask.type_as(x)
drop_mask.floor_()
return drop_mask * x / keep_prob
def forward(self, x):
z = x
if self.expansion_conv is not None:
x = self.expansion_conv(x)
x = self.depthwise_conv(x)
x = self.squeeze_excitation(x)
x = self.project_conv(x)
# Add identity skip
if x.shape == z.shape and self.with_skip:
if self.training and self.drop_connect_rate is not None:
x = self._drop_connect(x)
x += z
return x
```
And finally, we can implement generic `EfficientNet`:
```
from collections import OrderedDict
import math
def init_weights(module):
if isinstance(module, nn.Conv2d):
nn.init.kaiming_normal_(module.weight, a=0, mode='fan_out')
elif isinstance(module, nn.Linear):
init_range = 1.0 / math.sqrt(module.weight.shape[1])
nn.init.uniform_(module.weight, a=-init_range, b=init_range)
class EfficientNet(nn.Module):
def _setup_repeats(self, num_repeats):
return int(math.ceil(self.depth_coefficient * num_repeats))
def _setup_channels(self, num_channels):
num_channels *= self.width_coefficient
new_num_channels = math.floor(num_channels / self.divisor + 0.5) * self.divisor
new_num_channels = max(self.divisor, new_num_channels)
if new_num_channels < 0.9 * num_channels:
new_num_channels += self.divisor
return new_num_channels
def __init__(self, num_classes=100,
width_coefficient=1.0,
depth_coefficient=1.0,
se_rate=0.25,
dropout_rate=0.2,
drop_connect_rate=0.2):
super(EfficientNet, self).__init__()
self.width_coefficient = width_coefficient
self.depth_coefficient = depth_coefficient
self.divisor = 8
list_channels = [32, 16, 24, 40, 80, 112, 192, 320, 1280]
list_channels = [self._setup_channels(c) for c in list_channels]
list_num_repeats = [1, 2, 2, 3, 3, 4, 1]
list_num_repeats = [self._setup_repeats(r) for r in list_num_repeats]
expand_rates = [1, 6, 6, 6, 6, 6, 6]
strides = [1, 2, 2, 2, 1, 2, 1]
kernel_sizes = [3, 3, 5, 3, 5, 5, 3]
# Define stem:
self.stem = nn.Sequential(
nn.Conv2d(3, list_channels[0], kernel_size=3, stride=2, padding=1, bias=False),
nn.BatchNorm2d(list_channels[0], momentum=0.01, eps=1e-3),
Swish()
)
# Define MBConv blocks
blocks = []
counter = 0
num_blocks = sum(list_num_repeats)
for idx in range(7):
num_channels = list_channels[idx]
next_num_channels = list_channels[idx + 1]
num_repeats = list_num_repeats[idx]
expand_rate = expand_rates[idx]
kernel_size = kernel_sizes[idx]
stride = strides[idx]
drop_rate = drop_connect_rate * counter / num_blocks
name = "MBConv{}_{}".format(expand_rate, counter)
blocks.append((
name,
MBConv(num_channels, next_num_channels,
kernel_size=kernel_size, stride=stride, expand_rate=expand_rate,
se_rate=se_rate, drop_connect_rate=drop_rate)
))
counter += 1
for i in range(1, num_repeats):
name = "MBConv{}_{}".format(expand_rate, counter)
drop_rate = drop_connect_rate * counter / num_blocks
blocks.append((
name,
MBConv(next_num_channels, next_num_channels,
kernel_size=kernel_size, stride=1, expand_rate=expand_rate,
se_rate=se_rate, drop_connect_rate=drop_rate)
))
counter += 1
self.blocks = nn.Sequential(OrderedDict(blocks))
# Define head
self.head = nn.Sequential(
nn.Conv2d(list_channels[-2], list_channels[-1],
kernel_size=1, bias=False),
nn.BatchNorm2d(list_channels[-1], momentum=0.01, eps=1e-3),
Swish(),
nn.AdaptiveAvgPool2d(1),
Flatten(),
nn.Dropout(p=dropout_rate),
nn.Linear(list_channels[-1], num_classes)
)
self.apply(init_weights)
def forward(self, x):
f = self.stem(x)
f = self.blocks(f)
y = self.head(f)
return y
```
All EfficientNet models can be defined using the following parametrization:
```
# (width_coefficient, depth_coefficient, resolution, dropout_rate)
'efficientnet-b0': (1.0, 1.0, 224, 0.2),
'efficientnet-b1': (1.0, 1.1, 240, 0.2),
'efficientnet-b2': (1.1, 1.2, 260, 0.3),
'efficientnet-b3': (1.2, 1.4, 300, 0.3),
'efficientnet-b4': (1.4, 1.8, 380, 0.4),
'efficientnet-b5': (1.6, 2.2, 456, 0.4),
'efficientnet-b6': (1.8, 2.6, 528, 0.5),
'efficientnet-b7': (2.0, 3.1, 600, 0.5),
```
Let's define and train the third one: `EfficientNet-B0`
```
model = EfficientNet(num_classes=1000,
width_coefficient=1.0, depth_coefficient=1.0,
dropout_rate=0.2)
```
Number of parameters:
```
def print_num_params(model, display_all_modules=False):
total_num_params = 0
for n, p in model.named_parameters():
num_params = 1
for s in p.shape:
num_params *= s
if display_all_modules: print("{}: {}".format(n, num_params))
total_num_params += num_params
print("-" * 50)
print("Total number of parameters: {:.2e}".format(total_num_params))
print_num_params(model)
```
Let's compare the number of parameters with some of ResNets:
```
from torchvision.models.resnet import resnet18, resnet34, resnet50
print_num_params(resnet18(pretrained=False, num_classes=100))
print_num_params(resnet34(pretrained=False, num_classes=100))
print_num_params(resnet50(pretrained=False, num_classes=100))
```
### Model's graph with Tensorboard
We can optionally inspect model's graph with the code below. For that we need to install
`tensorboardX` package.
Otherwise go directly to the next section.
```
from tensorboardX.pytorch_graph import graph
import random
from IPython.display import clear_output, Image, display, HTML
def show_graph(graph_def):
"""Visualize TensorFlow graph."""
if hasattr(graph_def, 'as_graph_def'):
graph_def = graph_def.as_graph_def()
strip_def = graph_def
code = """
<script src="//cdnjs.cloudflare.com/ajax/libs/polymer/0.3.3/platform.js"></script>
<script>
function load() {{
document.getElementById("{id}").pbtxt = {data};
}}
</script>
<link rel="import" href="https://tensorboard.appspot.com/tf-graph-basic.build.html" onload=load()>
<div style="height:600px">
<tf-graph-basic id="{id}"></tf-graph-basic>
</div>
""".format(data=repr(str(strip_def)), id='graph'+str(random.randint(0, 1000)))
iframe = """
<iframe seamless style="width:1200px;height:620px;border:0" srcdoc="{}"></iframe>
""".format(code.replace('"', '"'))
display(HTML(iframe))
x = torch.rand(4, 3, 224, 224)
# Error : module 'torch.onnx' has no attribute 'set_training'
# uncomment when it will be fixed
# graph_def = graph(model, x, operator_export_type='RAW')
# Display in Firefox may not work properly. Use Chrome.
# show_graph(graph_def[0])
```
### Load pretrained weights
Let's load pretrained weights and check the model on a single image.
```
!mkdir /tmp/efficientnet_weights
!wget http://storage.googleapis.com/public-models/efficientnet-b0-08094119.pth -O/tmp/efficientnet_weights/efficientnet-b0-08094119.pth
from collections import OrderedDict
model_state = torch.load("/tmp/efficientnet_weights/efficientnet-b0-08094119.pth")
# A basic remapping is required
mapping = {
k: v for k, v in zip(model_state.keys(), model.state_dict().keys())
}
mapped_model_state = OrderedDict([
(mapping[k], v) for k, v in model_state.items()
])
model.load_state_dict(mapped_model_state, strict=False)
!wget https://raw.githubusercontent.com/lukemelas/EfficientNet-PyTorch/master/examples/simple/img.jpg -O/tmp/giant_panda.jpg
!wget https://raw.githubusercontent.com/lukemelas/EfficientNet-PyTorch/master/examples/simple/labels_map.txt -O/tmp/labels_map.txt
import json
with open("/tmp/labels_map.txt", "r") as h:
labels = json.load(h)
from PIL import Image
import torchvision.transforms as transforms
img = Image.open("/tmp/giant_panda.jpg")
# Preprocess image
image_size = 224
tfms = transforms.Compose([transforms.Resize(image_size),
transforms.CenterCrop(image_size),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),])
x = tfms(img).unsqueeze(0)
plt.imshow(img)
# Classify
model.eval()
with torch.no_grad():
y_pred = model(x)
# Print predictions
print('-----')
for idx in torch.topk(y_pred, k=5).indices.squeeze(0).tolist():
prob = torch.softmax(y_pred, dim=1)[0, idx].item()
print('{label:<75} ({p:.2f}%)'.format(label=labels[str(idx)], p=prob*100))
```
## Dataflow
Let's setup the dataflow:
- load CIFAR100 train and test datasets
- setup train/test image transforms
- setup train/test data loaders
According to the paper authors borrowed training settings from other publications and the dataflow for CIFAR100 is the following:
- input images to the network during training are resized to 224x224
- horizontally flipped randomly and augmented using cutout.
- each mini-batch contained 256 examples
```
from torchvision.datasets.cifar import CIFAR100
from torchvision.transforms import Compose, RandomCrop, Pad, RandomHorizontalFlip, Resize
from torchvision.transforms import ToTensor, Normalize
from torch.utils.data import Subset
path = "/tmp/cifar100"
from PIL.Image import BICUBIC
train_transform = Compose([
Resize(256, BICUBIC),
RandomCrop(224),
RandomHorizontalFlip(),
ToTensor(),
Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
test_transform = Compose([
Resize(224, BICUBIC),
ToTensor(),
Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
train_dataset = CIFAR100(root=path, train=True, transform=train_transform, download=True)
test_dataset = CIFAR100(root=path, train=False, transform=test_transform, download=False)
train_eval_indices = [random.randint(0, len(train_dataset) - 1) for i in range(len(test_dataset))]
train_eval_dataset = Subset(train_dataset, train_eval_indices)
len(train_dataset), len(test_dataset), len(train_eval_dataset)
from torch.utils.data import DataLoader
batch_size = 172
train_loader = DataLoader(train_dataset, batch_size=batch_size, num_workers=20,
shuffle=True, drop_last=True, pin_memory=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, num_workers=20,
shuffle=False, drop_last=False, pin_memory=True)
eval_train_loader = DataLoader(train_eval_dataset, batch_size=batch_size, num_workers=20,
shuffle=False, drop_last=False, pin_memory=True)
import torchvision.utils as vutils
# Plot some training images
batch = next(iter(train_loader))
plt.figure(figsize=(16, 8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(
vutils.make_grid(batch[0][:16], padding=2, normalize=True).cpu().numpy().transpose((1, 2, 0))
)
batch = None
torch.cuda.empty_cache()
```
## Finetunning model
As we are interested to finetune the model to CIFAR-100, we will replace the classification fully-connected layer (ImageNet-1000 vs CIFAR-100).
```
model.head[6].in_features, model.head[6].out_features
model.head[6] = nn.Linear(1280, 100)
model.head[6].in_features, model.head[6].out_features
```
We will finetune the model on GPU with AMP fp32/fp16 using nvidia/apex package.
```
assert torch.cuda.is_available()
assert torch.backends.cudnn.enabled, "NVIDIA/Apex:Amp requires cudnn backend to be enabled."
torch.backends.cudnn.benchmark = True
device = "cuda"
model = model.to(device)
```
Let's setup cross-entropy as criterion and SGD as optimizer.
We will split model parameters into 2 groups:
1) feature extractor (pretrained weights)
2) classifier (random weights)
and define different learning rates for these groups (via learning rate scheduler).
```
from itertools import chain
import torch.optim as optim
import torch.nn.functional as F
criterion = nn.CrossEntropyLoss()
lr = 0.01
optimizer = optim.SGD([
{
"params": chain(model.stem.parameters(), model.blocks.parameters()),
"lr": lr * 0.1,
},
{
"params": model.head[:6].parameters(),
"lr": lr * 0.2,
},
{
"params": model.head[6].parameters(),
"lr": lr
}],
momentum=0.9, weight_decay=0.001, nesterov=True)
from torch.optim.lr_scheduler import ExponentialLR
lr_scheduler = ExponentialLR(optimizer, gamma=0.975)
try:
from apex import amp
except ImportError:
raise ImportError("Please install apex from https://www.github.com/nvidia/apex to run this example.")
# Initialize Amp
model, optimizer = amp.initialize(model, optimizer, opt_level="O2", num_losses=1)
```
Next, let's define a single iteration function `update_fn`. This function is then used by `ignite.engine.Engine` to update model while running over the input data.
```
from ignite.utils import convert_tensor
def update_fn(engine, batch):
model.train()
x = convert_tensor(batch[0], device=device, non_blocking=True)
y = convert_tensor(batch[1], device=device, non_blocking=True)
y_pred = model(x)
# Compute loss
loss = criterion(y_pred, y)
with amp.scale_loss(loss, optimizer) as scaled_loss:
scaled_loss.backward()
optimizer.step()
return {
"batchloss": loss.item(),
}
```
Let's check `update_fn`
```
batch = next(iter(train_loader))
res = update_fn(engine=None, batch=batch)
batch = None
torch.cuda.empty_cache()
res
```
Now let's define a trainer and add some practical handlers:
- log to tensorboard: losses, metrics, lr
- progress bar
- models/optimizers checkpointing
```
from ignite.engine import Engine, Events, create_supervised_evaluator
from ignite.metrics import RunningAverage, Accuracy, Precision, Recall, Loss, TopKCategoricalAccuracy
from ignite.contrib.handlers import TensorboardLogger
from ignite.contrib.handlers.tensorboard_logger import OutputHandler, OptimizerParamsHandler
trainer = Engine(update_fn)
def output_transform(out):
return out['batchloss']
RunningAverage(output_transform=output_transform).attach(trainer, "batchloss")
from datetime import datetime
exp_name = datetime.now().strftime("%Y%m%d-%H%M%S")
log_path = "/tmp/finetune_efficientnet_cifar100/{}".format(exp_name)
tb_logger = TensorboardLogger(log_dir=log_path)
tb_logger.attach(trainer,
log_handler=OutputHandler('training', ['batchloss', ]),
event_name=Events.ITERATION_COMPLETED)
print("Experiment name: ", exp_name)
```
Let's setup learning rate scheduling:
```
trainer.add_event_handler(Events.EPOCH_COMPLETED, lambda engine: lr_scheduler.step())
# Log optimizer parameters
tb_logger.attach(trainer,
log_handler=OptimizerParamsHandler(optimizer, "lr"),
event_name=Events.EPOCH_STARTED)
from ignite.contrib.handlers import ProgressBar
# Iteration-wise progress bar
# ProgressBar(bar_format="").attach(trainer, metric_names=['batchloss',])
# Epoch-wise progress bar with display of training losses
ProgressBar(persist=True, bar_format="").attach(trainer,
event_name=Events.EPOCH_STARTED,
closing_event_name=Events.COMPLETED)
```
Let's create two evaluators to compute metrics on train/test images and log them to Tensorboard:
```
metrics = {
'Loss': Loss(criterion),
'Accuracy': Accuracy(),
'Precision': Precision(average=True),
'Recall': Recall(average=True),
'Top-5 Accuracy': TopKCategoricalAccuracy(k=5)
}
evaluator = create_supervised_evaluator(model, metrics=metrics,
device=device, non_blocking=True)
train_evaluator = create_supervised_evaluator(model, metrics=metrics,
device=device, non_blocking=True)
from ignite.handlers import global_step_from_engine
def run_evaluation(engine):
train_evaluator.run(eval_train_loader)
evaluator.run(test_loader)
trainer.add_event_handler(Events.EPOCH_STARTED(every=3), run_evaluation)
trainer.add_event_handler(Events.COMPLETED, run_evaluation)
# Log train eval metrics:
tb_logger.attach_output_handler(
train_evaluator,
event_name=Events.EPOCH_COMPLETED,
tag="training",
metric_names=list(metrics.keys()),
global_step_transform=global_step_from_engine(trainer)
)
# Log val metrics:
tb_logger.attach_output_handler(
evaluator,
event_name=Events.EPOCH_COMPLETED,
tag="test",
metric_names=list(metrics.keys()),
global_step_transform=global_step_from_engine(trainer)
)
```
Now let's setup the best model checkpointing, early stopping:
```
import logging
# Setup engine & logger
def setup_logger(logger):
handler = logging.StreamHandler()
formatter = logging.Formatter("%(asctime)s %(name)-12s %(levelname)-8s %(message)s")
handler.setFormatter(formatter)
logger.addHandler(handler)
logger.setLevel(logging.INFO)
from ignite.handlers import Checkpoint, DiskSaver, EarlyStopping, TerminateOnNan
trainer.add_event_handler(Events.ITERATION_COMPLETED, TerminateOnNan())
# Store the best model
def default_score_fn(engine):
score = engine.state.metrics['Accuracy']
return score
# Force filename to model.pt to ease the rerun of the notebook
disk_saver = DiskSaver(dirname=log_path)
best_model_handler = Checkpoint(to_save={'model': model},
save_handler=disk_saver,
filename_pattern="{name}.{ext}",
n_saved=1)
evaluator.add_event_handler(Events.COMPLETED, best_model_handler)
# Add early stopping
es_patience = 10
es_handler = EarlyStopping(patience=es_patience, score_function=default_score_fn, trainer=trainer)
evaluator.add_event_handler(Events.COMPLETED, es_handler)
setup_logger(es_handler.logger)
# Clear cuda cache between training/testing
def empty_cuda_cache(engine):
torch.cuda.empty_cache()
import gc
gc.collect()
trainer.add_event_handler(Events.EPOCH_COMPLETED, empty_cuda_cache)
evaluator.add_event_handler(Events.COMPLETED, empty_cuda_cache)
train_evaluator.add_event_handler(Events.COMPLETED, empty_cuda_cache)
num_epochs = 100
trainer.run(train_loader, max_epochs=num_epochs)
```
Finetunning results:
- Test dataset:
```
evaluator.state.metrics
```
- Training subset:
```
train_evaluator.state.metrics
```
Obviously, our training settings is not the optimal one and the delta between our result and the paper's one is about 5%.
## Inference
Let's load the best model and recompute evaluation metrics on test dataset with a very basic Test-Time-Augmentation to boost the performances.
```
best_model = EfficientNet()
best_model.load_state_dict(torch.load(log_path + "/model.pt"))
metrics = {
'Accuracy': Accuracy(),
'Precision': Precision(average=True),
'Recall': Recall(average=True),
}
def inference_update_with_tta(engine, batch):
best_model.eval()
with torch.no_grad():
x, y = batch
# Let's compute final prediction as a mean of predictions on x and flipped x
y_pred1 = best_model(x)
y_pred2 = best_model(x.flip(dims=(-1, )))
y_pred = 0.5 * (y_pred1 + y_pred2)
return y_pred, y
inferencer = Engine(inference_update_with_tta)
for name, metric in metrics.items():
metric.attach(inferencer, name)
ProgressBar(desc="Inference").attach(inferencer)
result_state = inferencer.run(test_loader, max_epochs=1)
```
Finally, we obtain similar scores:
```
result_state.metrics
```
| true |
code
| 0.74236 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/bkkaggle/pytorch-CycleGAN-and-pix2pix/blob/master/pix2pix.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Install
```
!git clone https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix
import os
os.chdir('pytorch-CycleGAN-and-pix2pix/')
!pip install -r requirements.txt
```
# Datasets
Download one of the official datasets with:
- `bash ./datasets/download_pix2pix_dataset.sh [cityscapes, night2day, edges2handbags, edges2shoes, facades, maps]`
Or use your own dataset by creating the appropriate folders and adding in the images. Follow the instructions [here](https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix/blob/master/docs/datasets.md#pix2pix-datasets).
```
!bash ./datasets/download_pix2pix_dataset.sh facades
```
# Pretrained models
Download one of the official pretrained models with:
- `bash ./scripts/download_pix2pix_model.sh [edges2shoes, sat2map, map2sat, facades_label2photo, and day2night]`
Or add your own pretrained model to `./checkpoints/{NAME}_pretrained/latest_net_G.pt`
```
!bash ./scripts/download_pix2pix_model.sh facades_label2photo
```
# Training
- `python train.py --dataroot ./datasets/facades --name facades_pix2pix --model pix2pix --direction BtoA`
Change the `--dataroot` and `--name` to your own dataset's path and model's name. Use `--gpu_ids 0,1,..` to train on multiple GPUs and `--batch_size` to change the batch size. Add `--direction BtoA` if you want to train a model to transfrom from class B to A.
```
!python train.py --dataroot ./datasets/facades --name facades_pix2pix --model pix2pix --direction BtoA --use_wandb
```
# Testing
- `python test.py --dataroot ./datasets/facades --direction BtoA --model pix2pix --name facades_pix2pix`
Change the `--dataroot`, `--name`, and `--direction` to be consistent with your trained model's configuration and how you want to transform images.
> from https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix:
> Note that we specified --direction BtoA as Facades dataset's A to B direction is photos to labels.
> If you would like to apply a pre-trained model to a collection of input images (rather than image pairs), please use --model test option. See ./scripts/test_single.sh for how to apply a model to Facade label maps (stored in the directory facades/testB).
> See a list of currently available models at ./scripts/download_pix2pix_model.sh
```
!ls checkpoints/
!python test.py --dataroot ./datasets/facades --direction BtoA --model pix2pix --name facades_label2photo_pretrained --use_wandb
```
# Visualize
```
import matplotlib.pyplot as plt
img = plt.imread('./results/facades_label2photo_pretrained/test_latest/images/100_fake_B.png')
plt.imshow(img)
img = plt.imread('./results/facades_label2photo_pretrained/test_latest/images/100_real_A.png')
plt.imshow(img)
img = plt.imread('./results/facades_label2photo_pretrained/test_latest/images/100_real_B.png')
plt.imshow(img)
```
| true |
code
| 0.618233 | null | null | null | null |
|
As the second step of this tutorial, we will train an image model. This step can be run in parallel with Step 3 (training the text model).
This notebook was run on an AWS p3.2xlarge
# Octopod Image Model Training Pipeline
```
%load_ext autoreload
%autoreload 2
import sys
sys.path.append('../../')
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim import lr_scheduler
from torch.utils.data import Dataset, DataLoader
```
Note: for images, we use the MultiInputMultiTaskLearner since we will send in the full image and a center crop of the image.
```
from octopod import MultiInputMultiTaskLearner, MultiDatasetLoader
from octopod.vision.dataset import OctopodImageDataset
from octopod.vision.models import ResnetForMultiTaskClassification
```
## Load in train and validation datasets
First we load in the csv's we created in Step 1.
Remember to change the path if you stored your data somewhere other than the default.
```
TRAIN_COLOR_DF = pd.read_csv('data/color_swatches/color_train.csv')
VALID_COLOR_DF = pd.read_csv('data/color_swatches/color_valid.csv')
TRAIN_PATTERN_DF = pd.read_csv('data/pattern_swatches/pattern_train.csv')
VALID_PATTERN_DF = pd.read_csv('data/pattern_swatches/pattern_valid.csv')
```
You will most likely have to alter this to however big your batches can be on your machine
```
batch_size = 64
```
We use the `OctopodImageDataSet` class to create train and valid datasets for each task.
Check out the documentation for infomation about the transformations.
```
color_train_dataset = OctopodImageDataset(
x=TRAIN_COLOR_DF['image_locs'],
y=TRAIN_COLOR_DF['simple_color_cat'],
transform='train',
crop_transform='train'
)
color_valid_dataset = OctopodImageDataset(
x=VALID_COLOR_DF['image_locs'],
y=VALID_COLOR_DF['simple_color_cat'],
transform='val',
crop_transform='val'
)
pattern_train_dataset = OctopodImageDataset(
x=TRAIN_PATTERN_DF['image_locs'],
y=TRAIN_PATTERN_DF['pattern_type_cat'],
transform='train',
crop_transform='train'
)
pattern_valid_dataset = OctopodImageDataset(
x=VALID_PATTERN_DF['image_locs'],
y=VALID_PATTERN_DF['pattern_type_cat'],
transform='val',
crop_transform='val'
)
```
We then put the datasets into a dictionary of dataloaders.
Each task is a key.
```
train_dataloaders_dict = {
'color': DataLoader(color_train_dataset, batch_size=batch_size, shuffle=True, num_workers=2),
'pattern': DataLoader(pattern_train_dataset, batch_size=batch_size, shuffle=True, num_workers=2),
}
valid_dataloaders_dict = {
'color': DataLoader(color_valid_dataset, batch_size=batch_size, shuffle=False, num_workers=8),
'pattern': DataLoader(pattern_valid_dataset, batch_size=batch_size, shuffle=False, num_workers=8),
}
```
The dictionary of dataloaders is then put into an instance of the Octopod `MultiDatasetLoader` class.
```
TrainLoader = MultiDatasetLoader(loader_dict=train_dataloaders_dict)
len(TrainLoader)
ValidLoader = MultiDatasetLoader(loader_dict=valid_dataloaders_dict, shuffle=False)
len(ValidLoader)
```
We need to create a dictionary of the tasks and the number of unique values so that we can create our model. This is a `new_task_dict` because we are training new tasks from scratch, but we could potentially have a mix of new and pretrained tasks. See the Octopod documentation for more details.
```
new_task_dict = {
'color': TRAIN_COLOR_DF['simple_color_cat'].nunique(),
'pattern': TRAIN_PATTERN_DF['pattern_type_cat'].nunique(),
}
new_task_dict
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print(device)
```
Create Model and Learner
===
These are completely new tasks so we use `new_task_dict`. If we had already trained a model on some tasks, we would use `pretrained_task_dict`.
And since these are new tasks, we set `load_pretrained_renset=True` to use the weights from Torch.
```
model = ResnetForMultiTaskClassification(
new_task_dict=new_task_dict,
load_pretrained_resnet=True
)
```
You will likely need to explore different values in this section to find some that work for your particular model.
```
lr_last = 1e-2
lr_main = 1e-4
optimizer = optim.Adam([
{'params': model.resnet.parameters(), 'lr': lr_main},
{'params': model.dense_layers.parameters(), 'lr': lr_last},
{'params': model.new_classifiers.parameters(), 'lr': lr_last},
])
exp_lr_scheduler = lr_scheduler.StepLR(optimizer, step_size= 4, gamma= 0.1)
loss_function_dict = {'color': 'categorical_cross_entropy', 'pattern': 'categorical_cross_entropy'}
metric_function_dict = {'color': 'multi_class_acc', 'pattern': 'multi_class_acc'}
learn = MultiInputMultiTaskLearner(model, TrainLoader, ValidLoader, new_task_dict, loss_function_dict, metric_function_dict)
```
Train model
===
As your model trains, you can see some output of how the model is performing overall and how it is doing on each individual task.
```
learn.fit(
num_epochs=10,
scheduler=exp_lr_scheduler,
step_scheduler_on_batch=False,
optimizer=optimizer,
device=device,
best_model=True
)
```
If you run the above cell and see an error like:
```python
RuntimeError: DataLoader worker (pid X) is killed by signal: Bus error. It is possible that dataloader's workers are out of shared memory. Please try to raise your shared memory limit.
```
Try lowering the `num_workers` to `0` for each `DataLoader` in `train_dataloaders_dict` and `valid_dataloaders_dict`.
Validate model
===
We provide a method on the learner called `get_val_preds`, which makes predictions on the validation data. You can then use this to analyze your model's performance in more detail.
```
pred_dict = learn.get_val_preds(device)
pred_dict
```
Save/Export Model
===
Once we are happy with our training we can save (or export) our model, using the `save` method (or `export`).
See the docs for the difference between `save` and `export`.
We will need the saved model later to use in the ensemble model
```
model.save(folder='models/', model_id='IMAGE_MODEL1')
model.export(folder='models/', model_id='IMAGE_MODEL1')
```
Now that we have an image model, we can move to `Step3_train_text_model`.
| true |
code
| 0.647492 | null | null | null | null |
|
# Improving Data Quality
**Learning Objectives**
1. Resolve missing values
2. Convert the Date feature column to a datetime format
3. Rename a feature column, remove a value from a feature column
4. Create one-hot encoding features
5. Understand temporal feature conversions
## Introduction
Recall that machine learning models can only consume numeric data, and that numeric data should be "1"s or "0"s. Data is said to be "messy" or "untidy" if it is missing attribute values, contains noise or outliers, has duplicates, wrong data, upper/lower case column names, and is essentially not ready for ingestion by a machine learning algorithm.
This notebook presents and solves some of the most common issues of "untidy" data. Note that different problems will require different methods, and they are beyond the scope of this notebook.
Each learning objective will correspond to a __#TODO__ in the [student lab notebook](https://github.com/GoogleCloudPlatform/training-data-analyst/blob/master/courses/machine_learning/deepdive2/launching_into_ml/labs/improve_data_quality.ipynb) -- try to complete that notebook first before reviewing this solution notebook.
```
!sudo chown -R jupyter:jupyter /home/jupyter/training-data-analyst
# Ensure the right version of Tensorflow is installed.
!pip freeze | grep tensorflow==2.1 || pip install tensorflow==2.1
```
Start by importing the necessary libraries.
### Import Libraries
```
import os
import pandas as pd # First, we'll import Pandas, a data processing and CSV file I/O library
import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
```
### Load the Dataset
The dataset is based on California's [Vehicle Fuel Type Count by Zip Code](https://data.ca.gov/dataset/vehicle-fuel-type-count-by-zip-codeSynthetic) report. The dataset has been modified to make the data "untidy" and is thus a synthetic representation that can be used for learning purposes.
Let's download the raw .csv data by copying the data from a cloud storage bucket.
```
if not os.path.isdir("../data/transport"):
os.makedirs("../data/transport")
!gsutil cp gs://cloud-training-demos/feat_eng/transport/untidy_vehicle_data.csv ../data/transport
!ls -l ../data/transport
```
### Read Dataset into a Pandas DataFrame
Next, let's read in the dataset just copied from the cloud storage bucket and create a Pandas DataFrame. We also add a Pandas .head() function to show you the top 5 rows of data in the DataFrame. Head() and Tail() are "best-practice" functions used to investigate datasets.
```
df_transport = pd.read_csv('../data/transport/untidy_vehicle_data.csv')
df_transport.head() # Output the first five rows.
```
### DataFrame Column Data Types
DataFrames may have heterogenous or "mixed" data types, that is, some columns are numbers, some are strings, and some are dates etc. Because CSV files do not contain information on what data types are contained in each column, Pandas infers the data types when loading the data, e.g. if a column contains only numbers, Pandas will set that column’s data type to numeric: integer or float.
Run the next cell to see information on the DataFrame.
```
df_transport.info()
```
From what the .info() function shows us, we have six string objects and one float object. Let's print out the first and last five rows of each column. We can definitely see more of the "string" object values now!
```
print(df_transport,5)
```
### Summary Statistics
At this point, we have only one column which contains a numerical value (e.g. Vehicles). For features which contain numerical values, we are often interested in various statistical measures relating to those values. We can use .describe() to see some summary statistics for the numeric fields in our dataframe. Note, that because we only have one numeric feature, we see only one summary stastic - for now.
```
df_transport.describe()
```
Let's investigate a bit more of our data by using the .groupby() function.
```
grouped_data = df_transport.groupby(['Zip Code','Model Year','Fuel','Make','Light_Duty','Vehicles'])
df_transport.groupby('Fuel').first() # Get the first entry for each month.
```
#### Checking for Missing Values
Missing values adversely impact data quality, as they can lead the machine learning model to make inaccurate inferences about the data. Missing values can be the result of numerous factors, e.g. "bits" lost during streaming transmission, data entry, or perhaps a user forgot to fill in a field. Note that Pandas recognizes both empty cells and “NaN” types as missing values.
Let's show the null values for all features in the DataFrame.
```
df_transport.isnull().sum()
```
To see a sampling of which values are missing, enter the feature column name. You'll notice that "False" and "True" correpond to the presence or abscence of a value by index number.
```
print (df_transport['Date'])
print (df_transport['Date'].isnull())
print (df_transport['Make'])
print (df_transport['Make'].isnull())
print (df_transport['Model Year'])
print (df_transport['Model Year'].isnull())
```
### What can we deduce about the data at this point?
First, let's summarize our data by row, column, features, unique, and missing values,
```
print ("Rows : " ,df_transport.shape[0])
print ("Columns : " ,df_transport.shape[1])
print ("\nFeatures : \n" ,df_transport.columns.tolist())
print ("\nUnique values : \n",df_transport.nunique())
print ("\nMissing values : ", df_transport.isnull().sum().values.sum())
```
Let's see the data again -- this time the last five rows in the dataset.
```
df_transport.tail()
```
### What Are Our Data Quality Issues?
1. **Data Quality Issue #1**:
> **Missing Values**:
Each feature column has multiple missing values. In fact, we have a total of 18 missing values.
2. **Data Quality Issue #2**:
> **Date DataType**: Date is shown as an "object" datatype and should be a datetime. In addition, Date is in one column. Our business requirement is to see the Date parsed out to year, month, and day.
3. **Data Quality Issue #3**:
> **Model Year**: We are only interested in years greater than 2006, not "<2006".
4. **Data Quality Issue #4**:
> **Categorical Columns**: The feature column "Light_Duty" is categorical and has a "Yes/No" choice. We cannot feed values like this into a machine learning model. In addition, we need to "one-hot encode the remaining "string"/"object" columns.
5. **Data Quality Issue #5**:
> **Temporal Features**: How do we handle year, month, and day?
#### Data Quality Issue #1:
##### Resolving Missing Values
Most algorithms do not accept missing values. Yet, when we see missing values in our dataset, there is always a tendency to just "drop all the rows" with missing values. Although Pandas will fill in the blank space with “NaN", we should "handle" them in some way.
While all the methods to handle missing values is beyond the scope of this lab, there are a few methods you should consider. For numeric columns, use the "mean" values to fill in the missing numeric values. For categorical columns, use the "mode" (or most frequent values) to fill in missing categorical values.
In this lab, we use the .apply and Lambda functions to fill every column with its own most frequent value. You'll learn more about Lambda functions later in the lab.
Let's check again for missing values by showing how many rows contain NaN values for each feature column.
```
# TODO 1a
df_transport.isnull().sum()
```
Run the cell to apply the lambda function.
```
# TODO 1b
df_transport = df_transport.apply(lambda x:x.fillna(x.value_counts().index[0]))
```
Let's check again for missing values.
```
# TODO 1c
df_transport.isnull().sum()
```
#### Data Quality Issue #2:
##### Convert the Date Feature Column to a Datetime Format
The date column is indeed shown as a string object. We can convert it to the datetime datatype with the to_datetime() function in Pandas.
```
# TODO 2a
df_transport['Date'] = pd.to_datetime(df_transport['Date'],
format='%m/%d/%Y')
# TODO 2b
df_transport.info() # Date is now converted.
```
Let's parse Date into three columns, e.g. year, month, and day.
```
df_transport['year'] = df_transport['Date'].dt.year
df_transport['month'] = df_transport['Date'].dt.month
df_transport['day'] = df_transport['Date'].dt.day
#df['hour'] = df['date'].dt.hour - you could use this if your date format included hour.
#df['minute'] = df['date'].dt.minute - you could use this if your date format included minute.
df_transport.info()
```
Next, let's confirm the Date parsing. This will also give us a another visualization of the data.
```
grouped_data = df_transport.groupby(['Make'])
df_transport.groupby('Fuel').first() # Get the first entry for each month.
```
Now that we have Dates as a integers, let's do some additional plotting.
```
plt.figure(figsize=(10,6))
sns.jointplot(x='month',y='Vehicles',data=df_transport)
#plt.title('Vehicles by Month')
```
#### Data Quality Issue #3:
##### Rename a Feature Column and Remove a Value.
Our feature columns have different "capitalizations" in their names, e.g. both upper and lower "case". In addition, there are "spaces" in some of the column names. In addition, we are only interested in years greater than 2006, not "<2006".
Let's remove all the spaces for feature columns by renaming them; we can also resolve the "case" problem too by making all the feature column names lower case.
```
# TODO 3a
df_transport.rename(columns = { 'Date': 'date', 'Zip Code':'zipcode', 'Model Year': 'modelyear', 'Fuel': 'fuel', 'Make': 'make', 'Light_Duty': 'lightduty', 'Vehicles': 'vehicles'}, inplace = True)
df_transport.head(2)
```
**Note:** Next we create a copy of the dataframe to avoid the "SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame" warning. Run the cell to remove the value '<2006' from the modelyear feature column.
```
# Here, we create a copy of the dataframe to avoid copy warning issues.
# TODO 3b
df = df_transport.loc[df_transport.modelyear != '<2006'].copy()
```
Next, confirm that the modelyear value '<2006' has been removed by doing a value count.
```
df['modelyear'].value_counts(0)
```
#### Data Quality Issue #4:
##### Handling Categorical Columns
The feature column "lightduty" is categorical and has a "Yes/No" choice. We cannot feed values like this into a machine learning model. We need to convert the binary answers from strings of yes/no to integers of 1/0. There are various methods to achieve this. We will use the "apply" method with a lambda expression. Pandas. apply() takes a function and applies it to all values of a Pandas series.
##### What is a Lambda Function?
Typically, Python requires that you define a function using the def keyword. However, lambda functions are anonymous -- which means there is no need to name them. The most common use case for lambda functions is in code that requires a simple one-line function (e.g. lambdas only have a single expression).
As you progress through the Course Specialization, you will see many examples where lambda functions are being used. Now is a good time to become familiar with them.
First, lets count the number of "Yes" and"No's" in the 'lightduty' feature column.
```
df['lightduty'].value_counts(0)
```
Let's convert the Yes to 1 and No to 0. Pandas. apply() . apply takes a function and applies it to all values of a Pandas series (e.g. lightduty).
```
df.loc[:,'lightduty'] = df['lightduty'].apply(lambda x: 0 if x=='No' else 1)
df['lightduty'].value_counts(0)
# Confirm that "lightduty" has been converted.
df.head()
```
#### One-Hot Encoding Categorical Feature Columns
Machine learning algorithms expect input vectors and not categorical features. Specifically, they cannot handle text or string values. Thus, it is often useful to transform categorical features into vectors.
One transformation method is to create dummy variables for our categorical features. Dummy variables are a set of binary (0 or 1) variables that each represent a single class from a categorical feature. We simply encode the categorical variable as a one-hot vector, i.e. a vector where only one element is non-zero, or hot. With one-hot encoding, a categorical feature becomes an array whose size is the number of possible choices for that feature.
Panda provides a function called "get_dummies" to convert a categorical variable into dummy/indicator variables.
```
# Making dummy variables for categorical data with more inputs.
data_dummy = pd.get_dummies(df[['zipcode','modelyear', 'fuel', 'make']], drop_first=True)
data_dummy.head()
# Merging (concatenate) original data frame with 'dummy' dataframe.
# TODO 4a
df = pd.concat([df,data_dummy], axis=1)
df.head()
# Dropping attributes for which we made dummy variables. Let's also drop the Date column.
# TODO 4b
df = df.drop(['date','zipcode','modelyear', 'fuel', 'make'], axis=1)
# Confirm that 'zipcode','modelyear', 'fuel', and 'make' have been dropped.
df.head()
```
#### Data Quality Issue #5:
##### Temporal Feature Columns
Our dataset now contains year, month, and day feature columns. Let's convert the month and day feature columns to meaningful representations as a way to get us thinking about changing temporal features -- as they are sometimes overlooked.
Note that the Feature Engineering course in this Specialization will provide more depth on methods to handle year, month, day, and hour feature columns.
First, let's print the unique values for "month" and "day" in our dataset.
```
print ('Unique values of month:',df.month.unique())
print ('Unique values of day:',df.day.unique())
print ('Unique values of year:',df.year.unique())
```
Next, we map each temporal variable onto a circle such that the lowest value for that variable appears right next to the largest value. We compute the x- and y- component of that point using sin and cos trigonometric functions. Don't worry, this is the last time we will use this code, as you can develop an input pipeline to address these temporal feature columns in TensorFlow and Keras - and it is much easier! But, sometimes you need to appreciate what you're not going to encounter as you move through the course!
Run the cell to view the output.
```
df['day_sin'] = np.sin(df.day*(2.*np.pi/31))
df['day_cos'] = np.cos(df.day*(2.*np.pi/31))
df['month_sin'] = np.sin((df.month-1)*(2.*np.pi/12))
df['month_cos'] = np.cos((df.month-1)*(2.*np.pi/12))
# Let's drop month, and day
# TODO 5
df = df.drop(['month','day','year'], axis=1)
# scroll left to see the converted month and day coluumns.
df.tail(4)
```
### Conclusion
This notebook introduced a few concepts to improve data quality. We resolved missing values, converted the Date feature column to a datetime format, renamed feature columns, removed a value from a feature column, created one-hot encoding features, and converted temporal features to meaningful representations. By the end of our lab, we gained an understanding as to why data should be "cleaned" and "pre-processed" before input into a machine learning model.
Copyright 2020 Google Inc.
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
| true |
code
| 0.254185 | null | null | null | null |
|
### Feature Scaling - Solution
With any distance based machine learning model (regularized regression methods, neural networks, and now kmeans), you will want to scale your data.
If you have some features that are on completely different scales, this can greatly impact the clusters you get when using K-Means.
In this notebook, you will get to see this first hand. To begin, let's read in the necessary libraries.
```
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn import preprocessing as p
%matplotlib inline
plt.rcParams['figure.figsize'] = (16, 9)
import helpers2 as h
import tests as t
# Create the dataset for the notebook
data = h.simulate_data(200, 2, 4)
df = pd.DataFrame(data)
df.columns = ['height', 'weight']
df['height'] = np.abs(df['height']*100)
df['weight'] = df['weight'] + np.random.normal(50, 10, 200)
```
`1.` Next, take a look at the data to get familiar with it. The dataset has two columns, and it is stored in the **df** variable. It might be useful to get an idea of the spread in the current data, as well as a visual of the points.
```
df.describe()
plt.scatter(df['height'], df['weight']);
```
Now that we've got a dataset, let's look at some options for scaling the data. As well as how the data might be scaled. There are two very common types of feature scaling that we should discuss:
**I. MinMaxScaler**
In some cases it is useful to think of your data in terms of the percent they are as compared to the maximum value. In these cases, you will want to use **MinMaxScaler**.
**II. StandardScaler**
Another very popular type of scaling is to scale data so that it has mean 0 and variance 1. In these cases, you will want to use **StandardScaler**.
It is probably more appropriate with this data to use **StandardScaler**. However, to get practice with feature scaling methods in python, we will perform both.
`2.` First let's fit the **StandardScaler** transformation to this dataset. I will do this one so you can see how to apply preprocessing in sklearn.
```
df_ss = p.StandardScaler().fit_transform(df) # Fit and transform the data
df_ss = pd.DataFrame(df_ss) #create a dataframe
df_ss.columns = ['height', 'weight'] #add column names again
plt.scatter(df_ss['height'], df_ss['weight']); # create a plot
```
`3.` Now it's your turn. Try fitting the **MinMaxScaler** transformation to this dataset. You should be able to use the previous example to assist.
```
df_mm = p.MinMaxScaler().fit_transform(df) # fit and transform
df_mm = pd.DataFrame(df_mm) #create a dataframe
df_mm.columns = ['height', 'weight'] #change the column names
plt.scatter(df_mm['height'], df_mm['weight']); #plot the data
```
`4.` Now let's take a look at how kmeans divides the dataset into different groups for each of the different scalings of the data. Did you end up with different clusters when the data was scaled differently?
```
def fit_kmeans(data, centers):
'''
INPUT:
data = the dataset you would like to fit kmeans to (dataframe)
centers = the number of centroids (int)
OUTPUT:
labels - the labels for each datapoint to which group it belongs (nparray)
'''
kmeans = KMeans(centers)
labels = kmeans.fit_predict(data)
return labels
labels = fit_kmeans(df, 10) #fit kmeans to get the labels
# Plot the original data with clusters
plt.scatter(df['height'], df['weight'], c=labels, cmap='Set1');
labels = fit_kmeans(df_mm, 10) #fit kmeans to get the labels
#plot each of the scaled datasets
plt.scatter(df_mm['height'], df_mm['weight'], c=labels, cmap='Set1');
labels = fit_kmeans(df_ss, 10)
plt.scatter(df_ss['height'], df_ss['weight'], c=labels, cmap='Set1');
```
**Different from what was stated in the video - In this case, the scaling did end up changing the results. In the video, the kmeans algorithm was not refit to each differently scaled dataset. It was only using the one clustering fit on every dataset. In this notebook, you see that clustering was recomputed with each scaling, which changes the results!**
| true |
code
| 0.533397 | null | null | null | null |
|
```
%load_ext watermark
%watermark -p torch,pytorch_lightning,torchmetrics,matplotlib
```
The three extensions below are optional, for more information, see
- `watermark`: https://github.com/rasbt/watermark
- `pycodestyle_magic`: https://github.com/mattijn/pycodestyle_magic
- `nb_black`: https://github.com/dnanhkhoa/nb_black
```
%load_ext pycodestyle_magic
%flake8_on --ignore W291,W293,E703,E402 --max_line_length=100
%load_ext nb_black
```
<a href="https://pytorch.org"><img src="https://raw.githubusercontent.com/pytorch/pytorch/master/docs/source/_static/img/pytorch-logo-dark.svg" width="90"/></a> <a href="https://www.pytorchlightning.ai"><img src="https://raw.githubusercontent.com/PyTorchLightning/pytorch-lightning/master/docs/source/_static/images/logo.svg" width="150"/></a>
# Multilayer Perceptron trained on MNIST
A simple multilayer perceptron [1][2] trained on MNIST [3].
### References
- [1] https://en.wikipedia.org/wiki/Multilayer_perceptron
- [2] L9.1 Multilayer Perceptron Architecture (24:24): https://www.youtube.com/watch?v=IUylp47hNA0
- [3] https://en.wikipedia.org/wiki/MNIST_database
## General settings and hyperparameters
- Here, we specify some general hyperparameter values and general settings.
```
HIDDEN_UNITS = (128, 256)
BATCH_SIZE = 256
NUM_EPOCHS = 10
LEARNING_RATE = 0.005
NUM_WORKERS = 4
```
- Note that using multiple workers can sometimes cause issues with too many open files in PyTorch for small datasets. If we have problems with the data loader later, try setting `NUM_WORKERS = 0` and reload the notebook.
## Implementing a Neural Network using PyTorch Lightning's `LightningModule`
- In this section, we set up the main model architecture using the `LightningModule` from PyTorch Lightning.
- In essence, `LightningModule` is a wrapper around a PyTorch module.
- We start with defining our neural network model in pure PyTorch, and then we use it in the `LightningModule` to get all the extra benefits that PyTorch Lightning provides.
```
import torch
import torch.nn.functional as F
# Regular PyTorch Module
class PyTorchModel(torch.nn.Module):
def __init__(self, input_size, hidden_units, num_classes):
super().__init__()
# Initialize MLP layers
all_layers = []
for hidden_unit in hidden_units:
layer = torch.nn.Linear(input_size, hidden_unit, bias=False)
all_layers.append(layer)
all_layers.append(torch.nn.ReLU())
input_size = hidden_unit
output_layer = torch.nn.Linear(
in_features=hidden_units[-1],
out_features=num_classes)
all_layers.append(output_layer)
self.layers = torch.nn.Sequential(*all_layers)
def forward(self, x):
x = torch.flatten(x, start_dim=1) # to make it work for image inputs
x = self.layers(x)
return x # x are the model's logits
# %load ../code_lightningmodule/lightningmodule_classifier_basic.py
import pytorch_lightning as pl
import torchmetrics
# LightningModule that receives a PyTorch model as input
class LightningModel(pl.LightningModule):
def __init__(self, model, learning_rate):
super().__init__()
self.learning_rate = learning_rate
# The inherited PyTorch module
self.model = model
if hasattr(model, "dropout_proba"):
self.dropout_proba = model.dropout_proba
# Save settings and hyperparameters to the log directory
# but skip the model parameters
self.save_hyperparameters(ignore=["model"])
# Set up attributes for computing the accuracy
self.train_acc = torchmetrics.Accuracy()
self.valid_acc = torchmetrics.Accuracy()
self.test_acc = torchmetrics.Accuracy()
# Defining the forward method is only necessary
# if you want to use a Trainer's .predict() method (optional)
def forward(self, x):
return self.model(x)
# A common forward step to compute the loss and labels
# this is used for training, validation, and testing below
def _shared_step(self, batch):
features, true_labels = batch
logits = self(features)
loss = torch.nn.functional.cross_entropy(logits, true_labels)
predicted_labels = torch.argmax(logits, dim=1)
return loss, true_labels, predicted_labels
def training_step(self, batch, batch_idx):
loss, true_labels, predicted_labels = self._shared_step(batch)
self.log("train_loss", loss)
# Do another forward pass in .eval() mode to compute accuracy
# while accountingfor Dropout, BatchNorm etc. behavior
# during evaluation (inference)
self.model.eval()
with torch.no_grad():
_, true_labels, predicted_labels = self._shared_step(batch)
self.train_acc(predicted_labels, true_labels)
self.log("train_acc", self.train_acc, on_epoch=True, on_step=False)
self.model.train()
return loss # this is passed to the optimzer for training
def validation_step(self, batch, batch_idx):
loss, true_labels, predicted_labels = self._shared_step(batch)
self.log("valid_loss", loss)
self.valid_acc(predicted_labels, true_labels)
self.log(
"valid_acc",
self.valid_acc,
on_epoch=True,
on_step=False,
prog_bar=True,
)
def test_step(self, batch, batch_idx):
loss, true_labels, predicted_labels = self._shared_step(batch)
self.test_acc(predicted_labels, true_labels)
self.log("test_acc", self.test_acc, on_epoch=True, on_step=False)
def configure_optimizers(self):
optimizer = torch.optim.Adam(self.parameters(), lr=self.learning_rate)
return optimizer
```
## Setting up the dataset
- In this section, we are going to set up our dataset.
### Inspecting the dataset
```
# %load ../code_dataset/dataset_mnist_check.py
from collections import Counter
from torchvision import datasets
from torchvision import transforms
from torch.utils.data import DataLoader
train_dataset = datasets.MNIST(
root="./data", train=True, transform=transforms.ToTensor(), download=True
)
train_loader = DataLoader(
dataset=train_dataset,
batch_size=BATCH_SIZE,
num_workers=NUM_WORKERS,
drop_last=True,
shuffle=True,
)
test_dataset = datasets.MNIST(
root="./data", train=False, transform=transforms.ToTensor()
)
test_loader = DataLoader(
dataset=test_dataset,
batch_size=BATCH_SIZE,
num_workers=NUM_WORKERS,
drop_last=False,
shuffle=False,
)
train_counter = Counter()
for images, labels in train_loader:
train_counter.update(labels.tolist())
test_counter = Counter()
for images, labels in test_loader:
test_counter.update(labels.tolist())
print("\nTraining label distribution:")
sorted(train_counter.items())
print("\nTest label distribution:")
sorted(test_counter.items())
```
### Performance baseline
- Especially for imbalanced datasets, it's pretty helpful to compute a performance baseline.
- In classification contexts, a useful baseline is to compute the accuracy for a scenario where the model always predicts the majority class -- we want our model to be better than that!
```
# %load ../code_dataset/performance_baseline.py
majority_class = test_counter.most_common(1)[0]
print("Majority class:", majority_class[0])
baseline_acc = majority_class[1] / sum(test_counter.values())
print("Accuracy when always predicting the majority class:")
print(f"{baseline_acc:.2f} ({baseline_acc*100:.2f}%)")
```
## A quick visual check
```
# %load ../code_dataset/plot_visual-check_basic.py
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import torchvision
for images, labels in train_loader:
break
plt.figure(figsize=(8, 8))
plt.axis("off")
plt.title("Training images")
plt.imshow(np.transpose(torchvision.utils.make_grid(
images[:64],
padding=2,
normalize=True),
(1, 2, 0)))
plt.show()
```
### Setting up a `DataModule`
- There are three main ways we can prepare the dataset for Lightning. We can
1. make the dataset part of the model;
2. set up the data loaders as usual and feed them to the fit method of a Lightning Trainer -- the Trainer is introduced in the following subsection;
3. create a LightningDataModule.
- Here, we will use approach 3, which is the most organized approach. The `LightningDataModule` consists of several self-explanatory methods, as we can see below:
```
# %load ../code_lightningmodule/datamodule_mnist_basic.py
from torch.utils.data.dataset import random_split
class DataModule(pl.LightningDataModule):
def __init__(self, data_path="./"):
super().__init__()
self.data_path = data_path
def prepare_data(self):
datasets.MNIST(root=self.data_path, download=True)
return
def setup(self, stage=None):
# Note transforms.ToTensor() scales input images
# to 0-1 range
train = datasets.MNIST(
root=self.data_path,
train=True,
transform=transforms.ToTensor(),
download=False,
)
self.test = datasets.MNIST(
root=self.data_path,
train=False,
transform=transforms.ToTensor(),
download=False,
)
self.train, self.valid = random_split(train, lengths=[55000, 5000])
def train_dataloader(self):
train_loader = DataLoader(
dataset=self.train,
batch_size=BATCH_SIZE,
drop_last=True,
shuffle=True,
num_workers=NUM_WORKERS,
)
return train_loader
def val_dataloader(self):
valid_loader = DataLoader(
dataset=self.valid,
batch_size=BATCH_SIZE,
drop_last=False,
shuffle=False,
num_workers=NUM_WORKERS,
)
return valid_loader
def test_dataloader(self):
test_loader = DataLoader(
dataset=self.test,
batch_size=BATCH_SIZE,
drop_last=False,
shuffle=False,
num_workers=NUM_WORKERS,
)
return test_loader
```
- Note that the `prepare_data` method is usually used for steps that only need to be executed once, for example, downloading the dataset; the `setup` method defines the dataset loading -- if we run our code in a distributed setting, this will be called on each node / GPU.
- Next, let's initialize the `DataModule`; we use a random seed for reproducibility (so that the data set is shuffled the same way when we re-execute this code):
```
torch.manual_seed(1)
data_module = DataModule(data_path='./data')
```
## Training the model using the PyTorch Lightning Trainer class
- Next, we initialize our model.
- Also, we define a call back to obtain the model with the best validation set performance after training.
- PyTorch Lightning offers [many advanced logging services](https://pytorch-lightning.readthedocs.io/en/latest/extensions/logging.html) like Weights & Biases. However, here, we will keep things simple and use the `CSVLogger`:
```
pytorch_model = PyTorchModel(
input_size=28*28,
hidden_units=HIDDEN_UNITS,
num_classes=10
)
# %load ../code_lightningmodule/logger_csv_acc_basic.py
from pytorch_lightning.callbacks import ModelCheckpoint
from pytorch_lightning.loggers import CSVLogger
lightning_model = LightningModel(pytorch_model, learning_rate=LEARNING_RATE)
callbacks = [
ModelCheckpoint(
save_top_k=1, mode="max", monitor="valid_acc"
) # save top 1 model
]
logger = CSVLogger(save_dir="logs/", name="my-model")
```
- Now it's time to train our model:
```
# %load ../code_lightningmodule/trainer_nb_basic.py
import time
trainer = pl.Trainer(
max_epochs=NUM_EPOCHS,
callbacks=callbacks,
progress_bar_refresh_rate=50, # recommended for notebooks
accelerator="auto", # Uses GPUs or TPUs if available
devices="auto", # Uses all available GPUs/TPUs if applicable
logger=logger,
deterministic=True,
log_every_n_steps=10,
)
start_time = time.time()
trainer.fit(model=lightning_model, datamodule=data_module)
runtime = (time.time() - start_time) / 60
print(f"Training took {runtime:.2f} min in total.")
```
## Evaluating the model
- After training, let's plot our training ACC and validation ACC using pandas, which, in turn, uses matplotlib for plotting (PS: you may want to check out [more advanced logger](https://pytorch-lightning.readthedocs.io/en/latest/extensions/logging.html) later on, which take care of it for us):
```
# %load ../code_lightningmodule/logger_csv_plot_basic.py
import pandas as pd
import matplotlib.pyplot as plt
metrics = pd.read_csv(f"{trainer.logger.log_dir}/metrics.csv")
aggreg_metrics = []
agg_col = "epoch"
for i, dfg in metrics.groupby(agg_col):
agg = dict(dfg.mean())
agg[agg_col] = i
aggreg_metrics.append(agg)
df_metrics = pd.DataFrame(aggreg_metrics)
df_metrics[["train_loss", "valid_loss"]].plot(
grid=True, legend=True, xlabel="Epoch", ylabel="Loss"
)
df_metrics[["train_acc", "valid_acc"]].plot(
grid=True, legend=True, xlabel="Epoch", ylabel="ACC"
)
plt.show()
```
- The `trainer` automatically saves the model with the best validation accuracy automatically for us, we which we can load from the checkpoint via the `ckpt_path='best'` argument; below we use the `trainer` instance to evaluate the best model on the test set:
```
trainer.test(model=lightning_model, datamodule=data_module, ckpt_path='best')
```
## Predicting labels of new data
- We can use the `trainer.predict` method either on a new `DataLoader` (`trainer.predict(dataloaders=...)`) or `DataModule` (`trainer.predict(datamodule=...)`) to apply the model to new data.
- Alternatively, we can also manually load the best model from a checkpoint as shown below:
```
path = trainer.checkpoint_callback.best_model_path
print(path)
lightning_model = LightningModel.load_from_checkpoint(path, model=pytorch_model)
lightning_model.eval();
```
- For simplicity, we reused our existing `pytorch_model` above. However, we could also reinitialize the `pytorch_model`, and the `.load_from_checkpoint` method would load the corresponding model weights for us from the checkpoint file.
- Now, below is an example applying the model manually. Here, pretend that the `test_dataloader` is a new data loader.
```
# %load ../code_lightningmodule/datamodule_testloader.py
test_dataloader = data_module.test_dataloader()
acc = torchmetrics.Accuracy()
for batch in test_dataloader:
features, true_labels = batch
with torch.no_grad():
logits = lightning_model(features)
predicted_labels = torch.argmax(logits, dim=1)
acc(predicted_labels, true_labels)
predicted_labels[:5]
```
- As an internal check, if the model was loaded correctly, the test accuracy below should be identical to the test accuracy we saw earlier in the previous section.
```
test_acc = acc.compute()
print(f'Test accuracy: {test_acc:.4f} ({test_acc*100:.2f}%)')
```
## Inspecting Failure Cases
- In practice, it is often informative to look at failure cases like wrong predictions for particular training instances as it can give us some insights into the model behavior and dataset.
- Inspecting failure cases can sometimes reveal interesting patterns and even highlight dataset and labeling issues.
```
# In the case of MNIST, the class label mapping
# is relatively trivial
class_dict = {0: 'digit 0',
1: 'digit 1',
2: 'digit 2',
3: 'digit 3',
4: 'digit 4',
5: 'digit 5',
6: 'digit 6',
7: 'digit 7',
8: 'digit 8',
9: 'digit 9'}
# %load ../code_lightningmodule/plot_failurecases_basic.py
# Append the folder that contains the
# helper_data.py, helper_plotting.py, and helper_evaluate.py
# files so we can import from them
import sys
sys.path.append("../../pytorch_ipynb")
from helper_plotting import show_examples
show_examples(
model=lightning_model, data_loader=test_dataloader, class_dict=class_dict
)
```
- In addition to inspecting failure cases visually, it is also informative to look at which classes the model confuses the most via a confusion matrix:
```
# %load ../code_lightningmodule/plot_confusion-matrix_basic.py
from torchmetrics import ConfusionMatrix
import matplotlib
from mlxtend.plotting import plot_confusion_matrix
cmat = ConfusionMatrix(num_classes=len(class_dict))
for x, y in test_dataloader:
with torch.no_grad():
pred = lightning_model(x)
cmat(pred, y)
cmat_tensor = cmat.compute()
cmat = cmat_tensor.numpy()
fig, ax = plot_confusion_matrix(
conf_mat=cmat,
class_names=class_dict.values(),
norm_colormap=matplotlib.colors.LogNorm()
# normed colormaps highlight the off-diagonals
# for high-accuracy models better
)
plt.show()
%watermark --iversions
```
| true |
code
| 0.852844 | null | null | null | null |
|
## 1. Meet Professor William Sharpe
<p>An investment may make sense if we expect it to return more money than it costs. But returns are only part of the story because they are risky - there may be a range of possible outcomes. How does one compare different investments that may deliver similar results on average, but exhibit different levels of risks?</p>
<p><img style="float: left ; margin: 5px 20px 5px 1px;" width="200" src="https://assets.datacamp.com/production/project_66/img/sharpe.jpeg"></p>
<p>Enter William Sharpe. He introduced the <a href="https://web.stanford.edu/~wfsharpe/art/sr/sr.htm"><em>reward-to-variability ratio</em></a> in 1966 that soon came to be called the Sharpe Ratio. It compares the expected returns for two investment opportunities and calculates the additional return per unit of risk an investor could obtain by choosing one over the other. In particular, it looks at the difference in returns for two investments and compares the average difference to the standard deviation (as a measure of risk) of this difference. A higher Sharpe ratio means that the reward will be higher for a given amount of risk. It is common to compare a specific opportunity against a benchmark that represents an entire category of investments.</p>
<p>The Sharpe ratio has been one of the most popular risk/return measures in finance, not least because it's so simple to use. It also helped that Professor Sharpe won a Nobel Memorial Prize in Economics in 1990 for his work on the capital asset pricing model (CAPM).</p>
<p>The Sharpe ratio is usually calculated for a portfolio and uses the risk-free interest rate as benchmark. We will simplify our example and use stocks instead of a portfolio. We will also use a stock index as benchmark rather than the risk-free interest rate because both are readily available at daily frequencies and we do not have to get into converting interest rates from annual to daily frequency. Just keep in mind that you would run the same calculation with portfolio returns and your risk-free rate of choice, e.g, the <a href="https://fred.stlouisfed.org/series/TB3MS">3-month Treasury Bill Rate</a>. </p>
<p>So let's learn about the Sharpe ratio by calculating it for the stocks of the two tech giants Facebook and Amazon. As benchmark we'll use the S&P 500 that measures the performance of the 500 largest stocks in the US. When we use a stock index instead of the risk-free rate, the result is called the Information Ratio and is used to benchmark the return on active portfolio management because it tells you how much more return for a given unit of risk your portfolio manager earned relative to just putting your money into a low-cost index fund.</p>
```
# Importing required modules
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Settings to produce nice plots in a Jupyter notebook
plt.style.use('fivethirtyeight')
%matplotlib inline
#stock_data =pd.read_csv('datasets/stock_data.csv')
# Reading in the data
stock_data = pd.read_csv('datasets/stock_data.csv',parse_dates=['Date'],index_col =['Date']).dropna()
benchmark_data = pd.read_csv('datasets/benchmark_data.csv',parse_dates=['Date'],
index_col=['Date']
).dropna()
#stock_data.Date.dtype
```
## 2. A first glance at the data
<p>Let's take a look the data to find out how many observations and variables we have at our disposal.</p>
```
# Display summary for stock_data
print('Stocks\n')
stock_data.info()
stock_data.head()
# Display summary for benchmark_data
print('\nBenchmarks\n')
benchmark_data.info()
benchmark_data.head()
```
## 3. Plot & summarize daily prices for Amazon and Facebook
<p>Before we compare an investment in either Facebook or Amazon with the index of the 500 largest companies in the US, let's visualize the data, so we better understand what we're dealing with.</p>
```
# visualize the stock_data
stock_data.plot(subplots = True, title ='Stock Data')
# summarize the stock_data
stock_data.describe()
```
## 4. Visualize & summarize daily values for the S&P 500
<p>Let's also take a closer look at the value of the S&P 500, our benchmark.</p>
```
# plot the benchmark_data
benchmark_data.plot(title = 'S&P 500' )
# summarize the benchmark_data
benchmark_data.describe()
```
## 5. The inputs for the Sharpe Ratio: Starting with Daily Stock Returns
<p>The Sharpe Ratio uses the difference in returns between the two investment opportunities under consideration.</p>
<p>However, our data show the historical value of each investment, not the return. To calculate the return, we need to calculate the percentage change in value from one day to the next. We'll also take a look at the summary statistics because these will become our inputs as we calculate the Sharpe Ratio. Can you already guess the result?</p>
```
# calculate daily stock_data returns
stock_returns = stock_data.pct_change()
stock_returns.head()
# plot the daily returns
stock_returns.plot()
# summarize the daily returnsstock_return
stock_returns.describe()
```
## 6. Daily S&P 500 returns
<p>For the S&P 500, calculating daily returns works just the same way, we just need to make sure we select it as a <code>Series</code> using single brackets <code>[]</code> and not as a <code>DataFrame</code> to facilitate the calculations in the next step.</p>
```
# calculate daily benchmark_data returns
sp_returns = benchmark_data['S&P 500'].pct_change()
# plot the daily returns
sp_returns.plot()
# summarize the daily returns
sp_returns.describe()
```
## 7. Calculating Excess Returns for Amazon and Facebook vs. S&P 500
<p>Next, we need to calculate the relative performance of stocks vs. the S&P 500 benchmark. This is calculated as the difference in returns between <code>stock_returns</code> and <code>sp_returns</code> for each day.</p>
```
# calculate the difference in daily returns
excess_returns = stock_returns.sub(sp_returns,axis =0)
excess_returns.head()
# plot the excess_returns
excess_returns.plot()
# summarize the excess_returns
excess_returns.describe()
```
## 8. The Sharpe Ratio, Step 1: The Average Difference in Daily Returns Stocks vs S&P 500
<p>Now we can finally start computing the Sharpe Ratio. First we need to calculate the average of the <code>excess_returns</code>. This tells us how much more or less the investment yields per day compared to the benchmark.</p>
```
# calculate the mean of excess_returns
# ... YOUR CODE FOR TASK 8 HERE ...
avg_excess_return = excess_returns.mean()
avg_excess_return
# plot avg_excess_retur(ns
avg_excess_return.plot.bar(title ='Mean of the Return')
```
## 9. The Sharpe Ratio, Step 2: Standard Deviation of the Return Difference
<p>It looks like there was quite a bit of a difference between average daily returns for Amazon and Facebook.</p>
<p>Next, we calculate the standard deviation of the <code>excess_returns</code>. This shows us the amount of risk an investment in the stocks implies as compared to an investment in the S&P 500.</p>
```
# calculate the standard deviations
sd_excess_return = excess_returns.std()
# plot the standard deviations
sd_excess_return.plot.bar(title ='Standard Deviation of the Return Difference')
```
## 10. Putting it all together
<p>Now we just need to compute the ratio of <code>avg_excess_returns</code> and <code>sd_excess_returns</code>. The result is now finally the <em>Sharpe ratio</em> and indicates how much more (or less) return the investment opportunity under consideration yields per unit of risk.</p>
<p>The Sharpe Ratio is often <em>annualized</em> by multiplying it by the square root of the number of periods. We have used daily data as input, so we'll use the square root of the number of trading days (5 days, 52 weeks, minus a few holidays): √252</p>
```
# calculate the daily sharpe ratio
daily_sharpe_ratio = avg_excess_return.div(sd_excess_return)
# annualize the sharpe ratio
annual_factor = np.sqrt(252)
annual_sharpe_ratio = daily_sharpe_ratio.mul(annual_factor)
# plot the annualized sharpe ratio
annual_sharpe_ratio.plot.bar(title ='Annualized Sharpe Ratio: Stocks vs S&P 500')
```
## 11. Conclusion
<p>Given the two Sharpe ratios, which investment should we go for? In 2016, Amazon had a Sharpe ratio twice as high as Facebook. This means that an investment in Amazon returned twice as much compared to the S&P 500 for each unit of risk an investor would have assumed. In other words, in risk-adjusted terms, the investment in Amazon would have been more attractive.</p>
<p>This difference was mostly driven by differences in return rather than risk between Amazon and Facebook. The risk of choosing Amazon over FB (as measured by the standard deviation) was only slightly higher so that the higher Sharpe ratio for Amazon ends up higher mainly due to the higher average daily returns for Amazon. </p>
<p>When faced with investment alternatives that offer both different returns and risks, the Sharpe Ratio helps to make a decision by adjusting the returns by the differences in risk and allows an investor to compare investment opportunities on equal terms, that is, on an 'apples-to-apples' basis.</p>
```
# Uncomment your choice.
buy_amazon = True
#buy_facebook = True
```
| true |
code
| 0.62601 | null | null | null | null |
|
```
import datetime
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.cross_validation import train_test_split
from ntflib import betantf
%matplotlib inline
sns.set(style="white")
```
## Defining functions for mapping and error
```
def mapper(array):
array = np.sort(array)
int_map = np.arange(len(np.unique(array))).astype(int)
dict_map = dict(zip(np.sort(np.unique(array)), int_map))
tmp = pd.Series(array)
res = tmp.map(lambda x: dict_map[x])
inv_dict_map = {v: k for k, v in dict_map.items()}
return res.values, inv_dict_map
def rmse(x, y):
return np.sqrt((x - y)**2.0).sum()
```
## Grabbing Movie Lens data
```
!wget http://files.grouplens.org/datasets/movielens/ml-1m.zip
!unzip ml-1m.zip
```
## Parsing data and cleaning it up for NTFLib
```
ratings = pd.read_table('ml-1m/ratings.dat', sep='::', names=['UserID', 'MovieID', 'Rating', 'Timestamp'])
ratings.Timestamp = ratings.Timestamp.map(lambda x: datetime.datetime.fromtimestamp(x).strftime('%Y-%m'))
# movies = pd.read_table('ml-1m/movies.dat', sep='::', names=['MovieID', 'Title', 'Genres'])
# users = pd.read_table('ml-1m/users.dat', sep='::', names=['UserID' ,'Gender', 'Age', 'Occupation::Zip-code'])
# Converting dates to integers
ratings['UserID'], inv_uid_dict = mapper(ratings['UserID'])
ratings['MovieID'], inv_mid_dict = mapper(ratings['MovieID'])
ratings['Timestamp'], inv_ts_dict = mapper(ratings['Timestamp'])
x_indices = ratings[['UserID', 'MovieID', 'Timestamp']].copy()
x_indices['UserID'] = x_indices['UserID'] - x_indices['UserID'].min()
x_indices['MovieID'] = x_indices['MovieID'] - x_indices['MovieID'].min()
x_indices['Timestamp'] = x_indices['Timestamp'] - x_indices['Timestamp'].min()
print x_indices.min()
x_indices = x_indices.values
x_vals = ratings['Rating'].values
print 'Number of unique movie IDs: {0}'.format(len(ratings['MovieID'].unique()))
print 'Max movie ID: {0}'.format(ratings['MovieID'].max())
indices_train, indices_test, val_train, val_test = train_test_split(
x_indices, x_vals, test_size=0.40, random_state=42)
shape_uid = len(np.unique(x_indices[:,0]))
shape_mid = len(np.unique(x_indices[:,1]))
shape_ts = len(np.unique(x_indices[:,2]))
shape = [shape_uid, shape_mid, shape_ts]
shape
indices_train
# shape = [len(np.unique(ratings[x])) for x in ['UserID', 'MovieID', 'Timestamp']]
bnf = betantf.BetaNTF(shape, n_components=5, n_iters=10)
before = bnf.score(indices_train, val_train)
initial = bnf.impute(x_indices)
reconstructed = bnf.fit(indices_train, val_train)
after = bnf.score()
assert(after < before)
debug
prediction = bnf.impute(indices_test)
rmse(prediction, val_test) / float(prediction.shape[0])
!cat ml-1m/README
```
| true |
code
| 0.357259 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/stephenadhi/nn-mpc/blob/main/EVALIDASI-testing.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import sys
sys.executable
import os
import matplotlib as mpl
import matplotlib.pyplot as plt
import random
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
import keras
from pandas import DataFrame
from pandas import read_csv
import math
from numpy import savetxt
from keras import layers
from tensorflow.keras.layers import Input, LSTM, Dense, Reshape, Dropout
from tensorflow.keras.models import Model, Sequential
from scipy.integrate import odeint, RK45
from tensorflow.keras.utils import plot_model
import timeit
tf.keras.backend.set_floatx('float64')
tf.keras.backend.clear_session()
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
try:
# Currently, memory growth needs to be the same across GPUs
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
logical_gpus = tf.config.experimental.list_logical_devices('GPU')
print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPUs")
except RuntimeError as e:
# Memory growth must be set before GPUs have been initialized
print(e)
```
## Mass-Spring-System
<img src="https://github.com/stephenadhi/nn-mpc/blob/main/mass-spring-damper.png?raw=1">
```
# Use ODEINT to solve the differential equations defined by the vector field
from scipy.integrate import odeint
def vectorfield(w, t, p):
"""
Defines the differential equations for the coupled spring-mass system.
Arguments:
w : vector of the state variables:
w = [x1,y1,x2,y2]
t : time
p : vector of the parameters:
p = [m1,m2,k1,k2,L1,L2,b1,b2]
"""
x1, v1, x2, v2, x3, v3 = w
m, k, kp, u1, u2, dist = p
# Create f = (x1',y1',x2',y2'):
f = [v1,
(k * ((-2 * x1) + x2) + kp * (-x1 ** 3 + (x2 - x1) ** 3)) / m + u1,
v2,
(k * (x1 - (2 * x2) + x3) + kp * ((x3 - x2) ** 3 - (x2 - x1) ** 3)) / m + u2,
v3,
(k * (x2 - x3) + kp * ((x2 - x3) ** 3)) / m + dist]
return f
```
# Use Best Training Data
```
df = pd.read_csv('u1000newage20000_0.001ssim.csv')
train_df = df
#val_df = df[int(0.5*n):int(1*n)]
val_df= pd.read_csv('u1000validationdatanewage5k_0.001ssim.csv')
test_df = pd.read_csv('u1000validationdatanewage5k_0.001ssim.csv')
#num_features = df.shape[1]
val_df.shape
train_mean = train_df.mean()
train_std = train_df.std()
train_mean
```
# Data preprocessing and NN model setup
```
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
#train_df = (train_df - train_df.min()) / (train_df.max() - train_df.min())
#val_df = (val_df - train_df.min()) / (train_df.max() - train_df.min())
#test_df = (test_df - train_df.min()) / (train_df.max() - train_df.min())
#plot
#df_std = (df - df.min()) / (df.max()-df.min())
df_std = (df - train_mean) / df.std()
#df_std.iloc[:,0:3] = df_std.iloc[:,0:3].values * 3
#df_std = (df - df.min()) / (df.max() - df.min())
df_std = df_std.astype('float64')
df_std = df_std.melt(var_name='States', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='States', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)
plt.savefig('Normalized.png', dpi=300)
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df,
#test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
def plot(self, plot_col, model=None, max_subplots=1):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(3, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Timestep ')
WindowGenerator.plot = plot
batchsize= 32
def make_dataset(self, data):
data = np.array(data, dtype=np.float64)
ds = tf.keras.preprocessing.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=False,
batch_size=batchsize,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
OUT_STEPS = 1
multi_window = WindowGenerator(input_width=1,
label_width=OUT_STEPS,
shift=OUT_STEPS,
label_columns= ['diff1','diff3']
)
multi_window.plot('diff1')
multi_window
for example_inputs, example_labels in multi_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
MAX_EPOCHS = 100
def compile(model, lr=0.001):
model.compile(loss=tf.losses.MeanSquaredError(),
optimizer=tf.optimizers.Adam(learning_rate=lr),
metrics=[tf.metrics.MeanSquaredError()],
experimental_steps_per_execution=10
)
def scheduler(epoch, lr):
if epoch > 100:
return lr * tf.math.exp(-0.01)
else: return lr
def fit(model, window, patience=150):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
callback = tf.keras.callbacks.LearningRateScheduler(scheduler)
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping,
# callback
]
)
return history
multi_val_performance = {}
multi_performance = {}
num_label=2
#set number of hidden nodes
n_hidden_nodes= 40
from functools import partial
multi_resdense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(n_hidden_nodes, activation=partial(tf.nn.leaky_relu, alpha=0.5)),
tf.keras.layers.Dense(OUT_STEPS*num_label,
kernel_initializer=tf.initializers.zeros
),
])
compile(multi_resdense_model,lr=0.001)
```
## Use best model - 40 hidden nodes
```
#Import best nodel
multi_resdense_model.load_weights('./checkpoints/0.001s20knewageresdense1-1batch32allep100lrelu40diff2u1000')
multi_window.plot('diff1',model=multi_resdense_model)
multi_window.plot('diff3',model=multi_resdense_model)
```
# Function to Standardize
```
xmean=train_mean[{'x1','x3'}]
xmean=xmean[['x1','x3']]
diffmean=train_mean[{'diff1','diff3'}]
diffmean=diffmean[['diff1','diff3']]
diffmean
xstd=train_std[{'x1','x3'}]
xstd=xstd[['x1','x3']]
diffstd=train_std[{'diff1','diff3'}]
diffstd=diffstd[['diff1','diff3']]
diffstd
def standardize(modelinput):
modelinput = (modelinput -train_mean.values) / train_std.values
return modelinput
def destandardize(modeloutput):
modeloutput = (modeloutput * train_std.values) + train_mean.values
return modeloutput
def denormalize(outputs):
outputs = outputs * diffstd + diffmean
return outputs
```
# Initial Setup
```
num_rollouts= 1
# Masses:
m = 0.5
# Spring constants
kp = 63.5
k = 217.0
# ODE solver parameters
abserr = 1.0e-8
relerr = 1.0e-6
scale=1
num_data= 4
interval= 0.001
stoptime = interval*(num_data)
np.random.seed(28)
hist= np.zeros((1,15))
hist[0,0:3]=[0,0,0]
dist = 200*(np.random.rand(num_data+1)-0.5)
#dist= np.zeros((num_data+1,1))
for roll in range(num_rollouts):
frames=0
#act1= 0*(np.random.rand(num_data+1)-0.5)
#act2= 0*(np.random.rand(num_data+1)-0.5)
act1 = np.zeros((num_data+1,1))
act2 = np.zeros((num_data+1,1))
#Initial states
w0 = np.zeros((1,6))
#w0= np.random.randn(1,6)
w0= w0.flatten()
prev = [[w0[0],w0[4]]]
value1= w0[0]
value3= w0[4]
# Pack up the parameters and initial conditions:
p = [m, k, kp, act1[0], dist[0], act2[0]]
# Call the ODE solver.
t1= np.array([0,interval])
wsol1 = odeint(vectorfield, w0, t1, args=(p,),
atol=abserr, rtol=relerr)
wsol1 = wsol1.flatten()
wcurr = np.array([wsol1[6:]])
w0=wsol1[6:]
diff1= w0[0] - value1
diff3= w0[4] - value3
diff= [[diff1, diff3]]
diff2=diff
#curr = np.hstack((np.array([[act1[1]]]),np.array([[dist[1]]]),np.array([[act2[1]]]),prev,diff2,diff,wcurr))
curr = np.hstack((np.array([act1[1]]),np.array([[dist[1]]]),np.array([act2[1]]),prev,diff2,diff, wcurr))
hist= np.vstack((hist, curr))
#print(w0)
prevv= prev
prev = [[w0[0],w0[4]]]
value11=value1
value33=value3
value1= w0[0]
value3= w0[4]
# Pack up the parameters and initial conditions:
p = [m, k, kp, act1[1], dist[1],act2[1]]
# Call the ODE solver.
t2= np.array([0+interval,interval+interval])
wsol1 = odeint(vectorfield, w0, t2, args=(p,),
atol=abserr, rtol=relerr)
wsol1 = wsol1.flatten()
wcurr = np.array([wsol1[6:]])
w0=wsol1[6:]
diff1= w0[0] - value1
diff3= w0[4] - value3
diff21= w0[0] - value11
diff23= w0[4] - value33
diff= [[diff1, diff3]]
diff2= [[diff21, diff23]]
#print(w0)
# curr = np.hstack((np.array([[act1[2]]]),np.array([[dist[2]]]),np.array([[act2[2]]]),prev,diff2,diff, wcurr))
curr = np.hstack((np.array([act1[2]]),np.array([[dist[2]]]),np.array([act2[2]]),prev,diff2,diff, wcurr))
hist= np.vstack((hist, curr))
lag=2
for ts in range(num_data-lag):
prevv = prev
t = np.array([stoptime * float(ts+lag) / (num_data), stoptime * float(ts + lag + 1) / (num_data)])
p = [m, k, kp, act1[ts+lag],dist[ts+lag], act2[ts+lag]]
# Call the ODE solver.
wsol1 = odeint(vectorfield, w0, t, args=(p,),atol=abserr, rtol=relerr)
wsol1 = wsol1.flatten()
prev = np.array([[wsol1[0],wsol1[4]]])
value11=value1
value33=value3
value1= wsol1[0]
value3= wsol1[4]
w0 = wsol1[6:]
#print(ts)
#print(w0)
diff1= w0[0] - value1
diff3= w0[4] - value3
diff21= w0[0] - value11
diff23= w0[4] - value33
diff= [[diff1, diff3]]
diff2= [[diff21, diff23]]
action= [act1[ts+lag+1],dist[ts+lag+1]]
#new = np.hstack((np.array([action]),np.array([[act2[ts+lag+1]]]),prev,diff2,diff, np.array([w0])))
new = np.hstack((np.array([act1[ts+lag+1]]),np.array([[dist[ts+lag+1]]]),np.array([act2[ts+lag+1]]),prev,diff2,diff, np.array([w0])))
# print("new: ",new)
hist = np.vstack((hist, new))
history=pd.DataFrame(data=hist,columns =["u1","dist.","u2","prev1","prev3","diff21","diff23","diff1","diff3","x1", "v1", "x2", "v2", "x3", "v3"])
historyy=pd.DataFrame(history[:])
history=historyy[-3:][{"u1","u2","diff21","diff23","dist.","diff1","diff3","x1","x3"}]
history=history[["u1","dist.","u2","x1","x3","diff21","diff23","diff1","diff3"]]
history=history.values
historyy
```
# **Simulating Control Strategy**
```
currentcost=10
horizon= 10
chor= int(horizon / 2)
ts=0
ref = np.ones((horizon,2))
ref[:,1]*=2
num_sim= 1
num_randactions=50
maxdeltau= 1000
maxact= 1000
minact= -maxact
scale=1
histo= np.zeros((3,9))
bestpred= np.zeros((horizon,2))
temp= history
#print("newtemp : ",temp)
savecost=np.zeros((num_sim,1))
start_time = timeit.default_timer()
for run in range(num_sim):
ts+=1
minJ=10000
bestaction= np.zeros((horizon,2))
#if currentcost > 0.5 and currentcost < 1:
# scale=0.8
#elif currentcost > 0.2 and currentcost < 0.5:
# scale=0.6
#elif currentcost > 0.1 and currentcost <0.2:
# scale=0.4
#print("scale: ", scale)
for jj in range (num_randactions):
histo[:]= temp[:]
prevaction= [histo[-1,0], histo[-1,2]]
action= np.ones((horizon,2)) * prevaction
for plan in range(chor):
actii= maxdeltau*2*(np.random.rand(1,2)-0.5)
action[plan:] += actii
if action[plan,0] > maxact:
action[plan:,0] = maxact
if action[plan,0] < minact:
action[plan:,0] = minact
if action[plan,1] > maxact:
action[plan:,1] = maxact
if action[plan,1] < minact:
action[plan:,1] = minact
# print("action: \n", action)
#print("histtemp: ", histo)
prednorm = np.zeros((horizon,2))
predstate = np.zeros((horizon,2))
#deltaaction= currentcost / 10000000 * np.sum((action[0]-prevaction)**2 + (action[2]-action[1])**2 + (action[1]-action[0])**2)
dist= 100*(np.random.rand(1)-0.5)
for kk in range(horizon):
histo[-1,0] = action[kk,0]
histo[-1,1] = disturb
histo[-1,2] = action[kk,1]
curr = histo[-1,3:5]
historstd=standardize(histo)
prednorm[kk,:]=denormalize(multi_resdense_model(np.array([historstd]))[0])
predstate[kk,:]= curr + prednorm[kk,:]
#print("currstate: ",histo[-1,3:5])
#print("currpreddiff: ", prednorm)
#print("predstate: ", predstate)
#histo[0:-1] = histo[1:]
#histo[-1,1]= disturb
histo[-1,3:5]= predstate[kk,:]
histo[-1,5:7]= histo[-1,-2:] + prednorm[kk,:]
histo[-1,-2:]= prednorm[kk,:]
predJ= np.sum((predstate - ref) ** 2)
if currentcost < 100:
#predJ += deltaaction
predJ+= 10*((predstate[horizon-1,0] - predstate[0,0])**2)*currentcost
predJ+= 10*((predstate[horizon-1,1] - predstate[0,1])**2)*currentcost
#penalize small change when large error
#if currentcost > 1:
# predJ -= 1000 * ((prednorm[5,1] - prednorm[0,1])**2)
#penalize big change when small error
#if currentcost < 0.5:
# predJ += 1000 * ((prednorm[5,1] - prednorm[0,1])**2)
#(prednorm[0,1] -ref[0,1])**2 + (prednorm[1,1] -ref[1,1])**2
#+ (prednorm[2,1] -ref[2,1])**2 + (prednorm[3,1] -ref[3,1])**2
#+ (prednorm[4,1] -ref[4,1])**2 + (prednorm[5,1] -ref[5,1])**2
#+ (prednorm[0,0] -ref[0,0])**2 + (prednorm[1,0] -ref[1,0])**2
#+ (prednorm[2,0] -ref[2,0])**2 + (prednorm[3,0] -ref[3,0])**2
#+ (prednorm[4,0] -ref[4,0])**2 + (prednorm[5,0] -ref[5,0])**2
#print(prednorm)
if predJ < minJ:
bestaction = action
minJ = predJ
bestpred= predstate
elapsed = timeit.default_timer() - start_time
print(elapsed)
thisishistory=pd.DataFrame(data=hist,columns =["u1","dist.","u2","prev1","prev3","diff21","diff23","diff1","diff3","x1", "v1", "x2", "v2", "x3", "v3"])
thisishistory
```
# Save to .CSV
```
#thisishistory.to_csv('dist50sim300-1000-1000-pen10xcost.csv',index=False)
thisishistory= pd.read_csv('1611changemassnodistchangerefreinf_startsim40000_train500-250_batch16sim300-1000-1000-pen5.csv')
thisishistory[40000:]
```
# Evaluate using Designed Metrics
```
actionshist= np.hstack([np.array([thisishistory.iloc[3:-1,0].values]).transpose(),np.array([thisishistory.iloc[3:-1,2].values]).transpose()])
actionshistory=pd.DataFrame(data=actionshist, columns=["u1","u2"])
actionshistory.insert(1,"prevu1", actionshistory.iloc[:,0].shift(1))
actionshistory.insert(3,"prevu2", actionshistory.iloc[:,2].shift(1))
diffu1= actionshistory["u1"] - actionshistory["prevu1"]
diffu2= actionshistory["u2"] - actionshistory["prevu2"]
actionshistory.insert(4,"diffu2", diffu2)
actionshistory.insert(2,"diffu1", diffu1)
deltaudt= actionshistory[["diffu1","diffu2"]]
deltaudt=deltaudt.dropna()
np.sqrt(deltaudt[40000:] ** 2).mean()
meanu=np.sqrt(np.square(thisishistory.iloc[40000:,:3])).mean()
meanu
thisishistory.min()
meandiff= np.sqrt(np.square(thisishistory.iloc[40000:,-2:])).mean()
meandiff
#action_sequence= thisishistory.iloc[:,0:3].values
#action_sequence=pd.DataFrame(action_sequence)
#action_sequence.to_csv('action_sequence.csv', index=False)
plot_out=['x1','x3']
thisishistory.iloc[40001]
RMSE= (np.sqrt(np.square(thisishistory[plot_out][40100:40300].values - [1,2]).mean()) + np.sqrt(np.square(thisishistory[plot_out][40400:40600].values - [0,0]).mean()))/2
RMSE
```
# Plotting
```
fig, axs = plt.subplots(3, sharex=False,figsize=(15,10))
x= range(600)
y1=thisishistory.iloc[-600:,3].values
y2=thisishistory.iloc[-600:,4].values
ref=np.ones((600,2))
ref[:,1]*=2
#both=np.hstack((y,ref))
z=thisishistory.iloc[-600:,4].values
uone= thisishistory.iloc[-600:,0].values
utwo= thisishistory.iloc[-600:,2].values
params = {'mathtext.default': 'regular' }
plt.rcParams.update(params)
#axs[0].set_title('System Outputs over Time', fontsize=20)
axs[0].plot(x, y1, label='$x_1$')
axs[0].plot(x, y2, label='$x_3$')
axs[0].plot(x, ref[:,0], 'k:',label= '$x_1,ref$')
axs[0].plot(x, ref[:,1], 'k:',label= '$x_3,ref$')
axs[1].plot(x, uone, 'k')
axs[2].plot(x, utwo,'k')
axs[0].set_ylabel("Position (m)", fontsize=12)
axs[1].set_ylabel("Actuator Force u1 (N)",fontsize=12)
axs[2].set_ylabel("Actuator Force u2 (N)", fontsize=12)
axs[2].set_xlabel("Timestep", fontsize=14)
#fig.legend(loc='upper right',bbox_to_anchor=(0.4, 0.26, 0.5, 0.62),fontsize=10)
fig.legend(loc='upper right',bbox_to_anchor=(0.4, 0.26, 0.50, 0.62),fontsize=10)
#plt.savefig('dist50sim300-1000-1000-pen10xcost.png', dpi=300)
fig, axs = plt.subplots(3, sharex=False,figsize=(15,10))
x= range(600)
y1=thisishistory.iloc[-600:,3].values
y2=thisishistory.iloc[-600:,4].values
ref=np.ones((600,2))
ref[:,1]*=2
ref[300:,:]=0
#both=np.hstack((y,ref))
z=thisishistory.iloc[-600:,4].values
uone= thisishistory.iloc[-600:,0].values
utwo= thisishistory.iloc[-600:,2].values
params = {'mathtext.default': 'regular' }
plt.rcParams.update(params)
#axs[0].set_title('System Outputs over Time', fontsize=20)
axs[0].plot(x, y1, label='$x_1$')
axs[0].plot(x, y2, label='$x_3$')
axs[0].plot(x, ref[:,0], 'k:',label= '$x_1,ref$')
axs[0].plot(x, ref[:,1], 'k:',label= '$x_3,ref$')
axs[1].plot(x, uone, 'k')
axs[2].plot(x, utwo,'k')
axs[0].set_ylabel("Position (m)", fontsize=12)
axs[1].set_ylabel("Actuator Force u1 (N)",fontsize=12)
axs[2].set_ylabel("Actuator Force u2 (N)", fontsize=12)
axs[2].set_xlabel("Timestep", fontsize=14)
#fig.legend(loc='upper right',bbox_to_anchor=(0.4, 0.26, 0.5, 0.62),fontsize=10)
fig.legend(loc='upper right',bbox_to_anchor=(0.4, 0.26, 0.5, 0.62),fontsize=10)
plt.savefig('changemassreinf.png', dpi=300)
axs[1].plot(x, uone, 'k')
axs[2].plot(x, utwo,'k')
axs[0].set_ylabel("Position (m)")
axs[0].set_xlabel("Timestep")
axs[1].set_ylabel("u1 (N)")
axs[2].set_ylabel("u2 (N)")
axs[2].set_xlabel("Timestep")
from matplotlib import rc
fig, axs = plt.subplots(2, sharex=True,figsize=(16,4))
x= range(600)
r1= np.sqrt(np.square(thisishistory[plot_out][-600:].values - [1,2]))[:,0]
r2= np.sqrt(np.square(thisishistory[plot_out][-600:].values - [1,2]))[:,1]
r= (r1+r2)/2
du1=deltaudt.iloc[-600:,0].values
du2=deltaudt.iloc[-600:,1].values
du=(du1+du2)/2
fig.suptitle(r'Control RMSE and Average $\Delta$u over Time')
axs[0].semilogy(x,r)
axs[1].plot(x,du)
axs[0].set_ylabel('RMSE')
axs[1].set_ylabel(r'Average $\Delta$u')
axs[1].set_xlabel("Time (ms)")
#axs[0].set_title("Position (m)")
#axs[0].plot(range(5000), aaa.iloc[:,3].values, 'B')
#plt.savefig('reinf_startsim10000_train500-250_batch16sim300-1000-1000-pen10xcost.png', dpi=300)
```
| true |
code
| 0.660665 | null | null | null | null |
|
# <div style="text-align: center">Linear Algebra for Data Scientists
<div style="text-align: center">One of the most common questions we get on <b>Data science</b> is:
<br>
How much maths do I need to learn to be a <b>data scientist</b>?
<br>
If you get confused and ask experts what should you learn at this stage, most of them would suggest / agree that you go ahead with Linear Algebra!
This is the third step of the [10 Steps to Become a Data Scientist](https://www.kaggle.com/mjbahmani/10-steps-to-become-a-data-scientist). and you can learn all of the thing you need for being a data scientist with Linear Algabra.</div>
<div style="text-align:center">last update: <b>12/12/2018</b></div>
You can Fork code and Follow me on:
> ###### [ GitHub](https://github.com/mjbahmani/10-steps-to-become-a-data-scientist)
> ###### [Kaggle](https://www.kaggle.com/mjbahmani/)
-------------------------------------------------------------------------------------------------------------
<b>I hope you find this kernel helpful and some <font color='blue'>UPVOTES</font> would be very much appreciated.</b>
-----------
<a id="top"></a> <br>
## Notebook Content
1. [Introduction](#1)
1. [Basic Concepts](#2)
1. [Notation ](#2)
1. [Matrix Multiplication](#3)
1. [Vector-Vector Products](#4)
1. [Outer Product of Two Vectors](#5)
1. [Matrix-Vector Products](#6)
1. [Matrix-Matrix Products](#7)
1. [Identity Matrix](#8)
1. [Diagonal Matrix](#9)
1. [Transpose of a Matrix](#10)
1. [Symmetric Metrices](#11)
1. [The Trace](#12)
1. [Norms](#13)
1. [Linear Independence and Rank](#14)
1. [Column Rank of a Matrix](#15)
1. [Row Rank of a Matrix](#16)
1. [Rank of a Matrix](#17)
1. [Subtraction and Addition of Metrices](#18)
1. [Inverse](#19)
1. [Orthogonal Matrices](#20)
1. [Range and Nullspace of a Matrix](#21)
1. [Determinant](#22)
1. [geometric interpretation of the determinant](#23)
1. [Tensors](#24)
1. [Hyperplane](#25)
1. [Eigenvalues and Eigenvectors](#30)
1. [Exercise](#31)
1. [Conclusion](#32)
1. [References](#33)
<a id="1"></a> <br>
# 1-Introduction
This is the third step of the [10 Steps to Become a Data Scientist](https://www.kaggle.com/mjbahmani/10-steps-to-become-a-data-scientist).
**Linear algebra** is the branch of mathematics that deals with **vector spaces**. good understanding of Linear Algebra is intrinsic to analyze Machine Learning algorithms, especially for **Deep Learning** where so much happens behind the curtain.you have my word that I will try to keep mathematical formulas & derivations out of this completely mathematical topic and I try to cover all of subject that you need as data scientist.
<img src='https://camo.githubusercontent.com/e42ea0e40062cc1e339a6b90054bfbe62be64402/68747470733a2f2f63646e2e646973636f72646170702e636f6d2f6174746163686d656e74732f3339313937313830393536333530383733382f3434323635393336333534333331383532382f7363616c61722d766563746f722d6d61747269782d74656e736f722e706e67' height=200 width=700>
<a id="top"></a> <br>
*Is there anything more useless or less useful than Algebra?*
**Billy Connolly**
## 1-1 Import
```
import matplotlib.patches as patch
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy import linalg
from sklearn import svm
import tensorflow as tf
import pandas as pd
import numpy as np
import glob
import sys
import os
```
## 1-2 Setup
```
%matplotlib inline
%precision 4
plt.style.use('ggplot')
np.set_printoptions(suppress=True)
```
<a id="1"></a> <br>
# 2- Basic Concepts
The following system of equations:
$\begin{equation}
\begin{split}
4 x_1 - 5 x_2 & = -13 \\
-2x_1 + 3 x_2 & = 9
\end{split}
\end{equation}$
We are looking for a unique solution for the two variables $x_1$ and $x_2$. The system can be described as:
\begin{align}
\dot{x} & = \sigma(y-x) \\
\dot{y} & = \rho x - y - xz \\
\dot{z} & = -\beta z + xy
\end{align}
$$
Ax=b
$$
as matrices:
$$A = \begin{bmatrix}
4 & -5 \\[0.3em]
-2 & 3
\end{bmatrix},\
b = \begin{bmatrix}
-13 \\[0.3em]
9
\end{bmatrix}$$
A **scalar** is an element in a vector, containing a real number **value**. In a vector space model or a vector mapping of (symbolic, qualitative, or quantitative) properties the scalar holds the concrete value or property of a variable.
A **vector** is an array, tuple, or ordered list of scalars (or elements) of size $n$, with $n$ a positive integer. The **length** of the vector, that is the number of scalars in the vector, is also called the **order** of the vector.
<img src='https://cnx.org/resources/ba7a89a854e2336c540409615dbf47aa44155c56/pic002.png' height=400 width=400>
<a id="top"></a> <br>
```
#3-dimensional vector in numpy
a = np.zeros((2, 3, 4))
#l = [[[ 0., 0., 0., 0.],
# [ 0., 0., 0., 0.],
# [ 0., 0., 0., 0.]],
# [[ 0., 0., 0., 0.],
# [ 0., 0., 0., 0.],
# [ 0., 0., 0., 0.]]]
a
# Declaring Vectors
x = [1, 2, 3]
y = [4, 5, 6]
print(type(x))
# This does'nt give the vector addition.
print(x + y)
# Vector addition using Numpy
z = np.add(x, y)
print(z)
print(type(z))
# Vector Cross Product
mul = np.cross(x, y)
print(mul)
```
**Vectorization** is the process of creating a vector from some data using some process.
Vectors of the length $n$ could be treated like points in $n$-dimensional space. One can calculate the distance between such points using measures like [Euclidean Distance](https://en.wikipedia.org/wiki/Euclidean_distance). The similarity of vectors could also be calculated using [Cosine Similarity](https://en.wikipedia.org/wiki/Cosine_similarity).
###### [Go to top](#top)
<a id="2"></a> <br>
## 3- Notation
A **matrix** is a list of vectors that all are of the same length. $A$ is a matrix with $m$ rows and $n$ columns, antries of $A$ are real numbers:
$A \in \mathbb{R}^{m \times n}$
A vector $x$ with $n$ entries of real numbers, could also be thought of as a matrix with $n$ rows and $1$ column, or as known as a **column vector**.
$x = \begin{bmatrix}
x_1 \\[0.3em]
x_2 \\[0.3em]
\vdots \\[0.3em]
x_n
\end{bmatrix}$
Representing a **row vector**, that is a matrix with $1$ row and $n$ columns, we write $x^T$ (this denotes the transpose of $x$, see above).
$x^T = \begin{bmatrix}
x_1 & x_2 & \cdots & x_n
\end{bmatrix}$
We use the notation $a_{ij}$ (or $A_{ij}$, $A_{i,j}$, etc.) to denote the entry of $A$ in the $i$th row and
$j$th column:
$A = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\[0.3em]
a_{21} & a_{22} & \cdots & a_{2n} \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix}$
We denote the $j$th column of $A$ by $a_j$ or $A_{:,j}$:
$A = \begin{bmatrix}
\big| & \big| & & \big| \\[0.3em]
a_{1} & a_{2} & \cdots & a_{n} \\[0.3em]
\big| & \big| & & \big|
\end{bmatrix}$
We denote the $i$th row of $A$ by $a_i^T$ or $A_{i,:}$:
$A = \begin{bmatrix}
-- & a_1^T & -- \\[0.3em]
-- & a_2^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_m^T & --
\end{bmatrix}$
A $n \times m$ matrix is a **two-dimensional** array with $n$ rows and $m$ columns.
###### [Go to top](#top)
<a id="3"></a> <br>
## 4-Matrix Multiplication
The result of the multiplication of two matrixes $A \in \mathbb{R}^{m \times n}$ and $B \in \mathbb{R}^{n \times p}$ is the matrix:
```
# initializing matrices
x = np.array([[1, 2], [4, 5]])
y = np.array([[7, 8], [9, 10]])
```
$C = AB \in \mathbb{R}^{m \times n}$
That is, we are multiplying the columns of $A$ with the rows of $B$:
$C_{ij}=\sum_{k=1}^n{A_{ij}B_{kj}}$
<img src='https://cdn.britannica.com/06/77706-004-31EE92F3.jpg'>
The number of columns in $A$ must be equal to the number of rows in $B$.
###### [Go to top](#top)
```
# using add() to add matrices
print ("The element wise addition of matrix is : ")
print (np.add(x,y))
# using subtract() to subtract matrices
print ("The element wise subtraction of matrix is : ")
print (np.subtract(x,y))
# using divide() to divide matrices
print ("The element wise division of matrix is : ")
print (np.divide(x,y))
# using multiply() to multiply matrices element wise
print ("The element wise multiplication of matrix is : ")
print (np.multiply(x,y))
```
<a id="4"></a> <br>
## 4-1 Vector-Vector Products
Inner or Dot **Product** of Two Vectors.
For two vectors $x, y \in \mathbb{R}^n$, the **inner product** or **dot product** $x^T y$ is a real number:
$x^T y \in \mathbb{R} = \begin{bmatrix}
x_1 & x_2 & \cdots & x_n
\end{bmatrix} \begin{bmatrix}
y_1 \\[0.3em]
y_2 \\[0.3em]
\vdots \\[0.3em]
y_n
\end{bmatrix} = \sum_{i=1}^{n}{x_i y_i}$
The **inner products** are a special case of matrix multiplication.
It is always the case that $x^T y = y^T x$.
##### Example
To calculate the inner product of two vectors $x = [1 2 3 4]$ and $y = [5 6 7 8]$, we can loop through the vector and multiply and sum the scalars (this is simplified code):
```
x = (1, 2, 3, 4)
y = (5, 6, 7, 8)
n = len(x)
if n == len(y):
result = 0
for i in range(n):
result += x[i] * y[i]
print(result)
```
It is clear that in the code above we could change line 7 to `result += y[i] * x[i]` without affecting the result.
###### [Go to top](#top)
We can use the *numpy* module to apply the same operation, to calculate the **inner product**. We import the *numpy* module and assign it a name *np* for the following code:
We define the vectors $x$ and $y$ using *numpy*:
```
x = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
print("x:", x)
print("y:", y)
```
We can now calculate the $dot$ or $inner product$ using the *dot* function of *numpy*:
```
np.dot(x, y)
```
The order of the arguments is irrelevant:
```
np.dot(y, x)
```
Note that both vectors are actually **row vectors** in the above code. We can transpose them to column vectors by using the *shape* property:
```
print("x:", x)
x.shape = (4, 1)
print("xT:", x)
print("y:", y)
y.shape = (4, 1)
print("yT:", y)
```
In fact, in our understanding of Linear Algebra, we take the arrays above to represent **row vectors**. *Numpy* treates them differently.
We see the issues when we try to transform the array objects. Usually, we can transform a row vector into a column vector in *numpy* by using the *T* method on vector or matrix objects:
###### [Go to top](#top)
```
x = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
print("x:", x)
print("y:", y)
print("xT:", x.T)
print("yT:", y.T)
```
The problem here is that this does not do, what we expect it to do. It only works, if we declare the variables not to be arrays of numbers, but in fact a matrix:
```
x = np.array([[1, 2, 3, 4]])
y = np.array([[5, 6, 7, 8]])
print("x:", x)
print("y:", y)
print("xT:", x.T)
print("yT:", y.T)
```
Note that the *numpy* functions *dot* and *outer* are not affected by this distinction. We can compute the dot product using the mathematical equation above in *numpy* using the new $x$ and $y$ row vectors:
###### [Go to top](#top)
```
print("x:", x)
print("y:", y.T)
np.dot(x, y.T)
```
Or by reverting to:
```
print("x:", x.T)
print("y:", y)
np.dot(y, x.T)
```
To read the result from this array of arrays, we would need to access the value this way:
```
np.dot(y, x.T)[0][0]
```
<a id="5"></a> <br>
## 4-2 Outer Product of Two Vectors
For two vectors $x \in \mathbb{R}^m$ and $y \in \mathbb{R}^n$, where $n$ and $m$ do not have to be equal, the **outer product** of $x$ and $y$ is:
$xy^T \in \mathbb{R}^{m\times n}$
The **outer product** results in a matrix with $m$ rows and $n$ columns by $(xy^T)_{ij} = x_i y_j$:
$xy^T \in \mathbb{R}^{m\times n} = \begin{bmatrix}
x_1 \\[0.3em]
x_2 \\[0.3em]
\vdots \\[0.3em]
x_n
\end{bmatrix} \begin{bmatrix}
y_1 & y_2 & \cdots & y_n
\end{bmatrix} = \begin{bmatrix}
x_1 y_1 & x_1 y_2 & \cdots & x_1 y_n \\[0.3em]
x_2 y_1 & x_2 y_2 & \cdots & x_2 y_n \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
x_m y_1 & x_m y_2 & \cdots & x_m y_n \\[0.3em]
\end{bmatrix}$
Some useful property of the outer product: assume $\mathbf{1} \in \mathbb{R}^n$ is an $n$-dimensional vector of scalars with the value $1$. Given a matrix $A \in \mathbb{R}^{m\times n}$ with all columns equal to some vector $x \in \mathbb{R}^m$, using the outer product $A$ can be represented as:
$A = \begin{bmatrix}
\big| & \big| & & \big| \\[0.3em]
x & x & \cdots & x \\[0.3em]
\big| & \big| & & \big|
\end{bmatrix} = \begin{bmatrix}
x_1 & x_1 & \cdots & x_1 \\[0.3em]
x_2 & x_2 & \cdots & x_2 \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
x_m &x_m & \cdots & x_m
\end{bmatrix} = \begin{bmatrix}
x_1 \\[0.3em]
x_2 \\[0.3em]
\vdots \\[0.3em]
x_m
\end{bmatrix} \begin{bmatrix}
1 & 1 & \cdots & 1
\end{bmatrix} = x \mathbf{1}^T$
```
x = np.array([[1, 2, 3, 4]])
print("x:", x)
print("xT:", np.reshape(x, (4, 1)))
print("xT:", x.T)
print("xT:", x.transpose())
```
Example
###### [Go to top](#top)
We can now compute the **outer product** by multiplying the column vector $x$ with the row vector $y$:
```
x = np.array([[1, 2, 3, 4]])
y = np.array([[5, 6, 7, 8]])
x.T * y
```
*Numpy* provides an *outer* function that does all that:
```
np.outer(x, y)
```
Note, in this simple case using the simple arrays for the data structures of the vectors does not affect the result of the *outer* function:
```
x = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
np.outer(x, y)
```
<a id="6"></a> <br>
## 4-3 Matrix-Vector Products
Assume a matrix $A \in \mathbb{R}^{m\times n}$ and a vector $x \in \mathbb{R}^n$ the product results in a vector $y = Ax \in \mathbb{R}^m$.
$Ax$ could be expressed as the dot product of row $i$ of matrix $A$ with the column value $j$ of vector $x$. Let us first consider matrix multiplication with a scalar:
###### [Go to top](#top)
$A = \begin{bmatrix}
1 & 2 \\[0.3em]
3 & 4
\end{bmatrix}$
We can compute the product of $A$ with a scalar $n = 2$ as:
$A = \begin{bmatrix}
1 * n & 2 * n \\[0.3em]
3 * n & 4 * n
\end{bmatrix} = \begin{bmatrix}
1 * 2 & 2 * 2 \\[0.3em]
3 * 2 & 4 * 2
\end{bmatrix} = \begin{bmatrix}
2 & 4 \\[0.3em]
6 & 8
\end{bmatrix} $
Using *numpy* this can be achieved by:
```
import numpy as np
A = np.array([[4, 5, 6],
[7, 8, 9]])
A * 2
```
Assume that we have a column vector $x$:
$x = \begin{bmatrix}
1 \\[0.3em]
2 \\[0.3em]
3
\end{bmatrix}$
To be able to multiply this vector with a matrix, the number of columns in the matrix must correspond to the number of rows in the column vector. The matrix $A$ must have $3$ columns, as for example:
$A = \begin{bmatrix}
4 & 5 & 6\\[0.3em]
7 & 8 & 9
\end{bmatrix}$
To compute $Ax$, we multiply row $1$ of the matrix with column $1$ of $x$:
$\begin{bmatrix}
4 & 5 & 6
\end{bmatrix}
\begin{bmatrix}
1 \\[0.3em]
2 \\[0.3em]
3
\end{bmatrix} = 4 * 1 + 5 * 2 + 6 * 3 = 32 $
We do the compute the dot product of row $2$ of $A$ and column $1$ of $x$:
$\begin{bmatrix}
7 & 8 & 9
\end{bmatrix}
\begin{bmatrix}
1 \\[0.3em]
2 \\[0.3em]
3
\end{bmatrix} = 7 * 1 + 8 * 2 + 9 * 3 = 50 $
The resulting column vector $Ax$ is:
$Ax = \begin{bmatrix}
32 \\[0.3em]
50
\end{bmatrix}$
Using *numpy* we can compute $Ax$:
```
A = np.array([[4, 5, 6],
[7, 8, 9]])
x = np.array([1, 2, 3])
A.dot(x)
```
We can thus describe the product writing $A$ by rows as:
<a id="top"></a> <br>
$y = Ax = \begin{bmatrix}
-- & a_1^T & -- \\[0.3em]
-- & a_2^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_m^T & --
\end{bmatrix} x = \begin{bmatrix}
a_1^T x \\[0.3em]
a_2^T x \\[0.3em]
\vdots \\[0.3em]
a_m^T x
\end{bmatrix}$
This means that the $i$th scalar of $y$ is the inner product of the $i$th row of $A$ and $x$, that is $y_i = a_i^T x$.
If we write $A$ in column form, then:
$y = Ax =
\begin{bmatrix}
\big| & \big| & & \big| \\[0.3em]
a_1 & a_2 & \cdots & a_n \\[0.3em]
\big| & \big| & & \big|
\end{bmatrix}
\begin{bmatrix}
x_1 \\[0.3em]
x_2 \\[0.3em]
\vdots \\[0.3em]
x_n
\end{bmatrix} =
\begin{bmatrix}
a_1
\end{bmatrix} x_1 +
\begin{bmatrix}
a_2
\end{bmatrix} x_2 + \dots +
\begin{bmatrix}
a_n
\end{bmatrix} x_n
$
In this case $y$ is a **[linear combination](https://en.wikipedia.org/wiki/Linear_combination)** of the *columns* of $A$, the coefficients taken from $x$.
The above examples multiply be the right with a column vector. One can multiply on the left by a row vector as well, $y^T = x^T A$ for $A \in \mathbb{R}^{m\times n}$, $x\in \mathbb{R}^m$, $y \in \mathbb{R}^n$. There are two ways to express $y^T$, with $A$ expressed by its columns, with $i$th scalar of $y^T$ corresponds to the inner product of $x$ and the $i$th column of $A$:
$y^T = x^T A = x^t \begin{bmatrix}
\big| & \big| & & \big| \\[0.3em]
a_1 & a_2 & \cdots & a_n \\[0.3em]
\big| & \big| & & \big|
\end{bmatrix} =
\begin{bmatrix}
x^T a_1 & x^T a_2 & \dots & x^T a_n
\end{bmatrix}$
One can express $A$ by rows, where $y^T$ is a linear combination of the rows of $A$ with the scalars from $x$.
$\begin{equation}
\begin{split}
y^T & = x^T A \\
& = \begin{bmatrix}
x_1 & x_2 & \dots & x_n
\end{bmatrix}
\begin{bmatrix}
-- & a_1^T & -- \\[0.3em]
-- & a_2^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_m^T & --
\end{bmatrix} \\
& = x_1 \begin{bmatrix}-- & a_1^T & --\end{bmatrix} + x_2 \begin{bmatrix}-- & a_2^T & --\end{bmatrix} + \dots + x_n \begin{bmatrix}-- & a_n^T & --\end{bmatrix}
\end{split}
\end{equation}$
###### [Go to top](#top)
<a id="7"></a> <br>
## 4-4 Matrix-Matrix Products
One can view matrix-matrix multiplication $C = AB$ as a set of vector-vector products. The $(i,j)$th entry of $C$ is the inner product of the $i$th row of $A$ and the $j$th column of $B$:
```
matrix1 = np.matrix(
[[0, 4],
[2, 0]]
)
matrix2 = np.matrix(
[[-1, 2],
[1, -2]]
)
matrix1 + matrix2
matrix1 - matrix2
```
### 4-4-1 Multiplication
To multiply two matrices with numpy, you can use the np.dot method:
```
np.dot(matrix1, matrix2)
matrix1 * matrix2
```
$C = AB =
\begin{bmatrix}
-- & a_1^T & -- \\[0.3em]
-- & a_2^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_m^T & --
\end{bmatrix}
\begin{bmatrix}
\big| & \big| & & \big| \\[0.3em]
b_1 & b_2 & \cdots & b_p \\[0.3em]
\big| & \big| & & \big|
\end{bmatrix} =
\begin{bmatrix}
a_1^T b_1 & a_1^T b_2 & \cdots & a_1^T b_p \\[0.3em]
a_2^T b_1 & a_2^T b_2 & \cdots & a_2^T b_p \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
a_m^T b_1 & a_m^T b_2 & \cdots & a_m^T b_p
\end{bmatrix}$
Here $A \in \mathbb{R}^{m\times n}$ and $B \in \mathbb{R}^{n\times p}$, $a_i \in \mathbb{R}^n$ and $b_j \in \mathbb{R}^n$, and $A$ is represented by rows, $B$ by columns.
If we represent $A$ by columns and $B$ by rows, then $AB$ is the sum of the outer products:
$C = AB =
\begin{bmatrix}
\big| & \big| & & \big| \\[0.3em]
a_1 & a_2 & \cdots & a_n \\[0.3em]
\big| & \big| & & \big|
\end{bmatrix}
\begin{bmatrix}
-- & b_1^T & -- \\[0.3em]
-- & b_2^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & b_n^T & --
\end{bmatrix}
= \sum_{i=1}^n a_i b_i^T
$
This means that $AB$ is the sum over all $i$ of the outer product of the $i$th column of $A$ and the $i$th row of $B$.
One can interpret matrix-matrix operations also as a set of matrix-vector products. Representing $B$ by columns, the columns of $C$ are matrix-vector products between $A$ and the columns of $B$:
$C = AB = A
\begin{bmatrix}
\big| & \big| & & \big| \\[0.3em]
b_1 & b_2 & \cdots & b_p \\[0.3em]
\big| & \big| & & \big|
\end{bmatrix} =
\begin{bmatrix}
\big| & \big| & & \big| \\[0.3em]
A b_1 & A b_2 & \cdots & A b_p \\[0.3em]
\big| & \big| & & \big|
\end{bmatrix}
$
In this interpretation the $i$th column of $C$ is the matrix-vector product with the vector on the right, i.e. $c_i = A b_i$.
Representing $A$ by rows, the rows of $C$ are the matrix-vector products between the rows of $A$ and $B$:
$C = AB = \begin{bmatrix}
-- & a_1^T & -- \\[0.3em]
-- & a_2^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_m^T & --
\end{bmatrix}
B =
\begin{bmatrix}
-- & a_1^T B & -- \\[0.3em]
-- & a_2^T B & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_n^T B & --
\end{bmatrix}$
The $i$th row of $C$ is the matrix-vector product with the vector on the left, i.e. $c_i^T = a_i^T B$.
#### Notes on Matrix-Matrix Products
**Matrix multiplication is associative:** $(AB)C = A(BC)$
**Matrix multiplication is distributive:** $A(B + C) = AB + AC$
**Matrix multiplication is, in general, not commutative;** It can be the case that $AB \neq BA$. (For example, if $A \in \mathbb{R}^{m\times n}$ and $B \in \mathbb{R}^{n\times q}$, the matrix product $BA$ does not even exist if $m$ and $q$ are not equal!)
###### [Go to top](#top)
<a id="8"></a> <br>
## 5- Identity Matrix
The **identity matrix** $I \in \mathbb{R}^{n\times n}$ is a square matrix with the value $1$ on the diagonal and $0$ everywhere else:
```
np.eye(4)
```
$I_{ij} = \left\{
\begin{array}{lr}
1 & i = j\\
0 & i \neq j
\end{array}
\right.
$
For all $A \in \mathbb{R}^{m\times n}$:
$AI = A = IA$
In the equation above multiplication has to be made possible, which means that in the portion $AI = A$ the dimensions of $I$ have to be $n\times n$, while in $A = IA$ they have to be $m\times m$.
We can generate an *identity matrix* in *numpy* using:
```
A = np.array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8],
[9, 10, 11]])
print("A:", A)
```
We can ask for the shape of $A$:
```
A.shape
```
The *shape* property of a matrix contains the $m$ (number of rows) and $n$ (number of columns) properties in a tuple, in that particular order. We can create an identity matrix for the use in $AI$ by using the $n$ value:
```
np.identity(A.shape[1], dtype="int")
```
Note that we specify the *dtype* parameter to *identity* as *int*, since the default would return a matrix of *float* values.
To generate an identity matrix for the use in $IA$ we would use the $m$ value:
```
np.identity(A.shape[0], dtype="int")
```
We can compute the dot product of $A$ and its identity matrix $I$:
```
n = A.shape[1]
I = np.array(np.identity(n, dtype="int"))
np.dot(A, I)
```
The same is true for the other direction:
```
m = A.shape[0]
I = np.array(np.identity(m, dtype="int"))
np.dot(I, A)
```
### 5-1 Inverse Matrices
```
inverse = np.linalg.inv(matrix1)
print(inverse)
```
<a id="9"></a> <br>
## 6- Diagonal Matrix
In the **diagonal matrix** non-diagonal elements are $0$, that is $D = diag(d_1, d_2, \dots{}, d_n)$, with:
$D_{ij} = \left\{
\begin{array}{lr}
d_i & i = j\\
0 & i \neq j
\end{array}
\right.
$
The identity matrix is a special case of a diagonal matrix: $I = diag(1, 1, \dots{}, 1)$.
In *numpy* we can create a *diagonal matrix* from any given matrix using the *diag* function:
```
import numpy as np
A = np.array([[0, 1, 2, 3],
[4, 5, 6, 7],
[8, 9, 10, 11],
[12, 13, 14, 15]])
np.diag(A)
```
An optional parameter *k* to the *diag* function allows us to extract the diagonal above the main diagonal with a positive *k*, and below the main diagonal with a negative *k*:
###### [Go to top](#top)
```
np.diag(A, k=1)
np.diag(A, k=-1)
```
<a id="10"></a> <br>
## 7- Transpose of a Matrix
**Transposing** a matrix is achieved by *flipping* the rows and columns. For a matrix $A \in \mathbb{R}^{m\times n}$ the transpose $A^T \in \mathbb{R}^{n\times m}$ is the $n\times m$ matrix given by:
$(A^T)_{ij} = A_{ji}$
Properties of transposes:
- $(A^T)^T = A$
- $(AB)^T = B^T A^T$
- $(A+B)^T = A^T + B^T$
```
a = np.array([[1, 2], [3, 4]])
a
a.transpose()
```
<a id="11"></a> <br>
## 8- Symmetric Matrices
Square metrices $A \in \mathbb{R}^{n\times n}$ are **symmetric**, if $A = A^T$.
$A$ is **anti-symmetric**, if $A = -A^T$.
For any matrix $A \in \mathbb{R}^{n\times n}$, the matrix $A + A^T$ is **symmetric**.
For any matrix $A \in \mathbb{R}^{n\times n}$, the matrix $A - A^T$ is **anti-symmetric**.
Thus, any square matrix $A \in \mathbb{R}^{n\times n}$ can be represented as a sum of a symmetric matrix and an anti-symmetric matrix:
$A = \frac{1}{2} (A + A^T) + \frac{1}{2} (A - A^T)$
The first matrix on the right, i.e. $\frac{1}{2} (A + A^T)$ is symmetric. The second matrix $\frac{1}{2} (A - A^T)$ is anti-symmetric.
$\mathbb{S}^n$ is the set of all symmetric matrices of size $n$.
$A \in \mathbb{S}^n$ means that $A$ is symmetric and of the size $n\times n$.
```
def symmetrize(a):
return a + a.T - np.diag(a.diagonal())
a = np.array([[1, 2], [3, 4]])
print(symmetrize(a))
```
<a id="12"></a> <br>
## 9-The Trace
The **trace** of a square matrix $A \in \mathbb{R}^{n\times n}$ is $tr(A)$ (or $trA$) is the sum of the diagonal elements in the matrix:
$trA = \sum_{i=1}^n A_{ii}$
Properties of the **trace**:
- For $A \in \mathbb{R}^{n\times n}$, $\mathrm{tr}A = \mathrm{tr}A^T$
- For $A,B \in \mathbb{R}^{n\times n}$, $\mathrm{tr}(A + B) = \mathrm{tr}A + \mathrm{tr}B$
- For $A \in \mathbb{R}^{n\times n}$, $t \in \mathbb{R}$, $\mathrm{tr}(tA) = t \mathrm{tr}A$
- For $A,B$ such that $AB$ is square, $\mathrm{tr}AB = \mathrm{tr}BA$
- For $A,B,C$ such that $ABC$ is square, $\mathrm{tr}ABC = \mathrm{tr}BCA = \mathrm{tr}CAB$, and so on for the product of more matrices.
###### [Go to top](#top)
```
a = np.arange(8).reshape((2,2,2))
np.trace(a)
print(np.trace(matrix1))
det = np.linalg.det(matrix1)
print(det)
a = np.array([[1, 2], [3, 4]])
a
a.transpose()
```
<a id="13"></a> <br>
# 10- Norms
a norm is a function that assigns a strictly positive length or size to each vector in a vector space—except for the zero vector, which is assigned a length of zero. A **seminorm**, on the other hand, is allowed to assign zero length to some non-zero vectors (in addition to the zero vector).
<a id="top"></a> <br>
The **norm** of a vector $x$ is $\| x\|$, informally the length of a vector.
Example: the Euclidean or $\mathscr{l}_2$ norm:
$\|x\|_2 = \sqrt{\sum_{i=1}^n{x_i^2}}$
Note: $\|x\|_2^2 = x^T x$
A **norm** is any function $f : \mathbb{R}^n \rightarrow \mathbb{R}$ that satisfies the following properties:
- For all $x \in \mathbb{R}^n$, $f(x) \geq 0$ (non-negativity)
- $f(x) = 0$ if and only if $x = 0$ (definiteness)
- For all $x \in \mathbb{R}^n$, $t \in \mathbb{R}$, $f(tx) = |t|\ f(x)$ (homogeneity)
- For all $x, y \in \mathbb{R}^n$, $f(x + y) \leq f(x) + f(y)$ (triangle inequality)
Norm $\mathscr{l}_1$:
$\|x\|_1 = \sum_{i=1}^n{|x_i|}$
How to calculate norm in python? **it is so easy**
###### [Go to top](#top)
```
v = np.array([1,2,3,4])
norm.median(v)
```
<a id="14"></a> <br>
# 11- Linear Independence and Rank
A set of vectors $\{x_1, x_2, \dots{}, x_n\} \subset \mathbb{R}^m$ is said to be **(linearly) independent** if no vector can be represented as a linear combination of the remaining vectors.
A set of vectors $\{x_1, x_2, \dots{}, x_n\} \subset \mathbb{R}^m$ is said to be **(lineraly) dependent** if one vector from this set can be represented as a linear combination of the remaining vectors.
For some scalar values $\alpha_1, \dots{}, \alpha_{n-1} \in \mathbb{R}$ the vectors $x_1, \dots{}, x_n$ are linerly dependent, if:
$\begin{equation}
x_n = \sum_{i=1}^{n-1}{\alpha_i x_i}
\end{equation}$
Example: The following vectors are lineraly dependent, because $x_3 = -2 x_1 + x_2$
$x_1 = \begin{bmatrix}
1 \\[0.3em]
2 \\[0.3em]
3
\end{bmatrix}
\quad
x_2 = \begin{bmatrix}
4 \\[0.3em]
1 \\[0.3em]
5
\end{bmatrix}
\quad
x_3 = \begin{bmatrix}
2 \\[0.3em]
-1 \\[0.3em]
-1
\end{bmatrix}
$
```
#How to find linearly independent rows from a matrix
matrix = np.array(
[
[0, 1 ,0 ,0],
[0, 0, 1, 0],
[0, 1, 1, 0],
[1, 0, 0, 1]
])
lambdas, V = np.linalg.eig(matrix.T)
# The linearly dependent row vectors
print (matrix[lambdas == 0,:])
```
<a id="15"></a> <br>
## 11-1 Column Rank of a Matrix
The **column rank** of a matrix $A \in \mathbb{R}^{m\times n}$ is the size of the largest subset of columns of $A$ that constitute a linear independent set. Informaly this is the number of linearly independent columns of $A$.
###### [Go to top](#top)
```
A = np.matrix([[1,3,7],[2,8,3],[7,8,1]])
np.linalg.matrix_rank(A)
from numpy.linalg import matrix_rank
matrix_rank(np.eye(4)) # Full rank matrix
I=np.eye(4); I[-1,-1] = 0. # rank deficient matrix
matrix_rank(I)
matrix_rank(np.ones((4,))) # 1 dimension - rank 1 unless all 0
matrix_rank(np.zeros((4,)))
```
<a id="16"></a> <br>
## 11-2 Row Rank of a Matrix
The **row rank** of a matrix $A \in \mathbb{R}^{m\times n}$ is the largest number of rows of $A$ that constitute a lineraly independent set.
<a id="17"></a> <br>
## 11-3 Rank of a Matrix
For any matrix $A \in \mathbb{R}^{m\times n}$, the column rank of $A$ is equal to the row rank of $A$. Both quantities are referred to collectively as the rank of $A$, denoted as $rank(A)$. Here are some basic properties of the rank:
###### [Go to top](#top)
- For $A \in \mathbb{R}^{m\times n}$, $rank(A) \leq \min(m, n)$. If $rank(A) = \min(m, n)$, then $A$ is said to be
**full rank**.
- For $A \in \mathbb{R}^{m\times n}$, $rank(A) = rank(A^T)$
- For $A \in \mathbb{R}^{m\times n}$, $B \in \mathbb{R}^{n\times p}$, $rank(AB) \leq \min(rank(A), rank(B))$
- For $A,B \in \mathbb{R}^{m\times n}$, $rank(A + B) \leq rank(A) + rank(B)$
```
from numpy.linalg import matrix_rank
print(matrix_rank(np.eye(4))) # Full rank matrix
I=np.eye(4); I[-1,-1] = 0. # rank deficient matrix
print(matrix_rank(I))
print(matrix_rank(np.ones((4,)))) # 1 dimension - rank 1 unless all 0
print (matrix_rank(np.zeros((4,))))
```
<a id="18"></a> <br>
# 12- Subtraction and Addition of Metrices
Assume $A \in \mathbb{R}^{m\times n}$ and $B \in \mathbb{R}^{m\times n}$, that is $A$ and $B$ are of the same size, to add $A$ to $B$, or to subtract $B$ from $A$, we add or subtract corresponding entries:
$A + B =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\[0.3em]
a_{21} & a_{22} & \cdots & a_{2n} \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix} +
\begin{bmatrix}
b_{11} & b_{12} & \cdots & b_{1n} \\[0.3em]
b_{21} & b_{22} & \cdots & b_{2n} \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
b_{m1} & b_{m2} & \cdots & b_{mn}
\end{bmatrix} =
\begin{bmatrix}
a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1n} + b_{1n} \\[0.3em]
a_{21} + b_{21} & a_{22} + b_{22} & \cdots & a_{2n} + b_{2n} \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
a_{m1} + b_{m1} & a_{m2} + b_{m2} & \cdots & a_{mn} + b_{mn}
\end{bmatrix}
$
The same is applies to subtraction:
$A - B =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\[0.3em]
a_{21} & a_{22} & \cdots & a_{2n} \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix} -
\begin{bmatrix}
b_{11} & b_{12} & \cdots & b_{1n} \\[0.3em]
b_{21} & b_{22} & \cdots & b_{2n} \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
b_{m1} & b_{m2} & \cdots & b_{mn}
\end{bmatrix} =
\begin{bmatrix}
a_{11} - b_{11} & a_{12} - b_{12} & \cdots & a_{1n} - b_{1n} \\[0.3em]
a_{21} - b_{21} & a_{22} - b_{22} & \cdots & a_{2n} - b_{2n} \\[0.3em]
\vdots & \vdots & \ddots & \vdots \\[0.3em]
a_{m1} - b_{m1} & a_{m2} - b_{m2} & \cdots & a_{mn} - b_{mn}
\end{bmatrix}
$
In Python using *numpy* this can be achieved using the following code:
```
import numpy as np
print("np.arange(9):", np.arange(9))
print("np.arange(9, 18):", np.arange(9, 18))
A = np.arange(9, 18).reshape((3, 3))
B = np.arange(9).reshape((3, 3))
print("A:", A)
print("B:", B)
```
The *numpy* function *arange* is similar to the standard Python function *range*. It returns an array with $n$ elements, specified in the one parameter version only. If we provide to parameters to *arange*, it generates an array starting from the value of the first parameter and ending with a value one less than the second parameter. The function *reshape* returns us a matrix with the corresponding number of rows and columns.
We can now add and subtract the two matrices $A$ and $B$:
```
A + B
A - B
```
<a id="19"></a> <br>
## 12-1 Inverse
The **inverse** of a square matrix $A \in \mathbb{R}^{n\times n}$ is $A^{-1}$:
$A^{-1} A = I = A A^{-1}$
Not all matrices have inverses. Non-square matrices do not have inverses by definition. For some square matrices $A$ the inverse might not exist.
$A$ is **invertible** or **non-singular** if $A^{-1}$ exists.
$A$ is **non-invertible** or **singular** if $A^{-1}$ does not exist.
<font color='red'>Note: **non-singular** means the opposite of **non-invertible**!</font>
For $A$ to have an inverse $A^{-1}$, $A$ must be **full rank**.
Assuming that $A,B \in \mathbb{R}^{n\times n}$ are non-singular, then:
- $(A^{-1})^{-1} = A$
- $(AB)^{-1} = B^{-1} A^{-1}$
- $(A^{-1})^T = (A^T)^{-1}$ (often simply $A^{-T}$)
###### [Go to top](#top)
<a id="20"></a> <br>
## 13- Orthogonal Matrices
Two vectors $x, y \in \mathbb{R}^n$ are **orthogonal** if $x^T y = 0$.
A vector $x \in \mathbb{R}^n$ is **normalized** if $\|x\|^2 = 1$.
A square matrix $U \in \mathbb{R}^{n\times n}$ is **orthogonal** if all its columns are orthogonal to each other and are **normalized**. The columns are then referred to as being **orthonormal**.
It follows immediately from the definition of orthogonality and normality that:
$U^T U = I = U U^T$
This means that the inverse of an orthogonal matrix is its transpose.
If U is not square - i.e., $U \in \mathbb{R}^{m\times n}$, $n < m$ - but its columns are still orthonormal, then $U^T U = I$, but $U U^T \neq I$.
We generally only use the term orthogonal to describe the case, where $U$ is square.
Another nice property of orthogonal matrices is that operating on a vector with an orthogonal matrix will not change its Euclidean norm. For any $x \in \mathbb{R}^n$, $U \in \mathbb{R}^{n\times n}$ orthogonal.
$\|U_x\|^2 = \|x\|^2$
```
#How to create random orthonormal matrix in python numpy
def rvs(dim=3):
random_state = np.random
H = np.eye(dim)
D = np.ones((dim,))
for n in range(1, dim):
x = random_state.normal(size=(dim-n+1,))
D[n-1] = np.sign(x[0])
x[0] -= D[n-1]*np.sqrt((x*x).sum())
# Householder transformation
Hx = (np.eye(dim-n+1) - 2.*np.outer(x, x)/(x*x).sum())
mat = np.eye(dim)
mat[n-1:, n-1:] = Hx
H = np.dot(H, mat)
# Fix the last sign such that the determinant is 1
D[-1] = (-1)**(1-(dim % 2))*D.prod()
# Equivalent to np.dot(np.diag(D), H) but faster, apparently
H = (D*H.T).T
return H
```
<a id="21"></a> <br>
## 14- Range and Nullspace of a Matrix
The **span** of a set of vectors $\{ x_1, x_2, \dots{}, x_n\}$ is the set of all vectors that can be expressed as
a linear combination of $\{ x_1, \dots{}, x_n \}$:
$\mathrm{span}(\{ x_1, \dots{}, x_n \}) = \{ v : v = \sum_{i=1}^n \alpha_i x_i, \alpha_i \in \mathbb{R} \}$
It can be shown that if $\{ x_1, \dots{}, x_n \}$ is a set of n linearly independent vectors, where each $x_i \in \mathbb{R}^n$, then $\mathrm{span}(\{ x_1, \dots{}, x_n\}) = \mathbb{R}^n$. That is, any vector $v \in \mathbb{R}^n$ can be written as a linear combination of $x_1$ through $x_n$.
The projection of a vector $y \in \mathbb{R}^m$ onto the span of $\{ x_1, \dots{}, x_n\}$ (here we assume $x_i \in \mathbb{R}^m$) is the vector $v \in \mathrm{span}(\{ x_1, \dots{}, x_n \})$, such that $v$ is as close as possible to $y$, as measured by the Euclidean norm $\|v − y\|^2$. We denote the projection as $\mathrm{Proj}(y; \{ x_1, \dots{}, x_n \})$ and can define it formally as:
$\mathrm{Proj}( y; \{ x_1, \dots{}, x_n \}) = \mathrm{argmin}_{v\in \mathrm{span}(\{x_1,\dots{},x_n\})}\|y − v\|^2$
The **range** (sometimes also called the columnspace) of a matrix $A \in \mathbb{R}^{m\times n}$, denoted $\mathcal{R}(A)$, is the the span of the columns of $A$. In other words,
$\mathcal{R}(A) = \{ v \in \mathbb{R}^m : v = A x, x \in \mathbb{R}^n\}$
Making a few technical assumptions (namely that $A$ is full rank and that $n < m$), the projection of a vector $y \in \mathbb{R}^m$ onto the range of $A$ is given by:
$\mathrm{Proj}(y; A) = \mathrm{argmin}_{v\in \mathcal{R}(A)}\|v − y\|^2 = A(A^T A)^{−1} A^T y$
<font color="red">See for more details in the notes page 13.</font>
The **nullspace** of a matrix $A \in \mathbb{R}^{m\times n}$, denoted $\mathcal{N}(A)$ is the set of all vectors that equal $0$ when multiplied by $A$, i.e.,
$\mathcal{N}(A) = \{ x \in \mathbb{R}^n : A x = 0 \}$
Note that vectors in $\mathcal{R}(A)$ are of size $m$, while vectors in the $\mathcal{N}(A)$ are of size $n$, so vectors in $\mathcal{R}(A^T)$ and $\mathcal{N}(A)$ are both in $\mathbb{R}^n$. In fact, we can say much more. It turns out that:
$\{ w : w = u + v, u \in \mathcal{R}(A^T), v \in \mathcal{N}(A) \} = \mathbb{R}^n$ and $\mathcal{R}(A^T) \cap \mathcal{N}(A) = \{0\}$
In other words, $\mathcal{R}(A^T)$ and $\mathcal{N}(A)$ are disjoint subsets that together span the entire space of
$\mathbb{R}^n$. Sets of this type are called **orthogonal complements**, and we denote this $\mathcal{R}(A^T) = \mathcal{N}(A)^\perp$.
###### [Go to top](#top)
<a id="22"></a> <br>
# 15- Determinant
The determinant of a square matrix $A \in \mathbb{R}^{n\times n}$, is a function $\mathrm{det} : \mathbb{R}^{n\times n} \rightarrow \mathbb{R}$, and is denoted $|A|$ or $\mathrm{det}A$ (like the trace operator, we usually omit parentheses).
<a id="23"></a> <br>
## 15-1 A geometric interpretation of the determinant
Given
$\begin{bmatrix}
-- & a_1^T & -- \\[0.3em]
-- & a_2^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_n^T & --
\end{bmatrix}$
consider the set of points $S \subset \mathbb{R}^n$ formed by taking all possible linear combinations of the row vectors $a_1, \dots{}, a_n \in \mathbb{R}^n$ of $A$, where the coefficients of the linear combination are all
between $0$ and $1$; that is, the set $S$ is the restriction of $\mathrm{span}( \{ a_1, \dots{}, a_n \})$ to only those linear combinations whose coefficients $\alpha_1, \dots{}, \alpha_n$ satisfy $0 \leq \alpha_i \leq 1$, $i = 1, \dots{}, n$. Formally:
$S = \{v \in \mathbb{R}^n : v = \sum_{i=1}^n \alpha_i a_i \mbox{ where } 0 \leq \alpha_i \leq 1, i = 1, \dots{}, n \}$
The absolute value of the determinant of $A$, it turns out, is a measure of the *volume* of the set $S$. The volume here is intuitively for example for $n = 2$ the area of $S$ in the Cartesian plane, or with $n = 3$ it is the common understanding of *volume* for 3-dimensional objects.
Example:
$A = \begin{bmatrix}
1 & 3 & 4\\[0.3em]
3 & 2 & 1\\[0.3em]
3 & 2 & 1
\end{bmatrix}$
The rows of the matrix are:
$a_1 = \begin{bmatrix}
1 \\[0.3em]
3 \\[0.3em]
3
\end{bmatrix}
\quad
a_2 = \begin{bmatrix}
3 \\[0.3em]
2 \\[0.3em]
2
\end{bmatrix}
\quad
a_3 = \begin{bmatrix}
4 \\[0.3em]
1 \\[0.3em]
1
\end{bmatrix}$
The set S corresponding to these rows is shown in:
<img src="http://mathworld.wolfram.com/images/equations/Determinant/NumberedEquation19.gif">
The figure above is an illustration of the determinant for the $2\times 2$ matrix $A$ above. Here, $a_1$ and $a_2$
are vectors corresponding to the rows of $A$, and the set $S$ corresponds to the shaded region (i.e., the parallelogram). The absolute value of the determinant, $|\mathrm{det}A| = 7$, is the area of the parallelogram.
For two-dimensional matrices, $S$ generally has the shape of a parallelogram. In our example, the value of the determinant is $|A| = −7$ (as can be computed using the formulas shown later), so the area of the parallelogram is $7$.
In three dimensions, the set $S$ corresponds to an object known as a parallelepiped (a three-dimensional box with skewed sides, such that every face has the shape of a parallelogram). The absolute value of the determinant of the $3 \times 3$ matrix whose rows define $S$ give the three-dimensional volume of the parallelepiped. In even higher dimensions, the set $S$ is an object known as an $n$-dimensional parallelotope.
Algebraically, the determinant satisfies the following three properties (from which all other properties follow, including the general formula):
- The determinant of the identity is $1$, $|I| = 1$. (Geometrically, the volume of a unit hypercube is $1$).
- Given a matrix $A \in \mathbb{R}^{n\times n}$, if we multiply a single row in $A$ by a scalar $t \in \mathbb{R}$, then the determinant of the new matrix is $t|A|$,<br/>
$\left| \begin{bmatrix}
-- & t a_1^T & -- \\[0.3em]
-- & a_2^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_m^T & --
\end{bmatrix}\right| = t|A|$<br/>
(Geometrically, multiplying one of the sides of the set $S$ by a factor $t$ causes the volume
to increase by a factor $t$.)
- If we exchange any two rows $a^T_i$ and $a^T_j$ of $A$, then the determinant of the new matrix is $−|A|$, for example<br/>
$\left| \begin{bmatrix}
-- & a_2^T & -- \\[0.3em]
-- & a_1^T & -- \\[0.3em]
& \vdots & \\[0.3em]
-- & a_m^T & --
\end{bmatrix}\right| = -|A|$
Several properties that follow from the three properties above include:
- For $A \in \mathbb{R}^{n\times n}$, $|A| = |A^T|$
- For $A,B \in \mathbb{R}^{n\times n}$, $|AB| = |A||B|$
- For $A \in \mathbb{R}^{n\times n}$, $|A| = 0$ if and only if $A$ is singular (i.e., non-invertible). (If $A$ is singular then it does not have full rank, and hence its columns are linearly dependent. In this case, the set $S$ corresponds to a "flat sheet" within the $n$-dimensional space and hence has zero volume.)
- For $A \in \mathbb{R}^{n\times n}$ and $A$ non-singular, $|A−1| = 1/|A|$
###### [Go to top](#top)
<a id="24"></a> <br>
# 16- Tensors
A [**tensor**](https://en.wikipedia.org/wiki/Tensor) could be thought of as an organized multidimensional array of numerical values. A vector could be assumed to be a sub-class of a tensor. Rows of tensors extend alone the y-axis, columns along the x-axis. The **rank** of a scalar is 0, the rank of a **vector** is 1, the rank of a **matrix** is 2, the rank of a **tensor** is 3 or higher.
###### [Go to top](#top)
```
A = tf.Variable(np.zeros((5, 5), dtype=np.float32), trainable=False)
new_part = tf.ones((2,3))
update_A = A[2:4,2:5].assign(new_part)
sess = tf.InteractiveSession()
tf.global_variables_initializer().run()
print(update_A.eval())
```
<a id="25"></a> <br>
# 17- Hyperplane
The **hyperplane** is a sub-space in the ambient space with one dimension less. In a two-dimensional space the hyperplane is a line, in a three-dimensional space it is a two-dimensional plane, etc.
Hyperplanes divide an $n$-dimensional space into sub-spaces that might represent clases in a machine learning algorithm.
```
np.random.seed(0)
X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
Y = [0] * 20 + [1] * 20
fig, ax = plt.subplots()
clf2 = svm.LinearSVC(C=1).fit(X, Y)
# get the separating hyperplane
w = clf2.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - (clf2.intercept_[0]) / w[1]
# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx2, yy2 = np.meshgrid(np.arange(x_min, x_max, .2),
np.arange(y_min, y_max, .2))
Z = clf2.predict(np.c_[xx2.ravel(), yy2.ravel()])
Z = Z.reshape(xx2.shape)
ax.contourf(xx2, yy2, Z, cmap=plt.cm.coolwarm, alpha=0.3)
ax.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.coolwarm, s=25)
ax.plot(xx,yy)
ax.axis([x_min, x_max,y_min, y_max])
plt.show()
```
<a id="31"></a> <br>
## 20- Exercises
let's do some exercise.
```
# Students may (probably should) ignore this code. It is just here to make pretty arrows.
def plot_vectors(vs):
"""Plot vectors in vs assuming origin at (0,0)."""
n = len(vs)
X, Y = np.zeros((n, 2))
U, V = np.vstack(vs).T
plt.quiver(X, Y, U, V, range(n), angles='xy', scale_units='xy', scale=1)
xmin, xmax = np.min([U, X]), np.max([U, X])
ymin, ymax = np.min([V, Y]), np.max([V, Y])
xrng = xmax - xmin
yrng = ymax - ymin
xmin -= 0.05*xrng
xmax += 0.05*xrng
ymin -= 0.05*yrng
ymax += 0.05*yrng
plt.axis([xmin, xmax, ymin, ymax])
# Again, this code is not intended as a coding example.
a1 = np.array([3,0]) # axis
a2 = np.array([0,3])
plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plot_vectors([a1, a2])
v1 = np.array([2,3])
plot_vectors([a1,v1])
plt.text(2,3,"(2,3)",fontsize=16)
plt.tight_layout()
#Matrices, Transformations and Geometric Interpretation
a1 = np.array([7,0]) # axis
a2 = np.array([0,5])
A = np.array([[2,1],[1,1]]) # transformation f in standard basis
v2 =np.dot(A,v1)
plt.figure(figsize=(8,8))
plot_vectors([a1, a2])
v1 = np.array([2,3])
plot_vectors([v1,v2])
plt.text(2,3,"v1 =(2,3)",fontsize=16)
plt.text(6,5,"Av1 = ", fontsize=16)
plt.text(v2[0],v2[1],"(7,5)",fontsize=16)
print(v2[1])
#Change to a Different Basis
e1 = np.array([1,0])
e2 = np.array([0,1])
B = np.array([[1,4],[3,1]])
plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plot_vectors([e1, e2])
plt.subplot(1,2,2)
plot_vectors([B.dot(e1), B.dot(e2)])
plt.Circle((0,0),2)
#plt.show()
#plt.tight_layout()
#Inner Products
e1 = np.array([1,0])
e2 = np.array([0,1])
A = np.array([[2,3],[3,1]])
v1=A.dot(e1)
v2=A.dot(e2)
plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plot_vectors([e1, e2])
plt.subplot(1,2,2)
plot_vectors([v1,v2])
plt.tight_layout()
#help(plt.Circle)
plt.Circle(np.array([0,0]),radius=1)
plt.Circle.draw
# using sqrt() to print the square root of matrix
print ("The element wise square root is : ")
print (np.sqrt(x))
```
<a id="32"></a> <br>
# 21-Conclusion
If you have made this far – give yourself a pat at the back. We have covered different aspects of **Linear algebra** in this Kernel. You are now finishing the **third step** of the course to continue, return to the [**main page**](https://www.kaggle.com/mjbahmani/10-steps-to-become-a-data-scientist/) of the course.
###### [Go to top](#top)
you can follow me on:
> ###### [ GitHub](https://github.com/mjbahmani/)
> ###### [Kaggle](https://www.kaggle.com/mjbahmani/)
<b>I hope you find this kernel helpful and some <font color='red'>UPVOTES</font> would be very much appreciated.<b/>
<a id="33"></a> <br>
# 22-References
1. [Linear Algbra1](https://github.com/dcavar/python-tutorial-for-ipython)
1. [Linear Algbra2](https://www.oreilly.com/library/view/data-science-from/9781491901410/ch04.html)
1. [GitHub](https://github.com/mjbahmani/10-steps-to-become-a-data-scientist)
>###### If you have read the notebook, you can follow next steps: [**Course Home Page**](https://www.kaggle.com/mjbahmani/10-steps-to-become-a-data-scientist)
| true |
code
| 0.366675 | null | null | null | null |
|
## SVM with Kernel trick to classify flowers!
As before we had issues with Logistic regression classifying Iris dataset, and we really want that trip, we will try with this Kernel trick to beat that non-linearity!!
This is from the excellent reference https://scikit-learn.org/stable/auto_examples/svm/plot_iris_svc.html#sphx-glr-auto-examples-svm-plot-iris-svc-py
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
def make_meshgrid(x, y, h=.02):
"""Create a mesh of points to plot in
Parameters
----------
x: data to base x-axis meshgrid on
y: data to base y-axis meshgrid on
h: stepsize for meshgrid, optional
Returns
-------
xx, yy : ndarray
"""
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Parameters
----------
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
# import some data to play with
iris = datasets.load_iris()
# Take the first two features. We could avoid this by using a two-dim dataset
X = iris.data[:, :2]
y = iris.target
# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0 # SVM regularization parameter
models = (svm.SVC(kernel='linear', C=C), #SVM with regularization
svm.LinearSVC(C=C, max_iter=10000), #SVM without regularization
svm.SVC(kernel='rbf', gamma=0.7, C=C), #SVM with Gaussian kernel
svm.SVC(kernel='poly', degree=3, gamma='auto', C=C)) #SVM with polynomial kernel!
models = (clf.fit(X, y) for clf in models)
# title for the plots
titles = ('SVC with linear kernel',
'LinearSVC (linear kernel)',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel')
# Set-up 2x2 grid for plotting.
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
for clf, title, ax in zip(models, titles, sub.flatten()):
plot_contours(ax, clf, xx, yy,
cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
```
| true |
code
| 0.834542 | null | null | null | null |
|
# HPV vaccination rates in Young Adults
## April 6, 2020
## University of Utah<br>Department of Biomedical Informatics
### Monika Baker<br>Betsy Campbell<br>Simone Longo
## Introduction
The <i>human papillomavirus</i> (HPV) is the most common sexually transmitted infection (STI) and affects 78 million Americans, primarily in their late teens and early twenties. While many HPV infections are benign, more severe cases can lead to lesions, warts, and a significantly increased risk of cancer. The WHO reports that nearly all cervical cancers as well as large proportions of cancers of other reproductive regions can be attributed to HPV infections. Forunately a vaccine exists to protect against the most virulent forms of HPV and is recommended for all people from as early as 9 up to 27 years old. If the immunization schedule is started early enough, the entire dose may be administered in two doses, however most cases require three vaccination rounds.
The CDC provides vaccination data as a proportion of adults aged 12-17 by state who have received each round of the HPV vaccination (link: https://www.cdc.gov/mmwr/volumes/65/wr/mm6533a4.htm#T3_down).
## Reading and Processing Data
```
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = 25, 15
plt.rcParams['font.size'] = 18
```
Get a quick overview of the data.
```
import pandas as pd
import seaborn as sns
data = pd.read_csv('hpv_melt.csv')
sns.barplot(x=data.vaccine, y=data.proportion)
```
From this plot, we immediately see that the proportion of HPV vaccinations decreases from one round of shots to the next. We also see a large difference between male and female rates.
```
from statannot import add_stat_annotation
melt_hpv = data
melt_hpv['gender'] = melt_hpv.vaccine.apply(lambda x: x.split('_')[-1])
melt_hpv['HPV_round'] = melt_hpv.vaccine.apply(lambda x: "".join(x.split('_')[:-1]))
order = list(set(melt_hpv.HPV_round))
boxpairs = [((order[0], 'fem'), (order[0], 'm')),
((order[1], 'fem'), (order[1], 'm')),
((order[2], 'fem'), (order[2], 'm'))]
ax = sns.boxplot(x="HPV_round", y="proportion", hue="gender", data=melt_hpv)
res = add_stat_annotation(ax, data=melt_hpv, x="HPV_round", y="proportion", hue="gender",
box_pairs=boxpairs, test='Mann-Whitney', loc='inside')
```
We can also see that differences between male and female proportions from one round to the next are also statistically significant.
### Comparing to Education Data
We first load the data from https://nces.ed.gov/programs/digest/d19/tables/dt19_203.40.asp?current=yes to obtain current enrollment information. This will be used to standardize spending and other statewide metrics on a per-pupil basis.
Total expenditures per state can be found here https://nces.ed.gov/programs/digest/d19/tables/dt19_236.30.asp?current=yes. In the following cells, the data from these 2 sources will be combined to show how HPV vaccination rates correlates to per-pupil education spending.
```
# Get total enrollment across states and territories after a little data cleaning
enrollment = pd.read_csv('enrollment.csv', header=None)
# standardize names
enrollment[0] = [i.strip().split('..')[0].strip() for i in enrollment[0]]
expenditures = pd.read_csv('expenditures.csv', header=None, index_col=0)
expenditures.index = [i.strip().split('..')[0].strip() for i in expenditures.index]
expenditures.iloc[:,0] = [int(str(i).replace(',','')) for i in expenditures.iloc[:,0]]
expenditures['enrollment'] = [int(str(i).replace(',','')) for i in enrollment.iloc[:,1]]
expenditures['CostPerStudent'] = expenditures.iloc[:,0] / expenditures.iloc[:,1]
expenditures.columns = ['expenditures', 'enrollment', 'CostPerStudent']
expenditures = expenditures.sort_index()
expenditures.sort_values(by='CostPerStudent').head()
df =pd.read_csv('hpv_clean_w_err.csv', index_col=0)
df.columns = ['State', *df.columns[1:]]
df = df.set_index('State')
hpv = df.iloc[:,3:9]
hpv['AverageHPV_Rate'] = df.mean(axis=1)
hpv = hpv.sort_index()
sns.scatterplot(y=hpv.AverageHPV_Rate, x=expenditures.CostPerStudent)
plot_trendline(y=hpv.AverageHPV_Rate, x=expenditures.CostPerStudent)
```
We see some weak correlation between higher spending per-pupil and higher HPV vaccination rates. This evidence is further validated by examining sexual education requirements.
The following sexual education data was taken from https://www.guttmacher.org/state-policy/explore/sex-and-hiv-education.
```
cdm = pd.read_csv('condoms.csv', header=None, index_col=0)
cdm[2] = [hpv.loc[x, 'AverageHPV_Rate'] for x in cdm.index]
#sns.boxplot(cdm[1], cdm[2])
cdm.columns = ['Required', 'AverageHPV_Rate']
mww_2g(cdm[cdm.Required == 0].AverageHPV_Rate, cdm[cdm.Required == 1].AverageHPV_Rate,
names=['NotRequired', 'Required'], col_names=['Average HPV Rate', 'Are condoms required in sex ed?'])
# Some helper functions
from statsmodels.formula.api import ols
import numpy as np
from scipy.stats import mannwhitneyu as mww
import itertools as it
def plot_trendline(x, y, c='r'):
data = {'x':x, 'y':y}
model = ols("y ~ x", data=data)
results = model.fit()
m = results.params[1]
b = results.params[0]
xax = np.linspace(x.min(), x.max(), 100)
yax = m * xax + b
plt.plot(xax, yax, c, label='y = {} x + {}\nR^2 = {}'.format(m, b, results.rsquared))
plt.legend(fontsize=24)
plt.show()
def mww_2g(g1, g2, names=None, col_names=['Value', 'Variable']):
if names is None:
name1 = g1.name
name2 = g2.name
else:
name1 = names[0]
name2 = names[1]
order = [name1, name2]
boxpairs = [(name1, name2)]
stat, pvalue = mww(g1, g2)
df = pd.DataFrame(zip(g1, it.repeat(name1)))
df = df.append(pd.DataFrame(zip(g2, it.repeat(name2))))
df.columns = col_names
plt.figure()
ax = sns.boxplot(data=df, x=col_names[1], y=col_names[0], order=order)
res = add_stat_annotation(ax, data=df, x=col_names[1], y=col_names[0],
box_pairs=boxpairs, perform_stat_test=False, pvalues=[pvalue],
test_short_name='Mann-Whitney-Wilcoxon', text_format='star', verbose=2, loc='inside')
```
| true |
code
| 0.446314 | null | null | null | null |
|
# **Model**
```
experiment_label = 'SVC04_na'
user_label = 'tay_donovan'
```
## **Aim**
Look for performance improvement in SVC model, by nullifying all negative values
## **Findings**
Findings for this notebook
```
#Initial imports
import pandas as pd
import numpy as np
import seaborn as sb
import matplotlib.pyplot as plt
import os
import sys
sys.path.append(os.path.abspath('..'))
from src.common_lib import DataReader, NBARawData
from sklearn.svm import SVC
```
## **Data input and cleansing**
```
#Load dataset using common function DataReader.read_data()
data_reader = DataReader()
# Load Raw Train Data
df_train = data_reader.read_data(NBARawData.TRAIN)
# Load Test Raw Data
df_test = data_reader.read_data(NBARawData.TEST)
#For train dataframe, remove redundant column 'Id_old'
cols_drop = ["Id", "Id_old"]
df_train.drop(cols_drop, axis=1, inplace=True)
df_train.columns = df_train.columns.str.strip()
df_train.describe
#For test dataframe, remove redundant column 'Id_old'
df_test.drop(cols_drop, axis=1, inplace=True)
df_test.columns = df_test.columns.str.strip()
df_test.describe
```
## **Negative values in dataset**
```
print(df_train.where(df_train < 0).count())
# Negative values do not make sense in this context
#Define negative cleaning function
def clean_negatives(strategy, df):
if strategy=='abs':
df = abs(df)
if strategy=='null':
df[df < 0] = 0
if strategy=='mean':
df[df < 0] = None
df.fillna(df.mean(), inplace=True)
return(df)
#Clean negative numbers
negatives_strategy = 'null'
df_train = clean_negatives(negatives_strategy, df_train)
df_test = clean_negatives(negatives_strategy, df_test)
```
## **Feature Correlation and Selection**
```
#Use Pearson Correlation to determine feature correlation
pearsoncorr = df_train.corr('pearson')
#Create heatmap of pearson correlation factors
fig, ax = plt.subplots(figsize=(10,10))
sb.heatmap(pearsoncorr,
xticklabels=pearsoncorr.columns,
yticklabels=pearsoncorr.columns,
cmap='RdBu_r',
annot=True,
linewidth=0.2)
#Drop correlated features w/ score over 0.9 - retain "MINS", "3P MADE","FTM","REB"
#selected_features = data_reader.select_feature_by_correlation(df_train)
```
## **Standard Scaling**
```
#Standardise scaling of all feature values
df_train_selected = df_train[selected_features]
#Apply scaler
scaler = StandardScaler()
df_cleaned = df_train_selected.copy()
target = df_cleaned.pop('TARGET_5Yrs')
df_train_cleaned = scaler.fit_transform(df_cleaned)
df_train_scaled = pd.DataFrame(df_train_cleaned)
df_train_scaled.columns = df_cleaned.columns
df_train_scaled['TARGET_5Yrs'] = target
# Split the training dataset using common function data_reader.splitdata
X_train, X_val, y_train, y_val = data_reader.split_data(df_train)
#X_train, X_val, y_train, y_val = data_reader.split_data(df_train_scaled)
```
## **Model Selection and Training**
```
#Create Optimised Model
optmodel = SVC()
#Use GridSearchCV to optimise parameters
from sklearn.model_selection import GridSearchCV
# defining parameter range
param_grid = {'C': [0.1, 1, 10, 100, 500],
'gamma': [1, 0.1, 0.01, 0.001, 0.0001],
'kernel': ['rbf']}
grid = GridSearchCV(SVC(probability=True), param_grid, refit = True, verbose = 3, scoring="roc_auc", n_jobs=-2)
# fitting the model for grid search
grid.fit(X_train, y_train)
#Print the optimised parameters
print(grid.best_params_)
#Create model with the optimised parameters
model = SVC(C=500, break_ties=False, class_weight='balanced', coef0=0.0,
decision_function_shape='ovr', degree=3,
gamma=0.0001, kernel='rbf', max_iter=-1,
probability=True, random_state=None, shrinking=True,
tol=0.001, verbose=False)
X_train.describe()
model.fit(X_train, y_train);
#Store model in /models
from joblib import dump
dump(model, '../models/' + experiment_label + '.joblib')
```
## **Model Evaluation**
```
#Create predictions for train and validation
y_train_preds = model.predict(X_train)
y_val_preds = model.predict(X_val)
#Evaluate train predictions
#from src.models.aj_metrics import confusion_matrix
from sklearn.metrics import roc_auc_score
from sklearn.metrics import plot_roc_curve, plot_precision_recall_curve
from sklearn.metrics import classification_report
sys.path.append(os.path.abspath('..'))
from src.models.aj_metrics import confusion_matrix
y_train_preds
#Training performance results
print("ROC AUC Score:")
print(roc_auc_score(y_train,y_train_preds))
print(classification_report(y_train, y_train_preds))
#Confusion matrix
print(confusion_matrix(y_train, y_train_preds))
#ROC Curve
plot_roc_curve(model,X_train, y_train)
#Precision Recall Curve
plot_precision_recall_curve(model,X_train,y_train)
#Validation performance analysis
print("ROC AUC Score:")
print(roc_auc_score(y_val,y_val_preds))
print("Confusion Matrix:")
print(classification_report(y_val, y_val_preds))
#Confusion matrix
print(confusion_matrix(y_train, y_train_preds))
#ROC Curve
plot_roc_curve(model,X_val, y_val)
#Precision Recall Curve
plot_precision_recall_curve(model,X_train,y_train)
```
## **Test output**
```
#Output predictions
X_test = df_test
y_test_preds = model.predict_proba(X_test)[:,1]
y_test_preds
output = pd.DataFrame({'Id': range(0,3799), 'TARGET_5Yrs': [p for p in y_test_preds]})
output.to_csv("../reports/" + user_label + "_submission_" + experiment_label + ".csv", index=False)
```
## **Outcome**
After outputting the predictions into kaggle, the final score was 0.70754
| true |
code
| 0.537891 | null | null | null | null |
|
# voila-interactive-football-pitch
This is a example widget served by `jupyter voila`. It combines `qgrid` and `bqplot` to create an interactive football pitch widget.
## Features
- Selected players on the pitch are highlighted in qgrid.
- Selected players selected in qgrid are marked on the pitch.
- Players are moveable on the pitch and their position is updated in qgrid.
```
import os
import ipywidgets as widgets
from bqplot import *
import numpy as np
import pandas as pd
import qgrid
# create DataFrame for team data
columns = ['name', 'id', 'x', 'y']
tottenham_players = [
['Lloris', 1, 0.1, 0.5],
['Trippier', 2, 0.2, 0.25],
['Alderweireld', 4, 0.2, 0.4],
['Vertonghen', 5, 0.2, 0.6],
['D. Rose', 3, 0.2, 0.75],
['Sissoko', 17, 0.3, 0.4],
['Winks', 8, 0.3, 0.6],
['Eriksen', 23, 0.4, 0.25],
['Alli', 20, 0.4, 0.5],
['Son', 7, 0.4, 0.75],
['H. Kane', 10, 0.45, 0.5]
]
temp_tottenham = pd.DataFrame.from_records(tottenham_players, columns=columns)
temp_tottenham['team'] = 'Tottenham Hotspur'
temp_tottenham['jersey'] = 'Blue'
liverpool_players = [
['Alisson', 13, 0.9, 0.5],
['Alexander-Arnold', 66, 0.8, 0.75],
['Matip', 32, 0.8, 0.6],
['van Dijk', 4, 0.8, 0.4],
['Robertson', 26, 0.8, 0.25],
['J. Henderson', 14, 0.7, 0.7],
['Fabinho', 3, 0.7, 0.5],
['Wijnaldum', 5, 0.7, 0.3],
['Salah', 11, 0.6, 0.75],
['Roberto Firmino', 9, 0.6, 0.5],
['Mané', 10, 0.6, 0.25]
]
temp_liverpool = pd.DataFrame.from_records(liverpool_players, columns=columns)
temp_liverpool['team'] = 'FC Liverpool'
temp_liverpool['jersey'] = 'Red'
teams = pd.concat([temp_tottenham, temp_liverpool], axis=0, ignore_index=True)
# Define bqplot Image mark
# read pitch image
image_path = os.path.abspath('pitch.png')
with open(image_path, 'rb') as f:
raw_image = f.read()
ipyimage = widgets.Image(value=raw_image, format='png')
scales_image = {'x': LinearScale(), 'y': LinearScale()}
axes_options = {'x': {'visible': False}, 'y': {'visible': False}}
image = Image(image=ipyimage, scales=scales_image, axes_options=axes_options)
# Full screen
image.x = [0, 1]
image.y = [0, 1]
# Define qgrid widget
qgrid.set_grid_option('maxVisibleRows', 10)
col_opts = {
'editable': False,
}
def on_row_selected(change):
"""callback for row selection: update selected points in scatter plot"""
filtered_df = qgrid_widget.get_changed_df()
team_scatter.selected = filtered_df.iloc[change.new].index.tolist()
qgrid_widget = qgrid.show_grid(teams, show_toolbar=False, column_options=col_opts)
qgrid_widget.observe(on_row_selected, names=['_selected_rows'])
qgrid_widget.layout = widgets.Layout(width='920px')
# Define scatter plot for team data
scales={'x': LinearScale(min=0, max=1), 'y': LinearScale(min=0, max=1)}
axes_options = {'x': {'visible': False}, 'y': {'visible': False}}
team_scatter = Scatter(x=teams['x'], y=teams['y'],
names=teams['name'],
scales= scales,
default_size=128,
interactions={'click': 'select'},
selected_style={'opacity': 1.0, 'stroke': 'Black'},
unselected_style={'opacity': 0.6},
axes_options=axes_options)
team_scatter.colors = teams['jersey'].values.tolist()
team_scatter.enable_move = True
# Callbacks
def change_callback(change):
qgrid_widget.change_selection(change.new)
def callback_update_qgrid(name, cell):
new_x = round(cell['point']['x'], 2)
new_y = round(cell['point']['y'], 2)
qgrid_widget.edit_cell(cell['index'], 'x', new_x)
qgrid_widget.edit_cell(cell['index'], 'y', new_y)
team_scatter.observe(change_callback, names=['selected'])
team_scatter.on_drag_end(callback_update_qgrid)
# Define football pitch widget
pitch_widget = Figure(marks=[image, team_scatter], padding_x=0, padding_y=0)
pitch_app = widgets.VBox([pitch_widget, qgrid_widget])
# Hack for increasing image size and keeping aspect ratio
width = 506.7
height = 346.7
factor = 1.8
pitch_widget.layout = widgets.Layout(width=f'{width*factor}px', height=f'{height*factor}px')
pitch_app
```
| true |
code
| 0.349449 | null | null | null | null |
|
### Structured Streaming with Kafka
In this notebook we'll examine how to connect Structured Streaming with Apache Kafka, a popular publish-subscribe system, to stream data from Wikipedia in real time, with a multitude of different languages.
#### Objectives:
* Learn About Kafka
* Learn how to establish a connection with Kafka
* Learn more aboutcreating visualizations
First, run the following cell to import the data and make various utilities available for our experimentation.
```
%run "./Includes/Classroom-Setup"
```
### 1.0. The Kafka Ecosystem
Kafka is software designed upon the **publish/subscribe** messaging pattern. Publish/subscribe messaging is where a sender (publisher) sends a message that is not specifically directed to any particular receiver (subscriber). The publisher classifies the message somehow, and the receiver subscribes to receive certain categories of messages. There are other usage patterns for Kafka, but this is the pattern we focus on in this course.
Publisher/subscriber systems typically have a central point where messages are published, called a **broker**. The broker receives messages from publishers, assigns offsets to them and commits messages to storage.
The Kafka version of a unit of data is an array of bytes called a **message**. A message can also contain a bit of information related to partitioning called a **key**. In Kafka, messages are categorized into **topics**.
#### 1.1. The Kafka Server
The Kafka server is fed by a separate TCP server that reads the Wikipedia edits, in real time, from the various language-specific IRC channels to which Wikimedia posts them. That server parses the IRC data, converts the results to JSON, and sends the JSON to a Kafka server, with the edits segregated by language. The various languages are **topics**. For example, the Kafka topic "en" corresponds to edits for en.wikipedia.org.
##### Required Options
When consuming from a Kafka source, you **must** specify at least two options:
1. The Kafka bootstrap servers, for example: `dsr.option("kafka.bootstrap.servers", "server1.databricks.training:9092")`
2. Some indication of the topics you want to consume.
#### 1.2. Specifying a Topic
There are three, mutually-exclusive, ways to specify the topics for consumption:
| Option | Value | Description | Example |
| ------------- | ---------------------------------------------- | -------------------------------------- | ------- |
| **subscribe** | A comma-separated list of topics | A list of topics to which to subscribe | `dsr.option("subscribe", "topic1")` <br/> `dsr.option("subscribe", "topic1,topic2,topic3")` |
| **assign** | A JSON string indicating topics and partitions | Specific topic-partitions to consume. | `dsr.dsr.option("assign", "{'topic1': [1,3], 'topic2': [2,5]}")`
| **subscribePattern** | A (Java) regular expression | A pattern to match desired topics | `dsr.option("subscribePattern", "e[ns]")` <br/> `dsr.option("subscribePattern", "topic[123]")`|
**Note:** In the example to follow, we're using the "subscribe" option to select the topics we're interested in consuming. We've selected only the "en" topic, corresponding to edits for the English Wikipedia. If we wanted to consume multiple topics (multiple Wikipedia languages, in our case), we could just specify them as a comma-separate list:
```dsr.option("subscribe", "en,es,it,fr,de,eo")```
There are other, optional, arguments you can give the Kafka source. For more information, see the <a href="https://people.apache.org//~pwendell/spark-nightly/spark-branch-2.1-docs/latest/structured-streaming-kafka-integration.html#" target="_blank">Structured Streaming and Kafka Integration Guide</a>
#### 1.3. The Kafka Schema
Reading from Kafka returns a `DataFrame` with the following fields:
| Field | Type | Description |
|------------------ | ------ |------------ |
| **key** | binary | The key of the record (not needed) |
| **value** | binary | Our JSON payload. We'll need to cast it to STRING |
| **topic** | string | The topic this record is received from (not needed) |
| **partition** | int | The Kafka topic partition from which this record is received (not needed). This server only has one partition. |
| **offset** | long | The position of this record in the corresponding Kafka topic partition (not needed) |
| **timestamp** | long | The timestamp of this record |
| **timestampType** | int | The timestamp type of a record (not needed) |
In the example below, the only column we want to keep is `value`.
**Note:** The default of `spark.sql.shuffle.partitions` is 200. This setting is used in operations like `groupBy`. In this case, we should be setting this value to match the current number of cores.
```
from pyspark.sql.functions import col
spark.conf.set("spark.sql.shuffle.partitions", sc.defaultParallelism)
kafkaServer = "server1.databricks.training:9092" # US (Oregon)
# kafkaServer = "server2.databricks.training:9092" # Singapore
editsDF = (spark.readStream # Get the DataStreamReader
.format("kafka") # Specify the source format as "kafka"
.option("kafka.bootstrap.servers", kafkaServer) # Configure the Kafka server name and port
.option("subscribe", "en") # Subscribe to the "en" Kafka topic
.option("startingOffsets", "earliest") # Rewind stream to beginning when we restart notebook
.option("maxOffsetsPerTrigger", 1000) # Throttle Kafka's processing of the streams
.load() # Load the DataFrame
.select(col("value").cast("STRING")) # Cast the "value" column to STRING
)
```
Let's display some data.
```
myStreamName = "lesson04a_ps"
display(editsDF, streamName = myStreamName)
```
Wait until stream is done initializing...
```
untilStreamIsReady(myStreamName)
```
Make sure to stop the stream before continuing.
```
stopAllStreams()
```
### 2.0. Use Kafka to Display the Raw Data
The Kafka server acts as a sort of "firehose" (or asynchronous buffer) and displays raw data. Since raw data coming in from a stream is transient, we'd like to save it to a more permanent data structure. The first step is to define the schema for the JSON payload.
**Note:** Only those fields of future interest are commented below.
```
from pyspark.sql.types import StructType, StructField, StringType, IntegerType, DoubleType, BooleanType
from pyspark.sql.functions import from_json, unix_timestamp
schema = StructType([
StructField("channel", StringType(), True),
StructField("comment", StringType(), True),
StructField("delta", IntegerType(), True),
StructField("flag", StringType(), True),
StructField("geocoding", StructType([ # (OBJECT): Added by the server, field contains IP address geocoding information for anonymous edit.
StructField("city", StringType(), True),
StructField("country", StringType(), True),
StructField("countryCode2", StringType(), True),
StructField("countryCode3", StringType(), True),
StructField("stateProvince", StringType(), True),
StructField("latitude", DoubleType(), True),
StructField("longitude", DoubleType(), True),
]), True),
StructField("isAnonymous", BooleanType(), True), # (BOOLEAN): Whether or not the change was made by an anonymous user
StructField("isNewPage", BooleanType(), True),
StructField("isRobot", BooleanType(), True),
StructField("isUnpatrolled", BooleanType(), True),
StructField("namespace", StringType(), True), # (STRING): Page's namespace. See https://en.wikipedia.org/wiki/Wikipedia:Namespace
StructField("page", StringType(), True), # (STRING): Printable name of the page that was edited
StructField("pageURL", StringType(), True), # (STRING): URL of the page that was edited
StructField("timestamp", StringType(), True), # (STRING): Time the edit occurred, in ISO-8601 format
StructField("url", StringType(), True),
StructField("user", StringType(), True), # (STRING): User who made the edit or the IP address associated with the anonymous editor
StructField("userURL", StringType(), True),
StructField("wikipediaURL", StringType(), True),
StructField("wikipedia", StringType(), True), # (STRING): Short name of the Wikipedia that was edited (e.g., "en" for the English)
])
```
Next we can use the function `from_json` to parse out the full message with the schema specified above.
```
from pyspark.sql.functions import col, from_json
jsonEdits = editsDF.select(
from_json("value", schema).alias("json")) # Parse the column "value" and name it "json"
```
When parsing a value from JSON, we end up with a single column containing a complex object. We can clearly see this by simply printing the schema.
```
jsonEdits.printSchema()
```
The fields of a complex object can be referenced with a "dot" notation as in: `col("json.geocoding.countryCode3")`
Since a large number of these fields/columns can become unwieldy, it's common to extract the sub-fields and represent them as first-level columns as seen below:
```
from pyspark.sql.functions import isnull, unix_timestamp
anonDF = (jsonEdits
.select(col("json.wikipedia").alias("wikipedia"), # Promoting from sub-field to column
col("json.isAnonymous").alias("isAnonymous"), # " " " " "
col("json.namespace").alias("namespace"), # " " " " "
col("json.page").alias("page"), # " " " " "
col("json.pageURL").alias("pageURL"), # " " " " "
col("json.geocoding").alias("geocoding"), # " " " " "
col("json.user").alias("user"), # " " " " "
col("json.timestamp").cast("timestamp")) # Promoting and converting to a timestamp
.filter(col("namespace") == "article") # Limit result to just articles
.filter(~isnull(col("geocoding.countryCode3"))) # We only want results that are geocoded
)
```
#### 2.1. Mapping Anonymous Editors' Locations
When you run the query, the default is a [live] html table. The geocoded information allows us to associate an anonymous edit with a country. We can then use that geocoded information to plot edits on a [live] world map. In order to create a slick world map visualization of the data, you'll need to click on the item below.
Under **Plot Options**, use the following:
* **Keys:** `countryCode3`
* **Values:** `count`
In **Display type**, use **World map** and click **Apply**.
<img src="https://files.training.databricks.com/images/eLearning/Structured-Streaming/plot-options-map-04.png"/>
By invoking a `display` action on a DataFrame created from a `readStream` transformation, we can generate a LIVE visualization!
**Note:** Keep an eye on the plot for a minute or two and watch the colors change.
```
mappedDF = (anonDF
.groupBy("geocoding.countryCode3") # Aggregate by country (code)
.count() # Produce a count of each aggregate
)
display(mappedDF, streamName = myStreamName)
```
Wait until stream is done initializing...
```
untilStreamIsReady(myStreamName)
```
Stop the streams.
```
stopAllStreams()
```
#### Review Questions
**Q:** What `format` should you use with Kafka?<br>
**A:** `format("kafka")`
**Q:** How do you specify a Kafka server?<br>
**A:** `.option("kafka.bootstrap.servers"", "server1.databricks.training:9092")`
**Q:** What verb should you use in conjunction with `readStream` and Kafka to start the streaming job?<br>
**A:** `load()`, but with no parameters since we are pulling from a Kafka server.
**Q:** What fields are returned in a Kafka DataFrame?<br>
**A:** Reading from Kafka returns a DataFrame with the following fields:
key, value, topic, partition, offset, timestamp, timestampType
Run the **`Classroom-Cleanup`** cell below to remove any artifacts created by this lesson.
```
%run "./Includes/Classroom-Cleanup"
```
##### Additional Topics & Resources
* <a href="http://spark.apache.org/docs/latest/structured-streaming-kafka-integration.html#creating-a-kafka-source-stream#" target="_blank">Create a Kafka Source Stream</a>
* <a href="https://kafka.apache.org/documentation/" target="_blank">Official Kafka Documentation</a>
* <a href="https://www.confluent.io/blog/okay-store-data-apache-kafka/" target="_blank">Use Kafka to store data</a>
| true |
code
| 0.700703 | null | null | null | null |
|
# DSCI 525 - Web and Cloud Computing
***Milestone 4:*** In this milestone, you will deploy the machine learning model you trained in milestone 3.
Milestone 4 checklist :
- [X] Use an EC2 instance.
- [X] Develop your API here in this notebook.
- [X] Copy it to ```app.py``` file in EC2 instance.
- [X] Run your API for other consumers and test among your colleagues.
- [X] Summarize your journey.
```
## Import all the packages that you need
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
```
## 1. Develop your API
rubric={mechanics:45}
You probably got how to set up primary URL endpoints from the ```sampleproject.ipynb notebook``` and have them process and return some data. Here we are going to create a new endpoint that accepts a POST request of the features required to run the machine learning model that you trained and saved in last milestone (i.e., a user will post the predictions of the 25 climate model rainfall predictions, i.e., features, needed to predict with your machine learning model). Your code should then process this data, use your model to make a prediction, and return that prediction to the user. To get you started with all this, I've given you a template which you should fill out to set up this functionality:
***NOTE:*** You won't be able to test the flask module (or the API you make here) unless you go through steps in ```2. Deploy your API```. However, here you can make sure that you develop all your functions and inputs properly.
```python
from flask import Flask, request, jsonify
import joblib
app = Flask(__name__)
# 1. Load your model here
model = joblib.load(...)
# 2. Define a prediction function
def return_prediction(...):
# format input_data here so that you can pass it to model.predict()
return model.predict(...)
# 3. Set up home page using basic html
@app.route("/")
def index():
# feel free to customize this if you like
return """
<h1>Welcome to our rain prediction service</h1>
To use this service, make a JSON post request to the /predict url with 5 climate model outputs.
"""
# 4. define a new route which will accept POST requests and return model predictions
@app.route('/predict', methods=['POST'])
def rainfall_prediction():
content = request.json # this extracts the JSON content we sent
prediction = return_prediction(...)
results = {...} # return whatever data you wish, it can be just the prediction
# or it can be the prediction plus the input data, it's up to you
return jsonify(results)
```
```
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from flask import Flask, request, jsonify
import joblib
app = Flask(__name__)
# 1. Load your model here
model = joblib.load('model.joblib')
# 2. Define a prediction function
def return_prediction(data):
# format input_data here so that you can pass it to model.predict()
return float(model.predict(np.array(data, ndmin = 2)))
# 3. Set up home page using basic html
@app.route("/")
def index():
# feel free to customize this if you like
return """
<h1>Welcome to our rain prediction service</h1>
To use this service, make a JSON post request to the /predict url with 25 climate model outputs.
"""
# 4. define a new route which will accept POST requests and return model predictions
@app.route('/predict', methods=['POST'])
def rainfall_prediction():
content = request.json # this extracts the JSON content we sent
prediction = return_prediction(content["data"])
results = {"Input": content["data"],
"Prediction": prediction} # return whatever data you wish, it can be just the prediction
# or it can be the prediction plus the input data, it's up to you
return jsonify(results)
```
## 2. Deploy your API
rubric={mechanics:40}
Once your API (app.py) is working we're ready to deploy it! For this, do the following:
1. SSH into your EC2 instance from milestone2. There are no issues if you want to spin another EC2 instance; if you plan to do so, make sure you terminate any other running instances.
2. Make a file `app.py` file in your instance and copy what you developed above in there.
2.1 You can use the linux editor using ```vi```. More details on vi Editor [here](https://www.guru99.com/the-vi-editor.html). I do recommend doing it this way and knowing some basics like ```:wq,:q!,dd``` will help.
2.2 Or else you can make a file in your laptop called app.py and copy it over to your EC2 instance using ```scp```. Eg: ```scp -r -i "ggeorgeAD.pem" ~/Desktop/worker.py ubuntu@ec2-xxx.ca-central-1.compute.amazonaws.com:~/```
3. Download your model from s3 to your EC2 instance.
4. Presumably you already have `pip` or `conda` installed on your instance from your previous milestone. You should use one of those package managers to install the dependencies of your API, like `flask`, `joblib`, `sklearn`, etc.
4.1. You have installed it in your TLJH using [Installing pip packages](https://tljh.jupyter.org/en/latest/howto/env/user-environment.html#installing-pip-packages). if you want to make it available to users outside of jupyterHub (which you want to in this case as we are logging into EC2 instance as user ```ubuntu``` by giving ```ssh -i privatekey ubuntu@<host_name>```) you can follow these [instructions](https://tljh.jupyter.org/en/latest/howto/env/user-environment.html#accessing-user-environment-outside-jupyterhub).
4.2. Alternatively you can install the required packages inside your terminal.
- Install conda:
wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh
bash Miniconda3-latest-Linux-x86_64.sh
- Install packages (there might be others):
conda install flask scikit-learn joblib
5. Now you're ready to start your service, go ahead and run `flask run --host=0.0.0.0 --port=8080`. This will make your service available at your EC2 instance's IP address on port 8080. Please make sure that you run this from where ```app.py``` and ```model.joblib``` resides.
6. You can now access your service by typing your EC2 instances public IPv4 address appened with `:8080` into a browswer, so something like `http://<your_EC2_ip>:8080`.
7. You should use `curl` to send a post request to your service to make sure it's working as expected.
>EG: curl -X POST http://your_EC2_ip:8080/predict -d '{"data":[1,2,3,4,53,11,22,37,41,53,11,24,31,44,53,11,22,35,42,53,12,23,31,42,53]}' -H "Content-Type: application/json"
8. Now, what happens if you exit your connection with the EC2 instance? Can you still reach your service?
9. There are several options we could use to help us persist our server even after we exit our shell session. We'll be using `screen`. `screen` will allow us to create a separate session within which we can run `flask` and which won't shut down when we exit the main shell session. Read [this](https://linuxize.com/post/how-to-use-linux-screen/) to learn more on ```screen```.
10. Now, create a new `screen` session (think of this as a new, separate shell), using: `screen -S myapi`. If you want to list already created sessions do ```screen -list```. If you want to get into an existing ```screen -x myapi```.
11. Within that session, start up your flask app. You can then exit the session by pressing `Ctrl + A then press D`. Here you are detaching the session, once you log back into EC2 instance you can attach it using ```screen -x myapi```.
12. Feel free to exit your connection with the EC2 instance now and try accessing your service again with `curl`. You should find that the service has now persisted!
13. ***CONGRATULATIONS!!!*** You have successfully got to the end of our milestones. Move to Task 3 and submit it.
## 3. Summarize your journey from Milestone 1 to Milestone 4
rubric={mechanics:10}
>There is no format or structure on how you write this. (also, no minimum number of words). It's your choice on how well you describe it.
Our Journey from Milestone 1 to Milestone 4:
In milestone 1, we attempted to clean and wrangle data for our model, but ran into speed issues locally depending on the machine that it was run on. We had issues with duplicating data through different iterations. Also, as part of this milestone we benchmarked each person’s computer when running the script to combine the data files.
In milestone 2, we set up our EC2 instance and repeated the same steps from Milestone 1, but ran into fewer issues with regards to speed. We moved the data to S3 bucket at the end of the milestone to store data. We also created logins for all users on Tiny Little Jupyter Hub (TLJH) so that we had the option to work individually. At this point, the data was ready to be applied to a model.
In milestone 3, we created our machine learning model on EC2 and then set up an EMR cluster which we accessed through `FoxyProxy Standard` in Firefox to help speed up hyperparameter optimization. Once we found the most optimal parameters, we applied those parameters to train and save the model to S3 in `joblib` format.
In milestone 4, we developed and deployed the API to access the model from Milestone 3 using `Flask`. We developed the app on our EC2 instance on TLJH and after installing the required dependencies, deployed using `screen` to get a persistent session so that it does not end after we close the Terminal. Finally, we used this to perform a prediction on sample input, as seen on the screenshot below.
https://github.com/UBC-MDS/DSCI_525_Group13_Rainfall/blob/main/img/m4_task2.png
<img src="../img/m4_task2.png" alt="result" style="width: 1000px;"/>
## 4. Submission instructions
rubric={mechanics:5}
In the textbox provided on Canvas please put a link where TAs can find the following-
- [X] This notebook with solution to ```1 & 3```
- [X] Screenshot from
- [X] Output after trying curl. Here is a [sample](https://github.ubc.ca/MDS-2020-21/DSCI_525_web-cloud-comp_students/blob/master/Milestones/milestone4/images/curl_deploy_sample.png). This is just an example; your input/output doesn't have to look like this, you can design the way you like. But at a minimum, it should show your prediction value.
| true |
code
| 0.636523 | null | null | null | null |
|
```
import keras
keras.__version__
```
# Deep Dream
This notebook contains the code samples found in Chapter 8, Section 2 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
----
[...]
## Implementing Deep Dream in Keras
We will start from a convnet pre-trained on ImageNet. In Keras, we have many such convnets available: VGG16, VGG19, Xception, ResNet50...
albeit the same process is doable with any of these, your convnet of choice will naturally affect your visualizations, since different
convnet architectures result in different learned features. The convnet used in the original Deep Dream release was an Inception model, and
in practice Inception is known to produce very nice-looking Deep Dreams, so we will use the InceptionV3 model that comes with Keras.
```
from keras.applications import inception_v3
from keras import backend as K
# We will not be training our model,
# so we use this command to disable all training-specific operations
K.set_learning_phase(0)
# Build the InceptionV3 network.
# The model will be loaded with pre-trained ImageNet weights.
model = inception_v3.InceptionV3(weights='imagenet',
include_top=False)
```
Next, we compute the "loss", the quantity that we will seek to maximize during the gradient ascent process. In Chapter 5, for filter
visualization, we were trying to maximize the value of a specific filter in a specific layer. Here we will simultaneously maximize the
activation of all filters in a number of layers. Specifically, we will maximize a weighted sum of the L2 norm of the activations of a
set of high-level layers. The exact set of layers we pick (as well as their contribution to the final loss) has a large influence on the
visuals that we will be able to produce, so we want to make these parameters easily configurable. Lower layers result in
geometric patterns, while higher layers result in visuals in which you can recognize some classes from ImageNet (e.g. birds or dogs).
We'll start from a somewhat arbitrary configuration involving four layers --
but you will definitely want to explore many different configurations later on:
```
# Dict mapping layer names to a coefficient
# quantifying how much the layer's activation
# will contribute to the loss we will seek to maximize.
# Note that these are layer names as they appear
# in the built-in InceptionV3 application.
# You can list all layer names using `model.summary()`.
layer_contributions = {
'mixed2': 0.2,
'mixed3': 3.,
'mixed4': 2.,
'mixed5': 1.5,
}
```
Now let's define a tensor that contains our loss, i.e. the weighted sum of the L2 norm of the activations of the layers listed above.
```
# Get the symbolic outputs of each "key" layer (we gave them unique names).
layer_dict = dict([(layer.name, layer) for layer in model.layers])
# Define the loss.
loss = K.variable(0.)
for layer_name in layer_contributions:
# Add the L2 norm of the features of a layer to the loss.
coeff = layer_contributions[layer_name]
activation = layer_dict[layer_name].output
# We avoid border artifacts by only involving non-border pixels in the loss.
scaling = K.prod(K.cast(K.shape(activation), 'float32'))
loss += coeff * K.sum(K.square(activation[:, 2: -2, 2: -2, :])) / scaling
```
Now we can set up the gradient ascent process:
```
# This holds our generated image
dream = model.input
# Compute the gradients of the dream with regard to the loss.
grads = K.gradients(loss, dream)[0]
# Normalize gradients.
grads /= K.maximum(K.mean(K.abs(grads)), 1e-7)
# Set up function to retrieve the value
# of the loss and gradients given an input image.
outputs = [loss, grads]
fetch_loss_and_grads = K.function([dream], outputs)
def eval_loss_and_grads(x):
outs = fetch_loss_and_grads([x])
loss_value = outs[0]
grad_values = outs[1]
return loss_value, grad_values
def gradient_ascent(x, iterations, step, max_loss=None):
for i in range(iterations):
loss_value, grad_values = eval_loss_and_grads(x)
if max_loss is not None and loss_value > max_loss:
break
print('...Loss value at', i, ':', loss_value)
x += step * grad_values
return x
```
Finally, here is the actual Deep Dream algorithm.
First, we define a list of "scales" (also called "octaves") at which we will process the images. Each successive scale is larger than
previous one by a factor 1.4 (i.e. 40% larger): we start by processing a small image and we increasingly upscale it:
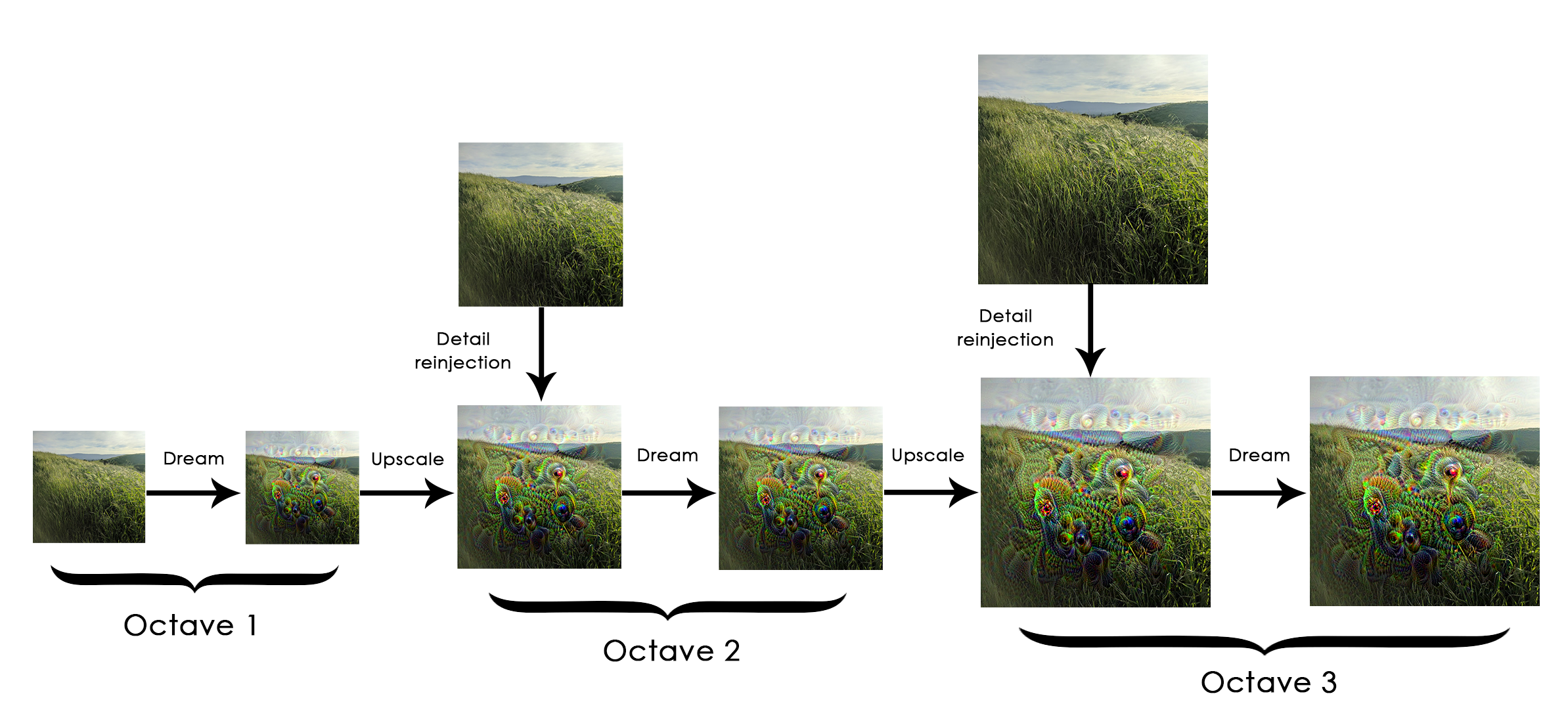
Then, for each successive scale, from the smallest to the largest, we run gradient ascent to maximize the loss we have previously defined,
at that scale. After each gradient ascent run, we upscale the resulting image by 40%.
To avoid losing a lot of image detail after each successive upscaling (resulting in increasingly blurry or pixelated images), we leverage a
simple trick: after each upscaling, we reinject the lost details back into the image, which is possible since we know what the original
image should look like at the larger scale. Given a small image S and a larger image size L, we can compute the difference between the
original image (assumed larger than L) resized to size L and the original resized to size S -- this difference quantifies the details lost
when going from S to L.
The code above below leverages the following straightforward auxiliary Numpy functions, which all do just as their name suggests. They
require to have SciPy installed.
```
import scipy
from keras.preprocessing import image
def resize_img(img, size):
img = np.copy(img)
factors = (1,
float(size[0]) / img.shape[1],
float(size[1]) / img.shape[2],
1)
return scipy.ndimage.zoom(img, factors, order=1)
def save_img(img, fname):
pil_img = deprocess_image(np.copy(img))
scipy.misc.imsave(fname, pil_img)
def preprocess_image(image_path):
# Util function to open, resize and format pictures
# into appropriate tensors.
img = image.load_img(image_path)
img = image.img_to_array(img)
img = np.expand_dims(img, axis=0)
img = inception_v3.preprocess_input(img)
return img
def deprocess_image(x):
# Util function to convert a tensor into a valid image.
if K.image_data_format() == 'channels_first':
x = x.reshape((3, x.shape[2], x.shape[3]))
x = x.transpose((1, 2, 0))
else:
x = x.reshape((x.shape[1], x.shape[2], 3))
x /= 2.
x += 0.5
x *= 255.
x = np.clip(x, 0, 255).astype('uint8')
return x
import numpy as np
# Playing with these hyperparameters will also allow you to achieve new effects
step = 0.01 # Gradient ascent step size
num_octave = 3 # Number of scales at which to run gradient ascent
octave_scale = 1.4 # Size ratio between scales
iterations = 20 # Number of ascent steps per scale
# If our loss gets larger than 10,
# we will interrupt the gradient ascent process, to avoid ugly artifacts
max_loss = 10.
# Fill this to the path to the image you want to use
base_image_path = '/home/ubuntu/data/original_photo_deep_dream.jpg'
# Load the image into a Numpy array
img = preprocess_image(base_image_path)
# We prepare a list of shape tuples
# defining the different scales at which we will run gradient ascent
original_shape = img.shape[1:3]
successive_shapes = [original_shape]
for i in range(1, num_octave):
shape = tuple([int(dim / (octave_scale ** i)) for dim in original_shape])
successive_shapes.append(shape)
# Reverse list of shapes, so that they are in increasing order
successive_shapes = successive_shapes[::-1]
# Resize the Numpy array of the image to our smallest scale
original_img = np.copy(img)
shrunk_original_img = resize_img(img, successive_shapes[0])
for shape in successive_shapes:
print('Processing image shape', shape)
img = resize_img(img, shape)
img = gradient_ascent(img,
iterations=iterations,
step=step,
max_loss=max_loss)
upscaled_shrunk_original_img = resize_img(shrunk_original_img, shape)
same_size_original = resize_img(original_img, shape)
lost_detail = same_size_original - upscaled_shrunk_original_img
img += lost_detail
shrunk_original_img = resize_img(original_img, shape)
save_img(img, fname='dream_at_scale_' + str(shape) + '.png')
save_img(img, fname='final_dream.png')
from matplotlib import pyplot as plt
plt.imshow(deprocess_image(np.copy(img)))
plt.show()
```
| true |
code
| 0.77806 | null | null | null | null |
|
# Interacting with Ethereum using web3.py and Jupyter Notebooks
Step by step guide for setting up a Jupyter notebook, connecting to an Ethereum node and working with a Smart Contract.
In this tutorial we are using Python 3, so make sure that **python** and **pip** are versioned correctly.
<hr>
## STEP 0: Getting tutorial materials
Grab a copy of the files that we use in this tutorial:
+ Using Git:
<code>git clone https://github.com/apguerrera/ethereum-notebooks.git</code>
+ Or download it manually from https://github.com/apguerrera/ethereum-notebooks
<hr>
## STEP 1: Installing dependencies
+ Install [Jupyter](https://jupyter.org/)
<code>pip install --upgrade pip</code>
<code>pip install jupyter</code>
+ Install [Web3.py](https://web3py.readthedocs.io/en/stable/), Python module for accessing Ethereum blockchain
<code>pip install web3</code>
+ Install [py-solc-x](https://pypi.org/project/py-solc-x/), Python module for compiling Solidity contracts
We use **py-solc-x** instead of **py-solc** to compile contracts, since py-solc doesn't support Solidity versions v.0.5.x.
Also **py-solc-x** provides an ability to choose between different Solidity compiler versions.
<code>pip install py-solc-x</code>
Note: the module itself doesn't contain **solc** executable, so let's install solc executable version 0.5.3 that we use in this tutorial
<code>python -m solcx.install v0.5.3</code>
+ To install Geth go to https://ethereum.org/cli and follow the instructions
<hr>
## STEP 2: Running local Geth node
+ Go to the project directory and run in your terminal:
<code>geth --dev --dev.period 2 --datadir ./testchain --rpc --rpccorsdomain ‘*’ --rpcport 8646 --rpcapi “eth,net,web3,debug” --port 32323 --maxpeers 0 console</code>
+ Or use <code>runGeth.sh</code> script which is doing exactly the same
<hr>
## STEP 3: Running Jupyter notebook
**If you're already viewing this notebook in Jupyter live mode, just skip this step.**
+ Open Jupyter notebooks by running the following in your terminal:
<code>jupyter notebook</code>
+ If you see an error message, try:
<code>jupyter-notebook</code>
It will open up a window in your browser. Here you need to go to the project folder and open <code>EthereumNotebookNew.ipynb</code>
<hr>
## STEP 4: Conecting to Web3
Web3 has a provider type that lets you connect to a local Ethereum node or endpoint such as [Infura](https://infura.io/).
In our example, we’ll be connecting to a local Geth node running from the /testchain directory, but can be set to any Ethereum node that web3 can connect to.
```
from web3 import Web3
w3 = Web3(Web3.IPCProvider('./testchain/geth.ipc'))
w3.isConnected() # if it's false, something went wrong
# check that all accounts were pulled from ./testchain directory successfuly
w3.eth.accounts
```
## STEP 5: Compiling contracts with py-solc-x
```
# compile contract using solcx and return contract interface
# arguments are filepath to the contract and name of the contract
def compile_contract(path, name):
compiled_contacts = solcx.compile_files([path])
contract_interface = compiled_contacts['{}:{}'.format(path, name)]
return contract_interface
contract_path = './contracts/WhiteList.sol'
contract_name = 'WhiteList'
contract_interface = compile_contract(contract_path, contract_name)
print(contract_interface)
# check that py-solc-x and solc are installed correctly
import solcx
solcx.get_installed_solc_versions()
```
## STEP 6: Deploying a contract to blockchain
In next steps we'll be using some functions from [/scripts/util.py](https://github.com/apguerrera/ethereum-notebooks/blob/master/scripts/util.py) and [/scripts/whitelist.py](https://github.com/apguerrera/ethereum-notebooks/blob/master/scripts/whitelist.py). It's **highly recommended** to check out this Python files to have better understanding of next steps.
Also we will pass **w3** instance as an argument to imported functions. We don't use **w3** as global variable since it's possible to have different endpoints thus having more than one w3 object in your program.
```
# import function that decrypts keystore file and returns account object
# check out tutorial directory in /scripts/util.py
from scripts.util import account_from_key
# compile contract, deploy it from account specified, then return transaction hash and contract interface
def deploy_contract(w3, account, path, name):
contract_interface = compile_contract(path, name)
contract = w3.eth.contract(abi=contract_interface['abi'], bytecode=contract_interface['bin'])
transaction = contract.constructor().buildTransaction({
'nonce': w3.eth.getTransactionCount(account.address),
'from': account.address
})
signed_transaction = w3.eth.account.signTransaction(transaction, account.privateKey)
tx_hash = w3.eth.sendRawTransaction(signed_transaction.rawTransaction)
return tx_hash.hex(), contract_interface
key_path = './testchain/keystore/UTC--2017-05-20T02-37-30.360937280Z--a00af22d07c87d96eeeb0ed583f8f6ac7812827e'
key_passphrase = '' # empty password for test keystore file, never do that in real life
account = account_from_key(w3, key_path, key_passphrase)
tx_hash, contract_interface = deploy_contract(w3, account, './contracts/WhiteList.sol', 'WhiteList')
tx_hash
```
Note: **deploy_contract doesn't return the address of created contract**, it returns hash of transaction made to create the contract
To get the address of the contract:
```
# import function that waits for deploy transaction to be included to block, and returns address of created contract
# check out tutorial directory in /scripts/util.py
from scripts.util import wait_contract_address
contract_address = wait_contract_address(w3, tx_hash)
contract_address
```
## STEP 7: Interacting with the contract
```
# import function that returns contract object using its address and ABI
# check out tutorial directory in /scripts/util.py
from scripts.util import get_contract
contract = get_contract(w3, contract_address, contract_interface['abi'])
contract.all_functions() # get all available functions of the contract
# check out /scripts/util.py and /scripts/whitelist.py
from scripts.whitelist import add_to_list
from scripts.util import wait_event
address_to_add = w3.eth.accounts[17]
tx_hash = add_to_list(w3, account, contract, [address_to_add])
event_added = wait_event(w3, contract, tx_hash, 'AccountListed')
if event_added:
print(event_added[0]['args'])
# check out /scripts/whitelist.py
from scripts.whitelist import is_in_list
is_in_list(account, contract, address_to_add) # check if address in whitelist
```
## Moving forward
Now you know how to compile Solidity contracts using **solc** and **py-solc-x**, deploy contracts using **Web3** and interact with them!
To see other code snippets and related information please check out [tutorial's GitHub repo](https://github.com/apguerrera/ethereum-notebooks/) and **WhitelistExample** notebook.
| true |
code
| 0.393443 | null | null | null | null |
|
# The Red Line Problem
Think Bayes, Second Edition
Copyright 2020 Allen B. Downey
License: [Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/)
```
# If we're running on Colab, install empiricaldist
# https://pypi.org/project/empiricaldist/
import sys
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
!pip install empiricaldist
# Get utils.py
import os
if not os.path.exists('utils.py'):
!wget https://github.com/AllenDowney/ThinkBayes2/raw/master/soln/utils.py
from utils import set_pyplot_params
set_pyplot_params()
```
The Red Line is a subway that connects Cambridge and Boston, Massachusetts. When I was working in Cambridge I took the Red Line from Kendall Square to South Station and caught the commuter rail to Needham. During rush hour Red Line trains run every 7–8 minutes, on average.
When I arrived at the station, I could estimate the time until the next train based on the number of passengers on the platform. If there were only a few people, I inferred that I just missed a train and expected to wait about 7 minutes. If there were more passengers, I expected the train to arrive sooner. But if there were a large number of passengers, I suspected that trains were not running on schedule, so I would go back to the street level and get a taxi.
While I was waiting for trains, I thought about how Bayesian estimation could help predict my wait time and decide when I should give up and take a taxi. This chapter presents the analysis I came up with.
This example is based on a project by Brendan Ritter and Kai Austin, who took a class with me at Olin College.
It was a chapter in the first edition of *Think Bayes*, I cut it from the second edition.
Before we get to the analysis, we have to make some modeling decisions. First, I will treat passenger arrivals as a Poisson process, which means I assume that passengers are equally likely to arrive at any time, and that they arrive at a rate, λ, measured in passengers per minute. Since I observe passengers during a short period of time, and at the same time every day, I assume that λ is constant.
On the other hand, the arrival process for trains is not Poisson. Trains to Boston are supposed to leave from the end of the line (Alewife station) every 7–8 minutes during peak times, but by the time they get to Kendall Square, the time between trains varies between 3 and 12 minutes.
To gather data on the time between trains, I wrote a script that downloads real-time data from the [MBTA](http://www.mbta.com/rider_tools/developers/), selects south-bound trains arriving at Kendall square, and records their arrival times in a database. I ran the script from 4 pm to 6 pm every weekday for 5 days, and recorded about 15 arrivals per day. Then I computed the time between consecutive arrivals.
Here are the gap times I recorded, in seconds.
```
observed_gap_times = [
428.0, 705.0, 407.0, 465.0, 433.0, 425.0, 204.0, 506.0, 143.0, 351.0,
450.0, 598.0, 464.0, 749.0, 341.0, 586.0, 754.0, 256.0, 378.0, 435.0,
176.0, 405.0, 360.0, 519.0, 648.0, 374.0, 483.0, 537.0, 578.0, 534.0,
577.0, 619.0, 538.0, 331.0, 186.0, 629.0, 193.0, 360.0, 660.0, 484.0,
512.0, 315.0, 457.0, 404.0, 740.0, 388.0, 357.0, 485.0, 567.0, 160.0,
428.0, 387.0, 901.0, 187.0, 622.0, 616.0, 585.0, 474.0, 442.0, 499.0,
437.0, 620.0, 351.0, 286.0, 373.0, 232.0, 393.0, 745.0, 636.0, 758.0,
]
```
I'll convert them to minutes and use `kde_from_sample` to estimate the distribution.
```
import numpy as np
zs = np.array(observed_gap_times) / 60
from utils import kde_from_sample
qs = np.linspace(0, 20, 101)
pmf_z = kde_from_sample(zs, qs)
```
Here's what it looks like.
```
from utils import decorate
pmf_z.plot()
decorate(xlabel='Time (min)',
ylabel='PDF',
title='Distribution of time between trains')
```
## The Update
At this point we have an estimate for the distribution of time between trains.
Now let's suppose I arrive at the station and see 10 passengers on the platform.
What distribution of wait times should I expect?
We'll answer this question in two steps.
* First, we'll derive the distribution of gap times as observed by a random arrival (me).
* Then we'll derive the distribution of wait times, conditioned on the number of passengers.
When I arrive at the station, I am more likely to arrive during a long gap than a short one.
In fact, the probability that I arrive during any interval is proportional to its duration.
If we think of `pmf_z` as the prior distribution of gap time, we can do a Bayesian update to compute the posterior.
The likelihood of my arrival during each gap is the duration of the gap:
```
likelihood = pmf_z.qs
```
So here's the first update.
```
posterior_z = pmf_z * pmf_z.qs
posterior_z.normalize()
```
Here's what the posterior distribution looks like.
```
pmf_z.plot(label='prior', color='C5')
posterior_z.plot(label='posterior', color='C4')
decorate(xlabel='Time (min)',
ylabel='PDF',
title='Distribution of time between trains')
```
Because I am more likely to arrive during a longer gap, the distribution is shifted to the right.
The prior mean is about 7.8 minutes; the posterior mean is about 8.9 minutes.
```
pmf_z.mean(), posterior_z.mean()
```
This shift is an example of the "inspection paradox", which [I wrote an article about](https://towardsdatascience.com/the-inspection-paradox-is-everywhere-2ef1c2e9d709).
As an aside, the Red Line schedule reports that trains run every 9 minutes during peak times. This is close to the posterior mean, but higher than the prior mean. I exchanged email with a representative of the MBTA, who confirmed that the reported time between trains is deliberately conservative in order to account for variability.
## Elapsed time
Elapsed time, which I call `x`, is the time between the arrival of the previous train and the arrival of a passenger.
Wait time, which I call `y`, is the time between the arrival of a passenger and the next arrival of a train.
I chose this notation so that
```
z = x + y.
```
Given the distribution of `z`, we can compute the distribution of `x`. I’ll start with a simple case and then generalize. Suppose the gap between trains is either 5 or 10 minutes with equal probability.
If we arrive at a random time, we arrive during a 5 minute gap with probability 1/3, or a 10 minute gap with probability 2/3.
If we arrive during a 5 minute gap, `x` is uniform from 0 to 5 minutes. If we arrive during a 10 minute gap, `x` is uniform from 0 to 10.
So the distribution of wait times is a weighted mixture of two uniform distributions.
More generally, if we have the posterior distribution of `z`, we can compute the distribution of `x` by making a mixture of uniform distributions.
We'll use the following function to make the uniform distributions.
```
from empiricaldist import Pmf
def make_elapsed_dist(gap, qs):
qs = qs[qs <= gap]
n = len(qs)
return Pmf(1/n, qs)
```
`make_elapsed_dist` takes a hypothetical gap and an array of possible times.
It selects the elapsed times less than or equal to `gap` and puts them into a `Pmf` that represents a uniform distribution.
I'll use this function to make a sequence of `Pmf` objects, one for each gap in `posterior_z`.
```
qs = posterior_z.qs
pmf_seq = [make_elapsed_dist(gap, qs) for gap in qs]
```
Here's an example that represents a uniform distribution from 0 to 0.6 minutes.
```
pmf_seq[3]
```
The last element of the sequence is uniform from 0 to 20 minutes.
```
pmf_seq[-1].plot()
decorate(xlabel='Time (min)',
ylabel='PDF',
title='Distribution of wait time in 20 min gap')
```
Now we can use `make_mixture` to make a weighted mixture of uniform distributions, where the weights are the probabilities from `posterior_z`.
```
from utils import make_mixture
pmf_x = make_mixture(posterior_z, pmf_seq)
pmf_z.plot(label='prior gap', color='C5')
posterior_z.plot(label='posterior gap', color='C4')
pmf_x.plot(label='elapsed time', color='C1')
decorate(xlabel='Time (min)',
ylabel='PDF',
title='Distribution of gap and elapsed times')
posterior_z.mean(), pmf_x.mean()
```
The mean elapsed time is 4.4 minutes, half the posterior mean of `z`.
And that makes sense, since we expect to arrive in the middle of the gap, on average.
## Counting passengers
Now let's take into account the number of passengers waiting on the platform.
Let's assume that passengers are equally likely to arrive at any time, and that they arrive at a rate, `λ`, that is known to be 2 passengers per minute.
Under those assumptions, the number of passengers who arrive in `x` minutes follows a Poisson distribution with parameter `λ x`
So we can use the SciPy function `poisson` to compute the likelihood of 10 passengers for each possible value of `x`.
```
from scipy.stats import poisson
lam = 2
num_passengers = 10
likelihood = poisson(lam * pmf_x.qs).pmf(num_passengers)
```
With this likelihood, we can compute the posterior distribution of `x`.
```
posterior_x = pmf_x * likelihood
posterior_x.normalize()
```
Here's what it looks like:
```
pmf_x.plot(label='prior', color='C1')
posterior_x.plot(label='posterior', color='C2')
decorate(xlabel='Time (min)',
ylabel='PDF',
title='Distribution of time since last train')
```
Based on the number of passengers, we think it has been about 5 minutes since the last train.
```
pmf_x.mean(), posterior_x.mean()
```
## Wait time
Now how long do we think it will be until the next train?
Based on what we know so far, the distribution of `z` is `posterior_z`, and the distribution of `x` is `posterior_x`.
Remember that we defined
```
z = x + y
```
If we know `x` and `z`, we can compute
```
y = z - x
```
So we can use `sub_dist` to compute the distribution of `y`.
```
posterior_y = Pmf.sub_dist(posterior_z, posterior_x)
```
Well, almost. That distribution contains some negative values, which are impossible.
But we can remove them and renormalize, like this:
```
nonneg = (posterior_y.qs >= 0)
posterior_y = Pmf(posterior_y[nonneg])
posterior_y.normalize()
```
Based on the information so far, here are the distributions for `x`, `y`, and `z`, shown as CDFs.
```
posterior_x.make_cdf().plot(label='posterior of x', color='C2')
posterior_y.make_cdf().plot(label='posterior of y', color='C3')
posterior_z.make_cdf().plot(label='posterior of z', color='C4')
decorate(xlabel='Time (min)',
ylabel='PDF',
title='Distribution of elapsed time, wait time, gap')
```
Because of rounding errors, `posterior_y` contains quantities that are not in `posterior_x` and `posterior_z`; that's why I plotted it as a CDF, and why it appears jaggy.
## Decision analysis
At this point we can use the number of passengers on the platform to predict the distribution of wait times. Now let’s get to the second part of the question: when should I stop waiting for the train and go catch a taxi?
Remember that in the original scenario, I am trying to get to South Station to catch the commuter rail. Suppose I leave the office with enough time that I can wait 15 minutes and still make my connection at South Station.
In that case I would like to know the probability that `y` exceeds 15 minutes as a function of `num_passengers`.
To answer that question, we can run the analysis from the previous section with range of `num_passengers`.
But there’s a problem. The analysis is sensitive to the frequency of long delays, and because long delays are rare, it is hard to estimate their frequency.
I only have data from one week, and the longest delay I observed was 15 minutes. So I can’t estimate the frequency of longer delays accurately.
However, I can use previous observations to make at least a coarse estimate. When I commuted by Red Line for a year, I saw three long delays caused by a signaling problem, a power outage, and “police activity” at another stop. So I estimate that there are about 3 major delays per year.
But remember that my observations are biased. I am more likely to observe long delays because they affect a large number of passengers. So we should treat my observations as a sample of `posterior_z` rather than `pmf_z`.
Here's how we can augment the observed distribution of gap times with some assumptions about long delays.
From `posterior_z`, I'll draw a sample of 260 values (roughly the number of work days in a year).
Then I'll add in delays of 30, 40, and 50 minutes (the number of long delays I observed in a year).
```
sample = posterior_z.sample(260)
delays = [30, 40, 50]
augmented_sample = np.append(sample, delays)
```
I'll use this augmented sample to make a new estimate for the posterior distribution of `z`.
```
qs = np.linspace(0, 60, 101)
augmented_posterior_z = kde_from_sample(augmented_sample, qs)
```
Here's what it looks like.
```
augmented_posterior_z.plot(label='augmented posterior of z', color='C4')
decorate(xlabel='Time (min)',
ylabel='PDF',
title='Distribution of time between trains')
```
Now let's take the analysis from the previous sections and wrap it in a function.
```
qs = augmented_posterior_z.qs
pmf_seq = [make_elapsed_dist(gap, qs) for gap in qs]
pmf_x = make_mixture(augmented_posterior_z, pmf_seq)
lam = 2
num_passengers = 10
def compute_posterior_y(num_passengers):
"""Distribution of wait time based on `num_passengers`."""
likelihood = poisson(lam * qs).pmf(num_passengers)
posterior_x = pmf_x * likelihood
posterior_x.normalize()
posterior_y = Pmf.sub_dist(augmented_posterior_z, posterior_x)
nonneg = (posterior_y.qs >= 0)
posterior_y = Pmf(posterior_y[nonneg])
posterior_y.normalize()
return posterior_y
```
Given the number of passengers when we arrive at the station, it computes the posterior distribution of `y`.
As an example, here's the distribution of wait time if we see 10 passengers.
```
posterior_y = compute_posterior_y(10)
```
We can use it to compute the mean wait time and the probability of waiting more than 15 minutes.
```
posterior_y.mean()
1 - posterior_y.make_cdf()(15)
```
If we see 10 passengers, we expect to wait a little less than 5 minutes, and the chance of waiting more than 15 minutes is about 1%.
Let's see what happens if we sweep through a range of values for `num_passengers`.
```
nums = np.arange(0, 37, 3)
posteriors = [compute_posterior_y(num) for num in nums]
```
Here's the mean wait as a function of the number of passengers.
```
mean_wait = [posterior_y.mean()
for posterior_y in posteriors]
import matplotlib.pyplot as plt
plt.plot(nums, mean_wait)
decorate(xlabel='Number of passengers',
ylabel='Expected time until next train',
title='Expected wait time based on number of passengers')
```
If there are no passengers on the platform when I arrive, I infer that I just missed a train; in that case, the expected wait time is the mean of `augmented_posterior_z`.
The more passengers I see, the longer I think it has been since the last train, and the more likely a train arrives soon.
But only up to a point. If there are more than 30 passengers on the platform, that suggests that there is a long delay, and the expected wait time starts to increase.
Now here's the probability that wait time exceeds 15 minutes.
```
prob_late = [1 - posterior_y.make_cdf()(15)
for posterior_y in posteriors]
plt.plot(nums, prob_late)
decorate(xlabel='Number of passengers',
ylabel='Probability of being late',
title='Probability of being late based on number of passengers')
```
When the number of passengers is less than 20, we infer that the system is operating normally, so the probability of a long delay is small. If there are 30 passengers, we suspect that something is wrong and expect longer delays.
If we are willing to accept a 5% chance of missing the connection at South Station, we should stay and wait as long as there are fewer than 30 passengers, and take a taxi if there are more.
Or, to take this analysis one step further, we could quantify the cost of missing the connection and the cost of taking a taxi, then choose the threshold that minimizes expected cost.
This analysis is based on the assumption that the arrival rate, `lam`, is known.
If it is not know precisely, but is estimated from data, we could represent our uncertainty about `lam` with a distribution, compute the distribution of `y` for each value of `lam`, and make a mixture to represent the distribution of `y`.
I did that in the version of this problem in the first edition of *Think Bayes*; I left it out here because it is not the focus of the problem.
| true |
code
| 0.763473 | null | null | null | null |
|
# Welcome to Safran Lab 1
Every day, more than 80,000 commercial flights take place around the world, operated by hundreds of airlines. For all aircraft take-off weight exceeding 27 tons, a regulatory constraint requires companies to systematically record and analyse all flight data, for the purpose of improving the safety of flights. Flight Data Monitoring strives to detect and prioritize deviations from standards set by the aircraft manufacturers, the authorities of civil aviation in the country, or even companies themselves. Such deviations, called events, are used to populate a database that enables companies to identify and monitor the risks inherent to these operations.
This notebook is designed to let you manipulate real aeronautical data, provided by the Safran Group. It is divided in two parts: the first part deals with the processing of raw data, you will be asked to visualize the data, understand what variables require processing and perform the processing for some of these variables. The second part deals with actual data analysis, and covers some interesting problems. We hope to give you some insights of the data scientist job and give you interesting and challenging questions.
<h1><div class="label label-success">Part 1: Data processing</div></h1>
## Loading raw data
** Context **
You will be provided with `780` flight records. Each is a full record of a flight starting at the beginning of the taxi out phase and terminating at the end of the taxi in phase. The sample rate is 1 Hz. Please be aware that due to side effects the very beginning of the record may be faulty. This is something to keep in mind when we will analyse the data.
Each flight data is a collection of time series resumed in a dataframe, the columns variables are described in the schema below:
| name | description | unit
|:-----:|:-------------:|:---:|
| TIME | elapsed seconds| second |
| LATP_1 | Latitude | degree ° |
| LONP_1 | Longitude | degree ° |
| RALT1 | Radio Altitude, sensor 1 | feet |
| RALT2 | Radio Altitude, sensor 2 | feet |
| RALT3 | Radio Altitude, sensor 3 | feet |
| ALT_STD | Relative Altitude | feet |
| HEAD | head | degree °|
| PITCH | pitch | degree ° |
| ROLL | roll | degree ° |
| IAS | Indicated Air Speed | m/s |
| N11 | speed N1 of the first engine | % |
| N21 | speed N2 of the first engine | % |
| N12 | speed N1 of the second engine | % |
| N22 | speed N2 of the second engine | % |
| AIR_GROUND | 1: ground, 0: air| boolean |
** Note ** : `TIME` represents the elapsed seconds from today midnight. You are not provided with an absolute time variable that would tell you the date and hour of the flights.
** Acquire expertise about aviation data **
You will need some expertise about the signification of the variables. Latitude and longitude are quite straightforward. Head, Pitch and Roll are standards orientation angles, check this [image](https://i.stack.imgur.com/65EKz.png) to be sure. RALT\* are coming from three different radio altimeters, they measure the same thing but have a lot of missing values and are valid only under a threshold altitude (around 5000 feet). Alt_std is the altitude measured from the pressure (it basically comes from a barometer), it is way less accurate that a radio altimeter but provides values for all altitudes. N1\* and N2\* are the rotational speeds of the engine sections expressed as a percentage of a nominal value. Some good links to check out to go deeper:
- [about phases of flight](http://www.fp7-restarts.eu/index.php/home/root/state-of-the-art/objectives/2012-02-15-11-58-37/71-book-video/parti-principles-of-flight/126-4-phases-of-a-flight)
- [pitch-roll-head](https://i.stack.imgur.com/65EKz.png)
- [about N\*\* variables I](http://aviation.stackexchange.com/questions/14690/what-are-n1-and-n2)
- [about N\*\* variables II](https://www.quora.com/Whats-N1-N2-in-aviation-And-how-is-the-value-of-100-N1-N2-determined)
- [how altimeters work](http://www.explainthatstuff.com/how-altimeters-work.html)
- [about runway naming](https://en.wikipedia.org/wiki/Runway#Naming)
```
# Set up
BASE_DIR = "/mnt/safran/TP1/data/"
from os import listdir
from os.path import isfile, join
import glob
import matplotlib as mpl
mpl.rcParams["axes.grid"] = True
import matplotlib.pylab as plt
%matplotlib inline
import numpy as np
import pandas as pd
pd.options.display.max_columns = 50
from datetime import datetime
from haversine import haversine
def load_data_from_directory(DATA_PATH, num_flights):
files_list = glob.glob(join(DATA_PATH, "*pkl"))
print("There are %d files in total" % len(files_list))
files_list = files_list[:num_flights]
print("We process %d files" % num_flights)
dfs = []
p = 0
for idx, f in enumerate(files_list):
if idx % int(len(files_list)/10) == 0:
print(str(p*10) + "%: [" + "#"*p + " "*(10-p) + "]", end="\r")
p += 1
dfs.append(pd.read_pickle(f))
print(str(p*10) + "%: [" + "#"*p + " "*(10-p) + "]", end="\r")
return dfs
```
<div class="label label-primary">Execute the cell below to load the data for part 1</div>
```
num_flights = 780
flights = load_data_from_directory(BASE_DIR + "part1/flights", num_flights)
for f in flights:
l = len(f)
new_idx = pd.date_range(start=pd.Timestamp("now").date(), periods=l, freq="S")
f.set_index(new_idx, inplace=True)
```
The data is loaded with pandas. Please take a look at the [pandas cheat sheet](https://github.com/pandas-dev/pandas/blob/master/doc/cheatsheet/Pandas_Cheat_Sheet.pdf) if you have any doubt. You are provided with 780 dataframes, each of them represents the records of the variables defined above during a whole flight.
`flights` is a list where each item is a dataframe storing the data of one flight. There is no particular ordering in this list. All the flights depart from the same airport and arrive at the same airport. These airports are hidden to you and you will soon understand how.
For example `flights[0]` is a dataframe, representing one flight.
```
# Give an alias to flights[0] for convenience
f = flights[0]
flights[0].head()
```
You can select a column by indexing by its name.
```
f["PITCH"].describe()
```
Use `iloc[]` to select by line number, either the whole dataframe to obtain all the variables of a dataframe...
```
f.iloc[50:60]
```
...or an individual series.
```
f["PITCH"].iloc[50:60]
```
Finally let's work out an example of visualization of a column.
```
# Create a figure and one subplot
fig, ax = plt.subplots()
# Give an alias to flights[0] for convenience
f = flights[0]
# Select PITCH column of f and plot the line on ax
f.PITCH.plot(title="the title", ax=ax)
```
## Visualization
To perform monitoring of flights, it is necessary to clean up the data. To start, it is important to visualize the data that is available, in order to understand better their properties and the problems associated with them (noise, statistical characteristics, features and other values).
For the following questions do not hesitate to resort to the documentation of pandas for plotting capabilities (for a [dataframe](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.plot.html) or for a [series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.plot.html))
<div class="alert alert-info">
<h3><div class="label label-default">Question 1</div> <div class="label label-info">Visualize all the variables</div></h3>
<br>
For an arbitrary flight, for example <code>flights[0]</code>, visualize all the variables. Would you rather use plot or scatter? Interpolate the data or not interpolate? Think about NaN values and how they are treated when we plot a series. Comment.
</div>
```
# LATP_1 LONP_1 HEAD PITCH ROLL IAS RALT1 RALT2 RALT3 ALT_STD N11 N21 N22 N12 AIR_GROUND
fig, axarr = plt.subplots(16,1, figsize=[10, 60])
f.LATP_1.plot(title='LATP_1', ax=axarr[1])
f.LONP_1.plot(title='LONP_1',ax=axarr[2])
f.HEAD.plot(title='HEAD',ax=axarr[3])
f.PITCH.plot(title='PITCH',ax=axarr[4])
f.ROLL.plot(title='ROLL',ax=axarr[5])
f.IAS.plot(title='IAS',ax=axarr[6])
f.RALT1.plot(title='RALT1',ax=axarr[7])
f.RALT2.plot(title='RALT2',ax=axarr[8])
f.RALT3.plot(title='RALT3',ax=axarr[9])
f.ALT_STD.plot(title='ALT_STD',ax=axarr[10])
f.N11.plot(title='N11',ax=axarr[11])
f.N12.plot(title='N12',ax=axarr[12])
f.N21.plot(title='N21',ax=axarr[13])
f.N22.plot(title='N22',ax=axarr[14])
f.AIR_GROUND.plot(title='AIR_GROUND',ax=axarr[15])
```
** Answer **
First of all we would use plots in order to visualise the trend in time of each variable alone. Scatter is vetter to understand the correlation between variables (without time in it).
For data that is empty we should interpolate (RALTs), and not for the rest.
We should inferpolate as a solution to the NaN values, but if there are too many NaNs it's not worth it, it may be better to join all three RALTs together
If it is interesting to see the variables for a given flight, it is more informative to view the set of values for all flights in order to understand what are the significant/normal values and what are those which are abnormal.
<div class="alert alert-info">
<h3><div class="label label-default">Question 2</div> <div class="label label-info">Visualize N21 variable for all flights</div></h3>
<br>
For the <code>N21</code> variable, for example, display all of the flights on the same figure. Use alpha parameter to add transparency to your plot. Is there any pattern? Comment the variabilities you observe.
</div>
```
for f in flights:
f.N21.plot(alpha=0.02, color='red', figsize=[15,9])
```
** Answer **
Even though they follow a clear pattern, there is a large variance. Nevertheless, there is a clear trend, with the ascention up to 00:30, cruise from then on and landing at the end.
Some variables must be analyzed together, such as latitude and longitude, otherwise the visualization information will be incomplete, we could be missing something.
<div class="alert alert-info">
<h3><div class="label label-default">Question 3</div> <div class="label label-info">Visualize latitude against longitude for all flights</div></h3>
<br>
Display the trajectories (<code>LONP_1</code>, <code>LATP_1</code>) of a subset of flights, for example 50 flights. What do you see? Keep in mind that the data during the beginning of the recording may be abnormal. What insight do you lose when you plot <code>LONP_1</code> against <code>LATP_1</code> ?
</div>
```
# fig, ax = plt.subplots(figsize=[16,16])
# for flight in flights[:50]:
# ax.plot(x=flight.LONP_1, y=flight.LATP_1, alpha=0.1)
# plt.show()
fig, ax = plt.subplots(figsize=[13, 13])
for f in flights[:50]:
f[10:].plot(x='LONP_1', y='LATP_1', ax=ax, alpha = 0.02, legend=False, kind='scatter')
ax.set_xlim(min(f.LONP_1[10:]), max(f.LONP_1[10:]))
ax.set_ylim(min(f.LATP_1[10:]), max(f.LATP_1[10:]))
```
** Answer **
We lose the time, not knowing how fast was the plane travelling. We also lose the height, meaning we have no clue about the takeoff-landing points (although we can have an approximate idea).
Keep in mind that our goal is to understand the nature and the inherent problems of our data, and its features. Proceed with the visual analysis of the data, looking at different features.
<div class="alert alert-info">
<h3><div class="label label-default">Question 4</div> <div class="label label-info">Recap variables that require pre-processing</div></h3>
<br>
Based on your observations as for now, what are the variables requiring processing? For each of these variables, specify the necessary pre-processing required prior to perform data analysis.
</div>
** Answer **
- **Longitude & Latitude**: Messy beginning and noisy signals with very high peaks. filtering it out would help.
- **RALTs**: Treatment of NaNs, maybe merging the three measurements.
- **HEAD**: There are some discontinuities, probably due to angle wrapping.
- **NXX and others**: they are quite clean, not need to processing
## Pre-processing
Data pre-processing is essential, in order to separate the errors due to measurement from "normal" data variability, which is representative of the phenomenon that interests us.
<div class="alert alert-info">
<h3><div class="label label-default">Question 5</div> <div class="label label-info">Smooth and filter out abnormal data in trajectories (LATP_1 and LONP_1)</div></h3>
<br>
Filter the flight trajectories (<code>LATP_1</code> and <code>LONP_1</code> variables). You can focus on the first 20 flights, that is <code>flights[:20]</code>. Display the trajectories before and after smoothing.
</div>
```
# This is a template code, fill in the blanks, or use your own code
# Give an alias to the first few flights for convenience
fs = flights[:20]
# Set up the figure to plot the trajectories before (ax0) and after smoothing (ax1)
fig, axes = plt.subplots(1, 2, figsize=(15, 8))
# Unpack the axes
ax0, ax1 = axes
# Iterate over fs and add two new smooth columns for each flight
for f in fs:
f["LATP_1_C"] = f.LATP_1.rolling(window=40).sum() # FILL IN THE BLANKS
f["LONP_1_C"] = f.LONP_1.rolling(window=40).sum()
# Iterate over fs and plot the trajectories before and after smoothing
for f in fs:
# Plot the raw trajectory on ax0
f.plot(kind="scatter", x="LATP_1", y="LONP_1", s=1, ax=ax0)
# Plot the smoothed trajectory on ax1
f.plot(kind="scatter", x="LATP_1_C", y="LONP_1_C", s=1, ax=ax1)
fig.tight_layout()
```
** Answer **
Just filtering with a window size of 40 secs and summing does the job
<div class="alert alert-info">
<h3><div class="label label-default">Question 6</div> <div class="label label-info">Pre-process HEAD, get rid off discontinuities</div></h3>
<br>
Angles are special variables because they "cycle" over their range of values. The <code>HEAD</code> variable shows artificial discontinuities: your goal is to eliminate (filter out) such discontinuities. The angle may no longer be between 0 and 360 degrees after the transformation but it will come very handy for some analysis later. Display the data before and after transformation. You can focus on one flight, for example <code>flights[0]</code>.
</div>
```
# Your code goes here ...
```
** Answer **
your answer here ...
<h1><div class="label label-success">Part 2: Analysis</div></h1>
We now turn to the data analysis task. In this part, we will use a **clean** dataset, which has been prepared for you; nevertheless, the functions you developed in the first part of the notebook can still be used to visualize and inspect the new data. Next, we display the schema of the new dataset you will use:
| name | description | unit |
|:-----:|:-------------:|:---:|
| TIME |elapsed seconds| second |
| **LATP_C** | **Latitude, Corrected**| ** degree ° **|
| **LONP_C** | **Longitude, Corrected**| ** degree ° **|
| **RALT_F** | **Radio Altitude, Fusioned**| ** feet ** |
| **ALT_STD_C** | **Relative Altitude, Corrected**| ** feet ** |
| **HEAD_C** | **head, Corrected**| ** degree ° ** |
| **HEAD_TRUE** | **head, without discontinuities**| ** degree ° ** |
| **PITCH_C** | **pitch, Corrected**| ** degree ° ** |
| **ROLL_C** | **roll, Corrected**| ** degree ° ** |
| **IAS_C** | **Indicated Air Speed, Corrected**| ** m/s ** |
| N11 | speed N1 of the first engine | % |
| N21 | speed N2 of the first engine | % |
| N12 | speed N1 of the second engine | % |
| N22 | speed N2 of the second engine | % |
| AIR_GROUND | 1: ground, 0: airr | boolean |
<div class="label label-primary">Execute the cell below to load the data for part 2</div>
```
num_flights = 780
flights = load_data_from_directory(BASE_DIR + "part2/flights/", num_flights)
for f in flights:
l = len(f)
new_idx = pd.date_range(start=pd.Timestamp("now").date(), periods=l, freq="S")
f.set_index(new_idx, inplace=True)
```
## Detection of phases of flight

In order to understand the different events that can happen, it is necessary to understand in what phase of the flight the aircraft is located. Indeed, an event that could be regarded as normal in a stage could be abnormal in another stage.
<div class="alert alert-info">
<h3><div class="label label-default">Question 7</div> <div class="label label-info">Detect take-off and touch-down phases</div></h3>
<br>
Using the clean dataset, detect the take-off phase and the touch-down of all flights. Among all the variables available, what is the variable that tells us the most easily when the take off happens? There is no trap here. Choose the best variable wisely and use it to detect the indices of take-off and touch-down. Plot <code>ALT_STD_C</code> 5 mins before and 5 mins after take-off to test your criterion. Do the same for touch-down.
</div>
```
plt.plot(f.RALT_F.diff(1).rolling(window=20).sum())
fig, ax = plt.subplots(1,2, figsize=[15,9])
ax[0].set_title('Takeoff')
ax[1].set_title('Landing')
for i,f in enumerate(flights):
takeoff = f.RALT_F.diff(1).rolling(window=20).sum().idxmax()
landing = f.RALT_F.diff(1).rolling(window=20).sum().idxmin()
ax[0].plot(f.loc[takeoff-360:takeoff+360].ALT_STD_C)
ax[1].plot(f.loc[landing-360:landing+360].ALT_STD_C)
plt.show()
```
** Answer **
Clearly the best variable would have been AIR_GROUND, a boolean that would tell us the exact moment when it starts flying. However, since we don't have access to it anymore, we are gonna use RALT_F, and by applying a difference of 5 seconds in the series while detecting the maximum and minimum we obtain the value.
<div class="alert alert-info">
<h3><div class="label label-default">Question 8</div> <div class="label label-info">HEAD during take-off and touch-down phases</div></h3>
<br>
Plot the <code>HEAD_C</code> variable between 20 seconds before the take-off until the take-off itself. Compute the mean of <code>HEAD_C</code> during this phase for each individual flight and do a boxplot of the distribution you obtain. Do the same for the touch-down. What do you observe? Is there something significant? Recall [how runways are named](https://en.wikipedia.org/wiki/Runway#Naming)
</div>
```
fig, ax = plt.subplots(1,2, figsize=[15,9])
ax[0].set_title('Takeoff HEAD_C')
ax[1].set_title('Landing HEAD_C')
meansTakeoff = []
meansLanding = []
for i,f in enumerate(flights):
takeoff = f.RALT_F.diff(1).rolling(window=20).sum().idxmax()
landing = f.RALT_F.diff(1).rolling(window=20).sum().idxmin()
meansTakeoff.append(f.loc[takeoff-20:takeoff].HEAD_C.mean())
meansLanding.append(f.loc[landing-20:landing].HEAD_C.mean())
df = pd.DataFrame(meansTakeoff)
df.plot.box(ax=ax[0])
df2 = pd.DataFrame(meansLanding)
df2.plot.box(ax=ax[1])
```
** Answer **
We see that the vast majority are below 100 degrees. if we divide by 10 we would be getting the most probable names for the runways the plane took.
Also, since the head degree in takeoff is in average smaller than the landing degree, the plane should be turning right in average during his trajectory
Next, we want to detect the moment that the aircraft completed its climb (top of climb) and the moment when the aircraft is in descent phase.
<div class="alert alert-info">
<h3><div class="label label-default">Question 9</div> <div class="label label-info">Detect top-of-climb and beginning of descent phases</div></h3>
<br>
Plot <code>ALT_STD_C</code> a minute before liftoff until five minutes after the top of climb. In another figure plot <code>ALT_STD_C</code> a minute before the beginning of descent until the touch-down. For information, a plane is considered:
<ul>
<li>in phase of climb if the altitude increases 30 feet/second for 20 seconds</li>
<li>in stable phase if the altitude does not vary more than 30 feet for 5 minutes</li>
<li>in phase of descent if the altitude decreases 30 feet/second for 20 seconds</li>
</ul>
</div>
```
# This is a template code, fill in the blanks, or use your own code
# Give an alias to flights[0] for convenience
f = flights[0]
f["CLIMB"] = f.ALT_STD_C.diff().rolling(window=20).sum() > 30
f["STABLE"] = f.ALT_STD_C.diff().rolling(window=300).sum() < 30
f["DESCENT"] = f.ALT_STD_C.diff().rolling(window=20).sum() < -30
f[f.CLIMB].ALT_STD_C.plot(color="C0", linestyle="none", marker=".", label="CLIMB") # plot climb phase
f[f.STABLE].ALT_STD_C.plot(color="C1", linestyle="none", marker=".", label="STABLE") # plot stable phase
f[f.DESCENT].ALT_STD_C.plot(color="C2", linestyle="none", marker=".", label="DESCENT") # plot descent phase
top_of_climb = f.CLIMB[-1]
beginning_of_descent = f.DESCENT[0]
plt.legend()
```
** Answer **
It works! some data is left out due to window size in stable areas.
<div class="alert alert-info">
<h3><div class="label label-default">Question 10</div> <div class="label label-info">Flight time</div></h3>
<br>
Using your criteria to detect the take-off and the touch-down, compute the duration of each flight, and plot the distribution you obtain (boxplot, histogram, kernel density estimation, use your best judgement). Comment the distribution.
</div>
```
dur_arr = []
for i,f in enumerate(flights):
takeoff = f.RALT_F.diff(1).rolling(window=20).sum().idxmax()
landing = f.RALT_F.diff(1).rolling(window=20).sum().idxmin()
dur_arr.append((landing.value-takeoff.value)/(1e+9))
df = pd.DataFrame(dur_arr)
df.plot.density(figsize=[15,9])
df.plot.hist(figsize=[15,9], bins=100)
```
** Answer **
Average is arround 6000 secs
## Problems
Note that the data that we are using in this notebook has been anonymized. This means that the trajectories of a flight have been modified to hide the real information about that flight. In particular, in the dataset we use in this notebook, trajectories have been modified by simple translation and rotation operations
<div class="alert alert-info">
<h3><div class="label label-default">Question 11</div> <div class="label label-danger">Challenge</div> <div class="label label-info">Find origin and destination airports</div></h3>
<br>
You are asked to find the departure and destination airports of the flights in the dataset. You are guided with sample code to load data from external resources and through several steps that will help you to narrow down the pairs of possible airports that fit with the anonymised data.
</div>
We begin by grabbing airport/routes/runways data available on the internet, for example [ourairports](http://ourairports.com/data) (for [airports](http://ourairports.com/data/airports.csv) and [runways](http://ourairports.com/data/runways.csv)) and [openflights](http://www.openflights.org/data.html) (for [routes](https://raw.githubusercontent.com/jpatokal/openflights/master/data/routes.dat)). These datasets would come useful. You can find the schema of the three datasets below and the code to load the data.
airports.csv
---------------
|var|description|
|:--:|:--:|
| ** ident ** | ** icao code **|
| type | type |
| name | airport name|
| ** latitude_deg **| ** latitude in ° **|
| ** longitude_deg **| ** longitude in ° **|
| elevation_ft | elevation in feet|
| ** iata_code ** | ** iata code ** |
routes.dat
---------------
|var|description|
|:--:|:--:|
|AIRLINE | 2-letter (IATA) or 3-letter (ICAO) code of the airline.|
|SOURCE_AIRPORT | 3-letter (IATA) code of the source airport.|
|DESTINATION_AIRPORT| 3-letter (IATA) code of the destination airport.|
runways.csv
---------------
|var|description|
|:--:|:--:|
|airport_ident | 4-letter (ICAO) code of the airport.|
| ** le_ident **| ** low-end runway identity **|
| le_elevation_ft | low-end runway elevation in feet |
| le_heading_degT | low-end runway heading in ° |
| ** he_ident **| ** high-end runway identity **|
| he_elevation_ft | high-end runway elevation in feet |
| ** he_heading_degT **|** high-end runway heading in ° **|
The code below has been done for you, it loads the three datasets mentionned and prepare the `pairs` dataframe.
```
# Load airports data from ourairports.com
airports = pd.read_csv("http://ourairports.com/data/airports.csv",
usecols=[1, 2, 3, 4, 5, 6, 13])
# Select large airports
large_airports = airports[(airports.type == "large_airport")]
print("There are " + str(len(large_airports)) +
" large airports in the world, let's focus on them")
print("airports columns:", airports.columns.values)
# Load routes data from openflights.com
routes = pd.read_csv("https://raw.githubusercontent.com/jpatokal/openflights/master/data/routes.dat",
header=0, usecols=[0, 2, 4],
names=["AIRLINE", "SOURCE_AIRPORT",
"DESTINATION_AIRPORT"])
print("routes columns:", routes.columns.values)
# Load runways data from ourairports.com
runways = pd.read_csv("http://ourairports.com/data/runways.csv", header=0,
usecols=[2, 8, 12, 14, 18],
dtype={
"le_ident": np.dtype(str),
"he_ident": np.dtype(str)
})
print("runways columns:", runways.columns.values)
# Create all pairs of large airports
la = large_airports
pairs = pd.merge(la.assign(i=0), la.assign(i=0), how="outer",
left_on="i", right_on="i", suffixes=["_origin", "_destination"])
# Compute haversine distance for all pairs of large airports
pairs["haversine_distance"] = pairs.apply(lambda x: haversine((x.latitude_deg_origin, x.longitude_deg_origin),
(x.latitude_deg_destination, x.longitude_deg_destination)), axis=1)
del pairs["type_origin"]
del pairs["type_destination"]
del pairs["i"]
pairs = pairs[pairs.ident_origin != pairs.ident_destination]
pairs = pairs.reindex_axis(["ident_origin", "ident_destination", "iata_code_origin", "iata_code_destination",
"haversine_distance",
"elevation_ft_origin", "elevation_ft_destination",
"latitude_deg_origin", "longitude_deg_origin",
"latitude_deg_destination", "longitude_deg_destination"], axis=1)
print("pairs columns:", pairs.columns.values)
```
<div class="label label-primary">Execute the cell below to load the data created by the code above</div>
```
airports = pd.read_pickle(BASE_DIR + "part2/airports.pkl")
large_airports = pd.read_pickle(BASE_DIR + "part2/large_airports.pkl")
routes = pd.read_pickle(BASE_DIR + "part2/routes.pkl")
runways = pd.read_pickle(BASE_DIR + "part2/runways.pkl")
pairs = pd.read_pickle(BASE_DIR + "part2/pairs.pkl")
print("There are " + str(len(large_airports)) +
" large airports in the world, let's focus on them")
# Plot all airports in longitude-latitude plane
plt.scatter(airports["longitude_deg"], airports["latitude_deg"], s=.1)
# Plot large airports in longitude-latitude plane
plt.scatter(large_airports["longitude_deg"], large_airports["latitude_deg"], s=.1)
plt.xlabel("latitude_deg")
plt.ylabel("longitude_deg")
plt.title("All airports (blue) \n large airports (red)")
print("airports columns:", airports.columns.values)
print("routes columns:", routes.columns.values)
print("runways columns:", runways.columns.values)
print("pairs columns:", pairs.columns.values)
```
You are provided with a dataframe of all pairs of large airports in the world: `pairs`
```
pairs.sample(5)
```
<div class="alert alert-info">
<h3><div class="label label-default">Question 11.1</div> <div class="label label-info"> Step 1</div></h3>
<br>
A first step towards the desanonymisation of the data is to use the distance between the airports. Each entry of `pairs` show the latitude and longitude of both airports and the haversine distance between them. Filter the possible pairs of airports by selecting airports that show a distance that is reasonably close to the distance you can compute with the anonymised data. How many pairs of airports do you have left?</div>
```
dist_arr = []
for i,f in enumerate(flights):
takeoff = f.RALT_F.diff(1).rolling(window=20).sum().idxmax()
landing = f.RALT_F.diff(1).rolling(window=20).sum().idxmin()
dist_arr.append(haversine((f.loc[takeoff].LATP_C, f.loc[takeoff].LONP_C), (f.loc[landing].LATP_C, f.loc[landing].LONP_C) ))
df= pd.DataFrame(dist_arr)
float(df.mean())
pairs2 = pairs[pairs.haversine_distance < float(df.mean())+100]
pairs3 = pairs2[pairs2.haversine_distance > float(df.mean())-100]
pairs3.describe()
pairs.describe()
```
** Answer **
We have reduced it to 6K possibilities by limiting it to the mean +-100 in haversine
<div class="alert alert-info">
<h3><div class="label label-default">Question 11.2</div> <div class="label label-info">Step 2</div></h3>
<br>
You should now have a significantly smaller dataframe of possible pairs of airports. The next step is to eliminate the pairs of airports that are connected by commercial flights. You have all the existing commercial routes in the dataset <code>routes</code>. Use this dataframe to eliminate the airports that are not connected. How many pairs of airports possible do you have left?
</div>
```
# This is template code cell, fill in the blanks, or use your own code
selected = pd.merge(pairs3,
routes,
how='inner',
left_on=["iata_code_origin", "iata_code_destination"],
right_on=["SOURCE_AIRPORT", "DESTINATION_AIRPORT"])
selected.describe()
```
** Answer **
Further down! up to 2.7K
<div class="alert alert-info">
<h3><div class="label label-default">Question 11.3</div> <div class="label label-info"> Step 3</div></h3>
<br>
You now have a list of pairs of airports that are at a reasonable distance with respect to the distance between the airports in the anonymised data and that are connected by a commercial route. We have explored variables in the anonymised data that have not been altered and that may help us to narrow down the possibilities even more. Can you see what variable you may use? What previous question can help you a lot? Choose your criterion and use it to eliminate to pairs of airports that does not fit to the anonymised data.
</div>
```
lat_arr1 = []
lat_arr2 = []
for i,f in enumerate(flights):
takeoff = f.RALT_F.diff(1).rolling(window=20).sum().idxmax()
landing = f.RALT_F.diff(1).rolling(window=20).sum().idxmin()
lat_arr1.append(f.loc[takeoff].LATP_C, f.loc[takeoff].LONP_C)
lat_arr2.append(f.loc[landing].LATP_C, f.loc[landing].LONP_C)
df1 = pd.DataFrame(lat_arr1)
df2 = pd.DataFrame(lat_arr2)
selected[selected.latitude_deg_origin < ...]
```
** Answer **
Clearly using the Latitude and Longitude should help greatly, filtering the same way we did before with the other data. No time to run it!
<div class="alert alert-info">
<h3><div class="label label-default">Question 11.4</div> <div class="label label-info">Step 4</div></h3>
<br>
Is there any other variables that can help discriminate more the airports?
</div>
```
# Your code goes here ...
```
** Answer **
your answer here ...
| true |
code
| 0.503113 | null | null | null | null |
|
```
from math import floor
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from src.LinearSimulator import Simulator, SimpleSSM
from src.control.SimpleMPC import MPC
from src.utils import set_seed
```
## Setup simulator and model
```
device = 'cpu'
set_seed(seed=0, use_cuda=False)
state_dim = 2
action_dim = 3
model = SimpleSSM(state_dim, action_dim).to(device)
simul = Simulator(state_dim, action_dim, noise=0.01).to(device)
A=np.array([[0.9, 0.1],
[0.1, 0.9]])
B=np.array([[1, -1],
[-1, 2],
[-2, 1]])
model.A.weight.data = torch.tensor(A, device=device).float()
simul.A.weight.data = torch.tensor(A, device=device).float()
model.B.weight.data = torch.tensor(B, device=device).float()
simul.B.weight.data = torch.tensor(B, device=device).float()
action_min = -1.0
action_max = +1.0
H = 5
T = 100
```
## Set target trajectory
```
x_ref = torch.ones((T, state_dim), device=device) * 2.0
recession_period = floor(T * 0.1)
x_ref[:recession_period, :] = 0
x_ref[-recession_period:, :] = 0
fig, axes = plt.subplots(2,1, sharex=True)
for i in range(2):
axes[i].plot(x_ref[:,i].to('cpu'),
color='C{}'.format(i),
label='state {} target'.format(i))
axes[i].set_xlabel('time')
axes[i].legend()
solver = MPC(model=model,
state_dim=state_dim,
action_dim=action_dim,
H=H,
action_min=action_min,
action_max=action_max).to(device)
x = torch.zeros((1,state_dim), device=device)
state_trajectory = []
action_trajectory = []
opt_results = []
for itr in range(T-H):
# Solve MPC problem
state_ref = x_ref[itr:itr+H,:]
state_ref = state_ref.unsqueeze(dim=0) # add batch dim
us, info = solver.solve(x0=x, target=state_ref, max_iter=2000)
action = us[:,0,:]
print("Step {:2d} | loss {:.7f} | solve : {}".format(itr, info['loss'], info['solve']))
# perform simulation with the optmized action
with torch.no_grad():
x = simul(x, action.view(1,-1))
action_trajectory.append(action)
state_trajectory.append(x)
opt_results.append(action)
controlled = np.concatenate(state_trajectory, axis=0)
fig, axes = plt.subplots(2,1, sharex=True)
for i in range(2):
axes[i].plot(x_ref[:,i].to('cpu'),
color='gray',
ls='--',
label='target'.format(i))
axes[i].plot(controlled[:,i],
color='C{}'.format(i),
label='controlled'.format(i))
axes[i].set_xlabel('time')
axes[i].legend()
```
| true |
code
| 0.759772 | null | null | null | null |
|
```
#load watermark
%load_ext watermark
%watermark -a 'Gopala KR' -u -d -v -p watermark,numpy,pandas,matplotlib,nltk,sklearn,tensorflow,theano,mxnet,chainer,seaborn,keras,tflearn,bokeh,gensim
import keras
keras.__version__
```
# A first look at a neural network
This notebook contains the code samples found in Chapter 2, Section 1 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
----
We will now take a look at a first concrete example of a neural network, which makes use of the Python library Keras to learn to classify
hand-written digits. Unless you already have experience with Keras or similar libraries, you will not understand everything about this
first example right away. You probably haven't even installed Keras yet. Don't worry, that is perfectly fine. In the next chapter, we will
review each element in our example and explain them in detail. So don't worry if some steps seem arbitrary or look like magic to you!
We've got to start somewhere.
The problem we are trying to solve here is to classify grayscale images of handwritten digits (28 pixels by 28 pixels), into their 10
categories (0 to 9). The dataset we will use is the MNIST dataset, a classic dataset in the machine learning community, which has been
around for almost as long as the field itself and has been very intensively studied. It's a set of 60,000 training images, plus 10,000 test
images, assembled by the National Institute of Standards and Technology (the NIST in MNIST) in the 1980s. You can think of "solving" MNIST
as the "Hello World" of deep learning -- it's what you do to verify that your algorithms are working as expected. As you become a machine
learning practitioner, you will see MNIST come up over and over again, in scientific papers, blog posts, and so on.
The MNIST dataset comes pre-loaded in Keras, in the form of a set of four Numpy arrays:
```
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
```
`train_images` and `train_labels` form the "training set", the data that the model will learn from. The model will then be tested on the
"test set", `test_images` and `test_labels`. Our images are encoded as Numpy arrays, and the labels are simply an array of digits, ranging
from 0 to 9. There is a one-to-one correspondence between the images and the labels.
Let's have a look at the training data:
```
train_images.shape
len(train_labels)
train_labels
```
Let's have a look at the test data:
```
test_images.shape
len(test_labels)
test_labels
```
Our workflow will be as follow: first we will present our neural network with the training data, `train_images` and `train_labels`. The
network will then learn to associate images and labels. Finally, we will ask the network to produce predictions for `test_images`, and we
will verify if these predictions match the labels from `test_labels`.
Let's build our network -- again, remember that you aren't supposed to understand everything about this example just yet.
```
from keras import models
from keras import layers
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))
```
The core building block of neural networks is the "layer", a data-processing module which you can conceive as a "filter" for data. Some
data comes in, and comes out in a more useful form. Precisely, layers extract _representations_ out of the data fed into them -- hopefully
representations that are more meaningful for the problem at hand. Most of deep learning really consists of chaining together simple layers
which will implement a form of progressive "data distillation". A deep learning model is like a sieve for data processing, made of a
succession of increasingly refined data filters -- the "layers".
Here our network consists of a sequence of two `Dense` layers, which are densely-connected (also called "fully-connected") neural layers.
The second (and last) layer is a 10-way "softmax" layer, which means it will return an array of 10 probability scores (summing to 1). Each
score will be the probability that the current digit image belongs to one of our 10 digit classes.
To make our network ready for training, we need to pick three more things, as part of "compilation" step:
* A loss function: the is how the network will be able to measure how good a job it is doing on its training data, and thus how it will be
able to steer itself in the right direction.
* An optimizer: this is the mechanism through which the network will update itself based on the data it sees and its loss function.
* Metrics to monitor during training and testing. Here we will only care about accuracy (the fraction of the images that were correctly
classified).
The exact purpose of the loss function and the optimizer will be made clear throughout the next two chapters.
```
network.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
```
Before training, we will preprocess our data by reshaping it into the shape that the network expects, and scaling it so that all values are in
the `[0, 1]` interval. Previously, our training images for instance were stored in an array of shape `(60000, 28, 28)` of type `uint8` with
values in the `[0, 255]` interval. We transform it into a `float32` array of shape `(60000, 28 * 28)` with values between 0 and 1.
```
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255
```
We also need to categorically encode the labels, a step which we explain in chapter 3:
```
from keras.utils import to_categorical
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
```
We are now ready to train our network, which in Keras is done via a call to the `fit` method of the network:
we "fit" the model to its training data.
```
network.fit(train_images, train_labels, epochs=2, batch_size=128)
```
Two quantities are being displayed during training: the "loss" of the network over the training data, and the accuracy of the network over
the training data.
We quickly reach an accuracy of 0.989 (i.e. 98.9%) on the training data. Now let's check that our model performs well on the test set too:
```
test_loss, test_acc = network.evaluate(test_images, test_labels)
print('test_acc:', test_acc)
```
Our test set accuracy turns out to be 97.8% -- that's quite a bit lower than the training set accuracy.
This gap between training accuracy and test accuracy is an example of "overfitting",
the fact that machine learning models tend to perform worse on new data than on their training data.
Overfitting will be a central topic in chapter 3.
This concludes our very first example -- you just saw how we could build and a train a neural network to classify handwritten digits, in
less than 20 lines of Python code. In the next chapter, we will go in detail over every moving piece we just previewed, and clarify what is really
going on behind the scenes. You will learn about "tensors", the data-storing objects going into the network, about tensor operations, which
layers are made of, and about gradient descent, which allows our network to learn from its training examples.
| true |
code
| 0.639624 | null | null | null | null |
|
**Copyright 2019 The TensorFlow Authors**.
Licensed under the Apache License, Version 2.0 (the "License").
# Generating Handwritten Digits with DCGAN
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/alpha/tutorials/generative/dcgan.ipynb">
<img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/tutorials/generative/dcgan.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/tutorials/generative/dcgan.ipynb">
<img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
View source on GitHub</a>
</td>
</table>
This tutorial demonstrates how to generate images of handwritten digits using a [Deep Convolutional Generative Adversarial Network](https://arxiv.org/pdf/1511.06434.pdf) (DCGAN). The code is written using the [Keras Sequential API](https://www.tensorflow.org/guide/keras) with a `tf.GradientTape` training loop.
## What are GANs?
[Generative Adversarial Networks](https://arxiv.org/abs/1406.2661) (GANs) are one of the most interesting ideas in computer science today. Two models are trained simultaneously by an adversarial process. A *generator* ("the artist") learns to create images that look real, while a *discriminator* ("the art critic") learns to tell real images apart from fakes.

During training, the *generator* progressively becomes better at creating images that look real, while the *discriminator* becomes better at telling them apart. The process reaches equilibrium when the *discriminator* can no longer distinguish real images from fakes.

This notebook demonstrate this process on the MNIST dataset. The following animation shows a series of images produced by the *generator* as it was trained for 50 epochs. The images begin as random noise, and increasingly resemble hand written digits over time.

To learn more about GANs, we recommend MIT's [Intro to Deep Learning](http://introtodeeplearning.com/) course.
```
# To generate GIFs
!pip install imageio
```
### Import TensorFlow and other libraries
```
!pip install tf-nightly-gpu-2.0-preview
import tensorflow as tf
print("You have version", tf.__version__)
assert tf.__version__ >= "2.0" # TensorFlow ≥ 2.0 required
from __future__ import absolute_import, division, print_function
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import os
import PIL
import tensorflow.keras.layers as layers
import time
from IPython import display
```
### Load and prepare the dataset
You will use the MNIST dataset to train the generator and the discriminator. The generator will generate handwritten digits resembling the MNIST data.
```
(train_images, train_labels), (_, _) = tf.keras.datasets.mnist.load_data()
train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')
train_images = (train_images - 127.5) / 127.5 # Normalize the images to [-1, 1]
BUFFER_SIZE = 60000
BATCH_SIZE = 256
# Batch and shuffle the data
train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
```
## Create the models
Both the generator and discriminator are defined using the [Keras Sequential API](https://www.tensorflow.org/guide/keras#sequential_model).
### The Generator
The generator uses `tf.keras.layers.Conv2DTranspose` (upsampling) layers to produce an image from a seed (random noise). Start with a `Dense` layer that takes this seed as input, then upsample several times until you reach the desired image size of 28x28x1. Notice the `tf.keras.layers.LeakyReLU` activation for each layer, except the output layer which uses tanh.
```
def make_generator_model():
model = tf.keras.Sequential()
model.add(layers.Dense(7*7*256, use_bias=False, input_shape=(100,)))
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
model.add(layers.Reshape((7, 7, 256)))
assert model.output_shape == (None, 7, 7, 256) # Note: None is the batch size
model.add(layers.Conv2DTranspose(128, (5, 5), strides=(1, 1), padding='same', use_bias=False))
assert model.output_shape == (None, 7, 7, 128)
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
model.add(layers.Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', use_bias=False))
assert model.output_shape == (None, 14, 14, 64)
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
model.add(layers.Conv2DTranspose(1, (5, 5), strides=(2, 2), padding='same', use_bias=False, activation='tanh'))
assert model.output_shape == (None, 28, 28, 1)
return model
```
Use the (as yet untrained) generator to create an image.
```
generator = make_generator_model()
noise = tf.random.normal([1, 100])
generated_image = generator(noise, training=False)
plt.imshow(generated_image[0, :, :, 0], cmap='gray')
```
### The Discriminator
The discriminator is a CNN-based image classifier.
```
def make_discriminator_model():
model = tf.keras.Sequential()
model.add(layers.Conv2D(64, (5, 5), strides=(2, 2), padding='same',
input_shape=[28, 28, 1]))
model.add(layers.LeakyReLU())
model.add(layers.Dropout(0.3))
model.add(layers.Conv2D(128, (5, 5), strides=(2, 2), padding='same'))
model.add(layers.LeakyReLU())
model.add(layers.Dropout(0.3))
model.add(layers.Flatten())
model.add(layers.Dense(1))
return model
```
Use the (as yet untrained) discriminator to classify the generated images as real or fake. The model will be trained to output positive values for real images, and negative values for fake images.
```
discriminator = make_discriminator_model()
decision = discriminator(generated_image)
print (decision)
```
## Define the loss and optimizers
Define loss functions and optimizers for both models.
```
# This method returns a helper function to compute cross entropy loss
cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True)
```
### Discriminator loss
This method quantifies how well the discriminator is able to distinguish real images from fakes. It compares the disciminator's predictions on real images to an array of 1s, and the disciminator's predictions on fake (generated) images to an array of 0s.
```
def discriminator_loss(real_output, fake_output):
real_loss = cross_entropy(tf.ones_like(real_output), real_output)
fake_loss = cross_entropy(tf.zeros_like(fake_output), fake_output)
total_loss = real_loss + fake_loss
return total_loss
```
### Generator loss
The generator's loss quantifies how well it was able to trick the discriminator. Intuitively, if the generator is performing well, the discriminator will classify the fake images as real (or 1). Here, we will compare the disciminators decisions on the generated images to an array of 1s.
```
def generator_loss(fake_output):
return cross_entropy(tf.ones_like(fake_output), fake_output)
```
The discriminator and the generator optimizers are different since we will train two networks separately.
```
generator_optimizer = tf.keras.optimizers.Adam(1e-4)
discriminator_optimizer = tf.keras.optimizers.Adam(1e-4)
```
### Save checkpoints
This notebook also demonstrates how to save and restore models, which can be helpful in case a long running training task is interrupted.
```
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
```
## Define the training loop
```
EPOCHS = 50
noise_dim = 100
num_examples_to_generate = 16
# We will reuse this seed overtime (so it's easier)
# to visualize progress in the animated GIF)
seed = tf.random.normal([num_examples_to_generate, noise_dim])
```
The training loop begins with generator receiving a random seed as input. That seed is used to produce an image. The discriminator is then used to classify real images (drawn from the training set) and fakes images (produced by the generator). The loss is calculated for each of these models, and the gradients are used to update the generator and discriminator.
```
# Notice the use of `tf.function`
# This annotation causes the function to be "compiled".
@tf.function
def train_step(images):
noise = tf.random.normal([BATCH_SIZE, noise_dim])
with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
generated_images = generator(noise, training=True)
real_output = discriminator(images, training=True)
fake_output = discriminator(generated_images, training=True)
gen_loss = generator_loss(fake_output)
disc_loss = discriminator_loss(real_output, fake_output)
gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables)
gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)
generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))
discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))
def train(dataset, epochs):
for epoch in range(epochs):
start = time.time()
for image_batch in dataset:
train_step(image_batch)
# Produce images for the GIF as we go
display.clear_output(wait=True)
generate_and_save_images(generator,
epoch + 1,
seed)
# Save the model every 15 epochs
if (epoch + 1) % 15 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print ('Time for epoch {} is {} sec'.format(epoch + 1, time.time()-start))
# Generate after the final epoch
display.clear_output(wait=True)
generate_and_save_images(generator,
epochs,
seed)
```
**Generate and save images**
```
def generate_and_save_images(model, epoch, test_input):
# Notice `training` is set to False.
# This is so all layers run in inference mode (batchnorm).
predictions = model(test_input, training=False)
fig = plt.figure(figsize=(4,4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i+1)
plt.imshow(predictions[i, :, :, 0] * 127.5 + 127.5, cmap='gray')
plt.axis('off')
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
```
## Train the model
Call the `train()` method defined above to train the generator and discriminator simultaneously. Note, training GANs can be tricky. It's important that the generator and discriminator do not overpower each other (e.g., that they train at a similar rate).
At the beginning of the training, the generated images look like random noise. As training progresses, the generated digits will look increasingly real. After about 50 epochs, they resemble MNIST digits. This may take about one minute / epoch with the default settings on Colab.
```
%%time
train(train_dataset, EPOCHS)
```
Restore the latest checkpoint.
```
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
```
## Create a GIF
```
# Display a single image using the epoch number
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
display_image(EPOCHS)
```
Use `imageio` to create an animated gif using the images saved during training.
```
with imageio.get_writer('dcgan.gif', mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
last = -1
for i,filename in enumerate(filenames):
frame = 2*(i**0.5)
if round(frame) > round(last):
last = frame
else:
continue
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
# A hack to display the GIF inside this notebook
os.rename('dcgan.gif', 'dcgan.gif.png')
```
Display the animated gif with all the mages generated during the training of GANs.
```
display.Image(filename="dcgan.gif.png")
```
## Next steps
This tutorial has shown the complete code necessary to write and train a GAN. As a next step, you might like to experiment with a different dataset, for example the Large-scale Celeb Faces Attributes (CelebA) dataset [available on Kaggle](https://www.kaggle.com/jessicali9530/celeba-dataset/home). To learn more about GANs we recommend the [NIPS 2016 Tutorial: Generative Adversarial Networks](https://arxiv.org/abs/1701.00160).
| true |
code
| 0.806396 | null | null | null | null |
|
# Detectron2 training notebook
Based on the [official Detectron 2 tutorial](
https://colab.research.google.com/drive/16jcaJoc6bCFAQ96jDe2HwtXj7BMD_-m5)
This is a notebook that can generate the model used for the image segmentation. It is intended to be used on google colab, but can easily be changed to run locally.
To run this notebook you need some extra files which are available in our google drive folder detectron2segment. The train and val folders, they contain images and their respective polygon annotations.
The output you need to save from this notebook is
- model_final.pth
- config.yml
These are used to run inference and should be placed in this folder
# Install detectron2
```
# install dependencies:
!pip install pyyaml==5.1
!gcc --version
# CUDA 10.2
!pip install torch==1.7.1 torchvision==0.8.2 torchaudio==0.7.2
# opencv is pre-installed on colab
import torch, torchvision
print(torch.__version__, torch.cuda.is_available())
!nvcc --version
# install detectron2: (Colab has CUDA 10.1 + torch 1.7)
# See https://detectron2.readthedocs.io/tutorials/install.html for instructions
import torch
assert torch.__version__.startswith("1.7") # please manually install torch 1.7 if Colab changes its default version
!pip install detectron2 -f https://dl.fbaipublicfiles.com/detectron2/wheels/cu101/torch1.7/index.html
exit(0) # After installation, you need to "restart runtime" in Colab. This line can also restart runtime
# Some basic setup:
# Setup detectron2 logger
import detectron2
from detectron2.utils.logger import setup_logger
setup_logger()
# import some common libraries
import numpy as np
import os, json, cv2, random
from google.colab.patches import cv2_imshow
# import some common detectron2 utilities
from detectron2 import model_zoo
from detectron2.engine import DefaultPredictor
from detectron2.config import get_cfg
from detectron2.utils.visualizer import Visualizer
from detectron2.data import MetadataCatalog, DatasetCatalog
```
# Run a pre-trained detectron2 model
We first download an image from the COCO dataset:
```
!wget http://images.cocodataset.org/val2017/000000439715.jpg -q -O input.jpg
im = cv2.imread("./input.jpg")
#im = cv2.imread("./drive/MyDrive/data/train/brace.jpg")
cv2_imshow(im)
```
Then, we create a detectron2 config and a detectron2 `DefaultPredictor` to run inference on this image.
```
cfg = get_cfg()
# add project-specific config (e.g., TensorMask) here if you're not running a model in detectron2's core library
cfg.merge_from_file(model_zoo.get_config_file("COCO-InstanceSegmentation/mask_rcnn_R_50_FPN_3x.yaml"))
cfg.MODEL.ROI_HEADS.SCORE_THRESH_TEST = 0.5 # set threshold for this model
# Find a model from detectron2's model zoo. You can use the https://dl.fbaipublicfiles... url as well
cfg.MODEL.WEIGHTS = model_zoo.get_checkpoint_url("COCO-InstanceSegmentation/mask_rcnn_R_50_FPN_3x.yaml")
predictor = DefaultPredictor(cfg)
outputs = predictor(im)
# We can use `Visualizer` to draw the predictions on the image.
v = Visualizer(im[:, :, ::-1], MetadataCatalog.get(cfg.DATASETS.TRAIN[0]), scale=1)
out = v.draw_instance_predictions(outputs["instances"].to("cpu"))
cv2_imshow(out.get_image()[:, :, ::-1])
# look at the outputs. See https://detectron2.readthedocs.io/tutorials/models.html#model-output-format for specification
print(outputs["instances"].pred_classes)
print(outputs["instances"].pred_boxes)
print(outputs["instances"].pred_masks[0])
import matplotlib.pyplot as plt
outputs["instances"].pred_masks[0].shape
im = cv2.imread("./input.jpg")
plt.imshow(outputs["instances"].pred_masks[0].cpu())
plt.imshow(im)
```
Extract relevant element
```
def extract(im):
mask2 = np.asarray(outputs["instances"].pred_masks[0].cpu())*1
mask3d = np.dstack((np.dstack((mask2, mask2)),mask2))*1
# mask by multiplication, clip to range 0 to 255 and make integer
result2 = (im * mask3d).clip(0, 255).astype(np.uint8)
result2[mask3d==0] = 255
box = np.asarray(outputs["instances"].pred_boxes[0].to('cpu').tensor[0],dtype=int)
crop_img = result2[box[1]:box[3], box[0]:box[2]]
return crop_img
crop_img = extract(im)
cv2_imshow(crop_img)
```
prøv den på et smykke
# Train on a custom dataset
```
# if your dataset is in COCO format, this cell can be replaced by the following three lines:
# from detectron2.data.datasets import register_coco_instances
# register_coco_instances("my_dataset_train", {}, "json_annotation_train.json", "path/to/image/dir")
# register_coco_instances("my_dataset_val", {}, "json_annotation_val.json", "path/to/image/dir")
```
På smykkerne
```
from google.colab import drive
drive.mount('/content/drive')
from detectron2.structures import BoxMode
from detectron2.data import DatasetCatalog, MetadataCatalog
def get_jewellery_dicts(directory):
"""
NB: the image labels used to train must have more than 6 vertices.
"""
classes = ['Jewellery']
dataset_dicts = []
i = 0
for filename in [file for file in os.listdir(directory) if file.endswith('.json')]:
json_file = os.path.join(directory, filename)
with open(json_file) as f:
img_anns = json.load(f)
record = {}
filename = os.path.join(directory, img_anns["imagePath"])
record["image_id"] = i
record["file_name"] = filename
record["height"] = 340
record["width"] = 510
i+=1
annos = img_anns["shapes"]
objs = []
for anno in annos:
px = [a[0] for a in anno['points']]
py = [a[1] for a in anno['points']]
poly = [(x, y) for x, y in zip(px, py)]
poly = [p for x in poly for p in x]
obj = {
"bbox": [np.min(px), np.min(py), np.max(px), np.max(py)],
"bbox_mode": BoxMode.XYXY_ABS,
"segmentation": [poly],
"category_id": classes.index(anno['label']),
"iscrowd": 0
}
objs.append(obj)
record["annotations"] = objs
dataset_dicts.append(record)
return dataset_dicts
for d in ["train", "val"]:
DatasetCatalog.register("Jewellery_" + d, lambda d=d: get_jewellery_dicts('/content/drive/MyDrive/detectron2segment/' + d))
MetadataCatalog.get("Jewellery_" + d).set(thing_classes=['Jewellery'])
jewellery_metadata = MetadataCatalog.get("Jewellery_train")
dataset_dicts = get_jewellery_dicts("drive/MyDrive/detectron2segment/train")
for d in random.sample(dataset_dicts, 3):
img = cv2.imread(d["file_name"])
visualizer = Visualizer(img[:, :, ::-1], metadata=jewellery_metadata, scale=0.5)
out = visualizer.draw_dataset_dict(d)
cv2_imshow(out.get_image()[:, :, ::-1])
#train
from detectron2.engine import DefaultTrainer
cfg = get_cfg()
cfg.merge_from_file(model_zoo.get_config_file("COCO-InstanceSegmentation/mask_rcnn_R_50_FPN_3x.yaml"))
cfg.DATASETS.TRAIN = ("Jewellery_train",)
cfg.DATASETS.TEST = ()
cfg.DATALOADER.NUM_WORKERS = 2
cfg.MODEL.WEIGHTS = model_zoo.get_checkpoint_url("COCO-InstanceSegmentation/mask_rcnn_R_50_FPN_3x.yaml") # Let training initialize from model zoo
cfg.SOLVER.IMS_PER_BATCH = 2
cfg.SOLVER.BASE_LR = 0.00025 # pick a good LR
cfg.SOLVER.MAX_ITER = 1000 # 1000 iterations seems good enough for this dataset
cfg.SOLVER.STEPS = [] # do not decay learning rate
cfg.MODEL.ROI_HEADS.BATCH_SIZE_PER_IMAGE = 128 # faster, and good enough for this toy dataset (default: 512)
cfg.MODEL.ROI_HEADS.NUM_CLASSES = 1 # only has one class (jewellery). (see https://detectron2.readthedocs.io/tutorials/datasets.html#update-the-config-for-new-datasets)
# NOTE: this config means the number of classes, but a few popular unofficial tutorials incorrect uses num_classes+1 here.
os.makedirs(cfg.OUTPUT_DIR, exist_ok=True)
trainer = DefaultTrainer(cfg)
trainer.resume_or_load(resume=False)
trainer.train()
# Inference should use the config with parameters that are used in training
# cfg now already contains everything we've set previously. We changed it a little bit for inference:
f = open('config.yml', 'w')
f.write(cfg.dump())
f.close()
# cfg.MODEL.WEIGHTS = "/content/drive/MyDrive/detectron2segment/model_final.pth"
cfg.MODEL.WEIGHTS = os.path.join(cfg.OUTPUT_DIR, "model_final.pth") # path to the model we just trained
cfg.MODEL.ROI_HEADS.SCORE_THRESH_TEST = 0.82 # set a custom testing threshold
predictor = DefaultPredictor(cfg)
from detectron2.utils.visualizer import ColorMode
dataset_dicts = get_jewellery_dicts("drive/MyDrive/detectron2segment/val")
for d in random.sample(dataset_dicts, 5):
im = cv2.imread(d["file_name"])
outputs = predictor(im) # format is documented at https://detectron2.readthedocs.io/tutorials/models.html#model-output-format
v = Visualizer(im[:, :, ::-1],
scale=0.5 # remove the colors of unsegmented pixels. This option is only available for segmentation models
)
out = v.draw_instance_predictions(outputs["instances"].to("cpu"))
cv2_imshow(out.get_image()[:, :, ::-1])
im = cv2.imread("test.jpg")
outputs = predictor(im) # format is documented at https://detectron2.readthedocs.io/tutorials/models.html#model-output-format
v = Visualizer(im[:, :, ::-1],
scale=0.5 # remove the colors of unsegmented pixels. This option is only available for segmentation models
)
out = v.draw_instance_predictions(outputs["instances"].to("cpu"))
cv2_imshow(out.get_image()[:, :, ::-1])
from detectron2.evaluation import COCOEvaluator, inference_on_dataset
from detectron2.data import build_detection_test_loader
evaluator = COCOEvaluator("Jewellery_val", ("bbox", "segm"), False, output_dir="./output/")
val_loader = build_detection_test_loader(cfg, "Jewellery_val")
print(inference_on_dataset(trainer.model, val_loader, evaluator))
# another equivalent way to evaluate the model is to use `trainer.test`
```
| true |
code
| 0.585338 | null | null | null | null |
|
# More Feature Engineering - Wide and Deep models
**Learning Objectives**
* Build a Wide and Deep model using the appropriate Tensorflow feature columns
## Introduction
In this notebook we'll use what we learned about feature columns to build a Wide & Deep model. Recall, that the idea behind Wide & Deep models is to join the two methods of learning through memorization and generalization by making a wide linear model and a deep learning model to accommodate both.
<img src='assets/wide_deep.png' width='80%'>
<sup>(image: https://ai.googleblog.com/2016/06/wide-deep-learning-better-together-with.html)</sup>
The Wide part of the model is associated with the memory element. In this case, we train a linear model with a wide set of crossed features and learn the correlation of this related data with the assigned label. The Deep part of the model is associated with the generalization element where we use embedding vectors for features. The best embeddings are then learned through the training process. While both of these methods can work well alone, Wide & Deep models excel by combining these techniques together.
```
# Ensure that we have Tensorflow 1.13 installed.
!pip3 freeze | grep tensorflow==1.13.1 || pip3 install tensorflow==1.13.1
import tensorflow as tf
import numpy as np
import shutil
print(tf.__version__)
```
## Load raw data
These are the same files created in the `create_datasets.ipynb` notebook
```
!gsutil cp gs://cloud-training-demos/taxifare/small/*.csv .
!ls -l *.csv
```
## Train and Evaluate input Functions
These are the same as before with one additional line of code: a call to `add_engineered_features()` from within the `_parse_row()` function.
```
CSV_COLUMN_NAMES = ["fare_amount","dayofweek","hourofday","pickuplon","pickuplat","dropofflon","dropofflat"]
CSV_DEFAULTS = [[0.0],[1],[0],[-74.0],[40.0],[-74.0],[40.7]]
def read_dataset(csv_path):
def _parse_row(row):
# Decode the CSV row into list of TF tensors
fields = tf.decode_csv(records = row, record_defaults = CSV_DEFAULTS)
# Pack the result into a dictionary
features = dict(zip(CSV_COLUMN_NAMES, fields))
# NEW: Add engineered features
features = add_engineered_features(features)
# Separate the label from the features
label = features.pop("fare_amount") # remove label from features and store
return features, label
# Create a dataset containing the text lines.
dataset = tf.data.Dataset.list_files(file_pattern = csv_path) # (i.e. data_file_*.csv)
dataset = dataset.flat_map(map_func = lambda filename:tf.data.TextLineDataset(filenames = filename).skip(count = 1))
# Parse each CSV row into correct (features,label) format for Estimator API
dataset = dataset.map(map_func = _parse_row)
return dataset
def train_input_fn(csv_path, batch_size = 128):
#1. Convert CSV into tf.data.Dataset with (features,label) format
dataset = read_dataset(csv_path)
#2. Shuffle, repeat, and batch the examples.
dataset = dataset.shuffle(buffer_size = 1000).repeat(count = None).batch(batch_size = batch_size)
return dataset
def eval_input_fn(csv_path, batch_size = 128):
#1. Convert CSV into tf.data.Dataset with (features,label) format
dataset = read_dataset(csv_path)
#2.Batch the examples.
dataset = dataset.batch(batch_size = batch_size)
return dataset
```
## Feature columns for Wide and Deep model
For the Wide columns, we will create feature columns of crossed features. To do this, we'll create a collection of Tensorflow feature columns to pass to the `tf.feature_column.crossed_column` constructor. The Deep columns will consist of numberic columns and any embedding columns we want to create.
```
# 1. One hot encode dayofweek and hourofday
fc_dayofweek = tf.feature_column.categorical_column_with_identity(key = "dayofweek", num_buckets = 7)
fc_hourofday = tf.feature_column.categorical_column_with_identity(key = "hourofday", num_buckets = 24)
# 2. Bucketize latitudes and longitudes
NBUCKETS = 16
latbuckets = np.linspace(start = 38.0, stop = 42.0, num = NBUCKETS).tolist()
lonbuckets = np.linspace(start = -76.0, stop = -72.0, num = NBUCKETS).tolist()
fc_bucketized_plat = tf.feature_column.bucketized_column(source_column = tf.feature_column.numeric_column(key = "pickuplon"), boundaries = lonbuckets)
fc_bucketized_plon = tf.feature_column.bucketized_column(source_column = tf.feature_column.numeric_column(key = "pickuplat"), boundaries = latbuckets)
fc_bucketized_dlat = tf.feature_column.bucketized_column(source_column = tf.feature_column.numeric_column(key = "dropofflon"), boundaries = lonbuckets)
fc_bucketized_dlon = tf.feature_column.bucketized_column(source_column = tf.feature_column.numeric_column(key = "dropofflat"), boundaries = latbuckets)
# 3. Cross features to get combination of day and hour
fc_crossed_day_hr = tf.feature_column.crossed_column(keys = [fc_dayofweek, fc_hourofday], hash_bucket_size = 24 * 7)
fc_crossed_dloc = tf.feature_column.crossed_column(keys = [fc_bucketized_dlat, fc_bucketized_dlon], hash_bucket_size = NBUCKETS * NBUCKETS)
fc_crossed_ploc = tf.feature_column.crossed_column(keys = [fc_bucketized_plat, fc_bucketized_plon], hash_bucket_size = NBUCKETS * NBUCKETS)
fc_crossed_pd_pair = tf.feature_column.crossed_column(keys = [fc_crossed_dloc, fc_crossed_ploc], hash_bucket_size = NBUCKETS**4)
```
We also add our engineered features that we used previously.
```
def add_engineered_features(features):
features["dayofweek"] = features["dayofweek"] - 1 # subtract one since our days of week are 1-7 instead of 0-6
features["latdiff"] = features["pickuplat"] - features["dropofflat"] # East/West
features["londiff"] = features["pickuplon"] - features["dropofflon"] # North/South
features["euclidean_dist"] = tf.sqrt(x = features["latdiff"]**2 + features["londiff"]**2)
return features
```
### Gather list of feature columns
Next we gather the list of wide and deep feature columns we'll pass to our Wide & Deep model in Tensorflow. To do this, we'll create a function `get_wide_deep` which will use our previously bucketized columns to collect crossed feature columns and sparse feature columns for our wide columns, and embedding feature columns and numeric features columns for the deep columns.
```
def get_wide_deep():
# Wide columns are sparse, have linear relationship with the output
wide_columns = [
# Feature crosses
fc_crossed_day_hr, fc_crossed_dloc,
fc_crossed_ploc, fc_crossed_pd_pair,
# Sparse columns
fc_dayofweek, fc_hourofday
]
# Continuous columns are deep, have a complex relationship with the output
deep_columns = [
# Embedding_column to "group" together ...
tf.feature_column.embedding_column(categorical_column = fc_crossed_pd_pair, dimension = 10),
tf.feature_column.embedding_column(categorical_column = fc_crossed_day_hr, dimension = 10),
# Numeric columns
tf.feature_column.numeric_column(key = "pickuplat"),
tf.feature_column.numeric_column(key = "pickuplon"),
tf.feature_column.numeric_column(key = "dropofflon"),
tf.feature_column.numeric_column(key = "dropofflat"),
tf.feature_column.numeric_column(key = "latdiff"),
tf.feature_column.numeric_column(key = "londiff"),
tf.feature_column.numeric_column(key = "euclidean_dist"),
tf.feature_column.indicator_column(categorical_column = fc_crossed_day_hr),
]
return wide_columns, deep_columns
```
## Serving Input Receiver function
Same as before except the received tensors are wrapped with `add_engineered_features()`.
```
def serving_input_receiver_fn():
receiver_tensors = {
'dayofweek' : tf.placeholder(dtype = tf.int32, shape = [None]), # shape is vector to allow batch of requests
'hourofday' : tf.placeholder(dtype = tf.int32, shape = [None]),
'pickuplon' : tf.placeholder(dtype = tf.float32, shape = [None]),
'pickuplat' : tf.placeholder(dtype = tf.float32, shape = [None]),
'dropofflat' : tf.placeholder(dtype = tf.float32, shape = [None]),
'dropofflon' : tf.placeholder(dtype = tf.float32, shape = [None]),
}
features = add_engineered_features(receiver_tensors) # 'features' is what is passed on to the model
return tf.estimator.export.ServingInputReceiver(features = features, receiver_tensors = receiver_tensors)
```
## Train and Evaluate (500 train steps)
The same as before, we'll train the model for 500 steps (sidenote: how many epochs do 500 trains steps represent?). Let's see how the engineered features we've added affect the performance. Note the use of `tf.estimator.DNNLinearCombinedRegressor` below.
```
%%time
OUTDIR = "taxi_trained_wd/500"
shutil.rmtree(path = OUTDIR, ignore_errors = True) # start fresh each time
tf.summary.FileWriterCache.clear() # ensure filewriter cache is clear for TensorBoard events file
tf.logging.set_verbosity(v = tf.logging.INFO) # so loss is printed during training
# Collect the wide and deep columns from above
wide_columns, deep_columns = get_wide_deep()
model = tf.estimator.DNNLinearCombinedRegressor(
model_dir = OUTDIR,
linear_feature_columns = wide_columns,
dnn_feature_columns = deep_columns,
dnn_hidden_units = [10,10], # specify neural architecture
config = tf.estimator.RunConfig(
tf_random_seed = 1, # for reproducibility
save_checkpoints_steps = 100 # checkpoint every N steps
)
)
# Add custom evaluation metric
def my_rmse(labels, predictions):
pred_values = tf.squeeze(input = predictions["predictions"], axis = -1)
return {"rmse": tf.metrics.root_mean_squared_error(labels = labels, predictions = pred_values)}
model = tf.contrib.estimator.add_metrics(estimator = model, metric_fn = my_rmse)
train_spec = tf.estimator.TrainSpec(
input_fn = lambda: train_input_fn("./taxi-train.csv"),
max_steps = 500)
exporter = tf.estimator.FinalExporter(name = "exporter", serving_input_receiver_fn = serving_input_receiver_fn) # export SavedModel once at the end of training
# Note: alternatively use tf.estimator.BestExporter to export at every checkpoint that has lower loss than the previous checkpoint
eval_spec = tf.estimator.EvalSpec(
input_fn = lambda: eval_input_fn("./taxi-valid.csv"),
steps = None,
start_delay_secs = 1, # wait at least N seconds before first evaluation (default 120)
throttle_secs = 1, # wait at least N seconds before each subsequent evaluation (default 600)
exporters = exporter) # export SavedModel once at the end of training
tf.estimator.train_and_evaluate(estimator = model, train_spec = train_spec, eval_spec = eval_spec)
```
### Results
Our RMSE for the Wide and Deep model is worse than for the DNN. However, we have only trained for 500 steps and it looks like the model is still learning. Just as before, let's run again, this time for 10x as many steps so we can give a fair comparison.
## Train and Evaluate (5,000 train steps)
Now, just as above, we'll execute a longer trianing job with 5,000 train steps using our engineered features and assess the performance.
```
%%time
OUTDIR = "taxi_trained_wd/5000"
shutil.rmtree(path = OUTDIR, ignore_errors = True) # start fresh each time
tf.summary.FileWriterCache.clear() # ensure filewriter cache is clear for TensorBoard events file
tf.logging.set_verbosity(v = tf.logging.INFO) # so loss is printed during training
# Collect the wide and deep columns from above
wide_columns, deep_columns = get_wide_deep()
model = tf.estimator.DNNLinearCombinedRegressor(
model_dir = OUTDIR,
linear_feature_columns = wide_columns,
dnn_feature_columns = deep_columns,
dnn_hidden_units = [10,10], # specify neural architecture
config = tf.estimator.RunConfig(
tf_random_seed = 1, # for reproducibility
save_checkpoints_steps = 100 # checkpoint every N steps
)
)
# Add custom evaluation metric
def my_rmse(labels, predictions):
pred_values = tf.squeeze(input = predictions["predictions"], axis = -1)
return {"rmse": tf.metrics.root_mean_squared_error(labels = labels, predictions = pred_values)}
model = tf.contrib.estimator.add_metrics(estimator = model, metric_fn = my_rmse)
train_spec = tf.estimator.TrainSpec(
input_fn = lambda: train_input_fn("./taxi-train.csv"),
max_steps = 5000)
exporter = tf.estimator.FinalExporter(name = "exporter", serving_input_receiver_fn = serving_input_receiver_fn) # export SavedModel once at the end of training
# Note: alternatively use tf.estimator.BestExporter to export at every checkpoint that has lower loss than the previous checkpoint
eval_spec = tf.estimator.EvalSpec(
input_fn = lambda: eval_input_fn("./taxi-valid.csv"),
steps = None,
start_delay_secs = 1, # wait at least N seconds before first evaluation (default 120)
throttle_secs = 1, # wait at least N seconds before each subsequent evaluation (default 600)
exporters = exporter) # export SavedModel once at the end of training
tf.estimator.train_and_evaluate(estimator = model, train_spec = train_spec, eval_spec = eval_spec)
```
### Results
Our RMSE is better but still not as good as the DNN we built. It looks like RMSE may still be reducing, but training is getting slow so we should move to the cloud if we want to train longer.
Also we haven't explored our hyperparameters much. Is our neural architecture of two layers with 10 nodes each optimal?
In the next notebook we'll explore this.
Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.668123 | null | null | null | null |
|
<h1 align = center><font size = 5>Image Procesing With Python(Matplotlib,Numpy and OpenCV)<font/></h1>
<h1>Introduction!</h1>
<h3>Welcome</h3>
<p>int this section, you will learn how to obtain the histogram from image, do normalization to image intesities, calculate cumulative histogram. By the end of this lab you will successfully learn histogram equalization</p>
### Prerequisite:
* [Python Tutorial](https://docs.python.org/3/tutorial/)
* [Numpy Tutorial](https://numpy.org/doc/stable/user/absolute_beginners.html)
* [Matplotlib Image Tutorial](https://matplotlib.org/tutorials/introductory/images.html#sphx-glr-tutorials-introductory-images-py)
<h2>Table of Contents</h2>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<ol>
<li><a href="#histogram_">Histogram Calculation</a>
<li><a href="#intensity_norm">Intensity Normalization</a></li>
<li><a href="#cummulative_histogram">Cummulative Histogram</a></li>
<li><a href="Histogram_eq">Histogram Equalization</a></li>
</ol>
</div>
<h2>what is the purpose of the histogram?</h2>
<P>describe the frequency of intensity values, brightness variation and show you how individual brightness levels are occupid in image, if the image was darker overall histogram would be concentrated towards black. and if the image was brighter, but with lower contrast. then the histogram would be thinner and concentrated near the whiter brightness levels. </p>
<p>histogram dipct the problem that originate during image acquistion, and reveal if there is much noise in the image, if the ideal histogram is known. we might want to remove this noisy </p>
### Import Packages.
```
import os # Miscellaneous operating system interface.
import numpy as np # linear algebra and scientific computing library.
import matplotlib.pyplot as plt # visualization package.
import matplotlib.image as mpimg # image reading and displaying package.
import cv2 # computer vision library.
%matplotlib inline
```
### list of images:
listing the images in the directory.
```
# images path
path = '..\..\images'
# list of images names
list_imgs = os.listdir(os.path.join(path,'img_proc'))
print(list_imgs)
```
### Reading Image:
* each image has a width and height (2-dim matrix).
* each coordinate is $I(u,v)$ we calling intenisty where `u` is row index and `v` is column index.
```
# display sample.
path = os.path.join(path,'img_proc',list_imgs[10])
image = mpimg.imread(path)
# printing image dimensions.
print(image.shape)
```
by taking a look to the result above we have image `2003` as width (rows) and `3000` as height (columns). in addition to the third element represent the colors channels `3`
### Convert Image to grayscale:
```
gray_img = cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)
# printing grayscale image dimension.
print(gray_img.shape)
```
above, we can see the result of printing image shape is little bit different. there are just two elements the width and height.
<br>
in grayscale image we just got 1 color channel.
#### elements of image datatype.
```
# depth of image is 8-bit grayscale
print(image.dtype)
```
#### Displaying the image.
```
# display sample.
plt.imshow(gray_img,cmap='gray')
plt.show()
```
## 1-Histogram Calculation:
### Grayscale image Histogram:
each single histogram is defined as where $h(i) = card\{(u,v)|I(u,v) = i\}$ $\forall$ $i \in [0,k-1]$
* $h(i)$ is the number of pixels in I with intensity value i
* $K = 2^8 = 256 - 1 = 255$
* $h(0),h(1),h(2),\dots,h(255)$
### Histogram Calcualtion Methods:
* Numpy Methods
* OpenCV Method.
* Matplotlib Method for calculating and visualizing in one step.
#### Numpy Methods.
```
# numpy method-1
un_val,occ_counts = np.unique(gray_img,return_counts = True)
plt.plot(un_val,occ_counts)
plt.show()
# histogram calculation with 'numpy.histogram()' function (method-2).
hist_np,_= np.histogram(gray_img.flatten(),256,[0,256])
plt.plot(hist_np)
plt.show()
```
#### OpenCV Method.
```
# histogram calculation opencv function with bins (method-4).
hist_cv = cv2.calcHist([gray_img],[0],None,[256],[0,256])
plt.plot(hist_cv)
plt.show()
```
#### Matplotlib Method.
```
# display the histogram (Matplotlib) method-3
fig,axes = plt.subplots(1,2,figsize=(12,8))
# display grayscale image and it's histogram.
axes[0].imshow(gray_img,cmap='gray')
axes[1].hist(gray_img.flatten(),256,[0,256])
# show the figure.
plt.show()
```
### 2-Intensity Normalization:
stretching the range of image intensities, simply instead of dealing with values ranging $[0-255]$ . the values will be ranging $[0,1]$.
<br>
here it's the equation: $N_{x,y} = \frac{O_{x,y}}{O_{max}}$
* $N_{x,y}$ $\rightarrow$ new image (output).
* $O_{x,y}$ $\rightarrow$ old image(input).
* $(x,y)\rightarrow$ is the Intensity or pixel coordinates
* $O_{max}$ $\rightarrow$ maximum value of intensities in the input image.
```
# image normalization
normalized_image = gray_img / float(gray_img.max())
# plotting figure.
fig, axes = plt.subplots(2,2,figsize=(12,8))
# display grayscale image and it's histogram.
axes[0][0].imshow(gray_img,cmap = 'gray')
axes[0][1].hist(gray_img.flatten(),256)
# display normalized grayscale image and it's histogram.
axes[1][0].imshow(normalized_image,cmap = 'gray')
axes[1][1].hist(normalized_image.flatten(),256)
# show the figure.
plt.show()
```
### 3-Cummulative Histogram:
derived from the ordinary histogram, and is useful when you performing certain image operations involving histogram e.g(Histogram Equlization). in other words we using to computer parameters for several common point operations.
<br>
<br>
here it's the mathemtical formula: $H(i) = \sum_{j=0}^i h(j)$ for $0 \leq i \lt k$, where $k = 2^8$
* H(i) the sum of all histogram values h(j) where $j \leq i$
* $H(k-1) = \sum_{j=0}^{k-1} h(j) = M \times N$ <br> where the total number of pixels in image is Width M and Height N
```
# method-1
_,hist = np.unique(gray_img,return_counts=True)
cum_hist = np.cumsum(hist)
plt.plot(cum_hist)
plt.show()
# cumulative histogram calculation.
hist_0,bins = np.histogram(gray_img.flatten(),256,[0,256])
cum_hist = hist_0.cumsum()
fig,axes = plt.subplots(1,2,figsize=(12,8))
axes[0].plot(hist_0)
axes[1].plot(cum_hist)
plt.show()
```
### 4-HIstogram Equalization:
<p>
nonlinear process aimed to highlight image brightness in away particularly suited to human visual analysis, and the produced picture with flatter histogram where all the levels equiprobable.
</p>
Here it's the first equation: $f_{eq}(a) = \lfloor {H}(a)\cdot \frac{K-1}{M \cdot N}\rfloor$
<br>
$E(q,O) = \frac{N_{max} - N_{min}}{N^2}\times\displaystyle\sum_{l=0}^ p O(l)$
<br>
$N_{x,y} = E(O_{x,y},O)$
* $E(q,O)$ $\rightarrow$ function take cummlative histogram and the image as input.
* $(N_{max} - N_{min})$ $\rightarrow$ $(K-1) = (2^8 - 1) = (256 -1) = 255$, $k = 255$ where $N_{max}$ is 255 and $N_{min} = 0$
* $l$ $\rightarrow$ each level value.
* $p \rightarrow$ is levels of the histogram.
* $\sum_{l = 0}^p O(l) \rightarrow$ cumulative histogram
* $N^2 \rightarrow$ image width and height $(M \times N)$
#### Numpy method.
```
# histogram equalization calculation.
hist_eq = cum_hist * (255/(gray_img.shape[0] * gray_img.shape[1]))
eq_image = hist_eq[gray_img]
# cumulative histogram calculation.
hist_0,bins = np.histogram(eq_image.flatten(),256,[0,256])
cum_hist = hist_0.cumsum()
fig, axes = plt.subplots(1,3,figsize=(16,8))
axes[0].imshow(eq_image,cmap='gray')
axes[1].hist(eq_image.flatten(),256)
axes[2].plot(cum_hist)
plt.show()
```
#### OpenCV Method.
```
# display the equalized histogram
eq_img_cv = cv2.equalizeHist(gray_img)
# cumulative histogram calculation.
hist_0,bins = np.histogram(eq_img_cv.flatten(),256,[0,256])
cum_hist = hist_0.cumsum()
fig,axes = plt.subplots(1,3,figsize=(16,8))
axes[0].imshow(eq_img_cv,cmap='gray')
axes[1].hist(eq_img_cv.flatten(),256)
axes[2].plot(cum_hist)
plt.show()
```
### About The Author:
this notebook written by Mohamed Salah Hassan Akel, Machine learning Engineer.
<hr>
<p>Copyright © 2020 Mohamed Akel Youtube Channel. This notebook and its source code are released under the terms of the <a href="">MIT License</a>.</p>
| true |
code
| 0.645679 | null | null | null | null |
|
# Extract features from clauses and sentences that need citations and those that do not
Author: Kiran Bhattacharyya
Revision: 5/11/18 - DRM - translate .py files into .ipynb, misc formatting
this code reads in two data files:
1. one contains sentences and clauses that need citations
2. the other contains sentences that do no
Then it filters the words in the sentence by parts of speech, and stems the words
It also calculates the occurance of the unique words and parts of speech in the two datasets
finally it saves these filtered data sets and the counts of the unique features in each dataset
```
# import relevant libraries
import nltk
import pandas as pd
import numpy as np
from nltk.stem.snowball import SnowballStemmer
# Create p_stemmer object
p_stemmer = SnowballStemmer("english", ignore_stopwords=True)
```
### load data which contain sentences that need citations and sentences that do not (are not claims)
```
needCite = pd.read_pickle('../Data/CitationNeeded.pkl') # need citations
noClaim = pd.read_pickle('../Data/NotACLaim.pkl') # do NOT need citations (are not claims)
```
### tokenize sentences into words and tag parts of speech
keep nouns (NN), adjectives (JJ), verbs (VB), adverbs (RB), numberical/cardinal (CD), determiner (DT)
features will include words that are any of the previous, the length of the sentence or clause
First for claim data:
5/16/18 DRM - removed .encode from thisWord to allow python 3 compatability.
```
needCite_filtSent = list() # list to store word tokenized and filtered sentences from citation needed list
needCite_wordTag = list() # list to store the part of speech of each word
noClaim_filtSent = list() # list to store word tokenized and filtered sentences from not a claim list
noClaim_wordTag = list() # list to store the part of speech of each word
allWordList = list() # list that stores all words in both data sentences
allPOSList = list() # list that stores all POS of all words in both datasets
for sent in needCite.CitationNeeded:
sent_token = nltk.word_tokenize(sent) # word tokenize the sentence
sent_pos = nltk.pos_tag(sent_token) # tag with part of speech
sent_filt_word = list() # create list to store filtered sentence words
sent_filt_pos = list() # create list to store the filtered parts of speech
for item in sent_pos: # for each item in the sentence
if len(item) > 1:
thisTag = item[1] # grab the part of speech
if 'NN' in thisTag or 'JJ' in thisTag or 'VB' in thisTag or 'RB' in thisTag or 'CD' in thisTag or 'DT' in thisTag: # if the tag is an approved part of speech
thisWord = item[0]
sent_filt_word.append(p_stemmer.stem(thisWord.lower()))
sent_filt_pos.append(thisTag)
allWordList.append(p_stemmer.stem(thisWord.lower()))
allPOSList.append(thisTag)
needCite_filtSent.append(sent_filt_word)
needCite_wordTag.append(sent_filt_pos)
needCite_filtSent[0:2]
needCite_wordTag[0:2]
len(needCite_filtSent)
for sent in noClaim.NotAClaim:
sent_token = nltk.word_tokenize(sent) # word tokenize the sentence
sent_pos = nltk.pos_tag(sent_token) # tag with part of speech
sent_filt_word = list() # create list to store filtered sentence words
sent_filt_pos = list() # create list to store the filtered parts of speech
for item in sent_pos: # for each item in the sentence
if len(item) > 1:
thisTag = item[1] # grab the part of speech
if 'NN' in thisTag or 'JJ' in thisTag or 'VB' in thisTag or 'RB' in thisTag or 'CD' in thisTag or 'DT' in thisTag: # if the tag is an approved part of speech
thisWord = item[0]
sent_filt_word.append(p_stemmer.stem(thisWord.lower()))
sent_filt_pos.append(thisTag)
allWordList.append(p_stemmer.stem(thisWord.lower()))
allPOSList.append(thisTag)
noClaim_filtSent.append(sent_filt_word)
noClaim_wordTag.append(sent_filt_pos)
noClaim_filtSent[0:2]
def test(a,b):
return a,b,a*b
[a,b,c]=test(3,4)
print(a,b,c)
```
### compute word occurances in sentences
```
import datetime
datetime.datetime.now()
## compute word occurances in sentences
uniqWords = list(set(allWordList)) # find all uniqwords in the dataset
wordOccur_claim = list() # list to store number of times word occurs in claim dataset
wordOccur_notClaim = list() # list to store number of times word occurs in not claim data set
for i in range(0,len(uniqWords)): # for each word
word = uniqWords[i]
numOfTimes = 0
for sent in needCite_filtSent:
if word in sent:
numOfTimes = numOfTimes + len([j for j, x in enumerate(sent) if x == word])
wordOccur_claim.append(numOfTimes)
numOfTimes = 0
for sent in noClaim_filtSent:
if word in sent:
numOfTimes = numOfTimes + len([j for j, x in enumerate(sent) if x == word])
wordOccur_notClaim.append(numOfTimes)
datetime.datetime.now()
```
start @ 6:05pm
```
import datetime
datetime.datetime.now()
```
### compute POS occurances in sentences
```
uniqPOS = list(set(allPOSList)) # find all uniqwords in the dataset
posOccur_claim = list() # for part of speech
posOccur_notClaim = list()
for i in range(0,len(uniqPOS)): # for each word
word = uniqPOS[i]
numOfTimes = 0
for sent in needCite_wordTag:
if word in sent:
numOfTimes = numOfTimes + len([j for j, x in enumerate(sent) if x == word])
posOccur_claim.append(numOfTimes)
numOfTimes = 0
for sent in noClaim_wordTag:
if word in sent:
numOfTimes = numOfTimes + len([j for j, x in enumerate(sent) if x == word])
posOccur_notClaim.append(numOfTimes)
```
### save all data
```
UniqWords = pd.DataFrame(
{'UniqueWords': uniqWords,
'WordOccurClaim': wordOccur_claim,
'WordOccurNotClaim': wordOccur_notClaim
})
UniqWords.to_pickle('../Data/UniqueWords.pkl')
UniqPOS = pd.DataFrame(
{'UniquePOS': uniqPOS,
'POSOccurClaim': posOccur_claim,
'POSOccurNotClaim': posOccur_notClaim
})
UniqPOS.to_pickle('../Data/UniquePOS.pkl')
NeedCite = pd.DataFrame(
{'NeedCiteWord': needCite_filtSent,
'NeedCitePOS': needCite_wordTag
})
NeedCite.to_pickle('../Data/NeedCiteFilt.pkl')
NotClaim = pd.DataFrame(
{'NotClaimWord': noClaim_filtSent,
'NotClaimPOS': noClaim_wordTag
})
NotClaim.to_pickle('../Data/NotClaimFilt.pkl')
```
| true |
code
| 0.241221 | null | null | null | null |
|
# Entanglement renormalization
One can open this notebook in Google Colab (is recommended)
[](https://colab.research.google.com/github/LuchnikovI/QGOpt/blob/master/docs/source/entanglement_renormalization.ipynb)
In the given tutorial, we show how the Riemannian optimization on the complex Stiefel manifold can be used to perform entanglement renormalization and find the ground state energy and the ground state itself of a many-body spin system at the point of quantum phase transition. First of all, let us import the necessary libraries.
```
import numpy as np
from scipy import integrate
import tensorflow as tf # tf 2.x
try:
import QGOpt as qgo
except ImportError:
!pip install git+https://github.com/LuchnikovI/QGOpt
import QGOpt as qgo
# TensorNetwork library
try:
import tensornetwork as tn
except ImportError:
!pip install tensornetwork
import tensornetwork as tn
import matplotlib.pyplot as plt
from tqdm import tqdm
tn.set_default_backend("tensorflow")
# Fix random seed to make results reproducable.
tf.random.set_seed(42)
```
## 1. Renormalization layer
First of all, one needs to define a renormalization (mera) layer. We use ncon API from TensorNetwork library for these purposes. The function mera_layer takes unitary and isometric tensors (building blocks) and performs renormalization of a local Hamiltonian as it is shown on the tensor diagram below (if the diagram is not displayed here, please open the notebook in Google Colab).

For more information about entanglement renormalization please see
Evenbly, G., & Vidal, G. (2009). Algorithms for entanglement renormalization. Physical Review B, 79(14), 144108.
Evenbly, G., & Vidal, G. (2014). Algorithms for entanglement renormalization: boundaries, impurities and interfaces. Journal of Statistical Physics, 157(4-5), 931-978.
For more information about ncon notation see for example
Pfeifer, R. N., Evenbly, G., Singh, S., & Vidal, G. (2014). NCON: A tensor network contractor for MATLAB. arXiv preprint arXiv:1402.0939.
```
@tf.function
def mera_layer(H,
U,
U_conj,
Z_left,
Z_right,
Z_left_conj,
Z_right_conj):
"""
Renormalizes local Hamiltonian.
Args:
H: complex valued tensor of shape (chi, chi, chi, chi),
input two-side Hamiltonian (a local term).
U: complex valued tensor of shape (chi ** 2, chi ** 2), disentangler
U_conj: complex valued tensor of shape (chi ** 2, chi ** 2),
conjugated disentangler.
Z_left: complex valued tensor of shape (chi ** 3, new_chi),
left isometry.
Z_right: complex valued tensor of shape (chi ** 3, new_chi),
right isometry.
Z_left_conj: complex valued tensor of shape (chi ** 3, new_chi),
left conjugated isometry.
Z_right_conj: complex valued tensor of shape (chi ** 3, new_chi),
right conjugated isometry.
Returns:
complex valued tensor of shape (new_chi, new_chi, new_chi, new_chi),
renormalized two side hamiltonian.
Notes:
chi is the dimension of an index. chi increases with the depth of mera, however,
at some point, chi is cut to prevent exponential growth of indices
dimensionality."""
# index dimension before renormalization
chi = tf.cast(tf.math.sqrt(tf.cast(tf.shape(U)[0], dtype=tf.float64)),
dtype=tf.int32)
# index dimension after renormalization
chi_new = tf.shape(Z_left)[-1]
# List of building blocks
list_of_tensors = [tf.reshape(Z_left, (chi, chi, chi, chi_new)),
tf.reshape(Z_right, (chi, chi, chi, chi_new)),
tf.reshape(Z_left_conj, (chi, chi, chi, chi_new)),
tf.reshape(Z_right_conj, (chi, chi, chi, chi_new)),
tf.reshape(U, (chi, chi, chi, chi)),
tf.reshape(U_conj, (chi, chi, chi, chi)),
H]
# structures (ncon notation) of three terms of ascending super operator
net_struc_1 = [[1, 2, 3, -3], [9, 11, 12, -4], [1, 6, 7, -1],
[10, 11, 12, -2], [3, 9, 4, 8], [7, 10, 5, 8], [6, 5, 2, 4]]
net_struc_2 = [[1, 2, 3, -3], [9, 11, 12, -4], [1, 2, 6, -1],
[10, 11, 12, -2], [3, 9, 4, 7], [6, 10, 5, 8], [5, 8, 4, 7]]
net_struc_3 = [[1, 2, 3, -3], [9, 10, 12, -4], [1, 2, 5, -1],
[8, 11, 12, -2], [3, 9, 4, 6], [5, 8, 4, 7], [7, 11, 6, 10]]
# sub-optimal contraction orders for three terms of ascending super operator
con_ord_1 = [4, 5, 8, 6, 7, 1, 2, 3, 11, 12, 9, 10]
con_ord_2 = [4, 7, 5, 8, 1, 2, 11, 12, 3, 6, 9, 10]
con_ord_3 = [6, 7, 4, 11, 8, 12, 10, 9, 1, 2, 3, 5]
# ncon
term_1 = tn.ncon(list_of_tensors, net_struc_1, con_ord_1)
term_2 = tn.ncon(list_of_tensors, net_struc_2, con_ord_2)
term_3 = tn.ncon(list_of_tensors, net_struc_3, con_ord_3)
return (term_1 + term_2 + term_3) / 3 # renormalized hamiltonian
# auxiliary functions that return initial isometries and disentanglers
@tf.function
def z_gen(chi, new_chi):
"""Returns random isometry.
Args:
chi: int number, input chi.
new_chi: int number, output chi.
Returns:
complex valued tensor of shape (chi ** 3, new_chi)."""
# one can use the complex Stiefel manfiold to generate a random isometry
m = qgo.manifolds.StiefelManifold()
return m.random((chi ** 3, new_chi), dtype=tf.complex128)
@tf.function
def u_gen(chi):
"""Returns the identity matrix of a given size (initial disentangler).
Args:
chi: int number.
Returns:
complex valued tensor of shape (chi ** 2, chi ** 2)."""
return tf.eye(chi ** 2, dtype=tf.complex128)
```
## 2. Transverse-field Ising (TFI) model hamiltonian and MERA building blocks
Here we define the Transverse-field Ising model Hamiltonian and building blocks (disentanglers and isometries) of MERA network that will be optimized.
First of all we initialize hyper parameters of MERA and TFI hamiltonian.
```
max_chi = 4 # max bond dim
num_of_layers = 5 # number of MERA layers (corresponds to 2*3^5 = 486 spins)
h_x = 1 # value of transverse field in TFI model (h_x=1 is the critical field)
```
One needs to define Pauli matrices. Here all Pauli matrices are represented as one tensor of size $3\times 2 \times 2$, where the first index enumerates a particular Pauli matrix, and the remaining two indices are matrix indices.
```
sigma = tf.constant([[[1j*0, 1 + 1j*0], [1 + 1j*0, 0*1j]],
[[0*1j, -1j], [1j, 0*1j]],
[[1 + 0*1j, 0*1j], [0*1j, -1 + 0*1j]]], dtype=tf.complex128)
```
Here we define local term of the TFI hamiltonian.
```
zz_term = tf.einsum('ij,kl->ikjl', sigma[2], sigma[2])
x_term = tf.einsum('ij,kl->ikjl', sigma[0], tf.eye(2, dtype=tf.complex128))
h = -zz_term - h_x * x_term
```
Here we define initial disentanglers, isometries, and state in the renormalized space.
```
# disentangler U and isometry Z in the first MERA layer
U = u_gen(2)
Z = z_gen(2, max_chi)
# lists with disentanglers and isometries in the rest of the layers
U_list = [u_gen(max_chi) for _ in range(num_of_layers - 1)]
Z_list = [z_gen(max_chi, max_chi) for _ in range(num_of_layers - 1)]
# lists with all disentanglers and isometries
U_list = [U] + U_list
Z_list = [Z] + Z_list
# initial state in the renormalized space (low dimensional in comparison
# with the dimensionality of the initial problem)
psi = tf.ones((max_chi ** 2, 1), dtype=tf.complex128)
psi = psi / tf.linalg.norm(psi)
# converting disentanglers, isometries, and initial state to real
# representation (necessary for the further optimizer)
U_list = list(map(qgo.manifolds.complex_to_real, U_list))
Z_list = list(map(qgo.manifolds.complex_to_real, Z_list))
psi = qgo.manifolds.complex_to_real(psi)
# wrapping disentanglers, isometries, and initial state into
# tf.Variable (necessary for the further optimizer)
U_var = list(map(tf.Variable, U_list))
Z_var = list(map(tf.Variable, Z_list))
psi_var = tf.Variable(psi)
```
## 3. Optimization of MERA
MERA parametrizes quantum state $\Psi(U, Z, \psi)$ of a spin system, where $U$ is a set of disentanglers, $Z$ is a set of isometries, and $\psi$ is a state in the renormalized space.
In order to find the ground state and its energy, we perform optimization of variational energy $$\langle\Psi(U, Z, \psi)|H_{\rm TFI}|\Psi(U, Z, \psi)\rangle\rightarrow \min_{U, \ Z, \ \psi \in {\rm Stiefel \ manifold}}$$
First of all, we define the parameters of optimization. In order to achieve better convergence, we decrease the learning rate with the number of iteration according to the exponential law.
```
iters = 3000 # number of iterations
lr_i = 0.6 # initial learning rate
lr_f = 0.05 # final learning rate
# learning rate is multiplied by this coefficient each iteration
decay = (lr_f / lr_i) ** (1 / iters)
```
Here we define an example of the complex Stiefel manifold necessary for Riemannian optimization and Riemannian Adam optimizer.
```
m = qgo.manifolds.StiefelManifold() # complex Stiefel manifold
opt = qgo.optimizers.RAdam(m, lr_i) # Riemannian Adam
```
Finally, we perform an optimization loop.
```
# this list will be filled by the value of variational energy per iteration
E_list = []
# optimization loop
for j in tqdm(range(iters)):
# gradient calculation
with tf.GradientTape() as tape:
# convert real valued variables back to complex valued tensors
U_var_c = list(map(qgo.manifolds.real_to_complex, U_var))
Z_var_c = list(map(qgo.manifolds.real_to_complex, Z_var))
psi_var_c = qgo.manifolds.real_to_complex(psi_var)
# initial local Hamiltonian term
h_renorm = h
# renormalization of a local Hamiltonian term
for i in range(len(U_var)):
h_renorm = mera_layer(h_renorm,
U_var_c[i],
tf.math.conj(U_var_c[i]),
Z_var_c[i],
Z_var_c[i],
tf.math.conj(Z_var_c[i]),
tf.math.conj(Z_var_c[i]))
# renormalizad Hamiltonian (low dimensional)
h_renorm = (h_renorm + tf.transpose(h_renorm, (1, 0, 3, 2))) / 2
h_renorm = tf.reshape(h_renorm, (max_chi * max_chi, max_chi * max_chi))
# energy
E = tf.cast((tf.linalg.adjoint(psi_var_c) @ h_renorm @ psi_var_c),
dtype=tf.float64)[0, 0]
# adding current variational energy to the list
E_list.append(E)
# gradients
grad = tape.gradient(E, U_var + Z_var + [psi_var])
# optimization step
opt.apply_gradients(zip(grad, U_var + Z_var + [psi_var]))
# learning rate update
opt._set_hyper("learning_rate", opt._get_hyper("learning_rate") * decay)
```
Here we compare exact ground state energy with MERA based value. We also plot how the difference between exact ground state energy and MERA-based energy evolves with the number of iteration.
```
# exact value of ground state energy in the critical point
N = 2 * (3 ** num_of_layers) # number of spins (for 5 layers one has 486 spins)
E0_exact_fin = -2 * (1 / np.sin(np.pi / (2 * N))) / N # exact energy per spin
plt.yscale('log')
plt.xlabel('iter')
plt.ylabel('err')
plt.plot(E_list - tf.convert_to_tensor(([E0_exact_fin] * len(E_list))), 'b')
print("MERA energy:", E_list[-1].numpy())
print("Exact energy:", E0_exact_fin)
```
| true |
code
| 0.801072 | null | null | null | null |
|
<table border="0">
<tr>
<td>
<img src="https://ictd2016.files.wordpress.com/2016/04/microsoft-research-logo-copy.jpg" style="width 30px;" />
</td>
<td>
<img src="https://www.microsoft.com/en-us/research/wp-content/uploads/2016/12/MSR-ALICE-HeaderGraphic-1920x720_1-800x550.jpg" style="width 100px;"/></td>
</tr>
</table>
# Double Machine Learning: Use Cases and Examples
Double Machine Learning (DML) is an algorithm that applies arbitrary machine learning methods
to fit the treatment and response, then uses a linear model to predict the response residuals
from the treatment residuals.
The EconML SDK implements the following DML classes:
* LinearDML: suitable for estimating heterogeneous treatment effects.
* SparseLinearDML: suitable for the case when $W$ is high dimensional vector and both the first stage and second stage estimate are linear.
In ths notebook, we show the performance of the DML on both synthetic data and observational data.
**Notebook contents:**
1. Example usage with single continuous treatment synthetic data
2. Example usage with single binary treatment synthetic data
3. Example usage with multiple continuous treatment synthetic data
4. Example usage with single continuous treatment observational data
5. Example usage with multiple continuous treatment, multiple outcome observational data
```
import econml
## Ignore warnings
import warnings
warnings.filterwarnings('ignore')
# Main imports
from econml.dml import DML, LinearDML,SparseLinearDML
# Helper imports
import numpy as np
from itertools import product
from sklearn.linear_model import Lasso, LassoCV, LogisticRegression, LogisticRegressionCV,LinearRegression,MultiTaskElasticNet,MultiTaskElasticNetCV
from sklearn.ensemble import RandomForestRegressor,RandomForestClassifier
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
import matplotlib
from sklearn.model_selection import train_test_split
%matplotlib inline
```
## 1. Example Usage with Single Continuous Treatment Synthetic Data and Model Selection
### 1.1. DGP
We use the data generating process (DGP) from [here](https://arxiv.org/abs/1806.03467). The DGP is described by the following equations:
\begin{align}
T =& \langle W, \beta\rangle + \eta, & \;\eta \sim \text{Uniform}(-1, 1)\\
Y =& T\cdot \theta(X) + \langle W, \gamma\rangle + \epsilon, &\; \epsilon \sim \text{Uniform}(-1, 1)\\
W \sim& \text{Normal}(0,\, I_{n_w})\\
X \sim& \text{Uniform}(0,1)^{n_x}
\end{align}
where $W$ is a matrix of high-dimensional confounders and $\beta, \gamma$ have high sparsity.
For this DGP,
\begin{align}
\theta(x) = \exp(2\cdot x_1).
\end{align}
```
# Treatment effect function
def exp_te(x):
return np.exp(2*x[0])
# DGP constants
np.random.seed(123)
n = 2000
n_w = 30
support_size = 5
n_x = 1
# Outcome support
support_Y = np.random.choice(np.arange(n_w), size=support_size, replace=False)
coefs_Y = np.random.uniform(0, 1, size=support_size)
epsilon_sample = lambda n: np.random.uniform(-1, 1, size=n)
# Treatment support
support_T = support_Y
coefs_T = np.random.uniform(0, 1, size=support_size)
eta_sample = lambda n: np.random.uniform(-1, 1, size=n)
# Generate controls, covariates, treatments and outcomes
W = np.random.normal(0, 1, size=(n, n_w))
X = np.random.uniform(0, 1, size=(n, n_x))
# Heterogeneous treatment effects
TE = np.array([exp_te(x_i) for x_i in X])
T = np.dot(W[:, support_T], coefs_T) + eta_sample(n)
Y = TE * T + np.dot(W[:, support_Y], coefs_Y) + epsilon_sample(n)
Y_train, Y_val, T_train, T_val, X_train, X_val, W_train, W_val = train_test_split(Y, T, X, W, test_size=.2)
# Generate test data
X_test = np.array(list(product(np.arange(0, 1, 0.01), repeat=n_x)))
```
### 1.2. Train Estimator
We train models in three different ways, and compare their performance.
#### 1.2.1. Default Setting
```
est = LinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor(),
random_state=123)
est.fit(Y_train, T_train, X=X_train, W=W_train)
te_pred = est.effect(X_test)
```
#### 1.2.2. Polynomial Features for Heterogeneity
```
est1 = SparseLinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor(),
featurizer=PolynomialFeatures(degree=3),
random_state=123)
est1.fit(Y_train, T_train, X=X_train, W=W_train)
te_pred1=est1.effect(X_test)
```
#### 1.2.3. Polynomial Features with regularization
```
est2 = DML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor(),
model_final=Lasso(alpha=0.1, fit_intercept=False),
featurizer=PolynomialFeatures(degree=10),
random_state=123)
est2.fit(Y_train, T_train, X=X_train, W=W_train)
te_pred2=est2.effect(X_test)
```
#### 1.2.4 Random Forest Final Stage
```
from econml.dml import ForestDML
# One can replace model_y and model_t with any scikit-learn regressor and classifier correspondingly
# as long as it accepts the sample_weight keyword argument at fit time.
est3 = ForestDML(model_y=RandomForestRegressor(),
model_t=RandomForestRegressor(),
discrete_treatment=False,
n_estimators=1000,
subsample_fr=.8,
min_samples_leaf=10,
min_impurity_decrease=0.001,
verbose=0, min_weight_fraction_leaf=.01)
est3.fit(Y_train, T_train, X=X_train, W=W_train)
te_pred3 = est3.effect(X_test)
est3.feature_importances_
```
### 1.3. Performance Visualization
```
plt.figure(figsize=(10,6))
plt.plot(X_test, te_pred, label='DML default')
plt.plot(X_test, te_pred1, label='DML polynomial degree=3')
plt.plot(X_test, te_pred2, label='DML polynomial degree=10 with Lasso')
plt.plot(X_test, te_pred3, label='ForestDML')
expected_te = np.array([exp_te(x_i) for x_i in X_test])
plt.plot(X_test, expected_te, 'b--', label='True effect')
plt.ylabel('Treatment Effect')
plt.xlabel('x')
plt.legend()
plt.show()
```
### 1.4. Model selection
For the three different models above, we can use score function to estimate the final model performance. The score is the MSE of the final stage Y residual, which can be seen as a proxy of the MSE of treatment effect.
```
score={}
score["DML default"] = est.score(Y_val, T_val, X_val, W_val)
score["DML polynomial degree=2"] = est1.score(Y_val, T_val, X_val, W_val)
score["DML polynomial degree=10 with Lasso"] = est2.score(Y_val, T_val, X_val, W_val)
score["ForestDML"] = est3.score(Y_val, T_val, X_val, W_val)
score
print("best model selected by score: ",min(score,key=lambda x: score.get(x)))
mse_te={}
mse_te["DML default"] = ((expected_te - te_pred)**2).mean()
mse_te["DML polynomial degree=2"] = ((expected_te - te_pred1)**2).mean()
mse_te["DML polynomial degree=10 with Lasso"] = ((expected_te - te_pred2)**2).mean()
mse_te["ForestDML"] = ((expected_te - te_pred3)**2).mean()
mse_te
print("best model selected by MSE of TE: ", min(mse_te, key=lambda x: mse_te.get(x)))
```
## 2. Example Usage with Single Binary Treatment Synthetic Data and Confidence Intervals
### 2.1. DGP
We use the following DGP:
\begin{align}
T \sim & \text{Bernoulli}\left(f(W)\right), &\; f(W)=\sigma(\langle W, \beta\rangle + \eta), \;\eta \sim \text{Uniform}(-1, 1)\\
Y = & T\cdot \theta(X) + \langle W, \gamma\rangle + \epsilon, & \; \epsilon \sim \text{Uniform}(-1, 1)\\
W \sim & \text{Normal}(0,\, I_{n_w}) & \\
X \sim & \text{Uniform}(0,\, 1)^{n_x}
\end{align}
where $W$ is a matrix of high-dimensional confounders, $\beta, \gamma$ have high sparsity and $\sigma$ is the sigmoid function.
For this DGP,
\begin{align}
\theta(x) = \exp( 2\cdot x_1 ).
\end{align}
```
# Treatment effect function
def exp_te(x):
return np.exp(2 * x[0])# DGP constants
np.random.seed(123)
n = 1000
n_w = 30
support_size = 5
n_x = 4
# Outcome support
support_Y = np.random.choice(range(n_w), size=support_size, replace=False)
coefs_Y = np.random.uniform(0, 1, size=support_size)
epsilon_sample = lambda n:np.random.uniform(-1, 1, size=n)
# Treatment support
support_T = support_Y
coefs_T = np.random.uniform(0, 1, size=support_size)
eta_sample = lambda n: np.random.uniform(-1, 1, size=n)
# Generate controls, covariates, treatments and outcomes
W = np.random.normal(0, 1, size=(n, n_w))
X = np.random.uniform(0, 1, size=(n, n_x))
# Heterogeneous treatment effects
TE = np.array([exp_te(x_i) for x_i in X])
# Define treatment
log_odds = np.dot(W[:, support_T], coefs_T) + eta_sample(n)
T_sigmoid = 1/(1 + np.exp(-log_odds))
T = np.array([np.random.binomial(1, p) for p in T_sigmoid])
# Define the outcome
Y = TE * T + np.dot(W[:, support_Y], coefs_Y) + epsilon_sample(n)
# get testing data
X_test = np.random.uniform(0, 1, size=(n, n_x))
X_test[:, 0] = np.linspace(0, 1, n)
```
### 2.2. Train Estimator
```
est = LinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestClassifier(min_samples_leaf=10),
discrete_treatment=True,
linear_first_stages=False,
n_splits=6)
est.fit(Y, T, X=X, W=W)
te_pred = est.effect(X_test)
lb, ub = est.effect_interval(X_test, alpha=0.01)
est2 = SparseLinearDML(model_y=RandomForestRegressor(),
model_t=RandomForestClassifier(min_samples_leaf=10),
discrete_treatment=True,
featurizer=PolynomialFeatures(degree=2),
linear_first_stages=False,
n_splits=6)
est2.fit(Y, T, X=X, W=W)
te_pred2 = est2.effect(X_test)
lb2, ub2 = est2.effect_interval(X_test, alpha=0.01)
est3 = ForestDML(model_y=RandomForestRegressor(),
model_t=RandomForestClassifier(min_samples_leaf=10),
discrete_treatment=True,
n_estimators=1000,
subsample_fr=.8,
min_samples_leaf=10,
min_impurity_decrease=0.001,
verbose=0, min_weight_fraction_leaf=.01,
n_crossfit_splits=6)
est3.fit(Y, T, X=X, W=W)
te_pred3 = est3.effect(X_test)
lb3, ub3 = est3.effect_interval(X_test, alpha=0.01)
est3.feature_importances_
```
### 2.3. Performance Visualization
```
expected_te=np.array([exp_te(x_i) for x_i in X_test])
plt.figure(figsize=(16,6))
plt.subplot(1, 3, 1)
plt.plot(X_test[:, 0], te_pred, label='LinearDML', alpha=.6)
plt.fill_between(X_test[:, 0], lb, ub, alpha=.4)
plt.plot(X_test[:, 0], expected_te, 'b--', label='True effect')
plt.ylabel('Treatment Effect')
plt.xlabel('x')
plt.legend()
plt.subplot(1, 3, 2)
plt.plot(X_test[:, 0], te_pred2, label='SparseLinearDML', alpha=.6)
plt.fill_between(X_test[:, 0], lb2, ub2, alpha=.4)
plt.plot(X_test[:, 0], expected_te, 'b--', label='True effect')
plt.ylabel('Treatment Effect')
plt.xlabel('x')
plt.legend()
plt.subplot(1, 3, 3)
plt.plot(X_test[:, 0], te_pred3, label='ForestDML', alpha=.6)
plt.fill_between(X_test[:, 0], lb3, ub3, alpha=.4)
plt.plot(X_test[:, 0], expected_te, 'b--', label='True effect')
plt.ylabel('Treatment Effect')
plt.xlabel('x')
plt.legend()
plt.show()
```
### 2.4. Other Inferences
#### 2.4.1 Effect Inferences
Other than confidence interval, we could also output other statistical inferences of the effect include standard error, z-test score and p value given each sample $X[i]$.
```
est.effect_inference(X_test[:10,]).summary_frame(alpha=0.1, value=0, decimals=3)
```
We could also get the population inferences given sample $X$.
```
est.effect_inference(X_test).population_summary(alpha=0.1, value=0, decimals=3, tol=0.001)
```
#### 2.4.2 Coefficient and Intercept Inferences
We could also get the coefficient and intercept inference for the final model when it's linear.
```
est.coef__inference().summary_frame()
est.intercept__inference().summary_frame()
est.summary()
```
## 3. Example Usage with Multiple Continuous Treatment Synthetic Data
### 3.1. DGP
We use the data generating process (DGP) from [here](https://arxiv.org/abs/1806.03467), and modify the treatment to generate multiple treatments. The DGP is described by the following equations:
\begin{align}
T =& \langle W, \beta\rangle + \eta, & \;\eta \sim \text{Uniform}(-1, 1)\\
Y =& T\cdot \theta_{1}(X) + T^{2}\cdot \theta_{2}(X) + \langle W, \gamma\rangle + \epsilon, &\; \epsilon \sim \text{Uniform}(-1, 1)\\
W \sim& \text{Normal}(0,\, I_{n_w})\\
X \sim& \text{Uniform}(0,1)^{n_x}
\end{align}
where $W$ is a matrix of high-dimensional confounders and $\beta, \gamma$ have high sparsity.
For this DGP,
\begin{align}
\theta_{1}(x) = \exp(2\cdot x_1)\\
\theta_{2}(x) = x_1^{2}\\
\end{align}
```
# DGP constants
np.random.seed(123)
n = 6000
n_w = 30
support_size = 5
n_x = 5
# Outcome support
support_Y = np.random.choice(np.arange(n_w), size=support_size, replace=False)
coefs_Y = np.random.uniform(0, 1, size=support_size)
epsilon_sample = lambda n: np.random.uniform(-1, 1, size=n)
# Treatment support
support_T = support_Y
coefs_T = np.random.uniform(0, 1, size=support_size)
eta_sample = lambda n: np.random.uniform(-1, 1, size=n)
# Generate controls, covariates, treatments and outcomes
W = np.random.normal(0, 1, size=(n, n_w))
X = np.random.uniform(0, 1, size=(n, n_x))
# Heterogeneous treatment effects
TE1 = np.array([x_i[0] for x_i in X])
TE2 = np.array([x_i[0]**2 for x_i in X]).flatten()
T = np.dot(W[:, support_T], coefs_T) + eta_sample(n)
Y = TE1 * T + TE2 * T**2 + np.dot(W[:, support_Y], coefs_Y) + epsilon_sample(n)
# Generate test data
X_test = np.random.uniform(0, 1, size=(100, n_x))
X_test[:, 0] = np.linspace(0, 1, 100)
```
### 3.2. Train Estimator
```
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.multioutput import MultiOutputRegressor
from sklearn.linear_model import ElasticNetCV
est = LinearDML(model_y=GradientBoostingRegressor(n_estimators=100, max_depth=3, min_samples_leaf=20),
model_t=MultiOutputRegressor(GradientBoostingRegressor(n_estimators=100,
max_depth=3,
min_samples_leaf=20)),
featurizer=PolynomialFeatures(degree=2, include_bias=False),
linear_first_stages=False,
n_splits=5)
T = T.reshape(-1,1)
est.fit(Y, np.concatenate((T, T**2), axis=1), X=X, W=W)
te_pred = est.const_marginal_effect(X_test)
lb, ub = est.const_marginal_effect_interval(X_test, alpha=0.01)
```
### 3.3. Performance Visualization
```
plt.figure(figsize=(10,6))
plt.plot(X_test[:, 0], te_pred[:, 0], label='DML estimate1')
plt.fill_between(X_test[:, 0], lb[:, 0], ub[:, 0], alpha=.4)
plt.plot(X_test[:, 0], te_pred[:, 1], label='DML estimate2')
plt.fill_between(X_test[:, 0], lb[:, 1], ub[:, 1], alpha=.4)
expected_te1 = np.array([x_i[0] for x_i in X_test])
expected_te2=np.array([x_i[0]**2 for x_i in X_test]).flatten()
plt.plot(X_test[:, 0], expected_te1, '--', label='True effect1')
plt.plot(X_test[:, 0], expected_te2, '--', label='True effect2')
plt.ylabel("Treatment Effect")
plt.xlabel("x")
plt.legend()
plt.show()
```
## 4. Example Usage with Single Continuous Treatment Observational Data
We applied our technique to Dominick’s dataset, a popular historical dataset of store-level orange juice prices and sales provided by University of Chicago Booth School of Business.
The dataset is comprised of a large number of covariates $W$, but researchers might only be interested in learning the elasticity of demand as a function of a few variables $x$ such
as income or education.
We applied the `LinearDML` to estimate orange juice price elasticity
as a function of income, and our results, unveil the natural phenomenon that lower income consumers are more price-sensitive.
### 4.1. Data
```
# A few more imports
import os
import pandas as pd
import urllib.request
from sklearn.preprocessing import StandardScaler
# Import the data
file_name = "oj_large.csv"
if not os.path.isfile(file_name):
print("Downloading file (this might take a few seconds)...")
urllib.request.urlretrieve("https://msalicedatapublic.blob.core.windows.net/datasets/OrangeJuice/oj_large.csv", file_name)
oj_data = pd.read_csv(file_name)
oj_data.head()
# Prepare data
Y = oj_data['logmove'].values
T = np.log(oj_data["price"]).values
scaler = StandardScaler()
W1 = scaler.fit_transform(oj_data[[c for c in oj_data.columns if c not in ['price', 'logmove', 'brand', 'week', 'store','INCOME']]].values)
W2 = pd.get_dummies(oj_data[['brand']]).values
W = np.concatenate([W1, W2], axis=1)
X=scaler.fit_transform(oj_data[['INCOME']].values)
## Generate test data
min_income = -1
max_income = 1
delta = (1 - (-1)) / 100
X_test = np.arange(min_income, max_income + delta - 0.001, delta).reshape(-1,1)
```
### 4.2. Train Estimator
```
est = LinearDML(model_y=RandomForestRegressor(),model_t=RandomForestRegressor())
est.fit(Y, T, X=X, W=W)
te_pred=est.effect(X_test)
```
### 4.3. Performance Visualization
```
# Plot Oranje Juice elasticity as a function of income
plt.figure(figsize=(10,6))
plt.plot(X_test, te_pred, label="OJ Elasticity")
plt.xlabel(r'Scale(Income)')
plt.ylabel('Orange Juice Elasticity')
plt.legend()
plt.title("Orange Juice Elasticity vs Income")
plt.show()
```
### 4.4. Confidence Intervals
We can also get confidence intervals around our predictions by passing an additional `inference` argument to `fit`. All estimators support bootstrap intervals, which involves refitting the same estimator repeatedly on subsamples of the original data, but `LinearDML` also supports a more efficient approach which can be achieved by leaving inference set to the default of `'auto'` or by explicitly passing `inference='statsmodels'`.
```
est.fit(Y, T, X=X, W=W)
te_pred=est.effect(X_test)
te_pred_interval = est.const_marginal_effect_interval(X_test, alpha=0.02)
# Plot Oranje Juice elasticity as a function of income
plt.figure(figsize=(10,6))
plt.plot(X_test.flatten(), te_pred, label="OJ Elasticity")
plt.fill_between(X_test.flatten(), te_pred_interval[0], te_pred_interval[1], alpha=.5, label="1-99% CI")
plt.xlabel(r'Scale(Income)')
plt.ylabel('Orange Juice Elasticity')
plt.title("Orange Juice Elasticity vs Income")
plt.legend()
plt.show()
```
## 5. Example Usage with Multiple Continuous Treatment, Multiple Outcome Observational Data
We use the same data, but in this case, we want to fit the demand of multiple brand as a function of the price of each one of them, i.e. fit the matrix of cross price elasticities. It can be done, by simply setting as $Y$ to be the vector of demands and $T$ to be the vector of prices. Then we can obtain the matrix of cross price elasticities.
\begin{align}
Y=[Logmove_{tropicana},Logmove_{minute.maid},Logmove_{dominicks}] \\
T=[Logprice_{tropicana},Logprice_{minute.maid},Logprice_{dominicks}] \\
\end{align}
### 5.1. Data
```
# Import the data
oj_data = pd.read_csv(file_name)
# Prepare data
oj_data['price'] = np.log(oj_data["price"])
# Transform dataset.
# For each store in each week, get a vector of logmove and a vector of logprice for each brand.
# Other features are store specific, will be the same for all brands.
groupbylist = ["store", "week", "AGE60", "EDUC", "ETHNIC", "INCOME",
"HHLARGE", "WORKWOM", "HVAL150",
"SSTRDIST", "SSTRVOL", "CPDIST5", "CPWVOL5"]
oj_data1 = pd.pivot_table(oj_data,index=groupbylist,
columns=oj_data.groupby(groupbylist).cumcount(),
values=['logmove', 'price'],
aggfunc='sum').reset_index()
oj_data1.columns = oj_data1.columns.map('{0[0]}{0[1]}'.format)
oj_data1 = oj_data1.rename(index=str,
columns={"logmove0": "logmove_T",
"logmove1": "logmove_M",
"logmove2":"logmove_D",
"price0":"price_T",
"price1":"price_M",
"price2":"price_D"})
# Define Y,T,X,W
Y = oj_data1[['logmove_T', "logmove_M", "logmove_D"]].values
T = oj_data1[['price_T', "price_M", "price_D"]].values
scaler = StandardScaler()
W=scaler.fit_transform(oj_data1[[c for c in groupbylist if c not in ['week', 'store', 'INCOME']]].values)
X=scaler.fit_transform(oj_data1[['INCOME']].values)
## Generate test data
min_income = -1
max_income = 1
delta = (1 - (-1)) / 100
X_test = np.arange(min_income, max_income + delta - 0.001, delta).reshape(-1, 1)
```
### 5.2. Train Estimator
```
est = LinearDML(model_y=MultiTaskElasticNetCV(cv=3, tol=1, selection='random'),
model_t=MultiTaskElasticNetCV(cv=3),
featurizer=PolynomialFeatures(1),
linear_first_stages=True)
est.fit(Y, T, X=X, W=W)
te_pred = est.const_marginal_effect(X_test)
```
### 5.3. Performance Visualization
```
# Plot Oranje Juice elasticity as a function of income
plt.figure(figsize=(18, 10))
dic={0:"Tropicana", 1:"Minute.maid", 2:"Dominicks"}
for i in range(3):
for j in range(3):
plt.subplot(3, 3, 3 * i + j + 1)
plt.plot(X_test, te_pred[:, i, j],
color="C{}".format(str(3 * i + j)),
label="OJ Elasticity {} to {}".format(dic[j], dic[i]))
plt.xlabel(r'Scale(Income)')
plt.ylabel('Orange Juice Elasticity')
plt.legend()
plt.suptitle("Orange Juice Elasticity vs Income", fontsize=16)
plt.show()
```
**Findings**: Look at the diagonal of the matrix, the TE of OJ prices are always negative to the sales across all the brand, but people with higher income are less price-sensitive. By contrast, for the non-diagonal of the matrix, the TE of prices for other brands are always positive to the sales for that brand, the TE is affected by income in different ways for different competitors. In addition, compare to previous plot, the negative TE of OJ prices for each brand are all larger than the TE considering all brand together, which means we would have underestimated the effect of price changes on demand.
### 5.4. Confidence Intervals
```
est.fit(Y, T, X=X, W=W)
te_pred = est.const_marginal_effect(X_test)
te_pred_interval = est.const_marginal_effect_interval(X_test, alpha=0.02)
# Plot Oranje Juice elasticity as a function of income
plt.figure(figsize=(18, 10))
dic={0:"Tropicana", 1:"Minute.maid", 2:"Dominicks"}
for i in range(3):
for j in range(3):
plt.subplot(3, 3, 3 * i + j + 1)
plt.plot(X_test, te_pred[:, i, j],
color="C{}".format(str(3 * i + j)),
label="OJ Elasticity {} to {}".format(dic[j], dic[i]))
plt.fill_between(X_test.flatten(), te_pred_interval[0][:, i, j],te_pred_interval[1][:, i,j], color="C{}".format(str(3*i+j)),alpha=.5, label="1-99% CI")
plt.xlabel(r'Scale(Income)')
plt.ylabel('Orange Juice Elasticity')
plt.legend()
plt.suptitle("Orange Juice Elasticity vs Income",fontsize=16)
plt.show()
```
| true |
code
| 0.634458 | null | null | null | null |
|
## Lecture 2: Models of Computation
Lecture by Erik Demaine
Video link here: [https://www.youtube.com/watch?v=Zc54gFhdpLA&list=PLUl4u3cNGP61Oq3tWYp6V_F-5jb5L2iHb&index=2](https://www.youtube.com/watch?v=Zc54gFhdpLA&list=PLUl4u3cNGP61Oq3tWYp6V_F-5jb5L2iHb&index=2)
### Problem statement:
Given two documents, **D1** and **D2**, find the distance between them
The distance **d(D1,D2)** can be defined in a number of ways, but we use the following definition:
* For a word 'w' in document D, D[w] is defined as the number of occurences of 'w' in D
* We create a vector for both documents D1 and D2 in this way
* Given both vectors, we compute the distance **d(D1,D2)** as the following steps:
- d'(D1,D2): Compute the **inner product** of these vectors
- ``d'(D1,D2) = sum(D1[w]*D2[w] for all w)``
- This works well, but fails when the documents are very long. We can normalize this by dividing it by the lengths of the vectors
- ``d''(D1,D2) = d'(D1,D2)/(|D1| * |D2|)``
- |D| is the length of document D in words
- This is also the cosine of the angle between the two vectors
- If we take the arccos value of d''(D1,D2), we get the angle between the two vector
- ``d(D1,D2) = arccos(d''(D1,D2))``
### Steps:
Calculating this requires broadly the following steps:
1. **Split document into words** - This can be done in a number of ways. The below list is not exhasutive
1. Go through the document, anytime you see a non alphanumeric character, start a new word
2. Use regex (can run in exponential time, so be very wary)
3. Use 'split'
2. **Find word frequencies** - Couple of ways to do this:
1. Sort the words, add to count
2. Go through words linearly, add to count dictionary
3. Compute distance as above
```
import os, glob
import copy, math
doc_dir="Sample Documents/"
doc_list=os.listdir(doc_dir)
```
#### Split document into words
```
def splitIntoWords(file_contents: str) -> list:
word_list=[]
curr_word=[]
for c in file_contents:
ord_c=ord(c)
if 65<=ord_c<=90 or 97<=ord_c<=122 or ord_c==39 or ord_c==44:
if ord_c==44 or ord_c==39:
continue
curr_word.append(c)
else:
if curr_word:
word_list.append("".join(curr_word).lower())
curr_word=[]
continue
#remember to append the last word
word_list.append("".join(curr_word).lower())
return word_list
assert len(doc_list)==2, "Invalid number of documents. Select any two"
for i, doc in enumerate(doc_list):
if i==0:
D1=splitIntoWords(open(doc_dir+doc,"r").read())
else:
D2=splitIntoWords(open(doc_dir+doc,"r").read())
```
#### Compute word count
```
def computeWordCount(word_list: list)-> dict:
'''
This functions computes word counts by checking to see if the word is in the count dictionary
If it is, then it increments that count by 1
Else, it sets the count to 1
'''
word_count={}
for word in word_list:
if word in word_count:
word_count[word]+=1
else:
word_count[word]=1
return word_count
def computeWordCountSort(word_list: list)-> dict:
'''
This method computes the word counts by first sorting the list lexicographically
If the word is the same as the previous one, it increments count by 1
Else, it sets the count to the computed value, resets count to 1 and sets the current word to the new one
'''
word_list.sort()
cur=word_list[0]
count=1
word_count={}
for word in word_list[1:]:
if word==cur:
count+=1
else:
word_count[cur]=count
count=1
cur=word
word_count[cur]=count
return word_count
```
The above functions are equivalent. You can use either of them to compute the word counts. Below, I use the ```computeWordCount()``` function
#### Compute distance
```
def dotProduct(vec1: dict, vec2: dict) -> float:
res=0.0
for key in set(list(vec1.keys())+list(vec2.keys())):
res+=vec1.get(key,0)*vec2.get(key,0)
return res
def dotProductFaster(vec1: dict, vec2:dict) -> float:
res=0.0
if len(vec1)>len(vec2):
smaller,larger=vec2,vec1
else:
smaller,larger=vec1,vec2
for key in smaller.keys():
res+=smaller[key]*larger.get(key,0)
return res
def normalize(word_list_doc1: list, word_list_doc2: list) -> int:
return len(word_list_doc1)*len(word_list_doc2)
def docdist(doc1, doc2):
D1=splitIntoWords(open(doc_dir+doc1,"r").read())
D2=splitIntoWords(open(doc_dir+doc2,"r").read())
D1_WC=computeWordCount(D1)
D2_WC=computeWordCount(D2)
#Use either of the two function below
#Time them to see which is faster
DotProductValue=dotProduct(D1_WC, D2_WC)
DotProductValueFaster= dotProductFaster(D1_WC, D2_WC)
normalizedDPValue=DotProductValueFaster/(normalize(D1,D2))
return math.acos(normalizedDPValue)
print(docdist(doc_list[0], doc_list[1]))
```
| true |
code
| 0.31877 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#VITS-Attentions" data-toc-modified-id="VITS-Attentions-1"><span class="toc-item-num">1 </span>VITS Attentions</a></span></li></ul></div>
```
# default_exp models.attentions
```
# VITS Attentions
```
# export
import copy
import math
import numpy as np
import torch
from torch import nn
from torch.nn import functional as F
from uberduck_ml_dev.models.common import LayerNorm
from uberduck_ml_dev.utils.utils import convert_pad_shape, subsequent_mask
class VITSEncoder(nn.Module):
def __init__(
self,
hidden_channels,
filter_channels,
n_heads,
n_layers,
kernel_size=1,
p_dropout=0.0,
window_size=4,
**kwargs
):
super().__init__()
self.hidden_channels = hidden_channels
self.filter_channels = filter_channels
self.n_heads = n_heads
self.n_layers = n_layers
self.kernel_size = kernel_size
self.p_dropout = p_dropout
self.window_size = window_size
self.drop = nn.Dropout(p_dropout)
self.attn_layers = nn.ModuleList()
self.norm_layers_1 = nn.ModuleList()
self.ffn_layers = nn.ModuleList()
self.norm_layers_2 = nn.ModuleList()
for i in range(self.n_layers):
self.attn_layers.append(
MultiHeadAttention(
hidden_channels,
hidden_channels,
n_heads,
p_dropout=p_dropout,
window_size=window_size,
)
)
self.norm_layers_1.append(LayerNorm(hidden_channels))
self.ffn_layers.append(
FFN(
hidden_channels,
hidden_channels,
filter_channels,
kernel_size,
p_dropout=p_dropout,
)
)
self.norm_layers_2.append(LayerNorm(hidden_channels))
def forward(self, x, x_mask):
attn_mask = x_mask.unsqueeze(2) * x_mask.unsqueeze(-1)
x = x * x_mask
for i in range(self.n_layers):
y = self.attn_layers[i](x, x, attn_mask)
y = self.drop(y)
x = self.norm_layers_1[i](x + y)
y = self.ffn_layers[i](x, x_mask)
y = self.drop(y)
x = self.norm_layers_2[i](x + y)
x = x * x_mask
return x
class Decoder(nn.Module):
def __init__(
self,
hidden_channels,
filter_channels,
n_heads,
n_layers,
kernel_size=1,
p_dropout=0.0,
proximal_bias=False,
proximal_init=True,
**kwargs
):
super().__init__()
self.hidden_channels = hidden_channels
self.filter_channels = filter_channels
self.n_heads = n_heads
self.n_layers = n_layers
self.kernel_size = kernel_size
self.p_dropout = p_dropout
self.proximal_bias = proximal_bias
self.proximal_init = proximal_init
self.drop = nn.Dropout(p_dropout)
self.self_attn_layers = nn.ModuleList()
self.norm_layers_0 = nn.ModuleList()
self.encdec_attn_layers = nn.ModuleList()
self.norm_layers_1 = nn.ModuleList()
self.ffn_layers = nn.ModuleList()
self.norm_layers_2 = nn.ModuleList()
for i in range(self.n_layers):
self.self_attn_layers.append(
MultiHeadAttention(
hidden_channels,
hidden_channels,
n_heads,
p_dropout=p_dropout,
proximal_bias=proximal_bias,
proximal_init=proximal_init,
)
)
self.norm_layers_0.append(LayerNorm(hidden_channels))
self.encdec_attn_layers.append(
MultiHeadAttention(
hidden_channels, hidden_channels, n_heads, p_dropout=p_dropout
)
)
self.norm_layers_1.append(LayerNorm(hidden_channels))
self.ffn_layers.append(
FFN(
hidden_channels,
hidden_channels,
filter_channels,
kernel_size,
p_dropout=p_dropout,
causal=True,
)
)
self.norm_layers_2.append(LayerNorm(hidden_channels))
def forward(self, x, x_mask, h, h_mask):
"""
x: decoder input
h: encoder output
"""
self_attn_mask = subsequent_mask(x_mask.size(2)).to(
device=x.device, dtype=x.dtype
)
encdec_attn_mask = h_mask.unsqueeze(2) * x_mask.unsqueeze(-1)
x = x * x_mask
for i in range(self.n_layers):
y = self.self_attn_layers[i](x, x, self_attn_mask)
y = self.drop(y)
x = self.norm_layers_0[i](x + y)
y = self.encdec_attn_layers[i](x, h, encdec_attn_mask)
y = self.drop(y)
x = self.norm_layers_1[i](x + y)
y = self.ffn_layers[i](x, x_mask)
y = self.drop(y)
x = self.norm_layers_2[i](x + y)
x = x * x_mask
return x
class MultiHeadAttention(nn.Module):
def __init__(
self,
channels,
out_channels,
n_heads,
p_dropout=0.0,
window_size=None,
heads_share=True,
block_length=None,
proximal_bias=False,
proximal_init=False,
):
super().__init__()
assert channels % n_heads == 0
self.channels = channels
self.out_channels = out_channels
self.n_heads = n_heads
self.p_dropout = p_dropout
self.window_size = window_size
self.heads_share = heads_share
self.block_length = block_length
self.proximal_bias = proximal_bias
self.proximal_init = proximal_init
self.attn = None
self.k_channels = channels // n_heads
self.conv_q = nn.Conv1d(channels, channels, 1)
self.conv_k = nn.Conv1d(channels, channels, 1)
self.conv_v = nn.Conv1d(channels, channels, 1)
self.conv_o = nn.Conv1d(channels, out_channels, 1)
self.drop = nn.Dropout(p_dropout)
if window_size is not None:
n_heads_rel = 1 if heads_share else n_heads
rel_stddev = self.k_channels**-0.5
self.emb_rel_k = nn.Parameter(
torch.randn(n_heads_rel, window_size * 2 + 1, self.k_channels)
* rel_stddev
)
self.emb_rel_v = nn.Parameter(
torch.randn(n_heads_rel, window_size * 2 + 1, self.k_channels)
* rel_stddev
)
nn.init.xavier_uniform_(self.conv_q.weight)
nn.init.xavier_uniform_(self.conv_k.weight)
nn.init.xavier_uniform_(self.conv_v.weight)
if proximal_init:
with torch.no_grad():
self.conv_k.weight.copy_(self.conv_q.weight)
self.conv_k.bias.copy_(self.conv_q.bias)
def forward(self, x, c, attn_mask=None):
q = self.conv_q(x)
k = self.conv_k(c)
v = self.conv_v(c)
x, self.attn = self.attention(q, k, v, mask=attn_mask)
x = self.conv_o(x)
return x
def attention(self, query, key, value, mask=None):
# reshape [b, d, t] -> [b, n_h, t, d_k]
b, d, t_s, t_t = (*key.size(), query.size(2))
query = query.view(b, self.n_heads, self.k_channels, t_t).transpose(2, 3)
key = key.view(b, self.n_heads, self.k_channels, t_s).transpose(2, 3)
value = value.view(b, self.n_heads, self.k_channels, t_s).transpose(2, 3)
scores = torch.matmul(query / math.sqrt(self.k_channels), key.transpose(-2, -1))
if self.window_size is not None:
assert (
t_s == t_t
), "Relative attention is only available for self-attention."
key_relative_embeddings = self._get_relative_embeddings(self.emb_rel_k, t_s)
rel_logits = self._matmul_with_relative_keys(
query / math.sqrt(self.k_channels), key_relative_embeddings
)
scores_local = self._relative_position_to_absolute_position(rel_logits)
scores = scores + scores_local
if self.proximal_bias:
assert t_s == t_t, "Proximal bias is only available for self-attention."
scores = scores + self._attention_bias_proximal(t_s).to(
device=scores.device, dtype=scores.dtype
)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e4)
if self.block_length is not None:
assert (
t_s == t_t
), "Local attention is only available for self-attention."
block_mask = (
torch.ones_like(scores)
.triu(-self.block_length)
.tril(self.block_length)
)
scores = scores.masked_fill(block_mask == 0, -1e4)
p_attn = F.softmax(scores, dim=-1) # [b, n_h, t_t, t_s]
p_attn = self.drop(p_attn)
output = torch.matmul(p_attn, value)
if self.window_size is not None:
relative_weights = self._absolute_position_to_relative_position(p_attn)
value_relative_embeddings = self._get_relative_embeddings(
self.emb_rel_v, t_s
)
output = output + self._matmul_with_relative_values(
relative_weights, value_relative_embeddings
)
output = (
output.transpose(2, 3).contiguous().view(b, d, t_t)
) # [b, n_h, t_t, d_k] -> [b, d, t_t]
return output, p_attn
def _matmul_with_relative_values(self, x, y):
"""
x: [b, h, l, m]
y: [h or 1, m, d]
ret: [b, h, l, d]
"""
ret = torch.matmul(x, y.unsqueeze(0))
return ret
def _matmul_with_relative_keys(self, x, y):
"""
x: [b, h, l, d]
y: [h or 1, m, d]
ret: [b, h, l, m]
"""
ret = torch.matmul(x, y.unsqueeze(0).transpose(-2, -1))
return ret
def _get_relative_embeddings(self, relative_embeddings, length):
max_relative_position = 2 * self.window_size + 1
# Pad first before slice to avoid using cond ops.
pad_length = max(length - (self.window_size + 1), 0)
slice_start_position = max((self.window_size + 1) - length, 0)
slice_end_position = slice_start_position + 2 * length - 1
if pad_length > 0:
padded_relative_embeddings = F.pad(
relative_embeddings,
convert_pad_shape([[0, 0], [pad_length, pad_length], [0, 0]]),
)
else:
padded_relative_embeddings = relative_embeddings
used_relative_embeddings = padded_relative_embeddings[
:, slice_start_position:slice_end_position
]
return used_relative_embeddings
def _relative_position_to_absolute_position(self, x):
"""
x: [b, h, l, 2*l-1]
ret: [b, h, l, l]
"""
batch, heads, length, _ = x.size()
# Concat columns of pad to shift from relative to absolute indexing.
x = F.pad(x, convert_pad_shape([[0, 0], [0, 0], [0, 0], [0, 1]]))
# Concat extra elements so to add up to shape (len+1, 2*len-1).
x_flat = x.view([batch, heads, length * 2 * length])
x_flat = F.pad(x_flat, convert_pad_shape([[0, 0], [0, 0], [0, length - 1]]))
# Reshape and slice out the padded elements.
x_final = x_flat.view([batch, heads, length + 1, 2 * length - 1])[
:, :, :length, length - 1 :
]
return x_final
def _absolute_position_to_relative_position(self, x):
"""
x: [b, h, l, l]
ret: [b, h, l, 2*l-1]
"""
batch, heads, length, _ = x.size()
# padd along column
x = F.pad(x, convert_pad_shape([[0, 0], [0, 0], [0, 0], [0, length - 1]]))
x_flat = x.view([batch, heads, length**2 + length * (length - 1)])
# add 0's in the beginning that will skew the elements after reshape
x_flat = F.pad(x_flat, convert_pad_shape([[0, 0], [0, 0], [length, 0]]))
x_final = x_flat.view([batch, heads, length, 2 * length])[:, :, :, 1:]
return x_final
def _attention_bias_proximal(self, length):
"""Bias for self-attention to encourage attention to close positions.
Args:
length: an integer scalar.
Returns:
a Tensor with shape [1, 1, length, length]
"""
r = torch.arange(length, dtype=torch.float32)
diff = torch.unsqueeze(r, 0) - torch.unsqueeze(r, 1)
return torch.unsqueeze(torch.unsqueeze(-torch.log1p(torch.abs(diff)), 0), 0)
class FFN(nn.Module):
def __init__(
self,
in_channels,
out_channels,
filter_channels,
kernel_size,
p_dropout=0.0,
activation=None,
causal=False,
):
super().__init__()
self.in_channels = in_channels
self.out_channels = out_channels
self.filter_channels = filter_channels
self.kernel_size = kernel_size
self.p_dropout = p_dropout
self.activation = activation
self.causal = causal
if causal:
self.padding = self._causal_padding
else:
self.padding = self._same_padding
self.conv_1 = nn.Conv1d(in_channels, filter_channels, kernel_size)
self.conv_2 = nn.Conv1d(filter_channels, out_channels, kernel_size)
self.drop = nn.Dropout(p_dropout)
def forward(self, x, x_mask):
x = self.conv_1(self.padding(x * x_mask))
if self.activation == "gelu":
x = x * torch.sigmoid(1.702 * x)
else:
x = torch.relu(x)
x = self.drop(x)
x = self.conv_2(self.padding(x * x_mask))
return x * x_mask
def _causal_padding(self, x):
if self.kernel_size == 1:
return x
pad_l = self.kernel_size - 1
pad_r = 0
padding = [[0, 0], [0, 0], [pad_l, pad_r]]
x = F.pad(x, convert_pad_shape(padding))
return x
def _same_padding(self, x):
if self.kernel_size == 1:
return x
pad_l = (self.kernel_size - 1) // 2
pad_r = self.kernel_size // 2
padding = [[0, 0], [0, 0], [pad_l, pad_r]]
x = F.pad(x, convert_pad_shape(padding))
return x
```
| true |
code
| 0.832032 | null | null | null | null |
|
## Data :
--> Date (date the crash had taken place)
--> Time (time the crash had taken place)
--> Location
--> Operator
--> Flight
--> Route
--> Type
--> Registration
--> cn/In - ?
--> Aboard - number of people aboard
--> Fatalities - lethal outcome
--> Ground - saved people
--> Summary - brief summary of the case
## Importing Libraries & getting Data
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# plt.style.use('dark_background')
from datetime import date ,timedelta ,datetime
import warnings
warnings.filterwarnings('ignore')
data = pd.read_csv('datasets/Airplane_Crashes_and_Fatalities_Since_1908.csv/Airplane_Crashes_and_Fatalities_Since_1908.csv')
data.head()
data.info()
```
## Handling Missing Values
```
def percent_missing_data(data):
missing_count = data.isnull().sum().sort_values(ascending=False)
missing_percent = 100 * data.isnull().sum().sort_values(ascending=False) / len(data)
missing_count = pd.DataFrame(missing_count[missing_count > 0])
missing_percent = pd.DataFrame(missing_percent[missing_percent > 0])
missing_values_table = pd.concat([missing_count, missing_percent], axis=1)
missing_values_table.columns = ["missing_count", "missing_percent"]
print('The dataset consists of {0} columns , out of which {1} have missing values.'.format(
data.shape[1], str(missing_values_table.shape[0])))
return missing_values_table
percent_missing_data(data)
sns.heatmap(data.isnull() ,yticklabels=False ,cbar=False ,cmap='viridis')
```
## Analysing Date & Time
```
data.Time.head() ,data.Date.head()
# replacing missing data in 'Time' column with 0.00
data['Time'] = data['Time'].replace(np.nan ,'00:00')
# changing format
data['Time'] = data['Time'].str.replace('c: ', '')
data['Time'] = data['Time'].str.replace('c:', '')
data['Time'] = data['Time'].str.replace('c', '')
data['Time'] = data['Time'].str.replace('12\'20', '12:20')
data['Time'] = data['Time'].str.replace('18.40', '18:40')
data['Time'] = data['Time'].str.replace('0943', '09:43')
data['Time'] = data['Time'].str.replace('22\'08', '22:08')
data['Time'] = data['Time'].str.replace('114:20', '00:00')
data['Time'] = data['Date'] + ' ' + data['Time']
def to_date(x):
return datetime.strptime(x, '%m/%d/%Y %H:%M')
data['Time'] = data['Time'].apply(to_date)
print('Date ranges from ' + str(data.Time.min()) + ' to ' + str(data.Time.max()))
data.Operator = data.Operator.str.upper()
data.head()
```
# Visualization
## Analysing Total Accidents per Year
```
temp = data.groupby(data.Time.dt.year)[['Date']].count()
temp = temp.rename(columns={'Date':'Count'})
plt.figure(figsize=(10,5))
plt.plot(temp.index ,'Count', data=temp, color='darkkhaki' ,marker='.',linewidth=1)
plt.xlabel('Year', fontsize=12)
plt.ylabel('Count', fontsize=12)
plt.title('Count of accidents by Year', loc='Center', fontsize=18)
plt.show()
```
## Analysing Total Accidents per Month, weekday & hour-of-day
```
import matplotlib.pylab as pl
import matplotlib.gridspec as gridspec
gs = gridspec.GridSpec(2,2)
plt.figure(figsize=(15,10) ,facecolor='#f7f7f7')
# 1st plot (month)
ax0 = pl.subplot(gs[0,:])
sns.barplot(data.groupby(data.Time.dt.month)[['Date']].count().index, 'Date', data=data.groupby(data.Time.dt.month)[['Date']].count(),color='coral',linewidth=2)
plt.xticks(data.groupby(data.Time.dt.month)[['Date']].count().index, [
'Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'])
plt.xlabel('Month' ,fontsize=10)
plt.ylabel('Count', fontsize=10)
plt.title('Count of Accidents by Month',loc='center', fontsize=14)
#====================================================================#
# 2nd plot (weekday)
ax1 = pl.subplot(gs[1,0])
sns.barplot(data.groupby(data.Time.dt.weekday)[['Date']].count().index, 'Date', data=data.groupby(data.Time.dt.weekday)[['Date']].count() ,color='deepskyblue' ,linewidth=1)
plt.xticks(data.groupby(data.Time.dt.weekday)[['Date']].count().index, [
'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun'])
plt.xlabel('Day of Week', fontsize=10)
plt.ylabel('Count', fontsize=10)
plt.title('Count of accidents by Day of Week', loc='Center', fontsize=14)
#====================================================================#
# 3rd plot (hour)
ax2 = pl.subplot(gs[1,1])
sns.barplot(data[data.Time.dt.hour != 0].groupby(data.Time.dt.hour)[['Date']].count().index, 'Date',
data=data[data.Time.dt.hour != 0].groupby(data.Time.dt.hour)[['Date']].count(), color='greenyellow', linewidth=1)
# plt.xticks(data.groupby(data.Time.dt.hour)[['Date']].count().index, [
# 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun'])
plt.xlabel('Hour', fontsize=10)
plt.ylabel('Count', fontsize=10)
plt.title('Count of accidents by Hour of Day', loc='Center', fontsize=14)
plt.tight_layout()
plt.show()
```
## Analysing Total Accidents based on Operator (Military)
```
temp = data.copy()
temp['isMilitary'] = temp.Operator.str.contains('MILITARY')
temp = temp.groupby('isMilitary')[['isMilitary']].count()
temp.index = ['Passenger' ,'Military']
temp_ = data.copy()
temp_['Military'] = temp_.Operator.str.contains('MILITARY')
temp_['Passenger'] = temp_.Military == False
temp_ = temp_.loc[:, ['Time', 'Military', 'Passenger']]
temp_ = temp_.groupby(temp_.Time.dt.year)[
['Military', 'Passenger']].aggregate(np.count_nonzero)
colors = ['tan', 'indianred']
plt.figure(figsize=(15, 6))
# 1st plot(pie-plot)
plt.subplot(1, 2, 1)
patches, texts = plt.pie(temp.isMilitary, colors=colors,
labels=temp.isMilitary, startangle=90)
plt.legend(patches, temp.index, loc="best", fontsize=10)
plt.axis('equal')
plt.title('Total number of accidents by Type of flight',
loc='Center', fontsize=14)
# 2nd plot
plt.subplot(1, 2, 2)
plt.plot(temp_.index, 'Military', data=temp_,
color='indianred', marker=".", linewidth=1)
plt.plot(temp_.index, 'Passenger', data=temp_,
color='tan', marker=".", linewidth=1)
plt.legend(fontsize=10)
plt.show()
```
## Analysing Fatalities vs Year
```
Fatalities = data.groupby(data.Time.dt.year).sum()
Fatalities['Proportion'] = Fatalities['Fatalities'] / Fatalities['Aboard']
plt.figure(figsize=(15, 6))
# 1st plot
plt.subplot(1, 2, 1)
plt.fill_between(Fatalities.index, 'Aboard',data=Fatalities, color="skyblue", alpha=0.2)
plt.plot(Fatalities.index, 'Aboard', data=Fatalities,marker=".", color="Slateblue", alpha=0.6, linewidth=1)
plt.fill_between(Fatalities.index, 'Fatalities',data=Fatalities, color="olive", alpha=0.2)
plt.plot(Fatalities.index, 'Fatalities', data=Fatalities,color="olive", marker=".", alpha=0.6, linewidth=1)
plt.legend(fontsize=10,loc='best')
plt.xlabel('Year', fontsize=10)
plt.ylabel('Amount of people', fontsize=10)
plt.title('Total number of people involved by Year', loc='Center', fontsize=14)
# 2nd plot
plt.subplot(1, 2, 2)
plt.plot(Fatalities.index, 'Proportion', data=Fatalities,marker=".", color='firebrick', linewidth=1)
plt.xlabel('Year', fontsize=10)
plt.ylabel('Ratio', fontsize=10)
plt.title('Fatalities / Total Ratio by Year', loc='Center', fontsize=14)
plt.tight_layout()
plt.show()
```
### So, 1970-1990 look like scary years in the history of air-flights with rise of deaths, but there might be also the rise of total amount of people flying by air, while actually proportion became lower.
### So, now analysing another dataset showing total number of flights or passengers
# Getting Data from new dataset
```
data_ = pd.read_csv('datasets/API_IS.AIR.DPRT_DS2_en_csv_v2_2766566/API_IS.AIR.DPRT_DS2_en_csv_v2_2766566.csv')
data_.head()
data_.columns
```
## Data Cleaning
```
data_ = data_.drop('Unnamed: 65',axis=1)
data_ = data_.drop(['Country Name', 'Country Code',
'Indicator Name', 'Indicator Code'], axis=1)
data_.head()
data_ = data_.replace(np.nan, 0)
data_ = pd.DataFrame(data_.sum())
data_.drop(data_.index[0:10])
data_ = data_['1970' :'2008']
data_.columns = ['Sum']
data_.index.name = 'Year'
data_.head()
Fatalities = Fatalities.reset_index()
Fatalities.Time = Fatalities.Time.apply(str)
Fatalities.index = Fatalities['Time']
del Fatalities['Time']
Fatalities = Fatalities['1970':'2008']
Fatalities = Fatalities[['Fatalities']]
Fatalities.head()
data_ = pd.concat([data_, Fatalities], axis=1)
data_['Ratio'] = data_['Fatalities'] / data_['Sum'] * 100
data_.Ratio.head()
```
# Visualization (data_)
## Analysing Amount of Passengers ,Total number of Fatalities per Year & Fatalities Ratio
```
gs = gridspec.GridSpec(3,3)
plt.figure(figsize=(30,10) ,facecolor='#f7f7f7')
ax0 = pl.subplot(gs[0,:])
plt.plot(data_.index ,'Sum' ,data=data_ ,marker='.' ,color='crimson',linewidth=1)
plt.xlabel('Year' ,fontsize=12)
plt.ylabel('Amount of passengers', loc='center', fontsize=12)
plt.title('Total amount of passengers by Year', loc='center', fontsize=16)
plt.xticks(rotation=90)
#---------------------------------------------------#
ax1 = pl.subplot(gs[1,:])
plt.plot(Fatalities.index, 'Fatalities', data=Fatalities,
marker='.', color='forestgreen', linewidth=1)
plt.xlabel('Year', fontsize=12)
plt.ylabel('Number of Fatalities', loc='center', fontsize=12)
plt.title('Total number of Fatalities by Year', loc='center', fontsize=16)
plt.xticks(rotation=90)
#---------------------------------------------------#
ax2 = pl.subplot(gs[2,:])
plt.plot(data_.index, 'Ratio', data=data_,
marker='.', color='darkorchid', linewidth=1)
plt.xlabel('Year', fontsize=12)
plt.ylabel('Ratio', loc='center', fontsize=12)
plt.title('Fatalities / Total amount of passegers Ratio by Year',
loc='center', fontsize=16)
plt.xticks(rotation=90)
#---------------------------------------------------#
plt.tight_layout()
plt.show()
```
## Analysing Ratio VS number of deaths
```
fig = plt.figure(figsize=(12, 6))
ax1 = fig.subplots()
ax1.plot(data_.index, 'Ratio', data=data_,
color='darkcyan', marker=".", linewidth=1)
ax1.set_xlabel('Year', fontsize=11)
for label in ax1.xaxis.get_ticklabels():
label.set_rotation(90)
ax1.set_ylabel('Ratio', fontsize=11)
ax1.tick_params('y')
ax2 = ax1.twinx()
ax2.plot(Fatalities.index, 'Fatalities', data=Fatalities,
color='hotpink', marker=".", linewidth=1)
ax2.set_ylabel('Number of fatalities', fontsize=11)
ax2.tick_params('y')
plt.title('Fatalities VS Ratio by Year', loc='Center', fontsize=14)
fig.tight_layout()
plt.show()
```
## Analysing Operator vs Fatality-Count
```
data.Operator = data.Operator.str.upper()
data.Operator = data.Operator.replace('A B AEROTRANSPORT' ,'AB AEROTRANSPORT')
total_count_operator = data.groupby('Operator')[['Operator']].count()
total_count_operator = total_count_operator.rename(columns={'Operator':'Count'})
total_count_operator = total_count_operator.sort_values(by='Count' ,ascending=False).head(20)
plt.figure(figsize=(12,6))
sns.barplot(x='Count' ,y=total_count_operator.index ,data=total_count_operator )
plt.xlabel('Count',fontsize=12)
plt.ylabel('Operator' ,fontsize=12)
plt.title('Total Count by Operator' ,loc='center', fontsize=14)
plt.show()
total_fatality_per_operator = data.groupby('Operator')[['Fatalities']].sum()
total_fatality_per_operator = total_fatality_per_operator.rename(columns={'Operator':'Fatalities'})
total_fatality_per_operator = total_fatality_per_operator.sort_values(by='Fatalities' ,ascending=False).head(20)
plt.figure(figsize=(12,6))
sns.barplot(x='Fatalities' ,y=total_fatality_per_operator.index ,data=total_fatality_per_operator )
plt.xlabel('Fatalities',fontsize=12)
plt.ylabel('Operator' ,fontsize=12)
plt.title('Total Fatalities per Operator' ,loc='center', fontsize=14)
plt.show()
```
## Analysing AEROFLOT (as they had the highest number of fatalities in all of the operators)
```
aeroflot = data[data.Operator =='AEROFLOT']
count_per_year = aeroflot.groupby(data.Time.dt.year)[['Date']].count()
count_per_year = count_per_year.rename(columns={'Date' : 'Count'})
plt.figure(figsize=(12,6))
plt.plot(count_per_year.index ,'Count' ,data=count_per_year ,marker='.' ,linewidth=1 ,color='darkslategray')
plt.xlabel('Year',fontsize=12)
plt.ylabel('Count',fontsize=12)
plt.title('Fatality Count of AEROFLOT (per year)',loc='Center',fontsize=14)
plt.show()
```
## Observations :
### --> Even so the number of crashes and fatalities is increasing, the number of flights is also increasing.
### --> And we could actually see that the ratio of fatalities/total amount of passengers trending down (for 2000s).
### --> However we can not make decisions about any Operator like "which airline is much safer to flight with" without knowledge of total amount flights.
### --> If Aeroflot has the largest number of crashes this doesn't mean that it is not worse to flight with because it might have the largest amount of flights.
| true |
code
| 0.463141 | null | null | null | null |
|
```
from IPython.core.display import HTML
HTML('''<style>
.container { width:100% !important; }
</style>
''')
```
# How to Check that a Formula is a Tautology
In this notebook we develop a function <tt>tautology</tt> that takes a formula $f$ from propositional logic and checks whether $f$ is a tautology. As we represent tautologies as nested tuples, we first have to import the parser for propositional logic.
```
import propLogParser as plp
```
As we represent propositional valuations as sets of variables, we need a function to compute all subsets of a given set. The module <tt>power</tt> provides a function called <tt>allSubsets</tt> such that for a given set $M$ the function call $\texttt{allSubsets}(M)$ computes a list containing all subsets of $M$, that is we have:
$$ \texttt{allSubsets}(M) = \bigl[A \mid A \in 2^M\bigr] $$
```
import power
power.allSubsets({'p', 'q'})
```
To be able to compute all propositional valuations for a given formula $f$ we first need to determine the set of all variables that occur in $f$. The function $\texttt{collectVars}(f)$ takes a formula $f$ from propositional logic and computes all propositional variables occurring in $f$. This function is defined recursively.
```
def collectVars(f):
"Collect all propositional variables occurring in the formula f."
if f[0] in ['⊤', '⊥']:
return set()
if isinstance(f, str):
return { f }
if f[0] == '¬':
return collectVars(f[1])
return collectVars(f[1]) | collectVars(f[2])
```
We have discussed the function <tt>evaluate</tt> previously. The call
$\texttt{evaluate}(f, I)$ takes a propsitional formula $f$ and a propositional valuation $I$, where $I$ is represented as a set of propositional variables. It evaluates $f$ given $I$.
```
def evaluate(f, I):
"""
Evaluate the propositional formula f using the propositional valuation I.
I is represented as a set of variables.
"""
if isinstance(f, str):
return f in I
if f[0] == '⊤': return True
if f[0] == '⊥': return False
if f[0] == '¬': return not evaluate(f[1], I)
if f[0] == '∧': return evaluate(f[1], I) and evaluate(f[2], I)
if f[0] == '∨': return evaluate(f[1], I) or evaluate(f[2], I)
if f[0] == '→': return not evaluate(f[1], I) or evaluate(f[2], I)
if f[0] == '↔': return evaluate(f[1], I) == evaluate(f[2], I)
```
Now we are ready to define the function $\texttt{tautology}(f)$ that takes a propositional formula $f$ and checks whether $f$ is a tautology. If $f$ is a tautology, the function returns <tt>True</tt>, otherwise a set of variables $I$ is returned such that $f$ evaluates to <tt>False</tt> if all variables in $I$ are <tt>True</tt>, while all variables not in $I$ are <tt>False</tt>.
```
def tautology(f):
"Check, whether the formula f is a tautology."
P = collectVars(f)
A = power.allSubsets(P)
if all(evaluate(f, I) for I in A):
return True
else:
return [I for I in A if not evaluate(f, I)][0]
```
The function $\texttt{test}(s)$ takes a string $s$ that can be parsed as a propositionl formula and checks whether this formula is a tautology.
```
def test(s):
f = plp.LogicParser(s).parse()
counterExample = tautology(f);
if counterExample == True:
print('The formula', s, 'is a tautology.')
else:
P = collectVars(f)
print('The formula ', s, ' is not a tautology.')
print('Counter example: ')
for x in P:
if x in counterExample:
print(x, "↦ True")
else:
print(x, "↦ False")
```
Let us run a few tests.
The first example is DeMorgan's rule.
```
test('¬(p ∨ q) ↔ ¬p ∧ ¬q')
test('(p → q) → (¬p → q) → q')
test('(p → q) → (¬p → ¬q)')
test('¬p ↔ (p → ⊥)')
```
| true |
code
| 0.458349 | null | null | null | null |
|
# Section: Encrypted Deep Learning
- Lesson: Reviewing Additive Secret Sharing
- Lesson: Encrypted Subtraction and Public/Scalar Multiplication
- Lesson: Encrypted Computation in PySyft
- Project: Build an Encrypted Database
- Lesson: Encrypted Deep Learning in PyTorch
- Lesson: Encrypted Deep Learning in Keras
- Final Project
# Lesson: Reviewing Additive Secret Sharing
_For more great information about SMPC protocols like this one, visit https://mortendahl.github.io. With permission, Morten's work directly inspired this first teaching segment._
```
import random
import numpy as np
BASE = 10
PRECISION_INTEGRAL = 8
PRECISION_FRACTIONAL = 8
Q = 293973345475167247070445277780365744413
PRECISION = PRECISION_INTEGRAL + PRECISION_FRACTIONAL
assert(Q > BASE**PRECISION)
def encode(rational):
upscaled = int(rational * BASE**PRECISION_FRACTIONAL)
field_element = upscaled % Q
return field_element
def decode(field_element):
upscaled = field_element if field_element <= Q/2 else field_element - Q
rational = upscaled / BASE**PRECISION_FRACTIONAL
return rational
# Explained by Leohard Feinar in Slack
# Here we want to encode negative numbers despite our number space is only between `0` and `Q-1`.
# Therefore we define that the half of the number space between `0` and `Q-1` is reserved for negative numbers,
# particularly the upper half of the number space between `Q/2` and `Q`
# therefore we check in the condition if our number is a positive number with
# `field_element <=Q/2`, then we simply return the number
# if the number is part of the negative number space, we make it negative by subtracting `Q`
def encrypt(secret):
first = random.randrange(Q)
second = random.randrange(Q)
third = (secret - first - second) % Q
return [first, second, third]
def decrypt(sharing):
return sum(sharing) % Q
def add(a, b):
c = list()
for i in range(len(a)):
c.append((a[i] + b[i]) % Q)
return tuple(c)
x = encrypt(encode(5.5))
x
y = encrypt(encode(2.3))
y
z = add(x,y)
z
decode(decrypt(z))
```
**Deal With Negative Value**
https://stackoverflow.com/questions/3883004/the-modulo-operation-on-negative-numbers-in-python
Unlike C or C++, Python's modulo operator (%) always return a number
having the same sign as the denominator (divisor).
`(-5) % 4 = (-2 × 4 + 3) % 4 = 3`
```
(-5) % 100 # -5 = -1 X 100 + 95
encode(-5)
n = encrypt(encode(-5))
n
decode(decrypt(n))
```
# Lesson: Encrypted Subtraction and Public/Scalar Multiplication
```
field = 23740629843760239486723
x = 5
bob_x_share = 2372385723 # random number
alices_x_share = field - bob_x_share + x
(bob_x_share + alices_x_share) % field
field = 10
x = 5
bob_x_share = 8
alice_x_share = field - bob_x_share + x
y = 1
bob_y_share = 9
alice_y_share = field - bob_y_share + y
((bob_x_share + alice_x_share) - (bob_y_share + alice_y_share)) % field
((bob_x_share - bob_y_share) + (alice_x_share - alice_y_share)) % field
bob_x_share + alice_x_share + bob_y_share + alice_y_share
bob_z_share = (bob_x_share - bob_y_share)
alice_z_share = (alice_x_share - alice_y_share)
(bob_z_share + alice_z_share) % field
def sub(a, b):
c = list()
for i in range(len(a)):
c.append((a[i] - b[i]) % Q)
return tuple(c)
field = 10
x = 5
bob_x_share = 8
alice_x_share = field - bob_x_share + x
y = 1
bob_y_share = 9
alice_y_share = field - bob_y_share + y
bob_x_share + alice_x_share
bob_y_share + alice_y_share
```
**Multiply by Public Number**
```
((bob_y_share * 3) + (alice_y_share * 3)) % field
def imul(a, scalar):
# logic here which can multiply by a public scalar
c = list()
for i in range(len(a)):
c.append((a[i] * scalar) % Q)
return tuple(c)
x = encrypt(encode(5.5))
x
z = imul(x, 3) # multiplier 3 is public
decode(decrypt(z))
```
# Lesson: Encrypted Computation in PySyft
```
import syft as sy
import torch as th
hook = sy.TorchHook(th)
from torch import nn, optim
bob = sy.VirtualWorker(hook, id="bob").add_worker(sy.local_worker)
alice = sy.VirtualWorker(hook, id="alice").add_worker(sy.local_worker)
secure_worker = sy.VirtualWorker(hook, id="secure_worker").add_worker(sy.local_worker)
x = th.tensor([1,2,3,4])
y = th.tensor([2,-1,1,0])
x = x.share(bob, alice, crypto_provider=secure_worker) # secure_worker provides randomly generated number
y = y.share(bob, alice, crypto_provider=secure_worker)
z = x + y
z.get()
z = x - y
z.get()
z = x * y
z.get()
z = x > y
z.get()
z = x < y
z.get()
z = x == y
z.get()
```
**With fix_precision**
```
x = th.tensor([1,2,3,4])
y = th.tensor([2,-1,1,0])
x = x.fix_precision().share(bob, alice, crypto_provider=secure_worker)
y = y.fix_precision().share(bob, alice, crypto_provider=secure_worker)
z = x + y
z.get().float_precision()
z = x - y
z.get().float_precision()
z = x * y
z.get().float_precision()
z = x > y
z.get().float_precision()
z = x < y
z.get().float_precision()
z = x == y
z.get().float_precision()
```
# Project: Build an Encrypted Database
```
# try this project here!
```
# Lesson: Encrypted Deep Learning in PyTorch
### Train a Model
```
from torch import nn
from torch import optim
import torch.nn.functional as F
# A Toy Dataset
data = th.tensor([[0,0],[0,1],[1,0],[1,1.]], requires_grad=True)
target = th.tensor([[0],[0],[1],[1.]], requires_grad=True)
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(2, 20)
self.fc2 = nn.Linear(20, 1)
def forward(self, x):
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
return x
# A Toy Model
model = Net()
def train():
# Training Logic
opt = optim.SGD(params=model.parameters(),lr=0.1)
for iter in range(20):
# 1) erase previous gradients (if they exist)
opt.zero_grad()
# 2) make a prediction
pred = model(data)
# 3) calculate how much we missed
loss = ((pred - target)**2).sum()
# 4) figure out which weights caused us to miss
loss.backward()
# 5) change those weights
opt.step()
# 6) print our progress
print(loss.data)
train()
model(data)
```
## Encrypt the Model and Data
```
encrypted_model = model.fix_precision().share(alice, bob, crypto_provider=secure_worker)
list(encrypted_model.parameters())
encrypted_data = data.fix_precision().share(alice, bob, crypto_provider=secure_worker)
encrypted_data
encrypted_prediction = encrypted_model(encrypted_data)
encrypted_prediction.get().float_precision()
```
# Lesson: Encrypted Deep Learning in Keras
## Step 1: Public Training
Welcome to this tutorial! In the following notebooks you will learn how to provide private predictions. By private predictions, we mean that the data is constantly encrypted throughout the entire process. At no point is the user sharing raw data, only encrypted (that is, secret shared) data. In order to provide these private predictions, Syft Keras uses a library called [TF Encrypted](https://github.com/tf-encrypted/tf-encrypted) under the hood. TF Encrypted combines cutting-edge cryptographic and machine learning techniques, but you don't have to worry about this and can focus on your machine learning application.
You can start serving private predictions with only three steps:
- **Step 1**: train your model with normal Keras.
- **Step 2**: secure and serve your machine learning model (server).
- **Step 3**: query the secured model to receive private predictions (client).
Alright, let's go through these three steps so you can deploy impactful machine learning services without sacrificing user privacy or model security.
Huge shoutout to the Dropout Labs ([@dropoutlabs](https://twitter.com/dropoutlabs)) and TF Encrypted ([@tf_encrypted](https://twitter.com/tf_encrypted)) teams for their great work which makes this demo possible, especially: Jason Mancuso ([@jvmancuso](https://twitter.com/jvmancuso)), Yann Dupis ([@YannDupis](https://twitter.com/YannDupis)), and Morten Dahl ([@mortendahlcs](https://github.com/mortendahlcs)).
_Demo Ref: https://github.com/OpenMined/PySyft/tree/dev/examples/tutorials_
## Train Your Model in Keras
To use privacy-preserving machine learning techniques for your projects you should not have to learn a new machine learning framework. If you have basic [Keras](https://keras.io/) knowledge, you can start using these techniques with Syft Keras. If you have never used Keras before, you can learn a bit more about it through the [Keras documentation](https://keras.io).
Before serving private predictions, the first step is to train your model with normal Keras. As an example, we will train a model to classify handwritten digits. To train this model we will use the canonical [MNIST dataset](http://yann.lecun.com/exdb/mnist/).
We borrow [this example](https://github.com/keras-team/keras/blob/master/examples/mnist_cnn.py) from the reference Keras repository. To train your classification model, you just run the cell below.
```
from __future__ import print_function
import tensorflow.keras as keras
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Flatten
from tensorflow.keras.layers import Conv2D, AveragePooling2D
from tensorflow.keras.layers import Activation
batch_size = 128
num_classes = 10
epochs = 2
# input image dimensions
img_rows, img_cols = 28, 28
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(10, (3, 3), input_shape=input_shape))
model.add(AveragePooling2D((2, 2)))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(AveragePooling2D((2, 2)))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(AveragePooling2D((2, 2)))
model.add(Activation('relu'))
model.add(Flatten())
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
## Save your model's weights for future private prediction
model.save('short-conv-mnist.h5')
```
## Step 2: Load and Serve the Model
Now that you have a trained model with normal Keras, you are ready to serve some private predictions. We can do that using Syft Keras.
To secure and serve this model, we will need three TFEWorkers (servers). This is because TF Encrypted under the hood uses an encryption technique called [multi-party computation (MPC)](https://en.wikipedia.org/wiki/Secure_multi-party_computation). The idea is to split the model weights and input data into shares, then send a share of each value to the different servers. The key property is that if you look at the share on one server, it reveals nothing about the original value (input data or model weights).
We'll define a Syft Keras model like we did in the previous notebook. However, there is a trick: before instantiating this model, we'll run `hook = sy.KerasHook(tf.keras)`. This will add three important new methods to the Keras Sequential class:
- `share`: will secure your model via secret sharing; by default, it will use the SecureNN protocol from TF Encrypted to secret share your model between each of the three TFEWorkers. Most importantly, this will add the capability of providing predictions on encrypted data.
- `serve`: this function will launch a serving queue, so that the TFEWorkers can can accept prediction requests on the secured model from external clients.
- `shutdown_workers`: once you are done providing private predictions, you can shut down your model by running this function. It will direct you to shutdown the server processes manually if you've opted to manually manage each worker.
If you want learn more about MPC, you can read this excellent [blog](https://mortendahl.github.io/2017/04/17/private-deep-learning-with-mpc/).
```
import numpy as np
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import AveragePooling2D, Conv2D, Dense, Activation, Flatten, ReLU, Activation
import syft as sy
hook = sy.KerasHook(tf.keras)
```
## Model
As you can see, we define almost the exact same model as before, except we provide a `batch_input_shape`. This allows TF Encrypted to better optimize the secure computations via predefined tensor shapes. For this MNIST demo, we'll send input data with the shape of (1, 28, 28, 1).
We also return the logit instead of softmax because this operation is complex to perform using MPC, and we don't need it to serve prediction requests.
```
num_classes = 10
input_shape = (1, 28, 28, 1)
model = Sequential()
model.add(Conv2D(10, (3, 3), batch_input_shape=input_shape))
model.add(AveragePooling2D((2, 2)))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(AveragePooling2D((2, 2)))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(AveragePooling2D((2, 2)))
model.add(Activation('relu'))
model.add(Flatten())
model.add(Dense(num_classes, name="logit"))
```
### Load Pre-trained Weights
With `load_weights` you can easily load the weights you have saved previously after training your model.
```
pre_trained_weights = 'short-conv-mnist.h5'
model.load_weights(pre_trained_weights)
```
## Step 3: Setup Your Worker Connectors
Let's now connect to the TFEWorkers (`alice`, `bob`, and `carol`) required by TF Encrypted to perform private predictions. For each TFEWorker, you just have to specify a host.
These workers run a [TensorFlow server](https://www.tensorflow.org/api_docs/python/tf/distribute/Server), which you can either manage manually (`AUTO = False`) or ask the workers to manage for you (`AUTO = True`). If choosing to manually manage them, you will be instructed to execute a terminal command on each worker's host device after calling `model.share()` below. If all workers are hosted on a single device (e.g. `localhost`), you can choose to have Syft automatically manage the worker's TensorFlow server.
```
AUTO = False
alice = sy.TFEWorker(host='localhost:4000', auto_managed=AUTO)
bob = sy.TFEWorker(host='localhost:4001', auto_managed=AUTO)
carol = sy.TFEWorker(host='localhost:4002', auto_managed=AUTO)
```
## Step 4: Split the Model Into Shares
Thanks to `sy.KerasHook(tf.keras)` you can call the `share` method to transform your model into a TF Encrypted Keras model.
If you have asked to manually manage servers above then this step will not complete until they have all been launched. Note that your firewall may ask for Python to accept incoming connection.
```
model.share(alice, bob, carol)
```
## Step 5: Launch 3 Servers
```
python -m tf_encrypted.player --config /tmp/tfe.config server0
python -m tf_encrypted.player --config /tmp/tfe.config server1
python -m tf_encrypted.player --config /tmp/tfe.config server2```
## Step 6: Serve the Model
Perfect! Now by calling `model.serve`, your model is ready to provide some private predictions. You can set `num_requests` to set a limit on the number of predictions requests served by the model; if not specified then the model will be served until interrupted.
```
model.serve(num_requests=3)
```
## Step 7: Run the Client
At this point open up and run the companion notebook: Section 4b - Encrytped Keras Client
## Step 8: Shutdown the Servers
Once your request limit above, the model will no longer be available for serving requests, but it's still secret shared between the three workers above. You can kill the workers by executing the cell below.
**Congratulations** on finishing Part 12: Secure Classification with Syft Keras and TFE!
```
model.shutdown_workers()
if not AUTO:
process_ids = !ps aux | grep '[p]ython -m tf_encrypted.player --config /tmp/tfe.config' | awk '{print $2}'
for process_id in process_ids:
!kill {process_id}
print("Process ID {id} has been killed.".format(id=process_id))
```
# Keystone Project - Mix and Match What You've Learned
Description: Take two of the concepts you've learned about in this course (Encrypted Computation, Federated Learning, Differential Privacy) and combine them for a use case of your own design. Extra credit if you can get your demo working with [WebSocketWorkers](https://github.com/OpenMined/PySyft/tree/dev/examples/tutorials/advanced/websockets-example-MNIST) instead of VirtualWorkers! Then take your demo or example application, write a blogpost, and share that blogpost in #general-discussion on OpenMined's slack!!!
Inspiration:
- This Course's Code: https://github.com/Udacity/private-ai
- OpenMined's Tutorials: https://github.com/OpenMined/PySyft/tree/dev/examples/tutorials
- OpenMined's Blog: https://blog.openmined.org
| true |
code
| 0.736661 | null | null | null | null |
|
# CAT10 BAYESIAN :D :D :D :D :D
```
import sys
from skopt import gp_minimize
from skopt.space import Real, Integer
from utils.post_processing import eurm_to_recommendation_list,eurm_remove_seed, shift_rec_list_cutoff
from utils.pre_processing import norm_max_row, norm_l1_row
from utils.evaluator import Evaluator
from utils.datareader import Datareader
from utils.ensembler import ensembler
from utils.definitions import *
import scipy.sparse as sps
import numpy as np
import os.path
```
# datareader, valutazione ed essenziali
```
dr = Datareader(verbose=False, mode = "offline", only_load="False")
ev = Evaluator(dr)
```
# cat10 > impostazioni da toccare
```
target_metric = 'ndcg'
best_score = 0
best_params = 0
norm = norm_max_row
verbose = True
# memory_on_disk= False
memory_on_notebook=True
```
### impostazioni da NON toccare
```
cat = 10
start_index = 9000
end_index = 10000
global_counter=0
x0 = None
y0 = None
```
# files e matrici
```
path = ROOT_DIR+'/npz_simo/'
cb_ar_file = path+"cb_ar_offline.npz"
cb_al_file = path+"cb_al_offline.npz"
cb_al_ar_file = path+"cb_al_offline.npz"
cf_ib_file = path+"cf_ib_offline.npz"
cf_ub_file = path+"cf_ub_offline.npz"
cb_ar = norm( eurm_remove_seed( sps.load_npz(cb_ar_file) ,dr)[start_index:end_index] )
cb_al = norm( eurm_remove_seed( sps.load_npz(cb_al_file) ,dr)[start_index:end_index] )
cb_al_ar = norm( eurm_remove_seed( sps.load_npz(cb_al_file) ,dr)[start_index:end_index] )
cf_ib = norm( eurm_remove_seed( sps.load_npz(cf_ib_file) ,dr)[start_index:end_index] )
cf_ub = norm( eurm_remove_seed( sps.load_npz(cf_ub_file) ,dr)[start_index:end_index] )
matrices_names = ['cb_ar', 'cb_al', 'cb_al_ar', 'cf_ib', 'cf_ub']
matrices_array = [ cb_ar, cb_al, cb_al_ar , cf_ib , cf_ub ]
matrices = dict(zip(matrices_names, matrices_array ))
```
# funzione obiettivo
il numero di matrici e l'ordine va rispettato
```
def obiettivo( x ):
global best_score,global_counter, best_params, x0, y0
# eurm = x[0]*cb_ar + x[1]*cb_al + x[2]*cf_ib + x[3]*cf_ub
eurm = sum( x[i]*matrix for i,matrix in enumerate(matrices_array))
# real objective function
ris = -ev.evaluate_single_metric(eurm_to_recommendation_list(eurm, cat=cat, remove_seed=False, verbose=False),
verbose=False,
cat=cat,
name="ens"+str(cat),
metric=target_metric,
level='track')
# memory variables
if x0 is None:
x0 = [[x]]
y0 = [ris]
else:
x0.append(x)
y0.append(ris)
global_counter+=1
if ris < best_score :
print("[NEW BEST]")
pretty_print(ris,x)
best_score= ris
best_params = x.copy()
best_params_dict = dict(zip(matrices_names,x.copy()))
elif verbose:
pretty_print(ris,x)
return ris
def pretty_print(ris, x):
print(global_counter,"RES:",ris, end="\tvals:\t")
for i in range(len(x)):
print(matrices_names[i],"%.2f" % (x[i]), end="\t")
print( )
```
# parameters
```
# The list of hyper-parameters we want to optimize. For each one we define the bounds,
# the corresponding scikit-learn parameter name, as well as how to sample values
# from that dimension (`'log-uniform'` for the learning rate)
space = [Real(0, 100, name=x) for x in matrices_names]
#"log-uniform",
space
res = gp_minimize(obiettivo, space,
base_estimator=None,
n_calls=300, n_random_starts=100,
acq_func='gp_hedge',
acq_optimizer='auto',
x0=x0, y0=y0,
random_state=None, verbose=False,
callback=None, n_points=10000,
n_restarts_optimizer=10,
xi=0.01, kappa=1.96,
noise='gaussian', n_jobs=-1)
best_score
best_params
```
# plot
```
from skopt.plots import plot_convergence, plot_objective
import skopt.plots
import matplotlib.pyplot as plt
%matplotlib inline
plot_convergence(res)
a = plot_objective(res)
['cb_ar', 'cb_al','cf_ib', 'cf_ub']
a = skopt.plots.plot_evaluations(res)
```
| true |
code
| 0.389198 | null | null | null | null |
|
<a id='1'></a>
# Import modules
```
import keras.backend as K
```
<a id='4'></a>
# Model Configuration
```
K.set_learning_phase(0)
# Input/Output resolution
RESOLUTION = 256 # 64x64, 128x128, 256x256
assert (RESOLUTION % 64) == 0, "RESOLUTION should be 64, 128, 256"
# Architecture configuration
arch_config = {}
arch_config['IMAGE_SHAPE'] = (RESOLUTION, RESOLUTION, 3)
arch_config['use_self_attn'] = True
arch_config['norm'] = "instancenorm" # instancenorm, batchnorm, layernorm, groupnorm, none
arch_config['model_capacity'] = "standard" # standard, lite
```
<a id='5'></a>
# Define models
```
from networks.faceswap_gan_model import FaceswapGANModel
model = FaceswapGANModel(**arch_config)
```
<a id='6'></a>
# Load Model Weights
```
model.load_weights(path="./models")
```
<a id='12'></a>
# Video Conversion
```
from converter.video_converter import VideoConverter
from detector.face_detector import MTCNNFaceDetector
mtcnn_weights_dir = "./mtcnn_weights/"
fd = MTCNNFaceDetector(sess=K.get_session(), model_path=mtcnn_weights_dir)
vc = VideoConverter()
vc.set_face_detector(fd)
vc.set_gan_model(model)
```
### Video conversion configuration
- `use_smoothed_bbox`:
- Boolean. Whether to enable smoothed bbox.
- `use_kalman_filter`:
- Boolean. Whether to enable Kalman filter.
- `use_auto_downscaling`:
- Boolean. Whether to enable auto-downscaling in face detection (to prevent OOM error).
- `bbox_moving_avg_coef`:
- Float point between 0 and 1. Smoothing coef. used when use_kalman_filter is set False.
- `min_face_area`:
- int x int. Minimum size of face. Detected faces smaller than min_face_area will not be transformed.
- `IMAGE_SHAPE`:
- Input/Output resolution of the GAN model
- `kf_noise_coef`:
- Float point. Increase by 10x if tracking is slow. Decrease by 1/10x if trakcing works fine but jitter occurs.
- `use_color_correction`:
- String of "adain", "adain_xyz", "hist_match", or "none". The color correction method to be applied.
- `detec_threshold`:
- Float point between 0 and 1. Decrease its value if faces are missed. Increase its value to reduce false positives.
- `roi_coverage`:
- Float point between 0 and 1 (exclusive). Center area of input images to be cropped (Suggested range: 0.85 ~ 0.95)
- `enhance`:
- Float point. A coef. for contrast enhancement in the region of alpha mask (Suggested range: 0. ~ 0.4)
- `output_type`:
- Layout format of output video: 1. [ result ], 2. [ source | result ], 3. [ source | result | mask ]
- `direction`:
- String of "AtoB" or "BtoA". Direction of face transformation.
```
options = {
# ===== Fixed =====
"use_smoothed_bbox": True,
"use_kalman_filter": True,
"use_auto_downscaling": False,
"bbox_moving_avg_coef": 0.65,
"min_face_area": 35 * 35,
"IMAGE_SHAPE": model.IMAGE_SHAPE,
# ===== Tunable =====
"kf_noise_coef": 3e-3,
"use_color_correction": "hist_match",
"detec_threshold": 0.7,
"roi_coverage": 0.9,
"enhance": 0.,
"output_type": 3,
"direction": "AtoB",
}
```
# Start video conversion
- `input_fn`:
- String. Input video path.
- `output_fn`:
- String. Output video path.
- `duration`:
- None or a non-negative float tuple: (start_sec, end_sec). Duration of input video to be converted
- e.g., setting `duration = (5, 7.5)` outputs a 2.5-sec-long video clip corresponding to 5s ~ 7.5s of the input video.
```
input_fn = "1.mp4"
output_fn = "OUTPUT_VIDEO.mp4"
duration = None
vc.convert(input_fn=input_fn, output_fn=output_fn, options=options, duration=duration)
```
| true |
code
| 0.618636 | null | null | null | null |
|
# Multilayer Perceptron
In the previous chapters, we showed how you could implement multiclass logistic regression (also called softmax regression)
for classifying images of clothing into the 10 possible categories.
To get there, we had to learn how to wrangle data,
coerce our outputs into a valid probability distribution (via `softmax`),
how to apply an appropriate loss function,
and how to optimize over our parameters.
Now that we’ve covered these preliminaries,
we are free to focus our attention on
the more exciting enterprise of designing powerful models
using deep neural networks.
## Hidden Layers
Recall that for linear regression and softmax regression,
we mapped our inputs directly to our outputs
via a single linear transformation:
$$
\hat{\mathbf{o}} = \mathrm{softmax}(\mathbf{W} \mathbf{x} + \mathbf{b})
$$
```
from IPython.display import SVG
SVG(filename='../img/singlelayer.svg')
```
If our labels really were related to our input data
by an approximately linear function, then this approach would be perfect.
But linearity is a *strong assumption*.
Linearity implies that for whatever target value we are trying to predict,
increasing the value of each of our inputs
should either drive the value of the output up or drive it down,
irrespective of the value of the other inputs.
Sometimes this makes sense!
Say we are trying to predict whether an individual
will or will not repay a loan.
We might reasonably imagine that all else being equal,
an applicant with a higher income
would be more likely to repay than one with a lower income.
In these cases, linear models might perform well,
and they might even be hard to beat.
But what about classifying images in FashionMNIST?
Should increasing the intensity of the pixel at location (13,17)
always increase the likelihood that the image depicts a pocketbook?
That seems ridiculous because we all know
that you cannot make sense out of an image
without accounting for the interactions among pixels.
### From one to many
As another case, consider trying to classify images
based on whether they depict *cats* or *dogs* given black-and-white images.
If we use a linear model, we'd basically be saying that
for each pixel, increasing its value (making it more white)
must always increase the probability that the image depicts a dog
or must always increase the probability that the image depicts a cat.
We would be making the absurd assumption that the only requirement
for differentiating cats vs. dogs is to assess how bright they are.
That approach is doomed to fail in a work
that contains both black dogs and black cats,
and both white dogs and white cats.
Teasing out what is depicted in an image generally requires
allowing more complex relationships between our inputs and outputs.
Thus we need models capable of discovering patterns
that might be characterized by interactions among the many features.
We can over come these limitations of linear models
and handle a more general class of functions
by incorporating one or more hidden layers.
The easiest way to do this is to stack
many layers of neurons on top of each other.
Each layer feeds into the layer above it, until we generate an output.
This architecture is commonly called a *multilayer perceptron*,
often abbreviated as *MLP*.
The neural network diagram for an MLP looks like this:
```
SVG(filename='../img/mlp.svg')
```
The multilayer perceptron above has 4 inputs and 3 outputs,
and the hidden layer in the middle contains 5 hidden units.
Since the input layer does not involve any calculations,
building this network would consist of
implementing 2 layers of computation.
The neurons in the input layer are fully connected
to the inputs in the hidden layer.
Likewise, the neurons in the hidden layer
are fully connected to the neurons in the output layer.
### From linear to nonlinear
We can write out the calculations that define this one-hidden-layer MLP in mathematical notation as follows:
$$
\begin{aligned}
\mathbf{h} & = \mathbf{W}_1 \mathbf{x} + \mathbf{b}_1 \\
\mathbf{o} & = \mathbf{W}_2 \mathbf{h} + \mathbf{b}_2 \\
\hat{\mathbf{y}} & = \mathrm{softmax}(\mathbf{o})
\end{aligned}
$$
By adding another layer, we have added two new sets of parameters,
but what have we gained in exchange?
In the model defined above, we do not achieve anything for our troubles!
That's because our hidden units are just a linear function of the inputs
and the outputs (pre-softmax) are just a linear function of the hidden units.
A linear function of a linear function is itself a linear function.
That means that for any values of the weights,
we could just collapse out the hidden layer
yielding an equivalent single-layer model using
$\mathbf{W} = \mathbf{W}_2 \mathbf{W}_1$ and $\mathbf{b} = \mathbf{W}_2 \mathbf{b}_1 + \mathbf{b}_2$.
$$\mathbf{o} = \mathbf{W}_2 \mathbf{h} + \mathbf{b}_2 = \mathbf{W}_2 (\mathbf{W}_1 \mathbf{x} + \mathbf{b}_1) + \mathbf{b}_2 = (\mathbf{W}_2 \mathbf{W}_1) \mathbf{x} + (\mathbf{W}_2 \mathbf{b}_1 + \mathbf{b}_2) = \mathbf{W} \mathbf{x} + \mathbf{b}$$
In order to get a benefit from multilayer architectures,
we need another key ingredient—a nonlinearity $\sigma$ to be applied to each of the hidden units after each layer's linear transformation.
The most popular choice for the nonlinearity these days is the rectified linear unit (ReLU) $\mathrm{max}(x,0)$.
After incorporating these non-linearities
it becomes impossible to merge layers.
$$
\begin{aligned}
\mathbf{h} & = \sigma(\mathbf{W}_1 \mathbf{x} + \mathbf{b}_1) \\
\mathbf{o} & = \mathbf{W}_2 \mathbf{h} + \mathbf{b}_2 \\
\hat{\mathbf{y}} & = \mathrm{softmax}(\mathbf{o})
\end{aligned}
$$
Clearly, we could continue stacking such hidden layers,
e.g. $\mathbf{h}_1 = \sigma(\mathbf{W}_1 \mathbf{x} + \mathbf{b}_1)$
and $\mathbf{h}_2 = \sigma(\mathbf{W}_2 \mathbf{h}_1 + \mathbf{b}_2)$
on top of each other to obtain a true multilayer perceptron.
Multilayer perceptrons can account for complex interactions in the inputs
because the hidden neurons depend on the values of each of the inputs.
It’s easy to design a hidden node that does arbitrary computation,
such as, for instance, logical operations on its inputs.
Moreover, for certain choices of the activation function
it’s widely known that multilayer perceptrons are universal approximators.
That means that even for a single-hidden-layer neural network,
with enough nodes, and the right set of weights,
we can model any function at all!
*Actually learning that function is the hard part.*
Moreover, just because a single-layer network *can* learn any function
doesn't mean that you should try to solve all of your problems with single-layer networks.
It turns out that we can approximate many functions
much more compactly if we use deeper (vs wider) neural networks.
We’ll get more into the math in a subsequent chapter,
but for now let’s actually build an MLP.
In this example, we’ll implement a multilayer perceptron
with two hidden layers and one output layer.
### Vectorization and mini-batch
As before, by the matrix $\mathbf{X}$, we denote a mini-batch of inputs.
The calculations to produce outputs from an MLP with two hidden layers
can thus be expressed:
$$
\begin{aligned}
\mathbf{H}_1 & = \sigma(\mathbf{W}_1 \mathbf{X} + \mathbf{b}_1) \\
\mathbf{H}_2 & = \sigma(\mathbf{W}_2 \mathbf{H}_1 + \mathbf{b}_2) \\
\mathbf{O} & = \mathrm{softmax}(\mathbf{W}_3 \mathbf{H}_2 + \mathbf{b}_3)
\end{aligned}
$$
With some abuse of notation, we define the nonlinearity $\sigma$
to apply to its inputs on a row-wise fashion, i.e. one observation at a time.
Note that we are also using the notation for *softmax* in the same way to denote a row-wise operation.
Often, as in this chapter, the activation functions that we apply to hidden layers are not merely row-wise, but component wise.
That means that after computing the linear portion of the layer,
we can calculate each nodes activation without looking at the values taken by the other hidden units.
This is true for most activation functions
(the batch normalization operation will be introduced in :numref:`chapter_batch_norm` is a notable exception to that rule).
## Activation Functions
Because they are so fundamental to deep learning, before going further,
let's take a brief look at some common activation functions.
### ReLU Function
As stated above, the most popular choice,
due to its simplicity of implementation
and its efficacy in training is the rectified linear unit (ReLU).
ReLUs provide a very simple nonlinear transformation.
Given the element $z$, the function is defined
as the maximum of that element and 0.
$$\mathrm{ReLU}(z) = \max(z, 0).$$
It can be understood that the ReLU function retains only positive elements and discards negative elements (setting those nodes to 0).
To get a better idea of what it looks like, we can plot it.
For convenience, we define a plotting function `xyplot`
to take care of the groundwork.
```
import sys
sys.path.insert(0, '..')
import numpy
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.autograd import Variable
def xyplot(x_vals,y_vals,name):
x_vals=x_vals.detach().numpy() # we can't directly use var.numpy() because varibles might
y_vals=y_vals.detach().numpy() # already required grad.,thus using var.detach().numpy()
plt.plot(x_vals,y_vals)
plt.xlabel('x')
plt.ylabel(name+'(x)')
```
Since relu is commomly used as activation function, PyTorch supports
the `relu` function as a basic native operator.
As you can see, the activation function is piece-wise linear.
```
x=Variable(torch.arange(-8.0,8.0,0.1,dtype=torch.float32).reshape(int(16/0.1),1),requires_grad=True)
y=torch.nn.functional.relu(x)
xyplot(x,y,'relu')
```
When the input is negative, the derivative of ReLU function is 0
and when the input is positive, the derivative of ReLU function is 1.
Note that the ReLU function is not differentiable
when the input takes value precisely equal to 0.
In these cases, we go with the left-hand-side (LHS) derivative
and say that the derivative is 0 when the input is 0.
We can get away with this because the input may never actually be zero.
There's an old adage that if subtle boundary conditions matter,
we are probably doing (*real*) mathematics, not engineering.
That conventional wisdom may apply here.
See the derivative of the ReLU function plotted below.
When we use .backward(), by default it is .backward(torch.Tensor([1])).This is useful when we are dealing with single scalar input.But here we are dealing with a vector input so we have to use this snippet.
```
y.backward(torch.ones_like(x),retain_graph=True)
xyplot(x,x.grad,"grad of relu")
```
Note that there are many variants to the ReLU function, such as the parameterized ReLU (pReLU) of [He et al., 2015](https://arxiv.org/abs/1502.01852). This variation adds a linear term to the ReLU, so some information still gets through, even when the argument is negative.
$$\mathrm{pReLU}(x) = \max(0, x) + \alpha \min(0, x)$$
The reason for using the ReLU is that its derivatives are particularly well behaved - either they vanish or they just let the argument through. This makes optimization better behaved and it reduces the issue of the vanishing gradient problem (more on this later).
### Sigmoid Function
The sigmoid function transforms its inputs which take values in $\mathbb{R}$ to the interval $(0,1)$.
For that reason, the sigmoid is often called a *squashing* function:
it squashes any input in the range (-inf, inf)
to some value in the range (0,1).
$$\mathrm{sigmoid}(x) = \frac{1}{1 + \exp(-x)}.$$
In the earliest neural networks, scientists
were interested in modeling biological neurons
which either *fire* or *don't fire*.
Thus the pioneers of this field, going all the way back to McCulloch and Pitts in the 1940s, were focused on thresholding units.
A thresholding function takes either value $0$
(if the input is below the threshold)
or value $1$ (if the input exceeds the threshold)
When attention shifted to gradient based learning,
the sigmoid function was a natural choice
because it is a smooth, differentiable approximation to a thresholding unit.
Sigmoids are still common as activation functions on the output units,
when we want to interpret the outputs as probabilities
for binary classification problems
(you can think of the sigmoid as a special case of the softmax)
but the sigmoid has mostly been replaced by the simpler and easier to train ReLU for most use in hidden layers.
In the "Recurrent Neural Network" chapter, we will describe
how sigmoid units can be used to control
the flow of information in a neural network
thanks to its capacity to transform the value range between 0 and 1.
See the sigmoid function plotted below.
When the input is close to 0, the sigmoid function
approaches a linear transformation.
```
x=Variable(torch.arange(-8.0,8.0,0.1,dtype=torch.float32).reshape(int(16/0.1),1),requires_grad=True)
y=torch.sigmoid(x)
xyplot(x,y,'sigmoid')
```
The derivative of sigmoid function is given by the following equation:
$$\frac{d}{dx} \mathrm{sigmoid}(x) = \frac{\exp(-x)}{(1 + \exp(-x))^2} = \mathrm{sigmoid}(x)\left(1-\mathrm{sigmoid}(x)\right).$$
The derivative of sigmoid function is plotted below.
Note that when the input is 0, the derivative of the sigmoid function
reaches a maximum of 0.25. As the input diverges from 0 in either direction, the derivative approaches 0.
```
y.backward(torch.ones_like(x),retain_graph=True)
xyplot(x,x.grad,'grad of sigmoid')
```
### Tanh Function
Like the sigmoid function, the tanh (Hyperbolic Tangent)
function also squashes its inputs,
transforms them into elements on the interval between -1 and 1:
$$\text{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}.$$
We plot the tanh function blow. Note that as the input nears 0, the tanh function approaches a linear transformation. Although the shape of the function is similar to the sigmoid function, the tanh function exhibits point symmetry about the origin of the coordinate system.
```
x=Variable(torch.arange(-8.0,8.0,0.1,dtype=torch.float32).reshape(int(16/0.1),1),requires_grad=True)
y=torch.tanh(x)
xyplot(x,y,"tanh")
```
The derivative of the Tanh function is:
$$\frac{d}{dx} \mathrm{tanh}(x) = 1 - \mathrm{tanh}^2(x).$$
The derivative of tanh function is plotted below.
As the input nears 0,
the derivative of the tanh function approaches a maximum of 1.
And as we saw with the sigmoid function,
as the input moves away from 0 in either direction,
the derivative of the tanh function approaches 0.
```
y.backward(torch.ones_like(x),retain_graph=True)
xyplot(x,x.grad,"grad of tanh")
```
In summary, we now know how to incorporate nonlinearities
to build expressive multilayer neural network architectures.
As a side note, your knowledge now already
puts you in command of the state of the art in deep learning, circa 1990.
In fact, you have an advantage over anyone working the 1990s,
because you can leverage powerful open-source deep learning frameworks
to build models rapidly, using only a few lines of code.
Previously, getting these nets training
required researchers to code up thousands of lines of C and Fortran.
## Summary
* The multilayer perceptron adds one or multiple fully-connected hidden layers between the output and input layers and transforms the output of the hidden layer via an activation function.
* Commonly-used activation functions include the ReLU function, the sigmoid function, and the tanh function.
## Exercises
1. Compute the derivative of the tanh and the pReLU activation function.
1. Show that a multilayer perceptron using only ReLU (or pReLU) constructs a continuous piecewise linear function.
1. Show that $\mathrm{tanh}(x) + 1 = 2 \mathrm{sigmoid}(2x)$.
1. Assume we have a multilayer perceptron *without* nonlinearities between the layers. In particular, assume that we have $d$ input dimensions, $d$ output dimensions and that one of the layers had only $d/2$ dimensions. Show that this network is less expressive (powerful) than a single layer perceptron.
1. Assume that we have a nonlinearity that applies to one minibatch at a time. What kinds of problems to you expect this to cause?
| true |
code
| 0.688076 | null | null | null | null |
|
# Numerical evaluation of the deflection of the beam
Number (code) of assignment: 5R4
Description of activity: H2 & H3
Report on behalf of:
name : Pieter van Halem
student number (4597591)
name : Dennis Dane
student number (4592239)
Data of student taking the role of contact person:
name : Pieter van Halem
email address : pietervanhalem@hotmail.com
# Function definition
In the first block are all the packages imported and constants defined. In the second block are all the functions for the numerical analyses defined. And the third block contains the two function for the bisect method. This is used in assignment 2.13.
```
import numpy as np
import scipy.sparse.linalg as sp_lg
import scipy.sparse as sp
import scipy as scp
import numpy.linalg as lg
import matplotlib.pyplot as plt
%matplotlib inline
EI = 2 * 10 ** 11 * (1/12) * 0.04 * 0.2 ** 3
L = 10
s = 2
xleft = 0.0
xright = L
yleft = 0.0
yright = 0.0
g = 9.8
def A(h, N):
d0 = np.ones(N)
d1 = np.ones(N-1)
d2 = np.ones(N-2)
A = (6*np.diag(d0,0) + -4*np.diag(d1,-1) + -4*np.diag(d1,1) + 1*np.diag(d2,-2) + 1*np.diag(d2,2))
A[0,0] = 5
A[N-1,N-1] = 5
return A * EI/(h ** 4)
def beig(h,N,x,yleft,yright, qM):
result = qM*np.ones(N)
return result
def bm(h,N,x,yleft,yright, qm):
result = np.zeros(N)
if(((L/2-s/2)/h).is_integer() == True):
for i in range(int((L/2-s/2)/h - 1),int((L/2+s/2)/h)):
if (i==int((L/2-s/2)/h - 1) or i == int((L/2+s/2)/h - 1)):
result[i] = result[i] + qm/2
else:
result[i] = result[i] + qm
return result
def bn(h,N,x):
result = np.zeros(N)
for i in range(int((L/2-s/2)/h -1),int((L/2+s/2)/h -1)):
result[i] = result[i] + 125 * np.pi* g * np.sin(np.pi*((h*(i+1)-4)/2))
return result
def solve(h,N,x,yleft,yright, k, qM, qm):
AA = A(h,N)
if k == 1:
bb = beig(h,N,x,yleft,yright, qM)
elif k == 2:
bb = bm(h,N,x,yleft,yright, qm)
elif k==3:
bb = beig(h,N,x,yleft,yright, qM)
bb = bb + bm(h,N,x,yleft,yright, qm)
elif k == 4:
bb = beig(h,N,x,yleft,yright, qM)
bb = bb + bn(h,N,x)
y = lg.solve(AA,bb)
result = np.concatenate(([yleft],y,[yright]))
return result
def main(N, k, qM = 611.52, qm = 2450.0):
h = (xright - xleft)/(N+1)
x = np.linspace(xleft,xright,N+2)
y = solve(h,N,x,yleft,yright,k, qM, qm)
return x,y
def plot(x,y):
plt.figure("Boundary value problem")
plt.plot(x,y,"k")
plt.xlabel("x")
plt.ylabel("y")
plt.title("De graph of the function y")
plt.legend("y", loc="best")
def table(x,y,N):
print ("{:>4}{:>11}{:>21}".format("k", "x_k", "y(x_k)"))
for k in range(0, N+2):
print ("{:4.0f}{:11.2f}{:23.7e}".format(k, x[k], y[k]))
def func(qm):
N = 199
x,y = main(N, 3,611.52, qm)
return np.max(y) - 0.03
def bisection(func, x1, x2, tol=0.01, nmax=10):
i = 0
for i in range(nmax):
xm = (1/2)*(x1 + x2)
fm = func(xm)
if func(xm) * func(x2) <= 0:
x1 = xm
else:
x2 = xm
i += 1
if np.abs(func(x1)) < tol:
break
if i == nmax:
a = str('Warning: the nmax is exeeded')
print(a)
return x1
```
# Assignment 2.11
Choose $h=1.0$ as grid size and make a table f the obtained numerical approximation of y. The table must give the deflection in 8-digit floating point format.
```
N = 9
x,y = main(N, 3)
table(x,y,len(y)-2)
```
# Assignment 2.12
Take $h=0.05$. Compute both $y$ and $yeig$. plot the obtained approximation of y as a function of x. plot $yeig$ in the same picture, distinguishing the different graphs visually. Where is the maximal deflection attain? With values take y and yeig at the midpoint of the beam?
```
N = 199
x,y = main(N, 1)
x2,y2222 = main(N, 3)
plt.figure("Boundary value problem")
plt.plot(x,y,"b", x2,y2222,"r")
plt.plot(x[np.argmax(y)],np.max(y),"xk", x2[np.argmax(y2222)],np.max(y2222),"xk")
plt.xlabel("x")
plt.ylabel("y")
plt.title("De graph of the function y")
plt.legend({"yeig","y", "maximal deflection"}, loc="best")
plt.gca().invert_yaxis()
plt.show()
print("The maximal deflection of yeig occurs at: x=",x[(np.argmax(y))])
print("The maximal deflection of y occurs at: x=",x2[(np.argmax(y2222))])
print()
print("The deflection in the midpoint of the beam is: yeig(5)= {:.7e}".format(np.max(y)))
print("The deflection in the midpoint of the beam is: y(5)= {:.7e}".format(np.max(y2222)))
```
# assignment 2.13
Determine the maximal mass $m$ allowed for, i.e. the mass leading to a deflection in the midpoint of the beam with a magnitude 0.03 (see original goal, formulated at the beginning of the assignment).
```
qmopt = bisection(func, 1000, 30000, tol = 1e-15, nmax = 100)
x,y = main(N, 3, qm = qmopt)
qmopt = qmopt*2/g
ymaxx = np.max(y)
print("The max value for m is:{:.7e}[kg] the deflection for this m is:{:.7e}".format(qmopt, ymaxx))
print("The truncation error is smaller than: 1e-15")
```
The maximal load $m$ is obtained with the bisect method. In this method we choose a tolerance of $1e-15$, such that the error is not visible in this notebook. We choose the Bisect method because it always converges. We couldn’t use the Newton Raphson method because the derivatives of the function are not known.
the defined functions are given in $ln[3]$
# Assignment 2.14
Determine $Am$ such that the total additional mass is again 500 kg. sketch the original load $qm$, i.e. (6) with m = 500, and the load qm in one figure.
To determine the value of Am we need to solve the following equation:
$$\int_{L/2-s/2}^{L/2+s/2} (Am*\sin(\pi*\frac{x-(L/2-s/2)}{s})) dx = 500$$
solving this equation results in:
$$ \frac{4}{\pi}Am = 500$$
$$ Am = 125\pi$$
```
x = np.linspace(4,6,100)
x2 = 4*np.ones(100)
x3 = 6*np.ones(100)
x4 = np.linspace(0,4,100)
x5 = np.linspace(6,10,100)
y1 = (500 * g / s)*np.ones(100)
y2 = 125 * np.pi* g * np.sin(np.pi*((x-4)/2))
y3 = np.linspace(0,500 * g / s,100)
y4 = np.zeros(100)
plt.plot(x,y2, 'r', x,y1, 'b', x2,y3,'b',x3,y3,'b', x4,y4,'b',x5,y4,'b')
plt.legend({"original","adapted"}, loc="best")
plt.xlim(0, 10);
```
# Assignment 2.15
Determine (using $h = 0.05$) the maximal deflection of the beam with the new load. Check whether this value is significantly different from the one obtained in exercise 12.
```
N=199
x,y = main(N, 4)
print("y(L/2) = {:.7e}".format(np.max(y)))
print("y2(L/2)-y1(L/2) = {:.7e} [m] = {:.7e} %".format(np.max(y) - np.max(y2222),(np.max(y) - np.max(y2222))/np.max(y) * 100 ) )
```
The deflection increases with approximately 0.14 mm with is 0.43% witch is not significant. However it is very logical that the deflection increases. because the load concentrates more in the centre, a larger moment is caused. This increases the deflection of the beam.
| true |
code
| 0.398436 | null | null | null | null |
|
# Model with character recognition - single model
Builds on `RNN-Morse-chars-dual` but tries a single model. In fact dit and dah sense could be duplicates of 'E' and 'T' character senses.env, chr and wrd separators are kept. Thus we just drop dit and dah senses from the raw labels.
## Create string
Each character in the alphabet should happen a large enough number of times. As a rule of thumb we will take some multiple of the number of characters in the alphabet. If the multiplier is large enough the probability of each character appearance will be even over the alphabet.
Seems to get better results looking at the gated graphs but procedural decision has to be tuned.
```
import MorseGen
morse_gen = MorseGen.Morse()
alphabet = morse_gen.alphabet14
print(132/len(alphabet))
morsestr = MorseGen.get_morse_str(nchars=132*7, nwords=27*7, chars=alphabet)
print(alphabet)
print(len(morsestr), morsestr)
```
## Generate dataframe and extract envelope
```
Fs = 8000
samples_per_dit = morse_gen.nb_samples_per_dit(Fs, 13)
n_prev = int((samples_per_dit/128)*12*2) + 1
print(f'Samples per dit at {Fs} Hz is {samples_per_dit}. Decimation is {samples_per_dit/128:.2f}. Look back is {n_prev}.')
label_df = morse_gen.encode_df_decim_str(morsestr, samples_per_dit, 128, alphabet)
env = label_df['env'].to_numpy()
print(type(env), len(env))
import numpy as np
def get_new_data(morse_gen, SNR_dB=-23, nchars=132, nwords=27, phrase=None, alphabet="ABC"):
if not phrase:
phrase = MorseGen.get_morse_str(nchars=nchars, nwords=nwords, chars=alphabet)
print(len(phrase), phrase)
Fs = 8000
samples_per_dit = morse_gen.nb_samples_per_dit(Fs, 13)
#n_prev = int((samples_per_dit/128)*19) + 1 # number of samples to look back is slightly more than a "O" a word space (3*4+7=19)
n_prev = int((samples_per_dit/128)*27) + 1 # number of samples to look back is slightly more than a "0" a word space (5*4+7=27)
print(f'Samples per dit at {Fs} Hz is {samples_per_dit}. Decimation is {samples_per_dit/128:.2f}. Look back is {n_prev}.')
label_df = morse_gen.encode_df_decim_tree(phrase, samples_per_dit, 128, alphabet)
# extract the envelope
envelope = label_df['env'].to_numpy()
# remove the envelope
label_df.drop(columns=['env'], inplace=True)
SNR_linear = 10.0**(SNR_dB/10.0)
SNR_linear *= 256 # Apply original FFT
print(f'Resulting SNR for original {SNR_dB} dB is {(10.0 * np.log10(SNR_linear)):.2f} dB')
t = np.linspace(0, len(envelope)-1, len(envelope))
power = np.sum(envelope**2)/len(envelope)
noise_power = power/SNR_linear
noise = np.sqrt(noise_power)*np.random.normal(0, 1, len(envelope))
# noise = butter_lowpass_filter(raw_noise, 0.9, 3) # Noise is also filtered in the original setup from audio. This empirically simulates it
signal = (envelope + noise)**2
signal[signal > 1.0] = 1.0 # a bit crap ...
return envelope, signal, label_df, n_prev
```
Try it...
```
import matplotlib.pyplot as plt
envelope, signal, label_df, n_prev = get_new_data(morse_gen, SNR_dB=-17, phrase=morsestr, alphabet=alphabet)
# Show
print(n_prev)
print(type(signal), signal.shape)
print(type(label_df), label_df.shape)
x0 = 0
x1 = 1500
plt.figure(figsize=(50,4+0.5*len(morse_gen.alphabet)))
plt.plot(signal[x0:x1]*0.7, label="sig")
plt.plot(envelope[x0:x1]*0.9, label='env')
plt.plot(label_df[x0:x1].dit*0.9 + 1.0, label='dit')
plt.plot(label_df[x0:x1].dah*0.9 + 1.0, label='dah')
plt.plot(label_df[x0:x1].ele*0.9 + 2.0, label='ele')
plt.plot(label_df[x0:x1].chr*0.9 + 2.0, label='chr', color="orange")
plt.plot(label_df[x0:x1].wrd*0.9 + 2.0, label='wrd')
plt.plot(label_df[x0:x1].nul*0.9 + 3.0, label='nul')
for i, a in enumerate(alphabet):
plt.plot(label_df[x0:x1][a]*0.9 + 4.0 + i, label=a)
plt.title("signal and labels")
plt.legend(loc=2)
plt.grid()
```
## Create data loader
### Define dataset
```
import torch
class MorsekeyingDataset(torch.utils.data.Dataset):
def __init__(self, morse_gen, device, SNR_dB=-23, nchars=132, nwords=27, phrase=None, alphabet="ABC"):
self.envelope, self.signal, self.label_df0, self.seq_len = get_new_data(morse_gen, SNR_dB=SNR_dB, phrase=phrase, alphabet=alphabet)
self.label_df = self.label_df0.drop(columns=['dit','dah'])
self.X = torch.FloatTensor(self.signal).to(device)
self.y = torch.FloatTensor(self.label_df.values).to(device)
def __len__(self):
return self.X.__len__() - self.seq_len
def __getitem__(self, index):
return (self.X[index:index+self.seq_len], self.y[index+self.seq_len])
def get_envelope(self):
return self.envelope
def get_signal(self):
return self.signal
def get_X(self):
return self.X
def get_labels(self):
return self.label_df
def get_labels0(self):
return self.label_df0
def get_seq_len(self):
return self.seq_len()
```
### Define keying data loader
```
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
train_chr_dataset = MorsekeyingDataset(morse_gen, device, -20, 132*5, 27*5, morsestr, alphabet)
train_chr_loader = torch.utils.data.DataLoader(train_chr_dataset, batch_size=1, shuffle=False) # Batch size must be 1
signal = train_chr_dataset.get_signal()
envelope = train_chr_dataset.get_envelope()
label_df = train_chr_dataset.get_labels()
label_df0 = train_chr_dataset.get_labels0()
print(type(signal), signal.shape)
print(type(label_df), label_df.shape)
x0 = 0
x1 = 1500
plt.figure(figsize=(50,3))
plt.plot(signal[x0:x1]*0.5, label="sig")
plt.plot(envelope[x0:x1]*0.9, label='env')
plt.plot(label_df[x0:x1].E*0.9 + 1.0, label='E')
plt.plot(label_df[x0:x1]["T"]*0.9 + 1.0, label='T')
plt.plot(label_df[x0:x1].ele*0.9 + 2.0, label='ele')
plt.plot(label_df[x0:x1].chr*0.9 + 2.0, label='chr')
plt.plot(label_df[x0:x1].wrd*0.9 + 2.0, label='wrd')
plt.title("keying - signal and labels")
plt.legend(loc=2)
plt.grid()
```
## Create model classes
```
import torch
import torch.nn as nn
class MorseLSTM(nn.Module):
"""
Initial implementation
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer_size).to(self.device))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq), 1, -1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(1, 1, self.hidden_layer_size).to(device),
torch.zeros(1, 1, self.hidden_layer_size).to(device)
)
class MorseBatchedLSTM(nn.Module):
"""
Initial implementation
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.input_size = input_size
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer_size).to(self.device))
self.m = nn.Softmax(dim=-1)
def forward(self, input_seq):
#print(len(input_seq), input_seq.shape, input_seq.view(-1, 1, 1).shape)
lstm_out, self.hidden_cell = self.lstm(input_seq.view(-1, 1, self.input_size), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return self.m(predictions[-1])
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(1, 1, self.hidden_layer_size).to(device),
torch.zeros(1, 1, self.hidden_layer_size).to(device)
)
class MorseLSTM2(nn.Module):
"""
LSTM stack
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6, dropout=0.2):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size, num_layers=2, dropout=dropout)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(2, 1, self.hidden_layer_size).to(self.device),
torch.zeros(2, 1, self.hidden_layer_size).to(self.device))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq), 1, -1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(2, 1, self.hidden_layer_size).to(device),
torch.zeros(2, 1, self.hidden_layer_size).to(device)
)
class MorseNoHLSTM(nn.Module):
"""
Do not keep hidden cell
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
def forward(self, input_seq):
h0 = torch.zeros(1, 1, self.hidden_layer_size).to(self.device)
c0 = torch.zeros(1, 1, self.hidden_layer_size).to(self.device)
lstm_out, _ = self.lstm(input_seq.view(len(input_seq), 1, -1), (h0, c0))
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
class MorseBiLSTM(nn.Module):
"""
Attempt Bidirectional LSTM: does not work
"""
def __init__(self, device, input_size=1, hidden_size=12, num_layers=1, num_classes=6):
super(MorseEnvBiLSTM, self).__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True, bidirectional=True)
self.fc = nn.Linear(hidden_size*2, num_classes) # 2 for bidirection
def forward(self, x):
# Set initial states
h0 = torch.zeros(self.num_layers*2, x.size(0), self.hidden_size).to(device) # 2 for bidirection
c0 = torch.zeros(self.num_layers*2, x.size(0), self.hidden_size).to(device)
# Forward propagate LSTM
out, _ = self.lstm(x.view(len(x), 1, -1), (h0, c0)) # out: tensor of shape (batch_size, seq_length, hidden_size*2)
# Decode the hidden state of the last time step
out = self.fc(out[:, -1, :])
return out[-1]
```
Create the keying model instance and print the details
```
morse_chr_model = MorseBatchedLSTM(device, hidden_layer_size=len(alphabet)*3, output_size=len(alphabet)+4).to(device) # This is the only way to get things work properly with device
morse_chr_loss_function = nn.MSELoss()
morse_chr_optimizer = torch.optim.Adam(morse_chr_model.parameters(), lr=0.001)
print(morse_chr_model)
print(morse_chr_model.device)
# Input and hidden tensors are not at the same device, found input tensor at cuda:0 and hidden tensor at cpu
for m in morse_chr_model.parameters():
print(m.shape, m.device)
X_t = torch.rand(n_prev)
X_t = X_t.cuda()
print("Input shape", X_t.shape, X_t.view(-1, 1, 1).shape)
print(X_t)
morse_chr_model(X_t)
import torchinfo
torchinfo.summary(morse_chr_model)
```
## Train model
```
it = iter(train_chr_loader)
X, y = next(it)
print(X.reshape(n_prev,1).shape, X[0].shape, y[0].shape)
print(X[0], y[0])
X, y = next(it)
print(X[0], y[0])
%%time
from tqdm.notebook import tqdm
epochs = 4
morse_chr_model.train()
for i in range(epochs):
train_losses = []
loop = tqdm(enumerate(train_chr_loader), total=len(train_chr_loader), leave=True)
for j, train in loop:
X_train = train[0][0]
y_train = train[1][0]
morse_chr_optimizer.zero_grad()
if morse_chr_model.__class__.__name__ in ["MorseLSTM", "MorseLSTM2", "MorseBatchedLSTM", "MorseBatchedLSTM2"]:
morse_chr_model.zero_hidden_cell() # this model needs to reset the hidden cell
y_pred = morse_chr_model(X_train)
single_loss = morse_chr_loss_function(y_pred, y_train)
single_loss.backward()
morse_chr_optimizer.step()
train_losses.append(single_loss.item())
# update progress bar
if j % 1000 == 0:
loop.set_description(f"Epoch [{i+1}/{epochs}]")
loop.set_postfix(loss=np.mean(train_losses))
print(f'final: {i+1:3} epochs loss: {np.mean(train_losses):6.4f}')
save_model = True
if save_model:
torch.save(morse_chr_model.state_dict(), 'models/morse_single_model')
else:
morse_chr_model.load_state_dict(torch.load('models/morse_single_model', map_location=device))
%%time
p_char_train = torch.empty(1,18).to(device)
morse_chr_model.eval()
loop = tqdm(enumerate(train_chr_loader), total=len(train_chr_loader))
for j, train in loop:
with torch.no_grad():
X_chr = train[0][0]
pred_val = morse_chr_model(X_chr)
p_char_train = torch.cat([p_char_train, pred_val.reshape(1,18)])
p_char_train = p_char_train[1:] # Remove garbge
print(p_char_train.shape) # t -> chars(t)
```
### Post process
- Move to CPU to ger chars(time)
- Transpose to get times(char)
```
p_char_train_c = p_char_train.cpu() # t -> chars(t) on CPU
p_char_train_t = torch.transpose(p_char_train_c, 0, 1).cpu() # c -> times(c) on CPU
print(p_char_train_c.shape, p_char_train_t.shape)
X_train_chr = train_chr_dataset.X.cpu()
label_df_chr = train_chr_dataset.get_labels()
l_alpha = label_df_chr[n_prev:].reset_index(drop=True)
plt.figure(figsize=(50,4+0.5*len(morse_gen.alphabet)))
plt.plot(l_alpha[x0:x1]["chr"]*(len(alphabet)+1)+2, label="ychr", alpha=0.2, color="black")
plt.plot(X_train_chr[x0+n_prev:x1+n_prev]*1.9, label='sig')
plt.plot(p_char_train_t[1][x0:x1]*0.9 + 2.0, label='c')
plt.plot(p_char_train_t[2][x0:x1]*0.9 + 2.0, label='w')
for i, a in enumerate(alphabet):
plt_a = plt.plot(p_char_train_t[i+4][x0:x1]*0.9 + 3.0 + i, label=a)
plt.plot(l_alpha[a][x0:x1]*0.5 + 3.0 + i, color=plt_a[0].get_color(), alpha=0.5)
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
```
## Test
### Test dataset and data loader
```
teststr = "AAAA USERS ARE USING EGGS AND GRAIN MONGO TEST MADAME WONDER WOMAN GOOD MAMA USSR WAS GREAT AAA"
test_chr_dataset = MorsekeyingDataset(morse_gen, device, -19, 132*5, 27*5, teststr, alphabet)
test_chr_loader = torch.utils.data.DataLoader(test_chr_dataset, batch_size=1, shuffle=False) # Batch size must be 1
```
### Run the model
```
p_chr_test = torch.empty(1,18).to(device)
morse_chr_model.eval()
loop = tqdm(enumerate(test_chr_loader), total=len(test_chr_loader))
for j, test in loop:
with torch.no_grad():
X_test = test[0]
pred_val = morse_chr_model(X_test[0])
p_chr_test = torch.cat([p_chr_test, pred_val.reshape(1,18)])
# drop first garbage sample
p_chr_test = p_chr_test[1:]
print(p_chr_test.shape)
p_chr_test_c = p_chr_test.cpu() # t -> chars(t) on CPU
p_chr_test_t = torch.transpose(p_chr_test_c, 0, 1).cpu() # c -> times(c) on CPU
print(p_chr_test_c.shape, p_chr_test_t.shape)
```
### Show results
```
X_test_chr = test_chr_dataset.X.cpu()
label_df_t = test_chr_dataset.get_labels()
l_alpha_t = label_df_t[n_prev:].reset_index(drop=True)
```
#### Raw results
Envelope reconstruction is obtained by combining the silences (env, chr, wrd) senses. To correct gap between chr and wrd a delayed copy of wrd is added. Eventually the envelope is truncated in the [0:1] interval. It appears on the second line in purple.
```
plt.figure(figsize=(100,4+0.5*len(morse_gen.alphabet)))
plt.plot(l_alpha_t[:]["chr"]*(len(alphabet)+1)+2, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.9, label='sig')
p_wrd_dly = p_chr_test_t[2][6:]
p_wrd_dly = torch.cat([p_wrd_dly, torch.zeros(6)])
p_env = 1.0 - p_chr_test_t[0] - p_chr_test_t[1] - (p_chr_test_t[2] + p_wrd_dly)
p_env[p_env < 0] = 0
p_env[p_env > 1] = 1
plt.plot(p_env*0.9 + 1.0, label='env', color="purple")
plt.plot(p_chr_test_t[1]*0.9 + 2.0, label='c', color="green")
plt.plot(p_chr_test_t[2]*0.9 + 2.0, label='w', color="red")
for i, a in enumerate(alphabet):
plt_a = plt.plot(p_chr_test_t[i+4,:]*0.9 + 3.0 + i, label=a)
plt.plot(l_alpha_t[a]*0.5 + 3.0 + i, color=plt_a[0].get_color(), linestyle="--")
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted.png')
p_chr_test_tn = p_chr_test_t.numpy()
ele_len = round(samples_per_dit*2 / 128)
win = np.ones(ele_len)/ele_len
p_chr_test_tlp = np.apply_along_axis(lambda m: np.convolve(m, win, mode='full'), axis=1, arr=p_chr_test_tn)
plt.figure(figsize=(100,4+0.5*len(morse_gen.alphabet)))
plt.plot(l_alpha_t[:]["chr"]*(len(alphabet)+1)+2, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.9, label='sig')
plt.plot(p_chr_test_tlp[1]*0.9 + 2.0, label='c', color="green")
plt.plot(p_chr_test_tlp[2]*0.9 + 2.0, label='w', color="red")
for i, a in enumerate(alphabet):
plt_a = plt.plot(p_chr_test_tlp[i+4,:]*0.9 + 3.0 + i, label=a)
plt.plot(l_alpha_t[a]*0.5 + 3.0 + i, color=plt_a[0].get_color(), linestyle="--")
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted.png')
```
#### Gated by character prediction
```
plt.figure(figsize=(100,4+0.5*len(morse_gen.alphabet)))
plt.plot(l_alpha_t["chr"]*(len(alphabet)+1)+2, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.9, label='sig')
plt.plot(p_chr_test_tlp[1]*0.9 + 1.0, label="cp", color="green")
plt.plot(p_chr_test_tlp[2]*0.9 + 1.0, label="wp", color="red")
for i, a in enumerate(alphabet):
line_a = p_chr_test_tlp[i+4] * p_chr_test_tlp[1]
plt_a = plt.plot(line_a*0.9 + 2.0 + i, label=a)
plt.plot(l_alpha_t[a]*0.5 + 2.0 + i, color=plt_a[0].get_color(), linestyle="--")
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted_gated.png')
plt.figure(figsize=(100,4+0.5*len(morse_gen.alphabet)))
plt.plot(l_alpha_t["chr"]*(len(alphabet))+2, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.9, label='sig')
plt.plot(p_chr_test_tlp[1]*0.9 + 1.0, label="cp", color="green")
line_wrd = p_chr_test_tlp[2]
plt.plot(line_wrd*0.9 + 1.0, color="red", linestyle="--")
line_wrd[line_wrd < 0.5] = 0
plt.plot(line_wrd*0.9 + 1.0, label="wp", color="red")
for i, a in enumerate(alphabet):
line_a = p_chr_test_tlp[i+4] * p_chr_test_tlp[1]
plt_a = plt.plot(line_a*0.9 + 2.0 + i, linestyle="--")
plt.plot(l_alpha_t[a]*0.3 + 2.0 + i, color=plt_a[0].get_color(), linestyle="--")
line_a[line_a < 0.3] = 0
plt.plot(line_a*0.9 + 2.0 + i, color=plt_a[0].get_color(), label=a)
plt.title("predictions thresholds")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted_thr.png')
```
## Procedural decision making
### take 2
```
class MorseDecoder2:
def __init__(self, alphabet, chr_len, wrd_len):
self.nb_alpha = len(alphabet)
self.alphabet = alphabet
self.chr_len = chr_len
self.wrd_len = wrd_len // 2
self.threshold = 0.25
self.chr_count = 0
self.wrd_count = 0
self.prevs = [0.0 for x in range(self.nb_alpha+3)]
self.res = ""
def new_samples(self, samples):
for i, s in enumerate(samples): # c, w, n, [alpha]
if i > 1:
t = s * samples[0] # gating for alpha characters
else:
t = s
if i == 1: # word separator
if t >= self.threshold and self.prevs[1] < self.threshold and self.wrd_count == 0:
self.wrd_count = self.wrd_len
self.res += " "
elif i > 1: # characters
if t >= self.threshold and self.prevs[i] < self.threshold and self.chr_count == 0:
self.chr_count = self.chr_len
if i > 2:
self.res += self.alphabet[i-3]
self.prevs[i] = t
if self.wrd_count > 0:
self.wrd_count -= 1
if self.chr_count > 0:
self.chr_count -= 1
chr_len = round(samples_per_dit*2 / 128)
wrd_len = round(samples_per_dit*4 / 128)
decoder = MorseDecoder2(alphabet, chr_len, wrd_len)
#p_chr_test_clp = torch.transpose(p_chr_test_tlp, 0, 1)
p_chr_test_clp = p_chr_test_tlp.transpose()
for s in p_chr_test_clp:
decoder.new_samples(s[1:]) # c, w, n, [alpha]
print(decoder.res)
```
### take 1
```
class MorseDecoder1:
def __init__(self, alphabet, chr_len, wrd_len):
self.nb_alpha = len(alphabet)
self.alphabet = alphabet
self.chr_len = chr_len
self.wrd_len = wrd_len
self.alpha = 0.3
self.threshold = 0.45
self.accum = [0.0 for x in range(self.nb_alpha+2)]
self.sums = [0.0 for x in range(self.nb_alpha+2)]
self.tests = [0.0 for x in range(self.nb_alpha+2)]
self.prevs = [0.0 for x in range(self.nb_alpha+2)]
self.counts = [0 for x in range(self.nb_alpha+2)]
self.res = ""
def new_samples(self, samples):
for i, s in enumerate(samples):
if i > 2:
t = s * samples[0] # gating for alpha characters
else:
t = s
# t = s
if i > 0:
j = i-1
t = self.alpha * t + (1 - self.alpha) * self.accum[j] # Exponential average does the low pass filtering
self.accum[j] = t
if t >= self.threshold and self.prevs[j] < self.threshold:
self.counts[j] = 0
if t > self.threshold:
self.sums[j] = self.sums[j] + t
self.tests[j] = 0.0
else:
blk_len = wrd_len if j == 0 else chr_len
if self.counts[j] > blk_len:
self.tests[j] = self.sums[j]
self.sums[j] = 0.0
self.counts[j] += 1
self.prevs[j] = t
if np.sum(self.tests) > 0.0:
ci = np.argmax(self.tests)
if ci == 0:
self.res += " "
elif ci > 1:
self.res += self.alphabet[ci - 2]
chr_len = round(samples_per_dit*2 / 128)
wrd_len = round(samples_per_dit*4 / 128)
decoder = MorseDecoder1(alphabet, chr_len, wrd_len)
for s in p_chr_test_c:
decoder.new_samples(s[1:]) # c, w, n, [alpha]
print(decoder.res)
```
| true |
code
| 0.584449 | null | null | null | null |
|
# Uniform longitudinal beam loading
```
%matplotlib notebook
import sys
sys.path.append('/Users/chall/research/github/rswarp/rswarp/utilities/')
import beam_analysis
import file_utils
from mpl_toolkits.mplot3d import Axes3D
import pickle
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
def svecplot(array):
fig = plt.figure(figsize = (8,8))
Q = plt.quiver(array[:,0],array[:,2],array[:,1],array[:,3])
plt.quiverkey(Q,0.0, 0.92, 0.002, r'$2', labelpos='W')
xmax = np.max(array[:,0])
xmin = np.min(array[:,0])
plt.xlim(1.5*xmin,1.5*xmax)
plt.ylim(1.5*xmin,1.5*xmax)
plt.show()
# Load simulation parameters
simulation_parameters = pickle.load(open("simulation_parameters.p", "rb"))
print simulation_parameters['timestep']
```
## Load and View Initial Distribution
```
f0 = file_utils.readparticles('diags/xySlice/hdf5/data00000001.h5')
step0 = beam_analysis.convertunits(f0['Electron'])
beam_analysis.plotphasespace(step0); # semicolon suppresses second plot
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111, projection='3d')
p = ax.scatter(step0[:,1]*1e3,step0[:,4],step0[:,3]*1e3)
ax.set_xlabel('x (mm)')
ax.set_ylabel('z (m)')
ax.set_zlabel('y (mm)')
plt.show()
```
## Load All Steps
```
full = file_utils.loadparticlefiles('diags/xySlice/hdf5/')
allSteps = []
for step in range(100,1400,100):
scon = beam_analysis.convertunits(full[step]['Electron'])
allSteps.append(full[step]['Electron'])
allSteps = np.array(allSteps)
# beam_analysis.plotphasespace(allSteps[10,:,:]):
```
# Magnetostatic Only Check
```
f0 = h5.File('diags/fields/magnetic/bfield00200.h5', 'r')
Bx = f0['data/200/meshes/B/r']
By = f0['data/200/meshes/B/t']
Bz = f0['data/200/meshes/B/z']
fig = plt.figure(figsize=(12,4))
ax = plt.gca()
xpoints = np.linspace(0,0.32,Bx[0,:,8].shape[0])
ax.plot(xpoints,By[0,:,15],label = "Bt from Sim")
ax.plot(xpoints[5:], -2 * 10.0e-6 * 1e-7 / (xpoints[5:]), label="Calc. Bt for r>R")
ax.plot(xpoints[0:16], -2 * 10e-6 * 1e-7 * (xpoints[0:16]) / 0.02**2, label="Calc. Bt for r<R")
ax.legend(loc=4)
plt.show()
fig = plt.figure(figsize=(8,8))
ax = plt.gca()
zslice = 10
ax.set_xlabel("y (m)")
ax.set_ylabel("x (m)")
ax.set_title("$B_%s$ for z=%s" % ('x',zslice))
cax = ax.imshow(By[0,:,:],cmap=plt.cm.viridis)
fig.colorbar(cax)
plt.tight_layout
plt.show()
```
# Electrostatic Only Check
```
# Calculate charge
I = 10e-6
L = 1.0
e = 1.6e-19
c = 3e8
beta = 0.56823
Ntot = int(I * L / e / (c * beta))
Qtot = Ntot * e
f0 = h5.File('diags/fields/electric/efield00200.h5', 'r')
Bx = f0['data/200/meshes/E/r']
By = f0['data/200/meshes/E/t']
Bz = f0['data/200/meshes/E/z']
fig = plt.figure(figsize=(12,4))
ax = plt.gca()
xpoints = np.linspace(0,0.32,Bx[0,:,8].shape[0])
ax.plot(xpoints,Bx[0,:,15],label = "Er from Sim")
ax.plot(xpoints[3:], -1 * Qtot / (2 * np.pi * 8.854e-12 * xpoints[3:]), label="Calc. Er for r>R")
ax.plot(xpoints[0:10], -1 * Qtot * (xpoints[0:10]) / (2 * np.pi * 8.854e-12 * 0.02**2), label="Calc. Er for r<R")
ax.legend(loc=4)
plt.show()
```
# E and B Static Solvers
```
f0 = h5.File('diags/fields/electric/efield00200.h5', 'r')
Ex = f0['data/200/meshes/E/r']
Ey = f0['data/200/meshes/E/t']
Ez = f0['data/200/meshes/E/z']
f0 = h5.File('diags/fields/magnetic/bfield00200.h5', 'r')
Bx = f0['data/200/meshes/B/r']
By = f0['data/200/meshes/B/t']
Bz = f0['data/200/meshes/B/z']
fig = plt.figure(figsize=(12,8))
xpoints = np.linspace(0,0.32,Bx[0,:,8].shape[0])
plt.subplot(211)
plt.plot(xpoints,By[0,:,15],label = "Er from Sim")
plt.plot(xpoints[3:], -2 * 10.0e-6 * 1e-7 / (xpoints[3:]), label="Calc. Bt for r>R")
plt.plot(xpoints[0:8], -2 * 10e-6 * 1e-7 * (xpoints[0:8]) / 0.02**2, label="Calc. Bt for r<R")
plt.legend(loc=4)
plt.title("Magnetic Field")
plt.subplot(212)
xpoints = np.linspace(0,0.32,Bx[0,:,8].shape[0])
plt.plot(xpoints,Ex[0,:,15],label = "Bt from Sim")
plt.plot(xpoints[3:], -1 * Qtot / (2 * np.pi * 8.854e-12 * xpoints[3:]), label="Calc. Er for r>R")
plt.plot(xpoints[0:8], -1 * Qtot * (xpoints[0:8]) / (2 * np.pi * 8.854e-12 * 0.02**2), label="Calc. Er for r<R")
plt.legend(loc=4)
plt.title("Electric Field")
plt.show()
```
| true |
code
| 0.479077 | null | null | null | null |
|
```
#hide
!pip install -Uqq fastbook
import fastbook
fastbook.setup_book()
#hide
from fastbook import *
```
# Image Classification
Now that you understand what deep learning is, what it's for, and how to create and deploy a model, it's time for us to go deeper! In an ideal world deep learning practitioners wouldn't have to know every detail of how things work under the hood… But as yet, we don't live in an ideal world. The truth is, to make your model really work, and work reliably, there are a lot of details you have to get right, and a lot of details that you have to check. This process requires being able to look inside your neural network as it trains, and as it makes predictions, find possible problems, and know how to fix them.
So, from here on in the book we are going to do a deep dive into the mechanics of deep learning. What is the architecture of a computer vision model, an NLP model, a tabular model, and so on? How do you create an architecture that matches the needs of your particular domain? How do you get the best possible results from the training process? How do you make things faster? What do you have to change as your datasets change?
We will start by repeating the same basic applications that we looked at in the first chapter, but we are going to do two things:
- Make them better.
- Apply them to a wider variety of types of data.
In order to do these two things, we will have to learn all of the pieces of the deep learning puzzle. This includes different types of layers, regularization methods, optimizers, how to put layers together into architectures, labeling techniques, and much more. We are not just going to dump all of these things on you, though; we will introduce them progressively as needed, to solve actual problems related to the projects we are working on.
## From Dogs and Cats to Pet Breeds
In our very first model we learned how to classify dogs versus cats. Just a few years ago this was considered a very challenging task—but today, it's far too easy! We will not be able to show you the nuances of training models with this problem, because we get a nearly perfect result without worrying about any of the details. But it turns out that the same dataset also allows us to work on a much more challenging problem: figuring out what breed of pet is shown in each image.
In <<chapter_intro>> we presented the applications as already-solved problems. But this is not how things work in real life. We start with some dataset that we know nothing about. We then have to figure out how it is put together, how to extract the data we need from it, and what that data looks like. For the rest of this book we will be showing you how to solve these problems in practice, including all of the intermediate steps necessary to understand the data that you are working with and test your modeling as you go.
We already downloaded the Pet dataset, and we can get a path to this dataset using the same code as in <<chapter_intro>>:
```
from fastai.vision.all import *
path = untar_data(URLs.PETS)
```
Now if we are going to understand how to extract the breed of each pet from each image we're going to need to understand how this data is laid out. Such details of data layout are a vital piece of the deep learning puzzle. Data is usually provided in one of these two ways:
- Individual files representing items of data, such as text documents or images, possibly organized into folders or with filenames representing information about those items
- A table of data, such as in CSV format, where each row is an item which may include filenames providing a connection between the data in the table and data in other formats, such as text documents and images
There are exceptions to these rules—particularly in domains such as genomics, where there can be binary database formats or even network streams—but overall the vast majority of the datasets you'll work with will use some combination of these two formats.
To see what is in our dataset we can use the `ls` method:
```
#hide
Path.BASE_PATH = path
path.ls()
```
We can see that this dataset provides us with *images* and *annotations* directories. The [website](https://www.robots.ox.ac.uk/~vgg/data/pets/) for the dataset tells us that the *annotations* directory contains information about where the pets are rather than what they are. In this chapter, we will be doing classification, not localization, which is to say that we care about what the pets are, not where they are. Therefore, we will ignore the *annotations* directory for now. So, let's have a look inside the *images* directory:
```
(path/"images").ls()
```
Most functions and methods in fastai that return a collection use a class called `L`. `L` can be thought of as an enhanced version of the ordinary Python `list` type, with added conveniences for common operations. For instance, when we display an object of this class in a notebook it appears in the format shown there. The first thing that is shown is the number of items in the collection, prefixed with a `#`. You'll also see in the preceding output that the list is suffixed with an ellipsis. This means that only the first few items are displayed—which is a good thing, because we would not want more than 7,000 filenames on our screen!
By examining these filenames, we can see how they appear to be structured. Each filename contains the pet breed, and then an underscore (`_`), a number, and finally the file extension. We need to create a piece of code that extracts the breed from a single `Path`. Jupyter notebooks make this easy, because we can gradually build up something that works, and then use it for the entire dataset. We do have to be careful to not make too many assumptions at this point. For instance, if you look carefully you may notice that some of the pet breeds contain multiple words, so we cannot simply break at the first `_` character that we find. To allow us to test our code, let's pick out one of these filenames:
```
fname = (path/"images").ls()[0]
```
The most powerful and flexible way to extract information from strings like this is to use a *regular expression*, also known as a *regex*. A regular expression is a special string, written in the regular expression language, which specifies a general rule for deciding if another string passes a test (i.e., "matches" the regular expression), and also possibly for plucking a particular part or parts out of that other string.
In this case, we need a regular expression that extracts the pet breed from the filename.
We do not have the space to give you a complete regular expression tutorial here,but there are many excellent ones online and we know that many of you will already be familiar with this wonderful tool. If you're not, that is totally fine—this is a great opportunity for you to rectify that! We find that regular expressions are one of the most useful tools in our programming toolkit, and many of our students tell us that this is one of the things they are most excited to learn about. So head over to Google and search for "regular expressions tutorial" now, and then come back here after you've had a good look around. The [book's website](https://book.fast.ai/) also provides a list of our favorites.
> a: Not only are regular expressions dead handy, but they also have interesting roots. They are "regular" because they were originally examples of a "regular" language, the lowest rung within the Chomsky hierarchy, a grammar classification developed by linguist Noam Chomsky, who also wrote _Syntactic Structures_, the pioneering work searching for the formal grammar underlying human language. This is one of the charms of computing: it may be that the hammer you reach for every day in fact came from a spaceship.
When you are writing a regular expression, the best way to start is just to try it against one example at first. Let's use the `findall` method to try a regular expression against the filename of the `fname` object:
```
re.findall(r'(.+)_\d+.jpg$', fname.name)
```
This regular expression plucks out all the characters leading up to the last underscore character, as long as the subsequence characters are numerical digits and then the JPEG file extension.
Now that we confirmed the regular expression works for the example, let's use it to label the whole dataset. fastai comes with many classes to help with labeling. For labeling with regular expressions, we can use the `RegexLabeller` class. In this example we use the data block API we saw in <<chapter_production>> (in fact, we nearly always use the data block API—it's so much more flexible than the simple factory methods we saw in <<chapter_intro>>):
```
pets = DataBlock(blocks = (ImageBlock, CategoryBlock),
get_items=get_image_files,
splitter=RandomSplitter(seed=42),
get_y=using_attr(RegexLabeller(r'(.+)_\d+.jpg$'), 'name'),
item_tfms=Resize(460),
batch_tfms=aug_transforms(size=224, min_scale=0.75))
dls = pets.dataloaders(path/"images")
```
One important piece of this `DataBlock` call that we haven't seen before is in these two lines:
```python
item_tfms=Resize(460),
batch_tfms=aug_transforms(size=224, min_scale=0.75)
```
These lines implement a fastai data augmentation strategy which we call *presizing*. Presizing is a particular way to do image augmentation that is designed to minimize data destruction while maintaining good performance.
## Presizing
We need our images to have the same dimensions, so that they can collate into tensors to be passed to the GPU. We also want to minimize the number of distinct augmentation computations we perform. The performance requirement suggests that we should, where possible, compose our augmentation transforms into fewer transforms (to reduce the number of computations and the number of lossy operations) and transform the images into uniform sizes (for more efficient processing on the GPU).
The challenge is that, if performed after resizing down to the augmented size, various common data augmentation transforms might introduce spurious empty zones, degrade data, or both. For instance, rotating an image by 45 degrees fills corner regions of the new bounds with emptyness, which will not teach the model anything. Many rotation and zooming operations will require interpolating to create pixels. These interpolated pixels are derived from the original image data but are still of lower quality.
To work around these challenges, presizing adopts two strategies that are shown in <<presizing>>:
1. Resize images to relatively "large" dimensions—that is, dimensions significantly larger than the target training dimensions.
1. Compose all of the common augmentation operations (including a resize to the final target size) into one, and perform the combined operation on the GPU only once at the end of processing, rather than performing the operations individually and interpolating multiple times.
The first step, the resize, creates images large enough that they have spare margin to allow further augmentation transforms on their inner regions without creating empty zones. This transformation works by resizing to a square, using a large crop size. On the training set, the crop area is chosen randomly, and the size of the crop is selected to cover the entire width or height of the image, whichever is smaller.
In the second step, the GPU is used for all data augmentation, and all of the potentially destructive operations are done together, with a single interpolation at the end.
<img alt="Presizing on the training set" width="600" caption="Presizing on the training set" id="presizing" src="images/att_00060.png">
This picture shows the two steps:
1. *Crop full width or height*: This is in `item_tfms`, so it's applied to each individual image before it is copied to the GPU. It's used to ensure all images are the same size. On the training set, the crop area is chosen randomly. On the validation set, the center square of the image is always chosen.
2. *Random crop and augment*: This is in `batch_tfms`, so it's applied to a batch all at once on the GPU, which means it's fast. On the validation set, only the resize to the final size needed for the model is done here. On the training set, the random crop and any other augmentations are done first.
To implement this process in fastai you use `Resize` as an item transform with a large size, and `RandomResizedCrop` as a batch transform with a smaller size. `RandomResizedCrop` will be added for you if you include the `min_scale` parameter in your `aug_transforms` function, as was done in the `DataBlock` call in the previous section. Alternatively, you can use `pad` or `squish` instead of `crop` (the default) for the initial `Resize`.
<<interpolations>> shows the difference between an image that has been zoomed, interpolated, rotated, and then interpolated again (which is the approach used by all other deep learning libraries), shown here on the right, and an image that has been zoomed and rotated as one operation and then interpolated just once on the left (the fastai approach), shown here on the left.
```
#hide_input
#id interpolations
#caption A comparison of fastai's data augmentation strategy (left) and the traditional approach (right).
dblock1 = DataBlock(blocks=(ImageBlock(), CategoryBlock()),
get_y=parent_label,
item_tfms=Resize(460))
dls1 = dblock1.dataloaders([(Path.cwd()/'images'/'grizzly.jpg')]*100, bs=8)
dls1.train.get_idxs = lambda: Inf.ones
x,y = dls1.valid.one_batch()
_,axs = subplots(1, 2)
x1 = TensorImage(x.clone())
x1 = x1.affine_coord(sz=224)
x1 = x1.rotate(draw=30, p=1.)
x1 = x1.zoom(draw=1.2, p=1.)
x1 = x1.warp(draw_x=-0.2, draw_y=0.2, p=1.)
tfms = setup_aug_tfms([Rotate(draw=30, p=1, size=224), Zoom(draw=1.2, p=1., size=224),
Warp(draw_x=-0.2, draw_y=0.2, p=1., size=224)])
x = Pipeline(tfms)(x)
#x.affine_coord(coord_tfm=coord_tfm, sz=size, mode=mode, pad_mode=pad_mode)
TensorImage(x[0]).show(ctx=axs[0])
TensorImage(x1[0]).show(ctx=axs[1]);
```
You can see that the image on the right is less well defined and has reflection padding artifacts in the bottom-left corner; also, the grass iat the top left has disappeared entirely. We find that in practice using presizing significantly improves the accuracy of models, and often results in speedups too.
The fastai library also provides simple ways to check your data looks right before training a model, which is an extremely important step. We'll look at those next.
### Checking and Debugging a DataBlock
We can never just assume that our code is working perfectly. Writing a `DataBlock` is just like writing a blueprint. You will get an error message if you have a syntax error somewhere in your code, but you have no guarantee that your template is going to work on your data source as you intend. So, before training a model you should always check your data. You can do this using the `show_batch` method:
```
dls.show_batch(nrows=1, ncols=3)
```
Take a look at each image, and check that each one seems to have the correct label for that breed of pet. Often, data scientists work with data with which they are not as familiar as domain experts may be: for instance, I actually don't know what a lot of these pet breeds are. Since I am not an expert on pet breeds, I would use Google images at this point to search for a few of these breeds, and make sure the images look similar to what I see in this output.
If you made a mistake while building your `DataBlock`, it is very likely you won't see it before this step. To debug this, we encourage you to use the `summary` method. It will attempt to create a batch from the source you give it, with a lot of details. Also, if it fails, you will see exactly at which point the error happens, and the library will try to give you some help. For instance, one common mistake is to forget to use a `Resize` transform, so you en up with pictures of different sizes and are not able to batch them. Here is what the summary would look like in that case (note that the exact text may have changed since the time of writing, but it will give you an idea):
```
#hide_output
pets1 = DataBlock(blocks = (ImageBlock, CategoryBlock),
get_items=get_image_files,
splitter=RandomSplitter(seed=42),
get_y=using_attr(RegexLabeller(r'(.+)_\d+.jpg$'), 'name'))
pets1.summary(path/"images")
```
```
Setting-up type transforms pipelines
Collecting items from /home/sgugger/.fastai/data/oxford-iiit-pet/images
Found 7390 items
2 datasets of sizes 5912,1478
Setting up Pipeline: PILBase.create
Setting up Pipeline: partial -> Categorize
Building one sample
Pipeline: PILBase.create
starting from
/home/sgugger/.fastai/data/oxford-iiit-pet/images/american_bulldog_83.jpg
applying PILBase.create gives
PILImage mode=RGB size=375x500
Pipeline: partial -> Categorize
starting from
/home/sgugger/.fastai/data/oxford-iiit-pet/images/american_bulldog_83.jpg
applying partial gives
american_bulldog
applying Categorize gives
TensorCategory(12)
Final sample: (PILImage mode=RGB size=375x500, TensorCategory(12))
Setting up after_item: Pipeline: ToTensor
Setting up before_batch: Pipeline:
Setting up after_batch: Pipeline: IntToFloatTensor
Building one batch
Applying item_tfms to the first sample:
Pipeline: ToTensor
starting from
(PILImage mode=RGB size=375x500, TensorCategory(12))
applying ToTensor gives
(TensorImage of size 3x500x375, TensorCategory(12))
Adding the next 3 samples
No before_batch transform to apply
Collating items in a batch
Error! It's not possible to collate your items in a batch
Could not collate the 0-th members of your tuples because got the following
shapes:
torch.Size([3, 500, 375]),torch.Size([3, 375, 500]),torch.Size([3, 333, 500]),
torch.Size([3, 375, 500])
```
You can see exactly how we gathered the data and split it, how we went from a filename to a *sample* (the tuple (image, category)), then what item transforms were applied and how it failed to collate those samples in a batch (because of the different shapes).
Once you think your data looks right, we generally recommend the next step should be using to train a simple model. We often see people put off the training of an actual model for far too long. As a result, they don't actually find out what their baseline results look like. Perhaps your probem doesn't need lots of fancy domain-specific engineering. Or perhaps the data doesn't seem to train the model all. These are things that you want to know as soon as possible. For this initial test, we'll use the same simple model that we used in <<chapter_intro>>:
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(2)
```
As we've briefly discussed before, the table shown when we fit a model shows us the results after each epoch of training. Remember, an epoch is one complete pass through all of the images in the data. The columns shown are the average loss over the items of the training set, the loss on the validation set, and any metrics that we requested—in this case, the error rate.
Remember that *loss* is whatever function we've decided to use to optimize the parameters of our model. But we haven't actually told fastai what loss function we want to use. So what is it doing? fastai will generally try to select an appropriate loss function based on what kind of data and model you are using. In this case we have image data and a categorical outcome, so fastai will default to using *cross-entropy loss*.
## Cross-Entropy Loss
*Cross-entropy loss* is a loss function that is similar to the one we used in the previous chapter, but (as we'll see) has two benefits:
- It works even when our dependent variable has more than two categories.
- It results in faster and more reliable training.
In order to understand how cross-entropy loss works for dependent variables with more than two categories, we first have to understand what the actual data and activations that are seen by the loss function look like.
### Viewing Activations and Labels
Let's take a look at the activations of our model. To actually get a batch of real data from our `DataLoaders`, we can use the `one_batch` method:
```
x,y = dls.one_batch()
```
As you see, this returns the dependent and independent variables, as a mini-batch. Let's see what is actually contained in our dependent variable:
```
y
```
Our batch size is 64, so we have 64 rows in this tensor. Each row is a single integer between 0 and 36, representing our 37 possible pet breeds. We can view the predictions (that is, the activations of the final layer of our neural network) using `Learner.get_preds`. This function either takes a dataset index (0 for train and 1 for valid) or an iterator of batches. Thus, we can pass it a simple list with our batch to get our predictions. It returns predictions and targets by default, but since we already have the targets, we can effectively ignore them by assigning to the special variable `_`:
```
preds,_ = learn.get_preds(dl=[(x,y)])
preds[0]
```
The actual predictions are 37 probabilities between 0 and 1, which add up to 1 in total:
```
len(preds[0]),preds[0].sum()
```
To transform the activations of our model into predictions like this, we used something called the *softmax* activation function.
### Softmax
In our classification model, we use the softmax activation function in the final layer to ensure that the activations are all between 0 and 1, and that they sum to 1.
Softmax is similar to the sigmoid function, which we saw earlier. As a reminder sigmoid looks like this:
```
plot_function(torch.sigmoid, min=-4,max=4)
```
We can apply this function to a single column of activations from a neural network, and get back a column of numbers between 0 and 1, so it's a very useful activation function for our final layer.
Now think about what happens if we want to have more categories in our target (such as our 37 pet breeds). That means we'll need more activations than just a single column: we need an activation *per category*. We can create, for instance, a neural net that predicts 3s and 7s that returns two activations, one for each class—this will be a good first step toward creating the more general approach. Let's just use some random numbers with a standard deviation of 2 (so we multiply `randn` by 2) for this example, assuming we have 6 images and 2 possible categories (where the first column represents 3s and the second is 7s):
```
#hide
torch.random.manual_seed(42);
acts = torch.randn((6,2))*2
acts
```
We can't just take the sigmoid of this directly, since we don't get rows that add to 1 (i.e., we want the probability of being a 3 plus the probability of being a 7 to add up to 1):
```
acts.sigmoid()
```
In <<chapter_mnist_basics>>, our neural net created a single activation per image, which we passed through the `sigmoid` function. That single activation represented the model's confidence that the input was a 3. Binary problems are a special case of classification problems, because the target can be treated as a single boolean value, as we did in `mnist_loss`. But binary problems can also be thought of in the context of the more general group of classifiers with any number of categories: in this case, we happen to have two categories. As we saw in the bear classifier, our neural net will return one activation per category.
So in the binary case, what do those activations really indicate? A single pair of activations simply indicates the *relative* confidence of the input being a 3 versus being a 7. The overall values, whether they are both high, or both low, don't matter—all that matters is which is higher, and by how much.
We would expect that since this is just another way of representing the same problem, that we would be able to use `sigmoid` directly on the two-activation version of our neural net. And indeed we can! We can just take the *difference* between the neural net activations, because that reflects how much more sure we are of the input being a 3 than a 7, and then take the sigmoid of that:
```
(acts[:,0]-acts[:,1]).sigmoid()
```
The second column (the probability of it being a 7) will then just be that value subtracted from 1. Now, we need a way to do all this that also works for more than two columns. It turns out that this function, called `softmax`, is exactly that:
``` python
def softmax(x): return exp(x) / exp(x).sum(dim=1, keepdim=True)
```
> jargon: Exponential function (exp): Literally defined as `e**x`, where `e` is a special number approximately equal to 2.718. It is the inverse of the natural logarithm function. Note that `exp` is always positive, and it increases _very_ rapidly!
Let's check that `softmax` returns the same values as `sigmoid` for the first column, and those values subtracted from 1 for the second column:
```
sm_acts = torch.softmax(acts, dim=1)
sm_acts
```
`softmax` is the multi-category equivalent of `sigmoid`—we have to use it any time we have more than two categories and the probabilities of the categories must add to 1, and we often use it even when there are just two categories, just to make things a bit more consistent. We could create other functions that have the properties that all activations are between 0 and 1, and sum to 1; however, no other function has the same relationship to the sigmoid function, which we've seen is smooth and symmetric. Also, we'll see shortly that the softmax function works well hand-in-hand with the loss function we will look at in the next section.
If we have three output activations, such as in our bear classifier, calculating softmax for a single bear image would then look like something like <<bear_softmax>>.
<img alt="Bear softmax example" width="280" id="bear_softmax" caption="Example of softmax on the bear classifier" src="images/att_00062.png">
What does this function do in practice? Taking the exponential ensures all our numbers are positive, and then dividing by the sum ensures we are going to have a bunch of numbers that add up to 1. The exponential also has a nice property: if one of the numbers in our activations `x` is slightly bigger than the others, the exponential will amplify this (since it grows, well... exponentially), which means that in the softmax, that number will be closer to 1.
Intuitively, the softmax function *really* wants to pick one class among the others, so it's ideal for training a classifier when we know each picture has a definite label. (Note that it may be less ideal during inference, as you might want your model to sometimes tell you it doesn't recognize any of the classes that it has seen during training, and not pick a class because it has a slightly bigger activation score. In this case, it might be better to train a model using multiple binary output columns, each using a sigmoid activation.)
Softmax is the first part of the cross-entropy loss—the second part is log likeklihood.
### Log Likelihood
When we calculated the loss for our MNIST example in the last chapter we used:
```python
def mnist_loss(inputs, targets):
inputs = inputs.sigmoid()
return torch.where(targets==1, 1-inputs, inputs).mean()
```
Just as we moved from sigmoid to softmax, we need to extend the loss function to work with more than just binary classification—it needs to be able to classify any number of categories (in this case, we have 37 categories). Our activations, after softmax, are between 0 and 1, and sum to 1 for each row in the batch of predictions. Our targets are integers between 0 and 36.
In the binary case, we used `torch.where` to select between `inputs` and `1-inputs`. When we treat a binary classification as a general classification problem with two categories, it actually becomes even easier, because (as we saw in the previous section) we now have two columns, containing the equivalent of `inputs` and `1-inputs`. So, all we need to do is select from the appropriate column. Let's try to implement this in PyTorch. For our synthetic 3s and 7s example, let's say these are our labels:
```
targ = tensor([0,1,0,1,1,0])
```
and these are the softmax activations:
```
sm_acts
```
Then for each item of `targ` we can use that to select the appropriate column of `sm_acts` using tensor indexing, like so:
```
idx = range(6)
sm_acts[idx, targ]
```
To see exactly what's happening here, let's put all the columns together in a table. Here, the first two columns are our activations, then we have the targets, the row index, and finally the result shown immediately above:
```
#hide_input
from IPython.display import HTML
df = pd.DataFrame(sm_acts, columns=["3","7"])
df['targ'] = targ
df['idx'] = idx
df['loss'] = sm_acts[range(6), targ]
t = df.style.hide_index()
#To have html code compatible with our script
html = t._repr_html_().split('</style>')[1]
html = re.sub(r'<table id="([^"]+)"\s*>', r'<table >', html)
display(HTML(html))
```
Looking at this table, you can see that the final column can be calculated by taking the `targ` and `idx` columns as indices into the two-column matrix containing the `3` and `7` columns. That's what `sm_acts[idx, targ]` is actually doing.
The really interesting thing here is that this actually works just as well with more than two columns. To see this, consider what would happen if we added an activation column for every digit (0 through 9), and then `targ` contained a number from 0 to 9. As long as the activation columns sum to 1 (as they will, if we use softmax), then we'll have a loss function that shows how well we're predicting each digit.
We're only picking the loss from the column containing the correct label. We don't need to consider the other columns, because by the definition of softmax, they add up to 1 minus the activation corresponding to the correct label. Therefore, making the activation for the correct label as high as possible must mean we're also decreasing the activations of the remaining columns.
PyTorch provides a function that does exactly the same thing as `sm_acts[range(n), targ]` (except it takes the negative, because when applying the log afterward, we will have negative numbers), called `nll_loss` (*NLL* stands for *negative log likelihood*):
```
-sm_acts[idx, targ]
F.nll_loss(sm_acts, targ, reduction='none')
```
Despite its name, this PyTorch function does not take the log. We'll see why in the next section, but first, let's see why taking the logarithm can be useful.
### Taking the Log
The function we saw in the previous section works quite well as a loss function, but we can make it a bit better. The problem is that we are using probabilities, and probabilities cannot be smaller than 0 or greater than 1. That means that our model will not care whether it predicts 0.99 or 0.999. Indeed, those numbers are so close together—but in another sense, 0.999 is 10 times more confident than 0.99. So, we want to transform our numbers between 0 and 1 to instead be between negative infinity and infinity. There is a mathematical function that does exactly this: the *logarithm* (available as `torch.log`). It is not defined for numbers less than 0, and looks like this:
```
plot_function(torch.log, min=0,max=4)
```
Does "logarithm" ring a bell? The logarithm function has this identity:
```
y = b**a
a = log(y,b)
```
In this case, we're assuming that `log(y,b)` returns *log y base b*. However, PyTorch actually doesn't define `log` this way: `log` in Python uses the special number `e` (2.718...) as the base.
Perhaps a logarithm is something that you have not thought about for the last 20 years or so. But it's a mathematical idea that is going to be really critical for many things in deep learning, so now would be a great time to refresh your memory. The key thing to know about logarithms is this relationship:
log(a*b) = log(a)+log(b)
When we see it in that format, it looks a bit boring; but think about what this really means. It means that logarithms increase linearly when the underlying signal increases exponentially or multiplicatively. This is used, for instance, in the Richter scale of earthquake severity, and the dB scale of noise levels. It's also often used on financial charts, where we want to show compound growth rates more clearly. Computer scientists love using logarithms, because it means that modification, which can create really really large and really really small numbers, can be replaced by addition, which is much less likely to result in scales that are difficult for our computers to handle.
> s: It's not just computer scientists that love logs! Until computers came along, engineers and scientists used a special ruler called a "slide rule" that did multiplication by adding logarithms. Logarithms are widely used in physics, for multiplying very big or very small numbers, and many other fields.
Taking the mean of the positive or negative log of our probabilities (depending on whether it's the correct or incorrect class) gives us the *negative log likelihood* loss. In PyTorch, `nll_loss` assumes that you already took the log of the softmax, so it doesn't actually do the logarithm for you.
> warning: Confusing Name, Beware: The nll in `nll_loss` stands for "negative log likelihood," but it doesn't actually take the log at all! It assumes you have _already_ taken the log. PyTorch has a function called `log_softmax` that combines `log` and `softmax` in a fast and accurate way. `nll_loss` is deigned to be used after `log_softmax`.
When we first take the softmax, and then the log likelihood of that, that combination is called *cross-entropy loss*. In PyTorch, this is available as `nn.CrossEntropyLoss` (which, in practice, actually does `log_softmax` and then `nll_loss`):
```
loss_func = nn.CrossEntropyLoss()
```
As you see, this is a class. Instantiating it gives you an object which behaves like a function:
```
loss_func(acts, targ)
```
All PyTorch loss functions are provided in two forms, the class just shown above, and also a plain functional form, available in the `F` namespace:
```
F.cross_entropy(acts, targ)
```
Either one works fine and can be used in any situation. We've noticed that most people tend to use the class version, and that's more often used in PyTorch's official docs and examples, so we'll tend to use that too.
By default PyTorch loss functions take the mean of the loss of all items. You can use `reduction='none'` to disable that:
```
nn.CrossEntropyLoss(reduction='none')(acts, targ)
```
> s: An interesting feature about cross-entropy loss appears when we consider its gradient. The gradient of `cross_entropy(a,b)` is just `softmax(a)-b`. Since `softmax(a)` is just the final activation of the model, that means that the gradient is proportional to the difference between the prediction and the target. This is the same as mean squared error in regression (assuming there's no final activation function such as that added by `y_range`), since the gradient of `(a-b)**2` is `2*(a-b)`. Because the gradient is linear, that means we won't see sudden jumps or exponential increases in gradients, which should lead to smoother training of models.
We have now seen all the pieces hidden behind our loss function. But while this puts a number on how well (or badly) our model is doing, it does nothing to help us know if it's actually any good. Let's now see some ways to interpret our model's predictions.
## Model Interpretation
It's very hard to interpret loss functions directly, because they are designed to be things computers can differentiate and optimize, not things that people can understand. That's why we have metrics. These are not used in the optimization process, but just to help us poor humans understand what's going on. In this case, our accuracy is looking pretty good already! So where are we making mistakes?
We saw in <<chapter_intro>> that we can use a confusion matrix to see where our model is doing well, and where it's doing badly:
```
#width 600
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix(figsize=(12,12), dpi=60)
```
Oh dear—in this case, a confusion matrix is very hard to read. We have 37 different breeds of pet, which means we have 37×37 entries in this giant matrix! Instead, we can use the `most_confused` method, which just shows us the cells of the confusion matrix with the most incorrect predictions (here, with at least 5 or more):
```
interp.most_confused(min_val=5)
```
Since we are not pet breed experts, it is hard for us to know whether these category errors reflect actual difficulties in recognizing breeds. So again, we turn to Google. A little bit of Googling tells us that the most common category errors shown here are actually breed differences that even expert breeders sometimes disagree about. So this gives us some comfort that we are on the right track.
We seem to have a good baseline. What can we do now to make it even better?
## Improving Our Model
We will now look at a range of techniques to improve the training of our model and make it better. While doing so, we will explain a little bit more about transfer learning and how to fine-tune our pretrained model as best as possible, without breaking the pretrained weights.
The first thing we need to set when training a model is the learning rate. We saw in the previous chapter that it needs to be just right to train as efficiently as possible, so how do we pick a good one? fastai provides a tool for this.
### The Learning Rate Finder
One of the most important things we can do when training a model is to make sure that we have the right learning rate. If our learning rate is too low, it can take many, many epochs to train our model. Not only does this waste time, but it also means that we may have problems with overfitting, because every time we do a complete pass through the data, we give our model a chance to memorize it.
So let's just make our learning rate really high, right? Sure, let's try that and see what happens:
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(1, base_lr=0.1)
```
That doesn't look good. Here's what happened. The optimizer stepped in the correct direction, but it stepped so far that it totally overshot the minimum loss. Repeating that multiple times makes it get further and further away, not closer and closer!
What do we do to find the perfect learning rate—not too high, and not too low? In 2015 the researcher Leslie Smith came up with a brilliant idea, called the *learning rate finder*. His idea was to start with a very, very small learning rate, something so small that we would never expect it to be too big to handle. We use that for one mini-batch, find what the losses are afterwards, and then increase the learning rate by some percentage (e.g., doubling it each time). Then we do another mini-batch, track the loss, and double the learning rate again. We keep doing this until the loss gets worse, instead of better. This is the point where we know we have gone too far. We then select a learning rate a bit lower than this point. Our advice is to pick either:
- One order of magnitude less than where the minimum loss was achieved (i.e., the minimum divided by 10)
- The last point where the loss was clearly decreasing
The learning rate finder computes those points on the curve to help you. Both these rules usually give around the same value. In the first chapter, we didn't specify a learning rate, using the default value from the fastai library (which is 1e-3):
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
lr_min,lr_steep = learn.lr_find()
print(f"Minimum/10: {lr_min:.2e}, steepest point: {lr_steep:.2e}")
```
We can see on this plot that in the range 1e-6 to 1e-3, nothing really happens and the model doesn't train. Then the loss starts to decrease until it reaches a minimum, and then increases again. We don't want a learning rate greater than 1e-1 as it will give a training that diverges like the one before (you can try for yourself), but 1e-1 is already too high: at this stage we've left the period where the loss was decreasing steadily.
In this learning rate plot it appears that a learning rate around 3e-3 would be appropriate, so let's choose that:
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(2, base_lr=3e-3)
```
> Note: Logarithmic Scale: The learning rate finder plot has a logarithmic scale, which is why the middle point between 1e-3 and 1e-2 is between 3e-3 and 4e-3. This is because we care mostly about the order of magnitude of the learning rate.
It's interesting that the learning rate finder was only discovered in 2015, while neural networks have been under development since the 1950s. Throughout that time finding a good learning rate has been, perhaps, the most important and challenging issue for practitioners. The soltuon does not require any advanced maths, giant computing resources, huge datasets, or anything else that would make it inaccessible to any curious researcher. Furthermore, Leslie Smith, was not part of some exclusive Silicon Valley lab, but was working as a naval researcher. All of this is to say: breakthrough work in deep learning absolutely does not require access to vast resources, elite teams, or advanced mathematical ideas. There is lots of work still to be done that requires just a bit of common sense, creativity, and tenacity.
Now that we have a good learning rate to train our model, let's look at how we can fine-tune the weights of a pretrained model.
### Unfreezing and Transfer Learning
We discussed briefly in <<chapter_intro>> how transfer learning works. We saw that the basic idea is that a pretrained model, trained potentially on millions of data points (such as ImageNet), is fine-tuned for some other task. But what does this really mean?
We now know that a convolutional neural network consists of many linear layers with a nonlinear activation function between each pair, followed by one or more final linear layers with an activation function such as softmax at the very end. The final linear layer uses a matrix with enough columns such that the output size is the same as the number of classes in our model (assuming that we are doing classification).
This final linear layer is unlikely to be of any use for us when we are fine-tuning in a transfer learning setting, because it is specifically designed to classify the categories in the original pretraining dataset. So when we do transfer learning we remove it, throw it away, and replace it with a new linear layer with the correct number of outputs for our desired task (in this case, there would be 37 activations).
This newly added linear layer will have entirely random weights. Therefore, our model prior to fine-tuning has entirely random outputs. But that does not mean that it is an entirely random model! All of the layers prior to the last one have been carefully trained to be good at image classification tasks in general. As we saw in the images from the [Zeiler and Fergus paper](https://arxiv.org/pdf/1311.2901.pdf) in <<chapter_intro>> (see <<img_layer1>> through <<img_layer4>>), the first few layers encode very general concepts, such as finding gradients and edges, and later layers encode concepts that are still very useful for us, such as finding eyeballs and fur.
We want to train a model in such a way that we allow it to remember all of these generally useful ideas from the pretrained model, use them to solve our particular task (classify pet breeds), and only adjust them as required for the specifics of our particular task.
Our challenge when fine-tuning is to replace the random weights in our added linear layers with weights that correctly achieve our desired task (classifying pet breeds) without breaking the carefully pretrained weights and the other layers. There is actually a very simple trick to allow this to happen: tell the optimizer to only update the weights in those randomly added final layers. Don't change the weights in the rest of the neural network at all. This is called *freezing* those pretrained layers.
When we create a model from a pretrained network fastai automatically freezes all of the pretrained layers for us. When we call the `fine_tune` method fastai does two things:
- Trains the randomly added layers for one epoch, with all other layers frozen
- Unfreezes all of the layers, and trains them all for the number of epochs requested
Although this is a reasonable default approach, it is likely that for your particular dataset you may get better results by doing things slightly differently. The `fine_tune` method has a number of parameters you can use to change its behavior, but it might be easiest for you to just call the underlying methods directly if you want to get some custom behavior. Remember that you can see the source code for the method by using the following syntax:
learn.fine_tune??
So let's try doing this manually ourselves. First of all we will train the randomly added layers for three epochs, using `fit_one_cycle`. As mentioned in <<chapter_intro>>, `fit_one_cycle` is the suggested way to train models without using `fine_tune`. We'll see why later in the book; in short, what `fit_one_cycle` does is to start training at a low learning rate, gradually increase it for the first section of training, and then gradually decrease it again for the last section of training.
```
learn.fine_tune??
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fit_one_cycle(3, 3e-3)
```
Then we'll unfreeze the model:
```
learn.unfreeze()
```
and run `lr_find` again, because having more layers to train, and weights that have already been trained for three epochs, means our previously found learning rate isn't appropriate any more:
```
learn.lr_find()
```
Note that the graph is a little different from when we had random weights: we don't have that sharp descent that indicates the model is training. That's because our model has been trained already. Here we have a somewhat flat area before a sharp increase, and we should take a point well before that sharp increase—for instance, 1e-5. The point with the maximum gradient isn't what we look for here and should be ignored.
Let's train at a suitable learning rate:
```
learn.fit_one_cycle(6, lr_max=1e-5)
```
This has improved our model a bit, but there's more we can do. The deepest layers of our pretrained model might not need as high a learning rate as the last ones, so we should probably use different learning rates for those—this is known as using *discriminative learning rates*.
### Discriminative Learning Rates
Even after we unfreeze, we still care a lot about the quality of those pretrained weights. We would not expect that the best learning rate for those pretrained parameters would be as high as for the randomly added parameters, even after we have tuned those randomly added parameters for a few epochs. Remember, the pretrained weights have been trained for hundreds of epochs, on millions of images.
In addition, do you remember the images we saw in <<chapter_intro>>, showing what each layer learns? The first layer learns very simple foundations, like edge and gradient detectors; these are likely to be just as useful for nearly any task. The later layers learn much more complex concepts, like "eye" and "sunset," which might not be useful in your task at all (maybe you're classifying car models, for instance). So it makes sense to let the later layers fine-tune more quickly than earlier layers.
Therefore, fastai's default approach is to use discriminative learning rates. This was originally developed in the ULMFiT approach to NLP transfer learning that we will introduce in <<chapter_nlp>>. Like many good ideas in deep learning, it is extremely simple: use a lower learning rate for the early layers of the neural network, and a higher learning rate for the later layers (and especially the randomly added layers). The idea is based on insights developed by [Jason Yosinski](https://arxiv.org/abs/1411.1792), who showed in 2014 that with transfer learning different layers of a neural network should train at different speeds, as seen in <<yosinski>>.
<img alt="Impact of different layers and training methods on transfer learning (Yosinski)" width="680" caption="Impact of different layers and training methods on transfer learning (courtesy of Jason Yosinski et al.)" id="yosinski" src="images/att_00039.png">
fastai lets you pass a Python `slice` object anywhere that a learning rate is expected. The first value passed will be the learning rate in the earliest layer of the neural network, and the second value will be the learning rate in the final layer. The layers in between will have learning rates that are multiplicatively equidistant throughout that range. Let's use this approach to replicate the previous training, but this time we'll only set the *lowest* layer of our net to a learning rate of 1e-6; the other layers will scale up to 1e-4. Let's train for a while and see what happens:
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fit_one_cycle(3, 3e-3)
learn.unfreeze()
learn.fit_one_cycle(12, lr_max=slice(1e-6,1e-4))
```
Now the fine-tuning is working great!
fastai can show us a graph of the training and validation loss:
```
learn.recorder.plot_loss()
```
As you can see, the training loss keeps getting better and better. But notice that eventually the validation loss improvement slows, and sometimes even gets worse! This is the point at which the model is starting to over fit. In particular, the model is becoming overconfident of its predictions. But this does *not* mean that it is getting less accurate, necessarily. Take a look at the table of training results per epoch, and you will often see that the accuracy continues improving, even as the validation loss gets worse. In the end what matters is your accuracy, or more generally your chosen metrics, not the loss. The loss is just the function we've given the computer to help us to optimize.
Another decision you have to make when training the model is for how long to train for. We'll consider that next.
### Selecting the Number of Epochs
Often you will find that you are limited by time, rather than generalization and accuracy, when choosing how many epochs to train for. So your first approach to training should be to simply pick a number of epochs that will train in the amount of time that you are happy to wait for. Then look at the training and validation loss plots, as shown above, and in particular your metrics, and if you see that they are still getting better even in your final epochs, then you know that you have not trained for too long.
On the other hand, you may well see that the metrics you have chosen are really getting worse at the end of training. Remember, it's not just that we're looking for the validation loss to get worse, but the actual metrics. Your validation loss will first get worse during training because the model gets overconfident, and only later will get worse because it is incorrectly memorizing the data. We only care in practice about the latter issue. Remember, our loss function is just something that we use to allow our optimizer to have something it can differentiate and optimize; it's not actually the thing we care about in practice.
Before the days of 1cycle training it was very common to save the model at the end of each epoch, and then select whichever model had the best accuracy out of all of the models saved in each epoch. This is known as *early stopping*. However, this is very unlikely to give you the best answer, because those epochs in the middle occur before the learning rate has had a chance to reach the small values, where it can really find the best result. Therefore, if you find that you have overfit, what you should actually do is retrain your model from scratch, and this time select a total number of epochs based on where your previous best results were found.
If you have the time to train for more epochs, you may want to instead use that time to train more parameters—that is, use a deeper architecture.
### Deeper Architectures
In general, a model with more parameters can model your data more accurately. (There are lots and lots of caveats to this generalization, and it depends on the specifics of the architectures you are using, but it is a reasonable rule of thumb for now.) For most of the architectures that we will be seeing in this book, you can create larger versions of them by simply adding more layers. However, since we want to use pretrained models, we need to make sure that we choose a number of layers that have already been pretrained for us.
This is why, in practice, architectures tend to come in a small number of variants. For instance, the ResNet architecture that we are using in this chapter comes in variants with 18, 34, 50, 101, and 152 layer, pretrained on ImageNet. A larger (more layers and parameters; sometimes described as the "capacity" of a model) version of a ResNet will always be able to give us a better training loss, but it can suffer more from overfitting, because it has more parameters to overfit with.
In general, a bigger model has the ability to better capture the real underlying relationships in your data, and also to capture and memorize the specific details of your individual images.
However, using a deeper model is going to require more GPU RAM, so you may need to lower the size of your batches to avoid an *out-of-memory error*. This happens when you try to fit too much inside your GPU and looks like:
```
Cuda runtime error: out of memory
```
You may have to restart your notebook when this happens. The way to solve it is to use a smaller batch size, which means passing smaller groups of images at any given time through your model. You can pass the batch size you want to the call creating your `DataLoaders` with `bs=`.
The other downside of deeper architectures is that they take quite a bit longer to train. One technique that can speed things up a lot is *mixed-precision training*. This refers to using less-precise numbers (*half-precision floating point*, also called *fp16*) where possible during training. As we are writing these words in early 2020, nearly all current NVIDIA GPUs support a special feature called *tensor cores* that can dramatically speed up neural network training, by 2-3x. They also require a lot less GPU memory. To enable this feature in fastai, just add `to_fp16()` after your `Learner` creation (you also need to import the module).
You can't really know ahead of time what the best architecture for your particular problem is—you need to try training some. So let's try a ResNet-50 now with mixed precision:
```
from fastai.callback.fp16 import *
learn = cnn_learner(dls, resnet50, metrics=error_rate).to_fp16()
learn.fine_tune(6, freeze_epochs=3)
```
You'll see here we've gone back to using `fine_tune`, since it's so handy! We can pass `freeze_epochs` to tell fastai how many epochs to train for while frozen. It will automatically change learning rates appropriately for most datasets.
In this case, we're not seeing a clear win from the deeper model. This is useful to remember—bigger models aren't necessarily better models for your particular case! Make sure you try small models before you start scaling up.
## Conclusion
In this chapter you learned some important practical tips, both for getting your image data ready for modeling (presizing, data block summary) and for fitting the model (learning rate finder, unfreezing, discriminative learning rates, setting the number of epochs, and using deeper architectures). Using these tools will help you to build more accurate image models, more quickly.
We also discussed cross-entropy loss. This part of the book is worth spending plenty of time on. You aren't likely to need to actually implement cross-entropy loss from scratch yourself in practice, but it's really important you understand the inputs to and output from that function, because it (or a variant of it, as we'll see in the next chapter) is used in nearly every classification model. So when you want to debug a model, or put a model in production, or improve the accuracy of a model, you're going to need to be able to look at its activations and loss, and understand what's going on, and why. You can't do that properly if you don't understand your loss function.
If cross-entropy loss hasn't "clicked" for you just yet, don't worry—you'll get there! First, go back to the last chapter and make sure you really understand `mnist_loss`. Then work gradually through the cells of the notebook for this chapter, where we step through each piece of cross-entropy loss. Make sure you understand what each calculation is doing, and why. Try creating some small tensors yourself and pass them into the functions, to see what they return.
Remember: the choices made in the implementation of cross-entropy loss are not the only possible choices that could have been made. Just like when we looked at regression we could choose between mean squared error and mean absolute difference (L1). If you have other ideas for possible functions that you think might work, feel free to give them a try in this chapter's notebook! (Fair warning though: you'll probably find that the model will be slower to train, and less accurate. That's because the gradient of cross-entropy loss is proportional to the difference between the activation and the target, so SGD always gets a nicely scaled step for the weights.)
## Questionnaire
1. Why do we first resize to a large size on the CPU, and then to a smaller size on the GPU?
1. If you are not familiar with regular expressions, find a regular expression tutorial, and some problem sets, and complete them. Have a look on the book's website for suggestions.
1. What are the two ways in which data is most commonly provided, for most deep learning datasets?
1. Look up the documentation for `L` and try using a few of the new methods is that it adds.
1. Look up the documentation for the Python `pathlib` module and try using a few methods of the `Path` class.
1. Give two examples of ways that image transformations can degrade the quality of the data.
1. What method does fastai provide to view the data in a `DataLoaders`?
1. What method does fastai provide to help you debug a `DataBlock`?
1. Should you hold off on training a model until you have thoroughly cleaned your data?
1. What are the two pieces that are combined into cross-entropy loss in PyTorch?
1. What are the two properties of activations that softmax ensures? Why is this important?
1. When might you want your activations to not have these two properties?
1. Calculate the `exp` and `softmax` columns of <<bear_softmax>> yourself (i.e., in a spreadsheet, with a calculator, or in a notebook).
1. Why can't we use `torch.where` to create a loss function for datasets where our label can have more than two categories?
1. What is the value of log(-2)? Why?
1. What are two good rules of thumb for picking a learning rate from the learning rate finder?
1. What two steps does the `fine_tune` method do?
1. In Jupyter Notebook, how do you get the source code for a method or function?
1. What are discriminative learning rates?
1. How is a Python `slice` object interpreted when passed as a learning rate to fastai?
1. Why is early stopping a poor choice when using 1cycle training?
1. What is the difference between `resnet50` and `resnet101`?
1. What does `to_fp16` do?
### Further Research
1. Find the paper by Leslie Smith that introduced the learning rate finder, and read it.
1. See if you can improve the accuracy of the classifier in this chapter. What's the best accuracy you can achieve? Look on the forums and the book's website to see what other students have achieved with this dataset, and how they did it.
| true |
code
| 0.694691 | null | null | null | null |
|
# Ingest Image Data
When working on computer vision tasks, you may be using a common library such as OpenCV, matplotlib, or pandas. Once we are moving to cloud and start your machine learning journey in Amazon Sagemaker, you will encounter new challenges of loading, reading, and writing files from S3 to a Sagemaker Notebook, and we will discuss several approaches in this section. Due to the size of the data we are dealing with, copying data into the instance is not recommended; you do not need to download data to the Sagemaker to train a model either. But if you want to take a look at a few samples from the image dataset and decide whether any transformation/pre-processing is needed, here are ways to do it.
### Image data: COCO (Common Objects in Context)
**COCO** is a large-scale object detection, segmentation, and captioning dataset. COCO has several features:
* Object segmentation
* Recognition in context
* Superpixel stuff segmentation
* 330K images (>200K labeled)
* 1.5 million object instances
* 80 object categories
* 91 stuff categories
* 5 captions per image
* 250,000 people with keypoints
## Set Up Notebook
```
%pip install -qU 'sagemaker>=2.15.0' 's3fs==0.4.2'
import io
import boto3
import sagemaker
import glob
import tempfile
# Get SageMaker session & default S3 bucket
sagemaker_session = sagemaker.Session()
bucket = sagemaker_session.default_bucket()
prefix = "image_coco/coco_val/val2017"
filename = "000000086956.jpg"
```
## Download image data and write to S3
**Note**: COCO data size is large so this could take around one minute or two. You can download partial files by using [COCOAPI](https://github.com/cocodataset/cocoapi). We recommend to go with a bigger storage instance when you start your notebook instance if you are experimenting with the full dataset.
```
# helper functions to upload data to s3
def write_to_s3(bucket, prefix, filename):
key = "{}/{}".format(prefix, filename)
return boto3.Session().resource("s3").Bucket(bucket).upload_file(filename, key)
# run this cell if you are in SageMaker Studio notebook
#!apt-get install unzip
!wget http://images.cocodataset.org/zips/val2017.zip -O coco_val.zip
# Uncompressing
!unzip -qU -o coco_val.zip -d coco_val
# upload the files to the S3 bucket, we only upload 20 images to S3 bucket to showcase how ingestion works
csv_files = glob.glob("coco_val/val2017/*.jpg")
for filename in csv_files[:20]:
write_to_s3(bucket, prefix, filename)
```
## Method 1: Streaming data from S3 to the SageMaker instance-memory
**Use AWS compatible Python Packages with io Module**
The easiest way to access your files in S3 without copying files into your instance storage is to use pre-built packages that already have implemented options to access data with a specified path string. Streaming means to read the object directly to memory instead of writing it to a file. As an example, the `matplotlib` library has a pre-built function `imread` that usually an URL or path to an image, but here we use S3 objects and BytesIO method to read the image. You can also go with `PIL` package.
```
import matplotlib.image as mpimage
import matplotlib.pyplot as plt
key = "{}/{}".format(prefix, filename)
image_object = boto3.resource("s3").Bucket(bucket).Object(key)
image = mpimage.imread(io.BytesIO(image_object.get()["Body"].read()), "jpg")
plt.figure(0)
plt.imshow(image)
from PIL import Image
im = Image.open(image_object.get()["Body"])
plt.figure(0)
plt.imshow(im)
```
## Method 2: Using temporary files on the SageMaker instance
Another way to work with your usual methods is to create temporary files on your SageMaker instance and feed them into the standard methods as a file path. Tempfiles provides automatic cleanup, meaning that creates temporary files that will be deleted as the file is closed.
```
tmp = tempfile.NamedTemporaryFile()
with open(tmp.name, "wb") as f:
image_object.download_fileobj(f)
f.seek(
0, 2
) # the file will be downloaded in a lazy fashion, so add this to the file descriptor
img = plt.imread(tmp.name)
print(img.shape)
plt.imshow(im)
```
## Method 3: Use AWS native methods
#### s3fs
[S3Fs](https://s3fs.readthedocs.io/en/latest/) is a Pythonic file interface to S3. It builds on top of botocore. The top-level class S3FileSystem holds connection information and allows typical file-system style operations like cp, mv, ls, du, glob, etc., as well as put/get of local files to/from S3.
```
import s3fs
fs = s3fs.S3FileSystem()
data_s3fs_location = "s3://{}/{}/".format(bucket, prefix)
# To List first file in your accessible bucket
fs.ls(data_s3fs_location)[0]
# open it directly with s3fs
data_s3fs_location = "s3://{}/{}/{}".format(bucket, prefix, filename) # S3 URL
with fs.open(data_s3fs_location) as f:
display(Image.open(f))
```
### Citation
Lin, Tsung-Yi, Maire, Michael, Belongie, Serge, Bourdev, Lubomir, Girshick, Ross, Hays, James, Perona, Pietro, Ramanan, Deva, Zitnick, C. Lawrence and Dollár, Piotr Microsoft COCO: Common Objects in Context. (2014). , cite arxiv:1405.0312Comment: 1) updated annotation pipeline description and figures; 2) added new section describing datasets splits; 3) updated author list .
| true |
code
| 0.226998 | null | null | null | null |
|
# Algorithms: linear classifier

This work by Jephian Lin is licensed under a [Creative Commons Attribution 4.0 International License](http://creativecommons.org/licenses/by/4.0/).
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
```
## Linear classifier
The concept of a linear classifier
is to find a line (or hyperplane)
that separates two groups data points
(each data points have labels either $1$ or $-1$).
The normal vector of this line (or hyperplane)
is then called the **linear classifier**.
The line (or hyperplane)
separates the space into two parts.
When a new data point is given,
we may check which part does this point belong to
and then predict the label.

### Linear classifier and inner product
Let ${\bf v}$ be a vector.
Then ${\bf v}$ separate the space into two parts,
$H_+ = \{{\bf p}\in\mathbb{R}^d: {\bf p}\cdot {\bf v} > 0\}$
and
$H_- = \{{\bf p}\in\mathbb{R}^d: {\bf p}\cdot {\bf v} < 0\}$.
Let $\{{\bf x}\}_{i=1}^N$ be a set of $N$ points
with each point labeled as $1$ or $-1$.
Let $y_i$ be the label of ${\bf x}_i$.
We say ${\bf v}$ is a **linear classifier** if
* ${\bf x}_i\cdot{\bf v} > 0 \iff y_i = 1$ for all $i$
* ${\bf x}_i\cdot{\bf v} < 0 \iff y_i = -1$ for all $i$
### `normal` being a linear classifier
Let `normal` be a vector.
Let `X` be a dataset of shape `(N, d)`.
(`X` has `N` samples with `d` features.)
Let `y` be the label of shape `(N, )`.
Through Numpy,
whether `normal` is a linear classifier
can be checked by
`np.all( np.sign(np.dot(X, normal))== y )`.
### `normal` not being a linear classifier
If `normal` is not a linear classifier,
then there must be a data point `X[i]` such that
`np.dot(X[i], normal)` and `y[i]` have the opposite signs.
Equivalently, `np.dot(X[i], normal) * y[i] < 0`.
In this case, we say
`normal` is not a linear classifier
witnessed by `X[i]` and `y[i]`.
### Algorithm
Let `X` be a dataset.
Each data point is labled by `1` or `-1`.
The label is recorded by `y`.
The goal is to find a normal vector `normal`
such that `np.sign(np.dot(X, normal))` is `y` (if possible).
1. Set `normal` as the zero vector (or any vector).
2. If `normal` is not a linear classifier witnessed by `X[i]` and `y[i]`,
then update `normal` by
* `normal -= X[i]` if `np.dot(X[i], normal) > 0` and `y[i] < 0`
* `normal += X[i]` if `np.dot(X[i], normal) > 0` and `y[i] < 0`
3. Repeat Step 2 until `normal` becomes a linear classifier.
Note:
The update process can be simplified into one line below.
```Python
normal = normal + y[i]*X[i]
```
### Pseudocode
**Input**:
a dataset `X` of shape `(N, d)` and
the label `y` of shape `(N,)`
(the label is either `1` or `-1`)
**Output**:
an array `normal = [c1 ... cd]`
such that `np.sign(np.dot(X, normal))` is `y`
```Python
normal = zero vector of dimension d (or any vector)
again = True
while again:
again = False
if `normal` is not a linear classifier
(witnessed by X[i] and y[i]):
update normal
again = True
```
##### Exercise
Given `d = 2`,
create a zero array `normal` of shape `(d, )`.
```
### your answer here
```
##### Exercise
Let `X = np.random.randn(100, 2)`,
`normal = np.random.randn(2)`, and
`y = np.random.choice([-1,1], 100)`.
Write a `for` loop to find every pair `X[i]` and `y[i]`
that witness `normal` not being a linear classifier.
```
### your asnwer here
```
##### Exercise
Following the setting of the previous exercise,
sometimes you just want to find
one pair of `X[i]` and `y[i]`
that witness `normal` not being a linear classifier.
Use `break` to stop the `for` loop when you find one.
```
### your asnwer here
```
##### Exercise
Obtain `X` and `y` by the code below.
```Python
X = np.random.randn(100, 2)
y = np.sign(np.dot(X, np.random.randn(2)))
```
```
### your answer here
```
##### Exercise
Write a function `linear_classifier(X, y)`
that returns a linear classifier `normal`.
```
### your answer here
```
##### Exercise
Let `X = np.random.randn(100, 2)` and
`normal = np.random.randn(2)`.
Compute the accuracy of `normal`.
That is, calculate the number of pairs `X[i]` and `y[i]`
such that `np.dot(X[i], normal)` and `y[i]` have the same sign,
and divide this number by the total number of samples
to get the accuracy.
```
### your answer here
```
##### Exercise
Add a new keyword `acc` to your `linear_classifier` function.
When `acc` is `True`,
print the current accuracy
whenever `normal` is updated.
```
### your answer here
```
##### Exercise
You `linear_classifier` can be very powerful.
Obtain the required settings below.
```Python
X = np.random.randn(100, 2)
y = np.sign(np.dot(X, np.random.randn(2)) + 0.1)
plt.scatter(X[:,0], X[:,1], c=y, cmap='viridis')
df = pd.DataFrame(X, columns=['x1', 'x2'])
df['1'] = 1
```
It is likely that `linear_classifier(X, y, acc=True)` never stops.
But `linear_classifier(df.values, y, acc=True)` will work.
Why? What is the meaning of the output?
```
### your answer here
```
##### Exercise
You `linear_classifier` can be very powerful.
Obtain the required settings below.
```Python
X = np.random.randn(100, 2)
y = np.sign(np.sum(X**2, axis=1) - 0.5)
plt.scatter(X[:,0], X[:,1], c=y, cmap='viridis')
df = pd.DataFrame(X, columns=['x1', 'x2'])
df['x1^2'] = df['x1']**2
df['x2^2'] = df['x2']**2
df['1'] = 1
```
It is likely that `linear_classifier(X, y, acc=True)` never stops.
But `linear_classifier(df.values, y, acc=True)` will work.
Why? What is the meaning of the output?
```
### your answer here
```
##### Sample code for a linear classifier passing through the origin
```
def linear_classifier(X, y, acc=False):
"""
Input:
X: array of shape (N, d) with N samples and d features
y: array of shape (N,); labels of points (-1 or 1)
Output:
an array normal = [c1, ..., cd] of shape (d,)
such that np.sign(np.dot(X, ans)) is y.
"""
N,d = X.shape
normal = np.array([0]*d, X.dtype)
again = True
while again:
again = False
for i in range(N):
row = X[i]
label = y[i]
if np.dot(row, normal) * label <= 0:
normal += label * row
again = True
break
if acc:
print((np.sign(np.dot(X, normal)) == y).mean())
return normal
N = 100
d = 2
X = np.random.randn(N, d)
y = np.sign(np.dot(X, np.random.randn(d)))
plt.scatter(X[:,0], X[:,1], c=y, cmap='viridis')
normal = linear_classifier(X, y, acc=True)
def draw_classifier_origin(X, y, normal):
"""
Input:
X, y: the X, y to be used for linear_classifier
normal: a normal vector
Output:
an illustration of the classifier
This function works only when X.shape[1] == 2.
"""
fig = plt.figure(figsize=(5,5))
ax = plt.axes()
### draw data points
ax.scatter(X[:,0], X[:,1], c=y, cmap='viridis')
### set boundary
xleft, xright = X[:,0].min(), X[:,0].max()
yleft, yright = X[:,1].min(), X[:,1].max()
xwidth = xright - xleft
ywidth = yright - yleft
width = max([xwidth, ywidth])
xleft, xright = xleft - (width-xwidth)/2, xright + (width-xwidth)/2
yleft, yright = yleft - (width-ywidth)/2, yright + (width-ywidth)/2
ax.set_xlim(xleft, xright)
ax.set_ylim(yleft, yright)
### draw normal vector and the line
length = np.sqrt(np.sum(normal ** 2))
c1,c2 = normal / length * (0.25*width)
ax.arrow(0, 0, c1, c2, color='red', head_width=0.05*width)
ax.plot([-4*width*c2, 4*width*c2], [4*width*c1, -4*width*c1], color='red')
# fig.savefig('linear_classifier.png')
draw_classifier_origin(X, y, normal)
```
| true |
code
| 0.579995 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/thomascong121/SocialDistance/blob/master/camera_colibration.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive')
%%capture
!pip install gluoncv
!pip install mxnet-cu101
import gluoncv
from gluoncv import model_zoo, data, utils
from matplotlib import pyplot as plt
import numpy as np
from collections import defaultdict
from mxnet import nd
import mxnet as mx
from skimage import io
import cv2
import os
img_path = '/content/drive/My Drive/social distance/0.png'
img = io.imread(img_path)
io.imshow(img)
io.show()
# keypoint = np.array([[739, 119], [990, 148], [614, 523], [229, 437]]).astype(float)
# keypoint *= 1.59
# keypoint = keypoint.astype(int)
# keypoint
keypoints = [(1175, 189), (1574, 235), (976, 831), (364, 694)]
```
```
import itertools
for i in keypoints:
cv2.circle(img, (i[0], i[1]), 10, (0, 0, 525), -1)
for i in itertools.combinations(keypoints, 2):
print(i)
cv2.line(img, (i[0][0], i[0][1]), (i[1][0], i[1][1]), (0, 255, 0), 2)
plt.imshow(img)
plt.show()
```
```
keypoints_birds_eye_view = [(700, 400), (1200, 400), (1200, 900), (700, 900)]
keypoint = np.float32(keypoints)
keypoints_birds_eye_view = np.float32(keypoints_birds_eye_view)
M = cv2.getPerspectiveTransform(keypoint, keypoints_birds_eye_view)
M
dst_img = cv2.warpPerspective(img, M, (img.shape[1], img.shape[0]))
plt.imshow(dst_img)
plt.show()
img = io.imread(img_path)
class Bird_eye_view_Transformer:
def __init__(self, keypoints, keypoints_birds_eye_view, actual_length, actual_width):
'''
keypoints input order
0 1
3 2
'''
self.keypoint = np.float32(keypoints)
self.keypoints_birds_eye_view = np.float32(keypoints_birds_eye_view)
self.M = cv2.getPerspectiveTransform(self.keypoint, self.keypoints_birds_eye_view)
self.length_ratio = actual_width/(keypoints_birds_eye_view[3][1] - keypoints_birds_eye_view[0][1])
self.width_ratio = actual_length/(keypoints_birds_eye_view[1][0] - keypoints_birds_eye_view[0][0])
def imshow(self, img):
dst_img = cv2.warpPerspective(img, self.M, (img.shape[1], img.shape[0]))
plt.imshow(dst_img)
plt.show()
keypoints = [(1175, 189), (1574, 235), (976, 831), (364, 694)]
keypoints_birds_eye_view = [(700, 400), (1200, 400), (1200, 900), (700, 900)]
actual_length = 10
actual_width = 5
transformer = Bird_eye_view_Transformer(keypoints, keypoints_birds_eye_view, actual_length, actual_width)
transformer.imshow(img)
```
| true |
code
| 0.479443 | null | null | null | null |
|
Text classification is the task of assigning a set of predefined categories to open-ended text. Text classifiers can be used to organize, structure, and categorize pretty much any kind of text – from documents, medical studies and files, and all over the web.We will classify the text into 9 categories.The 9 categories are:
- computer
- science
- politics
- sport
- automobile
- religion
- medicine
- sales
- alt.atheism
# Import Libraries
Let's first import all the required libraries
```
import os
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
import seaborn as sns
import plotly.graph_objects as go
import re
import string
import nltk
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn import svm
from time import time
from sklearn import linear_model
from sklearn import preprocessing
from sklearn.model_selection import StratifiedKFold
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn import model_selection
from sklearn.metrics import accuracy_score, precision_score, recall_score, plot_confusion_matrix, confusion_matrix, f1_score
from statistics import mean
import pickle
from tensorflow import keras
from keras import layers
from keras import losses
from keras import utils
from keras.layers.experimental.preprocessing import TextVectorization
from keras.callbacks import EarlyStopping
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.layers import Dense, Embedding, LSTM, SpatialDropout1D, Bidirectional, Dropout
from tensorflow.keras.models import load_model
import torch
from tqdm.notebook import tqdm
from transformers import BertTokenizer
from torch.utils.data import TensorDataset
from transformers import BertForSequenceClassification
from torch.utils.data import DataLoader, RandomSampler, SequentialSampler
from transformers import AdamW, get_linear_schedule_with_warmup
```
# Load Dataset
We will going to use the 20 news group dataset.Let's load the dataset in dataframe
```
dataset = fetch_20newsgroups(subset='train', remove=('headers', 'footers', 'quotes'), shuffle=True, random_state=42)
df = pd.DataFrame()
df['text'] = dataset.data
df['source'] = dataset.target
label=[]
for i in df['source']:
label.append(dataset.target_names[i])
df['label']=label
# first few rows of the dataset
df.head()
```
We will later use the label enocder to convert the labels (categorical value) into numeric value.So now, we will drop that column
```
# drop source column
df.drop(['source'],axis=1,inplace=True)
```
Let's see the count of each label
```
# value count
df['label'].value_counts()
```
In our dataset we have very less data in a each categorical label and there are 20 categories which are too much.We will combine the sub-categories
- So in politics we have mideast, guns and misc sub-topics we will replace all to politics
- We have sub-categories in sports, we will going to replace this also into sports
- We have two sub categories in religion, we will replace them to one
- We are going to make 9 categories in all
```
# replace to politics
df['label'].replace({'talk.politics.misc':'politics','talk.politics.guns':'politics',
'talk.politics.mideast':'politics'},inplace=True)
# replace to sport
df['label'].replace({'rec.sport.hockey':'sport','rec.sport.baseball':'sport'},inplace=True)
# replace to religion
df['label'].replace({'soc.religion.christian':'religion','talk.religion.misc':'religion'},inplace=True)
# replace to computer
df['label'].replace({'comp.windows.x':'computer','comp.sys.ibm.pc.hardware':'computer',
'comp.os.ms-windows.misc':'computer','comp.graphics':'computer',
'comp.sys.mac.hardware':'computer'},inplace=True)
# replace to sales
df['label'].replace({'misc.forsale':'sales'},inplace=True)
# replace to automobile
df['label'].replace({'rec.autos':'automobile','rec.motorcycles':'automobile'},inplace=True)
# replace to science
df['label'].replace({'sci.crypt':'science','sci.electronics':'science','sci.space':'science'},inplace=True)
# replace to medicine
df['label'].replace({'sci.med':'medicine'},inplace=True)
```
Let's see the number of unique targets
```
# number of targets
df['label'].nunique()
# value count
df['label'].value_counts()
```
We are going to make a number of words column in which there is the number of words in a particular text
```
df['Number_of_words'] = df['text'].apply(lambda x:len(str(x).split()))
df.head()
```
Check the basic stats of number of words, like maximum, minimum, average number of words
```
# basic stats
df['Number_of_words'].describe()
```
So the maximum number of words in our dataset is 11,765.Let's have a look at it
```
df[df['Number_of_words']==11765]
```
So maximu number of words text is belongs to electronics category.In our dataset we have some rows where there are no text at all i.e. the number of words is 0.We will drop those rows
```
no_text = df[df['Number_of_words']==0]
print(len(no_text))
# drop these rows
df.drop(no_text.index,inplace=True)
plt.style.use('ggplot')
plt.figure(figsize=(12,6))
sns.distplot(df['Number_of_words'],kde = False,color="red",bins=200)
plt.title("Frequency distribution of number of words for each text extracted", size=20)
```
# Data Pre-Processing
Now it's time to clean our dataset, we will lower the text, remove the text in square brackets, remove links and remove words containing numbers
```
# cleaning the text
def clean_text(text):
'''Make text lowercase, remove text in square brackets,remove links,remove punctuation
and remove words containing numbers.'''
text = text.lower()
text = re.sub('\[.*?\]', '', text)
text = re.sub('https?://\S+|www\.\S+', '', text)
text = re.sub('<.*?>+', '', text)
text = re.sub('[%s]' % re.escape(string.punctuation), '', text)
text = re.sub('\n', '', text)
text = re.sub('\w*\d\w*', '', text)
return text
# Applying the cleaning function to datasets
df['cleaned_text'] = df['text'].apply(lambda x: clean_text(x))
# updated text
df['cleaned_text'].head()
```
Let's convert our cleaned text into tokens
```
tokenizer=nltk.tokenize.RegexpTokenizer(r'\w+')
df['tokens'] = df['cleaned_text'].apply(lambda x:tokenizer.tokenize(x))
df.head()
```
Stopwords are those english words which do not add much meaning to a sentence.They are very commonly used words and we do not required those words. So we can remove those stopwords
```
# stopwords
stopwords.words('english')[0:5]
```
Let's check number of stopwords in nltk library
```
len(stopwords.words('english'))
```
Now we are going to remome the stopwords from the sentences
```
# removing stopwords
def remove_stopwords(text):
words = [w for w in text if w not in stopwords.words('english')]
return words
df['stopwordremove_tokens'] = df['tokens'].apply(lambda x : remove_stopwords(x))
df.head()
```
It's time to do lemmatization
```
# lemmatization
lem = WordNetLemmatizer()
def lem_word(x):
return [lem.lemmatize(w) for w in x]
df['lemmatized_text'] = df['stopwordremove_tokens'].apply(lem_word)
df.head()
```
Now we are going to combine our text, this is our final text
```
def combine_text(list_of_text):
'''Takes a list of text and combines them into one large chunk of text.'''
combined_text = ' '.join(list_of_text)
return combined_text
df['final_text'] = df['lemmatized_text'].apply(lambda x : combine_text(x))
df.head()
```
So we have cleaned the dataset and remove stopwords, it's possible that there are rows in which the text length is 0.We will find those rows and remove them
```
df['Final_no_of_words'] = df['final_text'].apply(lambda x:len(str(x).split()))
df.head()
# basic stats
df['Final_no_of_words'].describe()
# number of rows with text lenth = 0
print(len(df[df['Final_no_of_words']==0]))
# drop those rows
df.drop(df[df['Final_no_of_words']==0].index,inplace=True)
```
Now our text has been cleaned, we will convert the labels into numeric values using LableEncoder()
```
# label_encoder object knows how to understand word labels.
label_encoder = preprocessing.LabelEncoder()
# Encode labels in column 'species'.
df['target']= label_encoder.fit_transform(df['label'])
df['target'].unique()
```
# Dependent and Independent Variable
```
# dependent and independent variable
X = df['final_text']
y = df['target']
X.shape,y.shape
```
# Bag-of-Words
CountVectorizer is used to transform a given text into a vector on the basis of the frequency(count) of each word that occurs in the entire text.It involves counting the number of occurences each words appears in a document(text)
```
count_vectorizer = CountVectorizer()
count_vector = count_vectorizer.fit_transform(X)
print(count_vector[0].todense())
```
# Tf-Idf
Tf-Idf stands for Term Frequency-Inverse document frequency.It is a techinque to quantify a word in documents,we generally compute a weight to each word which signifies the importance of the word which signifies the importance of the word in the document and corpus
```
tfidf_vectorizer = TfidfVectorizer(min_df = 2,max_df = 0.5,ngram_range = (1,2))
tfidf = tfidf_vectorizer.fit_transform(X)
print(tfidf[0].todense())
```
# SMOTE technique to balance the dataset
So we can clearly see that our dataset is imbalanced dataset.We will use SMOTE technique to balance the dataset.SMOTE is an oversampling technique where the synthetic samples are generated for the minority class.The algorithm helps to overcome the overfitting problem posed by random sampling.
```
# count vector
smote = SMOTE(random_state = 402)
X_smote, Y_smote = smote.fit_resample(count_vector,y)
sns.countplot(Y_smote)
# tfidf
smote = SMOTE(random_state = 402)
X_smote_tfidf, Y_smote_tfidf = smote.fit_resample(tfidf,y)
sns.countplot(Y_smote_tfidf)
```
## Train-Test Split
```
# train-test split countvector
X_train, X_test, y_train, y_test = train_test_split(X_smote, Y_smote, test_size = 0.20, random_state = 0)
X_train.shape, X_test.shape,y_train.shape, y_test.shape
# train-test split tfidf
X_train_tfidf, X_test_tfidf, y_train_tfidf, y_test_tfidf = train_test_split(X_smote_tfidf, Y_smote_tfidf , test_size = 0.20, random_state = 0)
training_time_container = {'linear_svm_tfidf':0,'linear_svm':0,'mnb_naive_bayes_tfidf':0,
'mnb_naive_bayes':0,'random_forest_tfidf':0,'random_forest':0,
'logistic_reg':0,'logistic_reg_tfidf':0}
prediction_time_container = {'linear_svm_tfidf':0,'linear_svm':0,'mnb_naive_bayes_tfidf':0,
'mnb_naive_bayes':0,'random_forest_tfidf':0,'random_forest':0,
'logistic_reg':0,'logistic_reg_tfidf':0}
accuracy_container = {'linear_svm_tfidf':0,'linear_svm':0,'mnb_naive_bayes_tfidf':0,
'mnb_naive_bayes':0,'random_forest_tfidf':0,'random_forest':0,
'logistic_reg':0,'logistic_reg_tfidf':0}
```
# Logistic Regression
```
# on countvector
lg = LogisticRegression(C = 1.0)
#Fitting the model
t0=time()
lg.fit(X_train,y_train)
training_time_container['logistic_reg']=time()-t0
# Predicting the Test set results
t0 = time()
y_pred_lg = lg.predict(X_test)
prediction_time_container['logistic_reg']=time()-t0
lg_test_accuracy = accuracy_score(y_test,y_pred_lg)
accuracy_container['logistic_reg'] = lg_test_accuracy
print('Training Accuracy : ', accuracy_score(y_train,lg.predict(X_train)))
print('Testing Accuracy: ',lg_test_accuracy)
print("Training Time: ",training_time_container['logistic_reg'])
print("Prediction Time: ",prediction_time_container['logistic_reg'])
print(confusion_matrix(y_test,y_pred_lg))
# on tfidf
lg = LogisticRegression(C = 1.0)
#Fitting the model
t0=time()
lg.fit(X_train_tfidf,y_train_tfidf)
training_time_container['logistic_reg_tfidf']=time()-t0
# Predicting the Test set results
t0=time()
ypred_lg_tf = lg.predict(X_test_tfidf)
prediction_time_container['logistic_reg_tfidf']=time()-t0
lg_test_accuracy_tf = accuracy_score(y_test_tfidf,ypred_lg_tf)
accuracy_container['logistic_reg_tfidf'] = lg_test_accuracy_tf
print('Training Accuracy: ', accuracy_score(y_train_tfidf,lg.predict(X_train_tfidf)))
print('Testing Accuracy: ', lg_test_accuracy_tf)
print("Training Time: ",training_time_container['logistic_reg_tfidf'])
print("Prediction Time: ",prediction_time_container['logistic_reg_tfidf'])
print(confusion_matrix(y_test,ypred_lg_tf))
```
## Multinomial Naive Bayes
```
# on countvector
nb = MultinomialNB()
#Fitting the model
t0=time()
nb.fit(X_train,y_train)
training_time_container['mnb_naive_bayes']=time()-t0
# Predicting the Test set results
t0 = time()
y_pred_nb = nb.predict(X_test)
prediction_time_container['mnb_naive_bayes']=time()-t0
mnb_test_accuracy = accuracy_score(y_test,y_pred_nb)
accuracy_container['mnb_naive_bayes'] = mnb_test_accuracy
print('Training Accuracy : ', accuracy_score(y_train,nb.predict(X_train)))
print('Testing Accuracy: ',mnb_test_accuracy)
print("Training Time: ",training_time_container['mnb_naive_bayes'])
print("Prediction Time: ",prediction_time_container['mnb_naive_bayes'])
print(confusion_matrix(y_test,y_pred_nb))
# on tfidf
nb = MultinomialNB()
#Fitting the model
t0=time()
nb.fit(X_train_tfidf,y_train_tfidf)
training_time_container['mnb_naive_bayes_tfidf']=time()-t0
# Predicting the Test set results
t0=time()
ypred_nb_tf = nb.predict(X_test_tfidf)
prediction_time_container['mnb_naive_bayes_tfidf']=time()-t0
mnb_tfidf_test_accuracy = accuracy_score(y_test_tfidf,ypred_nb_tf)
accuracy_container['mnb_naive_bayes_tfidf'] = mnb_tfidf_test_accuracy
print('Training Accuracy: ', accuracy_score(y_train_tfidf,nb.predict(X_train_tfidf)))
print('Testing Accuracy: ',mnb_tfidf_test_accuracy )
print("Training Time: ",training_time_container['mnb_naive_bayes_tfidf'])
print("Prediction Time: ",prediction_time_container['mnb_naive_bayes_tfidf'])
print(confusion_matrix(y_test,ypred_nb_tf))
```
## SVM using Stochastic Gradient Descent
```
# Used hinge loss which gives linear Support Vector Machine. Also set the learning rate to 0.0001 (also the default value)
# which is a constant that's gets multiplied with the regularization term. For penalty, I've used L2 which is the standard
#regularizer for linear SVMs
# on countvector
svm_classifier = linear_model.SGDClassifier(loss='hinge',alpha=0.0001)
t0=time()
svm_classifier.fit(X_train,y_train)
training_time_container['linear_svm']=time()-t0
# Predicting the Test set results
t0=time()
y_pred_svm = svm_classifier.predict(X_test)
prediction_time_container['linear_svm']=time()-t0
svm_test_accuracy = accuracy_score(y_test,y_pred_svm)
accuracy_container['linear_svm'] = svm_test_accuracy
print('Training Accuracy : ', accuracy_score(y_train,svm_classifier.predict(X_train)))
print('Testing Accuracy: ',svm_test_accuracy )
print("Training Time: ",training_time_container['linear_svm'])
print("Prediction Time: ",prediction_time_container['linear_svm'])
print(confusion_matrix(y_test,y_pred_svm))
# on tfidf
svm_classifier = linear_model.SGDClassifier(loss='hinge',alpha=0.0001)
#Fitting the model
t0=time()
svm_classifier.fit(X_train_tfidf,y_train_tfidf)
training_time_container['linear_svm_tfidf']=time()-t0
# Predicting the Test set results
t0=time()
ypred_svm_tf = svm_classifier.predict(X_test_tfidf)
prediction_time_container['linear_svm_tfidf']=time()-t0
svm_test_accuracy_tf = accuracy_score(y_test_tfidf,ypred_svm_tf)
accuracy_container['linear_svm_tfdif'] = svm_test_accuracy_tf
print('Training Accuracy: ', accuracy_score(y_train_tfidf,svm_classifier.predict(X_train_tfidf)))
print('Testing Accuracy: ', svm_test_accuracy_tf)
print("Training Time: ",training_time_container['linear_svm_tfidf'])
print("Prediction Time: ",prediction_time_container['linear_svm_tfidf'])
print(confusion_matrix(y_test,ypred_svm_tf))
```
## RandomForest
```
# on count vectorizer
rf = RandomForestClassifier(n_estimators=50)
t0=time()
rf.fit(X_train,y_train)
training_time_container['random_forest']=time()-t0
# Predicting the Test set results
t0=time()
y_pred_rf = rf.predict(X_test)
prediction_time_container['random_forest']=time()-t0
rf_test_accuracy = accuracy_score(y_test,y_pred_rf)
accuracy_container['random_forest'] = rf_test_accuracy
print('Training Accuracy : ', accuracy_score(y_train,rf.predict(X_train)))
print('Testing Accuracy: ',rf_test_accuracy )
print("Training Time: ",training_time_container['random_forest'])
print("Prediction Time: ",prediction_time_container['random_forest'])
print(confusion_matrix(y_test,y_pred_rf))
# on tfidf
rf = RandomForestClassifier(n_estimators=50)
#Fitting the model
t0=time()
rf.fit(X_train_tfidf,y_train_tfidf)
training_time_container['random_forest_tfidf']=time()-t0
# Predicting the Test set results
t0=time()
ypred_rf_tf = rf.predict(X_test_tfidf)
prediction_time_container['random_forest_tfidf']=time()-t0
rf_test_accuracy_tf = accuracy_score(y_test_tfidf,ypred_rf_tf)
accuracy_container['random_forest_tfidf'] = rf_test_accuracy_tf
print('Training Accuracy: ', accuracy_score(y_train_tfidf,rf.predict(X_train_tfidf)))
print('Testing Accuracy: ',rf_test_accuracy_tf )
print("Training Time: ",training_time_container['random_forest_tfidf'])
print("Prediction Time: ",prediction_time_container['random_forest_tfidf'])
print(confusion_matrix(y_test,ypred_rf_tf ))
fig=go.Figure(data=[go.Bar(y=list(training_time_container.values()),x=list(training_time_container.keys()),
marker={'color':np.arange(len(list(training_time_container.values())))}
,text=list(training_time_container.values()), textposition='auto' )])
fig.update_layout(autosize=True ,plot_bgcolor='rgb(275, 275, 275)',
title="Comparison of Training Time of different classifiers",
xaxis_title="Machine Learning Models",
yaxis_title="Training time in seconds" )
fig.data[0].marker.line.width = 3
fig.data[0].marker.line.color = "black"
fig
fig=go.Figure(data=[go.Bar(y=list(prediction_time_container.values()),x=list(prediction_time_container.keys()),
marker={'color':np.arange(len(list(prediction_time_container.values())))}
,text=list(prediction_time_container.values()), textposition='auto' )])
fig.update_layout(autosize=True ,plot_bgcolor='rgb(275, 275, 275)',
title="Comparison of Prediction Time of different classifiers",
xaxis_title="Machine Learning Models",
yaxis_title="Prediction time in seconds" )
fig.data[0].marker.line.width = 3
fig.data[0].marker.line.color = "black"
fig
fig=go.Figure(data=[go.Bar(y=list(accuracy_container.values()),x=list(accuracy_container.keys()),
marker={'color':np.arange(len(list(accuracy_container.values())))}
,text=list(accuracy_container.values()), textposition='auto' )])
fig.update_layout(autosize=True ,plot_bgcolor='rgb(275, 275, 275)',
title="Comparison of Accuracy Scores of different classifiers",
xaxis_title="Machine Learning Models",
yaxis_title="Accuracy Scores" )
fig.data[0].marker.line.width = 3
fig.data[0].marker.line.color = "black"
fig
```
# Stratified K-fold CV
In machine learning, when we want to train our ML model we split our entire dataset into train set and test set using train test split class present in sklearn.Then we train our model on train set and test our model on test set. The problems that we face are, whenever we change the random_state parameter present in train_test_split(), we get different accuracy for different random_state and hence we can’t exactly point out the accuracy for our model.<br>
The solution for the this problem is to use K-Fold Cross-Validation. But K-Fold Cross Validation also suffer from second problem i.e. random sampling.<br>
The solution for both first and second problem is to use Stratified K-Fold Cross-Validation.Stratified k-fold cross-validation is same as just k-fold cross-validation, But in Stratified k-fold cross-validation, it does stratified sampling instead of random sampling.
## SVM
```
svm_skcv = linear_model.SGDClassifier(loss='hinge',alpha=0.0001)
# StratifiedKFold object.
skf = StratifiedKFold(n_splits=10, shuffle=True, random_state=1)
lst_accu_stratified_svm = []
for train_index, test_index in skf.split(X_smote_tfidf,Y_smote_tfidf):
x_train_fold, x_test_fold = X_smote_tfidf[train_index], X_smote_tfidf[test_index]
y_train_fold, y_test_fold = Y_smote_tfidf[train_index], Y_smote_tfidf[test_index]
svm_skcv.fit(x_train_fold, y_train_fold)
lst_accu_stratified_svm.append(svm_skcv.score(x_test_fold, y_test_fold))
# Print the output.
print('List of possible accuracy:', lst_accu_stratified_svm)
print('\nMaximum Accuracy That can be obtained from this model is:',max(lst_accu_stratified_svm)*100, '%')
print('\nMinimum Accuracy:', min(lst_accu_stratified_svm)*100, '%')
print('\nOverall Accuracy:',mean(lst_accu_stratified_svm)*100, '%')
```
## RandomForest
```
rf_skcv = RandomForestClassifier(n_estimators=50)
# StratifiedKFold object.
skf = StratifiedKFold(n_splits=10, shuffle=True, random_state=1)
lst_accu_stratified_rf = []
for train_index, test_index in skf.split(X_smote_tfidf,Y_smote_tfidf):
x_train_fold, x_test_fold = X_smote_tfidf[train_index], X_smote_tfidf[test_index]
y_train_fold, y_test_fold = Y_smote_tfidf[train_index], Y_smote_tfidf[test_index]
rf_skcv.fit(x_train_fold, y_train_fold)
lst_accu_stratified_rf.append(rf_skcv.score(x_test_fold, y_test_fold))
# Print the output.
print('List of possible accuracy:', lst_accu_stratified_rf)
print('\nMaximum Accuracy That can be obtained from this model is:', max(lst_accu_stratified_rf)*100, '%')
print('\nMinimum Accuracy:', min(lst_accu_stratified_rf)*100, '%')
print('\nOverall Accuracy:', mean(lst_accu_stratified_rf)*100, '%')
```
## Multinomial Naive Bayes
```
nb_skcv = MultinomialNB()
# StratifiedKFold object.
skf = StratifiedKFold(n_splits=10, shuffle=True, random_state=1)
lst_accu_stratified_nb = []
for train_index, test_index in skf.split(X_smote_tfidf,Y_smote_tfidf):
x_train_fold, x_test_fold = X_smote_tfidf[train_index], X_smote_tfidf[test_index]
y_train_fold, y_test_fold = Y_smote_tfidf[train_index], Y_smote_tfidf[test_index]
nb_skcv.fit(x_train_fold, y_train_fold)
lst_accu_stratified_nb.append(nb_skcv.score(x_test_fold, y_test_fold))
# Print the output.
print('List of possible accuracy:', lst_accu_stratified_nb)
print('\nMaximum Accuracy That can be obtained from this model is:', max(lst_accu_stratified_nb)*100, '%')
print('\nMinimum Accuracy:', min(lst_accu_stratified_nb)*100, '%')
print('\nOverall Accuracy:', mean(lst_accu_stratified_nb)*100, '%')
```
# Save the models
```
import joblib
# cv and tfidf
joblib.dump(count_vectorizer, open('cv.pkl', 'wb'),8)
joblib.dump(tfidf_vectorizer, open('tfidf.pkl', 'wb'),8)
# mnb
joblib.dump(nb, open('mnb.pkl', 'wb'),8)
# svm
joblib.dump(svm_classifier, open('svm.pkl', 'wb'),8)
# randomforest
joblib.dump(rf , open('rf.pkl', 'wb'),8)
```
# LSTM
We will not going to create RNN model due to its vanishing gradient problem instead of that we will going to create LSTM model.LSTMs have an additional state called ‘cell state’ through which the network makes adjustments in the information flow. The advantage of this state is that the model can remember or forget the leanings more selectively.
First of all we are going to do tokenization then we will generate sequence of n-grams.After that we will going to do padding.Padding is required because all the sentences are of different length so we need to make them of same length.We will going to do this by adding 0 in the end of the text with the help of pad_sequences function of keras
```
max_features = 6433 # the maximum number of words to keep, based on word frequency
tokenizer = Tokenizer(num_words=max_features )
tokenizer.fit_on_texts(df['cleaned_text'].values)
X = tokenizer.texts_to_sequences(df['cleaned_text'].values)
X = pad_sequences(X, padding = 'post', maxlen = 6433 )
X
X.shape[1]
Y = pd.get_dummies(df['label']).values
Y
X_train, X_test, Y_train, Y_test = train_test_split(X,Y, test_size = 0.25, random_state = 42,stratify = Y)
print(X_train.shape,Y_train.shape)
print(X_test.shape,Y_test.shape)
embid_dim = 300
lstm_out = 32
model = keras.Sequential()
model.add(Embedding(max_features, embid_dim, input_length = X.shape[1] ))
model.add(Bidirectional(LSTM(lstm_out)))
model.add(Dropout(0.4))
model.add(Dense(32, activation = 'relu'))
model.add(Dropout(0.4))
model.add(Dense(9,activation = 'softmax'))
model.summary()
```
So our model is created now it's time to train our model, we will going to use 10 epochs
```
batch_size = 128
earlystop = EarlyStopping(monitor='loss', min_delta=0, patience=3, verbose=0, mode='auto')
model.compile(loss = 'categorical_crossentropy', optimizer='adam',metrics = ['accuracy'])
history = model.fit(X_train, Y_train, epochs = 10, batch_size=batch_size, verbose = 1, validation_data= (X_test, Y_test),callbacks=[earlystop])
```
### Plot Accuracy and Loss
```
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'r', label='Training Loss')
plt.plot(epochs, val_loss, 'b', label='Validation Loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
### Save LSTM model
```
model.save('lstm.h5')
```
# BERT
So now we will going to make the bert model.In our kernel we have less memory so we will going to take 50% of our dataset
```
df_bert = df.sample(frac=0.5)
df_bert.reset_index(inplace=True)
df_bert['target'].value_counts()
```
So our dataset is imbalanced, we split the dataset in a stratified way
```
X_train, X_val, y_train, y_val = train_test_split(df_bert.index.values,
df_bert.target.values,
test_size=0.15,
random_state=42,
stratify=df_bert.target.values)
df_bert['data_type'] = ['not_set']*df_bert.shape[0]
df_bert.loc[X_train, 'data_type'] = 'train'
df_bert.loc[X_val, 'data_type'] = 'val'
```
Now we will construct the BERT Tokenizer.Based on wordpiece.We will intantiate a pre-trained model configuration to encode our data
```
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased',
do_lower_case=True)
```
- To convert all the titles from text into encoded form, we use a function called *batch_encode_plus* and we will proceed train and test data seperately.The first parameter inside the function is the text.
- *add_special_tokens = True* means the sequences will encoded with the special tokens realtive to their model
- *return_attention_mask=True* returns the attention mask according to the special tokenizer defined by *max_length* attribute
```
encoded_data_train = tokenizer.batch_encode_plus(
df_bert[df_bert.data_type=='train'].final_text.values,
add_special_tokens=True,
return_attention_mask=True,
pad_to_max_length=True,
max_length=256,
return_tensors='pt'
)
encoded_data_val = tokenizer.batch_encode_plus(
df_bert[df_bert.data_type=='val'].final_text.values,
add_special_tokens=True,
return_attention_mask=True,
pad_to_max_length=True,
max_length=256,
return_tensors='pt'
)
input_ids_train = encoded_data_train['input_ids']
attention_masks_train = encoded_data_train['attention_mask']
labels_train = torch.tensor(df_bert[df_bert.data_type=='train'].target.values)
input_ids_val = encoded_data_val['input_ids']
attention_masks_val = encoded_data_val['attention_mask']
labels_val = torch.tensor(df_bert[df_bert.data_type=='val'].target.values)
```
Now we got encoded dataset, we can create training data and validation data
```
dataset_train = TensorDataset(input_ids_train, attention_masks_train, labels_train)
dataset_val = TensorDataset(input_ids_val, attention_masks_val, labels_val)
# length of training and validation data
len(dataset_train), len(dataset_val)
```
We are treating each title as its unique sequence, so one sequence will be classified into one of the 12 labels
```
model = BertForSequenceClassification.from_pretrained("bert-base-uncased",
num_labels=12,
output_attentions=False,
output_hidden_states=False)
```
DataLoader combines a dataset and a sampler and provides an iterable over the given dataset.
```
batch_size = 3
dataloader_train = DataLoader(dataset_train,
sampler=RandomSampler(dataset_train),
batch_size=batch_size)
dataloader_validation = DataLoader(dataset_val,
sampler=SequentialSampler(dataset_val),
batch_size=batch_size)
optimizer = AdamW(model.parameters(),
lr=1e-5,
eps=1e-8)
epochs = 3
scheduler = get_linear_schedule_with_warmup(optimizer,
num_warmup_steps=0,
num_training_steps=len(dataloader_train)*epochs)
```
We will use f1 score as a performance metrics
```
def f1_score_func(preds, labels):
preds_flat = np.argmax(preds, axis=1).flatten()
labels_flat = labels.flatten()
return f1_score(labels_flat, preds_flat, average='weighted')
seed_val = 17
random.seed(seed_val)
np.random.seed(seed_val)
torch.manual_seed(seed_val)
torch.cuda.manual_seed_all(seed_val)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model.to(device)
print(device)
```
### Training loop
```
def evaluate(dataloader_val):
model.eval()
loss_val_total = 0
predictions, true_vals = [], []
for batch in dataloader_val:
batch = tuple(b.to(device) for b in batch)
inputs = {'input_ids': batch[0],
'attention_mask': batch[1],
'labels': batch[2],
}
with torch.no_grad():
outputs = model(**inputs)
loss = outputs[0]
logits = outputs[1]
loss_val_total += loss.item()
logits = logits.detach().cpu().numpy()
label_ids = inputs['labels'].cpu().numpy()
predictions.append(logits)
true_vals.append(label_ids)
loss_val_avg = loss_val_total/len(dataloader_val)
predictions = np.concatenate(predictions, axis=0)
true_vals = np.concatenate(true_vals, axis=0)
return loss_val_avg, predictions, true_vals
for epoch in tqdm(range(1, epochs+1)):
#model.train()
loss_train_total = 0
progress_bar = tqdm(dataloader_train, desc='Epoch {:1d}'.format(epoch), leave=False, disable=False)
for batch in progress_bar:
model.zero_grad()
batch = tuple(b.to(device) for b in batch)
inputs = {'input_ids': batch[0],
'attention_mask': batch[1],
'labels': batch[2],
}
outputs = model(**inputs)
loss = outputs[0]
loss_train_total += loss.item()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
optimizer.step()
scheduler.step()
progress_bar.set_postfix({'training_loss': '{:.3f}'.format(loss.item()/len(batch))})
tqdm.write(f'\nEpoch {epoch}')
loss_train_avg = loss_train_total/len(dataloader_train)
tqdm.write(f'Training loss: {loss_train_avg}')
val_loss, predictions, true_vals = evaluate(dataloader_validation)
val_f1 = f1_score_func(predictions, true_vals)
tqdm.write(f'Validation loss: {val_loss}')
tqdm.write(f'F1 Score (Weighted): {val_f1}')
```
| true |
code
| 0.506958 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Upload a Fairness Dashboard to Azure Machine Learning Studio
**This notebook shows how to generate and upload a fairness assessment dashboard from Fairlearn to AzureML Studio**
## Table of Contents
1. [Introduction](#Introduction)
1. [Loading the Data](#LoadingData)
1. [Processing the Data](#ProcessingData)
1. [Training Models](#TrainingModels)
1. [Logging in to AzureML](#LoginAzureML)
1. [Registering the Models](#RegisterModels)
1. [Using the Fairlearn Dashboard](#LocalDashboard)
1. [Uploading a Fairness Dashboard to Azure](#AzureUpload)
1. Computing Fairness Metrics
1. Uploading to Azure
1. [Conclusion](#Conclusion)
<a id="Introduction"></a>
## Introduction
In this notebook, we walk through a simple example of using the `azureml-contrib-fairness` package to upload a collection of fairness statistics for a fairness dashboard. It is an example of integrating the [open source Fairlearn package](https://www.github.com/fairlearn/fairlearn) with Azure Machine Learning. This is not an example of fairness analysis or mitigation - this notebook simply shows how to get a fairness dashboard into the Azure Machine Learning portal. We will load the data and train a couple of simple models. We will then use Fairlearn to generate data for a Fairness dashboard, which we can upload to Azure Machine Learning portal and view there.
### Setup
To use this notebook, an Azure Machine Learning workspace is required.
Please see the [configuration notebook](../../configuration.ipynb) for information about creating one, if required.
This notebook also requires the following packages:
* `azureml-contrib-fairness`
* `fairlearn==0.4.6`
* `joblib`
* `shap`
<a id="LoadingData"></a>
## Loading the Data
We use the well-known `adult` census dataset, which we load using `shap` (for convenience). We start with a fairly unremarkable set of imports:
```
from sklearn import svm
from sklearn.preprocessing import LabelEncoder, StandardScaler
from sklearn.linear_model import LogisticRegression
import pandas as pd
import shap
```
Now we can load the data:
```
X_raw, Y = shap.datasets.adult()
```
We can take a look at some of the data. For example, the next cells shows the counts of the different races identified in the dataset:
```
print(X_raw["Race"].value_counts().to_dict())
```
<a id="ProcessingData"></a>
## Processing the Data
With the data loaded, we process it for our needs. First, we extract the sensitive features of interest into `A` (conventionally used in the literature) and put the rest of the feature data into `X`:
```
A = X_raw[['Sex','Race']]
X = X_raw.drop(labels=['Sex', 'Race'],axis = 1)
X = pd.get_dummies(X)
```
Next, we apply a standard set of scalings:
```
sc = StandardScaler()
X_scaled = sc.fit_transform(X)
X_scaled = pd.DataFrame(X_scaled, columns=X.columns)
le = LabelEncoder()
Y = le.fit_transform(Y)
```
Finally, we can then split our data into training and test sets, and also make the labels on our test portion of `A` human-readable:
```
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test, A_train, A_test = train_test_split(X_scaled,
Y,
A,
test_size = 0.2,
random_state=0,
stratify=Y)
# Work around indexing issue
X_train = X_train.reset_index(drop=True)
A_train = A_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
A_test = A_test.reset_index(drop=True)
# Improve labels
A_test.Sex.loc[(A_test['Sex'] == 0)] = 'female'
A_test.Sex.loc[(A_test['Sex'] == 1)] = 'male'
A_test.Race.loc[(A_test['Race'] == 0)] = 'Amer-Indian-Eskimo'
A_test.Race.loc[(A_test['Race'] == 1)] = 'Asian-Pac-Islander'
A_test.Race.loc[(A_test['Race'] == 2)] = 'Black'
A_test.Race.loc[(A_test['Race'] == 3)] = 'Other'
A_test.Race.loc[(A_test['Race'] == 4)] = 'White'
```
<a id="TrainingModels"></a>
## Training Models
We now train a couple of different models on our data. The `adult` census dataset is a classification problem - the goal is to predict whether a particular individual exceeds an income threshold. For the purpose of generating a dashboard to upload, it is sufficient to train two basic classifiers. First, a logistic regression classifier:
```
lr_predictor = LogisticRegression(solver='liblinear', fit_intercept=True)
lr_predictor.fit(X_train, Y_train)
```
And for comparison, a support vector classifier:
```
svm_predictor = svm.SVC()
svm_predictor.fit(X_train, Y_train)
```
<a id="LoginAzureML"></a>
## Logging in to AzureML
With our two classifiers trained, we can log into our AzureML workspace:
```
from azureml.core import Workspace, Experiment, Model
ws = Workspace.from_config()
ws.get_details()
```
<a id="RegisterModels"></a>
## Registering the Models
Next, we register our models. By default, the subroutine which uploads the models checks that the names provided correspond to registered models in the workspace. We define a utility routine to do the registering:
```
import joblib
import os
os.makedirs('models', exist_ok=True)
def register_model(name, model):
print("Registering ", name)
model_path = "models/{0}.pkl".format(name)
joblib.dump(value=model, filename=model_path)
registered_model = Model.register(model_path=model_path,
model_name=name,
workspace=ws)
print("Registered ", registered_model.id)
return registered_model.id
```
Now, we register the models. For convenience in subsequent method calls, we store the results in a dictionary, which maps the `id` of the registered model (a string in `name:version` format) to the predictor itself:
```
model_dict = {}
lr_reg_id = register_model("fairness_linear_regression", lr_predictor)
model_dict[lr_reg_id] = lr_predictor
svm_reg_id = register_model("fairness_svm", svm_predictor)
model_dict[svm_reg_id] = svm_predictor
```
<a id="LocalDashboard"></a>
## Using the Fairlearn Dashboard
We can now examine the fairness of the two models we have training, both as a function of race and (binary) sex. Before uploading the dashboard to the AzureML portal, we will first instantiate a local instance of the Fairlearn dashboard.
Regardless of the viewing location, the dashboard is based on three things - the true values, the model predictions and the sensitive feature values. The dashboard can use predictions from multiple models and multiple sensitive features if desired (as we are doing here).
Our first step is to generate a dictionary mapping the `id` of the registered model to the corresponding array of predictions:
```
ys_pred = {}
for n, p in model_dict.items():
ys_pred[n] = p.predict(X_test)
```
We can examine these predictions in a locally invoked Fairlearn dashboard. This can be compared to the dashboard uploaded to the portal (in the next section):
```
from fairlearn.widget import FairlearnDashboard
FairlearnDashboard(sensitive_features=A_test,
sensitive_feature_names=['Sex', 'Race'],
y_true=Y_test.tolist(),
y_pred=ys_pred)
```
<a id="AzureUpload"></a>
## Uploading a Fairness Dashboard to Azure
Uploading a fairness dashboard to Azure is a two stage process. The `FairlearnDashboard` invoked in the previous section relies on the underlying Python kernel to compute metrics on demand. This is obviously not available when the fairness dashboard is rendered in AzureML Studio. The required stages are therefore:
1. Precompute all the required metrics
1. Upload to Azure
### Computing Fairness Metrics
We use Fairlearn to create a dictionary which contains all the data required to display a dashboard. This includes both the raw data (true values, predicted values and sensitive features), and also the fairness metrics. The API is similar to that used to invoke the Dashboard locally. However, there are a few minor changes to the API, and the type of problem being examined (binary classification, regression etc.) needs to be specified explicitly:
```
sf = { 'Race': A_test.Race, 'Sex': A_test.Sex }
from fairlearn.metrics._group_metric_set import _create_group_metric_set
dash_dict = _create_group_metric_set(y_true=Y_test,
predictions=ys_pred,
sensitive_features=sf,
prediction_type='binary_classification')
```
The `_create_group_metric_set()` method is currently underscored since its exact design is not yet final in Fairlearn.
### Uploading to Azure
We can now import the `azureml.contrib.fairness` package itself. We will round-trip the data, so there are two required subroutines:
```
from azureml.contrib.fairness import upload_dashboard_dictionary, download_dashboard_by_upload_id
```
Finally, we can upload the generated dictionary to AzureML. The upload method requires a run, so we first create an experiment and a run. The uploaded dashboard can be seen on the corresponding Run Details page in AzureML Studio. For completeness, we also download the dashboard dictionary which we uploaded.
```
exp = Experiment(ws, "notebook-01")
print(exp)
run = exp.start_logging()
try:
dashboard_title = "Sample notebook upload"
upload_id = upload_dashboard_dictionary(run,
dash_dict,
dashboard_name=dashboard_title)
print("\nUploaded to id: {0}\n".format(upload_id))
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()
```
Finally, we can verify that the dashboard dictionary which we downloaded matches our upload:
```
print(dash_dict == downloaded_dict)
```
<a id="Conclusion"></a>
## Conclusion
In this notebook we have demonstrated how to generate and upload a fairness dashboard to AzureML Studio. We have not discussed how to analyse the results and apply mitigations. Those topics will be covered elsewhere.
| true |
code
| 0.487063 | null | null | null | null |
|
# Heaps
## Overview
For this assignment you will start by modifying the heap data stucture implemented in class to allow it to keep its elements sorted by an arbitrary priority (identified by a `key` function), then use the augmented heap to efficiently compute the running median of a set of numbers.
## 1. Augmenting the Heap with a `key` function
The heap implementation covered in class is for a so-called "max-heap" — i.e., one where elements are organized such that the one with the maximum value can be efficiently extracted.
This limits our usage of the data structure, however. Our heap can currently only accommodate elements that have a natural ordering (i.e., they can be compared using the '`>`' and '`<`' operators as used in the implementation), and there's no way to order elements based on some partial or computed property.
To make our heap more flexible, you'll update it to allow a `key` function to be passed to its initializer. This function will be used to extract a value from each element added to the heap; these values, in turn, will be used to order the elements.
We can now easily create heaps with different semantics, e.g.,
- `Heap(len)` will prioritize elements based on their length (e.g., applicable to strings, sequences, etc.)
- `Heap(lambda x: -x)` can function as a *min-heap* for numbers
- `Heap(lambda x: x.prop)` will prioritize elements based on their `prop` attribute
If no `key` function is provided, the default max-heap behavior should be used — the "`lambda x:x`" default value for the `__init__` method does just that.
You will, at the very least, need to update the `_heapify` and `add` methods, below, to complete this assignment. (Note, also, that `pop_max` has been renamed `pop`, while `max` has been renamed `peek`, to reflect their more general nature.)
```
class Heap:
def __init__(self, key=lambda x:x):
self.data = []
self.key = key
@staticmethod
def _parent(idx):
return (idx-1)//2
@staticmethod
def _left(idx):
return idx*2+1
@staticmethod
def _right(idx):
return idx*2+2
def heapify(self, idx=0):
key = self.key
current = idx
left = Heap._left(current)
right = Heap._right(current)
limit = len(self.data)
maxidx = current
while True:
if left < limit and key(self.data[current]) < key(self.data[left]):
maxidx = left
if right < limit and key(self.data[maxidx]) < key(self.data[right]):
maxidx = right
if maxidx != current:
self.data[current], self.data[maxidx] = self.data[maxidx], self.data[current]
current = maxidx
left = Heap._left(current)
right = Heap._right(current)
else:
break
def add(self, x):
key = self.key
self.data.append(x)
current = len(self.data)-1
parent = Heap._parent(current)
while True:
if current != 0 and key(self.data[current]) > key(self.data[parent]):
self.data[current], self.data[parent] = self.data[parent], self.data[current]
current = parent
parent = Heap._parent(current)
else:
break
def peek(self):
return self.data[0]
def pop(self):
ret = self.data[0]
self.data[0] = self.data[len(self.data)-1]
del self.data[len(self.data)-1]
self.heapify()
return ret
def __bool__(self):
return len(self.data) > 0
def __len__(self):
return len(self.data)
def __repr__(self):
return repr(self.data)
# (1 point)
from unittest import TestCase
import random
tc = TestCase()
h = Heap()
random.seed(0)
for _ in range(10):
h.add(random.randrange(100))
tc.assertEqual(h.data, [97, 61, 65, 49, 51, 53, 62, 5, 38, 33])
# (1 point)
from unittest import TestCase
import random
tc = TestCase()
h = Heap(lambda x:-x)
random.seed(0)
for _ in range(10):
h.add(random.randrange(100))
tc.assertEqual(h.data, [5, 33, 53, 38, 49, 65, 62, 97, 51, 61])
# (2 points)
from unittest import TestCase
import random
tc = TestCase()
h = Heap(lambda s:len(s))
h.add('hello')
h.add('hi')
h.add('abracadabra')
h.add('supercalifragilisticexpialidocious')
h.add('0')
tc.assertEqual(h.data,
['supercalifragilisticexpialidocious', 'abracadabra', 'hello', 'hi', '0'])
# (2 points)
from unittest import TestCase
import random
tc = TestCase()
h = Heap()
random.seed(0)
lst = list(range(-1000, 1000))
random.shuffle(lst)
for x in lst:
h.add(x)
for x in range(999, -1000, -1):
tc.assertEqual(x, h.pop())
# (2 points)
from unittest import TestCase
import random
tc = TestCase()
h = Heap(key=lambda x:abs(x))
random.seed(0)
lst = list(range(-1000, 1000, 3))
random.shuffle(lst)
for x in lst:
h.add(x)
for x in reversed(sorted(range(-1000, 1000, 3), key=lambda x:abs(x))):
tc.assertEqual(x, h.pop())
```
## 2. Computing the Running Median
The median of a series of numbers is simply the middle term if ordered by magnitude, or, if there is no middle term, the average of the two middle terms. E.g., the median of the series [3, 1, 9, 25, 12] is **9**, and the median of the series [8, 4, 11, 18] is **9.5**.
If we are in the process of accumulating numerical data, it is useful to be able to compute the *running median* — where, as each new data point is encountered, an updated median is computed. This should be done, of course, as efficiently as possible.
The following function demonstrates a naive way of computing the running medians based on the series passed in as an iterable.
```
def running_medians_naive(iterable):
values = []
medians = []
for i, x in enumerate(iterable):
values.append(x)
values.sort()
if i%2 == 0:
medians.append(values[i//2])
else:
medians.append((values[i//2] + values[i//2+1]) / 2)
return medians
running_medians_naive([3, 1, 9, 25, 12])
running_medians_naive([8, 4, 11, 18])
```
Note that the function keeps track of all the values encountered during the iteration and uses them to compute the running medians, which are returned at the end as a list. The final running median, naturally, is simply the median of the entire series.
Unfortunately, because the function sorts the list of values during every iteration it is incredibly inefficient. Your job is to implement a version that computes each running median in O(log N) time using, of course, the heap data structure!
### Hints
- You will need to use two heaps for your solution: one min-heap, and one max-heap.
- The min-heap should be used to keep track of all values *greater than* the most recent running median, and the max-heap for all values *less than* the most recent running median — this way, the median will lie between the minimum value on the min-heap and the maximum value on the max-heap (both of which can be efficiently extracted)
- In addition, the difference between the number of values stored in the min-heap and max-heap must never exceed 1 (to ensure the median is being computed). This can be taken care of by intelligently `pop`-ping/`add`-ing elements between the two heaps.
```
def running_medians(iterable):
min_heap = Heap(lambda x:-x)
max_heap = Heap()
medians = []
for val in iterable:
try:
if middle != None:
if val >= middle:
min_heap.add(val)
max_heap.add(middle)
else:
min_heap.add(middle)
max_heap.add(val)
middle = None
medians.append((min_heap.peek() + max_heap.peek()) / 2)
else:
median = (min_heap.peek() + max_heap.peek()) / 2
if val >= median:
min_heap.add(val)
middle = min_heap.pop()
else:
max_heap.add(val)
middle = max_heap.pop()
medians.append(middle)
except:
middle = val
medians.append(middle)
return medians
# (2 points)
from unittest import TestCase
tc = TestCase()
tc.assertEqual([3, 2.0, 3, 6.0, 9], running_medians([3, 1, 9, 25, 12]))
# (2 points)
import random
from unittest import TestCase
tc = TestCase()
vals = [random.randrange(10000) for _ in range(1000)]
tc.assertEqual(running_medians_naive(vals), running_medians(vals))
# (4 points) MUST COMPLETE IN UNDER 10 seconds!
import random
from unittest import TestCase
tc = TestCase()
vals = [random.randrange(100000) for _ in range(100001)]
m_mid = sorted(vals[:50001])[50001//2]
m_final = sorted(vals)[len(vals)//2]
running = running_medians(vals)
tc.assertEqual(m_mid, running[50000])
tc.assertEqual(m_final, running[-1])
```
| true |
code
| 0.552057 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/DingLi23/s2search/blob/pipelining/pipelining/exp-csit/exp-csit_csit_shapley_value.ipynb" target="_blank"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### Experiment Description
> This notebook is for experiment \<exp-csit\> and data sample \<csit\>.
### Initialization
```
%reload_ext autoreload
%autoreload 2
import numpy as np, sys, os
sys.path.insert(1, '../../')
from shapley_value import compute_shapley_value, feature_key_list
sv = compute_shapley_value('exp-csit', 'csit')
```
### Plotting
```
import matplotlib.pyplot as plt
import numpy as np
from s2search_score_pdp import pdp_based_importance
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 5), dpi=200)
# generate some random test data
all_data = []
average_sv = []
sv_global_imp = []
for player_sv in [f'{player}_sv' for player in feature_key_list]:
all_data.append(sv[player_sv])
average_sv.append(pdp_based_importance(sv[player_sv]))
sv_global_imp.append(np.mean(np.abs(list(sv[player_sv]))))
# average_sv.append(np.std(sv[player_sv]))
# print(np.max(sv[player_sv]))
# plot violin plot
axs[0].violinplot(all_data,
showmeans=False,
showmedians=True)
axs[0].set_title('Violin plot')
# plot box plot
axs[1].boxplot(all_data,
showfliers=False,
showmeans=True,
)
axs[1].set_title('Box plot')
# adding horizontal grid lines
for ax in axs:
ax.yaxis.grid(True)
ax.set_xticks([y + 1 for y in range(len(all_data))],
labels=['title', 'abstract', 'venue', 'authors', 'year', 'n_citations'])
ax.set_xlabel('Features')
ax.set_ylabel('Shapley Value')
plt.show()
plt.rcdefaults()
fig, ax = plt.subplots(figsize=(12, 4), dpi=200)
# Example data
feature_names = ('title', 'abstract', 'venue', 'authors', 'year', 'n_citations')
y_pos = np.arange(len(feature_names))
# error = np.random.rand(len(feature_names))
# ax.xaxis.grid(True)
ax.barh(y_pos, average_sv, align='center', color='#008bfb')
ax.set_yticks(y_pos, labels=feature_names)
ax.invert_yaxis() # labels read top-to-bottom
ax.set_xlabel('PDP-based Feature Importance on Shapley Value')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
_, xmax = plt.xlim()
plt.xlim(0, xmax + 1)
for i, v in enumerate(average_sv):
margin = 0.05
ax.text(v + margin if v > 0 else margin, i, str(round(v, 4)), color='black', ha='left', va='center')
plt.show()
plt.rcdefaults()
fig, ax = plt.subplots(figsize=(12, 4), dpi=200)
# Example data
feature_names = ('title', 'abstract', 'venue', 'authors', 'year', 'n_citations')
y_pos = np.arange(len(feature_names))
# error = np.random.rand(len(feature_names))
# ax.xaxis.grid(True)
ax.barh(y_pos, sv_global_imp, align='center', color='#008bfb')
ax.set_yticks(y_pos, labels=feature_names)
ax.invert_yaxis() # labels read top-to-bottom
ax.set_xlabel('SHAP Feature Importance')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
_, xmax = plt.xlim()
plt.xlim(0, xmax + 1)
for i, v in enumerate(sv_global_imp):
margin = 0.05
ax.text(v + margin if v > 0 else margin, i, str(round(v, 4)), color='black', ha='left', va='center')
plt.show()
```
| true |
code
| 0.677487 | null | null | null | null |
|
# Intro to PyTorch
```
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(10)
V = torch.Tensor([1., 2., 3.])
M = torch.Tensor([[1., 2., 3.], [4.,5.,6.]])
torch.randn((2, 3, 4, 5)).view(12, -1)
data = autograd.Variable(torch.randn(2, 2))
print(data)
print(F.relu(data))
print(F.sigmoid(data))
print(data.view(-1))
print(F.softmax(data.view(-1)))
print(F.log_softmax(data.view(-1)))
```
## Logistic Regression with Bag of Words
```
data = [("me gusta comer en la cafeteria".split(), "SPANISH"),
("Give it to me".split(), "ENGLISH"),
("No creo que sea una buena idea".split(), "SPANISH"),
("No it is not a good idea to get lost at sea".split(), "ENGLISH")]
test_data = [("Yo creo que si".split(), "SPANISH"),
("it is lost on me".split(), "ENGLISH")]
# word_to_ix maps each word in the vocab to a unique integer, which will be its
# index into the Bag of words vector
word_to_ix = {}
for sent, _ in data + test_data:
for word in sent:
if word not in word_to_ix:
word_to_ix[word] = len(word_to_ix)
print(word_to_ix)
VOCAB_SIZE = len(word_to_ix)
NUM_LABELS = 2
class BoWClassifier(nn.Module): # inheriting from nn.Module!
def __init__(self, num_labels, vocab_size):
# calls the init function of nn.Module. Dont get confused by syntax,
# just always do it in an nn.Module
super(BoWClassifier, self).__init__()
# Define the parameters that you will need. In this case, we need A and b,
# the parameters of the affine mapping.
# Torch defines nn.Linear(), which provides the affine map.
# Make sure you understand why the input dimension is vocab_size
# and the output is num_labels!
self.linear = nn.Linear(vocab_size, num_labels)
# NOTE! The non-linearity log softmax does not have parameters! So we don't need
# to worry about that here
def forward(self, bow_vec):
# Pass the input through the linear layer,
# then pass that through log_softmax.
# Many non-linearities and other functions are in torch.nn.functional
return F.log_softmax(self.linear(bow_vec))
def make_bow_vector(sentence, word_to_ix):
vec = torch.zeros(len(word_to_ix))
for word in sentence:
vec[word_to_ix[word]] += 1
return vec.view(1, -1)
def make_target(label, label_to_ix):
return torch.LongTensor([label_to_ix[label]])
model = BoWClassifier(NUM_LABELS, VOCAB_SIZE)
# the model knows its parameters. The first output below is A, the second is b.
# Whenever you assign a component to a class variable in the __init__ function
# of a module, which was done with the line
# self.linear = nn.Linear(...)
# Then through some Python magic from the Pytorch devs, your module
# (in this case, BoWClassifier) will store knowledge of the nn.Linear's parameters
for param in model.parameters():
print(param)
# To run the model, pass in a BoW vector, but wrapped in an autograd.Variable
sample = data[0]
bow_vector = make_bow_vector(sample[0], word_to_ix)
log_probs = model(autograd.Variable(bow_vector))
print(log_probs)
label_to_ix = {"SPANISH": 0, "ENGLISH": 1}
# Run on test data before we train, just to see a before-and-after
for instance, label in test_data:
bow_vec = autograd.Variable(make_bow_vector(instance, word_to_ix))
log_probs = model(bow_vec)
print(log_probs)
# Print the matrix column corresponding to "creo"
print(next(model.parameters())[:, word_to_ix["creo"]])
loss_function = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
# Usually you want to pass over the training data several times.
# 100 is much bigger than on a real data set, but real datasets have more than
# two instances. Usually, somewhere between 5 and 30 epochs is reasonable.
for epoch in range(100):
for instance, label in data:
# Step 1. Remember that Pytorch accumulates gradients.
# We need to clear them out before each instance
model.zero_grad()
# Step 2. Make our BOW vector and also we must wrap the target in a
# Variable as an integer. For example, if the target is SPANISH, then
# we wrap the integer 0. The loss function then knows that the 0th
# element of the log probabilities is the log probability
# corresponding to SPANISH
bow_vec = autograd.Variable(make_bow_vector(instance, word_to_ix))
target = autograd.Variable(make_target(label, label_to_ix))
# Step 3. Run our forward pass.
log_probs = model(bow_vec)
# Step 4. Compute the loss, gradients, and update the parameters by
# calling optimizer.step()
loss = loss_function(log_probs, target)
loss.backward()
optimizer.step()
for instance, label in test_data:
bow_vec = autograd.Variable(make_bow_vector(instance, word_to_ix))
log_probs = model(bow_vec)
print(log_probs)
# Index corresponding to Spanish goes up, English goes down!
print(next(model.parameters())[:, word_to_ix["creo"]])
```
| true |
code
| 0.743698 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/teatime77/xbrl-reader/blob/master/notebook/sklearn.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### Matplotlibで日本語が表示できるようにします。
#### IPAフォントをインストールします。
```
!apt-get -y install fonts-ipafont-gothic
```
#### Matplotlibのフォントのキャッシュを再構築します。
```
import matplotlib
matplotlib.font_manager._rebuild()
```
#### <font color="red">キャッシュの再構築を有効にするために、ここでランタイムを再起動してください。</font>
### <font color="red">以下の中から予測したい項目のコメントをはずしてください。</font>
```
target = '売上高'
# target = '営業利益'
# target = '経常利益'
# target = '税引前純利益'
```
### <font color="red">グリッドサーチをする場合は、以下の変数の値をTrueにしてください。</font>
```
use_grid_search = False
```
### 選択した項目に対応するファイルをダウンロードします。
```
if target == '売上高':
! wget http://lkzf.info/xbrl/data/2020-04-08/preprocess-uriage.pickle
elif target == '営業利益':
! wget http://lkzf.info/xbrl/data/2020-04-08/preprocess-eigyo.pickle
elif target == '経常利益':
! wget http://lkzf.info/xbrl/data/2020-04-08/preprocess-keijo.pickle
elif target == '税引前純利益':
! wget http://lkzf.info/xbrl/data/2020-04-08/preprocess-jun.pickle
```
### CatBoostをインストールします。
```
! pip install catboost
```
### 必要なライブラリをインポートします。
```
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.linear_model import Ridge
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
from catboost import CatBoostRegressor
sns.set(font='IPAGothic')
```
### データを読み込みます。
```
import pickle
if target == '売上高':
file_name = 'preprocess-uriage.pickle'
elif target == '営業利益':
file_name = 'preprocess-eigyo.pickle'
elif target == '経常利益':
file_name = 'preprocess-keijo.pickle'
elif target == '税引前純利益':
file_name = 'preprocess-jun.pickle'
else:
assert False
with open(file_name, 'rb') as f:
data = pickle.load(f)
df = data['data_frame']
y_column = data['y_column']
```
### トレーニングデータとテストデータに分けます。
```
X_columns = [ x for x in df.columns if x != y_column ]
# トレーニングデータとテストデータに分けます。
X_train, X_test, y_train, y_test = train_test_split(df[X_columns], df[y_column], test_size=0.2, random_state=0)
```
### モデルを実行します。
```
from sklearn.model_selection import GridSearchCV
def run_model(model):
global y_test, y_pred
if use_grid_search and type(model) in [ RandomForestRegressor, XGBRegressor, LGBMRegressor, CatBoostRegressor ]:
# グリッドサーチをする場合
model = GridSearchCV(model, {'max_depth': [2,4,6], 'n_estimators': [50,100,200]}, verbose=2, n_jobs=-1)
# トレーニングデータで学習します。
result = model.fit(X_train, y_train)
if hasattr(result, 'best_params_'):
# 最適なパラメータがある場合
print ('best params =', result.best_params_)
# テストデータで予測します。
y_pred = model.predict(X_test)
# 平均二乗誤差を計算します。
accu1 = mean_squared_error(y_test, y_pred)
accu2 = mean_squared_error(y_test, [y_test.mean()] * len(y_test) )
# 平均絶対誤差を計算します。
accu3 = mean_absolute_error(y_test, y_pred)
accu4 = mean_absolute_error(y_test, [y_test.mean()] * len(y_test) )
print('\n平均二乗誤差 : %.4f ( %.4f ) 平均絶対誤差 : %.4f ( %.4f ) ※ カッコ内は全予測値を平均値で置き換えた場合\n' % (accu1, accu2, accu3, accu4))
if hasattr(model, 'feature_importances_'):
# 特徴量の重要度がある場合
# 重要度の順にソートします。
sorted_idx_names = sorted(enumerate(model.feature_importances_), key=lambda x: x[1], reverse=True)
print('特徴量の重要度')
for i, (idx, x) in enumerate(sorted_idx_names[:20]):
print(' %2d %.05f %s' % (i, 100 * x, X_train.columns[idx]))
# 正解と予測を散布図に表示します。
sns.jointplot(y_test, y_pred, kind="reg").set_axis_labels('正解', '予測')
```
### リッジ回帰
```
model = Ridge(alpha=.5)
run_model(model)
# 売上高の予測の場合、これくらいになるはず
# 平均二乗誤差 : 0.0645 ( 0.0667 ) 平均絶対誤差 : 0.1784 ( 0.1968 )
```
### サポートベクターマシン
```
model = SVR(kernel='rbf')
run_model(model)
# 売上高の予測の場合、これくらいになるはず
# 平均二乗誤差 : 0.0517 ( 0.0667 ) 平均絶対誤差 : 0.1670 ( 0.1968 )
```
### ランダムフォレスト
```
model = RandomForestRegressor(max_depth=6, n_estimators=200)
run_model(model)
# 売上高の予測の場合、これくらいになるはず
# 平均二乗誤差 : 0.0510 ( 0.0667 ) 平均絶対誤差 : 0.1680 ( 0.1968 )
```
### XGBoost
```
model = XGBRegressor(max_depth=2, n_estimators=200)
run_model(model)
# 売上高の予測の場合、これくらいになるはず
# 平均二乗誤差 : 0.0496 ( 0.0667 ) 平均絶対誤差 : 0.1642 ( 0.1968 )
```
### LightGBM
```
model = LGBMRegressor(objective='regression', num_leaves = 31, max_depth=4, n_estimators=50)
run_model(model)
# 売上高の予測の場合、これくらいになるはず
# 平均二乗誤差 : 0.0495 ( 0.0667 ) 平均絶対誤差 : 0.1645 ( 0.1968 )
```
### CatBoost
```
model = CatBoostRegressor(max_depth=2, n_estimators=200, verbose=0)
run_model(model)
# 売上高の予測の場合、これくらいになるはず
# 平均二乗誤差 : 0.0500 ( 0.0667 ) 平均絶対誤差 : 0.1646 ( 0.1968 )
```
| true |
code
| 0.301105 | null | null | null | null |
|

[](https://colab.research.google.com/github/JohnSnowLabs/spark-nlp-workshop/blob/master/tutorials/streamlit_notebooks/healthcare/NER_LAB.ipynb)
# **Detect lab results**
To run this yourself, you will need to upload your license keys to the notebook. Otherwise, you can look at the example outputs at the bottom of the notebook. To upload license keys, open the file explorer on the left side of the screen and upload `workshop_license_keys.json` to the folder that opens.
## 1. Colab Setup
Import license keys
```
import os
import json
with open('/content/spark_nlp_for_healthcare.json', 'r') as f:
license_keys = json.load(f)
license_keys.keys()
secret = license_keys['SECRET']
os.environ['SPARK_NLP_LICENSE'] = license_keys['SPARK_NLP_LICENSE']
os.environ['AWS_ACCESS_KEY_ID'] = license_keys['AWS_ACCESS_KEY_ID']
os.environ['AWS_SECRET_ACCESS_KEY'] = license_keys['AWS_SECRET_ACCESS_KEY']
sparknlp_version = license_keys["PUBLIC_VERSION"]
jsl_version = license_keys["JSL_VERSION"]
print ('SparkNLP Version:', sparknlp_version)
print ('SparkNLP-JSL Version:', jsl_version)
```
Install dependencies
```
# Install Java
! apt-get update -qq
! apt-get install -y openjdk-8-jdk-headless -qq > /dev/null
! java -version
# Install pyspark
! pip install --ignore-installed -q pyspark==2.4.4
# Install Spark NLP
! pip install --ignore-installed spark-nlp==$sparknlp_version
! python -m pip install --upgrade spark-nlp-jsl==$jsl_version --extra-index-url https://pypi.johnsnowlabs.com/$secret
```
Import dependencies into Python and start the Spark session
```
os.environ['JAVA_HOME'] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ['PATH'] = os.environ['JAVA_HOME'] + "/bin:" + os.environ['PATH']
import pandas as pd
from pyspark.ml import Pipeline
from pyspark.sql import SparkSession
import pyspark.sql.functions as F
import sparknlp
from sparknlp.annotator import *
from sparknlp_jsl.annotator import *
from sparknlp.base import *
import sparknlp_jsl
spark = sparknlp_jsl.start(secret)
```
## 2. Select the NER model and construct the pipeline
Select the NER model - Lab Results models: **ner_jsl, ner_jsl_enriched**
For more details: https://github.com/JohnSnowLabs/spark-nlp-models#pretrained-models---spark-nlp-for-healthcare
```
# You can change this to the model you want to use and re-run cells below.
# Lab models: ner_jsl, ner_jsl_enriched
MODEL_NAME = "ner_jsl"
```
Create the pipeline
```
document_assembler = DocumentAssembler() \
.setInputCol('text')\
.setOutputCol('document')
sentence_detector = SentenceDetector() \
.setInputCols(['document'])\
.setOutputCol('sentence')
tokenizer = Tokenizer()\
.setInputCols(['sentence']) \
.setOutputCol('token')
word_embeddings = WordEmbeddingsModel.pretrained('embeddings_clinical', 'en', 'clinical/models') \
.setInputCols(['sentence', 'token']) \
.setOutputCol('embeddings')
clinical_ner = NerDLModel.pretrained(MODEL_NAME, 'en', 'clinical/models') \
.setInputCols(['sentence', 'token', 'embeddings']) \
.setOutputCol('ner')
ner_converter = NerConverter()\
.setInputCols(['sentence', 'token', 'ner']) \
.setOutputCol('ner_chunk')
nlp_pipeline = Pipeline(stages=[
document_assembler,
sentence_detector,
tokenizer,
word_embeddings,
clinical_ner,
ner_converter])
empty_df = spark.createDataFrame([['']]).toDF("text")
pipeline_model = nlp_pipeline.fit(empty_df)
light_pipeline = LightPipeline(pipeline_model)
```
## 3. Create example inputs
```
# Enter examples as strings in this array
input_list = [
"""Tumor cells show no reactivity with cytokeratin AE1/AE3. No significant reactivity with CAM5.2 and no reactivity with cytokeratin-20 are seen. Tumor cells show partial reactivity with cytokeratin-7. PAS with diastase demonstrates no convincing intracytoplasmic mucin. No neuroendocrine differentiation is demonstrated with synaptophysin and chromogranin stains. Tumor cells show cytoplasmic and nuclear reactivity with S100 antibody. No significant reactivity is demonstrated with melanoma marker HMB-45 or Melan-A. Tumor cell nuclei (spindle cell and pleomorphic/giant cell carcinoma components) show nuclear reactivity with thyroid transcription factor marker (TTF-1). The immunohistochemical studies are consistent with primary lung sarcomatoid carcinoma with pleomorphic/giant cell carcinoma and spindle cell carcinoma components."""
]
```
## 4. Use the pipeline to create outputs
```
df = spark.createDataFrame(pd.DataFrame({"text": input_list}))
result = pipeline_model.transform(df)
```
## 5. Visualize results
Visualize outputs as data frame
```
exploded = F.explode(F.arrays_zip('ner_chunk.result', 'ner_chunk.metadata'))
select_expression_0 = F.expr("cols['0']").alias("chunk")
select_expression_1 = F.expr("cols['1']['entity']").alias("ner_label")
result.select(exploded.alias("cols")) \
.select(select_expression_0, select_expression_1).show(truncate=False)
result = result.toPandas()
```
Functions to display outputs as HTML
```
from IPython.display import HTML, display
import random
def get_color():
r = lambda: random.randint(128,255)
return "#%02x%02x%02x" % (r(), r(), r())
def annotation_to_html(full_annotation):
ner_chunks = full_annotation[0]['ner_chunk']
text = full_annotation[0]['document'][0].result
label_color = {}
for chunk in ner_chunks:
label_color[chunk.metadata['entity']] = get_color()
html_output = "<div>"
pos = 0
for n in ner_chunks:
if pos < n.begin and pos < len(text):
html_output += f"<span class=\"others\">{text[pos:n.begin]}</span>"
pos = n.end + 1
html_output += f"<span class=\"entity-wrapper\" style=\"color: black; background-color: {label_color[n.metadata['entity']]}\"> <span class=\"entity-name\">{n.result}</span> <span class=\"entity-type\">[{n.metadata['entity']}]</span></span>"
if pos < len(text):
html_output += f"<span class=\"others\">{text[pos:]}</span>"
html_output += "</div>"
display(HTML(html_output))
```
Display example outputs as HTML
```
for example in input_list:
annotation_to_html(light_pipeline.fullAnnotate(example))
```
| true |
code
| 0.395893 | null | null | null | null |
|
# Feature Transformation
Current state of transformations:
- alt: Currently fully transformed via `log(x + 1 - min(x))`. This appears to be acceptable in some circles but doubted in others.
- minimum_lap_time: Normalized by raceId, then used imputation by the median for outliers.
- average_lap_time: Normalized by raceId, then transformed using `log(x)`. Also used imputation by the median for outliers.
- PRCP: Ended up being transformed with `log(x + 1)`. Again, this appears to be acceptable in some circles but doubted in others.
## Set Up
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
%matplotlib inline
# Read in MasterData5.
master_data_url = 'https://raw.githubusercontent.com/georgetown-analytics/Formula1/main/data/processed/MasterData5.csv'
master_data = pd.read_csv(master_data_url, sep = ',', engine = 'python')
# Rename Completion Status to CompletionStatus.
master_data = master_data.rename(columns = {"Completion Status": "CompletionStatus"})
# Only include the final, decided features we'll be using in our models. Do not include identifiable features besides raceId and driverId.
features = master_data[['raceId', 'driverId', 'CompletionStatus', 'alt', 'grid', 'trackType2',
'average_lap_time', 'minimum_lap_time',
'year', 'PRCP', 'TAVG', 'isHistoric', 'oneHot_circuits_1',
'oneHot_circuits_2', 'oneHot_circuits_3', 'oneHot_circuits_4',
'oneHot_circuits_5', 'oneHot_circuits_6']]
# Rename trackType2 to trackType.
features = features.rename(columns = {"trackType2": "trackType"})
# Make trackType a string feature instead of numeric.
features["trackType"] = features.trackType.astype("str")
```
## Transform Features
We know from our `Variable_Distribution.csv` workbook that the features with positive skews that we need to transform are `alt` and `average_lap_time`. Features with outliers are `minimum_lap_time` and `PRCP`.
The site that has the code for using log to transform our features is here: https://towardsdatascience.com/feature-transformation-for-multiple-linear-regression-in-python-8648ddf070b8
### alt
The feature `alt`, or the altitude of each track, is positively skewed. You can see how below.
```
# Show the distribution of alt.
alt_dis = sns.displot(features, x = 'alt').set(title = "Distribution of Variable: alt")
# What does alt look like?
features['alt'].describe()
"""
Transform alt below using log(x + 1 - min(x)). These were suggested by the following sites:
https://blogs.sas.com/content/iml/2011/04/27/log-transformations-how-to-handle-negative-data-values.html
https://www.researchgate.net/post/can_we_replace-Inf_values_after_log_transformations_with_zero
"""
features['alt_trans'] = np.log(features['alt'] + 1 - min(features['alt']))
features.describe()
# Show the new distribution of alt.
alt_trans_dis = sns.displot(features, x = 'alt_trans').set(title = "Transformed Distribution of Variable: alt")
```
`alt` is still not exactly a normal distribution, but it is no longer skewed. This should help it perform better in our models.
### minimum_lap_time
Before we can deal with any outliers, we need to normalize the feature. Right now `minimum_lap_time` is not normalized across races, which is a problem because different races have different track lengths. In order to normalize this feature, we'll group by `raceId`, aggregate for the mean, and then join this new variable back up with our master data. From there we can find `normalized_minlaptime = minimum_lap_time / mean_minlaptime`.
```
# Group by raceId and aggregate for the mean.
raceId_min = master_data.groupby(['raceId'], as_index = False).agg({'minimum_lap_time':'mean'})
raceId_min.describe()
# Rename raceId_average's average_lap_time to mean_avglaptime.
raceId_min = raceId_min.rename(columns = {"minimum_lap_time": "mean_minlaptime"})
# Merge master_data with raceId_average by "raceId" to get avglaps_avg.
avglaps_min = pd.merge(master_data, raceId_min, on = "raceId")
avglaps_min.head()
# Normalize the average lap time by dividing average_lap_time by mean_avglaptime.
avglaps_min['normalized_minLapTime'] = avglaps_min['minimum_lap_time'] / avglaps_min['mean_minlaptime']
avglaps_min[['normalized_minLapTime', 'minimum_lap_time', 'mean_minlaptime']].describe()
```
Now that we have minimum lap time normalized, let's take a look at the distribution again. From the description above, with a large gap between the 75% quartile and the max, it looks like the data will still be skewed.
```
# Plot the distribution of our new variable.
norm_minlaptime_dist = sns.displot(avglaps_min, x = 'normalized_minLapTime').set(title = "Distribution of Variable: normalized_minLapTime")
# Plot a boxplot to find our outliers.
normmin_boxplt = sns.boxplot(data = avglaps_min, x = 'normalized_minLapTime').set(title = "Boxplot of Variable: normalized_minLapTime")
```
We have one significant outlier by 5.0, and three around the 2.0 to 3.5 range.
We'll go ahead and use imputation to deal with these outliers, as per this site (https://medium.com/analytics-vidhya/how-to-remove-outliers-for-machine-learning-24620c4657e8). We're essentially replacing our outliers' values with the medians. As Analytics Vidhya states, "median is appropriate because it is not affected by outliers." We also used Analytics Vidhya's code.
```
"""
Use Analytics Vidhya's code to create an if statement within a for loop to replace outliers above the
uppertail or below the lowertail with the median. Although Analytics Vidhya used 1.5 as their modifier,
we'll use 2.0 in order to try and collect less outliers while still allowing the distribution to normalize.
"""
for i in avglaps_min['normalized_minLapTime']:
Q1 = avglaps_min['normalized_minLapTime'].quantile(0.25)
Q3 = avglaps_min['normalized_minLapTime'].quantile(0.75)
IQR = Q3 - Q1
lowertail = Q1 - 2.0 * IQR
uppertail = Q3 + 2.0 * IQR
if i > uppertail or i < lowertail:
avglaps_min['normalized_minLapTime'] = avglaps_min['normalized_minLapTime'].replace(i, np.median(avglaps_min['normalized_minLapTime']))
# Plot a boxplot to find our outliers.
impnormmin_boxplt = sns.boxplot(data = avglaps_min, x = 'normalized_minLapTime').set(title = "Imputed Boxplot of Variable: normalized_minLapTime")
# Plot the new distribution of our new variable.
newnorm_minlaptime_dist = sns.displot(avglaps_min, x = 'normalized_minLapTime').set(title = "Imputed Distribution of Variable:\nnormalized_minLapTime")
```
We have a normalized feature with what appears to be a normal distribution! The one thing to worry about here is that there were so many outliers that had to be imputated, and that may cause a problem with our distribution.
### average_lap_time
Right now our `average_lap_time` is not normalized across races, which is a problem because different races have different track lengths. In order to normalize this feature, we'll group by `raceId`, aggregate for the mean, and then join this new variable back up with our master data. From there we can find `normalized_avglaptime = average_lap_time / mean_avglaptime`.
```
# Group by raceId and aggregate for the mean.
raceId_average = master_data.groupby(['raceId'], as_index = False).agg({'average_lap_time':'mean'})
raceId_average.describe()
# Rename raceId_average's average_lap_time to mean_avglaptime.
raceId_average = raceId_average.rename(columns = {"average_lap_time": "mean_avglaptime"})
# Merge master_data with raceId_average by "raceId" to get avglaps_avg.
avglaps_avg = pd.merge(master_data, raceId_average, on = "raceId")
avglaps_avg.head()
# Normalize the average lap time by dividing average_lap_time by mean_avglaptime.
avglaps_avg['normalized_avgLapTime'] = avglaps_avg['average_lap_time'] / avglaps_avg['mean_avglaptime']
avglaps_avg[['normalized_avgLapTime', 'average_lap_time', 'mean_avglaptime']].describe()
```
Now that we have average lap time normalized, let's take a look at the distribution again. From the description above, with a large gap between the 75% quartile and the max, it looks like the data will still be skewed.
```
# Plot the distribution of our new variable.
normalized_avglaptime_dist = sns.displot(avglaps_avg, x = 'normalized_avgLapTime').set(title = "Distribution of Variable: normalized_avgLapTime")
```
We can see that there appears to be a positive skew, so we'll use log(x) to transform the feature.
```
"""
Transform normalized_avgLapTime with log(x). This was suggested by Towards Data Science, linked above.
"""
avglaps_avg['normalized_avgLapTime'] = np.log(avglaps_avg['normalized_avgLapTime'])
avglaps_avg.describe()
# Plot the distribution of our transformed variable.
normalized_avglaptime_dist = sns.displot(avglaps_avg, x = 'normalized_avgLapTime').set(title = "Transformed Distribution of Variable: normalized_avgLapTime")
```
This looks much better, but we can see that there are still some extreme outliers.
```
"""
Use Analytics Vidhya's code to create an if statement within a for loop to replace outliers above the
uppertail or below the lowertail with the median. We'll use 2.5 as our modifier to try and collect less
outliers while still allowing the distribution to normalize.
"""
for i in avglaps_avg['normalized_avgLapTime']:
Q1 = avglaps_avg['normalized_avgLapTime'].quantile(0.25)
Q3 = avglaps_avg['normalized_avgLapTime'].quantile(0.75)
IQR = Q3 - Q1
lowertail = Q1 - 2.5 * IQR
uppertail = Q3 + 2.5 * IQR
if i > uppertail or i < lowertail:
avglaps_avg['normalized_avgLapTime'] = avglaps_avg['normalized_avgLapTime'].replace(i, np.median(avglaps_avg['normalized_avgLapTime']))
# Plot a boxplot to find our outliers.
impnormmin_boxplt = sns.boxplot(data = avglaps_avg, x = 'normalized_avgLapTime').set(title = "Transformed and Imputed Boxplot of Variable:\nnormalized_avgLapTime")
# Plot the new distribution of our new variable.
newnorm_minlaptime_dist = sns.displot(avglaps_avg, x = 'normalized_avgLapTime').set(title = "Transformed and Imputed Distribution of Variable:\nnormalized_avgLapTime")
```
We have a normalized feature with what appears to be a normal distribution! The one thing to worry about here is that there were so many outliers that had to be imputated, and that may cause a problem with our distribution.
### PRCP
```
# Plot a boxplot to find our outliers.
PRCP_boxplt = sns.boxplot(data = features, x = 'PRCP').set(title = "Distribution of Variable: PRCP")
```
We have one significant outlier.
```
# What does PRCP look like?
features['PRCP'].describe()
```
The high max with low 75% quartile definitely suggests a positive skew.
```
"""
Transform PRCP with log(x + 1). This was suggested by the following site:
https://discuss.analyticsvidhya.com/t/methods-to-deal-with-zero-values-while-performing-log-transformation-of-variable/2431/9
"""
features['PRCP_trans'] = np.log(features['PRCP'] + 1)
features.describe()
# Create a new variable distribution.
new2PRCP_dis = sns.displot(features, x = 'PRCP_trans').set(title = 'Transformed Distribution of Variable: PRCP')
# Plot a boxplot to find our outliers.
PRCPtrans_boxplt = sns.boxplot(data = features, x = 'PRCP_trans').set(title = "Transformed Boxplot of Variable: PRCP")
```
Although there still seem to be some outliers, they aren't as extreme as before.
## Rejoin the Features into One Dataset
Current locations of our features:
- `alt` and `alt_trans` are both in the `features` dataset
- `minimum_lap_time` and `normalized_minLapTime` are both in the `avglaps_min` dataset
- `average_lap_time` and `normalized_avgLapTime` are both in the `avglaps_avg` dataset
- `PRCP` and `PRCP_trans` are both in `features` dataset
```
# What columns are in features?
features.columns
```
We need to bring normalized_minLapTime and normalized_avgLapTime over to features.
```
# What columns are in avglaps_min?
avglaps_min.columns
# Select just the wanted features for a new dataset.
pref_minlapsdata = avglaps_min[["raceId", "driverId", "normalized_minLapTime"]]
pref_minlapsdata.describe()
# What columns are in avglaps_avg?
avglaps_avg.columns
# Select just the wanted features for a new dataset.
pref_avglapsdata = avglaps_avg[["raceId", "driverId", "normalized_avgLapTime"]]
pref_avglapsdata.describe()
# Merge features with pref_minlapsdata by "raceId" and "driverId" to get min_features.
min_features = pd.merge(features, pref_minlapsdata, on = ["raceId", "driverId"])
min_features.head()
# Merge min_features with pref_avglapsdata by "raceId" and "driverId" to get final_features.
final_features = pd.merge(min_features, pref_avglapsdata, on = ["raceId", "driverId"])
final_features.head()
```
### Create a csv file
```
# Use pandas.DataFrame.to_csv to read our final_features dataset into a new CSV file.
final_features.to_csv("./data/processed/final_features.csv", index = False)
```
| true |
code
| 0.607547 | null | null | null | null |
|
<b>Section One – Image Captioning with Tensorflow</b>
```
# load essential libraries
import math
import os
import tensorflow as tf
%pylab inline
# load Tensorflow/Google Brain base code
# https://github.com/tensorflow/models/tree/master/research/im2txt
from im2txt import configuration
from im2txt import inference_wrapper
from im2txt.inference_utils import caption_generator
from im2txt.inference_utils import vocabulary
# tell our function where to find the trained model and vocabulary
checkpoint_path = './model'
vocab_file = './model/word_counts.txt'
# this is the function we'll call to produce our captions
# given input file name(s) -- separate file names by a ,
# if more than one
def gen_caption(input_files):
# only print serious log messages
tf.logging.set_verbosity(tf.logging.FATAL)
# load our pretrained model
g = tf.Graph()
with g.as_default():
model = inference_wrapper.InferenceWrapper()
restore_fn = model.build_graph_from_config(configuration.ModelConfig(),
checkpoint_path)
g.finalize()
# Create the vocabulary.
vocab = vocabulary.Vocabulary(vocab_file)
filenames = []
for file_pattern in input_files.split(","):
filenames.extend(tf.gfile.Glob(file_pattern))
tf.logging.info("Running caption generation on %d files matching %s",
len(filenames), input_files)
with tf.Session(graph=g) as sess:
# Load the model from checkpoint.
restore_fn(sess)
# Prepare the caption generator. Here we are implicitly using the default
# beam search parameters. See caption_generator.py for a description of the
# available beam search parameters.
generator = caption_generator.CaptionGenerator(model, vocab)
captionlist = []
for filename in filenames:
with tf.gfile.GFile(filename, "rb") as f:
image = f.read()
captions = generator.beam_search(sess, image)
print("Captions for image %s:" % os.path.basename(filename))
for i, caption in enumerate(captions):
# Ignore begin and end words.
sentence = [vocab.id_to_word(w) for w in caption.sentence[1:-1]]
sentence = " ".join(sentence)
print(" %d) %s (p=%f)" % (i, sentence, math.exp(caption.logprob)))
captionlist.append(sentence)
return captionlist
testfile = 'test_images/ballons.jpeg'
figure()
imshow(imread(testfile))
capts = gen_caption(testfile)
input_files = 'test_images/ballons.jpeg,test_images/bike.jpeg,test_images/dog.jpeg,test_images/fireworks.jpeg,test_images/football.jpeg,test_images/giraffes.jpeg,test_images/headphones.jpeg,test_images/laughing.jpeg,test_images/objects.jpeg,test_images/snowboard.jpeg,test_images/surfing.jpeg'
capts = gen_caption(input_files)
```
<p><p><p><p><p>
<b>Retraining the image captioner</b>
```
# First download pretrained Inception (v3) model
import webbrowser
webbrowser.open("http://download.tensorflow.org/models/inception_v3_2016_08_28.tar.gz")
# Completely unzip tar.gz file to get inception_v3.ckpt,
# --recommend storing in im2txt/data directory
# Now gather and prepare the mscoco data
# Comment out cd magic command if already in data directory
%cd im2txt/data
# This command will take an hour or more to run typically.
# Note, you will need a lot of HD space (>100 GB)!
%run build_mscoco_data.py
# At this point you have files in im2txt/data/mscoco/raw-data that you can train
# on, or you can substitute your own data
%cd ..
# load needed modules
import tensorflow as tf
from im2txt import configuration
from im2txt import show_and_tell_model
# Define (but don't run yet) our captioning training function
def train():
model_config = configuration.ModelConfig()
model_config.input_file_pattern = input_file_pattern
model_config.inception_checkpoint_file = inception_checkpoint_file
training_config = configuration.TrainingConfig()
# Create training directory.
train_dir = train_dir
if not tf.gfile.IsDirectory(train_dir):
tf.logging.info("Creating training directory: %s", train_dir)
tf.gfile.MakeDirs(train_dir)
# Build the TensorFlow graph.
g = tf.Graph()
with g.as_default():
# Build the model.
model = show_and_tell_model.ShowAndTellModel(
model_config, mode="train", train_inception=train_inception)
model.build()
# Set up the learning rate.
learning_rate_decay_fn = None
if train_inception:
learning_rate = tf.constant(training_config.train_inception_learning_rate)
else:
learning_rate = tf.constant(training_config.initial_learning_rate)
if training_config.learning_rate_decay_factor > 0:
num_batches_per_epoch = (training_config.num_examples_per_epoch /
model_config.batch_size)
decay_steps = int(num_batches_per_epoch *
training_config.num_epochs_per_decay)
def _learning_rate_decay_fn(learning_rate, global_step):
return tf.train.exponential_decay(
learning_rate,
global_step,
decay_steps=decay_steps,
decay_rate=training_config.learning_rate_decay_factor,
staircase=True)
learning_rate_decay_fn = _learning_rate_decay_fn
# Set up the training ops.
train_op = tf.contrib.layers.optimize_loss(
loss=model.total_loss,
global_step=model.global_step,
learning_rate=learning_rate,
optimizer=training_config.optimizer,
clip_gradients=training_config.clip_gradients,
learning_rate_decay_fn=learning_rate_decay_fn)
# Set up the Saver for saving and restoring model checkpoints.
saver = tf.train.Saver(max_to_keep=training_config.max_checkpoints_to_keep)
# Run training.
tf.contrib.slim.learning.train(
train_op,
train_dir,
log_every_n_steps=log_every_n_steps,
graph=g,
global_step=model.global_step,
number_of_steps=number_of_steps,
init_fn=model.init_fn,
saver=saver)
# Initial training
input_file_pattern = 'im2txt/data/mscoco/train-?????-of-00256'
# change these if you put your stuff somewhere else
inception_checkpoint_file = 'im2txt/data/inception_v3.ckpt'
train_dir = 'im2txt/model'
# Don't train inception for initial run
train_inception = False
number_of_steps = 1000000
log_every_n_steps = 1
# Now run the training (warning: takes days-to-weeks!!!)
train()
# Fine tuning
input_file_pattern = 'im2txt/data/mscoco/train-?????-of-00256'
# change these if you put your stuff somewhere else
inception_checkpoint_file = 'im2txt/data/inception_v3.ckpt'
train_dir = 'im2txt/model'
# This will refine our results
train_inception = True
number_of_steps = 3000000
log_every_n_steps = 1
# Now run the training (warning: takes even longer than initial training!!!)
train()
# If you completed this, you can go back to the start of this notebook and
# point checkpoint_path and vocab_file to your generated files.
```
| true |
code
| 0.514095 | null | null | null | null |
|
```
import itertools
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import confusion_matrix, f1_score
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
```
# Load dataset
```
# Get data
import pandas as pd
from sklearn.datasets import load_iris
data = load_iris(as_frame=True)
dataset = data.frame
dataset.head()
# Print labels for target values
[print(f'{target}: {label}') for target, label in zip(data.target.unique(), data.target_names)]
# Process feature names
dataset.columns = [colname.strip(' (cm)').replace(' ', '_') for colname in dataset.columns.tolist()]
feature_names = dataset.columns.tolist()[:4]
feature_names
```
# Features engineering
```
dataset['sepal_length_to_sepal_width'] = dataset['sepal_length'] / dataset['sepal_width']
dataset['petal_length_to_petal_width'] = dataset['petal_length'] / dataset['petal_width']
dataset = dataset[[
'sepal_length', 'sepal_width', 'petal_length', 'petal_width',
'sepal_length_to_sepal_width', 'petal_length_to_petal_width',
'target'
]]
dataset.head()
```
# Split train/test dataset
```
test_size=0.2
train_dataset, test_dataset = train_test_split(dataset, test_size=test_size, random_state=42)
train_dataset.shape, test_dataset.shape
```
# Train
```
# Get X and Y
y_train = train_dataset.loc[:, 'target'].values.astype('int32')
X_train = train_dataset.drop('target', axis=1).values.astype('float32')
# Create an instance of Logistic Regression Classifier CV and fit the data
logreg = LogisticRegression(C=0.001, solver='lbfgs', multi_class='multinomial', max_iter=100)
logreg.fit(X_train, y_train)
```
# Evaluate
```
def plot_confusion_matrix(cm,
target_names,
title='Confusion matrix',
cmap=None,
normalize=True):
"""
given a sklearn confusion matrix (cm), make a nice plot
Arguments
---------
cm: confusion matrix from sklearn.metrics.confusion_matrix
target_names: given classification classes such as [0, 1, 2]
the class names, for example: ['high', 'medium', 'low']
title: the text to display at the top of the matrix
cmap: the gradient of the values displayed from matplotlib.pyplot.cm
see http://matplotlib.org/examples/color/colormaps_reference.html
plt.get_cmap('jet') or plt.cm.Blues
normalize: If False, plot the raw numbers
If True, plot the proportions
Usage
-----
plot_confusion_matrix(cm = cm, # confusion matrix created by
# sklearn.metrics.confusion_matrix
normalize = True, # show proportions
target_names = y_labels_vals, # list of names of the classes
title = best_estimator_name) # title of graph
Citiation
---------
http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html
"""
accuracy = np.trace(cm) / float(np.sum(cm))
misclass = 1 - accuracy
if cmap is None:
cmap = plt.get_cmap('Blues')
plt.figure(figsize=(8, 6))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
if target_names is not None:
tick_marks = np.arange(len(target_names))
plt.xticks(tick_marks, target_names, rotation=45)
plt.yticks(tick_marks, target_names)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
thresh = cm.max() / 1.5 if normalize else cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
if normalize:
plt.text(j, i, "{:0.4f}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
else:
plt.text(j, i, "{:,}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label\naccuracy={:0.4f}; misclass={:0.4f}'.format(accuracy, misclass))
plt.show()
# Get X and Y
y_test = test_dataset.loc[:, 'target'].values.astype('int32')
X_test = test_dataset.drop('target', axis=1).values.astype('float32')
prediction = logreg.predict(X_test)
cm = confusion_matrix(prediction, y_test)
f1 = f1_score(y_true = y_test, y_pred = prediction, average='macro')
# f1 score value
f1
plot_confusion_matrix(cm, data.target_names, normalize=False)
```
| true |
code
| 0.654453 | null | null | null | null |
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plotly.com/python/getting-started/) by downloading the client and [reading the primer](https://plotly.com/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plotly.com/python/getting-started/#initialization-for-online-plotting) or [offline](https://plotly.com/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plotly.com/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Vertical and Horizontal Lines Positioned Relative to the Axes
```
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Scatter(
x=[2, 3.5, 6],
y=[1, 1.5, 1],
text=['Vertical Line', 'Horizontal Dashed Line', 'Diagonal dotted Line'],
mode='text',
)
data = [trace0]
layout = {
'xaxis': {
'range': [0, 7]
},
'yaxis': {
'range': [0, 2.5]
},
'shapes': [
# Line Vertical
{
'type': 'line',
'x0': 1,
'y0': 0,
'x1': 1,
'y1': 2,
'line': {
'color': 'rgb(55, 128, 191)',
'width': 3,
},
},
# Line Horizontal
{
'type': 'line',
'x0': 2,
'y0': 2,
'x1': 5,
'y1': 2,
'line': {
'color': 'rgb(50, 171, 96)',
'width': 4,
'dash': 'dashdot',
},
},
# Line Diagonal
{
'type': 'line',
'x0': 4,
'y0': 0,
'x1': 6,
'y1': 2,
'line': {
'color': 'rgb(128, 0, 128)',
'width': 4,
'dash': 'dot',
},
},
]
}
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='shapes-lines')
```
#### Lines Positioned Relative to the Plot & to the Axes
```
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Scatter(
x=[2, 6],
y=[1, 1],
text=['Line positioned relative to the plot',
'Line positioned relative to the axes'],
mode='text',
)
data = [trace0]
layout = {
'xaxis': {
'range': [0, 8]
},
'yaxis': {
'range': [0, 2]
},
'shapes': [
# Line reference to the axes
{
'type': 'line',
'xref': 'x',
'yref': 'y',
'x0': 4,
'y0': 0,
'x1': 8,
'y1': 1,
'line': {
'color': 'rgb(55, 128, 191)',
'width': 3,
},
},
# Line reference to the plot
{
'type': 'line',
'xref': 'paper',
'yref': 'paper',
'x0': 0,
'y0': 0,
'x1': 0.5,
'y1': 0.5,
'line': {
'color': 'rgb(50, 171, 96)',
'width': 3,
},
},
]
}
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='shapes-line-ref')
```
#### Creating Tangent Lines with Shapes
```
import plotly.plotly as py
import plotly.graph_objs as go
import numpy as np
x0 = np.linspace(1, 3, 200)
y0 = x0 * np.sin(np.power(x0, 2)) + 1
trace0 = go.Scatter(
x=x0,
y=y0,
)
data = [trace0]
layout = {
'title': "$f(x)=x\\sin(x^2)+1\\\\ f\'(x)=\\sin(x^2)+2x^2\\cos(x^2)$",
'shapes': [
{
'type': 'line',
'x0': 1,
'y0': 2.30756,
'x1': 1.75,
'y1': 2.30756,
'opacity': 0.7,
'line': {
'color': 'red',
'width': 2.5,
},
},
{
'type': 'line',
'x0': 2.5,
'y0': 3.80796,
'x1': 3.05,
'y1': 3.80796,
'opacity': 0.7,
'line': {
'color': 'red',
'width': 2.5,
},
},
{
'type': 'line',
'x0': 1.90,
'y0': -1.1827,
'x1': 2.50,
'y1': -1.1827,
'opacity': 0.7,
'line': {
'color': 'red',
'width': 2.5,
},
},
]
}
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='tangent-line')
```
#### Rectangles Positioned Relative to the Axes
```
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Scatter(
x=[1.5, 4.5],
y=[0.75, 0.75],
text=['Unfilled Rectangle', 'Filled Rectangle'],
mode='text',
)
data = [trace0]
layout = {
'xaxis': {
'range': [0, 7],
'showgrid': False,
},
'yaxis': {
'range': [0, 3.5]
},
'shapes': [
# unfilled Rectangle
{
'type': 'rect',
'x0': 1,
'y0': 1,
'x1': 2,
'y1': 3,
'line': {
'color': 'rgba(128, 0, 128, 1)',
},
},
# filled Rectangle
{
'type': 'rect',
'x0': 3,
'y0': 1,
'x1': 6,
'y1': 2,
'line': {
'color': 'rgba(128, 0, 128, 1)',
'width': 2,
},
'fillcolor': 'rgba(128, 0, 128, 0.7)',
},
]
}
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='shapes-rectangle')
```
#### Rectangle Positioned Relative to the Plot & to the Axes
```
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Scatter(
x=[1.5, 3],
y=[2.5, 2.5],
text=['Rectangle reference to the plot',
'Rectangle reference to the axes'],
mode='text',
)
data = [trace0]
layout = {
'xaxis': {
'range': [0, 4],
'showgrid': False,
},
'yaxis': {
'range': [0, 4]
},
'shapes': [
# Rectangle reference to the axes
{
'type': 'rect',
'xref': 'x',
'yref': 'y',
'x0': 2.5,
'y0': 0,
'x1': 3.5,
'y1': 2,
'line': {
'color': 'rgb(55, 128, 191)',
'width': 3,
},
'fillcolor': 'rgba(55, 128, 191, 0.6)',
},
# Rectangle reference to the plot
{
'type': 'rect',
'xref': 'paper',
'yref': 'paper',
'x0': 0.25,
'y0': 0,
'x1': 0.5,
'y1': 0.5,
'line': {
'color': 'rgb(50, 171, 96)',
'width': 3,
},
'fillcolor': 'rgba(50, 171, 96, 0.6)',
},
]
}
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='shapes-rectangle-ref')
```
#### Highlighting Time Series Regions with Rectangle Shapes
```
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Scatter(
x=['2015-02-01', '2015-02-02', '2015-02-03', '2015-02-04', '2015-02-05',
'2015-02-06', '2015-02-07', '2015-02-08', '2015-02-09', '2015-02-10',
'2015-02-11', '2015-02-12', '2015-02-13', '2015-02-14', '2015-02-15',
'2015-02-16', '2015-02-17', '2015-02-18', '2015-02-19', '2015-02-20',
'2015-02-21', '2015-02-22', '2015-02-23', '2015-02-24', '2015-02-25',
'2015-02-26', '2015-02-27', '2015-02-28'],
y=[-14, -17, -8, -4, -7, -10, -12, -14, -12, -7, -11, -7, -18, -14, -14,
-16, -13, -7, -8, -14, -8, -3, -9, -9, -4, -13, -9, -6],
mode='lines',
name='temperature'
)
data = [trace0]
layout = {
# to highlight the timestamp we use shapes and create a rectangular
'shapes': [
# 1st highlight during Feb 4 - Feb 6
{
'type': 'rect',
# x-reference is assigned to the x-values
'xref': 'x',
# y-reference is assigned to the plot paper [0,1]
'yref': 'paper',
'x0': '2015-02-04',
'y0': 0,
'x1': '2015-02-06',
'y1': 1,
'fillcolor': '#d3d3d3',
'opacity': 0.2,
'line': {
'width': 0,
}
},
# 2nd highlight during Feb 20 - Feb 23
{
'type': 'rect',
'xref': 'x',
'yref': 'paper',
'x0': '2015-02-20',
'y0': 0,
'x1': '2015-02-22',
'y1': 1,
'fillcolor': '#d3d3d3',
'opacity': 0.2,
'line': {
'width': 0,
}
}
]
}
py.iplot({'data': data, 'layout': layout}, filename='timestamp-highlight')
```
#### Circles Positioned Relative to the Axes
```
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Scatter(
x=[1.5, 3.5],
y=[0.75, 2.5],
text=['Unfilled Circle',
'Filled Circle'],
mode='text',
)
data = [trace0]
layout = {
'xaxis': {
'range': [0, 4.5],
'zeroline': False,
},
'yaxis': {
'range': [0, 4.5]
},
'width': 800,
'height': 800,
'shapes': [
# unfilled circle
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'x0': 1,
'y0': 1,
'x1': 3,
'y1': 3,
'line': {
'color': 'rgba(50, 171, 96, 1)',
},
},
# filled circle
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'fillcolor': 'rgba(50, 171, 96, 0.7)',
'x0': 3,
'y0': 3,
'x1': 4,
'y1': 4,
'line': {
'color': 'rgba(50, 171, 96, 1)',
},
},
]
}
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='shapes-circle')
```
#### Highlighting Clusters of Scatter Points with Circle Shapes
```
import plotly.plotly as py
import plotly.graph_objs as go
import numpy as np
x0 = np.random.normal(2, 0.45, 300)
y0 = np.random.normal(2, 0.45, 300)
x1 = np.random.normal(6, 0.4, 200)
y1 = np.random.normal(6, 0.4, 200)
x2 = np.random.normal(4, 0.3, 200)
y2 = np.random.normal(4, 0.3, 200)
trace0 = go.Scatter(
x=x0,
y=y0,
mode='markers',
)
trace1 = go.Scatter(
x=x1,
y=y1,
mode='markers'
)
trace2 = go.Scatter(
x=x2,
y=y2,
mode='markers'
)
trace3 = go.Scatter(
x=x1,
y=y0,
mode='markers'
)
layout = {
'shapes': [
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'x0': min(x0),
'y0': min(y0),
'x1': max(x0),
'y1': max(y0),
'opacity': 0.2,
'fillcolor': 'blue',
'line': {
'color': 'blue',
},
},
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'x0': min(x1),
'y0': min(y1),
'x1': max(x1),
'y1': max(y1),
'opacity': 0.2,
'fillcolor': 'orange',
'line': {
'color': 'orange',
},
},
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'x0': min(x2),
'y0': min(y2),
'x1': max(x2),
'y1': max(y2),
'opacity': 0.2,
'fillcolor': 'green',
'line': {
'color': 'green',
},
},
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'x0': min(x1),
'y0': min(y0),
'x1': max(x1),
'y1': max(y0),
'opacity': 0.2,
'fillcolor': 'red',
'line': {
'color': 'red',
},
},
],
'showlegend': False,
}
data = [trace0, trace1, trace2, trace3]
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='clusters')
```
#### Venn Diagram with Circle Shapes
```
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Scatter(
x=[1, 1.75, 2.5],
y=[1, 1, 1],
text=['$A$', '$A+B$', '$B$'],
mode='text',
textfont=dict(
color='black',
size=18,
family='Arail',
)
)
data = [trace0]
layout = {
'xaxis': {
'showticklabels': False,
'showgrid': False,
'zeroline': False,
},
'yaxis': {
'showticklabels': False,
'showgrid': False,
'zeroline': False,
},
'shapes': [
{
'opacity': 0.3,
'xref': 'x',
'yref': 'y',
'fillcolor': 'blue',
'x0': 0,
'y0': 0,
'x1': 2,
'y1': 2,
'type': 'circle',
'line': {
'color': 'blue',
},
},
{
'opacity': 0.3,
'xref': 'x',
'yref': 'y',
'fillcolor': 'gray',
'x0': 1.5,
'y0': 0,
'x1': 3.5,
'y1': 2,
'type': 'circle',
'line': {
'color': 'gray',
},
}
],
'margin': {
'l': 20,
'r': 20,
'b': 100
},
'height': 600,
'width': 800,
}
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='venn-diagram')
```
#### SVG Paths
```
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Scatter(
x=[2, 1, 8, 8],
y=[0.25, 9, 2, 6],
text=['Filled Triangle',
'Filled Polygon',
'Quadratic Bezier Curves',
'Cubic Bezier Curves'],
mode='text',
)
data = [trace0]
layout = {
'xaxis': {
'range': [0, 9],
'zeroline': False,
},
'yaxis': {
'range': [0, 11],
'showgrid': False,
},
'shapes': [
# Quadratic Bezier Curves
{
'type': 'path',
'path': 'M 4,4 Q 6,0 8,4',
'line': {
'color': 'rgb(93, 164, 214)',
},
},
# Cubic Bezier Curves
{
'type': 'path',
'path': 'M 1,4 C 2,8 6,4 8,8',
'line': {
'color': 'rgb(207, 114, 255)',
},
},
# filled Triangle
{
'type': 'path',
'path': ' M 1 1 L 1 3 L 4 1 Z',
'fillcolor': 'rgba(44, 160, 101, 0.5)',
'line': {
'color': 'rgb(44, 160, 101)',
},
},
# filled Polygon
{
'type': 'path',
'path': ' M 3,7 L2,8 L2,9 L3,10, L4,10 L5,9 L5,8 L4,7 Z',
'fillcolor': 'rgba(255, 140, 184, 0.5)',
'line': {
'color': 'rgb(255, 140, 184)',
},
},
]
}
fig = {
'data': data,
'layout': layout,
}
py.iplot(fig, filename='shapes-path')
```
### Dash Example
[Dash](https://plotly.com/products/dash/) is an Open Source Python library which can help you convert plotly figures into a reactive, web-based application. Below is a simple example of a dashboard created using Dash. Its [source code](https://github.com/plotly/simple-example-chart-apps/tree/master/dash-shapesplot) can easily be deployed to a PaaS.
```
from IPython.display import IFrame
IFrame(src= "https://dash-simple-apps.plotly.host/dash-shapesplot/", width="100%", height="650px", frameBorder="0")
from IPython.display import IFrame
IFrame(src= "https://dash-simple-apps.plotly.host/dash-shapesplot/code", width="100%", height=500, frameBorder="0")
```
#### Reference
See https://plotly.com/python/reference/#layout-shapes for more information and chart attribute options!
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'shapes.ipynb', 'python/shapes/', 'Shapes | plotly',
'How to make SVG shapes in python. Examples of lines, circle, rectangle, and path.',
title = 'Shapes | plotly',
name = 'Shapes',
thumbnail='thumbnail/shape.jpg', language='python',
has_thumbnail='true', display_as='file_settings', order=32,
ipynb='~notebook_demo/14')
```
| true |
code
| 0.696346 | null | null | null | null |
|
```
import keras
keras.__version__
```
# 영화 리뷰 분류: 이진 분류 예제
이 노트북은 [케라스 창시자에게 배우는 딥러닝](https://tensorflow.blog/%EC%BC%80%EB%9D%BC%EC%8A%A4-%EB%94%A5%EB%9F%AC%EB%8B%9D/) 책의 3장 4절의 코드 예제입니다. 책에는 더 많은 내용과 그림이 있습니다. 이 노트북에는 소스 코드에 관련된 설명만 포함합니다.
----
2종 분류 또는 이진 분류는 아마도 가장 널리 적용된 머신 러닝 문제일 것입니다. 이 예제에서 리뷰 텍스트를 기반으로 영화 리뷰를 긍정과 부정로 분류하는 법을 배우겠습니다.
## IMDB 데이터셋
인터넷 영화 데이터베이스로부터 가져온 양극단의 리뷰 50,000개로 이루어진 IMDB 데이터셋을 사용하겠습니다. 이 데이터셋은 훈련 데이터 25,000개와 테스트 데이터 25,000개로 나뉘어 있고 각각 50%는 부정, 50%는 긍정 리뷰로 구성되어 있습니다.
왜 훈련 데이터와 테스트 데이터를 나눌까요? 같은 데이터에서 머신 러닝 모델을 훈련하고 테스트해서는 절대 안 되기 때문입니다! 모델이 훈련 데이터에서 잘 작동한다는 것이 처음 만난 데이터에서도 잘 동작한다는 것을 보장하지 않습니다. 중요한 것은 새로운 데이터에 대한 모델의 성능입니다(사실 훈련 데이터의 레이블은 이미 알고 있기 때문에 이를 예측하는 모델은 필요하지 않습니다). 예를 들어 모델이 훈련 샘플과 타깃 사이의 매핑을 모두 외워버릴 수 있습니다. 이런 모델은 처음 만나는 데이터에서 타깃을 예측하는 작업에는 쓸모가 없습니다. 다음 장에서 이에 대해 더 자세히 살펴보겠습니다.
MNIST 데이터셋처럼 IMDB 데이터셋도 케라스에 포함되어 있습니다. 이 데이터는 전처리되어 있어 각 리뷰(단어 시퀀스)가 숫자 시퀀스로 변환되어 있습니다. 여기서 각 숫자는 사전에 있는 고유한 단어를 나타냅니다.
다음 코드는 데이터셋을 로드합니다(처음 실행하면 17MB 정도의 데이터가 컴퓨터에 다운로드됩니다):
```
from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
```
매개변수 `num_words=10000`은 훈련 데이터에서 가장 자주 나타나는 단어 10,000개만 사용하겠다는 의미입니다. 드물게 나타나는 단어는 무시하겠습니다. 이렇게 하면 적절한 크기의 벡터 데이터를 얻을 수 있습니다.
변수 `train_data`와 `test_data`는 리뷰의 목록입니다. 각 리뷰는 단어 인덱스의 리스트입니다(단어 시퀀스가 인코딩된 것입니다). `train_labels`와 `test_labels`는 부정을 나타내는 0과 긍정을 나타내는 1의 리스트입니다:
```
train_data[0]
train_labels[0]
```
가장 자주 등장하는 단어 10,000개로 제한했기 때문에 단어 인덱스는 10,000을 넘지 않습니다:
```
max([max(sequence) for sequence in train_data])
```
재미 삼아 이 리뷰 데이터 하나를 원래 영어 단어로 어떻게 바꾸는지 보겠습니다:
```
# word_index는 단어와 정수 인덱스를 매핑한 딕셔너리입니다
word_index = imdb.get_word_index()
# 정수 인덱스와 단어를 매핑하도록 뒤집습니다
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
# 리뷰를 디코딩합니다.
# 0, 1, 2는 '패딩', '문서 시작', '사전에 없음'을 위한 인덱스이므로 3을 뺍니다
decoded_review = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]])
decoded_review
```
## 데이터 준비
신경망에 숫자 리스트를 주입할 수는 없습니다. 리스트를 텐서로 바꾸는 두 가지 방법이 있습니다:
* 같은 길이가 되도록 리스트에 패딩을 추가하고 `(samples, sequence_length)` 크기의 정수 텐서로 변환합니다. 그다음 이 정수 텐서를 다룰 수 있는 층을 신경망의 첫 번째 층으로 사용합니다(`Embedding` 층을 말하며 나중에 자세히 다루겠습니다).
* 리스트를 원-핫 인코딩하여 0과 1의 벡터로 변환합니다. 예를 들면 시퀀스 `[3, 5]`를 인덱스 3과 5의 위치는 1이고 그 외는 모두 0인 10,000차원의 벡터로 각각 변환합니다. 그다음 부동 소수 벡터 데이터를 다룰 수 있는 `Dense` 층을 신경망의 첫 번째 층으로 사용합니다.
여기서는 두 번째 방식을 사용하고 이해를 돕기 위해 직접 데이터를 원-핫 벡터로 만들겠습니다:
```
import numpy as np
def vectorize_sequences(sequences, dimension=10000):
# 크기가 (len(sequences), dimension))이고 모든 원소가 0인 행렬을 만듭니다
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1. # results[i]에서 특정 인덱스의 위치를 1로 만듭니다
return results
# 훈련 데이터를 벡터로 변환합니다
x_train = vectorize_sequences(train_data)
# 테스트 데이터를 벡터로 변환합니다
x_test = vectorize_sequences(test_data)
```
이제 샘플은 다음과 같이 나타납니다:
```
x_train[0]
```
레이블은 쉽게 벡터로 바꿀 수 있습니다:
```
# 레이블을 벡터로 바꿉니다
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
```
이제 신경망에 주입할 데이터가 준비되었습니다.
## 신경망 모델 만들기
입력 데이터가 벡터이고 레이블은 스칼라(1 또는 0)입니다. 아마 앞으로 볼 수 있는 문제 중에서 가장 간단할 것입니다. 이런 문제에 잘 작동하는 네트워크 종류는 `relu` 활성화 함수를 사용한 완전 연결 층(즉, `Dense(16, activation='relu')`)을 그냥 쌓은 것입니다.
`Dense` 층에 전달한 매개변수(16)는 은닉 유닛의 개수입니다. 하나의 은닉 유닛은 층이 나타내는 표현 공간에서 하나의 차원이 됩니다. 2장에서 `relu` 활성화 함수를 사용한 `Dense` 층을 다음과 같은 텐서 연산을 연결하여 구현하였습니다:
`output = relu(dot(W, input) + b)`
16개의 은닉 유닛이 있다는 것은 가중치 행렬 `W`의 크기가 `(input_dimension, 16)`이라는 뜻입니다. 입력 데이터와 `W`를 점곱하면 입력 데이터가 16 차원으로 표현된 공간으로 투영됩니다(그리고 편향 벡터 `b`를 더하고 `relu` 연산을 적용합니다). 표현 공간의 차원을 '신경망이 내재된 표현을 학습할 때 가질 수 있는 자유도'로 이해할 수 있습니다. 은닉 유닛을 늘리면 (표현 공간을 더 고차원으로 만들면) 신경망이 더욱 복잡한 표현을 학습할 수 있지만 계산 비용이 커지고 원치 않은 패턴을 학습할 수도 있습니다(훈련 데이터에서는 성능이 향상되지만 테스트 데이터에서는 그렇지 않은 패턴입니다).
`Dense` 층을 쌓을 때 두 가진 중요한 구조상의 결정이 필요합니다:
* 얼마나 많은 층을 사용할 것인가
* 각 층에 얼마나 많은 은닉 유닛을 둘 것인가
4장에서 이런 결정을 하는 데 도움이 되는 일반적인 원리를 배우겠습니다. 당분간은 저를 믿고 선택한 다음 구조를 따라 주세요.
* 16개의 은닉 유닛을 가진 두 개의 은닉층
* 현재 리뷰의 감정을 스칼라 값의 예측으로 출력하는 세 번째 층
중간에 있는 은닉층은 활성화 함수로 `relu`를 사용하고 마지막 층은 확률(0과 1 사이의 점수로, 어떤 샘플이 타깃 '1'일 가능성이 높다는 것은 그 리뷰가 긍정일 가능성이 높다는 것을 의미합니다)을 출력하기 위해 시그모이드 활성화 함수를 사용합니다. `relu`는 음수를 0으로 만드는 함수입니다. 시그모이드는 임의의 값을 [0, 1] 사이로 압축하므로 출력 값을 확률처럼 해석할 수 있습니다.
다음이 이 신경망의 모습입니다:

다음은 이 신경망의 케라스 구현입니다. 이전에 보았던 MNIST 예제와 비슷합니다:
```
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
```
마지막으로 손실 함수와 옵티마이저를 선택해야 합니다. 이진 분류 문제이고 신경망의 출력이 확률이기 때문에(네트워크의 끝에 시그모이드 활성화 함수를 사용한 하나의 유닛으로 된 층을 놓았습니다), `binary_crossentropy` 손실이 적합합니다. 이 함수가 유일한 선택은 아니고 예를 들어 `mean_squared_error`를 사용할 수도 있습니다. 확률을 출력하는 모델을 사용할 때는 크로스엔트로피가 최선의 선택입니다. 크로스엔트로피는 정보 이론 분야에서 온 개념으로 확률 분포 간의 차이를 측정합니다. 여기에서는 원본 분포와 예측 분포 사이를 측정합니다.
다음은 `rmsprop` 옵티마이저와 `binary_crossentropy` 손실 함수로 모델을 설정하는 단계입니다. 훈련하는 동안 정확도를 사용해 모니터링하겠습니다.
```
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
```
케라스에 `rmsprop`, `binary_crossentropy`, `accuracy`가 포함되어 있기 때문에 옵티마이저, 손실 함수, 측정 지표를 문자열로 지정하는 것이 가능합니다. 이따금 옵티마이저의 매개변수를 바꾸거나 자신만의 손실 함수, 측정 함수를 전달해야 할 경우가 있습니다. 전자의 경우에는 옵티마이저 파이썬 클래스를 사용해 객체를 직접 만들어 `optimizer` 매개변수에 전달하면 됩니다:
```
from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss='binary_crossentropy',
metrics=['accuracy'])
```
후자의 경우는 `loss`와 `metrics` 매개변수에 함수 객체를 전달하면 됩니다:
```
from keras import losses
from keras import metrics
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss=losses.binary_crossentropy,
metrics=[metrics.binary_accuracy])
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
```
## 훈련 검증
훈련하는 동안 처음 본 데이터에 대한 모델의 정확도를 측정하기 위해서는 원본 훈련 데이터에서 10,000의 샘플을 떼어서 검증 세트를 만들어야 합니다:
```
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]
```
이제 모델을 512개 샘플씩 미니 배치를 만들어 20번의 에포크 동안 훈련시킵니다(`x_train`과 `y_train` 텐서에 있는 모든 샘플에 대해 20번 반복합니다). 동시에 따로 떼어 놓은 10,000개의 샘플에서 손실과 정확도를 측정할 것입니다. 이렇게 하려면 `validation_data` 매개변수에 검증 데이터를 전달해야 합니다:
```
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
```
CPU를 사용해도 에포크마다 2초가 걸리지 않습니다. 전체 훈련은 20초 이상 걸립니다. 에포크가 끝날 때마다 10,000개의 검증 샘플 데이터에서 손실과 정확도를 계산하기 때문에 약간씩 지연됩니다.
`model.fit()` 메서드는 `History` 객체를 반환합니다. 이 객체는 훈련하는 동안 발생한 모든 정보를 담고 있는 딕셔너리인 `history` 속성을 가지고 있습니다. 한 번 확인해 보죠:
```
history_dict = history.history
history_dict.keys()
```
이 딕셔너리는 훈련과 검증하는 동안 모니터링할 측정 지표당 하나씩 모두 네 개의 항목을 담고 있습니다. 맷플롯립을 사용해 훈련과 검증 데이터에 대한 손실과 정확도를 그려 보겠습니다:
```
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
# ‘bo’는 파란색 점을 의미합니다
plt.plot(epochs, loss, 'bo', label='Training loss')
# ‘b’는 파란색 실선을 의미합니다
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf() # 그래프를 초기화합니다
acc = history_dict['acc']
val_acc = history_dict['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
```
점선은 훈련 손실과 정확도이고 실선은 검증 손실과 정확도입니다. 신경망의 무작위한 초기화 때문에 사람마다 결과거 조금 다를 수 있습니다.
여기에서 볼 수 있듯이 훈련 손실이 에포크마다 감소하고 훈련 정확도는 에포크마다 증가합니다. 경사 하강법 최적화를 사용했을 때 반복마다 최소화되는 것이 손실이므로 기대했던 대로입니다. 검증 손실과 정확도는 이와 같지 않습니다. 4번째 에포크에서 그래프가 역전되는 것 같습니다. 이것이 훈련 세트에서 잘 작동하는 모델이 처음 보는 데이터에 잘 작동하지 않을 수 있다고 앞서 언급한 경고의 한 사례입니다. 정확한 용어로 말하면 과대적합되었다고 합니다. 2번째 에포크 이후부터 훈련 데이터에 과도하게 최적화되어 훈련 데이터에 특화된 표현을 학습하므로 훈련 세트 이외의 데이터에는 일반화되지 못합니다.
이런 경우에 과대적합을 방지하기 위해서 3번째 에포크 이후에 훈련을 중지할 수 있습니다. 일반적으로 4장에서 보게 될 과대적합을 완화하는 다양한 종류의 기술을 사용할 수 있습니다.
처음부터 다시 새로운 신경망을 4번의 에포크 동안만 훈련하고 테스트 데이터에서 평가해 보겠습니다:
```
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)
results
```
아주 단순한 방식으로도 87%의 정확도를 달성했습니다. 최고 수준의 기법을 사용하면 95%에 가까운 성능을 얻을 수 있습니다.
## 훈련된 모델로 새로운 데이터에 대해 예측하기
모델을 훈련시킨 후에 이를 실전 환경에서 사용하고 싶을 것입니다. `predict` 메서드를 사용해서 어떤 리뷰가 긍정일 확률을 예측할 수 있습니다:
```
model.predict(x_test)
```
여기에서처럼 이 모델은 어떤 샘플에 대해 확신을 가지고 있지만(0.99 또는 그 이상, 0.01 또는 그 이하) 어떤 샘플에 대해서는 확신이 부족합니다(0.6, 0.4).
## 추가 실험
* 여기에서는 두 개의 은닉층을 사용했습니다. 한 개 또는 세 개의 은닉층을 사용하고 검증과 테스트 정확도에 어떤 영향을 미치는지 확인해 보세요.
* 층의 은닉 유닛을 추가하거나 줄여 보세요: 32개 유닛, 64개 유닛 등
* `binary_crossentropy` 대신에 `mse` 손실 함수를 사용해 보세요.
* `relu` 대신에 `tanh` 활성화 함수(초창기 신경망에서 인기 있었던 함수입니다)를 사용해 보세요.
다음 실험을 진행하면 여기에서 선택한 구조가 향상의 여지는 있지만 어느 정도 납득할 만한 수준이라는 것을 알게 것입니다!
## 정리
다음은 이 예제에서 배운 것들입니다:
* 원본 데이터를 신경망에 텐서로 주입하기 위해서는 꽤 많은 전처리가 필요합니다. 단어 시퀀스는 이진 벡터로 인코딩될 수 있고 다른 인코딩 방식도 있습니다.
* `relu` 활성화 함수와 함께 `Dense` 층을 쌓은 네트워크는 (감성 분류를 포함하여) 여러 종류의 문제에 적용할 수 있어서 앞으로 자주 사용하게 될 것입니다.
* (출력 클래스가 두 개인) 이진 분류 문제에서 네트워크는 하나의 유닛과 `sigmoid` 활성화 함수를 가진 `Dense` 층으로 끝나야 합니다. 이 신경망의 출력은 확률을 나타내는 0과 1 사이의 스칼라 값입니다.
* 이진 분류 문제에서 이런 스칼라 시그모이드 출력에 대해 사용할 손실 함수는 `binary_crossentropy`입니다.
* `rmsprop` 옵티마이저는 문제에 상관없이 일반적으로 충분히 좋은 선택입니다. 걱정할 거리가 하나 줄은 셈입니다.
* 훈련 데이터에 대해 성능이 향상됨에 따라 신경망은 과대적합되기 시작하고 이전에 본적 없는 데이터에서는 결과가 점점 나빠지게 됩니다. 항상 훈련 세트 이외의 데이터에서 성능을 모니터링해야 합니다.
| true |
code
| 0.775764 | null | null | null | null |
|
# Transfer learning with `braai`
`20200211` nb status: unfinished
We will fine-tune `braai` with transfer learning using the ZUDS survey as an example.
```
from astropy.io import fits
from astropy.visualization import ZScaleInterval
from bson.json_util import loads, dumps
import gzip
import io
from IPython import display
import json
from matplotlib.colors import LogNorm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from pandas.plotting import register_matplotlib_converters
from penquins import Kowalski
import tensorflow as tf
from tensorflow.keras.models import model_from_json, load_model
from tensorflow.keras.utils import normalize as tf_norm
import os
plt.style.use(['dark_background'])
register_matplotlib_converters()
%matplotlib inline
def load_model_helper(path, model_base_name):
"""
Build keras model using json-file with architecture and hdf5-file with weights
"""
with open(os.path.join(path, f'{model_base_name}.architecture.json'), 'r') as json_file:
loaded_model_json = json_file.read()
m = model_from_json(loaded_model_json)
m.load_weights(os.path.join(path, f'{model_base_name}.weights.h5'))
return m
def make_triplet(alert, normalize: bool = False, old_norm: bool = False, to_tpu: bool = False):
"""
Feed in alert packet
"""
cutout_dict = dict()
for cutout in ('science', 'template', 'difference'):
cutout_data = loads(dumps([alert[f'cutout{cutout.capitalize()}']]))[0]
# unzip
with gzip.open(io.BytesIO(cutout_data), 'rb') as f:
with fits.open(io.BytesIO(f.read())) as hdu:
data = hdu[0].data
# replace nans with zeros
cutout_dict[cutout] = np.nan_to_num(data)
# normalize
if normalize:
if not old_norm:
cutout_dict[cutout] /= np.linalg.norm(cutout_dict[cutout])
else:
# model <= d6_m7
cutout_dict[cutout] = tf_norm(cutout_dict[cutout])
# pad to 63x63 if smaller
shape = cutout_dict[cutout].shape
#print(shape)
if shape != (63, 63):
# print(f'Shape of {candid}/{cutout}: {shape}, padding to (63, 63)')
cutout_dict[cutout] = np.pad(cutout_dict[cutout], [(0, 63 - shape[0]), (0, 63 - shape[1])],
mode='constant', constant_values=1e-9)
triplet = np.zeros((63, 63, 3))
triplet[:, :, 0] = cutout_dict['science']
triplet[:, :, 1] = cutout_dict['template']
triplet[:, :, 2] = cutout_dict['difference']
if to_tpu:
# Edge TPUs require additional processing
triplet = np.rint(triplet * 128 + 128).astype(np.uint8).flatten()
return triplet
def plot_triplet(tr):
fig = plt.figure(figsize=(8, 2), dpi=120)
ax1 = fig.add_subplot(131)
ax1.axis('off')
interval = ZScaleInterval()
limits = interval.get_limits(triplet[:, :, 0])
# norm=LogNorm()
ax1.imshow(tr[:, :, 0], origin='upper', cmap=plt.cm.bone, vmin=limits[0], vmax=limits[1])
ax1.title.set_text('Science')
ax2 = fig.add_subplot(132)
ax2.axis('off')
limits = interval.get_limits(triplet[:, :, 1])
ax2.imshow(tr[:, :, 1], origin='upper', cmap=plt.cm.bone, vmin=limits[0], vmax=limits[1])
ax2.title.set_text('Reference')
ax3 = fig.add_subplot(133)
ax3.axis('off')
limits = interval.get_limits(triplet[:, :, 2])
ax3.imshow(tr[:, :, 2], origin='upper', cmap=plt.cm.bone, vmin=limits[0], vmax=limits[1])
ax3.title.set_text('Difference')
plt.show()
```
## Kowalski
Get some example triplets from Kowalski
```
with open('secrets.json', 'r') as f:
secrets = json.load(f)
k = Kowalski(username=secrets['kowalski']['username'],
password=secrets['kowalski']['password'])
connection_ok = k.check_connection()
print(f'Connection OK: {connection_ok}')
```
High `braai` version `d6_m9` scores:
```
q = {"query_type": "aggregate",
"query": {"catalog": "ZUDS_alerts",
"pipeline": [{'$match': {'classifications.braai': {'$gt': 0.9}}},
{'$project': {'candidate': 0, 'coordinates': 0}},
{'$sample': { 'size': 20 }}]
}
}
r = k.query(query=q)
high_braai = r['result_data']['query_result']
for alert in high_braai[-2:]:
triplet = make_triplet(alert, normalize=True, old_norm=False)
plot_triplet(triplet)
```
Low `braai` version `d6_m9` scores:
```
q = {"query_type": "aggregate",
"query": {"catalog": "ZUDS_alerts",
"pipeline": [{'$match': {'classifications.braai': {'$lt': 0.1}}},
{'$project': {'candidate': 0, 'coordinates': 0}},
{'$sample': { 'size': 20 }}]
}
}
r = k.query(query=q)
low_braai = r['result_data']['query_result']
for alert in low_braai[-2:]:
triplet = make_triplet(alert, normalize=True, old_norm=False)
plot_triplet(triplet)
```
## Load the model
```
model = load_model_helper(path='../models', model_base_name='d6_m9')
# remove the output layer, leave the feature extraction part
model_fe = tf.keras.Model(inputs=model.inputs, outputs=model.layers[-2].output)
for alert in low_braai[-2:]:
triplet = make_triplet(alert, normalize=True, old_norm=False)
tr = np.expand_dims(triplet, axis=0)
# get extracted features
features = model_fe.predict(tr)
print(features.shape)
# print(features)
output = tf.keras.layers.Dense(1, activation='sigmoid')(model_fe.output)
model_tl = tf.keras.Model(inputs=model_fe.inputs, outputs=output)
# mark layers as not trainable
for layer in model_tl.layers[:-1]:
layer.trainable = False
model_tl.summary()
```
| true |
code
| 0.602237 | null | null | null | null |
|
# Database Population & Querying
##### Using Pandas & SQLAlchemy to store and retrieve StatsBomb event data
---
```
import requests
import pandas as pd
import numpy as np
from tqdm import tqdm
from sqlalchemy import create_engine
```
In this example, we use SQLAlchemy's `create_engine` function to create a temporary database in memory.
We can use a similar approach to connect to other persistant local or remote databases. It's very flexible.
---
```
base_url = "https://raw.githubusercontent.com/statsbomb/open-data/master/data/"
comp_url = base_url + "matches/{}/{}.json"
match_url = base_url + "events/{}.json"
def parse_data(competition_id, season_id):
matches = requests.get(url=comp_url.format(competition_id, season_id)).json()
match_ids = [m['match_id'] for m in matches]
events = []
for match_id in tqdm(match_ids):
for e in requests.get(url=match_url.format(match_id)).json():
events.append(e)
return pd.json_normalize(events, sep='_')
```
This is pretty much the same `parse_data` function that we've seen in previous examples, but with a couple specific twists:
- We are storing entire events, not subsets of them.
- We are using `pd.json_normalize` to convert the hierarchical StatsBomb JSON data structure into something more tabular that can more easily be stored in a relational database.
---
```
competition_id = 43
season_id = 3
df = parse_data(competition_id, season_id)
location_columns = [x for x in df.columns.values if 'location' in x]
for col in location_columns:
for i, dimension in enumerate(["x", "y"]):
new_col = col.replace("location", dimension)
df[new_col] = df.apply(lambda x: x[col][i] if type(x[col]) == list else None, axis=1)
```
Because StatsBomb delivers x/y coordinates in an array (e.g. `[60.0, 40.0]`), we need to split them into separate columns so we can easily store the individual coordinates in a SQL database.
Unfortunately, this is a bit tricky, and we use a couple fun `Python` and `Pandas` tricks to our advantage.
First we determine which columns in the DataFrame are locations (with the list comprehension that generates the `location_columns` list).
Then we iterate through these columns, and each `dimension` (i.e. `x` and `y`), to create two new columns for each old column.
e.g. `pass_end_location` becomes `pass_end_x` and `pass_end_y`
Once we have the new column names, we use `df.apply` and a lambda function to grab the correct coordinate from each row. I recommend reading further on both **`df.apply`** and python **lambda functions** as they're a bit complicated, but fully worth learning about.
---
```
df = df[[c for c in df.columns if c not in location_columns]]
```
We use a list comprehension to generate a new subset of columns that we want in the DataFrame, excluding the old location columns.
---
```
columns_to_remove = ['tactics_lineup', 'related_events', 'shot_freeze_frame']
df = df[[c for c in df.columns if c not in columns_to_remove]]
```
In the same fashion, we're going to exclude the `tactics_lineup`, `related_events`, and `shot_freeze_frame` columns because their heirarcical data structures cannot easily be stored in a SQL database.
If you need these particular columns for analysis, you have to pull them out seperately.
> Note: _It's possible that you may need to exclude additional columns from the data specification if you're using a data set other than the World Cup 2018 data that we're using for this example._
---
```
engine = create_engine('sqlite://')
```
This creates a temporary SQLite3 database in memory, and provides an engine object that you can use to interact directly with it.
If you wish to use a persistant local or remote database, you can change the `uri` (i.e. `sqlite://`) to point elsewhere. For example, a `uri` for a local mysql database might look something like this: `mysql://user:password@127.0.0.1:3306/dbname`.
---
```
df.to_sql('events', engine)
```
This loads the content of our DataFrame into our SQLite3 database via the `engine` object, and puts the rows into new table named `events`.
> Note: **This takes a while**, 2-3 minutes on my local laptop.
---
```
top_passers = """
select player_name, count(*) as passes
from events
where 1=1
and type_name = "Pass"
group by player_id
order by count(*) desc
"""
pd.read_sql(top_passers, engine).head(10)
```
The demonstrates a basic SQL query that finds which players have attempted the most passes during the competition.
The query is fed into `pd.read_sql` along with the engine object to return the results.
---
```
top_xg = """
select player_name
, round(sum(shot_statsbomb_xg),2) as 'total xg'
from events
where 1=1
and type_name = "Shot"
group by player_id
order by 2 desc
"""
pd.read_sql(top_xg, engine).head(10)
```
Another example, this time demonstrating the results of a different question, but using a pretty similar SQL query to provide the solution.
---
---
Devin Pleuler 2020
| true |
code
| 0.26631 | null | null | null | null |
|
#### DS requests results via request/response cycle
A user can send a request to the domain owner to access a resource.
- The user can send a request by calling the `.request` method on the pointer.
- A `reason` needs to be passed on a parameter while requesting access to the data.
#### The user selects a dataset and perform some query
- The user selects a network and domain
- The logs into the domain and selects a dataset
- The user perform a query on the selected dataset pointer
```
import syft as sy
# Let's list the available dataset
sy.datasets
# We want to access the `Pneumonia Dataset`, let's connect to the RSNA domain
# Let's list the RSNA available networks
sy.networks
# Let's select the `WHO` network and list the available domains on the `WHO Network`.
who_network = sy.networks[1]
who_network.domains
# Let's select the `RSNA domain`
rsna_domain = who_network["e1640cc4af70422da1d60300724b1ee3"]
# Let's login into the rsna domain
rsna_domain_client = rsna_domain.login(email="sheldon@caltech.edu", password="bazinga")
# Let's select the pnuemonia dataset
pnuemonia_dataset = rsna_domain_client["fc650f14f6f7454b87d3ccd345c437b5"]
# Let's see the dataset
pnuemonia_dataset
# Let's select the lable tensors
label_ptr = pnuemonia_dataset["labels"]
# Let's calculate the unique labels in the dataset
unique_labels = label_ptr[:,0].unique()
```
#### The user fetches the results of their query
- The user can perform a `.get` operation to download the data of the variable locally.
- If a user tries to access a variable without publishing its results or without requesting it, then they receive a 403.
- If a user has requested a resource, then its denied by the DO, then the user receives a 403 on performing a get operation on the resource.
```
number_of_unique_labels = unique_labels.shape
# Let's access the labels
number_of_unique_labels.get()
# Let's request the results from the Domain Owner
number_of_unique_labels.request(reason="Know the number of unique labels in the dataset.")
```
#### The user views the request logs
- The user can list all the logs of all the requests send by them to a domain. **[P1]**
Following properties are visible to the user w.r.t to the logs (for data requests):
- Request Id (Unique id of the request)
- Request Date (Datetime on which the request was submitted. The datetime/timestamp are shown in UTC)
- Reason (The reason submitted to access the resource by requester)
- Result Id (The unique id of the reasource being requested)
- State (State of the request - Approved/Declined/Pending)
- Reviewer Comments (Comment provided by the reqeuest reviewer (DO) during request approval/deny)
- The user can filter through the logs via ID and Status. **[P2]**
```
# Let's check the status of our request logs
# A user can see only the request logs with state == `Pending`.
rsna_domain.requests
# If we want to see all the requests that are submitted to the domain,
rsna_domain.requests.all()
```
```
Some time has passed, let' check if our requests are approved or not.
```
```
# Let's check again for pending requests first....
rsna_domain.requests
# Let's check all the submitted requests
rsna_domain.requests.all()
# Great our requests are approved, let's get the information
unique_labels = number_of_unique_labels.get()
print(f"Unique Labels: {len(unique_labels)}")
# Filtering requests logs
# via Id (Get the request with the given request id)
rsna_domain.requests.filter(id="3ca9694c8e5d4214a1ed8025a1391c8c")
# or via Status (List all the logs with given status)
rsna_domain.requests.filter(status="Approved")
```
#### Dummy Data
```
import pandas as pd
from enum import Enum
import uuid
import torch
import datetime
import json
import numpy as np
class bcolors(Enum):
HEADER = "\033[95m"
OKBLUE = "\033[94m"
OKCYAN = "\033[96m"
OKGREEN = "\033[92m"
WARNING = "\033[93m"
FAIL = "\033[91m"
ENDC = "\033[0m"
BOLD = "\033[1m"
UNDERLINE = "\033[4m"
all_datasets = [
{
"Id": uuid.uuid4().hex,
"Name": "Diabetes Dataset",
"Tags": ["Health", "Classification", "Dicom"],
"Assets": '''["Images"] -> Tensor; ["Labels"] -> Tensor''',
"Description": "A large set of high-resolution retina images",
"Domain": "California Healthcare Foundation",
"Network": "WHO",
"Usage": 102,
"Added On": datetime.datetime.now().replace(month=1).strftime("%b %d %Y")
},
{
"Id": uuid.uuid4().hex,
"Name": "Canada Commodities Dataset",
"Tags": ["Commodities", "Canada", "Trade"],
"Assets": '''["ca-feb2021"] -> DataFrame''',
"Description": "Commodity Trade Dataset",
"Domain": "Canada Domain",
"Network": "United Nations",
"Usage": 40,
"Added On": datetime.datetime.now().replace(month=3, day=11).strftime("%b %d %Y")
},
{
"Id": uuid.uuid4().hex,
"Name": "Italy Commodities Dataset",
"Tags": ["Commodities", "Italy", "Trade"],
"Assets": '''["it-feb2021"] -> DataFrame''',
"Description": "Commodity Trade Dataset",
"Domain": "Italy Domain",
"Network": "United Nations",
"Usage": 23,
"Added On": datetime.datetime.now().replace(month=3).strftime("%b %d %Y")
},
{
"Id": uuid.uuid4().hex,
"Name": "Netherlands Commodities Dataset",
"Tags": ["Commodities", "Netherlands", "Trade"],
"Assets": '''["ne-feb2021"] -> DataFrame''',
"Description": "Commodity Trade Dataset",
"Domain": "Netherland Domain",
"Network": "United Nations",
"Usage": 20,
"Added On": datetime.datetime.now().replace(month=4, day=12).strftime("%b %d %Y")
},
{
"Id": uuid.uuid4().hex,
"Name": "Pnuemonia Dataset",
"Tags": ["Health", "Pneumonia", "X-Ray"],
"Assets": '''["X-Ray-Images"] -> Tensor; ["labels"] -> Tensor''',
"Description": "Chest X-Ray images. All provided images are in DICOM format.",
"Domain": "RSNA",
"Network": "WHO",
"Usage": 334,
"Added On": datetime.datetime.now().replace(month=1).strftime("%b %d %Y")
},
]
all_datasets_df = pd.DataFrame(all_datasets)
# Print available networks
available_networks = [
{
"Id": f"{uuid.uuid4().hex}",
"Name": "United Nations",
"Hosted Domains": 4,
"Hosted Datasets": 6,
"Description": "The UN hosts data related to the commodity and Census data.",
"Tags": ["Commodities", "Census", "Health"],
"Url": "https://un.openmined.org",
},
{
"Id": f"{uuid.uuid4().hex}",
"Name": "World Health Organisation",
"Hosted Domains": 3,
"Hosted Datasets": 5,
"Description": "WHO hosts data related to health sector of different parts of the worlds.",
"Tags": ["Virology", "Cancer", "Health"],
"Url": "https://who.openmined.org",
},
{
"Id": f"{uuid.uuid4().hex}",
"Name": "International Space Station",
"Hosted Domains": 2,
"Hosted Datasets": 4,
"Description": "ISS hosts data related to the topography of different exoplanets.",
"Tags": ["Exoplanets", "Extra-Terrestrial"],
"Url": "https://iss.openmined.org",
},
]
networks_df = pd.DataFrame(available_networks)
who_domains = [
{
"Id": f"{uuid.uuid4().hex}",
"Name": "California Healthcare Foundation",
"Hosted Datasets": 1,
"Description": "Health care systems",
"Tags": ["Clinical Data", "Healthcare"],
},
{
"Id": f"{uuid.uuid4().hex}",
"Name": "RSNA",
"Hosted Datasets": 1,
"Description": "Radiological Image Datasets",
"Tags": ["Dicom", "Radiology", "Health"],
},
]
who_domains_df = pd.DataFrame(who_domains)
pneumonia_dataset = [
{
"Asset Key": "[X-Ray-Images]",
"Type": "Tensor",
"Shape": "(40000, 7)"
},
{
"Asset Key": '[labels]',
"Type": "Tensor",
"Shape": "(40000, 5)"
},
]
print("""
Name: Pnuemonia Detection and Locationzation Dataset
Description: Chest X-Ray images. All provided images are in DICOM format.
""")
pneumonia_dataset_df = pd.DataFrame(pneumonia_dataset)
labels_data = np.random.randint(0, 2, size=(40000, 5))[:, 0]
label_tensors = torch.Tensor(labels_data)
authorization_error = f"""
{bcolors.FAIL.value}PermissionDenied:{bcolors.ENDC.value}
You don't have authorization to perform the `.get` operation.
You need to either `request` the results or `publish` the results.
"""
print(authorization_error)
request_uuid = uuid.uuid4().hex
request_submission = f"""
Your request has been submitted to the domain. Your request id is: {bcolors.BOLD.value}{request_uuid}
{bcolors.ENDC.value}You can check the status of your requests via `.requests`.
"""
print(request_submission)
requests_data = [
{
"Request Id": uuid.uuid4().hex,
"Request Date": datetime.datetime.now().strftime("%b %d %Y %I:%M%p"),
"Reason": "Know the number of unique labels in the dataset.",
"Result Id": uuid.uuid4().hex,
"State": "Pending",
"Reviewer Comments": "-",
},
{
"Request Id": uuid.uuid4().hex,
"Request Date": datetime.datetime.now().replace(day=19, hour=1).strftime("%b %d %Y %I:%M%p"),
"Reason": "Get the labels in the dataset.",
"Result Id": uuid.uuid4().hex,
"State": "Denied",
"Reviewer Comments": "Access to raw labels is not allowed",
}
]
requests_data_df = pd.DataFrame(requests_data)
approved_requests_data_df = requests_data_df.copy()
approved_requests_data_df["State"][0] = "Approved"
approved_requests_data_df["Reviewer Comments"][0] = "Looks good."
filtered_request_logs = approved_requests_data_df[:1]
```
| true |
code
| 0.6675 | null | null | null | null |
|
[](https://colab.research.google.com/github/cadCAD-org/demos/blob/master/tutorials/robots_and_marbles/robot-marbles-part-3/robot-marbles-part-3.ipynb)
# cadCAD Tutorials: The Robot and the Marbles, part 3
In parts [1](../robot-marbles-part-1/robot-marbles-part-1.ipynb) and [2](../robot-marbles-part-2/robot-marbles-part-2.ipynb) we introduced the 'language' in which a system must be described in order for it to be interpretable by cadCAD and some of the basic concepts of the library:
* State Variables
* Timestep
* State Update Functions
* Partial State Update Blocks
* Simulation Configuration Parameters
* Policies
In this notebook we'll look at how subsystems within a system can operate in different frequencies. But first let's copy the base configuration with which we ended Part 2. Here's the description of that system:
__The robot and the marbles__
* Picture a box (`box_A`) with ten marbles in it; an empty box (`box_B`) next to the first one; and __two__ robot arms capable of taking a marble from any one of the boxes and dropping it into the other one.
* The robots are programmed to take one marble at a time from the box containing the largest number of marbles and drop it in the other box. They repeat that process until the boxes contain an equal number of marbles.
* The robots act simultaneously; in other words, they assess the state of the system at the exact same time, and decide what their action will be based on that information.
```
%%capture
# Only run this cell if you need to install the libraries
# If running in google colab, this is needed.
!pip install cadcad matplotlib pandas numpy
# Import dependancies
# Data processing and plotting libraries
import pandas as pd
import numpy as np
from random import normalvariate
import matplotlib.pyplot as plt
# cadCAD specific libraries
from cadCAD.configuration.utils import config_sim
from cadCAD.configuration import Experiment
from cadCAD.engine import ExecutionContext, Executor
def p_robot_arm(params, substep, state_history, previous_state):
# Parameters & variables
box_a = previous_state['box_A']
box_b = previous_state['box_B']
# Logic
if box_b > box_a:
b_to_a = 1
elif box_b < box_a:
b_to_a = -1
else:
b_to_a = 0
# Output
return({'add_to_A': b_to_a, 'add_to_B': -b_to_a})
def s_box_A(params, substep, state_history, previous_state, policy_input):
# Parameters & variables
box_A_current = previous_state['box_A']
box_A_change = policy_input['add_to_A']
# Logic
box_A_new = box_A_current + box_A_change
# Output
return ('box_A', box_A_new)
def s_box_B(params, substep, state_history, previous_state, policy_input):
# Parameters & variables
box_B_current = previous_state['box_B']
box_B_change = policy_input['add_to_B']
# Logic
box_B_new = box_B_current + box_B_change
# Output
return ('box_B', box_B_new)
partial_state_update_blocks = [
{
'policies': {
'robot_arm_1': p_robot_arm,
'robot_arm_2': p_robot_arm
},
'variables': {
'box_A': s_box_A,
'box_B': s_box_B
}
}
]
MONTE_CARLO_RUNS = 1
SIMULATION_TIMESTEPS = 10
sim_config = config_sim(
{
'N': MONTE_CARLO_RUNS,
'T': range(SIMULATION_TIMESTEPS),
#'M': {} # This will be explained in later tutorials
}
)
initial_state = {
'box_A': 10, # box_A starts out with 10 marbles in it
'box_B': 0 # box_B starts out empty
}
from cadCAD import configs
del configs[:]
experiment = Experiment()
experiment.append_configs(
sim_configs=sim_config,
initial_state=initial_state,
partial_state_update_blocks=partial_state_update_blocks,
)
exec_context = ExecutionContext()
run = Executor(exec_context=exec_context, configs=configs)
(system_events, tensor_field, sessions) = run.execute()
df = pd.DataFrame(system_events)
# Create figure
fig = df.plot(x='timestep', y=['box_A','box_B'], marker='o', markersize=12,
markeredgewidth=4, alpha=0.7, markerfacecolor='black',
linewidth=5, figsize=(12,8), title="Marbles in each box as a function of time",
ylabel='Number of Marbles', grid=True, fillstyle='none',
xticks=list(df['timestep'].drop_duplicates()),
yticks=list(range(1+(df['box_A']+df['box_B']).max())));
```
# Asynchronous Subsystems
We have defined that the robots operate simultaneously on the boxes of marbles. But it is often the case that agents within a system operate asynchronously, each having their own operation frequencies or conditions.
Suppose that instead of acting simultaneously, the robots in our examples operated in the following manner:
* Robot 1: acts once every 2 timesteps
* Robot 2: acts once every 3 timesteps
One way to simulate the system with this change is to introduce a check of the current timestep before the robots act, with the definition of separate policy functions for each robot arm.
```
robots_periods = [2,3] # Robot 1 acts once every 2 timesteps; Robot 2 acts once every 3 timesteps
def get_current_timestep(cur_substep, previous_state):
if cur_substep == 1:
return previous_state['timestep']+1
return previous_state['timestep']
def robot_arm_1(params, substep, state_history, previous_state):
_robotId = 1
if get_current_timestep(substep, previous_state)%robots_periods[_robotId-1]==0: # on timesteps that are multiple of 2, Robot 1 acts
return p_robot_arm(params, substep, state_history, previous_state)
else:
return({'add_to_A': 0, 'add_to_B': 0}) # for all other timesteps, Robot 1 doesn't interfere with the system
def robot_arm_2(params, substep, state_history, previous_state):
_robotId = 2
if get_current_timestep(substep, previous_state)%robots_periods[_robotId-1]==0: # on timesteps that are multiple of 3, Robot 2 acts
return p_robot_arm(params, substep, state_history, previous_state)
else:
return({'add_to_A': 0, 'add_to_B': 0}) # for all other timesteps, Robot 1 doesn't interfere with the system
```
In the Partial State Update Blocks, the user specifies if state update functions will be run in series or in parallel and the policy functions that will be evaluated in that block
```
partial_state_update_blocks = [
{
'policies': { # The following policy functions will be evaluated and their returns will be passed to the state update functions
'robot_arm_1': robot_arm_1,
'robot_arm_2': robot_arm_2
},
'variables': { # The following state variables will be updated simultaneously
'box_A': s_box_A,
'box_B': s_box_B
}
}
]
from cadCAD import configs
del configs[:]
experiment = Experiment()
experiment.append_configs(
sim_configs=sim_config,
initial_state=initial_state,
partial_state_update_blocks=partial_state_update_blocks,
)
exec_context = ExecutionContext()
run = Executor(exec_context=exec_context, configs=configs)
(system_events, tensor_field, sessions) = run.execute()
df = pd.DataFrame(system_events)
# Create figure
fig = df.plot(x='timestep', y=['box_A','box_B'], marker='o', markersize=12,
markeredgewidth=4, alpha=0.7, markerfacecolor='black',
linewidth=5, figsize=(12,8), title="Marbles in each box as a function of time",
ylabel='Number of Marbles', grid=True, fillstyle='none',
xticks=list(df['timestep'].drop_duplicates()),
yticks=list(range(1+(df['box_A']+df['box_B']).max())));
```
Let's take a step-by-step look at what the simulation tells us:
* Timestep 1: the number of marbles in the boxes does not change, as none of the robots act
* Timestep 2: Robot 1 acts, Robot 2 doesn't; resulting in one marble being moved from box A to box B
* Timestep 3: Robot 2 acts, Robot 1 doesn't; resulting in one marble being moved from box A to box B
* Timestep 4: Robot 1 acts, Robot 2 doesn't; resulting in one marble being moved from box A to box B
* Timestep 5: the number of marbles in the boxes does not change, as none of the robots act
* Timestep 6: Robots 1 __and__ 2 act, as 6 is a multiple of 2 __and__ 3; resulting in two marbles being moved from box A to box B and an equilibrium being reached.
| true |
code
| 0.487856 | null | null | null | null |
|
# Data visualization with Matpotlib: Scatter plots
**Created by: Kirstie Whitaker**
**Created on: 29 July 2019**
In 2017 Michael Vendetti and I published a paper on *"Neuroscientific insights into the development of analogical reasoning"*.
The code to recreate the figures from processed data is available at https://github.com/KirstieJane/NORA_WhitakerVendetti_DevSci2017.
This tutorial is going to recreate figure 2 which outlines the behavioral results from the study.
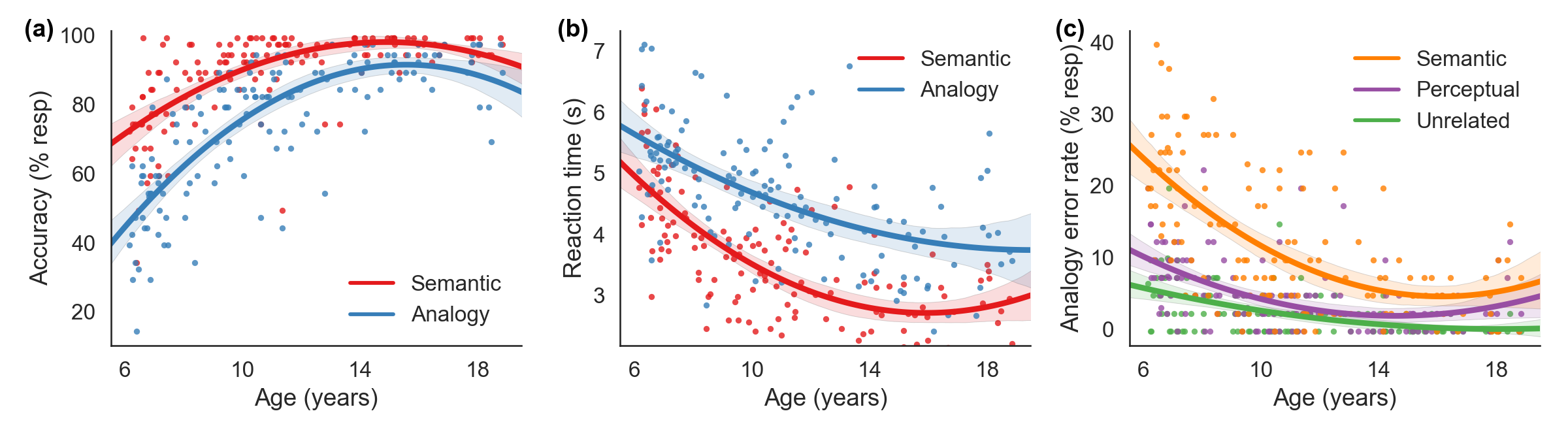
### Take what you need
The philosophy of the tutorial is that I'll start by making some very simple plots, and then enhance them up to "publication standard".
You should take _only the parts you need_ and leave the rest behind.
If you don't care about fancy legends, or setting the number of minor x ticks, then you can stop before we get to that part.
The goal is to have you leave the tutorial feeling like you know _how_ to get started writing code to visualize and customise your plots.
## Import modules
We're importing everything up here.
And they should all be listed in the [requirements.txt](requirements.txt) file in this repository.
Checkout the [README](README.md) file for more information on installing these packages.
```
from IPython.display import display
import matplotlib.lines as mlines
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import os
import pandas as pd
from statsmodels.formula.api import ols
import seaborn as sns
import string
```
## The task
In this study we asked children and adolescents (ages 6 to 18 years old) to lie in an fMRI scanner and complete an visual analogical reasoning task.
There were two types of questions.
* The **analogy** questions (shown in panel a in the figure below) asked "Which of the pictures at the bottom goes together with the 3rd picture *in the same way* that the two pictures at the top go together?"
* The **semantic** questions (shown in panel b in the figure below) were the control questions and the participants were simply asked asked "Which of the pictures below goes best with the picture at the top?"
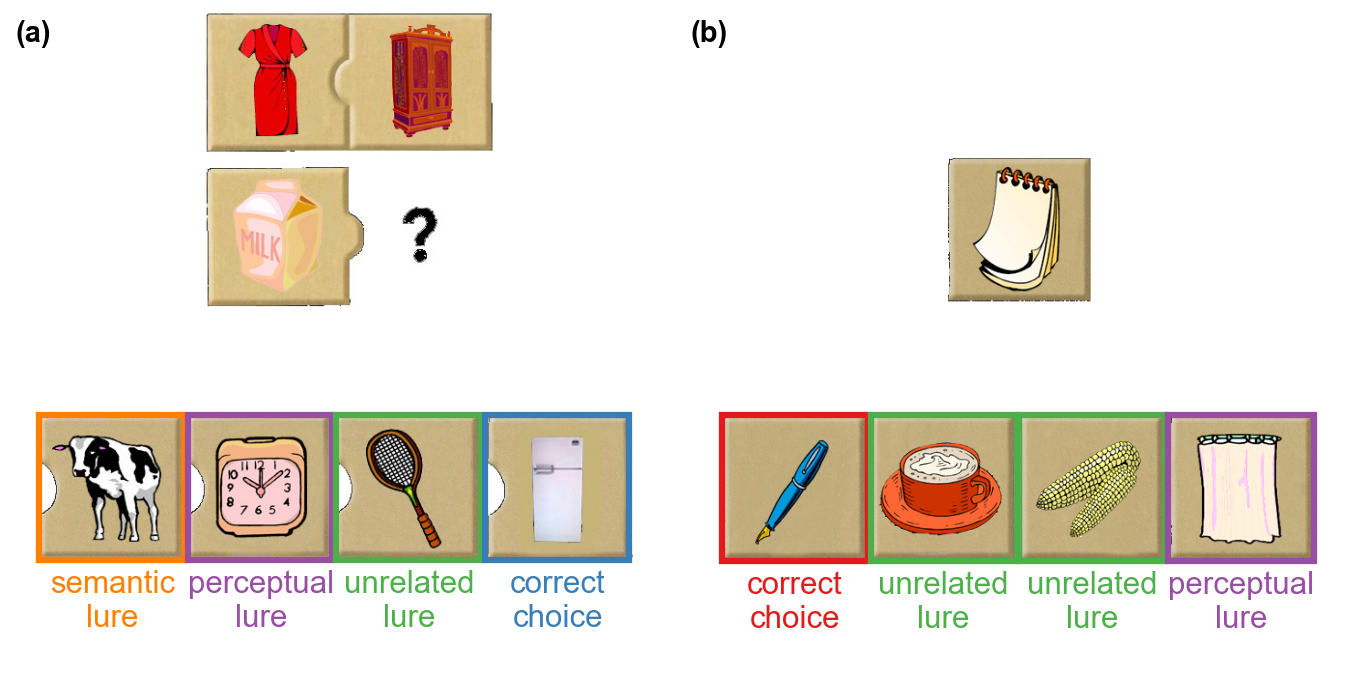
The answers to the **analogy** question are grouped into four different types:
* a **semantic** lure: milk comes from a cow...but that relationship is not the same as the one between dress and wardrobe
* a **perceptual** lure: the milk carton looks perceptually similar to the clock (but isn't semantically related)
* an **unrelate** lure: the tennis racket has nothing to do with any of the pictures at the top
* a **correct** answer: a dress is stored in a wardrobe, the milk is stored in the **fridge**
There are three answer types for the **semantic** question:
* a **correct** answer: the pen write on the notepad
* two **unrelated** lures: tea and sweetcorn have nothing to do with notepaper
* a **perceptual** lure: the shower curtain looks like the notepad (but isn't semantically related)
### Hypotheses
1. Accuracy on both tasks will increase (at a decreasing rate) with age, and accuracy will be higher for the semantic task compared to the analogy task.
2. Reaction time on both tasks will decrease (at a decreasing rate) with age, and reaction time will be smaller (faster) for the semantic task compared to the analogy task.
3. There will be more semantic errors than perceptual errors, and more perceptual errors than unrelated errors across all ages, although the number of errors will decrease with age (corresponding to an increase in accuracy).
## With great power comes great responsibility
I've listed some hypotheses above.
We can't confirm or reject them by visualizing the data.
Just because a line _looks_ like it is going up or down, doesn't mean it is statistically significantly doing so.
You can tell many stories with a picture...including ones that mislead people very easily.
Be careful!
## The data
The data is stored in the [DATA/WhitakerVendetti_BehavData.csv](https://github.com/KirstieJane/NORA_WhitakerVendetti_DevSci2017/blob/master/DATA/WhitakerVendetti_BehavData.csv) file in the [NORA_WhitakerVendetti_DevSci2017](https://github.com/KirstieJane/NORA_WhitakerVendetti_DevSci2017) GitHub repository.
I've made a copy of it in this repository so you don't have to go and get it from the web 😊
The important columns are:
* `subid_short`
* `Age_scan`
* `R1_percent_acc`
* `R2_percent_acc`
* `R1_meanRTcorr_cor`
* `R2_meanRTcorr_cor`
* `R2_percent_sem`
* `R2_percent_per`
* `R2_percent_dis`
The `R1` trials are the semantic trials (they have one relationship to process).
The `R2` trials are the analogy trials (they have two relationships to process).
**Accuracy** is the percentage of correct trials from all the trials a participant saw.
**Reaction time** is the mean RT of the _correct_ trials, corrected for some obvious outliers.
The **semantic**, **perceptual** and **unrelated** (née "distractor") errors are reported as percentages of all the trials the participant saw.
```
# Read in the data
df = pd.read_csv('data/WhitakerVendetti_BehavData.csv')
# Take a look at the first 5 rows
print ('====== Here are the first 5 rows ======')
display(df.head())
# Print all of the columns - its a big wide file 😬
print ('\n\n\n====== Here are all the columns in the file======')
display(df.columns)
# Lets just keep the columns we need
keep_cols = ['subid_short', 'Age_scan',
'R1_percent_acc', 'R2_percent_acc',
'R1_meanRTcorr_cor', 'R2_meanRTcorr_cor',
'R2_percent_sem', 'R2_percent_per', 'R2_percent_dis']
df = df.loc[:, keep_cols]
# And now lets see the summary information of this subset of the data
print ('\n\n\n====== Here are some summary statistics from the columns we need ======')
display(df.describe())
```
## A quick scatter plot
The first thing we'll do is take a look at our first hypothesis: that accuracy increase with age and that the analogy task is harder than the semantic task.
Lets start by making a scatter plot with **age** on the x axis and **semantic accuracy** on the y axis.
Cool, what about the accuracy on the analogy task?
That's nice, but it would probably be more useful if we put these two on the _same_ plot.
Woah, that was very clever!
Matplotlib didn't make two different plots, it assumed that I would want these two plots on the same axis because they were in the same cell.
If I had called `plt.show()` inbetween the two lines above I would have ended up with two plots:
## Being a little more explicit
The scatter plot above shows how easy it is to plot some data - for example to check whether you have any weird outliers or if the pattern of results generally looks the way you'd expect.
You can stop here if your goal is to explore the data ✨
But some times you'll want to have a bit more control over the plots, and for that we'll introduce the concepts of a matplotlib `figure` and an `axis`.
To be honest, we aren't really going to introduce them properly because that's a deeeeeep dive into the matplotlib object-orientated architecture.
There's a nice tutorial at [https://matplotlib.org/users/artists.html](https://matplotlib.org/users/artists.html), but all you need to know is that a **figure** is a figure - the canvas on which you'll make your beautiful visualisation - and it can contain multiple **axes** displaying different aspects or types of data.
In fact, that makes it a little easier to understand why the way that many people create a figure and an axis is to use the [`subplots`](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.subplots.html#matplotlib.pyplot.subplots) command.
(And here's a [stack overflow answer](https://stackoverflow.com/questions/34162443/why-do-many-examples-use-fig-ax-plt-subplots-in-matplotlib-pyplot-python) which explains it in a little more depth.)
If you run the command all by itself, you'll make an empty axis which takes up the whole figure area:
Lets add our plots to a figure:
Did you see that this time we changed `plt.scatter` to `ax.scatter`?
That's because we're being more specific about _where_ we want the data to be plotted.
Specifically, we want it on the first (only) axis in our figure.
We also got explicit about telling jupyter to show the plot with `plt.show()`.
You don't need this, but its good practice for when you start coding lots of plots all in one go and don't want them to all appear on the same axis 😂
## Let's add a regression line
In my paper I modelled the data with a quadratic (yeah, yeah, suboptimal, I know).
I used [`statsmodels`](https://www.statsmodels.org/stable/index.html) to fit the model and to get the predicted values.
```
# Add a column to our data frame for the Age_scan squared
df['Age_scan_sq'] = df['Age_scan']**2
# Semantic
formula_sem = 'R1_percent_acc ~ Age_scan_sq + Age_scan'
mod_sem = ols(formula=formula_sem, data=df)
results_sem = mod_sem.fit()
print(results_sem.summary())
predicted_sem = results_sem.predict()
print(predicted_sem)
# Analogy
formula_ana = 'R2_percent_acc ~ Age_scan_sq + Age_scan'
mod_ana = ols(formula=formula_ana, data=df)
results_ana = mod_ana.fit()
print(results_ana.summary())
predicted_ana = results_ana.predict()
print(predicted_ana)
```
Lets plot that modelled pattern on our scatter plot.
Hmmmm, that looks ok....but usually we'd draw these predicted values as a line rather than individual points.
And they'd be the same color.
To connect up the dots, we're going to use `ax.plot` instead of `ax.scatter`.
Woah! That's not right.
We forgot to sort the data into ascending order before we plotted it so we've connected all the points in the order that the participants joined the study....which is not a helpful ordering at all.
So instead, lets add the predicted values to our data frame and sort the data before we plot it:
```
df['R1_percent_acc_pred'] = predicted_sem
df['R2_percent_acc_pred'] = predicted_ana
df = df.sort_values(by='Age_scan', axis = 0)
```
Cool!
But those lines aren't very easy to see.
Let's make them a little thicker.
## Add a legend
These two lines aren't labelled!
We don't know which one is which.
So lets add a legend to the plot.
The function is called `ax.legend()` and we don't tell it the labels directly, we actually add those as _attributes_ of the scatter plots by adding `label`s.
So that's pretty cool.
Matplotlib hasn't added the regression lines to the legend, only the scatter plots, because they have labels.
The legend positioning is also very clever, matplotlib has put it in the location with the fewest dots!
Here's the [documentation](https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.legend.html) that shows you how to be explicit about where to put the legend.
The default value for `loc` is `best`, and we can happily keep that for the rest of this notebook.
If you really wanted to put it somewhere else, you can set the location explicitly.
For example, in the center on the right hand side.
## Change the colors
The fact that our semantic data (dots) and predicted values (line) are both blue, and that the analogy data are both orange, is a consequence of the order in which we've asked matplotlib to plot the data.
At the moment, matplotlib is coloring the first scatter plot with its first default color, and the second with the second default color.
Then when we give it a different type of plot (`plot` vs `scatter`) it starts the color cycle again.
(You can see the order of the colours in the [documentation of when they were introduced](https://matplotlib.org/3.1.1/users/dflt_style_changes.html#colors-in-default-property-cycle).)
If we move the order of the two regression lines the colours will change:
So that's no good!
Let's explicitly set the colors.
Cool....the colours are fixed....but wow those aren't nice to look at 😕
## Color management with Seaborn
[Seaborn](https://seaborn.pydata.org) is a Python data visualization library based on matplotlib.
It provides a high-level interface for drawing attractive and informative statistical graphics.
It does many beautiful things (a few of which we're going to explore) but it can sometimes be so clever that it becomes a little opaque.
If in doubt, remember that seaborn will almost always return an `axis` object for you, and you can change those settings just as you would in matplotlib.
One of the very nice things that seaborn does is manage colors easily.
The red and blue that I used in the published figure came from the ["Set1" Brewer color map](http://colorbrewer2.org/#type=qualitative&scheme=Set1&n=5).
We can get the RGB values for the colors in this qualitative color map from seaborn's `color_palette` function, and visualize them using the "palette plot" (`palplot`) function.
```
color_list = sns.color_palette("Set1", n_colors=5)
for color in color_list:
print(color)
sns.palplot(color_list)
```
Ok, now that we have our much nicer colors, let's change the red and blue in our accuracy plot.
## Really jazzing up the plot with seaborn
Another other two really beautiful things that seaborn can do is set the **context** of the plot, and the figure **style**.
There are lots of great examples in the [aesthetics tutorial](https://seaborn.pydata.org/tutorial/aesthetics.html) which I really encourage you to have a play around with.
Let's check out the `poster` context, with a `darkgrid` background.
Now that we've run the code above, lets re-make our scatter plot:
Wowzers trousers.
That's no good 😬
How about `notebook` context with a `ticks` background?
Fun, we've got back to the matplotlib default!
The settings have changed slightly since I wrote the original code in 2016, but I think the closest setting is `notebook` context with a `font_scale` of 1.5 and the `white` style.
When you run the `set_context` and `set_style` commands they become global settings for all plots that you subsequently make in the same notebook (or script).
Personally I load them in at the top of all my notebooks because I think they make the plots look nicer 💁♀️
Oh, and I like the plots [despined](https://seaborn.pydata.org/tutorial/aesthetics.html#removing-axes-spines) too, so lets do that real quick:
## Axis labels, limits and tick placement
### Labels
Our plots don't have any axis labels!
How will anyone know what they're looking at?!
Let's go ahead and label them 😸
### Limits
One of the things that's really nice to do is to be able to set the min and max values for a figure.
At the moment, matplotlib is guessing at a good place to start and stop the axes.
And it's doing a great job...but what if you wanted to show a subset of the data?
If the minimum or maxium age or reaction time values were different then you'd end up with slightly different dimensions on the x and y axes.
Let's see what it's guessing:
To be honest, its doing a great job.
I'd be inclined to leave it, but I wrote a little function to pad the axes by 5% of the data range and I think its useful for times when matplotlib isn't choosing sensibly, so let me show you how it works anyway.
```
def get_min_max(data, pad_percent=5):
"""
Calculate the range of the data by subtracting the minimum from the maximum value.
Subtract pad_percent of the range from the minimum value.
Add pad_percent of the range to the maximum value.
Default value for pad_percent is 5 which corresponds to 5%.
Return the padded min and max values.
"""
data_range = np.max(data) - np.min(data)
data_min = np.min(data) - (data_range * pad_percent/100.0)
data_max = np.max(data) + (data_range * pad_percent/100.0)
return data_min, data_max
```
You could set `pad_percent` to 0 to get rid of all the white space if you wanted to.
(You shouldn't though, it has cut off a bunch of the dots!)
### Tick placement
Seaborn and matplotlib have made a good guess at where to put the x and y ticks, but I don't think they're the most intuitive way of illustrating a 6 to 18 year age range.
So lets just put the ticks where I think they should be: at 6, 10, 14 and 18.
For the y ticks we can use the ticker `locator_params` to put them in the best place for getting a maximum of 6 ticks.
This is basically what matplotlib is already doing, but I'll show you the command just in case you want to use it in the future.
For example, if you wanted to force the plot to have 4 bins, you'd set `nbins` to 4:
And note that even when we set `nbins` to 6 (as I wrote in the original figure code), it actually only gives us 5 ticks, because matplotlib - correctly - can't find a sensible way to parse the range to give us 6 evenly spaced ticks on they y axis.
One quick point to remember here: the x and y axis **limits** are not the same as the **tick locations**.
The limits are the edges of the plot.
The tick locations are where the markers sit on the axes.
## Adding confidence intervals with seaborn
We're doing great.
Matplotlib has got us to a pretty nice looking plot.
But, a responsible visualization should have some error bars on it....and they are a pain to try to write ourselves.
So at this point, we're going to replace our `scatter` and `plot` functions (and all the code used to calculate the predicted values) with the wonderful [`regplot` function](https://seaborn.pydata.org/generated/seaborn.regplot.html) in seaborn.
Doh, that's not right.
We've fitted a straight line to data that is clearly reaching ceiling.
Fortunately, `regplot` take a parameter, `order=2`, to make the fitted line follow a quadratic function.
## Advanced legend-ing
Those dots in the legend aren't great: they look like they correspond to data points!
The following function replaces those dots with a line the same color as the colors we've used for the regplots.
I think this is some pretty hardcore matplotlib, and you _really_ only need it when you want to publish your figure.
There's a [matplotlib legend guide](https://matplotlib.org/3.1.1/tutorials/intermediate/legend_guide.html) if you want to dig into what's going on here...but be warned that it gets intense pretty quickly.
```
def add_line_to_legend(ax, color_list, label_list, loc='best', frameon=True):
"""
Add a legend that has lines instead of markers.
"""
line_list = []
for color, label in zip(color_list, label_list):
line_list += [mlines.Line2D([], [], color=color, marker=None, label=label)]
ax.legend(handles=line_list, loc=loc, frameon=frameon)
return ax
```
Yeaaaaah!
You did it!
The figure looks just like the published one.... except that that one has a bunch of other plots too!

## A second plot: Reaction time
A second hypothesis that we had was that participants would answer faster as they got older (reaction time would decrease) and that they would be **slower** (high RT) for the analogy trials.
These data are shown in the second panel in the published figure.
It's actually super similar to the first panel, we're just plotting two different variable from the data frame.
Let's see what happens if we change the plotting code to have a different variable:
🚀🌟🚀🌟🚀🌟🚀🌟🚀🌟🚀🌟
Fantastic!
We've made the second panel!
Just like that.
## Third plot: Errors
The third hypothesis that we want to test is that there are more semantic errors than perceptual errors, and more perceptual errors than unrelated errors.
As accuracy is increasing, the separate modelled lines (quadratic again) will all decrease.
## One function to plot them all
Do you remember how our figure plotting code was really similar across the three panels?
I think we can make a general function for our plots.
```
def visan_behav_plot(ax, behav_var_list, label_list, color_list, y_ax_label, legend_rev=False):
"""
Plot the visual analogy behavioural results on a given axis (ax)
"""
# Get the min and max values for the x and y axes
x_min, x_max = get_min_max(df['Age_scan'])
y_min, y_max = get_min_max(df[behav_var_list[0]])
if len(behav_var_list) > 1:
for behav_var in behav_var_list[1:]:
new_y_min, new_y_max = get_min_max(df[behav_var_list[-1]])
y_min, y_max = min(y_min, new_y_min), max(y_max, new_y_max)
# Loop over all the behavioural measures you want to plot
for behav_var, label, color in zip(behav_var_list, label_list, color_list):
sns.regplot(df['Age_scan'], df[behav_var],
label = label,
color = color,
ax = ax,
order = 2)
# Set the x and y tick locations
ax.set_xticks([6, 10, 14, 18])
ax.locator_params(nbins=6, axis='y')
# Set the x and y min and max axis limits
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
# Set the x and y labels
ax.set_xlabel('Age (years)')
ax.set_ylabel(y_ax_label)
# Add a legend
if legend_rev:
color_list = color_list[::-1]
label_list = label_list[::-1]
ax = add_line_to_legend(ax,
color_list,
label_list,
loc='best',
frameon=False)
sns.despine()
return ax
# Accuracy
fig, ax = plt.subplots()
ax = visan_behav_plot(ax,
['R1_percent_acc', 'R2_percent_acc'],
['Semantic', 'Analogy'],
color_list[:2],
'Accuracy (% resp)',
legend_rev=False)
plt.show()
# Reaction time
fig, ax = plt.subplots()
ax = visan_behav_plot(ax,
['R1_meanRTcorr_cor', 'R2_meanRTcorr_cor'],
['Semantic', 'Analogy'],
color_list[:2],
'Reaction time (s)',
legend_rev=False)
plt.show()
# Errors
fig, ax = plt.subplots()
ax = visan_behav_plot(ax,
['R2_percent_dis', 'R2_percent_per', 'R2_percent_sem'],
['Unrelated', 'Perceptual', 'Semantic'],
color_list[2:5],
'Reaction time (s)',
legend_rev=True)
plt.show()
```
## Three subplots
Our last step is to put these three plots into one figure.
We can use `subplots` to set the number of equally sized plots and `figsize` to set the dimensions of the figure.
Let's see what that looks like on its own.
One thing to note is that instead of getting just one axis back now, we get an **axis list** which allows us to iterate over the three panels.
```
if not os.path.isdir('figures'):
os.makedirs('figures')
```
### Save the figure
We can save this figure using `fig.savefig`.
## Panel labels
This is where I'm probably going a little overboard.
Setting the panel labels is definitely easier in any other picture editing software!!
But, it brings me great joy to make the figure entirely from code, so lets go ahead and use this function to add the panel labels.
```
def add_panel_labels_fig2(ax_list):
"""
Add panel labels (a, b, c) to the scatter plot.
Note that these positions have been calibrated by hand...
there isn't a good way to do it otherwise.
"""
x_list = [ -0.17, -0.1, -0.14 ]
y = 1.1
color='k'
fontsize=18
letters = string.ascii_lowercase
for i, ax in enumerate(ax_list):
ax.text(x_list[i], y,
'({})'.format(letters[i]),
fontsize=fontsize,
transform=ax.transAxes,
color=color,
horizontalalignment='center',
verticalalignment='center',
fontname='arial',
fontweight='bold'
)
return ax_list
fig, ax_list = plt.subplots(1, 3, figsize=(16,4.5))
# Accuracy
ax = ax_list[0]
ax = visan_behav_plot(ax,
['R1_percent_acc', 'R2_percent_acc'],
['Semantic', 'Analogy'],
color_list[:2],
'Accuracy (% resp)',
legend_rev=False)
# Reaction time
ax = ax_list[1]
ax = visan_behav_plot(ax,
['R1_meanRTcorr_cor', 'R2_meanRTcorr_cor'],
['Semantic', 'Analogy'],
color_list[:2],
'Reaction time (s)',
legend_rev=False)
# Errors
ax = ax_list[2]
ax = visan_behav_plot(ax,
['R2_percent_dis', 'R2_percent_per', 'R2_percent_sem'],
['Unrelated', 'Perceptual', 'Semantic'],
color_list[2:5],
'Analogy error rate (% resp)',
legend_rev=True)
ax_list = add_panel_labels_fig2(ax_list) # <-------- Add the panel labels
plt.tight_layout()
fig.savefig('figures/Figure2.png', dpi=150, bbox_inches=0)
plt.show()
```
## Congratulations!
We did it! 🎉🎉🎉
Look how similar these two figures look!
#### Figure 2 from GitHub repository

#### Figure 2 we've just made

## The end
Well done 💖
| true |
code
| 0.581065 | null | null | null | null |
|
# Live Data
The [HoloMap](../reference/containers/bokeh/HoloMap.ipynb) is a core HoloViews data structure that allows easy exploration of parameter spaces. The essence of a HoloMap is that it contains a collection of [Elements](http://build.holoviews.org/reference/index.html) (e.g. ``Image``s and ``Curve``s) that you can easily select and visualize.
HoloMaps hold fully constructed Elements at specifically sampled points in a multidimensional space. Although HoloMaps are useful for exploring high-dimensional parameter spaces, they can very quickly consume huge amounts of memory to store all these Elements. For instance, a hundred samples along four orthogonal dimensions would need a HoloMap containing a hundred *million* Elements, each of which could be a substantial object that takes time to create and costs memory to store. Thus ``HoloMaps`` have some clear limitations:
* HoloMaps may require the generation of millions of Elements before the first element can be viewed.
* HoloMaps can easily exhaust all the memory available to Python.
* HoloMaps can even more easily exhaust all the memory in the browser when displayed.
* Static export of a notebook containing HoloMaps can result in impractically large HTML files.
The ``DynamicMap`` addresses these issues by computing and displaying elements dynamically, allowing exploration of much larger datasets:
* DynamicMaps generate elements on the fly, allowing the process of exploration to begin immediately.
* DynamicMaps do not require fixed sampling, allowing exploration of parameters with arbitrary resolution.
* DynamicMaps are lazy in the sense they only compute as much data as the user wishes to explore.
Of course, these advantages come with some limitations:
* DynamicMaps require a live notebook server and cannot be fully exported to static HTML.
* DynamicMaps store only a portion of the underlying data, in the form of an Element cache and their output is dependent on the particular version of the executed code.
* DynamicMaps (and particularly their element caches) are typically stateful (with values that depend on patterns of user interaction), which can make them more difficult to reason about.
In addition to the different computational requirements of ``DynamicMaps``, they can be used to build sophisticated, interactive vizualisations that cannot be achieved using only ``HoloMaps``. This notebook demonstrates some basic examples and the [Responding to Events](./11-Responding_to_Events.ipynb) guide follows on by introducing the streams system. The [Custom Interactivity](./12-Custom_Interactivity.ipynb) shows how you can directly interact with your plots when using the Bokeh backend.
When DynamicMap was introduced in version 1.6, it supported multiple different 'modes' which have now been deprecated. This notebook demonstrates the simpler, more flexible and more powerful DynamicMap introduced in version 1.7. Users who have been using the previous version of DynamicMap should be unaffected as backwards compatibility has been preserved for the most common cases.
All this will make much more sense once we've tried out some ``DynamicMaps`` and showed how they work, so let's create one!
<center><div class="alert alert-info" role="alert">To visualize and use a <b>DynamicMap</b> you need to be running a live Jupyter server.<br>This guide assumes that it will be run in a live notebook environment.<br>
When viewed statically, DynamicMaps will only show the first available Element,<br> and will thus not have any slider widgets, making it difficult to follow the descriptions below.<br><br>
It's also best to run this notebook one cell at a time, not via "Run All",<br> so that subsequent cells can reflect your dynamic interaction with widgets in previous cells.</div></center>
## ``DynamicMap`` <a id='DynamicMap'></a>
Let's start by importing HoloViews and loading the extension:
```
import holoviews as hv
import numpy as np
hv.extension()
```
We will now create ``DynamicMap`` similar to the ``HoloMap`` introduced in the [Introductory guide](../getting_started/1-Introduction.ipynb). The ``HoloMap`` in that introduction consisted of ``Image`` elements defined by a function returning NumPy arrays called ``sine_array``. Here we will define a ``waves_image`` function that returns an array pattern parameterized by arbitrary ``alpha`` and ``beta`` parameters inside a HoloViews
[``Image``](../reference/elements/bokeh/Image.ipynb) element:
```
xvals = np.linspace(-4,0,202)
yvals = np.linspace(4,0,202)
xs,ys = np.meshgrid(xvals, yvals)
def waves_image(alpha, beta):
return hv.Image(np.sin(((ys/alpha)**alpha+beta)*xs))
waves_image(0,0) + waves_image(0,4)
```
Now we can demonstrate the possibilities for exploration enabled by the simplest declaration of a ``DynamicMap``.
### Basic ``DynamicMap`` declaration<a id='BasicDeclaration'></a>
A simple ``DynamicMap`` declaration looks identical to that needed to declare a ``HoloMap``. Instead of supplying some initial data, we will supply the ``waves_image`` function with key dimensions simply declaring the arguments of that function:
```
dmap = hv.DynamicMap(waves_image, kdims=['alpha', 'beta'])
dmap
```
This object is created instantly, but because it doesn't generate any `hv.Image` objects initially it only shows the printed representation of this object along with some information about how to display it. We will refer to a ``DynamicMap`` that doesn't have enough information to display itself as 'unbounded'.
The textual representation of all ``DynamicMaps`` look similar, differing only in the listed dimensions until they have been evaluated at least once.
#### Explicit indexing
Unlike a corresponding ``HoloMap`` declaration, this simple unbounded ``DynamicMap`` cannot yet visualize itself. To view it, we can follow the advice in the warning message. First we will explicitly index into our ``DynamicMap`` in the same way you would access a key on a ``HoloMap``:
```
dmap[0,1] + dmap.select(alpha=1, beta=2)
```
Note that the declared kdims are specifying the arguments *by position* as they do not match the argument names of the ``waves_image`` function. If you *do* match the argument names *exactly*, you can map a kdim position to any argument position of the callable. For instance, the declaration ``kdims=['freq', 'phase']`` would index first by frequency, then phase without mixing up the arguments to ``waves_image`` when indexing.
#### Setting dimension ranges
The second suggestion in the warning message was to supply dimension ranges using the ``redim.range`` method:
```
dmap.redim.range(alpha=(0,5.0), beta=(1,5.0))
```
Here each `hv.Image` object visualizing a particular sine ring pattern with the given parameters is created dynamically, whenever the slider is set to a new value. Any value in the allowable range can be requested by dragging the sliders or by tweaking the values using the left and right arrow keys.
Of course, we didn't have to use the ``redim.range`` method and we could have simply declared the ranges right away using explicit ``hv.Dimension`` objects. This would allow us to declare other dimension properties such as the step size used by the sliders: by default each slider can select around a thousand distinct values along its range but you can specify your own step value via the dimension ``step`` parameter. If you use integers in your range declarations, integer stepping will be assumed with a step size of one.
Note that whenever the ``redim`` method is used, a new ``DynamicMap`` is returned with the updated dimensions. In other words, the original ``dmap`` remains unbounded with default dimension objects.
#### Setting dimension values
The ``DynamicMap`` above allows exploration of *any* phase and frequency within the declared range unlike an equivalent ``HoloMap`` which would have to be composed of a finite set of samples. We can achieve a similar discrete sampling using ``DynamicMap`` by setting the ``values`` parameter on the dimensions:
```
dmap.redim.values(alpha=[0,1,2], beta=[0.1, 1.0, 2.5])
```
The sliders now snap to the specified dimension values and if you are running this live, the above cell should look like a [HoloMap](../reference/containers/bokeh/HoloMap.ipynb). ``DynamicMap`` is in fact a subclass of ``HoloMap`` with some crucial differences:
* You can now pick as many values of **alpha** or **beta** as allowed by the slider.
* What you see in the cell above will not be exported in any HTML snapshot of the notebook
We will now explore how ``DynamicMaps`` relate to ``HoloMaps`` including conversion operations between the two types. As we will see, there are other ways to display a ``DynamicMap`` without using explicit indexing or redim.
## Interaction with ``HoloMap``s
To explore the relationship between ``DynamicMap`` and ``HoloMap``, let's declare another callable to draw some shapes we will use in a new ``DynamicMap``:
```
def shapes(N, radius=0.5): # Positional keyword arguments are fine
paths = [hv.Path([[(radius*np.sin(a), radius*np.cos(a))
for a in np.linspace(-np.pi, np.pi, n+2)]],
extents=(-1,-1,1,1))
for n in range(N,N+3)]
return hv.Overlay(paths)
```
#### Sampling ``DynamicMap`` from a ``HoloMap``
When combining a ``HoloMap`` with a ``DynamicMap``, it would be very awkward to have to match the declared dimension ``values`` of the DynamicMap with the keys of the ``HoloMap``. Fortunately you don't have to:
```
%%opts Path (linewidth=1.5)
holomap = hv.HoloMap({(N,r):shapes(N, r) for N in [3,4,5] for r in [0.5,0.75]}, kdims=['N', 'radius'])
dmap = hv.DynamicMap(shapes, kdims=['N','radius'])
holomap + dmap
```
Here we declared a ``DynamicMap`` without using ``redim``, but we can view its output because it is presented alongside a ``HoloMap`` which defines the available keys. This convenience is subject to three particular restrictions:
* You cannot display a layout consisting of unbounded ``DynamicMaps`` only, because at least one HoloMap is needed to define the samples.
* The HoloMaps provide the necessary information required to sample the DynamicMap.
Note that there is one way ``DynamicMap`` is less restricted than ``HoloMap``: you can freely combine bounded ``DynamicMaps`` together in a ``Layout``, even if they don't share key dimensions.
Also notice that the ``%%opts`` cell magic allows you to style DynamicMaps in exactly the same way as HoloMaps. We will now use the ``%opts`` line magic to set the linewidths of all ``Path`` elements in the rest of the notebook:
```
%opts Path (linewidth=1.5)
```
#### Converting from ``DynamicMap`` to ``HoloMap``
Above we mentioned that ``DynamicMap`` is an instance of ``HoloMap``. Does this mean it has a ``.data`` attribute?
```
dtype = type(dmap.data).__name__
length = len(dmap.data)
print("DynamicMap 'dmap' has an {dtype} .data attribute of length {length}".format(dtype=dtype, length=length))
```
This is exactly the same sort of ``.data`` as the equivalent ``HoloMap``, except that its values will vary according to how much you explored the parameter space of ``dmap`` using the sliders above. In a ``HoloMap``, ``.data`` contains a defined sampling along the different dimensions, whereas in a ``DynamicMap``, the ``.data`` is simply the *cache*.
The cache serves two purposes:
* Avoids recomputation of an element should we revisit a particular point in the parameter space. This works well for categorical or integer dimensions, but doesn't help much when using continuous sliders for real-valued dimensions.
* Records the space that has been explored with the ``DynamicMap`` for any later conversion to a ``HoloMap`` up to the allowed cache size.
We can always convert *any* ``DynamicMap`` directly to a ``HoloMap`` as follows:
```
hv.HoloMap(dmap)
```
This is in fact equivalent to declaring a HoloMap with the same parameters (dimensions, etc.) using ``dmap.data`` as input, but is more convenient. Note that the slider positions reflect those we sampled from the ``HoloMap`` in the previous section.
Although creating a HoloMap this way is easy, the result is poorly controlled, as the keys in the DynamicMap cache are usually defined by how you moved the sliders around. If you instead want to specify a specific set of samples, you can easily do so by using the same key-selection semantics as for a ``HoloMap`` to define exactly which elements are to be sampled and put into the cache:
```
hv.HoloMap(dmap[{(2,0.3), (2,0.6), (3,0.3), (3,0.6)}])
```
Here we index the ``dmap`` with specified keys to return a *new* DynamicMap with those keys in its cache, which we then cast to a ``HoloMap``. This allows us to export specific contents of ``DynamicMap`` to static HTML which will display the data at the sampled slider positions.
The key selection above happens to define a Cartesian product, which is one of the most common ways to sample across dimensions. Because the list of such dimension values can quickly get very large when enumerated as above, we provide a way to specify a Cartesian product directly, which also works with ``HoloMaps``. Here is an equivalent way of defining the same set of four points in that two-dimensional space:
```
samples = hv.HoloMap(dmap[{2,3},{0.5,1.0}])
samples
samples.data.keys()
```
The default cache size of 500 Elements is relatively high so that interactive exploration will work smoothly, but you can reduce it using the ``cache_size`` parameter if you find you are running into issues with memory consumption. A bounded ``DynamicMap`` with ``cache_size=1`` requires the least memory, but will recompute a new Element every time the sliders are moved, making it less responsive.
#### Converting from ``HoloMap`` to ``DynamicMap``
We have now seen how to convert from a ``DynamicMap`` to a ``HoloMap`` for the purposes of static export, but why would you ever want to do the inverse?
Although having a ``HoloMap`` to start with means it will not save you memory, converting to a ``DynamicMap`` does mean that the rendering process can be deferred until a new slider value requests an update. You can achieve this conversion using the ``Dynamic`` utility as demonstrated here by applying it to the previously defined ``HoloMap`` called ``samples``:
```
from holoviews.util import Dynamic
dynamic = Dynamic(samples)
print('After apply Dynamic, the type is a {dtype}'.format(dtype=type(dynamic).__name__))
dynamic
```
In this particular example, there is no real need to use ``Dynamic`` as each frame renders quickly enough. For visualizations that are slow to render, using ``Dynamic`` can result in more responsive visualizations.
The ``Dynamic`` utility is very versatile and is discussed in more detail in the [Transforming Elements](./10-Transforming_Elements.ipynb) guide.
### Slicing ``DynamicMaps``
As we have seen we can either declare dimension ranges directly in the kdims or use the ``redim.range`` convenience method:
```
dmap = hv.DynamicMap(shapes, kdims=['N','radius']).redim.range(N=(2,20), radius=(0.5,1.0))
```
The declared dimension ranges define the absolute limits allowed for exploration in this continuous, bounded DynamicMap . That said, you can use the soft_range parameter to view subregions within that range. Setting the soft_range parameter on dimensions can be done conveniently using slicing:
```
sliced = dmap[4:8, :]
sliced
```
Notice that N is now restricted to the range 4:8. Open slices are used to release any ``soft_range`` values, which resets the limits back to those defined by the full range:
```
sliced[:, 0.8:1.0]
```
The ``[:]`` slice leaves the soft_range values alone and can be used as a convenient way to clone a ``DynamicMap``. Note that mixing slices with any other object type is not supported. In other words, once you use a single slice, you can only use slices in that indexing operation.
## Using groupby to discretize a DynamicMap
A DynamicMap also makes it easy to partially or completely discretize a function to evaluate in a complex plot. By grouping over specific dimensions that define a fixed sampling via the Dimension values parameter, the DynamicMap can be viewed as a ``GridSpace``, ``NdLayout``, or ``NdOverlay``. If a dimension specifies only a continuous range it can't be grouped over, but it may still be explored using the widgets. This means we can plot partial or completely discretized views of a parameter space easily.
#### Partially discretize
The implementation for all the groupby operations uses the ``.groupby`` method internally, but we also provide three higher-level convenience methods to group dimensions into an ``NdOverlay`` (``.overlay``), ``GridSpace`` (``.grid``), or ``NdLayout`` (``.layout``).
Here we will evaluate a simple sine function with three dimensions, the phase, frequency, and amplitude. We assign the frequency and amplitude discrete samples, while defining a continuous range for the phase:
```
xs = np.linspace(0, 2*np.pi,100)
def sin(ph, f, amp):
return hv.Curve((xs, np.sin(xs*f+ph)*amp))
kdims=[hv.Dimension('phase', range=(0, np.pi)),
hv.Dimension('frequency', values=[0.1, 1, 2, 5, 10]),
hv.Dimension('amplitude', values=[0.5, 5, 10])]
waves_dmap = hv.DynamicMap(sin, kdims=kdims)
```
Next we define the amplitude dimension to be overlaid and the frequency dimension to be gridded:
```
%%opts GridSpace [show_legend=True fig_size=200]
waves_dmap.overlay('amplitude').grid('frequency')
```
As you can see, instead of having three sliders (one per dimension), we've now laid out the frequency dimension as a discrete set of values in a grid, and the amplitude dimension as a discrete set of values in an overlay, leaving one slider for the remaining dimension (phase). This approach can help you visualize a large, multi-dimensional space efficiently, with full control over how each dimension is made visible.
#### Fully discretize
Given a continuous function defined over a space, we could sample it manually, but here we'll look at an example of evaluating it using the groupby method. Let's look at a spiral function with a frequency and first- and second-order phase terms. Then we define the dimension values for all the parameters and declare the DynamicMap:
```
%opts Path (linewidth=1 color=Palette('Blues'))
def spiral_equation(f, ph, ph2):
r = np.arange(0, 1, 0.005)
xs, ys = (r * fn(f*np.pi*np.sin(r+ph)+ph2) for fn in (np.cos, np.sin))
return hv.Path((xs, ys))
spiral_dmap = hv.DynamicMap(spiral_equation, kdims=['f','ph','ph2']).\
redim.values(f=np.linspace(1, 10, 10),
ph=np.linspace(0, np.pi, 10),
ph2=np.linspace(0, np.pi, 4))
```
Now we can make use of the ``.groupby`` method to group over the frequency and phase dimensions, which we will display as part of a GridSpace by setting the ``container_type``. This leaves the second phase variable, which we assign to an NdOverlay by setting the ``group_type``:
```
%%opts GridSpace [xaxis=None yaxis=None] Path [bgcolor='w' xaxis=None yaxis=None]
spiral_dmap.groupby(['f', 'ph'], group_type=hv.NdOverlay, container_type=hv.GridSpace)
```
This grid shows a range of frequencies `f` on the x axis, a range of the first phase variable `ph` on the `y` axis, and a range of different `ph2` phases as overlays within each location in the grid. As you can see, these techniques can help you visualize multidimensional parameter spaces compactly and conveniently.
## DynamicMaps and normalization
By default, a ``HoloMap`` normalizes the display of elements using the minimum and maximum values found across the ``HoloMap``. This automatic behavior is not possible in a ``DynamicMap``, where arbitrary new elements are being generated on the fly. Consider the following examples where the arrays contained within the returned ``Image`` objects are scaled with time:
```
%%opts Image {+axiswise}
ls = np.linspace(0, 10, 200)
xx, yy = np.meshgrid(ls, ls)
def cells(time):
return hv.Image(time*np.sin(xx+time)*np.cos(yy+time), vdims='Intensity')
dmap = hv.DynamicMap(cells, kdims='time').redim.range(time=(1,20))
dmap + dmap.redim.range(Intensity=(0,10))
```
Here we use ``+axiswise`` to see the behavior of the two cases independently. We see in **A** that when only the time dimension is given a range, no automatic normalization occurs (unlike a ``HoloMap``). In **B** we see that normalization is applied, but only when the value dimension ('Intensity') range has been specified.
In other words, ``DynamicMaps`` cannot support automatic normalization across their elements, but do support the same explicit normalization behavior as ``HoloMaps``. Values that are generated outside this range are simply clipped in accord with the usual semantics of explicit value dimension ranges.
Note that we always have the option of casting a ``DynamicMap`` to a ``HoloMap`` in order to automatically normalize across the cached values, without needing explicit value dimension ranges.
## Using DynamicMaps in your code
As you can see, ``DynamicMaps`` let you use HoloViews with a very wide range of dynamic data formats and sources, making it simple to visualize ongoing processes or very large data spaces.
Given unlimited computational resources, the functionality covered in this guide would match that offered by ``HoloMap`` but with fewer normalization options. ``DynamicMap`` actually enables a vast range of new possibilities for dynamic, interactive visualizations as covered in the [Responding to Events](./Responding_to_Events.ipynb) guide. Following on from that, the [Custom Interactivity](./12-Custom_Interactivity.ipynb) guide shows how you can directly interact with your plots when using the Bokeh backend.
| true |
code
| 0.461441 | null | null | null | null |
|
# Random numbers and simulation
You will learn how to use a random number generator with a seed and produce simulation results (**numpy.random**, **scipy.stats**), and calcuate the expected value of a random variable through Monte Carlo integration. You will learn how to save your results for later use (**pickle**). Finally, you will learn how to make your figures interactive (**ipywidgets**).
**Links:**
* [numpy.random](https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.random.html)
* [scipy.stats](https://docs.scipy.org/doc/scipy/reference/stats.html)
* [ipywidgets](https://ipywidgets.readthedocs.io/en/stable/examples/Widget%20List.html)
* datacamp on [pickle](https://www.datacamp.com/community/tutorials/pickle-python-tutorial)
**Imports:** We now import all the modules, we need for this notebook. Importing everything in the beginning makes it more clear what modules the notebook relies on.
```
import math
import pickle
import numpy as np
from scipy.stats import norm # normal distribution
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import ipywidgets as widgets
```
# Exchange economy with many consumers
Consider an **exchange economy** with
1. 2 goods, $(x_1,x_2)$
2. $N$ consumers indexed by $j \in \{1,2,\dots,N\}$
3. Preferences are Cobb-Douglas with uniformly *heterogenous* coefficients
$$
\begin{aligned}
u^{j}(x_{1},x_{2}) & = x_{1}^{\alpha_{j}}x_{2}^{1-\alpha_{j}}\\
& \,\,\,\alpha_{j}\sim\mathcal{U}(\underline{\mu},\overline{\mu})\\
& \,\,\,0<\underline{\mu}<\overline{\mu}<1
\end{aligned}
$$
4. Endowments are *homogenous* and given by
$$
\boldsymbol{e}^{j}=(e_{1}^{j},e_{2}^{j})=(k,1),\,k>0
$$
The implied **demand functions** are:
$$
\begin{aligned}
x_{1}^{\star j}(p_{1},p_{2},e^{j})&=&\alpha_{j}\frac{I}{p_{1}}=\alpha_{j}\frac{kp_{1}+p_{2}}{p_{1}} \\
x_{2}^{\star j}(p_{1},p_{2},e^{j})&=&(1-\alpha_{j})\frac{I}{p_{2}}=(1-\alpha_{j})\frac{kp_{1}+p_{2}}{p_{2}}
\end{aligned}
$$
The **equilibrium** for a random draw of $\alpha = \{\alpha_1,\alpha_2,\dots,\alpha_N\}$ is a set of **prices** $p_1$ and $p_2$ satifying:
$$
\begin{aligned}
x_1(p_1,p_2) = \sum_{j=1}^N x_{1}^{\star j}(p_{1},p_{2},e^{j}) &= \sum_{j=1}^N e_1^j = Nk \\
x_2(p_1,p_2) = \sum_{j=1}^N x_{2}^{\star j}(p_{1},p_{2},e^{j}) &= \sum_{j=1}^N e_2^j = N
\end{aligned}
$$
**Problem:** Solve for this equilibrium. But how do we handle the randomness? We need a random number generator (RNG).
**Warm-up**: Choose parameters and define demand functions.
```
# a. parameters
N = 1000
k = 2 # endowment
mu_low = 0.1 # lower bound on alpha
mu_high = 0.9 # upper bound on alpha
# b. demand functions
def demand_good_1_func(alpha,p1,p2,k):
I = k*p1+p2
return alpha*I/p1
def demand_good_2_func(alpha,p1,p2,k):
I = k*p1+p2
return (1-alpha)*I/p2
```
**Quizz:** take a quick [quizz](https://forms.office.com/Pages/ResponsePage.aspx?id=kX-So6HNlkaviYyfHO_6kckJrnVYqJlJgGf8Jm3FvY9UMFpSRTIzUlJKMkdFQlpIN1VZUE9EVTBaMSQlQCN0PWcu) regarding the demand functions.
# Random numbers
The two main approaches to generating random numbers are:
1. **Physical observations** of random processes (radioactive decay, atmospheric noise, roulette wheels, etc.)
2. **Algorithms** creating pseudo-random numbers
**Pseudo-random numbers** satisfy propoerties such that they are as good as random. It should be impossible (for all practical purposes) to calculate, or otherwise guess, from any given subsequence, any previous or future values in the sequence.
**More information:** See this [video](https://www.youtube.com/watch?v=C82JyCmtKWg&app=desktop#fauxfullscreen) by Infinite Series.
## Simple example: Middle-square method
Proposed by **John von Neumann**:
1. Start with a $N$ digit number
2. Square the number
3. Pad the number with leading zeros making it a $2N$ digit number
4. Extract the middle $N$ digits (*your random number*)
5. Return to step 1 to generate one more
> **Pro:** Simple and easy to implement. Conceptually somewhat similar to more advanced methods (e.g. *Mersenne-Twister* used by *numpy*).
>
> **Con:** Cycles can be no longer than $8^N$ periods. Many repeating cycles are very short. Internal state is directly observable.
>
> **Conclusion:** Can not be used in practice.
**Code:** An implementation in Python for $N = 4$ digit random integers:
```
def rng(number,max_iter=100):
already_seen = [] # list of seen numbers
i = 0
while number not in already_seen and i < max_iter:
already_seen.append(number)
squared = number**2
padded = str(squared).zfill(8) # add leading zeros
number = int(padded[2:6]) # extract middle 4 numbers
print(f"square = {squared:8d}, padded = {padded} -> {number:4d}")
i += 1
```
A reasonable cycle:
```
rng(4653)
```
A short cycle:
```
rng(540)
```
No cycle at all:
```
rng(3792)
```
## Numpy
Numpy provides various functions for drawing random numbers. We can, for example, draw random integers between 0 and 10000:
```
X = np.random.randint(0,10000,size=5)
print(X)
```
**Problem:** How can we reproduce our results the next time we open Python?
**Solution:** Use a seed! Choose the seed, and reset the random number generator:
```
print('set seed to 2000 and create numbers:')
np.random.seed(2000)
print(np.random.uniform(size=5))
print(np.random.uniform(size=5))
print('\nreset algorithm by stating the same seed again:')
np.random.seed(2000)
print(np.random.uniform(size=5))
```
> **Note:** The first and third draws above are exactly the same.
We can also **save and load the state** of the random number generator.
```
# a. save state
state = np.random.get_state()
# b. draw some random number
print('generate numbers from current state:')
print(np.random.uniform(size=5))
print(np.random.uniform(size=5))
# c. reset state
np.random.set_state(state)
# d. draw the same random numbers again
print('\ngenerate numbers from past state by reloading it:')
print(np.random.uniform(size=5))
print(np.random.uniform(size=5))
```
> **Note**: You should *only set the seed once* per program. Changing seed might brake randomness.
## Different distributions
Draw random numbers from various distributions:
```
X = np.random.normal(loc=0,scale=1,size=10**6)
Y = np.random.beta(a=5,b=2,size=10**6)
Z = np.random.uniform(low=-2,high=2,size=10**6)
vec = np.array([-2.5,-2.0,-1.5,-1.0,-0.5,0,0.5,1.0,1.5,2,2.5])
prob = (np.linspace(-1,1,vec.size)+0.1)**2 # all positive numbers
prob /= np.sum(prob) # make them sum to one
K = np.random.choice(vec,size=10**6,p=prob)
```
Plot the various distributions:
```
fig = plt.figure(dpi=100)
ax = fig.add_subplot(1,1,1)
ax.hist(X,bins=100,density=True,alpha=0.5,label='normal') # alpha < 1 = transparent
ax.hist(Y,bins=100,density=True,alpha=0.5,label='beta')
ax.hist(Z,bins=100,density=True,alpha=0.5,label='uniform')
ax.hist(K,bins=100,density=True,alpha=0.5,label='choice')
ax.set_xlim([-3,3])
ax.legend(loc='upper left'); # note: the ; stops output from being printed
```
**Task:** Follow this [link](https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.random.html). Choose a distribution and add it to the figure above.
## Analytical results
How close are our draws to a normal distribution?
```
from scipy.stats import norm
# a. create analytical distribution
loc_guess = 0.25
scale_guess = 0.75
# loc_guess, scale_guess = norm.fit(X)
F = norm(loc=loc_guess,scale=scale_guess)
rnd = F.rvs(5) # example: create 5 random draws from the distribution F
print(f'F pdf at 0.0: {F.pdf(0.0): 1.3f} \nF cdf at 0.0: {F.cdf(0.0): 1.3f}') # the object F has several useful functions available
# b. vector of x values
x_low = F.ppf(0.001) # x value where cdf is 0.001
x_high = F.ppf(0.999) # x value where cdf is 0.999
x = np.linspace(x_low,x_high,100)
# c. compare
fig = plt.figure(dpi=100)
ax = fig.add_subplot(1,1,1)
ax.plot(x,F.pdf(x),lw=2,label='estimated')
ax.hist(X,bins=100,density=True,histtype='stepfilled');
```
**Task:** Make the pdf fit the historgram.
## Permutations
```
class dice_cup:
def __init__(self,ndice):
self.ndice = ndice
def roll(self):
self.dice = np.random.randint(1,7,size=self.ndice)
print(self.dice)
def shuffle(self):
np.random.shuffle(self.dice)
print(self.dice)
def roll_and_sum(self):
self.roll()
print(self.dice.sum())
my_dice_cup = dice_cup(4)
my_dice_cup.roll()
my_dice_cup.shuffle()
my_dice_cup.roll_and_sum()
```
**Task:** Add a method ``roll_and_sum()`` to the class above, which rolls and print the sum of the dice. Compare the value of your roll to your neighbor.
*(You can delete the pass statement when starting to code. It's there to inform Python that roll_and_sum() is well defined as Python cannot handle a totally codeless function)*
# Demand
$$
x_1(p_1,p_2) = \sum_{j=1}^N x_{1}^{\star j}(p_{1},p_{2},e^{j}) = \alpha_{j}\frac{kp_{1}+p_{2}}{p_{1}}
$$
Find demand distribution and total demand:
```
def find_demand_good_1(alphas,p1,p2,k):
distr = demand_good_1_func(alphas,p1,p2,k) # Notice we are passing in arrays of alphas together with scalars! It works because of numpy broadcasting.
total = distr.sum()
return distr,total
```
Calculate for various prices:
```
# a. draw alphas
alphas = np.random.uniform(low=mu_low,high=mu_high,size=N)
# b. prices
p1_vec = [0.5,1,2,5]
p2 = 1
# c. demand
dists = np.empty((len(p1_vec),N))
totals = np.empty(len(p1_vec))
for i,p1 in enumerate(p1_vec):
dist,total = find_demand_good_1(alphas,p1,p2,k)
dists[i,:] = dist
totals[i] = total
```
Plot the results:
```
fig = plt.figure(figsize=(10,4))
ax_left = fig.add_subplot(1,2,1)
ax_left.set_title('Distributions of demand')
for i,p1 in enumerate(p1_vec):
ax_left.hist(dists[i],density=True,alpha=0.5,label=f'$p_1 = {p1}$')
ax_left.legend(loc='upper right')
ax_right = fig.add_subplot(1,2,2)
ax_right.set_title('Level of demand')
ax_right.grid(True)
ax_right.plot(p1_vec,totals)
```
# Interactive figures
Create a function constructing a figure:
```
def interactive_figure(alphas,p1,p2,k):
# a. calculations
dist,_total = find_demand_good_1(alphas,p1,p2,k)
# b. figure
fig = plt.figure(dpi=100)
ax = fig.add_subplot(1,1,1)
ax.hist(dist,density=True)
ax.set_xlim([0,4]) # fixed x range
ax.set_ylim([0,0.8]) # fixed y range
```
**Case 1:** Make it interactive with a **slider**
```
widgets.interact(interactive_figure,
alphas=widgets.fixed(alphas),
p1=widgets.FloatSlider(description="$p_1$", min=0.1, max=5, step=0.05, value=2),
p2=widgets.fixed(p2),
k=widgets.fixed(k)
);
```
**Case 2:** Make it interactive with a **textbox**:
```
widgets.interact(interactive_figure,
alphas=widgets.fixed(alphas),
p1=widgets.FloatText(description="$p_1$", value=2),
p2=widgets.fixed(p2),
k=widgets.fixed(k)
);
```
**Case 3:** Make it interactive with a **dropdown menu**
```
widgets.interact(interactive_figure,
alphas=widgets.fixed(alphas),
p1=widgets.Dropdown(description="$p_1$", options=[0.5,1,1.5,2.0,2.5,3], value=2),
p2=widgets.fixed(p2),
k=widgets.fixed(k)
);
```
**Task:** Add a slider for \\(k\\) to the interactive figure below.
```
# change this code
widgets.interact(interactive_figure,
alphas=widgets.fixed(alphas),
p1=widgets.FloatSlider(description="$p_1$", min=0.1, max=5, step=0.05, value=2),
p2=widgets.fixed(p2),
k=widgets.fixed(k)
);
```
# Equilibrium
The equilibrium conditions (demand = supply) were:
$$
\begin{aligned}
\sum_{j=1}^N x_{1}^{\star j}(p_{1},p_{2},e^{j}) &= Nk \Leftrightarrow Z_1 \equiv \sum_{j=1}^N x_{1}^{\star j}(p_{1},p_{2},e^{j}) - Nk = 0 \\
\sum_{j=1}^N x_{2}^{\star j}(p_{1},p_{2},e^{j}) &= N \Leftrightarrow Z_2 \equiv \sum_{j=1}^N x_{2}^{\star j}(p_{1},p_{2},e^{j}) - N = 0
\end{aligned}
$$
**Idea:** Solve the first equation. The second is then satisfied due to Walras's law.
**Excess demand functions:**
```
def excess_demand_good_1_func(alphas,p1,p2,k):
# a. demand
demand = np.sum(demand_good_1_func(alphas,p1,p2,k))
# b. supply
supply = k*alphas.size
# c. excess demand
excess_demand = demand-supply
return excess_demand
def excess_demand_good_2_func(alphas,p1,p2,k):
# a. demand
demand = np.sum(demand_good_2_func(alphas,p1,p2,k))
# b. supply
supply = alphas.size
# c. excess demand
excess_demand = demand-supply
return excess_demand
```
**Algorithm:**
First choose a tolerance $\epsilon > 0$ and an adjustment factor $\kappa$, and a guess on $p_1 > 0$.
Then find the equilibrium price by:
1. Calculate excess demand $Z_1 = \sum_{j=1}^N x_{1}^{\star j}(p_{1},p_{2},e^{j}) - Nk$
2. If $|Z_1| < \epsilon $ stop
3. If $|Z_1| \geq \epsilon $ set $p_1 = p_1 + \kappa \cdot \frac{Z_1}{N}$
4. Return to step 1
That is, if if excess demand is positive and far from 0, then increase the price. If excess demand is negative and far from 0, decrease the price.
```
def find_equilibrium(alphas,p1,p2,k,kappa=0.5,eps=1e-8,maxiter=500):
t = 0
while True:
# a. step 1: excess demand
Z1 = excess_demand_good_1_func(alphas,p1,p2,k)
# b: step 2: stop?
if np.abs(Z1) < eps or t >= maxiter:
print(f'{t:3d}: p1 = {p1:12.8f} -> excess demand -> {Z1:14.8f}')
break
# c. step 3: update p1
p1 = p1 + kappa*Z1/alphas.size
# d. step 4: print only every 25th iteration using the modulus operator
if t < 5 or t%25 == 0:
print(f'{t:3d}: p1 = {p1:12.8f} -> excess demand -> {Z1:14.8f}')
elif t == 5:
print(' ...')
t += 1
return p1
```
Find the equilibrium price:
```
p1 = 1.4
p2 = 1
kappa = 0.1
eps = 1e-8
p1 = find_equilibrium(alphas,p1,p2,k,kappa=kappa,eps=eps)
```
**Check:** Ensure that excess demand of both goods are (almost) zero.
```
Z1 = excess_demand_good_1_func(alphas,p1,p2,k)
Z2 = excess_demand_good_2_func(alphas,p1,p2,k)
print(Z1,Z2)
assert np.abs(Z1) < eps
assert np.abs(Z2) < eps
```
**Quizz:** take a quick quizz on the algorithm [here](https://forms.office.com/Pages/ResponsePage.aspx?id=kX-So6HNlkaviYyfHO_6kckJrnVYqJlJgGf8Jm3FvY9UMjRVRkEwQTRGVVJPVzRDS0dIV1VJWjhJVyQlQCN0PWcu)
# Numerical integration by Monte Carlo
Numerical integration is the task of computing
$$
\mathbb{E}[g(x)] \text{ where } x \sim F
$$
and $F$ is a known probability distribution and $g$ is a function.
Relying on the law of large numbers we approximate this integral with
$$
\mathbb{E}[g(x)] \approx \frac{1}{N}\sum_{i=1}^{N} g(x_i)
$$
where $x_i$ is drawn from $F$ using a random number generator. This is also called **numerical integration by Monte Carlo**.
**Monte Carlo function:**
```
def g(x):
return (x-1)**2
def MC(N,g,F):
X = F.rvs(size=N) # rvs = draw N random values from F
return np.mean(g(X))
```
**Example** with a normal distribution:
```
N = 1000
mu = 0.1
sigma = 0.5
F = norm(loc=mu,scale=sigma)
print(MC(N,g,F))
```
Function for drawning \\( K \\) Monte Carlo samples:
```
def MC_sample(N,g,F,K):
results = np.empty(K)
for i in range(K):
results[i] = MC(N,g,F)
return results
```
The variance across Monte Carlo samples falls with larger $N$:
```
K = 1000
for N in [10**2,10**3,10**4,10**5]:
results = MC_sample(N,g,F,K)
print(f'N = {N:8d}: {results.mean():.6f} (std: {results.std():.4f})')
```
## Advanced: Gauss-Hermite quadrature
**Problem:** Numerical integration by Monte Carlo is **slow**.
**Solution:** Use smarter integration formulas on the form
$$
\mathbb{E}[g(x)] \approx \sum_{i=1}^{n} w_ig(x_i)
$$
where $(x_i,w_i), \forall n \in \{1,2,\dots,N\}$, are called **quadrature nodes and weights** and are provided by some theoretical formula depending on the distribution of $x$.
**Example I, Normal:** If $x \sim \mathcal{N}(\mu,\sigma)$ then we can use [Gauss-Hermite quadrature](https://en.wikipedia.org/wiki/Gauss%E2%80%93Hermite_quadrature) as implemented below.
```
def gauss_hermite(n):
""" gauss-hermite nodes
Args:
n (int): number of points
Returns:
x (numpy.ndarray): nodes of length n
w (numpy.ndarray): weights of length n
"""
# a. calculations
i = np.arange(1,n)
a = np.sqrt(i/2)
CM = np.diag(a,1) + np.diag(a,-1)
L,V = np.linalg.eig(CM)
I = L.argsort()
V = V[:,I].T
# b. nodes and weights
x = L[I]
w = np.sqrt(math.pi)*V[:,0]**2
return x,w
def normal_gauss_hermite(sigma, n=7, mu=None, exp=False):
""" normal gauss-hermite nodes
Args:
sigma (double): standard deviation
n (int): number of points
mu (double,optinal): mean
exp (bool,optinal): take exp and correct mean (if not specified)
Returns:
x (numpy.ndarray): nodes of length n
w (numpy.ndarray): weights of length n
"""
if sigma == 0.0 or n == 1:
x = np.ones(n)
if mu is not None:
x += mu
w = np.ones(n)
return x,w
# a. GaussHermite
x,w = gauss_hermite(n)
x *= np.sqrt(2)*sigma
# b. log-normality
if exp:
if mu is None:
x = np.exp(x - 0.5*sigma**2)
else:
x = np.exp(x + mu)
else:
if mu is None:
x = x
else:
x = x + mu
w /= np.sqrt(math.pi)
return x,w
```
**Results:** Becuase the function is "nice", very few quadrature points are actually needed (*not generally true*).
```
for n in [1,2,3,5,7,9,11]:
x,w = normal_gauss_hermite(mu=mu,sigma=sigma,n=n)
result = np.sum(w*g(x))
print(f'n = {n:3d}: {result:.10f}')
```
**Example II, log-normal ([more info](https://en.wikipedia.org/wiki/Log-normal_distribution)):**
1. Let $\log x \sim \mathcal{N}(\mu,\sigma)$.
2. Gauss-Hermite quadrature nodes and weights can be used with the option `exp=True`.
3. To ensure $\mathbb{E}[x] = 1$ then $\mu = -0.5\sigma^2$.
```
z = np.random.normal(size=1_000_000,scale=sigma)
print('mean(x) when mu = 0')
x,w = normal_gauss_hermite(mu=0,sigma=sigma,n=7,exp=True)
print(f'MC: {np.mean(np.exp(z)):.4f}')
print(f'Gauss-Hermite: {np.sum(x*w):.4f}')
print('')
print('mean(x), mu = -0.5*sigma^2')
x,w = normal_gauss_hermite(sigma=sigma,n=7,exp=True)
print(f'MC: {np.mean(np.exp(z)-0.5*sigma**2):.4f}')
print(f'Gauss-Hermite: {np.sum(x*w):.4f}')
```
# Load and save
## Pickle
A good allround method for loading and saving is to use **pickle**. Here is how to save:
```
# a. variables
my_dict = {'a':1,'b':2}
my_vec = np.array([1,2,3])
my_tupple = (1,4,2)
# b. put them in a dictionary
my_data = {}
my_data['my_dict'] = my_dict
my_data['my_vec'] = my_vec
my_data['my_tupple'] = my_tupple
# c. save the dictionary in a file
with open(f'data.p', 'wb') as f: # wb = write binary
pickle.dump(my_data, f)
```
Delete the variables:
```
del my_dict
del my_vec
del my_tupple
```
Load the data again:
```
# a. try
try:
print(my_tupple)
except:
print('my_vec does not exist')
# b. load
with open(f'data.p', 'rb') as f: # rb = read binary
data = pickle.load(f)
my_dict = data['my_dict']
my_vec = data['my_vec']
my_tupple = data['my_tupple']
# c. try again
print(my_vec)
print(my_tupple)
```
## Saving with numpy
When only saving/loading **numpy arrays**, an alternative is to use ``np.savez`` (or ``np.savez_compressed``). This is typically faster than pickle.
Here is how to save some data:
```
my_data = {}
my_data['A'] = np.array([1,2,3])
my_data['B'] = np.zeros((5,8))
my_data['C'] = np.ones((7,3,8))
np.savez(f'data.npz', **my_data)
# '**' unpacks the dictionary
```
Here is how to load the data again:
```
# a. delete
del my_data
# a. load all
my_data = {}
with np.load(f'data.npz') as data_obj:
for key in data_obj.files:
my_data[key] = data_obj[key]
print(my_data['A'])
# b. load single array
X = np.load(f'data.npz')['A']
print(X)
```
# Summary
**This lecture:** We have talked about:
1. numpy.random: Drawing (pseudo-)random numbers (seed, state, distributions)
2. scipy.stats: Using analytical random distributions (ppf, pdf, cdf, rvs)
3. ipywidgets: Making interactive figures
4. pickle and np.savez: Saving and loading data
The method you learned for finding the equilibrium can be used in a lot of models. For example, a simple method can be applied with multiple goods.
**Your work:** Before solving Problem Set 2 read through this notebook and play around with the code.
**Next lecture:** Workflow and debugging. Go through these guides beforehand:
1. [Installing Python and VSCode](https://numeconcopenhagen.netlify.com//guides/python-setup)
2. [Running Python in JupyterLab](https://numeconcopenhagen.netlify.com//guides/jupyterlab)
3. [Running Python in VSCode](https://numeconcopenhagen.netlify.com//guides/vscode-basics)
You must have installed **git** and have a **GitHub account!** (step 2 in [Installing Python and VSCode](https://numeconcopenhagen.netlify.com//guides/python-setup)).
**Finally:** You can begin to think about who you want to work together with for the group assignments. We will talk more about inaugural project next-time.
| true |
code
| 0.467393 | null | null | null | null |
|
# Machine Learning and the MNC

[xkcd: Machine Learning](https://xkcd.com/1838/)
## About this Course
### Premises
1. Many machine learning methods are relevant and useful in a wide range of
academic and non-academic disciplines.
1. Machine learning should not be viewed as a black box.
1. It is important to know what job is performed by each cog - it is not
necessary to have the skills to construct the machine inside the (black) box.
1. You are interested in applying machine learning to real-world problems.
### Vision
By the end of the lecture you will:
- Understand fundamental machine learning concepts.
- Gain hands on experience by working on business-related use cases.
- Develop an understanding for typical challenges, be able to ask the right questions when assessing a model and be able to frame business related questions as ML projects.
### Challenges
Machine Learning is a very broad, deep and quickly developing field with progress being made in
both academia and industry at breathtaking pace.
Yet, fundamental concepts to not change and we will therefore focus on exactly these concept - at times at the price of not applying most state of the art tools or methods.
As understanding complex systems is greatly facilitated by gaining practical experience using them, this lecture takes a very hands on approach. In doing so, we will employ the the Python programming language and its Data Science and ML ecosystem. Yet again, for those unfamiliar with Python, learning a new programming language is always a challenge.
### Notes
While we will use Python as primary tool, the concepts discussed in this course are independent of the programming language. However, the employed libraries will help to maintain a high level perspective on the problem without the need to deal with numerical details.
### Literature
#### Introductory and Hands On
- [Hands-On Machine Learning with Scikit-Learn and TensorFlow](https://www.oreilly.com/library/view/hands-on-machine-learning/9781492032632/) *Concepts, Tools, and Techniques to Build Intelligent Systems*, easy to read, very hands on, uses [Python](http://python.org). Copies are available in the library.
- [An Introduction to Statistical Learning](http://faculty.marshall.usc.edu/gareth-james/ISL/) *with Applications in R*, easy to read, uses [R](https://www.r-project.org/), slightly more formal treatment than in the book above; available as PDF download.
#### More Formal
- [The Elements of Statistical Learning: Data Mining, Inference, and Prediction.](https://web.stanford.edu/~hastie/ElemStatLearn/), a classic, available as PDF download.
- [Pattern Recognition and Machine Learning](https://www.springer.com/gp/book/9780387310732), a classic, available as PDF download.
#### Online Resources and Courses
- [Scikit-learn's](https://scikit-learn.org/stable/user_guide.html) user guide features a wide range of examples and typically provides links to follow up information.
- [Coursera's](https://www.coursera.org/learn/machine-learning) offers courses both on Machine and Deep Learning.
- *And many (!) others.*
## About Machine Learning
### What are Machine Learning Use Cases?
In everyday life:
- Automatic face recognition
- Automatic text translation
- Automatic speech recognition
- Spam filter
- Recommendation systems
- ...
And elsewhere:
- Fraught detection
- Predictive maintenance
- Diagnosing diseases
- Sentiment/Topic analysis in texts
- ...
What do these applications have in common?
- Data
- Complexity
- Need to scale as data increases
- Need to evolve as data changes
- Need to learn from data
### What is Machine Learning?
\[ISL]:
> *Statistical learning* refers to a vast set of tools for *understanding data*.
\[HandsOn]:
> Machine Learning is the science (and art) of programming computers so they can *learn from data*.
### How does a Machine Learning Process look like?
#### Traditional Approach
<a href="https://www.oreilly.com/library/view/hands-on-machine-learning/9781491962282/ch01.html">
<img src="../images/handson/mlst_0101.png" alt="Traditional Approach" width="50%">
</a>
Comments:
- Writing rules may be hard if not outright impossible.
- Not clear how to update rules when new data arrives.
#### Machine Learning Approach
<a href="https://www.oreilly.com/library/view/hands-on-machine-learning/9781491962282/ch01.html">
<img src="../images/handson/mlst_0102.png" alt="Traditional Approach" width="50%">
</a>
Comments:
- Rule detection/specification is left to an algorithm.
- When new data arrives, the model is retrained.
Machine Learning systems be automated to incrementally improve over time.
<a href="https://www.oreilly.com/library/view/hands-on-machine-learning/9781491962282/ch01.html">
<img src="../images/handson/mlst_0103.png" alt="ML Approach" width="50%">
</a>
In addition, Machine Learning can be used to gain insights from data that is otherwise not available. It must no necessarily be *lots* of data.
<a href="https://www.oreilly.com/library/view/hands-on-machine-learning/9781491962282/ch01.html">
<img src="../images/handson/mlst_0104.png" alt="Traditional Approach" width="50%">
</a>
### What is Machine Learning good for?
\[HandsOn]:
> Machine Learning is great for:
> - Problems for which existing solutions require a lot of hand-tuning or long lists of rules: one Machine Learning algorithm can often simplify code and perform better
> - Complex problems for which there is no good solution at all using traditional approach: the best Machine Learning techniques can [may] find a solution.
> - Fluctuating environments: a Machine Learning system can adapt to new data.
> - Getting insights about problems and (large amounts of) data.
Machine Learning is typically used as part of a decision making process and may therefore be accompanied by (or even include) a cost benefit analysis.
## Python
> Python is an interpreted, high-level, general-purpose programming language.
> Created by Guido van Rossum and first released in 1991, Python's design philosophy emphasizes code readability [...].
> Its language constructs [...] aim to help programmers write clear, logical code for small and large-scale projects.
[Wikipedia](https://en.wikipedia.org/wiki/Python_(programming_language))
---
*Python has a very large scientific computing and Machine Learning ecosystem.*
## Machine Learning with Python
In this lecture, we will primarily use [scikit-learn](https://scikit-learn.org/stable/).
<a href="https://scikit-learn.org/stable/">
<img src="../images/sklearn/scikit-learn-logo-small.png" alt="scikit learn" width="20%">
</a>
Scikit-learn is a prominent, production-ready library used in both academia and industry with [endorsements](https://scikit-learn.org/stable/testimonials/testimonials.html) from e.g. [JPMorgan](https://www.jpmorgan.com/), [Spotify](https://www.spotify.com/), [Inria](https://www.inria.fr/), [Evernote](https://evernote.com/) and others.
One of the particular features is its very simple and uniform [API](https://en.wikipedia.org/wiki/Application_programming_interface) which allows to use a wide range of different models through very little different commands.
In addition, it provides a set of utilities typically needed for developing a Machine Learning system.
### Generic Use
Using scikit-learn typically involves at least the following steps:
```python
# 0. train test split
X_train, X_test, y_train, y_test = train_test_split(X, y)
# 1. choose a model
from sklearn.model_family import DesiredModel
# 2. instantiate a model with certain parameters
model = DesiredModel(model_parameters)
# 3. fit a model to the data
model.fit(X_train, y_train)
# 4. evaluate
model.score(X_test, y_test), model.score(X_train, y_train)
# 5. use the model to make a prediction
y_new = model.predict(X_new)
```
Although there are a lot of things going on in the background, the basic actions always take a form similar to this.
### A Simple Example
**Problem:**
- Input: 2D data, i.e. variables x1 and x2
- Output: binary, i.e. a variable y taking only values {0, 1} (=classes)
- Objective: separate input space according to class values
```
import matplotlib.pyplot as plt
from mlxtend.plotting import plot_decision_regions
from sklearn.datasets import make_moons
from sklearn.ensemble import RandomForestClassifier
def load_data(**wargs):
# experiment by setting the parameters to different values
# and observe the result
return make_moons(n_samples=200, noise=0.3, random_state=42)
def visualize_data(X, y):
fig, ax = plt.subplots()
ax.scatter(X[:, 0], X[:, 1], c=y)
return fig, ax
X, y = load_data()
visualize_data(X, y)
# SCIKIT-LEARN: start
# 1. chose a model
from sklearn.ensemble import RandomForestClassifier
# 2. set model parameters (perform parameter search e.g. using GridSearchCV)
model = RandomForestClassifier(n_estimators=100, random_state=42)
# 3. fit model
model.fit(X, y)
# 4. predict
model.predict(X)
# 5. inspect
plot_decision_regions(X, y, clf=model, legend=2)
# SCIKIT-LEARN: end
```
Observe how the model has successfully captured the shape of the data.
## A First Application
*Head over to the advertising notebook.*
| true |
code
| 0.609989 | null | null | null | null |
|
# How to Use Anomaly Detectors in Merlion
This notebook will guide you through using all the key features of anomaly detectors in Merlion. Specifically, we will explain
1. Initializing an anomaly detection model (including ensembles)
1. Training the model
1. Producing a series of anomaly scores with the model
1. Quantitatively evaluating the model
1. Visualizing the model's predictions
1. Saving and loading a trained model
1. Simulating the live deployment of a model using a `TSADEvaluator`
We will be using a single example time series for this whole notebook. We load and visualize it now:
```
import matplotlib.pyplot as plt
import numpy as np
from merlion.plot import plot_anoms
from merlion.utils import TimeSeries
from ts_datasets.anomaly import NAB
np.random.seed(1234)
# This is a time series with anomalies in both the train and test split.
# time_series and metadata are both time-indexed pandas DataFrames.
time_series, metadata = NAB(subset="realKnownCause")[3]
# Visualize the full time series
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
ax.plot(time_series)
# Label the train/test split with a dashed line & plot anomalies
ax.axvline(metadata[metadata.trainval].index[-1], ls="--", lw=2, c="k")
plot_anoms(ax, TimeSeries.from_pd(metadata.anomaly))
from merlion.utils import TimeSeries
# Get training split
train = time_series[metadata.trainval]
train_data = TimeSeries.from_pd(train)
train_labels = TimeSeries.from_pd(metadata[metadata.trainval].anomaly)
# Get testing split
test = time_series[~metadata.trainval]
test_data = TimeSeries.from_pd(test)
test_labels = TimeSeries.from_pd(metadata[~metadata.trainval].anomaly)
```
## Model Initialization
In this notebook, we will use three different anomaly detection models:
1. Isolation Forest (a classic anomaly detection model)
2. WindStats (an in-house model that divides each week into windows of a specified size, and compares time series values to the historical values in the appropriate window)
3. Prophet (Facebook's popular forecasting model, adapted for anomaly detection.
Let's start by initializing each of them:
```
# Import models & configs
from merlion.models.anomaly.isolation_forest import IsolationForest, IsolationForestConfig
from merlion.models.anomaly.windstats import WindStats, WindStatsConfig
from merlion.models.anomaly.forecast_based.prophet import ProphetDetector, ProphetDetectorConfig
# Import a post-rule for thresholding
from merlion.post_process.threshold import AggregateAlarms
# Import a data processing transform
from merlion.transform.moving_average import DifferenceTransform
# All models are initialized using the syntax ModelClass(config), where config
# is a model-specific configuration object. This is where you specify any
# algorithm-specific hyperparameters, any data pre-processing transforms, and
# the post-rule you want to use to post-process the anomaly scores (to reduce
# noisiness when firing alerts).
# We initialize isolation forest using the default config
config1 = IsolationForestConfig()
model1 = IsolationForest(config1)
# We use a WindStats model that splits each week into windows of 60 minutes
# each. Anomaly scores in Merlion correspond to z-scores. By default, we would
# like to fire an alert for any 4-sigma event, so we specify a threshold rule
# which achieves this.
config2 = WindStatsConfig(wind_sz=60, threshold=AggregateAlarms(alm_threshold=4))
model2 = WindStats(config2)
# Prophet is a popular forecasting algorithm. Here, we specify that we would like
# to pre-processes the input time series by applying a difference transform,
# before running the model on it.
config3 = ProphetDetectorConfig(transform=DifferenceTransform())
model3 = ProphetDetector(config3)
```
Now that we have initialized the individual models, we will also combine them in an ensemble. We set this ensemble's detection threshold to fire alerts for 4-sigma events (the same as WindStats).
```
from merlion.models.ensemble.anomaly import DetectorEnsemble, DetectorEnsembleConfig
ensemble_config = DetectorEnsembleConfig(threshold=AggregateAlarms(alm_threshold=4))
ensemble = DetectorEnsemble(config=ensemble_config, models=[model1, model2, model3])
```
## Model Training
All anomaly detection models (and ensembles) share the same API for training. The `train()` method returns the model's predicted anomaly scores on the training data. Note that you may optionally specify configs that modify the protocol used to train the model's post-rule! You may optionally specify ground truth anomaly labels as well (if you have them), but they are not needed. We give examples of all these behaviors below.
```
from merlion.evaluate.anomaly import TSADMetric
# Train IsolationForest in the default way, using the ground truth anomaly labels
# to set the post-rule's threshold
print(f"Training {type(model1).__name__}...")
train_scores_1 = model1.train(train_data=train_data, anomaly_labels=train_labels)
# Train WindStats completely unsupervised (this retains our anomaly detection
# default anomaly detection threshold of 4)
print(f"\nTraining {type(model2).__name__}...")
train_scores_2 = model2.train(train_data=train_data, anomaly_labels=None)
# Train Prophet with the ground truth anomaly labels, with a post-rule
# trained to optimize Precision score
print(f"\nTraining {type(model3).__name__}...")
post_rule_train_config_3 = dict(metric=TSADMetric.F1)
train_scores_3 = model3.train(
train_data=train_data, anomaly_labels=train_labels,
post_rule_train_config=post_rule_train_config_3)
# We consider an unsupervised ensemble, which combines the anomaly scores
# returned by the models & sets a static anomaly detection threshold of 3.
print("\nTraining ensemble...")
ensemble_post_rule_train_config = dict(metric=None)
train_scores_e = ensemble.train(
train_data=train_data, anomaly_labels=train_labels,
post_rule_train_config=ensemble_post_rule_train_config,
)
print("Done!")
```
## Model Inference
There are two ways to invoke an anomaly detection model: `model.get_anomaly_score()` returns the model's raw anomaly scores, while `model.get_anomaly_label()` returns the model's post-processed anomaly scores. The post-processing calibrates the anomaly scores to be interpretable as z-scores, and it also sparsifies them such that any nonzero values should be treated as an alert that a particular timestamp is anomalous.
```
# Here is a full example for the first model, IsolationForest
scores_1 = model1.get_anomaly_score(test_data)
scores_1_df = scores_1.to_pd()
print(f"{type(model1).__name__}.get_anomaly_score() nonzero values (raw)")
print(scores_1_df[scores_1_df.iloc[:, 0] != 0])
print()
labels_1 = model1.get_anomaly_label(test_data)
labels_1_df = labels_1.to_pd()
print(f"{type(model1).__name__}.get_anomaly_label() nonzero values (post-processed)")
print(labels_1_df[labels_1_df.iloc[:, 0] != 0])
print()
print(f"{type(model1).__name__} fires {(labels_1_df.values != 0).sum()} alarms")
print()
print("Raw scores at the locations where alarms were fired:")
print(scores_1_df[labels_1_df.iloc[:, 0] != 0])
print("Post-processed scores are interpretable as z-scores")
print("Raw scores are challenging to interpret")
```
The same API is shared for all models, including ensembles.
```
scores_2 = model2.get_anomaly_score(test_data)
labels_2 = model2.get_anomaly_label(test_data)
scores_3 = model3.get_anomaly_score(test_data)
labels_3 = model3.get_anomaly_label(test_data)
scores_e = ensemble.get_anomaly_score(test_data)
labels_e = ensemble.get_anomaly_label(test_data)
```
## Quantitative Evaluation
It is fairly transparent to visualize a model's predicted anomaly scores and also quantitatively evaluate its anomaly labels. For evaluation, we use specialized definitions of precision, recall, and F1 as revised point-adjusted metrics (see the technical report for more details). We also consider the mean time to detect anomalies.
In general, you may use the `TSADMetric` enum to compute evaluation metrics for a time series using the syntax
```
TSADMetric.<metric_name>.value(ground_truth=ground_truth, predict=anomaly_labels)
```
where `<metric_name>` is the name of the evaluation metric (see the API docs for details and more options), `ground_truth` is a time series of ground truth anomaly labels, and `anomaly_labels` is the output of `model.get_anomaly_label()`.
```
from merlion.evaluate.anomaly import TSADMetric
for model, labels in [(model1, labels_1), (model2, labels_2), (model3, labels_3), (ensemble, labels_e)]:
print(f"{type(model).__name__}")
precision = TSADMetric.Precision.value(ground_truth=test_labels, predict=labels)
recall = TSADMetric.Recall.value(ground_truth=test_labels, predict=labels)
f1 = TSADMetric.F1.value(ground_truth=test_labels, predict=labels)
mttd = TSADMetric.MeanTimeToDetect.value(ground_truth=test_labels, predict=labels)
print(f"Precision: {precision:.4f}")
print(f"Recall: {recall:.4f}")
print(f"F1: {f1:.4f}")
print(f"MTTD: {mttd}")
print()
```
Since the individual models are trained to optimize F1 directly, they all have low precision, high recall, and a mean time to detect of around 1 day. However, by instead training the individual models to optimize precision, and training a model combination unit to optimize F1, we are able to greatly increase the precision and F1 score, at the cost of a lower recall and higher mean time to detect.
## Model Visualization
Let's now visualize the model predictions that led to these outcomes. The option `filter_scores=True` means that we want to plot the post-processed anomaly scores (i.e. returned by `model.get_anomaly_label()`). You may instead specify `filter_scores=False` to visualize the raw anomaly scores.
```
for model in [model1, model2, model3]:
print(type(model).__name__)
fig, ax = model.plot_anomaly(
time_series=test_data, time_series_prev=train_data,
filter_scores=True, plot_time_series_prev=True)
plot_anoms(ax=ax, anomaly_labels=test_labels)
plt.show()
print()
```
So all the individual models generate quite a few false positives. Let's see how the ensemble does:
```
fig, ax = ensemble.plot_anomaly(
time_series=test_data, time_series_prev=train_data,
filter_scores=True, plot_time_series_prev=True)
plot_anoms(ax=ax, anomaly_labels=test_labels)
plt.show()
```
So the ensemble misses one of the three anomalies in the test split, but it also greatly reduces the number of false positives relative to the other models.
## Saving & Loading Models
All models have a `save()` method and `load()` class method. Models may also be loaded with the assistance of the `ModelFactory`, which works for arbitrary models. The `save()` method creates a new directory at the specified path, where it saves a `json` file representing the model's config, as well as a binary file for the model's state.
We will demonstrate these behaviors using our `IsolationForest` model (`model1`) for concreteness. Note that the config explicitly tracks the transform (to pre-process the data), the calibrator (to transform raw anomaly scores into z-scores), the thresholding rule (to sparsify the calibrated anomaly scores).
```
import json
import os
import pprint
from merlion.models.factory import ModelFactory
# Save the model
os.makedirs("models", exist_ok=True)
path = os.path.join("models", "isf")
model1.save(path)
# Print the config saved
pp = pprint.PrettyPrinter()
with open(os.path.join(path, "config.json")) as f:
print(f"{type(model1).__name__} Config")
pp.pprint(json.load(f))
# Load the model using Prophet.load()
model2_loaded = IsolationForest.load(dirname=path)
# Load the model using the ModelFactory
model2_factory_loaded = ModelFactory.load(name="IsolationForest", model_path=path)
```
We can do the same exact thing with ensembles! Note that the ensemble stores its underlying models in a nested structure. This is all reflected in the config.
```
# Save the ensemble
path = os.path.join("models", "ensemble")
ensemble.save(path)
# Print the config saved. Note that we've saved all individual models,
# and their paths are specified under the model_paths key.
pp = pprint.PrettyPrinter()
with open(os.path.join(path, "config.json")) as f:
print(f"Ensemble Config")
pp.pprint(json.load(f))
# Load the selector
selector_loaded = DetectorEnsemble.load(dirname=path)
# Load the selector using the ModelFactory
selector_factory_loaded = ModelFactory.load(name="DetectorEnsemble", model_path=path)
```
## Simulating Live Model Deployment
A typical model deployment scenario is as follows:
1. Train an initial model on some recent historical data, optionally with labels.
1. At a regular interval `retrain_freq` (e.g. once per week), retrain the entire model unsupervised (i.e. with no labels) on the most recent data.
1. Obtain the model's predicted anomaly scores for the time series values that occur between re-trainings. We perform this operation in batch, but a deployment scenario may do this in streaming.
1. Optionally, specify a maximum amount of data (`train_window`) that the model should use for training (e.g. the most recent 2 weeks of data).
We provide a `TSADEvaluator` object which simulates the above deployment scenario, and also allows a user to evaluate the quality of the forecaster according to an evaluation metric of their choice. We illustrate an example below using the ensemble.
```
# Initialize the evaluator
from merlion.evaluate.anomaly import TSADEvaluator, TSADEvaluatorConfig
evaluator = TSADEvaluator(model=ensemble, config=TSADEvaluatorConfig(retrain_freq="7d"))
# The kwargs we would provide to ensemble.train() for the initial training
# Note that we are training the ensemble unsupervised.
train_kwargs = {"anomaly_labels": None}
# We will use the default kwargs for re-training (these leave the
# post-rules unchanged, since there are no new labels)
retrain_kwargs = None
# We call evaluator.get_predict() to get the time series of anomaly scores
# produced by the anomaly detector when deployed in this manner
train_scores, test_scores = evaluator.get_predict(
train_vals=train_data, test_vals=test_data,
train_kwargs=train_kwargs, retrain_kwargs=retrain_kwargs
)
# Now let's evaluate how we did.
precision = evaluator.evaluate(ground_truth=test_labels, predict=test_scores, metric=TSADMetric.Precision)
recall = evaluator.evaluate(ground_truth=test_labels, predict=test_scores, metric=TSADMetric.Recall)
f1 = evaluator.evaluate(ground_truth=test_labels, predict=test_scores, metric=TSADMetric.F1)
mttd = evaluator.evaluate(ground_truth=test_labels, predict=test_scores, metric=TSADMetric.MeanTimeToDetect)
print("Ensemble Performance")
print(f"Precision: {precision:.4f}")
print(f"Recall: {recall:.4f}")
print(f"F1: {f1:.4f}")
print(f"MTTD: {mttd}")
print()
```
In this case, we see that by simply re-training the ensemble weekly in an unsupervised manner, we have increased the precision from $\frac{2}{5}$ to $\frac{2}{3}$, while leaving unchanged the recall and mean time to detect. This is due to data drift over time.
| true |
code
| 0.729676 | null | null | null | null |
|
```
artefact_prefix = '2_pytorch'
target = 'beer_style'
from dotenv import find_dotenv
from datetime import datetime
import pandas as pd
from pathlib import Path
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
from category_encoders.binary import BinaryEncoder
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, LabelEncoder, OneHotEncoder
from joblib import dump, load
# from src.data.sets import merge_categories
# from src.data.sets import save_sets
from src.data.sets import load_sets
# from src.data.sets import split_sets_random
# from src.data.sets import test_class_exclusion
# from src.models.performance import convert_cr_to_dataframe
from src.models.pytorch import PytorchClassification_2
from src.models.pytorch import get_device
from src.models.pytorch import train_classification
from src.models.pytorch import test_classification
from src.models.pytorch import PytorchDataset
from src.models.pipes import create_preprocessing_pipe
from src.visualization.visualize import plot_confusion_matrix
```
### Directory Set up
```
project_dir = Path(find_dotenv()).parent
data_dir = project_dir / 'data'
raw_data_dir = data_dir / 'raw'
interim_data_dir = data_dir / 'interim'
processed_data_dir = data_dir / 'processed'
reports_dir = project_dir / 'reports'
models_dir = project_dir / 'models'
processed_data_dir
```
### Load Save Data
```
## Panda Data type
from src.data.sets import load_sets
X_train, X_test, X_val, y_train, y_test, y_val = load_sets()
y_train['beer_style'].nunique()
X_train.head()
```
### Data Pipeline
```
pipe = Pipeline([
('bin_encoder', BinaryEncoder(cols=['brewery_name'])),
('scaler', StandardScaler())
])
X_train_trans = pipe.fit_transform(X_train)
X_val_trans = pipe.transform(X_val)
X_test_trans = pipe.transform(X_test)
X_train_trans.shape
n_features = X_train_trans.shape[1]
n_features
n_classes = y_train['beer_style'].nunique()
n_classes
```
### Encoding - Label
```
le = LabelEncoder()
y_train_trans = le.fit_transform(y_train)
y_val_trans = le.fit_transform(y_val)
y_test_trans = le.transform(y_test)
y_test_trans
```
### Convert to Pytorch Tensor
```
device = get_device()
device
train_dataset = PytorchDataset(X=X_train_trans, y=y_train_trans)
val_dataset = PytorchDataset(X=X_val_trans, y=y_val_trans)
test_dataset = PytorchDataset(X=X_test_trans, y=y_test_trans)
```
### Classification Model
```
model = PytorchClassification_2(n_features=n_features, n_classes=n_classes)
model.to(device)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
```
## Train the Model
```
N_EPOCHS = 20
BATCH_SIZE = 512
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 1, gamma=0.9)
start_time = datetime.now()
print(f'Started: {start_time}')
for epoch in range(N_EPOCHS):
train_loss, train_acc = train_classification(train_dataset,
model=model,
criterion=criterion,
optimizer=optimizer,
batch_size=BATCH_SIZE,
device=device,
scheduler=scheduler)
valid_loss, valid_acc = test_classification(val_dataset,
model=model,
criterion=criterion,
batch_size=BATCH_SIZE,
device=device)
print(f'Epoch: {epoch}')
print(f'\t(train)\tLoss: {train_loss:.4f}\t|\tAcc: {train_acc * 100:.1f}%')
print(f'\t(valid)\tLoss: {valid_loss:.4f}\t|\tAcc: {valid_acc * 100:.1f}%')
end_time = datetime.now()
runtime = end_time - start_time
print(f'Ended: {end_time}')
print(f'Runtime: {runtime}')
```
### Retrain the model with lesser EPOCH
```
N_EPOCHS = 20
BATCH_SIZE = 4096
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 1, gamma=0.9)
start_time = datetime.now()
print(f'Started: {start_time}')
for epoch in range(N_EPOCHS):
train_loss, train_acc = train_classification(train_dataset,
model=model,
criterion=criterion,
optimizer=optimizer,
batch_size=BATCH_SIZE,
device=device,
scheduler=scheduler)
valid_loss, valid_acc = test_classification(val_dataset,
model=model,
criterion=criterion,
batch_size=BATCH_SIZE,
device=device)
print(f'Epoch: {epoch}')
print(f'\t(train)\tLoss: {train_loss:.4f}\t|\tAcc: {train_acc * 100:.1f}%')
print(f'\t(valid)\tLoss: {valid_loss:.4f}\t|\tAcc: {valid_acc * 100:.1f}%')
end_time = datetime.now()
runtime = end_time - start_time
print(f'Ended: {end_time}')
print(f'Runtime: {runtime}')
```
### Prediction
```
model.to('cpu')
preds = model(test_dataset.X_tensor).argmax(1)
preds
model.to(device)
```
## Evaluation
### Classification Report
```
report = classification_report(y_test, le.inverse_transform(preds.cpu()))
print(report)
```
## Save Objects for Production
### Save model
```
path = models_dir / f'{artefact_prefix}_model'
torch.save(model, path.with_suffix('.torch'))
```
### Save Pipe Object
```
X = pd.concat([X_train, X_val, X_test])
prod_pipe = create_preprocessing_pipe(X)
path = models_dir / f'{artefact_prefix}_pipe'
dump(prod_pipe, path.with_suffix('.sav'))
```
### Save the label encoder
This is required to retrive the name of the beer_style.
```
path = models_dir / f'{artefact_prefix}_label_encoder'
dump(le, path.with_suffix('.sav'))
```
| true |
code
| 0.716591 | null | null | null | null |
|
# Monte Carlo experiments
The Monte Carlo method is a way of using random numbers to solve problems that can otherwise be quite complicated. Essentially, the idea is to replace uncertain values with a large list of values, assume those values have no uncertaintly, and compute a large list of results. Analysis of the results can often lead you to the solution to the original problem.
The following story is based on the Dart method, described in the following book by Thijsse, J. M. (2006), Computational Physics, Cambridge University Press, p. 273, ISBN 978-0-521-57588-1
### Approximating $\pi$
Let's use the Monte Carlo method to approximate $\pi$. First, the area of a circle is $A = \pi r^2,$
so that the unit circle ($r=1$) has an area $A = \pi$. Second, we define the square domain in which the unit circle just fits (2x2), and plot both:
```
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import uniform
def circle():
theta = np.linspace(0, 2*np.pi, num=1000)
x = [np.cos(n) for n in theta]
y = [np.sin(n) for n in theta]
return x, y
def square():
x = [-1,1,1,-1,-1]
y = [-1,-1,1,1,-1]
return x, y
plt.plot(*circle(), 'k')
plt.plot(*square(), 'k')
plt.axis('equal')
plt.show()
```
Consider a random point (x,y) inside the square.
**The probability that a random point from a square domain lies inside the biggest circle that fits inside the square is equal to the area of the circle divided by the area of the square.**
Our square is $2\times 2=4$ and our circle has an area of $\pi$, so if we pick many points, statistically, we expect $\pi/4$ of them to fall inside the circle.
### Our first few points
Let's create a function that will give us random points from a uniform distribution inside the square domain, and generate a few random points.
```
np.random.seed(seed=345) # remove/change the seed if you want different random numbers
def monte_carlo(n):
x = uniform.rvs(loc=-1, scale=2, size=n)
y = uniform.rvs(loc=-1, scale=2, size=n)
return x, y
mc_x, mc_y = monte_carlo(28)
plt.plot(*circle(), 'k')
plt.plot(*square(), 'k')
plt.scatter(mc_x, mc_y, c='green')
plt.axis('equal')
plt.show()
```
Let's colour the points depending on whether they are within 1 unit of the origin or not:
```
def dist(x, y):
return np.sqrt(x**2 + y**2)
def inside(x, y):
return dist(x, y) < 1
def outside(x, y):
return dist(x, y) > 1
np.random.seed(seed=345) # remove the command or change the value if you want different random numbers
x, y = monte_carlo(28)
ins = inside(x, y)
outs = outside(x, y)
plt.plot(*square(), 'k')
plt.plot(*circle(), 'k')
plt.scatter(x[ins], y[ins], c='blue',label=len(x[ins]))
plt.scatter(x[outs], y[outs], c='red', label=len(x[outs]))
plt.axis('equal')
plt.legend()
plt.show()
```
If you left the np.random seed as 345, and generated 28 points, then your output should have 22 blue points (inside the circle) and 6 red points (outside the circle).
So, if 22 out of 28 (around 76%) of the points are inside the circle, we can approximate $\pi$ from this.
$$
\begin{align}
\pi \approx 4(22/28) = 22/7 = 3.142857.
\end{align}
$$
$22/7$ is a common approximation of $\pi$, and this seed value happens to get us to this ratio. If you vary the random seed, however, you will see that this ratio for only a small number of points can vary quite a lot!
To produce a more robust approximation for $\pi$, we will need many more random points.
### 250 points
```
x, y = monte_carlo(250)
ins = inside(x, y)
outs = outside(x, y)
pi = 4 * len(x[ins])/len(x)
plt.plot(*square(), 'k')
plt.scatter(x[ins], y[ins], c='blue', label=len(x[ins]))
plt.scatter(x[outs], y[outs], c='red', label=len(x[outs]))
plt.axis('equal')
plt.legend()
plt.title('π ≈ {}'.format(pi))
plt.show()
```
### 1000 points
```
x, y = monte_carlo(1000)
ins = inside(x, y)
outs = outside(x, y)
pi = 4 * len(x[ins])/len(x)
plt.plot(*square(), 'k')
plt.scatter(x[ins], y[ins], c='blue', label=len(x[ins]))
plt.scatter(x[outs], y[outs], c='red', label=len(x[outs]))
plt.axis('equal')
plt.legend()
plt.title('π ≈ {}'.format(pi))
plt.show()
```
## 25000 points
```
x, y = monte_carlo(25000)
ins = inside(x, y)
outs = outside(x, y)
pi = 4 * len(x[ins])/len(x)
plt.plot(*square(), 'k')
plt.scatter(x[ins], y[ins], c='blue', label=len(x[ins]))
plt.scatter(x[outs], y[outs], c='red', label=len(x[outs]))
plt.axis('equal')
plt.legend()
plt.title('π ≈ {}'.format(pi))
plt.show()
```
With many points, you should see a completely blue circle in an otherwise red square, **and** a decent estimate of $\pi$.
## The mcerp3 package
There is a Python package, `mcerp3`, which handles Monte Carlo calculations automatically. It was originally written by Abraham Lee and has recently been updated by Paul Freeman to support Python3. This package is available on [PyPI](https://pypi.org/project/mcerp3/). If you want to use in this notebook in the cloud, you will have to do an install (which can take a bit of time):
```
#!pip install mcerp3 # or use conda install -y mcerp3 -c freemapa
!conda install -y mcerp3 -c freemapa
import mcerp3 as mc
from mcerp3.umath import sqrt
x = mc.U(-1, 1)
y = mc.U(-1, 1)
ins = sqrt(x**2 + y**2) < 1
print('percentage of points in the circle =', ins)
print('pi ≈', 4 * ins)
```
| true |
code
| 0.470493 | null | null | null | null |
|
# Part 2 - Advanced text classifiers
As seen in the past, we can create models that take advantage of counts of words and tf-idf scores and that yield some pretty accurate predictions. But it is possible to make use of several additional features to improve our classifier. In this learning unit we are going to check how we could use other data extracted from our text data to determine if an e-mail is 'spam' or 'not spam' (also known as ham). We are going to use a very well known Kaggle dataset for spam detection - [Kaggle Spam Collection](https://www.kaggle.com/uciml/sms-spam-collection-dataset).

This part will also introduce you to feature unions, a very useful way of combining different feature sets into your models. This scikit-learn class comes hand-in-hand with pipelines. Both allow you to delegate the work of combining and piping your transformer's outputs - your features - allowing you to create workflows in a very simple way.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.pipeline import Pipeline, FeatureUnion
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.preprocessing import StandardScaler
from nltk.corpus import stopwords
%matplotlib inline
warnings.simplefilter("ignore")
```
## 1 - Spam and Ham
As we mentioned before, we are going to try and come up with ways of detecting spam in the Kaggle Spam dataset. Let's load it and look into the data.
```
df = pd.read_csv('./datasets/spam.csv', encoding='latin1')
df.drop(["Unnamed: 2", "Unnamed: 3", "Unnamed: 4"], axis=1,inplace=True)
df.rename(columns={"v1":"label", "v2":"message"},inplace=True)
df.head()
```
You could think it should be quite easy to detect the spam text, since it is clearer to the human eye. I don't know about you, but I'm always suspicious of free stuff. There ain't no such thing as a free lunch (except for the ones in our hackathons).
But by now you should also know that what seems obvious in text to us is sometimes not as easy to detect by a model. So, what kind of features could you use for this? The most obvious one is the words themselves, which you already know how to use with your bag-of-words approach - using CountVectorizer or TfIdfVectorizer.
## 1.1 - Baseline
To start with, let's look at the target class distribution,
```
df.label.value_counts(normalize=True)
```
So, if we were to create a dumb classifier which always predicts "ham", we would get an accuracy of 86.6% for this dataset.
Let's get our baseline with the Bag-of-words approach. Here we are going to use a RandomForestClassifier, a powerful machine learning classifier that fits very well in this problem. You may remember this estimator from SLU13.
```
# Split in train and validation
train_data, test_data = train_test_split(df, test_size=0.2, random_state=42)
# Build the pipeline
text_clf = Pipeline([('tfidf', TfidfVectorizer()),
('classifier', RandomForestClassifier(random_state = 42))])
# Train the classifier
text_clf.fit(map(str, train_data['message'].values), train_data['label'].values)
predicted = text_clf.predict(map(str, test_data['message'].values))
np.mean(predicted == test_data['label'])
```
Powerful words, no?
Our next step is to include other features.
## 1.2 - Adding extra features
But, beside this vectorization as a bag-of-words, let's understand if our classifier can be fed other signals we can retrieve from the text. Let's check for example the *length of the message*. We'll first compute it and add it as a feature in our dataframe.
```
df['length'] = df['message'].map(len)
df.head()
```
**Is this feature useful?**
Since this is only one numerical feature, we can just simply plot its distribution in our data. Let's evaluate the length distribution for "Spam" and "Ham"
```
ax_list = df.hist(column='length', by='label', bins=50,figsize=(12,4))
ax_list[0].set_xlim((0,300))
ax_list[1].set_xlim((0,300))
```
Seems quite different, right? So you would guess this feature should be helpful in your classifier.
But let's actually check this feature through the use of a text classifier. Now for the tricky parts.
### Preprocessing
If BLU7 is still fresh on you, you remember that when using pipelines we just fed it the text column. In fact, we could feed it more than one column, but the standard preprocessing applies the same preprocessing to the whole dataset. For our heterogeneous data, this doesn't quite work.
So what can we do if we want to have a pipeline using several different features from several different columns? We can't apply the same methods to everything right? So first thing we can do is to create a selector transformer that simply returns the right column in the dataset by the key value(s) you pass.
You can find below two such transformers: `TextSelector` for text columns and `NumberSelector` for number columns. Note that the only difference between them is the return type.
```
class Selector(BaseEstimator, TransformerMixin):
"""
Transformer to select a column from the dataframe to perform additional transformations on
"""
def __init__(self, key):
self.key = key
def fit(self, X, y=None):
return self
class TextSelector(Selector):
"""
Transformer to select a single column from the data frame to perform additional transformations on
Use on text columns in the data
"""
def transform(self, X):
return X[self.key]
class NumberSelector(Selector):
"""
Transformer to select a single column from the data frame to perform additional transformations on
Use on numeric columns in the data
"""
def transform(self, X):
return X[[self.key]]
```
And then we define pipelines tailored for each of our cases.
```
text = Pipeline([
('selector', TextSelector("message")),
('tfidf', TfidfVectorizer())
])
length = Pipeline([
('selector', NumberSelector("length")),
('standard', StandardScaler())
])
```
Notice that we used the `StandardScaler`. The use of this scaler (scales the feature to zero mean and unit variance) is because we don't want to have different feature scales in our classifier. Most of classification algorithms expect the features to be in the same scale!
You might be wondering now:
> *How does this solve my problem... now I have two pipelines and although I can feed my whole dataset they are separate pipelines... does this help at all?*
In fact, if you were to run them separately this would not be that helpful, since you would have to add the classifier at the end of each. It seems like we are missing only one piece, a way to combine steps in parallel and not in sequence. This is where feature unions come in!
## 1.3 - Feature Unions
While pipelines define a cascaded workflow, feature unions allow you to parallelize your workflows and have several transformations applied in parallel to your pipeline. The image below presents a simple pipeline, in sequence:
<img src="./media/pipeline.png" width="40%">
While the following one presents what it is called a feature union:
<img src="./media/unions.png" width="70%">
The latter is quite simple to define in scikit-learn, as follows:
```
# Feature Union allow use to use multiple distinct features in our classifier
feats = FeatureUnion([('text', text),
('length', length)])
```
Now you can use this combination of pipelines and feature unions inside a new pipeline!
<img src="./media/pipelines_dawg.png" width="45%">
We then get our final flow, from which we can extract the classification score.
```
# Split in train and validation
train_data, test_data = train_test_split(df, test_size=0.2, random_state=42)
pipeline = Pipeline([
('features',feats),
('classifier', RandomForestClassifier(random_state = 42)),
])
pipeline.fit(train_data, train_data.label)
preds = pipeline.predict(test_data)
np.mean(preds == test_data.label)
```
Our new feature does help! We got a slightly improvement from a baseline that was already quite high. Nicely done. Let's now play with other more complex text features and see if we can maximize our classification score even more.
## 1.4 - Advanced features
What kind of features can you think of?
You could start by just having the number of words, in the same way that we had the character length of the sentence:
```
df['words'] = df['message'].str.split().map(len)
```
Remember BLU7? Remember stopwords?
<img src="./media/stopwords.png" width="40%">
Let's count only words that are not stopwords, since these are normally less relevant.
```
stop_words = set(stopwords.words('english'))
df['words_not_stopword'] = df['message'].apply(lambda x: len([t for t in x.split() if t not in stop_words]))
```
In the same way, we can apply counts conditioned on other different characteristics, like counting the number of commas in the sentence or the number of words that are uppercased or capitalized:
```
df['commas'] = df['message'].str.count(',')
df['upper'] = df['message'].map(lambda x: map(str.isupper, x)).map(sum)
df['capitalized'] = df['message'].map(lambda x: map(str.istitle, x)).map(sum)
```
We can also model the type of words by their length, for example:
```
#get the average word length
df['avg_word_length'] = df['message'].apply(lambda x: np.mean([len(t) for t in x.split() if t not in stop_words]) if len([len(t) for t in x.split(' ') if t not in stop_words]) > 0 else 0)
```
Let's take a look then at our output data frame, and all the features we added:
```
df.head()
```
And now we can use the Feature Unions that we learned about to merge all these together. We'll split the data, create pipelines for all our new features and get their unions. Easy, right?
```
words = Pipeline([
('selector', NumberSelector(key='words')),
('standard', StandardScaler())
])
words_not_stopword = Pipeline([
('selector', NumberSelector(key='words_not_stopword')),
('standard', StandardScaler())
])
avg_word_length = Pipeline([
('selector', NumberSelector(key='avg_word_length')),
('standard', StandardScaler())
])
commas = Pipeline([
('selector', NumberSelector(key='commas')),
('standard', StandardScaler()),
])
upper = Pipeline([
('selector', NumberSelector(key='upper')),
('standard', StandardScaler()),
])
capitalized = Pipeline([
('selector', NumberSelector(key='capitalized')),
('standard', StandardScaler()),
])
feats = FeatureUnion([('text', text),
('length', length),
('words', words),
('words_not_stopword', words_not_stopword),
('avg_word_length', avg_word_length),
('commas', commas),
('upper', upper),
('capitalized', capitalized)])
feature_processing = Pipeline([('feats', feats)])
```
We ended with our classifier so let's run it and get our classification score.
*Drumroll, please.*
```
# Split in train and validation
train_data, test_data = train_test_split(df, test_size=0.2, random_state=42)
pipeline = Pipeline([
('features',feats),
('classifier', RandomForestClassifier(random_state = 42)),
])
pipeline.fit(train_data, train_data.label)
preds = pipeline.predict(test_data)
np.mean(preds == test_data.label)
```
<img src="./media/sad.png" width="40%">
Although we are still above the baseline, we didn't surpass by much the score of using just the text and its length. But don't despair, with all the tools from BLU7, BLU8 and the first part of this BLU you are already perfectly equipped to find yet new features and to analyze if they are good or not. Even to integrate your pipelines with dimensionality reduction techniques that might find your meaningful features among all these.
## 2 - Other classifiers
New approaches in text processing have arised with new machine learning methods known as deep learning. The usage of deep learning methods is out of the scope for this BLU, but it is important that the reader is aware of the potential of such methods to improve over traditional machine learning algorithms. In particular, we suggest the knowledge about two different classifiers besides sklearn.
* [StarSpace](https://github.com/facebookresearch/StarSpace)
* [Vowpal Wabbit classifier](https://github.com/JohnLangford/vowpal_wabbit/wiki)
### Additional Pointers
* https://www.kaggle.com/baghern/a-deep-dive-into-sklearn-pipelines
* http://zacstewart.com/2014/08/05/pipelines-of-featureunions-of-pipelines.html
* http://michelleful.github.io/code-blog/2015/06/20/pipelines/
* http://scikit-learn.org/stable/auto_examples/hetero_feature_union.html#sphx-glr-auto-examples-hetero-feature-union-py
## 3 - Final remarks
And we are at the end of our NLP specialization. It saddens me, but it is time to say goodbye.
Throughout these BLUs you learned:
* How to process text
* Typicall text features used in classification tasks
* State of the art techniques to encode text
* Methods to analyze feature importance
* Methods to perform feature reduction
* How to design pipelines and combine different features inside them
You are now armed with several tools to perform text classification and much more in NLP. Don't forget to review all of this for the NLP hackathon, and to do your best in the Exercises.
<img src="./media/so_long.jpg" width="40%">
| true |
code
| 0.628835 | null | null | null | null |
|
```
import oommfc as oc
import discretisedfield as df
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import colorsys
plt.style.use('styles/lato_style.mplstyle')
def convert_to_RGB(hls_color):
return np.array(colorsys.hls_to_rgb(hls_color[0] / (2 * np.pi),
hls_color[1],
hls_color[2]))
def generate_RGBs(field_data):
"""
field_data :: (n, 3) array
"""
hls = np.ones_like(field_data)
hls[:, 0] = np.arctan2(field_data[:, 1],
field_data[:, 0]
)
hls[:, 0][hls[:, 0] < 0] = hls[:, 0][hls[:, 0] < 0] + 2 * np.pi
hls[:, 1] = 0.5 * (field_data[:, 2] + 1)
rgbs = np.apply_along_axis(convert_to_RGB, 1, hls)
# Redefine colours less than zero
# rgbs[rgbs < 0] += 2 * np.pi
return rgbs
```
Initial states:
```
R = 30e-9 # bubble radius
w = 30e-9 # dw width
a = 130 * np.pi / 180
def init_m_lattice(pos):
xm, ym = 160e-9, 100e-9
for xc, yc in [[0, 0], [-xm, -ym], [xm, -ym], [xm, ym], [-xm, ym]]:
x, y = pos[0] - xc, pos[1] - yc
r = np.sqrt(x ** 2 + y ** 2)
phi = np.arctan2(y, x)
if r <= R:
if (phi < 10 * np.pi / 180) or (phi < 0 and phi > -170 * np.pi / 180):
factor = 1
else:
factor = -1
sech = 1 / np.cosh(np.pi * (r - R) / w)
mx = factor * sech * (-np.sin(phi + a))
my = factor * sech * (np.cos(phi + a))
mz = 1 - (mx ** 2 + my ** 2)
# if r < R:
# mz = -(1 - (mx ** 2 + my ** 2))
# else:
# mz = (1 - (mx ** 2 + my ** 2))
return (mx, my, mz)
return (0, 0, 1)
def init_m(pos):
x, y = pos[0], pos[1]
r = np.sqrt(x ** 2 + y ** 2)
phi = np.arctan2(y, x)
if (phi < 10 * np.pi / 180) or (phi < 0 and phi > -170 * np.pi / 180):
factor = 1
else:
factor = -1
sech = 1 / np.cosh(np.pi * (r - R) / w)
mx = factor * sech * (-np.sin(phi + a))
my = factor * sech * (np.cos(phi + a))
# mz = 1 - (mx ** 2 + my ** 2)
if r < R:
mz = -(1 - (mx ** 2 + my ** 2))
else:
mz = (1 - (mx ** 2 + my ** 2))
return (mx, my, mz)
def init_dot(pos):
x, y = pos[0], pos[1]
r = np.sqrt(x ** 2 + y ** 2)
if r < R:
mz = -1
else:
mz = 1
return (0, 0, mz)
def init_type2bubble(pos):
R = 80e-9
x, y = pos[0], pos[1]
r = np.sqrt(x ** 2 + y ** 2)
phi = np.arctan2(y, x) + 0.5 * np.pi
k = np.pi / R
if r < R and y > 0:
m = (np.sin(k * r) * np.cos(phi), np.sin(k * r) * np.sin(phi), -np.cos(k * r))
elif r < R and y < 0:
m = (-np.sin(k * r) * np.cos(phi), -np.sin(k * r) * np.sin(phi), -np.cos(k * r))
else:
m = (0, 0, 1)
return m
def init_type2bubble_bls(pos):
R = 80e-9
x, y = pos[0], pos[1]
r = np.sqrt(x ** 2 + y ** 2)
phi = np.arctan2(y, x)
phi_b = np.arctan2(y, x) + 0.5 * np.pi
k = np.pi / R
if r < R and y > 0 and phi < np.pi * 0.5:
m = (-np.sin(k * r) * np.cos(phi_b), -np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
elif r < R and y > 0 and phi > np.pi * 0.5:
m = (np.sin(k * r) * np.cos(phi_b), np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
elif r < R and y < 0 and np.abs(phi) > np.pi * 0.5:
m = (-np.sin(k * r) * np.cos(phi_b), -np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
elif r < R and y < 0 and np.abs(phi) < np.pi * 0.5:
m = (np.sin(k * r) * np.cos(phi_b), np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
else:
m = (0, 0, 1)
return m
def init_type2bubble_bls_II(pos):
R = 80e-9
x, y = pos[0], pos[1]
r = np.sqrt(x ** 2 + y ** 2)
phi = np.arctan2(y, x)
phi_b = np.arctan2(y, x) + 0.5 * np.pi
k = np.pi / R
if r < R and y > 0:
m = (np.sin(k * r) * np.cos(phi_b), np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
elif r < R and y < 0:
m = (-np.sin(k * r) * np.cos(phi_b), -np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
else:
m = (0, 0, 1)
return m
def init_type2bubble_neel(pos):
R = 80e-9
x, y = pos[0], pos[1]
r = np.sqrt(x ** 2 + y ** 2)
phi = np.arctan2(y, x)
phi_b = np.arctan2(y, x)
k = np.pi / R
if r < R and y > 0 and phi < np.pi * 1:
m = (-np.sin(k * r) * np.cos(phi_b), -np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
elif r < R and y > 0 and phi > np.pi * 1:
m = (np.sin(k * r) * np.cos(phi_b), np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
elif r < R and y < 0 and np.abs(phi) > np.pi * 1:
m = (-np.sin(k * r) * np.cos(phi_b), -np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
elif r < R and y < 0 and np.abs(phi) < np.pi * 1:
m = (np.sin(k * r) * np.cos(phi_b), np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
else:
m = (0, 0, 1)
return m
def init_type2bubble_neel_II(pos):
R = 80e-9
x, y = pos[0], pos[1]
r = np.sqrt(x ** 2 + y ** 2)
phi = np.arctan2(y, x)
phi_b = np.arctan2(y, x)
k = np.pi / R
if r < R and y > 0:
m = (np.sin(k * r) * np.cos(phi_b), np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
elif r < R and y < 0:
m = (-np.sin(k * r) * np.cos(phi_b), -np.sin(k * r) * np.sin(phi_b), -np.cos(k * r))
else:
m = (0, 0, 1)
return m
np.random.seed(42)
def init_random(pos):
m = 2 * np.random.random((1, 3)) - 1
return m
mu0 = 4 * np.pi * 1e-7
# A = 12e-12
# Ms = 5.37e5
# Ku = 187952
# B = 180e-3
A = 20e-12
Ms = 0.648 / mu0
Ku = A / 2.3e-16
# Apply field in an angle
B = 0.2
theta_B = 0 * np.pi / 180
phi_B = 0 * np.pi / 180
print('lex = ', np.sqrt(2 * A / (mu0 * Ms ** 2)))
mesh = oc.Mesh(p1=(-400e-9, -400e-9, -50e-9), p2=(400e-9, 400e-9, 50e-9),
cell=(5e-9, 5e-9, 5e-9))
system = oc.System(name='oommf_typeII_bubble')
# Add interactions
system.hamiltonian = (oc.Exchange(A=A) + oc.UniaxialAnisotropy(K1=Ku, u=(0, 0, 1))
+ oc.Demag()
+ oc.Zeeman((np.cos(phi_B) * np.sin(theta_B) * B / mu0,
np.sin(phi_B) * np.sin(theta_B) * B / mu0,
np.cos(theta_B) * B / mu0))
)
system.m = df.Field(mesh, value=init_m, norm=Ms)
f, ax = plt.subplots(ncols=1, figsize=(8, 8))
system.m.plot_plane('z', ax=ax)
```
Relax the system:
```
md = oc.MinDriver()
md.drive(system)
```
Extract the simulation data:
```
# A list of tuples with the coordinates in the order of systems[2]
coordinates = list(system.m.mesh.coordinates)
# Turn coordinates into a (N, 3) array and save in corresponding variables
# scaled in nm
coordinates = np.array(coordinates)
x_oommf, y_oommf, z_oommf = coordinates[:, 0] * 1e9, coordinates[:, 1] * 1e9, coordinates[:, 2] * 1e9
xs, ys, zs = np.unique(x_oommf), np.unique(y_oommf), np.unique(z_oommf)
# phi_oommf = np.arctan2(y_oommf, x_oommf)
# Get the magnetisation for every coordinate in the magnetisation list
values = []
for c in coordinates:
values.append(system.m(c))
values = np.array(values)
# Save them in the corresponding row and column of the m list
# mx, my, mz:
mx, my, mz = (values[:, 0] / Ms, values[:, 1] / Ms,values[:, 2] / Ms)
# mphi = lambda z_i: (-mx_O * np.sin(phi_O) + my_O * np.cos(phi_O))[_filter_y_O(z_i)]
# mr = lambda z_i: (mx_O * np.cos(phi_O) + my_O * np.sin(phi_O))[_filter_y_O(z_i)]
# Optionally save the data:
#
# np.savetxt('coordinates_typeIIbubble_800nmx800nmx100nm.txt', coordinates)
# np.savetxt('mx_typeIIbubble_800nmx800nmx100nm.txt', mx)
# np.savetxt('my_typeIIbubble_800nmx800nmx100nm.txt', my)
# np.savetxt('mz_typeIIbubble_800nmx800nmx100nm.txt', mz)
# Make an average through the thickness
z_filter = z_oommf == np.unique(z_oommf)[0]
av_map_x = np.copy(np.zeros_like(mx[z_filter]))
av_map_y = np.copy(np.zeros_like(mx[z_filter]))
av_map_z = np.copy(np.zeros_like(mx[z_filter]))
for layer in np.unique(z_oommf)[:]:
z_filter = z_oommf == layer
av_map_x += mx[z_filter]
av_map_y += my[z_filter]
av_map_z += mz[z_filter]
av_map_x /= len(np.unique(z_oommf)[:])
av_map_y /= len(np.unique(z_oommf)[:])
av_map_z /= len(np.unique(z_oommf)[:])
```
Plot the the system at the bottom layer:
```
f, ax = plt.subplots(ncols=1, figsize=(8, 8))
z_filter = z_oommf == np.unique(z_oommf)[0]
rgb_map = generate_RGBs(np.column_stack((mx, my, mz)))
plt.scatter(x_oommf[z_filter], y_oommf[z_filter], c=rgb_map[z_filter])
# plt.scatter(x_oommf, y_oommf, c=rgb_map)
# Arrows filter
arr_fltr_tmp = np.zeros(len(xs))
arr_fltr_tmp[::6] = 1
arr_fltr = np.zeros_like(x_oommf[z_filter]).reshape(len(xs), -1)
arr_fltr[::6] = arr_fltr_tmp
arr_fltr = arr_fltr.astype(np.bool).reshape(-1,)
plt.quiver(x_oommf[z_filter][arr_fltr], y_oommf[z_filter][arr_fltr],
mx[z_filter][arr_fltr], my[z_filter][arr_fltr],
scale=None)
# plt.savefig('oommf_bubble_tilted_30deg_y-axis-neg.jpg', dpi=300, bbox_inches='tight')
```
Plot the average:
```
f, ax = plt.subplots(ncols=1, figsize=(8, 8))
z_filter = z_oommf == np.unique(z_oommf)[0]
rgb_map = generate_RGBs(np.column_stack((av_map_x, av_map_y, av_map_z)))
plt.scatter(x_oommf[z_filter], y_oommf[z_filter], c=rgb_map)
# Arrows filter
arr_fltr_tmp = np.zeros(len(xs))
arr_fltr_tmp[::6] = 1
arr_fltr = np.zeros_like(x_oommf[z_filter]).reshape(len(xs), -1)
arr_fltr[::6] = arr_fltr_tmp
arr_fltr = arr_fltr.astype(np.bool).reshape(-1,)
plt.quiver(x_oommf[z_filter][arr_fltr], y_oommf[z_filter][arr_fltr],
av_map_x[arr_fltr], av_map_y[arr_fltr],
scale=None)
# plt.savefig('av_map_thickness_quiver.jpg', dpi=300, bbox_inches='tight')
```
| true |
code
| 0.263931 | null | null | null | null |
|
# Autoencoder
In this notebook we will
```
from keras.layers import Input, Dense
from keras.models import Model
import matplotlib.pyplot as plt
import matplotlib.colors as mcol
from matplotlib import cm
def graph_colors(nx_graph):
#cm1 = mcol.LinearSegmentedColormap.from_list("MyCmapName",["blue","red"])
#cm1 = mcol.Colormap('viridis')
cnorm = mcol.Normalize(vmin=0,vmax=9)
cpick = cm.ScalarMappable(norm=cnorm,cmap='Set1')
cpick.set_array([])
val_map = {}
for k,v in nx.get_node_attributes(nx_graph,'attr').items():
#print(v)
val_map[k]=cpick.to_rgba(v)
#print(val_map)
colors=[]
for node in nx_graph.nodes():
#print(node,val_map.get(str(node), 'black'))
colors.append(val_map[node])
return colors
```
##### 1 Write a function that builds a simple autoencoder
The autoencoder must have a simple Dense layer with relu activation. The number of node of the dense layer is a parameter of the function
The function must return the entire autoencoder model as well as the encoder and the decoder
##### Load the mnist dataset
##### 2. Buil the autoencoder with a embedding size of 32 and print the number of parameters of the model. What do they relate to ?
##### 3. Fit the autoencoder using 32 epochs with a batch size of 256
##### 4. Using the history module of the autoencoder write a function that plots the learning curves with respect to the epochs on the train and test set. What can you say about these learning curves ? Give also the last loss on the test set
##### 5. Write a function that plots a fix number of example of the original images on the test as weel as their reconstruction
### Nearest neighbours graphs
The goal of this part is to visualize the neighbours graph in the embedding. It corresponds the the graph of the k-nearest neighbours using the euclidean distance of points the element in the embedding
```
from sklearn.neighbors import kneighbors_graph
import networkx as nx
def plot_nearest_neighbour_graph(encoder,x_test,y_test,ntest=100,p=3): #to explain
X=encoder.predict(x_test[1:ntest])
y=y_test[1:ntest]
A = kneighbors_graph(X, p, mode='connectivity', include_self=True)
G=nx.from_numpy_array(A.toarray())
nx.set_node_attributes(G,dict(zip(range(ntest),y)),'attr')
fig, ax = plt.subplots(figsize=(10,10))
pos=nx.layout.kamada_kawai_layout(G)
nx.draw(G,pos=pos
,with_labels=True
,labels=nx.get_node_attributes(G,'attr')
,node_color=graph_colors(G))
plt.tight_layout()
plt.title('Nearest Neighbours Graph',fontsize=15)
plt.show()
```
### Reduce the dimension of the embedding
##### 6. Rerun the previous example using an embedding dimension of 16
## Adding sparsity
##### 7. In this part we will add sparisity over the weights on the embedding layer. Write a function that build such a autoencoder (using a l1 regularization with a configurable regularization parameter and using the same autoencoder architecture that before)
# Deep autoencoder
# Convolutionnal autoencoder
# Application to denoising
| true |
code
| 0.671444 | null | null | null | null |
|
## Frauchiger-Renner thought experiment in the collapse theories
### Installation instruction
It is recommended that you clone the qthought repository to your local machine and then run
in the qthought folder.
If you did not pip install qthought, you can use the following quick-fix by uncommenting and adapting to your local file path
```
#import sys
#import os
# to run the example, set the following path to the folder path of qthought on your machine
#sys.path.append(os.path.abspath('/Users/nuri/qthought/qthought'))
```
### Defining the protocol
The code below implements the Frauchiger Renner paradox with a collapse theory prescription of measurement, where agents treat each measurement as a collapse, and the setup can be represented as a branching tree of outcomes. In this case, we see that the paradox arising in the original paper does not take place. Prior to reading this, it is recommended to take a look at the PDF description file Frauchiger-Renner example.
First, we import the ProjectQ operations needed for the protocol: the required single-qubit gates and the control. We also import *Protocol* and *ProtocolStep* classes to be able to define steps of the protocol; *QuantumSystem* to operate quantum systems of different dimensionality; *Agent* class and all functions from the *collapse_theory* module; *consistency* class to be able to chain agents' statements. Additionally, we import *InitR* function which initializes a qubit in the state $\frac{1}{\sqrt{3}} |0> + \sqrt{\frac{2}{3}} |1>$.
```
import warnings
warnings.filterwarnings('ignore')
import numpy as np
from projectq.ops import H, X, Measure
from projectq.meta import Control
from qthought.protocol import ProtocolStep
from qthought.quantumsystem import QuantumSystem
from qthought.agents import InferenceTable
from qthought.interpretations.collapse_theory import *
from qthought.FrauchigerRennerExample.FR_protocol import InitR
from qthought.logicalReasoning.consistency import consistency
```
The first action of the protocol (at time $t=1$) is the initilization of the qubit $R$ Alice has in her lab in the state $\frac{1}{\sqrt{3}} |0> + \sqrt{\frac{2}{3}} |1>$. After defining the action, we define the step of the protocol by specifying: domain of action; written description of the action, which will be used for printouts during the run; time of the step; and which action variable being described.
```
# Step 1: Initialize r
# ----------------------------------------------------------
@enable_branching()
def step1_action(qsys):
"""Prepares the subsystem `r` of a `QuantumSystem` in the Frauchiger-Renner initial state."""
InitR | qsys['r']
step1 = ProtocolStep(domain={'Qubit': ['r']},
descr='Initialize R',
time=1,
action=step1_action)
```
At $t=2$, Alice measures $R$ and writes the result in her memory.
```
# Step 2: Alice observes r
# ----------------------------------------------------------
@enable_branching(collapse_system='r')
def step2_action(qsys):
observe(qsys['Alice_memory'], qsys['r'])
step2 = ProtocolStep(domain={'AgentMemory(1)': ['Alice'],
'Qubit': ['r']},
descr='ALICE observes R',
time=2,
action=step2_action)
```
At $t=3$, Alice makes an inference based on her outcome.
```
# Step 3: Alice makes inference
# ----------------------------------------------------------
@enable_branching()
def step3_action(qsys):
qsys['Alice'].make_inference()
step3 = ProtocolStep(domain={'Agent(1,1)': ['Alice']},
descr='ALICE makes an inference',
time=3,
action=step3_action)
```
At $t=4$, Alice prepares the qubit $S$ based on her outcome: in the state $|0>$ if she obtain $a=0$, and in the state $\frac{1}{\sqrt{2}} |0> + \frac{1}{\sqrt{2}} |1>$ if she got $a=1$.
```
# Step 4: Alice prepares S
# ----------------------------------------------------------
@enable_branching()
def step4_action(qsys):
with Control(qsys['eng'], qsys['Alice_memory']):
H | qsys['s']
step4 = ProtocolStep(domain={'Qubit': ['s'],
'AgentMemory(1)': ['Alice']},
descr='Apply H to S controlled on ALICE_MEMORY',
time=4,
action=step4_action)
```
At $t=5$, Bob measures $S$ and writes the result down to his memory.
```
# Step 5: Bob measures S
# ----------------------------------------------------------
@enable_branching(collapse_system='s')
def step5_action(qsys):
observe(qsys['Bob_memory'], qsys['s'])
step5 = ProtocolStep(domain={'Qubit': ['s'],
'AgentMemory(1)': ['Bob']},
descr='BOB measures S',
time=5,
action=step5_action)
```
At $t=6$, Bob makes an inference based on his outcome.
```
# Step 6: Bob makes inference
# ----------------------------------------------------------
@enable_branching()
def step6_action(qsys):
qsys['Bob'].make_inference()
step6 = ProtocolStep(domain={'Agent(1,1)': ['Bob']},
descr='BOB makes an inference',
time=6,
action=step6_action)
```
At $t=7$, we need to reverse Alice's reasoning process for Ursula to be able to measure in the $|ok>$, $|fail>$ basis.
```
# Step 7: Reverse inference making in Alice
# ----------------------------------------------------------
@enable_branching()
def step7_action(qsys):
qsys['Alice'].make_inference(reverse=True)
observe(qsys['Alice_memory'], qsys['r'], reverse=True)
step7 = ProtocolStep(domain={'Agent(1,1)': ['Alice']},
descr='Reverse Alice reasoning (Step1: in ok --> 1(R)',
time=7,
action=step7_action)
```
Ursula measures Alice's lab in the $|ok>$, $|fail>$ basis (~ Bell basis). To do so, we first apply a Hadamard gate on $R$ at $t=8$, and then measure it in computational basis at $t=9$.
```
# Step 8: Hadamard on r
# ----------------------------------------------------------
@enable_branching()
def step8_action(qsys):
H | qsys['r']
step8 = ProtocolStep(domain={'Qubit': ['r']},
descr='Perform Hadamard on R (Step2: in ok --> 1(R)',
time=8,
action=step8_action)
# Step 9: Ursula measures Alices lab
# ----------------------------------------------------------
@enable_branching(collapse_system='r')
def step9_action(qsys):
observe(qsys['Ursula_memory'], qsys['r'])
step9 = ProtocolStep(domain={'Qubit': ['r'],
'AgentMemory(1)': ['Ursula']},
descr='URSULA measures ALICEs lab (i.e. r)',
time=9,
action=step9_action)
```
Ursula reasons based on her outcome at $t=10$, and announces it at $t=11$.
```
# Step 10: Ursula makes an inference
# ----------------------------------------------------------
@enable_branching()
def step10_action(qsys):
qsys['Ursula'].make_inference()
step10 = ProtocolStep(domain={'Agent(1,1)': ['Ursula']},
descr='URSULA makes inference',
time=10,
action=step10_action)
# Step 11: Ursula announces her prediction
# ----------------------------------------------------------
@enable_branching()
def step11_action(qsys):
Measure | qsys['Ursula_prediction']
print('!Measurement made on Ursula_prediction!')
print('Ursula prediction:', readout([qsys['Ursula_prediction']]))
step11 = ProtocolStep(domain={'Agent(1,1)': ['Ursula']},
descr='URSULA announces her prediction',
time=11,
action=step11_action)
```
Now we repeat the same procedure for Wigner measuring Bob's lab. First, we reverse Bob's reasoning process at $t=12$.
```
# Step 12: Reverse Bob's reasoning
# ----------------------------------------------------------
@enable_branching()
def step12_action(qsys):
qsys['Bob'].make_inference(reverse=True)
# qsys['Bob'].observe(qsys['s'], reverse=True)
observe(qsys['Bob_memory'], qsys['s'], reverse=True)
step12 = ProtocolStep(domain={'Agent(1,1)': ['Bob']},
descr='Reverse BOBs inference procedure',
time=12,
action=step12_action)
```
Wigner measures Bob's lab in the $|ok>$, $|fail>$ basis (~ Bell basis). To do so, we first apply a Hadamard gate on $S$ at $t=13$, measure it in computational basis at $t=14$, and subsequently check if Wigner gets outcome "ok".
```
# Step 13: Apply Hadamard on s
# ----------------------------------------------------------
@enable_branching()
def step13_action(qsys):
H | qsys['s']
step13 = ProtocolStep(domain={'Qubit': ['s']},
descr='Apply Hadamard on S, i.e. transform system S+BOB: ok --> 1(s) ',
time=13,
action=step13_action)
# Step 14: Check if Bob is in ok state
# ----------------------------------------------------------
def step14_action(qsys):
Measure | qsys['s']
print('!Measurement made on s!')
print('s-state:', readout([qsys['s']]))
step14 = ProtocolStep(domain={'Agent(1,1)': ['Bob']},
descr='Check if Bob+s is in ok state (corresponding to s: 1)',
time=14,
action=step14_action)
```
### Building up inference tables
Now we construct the inference tables according to which the inference qubits of different agents are initialized. First, we consider the inference table of Alice: she has to reason about Wigner's outcome, and for that we need to include the steps of what is happening in the Bob's lab ($t=5,6$), and Wigner's actions ($t=12,13$).
```
p_TA_steps = [step1, step2, step4, step5, step6,
step12, step13]
p_TA = sum(p_TA_steps)
p_TA
```
Alice makes a forward inference about a measurement outcome later in the experiment -- and none of her conclusions are deterministic!
```
TA = forward_inference(p_TA,
subsys_x='Alice_memory', t_x=2,
subsys_y='s', t_y=13,
silent=False)
TA
```
Now Bob reasons about Alice, making a backward inference about a measurement outcome earlier in the experiment.
```
p_TB_steps = [step1, step2, step4, step5]
p_TB = sum(p_TB_steps)
p_TB
TB = backward_inference(p_TB,
subsys_x='Alice_memory', t_x=2,
subsys_y='Bob_memory', t_y=5,
silent=False)
TB
```
Ursula reasons about Bob, using backward inference as well.
```
p_TU_steps = [step1, step2, step3, step4, step5,
step6, step7, step8 ,step9]
p_TU = sum(p_TU_steps)
p_TU
TU = backward_inference(p_TU,
subsys_x='Bob_memory', t_x=5,
subsys_y='Ursula_memory', t_y=9,
silent=False)
TU
```
### Combining the inference tables with consistency
Now the consistency rules come to play. They tell us how to combine the obtained inference tables -- in this case we don't have any special restrictions, as we use the classical modal logic where we are always free to conclude $A \Rightarrow C$ from knowing $A \Rightarrow B$ and $B \Rightarrow C$, regardless of which agent has produced the statement.
```
TA_final = TA
TB_final = consistency(TB, TA)
TU_final = consistency(TU, TB_final)
print(TA_final)
print(TB_final)
print(TU_final)
```
### Running the full protocol
Now we are ready to run the full protocol, and see if the "winning condition" (getting the inconsistency) is satisfied. In this case, no inferences can be made with probability 1, so the inconsistency ("winning condition") is never satisfied.
```
steps = [step1, step2, step3, step4, step5,
step6, step7, step8, step9, step10,
step12, step13]
p = sum(steps)
p
print('-'*70)
print('Requiring quantum system:')
qsys = QuantumSystem(p.get_requirements())
no_prediction_state = 1
qsys.print_wavefunction()
print('-'*70)
print('Initialize inference system')
qsys['Alice'].set_inference_table(TA_final, no_prediction_state)
qsys['Bob'].set_inference_table(TB_final, no_prediction_state)
qsys['Ursula'].set_inference_table(TU_final, no_prediction_state)
qsys['Alice'].prep_inference()
qsys['Bob'].prep_inference()
qsys['Ursula'].prep_inference()
qsys.print_wavefunction()
qtree = QuantumTree(qsys)
print('-'*70)
print('Run protocol:')
p.run_manual(qtree, silent=False)
print('-'*70)
print('Perform final measurements.')
states = to_flat_unique(get_possible_outcomes(qtree, 'all'))
possible_final_states = [np.binary_repr(a, len(qtree[0])) for a in states]
print('Possible outcome states:')
for state in possible_final_states:
state = state[::-1] # transform state to internal representation
print('--------------------------')
ok_bar = bool(int(state[qtree.get_position(0, 'Ursula_memory')[0]])) # True, iff Ursula_memory == 1
ok = bool(int(state[qtree.get_position(0, 's')[0]])) # True, iff s == 1
Upred = state[qtree.get_position(0, 'Ursula_prediction')[0]] # Ursula prediction state: 1 - cannot say,0 - fail
if ok_bar and ok: print('XXXXXXXXXXX WINNING XXXXXXXXXXXXX')
print('U. predicts fail:'.ljust(10), bool(1-int(Upred)))
print('ok_bar'.ljust(10), ok_bar)
print('ok'.ljust(10), ok)
if ok_bar and ok:
print('Winning state:', state[::-1])
print('XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX')
```
| true |
code
| 0.547162 | null | null | null | null |
|
# 2. Tool to identify some components that have caused the electrical events
<p> This jupyter notebook was used to manually identify some of the componennts that have caused the electrical events, that were previously hand-labeled. The components identified are <b> pumps, grinders (motor) and heaters </b>in the coffeemaker. </p> <b> This is the second notebook in the labeling pipeline of CREAM. </b>
<div class="alert alert-info">
<h3>Instructions for using this notebook</h3>
<p> In the following, we load the electrical events that have been previously labeled with the "1_electrical_events_labeling_tool.ipynb" notebook. </p>
<p> Proceed at the end of the notebook with the corresponding cell for the labeling. Follow the instructions given there. </p>
## Imports
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import h5py
import pandas as pd
import os
import sys
from pathlib import Path
from datetime import datetime
from datetime import timedelta
import math
import pdb
import scipy
# Add project path to path for import
project_path = os.path.abspath("..")
if project_path not in sys.path:
sys.path.append(project_path)
# Add module path to path for import
module_path = os.path.abspath("../data_utility/data_utility.py")
if module_path not in sys.path:
sys.path.append(module_path)
from data_utility import CREAM_Day # class to work with a day of the CREAM Dataset
%matplotlib notebook
# Intentional replication is necessary
%matplotlib notebook
%load_ext autoreload
# Reload all modules every time before executing the Python code typed.
%autoreload 2
# Import some graphical modules
from IPython.display import display, clear_output
from ipywidgets import Button, Layout, ButtonStyle, HBox, VBox, widgets, Output
from IPython.display import SVG, display, clear_output
import subprocess
import glob
```
## Global Functions
```
def plot_event_window(event_timestamp:pd.Timestamp, window_size, current_CREAM_day:CREAM_Day, concurrent_events_dict):
"""
Plots a window of window_size in each direction around the event_timestamp.
The event_timestamp marks the beginning of the minute where the event stopped.
So instead of directly using the event_timestamp, we plot the event_timestamp + 59 seconds
to mark the end of the minute in that the event stopped.
Therefore the event has happended before the point that is marked as a bold red line.
The current signal of the coffee maker is plotted.
The event type is the label the event gets.
If a concurrent_events_dict is provided, with the keys being the name of the event list and the values being the event dataframes,
all other events that happen within the window of interest are also plotted.
Appliance events are bold orange lines.
Other events are dashed red lines.
"""
# Import and set globals necessary for the click functions
global EVENT_TIMESTAMP
global WINDOW_START_TS
global COMPONENTS_DF
# Instead of taking the event timestamp directly we take the END of the minute
end_event_timestamp = event_timestamp + timedelta(seconds=59)
# Tackle border cases of the timestamp
if end_event_timestamp - timedelta(seconds=window_size) < current_CREAM_day.minimum_request_timestamp: # in case we are at the beginning of the day
duration_to_left = end_event_timestamp - current_CREAM_day.minimum_request_timestamp
duration_to_left = duration_to_left.total_seconds() # amount of data that we load now to the left of the current timestmap
duration_to_right = window_size #to the right we can load the full window
elif end_event_timestamp + timedelta(seconds=window_size) > current_CREAM_day.maximum_request_timestamp: # in case we are at the end of the day
duration_to_right = current_CREAM_day.maximum_request_timestamp - end_event_timestamp
duration_to_right = duration_to_right.total_seconds() #amount of data that we load now to the right of the current timestamp
duration_to_left = window_size #to the left we can load the full window
else: # if we have anough datapoints to the left and to the right to load the full WINDOW_SIZE in each direction
duration_to_left = window_size
duration_to_right = window_size
# Create the start- and end-timestamp and compute the overall duration of the window
duration = duration_to_left + duration_to_right
start_ts = end_event_timestamp - timedelta(seconds=duration_to_left)
end_ts = end_event_timestamp + timedelta(seconds=duration_to_right)
# Load the data
voltage, current = current_CREAM_day.load_time_frame(start_datetime=start_ts, duration=duration) #and WINDOW_SIZE seconds after the event
# Compute the index of the event, using the timestamp
end_event_index = current_CREAM_day.get_index_from_timestamp(start_ts, end_event_timestamp)
fig, ax = plt.subplots(1,1)
fig.canvas.mpl_connect('button_press_event', onclick) #append event to figure
xticks = np.arange(len(current))
ax.plot(xticks, current, markersize=0.1, alpha=0.6)
ax.tick_params(axis='x', rotation=90) #rotate the xlabels
if np.max(current) < 1: #in case of noise, show an appropriate range
ax.set_ylim([-6,6])
# Plot the event line
ax.axvline(end_event_index, color="red", linewidth=1.5)
# Add other events that happend within the window
if len(concurrent_events_dict) > 0:
for event_list_name, concurrent_events_df in concurrent_events_dict.items():
# If an already refined timestamp list (either product, or maintenance) is provided, one
# can plot the detailed end timestamps instead of the coarse grained ones that are not refined yet
if "End_Timestamp" in concurrent_events_df.columns:
ts_column_name = "End_Timestamp"
else:
ts_column_name = "Timestamp"
concurrent_events_df_roi = concurrent_events_df[(concurrent_events_df[ts_column_name] <= end_ts) & (concurrent_events_df[ts_column_name] >= start_ts)]
if len(concurrent_events_df_roi) > 0:
for i, row in concurrent_events_df_roi.iterrows():
# Get the event index
i = current_CREAM_day.get_index_from_timestamp(start_ts, row[ts_column_name])
# Some plotting adjustments, depending on the type of event that is plotted
if "component" in event_list_name:
color ="orange"
linewidth=1.5
else: # in case of product or maintenance events
color="red"
if "product" in event_list_name:
if "Product" in concurrent_events_df_roi.columns:
label = row.Product
elif "Event_Type" in concurrent_events_df_roi.columns:
label= row.Event_Type
else:
label = "unspecified"
linewidth=1.2
elif "maintenance" in event_list_name:
if "Activity" in concurrent_events_df_roi.columns:
label = row.Activity
elif "Event_Type" in concurrent_events_df_roi.columns:
label= row.Event_Type
else:
label = "unspecified"
linewidth=1.2
else:
label = "Unknown"
linewidth=0.6
# Plot the line
ax.axvline(i, color=color, linestyle=":", label=label, linewidth=linewidth)
if len(COMPONENTS_DF) > 1:
# use mask here because of misaligned indices
mask = (COMPONENTS_DF.Timestamp <= end_ts) & (COMPONENTS_DF.Timestamp >= start_ts)
concurrent_events_df_roi = COMPONENTS_DF.loc[mask.values]
concurrent_events_df_roi = concurrent_events_df_roi[concurrent_events_df_roi.Component!="unlabeled"] #only take the ones with an already labeled component
if len(concurrent_events_df_roi) > 0:
for i, row in concurrent_events_df_roi.iterrows():
i = current_CREAM_day.get_index_from_timestamp(start_ts, row.Timestamp)
ax.axvline(i, color="green", linestyle=":", label="already labeled end " + str(i))
# add time information to plot
samples_per_minute = current_CREAM_day.sampling_rate * 60 #every 60 seconds
if len(current) % samples_per_minute == 0: #just in case the parameters are changed and there are no full minutes in the signals
step = len(current) / samples_per_minute
for i in range(0, int(step+1)):
ax.axvline(i*samples_per_minute, color="black", ymax=0.1)
fig.suptitle("Event :" + "\n" + str(str(start_ts) + " - " + str(end_ts)))
ax.legend(loc='upper right')
EVENT_TIMESTAMP = event_timestamp
WINDOW_START_TS = start_ts
return fig, ax
```
## Global Variables
```
EVENT_INDEX = int(0) # index of the EVENTS_TO_LABEL_DF that the programm is currently at
EVENTS_TO_LABEL_DF = None # dataframe of the list of events to label
EVENT_TIMESTAMP = None # timestamp of the event that is in the current focus
WINDOW_START_TS = None # start timestamp of the window we are currently looking at
LAST_EVENT_CLICKED_LOC_LIST = [] # list of the locs of the last events clicked
LABELED_TIMESTAMP = None # the labeled timestamp
WINDOW_SIZE = int(120) # seconds, the window size in each direction around and event to be displayed
ALL_DAYS = ["2018-08-23" , "2018-08-24" , "2018-08-25", "2018-08-26" , "2018-08-27" , "2018-08-28" ,
"2018-08-29", "2018-08-30", "2018-08-31", "2018-09-01", "2018-09-02" , "2018-09-03" , "2018-09-04" ,
"2018-09-05", "2018-09-06", "2018-09-07", "2018-09-08" , "2018-09-09" , "2018-09-10", "2018-09-11", "2018-09-12"
"2018-09-13" ,"2018-09-14" ,"2018-09-15" , "2018-09-16", "2018-09-17", "2018-09-18","2018-09-19" , "2018-09-20" ,
"2018-09-21" , "2018-09-22" , "2018-09-23" ,"2018-09-24" ,"2018-09-25" ,"2018-09-26" , "2018-09-27", "2018-09-28" ,
"2018-09-29" , "2018-09-30" , "2018-10-01" ,"2018-10-02" , "2018-10-03" ,"2018-10-04", "2018-10-05" , "2018-10-06" ,
"2018-10-07", "2018-10-08" ]
```
## Widget functions for the UI
```
closest_event_loc = None
timestamp_clicked = None
def onclick(event):
"""
Function to be executed in case of a click event at a figure.
"""
global COMPONENTS_DF # Dataframe containing the component events
global COMPONENT_NAME # Name of the component currently labeled
global LAST_EVENT_CLICKED_LOC_LIST # list of locs of the last events clicked, used for deleting last click in case of errors
global EVENT_TIMESTAMP #timestamp of the event of interest that was autoamticcaly generated
global WINDOW_START_TS #start timestamp of the window we are currently looking at
global current_CREAM_day #object representing the current day in the CREAM dataset
global EVENT_INDEX # index of the EVENTS_TO_LABEL_DF that the programm is currently at
global closest_event_loc
global timestamp_clicked
# Take the event index from the click, convert it to a timestamp
timestamp_clicked = current_CREAM_day.get_timestamp_from_index(WINDOW_START_TS, math.floor(event.xdata))
if timestamp_clicked > EVENT_TIMESTAMP + timedelta(seconds=60):
print("The red timestamp is generated after the event is completed! Hence, do not place the click after it!")
return
event_before = COMPONENTS_DF[COMPONENTS_DF.Timestamp <= timestamp_clicked].iloc[-1]
event_after = COMPONENTS_DF[COMPONENTS_DF.Timestamp > timestamp_clicked].iloc[0]
delta_before = timestamp_clicked - event_before.Timestamp
delta_before = delta_before.total_seconds()
delta_after = event_after.Timestamp - timestamp_clicked
delta_after = delta_after.total_seconds()
if delta_before <= delta_after:
closest_event_loc = event_before.name
else:
closest_event_loc = event_after.name
COMPONENTS_DF.at[closest_event_loc, "Component"] = COMPONENT_NAME
# Store the loc to enable the delete function in case of errors
LAST_EVENT_CLICKED_LOC_LIST.append(closest_event_loc)
# Increment the index we are currently looking at
EVENT_INDEX += 1
return
def display_initial_event(event_index_p=0):
"""
Display the start event. This is set to 0 as per default!
In case of interruptions in the labeling process or in case of errors, you can restart labeling at
an arbitrary index using the event_index_p paramter.
"""
global COMPONENTS_DF # Dataframe containing the component events
global COMPONENT_NAME # Name of the component currently labeled
global LAST_EVENT_CLICKED_LOC_LIST # loc of the last event clicked, used for deleting last click in case of errors
global CONCURRENT_EVENTS_DICT # dictionary containg the events happening concurrently, used for plotting
global EVENTS_TO_LABEL_DF # dataframe of the list of events to label
global EVENT_INDEX # event index we are currently processing
global FIG # global figure object
global AX # global axis object
global current_CREAM_day # global CREAM_day object
global WINDOW_SIZE # global WINDOW_SIZE
plt.clf()
clear_output()
if EVENT_INDEX > len(EVENTS_TO_LABEL_DF)-1:
print("THIS WAS THE LAST EVENT! YOU ARE DONE!")
return
# For the timestamp we need to check if we need to create the corresponding CREAM_Day object, or if it already exists
event_timestamp = EVENTS_TO_LABEL_DF.iloc[EVENT_INDEX].Timestamp
event_date = str(EVENTS_TO_LABEL_DF.iloc[EVENT_INDEX].Date)
if current_CREAM_day.day_date != event_date: # if the event does not lie withing the current CREAM_day object, create a new one
day_path = os.path.join(PATH_TO_DATA, event_date)
current_CREAM_day = CREAM_Day(cream_day_location=day_path,use_buffer=True, buffer_size_files=2)
FIG, AX = plot_event_window(event_timestamp = EVENTS_TO_LABEL_DF.iloc[EVENT_INDEX].Timestamp,
window_size = WINDOW_SIZE,
current_CREAM_day = current_CREAM_day,
concurrent_events_dict = CONCURRENT_EVENTS_DICT)
FIG.show()
display(button_box)
def on_next_clicked(event):
global LABEL_DESTINATION_PATH #location where the event labels will be stored, is user specified
global WINDOW_START_TS #start timestamp of the window we are currently looking at
global COMPONENTS_DF # Dataframe containing the component events
global COMPONENT_NAME # Name of the component currently labeled
global LAST_EVENT_CLICKED_LOC_LIST # loc of the last event clicked, used for deleting last click in case of errors
global CONCURRENT_EVENTS_DICT # dictionary containg the events happening concurrently, used for plotting
global EVENTS_TO_LABEL_DF # dataframe of the list of events to label
global EVENT_INDEX # event index we are currently processing
global FIG # global figure object
global AX # global axis object
global current_CREAM_day # global CREAM_day object
global WINDOW_SIZE # global WINDOW_SIZE
save_labels(destination=LABEL_DESTINATION_PATH) #save it
plt.clf()
clear_output()
if EVENT_INDEX > len(EVENTS_TO_LABEL_DF)-1:
print("THIS WAS THE LAST EVENT! YOU ARE DONE!")
return
print("This is event number " + str(EVENT_INDEX) + " of " + str(len(EVENTS_TO_LABEL_DF)))
# For the timestamp we need to check if we need to create the corresponding CREAM_Day object, or if it already exists
event_timestamp = EVENTS_TO_LABEL_DF.iloc[EVENT_INDEX].Timestamp
event_date = str(EVENTS_TO_LABEL_DF.iloc[EVENT_INDEX].Date)
if current_CREAM_day.day_date != event_date: # if the event does not lie withing the current CREAM_day object, create a new one
day_path = os.path.join(PATH_TO_DATA, event_date)
current_CREAM_day = CREAM_Day(cream_day_location=day_path,use_buffer=True, buffer_size_files=2)
FIG, AX = plot_event_window(event_timestamp = EVENTS_TO_LABEL_DF.iloc[EVENT_INDEX].Timestamp,
window_size = WINDOW_SIZE,
current_CREAM_day = current_CREAM_day,
concurrent_events_dict = CONCURRENT_EVENTS_DICT)
FIG.show()
display(button_box)
def save_labels(destination: str):
global EVENT_INDEX
global COMPONENTS_DF
global COMPONENT_NAME
filename = "labeled_component_events.csv"
if EVENT_INDEX % 10 == 0 and EVENT_INDEX > 0: #every 10 events: before storing the new file, save the old one
os.rename(os.path.join(destination, filename), os.path.join(destination, "previous_component_event_labels.csv"))
#Store the new one
COMPONENTS_DF.to_csv(os.path.join(destination, filename), index=False)
def on_delete_clicked(event):
"""
Deletes the last click from every key in the event_dictionary and returns to the previous window
"""
global COMPONENTS_DF # Dataframe containing the component events
global COMPONENT_NAME # Name of the component currently labeled
global LAST_EVENT_CLICKED_LOC_LIST # loc of the last event clicked, used for deleting last click in case of errors
global CONCURRENT_EVENTS_DICT # dictionary containg the events happening concurrently, used for plotting
global EVENTS_TO_LABEL_DF # dataframe of the list of events to label
global EVENT_INDEX # event index we are currently processing
global FIG # global figure object
global AX # global axis object
if EVENT_INDEX <= 0 or LAST_EVENT_CLICKED_LOC_LIST is None: #we arrived at the first event again
print("This is the first event, you can not go further back in time!")
return
COMPONENTS_DF.at[LAST_EVENT_CLICKED_LOC_LIST[EVENT_INDEX], "Component"] = "unlabeled"
EVENT_INDEX = EVENT_INDEX - 1 # adjust EVENT_INDEX
FIG, AX = plot_event_window(event_timestamp = EVENTS_TO_LABEL_DF[EVENT_INDEX].Timestamp,
window_size = WINDOW_SIZE,
current_CREAM_day = current_CREAM_day,
concurrent_events_dict = CONCURRENT_EVENTS_DICT)
# Now display the previous event
plt.clf()
clear_output()
print("The current Event Index is " + str(EVENT_INDEX))
FIG.show()
display(button_box)
return EVENT_DICTIONARY
```
# Only touch this area in the notebook to alter variables like, for example, the path to the dataset
<div class="alert alert-danger">
<h3>//ToDo</h3>'
<p>Please specify the component name to label. </p>
</div>
```
COMPONENT_NAME = "millingplant" # 'pump', 'heater'
```
<div class="alert alert-danger">
<h3>//ToDo</h3>
<p>Please specify the path to the main-folder of "CREAM". </p>
</div>
```
PATH_TO_DATA = os.path.abspath(os.path.join("..", "..", "Datasets", "CREAM"))
```
<div class="alert alert-danger">
<h3>//ToDo</h3>
<p>Please specify the path to location where you want to store the labels. </p>
</div>
```
LABEL_DESTINATION_PATH = os.path.abspath(os.path.join("..", "..", "Datasets", "CREAM", "tmp"))
```
## Execute this cell to load the raw electrical events
<p> In the following, we load the electrical events that have been previously labeled with the "1_electrical_events_labeling_tool.ipynb" notebook. </p>
<p> Furthermore, we load the raw product and maintenance events, that contain the timestamps with a per minute precision </p>
```
#necessary for the plotting
# Load the events
day_path = os.path.join(PATH_TO_DATA, "2018-08-24") #arbitrary day to initialize the object
current_CREAM_day = CREAM_Day(cream_day_location=day_path,use_buffer=True, buffer_size_files=2)
# Load the electrical component events (the raw ones)
#COMPONENTS_DF = current_CREAM_day.load_component_events(os.path.join(PATH_TO_DATA, "raw_coffee_maker_logs", "raw_component_events.csv"), raw_file=True, filter_day=False)
# Load the product and the maintenance events (the raw ones, per minute events) and filter for the day
all_maintenance_events = current_CREAM_day.load_machine_events(os.path.join(PATH_TO_DATA, "raw_coffee_maker_logs", "raw_maintenance_events.csv"), raw_file=True, filter_day=False)
all_product_events = current_CREAM_day.load_machine_events(os.path.join(PATH_TO_DATA, "raw_coffee_maker_logs", "raw_product_events.csv"), raw_file=True, filter_day=False)
# Initalize the dictionary that is used to determine concurrent_events in the plot method
CONCURRENT_EVENTS_DICT = {"product_events" : all_product_events, "maintenance_events" : all_maintenance_events}
```
## Execute this cell to add the "Component" column to the raw_component events from labeling step 1
```
if "Component" not in COMPONENTS_DF.columns: #only if the column has not been created before
COMPONENTS_DF["Component"] = "unlabeled"
```
# Execute this cell to start the labeling
<p> Click into the figure as close as possible to the event you want to label. The closest event to your click
is then labeled accordingly. </p>
<p> To ease labeling and to raise awareness for concurrent events the follwoing lines are displayed: </p>
<p> Appliance event labels are shown in dashed orange lines </p>
<p> Any other product or maintenance event is show with a dashed red line </p>
<p> <b> The red line marks the point by that the event has to be finished latest! </b> </p>
<p> The short black lines represent one minute steps </p>
<p> If you think you are done with this event, click the green <b> "next" </b> button to load the next event and save the previous one </p>
<p> If you have selected <b> "next" </b> accidentially or still to remove the event you have labeled from the previous event, select the red <b> "delete last entry" </b >button </p>
<div class="alert alert-info">
<h4>Empty Figure or not in interactive mode</h4>
<p>If the plot does not load or is not in the interactive mode, reexecute the cell or reexcute the import cell</p>
</div>
<div class="alert alert-danger">
<h3> Do not use the zoom and other capabilities from the plot toolbar</h3>
<p>Clicks when zooming etc. also get registred as clicks for labels!</p>
</div>
```
if COMPONENT_NAME == "millingplant":
#build the events_to_label and the concurrent_events dict (schauen ob das schon gefilterted erwartet wird!)
EVENTS_TO_LABEL_DF = None # dataframe of the list of events to label
EVENTS_TO_LABEL_DF = all_maintenance_events[(all_maintenance_events.Activity == 'MillingPlantEspresso') |
(all_maintenance_events.Activity == 'MillingPlantCoffee')]
# sample a random subset, because there are a lot of them
np.random.seed(42)
sample_size = int(len(EVENTS_TO_LABEL_DF) * 0.15)
events_to_label_subset = np.random.choice(EVENTS_TO_LABEL_DF.index, sample_size, replace=False)
EVENTS_TO_LABEL_DF = EVENTS_TO_LABEL_DF.loc[events_to_label_subset]
EVENTS_TO_LABEL_DF.sort_index(inplace=True) #sort by index
print("Proceed with the labeleling of the millingplant events below!")
# Create and register Buttons
next_button = Button(description="Next -> ",style=ButtonStyle(button_color='green'))
delete_button = Button(description=" <- Delete last entry",style=ButtonStyle(button_color='red'))
button_box = HBox([next_button, delete_button])
next_button.on_click(on_next_clicked)
delete_button.on_click(on_delete_clicked)
# Display first event --> event_index is set to zero for the start
# In case of erros or interruptions, provide another event index to the display_initial_event function
display_initial_event(event_index_p=0)
elif COMPONENT_NAME == "pump":
EVENTS_TO_LABEL_DF = all_product_events[all_product_events.Product == 'hot_water']
EVENTS_TO_LABEL_DF.sort_index(inplace=True) #sort by index
print("Proceed with the labeling of the pump events below!")
# Create and register Buttons
next_button = Button(description="Next -> ",style=ButtonStyle(button_color='green'))
delete_button = Button(description=" <- Delete last entry",style=ButtonStyle(button_color='red'))
button_box = HBox([next_button, delete_button])
next_button.on_click(on_next_clicked)
delete_button.on_click(on_delete_clicked)
# Display first event --> event_index is set to zero for the start
# In case of erros or interruptions, provide another event index to the display_initial_event function
display_initial_event(event_index_p=0)
elif COMPONENT_NAME == "heater":
# Simply select all the events on saturdays to be heater events. we only label the on-events
# We have investigated the data (product events) and no other events can be found on saturdays
# Get the Saturday dates
day_information_df = current_CREAM_day.get_weekday_information(date=ALL_DAYS)
saturdays = day_information_df[day_information_df.Weekday == "Saturday"].Date.values
# Filter for the On-Events and the saturdays in the component events
mask = (COMPONENTS_DF.Event_Type == "On") & (COMPONENTS_DF.Date.isin(saturdays))
COMPONENTS_DF.at[mask, "Component"] = "heater"
# To signal that everything is finished
EVENTS_TO_LABEL_DF = []
print("The heating events have been labeled and saved!")
else:
raise ValueError("Component name is not available! Please use either millingplant, heater or pump")
```
| true |
code
| 0.48621 | null | null | null | null |
|
# Feature importance per signature type
This notebooks analyses which characters are more important for each individual signature type. In other words, what makes each cluster unique compared to all the other.
```
import numpy as np
import pandas as pd
import geopandas as gpd
import dask.dataframe
import matplotlib.pyplot as plt
import urbangrammar_graphics as ugg
import seaborn as sns
from matplotlib.lines import Line2D
from sklearn.ensemble import RandomForestClassifier
%time standardized_form = dask.dataframe.read_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/form/standardized/").set_index('hindex')
%time stand_fn = dask.dataframe.read_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/function/standardized/")
%time data = dask.dataframe.multi.concat([standardized_form, stand_fn], axis=1).replace([np.inf, -np.inf], np.nan).fillna(0)
%time data = data.drop(columns=["keep_q1", "keep_q2", "keep_q3"])
%time data = data.compute()
labels_l1 = pd.read_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/KMeans10GB.pq")
labels_l2_9 = pd.read_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/clustergram_cl9_labels.pq")
labels_l2_2 = pd.read_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/subclustering_cluster2_k3.pq")
labels = labels_l1.copy()
labels.loc[labels.kmeans10gb == 9, 'kmeans10gb'] = labels_l2_9['9'].values + 90
labels.loc[labels.kmeans10gb == 2, 'kmeans10gb'] = labels_l2_2['subclustering_cluster2_k3'].values + 20
outliers = [98, 93, 96, 97]
mask = ~labels.kmeans10gb.isin(outliers)
```
## Feature importance per cluster
```
labels.kmeans10gb.unique()
imps = pd.DataFrame()
for cluster in labels.kmeans10gb.unique():
if cluster not in outliers:
cluster_bool = labels.loc[mask]['kmeans10gb'].apply(lambda x: 1 if x == cluster else 0)
clf = RandomForestClassifier(n_estimators=10, n_jobs=-1, random_state=42, verbose=1)
clf = clf.fit(data.loc[mask].values, cluster_bool.values)
importances = pd.Series(clf.feature_importances_, index=data.columns).sort_values(ascending=False)
imps[f'cluster_{cluster}'] = importances.head(50).index.values
imps[f'cluster_{cluster}_vals'] = importances.head(50).values
chars = [c for c in imps.columns if 'vals' not in c]
imps[sorted(chars)]
imps.to_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/per_cluster_importance.pq")
ims = pd.read_parquet("../../urbangrammar_samba/spatial_signatures/clustering_data/per_cluster_importance.pq")
names.columns
n_chars = 10
names = ims[[c for c in ims.columns if "_vals" not in c]].head(n_chars)
values = ims[[c for c in ims.columns if "_vals" in c]].head(n_chars)
coded = {
'population': 'func_population',
'night_lights': 'func_night_lights',
'A, B, D, E. Agriculture, energy and water': 'func_workplace_abde',
'C. Manufacturing': 'func_workplace_c',
'F. Construction': 'func_workplace_f',
'G, I. Distribution, hotels and restaurants': 'func_workplace_gi',
'H, J. Transport and communication': 'func_workplace_hj',
'K, L, M, N. Financial, real estate, professional and administrative activities': 'func_workplace_klmn',
'O,P,Q. Public administration, education and health': 'func_workplace_opq',
'R, S, T, U. Other': 'func_workplace_rstu',
'Code_18_124': 'func_corine_124',
'Code_18_211': 'func_corine_211',
'Code_18_121': 'func_corine_121',
'Code_18_421': 'func_corine_421',
'Code_18_522': 'func_corine_522',
'Code_18_142': 'func_corine_142',
'Code_18_141': 'func_corine_141',
'Code_18_112': 'func_corine_112',
'Code_18_231': 'func_corine_231',
'Code_18_311': 'func_corine_311',
'Code_18_131': 'func_corine_131',
'Code_18_123': 'func_corine_123',
'Code_18_122': 'func_corine_122',
'Code_18_512': 'func_corine_512',
'Code_18_243': 'func_corine_243',
'Code_18_313': 'func_corine_313',
'Code_18_412': 'func_corine_412',
'Code_18_321': 'func_corine_321',
'Code_18_322': 'func_corine_322',
'Code_18_324': 'func_corine_324',
'Code_18_111': 'func_corine_111',
'Code_18_423': 'func_corine_423',
'Code_18_523': 'func_corine_523',
'Code_18_312': 'func_corine_312',
'Code_18_133': 'func_corine_133',
'Code_18_333': 'func_corine_333',
'Code_18_332': 'func_corine_332',
'Code_18_411': 'func_corine_411',
'Code_18_132': 'func_corine_132',
'Code_18_222': 'func_corine_222',
'Code_18_242': 'func_corine_242',
'Code_18_331': 'func_corine_331',
'Code_18_511': 'func_corine_511',
'Code_18_334': 'func_corine_334',
'Code_18_244': 'func_corine_244',
'Code_18_521': 'func_corine_521',
'mean': 'func_ndvi',
'supermarkets_nearest': 'func_supermarkets_nearest',
'supermarkets_counts': 'func_supermarkets_counts',
'listed_nearest': 'func_listed_nearest',
'listed_counts': 'func_listed_counts',
'fhrs_nearest': 'func_fhrs_nearest',
'fhrs_counts': 'func_fhrs_counts',
'culture_nearest': 'func_culture_nearest',
'culture_counts': 'func_culture_counts',
'nearest_water': 'func_water_nearest',
'nearest_retail_centre': 'func_retail_centrenearest',
'sdbAre': 'form_sdbAre',
'sdbPer': 'form_sdbPer',
'sdbCoA': 'form_sdbCoA',
'ssbCCo': 'form_ssbCCo',
'ssbCor': 'form_ssbCor',
'ssbSqu': 'form_ssbSqu',
'ssbERI': 'form_ssbERI',
'ssbElo': 'form_ssbElo',
'ssbCCM': 'form_ssbCCM',
'ssbCCD': 'form_ssbCCD',
'stbOri': 'form_stbOri',
'sdcLAL': 'form_sdcLAL',
'sdcAre': 'form_sdcAre',
'sscCCo': 'form_sscCCo',
'sscERI': 'form_sscERI',
'stcOri': 'form_stcOri',
'sicCAR': 'form_sicCAR',
'stbCeA': 'form_stbCeA',
'mtbAli': 'form_mtbAli',
'mtbNDi': 'form_mtbNDi',
'mtcWNe': 'form_mtcWNe',
'mdcAre': 'form_mdcAre',
'ltcWRE': 'form_ltcWRE',
'ltbIBD': 'form_ltbIBD',
'sdsSPW': 'form_sdsSPW',
'sdsSWD': 'form_sdsSWD',
'sdsSPO': 'form_sdsSPO',
'sdsLen': 'form_sdsLen',
'sssLin': 'form_sssLin',
'ldsMSL': 'form_ldsMSL',
'mtdDeg': 'form_mtdDeg',
'lcdMes': 'form_lcdMes',
'linP3W': 'form_linP3W',
'linP4W': 'form_linP4W',
'linPDE': 'form_linPDE',
'lcnClo': 'form_lcnClo',
'ldsCDL': 'form_ldsCDL',
'xcnSCl': 'form_xcnSCl',
'mtdMDi': 'form_mtdMDi',
'lddNDe': 'form_lddNDe',
'linWID': 'form_linWID',
'stbSAl': 'form_stbSAl',
'sddAre': 'form_sddAre',
'sdsAre': 'form_sdsAre',
'sisBpM': 'form_sisBpM',
'misCel': 'form_misCel',
'mdsAre': 'form_mdsAre',
'lisCel': 'form_lisCel',
'ldsAre': 'form_ldsAre',
'ltcRea': 'form_ltcRea',
'ltcAre': 'form_ltcAre',
'ldeAre': 'form_ldeAre',
'ldePer': 'form_ldePer',
'lseCCo': 'form_lseCCo',
'lseERI': 'form_lseERI',
'lseCWA': 'form_lseCWA',
'lteOri': 'form_lteOri',
'lteWNB': 'form_lteWNB',
'lieWCe': 'form_lieWCe',
}
types = {
0: "Countryside agriculture",
1: "Accessible suburbia",
3: "Open sprawl",
4: "Wild countryside",
5: "Warehouse/Park land",
6: "Gridded residential quarters",
7: "Urban buffer",
8: "Disconnected suburbia",
20: "Dense residential neighbourhoods",
21: "Connected residential neighbourhoods",
22: "Dense urban neighbourhoods",
90: "Local urbanity",
91: "Concentrated urbanity",
92: "Regional urbanity",
94: "Metropolitan urbanity",
95: "Hyper concentrated urbanity",
93: "outlier",
96: "outlier",
97: "outlier",
98: "outlier",
}
def cmap(name):
if "_q" in name:
name = name[:-3]
if coded[name][:4] == "form":
return ugg.COLORS[1]
if coded[name][:4] == "func":
return ugg.COLORS[4]
raise ValueError()
x = np.repeat(np.arange(0, 16), n_chars)
y = np.tile(np.arange(0, n_chars), 16) * - 1
colors = names.applymap(cmap).values.T.flatten()
alpha = values.values.T.flatten() / values.values.T.flatten().max()
ticks = [types[int(c[8:])] for c in names.columns]
fig, ax = plt.subplots(figsize=(16, n_chars))
ax.scatter(x, y, alpha=alpha, color=colors, marker="s", s=2500)
plt.tight_layout()
# ax.set_axis_off()
plt.xticks(np.arange(0, 16), ticks, rotation='vertical')
plt.yticks([0, -9], ["top predictor", "10th predictor"])
sns.despine(left=True, bottom=True)
# plt.savefig("figs/feature_imp_10.pdf")
```
| true |
code
| 0.46132 | null | null | null | null |
|
# Contents
* [Plot](#Plot)
* [Subplot](#Subplot)
* [Placement of ticks and custom tick labels](#Placement-of-ticks-and-custom-tick-labels)
* [Annotate](#Annotate)
* [Axis Grid](#Axis-Grid)
* [Axis spines](#Axis-spines)
* [Twin axes](#Twin-axes)
* [Axes where x and y is zero](#Axes-where-x-and-y-is-zero)
* [Figure](#Figure)
* [Figure size and aspect ratio (DPI)](#Figure-size-and-aspect-ratio-(DPI))
* [Saving figures](#Saving-figures)
* [Setting colors, linewidths, linetypes](#Setting-colors,-linewidths,-linetypes)
* [Scatter](#Scatter)
* [Histogram](#Histogram)
* [Other 2D plot styles](#Other-2D-plot-styles)
* [Colormap and contour figures](#Colormap-and-contour-figures)
* [Pcolor](#Pcolor)
* [Imshow](#Imshow)
* [Box Plot](#Box-Plot)
* [Referans Link](#Referans-Link)
```
import numpy as np
import matplotlib.pyplot as plt
#jupyter-notebook için bu satıra yazılmalıdır.
%matplotlib inline
```
## Plot
```
plt.plot([1,2,3,4]) #Çizgi çizmede kullanılır.
plt.ylabel("number") #Y eksenine isim verir.
plt.xlabel("time") #X eksenine isim verir.
plt.show() #Grafiği gösterir.
plt.plot([1,2,3,4],[1,4,9,16]) #ilk matris x, ikinci matris y eksenindedir.
plt.show()
plt.plot([1,2,3,4],[1,4,9,16],'ro') #r:kırmızı, o: daire
plt.axis([0,6,0,20]) #eksenlerin uzunluğu ayarlandı.
plt.show()
x=np.linspace(0,5,11)
y=x**2
print x
print y
plt.plot(x, y, 'r') # 'r' is the color red
plt.xlabel('X Axis Title Here')
plt.ylabel('Y Axis Title Here')
plt.title('String Title Here')
plt.show()
#linewidth: çizgi genişliği
plt.plot(x,y,'r--',linewidth=5.0)
plt.text(2.5, 10, r"$y=x^2$", fontsize=50, color="blue")
plt.show()
t=np.arange(0,5,0.2)
#r: red, b:blue, g:green
#--: kesikli çizgi, ^: üçgen, s:square(kare)
plt.plot(t,t,'r--', label = "t")
plt.plot(t,t**2,'bs', label = "t^2")
plt.plot(t,t**3, "g^", label = "t^3")
plt.legend() #açıklama kısmını çizer.
plt.show()
```
## Subplot
```
# plt.subplot(nrows, ncols, plot_number)
plt.subplot(1,2,1)
plt.plot(x, y, 'r--')
plt.subplot(1,2,2)
plt.plot(y, x, 'g*-');
# Use similar to plt.figure() except use tuple unpacking to grab fig and axes
# Empty canvas of 1 by 2 subplots
fig, axes = plt.subplots(nrows=1, ncols=3)
for ax in axes:
ax.plot(x, y, 'g')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('title')
fig.tight_layout() #Bu, örtüşen içerik olmaması için şekil tuvalindeki eksenlerin konumlarını otomatik olarak ayarlar.
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
axes[0].plot(x, x**2, x, x**3)
axes[0].set_title("default axes ranges")
axes[1].plot(x, x**2, x, x**3)
axes[1].axis('tight')
axes[1].set_title("tight axes")
axes[2].plot(x, x**2, x, x**3)
axes[2].set_ylim([0, 60])
axes[2].set_xlim([2, 5])
axes[2].set_title("custom axes range");
def f(t):
return np.exp(-t) * np.cos(2*np.pi*t)
t1 = np.arange(0.0, 5.0, 0.1)
t2 = np.arange(0.0, 5.0, 0.02)
plt.figure(1)
plt.subplot(211)
plt.plot(t1, f(t1), 'bo', t2, f(t2), 'k')
plt.subplot(212)
plt.plot(t2, np.cos(2*np.pi*t2), 'r--')
plt.show()
```
### Placement of ticks and custom tick labels
```
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(x, x**2, x, x**3, lw=10)
ax.set_xticks([1, 2, 3, 4, 5])
ax.set_xticklabels([r'$\alpha$', r'$\beta$', r'$\gamma$', r'$\delta$', r'$\epsilon$'], fontsize=20)
yticks = [0, 50, 100, 150]
ax.set_yticks(yticks)
ax.set_yticklabels(["$%.1f$" % y for y in yticks], fontsize=18); # use LaTeX formatted labels
```
### Annotate
```
ax = plt.subplot(111)
t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
plt.plot(t, s, lw=2)
plt.annotate('local max', xy=(2, 1), xytext=(3, 1.5),
arrowprops=dict(facecolor='black', shrink=0.05),
)
plt.ylim(-2, 2) #Y eksenini boyutlandırdı.
plt.show()
```
### Axis Grid
```
fig, axes = plt.subplots(1, 2, figsize=(10,3))
# default grid appearance
axes[0].plot(x, x**2, x, x**3, lw=2)
axes[0].grid(True)
# custom grid appearance
axes[1].plot(x, x**2, x, x**3, lw=2)
axes[1].grid(color='b', alpha=0.5, linestyle='dashed', linewidth=3)
```
### Axis spines
```
fig, ax = plt.subplots(figsize=(6,2))
ax.spines['bottom'].set_color('blue')
ax.spines['top'].set_color('blue')
ax.spines['left'].set_color('red')
ax.spines['left'].set_linewidth(4)
# turn off axis spine to the right
ax.spines['right'].set_color("none")
ax.yaxis.tick_left() # only ticks on the left side
```
### Twin axes
```
fig, ax1 = plt.subplots()
ax1.plot(x, x**2, lw=2, color="blue")
ax1.set_ylabel(r"area $(m^2)$", fontsize=18, color="blue")
for label in ax1.get_yticklabels():
label.set_color("blue")
ax2 = ax1.twinx()
ax2.plot(x, x**3, lw=2, color="red")
ax2.set_ylabel(r"volume $(m^3)$", fontsize=18, color="red")
for label in ax2.get_yticklabels():
label.set_color("red")
```
### Axes where x and y is zero
```
fig, ax = plt.subplots()
ax.spines['right'].set_color('green')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0)) # set position of x spine to x=0
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0)) # set position of y spine to y=0
xx = np.linspace(-0.75, 1., 100)
ax.plot(xx, xx**3);
```
## Figure
```
fig = plt.figure()
help(fig.add_axes)
x=np.linspace(0,5,11)
y=x**2
# Create Figure (empty canvas)
fig = plt.figure()
# Add set of axes to figure
axes = fig.add_axes([0.1, 0.1, 0.8, 0.8]) # left, bottom, width, height (range 0 to 1)
# Plot on that set of axes
axes.plot(x, y, 'b')
axes.set_xlabel('Set X Label') # Notice the use of set_ to begin methods
axes.set_ylabel('Set y Label')
axes.set_title('Set Title')
# Creates blank canvas
fig = plt.figure()
axes1 = fig.add_axes([0.1, 0.1, 0.8, 0.8]) # main axes
axes2 = fig.add_axes([0.2, 0.5, 0.4, 0.3]) # inset axes
# Larger Figure Axes 1
axes1.plot(x, y, 'b')
axes1.set_xlabel('X_label_axes1')
axes1.set_ylabel('Y_label_axes1')
axes1.set_title('Axes 1 Title')
# Insert Figure Axes 2
axes2.plot(y, x, 'r')
axes2.set_xlabel('X_label_axes2')
axes2.set_ylabel('Y_label_axes2')
axes2.set_title('Axes 2 Title');
x = np.linspace(0,2*np.pi,20)
y = np.linspace(0,5,20)
print x
print y
# Create Figure (empty canvas)
fig = plt.figure()
# Add set of axes to figure
axes = fig.add_axes([0.1, 0.1, 0.9, 0.9], projection='polar') # left, bottom, width, height (range 0 to 1)
# Plot on that set of axes
axes.plot(x, y, 'b')
axes.set_xlabel('Set X Label')
axes.set_ylabel('Set y Label')
axes.set_title('Set Title');
```
### Figure size and aspect ratio (DPI)
```
x=np.linspace(0,5,11)
y=x**2
fig, axes = plt.subplots(figsize=(10,4), dpi=100)
axes.plot(x, y, 'r')
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_title('title');
```
## Saving figures
```
fig.savefig("filename.png", dpi=200)
```
## Setting colors, linewidths, linetypes
```
fig, ax = plt.subplots(figsize=(12,6))
ax.plot(x, x+1, color="red", linewidth=0.25)
ax.plot(x, x+2, color="red", linewidth=0.50)
ax.plot(x, x+3, color="red", linewidth=1.00)
ax.plot(x, x+4, color="red", linewidth=2.00)
# possible linestype options ‘-‘, ‘–’, ‘-.’, ‘:’, ‘steps’
ax.plot(x, x+5, color="green", lw=3, linestyle='-')
ax.plot(x, x+6, color="green", lw=3, ls='-.')
ax.plot(x, x+7, color="green", lw=3, ls=':')
# custom dash
line, = ax.plot(x, x+8, color="black", lw=4.50)
line.set_dashes([5, 10, 15, 10]) # format: line length, space length, ...
# possible marker symbols: marker = '+', 'o', '*', 's', ',', '.', '1', '2', '3', '4', ...
ax.plot(x, x+ 9, color="blue", lw=3, ls='-', marker='+')
ax.plot(x, x+10, color="blue", lw=3, ls='--', marker='o')
ax.plot(x, x+11, color="blue", lw=3, ls='-', marker='s')
ax.plot(x, x+12, color="blue", lw=3, ls='--', marker='1')
# marker size and color
ax.plot(x, x+13, color="purple", lw=1, ls='-', marker='o', markersize=20)
ax.plot(x, x+14, color="purple", lw=1, ls='-', marker='o', markersize=4)
ax.plot(x, x+15, color="purple", lw=1, ls='-', marker='o', markersize=8, markerfacecolor="red")
ax.plot(x, x+16, color="purple", lw=1, ls='-', marker='s', markersize=8,
markerfacecolor="yellow", markeredgewidth=3, markeredgecolor="green");
```
## Scatter
```
plt.scatter(x,y)
data={'a':np.arange(50),
'c':np.random.randint(0,50,50),
'd':np.random.randn(50)}
data['b']=data['a']+10*np.random.randn(50)
data['d']=np.abs(data['d'])*100
#c:color, s:çap
plt.scatter('a','b',c='c',s='d',data=data) #daireler çizer.
plt.xlabel('a degerleri')
plt.ylabel('y degerleri')
plt.show()
```
### Histogram
```
# A histogram
n = np.random.randn(100000)
fig, axes = plt.subplots(1, 2, figsize=(12,4))
axes[0].hist(n)
axes[0].set_title("Default histogram")
axes[0].set_xlim((min(n), max(n)))
axes[1].hist(n, cumulative=True, bins=50)
axes[1].set_title("Cumulative detailed histogram")
axes[1].set_xlim((min(n), max(n)));
mu, sigma=100, 15
x=mu+sigma*np.random.randn(10000)
n,bins,patches=plt.hist(x,50,density=True,facecolor='g',alpha=0.75) #Histogram çizer.
plt.xlabel('Smarts')
plt.ylabel('Probability')
plt.title('Histogram of IQ')
plt.text(60, .025, r'$\mu=100,\ \sigma=15$') #Grafik üzerine yazar.
plt.axis([40, 160, 0, 0.03]) #Eksenleri boyutlandırdı.
plt.grid(True) #Kalvuz çizgileri
plt.show()
```
## Other 2D plot styles
```
names = ['group_a', 'group_b', 'group_c']
values = [1, 10, 100]
plt.figure(1, figsize=(9, 5)) #figürü boyutlandırdık.
plt.subplot(131) #figürü 1 satır 3 sütuna böler.
plt.bar(names, values) #Sütun grafiği
plt.title('Sutun Grafigi') #başlık ekler.
plt.subplot(132)
plt.scatter(names, values)
plt.title('Nokta Grafigi')
plt.subplot(133)
plt.plot(names, values)
plt.title('Cizgi Grafigi')
plt.suptitle('Categorical Plotting') #Başlık ekler.
plt.show()
n = np.array([0,1,2,3,4,5])
fig, axes = plt.subplots(1, 4, figsize=(12,3))
axes[0].scatter(xx, xx + 0.25*np.random.randn(len(xx)))
axes[0].set_title("scatter")
axes[1].step(n, n**2, lw=2)
axes[1].set_title("step")
axes[2].bar(n, n**2, align="center", width=0.5, alpha=0.5)
axes[2].set_title("bar")
axes[3].fill_between(x, x**2, x**3, color="green", alpha=0.5);
axes[3].set_title("fill_between");
```
## Colormap and contour figures
```
alpha = 0.7
phi_ext = 2 * np.pi * 0.5
def flux_qubit_potential(phi_m, phi_p):
return 2 + alpha - 2 * np.cos(phi_p) * np.cos(phi_m) - alpha * np.cos(phi_ext - 2*phi_p)
phi_m = np.linspace(0, 2*np.pi, 100)
phi_p = np.linspace(0, 2*np.pi, 100)
X,Y = np.meshgrid(phi_p, phi_m)
Z = flux_qubit_potential(X, Y).T
```
### Pcolor
```
fig, ax = plt.subplots()
p = ax.pcolor(X/(2*np.pi), Y/(2*np.pi), Z, cmap=plt.cm.RdBu, vmin=abs(Z).min(), vmax=abs(Z).max())
cb = fig.colorbar(p, ax=ax)
```
### Imshow
```
fig, ax = plt.subplots()
im = ax.imshow(Z, cmap=plt.cm.RdBu, vmin=abs(Z).min(), vmax=abs(Z).max(), extent=[0, 1, 0, 1])
im.set_interpolation('bilinear')
cb = fig.colorbar(im, ax=ax)
```
### Contour
```
fig, ax = plt.subplots()
cnt = ax.contour(Z, cmap=plt.cm.RdBu, vmin=abs(Z).min(), vmax=abs(Z).max(), extent=[0, 1, 0, 1])
```
## Box Plot
```
data = [np.random.normal(0, std, 100) for std in range(1, 4)]
# rectangular box plot
plt.boxplot(data,vert=True,patch_artist=True);
```
## Referans Link
### https://matplotlib.org/tutorials/introductory/pyplot.html
### https://matplotlib.org/gallery.html
### https://www.southampton.ac.uk/~fangohr/training/python/notebooks/Matplotlib.html
### http://www.labri.fr/perso/nrougier/teaching/matplotlib/
| true |
code
| 0.488161 | null | null | null | null |
|
## Dogs v Cats super-charged!
```
# Put these at the top of every notebook, to get automatic reloading and inline plotting
%reload_ext autoreload
%autoreload 2
%matplotlib inline
# This file contains all the main external libs we'll use
from fastai.imports import *
from fastai.transforms import *
from fastai.conv_learner import *
from fastai.model import *
from fastai.dataset import *
from fastai.sgdr import *
from fastai.plots import *
PATH = "data/dogscats/"
sz=299
arch=resnext50
bs=28
tfms = tfms_from_model(arch, sz, aug_tfms=transforms_side_on, max_zoom=1.1)
data = ImageClassifierData.from_paths(PATH, tfms=tfms, bs=bs, num_workers=4)
learn = ConvLearner.pretrained(arch, data, precompute=True, ps=0.5)
learn.fit(1e-2, 1)
learn.precompute=False
learn.fit(1e-2, 2, cycle_len=1)
learn.unfreeze()
lr=np.array([1e-4,1e-3,1e-2])
learn.fit(lr, 3, cycle_len=1)
learn.save('224_all_50')
learn.load('224_all_50')
log_preds,y = learn.TTA()
probs = np.mean(np.exp(log_preds),0)
accuracy_np(probs,y)
```
## Analyzing results
```
preds = np.argmax(probs, axis=1)
probs = probs[:,1]
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y, preds)
plot_confusion_matrix(cm, data.classes)
def rand_by_mask(mask): return np.random.choice(np.where(mask)[0], 4, replace=False)
def rand_by_correct(is_correct): return rand_by_mask((preds == data.val_y)==is_correct)
def plot_val_with_title(idxs, title):
imgs = np.stack([data.val_ds[x][0] for x in idxs])
title_probs = [probs[x] for x in idxs]
print(title)
return plots(data.val_ds.denorm(imgs), rows=1, titles=title_probs)
def plots(ims, figsize=(12,6), rows=1, titles=None):
f = plt.figure(figsize=figsize)
for i in range(len(ims)):
sp = f.add_subplot(rows, len(ims)//rows, i+1)
sp.axis('Off')
if titles is not None: sp.set_title(titles[i], fontsize=16)
plt.imshow(ims[i])
def load_img_id(ds, idx): return np.array(PIL.Image.open(PATH+ds.fnames[idx]))
def plot_val_with_title(idxs, title):
imgs = [load_img_id(data.val_ds,x) for x in idxs]
title_probs = [probs[x] for x in idxs]
print(title)
return plots(imgs, rows=1, titles=title_probs, figsize=(16,8))
def most_by_mask(mask, mult):
idxs = np.where(mask)[0]
return idxs[np.argsort(mult * probs[idxs])[:4]]
def most_by_correct(y, is_correct):
mult = -1 if (y==1)==is_correct else 1
return most_by_mask((preds == data.val_y)==is_correct & (data.val_y == y), mult)
plot_val_with_title(most_by_correct(0, False), "Most incorrect cats")
plot_val_with_title(most_by_correct(1, False), "Most incorrect dogs")
```
| true |
code
| 0.59013 | null | null | null | null |
|
# TF Ranking
In this Notebook, we run through a simplified example to highlight some of the features of the TF Ranking library and demonstrate an end-to-end execution.
The general recipe is a short list of four main steps:
1. Compose a function to **read** input data and prepare a Tensorflow Dataset;
2. Define a **scoring** function that, given a (set of) query-document feature vector(s), produces a score indicating the query's level of relevance to the document;
3. Create a **loss** function that measures how far off the produced scores from step (2) are from the ground truth; and,
4. Define evaluation **metrics**.
A final step makes use of standard Tensorflow API to create, train, and evaluate a model.
We have included in the TF Ranking library a default implementation of data readers (in the `tensorflow_ranking.data` module), loss functions (in `tensorflow_ranking.losses`), and popular evaluation metrics (in `tensorflow_ranking.metrics`) that may be further tailored to your needs as we shall show later in this Notebook.
### Preparation
In what follows, we will assume the existence of a dataset that is split into training and test sets and that are stored at `data/train.txt` and `data/test.txt` respectively. We further assume that the dataset is in the LibSVM format and lines in the training and test files are sorted by query ID -- an assumption that holds for many popular learning-to-rank benchmark datasets.
We have included in our release a toy (randomly generated) dataset in the `data/` directory. However, to learn a more interesting model, you may copy your dataset of choice to the `data/` directory. Please ensure the format of your dataset conforms to the requirements above. Alternatively, you may edit this Notebook to plug in a customized input pipeline for a non-comformant dataset.
# Get Started with TF Ranking
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/ranking/blob/master/tensorflow_ranking/examples/tf_ranking_libsvm.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/ranking/blob/master/tensorflow_ranking/examples/tf_ranking_libsvm.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
### Dependencies and Global Variables
Let us start by importing libraries that will be used throughout this Notebook. We also enable the "eager execution" mode for convenience and demonstration purposes.
```
! pip install tensorflow_ranking
import tensorflow as tf
import tensorflow_ranking as tfr
tf.enable_eager_execution()
tf.executing_eagerly()
```
Next, we will download a dummy dataset in LibSVM format.Note that you can replace these datasets with public or custom datasets.
We also define some global parameters.
```
! wget -O "/tmp/train.txt" "https://raw.githubusercontent.com/tensorflow/ranking/master/tensorflow_ranking/examples/data/train.txt"
! wget -O "/tmp/test.txt" "https://raw.githubusercontent.com/tensorflow/ranking/master/tensorflow_ranking/examples/data/test.txt"
# Store the paths to files containing training and test instances.
# As noted above, we will assume the data is in the LibSVM format
# and that the content of each file is sorted by query ID.
_TRAIN_DATA_PATH="/tmp/train.txt"
_TEST_DATA_PATH="/tmp/test.txt"
# Define a loss function. To find a complete list of available
# loss functions or to learn how to add your own custom function
# please refer to the tensorflow_ranking.losses module.
_LOSS="pairwise_logistic_loss"
# In the TF-Ranking framework, a training instance is represented
# by a Tensor that contains features from a list of documents
# associated with a single query. For simplicity, we fix the shape
# of these Tensors to a maximum list size and call it "list_size,"
# the maximum number of documents per query in the dataset.
# In this demo, we take the following approach:
# * If a query has fewer documents, its Tensor will be padded
# appropriately.
# * If a query has more documents, we shuffle its list of
# documents and trim the list down to the prescribed list_size.
_LIST_SIZE=100
# The total number of features per query-document pair.
# We set this number to the number of features in the MSLR-Web30K
# dataset.
_NUM_FEATURES=136
# Parameters to the scoring function.
_BATCH_SIZE=32
_HIDDEN_LAYER_DIMS=["20", "10"]
```
### Input Pipeline
The first step to construct an input pipeline that reads your dataset and produces a `tensorflow.data.Dataset` object. In this example, we will invoke a LibSVM parser that is included in the `tensorflow_ranking.data` module to generate a `Dataset` from a given file.
We parameterize this function by a `path` argument so that the function can be used to read both training and test data files.
```
def input_fn(path):
train_dataset = tf.data.Dataset.from_generator(
tfr.data.libsvm_generator(path, _NUM_FEATURES, _LIST_SIZE),
output_types=(
{str(k): tf.float32 for k in range(1,_NUM_FEATURES+1)},
tf.float32
),
output_shapes=(
{str(k): tf.TensorShape([_LIST_SIZE, 1])
for k in range(1,_NUM_FEATURES+1)},
tf.TensorShape([_LIST_SIZE])
)
)
train_dataset = train_dataset.shuffle(1000).repeat().batch(_BATCH_SIZE)
return train_dataset.make_one_shot_iterator().get_next()
```
### Scoring Function
Next, we turn to the scoring function which is arguably at the heart of a TF Ranking model. The idea is to compute a relevance score for a (set of) query-document pair(s). The TF-Ranking model will use training data to learn this function.
Here we formulate a scoring function using a feed forward network. The function takes the features of a single example (i.e., query-document pair) and produces a relevance score.
```
def example_feature_columns():
"""Returns the example feature columns."""
feature_names = [
"%d" % (i + 1) for i in range(0, _NUM_FEATURES)
]
return {
name: tf.feature_column.numeric_column(
name, shape=(1,), default_value=0.0) for name in feature_names
}
def make_score_fn():
"""Returns a scoring function to build `EstimatorSpec`."""
def _score_fn(context_features, group_features, mode, params, config):
"""Defines the network to score a documents."""
del params
del config
# Define input layer.
example_input = [
tf.layers.flatten(group_features[name])
for name in sorted(example_feature_columns())
]
input_layer = tf.concat(example_input, 1)
cur_layer = input_layer
for i, layer_width in enumerate(int(d) for d in _HIDDEN_LAYER_DIMS):
cur_layer = tf.layers.dense(
cur_layer,
units=layer_width,
activation="tanh")
logits = tf.layers.dense(cur_layer, units=1)
return logits
return _score_fn
```
### Evaluation Metrics
We have provided an implementation of popular Information Retrieval evalution metrics in the TF Ranking library.
```
def eval_metric_fns():
"""Returns a dict from name to metric functions.
This can be customized as follows. Care must be taken when handling padded
lists.
def _auc(labels, predictions, features):
is_label_valid = tf_reshape(tf.greater_equal(labels, 0.), [-1, 1])
clean_labels = tf.boolean_mask(tf.reshape(labels, [-1, 1], is_label_valid)
clean_pred = tf.boolean_maks(tf.reshape(predictions, [-1, 1], is_label_valid)
return tf.metrics.auc(clean_labels, tf.sigmoid(clean_pred), ...)
metric_fns["auc"] = _auc
Returns:
A dict mapping from metric name to a metric function with above signature.
"""
metric_fns = {}
metric_fns.update({
"metric/ndcg@%d" % topn: tfr.metrics.make_ranking_metric_fn(
tfr.metrics.RankingMetricKey.NDCG, topn=topn)
for topn in [1, 3, 5, 10]
})
return metric_fns
```
### Putting It All Together
We are now ready to put all of the components above together and create an `Estimator` that can be used to train and evaluate a model.
```
def get_estimator(hparams):
"""Create a ranking estimator.
Args:
hparams: (tf.contrib.training.HParams) a hyperparameters object.
Returns:
tf.learn `Estimator`.
"""
def _train_op_fn(loss):
"""Defines train op used in ranking head."""
return tf.contrib.layers.optimize_loss(
loss=loss,
global_step=tf.train.get_global_step(),
learning_rate=hparams.learning_rate,
optimizer="Adagrad")
ranking_head = tfr.head.create_ranking_head(
loss_fn=tfr.losses.make_loss_fn(_LOSS),
eval_metric_fns=eval_metric_fns(),
train_op_fn=_train_op_fn)
return tf.estimator.Estimator(
model_fn=tfr.model.make_groupwise_ranking_fn(
group_score_fn=make_score_fn(),
group_size=1,
transform_fn=None,
ranking_head=ranking_head),
params=hparams)
```
Let us instantiate and initialize the `Estimator` we defined above.
```
hparams = tf.contrib.training.HParams(learning_rate=0.05)
ranker = get_estimator(hparams)
```
Now that we have a correctly initialized `Estimator`, we will train a model using the training data. We encourage you to experiment with different number of steps here and below.
```
ranker.train(input_fn=lambda: input_fn(_TRAIN_DATA_PATH), steps=100)
```
Finally, let us evaluate our model on the test set.
```
ranker.evaluate(input_fn=lambda: input_fn(_TEST_DATA_PATH), steps=100)
```
### Visualization
The train and evaluation steps above by default store checkpoints, metrics, and other useful information about your network to a temporary directory on disk. We encourage you to visualize this data using [Tensorboard](http://www.tensorflow.org/guide/summaries_and_tensorboard). In particular, you can launch Tensorboard and point it to where your model data is stored as follows:
First, let's find out the path to the log directory created by the process above.
```
ranker.model_dir
```
Launch Tensorboard in shell using:
$ tensorboard --logdir=<ranker.model_dir output>
| true |
code
| 0.877345 | null | null | null | null |
|
<!--BOOK_INFORMATION-->
<a href="https://www.packtpub.com/big-data-and-business-intelligence/machine-learning-opencv" target="_blank"><img align="left" src="data/cover.jpg" style="width: 76px; height: 100px; background: white; padding: 1px; border: 1px solid black; margin-right:10px;"></a>
*This notebook contains an excerpt from the book [Machine Learning for OpenCV](https://www.packtpub.com/big-data-and-business-intelligence/machine-learning-opencv) by Michael Beyeler.
The code is released under the [MIT license](https://opensource.org/licenses/MIT),
and is available on [GitHub](https://github.com/mbeyeler/opencv-machine-learning).*
*Note that this excerpt contains only the raw code - the book is rich with additional explanations and illustrations.
If you find this content useful, please consider supporting the work by
[buying the book](https://www.packtpub.com/big-data-and-business-intelligence/machine-learning-opencv)!*
<!--NAVIGATION-->
< [Combining Decision Trees Into a Random Forest](10.02-Combining-Decision-Trees-Into-a-Random-Forest.ipynb) | [Contents](../README.md) | [Implementing AdaBoost](10.04-Implementing-AdaBoost.ipynb) >
# Using Random Forests for Face Recognition
A popular dataset that we haven't talked much about yet is the **Olivetti face dataset**.
The Olivetti face dataset was collected in 1990 by AT&T Laboratories Cambridge. The
dataset comprises facial images of 40 distinct subjects, taken at different times and under
different lighting conditions. In addition, subjects varied their facial expression
(open/closed eyes, smiling/not smiling) and their facial details (glasses/no glasses).
Images were then quantized to 256 grayscale levels and stored as unsigned 8-bit integers.
Because there are 40 distinct subjects, the dataset comes with 40 distinct target labels.
Recognizing faces thus constitutes an example of a **multiclass classification** task.
## Loading the dataset
Like many other classic datasets, the Olivetti face dataset can be loaded using scikit-learn:
```
from sklearn.datasets import fetch_olivetti_faces
dataset = fetch_olivetti_faces()
X = dataset.data
y = dataset.target
```
Although the original images consisted of 92 x 112 pixel images, the version available
through scikit-learn contains images downscaled to 64 x 64 pixels.
To get a sense of the dataset, we can plot some example images. Let's pick eight indices
from the dataset in a random order:
```
import numpy as np
np.random.seed(21)
idx_rand = np.random.randint(len(X), size=8)
```
We can plot these example images using Matplotlib, but we need to make sure we reshape
the column vectors to 64 x 64 pixel images before plotting:
```
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(14, 8))
for p, i in enumerate(idx_rand):
plt.subplot(2, 4, p + 1)
plt.imshow(X[i, :].reshape((64, 64)), cmap='gray')
plt.axis('off')
```
You can see how all the faces are taken against a dark background and are upright. The
facial expression varies drastically from image to image, making this an interesting
classification problem. Try not to laugh at some of them!
## Preprocessing the dataset
Before we can pass the dataset to the classifier, we need to preprocess it following the best
practices from [Chapter 4](04.00-Representing-Data-and-Engineering-Features.ipynb), *Representing Data and Engineering Features*.
Specifically, we want to make sure that all example images have the same mean grayscale
level:
```
n_samples, n_features = X.shape
X -= X.mean(axis=0)
```
We repeat this procedure for every image to make sure the feature values of every data
point (that is, a row in `X`) are centered around zero:
```
X -= X.mean(axis=1).reshape(n_samples, -1)
```
The preprocessed data can be visualized using the preceding code:
```
plt.figure(figsize=(14, 8))
for p, i in enumerate(idx_rand):
plt.subplot(2, 4, p + 1)
plt.imshow(X[i, :].reshape((64, 64)), cmap='gray')
plt.axis('off')
plt.savefig('olivetti-pre.png')
```
## Training and testing the random forest
We continue to follow our best practice to split the data into training and test sets:
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, random_state=21
)
```
Then we are ready to apply a random forest to the data:
```
import cv2
rtree = cv2.ml.RTrees_create()
```
Here we want to create an ensemble with 50 decision trees:
```
num_trees = 50
eps = 0.01
criteria = (cv2.TERM_CRITERIA_MAX_ITER + cv2.TERM_CRITERIA_EPS,
num_trees, eps)
rtree.setTermCriteria(criteria)
```
Because we have a large number of categories (that is, 40), we want to make sure the
random forest is set up to handle them accordingly:
```
rtree.setMaxCategories(len(np.unique(y)))
```
We can play with other optional arguments, such as the number of data points required in a
node before it can be split:
```
rtree.setMinSampleCount(2)
```
However, we might not want to limit the depth of each tree. This is again, a parameter we
will have to experiment with in the end. But for now, let's set it to a large integer value,
making the depth effectively unconstrained:
```
rtree.setMaxDepth(1000)
```
Then we can fit the classifier to the training data:
```
rtree.train(X_train, cv2.ml.ROW_SAMPLE, y_train);
```
We can check the resulting depth of the tree using the following function:
```
rtree.getMaxDepth()
```
This means that although we allowed the tree to go up to depth 1000, in the end only 25
layers were needed.
The evaluation of the classifier is done once again by predicting the labels first (`y_hat`) and
then passing them to the `accuracy_score` function:
```
_, y_hat = rtree.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_hat)
```
We find 87% accuracy, which turns out to be much better than with a single decision tree:
```
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(random_state=21, max_depth=25)
tree.fit(X_train, y_train)
tree.score(X_test, y_test)
```
Not bad! We can play with the optional parameters to see if we get better. The most
important one seems to be the number of trees in the forest. We can repeat the experiment
with a forest made from 100 trees:
```
num_trees = 100
eps = 0.01
criteria = (cv2.TERM_CRITERIA_MAX_ITER + cv2.TERM_CRITERIA_EPS,
num_trees, eps)
rtree.setTermCriteria(criteria)
rtree.train(X_train, cv2.ml.ROW_SAMPLE, y_train);
_, y_hat = rtree.predict(X_test)
accuracy_score(y_test, y_hat)
```
With this configuration, we get 91% accuracy!
Another interesting use case of decision tree ensembles is Adaptive Boosting or AdaBoost.
<!--NAVIGATION-->
< [Combining Decision Trees Into a Random Forest](10.02-Combining-Decision-Trees-Into-a-Random-Forest.ipynb) | [Contents](../README.md) | [Implementing AdaBoost](10.04-Implementing-AdaBoost.ipynb) >
| true |
code
| 0.776077 | null | null | null | null |
|
Basis Pursuit DeNoising
=======================
This example demonstrates the use of class [admm.bpdn.BPDN](http://sporco.rtfd.org/en/latest/modules/sporco.admm.bpdn.html#sporco.admm.bpdn.BPDN) to solve the Basis Pursuit DeNoising (BPDN) problem [[16]](http://sporco.rtfd.org/en/latest/zreferences.html#id16)
$$\mathrm{argmin}_\mathbf{x} \; (1/2) \| D \mathbf{x} - \mathbf{s} \|_2^2 + \lambda \| \mathbf{x} \|_1 \;,$$
where $D$ is the dictionary, $\mathbf{x}$ is the sparse representation, and $\mathbf{s}$ is the signal to be represented. In this example the BPDN problem is used to estimate the reference sparse representation that generated a signal from a noisy version of the signal.
```
from __future__ import print_function
from builtins import input
import numpy as np
from sporco.admm import bpdn
from sporco import util
from sporco import plot
plot.config_notebook_plotting()
```
Configure problem size, sparsity, and noise level.
```
N = 512 # Signal size
M = 4*N # Dictionary size
L = 32 # Number of non-zero coefficients in generator
sigma = 0.5 # Noise level
```
Construct random dictionary, reference random sparse representation, and test signal consisting of the synthesis of the reference sparse representation with additive Gaussian noise.
```
# Construct random dictionary and random sparse coefficients
np.random.seed(12345)
D = np.random.randn(N, M)
x0 = np.zeros((M, 1))
si = np.random.permutation(list(range(0, M-1)))
x0[si[0:L]] = np.random.randn(L, 1)
# Construct reference and noisy signal
s0 = D.dot(x0)
s = s0 + sigma*np.random.randn(N,1)
```
Set BPDN solver class options.
```
opt = bpdn.BPDN.Options({'Verbose': False, 'MaxMainIter': 500,
'RelStopTol': 1e-3, 'AutoRho': {'RsdlTarget': 1.0}})
```
Select regularization parameter $\lambda$ by evaluating the error in recovering the sparse representation over a logarithmicaly spaced grid. (The reference representation is assumed to be known, which is not realistic in a real application.) A function is defined that evalues the BPDN recovery error for a specified $\lambda$, and this function is evaluated in parallel by [sporco.util.grid_search](http://sporco.rtfd.org/en/latest/modules/sporco.util.html#sporco.util.grid_search).
```
# Function computing reconstruction error at lmbda
def evalerr(prm):
lmbda = prm[0]
b = bpdn.BPDN(D, s, lmbda, opt)
x = b.solve()
return np.sum(np.abs(x-x0))
# Parallel evalution of error function on lmbda grid
lrng = np.logspace(1, 2, 20)
sprm, sfvl, fvmx, sidx = util.grid_search(evalerr, (lrng,))
lmbda = sprm[0]
print('Minimum ℓ1 error: %5.2f at 𝜆 = %.2e' % (sfvl, lmbda))
```
Once the best $\lambda$ has been determined, run BPDN with verbose display of ADMM iteration statistics.
```
# Initialise and run BPDN object for best lmbda
opt['Verbose'] = True
b = bpdn.BPDN(D, s, lmbda, opt)
x = b.solve()
print("BPDN solve time: %.2fs" % b.timer.elapsed('solve'))
```
Plot comparison of reference and recovered representations.
```
plot.plot(np.hstack((x0, x)), title='Sparse representation',
lgnd=['Reference', 'Reconstructed'])
```
Plot lmbda error curve, functional value, residuals, and rho
```
its = b.getitstat()
fig = plot.figure(figsize=(15, 10))
plot.subplot(2, 2, 1)
plot.plot(fvmx, x=lrng, ptyp='semilogx', xlbl='$\lambda$',
ylbl='Error', fig=fig)
plot.subplot(2, 2, 2)
plot.plot(its.ObjFun, xlbl='Iterations', ylbl='Functional', fig=fig)
plot.subplot(2, 2, 3)
plot.plot(np.vstack((its.PrimalRsdl, its.DualRsdl)).T,
ptyp='semilogy', xlbl='Iterations', ylbl='Residual',
lgnd=['Primal', 'Dual'], fig=fig)
plot.subplot(2, 2, 4)
plot.plot(its.Rho, xlbl='Iterations', ylbl='Penalty Parameter', fig=fig)
fig.show()
```
| true |
code
| 0.793646 | null | null | null | null |
|
## Tools that we will use
- **Pip**
Python's official package manager, and is most commonly used to install packages published on the Python Package Index (PyPI).
Run:
```bash
pip --version
```
- **Conda**
Anaconda package manager that automates the process of installing, updating, and removing packages.
`pip` is a general-purpose manager for Python packages; `conda` is a language-agnostic cross-platform environment manager.
Run:
```bash
conda info
conda env list
where conda # this output should be in your PATH variable
```
See *Conda_Cheatsheet.pdf* inside the Student_Resources for more useful commands.
- **Anaconda**
Free and open source distribution that comes with a lot of tools right of the box, it comes with either Python or R, a package manager called conda, and a lot of other libraries and packages pre-installed, these packages are usually related to analytics and scientific and help to plot and compute large amounts of data.
Anaconda is an option that people prefer because it simplify issues related to installing different python version of python, creating different environments, privileges issues, etc.
If you are on Windows, use Anaconda Prompt instead of Windows Command Prompt.
Run
```bash
where anaconda
```
- **Jupyter**
*Project Jupyter* was created from *iPython Notebooks* with the intention to be robust and language agnostic (Julia, and R notebooks).Designed for creating reproducible computational narratives.
*JupyterLab* is an interactive development environment for working with notebooks, code and data. JupyterLab has full support for Jupyter notebooks. Additionally, JupyterLab enables you to use text editors, terminals, data file viewers, and other custom components side by side with notebooks in a tabbed work area.
- **Git**
To publish workshop’s sections (.ipynb files)
https://help.github.com/articles/working-with-jupyter-notebook-files-on-github/
- **Python**
Interpreted cross-platform high-level programming language for general-purpose programming.
Useful commands:
```bash
where python # this output should be in your PATH variable
python hello_world.py #to run a script
python hello_human.py Victor
```
## Tools that we will not be using
- **Miniconda**
Another software distribution Miniconda is essentially an installer for an empty conda environment, containing only Conda and Python, so that you can install what you need from scratch.
- **IPython**
Currently, IPython fulfill 2 roles: being the python backend to the jupyter notebook, (aka kernel) and an interactive python shell.
## To run a command on Jupyter Notebook:
```
%run hello_world.py
%run hello_human.py Victor
```
| true |
code
| 0.882959 | null | null | null | null |
|
# Bring your own pipe-mode algorithm to Amazon SageMaker
_**Create a Docker container for training SageMaker algorithms using Pipe-mode**_
---
## Contents
1. [Overview](#Overview)
1. [Preparation](#Preparation)
1. [Permissions](#Permissions)
1. [Code](#Code)
1. [train.py](#train.py)
1. [Dockerfile](#Dockerfile)
1. [Customize](#Customize)
1. [Train](#Train)
1. [Conclusion](#Conclusion)
---
## Overview
SageMaker Training supports two different mechanisms with which to transfer training data to a training algorithm: File-mode and Pipe-mode.
In File-mode, training data is downloaded to an encrypted EBS volume prior to commencing training. Once downloaded, the training algorithm trains by reading the downloaded training data files.
On the other hand, in Pipe-mode, the input data is transferred to the algorithm while it is training. This poses a few significant advantages over File-mode:
* In File-mode, training startup time is proportional to size of the input data. In Pipe-mode, the startup delay is constant, independent of the size of the input data. This translates to much faster training startup for training jobs with large GB/PB-scale training datasets.
* You do not need to allocate (and pay for) a large disk volume to be able to download the dataset.
* Throughput on IO-bound Pipe-mode algorithms can be multiple times faster than on equivalent File-mode algorithms.
However, these advantages come at a cost - a more complicated programming model than simply reading from files on a disk. This notebook aims to clarify what you need to do in order to use Pipe-mode in your custom training algorithm.
---
## Preparation
_This notebook was created and tested on an ml.t2.medium notebook instance._
Let's start by specifying:
- S3 URIs `s3_training_input` and `s3_model_output` that you want to use for training input and model data respectively. These should be within the same region as the Notebook Instance, training, and hosting. Since the "algorithm" you're building here doesn't really have any specific data-format, feel free to point `s3_training_input` to any s3 dataset you have, the bigger the dataset the better to test the raw IO throughput performance. For this example, the Boston Housing dataset will be copied over to your s3 bucket.
- The `training_instance_type` to use for training. More powerful instance types have more CPU and bandwidth which would result in higher throughput.
- The IAM role arn used to give training access to your data.
### Permissions
Running this notebook requires permissions in addition to the normal `SageMakerFullAccess` permissions. This is because you'll be creating a new repository in Amazon ECR. The easiest way to add these permissions is simply to add the managed policy `AmazonEC2ContainerRegistryFullAccess` to the role that you used to start your notebook instance. There's no need to restart your notebook instance when you do this, the new permissions will be available immediately.
```
import boto3
import pandas as pd
import sagemaker
# to load the boston housing dataset
from sklearn.datasets import *
# Get SageMaker session & default S3 bucket
role = sagemaker.get_execution_role()
sagemaker_session = sagemaker.Session()
region = sagemaker_session.boto_region_name
s3 = sagemaker_session.boto_session.resource("s3")
bucket = sagemaker_session.default_bucket() # replace with your own bucket name if you have one
# helper functions to upload data to s3
def write_to_s3(filename, bucket, prefix):
filename_key = filename.split(".")[0]
key = "{}/{}/{}".format(prefix, filename_key, filename)
return s3.Bucket(bucket).upload_file(filename, key)
def upload_to_s3(bucket, prefix, filename):
url = "s3://{}/{}/{}".format(bucket, prefix, filename)
print("Writing data to {}".format(url))
write_to_s3(filename, bucket, prefix)
```
If you have a larger dataset you want to try, here is the place to swap in your dataset.
```
filename = "boston_house.csv"
# Download files from sklearns.datasets
tabular_data = load_boston()
tabular_data_full = pd.DataFrame(tabular_data.data, columns=tabular_data.feature_names)
tabular_data_full["target"] = pd.DataFrame(tabular_data.target)
tabular_data_full.to_csv(filename, index=False)
```
Upload the dataset to your bucket. You'll find it with the 'pipe_bring_your_own/training' prefix.
```
prefix = "pipe_bring_your_own/training"
training_data = "s3://{}/{}".format(bucket, prefix)
print("Training data in {}".format(training_data))
upload_to_s3(bucket, prefix, filename)
```
## Code
For the purposes of this demo you're going to write an extremely simple “training” algorithm in Python. In essence it will conform to the specifications required by SageMaker Training and will read data in Pipe-mode but will do nothing with the data, simply reading it and throwing it away. You're doing it this way to be able to illustrate only exactly what's needed to support Pipe-mode without complicating the code with a real training algorithm.
In Pipe-mode, data is pre-fetched from S3 at high-concurrency and throughput and streamed into Unix Named Pipes (aka FIFOs) - one FIFO per Channel per epoch. The algorithm must open the FIFO for reading and read through to <EOF> (or optionally abort mid-stream) and close its end of the file descriptor when done. It can then optionally wait for the next epoch's FIFO to get created and commence reading, iterating through epochs until it has achieved its completion criteria.
For this example, you'll need two supporting files:
### train.py
`train.py` simply iterates through 5 epochs on the `training` Channel. Each epoch involves reading the training data stream from a FIFO named `/opt/ml/input/data/training_${epoch}`. At the end of the epoch the code simply iterates to the next epoch, waits for the new epoch's FIFO to get created and continues on.
A lot of the code in `train.py` is merely boilerplate code, dealing with printing log messages, trapping termination signals etc. The main code that iterates through reading each epoch's data through its corresponding FIFO is the following:
```
!pygmentize train.py
```
### Dockerfile
You can use any of the preconfigured Docker containers that SageMaker provides, or build one from scratch. This example uses the [PyTorch - AWS Deep Learning Container](https://github.com/aws/deep-learning-containers/blob/master/available_images.md), then adds `train.py`, and finally runs `train.py` when the entrypoint is launched. To learn more about bring your own container training options, see the [Amazon SageMaker Training Toolkit](https://github.com/aws/sagemaker-training-toolkit).
```
%cat Dockerfile
```
## Customize
To fetch the PyTorch AWS Deep Learning Container (DLC), first login to ECR.
```
%%sh
aws ecr get-login-password --region us-east-1 | docker login --username AWS --password-stdin 763104351884.dkr.ecr.us-east-1.amazonaws.com
```
Next, build your custom docker container, tagging it with the name "pipe_bring_your_own".
```
%%sh
docker build -t pipe_bring_your_own .
```
With the container built, you can now tag it with the full name you will need when calling it for training (`ecr_image`). Then upload your custom container to ECR.
```
account = !aws sts get-caller-identity --query Account --output text
algorithm_name = "pipe_bring_your_own"
ecr_image = '{}.dkr.ecr.{}.amazonaws.com/{}:latest'.format(account[0], region, algorithm_name)
print('ecr_image: {}'.format(ecr_image))
ecr_client = boto3.client('ecr')
try:
response = ecr_client.describe_repositories(
repositoryNames=[
algorithm_name,
],
)
print("Repo exists...")
except Exception as e:
create_repo = ecr_client.create_repository(repositoryName=algorithm_name)
print("Created repo...")
!docker tag {algorithm_name} {ecr_image}
!docker push {ecr_image}
```
## Train
Now, you will use the `Estimator` function and pass in the information needed to run the training container in SageMaker.
Note that `input_mode` is the parameter required for you to set pipe mode for this training run. Also note that the `base_job_name` doesn't let you use underscores, so that's why you're using dashes.
```
from sagemaker.estimator import Estimator
estimator = Estimator(
image_uri=ecr_image,
role=role,
base_job_name="pipe-bring-your-own-test",
instance_count=1,
instance_type="ml.c4.xlarge",
input_mode="Pipe",
)
# Start training
estimator.fit(training_data)
```
Note the throughput logged by the training logs above. By way of comparison a File-mode algorithm will achieve at most approximately 150MB/s on a high-end `ml.c5.18xlarge` and approximately 75MB/s on a `ml.m4.xlarge`.
---
## Conclusion
There are a few situations where Pipe-mode may not be the optimum choice for training in which case you should stick to using File-mode:
* If your algorithm needs to backtrack or skip ahead within an epoch. This is simply not possible in Pipe-mode since the underlying FIFO cannot not support `lseek()` operations.
* If your training dataset is small enough to fit in memory and you need to run multiple epochs. In this case may be quicker and easier just to load it all into memory and iterate.
* Your training dataset is not easily parse-able from a streaming source.
In all other scenarios, if you have an IO-bound training algorithm, switching to Pipe-mode may give you a significant throughput-boost and will reduce the size of the disk volume required. This should result in both saving you time and reducing training costs.
You can read more about building your own training algorithms in the [SageMaker Training documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/your-algorithms-training-algo.html).
| true |
code
| 0.416945 | null | null | null | null |
|
# DNA complement and reverse
This notebook was used to benchmark the different approach of computing
the complement of a sequence.
Takes about 15ms to analyse a 1e7 long sequence.
```
# First, let us create a sequence.
from biokit.sequence.benchmark import SequenceBenchmark
def create_sequence(expectedLength=1e6):
s = SequenceBenchmark()
return s.create_sequence(expectedLength)
sequence = create_sequence(1e7)
```
## BioPython
```
from Bio.Seq import Seq
from Bio.Alphabet import IUPAC
from Bio.SeqUtils import GC
seq1 = Seq(sequence, IUPAC.unambiguous_dna)
GC(seq1)
%%timeit -n 3
seq1 = Seq(sequence, IUPAC.unambiguous_dna)
res = seq1.complement()
len(seq1)
```
## Python with lists
```
class DNAList(object):
bases = ["A", "C", "T", "G"]
cbases = {"T":"A", "G":"C", "A":"T", "C":"G"}
def __init__(self, data):
self.data = data[:]
def get_complement(self):
res = "".join((self.cbases[x] for x in self))
return res
def __getitem__(self, index):
if type(index) == slice:
return "".join(self.data[index])
return self.data[index]
seq2 = DNAList(sequence[0:1000000]) # slow
%%timeit -n 3
res = seq2.get_complement()
```
## Python with strings
This is a simplified version of what is done in BioPython and BioKit
```
import string
# with strings as ACGT / TGCA, there is no improvment
trans = bytes.maketrans(b'ACGTagct', b'TGCAtgca')
class DNA(object):
def __init__(self, sequence):
self.sequence = sequence
def complement(self):
return self.sequence.translate(trans)
d = DNA(sequence)
%%timeit -n 3
res = d.complement()
#fh = open("test.fasta", "w")
#fh.write(res)
#fh.close()
```
## Another way with Pandas?
```
import pandas as pd
d = pd.Series(sequence)
# here we just store the sequence so the timeseries is
# just a container. Instanciation is 50 times longer
# than a simple class storing the sequence as a string though
trans = bytes.maketrans(b'ACGTacgt', b'TGCAtgca')
%%timeit -n 3
res = "".join(d).translate(trans)
```
## BioKit
```
from biokit.sequence import dna
d = dna.DNA(sequence)
%%timeit -n 10
# maketrans
d.get_complement()
```
## cython test
- Cythonise does not make it faster. probably the reason being that maketrans is alredy optimised
- THe code below provides a cython version of the code implemented earlier (CyTransSeq) and a cythonised version of a dictionary implementation.
- Neither are faster than the maketrans
- lookup and lut table do not help either
- references: http://nbviewer.ipython.org/urls/gist.github.com/Jorge-C/d51b48d3e18897c46ea2/raw/73d7e11e4b72d6ba90e0021931afa230e63031e9/cython+sequences.ipynb?create=1
```
%load_ext cython
%%cython --annotate
# source http://nbviewer.ipython.org/urls/gist.github.com/Jorge-C/d51b48d3e18897c46ea2/raw/73d7e11e4b72d6ba90e0021931afa230e63031e9/cython+sequences.ipynb?create=1
cimport cython
import numpy as np
cimport numpy as cnp
table = bytes.maketrans(b'ACGTacgt',
b'TGCAtgca')
cdef class CyTransSeq(object):
"""Simply defining the class as a cython one, uses translation table"""
cdef public str seq
def __cinit__(self, seq):
self.seq = seq
cpdef rc(self):
return list(reversed(self.seq.translate(table)))
cpdef complement(self):
return self.seq.translate(table)
cdef class CySeq(object):
"""Translation using a dict, cythonized"""
_complement_map = {
'A': 'T', 'C':'G', 'G':'C', 'T':'A',
'a': 't', 'c':'g', 'g':'c', 't':'a'}
cdef public str seq
def __cinit__(self, seq):
self.seq = seq
cdef _rc(self):
result = []
for base in reversed(self.seq):
result.append(self._complement_map[base])
return result
cdef _complement1(self):
result = []
for base in self.seq:
result.append(self._complement_map[base])
return result
def complement1(self):
return self._complement1()
def complement2(self):
return self._complement2()
cdef _complement2(self):
return [self._complement_map[base] for base in self.seq]
def rc(self):
return self._rc()
seq = CyTransSeq(sequence)
%%timeit -n 3
res = seq.complement()
```
## Plot
```
import matplotlib as plt
%matplotlib
import pylab
N = [1e5, 1e6, 5e6, 1e7, 5e7, 1e8]
import time
timesBioKit = []
timesC = []
timesBio = []
timesCyt = []
for el in N:
# BioKit
factor = int(el / 50.) #100 is the length of the small string
subseq = "AGCTTTTCATTCTGACTGCAACGGGCAATATGTCAGTGTCTCGTTGCAAA"
sequence_in = "".join([subseq]*factor)
seq = dna.DNA(sequence_in)
t1 = time.time()
res = seq.get_complement()
t2 = time.time()
timesBioKit.append(t2-t1)
#t1 = time.time()
#res = seq.get_complement_c()
#t2 = time.time()
#timesC.append(t2-t1)
# biopython
seqbio = Seq(sequence_in, IUPAC.unambiguous_dna)
t1 = time.time()
seqbio.complement()
t2 = time.time()
timesBio.append(t2-t1)
# cython
seqcyt = CyTransSeq(sequence_in)
t1 = time.time()
seqcyt.complement()
t2 = time.time()
timesCyt.append(t2-t1)
print(el)
%pylab inline
pylab.clf()
pylab.loglog(N, timesBioKit, 'o-', N, timesBio, 'gx-',
N, timesCyt,
'ko-')
pylab.legend(['timesBioKit', 'timesBio', 'times Cython'],
loc='best')
```
| true |
code
| 0.602617 | null | null | null | null |
|
# Gentle Introduction to Pytorch Autograd with Linear Regression
#### By Michael Przystupa
** By the end of this tutorial students will be able to:**:
- Analytically solve a linear regression
- Explain what pytorch automatically handles with it's autograd library
- Construct a linear model using the pytorch module
## Introduction
Linear regression is a fairly common practise and is a good starting place with introducing you building models using the pytorch library. We'll start by showing how analytically you can solve linear regression analytically which we can use to compare how our pytorch model compares.
First, let's import the libraries we'll need:
```
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
#just your typical imports in python
```
## The Data Set
We'll be working with a toy dataset which is just a linear function with added guassian noise:
\begin{equation}
f(x) = ax + b + N(0, 1)
\end{equation}
In real machine learning, your data won't be so nice, but we want something we can easily look at to get some intuition about how the model works.
** note ** : In general, we do not KNOW the function our data came from. That's why we want to build models to try and approximate something that looks like our data COULD have come from it.
```
def f( x, a= 2.0, b = 1.0, add_noise=True):
if add_noise:
n = np.random.normal(0.0, 1.0)
else:
n = 0.0
return a * x + b + n
X = np.linspace(-5.0, 5.0, num= 200)
y = np.array([f(x) for x in X])
plt.plot(X, y, 'g^')
plt.show()
```
## Analytically
Clearly, there is some relationship in this data, and we'd like to represent this some how with a function of the form
\begin{equation}
w_{1} x + w_{2} = \hat y
\end{equation}
In machine learning, to find these w's we generally want to have some objective to see how good the weights are. One example is minimizing the mean-squared error which for our equation looks like this:
\begin{equation}
Objective(w) = \sum_{i=1}^{n} (w_{1} x_{i} + w_{2} + - y_{i}) ^{2}
\end{equation}
You'll have to trust me on this, but we can solve this directly by doing the following manipulation:
\begin{equation}
w = (X^{t} X)^{-1} (X^{t} y)
\end{equation}
where X is our data matrix and y is our labels, and w is our weights we want to parameterize
```
# Solving problem analytically:
X = np.stack((X, np.ones(X.shape[0])), axis=1) #this is so we have w_{2}
y = np.array([y]).transpose() # has to do with shape of data
X_t = X.transpose()
#Calculating each of the components
X_tX = np.matmul(X_t, X)
X_ty = np.matmul(X_t, y)
w = np.matmul(np.linalg.inv(X_tX) , (X_ty))
#this will show the best weights we can do with the data
print('w_0 = {}, w_1 = {}'.format(w[0], w[1]))
#Plotting our approximations of true values
#lambda is a key word in python for defining smaller functions
lin_model = lambda x : f(x, w[0], w[1], add_noise=False)
y_hat = [lin_model(x) for x in X[:,0]]
plt.plot(X[:,0], y, 'g^')
plt.plot(X[:,0], y_hat, 'r--')
plt.show()
```
This is all well and good...if you can calculate your inverse. In that case, you're going to have to get creative and do some optimization.
## Stochastic Gradient Descent (S.G.D)
This can be fairly math heavy, but here's the gist of what we're going to do:
\begin{equation}
w = w - \alpha * \nabla Objective(w)
\end{equation}
where $\alpha$ is referred to as the learning rate and is the amount we will update our current weights by at each step and $\nabla Objective(w)$ means we want to take the gradient with respect to our loss. One minor thing with this is that in S.G.D. we are making updates based off single examples in our data and this is done usually for performance reasons (although there is theory about why it works well too).
Maybe this all seems a little scary, particularly if you're not sure what a gradient is. Thankfully, pytorch makes it so you don't need to pull out your old calculus textbook and handles calculating these for us as we'll see.
## Pytorch's autograd system
The most useful part of pytorch is the autograd system. The gist of it is that it will automatically calculate gradients for any operations done on a pytorch tensor, so we have to say good bye to our good friend numpy, which is easy to do:
```
X = torch.from_numpy(X).float()
y = torch.from_numpy(y).float()
# Now, to do SGD we'll need a learning rate and an initial set of weights:
alpha = 1e-3
w = torch.randn(2, requires_grad=True) #requires grad is key to do this
```
To use pytorch's autograd feature, we're going to calculate the prediction with our current weights and call backward on our loss function. When you call .backward() on a tensor of interest, it calculates the gradient and we can access it with the .grad field of tensors to do our update
```
order = torch.randperm(X.size()[0])
#redefine our linear model to use the tensor version of w
for _ in range(0, 10):
total_loss = 0.0
for i in order:
x = X[i,:]
y_hat = torch.matmul(x, w) #ax + b esentially
loss = F.mse_loss(y_hat[0], y[i,0]) #our objective function
loss.backward() #where our gradients get calculated
total_loss += loss.item()
with torch.no_grad():
w -= alpha * w.grad
w.grad.zero_()
print('Loss on epoch {}: {}'.format(_, total_loss / X.size()[0]))
print(w)
X = X.numpy()
y = y.numpy()
w = w.detach().numpy()
lin_model = lambda x : f(x, w[0], w[1], add_noise=False)
y_hat = [lin_model(x) for x in X[:,0]]
plt.plot(X[:,0], y, 'g^')
plt.plot(X[:,0], y_hat, 'r--')
plt.show()
```
As we can see, our model now performsabout the same as our analytical solution, but the advantage is that doing it this way is always possible and doesn't rely on our inverse having to exist.
## Going full Pytorch
Now the above loop was to illustrate what pytorch is doing. We cheated a little bit by also using the .backward() call instead of calculating it our selves, but that's the reason WHY these deep learning frameworks are great, because you don't HAVE to do this all by hand.
```
X = torch.from_numpy(X).float()
y = torch.from_numpy(y).float()
class LinRegression(nn.Module):
def __init__(self):
super(LinRegression, self).__init__()
self.linear = nn.Linear(2, 1, bias=False )
#the bias term is generally set to True, but we added the 1's column to x
def forward(self, x):
return self.linear(x)
model = LinRegression()
sgd = optim.SGD(model.parameters(), lr=1e-3)
order = torch.randperm(X.size()[0])
for _ in range(0, 10):
total_loss = 0.0
for i in order:
x = X[i,:]
y_hat = model(x)
loss = F.mse_loss(y_hat[0], y[i,0]) #our objective function
loss.backward() #where our gradients get calculated
total_loss += loss.item()
sgd.step()
sgd.zero_grad()
print('Loss on epoch {}: {}'.format(_, total_loss / X.size()[0]))
y_hat = model(X)
y_hat = y_hat.detach().numpy()
X = X.numpy()
y = y.numpy()
plt.plot(X[:,0], y, 'g^')
plt.plot(X[:,0], y_hat, 'r--')
plt.show()
```
## Conclusions
In this tutorial we've seen how to solve linear regression using pytorch's autograd system and how to build models with pytorch. We saw several pytorch packages including torch, torch.optim, torch.nn, and torch.nn.functional. We then saw how to use these modules together to train our model.
## Exercise: Logistic Regression
Logistic regression is a sort of extension of linear regression for the classification setting.
Using what you've seen in this tutorial and class, build a logistic regression model to train a model for the following toy dataset:
```
def f(x):
if x > 0.0:
return 1.0
else:
return 0.0
X = np.linspace(-5.0, 5.0, num= 200)
y = np.array([f(x) for x in X])
plt.plot(X, y, 'g^')
plt.show()
#starter code:
X = torch.from_numpy(X)
y = torch.from_numpy(y)
class LogisticRegression(nn.Module):
def __init__(self):
super(LogisticRegression, self).__init__()
#insert code here
def forward(self, x):
#insert code
return x
# some set-up
order = torch.randperm(X.size()[0])
#training loop
for _ in range(0, 10):
total_loss = 0.0
for i in order:
x = X[i]
y_hat = model(x)
#insert call to loss function here
loss.backward() #where our gradients get calculated
total_loss += loss.item()
sgd.step()
sgd.zero_grad()
print('Loss on epoch {}: {}'.format(_, total_loss / X.size()[0]))
y_hat = model(X)
y_hat = y_hat.detach().numpy()
X = X.numpy()
y = y.numpy()
plt.plot(X[:,0], y, 'g^')
plt.plot(X[:,0], y_hat, 'r--')
plt.show()
```
| true |
code
| 0.83952 | null | null | null | null |
|
In this demo, we use knowledge distillation to train a ResNet-18 model for image classification. We will show how to provide teacher model, student model, data loaders, inference pipeline and other arguments to the toolkit and start knowledge distillation training.
```
!pip install pytorch-lightning
```
## Download the toolkit
```
!git clone https://github.com/georgian-io/Knowledge-Distillation-Toolkit.git
%cd Knowledge-Distillation-Toolkit/
import yaml
from collections import ChainMap
import torch
import torch.nn.functional as F
from torchvision.models.resnet import ResNet, BasicBlock
from torchvision import datasets, transforms
from knowledge_distillation.kd_training import KnowledgeDistillationTraining
```
## Define the student model and teacher model
```
class StudentModel(ResNet):
def __init__(self):
super(StudentModel, self).__init__(BasicBlock, [2, 2, 2, 2], num_classes=10) #ResNet18
self.conv1 = torch.nn.Conv2d(1, 64,
kernel_size=(7, 7),
stride=(2, 2),
padding=(3, 3), bias=False)
def forward(self, batch, temperature=1):
logits = super(StudentModel, self).forward(batch)
logits = logits / temperature
prob = F.softmax(logits, dim=0)
log_prob = F.log_softmax(logits, dim=0)
return {"logits":logits, "prob":prob, "log_prob":log_prob}
class TeacherModel(ResNet):
def __init__(self):
super(TeacherModel, self).__init__(BasicBlock, [3, 4, 6, 3], num_classes=10) #ResNet34
self.conv1 = torch.nn.Conv2d(1, 64,
kernel_size=(7, 7),
stride=(2, 2),
padding=(3, 3), bias=False)
def forward(self, batch, temperature=1):
logits = super(TeacherModel, self).forward(batch)
logits = logits / temperature
prob = F.softmax(logits, dim=0)
log_prob = F.log_softmax(logits, dim=0)
return {"logits":logits, "prob":prob, "log_prob":log_prob}
```
## Define the inference pipeline
```
class inference_pipeline:
def __init__(self, device):
self.device = device
def run_inference_pipeline(self, model, data_loader):
accuracy = 0
model.eval()
with torch.no_grad():
for i, data in enumerate(data_loader):
X, y = data[0].to(self.device), data[1].to(self.device)
outputs = model(X)
predicted = torch.max(outputs["prob"], 1)[1]
accuracy += predicted.eq(y.view_as(predicted)).sum().item()
accuracy = accuracy / len(data_loader.dataset)
return {"inference_result": accuracy}
def get_data_for_kd_training(batch):
data = torch.cat([sample[0] for sample in batch], dim=0)
data = data.unsqueeze(1)
return data,
```
## Read from demo_config.yaml, which contains all argument set up
```
config = yaml.load(open('./examples/resnet_compression_demo/demo_config.yaml','r'), Loader=yaml.FullLoader)
device = torch.device("cuda")
```
## Create training and validation data loaders
We will use the MNIST dataset
```
# Create data loaders for training and validation
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
train_kwargs = {'batch_size': 16, 'num_workers': 0}
test_kwargs = {'batch_size': 1000, 'num_workers': 0}
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
test_dataset = datasets.MNIST('./data', train=False, transform=transform)
train_data_loader = torch.utils.data.DataLoader(train_dataset, collate_fn=get_data_for_kd_training, **train_kwargs)
test_loader = torch.utils.data.DataLoader(test_dataset, **test_kwargs)
val_data_loaders = {"accuracy_on_validation_set": test_loader}
```
## Create an instance of inference pipeline
```
# Create inference pipeline for validating the student model
inference_pipeline_example = inference_pipeline(device)
```
## Create an instance of student model and teacher model
```
# Create student and teacher model
student_model = StudentModel()
teacher_model = TeacherModel()
teacher_model.load_state_dict(torch.load("./examples/resnet_compression_demo/trained_model/resnet34_teacher.pt"))
```
## Pass data loaders, student and teacher model, inference pipeline and other argument set up into `KnowledgeDistillationTraining`
```
# Train a student model with knowledge distillation and get its performance on dev set
KD_resnet = KnowledgeDistillationTraining(train_data_loader = train_data_loader,
val_data_loaders = val_data_loaders,
inference_pipeline = inference_pipeline_example,
student_model = student_model,
teacher_model = teacher_model,
num_gpu_used = config["knowledge_distillation"]["general"]["num_gpu_used"],
final_loss_coeff_dict = config["knowledge_distillation"]["final_loss_coeff"],
logging_param = ChainMap(config["knowledge_distillation"]["general"],
config["knowledge_distillation"]["optimization"],
config["knowledge_distillation"]["final_loss_coeff"],
config["knowledge_distillation"]["pytorch_lightning_trainer"]),
**ChainMap(config["knowledge_distillation"]["optimization"],
config["knowledge_distillation"]["pytorch_lightning_trainer"],
config["knowledge_distillation"]["comet_info"])
)
```
## Start knowledge distillation training
```
KD_resnet.start_kd_training()
```
As the above output shows, validation accuracy of the student model improves in every training epoch
```
```
| true |
code
| 0.876529 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.