prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# NLP Techniques
## Input -> clean data, check if the data makes sense
## NLP Techniques -> specifically designed for text data
## Output -> plot can help to check if we have what we are looking for
### 1) Sentiment Analysis
### We use the Corpus(original text) to have all words
### We use TextBlob (nltk)
### We use Naive Bayes (statistical methods)
```
# Polarity Subjectivity
# -1(Negative) <----------->(Positive)+1 0(Objective-fact)<---------------->(Subjective-Opion+1)
from textblob import TextBlob
TextBlob("I love Python").sentiment
TextBlob("great").sentiment # it took the average of the word great
TextBlob("not great").sentiment # generally when the word not is infront of word it is Negative
import pandas as pd
data = pd.read_pickle('files\\corpus.pkl')
#df_data_clean['transcript']['Dave']
pol = lambda x: TextBlob(x).sentiment.polarity
sub = lambda x: TextBlob(x).sentiment.subjectivity
data['Polarity'] = data['transcript'].apply(pol)
data['Subjectivity'] = data['transcript'].apply(sub)
data
# Lets plot the results
import matplotlib.pyplot as plt
plt.figure(figsize=(10,8))
for comedian in data.index:
x = data['Polarity'][comedian]
y = data['Subjectivity'][comedian]
plt.text(x+.001,y+.001, comedian, fontsize=8)
plt.xlim(-.001,.12)
plt.scatter(x,y)
plt.xlabel(f"Negative <-----------> Positive\nPolarity")
plt.ylabel(f"Fact <----------->Opion\nSubjectivity")
```
### 2) Topic Modeling
### We use the Document-Term Matrix(words) the order does not matter
### We use gensim
### We use Latent Dirichlet Allocation(LDA) L(hidden), D(type of probability distribution)
### We use nltk for some parts of speech tagging
#### Example
#### I like bananas and oranges Topic A - 100%
#### Frogs and fish live in ponds Topic B - 100%
#### Kittens and puppies are fluffy Topic B - 100%
#### I had spinach and apple smothie Topic A - 100%
#### My kitten loves kale Topic A - 60% and Topic B - 40%
#### Topic A-> 40% banana, 30% kale, 10% breakfast... Food
#### TOpic B-> 30% kitten, 20% puppy, 10% frog, 5% cute... Animal
#### Every document is a mix of Topics
#### Every topic is a mix of words
```
# Using gensin to do all the work behind the separation of topic and words
# We need to inform the document-term matrix, number of topics and number of iterations
data = pd.read_pickle('files\\dtm_stop.pkl')
data
# to use gensim first install -> conda install -c conda-forge gensim
from gensim import matutils, models
import scipy.sparse
tdm = data.transpose()
tdm.head()
# we need to put the document-term matrix into a new gensim format
# from df -> sparse matrix
sparse_counts = scipy.sparse.csr_matrix(tdm)
corpus = matutils.Sparse2Corpus(sparse_counts)
corpus
# gensim requires dictionary of the all terms and theirs respective location in the term-document matrix
import pickle
cv = pickle.load(open("files\\cv_stop.pkl","rb"))
id2word = dict((v,k) for k, v in cv.vocabulary_.items())
```
# Attempt #1 - Topics in generall
```
# now we need to specify 2 other parameters as well
# the number of topics and the number of passes
lda = models.LdaModel(corpus=corpus, id2word=id2word, num_topics=4, passes=10)
lda.print_topics()
```
# Attempt #2 - Only Nouns
```
# create a function to pull out nouns from a string of text
from nltk import word_tokenize, pos_tag
def nouns(text):
'''Give a string of text, tokenize the text and pull out only the nouns'''
is_noun = lambda pos:pos[:2] == "NN"
tokenized = word_tokenize(text)
all_nouns = [word for word,pos in pos_tag(tokenized) if is_noun(pos)]
return ' '.join(all_nouns)
# read the cleaned data, before the CounterVectorizer step
data_clean = pd.read_pickle('files\\data_clean.pkl')
data_clean
# apply the nouns function to the transcript to filter only nouns
data_nouns = pd.DataFrame(data_clean.transcript.apply(nouns))
data_nouns
# now whe know some other stopwords related to the nouns
# Lets update our document-term matrix with the new list of stop words
from sklearn.feature_extraction import text
from sklearn.feature_extraction.text import CountVectorizer
# another word to stopwords
add_stop_words = ['like','im','know','just','thats','people','youre','think','yeah','said','year','years','yes']
# add new stop words
stop_words = text.ENGLISH_STOP_WORDS.union(add_stop_words)
# re-create document-term matrix
cvn = CountVectorizer(stop_words=stop_words) # using the new stopwords
data_cvn = cvn.fit_transform(data_nouns.transcript) # apply into column transcript
data_dtmn = pd.DataFrame(data_cvn.toarray(),columns=cvn.get_feature_names()) # create another df with the words and frequency
data_dtmn.index = data_nouns.index # use the index from df
data_dtmn
# create the gensim corpus
corpusn = matutils.Sparse2Corpus(scipy.sparse.csr_matrix(data_dtmn.transpose()))
# create the vocabulary dictionary
id2wordn = dict((v,k) for k,v in cvn.vocabulary_.items())
# lets start with 4 topics
ldan = models.LdaModel(corpus=corpusn, num_topics=4, id2word=id2wordn, passes=10)
ldan.print_topics()
```
# Attempt #3 - Only Nouns/Adjectives
```
def nouns_adj(text):
'''Give a string of text, tokenize the text and pull out only the nouns or adjetives'''
is_noun_adj = lambda pos:pos[:2] == "NN" or pos[:2] == "JJ"
tokenized = word_tokenize(text)
nouns_adj = [word for word,pos in pos_tag(tokenized) if is_noun_adj(pos)]
return ' '.join(nouns_adj)
# apply the nouns function to the transcript to filter only nouns or adjetives
data_nouns_adj = pd.DataFrame(data_clean.transcript.apply(nouns_adj))
data_nouns_adj
# create a new document-term matrix using only nouns and adjectives, remore common words
# re-create document-term matrix
cvna = CountVectorizer(stop_words=stop_words, max_df=.8) # using the new stopwords
data_cvna = cvna.fit_transform(data_nouns_adj.transcript) # apply into column transcript
data_dtmna = pd.DataFrame(data_cvna.toarray(),columns=cvna.get_feature_names()) # create another df with the words and frequency
data_dtmna.index = data_nouns_adj.index # use the index from df
data_dtmna
# create the gensim corpus
corpusna = matutils.Sparse2Corpus(scipy.sparse.csr_matrix(data_dtmna.transpose()))
# create the vocabulary dictionary
id2wordna = dict((v,k) for k,v in cvna.vocabulary_.items())
# lets start with 4 topics
ldana = models.LdaModel(corpus=corpusna, num_topics=4, id2word=id2wordna, passes=10)
ldana.print_topics()
```
# Identify Topics in Each Document
```
# Our final LDA model
ldna = models.LdaModel(corpus=corpusna, num_topics=4, id2word=id2wordna, passes=80)
ldana.print_topics()
```
### Topics
#### Topic 0: train,wife,chinese,asian
#### Topic 1: indian, russel, asian, chinese
#### Topic 2: coronavirus, mask, helicopter, president, meeting, cold
#### Topic 3: indian, russel, nose, son, india
```
# Now, take a look at which topic each transcript contains
corpus_transformed = ldana[corpusna]
list(zip([a for [(a,b)] in corpus_transformed], data_dtmna.index))
```
### Topics
#### Topic 0: train,wife,chinese,asian ->Ronny
#### Topic 1: indian, russel, asian, chinese ->Nobody
#### Topic 2: coronavirus, mask, helicopter, president, meeting, cold ->Dave
#### Topic 3: indian, russel, nose, son, india ->Russel
| true |
code
| 0.442155 | null | null | null | null |
|
# Text Similarity
<div class="alert alert-info">
This tutorial is available as an IPython notebook at [Malaya/example/similarity](https://github.com/huseinzol05/Malaya/tree/master/example/similarity).
</div>
<div class="alert alert-info">
This module trained on both standard and local (included social media) language structures, so it is save to use for both.
</div>
```
%%time
import malaya
string1 = 'Pemuda mogok lapar desak kerajaan prihatin isu iklim'
string2 = 'Perbincangan isu pembalakan perlu babit kerajaan negeri'
string3 = 'kerajaan perlu kisah isu iklim, pemuda mogok lapar'
string4 = 'Kerajaan dicadang tubuh jawatankuasa khas tangani isu alam sekitar'
news1 = 'Tun Dr Mahathir Mohamad mengakui pembubaran Parlimen bagi membolehkan pilihan raya diadakan tidak sesuai dilaksanakan pada masa ini berikutan isu COVID-19'
tweet1 = 'DrM sembang pilihan raya tak boleh buat sebab COVID 19'
```
### Calculate similarity using doc2vec
We can use any word vector interface provided by Malaya to use doc2vec similarity interface.
Important parameters,
1. `aggregation`, aggregation function to accumulate word vectors. Default is `mean`.
* ``'mean'`` - mean.
* ``'min'`` - min.
* ``'max'`` - max.
* ``'sum'`` - sum.
* ``'sqrt'`` - square root.
2. `similarity` distance function to calculate similarity. Default is `cosine`.
* ``'cosine'`` - cosine similarity.
* ``'euclidean'`` - euclidean similarity.
* ``'manhattan'`` - manhattan similarity.
#### Using word2vec
I will use `load_news`, word2vec from wikipedia took a very long time. wikipedia much more accurate.
```
vocab_news, embedded_news = malaya.wordvector.load_news()
w2v = malaya.wordvector.load(embedded_news, vocab_news)
doc2vec = malaya.similarity.doc2vec(w2v)
```
#### predict for 2 strings
```
doc2vec.predict_proba([string1], [string2], aggregation = 'mean', soft = False)
```
#### predict batch of strings
```
doc2vec.predict_proba([string1, string2], [string3, string4])
```
#### visualize heatmap
```
doc2vec.heatmap([string1, string2, string3, string4])
```
Different similarity function different percentage.
### Calculate similarity using deep encoder
We can use any encoder models provided by Malaya to use encoder similarity interface, example, BERT, XLNET, and skip-thought. Again, these encoder models not trained to do similarity classification, it just encode the strings into vector representation.
Important parameters,
1. `similarity` distance function to calculate similarity. Default is `cosine`.
* ``'cosine'`` - cosine similarity.
* ``'euclidean'`` - euclidean similarity.
* ``'manhattan'`` - manhattan similarity.
#### using xlnet
```
xlnet = malaya.transformer.load(model = 'xlnet')
encoder = malaya.similarity.encoder(xlnet)
```
#### predict for 2 strings
```
encoder.predict_proba([string1], [string2])
```
#### predict batch of strings
```
encoder.predict_proba([string1, string2, news1, news1], [string3, string4, husein, string1])
```
#### visualize heatmap
```
encoder.heatmap([string1, string2, string3, string4])
```
### List available Transformer models
```
malaya.similarity.available_transformer()
```
We trained on [Quora Question Pairs](https://github.com/huseinzol05/Malay-Dataset#quora), [translated SNLI](https://github.com/huseinzol05/Malay-Dataset#snli) and [translated MNLI](https://github.com/huseinzol05/Malay-Dataset#mnli)
Make sure you can check accuracy chart from here first before select a model, https://malaya.readthedocs.io/en/latest/Accuracy.html#similarity
**You might want to use ALXLNET, a very small size, 49MB, but the accuracy is still on the top notch.**
### Load transformer model
In this example, I am going to load `alxlnet`, feel free to use any available models above.
```
model = malaya.similarity.transformer(model = 'alxlnet')
```
### Load Quantized model
To load 8-bit quantized model, simply pass `quantized = True`, default is `False`.
We can expect slightly accuracy drop from quantized model, and not necessary faster than normal 32-bit float model, totally depends on machine.
```
quantized_model = malaya.similarity.transformer(model = 'alxlnet', quantized = True)
```
#### predict batch
```python
def predict_proba(self, strings_left: List[str], strings_right: List[str]):
"""
calculate similarity for two different batch of texts.
Parameters
----------
string_left : List[str]
string_right : List[str]
Returns
-------
result : List[float]
"""
```
you need to give list of left strings, and list of right strings.
first left string will compare will first right string and so on.
similarity model only supported `predict_proba`.
```
model.predict_proba([string1, string2, news1, news1], [string3, string4, tweet1, string1])
quantized_model.predict_proba([string1, string2, news1, news1], [string3, string4, tweet1, string1])
```
#### visualize heatmap
```
model.heatmap([string1, string2, string3, string4])
```
### Vectorize
Let say you want to visualize sentences in lower dimension, you can use `model.vectorize`,
```python
def vectorize(self, strings: List[str]):
"""
Vectorize list of strings.
Parameters
----------
strings : List[str]
Returns
-------
result: np.array
"""
```
```
texts = [string1, string2, string3, string4, news1, tweet1]
r = quantized_model.vectorize(texts)
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
tsne = TSNE().fit_transform(r)
tsne.shape
plt.figure(figsize = (7, 7))
plt.scatter(tsne[:, 0], tsne[:, 1])
labels = texts
for label, x, y in zip(
labels, tsne[:, 0], tsne[:, 1]
):
label = (
'%s, %.3f' % (label[0], label[1])
if isinstance(label, list)
else label
)
plt.annotate(
label,
xy = (x, y),
xytext = (0, 0),
textcoords = 'offset points',
)
```
### Stacking models
More information, you can read at https://malaya.readthedocs.io/en/latest/Stack.html
If you want to stack zero-shot classification models, you need to pass labels using keyword parameter,
```python
malaya.stack.predict_stack([model1, model2], List[str], strings_right = List[str])
```
We will passed `strings_right` as `**kwargs`.
```
alxlnet = malaya.similarity.transformer(model = 'alxlnet')
albert = malaya.similarity.transformer(model = 'albert')
tiny_bert = malaya.similarity.transformer(model = 'tiny-bert')
malaya.stack.predict_stack([alxlnet, albert, tiny_bert], [string1, string2, news1, news1],
strings_right = [string3, string4, tweet1, string1])
```
| true |
code
| 0.565239 | null | null | null | null |
|
### Machine Learning for Engineers: [DecisionTree](https://www.apmonitor.com/pds/index.php/Main/DecisionTree)
- [Decision Tree](https://www.apmonitor.com/pds/index.php/Main/DecisionTree)
- Source Blocks: 4
- Description: Introduction to Decision Tree
- [Course Overview](https://apmonitor.com/pds)
- [Course Schedule](https://apmonitor.com/pds/index.php/Main/CourseSchedule)
```
from sklearn.tree import DecisionTreeClassifier
dtree = DecisionTreeClassifier(max_depth=10,random_state=101,\
max_features=None,min_samples_leaf=5)
dtree.fit(XA,yA)
yP = dtree.predict(XB)
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier(max_depth=10,random_state=101,\
max_features=None,min_samples_leaf=5)
# The digits dataset
digits = datasets.load_digits()
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
# Split into train and test subsets (50% each)
X_train, X_test, y_train, y_test = train_test_split(
data, digits.target, test_size=0.5, shuffle=False)
# Learn the digits on the first half of the digits
classifier.fit(X_train, y_train)
# Test on second half of data
n = np.random.randint(int(n_samples/2),n_samples)
print('Predicted: ' + str(classifier.predict(digits.data[n:n+1])[0]))
# Show number
plt.imshow(digits.images[n], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
# Split a dataset based on an attribute and an attribute value
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
# Calculate the Gini index for a split dataset
def gini_index(groups, classes):
# count all samples at split point
n_instances = float(sum([len(group) for group in groups]))
# sum weighted Gini index for each group
gini = 0.0
for group in groups:
size = float(len(group))
# avoid divide by zero
if size == 0:
continue
score = 0.0
# score the group based on the score for each class
for class_val in classes:
p = [row[-1] for row in group].count(class_val) / size
score += p * p
# weight the group score by its relative size
gini += (1.0 - score) * (size / n_instances)
return gini
# Select the best split point for a dataset
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1):
for row in dataset:
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
if gini < b_score:
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
# Create a terminal node value
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key=outcomes.count)
# Create child splits for a node or make terminal
def split(node, max_depth, min_size, depth):
left, right = node['groups']
del(node['groups'])
# check for a no split
if not left or not right:
node['left'] = node['right'] = to_terminal(left + right)
return
# check for max depth
if depth >= max_depth:
node['left'], node['right'] = to_terminal(left), to_terminal(right)
return
# process left child
if len(left) <= min_size:
node['left'] = to_terminal(left)
else:
node['left'] = get_split(left)
split(node['left'], max_depth, min_size, depth+1)
# process right child
if len(right) <= min_size:
node['right'] = to_terminal(right)
else:
node['right'] = get_split(right)
split(node['right'], max_depth, min_size, depth+1)
# Build a decision tree
def build_tree(train, max_depth, min_size):
root = get_split(train)
split(root, max_depth, min_size, 1)
return root
# Print a decision tree
def print_tree(node, depth=0):
if isinstance(node, dict):
print('%s[X%d < %.3f]' % ((depth*' ', (node['index']+1), node['value'])))
print_tree(node['left'], depth+1)
print_tree(node['right'], depth+1)
else:
print('%s[%s]' % ((depth*' ', node)))
dataset = [[2.771244718,1.784783929,0],
[1.728571309,1.169761413,0],
[3.678319846,2.81281357,0],
[3.961043357,2.61995032,0],
[2.999208922,2.209014212,0],
[7.497545867,3.162953546,1],
[9.00220326,3.339047188,1],
[7.444542326,0.476683375,1],
[10.12493903,3.234550982,1],
[6.642287351,3.319983761,1]]
tree = build_tree(dataset, 1, 1)
print_tree(tree)
# Make a prediction with a decision tree
def predict(node, row):
if row[node['index']] < node['value']:
if isinstance(node['left'], dict):
return predict(node['left'], row)
else:
return node['left']
else:
if isinstance(node['right'], dict):
return predict(node['right'], row)
else:
return node['right']
# predict with a stump
stump = {'index': 0, 'right': 1, 'value': 6.642287351, 'left': 0}
for row in dataset:
prediction = predict(stump, row)
print('Expected=%d, Got=%d' % (row[-1], prediction))
```
| true |
code
| 0.514888 | null | null | null | null |
|
### Stock Market Prediction And Forecasting Using Stacked LSTM
### Import the Libraries
```
import numpy as np
import pandas as pd
from pandas_datareader import data, wb
from pandas.util.testing import assert_frame_equal
import matplotlib.pyplot as plt
import seaborn as sns
import tensorflow as tf
import math
import datetime
import plotly
import cufflinks as cf
cf.go_offline()
%matplotlib inline
```
### Set Duration
```
start = datetime.datetime(2015, 7, 11)
end = datetime.datetime(2020, 7, 11)
```
### Import the data using DataReader
```
df = data.DataReader("GOOG",'yahoo',start,end)
df.head()
df.tail()
```
### Exploratory Data Analysis
#### Maximum Closing Rate
```
df.xs(key='Close',axis=1).max()
```
#### Visualization (Closing Rate)
```
df.xs(key='Close',axis=1).iplot()
```
#### 30-day Moving Average for Close Price
```
plt.figure(figsize=(12,5))
df['Close'].loc['2019-07-10':'2020-07-10'].rolling(window=30).mean().plot(label='30 Day Moving Avg.')
df['Close'].loc['2019-07-10':'2020-07-10'].plot(label='Close')
plt.legend()
df0 = df[['Open','High','Low','Close']].loc['2019-07-10':'2020-07-10']
df0.iplot(kind='candle')
df['Close'].loc['2019-07-10':'2020-07-10'].ta_plot(study='sma',periods=[9,18,27])
```
#### Let's Reset the Index to Close
```
df1=df.reset_index()['Close']
df1
```
#### Using MinMaxScaler
```
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler(feature_range=(0,1))
df1=scaler.fit_transform(np.array(df1).reshape(-1,1))
print(df1)
```
#### Splitting the Close data into Train and Test sets
```
training_size=int(len(df1)*0.70)
test_size=len(df1)-training_size
train_data,test_data=df1[0:training_size,:],df1[training_size:len(df1),:1]
training_size,test_size
train_data
# convert an array of values into a dataset matrix
def create_dataset(dataset, time_step=1):
dataX, dataY = [], []
for i in range(len(dataset)-time_step-1):
a = dataset[i:(i+time_step), 0] ###i=0, 0,1,2,3-----99 100
dataX.append(a)
dataY.append(dataset[i + time_step, 0])
return np.array(dataX), np.array(dataY)
# reshape into X=t,t+1,t+2,t+3 and Y=t+4
time_step = 100
X_train, y_train = create_dataset(train_data, time_step)
X_test, y_test = create_dataset(test_data, time_step)
print(X_train.shape), print(y_train.shape)
print(X_test.shape), print(y_test.shape)
# reshape input to be [samples, time steps, features] which is required for LSTM
X_train =X_train.reshape(X_train.shape[0],X_train.shape[1] , 1)
X_test = X_test.reshape(X_test.shape[0],X_test.shape[1] , 1)
```
### Stacked LSTM Model
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import LSTM
model=Sequential()
model.add(LSTM(50,return_sequences=True,input_shape=(100,1)))
model.add(LSTM(50,return_sequences=True))
model.add(LSTM(50))
model.add(Dense(1))
model.compile(loss='mean_squared_error',optimizer='adam')
model.summary()
model.summary()
model.fit(X_train,y_train,validation_data=(X_test,y_test),epochs=100,batch_size=64,verbose=1)
```
### Lets Predict
```
train_predict=model.predict(X_train)
test_predict=model.predict(X_test)
# Transformback to original form
train_predict=scaler.inverse_transform(train_predict)
test_predict=scaler.inverse_transform(test_predict)
### Calculate RMSE performance metrics
from sklearn.metrics import mean_squared_error
math.sqrt(mean_squared_error(y_train,train_predict))
### Test Data RMSE
math.sqrt(mean_squared_error(y_test,test_predict))
```
### Let's Visualize the Predictions
```
# shift train predictions for plotting
look_back=100
trainPredictPlot = np.empty_like(df1)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[look_back:len(train_predict)+look_back, :] = train_predict
# shift test predictions for plotting
testPredictPlot = np.empty_like(df1)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(train_predict)+(look_back*2)+1:len(df1)-1, :] = test_predict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(df1))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
len(test_data)
x_input=test_data[278:].reshape(1,-1)
x_input.shape
temp_input=list(x_input)
temp_input=temp_input[0].tolist()
temp_input
# demonstrate prediction for next 10 days
from numpy import array
lst_output=[]
n_steps=100
i=0
while(i<30):
if(len(temp_input)>100):
#print(temp_input)
x_input=np.array(temp_input[1:])
print("{} day input {}".format(i,x_input))
x_input=x_input.reshape(1,-1)
x_input = x_input.reshape((1, n_steps, 1))
#print(x_input)
yhat = model.predict(x_input, verbose=0)
print("{} day output {}".format(i,yhat))
temp_input.extend(yhat[0].tolist())
temp_input=temp_input[1:]
#print(temp_input)
lst_output.extend(yhat.tolist())
i=i+1
else:
x_input = x_input.reshape((1, n_steps,1))
yhat = model.predict(x_input, verbose=0)
print(yhat[0])
temp_input.extend(yhat[0].tolist())
print(len(temp_input))
lst_output.extend(yhat.tolist())
i=i+1
print(lst_output)
```
### Predictions for Next 30 Days
```
day_new=np.arange(1,101)
day_pred=np.arange(101,131)
len(df1)
plt.plot(day_new,scaler.inverse_transform(df1[1160:]))
plt.plot(day_pred,scaler.inverse_transform(lst_output))
df3=df1.tolist()
df3.extend(lst_output)
plt.plot(df3[1200:])
df3=scaler.inverse_transform(df3).tolist()
plt.plot(df3)
```
**CONCLUSION:** Here, we can see that the predictions seem to be close to Perfect. The Error rates are pretty low which acts as a good sign for our model.
| true |
code
| 0.574156 | null | null | null | null |
|
```
%matplotlib inline
import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt
```
### Skewness
---
The <font color='red'>skewness</font> of a random variable is defined as
\begin{equation*}
\beta_1 = \mathrm{E}\left[\left(\frac{X-\mu}{\sigma}\right)^3\right],
\end{equation*}
where $\mu=\mathrm{E}[X]$ and $\sigma^2=\mathrm{Var}[X]$.
The skewness $\beta_1$ tells whether the distribution is symmetric around the mean $\mu$ or not.
+ If $\beta_1>0$, the distribution has a longer tail on the right.
+ If $\beta_1<0$, the distribution has a longer tail on the left.
+ If $\beta_1=0$, the distribution is symmetric around the mean $\mu$.
```
fig1 = plt.figure(num=1, facecolor='w')
x = np.linspace(-5.0, 5.0, 201)
plt.plot(x, st.skewnorm.pdf(x, 8.0, loc=-3.0, scale=2.0), 'b-', label='Positive Skew')
plt.plot(x, st.skewnorm.pdf(x, -8.0, loc=3.0, scale=2.0), 'r-', label='Negative Skew')
plt.plot(x, st.norm.pdf(x), 'g-', label='Symmetric')
plt.xlim((-5.0, 7.0))
plt.ylim((0.0, 0.42))
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend(loc='upper right', frameon=False)
# plt.savefig('ms_fig_skewness.eps', dpi=600)
plt.show()
```
### Skew Normal Distribution
$$
f(x|\alpha,\mu,\sigma) = \frac{2}{\sigma}\phi\left(\frac{x-\mu}{\sigma}\right)\Phi\left(\frac{\alpha(x-\mu)}{\sigma}\right),
$$
where
$$
\phi(x) = \frac1{\sqrt{2\pi}}e^{-\frac{x^2}2},\quad
\Phi(x) = \int_{-\infty}^x\phi(z)dx.
$$
Reference:
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.skewnorm.html
### Kurtosis
---
The <fond color='red'>kurtosis</font> of a random variable is defined as
$$
\beta_2 = \mathrm{E}\left[\left(\frac{X-\mu}{\sigma}\right)^4\right],
$$
where $\mu=\mathbf{E}[X]$ and $\sigma^2=\mathrm{Var}[X]$.
The kurtosis $\beta_2$ is a measurement of thickness/heaveiness of the tail.
Note that the kurtosis of the normal distribution is 3. Since the kurtosis of the normal distribution is 3, $\beta_2-3$ is often used as a measurement on whether the distribution has a thicker tail than the normal distribution, which is called the <font color='red'>excess kurtosis</font>.
+ If $\beta_2>3$, the distribution has a thicker tail (<font color='red'>leptokurtic</font>).
+ If $\beta_2<3$, the distribution has a thinner tail (<font color='red'>platykurtic</font>).
```
from scipy.special import gamma
fig2 = plt.figure(num=2, facecolor='w')
x = np.linspace(-5.0, 5.0, 201)
plt.plot(x, st.gennorm.pdf(x, 1.0, scale=np.sqrt(gamma(1.0)/gamma(3.0))),
'b-', label='Leptokurtic')
plt.plot(x, st.gennorm.pdf(x, 8.0, scale=np.sqrt(gamma(1.0/8.0)/gamma(3.0/8.0))),
'r-', label='Platykurtic')
plt.plot(x, st.norm.pdf(x), 'g-', label='Normal')
plt.xlim((-5.0, 5.0))
plt.ylim((0.0, 0.73))
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend(loc='upper right', frameon=False)
# plt.savefig('ms_fig_kurtosis.eps', dpi=600)
plt.show()
```
### Generalized Normal (Error) Distribution
$$
f(x|\beta,\mu,\sigma) = \frac{\beta}{2\sigma\Gamma(1/\beta)}\exp\left[-\left|\frac{x-\mu}{\sigma}\right|^\beta\right].
$$
Reference:
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.gennorm.html
| true |
code
| 0.648299 | null | null | null | null |
|
# Composite
Can a composite pattern make templating easier?
## Templating
There are three template targets:
* plain text
* PDF
* Word
That's because some of the uses for this are lawyers that use Word documents.
I'm building the templating system up from low principles, because everyone tries to start in the middle and I've never found or built a templating system that I've been satisfied with. That's partly because it's an end-user product that's quite finicky. In a tool where you can do anything, anything we do to it can have brittle consequences.
Still, the goal is to provide merged documents in a safe way.
## Workflow
A good system will have:
* a valid source document
* a valid set of instructions to merge
* validation on inputs, even partial ones
* conditional sections of documents, based on the dataset
* incremental control over merging (partial merges OK)
* clear instructions when something failed
* document lifecycle, including versions
* the ability to target text, PDF, and Word
* support from the document and inputs to clean up and guide the process
If that's what I want generally, a composite only adds a tree to the system.
## Embedments
Embedments are basically fields, with foreign code and some smart collections of operations. Using a composite of embedments, we are saying there's a tree of instructions, one instruction per field. That may be the wrong way to think of the problem, considering the real problem defined in Workflow.
The Composite comes from the GoF Composite Pattern. The Embedment comes from Martin Fowler's Domain Specific Languages.
## Basic Model
The basic model uses a Component, Composite, and Leaf to create an operational workflow.
The original source on this can be [found here](https://sourcemaking.com/design_patterns/composite/python/1)
```
import abc
class Component(metaclass=abc.ABCMeta):
@abc.abstractmethod
def operation(self):
pass
class Composite(Component):
def __init__(self):
self._children = set()
def operation(self):
for child in self._children:
child.operation()
def add(self, component):
self._children.add(component)
def remove(self, component):
self._children.discard(component)
class Leaf(Component):
def operation(self):
pass
class L1(Leaf):
def operation(self):
print(id(self))
composite = Composite()
composite.add(L1())
composite.add(L1())
composite.operation()
root = Composite()
b1 = Composite()
l1 = L1()
l2 = L1()
b1.add(l1)
b1.add(l2)
root.add(b1)
b2 = Composite()
b2.add(l2)
root.add(b2)
root.operation()
```
### Making Sense
Strengths:
* a leaf can work with state
* Component can be state smart
Modifications:
* can pass/share state so leaves can work from a collective state
* work with a tree and a builder of some sort
```
import re
import abc
from collections.abc import Iterable
from functools import partial
def listify(o):
if o is None: return []
if isinstance(o, list): return o
if isinstance(o, str): return [o]
if isinstance(o, dict): return [o]
if isinstance(o, Iterable): return list(o)
return [o]
class Component(metaclass=abc.ABCMeta):
@abc.abstractmethod
def __call__(self):
pass
class Composite(Component):
@classmethod
def build(cls, components, **kw):
return cls(**kw).add(components)
def __init__(self, **kw):
self._children = []
self.sort_key = kw.get('key')
@property
def sorter(self):
if self.sort_key is None: return sorted
return partial(sorted, key=self.sort_key)
def add(self, components):
if not isinstance(components, Iterable): components = [components]
self._children = list(self.sorter(self._children + components))
return self
def remove(self, components):
if not isinstance(components, Iterable): components = [components]
for component in components:
self._children.remove(component)
return self
@property
def length(self):
return sum([child.length for child in self._children])
def __call__(self, *a, **kw):
for child in self._children:
child(*a, **kw)
def __repr__(self):
return f"{self.__class__.__name__}: {self.length} leaves"
class Leaf(Composite):
@classmethod
def hydrate(cls, item):
if isinstance(item, cls): return item
if isinstance(item, dict): return cls(**item)
return cls(item)
@classmethod
def build(cls, items):
items = listify(items)
leaves = [cls.hydrate(item) for item in items]
return Composite.build(leaves)
length = 1
def __call__(self, *a, **kw):
pass
class NaiveEmbedment(Leaf):
def __init__(self, name=None, pattern=None, **kw):
self.name = name
self.pattern = re.compile(name if pattern is None else pattern)
self.kw = kw
def __call__(self, document, replacement, *a, **kw):
return re.sub(self.pattern, replacement, document)
def __repr__(self):
return f"{self.__call__.__name__}: {self.name} {self.pattern}"
class InsertEmbedment(Leaf):
@classmethod
def build(cls, items):
items = listify(items)
leaves = [cls.hydrate(item) for item in items]
return Composite.build(leaves, key=lambda e: e.location)
def __init__(self, location, name=None, **kw):
self.location = location
self.name = name
self.offset = kw.get('offset', 0)
self.kw = kw
def __call__(self, document, text, *a, **kw):
offset = kw.get('offset', self.offset)
position = self.location + offset
self.offset = offset + len(text)
result = document[:position] + text + document[position:]
print(result)
return result
def __repr__(self):
return f"{self.__class__.__name__} {self.location}"
r = re.compile('foo')
doc = "foo bar baz foo bar foo"
NaiveEmbedment('foo')(doc, 'ccc')
s = InsertEmbedment.build([15, 10, 5])
s(doc, 'abc')
s = InsertEmbedment(12, name='incomplete')
print(s(doc, 'xxx '))
s.offset
```
### Making Sense
So, the embedment composite is different:
* uses call
* has some builders and a hydration mechanism
* addresses a sort
This makes it easier to assemble, but it's still lacking clarity:
* all the steps?
* error control?
* executable/valid?
* state/incremental process?
Also, it's hard to say what an embedment should be doing. There's the possiblity of knowing a location, or a slice that should be replaced, but that's difficult. It might be right to have a difficult embedment if the environment needs to learn those kinds of things, and it's easier to get a slice or a location from another tool. Compared to a Jinja template, though, it's opaque. There needs to be confidence from the other tool that this is the right way to address the source document.
This makes sense for use cases like:
* Given a text document, want to programatically build a template rather than pre-build it.
* Given a PDF document, want to create an overlay set of fields.
* Given a document and an ML model, I want to see if I can build a fieldset and survey pair.
## Embedments Composite
Embedments is a verb for what a field does. It applies code to embed itself.
* All embedments work on documents.
* Allow embedments to have an order.
* A simple embedment can apply text to a position in the document.
* The position is relative to the original location, or something easier to use.
```
class TextEmbedment:
def __init__(self, *a, **kw):
self.kw = kw
@property
def prior_offset(self):
return self.kw.get('offset', 0)
@property
def posterior_offset(self):
if hasattr(self, 'text'):
length = len(self.text)
else:
lengt = 0
return self.offset + length
def _get(self, name):
return getattr(self, name) + self.prior_offset
class PlainEmbedment(TextEmbedment):
def __init__(self, position, text, **kw):
self.position = position
self.text = text
self.kw = kw
def __call__(self, document):
position = self._get('position')
return document[:position] + self.text + document[position:]
class ReplacingEmbedment(TextEmbedment):
def __init__(self, begin, end, text, **kw):
self.begin = begin
self.end = end
self.text = text
self.kw = kw
def __call__(self, document):
begin = self._get('begin')
end = self._get('end')
return document[:begin] + self.text + document[end:]
document = "This is a document."
embedment = PlainEmbedment(10, 'nice ')
assert embedment(document) == "This is a nice document."
embedment = ReplacingEmbedment(8, 9, 'one fine')
assert embedment(document) == 'This is one fine document.'
```
### Making Sense
If I know where something goes, I can apply it. Therefore:
* Learn where something goes by an easier standard (encode what I know when I decide to add a field).
* Create a chain of embedments.
* Store and use the incrementing offset to apply the embedment to the right location.
* Use validation and error control throughout.
## Regular Expression Field Identity
I'm thinking that a hint could be used in a document. Say, field1 is a document marker. I can create a regular expression with a function and then ensure it's unique. If it's a stable identifier, great. If not, use the keywords to make a better regular expression. Default keywords make it obvious what I'm looking for.
I need an obvious way to see how these locations are being developed. Transparency.
```
import re
def match_count(r, doc, **kw):
if not isinstance(r, re.Pattern): r = re.compile(r)
return len(r.findall(doc))
def is_stable(r, docs, **kw):
if not isinstance(docs, list): docs = [docs]
counts = [match_count(r, doc) == 1 for doc in docs]
return all(counts)
def location_for(r, doc, **kw):
if not isinstance(r, re.Pattern): r = re.compile(r)
if not is_stable(r, doc, **kw): return (0, 0)
return r.search(doc).span()
def insertion_point_for(r, doc, **kw):
begin, _end = location_for(r, doc, **kw)
return begin
def replacing_embedment(r, value, doc, **kw):
begin, end = location_for(r, doc, **kw)
return ReplacingEmbedment(begin, end, value)
doc = "uber super duper doc"
field = "super"
r = re.compile(field)
assert match_count(r, doc) == 1
assert match_count(field, doc) == 1
assert is_stable(field, doc)
assert is_stable('uper', doc) is False
assert location_for(r, doc) == (5, 10)
e = replacing_embedment(r, 'fantastic', doc)
# e('fantastic', doc)
e(doc)
```
### FIXME
Fix this: an embedment without the replacement? I don't like this, but it's almost there.
## Jinja Templates
I can create templates out of Jinja instead.
Benefits:
* no guesswork on fields
* loops, conditions, logic
* stable, well-executed
Costs:
* larger framework
* not a stepping stone to PDF models
### Not Here
I'm not going to fully explore Jinja templates here. I don't want to leave that stuff in this lab right now. Better to come back to this, but leaving notes here. The template I threw away came from the [Jinja documentation](https://jinja.palletsprojects.com/en/2.11.x/).
```
# from jinja2 import Environment, PackageLoader, select_autoescape
# title = "Some Title"
# class User:
# def __init__(self, url, username):
# self.url = url
# self.username = username
# users = [User('http://example.com', 'Some User')]
# env = Environment(
# loader=PackageLoader('slip_box', 'templates'),
# autoescape=select_autoescape(['html', 'xml'])
# )
# template = env.get_template('test.html')
# print(template.render(title=title, users=users))
```
| true |
code
| 0.695648 | null | null | null | null |
|
<h1> Preprocessing using tf.transform and Dataflow </h1>
This notebook illustrates:
<ol>
<li> Creating datasets for Machine Learning using tf.transform and Dataflow
</ol>
<p>
While Pandas is fine for experimenting, for operationalization of your workflow, it is better to do preprocessing in Apache Beam. This will also help if you need to preprocess data in flight, since Apache Beam also allows for streaming.
<p>
Only specific combinations of TensorFlow/Beam are supported by tf.transform. So make sure to get a combo that is.
* TFT 0.4.0
* TF 1.4 or higher
* Apache Beam [GCP] 2.2.0 or higher
```
%bash
pip uninstall -y google-cloud-dataflow
pip install --upgrade --force tensorflow_transform==0.4.0 apache-beam[gcp]
%bash
pip freeze | grep -e 'flow\|beam'
```
You need to restart your kernel to register the new installs running the below cells
```
import tensorflow as tf
import apache_beam as beam
print(tf.__version__)
# change these to try this notebook out
BUCKET = 'cloud-training-demos-ml'
PROJECT = 'cloud-training-demos'
REGION = 'us-central1'
import os
os.environ['BUCKET'] = BUCKET
os.environ['PROJECT'] = PROJECT
os.environ['REGION'] = REGION
!gcloud config set project $PROJECT
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/; then
gsutil mb -l ${REGION} gs://${BUCKET}
fi
```
<h2> Save the query from earlier </h2>
The data is natality data (record of births in the US). My goal is to predict the baby's weight given a number of factors about the pregnancy and the baby's mother. Later, we will want to split the data into training and eval datasets. The hash of the year-month will be used for that.
```
query="""
SELECT
weight_pounds,
is_male,
mother_age,
mother_race,
plurality,
gestation_weeks,
mother_married,
ever_born,
cigarette_use,
alcohol_use,
FARM_FINGERPRINT(CONCAT(CAST(YEAR AS STRING), CAST(month AS STRING))) AS hashmonth
FROM
publicdata.samples.natality
WHERE year > 2000
"""
import google.datalab.bigquery as bq
df = bq.Query(query + " LIMIT 100").execute().result().to_dataframe()
df.head()
```
<h2> Create ML dataset using tf.transform and Dataflow </h2>
<p>
Let's use Cloud Dataflow to read in the BigQuery data and write it out as CSV files. Along the way, let's use tf.transform to do scaling and transforming. Using tf.transform allows us to save the metadata to ensure that the appropriate transformations get carried out during prediction as well.
<p>
Note that after you launch this, the notebook won't show you progress. Go to the GCP webconsole to the Dataflow section and monitor the running job. It took about <b>30 minutes</b> for me. If you wish to continue without doing this step, you can copy my preprocessed output:
<pre>
gsutil -m cp -r gs://cloud-training-demos/babyweight/preproc_tft gs://your-bucket/
</pre>
```
%writefile requirements.txt
tensorflow-transform==0.4.0
import datetime
import apache_beam as beam
import tensorflow_transform as tft
from tensorflow_transform.beam import impl as beam_impl
def preprocess_tft(inputs):
import copy
import numpy as np
def center(x):
return x - tft.mean(x)
result = copy.copy(inputs) # shallow copy
result['mother_age_tft'] = center(inputs['mother_age'])
result['gestation_weeks_centered'] = tft.scale_to_0_1(inputs['gestation_weeks'])
result['mother_race_tft'] = tft.string_to_int(inputs['mother_race'])
return result
#return inputs
def cleanup(rowdict):
import copy, hashlib
CSV_COLUMNS = 'weight_pounds,is_male,mother_age,mother_race,plurality,gestation_weeks,mother_married,cigarette_use,alcohol_use'.split(',')
STR_COLUMNS = 'key,is_male,mother_race,mother_married,cigarette_use,alcohol_use'.split(',')
FLT_COLUMNS = 'weight_pounds,mother_age,plurality,gestation_weeks'.split(',')
# add any missing columns, and correct the types
def tofloat(value, ifnot):
try:
return float(value)
except (ValueError, TypeError):
return ifnot
result = {
k : str(rowdict[k]) if k in rowdict else 'None' for k in STR_COLUMNS
}
result.update({
k : tofloat(rowdict[k], -99) if k in rowdict else -99 for k in FLT_COLUMNS
})
# modify opaque numeric race code into human-readable data
races = dict(zip([1,2,3,4,5,6,7,18,28,39,48],
['White', 'Black', 'American Indian', 'Chinese',
'Japanese', 'Hawaiian', 'Filipino',
'Asian Indian', 'Korean', 'Samaon', 'Vietnamese']))
if 'mother_race' in rowdict and rowdict['mother_race'] in races:
result['mother_race'] = races[rowdict['mother_race']]
else:
result['mother_race'] = 'Unknown'
# cleanup: write out only the data we that we want to train on
if result['weight_pounds'] > 0 and result['mother_age'] > 0 and result['gestation_weeks'] > 0 and result['plurality'] > 0:
data = ','.join([str(result[k]) for k in CSV_COLUMNS])
result['key'] = hashlib.sha224(data).hexdigest()
yield result
def preprocess(query, in_test_mode):
import os
import os.path
import tempfile
import tensorflow as tf
from apache_beam.io import tfrecordio
from tensorflow_transform.coders import example_proto_coder
from tensorflow_transform.tf_metadata import dataset_metadata
from tensorflow_transform.tf_metadata import dataset_schema
from tensorflow_transform.beam.tft_beam_io import transform_fn_io
job_name = 'preprocess-babyweight-features' + '-' + datetime.datetime.now().strftime('%y%m%d-%H%M%S')
if in_test_mode:
import shutil
print 'Launching local job ... hang on'
OUTPUT_DIR = './preproc_tft'
shutil.rmtree(OUTPUT_DIR, ignore_errors=True)
else:
print 'Launching Dataflow job {} ... hang on'.format(job_name)
OUTPUT_DIR = 'gs://{0}/babyweight/preproc_tft/'.format(BUCKET)
import subprocess
subprocess.call('gsutil rm -r {}'.format(OUTPUT_DIR).split())
options = {
'staging_location': os.path.join(OUTPUT_DIR, 'tmp', 'staging'),
'temp_location': os.path.join(OUTPUT_DIR, 'tmp'),
'job_name': job_name,
'project': PROJECT,
'max_num_workers': 24,
'teardown_policy': 'TEARDOWN_ALWAYS',
'no_save_main_session': True,
'requirements_file': 'requirements.txt'
}
opts = beam.pipeline.PipelineOptions(flags=[], **options)
if in_test_mode:
RUNNER = 'DirectRunner'
else:
RUNNER = 'DataflowRunner'
# set up metadata
raw_data_schema = {
colname : dataset_schema.ColumnSchema(tf.string, [], dataset_schema.FixedColumnRepresentation())
for colname in 'key,is_male,mother_race,mother_married,cigarette_use,alcohol_use'.split(',')
}
raw_data_schema.update({
colname : dataset_schema.ColumnSchema(tf.float32, [], dataset_schema.FixedColumnRepresentation())
for colname in 'weight_pounds,mother_age,plurality,gestation_weeks'.split(',')
})
raw_data_metadata = dataset_metadata.DatasetMetadata(dataset_schema.Schema(raw_data_schema))
def read_rawdata(p, step, test_mode):
if step == 'train':
selquery = 'SELECT * FROM ({}) WHERE MOD(ABS(hashmonth),4) < 3'.format(query)
else:
selquery = 'SELECT * FROM ({}) WHERE MOD(ABS(hashmonth),4) = 3'.format(query)
if in_test_mode:
selquery = selquery + ' LIMIT 100'
#print 'Processing {} data from {}'.format(step, selquery)
return (p
| '{}_read'.format(step) >> beam.io.Read(beam.io.BigQuerySource(query=selquery, use_standard_sql=True))
| '{}_cleanup'.format(step) >> beam.FlatMap(cleanup)
)
# run Beam
with beam.Pipeline(RUNNER, options=opts) as p:
with beam_impl.Context(temp_dir=os.path.join(OUTPUT_DIR, 'tmp')):
# analyze and transform training
raw_data = read_rawdata(p, 'train', in_test_mode)
raw_dataset = (raw_data, raw_data_metadata)
transformed_dataset, transform_fn = (
raw_dataset | beam_impl.AnalyzeAndTransformDataset(preprocess_tft))
transformed_data, transformed_metadata = transformed_dataset
_ = transformed_data | 'WriteTrainData' >> tfrecordio.WriteToTFRecord(
os.path.join(OUTPUT_DIR, 'train'),
coder=example_proto_coder.ExampleProtoCoder(
transformed_metadata.schema))
# transform eval data
raw_test_data = read_rawdata(p, 'eval', in_test_mode)
raw_test_dataset = (raw_test_data, raw_data_metadata)
transformed_test_dataset = (
(raw_test_dataset, transform_fn) | beam_impl.TransformDataset())
transformed_test_data, _ = transformed_test_dataset
_ = transformed_test_data | 'WriteTestData' >> tfrecordio.WriteToTFRecord(
os.path.join(OUTPUT_DIR, 'eval'),
coder=example_proto_coder.ExampleProtoCoder(
transformed_metadata.schema))
_ = (transform_fn
| 'WriteTransformFn' >>
transform_fn_io.WriteTransformFn(os.path.join(OUTPUT_DIR, 'metadata')))
job = p.run()
if in_test_mode:
job.wait_until_finish()
print "Done!"
preprocess(query, in_test_mode=False)
%bash
gsutil ls gs://${BUCKET}/babyweight/preproc_tft/*-00000*
```
Copyright 2017 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.372334 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/rim-yu/Keras-GAN/blob/master/team_project_dcgan.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
https://blog.naver.com/dong961015/221839396386 참고하였음.
```
from __future__ import print_function, division
from keras.datasets import mnist
from keras.layers import Input, Dense, Reshape, Flatten, Dropout
from keras.layers import BatchNormalization, Activation, ZeroPadding2D
from keras.layers.advanced_activations import LeakyReLU
from keras.layers.convolutional import UpSampling2D, Conv2D
from keras.models import Sequential, Model
from keras.optimizers import Adam
from keras.preprocessing import image
import glob
import matplotlib.pyplot as plt
import sys
import numpy as np
# 드라이브 마운트 후
path = glob.glob("/content/drive/Shared drives/team-project/team-project_rim/texts_jpg_original/*.jpg")
def load_image(path):
image_list = np.zeros((len(path), 28, 28, 1))
for i, fig in enumerate(path):
# target_size = (세로길이, 가로길이)
img = image.load_img(fig, color_mode='grayscale', target_size=(28, 28))
x = image.img_to_array(img).astype('float32')
image_list[i] = x
return image_list
a = image.load_img("/content/drive/Shared drives/team-project/team-project_rim/texts_jpg_original/GimhaeGayaR.jpg", color_mode='grayscale', target_size=(28, 28))
b = image.img_to_array(a).astype('float32')
print(b.shape)
a
class DCGAN():
def __init__(self):
# Input shape
self.img_rows = 28
self.img_cols = 28
self.channels = 1
self.img_shape = (self.img_rows, self.img_cols, self.channels)
self.latent_dim = 100
optimizer = Adam(0.0002, 0.5)
# Build and compile the discriminator
self.discriminator = self.build_discriminator()
self.discriminator.compile(loss='binary_crossentropy',
optimizer=optimizer,
metrics=['accuracy'])
# Build the generator
self.generator = self.build_generator()
# The generator takes noise as input and generates imgs
z = Input(shape=(self.latent_dim,))
img = self.generator(z)
# For the combined model we will only train the generator
self.discriminator.trainable = False
# The discriminator takes generated images as input and determines validity
valid = self.discriminator(img)
# The combined model (stacked generator and discriminator)
# Trains the generator to fool the discriminator
self.combined = Model(z, valid)
self.combined.compile(loss='binary_crossentropy', optimizer=optimizer)
def build_generator(self):
model = Sequential()
model.add(Dense(128 * 7 * 7, activation="relu", input_dim=self.latent_dim))
model.add(Reshape((7, 7, 128)))
model.add(UpSampling2D())
model.add(Conv2D(128, kernel_size=3, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(Activation("relu"))
model.add(UpSampling2D())
model.add(Conv2D(64, kernel_size=3, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(Activation("relu"))
model.add(Conv2D(self.channels, kernel_size=3, padding="same"))
model.add(Activation("tanh"))
model.summary()
noise = Input(shape=(self.latent_dim,))
img = model(noise)
return Model(noise, img)
def build_discriminator(self):
model = Sequential()
model.add(Conv2D(32, kernel_size=3, strides=2, input_shape=self.img_shape, padding="same"))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(64, kernel_size=3, strides=2, padding="same"))
model.add(ZeroPadding2D(padding=((0,1),(0,1))))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(128, kernel_size=3, strides=2, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(256, kernel_size=3, strides=1, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(1, activation='sigmoid'))
model.summary()
img = Input(shape=self.img_shape)
validity = model(img)
return Model(img, validity)
def train(self, epochs, batch_size=128, save_interval=50):
# Load the dataset
X_train = load_image(path)
# Rescale -1 to 1
X_train = X_train / 127.5 - 1.
X_train = np.expand_dims(X_train, axis=3)
# Adversarial ground truths
valid = np.ones((batch_size, 1))
fake = np.zeros((batch_size, 1))
for epoch in range(epochs):
# ---------------------
# Train Discriminator
# ---------------------
# Select a random half of images
idx = np.random.randint(0, X_train.shape[0], batch_size)
imgs = X_train[idx]
# Sample noise and generate a batch of new images
noise = np.random.normal(0, 1, (batch_size, self.latent_dim))
gen_imgs = self.generator.predict(noise)
# Train the discriminator (real classified as ones and generated as zeros)
d_loss_real = self.discriminator.train_on_batch(imgs, valid)
d_loss_fake = self.discriminator.train_on_batch(gen_imgs, fake)
d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)
# ---------------------
# Train Generator
# ---------------------
# Train the generator (wants discriminator to mistake images as real)
g_loss = self.combined.train_on_batch(noise, valid)
# Plot the progress
print ("%d [D loss: %f, acc.: %.2f%%] [G loss: %f]" % (epoch, d_loss[0], 100*d_loss[1], g_loss))
# If at save interval => save generated image samples
if epoch % save_interval == 0:
self.save_imgs(epoch)
def save_imgs(self, epoch):
r, c = 5, 5
noise = np.random.normal(0, 1, (r * c, self.latent_dim))
gen_imgs = self.generator.predict(noise)
# Rescale images 0 - 1
gen_imgs = 0.5 * gen_imgs + 0.5
fig, axs = plt.subplots(r, c)
cnt = 0
for i in range(r):
for j in range(c):
axs[i,j].imshow(gen_imgs[cnt, :,:,0], cmap='gray')
axs[i,j].axis('off')
cnt += 1
#fig.savefig("images/mnist_%d.png" % epoch)
fig.savefig("/content/drive/My Drive/team-project/images/picture_%d.png" % epoch)
plt.close()
if __name__ == '__main__':
dcgan = DCGAN()
dcgan.train(epochs=4000, batch_size=32, save_interval=50)
class DCGAN():
def __init__(self):
# 들어올 이미지 사이즈 설정
self.img_rows = 28
self.img_cols = 28
self.channels = 1
self.img_shape = (self.img_rows, self.img_cols, self.channels)
self.latent_dim = 100
optimizer = Adam(0.0002, 0.5)
# Build and compile the discriminator
self.discriminator = self.build_discriminator()
self.discriminator.compile(loss='binary_crossentropy',
optimizer=optimizer,
metrics=['accuracy'])
# Build the generator
self.generator = self.build_generator()
# The generator takes noise as input and generates imgs
z = Input(shape=(self.latent_dim,))
img = self.generator(z)
# For the combined model we will only train the generator
self.discriminator.trainable = False
# The discriminator takes generated images as input and determines validity
valid = self.discriminator(img)
# The combined model (stacked generator and discriminator)
# Trains the generator to fool the discriminator
self.combined = Model(z, valid)
self.combined.compile(loss='binary_crossentropy', optimizer=optimizer)
def build_generator(self):
model = Sequential()
model.add(Dense(128 * 64 * 64, activation="relu", input_dim=self.latent_dim))
model.add(Reshape((64, 64, 128)))
model.add(UpSampling2D())
model.add(Conv2D(128, kernel_size=3, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(Activation("relu"))
model.add(UpSampling2D())
model.add(Conv2D(64, kernel_size=3, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(Activation("relu"))
model.add(Conv2D(self.channels, kernel_size=3, padding="same"))
model.add(Activation("tanh"))
model.summary()
noise = Input(shape=(self.latent_dim,))
img = model(noise)
return Model(noise, img)
def build_discriminator(self):
model = Sequential()
model.add(Conv2D(32, kernel_size=3, strides=2, input_shape=self.img_shape, padding="same"))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(64, kernel_size=3, strides=2, padding="same"))
model.add(ZeroPadding2D(padding=((0,1),(0,1))))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(128, kernel_size=3, strides=2, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(256, kernel_size=3, strides=1, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(1, activation='sigmoid'))
model.summary()
img = Input(shape=self.img_shape)
validity = model(img)
return Model(img, validity)
def train(self, epochs, batch_size=128, save_interval=50):
# Load the dataset
X_train=load_image(path)
# Rescale -1 to 1
X_train = X_train / 127.5 - 1.
# Adversarial ground truths
valid = np.ones((batch_size, 1))
fake = np.zeros((batch_size, 1))
for epoch in range(epochs):
# ---------------------
# Train Discriminator
# ---------------------
# Select a random half of images
idx = np.random.randint(0, X_train.shape[0], batch_size)
imgs = X_train[idx]
# Sample noise and generate a batch of new images
noise = np.random.normal(0, 1, (batch_size, self.latent_dim))
gen_imgs = self.generator.predict(noise)
# Train the discriminator (real classified as ones and generated as zeros)
d_loss_real = self.discriminator.train_on_batch(imgs, valid)
d_loss_fake = self.discriminator.train_on_batch(gen_imgs, fake)
d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)
# ---------------------
# Train Generator
# ---------------------
# Train the generator (wants discriminator to mistake images as real)
g_loss = self.combined.train_on_batch(noise, valid)
# Plot the progress
print ("%d [D loss: %f, acc.: %.2f%%] [G loss: %f]" % (epoch, d_loss[0], 100*d_loss[1], g_loss))
# If at save interval => save generated image samples
if epoch % save_interval == 0:
self.save_imgs(epoch)
#생성되는 이미지를 epoch50번 할때마다 저장
def save_imgs(self, epoch):
r, c = 5, 5
noise = np.random.normal(0, 1, (r * c, self.latent_dim))
gen_imgs = self.generator.predict(noise)
# Rescale images 0 - 1
gen_imgs = 0.5 * gen_imgs + 0.5
fig, axs = plt.subplots(r, c)
cnt = 0
for i in range(r):
for j in range(c):
axs[i,j].imshow(gen_imgs[cnt, :,:,0], cmap='gray')
axs[i,j].axis('off')
cnt += 1
plt.savefig("/content/drive/My Drive/team-project/images/picture_%d.png" % epoch)
plt.close()
if __name__ == '__main__':
dcgan = DCGAN()
dcgan.train(epochs=4000, batch_size=32, save_interval=50)
```
| true |
code
| 0.839487 | null | null | null | null |
|
# Variational Monte Carlo with Neural Networks
In this tutorial we will use NetKet to obtain the ground state of the J1-J2 model in one-dimension with periodic boundary conditions, using a Neural Network variational wave-function. The Hamiltonian of the model is given by:
$$ H = \sum_{i=1}^{L} J_{1}\vec{\sigma}_{i} \cdot \vec{\sigma}_{i+1} + J_{2} \vec{\sigma}_{i} \cdot \vec{\sigma}_{i+2} $$
where the sum is over sites of the 1-D chain. Here $\vec{\sigma}=(\sigma^x,\sigma^y,\sigma^z)$ is the vector of Pauli matrices.
We will also explore some useful functionalities provided by the package.
## Objectives:
1. Defining custom Hamiltonians
2. Defining the machine (variational ansatz)
3. Variational Monte Carlo Optimisation
4. Measuring observables
5. Data Visualisation
6. Sanity Check: Exact Diagonalisation
Let's start.
```
# ensure we run on the CPU
import os
os.environ["JAX_PLATFORM_NAME"] = "cpu"
# Import netket library
import netket as nk
# Helper libraries
import numpy as np
import matplotlib.pyplot as plt
```
## 1) Defining a Custom Hamiltonian
The first thing to do is to define the graph (lattice) on which to specify the Hamiltonian. Here we would like to build a one-dimensional graph with both nearest and next nearest neighbour bonds. The graph is created in the ``nk.graph.CustomGraph`` class. To initialise the class we simply provide a list of edges in the ``[[site_i, site_j, edge_color], ...]``
```
#Couplings J1 and J2
J = [1, 0.2]
L = 14
# Define custom graph
edge_colors = []
for i in range(L):
edge_colors.append([i, (i+1)%L, 1])
edge_colors.append([i, (i+2)%L, 2])
# Define the netket graph object
g = nk.graph.Graph(edges=edge_colors)
```
We specify a different ``color`` for each type of bond so as to define a different operator for each of them.
Next, we define the relevant bond operators.
```
#Sigma^z*Sigma^z interactions
sigmaz = [[1, 0], [0, -1]]
mszsz = (np.kron(sigmaz, sigmaz))
#Exchange interactions
exchange = np.asarray([[0, 0, 0, 0], [0, 0, 2, 0], [0, 2, 0, 0], [0, 0, 0, 0]])
bond_operator = [
(J[0] * mszsz).tolist(),
(J[1] * mszsz).tolist(),
(-J[0] * exchange).tolist(),
(J[1] * exchange).tolist(),
]
bond_color = [1, 2, 1, 2]
```
**Side Remark**: Notice the minus sign in front of the exchange. This is simply a basis rotation corresponding to the Marshall sign rule (as an exercise, change the sign of this exchange and observe that the exact diagonalization results in Section 6 do not change). The goal of this basis rotation is to speed up the convergence of the Monte Carlo simulations of the wave-function (by providing a good variational sign structure to start with), but in principle the converged results should be identical in both bases. Note further that this sign change is useful at low frustration (such as here $J_2=0.2$), but may actually be not optimal at stronger frustration. As a bonus exercise, repeat the calculation with $J_2=0.8$, and see which basis (*i.e.* which sign in front of the exchange) leads to faster convergence.
Before defining the Hamiltonian, we also need to specify the Hilbert space. For our case, this would be the chain spin-half degrees of freedom.
```
# Spin based Hilbert Space
hi = nk.hilbert.Spin(s=0.5, total_sz=0.0, N=g.n_nodes)
```
Note that we impose here the total magnetization to be zero (it turns out to be the correct magnetization for the ground-state). As an exercise, check that the energy of the lowest state in other magnetization sectors is larger.
Next, we define the custom graph Hamiltonian using the ``nk.operator.GraphOperator`` class, by providing the hilbert space ``hi``, the bond operators ``bondops=bond_operator`` and the corresponding bond color ``bondops_colors=bond_color``. The information about the graph (bonds and bond colors) are contained within the ``nk.hilbert.Spin`` object ``hi``.
```
# Custom Hamiltonian operator
op = nk.operator.GraphOperator(hi, graph=g, bond_ops=bond_operator, bond_ops_colors=bond_color)
```
## 2) Defining the Machine
For this tutorial, we shall use the most common type of neural network: fully connected feedforward neural network ``nk.machine.FFNN``. Other types of neural networks available will be discussed in other tutorials.
```
import netket.nn as nknn
import jax.numpy as jnp
class FFNN(nknn.Module):
@nknn.compact
def __call__(self, x):
x = nknn.Dense(features=2*x.shape[-1], use_bias=True, dtype=np.complex128, kernel_init=nknn.initializers.normal(stddev=0.01), bias_init=nknn.initializers.normal(stddev=0.01))(x)
x = nknn.log_cosh(x)
x = jnp.sum(x, axis=-1)
return x
model = FFNN()
```
## 3) Variational Monte Carlo Optimisation
We have now set up our model (Hamiltonian, Graph, Hilbert Space) and can proceed to optimise the variational ansatz we chose, namely the ``ffnn`` machine.
To setup the variational Monte Carlo optimisation tool, we have to provide a sampler ``nk.sampler`` and an optimizer ``nk.optimizer``.
```
# We shall use an exchange Sampler which preserves the global magnetization (as this is a conserved quantity in the model)
sa = nk.sampler.MetropolisExchange(hilbert=hi, graph=g, d_max = 2)
# Construct the variational state
vs = nk.variational.MCState(sa, model, n_samples=1000)
# We choose a basic, albeit important, Optimizer: the Stochastic Gradient Descent
opt = nk.optimizer.Sgd(learning_rate=0.01)
# Stochastic Reconfiguration
sr = nk.optimizer.SR(diag_shift=0.01)
# We can then specify a Variational Monte Carlo object, using the Hamiltonian, sampler and optimizers chosen.
# Note that we also specify the method to learn the parameters of the wave-function: here we choose the efficient
# Stochastic reconfiguration (Sr), here in an iterative setup
gs = nk.VMC(hamiltonian=op, optimizer=opt, variational_state=vs, preconditioner=sr)
```
## 4) Measuring Observables
Before running the optimization, it can be helpful to add some observables to keep track off during the optimization. For our purpose, let us measure the antiferromagnetic structure factor, defined as:
$$ \frac{1}{L} \sum_{ij} \langle \hat{\sigma}_{i}^z \cdot \hat{\sigma}_{j}^z\rangle e^{i\pi(i-j)}$$.
```
# We need to specify the local operators as a matrix acting on a local Hilbert space
sf = []
sites = []
structure_factor = nk.operator.LocalOperator(hi, dtype=complex)
for i in range(0, L):
for j in range(0, L):
structure_factor += (nk.operator.spin.sigmaz(hi, i)*nk.operator.spin.sigmaz(hi, j))*((-1)**(i-j))/L
```
Once again, notice that we had to multiply the exchange operator (matrix) by some factor. This is to account for the Marshall basis rotation we made in our model.
We can now optimize our variational ansatz. The optimization data for each iteration will be stored in a log file, which contains the following information:
1. Mean, variance and uncertainty in the Energy $ \langle \hat{H} \rangle $
2. Mean, variance and uncertainty in the Energy Variance, $ \langle\hat{H}^{2}\rangle-\langle \hat{H}\rangle^{2}$.
3. Acceptance rates of the sampler
4. Mean, variance and uncertainty of observables (if specified)
Now let's learn the ground-state!
```
# Run the optimization protocol
gs.run(out='test', n_iter=600, obs={'Structure Factor': structure_factor})
```
## 5) Data Visualisation
Now that we have optimized our machine to find the ground state of the $J_1-J_2$ model, let's look at what we have.
The relevant data are stored in the ".log" file while the optimized parameters are in the ".wf" file. The files are all in json format.
We shall extract the energy as well as specified observables (antiferromagnetic structure factor in our case) from the ".log" file.
```
# Load the data from the .log file
import json
data=json.load(open("test.log"))
iters = data['Energy']['iters']
energy=data['Energy']['Mean']['real']
sf=data['Structure Factor']['Mean']['real']
fig, ax1 = plt.subplots()
ax1.plot(iters, energy, color='blue', label='Energy')
ax1.set_ylabel('Energy')
ax1.set_xlabel('Iteration')
ax2 = ax1.twinx()
ax2.plot(iters, np.array(sf), color='green', label='Structure Factor')
ax2.set_ylabel('Structure Factor')
ax1.legend(loc=2)
ax2.legend(loc=1)
plt.show()
```
Let's also compute the average of those quantities (energy and neel order) over the last 50 iterations where the optimization seems to have converged.
```
print(r"Structure factor = {0:.3f}({1:.3f})".format(np.mean(sf[-50:]),
np.std(np.array(sf[-50:]))/np.sqrt(50)))
print(r"Energy = {0:.3f}({1:.3f})".format(np.mean(energy[-50:]), np.std(energy[-50:])/(np.sqrt(50))))
```
## 6) Sanity Check: Exact Diagonalisation
Now that we have obtained some results using VMC, it is a good time to check the quality of our results (at least for small system sizes). For this purpose, Netket provides exact diagonalisation tools.
```
E_gs, ket_gs = nk.exact.lanczos_ed(op, compute_eigenvectors=True)
structure_factor_gs = (ket_gs.T.conj()@structure_factor.to_linear_operator()@ket_gs).real[0,0]
```
Here we have specified that we want the corresponding eigenvector (in order to compute observables).
```
print("Exact Ground-state Structure Factor: {0:.3f}".format(structure_factor_gs))
print("Exact ground state energy = {0:.3f}".format(E_gs[0]))
```
So we see that the both energy and the structure factor we obtained is in agreement with the value obtained via exact diagonalisation.
| true |
code
| 0.687119 | null | null | null | null |
|
「PyTorch入門 8. クイックスタート」
===============================================================
【原題】Learn the Basics
【原著】
[Suraj Subramanian](https://github.com/suraj813)、[Seth Juarez](https://github.com/sethjuarez/) 、[Cassie Breviu](https://github.com/cassieview/) 、[Dmitry Soshnikov](https://soshnikov.com/)、[Ari Bornstein](https://github.com/aribornstein/)
【元URL】https://pytorch.org/tutorials/beginner/basics/quickstart_tutorial.html
【翻訳】電通国際情報サービスISID AIトランスフォーメーションセンター 小川 雄太郎
【日付】2021年03月20日
【チュトーリアル概要】
本チュートリアルでは、機械学習を実行するためのPyTorchの各APIを紹介します。詳細を知りたい方は、各セクションのリンク先をご参照ください。
---
【注意】
ディープラーニングフレームワークの経験があり、ディープラーニングの実装に慣れている方は、本チュートリアルをまず確認し、PyTorchのAPIに慣れてください。
<br>
ディープラーニングフレームワークを利用した実装に初めて取り組む方は、本チュートリアルからではなく、
[「PyTorch入門 1. テンソル」](https://colab.research.google.com/github/YutaroOgawa/pytorch_tutorials_jp/blob/main/notebook/0_Learn%20the%20Basics/1_1_tensor_tutorial_jp.ipynb)から、1 stepずつ進めてください。
---
データの取り扱い
-----------------
PyTorchではデータを取り扱う際に、基本的な要素が2つ存在します。
``torch.utils.data.Dataset``と``torch.utils.data.DataLoader``です。
<br>
``Dataset`` は各ラベルと、それに対応するサンプルデータを保持します。
``DataLoader`` は``Dataset``をイテレーティブに(=反復処理可能に)操作できるようラップしたものになります。
<br>
(詳細)
https://pytorch.org/docs/stable/data.html
```
%matplotlib inline
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor, Lambda, Compose
import matplotlib.pyplot as plt
```
PyTorchには以下に示すようなドメイン固有のライブラリが存在し、それぞれにデータセットが用意されています。
本チュートリアルでは、TorchVisionのデータセットを使用します。
- [TorchText](https://pytorch.org/text/stable/index.html)
- [TorchVision](https://pytorch.org/vision/stable/index.html)
- [TorchAudio](https://pytorch.org/audio/stable/index.html)
``torchvision.datasets`` モジュールには、画像データの ``Dataset`` オブジェクトがたくさん用意されています。
例えば、CIFAR, COCOなどです ([データセット一覧はこちらから](https://pytorch.org/docs/stable/torchvision/datasets.html))。
本チュートリアルでは、FashionMNISTデータセットを使用します。
TorchVisionの すべての``Dataset`` には2つの引数があります。
``transform`` と ``target_transform`` であり、それぞれサンプルとラベルの変換処理を行います。
```
# 訓練データをdatasetsからダウンロード
training_data = datasets.FashionMNIST(
root="data",
train=True,
download=True,
transform=ToTensor(),
)
# テストデータをdatasetsからダウンロード
test_data = datasets.FashionMNIST(
root="data",
train=False,
download=True,
transform=ToTensor(),
)
```
DataLoaderの引数としてDatasetを渡します。
DataLoaderはDatasetをイテレート処理できるようにラップしたものです。
バッチ処理、サンプリング、シャッフル、マルチプロセスでのデータ読み込み等をサポートしています。
以下では、バッチサイズを64と定義します。
つまり、データローダの反復要素は、64個の特徴量とラベルから構成されるバッチを返すことになります。
```
batch_size = 64
# データローダーの作成
train_dataloader = DataLoader(training_data, batch_size=batch_size)
test_dataloader = DataLoader(test_data, batch_size=batch_size)
for X, y in test_dataloader:
print("Shape of X [N, C, H, W]: ", X.shape)
print("Shape of y: ", y.shape, y.dtype)
break
```
さらなる詳細は、[「PyTorch入門 2. データセットとデータローダー」](https://colab.research.google.com/github/YutaroOgawa/pytorch_tutorials_jp/blob/main/notebook/0_Learn%20the%20Basics/0_2_data_tutorial_jp.ipynb
)をご覧ください。
--------------
モデルの構築
------------------
PyTorchでニューラルネットワークの形を定義する際には、[nn.Module](https://pytorch.org/docs/stable/generated/torch.nn.Module.html)を継承します。
``__init__`` 関数で、ネットワークの各レイヤーを定義し、データの順伝搬を``forward`` 関数に定義します。
なお処理を高速化するために、可能であればニューラルネットワークをGPU上へ移動させます。
```
# 訓練に際して、可能であればGPU(cuda)を設定します。GPUが搭載されていない場合はCPUを使用します
device = "cuda" if torch.cuda.is_available() else "cpu"
print("Using {} device".format(device))
# modelを定義します
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(28*28, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 10),
nn.ReLU()
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = NeuralNetwork().to(device)
print(model)
```
さらなる詳細は、[「PyTorch入門 4. モデル構築」](https://colab.research.google.com/github/YutaroOgawa/pytorch_tutorials_jp/blob/main/notebook/0_Learn%20the%20Basics/0_4_buildmodel_tutorial_js.ipynb
)をご覧ください。
--------------
モデルパラメータの最適化
----------------------------------------
ニューラルネットワークモデルを訓練するためには、
損失関数:[loss function](<https://pytorch.org/docs/stable/nn.html#loss-functions)と、最適化手法:[optimizer](https://pytorch.org/docs/stable/optim.html)が必要です。
```
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
```
1回の訓練ループにおいてモデルは、まず訓練データのバッチに対して推論を実行して損失誤差を計算し、
その後、損失誤差をバックプロパゲーションして、モデルパラメータを更新します。
```
def train(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
for batch, (X, y) in enumerate(dataloader):
X, y = X.to(device), y.to(device)
# 損失誤差を計算
pred = model(X)
loss = loss_fn(pred, y)
# バックプロパゲーション
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch % 100 == 0:
loss, current = loss.item(), batch * len(X)
print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
```
また、モデルがうまく学習していることを確認するために、テストデータセットに対するモデルの性能も確認します。
```
def test(dataloader, model):
size = len(dataloader.dataset)
model.eval()
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
X, y = X.to(device), y.to(device)
pred = model(X)
test_loss += loss_fn(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= size
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
```
訓練プロセスでは複数イテレーションを実行します。
各エポックの間、モデルはより良い予測ができるようにパラメータを学習します。
エポックごとにモデルの正解率と損失を出力して、正解率が向上し、損失が低下していっているかを確認します。
```
epochs = 5
for t in range(epochs):
print(f"Epoch {t+1}\n-------------------------------")
train(train_dataloader, model, loss_fn, optimizer)
test(test_dataloader, model)
print("Done!")
```
さらなる詳細は、[「PyTorch入門 6. 最適化」](https://colab.research.google.com/github/YutaroOgawa/pytorch_tutorials_jp/blob/main/notebook/0_Learn%20the%20Basics/0_6_optimization_tutorial_js.ipynb)をご覧ください。
--------------
モデルの保存
-------------
モデルを保存する一般的な方法は、モデルの内部状態の辞書(モデルのパラメータを含む)をシリアル化する手法です。
```
torch.save(model.state_dict(), "model.pth")
print("Saved PyTorch Model State to model.pth")
```
---
モデルの読み込み
----------------------------
モデルの読み込む際には、まずモデルの構造を再作成し、そのインスタンスに、保存しておいた状態辞書をロードします。
```
model = NeuralNetwork()
model.load_state_dict(torch.load("model.pth"))
```
これでモデルは推論可能な状態です。
```
classes = [
"T-shirt/top",
"Trouser",
"Pullover",
"Dress",
"Coat",
"Sandal",
"Shirt",
"Sneaker",
"Bag",
"Ankle boot",
]
model.eval()
x, y = test_data[0][0], test_data[0][1]
with torch.no_grad():
pred = model(x)
predicted, actual = classes[pred[0].argmax(0)], classes[y]
print(f'Predicted: "{predicted}", Actual: "{actual}"')
```
さらなる詳細は、[「PyTorch入門 7. モデルの保存・読み込み」](https://colab.research.google.com/github/YutaroOgawa/pytorch_tutorials_jp/blob/main/notebook/0_Learn%20the%20Basics/0_7_saveloadrun_tutorial_js.ipynb)をご覧ください。
以上。
| true |
code
| 0.781497 | null | null | null | null |
|
```
# helper functions
def plot_dataset(X, y, axes):
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.axis(axes)
plt.grid(True, which='both')
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
def plot_predictions(clf, axes):
x0s = np.linspace(axes[0], axes[1], 100)
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(x0s, x1s)
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
import matplotlib.pyplot as plt
import numpy as np
```
### Linear SVM Classification
You can think of an SVM classifier as fitting the widest possible street (represented by the parallel dashed lines) between the classes. This is called **large margin classification**.
Adding more training instances “off the street” will not affect the decision boundary at all: it is fully determined (or "supported") by the instances located on the
edge of the street. These instances are called the support vectors
SVMs are sensitive to the feature scales.
### Soft Margin Classification
If we strictly impose that all instances be off the street and on the right side, this is called **hard margin classification**. There are two main issues with hard margin classification. First, it only works if the data is linearly separable, and second it is quite sensitive to outliers
The objective is to find a good balance between keeping the street as large as possible and limiting the margin violations (i.e., instances that end up in the middle of the street or even on the wrong side). This is called so **margin classification**.
In Scikit-Learn’s SVM classes, you can control this balance using the C hyperparameter: a smaller C value leads to a wider street but more margin violations.
Using a high C value the classifier makes fewer margin violations but ends up with a smaller margin.
```
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]
y = (iris["target"] == 2).astype(np.float64)
svm_clf = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge")),
])
svm_clf.fit(X, y)
svm_clf.predict([[5.5, 1.7]])
```
### Nonlinear SVM Classification
Although linear SVM classifiers are efficient and work surprisingly well in many cases, many datasets are not even close to being linearly separable. One approach to handling nonlinear datasets is to add more features, such as polynomial features (as you did in Chapter 4); in some cases this can result in a linearly separable dataset.
```
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", max_iter=5000, random_state=42))
])
polynomial_svm_clf.fit(X, y)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
```
### Polynomial kernel
Adding polynomial features is simple to implement and can work great with all sorts of Machine Learning algorithms (not just SVMs), but at a low polynomial degree it cannot deal with very complex datasets, and with a high polynomial degree it creates a huge number of features, making the model too slow.
Fortunately, when using SVMs you can apply an almost miraculous mathematical technique called the kernel trick.
It makes it possible to get the same result as if you added many polynomial features, even with very highdegree polynomials, without actually having to add them. So there is no combinatorial explosion of the number of features since you don’t actually add any features. This trick is implemented by the SVC class.
```
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
```
The hyperparameter **coef0** controls how much the model is influenced by highdegree polynomials versus low-degree polynomials.
```
poly_kernel_svm_clf.fit(X, y)
poly100_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
poly100_kernel_svm_clf.fit(X, y)
fig, axes = plt.subplots(ncols=2, figsize=(11, 4), sharey=True)
plt.sca(axes[0])
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.45, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.4, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)
plt.sca(axes[1])
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.45, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.4, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)
plt.ylabel("")
```
### Adding Similarity Features
Another technique to tackle nonlinear problems is to add features computed using a ***similarity function*** that measures how much each instance resembles a particular ***landmark***
let’s define the similarity function to be the ***Gaussian Radial Basis Function (RBF)***
$\phi_{\gamma}(\mathbf{x}, ℓ) = exp \ (-\gamma \left\lVert \mathbf{x} - ℓ \right\rVert^2)$
It is a bell-shaped function varying from 0 (very far away from the landmark) to 1 (at
the landmark).
```
def gaussian_rbf(x, landmark, gamma):
return np.exp(-gamma * np.linalg.norm(x - landmark)**2)
print(gaussian_rbf(-1, -2, 0.3))
print(gaussian_rbf(-1, 1, 0.3))
```
Selecting the landmarks: The simplest approach is to create a
landmark at the location of each and every instance in the dataset. This creates many dimensions and thus increases the chances that the transformed training set will be linearly separable. The downside is that a training set with $m$ instances and $n$ features gets transformed into a training set with $m$ instances and $m$ features (assuming you drop the original features). If your training set is very large, you end up with an equally large number of features.
### Gaussian RBF Kernel
Just like the polynomial features method, the similarity features method can be useful with any Machine Learning algorithm, but it may be computationally expensive to compute all the additional features, especially on large training sets. However, once again the kernel trick does its SVM magic: it makes it possible to obtain a similar result as if you had added many similarity features, without actually having to add them.
```
rbf_kernel_svm_clf = Pipeline([
("scalar", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)
from sklearn.svm import SVC
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)
svm_clfs = []
for gamma, C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
])
rbf_kernel_svm_clf.fit(X, y)
svm_clfs.append(rbf_kernel_svm_clf)
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10.5, 7), sharex=True, sharey=True)
for i, svm_clf in enumerate(svm_clfs):
plt.sca(axes[i // 2, i % 2])
plot_predictions(svm_clf, [-1.5, 2.45, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.45, -1, 1.5])
gamma, C = hyperparams[i]
plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
if i in (0, 1):
plt.xlabel("")
if i in (1, 3):
plt.ylabel("")
```
### Regression
The SVM algorithm is quite versatile: not only does it support linear and nonlinear classification, but it also supports linear and nonlinear regression. The trick is to reverse the objective: >> instead of trying to fit the largest possible street between two classes while limiting margin violations, SVM Regression tries to fit as many instances as possible on the street while limiting margin violations (i.e., instances of the street). The width of the street is controlled by a hyperparameter $ϵ$.
```
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1)).ravel()
from sklearn.svm import LinearSVR
svm_reg1 = LinearSVR(epsilon=1.5, random_state=42)
svm_reg2 = LinearSVR(epsilon=0.5, random_state=42)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)
def find_support_vectors(svm_reg, X, y):
y_pred = svm_reg.predict(X)
off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
return np.argwhere(off_margin)
svm_reg1.support_ = find_support_vectors(svm_reg1, X, y)
svm_reg2.support_ = find_support_vectors(svm_reg2, X, y)
eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])
def plot_svm_regression(svm_reg, X, y, axes):
x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
y_pred = svm_reg.predict(x1s)
plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
plt.plot(X, y, "bo")
plt.xlabel(r"$x_1$", fontsize=18)
plt.legend(loc="upper left", fontsize=18)
plt.axis(axes)
fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_reg1, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.annotate(
'', xy=(eps_x1, eps_y_pred), xycoords='data',
xytext=(eps_x1, eps_y_pred - svm_reg1.epsilon),
textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
)
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.sca(axes[1])
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)
plt.show()
```
Adding more training instances within the margin does not affect the model’s predictions; thus, the model is said to be $ϵ-insensitive$.
```
# Non-linear regression tasks
np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()
from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", degree=2, C=100,
epsilon=0.1, gamma="scale")
svm_poly_reg.fit(X, y)
from sklearn.svm import SVR
svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1, gamma="scale")
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)
fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.sca(axes[1])
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)
plt.show()
```
| true |
code
| 0.650134 | null | null | null | null |
|
# 1. Description
This notebook will performe the subgrouping algorithm shown in Figure S1 in the paper "Prediction of the ICU mortality based on the missing events.".
# 2. Before running...
Before proceeding the followings, plaease solve the python environment accordingly first. This program requires the following libraries.
```
import pandas as pd # 1.2.1
import itertools
```
Then please put the related files at the appropriate directory so that the program reaches the input files. To test if you correctly set the input files, run the below. If you could, the cell would not end without errors.
```
input_ids = set(pd.read_csv("ids/004_sepsis_aps_4226.csv", header=None).iloc[:,0].tolist())
len(input_ids) # 4226
eICU_file = {}
eICU_file['apacheApsVar'] = pd.read_csv('data/apacheApsVar.csv')
eICU_file['apachePatientResult'] = pd.read_csv('data/apachePatientResult.csv')
eICU_file['apachePredVar'] = pd.read_csv('data/apachePredVar.csv')
eICU_file['patient'] = pd.read_csv('data/patient.csv')
```
For preparing the file "004_sepsis_aps_4226.csv", please follow this notebook (1_the_sepsis_group_and_non_sepsis_group.ipynb).<br>
<br>
For getting the eICU files, please see "https://www.usa.philips.com/healthcare/solutions/enterprise-telehealth/eri" or "https://eicu-crd.mit.edu/gettingstarted/access/".
# 3. Class definition
```
class status():
def __init__(self, df):
# df
self.df = df
self.df_thistime = pd.DataFrame([], columns=df.columns)
self.df_next = df
# ID
self.ids_all = set(df.patientunitstayid)
self.ids_thistime = set([])
self.ids_next = self.ids_all
# parameter
self.target = []
def remove(self, target):
self.target += target
# Update ID
tmp = set(self.df_next.drop(target, axis=1).where(self.df_next>=0).dropna().patientunitstayid)
self.ids_thistime |= tmp
self.ids_next -= tmp
# df thistime
self.df_thistime = self.df.drop(self.target, axis=1)
self.df_thistime = self.df_thistime.query("patientunitstayid in @ self.ids_thistime")
# df_next
self.df_next = self.df_next.drop(target, axis=1)
self.df_next = self.df_next.query("patientunitstayid in @ self.ids_next")
def get_next(self, depth):
# 1st and Last columns are not paramters
parameters = self.df_next.columns[1:-1]
# depth : the number of parameters to be excluded at once
combinations = [list(i) for i in itertools.combinations(parameters, depth)]
# # of non-NaN-records
num_non_nan = pd.DataFrame({
"__".join(comb) : [len(self.df_next.drop(comb, axis=1).where(self.df_next>=0).dropna())]
for comb in combinations
}).T
# "1 <= # of non-NaN-records < # of pids" is ideal.
tf = num_non_nan.applymap(lambda x : 1 <= x <= len(self.df_next) - 1)
if tf.any().any():
tmp = num_non_nan[tf]
return tmp.idxmax()[0]
else:
# "# of non-NaN-records == # of pids" is acceptable.
tf = num_non_nan.applymap(lambda x : 1 <= x <= len(self.df_next))
if tf.any().any():
tmp = num_non_nan[tf]
return tmp.idxmax()[0]
else:
# If there's no more parameteres, return nan
if len(parameters) == 1:
return "nan"
# If there's only NaN records, return ""
else:
return ""
```
# 4. Prepare DataFrame
## 4.1. Definition of variables used in this study
```
len(eICU_file['apachePatientResult'][eICU_file['apachePatientResult']["apacheversion"]=="IV"])
eICU_parm = {}
eICU_parm['apacheApsVar'] = [
'patientunitstayid',
'intubated',
'vent',
'dialysis',
'eyes',
'motor',
'verbal',
'meds',
'urine',
'wbc',
'temperature',
'respiratoryrate',
'sodium',
'heartrate',
'meanbp',
'ph',
'hematocrit',
'creatinine',
'albumin',
'pao2',
'pco2',
'bun',
'glucose',
'bilirubin',
'fio2'
]
eICU_parm['apachePatientResult'] = [
'patientunitstayid',
'apachescore',
'predictedicumortality',
'predictediculos',
'predictedhospitalmortality',
'predictedhospitallos',
'preopmi',
'preopcardiaccath',
'ptcawithin24h',
'predventdays'
]
eICU_parm['apachePredVar'] = [
'patientunitstayid',
'gender',
'teachtype',
'bedcount',
'graftcount',
'age',
'thrombolytics',
'aids',
'hepaticfailure',
'lymphoma',
'metastaticcancer',
'leukemia',
'immunosuppression',
'cirrhosis',
'ima',
'midur',
'ventday1',
'oobventday1',
'oobintubday1',
'diabetes'
]
eICU_parm['patient'] = [
'patientunitstayid',
'hospitalid',
'admissionheight',
'hospitaladmitoffset',
'admissionweight'
]
```
## 4.2. DataFrame
```
#========================================
# select columns and ids for each file
#========================================
eICU_df = {}
eICU_df['apacheApsVar'] = eICU_file['apacheApsVar'][eICU_parm['apacheApsVar']].query("patientunitstayid in @ input_ids")
eICU_df['apachePatientResult'] = eICU_file['apachePatientResult'][eICU_parm['apachePatientResult']].query("patientunitstayid in @ input_ids")
eICU_df['apachePredVar'] = eICU_file['apachePredVar'][eICU_parm['apachePredVar']].query("patientunitstayid in @ input_ids")
eICU_df['patient'] = eICU_file['patient'][eICU_parm['patient']].query("patientunitstayid in @ input_ids")
#========================================
# make column names unique
#========================================
# (column name -> filename + column name)
eICU_df['apacheApsVar'].columns = [
'apacheApsVar_' + parm if not parm=="patientunitstayid" else "patientunitstayid"
for parm in eICU_df['apacheApsVar'].columns
]
eICU_df['apachePatientResult'].columns = [
'apachePatientResult_' + parm if not parm=="patientunitstayid" else "patientunitstayid"
for parm in eICU_df['apachePatientResult'].columns
]
eICU_df['apachePredVar'].columns = [
'apachePredVar_' + parm if not parm=="patientunitstayid" else "patientunitstayid"
for parm in eICU_df['apachePredVar'].columns
]
eICU_df['patient'].columns = [
'patient_' + parm if not parm=="patientunitstayid" else "patientunitstayid"
for parm in eICU_df['patient'].columns
]
#========================================
# Make X
#========================================
# 1st column : key (patientunitstayid)
key = pd.DataFrame(list(input_ids), columns=["patientunitstayid"])
# 2nd~ column : parameters
key_X = pd.merge(key, eICU_df['apacheApsVar'], on="patientunitstayid")
key_X = pd.merge(key_X, eICU_df['apachePatientResult'], on="patientunitstayid")
key_X = pd.merge(key_X, eICU_df['apachePredVar'], on="patientunitstayid")
key_X = pd.merge(key_X, eICU_df['patient'], on="patientunitstayid")
#========================================
# Make X_y (df)
#========================================
# Last column : DEAD(=1) or ALIVE(=0)
y = eICU_file["apachePatientResult"][['patientunitstayid', 'actualicumortality']].replace('ALIVE',0).replace('EXPIRED',1)
key_X_y = pd.merge(key_X, y, on="patientunitstayid")
#========================================
# Rename
#========================================
df = key_X_y
len(df)
```
# 5. Subgrouping
```
df_status = status(df)
k=1
print("# of INPUT : ", len(df_status.ids_all), " patientunitstayids", "\n\n")
while 1:
print("##################################")
print(" Subgroup ",k)
print("##################################")
print("\n")
print("Checking the inputs...")
print("\n")
parms_tobe_excluded = []
#========================================
# Get Subgroup
#========================================
while not(500 <= len(df_status.ids_thistime) <= 2000):
parms = ""
# upto 3 parameters taken into account
for i in range(1,4):
parms = df_status.get_next(i)
# if parameters are found
if parms != "":
break
# If no paramteres found, Output "Time out" and Stop.
if parms == "":
print("Time Out\n")
df_status.df_next = pd.DataFrame()
break
# If too many nan, Output "Interpolation needed" and Stop
if parms == "nan":
print("Interpolation needed\n")
df_status.df_next = pd.DataFrame()
break
# Change format
parms = parms.split("__")
# Update
df_status.remove(parms)
parms_tobe_excluded += parms
print("--> ", [i.split("_")[1] for i in parms], " is/are selected to be excluded.\n")
print("--> ", ", ".join([i.split("_")[1] for i in parms_tobe_excluded]), " was/were excluded in the end.\n")
parms_tobe_excluded = []
df_A = pd.DataFrame()
if 500 <= len(df_status.ids_next):
print("--> ", len(df_status.ids_thistime), " patientunitstayids survived.\n")
df_A = df_status.df_thistime
df_status = status(df_status.df_next)
else:
# The rests pids are picked up and merged into thistime.
print("--> ", len(df_status.ids_thistime)+len(df_status.ids_next), " patientunitstayids survived.\n")
df_A = pd.concat([df_status.df_thistime, df_status.df_next])
df_status.ids_next = set([])
df_status.df_next = df_status.df_next.query("patientunitstayid in @ df_status.ids_next")
df_A = df_A.where(df_A>=0).dropna()
k+=1
if len(df_status.df_next) == 0:
break
```
| true |
code
| 0.219212 | null | null | null | null |
|
### TCLab Overview

### Generate Step Test Data
```
import numpy as np
import pandas as pd
import tclab
import time
import os.path
# generate step test data on Arduino
filename = 'data.csv'
# redo data collection?
redo = False
# check if file already exists
if os.path.isfile(filename) and (not redo):
print('File: '+filename+' already exists.')
print('Change redo=True to collect data again')
print('TCLab should be at room temperature at start')
else:
# heater steps
Q1d = np.zeros(601)
Q1d[10:200] = 80
Q1d[200:280] = 20
Q1d[280:400] = 70
Q1d[400:] = 50
Q2d = np.zeros(601)
Q2d[120:320] = 100
Q2d[320:520] = 10
Q2d[520:] = 80
# Connect to Arduino
a = tclab.TCLab()
fid = open(filename,'w')
fid.write('Time,Q1,Q2,T1,T2\n')
fid.close()
# run step test (10 min)
for i in range(601):
# set heater values
a.Q1(Q1d[i])
a.Q2(Q2d[i])
print('Time: ' + str(i) + \
' Q1: ' + str(Q1d[i]) + \
' Q2: ' + str(Q2d[i]) + \
' T1: ' + str(a.T1) + \
' T2: ' + str(a.T2))
# wait 1 second
time.sleep(1)
fid = open(filename,'a')
fid.write(str(i)+','+str(Q1d[i])+','+str(Q2d[i])+',' \
+str(a.T1)+','+str(a.T2)+'\n')
# close connection to Arduino
a.close()
fid.close()
```
### Plot Step Test Data
```
import matplotlib.pyplot as plt
%matplotlib inline
# read data file
filename = 'data.csv'
data = pd.read_csv(filename)
# plot measurements
plt.figure(figsize=(10,7))
plt.subplot(2,1,1)
plt.plot(data['Time'],data['Q1'],'r-',label='Heater 1')
plt.plot(data['Time'],data['Q2'],'b--',label='Heater 2')
plt.ylabel('Heater (%)')
plt.legend(loc='best')
plt.subplot(2,1,2)
plt.plot(data['Time'],data['T1'],'r.',label='Temperature 1')
plt.plot(data['Time'],data['T2'],'b.',label='Temperature 2')
plt.ylabel(r'Temperature ($^oC$)')
plt.legend(loc='best')
plt.xlabel('Time (sec)')
plt.savefig('data.png')
plt.show()
```
### Physics-based Model Prediction
```
!pip install gekko
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from gekko import GEKKO
from scipy.integrate import odeint
from scipy.interpolate import interp1d
# Import data
try:
# try to read local data file first
filename = 'data.csv'
data = pd.read_csv(filename)
except:
filename = 'http://apmonitor.com/pdc/uploads/Main/tclab_data2.txt'
data = pd.read_csv(filename)
# Fit Parameters of Energy Balance
m = GEKKO() # Create GEKKO Model
# Parameters to Estimate
U = m.FV(value=10,lb=1,ub=20)
Us = m.FV(value=20,lb=5,ub=40)
alpha1 = m.FV(value=0.01,lb=0.001,ub=0.03) # W / % heater
alpha2 = m.FV(value=0.005,lb=0.001,ub=0.02) # W / % heater
tau = m.FV(value=10.0,lb=5.0,ub=60.0)
# Measured inputs
Q1 = m.Param()
Q2 = m.Param()
Ta =23.0+273.15 # K
mass = 4.0/1000.0 # kg
Cp = 0.5*1000.0 # J/kg-K
A = 10.0/100.0**2 # Area not between heaters in m^2
As = 2.0/100.0**2 # Area between heaters in m^2
eps = 0.9 # Emissivity
sigma = 5.67e-8 # Stefan-Boltzmann
TH1 = m.SV()
TH2 = m.SV()
TC1 = m.CV()
TC2 = m.CV()
# Heater Temperatures in Kelvin
T1 = m.Intermediate(TH1+273.15)
T2 = m.Intermediate(TH2+273.15)
# Heat transfer between two heaters
Q_C12 = m.Intermediate(Us*As*(T2-T1)) # Convective
Q_R12 = m.Intermediate(eps*sigma*As*(T2**4-T1**4)) # Radiative
# Energy balances
m.Equation(TH1.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T1) \
+ eps * sigma * A * (Ta**4 - T1**4) \
+ Q_C12 + Q_R12 \
+ alpha1*Q1))
m.Equation(TH2.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T2) \
+ eps * sigma * A * (Ta**4 - T2**4) \
- Q_C12 - Q_R12 \
+ alpha2*Q2))
# Conduction to temperature sensors
m.Equation(tau*TC1.dt() == TH1-TC1)
m.Equation(tau*TC2.dt() == TH2-TC2)
# Options
# STATUS=1 allows solver to adjust parameter
U.STATUS = 1
Us.STATUS = 1
alpha1.STATUS = 1
alpha2.STATUS = 1
tau.STATUS = 1
Q1.value=data['Q1'].values
Q2.value=data['Q2'].values
TH1.value=data['T1'].values[0]
TH2.value=data['T2'].values[0]
TC1.value=data['T1'].values
TC1.FSTATUS = 1 # minimize fstatus * (meas-pred)^2
TC2.value=data['T2'].values
TC2.FSTATUS = 1 # minimize fstatus * (meas-pred)^2
m.time = data['Time'].values
m.options.IMODE = 5 # MHE
m.options.EV_TYPE = 2 # Objective type
m.options.NODES = 2 # Collocation nodes
m.options.SOLVER = 3 # IPOPT
m.solve(disp=False) # Solve
# Parameter values
print('U : ' + str(U.value[0]))
print('Us : ' + str(Us.value[0]))
print('alpha1: ' + str(alpha1.value[0]))
print('alpha2: ' + str(alpha2.value[-1]))
print('tau: ' + str(tau.value[0]))
sae = 0.0
for i in range(len(data)):
sae += np.abs(data['T1'][i]-TC1.value[i])
sae += np.abs(data['T2'][i]-TC2.value[i])
print('SAE Energy Balance: ' + str(sae))
# Create plot
plt.figure(figsize=(10,7))
ax=plt.subplot(2,1,1)
ax.grid()
plt.plot(data['Time'],data['T1'],'r.',label=r'$T_1$ measured')
plt.plot(m.time,TC1.value,color='black',linestyle='--',\
linewidth=2,label=r'$T_1$ energy balance')
plt.plot(data['Time'],data['T2'],'b.',label=r'$T_2$ measured')
plt.plot(m.time,TC2.value,color='orange',linestyle='--',\
linewidth=2,label=r'$T_2$ energy balance')
plt.ylabel(r'T ($^oC$)')
plt.legend(loc=2)
ax=plt.subplot(2,1,2)
ax.grid()
plt.plot(data['Time'],data['Q1'],'r-',\
linewidth=3,label=r'$Q_1$')
plt.plot(data['Time'],data['Q2'],'b:',\
linewidth=3,label=r'$Q_2$')
plt.ylabel('Heaters')
plt.xlabel('Time (sec)')
plt.legend(loc='best')
plt.savefig('Physics_fit.png')
```
### Determine FOPDT Parameters with Graphical Fit Widget
```
import numpy as np
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import ipywidgets as wg
from IPython.display import display
# try to read local data file first
try:
filename = 'data.csv'
data = pd.read_csv(filename)
except:
filename = 'http://apmonitor.com/pdc/uploads/Main/tclab_data2.txt'
data = pd.read_csv(filename)
n = 601 # time points to plot
tf = 600.0 # final time
# Use expected room temperature for initial condition
#y0 = [23.0,23.0]
# Use initial condition
y0d = [data['T1'].values[0],data['T2'].values[0]]
# load data
Q1 = data['Q1'].values
Q2 = data['Q2'].values
T1 = data['T1'].values
T2 = data['T2'].values
T1p = np.ones(n)*y0d[0]
T2p = np.ones(n)*y0d[1]
def process(y,t,u1,u2,Kp,Kd,taup):
y1,y2 = y
dy1dt = (1.0/taup) * (-(y1-y0d[0]) + Kp * u1 + Kd * (y2-y1))
dy2dt = (1.0/taup) * (-(y2-y0d[1]) + (Kp/2.0) * u2 + Kd * (y1-y2))
return [dy1dt,dy2dt]
def fopdtPlot(Kp,Kd,taup,thetap):
y0 = y0d
t = np.linspace(0,tf,n) # create time vector
iae = 0.0
# loop through all time steps
for i in range(1,n):
# simulate process for one time step
ts = [t[i-1],t[i]] # time interval
inputs = (Q1[max(0,i-int(thetap))],Q2[max(0,i-int(thetap))],Kp,Kd,taup)
y = odeint(process,y0,ts,args=inputs)
y0 = y[1] # record new initial condition
T1p[i] = y0[0]
T2p[i] = y0[1]
iae += np.abs(T1[i]-T1p[i]) + np.abs(T2[i]-T2p[i])
# plot FOPDT response
plt.figure(1,figsize=(15,7))
plt.subplot(2,1,1)
plt.plot(t,T1,'r.',linewidth=2,label='Temperature 1 (meas)')
plt.plot(t,T2,'b.',linewidth=2,label='Temperature 2 (meas)')
plt.plot(t,T1p,'r--',linewidth=2,label='Temperature 1 (pred)')
plt.plot(t,T2p,'b--',linewidth=2,label='Temperature 2 (pred)')
plt.ylabel(r'T $(^oC)$')
plt.text(200,20,'Integral Abs Error: ' + str(np.round(iae,2)))
plt.text(400,35,r'$K_p$: ' + str(np.round(Kp,0)))
plt.text(400,30,r'$K_d$: ' + str(np.round(Kd,0)))
plt.text(400,25,r'$\tau_p$: ' + str(np.round(taup,0)) + ' sec')
plt.text(400,20,r'$\theta_p$: ' + str(np.round(thetap,0)) + ' sec')
plt.legend(loc=2)
plt.subplot(2,1,2)
plt.plot(t,Q1,'b--',linewidth=2,label=r'Heater 1 ($Q_1$)')
plt.plot(t,Q2,'r:',linewidth=2,label=r'Heater 2 ($Q_2$)')
plt.legend(loc='best')
plt.xlabel('time (sec)')
Kp_slide = wg.FloatSlider(value=0.5,min=0.1,max=1.5,step=0.05)
Kd_slide = wg.FloatSlider(value=0.0,min=0.0,max=1.0,step=0.05)
taup_slide = wg.FloatSlider(value=50.0,min=50.0,max=250.0,step=5.0)
thetap_slide = wg.FloatSlider(value=0,min=0,max=30,step=1)
wg.interact(fopdtPlot, Kp=Kp_slide, Kd=Kd_slide, taup=taup_slide,thetap=thetap_slide)
print('FOPDT Simulator: Adjust Kp, Kd, taup, and thetap ' + \
'to achieve lowest Integral Abs Error')
```
### Determine FOPDT Parameters with Optimization
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.optimize import minimize
from scipy.interpolate import interp1d
# initial guesses
x0 = np.zeros(4)
x0[0] = 0.8 # Kp
x0[1] = 0.2 # Kd
x0[2] = 150.0 # taup
x0[3] = 10.0 # thetap
# Import CSV data file
# try to read local data file first
try:
filename = 'data.csv'
data = pd.read_csv(filename)
except:
filename = 'http://apmonitor.com/pdc/uploads/Main/tclab_data2.txt'
data = pd.read_csv(filename)
Q1_0 = data['Q1'].values[0]
Q2_0 = data['Q2'].values[0]
T1_0 = data['T1'].values[0]
T2_0 = data['T2'].values[0]
t = data['Time'].values - data['Time'].values[0]
Q1 = data['Q1'].values
Q2 = data['Q2'].values
T1 = data['T1'].values
T2 = data['T2'].values
# specify number of steps
ns = len(t)
delta_t = t[1]-t[0]
# create linear interpolation of the u data versus time
Qf1 = interp1d(t,Q1)
Qf2 = interp1d(t,Q2)
# define first-order plus dead-time approximation
def fopdt(T,t,Qf1,Qf2,Kp,Kd,taup,thetap):
# T = states
# t = time
# Qf1 = input linear function (for time shift)
# Qf2 = input linear function (for time shift)
# Kp = model gain
# Kd = disturbance gain
# taup = model time constant
# thetap = model time constant
# time-shift Q
try:
if (t-thetap) <= 0:
Qm1 = Qf1(0.0)
Qm2 = Qf2(0.0)
else:
Qm1 = Qf1(t-thetap)
Qm2 = Qf2(t-thetap)
except:
Qm1 = Q1_0
Qm2 = Q2_0
# calculate derivative
dT1dt = (-(T[0]-T1_0) + Kp*(Qm1-Q1_0) + Kd*(T[1]-T[0]))/taup
dT2dt = (-(T[1]-T2_0) + (Kp/2.0)*(Qm2-Q2_0) + Kd*(T[0]-T[1]))/taup
return [dT1dt,dT2dt]
# simulate FOPDT model
def sim_model(x):
# input arguments
Kp,Kd,taup,thetap = x
# storage for model values
T1p = np.ones(ns) * T1_0
T2p = np.ones(ns) * T2_0
# loop through time steps
for i in range(0,ns-1):
ts = [t[i],t[i+1]]
T = odeint(fopdt,[T1p[i],T2p[i]],ts,args=(Qf1,Qf2,Kp,Kd,taup,thetap))
T1p[i+1] = T[-1,0]
T2p[i+1] = T[-1,1]
return T1p,T2p
# define objective
def objective(x):
# simulate model
T1p,T2p = sim_model(x)
# return objective
return sum(np.abs(T1p-T1)+np.abs(T2p-T2))
# show initial objective
print('Initial SSE Objective: ' + str(objective(x0)))
print('Optimizing Values...')
# optimize without parameter constraints
#solution = minimize(objective,x0)
# optimize with bounds on variables
bnds = ((0.4, 1.5), (0.1, 0.5), (50.0, 200.0), (0.0, 30.0))
solution = minimize(objective,x0,bounds=bnds,method='SLSQP')
# show final objective
x = solution.x
iae = objective(x)
Kp,Kd,taup,thetap = x
print('Final SSE Objective: ' + str(objective(x)))
print('Kp: ' + str(Kp))
print('Kd: ' + str(Kd))
print('taup: ' + str(taup))
print('thetap: ' + str(thetap))
# save fopdt.txt file
fid = open('fopdt.txt','w')
fid.write(str(Kp)+'\n')
fid.write(str(Kd)+'\n')
fid.write(str(taup)+'\n')
fid.write(str(thetap)+'\n')
fid.write(str(T1_0)+'\n')
fid.write(str(T2_0)+'\n')
fid.close()
# calculate model with updated parameters
T1p,T2p = sim_model(x)
plt.figure(1,figsize=(15,7))
plt.subplot(2,1,1)
plt.plot(t,T1,'r.',linewidth=2,label='Temperature 1 (meas)')
plt.plot(t,T2,'b.',linewidth=2,label='Temperature 2 (meas)')
plt.plot(t,T1p,'r--',linewidth=2,label='Temperature 1 (pred)')
plt.plot(t,T2p,'b--',linewidth=2,label='Temperature 2 (pred)')
plt.ylabel(r'T $(^oC)$')
plt.text(200,20,'Integral Abs Error: ' + str(np.round(iae,2)))
plt.text(400,35,r'$K_p$: ' + str(np.round(Kp,1)))
plt.text(400,30,r'$K_d$: ' + str(np.round(Kd,1)))
plt.text(400,25,r'$\tau_p$: ' + str(np.round(taup,0)) + ' sec')
plt.text(400,20,r'$\theta_p$: ' + str(np.round(thetap,0)) + ' sec')
plt.legend(loc=2)
plt.subplot(2,1,2)
plt.plot(t,Q1,'b--',linewidth=2,label=r'Heater 1 ($Q_1$)')
plt.plot(t,Q2,'r:',linewidth=2,label=r'Heater 2 ($Q_2$)')
plt.legend(loc='best')
plt.xlabel('time (sec)')
plt.savefig('fopdt_opt.png')
plt.show()
```
### Design 2 PID Controllers for T1 and T2
```
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import ipywidgets as wg
from IPython.display import display
n = 601 # time points to plot
tf = 600.0 # final time
# Load TCLab FOPDT
fid = open('fopdt.txt','r')
Kp = float(fid.readline())
Kd = float(fid.readline())
taup = float(fid.readline())
thetap = float(fid.readline())
T1_0 = float(fid.readline())
T2_0 = float(fid.readline())
fid.close()
y0 = [T1_0,T2_0]
Kff = -Kp/Kd
def process(y,t,u1,u2):
y1,y2 = y
dy1dt = (1.0/taup) * (-(y1-y0[0]) + Kp * u1 + Kd * (y2-y1))
dy2dt = (1.0/taup) * (-(y2-y0[1]) + (Kp/2.0) * u2 + Kd * (y1-y2))
return [dy1dt,dy2dt]
def pidPlot(Kc,tauI,tauD,Kff):
y0 = [23.0,23.0]
t = np.linspace(0,tf,n) # create time vector
P1 = np.zeros(n) # initialize proportional term
I1 = np.zeros(n) # initialize integral term
D1 = np.zeros(n) # initialize derivative term
FF1 = np.zeros(n) # initialize feedforward term
e1 = np.zeros(n) # initialize error
P2 = np.zeros(n) # initialize proportional term
I2 = np.zeros(n) # initialize integral term
D2 = np.zeros(n) # initialize derivative term
FF2 = np.zeros(n) # initialize feedforward term
e2 = np.zeros(n) # initialize error
OP1 = np.zeros(n) # initialize controller output
OP2 = np.zeros(n) # initialize disturbance
PV1 = np.ones(n)*y0[0] # initialize process variable
PV2 = np.ones(n)*y0[1] # initialize process variable
SP1 = np.ones(n)*y0[0] # initialize setpoint
SP2 = np.ones(n)*y0[1] # initialize setpoint
SP1[10:] = 60.0 # step up
SP1[400:] = 40.0 # step up
SP2[150:] = 50.0 # step down
SP2[350:] = 35.0 # step down
Kc1 = Kc
Kc2 = Kc*2.0
Kff1 = Kff
Kff2 = Kff*2.0
iae = 0.0
# loop through all time steps
for i in range(1,n):
# simulate process for one time step
ts = [t[i-1],t[i]] # time interval
heaters = (OP1[max(0,i-int(thetap))],OP2[max(0,i-int(thetap))])
y = odeint(process,y0,ts,args=heaters)
y0 = y[1] # record new initial condition
# calculate new OP with PID
PV1[i] = y[1][0] # record T1 PV
PV2[i] = y[1][1] # record T2 PV
iae += np.abs(SP1[i]-PV1[i]) + np.abs(SP2[i]-PV2[i])
dt = t[i] - t[i-1] # calculate time step
# PID for loop 1
e1[i] = SP1[i] - PV1[i] # calculate error = SP - PV
P1[i] = Kc1 * e1[i] # calculate proportional term
I1[i] = I1[i-1] + (Kc1/tauI) * e1[i] * dt # calculate integral term
D1[i] = -Kc * tauD * (PV1[i]-PV1[i-1])/dt # calculate derivative
FF1[i] = Kff1 * (PV2[i]-PV1[i])
OP1[i] = P1[i] + I1[i] + D1[i] + FF1[i] # calculate new output
if OP1[i]>=100:
OP1[i] = 100.0
I1[i] = I1[i-1] # reset integral
if OP1[i]<=0:
OP1[i] = 0.0
I1[i] = I1[i-1] # reset integral
# PID for loop 2
e2[i] = SP2[i] - PV2[i] # calculate error = SP - PV
P2[i] = Kc2 * e2[i] # calculate proportional term
I2[i] = I2[i-1] + (Kc2/tauI) * e2[i] * dt # calculate integral term
D2[i] = -Kc2 * tauD * (PV2[i]-PV2[i-1])/dt # calculate derivative
FF2[i] = Kff2 * (PV1[i]-PV2[i])
OP2[i] = P2[i] + I2[i] + D2[i] + FF2[i] # calculate new output
if OP2[i]>=100:
OP2[i] = 100.0
I2[i] = I2[i-1] # reset integral
if OP2[i]<=0:
OP2[i] = 0.0
I2[i] = I2[i-1] # reset integral
# plot PID response
plt.figure(1,figsize=(15,7))
plt.subplot(2,2,1)
plt.plot(t,SP1,'k-',linewidth=2,label='Setpoint 1 (SP)')
plt.plot(t,PV1,'r:',linewidth=2,label='Temperature 1 (PV)')
plt.ylabel(r'T $(^oC)$')
plt.text(100,35,'Integral Abs Error: ' + str(np.round(iae,2)))
plt.text(400,35,r'$K_{c1}$: ' + str(np.round(Kc,1)))
plt.text(400,30,r'$\tau_I$: ' + str(np.round(tauI,0)) + ' sec')
plt.text(400,25,r'$\tau_D$: ' + str(np.round(tauD,0)) + ' sec')
plt.text(400,20,r'$K_{ff}$: ' + str(np.round(Kff1,2)))
plt.ylim([15,70])
plt.legend(loc=1)
plt.subplot(2,2,2)
plt.plot(t,SP2,'k-',linewidth=2,label='Setpoint 2 (SP)')
plt.plot(t,PV2,'r:',linewidth=2,label='Temperature 2 (PV)')
plt.ylabel(r'T $(^oC)$')
plt.text(20,65,r'$K_{c2}$: ' + str(np.round(Kc*2,1)))
plt.text(20,60,r'$\tau_I$: ' + str(np.round(tauI,0)) + ' sec')
plt.text(20,55,r'$\tau_D$: ' + str(np.round(tauD,0)) + ' sec')
plt.text(20,50,r'$K_{ff}$: ' + str(np.round(Kff2,2)))
plt.ylim([15,70])
plt.legend(loc=1)
plt.subplot(2,2,3)
plt.plot(t,OP1,'b--',linewidth=2,label='Heater 1 (OP)')
plt.legend(loc='best')
plt.xlabel('time (sec)')
plt.subplot(2,2,4)
plt.plot(t,OP2,'b--',linewidth=2,label='Heater 2 (OP)')
plt.legend(loc='best')
plt.xlabel('time (sec)')
print('PID with Feedforward Simulator: Adjust Kc, tauI, tauD, and Kff ' + \
'to achieve lowest Integral Abs Error')
# ITAE Setpoint Tracking PI Tuning
Kc = (0.586/Kp)*(thetap/taup)**(-0.916); tauI = taup/(1.03-0.165*(thetap/taup))
print(f'ITAE Recommended: Kc={Kc:4.2f}, tauI={tauI:5.1f}, tauD=0, Kff={Kff:4.2f}')
# IMC Aggressive PID Tuning
tauc = max(0.1*taup,0.8*thetap); Kc = (1/Kp)*(taup+0.5*taup)/(tauc+0.5*thetap)
tauI = taup+0.5*thetap; tauD = taup*thetap/(2*taup+thetap); Kff=-Kd/Kp
print(f'IMC Recommended: Kc={Kc:4.2f}, tauI={tauI:5.1f}, tauD={tauD:4.2f}, Kff={Kff:4.2f}')
Kc_slide = wg.FloatSlider(value=Kc,min=0.0,max=50.0,step=1.0)
tauI_slide = wg.FloatSlider(value=tauI,min=20.0,max=250.0,step=1.0)
tauD_slide = wg.FloatSlider(value=tauD,min=0.0,max=20.0,step=1.0)
Kff_slide = wg.FloatSlider(value=Kff,min=-0.5,max=0.5,step=0.1)
wg.interact(pidPlot, Kc=Kc_slide, tauI=tauI_slide, tauD=tauD_slide,Kff=Kff_slide)
print('')
```
### Test Interacting PID Controllers with TCLab
```
import tclab
import numpy as np
import time
import matplotlib.pyplot as plt
from scipy.integrate import odeint
#-----------------------------------------
# PID controller performance for the TCLab
#-----------------------------------------
# PID Parameters
Kc = 5.0
tauI = 120.0 # sec
tauD = 2.0 # sec
Kff = -0.3
# Animate Plot?
animate = True
if animate:
try:
from IPython import get_ipython
from IPython.display import display,clear_output
get_ipython().run_line_magic('matplotlib', 'inline')
ipython = True
print('IPython Notebook')
except:
ipython = False
print('Not IPython Notebook')
#-----------------------------------------
# PID Controller with Feedforward
#-----------------------------------------
# inputs ---------------------------------
# sp = setpoint
# pv = current temperature
# pv_last = prior temperature
# ierr = integral error
# dt = time increment between measurements
# outputs --------------------------------
# op = output of the PID controller
# P = proportional contribution
# I = integral contribution
# D = derivative contribution
def pid(sp,pv,pv_last,ierr,dt,d,cid):
# Parameters in terms of PID coefficients
if cid==1:
# controller 1
KP = Kc
Kf = Kff
else:
# controller 2
KP = Kc * 2.0
Kf = Kff * 2.0
KI = Kc/tauI
KD = Kc*tauD
# ubias for controller (initial heater)
op0 = 0
# upper and lower bounds on heater level
ophi = 100
oplo = 0
# calculate the error
error = sp-pv
# calculate the integral error
ierr = ierr + KI * error * dt
# calculate the measurement derivative
dpv = (pv - pv_last) / dt
# calculate the PID output
P = KP * error
I = ierr
D = -KD * dpv
FF = Kff * d
op = op0 + P + I + D + FF
# implement anti-reset windup
if op < oplo or op > ophi:
I = I - KI * error * dt
# clip output
op = max(oplo,min(ophi,op))
# return the controller output and PID terms
return [op,P,I,D,FF]
# save txt file with data and set point
# t = time
# u1,u2 = heaters
# y1,y2 = tempeatures
# sp1,sp2 = setpoints
def save_txt(t, u1, u2, y1, y2, sp1, sp2):
data = np.vstack((t, u1, u2, y1, y2, sp1, sp2)) # vertical stack
data = data.T # transpose data
top = ('Time,Q1,Q2,T1,T2,TSP1,TSP2')
np.savetxt('validate.txt', data, delimiter=',',\
header=top, comments='')
# Connect to Arduino
a = tclab.TCLab()
# Wait until temperature is below 25 degC
print('Check that temperatures are < 25 degC before starting')
i = 0
while a.T1>=25.0 or a.T2>=25.0:
print(f'Time: {i} T1: {a.T1} T2: {a.T2}')
i += 10
time.sleep(10)
# Turn LED on
print('LED On')
a.LED(100)
# Run time in minutes
run_time = 10.0
# Number of cycles
loops = int(60.0*run_time)
tm = np.zeros(loops)
# Heater set point steps
Tsp1 = np.ones(loops) * a.T1
Tsp2 = np.ones(loops) * a.T2 # set point (degC)
Tsp1[10:] = 60.0 # step up
Tsp1[400:] = 40.0 # step down
Tsp2[150:] = 50.0 # step up
Tsp2[350:] = 35.0 # step down
T1 = np.ones(loops) * a.T1 # measured T (degC)
T2 = np.ones(loops) * a.T2 # measured T (degC)
# impulse tests (0 - 100%)
Q1 = np.ones(loops) * 0.0
Q2 = np.ones(loops) * 0.0
if not animate:
print('Running Main Loop. Ctrl-C to end.')
print(' Time SP1 PV1 Q1 SP2 PV2 Q2 IAE')
print(('{:6.1f} {:6.2f} {:6.2f} ' + \
'{:6.2f} {:6.2f} {:6.2f} {:6.2f} {:6.2f}').format( \
tm[0],Tsp1[0],T1[0],Q1[0],Tsp2[0],T2[0],Q2[0],0.0))
# Main Loop
start_time = time.time()
prev_time = start_time
dt_error = 0.0
# Integral error
ierr1 = 0.0
ierr2 = 0.0
# Integral absolute error
iae = 0.0
if not ipython:
plt.figure(figsize=(10,7))
plt.ion()
plt.show()
try:
for i in range(1,loops):
# Sleep time
sleep_max = 1.0
sleep = sleep_max - (time.time() - prev_time) - dt_error
if sleep>=1e-4:
time.sleep(sleep-1e-4)
else:
print('exceeded max cycle time by ' + str(abs(sleep)) + ' sec')
time.sleep(1e-4)
# Record time and change in time
t = time.time()
dt = t - prev_time
if (sleep>=1e-4):
dt_error = dt-sleep_max+0.009
else:
dt_error = 0.0
prev_time = t
tm[i] = t - start_time
# Read temperatures in Kelvin
T1[i] = a.T1
T2[i] = a.T2
# Disturbances
d1 = T1[i] - 23.0
d2 = T2[i] - 23.0
# Integral absolute error
iae += np.abs(Tsp1[i]-T1[i]) + np.abs(Tsp2[i]-T2[i])
# Calculate PID output
[Q1[i],P,ierr1,D,FF] = pid(Tsp1[i],T1[i],T1[i-1],ierr1,dt,d2,1)
[Q2[i],P,ierr2,D,FF] = pid(Tsp2[i],T2[i],T2[i-1],ierr2,dt,d1,2)
# Write output (0-100)
a.Q1(Q1[i])
a.Q2(Q2[i])
if not animate:
# Print line of data
print(('{:6.1f} {:6.2f} {:6.2f} ' + \
'{:6.2f} {:6.2f} {:6.2f} {:6.2f} {:6.2f}').format( \
tm[i],Tsp1[i],T1[i],Q1[i],Tsp2[i],T2[i],Q2[i],iae))
else:
if ipython:
plt.figure(figsize=(10,7))
else:
plt.clf()
# Update plot
ax=plt.subplot(2,1,1)
ax.grid()
plt.plot(tm[0:i],Tsp1[0:i],'k--',label=r'$T_1$ set point')
plt.plot(tm[0:i],T1[0:i],'b.',label=r'$T_1$ measured')
plt.plot(tm[0:i],Tsp2[0:i],'k-',label=r'$T_2$ set point')
plt.plot(tm[0:i],T2[0:i],'r.',label=r'$T_2$ measured')
plt.ylabel(r'Temperature ($^oC$)')
plt.text(0,65,'IAE: ' + str(np.round(iae,2)))
plt.legend(loc=4)
plt.ylim([15,70])
ax=plt.subplot(2,1,2)
ax.grid()
plt.plot(tm[0:i],Q1[0:i],'b-',label=r'$Q_1$')
plt.plot(tm[0:i],Q2[0:i],'r:',label=r'$Q_2$')
plt.ylim([-10,110])
plt.ylabel('Heater (%)')
plt.legend(loc=1)
plt.xlabel('Time (sec)')
if ipython:
clear_output(wait=True)
display(plt.gcf())
else:
plt.draw()
plt.pause(0.05)
# Turn off heaters
a.Q1(0)
a.Q2(0)
a.close()
# Save text file
save_txt(tm,Q1,Q2,T1,T2,Tsp1,Tsp2)
# Save Plot
if not animate:
plt.figure(figsize=(10,7))
ax=plt.subplot(2,1,1)
ax.grid()
plt.plot(tm,Tsp1,'k--',label=r'$T_1$ set point')
plt.plot(tm,T1,'b.',label=r'$T_1$ measured')
plt.plot(tm,Tsp2,'k-',label=r'$T_2$ set point')
plt.plot(tm,T2,'r.',label=r'$T_2$ measured')
plt.ylabel(r'Temperature ($^oC$)')
plt.text(0,65,'IAE: ' + str(np.round(iae,2)))
plt.legend(loc=4)
ax=plt.subplot(2,1,2)
ax.grid()
plt.plot(tm,Q1,'b-',label=r'$Q_1$')
plt.plot(tm,Q2,'r:',label=r'$Q_2$')
plt.ylabel('Heater (%)')
plt.legend(loc=1)
plt.xlabel('Time (sec)')
plt.savefig('PID_Control.png')
# Allow user to end loop with Ctrl-C
except KeyboardInterrupt:
# Disconnect from Arduino
a.Q1(0)
a.Q2(0)
print('Shutting down')
a.close()
save_txt(tm[0:i],Q1[0:i],Q2[0:i],T1[0:i],T2[0:i],Tsp1[0:i],Tsp2[0:i])
plt.savefig('PID_Control.png')
# Make sure serial connection closes with an error
except:
# Disconnect from Arduino
a.Q1(0)
a.Q2(0)
print('Error: Shutting down')
a.close()
save_txt(tm[0:i],Q1[0:i],Q2[0:i],T1[0:i],T2[0:i],Tsp1[0:i],Tsp2[0:i])
plt.savefig('PID_Control.png')
raise
print('PID test complete')
print('Kc: ' + str(Kc))
print('tauI: ' + str(tauI))
print('tauD: ' + str(tauD))
print('Kff: ' + str(Kff))
```
| true |
code
| 0.354978 | null | null | null | null |
|
# <font color='orange'>Word2Vec Introduction </font>
The Natural Languahe Processing for data science that was introduced in class discusses the ideas of topics as Bag of words and N-grams with a key note by professor mentioning “this lecture may be subject to change in the upcoming years, as massive improvements in “off-the-shelf” language understanding are ongoing.” This tutorial will introduce you to one such deep learning method known as Word2Vec which aims to learn the meaning of the words rather than relying on heuristic approaches.
Limiting the scope of the tutorial and not going into deeper mathematics, word2vec can be explained as a model where each word is represented as a vector in N dimensional space. During the initialization stage, the vocabulary of corpus can be randomly initialized as vectors with some values. Then, using vector addition, if we add tiny bit of one vector to another, the vector moves closer to each other and similarly subtraction results in moving further away from one another. So while training a model we can pull the vector closer to words that it co occurs with within a specified window and away from all the other words. So in the end of the training words that are similar in meaning end up clustering nearby each other and many more patterns arises automatically.
## <font color='orange'>Technique</font>
Word2Vec uses a technique called <b>skip-gram with negative sampling</b> to map the semantic space of a text corpus. I have tried to explain this using a passage taken from dataset used in our tutorial.
“This system is sometimes known as a presidential system because the government is answerable<font color='green'> <i>solely and exclusively to a </i></font><font color='red'><i><b> 'presiding' </b></i></font><font color='green'><i>activist head of state, and</i></font> is selected by and on occasion dismissed by the head of state without reference to the legislature.”
<b>Step 1</b>
Let’s take a word from above passage as target and number of words occurring close to the target as context (five words on either side of target).
<i>Target</i> = presiding
<i>Context</i> = solely and exclusively to a; activist head of state, and
<b>Step 2</b>
Each of the word in the above paragragh should be represented as a vector in n dimensional space. In the beginning, these vector values can be randomly initialized.
Note: The dimension can be decided at the time of model creation, given as one of the parameters of models
<b>Step 3</b>
Our goal is to get the target and context closer to each other in vector space. This can be done by taking the target and context vectors and pulling them together by a small amount by maximizing the log transformation of the dot product of the target and the context vectors.
<b>Step 4</b>
Another motive is to move target vector away from words that are not in it’s context. To achieve this, words are randomly sampled from rest of the corpus and they are pushed away from target vector by minimizing the log transformation of the dot product of the target and the non context sample words.
The above four steps is repeated for each target word. In the end the vectors that are often used together will be pulled towards each other and vectors for words that are rarely used together will be pushed apart.
In our example if notion of ‘presiding’ resembles ‘activist head’ often in corpus then vectors for these two concepts will be close to one another.
## <font color='blue'>Data Collection</font>
I used [ClueWeb datasets](http://lemurproject.org/clueweb12/) which consists of around (50 million Wikipedia documents) and indexed them using [Apache Lucene](https://lucene.apache.org/core/). After Indexing, I used Lucene Search Engine to extract the top 1000 documents for query "president united states". These documents are then stored in a local file "wikidocs"
I am using these 1000 documents to build the word2vec model to find the interested relationships between words.
Please note that the entire process of indexing and retrieving the documents is beyond the scope of the tutorial.
The file wikidocs can be downloaded from https://www.dropbox.com/s/rnu33c4j6ywnu6z/wikidocs?dl=0. Make sure to save the file in same directory as the notebook.
```
#Load the documents extracted from wikipedia corpus
with open("wikidocs") as f:
html = f.read()
html = unicode(html, errors='replace')
#Printing the lenght of the corpus
print("The lenght of corpus is "+str(len(html))+".")
```
## <font color='blue'> Install Libraries</font>
The data collected is in the form of xml which needs to be cleaned to plain text format. I am using BeautifulSoup libraries to parse the wikipedia documents and nltk tokenizer to convert them to tokens.
Please note that these libraries are already been introduced in class and used in homeworks. Hence, running the below command should work for you.
```
import urllib
import re
import pandas as pd
import nltk.data
from nltk.corpus import stopwords
from bs4 import BeautifulSoup
nltk.download('punkt')
```
## <font color='blue'> Parsing </font>
<b>Convert the docs into list of sentences</b>
Word2Vec toolkit in python expects input in the form of a list of sentences, each of which is a list of words.
<b>Remove punctuation and lowercase all words</b>
The words are converted into lowecase and punctuations are removed using regular expressions.
<b>Stopwords</b>
Removal of stopwords is optional. It is better to not remove stopwords for word2vec algorithm for the first train as the algorithm relies on the broader context of the sentence in order to produce high-quality word vectors. However, if results are not satisfactory, the model can be trained again by removing stop words.
```
# Function to convert a document to a sequence of words,
# optionally removing stop words.
# Returns a list of words.
def review_to_wordlist(review, remove_stopwords=False):
# 1. Remove HTML
review_text = BeautifulSoup(review,"lxml").get_text()
review_text = review_text.encode('utf-8')
# 2. Remove non-letters
review_text = re.sub("[^a-zA-Z]"," ", review_text)
# 3. Convert words to lower case and split them
words = review_text.lower()
words = words.split()
# 4. Optionally remove stop words (false by default)
if remove_stopwords:
stops = stopwords.words("english")
stops = set(stops)
words = [w for w in words if not w in stops]
# 5. Return a list of words
return(words)
```
Function to split a document into parsed sentences using NLTK tokenizer.
```
# Function to split a review into parsed sentences. Returns a
# list of sentences, where each sentence is a list of words
def review_to_sentences( review, tokenizer, remove_stopwords=False):
# 1. Use the NLTK tokenizer to split the paragraph into sentences
raw_sentences = tokenizer.tokenize(review.strip())
# 2. Loop over each sentence
sentences = []
for raw_sentence in raw_sentences:
# If a sentence is empty, skip it
if len(raw_sentence) > 0:
# Otherwise, call review_to_wordlist to get a list of words
sentences.append( review_to_wordlist( raw_sentence, \
remove_stopwords ))
# Return the list of sentences (each sentence is a list of words,
# so this returns a list of lists
return sentences
```
Now we apply these functions to our Wikipedia Corpus
```
#Parse documents to create list of sentences
tokenizer = nltk.data.load('nltk:tokenizers/punkt/english.pickle')
sentences = review_to_sentences(html, tokenizer)
print("There are " + str(len(sentences)) + " sentences in our corpus.")
```
Let's observe what a sentence looks like after parsing it through above functions.
```
sentences[100]
```
# <font color='green'>Generating Word2Vec Model</font>
## <font color='red'> Installing the libraries</font>
You can install gensim using pip:
$ pip install --upgrade gensim
If this fail, make sure you’re installing into a writeable location (or use sudo), and have following dependencies.
Python >= 2.6
NumPy >= 1.3
SciPy >= 0.7
Alternatively, you can use conda package to install gensim, which takes care of all the dependencies.
$ conda install -c anaconda gensim=0.12.4
## <font color='red'>Load libraries for word2vec</font>
After you run all the installs, make sure the following commands work for you:
```
import gensim
from gensim.models import word2vec
from gensim.models import Phrases
from gensim.models import Word2Vec
import logging
```
## <font color='red'>Training the Model </font>
## Logging
Import the built-in logging module and configure it so that Word2Vec creates nice output messages
```
#Using built in logging
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s',\
level=logging.INFO)
```
## Parameters for model
The Word2Vec model requires some parameters for initialization.
<b>size</b>
Size is number of dimensions you want for word vectors. If you have an idea about how many topics the corpus cover, you can use that as size here. For wikipedia documents I use around 50-100. Usually, you will need to experiment with this value and pick the one which gives you best result.
<b>min_count</b>
Terms that occur less than min_count are ignored in calculations. This reduce noise in the vector space. I have used 10 for my experiment. Usually for bigger corpus size, you can experiment with higher values.
<b>window</b>
The maximum distance between the current and predicted word within a sentence. This is explained in the technique section of the tutorial.
<b>downsampling</b>
Threshold for configuring which higher-frequency words are randomly downsampled. Useful range is (0, 1e-5)
```
# Set values for various parameters
num_features = 200 # Word vector dimensionality
min_word_count = 10 # Minimum word count
num_workers = 4 # Number of threads to run in parallel
context = 10 # Context window size
downsampling = 1e-3 # Downsample setting for frequent words
```
## Initialize and train the model
Train the model using the above parameters. This might take some time
```
print "Training model..."
model = word2vec.Word2Vec(sentences, workers=num_workers, \
size=num_features, min_count = min_word_count, \
window = context, sample = downsampling)
```
If you don’t plan to train the model any further, calling init_sims will be better for memory.
```
model.init_sims(replace=True)
```
## <font color='red'>Storing & Loading Models</font>
It can be helpful to create a meaningful model name and save the model for later use.
You can load it later using Word2Vec.load()
```
#You can save the model using meaningful name
model_name = "wiki_100features_15word_count"
model.save(model_name)
#Loading the saved model
word2vec_model = gensim.models.Word2Vec.load("wiki_100features_15word_count")
```
## <font color='red'>Investigate the vocabulary</font>
You can either use model.index2word which gives list of all the terms in vocabulary. Or model.vocab.keys() which gives keys of all the terms used in the model.
```
#List of all the vcabulary terms
vocab = model.index2word
print "Lenght of vocabulary =",len(vocab)
print vocab[20:69]
```
Check if the word ‘obama’ exists in the vocabulary:
```
'obama' in model.vocab
```
Check if the word 'beyonce’ exists in the vocabulary:
```
'beyonce' in model.vocab
```
The vector representation of word ‘obama’ looks like this:
```
model['obama']
```
Let's test the words similar to "obama"
```
model.most_similar('obama', topn=10)
```
## <font color='red'>Phrases</font>
We can use gensim models.phrases in order to detect common phrases from sentences. For example two single words "new" and "york" can be combined as one word "new york".
```
bigram = gensim.models.Phrases(sentences)
```
Generte the model using above bigram.
```
new_model = Word2Vec(bigram[sentences], workers=num_workers, \
size=num_features, min_count = min_word_count, \
window = context, sample = downsampling)
```
Let's access the new vocabulary.
```
vocab = new_model.vocab.keys()
vocab = list(vocab)
print "Lenght of new vocabulary =",len(vocab)
print vocab[15:55]
```
Check if the word 'dominican republic’ exists in the vocabulary:
```
'dominican_republic' in new_model.vocab
```
Let’s assess the relationship of words in our semantic vector space. For example, which words are most similar to the word ‘republic’?
```
new_model.most_similar('republic', topn=10)
```
What about the phrase "dominican republic"?
```
new_model.most_similar('dominican_republic', topn=10)
```
Does the results differ if we exclude the relationship between republic and dominican_republic?
```
new_model.most_similar(positive=['republic'], negative=['dominican_republic'], topn=10)
```
## <font color='red'>Query Expansion</font>
One of the applications of word embedding is that it can be used in search engine in order to expand the query terms in order to produce better results.
If you recall previously, the wikipedia documents are extracted from Lucene Search using the query "president united states". Now, let's use these three query terms to obtain expanded terms closest to query.
Note: This idea is taken from the paper: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/06/acl2016.pdf
Below function take each term in vocabulary and compare it to each term of query in terms of similarity score. The similarity scores are added for all terms and top k terms are returned.
```
#Function to expand a query term
def expand_term(query,k):
#Get the vocab of model
vocab = new_model.index2word
vocab = set(vocab)
term_score = {}
#Split the query terms
query_list = query.split()
#Convert the query to lower case
query_list = [element.lower() for element in query_list]
#Remove stop words from query
stops = stopwords.words("english")
stops = set(stops)
query = [word for word in query_list if word not in stops]
#Filter the vocab to remove stopwords
filter_vocab = [word for word in vocab if word not in stops]
#Calculate each score for terms in vocab
for term in filter_vocab:
term_score[term] = 0.0
for q in query:
if term in term_score:
term_score[term] += new_model.similarity(q,term)
else:
term_score[term] = new_model.similarity(q,term)
#Sort the top k terms of dict term_score
sorted_k_terms = sorted(term_score.iteritems(), key=lambda x:-x[1])[:k]
sorted_k_terms = dict(sorted_k_terms)
#join the query term
q_term = ' '.join(query)
#Return the expanded terms of query
return sorted_k_terms.keys()
```
Now, let's test our function to check the result for query "president united states"
```
query = "president united states"
k = 15 #k defines number of expanded terms
result = expand_term(query,k)
print result
```
Now let's try for "republic constitution"
```
query = "republic constitution"
k = 15 #k defines number of expanded terms
result = expand_term(query,k)
print result
```
## <font color='orange'>Applications</font>
Word2Vec model as described in this tutorial capture semantic and syntactic relationships among words in corpus. Hence, it can be used in search engines for synonyms, query expansion as well as recommendations (for example, recommending similar movies).
In our experiments, word embeddings do not seem to provide enough discriminative power between related but distinct concepts. This could be due to smaller corpus size as well as word embeddings are in it's initial stage of development. Hence, there is a huge scope for improvements in the above technique for it to be fully utilized in commercial applications.
This being said, word2vec are exteremely interesting and it's lot of fun to explore the relationships amongst different words.
## <font color='orange'>Refrences</font>
[Google's code, writeup, and the accompanying papers](https://code.google.com/archive/p/word2vec/)
[Efficient Estimation of Word Representations in Vector Space](https://arxiv.org/pdf/1301.3781.pdf)
[Distributed Representations of Words and Phrases and their Compositionality](https://arxiv.org/pdf/1310.4546.pdf)
[Presentation on word2vec by Tomas Mikolov from Google](https://docs.google.com/file/d/0B7XkCwpI5KDYRWRnd1RzWXQ2TWc/edit)
| true |
code
| 0.330458 | null | null | null | null |
|
###### The probability of an eccentricity GIVEN that a planet is transiting (P(e|b)) and the probability of a longitude of periastron GIVEN that a planet is transiting (P(w|b)) are different than P(e) and P(w).
https://academic.oup.com/mnras/article/444/3/2263/1053015
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from tqdm import tqdm
from astropy.table import Table
import astropy.units as u
import matplotlib
# Using `batman` to create & fit fake transit
import batman
# Using astropy BLS and scipy curve_fit to fit transit
from astropy.timeseries import BoxLeastSquares
from scipy.optimize import curve_fit
import scipy.optimize as opt
# Using emcee & corner to find and plot (e, w) distribution
import emcee
import corner
# And importing `photoeccentric`
import photoeccentric as ph
# Random stuff
import scipy.constants as c
from scipy.stats import rayleigh
import os
from pathlib import Path
%load_ext autoreload
%autoreload 2
%matplotlib inline
plt.rcParams['figure.figsize'] = [12, 8]
def find_nearest(array, value):
array = np.asarray(array)
idx = (np.abs(array - value)).argmin()
return array[idx]
def mode(dist):
"""Gets mode of a histogram.
Parameters
----------
dist: array
Distribution
Returns
-------
mode: float
Mode
"""
#n, bins = np.histogram(dist, bins=np.linspace(np.nanmin(dist), np.nanmax(dist), 100))
n, bins = np.histogram(dist, bins=np.linspace(np.nanmin(dist), np.nanmax(dist), 500))
mode = bins[np.nanargmax(n)]
return mode
```
# UNIFORM DISTRIBUTION
```
distpath_uniform = "/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/photoeccentric/notebooks/hpgresults/uniform_dist/results_w_-90to270/"
truee = []
truew = []
edist_uniform = []
for subdir, dirs, files in os.walk(distpath_uniform):
try:
trueparams = subdir.split("/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/photoeccentric/notebooks/hpgresults/uniform_dist/results_w_-90to270/e_",1)[1]
truee.append(float(trueparams.split('_w_')[0]))
truew.append(float(trueparams.split('_w_')[1]))
except IndexError:
continue
for file in files:
if 'distributions' in file:
distpath = os.path.join(subdir, file)
edist_uniform.append(np.genfromtxt(distpath, delimiter=','))
truee = np.array(truee)
truew = np.array(truew)
edist_uniform = np.array(edist_uniform)
fite = []
fitw = []
fitg = []
es_uniform = []
ws_uniform = []
gs_uniform = []
for i in range(len(edist_uniform)):
es_uniform.append(edist_uniform[i][:,0])
fite.append(ph.mode(edist_uniform[i][:,0]))
ws_uniform.append(edist_uniform[i][:,1])
fitw.append(ph.mode(edist_uniform[i][:,1]))
gs_uniform.append(edist_uniform[i][:,2])
fitg.append(ph.mode(edist_uniform[i][:,2]))
fite = np.array(fite)
es_uniform = np.array(es_uniform)
fitw = np.array(fitw)
ws_uniform = np.array(ws_uniform)
fitg = np.array(fitg)
gs_uniform = np.array(gs_uniform)
# for i in range(len(es_uniform)):
# plt.hist(es_uniform[i], alpha=0.3, density=True, stacked=True);
# plt.xlabel('Fit E Distributions')
# plt.title('All E distributions (sample ~500)')
# plt.cla()
# for i in range(len(ws_uniform)):
# plt.hist(ws_uniform[i], alpha=0.3, density=True, stacked=True);
# plt.xlabel('Fit w Distributions (deg)')
# plt.title('All w distributions (sample ~800)')
plt.cla()
fz = 15
plt.hist2d(ws_uniform.flatten(), es_uniform.flatten(), bins=[20,20], cmap='Blues', density=True);
plt.colorbar(label='Rel. Density')
plt.scatter(truew, truee, marker='o', s=15, c='palevioletred', label='True Params')
plt.scatter(fitw, fite, marker='X', s=15, c='mediumaquamarine', label='Fit Params (Mode)')
plt.legend(fontsize=fz)
plt.xlabel('$\omega$', fontsize=fz)
plt.ylabel('$e$', fontsize=fz)
plt.title('Fit $(e,w)$ Heatmap From Uniform Distribubtion', fontsize=fz)
plt.savefig('Fit_EW_heatmap_uniform_new.png')
randint = int(np.random.randint(0, len(es_uniform), 1))
for i in range(len(es_uniform)):
plt.cla()
plt.hist2d(ws_uniform[i], es_uniform[i], cmap='Blues', bins=[13,10]);
plt.scatter(truew[i], truee[i], c='r', s=100, label='True')
plt.scatter(fitw[i], fite[i], c='g', marker='X', s=100, label='Fit')
plt.xlim(-90, 270)
plt.ylim(0, 1)
plt.xlabel(r'$\omega$', fontsize=20)
plt.ylabel('$e$', fontsize=20)
plt.title('$e$ = ' + str(truee[i]) + '; $\omega$ = ' + str(truew[i]), fontsize=20)
plt.legend()
plt.savefig('all_new_heatmaps/e_' + str(truee[i]) + '_w_' + str(truew[i]) + 'singleheatmap.png')
wuniform = np.random.uniform(-90, 270, 50)
inds = []
for i in range(len(wuniform)):
inds.append(int(np.argwhere(fitw == find_nearest(fitw, wuniform[i]))[0]))
euni = truee[inds].flatten()
wuni = truew[inds].flatten()
efuni = fite[inds].flatten()
wfuni = fitw[inds].flatten()
edistuni = np.array(es_uniform[inds]).flatten()
wdistuni = np.array(ws_uniform[inds]).flatten()
def deltallike(g, gerr, truee, truew, fite, fitw):
model_fit = (1+e*np.sin(w*(np.pi/180.)))/np.sqrt(1-e**2)
sigma2_fit = gerr ** 2
loglike_fit = -0.5 * np.sum((g - model_fit) ** 2 / sigma2_fit + np.log(sigma2_fit))
model_true = (1+truee*np.sin(truew*(np.pi/180.)))/np.sqrt(1-truee**2)
sigma2_true = gerr ** 2
loglike_true = -0.5 * np.sum((g - model_true) ** 2 / sigma2_true + np.log(sigma2_true))
llike = np.abs(loglike_fit-loglike_true)
return llike
llike = []
for i in range(len(truee)):
g = ph.mode(gs_uniform[i])
e = ph.mode(es_uniform[i])
w = ph.mode(ws_uniform[i])
gerr = np.nanstd(gs_uniform[i])
llike.append(deltallike(g, gerr, truee[i], truew[i], e, w))
llike = np.array(llike)
llikeuni = llike[inds]
plt.cla()
fz = 15
plt.hist2d(wdistuni, edistuni, bins=[20,20], cmap='Blues')#, norm=matplotlib.colors.LogNorm());
#plt.clim(vmax=4000.0)
plt.colorbar(label='Rel. Density')
plt.scatter(wuni, euni, marker='o', s=80, c='palevioletred', label='True Params')
plt.scatter(wfuni, efuni, marker='X', s=80, c='mediumaquamarine', label='Fit Params')
plt.legend(fontsize=fz)
plt.xlabel('$w$', fontsize=fz)
plt.ylabel('$e$', fontsize=fz)
plt.title('50 Fit $w$s Pulled Uniformly', fontsize=fz)
plt.savefig('heatmap_truee_uniformwfit_50_611.png')
#euni,wuni
plt.cla()
fz = 15
plt.hist2d(wdistuni, edistuni, bins=[20,10], cmap='Blues')#, norm=matplotlib.colors.LogNorm());
#plt.clim(vmax=4000.0)
plt.colorbar(label='Rel. Density')
plt.scatter(wuni, euni, marker='o', s=80, c=llikeuni, label='True Params', cmap='Reds')#, norm=matplotlib.colors.LogNorm())
plt.colorbar(label='"log Likelihood"')
#plt.scatter(wfuni, efuni, marker='X', s=80, c='mediumaquamarine', label='Fit Params')
plt.legend(fontsize=fz)
plt.xlabel('$w$', fontsize=fz)
plt.ylabel('$e$', fontsize=fz)
plt.title('50 Fit $w$s Pulled Uniformly', fontsize=fz)
plt.savefig('heatmap_truee_uniformwfit50_llike_new_611.png')
plt.cla()
fz = 15
plt.hist2d(wdistuni, edistuni, bins=[20,10], cmap='Blues')#, norm=matplotlib.colors.LogNorm());
#plt.clim(vmax=4000.0)
plt.colorbar(label='Rel. Density')
plt.scatter(wfuni, efuni, marker='X', s=80, c=llikeuni, label='Fit Params', cmap='Greens')#, norm=matplotlib.colors.LogNorm())
plt.colorbar(label='DELTA Log Like')
plt.legend(fontsize=fz)
plt.xlabel('$w$', fontsize=fz)
plt.ylabel('$e$', fontsize=fz)
plt.title('50 Fit $w$s Pulled Uniformly', fontsize=fz)
plt.savefig('heatmap_truee_uniformwfit50_lfitslike_new_611.png')
plt.cla()
fz = 15
cmap = plt.cm.Reds
plt.hist2d(ws_uniform.flatten(), es_uniform.flatten(), bins=[20,20], cmap='Blues', density=True)#norm=matplotlib.colors.LogNorm());
plt.colorbar(label='Rel. Density')
plt.scatter(truew, truee, marker='o', s=15, c=llike, label='True Params', cmap=cmap, norm=matplotlib.colors.LogNorm())
plt.colorbar(label='$\Delta$ Ln Likelihood')
#plt.clim(vmin=0, vmax=700)
#plt.scatter(fitw, fite, marker='x', s=15, c='mediumaquamarine', label='Fit Params')
plt.legend(fontsize=fz)
plt.xlabel('$\omega$', fontsize=fz)
plt.ylabel('$e$', fontsize=fz)
plt.title('Fit $(e,w)$ Heatmap From Uniform Distribubtion', fontsize=fz)
#plt.savefig('heatmap_llike_colorbar_new.png')
plt.cla()
fz = 15
cmap = plt.cm.Greens
plt.hist2d(ws_uniform.flatten(), es_uniform.flatten(), bins=[20,20], cmap='Blues', density=True)#, norm=matplotlib.colors.LogNorm());
plt.colorbar(label='Rel. Density')
plt.scatter(fitw, fite, marker='X', s=15, c=llike, label='Fit Params', cmap=cmap)
plt.colorbar(label='$\Delta$ Ln Likelihood')
plt.clim(vmin=0, vmax=700)
plt.legend(fontsize=fz)
plt.xlabel('$\omega$', fontsize=fz)
plt.ylabel('$e$', fontsize=fz)
plt.title('Fit $(e,w)$ Heatmap From Uniform Distribubtion', fontsize=fz)
plt.savefig('heatmap_llike_colorbar_fit_new.png')
plt.hist(edistuni, color='cornflowerblue', bins=np.arange(0, 1, 0.1), density=True, stacked=True)
plt.xlabel('$e$', fontsize=fz)
plt.ylabel('Rel. Density')
plt.title('e distribution')
```
# GAUSSIAN DISTRIBUTION
```
# e_rand = np.random.normal(0.4, 0.1, size=n)
# w_rand = np.random.normal(0.0, 45.0, size=n)
trueew_gaussian = pd.read_csv('/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/photoeccentric/notebooks/plots_hpg/gaussian/fitew.txt', index_col=False)
distpath_gaussian = "/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/photoeccentric/notebooks/plots_hpg/gaussian/edists/"
paths = sorted(Path(distpath_gaussian).iterdir(), key=os.path.getmtime)
paths.reverse()
edist_gaussian = []
for file in paths:
fname = os.path.join(distpath_gaussian, file)
try:
edist_gaussian.append(np.genfromtxt(fname, delimiter=','))
except UnicodeDecodeError:
pass
es_gaussian = []
ws_gaussian = []
gs_gaussian = []
for i in range(len(edist_gaussian)):
es_gaussian.append(edist_gaussian[i][:,0])
ws_gaussian.append(edist_gaussian[i][:,1])
gs_gaussian.append(edist_gaussian[i][:,2])
es_gaussian = np.array(es_gaussian)
fite = []
plt.cla()
for i in range(len(es_gaussian)):
fite.append(mode(es_gaussian[i]))
plt.hist(es_gaussian[i], alpha=0.3, density=True, stacked=True);
fite = np.array(fite)
plt.xlabel('Fit E Distributions')
plt.title('All E distributions (sample ~800)')
ws_gaussian = np.array(ws_gaussian)
fitw = []
plt.cla()
for i in range(len(ws_gaussian)):
fitw.append(mode(ws_gaussian[i]))
plt.hist(ws_gaussian[i], alpha=0.3, density=True, stacked=True);
fitw = np.array(fitw)
plt.xlabel('Fit w Distributions (deg)')
plt.title('All w distributions (sample ~800)')
truew = np.array(trueew_gaussian['truew'])
truee = np.array(trueew_gaussian['truee'])
len(truee)
for i in range(len(fitw)):
if fitw[i] > 90:
fitw[i] = fitw[i]-180
plt.cla()
fz = 15
cmap = plt.cm.Blues
cmap.set_bad(color='white')
plt.hist2d(ws_gaussian.flatten(), es_gaussian.flatten(), bins=[22,10], cmap=cmap, norm=matplotlib.colors.LogNorm());
plt.colorbar(label='Rel. Density')
plt.scatter(truew, truee, marker='o', s=15, c='palevioletred', label='True Params')
plt.scatter(fitw, fite, marker='x', s=15, c='mediumaquamarine', label='Fit Params (Mode)')
plt.legend(fontsize=fz)
plt.xlim(-90, 90)
plt.xlabel('$\omega$', fontsize=fz)
plt.ylabel('$e$', fontsize=fz)
plt.title('Fit $(e,w)$ Heatmap From gaussian Distribubtion', fontsize=fz)
plt.savefig('Fit_EW_heatmap_gaussian.png')
wgaussian = np.random.uniform(-90, 90, 2)
inds = []
for i in range(len(wgaussian)):
inds.append(int(np.argwhere(fitw == find_nearest(fitw, wgaussian[i]))[0]))
euni = truee[inds].flatten()
wuni = truew[inds].flatten()
efuni = fite[inds].flatten()
wfuni = fitw[inds].flatten()
edistuni = np.array(es_gaussian[inds]).flatten()
wdistuni = np.array(ws_gaussian[inds]).flatten()
llike = []
for i in range(len(fite)):
counts, wbins, ebins = np.histogram2d(ws_gaussian[i], es_gaussian[i], bins=15);
llike.append(counts[np.digitize(truew[i], wbins)-1, np.digitize(truee[i], ebins)-1])
llike = np.array(llike)
llikeuni = llike[inds]
plt.cla()
fz = 15
plt.hist2d(wdistuni, edistuni, bins=[25,10], cmap='Blues', norm=matplotlib.colors.LogNorm());
plt.xlim(-90, 90)
#plt.clim(vmax=4000.0)
plt.colorbar(label='Rel. Density')
plt.scatter(wuni, euni, marker='o', s=80, c='palevioletred', label='True Params')
plt.scatter(wfuni, efuni, marker='X', s=80, c='mediumaquamarine', label='Fit Params')
plt.legend(fontsize=fz)
plt.xlabel('$w$', fontsize=fz)
plt.ylabel('$e$', fontsize=fz)
plt.title('50 Fit $w$s Pulled gaussianly', fontsize=fz)
plt.savefig('heatmap_truee_gaussianwfit_50.png')
```
| true |
code
| 0.622775 | null | null | null | null |
|
# Chapter 5 - Resampling Methods
- [Load dataset](#Load-dataset)
- [Cross-Validation](#5.1-Cross-Validation)
```
# %load ../standard_import.txt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.linear_model as skl_lm
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split, LeaveOneOut, KFold, cross_val_score
from sklearn.preprocessing import PolynomialFeatures
%matplotlib inline
plt.style.use('seaborn-white')
```
### Load dataset
Dataset available on http://www-bcf.usc.edu/~gareth/ISL/data.html
```
df1 = pd.read_csv('Data/Auto.csv', na_values='?').dropna()
df1.info()
```
## 5.1 Cross-Validation
### Figure 5.2 - Validation Set Approach
Using Polynomial feature generation in scikit-learn<BR>
http://scikit-learn.org/dev/modules/preprocessing.html#generating-polynomial-features
```
t_prop = 0.5
p_order = np.arange(1,11)
r_state = np.arange(0,10)
X, Y = np.meshgrid(p_order, r_state, indexing='ij')
Z = np.zeros((p_order.size,r_state.size))
regr = skl_lm.LinearRegression()
# Generate 10 random splits of the dataset
for (i,j),v in np.ndenumerate(Z):
poly = PolynomialFeatures(int(X[i,j]))
X_poly = poly.fit_transform(df1.horsepower.values.reshape(-1,1))
X_train, X_test, y_train, y_test = train_test_split(X_poly, df1.mpg.ravel(),
test_size=t_prop, random_state=Y[i,j])
regr.fit(X_train, y_train)
pred = regr.predict(X_test)
Z[i,j]= mean_squared_error(y_test, pred)
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(10,4))
# Left plot (first split)
ax1.plot(X.T[0],Z.T[0], '-o')
ax1.set_title('Random split of the data set')
# Right plot (all splits)
ax2.plot(X,Z)
ax2.set_title('10 random splits of the data set')
for ax in fig.axes:
ax.set_ylabel('Mean Squared Error')
ax.set_ylim(15,30)
ax.set_xlabel('Degree of Polynomial')
ax.set_xlim(0.5,10.5)
ax.set_xticks(range(2,11,2));
```
### Figure 5.4
```
p_order = np.arange(1,11)
r_state = np.arange(0,10)
# LeaveOneOut CV
regr = skl_lm.LinearRegression()
loo = LeaveOneOut()
loo.get_n_splits(df1)
scores = list()
for i in p_order:
poly = PolynomialFeatures(i)
X_poly = poly.fit_transform(df1.horsepower.values.reshape(-1,1))
score = cross_val_score(regr, X_poly, df1.mpg, cv=loo, scoring='neg_mean_squared_error').mean()
scores.append(score)
# k-fold CV
folds = 10
elements = len(df1.index)
X, Y = np.meshgrid(p_order, r_state, indexing='ij')
Z = np.zeros((p_order.size,r_state.size))
regr = skl_lm.LinearRegression()
for (i,j),v in np.ndenumerate(Z):
poly = PolynomialFeatures(X[i,j])
X_poly = poly.fit_transform(df1.horsepower.values.reshape(-1,1))
kf_10 = KFold(n_splits=folds, random_state=Y[i,j])
Z[i,j] = cross_val_score(regr, X_poly, df1.mpg, cv=kf_10, scoring='neg_mean_squared_error').mean()
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(10,4))
# Note: cross_val_score() method return negative values for the scores.
# https://github.com/scikit-learn/scikit-learn/issues/2439
# Left plot
ax1.plot(p_order, np.array(scores)*-1, '-o')
ax1.set_title('LOOCV')
# Right plot
ax2.plot(X,Z*-1)
ax2.set_title('10-fold CV')
for ax in fig.axes:
ax.set_ylabel('Mean Squared Error')
ax.set_ylim(15,30)
ax.set_xlabel('Degree of Polynomial')
ax.set_xlim(0.5,10.5)
ax.set_xticks(range(2,11,2));
```
| true |
code
| 0.662551 | null | null | null | null |
|
This is a notebook with all experiments in the DEDPUL paper on behcnmark data sets: UCI, MNIST, CIFAR-10.
At the end of the notebook you can play with DEDPUL on specific data sets.
```
import numpy as np
import pandas as pd
from scipy.stats import norm, laplace
import torch.nn as nn
import torch.optim as optim
import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn.functional as F
import pickle
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from matplotlib.lines import Line2D
%matplotlib inline
from IPython import display
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
import random
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import cross_val_score, train_test_split
from scipy.stats import gaussian_kde
from sklearn.mixture import GaussianMixture
from sklearn.metrics import accuracy_score, log_loss, mean_absolute_error, mean_squared_error, brier_score_loss
from sklearn.metrics import precision_score, recall_score, roc_auc_score, balanced_accuracy_score
from sklearn.model_selection import StratifiedKFold
from sklearn.decomposition import PCA
from sklearn.svm import OneClassSVM
from scipy.stats import linregress
from scipy.optimize import minimize
from scipy.stats import t
from statsmodels.stats.multitest import multipletests
from keras.layers import Dense, Dropout, Input, BatchNormalization
from keras.models import Model, Sequential
from keras.optimizers import Adam
from keras.losses import binary_crossentropy
from keras.callbacks import EarlyStopping
from algorithms import *
from utils import *
from KMPE import *
from NN_functions import *
from torchvision.datasets import MNIST
from tqdm import tqdm_notebook as tqdm
# from tqdm import tqdm as tqdm
import warnings
warnings.filterwarnings('ignore')
```
# Data
```
def read_data(data_mode, truncate=None, random_state=None):
if data_mode == 'bank':
df = pd.read_csv('UCI//bank//bank-full.csv', sep=';')
df['balance'] = normalize_col(df['balance'])
df = dummy_encode(df)
df.rename(columns={'y': 'target'}, inplace=True)
elif data_mode == 'concrete':
df = pd.read_excel('UCI//concrete//Concrete_Data.xls')
df = normalize_cols(df)
df.rename(columns={'Concrete compressive strength(MPa, megapascals) ': 'target'}, inplace=True)
df['target'] = reg_to_class(df['target'])
elif data_mode == 'housing':
df = pd.read_fwf('UCI//housing//housing.data.txt', header=None)
df = normalize_cols(df)
df.rename(columns={13: 'target'}, inplace=True)
df['target'] = reg_to_class(df['target'])
elif data_mode == 'landsat':
df = pd.read_csv('UCI//landsat//sat.trn.txt', header=None, sep=' ')
df = pd.concat([df, pd.read_csv('UCI//landsat//sat.tst.txt', header=None, sep=' ')])
df = normalize_cols(df, columns=[x for x in range(36)])
df.rename(columns={36: 'target'}, inplace=True)
df['target'] = mul_to_bin(df['target'])
elif data_mode == 'mushroom':
df = pd.read_csv('UCI//mushroom//agaricus-lepiota.data.txt', header=None)
df = dummy_encode(df)
df.rename(columns={0: 'target'}, inplace=True)
elif data_mode == 'pageblock':
df = pd.read_fwf('UCI//pageblock//page-blocks.data', header=None)
df = normalize_cols(df, columns=[x for x in range(10)])
df.rename(columns={10: 'target'}, inplace=True)
df['target'] = mul_to_bin(df['target'], 1)
elif data_mode == 'shuttle':
df = pd.read_csv('UCI//shuttle//shuttle.trn', header=None, sep=' ')
df = pd.concat([df, pd.read_csv('UCI//shuttle//shuttle.tst.txt', header=None, sep=' ')])
df = normalize_cols(df, columns=[x for x in range(9)])
df.rename(columns={9: 'target'}, inplace=True)
df['target'] = mul_to_bin(df['target'], 1)
elif data_mode == 'spambase':
df = pd.read_csv('UCI//spambase//spambase.data.txt', header=None, sep=',')
df = normalize_cols(df, columns=[x for x in range(57)])
df.rename(columns={57: 'target'}, inplace=True)
elif data_mode == 'wine':
df = pd.read_csv('UCI//wine//winequality-red.csv', sep=';')
df_w = pd.read_csv('UCI//wine//winequality-white.csv', sep=';')
df['target'] = 1
df_w['target'] = 0
df = pd.concat([df, df_w])
df = normalize_cols(df, [x for x in df.columns if x != 'target'])
elif data_mode.startswith('mnist'):
data = MNIST('mnist', download=True, train=True)
data_test = MNIST('mnist', download=True, train=False)
df = data.train_data
target = data.train_labels
df_test = data_test.test_data
target_test = data_test.test_labels
df = pd.DataFrame(torch.flatten(df, start_dim=1).detach().numpy())
df_test = pd.DataFrame(torch.flatten(df_test, start_dim=1).detach().numpy())
df = pd.concat([df, df_test])
df = normalize_cols(df)
target = pd.Series(target.detach().numpy())
target_test = pd.Series(target_test.detach().numpy())
target = pd.concat([target, target_test])
if data_mode == 'mnist_1':
target[target % 2 == 0] = 0
target[target != 0] = 1
elif data_mode == 'mnist_2':
target[target < 5] = 0
target[target >= 5] = 1
elif data_mode == 'mnist_3':
target[target.isin({0, 3, 5, 6, 7})] = 0
target[target.isin({1, 2, 4, 8, 9})] = 1
df['target'] = target
elif data_mode.startswith('cifar10'):
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
# trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
# shuffle=True, num_workers=2)
data = trainset.data
target = trainset.targets
# if truncate is not None and truncate < trainset.data.shape[0]:
# np.random.seed(random_state)
# mask = np.random.choice(np.arange(trainset.data.shape[0]), truncate, replace=False)
# np.random.seed(None)
# data = trainset.data[mask]
# target = trainset.targets[mask]
data = data / 128 - 1
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
target = pd.Series(target)
target[target.isin([0, 1, 8, 9])] = 1
target[target != 1] = 0
df = pd.DataFrame(data.reshape(data.shape[0], -1))
df['target'] = target
# 1 = N, 0 = P
df['target'] = 1 - df['target']
if truncate is not None and truncate < df.shape[0]:
if truncate > 1:
df = df.sample(n=truncate, random_state=random_state)
elif truncate > 0:
df = df.sample(frac=truncate, random_state=random_state)
return df
def make_pu(df, data_mode, alpha=0.5, random_state=None):
df['target_pu'] = df['target']
n_pos, n_pos_to_mix, n_neg_to_mix = shapes[data_mode][alpha]
df_pos = df[df['target'] == 0].sample(n=n_pos+n_pos_to_mix, random_state=random_state, replace=False).reset_index(drop=True)
df_neg = df[df['target'] == 1].sample(n=n_neg_to_mix, random_state=random_state, replace=False).reset_index(drop=True)
df_pos.loc[df_pos.sample(n=n_pos_to_mix, random_state=random_state, replace=False).index, 'target_pu'] = 1
return pd.concat([df_pos, df_neg]).sample(frac=1).reset_index(drop=True)
shapes = {'bank': {0.95: (1000, int(39922 / 19), 39922),
0.75: (1000, 4289, 4289*3),
0.50: (1000, 4289, 4289),
0.25: (1000, 4289, int(4289 / 3)),
0.05: (1000, 4289, int(4289 / 19))},
'concrete': {0.95: (100, int(540 / 19), 540),
0.75: (100, 180, 540),
0.50: (100, 390, 390),
0.25: (100, 390, 130),
0.05: (100, 380, 20)},
'housing': {0.95: (194, 15, 297),
0.75: (110, 99, 297),
0.50: (50, 159, 159),
0.25: (50, 159, 53),
0.05: (57, 152, 8)},
'landsat': {0.95: (1000, 189, 3594),
0.75: (1000, 1000, 3000),
0.50: (1000, 1841, 1841),
0.25: (1000, 1841, int(1841 / 3)),
0.05: (1000, 1841, int(1841 / 19))},
'mushroom': {0.95: (1000, 200, 3800),
0.75: (1000, 1000, 3000),
0.50: (1000, 2000, 2000),
0.25: (1000, 2916, 972),
0.05: (990, 2926, 154)},
'pageblock': {0.95: (100, 234, 4446),
0.75: (100, 460, 1380),
0.50: (100, 460, 460),
0.25: (101, 459, 153),
0.05: (104, 456, 24)},
'shuttle': {0.95: (1000, int(45586 / 19), 45586),
0.75: (1000, 11414, 11414 * 3),
0.50: (1000, 11414, 11414),
0.25: (1000, 11414, int(11414 / 3)),
0.05: (1000, 11414, int(11414 / 19))},
'spambase': {0.95: (400, 147, 2788),
0.75: (400, 929, 2788),
0.50: (400, 1413, 1413),
0.25: (400, 1413, 471),
0.05: (407, 1406, 74)},
'wine': {0.95: (500, int(4898 / 19), 4898),
0.75: (500, 1099, 1099 * 3),
0.50: (500, 1099, 1099),
0.25: (500, 1099, int(1099 / 3)),
0.05: (500, 1099, int(1099 / 19))},
'mnist_1': {0.95: (1000, int(34418 / 19), 34418),
0.75: (1000, int(34418 / 3), 34418),
0.50: (1000, 34418, 34418),
0.25: (1000, 34582, int(34582 / 3)),
0.05: (1000, 34582, int(34582 / 19))},
'cifar10': {0.95: (1000, int(30000 / 19), 30000),
0.75: (1000, 10000, 30000),
0.50: (1000, 19000, 19000),
0.25: (1000, 19000, int(19000 / 3)),
0.05: (1000, 19000, int(19000 / 19))}}
LRS = {
'bank': 5e-4,
'concrete': 1e-4,
'housing': 1e-4,
'landsat': 1e-5,
'mushroom': 1e-4,
'pageblock': 1e-4,
'shuttle': 1e-4,
'spambase': 1e-5,
'wine': 5e-5,
'mnist_1': 1e-4,
'mnist_2': 1e-4,
'mnist_3': 1e-4,
'cifar10': 1e-4,
}
```
# DEDPUL, EN, and nnPU
```
def experiment_uci(datasets=None, alphas=None, n_networks=1, n_rep=10, find_alpha=False):
if alphas is None:
alphas = [0.05, 0.25, 0.5, 0.75, 0.95]
if datasets is None:
datasets = [
'bank', 'concrete', 'mushroom', 'pageblock', 'landsat', 'shuttle', 'spambase', 'wine',
'mnist_1',
'cifar10',
]
results = []
fixed_alpha = None
for dataset in tqdm(datasets):
for alpha in tqdm(shapes[dataset].keys()):
if alpha not in alphas:
continue
n_pos, n_pos_to_mix, n_neg_to_mix = shapes[dataset][alpha]
n_mix = n_pos_to_mix + n_neg_to_mix
real_alpha = n_neg_to_mix / n_mix
for i in tqdm(range(n_rep)):
df = read_data(dataset, truncate=None, random_state=i)
df = make_pu(df, dataset, alpha, random_state=i)
data = df.drop(['target', 'target_pu'], axis=1).values
all_conv = False
n_neurons = 512
if dataset == 'cifar10':
data = np.swapaxes(data.reshape(data.shape[0], 32, 32, 3), 1, 3)
all_conv = True
n_neurons = 128
target_pu = df['target_pu'].values
target_mix = df.loc[df['target_pu'] == 1, 'target'].values
if not find_alpha:
fixed_alpha = real_alpha
res = dict()
try:
res = estimate_poster_cv(data, target_pu, estimator='ntc_methods', alpha=fixed_alpha,
estimate_poster_options={'disp': False, 'alpha_as_mean_poster': True},
estimate_diff_options={
'MT': False, 'MT_coef': 0.25, 'decay_MT_coef': False, 'tune': False,
'bw_mix': 0.05, 'bw_pos': 0.1, 'threshold': 'mid',
'n_gauss_mix': 20, 'n_gauss_pos': 10,
'bins_mix': 20, 'bins_pos': 20, 'k_neighbours': None,},
estimate_preds_cv_options={
'n_networks': n_networks,
'cv': 5,
'random_state': i*n_networks,
'hid_dim': n_neurons,
'n_hid_layers': 1,
'lr': LRS[dataset],
'l2': 1e-4,
'bn': True,
'all_conv': all_conv,
},
train_nn_options = {
'n_epochs': 250, 'loss_function': 'log', 'batch_size': 64,
'n_batches': None, 'n_early_stop': 7, 'disp': False,
},
### catboost
# estimate_preds_cv_options={
# 'n_networks': n_networks,
# 'cv': 5,
# 'random_state': i*n_networks,
# 'n_early_stop': 25,
# 'catboost_params': {
# 'iterations': 500, 'depth': 8, 'learning_rate': 0.02,
# 'l2_leaf_reg': 10,
# },
# },
)
res['nnre_sigmoid'] = estimate_poster_cv(
data, target_pu, estimator='nnre', alpha=real_alpha,
estimate_preds_cv_options={
'n_networks': n_networks,
'cv': 5,
'random_state': i*n_networks,
'hid_dim': n_neurons,
'n_hid_layers': 1,
'lr': LRS[dataset],
'l2': 1e-4,
'bn': True,
'all_conv': all_conv,
},
train_nn_options = {
'n_epochs': 250, 'loss_function': 'sigmoid', 'batch_size': 64,
'n_batches': None, 'n_early_stop': 10, 'disp': False,
'beta': 0, 'gamma': 1,
},
)
res['nnre_brier'] = estimate_poster_cv(
data, target_pu, estimator='nnre', alpha=real_alpha,
estimate_preds_cv_options={
'n_networks': n_networks,
'cv': 5,
'random_state': i*n_networks,
'hid_dim': n_neurons,
'n_hid_layers': 1,
'lr': LRS[dataset],
'l2': 1e-4,
'bn': True,
'all_conv': all_conv,
},
train_nn_options = {
'n_epochs': 250, 'loss_function': 'brier', 'batch_size': 64,
'n_batches': None, 'n_early_stop': 10, 'disp': False,
'beta': 0, 'gamma': 1,
},
)
except:
print(f'dataset = {dataset}, i = {i} failed')
continue
for key in res.keys():
est_alpha, poster = res[key]
cur_result = [dataset, key, i, n_mix, n_pos, alpha, real_alpha, est_alpha]
if poster is not None:
cur_result.append(np.mean(poster))
cur_result.append(accuracy_score(target_mix, poster.round()))
cur_result.append(roc_auc_score(target_mix, poster))
cur_result.append(log_loss(target_mix, poster))
cur_result.append(precision_score(target_mix, poster.round()))
cur_result.append(recall_score(target_mix, poster.round()))
cur_result.append(balanced_accuracy_score(target_mix, poster.round()))
cur_result.append(brier_score_loss(target_mix, poster))
results.append(cur_result)
df_results = pd.DataFrame(results, columns=['dataset', 'estimator', 'random_state',
'n_mix', 'n_pos', 'alpha', 'real_alpha', 'est_alpha', 'mean_poster',
'accuracy', 'roc', 'log_loss', 'precision', 'recall',
'accuracy_balanced', 'brier_score',])
return df_results
res = experiment_uci()
res = res.round(5)
res.to_csv('exp_uci_new.csv', index=False, sep=';', decimal=',')
```
# KMPE
```
def experiment_uci_KM(datasets=None, alphas=None, n_rep=10, max_sample=4000):
if alphas is None:
alphas = [0.05, 0.25, 0.5, 0.75, 0.95]
if datasets is None:
datasets = ['bank', 'concrete', 'landsat', 'mushroom', 'pageblock', 'shuttle', 'spambase', 'wine',
'mnist_1',
'cifar10',]
results = []
for dataset in tqdm(datasets):
for alpha in tqdm(shapes[dataset].keys()):
if alpha not in alphas:
continue
n_pos, n_pos_to_mix, n_neg_to_mix = shapes[dataset][alpha]
n_mix = n_pos_to_mix + n_neg_to_mix
real_alpha = n_neg_to_mix / n_mix
for i in tqdm(range(n_rep)):
df = read_data(dataset, truncate=None, random_state=i)
df = make_pu(df, dataset, alpha, random_state=i)
if dataset in {'mnist_1', 'mnist_2', 'mnist_3', 'cifar10'}:
pca = PCA(50)
data = pca.fit_transform(df.drop(['target', 'target_pu'], axis=1).values)
else:
data = df.drop(['target', 'target_pu'], axis=1).values
target_pu = df['target_pu'].values
target_mix = df.loc[df['target_pu'] == 1, 'target'].values
data_pos = data[target_pu == 0]
data_mix = data[target_pu == 1][np.random.randint(0, int(target_pu.sum()),
min(max_sample - int((1-target_pu).sum()),
int(target_pu.sum())))]
try:
KM_2 = 1 - wrapper(data_mix, data_pos, disp=False,
KM_1=False, KM_2=True, lambda_lower_bound=0.5, lambda_upper_bound=10)
except ValueError as e:
KM_2 = np.NaN
print(e)
cur_result = [dataset, i, n_mix, n_pos, alpha, real_alpha, KM_2]
results.append(cur_result)
df_results = pd.DataFrame(results, columns=['dataset', 'random_state', 'n_mix', 'n_pos', 'alpha', 'real_alpha',
'est_alpha'])
df_results['estimator'] = 'KM'
return df_results
res_KM = experiment_uci_KM(datasets=None, alphas=None, n_rep=10)
res_KM = res_KM.round(5)
res_KM.to_csv('exp_KMPE_uci.csv', index=False, sep=';', decimal=',')
```
# TIcE
```
from TIcE import tice, tice_c_to_alpha, min_max_scale
def experiment_uci_TIcE(datasets=None, alphas=None, n_rep=10, NTC=False):
if alphas is None:
alphas = [0.05, 0.25, 0.5, 0.75, 0.95]
if datasets is None:
datasets = [
'bank', 'concrete', 'mushroom',
'landsat', 'pageblock', 'shuttle', 'spambase', 'wine',
'mnist_1',
'cifar10'
]
results = []
for dataset in tqdm(datasets):
for alpha in tqdm(shapes[dataset].keys()):
if alpha not in alphas:
continue
n_pos, n_pos_to_mix, n_neg_to_mix = shapes[dataset][alpha]
n_mix = n_pos_to_mix + n_neg_to_mix
real_alpha = n_neg_to_mix / n_mix
for i in tqdm(range(n_rep)):
df = read_data(dataset, truncate=None, random_state=i)
df = make_pu(df, dataset, alpha, random_state=i)
data = df.drop(['target', 'target_pu'], axis=1).values
target_pu = df['target_pu'].values
target_mix = df.loc[df['target_pu'] == 1, 'target'].values
gamma = target_pu.sum() / target_pu.shape[0]
if NTC:
if dataset == 'cifar10':
data = np.swapaxes(data.reshape(data.shape[0], 32, 32, 3), 1, 3)
data = estimate_preds_cv(
data, target_pu, cv=5, all_conv=(dataset == 'cifar10'),
n_networks=1, hid_dim=512, n_hid_layers=1, lr=LRS[dataset], bn=True, l2=1e-4,
train_nn_options={'n_epochs': 200, 'metric': roc_auc_loss, 'batch_size': 64,
'n_batches': None, 'n_early_stop': 10, 'disp': False,
'loss_function': 'log'}).reshape(-1, 1)
else:
if dataset in {'mnist_1', 'mnist_2', 'mnist_3', 'cifar10'}:
pca = PCA(200)
data = pca.fit_transform(data)
data = min_max_scale(data)
c = tice(data, 1 - target_pu, 10, np.random.randint(5, size=len(data)),
delta=.2 maxSplits=500, minT=10, n_splits=3)[0]
alpha_tice = tice_c_to_alpha(c, gamma)
cur_result = [dataset, i, n_mix, n_pos, alpha, real_alpha, alpha_tice]
results.append(cur_result)
df_results = pd.DataFrame(results, columns=['dataset', 'random_state', 'n_mix', 'n_pos', 'alpha', 'real_alpha',
'est_alpha'])
df_results['estimator'] = 'tice'
return df_results
res_tice = experiment_uci_TIcE(NTC=False, n_rep=10)
res_tice = res_tice.round(5)
res_tice['est_alpha'][res_tice['est_alpha'] < 0] = 0
res_tice.to_csv('TIcE_uci.csv', index=False, sep=';', decimal=',')
```
# The data set with all results
```
# this is a merged data set with all experiments with all methods
res = pd.read_csv('exp_uci_new_merged.csv', sep=';', decimal=',')
res['alpha_mae'] = (res['real_alpha'] - res['est_alpha']).abs()
res_grouped = res.groupby(['dataset', 'n_mix', 'n_pos', 'alpha', 'estimator']).mean().drop(
['est_alpha', 'random_state'], axis=1).reset_index()
res_pivot_alpha = res_grouped.pivot_table(index=['dataset', 'alpha'], columns=['estimator'], values='alpha_mae')
metric = 'accuracy'
res_pivot_roc = res_grouped.pivot_table(index=['dataset', 'alpha'], columns=['estimator'], values=metric)
res_pivot_roc = 1 - res_pivot_roc
res_pivot_roc = clean_columns_poster(res_pivot_roc)
res_pivot_alpha.reset_index(inplace=True)
res_pivot_alpha.loc[res_pivot_alpha['dataset'] == 'mnist_1', 'dataset'] = 'mnist'
res_pivot_alpha.set_index(['dataset', 'alpha'], inplace=True)
res_pivot_roc.reset_index(inplace=True)
res_pivot_roc.loc[res_pivot_roc['dataset'] == 'mnist_1', 'dataset'] = 'mnist'
res_pivot_roc.set_index(['dataset', 'alpha'], inplace=True)
```
# Plots
```
# To switch between comparison of DEDPUL with SOTA and ablations of DEDPUL, comment lines under #1 and
# uncomment lines under #2
def plot_results_uci(res_plt, datasets=None, ylims=None, reverse_alpha=False, save_name=None, dpi=200,
alpha_mode=True):
if reverse_alpha:
# by default all estimates are computed for negative priors; here convert them to positive priors
res_plt['alpha'] = 1 - res_plt['alpha']
if ylims is None:
ylims = dict()
if datasets is None:
datasets = ['bank', 'concrete', 'mushroom', 'landsat', 'pageblock', 'shuttle',
'spambase', 'wine', 'mnist', 'cifar10']
fig = plt.figure(0)
fig.set_size_inches(w=35, h=14)
for i in range(10):
try:
dataset = datasets[i]
except:
break
res_plt_cur = res_plt[res_plt['dataset'] == dataset]
plt.subplot2grid((2, 5), (i//5,i%5), colspan=1, rowspan=1)
plt.title(dataset, fontdict={'fontsize': 23})
if not alpha_mode:
pass
# 1
plt.plot(res_plt_cur['alpha'], res_plt_cur['nnre_brier'], color='purple', marker='v', ls='--')
plt.plot(res_plt_cur['alpha'], res_plt_cur['nnre_sigmoid'], color='brown', marker='^', ls='-.')
else:
pass
# 1
plt.plot(res_plt_cur['alpha'], res_plt_cur['KM'], 'rs--')
plt.plot(res_plt_cur['alpha'], res_plt_cur['tice'], c='g', marker='v', ls='-.')
plt.plot(res_plt_cur['alpha'], res_plt_cur['tice+ntc'], c='b', marker='*', ls='-.')
# 2
# plt.plot(res_plt_cur['alpha'], res_plt_cur['baseline_dedpul'], c='r', marker='*', ls='--')
plt.plot(res_plt_cur['alpha'], res_plt_cur['dedpul'], 'ko-')
# 1
plt.plot(res_plt_cur['alpha'], res_plt_cur['e1_en'], c='orange', marker='x', ls=':')
# 2
# plt.plot(res_plt_cur['alpha'], res_plt_cur['cat'], c='g', marker='*', ls='--')
# plt.plot(res_plt_cur['alpha'], res_plt_cur['dedpul_GMM'], c='purple', marker='*', ls='-.')
# plt.plot(res_plt_cur['alpha'], res_plt_cur['dedpul_hist'], c='b', marker='*', ls='-.')
# plt.plot(res_plt_cur['alpha'], res_plt_cur['dedpul_no_heur'], c='darkcyan', marker='*', ls=':')
plt.xlim(0, 1)
plt.yticks([0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5], fontsize='xx-large')
plt.xticks(res_plt_cur['alpha'].unique(), fontsize='xx-large')
if dataset in ylims.keys():
plt.ylim(0, ylims[dataset])
if i >= 5:
plt.xlabel(r'$\alpha$', fontsize='xx-large')
if i% 5 == 0:
if not alpha_mode:
plt.ylabel('1 - accuracy', fontsize='xx-large')
else:
plt.ylabel(r'$\left|\alpha - \widetilde{\alpha}^*\right|$', fontsize='xx-large')
if dataset == 'mushroom':
if not alpha_mode:
# 1
plt.legend(handles=(Line2D([], [], linestyle=':', color='orange', marker='x'),
Line2D([], [], color='purple', marker='v', ls='--'),
Line2D([], [], color='brown', marker='^', ls='-.'),
Line2D([], [], linestyle='-', color='k', marker='o')),
labels=('EN', 'nnPU-brier', 'nnPU-sigmoid', 'DEDPUL'), loc='upper left', fontsize='xx-large')
# 2
# plt.legend(handles=(Line2D([], [], linestyle='-', color='k', marker='o'),
# Line2D([], [], linestyle='--', color='g', marker='*'),
# Line2D([], [], linestyle='-.', color='purple', marker='*'),
# Line2D([], [], linestyle='-.', color='b', marker='*'),
# Line2D([], [], linestyle=':', color='darkcyan', marker='*')),
# labels=('DEDPUL', 'catboost', 'GMM', 'hist', 'no_smooth'),
# loc='upper left', fontsize='xx-large')
else:
# 1
plt.legend(handles=(Line2D([], [], linestyle=':', color='orange', marker='x'),
Line2D([], [], c='g', marker='v', ls='-.'),
Line2D([], [], c='b', marker='*', ls='-.'),
Line2D([], [], linestyle='--', color='r', marker='s'),
Line2D([], [], linestyle='-', color='k', marker='o'),
),
labels=('EN', 'TIcE', 'NTC+TIcE', 'KM2', 'DEDPUL'),
loc='upper left', fontsize='xx-large')
# 2
# plt.legend(handles=(Line2D([], [], linestyle='-', color='k', marker='o'),
# Line2D([], [], linestyle='--', color='r', marker='*'),
# Line2D([], [], linestyle='--', color='g', marker='*'),
# Line2D([], [], linestyle='-.', color='purple', marker='*'),
# Line2D([], [], linestyle='-.', color='b', marker='*'),
# Line2D([], [], linestyle=':', color='darkcyan', marker='*')),
# labels=('DEDPUL', 'simple_alpha', 'catboost', 'GMM', 'hist', 'no_smooth'),
# loc='upper center', fontsize='xx-large')
if save_name:
plt.savefig(save_name + '.png', dpi=dpi)
plot_results_uci(res_pivot_alpha.copy().reset_index(), reverse_alpha=True, alpha_mode=True,
ylims={'bank': 0.4,
'concrete': 0.5,
'landsat': 0.5,
'mushroom': 0.3,
'pageblock': 0.4,
'shuttle': 0.1,
'spambase': 0.5,
'wine': 0.5,
'mnist': 0.5,
'cifar10': 0.5},
# # save_name='uci_alpha_new',
# ylims={'bank': 0.2,
# 'concrete': 0.45,
# 'landsat': 0.16,
# 'mushroom': 0.3,
# 'pageblock': 0.5,
# 'shuttle': 0.2,
# 'spambase': 0.25,
# 'wine': 0.35,
# 'mnist': 0.15,
# 'cifar10': 0.25},
# # save_name='uci_alpha_new_ablation',
)
plot_results_uci(res_pivot_roc.copy().reset_index(), reverse_alpha=True, alpha_mode=False,
ylims={'bank': 0.25,
'concrete': 0.4,
'landsat': 0.15,
'mushroom': 0.1,
'pageblock': 0.25,
'shuttle': 0.05,
'spambase': 0.25,
'wine': 0.05,
'mnist': 0.2,
'cifar10': 0.35},
# # save_name='uci_ac_new',
# ylims={'bank': 0.25,
# 'concrete': 0.3,
# 'landsat': 0.1,
# 'mushroom': 0.05,
# 'pageblock': 0.2,
# 'shuttle': 0.05,
# 'spambase': 0.2,
# 'wine': 0.05,
# 'mnist': 0.15,
# 'cifar10': 0.25},
# # save_name='uci_ac_new_ablation',
)
```
# DEDPUL on specific single data sets
```
# data_mode = 'bank' # 0.11, (5289, 39922, 45211)
# data_mode = 'concrete' # 0.47, (490, 540, 1030)
# data_mode = 'housing' # 0.41, (209, 297, 506)
# data_mode = 'landsat' # 0.44, (2841, 3594, 6435)
data_mode = 'mushroom' # 0.48, (3916, 4208, 8124)
# data_mode = 'pageblock' # 0.1, (560, 4913, 5473)
# data_mode = 'shuttle' # 0.21, (12414, 45586, 58000)
# data_mode = 'spambase' # 0.39, (1813, 2788, 4601)
# data_mode = 'wine' # 0.24, (1599, 4898, 6497)
# data_mode = 'mnist_1' # 0.51, (35582, 34418, 70000)
# data_mode = 'cifar10' # 0.4, (20000, 30000, 50000)
alpha = 0.25
df = read_data(data_mode, truncate=None)
df = make_pu(df, data_mode, alpha=alpha, random_state=None)
alpha = ((df['target'] == 1).sum() / (df['target_pu'] == 1).sum()).item()
gamma = (df['target_pu'] == 1).sum() / df.shape[0]
print(df.shape)
print('alpha =', alpha)
data = df.drop(['target', 'target_pu'], axis=1).values
all_conv = False
if data_mode == 'cifar10':
data = np.swapaxes(data.reshape(data.shape[0], 32, 32, 3), 1, 3)
all_conv = True
target = df['target_pu'].values
preds = estimate_preds_cv(data, target, cv=3, bayes=False, random_state=42, all_conv=all_conv,
n_networks=1, hid_dim=512, n_hid_layers=1, lr=LRS[data_mode], l2=1e-4, bn=True,
train_nn_options={'n_epochs': 500, 'bayes_weight': 1e-5,
'batch_size': 64, 'n_batches': None, 'n_early_stop': 7,
'disp': True, 'loss_function': 'log',
'metric': roc_auc_loss, 'stop_by_metric': False})
# preds = estimate_preds_cv_catboost(
# data, target, cv=5, n_networks=1, random_state=42, n_early_stop=20, verbose=True,
# catboost_params={
# 'iterations': 500, 'depth': 8, 'learning_rate': 0.02, 'l2_leaf_reg': 10,
# },
# )
print('ac', accuracy_score(df['target_pu'], preds.round()))
# print('bac', balanced_accuracy_score(df['target_pu'], preds.round()))
print('roc', roc_auc_score(df['target_pu'], preds))
print('brier', brier_score_loss(df['target_pu'], preds))
bw_mix = 0.05
bw_pos = 0.1
MT_coef = 0.25
threshold = (preds[df['target_pu'].values==1].mean()+preds[df['target_pu'].values==0].mean())/2
threshold_h = preds[df['target_pu'].values==1].mean()
threshold_l = preds[df['target_pu'].values==0].mean()
k_neighbours = df.shape[0] // 20
diff = estimate_diff(preds, df['target_pu'].values, bw_mix, bw_pos, 'logit', threshold, k_neighbours,
MT=False, MT_coef=MT_coef, tune=False)
test_alpha, poster = estimate_poster_em(diff, mode='dedpul', converge=True, nonconverge=True,
max_diff=0.05, step=0.0025, alpha_as_mean_poster=True,
# alpha=alpha,
)
print('alpha:', test_alpha, '\nmean_poster:', np.mean(poster), '\ncons_alpha:', alpha,
'\nbaseline alpha:', 1-min(1/diff))
# print('log_loss:',
# log_loss(df.loc[df['target_pu']==1, 'target'], poster))
print('accuracy:',
accuracy_score(df.loc[df['target_pu']==1, 'target'], poster.round()))
print('balanced_accuracy:',
balanced_accuracy_score(df.loc[df['target_pu']==1, 'target'], poster.round()))
print('precision:',
precision_score(df.loc[df['target_pu']==1, 'target'], poster.round()))
print('recall:',
recall_score(df.loc[df['target_pu']==1, 'target'], poster.round()))
print('roc-auc:',
roc_auc_score(df.loc[df['target_pu']==1, 'target'], poster))
# print('MAE:',
# mean_absolute_error(df.loc[df['target_pu']==1, 'target'], poster))
# print('RMSE:',
# np.sqrt(mean_squared_error(df.loc[df['target_pu']==1, 'target'], poster)))
```
| true |
code
| 0.579519 | null | null | null | null |
|
# Data visualization of iris Dataset
this is exploration of iris dataset using python visualizing modules
for more info :- https://en.wikipedia.org/wiki/Iris_(plant)
```
# importing dapendent libraries
import numpy as np
import pandas as pd
#The subprocess module allows you to spawn new processes, connect to their input/output/error pipes, and obtain their return codes. This module intends to replace several older modules and functions:
# os.system ,os.spawn* ,os.popen* ,popen2.* , commands.*
from subprocess import check_output
%matplotlib inline
import pandas as pd
import warnings # in case due to compatiblity issues posed by the data visualization libraries
import seaborn as sns # graph visualization library
import matplotlib.pyplot as plt
sns.set(style="darkgrid",color_codes = True)
#loading the flower dataset
iris = pd.read_csv("Iris.csv")
#now for checking the dataframe of a particular type of species
iris_ve = iris.loc[iris['Species']== "Iris-versicolor"]
iris_ve.describe()
#finding the statistics of species and their count
iris["Species"].value_counts()
#plotting the species according to the diffrent features displayed by the dataframe
sns.FacetGrid(iris,hue="Species",size = 10)\
.map(plt.scatter,"SepalWidthCm","PetalWidthCm") \
.add_legend()
#now plotting between sepal length and petal length
sns.FacetGrid(iris,hue="Species",size = 10)\
.map(plt.scatter,"SepalLengthCm","PetalLengthCm") \
.add_legend()
# thus the above two plots shows that sepal and petal length have more linear relation and can be classified
# now plotting multivariable visualization
# for more info , comsult https://pandas.pydata.org/pandas-docs/stable/visualization.html
from pandas.tools.plotting import parallel_coordinates
#just plotting the diffrent species accoring to the diffrent features ,one taken at a time
r = parallel_coordinates(iris.drop("Id",axis=1),"Species")
import matplotlib
r.savefig(fname, dpi=None, facecolor='w', edgecolor='w',
orientation='portrait', papertype=None, format=None,
transparent=False, bbox_inches=None, pad_inches=0.1,
frameon=None)
#plotting the figure with the paragraph
ax = df.plot()
fig = ax.get_figure()
fig.savefig('plot.png')
#now using bokeh library to plot bar and plotting diffrent species according to their color , length
from bokeh.plotting import figure, output_notebook, show
N = 4000
#x = np.random.random(size=N) * 100
#y = np.random.random(size=N) * 100
x = iris.PetalLengthCm
y = iris.SepalLengthCm
radii = np.random.random(size=N) * 1.5
colors = ["#%02x%02x%02x" % (int(r), int(g), 150) for r, g in zip(np.floor(50+2*x), np.floor(30+2*y))]
output_notebook()
Plots="resize,crosshair,pan,wheel_zoom,box_zoom,reset,tap,previewsave,box_select,poly_select,lasso_select"
p = figure(tools=Plots)
p.scatter(x,y,radius=0.02, fill_alpha=0.9,line_color=None)
#just testing the plotting of the Petal length and sepal length ( although quite odd)
show(p)
#showing histogram plot having the count of species according to length
from bokeh.charts import Histogram
hist = Histogram(iris, values="PetalLengthCm", color="Species", legend="top_right", bins=12)
show(hist)
from bokeh.charts import Bar, output_file, show
p = Bar(iris, label='PetalLengthCm', values='PetalWidthCm', agg='median', group='Species',
title="Y = Median PetalWidthCm X PetalLengthCm, grouped by Species", legend='top_right')
show(p)
```
# traning model on iris data-set using knn classifier to predict the species using there features
```
#here we will be using the sklearn library which has prebuild many machine learning methods and datasets
from sklearn.datasets import load_iris
iris = load_iris()
#store the values of data in X
X = iris.data
# store the output trained answers in Y
y = iris.target
#importing the knn clasifier function
from sklearn.neighbors import KNeighborsClassifier
# now we will "Instantiate" the "estimator"
#where
# "Estimator" is scikit-learn's term for model
# "Instantiate" means "make an instance of"
knn = KNeighborsClassifier(n_neighbors=1)
print(knn)
# now fiiting the input ufeatures and observed outputs and fitting the data
knn.fit(X,y)
#Now for predicting the outputs , passing the matrix of values
X_new = [[3, 5, 4, 2], [5, 4, 3, 2]]
knn.predict(X_new)
```
| true |
code
| 0.646655 | null | null | null | null |
|
## Plot Scoreboard Using Python and Plotly
##### ABOUT THE AUTHOR:
This notebook was contributed by [Plotly user Emilia Petrisor](https://plot.ly/~empet). You can follow Emilia on Twitter [@mathinpython](https://twitter.com/mathinpython) or [Github](https://github.com/empet).
### Two Scoreboards for Republican Presidential Candidates
Starting with August 6, 2015, The New York Times updates from time to time a scoreboard for the republican presidential [candidates](http://www.nytimes.com/interactive/2015/08/06/upshot/2016-republican-presidential-candidates-dashboard.html).
In this IPython (Jupyter) Notebook we generate the scoreboard published on August 14, respectively August 17, as [Heatmap(s)](https://plot.ly/python/heatmaps/) objects in Python Plotly.
Inspecting the web page [source code](view-source:http://www.nytimes.com/interactive/2015/08/06/upshot/2016-republican-presidential-candidates-dashboard.html?abt=0002&abg=0)
we found out that the scoreboard heatmap in The New York Times is generated with [http://colorzilla.com/gradient-editor/]( http://colorzilla.com/gradient-editor/).
To identify the color code of each of the 16 colors defining the color gradient in The New York Times dashboard we install `ColorZilla`
[Chrome extension](https://chrome.google.com/webstore/detail/colorzilla/bhlhnicpbhignbdhedgjhgdocnmhomnp?hl=en).
When the *newtimes* page is opened, we choose the *Web page color analyzer* in the `ColorZilla` menu and read
succesively the color codes.
The corresponding [Plotly colorscale](https://plot.ly/python/heatmaps-contours-and-2dhistograms-tutorial/#Custom-color-scales-in-Plotly) is defined as follows:
```
newyorktimes_cs=[[0.0, '#8B0000'],
[0.06666666666666667, '#9E051B'],
[0.13333333333333333, '#B0122C'],
[0.2, '#C0223B'],
[0.26666666666666666, '#CF3447'],
[0.3333333333333333, '#DB4551'],
[0.4, '#E75758'],
[0.4666666666666667, '#F06A5E'],
[0.5333333333333333, '#F87D64'],
[0.6, '#FE906A'],
[0.6666666666666666, '#FFA474'],
[0.7333333333333333, '#FFB880'],
[0.8, '#FFCB91'],
[0.8666666666666667, '#FFDEA7'],
[0.9333333333333333, '#FFEEC1'],
[1.0, '#FFFFE0']]
```
Below we give the table of rankings as for 14 August, by the factors in the list with the same name.
```
tab_vals14=[[1,2,3,4,5,6,6,8,9,9,9,12,13,13,13,13],
[1,7,5,12,5,4,12,7,2,3,12,7,7,12,7,12],
[4,7,2,1,10,5,6,7,9,12,3,14,12,11,15,16],
[2,9,4,1,3,8,10,11,6,5,6,14,14,12,14,13],
[1,3,4,14,8,2,13,12,7,6,9,16,5,10,12,15]]
candidates=['Bush', 'Rubio', 'Walker', 'Trump', 'Kasich', 'Cruz', 'Fiorina', 'Huckabee', 'Paul']+\
['Christie', 'Carson', 'Santorum', 'Perry', 'Jindal', 'Graham', 'Pataki']
factors=['Prediction Market', 'NationalEndorsements', 'Iowa Polls']+\
['New Hampshire Polls', 'Money Raised']
```
First we define a simple Plotly Heatmap:
```
import plotly.plotly as py
from plotly.graph_objs import *
data14=Data([Heatmap(z=tab_vals14,
y=factors,
x=candidates,
colorscale=newyorktimes_cs,
showscale=False
)])
width = 900
height =450
anno_text="Data source:\
<a href='http://www.nytimes.com/interactive/2015/08/06/upshot/\
2016-republican-presidential-candidates-dashboard.html'> [1]</a>"
title = "A scoreboard for republican candidates as of August 14, 2015"
layout = Layout(
title=' ',
font=Font(
family='Balto, sans-serif',
size=12,
color='rgb(68,68,68)'
),
showlegend=False,
xaxis=XAxis(
title='',
showgrid=True,
side='top'
),
yaxis=YAxis(
title='',
autorange='reversed',
showgrid=True,
autotick=False,
dtick=1
),
autosize=False,
height=height,
width=width,
margin=Margin(
l=135,
r=40,
b=85,
t=170
)
)
annotations = Annotations([
Annotation(
showarrow=False,
text=anno_text,
xref='paper',
yref='paper',
x=0,
y=-0.1,
xanchor='left',
yanchor='bottom',
font=Font(
size=11 )
)])
fig=Figure(data=data14, layout=layout)
fig['layout'].update(
title=title,
annotations=annotations
)
py.sign_in('empet', 'my_api_key')
py.iplot(fig,filename='Heatmap-republican-candidates-14')
```
Now we go further and update the above Figure with data available on August 17, and moreover we annotate the Heatmap, displaying the candidate ranking on each cell.
```
tab_vals17=[[1,2,3,4,5,6,7,7,9,9,11,11,13,13,13,13],
[1,7,5,12,5,4,7,12,2,12,3, 7,7,12,7,12],
[4,7,2,1,10,5,7, 6, 9,3, 12, 14,12,11,15,16],
[2,9,4,1,3,8,11, 10, 6,6, 5, 14,14,12,14,13],
[1,3,4,14,8,2,12, 13, 7,9, 6,16,5,10,11,15]]
candidates17=['Bush', 'Rubio', 'Walker', 'Trump', 'Kasich', 'Cruz', 'Huckabee', 'Fiorina','Paul']+\
['Carson', 'Christie', 'Santorum', 'Perry', 'Jindal', 'Graham', 'Pataki']
```
The first row in `tab_vals17` changed relative to the same row in `tab_vals14`, by swapping their positions the candidates (Fiorina, Huckabee) and (Christie, Carson), and correspondingly the other rows.
```
fig['data'].update(Data([Heatmap(z=tab_vals17,
y=factors,
x=candidates17,
colorscale=newyorktimes_cs,
showscale=False
)]))
for i, row in enumerate(tab_vals17):
for j, val in enumerate(row):
annotations.append(
Annotation(
text=str(val),
x=candidates[j], y=factors[i],
xref='x1', yref='y1',
font=dict(color='white' if tab_vals17[i][j]<12 else 'rgb(150,150,150)'),
showarrow=False))
fig['layout'].update(
title="A scoreboard for republican candidates as of August 17, 2015 <br> Annotated heatmap",
annotations=annotations
)
py.iplot(fig,filename='Annotated heatmap-republican-candidates-17')
from IPython.core.display import HTML
def css_styling():
styles = open("./custom.css", "r").read()
return HTML(styles)
css_styling()
from IPython.display import HTML, display
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="https://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
import publisher
publisher.publish('scoreboard-republican-candidates', '/ipython-notebooks/scoreboard-heatmaps/',
'Two Scoreboards for Republican Presidential Candidates',
'Plot Scoreboard Using Python and Plotly')
```
| true |
code
| 0.467575 | null | null | null | null |
|
## AUC in CatBoost
[](https://colab.research.google.com/github/catboost/catboost/tree/master/catboost/tutorial/metrics/AUC_tutorial.ipynb)
The tutorial is dedicated to The Area Under the Receiver Operating Characteristic (ROC) Curve (AUC) and it's implementations in CatBoost for binary classification, multiclass classification and ranking problems.
### Library installation
```
!pip install --upgrade catboost
!pip install --upgrade ipywidgets
!pip install shap
!pip install --upgrade sklearn
# !pip install --upgrade numpy
!jupyter nbextension enable --py widgetsnbextension
import catboost
print(catboost.__version__)
!python --version
import pandas as pd
import os
import numpy as np
np.set_printoptions(precision=4)
import catboost
import sklearn
import matplotlib.pyplot as plt
from catboost import datasets, Pool
from catboost.utils import get_roc_curve, eval_metric
from sklearn import metrics
from sklearn.model_selection import train_test_split
```
### About AUC
The **ROC curve** shows the *model's ability to distinguishing between classes*.
The model which randomly assigns a class to object is a 'bad' classifier and has a diagonal ROC curve. The better is the classifier, the higher is the ROC curve. The ROC curve is plotted with TPR, [True Positive Rate](https://en.wikipedia.org/wiki/Receiver_operating_characteristic#Basic_concept), on the y-axis against the FPR, [False Positive Rate](https://en.wikipedia.org/wiki/Receiver_operating_characteristic#Basic_concept), on the x-axis. The curve also could be interpreted in terms of [Sensitivity and Specificity](https://en.wikipedia.org/wiki/Sensitivity_and_specificity) of the model with Sensitivity on the y-axis and (1-Specificity) on the x-axis.
Building and visualizing the ROC curve could be used *to measure classification algorithm performance with different probability boundaries* and *select the probability boundary* required to achieve the specified false-positive or false-negative rate.
**AUC** is the Area Under the ROC Curve. The best AUC = 1 for a model that ranks all the objects right (all objects with class 1 are assigned higher probabilities then objects of class 0). AUC for the 'bad' classifier is equal to 0.5.
AUC is used for binary classification, multiclass classification, and ranking problems. *AUC measures the proportion of correctly ordered objects and the capability of the model to distinguish between the classes*.
The AUC has an important statistical property: the *AUC of a classifier is equivalent to the probability that the classifier will rank a randomly chosen positive instance higher than a randomly chosen negative instance*.
### CatBoost implementation
CatBoost implements AUC for [binary classification](https://catboost.ai/docs/concepts/loss-functions-classification.html), [multiclassification](https://catboost.ai/docs/concepts/loss-functions-multiclassification.html) and [ranking](https://catboost.ai/docs/concepts/loss-functions-ranking.html) problems. AUC is used during training to detect overfitting and select the best model. AUC is also used as a metric for predictions evaluation and comparison with [utils.eval_metric](https://https://catboost.ai/docs/concepts/python-reference_utils_eval_metric.html). See examples of models fitting and AUC calculation with CatBoost in the section [How to use AUC in Catboost on real datasets?](#scrollTo=BP1nOBpvFzPV)
### Useful links
* Read more about ROC on [Wikipedia](https://en.wikipedia.org/wiki/Receiver_operating_characteristic).
* To get an understanding of the ROC curve building from scratch see [the article](https://people.inf.elte.hu/kiss/11dwhdm/roc.pdf).
* To get an understanding of AUC$\mu$ for multiclass classification see [the article](http://proceedings.mlr.press/v97/kleiman19a/kleiman19a.pdf).
# Binary classification
## Calculation rules for binary classification
AUC for binary classification is calculated according to the following formula:
$$
AUC = \frac{\sum_{t_i = 0, t_j = 1} I(a_i, a_j) w_i w_j}{\sum_{t_i = 0, t_j = 1}{w_i w_j}},
$$
where $a_i, a_j$ - predictions (probabilities) of objects to belong to the class 1 given by the algorithm.
The sum is calculated on all pairs of objects $i, j$ such that:
$t_i = 0, t_j = 1$ where $t$ is true true class label.
$I$ is an indicator function equal to 1 if objects $i, j$ are ordered correctly:
$$
I(a_i, a_j) =
\begin{cases}
1 & \quad \text{if } a_i < a_j\\
0.5 & \quad \text{if } a_i = a_j\\
0 & \quad \text{if } a_i > a_j\\
\end{cases}
$$
A user could assign weights to each object to specify the importance of each object in metric calculation.
## Simple example of AUC calculation for binary classification
Let's look at a simple example of ROC curve building and AUC calculation:
We have a sample of 10 objects, 4 from class 1 and 6 from class 0 ('class' column). All objects are equally important (weights = 1).
Assume we predicted probabilities of objects to come from class 1 ('prediction' column).
```
toy_example = pd.DataFrame({'class': [1, 1, 1, 1, 0, 0, 0, 0, 0, 0], 'prediction': [0.9, 0.4, 0.6, 0.2, 0.8, 0.25, 0.15, 0.4, 0.3, 0.1]})
```
To build the ROC curve we need to sort the dataset in descending order of predicted probabilities.
```
toy_example.sort_values(by='prediction', ascending=False, inplace=True)
toy_example
```
The denominator $\sum_{t_i = 0, t_j = 1}{w_i w_j}$ is equal to the number of pairs of objects $i, j$ such that true class $t_i = 0, t_j = 1$. As there are 4 objects from class 1 and 6 objects from class 0, the denominator is equal to 24.
For each object from class 1 count the number of objects from class 0, which are below (has less probability) in the sorted dataset.
We add +1 of objects ordered correctly (e.g. objects with IDs 0 and 4) and +0.5 if probabilities are equal (e.g. objects with IDs 1 and 7).
For example, the object with ID = 1 adds +4.5 to AUC numerator as correctly ordered with objects with IDs: 8, 3, 6, 9 and has equal prediction with object 7:

```
denominator = sum(toy_example['class'] == 1) * sum(toy_example['class'] == 0)
numerator = (6 + 5 + 4.5 + 2)
manually_calculated_auc = numerator / denominator
print('Example of manually calculated ROC AUC = {0:.4f}'.format(manually_calculated_auc))
```
Let's calculate the same metric with Catboost and ensure everything is right:
```
catboost_auc = eval_metric(toy_example['class'], toy_example['prediction'], 'AUC')[0]
print('Example of ROC AUC calculated with CatBoost = {0:.4f}'.format(catboost_auc))
```
## ROC curve
To build a ROC curve put the number of objects of class 1 ($n_1$) in the square with side 1 along the $ y $-axis, and the number of objects of class 0 ($n_0$) along the $ x $-axis.
Going by the list of target labels sorted by model predictions in descending order will add $\frac{1}{n_1}$ along the $y$-axis encountering an object of class 1 and $\frac{1}{n_0}$ along the $x$-axis encountering an object of class 0.
Let's get FPR, TPR with sklearn and visualize the curve.
```
toy_example
```
Going from top to bottom by the 'class' column we go up on the plot if the class is 1 or right if the class is 0. When we meet objects with equal prediction add the number of 1 along y and the number of 0 along x and go by the diagonal of the rectangle.
```
fpr, tpr, _ = sklearn.metrics.roc_curve(toy_example['class'], toy_example['prediction'])
plt.figure()
lw = 2
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve')
plt.fill_between(fpr, tpr, y2=0, color='darkorange', alpha=0.3, label='Area Under Curve (area = %0.2f)' % catboost_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic curve example')
plt.legend(loc="lower right")
plt.show()
```
Let's have a look at the toy_example objects and understand how each object impacted the ROC curve:

## AUC: Calculation with weights
CatBoost allows us to assign a weight to each object in the dataset for AUC calculation according to [the formula above](#scrollTo=4RbdSB4EMBZs). If no weights assigned, all weights are equal to 1 and thus AUC is proportional to the number of correctly ordered pairs. If weights assigned this property is changed.
Weights are useful for unbalanced datasets. If there is a class or a group of objects with a small number of samples in the train dataset it could be reasonable to increase the weights for corresponding objects.
For example if we assign weight 10 to one object it can be understood as adding 9 of the same objects to the dataset.
Let's calculate AUC for an example of the wrong and right classification of one important object with weight = 10.
```
toy_example['weight'] = 1
roc_auc = catboost.utils.eval_metric(toy_example['class'], toy_example['prediction'], 'AUC', weight=toy_example['weight'])[0]
print('ROC AUC with default weights = {0:.4f}'.format(roc_auc))
# seting weight=10 to important object with correct ordering
toy_example.iloc[0, 2] = 10
toy_example
roc_auc = catboost.utils.eval_metric(toy_example['class'], toy_example['prediction'], 'AUC', weight=toy_example['weight'])[0]
print('AUC: = {0:.4f}'.format(roc_auc))
print('Important object is correctly ordered, AUC increases')
# set weight=10 to important object with wrong ordering
toy_example['weight'] = 1
toy_example.iloc[1, 2] = 10
toy_example
roc_auc = catboost.utils.eval_metric(toy_example['class'], toy_example['prediction'], 'AUC', weight=toy_example['weight'])[0]
print('AUC: = {0:.4f}'.format(roc_auc))
print('Important object is incorrectly ordered, AUC decreases')
```
# AUC for multiclass classification
There are two AUC metrics implemented for multiclass classification in Catboost.
The first is **OneVsAll**. AUC value is calculated separately for each class according to the binary classification calculation principles.
The second is **AUC$\mu$**, which is designed to meet the following properties:
* Property 1. If a model gives the correct label the highest probability
on every example, then AUC = 1
* Property 2. Random guessing on examples yields AUC = 0.5
* Property 3. AUC is insensitive to class skew
AUC$\mu$ could be interpreted as an average of pairwise AUCs between the classes. Details could be found in the [article](http://proceedings.mlr.press/v97/kleiman19a/kleiman19a.pdf).
### OneVsAll AUC
OneVsAll AUC in Catboost returns $n$ AUC values for $n$-class classification. The value is calculated separately for each class $k$ numbered from $0$ to $K–1$ according [to the binary classification calculation rules](#scrollTo=4RbdSB4EMBZs). The objects of class $k$ are considered positive, while all others are considered negative.
Let's create a small example and calculate OneVsAll AUC for 3 classes.
```
classes = [0, 1, 1, 0, 1, 1, 1, 0, 1, 2]
probas =\
np.array([[0.4799, 0.3517, 0.3182, 0.3625, 0.336 , 0.3034, 0.4284, 0.5497, 0.231 , 0.27 ],
[0.2601, 0.3052, 0.3637, 0.3742, 0.3808, 0.3995, 0.3038, 0.2258, 0.264 , 0.4581],
[0.2601, 0.3431, 0.3182, 0.2633, 0.2832, 0.2971, 0.2678, 0.2245,0.506 , 0.271 ]])
```
Let's calculate ROC AUC for each class using binary classification rules:
```
one_vs_all_df_example = pd.DataFrame({'class_0': classes, 'class_1': classes, 'class_2': classes, 'probability_of_0': probas[0, :], 'probability_of_1': probas[1, :], 'probability_of_2': probas[2, :]})
one_vs_all_df_example.loc[one_vs_all_df_example['class_0'] != 0, 'class_0'] = -1
one_vs_all_df_example.loc[one_vs_all_df_example['class_0'] == 0, 'class_0'] = 1
one_vs_all_df_example.loc[one_vs_all_df_example['class_0'] == -1, 'class_0'] = 0
one_vs_all_df_example.loc[one_vs_all_df_example['class_1'] != 1, 'class_1'] = 0
one_vs_all_df_example.loc[one_vs_all_df_example['class_1'] == 1, 'class_1'] = 1
one_vs_all_df_example.loc[one_vs_all_df_example['class_2'] != 2, 'class_2'] = 0
one_vs_all_df_example.loc[one_vs_all_df_example['class_2'] == 2, 'class_2'] = 1
one_vs_all_df_example
roc_aucs = []
for i in range(3):
roc_aucs.append(catboost.utils.eval_metric(one_vs_all_df_example['class_' + str(i)], one_vs_all_df_example['probability_of_' + str(i)], 'AUC')[0])
print('Binary Classification ROC AUC for class {0} = {1:.4f}'.format(i, roc_aucs[-1]))
```
Let's calculate the same metric with OneVsAll Catboost AUC and ensure everything is right:
```
aucs = eval_metric(classes, probas, 'AUC:type=OneVsAll')
for i in range(len(aucs)):
print('OneVsAll ROC AUC for class {0} = {1:.4f}'.format(i, aucs[i]))
```
#### Visualizing ROC curves
```
plt.figure()
lw = 2
colors = ['r', 'y', 'c']
for i in range(3):
fpr, tpr, _ = sklearn.metrics.roc_curve(one_vs_all_df_example['class_' + str(i)], one_vs_all_df_example['probability_of_' + str(i)])
plt.plot(fpr, tpr, color=colors[i],
lw=lw, label='ROC curve for class {0}, area = {1:.4f}'.format(i, roc_aucs[i]), alpha=0.5)
plt.fill_between(fpr, tpr, y2=0, color=colors[i], alpha=0.1)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic curve example')
plt.legend(loc="lower right")
plt.show()
```
#### OneVsAll AUC with weights
```
# setting a big weight to incorrectly classified object of class 1 (misclassified as 2)
AUCs = eval_metric(classes, probas, weight=[1, 1, 1, 1, 1, 1, 1, 1, 10, 1], metric='AUC:type=OneVsAll')
print('CalBoost OneVsAll AUC with weights:')
print('AUC:class=0 = {0:.4f}, AUC:class=1 = {1:.4f}, AUC:class=2 = {2:.4f}'.format(AUCs[0], AUCs[1], AUCs[2]))
# setting a big weight to correctly classified object of class 0
AUCs = eval_metric(classes, probas, weight=[10, 1, 1, 1, 1, 1, 1, 1, 1, 1], metric='AUC:type=OneVsAll')
print('CalBoost OneVsAll AUC with weights:')
print('AUC:class=0 = {0:.4f}, AUC:class=1 = {1:.4f}, AUC:class=2 = {2:.4f}'.format(AUCs[0], AUCs[1], AUCs[2]))
```
Weights of the objects would affect AUC values for all classes as all objects of the other classes are used in the calculation as objects of class 0.
OneVsAll AUC measures the ability of the classifier to distinguish objects of one class from another.
An advantage of OneVsAll is the ability to monitor performance on different classes separately.
## AUC$\mu$
AUC$\mu$ could be simply used as an evaluation metric to prevent overfitting, while OneVsAll AUC could not as it contains a metric value for each class and AUCs for different classes may vary inconsistently during training.
Let's have a look at the AUC$\mu$ formula:
$$
AUC\mu = \frac{2}{K(K - 1)}\sum_{i<j} S(i, j)
$$
$K$ is a number of classes, $i < j ≤ K$ are the classes' numbers.
$S(i, j)$ is a separability measure between classes $i$ and $j$ defined as:
$$
S(i, j) = \frac{1}{n_i n_j}\sum_{a \in D_i, b \in D_j} \hat{I} \circ O(y^{(a)}, y^{(b)}, \hat{p}^{(a)}, \hat{p}^{(b)}, v_{i, j}),
$$
where
* $\hat I$ is indicator function applied to results of $O$, which returns 1 if $O$ returns a positive value, 0 if $O$ returns a negative value, and 0.5 if $O$ returns 0.
* $O$ is an orientation function indicating if the two instances are ordered correctly, incorrectly, or tied. $O$ returns a positive value if the predictions are ranked correctly, a negative
value if they are ranked incorrectly, and 0 if their rank is
tied.
* $a$, $b$ are objects from classes $i$, $j$ respectively,
* $\hat{p}^{(a)}$, $\hat{p}^{(b)}$ are vectors of predicted probabilities of the object to belong to the classes,
* $y^{(a)}$, $y^{(b)}$ are true labels of objects $a$, $b$ (one-hot vectors),
* $v_{i, j}$ is a two-class decision hyperplane normal vector.
$O$ is caclulates as following:
$O(y^{(a)}, y^{(b)}, \hat{p}^{(a)}, \hat{p}^{(b)}, v_{i, j}) = v_{i, j} (y^{(a)} - y^{(b)}) v_{i, j} (\hat{p}^{(a)} - \hat{p}^{(b)})$
Vectors $v_{i, j}$ come from misclassification cost matrix $A$, which is defined manually following the learning task.
$v_{i,j} = A_{i,.} - A_{j,.}$
$A_{i,j}$ is the cost of classifying an instance as class $i$
when its true class is $j$. Then $A$ defines a partition on the
$(K − 1)$−simplex and induces decision boundaries between
the $K$ classes.
Default misclassification cost matrix values are 1 everywhere, except the diagonal where they are 0. It is called the argmax partition
matrix as it assigns a class with maximal probability.
Here is a partition for a 3-class classification problem with the argmax partition matrix A. For a user-defined partition matrix the boundaries (marked by arrows) are shifted.

Follow [the article](http://proceedings.mlr.press/v97/kleiman19a/kleiman19a.pdf) for more details.
CatBoost allows us to set the misclassification cost matrix $A$ and objects' weights to calculate $AUC\mu$.
Let's calculate $AUC\mu$ for a very small example with 3 classes and 4 objects:
```
classes = np.array([2, 1, 0, 2])
y = np.array([[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 0, 1]])
probas = np.array([[0.3, 0.5, 0.2], [0.4, 0.5, 0.1], [0.4, 0.15, 0.45], [0.05, 0.5, 0.45]])
K = 3
A = np.array([[0, 1, 1], [1, 0, 1], [1, 1, 0]])
def get_I(value):
if value > 0:
return 1
elif value == 0:
return 0.5
return 0
```
Let's compute $S(i, j)$ for each ordered classes' pair:
```
# i = 0 (objects: y_2), j = 1 (objects: y_1)
v_01 = A[0, :] - A[1, :]
s_01 = get_I(v_01.dot(y[2] - y[1]) * v_01.dot(probas[2] - probas[1]))
# i = 0 (objects: y_2), j = 2 (objects: y_0, y_3)
v_02 = A[0, :] - A[2, :]
s_02 = 1 / (1 * 2) * (get_I(v_02.dot(y[2] - y[0]) * v_02.dot(probas[2] - probas[0])) + \
get_I(v_02.dot(y[2] - y[3]) * v_02.dot(probas[2] - probas[3])))
# i = 1 (objects: y_1), j = 2 (objects: y_0, y_3)
v_12 = A[1, :] - A[2, :]
s_12 = 1 / (1 * 2) * (get_I(v_12.dot(y[1] - y[0]) * v_02.dot(probas[1] - probas[0])) + \
get_I(v_12.dot(y[1] - y[3]) * v_02.dot(probas[1] - probas[3])))
AUC_mu = 2 / (K * (K - 1)) * (s_01 + s_02 + s_12)
print('AUC_mu = {:.4f}'.format(AUC_mu))
```
Let's calculate the same metric with Catboost $AUC\mu$ and ensure everything is right:
```
print('Catboost AUC_mu = {:.4f}'.format(eval_metric(classes, probas.T, 'AUC:type=Mu')[0]))
```
Let's calculate OneVsAll AUC for the same data:
```
AUCs = eval_metric(classes, probas.T, metric='AUC:type=OneVsAll')
print('AUC:class=0 = {0:.4f}, AUC:class=1 = {1:.4f}, AUC:class=2 = {2:.4f}'.format(AUCs[0], AUCs[1], AUCs[2]))
```
As we can see OneVsAll AUC and $AUC\mu$ are pretty high, but actually algorithm performance is bad, accuracy is 0.25. Thus it is reasonable to evaluate other important metrics during training.
```
print('Accuracy = {:.4f}'.format(eval_metric(classes, probas.T, metric='Accuracy')[0]))
```
#### $AUC\mu$ with misclassification cost matrix and weights
```
AUC = eval_metric(classes, probas.T, weight=[1, 10, 1, 1], metric='AUC:type=Mu;misclass_cost_matrix=0/0.5/2/1/0/1/0/0.5/0')
print('Catboost AUC_mu with weights = {:.4f}'.format(AUC[0]))
```
$AUC\mu$ is a good generalizing metric to estimate algorithm ability to separate classes in multiclassification problems. See more about different approaches to multiclass AUC calculation and their properties in section 4.3 of [the article](http://proceedings.mlr.press/v97/kleiman19a/kleiman19a.pdf).
AUC$\mu$ could be interpreted as an average of pairwise AUCs between the classes. AUC$\mu$ is a single value unlike OneVsAll AUC and thus it could be used as an evaluation metric during training for overfitting detection and trees pruning.
# AUC for ranking
There are two variants of AUC for Ranking in CatBoost.
### The Classic AUC
is used for models with Logloss and CrossEntropy loss functions. It has the same formula as AUC for binary classification:
$$
\frac{\sum I(a_i, a_j) w_i w_j}{\sum{w_i w_j}}
$$
$a_i, a_j$ - predicted rank of objects i, j.
The sum is calculated on all pairs of objects $i, j$ such that:
$t_i = 0, t_j = 1$ where $t$ is relevance.
$$
I(a_i, a_j) =
\begin{cases}
1 & \quad \text{if } a_i < a_j\\
0.5 & \quad \text{if } a_i = a_j\\
0 & \quad \text{if } a_i > a_j\\
\end{cases}
$$
The formula above suits for simple tasks with target values equal to 1 and 0. What if we have more target values?
If the target type is not binary, then every object $i$ with target value $t$ and weight $w$ is replaced with two objects for the metric calculation:
* $\sigma_1$ with weight $wt$ and target value 1
* $\sigma_2$ with weight $w(1 - t)$ and target value 0.
Target values must be in the range [0; 1].
Let's calculate Classic AUC for Ranking for a small example. Assume we have 2 documents, 2 requests, corresponding relevances in the range [1, 5] and predicted relevance in the range [0, 1]:
```
rank_df = pd.DataFrame({'request_id': [1, 1, 2, 2], 'doc_id': [1, 2, 1, 2], 'relevance': [2, 5, 4, 1], 'pred':[0.3, 0.7, 0.2, 0.6], 'weight': [1, 1, 1, 1]})
#map relevence to [0, 1]
rank_df.loc[:, 'relevance'] /= 5
rank_df.sort_values(by='pred', axis=0, inplace=True)
rank_df
```
Let's create objects $\sigma$ required for calculation and update weights:
```
rank_df_sigma = pd.concat([
rank_df,rank_df
],ignore_index=True)
rank_df_sigma['new_relevance'] = 0
rank_df_sigma.loc[:3, 'new_relevance'] = 1
rank_df_sigma['new_weight'] = rank_df_sigma['weight']
rank_df_sigma.loc[rank_df_sigma['new_relevance'] == 1, 'new_weight'] = rank_df_sigma['relevance'] * rank_df_sigma['weight']
rank_df_sigma.loc[rank_df_sigma['new_relevance'] == 0, 'new_weight'] = (1 - rank_df_sigma['relevance']) * rank_df_sigma['weight']
rank_df_sigma.sort_values(by='pred', axis=0, ascending=False, inplace=True)
rank_df_sigma
```
Let's calculate AUC:
```
# finding sum of weights for denominator
weights1 = rank_df_sigma.loc[rank_df_sigma['new_relevance'] == 1, 'new_weight'].to_numpy()
weights0 = rank_df_sigma.loc[rank_df_sigma['new_relevance'] == 0, 'new_weight'].to_numpy()
```
Calculation details for object #3:

```
denominator = np.sum(weights1.reshape(-1, 1)@weights0.reshape(1, -1))
# for each object of class 1 find objects of class 0 below and add composition of weights and indicatior function to the numerator
numerator = 1 * (0.8 + 0.6 + 0.2) + 0.2 * (0.8 * 0.5 + 0.6 + 0.2) + 0.4 * (0.6 * 0.5 + 0.2) + 0.8 * 0.2 * 0.5
manually_calculated_auc = numerator / denominator
print('Example of manually calculated Classic ROC AUC for ranking = {0:.4f}'.format(manually_calculated_auc))
print('CatBoost Classic ROC AUC for ranking = {0:.4f}'.format(eval_metric(rank_df['relevance'], rank_df['pred'], 'AUC:type=Classic')[0]))
```
## Ranking AUC
Ranking AUC is used for ranking loss functions.
$$
\frac{\sum I(a_i, a_j) w_i w_j}{\sum{w_i w_j}}
$$
$a_i, a_j$ - predicted rank of objects i, j.
The sum is calculated on all pairs of objects $i, j$ such that:
$t_i < t_j$ where $t$ is relevance.
$$
I(a_i, a_j) =
\begin{cases}
1 & \quad \text{if } a_i < a_j\\
0.5 & \quad \text{if } a_i = a_j\\
0 & \quad \text{if } a_i > a_j\\
\end{cases}
$$
Let's compute Ranking AUC for the small example above:
```
rank_df.sort_values(by='relevance', axis=0, inplace=True, ascending=False)
rank_df
```
Calculation details:

```
n = rank_df['relevance'].unique().shape[0]
denominator = (n * (n-1)) / 2 #number of ordered pairs
# for object #1 three object below are less relevant by real relevance and predictions, the other are incorrectly ranked
numerator = 3
manually_calculated_auc = numerator / denominator
print('Example of manually calculated Ranking ROC AUC = {0:.4f}'.format(manually_calculated_auc))
print('CatBoost Ranking ROC AUC = {0:.4f}'.format(eval_metric(rank_df['relevance'], rank_df['pred'], 'AUC:type=Ranking', group_id=rank_df['request_id'])[0]))
```
Ranking AUC is directly measuring the quantity of correctly ranked pairs. The problem is the metric is calculated regardless of groups. In our example, we have groups (requests) and we may want to measure quality inside the groups, but currently, AUC is calculated over the dataset and AUC penalizes us if, for example, top-one document for one request is ranked lower than top-one for another document while true ranks are opposite (but still top-one for each document).
One more problem of AUC for Ranking is that it does not distinguish the top object from the others. If we have a lot of irrelevant documents, which are ranked irrelevant by the model, but bad ranking in top-10, AUC could still be high because of that "tail" of irrelevant objects, ranked lower than relevant.
#Overview
AUC is a widely used metric to measure the ability of a model to distinguish classes and correctly order objects from different classes / with different relevance. AUC is not differentiable and thus cannot be used as a loss function, but it is pretty informative and useful as a metric.
We have examined the following AUC types:
* AUC for binary classification. It is a classical metric, which measures the model quality. ROC curve allows selecting the probability threshold to meet required False Positive or False Negative Rates.
* AUC for multiclass classification: OneVsAll and $AUC\mu$. OneVsAll AUC helps to control algorithm performance for each class, but can not be used as a metric to prevent overfitting. On the contrary, $AUC\mu$ is good as a generalizing metric, but will not detect a problem with one class.
* AUC for ranking: Classic AUC and Ranking AUC. AUC suits for ranking tasks because it is designed to measure how the algorithm distinguishes between classes and it is simply transferring to distinguishing between relevant and irrelevant objects. But AUC does not take into account that in ranking problems the first $n$ positions are very important and treats each correctly ordered pair of documents equally.
# How to use AUC in Catboost on real datasets?
AUC implemented in CatBoost allows using weights to consider object and classes' importance in metric calculation.
You can use AUC in Catboost during training as a validation metric to prevent overfitting and select the best model and as a metric to compare different models' results.
Let's consider an example of using AUC for a multiclassification task.
### AUC for multiclass classification
#### Loading dataset
We will use the [Wine recognition dataset](https://scikit-learn.org/stable/datasets/index.html#wine-dataset ) for multiclass classification problem
```
!wget https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data
columns = ['Class', 'Alcohol', 'Malic_acid', 'Ash', 'Alcalinity_of_ash', 'Magnesium', 'Total_phenols', 'Flavanoids', 'Nonflavanoid_phenols', 'Proanthocyanins', 'Color_intensity', 'Hue', 'OD280OD315_of_diluted_wines', 'Proline']
train_df = pd.read_csv('wine.data', names=columns)
train_df.head(5)
```
#### Creating pool
```
y = train_df['Class']
X = train_df.drop(columns='Class')
y.unique()
from sklearn.model_selection import train_test_split
X_train, X_validation, y_train, y_validation = train_test_split(X, y, train_size=0.5, random_state=42)
train_pool = Pool(X_train, y_train)
validation_pool = Pool(X_validation, y_validation)
```
#### Training model
```
from catboost import CatBoostClassifier
model = CatBoostClassifier(
iterations=20,
eval_metric='AUC',
custom_metric=['AUC:type=OneVsAll;hints=skip_train~false', 'Accuracy'],
# metric_period=10,
loss_function='MultiClass',
train_dir='model_dir',
random_seed=42)
model.fit(
train_pool,
eval_set=validation_pool,
verbose=True,
);
```
Model is shrinked to the first best $AUC\mu$ value (17 iteration)
#### Calculating metrics
```
AUCs = model.eval_metrics(validation_pool, metrics=['AUC:type=Mu', 'AUC:type=OneVsAll'])
print('AUC:type=OneVsAll:')
print('AUC:class=0 = {0:.4f}, AUC:class=1 = {1:.4f}, AUC:class=2 = {2:.4f}'.format(AUCs['AUC:class=0'][-1], AUCs['AUC:class=1'][-1], AUCs['AUC:class=2'][-1]))
print('\nAUC:type=Mu:')
print('AUC:type=Mu = {0:.5f}'.format(AUCs['AUC:type=Mu'][-1]))
```
Using weigths and misclassification cost matrix:
```
weights = np.random.rand(X_validation.shape[0])
weights[10] = 100
validation_pool = Pool(X_validation, y_validation, weight=weights)
AUC = model.eval_metrics(validation_pool, metrics=['AUC:type=Mu', 'AUC:type=Mu;use_weights=True', 'AUC:type=Mu;misclass_cost_matrix=0/0.5/2/1/0/1/0/0.5/0;use_weights=True'])
print('AUC:type=Mu = {0:.5f}'.format(AUC['AUC:type=Mu'][-1]))
print('AUC:type=Mu;use_weights=True = {0:.5f}'.format(AUC['AUC:use_weights=true;type=Mu'][-1]))
print('AUC:use_weights=true;type=Mu;misclass_cost_matrix = {0:.5f}'.format(AUC['AUC:use_weights=true;type=Mu;misclass_cost_matrix=0/0.5/2/1/0/1/0/0.5/0'][-1]))
```
| true |
code
| 0.57946 | null | null | null | null |
|
# Creating Keras DNN model
**Learning Objectives**
1. Create input layers for raw features
1. Create feature columns for inputs
1. Create DNN dense hidden layers and output layer
1. Build DNN model tying all of the pieces together
1. Train and evaluate
## Introduction
In this notebook, we'll be using Keras to create a DNN model to predict the weight of a baby before it is born.
We'll start by defining the CSV column names, label column, and column defaults for our data inputs. Then, we'll construct a tf.data Dataset of features and the label from the CSV files and create inputs layers for the raw features. Next, we'll set up feature columns for the model inputs and build a deep neural network in Keras. We'll create a custom evaluation metric and build our DNN model. Finally, we'll train and evaluate our model.
Each learning objective will correspond to a __#TODO__ in the [student lab notebook](https://github.com/GoogleCloudPlatform/training-data-analyst/tree/master/courses/machine_learning/deepdive2/end_to_end_ml/labs/keras_dnn_babyweight.ipynb) -- try to complete that notebook first before reviewing this solution notebook.
## Set up environment variables and load necessary libraries
```
!sudo chown -R jupyter:jupyter /home/jupyter/training-data-analyst
!pip install --user google-cloud-bigquery==1.25.0
```
**Note**: Restart your kernel to use updated packages.
Kindly ignore the deprecation warnings and incompatibility errors related to google-cloud-storage.
Import necessary libraries.
```
from google.cloud import bigquery
import pandas as pd
import datetime
import os
import shutil
import matplotlib.pyplot as plt
import tensorflow as tf
print(tf.__version__)
```
Set environment variables so that we can use them throughout the notebook.
```
%%bash
export PROJECT=$(gcloud config list project --format "value(core.project)")
echo "Your current GCP Project Name is: "$PROJECT
PROJECT = "cloud-training-demos" # Replace with your PROJECT
```
## Create ML datasets by sampling using BigQuery
We'll begin by sampling the BigQuery data to create smaller datasets. Let's create a BigQuery client that we'll use throughout the lab.
```
bq = bigquery.Client(project = PROJECT)
```
We need to figure out the right way to divide our hash values to get our desired splits. To do that we need to define some values to hash within the module. Feel free to play around with these values to get the perfect combination.
```
modulo_divisor = 100
train_percent = 80.0
eval_percent = 10.0
train_buckets = int(modulo_divisor * train_percent / 100.0)
eval_buckets = int(modulo_divisor * eval_percent / 100.0)
```
We can make a series of queries to check if our bucketing values result in the correct sizes of each of our dataset splits and then adjust accordingly. Therefore, to make our code more compact and reusable, let's define a function to return the head of a dataframe produced from our queries up to a certain number of rows.
```
def display_dataframe_head_from_query(query, count=10):
"""Displays count rows from dataframe head from query.
Args:
query: str, query to be run on BigQuery, results stored in dataframe.
count: int, number of results from head of dataframe to display.
Returns:
Dataframe head with count number of results.
"""
df = bq.query(
query + " LIMIT {limit}".format(
limit=count)).to_dataframe()
return df.head(count)
```
For our first query, we're going to use the original query above to get our label, features, and columns to combine into our hash which we will use to perform our repeatable splitting. There are only a limited number of years, months, days, and states in the dataset. Let's see what the hash values are. We will need to include all of these extra columns to hash on to get a fairly uniform spread of the data. Feel free to try less or more in the hash and see how it changes your results.
```
# Get label, features, and columns to hash and split into buckets
hash_cols_fixed_query = """
SELECT
weight_pounds,
is_male,
mother_age,
plurality,
gestation_weeks,
year,
month,
CASE
WHEN day IS NULL THEN
CASE
WHEN wday IS NULL THEN 0
ELSE wday
END
ELSE day
END AS date,
IFNULL(state, "Unknown") AS state,
IFNULL(mother_birth_state, "Unknown") AS mother_birth_state
FROM
publicdata.samples.natality
WHERE
year > 2000
AND weight_pounds > 0
AND mother_age > 0
AND plurality > 0
AND gestation_weeks > 0
"""
display_dataframe_head_from_query(hash_cols_fixed_query)
```
Using `COALESCE` would provide the same result as the nested `CASE WHEN`. This is preferable when all we want is the first non-null instance. To be precise the `CASE WHEN` would become `COALESCE(wday, day, 0) AS date`. You can read more about it [here](https://cloud.google.com/bigquery/docs/reference/standard-sql/conditional_expressions).
Next query will combine our hash columns and will leave us just with our label, features, and our hash values.
```
data_query = """
SELECT
weight_pounds,
is_male,
mother_age,
plurality,
gestation_weeks,
FARM_FINGERPRINT(
CONCAT(
CAST(year AS STRING),
CAST(month AS STRING),
CAST(date AS STRING),
CAST(state AS STRING),
CAST(mother_birth_state AS STRING)
)
) AS hash_values
FROM
({CTE_hash_cols_fixed})
""".format(CTE_hash_cols_fixed=hash_cols_fixed_query)
display_dataframe_head_from_query(data_query)
```
The next query is going to find the counts of each of the unique 657484 `hash_values`. This will be our first step at making actual hash buckets for our split via the `GROUP BY`.
```
# Get the counts of each of the unique hash of our splitting column
first_bucketing_query = """
SELECT
hash_values,
COUNT(*) AS num_records
FROM
({CTE_data})
GROUP BY
hash_values
""".format(CTE_data=data_query)
display_dataframe_head_from_query(first_bucketing_query)
```
The query below performs a second layer of bucketing where now for each of these bucket indices we count the number of records.
```
# Get the number of records in each of the hash buckets
second_bucketing_query = """
SELECT
ABS(MOD(hash_values, {modulo_divisor})) AS bucket_index,
SUM(num_records) AS num_records
FROM
({CTE_first_bucketing})
GROUP BY
ABS(MOD(hash_values, {modulo_divisor}))
""".format(
CTE_first_bucketing=first_bucketing_query, modulo_divisor=modulo_divisor)
display_dataframe_head_from_query(second_bucketing_query)
```
The number of records is hard for us to easily understand the split, so we will normalize the count into percentage of the data in each of the hash buckets in the next query.
```
# Calculate the overall percentages
percentages_query = """
SELECT
bucket_index,
num_records,
CAST(num_records AS FLOAT64) / (
SELECT
SUM(num_records)
FROM
({CTE_second_bucketing})) AS percent_records
FROM
({CTE_second_bucketing})
""".format(CTE_second_bucketing=second_bucketing_query)
display_dataframe_head_from_query(percentages_query)
```
We'll now select the range of buckets to be used in training.
```
# Choose hash buckets for training and pull in their statistics
train_query = """
SELECT
*,
"train" AS dataset_name
FROM
({CTE_percentages})
WHERE
bucket_index >= 0
AND bucket_index < {train_buckets}
""".format(
CTE_percentages=percentages_query,
train_buckets=train_buckets)
display_dataframe_head_from_query(train_query)
```
We'll do the same by selecting the range of buckets to be used evaluation.
```
# Choose hash buckets for validation and pull in their statistics
eval_query = """
SELECT
*,
"eval" AS dataset_name
FROM
({CTE_percentages})
WHERE
bucket_index >= {train_buckets}
AND bucket_index < {cum_eval_buckets}
""".format(
CTE_percentages=percentages_query,
train_buckets=train_buckets,
cum_eval_buckets=train_buckets + eval_buckets)
display_dataframe_head_from_query(eval_query)
```
Lastly, we'll select the hash buckets to be used for the test split.
```
# Choose hash buckets for testing and pull in their statistics
test_query = """
SELECT
*,
"test" AS dataset_name
FROM
({CTE_percentages})
WHERE
bucket_index >= {cum_eval_buckets}
AND bucket_index < {modulo_divisor}
""".format(
CTE_percentages=percentages_query,
cum_eval_buckets=train_buckets + eval_buckets,
modulo_divisor=modulo_divisor)
display_dataframe_head_from_query(test_query)
```
In the below query, we'll `UNION ALL` all of the datasets together so that all three sets of hash buckets will be within one table. We added `dataset_id` so that we can sort on it in the query after.
```
# Union the training, validation, and testing dataset statistics
union_query = """
SELECT
0 AS dataset_id,
*
FROM
({CTE_train})
UNION ALL
SELECT
1 AS dataset_id,
*
FROM
({CTE_eval})
UNION ALL
SELECT
2 AS dataset_id,
*
FROM
({CTE_test})
""".format(CTE_train=train_query, CTE_eval=eval_query, CTE_test=test_query)
display_dataframe_head_from_query(union_query)
```
Lastly, we'll show the final split between train, eval, and test sets. We can see both the number of records and percent of the total data. It is really close to that we were hoping to get.
```
# Show final splitting and associated statistics
split_query = """
SELECT
dataset_id,
dataset_name,
SUM(num_records) AS num_records,
SUM(percent_records) AS percent_records
FROM
({CTE_union})
GROUP BY
dataset_id,
dataset_name
ORDER BY
dataset_id
""".format(CTE_union=union_query)
display_dataframe_head_from_query(split_query)
```
Now that we know that our splitting values produce a good global splitting on our data, here's a way to get a well-distributed portion of the data in such a way that the train, eval, test sets do not overlap and takes a subsample of our global splits.
```
# every_n allows us to subsample from each of the hash values
# This helps us get approximately the record counts we want
every_n = 1000
splitting_string = "ABS(MOD(hash_values, {0} * {1}))".format(every_n, modulo_divisor)
def create_data_split_sample_df(query_string, splitting_string, lo, up):
"""Creates a dataframe with a sample of a data split.
Args:
query_string: str, query to run to generate splits.
splitting_string: str, modulo string to split by.
lo: float, lower bound for bucket filtering for split.
up: float, upper bound for bucket filtering for split.
Returns:
Dataframe containing data split sample.
"""
query = "SELECT * FROM ({0}) WHERE {1} >= {2} and {1} < {3}".format(
query_string, splitting_string, int(lo), int(up))
df = bq.query(query).to_dataframe()
return df
train_df = create_data_split_sample_df(
data_query, splitting_string,
lo=0, up=train_percent)
eval_df = create_data_split_sample_df(
data_query, splitting_string,
lo=train_percent, up=train_percent + eval_percent)
test_df = create_data_split_sample_df(
data_query, splitting_string,
lo=train_percent + eval_percent, up=modulo_divisor)
print("There are {} examples in the train dataset.".format(len(train_df)))
print("There are {} examples in the validation dataset.".format(len(eval_df)))
print("There are {} examples in the test dataset.".format(len(test_df)))
```
## Preprocess data using Pandas
We'll perform a few preprocessing steps to the data in our dataset. Let's add extra rows to simulate the lack of ultrasound. That is we'll duplicate some rows and make the `is_male` field be `Unknown`. Also, if there is more than child we'll change the `plurality` to `Multiple(2+)`. While we're at it, we'll also change the plurality column to be a string. We'll perform these operations below.
Let's start by examining the training dataset as is.
```
train_df.head()
```
Also, notice that there are some very important numeric fields that are missing in some rows (the count in Pandas doesn't count missing data)
```
train_df.describe()
```
It is always crucial to clean raw data before using in machine learning, so we have a preprocessing step. We'll define a `preprocess` function below. Note that the mother's age is an input to our model so users will have to provide the mother's age; otherwise, our service won't work. The features we use for our model were chosen because they are such good predictors and because they are easy enough to collect.
```
def preprocess(df):
""" Preprocess pandas dataframe for augmented babyweight data.
Args:
df: Dataframe containing raw babyweight data.
Returns:
Pandas dataframe containing preprocessed raw babyweight data as well
as simulated no ultrasound data masking some of the original data.
"""
# Clean up raw data
# Filter out what we don"t want to use for training
df = df[df.weight_pounds > 0]
df = df[df.mother_age > 0]
df = df[df.gestation_weeks > 0]
df = df[df.plurality > 0]
# Modify plurality field to be a string
twins_etc = dict(zip([1,2,3,4,5],
["Single(1)",
"Twins(2)",
"Triplets(3)",
"Quadruplets(4)",
"Quintuplets(5)"]))
df["plurality"].replace(twins_etc, inplace=True)
# Clone data and mask certain columns to simulate lack of ultrasound
no_ultrasound = df.copy(deep=True)
# Modify is_male
no_ultrasound["is_male"] = "Unknown"
# Modify plurality
condition = no_ultrasound["plurality"] != "Single(1)"
no_ultrasound.loc[condition, "plurality"] = "Multiple(2+)"
# Concatenate both datasets together and shuffle
return pd.concat(
[df, no_ultrasound]).sample(frac=1).reset_index(drop=True)
```
Let's process the train, eval, test set and see a small sample of the training data after our preprocessing:
```
train_df = preprocess(train_df)
eval_df = preprocess(eval_df)
test_df = preprocess(test_df)
train_df.head()
train_df.tail()
```
Let's look again at a summary of the dataset. Note that we only see numeric columns, so `plurality` does not show up.
```
train_df.describe()
```
## Write to .csv files
In the final versions, we want to read from files, not Pandas dataframes. So, we write the Pandas dataframes out as csv files. Using csv files gives us the advantage of shuffling during read. This is important for distributed training because some workers might be slower than others, and shuffling the data helps prevent the same data from being assigned to the slow workers.
```
# Define columns
columns = ["weight_pounds",
"is_male",
"mother_age",
"plurality",
"gestation_weeks"]
# Write out CSV files
train_df.to_csv(
path_or_buf="train.csv", columns=columns, header=False, index=False)
eval_df.to_csv(
path_or_buf="eval.csv", columns=columns, header=False, index=False)
test_df.to_csv(
path_or_buf="test.csv", columns=columns, header=False, index=False)
%%bash
wc -l *.csv
%%bash
head *.csv
%%bash
tail *.csv
%%bash
ls *.csv
%%bash
head -5 *.csv
```
## Create Keras model
### Set CSV Columns, label column, and column defaults.
Now that we have verified that our CSV files exist, we need to set a few things that we will be using in our input function.
* `CSV_COLUMNS` is going to be our header name of our column. Make sure that they are in the same order as in the CSV files
* `LABEL_COLUMN` is the header name of the column that is our label. We will need to know this to pop it from our features dictionary.
* `DEFAULTS` is a list with the same length as `CSV_COLUMNS`, i.e. there is a default for each column in our CSVs. Each element is a list itself with the default value for that CSV column.
```
# Determine CSV, label, and key columns
# Create list of string column headers, make sure order matches.
CSV_COLUMNS = ["weight_pounds",
"is_male",
"mother_age",
"plurality",
"gestation_weeks"]
# Add string name for label column
LABEL_COLUMN = "weight_pounds"
# Set default values for each CSV column as a list of lists.
# Treat is_male and plurality as strings.
DEFAULTS = [[0.0], ["null"], [0.0], ["null"], [0.0]]
```
### Make dataset of features and label from CSV files.
Next, we will write an input_fn to read the data. Since we are reading from CSV files we can save ourselves from trying to recreate the wheel and can use `tf.data.experimental.make_csv_dataset`. This will create a CSV dataset object. However we will need to divide the columns up into features and a label. We can do this by applying the map method to our dataset and popping our label column off of our dictionary of feature tensors.
```
def features_and_labels(row_data):
"""Splits features and labels from feature dictionary.
Args:
row_data: Dictionary of CSV column names and tensor values.
Returns:
Dictionary of feature tensors and label tensor.
"""
label = row_data.pop(LABEL_COLUMN)
return row_data, label # features, label
def load_dataset(pattern, batch_size=1, mode='eval'):
"""Loads dataset using the tf.data API from CSV files.
Args:
pattern: str, file pattern to glob into list of files.
batch_size: int, the number of examples per batch.
mode: 'train' | 'eval' to determine if training or evaluating.
Returns:
`Dataset` object.
"""
# Make a CSV dataset
dataset = tf.data.experimental.make_csv_dataset(
file_pattern=pattern,
batch_size=batch_size,
column_names=CSV_COLUMNS,
column_defaults=DEFAULTS,
ignore_errors=True)
# Map dataset to features and label
dataset = dataset.map(map_func=features_and_labels) # features, label
# Shuffle and repeat for training
if mode == 'train':
dataset = dataset.shuffle(buffer_size=1000).repeat()
# Take advantage of multi-threading; 1=AUTOTUNE
dataset = dataset.prefetch(buffer_size=1)
return dataset
```
### Create input layers for raw features.
We'll need to get the data to read in by our input function to our model function, but just how do we go about connecting the dots? We can use Keras input layers [(tf.Keras.layers.Input)](https://www.tensorflow.org/api_docs/python/tf/keras/Input) by defining:
* shape: A shape tuple (integers), not including the batch size. For instance, shape=(32,) indicates that the expected input will be batches of 32-dimensional vectors. Elements of this tuple can be None; 'None' elements represent dimensions where the shape is not known.
* name: An optional name string for the layer. Should be unique in a model (do not reuse the same name twice). It will be autogenerated if it isn't provided.
* dtype: The data type expected by the input, as a string (float32, float64, int32...)
```
# TODO 1
def create_input_layers():
"""Creates dictionary of input layers for each feature.
Returns:
Dictionary of `tf.Keras.layers.Input` layers for each feature.
"""
inputs = {
colname: tf.keras.layers.Input(
name=colname, shape=(), dtype="float32")
for colname in ["mother_age", "gestation_weeks"]}
inputs.update({
colname: tf.keras.layers.Input(
name=colname, shape=(), dtype="string")
for colname in ["is_male", "plurality"]})
return inputs
```
### Create feature columns for inputs.
Next, define the feature columns. `mother_age` and `gestation_weeks` should be numeric. The others, `is_male` and `plurality`, should be categorical. Remember, only dense feature columns can be inputs to a DNN.
```
# TODO 2
def categorical_fc(name, values):
"""Helper function to wrap categorical feature by indicator column.
Args:
name: str, name of feature.
values: list, list of strings of categorical values.
Returns:
Indicator column of categorical feature.
"""
cat_column = tf.feature_column.categorical_column_with_vocabulary_list(
key=name, vocabulary_list=values)
return tf.feature_column.indicator_column(categorical_column=cat_column)
def create_feature_columns():
"""Creates dictionary of feature columns from inputs.
Returns:
Dictionary of feature columns.
"""
feature_columns = {
colname : tf.feature_column.numeric_column(key=colname)
for colname in ["mother_age", "gestation_weeks"]
}
feature_columns["is_male"] = categorical_fc(
"is_male", ["True", "False", "Unknown"])
feature_columns["plurality"] = categorical_fc(
"plurality", ["Single(1)", "Twins(2)", "Triplets(3)",
"Quadruplets(4)", "Quintuplets(5)", "Multiple(2+)"])
return feature_columns
```
### Create DNN dense hidden layers and output layer.
So we've figured out how to get our inputs ready for machine learning but now we need to connect them to our desired output. Our model architecture is what links the two together. Let's create some hidden dense layers beginning with our inputs and end with a dense output layer. This is regression so make sure the output layer activation is correct and that the shape is right.
```
# TODO 3
def get_model_outputs(inputs):
"""Creates model architecture and returns outputs.
Args:
inputs: Dense tensor used as inputs to model.
Returns:
Dense tensor output from the model.
"""
# Create two hidden layers of [64, 32] just in like the BQML DNN
h1 = tf.keras.layers.Dense(64, activation="relu", name="h1")(inputs)
h2 = tf.keras.layers.Dense(32, activation="relu", name="h2")(h1)
# Final output is a linear activation because this is regression
output = tf.keras.layers.Dense(
units=1, activation="linear", name="weight")(h2)
return output
```
### Create custom evaluation metric.
We want to make sure that we have some useful way to measure model performance for us. Since this is regression, we would like to know the RMSE of the model on our evaluation dataset, however, this does not exist as a standard evaluation metric, so we'll have to create our own by using the true and predicted labels.
```
def rmse(y_true, y_pred):
"""Calculates RMSE evaluation metric.
Args:
y_true: tensor, true labels.
y_pred: tensor, predicted labels.
Returns:
Tensor with value of RMSE between true and predicted labels.
"""
return tf.sqrt(tf.reduce_mean((y_pred - y_true) ** 2))
```
### Build DNN model tying all of the pieces together.
Excellent! We've assembled all of the pieces, now we just need to tie them all together into a Keras Model. This is a simple feedforward model with no branching, side inputs, etc. so we could have used Keras' Sequential Model API but just for fun we're going to use Keras' Functional Model API. Here we will build the model using [tf.keras.models.Model](https://www.tensorflow.org/api_docs/python/tf/keras/Model) giving our inputs and outputs and then compile our model with an optimizer, a loss function, and evaluation metrics.
```
# TODO 4
def build_dnn_model():
"""Builds simple DNN using Keras Functional API.
Returns:
`tf.keras.models.Model` object.
"""
# Create input layer
inputs = create_input_layers()
# Create feature columns
feature_columns = create_feature_columns()
# The constructor for DenseFeatures takes a list of numeric columns
# The Functional API in Keras requires: LayerConstructor()(inputs)
dnn_inputs = tf.keras.layers.DenseFeatures(
feature_columns=feature_columns.values())(inputs)
# Get output of model given inputs
output = get_model_outputs(dnn_inputs)
# Build model and compile it all together
model = tf.keras.models.Model(inputs=inputs, outputs=output)
model.compile(optimizer="adam", loss="mse", metrics=[rmse, "mse"])
return model
print("Here is our DNN architecture so far:\n")
model = build_dnn_model()
print(model.summary())
```
We can visualize the DNN using the Keras plot_model utility.
```
tf.keras.utils.plot_model(
model=model, to_file="dnn_model.png", show_shapes=False, rankdir="LR")
```
## Run and evaluate model
### Train and evaluate.
We've built our Keras model using our inputs from our CSV files and the architecture we designed. Let's now run our model by training our model parameters and periodically running an evaluation to track how well we are doing on outside data as training goes on. We'll need to load both our train and eval datasets and send those to our model through the fit method. Make sure you have the right pattern, batch size, and mode when loading the data.
```
# TODO 5
TRAIN_BATCH_SIZE = 32
NUM_TRAIN_EXAMPLES = 10000 * 5 # training dataset repeats, it'll wrap around
NUM_EVALS = 5 # how many times to evaluate
# Enough to get a reasonable sample, but not so much that it slows down
NUM_EVAL_EXAMPLES = 10000
trainds = load_dataset(
pattern="train*",
batch_size=TRAIN_BATCH_SIZE,
mode='train')
evalds = load_dataset(
pattern="eval*",
batch_size=1000,
mode='eval').take(count=NUM_EVAL_EXAMPLES // 1000)
steps_per_epoch = NUM_TRAIN_EXAMPLES // (TRAIN_BATCH_SIZE * NUM_EVALS)
logdir = os.path.join(
"logs", datetime.datetime.now().strftime("%Y%m%d-%H%M%S"))
tensorboard_callback = tf.keras.callbacks.TensorBoard(
log_dir=logdir, histogram_freq=1)
history = model.fit(
trainds,
validation_data=evalds,
epochs=NUM_EVALS,
steps_per_epoch=steps_per_epoch,
callbacks=[tensorboard_callback])
```
### Visualize loss curve
```
# Plot
import matplotlib.pyplot as plt
nrows = 1
ncols = 2
fig = plt.figure(figsize=(10, 5))
for idx, key in enumerate(["loss", "rmse"]):
ax = fig.add_subplot(nrows, ncols, idx+1)
plt.plot(history.history[key])
plt.plot(history.history["val_{}".format(key)])
plt.title("model {}".format(key))
plt.ylabel(key)
plt.xlabel("epoch")
plt.legend(["train", "validation"], loc="upper left");
```
### Save the model
```
OUTPUT_DIR = "babyweight_trained"
shutil.rmtree(OUTPUT_DIR, ignore_errors=True)
EXPORT_PATH = os.path.join(
OUTPUT_DIR, datetime.datetime.now().strftime("%Y%m%d%H%M%S"))
tf.saved_model.save(
obj=model, export_dir=EXPORT_PATH) # with default serving function
print("Exported trained model to {}".format(EXPORT_PATH))
!ls $EXPORT_PATH
```
Copyright 2020 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.727461 | null | null | null | null |
|
**author**: lukethompson@gmail.com<br>
**date**: 8 Oct 2017<br>
**language**: Python 3.5<br>
**license**: BSD3<br>
## sequence_prevalence.ipynb
```
import pandas as pd
import numpy as np
import locale
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
locale.setlocale(locale.LC_ALL, 'en_US')
def list_otu_studies(df, index):
return(set([x.split('.')[0] for x in df.loc[index]['list_samples'].split(',')]))
locale.format("%d", 1255000, grouping=True)
```
## QC-filtered samples
```
path_otus = '../../data/sequence-lookup/otu_summary.emp_deblur_90bp.qc_filtered.rare_5000.tsv' # gunzip first
num_samples = '24,910'
num_studies = '96'
df_otus = pd.read_csv(path_otus, sep='\t', index_col=0)
df_otus['studies'] = [list_otu_studies(df_otus, index) for index in df_otus.index]
df_otus['num_studies'] = [len(x) for x in df_otus.studies]
df_otus.shape
df_otus.num_samples.max()
(df_otus.num_samples > 100).value_counts() / 307572
(df_otus.num_studies > 10).value_counts() / 307572
df_otus.num_studies.max()
```
### Per-study endemism
Objective: Determine the number of OTUs that are study-dependent (or EMPO-dependent). For a given OTU, is it found in only one study's samples or in multiple studies (Venn diagram)?
```
df_otus.num_studies.max()
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12,4))
ax[0].hist(df_otus.num_studies, bins=np.concatenate(([], np.arange(1, 110, 1))))
ax[0].set_xlim([0, 98])
ax[0].set_xticks(np.concatenate((np.array([1.5]), np.arange(10.5, 92, 10))))
ax[0].set_xticklabels(['1', '10', '20', '30', '40', '50', '60', '70', '80', '90']);
ax[1].hist(df_otus.num_studies, bins=np.concatenate(([], np.arange(1, 110, 1))))
ax[1].set_yscale('log')
ax[1].set_ylim([5e-1, 1e6])
ax[1].set_xlim([0, 98])
ax[1].set_xticks(np.concatenate((np.array([1.5]), np.arange(10.5, 92, 10))))
ax[1].set_xticklabels(['1', '10', '20', '30', '40', '50', '60', '70', '80', '90']);
fig.text(0.5, 0.0, 'Number of studies a tag sequence was observed in (out of %s)' % num_studies, ha='center', va='center')
fig.text(0.0, 0.5, 'Number of tag sequences (out of %s)' % locale.format("%d", df_otus.shape[0], grouping=True),
ha='center', va='center', rotation='vertical')
exactly1 = df_otus.num_studies.value_counts()[1]
num_otus = df_otus.shape[0]
# fig.text(0.3, 0.51, '%s tag sequences (%.1f%%) found in only a single study\n\n\n\n\n\n%s tag sequences (%.1f%%) found in >1 study' %
# (locale.format("%d", exactly1, grouping=True),
# (exactly1/num_otus*100),
# locale.format("%d", num_otus-exactly1, grouping=True),
# ((num_otus-exactly1)/num_otus*100)),
# ha='center', va='center', fontsize=10)
plt.tight_layout()
plt.savefig('hist_endemism_90bp_qcfiltered.pdf', bbox_inches='tight')
```
### Per-sample endemism
```
fig = plt.figure(figsize=(12,4))
plt.subplot(121)
mybins = np.concatenate(([], np.arange(1, 110, 1)))
n, bins, patches = plt.hist(df_otus.num_samples, bins=mybins)
plt.axis([0, 92, 0, 4.5e4])
plt.xticks(np.concatenate((np.array([1.5]), np.arange(10.5, 92, 10))),
['1', '10', '20', '30', '40', '50', '60', '70', '80', '90']);
plt.subplot(122)
mybins = np.concatenate(([], np.arange(1, max(df_otus.num_samples)+100, 100)))
n, bins, patches = plt.hist(df_otus.num_samples, bins=mybins)
plt.yscale('log')
plt.axis([-100, 9200, 5e-1, 10e5])
plt.xticks([50, 1050, 2050, 3050, 4050, 5050, 6050, 7050, 8050, 9050],
['1-100', '1001-1100', '2001-2100', '3001-3100', '4001-4100',
'5001-5100', '6001-6100', '7001-7100', '8001-8100', '9001-9100'],
rotation=45, ha='right');
fig.text(0.5, 0.0, 'Number of samples a tag sequence was observed in (out of %s)' % num_samples, ha='center', va='center')
fig.text(0.0, 0.6, 'Number of tag sequences (out of %s)' % locale.format("%d", df_otus.shape[0], grouping=True),
ha='center', va='center', rotation='vertical')
exactly1 = df_otus.num_samples.value_counts()[1]
num_otus = df_otus.shape[0]
# fig.text(0.3, 0.6, '%s sequences (%.1f%%) found in only a single sample\n\n\n\n\n\n%s sequences (%.1f%%) found in >1 sample' %
# (locale.format("%d", exactly1, grouping=True),
# (exactly1/num_otus*100),
# locale.format("%d", num_otus-exactly1, grouping=True),
# ((num_otus-exactly1)/num_otus*100)),
# ha='center', va='center', fontsize=10)
plt.tight_layout()
plt.savefig('hist_otus_90bp_qcfiltered.pdf', bbox_inches='tight')
```
### Abundance vs. prevalence
```
plt.scatter(df_otus.num_samples, df_otus.total_obs, alpha=0.1)
plt.xscale('log')
plt.yscale('log')
plt.xlabel('Number of samples a tag sequence was observed in (out of %s)' % num_samples)
plt.ylabel('Total number of tag sequence observations')
plt.savefig('scatter_otus_90bp_qcfiltered.png')
```
## Subset 2k
```
path_otus = '../../data/sequence-lookup/otu_summary.emp_deblur_90bp.subset_2k.rare_5000.tsv' # gunzip first
num_samples = '2000'
df_otus = pd.read_csv(path_otus, sep='\t', index_col=0)
df_otus['studies'] = [list_otu_studies(df_otus, index) for index in df_otus.index]
df_otus['num_studies'] = [len(x) for x in df_otus.studies]
df_otus.num_samples.max()
df_otus.num_samples.value_counts().head()
plt.figure(figsize=(12,3))
mybins = np.concatenate(([-8.99, 1.01], np.arange(10, max(df_otus.num_samples), 10)))
n, bins, patches = plt.hist(df_otus.num_samples, bins=mybins)
plt.yscale('log')
plt.axis([-10, 600, 5e-1, 1e6])
plt.xticks([-4, 5.5, 15.5, 104.5, 204.5, 304.5, 404.5, 474.5, 574.5],
['exactly 1', '2-9', '10-19', '100-109', '200-209', '300-309', '400-409', '470-479', '570-579'],
rotation=45, ha='right', fontsize=9);
plt.xlabel('Number of samples OTU observed in (out of %s)' % num_samples)
plt.ylabel('Number of OTUs (out of %s)' % df_otus.shape[0])
plt.savefig('hist_otus_90bp_subset2k.pdf')
plt.scatter(df_otus.num_samples, df_otus.total_obs, alpha=0.1)
plt.xscale('log')
plt.yscale('log')
plt.xlabel('Number of samples OTU observed in (out of %s)' % num_samples)
plt.ylabel('Total number of OTU observations')
plt.savefig('scatter_otus_90bp_subset2k.png')
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12,4))
ax[0].hist(df_otus.num_studies, bins=df_otus.num_studies.max())
ax[1].hist(df_otus.num_studies, bins=df_otus.num_studies.max())
ax[1].set_yscale('log')
ax[1].set_ylim([5e-1, 1e6])
fig.text(0.5, 0.03, 'Number of studies OTU found in (out of %s)' % num_samples, ha='center', va='center')
fig.text(0.07, 0.5, 'Number of OTUs', ha='center', va='center', rotation='vertical')
exactly1 = df_otus.num_studies.value_counts()[1]
num_otus = df_otus.shape[0]
fig.text(0.3, 0.5, '%s OTUs (%.1f%%) found in only a single study\n\n\n\n\n\n\n\n\n%s OTUs (%.1f%%) found in >1 study' %
(locale.format("%d", exactly1, grouping=True),
(exactly1/num_otus*100),
locale.format("%d", num_otus-exactly1, grouping=True),
((num_otus-exactly1)/num_otus*100)),
ha='center', va='center', fontsize=10)
plt.savefig('hist_endemism_90bp_subset2k.pdf')
```
| true |
code
| 0.521349 | null | null | null | null |
|
## In the last chapter, you learned how to graphically explore data. In this chapter, you will compute useful summary statistics, which serve to concisely describe salient features of a data set with a few numbers.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
import warnings
warnings.filterwarnings('ignore')
data = load_iris()
df = pd.DataFrame(data['data'])
df.columns = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
df['species'] = ''
df['species'][:50] = 'setosa'
df['species'][50:100] = 'versicolor'
df['species'][100:150] = 'virginica'
df.head()
versicolor_petal_length = df[df['species']=='versicolor']['petal length (cm)'].values
setosa_petal_length = df[df['species'] == 'setosa']['petal length (cm)'].values
virginica_petal_length = df[df['species'] == 'virginica']['petal length (cm)'].values
```
## Computing means
The mean of all measurements gives an indication of the typical magnitude of a measurement. It is computed using np.mean().
```
# Compute the mean: mean_length_vers
mean_length_vers = np.mean(versicolor_petal_length)
mean_length_vers
```
## Computing percentiles
In this exercise, you will compute the percentiles of petal length of Iris versicolor
```
# Specify array of percentiles: percentiles
percentiles = np.array([2.5, 25, 50, 75, 97.5])
# Compute percentiles: ptiles_vers
ptiles_vers = np.percentile(versicolor_petal_length, percentiles)
ptiles_vers
```
## Comparing percentiles to ECDF
To see how the percentiles relate to the ECDF, you will plot the percentiles of Iris versicolor petal lengths you calculated in the last exercise on the ECDF plot you generated in chapter 1. The percentile variables from the previous exercise are available in the workspace as ptiles_vers and percentiles.
Note that to ensure the Y-axis of the ECDF plot remains between 0 and 1, you will need to rescale the percentiles array accordingly - in this case, dividing it by 100.
```
#!pip install ipynb
from ipynb.fs.full.Module1_Graphical_exploratory_data_analysis import ecdf;
x_vers, y_vers = ecdf(versicolor_petal_length)
# Plot the ECDF
plt.figure(figsize = (8,6))
plt.plot(x_vers, y_vers, '.')
plt.xlabel('petal length (cm)')
plt.ylabel('ECDF')
# Overlay percentiles as red x's
plt.plot(ptiles_vers, percentiles/100, marker='D', color='red',
linestyle='none')
```
## Box-and-whisker plot
Making a box plot for the petal lengths is unnecessary because the iris data set is not too large and the bee swarm plot works fine. However, it is always good to get some practice. Make a box plot of the iris petal lengths. You have a pandas DataFrame, df, which contains the petal length data, in your namespace. Inspect the data frame df in the IPython shell using df.head() to make sure you know what the pertinent columns are.
```
# Create box plot with Seaborn's default settings
sns.boxplot(x = 'species', y = 'petal length (cm)' ,data = df)
# Label the axes
plt.xlabel('species')
plt.ylabel('petal length (cm)')
```
## Computing the variance
It is important to have some understanding of what commonly-used functions are doing under the hood. Though you may already know how to compute variances, this is a beginner course that does not assume so. In this exercise, we will explicitly compute the variance of the petal length of Iris veriscolor using the equations. We will then use np.var() to compute it.
__Instructions__
- Create an array called differences that is the difference between the petal lengths (versicolor_petal_length) and the mean petal length. The variable versicolor_petal_length is already in your namespace as a NumPy array so you can take advantage of NumPy's vectorized operations.
- Square each element in this array. For example, x**2 squares each element in the array x. Store the result as diff_sq.
- Compute the mean of the elements in diff_sq using np.mean(). Store the result as variance_explicit.
- Compute the variance of versicolor_petal_length using np.var(). Store the result as variance_np.
- Print both variance_explicit and variance_np in one print call to make sure they are consistent.
```
# Array of differences to mean: differences
differences = np.array(versicolor_petal_length - np.mean(versicolor_petal_length))
# Square the differences: diff_sq
diff_sq = differences**2
# Compute the mean square difference: variance_explicit
variance_explicit = np.mean(diff_sq)
# Compute the variance using NumPy: variance_np
variance_np = np.var(versicolor_petal_length)
# Print the results
variance_explicit ,variance_np
```
## The standard deviation and the variance
The standard deviation is the square root of the variance. You will see this for yourself by computing the standard deviation using np.std() and comparing it to what you get by computing the variance with np.var() and then computing the square root.
```
# Compute the variance: variance
variance = np.var(versicolor_petal_length)
# Print the square root of the variance
print(np.sqrt(variance))
# Print the standard deviation
print(np.std(versicolor_petal_length))
```
## Scatter plots
When you made bee swarm plots, box plots, and ECDF plots in previous exercises, you compared the petal lengths of different species of iris. But what if you want to compare two properties of a single species? This is exactly what we will do in this exercise. We will make a scatter plot of the petal length and width measurements of Anderson's Iris versicolor flowers. If the flower scales (that is, it preserves its proportion as it grows), we would expect the length and width to be correlated.
```
versicolor_petal_width = df[df['species']=='versicolor']['petal width (cm)'].values
setosa_petal_width = df[df['species'] == 'setosa']['petal width (cm)'].values
virginica_petal_width = df[df['species'] == 'virginica']['petal width (cm)'].values
# Make a scatter plot
plt.plot(versicolor_petal_length, versicolor_petal_width, marker = '.', linestyle = 'none')
# Label the axes
plt.xlabel('petal length(cm)')
plt.ylabel('petal width (cm)')
```
## Computing the covariance
The covariance may be computed using the Numpy function np.cov(). For example, we have two sets of data x and y, np.cov(x, y) returns a 2D array where entries [0,1] and [1,0] are the covariances. Entry [0,0] is the variance of the data in x, and entry [1,1] is the variance of the data in y. This 2D output array is called the covariance matrix, since it organizes the self- and covariance.
__Instructions__
- Use np.cov() to compute the covariance matrix for the petal length (versicolor_petal_length) and width (versicolor_petal_width) of I. versicolor.
- Print the covariance matrix.
- Extract the covariance from entry [0,1] of the covariance matrix. Note that by symmetry, entry [1,0] is the same as entry [0,1].
```
# Compute the covariance matrix: covariance_matrix
covariance_matrix = np.cov(versicolor_petal_length, versicolor_petal_width)
# Print covariance matrix
print(covariance_matrix)
# Extract covariance of length and width of petals: petal_cov
petal_cov = covariance_matrix[0,1]
# Print the length/width covariance
print(petal_cov)
```
## Computing the Pearson correlation coefficient
the Pearson correlation coefficient, also called the Pearson r, is often easier to interpret than the covariance. It is computed using the np.corrcoef() function. Like np.cov(), it takes two arrays as arguments and returns a 2D array. Entries [0,0] and [1,1] are necessarily equal to 1 (can you think about why?), and the value we are after is entry [0,1].
In this exercise, you will write a function, pearson_r(x, y) that takes in two arrays and returns the Pearson correlation coefficient. You will then use this function to compute it for the petal lengths and widths of I. versicolor.
```
def pearson_r(x, y):
"""Compute Pearson correlation coefficient between two arrays."""
# Compute correlation matrix: corr_mat
corr_mat = np.corrcoef(x, y)
# Return entry [0,1]
return corr_mat[0,1]
# Compute Pearson correlation coefficient for I. versicolor
r = pearson_r(versicolor_petal_width, versicolor_petal_length)
# Print the result
r
```
| true |
code
| 0.72086 | null | null | null | null |
|
⊕ [Tutorial: Python in 10 Minutes - ArangoDB database](https://www.arangodb.com/tutorials/tutorial-python/)
```
from pyArango.connection import *
conn = Connection(username="root", password="")
```
When this code executes, it initializes the server connection on the conn variable. By default, pyArango attempts to establish a connection to http://127.0.0.1:8529. That is, it wants to initialize a remote connection to your local host on port 8529. If you are hosting ArangoDB on a different server or use a different port, you need to set these options when you instantiate the Connection class.
```
# db = conn.createDatabase(name="school")
db = conn["school"]
db
>>> studentsCollection = db.createCollection(name="Students")
>>> db["Students"]
```
## 创建集合
ArangoDB将文档和边缘分组到集合中。这类似于关系数据库中表的概念,但关键的区别是集合是无模式的。
在pyArango中,您可以通过调用createCollection()给定数据库上的方法来创建集合。例如,在上一节中,您创建了一个school数据库。您可能希望为该学生提供该数据库的集合。
```
# >>> studentsCollection = db.createCollection(name="Students")
>>> db["Students"]
```
## 创建文档
设置数据库和集合后,您可以开始向它们添加数据。继续与Relational数据库进行比较,其中集合是表,文档是该表上的一行。但是,与行不同,文档是无模式的。您可以包含应用程序所需的任何值排列。
例如,将学生添加到集合中:
```
>>> doc1 = studentsCollection.createDocument()
>>> doc1["name"] = "John Smith"
>>> doc1
>>> doc2 = studentsCollection.createDocument()
>>> doc2["firstname"] = "Emily"
>>> doc2["lastname"] = "Bronte"
>>> doc2
```
该文档显示_id为“无”,因为您尚未将其保存到ArangoDB。这意味着变量存在于Python代码中,但不存在于数据库中。ArangoDB _id通过将集合名称与值配对来构造值_key。它还为您处理分配,您只需设置密钥并保存文档。
```
>>> doc1._key = "johnsmith"
>>> doc1.save()
>>> doc1
studentsCollection["johnsmith"]
```
您可能希望从数据库中删除文档。这可以通过该delete()方法完成。
```
>>> tom = studentsCollection["johnsmith"]
>>> tom.delete()
# >>> studentsCollection["johnsmith"]
students = [('Oscar', 'Wilde', 3.5), ('Thomas', 'Hobbes', 3.2),
('Mark', 'Twain', 3.0), ('Kate', 'Chopin', 3.8), ('Fyodor', 'Dostoevsky', 3.1),
('Jane', 'Austen',3.4), ('Mary', 'Wollstonecraft', 3.7), ('Percy', 'Shelley', 3.5),
('William', 'Faulkner', 3.8), ('Charlotte', 'Bronte', 3.0)]
for (first, last, gpa) in students:
doc = studentsCollection.createDocument()
doc['name'] = "%s %s" % (first, last)
doc['gpa'] = gpa
doc['year'] = 2017
doc._key = ''.join([first, last]).lower()
doc.save()
# 访问数据库中的文档。最简单的方法是使用_key值。
def report_gpa(document):
print("Student: %s" % document['name'])
print("GPA: %s" % document['gpa'])
kate = studentsCollection['katechopin']
report_gpa(kate)
# 当您从ArangoDB中读取文档到您的应用程序时,您将创建该文档的本地副本。然后,您可以对文档进行操作,对其进行任何更改,然后使用该save()方法将结果推送到数据库。
def update_gpa(key, new_gpa):
doc = studentsCollection[key]
doc['gpa'] = new_gpa
doc.save()
# 您可能希望对给定集合中的所有文档进行操作。使用该fetchAll()方法,您可以检索并迭代文档列表。例如,假设这是学期结束,你想知道哪些学生的平均成绩高于3.5:
def top_scores(col, gpa):
print("Top Soring Students:")
for student in col.fetchAll():
if student['gpa'] >= gpa:
print("- %s" % student['name'])
top_scores(studentsCollection, 3.5)
```
## AQL用法
除了上面显示的Python方法之外,ArangoDB还提供了一种查询语言(称为AQL),用于检索和修改数据库上的文档。在pyArango中,您可以使用该AQLQuery()方法发出这些查询。
例如,假设您要检索ArangoDB中所有文档的密钥:
```
aql = "FOR x IN Students RETURN x._key"
queryResult = db.AQLQuery(aql, rawResults=True, batchSize=100)
for key in queryResult:
print(key)
```
在上面的示例中,该AQLQuery()方法将AQL查询作为参数,并带有两个附加选项:
* rawResults 定义是否需要查询返回的实际结果。
* batchSize 当查询返回的结果多于给定值时,pyArango驱动程序会自动请求新批次。
请记住,文件的顺序不能保证。如果您需要按特定顺序排列结果,请在AQL查询中添加sort子句。
⊕ [Graph | Example AQL Queries for Graphs | Cookbook | ArangoDB Documentation](https://www.arangodb.com/docs/stable/cookbook/graph-example-actors-and-movies.html)
During this solution we will be using arangosh to create and query the data. All the AQL queries are strings and can simply be copied over to your favorite driver instead of arangosh.
Create a Test Dataset in arangosh: ...
示例是使用nodejs编写的.
## 使用AQL插入文档
与上面的文档创建类似,您也可以使用AQL将文档插入ArangoDB。这是通过INSERT使用bindVars该AQLQuery()方法选项的语句完成的。
```
>>> doc = {'_key': 'denisdiderot', 'name': 'Denis Diderot', 'gpa': 3.7}
>>> bind = {"doc": doc}
>>> aql = "INSERT @doc INTO Students LET newDoc = NEW RETURN newDoc"
>>> queryResult = db.AQLQuery(aql, bindVars=bind)
queryResult[0]
```
## 使用AQL更新文档
如果数据库中已存在文档并且您想要修改该文档中的数据,则可以使用该UPDATE语句。例如,假设您在CSV文件中收到学生的更新成绩点平均值。
首先,检查其中一个学生的GPA以查看旧值:
```
db["Students"]["katechopin"]
# 然后遍历文件,更新每个学生的GPA:
with open("grades.csv", "r") as f:
grades = f.read().split(',')
for key,gpa in grades.items():
doc = {"gpa": float(gpa)}
bind = {"doc": doc, "key": key}
aql = "UPDATE @key WITH @doc IN Stdents LET pdated NEW RETRN updated"
db.AQLQuery(aql, bindVars=bind)
# 最后,再次检查学生的GPA。
db["Students"]["katechopin"]
```
| true |
code
| 0.237686 | null | null | null | null |
|
# Multiple linear regression model
### Let's mimic the process of building our trading model of SPY, base on the historical data of different stock markets
```
import pandas as pd
import statsmodels.formula.api as smf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
# import all stock market data into DataFrame
aord = pd.DataFrame.from_csv('../data/indice/ALLOrdinary.csv')
nikkei = pd.DataFrame.from_csv('../data/indice/Nikkei225.csv')
hsi = pd.DataFrame.from_csv('../data/indice/HSI.csv')
daxi = pd.DataFrame.from_csv('../data/indice/DAXI.csv')
cac40 = pd.DataFrame.from_csv('../data/indice/CAC40.csv')
sp500 = pd.DataFrame.from_csv('../data/indice/SP500.csv')
dji = pd.DataFrame.from_csv('../data/indice/DJI.csv')
nasdaq = pd.DataFrame.from_csv('../data/indice/nasdaq_composite.csv')
spy = pd.DataFrame.from_csv('../data/indice/SPY.csv')
nasdaq.head()
```
## Step 1: Data Munging
```
# Due to the timezone issues, we extract and calculate appropriate stock market data for analysis
# Indicepanel is the DataFrame of our trading model
indicepanel=pd.DataFrame(index=spy.index)
indicepanel['spy']=spy['Open'].shift(-1)-spy['Open']
indicepanel['spy_lag1']=indicepanel['spy'].shift(1)
indicepanel['sp500']=sp500["Open"]-sp500['Open'].shift(1)
indicepanel['nasdaq']=nasdaq['Open']-nasdaq['Open'].shift(1)
indicepanel['dji']=dji['Open']-dji['Open'].shift(1)
indicepanel['cac40']=cac40['Open']-cac40['Open'].shift(1)
indicepanel['daxi']=daxi['Open']-daxi['Open'].shift(1)
indicepanel['aord']=aord['Close']-aord['Open']
indicepanel['hsi']=hsi['Close']-hsi['Open']
indicepanel['nikkei']=nikkei['Close']-nikkei['Open']
indicepanel['Price']=spy['Open']
indicepanel.head()
# Lets check whether do we have NaN values in indicepanel
indicepanel.isnull().sum()
# We can use method 'fillna()' from dataframe to forward filling the Nan values
# Then we can drop the reminding Nan values
indicepanel = indicepanel.fillna(method='ffill')
indicepanel = indicepanel.dropna()
# Lets check whether do we have Nan values in indicepanel now
indicepanel.isnull().sum()
# save this indicepanel for part 4.5
path_save = '../data/indice/indicepanel.csv'
indicepanel.to_csv(path_save)
print(indicepanel.shape)
```
## Step 2: Data Spliting
```
#split the data into (1)train set and (2)test set
Train = indicepanel.iloc[-2000:-1000, :]
Test = indicepanel.iloc[-1000:, :]
print(Train.shape, Test.shape)
```
## Step 3: Explore the train data set
```
# Generate scatter matrix among all stock markets (and the price of SPY) to observe the association
from pandas.tools.plotting import scatter_matrix
sm = scatter_matrix(Train, figsize=(10, 10))
```
## Step 4: Check the correlation of each index between spy
```
# Find the indice with largest correlation
corr_array = Train.iloc[:, :-1].corr()['spy']
print(corr_array)
formula = 'spy~spy_lag1+sp500+nasdaq+dji+cac40+aord+daxi+nikkei+hsi'
lm = smf.ols(formula=formula, data=Train).fit()
lm.summary()
```
## Step 5: Make prediction
```
Train['PredictedY'] = lm.predict(Train)
Test['PredictedY'] = lm.predict(Test)
plt.scatter(Train['spy'], Train['PredictedY'])
```
## Step 6: Model evaluation - Statistical standard
We can measure the performance of our model using some statistical metrics - **RMSE**, **Adjusted $R^2$ **
```
# RMSE - Root Mean Squared Error, Adjusted R^2
def adjustedMetric(data, model, model_k, yname):
data['yhat'] = model.predict(data)
SST = ((data[yname] - data[yname].mean())**2).sum()
SSR = ((data['yhat'] - data[yname].mean())**2).sum()
SSE = ((data[yname] - data['yhat'])**2).sum()
r2 = SSR/SST
adjustR2 = 1 - (1-r2)*(data.shape[0] - 1)/(data.shape[0] -model_k -1)
RMSE = (SSE/(data.shape[0] -model_k -1))**0.5
return adjustR2, RMSE
def assessTable(test, train, model, model_k, yname):
r2test, RMSEtest = adjustedMetric(test, model, model_k, yname)
r2train, RMSEtrain = adjustedMetric(train, model, model_k, yname)
assessment = pd.DataFrame(index=['R2', 'RMSE'], columns=['Train', 'Test'])
assessment['Train'] = [r2train, RMSEtrain]
assessment['Test'] = [r2test, RMSEtest]
return assessment
# Get the assement table fo our model
assessTable(Test, Train, lm, 9, 'spy')
```
| true |
code
| 0.374076 | null | null | null | null |
|
# Imports and Simulation Parameters
```
import numpy as np
import math
import cmath
import scipy
import scipy.integrate
import sys
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
hbar = 1.0 / (2.0 * np.pi)
ZERO_TOLERANCE = 10**-6
MAX_VIBRATIONAL_STATES = 200
STARTING_GROUND_STATES = 5
STARTING_EXCITED_STATES = 5
time_scale_set = 10 #will divide the highest energy to give us the time step
low_frequency_cycles = 25.0 #will multiply the frequency of the lowest frequency mode to get the max time
#See if a factorial_Storage dictionary exists already and if not, create one
try:
a = factorial_storage
except:
factorial_storage = {}
```
# Defining Parameters of the System
```
energy_g = 0
energy_gamma = .1
energy_e = 0
energy_epsilon = .31
Huang_Rhys_Parameter = .80
S = Huang_Rhys_Parameter
#bookkeeping
overlap_storage = {}
electronic_energy_gap = energy_e + .5*energy_epsilon - (energy_g + .5 * energy_gamma)
min_energy = energy_g + energy_gamma * .5
mu_0 = 1.0
```
If we set the central frequency of a pulse at the 0->0 transition, and we decide we care about the ratio of the 0->1 transition to the 0->0 transition and set that to be $\tau$ then the desired pulse width will be
\begin{align}
\sigma &= \sqrt{-\frac{2 \ln (\tau)}{\omega_{\epsilon}^2}}
\end{align}
```
def blank_wavefunction(number_ground_states, number_excited_states):
return np.zeros((number_ground_states + number_excited_states))
def perturbing_function(time):
# stdev = 30000.0 * dt #very specific to 0->0 transition!
stdev = 3000.0 * dt #clearly has a small amount of amplitude on 0->1 transition
center = 6 * stdev
return np.cos(electronic_energy_gap*(time - center) / hbar)*np.exp( - (time - center)**2 / (2 * stdev**2)) / stdev
def time_function_handle_from_tau(tau_proportion):
stdev = np.sqrt( -2.0 * np.log(tau_proportion) / (energy_epsilon/hbar)**2)
center = 6 * stdev
return center, stdev, lambda t: np.cos(electronic_energy_gap*(t - center) / hbar)*np.exp( - (t - center)**2 / (2 * stdev**2)) / stdev
def time_function_handle_from_tau_and_kappa(tau_proportion, kappa_proportion):
stdev = np.sqrt( -2.0 * np.log(tau_proportion) / (energy_epsilon/hbar)**2)
center = 6 * stdev
return center, stdev, lambda t: kappa_proportion * energy_gamma * np.cos(electronic_energy_gap*(t - center) / hbar)*np.exp( - (t - center)**2 / (2 * stdev**2)) / stdev
def perturbing_function_define_tau(time, tau_proportion):
center, stdev, f = time_function_handle_from_tau(tau_proportion)
return f(time)
```
# Defining Useful functions
$ O_{m}^{n} = \left(-1\right)^{n} \sqrt{\frac{e^{-S}S^{m+n}}{m!n!}} \sum_{j=0}^{\min \left( m,n \right)} \frac{m!n!}{j!(m-j)!(n-j)!}(-1)^j S^{-j} $
```
def factorial(i):
if i in factorial_storage:
return factorial_storage[i]
if i <= 1:
return 1.0
else:
out = factorial(i - 1) * i
factorial_storage[i] = out
return out
def ndarray_factorial(i_array):
return np.array([factorial(i) for i in i_array])
def overlap_function(ground_quantum_number, excited_quantum_number):
m = ground_quantum_number
n = excited_quantum_number
if (m,n) in overlap_storage:
return overlap_storage[(m,n)]
output = (-1)**n
output *= math.sqrt(math.exp(-S) * S**(m + n) /(factorial(m) * factorial(n)) )
j_indeces = np.array(range(0, min(m,n) + 1))
j_summation = factorial(m) * factorial(n) * np.power(-1.0, j_indeces) * np.power(S, -j_indeces)
j_summation = j_summation / (ndarray_factorial(j_indeces) * ndarray_factorial( m - j_indeces) * ndarray_factorial(n - j_indeces) )
output *= np.sum(j_summation)
overlap_storage[(m,n)] = output
return output
```
# Solving the Differential Equation
\begin{align*}
\left(\frac{d G_a(t)}{dt} + \frac{i}{\hbar}\Omega_{(a)}\right) &=-E(t)\frac{i}{\hbar} \sum_{b} E_b(t) \mu_{a}^{b}\\
\left(\frac{d E_b(t)}{dt} + \frac{i}{\hbar} \Omega^{(b)} \right) &=-E(t)\frac{i}{\hbar} \sum_{a} G_a(t) \mu_{a}^{b}
\end{align*}
Or in a more compact form:
\begin{align*}
\frac{d}{dt}\begin{bmatrix}
G_a(t) \\
E_b(t)
\end{bmatrix}
= -\frac{i}{\hbar}
\begin{bmatrix}
\Omega_{(a)} & E(t) \mu_{a}^{b} \\
E(t) \mu_{a}^{b} & \Omega^{b}
\end{bmatrix}
\cdot
\begin{bmatrix}
G_a(t) \\
E_b(t)
\end{bmatrix}
\end{align*}
```
def ode_diagonal_matrix(number_ground_states, number_excited_states):
#Define the Matrix on the RHS of the above equation
ODE_DIAGONAL_MATRIX = np.zeros((number_ground_states + number_excited_states, number_ground_states + number_excited_states), dtype=np.complex)
#set the diagonals
for ground_i in range(number_ground_states):
ODE_DIAGONAL_MATRIX[ground_i, ground_i] = -1.0j * (energy_g + energy_gamma * (ground_i + .5)) / hbar
for excited_i in range(number_excited_states):
excited_index = excited_i + number_ground_states #the offset since the excited states comes later
ODE_DIAGONAL_MATRIX[excited_index, excited_index] = -1.0j * (energy_e + energy_epsilon * (excited_i + .5)) / hbar
return ODE_DIAGONAL_MATRIX
#now for the off-diagonals
def mu_matrix(c, number_ground_states, number_excited_states):
MU_MATRIX = np.zeros((number_ground_states, number_excited_states), dtype = np.complex)
for ground_a in range(number_ground_states):
for excited_b in range(number_excited_states):
new_mu_entry = overlap_function(ground_a, excited_b)
if ground_a >0:
new_mu_entry += c * math.sqrt(ground_a) * overlap_function(ground_a - 1, excited_b)
new_mu_entry += c * math.sqrt(ground_a+1) * overlap_function(ground_a + 1, excited_b)
MU_MATRIX[ground_a, excited_b] = new_mu_entry
return MU_MATRIX
def ode_off_diagonal_matrix(c_value, number_ground_states, number_excited_states):
output = np.zeros((number_ground_states + number_excited_states, number_ground_states + number_excited_states), dtype=np.complex)
MU_MATRIX = mu_matrix(c_value, number_ground_states, number_excited_states)
output[0:number_ground_states, number_ground_states:] = -1.0j * mu_0 * MU_MATRIX / hbar
output[number_ground_states:, 0:number_ground_states] = -1.0j * mu_0 * MU_MATRIX.T / hbar
return output
def IR_transition_dipoles(number_ground_states, number_excited_states):
"outputs matrices to calculate ground and excited state IR emission spectra. Can be combined for total"
output_g = np.zeros((number_ground_states + number_excited_states, number_ground_states + number_excited_states), dtype=np.complex)
output_e = np.zeros((number_ground_states + number_excited_states, number_ground_states + number_excited_states), dtype=np.complex)
for ground_a in range(number_ground_states):
try:
output_g[ground_a, ground_a + 1] = math.sqrt(ground_a + 1)
output_g[ground_a + 1, ground_a] = math.sqrt(ground_a + 1)
except:
pass
try:
output_g[ground_a, ground_a - 1] = math.sqrt(ground_a)
output_g[ground_a - 1, ground_a] = math.sqrt(ground_a)
except:
pass
for excited_a in range(number_excited_states):
matrix_index_e = number_ground_states + excited_a -1 #because of how 'number_ground_states' is defined
try:
output_e[matrix_index_e, matrix_index_e + 1] = math.sqrt(excited_a + 1)
output_e[matrix_index_e + 1, matrix_index_e] = math.sqrt(excited_a + 1)
except:
pass
try:
output_e[matrix_index_e, matrix_index_e - 1] = math.sqrt(excited_a)
output_e[matrix_index_e - 1, matrix_index_e] = math.sqrt(excited_a)
except:
pass
return output_g, output_e
```
\begin{align*}
\mu(x) &= \mu_0 \left(1 + \lambda x \right) \\
&= \mu_0 \left(1 + c\left(a + a^{\dagger} \right) \right) \\
\mu_{a}^{b} &= \mu_0\left(O_{a}^{b} + c\left(\sqrt{a}O_{a-1}^{b} + \sqrt{a+1}O_{a+1}^{b}\right) \right)
\end{align*}
```
class VibrationalStateOverFlowException(Exception):
def __init__(self):
pass
def propagate_amplitude_to_end_of_perturbation(c_value, ratio_01_00, kappa=1, starting_ground_states=STARTING_GROUND_STATES, starting_excited_states=STARTING_EXCITED_STATES):
center_time, stdev, time_function = time_function_handle_from_tau_and_kappa(ratio_01_00, kappa)
ending_time = center_time + 8.0 * stdev
number_ground_states = starting_ground_states
number_excited_states = starting_excited_states
while number_excited_states + number_ground_states < MAX_VIBRATIONAL_STATES:
#define time scales
max_energy = energy_e + energy_epsilon * (.5 + number_excited_states) + kappa * energy_gamma * mu_0
dt = 1.0 / (time_scale_set * max_energy)
ODE_DIAGONAL = ode_diagonal_matrix(number_ground_states, number_excited_states)
ODE_OFF_DIAGONAL = ode_off_diagonal_matrix(c_value, number_ground_states, number_excited_states)
def ODE_integrable_function(time, coefficient_vector):
ODE_TOTAL_MATRIX = ODE_OFF_DIAGONAL * time_function(time) + ODE_DIAGONAL
return np.dot(ODE_TOTAL_MATRIX, coefficient_vector)
#define the starting wavefuntion
initial_conditions = blank_wavefunction(number_ground_states, number_excited_states)
initial_conditions[0] = 1
#create ode solver
current_time = 0.0
ode_solver = scipy.integrate.complex_ode(ODE_integrable_function)
ode_solver.set_initial_value(initial_conditions, current_time)
#Run it
results = []
try: #this block catches an overflow into the highest ground or excited vibrational state
while current_time < ending_time:
# print(current_time, ZERO_TOLERANCE)
#update time, perform solution
current_time = ode_solver.t+dt
new_result = ode_solver.integrate(current_time)
results.append(new_result)
#make sure solver was successful
if not ode_solver.successful():
raise Exception("ODE Solve Failed!")
#make sure that there hasn't been substantial leakage to the highest excited states
re_start_calculation = False
if abs(new_result[number_ground_states - 1])**2 >= ZERO_TOLERANCE:
number_ground_states +=1
# print("Increasing Number of Ground vibrational states to %i " % number_ground_states)
re_start_calculation = True
if abs(new_result[-1])**2 >= ZERO_TOLERANCE:
number_excited_states +=1
# print("Increasing Number of excited vibrational states to %i " % number_excited_states)
re_start_calculation = True
if re_start_calculation:
raise VibrationalStateOverFlowException()
except VibrationalStateOverFlowException:
#Move on and re-start the calculation
continue
#Finish calculating
results = np.array(results)
return results, number_ground_states, number_excited_states
raise Exception("NEEDED TOO MANY VIBRATIONAL STATES! RE-RUN WITH DIFFERENT PARAMETERS!")
def get_average_quantum_number_time_series(c_value, ratio_01_00, kappa=1, starting_ground_states=STARTING_GROUND_STATES, starting_excited_states=STARTING_EXCITED_STATES):
results, number_ground_states, number_excited_states = propagate_amplitude_to_end_of_perturbation(c_value, ratio_01_00, kappa, starting_ground_states, starting_excited_states)
probabilities = np.abs(results)**2
#calculate the average_vibrational_quantum_number series
average_ground_quantum_number = probabilities[:,0:number_ground_states].dot(np.array(range(number_ground_states)) )
average_excited_quantum_number = probabilities[:,number_ground_states:].dot(np.array(range(number_excited_states)))
return average_ground_quantum_number, average_excited_quantum_number, results, number_ground_states, number_excited_states
def IR_emission_spectrum_after_excitation(c_value, ratio_01_00, kappa=1, starting_ground_states=STARTING_GROUND_STATES, starting_excited_states=STARTING_EXCITED_STATES):
center_time, stdev, time_function = time_function_handle_from_tau_and_kappa(ratio_01_00, kappa)
perturbation_ending_time = center_time + 8.0 * stdev
simulation_ending_time = perturbation_ending_time + low_frequency_cycles * hbar/min_energy
number_ground_states = starting_ground_states
number_excited_states = starting_excited_states
while number_excited_states + number_ground_states < MAX_VIBRATIONAL_STATES:
ir_transDipole_g, ir_transDipole_e = IR_transition_dipoles(number_ground_states, number_excited_states)
time_emission_g = [0]
time_emission_e = [0]
#define time scales
e = energy_e + energy_epsilon * (.5 + number_excited_states)
g = energy_g + energy_gamma* (.5 + number_ground_states)
plus = e + g
minus = e - g
J = kappa * energy_gamma * mu_0
max_split_energy = plus + math.sqrt(minus**2 + 4 * J**2)
max_energy = max_split_energy * .5
dt = 1.0 / (time_scale_set * max_energy)
time_values = np.arange(0, simulation_ending_time, dt)
ODE_DIAGONAL = ode_diagonal_matrix(number_ground_states, number_excited_states)
ODE_OFF_DIAGONAL = ode_off_diagonal_matrix(c_value, number_ground_states, number_excited_states)
def ODE_integrable_function(time, coefficient_vector):
ODE_TOTAL_MATRIX = ODE_OFF_DIAGONAL * time_function(time) + ODE_DIAGONAL
return np.dot(ODE_TOTAL_MATRIX, coefficient_vector)
def ODE_jacobean(time, coefficient_vector):
ODE_TOTAL_MATRIX = ODE_OFF_DIAGONAL * time_function(time) + ODE_DIAGONAL
return ODE_TOTAL_MATRIX
#define the starting wavefuntion
initial_conditions = blank_wavefunction(number_ground_states, number_excited_states)
initial_conditions[0] = 1
#create ode solver
current_time = 0.0
try:
del ode_solver
except:
pass
# ode_solver = scipy.integrate.complex_ode(ODE_integrable_function)
ode_solver = scipy.integrate.complex_ode(ODE_integrable_function, jac = ODE_jacobean)
# ode_solver.set_integrator("lsoda")
ode_solver.set_integrator("vode", with_jacobian=True)
ode_solver.set_initial_value(initial_conditions, current_time)
#Run it
results = []
try: #this block catches an overflow into the highest ground or excited vibrational state
while current_time < simulation_ending_time:
# print(current_time, ZERO_TOLERANCE)
#update time, perform solution
current_time = ode_solver.t+dt
new_result = ode_solver.integrate(current_time)
results.append(new_result)
#make sure solver was successful
if not ode_solver.successful():
raise Exception("ODE Solve Failed!")
if current_time < perturbation_ending_time:
#make sure that there hasn't been substantial leakage to the highest excited states
re_start_calculation = False
if abs(new_result[number_ground_states - 1])**2 >= ZERO_TOLERANCE:
number_ground_states +=1
# print("Increasing Number of Ground vibrational states to %i " % number_ground_states)
re_start_calculation = True
if abs(new_result[-1])**2 >= ZERO_TOLERANCE:
number_excited_states +=1
# print("Increasing Number of excited vibrational states to %i " % number_excited_states)
re_start_calculation = True
if re_start_calculation:
raise VibrationalStateOverFlowException()
#calculate IR emission
time_emission_g.append(np.conj(new_result).T.dot(ir_transDipole_g.dot(new_result)))
time_emission_e.append(np.conj(new_result).T.dot(ir_transDipole_e.dot(new_result)))
#on to next time value...
except VibrationalStateOverFlowException:
#Move on and re-start the calculation
continue
#Finish calculating
results = np.array(results)
n_t = len(time_emission_e)
time_emission_g = np.array(time_emission_g)
time_emission_e = np.array(time_emission_e)
filter_x = np.array(range(n_t))
filter_center = n_t / 2.0
filter_sigma = n_t / 10.0
filter_values = np.exp(-(filter_x - filter_center)**2 / (2 * filter_sigma**2))
frequencies = np.fft.fftshift(np.fft.fftfreq(time_emission_g.shape[0], d= dt))
frequency_emission_g = dt * np.fft.fftshift(np.fft.fft(time_emission_g * filter_values))
frequency_emission_e = dt * np.fft.fftshift(np.fft.fft(time_emission_e * filter_values))
return results, frequencies, frequency_emission_g, frequency_emission_e, number_ground_states, number_excited_states
raise Exception("NEEDED TOO MANY VIBRATIONAL STATES! RE-RUN WITH DIFFERENT PARAMETERS!")
c_values = np.logspace(-4, np.log10(1), 5)
tau_values = np.logspace(-4, np.log10(.95), 10)
kappa_values = np.logspace(-2, np.log10(5), 20)
number_calcs = c_values.shape[0] * tau_values.shape[0] * kappa_values.shape[0]
heating_results_ground = np.zeros((kappa_values.shape[0], tau_values.shape[0], c_values.shape[0]))
ir_amplitudes = np.zeros(heating_results_ground.shape)
heating_results_excited = np.zeros(heating_results_ground.shape)
# Keep track of the IR Spectrum
n_g = STARTING_GROUND_STATES
n_e = STARTING_EXCITED_STATES
counter = 1
# we will use the value of c as a bellweather for how many starting states to work with.
c_to_ng = {}
c_to_ne = {}
for i_kappa, kappa in enumerate(kappa_values):
# as we increase in both tau and
for i_tau, tau in enumerate(tau_values):
for i_c, c in enumerate(c_values):
try:
n_g = c_to_ng[c]
n_e = c_to_ne[c]
except:
n_g = STARTING_GROUND_STATES
n_e = STARTING_EXCITED_STATES
c_to_ng[c] = n_g
c_to_ne[c] = n_e
sys.stdout.flush()
sys.stdout.write("\r%i / %i Calculating kappa=%f, c=%f, tau=%f at n_g = %i and n_e=%i..." %(counter, number_calcs, kappa, c, tau, n_g, n_e))
# print("\r%i / %i Calculating kappa=%f, c=%f, tau=%f at n_g = %i and n_e=%i..." %(counter, number_calcs, kappa, c, tau, n_g, n_e))
# n_bar_g, n_bar_e, results, num_g, num_e = get_average_quantum_number_time_series(c,
# tau,
# kappa,
# starting_ground_states = n_g,
# starting_excited_states = n_e)
# heating_results_ground[i_kappa, i_tau, i_c] = n_bar_g[-1]
# heating_results_excited[i_kappa, i_tau, i_c] = n_bar_e[-1]
_, frequencies, emission_g, emission_e, num_g, num_e = IR_emission_spectrum_after_excitation(c,
tau,
kappa,
starting_ground_states = n_g,
starting_excited_states = n_e)
if num_g > c_to_ng[c]:
c_to_ng[c] = num_g
if num_e > c_to_ne[c]:
c_to_ne[c] = num_e
vibrational_frequency_index = np.argmin(np.abs(energy_gamma - frequencies))
ir_power = np.abs(emission_g[vibrational_frequency_index])**2
ir_amplitudes[i_kappa, i_tau, i_c] = ir_power
counter +=1
# plt.figure()
# plt.title(r"$\kappa{}, \tau={}, c={}".format(kappa, tau, c))
# plt.plot(frequencies, emission_g)
# plt.xlim(0, 2)
# decreased dt, does that keep these parameters from failing? last one is 600 / 800 Calculating kappa=8.858668, c=0.750000, tau=0.850000
for i_kappa, kappa in enumerate(kappa_values):
for i_tau, tau in enumerate(tau_values):
ir_power = ir_amplitudes[i_kappa, i_tau, :]
plt.loglog(c_values, ir_power, "*-")
plt.xlabel(r"$c$")
plt.figure()
for i_kappa, kappa in enumerate(kappa_values):
for i_c, c in enumerate(c_values):
ir_power = ir_amplitudes[i_kappa, :, i_c]
plt.loglog(tau_values, ir_power, "*-")
plt.xlabel(r"$\tau$")
plt.figure()
for i_tau, tau in enumerate(tau_values):
for i_c, c in enumerate(c_values):
# for i_c in [0,-1]:
ir_power = ir_amplitudes[:, i_tau, i_c]
# plt.loglog(kappa_values, ir_power, ["blue", "red"][i_c])
plt.loglog(kappa_values, ir_power)
plt.xlabel(r"$\kappa$")
# plt.xlim(-.1, 1.1)
# plt.ylim(-10, 500)
c_log = np.log10(c_values)
tau_log = np.log10(tau_values)
kappa_log = np.log10(kappa_values)
log_ir_amplitudes = np.log(ir_amplitudes)
num_levels = 100
contours = np.linspace(np.min(log_ir_amplitudes), np.max(log_ir_amplitudes), num_levels)
# for i_kappa, kappa in enumerate(kappa_values):
# ir_power = log_ir_amplitudes[i_kappa, :, :]
# plt.figure()
# plt.contourf(c_log, tau_log, ir_power, contours)
# plt.title(r"$\kappa = {}$".format(kappa))
# plt.ylabel(r"$c$")
# plt.xlabel(r"$\tau$")
# plt.colorbar()
for i_tau, tau in enumerate(tau_values):
ir_power = log_ir_amplitudes[:, i_tau, :]
plt.figure()
plt.contourf(c_log, kappa_log, ir_power, contours)
plt.title(r"$\tau = {}$".format(tau))
plt.ylabel(r"$\kappa$")
plt.xlabel(r"$c$")
plt.colorbar()
for i_c, c in enumerate(c_values):
ir_power = log_ir_amplitudes[:, :, i_c]
plt.figure()
plt.contourf(tau_log, kappa_log, ir_power, contours)
plt.title(r"$c = {}$".format(c))
plt.ylabel(r"$\kappa$")
plt.xlabel(r"$\tau$")
plt.colorbar()
np.linspace()
```
| true |
code
| 0.551272 | null | null | null | null |
|
# Chunking strategies for a Wide-ResNet
This tutorial shows how to utilize a hypernet container [HContainer](../hnets/hnet_container.py) and class [StructuredHMLP](../hnets/structured_mlp_hnet.py) (a certain kind of hypernetwork that allows *smart* chunking) in combination with a Wide-ResNet [WRN](../mnets/wide_resnet.py).
```
# Ensure code of repository is visible to this tutorial.
import sys
sys.path.insert(0, '..')
import numpy as np
import torch
from hypnettorch.hnets.structured_hmlp_examples import wrn_chunking
from hypnettorch.hnets import HContainer, StructuredHMLP
from hypnettorch.mnets import WRN
```
## Instantiate a WRN-28-10-B(3,3)
First, we instantiate a WRN-28-10 (i.e., a WRN containing $28$ convolutional layers (and an additional fully-connected output layer) and a widening factor $k=10$) with no internal weights (`no_weights=True`). Thus, it's weights are expected to originate externally (in our case from a hypernetwork) and to be passed to its `forward` method.
In particular, we are interested in instantiating a network that matches the one used in the study [Sacramento et al., "Economical ensembles with hypernetworks", 2020](https://arxiv.org/abs/2007.12927) (accessed August 18th, 2020). Therefore, the convolutional layers won't have bias terms (but the final fully-connected layer will).
```
net = WRN(in_shape=(32, 32, 3), num_classes=10, n=4, k=10,
num_feature_maps=(16, 16, 32, 64), use_bias=False,
use_fc_bias=True, no_weights=False, use_batch_norm=True,
dropout_rate=-1)
```
## Reproduce the chunking strategy from Sacramento et al.
We first design a hypernetwork that matches the chunking strategy described in [Sacramento et al.](https://arxiv.org/abs/2007.12927). Thus, not all parameters are produced by a hypernetwork. Batchnorm weights will be shared among conditions (in their case, each condition represents one ensemble member), while the output layer weights will be condition-specific (ensemble-member-specific). The remaining weight are produced via linear hypernetworks (no bias terms in the hypernets) using a specific chunking strategy, which is described in the paper and in the docstring of function [wrn_chunking](../hnets/structured_hmlp_examples.py). To realize the mixture between shared weights (batchnorm), condition-specific weights (output weights) and hypernetwork-produced weights, we employ the special hypernetwork class [HContainer](../hnets/hnet_container.py).
We first create an instance of class [StructuredHMLP](../hnets/structured_mlp_hnet.py) for all hypernetwork-produced weights.
```
# Number of conditions (ensemble members). Arbitrarily chosen!
num_conds = 10
# Split the network's parameter shapes into shapes corresponding to batchnorm-weights,
# hypernet-produced weights and output weights.
# Here, we make use of implementation specific knowledge, which could also be retrieved
# via the network's "param_shapes_meta" attribute, which contains meta information
# about all parameters.
bn_shapes = net.param_shapes[:2*len(net.batchnorm_layers)] # Batchnorm weight shapes
hnet_shapes = net.param_shapes[2*len(net.batchnorm_layers):-2] # Conv layer weight shapes
out_shapes = net.param_shapes[-2:] # Output layer weight shapes
# This function already defines the network chunking in the same way the paper
# specifies it.
chunk_shapes, num_per_chunk, assembly_fct = wrn_chunking(net, ignore_bn_weights=True,
ignore_out_weights=True,
gcd_chunking=False)
# Taken from table S1 in the paper.
chunk_emb_sizes = [10, 7, 14, 14, 14, 7, 7, 7]
# Important, the underlying hypernetworks should be linear, i.e., no hidden layers:
# ``layers': []``
# They also should not use bias vectors -> hence, weights are simply generated via a
# matrix vector product (chunk embedding input times hypernet, which is a weight matrix).
# Note, we make the chunk embeddings conditional and tell the hypernetwork, that
# it doesn't have to expect any other input except those learned condition-specific
# embeddings.
shnet = StructuredHMLP(hnet_shapes, chunk_shapes, num_per_chunk, chunk_emb_sizes,
{'layers': [], 'use_bias': False}, assembly_fct,
cond_chunk_embs=True, uncond_in_size=0,
cond_in_size=0, num_cond_embs=num_conds)
```
Now, we combine the above produce `shnet` with shared batchnorm weights and condition-specific output weights in an instance of class [HContainer](../hnets/hnet_container.py), which will represent the final hypernetwork.
```
# We first have to create a simple function handle that tells the `HContainer` how to
# recombine the batchnorm-weights, hypernet-produced weights and output weights.
def simple_assembly_func(list_of_hnet_tensors, uncond_tensors, cond_tensors):
# `list_of_hnet_tensors`: Contains outputs of all linear hypernets (conv
# layer weights).
# `uncond_tensors`: Contains the single set of shared batchnorm weights.
# `cond_tensors`: Contains the condition-specific output weights.
return uncond_tensors + list_of_hnet_tensors[0] + cond_tensors
hnet = HContainer(net.param_shapes, simple_assembly_func, hnets=[shnet],
uncond_param_shapes=bn_shapes, cond_param_shapes=out_shapes,
num_cond_embs=num_conds)
```
Create sample predictions for 3 different ensemble members.
```
# Batch of inputs.
batch_size = 1
x = torch.rand((batch_size, 32*32*3))
# Which ensemble members to consider?
cond_ids = [2,3,7]
# Generate weights for ensemble members defined above.
weights = hnet.forward(cond_id=cond_ids)
# Compute prediction for each ensemble member.
for i in range(len(cond_ids)):
pred = net.forward(x, weights=weights[i])
# Apply softmax.
pred = torch.nn.functional.softmax(pred, dim=1).cpu().detach().numpy()
print('Prediction of ensemble member %d: %s' \
% (cond_ids[i], np.array2string(pred, precision=3, separator=', ')))
```
## Create a batch-ensemble network
Now, we consider the special case where all parameters are shared except for batchnorm weights and output weights. Thus, no "hypernetwork" are required. Though, we use the class [HContainer](../hnets/hnet_container.py) for convinience.
```
def simple_assembly_func2(list_of_hnet_tensors, uncond_tensors, cond_tensors):
# `list_of_hnet_tensors`: None
# `uncond_tensors`: Contains all conv layer weights.
# `cond_tensors`: Contains the condition-specific batchnorm and output weights.
return cond_tensors[:-2] + uncond_tensors + cond_tensors[-2:]
hnet2 = HContainer(net.param_shapes, simple_assembly_func2, hnets=None,
uncond_param_shapes=hnet_shapes,
cond_param_shapes=bn_shapes+out_shapes,
num_cond_embs=num_conds)
# Batch of inputs.
batch_size = 1
x = torch.rand((batch_size, 32*32*3))
# Which ensemble members to consider?
cond_ids = [2,3,7]
# Generate weights for ensemble members defined above.
weights = hnet2.forward(cond_id=cond_ids)
# Compute prediction for each ensemble member.
for i in range(len(cond_ids)):
pred = net.forward(x, weights=weights[i])
# Apply softmax.
pred = torch.nn.functional.softmax(pred, dim=1).cpu().detach().numpy()
print('Prediction of ensemble member %d: %s' \
% (cond_ids[i], np.array2string(pred, precision=3, separator=', ')))
```
| true |
code
| 0.811097 | null | null | null | null |
|
```
%matplotlib inline
from NewsFlow import *
from VisualTools import *
%load_ext autoreload
%autoreload 2
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
from matplotlib.patches import Patch
from matplotlib.lines import Line2D
from matplotlib.colors import LinearSegmentedColormap
```
# Basic use
The `NewsFlow` can be simulated in many different ways using various input parameters. Nevertheless, at the very least, its basic use requires specifying the following input parameters:
- population layer $\mathcal{G}_R = (\mathcal{R}, E_R)$ in the form of an (unweighted undirected) `igraph.Graph` graph,
- the initial number $R^F(0) \in [1, R-1]$ of consumers of false news in the form of an `int` variable `F0`,
- the rate $\eta$ of per-capita news-alignment events (these rewire the inter-layer coupling) in the form of a `double` variable `eta`,
- the basic spreading rate $\lambda^F$ regulating edge-balancing events towards the false state in the form of a `double` variable `lambda_F`.
For example:
```
g = ig.Graph.Barabasi(n=1000, m=20, power=-2.5) # generates a Barabási-Albert graph on 1000 vertices
time_range, list_polarised, list_rhoF, list_FT_edges = newsFlow(g=g, F0=500, eta=10, lambda_F=0.5)
```
Notice that the execution terminated at $t_n$ due to the sample variance in either the number of unbalanced (active) edges $\lvert E^{FT}(t_n) \rvert$ or the number of polarised individuals $P(t_n)$ over the sliding window of length `window_size` dropping below the permitted tolerance `tol`.
One could instead specify an upper limit on the simulation time by providing an `int` variable `t_max`, e.g.,
```
time_range, list_polarised, list_rhoF, list_FT_edges = newsFlow(g=g, F0=500, eta=10, lambda_F=0.5,
t_max=100)
```
Or, one could use *both* termination conditions by feeding in the upper limit on the simulation time `t_max` as well as the arguments `window_size` and/or `tol` customising the computation of the sliding-window variances (note that one can always tweak either or both of these parameters).
```
time_range, list_polarised, list_rhoF, list_FT_edges = newsFlow(g=g, F0=500, eta=10, lambda_F=0.5,
t_max=100, window_size=200, tol=0.0001)
```
However, in order to make sense of the simulation outcomes, one might want to make use of the visualisation tools provided in the script `VisualTools`.
In the [following section](#sfreq0) of the tutorial we focus solely on the default value of the sampling frequency `sfreq`, i.e., `sfreq == 0`. This comes in handy when one is interested in the detailed time evolution of the system at the macro level.
Next, we take a peek at the case of `sfreq < 0`. This choice is especially helpful when only the final simulation state (at the macro level) is required. [Section](#sfreql0) provides related visual aids.
Finally, the [last section](#sfreqg0) is dedicated to examples where the particular choice of `sfreq > 0` matters even more and at last justifies its name. Here, one can find a selection of functions which illustrate the time evolution (with a sampling frequency of `sfreq`) at the micro scale, that is, at the level of individual news providers and individual news consumers.
## Default value of the sampling frequency `sfreq`: `sfreq == 0`
<a id='sfreq0'></a>
```
_ = plot_newsFlow(N=1000, F0=500, eta=10, lambda_F=0.5)
data = time_evolution_F0(N=300, list_F0=[3, 30, 75, 150], lambda_F=2, eta=20, t_max=100)
colours = ['limegreen', 'darkgray', 'gray', 'crimson']
draw_time_evolution_F0(data=data, colours=colours, inset_lims=[0.05, 1, 0.1, 0.2], inset_width=2)
data = time_evolution_lambda_F_eta(N=500, F0=150, list_lambdaF=[0.2, 1, 5], list_eta=[10, 20, 50])
legend_elements = [Patch(color='limegreen', label=r'$\lambda^F = 0.2$'),
Patch(color='gray', label=r'$\lambda^F = 1$'),
Patch(color='crimson', label=r'$\lambda^F = 5$'),
Line2D([], [], color='dimgray', label='$\eta = 10$', linestyle='dotted',
markerfacecolor='dimgray'),
Line2D([], [], color='dimgray', label='$\eta = 20$', linestyle='dashed',
markerfacecolor='dimgray'),
Line2D([], [], color='dimgray', label='$\eta = 50$', linestyle='solid',
markerfacecolor='dimgray')]
colours = {0.2: 'limegreen', 1: 'gray', 5: 'crimson'}
linestyles = {10: 'dotted', 20: 'dashed', 50: 'solid'}
alphas = {10: 0.3, 20: 0.6, 50: 0.9}
draw_time_evolution_lambda_F_eta(data=data, colours=colours, linestyles=linestyles, alphas=alphas,
legend_elements=legend_elements)
```
## Sampling frequency `sfreq < 0`
<a id='sfreql0'></a>
```
final_polarised, final_rhoF, final_FT_edges = rho_heatmaps(N=300, F0=150,
lambdaF_list=[0.25, 0.5, 1, 2, 4],
eta_list=[10, 20, 30, 40, 50],
rep=10, tol=0.02)
draw_heatmap(data=final_polarised, title=r'Final density $\rho^P$ of polarised individuals',
cmap=sns.light_palette((210, 90, 60), input="husl"), markCells=[[1,0], [0,2]])
cmap = LinearSegmentedColormap.from_list(name='rhoF',
colors=['limegreen', 'lightgreen', 'whitesmoke', 'lightcoral', 'crimson'], N=300)
draw_heatmap(data=final_rhoF, title=r'Final density $\rho^F$ of individuals in the false state',
cmap=cmap, markCells=[[1,1], [2,2]], vmin=0.00, vmax=1.00, center=0.50)
draw_heatmap(data=final_FT_edges, title=r'Final density $\rho^{FT}$ of unbalanced edges',
cmap=sns.light_palette((210, 90, 60), input="husl"), markCells=[[3,2], [2,1], [1,4]])
data = rho_lambdaF(list_N=[200, 400, 600], list_rhoF0=[0.01, 0.10, 0.25, 0.5], rep=1,
list_lambdaF=[0.25, 0.5, 1, 2, 4], eta=5, t_max=100)
colours = {0.01: 'limegreen', 0.1: 'darkgray', 0.25: 'gray', 0.5: 'crimson'}
markers = {200: 'v', 400: 's', 600: '^'}
legend_elements = [Patch(color='limegreen', label=r'$\rho^F(0) = 0.01$'),
Patch(color='darkgray', label=r'$\rho^F(0) = 0.10$'),
Patch(color='gray', label=r'$\rho^F(0) = 0.25$'),
Patch(color='crimson', label=r'$\rho^F(0) = 0.50$'),
Line2D([], [], marker='v', color='dimgray', label='R = 200', linestyle='None',
markerfacecolor='dimgray', markersize=8),
Line2D([], [], marker='s', color='dimgray', label='R = 400', linestyle='None',
markerfacecolor='dimgray', markersize=8),
Line2D([], [], marker='^', color='dimgray', label='R = 600', linestyle='None',
markerfacecolor='dimgray', markersize=8)]
plot_densities_lambdaF(data=data, colours=colours, markers=markers, legend_elements=legend_elements)
data = rho_eta(list_N=[200, 400, 600], list_rhoF0=[0.01, 0.10, 0.25, 0.5], rep=1,
list_eta=[1, 30, 50], lambda_F=2, t_max=50)
plot_densities_eta(data=data, colours=colours, markers=markers, legend_elements=legend_elements)
```
## Sampling frequency `sfreq > 0`
<a id='sfreqg0'></a>
```
data = get_media_repertoire(N=500, lambda_F=1, eta=50, sfreq=10, t_max=50)
media_repertoire(data=data)
public_scatter(data=data)
subscription(data=data)
data = get_media_subscriptions(N=500, lambda_F=1, eta=50, sfreq=10, t_max=100)
media_subscriptions(data=data)
media_scatter(data=data)
readership(data=data)
```
| true |
code
| 0.600657 | null | null | null | null |
|

**[MiCMOR](https://micmor.kit.edu) [SummerSchool "Environmental Data Science: From Data Exploration to Deep Learning"](https://micmor.kit.edu/sites/default/files/MICMoR%20Summer%20School%202019%20Flyer.pdf)**
IMK-IFU KIT Campus Alpin, Sept. 4 - 13 2019, Garmisch-Partenkirchen, Germany.
---
# Basic plotting in Python: Matplotlib
**Note:** Parts of this notebook are inspired by the Notebook of Chapter 9 of the excellent [Python for Data Analysis Book](https://www.oreilly.com/library/view/python-for-data/9781491957653/) by Wes McKinney (the creator of pandas).
The original notebook is located [here](https://nbviewer.jupyter.org/github/pydata/pydata-book/blob/2nd-edition/ch09.ipynb).
The core plotting layer for most python plotting libs is [matplotlib](https://matplotlib.org).
Initially, it was modeled after the Matlab plotting routines. It's been
around for a long time and is very solid but may seem a bit clunky at first.
Some of the more modern packages have nicer visuals by default, but you can tweak
matplotlib a lot and can also make it look more modern. Furthermore, a lot of the
other packages will use matplotlib as a back-end. This is nice since you then can alter
them as you would with pure matplotlib plots.
What also makes it a bit confusing for newcomers is a) that it's pretty low level and that b)
it can be used with two paradigms: the matlab-style state-based model and the object-oriented (OO) model.
```
%matplotlib inline
%load_ext autoreload
%autoreload 2
import matplotlib.pylab as plt
import numpy as np
```
## The two Matplotlib Plotting APIs
Just a brief comparison...
### MATLAB-style stateful plotting flavor
This interface is stateful (it keeps track of the "current" figure and axes, you can get a reference to them with `plt.gcf()` (get current figure) and `plt.gca()` (get current axes).
The interface is fast and convenient for simple plots. However, it can be nasty for more complex pots (i.e. mulitple panels). IMHO, do not use this for your work. The OO-style is almost as easy to use and much more powerful... However, you often might want to mix it in so it's good to know.
```
# some data
x = np.linspace(0, 10, 100)
# create a plot figure
plt.figure()
# create the first of two panels and set current axis
plt.subplot(2, 1, 1) # (rows, columns, panel number)
plt.plot(x, np.sin(x))
# create the second panel and set current axis
plt.subplot(2, 1, 2)
plt.plot(x, np.cos(x));
```
### Object-oriented flavor
```
# First create a grid of plots
# ax will be an array of two Axes objects
fig, ax = plt.subplots(2)
# Call plot() method on the appropriate object
ax[0].plot(x, np.sin(x))
ax[1].plot(x, np.cos(x));
```
## The Basics
**Note:** It's quite common to mix and match the two interface styles.
### Figures and subplots
As you can see, we always start with `figure`, `subplot` and `axes` objects. You can think of figure
as the canvas and axes as an individual plot with its x/y-axis, ticks, labels and the actual plots. A figure can be composed by multiple subplots which each being addressed by its own axis.
```
# the manual way to compose a figure with three subplots
fig = plt.figure()
# the numbers are: row, column, number of plot
ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
```
Matlotlib (MPL) uses a code to represent linestyle, cymbols or color. Here, we want a black (`k`) dashed (`--`) line.
```
plt.plot(np.random.randn(50).cumsum(), 'k--');
```
Now we do a more complicated plot. It is composed of two subplots, with a histogram on the left and a scatter plot on the right. We specify a plot size of 14x4 inches.
We also use 20 bins for the histogram and fill the bars with black (30% opacity).
```
fig = plt.figure(figsize=(14,4))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
ax1.hist(np.random.randn(100), bins=20, color='k', alpha=0.3)
ax2.scatter(np.arange(30), np.arange(30) + 3 * np.random.randn(30));
plt.close('all')
```
A more common way to create a figure with subplots is:
```python
fig, axes = plt.subplots(2, 3)
```
This would create a figure with 6 subplots (2 rows, 3 columns).
Now, let's compose a 2x2 plot with shared axes and histograms. We also adjust the space between the plots for a more compact plot.
```
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True)
for i in range(2):
for j in range(2):
axes[i, j].hist(np.random.randn(500), bins=50, color='k', alpha=0.5)
plt.subplots_adjust(wspace=0, hspace=0)
```
## Colors, Markers and line styles
As mentioned above, you can adjust markers and styles with a special syntax. `ko--` would create a ine plot (dashed) with marker circles in black.
```
from numpy.random import randn
plt.plot(randn(30).cumsum(), 'ko--');
plt.close('all')
```
You can combine multiple plots into an axis and create a legend that's composed from labels attached to the plot commands...
```
data = np.random.randn(30).cumsum()
plt.plot(data, 'k--', label='Default')
plt.plot(data, 'k-', drawstyle='steps-post', label='steps-post')
plt.legend(loc='best');
```
## Ticks, labels and legends
Se can customize all parts of the plots. I.e., we can set custom ticks and labels.
```
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(np.random.randn(1000).cumsum())
# now we define custom tick positions and tick labels
ticks = ax.set_xticks([0, 250, 500, 750, 1000])
labels = ax.set_xticklabels(['one', 'two', 'three', 'four', 'five'],
rotation=30, fontsize='small')
# set a title and an axis label
ax.set_title('My first matplotlib plot')
ax.set_xlabel('Stages');
```
As previously shown above, it's easy to add legends (see the guide [[here]](https://matplotlib.org/3.1.1/tutorials/intermediate/legend_guide.html) for more details...
```
from numpy.random import randn
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(randn(1000).cumsum(), 'k', label='one')
ax.plot(randn(1000).cumsum(), 'k--', label='two')
ax.plot(randn(1000).cumsum(), 'k.', label='three');
# add legend to the best location (repart the plot by
# running the cell multiple times to see it in action)
ax.legend(loc='best');
```
## Saving files to disk
It's easy to save the figure to disc. You can specify the file type to `pdf` or `png`:
```python
# plot my stuff, then...
plt.savefig('figure.png', dpi=400, bbox_inches='tight')
# and as a pdf
plt.savefig('figure.pdf', bbox_inches='tight')
```
`bbox_inches='tight'` is required to avoid unnecessary whitespace around figures...
### Change the plot style
As this is a common complaint about matplotlib: you can actually style your plots in matplotlib.
```python
plt.style.use('seaborn-whitegrid')
```
Below are some examples (source - also click for more examples: https://matplotlib.org/3.1.1/gallery/style_sheets/style_sheets_reference.html):



And a note on confusing differences in the API.
Consider this simple plot:
```
x = np.linspace(0, 10, 30)
y = np.sin(x)
plt.plot(x, y, 'o', color='black');
```
Matplotlib can be used with a bit of an archaic syntax for specifying linstyles, symbols and colors in very short argument form.
Take a look at this example:
```
plt.plot(x, y, 'o-k');
```
This could also be written as:
```
plt.plot(x, y, 'o', ls='-', c='k');
```
Or even more verbose (but actually readable):
```
plt.plot(x, y, 'o', linestyle='-', color='black');
```
Use scatter instead of plot if you want to control aspects of the points with data...
```
rng = np.random.RandomState(0)
x = rng.randn(100)
y = rng.randn(100)
colors = rng.rand(100)
sizes = 1000 * rng.rand(100)
plt.scatter(x, y, c=colors, s=sizes, alpha=0.3,
cmap='viridis')
plt.colorbar(); # show color scale
```
This is much more versatile and already halfway towards the more modern plottings libraries.
## Closing early...
We have to leave it at that since we cannot dive well into `matplotlib` in this course. We will use mostly
other libraries to get results fast, but some matplotlib might crop up occasionally.
However, you can always - and should - consult the excellent matplotlib documentation/ gallery with its vast number of
examples.
[Matplotlib gallery](https://matplotlib.org/gallery/index.html)
| true |
code
| 0.683604 | null | null | null | null |
|
[View in Colaboratory](https://colab.research.google.com/github/whongyi/openrec/blob/master/tutorials/Youtube_Recommender_example.ipynb)
<p align="center">
<img src ="https://recsys.acm.org/wp-content/uploads/2017/07/recsys-18-small.png" height="40" /> <font size="4">Recsys 2018 Tutorial</font>
</p>
<p align="center">
<font size="4"><b>Modularizing Deep Neural Network-Inspired Recommendation Algorithms</b></font>
</p>
<p align="center">
<font size="4">Hands on: Customizing Deep YouTube Video Recommendation. Youtube example</font>
</p>
# the Youtube Recommender
The training graph of YouTube-Rec can be decomposed as follows.
<p align="center">
<img src ="https://s3.amazonaws.com/cornell-tech-sdl-openrec/tutorials/youtube_rec_module.png" height="600" />
</p>
* **inputgraph**: user demographis, item consumption history and the groundtruth label.
* **usergraph**: extract user-specific latent factor.
* **itemgraph**: extract latent factors for items.
* **interactiongraph**: uses MLP and softmax to model user-item interactions.
After defining subgraphs, their interfaces and connections need to be specified. A sample specification of YouTube-Rec can be as follows.
<p align="center">
<img src ="https://s3.amazonaws.com/cornell-tech-sdl-openrec/tutorials/youtube_rec.png" height="300" />
</p>
# Install OpenRec and download dataset
```
!pip install openrec
import urllib.request
dataset_prefix = 'http://s3.amazonaws.com/cornell-tech-sdl-openrec'
urllib.request.urlretrieve('%s/lastfm/lastfm_test.npy' % dataset_prefix,
'lastfm_test.npy')
urllib.request.urlretrieve('%s/lastfm/lastfm_train.npy' % dataset_prefix,
'lastfm_train.npy')
urllib.request.urlretrieve('%s/lastfm/user_feature.npy' % dataset_prefix,
'user_feature.npy')
```
# Your task
- understand reuse and extend an exsiting recommender
- fill in the placeholders in the implementation of the `YouTubeRec` function
- successfully run the experimental code with the recommender you just built.
```
from openrec.recommenders import VanillaYouTubeRec # load the vanilla version and extend it with user demographic informaton
from openrec.modules.extractions import LatentFactor
from openrec.modules.interactions import MLPSoftmax
import tensorflow as tf
def Tutorial_YouTubeRec(batch_size, user_dict, item_dict, dim_user_embed, dim_item_embed,
max_seq_len, l2_reg_embed=None, l2_reg_mlp=None, dropout=None,
init_model_dir=None, save_model_dir='Youtube/', train=True, serve=False):
rec = VanillaYouTubeRec(batch_size=batch_size,
dim_item_embed=dim_item_embed['id'],
max_seq_len=max_seq_len,
total_items=item_dict['id'],
l2_reg_embed=l2_reg_embed,
l2_reg_mlp=l2_reg_embed,
dropout=dropout,
init_model_dir=init_model_dir,
save_model_dir=save_model_dir,
train=train,
serve=serve)
@rec.traingraph.inputgraph.extend(outs=['user_gender', 'user_geo'])
def add_train_feature(subgraph):
subgraph['user_gender'] = tf.placeholder(tf.int32, shape=[batch_size], name='user_gender')
subgraph['user_geo'] = tf.placeholder(tf.int32, shape=[batch_size], name='user_geo')
subgraph.update_global_input_mapping({'user_gender': subgraph['user_gender'],
'user_geo': subgraph['user_geo']})
@rec.servegraph.inputgraph.extend(outs=['user_gender', 'user_geo'])
def add_serve_feature(subgraph):
subgraph['user_gender'] = tf.placeholder(tf.int32, shape=[None], name='user_gender')
subgraph['user_geo'] = tf.placeholder(tf.int32, shape=[None], name='user_geo')
subgraph.update_global_input_mapping({'user_gender': subgraph['user_gender'],
'user_geo': subgraph['user_geo']})
@rec.traingraph.usergraph(ins=['user_gender', 'user_geo'], outs=['user_vec'])
@rec.servegraph.usergraph(ins=['user_gender', 'user_geo'], outs=['user_vec'])
def user_graph(subgraph):
_, user_gender = LatentFactor(l2_reg=l2_reg_embed,
shape=[user_dict['gender'], dim_user_embed['gender']],
id_=subgraph['user_gender'],
subgraph=subgraph,
init='normal',
scope='user_gender')
_, user_geo = LatentFactor(l2_reg=l2_reg_embed,
shape=[user_dict['geo'], dim_user_embed['geo']],
id_=subgraph['user_geo'],
subgraph=subgraph,
init='normal',
scope='user_geo')
subgraph['user_vec'] = tf.concat([user_gender, user_geo], axis=1)
@rec.traingraph.interactiongraph(ins=['user_vec', 'seq_item_vec', 'seq_len', 'label'])
def train_interaction_graph(subgraph):
MLPSoftmax(user=subgraph['user_vec'],
item=subgraph['seq_item_vec'],
seq_len=subgraph['seq_len'],
max_seq_len=max_seq_len,
dims=[dim_user_embed['total'] + dim_item_embed['total'], item_dict['id']],
l2_reg=l2_reg_mlp,
labels=subgraph['label'],
dropout=dropout,
train=True,
subgraph=subgraph,
scope='MLPSoftmax')
@rec.servegraph.interactiongraph(ins=['user_vec', 'seq_item_vec', 'seq_len'])
def serve_interaction_graph(subgraph):
MLPSoftmax(user=subgraph['user_vec'],
item=subgraph['seq_item_vec'],
seq_len=subgraph['seq_len'],
max_seq_len=max_seq_len,
dims=[dim_user_embed['total'] + dim_item_embed['total'], item_dict['id']],
l2_reg=l2_reg_mlp,
train=False,
subgraph=subgraph,
scope='MLPSoftmax')
@rec.traingraph.connector.extend
@rec.servegraph.connector.extend
def connect(graph):
graph.usergraph['user_gender'] = graph.inputgraph['user_gender']
graph.usergraph['user_geo'] = graph.inputgraph['user_geo']
graph.interactiongraph['user_vec'] = graph.usergraph['user_vec']
return rec
```
# Experiement
We will use the recommender you implemented to run a toy experiement on the LastFM dataset.
## load lastfm dataset
```
import numpy as np
train_data = np.load('lastfm_train.npy')
test_data = np.load('lastfm_test.npy')
user_feature = np.load('user_feature.npy')
total_users = 992
total_items = 14598
user_dict = {'gender': 3,
'geo': 67}
item_dict = {'id': total_items}
user_feature[:10], test_data[:10]
```
## preprocessing dataset
```
from openrec.utils import Dataset
train_dataset = Dataset(train_data, total_users, total_items,
sortby='ts', name='Train')
test_dataset = Dataset(test_data, total_users, total_items,
sortby='ts', name='Test')
```
## hyperparameters and training parameters
```
dim_user_embed = {'geo': 40, # dimension of user geographic embedding
'gender': 10, # dimension of user gender embedding
'total': 50}
dim_item_embed = {'id': 50, 'total': 50} # dimension of item embedding
max_seq_len = 100 # the maxium length of user's listen history
total_iter = int(1e3) # iterations for training
batch_size = 100 # training batch size
eval_iter = 100 # iteration of evaluation
save_iter = eval_iter # iteration of saving model
```
## define sampler
We use `YouTubeSampler` and `YouTubeEvaluationSampler` to sample sequences of training and testing samples.
```
from openrec.utils.samplers import YouTubeSampler, YouTubeEvaluationSampler
train_sampler = YouTubeSampler(user_feature=user_feature,
batch_size=batch_size,
max_seq_len=max_seq_len,
dataset=train_dataset,
num_process=1)
test_sampler = YouTubeEvaluationSampler(user_feature=user_feature,
dataset=test_dataset,
max_seq_len=max_seq_len)
```
## define evaluator
```
from openrec.utils.evaluators import AUC, Recall
auc_evaluator = AUC()
recall_evaluator = Recall(recall_at=[100, 200, 300, 400, 500])
```
## define model trainer
we used the Vanilla version of the Youtube recommender to train our model.
```
from openrec import ModelTrainer
model = Tutorial_YouTubeRec(batch_size=batch_size,
user_dict=user_dict,
item_dict=item_dict,
max_seq_len=max_seq_len,
dim_item_embed=dim_item_embed,
dim_user_embed=dim_user_embed,
save_model_dir='youtube_recommender/',
train=True, serve=True)
model_trainer = ModelTrainer(model=model)
```
## training and testing
```
model_trainer.train(total_iter=total_iter,
eval_iter=eval_iter,
save_iter=save_iter,
train_sampler=train_sampler,
eval_samplers=[test_sampler],
evaluators=[auc_evaluator, recall_evaluator])
```
| true |
code
| 0.708944 | null | null | null | null |
|
```
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras import utils, regularizers, callbacks, backend
from tensorflow.keras.layers import Input, Dense, Activation, ZeroPadding1D, BatchNormalization, Flatten, Reshape, Conv1D, MaxPooling1D, Dropout, Add, LSTM, Embedding
from tensorflow.keras.initializers import glorot_normal, glorot_uniform
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.models import Model, load_model
from astropy.io import fits
from IPython.display import YouTubeVideo
from tools.resample_flux import trapz_rebin
from tensorflow.keras.utils import to_categorical
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
```
# <span style="color:#3E2D80">Creando un cerebro artifical para encontrar la más temperamental de las bestias astronómicas</span>
Si crees que Nueva York es un lugar ajetreado, ¡piénsalo de nuevo! El espacio está lleno de cosas que chocan continuamente en la noche. Durante su estudio de cinco años, DESI tendrá la oportunidad de atrapar a miles de las bestias astronómicas más temperamentales del Universo, desde [estrellas en explosión](https://es.wikipedia.org/wiki/Supernova) a [fusionando estrellas de neutrones y estrellas negras agujeros](https://es.wikipedia.org/wiki/Kilonova) y [estrellas destrozadas por agujeros negros](https://es.wikipedia.org/wiki/Evento_de_disrupci%C3%B3n_de_marea), sin mencionar una larga lista de otros eventos fantásticos.
Los científicos de DESI son inteligentes, ¡pero ni siquiera ellos pueden identificar todos estos casi > 30 millones de espectros! Afortunadamente, tenemos expertos que saben cómo crear cerebros artificiales, o redes neuronales, construidas para especializarse en tareas como esta. En este cuaderno, [Segev Ben Zvi](https://www.pas.rochester.edu/~sybenzvi/),
<img src="../desihigh/images/Segev.jpg" alt="Drawing" style="width: 400px;"/>
nos pondrá al día con el aprendizaje automático de vanguardia y cómo se usa en esta búsqueda. Las supernovas (de tipo Ia) son las más críticas para la cosmología, así que primero nos centraremos en cómo identificarlas (a simple vista), ¡luego enseñaremos a trozos de silicio a hacerlo!
### Supernovas de colapso del núcleo
En casi todos los casos, las supernovas son la etapa final del ciclo de vida de las estrellas más masivas (> 10 $ M_{\odot} $, 10 veces mayor que la masa del Sol). Finalmente, el combustible disponible que sostiene la fusión nuclear en el núcleo se agota y la energía utilizada para soportar la capa más externa desaparece. Entonces, inevitablemente, la estrella colapsa por su propio peso en una violenta explosión que dura solo una fracción de segundo. Una estrella de neutrones quedará atrás o, si la estrella progenitora es lo suficientemente masiva, incluso un [agujero negro](https://es.wikipedia.org/wiki/Agujero_negro).
```
YouTubeVideo('o-Psuz7u5OI', width=800, height=400)
```
### Supernovas binarias
No todas las supernovas surgen debido al colapso del núcleo. En sistemas binarios con una enana blanca compacta y una estrella envejecida (secuencia principal), la enana blanca puede atraer material gravitacionalmente desde la capa de su compañera. Si se acumula suficiente material en la superficie de la enana blanca para que su masa total exceda el [límite de Chandrasekhar](https://es.wikipedia.org/wiki/L%C3%ADmite_de_Chandrasekhar), 1.44 $ M_\odot $, entonces ocurre una reacción nuclear descontrolada que hace explotar la Enana Blanca en una explosión intensamente brillante. ¡Estas llamadas supernovas de tipo Ia son la razón por la que descubrimos la Energía Oscura en primer lugar!
<img src="../desihigh/images/type1a.jpg" alt="Drawing" style="width: 400px;"/>
Estos diferentes tipos de supernova se distinguen por su brillo cambiante con el tiempo, su _'curva de luz'_, pero si tenemos el espectro de la supernova, es mucho menos probable que cometamos un error. Cada espectro de supernova tiene líneas muy amplias distintas tanto en emisión como en absorción (Si II, H $\alpha$, Ca II, etc.), del gas caliente que escapa de la explosión central a alta velocidad. Estas "huellas" permiten distinguir los distintos tipos.
<img src="../desihigh/images/sne_filippenko.png" width="600px"/>
¿Puedes decir qué es diferente entre estos cuatro ejemplos? ¿Tienen líneas en común y diferencias? Durante muchas décadas, los astrónomos han seguido esta lógica y la han dividido en una clasificación de supernovas, lo que nos dice el mecanismo detrás de su origen.
<img src="../desihigh/images/SupernovaeClassification.png" width="600px"/>
Por ejemplo, una supernovas de tipo Ib no muestra líneas de hidrógeno (H), pero sí las de helio.
## Cátalogo de Galaxias Brillantes de DESI (Bright Galaxy Survey)
Para ser lo suficientemente brillantes como para ser detectadas, las supernovas deben vivir en una galaxia relativamente cercana, como Messier 101,
<img src="../desihigh/images/type1aBGS.jpg" alt="Drawing" style="width: 400px;"/>
Con su estudio de diez millones de galaxias en el Universo _local_, el DESI Bright Galaxy Survey será perfecto para encontrarlas, ya que la luz recolectada por cualquier fibra dada será el total de la galaxia y la luz de una supernova potencial,
<img src="../desihigh/images/Messier101.png" alt="Drawing" style="width: 400px;"/>
donde vemos la misma galaxia Messier 101 en las imágenes Legacy de DESI y el área sobre la cual la luz es recolectada por las fibras (círculos). No sabremos de antemano si hay supernovas allí, por supuesto, así que esto solo funciona ya que DESI observará muchas galaxias y la tasa de supernovas en el Universo es relativamente alta, ¡así que tenemos buenas probabilidades!
Veamos cómo se ve esto en la práctica.
### ¿Qué ve DESI?
```
# Abrimos el archivo y vemos su contenido básico
hdus = fits.open('../desihigh/dat/bgs-supernovae.fits')
hdus.info()
```
Here _WAVE_ is simply an array of the observed wavelengths,
```
hdus['WAVE'].data
```
_FLUX_ es la intensidad de luz observada y _IVAR_ es $ (1\ / \ \rm{varianza \ esperada }) $ del flujo, es decir, de esto podemos derivar el error en este flujo observado. ¿Puedes pensar cómo? Dada la forma,
```
hdus['FLUX'].data.shape
```
vemos que tenemos el flujo medido a las mismas longitudes de onda que las de arriba, para seis objetivos.
```
# Graficamos todos los espectros en la misma cuadrícula de longitud de onda.
fig, axes = plt.subplots(2,3, figsize=(8,5), sharex=True, sharey=True, tight_layout=True)
for i, ax in enumerate(axes.flatten()):
wave = hdus['WAVE'].data
flux = hdus['FLUX'].data[i]
ivar = hdus['IVAR'].data[i]
spec = hdus['SPECTYPE'].data[i][0]
ax.plot(wave, flux, alpha=0.5)
ax.set(xlim=(3600, 9800), ylim=(-10,50),
title=spec)
axes[0,0].set(ylabel=r'Flux [$10^{-17}$ erg cm$^{-2}$ s$^{-1}$ $\AA^{-1}$]');
axes[1,0].set(ylabel=r'Flux [$10^{-17}$ erg cm$^{-2}$ s$^{-1}$ $\AA^{-1}$]');
for i in range(0,3):
axes[1,i].set(xlabel=r'Observed wavelength [$\AA$]')
```
Estos son los flujos observados por una fibra determinada de DESI, después de haber removido la luz conocida de la atmósfera. En la parte superior izquierda, tenemos la luz emitida por una galaxia BGS típica. Los otros paneles contienen la luz de la galaxia de un tipo específico de supernovas en cada caso. ¡Lo primero que hay que notar es que esto es _mucho_ menos claro de lo que esperábamos del espectro de ejemplo anterior!
Entonces, ¿cómo podemos confirmar que la luz de las supernovas de cada tipo (Ib, Ic, IIn, IIP) está realmente allí, como se confirma?
## Menos es más
Nuestro "problema" es que DESI mide la cantidad de luz en intervalos muy pequeños en longitud de onda (o color), debido a su alta resolución. Los espectros de objetivos específicos, en este caso supernovas, pueden no cambiar mucho en un intervalo de longitud de onda pequeño, por lo que terminamos con muchas mediciones _ruidosas_ de la misma cosa: la intensidad de la luz en un color o longitud de onda promedio.
Esto es _genial_, ya que podemos ser inteligentes y simplemente combinar estas medidas para obtener un valor promedio que es mucho más _preciso_.
```
# Graficamos todos los espectros en la misma cuadrícula de longitud de onda.
fig, axes = plt.subplots(2,3, figsize=(15,8), sharex=True, sharey=True, tight_layout=True)
# Remuestreamos el flujo en una nueva cuadrícula de longitud de onda con solo 100 bins.
coarse_wave = np.linspace(3600, 9800, 101)
for i, ax in enumerate(axes.flatten()):
wave = hdus['WAVE'].data
flux = hdus['FLUX'].data[i]
ivar = hdus['IVAR'].data[i]
spec = hdus['SPECTYPE'].data[i][0]
ax.plot(wave, flux, alpha=0.5)
fl = trapz_rebin(wave, flux, edges=coarse_wave)
ax.plot(coarse_wave[:-1], fl, 'k-', alpha=0.2)
ax.set(xlim=(3600, 9800), ylim=(-10,50),
title=spec)
axes[0,0].set(ylabel=r'flux [$10^{-17}$ erg cm$^{-2}$ s$^{-1}$ $\AA^{-1}$]');
axes[1,0].set(ylabel=r'flux [$10^{-17}$ erg cm$^{-2}$ s$^{-1}$ $\AA^{-1}$]');
for i in range(0,3):
axes[1,i].set(xlabel=r'Observed wavelength [$\AA$]')
```
¡Y ahora vemos mucho mejor los deeps característicos, o líneas de absorción, de las supernovas! Por supuesto, este no es el único enfoque. Podríamos haber usado estadísticas y los datos originales 'no agrupados', pero las cosas siempre son mejores cuando son más transparentes. Sin embargo, sigue siendo complicado, ya que la velocidad de la estrella significa que las líneas de absorción no estarán donde las esperaríamos normalmente. En este sentido, hay _dos corrimientos al rojo_ en el espectro.
Así que hemos identificado con éxito una (¡simulada, por ahora!) Supernovas DESI, pero nunca pudimos inspeccionar visualmente el estudio completo de esta manera. Necesitamos un método más eficiente...
## Un cerebro artificial: donde la anatomía se encuentra con la astronomía
<img src="../desihigh/images/AIBrain.jpg" alt="Drawing" style="width: 600px;"/>
Dada la increíble capacidad del cerebro humano, ¿a quién no se le ocurriría intentar comprenderlo y reproducirlo? Se logró un gran progreso en la década de 1940 con modelos simples que llevaron a los modelos de vanguardia de _aprendizaje profundo_ que han sido fundamentales para Google, Amazon y otras tecnologías hoy en día gigantes.
En las neuronas biológicas, las dendritas reciben señales de entrada de _miles_ de neuronas vecinas. Estas señales se _combinan_ en el núcleo y pasan a un axón. Solo si la señal combinada es _mayor que un valor de umbral_, entonces el axón liberará una señal prescrita.
<img src="../desihigh/images/Dendrite.jpg" alt="Drawing" style="width: 600px;"/>
Este simple paso final es donde ocurre la magia. Antes de esto, la señal de salida es una simple suma ponderada de las señales de entrada, p. Ej. $ y = a \ cdot x + b $. Las posibilidades de esta configuración son relativamente limitadas.
El umbral hace que la señal sea _no lineal_, de modo que cuando la señal de entrada cambia en una _cantidad pequeña, dx_, la señal de salida puede cambiar en _mucho_. Esto, junto con el _gran número_ de neuronas (relativamente simples) en el cerebro permite un potencial casi ilimitado, representado por el rango de posibilidades de salida o ideas que pueden formarse. Mientras lees esto, hay _100 mil millones_ de neuronas que pueden disparar su imaginación. ¡Quién sabe lo que se te ocurra!
### Potencial ilimitado
El aprendizaje automático 'profundo' es donde estas ideas relativamente simples se encuentran con la potencia informática bruta que nos otorgó [John von Neumann](https://es.wikipedia.org/wiki/John_von_Neumann), [John Bardeen](https://es.wikipedia.org/wiki/John_Bardeen), ... Las cosas realmente despegaron cuando salió a la luz el [martillo](https://es.wikipedia.org/wiki/Unidad_de_procesamiento_gr%C3%A1fico) adecuado para el problema.
En un equipo, pero en esencia, la misma estructura, podemos tener una serie de valores de entrada, $ x_1, x_2, ... $, como lo que sería recogido por las dendritas, que se ponderan y se suma, $ a_1 \ cdot x 1 + a2 \ cdot x_2 + ... + b_1 \ cdot _ x2 + ... $ como en el axón. Esto puede suceder varias veces, en una serie de 'capas ocultas', donde la salida de la capa anterior actúa como entrada de la siguiente. En cualquier etapa, aunque normalmente es la última, la "magia" podría ser introducida, o de forma similar, en una capa determinada. Por lo general, esto se conoce como "activación", en analogía con el disparo de un axón.
<img src="../desihigh/images/network.jpg" width="600px"/>
De antemano, o _a priori_, no tenemos idea de cuál debería ser el peso de nuestra 'red neuronal' artificial para un problema dado. La capacidad de la configuración está representada por el número de salidas diferentes que se pueden generar cuando cualquier peso determinado produce un nuevo número aleatorio, el resultado de lo que normalmente Será algo sin sentido para una entrada dada.
Pero si podemos definir el "éxito", como la satisfacción después de una buena comida o una broma, entonces podemos inculcar el "buen comportamiento" en los pesos. Introducimos repetidamente la red en un rango de escenarios diferentes y permitimos que los pesos, $ a_1, ..., b_1, ... $, o entidad, se refinen a aquellos que logran el _mayor éxito_, según se define en comparación con el 'verdad'. De esta manera, podemos replicar cientos de generaciones de [selección natural](https://es.wikipedia.org/wiki/Selecci%C3%B3n_natural) en una fracción de segundo.
### Si la vida fuera tan simple
El atractivo del aprendizaje profundo es claro, al igual que su potencial: ¿cuántas veces te has equivocado en tu vida? Claro, siempre estamos aprendiendo, pero la ciencia generalmente se basa en lo que sabemos y lo que no, dentro de lo razonable. No sobrevivirás demasiado tiempo en el campo si predices una respuesta diferente a la que tenías seis meses antes, ¡a pesar de lo mucho que hayas aprendido!
En otras palabras, lo más importante es saber lo que puedes decir _con confianza_. Normalmente, las redes neuronales harán una predicción definitiva, sin tener idea de su confianza y crecimiento potencial. Como tal, podríamos revisar nuestra ambición ...
### Potencial Limitado
Habiendo admitido nuestro potencial mundano, podríamos sacrificar algo de nuestra capacidad de ser perfectos, a favor de limitar el _potencial de equivocarnos_. Esto puede ser práctico, ya que una red con una gran cantidad de pesos puede ser infalible dada una potencia informática infinita, pero de lo contrario sería un desafío enorme.
Uno de los medios más efectivos para limitar el número de pesos en nuestra red y, por lo tanto, la posibilidad de estar equivocados, es reemplazar capas ocultas 'completamente conectadas' de pesos arbitrarios con capas 'convolucionales'. Una convolución simplemente reemplaza una cantidad de píxeles vecinos con un promedio ponderado, como en este caso.
<img src="../desihigh/images/CMB-lensing.jpg" width="600px"/>
Así, no es algo muy diferente a una capa completamente conectada. Sin embargo, difiere en que los pesos aplicados dentro de la imagen son _constantes en toda la imagen_. En otras palabras, una capa "completamente conectada" permite un tamaño, forma y tipo de vidrio diferentes en cualquier posición dada de una imagen. Al restringirnos a 'un vaso', reducimos en gran medida el potencial de la red, tanto en su capacidad para tener razón como para estar equivocado.
De esta manera, hemos recurrido a [filtros adaptados](https://es.wikipedia.org/wiki/Filtro_adaptado) arbitrarios, conocidos pronto por la invención del radar y el sonar. Eso no quiere decir que no tengamos algunas capas completamente conectadas, lo que podría detectar anomalías que no son consistentes en una imagen determinada.
## El Evento Principal
Primero, simplemente abramos nuestro archivo de datos y enumeremos el resultado.
```
spectra = np.load('../desihigh/dat/sn_simspectra.npz')
spectra.files
```
y descomprímamoslo en algo más explícito,
```
wave = spectra['wave']
# Host galaxy.
host_fluxes = spectra['hosts']
snia_fluxes = spectra['snia']
snib_fluxes = spectra['snib']
snic_fluxes = spectra['snic']
snii_fluxes = spectra['sniip']
```
Como anteriormente, esto es simplemente espectros de galaxias (hospedaje de nuestras supernovas) de ejemplo, junto con ejemplos que contienen clases específicas de supernovas. Para ser concretos, tracemos un espectro de cada uno.
```
fig, axes = plt.subplots(2,3, figsize = (12,7), tight_layout=True, sharex=True, sharey=True)
ax = axes[0,0]
ax.plot(wave, host_fluxes[0])
ax.set(ylabel='normalized flux',
title='BGS host galaxy')
ax = axes[0,1]
ax.plot(wave, snia_fluxes[0])
ax.set(title='Host + SN Ia')
ax = axes[0,2]
ax.plot(wave, snib_fluxes[0])
ax.set(title='Host + SN Ib')
ax = axes[1,0]
ax.plot(wave, snic_fluxes[0])
ax.set(xlabel=r'Rest frame wavelength [$\AA$]',
ylabel='Normalized flux',
title='Host + SN Ic')
ax = axes[1,1]
ax.plot(wave, snii_fluxes[0])
ax.set(xlabel=r'rest frame wavelength [$\AA$]',
title='Host + SN IIP')
axes[1,2].axis('off');
```
Hay muchas posibilidades entre las que le estamos pidiendo a la red que busque. Para facilitar las cosas, estos espectros se han _precondicionado_. Para lograr esto, hemos: eliminado el efecto del corrimiento al rojo del espectro observado;
promediado en los contenedores vecinos, como anteriormente; renormalizado los flujos para que se encuentren entre [0, 1]; por lo tanto, ignoramos el brillo de las supernovas al determinar su tipo.
## Creando un cerebro artificial para encontrar las bestias astronómicas más temperamentales
Primero crearemos nuestro cerebro artificial y luego diseñaremos desafíos que pueda intentar repetidamente y _aprender_. Si usamos todos nuestros datos para crear los desafíos, entonces no tenemos datos externos para probar qué tan bien está funcionando la red; este sería un ejemplo clásico de [sobreajuste](https://es.wikipedia.org/wiki/Sobreajuste).
Para evitar esto, dividiremos nuestros datos en conjuntos de *entrenamiento* (train) y *validación* (test). Finalmente, para ser amigable con la computadora, asignaremos _etiquetas enteras_ simples a los tipos que esperamos que la red pueda adivinar: (host, Ia, Ib, Ic, IIp) = (0,1,2,3,4) respectivamente.
```
# Divide los datos en variables x y y, donde x = espectros y y = nuestras etiquetas.
nbins = len(wave)
x = np.concatenate([host_fluxes,
snia_fluxes,
snib_fluxes,
snic_fluxes,
snii_fluxes
]).reshape(-1, nbins, 1)
y = to_categorical(
np.concatenate([np.full(len(host_fluxes), 0),
np.full(len(snia_fluxes), 1),
np.full(len(snib_fluxes), 2),
np.full(len(snic_fluxes), 3),
np.full(len(snii_fluxes), 4)
]))
x.shape, y.shape
# Dividiendo entre *entrenamiento* (train) y *validación* (test).
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.333)
```
### La red
Inicializaremos una red con un potencial limitado por tres capas convolucionales. Podría tener menos o más, según lo determinado por los pros y los contras anteriores. También vamos a optimizar la red en función de su _exactitud_, una métrica que maximiza el número de predicciones de la red que coinciden con la verdad. También podríamos entrenar en otras métricas como _precision_, que minimiza la cantidad de predicciones falsas; parece que debería ser lo mismo, pero [no](https://es.wikipedia.org/wiki/Precisi%C3%B3n_y_exhaustividad).
```
def network(input_shape, ncat, learning_rate=0.0005, reg=0.003, dropout=0.7, seed=None):
"""Definimos la estructura de la red convolucional.
Párametros
----------
input_shape : int
Forma del espectro de entrada.
ncat : int
Numero de categorias o clases.
learning_rate : float
Tasa de Aprendizaje.
reg : float
Factor de Regularización.
dropout : float
Factor de perdida.
seed : int
Semilla de inicialización
Retorno
-------
modelo : tensorflow.keras.Model
Una instancia modelo de la red.
"""
X_input = Input(input_shape, name='Input_Spec')
# Primera capa convolucional
with backend.name_scope('Conv_1'):
X = Conv1D(filters=8, kernel_size=5, strides=1, padding='same',
kernel_regularizer=regularizers.l2(reg),
bias_initializer='zeros',
kernel_initializer=glorot_normal(seed))(X_input)
X = BatchNormalization(axis=2)(X)
X = Activation('relu')(X)
X = MaxPooling1D(pool_size= 2)(X)
# Segunda capa convolucional
with backend.name_scope('Conv_2'):
X = Conv1D(filters=16, kernel_size=5, strides=1, padding='same',
kernel_regularizer=regularizers.l2(reg),
bias_initializer='zeros',
kernel_initializer=glorot_normal(seed))(X)
X = BatchNormalization(axis=2)(X)
X = Activation('relu')(X)
X = MaxPooling1D(2)(X)
# Tercera capa convolucional
with backend.name_scope('Conv_3'):
X = Conv1D(filters=32, kernel_size=5, strides=1, padding='same',
kernel_regularizer=regularizers.l2(reg),
bias_initializer='zeros',
kernel_initializer=glorot_normal(seed))(X)
X = BatchNormalization(axis=2)(X)
X = Activation('relu')(X)
X = MaxPooling1D(2)(X)
# Capa aplanada completamente conectada
with backend.name_scope('Dense_Layer'):
X = Flatten()(X)
X = Dense(256, kernel_regularizer=regularizers.l2(reg),
activation='relu')(X)
X = Dropout(rate=dropout, seed=seed)(X)
# Capa de salida con activación sigmoide
with backend.name_scope('Output_Layer'):
X = Dense(ncat, kernel_regularizer=regularizers.l2(reg),
activation='sigmoid',name='Output_Classes')(X)
model = Model(inputs=X_input, outputs=X, name='SNnet')
# Configura el optimizador, la función de pérdida y las métricas de optimización.
model.compile(optimizer=Adam(lr=learning_rate), loss='categorical_crossentropy',
metrics=['accuracy'])
return model
# Definiremos la red aquí.
# La forma de entrada tendrá nbins = 150 bins de longitud de onda.
# El número de categorías está definido por la forma de nuestro vector y.
# Deberíamos tener cinco categorías (hosts, SN Ia, Ib, Ic y IIP).
cnn_model = network((nbins, 1), ncat=y.shape[1])
cnn_model.summary()
```
Considere esto por un minuto. En total, hay 152,405 valores separados que se pueden entrenar en esta red. Eso es un poco menos de los ~10 mil millones en el suyo, ¡pero aún es mucho! Esto significa que existe un potencial considerable para que la red obtenga muy buenos espectros distintivos de candidatos a supernovas, pero que se necesitará mucho aprendizaje para obtener resultados sensibles.
### De pie sobre tus propios pies
Ahora, deja que suceda la magia. Dejaremos que la red aborde los desafíos y diseñe sus pesos, o neuronas, para maximizar la satisfacción o su capacidad para tener éxito.
```
history = cnn_model.fit(x_train, y_train, batch_size=50, epochs=125, validation_data=(x_test, y_test), shuffle=True)
```
### ¿Pro o no pro?
Cada vez que la red intenta aprender, el desafío se conoce como una "época". A medida que aprende, deberíamos preocuparnos por la pérdida: una medida de qué tan mal la red está identificando nuestros espectros, que queremos minimizar. Considerando que, la precisión mide qué tan bien lo hace la red para identificar las cinco clases diferentes simuladas, siendo esto lo que queremos maximizar.
```
fig, axes = plt.subplots(1,2, figsize=(12,5), sharex=True)
nepoch = len(history.history['loss'])
epochs = np.arange(1, nepoch+1)
ax = axes[0]
ax.plot(epochs, history.history['accuracy'], label='acc')
ax.plot(epochs, history.history['val_accuracy'], label='val_acc')
ax.set(xlabel='Training epoch',
ylabel='Accuracy',
xlim=(0, nepoch),
ylim=(0.,1.0)
)
ax.legend(fontsize=12, loc='best')
ax.grid(ls=':')
ax = axes[1]
ax.plot(epochs, history.history['loss'], label='loss')
ax.plot(epochs, history.history['val_loss'], label='val_loss')
ax.set(xlabel='Training epoch',
ylabel='Loss',
xlim=(0, nepoch),
# ylim=(0.,2.0)
)
ax.legend(fontsize=12, loc='best')
ax.grid(ls=':')
fig.tight_layout();
```
Podemos ver que la red aprendió inicialmente muy rápido, pero la mejora se ralentizó alrededor de 50 épocas más o menos. En este punto, la precisión alcanzada fue de alrededor del 70%, ¡así que no está mal!
### Matriz de confusión
En este tipo de clasificación, otra forma de medir el éxito es mediante la _matriz de confusión_,
```
# Vamos a utilizar la muestra de prueba para probar las predicciones de nuestra
# CNN entrenada ahora que ha "aprendido" a distinguir los diferentes tipos de
# supernovas. Esto no es ideal ... deberíamos tener una tercer
# muestra independiente de las muestras de entrenamiento y prueba.
y_pred = cnn_model.predict(x_test)
# En el clasificador de clases múltiples, evalue el máximo de
# coincidencias en la matriz de salida de valores.
cm = confusion_matrix(y_test.argmax(axis=1), y_pred.argmax(axis=1))
cmnorm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
fig, ax = plt.subplots(1,1, figsize=(8,7))
im = ax.imshow(cmnorm, cmap='Blues', vmin=0, vmax=1)
cb = ax.figure.colorbar(im, ax=ax, fraction=0.046, pad=0.04)
cb.set_label('Fracción Correcta')
labels = ['Hosts', 'SN Ia', 'SN Ib', 'SN Ic', 'SN IIP']
ax.set(aspect='equal',
xlabel='Clase Predicha',
xticks=np.arange(cm.shape[1]),
xticklabels=labels,
ylabel='Clase Verdadera',
yticks=np.arange(cm.shape[1]),
yticklabels=labels)
thresh = 0.5*cm.max()
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j, i, '{:.3f}\n({:d})'.format(cmnorm[i,j], cm[i,j]),
ha='center', va='center',
color='black' if cm[i,j] < thresh else 'white')
fig.tight_layout()
```
Si la CNN es perfecta para clasificar todas las categorías, entonces la entrada 'Etiqueta verdadera' y la salida de 'Etiqueta predicha' de la red coincidirían siempre. En este caso, solo los cuadrados diagonales aparecerían rellenos en la matriz; El resto estaría en blanco.
En nuestro caso, vemos que la CNN es realmente buena para clasificar el tipo Ia; promedio en la clasificación de tipo IIP; y mediocre en la clasificación de Ib y Ic supernvoae. Parece estar mezclando el tipo Ib y el Ic, y afirma incorrectamente que el 10% de las galaxias anfitrionas contienen en realidad una supernova de tipo Ib. ¡Ups!
Finalmente, es notable que hemos completado el círculo, por supuesto, como el silicio fundamental para los transitores en el que se realizará este cálculo una vez que se originó en las mismas supernovas que estamos buscando.
## ¿Puedes hacerlo mejor?
Una de las cosas fascinantes del aprendizaje automático es que se trata de un número ilimitado de cosas que se pueden modificar y que podrían mejorar el rendimiento. El arte es saber qué cosas pueden mejorar las cosas para un problema dado.
_Aumentar el tamaño del conjunto de entrenamiento_: podríamos creer que hemos proporcionado datos insuficientes para que la red aprenda. Tenemos más disponibles en el _conjunto de validación_ que podríamos agregar, pero ¿a qué costo? Si la red mejora, ¿es real o simplemente está sobreajustada? Sin embargo, puede intentar cambiar a una 'división 80-20'.
_Personalizar la tasa de aprendizaje y abandono_: la rapidez con la que la CNN reacciona a los nuevos datos está determinada por una _tasa de aprendizaje preestablecida_: hay un equilibrio que hay que mantener para resolver mejor los problemas nuevos, sin dejar de hacerlo bien en los viejos; Esto a menudo se conoce como "histéresis" dentro de la física, en analogía con efectos similares en el magnetismo. Puede intentar cambiar la tasa de aprendizaje en la $\tt{red}$ anterior.
_Cambio de la 'arquitectura'_: hemos limitado la red a tres capas, podríamos agregar más o menos. ¿Encuentra alguna diferencia significativa?
## Entonces, te gusta el aprendizaje automático ...
Bueno, ¡estás muy bien preparado para los probables éxitos y desafíos del próximo siglo! Existe una gran cantidad de material, pero lo siguiente es muy recomendable: [Neural Networks and Deep Learning](http://neuralnetworksanddeeplearning.com/), [3blue1brown: Neural Networks](https://youtu.be/aircAruvnKk) y [Aprendizaje profundo con Python](https://www.amazon.com/Deep-Learning-Python-Francois-Chollet/dp/1617294438).
Realmente el aprendizaje automático tiene el potencial de cambiar todo, como se ha demostrado asombrosamente [recientemente](https://www.nature.com/articles/d41586-020-03348-4).
| true |
code
| 0.672332 | null | null | null | null |
|
Filter pipelines
================
This example shows how to use the `pymia.filtering` package to set up image filter pipeline and apply it to an image.
The pipeline consists of a gradient anisotropic diffusion filter followed by a histogram matching. This pipeline will be applied to a T1-weighted MR image and a T2-weighted MR image will be used as a reference for the histogram matching.
<div class="alert alert-warning">
Tip
This example is available as Jupyter notebook at [./examples/filtering/basic.ipynb](https://github.com/rundherum/pymia/blob/master/examples/filtering/basic.ipynb) and Python script at [./examples/filtering/basic.py](https://github.com/rundherum/pymia/blob/master/examples/filtering/basic.py).
</div>
<div class="alert alert-info">
Note
To be able to run this example:
- Get the example data by executing [./examples/example-data/pull_example_data.py](https://github.com/rundherum/pymia/blob/master/examples/example-data/pull_example_data.py).
- Install matplotlib (`pip install matplotlib`).
</div>
Import the required modules.
```
import glob
import os
import matplotlib.pyplot as plt
import pymia.filtering.filter as flt
import pymia.filtering.preprocessing as prep
import SimpleITK as sitk
```
Define the path to the data.
```
data_dir = '../example-data'
```
Let us create a list with the two filters, a gradient anisotropic diffusion filter followed by a histogram matching.
```
filters = [
prep.GradientAnisotropicDiffusion(time_step=0.0625),
prep.HistogramMatcher()
]
histogram_matching_filter_idx = 1 # we need the index later to update the HistogramMatcher's parameters
```
Now, we can initialize the filter pipeline.
```
pipeline = flt.FilterPipeline(filters)
```
We can now loop over the subjects of the example data. We will both load the T1-weighted and T2-weighted MR images and execute the pipeline on the T1-weighted MR image. Note that for each subject, we update the parameters for the histogram matching filter to be the corresponding T2-weighted image.
```
# get subjects to evaluate
subject_dirs = [subject for subject in glob.glob(os.path.join(data_dir, '*')) if os.path.isdir(subject) and os.path.basename(subject).startswith('Subject')]
for subject_dir in subject_dirs:
subject_id = os.path.basename(subject_dir)
print(f'Filtering {subject_id}...')
# load the T1- and T2-weighted MR images
t1_image = sitk.ReadImage(os.path.join(subject_dir, f'{subject_id}_T1.mha'))
t2_image = sitk.ReadImage(os.path.join(subject_dir, f'{subject_id}_T2.mha'))
# set the T2-weighted MR image as reference for the histogram matching
pipeline.set_param(prep.HistogramMatcherParams(t2_image), histogram_matching_filter_idx)
# execute filtering pipeline on the T1-weighted image
filtered_t1_image = pipeline.execute(t1_image)
# plot filtering result
slice_no_for_plot = t1_image.GetSize()[2] // 2
fig, axs = plt.subplots(1, 2)
axs[0].imshow(sitk.GetArrayFromImage(t1_image[:, :, slice_no_for_plot]), cmap='gray')
axs[0].set_title('Original image')
axs[1].imshow(sitk.GetArrayFromImage(filtered_t1_image[:, :, slice_no_for_plot]), cmap='gray')
axs[1].set_title('Filtered image')
fig.suptitle(f'{subject_id}', fontsize=16)
plt.show()
```
Visually, we can clearly see the smoothing of the filtered image due to the anisotrophic filtering. Also, the image intensities are brighter due to the histogram matching.
| true |
code
| 0.692278 | null | null | null | null |
|
# Amazon SageMaker Multi-Model Endpoints using Scikit Learn
*이 노트북은 [Amazon SageMaker Multi-Model Endpoints using Scikit Learn (영문 원본)](https://github.com/awslabs/amazon-sagemaker-examples/blob/master/advanced_functionality/multi_model_sklearn_home_value/sklearn_multi_model_endpoint_home_value.ipynb) 의 한국어 번역입니다.*
고객들은 [Amazon SageMaker 멀티 모델 엔드포인트(multi-model endpoints)](https://docs.aws.amazon.com/sagemaker/latest/dg/multi-model-endpoints.html)를 사용하여 최대 수천 개의 모델을 완벽하게 호스팅하는 엔드포인트를 생성할 수 있습니다. 이러한 엔드포인트는 공통 추론 컨테이너(common inference container)에서 제공할 수 있는 많은 모델 중 하나를 온디맨드(on demand)로 호출할 수 있어야 하고 자주 호출되지 않는 모델이 약간의 추가 대기 시간(latency) 허용이 가능한 사례들에 적합합니다. 지속적으로 낮은 추론 대기 시간이 필요한 애플리케이션의 경우 기존의 엔드포인트가 여전히 최선의 선택입니다.
High level에서 Amazon SageMaker는 필요에 따라 멀티 모델 엔드포인트에 대한 모델 로딩 및 언로딩을 관리합니다. 특정 모델에 대한 호출 요청이 발생하면 Amazon SageMaker는 해당 모델에 할당된 인스턴스로 요청을 라우팅하고 S3에서 모델 아티팩트(model artifacts)를 해당 인스턴스로 다운로드한 다음 컨테이너의 메모리에 모델 로드를 시작합니다. 로딩이 완료되면 Amazon SageMaker는 요청된 호출을 수행하고 결과를 반환합니다. 모델이 선택된 인스턴스의 메모리에 이미 로드되어 있으면 다운로드 및 로딩 단계들을 건너 뛰고 즉시 호출이 수행됩니다.
멀티 모델 엔드포인트 작성 및 사용 방법을 보여주기 위해, 이 노트북은 단일 위치의 주택 가격을 예측하는 Scikit Learn 모델을 사용하는 예시를 제공합니다. 이 도메인은 멀티 모델 엔드포인트를 쉽게 실험하기 위한 간단한 예제입니다.
Amazon SageMaker 멀티 모델 엔드포인트 기능은 컨테이너를 가져 오는 프레임워크를 포함한 모든 머신 러닝 프레임워크 및 알고리즘에서 작동하도록 설계되었습니다.
### Contents
1. [Build and register a Scikit Learn container that can serve multiple models](#Build-and-register-a-Scikit-Learn-container-that-can-serve-multiple-models)
1. [Generate synthetic data for housing models](#Generate-synthetic-data-for-housing-models)
1. [Train multiple house value prediction models](#Train-multiple-house-value-prediction-models)
1. [Import models into hosting](#Import-models-into-hosting)
1. [Deploy model artifacts to be found by the endpoint](#Deploy-model-artifacts-to-be-found-by-the-endpoint)
1. [Create the Amazon SageMaker model entity](#Create-the-Amazon-SageMaker-model-entity)
1. [Create the multi-model endpoint](#Create-the-multi-model-endpoint)
1. [Exercise the multi-model endpoint](#Exercise-the-multi-model-endpoint)
1. [Dynamically deploy another model](#Dynamically-deploy-another-model)
1. [Invoke the newly deployed model](#Invoke-the-newly-deployed-model)
1. [Updating a model](#Updating-a-model)
1. [Clean up](#Clean-up)
## Build and register a Scikit Learn container that can serve multiple models
```
!pip install -qU awscli boto3 sagemaker
```
추론 컨테이너가 멀티 모델 엔드 포인트에서 여러 모델을 제공하려면 특정 모델의 로드(load), 나열(list), 가져오기(get), 언로드(unload) 및 호출(invoke)을 위한 [추가 API](https://docs.aws.amazon.com/sagemaker/latest/dg/build-multi-model-build-container.html)를 구현해야 합니다.
[SageMaker Scikit Learn 컨테이너 저장소의 'mme' branch](https://github.com/aws/sagemaker-scikit-learn-container/tree/mme)는 멀티 모델 엔드포인트에 필요한 추가 컨테이너 API를 구현하는 HTTP 프론트엔드를 제공하는 프레임워크인 [Multi Model Server](https://github.com/awslabs/multi-model-server)를 사용하도록 SageMaker의 Scikit Learn 프레임워크 컨테이너를 조정하는 방법에 대한 예제 구현입니다. 또한 사용자 정의 프레임워크 (본 예시에서는 Scikit Learn 프레임워크)를 사용하여 모델을 제공하기 위한 플러그 가능한 백엔드 핸들러(pluggable backend handler)를 제공합니다.
이 branch를 사용하여 모든 멀티 모델 엔드 포인트 컨테이너 요구 사항을 충족하는 Scikit Learn 컨테이너를 구축한 다음 해당 이미지를 Amazon Elastic Container Registry(ECR)에 업로드합니다. 이미지를 ECR에 업로드하면 새로운 ECR 저장소가 생성될 수 있으므로 이 노트북에는 일반 `SageMakerFullAccess` 권한 외에 권한이 필요합니다. 이러한 권한을 추가하는 가장 쉬운 방법은 관리형 정책 `AmazonEC2ContainerRegistryFullAccess`를 노트북 인스턴스를 시작하는 데 사용한 역할(role)에 추가하는 것입니다. 이 작업을 수행할 때 노트북 인스턴스를 다시 시작할 필요가 없으며 새 권한을 즉시 사용할 수 있습니다.
```
ALGORITHM_NAME = 'multi-model-sklearn'
%%sh -s $ALGORITHM_NAME
algorithm_name=$1
account=$(aws sts get-caller-identity --query Account --output text)
# Get the region defined in the current configuration (default to us-west-2 if none defined)
region=$(aws configure get region)
ecr_image="${account}.dkr.ecr.${region}.amazonaws.com/${algorithm_name}:latest"
# If the repository doesn't exist in ECR, create it.
aws ecr describe-repositories --repository-names "${algorithm_name}" > /dev/null 2>&1
if [ $? -ne 0 ]
then
aws ecr create-repository --repository-name "${algorithm_name}" > /dev/null
fi
# Get the login command from ECR and execute it directly
$(aws ecr get-login --region ${region} --no-include-email --registry-ids ${account})
# Build the docker image locally with the image name and then push it to ECR
# with the full image name.
# First clear out any prior version of the cloned repo
rm -rf sagemaker-scikit-learn-container/
# Clone the sklearn container repo
git clone --single-branch --branch mme https://github.com/aws/sagemaker-scikit-learn-container.git
cd sagemaker-scikit-learn-container/
# Build the "base" container image that encompasses the installation of the
# scikit-learn framework and all of the dependencies needed.
docker build -q -t sklearn-base:0.20-2-cpu-py3 -f docker/0.20-2/base/Dockerfile.cpu --build-arg py_version=3 .
# Create the SageMaker Scikit-learn Container Python package.
python setup.py bdist_wheel --universal
# Build the "final" container image that encompasses the installation of the
# code that implements the SageMaker multi-model container requirements.
docker build -q -t ${algorithm_name} -f docker/0.20-2/final/Dockerfile.cpu .
docker tag ${algorithm_name} ${ecr_image}
docker push ${ecr_image}
```
## Generate synthetic data for housing models
```
import numpy as np
import pandas as pd
import json
import datetime
import time
from time import gmtime, strftime
import matplotlib.pyplot as plt
NUM_HOUSES_PER_LOCATION = 1000
LOCATIONS = ['NewYork_NY', 'LosAngeles_CA', 'Chicago_IL', 'Houston_TX', 'Dallas_TX',
'Phoenix_AZ', 'Philadelphia_PA', 'SanAntonio_TX', 'SanDiego_CA', 'SanFrancisco_CA']
PARALLEL_TRAINING_JOBS = 4 # len(LOCATIONS) if your account limits can handle it
MAX_YEAR = 2019
def gen_price(house):
_base_price = int(house['SQUARE_FEET'] * 150)
_price = int(_base_price + (10000 * house['NUM_BEDROOMS']) + \
(15000 * house['NUM_BATHROOMS']) + \
(15000 * house['LOT_ACRES']) + \
(15000 * house['GARAGE_SPACES']) - \
(5000 * (MAX_YEAR - house['YEAR_BUILT'])))
return _price
def gen_random_house():
_house = {'SQUARE_FEET': int(np.random.normal(3000, 750)),
'NUM_BEDROOMS': np.random.randint(2, 7),
'NUM_BATHROOMS': np.random.randint(2, 7) / 2,
'LOT_ACRES': round(np.random.normal(1.0, 0.25), 2),
'GARAGE_SPACES': np.random.randint(0, 4),
'YEAR_BUILT': min(MAX_YEAR, int(np.random.normal(1995, 10)))}
_price = gen_price(_house)
return [_price, _house['YEAR_BUILT'], _house['SQUARE_FEET'],
_house['NUM_BEDROOMS'], _house['NUM_BATHROOMS'],
_house['LOT_ACRES'], _house['GARAGE_SPACES']]
COLUMNS = ['PRICE', 'YEAR_BUILT', 'SQUARE_FEET', 'NUM_BEDROOMS',
'NUM_BATHROOMS', 'LOT_ACRES', 'GARAGE_SPACES']
def gen_houses(num_houses):
_house_list = []
for i in range(num_houses):
_house_list.append(gen_random_house())
_df = pd.DataFrame(_house_list,
columns=COLUMNS)
return _df
```
## Train multiple house value prediction models
```
import sagemaker
from sagemaker import get_execution_role
from sagemaker.predictor import csv_serializer
import boto3
sm_client = boto3.client(service_name='sagemaker')
runtime_sm_client = boto3.client(service_name='sagemaker-runtime')
s3 = boto3.resource('s3')
s3_client = boto3.client('s3')
sagemaker_session = sagemaker.Session()
role = get_execution_role()
ACCOUNT_ID = boto3.client('sts').get_caller_identity()['Account']
REGION = boto3.Session().region_name
BUCKET = sagemaker_session.default_bucket()
SCRIPT_FILENAME = 'script.py'
USER_CODE_ARTIFACTS = 'user_code.tar.gz'
MULTI_MODEL_SKLEARN_IMAGE = '{}.dkr.ecr.{}.amazonaws.com/{}:latest'.format(ACCOUNT_ID, REGION,
ALGORITHM_NAME)
DATA_PREFIX = 'DEMO_MME_SCIKIT'
HOUSING_MODEL_NAME = 'housing'
MULTI_MODEL_ARTIFACTS = 'multi_model_artifacts'
TRAIN_INSTANCE_TYPE = 'ml.m4.xlarge'
ENDPOINT_INSTANCE_TYPE = 'ml.m4.xlarge'
```
### Split a given dataset into train, validation, and test
```
from sklearn.model_selection import train_test_split
SEED = 7
SPLIT_RATIOS = [0.6, 0.3, 0.1]
def split_data(df):
# split data into train and test sets
seed = SEED
val_size = SPLIT_RATIOS[1]
test_size = SPLIT_RATIOS[2]
num_samples = df.shape[0]
X1 = df.values[:num_samples, 1:] # keep only the features, skip the target, all rows
Y1 = df.values[:num_samples, :1] # keep only the target, all rows
# Use split ratios to divide up into train/val/test
X_train, X_val, y_train, y_val = \
train_test_split(X1, Y1, test_size=(test_size + val_size), random_state=seed)
# Of the remaining non-training samples, give proper ratio to validation and to test
X_test, X_test, y_test, y_test = \
train_test_split(X_val, y_val, test_size=(test_size / (test_size + val_size)),
random_state=seed)
# reassemble the datasets with target in first column and features after that
_train = np.concatenate([y_train, X_train], axis=1)
_val = np.concatenate([y_val, X_val], axis=1)
_test = np.concatenate([y_test, X_test], axis=1)
return _train, _val, _test
```
### Launch a single training job for a given housing location
모델 학습 시, 기존 SageMaker 모델과 동일한 방식으로 학습하기 때문에 멀티 모델 엔트 포인트에 특화된 기능을 따로 구현하실 필요가 없습니다.
```
%%writefile $SCRIPT_FILENAME
import argparse
import os
import glob
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.externals import joblib
# inference functions ---------------
def model_fn(model_dir):
print('loading model.joblib from: {}'.format(model_dir))
_loaded_model = joblib.load(os.path.join(model_dir, 'model.joblib'))
return _loaded_model
if __name__ =='__main__':
print('extracting arguments')
parser = argparse.ArgumentParser()
# hyperparameters sent by the client are passed as command-line arguments to the script.
# to simplify the demo we don't use all sklearn RandomForest hyperparameters
parser.add_argument('--n-estimators', type=int, default=10)
parser.add_argument('--min-samples-leaf', type=int, default=3)
# Data, model, and output directories
parser.add_argument('--model-dir', type=str, default=os.environ.get('SM_MODEL_DIR'))
parser.add_argument('--train', type=str, default=os.environ.get('SM_CHANNEL_TRAIN'))
parser.add_argument('--validation', type=str, default=os.environ.get('SM_CHANNEL_VALIDATION'))
parser.add_argument('--model-name', type=str)
args, _ = parser.parse_known_args()
print('reading data')
print('model_name: {}'.format(args.model_name))
train_file = os.path.join(args.train, args.model_name + '_train.csv')
train_df = pd.read_csv(train_file)
val_file = os.path.join(args.validation, args.model_name + '_val.csv')
test_df = pd.read_csv(os.path.join(val_file))
print('building training and testing datasets')
X_train = train_df[train_df.columns[1:train_df.shape[1]]]
X_test = test_df[test_df.columns[1:test_df.shape[1]]]
y_train = train_df[train_df.columns[0]]
y_test = test_df[test_df.columns[0]]
# train
print('training model')
model = RandomForestRegressor(
n_estimators=args.n_estimators,
min_samples_leaf=args.min_samples_leaf,
n_jobs=-1)
model.fit(X_train, y_train)
# print abs error
print('validating model')
abs_err = np.abs(model.predict(X_test) - y_test)
# print couple perf metrics
for q in [10, 50, 90]:
print('AE-at-' + str(q) + 'th-percentile: '
+ str(np.percentile(a=abs_err, q=q)))
# persist model
path = os.path.join(args.model_dir, 'model.joblib')
joblib.dump(model, path)
print('model persisted at ' + path)
# can test the model locally
# ! python script.py --n-estimators 100 \
# --min-samples-leaf 2 \
# --model-dir ./ \
# --model-name 'NewYork_NY' \
# --train ./data/NewYork_NY/train/ \
# --validation ./data/NewYork_NY/val/
# from sklearn.externals import joblib
# regr = joblib.load('./model.joblib')
# _start_time = time.time()
# regr.predict([[0.0, 0.0, 0.0, 0.0, 0.0, 0.0]])
# _duration = time.time() - _start_time
# print('took {:,d} ms'.format(int(_duration * 1000)))
from sagemaker.sklearn.estimator import SKLearn
def launch_training_job(location):
# clear out old versions of the data
_s3_bucket = s3.Bucket(BUCKET)
_full_input_prefix = '{}/model_prep/{}'.format(DATA_PREFIX, location)
_s3_bucket.objects.filter(Prefix=_full_input_prefix + '/').delete()
# upload the entire set of data for all three channels
_local_folder = 'data/{}'.format(location)
_inputs = sagemaker_session.upload_data(path=_local_folder,
key_prefix=_full_input_prefix)
print('Training data uploaded: {}'.format(_inputs))
_job = 'mme-{}'.format(location.replace('_', '-'))
_full_output_prefix = '{}/model_artifacts/{}'.format(DATA_PREFIX,
location)
_s3_output_path = 's3://{}/{}'.format(BUCKET, _full_output_prefix)
_estimator = SKLearn(
entry_point=SCRIPT_FILENAME, role=role,
train_instance_count=1, train_instance_type=TRAIN_INSTANCE_TYPE,
framework_version='0.20.0',
output_path=_s3_output_path,
base_job_name=_job,
metric_definitions=[
{'Name' : 'median-AE',
'Regex': 'AE-at-50th-percentile: ([0-9.]+).*$'}],
hyperparameters = {'n-estimators' : 100,
'min-samples-leaf': 3,
'model-name' : location})
DISTRIBUTION_MODE = 'FullyReplicated'
_train_input = sagemaker.s3_input(s3_data=_inputs+'/train',
distribution=DISTRIBUTION_MODE, content_type='csv')
_val_input = sagemaker.s3_input(s3_data=_inputs+'/val',
distribution=DISTRIBUTION_MODE, content_type='csv')
_remote_inputs = {'train': _train_input, 'validation': _val_input}
_estimator.fit(_remote_inputs, wait=False)
return _estimator.latest_training_job.name
```
### Kick off a model training job for each housing location
```
def save_data_locally(location, train, val, test):
_header = ','.join(COLUMNS)
os.makedirs('data/{}/train'.format(location))
np.savetxt( 'data/{0}/train/{0}_train.csv'.format(location), train, delimiter=',', fmt='%.2f')
os.makedirs('data/{}/val'.format(location))
np.savetxt( 'data/{0}/val/{0}_val.csv'.format(location), val, delimiter=',', fmt='%.2f')
os.makedirs('data/{}/test'.format(location))
np.savetxt( 'data/{0}/test/{0}_test.csv'.format(location), test, delimiter=',', fmt='%.2f')
import shutil
import os
training_jobs = []
shutil.rmtree('data', ignore_errors=True)
for loc in LOCATIONS[:PARALLEL_TRAINING_JOBS]:
_houses = gen_houses(NUM_HOUSES_PER_LOCATION)
_train, _val, _test = split_data(_houses)
save_data_locally(loc, _train, _val, _test)
_job = launch_training_job(loc)
training_jobs.append(_job)
print('{} training jobs launched: {}'.format(len(training_jobs), training_jobs))
```
### Wait for all model training to finish
```
def wait_for_training_job_to_complete(job_name):
print('Waiting for job {} to complete...'.format(job_name))
_resp = sm_client.describe_training_job(TrainingJobName=job_name)
_status = _resp['TrainingJobStatus']
while _status=='InProgress':
time.sleep(60)
_resp = sm_client.describe_training_job(TrainingJobName=job_name)
_status = _resp['TrainingJobStatus']
if _status == 'InProgress':
print('{} job status: {}'.format(job_name, _status))
print('DONE. Status for {} is {}\n'.format(job_name, _status))
# wait for the jobs to finish
for j in training_jobs:
wait_for_training_job_to_complete(j)
```
## Import models into hosting
멀티 모델 엔드포인트의 가장 큰 차이점은 모델 엔티티(Model entity)를 작성할 때 컨테이너의 `MultiModel`은 엔드포인트에서 호출할 수 있는 모델 아티팩트가 있는 S3 접두부(prefix)입니다. 나머지 S3 경로는 실제로 모델을 호출할 때 지정됩니다. 슬래시로 위치를 닫아야 하는 점을 기억해 주세요.
컨테이너의 `Mode`는 컨테이너가 여러 모델을 호스팅함을 나타내기 위해 `MultiModel`로 지정됩니다.
### Deploy model artifacts to be found by the endpoint
상술한 바와 같이, 멀티 모델 엔드 포인트는 S3의 특정 위치에서 모델 아티팩트를 찾도록 구성됩니다. 학습된 각 모델에 대해 모델 아티팩트를 해당 위치에 복사합니다.
이 예에서는 모든 모델들을 단일 폴더에 저장합니다. 멀티 모델 엔드 포인트의 구현은 임의의 폴더 구조를 허용할 만큼 유연합니다. 예를 들어 일련의 하우징 모델의 경우 각 지역마다 최상위 폴더가 있을 수 있으며 모델 아티팩트는 해당 지역 폴더로 복사됩니다. 이러한 모델을 호출할 때 참조되는 대상 모델에는 폴더 경로가 포함됩니다. 예를 들어 `northeast/Boston_MA.tar.gz`입니다.
```
import re
def parse_model_artifacts(model_data_url):
# extract the s3 key from the full url to the model artifacts
_s3_key = model_data_url.split('s3://{}/'.format(BUCKET))[1]
# get the part of the key that identifies the model within the model artifacts folder
_model_name_plus = _s3_key[_s3_key.find('model_artifacts') + len('model_artifacts') + 1:]
# finally, get the unique model name (e.g., "NewYork_NY")
_model_name = re.findall('^(.*?)/', _model_name_plus)[0]
return _s3_key, _model_name
# make a copy of the model artifacts from the original output of the training job to the place in
# s3 where the multi model endpoint will dynamically load individual models
def deploy_artifacts_to_mme(job_name):
_resp = sm_client.describe_training_job(TrainingJobName=job_name)
_source_s3_key, _model_name = parse_model_artifacts(_resp['ModelArtifacts']['S3ModelArtifacts'])
_copy_source = {'Bucket': BUCKET, 'Key': _source_s3_key}
_key = '{}/{}/{}.tar.gz'.format(DATA_PREFIX, MULTI_MODEL_ARTIFACTS, _model_name)
print('Copying {} model\n from: {}\n to: {}...'.format(_model_name, _source_s3_key, _key))
s3_client.copy_object(Bucket=BUCKET, CopySource=_copy_source, Key=_key)
return _key
```
*의도적으로 첫 번째 모델을 복사하지 않는다는 점을 유의해 주세요.*. 첫 번째 모델은 향후 실습 과정에서 복사하여 이미 실행 중인 엔드포인트에 새 모델을 동적으로 추가하는 방법을 보여주기 위함입니다.
```
# First, clear out old versions of the model artifacts from previous runs of this notebook
s3 = boto3.resource('s3')
s3_bucket = s3.Bucket(BUCKET)
full_input_prefix = '{}/multi_model_artifacts'.format(DATA_PREFIX)
print('Removing old model artifacts from {}'.format(full_input_prefix))
filter_resp = s3_bucket.objects.filter(Prefix=full_input_prefix + '/').delete()
# copy every model except the first one
for job in training_jobs[1:]:
deploy_artifacts_to_mme(job)
```
### Create the Amazon SageMaker model entity
`boto3`을 사용하여 모델 엔터티를 만듭니다. 단일 모델을 설명하는 대신 멀티 모델 시맨틱(semantics)의 사용을 나타내며 모든 특정 모델 아티팩트의 소스 위치를 식별합니다.
```
# When using multi-model endpoints with the Scikit Learn container, we need to provide an entry point for
# inference that will at least load the saved model. This function uploads a model artifact containing such a
# script. This tar.gz file will be fed to the SageMaker multi-model creation and pointed to by the
# SAGEMAKER_SUBMIT_DIRECTORY environment variable.
def upload_inference_code(script_file_name, prefix):
_tmp_folder = 'inference-code'
if not os.path.exists(_tmp_folder):
os.makedirs(_tmp_folder)
!tar -czvf $_tmp_folder/$USER_CODE_ARTIFACTS $script_file_name > /dev/null
_loc = sagemaker_session.upload_data(_tmp_folder,
key_prefix='{}/{}'.format(prefix, _tmp_folder))
return _loc + '/' + USER_CODE_ARTIFACTS
def create_multi_model_entity(multi_model_name, role):
# establish the place in S3 from which the endpoint will pull individual models
_model_url = 's3://{}/{}/{}/'.format(BUCKET, DATA_PREFIX, MULTI_MODEL_ARTIFACTS)
_container = {
'Image': MULTI_MODEL_SKLEARN_IMAGE,
'ModelDataUrl': _model_url,
'Mode': 'MultiModel',
'Environment': {
'SAGEMAKER_PROGRAM' : SCRIPT_FILENAME,
'SAGEMAKER_SUBMIT_DIRECTORY' : upload_inference_code(SCRIPT_FILENAME, DATA_PREFIX)
}
}
create_model_response = sm_client.create_model(
ModelName = multi_model_name,
ExecutionRoleArn = role,
Containers = [_container])
return _model_url
multi_model_name = '{}-{}'.format(HOUSING_MODEL_NAME, strftime('%Y-%m-%d-%H-%M-%S', gmtime()))
model_url = create_multi_model_entity(multi_model_name, role)
print('Multi model name: {}'.format(multi_model_name))
print('Here are the models that the endpoint has at its disposal:')
!aws s3 ls --human-readable --summarize $model_url
```
### Create the multi-model endpoint
멀티 모델 엔드포인트에 대한 SageMaker 엔드포인트 설정(config)에는 특별한 것이 없습니다. 예상 예측 워크로드에 적합한 인스턴스 유형과 인스턴스 수를 고려해야 합니다. 개별 모델의 수와 크기에 따라 메모리 요구 사항이 변동합니다.
엔드포인트 설정이 완료되면 엔드포인트 생성(creation)은 간단합니다.
```
endpoint_config_name = multi_model_name
print('Endpoint config name: ' + endpoint_config_name)
create_endpoint_config_response = sm_client.create_endpoint_config(
EndpointConfigName = endpoint_config_name,
ProductionVariants=[{
'InstanceType': ENDPOINT_INSTANCE_TYPE,
'InitialInstanceCount': 1,
'InitialVariantWeight': 1,
'ModelName' : multi_model_name,
'VariantName' : 'AllTraffic'}])
endpoint_name = multi_model_name
print('Endpoint name: ' + endpoint_name)
create_endpoint_response = sm_client.create_endpoint(
EndpointName=endpoint_name,
EndpointConfigName=endpoint_config_name)
print('Endpoint Arn: ' + create_endpoint_response['EndpointArn'])
print('Waiting for {} endpoint to be in service...'.format(endpoint_name))
waiter = sm_client.get_waiter('endpoint_in_service')
waiter.wait(EndpointName=endpoint_name)
```
## Exercise the multi-model endpoint
### Invoke multiple individual models hosted behind a single endpoint
여기서 여러분은 특정 위치 기반 주택 모델을 무작위로 선택하는 것을 반복합니다. 주어진 모델의 첫번째 호출에 대해 지불된 콜드 스타트(cold start) 비용이 과금된다는 점을 알아 두세요. 동일한 모델의 후속 호출은 이미 메모리에 로드된 모델을 활용합니다.
```
def predict_one_house_value(features, model_name):
print('Using model {} to predict price of this house: {}'.format(full_model_name,
features))
_float_features = [float(i) for i in features]
_body = ','.join(map(str, _float_features)) + '\n'
_start_time = time.time()
_response = runtime_sm_client.invoke_endpoint(
EndpointName=endpoint_name,
ContentType='text/csv',
TargetModel=full_model_name,
Body=_body)
_predicted_value = json.loads(_response['Body'].read())[0]
_duration = time.time() - _start_time
print('${:,.2f}, took {:,d} ms\n'.format(_predicted_value, int(_duration * 1000)))
# iterate through invocations with random inputs against a random model showing results and latency
for i in range(10):
model_name = LOCATIONS[np.random.randint(1, len(LOCATIONS[:PARALLEL_TRAINING_JOBS]))]
full_model_name = '{}.tar.gz'.format(model_name)
predict_one_house_value(gen_random_house()[1:], full_model_name)
```
### Dynamically deploy another model
여기서 신규 모델의 동적 로딩의 힘을 볼 수 있습니다. 이전에 모델을 배포할 때 의도적으로 첫 번째 모델을 복사하지 않았습니다. 이제 추가 모델을 배포하고 다중 모델 엔드 포인트를 통해 즉시 모델을 호출할 수 있습니다. 이전 모델과 마찬가지로 엔드포인트가 모델을 다운로드하고 메모리에 로드하는 데 시간이 걸리므로 새 모델을 처음 호출하는 데 시간이 약간 더 걸린다는 점을 명심해 주세요.
```
# add another model to the endpoint and exercise it
deploy_artifacts_to_mme(training_jobs[0])
```
### Invoke the newly deployed model
엔드포인트 업데이트 또는 재시작 없이 새로 배포된 모델들로 호출을 수행해 보세요.
```
print('Here are the models that the endpoint has at its disposal:')
!aws s3 ls $model_url
model_name = LOCATIONS[0]
full_model_name = '{}.tar.gz'.format(model_name)
for i in range(5):
features = gen_random_house()
predict_one_house_value(gen_random_house()[1:], full_model_name)
```
### Updating a model
모델을 업데이트하려면 위와 동일한 방법으로 새 모델로 추가하세요. 예를 들어,`NewYork_NY.tar.gz` 모델을 재학습하고 호출을 시작하려는 경우 업데이트된 모델 아티팩트를 S3 접두어(prefix) 뒤에 `NewYork_NY_v2.tar.gz`와 같은 새로운 이름으로 업로드한 다음 `NewYork_NY.tar.gz` 대신`NewYork_NY_v2.tar.gz`를 호출하도록 `TargetModel` 필드를 변경하세요. 모델의 이전 버전이 여전히 컨테이너 또는 엔드포인트 인스턴스의 스토리지 볼륨에 로드될 수 있으므로 Amazon S3에서 모델 아티팩트를 덮어 쓰지 않으려고 합니다. 그러면 새 모델 호출 시 이전 버전의 모델을 호출할 수 있습니다.
또는, 엔드포인트를 중지하고 새로운 모델 셋을 재배포할 수 있습니다.
## Clean up
더 이상 사용하지 않는 엔드포인트에 대한 요금이 청구되지 않도록 리소스를 정리합니다.
```
# shut down the endpoint
sm_client.delete_endpoint(EndpointName=endpoint_name)
# and the endpoint config
sm_client.delete_endpoint_config(EndpointConfigName=endpoint_config_name)
# delete model too
sm_client.delete_model(ModelName=multi_model_name)
```
| true |
code
| 0.447219 | null | null | null | null |
|
# Análise Financeira com Python
### Objetivo:
Vamos dividir essa mentoria em 2 etapas:
Etapa 1 - Usar o Python para puxar dados da Web de cotação de qualquer ação e analisar o resultado de uma carteira
Etapa 2 - Puxar indicadores de empresas diferentes e fazer a comparação entre elas para escolhar "qual a melhor empresa"
### Disclamer Importante
Não sou analista, influencer, agente autônomo, sábio ou nada de finanças ou ações. Temos 1 objetivo aqui e apenas 1: aprender como usar o Python para fazer o que a gente quiser.
Então não se preocupe com "erros teóricos" ou ainda com o resultado de qualquer tipo de análise. O nosso objetivo aqui é treinar Python
### Parte 1 - Carteira de Investimentos
- Vamos pegar uma carteira teórica completa e calcular o rendimento dela ao longo de 2020 e comparar com os principais indicadores (CDI, IBOV, IPCA). No caso vamos usar o IBOV, mas o procedimento para os outros indicadores é semelhante
- Carteira: R$100.000, divididos da seguinte maneira em 01/01/2020:
- 30% Ações Brasileiras - Arquivo Carteira
- 10% SMAL11 - Arquivo Carteira
- 10% FII - Arquivo Carteira
- 50% Tesouro Selic
```
#importando as bibliotecas
import pandas as pd
import matplotlib.pyplot as plt
#importando a carteira
carteira = pd.read_excel('CarteiraMentoria.xlsx')
display(carteira)
# código do matplotlib que faz os dois gráficos ficarem um do lado do outro
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
#vamos ver a distribuição da carteira por ativos
# .plot.pie -> mostra um gráfico de pizza
# ax=ax1 -> mostra que esse gráfico é o ax1 para o matplotlib
# ax=ax2 -> mostra que esse gráfico é o ax2 para o matplotlib
# labels -> são os rótulos
# y -> são os valores que vão ser mostrados
# legend=False -> ele mostraria uma legenda para o gráfico, mas não precisa nesse caso
# title -> título
# figsize -> mexe no tamanho do gráfico com largura e altura
# autopct -> adiciona o percentual
grafico1 = carteira.plot.pie(ax=ax1, labels=carteira['Ativos'], y='Valor Investido', legend=False, title='Distribuição de Ativos da Carteira', figsize=(15, 5), autopct="%.1f%%")
# .set_ylabel('') -> tira a legenda do eixo y
grafico1.set_ylabel('')
# vai pegar as linhas da coluna 'Tipo' e vai somar
grafico2 = carteira.groupby('Tipo').sum().plot.pie(ax=ax2, y='Valor Investido', legend=False, title='Distribuição de Classe de Ativos da Carteira', figsize=(15, 5), autopct="%.1f%%")
grafico2.set_ylabel('')
```
#### Pegando as Cotações ao Longo de 2020
- IBOV
```
# permite pegar cotações do yahoo finances
import pandas_datareader.data as web
# web.DataReader -> comando para pegar as cotações
# ticker -> exemplo: ^BVSP
# local de onde pega as informações -> exemplo: yahoo
# início -> start
# fim -> end
ibov_df = web.DataReader('^BVSP', data_source='yahoo', start='2020-01-01', end='2020-12-10')
display(ibov_df)
#print(ibov_df.info())
# mostrando o gráfico
ibov_df['Adj Close'].plot(figsize=(15, 5))
```
- Da nossa carteira
```
carteira_df = pd.DataFrame()
# para cada ativo da tabela 'Ativos' vai pegar os valores que não tem 'Tesouro' no ativo
# criou um dataframe chamado carteira_df, vai adicionar cada ativo nessa carteira
for ativo in carteira['Ativos']:
if 'Tesouro' not in ativo:
carteira_df[ativo] = web.DataReader('{}.SA'.format(ativo), data_source='yahoo', start='2020-01-01', end='2020-12-10')['Adj Close']
# para consertar o problema abaixo usou o método ffill que preenche o valor vazio com o valor anterior
carteira_df = carteira_df.ffill()
# analisou para ver se tem valores faltando no non-null (os valores não estão iguais)
print(carteira_df.info())
# mostrando a tabela
display(carteira_df)
```
- Do Tesouro Selic:
```
# podemos ler um arquivo csv da internet
link = 'https://www.tesourotransparente.gov.br/ckan/dataset/df56aa42-484a-4a59-8184-7676580c81e3/resource/796d2059-14e9-44e3-80c9-2d9e30b405c1/download/PrecoTaxaTesouroDireto.csv'
# passando o link e tratando a tabela
# decimal -> troca as vírgulas pelo ponto nos números
tesouro_df = pd.read_csv(link, sep=';', decimal=',')
# transformando a coluna em datetime
tesouro_df['Data Base'] = pd.to_datetime(tesouro_df['Data Base'], format='%d/%m/%Y')
# pegando a linha a coluna 'Tipo Titulo' for igual a 'Tesouro Selic' e todas as colunas
tesouro_df = tesouro_df.loc[tesouro_df['Tipo Titulo']=='Tesouro Selic', :]
# mostrando a tabela
display(tesouro_df)
```
- Juntar o tesouro selic na nossa carteira
```
# renomeando a coluna 'Data Base' para 'Date' porque essa coluna precisa ter o nome igual da coluna do ibov_df
tesouro_df = tesouro_df.rename(columns={'Data Base': 'Date'})
# juntando as colunas 'Data' e 'Pu Base Manha' do tesouro_df com a carteira_df
# on -> passa a coluna que é igual nas duas tabelas
# how -> diz que a tabela da carteira vai ficar na esquerda
carteira_df = carteira_df.merge(tesouro_df[['Date', 'PU Base Manha']], on='Date', how='left')
# mostrando a tabela
display(carteira_df)
# renomeando o nome da coluna
carteira_df = carteira_df.rename(columns={'PU Base Manha': 'Tesouro Selic'})
# ffill vai preencher o valor vazio com o valor anterior
carteira_df = carteira_df.ffill()
# mostrando a tabela
display(carteira_df)
```
- Calcular o valor investido
```
valor_investido = carteira_df.copy()
for ativo in carteira['Ativos']:
# vai multiplicar o preço investido pela quantidade
valor_investido[ativo] = valor_investido[ativo] * carteira.loc[carteira['Ativos']==ativo, 'Qtde'].values[0]
# transformando a coluna 'Date' em índice porque não queremos somar ela
valor_investido = valor_investido.set_index('Date')
# criando uma coluna 'Total' e somando as linhas (axis=1)
valor_investido['Total'] = valor_investido.sum(axis=1)
# mostrando a tabela
display(valor_investido)
# é necessário normalizar os dados para começarem do mesmo ponto no gráfico
# o valor investido normalizado é o valor investido / primeira linha valor investido
valor_investido_norm = valor_investido / valor_investido.iloc[0]
# o ibov normalizado é o ibov / primeira linha do ibov
ibov_df_norm = ibov_df / ibov_df.iloc[0]
# mostrando os gráficos
valor_investido_norm['Total'].plot(figsize=(15, 5), label='Carteira')
ibov_df_norm['Adj Close'].plot(label='IBOV')
# mostrando a legenda
plt.legend()
# rentabilidade é o último valor investido normalizado divido pelo primeiro valor investido normalizado -1
rentabilidade_carteira = valor_investido_norm['Total'].iloc[-1] - 1
rentabilidade_ibov = ibov_df_norm['Adj Close'].iloc[-1] - 1
print('Rentabilidade da Carteira {:.1%}'.format(rentabilidade_carteira))
print('Rentabilidade do Ibovespa {:.1%}'.format(rentabilidade_ibov))
```
### Parte 2 - Comparativo entre Ativos
Créditos: https://simply-python.com/2019/01/16/retrieving-stock-statistics-from-yahoo-finance-using-python/
```
tgt_website = r'https://sg.finance.yahoo.com/quote/PETR4.SA/key-statistics?p=PETR4.SA'
def get_key_stats(tgt_website, ticker):
# lendo todas as tabelas desse página html
df_list = pd.read_html(tgt_website)
result_df = df_list[0]
# para cada tabela adiciona uma tabela na outra
for df in df_list[1:]:
result_df = result_df.append(df)
# o nome da coluna 1 é renomeado para 'ticker'
result_df = result_df.rename(columns={1: ticker})
# vai transpor a tabela com o 'T' (vai deixar a tabela mais organizada)
return result_df.set_index(0).T
df_petr4 = get_key_stats(tgt_website, 'PETR4')
display(df_petr4)
```
- Comparando as ações de:
1. Magazine Luiza (MGLU3)
2. Lojas Americanas (LAME4)
3. Via Varejo (VVAR3)
```
acoes = ['MGLU3', 'LAME4', 'VVAR3']
# criando um dataframe
estatiscas_empresas = pd.DataFrame()
# para cada ação na lista de ações vai passar um link onde vai ter o nome de cada ação no link
for acao in acoes:
link = f'https://sg.finance.yahoo.com/quote/{acao}.SA/key-statistics?p={acao}.SA'
# vai pegar as key stats
df = get_key_stats(link, acao)
estatiscas_empresas = estatiscas_empresas.append(df)
display(estatiscas_empresas)
print(list(estatiscas_empresas.columns))
```
#### Price/sales (ttm)
```
import seaborn as sns
# mostra um gráfico de barras
# é necessário passar o valor de 'x' e o valor de 'y'
sns.barplot(x=estatiscas_empresas.index, y=estatiscas_empresas['Price/sales (ttm)'])
```
#### Enterprise value / EBITDA
```
sns.barplot(x=estatiscas_empresas.index, y=estatiscas_empresas['Enterprise value/EBITDA 6'])
```
| true |
code
| 0.375535 | null | null | null | null |
|
# Training HOG-based AU detectors
*written by Tiankang Xie*
In the tutorial we will demonstrate how to train the HOG-based AU models as described in our paper.
The tutorial is split into 3 parts, where the first part demonstrates how to extract hog features from the dataset,
and the second part demonstrates how to use the extracted hogs to perform statistical learning, the third part will be
to demonstrate how to test the trained models with additional test data
## Part 1: Extracting HOGs and Landmarks
```
from PIL import Image, ImageOps
import math
from scipy.spatial import ConvexHull
from skimage.morphology.convex_hull import grid_points_in_poly
from feat import Detector
from feat.tests.utils import get_test_data_path
import os
import matplotlib.pyplot as plt
## EXTRACT HOGS
from skimage import data, exposure
from skimage.feature import hog
from tqdm import tqdm
import cv2
import pandas as pd
import csv
import numpy as np
def align_face_68pts(img, img_land, box_enlarge, img_size=112):
"""
Adapted from https://github.com/ZhiwenShao/PyTorch-JAANet by Zhiwen Shao, modified by Tiankang Xie
img: image
img_land: landmarks 68
box_enlarge: relative size of face
img_size = 112
"""
leftEye0 = (img_land[2 * 36] + img_land[2 * 37] + img_land[2 * 38] + img_land[2 * 39] + img_land[2 * 40] +
img_land[2 * 41]) / 6.0
leftEye1 = (img_land[2 * 36 + 1] + img_land[2 * 37 + 1] + img_land[2 * 38 + 1] + img_land[2 * 39 + 1] +
img_land[2 * 40 + 1] + img_land[2 * 41 + 1]) / 6.0
rightEye0 = (img_land[2 * 42] + img_land[2 * 43] + img_land[2 * 44] + img_land[2 * 45] + img_land[2 * 46] +
img_land[2 * 47]) / 6.0
rightEye1 = (img_land[2 * 42 + 1] + img_land[2 * 43 + 1] + img_land[2 * 44 + 1] + img_land[2 * 45 + 1] +
img_land[2 * 46 + 1] + img_land[2 * 47 + 1]) / 6.0
deltaX = (rightEye0 - leftEye0)
deltaY = (rightEye1 - leftEye1)
l = math.sqrt(deltaX * deltaX + deltaY * deltaY)
sinVal = deltaY / l
cosVal = deltaX / l
mat1 = np.mat([[cosVal, sinVal, 0], [-sinVal, cosVal, 0], [0, 0, 1]])
mat2 = np.mat([[leftEye0, leftEye1, 1], [rightEye0, rightEye1, 1], [img_land[2 * 30], img_land[2 * 30 + 1], 1],
[img_land[2 * 48], img_land[2 * 48 + 1], 1], [img_land[2 * 54], img_land[2 * 54 + 1], 1]])
mat2 = (mat1 * mat2.T).T
cx = float((max(mat2[:, 0]) + min(mat2[:, 0]))) * 0.5
cy = float((max(mat2[:, 1]) + min(mat2[:, 1]))) * 0.5
if (float(max(mat2[:, 0]) - min(mat2[:, 0])) > float(max(mat2[:, 1]) - min(mat2[:, 1]))):
halfSize = 0.5 * box_enlarge * float((max(mat2[:, 0]) - min(mat2[:, 0])))
else:
halfSize = 0.5 * box_enlarge * float((max(mat2[:, 1]) - min(mat2[:, 1])))
scale = (img_size - 1) / 2.0 / halfSize
mat3 = np.mat([[scale, 0, scale * (halfSize - cx)], [0, scale, scale * (halfSize - cy)], [0, 0, 1]])
mat = mat3 * mat1
aligned_img = cv2.warpAffine(img, mat[0:2, :], (img_size, img_size), cv2.INTER_LINEAR, borderValue=(128, 128, 128))
land_3d = np.ones((int(len(img_land)/2), 3))
land_3d[:, 0:2] = np.reshape(np.array(img_land), (int(len(img_land)/2), 2))
mat_land_3d = np.mat(land_3d)
new_land = np.array((mat * mat_land_3d.T).T)
new_land = np.array(list(zip(new_land[:,0], new_land[:,1]))).astype(int)
return aligned_img, new_land
def extract_hog(image, detector):
im = cv2.imread(image)
detected_faces = np.array(detector.detect_faces(im)[0])
im = np.asarray(im)
detected_faces = np.array(detector.detect_faces(np.array(im))[0])
detected_faces = detected_faces.astype(int)
points = detector.detect_landmarks(np.array(im), [detected_faces])[0].astype(int)
aligned_img, points = align_face_68pts(im, points.flatten(), 2.5)
hull = ConvexHull(points)
mask = grid_points_in_poly(shape=np.array(aligned_img).shape,
verts= list(zip(points[hull.vertices][:,1], points[hull.vertices][:,0])) # for some reason verts need to be flipped
)
mask[0:np.min([points[0][1], points[16][1]]), points[0][0]:points[16][0]] = True
aligned_img[~mask] = 0
resized_face_np = aligned_img
fd, hog_image = hog(resized_face_np, orientations=8, pixels_per_cell=(8, 8),
cells_per_block=(2, 2), visualize=True, multichannel=True)
return fd, points.flatten(), resized_face_np, hog_image
# Initialize a detector class to detect landmarks and bounding box
A01 = Detector(face_model='RetinaFace',emotion_model=None, landmark_model="mobilenet", au_model=None) #initialize model
master_file = pd.read_csv("/home/tiankang/AU_Dataset/DISFA/toy_disfa.csv",index_col=0)
print(master_file)
# Make sure that in the master file you have a column (called original_path), which points to the path of the images
write_path = "/home/tiankang/AU_Dataset/OpenFace/tutorial" # This is the path where you store all hog and landmark files
master_file["Marked"] = True # THis mark column serves to check whether each image can be correctly processed by the algorithm.
with open(write_path+'hogs_file.csv', "w", newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerow(list(range(5408)))
with open(write_path+'new_landmarks_files.csv', "w", newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerow(list(range(136)))
for ix in tqdm(range(master_file.shape[0])):
try:
imageURL = master_file['original_path'][ix]
fd, landpts, cropped_img, hogs = extract_hog(imageURL, detector=A01)
with open(write_path+'hogs_file.csv', "a+", newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerow(fd)
with open(write_path+'new_landmarks_files.csv', "a+", newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerow(landpts.flatten())
except:
master_file['Marked'][ix] = False
print("failed to load",imageURL)
continue;
# Try to visualize one subject
plt.imshow(hogs)
plt.show()
# Save the master file
master_file.to_csv(write_path+"HOG_master_file.csv")
```
## Part 2: Train Models with Hog
```
import pandas as pd
import numpy as np
from sklearn.metrics import classification_report
from sklearn.svm import LinearSVC, SVC
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
from tqdm import tqdm
from sklearn.metrics import f1_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
# Load in y labels from the stored master file
master_file_hog = pd.read_csv(write_path+"HOG_master_file.csv", index_col=0)
master_file_hog = master_file_hog[master_file_hog['Marked']==True]
master_file_hog.reset_index(drop=True,inplace=True)
print(master_file_hog.head())
# We see that there are 9 possible AUs
AU_nums = [1,2,4,6,9,12,17,25,26]
AU_LABELS = ['AU'+str(i) for i in AU_nums]
master_ylabels = master_file_hog[AU_LABELS]
print(master_ylabels)
# Load in hogs and landmarks
hogs_vals = pd.read_csv(write_path+"hogs_file.csv")
landmarks_ts = pd.read_csv(write_path+"new_landmarks_files.csv")
print(hogs_vals.shape)
print(landmarks_ts.shape)
# Perform PCA on the hogs and concatenate it with landmarks
scaler = StandardScaler()
hogs_cbd_std = scaler.fit_transform(hogs_vals)
pca = PCA(n_components = 0.95, svd_solver = 'full')
hogs_transformed = pca.fit_transform(hogs_cbd_std)
x_features = np.concatenate((hogs_transformed,landmarks_ts),1)
print(x_features.shape)
# Train a classifier
def balanced_sample_maker(X, y, sample_size, random_seed=None):
""" return a balanced data set by sampling all classes with sample_size
current version is developed on assumption that the positive
class is the minority.
Parameters:
===========
X: {numpy.ndarrray}
y: {numpy.ndarray}
"""
uniq_levels = np.unique(y)
uniq_counts = {level: sum(y == level) for level in uniq_levels}
if not random_seed is None:
np.random.seed(random_seed)
# find observation index of each class levels
groupby_levels = {}
for ii, level in enumerate(uniq_levels):
obs_idx = [idx for idx, val in enumerate(y) if val == level]
groupby_levels[level] = obs_idx
# oversampling on observations of each label
balanced_copy_idx = []
for gb_level, gb_idx in groupby_levels.items():
over_sample_idx = np.random.choice(gb_idx, size=sample_size, replace=True).tolist()
balanced_copy_idx+=over_sample_idx
np.random.shuffle(balanced_copy_idx)
return (X[balanced_copy_idx, :], y[balanced_copy_idx], balanced_copy_idx)
def _return_SVM(hog_feature_cbd, y):
(balX, baly, idx) = balanced_sample_maker(hog_feature_cbd, y, sample_size = np.sum(y==1), random_seed=1)
# Scale HOG features
#balXstd = scaler.fit_transform(balX)
balXstd = balX
# Fit model
clf = LinearSVC(C = 1e-6, max_iter=1200) # Change parameter here
clf.fit(X=balXstd, y=baly)
print("Training report:", classification_report(baly, clf.predict(balXstd)))
return(clf)
def _return_RF(hog_feature_cbd,y):
#print(np.isnan(hog_feature_cbd).sum())
(balX, baly, idx) = balanced_sample_maker(hog_feature_cbd, y, sample_size = np.sum(y==1), random_seed=1)
balXstd = balX
clf = RandomForestClassifier(random_state=0, n_estimators=140,max_depth=15,min_samples_split=20,min_samples_leaf=20) #Change parameter here
clf.fit(X=balXstd, y=baly)
print("Training report:", classification_report(baly, clf.predict(balXstd)))
return(clf)
def _return_Logistic(hog_feature_cbd, y):
(balX, baly, idx) = balanced_sample_maker(hog_feature_cbd, y, sample_size = np.sum(y==1), random_seed=1)
balXstd = balX
# Fit model
clf = LogisticRegression(random_state=0) # Change parameter here
clf.fit(X=balXstd, y=baly)
print("Training report:", classification_report(baly, clf.predict(balXstd)))
return(clf)
def fit_transform_test(hog_features, au_matrix, AuNum_list, method='SVM'):
all_svm_params = {}
scaler = StandardScaler()
for AuNum in AuNum_list:
print("==========", "processing AU:",AuNum,'====================')
y = au_matrix[AuNum]
y = y.values.ravel()
if method == 'SVM':
new_clf = _return_SVM(hog_feature_cbd=hog_features, y = y)
elif method == 'RF':
new_clf = _return_RF(hog_feature_cbd=hog_features, y = y)
elif method == 'Logistic':
new_clf = _return_Logistic(hog_feature_cbd=hog_features, y = y)
all_svm_params[AuNum] = new_clf
return(all_svm_params)
trained_svm = fit_transform_test(hog_features=x_features,au_matrix=master_ylabels,AuNum_list=AU_LABELS, method='SVM')
```
## 3. Validate the results on benchmark data
```
# If we have a test data:
test_master_file = pd.read_csv("/home/tiankang/AU_Dataset/DISFA/toy_test.csv",index_col=0)
print(test_master_file.head())
# We will again process the HOGs ad landmarks for test data
write_path = "/home/tiankang/AU_Dataset/OpenFace/tutorial" # This is the path where you store all hog and landmark files
master_file["Marked"] = True # THis mark column serves to check whether each image can be correctly processed by the algorithm.
with open(write_path+'hogs_file_test.csv', "w", newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerow(list(range(5408)))
with open(write_path+'new_landmarks_files_test.csv', "w", newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerow(list(range(136)))
for ix in tqdm(range(master_file.shape[0])):
try:
imageURL = master_file['original_path'][ix]
fd, landpts, cropped_img, hogs = extract_hog(imageURL, detector=A01)
with open(write_path+'hogs_file_test.csv', "a+", newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerow(fd)
with open(write_path+'new_landmarks_files_test.csv', "a+", newline='') as csvfile:
writer = csv.writer(csvfile, delimiter=',')
writer.writerow(landpts.flatten())
except:
master_file['Marked'][ix] = False
print("failed to load",imageURL)
continue;
# Save the master file
master_file.to_csv(write_path+"HOG_master_file_test.csv")
# Load in y labels from the stored master file
master_file_hog_test = pd.read_csv(write_path+"HOG_master_file_test.csv", index_col=0)
master_file_hog_test = master_file_hog_test[master_file_hog_test['Marked']==True]
master_file_hog_test.reset_index(drop=True,inplace=True)
print(master_file_hog_test.head())
# We see that there are 9 possible AUs
AU_nums = [1,2,4,6,9,12,17,25,26]
AU_LABELS = ['AU'+str(i) for i in AU_nums]
master_ylabels_test = master_file_hog_test[AU_LABELS]
print(master_ylabels_test)
# Load in hogs and landmarks
hogs_test = pd.read_csv(write_path+"hogs_file_test.csv")
landmarks_test = pd.read_csv(write_path+"new_landmarks_files_test.csv")
print(hogs_test.shape)
print(landmarks_test.shape)
# Perform PCA on the hogs and concatenate it with landmarks
# Use the previous PCA and scalar
hogs_test_std = scaler.fit_transform(hogs_test)
hogs_test_transformed = pca.fit_transform(hogs_test_std)
x_features_test = np.concatenate((hogs_test_transformed,landmarks_test),1)
print(x_features_test.shape)
for AU_m in trained_svm:
clf = trained_svm[AU_m]
pred_y = clf.predict(X=x_features_test)
print("prediction result for AU:", AU_m)
print("Training report:", classification_report(master_ylabels_test[AU_m], pred_y))
print("f1_score:",f1_score(master_ylabels_test[AU_m], pred_y))
```
| true |
code
| 0.48621 | null | null | null | null |
|
# Import libraries
We will make extensive use of `pandas` and `LightGBM` throughout this demo. `pickle` will be used to save and load model files
```
import lightgbm as lgb
import pandas as pd
import numpy as np
import csv
import pickle
from sklearn.metrics import mean_squared_error
import matplotlib
%matplotlib inline
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 4
```
# Slack channel notifications
Import `SlackClient` and create basic function that will post a Slack notification in `channel` when code is finished running
```
from slackclient import SlackClient
def slack_message(message, channel):
token = 'your_token'
sc = SlackClient(token)
sc.api_call('chat.postMessage', channel=channel,
text=message, username='My Sweet Bot',
icon_emoji=':upside_down_face:')
```
# Import data and set data types
Set working directory and ensure schema is correct before importing train and test sets. `infer_datetime_format` automatically reads the date column `dates` - check this is correct afterwards, but it is usually pretty smart
```
data_dir = '/your/directory/'
data_file = data_dir + 'data_file'
data = pd.read_csv(data_file, sep = "\t", parse_dates = ['dates'], infer_datetime_format = True)
```
# Combine train and test set
Combine `train` and `test` data sets before parsing through dense vector encoding. This is especially important because we want to maintain the same set of columns across both train and test sets. These can be inconsistent if a particular level of a categorical variable is present in one data set but not the other
* `cat_cols` are categorical columns that will be used in model training
* `index_cols` are columns that are used for indexing purposes and will not be fit in the model
* `pred_cols` are the response variable columns
* `num_cols` are the numeric columns that will be used in model training
```
cat_cols = ['ATTRIBUTE_1','ATTRIBUTE_2','ATTRIBUTE_3']
index_cols = ['FACTOR_1','FACTOR_2','FACTOR_3']
pred_cols = ['RESPONSE']
num_cols = [x for x in list(data.columns.values) if x not in cat_cols if x not in fac_cols if x not in pred_cols]
```
# Convert categorial variables to dense vectors
```
data_cat = pd.DataFrame(data[cat_cols])
for feature in cat_cols: # Loop through all columns in the dataframe
if data_cat[feature].dtype == 'object': # Only apply for columns with categorical strings
data_cat[feature] = pd.Categorical(data[feature]).codes # Replace strings with an integer
```
# Prepare final dataframe before resplitting into train and test sets
Importantly, we want to ensure that `train_final` and `test_final` are the same rows of data as `train` and `test`. `DATE_SPLIT` is the date we want to use to split our train and test sets
```
data_num = data[num_cols]
data_final = pd.concat([data_cat, data_num], axis=1)
data_final['DATE'] = data['DATE']
data_final['RESPONSE'] = data['RESPONSE']
print data_final.shape
train_final = data_final[data_final['DATE'] <= 'DATE_SPLIT']
test_final = data_final[data_final['DATE'] >= 'DATE_SPLIT' ]
print(train_final.shape)
print(test_final.shape)
train = data[data['DATE'] <= 'DATE_SPLIT']
test = data[data['DATE'] >= 'DATE_SPLIT' ]
print(train.shape)
print(test.shape)
```
# Create design matrix and response vector
```
y_train = train_final['RESPONSE']
y_test = test_final['RESPONSE']
x_train = train_final.drop(['RESPONSE','DATE'], axis=1)
x_test = test_final.drop(['RESPONSE','DATE'], axis=1)
print x_train.columns.values
```
# Create Dataset objects for LightGBM
```
lgb_train = lgb.Dataset(data = x_train, label = y_train, free_raw_data = False)
lgb_test = lgb.Dataset(data = x_test, label = y_test, reference = lgb_train, free_raw_data = False)
```
# Set hyperparameters for LightGBM
Set hyperparameters for training GBM. LightGBM grows each tree in a leaf-wise fashion, compared to other algorithms like XGBoost which grows each tree level-wise. LightGBM will choose the leaf with the highest delta loss to grow, leading to greater loss reductions compared to level-wise algorithms.
We need to specify the `num_leaves` parameter, which controls the maximum number of leaves a base learner can grow. `max_depth` can also be used to control for maximum tree depth, since leaf-wise growth may cause over-fitting when the dataset is small. A separate `max_depth` parameter has not been set here, but can be implemented by simply changing the `max_depth` value in `params`.
We implement the DART algorithm here, instead of a traditional Gradient Boosting Decision Tree. More information about DART can be found here: https://arxiv.org/pdf/1505.01866.pdf
```
depth = 8
num_leaves = 2**depth - 1
params = {'boosting_type': 'dart',
'objective': 'regression',
'metric': 'l2',
'num_leaves': num_leaves,
'max_depth': -1,
'learning_rate': 0.02,
'n_estimators': 1000,
'min_split_gain': 0.05,
'min_child_weight': 0.5,
'subsample': 0.8,
'colsample_bytree': 0.8,
'reg_alpha': 0.2,
'reg_lambda': 0.2,
'drop_rate': 0.2,
'skip_drop': 0.8,
'max_drop': 200,
'seed': 100,
'silent': False
}
```
# Run cross-validation with set hyperparameters
Early stopping rounds have also been implemented, so we can be ambitious and increase `n_estimators` to `1000`. We will use the best tree to fit the final GBM
```
num_boost_round = 1000
early_stopping_rounds = 10
nfold = 5
evals_result = {}
gbmCV = lgb.cv(params,
train_set = lgb_train,
num_boost_round = num_boost_round,
nfold = nfold,
early_stopping_rounds = early_stopping_rounds,
verbose_eval = True
)
slack_message("Cross validation completed!", 'channel')
```
# Train GBM
Train model using the best tree found from cross-validation. Here, we record the test results at each boosting iteration
```
num_boost_round = len(gbmCV['l2-mean'])
gbm = lgb.train(params,
train_set = lgb_train,
num_boost_round = num_boost_round,
valid_sets = [lgb_test],
valid_names = ['eval'],
evals_result = evals_result,
verbose_eval = True
)
slack_message("Booster object completed!", 'channel')
```
# Plot feature importance and print values
Plot the top 30 features by `split` importance. Create dataframe that records the `split` and `gain` of each feature
```
lgb.plot_importance(gbm, max_num_features = 30, importance_type='split')
importance = pd.DataFrame()
importance['Feature'] = x_train.columns.values
importance['ImportanceWeight'] = gbm.feature_importance(importance_type = 'split')
importance['ImportanceGain'] = gbm.feature_importance(importance_type = 'gain')
importance.sort_values(by = 'ImportanceWeight', ascending = False, inplace = True)
importance.head()
```
# Plot L2 during training
Plot the test results at each boosting iteration
```
lgb.plot_metric(evals_result, metric='l2')
```
# Produce predictions for train and test sets before measuring accuracy
Calculate predictions for both train and test sets, and then calculate MSE and RMSE for both datasets
```
gbm_train_preds = gbm.predict(x_train, num_iteration = gbm.best_iteration)
gbm_test_preds = gbm.predict(x_test, num_iteration = gbm.best_iteration)
print gbm_train_preds.shape
print gbm_test_preds.shape
print "\nModel Report"
print "MSE Train : %f" % mean_squared_error(y_train, gbm_train_preds)
print "MSE Test: %f" % mean_squared_error(y_test, gbm_test_preds)
print "RMSE Train: %f" % mean_squared_error(y_train, gbm_train_preds)**0.5
print "RMSE Test: %f" % mean_squared_error(y_test, gbm_test_preds)**0.5
```
# Save model file and write .csv files to working directory
Save LightGBM model file for future reference. Similar function to load previously saved files is commented out below. Then, write all files to the working directory
```
pickle.dump(gbm, open("gbm.pickle.dat", "wb"))
# gbm = pickle.load(open("gbm.pickle.dat", "rb"))
# gbm_train_preds = gbm.predict(x_train)
# gbm_test_preds = gbm.predict(x_test)
# print "\nModel Report"
# print "MSE Train : %f" % mean_squared_error(y_train, gbm_train_preds)
# print "MSE Test: %f" % mean_squared_error(y_test, gbm_test_preds)
# print "RMSE Train: %f" % mean_squared_error(y_train, gbm_train_preds)**0.5
# print "RMSE Test: %f" % mean_squared_error(y_test, gbm_test_preds)**0.5
train_preds = pd.DataFrame(gbm_train_preds)
test_preds = pd.DataFrame(gbm_test_preds)
train_preds.columns = ['RESPONSE']
test_preds.column = ['RESPONSE']
train.to_csv('LGBM Train.csv', sep=',')
train_preds.to_csv('LGBM Train Preds.csv', sep=',')
test.to_csv('LGBM Test.csv', sep=',')
test_preds.to_csv('LGBM Test Preds.csv', sep=',')
importance.to_csv('LGBM Feature Importance.csv', index = False)
slack_message("Files saved!", 'channel')
```
| true |
code
| 0.299489 | null | null | null | null |
|
# Boltzmann Wealth Model
```
from mesa import Agent, Model
from mesa.time import RandomActivation #activation order of agents matters but
#there are 3 implementations - Random, Simultaneous
%matplotlib inline
import matplotlib.pyplot as plt
import random
#import seaborn as sns
from mesa.space import MultiGrid
from mesa.datacollection import DataCollector
```
## Establishes Agent Class
1. Attributes (wealth) whe agent is initialized
2. move - move through multigrid
3. give money - identify neighbors, give money
4. Step which is action agent takes each time iteration
```
# Set up initial agents this is where you typically assign your attirbutes for each agent object
class MoneyAgent(Agent):
""" An agent with fixed initial wealth."""
def __init__(self, unique_id, model):
super().__init__(unique_id, model)
self.wealth = 1
def move(self):
possible_steps = self.model.grid.get_neighborhood(
self.pos,
moore=True,
include_center=False)
new_position = random.choice(possible_steps)
self.model.grid.move_agent(self, new_position)
def give_money(self):
cellmates = self.model.grid.get_cell_list_contents([self.pos])
if len(cellmates) > 1:
other = random.choice(cellmates)
other.wealth += 1
self.wealth -= 1
def step(self):
self.move()
if self.wealth > 0:
self.give_money()
```
# Model class retains all agents and runs each step of the model
# Contains
1. activation object - randomly shuffle agent order each step
2. world (i.e. multigrid) -allows more than one agent on a spot
3. data collector - collects data on agents
4. agent population
5. gini coefficient function - kept outside class for batch runner/ model class interaction
6. step function for model
```
def compute_gini(model):
agent_wealths = [agent.wealth for agent in model.schedule.agents]
x = sorted(agent_wealths)
N = model.num_agents
B = sum( xi * (N-i) for i,xi in enumerate(x) ) / (N*sum(x))
return (1 + (1/N) - 2*B)
# Your model class which stores all your agents
class MoneyModel(Model):
"""A model with some number of agents."""
def __init__(self, N, width, height):
self.num_agents = N
self.grid = MultiGrid(width, height, True)
self.schedule = RandomActivation(self)
# create a datacollector to caputre key metric
self.datacollector = DataCollector(
model_reporters={"Gini": compute_gini}, # A function to call
agent_reporters={"Wealth": "wealth"}) # An agent attribute
# Create population of agents
for i in range(self.num_agents):
a = MoneyAgent(i, self)
self.schedule.add(a)
# Add the agent to a random grid cell
x = random.randrange(self.grid.width)
y = random.randrange(self.grid.height)
self.grid.place_agent(a, (x, y))
def step(self):
self.datacollector.collect(self)
self.schedule.step()
```
## Run the model and plot the results
## Runs 50 Agents in a 10 X 10 grid
```
model = MoneyModel(100, 10, 10)
for i in range(100):
model.step()
```
# Plot Location and Wealth
```
import numpy as np
plt.figure(figsize=(10,10))
agent_counts = np.zeros((model.grid.width, model.grid.height))
for cell in model.grid.coord_iter():
cell_content, x, y = cell
agent_count = len(cell_content)
agent_counts[x][y] = agent_count
plt.imshow(agent_counts, interpolation='nearest')
plt.colorbar()
# If running from a text editor or IDE, remember you'll need the following:
```
# Plot Gini Coefficient - g coefficient by step
```
plt.figure(figsize=(10,10))
gini = model.datacollector.get_model_vars_dataframe()
plt.plot(gini)
```
# See Dataframe of Plot
```
agent_wealth = model.datacollector.get_agent_vars_dataframe()
agent_wealth
```
# Plot Histogram of Step
```
plt.figure(figsize=(10,10))
end_wealth = agent_wealth.xs(19, level="Step")["Wealth"] # .xs is a pandas dataframe to get a cross section of the frame
plt.hist(end_wealth, bins=range(agent_wealth.Wealth.max()+1))
```
# Plot Path of One Agent
```
plt.figure(figsize=(10,10))
one_agent_wealth = agent_wealth.xs(20, level="AgentID")
plt.plot(one_agent_wealth)
```
## BATCH RUNNER
Adds one element - self.running = True
```
from mesa.batchrunner import BatchRunner
class MoneyModel(Model):
"""A model with some number of agents."""
def __init__(self, N, width, height):
self.num_agents = N
self.grid = MultiGrid(width, height, True)
self.schedule = RandomActivation(self)
self.running = True
# create a datacollector to caputre key metric
self.datacollector = DataCollector(
model_reporters={"Gini": compute_gini}, # A function to call
agent_reporters={"Wealth": "wealth"}) # An agent attribute
# Create population of agents
for i in range(self.num_agents):
a = MoneyAgent(i, self)
self.schedule.add(a)
# Add the agent to a random grid cell
x = random.randrange(self.grid.width)
y = random.randrange(self.grid.height)
self.grid.place_agent(a, (x, y))
def step(self):
self.datacollector.collect(self)
self.schedule.step()
fixed_params = {"width": 10,
"height": 10}
variable_params = {"N": range(10, 500, 10)}
batch_run = BatchRunner(MoneyModel,
fixed_parameters=fixed_params,
variable_parameters=variable_params,
iterations=5,
max_steps=100,
model_reporters={"Gini": compute_gini})
batch_run.run_all()
plt.figure(figsize=(10,10))
run_data = batch_run.get_model_vars_dataframe()
run_data.head()
plt.scatter(run_data.N, run_data.Gini)
```
| true |
code
| 0.834373 | null | null | null | null |
|
# Behringer X-Touch Mini
This notebook can be downloaded [here](https://github.com/jupyter-widgets/midicontrols/blob/master/examples/Example.ipynb).
Because Chrome is the only browser that implements the [Web MIDI API](https://developer.mozilla.org/en-US/docs/Web/API/MIDIAccess), this package only works in Chrome. Firefox has [recent discussion](https://bugzilla.mozilla.org/show_bug.cgi?id=836897) on how to move forward with implementing this standard.
Each midi controller needs a custom implementation exposing the interface for that specific midi controller as buttons, knobs, faders, etc. Currently we support the [Behringer X-Touch Mini](https://www.behringer.com/Categories/Behringer/Computer-Audio/Desktop-Controllers/X-TOUCH-MINI/p/P0B3M#googtrans(en|en)) controller, which is currently available for around \$60.
```
from ipymidicontrols import XTouchMini, xtouchmini_ui
x = XTouchMini()
```
We can work directly with the controls to assign values, listen for value changes, etc., just like a normal widget. Run the cell below, then turn the first knob or press the upper left button. You should see the values below update. Note that the button value toggles when held down, and the light on the physical button reflects this state, where true means light on, false means light off.
```
left_knob = x.rotary_encoders[0]
upper_left_button = x.buttons[0]
display(left_knob)
display(upper_left_button)
```
You can also adjust the values from Python and the changes are reflected in the kernel.
```
left_knob.value = 50
```
## Rotary encoders (knobs)
Rotary encoders (i.e., knobs) have a min and max that can be set.
```
left_knob.min=0
left_knob.max=10
```
Knobs have a variety of ways to display the value in the lights around the knob. If your value represents a deviation from some reference, you might use the `'trim'` light mode. If your value represents the width of a symmetric range around some reference, you might use the `'spread'` light mode.
```
# light_mode can be 'single', 'wrap', 'trim', 'spread'
left_knob.light_mode = 'spread'
```
We'll set the min/max back to the default (0, 100) range for the rest of the example for consistency with other knobs.
```
left_knob.min = 0
left_knob.max = 100
```
## Buttons
Since the button has a True/False state, and holding down the button momentarily toggles the state, if we set the button to True when it is not held down, we reverse the toggling (i.e., it is now True by default, and pressing it toggles it to False).
```
upper_left_button.value = True
# Now press the button to see it toggle to false.
```
We can change this toggling behavior in the button by setting the button `mode`. It defaults to `'momentary'`, which means the button state toggles only when the button is held down. Setting `mode` to `'toggle'` makes the button toggle its value each time it is pressed. Run the following cell and press the button several times. Notice how the toggle behavior is different.
```
upper_left_button.mode = 'toggle'
```
Each rotary encoder can also be pressed as a button and the toggle mode can be set as well. Run the cell below and press the left knob.
```
left_knob_button = x.rotary_buttons[0]
left_knob_button.mode = 'toggle'
display(left_knob_button)
```
## Faders
The fader can send its value to Python and has `min`, `max`, and `value` properties.
```
fader = x.faders[0]
display(fader)
```
Because the X-Touch Mini does not have motorized faders, the fader cannot be moved to represent a value set from Python. Any value set from Python is overridden by the next fader movement.
## Listening to changes
As with any widget, we can observe changes from any control to run a function.
```
from ipywidgets import Output
out = Output()
@out.capture()
def f(change):
print('upper left button is %s'%(change.new))
upper_left_button.observe(f, 'value')
display(out)
```
## Linking to other widgets
You can synchronize these widgets up to other widgets using `link()` to give a nicer GUI. Run the cell below and then try turning the left knob or pressing the upper left button. Also try adjusting the slider and checkbox below to see that the values are synchronized both ways.
```
from ipywidgets import link, IntSlider, Checkbox, VBox
slider = IntSlider(description="Left knob", min=left_knob.min, max=left_knob.max)
checkbox = Checkbox(description="Upper left button")
link((left_knob, 'value'), (slider, 'value'))
link((upper_left_button, 'value'), (checkbox, 'value'))
display(VBox([slider, checkbox]))
```
This package includes a convenience function, `xtouchmini_ux()`, to link each control up to a slider or checkbox widget in a GUI that roughly approximates the physical layout.
```
xtouchmini_ui(x)
```
## Experimenting with options
Let's set various controls to explore the available button and knob light modes, as well as some random values to see what they look like on the controller.
```
for b in x.buttons:
b.mode='toggle'
for b in x.rotary_buttons[:4]:
b.mode='toggle'
for b in x.rotary_buttons[4:]:
b.mode='momentary'
for b in x.side_buttons:
b.mode='momentary'
for b, mode in zip(x.rotary_encoders, ['single', 'single', 'trim', 'trim', 'wrap', 'wrap', 'spread', 'spread']):
b.light_mode = mode
# Set some random values
import secrets
for b in x.buttons:
b.value=secrets.choice([False, True])
for b in x.rotary_encoders:
b.value = secrets.randbelow(101)
```
## Clearing values
Finally, let's clear all of the values.
```
# Clear all values
for b in x.buttons:
b.value = False
for b in x.rotary_buttons:
b.value = False
for b in x.rotary_encoders:
b.value = 0
```
| true |
code
| 0.297311 | null | null | null | null |
|
# PyTorch Image Captioning model for time series
This notebook demonstrates how to use an image-captioning model for time-series prediction. The data set is based on the NASDAQ 100 data provided in "[A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction](https://arxiv.org/pdf/1704.02971.pdf)".
The code reuses the same sampling code from Chandler Zuo's [blog](http://chandlerzuo.github.io/blog/2017/11/darnn).
The image captioning model was based off of the following PyTorch [tutorial](https://github.com/yunjey/pytorch-tutorial/tree/master/tutorials/03-advanced/image_captioning) on image captioning.
```
import torch
from torch import nn
from torch.autograd import Variable
from torch import optim
import torch.nn.functional as F
import matplotlib
# matplotlib.use('Agg')
%matplotlib notebook
import os
import datetime as dt
import itertools
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
use_cuda = torch.cuda.is_available()
# use_cuda = False
print("Is CUDA available? ", use_cuda)
```
### Logger set up
```
import logging
modelName = "cnn_lstm"
# check if results directory exists
if not os.path.isdir("./results/%s" %(modelName)):
os.makedirs("./results/%s" %(modelName))
logger = logging.getLogger(__name__)
logger.setLevel(logging.INFO)
dlogger = logging.getLogger(__name__)
dlogger.setLevel(logging.DEBUG)
# create file handler
log = logging.FileHandler("./results/%s/%s_results.log" %(modelName, modelName))
log.setLevel(logging.INFO)
debug_log = logging.FileHandler("./results/%s/%s_debug.log" %(modelName, modelName))
debug_log.setLevel(logging.DEBUG)
logger.addHandler(log)
dlogger.addHandler(debug_log)
```
### Encoder: CNN
```
class EncoderCNN(nn.Module):
def __init__(self, input_dim=1, channel_size=64, batch_size=10, T=100, feature_size=81):
super(EncoderCNN, self).__init__()
self.input_dim = input_dim # num channels
self.batch_size = batch_size
self.channel_size = channel_size
self.T = T
self.feature_size = feature_size
# (N, C, H, W) = (num_batch, features, history, stocks)
# Conv2d - out:(N, 64, 100, 81), kernel(3, 5) stride:1
# added a linear layer to shrink the num stocks lower due to memory
self.small_feature_size = 10
self.first_linear = nn.Linear(feature_size, self.small_feature_size)
self.first_cnn_layer = nn.Sequential(
nn.Conv2d(input_dim, channel_size, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.Dropout(0.2))
# Conv2d - out:(N, 64, 100, 81), kernel(3,5) stride:1
self.second_cnn_layer = nn.Sequential(
nn.Conv2d(channel_size, channel_size, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.Dropout(0.2))
# dense layer - in: (N, 100*64*81), out: (N, 100*81)
self.first_dense_layer = nn.Sequential(
nn.Linear(T*self.small_feature_size*channel_size, T*self.feature_size),
nn.ReLU(),
nn.Dropout(0.2))
def forward(self, xt):
# conv2d input (N, 1, H, W) expects (N, C, H, W)
# print("x: ", xt.size())
N = xt.size(0)
# lin: in (N, 1, H, W) out: (N, 1, H, 10)
out = self.first_linear(xt)
# print("cnn: linear: ", out.size())
# cnn: in (N, 1, H, 10) out: (N, C, H, 10)
out = self.first_cnn_layer(out)
# print("cnn: first_layer output: ", out.size())
# cnn: in (N, C, H, 10) out: (N, C, H, 10)
out = self.second_cnn_layer(out)
# print("cnn: second_layer output: ", out.size())
# reshape for linear layer
out = out.view(N, self.T*self.small_feature_size*self.channel_size)
# print("flatten: ", out.size())
# first dense layer in: (N, C*H*W) out: (N, H*W)
out = self.first_dense_layer(out)
# print("first dense layer output: ", out.size())
# reshape output for (N, T, W)
out = out.reshape(out.size(0), self.T, self.feature_size)
# print("reshape out: ", out.size())
return out
```
### Decoder: LSTM
```
class DecoderLSTM(nn.Module):
def __init__(self, feature_size, decoder_hidden_size, T=100, num_layers=2):
super(DecoderLSTM, self).__init__()
self.T = T
self.feature_size = feature_size
self.decoder_hidden_size = decoder_hidden_size
# print("decoder: decoder_hidden_size: ", decoder_hidden_size)
# lstm - in: (N, T, W) out: (N, T, H)
self.lstm_layer = nn.LSTM(feature_size, decoder_hidden_size,
num_layers=num_layers,
dropout=0.2,
batch_first=True)
# dense layer - in: (N, T*H), out: (N, T*H)
self.dense_layer = nn.Sequential(
nn.Linear(T*(decoder_hidden_size+1), T*(decoder_hidden_size+1)),
nn.ReLU(),
nn.Dropout(0.2))
# final layer - in: (N, T*H) out:(N, 1)
self.final_layer = nn.Linear(T*(decoder_hidden_size+1), 1)
# log info
logger.info("decoder - feature_size: %s hidden_size: %s T: %s" \
%(feature_size, decoder_hidden_size, T))
def forward(self, features, y_history):
# x (N, T, W) y_history (N, T, 1)
# print("features: ", features.size())
# print("y_history: ", y_history.size())
# lstm layer in: (N, T, W) out: (N, T, H)
out, lstm_out = self.lstm_layer(features)
# print("lstm layer: ", out.size())
# clipping to eliminate nan's from lstm
out.register_hook(lambda x: x.clamp(min=-100, max=100))
# combine with y_history
out = torch.cat((out, y_history), dim=2)
# print("out cat: ", out.size())
# flatten in: (N, T, H) out: (N, T*(H=1))
out = out.contiguous().view(-1, out.size(1)*out.size(2))
# print("out flatten: ", out.size())
# final layer in: (N, T*(H+1)), out: (N, 1)
out = self.final_layer(out)
# print("final layer: ", out.size())
return out
def init_hidden(self, x):
return Variable(x.data.new(1, x.size(0), self.decoder_hidden_size).zero_())
```
### Train & Test
```
# Train the model
class cnn_lstm:
def __init__(self, file_data, decoder_hidden_size = 64, T = 10,
input_dim= 1, channel_size = 64, feature_size = 81,
learning_rate = 0.01, batch_size = 128, parallel = False, debug = False):
self.T = T
dat = pd.read_csv(file_data, nrows = 100 if debug else None)
print("Shape of data: %s.\nMissing in data: %s" %(dat.shape, dat.isnull().sum().sum()))
self.X = dat[[x for x in dat.columns if x != 'NDX']][:-1].as_matrix()
# drop last row since using forward y
y = dat.NDX.shift(-1).values
self.y = y[:-1].reshape((-1, 1))
print("X shape", self.X.shape)
print("y shape", self.y.shape)
self.batch_size = batch_size
if use_cuda:
#input_dim=1, channel_size=64, batch_size=10, T=100, feature_size=81)
self.encoder = EncoderCNN(input_dim=input_dim, channel_size=channel_size,
batch_size=batch_size, T=T, feature_size=feature_size).cuda()
# feature_size, decoder_hidden_size, T=100, num_layers=2)
self.decoder = DecoderLSTM(feature_size, decoder_hidden_size, T=T, num_layers=2).cuda()
else:
self.encoder = EncoderCNN(input_dim=input_dim, channel_size=channel_size,
batch_size=batch_size, T=T, feature_size=feature_size).cpu()
self.decoder = DecoderLSTM(feature_size, decoder_hidden_size, T=T, num_layers=2).cpu()
if parallel:
self.encoder = nn.DataParallel(self.encoder)
self.decoder = nn.DataParallel(self.decoder)
self.encoder_optimizer = optim.Adam(params = filter(lambda p: p.requires_grad, self.encoder.parameters()),
lr = learning_rate)
self.decoder_optimizer = optim.Adam(params = filter(lambda p: p.requires_grad, self.decoder.parameters()),
lr = learning_rate)
self.train_size = int(self.X.shape[0] * 0.7)
self.train_mean = np.mean(self.y[:self.train_size])
print("train mean: %s" %(self.train_mean))
self.y = self.y - self.train_mean # Question: why Adam requires data to be normalized?
print("Training size: %s" %(self.train_size))
logger.info("Training size: %s" %(self.train_size))
def train(self, n_epochs = 10):
iter_per_epoch = int(np.ceil(self.train_size * 1. / self.batch_size))
print("Iterations per epoch: %s ~ %s" %(self.train_size * 1. / self.batch_size, iter_per_epoch))
logger.info("Iterations per epoch: %s ~ %s" %(self.train_size * 1. / self.batch_size, iter_per_epoch))
self.iter_losses = np.zeros(n_epochs * iter_per_epoch)
self.epoch_losses = np.zeros(n_epochs)
self.loss_func = nn.MSELoss()
n_iter = 0
learning_rate = 1.
for i in range(n_epochs):
print("\n-------------------------------------------")
print("Epoch: ", i)
logger.info("\n-------------------------------------------")
logger.info("Epoch: %s" %(i))
perm_idx = np.random.permutation(self.train_size - self.T)
j = 0
while j < self.train_size - self.T:
batch_idx = perm_idx[j:(j + self.batch_size)]
X = np.zeros((len(batch_idx), self.T, self.X.shape[1]))
y_history = np.zeros((len(batch_idx), self.T))
y_target = self.y[batch_idx + self.T]
for k in range(len(batch_idx)):
X[k, :, :] = self.X[batch_idx[k] : (batch_idx[k] + self.T), :]
# y_history[k, :] (T-1,)
y_history[k, :] = self.y[batch_idx[k] : (batch_idx[k] + self.T)].flatten()
# train
loss = self.train_iteration(X, y_history, y_target)
# print("loss: ", loss.item())
self.iter_losses[int(i * iter_per_epoch + j / self.batch_size)] = loss
if (j / self.batch_size) % 50 == 0:
print("\tbatch: %s loss: %s" %(j / self.batch_size, loss))
logger.info("\tbatch: %s loss: %s" %(j / self.batch_size, loss))
j += self.batch_size
n_iter += 1
# decrease learplt.savefig("./results/%s/predi")plt.savefig("./results/%s/predi")ning rate
if n_iter % 10000 == 0 and n_iter > 0:
for param_group in self.encoder_optimizer.param_groups:
param_group['lr'] = param_group['lr'] * 0.9
logger.info("encoder learning rate: ", param_group["lr"])
for param_group in self.decoder_optimizer.param_groups:
param_group['lr'] = param_group['lr'] * 0.9
logger.info("decoder learning rate: ", param_group["lr"])
self.epoch_losses[i] = np.mean(self.iter_losses[range(i * iter_per_epoch, (i + 1) * iter_per_epoch)])
if i % 10 == 0:
print("Epoch %s, loss: %s" %(i, self.epoch_losses[i]))
logger.info("Epoch %s, loss: %s" %(i, self.epoch_losses[i]))
if i % 10 == 0:
print("\n Predict")
y_train_pred = self.predict(on_train = True)
y_test_pred = self.predict(on_train = False)
y_pred = np.concatenate((y_train_pred, y_test_pred))
y_pred = y_train_pred
plt.figure()
plt.plot(range(1, 1 + len(self.y)), self.y, label = "True")
plt.plot(range(self.T , len(y_train_pred) + self.T), y_train_pred, label = 'Predicted - Train')
plt.plot(range(self.T + len(y_train_pred) , len(self.y) + 1), y_test_pred, label = 'Predicted - Test')
plt.legend(loc = 'upper left')
plt.show()
plt.savefig("./results/%s/predict_%s_epoch%s.png" %(modelName, modelName, i), bbox_inches="tight")
def train_iteration(self, X, y_history, y_target):
# zero gradient - original code placemenet
self.encoder_optimizer.zero_grad()
self.decoder_optimizer.zero_grad()
# define variables
if use_cuda:
Xt = Variable(torch.from_numpy(X).type(torch.FloatTensor).cuda())
yht = Variable(torch.from_numpy(y_history).type(torch.FloatTensor).cuda())
y_true = Variable(torch.from_numpy(y_target).type(torch.FloatTensor).cuda())
else:
Xt = Variable(torch.from_numpy(X).type(torch.FloatTensor).cpu())
yht = Variable(torch.from_numpy(y_history).type(torch.FloatTensor).cpu())
y_true = Variable(torch.from_numpy(y_target).type(torch.FloatTensor).cpu())
# run models get prediction
# Xt (N, C, H, W)
Xt = Xt.view(Xt.size(0), 1, Xt.size(1), Xt.size(2))
# yht (N, T, 1)
yht = yht.unsqueeze(2)
features = self.encoder(Xt)
y_pred = self.decoder(features, yht)
# loss
loss = self.loss_func(y_pred, y_true)
loss.backward()
# optimizer
self.encoder_optimizer.step()
self.decoder_optimizer.step()
return loss.item()
def predict(self, on_train = False):
if on_train:
y_pred = np.zeros(self.train_size - self.T + 1)
print("PREDICT train")
else:
y_pred = np.zeros(self.X.shape[0] - self.train_size)
print("PREDICT test")
i = 0
while i < len(y_pred):
batch_idx = np.array(range(len(y_pred)))[i : (i + self.batch_size)]
X = np.zeros((len(batch_idx), self.T, self.X.shape[1]))
y_history = np.zeros((len(batch_idx), self.T))
for j in range(len(batch_idx)):
if on_train:
X[j, :, :] = self.X[range(batch_idx[j], batch_idx[j] + self.T), :]
y_history[j, :] = self.y[range(batch_idx[j], batch_idx[j]+ self.T)].flatten()
else:
X[j, :, :] = self.X[range(batch_idx[j] + self.train_size - self.T, batch_idx[j] + self.train_size), :]
y_history[j, :] = self.y[range(batch_idx[j] + self.train_size - self.T, batch_idx[j]+ self.train_size)].flatten()
if use_cuda:
Xt = Variable(torch.from_numpy(X).type(torch.FloatTensor).cuda())
yht = Variable(torch.from_numpy(y_history).type(torch.FloatTensor).cuda())
# Xt (N, C, H, W)
Xt = Xt.view(Xt.size(0), 1, Xt.size(1), Xt.size(2))
# yht (N, T, 1)
yht = yht.unsqueeze(2)
features = self.encoder(Xt)
pred_cuda = self.decoder(features, yht)
y_pred[i:(i+self.batch_size)] = pred_cuda.cpu().data.numpy()[:, 0]
else:
Xt = Variable(torch.from_numpy(X).type(torch.FloatTensor).cpu())
yht = Variable(torch.from_numpy(y_history).type(torch.FloatTensor).cpu())
# Xt (N, C, H, W)
Xt = Xt.view(Xt.size(0), 1, Xt.size(1), Xt.size(2))
# yht (N, T, 1)
yht = yht.unsqueeze(2)
features = self.encoder(Xt)
y_pred[i:(i + self.batch_size)] = self.decoder(features, yht).data.numpy()[:, 0]
i += self.batch_size
return y_pred
index_file = "./nasdaq100/small/nasdaq100_padding.csv"
# file_data, decoder_hidden_size = 64, T = 10,
# input_dim= 1, channel_size = 64, feature_size = 81,
# learning_rate = 0.01, batch_size = 128, parallel = False, debug = False)
model = cnn_lstm(file_data=index_file, decoder_hidden_size = 100, T = 50,
input_dim = 1, channel_size = 64, feature_size = 81,
learning_rate = 0.01, batch_size = 128, parallel = False, debug = False)
model.train(n_epochs = 100)
y_train = model.predict(on_train=True)
y_pred = model.predict(on_train=False)
plt.figure()
plt.semilogy(range(len(model.iter_losses)), model.iter_losses)
plt.show()
plt.savefig("./results/%s/iter_losses_%s.png" %(modelName, modelName), bbox_inches="tight")
plt.figure()
plt.semilogy(range(len(model.epoch_losses)), model.epoch_losses)
plt.show()
plt.savefig("./results/%s/epoch_losses_%s.png" %(modelName, modelName), bbox_inches="tight")
plt.figure()
plt.semilogy(range(len(model.iter_losses)), model.iter_losses)
plt.show()
plt.savefig("./results/%s/iter_losses_%s.png" %(modelName, modelName), bbox_inches="tight")
plt.figure()
plt.semilogy(range(len(model.epoch_losses)), model.epoch_losses)
plt.show()
plt.savefig("./results/%s/epoch_losses_%s.png" %(modelName, modelName), bbox_inches="tight")
plt.figure()
plt.plot(model.y[model.train_size:], label = "True")
plt.plot(y_pred, label = 'Predicted', linestyle="--", )
plt.legend(loc = 'upper left')
plt.title("Test Results")
plt.show()
plt.savefig("./results/%s/predict_%s.png" %(modelName, modelName), bbox_inches="tight")
print("train_mean: ", model.train_mean)
y_true = model.y[model.train_size:].flatten() + model.train_mean
ydf = pd.DataFrame({"pred":y_pred + model.train_mean, "true":y_true})
ydf.to_csv("./results/%s/price_predictions_%s.csv" %(modelName, modelName))
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(ydf.true, ydf.pred)
print("average test mse: %s" %(mse))
y_train_true = model.y[:len(y_train)].flatten() + model.train_mean
ytrain_df = pd.DataFrame({"pred":y_train + model.train_mean, "true":y_train_true})
mse = mean_squared_error(ytrain_df.true, ytrain_df.pred)
print("average train mse: %s" %(mse))
# pre announcement
pre_mse = mean_squared_error(ydf.true.loc[:9259], ydf.pred.loc[:9259])
post_mse = mean_squared_error(ydf.true.loc[9259:], ydf.pred.loc[9259:])
print("pre_mse: %s" %(pre_mse))
print("post mse: %s" %(post_mse))
```
| true |
code
| 0.778755 | null | null | null | null |
|
# My First Neural Network, Part 2. Bias and CE Loss
> Bias and cross-entropy loss
- toc: true
- branch: master
- badges: true
- comments: true
- metadata_key1: metadata_value1
- metadata_key2: metadata_value2
- image: https://i.imgur.com/5CbsjVW.png
- description: Bias and cross-entropy loss
- redirect_to: https://drscotthawley.github.io/blog/2019/02/04/My-First-NN-Part-2.html
Links to lessons:
[Part 0](https://drscotthawley.github.io/Following-Gravity/),
[Part 1](https://colab.research.google.com/drive/1CPueDKDYOC33U_0qHxBhsDPpzYMpD8c8),
[Part 2](https://colab.research.google.com/drive/1O9xcdAQUxo7KdVhbggqLCvabc77Rj-yH),
[Part 3](https://colab.research.google.com/drive/1UZDEK-3v-SWxpDYBfamBoD4xhy7H2DEZ#scrollTo=14tOCcvT_a0I)
Moving on from our [our previous notebook](https://colab.research.google.com/drive/1CPueDKDYOC33U_0qHxBhsDPpzYMpD8c8), we will investigate three things we could do to improve the models developed previously:
1. Add a bias term
2. Use a different loss function
3. Add more layers to the network *(postponed to next lesson)*
## 1. Add a bias term
Our weighted sums did not include any constant offset or "bias" term. This may be fine for some data, but not for many others.
For example, in a simple linear model $y = mx+b$, the choice of $b=0$ limits the model's ability to accurately fit some data.

That is effectively what we did with our weighted sum $\sum_j X_{ij}w_j$: there was no constant offset. To correct this lack, we could add a new variable $b$ and make our weighted sum $b + \sum_j X_{ij}w_j$. Equivalently, and more conveniently for the purposes of coding, we could put an additional column of 1's in the input $X$, and a new row to our weight matrix $w$. By convention, this is usually done with the zeroth element, so that $X_{i0}=1$ and the columns of $X$ are moved to the right, and $w_0 = b$ will be the new constant offset (because $1*w_0 = w_0$.)
For the first problem (Trask's first problem), this change makes our new matrix equation look like (with new bias terms in red)
$$
f\left(
\overbrace{
\left[ {\begin{array}{ccc}
\color{red}1 & 0 & 0 & 1 \\
\color{red}1 & 0 & 1 & 1\\
\color{red}1 & 1 & 0 & 1\\
\color{red}1 & 1 & 1 & 1\\
\end{array} } \right]
}^\text{X}
\overbrace{
\left[ {\begin{array}{c}
\color{red}{w_0} \\
w_1\\
w_2\\
w_3
\end{array} } \right]
}^{w}
\right)
=
\overbrace{
\left[ {\begin{array}{c}
0 \\
0 \\
1 \\
1 \\
\end{array} } \right]
}^{\tilde{Y}}
$$
***Foreshadowing***: *Note that in this problem, the rightmost column of $X$ already was a column of all 1's, and so already has something akin to a bias. Thus, adding a new column of all 1's will not add any information, and so for this problem we expect that adding the bias won't improve the model performance.)*
With this change, we can still write our weighted sum as $\sum_j X_{ij}w_j$, it's just that $j$ now runs over 0..3 instead of 0..2. To emphasize: We can leave the rest of our code the same as before, provided we change $X$ by adding a column of 1's.
In terms of coding the change to $X$, we can either rewrite it by hand, or pull a numpy trick:
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# old data
X = np.array([ [0,0,1],
[0,1,1],
[1,0,1],
[1,1,1] ])
# add a column of 1's
new_col = np.ones((X.shape[0],1)) # array of 1s, w/ same # of rows as X, 1 col wide
X_bias = np.hstack((new_col,X)) # stack them horizontally
print(X_bias)
```
Let's compare our the use of the bias term without. We'll define functions for the gradient descent and for the plotting of the loss history, so we can call these again later in this lesson.
```
Y = np.array([[0,0,1,1]]).T # target output dataset
def sigmoid(x,deriv=False):
if(deriv==True):
return x*(1-x)
return 1/(1+np.exp(-x))
def calc_loss(Y_pred, Y, X, w, activ, loss_type="mse"): # MSE loss
diff = Y_pred - Y
loss = (diff**2).mean()
gradient = np.dot( X.T, diff*activ(Y_pred, deriv=True)) # for weight update
return loss, gradient
def fit(X, Y, activ, use_bias=True, alpha=3.0, maxiter=10000, loss_type='mse'):
"""
fit: Generic routine for doing our gradient decent
Required arguments:
X: input matrix
Y: target output
activ: reference to an activation function
Keywork arguments (optional):
use_bias: Flag for whether to use bias in the model
alpha: learning rate. Tip: Use the largest alpha 'you can get away with'
maxiter: maximum number of iterations
loss_type: Set to MSE for now but we'll extend this later.
"""
if use_bias: # add a column of 1's to X
new_col = np.ones((X.shape[0],1))
X = np.hstack((new_col,X))
# Define weights
np.random.seed(1) # for reproducibility
if activ == sigmoid:
w = 2*np.random.random((X.shape[1],Y.shape[1])) - 1 # -1..1
else:
w = np.random.random((X.shape[1],Y.shape[1]))/10 # only positive weights (for later)
loss_hist = [] # start with an empty list
for iter in range(maxiter):
Y_pred = activ(np.dot(X,w)) # compute prediction, i.e. tilde{Y}
loss, gradient = calc_loss(Y_pred, Y, X, w, activ, loss_type)
loss_hist.append(loss) # add to the history of the loss
w -= alpha * gradient # weight update
return w, Y_pred, loss_hist # send these values back
# Now call the fit function twice, to compare with and without bias:
w_old, Y_pred_old, loss_hist_old = fit(X, Y, sigmoid, use_bias=False)
w_new, Y_pred_new, loss_hist_new = fit(X, Y, sigmoid)
# Plot the results. Make a function so we can call this again later
def plot_new_old(loss_hist_old, loss_hist_new, labels=["no bias", "with bias"]):
plt.loglog(loss_hist_old, label=labels[0])
plt.loglog(loss_hist_new, label=labels[1])
plt.xlabel("Iteration")
plt.ylabel("MSE Loss (monitoring)")
plt.legend()
plt.show()
plot_new_old(loss_hist_old, loss_hist_new)
# And print the final answers:
print("No bias: Y_pred =",Y_pred_old)
print("With bias: Y_pred =",Y_pred_new)
```
As expected, *for this problem*, the inclusion of bias didn't make any significant difference. Let's try the same thing for the 7-segment display problem from Part 1. And let's try two different runs, one with sigmoid activation, and another with ReLU:
```
X_7seg = np.array([ [1,1,1,1,1,1,0,1], # 0
[0,1,1,0,0,0,0,1], # 1
[1,1,0,1,1,0,1,1], # 2
[1,1,1,1,0,0,1,1], # 3
[0,1,1,0,0,1,1,1], # 4
[1,0,1,1,0,1,1,1], # 5
[1,0,1,1,1,1,1,1], # 6
[1,1,1,0,0,0,0,1], # 7
[1,1,1,1,1,1,1,1], # 8
[1,1,1,1,0,1,1,1] # 9
])
Y_7seg = np.eye(10)
X, Y = X_7seg, Y_7seg
def relu(x,deriv=False): # relu activation
if(deriv==True):
return 1*(x>0)
return x*(x>0)
# Call the fit routine twice, once for sigmoid activation, once for relu
for activ in [sigmoid, relu]:
print("\n\n--------- activ = ",activ)
alpha = 0.5 if activ == sigmoid else 0.005 # assign learning rate
w_old, Y_pred_old, loss_hist_old = fit(X, Y, activ, alpha=alpha, use_bias=False)
w_new, Y_pred_new, loss_hist_new = fit(X, Y, activ, alpha=alpha)
# Report results
plot_new_old(loss_hist_old, loss_hist_new)
np.set_printoptions(formatter={'float': lambda x: "{0:0.2f}".format(x)}) # 2 sig figs
print("No bias: Y_pred =\n",Y_pred_old)
print("With bias: Y_pred =\n",Y_pred_new)
```
...So for this problem, it seems that adding the bias gave us a bit more accuracy, both for the sigmoid and relu activations. *Note: in this example, the learning rates were chosen by experiment; you should get in the habit of going back and experimenting with different learning rates.*
## Video Interlude: Logistic Regression
What we've been doing up until now has been a "classification" problem, with "yes"/"no" answers represented by 1's and 0's. This sort of operation is closely associated with the statistical method of Logistic Regression. It is akin to linear regression but with a sigmoid activation function. When doing Logistic Regression, one optimizes to fit by finding the maximum "likelihood" of a given model being correct.
To gain some insight on Logistic Regression, watch [this SatsQuest video](https://www.youtube.com/watch?v=yIYKR4sgzI8). (You can ignore his remarks about his preceding video, "R squared" and "p-value", etc.)
In what follows, we will be *minimizing* the *negative* of the *logarithm* of the likelihood, a quantity typically known as the Cross-Entropy loss. (This same quantity is also the non-constant part of the "Kullback-Leibler Divergence" or "K-L divergence," so you may hear it called that sometimes.)
## 2. Use a different loss function: Cross-Entropy loss
Let's return to Trask's first problem for which there is only one target per data point (row) of input, namely a target of 0 or 1. In this case, using the sigmoid function for this classification problem is one of [logistic regression](https://www.youtube.com/watch?v=yIYKR4sgzI8), even though we hadn't it identified it as such.
We've been using mean squared error (MSE) loss, but other loss functions exist. In particular, for outputs which are either "yes" or "no" such as the *classification problem* we are solving, a function called "[cross entropy](https://ml-cheatsheet.readthedocs.io/en/latest/loss_functions.html#cross-entropy)" is typically preferred. The cross-entropy loss is written like this:
$$L_{CE} = -\sum_i \left[ Y_i\log(\tilde{Y}_i) + (1-Y_i)\log(1-\tilde{Y}_i) \right]$$
Note that since the function $\log(x)$ is undefined for $x\le0$, we need to make sure $0<\tilde{Y}_i<1$ for all $i$. One way to ensure this is to use sigmoid activation! Thus, for classification problems, it is very common to see sigmoid activation (or its multi-class relative "[softmax](http://dataaspirant.com/2017/03/07/difference-between-softmax-function-and-sigmoid-function/)") immediately before the output, even for many-layer neural networks with all kinds of other activations in other places.
To use the CE loss with gradient descent, we need its derivative with respect to the weights. First let's write the CE loss in terms of the inputs $X$, weights $w$ and activation function $f$:
...wait, for compactness, let's write the weighted sum as $S_i = \sum_j X_{ij}w_j$. Ok, now going forward....
$$L_{CE} = -\sum_i\left[ Y_i\log\left(f\left(S_i \right)\right) + (1-Y_i)\log\left(1- f\left(S_{i}\right)\right) \right]$$
For any function $g(x)$, the derivative of $\log(g(x))$ with respect to x is just $1/g*(du/dx)$, so our partial derivatives with respect to weights look like
$${\partial L_{CE}\over \partial w_j} = -\sum_i\left[ {Y_i\over\tilde{Y_i}}{\partial f(S_i)\over \partial w_j} -
{1-Y_i\over 1-\tilde{Y}_i} {\partial f(S_i)\over \partial w_j} \right]\\
= -\sum_i {\partial f(S_i) \over \partial S_i}{\partial S_i\over\partial w_j} \left[ {Y_i\over\tilde{Y_i}} -
{1-Y_i\over 1-\tilde{Y}_i} \right]
$$
And if we multiply by $2/N$, we can write this as
$$
{\partial L_{CE}\over \partial w_j}
= {2\over N} \sum_{i=0}^{N-1} {\partial f(S_i) \over \partial S_i}X_{ij}
\left[
{\tilde{Y_i}-Y_i\over \tilde{Y_i}(1-\tilde{Y_i}) }\right]$$
This is similar to the partial derivatives for our MSE loss, except the term in the denominator is new. To see this more clearly,
recall that the weight update for MSE (from Part 1) was
$$
w := w - \alpha X^T \cdot \left( [\tilde{Y}-Y]*\tilde{Y}*(1-\tilde{Y})\right)
$$
whereas for CE we actually get a bit of a simplification because the term in the denominator cancels with a similar term in the numerator:
$$
w := w - \alpha X^T \cdot \left( [\tilde{Y}-Y]*\tilde{Y}*(1-\tilde{Y})\right) / (\tilde{Y}*(1-\tilde{Y})) \\
w := w - \alpha X^T \cdot [\tilde{Y}-Y].
$$
Thus despite all this seeming complication, our CE weight update is actually simpler than what it was before as MSE!
Let's try this out with code now:
```
# we'll "overwrite" the earlier calc_loss function
def calc_loss(Y_pred, Y, X, w, activ, loss_type='ce'):
diff = Y_pred - Y
loss = (diff**2).mean() # MSE loss
if 'ce' == loss_type:
diff = diff / (Y_pred*(1-Y_pred)) # use this for gradient
#loss = -(Y*np.log(Y_tilde) + (1-Y)*np.log1p(-Y_tilde)).mean() # CE Loss
# Actually we don't care what the loss itself is.
# Let's use MSE loss for 'monitoring' regardless, so we can compare the
# effects of using different gradients-of-loss functions
gradient = np.dot( X.T, diff*activ(Y_pred, deriv=True)) # same as before
return loss, gradient
#----
X = X_bias
Y = np.array([[0,0,1,1]]).T # target output dataset
# Compare old and new
w_mse, Y_pred_mse, loss_hist_mse = fit(X, Y, sigmoid, alpha=0.5, loss_type='mse')
w_ce, Y_pred_ce, loss_hist_ce = fit(X, Y, sigmoid, alpha=0.5, loss_type='ce') # fit
plot_new_old(loss_hist_mse, loss_hist_ce, ["MSE, with bias", "CE, with bias"])
# And print the final answers:
print("MSE _loss: Y_pred =\n",Y_pred_mse)
print("CE loss: Y_pred =\n",Y_pred_ce)
```
This works a lot better! To understand why, note that the gradients for MSE loss scale like
$$[\tilde{Y}-Y]*\tilde{Y}*(1-\tilde{Y})$$ and thus **these gradients go to zero** as $\tilde{Y}\rightarrow 0$, and/or $\tilde{Y}\rightarrow 1$, which makes training **very slow**! In contrast, the extra denominator in the CE gradients effectively cancels out this behavior, leaving the remaining term of
$$[\tilde{Y}-Y]$$ which varies *linearly* with the difference from the target value. This makes training much more efficient.
```
# Aside: What happens if we try ReLU activation with CE loss? Bad things, probably.
# Recall that ReLU maps negative numbers to 0, and isn't bounded from above.
# Thus the "denominator" in the 'diff term' in our earlier code will tend to 'explode'.
# Put differently, note that log(x) is undefined for x=0, as is log(1-x) for x=1.
w_relu_ce, Y_pred_relu_ce, loss_hist_relu_ce = fit(X, Y, relu, alpha=0.001, loss_type='ce')
plot_new_old(loss_hist_ce, loss_hist_relu_ce, ["CE, sigmoid", "CE, ReLU"])
```
# Excercise:
Do the same comparison for the 7-segment display problem: Make a plot showing a comparison of the loss history use MSE loss vs. using CE loss. And print out the final values of `Y_pred` for each. Use a learning rate of 0.5 and sigmoid activation, with bias.
Take a screenshot of the output and upload it to your instructor.
(*Note:* for the 7-segment display, since the target $Y$ has multiple columns, we should "normalize" the output in order to be able to properly interpret the output values $\tilde{Y}$ as probabilities. To do so, we would use a `softmax` activation. For now, we haven't bothered with this because it would add a bit more math, and is not actually necessary to solve this problem. )
Next time: [Part 3: Multi-Layer Networks and Backpropagation](https://colab.research.google.com/drive/1UZDEK-3v-SWxpDYBfamBoD4xhy7H2DEZ#scrollTo=14tOCcvT_a0I)
| true |
code
| 0.546194 | null | null | null | null |
|
# Instaquery
In this notebook, we'll define an `instaquery()` function that lets you:
1. define a renderer (plot, table, print, etc.)
2. filter the data using `pandas.query` syntax
3. specify a column to group-by
This tiny function can be handy for quick, throwaway exploration that you do not want captured permanently in the notebook (e.g., exploration off the primary track).
```
%matplotlib inline
from IPython.display import display, Image
from IPython.html.widgets import interact_manual
def instaquery(df, renderer=lambda df, by: display(df)):
'''
Creates an interactive query widget with an optional custom renderer.
df: DataFrame to query
renderer: Render function of the form lambda df, by where df is the subset of the DataFrame rows
matching the query and by is the column selected for a group-by option. The default render
function simply displays the rows matching the query and ignores the group-by.
'''
by_vals = tuple(['---'] + list(df.columns))
@interact_manual(query='', by=by_vals)
def instaquery(query, by):
'''Inner function that gets called when the user interacts with the widgets.'''
try:
sub_df = df.query(query)
except Exception:
sub_df = df
# replace sentinel with None
by = None if by == '---' else by
renderer(sub_df, by)
```
It doesn't look like much, but hers's a screenshot of just one thing it can do.
```
Image('./instaquery.png', retina=True, )
```
## Example #1: Pair Plot of Iris Data
Let's use it to render seaborn pairplots for the class iris dataset first.
```
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import seaborn as sns
df = sns.load_dataset('iris')
df.head()
```
We initialize the instaquery with the iris DataFrame and a custom render function. In our function, we render plots of all pairwise column combinations. We color points / bars by a selected column.
1. Run the cell below. Then hit *Run instaquery*. You should see the pairwise plots for the full dataset.
2. Next, select `species` in the *by* dropdown and click *Run instaquery* again. You still see the full dataset, but with each feature vector color coded according to its `species` category.
4. Finally, enter the query string `petal_width > 0.5 and petal_length < 5` and click *Run instaquery*. Now you only see the data that fall within the query parameters colorized according to species.
```
instaquery(df, lambda df, by: sns.pairplot(df, size=2.5, hue=by))
```
## Example #2: Pair Plot of Select Tip Columns
Now let's switch to another dataset, but and customize the pairwise plots a bit.
```
df = sns.load_dataset('tips')
```
In this dataset, not all columns have numeric values. Since we're interested in using `pairplot`, we need to filter out some columns from our pairings. But, at the same time, we gain more categorical columns to use for grouping.
```
df.head()
```
In this invocation of `instaquery`, we pass a fixed list of columns of interest for ploitting. We also specify the plot fill opacity since our data is denser than in the iris dataset.
1. Try coloring by `sex`, `day`, `smoker`, etc.
2. When coloring by `day`, try the query `total_bill * 0.15 < tip`. This plots customer tips greater than 15% of the total bill amount colored by day.
```
instaquery(df, lambda df, by: sns.pairplot(df, vars=['tip', 'total_bill', 'size'], size=3.5, hue=by, plot_kws={'alpha' : 0.7}))
```
## Example #3: Description of Tip Groups
As a final example, we cease plotting and use a different renderer: a pandas table giving the basic summary stats of all numeric columns, optionally grouped by a column.
1. Try *Run instaquery* with no values first.
2. Try grouping by `sex`.
3. Try grouping by `sex` with the query `time == 'Lunch'`.
```
instaquery(df, lambda df, by: display(df.groupby(by).describe()) if by else display(df.describe()))
```
## Homework: Violin Plot Renderer
Try to implement a violin plot renderer that compares the distribution of tips grouped by a column of choice. Here's a hint in the form of a static violin plot.
```
sns.violinplot(df.tip, df.sex)
```
<div class="alert" style="border: 1px solid #aaa; background: radial-gradient(ellipse at center, #ffffff 50%, #eee 100%);">
<div class="row">
<div class="col-sm-1"><img src="https://knowledgeanyhow.org/static/images/favicon_32x32.png" style="margin-top: -6px"/></div>
<div class="col-sm-11">This notebook was created using <a href="https://knowledgeanyhow.org">IBM Knowledge Anyhow Workbench</a>. To learn more, visit us at <a href="https://knowledgeanyhow.org">https://knowledgeanyhow.org</a>.</div>
</div>
</div>
| true |
code
| 0.517754 | null | null | null | null |
|
# MAT281 - Laboratorio N°11
<a id='p1'></a>
## I.- Problema 01
Lista de actos delictivos registrados por el Service de police de la Ville de Montréal (SPVM).
<img src="http://henriquecapriles.com/wp-content/uploads/2017/02/femina_detenida-1080x675.jpg" width="480" height="360" align="center"/>
El conjunto de datos en estudio `interventionscitoyendo.csv` corresponde a todos los delitos entre 2015 y agosto de 2020en Montreal. Cada delito está asociado en grandes categorías, y hay información sobre la ubicación, el momento del día, etc.
> **Nota**: Para más información seguir el siguiente el [link](https://donnees.montreal.ca/ville-de-montreal/actes-criminels).
```
# librerias
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from statsmodels.tsa.statespace.sarimax import SARIMAX
from metrics_regression import *
# graficos incrustados
plt.style.use('fivethirtyeight')
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
# parametros esteticos de seaborn
sns.set_palette("deep", desat=.6)
sns.set_context(rc={"figure.figsize": (12, 4)})
# read data
validate_categorie = [
'Introduction', 'Méfait','Vol dans / sur véhicule à moteur', 'Vol de véhicule à moteur',
]
df = pd.read_csv(os.path.join("data","interventionscitoyendo.csv"), sep=",", encoding='latin-1')
df.columns = df.columns.str.lower()
df['date'] = pd.to_datetime(df['date'], format='%Y-%m-%d')
df = df.loc[lambda x: x['categorie'].isin(validate_categorie)]
df = df.sort_values(['categorie','date'])
df.head()
```
Como tenemos muchos datos por categoría a nivel de día, agruparemos a nivel de **semanas** y separaremos cada serie temporal.
```
cols = ['date','pdq']
y_s1 = df.loc[lambda x: x.categorie == validate_categorie[0] ][cols].set_index('date').resample('W').mean()
y_s2 = df.loc[lambda x: x.categorie == validate_categorie[1] ][cols].set_index('date').resample('W').mean()
y_s3 = df.loc[lambda x: x.categorie == validate_categorie[2] ][cols].set_index('date').resample('W').mean()
y_s4 = df.loc[lambda x: x.categorie == validate_categorie[3] ][cols].set_index('date').resample('W').mean()
```
El objetivo de este laboratorio es poder realizar un análisis completo del conjunto de datos en estudio, para eso debe responder las siguientes preguntas:
1. Realizar un gráfico para cada serie temporal $y\_{si}, i =1,2,3,4$.
```
# graficar datos
y_s1.plot(figsize=(15, 3),color = 'blue')
y_s2.plot(figsize=(15, 3),color = 'red')
y_s3.plot(figsize=(15, 3),color = 'green')
y_s4.plot(figsize=(15, 3),color = 'pink')
plt.show()
```
2. Escoger alguna serie temporal $y\_{si}, i =1,2,3,4$. Luego:
* Realice un análisis exploratorio de la serie temporal escogida
* Aplicar el modelo de pronóstico $SARIMA(p,d,q)x(P,D,Q,S)$, probando varias configuraciones de los hiperparámetros. Encuentre la mejor configuración. Concluya.
* Para el mejor modelo encontrado, verificar si el residuo corresponde a un ruido blanco.
> **Hint**: Tome como `target_date` = '2021-01-01'. Recuerde considerar que su columna de valores se llama `pdq`.
# EDA
```
y_s1.head()
y_s1.sort_values(['date'])
y_s1.describe().T
# diagrama de caja y bigotes
fig, ax = plt.subplots(figsize=(15,6))
sns.boxplot(y_s1.index.year, y_s1.pdq, ax=ax)
plt.show()
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
from matplotlib import pyplot
pyplot.figure(figsize=(12,9))
# acf
pyplot.subplot(211)
plot_acf(y_s1.pdq, ax=pyplot.gca(), lags = 30)
#pacf
pyplot.subplot(212)
plot_pacf(y_s1.pdq, ax=pyplot.gca(), lags = 30)
pyplot.show()
from pylab import rcParams
import statsmodels.api as sm
import matplotlib.pyplot as plt
rcParams['figure.figsize'] = 18, 8
decomposition = sm.tsa.seasonal_decompose(y_s1, model='multiplicative')
fig = decomposition.plot()
plt.show()
```
# Modelo SARIMA
```
# creando clase SarimaModels
class SarimaModels:
def __init__(self,params):
self.params = params
@property
def name_model(self):
return f"SARIMA_{self.params[0]}X{self.params[1]}".replace(' ','')
@staticmethod
def test_train_model(y,date):
mask_ds = y.index < date
y_train = y[mask_ds]
y_test = y[~mask_ds]
return y_train, y_test
def fit_model(self,y,date):
y_train, y_test = self.test_train_model(y,date )
model = SARIMAX(y_train,
order=self.params[0],
seasonal_order=self.params[1],
enforce_stationarity=False,
enforce_invertibility=False)
model_fit = model.fit(disp=0)
return model_fit
def df_testig(self,y,date):
y_train, y_test = self.test_train_model(y,date )
model = SARIMAX(y_train,
order=self.params[0],
seasonal_order=self.params[1],
enforce_stationarity=False,
enforce_invertibility=False)
model_fit = model.fit(disp=0)
start_index = y_test.index.min()
end_index = y_test.index.max()
preds = model_fit.get_prediction(start=start_index,end=end_index, dynamic=False)
df_temp = pd.DataFrame(
{
'y':y_test['pdq'],
'yhat': preds.predicted_mean
}
)
return df_temp
def metrics(self,y,date):
df_temp = self.df_testig(y,date)
df_metrics = summary_metrics(df_temp)
df_metrics['model'] = self.name_model
return df_metrics
# definir parametros
import itertools
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
params = list(itertools.product(pdq,seasonal_pdq))
target_date = '2021-01-01'
# iterar para los distintos escenarios
frames = []
for param in params:
try:
sarima_model = SarimaModels(param)
df_metrics = sarima_model.metrics(y_s1,target_date)
frames.append(df_metrics)
except:
pass
# juntar resultados de las métricas y comparar
df_metrics_result = pd.concat(frames)
df_metrics_result.sort_values(['mae','mape'])
param = [(0,0,0),(1,0,1,12)]
sarima_model = SarimaModels(param)
model_fit = sarima_model.fit_model(y_s1,target_date)
best_model = sarima_model.df_testig(y_s1,target_date)
best_model.head()
# graficar mejor modelo
preds = best_model['yhat']
ax = y_s1['2020':].plot(label='observed')
preds.plot(ax=ax, label='Forecast', alpha=.7, figsize=(14, 7))
ax.set_xlabel('Date')
ax.set_ylabel('PDQ')
plt.legend()
plt.show()
```
**Conclusión**: La configuración la cual minimiza el modelo según mae y mape, a pesar de ser el mejor, no es un buen modelo de pronostico SARIMA.
# Verificación de ruido blanco
```
# resultados del error
model_fit.plot_diagnostics(figsize=(16, 8))
plt.show()
```
* **gráfico standarized residual**:En este caso se observa que esta nueva serie de tiempo corresponde a una serie estacionaria que oscila entorno al cero, por lo tanto es un ruido blanco.
* **gráfico histogram plus estimated density**: En este caso, el histograma es muy similar al histograma de una variable N(0,1), por lo que es ruido blanco.
* **gráfico correlogramse**: observa que no hay correlación entre ninguna de las variables, por lo que se puedan dar indicios de independencia entre las variables.
**Conclusión:** Dados los graficos de los errores asociados al modelo, se concluye que el error asociado al modelo en estudio corresponde a un ruido blanco.
| true |
code
| 0.58255 | null | null | null | null |
|
# geotiff2csv
Extraire une portion de GeoTiff en utilisant la librairie Gdal.
## Introduction
Le **GeoTiff** est un format d'image fréquemment utilisé pour stocker des **données géo-référencées**.
Le format GeoTiff est, par exemple, utilisé pour la mise à disposition de [Corine Land Cover](https://land.copernicus.eu/pan-european/corine-land-cover)(**CLC**).
Dans le cas de CLC, à chaque **Pixel** de l'image correspond un **hectare** de terrain. A chaque Pixel est associé un code. Dans le cas de CLC, il s'agit d'un code d'occupation du sol (Land Use).
CLC couvre 39 états. Les fichiers GeoTiff fournis par l'Agence Européenne de l'environnement sont très gros. Il y a un fichier par année. Chaque fichier fait environ 200 MB.
Un GeoTiff est une image qui peut facilement être importée sous la forme d'une **matrice**. Dans le cas de CLC, la matrice est énorme puisqu'elle compte **65.000 lignes** pour **46.000 colonnes**, ce qui fait 65.000 * 46.000 = 2.99 milliards de pixels! Il s'agit vraiment d'une très grosse matrice!
Nous ne nous intéressons, pour l'instant, qu'aux données belges. L'idée est d'extraire de cette grosse matrice, une sous-matrice qui comporte tous les pixels relatifs à la Belgique. Nous aurons, bien sûr, dans notre sous-matrice, quelques éléments (pixels) qui ne concernent pas la Belgique, puisque notre pays n'a pas une forme "rectangulaire".
Pour extraire des informations d'un GeoTiff, nous pouvons utiliser la librairie [Gdal](https://en.wikipedia.org/wiki/GDAL).
## Tiff
Le Tiff est un format pour le stockage d'images matricielles. On parle aussi de "raster" en anglais. Voici une image extraite de Wikipédia et qui montre différents éléments (ou pixels) qui composent une image matricielle.

## GeoTiff
Un GeoTiff est une image au format Tiff auquel on a ajouté des **méta-données de géo-référencement**. De la documentation sur le *format GeoTiff* est disponible à l'adresse [https://www.gdal.org/frmt_gtiff.html](https://www.gdal.org/frmt_gtiff.html).
Lorsque nous importons un GeoTiff en Python, nous obtenons une matrice. L'élément de la matrice situé à l'intersection de la $L^{ème}$ ligne et de la $P^{ème}$ colonne est identifié à l'aide du couple $(L,P)$.
Les méta-données stockées dans les fichiers Corine Land Cover nous permettent de transformer un couple $(L,P)$ en coordonnées géographiques $(X,Y)$. Nous ferons en sorte que ces coordonnées correspondent au centroïde de l'hectare correspondant au pixel situé en $(L,P)$.
Le système de projection utilisé par CLC est l'ETRS89 LAEA. **LAEA** est un acronyme pour **Lambert Azimuthal Equal Area**.
## Géoréférencement
Le géoréférencement est l'action qui consiste à associer les coordonnées $(L,P)$ aux coordonnées $(X,Y)$.
## Gdal
Pour extraire des informations d'un GeoTiff, nous pouvons utiliser la librairie [Gdal](https://en.wikipedia.org/wiki/GDAL). Il s'agit d'une librairie qui est utilisée par un très grand nombre de logiciels (ArcGis, QGis, ...).
La documentation est disponible à l'adresse [https://www.gdal.org/classGDALDataset.html](https://www.gdal.org/classGDALDataset.html).
Fonction intéressantes du package Gdal (pas toutes utilisées ic):
* myRaster.GetProjectionRef()
* myRaster.RasterCount
* myBand=myRaster.GetRasterBand(1)
* myBand.DataType
* myBand.XSize,myBand.YSize
* myRaster.GetGeoTransform()
* myBand.GetNoDataValue()
## Bounding box
Nous pouvons utiliser [BBox finder](http://bboxfinder.com/#49.425267,2.427979,51.553167,6.553345) pour identifier un rectangle qui entoure la Belgique (ou une autre unité administrative).
Exemple de Bounding Boxes:
- Belgium: **(3795050, 2939950)->(4067050, 3169950)**
- Rixensart: **(3919063,3067640)->(3952705,3091820)**
# Paramètres
```
# Input files
CorineGeoTiffDirectory='/home/yoba/DataScience/data/Open-Data/clc'
CorineGeoTiff={
1990:'{}/1990/CLC1990_CLC1990_V2018_20b2.tif'.format(CorineGeoTiffDirectory),
2000:'{}/2000/CLC2006_CLC2000_V2018_20b2.tif'.format(CorineGeoTiffDirectory),
2006:'{}/2006/CLC2012_CLC2006_V2018_20b2.tif'.format(CorineGeoTiffDirectory),
2012:'{}/2012/CLC2018_CLC2012_V2018_20b2.tif'.format(CorineGeoTiffDirectory),
2018:'{}/2018/clc2018_clc2018_V2018.20b2.tif'.format(CorineGeoTiffDirectory)
}
# Bounding box
x1,y1=3795050,2939950
x2,y2=4067050,3169950
# Output directory
CorineCsvDirectory='/home/yoba/DataScience/data/StatisticalProducts/clc/bbox'
```
# Imports
```
import numpy as np
import pandas as pd
from osgeo import gdal
from numpy.linalg import inv
```
# Fonctions
## Transformer des (X,Y) en (L,P)
```
def xy2pixel(padfTransform,Xp,Yp)-> '(pixel,line) coordinates':
"""
Transforming projection coordinates (Xp,Yp) to pixel/line (P,L) raster space.
"""
pixel2xy=np.array([[padfTransform[1], padfTransform[2]],
[padfTransform[4], padfTransform[5]]])
xy2pixel=inv(pixel2xy)
a = np.matmul(xy2pixel,np.array([[Xp-padfTransform[0]],
[Yp-padfTransform[3]]]))
result=(a-np.array([[0.5],[0.5]])).tolist()
return {'pixel':int(result[0][0]),'line':int(result[1][0])}
```
## Transformer des (L,P) en (X,Y)
```
def pixel2xy(padfTransform,P:'pixel (column)',L:'line')->'(x,y) coordinates':
"""
Transforming pixel/line (P,L) raster space to projection coordinates (Xp,Yp).
In a north up image, padfTransform[1] is the pixel width, and padfTransform[5]
is the pixel height. The upper left corner of the upper left pixel is at
position (padfTransform[0],padfTransform[3]).
The padTransform vector is stored in the metadata portion of the geoTiff. We can
extract it using the GetGetTransform() method.
"""
Xp = padfTransform[0] + (P+0.5) * padfTransform[1] + (L+0.5) * padfTransform[2]
Yp = padfTransform[3] + (P+0.5) * padfTransform[4] + (L+0.5) * padfTransform[5]
return (Xp,Yp)
def geotiff2csv(year):
inputFile=CorineGeoTiff[year]
outputFile=f'{CorineCsvDirectory}/clc-({x1},{y1})-({x2},{y2})-{year}.csv'
# Opening a GeoTiff does not import it into memory. In the end, we have a "link"
myRaster = gdal.Open(inputFile)
# "Connect" to first band - There is only one band in CLC files
myBand=myRaster.GetRasterBand(1)
# Identify portion of geotiff to extract
lowerLeftCorner =xy2pixel(myRaster.GetGeoTransform(),x1,y1)
upperRightCorner=xy2pixel(myRaster.GetGeoTransform(),x2,y2)
# Extract
pixelOffset = lowerLeftCorner['pixel']
pixelWindowSize = upperRightCorner['pixel']-lowerLeftCorner['pixel']
lineOffset = upperRightCorner['line']
lineWindowSize = lowerLeftCorner['line']-upperRightCorner['line']
myBBox=myBand.ReadAsArray(xoff = pixelOffset ,
yoff = lineOffset ,
win_xsize = pixelWindowSize ,
win_ysize = lineWindowSize )
# Get rid of "No Data" values
L,P = np.where( myBBox != myBand.GetNoDataValue() )
data_vals = np.extract(myBBox != myBand.GetNoDataValue(), myBBox)
# Transform (P,L) to (X,Y) coordinates
XY=pixel2xy(myRaster.GetGeoTransform(),pixelOffset+P,lineOffset+L)
# Export results
myDataFrame=pd.DataFrame({'X':XY[0],'Y':XY[1],'VALUE':data_vals})
myDataFrame.to_csv(outputFile,index=False,sep='|')
```
# Functions calls
```
for y in [1990,2000,2006,2012,2018]:
geotiff2csv(y)
```
| true |
code
| 0.477798 | null | null | null | null |
|
# T81-558: Applications of Deep Neural Networks
**Module 7: Convolutional Neural Networks.**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), School of Engineering and Applied Science, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module Video Material
Main video lecture:
* [Part 7.1: Data Sets for Computer Vision](https://www.youtube.com/watch?v=u8xn393mDPM&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN&index=21)
* [Part 7.2: Convolution Neural Network](https://www.youtube.com/watch?v=cf6FDLFNWEk&index=22&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN)
* [Part 7.3: Using Convolutional Neural Networks (CNNs) in Keras and TensorFlo](https://www.youtube.com/watch?v=LSSH_NdXwhU&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN&index=23)
Weekly video update:
* [Weekly Update #7, Feb 25, 2018](https://youtu.be/KquKVOXU2bc)
# Helpful Functions
You will see these at the top of every module. These are simply a set of reusable functions that we will make use of. Each of them will be explained as the semester progresses. They are explained in greater detail as the course progresses. Class 4 contains a complete overview of these functions.
```
from sklearn import preprocessing
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import shutil
import os
import requests
import base64
# Encode text values to dummy variables(i.e. [1,0,0],[0,1,0],[0,0,1] for red,green,blue)
def encode_text_dummy(df, name):
dummies = pd.get_dummies(df[name])
for x in dummies.columns:
dummy_name = "{}-{}".format(name, x)
df[dummy_name] = dummies[x]
df.drop(name, axis=1, inplace=True)
# Encode text values to a single dummy variable. The new columns (which do not replace the old) will have a 1
# at every location where the original column (name) matches each of the target_values. One column is added for
# each target value.
def encode_text_single_dummy(df, name, target_values):
for tv in target_values:
l = list(df[name].astype(str))
l = [1 if str(x) == str(tv) else 0 for x in l]
name2 = "{}-{}".format(name, tv)
df[name2] = l
# Encode text values to indexes(i.e. [1],[2],[3] for red,green,blue).
def encode_text_index(df, name):
le = preprocessing.LabelEncoder()
df[name] = le.fit_transform(df[name])
return le.classes_
# Encode a numeric column as zscores
def encode_numeric_zscore(df, name, mean=None, sd=None):
if mean is None:
mean = df[name].mean()
if sd is None:
sd = df[name].std()
df[name] = (df[name] - mean) / sd
# Convert all missing values in the specified column to the median
def missing_median(df, name):
med = df[name].median()
df[name] = df[name].fillna(med)
# Convert all missing values in the specified column to the default
def missing_default(df, name, default_value):
df[name] = df[name].fillna(default_value)
# Convert a Pandas dataframe to the x,y inputs that TensorFlow needs
def to_xy(df, target):
result = []
for x in df.columns:
if x != target:
result.append(x)
# find out the type of the target column. Is it really this hard? :(
target_type = df[target].dtypes
target_type = target_type[0] if hasattr(target_type, '__iter__') else target_type
# Encode to int for classification, float otherwise. TensorFlow likes 32 bits.
if target_type in (np.int64, np.int32):
# Classification
dummies = pd.get_dummies(df[target])
return df.as_matrix(result).astype(np.float32), dummies.as_matrix().astype(np.float32)
else:
# Regression
return df.as_matrix(result).astype(np.float32), df.as_matrix([target]).astype(np.float32)
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return "{}:{:>02}:{:>05.2f}".format(h, m, s)
# Regression chart.
def chart_regression(pred,y,sort=True):
t = pd.DataFrame({'pred' : pred, 'y' : y.flatten()})
if sort:
t.sort_values(by=['y'],inplace=True)
a = plt.plot(t['y'].tolist(),label='expected')
b = plt.plot(t['pred'].tolist(),label='prediction')
plt.ylabel('output')
plt.legend()
plt.show()
# Remove all rows where the specified column is +/- sd standard deviations
def remove_outliers(df, name, sd):
drop_rows = df.index[(np.abs(df[name] - df[name].mean()) >= (sd * df[name].std()))]
df.drop(drop_rows, axis=0, inplace=True)
# Encode a column to a range between normalized_low and normalized_high.
def encode_numeric_range(df, name, normalized_low=-1, normalized_high=1,
data_low=None, data_high=None):
if data_low is None:
data_low = min(df[name])
data_high = max(df[name])
df[name] = ((df[name] - data_low) / (data_high - data_low)) \
* (normalized_high - normalized_low) + normalized_low
# This function submits an assignment. You can submit an assignment as much as you like, only the final
# submission counts. The paramaters are as follows:
# data - Pandas dataframe output.
# key - Your student key that was emailed to you.
# no - The assignment class number, should be 1 through 1.
# source_file - The full path to your Python or IPYNB file. This must have "_class1" as part of its name.
# . The number must match your assignment number. For example "_class2" for class assignment #2.
def submit(data,key,no,source_file=None):
if source_file is None and '__file__' not in globals(): raise Exception('Must specify a filename when a Jupyter notebook.')
if source_file is None: source_file = __file__
suffix = '_class{}'.format(no)
if suffix not in source_file: raise Exception('{} must be part of the filename.'.format(suffix))
with open(source_file, "rb") as image_file:
encoded_python = base64.b64encode(image_file.read()).decode('ascii')
ext = os.path.splitext(source_file)[-1].lower()
if ext not in ['.ipynb','.py']: raise Exception("Source file is {} must be .py or .ipynb".format(ext))
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key':key}, json={'csv':base64.b64encode(data.to_csv(index=False).encode('ascii')).decode("ascii"),
'assignment': no, 'ext':ext, 'py':encoded_python})
if r.status_code == 200:
print("Success: {}".format(r.text))
else: print("Failure: {}".format(r.text))
```
# Computer Vision
This class will focus on computer vision. There are some important differences and similarities with previous neural networks.
* We will usually use classification, though regression is still an option.
* The input to the neural network is now 3D (height, width, color)
* Data are not transformed, no zscores or dummy variables.
* Processing time is much longer.
* We now have different layer times: dense layers (just like before), convolution layers and max pooling layers.
* Data will no longer arrive as CSV files. TensorFlow provides some utilities for going directly from image to the input for a neural network.
# Computer Vision Data Sets
There are many data sets for computer vision. Two of the most popular are the MNIST digits data set and the CIFAR image data sets.
## MNIST Digits Data Set
The [MNIST Digits Data Set](http://yann.lecun.com/exdb/mnist/) is very popular in the neural network research community. A sample of it can be seen here:

This data set was generated from scanned forms.

## CIFAR Data Set
The [CIFAR-10 and CIFAR-100](https://www.cs.toronto.edu/~kriz/cifar.html) datasets are also frequently used by the neural network research community.

The CIFAR-10 data set contains low-rez images that are divided into 10 classes. The CIFAR-100 data set contains 100 classes in a hierarchy.
# Other Resources
* [Imagenet:Large Scale Visual Recognition Challenge 2014](http://image-net.org/challenges/LSVRC/2014/index)
* [Andrej Karpathy](http://cs.stanford.edu/people/karpathy/) - PhD student/instructor at Stanford.
* [CS231n Convolutional Neural Networks for Visual Recognition](http://cs231n.stanford.edu/) - Stanford course on computer vision/CNN's.
* [CS231n - GitHub](http://cs231n.github.io/)
* [ConvNetJS](http://cs.stanford.edu/people/karpathy/convnetjs/) - Javascript library for deep learning.
# Convolutional Neural Networks (CNNs)
The convolutional neural network (CNN) is a neural network technology that has profoundly impacted the area of computer vision (CV). Fukushima (1980) introduced the original concept of a convolutional neural network, and LeCun, Bottou, Bengio & Haffner (1998) greatly improved this work. From this research, Yan LeCun introduced the famous LeNet-5 neural network architecture. This class follows the LeNet-5 style of convolutional neural network.
**A LeNET-5 Network (LeCun, 1998)**

So far we have only seen one layer type (dense layers). By the end of this course we will have seen:
* **Dense Layers** - Fully connected layers. (introduced previously)
* **Convolution Layers** - Used to scan across images. (introduced this class)
* **Max Pooling Layers** - Used to downsample images. (introduced this class)
* **Dropout Layer** - Used to add regularization. (introduced next class)
## Convolution Layers
The first layer that we will examine is the convolutional layer. We will begin by looking at the hyper-parameters that you must specify for a convolutional layer in most neural network frameworks that support the CNN:
* Number of filters
* Filter Size
* Stride
* Padding
* Activation Function/Non-Linearity
The primary purpose for a convolutional layer is to detect features such as edges, lines, blobs of color, and other visual elements. The filters can detect these features. The more filters that we give to a convolutional layer, the more features it can detect.
A filter is a square-shaped object that scans over the image. A grid can represent the individual pixels of a grid. You can think of the convolutional layer as a smaller grid that sweeps left to right over each row of the image. There is also a hyper parameter that specifies both the width and height of the square-shaped filter. Figure 10.1 shows this configuration in which you see the six convolutional filters sweeping over the image grid:
A convolutional layer has weights between it and the previous layer or image grid. Each pixel on each convolutional layer is a weight. Therefore, the number of weights between a convolutional layer and its predecessor layer or image field is the following:
```
[FilterSize] * [FilterSize] * [# of Filters]
```
For example, if the filter size were 5 (5x4) for 10 filters, there would be 250 weights.
You need to understand how the convolutional filters sweep across the previous layer’s output or image grid. Figure 10.2 illustrates the sweep:

The above figure shows a convolutional filter with a size of 4 and a padding size of 1. The padding size is responsible for the boarder of zeros in the area that the filter sweeps. Even though the image is actually 8x7, the extra padding provides a virtual image size of 9x8 for the filter to sweep across. The stride specifies the number of positions at which the convolutional filters will stop. The convolutional filters move to the right, advancing by the number of cells specified in the stride. Once the far right is reached, the convolutional filter moves back to the far left, then it moves down by the stride amount and
continues to the right again.
Some constraints exist in relation to the size of the stride. Obviously, the stride cannot be 0. The convolutional filter would never move if the stride were set to 0. Furthermore, neither the stride, nor the convolutional filter size can be larger than the previous grid. There are additional constraints on the stride (s), padding (p) and the filter width (f) for an image of width (w). Specifically, the convolutional filter must be able to start at the far left or top boarder, move a certain number of strides, and land on the far right or bottom boarder. The following equation shows the number of steps a convolutional operator
must take to cross the image:
$ steps = \frac{w - f + 2p}{s+1} $
The number of steps must be an integer. In other words, it cannot have decimal places. The purpose of the padding (p) is to be adjusted to make this equation become an integer value.
## Max Pooling Layers
Max-pool layers downsample a 3D box to a new one with smaller dimensions. Typically, you can always place a max-pool layer immediately following convolutional layer. The LENET shows the max-pool layer immediately after layers C1 and C3. These max-pool layers progressively decrease the size of the dimensions of the 3D boxes passing through them. This technique can avoid overfitting (Krizhevsky, Sutskever & Hinton, 2012).
A pooling layer has the following hyper-parameters:
* Spatial Extent (f )
* Stride (s)
Unlike convolutional layers, max-pool layers do not use padding. Additionally, max-pool layers have no weights, so training does not affect them. These layers simply downsample their 3D box input. The 3D box output by a max-pool layer will have a width equal to this equation:
$ w_2 = \frac{w_1 - f}{s + 1} $
The height of the 3D box produced by the max-pool layer is calculated similarly with this equation:
$ h_2 = \frac{h_1 - f}{s + 1} $
The depth of the 3D box produced by the max-pool layer is equal to the depth the 3D box received as input. The most common setting for the hyper-parameters of a max-pool layer are f =2 and s=2. The spatial extent (f) specifies that boxes of 2x2 will be scaled down to single pixels. Of these four pixels, the pixel with the maximum value will represent the 2x2 pixel in the new grid. Because squares of size 4 are replaced with size 1, 75% of the pixel information is lost. The following figure shows this transformation as a 6x6 grid becomes a 3x3:

Of course, the above diagram shows each pixel as a single number. A grayscale image would have this characteristic. For an RGB image, we usually take the average of the three numbers to determine which pixel has the maximum value.
[More information on CNN's](http://cs231n.github.io/convolutional-networks/)
# TensorFlow with CNNs
The following sections describe how to use TensorFlow/Keras with CNNs.
# Access to Data Sets
Keras provides built in access classes for MNIST. It is important to note that MNIST data arrives already separated into two sets:
* **train** - Neural network will be trained with this.
* **test** - Used for validation.
```
import keras
from keras.callbacks import EarlyStopping
from keras.layers import Dense, Dropout
from keras import regularizers
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print("Shape of x_train: {}".format(x_train.shape))
print("Shape of y_train: {}".format(y_train.shape))
print()
print("Shape of x_test: {}".format(x_test.shape))
print("Shape of y_test: {}".format(y_test.shape))
```
# Display the Digits
The following code shows what the MNIST files contain.
```
# Display as text
from IPython.display import display
import pandas as pd
print("Shape for dataset: {}".format(x_train.shape))
print("Labels: {}".format(y_train))
# Single MNIST digit
single = x_train[0]
print("Shape for single: {}".format(single.shape))
display(pd.DataFrame(single.reshape(28,28)))
# Display as image
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
digit = 105 # Change to choose new digit
a = x_train[digit]
plt.imshow(a, cmap='gray', interpolation='nearest')
print("Image (#{}): Which is digit '{}'".format(digit,y_train[digit]))
```
# Define CNN
```
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
batch_size = 128
num_classes = 10
epochs = 12
# input image dimensions
img_rows, img_cols = 28, 28
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print("Training samples: {}".format(x_train.shape[0]))
print("Test samples: {}".format(x_test.shape[0]))
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])
```
## Training/Fitting CNN
The following code will train the CNN for 20,000 steps. This can take awhile, you might want to scale the step count back. GPU training can help. My results:
* CPU Training Time: Elapsed time: 1:50:13.10
* GPU Training Time: Elapsed time: 0:13:43.06
```
import tensorflow as tf
import time
start_time = time.time()
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=2,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))
elapsed_time = time.time() - start_time
print("Elapsed time: {}".format(hms_string(elapsed_time)))
```
## Evaluate Accuracy
Note, if you are using a GPU you might get the **ResourceExhaustedError**. This occurs because the GPU might not have enough ram to predict the entire data set at once.
```
# Predict using either GPU or CPU, send the entire dataset. This might not work on the GPU.
# Set the desired TensorFlow output level for this example
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))
```
GPUs are most often used for training rather than prediction. For prediction either disable the GPU or just predict on a smaller sample. If your GPU has enough memory, the above prediction code may work just fine. If not, just prediction on a sample with the following code:
```
from sklearn import metrics
# For GPU just grab the first 100 images
small_x = x_test[1:100]
small_y = y_test[1:100]
small_y2 = np.argmax(small_y,axis=1)
pred = model.predict(small_x)
pred = np.argmax(pred,axis=1)
score = metrics.accuracy_score(small_y2, pred)
print('Accuracy: {}'.format(score))
```
# Latest Advances in CNN's
He, K., Zhang, X., Ren, S., & Sun, J. (2016). [Deep residual learning for image recognition](https://arxiv.org/abs/1512.03385). In *Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition* (pp. 770-778).
* [Caffee ResNet GitHub](https://github.com/KaimingHe/deep-residual-networks)
* [ResNet in TensorFlow](https://github.com/tensorflow/models/blob/master/resnet/resnet_model.py)
Geoffrey Hinton is suggesting that we might be [doing computer vision wrong](https://www.wired.com/story/googles-ai-wizard-unveils-a-new-twist-on-neural-networks/) and has introduced two new papers about an old technique called Capsule Neural Networks:
* Sabour, S., Frosst, N., & Hinton, G. E. (2017). [Dynamic Routing Between Capsules](https://arxiv.org/abs/1710.09829). arXiv preprint arXiv:1710.09829.
* [Matrix capsules with EM routing](https://openreview.net/forum?id=HJWLfGWRb¬eId=HJWLfGWRb) - ICLR 2018 Blind Submission
# Module 7 Assignment
You can find the first assignmeht here: [assignment 7](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/assignments/assignment_yourname_class7.ipynb)
| true |
code
| 0.501465 | null | null | null | null |
|
```
import numpy as np
from keras.models import Model
from keras.layers import Input
from keras.layers.recurrent import SimpleRNN
from keras import backend as K
import json
from collections import OrderedDict
def format_decimal(arr, places=6):
return [round(x * 10**places) / 10**places for x in arr]
DATA = OrderedDict()
```
### SimpleRNN
**[recurrent.SimpleRNN.0] units=4, activation='tanh'**
Note dropout_W and dropout_U are only applied during training phase
```
data_in_shape = (3, 6)
rnn = SimpleRNN(4, activation='tanh')
layer_0 = Input(shape=data_in_shape)
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3400 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U', 'b']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.0'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[recurrent.SimpleRNN.1] units=5, activation='sigmoid'**
Note dropout_W and dropout_U are only applied during training phase
```
data_in_shape = (8, 5)
rnn = SimpleRNN(5, activation='sigmoid')
layer_0 = Input(shape=data_in_shape)
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3500 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U', 'b']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.1'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[recurrent.SimpleRNN.2] units=4, activation='tanh', return_sequences=True**
Note dropout_W and dropout_U are only applied during training phase
```
data_in_shape = (7, 6)
rnn = SimpleRNN(4, activation='tanh', return_sequences=True)
layer_0 = Input(shape=data_in_shape)
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3600 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U', 'b']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.2'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[recurrent.SimpleRNN.3] units=4, activation='tanh', return_sequences=False, go_backwards=True**
Note dropout_W and dropout_U are only applied during training phase
```
data_in_shape = (7, 6)
rnn = SimpleRNN(4, activation='tanh', return_sequences=False, go_backwards=True)
layer_0 = Input(shape=data_in_shape)
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3700 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U', 'b']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.3'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[recurrent.SimpleRNN.4] units=4, activation='tanh', return_sequences=True, go_backwards=True**
Note dropout_W and dropout_U are only applied during training phase
```
data_in_shape = (7, 6)
rnn = SimpleRNN(4, activation='tanh', return_sequences=True, go_backwards=True)
layer_0 = Input(shape=data_in_shape)
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3800 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U', 'b']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.4'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[recurrent.SimpleRNN.5] units=4, activation='tanh', return_sequences=False, go_backwards=False, stateful=True**
Note dropout_W and dropout_U are only applied during training phase
**To test statefulness, model.predict is run twice**
```
data_in_shape = (7, 6)
rnn = SimpleRNN(4, activation='tanh', return_sequences=False, go_backwards=False, stateful=True)
layer_0 = Input(batch_shape=(1, *data_in_shape))
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3800 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U', 'b']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.5'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[recurrent.SimpleRNN.6] units=4, activation='tanh', return_sequences=True, go_backwards=False, stateful=True**
Note dropout_W and dropout_U are only applied during training phase
**To test statefulness, model.predict is run twice**
```
data_in_shape = (7, 6)
rnn = SimpleRNN(4, activation='tanh', return_sequences=True, go_backwards=False, stateful=True)
layer_0 = Input(batch_shape=(1, *data_in_shape))
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3810 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U', 'b']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.6'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[recurrent.SimpleRNN.7] units=4, activation='tanh', return_sequences=False, go_backwards=True, stateful=True**
Note dropout_W and dropout_U are only applied during training phase
**To test statefulness, model.predict is run twice**
```
data_in_shape = (7, 6)
rnn = SimpleRNN(4, activation='tanh', return_sequences=False, go_backwards=True, stateful=True)
layer_0 = Input(batch_shape=(1, *data_in_shape))
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3820 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U', 'b']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.7'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[recurrent.SimpleRNN.8] units=4, activation='tanh', use_bias=False, return_sequences=True, go_backwards=True, stateful=True**
Note dropout_W and dropout_U are only applied during training phase
**To test statefulness, model.predict is run twice**
```
data_in_shape = (7, 6)
rnn = SimpleRNN(4, activation='tanh', use_bias=False, return_sequences=True, go_backwards=True, stateful=True)
layer_0 = Input(batch_shape=(1, *data_in_shape))
layer_1 = rnn(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(3830 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
weight_names = ['W', 'U']
for w_i, w_name in enumerate(weight_names):
print('{} shape:'.format(w_name), weights[w_i].shape)
print('{}:'.format(w_name), format_decimal(weights[w_i].ravel().tolist()))
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['recurrent.SimpleRNN.8'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
### export for Keras.js tests
```
print(json.dumps(DATA))
```
| true |
code
| 0.417004 | null | null | null | null |
|
<h1>Model Evaluation and Selection</h1>
**Agenda**
- **Regression Evaluation**
- What is the usage of **classification accuracy**?
- How does a **confusion matrix** describe the performance of a classifier?
- **Precision, Recall, F1-score** and **Fb-Score**
- **ROC, AUC curve**
- Evaluation measures for **multi-class** classification
- **Overfitting** and **Underfitting**
- **Cross-Validation**
- **Learning Curves**
- Searching for optimal tuning parameters using **Grid Search** and **Random Search**
**Load Libs**
```
from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import warnings; warnings.filterwarnings('ignore')
```
## Regression Evaluation
```
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
Dataset = load_boston()
X,y = Dataset.data, Dataset.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42, test_size=.3)
clf = LinearRegression().fit(X_train, y_train)
y_pred = clf.predict(X_test)
```
### Mean Absolute Error
<img src='img/eq.jpg' >
<img src='img/mae.png' >
```
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)
```
### Mean Squared Error
<img src="img/eq2.jpg">
```
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred)
```
### R2 Score
<img src='img/r2.png' >
```
from sklearn.metrics import r2_score
r2_score(y_test, y_pred)
```
## Classification Evaluation
### Imbalanced-Data Classification Accuracy
**Dataset Link:** https://www.kaggle.com/mlg-ulb/creditcardfraud <br>
**Alternatively** unzip credit_card_fraud.rar
```
Dataset = pd.read_csv('credit_card_fraud.csv')
print(Dataset.shape)
Dataset.head(10)
X = Dataset.iloc[:,:-1]
target = Dataset.iloc[:,Dataset.shape[1]-1]
target_count = target.value_counts()
print('Not Fraud:', target_count[0])
print('Fraud:', target_count[1])
target_count.plot(kind='bar', title='Count (target)');
```
<img src="img/f2.png">
**Logistic Regression**
```
X_train, X_test, y_train, y_test = train_test_split(X, target, random_state=42, test_size=.3)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(random_state = 42).fit(X_train, y_train)
y_pred = lr.fit(X_train, y_train).predict(X_test)
from sklearn import metrics
print("Accurcy Score: {0}".format(metrics.accuracy_score(y_test, y_pred)))
```
**Dummy Classifiers**
<img src="img/f3.png">
```
from sklearn.dummy import DummyClassifier
dummy_majority = DummyClassifier(strategy = 'most_frequent').fit(X_train, y_train)
y_dummy_predictions = dummy_majority.predict(X_test)
print("Dummy Score: {0}".format(dummy_majority.score(X_test, y_test)))
```
**Accuracy**
<img src="img/acc.png">
### Confusion matrix
**Example**
<img src="img/conf_ex2.png">
<img src='img/conf_eq.png' >
**Confusion Matrix of Dummy Classifer**
```
from sklearn.metrics import confusion_matrix
confusion_dummy = confusion_matrix(y_true=y_test, y_pred=y_dummy_predictions)
print(pd.DataFrame(data=confusion_dummy,
index=["Actuall Not Fraud","Actuall Fraud"],
columns =["Predicted Not Fraud","Predicted Fraud"]))
labels = ['Not Fraud', 'Fraud']
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(confusion_dummy, cmap=plt.cm.Blues)
fig.colorbar(cax)
ax.set_xticklabels([''] + labels)
ax.set_yticklabels([''] + labels)
plt.xlabel('Predicted')
plt.ylabel('Actuall')
plt.show()
```
**Confusion Matrix of Logistic regression**
```
confusion = confusion_matrix(y_true=y_test, y_pred=y_pred)
print(pd.DataFrame(data=confusion,
index=["Actuall Not Fraud","Actuall Fraud"],
columns =["Predicted Not Fraud","Predicted Fraud"]))
labels = ['Not Fraud', 'Fraud']
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(confusion, cmap=plt.cm.Blues)
fig.colorbar(cax)
ax.set_xticklabels([''] + labels)
ax.set_yticklabels([''] + labels)
plt.xlabel('Predicted')
plt.ylabel('Actuall')
plt.show()
```
### Precision
How many of the predicted positive examples are really positive?
<img src='img/pre.png' >
### Recall (Sensitivity)
When the actual value is positive, how often is the prediction correct?
<img src='img/re.png' >
<br>
**Trading Off Precision and Recall**<br>
Can be achieved by e.g. varying decision **threshold** of a classifier.
- Suppose we want to predict y=1 only if very **confident**
- Higher threshold, higher precision, lower recall.
- Suppose we want to **avoid missing** positive examples
- Lower threshold, higher recall, lower precision.
**Which metrics should you focus on?**
- Choice of metric depends on your **business objective**
- **Spam filter** (positive class is "spam"): Optimize for **precision or specificity** because false negatives (spam goes to the inbox) are more acceptable than false positives (non-spam is caught by the spam filter)
- **Fraudulent transaction detector** (positive class is "fraud"): Optimize for **Recall (sensitivity)** because false positives (normal transactions that are flagged as possible fraud) are more acceptable than false negatives (fraudulent transactions that are not detected)
<br>
### F1-Score
**F1-Score** is the **Harmonic Mean** between precision and recall
<img src='img/f1-score.png' >
### Fb-Score
Gives a percentage more **importance/weight** to either **precision** or **recall**
<img src='img/fb-score.png' >
```
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print("Score of Logistic Regression Classifer:")
print(pd.DataFrame(data=[accuracy_score(y_test, y_pred),
precision_score(y_test, y_pred),
recall_score(y_test, y_pred),
f1_score(y_test, y_pred)],
index=["Accuracy","Precision","Recall","F1-Score"],
columns =["Value"]))
print("Score of Dummy Regression Classifer:")
print(pd.DataFrame(data=[accuracy_score(y_test, y_dummy_predictions),
precision_score(y_test, y_dummy_predictions),
recall_score(y_test, y_dummy_predictions),
f1_score(y_test, y_dummy_predictions)],
index=["Accuracy","Precision","Recall","F1-Score"],
columns =["Value"]))
from sklearn.metrics import classification_report
print("Score of Logistic Regression Classifier:")
print(classification_report(y_test, y_pred, target_names=['Not Fraud', 'Fraud']))
print("Score of Dummy Classifier:")
print(classification_report(y_test, y_dummy_predictions, target_names=['Not Fraud', 'Fraud']))
from sklearn.metrics import fbeta_score
print("Fb-Score: {:.2f}".format(fbeta_score(y_test, y_pred, average='macro', beta=2)))
print("Fb-Score: {:.2f}".format(fbeta_score(y_test, y_pred, average='macro', beta=1)))
for THRESHOLD in np.arange(0.1, 1.0, 0.1):
preds = np.where(lr.predict_proba(X_test)[:,1] > THRESHOLD, 1, 0)
print ("THRESHOLD= {:.1f}".format(THRESHOLD))
print(pd.DataFrame(data=[precision_score(y_test, preds),
recall_score(y_test, preds),],
index=["Precision", "Recall"],
columns =["Value"]))
print()
print()
```
### ROC curves, Area-Under-Curve (AUC)
**Recall (Sensitivity)**
**When the actual value is positive, how often is the prediction correct?**
<img src='img/re.png' >
**Specificity**
**When the actual value is negative, how often is the prediction correct?**
<img src='img/spec.png'>
```
from sklearn.metrics import roc_curve, auc
y_score_lr = lr.fit(X_train, y_train).decision_function(X_test)
fpr_lr, tpr_lr, _ = roc_curve(y_test, y_score_lr)
plt.figure(num=None, figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.xlim([-0.01, 1.00])
plt.ylim([-0.01, 1.01])
plt.plot(fpr_lr, tpr_lr, lw=3, label='AUC: {:0.2f})'.format(metrics.roc_auc_score(y_test, y_score_lr)))
plt.xlabel('False Positive Rate (Specifity)', fontsize=16)
plt.ylabel('True Positive Rate (Sensitivity)', fontsize=16)
plt.title('ROC curve', fontsize=16)
plt.legend(loc='lower right', fontsize=13)
plt.plot([0, 1], [0, 1], color='navy', lw=3, linestyle='--')
plt.axes().set_aspect('equal')
plt.show()
```
**AUC = 0 (worst) AUC = 1 (best)**
**ROC/AUC advantages:**
- Does not require you to **set a classification threshold**
- Still useful when there is **high class imbalance**
- Gives a **single number** for easy comparison.
## Evaluation measures for multi-class classification
**Data Preparation**
```
from sklearn.ensemble import RandomForestClassifier
import seaborn as sns
from sklearn.datasets import fetch_olivetti_faces
dataset = fetch_olivetti_faces()
X, y = dataset.data, dataset.target
X_train_mc, X_test_mc, y_train_mc, y_test_mc = train_test_split(X, y, random_state=0)
```
**Classification**
```
clf = RandomForestClassifier(n_estimators=200, max_depth=15,
random_state=42).fit(X_train_mc, y_train_mc)
clf_predicted_mc = clf.predict(X_test_mc)
```
**Confusion Matrix**
```
confusion_mc = confusion_matrix(y_test_mc, clf_predicted_mc)
df_cm = pd.DataFrame(confusion_mc,
index = [i for i in range(0,confusion_mc.shape[0])], columns = [i for i in range(0,confusion_mc.shape[1])])
plt.figure(num=None, figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
sns.heatmap(df_cm, annot=True)
plt.title('Random Forest Classifier \nAccuracy:{0:.3f}'.format(accuracy_score(y_test_mc,
clf_predicted_mc)))
plt.ylabel('Actuall label')
plt.xlabel('Predicted label')
print(classification_report(y_test_mc, clf_predicted_mc))
```
## Overfitting and Underfitting
- Machine Learning models have one sole purpose; to generalize well.<br>
- A model that **generalizes** well is a model that is neither **underfit** nor **overfit.**
- **Generalization** is the model’s ability to give sensible outputs to sets of input that it has never seen before.
```
from sklearn.tree import DecisionTreeRegressor
# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))
# Plot the results
plt.figure(num=None, figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.scatter(X, y, s=20, edgecolor="black",
c="darkorange", label="data")
plt.xlabel("data")
plt.ylabel("target")
plt.title("Data")
plt.legend()
plt.show()
```
<br>
<br>
**Overfitting** is the case where the overall cost is really small, but the generalization of the model is unreliable. This is due to the model learning “too much” from the training data set.
```
# Fit regression model
clf = DecisionTreeRegressor(max_depth=15)
clf.fit(X, y)
# Predict
y_1 = clf.predict(X)
# Plot the results
plt.figure(num=None, figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.scatter(X, y, s=20, edgecolor="black",
c="darkorange", label="data")
plt.plot(X, y_1, color="cornflowerblue",
label="max_depth=15", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Overfitting")
plt.legend()
plt.show()
```
**Overfitting** happens when the model is too complex relative to the amount and noisiness of the training data.<br><br>
**Possible Solutions:**
- Simplify the model by selecting one with fewer parameters.
- Gather more training data.
- Reduce the noise in the training data.
- Apply Cross- Validation.
<br>
<br>
**Underfitting** is the case where the model has “ not learned enough” from the training data, resulting in low generalization and unreliable predictions.
```
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0, test_size=0.9)
# Fit regression model
clf = DecisionTreeRegressor(max_depth=1)
clf.fit(X_train, y_train)
# Predict
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = clf.predict(X_test)
# Plot the results
plt.figure(num=None, figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.scatter(X, y, s=20, edgecolor="black",
c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",
label="max_depth=1", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Underfitting")
plt.legend()
plt.show()
```
**Underfitting** occurs when your model is too simple to learn the underlying structure of the data.<br><br>
**Possible Solutions:**
- Selecting a more powerful model, with more parameters.
- Feeding better features to the learning algorithm.
- Reducing the constraints on the model,
<br>
<br>
## Model selection using evaluation metrics
**Train/test on same data**
- Typically overfits and likely won't generalize well to new data.
- **Not recommended**
### Single train/test split (Holdout)
- Fast and simple.
- In most patterns we don't have the **luxury** of large data set.
- Generally, this split will be close to 80% of the data for training and 20% of the data for testing.
- Splitting the data set into training and testing sets will leave us with either **insufficient training or testing patterns**.
- Clearly the testing data set contains **useful information** for learning. Yet, they are **ignored** and not used for training purposes in the data splitting error rate estimation method.
- If dataset is not completely even. In splitting our dataset we may end up splitting it in such a way that our training set is very different from the test
<img src='img/holdout.png'>
```
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
digits = load_breast_cancer()
X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2 , random_state=2233)
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
print(classification_report(y_test, y_pred))
```
### K-fold cross-validation
- K train-test splits.
- Average metric over all splits.
- Randomly split our dataset into K equally sized parts.
<br>
<br>
**K-fold cross-validation algorithm**
1. Split the dataset into K **equal** partitions (or "folds").
2. Use fold 1 as the **testing set** and the union of the other folds as the **training set**.
3. Calculate **testing accuracy**.
4. Repeat steps 2 and 3 K times, using a **different fold** as the testing set each time.
5. Use the **average testing accuracy** as the estimate of out-of-sample accuracy.
<img src='img/k1.png'>
```
data = load_breast_cancer()
X, y = data.data, data.target
from sklearn.model_selection import cross_val_score
knn = KNeighborsClassifier(n_neighbors=5)
# use recall as scoring metric
scores = cross_val_score(knn, X, y, cv=5, scoring = 'f1')
print('Cross-validation (F1-Score)', scores)
print("Average cross-validation score (F1-Score) : {:.3f}".format(scores.mean()))
print()
```
### RepeatedKFold
- the most robust of cross validation methods.
- Similar to K-Fold, we set a value for K which signifies the number of times we will train our model. However, in this case K will not represent the number of equally sized partitions.
- on each training iteration, we randomly select points to be for the testing set.
- The advantage of this method over K-Fold is that the proportion of the train-test split is not dependent on the number of iterations.
- The disadvantage of this method is that some points may never be selected to be in the test subset at all — at the same time, some points might be selected multiple times.
<img src='k2.png' >
```
from sklearn.metrics import f1_score
from sklearn.model_selection import RepeatedKFold
data = load_breast_cancer()
X, y = data.data, data.target
rkf = RepeatedKFold(n_splits=5, n_repeats=2, random_state=42)
l = []
knn = KNeighborsClassifier(n_neighbors=5)
for train_index, test_index in rkf.split(X):
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
l.append(f1_score(y_test, y_pred))
print('RepeatedKFold (F1-Score)', l)
print("Average RepeatedKFold score (F1-Score) : {:.3f}".format(sum(l) / len(l)))
```
<br>
<br>
### Learning Curves
- **Train Learning Curve:** Learning curve calculated from the training dataset that gives an idea of how well the model is learning.
- **Validation Learning Curve:** Learning curve calculated from a hold-out validation dataset that gives an idea of how well the model is generalizing.
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
from sklearn.tree import DecisionTreeClassifier
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=None, train_sizes=np.linspace(.1, 1.0, 5)):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="validation score")
plt.legend(loc="best")
return plt
digits = load_digits()
X, y = digits.data, digits.target
```
**Underfitting:** A model of a given complexity will underfit a large dataset: this means that the training score will decrease, but the validation score will increase
<br>
1. Example of Training Learning Curve Showing an Underfit Model That Requires Further Training
```
title = "Learning Curves (Naive Bayes)"
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01))
```
2. Example of Training Learning Curve Showing An Underfit Model That Does Not Have Sufficient Capacity
```
title = "Learning Curves (SVC)"
estimator = SVC(gamma=0.1)
plot_learning_curve(estimator, title, X, y)
plt.show()
```
**Overfitting:** A model of a given complexity will overfit a small dataset: this means the training score will be relatively high, while the validation score increases to a point and begins decreasing again.
```
title = "Learning Curves (Decision Tree)"
cv = ShuffleSplit(n_splits=10, test_size=0.001, random_state=0)
estimator = DecisionTreeClassifier(random_state=42, max_depth=100)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv)
plt.show()
```
**Good Fit:** A model will never, except by chance, give a better score to the validation set than the training set: this means the curves should keep getting closer together but never cross.
```
title = "Learning Curves (SVC)"
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv)
plt.show()
```
### Searching for optimal tuning parameters using Grid Search and Random Search
#### Grid Search
<img src='grid.png' >
```
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
dataset = load_digits()
X, y = dataset.data, dataset.target == 1
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
clf = SVC(kernel='rbf')
grid_values = {'C': [ 0.01, 0.1, 1, 10, 100],
'gamma': [ 0.005, 0.01, 0.05, 0.1, 1, 10, 100]}
grid_clf = GridSearchCV(clf, param_grid = grid_values,cv=5, scoring = 'f1_micro')
grid_clf.fit(X_train, y_train)
y_decision_fn_scores = grid_clf.decision_function(X_test)
print('Grid best score (F1): {:.2f}'.format(grid_clf.best_score_))
print('Grid best parameter (max. F1): ', grid_clf.best_params_)
print('Grid best Estimator: ',grid_clf.best_estimator_)
```
#### Random Search
<img src='rand.png' >
```
from sklearn.model_selection import RandomizedSearchCV
from sklearn.neighbors import KNeighborsClassifier
param_dist = dict(n_neighbors=list(range(1, 200)), weights=['uniform', 'distance']
,algorithm =['auto', 'ball_tree', 'kd_tree', 'brute']
,leaf_size=list(range(1, 70)), p = [1,2]
)
knn = KNeighborsClassifier()
rand = RandomizedSearchCV(knn, param_dist, cv=5, scoring='f1_micro', n_iter=100)
rand.fit(X_train, y_train)
y_decision_fn_scores = rand.predict(X_test)
print('Grid best score (F1): {:.2f}'.format(rand.best_score_))
print('Grid best parameter (max. F1): ', rand.best_params_)
print('Grid best Estimator: ',rand.best_estimator_)
```
#### Grid Search vs Random Search
<img src='com.png' >
**Grid Search**
- Works best for lower dimensional data.
- finds the optimal parameter.
- Finds the best soultion.
- Slower.
**Random Search**
- Works best for higher dimensional data.
- The optimal parameter is not found since we do not have it in our grid.
- Finds the near best solution.
- Faster.
<br><br><br><br>
**Comments or Questions?**
- Email: <baghdady.usama@gmail.com>
- Linkedin: www.linkedin.com/in/usama-albaghdady-76944057
- Facebook: www.facebook.com/baghdady.usama
| true |
code
| 0.683314 | null | null | null | null |
|
# To evaluta the network of classifer, we trained the model on GTSRB dataset
Thanks for the great selfless tutorial: https://chsasank.github.io/keras-tutorial.html
```
import numpy as np
from skimage import io, color, exposure, transform
from sklearn.cross_validation import train_test_split
import os
import glob
import h5py
from time import time
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential, model_from_json
from keras.layers import Dense, Dropout, Activation, Flatten, BatchNormalization, Merge
from keras.layers import Convolution2D, MaxPooling2D, AveragePooling2D
from keras.optimizers import SGD, Adam, RMSprop
from keras.utils import np_utils
from keras.callbacks import LearningRateScheduler, ModelCheckpoint, TensorBoard, ReduceLROnPlateau
from keras.regularizers import l2
from keras import backend as K
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# for auto-reloading external modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
NUM_CLASSES = 43
IMG_SIZE = 48
```
## Function to preprocess the image:
```
def preprocess_img(img):
# Histogram normalization in y
# hsv = color.rgb2hsv(img)
# hsv[:,:,2] = exposure.equalize_hist(hsv[:,:,2])
# img = color.hsv2rgb(hsv)
# central scrop
min_side = min(img.shape[:-1])
centre = img.shape[0]//2, img.shape[1]//2
img = img[centre[0]-min_side//2:centre[0]+min_side//2,
centre[1]-min_side//2:centre[1]+min_side//2,
:]
# //代表 整数除法
# rescale to standard size
img = transform.resize(img, (IMG_SIZE, IMG_SIZE))
# 注意对于tensorflow和theano通道顺序的不同
# roll color axis to axis 0
#img = np.rollaxis(img,-1)
return img
def get_class(img_path):
return int(img_path.split('/')[-2])
```
## Preprocess all training images into a numpy array
```
try:
with h5py.File('X.h5') as hf:
X, Y = hf['imgs'][:], hf['labels'][:]
print("Loaded images from X.h5")
except (IOError,OSError, KeyError):
print("Error in reading X.h5. Processing all images...")
root_dir = '/home/jia/Desktop/traffic_sign_keras1.2/GTSRB_Train_images/Final_Training/Images/'
imgs = []
labels = []
all_img_paths = glob.glob(os.path.join(root_dir, '*/*.ppm'))
#打乱图片路径顺序
np.random.shuffle(all_img_paths)
for img_path in all_img_paths:
try:
img = preprocess_img(io.imread(img_path))
# io.imread 读入的数据是 uint8
label = get_class(img_path)
imgs.append(img)
labels.append(label)
if len(imgs)%1000 == 0: print("Processed {}/{}".format(len(imgs), len(all_img_paths)))
except (IOError, OSError):
print('missed', img_path)
pass
X = np.array(imgs, dtype='float32')
Y = np.eye(NUM_CLASSES, dtype='uint8')[labels]
# Y = ***[labels] 生成one-hot编码的方式
with h5py.File('X.h5','w') as hf:
hf.create_dataset('imgs', data=X)
hf.create_dataset('labels', data=Y)
```
# Load and Preprocess Test images
```
try:
with h5py.File('X_test.h5') as hf:
X_test, y_test = hf['imgs'][:], hf['labels'][:]
print("Loaded images from X_test.h5")
except (IOError,OSError, KeyError):
print("Error in reading X.h5. Processing all images...")
import pandas as pd
test = pd.read_csv('/home/jia/Desktop/traffic_sign_keras1.2/GTSRB_Test_images/Final_Test/Images/GT-final_test.csv',sep=';')
X_test = []
y_test = []
i = 0
for file_name, class_id in zip(list(test['Filename']), list(test['ClassId'])):
img_path = os.path.join('/home/jia/Desktop/CS231N_AND_traffic_sign_keras1.2/GTSRB_Test_images/Final_Test/Images/',file_name)
X_test.append(preprocess_img(io.imread(img_path)))
y_test.append(class_id)
X_test = np.array(X_test, dtype='float32')
y_test = np.array(y_test, dtype='uint8')
with h5py.File('X_test.h5','w') as hf:
hf.create_dataset('imgs', data=X_test)
hf.create_dataset('labels', data=y_test)
index=np.zeros(1307, dtype='int')
for i in range(1307):
index[i]=i*30+np.random.randint(0,30)
X_val = X[index]
y_val = Y[index]
# creat the training index1
index1=np.setdiff1d(np.array(range(39210)), index, assume_unique=True)
X_train=X[index1]
y_train=Y[index1]
normalize = 0
# Normalize the data: subtract the mean image
if normalize:
mean_image = np.mean(X_train, axis=0)
X_train -= mean_image
X_val -= mean_image
X_test -= mean_image
print 'Train data shape: ', X_train.shape
print 'Train labels shape: ', y_train.shape
print 'Validation data shape: ', X_val.shape
print 'Validation labels shape: ', y_val.shape
print 'Test data shape: ', X_test.shape
print 'Test labels shape: ', y_test.shape
```
# Show Traffic Sign Examples
```
# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = [8, 11, 14,16, 26, 33, 38]
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_test == cls) #返回扁平化数组之后非0元素的index, y是数字标签
idxs = np.random.choice(idxs, samples_per_class, replace=False) #replace=False 使得随即选取的没有重复的
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
img=X_test[idx].copy()
plt.imshow(img) #X原始是float64,图像显示要变成uint8
plt.axis('off') #取消axis的显示
if i == 0:
plt.title(cls)
foo_fig = plt.gcf() # 'get current figure'
#foo_fig.savefig('foo.eps', format='eps', dpi=1000)
foo_fig.savefig('jiatong.png', format='png', dpi=300)
plt.close()
```
# Initialization of Weights
```
from keras import backend as K
import numpy as np
def my_init(shape, name=None):
value = np.random.random(shape)
return K.variable(value, name=name)
```
# Define Keras model
```
# 注意keras使用tensorflow和thano不同后台, 数据输入的通道顺序不同哦
def cnn_model():
branch_0= Sequential()
branch_1 = Sequential()
model0 = Sequential()
model = Sequential()
# ********************************************** 48*48
model0.add(Convolution2D(32, 3, 3, border_mode='same', init='he_normal' , input_shape=(IMG_SIZE, IMG_SIZE, 3)))
model0.add(BatchNormalization(epsilon=1e-06, axis=3))
model0.add(Activation('relu'))
model0.add(Convolution2D(48, 7, 1, border_mode='same', init='he_normal'))
model0.add(BatchNormalization(epsilon=1e-06, axis=3))
model0.add(Activation('relu'))
model0.add(Convolution2D(48, 1, 7, border_mode='same', init='he_normal'))
model0.add(BatchNormalization(epsilon=1e-06, axis=3))
model0.add(Activation('relu'))
model0.add(MaxPooling2D(pool_size=(2, 2)))
model0.add(Dropout(0.2))
# ****************************************** 24*24
branch_0.add(model0)
branch_1.add(model0)
branch_0.add(Convolution2D(64, 3, 1, border_mode='same', init='he_normal'))
branch_0.add(BatchNormalization(epsilon=1e-06, axis=3))
branch_0.add(Activation('relu'))
branch_0.add(Convolution2D(64, 1, 3, border_mode='same', init='he_normal'))
branch_0.add(BatchNormalization(epsilon=1e-06, axis=3))
branch_0.add(Activation('relu'))
branch_1.add(Convolution2D(64, 1, 7, border_mode='same', init='he_normal'))
branch_1.add(BatchNormalization(epsilon=1e-06, axis=3))
branch_1.add(Activation('relu'))
branch_1.add(Convolution2D(64, 7, 1, border_mode='same', init='he_normal'))
branch_1.add(BatchNormalization(epsilon=1e-06, axis=3))
branch_1.add(Activation('relu'))
model.add(Merge([branch_0, branch_1], mode='concat', concat_axis=-1))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.2))
# ******************************************* 12*12
model.add(Convolution2D(128, 3, 3, border_mode='same', init='he_normal'))
model.add(BatchNormalization(epsilon=1e-06, axis=3))
model.add(Activation('relu'))
model.add(Convolution2D(256, 3, 3, border_mode='same', init='he_normal')) # 之前是256个滤波器
model.add(BatchNormalization(epsilon=1e-06, axis=3))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.3))
# *************************************** 6*6
model.add(Flatten())
model.add(Dense(256, init='he_normal'))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(0.4))
model.add(Dense(NUM_CLASSES, activation='softmax', init='he_normal'))
return model
model = cnn_model()
# let's train the model using SGD + momentum (how original).
lr = 0.001
sgd = SGD(lr=lr, decay=1e-6, momentum=0.9, nesterov=True)
adm = Adam(lr=0.001, decay=1e-6) #之前没有设置decay
model.compile(loss='categorical_crossentropy',
optimizer=adm,
metrics=['accuracy'])
def lr_schedule(epoch):
return lr * (0.1 ** int(epoch/10))
```
# Plot and Save the model
```
from keras.utils.visualize_util import plot
plot(model, to_file='model.png')
```
# Start Training
```
batch_size = 16
nb_epoch = 30
t1=time()
history = model.fit(X_train, y_train, batch_size=batch_size,
nb_epoch=nb_epoch,
validation_data=(X_val, y_val),
shuffle = True
)
t2=time()
print (t2-t1)
```
# Test on the Test Dataset
```
t1=time()
y_pred = model.predict_classes(X_test)
t2=time()
acc = np.mean(y_pred==y_test)
print("Test accuracy = {}".format(acc))
print (t2-t1)
```
# Plot the Training History
```
plt.figure(figsize=(6,5))
plt.plot(history.history['loss'], '-o')
plt.plot(history.history['val_loss'], '-x')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'], loc='upper right')
plt.show()
plt.figure(figsize=(6,5))
plt.plot(history.history['acc'], '-o')
plt.plot(history.history['val_acc'], '-x')
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train_acc', 'val_acc'], loc='lower right')
plt.show()
```
# Load Test data
```
# 将类别标签转换成为 one-hot 编码, 如果需要的话
#from keras.utils.np_utils import to_categorical
#y_test1 = to_categorical(y_test, 43)
```
# With Data augmentation
```
from sklearn.cross_validation import train_test_split
datagen = ImageDataGenerator(featurewise_center=False,
featurewise_std_normalization=False,
width_shift_range=0.1,
height_shift_range=0.1,
zoom_range=0.2,
shear_range=0.1,
rotation_range=10.,)
datagen.fit(X_train)
# # Reinstallise models
# model = cnn_model()
# # let's train the model using SGD + momentum (how original).
# lr = 0.001
# sgd = SGD(lr=lr, decay=1e-6, momentum=0.9, nesterov=True)
# model.compile(loss='categorical_crossentropy',
# optimizer=adm,
# metrics=['accuracy'])
# def lr_schedule(epoch):
# return lr*(0.1**int(epoch/10))
```
# Training based on the former model
```
nb_epoch = 200
history2=model.fit_generator(datagen.flow(X_train, y_train, batch_size=batch_size),
samples_per_epoch=X_train.shape[0],
nb_epoch=nb_epoch,
validation_data=(X_val, y_val),
callbacks=[ReduceLROnPlateau('val_loss', factor=0.2, patience=20, verbose=1, mode='auto'),
ModelCheckpoint('model_final.h5',save_best_only=True)]
)
model.save('my_model_99.66.h5')
t1=time()
y_pred = model.predict_classes(X_test)
t2=time()
acc = np.mean(y_pred==y_test)
print("Test accuracy = {}".format(acc))
print (t2-t1)
model.summary()
model.count_params()
```
| true |
code
| 0.452536 | null | null | null | null |
|
### Import Numpy & Math libraries
```
import numpy as np
import math
```
### Assuming a 200 Layer Neural Network
#### Let's see what happens to the Mean and Std-Dev at the end of 200 layer computations when we randomly initialize from a standard distribution (Using np.random.randn)
```
x = np.random.randn(256)
for i in range(200):
a = np.random.randn(256, 256)
x = np.matmul(a, x)
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}'.format(x.std()))
```
#### Above results show that the activations blew and the mean & std-dev are too high. Let's see after which layer this actually happened...
```
x = np.random.randn(256)
for i in range(200):
a = np.random.randn(256, 256)
x = np.matmul(a, x)
if np.isinf(x.std()):
break
print('Layer : {}'.format(i))
```
#### At Layer 127, the std-dev went close to inf!!!
#### Let's see if we initialize it too low, having a std-dev of 0.01
```
x = np.random.randn(256)
for i in range(200):
a = np.random.randn(256, 256) * 0.01
x = np.matmul(a, x)
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}'.format(x.std()))
```
#### As we can see, the values are too low and have vanished completely!!!
#### The matrix product of our inputs x and weight matrix a that we initialized from a standard normal distribution will, on average, have a standard deviation very close to the square root of the number of input connections i.e √256
```
for i in range(200):
x = np.random.randn(256)
a = np.random.randn(256, 256)
y = np.matmul(a, x)
print('Mean : {}'.format(y.mean()))
print('Std-Dev : {}'.format(y.std()))
print('Sqrt of 256 : {}'.format(math.sqrt(256)))
```
#### We see a Std-Dev of 0 when we initialize with 1 as parameter for the standard normal distribution
```
for i in range(200):
x = np.random.randn(1)
a = np.random.randn(1)
y = np.matmul(a, x)
print('Mean : {}'.format(y.mean()))
print('Std-Dev : {}'.format(y.std()))
```
#### If we first scale the weight matrix a by dividing all its randomly chosen values by √256, the element-wise multiplication that fills in one element of the outputs y would now, on average, have a variance of only 1/√256.
```
for i in range(200):
x = np.random.randn(256)
a = np.random.randn(256, 256) * math.sqrt(1./256)
y = np.matmul(a, x)
print('Mean : {}'.format(y.mean()))
print('Std-Dev : {}\n'.format(y.std()))
```
#### Let's scale the weights by 1/√n, where n is the number of network input connections at a layer (256 in our case)
```
x = np.random.randn(256)
for i in range(200):
a = np.random.randn(256, 256) * math.sqrt(1./256)
x = np.matmul(a, x)
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
#### Voila!!! Certainly did not explode at the end of 200 layers also!!!
#### Let's see what happens if we scale the weights and have a network size of 1000
```
x = np.random.randn(256)
for i in range(1000):
a = np.random.randn(256, 256) * math.sqrt(1./256)
x = np.matmul(a, x)
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
#### Certainly impressive results, they are not yet blown even after 1000 layer
### Let's attach activation functions and look at the results
```
def tanh(x):
return np.tanh(x)
def sigmoid(x):
s = 1.0/(1 + np.exp(-x))
return s
def ReLU(x):
r = np.maximum(0, x)
return r
```
#### Tanh Activation + Standard Normal Distribution
```
x = np.random.randn(256)
for i in range(200):
a = np.random.randn(256, 256) * math.sqrt(1./256)
x = tanh(np.matmul(a, x))
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
#### Sigmoid Activation + Standard Normal Distribution
```
x = np.random.randn(256)
for i in range(200):
a = np.random.randn(256, 256) * math.sqrt(1./256)
x = sigmoid(np.matmul(a, x))
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
#### Conceptually, it makes sense that when using activation functions that are symmetric about zero and have outputs inside [-1,1], such as softsign and tanh, we’d want the activation outputs of each layer to have a mean of 0 and a standard deviation around 1, on average. Let's see if applied to ReLU
#### ReLU + Standard Normal Distribution fails drastically
```
x = np.random.randn(256)
for i in range(200):
a = np.random.randn(256, 256) * math.sqrt(1./256)
x = ReLU(np.matmul(a, x))
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
#### In ReLU the Std-dev is quite close to the square root of the number of input connections, divided by the square root of two, or √256/√2 here
```
for i in range(200):
x = np.random.randn(256)
a = np.random.randn(256, 256)
y = ReLU(np.matmul(a, x))
print('Mean : {}'.format(y.mean()))
print('Std-Dev : {}\n'.format(y.std()))
math.sqrt(256/2)
```
#### Scaling the weights by this number i.e. 2 will help our cause. One more reason of choosing two is increase the influence by 2 as half of the weights are lost when f(x)<0
```
x = np.random.randn(256)
for i in range(200):
a = np.random.randn(256, 256) * math.sqrt(2./256)
x = ReLU(np.matmul(a, x))
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
#### Tanh + Uniform Normal Distribution fails drastically
```
x = np.random.randn(256)
for i in range(200):
a = np.random.uniform(-1, 1, (256, 256)) * math.sqrt(1./256)
x = tanh(np.matmul(a, x))
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
#### Xavier Initialization + Tanh works well
```
x = np.random.randn(256)
for i in range(200):
a = np.random.uniform(-1, 1, (256, 256)) * math.sqrt(6./(256 + 256))
x = tanh(np.matmul(a, x))
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
#### Xavier Initialization + ReLU fails!
```
x = np.random.randn(256)
for i in range(200):
a = np.random.uniform(-1, 1, (256, 256)) * math.sqrt(6./(256 + 256))
x = ReLU(np.matmul(a, x))
print('Mean : {}'.format(x.mean()))
print('Std-Dev : {}\n'.format(x.std()))
```
## Summary
#### Xavier Init with ReLU fails
#### Xavier Init and Std Normal Distribution with all zero-centered activations will work well (Tanh, Sigmoid etc)
#### Std Normal Distribution scaled by sqrt(2/n) with ReLU works well where n is no. of neurons
| true |
code
| 0.391871 | null | null | null | null |
|
# 準ニュートン法
引き続き、非線形最適化の手法について学習していきましょう。
今回は、ニュートン法においてその計算が必要であったヘッセ行列(の逆行列) の近似を、計算の過程で並行して求めることで、ニュートン法のような高速な収束性を、より少ない計算量で行うことのできる、**準ニュートン法**について扱います。
準ニュートン法に於けるヘッセ行列(の逆行列) の近似公式はいくつも知られていますが、ここではAnaconda に標準で添付されているSciPy において提供される、BFGS(Broyden-Fletcher-Goldfarb-Shanno) 公式による準ニュートン法について、その生成点列の挙動を確認しましょう。
```
import numpy as np
from scipy.optimize import line_search
def sdm(xk, iter=15):
sequence = [xk]
for k in range(iter):
dk = -jac(xk)
alpha = line_search(fun, jac, xk, dk)[0]
xk = xk + alpha * dk
sequence.append(xk)
return np.array(sequence)
```
## 目的関数
今回も、前々回、前回と扱ってきた、
\begin{align*}
f(x_0, x_1):=\sin\left(\frac{1}{2}x_0^2-\frac{1}{4}x_1^2+3\right)\cos(2x_0+1-e^{x_1})
\end{align*}
を目的関数として考えましょう。
この関数は、前回確認した通り、下記のような複雑な形状をしていました。
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(8, 6), dpi=80)
ax = plt.axes(projection='3d')
X, Y = np.meshgrid(np.linspace(-1, 1, 100), np.linspace(-1, 1, 100))
Z = np.array([[np.sin((x ** 2) / 2 - (y ** 2 ) / 4 + 3) * np.cos(2 * x + 1 - np.exp(y)) for x, y in zip(vx, vy)] for vx, vy in zip(X, Y)])
ax.plot_surface(X, Y, Z, cmap='plasma')
```
この目的関数`fun` およびその勾配`jac` は、それぞれ下記のようにSymPy を用いてPython 関数として導出することができました。
後にNewton 法とも結果の比較を行うために、ヘッセ行列`hess` も同時に求めておきましょう。
```
import numpy as np
from sympy import symbols, sin, cos, exp, diff
_x, _y = symbols('x, y')
F = sin((_x ** 2) / 2 - (_y ** 2) / 4 + 3) * cos(2 * _x + 1 - exp(_y))
FdX, FdY = diff(F, _x), diff(F, _y)
FdXdX, FdXdY = diff(FdX, _x), diff(FdX, _y)
FdYdX, FdYdY = diff(FdY, _x), diff(FdY, _y)
def fun(x):
p = {_x: x[0], _y: x[1]}
return float(F.subs(p))
def jac(x):
p = {_x: x[0], _y: x[1]}
return np.array([FdX.subs(p), FdY.subs(p)], dtype=np.float)
def hess(x):
p = {_x: x[0], _y: x[1]}
return np.array([[FdXdX.subs(p), FdXdY.subs(p)],
[FdYdX.subs(p), FdYdY.subs(p)]], dtype=np.float)
```
## BFGS 公式による準ニュートン法
それでは早速、実験をしてみましょう。
BFGS 公式による準ニュートン法は、下記の関数により実行することができます。
```python
from scipy.optimize import minimize
x = minimize(fun, x0, method='bfgs', jac=jac).x
```
前回の信頼領域法と同様に、``scipy.optimize`` モジュールの``minimize`` 関数より、最適化アルゴリズムを呼び出すことができます。
信頼領域法と異なり、ヘッセ行列を指定する必要はなく、目的関数``fun``、初期点``x0`` および勾配``jac`` を与えることで実行できます。
それでは早速、生成点列の挙動を確認してみましょう。
初期点は前回までと同様に、$x^{(0)}:=(-0.3, 0.2)^\top$ を与えるものとします。
ここでは、比較のため、最急降下法とニュートン法による生成点列も同時にプロットしてみましょう。
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize, line_search
def newton(xk, iter=15):
sequence = [xk]
return np.array(sequence)
X, Y = np.meshgrid(np.linspace(-1, 1, 100), np.linspace(-1, 1, 100))
plt.ylim(-1, 1)
plt.xlim(-1, 1)
Z = np.array([[np.sin((x ** 2) / 2 - (y ** 2 ) / 4 + 3) * np.cos(2 * x + 1 - np.exp(y)) for x, y in zip(vx, vy)] for vx, vy in zip(X, Y)])
plt.contour(X, Y, Z, cmap='plasma', levels=np.linspace(np.min(Z), np.max(Z), 15))
sequence = [np.array([-0.3, 0.2])]
for k in range(15):
dk = -jac(sequence[-1])
alpha = line_search(fun, jac, sequence[-1], dk)[0]
sequence.append(sequence[-1] + alpha * dk)
sequence = np.array(sequence)
plt.plot(sequence[:, 0], sequence[:, 1], marker='o', label='sdm')
sequence = [np.array([-0.3, 0.2])]
for k in range(15):
sequence.append(sequence[-1] + np.linalg.solve(hess(sequence[-1]), -jac(sequence[-1])))
sequence = np.array(sequence)
plt.plot(sequence[:, 0], sequence[:, 1], marker='v', label='newton')
sequence = [np.array([-0.3, 0.2])]
minimize(fun, sequence[0], method='bfgs', jac=jac, callback=lambda xk: sequence.append(xk))
sequence = np.array(sequence)
plt.plot(sequence[:, 0], sequence[:, 1], marker='^', label='bfgs')
plt.legend()
```
準ニュートン法による生成点列は、多少の振動こそ起きていますが、最急降下法(sdm) のような極端な振動はなく、しかしニュートン法(newton) のように発散はせずに、比較的効率的に最適解へ収束していることが見て取れます。
## 参考文献
* 福島雅夫著『新版 数理計画入門』(朝倉書店; 2011)
* 矢部博著『工学基礎 最適化とその応用』(数理工学社; 2006)
* J. Nocedal, S. J. Wright: Numerical Optimization (2nd ed.), Springer (2006)
* [Gradient descent - Wikipedia](https://en.wikipedia.org/wiki/Gradient_descent) (目的関数はこのページのものを使用しました。)
| true |
code
| 0.497437 | null | null | null | null |
|
# DAG Creation and Submission
Launch this tutorial in a Jupyter Notebook on Binder:
[](https://mybinder.org/v2/gh/htcondor/htcondor-python-bindings-tutorials/master?urlpath=lab/tree/DAG-Creation-And-Submission.ipynb)
In this tutorial, we will learn how to use `htcondor.dags` to create and submit an HTCondor DAGMan workflow.
Our goal will be to create an image of the Mandelbrot set.
This is a perfect problem for high-throughput computing because each point in the image can be calculated completely independently of any other point, so we are free to divide the image creation up into patches, each created by a single HTCondor job.
DAGMan will enter the picture to coordinate stitching the image patches we create back into a single image.
## Making a Mandelbrot set image locally
We'll use `goatbrot` (https://github.com/beejjorgensen/goatbrot) to make the image.
`goatbrot` can be run from the command line, and takes a series of options to specify which part of the Mandelbrot set to draw, as well as the properties of the image itself.
`goatbrot` options:
- `-i 1000` The number of iterations.
- `-c 0,0` The center point of the image region.
- `-w 3` The width of the image region.
- `-s 1000,1000` The pixel dimensions of the image.
- `-o test.ppm` The name of the output file to generate.
We can run a shell command from Jupyter by prefixing it with a `!`:
```
! ./goatbrot -i 10 -c 0,0 -w 3 -s 500,500 -o test.ppm
! convert test.ppm test.png
```
Let's take a look at the test image. It won't be very good, because we didn't run for very many iterations.
We'll use HTCondor to produce a better image!
```
from IPython.display import Image
Image('test.png')
```
## What is the workflow?
We can parallelize this calculation by drawing rectangular sub-regions of the full region ("tiles") we want and stitching them together into a single image using `montage`.
Let's draw this out as a graph, showing how data (image patches) will flow through the system.
(Don't worry about this code, unless you want to know how to make dot diagrams in Python!)
```
from graphviz import Digraph
import itertools
num_tiles_per_side = 2
dot = Digraph()
dot.node('montage')
for x, y in itertools.product(range(num_tiles_per_side), repeat = 2):
n = f'tile_{x}-{y}'
dot.node(n)
dot.edge(n, 'montage')
dot
```
Since we can chop the image up however we'd like, we have as many tiles per side as we'd like (try changing `num_tiles_per_side` above).
The "shape" of the DAG is the same: there is a "layer" of `goatbrot` jobs that calculate tiles, which all feed into `montage`.
Now that we know the structure of the problem, we can start describing it to HTCondor.
## Describing `goatbrot` as an HTCondor job
We describe a job using a `Submit` object.
It corresponds to the submit *file* used by the command line tools.
It mostly behaves like a standard Python dictionary, where the keys and values correspond to submit descriptors.
```
import htcondor
tile_description = htcondor.Submit(
executable = 'goatbrot', # the program we want to run
arguments = '-i 10000 -c $(x),$(y) -w $(w) -s 500,500 -o tile_$(tile_x)-$(tile_y).ppm', # the arguments to pass to the executable
log = 'mandelbrot.log', # the HTCondor job event log
output = 'goatbrot.out.$(tile_x)_$(tile_y)', # stdout from the job goes here
error = 'goatbrot.err.$(tile_x)_$(tile_y)', # stderr from the job goes here
request_cpus = '1', # resource requests; we don't need much per job for this problem
request_memory = '128MB',
request_disk = '1GB',
)
print(tile_description)
```
Notice the heavy use of macros like `$(x)` to specify the tile.
Those aren't built-in submit macros; instead, we will plan on passing their values in through **vars**.
Vars will let us customize each individual job in the tile layer by filling in those macros individually.
Each job will recieve a dictionary of macro values; our next goal is to make a list of those dictionaries.
We will do this using a function that takes the number of tiles per side as an argument.
As mentioned above, the **structure** of the DAG is the same no matter how "wide" the tile layer is.
This is why we define a function to produce the tile vars instead of just calculating them once: we can vary the width of the DAG by passing different arguments to `make_tile_vars`.
More customizations could be applied to make different images (for example, you could make it possible to set the center point of the image).
```
def make_tile_vars(num_tiles_per_side, width = 3):
width_per_tile = width / num_tiles_per_side
centers = [
width_per_tile * (n + 0.5 - (num_tiles_per_side / 2))
for n in range(num_tiles_per_side)
]
vars = []
for (tile_y, y), (tile_x, x) in itertools.product(enumerate(centers), repeat = 2):
var = dict(
w = width_per_tile,
x = x,
y = -y, # image coordinates vs. Cartesian coordinates
tile_x = str(tile_x).rjust(5, '0'),
tile_y = str(tile_y).rjust(5, '0'),
)
vars.append(var)
return vars
tile_vars = make_tile_vars(2)
for var in tile_vars:
print(var)
```
If we want to increase the number of tiles per side, we just pass in a larger number.
Because the `tile_description` is **parameterized** in terms of these variables, it will work the same way no matter what we pass in as `vars`.
```
tile_vars = make_tile_vars(4)
for var in tile_vars:
print(var)
```
## Describing montage as an HTCondor job
Now we can write the `montage` job description.
The problem is that the arguments and input files depend on how many tiles we have, which we don't know ahead-of-time.
We'll take the brute-force approach of just writing a function that takes the tile `vars` we made in the previous section and using them to build the `montage` job description.
Not that some of the work of building up the submit description is done in Python.
This is a major advantage of communicating with HTCondor via Python: you can do the hard work in Python instead of in submit language!
One area for possible improvement here is to remove the duplication of the format of the input file names, which is repeated here from when it was first used in the `goatbrot` submit object. When building a larger, more complicated workflow, it is important to reduce duplication of information to make it easier to modify the workflow in the future.
```
def make_montage_description(tile_vars):
num_tiles_per_side = int(len(tile_vars) ** .5)
input_files = [f'tile_{d["tile_x"]}-{d["tile_y"]}.ppm' for d in tile_vars]
return htcondor.Submit(
executable = '/usr/bin/montage',
arguments = f'{" ".join(input_files)} -mode Concatenate -tile {num_tiles_per_side}x{num_tiles_per_side} mandelbrot.png',
transfer_input_files = ', '.join(input_files),
log = 'mandelbrot.log',
output = 'montage.out',
error = 'montage.err',
request_cpus = '1',
request_memory = '128MB',
request_disk = '1GB',
)
montage_description = make_montage_description(make_tile_vars(2))
print(montage_description)
```
## Describing the DAG using `htcondor.dags`
Now that we have the job descriptions, all we have to do is use `htcondor.dags` to tell DAGMan about the dependencies between them.
`htcondor.dags` is a subpackage of the HTCondor Python bindings that lets you write DAG descriptions using a higher-level language than raw DAG description file syntax.
Incidentally, it also lets you use Python to drive the creation process, increasing your flexibility.
**Important Concept:** the code from `dag = dags.DAG()` onwards only defines the **topology** (or **structure**) of the DAG.
The `tile` layer can be flexibly grown or shrunk by adjusting the `tile_vars` without changing the topology, and this can be clearly expressed in the code.
The `tile_vars` are driving the creation of the DAG. Try changing `num_tiles_per_side` to some other value!
```
from htcondor import dags
num_tiles_per_side = 2
# create the tile vars early, since we need to pass them to multiple places later
tile_vars = make_tile_vars(num_tiles_per_side)
dag = dags.DAG()
# create the tile layer, passing in the submit description for a tile job and the tile vars
tile_layer = dag.layer(
name = 'tile',
submit_description = tile_description,
vars = tile_vars,
)
# create the montage "layer" (it only has one job in it, so no need for vars)
# note that the submit description is created "on the fly"!
montage_layer = tile_layer.child_layer(
name = 'montage',
submit_description = make_montage_description(tile_vars),
)
```
We can get a textual description of the DAG structure by calling the `describe` method:
```
print(dag.describe())
```
## Write the DAG to disk
We still need to write the DAG to disk to get DAGMan to work with it.
We also need to move some files around so that the jobs know where to find them.
```
from pathlib import Path
import shutil
dag_dir = (Path.cwd() / 'mandelbrot-dag').absolute()
# blow away any old files
shutil.rmtree(dag_dir, ignore_errors = True)
# make the magic happen!
dag_file = dags.write_dag(dag, dag_dir)
# the submit files are expecting goatbrot to be next to them, so copy it into the dag directory
shutil.copy2('goatbrot', dag_dir)
print(f'DAG directory: {dag_dir}')
print(f'DAG description file: {dag_file}')
```
## Submit the DAG via the Python bindings
Now that we have written out the DAG description file, we can submit it for execution using the standard Python bindings submit mechanism.
The `Submit` class has a static method which can read a DAG description and generate a corresponding `Submit` object:
```
dag_submit = htcondor.Submit.from_dag(str(dag_file), {'force': 1})
print(dag_submit)
```
Now we can enter the DAG directory and submit the DAGMan job, which will execute the graph:
```
import os
os.chdir(dag_dir)
schedd = htcondor.Schedd()
with schedd.transaction() as txn:
cluster_id = dag_submit.queue(txn)
print(f"DAGMan job cluster is {cluster_id}")
os.chdir('..')
```
Let's wait for the DAGMan job to complete by reading it's event log:
```
dag_job_log = f"{dag_file}.dagman.log"
print(f"DAG job log file is {dag_job_log}")
# read events from the log, waiting forever for the next event
dagman_job_events = htcondor.JobEventLog(str(dag_job_log)).events(None)
# this event stream only contains the events for the DAGMan job itself, not the jobs it submits
for event in dagman_job_events:
print(event)
# stop waiting when we see the terminate event
if event.type is htcondor.JobEventType.JOB_TERMINATED and event.cluster == cluster_id:
break
```
Let's look at the final image!
```
Image(dag_dir / "mandelbrot.png")
```
| true |
code
| 0.243103 | null | null | null | null |
|
## Reading/writing files
### BIOINF 575 - Fall 2020
### Functions recap - important functions continued
#### RECAP & RESOURCES
#### RECAP
```python
# FUNCTIONS
# DEFINITION - creating a function
def function_name(arg1, arg2, darg=None):
# instructions to compute result
return result
# CALL - running a function
function_result = function_name(val1, val2, dval)
```
* <b>A function doesn't need to have arguments to work</b>
* <b>`return` statments exit the function while passing on the data</b>
* <b>if there is no `return` statement None is returned</b>
* <b>Defining a function does not run a function. </b>
* <b>To run a function, it must be called using `([args])` after the function name</b>
```python
function_name(val1, val2, [dval])
```
#### RESOURCES
FUNCTIONS
https://docs.python.org/3/tutorial/introduction.html
https://docs.python.org/3/library/functions.html
https://www.python.org/dev/peps/pep-0257/
https://www.tutorialspoint.com/python3/python_functions.htm
https://www.geeksforgeeks.org/functions-in-python/
https://github.com/Pierian-Data/Complete-Python-3-Bootcamp/tree/master/03-Methods%20and%20Functions
READING & WRITING FILES
https://docs.python.org/3/tutorial/inputoutput.html#reading-and-writing-files
https://www.tutorialspoint.com/python/python_files_io.htm
https://www.geeksforgeeks.org/reading-writing-text-files-python/
https://www.w3schools.com/python/python_file_write.asp
https://www.python-course.eu/python3_file_management.php
https://colab.research.google.com/github/computationalcore/introduction-to-python/blob/master/notebooks/4-files/PY0101EN-4-1-ReadFile.ipynb
https://github.com/aushafy/Python-Write-and-Read-File
https://eeob-biodata.github.io/BCB546X-Fall2017/Week_09/additional-lesson/
---
### Function Examples
___
##### <b>`*args`</b> - unkown no. of arguments - unpack collection of argument values
##### <b>`**kargs`</b> - unkown no. of arguments - unpack mapping of names and values
```
x = 20
print(*("EGFR", "TP53", "AAACGTTA", 30, [x, 60]))
print("EGFR", "TP53", "AAACGTTA", 30, [x, 60])
def test_karg(**keys_args_dict):
for name,value in keys_args_dict.items():
print("name = ", name)
print("value = ", value)
test_karg(**{"gene":"EGFR", "expression": 20,"transcript_no": 4})
test_karg(gene = "EGFR", expression = 20, transcript_no = 4)
```
___
##### <b>`Recursive`</b> function - function that calls itself
```
test_list = ["CGTA", "CCCT", "GGGA", "ACGG"]
def display_elements(seq_list, pos):
if pos <= len(seq_list)-1:
print(seq_list[pos])
display_elements(seq_list, pos + 1)
display_elements(test_list, 0)
```
____
##### <b>`lambda` function</b> - anonymous function - it has no name
Should be used only with simple expressions
https://docs.python.org/3/reference/expressions.html#lambda<br>
https://www.geeksforgeeks.org/python-lambda-anonymous-functions-filter-map-reduce/<br>
https://realpython.com/python-lambda/<br>
`lambda arguments : expression`
A lambda function can take <b>any number of arguments<b>, but must always have <b>only one expression</b>.
```
compute_expression = lambda x, y: x + y + x*y
compute_expression(2, 3)
```
____
### Useful functions
#### Built-in functions
https://docs.python.org/3/library/functions.html
##### <b>`zip(*iterables)`</b> - make an iterator that aggregates respective elements from each of the iterables.
https://docs.python.org/3/library/functions.html#zip
##### <b>`map(function, iterable, ...)`</b> - apply function to every element of an iterable - return iterable with results
https://docs.python.org/3/library/functions.html#map
##### <b>`filter(function, iterable)`</b> - apply function (bool result) to every element of an iterable - return the elements from the input iterable for which the function returns True
https://docs.python.org/3/library/functions.html#filter
##### <b>`functools.reduce(function, iterable[, initializer])`</b> - apply function to every element of an iterable to reduce the iterable to a single value
https://docs.python.org/3/library/functools.html#functools.reduce
```
combined_res = zip([10,20,30],["ACT","GGT","AACT"],[True,False,True])
combined_res
for element in combined_res:
print(element)
list(combined_res)
# unzip list
x, y, z = zip(*[(3,4,7), (12,15,19), (30,60,90)])
print(x, y, z)
```
_____
```
map(abs,[-2,0,-5,6,-7])
list(map(abs,[-2,0,-5,6,-7]))
```
https://www.geeksforgeeks.org/python-map-function/
```
numbers1 = [1, 2, 3]
numbers2 = [4, 5, 6]
result = map(lambda x, y: x + y, numbers1, numbers2)
list(result)
```
____
Use a lambda function and the map function to compute a result from the followimg 3 lists.<br>
If the element in the third list is divisible by 3 return 3*x, otherwise return 2*y.
```
numbers1 = [1, 2, 3, 4, 5, 6]
numbers2 = [7, 8, 9, 10, 11, 12]
numbers3 = [13, 14, 15, 16, 17, 18]
result = map(lambda x, y, z: 3*x if z%3 ==0 else 2*y, \
numbers1, numbers2, numbers3)
list(result)
def compute_res(x,y,z):
res = None
if z%3 == 0:
res = 3*x
else:
res = 2*y
return res
result = map(compute_res, numbers1, numbers2, numbers3)
list(result)
```
____
```
test_list = [3,4,5,6,7]
result = filter(lambda x: x > 4, test_list)
result
list(result)
# Filter to remove empty structures or 0
test_list = [3, 0, 5, None, 7, "", "AACG", []]
result = filter(bool, test_list)
list(result)
```
____
```
from functools import reduce
reduce(lambda x,y: x+y, [47,11,42,13])
```
<img src = https://www.python-course.eu/images/reduce_diagram.png width=300/>
https://www.python-course.eu/lambda.php
https://www.geeksforgeeks.org/reduce-in-python/
https://www.tutorialsteacher.com/python/python-reduce-function
```
test_list = [1,2,3,4,5,6]
# compute factorial of n
n=5
reduce(lambda x, y: x*y, range(1, n+1))
```
_____
### Input/Output and File Handling
#### Reading user input: the `input()` function
```
# reads text, evaluates expression
res = input()
while res != "STOP":
print("input", res)
res = input()
```
File is a named location on disk to store related information
It is used to permanently store data in a non-volatile memory (e.g. hard disk)<br>
https://www.programiz.com/python-programming/file-operation
#### Open a file for reading or writing
https://docs.python.org/3/library/functions.html#open
```python
open(file, mode='r', buffering=-1, encoding=None, errors=None, newline=None, closefd=True, opener=None)
fileObj = open(fileName, ‘r’) # open file for reading, r+
fileObj = open(fileName, ‘w’) # open file for writing, w+
fileObj = open(fileName, ‘a’) # open file for appending, a+
```
(Note: fileName must be a string or reference to one)
The file object is iterable by line
```
#help(open)
```
<b>Write</b>
```
# open file and write lines into a file
test_file = open("test.txt", mode = "w")
test_file.write("Writing some text.\n")
test_file.write("Writing another line.")
test_file.close()
for elem in dir(test_file):
if "_" not in elem:
print(elem)
```
<b>Close file</b>
```
# close()
help(test_file.close)
```
<b>Read</b>
```
# open file and read file contents
test_file = open("test.txt", "r")
res = test_file.read()
print(res)
test_file.close()
```
<b>Read line</b>
```
test_file = open("test.txt", "r")
res = test_file.readlines()
print(res)
test_file.close()
```
<b>Go at position</b>
```
# seek
test_file = open("test.txt", "r")
test_file.seek(10)
res = test_file.readline()
print(res)
print(test_file.tell())
test_file.close()
```
<b>Return current position</b>
```
# tell
```
### Context manager
<b>with: give code context</b>
The special part about with is when it is paired with file handling or database access functionality
```
# Without with
test_file = open("test.txt",'r')
print(test_file.read())
test_file.close()
# With with :)
with open("test.txt",'r') as test_file:
print(test_file.read())
```
The file is opened and processed. <br>
As soon as you exit the with statement, <b>the file is closed automatically</b>.
```
# parsing files
def parse_line(line):
return line.strip().split(" ")
with open("test.txt",'r') as test_file:
line = test_file.readline()
while (line != ""):
print(parse_line(line))
line = test_file.readline()
```
### <font color = "red">Exercise</font>:
Open the file test.txt and add 10 lines in a for loop.
The line should contain: Line index
Line 0
Line 1
https://www.tutorialspoint.com/python/python_files_io.htm
https://www.tutorialspoint.com/python/file_methods.htm
_____
### NumPy - Numeric python <img src="https://upload.wikimedia.org/wikipedia/commons/thumb/1/1a/NumPy_logo.svg/1200px-NumPy_logo.svg.png" alt="NumPy logo" width = "100">
NumPy (np) is the premier Python package for scientific computing
https://numpy.org
Its powerful comes from the <b>N-dimensional array object</b>
np is a *lower*-level numerical computing library.
This means that, while you can use it directly, most of its power comes from the packages built on top of np:
* Pandas (*Pan*els *Da*tas)
* Scikit-learn (machine learning)
* Scikit-image (image processing)
* OpenCV (computer vision)
* more...
<b>Importing NumPy<br>
Convention: use np alias</b>
```
import numpy as np
```
<img src="https://www.oreilly.com/library/view/elegant-scipy/9781491922927/assets/elsp_0105.png" alt="data structures" width="500">
<b>NumPy basics</b>
Arrays are designed to:
* handle vectorized operations lists are not
* if you apply a function it is performed on every item in the array, rather than on the whole array object
* store multiple items <b>of the same data type</b>
* have 0-based indexing
* Missing values can be represented using `np.nan` object
* the object `np.inf` represents infinite
* Array size cannot be changed, should create a new array
* An equivalent numpy array occupies much less space than a python list of lists
<b>Create Array</b><br>
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.creation.html
```
# Build array from Python list
vector = np.array([1,2,3])
vector
# matrix with zeros
np.zeros((3,4), dtype = int)
# matrix with 1s
np.ones((3,4), dtype=int)
# matrix with a constant value
value = 20
np.full((3,4), value)
# Create a 4x4 identity matrix
np.eye(4)
# arange - numpy range
np.arange(10, 30, 2)
# evenly spaced numbers over a specified interval
ev_array = np.linspace(1, 10, 20)
print(ev_array)
ev_array.shape
```
<b>Random data</b><br>
https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.random.html
```
# Create an array filled with random values
np.random.random((3,4))
# Create an array filled with random values from the standard normal distribution
np.random.randn(3,4)
# Generate the same random numbers every time
# Set seed
np.random.seed(10)
np.random.randn(3,4)
np.random.seed(10)
print(np.random.randn(3,4))
print(np.random.randn(3,4))
np.random.seed(100)
print(np.random.randn(3,4))
```
```python
# Create the random state
rs = np.random.RandomState(100)
```
<b>Basic array attributes:</b>
* shape: array dimension
* size: Number of elements in array
* ndim: Number of array dimension (len(arr.size))
* dtype: Data-type of the array
* T: The transpose of the array
```
matrix = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
matrix
# let's check them out
matrix.shape
matrix.size
matrix = np.array([[[1,2],[2,3],[3,4]],[[4,5],[4,6],[6,7]]])
matrix.ndim
matrix.dtype
matrix.T
matrix
```
<b>Reshaping</b>
```
matrix
# Reshaping
matrix_reshaped = matrix.reshape(2,6)
matrix_reshaped
```
<b>Slicing/Indexing</b>
```
# List-like
matrix_reshaped[1][1]
matrix_reshaped[1,3]
matrix_reshaped[1,:3]
matrix_reshaped[:2,:3]
# iterrating ... let's print the elements of matrix_reshaped
nrows = matrix_reshaped.shape[0]
ncols = matrix_reshaped.shape[1]
for i in range(nrows):
for j in range(ncols):
print(matrix_reshaped[i,j])
# Fun arrays
checkers_board = np.zeros((8,8),dtype=int)
checkers_board[1::2,::2] = 1
checkers_board[::2,1::2] = 1
print(checkers_board)
```
Create a 2d array with 1 on the border and 0 inside
```
boarder_array = np.zeros((8,8),dtype=int)
boarder_array[0,:] = 1
boarder_array
boarder_array = np.ones((8,8),dtype=int)
boarder_array[1:-1,1:-1] = 0
boarder_array
boarder_array[:,-1]
```
<b>Performance</b>
test_list = list(range(int(1e6)))
<br>
test_vector = np.array(test_list)
```
test_list = list(range(int(1e6)))
test_vector = np.array(test_list)
%%timeit
sum(test_list)
%%timeit
np.sum(test_vector)
```
https://numpy.org/devdocs/user/quickstart.html#universal-functions
<b>Matrix operations</b>
https://www.tutorialspoint.com/matrix-manipulation-in-python<br>
Arithmetic operators on arrays apply elementwise. <br>
A new array is created and filled with the result.
<b>Array broadcasting</b><br>
https://docs.scipy.org/doc/numpy/user/basics.broadcasting.html<br>
The term broadcasting describes how numpy treats arrays with different shapes during arithmetic operations. <br>
Subject to certain constraints, the smaller array is “broadcast” across the larger array so that they have compatible shapes.
<img src = "https://www.tutorialspoint.com/numpy/images/array.jpg" height=10/>
https://www.tutorialspoint.com/numpy/numpy_broadcasting.htm
```
matrix
np.array([1,2,3,4]).reshape(4,1)
matrix + np.array([1,2,3,4]).reshape(4,1)
matrix + np.array([1,2,3])
matrix * np.array([1,2,3,4]).reshape(4,1)
matrix2 = np.array([[1,2,3],[5,6,7],[1,1,1],[2,2,2]])
matrix2
matrix * matrix2
# matrix multiplication
matrix.dot(np.array([1,2,3]).reshape(3,1))
# matrix multiplication - more recently
matrix@(np.array([1,2,3]).reshape(3,1))
# stacking arrays together
np.vstack((matrix,matrix2))
np.hstack((matrix,matrix2))
# splitting arrays
np.vsplit(matrix,2)
np.hsplit(matrix,(2,3))
```
<b>Copy</b>
```
matrix
# shallow copy - looks at the same data
matrix_copy = matrix
matrix_copy1 = matrix.view()
print(matrix_copy)
print(matrix_copy1)
print(matrix)
print(matrix_copy)
print(matrix_copy1)
matrix_copy1[0,0] = 5
# deep copy
matrix_copy2 = matrix.copy()
print(matrix_copy2)
matrix_copy2[0,0] = 7
print(matrix)
print(matrix_copy)
print(matrix_copy1)
print(matrix_copy2)
```
<b>More matrix computation</b>
```
# conditional subsetting
matrix[(6 < matrix[:,0])]
matrix[(4 <= matrix[:,0]) & (matrix[:,0] <= 7)
& (2 <= matrix[:,1]) & (matrix[:,1] <= 7),]
matrix
# col mean
matrix.mean(axis = 0)
# row mean
matrix.mean(axis = 1)
# unique values and counts
matrix = np.random.random((3,4), )
matrix = np.array([[ 5, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
uvals, counts = np.unique(matrix, return_counts=True)
print(uvals,counts)
```
https://www.w3resource.com/python-exercises/numpy/index.php
Create a matrix of 5 rows and 6 columns with numbers from 1 to 30.
Add 2 to the odd values of the array.
```
matrix = np.arange(1,31).reshape(5,6)
matrix[matrix%2==1 ] += 2
matrix
```
Normalize the values in the matrix. Substract the mean and divide by the standard deviation.
```
mat_mean = np.mean(matrix)
mat_std = np.std(matrix)
matrix_norm = (matrix - mat_mean)/mat_std
matrix_norm
matrix
```
Create a random array (5 by 3) and compute:
* the sum of all elements
* the sum of the rows
* the sum of the columns
```
matrix = np.random.rand(5,3)
print(matrix)
matrix.sum()
matrix.sum(1)
matrix.sum(0)
#Given a set of Gene Ontology (GO) terms and the genes that are associated with these terms find the gene
#that is associated with the most GO terms
go_terms=np.array(["cellular response to nicotine",
"cellular response to hypoxia",
"cellular response to lipid"])
genes=np.array(["BAD","KCNJ11","MSX1","CASR","ZFP36L1"])
assoc_matrix = np.array([[1,1,0,1,0],[1,0,0,1,1],[1,0,0,0,0]])
print(assoc_matrix)
max(assoc_matrix.sum(0))
genes[0]
```
| true |
code
| 0.244927 | null | null | null | null |
|
# <p style="text-align: center;"> Social Butterfly - Umbrella Academy - After Metadata </p>

```
from IPython.display import HTML
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
The raw code for this IPython notebook is by default hidden for easier reading.
To toggle on/off the raw code, click <a href="javascript:code_toggle()">here</a>.''')
```
# <p style="text-align: center;"> Table of Contents </p>
- ## 1. [Introduction](#Introduction)
- ### 1.1 [Abstract](#abstract)
- ### 1.2 [Importing Libraries](#importing_libraries)
- ### 1.3 [Streaming](#streaming)
- ### 1.3.1[Setting up Stream Listener](#stream_listener)
- ### 1.3.2[Starting the Listener](#starting_the_listener)
- ### 1.3.3[Making a Dataframe](#making_dataframe)
- ### 1.4 [Dataset Summary](#dataset_summary)
- ### 1.5 [Dataset Cleaning](#dataset_cleaning)
- ### 1.5.1[Functions to clean data](#functions_for_cleaning)
- ## 2. [Wordclouds](#wordclouds)
- ### 2.1 [Number of words in a text](#number_of_words)
- ### 2.2 [Generating Wordclouds](#Generating_Wordclouds)
- ### 2.3 [Masking the wordcloud](#masking_wordcloud)
- ### 2.4 [Preparing Wordclouds](#preparing_wordcloud)
- ### 2.5 [Function for Building a GIF](#gif_building)
- ## 3. [LSTM](#lstm)
- ### 3.1 [Creating character/word mappings](#char_and_word_mapping)
- ### 3.2 [Creating set of words](#creating_set_words)
- ### 3.3 [Creating sequences](#creating_sequences)
- ### 3.4 [Saving Tokens](#Saving_Tokens)
- ### 3.5 [Integer Encoding Sequences](#Integer_Encoding)
- ### 3.6 [Defining the Model](#defining_model)
- ### 3.7 [Generating Sequences](#generating_sequence)
- ### 3.7.1[Deeper_LSTM_Model](#DeeperModel)
- ## 4. [Conclusion](#Conclusion)
- ## 5. [Scope](#Scope)
- ## 6. [Contribution](#Contribution)
- ## 7. [Citation](#Citation)
- ## 8. [License](#License)
# <p style="text-align: center;"> 1.0 Introduction </p> <a id='Introduction'></a>
# 1.1 Abstract <a id='abstract'></a>
Now that we have collected the Metadata in the previous notebook(go to the [Link](./Umbrella_Academy_INFO6105_Collecting_Metadata.ipynb) if you haven't seen it yet). We can now stream data from twitter using these most occuring hashtags.
In this notebook we will be scrapping data using the hashtags we scrapped in Collecting Metadata (Part 1) , using a real time streaming listener. For this data being scrapped we won't be using retweets and the conditional requirement is that dataset should be large enough in order fo us to build the model. What are we trying to build a model for?
Our idea builds from the fact that creating content that too fastly and the one which can become popular as it gets posted and adds a x-factor to one's social media handle is quite hard , because there is so much data every where that one thing or other correlats with one another. Also, Creating content that doesn’t get popular and is not ranked well is a wasted expense. However, producing a blog post becomes popular and ranks highly is a wise investment. Repeating the same process will give you a consistent basis for a serious competitive advantage.
Most people feel that optimizing content manually is a tedious and time consuming process. But it doesn’t have to be that way. We can incorporate content optimization into content creation workflow. In our project , we are somehow trying to work on a similar idea in order to create model which optimizes the content for social platform i.e social butterfly, by experimenting on other available platforms like twitter ,instagram etc. We are using a series of neural network i.e LSTM for doing the same.
[Back to top](#Introduction)
# 1.2 Importing Libraries <a id='importing_libraries'></a>
In this step, we import libraries that we need for this notebook. A few basic libraries like numpy, pandas, matplotlib etc are used. Other libraries like tweepy, json, csv are used to collect data from twitter and save them as a json and csv file. Libraries like base
[Back to top](#Introduction)
```
#Data Extraction and saving
import json
from json import dumps, loads
from pandas.io.json import json_normalize as jn
import tweepy
import csv
#Plotting and visualization
import matplotlib.pyplot as plt
#To encode and decode strings
import codecs
#Tweepy streaming
from tweepy.streaming import StreamListener
from tweepy import OAuthHandler
from tweepy import Stream
# diving into NLP tasks such as noun phrase extraction, sentiment analysis, classification, translation, and more.
from textblob import TextBlob
#time based and os dependent functionality
import time
import os
import sys
#Basic Python arrays and dataframe
import numpy as np
import pandas as pd
#regex string commands and converting images to bas64 form
import re,string
import base64
from scipy.misc import imread
#Library for wordcloud
from wordcloud import WordCloud, STOPWORDS,ImageColorGenerator
#Python gif and animation
from IPython.display import HTML
from matplotlib.pyplot import *
from matplotlib import cm
from matplotlib import animation
from matplotlib import rc, animation
rc('animation', html='html5')
import io
import imageio
#LSTM libraries
from keras.layers import Embedding
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
from keras.layers import LSTM
from keras.utils import np_utils
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.callbacks import ModelCheckpoint
from keras.utils import np_utils
import pickle
from random import randint
#Ignore warnings in outputs
import warnings; warnings.simplefilter('ignore')
#Twitter Credentials
twitter_cred = dict()
twitter_cred['CONSUMER_KEY'] = ''
twitter_cred['CONSUMER_SECRET'] = ''
twitter_cred['ACCESS_KEY'] = ''
twitter_cred['ACCESS_SECRET'] = ''
# Saving the Twitter Credentials to a json file
script_dir = os.path.dirname('__file__')
file_path = os.path.join(script_dir, 'JSON_and_CSV_Files/twitter_credentials.json')
with open(file_path, 'w') as secret_info:
json.dump(twitter_cred, secret_info, indent=4, sort_keys=True)
with open('JSON_and_CSV_Files/twitter_credentials.json') as cred_data:
info = json.load(cred_data)
consumer_key = info['CONSUMER_KEY']
consumer_secret = info['CONSUMER_SECRET']
access_key = info['ACCESS_KEY']
access_secret = info['ACCESS_SECRET']
# Create the api endpoint
auth = tweepy.OAuthHandler(consumer_key, consumer_secret)
api = tweepy.API(auth)
```
# 1.3 Streaming <a id='streaming'></a>
For collecting Metadata, we used user inputs for how many tweets should be collected and which hashtags should be scraped. However in this part, we'll use the most occuring hashtags as input and run it for a longer time (5 hours or more).
[Back to top](#Introduction)
# 1.3.1 Setting up Stream Listener<a id='stream_listener'></a>
Here we'll set up a Stream Listener which will save the scraped tweets in a json file. We will also make sure that the tweets that we're collecting are not Retweets as there could be multiple retweets with the same content, which would make the content redundant.
[Back to top](#streaming)
```
start_time = time.time()
class MyListener(StreamListener):
def __init__(self, start_time, time_limit=60):
self.time = start_time
self.limit = time_limit
self.tweet_data = []
self.saveFile = open('JSON_and_CSV_Files/raw_tweets.json', 'a', encoding='utf-8')
def on_data(self, data):
if (time.time() - self.time) < self.limit:
decoded = json.loads(data)
if not decoded['text'].startswith('RT'):
try:
self.tweet_data.append(data)
saveFile = open('JSON_and_CSV_Files/raw_tweets.json', 'w', encoding='utf-8')
saveFile.write(u'[\n')
saveFile.write(','.join(self.tweet_data))
saveFile.write(u'\n]')
saveFile.close()
#exit()
return True
except BaseException as e:
print("Error on_data: %s" % str(e))
time.sleep(5)
return True
else:
self.saveFile.close()
return False
def on_error(self, status):
print(status)
return True
#if __name__ == '__main__':
#MyListener = MyListener()
#auth = OAuthHandler(consumer_key, consumer_secret)
#auth.set_access_token(access_key, access_secret)
#stream = Stream(auth,MyListener )
#stream.filter(track=['#ML', '#Datascience', '#Arima'])
```
# 1.3.2 Starting the Listener<a id='starting_the_listener'></a>
In this step we start the stream listener for the given timeframe. We also filter our stream such that it only collects data on the given hashtags. We also restrict the language to english so as to not deal with non-ascii characters.
[Back to top](#streaming)
```
#MyListener = MyListener()
#auth = OAuthHandler(consumer_key, consumer_secret)
#auth.set_access_token(access_key, access_secret)
#stream = Stream(auth,MyListener(start_time, time_limit=18000) )
#stream.filter(track=['#ML', '#AI', '#deeplearning'],languages =["en"])
```
# 1.3.3 Making a Dataframe<a id='making_dataframe'></a>
In this step we will normalize the json file that we have, since it is in nested form(JSON Object inside a JSON Object). After this we save the file to a dataframe, since it is easier to work with a Pandas' Dataframe.
[Back to top](#streaming)
```
# data=open('raw_tweets.json', 'r', encoding='utf-8')
# df = pandas.io.json.json_normalize(data)
# df.columns = df.columns.map(lambda x: x.split(".")[-1])
# df.head()
with open('JSON_and_CSV_Files/raw_tweets.json', 'r', encoding="utf-8") as json_file:
json_work = json.load(json_file)
df = pd.io.json.json_normalize(json_work)
```
Since we'll be working with only the text values in our algorithm, we don't need any other extracted columns. So we select only the column 'text'.
```
#Setting our source for text generation
df_clean=df['text']
#Making the dataframe
df_cleans=pd.DataFrame({'text':df_clean})
```
# 1.4 Dataset Summary <a id='dataset_summary'></a>
Since this dataset is scraped from twitter, it is bound to have some irregular values. In this step we check the summary of the dataset by checking the first 5 columns of the scraped data, checking the data types of the columns and checking the summary of the dataset.
[Back to top](#Introduction)
```
df_cleans.head()
df_cleans.info()
df_cleans.describe()
```
# 1.5 Dataset Cleaning <a id='dataset_cleaning'></a>
Since this dataset is scraped from twitter, it is bound to have some irregular values. By seeing the summary of our dataset we have gained some important insight about the type of data, and we need to clean the data to be able to further process it.
[Back to top](#Introduction)
### 1.5.1 Functions to clean data <a id='functions_for_cleaning'></a>
We have created a wide array of functions to clean the data by removing hashtags and other entities in the text ('@', 'â'..). Then we have removed all non-ascii characters from the text and also removed all Emojis. Along with this we are also extracting hashtags from the tweets and saving them in a seperate column
[Back to top](#dataset_cleaning)
```
def remove_RT(x):
if x=="RT ":
return " "
#return str(x.replace('b\'RT ',''))
def strip_links(text):
link_regex = re.compile('((https?):((//)|(\\\\))+([\w\d:#@%/;$()~_?\+-=\\\.&](#!)?)*)', re.DOTALL)
links = re.findall(link_regex, text)
#cleanString = re.sub('\W+','', string )
for link in links:
text = text.replace(link[0], ', ')
#text = text.replace(cleanString, '')
return text
def strip_all_entities(text):
entity_prefixes = ['@','#']
for separator in string.punctuation:
if separator not in entity_prefixes :
text = text.replace(separator,' ')
words = []
for word in text.split():
word = word.strip()
if word:
if word[0] not in entity_prefixes:
words.append(word)
return ' '.join(words)
def removeNonAscii(s): return "".join(i for i in s if ord(i)<128)
df_cleans['TextNoMentions']=df_cleans['text'].str.replace('RT', ' ')
df_cleans['TextNoMentions']=df_cleans['TextNoMentions'].str.replace('#', '', case=False)
#df_cleans['TextNoLinks']=df_cleans['text'].apply(strip_links)
df_cleans['TextNoMentions']=df_cleans['TextNoMentions'].str.replace('http\S+|www.\S+', '', case=False)
#df_cleans['TextNoEntities']=df_cleans['TextNoLinks'].apply(strip_all_entities)
df_cleans['TextNoMentions']=df_cleans['TextNoMentions'].apply(strip_all_entities)
df_cleans['TextNoMentions']=df_cleans['TextNoMentions'].apply(removeNonAscii)
a=df_cleans['TextNoMentions'].unique()
a=a.tolist()
df_cleaner=pd.DataFrame({'text':a})
df_cleaner.head()
df_cleaner['text']=df_cleaner['text'].str.lower()
```
# <p style="text-align: center;"> 2.0 Wordclouds </p> <a id='wordclouds'></a>
[Back to top](#Introduction)
# 2.1 Number of words in a text <a id='number_of_words'></a>
[Back to top](#wordclouds)
```
# Lets check the avg number of words in text written by each author in a histogram
def word_count(row):
"""function to calculate the count of words in a given text """
text = row['text']
text_splited = text.split(' ')
word_count = text_splited.__len__()
return word_count
df_cleaner['word_count'] = ''
df_cleaner['word_count'] = df_cleaner.apply(lambda row: word_count(row), axis =1)
df_cleaner.head()
```
# 2.2 Generating Wordclouds <a id='Generating_Wordclouds'></a>
[Back to top](#wordclouds)
```
#mws = df_cleaner["text"].values
wc = WordCloud(background_color="white", max_words=5000,
stopwords=STOPWORDS, max_font_size= 50)
# generate word cloud
wc.generate(" ".join(df_cleaner.text.values))
# show
plt.figure(figsize=(16,13))
plt.imshow(wc, interpolation='bilinear')
plt.title("words from all author", fontsize=14,color='seagreen')
plt.axis("off")
```
# 2.3 Masking the wordcloud <a id='masking_wordcloud'></a>
[Back to top](#wordclouds)
```
def base_64(input_image):
""" Function to convert the image to base64 """
image = open(input_image, 'rb') #open binary file in read mode
image_read = image.read()
output_base64 = base64.encodebytes(image_read)
return output_base64
def codecs_img(input_image,base64_image):
"""Generate the Mask for EAP """
f1 = open(input_image, "wb")
f1.write(codecs.decode(base64_image,'base64'))
f1.close()
img1 = imageio.imread(input_image)
#img = img1.resize((980,1000))
#imgplot=plt.imshow(img1)
#plt.show()
hcmask=img1
return hcmask
mask = base_64('Images/Wordcloud/mask.png')
img1 = base_64('Images/Wordcloud/1.png')
img2 = base_64('Images/Wordcloud/2.png')
img3 = base_64('Images/Wordcloud/3.png')
img4 = base_64('Images/Wordcloud/4.png')
hcmask1 = codecs_img('Images/Wordcloud/mask.png' , mask)
hcmask2 = codecs_img('Images/Wordcloud/1.png' , img1)
hcmask3 = codecs_img('Images/Wordcloud/2.png' , img2)
hcmask4 = codecs_img('Images/Wordcloud/3.png' , img3)
hcmask5 = codecs_img('Images/Wordcloud/4.png' , img4)
```
Updating the stopwords because data from twitter has a few terms which appear over and over again,
which have no relevance to our text like 'gt' which is an acronym for go to, it is added before a link,
so along with removing links, we must also remove these words
```
Stopwords_Updated = ('amp', 'gt', 'via' ,'de', 'https')
STOPWORDS=STOPWORDS.union(Stopwords_Updated)
mask = df_cleaner['text'].values
def generate_wordcloud(words, mask):
""" Generating Word Clouds """
word_cloud = WordCloud(width = 512, height = 512, background_color='white', stopwords=STOPWORDS, mask=mask, max_font_size= 45).generate(" ".join(words))
plt.figure(figsize=(10,8))
image_colors = ImageColorGenerator(mask)
plt.imshow(word_cloud, interpolation='bilinear') # interpolation(helps in masking)
plt.axis('off')
plt.tight_layout(pad=0)
plt.show()
generate_wordcloud(mask,hcmask1)
```
# 2.4 Preparing Wordclouds <a id='preparing_wordcloud'></a>
[Back to top](#wordclouds)
```
def generate_wordclouds_gif(words, mask, wc_list):
""" Generating Word Clouds """
word_cloud = WordCloud(width = 512, height = 512, background_color='white', stopwords=STOPWORDS, mask=mask, max_font_size= 45).generate(" ".join(words))
wc_list.append(word_cloud)
return wc_list
%%capture
wc_list=[]
generate_wordclouds_gif(mask, hcmask2, wc_list)
generate_wordclouds_gif(mask, hcmask3, wc_list)
generate_wordclouds_gif(mask, hcmask4, wc_list)
generate_wordclouds_gif(mask, hcmask5, wc_list)
generate_wordclouds_gif(mask, hcmask5, wc_list)
generate_wordclouds_gif(mask, hcmask4, wc_list)
generate_wordclouds_gif(mask, hcmask3, wc_list)
generate_wordclouds_gif(mask, hcmask2, wc_list)
```
# 2.5 Function for Building a GIF <a id='gif_building'></a>
[Back to top](#wordclouds)
```
start = time.time()
def build_gif(imgs = wc_list, show_gif=False, save_gif=True, title=''):
"""function to create a gif of heatmaps"""
fig, ax = plt.subplots(nrows=1,ncols=1,figsize=(21,15))
ax.set_axis_off()
author_range = ["A", "B", "C", "D", "E", "F", "G", "H"]
def show_im(pairs):
ax.clear()
ax.set_title(str((pairs[0])))
ax.imshow(pairs[1])
ax.set_axis_off()
pairs = list(zip(author_range, imgs))
im_ani = matplotlib.animation.FuncAnimation(fig, show_im, pairs,interval=450, repeat_delay=0, blit=False, repeat=True)
plt.cla()
from IPython.display import HTML
HTML(im_ani.to_html5_video())
if save_gif:
im_ani.save('Images/GIFs/animation1.gif', writer='pillow') #, writer='imagemagick'
if show_gif:
plt.show()
return
end = time.time()
print("Time taken by above cell is {}".format(end-start))
%%capture
start = time.time()
build_gif()
end = time.time()
print(end-start)
filename = 'Images/GIFs/animation1.gif'
video = io.open(filename, 'r+b').read()
encoded = base64.b64encode(video)
HTML(data='''<img src="data:image/gif;base64,{0}" type="gif" />'''.format(encoded.decode('ascii')))
```
# <p style="text-align: center;"> 3.0 LSTM</p> <a id='lstm'></a>
[Back to top](#Introduction)
A language model can predict the probability of the next word in the sequence, based on the words already observed in the sequence.
**Neural network models** are a preferred method for developing statistical language models because they can use a distributed representation where different words with similar meanings have similar representation and because they can use a large context of recently observed words when making predictions.
In this section, we will develop a simple LSTM network to learn sequences of characters from the tweets we scrapped. In the next section we will use this model to generate new sequences of words.
But Before that lets look at how LSTM works.
A **recurrent neural network** (RNN) is a class of artificial neural network where connections between nodes form a directed graph along a temporal sequence. This allows it to exhibit temporal dynamic behavior. Unlike feedforward neural networks, RNNs can use their internal state (memory) to process sequences of inputs. This makes them applicable to tasks such as unsegmented, connected handwriting recognition or speech recognition.One of the appeals of RNNs is the idea that they might be able to connect previous information to the present task. Sometimes we only want to look at the current information (recent) to perform present task and past information is of not much use to our result, but in case of language modeling , where context is important at times and not important at other times the situation becomes trickier. In cases , where the gap between relevant information and the place where it's needed is small, RNN are useful because they can learn to use past information. But there are also cases where we need more context, the gap becomes large between two informations, RNNs is unable to learn to connect the information. **And that's when LSTM comes in play**

**Long Short Term Memory** networks – usually just called “LSTMs” – are a special kind of RNN, capable of learning long-term dependencies. LSTMs are explicitly designed to avoid the long-term dependency problem. Remembering information for long periods of time is practically their default behavior
### All recurrent neural networks have the form of a chain of repeating modules of neural network. In standard RNNs, this repeating module will have a very simple structure, such as a single tanh layer.***

### LSTMs also have this chain like structure, but the repeating module has a different structure. Instead of having a single neural network layer, there are four, interacting in a very special way.***

### How LSTM Works?
**Lets first look at the notations used in the chain like structure(it's not that complex)**

In the above diagram, each line carries an entire vector, from the output of one node to the inputs of others.
> **Pink circles** represent pointwise operations, like vector addition
> **Yellow boxes** are learned neural network layers.
> **Lines** merging denote concatenation
> **Line** forking denote its content being copied and
> The **copies** going to different locations
LSTM is a chain like structure containing various cells , each represented by green box in above diagram. The most important thing in LSTMs is the cell state i.e the horizontal line running through the top of the diagram. The cell state is kind of like a conveyor belt. It runs straight down the entire chain, with only some minor linear interactions. It’s very easy for information to just flow along it unchanged.

The LSTM does has the ability to remove or add information to the cell state, carefully regulated by structures called gates. Gates are a way to optionally let information through. They are composed out of a sigmoid neural net layer and a pointwise multiplication operation. The sigmoid layer outputs numbers between zero and one, describing how much of each component should be let through. A value of zero means “let nothing through,” while a value of one means “let everything through!”

An LSTM has three of these gates, to protect and control the cell state.
#### Step by Step LSTM
1. The first step in LSTM is to decide what information we are going to discard from the cell state. This decison is made by sigmoid layer. It looks at ***ht-1 and xt***, and outputs a number between 0 and 1 for each number in the cell state ***Ct−1***.
> 1 represents “keep this” while a 0 represents “get rid of this.”

2. The next step is to decide what new information we’re going to store in the cell state. This has two parts.
>First, a sigmoid layer called the “input gate layer” decides which values we’ll update and which we will reject.
>Next, a tanh layer creates a vector of new values, **C̃t**, that could be added to the new state.

**Next step, combine these two to create an update to the state.**
3. Then we update the old cell state, **Ct−1**, into the new cell state **Ct**.
We multiply the old state by **ft**, forgetting the things we decided to forget earlier. Then we add **it∗C̃t** . This is the new values, scaled by how much we decided to update each state value.

4. Finally, we need to decide what we’re going to output. This output will be based on our cell state, but will be a filtered version. First, we run a sigmoid layer which decides what parts of the cell state we’re going to output. Then, we put the cell state through tanh (to push the values to be between −1 and 1) and multiply it by the output of the sigmoid gate, so that we only output the parts we decided to.

## Lets work it out!! Lets try making a model based on LSTM

The language model will be statistical and will predict the probability of each word given an input sequence of text. The predicted word will be fed in as input to in turn generate the next word.
A key design decision is how long the input sequences should be. They need to be long enough to allow the model to learn the context for the words to predict. This input length will also define the length of seed text used to generate new sequences when we use the model.
# 3.1 Creating character/word mappings <a id='char_and_word_mapping'></a>
[Back to top](#lstm)
We need to transform the raw text into a sequence of tokens or words that we can use as a source to train the model.
We will be removing following from our given input texts
> 1. Replace ‘–‘ with a white space so we can split words better.
> 2. Split words based on white space.
> 3. Remove all punctuation from words to reduce the vocabulary size (e.g. ‘What?’ becomes ‘What’).
> 4. Remove all words that are not alphabetic to remove standalone punctuation tokens.
> 5. Normalize all words to lowercase to reduce the vocabulary size.
Vocabulary size is a big deal with language modeling. A smaller vocabulary results in a smaller model that trains faster.
#### We can run this cleaning operation on our loaded document and print out some of the tokens
```
# turn a doc into clean tokens
def clean_doc(row):
# replace '--' with a space ' '
text = row['text']
text = text.replace('--', ' ')
# split into tokens by white space
tokens = text.split()
# remove punctuation from each token
table = str.maketrans('', '', string.punctuation)
tokens = [w.translate(table) for w in tokens]
# remove remaining tokens that are not alphabetic
tokens = [word for word in tokens if word.isalpha()]
# make lower case
tokens = [word.lower() for word in tokens]
return tokens
df_cleaner['token'] = df_cleaner.apply(lambda row: clean_doc(row), axis =1)
#loaded document as an argument and returns an array of clean tokens.
df_cleaner.head()
```
# 3.2 Creating set of words <a id='creating_set_words'></a>
[Back to top](#lstm)
```
#creating a set of all words in the text columns
def list_creation(list_trial):
list_trial=list_trial.tolist()
result_trial = set(x for l in list_trial for x in l)
#print (result_set)
return (result_trial)
df_tokens=list_creation(df_cleaner['token'])
df_tokens_=set(df_tokens)
print('Total Tokens: %d' % len(df_tokens))
print('Unique Tokens: %d' % len(df_tokens_))
```
# 3.3 Creating sequences <a id='creating_sequences'></a>
We are training a statistical language model from the prepared data. It has a few unique characteristics:
> 1. It uses a distributed representation for words so that different words with similar meanings will have a similar representation.
> 2. It learns the representation at the same time as learning the model.
> 3. It learns to predict the probability for the next word using the context of the last 100 words.
We will be using the concept of an Embedding Layer to learn the representation of words, and a Long Short-Term Memory (LSTM) recurrent neural network to learn to predict words based on their context.Steps are as follow
1. Firstly we will be organizing the long list of tokens into sequences of n input words and 1 output word. That is, sequences of n+1 words. We can do this by iterating over the list of tokens from token n+1 onwards and taking the prior n tokens as a sequence, then repeating this process to the end of the list of tokens. For our example we will be using a sequence of 11 words
[Back to top](#lstm)
```
# organize into sequences of tokens
length = 11 + 1
sequences = list()
df_tokens=list(df_tokens)
for i in range(length, len(df_tokens)):
# select sequence of tokens
seq = df_tokens[i-length:i]
# convert into a line
line = ' '.join(seq)
# store
sequences.append(line)
print('Total Sequences: %d' % len(sequences))
#use sequences for modeling
```
# 3.4 Saving Tokens and Loading Tokens <a id='Saving_Tokens'></a>
## One Dialog per line
[Back to top](#lstm)
```
# save tokens to file, one dialog per line
def save_doc(lines, filename):
data = '\n'.join(lines)
file = open(filename, 'w')
file.write(data)
file.close()
## loads tokens to file, one dialog per line
def load_doc(filename):
# open the file as read only
file = open(filename, 'r')
# read all text
text = file.read()
# close the file
file.close()
return text
out_filename = 'LSTM_Files/republic_sequences.txt'
save_doc(sequences, out_filename)
# load
in_filename = 'LSTM_Files/republic_sequences.txt'
doc = load_doc(in_filename)
lines = doc.split('\n')
```
# 3.5 Integer Encoding Sequences <a id='Integer_Encoding'></a>
[Back to top](#lstm)
The word embedding layer expects input sequences to be comprised of integers. We can map each word in our vocabulary to a unique integer and encode our input sequences. Later, when we make predictions, we can convert the prediction to numbers and look up their associated words in the same mapping.
To do this encoding, we will use the Tokenizer class in the Keras API.
>1. First, the Tokenizer must be trained on the entire training dataset, which means it finds all of the unique words in the data and assigns each a unique integer.
>2. We can then use the fit Tokenizer to encode all of the training sequences, converting each sequence from a list of words to a list of integers.
```
# integer encode sequences of words
tokenizer = Tokenizer()
tokenizer.fit_on_texts(lines)
sequences = tokenizer.texts_to_sequences(lines)
```
## Word Index
We can access the mapping of words to integers as a dictionary attribute called word_index on the Tokenizer object. We need to know the size of the vocabulary for defining the embedding layer later. We can determine the vocabulary by calculating the size of the mapping dictionary.
Words are assigned values from 1 to the total number of words .The Embedding layer needs to allocate a vector representation for each word in this vocabulary from index 1 to the largest index and because indexing of arrays is zero-offset, the index of the word at the end of the vocabulary will be n, that means the array must be n+1 in length.
when specifying the vocabulary size to the Embedding layer, we specify it as 1 larger than the actual vocabulary.
```
# vocabulary size
vocab_size = len(tokenizer.word_index) + 1
```
### Input and Output Sequences
Now encoding of sequence is done, so we need to know the input (X) and output (y) elememts. We do that by array slicing. We have used one hot encoding for output word, converting it from an integer to a vector of 0 values, 1 for each word in vocabulary,indicating 1 to specific word at the index of words .
We have done this , so that the model learns to predict the probability distribution for the next word and the ground truth from which to learn from is 0 for all words except the actual word that comes next.
Keras provides the to_categorical() that can be used to one hot encode the output words for each input-output sequence pair.
***Finally, we need to specify to the Embedding layer how long input sequences are. A good generic way to specify that is to use the second dimension (number of columns) of the input data’s shape. That way, if you change the length of sequences when preparing data, you do not need to change this data loading code; it is generic.***
```
sequences = np.asarray(sequences)
X, y = sequences[:,:-1], sequences[:,-1]
seq_length = X.shape[1]
y = np_utils.to_categorical(y, num_classes=vocab_size)
```
# 3.6 Defining the Model <a id='defining_model'></a>
[Back to top](#lstm)
We will be fitting and training our model now. The learned embedding needs to know the size of the vocabulary and the length of input sequences as previously discussed. It also has a parameter to specify how many dimensions will be used to represent each word. That is, the size of the embedding vector space. We will use a two LSTM hidden layers with 200 memory cells each. More memory cells and a deeper network may achieve better results.
```
# define model
model = Sequential()
model.add(Embedding(vocab_size, 75, input_length=seq_length))
model.add(LSTM(100, return_sequences=True))
model.add(LSTM(100))
model.add(Dense(100, activation='relu'))
model.add(Dense(vocab_size, activation='softmax'))
print(model.summary())
```
#### Important Points to Note:-
>A dense fully connected layer with 200 neurons connects to the LSTM hidden layers to interpret the features extracted from the sequence. The output layer predicts the next word as a single vector the size of the vocabulary with a probability for each word in the vocabulary. A softmax activation function is used to ensure the outputs have the characteristics of normalized probabilities.
>Our model is learning a multi-class classification and this is the suitable loss function for this type of problem. The efficient Adam implementation to mini-batch gradient descent is used and accuracy is evaluated of the model.
>Finally, the model is fit on the data for 100 training epochs with a modest batch size of 128 to speed things up.
#### Model Parameters:-
>Activation Function: We have used ReLU as the activation function. ReLU is a non-linear activation function, which helps complex relationships in the data to be captured by the model.
>Optimiser: We use adam optimiser, which is an adaptive learning rate optimiser.
>Loss function: We will train a network to output a probability over the 10 classes using Cross-Entropy loss, also called Softmax Loss. It is very useful for multi-class classification.
```
%%capture
# compile model
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit model
MODEL=model.fit(X, y, batch_size=128, epochs=100)
```
#### We use the Keras model API to save the model to the file ‘model.h5‘ in the current working directory.
Our model is all trained now and can be utilised to generate new sequences of texts that have same statistical properties, although it might be difficult but then nothing is impossible.
We need the text so that we can choose a source sequence as input to the model for generating a new sequence of text.
The model will require 100 words as input. We will need to specify the expected length of input. We can determine this from the input sequences by calculating the length of one line of the loaded data and subtracting 1 for the expected output word that is also on the same line.
```
# save the model to file
model.save('LSTM_Files/model.h5')
# save the tokenizer
output = open('LSTM_Files/myfile.pkl', 'wb')
pickle.dump(tokenizer, output)
output.close()
#pkl_file = open('tokenizer.pkl', 'rb')
#mydict2 = pickle.load(pkl_file)
#pkl_file.close()
seq_length = len(lines[0].split()) - 1 ####sequence lenght that we will feed
```

# 3.6 Generating Sequences <a id='generating_sequence'></a>
Preparing a seed input, which is randomly done
```
seed_text = lines[randint(0,len(lines))]
print(seed_text + '\n')
```
Basis to understand the following present given underneath
>1. First, the seed text must be encoded to integers using the same tokenizer that we used when training the model.
>Following line in code shows us this encoded = tokenizer.texts_to_sequences([in_text])[0]
>2. The model can predict the next word directly by calling model.predict_classes() that will return the index of the word with the highest probability. (represented by yhat). Look up the index in the Tokenizers mapping to get the associated word.
>3. Then we will be appending this word to the seed text and repeat the process.
>4. The input sequence is going to get too long. We can truncate it to the desired length after the input sequence has been encoded to integers. Keras provides the pad_sequences() function that we can use to perform this truncation.
```
def generate_seq(model, tokenizer, seq_length, seed_text, n_words):
result = list()
in_text = seed_text
# generate a fixed number of words
for _ in range(n_words):
# encode the text as integer
encoded = tokenizer.texts_to_sequences([in_text])[0]
# truncate sequences to a fixed length
encoded = pad_sequences([encoded], maxlen=seq_length, truncating='pre')
# predict probabilities for each word
yhat = model.predict_classes(encoded, verbose=0)
# map predicted word index to word
out_word = ''
for word, index in tokenizer.word_index.items():
if index == yhat:
out_word = word
break
# append to input
in_text += ' ' + out_word
result.append(out_word)
return ' '.join(result)
```
#### Generate a sequence of new words given some seed text.
```
# generate new text
generated = generate_seq(model, tokenizer, seq_length, seed_text, 50)
print(generated)
```
#### BLEU (bilingual evaluation understudy) is an algorithm for evaluating the quality of text which has been machine-translated from one natural language to another. Quality is considered to be the correspondence between a machine's output and that of a human: "the closer a machine translation is to a professional human translation, the better it is" – this is the central idea behind BLEU.[1][2] BLEU was one of the first metrics to claim a high correlation with human judgements of quality,[3][4] and remains one of the most popular automated and inexpensive metrics.
```
## for calculation of bleu score
from nltk.translate.bleu_score import sentence_bleu
score = sentence_bleu(generated, seed_text)
```
### 3.7.1 Deeper LSTM Model <a id='DeeperModel'></a>
We will be creating a set of all of the distinct characters in the loaded document, then we will be creating a map of each character to a unique integer.
```
# load ascii text and covert to lowercase
doc = load_doc(in_filename)
lines = doc.split('\n')
# create mapping of unique chars to integers, and a reverse mapping
chars = sorted(list(set(doc)))
char_to_int = dict((c, i) for i, c in enumerate(chars))
int_to_char = dict((i, c) for i, c in enumerate(chars))
```
Summary of loaded data
```
# summarize the loaded data
n_chars = len(doc)
n_vocab = len(chars)
print ("Total Characters: ", n_chars)
print ("Total Vocab: ", n_vocab)
```
Each training pattern of the network is comprised of let say 100 time steps of one character (X) followed by one character output (y). When creating these sequences, we slide this window along the whole document one character at a time, allowing each character a chance to be learned from the 100 characters that preceded it (except the first 100 characters of course).
#### Prepare the dataset of input to output pairs encoded as integers
```
# prepare the dataset of input to output pairs encoded as integers
seq_length = 100
dataX = []
dataY = []
for i in range(0, n_chars - seq_length, 1):
seq_in = doc[i:i + seq_length]
seq_out = doc[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
n_patterns = len(dataX)
print ("Total Patterns: ", n_patterns)
```
#### One Hot Encoding of output variable
```
# reshape X to be [samples, time steps, features]
X = np.reshape(dataX, (n_patterns, seq_length, 1))
# normalize
X = X / float(n_vocab)
# one hot encode the output variable
y = np_utils.to_categorical(dataY)
```
#### Define the LSTM model
>The network is slow to train (about 300 seconds per epoch on an Nvidia K520 GPU). Because of the slowness and because of our optimization requirements, we will use model checkpointing to record all of the network weights to file each time an improvement in loss is observed at the end of the epoch. We will use the best set of weights (lowest loss) to instantiate our generative model in the next section.
```
# define the LSTM model
model = Sequential()
model.add(LSTM(256, input_shape=(X.shape[1], X.shape[2])))
model.add(Dropout(0.2))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam')
# define the checkpoint
filepath="LSTM_Files/weights-improvement-{epoch:02d}-{loss:.4f}.hdf5"
checkpoint = ModelCheckpoint(filepath, monitor='loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
# fit the model
model.fit(X, y, epochs=2, batch_size=128, callbacks=callbacks_list)
```
#### After running this piece of code , we will have a number of weight checkpoint files in the local directory. We can delete them all except the one with the smallest loss value.
```
# load the network weights
filename = "LSTM_Files/weights-improvement-02-2.7259.hdf5"
model.load_weights(filename)
model.compile(loss='categorical_crossentropy', optimizer='adam')
```
#### Generate Text using deeper network (LSTM)
```
# pick a random seed
start = np.random.randint(0, len(dataX)-1)
pattern = dataX[start]
print ("Seed:")
print ("\"", ''.join([int_to_char[value] for value in pattern]), "\"")
# generate characters
for i in range(1000):
x = np.reshape(pattern, (1, len(pattern), 1))
x = x / float(n_vocab)
prediction = model.predict(x, verbose=0)
index = np.argmax(prediction)
result = int_to_char[index]
seq_in = [int_to_char[value] for value in pattern]
sys.stdout.write(result)
pattern.append(index)
pattern = pattern[1:len(pattern)]
print ("\nDone.")
```

# <p style="text-align: center;">Conclusion<p><a id='Conclusion'></a>
1. We are not interested in the most accurate (classification accuracy) model of the training dataset. The model is the one that predicts each character in the training dataset perfectly. Instead we are interested in a generalization of the dataset that minimizes the chosen loss function. We are seeking a balance between generalization and overfitting but short of memorization.
2. As of now we are able to generate text, which seems much more gibberish but is making sense in some parts, the text generated can be tuned by adding different dense layers , building complex neuron network and by increasing epochs and decreasing the batch size.
3. Still working on BLEU and Meteor score though we are able to calculate it , it gives us a low value because the text that is being generated as of now is a bit gibberish and will yield a low value, ideally the score for BLEU should be between 0.0 to 1.0 and we got a value of 1.276854e-89, which is low , so if modeling is tweaked it may yield good results, this is still being worked upon
4. Model can also perform well , if we take a large vocab size and our input seed lenght is good enough, although time consuming, but output can vary differently if we experiment it in that way.
5. Adding weights to model with better accuracy results results in making a model (deeper and denser one better), we can keep on iterating that ways.
6. The collected data can be tested upon to find its sentiment by our third project notebook (sentiment analysis part 3)
[Back to top](#Introduction)
# <p style="text-align: center;">Future Scope<p><a id='Scope'></a>
1. Still working on BLEU and Meteor score though we are able to calculate it , it gives us a low value because the text that is being generated as of now is a bit gibberish and will yield a low value, ideally the score for BLEU should be between 0.0 to 1.0 and we got a value of 1.276854e-89, which is low , so if modeling is tweaked it may yield good results, this is still being worked upon
2. Train the model more by increasing the epochs & decreasing the batch size
3. Try different RNN and compare which is better
4. Try to train the data with more than 1 sources
5. Predict less characters for output
6. Do it on data collected through scraping of article websites , will yield better results
7. We can try to employ GANs , works good for image , can also be tried for texts
The next part of the project is[Sentiment Analysis](Umbrella_Academy_INFO6105_Sentiment_Analysis.ipynb). Please click the link to follow to the next notebook.
# <p style="text-align: center;">Contribution<p><a id='Contribution'></a>
- Code by self : 60%
- Code from external Sources : 40%
[Back to top](#Introduction)
# Citation:
1. https://github.com/abdulfatir/twitter-sentiment-analysis/blob/master/code/preprocess.py
2. https://stackoverflow.com/questions/8282553/removing-character-in-list-of-strings
3. https://github.com/bear/python-twitter/blob/master/twitter/parse_tweet.py
4. https://gist.github.com/dreikanter/2787146
5. https://docs.python.org/3.4/howto/unicode.html
6. https://www.kaggle.com/eliasdabbas/extract-entities-from-social-media-posts
7. https://machinelearningmastery.com/text-generation-lstm-recurrent-neural-networks-python-keras/
8. https://machinelearningmastery.com/how-to-develop-a-word-level-neural-language-model-in-keras/
[Back to top](#Introduction)
# <p style="text-align: center;">License<p><a id='License'></a>
Copyright (c) 2019 Manali Sharma, Rushabh Nisher
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
[Back to top](#Introduction)
| true |
code
| 0.305963 | null | null | null | null |
|
# TopicBank Demo
The notebook contains a demonstration of the [TopicBank approach](https://github.com/machine-intelligence-laboratory/OptimalNumberOfTopics/tree/master/topnum/search_methods/topic_bank) for finding an appropriate number of topics.
Dataset used for demonstration is [20 Newsgroups](http://qwone.com/~jason/20Newsgroups/), preprocessed in a way described in the notebook [Making-Decorrelation-and-Topic-Selection-Friends.ipynb](https://github.com/machine-intelligence-laboratory/TopicNet/blob/master/topicnet/demos/Making-Decorrelation-and-Topic-Selection-Friends.ipynb).
```
# General imports
import numpy as np
import os
from scipy.stats import gaussian_kde
from matplotlib import pyplot as plt
%matplotlib inline
# Making `topnum` module visible for Python
import sys
sys.path.insert(0, '..')
# Optimal number of topics
from topnum.data.vowpal_wabbit_text_collection import VowpalWabbitTextCollection
from topnum.search_methods import TopicBankMethod
```
## Data
In the folder below must reside the necessary data file in Vowpal Wabbit format.
```
DATA_FOLDER_PATH = 'data'
os.listdir(DATA_FOLDER_PATH)
vw_file_path = os.path.join(
DATA_FOLDER_PATH,
'twenty_newsgroups__vw__natural_order.txt'
)
```
Checking if all OK with data, what modalities does the collection have.
```
! head -n 7 $vw_file_path
```
Defining a text collection entity, which is to be passed to topic number search method later:
```
text_collection = VowpalWabbitTextCollection(
vw_file_path,
main_modality='@text'
)
```
Let's transform this collection to the TopicNet's Dataset (so as to look at it more easily).
```
dataset = text_collection._to_dataset()
dataset._data.shape
dataset._data.head()
```
The searching method itself.
It has several parameters: some are specific for the renormalization approach, some are common for all the search methods presented in `topnum` module.
```
optimizer = TopicBankMethod(
data = dataset, # `text_collection` also would be fine here
min_df_rate=0.001, # excluding too rare words from text collection's vocabulary
max_num_models = 100, # number of models for collecting topics
one_model_num_topics = 100, # number of topics in one model
num_fit_iterations = 100, # 100 or 200 surely might be enough
topic_score_threshold_percentile = 90 # 10% of the best model topics according to the score are going to be considered as good
)
```
Fulfilling the search:
```
%%time
optimizer.search_for_optimum(text_collection)
```
The search method's result may be accessed as `optimizer._result`.
Let's see what is available here:
```
list(optimizer._result.keys())
```
Point estimate of the number of topics and standard deviation (std) over the restarts (`num_restarts`):
```
result_key_optimum = 'optimum'
result_key_optimum_std = 'optimum_std'
print(
f'Optimum: {optimizer._result[result_key_optimum]} topics.' +
f' Std: {optimizer._result[result_key_optimum_std]}'
)
```
The number of topics appeared to be $20$!
So, the method worked pretty well for this particular dataset.
```
result_key_bank_scores = 'bank_scores'
result_key_bank_topic_scores = 'bank_topic_scores'
result_key_model_scores = 'model_scores'
result_key_model_topic_scores = 'model_topic_scores'
print(
'Num iterations:',
len(optimizer._result[result_key_bank_scores])
)
print(
'...same as:',
len(optimizer._result[result_key_model_scores])
)
print(
'...and:',
len(optimizer._result[result_key_model_topic_scores])
)
print(
'Final number of topics:',
len(optimizer._result[result_key_bank_topic_scores])
)
```
Let us look at the first elements in the result values:
```
# Scores for the bank as topic model
list(optimizer._result[result_key_bank_scores])[0]
# Averaged scores for bank topics for the particular iteration
list(optimizer._result[result_key_bank_topic_scores])[0]
# Scores for the model trained during the iteration
list(optimizer._result[result_key_model_scores])[0]
# Scores for each topic of the current model
list(optimizer._result[result_key_model_topic_scores])[0][:3]
```
Using the saved scores one may analyze the process.
For example, how the perplexity changes for the bank during its creation:
```
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
x = range(len(list(optimizer._result[result_key_bank_scores])))
y = [s['perplexity_score'] for s in optimizer._result[result_key_bank_scores]]
ax.scatter(x, y, s=100)
ax.set_xlabel('Iteration (number of models)')
ax.set_ylabel('Perplexity')
ax.grid(True)
plt.show()
```
And the perplexity for ordinary models:
```
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
x = range(len(list(optimizer._result[result_key_model_scores])))
y = [s['perplexity_score'] for s in optimizer._result[result_key_model_scores]]
ax.scatter(x, y, s=100)
ax.set_xlabel('Iteration (number of models)')
ax.set_ylabel('Perplexity of the model')
ax.grid(True)
plt.show()
```
And another score worth looking at — topic coherence (for example, intratext), as a measure of topic interpretability:
```
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
score_name = 'intratext_coherence_score'
x = range(len(list(optimizer._result[result_key_bank_topic_scores])))
y_bank = [
s[score_name]
for s in optimizer._result[result_key_bank_topic_scores]
]
y_model = [
s[score_name]
for model_scores in optimizer._result[result_key_model_topic_scores]
for s in model_scores
]
y_model = [v if v is not None else 0.0 for v in y_model]
gauss_for_bank = gaussian_kde(y_bank)
gauss_for_models = gaussian_kde(y_model)
x = np.arange(-0.01, 0.2, 0.001)
ax.plot(x, gauss_for_bank(x), color='b', lw=5, label='topic bank')
ax.plot(x, gauss_for_models(x), color='r', lw=5, label='ordinary model')
ax.set_xlabel('Coherence value')
ax.set_ylabel('KDE')
ax.legend()
ax.grid(True)
plt.show()
```
Distance of newly added topic to the nearest topic already in the bank:
```
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
x = range(len(list(optimizer._result[result_key_bank_topic_scores])))
y = [s['distance_to_nearest'] for s in optimizer._result[result_key_bank_topic_scores]]
ax.scatter(x, y, s=100)
ax.set_xlabel('Iteration (number of models)')
ax.set_ylabel('Perplexity of the model')
ax.grid(True)
plt.show()
```
As the bank growths, this distance value shrinks.
| true |
code
| 0.656658 | null | null | null | null |
|
# Investigation into Sklearn Pipelines for Scaling and Model Selection
Using http://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html
and data https://archive.ics.uci.edu/ml/datasets/APS+Failure+at+Scania+Trucks
```
import numpy as np
import pandas as pd
import re
import os
from pandas.plotting import scatter_matrix
get_ipython().magic(u'env OMP_NUM_THREADS=2')
from IPython.display import display, HTML
import sklearn
import sklearn.model_selection
import requests
import io
import random
# Set the ransom seed used for the whole program to allow reprocibility
np.random.seed(3214412)
DEBUG = True # If true, pull a sample of the dataset for development
local_archive = "aps_failure_training_set.csv"
if not os.path.exists(local_archive):
print("Downloading contents")
data_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/00421/aps_failure_training_set.csv"
contents=requests.get(data_url).content
# First 20 rows of the file is a header with licensing info
# The header with column names is on row 21
raw_data_df=pd.read_csv(io.StringIO(contents.decode('utf-8')), skiprows=20, na_values="na")
raw_data_df.to_csv(local_archive, index=False)
else:
print("Loading from local")
raw_data_df=pd.read_csv(local_archive, na_values="na")
raw_data_df.head()
# This is a poc on sklearn-pipelines so drop down to 10 columns
# Grab the 10 columns with the least number of null values and column "class"
data_df = raw_data_df[raw_data_df.isnull().sum().sort_values()[:11].index].dropna()
data_df.head()
print("Count of rows: {}".format(data_df.shape[0]))
print("Count of rows with class 'neg': {}".format(data_df[data_df['class'] == 'neg']['class'].shape[0]))
print("Count of rows with class 'pos': {}".format(data_df[data_df['class'] == 'pos']['class'].shape[0]))
# Describe all the columns at once
display(pd.concat([data_df[col].describe().to_frame(name=col) for col in data_df.columns if col != 'class'], axis=1))
display(data_df['class'].value_counts())
```
## Pipeline POC work
```
train_df = data_df.drop(labels=['class'], axis=1)
labels_srs = data_df['class']
```
### Basic scaling
```
from sklearn.preprocessing import StandardScaler
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.pipeline import Pipeline
from sklearn import svm
scaling = StandardScaler()
svm_model = svm.SVC(kernel='linear')
chi_f_selection = SelectKBest(score_func=chi2, k=8)
pipeline_model = Pipeline([
('chi_selection', chi_f_selection),
('scaling', scaling),
('svc', svm_model)])
fit_model = pipeline_model.fit(train_df, labels_srs)
# Now try it out
print("score: {}".format(fit_model.score(train_df, y=labels_srs)))
print("Sample of Predictions:\n{}".format(fit_model.predict(train_df.sample(n=50))))
```
### Grid Search over Pipeline paramaters
1. Feature selection functions and parameters
```
from sklearn.feature_selection import SelectKBest, chi2, f_classif, f_regression
from sklearn.model_selection import GridSearchCV
scaling = StandardScaler()
svm_model = svm.SVC(kernel='linear')
chi_f_selection = SelectKBest(score_func=chi2, k=8)
pipeline_model = Pipeline([
('chi_selection', chi_f_selection),
('scaling', scaling),
('svc', svm_model)])
# Commented a few options out in the interest of POC and time
param_grid = [
{
'chi_selection__score_func': [chi2], #, f_regression, f_classif],
'scaling__with_mean': [True],#, False],
'scaling__with_std': [True],#, False],
'svc__C': [0.5]#, 1, 5, 10]
}
]
grid = GridSearchCV(pipeline_model, cv=3, n_jobs=3, param_grid=param_grid)
grid_fit_model = grid.fit(train_df, labels_srs)
# Now try it out
print("score: {}".format(grid_fit_model.score(train_df, y=labels_srs)))
print("Sample of Predictions:\n{}".format(grid_fit_model.predict(train_df.sample(n=50))))
print("Best Parameters")
grid_fit_model.best_params_
```
### Cross Validation score prediction
```
from sklearn.model_selection import cross_val_score
cross_val_score(grid_fit_model, train_df, labels_srs, cv=3)
```
## Bootstrapping
```
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
scaling = StandardScaler()
dtc_model = DecisionTreeClassifier()
ab_dtc_model = AdaBoostClassifier(dtc_model)
chi_f_selection = SelectKBest(score_func=chi2, k=8)
pipeline_model = Pipeline([
('chi_selection', chi_f_selection),
('scaling', scaling),
('boost', ab_dtc_model)])
# Commented a few options out in the interest of POC and time
param_grid = [
{
'chi_selection__score_func': [chi2], #, f_regression, f_classif],
'scaling__with_mean': [True],#, False],
'scaling__with_std': [True],#, False],
'boost__n_estimators': [10, 50, 200],
'boost__base_estimator': [DecisionTreeClassifier(max_depth=1, min_samples_leaf=1),
DecisionTreeClassifier(max_depth=5, min_samples_leaf=3)]
}
]
grid = GridSearchCV(pipeline_model, cv=3, n_jobs=6, param_grid=param_grid)
grid_fit_model = grid.fit(train_df, labels_srs)
# Now try it out
print("score: {}".format(grid_fit_model.score(train_df, y=labels_srs)))
print("Sample of Predictions:\n{}".format(grid_fit_model.predict(train_df.sample(n=50))))
print("Best Parameters")
grid_fit_model.best_params_
```
## Model Selection
```
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
classifiers = dict(
knn3=KNeighborsClassifier(3),
svc=SVC(kernel="linear", C=0.025),
tree=DecisionTreeClassifier(max_depth=5),
forest=RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1),
boost=AdaBoostClassifier()
)
from sklearn.preprocessing import StandardScaler
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.pipeline import Pipeline
from sklearn import svm
scaling = StandardScaler()
svm_model = svm.SVC(kernel='linear')
chi_f_selection = SelectKBest(score_func=chi2, k=8)
def get_score(name, model):
pipeline_model = Pipeline([
('chi_selection', chi_f_selection),
('scaling', scaling),
(name, model)])
fit_model = pipeline_model.fit(train_df, labels_srs)
score = fit_model.score(train_df, y=labels_srs)
return score
results = {name: get_score(name, model) for name, model in classifiers.items()}
for name, score in results.items():
print("{name}: score={score}".format(name=name, score=score))
```
| true |
code
| 0.532668 | null | null | null | null |
|
# Tile Coding
---
Tile coding is an innovative way of discretizing a continuous space that enables better generalization compared to a single grid-based approach. The fundamental idea is to create several overlapping grids or _tilings_; then for any given sample value, you need only check which tiles it lies in. You can then encode the original continuous value by a vector of integer indices or bits that identifies each activated tile.
### 1. Import the Necessary Packages
```
# Import common libraries
import sys
import gym
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import time
import copy
# Set plotting options
%matplotlib inline
plt.style.use('ggplot')
np.set_printoptions(precision=3, linewidth=120)
```
### 2. Specify the Environment, and Explore the State and Action Spaces
We'll use [OpenAI Gym](https://gym.openai.com/) environments to test and develop our algorithms. These simulate a variety of classic as well as contemporary reinforcement learning tasks. Let's begin with an environment that has a continuous state space, but a discrete action space.
```
# Create an environment
env = gym.make('Acrobot-v1')
env.seed(505);
# Explore state (observation) space
print("State space:", env.observation_space)
print("- low:", env.observation_space.low)
print("- high:", env.observation_space.high)
# Explore action space
print("Action space:", env.action_space)
state = env.reset()
score = 0
start_time = time.time()
n_steps = 0
while True:
n_steps += 1
action = env.action_space.sample()
env.render()
state, reward, done, _ = env.step(action)
score += reward
if done:
break
print(n_steps, 'steps in', round(time.time() - start_time, 3), 'seconds')
print('Final score:', score)
env.close()
```
Note that the state space is multi-dimensional, with most dimensions ranging from -1 to 1 (positions of the two joints), while the final two dimensions have a larger range. How do we discretize such a space using tiles?
### 3. Tiling
Let's first design a way to create a single tiling for a given state space. This is very similar to a uniform grid! The only difference is that you should include an offset for each dimension that shifts the split points.
For instance, if `low = [-1.0, -5.0]`, `high = [1.0, 5.0]`, `bins = (10, 10)`, and `offsets = (-0.1, 0.5)`, then return a list of 2 NumPy arrays (2 dimensions) each containing the following split points (9 split points per dimension):
```
[array([-0.9, -0.7, -0.5, -0.3, -0.1, 0.1, 0.3, 0.5, 0.7]),
array([-3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5])]
```
Notice how the split points for the first dimension are offset by `-0.1`, and for the second dimension are offset by `+0.5`. This might mean that some of our tiles, especially along the perimeter, are partially outside the valid state space, but that is unavoidable and harmless.
```
def create_tiling_grid(low, high, bins=(10, 10), offsets=(0.0, 0.0)):
"""Define a uniformly-spaced grid that can be used for tile-coding a space.
Parameters
----------
low : array_like
Lower bounds for each dimension of the continuous space.
high : array_like
Upper bounds for each dimension of the continuous space.
bins : tuple
Number of bins or tiles along each corresponding dimension.
offsets : tuple
Split points for each dimension should be offset by these values.
Returns
-------
grid : list of array_like
A list of arrays containing split points for each dimension.
"""
assert len(low) == len(high) == len(bins) == len(offsets),\
"all lengths must match: given lengths are {}, {}, {}, {}".format(len(low), len(high), len(bins), len(offsets))
return [np.linspace(start=low[dim], stop=high[dim], num=bins[dim] + 1)[1:-1] + offsets[dim] for dim in range(len(bins))]
low = [-1.0, -5.0]
high = [1.0, 5.0]
create_tiling_grid(low, high, bins=(10, 10), offsets=(-0.1, 0.5)) # [test]
```
You can now use this function to define a set of tilings that are a little offset from each other.
```
def create_tilings(low, high, tiling_specs):
"""Define multiple tilings using the provided specifications.
Parameters
----------
low : array_like
Lower bounds for each dimension of the continuous space.
high : array_like
Upper bounds for each dimension of the continuous space.
tiling_specs : list of tuples
A sequence of (bins, offsets) to be passed to create_tiling_grid().
Returns
-------
tilings : list
A list of tilings (grids), each produced by create_tiling_grid().
"""
return [create_tiling_grid(low, high, bins, offsets) for bins, offsets in tiling_specs]
# Tiling specs: [(<bins>, <offsets>), ...]
tiling_specs = [((10, 10), (-0.066, -0.33)),
((10, 10), (0.0, 0.0)),
((10, 10), (0.066, 0.33))]
tilings = create_tilings(low, high, tiling_specs)
```
It may be hard to gauge whether you are getting desired results or not. So let's try to visualize these tilings.
```
from matplotlib.lines import Line2D
plt.rcParams['figure.facecolor'] = 'w'
def visualize_tilings(tilings):
"""Plot each tiling as a grid."""
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
linestyles = ['-', '--', ':']
legend_lines = []
fig, ax = plt.subplots(figsize=(10, 10))
for i, grid in enumerate(tilings):
for x in grid[0]:
l = ax.axvline(x=x, color=colors[i % len(colors)], linestyle=linestyles[i % len(linestyles)], label=i)
for y in grid[1]:
l = ax.axhline(y=y, color=colors[i % len(colors)], linestyle=linestyles[i % len(linestyles)])
legend_lines.append(l)
ax.grid(False)
ax.legend(legend_lines, ["Tiling #{}".format(t) for t in range(len(legend_lines))], facecolor='white', framealpha=0.9)
ax.set_title("Tilings")
return ax # return Axis object to draw on later, if needed
visualize_tilings(tilings);
```
Great! Now that we have a way to generate these tilings, we can next write our encoding function that will convert any given continuous state value to a discrete vector.
### 4. Tile Encoding
Implement the following to produce a vector that contains the indices for each tile that the input state value belongs to. The shape of the vector can be the same as the arrangment of tiles you have, or it can be ultimately flattened for convenience.
You can use the same `discretize()` function here from grid-based discretization, and simply call it for each tiling.
```
def discretize(sample, grid):
"""Discretize a sample as per given grid.
Parameters
----------
sample : array_like
A single sample from the (original) continuous space.
grid : list of array_like
A list of arrays containing split points for each dimension.
Returns
-------
discretized_sample : array_like
A sequence of integers with the same number of dimensions as sample.
"""
return tuple(int(np.digitize(sample_point, corresponding_grid))
for sample_point, corresponding_grid in zip(sample, grid))
def tile_encode(sample, tilings, flatten=False):
"""Encode given sample using tile-coding.
Parameters
----------
sample : array_like
A single sample from the (original) continuous space.
tilings : list
A list of tilings (grids), each produced by create_tiling_grid().
flatten : bool
If true, flatten the resulting binary arrays into a single long vector.
Returns
-------
encoded_sample : list or array_like
A list of binary vectors, one for each tiling, or flattened into one.
"""
encoded_sample = [discretize(sample, grid) for grid in tilings]
return np.concatenate(encoded_sample) if flatten else encoded_sample
# Test with some sample values
samples = [(-1.2 , -5.1 ),
(-0.75, 3.25),
(-0.5 , 0.0 ),
( 0.25, -1.9 ),
( 0.15, -1.75),
( 0.75, 2.5 ),
( 0.7 , -3.7 ),
( 1.0 , 5.0 )]
encoded_samples = [tile_encode(sample, tilings) for sample in samples]
print("\nSamples:", repr(samples), sep="\n")
print("\nEncoded samples:", repr(encoded_samples), sep="\n")
```
Note that we did not flatten the encoding above, which is why each sample's representation is a pair of indices for each tiling. This makes it easy to visualize it using the tilings.
```
from matplotlib.patches import Rectangle
def visualize_encoded_samples(samples, encoded_samples, tilings, low=None, high=None):
"""Visualize samples by activating the respective tiles."""
samples = np.array(samples) # for ease of indexing
# Show tiling grids
ax = visualize_tilings(tilings)
# If bounds (low, high) are specified, use them to set axis limits
if low is not None and high is not None:
ax.set_xlim(low[0], high[0])
ax.set_ylim(low[1], high[1])
else:
# Pre-render (invisible) samples to automatically set reasonable axis limits, and use them as (low, high)
ax.plot(samples[:, 0], samples[:, 1], 'o', alpha=0.0)
low = [ax.get_xlim()[0], ax.get_ylim()[0]]
high = [ax.get_xlim()[1], ax.get_ylim()[1]]
# Map each encoded sample (which is really a list of indices) to the corresponding tiles it belongs to
tilings_extended = [np.hstack((np.array([low]).T, grid, np.array([high]).T)) for grid in tilings] # add low and high ends
tile_centers = [(grid_extended[:, 1:] + grid_extended[:, :-1]) / 2 for grid_extended in tilings_extended] # compute center of each tile
tile_toplefts = [grid_extended[:, :-1] for grid_extended in tilings_extended] # compute topleft of each tile
tile_bottomrights = [grid_extended[:, 1:] for grid_extended in tilings_extended] # compute bottomright of each tile
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
for sample, encoded_sample in zip(samples, encoded_samples):
for i, tile in enumerate(encoded_sample):
# Shade the entire tile with a rectangle
topleft = tile_toplefts[i][0][tile[0]], tile_toplefts[i][1][tile[1]]
bottomright = tile_bottomrights[i][0][tile[0]], tile_bottomrights[i][1][tile[1]]
ax.add_patch(Rectangle(topleft, bottomright[0] - topleft[0], bottomright[1] - topleft[1],
color=colors[i], alpha=0.33))
# In case sample is outside tile bounds, it may not have been highlighted properly
if any(sample < topleft) or any(sample > bottomright):
# So plot a point in the center of the tile and draw a connecting line
cx, cy = tile_centers[i][0][tile[0]], tile_centers[i][1][tile[1]]
ax.add_line(Line2D([sample[0], cx], [sample[1], cy], color=colors[i]))
ax.plot(cx, cy, 's', color=colors[i])
# Finally, plot original samples
ax.plot(samples[:, 0], samples[:, 1], 'o', color='r')
ax.margins(x=0, y=0) # remove unnecessary margins
ax.set_title("Tile-encoded samples")
return ax
visualize_encoded_samples(samples, encoded_samples, tilings);
```
Inspect the results and make sure you understand how the corresponding tiles are being chosen. Note that some samples may have one or more tiles in common.
### 5. Q-Table with Tile Coding
The next step is to design a special Q-table that is able to utilize this tile coding scheme. It should have the same kind of interface as a regular table, i.e. given a `<state, action>` pair, it should return a `<value>`. Similarly, it should also allow you to update the `<value>` for a given `<state, action>` pair (note that this should update all the tiles that `<state>` belongs to).
The `<state>` supplied here is assumed to be from the original continuous state space, and `<action>` is discrete (and integer index). The Q-table should internally convert the `<state>` to its tile-coded representation when required.
```
class QTable:
"""Simple Q-table."""
def __init__(self, state_size, action_size):
"""Initialize Q-table.
Parameters
----------
state_size : tuple
Number of discrete values along each dimension of state space.
action_size : int
Number of discrete actions in action space.
"""
self.state_size = state_size
self.action_size = action_size
self.q_table = np.zeros(state_size + (action_size,))
def __getitem__(self, key):
return self.q_table[key]
class TiledQTable:
"""Composite Q-table with an internal tile coding scheme."""
def __init__(self, low, high, tiling_specs, action_size):
"""Create tilings and initialize internal Q-table(s).
Parameters
----------
low : array_like
Lower bounds for each dimension of state space.
high : array_like
Upper bounds for each dimension of state space.
tiling_specs : list of tuples
A sequence of (bins, offsets) to be passed to create_tilings() along with low, high.
action_size : int
Number of discrete actions in action space.
"""
self.tilings = create_tilings(low, high, tiling_specs)
self.state_sizes = [tuple(len(splits) + 1 for splits in tiling_grid) for tiling_grid in self.tilings]
self.__first_indices = np.cumsum([0] + [np.prod(state_size) for state_size in self.state_sizes[:-1]])
self.__strides = np.array([tuple(np.prod(state_size[i:]) for i in range(1, len(state_size))) + (1,) for state_size in self.state_sizes])
self.action_size = action_size
# self.q_tables = [QTable(state_size, self.action_size) for state_size in self.state_sizes]
self.__flat_q_tables = np.zeros((self.__first_indices[-1] + np.prod(self.state_sizes[-1]), action_size))
@property
def q_tables(self):
start_ends = [tuple(self.__first_indices[i:i+2]) for i in range(len(self.__first_indices) - 1)] + [(self.__first_indices[-1], None)]
return [self.__flat_q_tables[start_end[0]:start_end[1]].reshape(state_size + (self.action_size,))
for state_size, start_end in zip(self.state_sizes, start_ends)]
@q_tables.setter
def q_tables(self, q_tables):
if isinstance(q_tables, (tuple, list)):
if len(q_tables) == len(self.q_tables):
for i, (old_q_table, new_q_table) in enumerate(zip(self.q_tables, new_q_table)):
if old_q_table.shape != new_q_table.shape:
raise RuntimeError("all Q tables must have the same dimensionality"\
"as the original ones: mismatch found in index {}"\
" - New {}, Old {}".format(i, new_q_table.shape, old_q_table.shape))
for old_q_table, new_q_table in zip(self.q_tables, new_q_table):
old_q_table[:] = new_q_table
else:
if q_tables.shape != self.__flat_q_tables.shape:
raise RuntimeError("the given Q table array must have the same dimensions as the "\
"original state-flattened Q table: given - {}, original - {}"\
.format(q_tables.shape, self.__flat_q_tables.shape))
self.__flat_q_tables = q_tables
def get(self, state, action):
"""Get Q-value for given <state, action> pair.
Parameters
----------
state : array_like
Vector representing the state in the original continuous space.
action : int
Index of desired action.
Returns
-------
value : float
Q-value of given <state, action> pair, averaged from all internal Q-tables.
"""
# tile_indices = tile_encode(state, self.tilings)
# return np.mean([q_table.q_table[tile_idx] for q_table, tile_idx in zip(self.q_tables, tile_indices)])
state_indices = np.sum(tile_encode(state, self.tilings) * self.__strides, axis=1, keepdims=False) + self.__first_indices
return np.mean(self.__flat_q_tables[state_indices, action])
def get_action_values(self, state):
"""Get all Q-values for given state.
Parameters
----------
state : array_like
Vector representing the state in the original continuous space.
Returns
-------
value : ndarray
Q-values of given state, averaged from all internal Q-tables.
"""
state_indices = np.sum(tile_encode(state, self.tilings) * self.__strides, axis=1, keepdims=False) + self.__first_indices
return np.mean(self.__flat_q_tables[state_indices], axis=0)
def update(self, state, action, value, alpha=0.1):
"""Soft-update Q-value for given <state, action> pair to value.
Instead of overwriting Q(state, action) with value, perform soft-update:
Q(state, action) = alpha * value + (1.0 - alpha) * Q(state, action)
Parameters
----------
state : array_like
Vector representing the state in the original continuous space.
action : int
Index of desired action.
value : float
Desired Q-value for <state, action> pair.
alpha : float
Update factor to perform soft-update, in [0.0, 1.0] range.
"""
# tile_indices = tile_encode(state, self.tilings)
# for q_table, tile_idx in zip(self.q_tables, tile_indices):
# q_table.q_table[tile_idx] += alpha * (value - q_table.q_table[tile_idx])
state_indices = np.sum(tile_encode(state, self.tilings) * self.__strides, axis=1, keepdims=False) + self.__first_indices
self.__flat_q_tables[state_indices, action] += alpha * (value - self.__flat_q_tables[state_indices, action])
# Test with a sample Q-table
tq = TiledQTable(low, high, tiling_specs, 2)
s1 = 3; s2 = 4; a = 0; q = 1.0
print("[GET] Q({}, {}) = {}".format(samples[s1], a, tq.get(samples[s1], a))) # check value at sample = s1, action = a
print("[UPDATE] Q({}, {}) = {}".format(samples[s2], a, q)); tq.update(samples[s2], a, q) # update value for sample with some common tile(s)
print("[GET] Q({}, {}) = {}".format(samples[s1], a, tq.get(samples[s1], a))) # check value again, should be slightly updated
print(len(tq.q_tables))
print(*(q.shape for q in tq.q_tables))
```
If you update the q-value for a particular state (say, `(0.25, -1.91)`) and action (say, `0`), then you should notice the q-value of a nearby state (e.g. `(0.15, -1.75)` and same action) has changed as well! This is how tile-coding is able to generalize values across the state space better than a single uniform grid.
### 6. Implement a Q-Learning Agent using Tile-Coding
Now it's your turn to apply this discretization technique to design and test a complete learning agent!
```
class QLearningAgent:
"""Q-Learning agent that can act on a continuous state space by discretizing it."""
def __init__(self, env, tq, alpha=0.02, alpha_decay_rate=None, min_alpha=None, gamma=0.99,
epsilon=1.0, epsilon_decay_rate=0.9995, min_epsilon=.01, seed=0):
"""Initialize variables, create grid for discretization."""
# Environment info
self.env = env
self.tq = tq
self.state_sizes = tq.state_sizes # list of state sizes for each tiling
self.action_size = self.env.action_space.n # 1-dimensional discrete action space
self.seed = np.random.seed(seed)
print("Environment:", self.env)
print("State space sizes:", self.state_sizes)
print("Action space size:", self.action_size)
# Learning parameters
self.alpha = self.initial_alpha = alpha # learning rate
self.alpha_decay_rate = alpha_decay_rate if alpha_decay_rate else 1.0
self.min_alpha = min_alpha if min_alpha else 0.
self.gamma = gamma # discount factor
self.epsilon = self.initial_epsilon = epsilon # initial exploration rate
self.epsilon_decay_rate = epsilon_decay_rate # how quickly should we decrease epsilon
self.min_epsilon = min_epsilon
def reset_episode(self, state):
"""Reset variables for a new episode."""
# Gradually decrease exploration rate
self.epsilon *= self.epsilon_decay_rate
self.epsilon = max(self.epsilon, self.min_epsilon)
self.alpha *= self.alpha_decay_rate
self.alpha = max(self.alpha, self.min_alpha)
self.last_state = state
# Q_s = [self.tq.get(state, action) for action in range(self.action_size)]
Q_s = self.tq.get_action_values(state)
self.last_action = np.argmax(Q_s)
return self.last_action
def reset_learning(self, alpha=None):
"""Reset learning rate used when training."""
self.alpha = alpha if alpha is not None else self.initial_alpha
def reset_exploration(self, epsilon=None):
"""Reset exploration rate used when training."""
self.epsilon = epsilon if epsilon is not None else self.initial_epsilon
def act(self, state, reward=None, done=None, mode='train'):
"""Pick next action and update internal Q table (when mode != 'test')."""
# Q_s = [self.tq.get(state, action) for action in range(self.action_size)]
Q_s = self.tq.get_action_values(state)
# Pick the best action from Q table
greedy_action = np.argmax(Q_s)
if mode == 'test':
# Test mode: Simply produce an action
action = greedy_action
else:
# Train mode (default): Update Q table, pick next action
# Note: We update the Q table entry for the *last* (state, action) pair with current state, reward
value = reward + self.gamma * max(Q_s)
self.tq.update(self.last_state, self.last_action, value, self.alpha)
# Exploration vs. exploitation
do_exploration = np.random.uniform(0, 1) < self.epsilon
if do_exploration:
# Pick a random action
action = np.random.randint(0, self.action_size)
else:
# Pick the greedy action
action = greedy_action
# Roll over current state, action for next step
self.last_state = state
self.last_action = action
return action
n_bins = 15
bins = tuple([n_bins]*env.observation_space.shape[0])
offset_pos = (env.observation_space.high - env.observation_space.low)/(3*n_bins)
tiling_specs = [(bins, -3 * offset_pos),
(bins, -2 * offset_pos),
(bins, -offset_pos),
(bins, tuple([0.0]*env.observation_space.shape[0])),
(bins, offset_pos),
(bins, 2 * offset_pos),
(bins, 3 * offset_pos)]
tq = TiledQTable(env.observation_space.low,
env.observation_space.high,
tiling_specs,
env.action_space.n)
def get_decay_rate(initial, final, duration):
return (final / initial) ** (1 / duration)
initial_alpha = 0.05
final_alpha = 0.05
alpha_decay_duration = 300
alpha_decay_rate = get_decay_rate(initial_alpha, final_alpha, alpha_decay_duration)
print("Alpha decay rate:", alpha_decay_rate)
initial_epsilon = 1.0
final_epsilon = 0.001
epsilon_decay_duration = 30000
epsilon_decay_rate = get_decay_rate(initial_epsilon, final_epsilon, epsilon_decay_duration)
print("Epsilon decay rate:", epsilon_decay_rate)
agent = QLearningAgent(env, tq,
alpha=initial_alpha, # 0.02
alpha_decay_rate=alpha_decay_rate, # None
min_alpha=0.00001, # None
gamma=0.99, # 0.99
epsilon=initial_epsilon, # 1.0
epsilon_decay_rate=epsilon_decay_rate, # 0.9995
min_epsilon=0.00001) # 0.01
def run(agent, env, num_episodes=10000, mode='train', alpha_resets=None, epsilon_resets=None, print_every=100):
"""Run agent in given reinforcement learning environment and return scores."""
alpha_reset_at, alpha_reset_vals, alpha_new_decay_rates = zip(*alpha_resets) if alpha_resets else ([], [], [])
epsilon_reset_at, epsilon_reset_vals, epsilon_new_decay_rates = zip(*epsilon_resets) if epsilon_resets else ([], [], [])
scores = []
max_avg_score = avg_score = -np.inf
best_score = max_avg_score
best_agent = copy.deepcopy(agent)
for i_episode in range(1, num_episodes+1):
# Initialize episode
state = env.reset()
action = agent.reset_episode(state)
total_reward = 0
done = False
# Roll out steps until done
while not done:
state, reward, done, info = env.step(action)
total_reward += reward
action = agent.act(state, reward, done, mode)
# Save final score
scores.append(total_reward)
# Print episode stats
if mode == 'train':
if total_reward > best_score:
best_score = total_reward
best_agent = copy.deepcopy(agent)
if i_episode in alpha_reset_at:
new_alpha = alpha_reset_vals[alpha_reset_at.index(i_episode)]
agent.reset_learning(new_alpha)
new_decay = alpha_new_decay_rates[alpha_reset_at.index(i_episode)]
if new_decay:
agent.alpha_decay_rate = new_decay
if i_episode in epsilon_reset_at:
new_epsilon = epsilon_reset_vals[epsilon_reset_at.index(i_episode)]
agent.reset_exploration(new_epsilon)
new_decay = epsilon_new_decay_rates[epsilon_reset_at.index(i_episode)]
if new_decay:
agent.epsilon_decay_rate = new_decay
if len(scores) > 100:
avg_score = np.mean(scores[-100:])
if avg_score > max_avg_score:
max_avg_score = avg_score
if i_episode % print_every == 0:
print("\rEpisode {}/{} | Max Average Score: {} | Current Average Score: {} | Current Alpha: {} | Current Epsilon: {}"\
.format(i_episode, num_episodes, max_avg_score, avg_score, agent.alpha, agent.epsilon), end="")
sys.stdout.flush()
return scores, best_agent
# agent.initial_alpha
# agent.initial_epsilon
alpha_resets = [(1, 0.02, 1.0)]
epsilon_resets = [(1, 1.0, get_decay_rate(1.0, 0.00001, 30000))]
scores, best_agent = run(agent, env, num_episodes=30000, alpha_resets=alpha_resets, epsilon_resets=epsilon_resets, print_every=10)
def plot_scores(scores, rolling_window=100):
"""Plot scores and optional rolling mean using specified window."""
plt.figure(figsize=(12, 12)); plt.plot(scores); plt.title("Scores");
rolling_mean = pd.Series(scores).rolling(rolling_window).mean()
plt.plot(rolling_mean);
return rolling_mean
rolling_mean = plot_scores(scores)
frames_per_second = 30
second_per_frame = 1 / frames_per_second
state = env.reset()
score = 0
t0 = time.time()
while True:
action = agent.act(state, mode='test')
env.render()
state, reward, done, _ = env.step(action)
score += reward
temporal_time_diff = time.time() - t0
if temporal_time_diff < second_per_frame:
time.sleep(second_per_frame - temporal_time_diff)
t0 = time.time()
if done:
break
print('Final score:', score)
env.close()
```
---
| true |
code
| 0.727156 | null | null | null | null |
|
# The Finite Element Mesh
The finite element mesh is a fundamental construct for Underworld models. This notebook will go through different examples of what can be done with Underworld's mesh object.
#### Overview:
1. Creating, visualising and accessing a mesh object.
2. Modifing a mesh.
3. Loading and saving meshes.
**Keywords:** meshes, mesh geometry, loading data
**References**
1. Moresi, L., Dufour, F., Muhlhaus, H.B., 2002. Mantle convection modeling with viscoelastic/brittle lithosphere: Numerical methodology and plate tectonic modeling. Pure Appl. Geophys. 159 (10), 2335–2356.
2. Moresi, L., Dufour, F., Muhlhaus, H.B., 2003. A Lagrangian integration point finite element method for large deformation modeling of viscoelastic geomaterials. J. Comput. Phys. 184, 476–497.
3. Moresi, L., Quenette, S., Lemiale, V., Meriaux, C., Appelbe, B., Muhlhaus, H.-B., 2007. Computational approaches to studying non-linear dynamics of the crust and mantle. Physics of the Earth and Planetary Interiors 163, 69–82.
```
import underworld as uw
import glucifer
```
## Creating, visualising and accessing a mesh object
```
# create an 8x8 rectalinear element mesh
# range x:[0.0,2.0], y:[0.0,1.0]
mesh = uw.mesh.FeMesh_Cartesian( elementType = ("Q1"),
elementRes = (8, 8),
minCoord = (0.0, 0.0),
maxCoord = (2.0, 1.0) )
# visualising the result
figMesh = glucifer.Figure(figsize=(1200,600))
figMesh.append( glucifer.objects.Mesh(mesh, nodeNumbers=True) )
figMesh.show()
# The meshes' node geometry data can be directly read via numpy arrays `mesh.data`
node_id = 1
print "Coordinate of mesh point {} is {}". format(node_id, mesh.data[node_id])
# Sets of node indexes that define boundaries are contained under the `mesh.specialSets` dictionary
print mesh.specialSets.keys()
# The left vertical wall is defined 'MinI_VertexSet'
print mesh.specialSets['MinI_VertexSet']
# The right vertical wall is defined 'MaxI_VertexSet
# The upper horizontal wall is defined 'MaxJ_VertexSet
# The lower horizontal wall is defined 'MinJ_VertexSet
```
#### Element types
The `elementType` input argument for a mesh defines the element shape functions. Shape functions define the polynomial order of finite element mesh.
Underworld currently supports these element types:
* Q2: quadratic elements
* Q1: linear elements
* dP1c: discontinuous linear elements.
* dQ0: discontinuous constant elements. (i.e. 1 node in the centre of the element)
#### Mixed elements
The mesh object allow for up to 2 element types to be defined for a single mesh. This is initialised by passing a string to the `elementType` argument of the following form:
* Q2/dpc1
* Q2/Q1
* Q1/dQ0
For a definition of finite element naming conventions used in Underworld see [here](https://femtable.org/femtable.pdf)
Let us now create a 2D mesh object with mixed elements (for 3D simply add an extra term in the tuples for the ``elementRes``, ``minCoord`` and ``maxCoord``).
```
mesh2 = uw.mesh.FeMesh_Cartesian( elementType = ("Q2/dpc1"),
elementRes = (4, 4),
minCoord = (0., 0.),
maxCoord = (2., 1.))
figMesh2 = glucifer.Figure(figsize=(1200,600))
figMesh2.append( glucifer.objects.Mesh(mesh2.subMesh, nodeNumbers=True) )
figMesh2.append( glucifer.objects.Mesh(mesh2, nodeNumbers=True, segmentsPerEdge=4) )
figMesh2.show()
# The mesh data for the 2nd element type can be accessed via the `mesh.subMesh`.
print(' Number of mesh points (Total) = {0:2d}'.format(len(mesh2.data)))
print(' Number of submesh points = {0:2d}'.format(len(mesh2.subMesh.data)))
```
## Deforming the mesh
By default the mesh data is read only. The following cell will unlock the mesh and displace a single node of the mesh in the positive x direction.
```
with mesh.deform_mesh():
mesh.data[40][0] += 0.025
figMesh.show()
```
Deforming meshes allows us to increase resolution where it is needed most. For example at the top of the simulation domain by redefining the vertical mesh coordinate to be $z := \sqrt{z}$
```
mesh.reset() # restore the mesh to the original configuration specified by elementType
with mesh.deform_mesh():
for index, coord in enumerate(mesh.data):
mesh.data[index][1] = mesh.data[index][1]**0.5
figMesh.show()
```
## Saving and loading meshes
Mesh coordinate data can be saved in hdf5 format using the ``save`` method attached to the ``mesh`` class. The following line will save the mesh to a file.
```
mesh.save('deformedMesh.h5')
```
To check that this has worked we will re-create the mesh, plot and then reload the saved mesh.
```
mesh = uw.mesh.FeMesh_Cartesian( elementType = ("Q1"),
elementRes = (8, 8),
minCoord = (0.0, 0.0),
maxCoord = (2.0, 1.0))
figMesh = glucifer.Figure(figsize=(1200,600))
figMesh.append( glucifer.objects.Mesh(mesh, nodeNumbers=True) )
figMesh.show()
```
Now load the mesh and display:
```
mesh.load('deformedMesh.h5')
figMesh.show()
```
| true |
code
| 0.709 | null | null | null | null |
|
# Demo of MUMBO for multi-fidelity Bayesian Optimisation
This notebook provides a demo of the MUlti-task Max-value Bayesian Optimisation (MUMBO) acquisition function of Moss et al [2020].
https://arxiv.org/abs/2006.12093
MUMBO provides the high perfoming optimization of other entropy-based acquisitions. However, unlike the standard entropy-search for multi-fidelity optimization, MUMBO requires a fraction of the computational cost. MUMBO is a multi-fidelity (or multi-task) extension of max-value entropy search also availible in Emukit.
Our implementation of MUMBO is controlled by two parameters: "num_samples" and "grid_size". "num_samples" controls how many mote-carlo samples we use to calculate entropy reductions. As we only approximate a 1-d integral, "num_samples" does not need to be large or be increased for problems with large d (unlike standard entropy-search). We recomend values between 5-15. "grid_size" controls the coarseness of the grid used to approximate the distribution of our max value and so must increase with d. We recommend 10,000*d. Note that as the grid must only be calculated once per BO step, the choice of "grid_size" does not have a large impact on computation time.
```
### General imports
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import colors as mcolors
import GPy
import time
np.random.seed(12345)
### Emukit imports
from emukit.test_functions.forrester import multi_fidelity_forrester_function
from emukit.core.loop.user_function import UserFunctionWrapper
from emukit.multi_fidelity.convert_lists_to_array import convert_x_list_to_array
from emukit.bayesian_optimization.acquisitions.entropy_search import MultiInformationSourceEntropySearch
from emukit.bayesian_optimization.acquisitions.max_value_entropy_search import MUMBO
from emukit.core.acquisition import Acquisition
from emukit.multi_fidelity.models.linear_model import GPyLinearMultiFidelityModel
from emukit.multi_fidelity.kernels.linear_multi_fidelity_kernel import LinearMultiFidelityKernel
from emukit.multi_fidelity.convert_lists_to_array import convert_xy_lists_to_arrays
from emukit.core import ParameterSpace, ContinuousParameter, InformationSourceParameter
from emukit.model_wrappers import GPyMultiOutputWrapper
from GPy.models.gp_regression import GPRegression
### --- Figure config
LEGEND_SIZE = 15
```
Set up our toy problem (1D optimisation of the forrester function with two fidelity levels) and collect 6 initial points at low fidelity and 3 at high fidelitly.
```
# Load function
# The multi-fidelity Forrester function is already wrapped as an Emukit UserFunction object in
# the test_functions package
forrester_fcn, _ = multi_fidelity_forrester_function()
forrester_fcn_low = forrester_fcn.f[0]
forrester_fcn_high = forrester_fcn.f[1]
# Assign costs
low_fidelity_cost = 1
high_fidelity_cost = 10
# Plot the function s
x_plot = np.linspace(0, 1, 200)[:, None]
y_plot_low = forrester_fcn_low(x_plot)
y_plot_high = forrester_fcn_high(x_plot)
plt.plot(x_plot, y_plot_low, 'b')
plt.plot(x_plot, y_plot_high, 'r')
plt.legend(['Low fidelity', 'High fidelity'])
plt.xlim(0, 1)
plt.title('High and low fidelity Forrester functions')
plt.xlabel('x')
plt.ylabel('y');
# Collect and plot initial samples
np.random.seed(123)
x_low = np.random.rand(6)[:, None]
x_high = x_low[:3]
y_low = forrester_fcn_low(x_low)
y_high = forrester_fcn_high(x_high)
plt.scatter(x_low,y_low)
plt.scatter(x_high,y_high)
```
Fit our linear multi-fidelity GP model to the observed data.
```
x_array, y_array = convert_xy_lists_to_arrays([x_low, x_high], [y_low, y_high])
kern_low = GPy.kern.RBF(1)
kern_low.lengthscale.constrain_bounded(0.01, 0.5)
kern_err = GPy.kern.RBF(1)
kern_err.lengthscale.constrain_bounded(0.01, 0.5)
multi_fidelity_kernel = LinearMultiFidelityKernel([kern_low, kern_err])
gpy_model = GPyLinearMultiFidelityModel(x_array, y_array, multi_fidelity_kernel, 2)
gpy_model.likelihood.Gaussian_noise.fix(0.1)
gpy_model.likelihood.Gaussian_noise_1.fix(0.1)
model = GPyMultiOutputWrapper(gpy_model, 2, 5, verbose_optimization=False)
model.optimize()
```
Define acqusition functions for multi-fidelity problems
```
# Define cost of different fidelities as acquisition function
class Cost(Acquisition):
def __init__(self, costs):
self.costs = costs
def evaluate(self, x):
fidelity_index = x[:, -1].astype(int)
x_cost = np.array([self.costs[i] for i in fidelity_index])
return x_cost[:, None]
@property
def has_gradients(self):
return True
def evaluate_with_gradients(self, x):
return self.evalute(x), np.zeros(x.shape)
parameter_space = ParameterSpace([ContinuousParameter('x', 0, 1), InformationSourceParameter(2)])
cost_acquisition = Cost([low_fidelity_cost, high_fidelity_cost])
es_acquisition = MultiInformationSourceEntropySearch(model, parameter_space) / cost_acquisition
mumbo_acquisition = MUMBO(model, parameter_space, num_samples=5, grid_size=500) / cost_acquisition
```
Lets plot the resulting acqusition functions (MUMBO and standard entropy search for multi-fidelity BO) for the chosen model on the collected data. Note that MES takes a fraction of the time of ES to compute (plotted on a log scale). This difference becomes even more apparent as you increase the dimensions of the sample space.
```
x_plot_low = np.concatenate([np.atleast_2d(x_plot), np.zeros((x_plot.shape[0], 1))], axis=1)
x_plot_high = np.concatenate([np.atleast_2d(x_plot), np.ones((x_plot.shape[0], 1))], axis=1)
t_0=time.time()
es_plot_low = es_acquisition.evaluate(x_plot_low)
es_plot_high = es_acquisition.evaluate(x_plot_high)
t_es=time.time()-t_0
mumbo_plot_low = mumbo_acquisition.evaluate(x_plot_low)
mumbo_plot_high = mumbo_acquisition.evaluate(x_plot_high)
t_mumbo=time.time()-t_es-t_0
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.plot(x_plot, es_plot_low , "blue")
ax1.plot(x_plot, es_plot_high, "red")
ax1.set_title("Multi-fidelity Entropy Search")
ax1.set_xlabel(r"$x$")
ax1.set_ylabel(r"$\alpha(x)$")
ax1.set_xlim(0, 1)
ax2.plot(x_plot, mumbo_plot_low , "blue", label="Low fidelity evaluations")
ax2.plot(x_plot, mumbo_plot_high , "red",label="High fidelity evaluations")
ax2.legend(loc="upper right")
ax2.set_title("MUMBO")
ax2.set_xlabel(r"$x$")
ax2.set_ylabel(r"$\alpha(x)$")
ax2.set_xlim(0, 1)
plt.tight_layout()
plt.figure()
plt.bar(["es","MUMBO"],[t_es,t_mumbo])
plt.xlabel("Acquisition Choice")
plt.yscale('log')
plt.ylabel("Calculation Time (secs)")
```
| true |
code
| 0.88225 | null | null | null | null |
|
```
#hide
!pip install -Uqq fastbook
import fastbook
fastbook.setup_book()
#hide
from fastai.vision.all import *
from fastbook import *
matplotlib.rc('image', cmap='Greys')
```
# Under the Hood: Training a Digit Classifier
Having seen what it looks like to actually train a variety of models in Chapter 2, let’s now look under the hood and see exactly what is going on. We’ll start by using computer vision to introduce fundamental tools and concepts for deep learning.
To be exact, we'll discuss the roles of arrays and tensors and of broadcasting, a powerful technique for using them expressively. We'll explain stochastic gradient descent (SGD), the mechanism for learning by updating weights automatically. We'll discuss the choice of a loss function for our basic classification task, and the role of mini-batches. We'll also describe the math that a basic neural network is actually doing. Finally, we'll put all these pieces together.
In future chapters we’ll do deep dives into other applications as well, and see how these concepts and tools generalize. But this chapter is about laying foundation stones. To be frank, that also makes this one of the hardest chapters, because of how these concepts all depend on each other. Like an arch, all the stones need to be in place for the structure to stay up. Also like an arch, once that happens, it's a powerful structure that can support other things. But it requires some patience to assemble.
Let's begin. The first step is to consider how images are represented in a computer.
## Pixels: The Foundations of Computer Vision
In order to understand what happens in a computer vision model, we first have to understand how computers handle images. We'll use one of the most famous datasets in computer vision, [MNIST](https://en.wikipedia.org/wiki/MNIST_database), for our experiments. MNIST contains images of handwritten digits, collected by the National Institute of Standards and Technology and collated into a machine learning dataset by Yann Lecun and his colleagues. Lecun used MNIST in 1998 in [Lenet-5](http://yann.lecun.com/exdb/lenet/), the first computer system to demonstrate practically useful recognition of handwritten digit sequences. This was one of the most important breakthroughs in the history of AI.
## Sidebar: Tenacity and Deep Learning
The story of deep learning is one of tenacity and grit by a handful of dedicated researchers. After early hopes (and hype!) neural networks went out of favor in the 1990's and 2000's, and just a handful of researchers kept trying to make them work well. Three of them, Yann Lecun, Yoshua Bengio, and Geoffrey Hinton, were awarded the highest honor in computer science, the Turing Award (generally considered the "Nobel Prize of computer science"), in 2018 after triumphing despite the deep skepticism and disinterest of the wider machine learning and statistics community.
Geoff Hinton has told of how even academic papers showing dramatically better results than anything previously published would be rejected by top journals and conferences, just because they used a neural network. Yann Lecun's work on convolutional neural networks, which we will study in the next section, showed that these models could read handwritten text—something that had never been achieved before. However, his breakthrough was ignored by most researchers, even as it was used commercially to read 10% of the checks in the US!
In addition to these three Turing Award winners, there are many other researchers who have battled to get us to where we are today. For instance, Jurgen Schmidhuber (who many believe should have shared in the Turing Award) pioneered many important ideas, including working with his student Sepp Hochreiter on the long short-term memory (LSTM) architecture (widely used for speech recognition and other text modeling tasks, and used in the IMDb example in <<chapter_intro>>). Perhaps most important of all, Paul Werbos in 1974 invented back-propagation for neural networks, the technique shown in this chapter and used universally for training neural networks ([Werbos 1994](https://books.google.com/books/about/The_Roots_of_Backpropagation.html?id=WdR3OOM2gBwC)). His development was almost entirely ignored for decades, but today it is considered the most important foundation of modern AI.
There is a lesson here for all of us! On your deep learning journey you will face many obstacles, both technical, and (even more difficult) posed by people around you who don't believe you'll be successful. There's one *guaranteed* way to fail, and that's to stop trying. We've seen that the only consistent trait amongst every fast.ai student that's gone on to be a world-class practitioner is that they are all very tenacious.
## End sidebar
For this initial tutorial we are just going to try to create a model that can classify any image as a 3 or a 7. So let's download a sample of MNIST that contains images of just these digits:
```
path = untar_data(URLs.MNIST_SAMPLE)
#hide
Path.BASE_PATH = path
```
We can see what's in this directory by using `ls`, a method added by fastai. This method returns an object of a special fastai class called `L`, which has all the same functionality of Python's built-in `list`, plus a lot more. One of its handy features is that, when printed, it displays the count of items, before listing the items themselves (if there are more than 10 items, it just shows the first few):
```
path.ls()
```
The MNIST dataset follows a common layout for machine learning datasets: separate folders for the training set and the validation set (and/or test set). Let's see what's inside the training set:
```
(path/'train').ls()
```
There's a folder of 3s, and a folder of 7s. In machine learning parlance, we say that "3" and "7" are the *labels* (or targets) in this dataset. Let's take a look in one of these folders (using `sorted` to ensure we all get the same order of files):
```
threes = (path/'train'/'3').ls().sorted()
sevens = (path/'train'/'7').ls().sorted()
threes
```
As we might expect, it's full of image files. Let’s take a look at one now. Here’s an image of a handwritten number 3, taken from the famous MNIST dataset of handwritten numbers:
```
im3_path = threes[1]
im3 = Image.open(im3_path)
im3
```
Here we are using the `Image` class from the *Python Imaging Library* (PIL), which is the most widely used Python package for opening, manipulating, and viewing images. Jupyter knows about PIL images, so it displays the image for us automatically.
In a computer, everything is represented as a number. To view the numbers that make up this image, we have to convert it to a *NumPy array* or a *PyTorch tensor*. For instance, here's what a section of the image looks like, converted to a NumPy array:
```
array(im3)[4:10,4:10]
```
The `4:10` indicates we requested the rows from index 4 (included) to 10 (not included) and the same for the columns. NumPy indexes from top to bottom and left to right, so this section is located in the top-left corner of the image. Here's the same thing as a PyTorch tensor:
```
tensor(im3)[4:10,4:10]
```
We can slice the array to pick just the part with the top of the digit in it, and then use a Pandas DataFrame to color-code the values using a gradient, which shows us clearly how the image is created from the pixel values:
```
#hide_output
im3_t = tensor(im3)
df = pd.DataFrame(im3_t[4:15,4:22])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')
```
<img width="453" id="output_pd_pixels" src="images/att_00058.png">
You can see that the background white pixels are stored as the number 0, black is the number 255, and shades of gray are between the two. The entire image contains 28 pixels across and 28 pixels down, for a total of 784 pixels. (This is much smaller than an image that you would get from a phone camera, which has millions of pixels, but is a convenient size for our initial learning and experiments. We will build up to bigger, full-color images soon.)
So, now you've seen what an image looks like to a computer, let's recall our goal: create a model that can recognize 3s and 7s. How might you go about getting a computer to do that?
> Warning: Stop and Think!: Before you read on, take a moment to think about how a computer might be able to recognize these two different digits. What kinds of features might it be able to look at? How might it be able to identify these features? How could it combine them together? Learning works best when you try to solve problems yourself, rather than just reading somebody else's answers; so step away from this book for a few minutes, grab a piece of paper and pen, and jot some ideas down…
## First Try: Pixel Similarity
So, here is a first idea: how about we find the average pixel value for every pixel of the 3s, then do the same for the 7s. This will give us two group averages, defining what we might call the "ideal" 3 and 7. Then, to classify an image as one digit or the other, we see which of these two ideal digits the image is most similar to. This certainly seems like it should be better than nothing, so it will make a good baseline.
> jargon: Baseline: A simple model which you are confident should perform reasonably well. It should be very simple to implement, and very easy to test, so that you can then test each of your improved ideas, and make sure they are always better than your baseline. Without starting with a sensible baseline, it is very difficult to know whether your super-fancy models are actually any good. One good approach to creating a baseline is doing what we have done here: think of a simple, easy-to-implement model. Another good approach is to search around to find other people that have solved similar problems to yours, and download and run their code on your dataset. Ideally, try both of these!
Step one for our simple model is to get the average of pixel values for each of our two groups. In the process of doing this, we will learn a lot of neat Python numeric programming tricks!
Let's create a tensor containing all of our 3s stacked together. We already know how to create a tensor containing a single image. To create a tensor containing all the images in a directory, we will first use a Python list comprehension to create a plain list of the single image tensors.
We will use Jupyter to do some little checks of our work along the way—in this case, making sure that the number of returned items seems reasonable:
```
seven_tensors = [tensor(Image.open(o)) for o in sevens]
three_tensors = [tensor(Image.open(o)) for o in threes]
len(three_tensors),len(seven_tensors)
```
> note: List Comprehensions: List and dictionary comprehensions are a wonderful feature of Python. Many Python programmers use them every day, including the authors of this book—they are part of "idiomatic Python." But programmers coming from other languages may have never seen them before. There are a lot of great tutorials just a web search away, so we won't spend a long time discussing them now. Here is a quick explanation and example to get you started. A list comprehension looks like this: `new_list = [f(o) for o in a_list if o>0]`. This will return every element of `a_list` that is greater than 0, after passing it to the function `f`. There are three parts here: the collection you are iterating over (`a_list`), an optional filter (`if o>0`), and something to do to each element (`f(o)`). It's not only shorter to write but way faster than the alternative ways of creating the same list with a loop.
We'll also check that one of the images looks okay. Since we now have tensors (which Jupyter by default will print as values), rather than PIL images (which Jupyter by default will display as images), we need to use fastai's `show_image` function to display it:
```
show_image(three_tensors[1]);
```
For every pixel position, we want to compute the average over all the images of the intensity of that pixel. To do this we first combine all the images in this list into a single three-dimensional tensor. The most common way to describe such a tensor is to call it a *rank-3 tensor*. We often need to stack up individual tensors in a collection into a single tensor. Unsurprisingly, PyTorch comes with a function called `stack` that we can use for this purpose.
Some operations in PyTorch, such as taking a mean, require us to *cast* our integer types to float types. Since we'll be needing this later, we'll also cast our stacked tensor to `float` now. Casting in PyTorch is as simple as typing the name of the type you wish to cast to, and treating it as a method.
Generally when images are floats, the pixel values are expected to be between 0 and 1, so we will also divide by 255 here:
```
stacked_sevens = torch.stack(seven_tensors).float()/255
stacked_threes = torch.stack(three_tensors).float()/255
stacked_threes.shape
```
Perhaps the most important attribute of a tensor is its *shape*. This tells you the length of each axis. In this case, we can see that we have 6,131 images, each of size 28×28 pixels. There is nothing specifically about this tensor that says that the first axis is the number of images, the second is the height, and the third is the width—the semantics of a tensor are entirely up to us, and how we construct it. As far as PyTorch is concerned, it is just a bunch of numbers in memory.
The *length* of a tensor's shape is its rank:
```
len(stacked_threes.shape)
```
It is really important for you to commit to memory and practice these bits of tensor jargon: _rank_ is the number of axes or dimensions in a tensor; _shape_ is the size of each axis of a tensor.
> A: Watch out because the term "dimension" is sometimes used in two ways. Consider that we live in "three-dimensonal space" where a physical position can be described by a 3-vector `v`. But according to PyTorch, the attribute `v.ndim` (which sure looks like the "number of dimensions" of `v`) equals one, not three! Why? Because `v` is a vector, which is a tensor of rank one, meaning that it has only one _axis_ (even if that axis has a length of three). In other words, sometimes dimension is used for the size of an axis ("space is three-dimensional"); other times, it is used for the rank, or the number of axes ("a matrix has two dimensions"). When confused, I find it helpful to translate all statements into terms of rank, axis, and length, which are unambiguous terms.
We can also get a tensor's rank directly with `ndim`:
```
stacked_threes.ndim
```
Finally, we can compute what the ideal 3 looks like. We calculate the mean of all the image tensors by taking the mean along dimension 0 of our stacked, rank-3 tensor. This is the dimension that indexes over all the images.
In other words, for every pixel position, this will compute the average of that pixel over all images. The result will be one value for every pixel position, or a single image. Here it is:
```
mean3 = stacked_threes.mean(0)
show_image(mean3);
```
According to this dataset, this is the ideal number 3! (You may not like it, but this is what peak number 3 performance looks like.) You can see how it's very dark where all the images agree it should be dark, but it becomes wispy and blurry where the images disagree.
Let's do the same thing for the 7s, but put all the steps together at once to save some time:
```
mean7 = stacked_sevens.mean(0)
show_image(mean7);
```
Let's now pick an arbitrary 3 and measure its *distance* from our "ideal digits."
> stop: Stop and Think!: How would you calculate how similar a particular image is to each of our ideal digits? Remember to step away from this book and jot down some ideas before you move on! Research shows that recall and understanding improves dramatically when you are engaged with the learning process by solving problems, experimenting, and trying new ideas yourself
Here's a sample 3:
```
a_3 = stacked_threes[1]
show_image(a_3);
```
How can we determine its distance from our ideal 3? We can't just add up the differences between the pixels of this image and the ideal digit. Some differences will be positive while others will be negative, and these differences will cancel out, resulting in a situation where an image that is too dark in some places and too light in others might be shown as having zero total differences from the ideal. That would be misleading!
To avoid this, there are two main ways data scientists measure distance in this context:
- Take the mean of the *absolute value* of differences (absolute value is the function that replaces negative values with positive values). This is called the *mean absolute difference* or *L1 norm*
- Take the mean of the *square* of differences (which makes everything positive) and then take the *square root* (which undoes the squaring). This is called the *root mean squared error* (RMSE) or *L2 norm*.
> important: It's Okay to Have Forgotten Your Math: In this book we generally assume that you have completed high school math, and remember at least some of it... But everybody forgets some things! It all depends on what you happen to have had reason to practice in the meantime. Perhaps you have forgotten what a _square root_ is, or exactly how they work. No problem! Any time you come across a maths concept that is not explained fully in this book, don't just keep moving on; instead, stop and look it up. Make sure you understand the basic idea, how it works, and why we might be using it. One of the best places to refresh your understanding is Khan Academy. For instance, Khan Academy has a great [introduction to square roots](https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:rational-exponents-radicals/x2f8bb11595b61c86:radicals/v/understanding-square-roots).
Let's try both of these now:
```
dist_3_abs = (a_3 - mean3).abs().mean()
dist_3_sqr = ((a_3 - mean3)**2).mean().sqrt()
dist_3_abs,dist_3_sqr
dist_7_abs = (a_3 - mean7).abs().mean()
dist_7_sqr = ((a_3 - mean7)**2).mean().sqrt()
dist_7_abs,dist_7_sqr
```
In both cases, the distance between our 3 and the "ideal" 3 is less than the distance to the ideal 7. So our simple model will give the right prediction in this case.
PyTorch already provides both of these as *loss functions*. You'll find these inside `torch.nn.functional`, which the PyTorch team recommends importing as `F` (and is available by default under that name in fastai):
```
F.l1_loss(a_3.float(),mean7), F.mse_loss(a_3,mean7).sqrt()
```
Here `mse` stands for *mean squared error*, and `l1` refers to the standard mathematical jargon for *mean absolute value* (in math it's called the *L1 norm*).
> S: Intuitively, the difference between L1 norm and mean squared error (MSE) is that the latter will penalize bigger mistakes more heavily than the former (and be more lenient with small mistakes).
> J: When I first came across this "L1" thingie, I looked it up to see what on earth it meant. I found on Google that it is a _vector norm_ using _absolute value_, so looked up _vector norm_ and started reading: _Given a vector space V over a field F of the real or complex numbers, a norm on V is a nonnegative-valued any function p: V → \[0,+∞) with the following properties: For all a ∈ F and all u, v ∈ V, p(u + v) ≤ p(u) + p(v)..._ Then I stopped reading. "Ugh, I'll never understand math!" I thought, for the thousandth time. Since then I've learned that every time these complex mathy bits of jargon come up in practice, it turns out I can replace them with a tiny bit of code! Like, the _L1 loss_ is just equal to `(a-b).abs().mean()`, where `a` and `b` are tensors. I guess mathy folks just think differently than me... I'll make sure in this book that every time some mathy jargon comes up, I'll give you the little bit of code it's equal to as well, and explain in common-sense terms what's going on.
We just completed various mathematical operations on PyTorch tensors. If you've done some numeric programming in PyTorch before, you may recognize these as being similar to NumPy arrays. Let's have a look at those two very important data structures.
### NumPy Arrays and PyTorch Tensors
[NumPy](https://numpy.org/) is the most widely used library for scientific and numeric programming in Python. It provides very similar functionality and a very similar API to that provided by PyTorch; however, it does not support using the GPU or calculating gradients, which are both critical for deep learning. Therefore, in this book we will generally use PyTorch tensors instead of NumPy arrays, where possible.
(Note that fastai adds some features to NumPy and PyTorch to make them a bit more similar to each other. If any code in this book doesn't work on your computer, it's possible that you forgot to include a line like this at the start of your notebook: `from fastai.vision.all import *`.)
But what are arrays and tensors, and why should you care?
Python is slow compared to many languages. Anything fast in Python, NumPy, or PyTorch is likely to be a wrapper for a compiled object written (and optimized) in another language—specifically C. In fact, **NumPy arrays and PyTorch tensors can finish computations many thousands of times faster than using pure Python.**
A NumPy array is a multidimensional table of data, with all items of the same type. Since that can be any type at all, they can even be arrays of arrays, with the innermost arrays potentially being different sizes—this is called a "jagged array." By "multidimensional table" we mean, for instance, a list (dimension of one), a table or matrix (dimension of two), a "table of tables" or "cube" (dimension of three), and so forth. If the items are all of some simple type such as integer or float, then NumPy will store them as a compact C data structure in memory. This is where NumPy shines. NumPy has a wide variety of operators and methods that can run computations on these compact structures at the same speed as optimized C, because they are written in optimized C.
A PyTorch tensor is nearly the same thing as a NumPy array, but with an additional restriction that unlocks some additional capabilities. It's the same in that it, too, is a multidimensional table of data, with all items of the same type. However, the restriction is that a tensor cannot use just any old type—it has to use a single basic numeric type for all components. For example, a PyTorch tensor cannot be jagged. It is always a regularly shaped multidimensional rectangular structure.
The vast majority of methods and operators supported by NumPy on these structures are also supported by PyTorch, but PyTorch tensors have additional capabilities. One major capability is that these structures can live on the GPU, in which case their computation will be optimized for the GPU and can run much faster (given lots of values to work on). In addition, PyTorch can automatically calculate derivatives of these operations, including combinations of operations. As you'll see, it would be impossible to do deep learning in practice without this capability.
> S: If you don't know what C is, don't worry as you won't need it at all. In a nutshell, it's a low-level (low-level means more similar to the language that computers use internally) language that is very fast compared to Python. To take advantage of its speed while programming in Python, try to avoid as much as possible writing loops, and replace them by commands that work directly on arrays or tensors.
Perhaps the most important new coding skill for a Python programmer to learn is how to effectively use the array/tensor APIs. We will be showing lots more tricks later in this book, but here's a summary of the key things you need to know for now.
To create an array or tensor, pass a list (or list of lists, or list of lists of lists, etc.) to `array()` or `tensor()`:
```
data = [[1,2,3],[4,5,6]]
arr = array (data)
tns = tensor(data)
arr # numpy
tns # pytorch
```
All the operations that follow are shown on tensors, but the syntax and results for NumPy arrays is identical.
You can select a row (note that, like lists in Python, tensors are 0-indexed so 1 refers to the second row/column):
```
tns[1]
```
or a column, by using `:` to indicate *all of the first axis* (we sometimes refer to the dimensions of tensors/arrays as *axes*):
```
tns[:,1]
```
You can combine these with Python slice syntax (`[start:end]` with `end` being excluded) to select part of a row or column:
```
tns[1,1:3]
```
And you can use the standard operators such as `+`, `-`, `*`, `/`:
```
tns+1
```
Tensors have a type:
```
tns.type()
```
And will automatically change type as needed, for example from `int` to `float`:
```
tns*1.5
```
So, is our baseline model any good? To quantify this, we must define a metric.
## Computing Metrics Using Broadcasting
Recall that a metric is a number that is calculated based on the predictions of our model, and the correct labels in our dataset, in order to tell us how good our model is. For instance, we could use either of the functions we saw in the previous section, mean squared error, or mean absolute error, and take the average of them over the whole dataset. However, neither of these are numbers that are very understandable to most people; in practice, we normally use *accuracy* as the metric for classification models.
As we've discussed, we want to calculate our metric over a *validation set*. This is so that we don't inadvertently overfit—that is, train a model to work well only on our training data. This is not really a risk with the pixel similarity model we're using here as a first try, since it has no trained components, but we'll use a validation set anyway to follow normal practices and to be ready for our second try later.
To get a validation set we need to remove some of the data from training entirely, so it is not seen by the model at all. As it turns out, the creators of the MNIST dataset have already done this for us. Do you remember how there was a whole separate directory called *valid*? That's what this directory is for!
So to start with, let's create tensors for our 3s and 7s from that directory. These are the tensors we will use to calculate a metric measuring the quality of our first-try model, which measures distance from an ideal image:
```
valid_3_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'3').ls()])
valid_3_tens = valid_3_tens.float()/255
valid_7_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'7').ls()])
valid_7_tens = valid_7_tens.float()/255
valid_3_tens.shape,valid_7_tens.shape
```
It's good to get in the habit of checking shapes as you go. Here we see two tensors, one representing the 3s validation set of 1,010 images of size 28×28, and one representing the 7s validation set of 1,028 images of size 28×28.
We ultimately want to write a function, `is_3`, that will decide if an arbitrary image is a 3 or a 7. It will do this by deciding which of our two "ideal digits" this arbitrary image is closer to. For that we need to define a notion of distance—that is, a function that calculates the distance between two images.
We can write a simple function that calculates the mean absolute error using an experssion very similar to the one we wrote in the last section:
```
def mnist_distance(a,b): return (a-b).abs().mean((-1,-2))
mnist_distance(a_3, mean3)
```
This is the same value we previously calculated for the distance between these two images, the ideal 3 `mean_3` and the arbitrary sample 3 `a_3`, which are both single-image tensors with a shape of `[28,28]`.
But in order to calculate a metric for overall accuracy, we will need to calculate the distance to the ideal 3 for _every_ image in the validation set. How do we do that calculation? We could write a loop over all of the single-image tensors that are stacked within our validation set tensor, `valid_3_tens`, which has a shape of `[1010,28,28]` representing 1,010 images. But there is a better way.
Something very interesting happens when we take this exact same distance function, designed for comparing two single images, but pass in as an argument `valid_3_tens`, the tensor that represents the 3s validation set:
```
valid_3_dist = mnist_distance(valid_3_tens, mean3)
valid_3_dist, valid_3_dist.shape
```
Instead of complaining about shapes not matching, it returned the distance for every single image as a vector (i.e., a rank-1 tensor) of length 1,010 (the number of 3s in our validation set). How did that happen?
Take another look at our function `mnist_distance`, and you'll see we have there the subtraction `(a-b)`. The magic trick is that PyTorch, when it tries to perform a simple subtraction operation between two tensors of different ranks, will use *broadcasting*. That is, it will automatically expand the tensor with the smaller rank to have the same size as the one with the larger rank. Broadcasting is an important capability that makes tensor code much easier to write.
After broadcasting so the two argument tensors have the same rank, PyTorch applies its usual logic for two tensors of the same rank: it performs the operation on each corresponding element of the two tensors, and returns the tensor result. For instance:
```
tensor([1,2,3]) + tensor([1,1,1])
```
So in this case, PyTorch treats `mean3`, a rank-2 tensor representing a single image, as if it were 1,010 copies of the same image, and then subtracts each of those copies from each 3 in our validation set. What shape would you expect this tensor to have? Try to figure it out yourself before you look at the answer below:
```
(valid_3_tens-mean3).shape
```
We are calculating the difference between our "ideal 3" and each of the 1,010 3s in the validation set, for each of 28×28 images, resulting in the shape `[1010,28,28]`.
There are a couple of important points about how broadcasting is implemented, which make it valuable not just for expressivity but also for performance:
- PyTorch doesn't *actually* copy `mean3` 1,010 times. It *pretends* it were a tensor of that shape, but doesn't actually allocate any additional memory
- It does the whole calculation in C (or, if you're using a GPU, in CUDA, the equivalent of C on the GPU), tens of thousands of times faster than pure Python (up to millions of times faster on a GPU!).
This is true of all broadcasting and elementwise operations and functions done in PyTorch. *It's the most important technique for you to know to create efficient PyTorch code.*
Next in `mnist_distance` we see `abs`. You might be able to guess now what this does when applied to a tensor. It applies the method to each individual element in the tensor, and returns a tensor of the results (that is, it applies the method "elementwise"). So in this case, we'll get back 1,010 matrices of absolute values.
Finally, our function calls `mean((-1,-2))`. The tuple `(-1,-2)` represents a range of axes. In Python, `-1` refers to the last element, and `-2` refers to the second-to-last. So in this case, this tells PyTorch that we want to take the mean ranging over the values indexed by the last two axes of the tensor. The last two axes are the horizontal and vertical dimensions of an image. After taking the mean over the last two axes, we are left with just the first tensor axis, which indexes over our images, which is why our final size was `(1010)`. In other words, for every image, we averaged the intensity of all the pixels in that image.
We'll be learning lots more about broadcasting throughout this book, especially in <<chapter_foundations>>, and will be practicing it regularly too.
We can use `mnist_distance` to figure out whether an image is a 3 or not by using the following logic: if the distance between the digit in question and the ideal 3 is less than the distance to the ideal 7, then it's a 3. This function will automatically do broadcasting and be applied elementwise, just like all PyTorch functions and operators:
```
def is_3(x): return mnist_distance(x,mean3) < mnist_distance(x,mean7)
```
Let's test it on our example case:
```
is_3(a_3), is_3(a_3).float()
```
Note that when we convert the Boolean response to a float, we get `1.0` for `True` and `0.0` for `False`. Thanks to broadcasting, we can also test it on the full validation set of 3s:
```
is_3(valid_3_tens)
```
Now we can calculate the accuracy for each of the 3s and 7s by taking the average of that function for all 3s and its inverse for all 7s:
```
accuracy_3s = is_3(valid_3_tens).float() .mean()
accuracy_7s = (1 - is_3(valid_7_tens).float()).mean()
accuracy_3s,accuracy_7s,(accuracy_3s+accuracy_7s)/2
```
This looks like a pretty good start! We're getting over 90% accuracy on both 3s and 7s, and we've seen how to define a metric conveniently using broadcasting.
But let's be honest: 3s and 7s are very different-looking digits. And we're only classifying 2 out of the 10 possible digits so far. So we're going to need to do better!
To do better, perhaps it is time to try a system that does some real learning—that is, that can automatically modify itself to improve its performance. In other words, it's time to talk about the training process, and SGD.
## Stochastic Gradient Descent (SGD)
Do you remember the way that Arthur Samuel described machine learning, which we quoted in <<chapter_intro>>?
> : Suppose we arrange for some automatic means of testing the effectiveness of any current weight assignment in terms of actual performance and provide a mechanism for altering the weight assignment so as to maximize the performance. We need not go into the details of such a procedure to see that it could be made entirely automatic and to see that a machine so programmed would "learn" from its experience.
As we discussed, this is the key to allowing us to have a model that can get better and better—that can learn. But our pixel similarity approach does not really do this. We do not have any kind of weight assignment, or any way of improving based on testing the effectiveness of a weight assignment. In other words, we can't really improve our pixel similarity approach by modifying a set of parameters. In order to take advantage of the power of deep learning, we will first have to represent our task in the way that Arthur Samuel described it.
Instead of trying to find the similarity between an image and an "ideal image," we could instead look at each individual pixel and come up with a set of weights for each one, such that the highest weights are associated with those pixels most likely to be black for a particular category. For instance, pixels toward the bottom right are not very likely to be activated for a 7, so they should have a low weight for a 7, but they are likely to be activated for an 8, so they should have a high weight for an 8. This can be represented as a function and set of weight values for each possible category—for instance the probability of being the number 8:
```
def pr_eight(x,w) = (x*w).sum()
```
Here we are assuming that `x` is the image, represented as a vector—in other words, with all of the rows stacked up end to end into a single long line. And we are assuming that the weights are a vector `w`. If we have this function, then we just need some way to update the weights to make them a little bit better. With such an approach, we can repeat that step a number of times, making the weights better and better, until they are as good as we can make them.
We want to find the specific values for the vector `w` that causes the result of our function to be high for those images that are actually 8s, and low for those images that are not. Searching for the best vector `w` is a way to search for the best function for recognising 8s. (Because we are not yet using a deep neural network, we are limited by what our function can actually do—we are going to fix that constraint later in this chapter.)
To be more specific, here are the steps that we are going to require, to turn this function into a machine learning classifier:
1. *Initialize* the weights.
1. For each image, use these weights to *predict* whether it appears to be a 3 or a 7.
1. Based on these predictions, calculate how good the model is (its *loss*).
1. Calculate the *gradient*, which measures for each weight, how changing that weight would change the loss
1. *Step* (that is, change) all the weights based on that calculation.
1. Go back to the step 2, and *repeat* the process.
1. Iterate until you decide to *stop* the training process (for instance, because the model is good enough or you don't want to wait any longer).
These seven steps, illustrated in <<gradient_descent>>, are the key to the training of all deep learning models. That deep learning turns out to rely entirely on these steps is extremely surprising and counterintuitive. It's amazing that this process can solve such complex problems. But, as you'll see, it really does!
```
#id gradient_descent
#caption The gradient descent process
#alt Graph showing the steps for Gradient Descent
gv('''
init->predict->loss->gradient->step->stop
step->predict[label=repeat]
''')
```
There are many different ways to do each of these seven steps, and we will be learning about them throughout the rest of this book. These are the details that make a big difference for deep learning practitioners, but it turns out that the general approach to each one generally follows some basic principles. Here are a few guidelines:
- Initialize:: We initialize the parameters to random values. This may sound surprising. There are certainly other choices we could make, such as initializing them to the percentage of times that pixel is activated for that category—but since we already know that we have a routine to improve these weights, it turns out that just starting with random weights works perfectly well.
- Loss:: This is what Samuel referred to when he spoke of *testing the effectiveness of any current weight assignment in terms of actual performance*. We need some function that will return a number that is small if the performance of the model is good (the standard approach is to treat a small loss as good, and a large loss as bad, although this is just a convention).
- Step:: A simple way to figure out whether a weight should be increased a bit, or decreased a bit, would be just to try it: increase the weight by a small amount, and see if the loss goes up or down. Once you find the correct direction, you could then change that amount by a bit more, and a bit less, until you find an amount that works well. However, this is slow! As we will see, the magic of calculus allows us to directly figure out in which direction, and by roughly how much, to change each weight, without having to try all these small changes. The way to do this is by calculating *gradients*. This is just a performance optimization, we would get exactly the same results by using the slower manual process as well.
- Stop:: Once we've decided how many epochs to train the model for (a few suggestions for this were given in the earlier list), we apply that decision. This is where that decision is applied. For our digit classifier, we would keep training until the accuracy of the model started getting worse, or we ran out of time.
Before applying these steps to our image classification problem, let's illustrate what they look like in a simpler case. First we will define a very simple function, the quadratic—let's pretend that this is our loss function, and `x` is a weight parameter of the function:
```
def f(x): return x**2
```
Here is a graph of that function:
```
plot_function(f, 'x', 'x**2')
```
The sequence of steps we described earlier starts by picking some random value for a parameter, and calculating the value of the loss:
```
plot_function(f, 'x', 'x**2')
plt.scatter(-1.5, f(-1.5), color='red');
```
Now we look to see what would happen if we increased or decreased our parameter by a little bit—the *adjustment*. This is simply the slope at a particular point:
<img alt="A graph showing the squared function with the slope at one point" width="400" src="images/grad_illustration.svg"/>
We can change our weight by a little in the direction of the slope, calculate our loss and adjustment again, and repeat this a few times. Eventually, we will get to the lowest point on our curve:
<img alt="An illustration of gradient descent" width="400" src="images/chapter2_perfect.svg"/>
This basic idea goes all the way back to Isaac Newton, who pointed out that we can optimize arbitrary functions in this way. Regardless of how complicated our functions become, this basic approach of gradient descent will not significantly change. The only minor changes we will see later in this book are some handy ways we can make it faster, by finding better steps.
### Calculating Gradients
The one magic step is the bit where we calculate the gradients. As we mentioned, we use calculus as a performance optimization; it allows us to more quickly calculate whether our loss will go up or down when we adjust our parameters up or down. In other words, the gradients will tell us how much we have to change each weight to make our model better.
You may remember from your high school calculus class that the *derivative* of a function tells you how much a change in its parameterss will change its result. If not, don't worry, lots of us forget calculus once high school is behind us! But you will have to have some intuitive understanding of what a derivative is before you continue, so if this is all very fuzzy in your head, head over to Khan Academy and complete the [lessons on basic derivatives](https://www.khanacademy.org/math/differential-calculus/dc-diff-intro). You won't have to know how to calculate them yourselves, you just have to know what a derivative is.
The key point about a derivative is this: for any function, such as the quadratic function we saw in the previous section, we can calculate its derivative. The derivative is another function. It calculates the change, rather than the value. For instance, the derivative of the quadratic function at the value 3 tells us how rapidly the function changes at the value 3. More specifically, you may recall that gradient is defined as *rise/run*, that is, the change in the value of the function, divided by the change in the value of the parameter. When we know how our function will change, then we know what we need to do to make it smaller. This is the key to machine learning: having a way to change the parameters of a function to make it smaller. Calculus provides us with a computational shortcut, the derivative, which lets us directly calculate the gradients of our functions.
One important thing to be aware of is that our function has lots of weights that we need to adjust, so when we calculate the derivative we won't get back one number, but lots of them—a gradient for every weight. But there is nothing mathematically tricky here; you can calculate the derivative with respect to one weight, and treat all the other ones as constant, then repeat that for each other weight. This is how all of the gradients are calculated, for every weight.
We mentioned just now that you won't have to calculate any gradients yourself. How can that be? Amazingly enough, PyTorch is able to automatically compute the derivative of nearly any function! What's more, it does it very fast. Most of the time, it will be at least as fast as any derivative function that you can create by hand. Let's see an example.
First, let's pick a tensor value which we want gradients at:
```
xt = tensor(3.).requires_grad_()
```
Notice the special method `requires_grad_`? That's the magical incantation we use to tell PyTorch that we want to calculate gradients with respect to that variable at that value. It is essentially tagging the variable, so PyTorch will remember to keep track of how to compute gradients of the other, direct calculations on it that you will ask for.
> a: This API might throw you off if you're coming from math or physics. In those contexts the "gradient" of a function is just another function (i.e., its derivative), so you might expect gradient-related APIs to give you a new function. But in deep learning, "gradients" usually means the _value_ of a function's derivative at a particular argument value. The PyTorch API also puts the focus on the argument, not the function you're actually computing the gradients of. It may feel backwards at first, but it's just a different perspective.
Now we calculate our function with that value. Notice how PyTorch prints not just the value calculated, but also a note that it has a gradient function it'll be using to calculate our gradients when needed:
```
yt = f(xt)
yt
```
Finally, we tell PyTorch to calculate the gradients for us:
```
yt.backward()
```
The "backward" here refers to *backpropagation*, which is the name given to the process of calculating the derivative of each layer. We'll see how this is done exactly in chapter <<chapter_foundations>>, when we calculate the gradients of a deep neural net from scratch. This is called the "backward pass" of the network, as opposed to the "forward pass," which is where the activations are calculated. Life would probably be easier if `backward` was just called `calculate_grad`, but deep learning folks really do like to add jargon everywhere they can!
We can now view the gradients by checking the `grad` attribute of our tensor:
```
xt.grad
```
If you remember your high school calculus rules, the derivative of `x**2` is `2*x`, and we have `x=3`, so the gradients should be `2*3=6`, which is what PyTorch calculated for us!
Now we'll repeat the preceding steps, but with a vector argument for our function:
```
xt = tensor([3.,4.,10.]).requires_grad_()
xt
```
And we'll add `sum` to our function so it can take a vector (i.e., a rank-1 tensor), and return a scalar (i.e., a rank-0 tensor):
```
def f(x): return (x**2).sum()
yt = f(xt)
yt
```
Our gradients are `2*xt`, as we'd expect!
```
yt.backward()
xt.grad
```
The gradients only tell us the slope of our function, they don't actually tell us exactly how far to adjust the parameters. But it gives us some idea of how far; if the slope is very large, then that may suggest that we have more adjustments to do, whereas if the slope is very small, that may suggest that we are close to the optimal value.
### Stepping With a Learning Rate
Deciding how to change our parameters based on the values of the gradients is an important part of the deep learning process. Nearly all approaches start with the basic idea of multiplying the gradient by some small number, called the *learning rate* (LR). The learning rate is often a number between 0.001 and 0.1, although it could be anything. Often, people select a learning rate just by trying a few, and finding which results in the best model after training (we'll show you a better approach later in this book, called the *learning rate finder*). Once you've picked a learning rate, you can adjust your parameters using this simple function:
```
w -= gradient(w) * lr
```
This is known as *stepping* your parameters, using an *optimizer step*.
If you pick a learning rate that's too low, it can mean having to do a lot of steps. <<descent_small>> illustrates that.
<img alt="An illustration of gradient descent with a LR too low" width="400" caption="Gradient descent with low LR" src="images/chapter2_small.svg" id="descent_small"/>
But picking a learning rate that's too high is even worse—it can actually result in the loss getting *worse*, as we see in <<descent_div>>!
<img alt="An illustration of gradient descent with a LR too high" width="400" caption="Gradient descent with high LR" src="images/chapter2_div.svg" id="descent_div"/>
If the learning rate is too high, it may also "bounce" around, rather than actually diverging; <<descent_bouncy>> shows how this has the result of taking many steps to train successfully.
<img alt="An illustation of gradient descent with a bouncy LR" width="400" caption="Gradient descent with bouncy LR" src="images/chapter2_bouncy.svg" id="descent_bouncy"/>
Now let's apply all of this in an end-to-end example.
### An End-to-End SGD Example
We've seen how to use gradients to find a minimum. Now it's time to look at an SGD example and see how finding a minimum can be used to train a model to fit data better.
Let's start with a simple, synthetic, example model. Imagine you were measuring the speed of a roller coaster as it went over the top of a hump. It would start fast, and then get slower as it went up the hill; it would be slowest at the top, and it would then speed up again as it went downhill. You want to build a model of how the speed changes over time. If you were measuring the speed manually every second for 20 seconds, it might look something like this:
```
time = torch.arange(0,20).float(); time
speed = torch.randn(20)*3 + 0.75*(time-9.5)**2 + 1
plt.scatter(time,speed);
```
We've added a bit of random noise, since measuring things manually isn't precise. This means it's not that easy to answer the question: what was the roller coaster's speed? Using SGD we can try to find a function that matches our observations. We can't consider every possible function, so let's use a guess that it will be quadratic; i.e., a function of the form `a*(time**2)+(b*time)+c`.
We want to distinguish clearly between the function's input (the time when we are measuring the coaster's speed) and its parameters (the values that define *which* quadratic we're trying). So, let's collect the parameters in one argument and thus separate the input, `t`, and the parameters, `params`, in the function's signature:
```
def f(t, params):
a,b,c = params
return a*(t**2) + (b*t) + c
```
In other words, we've restricted the problem of finding the best imaginable function that fits the data, to finding the best *quadratic* function. This greatly simplifies the problem, since every quadratic function is fully defined by the three parameters `a`, `b`, and `c`. Thus, to find the best quadratic function, we only need to find the best values for `a`, `b`, and `c`.
If we can solve this problem for the three parameters of a quadratic function, we'll be able to apply the same approach for other, more complex functions with more parameters—such as a neural net. Let's find the parameters for `f` first, and then we'll come back and do the same thing for the MNIST dataset with a neural net.
We need to define first what we mean by "best." We define this precisely by choosing a *loss function*, which will return a value based on a prediction and a target, where lower values of the function correspond to "better" predictions. For continuous data, it's common to use *mean squared error*:
```
def mse(preds, targets): return ((preds-targets)**2).mean()
```
Now, let's work through our 7 step process.
#### Step 1: Initialize the parameters
First, we initialize the parameters to random values, and tell PyTorch that we want to track their gradients, using `requires_grad_`:
```
params = torch.randn(3).requires_grad_()
#hide
orig_params = params.clone()
```
#### Step 2: Calculate the predictions
Next, we calculate the predictions:
```
preds = f(time, params)
```
Let's create a little function to see how close our predictions are to our targets, and take a look:
```
def show_preds(preds, ax=None):
if ax is None: ax=plt.subplots()[1]
ax.scatter(time, speed)
ax.scatter(time, to_np(preds), color='red')
ax.set_ylim(-300,100)
show_preds(preds)
```
This doesn't look very close—our random parameters suggest that the roller coaster will end up going backwards, since we have negative speeds!
#### Step 3: Calculate the loss
We calculate the loss as follows:
```
loss = mse(preds, speed)
loss
```
Our goal is now to improve this. To do that, we'll need to know the gradients.
#### Step 4: Calculate the gradients
The next step is to calculate the gradients. In other words, calculate an approximation of how the parameters need to change:
```
loss.backward()
params.grad
params.grad * 1e-5
```
We can use these gradients to improve our parameters. We'll need to pick a learning rate (we'll discuss how to do that in practice in the next chapter; for now we'll just use 1e-5, or 0.00001):
```
params
```
#### Step 5: Step the weights.
Now we need to update the parameters based on the gradients we just calculated:
```
lr = 1e-5
params.data -= lr * params.grad.data
params.grad = None
```
> a: Understanding this bit depends on remembering recent history. To calculate the gradients we call `backward` on the `loss`. But this `loss` was itself calculated by `mse`, which in turn took `preds` as an input, which was calculated using `f` taking as an input `params`, which was the object on which we originally called `required_grads_`—which is the original call that now allows us to call `backward` on `loss`. This chain of function calls represents the mathematical composition of functions, which enables PyTorch to use calculus's chain rule under the hood to calculate these gradients.
Let's see if the loss has improved:
```
preds = f(time,params)
mse(preds, speed)
```
And take a look at the plot:
```
show_preds(preds)
```
We need to repeat this a few times, so we'll create a function to apply one step:
```
def apply_step(params, prn=True):
preds = f(time, params)
loss = mse(preds, speed)
loss.backward()
params.data -= lr * params.grad.data
params.grad = None
if prn: print(loss.item())
return preds
```
#### Step 6: Repeat the process
Now we iterate. By looping and performing many improvements, we hope to reach a good result:
```
for i in range(10): apply_step(params)
#hide
params = orig_params.detach().requires_grad_()
```
The loss is going down, just as we hoped! But looking only at these loss numbers disguises the fact that each iteration represents an entirely different quadratic function being tried, on the way to finding the best possible quadratic function. We can see this process visually if, instead of printing out the loss function, we plot the function at every step. Then we can see how the shape is approaching the best possible quadratic function for our data:
```
_,axs = plt.subplots(1,4,figsize=(12,3))
for ax in axs: show_preds(apply_step(params, False), ax)
plt.tight_layout()
```
#### Step 7: stop
We just decided to stop after 10 epochs arbitrarily. In practice, we would watch the training and validation losses and our metrics to decide when to stop, as we've discussed.
### Summarizing Gradient Descent
```
#hide_input
#id gradient_descent
#caption The gradient descent process
#alt Graph showing the steps for Gradient Descent
gv('''
init->predict->loss->gradient->step->stop
step->predict[label=repeat]
''')
```
To summarize, at the beginning, the weights of our model can be random (training *from scratch*) or come from a pretrained model (*transfer learning*). In the first case, the output we will get from our inputs won't have anything to do with what we want, and even in the second case, it's very likely the pretrained model won't be very good at the specific task we are targeting. So the model will need to *learn* better weights.
We begin by comparing the outputs the model gives us with our targets (we have labeled data, so we know what result the model should give) using a *loss function*, which returns a number that we want to make as low as possible by improving our weights. To do this, we take a few data items (such as images) from the training set and feed them to our model. We compare the corresponding targets using our loss function, and the score we get tells us how wrong our predictions were. We then change the weights a little bit to make it slightly better.
To find how to change the weights to make the loss a bit better, we use calculus to calculate the *gradients*. (Actually, we let PyTorch do it for us!) Let's consider an analogy. Imagine you are lost in the mountains with your car parked at the lowest point. To find your way back to it, you might wander in a random direction, but that probably wouldn't help much. Since you know your vehicle is at the lowest point, you would be better off going downhill. By always taking a step in the direction of the steepest downward slope, you should eventually arrive at your destination. We use the magnitude of the gradient (i.e., the steepness of the slope) to tell us how big a step to take; specifically, we multiply the gradient by a number we choose called the *learning rate* to decide on the step size. We then *iterate* until we have reached the lowest point, which will be our parking lot, then we can *stop*.
All of that we just saw can be transposed directly to the MNIST dataset, except for the loss function. Let's now see how we can define a good training objective.
## The MNIST Loss Function
We already have our dependent variables `x`—these are the images themselves. We'll concatenate them all into a single tensor, and also change them from a list of matrices (a rank-3 tensor) to a list of vectors (a rank-2 tensor). We can do this using `view`, which is a PyTorch method that changes the shape of a tensor without changing its contents. `-1` is a special parameter to `view` that means "make this axis as big as necessary to fit all the data":
```
train_x = torch.cat([stacked_threes, stacked_sevens]).view(-1, 28*28)
```
We need a label for each image. We'll use `1` for 3s and `0` for 7s:
```
train_y = tensor([1]*len(threes) + [0]*len(sevens)).unsqueeze(1)
train_x.shape,train_y.shape
```
A `Dataset` in PyTorch is required to return a tuple of `(x,y)` when indexed. Python provides a `zip` function which, when combined with `list`, provides a simple way to get this functionality:
```
dset = list(zip(train_x,train_y))
x,y = dset[0]
x.shape,y
valid_x = torch.cat([valid_3_tens, valid_7_tens]).view(-1, 28*28)
valid_y = tensor([1]*len(valid_3_tens) + [0]*len(valid_7_tens)).unsqueeze(1)
valid_dset = list(zip(valid_x,valid_y))
```
Now we need an (initially random) weight for every pixel (this is the *initialize* step in our seven-step process):
```
def init_params(size, std=1.0): return (torch.randn(size)*std).requires_grad_()
weights = init_params((28*28,1))
```
The function `weights*pixels` won't be flexible enough—it is always equal to 0 when the pixels are equal to 0 (i.e., its *intercept* is 0). You might remember from high school math that the formula for a line is `y=w*x+b`; we still need the `b`. We'll initialize it to a random number too:
```
bias = init_params(1)
```
In neural networks, the `w` in the equation `y=w*x+b` is called the *weights*, and the `b` is called the *bias*. Together, the weights and bias make up the *parameters*.
> jargon: Parameters: The _weights_ and _biases_ of a model. The weights are the `w` in the equation `w*x+b`, and the biases are the `b` in that equation.
We can now calculate a prediction for one image:
```
(train_x[0]*weights.T).sum() + bias
```
While we could use a Python `for` loop to calculate the prediction for each image, that would be very slow. Because Python loops don't run on the GPU, and because Python is a slow language for loops in general, we need to represent as much of the computation in a model as possible using higher-level functions.
In this case, there's an extremely convenient mathematical operation that calculates `w*x` for every row of a matrix—it's called *matrix multiplication*. <<matmul>> shows what matrix multiplication looks like.
<img alt="Matrix multiplication" width="400" caption="Matrix multiplication" src="images/matmul2.svg" id="matmul"/>
This image shows two matrices, `A` and `B`, being multiplied together. Each item of the result, which we'll call `AB`, contains each item of its corresponding row of `A` multiplied by each item of its corresponding column of `B`, added together. For instance, row 1, column 2 (the orange dot with a red border) is calculated as $a_{1,1} * b_{1,2} + a_{1,2} * b_{2,2}$. If you need a refresher on matrix multiplication, we suggest you take a look at the [Intro to Matrix Multiplication](https://youtu.be/kT4Mp9EdVqs) on *Khan Academy*, since this is the most important mathematical operation in deep learning.
In Python, matrix multiplication is represented with the `@` operator. Let's try it:
```
def linear1(xb): return xb@weights + bias
preds = linear1(train_x)
preds
```
The first element is the same as we calculated before, as we'd expect. This equation, `batch@weights + bias`, is one of the two fundamental equations of any neural network (the other one is the *activation function*, which we'll see in a moment).
Let's check our accuracy. To decide if an output represents a 3 or a 7, we can just check whether it's greater than 0, so our accuracy for each item can be calculated (using broadcasting, so no loops!) with:
```
corrects = (preds>0.0).float() == train_y
corrects
corrects.float().mean().item()
```
Now let's see what the change in accuracy is for a small change in one of the weights:
```
weights[0] *= 1.0001
preds = linear1(train_x)
((preds>0.0).float() == train_y).float().mean().item()
```
As we've seen, we need gradients in order to improve our model using SGD, and in order to calculate gradients we need some *loss function* that represents how good our model is. That is because the gradients are a measure of how that loss function changes with small tweaks to the weights.
So, we need to choose a loss function. The obvious approach would be to use accuracy, which is our metric, as our loss function as well. In this case, we would calculate our prediction for each image, collect these values to calculate an overall accuracy, and then calculate the gradients of each weight with respect to that overall accuracy.
Unfortunately, we have a significant technical problem here. The gradient of a function is its *slope*, or its steepness, which can be defined as *rise over run*—that is, how much the value of the function goes up or down, divided by how much we changed the input. We can write this in mathematically as: `(y_new - y_old) / (x_new - x_old)`. This gives us a good approximation of the gradient when `x_new` is very similar to `x_old`, meaning that their difference is very small. But accuracy only changes at all when a prediction changes from a 3 to a 7, or vice versa. The problem is that a small change in weights from `x_old` to `x_new` isn't likely to cause any prediction to change, so `(y_new - y_old)` will almost always be 0. In other words, the gradient is 0 almost everywhere.
A very small change in the value of a weight will often not actually change the accuracy at all. This means it is not useful to use accuracy as a loss function—if we do, most of the time our gradients will actually be 0, and the model will not be able to learn from that number.
> S: In mathematical terms, accuracy is a function that is constant almost everywhere (except at the threshold, 0.5), so its derivative is nil almost everywhere (and infinity at the threshold). This then gives gradients that are 0 or infinite, which are useless for updating the model.
Instead, we need a loss function which, when our weights result in slightly better predictions, gives us a slightly better loss. So what does a "slightly better prediction" look like, exactly? Well, in this case, it means that if the correct answer is a 3 the score is a little higher, or if the correct answer is a 7 the score is a little lower.
Let's write such a function now. What form does it take?
The loss function receives not the images themselves, but the predictions from the model. Let's make one argument, `prds`, of values between 0 and 1, where each value is the prediction that an image is a 3. It is a vector (i.e., a rank-1 tensor), indexed over the images.
The purpose of the loss function is to measure the difference between predicted values and the true values — that is, the targets (aka labels). Let's make another argument, `trgts`, with values of 0 or 1 which tells whether an image actually is a 3 or not. It is also a vector (i.e., another rank-1 tensor), indexed over the images.
So, for instance, suppose we had three images which we knew were a 3, a 7, and a 3. And suppose our model predicted with high confidence (`0.9`) that the first was a 3, with slight confidence (`0.4`) that the second was a 7, and with fair confidence (`0.2`), but incorrectly, that the last was a 7. This would mean our loss function would receive these values as its inputs:
```
trgts = tensor([1,0,1])
prds = tensor([0.9, 0.4, 0.2])
```
Here's a first try at a loss function that measures the distance between `predictions` and `targets`:
```
def mnist_loss(predictions, targets):
return torch.where(targets==1, 1-predictions, predictions).mean()
```
We're using a new function, `torch.where(a,b,c)`. This is the same as running the list comprehension `[b[i] if a[i] else c[i] for i in range(len(a))]`, except it works on tensors, at C/CUDA speed. In plain English, this function will measure how distant each prediction is from 1 if it should be 1, and how distant it is from 0 if it should be 0, and then it will take the mean of all those distances.
> note: Read the Docs: It's important to learn about PyTorch functions like this, because looping over tensors in Python performs at Python speed, not C/CUDA speed! Try running `help(torch.where)` now to read the docs for this function, or, better still, look it up on the PyTorch documentation site.
Let's try it on our `prds` and `trgts`:
```
torch.where(trgts==1, 1-prds, prds)
```
You can see that this function returns a lower number when predictions are more accurate, when accurate predictions are more confident (higher absolute values), and when inaccurate predictions are less confident. In PyTorch, we always assume that a lower value of a loss function is better. Since we need a scalar for the final loss, `mnist_loss` takes the mean of the previous tensor:
```
mnist_loss(prds,trgts)
```
For instance, if we change our prediction for the one "false" target from `0.2` to `0.8` the loss will go down, indicating that this is a better prediction:
```
mnist_loss(tensor([0.9, 0.4, 0.8]),trgts)
```
One problem with `mnist_loss` as currently defined is that it assumes that predictions are always between 0 and 1. We need to ensure, then, that this is actually the case! As it happens, there is a function that does exactly that—let's take a look.
### Sigmoid
The `sigmoid` function always outputs a number between 0 and 1. It's defined as follows:
```
def sigmoid(x): return 1/(1+torch.exp(-x))
```
Pytorch defines an accelerated version for us, so we don’t really need our own. This is an important function in deep learning, since we often want to ensure values are between 0 and 1. This is what it looks like:
```
plot_function(torch.sigmoid, title='Sigmoid', min=-4, max=4)
```
As you can see, it takes any input value, positive or negative, and smooshes it onto an output value between 0 and 1. It's also a smooth curve that only goes up, which makes it easier for SGD to find meaningful gradients.
Let's update `mnist_loss` to first apply `sigmoid` to the inputs:
```
def mnist_loss(predictions, targets):
predictions = predictions.sigmoid()
return torch.where(targets==1, 1-predictions, predictions).mean()
```
Now we can be confident our loss function will work, even if the predictions are not between 0 and 1. All that is required is that a higher prediction corresponds to higher confidence an image is a 3.
Having defined a loss function, now is a good moment to recapitulate why we did this. After all, we already had a metric, which was overall accuracy. So why did we define a loss?
The key difference is that the metric is to drive human understanding and the loss is to drive automated learning. To drive automated learning, the loss must be a function that has a meaningful derivative. It can't have big flat sections and large jumps, but instead must be reasonably smooth. This is why we designed a loss function that would respond to small changes in confidence level. This requirement means that sometimes it does not really reflect exactly what we are trying to achieve, but is rather a compromise between our real goal, and a function that can be optimized using its gradient. The loss function is calculated for each item in our dataset, and then at the end of an epoch the loss values are all averaged and the overall mean is reported for the epoch.
Metrics, on the other hand, are the numbers that we really care about. These are the values that are printed at the end of each epoch that tell us how our model is really doing. It is important that we learn to focus on these metrics, rather than the loss, when judging the performance of a model.
### SGD and Mini-Batches
Now that we have a loss function that is suitable for driving SGD, we can consider some of the details involved in the next phase of the learning process, which is to change or update the weights based on the gradients. This is called an *optimization step*.
In order to take an optimization step we need to calculate the loss over one or more data items. How many should we use? We could calculate it for the whole dataset, and take the average, or we could calculate it for a single data item. But neither of these is ideal. Calculating it for the whole dataset would take a very long time. Calculating it for a single item would not use much information, so it would result in a very imprecise and unstable gradient. That is, you'd be going to the trouble of updating the weights, but taking into account only how that would improve the model's performance on that single item.
So instead we take a compromise between the two: we calculate the average loss for a few data items at a time. This is called a *mini-batch*. The number of data items in the mini-batch is called the *batch size*. A larger batch size means that you will get a more accurate and stable estimate of your dataset's gradients from the loss function, but it will take longer, and you will process fewer mini-batches per epoch. Choosing a good batch size is one of the decisions you need to make as a deep learning practitioner to train your model quickly and accurately. We will talk about how to make this choice throughout this book.
Another good reason for using mini-batches rather than calculating the gradient on individual data items is that, in practice, we nearly always do our training on an accelerator such as a GPU. These accelerators only perform well if they have lots of work to do at a time, so it's helpful if we can give them lots of data items to work on. Using mini-batches is one of the best ways to do this. However, if you give them too much data to work on at once, they run out of memory—making GPUs happy is also tricky!
As we saw in our discussion of data augmentation in <<chapter_production>>, we get better generalization if we can vary things during training. One simple and effective thing we can vary is what data items we put in each mini-batch. Rather than simply enumerating our dataset in order for every epoch, instead what we normally do is randomly shuffle it on every epoch, before we create mini-batches. PyTorch and fastai provide a class that will do the shuffling and mini-batch collation for you, called `DataLoader`.
A `DataLoader` can take any Python collection and turn it into an iterator over many batches, like so:
```
coll = range(15)
dl = DataLoader(coll, batch_size=5, shuffle=True)
list(dl)
```
For training a model, we don't just want any Python collection, but a collection containing independent and dependent variables (that is, the inputs and targets of the model). A collection that contains tuples of independent and dependent variables is known in PyTorch as a `Dataset`. Here's an example of an extremely simple `Dataset`:
```
ds = L(enumerate(string.ascii_lowercase))
ds
```
When we pass a `Dataset` to a `DataLoader` we will get back many batches which are themselves tuples of tensors representing batches of independent and dependent variables:
```
dl = DataLoader(ds, batch_size=6, shuffle=True)
list(dl)
```
We are now ready to write our first training loop for a model using SGD!
## Putting It All Together
It's time to implement the process we saw in <<gradient_descent>>. In code, our process will be implemented something like this for each epoch:
```python
for x,y in dl:
pred = model(x)
loss = loss_func(pred, y)
loss.backward()
parameters -= parameters.grad * lr
```
First, let's re-initialize our parameters:
```
weights = init_params((28*28,1))
bias = init_params(1)
```
A `DataLoader` can be created from a `Dataset`:
```
dl = DataLoader(dset, batch_size=256)
xb,yb = first(dl)
xb.shape,yb.shape
```
We'll do the same for the validation set:
```
valid_dl = DataLoader(valid_dset, batch_size=256)
```
Let's create a mini-batch of size 4 for testing:
```
batch = train_x[:4]
batch.shape
preds = linear1(batch)
preds
loss = mnist_loss(preds, train_y[:4])
loss
```
Now we can calculate the gradients:
```
loss.backward()
weights.grad.shape,weights.grad.mean(),bias.grad
```
Let's put that all in a function:
```
def calc_grad(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()
```
and test it:
```
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
```
But look what happens if we call it twice:
```
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
```
The gradients have changed! The reason for this is that `loss.backward` actually *adds* the gradients of `loss` to any gradients that are currently stored. So, we have to set the current gradients to 0 first:
```
weights.grad.zero_()
bias.grad.zero_();
```
> note: Inplace Operations: Methods in PyTorch whose names end in an underscore modify their objects _in place_. For instance, `bias.zero_()` sets all elements of the tensor `bias` to 0.
Our only remaining step is to update the weights and biases based on the gradient and learning rate. When we do so, we have to tell PyTorch not to take the gradient of this step too—otherwise things will get very confusing when we try to compute the derivative at the next batch! If we assign to the `data` attribute of a tensor then PyTorch will not take the gradient of that step. Here's our basic training loop for an epoch:
```
def train_epoch(model, lr, params):
for xb,yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_()
```
We also want to check how we're doing, by looking at the accuracy of the validation set. To decide if an output represents a 3 or a 7, we can just check whether it's greater than 0. So our accuracy for each item can be calculated (using broadcasting, so no loops!) with:
```
(preds>0.0).float() == train_y[:4]
```
That gives us this function to calculate our validation accuracy:
```
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds>0.5) == yb
return correct.float().mean()
```
We can check it works:
```
batch_accuracy(linear1(batch), train_y[:4])
```
and then put the batches together:
```
def validate_epoch(model):
accs = [batch_accuracy(model(xb), yb) for xb,yb in valid_dl]
return round(torch.stack(accs).mean().item(), 4)
validate_epoch(linear1)
```
That's our starting point. Let's train for one epoch, and see if the accuracy improves:
```
lr = 1.
params = weights,bias
train_epoch(linear1, lr, params)
validate_epoch(linear1)
```
Then do a few more:
```
for i in range(20):
train_epoch(linear1, lr, params)
print(validate_epoch(linear1), end=' ')
```
Looking good! We're already about at the same accuracy as our "pixel similarity" approach, and we've created a general-purpose foundation we can build on. Our next step will be to create an object that will handle the SGD step for us. In PyTorch, it's called an *optimizer*.
### Creating an Optimizer
Because this is such a general foundation, PyTorch provides some useful classes to make it easier to implement. The first thing we can do is replace our `linear1` function with PyTorch's `nn.Linear` module. A *module* is an object of a class that inherits from the PyTorch `nn.Module` class. Objects of this class behave identically to standard Python functions, in that you can call them using parentheses and they will return the activations of a model.
`nn.Linear` does the same thing as our `init_params` and `linear` together. It contains both the *weights* and *biases* in a single class. Here's how we replicate our model from the previous section:
```
linear_model = nn.Linear(28*28,1)
```
Every PyTorch module knows what parameters it has that can be trained; they are available through the `parameters` method:
```
w,b = linear_model.parameters()
w.shape,b.shape
```
We can use this information to create an optimizer:
```
class BasicOptim:
def __init__(self,params,lr): self.params,self.lr = list(params),lr
def step(self, *args, **kwargs):
for p in self.params: p.data -= p.grad.data * self.lr
def zero_grad(self, *args, **kwargs):
for p in self.params: p.grad = None
```
We can create our optimizer by passing in the model's parameters:
```
opt = BasicOptim(linear_model.parameters(), lr)
```
Our training loop can now be simplified to:
```
def train_epoch(model):
for xb,yb in dl:
calc_grad(xb, yb, model)
opt.step()
opt.zero_grad()
```
Our validation function doesn't need to change at all:
```
validate_epoch(linear_model)
```
Let's put our little training loop in a function, to make things simpler:
```
def train_model(model, epochs):
for i in range(epochs):
train_epoch(model)
print(validate_epoch(model), end=' ')
```
The results are the same as in the previous section:
```
train_model(linear_model, 20)
```
fastai provides the `SGD` class which, by default, does the same thing as our `BasicOptim`:
```
linear_model = nn.Linear(28*28,1)
opt = SGD(linear_model.parameters(), lr)
train_model(linear_model, 20)
```
fastai also provides `Learner.fit`, which we can use instead of `train_model`. To create a `Learner` we first need to create a `DataLoaders`, by passing in our training and validation `DataLoader`s:
```
dls = DataLoaders(dl, valid_dl)
```
To create a `Learner` without using an application (such as `cnn_learner`) we need to pass in all the elements that we've created in this chapter: the `DataLoaders`, the model, the optimization function (which will be passed the parameters), the loss function, and optionally any metrics to print:
```
learn = Learner(dls, nn.Linear(28*28,1), opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)
```
Now we can call `fit`:
```
learn.fit(10, lr=lr)
```
As you can see, there's nothing magic about the PyTorch and fastai classes. They are just convenient pre-packaged pieces that make your life a bit easier! (They also provide a lot of extra functionality we'll be using in future chapters.)
With these classes, we can now replace our linear model with a neural network.
## Adding a Nonlinearity
So far we have a general procedure for optimizing the parameters of a function, and we have tried it out on a very boring function: a simple linear classifier. A linear classifier is very constrained in terms of what it can do. To make it a bit more complex (and able to handle more tasks), we need to add something nonlinear between two linear classifiers—this is what gives us a neural network.
Here is the entire definition of a basic neural network:
```
def simple_net(xb):
res = xb@w1 + b1
res = res.max(tensor(0.0))
res = res@w2 + b2
return res
```
That's it! All we have in `simple_net` is two linear classifiers with a `max` function between them.
Here, `w1` and `w2` are weight tensors, and `b1` and `b2` are bias tensors; that is, parameters that are initially randomly initialized, just like we did in the previous section:
```
w1 = init_params((28*28,30))
b1 = init_params(30)
w2 = init_params((30,1))
b2 = init_params(1)
```
The key point about this is that `w1` has 30 output activations (which means that `w2` must have 30 input activations, so they match). That means that the first layer can construct 30 different features, each representing some different mix of pixels. You can change that `30` to anything you like, to make the model more or less complex.
That little function `res.max(tensor(0.0))` is called a *rectified linear unit*, also known as *ReLU*. We think we can all agree that *rectified linear unit* sounds pretty fancy and complicated... But actually, there's nothing more to it than `res.max(tensor(0.0))`—in other words, replace every negative number with a zero. This tiny function is also available in PyTorch as `F.relu`:
```
plot_function(F.relu)
```
> J: There is an enormous amount of jargon in deep learning, including terms like _rectified linear unit_. The vast vast majority of this jargon is no more complicated than can be implemented in a short line of code, as we saw in this example. The reality is that for academics to get their papers published they need to make them sound as impressive and sophisticated as possible. One of the ways that they do that is to introduce jargon. Unfortunately, this has the result that the field ends up becoming far more intimidating and difficult to get into than it should be. You do have to learn the jargon, because otherwise papers and tutorials are not going to mean much to you. But that doesn't mean you have to find the jargon intimidating. Just remember, when you come across a word or phrase that you haven't seen before, it will almost certainly turn to be referring to a very simple concept.
The basic idea is that by using more linear layers, we can have our model do more computation, and therefore model more complex functions. But there's no point just putting one linear layout directly after another one, because when we multiply things together and then add them up multiple times, that could be replaced by multiplying different things together and adding them up just once! That is to say, a series of any number of linear layers in a row can be replaced with a single linear layer with a different set of parameters.
But if we put a nonlinear function between them, such as `max`, then this is no longer true. Now each linear layer is actually somewhat decoupled from the other ones, and can do its own useful work. The `max` function is particularly interesting, because it operates as a simple `if` statement.
> S: Mathematically, we say the composition of two linear functions is another linear function. So, we can stack as many linear classifiers as we want on top of each other, and without nonlinear functions between them, it will just be the same as one linear classifier.
Amazingly enough, it can be mathematically proven that this little function can solve any computable problem to an arbitrarily high level of accuracy, if you can find the right parameters for `w1` and `w2` and if you make these matrices big enough. For any arbitrarily wiggly function, we can approximate it as a bunch of lines joined together; to make it closer to the wiggly function, we just have to use shorter lines. This is known as the *universal approximation theorem*. The three lines of code that we have here are known as *layers*. The first and third are known as *linear layers*, and the second line of code is known variously as a *nonlinearity*, or *activation function*.
Just like in the previous section, we can replace this code with something a bit simpler, by taking advantage of PyTorch:
```
simple_net = nn.Sequential(
nn.Linear(28*28,30),
nn.ReLU(),
nn.Linear(30,1)
)
```
`nn.Sequential` creates a module that will call each of the listed layers or functions in turn.
`nn.ReLU` is a PyTorch module that does exactly the same thing as the `F.relu` function. Most functions that can appear in a model also have identical forms that are modules. Generally, it's just a case of replacing `F` with `nn` and changing the capitalization. When using `nn.Sequential`, PyTorch requires us to use the module version. Since modules are classes, we have to instantiate them, which is why you see `nn.ReLU()` in this example.
Because `nn.Sequential` is a module, we can get its parameters, which will return a list of all the parameters of all the modules it contains. Let's try it out! As this is a deeper model, we'll use a lower learning rate and a few more epochs.
```
learn = Learner(dls, simple_net, opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)
#hide_output
learn.fit(40, 0.1)
```
We're not showing the 40 lines of output here to save room; the training process is recorded in `learn.recorder`, with the table of output stored in the `values` attribute, so we can plot the accuracy over training as:
```
plt.plot(L(learn.recorder.values).itemgot(2));
```
And we can view the final accuracy:
```
learn.recorder.values[-1][2]
```
At this point we have something that is rather magical:
1. A function that can solve any problem to any level of accuracy (the neural network) given the correct set of parameters
1. A way to find the best set of parameters for any function (stochastic gradient descent)
This is why deep learning can do things which seem rather magical such fantastic things. Believing that this combination of simple techniques can really solve any problem is one of the biggest steps that we find many students have to take. It seems too good to be true—surely things should be more difficult and complicated than this? Our recommendation: try it out! We just tried it on the MNIST dataset and you have seen the results. And since we are doing everything from scratch ourselves (except for calculating the gradients) you know that there is no special magic hiding behind the scenes.
### Going Deeper
There is no need to stop at just two linear layers. We can add as many as we want, as long as we add a nonlinearity between each pair of linear layers. As you will learn, however, the deeper the model gets, the harder it is to optimize the parameters in practice. Later in this book you will learn about some simple but brilliantly effective techniques for training deeper models.
We already know that a single nonlinearity with two linear layers is enough to approximate any function. So why would we use deeper models? The reason is performance. With a deeper model (that is, one with more layers) we do not need to use as many parameters; it turns out that we can use smaller matrices with more layers, and get better results than we would get with larger matrices, and few layers.
That means that we can train the model more quickly, and it will take up less memory. In the 1990s researchers were so focused on the universal approximation theorem that very few were experimenting with more than one nonlinearity. This theoretical but not practical foundation held back the field for years. Some researchers, however, did experiment with deep models, and eventually were able to show that these models could perform much better in practice. Eventually, theoretical results were developed which showed why this happens. Today, it is extremely unusual to find anybody using a neural network with just one nonlinearity.
Here what happens when we train an 18-layer model using the same approach we saw in <<chapter_intro>>:
```
dls = ImageDataLoaders.from_folder(path)
learn = cnn_learner(dls, resnet18, pretrained=False,
loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(1, 0.1)
```
Nearly 100% accuracy! That's a big difference compared to our simple neural net. But as you'll learn in the remainder of this book, there are just a few little tricks you need to use to get such great results from scratch yourself. You already know the key foundational pieces. (Of course, even once you know all the tricks, you'll nearly always want to work with the pre-built classes provided by PyTorch and fastai, because they save you having to think about all the little details yourself.)
## Jargon Recap
Congratulations: you now know how to create and train a deep neural network from scratch! We've gone through quite a few steps to get to this point, but you might be surprised at how simple it really is.
Now that we are at this point, it is a good opportunity to define, and review, some jargon and key concepts.
A neural network contains a lot of numbers, but they are only of two types: numbers that are calculated, and the parameters that these numbers are calculated from. This gives us the two most important pieces of jargon to learn:
- Activations:: Numbers that are calculated (both by linear and nonlinear layers)
- Parameters:: Numbers that are randomly initialized, and optimized (that is, the numbers that define the model)
We will often talk in this book about activations and parameters. Remember that they have very specific meanings. They are numbers. They are not abstract concepts, but they are actual specific numbers that are in your model. Part of becoming a good deep learning practitioner is getting used to the idea of actually looking at your activations and parameters, and plotting them and testing whether they are behaving correctly.
Our activations and parameters are all contained in *tensors*. These are simply regularly shaped arrays—for example, a matrix. Matrices have rows and columns; we call these the *axes* or *dimensions*. The number of dimensions of a tensor is its *rank*. There are some special tensors:
- Rank zero: scalar
- Rank one: vector
- Rank two: matrix
A neural network contains a number of layers. Each layer is either *linear* or *nonlinear*. We generally alternate between these two kinds of layers in a neural network. Sometimes people refer to both a linear layer and its subsequent nonlinearity together as a single layer. Yes, this is confusing. Sometimes a nonlinearity is referred to as an *activation function*.
<<dljargon1>> summarizes the key concepts related to SGD.
```asciidoc
[[dljargon1]]
.Deep learning vocabulary
[options="header"]
|=====
| Term | Meaning
|ReLU | Function that returns 0 for negative numbers and doesn't change positive numbers.
|Mini-batch | A smll group of inputs and labels gathered together in two arrays. A gradient descent step is updated on this batch (rather than a whole epoch).
|Forward pass | Applying the model to some input and computing the predictions.
|Loss | A value that represents how well (or badly) our model is doing.
|Gradient | The derivative of the loss with respect to some parameter of the model.
|Backward pass | Computing the gradients of the loss with respect to all model parameters.
|Gradient descent | Taking a step in the directions opposite to the gradients to make the model parameters a little bit better.
|Learning rate | The size of the step we take when applying SGD to update the parameters of the model.
|=====
```
> note: _Choose Your Own Adventure_ Reminder: Did you choose to skip over chapters 2 & 3, in your excitement to peek under the hood? Well, here's your reminder to head back to chapter 2 now, because you'll be needing to know that stuff very soon!
## Questionnaire
1. How is a grayscale image represented on a computer? How about a color image?
1. How are the files and folders in the `MNIST_SAMPLE` dataset structured? Why?
1. Explain how the "pixel similarity" approach to classifying digits works.
1. What is a list comprehension? Create one now that selects odd numbers from a list and doubles them.
1. What is a "rank-3 tensor"?
1. What is the difference between tensor rank and shape? How do you get the rank from the shape?
1. What are RMSE and L1 norm?
1. How can you apply a calculation on thousands of numbers at once, many thousands of times faster than a Python loop?
1. Create a 3×3 tensor or array containing the numbers from 1 to 9. Double it. Select the bottom-right four numbers.
1. What is broadcasting?
1. Are metrics generally calculated using the training set, or the validation set? Why?
1. What is SGD?
1. Why does SGD use mini-batches?
1. What are the seven steps in SGD for machine learning?
1. How do we initialize the weights in a model?
1. What is "loss"?
1. Why can't we always use a high learning rate?
1. What is a "gradient"?
1. Do you need to know how to calculate gradients yourself?
1. Why can't we use accuracy as a loss function?
1. Draw the sigmoid function. What is special about its shape?
1. What is the difference between a loss function and a metric?
1. What is the function to calculate new weights using a learning rate?
1. What does the `DataLoader` class do?
1. Write pseudocode showing the basic steps taken in each epoch for SGD.
1. Create a function that, if passed two arguments `[1,2,3,4]` and `'abcd'`, returns `[(1, 'a'), (2, 'b'), (3, 'c'), (4, 'd')]`. What is special about that output data structure?
1. What does `view` do in PyTorch?
1. What are the "bias" parameters in a neural network? Why do we need them?
1. What does the `@` operator do in Python?
1. What does the `backward` method do?
1. Why do we have to zero the gradients?
1. What information do we have to pass to `Learner`?
1. Show Python or pseudocode for the basic steps of a training loop.
1. What is "ReLU"? Draw a plot of it for values from `-2` to `+2`.
1. What is an "activation function"?
1. What's the difference between `F.relu` and `nn.ReLU`?
1. The universal approximation theorem shows that any function can be approximated as closely as needed using just one nonlinearity. So why do we normally use more?
### Further Research
1. Create your own implementation of `Learner` from scratch, based on the training loop shown in this chapter.
1. Complete all the steps in this chapter using the full MNIST datasets (that is, for all digits, not just 3s and 7s). This is a significant project and will take you quite a bit of time to complete! You'll need to do some of your own research to figure out how to overcome some obstacles you'll meet on the way.
| true |
code
| 0.612541 | null | null | null | null |
|
# MNIST DATA with Convolutional Neural Network
## 1. Import Packages
```
import input_data
import numpy as np
import matplotlib.pylab as plt
import tensorflow as tf
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.models import load_model
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
```
## 2. Explore MNIST Data
```
mnist_images = input_data.read_data_sets("./mnist_data", one_hot=False)
# Example of a picture
pic,real_values = mnist_images.train.next_batch(25)
index = 11 # changeable with 0 ~ 24 integer
image = pic[index,:]
image = np.reshape(image,[28,28])
plt.imshow(image)
plt.show()
# Explore MNIST data
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
image = np.reshape(pic[i,:] , [28,28])
plt.imshow(image)
plt.xlabel(real_values[i])
plt.show()
```
## 3. Make Dataset
```
# Download Data : http://yann.lecun.com/exdb/mnist/
# Data input script : https://github.com/tensorflow/tensorflow/tree/master/tensorflow/examples/tutorials/mnist
mnist = input_data.read_data_sets("./samples/MNIST_data/", one_hot=True)
print("the number of train examples :" , mnist.train.num_examples)
print("the number of test examples :" , mnist.test.num_examples)
x_train = mnist.train.images.reshape(55000, 28, 28, 1)
x_test = mnist.test.images.reshape(10000, 28, 28, 1)
y_train = mnist.train.labels
y_test = mnist.test.labels
```
## 4. Building my neural network in tensorflow
```
batch_size = 128
num_classes = 10
epochs = 50
model = Sequential()
model.add(Conv2D(32, kernel_size=(5, 5), strides=(1, 1), padding='same',
activation='relu',
input_shape=(28,28,1)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, (5, 5), activation='relu', padding='same'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(1024, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
hist = model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
```
## 5. Calculate Accuracy
```
score1 = model.evaluate(x_train, y_train, verbose=0)
score2 = model.evaluate(x_test, y_test, verbose=0)
print('Train accuracy:', score1[1])
print('Test accuracy:', score2[1])
```
## 6. Check a prediction
```
predictions = model.predict(x_test)
predictions[101]
print(np.argmax(predictions[101])) # highest confidence
# This model is convinced that this image is "1"
plt.imshow(x_test[101].reshape(28,28))
```
## 7. Save model
```
# Save model
model_json = model.to_json()
with open("model.json", "w") as json_file :
json_file.write(model_json)
# Save model weights
model.save_weights("model_weight.h5")
print("Saved model to disk")
# evaluate
loaded_model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
train_score = loaded_model.evaluate(x_train, y_train, verbose=0)
test_score = loaded_model.evaluate(x_test, y_test, verbose=0)
print('training accuracy : ' + str(train_score[1]))
print('test accuracy : ' + str(test_score[1]))
```
| true |
code
| 0.694056 | null | null | null | null |
|
```
%matplotlib inline
```
Magnetostatic Fields
=====================
An example of using PlasmaPy's `Magnetostatic` class in `physics` subpackage.
```
from plasmapy.formulary import magnetostatics
from plasmapy.plasma.sources import Plasma3D
import numpy as np
import astropy.units as u
import matplotlib.pyplot as plt
```
Some common magnetostatic fields can be generated and added to a plasma object.
A dipole
```
dipole = magnetostatics.MagneticDipole(np.array([0, 0, 1])*u.A*u.m*u.m, np.array([0, 0, 0])*u.m)
print(dipole)
```
initialize a a plasma, where the magnetic field will be calculated on
```
plasma = Plasma3D(domain_x=np.linspace(-2, 2, 30) * u.m,
domain_y=np.linspace(0, 0, 1) * u.m,
domain_z=np.linspace(-2, 2, 20) * u.m)
```
add the dipole field to it
```
plasma.add_magnetostatic(dipole)
X, Z = plasma.grid[0, :, 0, :], plasma.grid[2, :, 0, :]
U = plasma.magnetic_field[0, :, 0, :].value.T # because grid uses 'ij' indexing
W = plasma.magnetic_field[2, :, 0, :].value.T # because grid uses 'ij' indexing
plt.figure()
plt.axis('square')
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.title('Dipole field in x-z plane, generated by a dipole pointing in the z direction')
plt.streamplot(plasma.x.value, plasma.z.value, U, W)
```
```
cw = magnetostatics.CircularWire(np.array([0, 0, 1]), np.array([0, 0, 0])*u.m, 1*u.m, 1*u.A)
print(cw)
```
initialize a a plasma, where the magnetic field will be calculated on
```
plasma = Plasma3D(domain_x=np.linspace(-2, 2, 30) * u.m,
domain_y=np.linspace(0, 0, 1) * u.m,
domain_z=np.linspace(-2, 2, 20) * u.m)
```
add the circular coil field to it
```
plasma.add_magnetostatic(cw)
X, Z = plasma.grid[0, :, 0, :], plasma.grid[2, :, 0, :]
U = plasma.magnetic_field[0, :, 0, :].value.T # because grid uses 'ij' indexing
W = plasma.magnetic_field[2, :, 0, :].value.T # because grid uses 'ij' indexing
plt.figure()
plt.axis('square')
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.title('Circular coil field in x-z plane, generated by a circular coil in the x-y plane')
plt.streamplot(plasma.x.value, plasma.z.value, U, W)
```
```
gw_cw = cw.to_GeneralWire()
# the calculated magnetic field is close
print(gw_cw.magnetic_field([0, 0, 0]) - cw.magnetic_field([0, 0, 0]))
```
```
iw = magnetostatics.InfiniteStraightWire(np.array([0, 1, 0]), np.array([0, 0, 0])*u.m, 1*u.A)
print(iw)
```
initialize a a plasma, where the magnetic field will be calculated on
```
plasma = Plasma3D(domain_x=np.linspace(-2, 2, 30) * u.m,
domain_y=np.linspace(0, 0, 1) * u.m,
domain_z=np.linspace(-2, 2, 20) * u.m)
# add the infinite straight wire field to it
plasma.add_magnetostatic(iw)
X, Z = plasma.grid[0, :, 0, :], plasma.grid[2, :, 0, :]
U = plasma.magnetic_field[0, :, 0, :].value.T # because grid uses 'ij' indexing
W = plasma.magnetic_field[2, :, 0, :].value.T # because grid uses 'ij' indexing
plt.figure()
plt.title('Dipole field in x-z plane, generated by a infinite straight wire '
'pointing in the y direction')
plt.axis('square')
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.streamplot(plasma.x.value, plasma.z.value, U, W)
```
| true |
code
| 0.61086 | null | null | null | null |
|
# Home Work Assignment 3: Bootstrap
```
import numpy as np
import pandas as pd
df = pd.read_csv('star_dataset.csv')
df.head()
```
Best partition from previous work is determined by the following parameters.
```
n_cluster = 4
random_state = 9
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
quantitative_columns = ['Temperature (K)', 'Luminosity(L/Lo)', 'Radius(R/Ro)', 'Absolute magnitude(Mv)']
X = df[quantitative_columns]
X = StandardScaler().fit_transform(X)
kmeans = KMeans(n_clusters=n_cluster, n_init=1, max_iter=500, init='random',
tol=1e-4, algorithm='full', random_state=random_state)
kmeans.fit(X)
df['cluster_id'] = kmeans.labels_
df.head(10)
```
### 1. Take a feature, find the 95% confidence interval for its grand mean by using bootstrap
```
def bootstrap(data, K):
data = np.asarray(data)
N = len(data)
means = []
for _ in range(K):
idxs = np.random.choice(N, N, replace=True)
mean = data[idxs].mean()
means.append(mean)
return np.asarray(means)
def confidence_interval(means, pivotal=True):
if pivotal is True:
left = means.mean() - 1.96 * means.std()
right = means.mean() + 1.96 * means.std()
else:
left = np.percentile(means, 2.5)
right = np.percentile(means, 97.5)
return sorted([abs(left), abs(right)])
print('mean: {:.2f}'.format(df['Temperature (K)'].mean()))
print('no-pivotal: [{:.2f}, {:.2f}]'.format(*confidence_interval(bootstrap(df['Temperature (K)'], 1000), pivotal=False)))
print('pivotal: [{:.2f}, {:.2f}]'.format(*confidence_interval(bootstrap(df['Temperature (K)'], 1000), pivotal=True)))
```
### 2. Compare the within-cluster means for one of the features between two clusters using bootstrap
```
cluster_0 = df[df['cluster_id'] == 0]
cluster_1 = df[df['cluster_id'] == 1]
data = bootstrap(cluster_0['Temperature (K)'], 1000) - bootstrap(cluster_1['Temperature (K)'], 1000)
print('no-pivotal: [{:.2f}, {:.2f}]'.format(*confidence_interval(data, pivotal=False)))
print('pivotal: [{:.2f}, {:.2f}]'.format(*confidence_interval(data, pivotal=True)))
```
### 3. Take a cluster, and compare the grand mean with the within- cluster mean for the feature by using bootstrap
```
cluster_0 = df
cluster_1 = df[df['cluster_id'] == 1]
data = bootstrap(cluster_0['Temperature (K)'], 1000) - bootstrap(cluster_1['Temperature (K)'], 1000)
print('no-pivotal: [{:.2f}, {:.2f}]'.format(*confidence_interval(data, pivotal=False)))
print('pivotal: [{:.2f}, {:.2f}]'.format(*confidence_interval(data, pivotal=True)))
```
| true |
code
| 0.38194 | null | null | null | null |
|
# Random Signals
*This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*
## Cumulative Distribution Functions
A random process can be characterized by the statistical properties of its amplitude values. [Cumulative distribution functions](https://en.wikipedia.org/wiki/Cumulative_distribution_function) (CDFs) are one possibility to do so.
### Univariate Cumulative Distribution Function
The univariate CDF $P_x(\theta, k)$ of a continuous-amplitude real-valued random signal $x[k]$ is defined as
\begin{equation}
P_x(\theta, k) := \Pr \{ x[k] \leq \theta\}
\end{equation}
where $\Pr \{ \cdot \}$ denotes the probability that the given condition holds. The univariate CDF quantifies the probability that for the entire ensemble and for a fixed time index $k$ the amplitude $x[k]$ is smaller or equal to $\theta$. The term '*univariate*' reflects the fact that only one random process is considered.
The CDF shows the following properties which can be concluded directly from its definition
\begin{equation}
\lim_{\theta \to -\infty} P_x(\theta, k) = 0
\end{equation}
and
\begin{equation}
\lim_{\theta \to \infty} P_x(\theta, k) = 1
\end{equation}
The former property results from the fact that all amplitude values $x[k]$ are larger than $- \infty$, the latter from the fact that all amplitude values lie within $- \infty$ and $\infty$. The univariate CDF $P_x(\theta, k)$ is furthermore a non-decreasing function.
The probability that $\theta_1 < x[k] \leq \theta_2$ is given as
\begin{equation}
\Pr \{\theta_1 < x[k] \leq \theta_2\} = P_x(\theta_2, k) - P_x(\theta_1, k)
\end{equation}
Hence, the probability that a continuous-amplitude random signal takes a specific value $x[k]=\theta$ is zero when calculated by means of the CDF. This motivates the definition of probability density functions introduced later.
### Bivariate Cumulative Distribution Function
The statistical dependencies between two signals are frequently of interest in statistical signal processing. The bivariate or joint CDF $P_{xy}(\theta_x, \theta_y, k_x, k_y)$ of two continuous-amplitude real-valued random signals $x[k]$ and $y[k]$ is defined as
\begin{equation}
P_{xy}(\theta_x, \theta_y, k_x, k_y) := \Pr \{ x[k_x] \leq \theta_x \wedge y[k_y] \leq \theta_y \}
\end{equation}
The joint CDF quantifies the probability for the entire ensemble of sample functions that for a fixed $k_x$ the amplitude value $x[k_x]$ is smaller or equal to $\theta_x$ and that for a fixed $k_y$ the amplitude value $y[k_y]$ is smaller or equal to $\theta_y$. The term '*bivariate*' reflects the fact that two random processes are considered. The bivariate CDF can also be used to characterize the statistical properties of one random signal $x[k]$ at two different time-instants $k_x$ and $k_y$ by setting $y[k] = x[k]$
\begin{equation}
P_{xx}(\theta_1, \theta_2, k_1, k_2) := \Pr \{ x[k_1] \leq \theta_1 \wedge y[k_2] \leq \theta_2 \}
\end{equation}
The definition of the bivariate CDF can be extended straightforward to the case of more than two random variables. The resulting CDF is termed as multivariate CDF.
## Probability Density Functions
[Probability density functions](https://en.wikipedia.org/wiki/Probability_density_function) (PDFs) describe the probability for one or multiple random signals to take on a specific value. Again the univariate case is discussed first.
### Univariate Probability Density Function
The univariate PDF $p_x(\theta, k)$ of a continuous-amplitude real-valued random signal $x[k]$ is defined as the derivative of the univariate CDF
\begin{equation}
p_x(\theta, k) = \frac{\partial}{\partial \theta} P_x(\theta, k)
\end{equation}
Due to the properties of the CDF and the definition of the PDF, it shows the following properties
\begin{equation}
p_x(\theta, k) \geq 0
\end{equation}
and
\begin{equation}
\int\limits_{-\infty}^{\infty} p_x(\theta, k) \, \mathrm{d}\theta = P_x(\infty, k) = 1
\end{equation}
The univariate PDF has only positive values and the area below the PDF is equal to one.
Due to the definition of the PDF as derivative of the CDF, the CDF can be computed from the PDF by integration
\begin{equation}
P_x(\theta, k) = \int\limits_{-\infty}^{\theta} p_x(\theta, k) \, \mathrm{d}\theta
\end{equation}
#### Example - Estimate of an univariate PDF by the histogram
In the process of calculating a [histogram](https://en.wikipedia.org/wiki/Histogram), the entire range of amplitude values of a random signal is split into a series of intervals (bins). For a given random signal the number of samples is counted which fall into one of these intervals. This is repeated for all intervals. The counts are finally normalized with respect to the total number of samples. This process constitutes a numerical estimation of the PDF of a random process.
In the following example the histogram of an ensemble of random signals is computed for each time index $k$. The CDF is computed by taking the cumulative sum over the histogram bins. This constitutes a numerical approximation of above integral
\begin{equation}
\int\limits_{-\infty}^{\theta} p_x(\theta, k) \approx \sum_{i=0}^{N} p_x(\theta_i, k) \, \Delta\theta_i
\end{equation}
where $p_x(\theta_i, k)$ denotes the $i$-th bin of the PDF and $\Delta\theta_i$ its width.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
K = 32 # number of temporal samples
N = 10000 # number of sample functions
bins = 100 # number of bins for the histogram
# draw sample functions from a random process
np.random.seed(2)
x = np.random.normal(size=(N, K))
x += np.tile(np.cos(2*np.pi/K*np.arange(K)), [N, 1])
# compute the histogram
px = np.zeros((bins, K))
for k in range(K):
px[:, k], edges = np.histogram(x[:, k], bins=bins, range=(-4,4), density=True)
# compute the CDF
Px = np.cumsum(px, axis=0) * 8/bins
# plot the PDF
plt.figure(figsize=(10,6))
plt.pcolor(np.arange(K), edges, px)
plt.title(r'Estimated PDF $\hat{p}_x(\theta, k)$')
plt.xlabel(r'$k$')
plt.ylabel(r'$\theta$')
plt.colorbar()
plt.autoscale(tight=True)
# plot the CDF
plt.figure(figsize=(10,6))
plt.pcolor(np.arange(K), edges, Px, vmin=0, vmax=1)
plt.title(r'Estimated CDF $\hat{P}_x(\theta, k)$')
plt.xlabel(r'$k$')
plt.ylabel(r'$\theta$')
plt.colorbar()
plt.autoscale(tight=True)
```
**Exercise**
* Change the number of sample functions `N` or/and the number of `bins` and rerun the examples. What changes? Why?
In numerical simulations of random processes only a finite number of sample functions and temporal samples can be considered. This holds also for the number of intervals (bins) used for the histogram. As a result, numerical approximations of the CDF/PDF will be subject to statistical uncertainties that typically will become smaller if the number of sample functions `N` is increased.
### Bivariate Probability Density Function
The bivariate or joint PDF $p_{xy}(\theta_x, \theta_y, k_x, k_y)$ of two continuous-amplitude real-valued random signals $x[k]$ and $y[k]$ is defined as
\begin{equation}
p_{xy}(\theta_x, \theta_y, k_x, k_y) := \frac{\partial^2}{\partial \theta_x \partial \theta_y} P_{xy}(\theta_x, \theta_y, k_x, k_y)
\end{equation}
The bivariate PDF quantifies the joint probability that $x[k]$ takes the value $\theta_x$ and that $y[k]$ takes the value $\theta_y$ for the entire ensemble of sample functions.
If $x[k] = y[k]$ the bivariate PDF $p_{xx}(\theta_1, \theta_2, k_1, k_2)$ describes the probability that the random signal $x[k]$ takes the value $\theta_1$ at time instance $k_1$ and the value $\theta_2$ at time instance $k_2$. Hence, $p_{xx}(\theta_1, \theta_2, k_1, k_2)$ provides insights into the temporal dependencies of a random signal $x[k]$.
This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Digital Signal Processing - Lecture notes featuring computational examples, 2016*.
| true |
code
| 0.703129 | null | null | null | null |
|
## Image Classification Problems - Warm-Up
In the following set of tutorials, we will focus on a particular class of problems, namely supervised classification, as a typical example for machine learning application use cases. Generally, in classification the task is to assign data items to a fixed set of categories, or in other words classes. While this might sound like an easy task for trivial problems such as deciding if someone is of legal age given their birthday, other classification problems are much harder. Consider for example the problem of identifying in a gray-scale satellite image, what land-cover type, e.g. road, house, field, etc., one can see. There are a number of challenges involved in this problem, objects may have different shapes, might be partially covered by cloud shadows or simply have varying colors. Writing a rule-based algorithm for such a problem is close to impossible.
Therefore, we would want to employ a data-driven approach instead and stochastically infer reasonable respresentations for each data-item and class from manually annotated examples (the supervisor). This approach is so flexible that it can be mapped to a large number of application scenarios by providing input data with its corresponding encoded pattern labels (i.e. the annotations). As part of this tutorial, we will study one examplery use case - image classification. For a number of images, we will predict, what object is depicted in it.
For teaching purposes, we will use the battle-test MNIST database [1]. It contains 70.000 images with 28x28 pixels of hand-written digits, collected by US-American National Institute of Standard and Technology. The classification task is to decide what digit can be seen in each of these images. You should notice throughout the tutorial session that the presented approaches can be easily transferred to other application domains, like for example the initially presented satellite image scenario.
### Setup
In line with the presented tutorial series, we will make use of the Python programming language and a number of additionally downloadable packages. Some of you might already be familiar with these, so you might want to skip ahead to the next section.
For those of you that are new to Python, you might an enjoy a (very) brief overview of the packages, we are going to use:
* **h5py [3]** - a module that allows us to process HDF5 [2] files.
* **numpy [4]** - a library for efficient manipulation of multi-dimensional arrays, matrices and mathemical operations.
* **matplotlib [5]** - a plotting library, which we will use to create 2D plots and display images.
```
import h5py
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
```
### Loading the Data
The entire MNIST database of images including labels is approximately 220 MB in size. During the tutorials you are going to work on the entire dataset. For pratical purposes we have stored the images and labels in an HDF5 file. This is a specifialized data format that originates from the area of high-performance computing (HPC). It is highly optimized for scenarios in which large amounts of data are read and write from disk (potentially in parallel).
HDF5 is particular suited for (semi-)structured data, like vector, matrices or other multi-dimensional arrays. Moreover, HDF5 also provides advanced compressing algorithms reducing the effective size of the MNIST database on disk to roughly 18 MB. At the same time the access to HDF5 files is straight-forward. Within each HDF5 file there is a structure akin to a file-system and its pathes under which data can be stored, respectively read. In our HDF5 file the images of the MNIST dataset can be found in the path (it is actually called a dataset) 'data' and the labels in the dataset 'labels'.
```
def load_data(path='mnist.h5'):
"""
Loads a dataset and its supervisor labels from the HDF5 file specified by the path.
It is assumed that the HDF5 dataset containing the data is called 'data' and the labels are called 'labels'.
Parameters
----------
path : str, optional
The absolute or relative path to the HDF5 file, defaults to mnist.h5.
Returns
-------
data_and_labels : tuple(np.array[samples, width, height], np.array[samples])
a tuple with two numpy array containing the data and labels
"""
with h5py.File(path, 'r') as handle:
return np.array(handle['/data']), np.array(handle['/labels'])
data, labels = load_data()
data.shape, labels.shape
```
### Getting Familiar with the MNIST Dataset
Let's have a look on some of the images, to get a feel for what they look like. Each of them has only a single color gray channel, i.e. is black-and-white.
```
def show_examples(data, width=10, height=6):
"""
Displays a number of example images from a given dataset.
The images are arranged in a rectangular grid with a specified width and height.
Parameters
----------
data : np.array[samples, width, height]
The dataset containing the images.
width : int, optional
How wide the rectangular image grid shall be, defaults to ten.
height : int, optional
How high the rectangular image grid shall, defaults to six.
"""
index = 0
figure, axes = plt.subplots(height, width, figsize=(16, 9), sharex=True, sharey=True)
for h in range(height):
for w in range(width):
axis = axes[h][w]
axis.grid(False)
axis.imshow(data[index], cmap='gist_gray')
index += 1
plt.show()
show_examples(data)
```
### A Slightly Deeper Look
In data-driven application use cases it is usually beneficial to get understanding about the properties of the utilized datasets. This is not only necessary to preprocess the data properly, e.g. clean missing values or normalize each of the feature axis to be on the same scale, but also to be able to fine-tune the machine learning algorithm parameters.
The MNIST dataset is fortunately nicely preprocessed and each feature, i.e. the pixel values, are all within the same range. Therefore, we do not need for the sake of this tutorial to perform any further preprocessing. However, it would be good see whether some of the patterns, meaning the digits, are underrepresented. If so, this would not only mean that we should pay close attention, how we evaluate the model, but also, how effective each of the classes may be learned. Let's have a look.
```
def count_digits(labels):
"""
Counts how often each of the individual labels, i.e. each digit, occurs in the dataset.
Parameters
----------
labels : np.array[samples]
The labels for each data item.
Returns
-------
counts : dict[unique_classes -> int]
A mapping between each unique class label and its absolute occurrence count.
"""
return dict(enumerate(np.bincount(labels)))
count_digits(labels)
```
All of the classes seem to be more or less evenly distributed. We can only observe a slight bias towards the digits *1*, *3* and *7* as well as a slight underrepresentation of number *5*. Including more samples depicting *1* and *7* seems like a logical precaution due to their similarity. In practice, we must later carefully investigate how much this skew affects our machine learning model performance.
Since all of the images of the digits in the MNIST database are centered and only have a single color channel, we should be able to compute an "average" digits for each of them.
```
def average_images(data, labels):
"""
Averages all the data items that are of the same class and returns the resulting 'mean items'.
Parameters
----------
data : np.array[samples, width, height]
The dataset containing the images.
labels : np.array[samples]
The corresponding labels for each data item.
Returns
-------
mean_items : np.array[unique_classes, width, height]
The 'mean items' for each unique class in the labels
"""
classes = np.unique(labels).shape[0]
averages = np.zeros((classes, data.shape[1], data.shape[2],))
for digit in range(classes):
averages[digit] = data[labels == digit].mean(axis=0)
return averages
show_examples(average_images(data, labels), width=5, height=2)
```
The average numbers still clearly resemble their corresponding individuals. Some of them are a little more fuzzy than others so, e.g. *4* or *9*, highlighting the sample variance and the necessity for a stochastic learning approach. Moreover, one can also clearly see that the digits are American-styled, e.g. missing diagonal slash for the *1* or cross bar for the *7*.
### References
[1] **The MNIST database of handwritten digits**, *Yann LeCun, Corinna Cortes, Christopher J. C. Burges*, [external link](http://yann.lecun.com/exdb/mnist/).
[2] **Hierarchical Data Format, version 5**, *The HDF Group*, [external link](http://www.hdfgroup.org/HDF5/).
[3] **HDF5 for Python**, *Andrew Collette*, O'Reilly, (2008), [documentation, external link](http://docs.h5py.org/en/latest/index.html).
[4] **A guide to NumPy**, *Travis E, Oliphant*, Trelgol Publishing, (2006), [documentation, external link](https://docs.scipy.org/doc/numpy-1.14.0/).
[5] **Matplotlib: A 2D graphics environment**, *John D. Hunter, J. D.*, Computing In Science & Engineering, vol. 9, issue 3, 90-95, (2007), [documentation, external link](https://matplotlib.org/).
| true |
code
| 0.802459 | null | null | null | null |
|
**Notas para contenedor de docker:**
Comando de docker para ejecución de la nota de forma local:
nota: cambiar `<ruta a mi directorio>` por la ruta de directorio que se desea mapear a `/datos` dentro del contenedor de docker.
```
docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_numerical -p 8888:8888 -p 8786:8786 -p 8787:8787 -d palmoreck/jupyterlab_numerical:1.1.0
```
password para jupyterlab: `qwerty`
Detener el contenedor de docker:
```
docker stop jupyterlab_numerical
```
Documentación de la imagen de docker `palmoreck/jupyterlab_numerical:1.1.0` en [liga](https://github.com/palmoreck/dockerfiles/tree/master/jupyterlab/numerical).
---
Esta nota utiliza métodos vistos en [1.5.Integracion_numerica](https://github.com/ITAM-DS/analisis-numerico-computo-cientifico/blob/master/temas/I.computo_cientifico/1.5.Integracion_numerica.ipynb)
Documentación de [cython](https://cython.org/):
* [Basic Tutorial](https://cython.readthedocs.io/en/latest/src/tutorial/cython_tutorial.html)
* [Source Files and Compilation](https://cython.readthedocs.io/en/latest/src/userguide/source_files_and_compilation.html)
* [Compiling with a Jupyter Notebook](https://cython.readthedocs.io/en/latest/src/userguide/source_files_and_compilation.html#compiling-with-a-jupyter-notebook)
**La siguiente celda muestra el modo de utilizar el comando magic de `%pip` para instalar paquetes desde jupyterlab.** Ver [liga](https://ipython.readthedocs.io/en/stable/interactive/magics.html#built-in-magic-commands) para magic commands.
Instalamos cython:
```
%pip install -q --user cython
```
La siguiente celda reiniciará el kernel de **IPython** para cargar los paquetes instalados en la celda anterior. Dar **Ok** en el mensaje que salga y continuar con el contenido del notebook.
```
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
```
# Cython y el por qué compilar a código de máquina
De las opciones más sencillas que tenemos a nuestra disposición para resolver bottlenecks en nuestro programa es hacer que nuestro código haga menos trabajo. ¿Cómo podemos hacer esto? <- compilando nuestro código a código de máquina para que el código en Python ejecute menos instrucciones.
**¿Por qué puede ser lenta la ejecución de un bloque de código en Python (o en algún otro lenguaje tipo intérprete)?** La verificación de tipo de datos (si son `int`, `double` o `string`), los objetos temporales que se crean por tipo de dato (un objeto tipo `int` en Python tiene asociado un objeto de alto nivel con el que interactuamos pero que causa overhead) y las llamadas a funciones de alto nivel (por ejemplo las que ayudan a almacenar al objeto en memoria) son tres de las fuentes que hacen a Python (y a otro lenguaje tipo intérprete como `R` o `Matlab`) lento. También otras fuentes que responden la pregunta son:
* Desde el punto de vista de la memoria de la máquina, el número de referencias a un objeto y las copias entre objetos.
* No es posible vectorizar un cálculo sin el uso de extensiones (por ejemplo paquetes como `numpy`).
Un paquete para resolver lo anterior es Cython que requiere que escribamos en un lenguaje híbrido entre Python y C. Si bien a l@s integrantes de un equipo de desarrollo que no saben C éste cambio reducirá la velocidad de desarrollo, en la práctica si se tiene un bottleneck que no ha podido resolverse con herramientas como el cómputo en paralelo o vectorización, se recomienda utilizar Cython para regiones pequeñas del código y resolver el bottleneck del programa.
Cython es un compilador que convierte *type-annotated Python* y *C like* (instrucciones escritas en Python pero en una forma tipo lenguaje C) en un módulo compilado que funciona como una extensión de Python. Este módulo puede ser importado como un módulo regular de Python utilizando `import`.
Además Cython tiene ya un buen tiempo en la comunidad (2007 aprox.), es altamente usado y es de las herramientas preferidas para código tipo *CPU-bound* (un gran porcentaje del código es uso de CPU vs uso de memoria o I/O). También soporta a la [API OpenMP](https://www.openmp.org/) que veremos en el capítulo de cómputo en paralelo para aprovechar los múltiples cores o CPU's de una máquina.
Para ver más historia de Cython ir a la referencia 1. de esta nota o a la [liga](https://en.wikipedia.org/wiki/Cython).
# ¿Qué tipo de ganancias en velocidad podemos esperar al usar Cython?
* Código en el que se tengan muchos loops (por ejemplo ciclos `for`) en los que se realizan operaciones matemáticas típicamente no vectorizadas o que no pueden vectorizarse*. Esto es, códigos en los que las instrucciones son básicamente sólo Python sin utilizar paquetes externos. Además, si en el ciclo las variables no cambian de su tipo (por ejemplo de `int` a `float`) entonces es una blanco perfecto para ganancia en velocidad al compilar a código de máquina.
*Si tu código de Python llama a operaciones vectorizadas vía `numpy` podría ser que no se ejecute más rápido tu código después de compilarlo.
* No esperamos tener un *speedup* después de compilar para llamadas a librerías externas (por ejemplo a expresiones regulares, operaciones con `string`s o a una base de datos). Programas que tengan alta carga de I/O también es poco probable que muestren ganancias significativas.
En general es poco probable que tu código compilado se ejecute más rápido que un código en C "bien aceitado" y también es poco probable que se ejecute más lento. Es muy posible que el código C generado desde tu Python pueda alcanzar las velocidades de un código escrito en C, a menos que la persona que programó en C tenga un gran conocimiento de formas de hacer que el código de C se ajuste a la arquitectura de la máquina sobre la que se ejecutan los códigos.
**No olvidar:** es importante fijar de forma aproximada el tiempo objetivo que se desea alcanzar para un código que escribamos. Si bien el perfilamiento y la compilación son herramientas para resolver los bottlenecks, debemos tomar en cuenta el tiempo objetivo fijado y ser práctic@s en el desarrollo, no podemos por siempre estar optimizando nuestro código.
# Ejemplo
Cython puede utilizarse vía un script `setup.py` que compila un módulo pero también puede utilizarse en `IPython` vía un comando `magic`.
```
import math
import time
from scipy.integrate import quad
```
## Vía un script `setup.py`
Para este caso requerimos tres archivos:
1) El código escrito en Python que será compilado en un archivo con extensión `.pyx`.
2) Un archivo `setup.py` que contiene las instrucciones para llamar a Cython y cree el módulo compilado.
3) El código escrito en Python que importará el módulo compilado (puede pensarse como nuestro `main`).
1) Función a compilar en un archivo `.pyx`:
```
%%file Rcf_cython.pyx
def Rcf(f,a,b,n): #Rcf: rectángulo compuesto para f
"""
Compute numerical approximation using rectangle or mid-point method in
an interval.
Nodes are generated via formula: x_i = a+(i+1/2)h_hat for i=0,1,...,n-1 and h_hat=(b-a)/n
Args:
f (lambda expression): lambda expression of integrand
a (int): left point of interval
b (int): right point of interval
n (int): number of subintervals
Returns:
Rcf (float)
"""
h_hat=(b-a)/n
nodes=[a+(i+1/2)*h_hat for i in range(0,n)]
sum_res=0
for node in nodes:
sum_res=sum_res+f(node)
return h_hat*sum_res
```
2) Archivo `setup.py` que contiene las instrucciones para el build:
```
%%file setup.py
from distutils.core import setup
from distutils.extension import Extension
from Cython.Distutils import build_ext
setup(cmdclass = {'build_ext': build_ext},
ext_modules = [Extension("Rcf_compiled",
["Rcf_cython.pyx"])]
)
```
Compilar desde la línea de comandos:
```
%%bash
python3 setup.py build_ext --inplace #inplace para compilar el módulo en el directorio
#actual
```
**Notas:**
* La compilación debe hacerse cada vez que se modifica el código de la función `Rcf` del archivo `Rcf_cython.pyx` o cambia el `setup.py`.
* Obsérvese en el directorio donde se encuentra la nota que se generó un archivo `Rcf_cython.c`.
3) Importar módulo compilado y ejecutarlo:
```
f=lambda x: math.exp(-x**2) #using math library
import Rcf_compiled
n=10**6
start_time = time.time()
aprox=Rcf_compiled.Rcf(f,0,1,n)
end_time = time.time()
aprox
secs = end_time-start_time
print("Rcf tomó",secs,"segundos" )
```
**Recuérdese** revisar el error relativo:
```
def err_relativo(aprox, obj):
return math.fabs(aprox-obj)/math.fabs(obj) #obsérvese el uso de la librería math
obj, err = quad(f, 0, 1)
err_relativo(aprox,obj)
```
**Ejercicio:** investigar por qué se tiene un error relativo del orden de $10^{-7}$ y no de mayor precisión como se verá más abajo con el archivo `Rcf_cython2.pyx`.
```
%timeit -n 5 -r 10 Rcf_compiled.Rcf(f,0,1,n)
```
**Obs:** El error relativo anterior es más grande del que se obtenía anteriomente, por ello se utilizará el módulo `cythonize` (haciendo pruebas e investigando un poco se obtuvo la precisión de antes).
```
%%file Rcf_cython2.pyx
def Rcf(f,a,b,n): #Rcf: rectángulo compuesto para f
"""
Compute numerical approximation using rectangle or mid-point method in
an interval.
Nodes are generated via formula: x_i = a+(i+1/2)h_hat for i=0,1,...,n-1 and h_hat=(b-a)/n
Args:
f (lambda expression): lambda expression of integrand
a (int): left point of interval
b (int): right point of interval
n (int): number of subintervals
Returns:
Rcf (float)
"""
h_hat=(b-a)/n
nodes=[a+(i+1/2)*h_hat for i in range(0,n)]
sum_res=0
for node in nodes:
sum_res=sum_res+f(node)
return h_hat*sum_res
%%file setup2.py
from distutils.core import setup
from Cython.Build import cythonize
setup(ext_modules = cythonize("Rcf_cython2.pyx",
compiler_directives={'language_level' : 3})
)
#es posible que la solución del ejercicio anterior tenga que ver con el Warning
#y uso de la directiva language_level
%%bash
python3 setup2.py build_ext --inplace
import Rcf_cython2
n=10**6
start_time = time.time()
aprox=Rcf_cython2.Rcf(f,0,1,n)
end_time = time.time()
aprox
secs = end_time-start_time
print("Rcf tomó",secs,"segundos" )
```
Revisar error relativo:
```
err_relativo(aprox,obj)
```
## Vía el comando magic `%cython`
```
%load_ext Cython
%%cython
def Rcf(f,a,b,n): #Rcf: rectángulo compuesto para f
"""
Compute numerical approximation using rectangle or mid-point method in
an interval.
Nodes are generated via formula: x_i = a+(i+1/2)h_hat for i=0,1,...,n-1 and h_hat=(b-a)/n
Args:
f (lambda expression): lambda expression of integrand
a (int): left point of interval
b (int): right point of interval
n (int): number of subintervals
Returns:
Rcf (float)
"""
h_hat=(b-a)/n
nodes=[a+(i+1/2)*h_hat for i in range(0,n)]
sum_res=0
for node in nodes:
sum_res=sum_res+f(node)
return h_hat*sum_res
n=10**6
start_time = time.time()
aprox=Rcf(f,0,1,n)
end_time = time.time()
secs = end_time-start_time
print("Rcf tomó",secs,"segundos" )
err_relativo(aprox,obj)
%timeit -n 5 -r 10 Rcf(f,0,1,n)
```
# Cython Annotations para analizar un bloque de código
Cython tiene una opción de *annotation* que generará un archivo con extensión `.html` que se puede visualizar en jupyterlab o en un browser.
Cada línea puede ser expandida haciendo un doble click que mostrará el código C generado. Líneas más amarillas refieren a más llamadas en la máquina virtual de Python (por máquina virtual de Python entiéndase la maquinaria que utiliza Python para traducir el lenguaje de alto nivel a [bytecode](https://en.wikipedia.org/wiki/Bytecode) ), mientras que líneas más blancas significan "más código en C y no Python". El objetivo es remover la mayor cantidad de líneas amarillas posibles (pues típicamente son costosas en tiempo y si las líneas están dentro de loops son todavía más costosas) y terminar con códigos cuyas annotations sean lo más blancas posibles. Concentra tu atención en las líneas que son amarillas y están dentro de los loops, no pierdas tu tiempo en líneas amarillas que están fuera de loops y que no causan una ejecución lenta (para identificar esto perfila tu código).
## Vía línea de comando:
```
%%bash
$HOME/.local/bin/cython -a Rcf_cython.pyx
```
Ver archivo creado: `Rcf_cython.html`
## Vía comando de magic y flag `-a`:
```
%%cython?
%%cython -a
def Rcf(f,a,b,n): #Rcf: rectángulo compuesto para f
"""
Compute numerical approximation using rectangle or mid-point method in
an interval.
Nodes are generated via formula: x_i = a+(i+1/2)h_hat for i=0,1,...,n-1 and h_hat=(b-a)/n
Args:
f (lambda expression): lambda expression of integrand
a (int): left point of interval
b (int): right point of interval
n (int): number of subintervals
Returns:
Rcf (float)
"""
h_hat=(b-a)/n
nodes=[a+(i+1/2)*h_hat for i in range(0,n)]
sum_res=0
for node in nodes:
sum_res=sum_res+f(node)
return h_hat*sum_res
```
<img src="https://dl.dropboxusercontent.com/s/0fjkhg66rl0v2n0/output_cython_1.png?dl=0" heigth="500" width="500">
**Nota:** la imagen anterior es un screenshot que generé ejecutando la celda anterior.
**Obs:** para este ejemplo la línea $18$ es muy amarilla y está dentro del loop. Recuérdese de la nota [1.6.Perfilamiento_Python.ipynb](https://github.com/ITAM-DS/analisis-numerico-computo-cientifico/blob/master/temas/I.computo_cientifico/1.6.Perfilamiento_Python.ipynb) que es una línea en la que se gasta parte del tiempo total de ejecución del código.
Una primera opción que tenemos es crear los nodos para el método de integración dentro del loop y separar el llamado a la *list comprehension* `nodes=[a+(i+1/2)*h_hat for i in range(0,n)]`:
```
%%cython -a
def Rcf2(f,a,b,n): #Rcf: rectángulo compuesto para f
"""
Compute numerical approximation using rectangle or mid-point method in
an interval.
Nodes are generated via formula: x_i = a+(i+1/2)h_hat for i=0,1,...,n-1 and h_hat=(b-a)/n
Args:
f (lambda expression): lambda expression of integrand
a (int): left point of interval
b (int): right point of interval
n (int): number of subintervals
Returns:
Rcf (float)
"""
h_hat=(b-a)/n
sum_res=0
for i in range(0,n):
x=a+(i+1/2.0)*h_hat
sum_res+=f(x)
return h_hat*sum_res
```
<img src="https://dl.dropboxusercontent.com/s/d5atbbiivsh2mgk/output_cython_2.png?dl=0" heigth="500" width="500">
**Nota:** la imagen anterior es un screenshot que generé ejecutando la celda anterior.
```
n=10**6
start_time = time.time()
aprox=Rcf2(f,0,1,n)
end_time = time.time()
secs = end_time-start_time
print("Rcf2 tomó",secs,"segundos" )
err_relativo(aprox,obj)
%timeit -n 5 -r 10 Rcf2(f,0,1,n)
```
**Obs:** para este ejemplo las líneas $17$ y $18$ son muy amarillas y están dentro del loop. Además son líneas que involucran tipos de datos que no cambiarán en la ejecución de cada loop. Nos enfocamos a hacerlas más blancas... Una primera opción es **declarar los tipos de objetos** que están involucrados en el loop utilizando la sintaxis `cdef`:
```
%%cython -a
def Rcf3(f,double a,double b,unsigned int n): #obsérvese la declaración de los tipos
"""
Compute numerical approximation using rectangle or mid-point method in
an interval.
Nodes are generated via formula: x_i = a+(i+1/2)h_hat for i=0,1,...,n-1 and h_hat=(b-a)/n
Args:
f (lambda expression): lambda expression of integrand
a (int): left point of interval
b (int): right point of interval
n (int): number of subintervals
Returns:
Rcf (float)
"""
cdef unsigned int i #obsérvese la declaración de los tipos
cdef double x,sum_res, h_hat #obsérvese la declaración de los tipos
h_hat=(b-a)/n
sum_res=0
for i in range(0,n):
x=a+(i+1/2.0)*h_hat
sum_res+=f(x)
return h_hat*sum_res
```
<img src="https://dl.dropboxusercontent.com/s/ttxyxbkbmtxptdt/output_cython_3.png?dl=0" heigth="500" width="500">
**Nota:** la imagen anterior es un screenshot que generé ejecutando la celda anterior.
```
n=10**6
start_time = time.time()
aprox=Rcf3(f,0,1,n)
end_time = time.time()
secs = end_time-start_time
print("Rcf3 tomó",secs,"segundos" )
err_relativo(aprox,obj)
%timeit -n 5 -r 10 Rcf3(f,0,1,n)
```
**Obs:** al definir tipos éstos sólo serán entendidos por Cython y **no por Python**. Cython utiliza estos tipos para convertir el código de Python a objetos de C, éstos objetos no tienen que convertirse de vuelta a objetos de Python. Entonces perdemos flexibilidad pero ganamos velocidad.
Y podemos bajar más el tiempo al definir la función que será utilizada:
```
%%cython -a
import math
def Rcf4(double a,double b,unsigned int n): #Rcf: rectángulo compuesto para f
"""
Compute numerical approximation using rectangle or mid-point method in
an interval.
Nodes are generated via formula: x_i = a+(i+1/2)h_hat for i=0,1,...,n-1 and h_hat=(b-a)/n
Args:
f (lambda expression): lambda expression of integrand
a (int): left point of interval
b (int): right point of interval
n (int): number of subintervals
Returns:
Rcf (float)
"""
cdef unsigned int i
cdef double x,sum_res, h_hat
h_hat=(b-a)/n
sum_res=0
for i in range(0,n):
x=a+(i+1/2.0)*h_hat
sum_res+=math.exp(-x**2)
return h_hat*sum_res
```
<img src="https://dl.dropboxusercontent.com/s/a5upwaoveixxuza/output_cython_4.png?dl=0" heigth="500" width="500">
**Nota:** la imagen anterior es un screenshot que generé ejecutando la celda anterior.
```
n=10**6
start_time = time.time()
aprox=Rcf4(0,1,n)
end_time = time.time()
secs = end_time-start_time
print("Rcf4 tomó",secs,"segundos" )
err_relativo(aprox,obj)
%timeit -n 5 -r 10 Rcf4(0,1,n)
```
**Obs:** estamos ganando velocidad pues el compilador de C `gcc` puede optimizar funciones de bajo nivel para operar en los bytes que están asociados a las variables y no realiza llamadas a la máquina virtual de Python.
**Ejercicios**
1. Realiza el análisis con las herramientas revisadas en esta nota para las reglas del trapecio y de Simpson de la nota [1.5.Integracion_numerica](https://github.com/ITAM-DS/analisis-numerico-computo-cientifico/blob/master/temas/I.computo_cientifico/1.5.Integracion_numerica.ipynb).
**Referencias**
1. M. Gorelick, I. Ozsvald, High Performance Python, O'Reilly Media, 2014.
| true |
code
| 0.614278 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/reallygooday/60daysofudacity/blob/master/Linear_Regression2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Link to Colab Jupyter Notebook: https://colab.research.google.com/drive/19QYWp_lExrN65b6OesWS9NNA7x0fHKmq#scrollTo=KOl9mFXs7ja8
# Deep Learning using PyTorch
Implementing Machine Learning based algorithm to train Linear Model to fit a set of data points.
Getting comfortable making predictions by using Linear Model.
Machine Leraning is the concept of building algorithms that can learn based on experience to detect and predict meaningful patterns.
In Supervised Learning, algorithms are trained to make use of labeled data. Once introduced to new input, the algoritms are able to predict a corresponding output.
```
# import relevant Torch Library
!pip3 install torch
import torch
from torch.nn import Linear
w = torch.tensor(3.0, requires_grad=True) #weight
b = torch.tensor(1.0, requires_grad=True)#bias
def forward(x): # forward-function with one argument
y =w*x + b
return y
x =torch.tensor(2)
forward(x)
x = torch.tensor([[4],[7]]) # making predictins for 4 and 7, two separate inputs
forward(x)
```
* 13 is prediction for 4;
* 22 is prediction for 7
```
torch.manual_seed(1) # set a seed for generating random number for the Linear Class
model = Linear(in_features =1, out_features=1) # for every single input calculate single ouput
print(model.bias, model.weight) # obtain the optimal parameters to fit the data
x = torch.tensor([2.0]) # float number
# passing x as input
# passing multiple input
x = torch.tensor([[2.0],[3.3]])
model(x)
import torch.nn as nn
# Linear Regression Class
# creating objects, new instances of Linear Regression Class
# class is followed by init method(constructer, initializer)
class LR(nn.Module):
def __init__(self,input_size,output_size):
super().__init__() # template to create custom class
self.Linear = nn.Linear(input_size,output_size)
def forward(self, x):
pred = self.Linear(x)
return pred
torch.manual_seed(1)
model = LR(1,1)
print(list(model.parameters()))
```
weight equals 0.5153
bias equals -0.4414
```
x = torch.tensor([1.0]) # single input, single output
print(model.forward(x))
x = torch.tensor([[1.0],[2.0]]) # multiple input, multiple output
print(model.forward(x))
```
# Train model to fit a dataset.
```
import matplotlib.pyplot as plt
x = torch.randn(100,1)*10 # returns a tensor filled with random numbers
y = x
print(x)
```
Each datapoint is characterized by X and Y coordinates.
Fitting a linear model into a straight line of data points.
```
x = torch.randn(100,1)*10
y = x # output equals input
plt.plot(x.numpy(), y.numpy())
```
This results in a straight line of datapoints.
# Creating noisy dataset.
Adding noise to output to each Y value and shift upwards and downwards.
Noise will be normally distributed accross the entire range.
```
x = torch.randn(100,1)*10
y = x + 3*torch.randn(100,1) # multiply noise ratio by 3 to make noise reasonably significant
plt.plot(x.numpy(), y.numpy(), 'o')
plt.ylabel('Y')
plt.xlabel('X')
class LR(nn.Module):
def __init__(self,input_size,output_size):
super().__init__() # template to create custom class
self.Linear = nn.Linear(input_size,output_size)
def forward(self, x):
pred = self.Linear(x)
return pred
torch.manual_seed(1)
model = LR(1,1)
print(model)
print(list(model.parameters()))
[w,b] = model.parameters()
w1=w[0][0].item()
b1=b[0].item()
print(w1,b1)
# parameters, tensor values
[w,b] = model.parameters()
print(w,b)
w1=w[0][0]
b1=b[0]
print(w1,b1)
def get_params():
return()
# parameters, tensor values
[w,b] = model.parameters()
w1=w[0][0]
b1=b[0]
print(w1,b1)
def get_params():
return(w[0][0].item(), b[0].item())
```
# Plot Linear Model alongside datapoints.
Determine numerical expression for x1 and y1.
```
import numpy as np
def plot_fit(title):
plt.title = title
w1,b1 = get_params()
x1 = np.array([-30, 30])
y1 = w1*x1 + b1
plt.plot(x1, y1,'r')
plt.scatter(x,y)
plt.show()
plot_fit('Initial Model')
```
The line doesn't fit data. It would be better to use Gradient Descent Algorithn to adjust parameters.
```
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)
epochs =100
losses = []
for i in range(epochs):
y_pred = model.forward(x)
loss = criterion(y_pred, y)
print('epochs:', i, 'loss:', loss.item())
losses.append(loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
plot_fit('Trained Model')
The Linear Model has been trained to fit training data using gradient descent.
```
| true |
code
| 0.814809 | null | null | null | null |
|
# Block Move in Fixed Time
Here, we look at a problem called "Block Move". Block Move is a very simple optimal control problem defined by Matthew Kelly in the paper *[An Introduction to Trajectory Optimization: How to Do Your Own Direct Collocation](https://epubs.siam.org/doi/10.1137/16M1062569)*.
The basics of the problem are this:
-----
Suppose we have a block with a unit mass on a frictionless surface; the block can slide forward and backwards along a number line $x$. At $t=0$, the block starts at $x=0$ with velocity $v=0$. At $t=1$, we want the block to have moved to $x=1$ and again be stationary with $v=0$.
We are allowed to apply any amount of force $u(t)$ to the block, but we want to find the path that minimizes the amount of "effort" applied. We measure "effort" as the integral $\int_0^1 u(t)^2\ dt$.
What should our force input $u(t)$ be?
-----
Let's solve the problem. First, we do some boilerplate setup:
```
import aerosandbox as asb
import aerosandbox.numpy as np
opti = asb.Opti()
n_timesteps = 300
mass_block = 1
```
Then, we define our time vector, our state vectors, and our force vector.
```
time = np.linspace(0, 1, n_timesteps)
position = opti.variable(
init_guess=np.linspace(0, 1, n_timesteps) # Guess a trajectory that takes us there linearly.
)
velocity = opti.derivative_of(
position,
with_respect_to=time,
derivative_init_guess=1, # Guess a velocity profile that is uniform over time.
)
force = opti.variable(
init_guess=np.linspace(1, -1, n_timesteps), # Guess that the force u(t) goes from 1 to -1 over the time window.
n_vars=n_timesteps
)
```
We can't forget to constrain the derivative of velocity to be equal to the acceleration!
```
opti.constrain_derivative(
variable=velocity,
with_respect_to=time,
derivative=force / mass_block, # F = ma
)
```
Now, we compute the amount of effort expended using a numerical integral:
```
effort_expended = np.sum(
np.trapz(force ** 2) * np.diff(time)
)
opti.minimize(effort_expended)
```
Can't forget to add those boundary conditions!
Some notes:
* *"Wait, isn't $x=0$ an initial condition, not a boundary condition?"* There is no mathematical difference between *initial conditions* and *boundary conditions*. We use the phrase "boundary conditions" to refer to both. This helps eliminate any confusion between "initial conditions" and "initial guesses".
* *"Wait, what's the difference between initial conditions and initial guesses?"* "Initial conditions" are really just boundary conditions that happen to be applied at the boundary $t=0$. "Initial guesses" are our best guess for each of our design variables - basically, our best guess for the optimal trajectory. It is so important that the distinction be understood! Again, we use the "boundary conditions" catch-all rather than "initial conditions" to help reinforce this distinction.
Now for those boundary conditions:
```
opti.subject_to([
position[0] == 0,
position[-1] == 1,
velocity[0] == 0,
velocity[-1] == 0,
])
```
Now, we solve.
```
sol = opti.solve()
```
This actually solves in just one iteration because it is an unconstrained quadratic program.
Let's plot what our solution looks like:
```
import matplotlib.pyplot as plt
import seaborn as sns
fig, ax = plt.subplots(1, 1, figsize=(6.4, 4.8), dpi=200)
plt.plot(sol.value(time), sol.value(position))
plt.xlabel(r"Time")
plt.ylabel(r"Position")
plt.title(r"Position")
plt.tight_layout()
plt.show()
fig, ax = plt.subplots(1, 1, figsize=(6.4, 4.8), dpi=200)
plt.plot(sol.value(time), sol.value(velocity))
plt.xlabel(r"Time")
plt.ylabel(r"Velocity")
plt.title(r"Velocity")
plt.tight_layout()
plt.show()
fig, ax = plt.subplots(1, 1, figsize=(6.4, 4.8), dpi=200)
plt.plot(sol.value(time), sol.value(force))
plt.xlabel(r"Time")
plt.ylabel(r"Force")
plt.title(r"Force")
plt.tight_layout()
plt.show()
```
That makes sense! We can actually prove optimality of these functions here using calculus of variations; see Appendix B of the Kelly paper for more details.
| true |
code
| 0.691028 | null | null | null | null |
|
## Basic training functionality
```
from fastai.basic_train import *
from fastai.gen_doc.nbdoc import *
from fastai.vision import *
from fastai.distributed import *
```
[`basic_train`](/basic_train.html#basic_train) wraps together the data (in a [`DataBunch`](/basic_data.html#DataBunch) object) with a PyTorch model to define a [`Learner`](/basic_train.html#Learner) object. Here the basic training loop is defined for the [`fit`](/basic_train.html#fit) method. The [`Learner`](/basic_train.html#Learner) object is the entry point of most of the [`Callback`](/callback.html#Callback) objects that will customize this training loop in different ways. Some of the most commonly used customizations are available through the [`train`](/train.html#train) module, notably:
- [`Learner.lr_find`](/train.html#lr_find) will launch an LR range test that will help you select a good learning rate.
- [`Learner.fit_one_cycle`](/train.html#fit_one_cycle) will launch a training using the 1cycle policy to help you train your model faster.
- [`Learner.to_fp16`](/train.html#to_fp16) will convert your model to half precision and help you launch a training in mixed precision.
```
show_doc(Learner, title_level=2)
```
The main purpose of [`Learner`](/basic_train.html#Learner) is to train `model` using [`Learner.fit`](/basic_train.html#Learner.fit). After every epoch, all *metrics* will be printed and also made available to callbacks.
The default weight decay will be `wd`, which will be handled using the method from [Fixing Weight Decay Regularization in Adam](https://arxiv.org/abs/1711.05101) if `true_wd` is set (otherwise it's L2 regularization). If `true_wd` is set it will affect all optimizers, not only Adam. If `bn_wd` is `False`, then weight decay will be removed from batchnorm layers, as recommended in [Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour](https://arxiv.org/abs/1706.02677). If `train_bn`, batchnorm layer learnable params are trained even for frozen layer groups.
To use [discriminative layer training](#Discriminative-layer-training), pass a list of [`nn.Module`](https://pytorch.org/docs/stable/nn.html#torch.nn.Module) as `layer_groups`; each [`nn.Module`](https://pytorch.org/docs/stable/nn.html#torch.nn.Module) will be used to customize the optimization of the corresponding layer group.
If `path` is provided, all the model files created will be saved in `path`/`model_dir`; if not, then they will be saved in `data.path`/`model_dir`.
You can pass a list of [`callback`](/callback.html#callback)s that you have already created, or (more commonly) simply pass a list of callback functions to `callback_fns` and each function will be called (passing `self`) on object initialization, with the results stored as callback objects. For a walk-through, see the [training overview](/training.html) page. You may also want to use an [application](applications.html) specific model. For example, if you are dealing with a vision dataset, here the MNIST, you might want to use the [`cnn_learner`](/vision.learner.html#cnn_learner) method:
```
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = cnn_learner(data, models.resnet18, metrics=accuracy)
```
### Model fitting methods
```
show_doc(Learner.lr_find)
```
Runs the learning rate finder defined in [`LRFinder`](/callbacks.lr_finder.html#LRFinder), as discussed in [Cyclical Learning Rates for Training Neural Networks](https://arxiv.org/abs/1506.01186).
```
learn.lr_find()
learn.recorder.plot()
show_doc(Learner.fit)
```
Uses [discriminative layer training](#Discriminative-layer-training) if multiple learning rates or weight decay values are passed. To control training behaviour, use the [`callback`](/callback.html#callback) system or one or more of the pre-defined [`callbacks`](/callbacks.html#callbacks).
```
learn.fit(1)
show_doc(Learner.fit_one_cycle)
```
Use cycle length `cyc_len`, a per cycle maximal learning rate `max_lr`, momentum `moms`, division factor `div_factor`, weight decay `wd`, and optional callbacks [`callbacks`](/callbacks.html#callbacks). Uses the [`OneCycleScheduler`](/callbacks.one_cycle.html#OneCycleScheduler) callback. Please refer to [What is 1-cycle](/callbacks.one_cycle.html#What-is-1cycle?) for a conceptual background of 1-cycle training policy and more technical details on what do the method's arguments do.
```
learn.fit_one_cycle(1)
```
### See results
```
show_doc(Learner.predict)
```
`predict` can be used to get a single prediction from the trained learner on one specific piece of data you are interested in.
```
learn.data.train_ds[0]
```
Each element of the dataset is a tuple, where the first element is the data itself, while the second element is the target label. So to get the data, we need to index one more time.
```
data = learn.data.train_ds[0][0]
data
pred = learn.predict(data)
pred
```
The first two elements of the tuple are, respectively, the predicted class and label. Label here is essentially an internal representation of each class, since class name is a string and cannot be used in computation. To check what each label corresponds to, run:
```
learn.data.classes
```
So category 0 is 3 while category 1 is 7.
```
probs = pred[2]
```
The last element in the tuple is the predicted probabilities. For a categorization dataset, the number of probabilities returned is the same as the number of classes; `probs[i]` is the probability that the `item` belongs to `learn.data.classes[i]`.
```
learn.data.valid_ds[0][0]
```
You could always check yourself if the probabilities given make sense.
```
show_doc(Learner.get_preds)
```
It will run inference using the learner on all the data in the `ds_type` dataset and return the predictions; if `n_batch` is not specified, it will run the predictions on the default batch size. If `with_loss`, it will also return the loss on each prediction.
Here is how you check the default batch size.
```
learn.data.batch_size
preds = learn.get_preds()
preds
```
The first element of the tuple is a tensor that contains all the predictions.
```
preds[0]
```
While the second element of the tuple is a tensor that contains all the target labels.
```
preds[1]
preds[1][0]
```
For more details about what each number mean, refer to the documentation of [`predict`](/basic_train.html#predict).
Since [`get_preds`](/basic_train.html#get_preds) gets predictions on all the data in the `ds_type` dataset, here the number of predictions will be equal to the number of data in the validation dataset.
```
len(learn.data.valid_ds)
len(preds[0]), len(preds[1])
```
To get predictions on the entire training dataset, simply set the `ds_type` argument accordingly.
```
learn.get_preds(ds_type=DatasetType.Train)
```
To also get prediction loss along with the predictions and the targets, set `with_loss=True` in the arguments.
```
learn.get_preds(with_loss=True)
```
Note that the third tensor in the output tuple contains the losses.
```
show_doc(Learner.validate)
```
Return the calculated loss and the metrics of the current model on the given data loader `dl`. The default data loader `dl` is the validation dataloader.
You can check the default metrics of the learner using:
```
str(learn.metrics)
learn.validate()
learn.validate(learn.data.valid_dl)
learn.validate(learn.data.train_dl)
show_doc(Learner.show_results)
```
Note that the text number on the top is the ground truth, or the target label, the one in the middle is the prediction, while the image number on the bottom is the image data itself.
```
learn.show_results()
learn.show_results(ds_type=DatasetType.Train)
show_doc(Learner.pred_batch)
```
Note that the number of predictions given equals to the batch size.
```
learn.data.batch_size
preds = learn.pred_batch()
len(preds)
```
Since the total number of predictions is too large, we will only look at a part of them.
```
preds[:10]
item = learn.data.train_ds[0][0]
item
batch = learn.data.one_item(item)
batch
learn.pred_batch(batch=batch)
show_doc(Learner.interpret, full_name='interpret')
jekyll_note('This function only works in the vision application.')
```
For more details, refer to [ClassificationInterpretation](/vision.learner.html#ClassificationInterpretation)
### Model summary
```
show_doc(Learner.summary)
```
### Test time augmentation
```
show_doc(Learner.TTA, full_name = 'TTA')
```
Applies Test Time Augmentation to `learn` on the dataset `ds_type`. We take the average of our regular predictions (with a weight `beta`) with the average of predictions obtained through augmented versions of the training set (with a weight `1-beta`). The transforms decided for the training set are applied with a few changes `scale` controls the scale for zoom (which isn't random), the cropping isn't random but we make sure to get the four corners of the image. Flipping isn't random but applied once on each of those corner images (so that makes 8 augmented versions total).
### Gradient clipping
```
show_doc(Learner.clip_grad)
```
### Mixed precision training
```
show_doc(Learner.to_fp16)
```
Uses the [`MixedPrecision`](/callbacks.fp16.html#MixedPrecision) callback to train in mixed precision (i.e. forward and backward passes using fp16, with weight updates using fp32), using all [NVIDIA recommendations](https://docs.nvidia.com/deeplearning/sdk/mixed-precision-training/index.html) for ensuring speed and accuracy.
```
show_doc(Learner.to_fp32)
```
### Distributed training
If you want to use ditributed training or [`torch.nn.DataParallel`](https://pytorch.org/docs/stable/nn.html#torch.nn.DataParallel) these will directly wrap the model for you.
```
show_doc(Learner.to_distributed, full_name='to_distributed')
show_doc(Learner.to_parallel, full_name='to_parallel')
```
### Discriminative layer training
When fitting a model you can pass a list of learning rates (and/or weight decay amounts), which will apply a different rate to each *layer group* (i.e. the parameters of each module in `self.layer_groups`). See the [Universal Language Model Fine-tuning for Text Classification](https://arxiv.org/abs/1801.06146) paper for details and experimental results in NLP (we also frequently use them successfully in computer vision, but have not published a paper on this topic yet). When working with a [`Learner`](/basic_train.html#Learner) on which you've called `split`, you can set hyperparameters in four ways:
1. `param = [val1, val2 ..., valn]` (n = number of layer groups)
2. `param = val`
3. `param = slice(start,end)`
4. `param = slice(end)`
If we chose to set it in way 1, we must specify a number of values exactly equal to the number of layer groups. If we chose to set it in way 2, the chosen value will be repeated for all layer groups. See [`Learner.lr_range`](/basic_train.html#Learner.lr_range) for an explanation of the `slice` syntax).
Here's an example of how to use discriminative learning rates (note that you don't actually need to manually call [`Learner.split`](/basic_train.html#Learner.split) in this case, since fastai uses this exact function as the default split for `resnet18`; this is just to show how to customize it):
```
# creates 3 layer groups
learn.split(lambda m: (m[0][6], m[1]))
# only randomly initialized head now trainable
learn.freeze()
learn.fit_one_cycle(1)
# all layers now trainable
learn.unfreeze()
# optionally, separate LR and WD for each group
learn.fit_one_cycle(1, max_lr=(1e-4, 1e-3, 1e-2), wd=(1e-4,1e-4,1e-1))
show_doc(Learner.lr_range)
```
Rather than manually setting an LR for every group, it's often easier to use [`Learner.lr_range`](/basic_train.html#Learner.lr_range). This is a convenience method that returns one learning rate for each layer group. If you pass `slice(start,end)` then the first group's learning rate is `start`, the last is `end`, and the remaining are evenly geometrically spaced.
If you pass just `slice(end)` then the last group's learning rate is `end`, and all the other groups are `end/10`. For instance (for our learner that has 3 layer groups):
```
learn.lr_range(slice(1e-5,1e-3)), learn.lr_range(slice(1e-3))
show_doc(Learner.unfreeze)
```
Sets every layer group to *trainable* (i.e. `requires_grad=True`).
```
show_doc(Learner.freeze)
```
Sets every layer group except the last to *untrainable* (i.e. `requires_grad=False`).
What does '**the last layer group**' mean?
In the case of transfer learning, such as `learn = cnn_learner(data, models.resnet18, metrics=error_rate)`, `learn.model`will print out two large groups of layers: (0) Sequential and (1) Sequental in the following structure. We can consider the last conv layer as the break line between the two groups.
```
Sequential(
(0): Sequential(
(0): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace)
...
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
)
(1): Sequential(
(0): AdaptiveConcatPool2d(
(ap): AdaptiveAvgPool2d(output_size=1)
(mp): AdaptiveMaxPool2d(output_size=1)
)
(1): Flatten()
(2): BatchNorm1d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(3): Dropout(p=0.25)
(4): Linear(in_features=1024, out_features=512, bias=True)
(5): ReLU(inplace)
(6): BatchNorm1d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(7): Dropout(p=0.5)
(8): Linear(in_features=512, out_features=12, bias=True)
)
)
```
`learn.freeze` freezes the first group and keeps the second or last group free to train, including multiple layers inside (this is why calling it 'group'), as you can see in `learn.summary()` output. How to read the table below, please see [model summary docs](/callbacks.hooks.html#model_summary).
```
======================================================================
Layer (type) Output Shape Param # Trainable
======================================================================
...
...
...
______________________________________________________________________
Conv2d [1, 512, 4, 4] 2,359,296 False
______________________________________________________________________
BatchNorm2d [1, 512, 4, 4] 1,024 True
______________________________________________________________________
AdaptiveAvgPool2d [1, 512, 1, 1] 0 False
______________________________________________________________________
AdaptiveMaxPool2d [1, 512, 1, 1] 0 False
______________________________________________________________________
Flatten [1, 1024] 0 False
______________________________________________________________________
BatchNorm1d [1, 1024] 2,048 True
______________________________________________________________________
Dropout [1, 1024] 0 False
______________________________________________________________________
Linear [1, 512] 524,800 True
______________________________________________________________________
ReLU [1, 512] 0 False
______________________________________________________________________
BatchNorm1d [1, 512] 1,024 True
______________________________________________________________________
Dropout [1, 512] 0 False
______________________________________________________________________
Linear [1, 12] 6,156 True
______________________________________________________________________
Total params: 11,710,540
Total trainable params: 543,628
Total non-trainable params: 11,166,912
```
```
show_doc(Learner.freeze_to)
```
From above we know what is layer group, but **what exactly does `freeze_to` do behind the scenes**?
The `freeze_to` source code can be understood as the following pseudo-code:
```python
def freeze_to(self, n:int)->None:
for g in self.layer_groups[:n]: freeze
for g in self.layer_groups[n:]: unfreeze
```
In other words, for example, `freeze_to(1)` is to freeze layer group 0 and unfreeze the rest layer groups, and `freeze_to(3)` is to freeze layer groups 0, 1, and 2 but unfreeze the rest layer groups (if there are more layer groups left).
Both `freeze` and `unfreeze` [sources](https://github.com/fastai/fastai/blob/master/fastai/basic_train.py#L216) are defined using `freeze_to`:
- When we say `freeze`, we mean that in the specified layer groups the [`requires_grad`](/torch_core.html#requires_grad) of all layers with weights (except BatchNorm layers) are set `False`, so the layer weights won't be updated during training.
- when we say `unfreeze`, we mean that in the specified layer groups the [`requires_grad`](/torch_core.html#requires_grad) of all layers with weights (except BatchNorm layers) are set `True`, so the layer weights will be updated during training.
```
show_doc(Learner.split)
```
A convenience method that sets `layer_groups` based on the result of [`split_model`](/torch_core.html#split_model). If `split_on` is a function, it calls that function and passes the result to [`split_model`](/torch_core.html#split_model) (see above for example).
### Saving and loading models
Simply call [`Learner.save`](/basic_train.html#Learner.save) and [`Learner.load`](/basic_train.html#Learner.load) to save and load models. Only the parameters are saved, not the actual architecture (so you'll need to create your model in the same way before loading weights back in). Models are saved to the `path`/`model_dir` directory.
```
show_doc(Learner.save)
```
If argument `name` is a pathlib object that's an absolute path, it'll override the default base directory (`learn.path`), otherwise the model will be saved in a file relative to `learn.path`.
```
learn.save("trained_model")
learn.save("trained_model", return_path=True)
show_doc(Learner.load)
```
This method only works after `save` (don't confuse with `export`/[`load_learner`](/basic_train.html#load_learner) pair).
If the `purge` argument is `True` (default) `load` internally calls `purge` with `clear_opt=False` to presever `learn.opt`.
```
learn = learn.load("trained_model")
```
### Deploying your model
When you are ready to put your model in production, export the minimal state of your [`Learner`](/basic_train.html#Learner) with:
```
show_doc(Learner.export)
```
If argument `fname` is a pathlib object that's an absolute path, it'll override the default base directory (`learn.path`), otherwise the model will be saved in a file relative to `learn.path`.
Passing `destroy=True` will destroy the [`Learner`](/basic_train.html#Learner), freeing most of its memory consumption. For specifics see [`Learner.destroy`](/basic_train.html#Learner.destroy).
This method only works with the [`Learner`](/basic_train.html#Learner) whose [`data`](/vision.data.html#vision.data) was created through the [data block API](/data_block.html).
Otherwise, you will have to create a [`Learner`](/basic_train.html#Learner) yourself at inference and load the model with [`Learner.load`](/basic_train.html#Learner.load).
```
learn.export()
learn.export('trained_model.pkl')
path = learn.path
path
show_doc(load_learner)
```
This function only works after `export` (don't confuse with `save`/`load` pair).
The `db_kwargs` will be passed to the call to `databunch` so you can specify a `bs` for the test set, or `num_workers`.
```
learn = load_learner(path)
learn = load_learner(path, 'trained_model.pkl')
```
WARNING: If you used any customized classes when creating your learner, you must first define these classes first before executing [`load_learner`](/basic_train.html#load_learner).
You can find more information and multiple examples in [this tutorial](/tutorial.inference.html).
### Freeing memory
If you want to be able to do more without needing to restart your notebook, the following methods are designed to free memory when it's no longer needed.
Refer to [this tutorial](/tutorial.resources.html) to learn how and when to use these methods.
```
show_doc(Learner.purge)
```
If `learn.path` is read-only, you can set `model_dir` attribute in Learner to a full `libpath` path that is writable (by setting `learn.model_dir` or passing `model_dir` argument in the [`Learner`](/basic_train.html#Learner) constructor).
```
show_doc(Learner.destroy)
```
If you need to free the memory consumed by the [`Learner`](/basic_train.html#Learner) object, call this method.
It can also be automatically invoked through [`Learner.export`](/basic_train.html#Learner.export) via its `destroy=True` argument.
### Other methods
```
show_doc(Learner.init)
```
Initializes all weights (except batchnorm) using function `init`, which will often be from PyTorch's [`nn.init`](https://pytorch.org/docs/stable/nn.html#torch-nn-init) module.
```
show_doc(Learner.mixup)
```
Uses [`MixUpCallback`](/callbacks.mixup.html#MixUpCallback).
```
show_doc(Learner.backward)
show_doc(Learner.create_opt)
```
You generally won't need to call this yourself - it's used to create the [`optim`](https://pytorch.org/docs/stable/optim.html#module-torch.optim) optimizer before fitting the model.
```
show_doc(Learner.dl)
learn.dl()
learn.dl(DatasetType.Train)
show_doc(Recorder, title_level=2)
```
A [`Learner`](/basic_train.html#Learner) creates a [`Recorder`](/basic_train.html#Recorder) object automatically - you do not need to explicitly pass it to `callback_fns` - because other callbacks rely on it being available. It stores the smoothed loss, hyperparameter values, and metrics for each batch, and provides plotting methods for each. Note that [`Learner`](/basic_train.html#Learner) automatically sets an attribute with the snake-cased name of each callback, so you can access this through `Learner.recorder`, as shown below.
### Plotting methods
```
show_doc(Recorder.plot)
```
This is mainly used with the learning rate finder, since it shows a scatterplot of loss vs learning rate.
```
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = cnn_learner(data, models.resnet18, metrics=accuracy)
learn.lr_find()
learn.recorder.plot()
show_doc(Recorder.plot_losses)
```
Note that validation losses are only calculated once per epoch, whereas training losses are calculated after every batch.
```
learn.fit_one_cycle(5)
learn.recorder.plot_losses()
show_doc(Recorder.plot_lr)
learn.recorder.plot_lr()
learn.recorder.plot_lr(show_moms=True)
show_doc(Recorder.plot_metrics)
```
Note that metrics are only collected at the end of each epoch, so you'll need to train at least two epochs to have anything to show here.
```
learn.recorder.plot_metrics()
```
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality. Refer to [`Callback`](/callback.html#Callback) for more details.
```
show_doc(Recorder.on_backward_begin)
show_doc(Recorder.on_batch_begin)
show_doc(Recorder.on_epoch_end)
show_doc(Recorder.on_train_begin)
```
### Inner functions
The following functions are used along the way by the [`Recorder`](/basic_train.html#Recorder) or can be called by other callbacks.
```
show_doc(Recorder.add_metric_names)
show_doc(Recorder.format_stats)
```
## Module functions
Generally you'll want to use a [`Learner`](/basic_train.html#Learner) to train your model, since they provide a lot of functionality and make things easier. However, for ultimate flexibility, you can call the same underlying functions that [`Learner`](/basic_train.html#Learner) calls behind the scenes:
```
show_doc(fit)
```
Note that you have to create the [`Optimizer`](https://pytorch.org/docs/stable/optim.html#torch.optim.Optimizer) yourself if you call this function, whereas [`Learn.fit`](/basic_train.html#fit) creates it for you automatically.
```
show_doc(train_epoch)
```
You won't generally need to call this yourself - it's what [`fit`](/basic_train.html#fit) calls for each epoch.
```
show_doc(validate)
```
This is what [`fit`](/basic_train.html#fit) calls after each epoch. You can call it if you want to run inference on a [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) manually.
```
show_doc(get_preds)
show_doc(loss_batch)
```
You won't generally need to call this yourself - it's what [`fit`](/basic_train.html#fit) and [`validate`](/basic_train.html#validate) call for each batch. It only does a backward pass if you set `opt`.
## Other classes
```
show_doc(LearnerCallback, title_level=3)
show_doc(RecordOnCPU, title_level=3)
```
## Open This Notebook
<button style="display: flex; align-item: center; padding: 4px 8px; font-size: 14px; font-weight: 700; color: #1976d2; cursor: pointer;" onclick="window.location.href = 'https://console.cloud.google.com/mlengine/notebooks/deploy-notebook?q=download_url%3Dhttps%253A%252F%252Fraw.githubusercontent.com%252Ffastai%252Ffastai%252Fmaster%252Fdocs_src%252Fbasic_train.ipynb';"><img src="https://www.gstatic.com/images/branding/product/1x/cloud_24dp.png" /><span style="line-height: 24px; margin-left: 10px;">Open in GCP Notebooks</span></button>
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(Learner.tta_only)
show_doc(Learner.TTA)
show_doc(RecordOnCPU.on_batch_begin)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.837371 | null | null | null | null |
|
```
#1. Use matplotlib to plot the following equation:
# y = x^2 -x + 2
#You'll need to write the code that generates the x and y points.
#Add an anotation for the point 0, 0, the origin.
import matplotlib.pyplot as plt
x = list(range(-50, 50))
# generate our y values
y = [(n ** 2 - n + 2) for n in x]
plt.plot(x, y)
# title
plt.title('$y = x^{2} - x + 2$')
# annotate the origin
plt.annotate('Origin', xy=(0, 0), xytext=(-5, 500))
plt.show()
#2. Create and label 4 separate charts for the following equations
#(choose a range for x that makes sense):
y = √x
y = x^3
y= 2^x
y= 1/(x +1)
from math import sqrt
# When sqrt involved x cannot be less than 0
x = list(range(0, 50))
# generate y
y = [sqrt(n) for n in x]
plt.plot(x, y)
plt.title('$\sqrt{x}$')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
#Plot x ** 3
# range of x
x = list(range(-10, 10))
# generate y
y = [n ** 3 for n in x]
plt.plot(x, y)
plt.title('$x^{3}$')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
#Plot y= 2 ** x
# set range for x
x = list(range(-10, 10))
# generate y
y = [2 ** n for n in x]
# plot x and y
plt.plot(x, y)
plt.title('$2^{x}$')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
#Plot y= 1/(x +1)
# set range for x
x = list(range(0, 10))
# generate y
y = [1/(n +1) for n in x]
# plot x and y
plt.plot(x, y)
plt.title('$1/(x +1)$')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
#3. Combine the figures you created in the last step into one large figure with 4 subplots.
plt.figure(figsize = (20, 10))
# plot $\sqrt{x}$
plt.subplot(2, 2, 1)
# # When sqrt involved x cannot be less than 0
x = list(range(0, 50))
# generate y
y = [sqrt(n) for n in x]
plt.plot(x, y)
plt.title('$\sqrt{x}$')
plt.ylabel('$y$')
# plot x ** 3
plt.subplot(2, 2, 2)
# range of x
x = list(range(-10, 10))
# generate y
y = [n ** 3 for n in x]
plt.plot(x, y)
plt.title('$x^{3}$')
plt.xlabel('$x$')
# plot y= 2 ** x
plt.subplot(2, 2, 3)
# set range for x
x = list(range(-10, 10))
# generate y
y = [2 ** n for n in x]
# plot x and y
plt.plot(x, y)
plt.title('$2^{x}$')
plt.xlabel('$x$')
plt.ylabel('$y$')
#Plot y= 1/(x +1)
plt.subplot(2,2,4)
# set range for x
x = list(range(0, 10))
# generate y
y = [1/(n +1) for n in x]
# plot x and y
plt.plot(x, y)
plt.title('$1/(x +1)$')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
#4. Combine the figures you created in the last step into :
#-- One figure where each of the 4 equations has a different color for the points.
#-- Be sure to include a legend and an appropriate title for the figure.
x = list(range(0, 30))
# generate y for each fucntion
y1 = [sqrt(n) for n in x]
y2 = [n**3 for n in x]
y3 = [2**n for n in x]
y4 = [1/(n +1) for n in x]
plt.plot(x, y1, c='slategray', label='$\sqrt{x}$', alpha=0.7)
plt.plot(x, y2, c='cadetblue', label='$x^{3}$', alpha=0.6)
plt.plot(x, y3, c='firebrick', label='$2^{x}$', alpha=0.5)
plt.plot(x, y4, c='darkgoldenrod', label='$1/(x +1)$', alpha=0.5)
plt.ylim(0, 15)
plt.xlim(0, 15)
plt.ylabel('$y$')
plt.xlabel('$x$')
plt.title('All Figures Combined')
plt.legend()
plt.show()
```
| true |
code
| 0.734672 | null | null | null | null |
|
```
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
```
# Graphical Representations of Data
By Evgenia "Jenny" Nitishinskaya, Maxwell Margenot, and Delaney Granizo-Mackenzie.
Part of the Quantopian Lecture Series:
* [www.quantopian.com/lectures](https://www.quantopian.com/lectures)
* [github.com/quantopian/research_public](https://github.com/quantopian/research_public)
Notebook released under the Creative Commons Attribution 4.0 License.
Representing data graphically can be incredibly useful for learning how the data behaves and seeing potential structure or flaws. Care should be taken, as humans are incredibly good at seeing only evidence that confirms our beliefs, and visual data lends itself well to that. Plots are good to use when formulating a hypothesis, but should not be used to test a hypothesis.
We will go over some common plots here.
```
# Import our libraries
# This is for numerical processing
import numpy as np
# This is the library most commonly used for plotting in Python.
# Notice how we import it 'as' plt, this enables us to type plt
# rather than the full string every time.
import matplotlib.pyplot as plt
```
## Getting Some Data
If we're going to plot data we need some data to plot. We'll get the pricing data of Apple (000333) and Microsoft (000001) to use in our examples.
### Data Structure
Knowing the structure of your data is very important. Normally you'll have to do a ton work molding your data into the form you need for testing. Quantopian has done a lot of cleaning on the data, but you still need to put it into the right shapes and formats for your purposes.
In this case the data will be returned as a pandas dataframe object. The rows are timestamps, and the columns are the two assets, 000333 and 000001.
```
from zipline.component.data import load_bars
start = '2014-01-01'
end = '2015-01-01'
data = load_bars(['000001', '000333'], start=start, end=end)
data.head()
```
Indexing into the data with `data['000333']` will yield an error because the type of the columns are equity objects and not simple strings. Let's change that using this little piece of Python code. Don't worry about understanding it right now, unless you do, in which case congratulations.
```
data.head()
```
Much nicer, now we can index. Indexing into the 2D dataframe will give us a 1D series object. The index for the series is timestamps, the value upon index is a price. Similar to an array except instead of integer indecies it's times.
```
data['000001'].head()
```
## 柱状图(Histogram)
A histogram is a visualization of how frequent different values of data are. By displaying a frequency distribution using bars, it lets us quickly see where most of the observations are clustered. The height of each bar represents the number of observations that lie in each interval. You can think of a histogram as an empirical and discrete Propoability Density Function (PDF).
```
# Plot a histogram using 20 bins
plt.hist(data['000001'], bins=20)
plt.xlabel('Price')
plt.ylabel('Number of Days Observed')
plt.title('Frequency Distribution of 000001 Prices, 2014')
```
### Returns Histogram
In finance rarely will we look at the distribution of prices. The reason for this is that prices are non-stationary and move around a lot. For more info on non-stationarity please see [this lecture](https://www.quantopian.com/lectures/integration-cointegration-and-stationarity). Instead we will use daily returns. Let's try that now.
```
# Remove the first element because percent change from nothing to something is NaN
R = data['000001'].pct_change()[1:]
# Plot a histogram using 20 bins
plt.hist(R, bins=20)
plt.xlabel('Return')
plt.ylabel('观察日期数量')
plt.title('Frequency Distribution of 000001 Returns, 2014');
```
The graph above shows, for example, that the daily returns of 000001 were above 0.03 on fewer than 5 days in 2014. Note that we are completely discarding the dates corresponding to these returns.
#####IMPORTANT: Note also that this does not imply that future returns will have the same distribution.
### Cumulative Histogram (Discrete Estimated CDF)
An alternative way to display the data would be using a cumulative distribution function, in which the height of a bar represents the number of observations that lie in that bin or in one of the previous ones. This graph is always nondecreasing since you cannot have a negative number of observations. The choice of graph depends on the information you are interested in.
```
# Remove the first element because percent change from nothing to something is NaN
R = data['000001'].pct_change()[1:]
# Plot a histogram using 20 bins
plt.hist(R, bins=20, cumulative=True)
plt.xlabel('Return')
plt.ylabel('Number of Days Observed')
plt.title('Cumulative Distribution of 000001 Returns, 2014');
```
## Scatter plot
A scatter plot is useful for visualizing the relationship between two data sets. We use two data sets which have some sort of correspondence, such as the date on which the measurement was taken. Each point represents two corresponding values from the two data sets. However, we don't plot the date that the measurements were taken on.
```
plt.scatter(data['000001'], data['000333'])
plt.xlabel('平安银行')
plt.ylabel('美的集团')
plt.title('Daily Prices in 2014');
R_000001 = data['000001'].pct_change()[1:]
R_000333 = data['000333'].pct_change()[1:]
plt.scatter(R_000001, R_000333)
plt.xlabel('000001')
plt.ylabel('000333')
plt.title('Daily Returns in 2014')
```
# Line graph
A line graph can be used when we want to track the development of the y value as the x value changes. For instance, when we are plotting the price of a stock, showing it as a line graph instead of just plotting the data points makes it easier to follow the price over time. This necessarily involves "connecting the dots" between the data points, which can mask out changes that happened between the time we took measurements.
```
plt.plot(data['000001'])
plt.plot(data['000333'])
plt.ylabel('Price')
plt.legend(['000001', '000333']);
# Remove the first element because percent change from nothing to something is NaN
R = data['000001'].pct_change()[1:]
plt.plot(R)
plt.ylabel('Return')
plt.title('000001 Returns')
```
## Never Assume Conditions Hold
Again, whenever using plots to visualize data, do not assume you can test a hypothesis by looking at a graph. Also do not assume that because a distribution or trend used to be true, it is still true. In general much more sophisticated and careful validation is required to test whether models hold, plots are mainly useful when initially deciding how your models should work.
*This presentation is for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation for any security; nor does it constitute an offer to provide investment advisory or other services by Quantopian, Inc. ("Quantopian"). Nothing contained herein constitutes investment advice or offers any opinion with respect to the suitability of any security, and any views expressed herein should not be taken as advice to buy, sell, or hold any security or as an endorsement of any security or company. In preparing the information contained herein, Quantopian, Inc. has not taken into account the investment needs, objectives, and financial circumstances of any particular investor. Any views expressed and data illustrated herein were prepared based upon information, believed to be reliable, available to Quantopian, Inc. at the time of publication. Quantopian makes no guarantees as to their accuracy or completeness. All information is subject to change and may quickly become unreliable for various reasons, including changes in market conditions or economic circumstances.*
| true |
code
| 0.648355 | null | null | null | null |
|
## DR = (Digit Recognizer)
- https://www.kaggle.com/c/digit-recognizer
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import tensorflow as tf
import time
train = pd.read_csv("./input/train.csv")
test = pd.read_csv("./input/test.csv")
train.describe()
train.shape
train.head()
learning_rate = 0.0001
total_train = 2500
drop_out = 0.7
batch_size = 50
VALIDATION_SIZE = 2000
IMAGE_TO_DISPLAY = 10
```
## 784 = 28 x 28
```
images = train.iloc[:,1:].values
images = images.astype(np.float)
print(images)
images = np.multiply(images, 1.0 / 255.0)
print(len(images))
print('images({0[0]},{0[1]})'.format(images.shape))
```
- image에서 1번 성분 추출
```
image_size = images.shape[1]
print(image_size)
```
- ceil 반올림 개념
```
image_width = image_height = np.ceil(np.sqrt(image_size)).astype(np.uint8)
print ('image_width => {0}\nimage_height => {1}'.format(image_width,image_height))
image_01 = images[400].reshape(image_width,image_height)
plt.axis('off')
plt.imshow(image_01, cmap = cm.binary)
plt.show()
# display image
def display(img):
# (784) => (28,28)
one_image = img.reshape(image_width,image_height)
plt.axis('off')
plt.imshow(one_image, cmap=cm.binary_r)
plt.show()
# output image
display(images[IMAGE_TO_DISPLAY])
labels_flat = train[[0]].values.ravel()
print(labels_flat)
print('labels_flat({0})'.format(len(labels_flat)))
print ('labels_flat[{0}] => {1}'.format(IMAGE_TO_DISPLAY,labels_flat[IMAGE_TO_DISPLAY]))
labels_count = np.unique(labels_flat).shape[0]
print('labels_count => {0}'.format(labels_count))
def dense_to_one_hot(labels_dense, num_classes):
num_labels = labels_dense.shape[0]
index_offset = np.arange(num_labels) * num_classes
labels_one_hot = np.zeros((num_labels, num_classes))
labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1
return labels_one_hot
labels = dense_to_one_hot(labels_flat, labels_count)
labels = labels.astype(np.uint8)
print('labels({0[0]},{0[1]})'.format(labels.shape))
print ('labels[{0}] => {1}'.format(IMAGE_TO_DISPLAY,labels[IMAGE_TO_DISPLAY]))
```
## Data process for tensorflow
```
validation_images = images[:VALIDATION_SIZE]
validation_labels = labels[:VALIDATION_SIZE]
train_images = images[VALIDATION_SIZE:]
train_labels = labels[VALIDATION_SIZE:]
print('train_images({0[0]},{0[1]})'.format(train_images.shape))
print('validation_images({0[0]},{0[1]})'.format(validation_images.shape))
```
# Model
```
#images
X = tf.placeholder(tf.float32, shape=[None, image_size])
#labels
Y = tf.placeholder(tf.float32, shape=[None, labels_count])
weight_01 = tf.Variable(tf.truncated_normal([5,5,1,32],stddev=0.1))
bias_01 = tf.Variable(tf.constant(0.1,shape=[32]))
print(weight_01)
print(bias_01)
```
- The convolution computes 32 features for each 5x5 patch. Its weight tensor has a shape of [5, 5, 1, 32].
- tf.reshpte[-1(None), 넓이, 높이, 밀도]
```
image = tf.reshape(X, [-1, image_width, image_height,1])
print(image.get_shape())
con2d_01 = tf.nn.conv2d(image, weight_01, strides=[1,1,1,1], padding='SAME')
print(con2d_01.shape)
con2d_01 = con2d_01 + bias_01
print(con2d_01.shape)
con2d_01 = tf.nn.relu(con2d_01)
print(con2d_01.shape)
con2d_01_mp = tf.nn.max_pool(con2d_01, ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
print(con2d_01_mp.get_shape())
layer_01 = tf.reshape(con2d_01, (-1, image_height, image_width, 4, 8))
print(layer_01.shape)
layer_01 = tf.transpose(layer_01, (0, 3, 1, 4,2))
print(layer_01.shape)
layer_01 = tf.reshape(layer_01, (-1, image_height * 4, image_width * 8))
print(layer_01.shape)
weight_02 = tf.Variable(tf.truncated_normal([5,5,32,64],stddev=0.1))
bias_02 = tf.Variable(tf.constant(0.1,shape=[64]))
print(weight_02)
print(bias_02)
con2d_02 = tf.nn.conv2d(con2d_01_mp, weight_02, strides=[1,1,1,1], padding='SAME')
print(con2d_02.shape)
con2d_02 = con2d_02 + bias_02
print(con2d_02.shape)
con2d_02 = tf.nn.relu(con2d_02)
print(con2d_02.shape)
con2d_02_mp = tf.nn.max_pool(con2d_02, ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
print(con2d_02_mp.get_shape())
layer_02 = tf.reshape(con2d_02, (-1, 14, 14, 4 ,16))
print(layer_02.shape)
layer_02 = tf.transpose(layer_02, (0, 3, 1, 4,2))
print(layer_02.shape)
layer_02 = tf.reshape(layer_02, (-1, 14*4, 14*16))
print(layer_02.shape)
weight_03 = tf.Variable(tf.truncated_normal([7*7*64, 1024],stddev=0.1))
bias_03 = tf.Variable(tf.constant(0.1,shape=[1024]))
print(weight_03)
print(weight_03.shape)
print(bias_03)
print(bias_03.shape)
con2d_02_mp_flat = tf.reshape(con2d_02_mp, [-1, 7*7*64])
print(con2d_02_mp_flat.shape)
hypothesis = tf.nn.relu(tf.matmul(con2d_02_mp_flat, weight_03) + bias_03)
print(hypothesis)
print(hypothesis.shape)
keep_prob = tf.placeholder(tf.float32)
hypothesis_do = tf.nn.dropout(hypothesis, keep_prob=keep_prob)
# labels_count = 10
weight_04 = tf.Variable(tf.truncated_normal([1024, labels_count],stddev=0.1))
bias_04 = tf.Variable(tf.constant(0.1,shape=[labels_count]))
print(weight_04)
print(weight_04.shape)
print(bias_04)
print(bias_04.shape)
output = tf.nn.softmax(tf.matmul(hypothesis_do, weight_04) + bias_04)
print(output.shape)
cost = - tf.reduce_sum(Y * tf.log(output))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
```
# 정확도
```
prediction = tf.equal(tf.argmax(Y,1), tf.argmax(output,1))
accuracy = tf.reduce_mean(tf.cast(prediction, tf.float32))
predict = tf.argmax(Y,1)
```
## Training
```
epochs_completed = 0
index_in_epoch = 0
num_examples = train_images.shape[0]
def next_batch(batch_size):
global train_images
global train_labels
global index_in_epoch
global epochs_completed
start = index_in_epoch
index_in_epoch += batch_size
# when all trainig data have been already used, it is reorder randomly
if index_in_epoch > num_examples:
# finished epoch
epochs_completed += 1
# shuffle the data
perm = np.arange(num_examples)
np.random.shuffle(perm)
train_images = train_images[perm]
train_labels = train_labels[perm]
# start next epoch
start = 0
index_in_epoch = batch_size
assert batch_size <= num_examples
end = index_in_epoch
return train_images[start:end], train_labels[start:end]
init = tf.global_variables_initializer()
sess = tf.InteractiveSession()
sess.run(init)
train_accuracies = []
validation_accuracies = []
x_range = []
display_step=1
"""
learning_rate = 0.0001
total_train = 2500
drop_out = 0.7
batch_size = 50
VALIDATION_SIZE = 2000
IMAGE_TO_DISPLAY = 10
"""
start_time = time.time()
for i in range(total_train):
batch_xs, batch_ys = next_batch(batch_size)
if i%display_step == 0 or (i+1) == total_train:
train_accuracy = accuracy.eval(feed_dict={X:batch_xs, Y: batch_ys, keep_prob: 1.0})
if(VALIDATION_SIZE):
validation_accuracy = accuracy.eval(feed_dict={ X: validation_images[0:batch_size],
Y: validation_labels[0:batch_size],
keep_prob: 1.0})
print('training_accuracy / validation_accuracy => %.2f / %.2f for step %d'%(train_accuracy, validation_accuracy, i))
validation_accuracies.append(validation_accuracy)
else:
print('training_accuracy => %.4f for step %d'%(train_accuracy, i))
train_accuracies.append(train_accuracy)
x_range.append(i)
if i%(display_step*10) == 0 and i:
display_step *= 10
sess.run(optimizer, feed_dict={X: batch_xs, Y: batch_ys, keep_prob: drop_out})
estimated_time = time.time() - start_time
print(estimated_time, "[second]")
if(VALIDATION_SIZE):
validation_accuracy = accuracy.eval(feed_dict={X: validation_images,
Y: validation_labels,
keep_prob: 1.0})
print('validation_accuracy => %.4f'%validation_accuracy)
plt.plot(x_range, train_accuracies,'-b', label='Training')
plt.plot(x_range, validation_accuracies,'-g', label='Validation')
plt.legend(loc='lower right', frameon=False)
plt.ylim(ymax = 1.1, ymin = 0.7)
plt.ylabel('accuracy')
plt.xlabel('step')
plt.show()
```
# Result
- accuracy = 98.5%
- estimated time = 25.9[s]
# Train에 대한 Test
```
test = test.astype(np.float)
```
- 0~255까지의 수를 0과 1 사이의 값으로 normalize
```
test = np.multiply(test, 1.0/255.0)
print(test.shape)
prediction_lables = np.zeros(test.shape[0])
print(prediction_lables)
layer1_grid = layer_01.eval(feed_dict={X: test[7:7+1], keep_prob: 1.0})
plt.axis('off')
plt.imshow(layer1_grid[0], cmap=cm.seismic )
plt.show()
sess.close()
```
| true |
code
| 0.54698 | null | null | null | null |
|
<img src="../../../images/qiskit-heading.png" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" width="500 px" align="left">
## _*Comparing Classical and Quantum Finite Automata (QFA)*_
Finite Automaton has been a mathematical model for computation since its invention in the 1940s. The purpose of a Finite State Machine is to recognize patterns within an input taken from some character set and accept or reject the input based on whether the pattern defined by the machine occurs in the input. The machine requires a list of states, the initial state, and the conditions for each transition from state to state. Such classical examples are vending machines, coin-operated turnstiles, elevators, traffic lights, etc.
In the classical algorithm, the sequence begins in the start state, and will only make a transition if the next character in the input string matches the label on the transition from the current to the next state. The machine will continue making transitions on each input character until no move is possible. The string will be accepted if its final state is in the accept state and will be rejected if its final state is anywhere else.
As for Quantum Finite Automata (QFA), the machine works by accepting a finite-length string of letters from a finite alphabet and utilizing quantum properties such as superposition to assign the string a probability of being in either the accept or reject state.
***
### Contributors
Kaitlin Gili, Rudy Raymond
## Prime Divisibility Algorithm
Let's say that we have a string with $ a^i $ letters and we want to know whether the string is in the language $ L $ where $ L $ = {$ a^i $ | $ i $ is divisble by $ p $} and $ p $ is a prime number. If $ i $ is divisible by $ p $, we want to accept the string into the language, and if not, we want to reject it.
$|0\rangle $ and $ |1\rangle $ serve as our accept and reject states.
Classically, this algorithm requires a minimum of $ log(p) $ bits to store the information, whereas the quantum algorithm only requires $ log(log(p)) $ qubits. For example, using the highest known prime integer, the classical algorithm requires **a minimum of 77,232,917 bits**, whereas the quantum algorithm **only requires 27 qubits**.
## Introduction <a id='introduction'></a>
The algorithm in this notebook follows that in [Ambainis et al. 1998](https://arxiv.org/pdf/quant-ph/9802062.pdf). We assume that we are given a string and a prime integer. If the user does not input a prime number, the output will be a ValueError. First, we demonstrate a simpler version of the quantum algorithm that uses $ log(p) $ qubits to store the information. Then, we can use this to more easily understand the quantum algorithm that requires only $ log(log(p)) $ qubits.
## The Algorithm for Log(p) Qubits
The algorithm is quite simple as follows.
1. Prepare quantum and classical registers for $ log(p) $ qubits initialized to zero.
$$ |0\ldots 0\rangle $$
2. Prepare $ log(p) $ random numbers k in the range {$ 1 $... $ p-1 $}. These numbers will be used to decrease the probability of a string getting accepted when $ i $ does not divide $ p $.
3. Perform a number of $ i $ Y-Rotations on each qubit, where $ \theta $ is initially zero and $ \Phi $ is the angle of rotation for each unitary. $$ \Phi = \frac{2 \pi k}{p} $$
4. In the final state:
$$ \cos \theta |0\rangle + \sin \theta |1\rangle $$
$$ \theta = \frac{2 \pi k} p {i} $$
5. Measure each of the qubits in the classical register. If $ i $ divides $ p $, $ \cos \theta $ will be one for every qubit and the state will collapse to $ |0\rangle $ to demonstrate an accept state with a probability of one. Otherwise, the output will consist of a small probability of accepting the string into the language and a higher probability of rejecting the string.
## The Circuit <a id="circuit"></a>
We now implement the QFA Prime Divisibility algorithm with QISKit by first preparing the environment.
```
# useful additional packages
import random
import math
from sympy.ntheory import isprime
# importing QISKit
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import Aer, IBMQ, execute
from qiskit.wrapper.jupyter import *
from qiskit.backends.ibmq import least_busy
from qiskit.tools.visualization import matplotlib_circuit_drawer as circuit_drawer
from qiskit.tools.visualization import plot_histogram, qx_color_scheme
IBMQ.load_accounts()
sim_backend = Aer.get_backend('qasm_simulator')
device_backend = least_busy(IBMQ.backends(operational=True, simulator=False))
device_coupling = device_backend.configuration()['coupling_map']
```
We then use QISKit to program the algorithm.
```
#Function that takes in a prime number and a string of letters and returns a quantum circuit
def qfa_algorithm(string, prime):
if isprime(prime) == False:
raise ValueError("This number is not a prime") #Raises a ValueError if the input prime number is not prime
else:
n = math.ceil((math.log(prime))) #Rounds up to the next integer of the log(prime)
qr = QuantumRegister(n) #Creates a quantum register of length log(prime) for log(prime) qubits
cr = ClassicalRegister(n) #Creates a classical register for measurement
qfaCircuit = QuantumCircuit(qr, cr) #Defining the circuit to take in the values of qr and cr
for x in range(n): #For each qubit, we want to apply a series of unitary operations with a random int
random_value = random.randint(1,prime - 1) #Generates the random int for each qubit from {1, prime -1}
for letter in string: #For each letter in the string, we want to apply the same unitary operation to each qubit
qfaCircuit.ry((2*math.pi*random_value) / prime, qr[x]) #Applies the Y-Rotation to each qubit
qfaCircuit.measure(qr[x], cr[x]) #Measures each qubit
return qfaCircuit #Returns the created quantum circuit
```
The qfa_algorithm function returns the Quantum Circuit qfaCircuit.
## Experiment with Simulators
We can run the above circuit on the simulator.
```
#A function that returns a string saying if the string is accepted into the language or rejected
def accept(parameter):
states = list(result.get_counts(parameter))
for s in states:
for integer in s:
if integer == "1":
return "Reject: the string is not accepted into the language"
return "Accept: the string is accepted into the language"
```
Insert your own parameters and try even larger prime numbers.
```
range_lower = 0
range_higher = 36
prime_number = 11
for length in range(range_lower,range_higher):
params = qfa_algorithm("a"* length, prime_number)
job = execute(params, sim_backend, shots=1000)
result = job.result()
print(accept(params), "\n", "Length:",length," " ,result.get_counts(params))
```
### Drawing the circuit of the QFA
Below is the snapshop of the QFA for reading the bitstring of length $3$. It can be seen that there are independent QFAs each of which performs $Y$ rotation for $3$ times.
```
circuit_drawer(qfa_algorithm("a"* 3, prime_number), style=qx_color_scheme())
```
## The Algorithm for Log(Log(p)) Qubits
The algorithm is quite simple as follows.
1. Prepare a quantum register for $ log(log(p)) + 1 $ qubits initialized to zero. The $ log(log(p))$ qubits will act as your control bits and the 1 extra will act as your target bit. Also prepare a classical register for 1 bit to measure the target.
$$ |0\ldots 0\rangle |0\rangle $$
2. Hadamard the control bits to put them in a superposition so that we can perform multiple QFA's at the same time.
3. For each of $s $ states in the superposition, we can perform an individual QFA with the control qubits acting as the random integer $ k $ from the previous algorithm. Thus, we need $ n $ values from $ 1... log(p)$ for $ k $. For each letter $ i $ in the string, we perform a controlled y-rotation on the target qubit, where $ \theta $ is initially zero and $ \Phi $ is the angle of rotation for each unitary. $$ \Phi = \frac{2 \pi k_{s}}{p} $$
4. The target qubit in the final state:
$$ \cos \theta |0\rangle + \sin \theta |1\rangle $$
$$ \theta = \sum_{s=0}^n \frac{2 \pi k_{s}} p {i} $$
5. Measure the target qubit in the classical register. If $ i $ divides $ p $, $ \cos \theta $ will be one for every QFA and the state of the target will collapse to $ |0\rangle $ to demonstrate an accept state with a probability of one. Otherwise, the output will consist of a small probability of accepting the string into the language and a higher probability of rejecting the string.
## The Circuit <a id="circuit"></a>
We then use QISKit to program the algorithm.
```
#Function that takes in a prime number and a string of letters and returns a quantum circuit
def qfa_controlled_algorithm(string, prime):
if isprime(prime) == False:
raise ValueError("This number is not a prime") #Raises a ValueError if the input prime number is not prime
else:
n = math.ceil((math.log(math.log(prime,2),2))) #Represents log(log(p)) control qubits
states = 2 ** (n) #Number of states that the qubits can represent/Number of QFA's to be performed
qr = QuantumRegister(n+1) #Creates a quantum register of log(log(prime)) control qubits + 1 target qubit
cr = ClassicalRegister(1) #Creates a classical register of log(log(prime)) control qubits + 1 target qubit
control_qfaCircuit = QuantumCircuit(qr, cr) #Defining the circuit to take in the values of qr and cr
for q in range(n): #We want to take each control qubit and put them in a superposition by applying a Hadamard Gate
control_qfaCircuit.h(qr[q])
for letter in string: #For each letter in the string, we want to apply a series of Controlled Y-rotations
for q in range(n):
control_qfaCircuit.cu3(2*math.pi*(2**q)/prime, 0, 0, qr[q], qr[n]) #Controlled Y on Target qubit
control_qfaCircuit.measure(qr[n], cr[0]) #Measure the target qubit
return control_qfaCircuit #Returns the created quantum circuit
```
The qfa_algorithm function returns the Quantum Circuit control_qfaCircuit.
## Experiment with Simulators
We can run the above circuit on the simulator.
```
for length in range(range_lower,range_higher):
params = qfa_controlled_algorithm("a"* length, prime_number)
job = execute(params, sim_backend, shots=1000)
result = job.result()
print(accept(params), "\n", "Length:",length," " ,result.get_counts(params))
```
### Drawing the circuit of the QFA
Below is the snapshot of the QFA for reading the bitstring of length $3$. It can be seen that there is a superposition of QFAs instead of independent QFAs.
```
circuit_drawer(qfa_controlled_algorithm("a"* 3, prime_number), style=qx_color_scheme())
```
## Experimenting with Real Devices
Real-device backends have errors and if the above QFAs are executed on the noisy backends, errors in rejecting strings that should have been accepted can happen. Let us see how well the real-device backends can realize the QFAs.
Let us look an example when the QFA should reject the bitstring because the length of the bitstring is not divisible by the prime number.
```
prime_number = 3
length = 2 # set the length so that it is not divisible by the prime_number
print("The length of a is", length, " while the prime number is", prime_number)
qfa1 = qfa_controlled_algorithm("a"* length, prime_number)
%%qiskit_job_status
HTMLProgressBar()
job = execute(qfa1, backend=device_backend, coupling_map=device_coupling, shots=100)
result = job.result()
plot_histogram(result.get_counts())
```
In the above, we can see that the probability of observing "1" is quite significant. Let us see how the circuit looks like.
```
circuit_drawer(qfa1, style=qx_color_scheme())
```
Now, let us see what happens when the QFAs should accept the input string.
```
print_number = length = 3 # set the length so that it is divisible by the prime_number
print("The length of a is", length, " while the prime number is", prime_number)
qfa2 = qfa_controlled_algorithm("a"* length, prime_number)
%%qiskit_job_status
HTMLProgressBar()
job = execute(qfa2, backend=device_backend, coupling_map=device_coupling, shots=100)
result = job.result()
plot_histogram(result.get_counts())
```
The error of rejecting the bitstring is equal to the probability of observing "1" which can be checked from the above histogram. We can see that the noise of real-device backends prevents us to have a correct answer. It is left as future work on how to mitigate errors of the backends in the QFA models.
```
circuit_drawer(qfa2, style=qx_color_scheme())
```
| true |
code
| 0.652352 | null | null | null | null |
|
# Artificial Neural Network in Python with Keras
In this program we construct an Artificial Neuron Network model. The aim is to build a classification model to predict if a certain customer will leave the bank services in the six months.
**Dataset Description**
For this problem we have a Dataset composed by 10000 instances (rows) and 14 features (columns). As the objective is to predict the probability of a client will leave the bank service, in our dataset the last column corresponds to the response. The others columns are the features (independent variables) that we consider to build and training the model, these columns are: RowNumber, CustomerId, Surname, CreditScore, Geography, Gender, Age, Tenure, Balance, NumOfProducts, HasCrCard, IsActiveMember, EstimatedSalary, Exited.
## Importing Libraries
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
```
## Importing the Dataset
```
dataset = pd.read_csv('Churn_Modelling.csv')
dataset.head()
```
### Visualizing the categorical variables
```
dataset['Gender'].value_counts()
dataset['Gender'].value_counts().plot.bar()
dataset.Geography.value_counts()
dataset.Geography.value_counts().plot.bar()
```
### Visualizing the Numerical Variables
```
dataset['Age'].hist(bins=10)
dataset.dtypes
sns.pairplot(dataset, hue = 'Exited',
vars = ['CreditScore', 'Age', 'Balance', 'EstimatedSalary'] )
```
### Correlation with the response variable
```
dataset_n = dataset.drop(columns=['RowNumber', 'CustomerId', 'Surname', 'Geography', 'Gender',
'Tenure', 'NumOfProducts', 'HasCrCard', 'IsActiveMember', 'Exited'])
dataset_n.corrwith(dataset.Exited).plot.bar(
figsize = (20, 10), title = "Correlation with Exited", fontsize = 15,
rot = 45, grid = True)
```
### Correlation Between Numerical Variables
```
## Correlation Matrix
sns.set(style="white")
# Compute the correlation matrix
corr = dataset_n.corr()
# Generate a mask for the upper triangle
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(10, 20))
# Generate a custom diverging colormap
cmap = sns.diverging_palette(220, 10, as_cmap=True)
# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=.1, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, annot = True)
```
### Feature Engineering
```
sns.histplot(data=dataset, x='Age', hue='Exited', kde = True)
sns.histplot(data=dataset[dataset['Exited'] == 1], x='Age', hue='Exited', bins = 7, kde = True)
sns.histplot(data=dataset[dataset['Exited'] == 0], x='Age', hue='Exited', bins = 6, kde = True)
def category_age(Age):
if (Age <=28):
return 0
elif(Age > 28) & (Age <= 38):
return 1
elif(Age > 38) & (Age <= 58):
return 2
#elif(Age > 40) & (Age <= 50):
# return 3
#elif(Age > 50) & (Age <= 60):
# return 4
else:
return 3
#dataset['Age'] = dataset['Age'].map(category_age)
dataset[dataset['Exited'] == 1]['Age'].value_counts()
sns.histplot(data=dataset[dataset['Exited'] == 1], x='Age', hue='Exited', kde = True)
dataset.columns
```
### Excluding not important columns
```
dataset = dataset.drop(columns=['RowNumber', 'CustomerId', 'Surname'])
```
### Encoding Categorical Data
```
dataset['Gender'] = dataset['Gender'].astype('category').cat.codes
```
### One Hot Econding
```
dataset = pd.get_dummies(dataset)
dataset.head()
response = dataset['Exited']
dataset = dataset.drop(columns=['Exited'])
response.head()
```
### Splitting the Dataset into train and test set
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(dataset, response, test_size = 0.2, random_state = 0)
```
### Feature Scaling
In almost ANN models we must to apply feature scale.
```
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train_bckp = pd.DataFrame(sc_X.fit_transform(X_train))
X_test_bckp = pd.DataFrame(sc_X.transform(X_test))
X_train_bckp.columns = X_train.columns.values
X_test_bckp.columns = X_test.columns.values
X_train_bckp.index = X_train.index.values
X_test_bckp.index = X_test.index.values
X_train = X_train_bckp
X_test = X_test_bckp
```
## Building the Neural Networks
EXPLAIN IN MORE DETAIL WHAT IS AN ANN, WHICH STEP WE NEED AND SO ON
### Importing the Keras library
```
import keras
from keras.models import Sequential # To initialize the ANN
from keras.layers import Dense # To creat the hidden layers
```
### Initiating the ANN
```
classifier = Sequential() # To initiate the ANN
```
### Creating the Layers
```
classifier.add(Dense(units=6, activation='relu',
kernel_initializer= 'uniform',
input_dim=X_train.shape[1])) # Creating the hidden layer
classifier.add(Dense(units=6, activation='relu',
kernel_initializer= 'uniform')) # Creating the hidden layer
classifier.add(Dense(units=1, activation='sigmoid',
kernel_initializer= 'uniform')) # Creating the hidden layer
```
### Compiling the ANN
```
classifier.compile(optimizer='adam', loss='binary_crossentropy',
metrics=['accuracy'])
```
## Training the ANN
```
classifier.fit(X_train, y_train, batch_size=32, epochs=100)
```
### Predicting a New Result
```
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)
```
### Making the Confusion Matrix
```
from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
score_train = classifier.evaluate(X_train, y_train)
score_test = classifier.evaluate(X_test, y_test)
print(score_train)
print(score_test)
```
## Evaluating the model
Here we are going to proceed with a k-fold cross validation. We need to create a new function.
def build_classifier(optimizer='adam'):
classifier = Sequential()
classifier.add(Dense(units = 6, kernel_initializer = 'uniform', activation = 'relu', input_dim = X.shape[1]))
classifier.add(Dense(units = 6, kernel_initializer = 'uniform', activation = 'relu'))
classifier.add(Dense(units = 1, kernel_initializer = 'uniform', activation = 'sigmoid'))
classifier.compile(optimizer = optimizer, loss = 'binary_crossentropy', metrics = ['accuracy'])
return classifier
### K-Fold Cross Validation
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import cross_val_score
classifier = KerasClassifier(build_fn = build_classifier, batch_size = 32, epochs = 100)
accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train,
cv = 10, n_jobs = -1)
mean = accuracies.mean()
variance = accuracies.std()
print(mean)
print(variance)
## Tuning the Model
from sklearn.model_selection import GridSearchCV
classifier = KerasClassifier(build_fn = build_classifier)
parameters = {'batch_size': [8, 16, 32, 64],
'epochs': [100, 500],
'optimizer': ['adam', 'rmsprop']}
grid_search = GridSearchCV(estimator = classifier,
param_grid = parameters,
scoring = 'accuracy',
cv = 10, n_jobs = -1)
grid_search = grid_search.fit(X_train, y_train)
best_parameters = grid_search.best_params_
best_accuracy = grid_search.best_score_
print(best_parameters)
best_accuracy
| true |
code
| 0.648689 | null | null | null | null |
|
# Writing Functions in Python
**by [Richard W. Evans](https://sites.google.com/site/rickecon/), June 2019**
Python has many [built-in functions](https://docs.python.org/3/library/functions.html). Functions are objects that accept a specific set of inputs, perform operations on those inputs, and return a set of outputs based on those inputs. Python is a language that focuses on functions. Further, the importing of packages expands the set of functions available to the user.
In this notebook, we learn the basics of writing a function in Python, some best practices about docstrings and documentation, and some of the art of using functions to make your code modular. **Modularity** of code is the principle of writing functions for operations that occur multiple times so that a change to that operation only has to be changed once in the code rather than in every instance of the operation. Furthermore, the principle of code modularity also make it easier to take pieces of your code and plug them into other projects as well as combining other projects with your code.
## 1. The form of a Python function
You can define a function in a Python module or script by using the `def` keyword followed by the function name, a parenthesized list of inputs, and a colon `:`. You then include the operations you want your function to perform by typing lines of executable code, each of which begins with an indent of four spaces. Finally, if you want your function to return any objects, those objects are listed in a comma-separated list following the `return` keyword as the last indented line of the function.
The following function concatenates two strings into one string.
```
def string2together(str1, str2):
'''
--------------------------------------------------------------------
This function concatenates two strings as one string with a space
separating them.
--------------------------------------------------------------------
INPUTS:
str1 = string, first string argument passed into function
str2 = string, second string argument passed into function
OTHER FUNCTIONS AND FILES CALLED BY THIS FUNCTION: None
OBJECTS CREATED WITHIN THIS FUNCTION:
big_string = string, combination of str1 and str2 with a space
between them
FILES CREATED BY THIS FUNCTION: None
RETURNS: big_string
--------------------------------------------------------------------
'''
big_string = str1 + ' ' + str2
return big_string
myfirstname = "Rick"
mylastname = "Evans"
fullname = string2together(myfirstname, mylastname)
fullname
```
Note first how extensive the documentation is for this function. The function `string2together` has only two lines of executable code in it. The rest is docstring. We will talk about docstrings and commenting more in Section 3 of this notebook.
Also note that we could have written that function `string2together` with only one line of executable code by combining the two lines in the following way: `return str1 + ' ' + str2`. It is best to keep the return statement clean by only returning objects that have already been created in the body of the function. This makes the function's operation more accessible and transparent.
Note that, despite the simplicity, this function would be extremely valuable if it were used multiple times in a bigger set of operations. Imagine a process that concatenated two strings with a space in between many times. Now assume you wanted to change some of those instances to be reversed order with a comma separating them. This could be done quickly by changing the one instance of this function rather than each time the operation is called. More on this in Section 4 on modularity.
## 2. Some Python function workflows
### 2.1 Modules and scripts
This approach separates the top-level operations (such as the declaration of exogenous parameter values or analysis of results) from the operations that generate the results. In this approach all declaration of parameter values and final analysis of results is done in a Python script (e.g., `script.py`). The script has no function definitions. It only calls the functions it must use from the module.
The module is a Python script (e.g., `module.py`) that does not execute any operations on its own. The module is simply a collection of function definitions that can be imported into other scripts or modules. The following pseudocode is an example of a script.
```python
import whateverlibraries as wel
import module as mod
...
# Declare parameter values and any other stuff
...
# Call some functions from module.py
val1 = md.func1(val2, val3)
val4 = md.func2(val5, val1)
```
The module `module.py` has at least two functions defined in it: `func1` and `func2`. By having these functions imported from the module, they can be differentiated by the `md.` prefix from other functions from other modules or from the script itself that might have the same name.
### 2.2 Scripts with "if __name__ == '__main__':"
Suppose you write a module that has in it only functions. You can place the `if __name__ == '__main__':` construct at the end of the module, and every command indented underneath it will execute when the module is run as a script. `'__main__'` is the name of the scope in which top-level code executes.
```python
# This code is part of a module entitled 'module1.py'
def simplesum(val1, val2):
the_sum = val1 + val2
return the_sum
if __name__ == "__main__":
# execute only if run as a script
myheight = 5.9
mydadsheight = 6.0
tot_height = simplesum(myheight, mydadsheight)
```
You could execute the code that calculates the variable `tot_height` by running `module1.py` as a script (typing `python module1.py` from the terminal or `run module1.py` from ipython).
This method is often prefered to having functions and executable script lines in the same function as is described in Section 2.3. The reason is that, in this method using the `if __name__ == '__main__':` construct, all the commands are inside of functions.
### 2.3 Functions and executable commands in script
You can declare functions and run executable lines outside of functions in the same script. This is commonly done in small projects, although many developers feel that following the method from Section 2.2 is a better practice.
```
import numpy as np
# Declare parameters
myheight = 5.9
mydadsheight = 6.0
def simplesum(val1, val2):
the_sum = val1 + val2
return the_sum
tot_height = simplesum(myheight, mydadsheight)
tot_height
```
## 3. Function documentation
Every function should be well documented. The form of exact function docstrings has not yet been fully regularized in the Python community, but some key principles apply. It is ideal to give carefully organized and easily accessible information in your docstrings and in-line comments such that an outside user can quickly understand what your function is doing.
Good documentation can save you time in the long-run (but almost certainly not in the short run) by giving a nice roadmap for debugging code later on if a problem arises. Furthermore, you might sometimes forget what you were originally trying to do with a particular piece of code, and the documentation will remind you. Lastly, well-documented code is essential for other researchers to be able to collaborate with you.
Comments in the code are descriptive lines that are not executed by the interpreter. You can comment code in three ways. Brackets of three double quotes `""" """` or brackets of three single quotes `''' '''` will comment out large blocks of text. The pound sign `#` will comment out a single line of text or a partial line of text.
```
print(3 + 7)
# print("You're not the best!")
print("You're the best!")
'''
In the following code snippet, I will
print out what most other people think
of me. But I might want to change it
by uncommenting and commenting out particular
lines.
'''
print("You're the best.")
# print("You're not the best.")
```
### 3.1 The function docstring
The function docstring is a block of text commented out by three bracketing quotes `''' '''` or `""" """`. Docstrings that immediately follow a function are often brought up as the automatic function help or description in advanced text editors and ipython development environments (IDEs). As such, the docstring is an essential description and roadmap for a function. Below is an example of a function that takes as an input a scalar that represents the number of seconds some procedure took.
```
def print_time(seconds, type):
'''
--------------------------------------------------------------------
Takes a total amount of time in seconds and prints it in terms of
more readable units (days, hours, minutes, seconds)
--------------------------------------------------------------------
INPUTS:
seconds = scalar > 0, total amount of seconds
type = string, description of the type of computation
OTHER FUNCTIONS AND FILES CALLED BY THIS FUNCTION:
OBJECTS CREATED WITHIN FUNCTION:
secs = scalar > 0, remainder number of seconds
mins = integer >= 1, remainder number of minutes
hrs = integer >= 1, remainder number of hours
days = integer >= 1, number of days
FILES CREATED BY THIS FUNCTION: None
RETURNS: Nothing
--------------------------------------------------------------------
'''
if seconds < 60: # seconds
secs = round(seconds, 4)
print(type + ' computation time: ' + str(secs) + ' sec')
elif seconds >= 60 and seconds < 3600: # minutes
mins = int(seconds / 60)
secs = round(((seconds / 60) - mins) * 60, 1)
print(type + ' computation time: ' + str(mins) + ' min, ' +
str(secs) + ' sec')
elif seconds >= 3600 and seconds < 86400: # hours
hrs = int(seconds / 3600)
mins = int(((seconds / 3600) - hrs) * 60)
secs = round(((seconds / 60) - hrs * 60 - mins) * 60, 1)
print(type + ' computation time: ' + str(hrs) + ' hrs, ' +
str(mins) + ' min, ' + str(secs) + ' sec')
elif seconds >= 86400: # days
days = int(seconds / 86400)
hrs = int(((seconds / 86400) - days) * 24)
mins = int(((seconds / 3600) - days * 24 - hrs) * 60)
secs = round(
((seconds / 60) - days * 24 * 60 - hrs * 60 - mins) * 60, 1)
print(type + ' computation time: ' + str(days) + ' days, ' +
str(hrs) + ' hrs, ' + str(mins) + ' min, ' +
str(secs) + ' sec')
print_time(98765, 'Simulation')
```
Notice the docstring after the definition line of the function. It starts out with a general description of what the function does. Then it describes the inputs to the function, any other functions that this function calls, any objects created by this function, any files saved by this function, and the objects that the function returns. In this case, the function does not return any objects. It just prints output to the terminal.
You will also notice the in-line comments after each `if` statement. These comments describe what particular sections of the code are doing.
### 3.2 In-line comments
You see examples of in-line comments in the `print_time()` function above. In-line comments can be helpful for describing the flow of operations or logic within a function. They act as road signs along the way to a functions completion.
## 4. Function modularity
A principle in writing Python code is to make functions for each piece that gets used multiple times. This is where the art of good code writing is evident. Here are some questions that the developer must answer.
1. How many times must an operation be repeated before it merits its own function?
2. How complicated must an operation be to merit its own function?
3. Which groups of operations are best grouped together as functions?
## 5. Lambda functions
The keyword `lambda` is a shortcut for creating one-line functions in Python.
```
f = lambda x: 6 * (x ** 3) + 4 * (x ** 2) - x + 3
f(10)
g = lambda x, y, z: x + y ** 2 - z ** 3
g(1, 2, 3)
```
## 6. Generalized function input
Sometimes you will want to define a function that has a variable number of input arguments. Python's function syntax includes two variable length input objects: `*args` and `*kwargs`. `*args` is a list of the positional arguments, and `*kwargs` is a dictionary mapping the keywords to their argument. This is the most general forma of a function definition.
```
def report(*args, **kwargs):
for i, arg in enumerate(args):
print('Argument ' + str(i) + ':', arg)
for key in kwargs:
print("Keyword", key, "->", kwargs[key])
report("TK", 421, exceptional=False, missing=True)
```
Passing arguments or dictionaries through the variable length `*args` or `*kwargs` objects is often desireable for the targets of SciPy's root finders, solvers, and minimizers.
## 7. Some function best practices
1. Don't use global variables. Always explicitly pass everything in to a function that the function requires to execute.
2. Don't pass input arguments into a function that do not get used. This principle is helpful when one needs to debug code.
3. Don't create objects in the return line of a function. Even though it is easier and you can often write an entire function in one return line, it is much cleaner and more transparent to create all of your objects in the body of a function and only return objects that have already been created.
## References
* [Python labs](http://www.acme.byu.edu/?page_id=2067), Applied and Computational Mathematics Emphasis (ACME), Brigham Young University.
| true |
code
| 0.485844 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
from keras.layers import Input, Dense
from keras.models import Model
from keras.datasets import fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
x_train.shape, x_test.shape, type(x_train)
plt.imshow(x_train[1], cmap='binary')
# Size of encoded representation
# 32 floats denotes a compression factor of 24.5 assuming input is 784 float
# we have 32*32 or 1024 floats
encoding_dim = 32
#Input placeholder
input_img = Input(shape=(784,))
#Encoded representation of input image
encoded = Dense(encoding_dim, activation='relu', activity_regularizer=regularizers.l1(10e-5))(input_img)
# Decode is lossy reconstruction of input
decoded = Dense(784, activation='sigmoid')(encoded)
# This autoencoder will map input to reconstructed output
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
autoencoder.summary()
''' The seperate encoder network '''
# Define a model which maps input images to the latent space
encoder_network = Model(input_img, encoded)
# Visualize network
encoder_network.summary()
''' The seperate decoder network '''
# Placeholder to recieve the encoded (32-dimensional) representation as input
encoded_input = Input(shape=(encoding_dim,))
# Decoder layer, retrieved from the aucoencoder model
decoder_layer = autoencoder.layers[-1]
# Define the decoder model, mapping the latent space to the output layer
decoder_network = Model(encoded_input, decoder_layer(encoded_input))
# Visualize network
decoder_network.summary()
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
# Normalize pixel values
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
# Flatten images to 2D arrays
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
# Print out the shape
print(x_train.shape)
print(x_test.shape)
plt.imshow(x_train[1].reshape(28,28))
autoencoder.fit(x_train, x_train,
epochs=50,
batch_size=256,
shuffle=True,
validation_data=(x_test, x_test))
# Time to encode some images
encoded_imgs = encoder_network.predict(x_test)
# Then decode them
decoded_imgs = decoder_network.predict(encoded_imgs)
# use Matplotlib (don't ask)
import matplotlib.pyplot as plt
plt.figure(figsize=(22, 6))
num_imgs = 9
for i in range(n):
# display original
ax = plt.subplot(2, num_imgs, i + 1)
true_img = x_test[i].reshape(28, 28)
plt.imshow(true_img)
# display reconstruction
ax = plt.subplot(2, num_imgs, i + 1 + num_imgs)
reconstructed_img = decoded_imgs[i].reshape(28,28)
plt.imshow(reconstructed_img)
plt.show()
```
| true |
code
| 0.732596 | null | null | null | null |
|
# VGG-16 on CIFAR-10
### Imports
```
import time
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets
from torchvision import transforms
from torch.utils.data import DataLoader
if torch.cuda.is_available():
torch.backends.cudnn.deterministic = True
```
### Settings and Dataset
```
# Device
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Hyperparameters
random_seed = 1
learning_rate = 0.001
num_epochs = 10
batch_size = 128
torch.manual_seed(random_seed)
# Architecture
num_features = 784
num_classes = 10
# Data
train_dataset = datasets.CIFAR10(root='data',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = datasets.CIFAR10(root='data',
train=False,
transform=transforms.ToTensor())
train_loader = DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
# Checking the dataset
for images, labels in train_loader:
print('Image batch dimensions:', images.shape)
print('Image label dimensions:', labels.shape)
break
```
### Model
```
class VGG16(nn.Module):
def __init__(self, num_classes):
super(VGG16, self).__init__()
self.block_1 = nn.Sequential(
nn.Conv2d(in_channels=3,
out_channels=64,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=64,
out_channels=64,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.block_2 = nn.Sequential(
nn.Conv2d(in_channels=64,
out_channels=128,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=128,
out_channels=128,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.block_3 = nn.Sequential(
nn.Conv2d(in_channels=128,
out_channels=256,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256,
out_channels=256,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256,
out_channels=256,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.block_4 = nn.Sequential(
nn.Conv2d(in_channels=256,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.block_5 = nn.Sequential(
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.classifier = nn.Sequential(
nn.Linear(512, 4096),
nn.ReLU(True),
nn.Linear(4096, 4096),
nn.ReLU(True),
nn.Linear(4096, num_classes)
)
for m in self.modules():
if isinstance(m, torch.nn.Conv2d) or isinstance(m, torch.nn.Linear):
nn.init.kaiming_uniform_(m.weight, mode='fan_in', nonlinearity='relu')
if m.bias is not None:
m.bias.detach().zero_()
def forward(self, x):
x = self.block_1(x)
x = self.block_2(x)
x = self.block_3(x)
x = self.block_4(x)
x = self.block_5(x)
x = torch.flatten(x, 1)
logits = self.classifier(x)
probas = F.softmax(logits, dim=1)
return logits, probas
model = VGG16(num_classes)
model.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
```
### Training
```
def compute_accuracy(model, data_loader):
model.eval()
correct_pred, num_examples = 0, 0
for i, (features, targets) in enumerate(data_loader):
features = features.to(device)
targets = targets.to(device)
logits, probas = model(features)
_, predicted_labels = torch.max(probas, 1)
num_examples += targets.size(0)
correct_pred += (predicted_labels == targets).sum()
return correct_pred.float()/num_examples * 100
for epoch in range(num_epochs):
model.train()
for batch_idx, (features, targets) in enumerate(train_loader):
features = features.to(device)
targets = targets.to(device)
# Forward and Backprop
logits, probas = model(features)
cost = F.cross_entropy(logits, targets)
optimizer.zero_grad()
cost.backward()
# update model paramets
optimizer.step()
# Logging
if not batch_idx % 50:
print ('Epoch: %03d/%03d | Batch %04d/%04d | Cost: %.4f'
%(epoch+1, num_epochs, batch_idx,
len(train_loader), cost))
model.eval()
with torch.set_grad_enabled(False):
print('Epoch: %03d/%03d | Train: %.3f%% ' %(
epoch+1, num_epochs,
compute_accuracy(model, train_loader)))
```
### Evaluation
```
with torch.set_grad_enabled(False):
print('Test accuracy: %.2f%%' % (compute_accuracy(model, test_loader)))
```
| true |
code
| 0.800283 | null | null | null | null |
|
```
import tensorflow as tf
from tensorflow import keras
print( 'Tensorflow : ',tf.__version__)
print( ' |-> Keras : ',keras.__version__)
```
# 5.1 - Introduction to convnets
This notebook contains the code sample found in Chapter 5, Section 1 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
----
First, let's take a practical look at a very simple convnet example. We will use our convnet to classify MNIST digits, a task that you've already been
through in Chapter 2, using a densely-connected network (our test accuracy then was 97.8%). Even though our convnet will be very basic, its
accuracy will still blow out of the water that of the densely-connected model from Chapter 2.
The 6 lines of code below show you what a basic convnet looks like. It's a stack of `Conv2D` and `MaxPooling2D` layers. We'll see in a
minute what they do concretely.
Importantly, a convnet takes as input tensors of shape `(image_height, image_width, image_channels)` (not including the batch dimension).
In our case, we will configure our convnet to process inputs of size `(28, 28, 1)`, which is the format of MNIST images. We do this via
passing the argument `input_shape=(28, 28, 1)` to our first layer.
```
from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
```
Let's display the architecture of our convnet so far:
```
model.summary()
```
You can see above that the output of every `Conv2D` and `MaxPooling2D` layer is a 3D tensor of shape `(height, width, channels)`. The width
and height dimensions tend to shrink as we go deeper in the network. The number of channels is controlled by the first argument passed to
the `Conv2D` layers (e.g. 32 or 64).
The next step would be to feed our last output tensor (of shape `(3, 3, 64)`) into a densely-connected classifier network like those you are
already familiar with: a stack of `Dense` layers. These classifiers process vectors, which are 1D, whereas our current output is a 3D tensor.
So first, we will have to flatten our 3D outputs to 1D, and then add a few `Dense` layers on top:
```
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
```
We are going to do 10-way classification, so we use a final layer with 10 outputs and a softmax activation. Now here's what our network
looks like:
```
model.summary()
```
As you can see, our `(3, 3, 64)` outputs were flattened into vectors of shape `(576,)`, before going through two `Dense` layers.
Now, let's train our convnet on the MNIST digits. We will reuse a lot of the code we have already covered in the MNIST example from Chapter
2.
```
from keras.datasets import mnist
from keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=64)
```
Let's evaluate the model on the test data:
```
test_loss, test_acc = model.evaluate(test_images, test_labels)
test_acc
```
While our densely-connected network from Chapter 2 had a test accuracy of 97.8%, our basic convnet has a test accuracy of 99.3%: we
decreased our error rate by 68% (relative). Not bad!
| true |
code
| 0.790156 | null | null | null | null |
|
# Functions - Best practices
In this notebook we will discuss a bit about what are the best practices of documenting and writing functions. These topics won't be graded but they will give you a general idea of what to do once you start developing in real-world. They are also usable throughout any programming language.
The following are just initial ideas for you to think about and use during the course. Commenting, what to comment and how to comment are open-ended discussions and different people have different opinions. Just make sure, pretty please 🙏, that you comment and document what you don't know. I can't stress this enough, **You don't know how many times people had to refactor code and redo everything just because they forgot what it did.**
## Comments
Everyone likes comments and everyone knows that they are important. Leaving comments in the code allows others to understand our thought process and allows you to return to the code, after some days, and still understand what the hell you were trying to do at that time. I know it sounds troublesome and you think that you will remember what you were doing, but trust me when I say this:
### You won't remember everything so might as well add some comments
Initially, and after reading all these warnings your thought process will likely be

But **be careful!** If you start commenting everything like in the function `adding_function` below, most of your comments will feel like noise and the important comments will be lost in the spam
```
# Example of spammy comments
def adding_function(int_1, int_2):
# This function adds two integers -> as the name and parameters already suggest, useless comment
# Adding variables a+b -> useless as well, any person that sees this knows that it's an adding operation
result = int_1 + int_2
#returns the result of the sum made above -> we know already 😂
return result
# In this case the code is very self-descriptive, so it may not need any comments really
```
When taking comments into consideration, and this will be hard at first, you need to find balance between over-commenting and commenting what is needed. Your variables should also be descriptive of what you are trying to achieve
```
import re
def sanitize_string(string):
if type(string) is not str:
# No need for a comment, you understand by the print and condition what is happening here
print("Not a string!")
return
# Wow, what the *!F$% is this next piece of code doing?
# -> Maybe I should document this for other people and myself in the future!
# regex, removes any character that is not a space, number or letter
clean_string = re.sub('[^A-Za-z0-9 ]+', '', string)
# this you probably know, but if you don't -> comment!
# It lowercases the string
return clean_string.lower()
weird_string = "^*ººHe'?llo Woç.,-rld!"
sanitize_string(weird_string)
sanitize_string(2)
```
<div>
<img alt="perfectly balanced", src="./assets/perfectly_balanced.jpeg" width="400">
</div>
Commenting is completely up to the programmer. It's **your responsability** to know what you are doing and to make sure that the people who are reading your code understand what you were doing at the time of writing!
* Use clear, descriptive variables!
* Use clear, descriptive function names - `function_one` doesn't add any information on what it does!
* If you are making any assumption inside the code - document it!
* If you are fixing an edge case (i.e., a very specific problem/condition of your solution) - document it!
* If you feel that it's not clear what you have done - leave a comment!
* Don't add comments to every line of the program describing every single thing you do, most of them probably won't add any value
## Docstrings
Python documentation strings - docstrings - are a way of providing a convenient and constant way of writing a description to any type of functions, classes and methods (the last two you will learn later on). There are several ways of writing docstrings, I'll introduce you to a specific one but in general they all tend to rotate around the same idea which is - **document and comment your function!**
Usually every function should state its purpose and give a general description of what it receives (parameters) and what it returns. Moreover, some IDEs - like VSCode, not Jupyter - already come with this option so usually if you write `"""` and click enter after a function it will create a docstring for you to fill
Example shown below
<div>
<img alt="docstring_1", src="./assets/docstring_01.png" width="600">
</div>
After pressing Enter this is what shows up!
<div>
<img alt="docstring_2", src="./assets/docstring_02.png" width="600">
</div>
Pretty cool right?! Some IDEs already give you all the tools to employ Docstrings so there is really no excuse!
**Note:** You may need to activate this feature on your IDE. For VSCode you might need to install this plugin: https://marketplace.visualstudio.com/items?itemName=njpwerner.autodocstring -> check its example for a detailed video on how to do this
Using function `sanitize_string` as an example:
```
def sanitize_string(string):
"""
Cleans a string by removing any characters that are not spaces, numbers or letters. returns it in lowercase
:param string: string to be cleaned
:return: sanitized string
"""
if type(string) is not str:
print("Not a string!")
return
# removes any character that is not a space, number or letter
clean_string = re.sub('[^A-Za-z0-9 ]+', '', string)
return clean_string.lower()
```
In conclusion, docstrings are a really good way of documenting every function you use on a program! Keeping it constant throughout all functions leads to a very organised commenting. Moreover (and this is the fun interesting part!), there are tools - like [Sphinx](https://www.sphinx-doc.org/en/master/) - that you can use that transform all these docstring comments into a web documentation page automatically!
For a real life example, the [Numpy documentation page](https://numpy.org/doc/stable/reference/) (a really valuable tool for data scientists!) was created automatically by using Sphinx with docstrings!
There are many many more stuff that can be done here but I don't want to kill you with information overload. If you focus on these two topics it will be of great help to you in the future! Thank you for reading this, have an appreciation meme!
<div>
<img alt="love_python", src="./assets/program_python.png" width="400">
</div>
| true |
code
| 0.631935 | null | null | null | null |
|
# Bayesian optimization
*Selected Topics in Mathematical Optimization: 2017-2018*
**Michiel Stock** ([email](michiel.stock@ugent.be))

```
import numpy as np
import sympy as sp
sp.init_printing()
from numpy import sin, exp, cos
from sklearn.preprocessing import normalize
from scipy.stats import norm
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
%matplotlib inline
np.random.seed(3)
blue = '#264653'
green = '#2a9d8f'
yellow = '#e9c46a'
orange = '#f4a261'
red = '#e76f51'
black = '#50514F'
```
## Motivation
**Goal**:
Solve
$$
\mathbf{x}^* = \text{arg min}_\mathbf{x}\, f(\mathbf{x})
$$
when every evaluation of $f(\mathbf{x})$ is *expensive*.
**Example 1**:
*Dark art* of selecting the right hyperparameters for a machine learning model. Ditto for many optimization methods!

**Example 2**:
*Model calibration* to find the right parameters or structure of a mechanistic model.
**Example 3**:
Experimentation for improvement (drug design, product development, new cooking recipes...):
1. Gather data
2. Make model
3. Select new experiments for testing in the lab
4. Repeat
## Leading example
Damped spring mass system.

Model:
$$
m\ddot{y}(t) + \gamma \dot{y}(t) + k y(t) = 0\,,
$$
with:
- $m$: the mass (1 kg)
- $\gamma$: friction parameter (unknown)
- $k$: the spring constant (unknown)
Can be simulated (here exact solution known).
```
def damped_oscillator(t_vals, g, k, m=1, sigma=0, x0=1):
if g**2 > 4*k*m:
l1 = (-g**2 + (g**2 - 4*k*m)**0.5) / (2 * m)
l2 = (-g**2 - (g**2 - 4*k*m)**0.5) / (2 * m)
c1, c2 = np.linalg.solve([[1, 1], [l1, l2]], [[x0], [0]]).flatten()
y_vals = c1 * exp(t_vals * l1) + c2 * exp(t_vals * l2)
elif g**2 == 4*k*m:
l1 = - g / (2 * m)
c1, c2 = np.linalg.solve([[1, 0], [l1, 1]], [[x0], [0]]).flatten()
y_vals = c1 * exp(t_vals * l1) + c2 * t_vals * exp(t_vals * l1)
else:
alpha = - g / (2 * m)
beta = (4 * m * k - g**2)**0.5 / (2 * m)
c1, c2 = np.linalg.solve([[1, 0], [alpha, beta]], [[x0], [0]]).flatten()
y_vals = exp(alpha * t_vals) * (c1 * cos(beta * t_vals) + c2 * sin(beta * t_vals))
return y_vals + np.random.randn(len(t_vals)) * sigma
fig, ax = plt.subplots()
t_vals = np.linspace(0, 5, num = 1000)
for g in np.logspace(-2, 2, num=4):
for k in np.logspace(-2, 2, num=4):
y_vals = damped_oscillator(t_vals, g=g, k=k)
ax.plot(t_vals, y_vals)
ax.set_xlabel('$t$')
ax.set_ylabel('$y(t)$')
```
## Finding the best model parameters
We perform some experiments, and have 20 noisy measurements.
```
# parameters
m=1 # known
kstar=7 # unknown
gstar=1 # unknown
# noisy observations
t_meas = np.linspace(0, 5, num=20)
y_obs = damped_oscillator(t_meas, g=gstar, k=kstar, m=m, sigma=0.15)
# true function
t_vals = np.linspace(0, 5, num = 1000)
y_vals = damped_oscillator(t_vals, g=gstar, k=kstar, m=m)
fig, ax = plt.subplots()
ax.plot(t_vals, y_vals, c=blue, label='unknown parametrized function')
ax.scatter(t_meas, y_obs, c=red, label='noisy observations')
ax.set_xlabel('$t$')
ax.set_ylabel('$y(t)$')
ax.legend(loc=0)
```
For a given $\gamma$ and $k$, compute the mean squared error:
$$
MSE(\gamma, k) = \frac{1}{20} \sum_{i=1}^{20} (y(t_i) - \hat{y}(t_i, \gamma, k))^2
$$
Best parameters obtained by:
$$
\gamma^*, k^* = \text{arg min}_{\gamma, k} MSE(\gamma, k)
$$
```
def get_mse(g, k):
"""
Computes the mean squared error for a given gamma and k.
"""
y_sim = damped_oscillator(t_meas, g=g, k=k)
return np.log10(np.mean((y_sim - y_obs)**2))
```
Since gamma and kappa are positive values for which we do not know the scale, it makes sense to work with the logarithm of these paramaters.
```
g_vals = np.logspace(-2, 2, num=100)
k_vals = np.logspace(-2, 2, num=100)
mse_pars = np.zeros((len(g_vals), len(k_vals)))
for i, g in enumerate(g_vals):
for j, k in enumerate(k_vals):
mse_pars[i, j] = get_mse(g=g, k=k)
```
Because the example is simple, we can search the complete space for the best parameters.
```
G, K = np.meshgrid(g_vals, k_vals)
fig, ax = plt.subplots(figsize=(6, 6))
ax.contourf(K, G, mse_pars.T)
ax.set_xlabel('$k$')
ax.set_ylabel('$g$')
ax.scatter(kstar, gstar, c='y')
ax.loglog()
```
In general, it is *not* possible to sample the whole parameter space. If the model is really complex, even a single evalutation might be expensive! What if we only can test a limited number of parameter combinations?
## Grid search vs. random search
```
param_grid = np.array([[g, k] for k in np.logspace(-1.5, 1.5, num=4) for g in np.logspace(-1.5, 1.5, num=4)])
param_random = 10**np.random.uniform(-2, 2, size=(16, 2))
fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 5))
ax0.scatter(param_grid[:,0], param_grid[:,1], c=red, label='samples')
ax0.set_title('Grid')
ax1.scatter(param_random[:,0], param_random[:,1], c=red, label='samples')
ax1.set_title('Random')
for ax in (ax1, ax0):
ax.scatter(kstar, gstar, c=yellow, label='optimal parameters')
ax.loglog()
ax.set_xlabel('$k$')
ax.set_ylabel('$\gamma$')
ax.set_ylim([1e-2, 1e2])
ax.set_xlim([1e-2, 1e2])
ax.legend(loc=0)
```
> **Don't use grid search!**
```
# evaluate instances
simulated_parameters = param_random
#simulated_parameters = param_grid
mse_obs = np.array([get_mse(g=g, k=k) for g, k in simulated_parameters])
mse_obs
```
## Surrogate modelling with Gaussian processes
Predict the performance of *new* parameter combinations using a surrogate model.
(From here on onwards, $\mathbf{x}\in\mathcal{X}$ is used to denote the parameters)
Gaussian process:
- learn a function of the form $f: \mathcal{X}\rightarrow \mathbb{R}$
- nonlinear model, uses a positive-definite covariance function $K:\mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}$
- Bayesian method: prior on function and use Bayes' theorem to condition on observed data
- can be updated if more date becomes available (online learning)
- fully probabilistic, in theory no tuning!
The model return for a given instance $\mathcal{x}$:
- $\mu(\mathbf{x})$: expected value;
- $\sigma(\mathbf{x})$: standard deviation.
For a brief, but well-founded overview of Gaussian processes, consult the [chapter](http://www.inference.org.uk/mackay/gpB.pdf) in the book of MacKay.
```
gaussian_process = GaussianProcessRegressor(alpha=1e-3)
# take logarithm of MSE and the parameters to obtain better scaling
gaussian_process.fit(np.log10(simulated_parameters), mse_obs)
instance = np.log10([[3, 0.1]])
mu, sigma = gaussian_process.predict(instance, return_std=True)
print('Predicted MSE: {} ({})'.format(mu[0], sigma[0]))
```
Explore whole parameter space.
```
mu_mse = np.zeros_like(mse_pars)
std_mse = np.zeros_like(mse_pars)
for i, g in enumerate(g_vals):
for j, k in enumerate(k_vals):
instance = np.log10([[g, k]])
mu, sigma = gaussian_process.predict(instance, return_std=True)
mu_mse[i, j] = mu[:]
std_mse[i, j] = sigma[:]
fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 5))
ax0.contourf(K, G, mu_mse.T)
ax0.set_title('Estimated MSE')
ax1.contourf(K, G, std_mse.T)
ax1.set_title('Std MSE')
for ax in (ax0, ax1):
ax.set_xlabel('$k$')
ax.set_ylabel('$\gamma$')
ax.loglog()
ax.scatter(kstar, gstar, c=yellow)
ax.scatter(simulated_parameters[:,0], simulated_parameters[:,1], c=red)
```
Slice for $k=1$.
```
k_slice = np.column_stack((np.logspace(-2, 2, num=100), [1]*100))
# expected mse, std
mu, sigma = gaussian_process.predict(np.log10(k_slice), return_std=True)
fig, ax = plt.subplots()
ax.plot(k_slice[:,0], mu, c=green, label='expected value')
ax.plot(k_slice[:,0], mu-2*sigma, c=orange, ls='--', label='95% interval')
ax.plot(k_slice[:,0], mu+2*sigma, c=orange, ls='--')
ax.semilogx()
ax.set_xlabel('$\gamma$')
ax.set_ylabel('predicted MSE')
ax.legend(loc=0)
```
## Acquisition functions
How to choose points to simulate/test?
Acquisition function $a:\mathcal{X}\rightarrow\mathbb{R}^+$, determines how 'interesting' a point is to explore.
Choose
$$
\mathbf{x}_\text{next} = \text{arg max}_\mathbf{x} a(\mathbf{x})\,.
$$
Trade-off between *exploration* and *exploitation*.
**Probability of Improvement**
$$
a_\text{PI}(\mathbf{x}) = P(f(\mathbf{x})<f(\mathbf{x}_\text{best}) ) = \Phi(\gamma(\mathbf{x}))\,,
$$
with $\Phi(\cdot)$ the CDF of a standard normal distirbution and
$$
\gamma(\mathbf{x})= \frac{f(x_\text{best}) - \mu(\mathbf{x})}{\sigma(\mathbf{x})}\,.
$$
```
def calculate_gamma(mu, sigma, fbest):
return (fbest - mu) / sigma
def probability_improvement(mu, sigma, fbest=np.min(mse_obs)):
"""
Calculates probability of improvement.
"""
gamma_values = calculate_gamma(mu, sigma, fbest)
return norm.cdf(gamma_values)
```
**Expected Improvement**
$$
a_\text{EI}(\mathbf{x}) = E[\max(f(\mathbf{x}) - f(\mathbf{x}_\text{best}), 0)] = \sigma(\mathbf{x})(\gamma(\mathbf{x})\Phi(\gamma(\mathbf{x})) + \phi(\gamma(\mathbf{x}))\,,
$$
with $\phi(\cdot)$ the PDF of a standard normal distirbution.
```
def expected_improvement(mu, sigma, fbest=np.min(mse_obs)):
"""
Calculates expected improvement.
"""
gamma_values = calculate_gamma(mu, sigma, fbest)
return sigma * (gamma_values * norm.cdf(gamma_values) + norm.pdf(gamma_values))
```
**GP Lower Confidence Limit**
$$
a_\text{LCB} = \mu(\mathbf{x}) - \kappa \sigma(\mathbf{x})\,,
$$
with $\kappa$ a parameter determining the tightness of the bound.
```
def lower_confidence_bound(mu, sigma, kappa=2):
"""
Calculates lower confidence bound.
Made negative: maximizing acquisition function!
"""
return - (mu - kappa * sigma)
def plot_acquisitions():
fig, (ax0, ax1, ax2, ax3) = plt.subplots(nrows=4, sharex=True, figsize=(8, 10))
# plot mu and sigma
ax0.plot(k_slice[:,0], mu, c=green, label='expected value')
ax0.plot(k_slice[:,0], mu-2*sigma, c=orange, ls='--', label='95% interval')
ax0.plot(k_slice[:,0], mu+2*sigma, c=orange, ls='--')
ax0.semilogx()
ax0.set_ylabel('predicted\nMSE')
# plot information gains
ax1.plot(k_slice[:,0], probability_improvement(mu, sigma), c=blue, label='PI')
ax1.set_ylabel('PI')
ax2.plot(k_slice[:,0], expected_improvement(mu, sigma), c=blue, label='EI')
ax2.set_ylabel('EI')
ax3.plot(k_slice[:,0], lower_confidence_bound(mu, sigma), c=blue, label='LCB')
ax3.set_ylabel('LCB')
ax3.set_xlabel('$\gamma$')
plot_acquisitions()
PI = np.zeros_like(mse_pars)
EI = np.zeros_like(mse_pars)
LCB = np.zeros_like(mse_pars)
for i, g in enumerate(g_vals):
for j, k in enumerate(k_vals):
instance = np.log10([[g, k]])
mu, sigma = gaussian_process.predict(instance, return_std=True)
mu = mu[:]
sigma = sigma[:]
PI[i,j] = probability_improvement(mu, sigma)
EI[i,j] = expected_improvement(mu, sigma)
LCB[i,j] = lower_confidence_bound(mu, sigma)
def show_acquisition_contourf(ax0, ax1, ax2):
ax0.contourf(K, G, PI.T)
ax0.set_title('PI')
ax0.scatter(simulated_parameters[:,0], simulated_parameters[:,1], c=red)
ax1.contourf(K, G, EI.T)
ax1.set_title('EI')
ax1.scatter(simulated_parameters[:,0], simulated_parameters[:,1], c=red)
ax2.contourf(K, G, LCB.T)
ax2.set_title('LCB')
ax2.scatter(simulated_parameters[:,0], simulated_parameters[:,1], c=red)
for ax in (ax0, ax1, ax2):
ax.set_xlabel('$k$')
ax.set_ylabel('$\gamma$')
ax.loglog()
ax.scatter(kstar, gstar, c=yellow)
ax.scatter(simulated_parameters[:,0], simulated_parameters[:,1], c=red)
fig, (ax0, ax1, ax2) = plt.subplots(ncols=3, figsize=(13, 5))
show_acquisition_contourf(ax0, ax1, ax2)
```
Use Gaussian process model to select new points to evaluate!
## Gradient-based optimization for finding next point
If we assume that evaluating points from the Gaussian process surogate model is much cheaper than evaluating the true function, we can either use an exhaustive sampling of this space (if the dimension is not too large) or use a gradient-based optimizer to find a maximizer of the acquisition function.
```
from scipy.optimize import minimize
neg_acquisition = lambda parameter : -probability_improvement(*gaussian_process.predict(parameter.reshape((1,2)),
return_std=True))
# start from best previous point
f0, x0 = min(zip(mse_obs, simulated_parameters))
result = minimize(neg_acquisition, x0=x0,
bounds=[(-2, 2), (-2, 2)])
xnew = result.x
result
print('New parameters to try: {}'.format(10**xnew))
```
## Concluding remarks
**Remark 1**
Gaussian process model usually continuous and differentiable w.r.t. $\mathbf{x}$:
- $\nabla \mu(\mathbf{x})$
- $\nabla \sigma(\mathbf{x})$
gradient-based optimization!
**Ramark 2**
Use of correlation between instances:
```
param_random = 10**np.random.uniform(-2, 2, size=(20, 2))
mu, cov = gaussian_process.predict(np.log10(param_random), return_cov=True)
fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(8, 4))
ax0.plot(10**mu)
ax0.set_ylabel('estimated MSE')
ax1.imshow(cov, interpolation='nearest', cmap='hot')
ax1.set_title('Covariance')
```
Use coviance to select a *set* of informative instances to explore!
**Remark 3**
Some instances will differ in execution times:
- regularization size (machine learning)
- learning rate (machine learning)
- number of parameters
- grid size approximation (mechanistic modelling)
Better optimize *expected improvement per second*. Use a model of expected duration (second Gaussian process).
## References
Snoek, J., Larochelle, H., Adams, R. '*Practical Bayesian optimization of machine learning algorithms*'. Advances in Neural Information Processing Systems (2012)
Rasmussen, C., Williams, C., '*Gaussian Processes for Machine Learning*'. The MIT Press (2006)
| true |
code
| 0.631594 | null | null | null | null |
|
# Using Amazon Elastic Inference with MXNet on an Amazon SageMaker Notebook Instance
This notebook demonstrates how to enable and utilize Amazon Elastic Inference with our predefined SageMaker MXNet containers.
Amazon Elastic Inference (EI) is a resource you can attach to your Amazon EC2 instances to accelerate your deep learning (DL) inference workloads. EI allows you to add inference acceleration to an Amazon SageMaker hosted endpoint or Jupyter notebook for a fraction of the cost of using a full GPU instance. For more information please visit: https://docs.aws.amazon.com/sagemaker/latest/dg/ei.html
This notebook is an adaption of the [SageMaker MXNet MNIST notebook](https://github.com/awslabs/amazon-sagemaker-examples/blob/master/sagemaker-python-sdk/mxnet_mnist/mxnet_mnist.ipynb), with modifications showing the changes needed to enable and use EI with MXNet on SageMaker.
1. [Using Amazon Elastic Inference with MXNet on an Amazon SageMaker Notebook Instance](#Using-Amazon-Elastic-Inference-with-MXNet-on-an-Amazon-SageMaker-Notebook-Instance)
1. [MNIST dataset](#MNIST-dataset)
1. [Setup](#Setup)
1. [The training script](#The-training-script)
1. [SageMaker's MXNet estimator class](#SageMaker's-MXNet-estimator-class)
1. [Running the Training job](#Running-the-Training-job)
1. [Creating an inference endpoint and attaching an EI accelerator](#Creating-an-inference-endpoint-and-attaching-an-EI-accelerator)
1. [How our models are loaded](#How-our-models-are-loaded)
1. [Using EI with a SageMaker notebook instance](#Using-EI-with-a-SageMaker-notebook-instance)
1. [Making an inference request locally](#Making-an-inference-request-locally)
1. [Delete the Endpoint](#Delete-the-endpoint)
If you are familiar with SageMaker and already have a trained model, skip ahead to the [Creating-an-inference-endpoint section](#Creating-an-inference-endpoint-with-EI)
For this example, we will be utilizing the SageMaker Python SDK, which makes it easy to train and deploy MXNet models. In this example, we train a simple neural network using the Apache MXNet [Module API](https://mxnet.apache.org/api/python/module/module.html) and the MNIST dataset.
### MNIST dataset
The MNIST dataset is widely used for handwritten digit classification, and consists of 70,000 labeled 28x28 pixel grayscale images of hand-written digits. The dataset is split into 60,000 training images and 10,000 test images. There are 10 classes (one for each of the 10 digits). The task at hand is to train a model using the 60,000 training images and subsequently test its classification accuracy on the 10,000 test images.
### Setup
Let's start by creating a SageMaker session and specifying the IAM role arn used to give training and hosting access to your data. See the [documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-roles.html) for how to create these. Note, if more than one role is required for notebook instances, training, and/or hosting, please replace the `sagemaker.get_execution_role()` with a the appropriate full IAM role arn string(s).
```
import sagemaker
role = sagemaker.get_execution_role()
```
This notebook shows how to use the SageMaker Python SDK to run your code in a local container before deploying to SageMaker's managed training or hosting environments. Just change your estimator's instance_type to local or local_gpu. For more information, see [local mode](https://github.com/aws/sagemaker-python-sdk#local-mode).
To use Amazon Elastic Inference locally change your `accelerator_type` to `local_sagemaker_notebook` when calling `deploy()`.
***`local_sagemaker_notebook` will only work if you created your notebook instance with an EI accelerator attached to it.***
In order to use this feature you'll need to install docker-compose (and nvidia-docker if training with a GPU). Running following script will install docker-compose or nvidia-docker-compose and configure the notebook environment for you.
Note, you can only run a single local notebook at a time.
```
!/bin/bash ./setup.sh
```
### The training script
The ``mnist_ei.py`` script provides all the code we need for training and hosting a SageMaker model. The script also checkpoints the model at the end of every epoch and saves the model graph, params and optimizer state in the folder `/opt/ml/checkpoints`. If the folder path does not exist then it will skip checkpointing. The script we will use is adaptated from Apache MXNet [MNIST tutorial](https://mxnet.incubator.apache.org/tutorials/python/mnist.html).
```
!pygmentize mnist_ei.py
```
### SageMaker's MXNet estimator class
The SageMaker ```MXNet``` estimator allows us to run single machine or distributed training in SageMaker, using CPU or GPU-based instances.
When we create the estimator, we pass in the filename of our training script, the name of our IAM execution role, and the S3 locations we defined in the setup section. We also provide a few other parameters. ``instance_count`` and ``instance_type`` determine the number and type of SageMaker instances that will be used for the training job. The ``hyperparameters`` parameter is a ``dict`` of values that will be passed to your training script -- you can see how to access these values in the ``mnist_ei.py`` script above.
For this example, we will train our model on the local instance this notebook is running on. This is achieved by using `local` for `instance_type`. By passing local, training will be done inside of a Docker container on this notebook instance.
```
from sagemaker.mxnet import MXNet
mnist_estimator = MXNet(
entry_point="mnist_ei.py",
role=role,
instance_count=1,
instance_type="local",
framework_version="1.7.0",
py_version="py3",
hyperparameters={"learning-rate": 0.1},
)
```
### Running the Training job
After we've constructed our MXNet object, we can fit it using data stored in S3. Below we run SageMaker training on two input channels: **train** and **test**.
During training, SageMaker makes this data stored in S3 available in the local filesystem where the mnist script is running. The ```mnist_ei.py``` script simply loads the train and test data from disk.
```
%%time
import boto3
region = boto3.Session().region_name
train_data_location = "s3://sagemaker-sample-data-{}/mxnet/mnist/train".format(region)
test_data_location = "s3://sagemaker-sample-data-{}/mxnet/mnist/test".format(region)
mnist_estimator.fit({"train": train_data_location, "test": test_data_location})
```
### Creating an inference endpoint and attaching an EI accelerator
After training, we use the ``MXNet`` estimator object to build and deploy an ``MXNetPredictor``. This creates a Sagemaker endpoint -- a hosted prediction service that we can use to perform inference.
The arguments to the ``deploy`` allows us to set the following:
* `instance_count` - how many instances to back the endpoint.
* `instance_type` - which EC2 instance type to use for the endpoint. For information on supported instance, please check [here](https://aws.amazon.com/sagemaker/pricing/instance-types/).
* `accelerator_type` - determines which EI accelerator type to attach to each of our instances. The supported types of accelerators can be found here: https://aws.amazon.com/sagemaker/pricing/instance-types/
### How our models are loaded
You should provide your custom `model_fn` to use EI accelerator attached to your endpoint. An example of `model_fn` implementation is as follows:
```python
def model_fn(model_dir):
ctx = mx.cpu()
sym, args, aux = mx.model.load_checkpoint(os.path.join(model_dir, 'model'), 0)
sym = sym.optimize_for('EIA')
mod = mx.mod.Module(symbol=sym, context=ctx, data_names=data_names, label_names=None)
mod.bind(for_training=False, data_shapes=data_shapes)
mod.set_params(args, aux, allow_missing=True)
return mod
```
Check ``mnist_ei.py`` above for the specific implementation of `model_fn()` in this notebook example.
In **EI MXNet 1.5.1 and earlier**, the predefined SageMaker MXNet containers have a default `model_fn`, which determines how your model is loaded. The default `model_fn` loads an MXNet Module object with a context based on the instance type of the endpoint.
If an EI accelerator is attached to your endpoint and a custom `model_fn` isn't provided, then the default `model_fn` will load the MXNet Module object. This default `model_fn` works with the default `save` function. If a custom `save` function was defined, then you may need to write a custom `model_fn` function. For more information on `model_fn`, see [this documentation for using MXNet with SageMaker](https://sagemaker.readthedocs.io/en/stable/using_mxnet.html#load-a-model).
For examples on how to load and serve a MXNet Module object explicitly, please see our [predefined default `model_fn` for MXNet](https://github.com/aws/sagemaker-mxnet-serving-container/blob/master/src/sagemaker_mxnet_serving_container/default_inference_handler.py#L36).
### Using EI with a SageMaker notebook instance
Here we're going to utilize the EI accelerator attached to our local SageMaker notebook instance. This can be done by using `local_sagemaker_notebook` as the value for `accelerator_type`. This will make an inference request against the MXNet endpoint running on this Notebook Instance with an attached EI.
An EI accelerator must be attached in order to make inferences using EI.
As of now, an EI accelerator attached to a notebook will initialize for the first deep learning framework used to inference against EI. If you wish to use EI with another deep learning framework, please either restart or create a new notebook instance with the new EI.
***`local_sagemaker_notebook` will only work if you created your notebook instance with an EI accelerator attached to it.***
***Please restart or create a new notebook instance if you wish to use EI with a different framework than the first framework used on this notebook instance as specified when calling `deploy()` with `local_sagemaker_notebook`for `accelerator_type`.***
```
%%time
predictor = mnist_estimator.deploy(
initial_instance_count=1, instance_type="local", accelerator_type="local_sagemaker_notebook"
)
```
The request handling behavior of the Endpoint is determined by the ``mnist_ei.py`` script. In this case, the script doesn't include any request handling functions, so the Endpoint will use the default handlers provided by SageMaker. These default handlers allow us to perform inference on input data encoded as a multi-dimensional JSON array.
### Making an inference request locally
Now that our Endpoint is deployed and we have a ``predictor`` object, we can use it to classify handwritten digits.
To see inference in action, draw a digit in the image box below. The pixel data from your drawing will be loaded into a ``data`` variable in this notebook.
*Note: after drawing the image, you'll need to move to the next notebook cell.*
```
from IPython.display import HTML
HTML(open("input.html").read())
```
Now we can use the ``predictor`` object to classify the handwritten digit:
```
%%time
response = predictor.predict(data)
print("Raw prediction result:")
print(response)
labeled_predictions = list(zip(range(10), response[0]))
print("Labeled predictions: ")
print(labeled_predictions)
labeled_predictions.sort(key=lambda label_and_prob: 1.0 - label_and_prob[1])
print("Most likely answer: {}".format(labeled_predictions[0]))
```
### Delete the endpoint
After you have finished with this example, remember to delete the prediction endpoint to release the instance(s) associated with it.
```
print("Endpoint name: " + predictor.endpoint)
import sagemaker
predictor.delete_endpoint()
```
| true |
code
| 0.44559 | null | null | null | null |
|
# Translator: Go from moment representation to ExpFam-representation
This task is about taking a distribution represented by its moment-parameters, translate it into the exponential family representation, and compare the two by plotting them. We will focus on Gaussians and Gamma-distributed variables here, but this exercise an be done for any exp.fam. distribution.
**Imports**
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, gamma
from scipy.special import gammaln
```
**Helper function**
Take representation of an exp.fam. distribution and a function to plot the moment-pdf
```
def plot_pdf(x, h, T, eta, A, moment_pdf):
"""
Put the pieces of an exp.fam.representation together and compare with the moment-representation.
:param x: The values for which we will evaluate the two functions
-- a list of x-values for which the pdf's are calculated
:param h: The log-base measure. This is a *function* that can be evaluated at any x, and for each x return a scalar
:param T: The sufficient statistics function. This is again a *Æfunction*. Takes a vector as input and
return a matrix (the vector of sufficient statistics for each value of the x-vector)
:param eta: Natural parameters. This is a vector, constant in x so not a function.
:param A: The log partition function. This is defined by the parameterization,
hence not a function in the implementation.
:param moment_pdf: A function that generates the pdf using moment parameters (so, a "pointer" to a built-in)
:return: Nothing.
"""
log_exp_fam = h(x) + np.matmul(eta, T(x)) - A # Put together the log-pdf of the exp.fam. distribution
plt.plot(x, np.exp(log_exp_fam), "b-") # Plot it
plt.plot(x, moment_pdf(x), "r--") # Plot the "gold-standard"
plt.title('Moment PDF (red) and ExpFam pdf (blue). Hopefully identical')
plt.show()
```
## EXAMPLE: GAUSSIAN
**Define the starting-point**, that is, define the moment-parameters, the range for which 98% of the probability mass resides, and the pdf-function
```
# Moment parameters
sigma = 3.
mu = -1.
# Choose x to cover most of the are where the distribution has probability mass
x = np.linspace(norm.ppf(0.01, loc=mu, scale=sigma),
norm.ppf(0.99, loc=mu, scale=sigma), 25)
# The comparison: Gauss pdf using the moment parameters
def normal_pdf_function(x):
return norm.pdf(x, loc=mu, scale=sigma)
```
### Define the exp.fam. representation
**Log base measure:** For the Gaussian, $h(x) = -.5\log(2\pi)$. It is constant in $x$ for the Gaussian distribution,
but is defined as a function in the implementation anyway, because the log base measure is a function in general.
```
def log_base_measure_func(x):
return -.5 * np.log(2*np.pi)
```
**Sufficient statistics:** For the gaussian, $T(x) = [x, x^2]$. Note that if
`x` is a vector/list this function should return an array
```
def T_func(x):
# Define storage space
ans = np.zeros((2, x.shape[0]))
# Fill in values
ans[0, :] = x
ans[1, :] = x * x
return ans
```
**Natural parameters:** Defined from the moment parameters, and for the Gaussian it is
$[\frac{\mu}{\sigma^2}, -\frac{1}{2\sigma^2}]$.
```
natural_parameters = np.array([mu/(sigma*sigma), -.5/(sigma*sigma)])
```
**Log partition function:** Can be defined from moment parameters $(\mu, \sigma)$
or alternatively from natural parameters. Here we use $A=\frac{\mu^2}{2\sigma^2} + \log|\sigma|$.
```
log_partition = mu*mu/(2*sigma*sigma) + np.log(sigma)
```
### Plot the exp-fam we generated, and compare to the moment-parameterized PDF
Note how functions are passed on, e.g. `h=log_base_measure_func` will ensure that `h(x)`can be called from `plot_pdf` with the `x` that is defined in the scope fo that function.
```
plot_pdf(x=x, h=log_base_measure_func, T=T_func,
eta=natural_parameters, A=log_partition,
moment_pdf=normal_pdf_function)
```
## And now the Gamma-distruibution
Start by setting up. We can later play with alpha and beta
```
# Moment parameters
alpha = 2.
beta = 3.
# Choose x as the range that covers 98% prob.mass
x = np.linspace(gamma.ppf(0.01, a=alpha, scale=1/beta),
gamma.ppf(0.99, a=alpha, scale=1/beta), 25)
# Calculate moment-parameter pdf
def gamma_pdf_func(x):
return gamma.pdf(x, a=alpha, scale=1/beta)
```
### Make the ExpFam representation
Information about the Gamma can be found
[here](https://en.wikipedia.org/wiki/Exponential_family#Table_of_distributions "here")
or in the slides.
```
# Log base measure: $h(x) = 0$. It is constant in x, but is defined as a function anyway
def log_base_measure_func(x):
return 0
# Sufficient statistics: $T(x) = [\log(x), x]$.
# If x is an array this function should return an array
def T_func(x):
# Define storage space
ans = np.zeros((2, x.shape[0]))
# Fill in values
ans[0, :] = np.log(x)
ans[1, :] = x
return ans
# Natural parameters: Defined from the moment parameters
natural_parameters = np.array([alpha - 1, -beta])
# Log partition function. Can be defined from moment parameters alpha, beta
# or alternatively from natural parameters [eta1, eta2]
log_partition = gammaln(alpha) - alpha * np.log(beta)
```
**Test by generating a plot**
```
plot_pdf(x=x, h=log_base_measure_func, T=T_func,
eta=natural_parameters, A=log_partition, moment_pdf=gamma_pdf_func)
```
| true |
code
| 0.782714 | null | null | null | null |
|
<img src="https://upload.wikimedia.org/wikipedia/en/a/a1/Visma_logo.jpg"
align="right"
width="30%"
alt="Visma logo">
Semi supervised learning (Still under development!)
=============
<img src="http://www.rm.dk/siteassets/regional-udvikling/digitalisering/dabai/dabai-logo.png"
align="right"
width="20%"
alt="DABAI logo">
The first set of methods cover the principals from the following summary: http://sci2s.ugr.es/ssl
A batch-generative method, consisting of Kmeans and Logistic Regression, is implemented to cover a naive approach. This experiment is compared to a baseline whice consists of only Logistic Regression.
```
%run -i initilization.py
from pyspark.sql import functions as F
from pyspark.ml import clustering
from pyspark.ml import feature
from pyspark.sql import DataFrame
from pyspark.sql import Window
from pyspark.ml import Pipeline
from pyspark.ml import classification
from pyspark.ml.evaluation import BinaryClassificationEvaluator
from pyspark.ml.tuning import ParamGridBuilder, CrossValidator
from shared import Plot2DGraphs, create_dummy_data
from semisupervised import batch_generative_model
```
##### Add some parameters in order to generate a dataset
```
mean_1 = [3.0, 3.0]
std_1 = [2, 2]
mean_2 = [-3.0, -3.0]
std_2 = [1. , 1.0]
n_1 = 300
n_2 = 300
n = [n_1, n_2]
mean = [mean_1, mean_2]
std = [std_1, std_2]
```
### An initial method to semi supervised learning
The following cells are ment to be a data creation method along with an initial try on generate model for semi supervised learning.
```
def compute_error_rate(data_frame, truth_label='real_label', found_label='prediction'):
"""
"""
df_stats = (data_frame
.groupBy([truth_label, found_label])
.agg(F.count('prediction').alias('Prediction Count'))
)
n = (df_stats
.select(F.sum(F.col('Prediction Count')).alias('n'))
.collect()[0]['n']
)
wrong_guess = (df_stats
.filter((F.col(truth_label) != F.col(found_label)))
.select(F.sum(F.col('Prediction Count')).alias('errors'))
.collect()[0]['errors']
)
df_stats.show()
print(n)
print(wrong_guess)
print('Error-rate: {}'.format(wrong_guess/n))
```
###### Create the labled dataset, and with 1% used lables and the rest is set to NAN.
```
tester = create_dummy_data.create_labeled_data_with_clusters(n, mean, std, 0.01)
df_tester = spark.createDataFrame(tester)
```
The dataset with lables and available lables plotted
```
Plot2DGraphs.plot_known_and_unknown_data(tester)
```
###### The initial try at classifying the data, using logistic regression
```
df_train = df_tester.filter((F.col('used_label') != np.NaN))
df_test = df_tester.filter((F.col('used_label') == np.NaN))
vec_assembler = feature.VectorAssembler(
inputCols=['x','y'],
outputCol='features')
lg = classification.LogisticRegression(
featuresCol=vec_assembler.getOutputCol(),
labelCol='used_label')
pipeline = Pipeline(stages=[vec_assembler, lg])
# CrossValidation gets build here!
param_grid = (ParamGridBuilder()
.addGrid(lg.regParam, [0.1, 0.01])
.build()
)
evaluator = BinaryClassificationEvaluator(
rawPredictionCol=lg.getRawPredictionCol(),
labelCol=lg.getLabelCol())
cross_validator = CrossValidator(
estimator=pipeline,
estimatorParamMaps=param_grid,
evaluator=evaluator,
numFolds=3)
cross_validator_model = cross_validator.fit(df_train)
df_without_semisupervised = cross_validator_model.transform(df_test)
Plot2DGraphs.plot_known_and_unknown_data(
df_without_semisupervised.toPandas(),
labelCol='prediction')
compute_error_rate(df_without_semisupervised)
```
##### Lets take a look at the semi supervised approach
This simplifyed version uses KMeans and Logistic Regression. In the future, the obvious thing to do is either create a user active system or use an ensembled approach
```
df_output = batch_generative_model.semi_supervised_batch_single_classifier_generate_approach(df_tester,['x','y'])
df_output.limit(5).toPandas()
compute_error_rate(df_output)
Plot2DGraphs.plot_known_and_unknown_data(df_output.toPandas(), labelCol='prediction')
df = spark.read.parquet('/home/svanhmic/workspace/data/DABAI/sparkdata/parquet/double_helix.parquet/')
df.write.csv('/home/svanhmic/workspace/data/DABAI/sparkdata/csv/double_helix.csv/')
```
| true |
code
| 0.490358 | null | null | null | null |
|
# Using EMI-FastGRNN on the HAR Dataset
This is a very simple example of how the existing EMI-FastGRNN implementation can be used on the HAR dataset. We illustrate how to train a model that predicts on 48 step sequence in place of the 128 length baselines while attempting to predict early. For more advanced use cases which involves more sophisticated computation graphs or loss functions, please refer to the doc strings provided with the released code.
In the preprint of our work, we use the terms *bag* and *instance* to refer to the RNN input sequence of original length and the shorter ones we want to learn to predict on, respectively. In the code though, *bag* is replaced with *instance* and *instance* is replaced with *sub-instance*. We will use the term *instance* and *sub-instance* interchangeably.
The network used here is a simple RNN + Linear classifier network.
The UCI [Human Activity Recognition](https://archive.ics.uci.edu/ml/datasets/human+activity+recognition+using+smartphones) dataset.
```
from __future__ import print_function
import os
import sys
import tensorflow as tf
import numpy as np
sys.path.insert(0, '../../')
os.environ['CUDA_VISIBLE_DEVICES'] ='1'
# FastGRNN and FastRNN imports
from edgeml.graph.rnn import EMI_DataPipeline
from edgeml.graph.rnn import EMI_FastGRNN
from edgeml.graph.rnn import EMI_FastRNN
from edgeml.trainer.emirnnTrainer import EMI_Trainer, EMI_Driver
import edgeml.utils
```
Let us set up some network parameters for the computation graph.
```
# Network parameters for our FastGRNN + FC Layer
NUM_HIDDEN = 16
NUM_TIMESTEPS = 48
NUM_FEATS = 9
FORGET_BIAS = 1.0
NUM_OUTPUT = 6
USE_DROPOUT = False
KEEP_PROB = 0.9
# Non-linearities can be chosen among "tanh, sigmoid, relu, quantTanh, quantSigm"
UPDATE_NL = "quantTanh"
GATE_NL = "quantSigm"
# Ranks of Parameter matrices for low-rank parameterisation to compress models.
WRANK = 5
URANK = 6
# For dataset API
PREFETCH_NUM = 5
BATCH_SIZE = 32
# Number of epochs in *one iteration*
NUM_EPOCHS = 3
# Number of iterations in *one round*. After each iteration,
# the model is dumped to disk. At the end of the current
# round, the best model among all the dumped models in the
# current round is picked up..
NUM_ITER = 4
# A round consists of multiple training iterations and a belief
# update step using the best model from all of these iterations
NUM_ROUNDS = 10
# A staging direcory to store models
MODEL_PREFIX = '/tmp/models/model-fgrnn'
```
# Loading Data
Please make sure the data is preprocessed to a format that is compatible with EMI-RNN. `tf/examples/EMI-RNN/fetch_har.py` can be used to download and setup the HAR dataset.
```
# Loading the data
x_train, y_train = np.load('./HAR/48_16/x_train.npy'), np.load('./HAR/48_16/y_train.npy')
x_test, y_test = np.load('./HAR/48_16/x_test.npy'), np.load('./HAR/48_16/y_test.npy')
x_val, y_val = np.load('./HAR/48_16/x_val.npy'), np.load('./HAR/48_16/y_val.npy')
# BAG_TEST, BAG_TRAIN, BAG_VAL represent bag_level labels. These are used for the label update
# step of EMI/MI RNN
BAG_TEST = np.argmax(y_test[:, 0, :], axis=1)
BAG_TRAIN = np.argmax(y_train[:, 0, :], axis=1)
BAG_VAL = np.argmax(y_val[:, 0, :], axis=1)
NUM_SUBINSTANCE = x_train.shape[1]
print("x_train shape is:", x_train.shape)
print("y_train shape is:", y_train.shape)
print("x_test shape is:", x_val.shape)
print("y_test shape is:", y_val.shape)
```
# Computation Graph

The *EMI-RNN* computation graph is constructed out of the following three mutually disjoint parts ('modules'):
1. `EMI_DataPipeline`: An efficient data input pipeline that using the Tensorflow Dataset API. This module ingests data compatible with EMI-RNN and provides two iterators for a batch of input data, $x$ and label $y$.
2. `EMI_RNN`: The 'abstract' `EMI-RNN` class defines the methods and attributes required for the forward computation graph. An implementation based on FastGRNN - `EMI_FastGRNN` is used in this document, though the user is free to implement his own computation graphs compatible with `EMI-RNN`. This module expects two Dataset API iterators for $x$-batch and $y$-batch as inputs and constructs the forward computation graph based on them. Every implementation of this class defines an `output` operation - the output of the forward computation graph.
3. `EMI_Trainer`: An instance of `EMI_Trainer` class which defines the loss functions and the training routine. This expects an `output` operator from an `EMI-RNN` implementation and attaches loss functions and training routines to it.
To build the computation graph, we create an instance of all the above and then connect them together.
Note that, the `EMI_FastGRNN` class is an implementation that uses an FastGRNN cell and pushes the FastGRNN output at each step to a secondary classifier for classification. This secondary classifier is not implemented as part of `EMI_FastGRNN` and is left to the user to define by overriding the `createExtendedGraph` method, and the `restoreExtendedgraph` method.
For the purpose of this example, we will be using a simple linear layer as a secondary classifier.
```
# Define the linear secondary classifier
def createExtendedGraph(self, baseOutput, *args, **kwargs):
W1 = tf.Variable(np.random.normal(size=[NUM_HIDDEN, NUM_OUTPUT]).astype('float32'), name='W1')
B1 = tf.Variable(np.random.normal(size=[NUM_OUTPUT]).astype('float32'), name='B1')
y_cap = tf.add(tf.tensordot(baseOutput, W1, axes=1), B1, name='y_cap_tata')
self.output = y_cap
self.graphCreated = True
def restoreExtendedGraph(self, graph, *args, **kwargs):
y_cap = graph.get_tensor_by_name('y_cap_tata:0')
self.output = y_cap
self.graphCreated = True
def feedDictFunc(self, keep_prob=None, inference=False, **kwargs):
if inference is False:
feedDict = {self._emiGraph.keep_prob: keep_prob}
else:
feedDict = {self._emiGraph.keep_prob: 1.0}
return feedDict
EMI_FastGRNN._createExtendedGraph = createExtendedGraph
EMI_FastGRNN._restoreExtendedGraph = restoreExtendedGraph
if USE_DROPOUT is True:
EMI_FastGRNN.feedDictFunc = feedDictFunc
inputPipeline = EMI_DataPipeline(NUM_SUBINSTANCE, NUM_TIMESTEPS, NUM_FEATS, NUM_OUTPUT)
emiFastGRNN = EMI_FastGRNN(NUM_SUBINSTANCE, NUM_HIDDEN, NUM_TIMESTEPS, NUM_FEATS, wRank=WRANK, uRank=URANK,
gate_non_linearity=GATE_NL, update_non_linearity=UPDATE_NL, useDropout=USE_DROPOUT)
emiTrainer = EMI_Trainer(NUM_TIMESTEPS, NUM_OUTPUT, lossType='xentropy')
```
Now that we have all the elementary parts of the computation graph setup, we connect them together to form the forward graph.
```
tf.reset_default_graph()
g1 = tf.Graph()
with g1.as_default():
# Obtain the iterators to each batch of the data
x_batch, y_batch = inputPipeline()
# Create the forward computation graph based on the iterators
y_cap = emiFastGRNN(x_batch)
# Create loss graphs and training routines
emiTrainer(y_cap, y_batch)
```
# EMI Driver
The `EMI_Driver` implements the `EMI_RNN` algorithm. For more information on how the driver works, please refer to `tf/docs/EMI-RNN.md`. Note that, during the training period, the accuracy printed is instance level accuracy with the current label information as target. Bag level accuracy, with which we are actually concerned, is calculated after the training ends.
```
with g1.as_default():
emiDriver = EMI_Driver(inputPipeline, emiFastGRNN, emiTrainer)
emiDriver.initializeSession(g1)
y_updated, modelStats = emiDriver.run(numClasses=NUM_OUTPUT, x_train=x_train,
y_train=y_train, bag_train=BAG_TRAIN,
x_val=x_val, y_val=y_val, bag_val=BAG_VAL,
numIter=NUM_ITER, keep_prob=KEEP_PROB,
numRounds=NUM_ROUNDS, batchSize=BATCH_SIZE,
numEpochs=NUM_EPOCHS, modelPrefix=MODEL_PREFIX,
fracEMI=0.5, updatePolicy='top-k', k=1)
```
# Evaluating the trained model

## Accuracy
Since the trained model predicts on a smaller 48-step input while our test data has labels for 128 step inputs (i.e. bag level labels), evaluating the accuracy of the trained model is not straight forward. We perform the evaluation as follows:
1. Divide the test data also into sub-instances; similar to what was done for the train data.
2. Obtain sub-instance level predictions for each bag in the test data.
3. Obtain bag level predictions from sub-instance level predictions. For this, we use our estimate of the length of the signature to estimate the expected number of sub-instances that would be non negative - $k$ illustrated in the figure. If a bag has $k$ consecutive sub-instances with the same label, that becomes the label of the bag. All other bags are labeled negative.
4. Compare the predicted bag level labels with the known bag level labels in test data.
## Early Savings
Early prediction is accomplished by defining an early prediction policy method. This method receives the prediction at each step of the learned FastGRNN for a sub-instance as input and is expected to return a predicted class and the 0-indexed step at which it made this prediction. This is illustrated below in code.
```
# Early Prediction Policy: We make an early prediction based on the predicted classes
# probability. If the predicted class probability > minProb at some step, we make
# a prediction at that step.
def earlyPolicy_minProb(instanceOut, minProb, **kwargs):
assert instanceOut.ndim == 2
classes = np.argmax(instanceOut, axis=1)
prob = np.max(instanceOut, axis=1)
index = np.where(prob >= minProb)[0]
if len(index) == 0:
assert (len(instanceOut) - 1) == (len(classes) - 1)
return classes[-1], len(instanceOut) - 1
index = index[0]
return classes[index], index
def getEarlySaving(predictionStep, numTimeSteps, returnTotal=False):
predictionStep = predictionStep + 1
predictionStep = np.reshape(predictionStep, -1)
totalSteps = np.sum(predictionStep)
maxSteps = len(predictionStep) * numTimeSteps
savings = 1.0 - (totalSteps / maxSteps)
if returnTotal:
return savings, totalSteps
return savings
k = 2
predictions, predictionStep = emiDriver.getInstancePredictions(x_test, y_test, earlyPolicy_minProb, minProb=0.99)
bagPredictions = emiDriver.getBagPredictions(predictions, minSubsequenceLen=k, numClass=NUM_OUTPUT)
print('Accuracy at k = %d: %f' % (k, np.mean((bagPredictions == BAG_TEST).astype(int))))
print('Additional savings: %f' % getEarlySaving(predictionStep, NUM_TIMESTEPS))
# A slightly more detailed analysis method is provided.
df = emiDriver.analyseModel(predictions, BAG_TEST, NUM_SUBINSTANCE, NUM_OUTPUT)
```
## Picking the best model
The `EMI_Driver.run()` method, upon finishing, returns a list containing information about the best models after each EMI-RNN round. This can be used to identify the best model (based on validation accuracy) at the end of each round - illustrated below.
```
devnull = open(os.devnull, 'r')
for val in modelStats:
round_, acc, modelPrefix, globalStep = val
emiDriver.loadSavedGraphToNewSession(modelPrefix, globalStep, redirFile=devnull)
predictions, predictionStep = emiDriver.getInstancePredictions(x_test, y_test, earlyPolicy_minProb,
minProb=0.99, keep_prob=1.0)
bagPredictions = emiDriver.getBagPredictions(predictions, minSubsequenceLen=k, numClass=NUM_OUTPUT)
print("Round: %2d, Validation accuracy: %.4f" % (round_, acc), end='')
print(', Test Accuracy (k = %d): %f, ' % (k, np.mean((bagPredictions == BAG_TEST).astype(int))), end='')
print('Additional savings: %f' % getEarlySaving(predictionStep, NUM_TIMESTEPS))
```
| true |
code
| 0.694847 | null | null | null | null |
|
# Feature Selection
* ` skelearn.feaeture_selection ` module can be used for feature selection / dimensionality reduction.
* This helps to imporve the accuracy score or performance while dealing with large dimensional data.
https://scikit-learn.org/stable/modules/feature_selection.html
## Removing features with low variance
* Variance thresholding method can be used to remove features having low variance.
* Set a particular variance threshold for a given attribute.
* ` VarianceThreshold ` will remove the column having variance less than the given threshold.
* By default ` VarianceThreshold ` removes the columns having zero variance.
```
from sklearn.feature_selection import VarianceThreshold
X = [[0,0,1], [0,1,0], [1,0,0], [0,1,1], [0,1,0], [0,1,1]]
sel = VarianceThreshold(threshold = 0.16)
sel.fit_transform(X)
```
## Univariate Feature Selection
* Univariate Feature Selection works by considering statistical tests.
* It is prepreocessing step before estimator
* Use the ` SelectBest ` and apply ` fit_transform `
* ` Select_best ` removes all the ` k ` highest scoring features
* ` SelectPercentile ` removes all but a user-specified highest scoring percentage of feature.
* Using common univariate statistical tests for each feature: false positive rate ` SelectFpr `, false discovery rate ` SelectFdr `, or famaily wise error ` SelectFwe `
* Let us perform $ \chi^2 $ test to the samples to retrieve only the two best features
```
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
iris = load_iris()
X, y = iris.data, iris.target
print(X.shape)
SB = SelectKBest(chi2, k=2)
X_new = SB.fit_transform(X,y)
print(X_new.shape)
```
* These objects take input a scoring function and return univariate scores or p-values
* Some guidelines: -
* For regresiion: - `f_regrssion` , ` mutual_info_regression `
* For classification: - ` chi2 ` , ` f_classif `, ` mutual_info_classif `
* The methods based on F-test estimate the degree of linear dependency between two random varaibles.
* Mututal information methods can capture any kind of statistical dependency, but they are non parametric and require more samples for accurate estimation
## Recursive Feature Elimination
* Given an external estimator that assigns weights to features, recursive feature elimination is to select features by recursively considering smaller and smaller sets of features.
* First, the estimator is trained on the inital set of features and the importance of the features is obtained using the ` coef_ ` method or through the ` feature_importances_ ` attribute.
* Then, the least important features are pruned from current set of features.
* This procedure is repeated on the pruned set unitil the desired number of features to be selected are eventually reached.
### E.g. Recursive feature elimination
```
from sklearn.datasets import make_friedman1
from sklearn.feature_selection import RFE
from sklearn.svm import SVR
X,y = make_friedman1(n_samples = 50, n_features=10, random_state = 0)
estimator = SVR(kernel = 'linear')
print(X.shape)
# The classifier must support the coef_ or feature_importances_ attributes
# Estimator denotes the estimator which we are using
# n_feaures denotes the maximum number of features that we are want to choose
# step denotes the amount of features to be removed at end of every iteration
selector = RFE(estimator, n_features_to_select= 5, step=1)
selector = selector.fit(X,y)
# Use selector.support_ do display the mask of features, that is which features were selected
print(selector.support_)
# Use selectior.ranking_ to correspond to the ranking of the ith position of the feature
# Best features are ranked as 1
print(selector.ranking_)
```
### E.g. Recursive feature elimination using cross-validation
Feature ranking using cross-validation selection of best number of features
```
from sklearn.datasets import make_friedman1
from sklearn.feature_selection import RFECV
from sklearn.svm import SVR
X, y = make_friedman1(n_samples = 50, n_features = 10, random_state=0)
estimator = SVR(kernel = 'linear')
# cv denotes number of times we do cross_validation
selector = RFECV(estimator, min_features_to_select=5, cv = 5)
selector = selector.fit(X,y)
selector.support_
selector.ranking_
```
## Feature selection using SelectFromModel
* ` SelectFromModel ` is a meta-transformer that helps can be used with any estimator having ` coef_ ` or ` features_importance_ ` attribute after fitting.
* The features are considered unimportant are removed, if the corresponding `coef_` or ` features_importance_ ` values are below the providied ` threshold ` parameter.
* Apart from specifying the threshold numerically, there are built-in hueristics for finding for finding a threshold using a string argument such as "mean", "mode" or "median".
### L1-based feature Selection
* Linear models penalized with L1 norm have sparse solutions.
* When the goal is to reduce the dimensionality of the data to use with another classifier then they can be used along with the ` feature_selection.SelectFromModel ` to select the non-zero coefficients.
* In particular, sparse estimators useful for this purpose are the 1 ` linear_model.Lasso ` for regression, and of ` linear_model.LogisticRegression `and ` svm.LinearSVC ` for classification
```
from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
iris = load_iris()
X,y = iris.data, iris.target
print(X.shape)
lsvc = LinearSVC(C = 0.01, penalty = "l1", dual = False, max_iter = 2500)
lsvc = lsvc.fit(X,y)
# Estimator contains the name of estimator we are trying to fit
# Whether a prefit model is expected to be passed into the constructor directly or not.
# If True, transform must be called directly and SelectFromModel cannot be used with cross_val_score,
# GridSearchCV and similar utilities that clone the estimator.
# Otherwise train the model using fit and then transform to do feature selection.
model = SelectFromModel(lsvc, prefit = True)
X_new = model.transform(X)
print(X_new.shape)
```
* With SVMs and logistic-regression, the parameter C controls the sparsity: the smaller C the fewer features selected.
* With Lasso, the higher the alpha parameter, the fewer features selected.
### Tree-based feature Selection
* Tree-based estimator can be used to compute the feature importances which in turn can be used to dicared the irrelevant features
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
iris = load_iris()
X, y = iris.data, iris.target
print(X.shape)
clf = RandomForestClassifier(n_estimators=100, n_jobs = -1, random_state=0)
clf = clf.fit(X,y)
clf.feature_importances_
model = SelectFromModel(clf, threshold = 0.3, prefit = True)
X_new = model.transform(X)
print(X_new.shape)
```
## Feature Selection as Part of ML Pipeline
* Feature selection is usually used as a prepreocessing step before doing actual learning.
* Recommended way to do this is use ` sklearn.pipeline.Pipeline `
```
from sklearn.pipeline import Pipeline
clf = Pipeline([
('feature_selection', SelectFromModel(LinearSVC(max_iter = 8000))),
('classification', RandomForestClassifier(n_estimators = 100))
])
clf = clf.fit(X,y)
```
* In this snippet we make use of `sklearn.svm.LinearSVC` with ` SelectfromModel `.
* ` SelectfromModel ` selects the important feature and passes it to `RandomForestClassifier`.
* `RandomForestClassifer` trains only on the relevant input given by the pipeline
| true |
code
| 0.806338 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/TeachingTextMining/TextClassification/blob/main/01-SA-Pipeline/01-SA-Pipeline-Reviews.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Entrenamiento y ejecución de un pipeline de clasificación textual
La clasificación de textos consiste en, dado un texto, asignarle una entre varias categorías. Algunos ejemplos de esta tarea son:
- dado un tweet, categorizar su connotación como positiva, negativa o neutra.
- dado un post de Facebook, clasificarlo como portador de un lenguaje ofensivo o no.
En la actividad exploraremos cómo crear un pipeline y entrenarlo para clasificar reviews de [IMDB](https://www.imdb.com/) sobre películas en las categorías \[$positive$, $negative$\]
Puede encontrar más información sobre este problema en [Kaggle](https://www.kaggle.com/lakshmi25npathi/imdb-dataset-of-50k-movie-reviews) y en [Large Movie Review Datase](http://ai.stanford.edu/~amaas/data/sentiment/).
**Instrucciones:**
- siga las indicaciones y comentarios en cada apartado.
**Después de esta actividad nos habremos familiarizado con:**
- algunos tipos de características ampliamente utilizadas en la clasificación de textos.
- cómo construir un pipeline para la clasificación de textos utilizando [scikit-learn](https://scikit-learn.org/stable/).
- utilizar este pipeline para clasificar nuevos textos.
**Requerimientos**
- python 3.6 - 3.8
- pandas
- plotly
<a name="sec:setup"></a>
### Instalación de librerías e importación de dependencias.
Para comenzar, es preciso instalar e incluir las librerías necesarias. En este caso, el entorno de Colab incluye las necesarias.
Ejecute la siguiente casilla prestando atención a las explicaciones dadas en los comentarios.
```
# reset environment
%reset -f
# para construir gráficas y realizar análisis exploratorio de los datos
import plotly.graph_objects as go
import plotly.figure_factory as ff
import plotly.express as px
# para cargar datos y realizar pre-procesamiento básico
import pandas as pd
from collections import Counter
# para pre-procesamiento del texto y extraer características
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from nltk.stem.snowball import EnglishStemmer
# algoritmos de clasificación
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import BernoulliNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
# para construir pipelines
from sklearn.pipeline import Pipeline
# para evaluar los modelos
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix, roc_curve, auc
from sklearn.utils.multiclass import unique_labels
# para guardar el modelo
import pickle
print('Done!')
```
#### Definición de funciones y variables necesarias para el pre-procesamiento de datos
Antes de definir el pipeline definiremos algunas variables útiles como el listado de stop words y funciones para cargar los datos, entrenar el modelo etc.
```
#listado de stopwords. Este listado también se puede leer desde un fichero utilizando la función read_corpus
stop_words=['i','me','my','myself','we','our','ours','ourselves','you','your','yours','yourself','yourselves',
'he','him','his','himself','she','her','hers','herself','it','its','itself','they','them','their',
'theirs','themselves','what','which','who','whom','this','that','these','those','am','is','are',
'was','were','be','been','being','have','has','had','having','do','does','did','doing','a','an',
'the','and','but','if','or','because','as','until','while','of','at','by','for','with','about',
'against','between','into','through','during','before','after','above','below','to','from','up',
'down','in','out','on','off','over','under','again','further','then','once','here','there','when',
'where','why','how','all','any','both','each','few','more','most','other','some','such','no','nor',
'not','only','own','same','so','than','too','very','s','t','can','will','just','don','should','now', 'ever']
# función auxiliar utilizada por CountVectorizer para procesar las frases
def english_stemmer(sentence):
stemmer = EnglishStemmer()
analyzer = CountVectorizer(binary=False, analyzer='word', stop_words=stop_words,
ngram_range=(1, 1)).build_analyzer()
return (stemmer.stem(word) for word in analyzer(sentence))
# guarda un pipeline entrenado
def save_model(model, modelName = "pickle_model.pkl"):
pkl_filename = modelName
with open(pkl_filename, 'wb') as file:
pickle.dump(model, file)
# carga un pipeline entrenado y guardado previamente
def load_model(rutaModelo = "pickle_model.pkl"):
# Load from file
with open(rutaModelo, 'rb') as file:
pickle_model = pickle.load(file)
return pickle_model
# función auxiliar para realizar predicciones con el modelo
def predict_model(model, data, pref='m'):
"""
data: list of the text to predict
pref: identificador para las columnas (labels_[pref], scores_[pref]_[class 1], etc.)
"""
res = {}
scores = None
labels = model.predict(data)
if hasattr(model, 'predict_proba'):
scores = model.predict_proba(data)
# empaquetar scores dentro de un diccionario que contiene labels, scores clase 1, scores clase 2, .... El nombre de la clase se normaliza a lowercase
res = {f'scores_{pref}_{cls.lower()}':score for cls, score in zip(model.classes_, [col for col in scores.T])}
# añadir datos relativos a la predicción
res[f'labels_{pref}'] = labels
# convertir a dataframe ordenando las columnas primero el label y luego los scores por clase, las clases ordenadas alfabeticamente.
res = pd.DataFrame(res, columns=sorted(list(res.keys())))
return res
# función auxiliar que evalúa los resultados de una clasificación
def evaluate_model(y_true, y_pred, y_score=None, pos_label='positive'):
"""
"""
print('==== Sumario de la clasificación ==== ')
print(classification_report(y_true, y_pred))
print('Accuracy -> {:.2%}\n'.format(accuracy_score(y_true, y_pred)))
# graficar matriz de confusión
display_labels = sorted(unique_labels(y_true, y_pred), reverse=True)
cm = confusion_matrix(y_true, y_pred, labels=display_labels)
z = cm[::-1]
x = display_labels
y = x[::-1].copy()
z_text = [[str(y) for y in x] for x in z]
fig_cm = ff.create_annotated_heatmap(z, x=x, y=y, annotation_text=z_text, colorscale='Viridis')
fig_cm.update_layout(
height=400, width=400,
showlegend=True,
margin={'t':150, 'l':0},
title={'text' : 'Matriz de Confusión', 'x':0.5, 'xanchor': 'center'},
xaxis = {'title_text':'Valor Real', 'tickangle':45, 'side':'top'},
yaxis = {'title_text':'Valor Predicho', 'tickmode':'linear'},
)
fig_cm.show()
# curva roc (definido para clasificación binaria)
fig_roc = None
if y_score is not None:
fpr, tpr, thresholds = roc_curve(y_true, y_score, pos_label=pos_label)
fig_roc = px.area(
x=fpr, y=tpr,
title={'text' : f'Curva ROC (AUC={auc(fpr, tpr):.4f})', 'x':0.5, 'xanchor': 'center'},
labels=dict(x='Ratio Falsos Positivos', y='Ratio Verdaderos Positivos'),
width=400, height=400
)
fig_roc.add_shape(type='line', line=dict(dash='dash'), x0=0, x1=1, y0=0, y1=1)
fig_roc.update_yaxes(scaleanchor="x", scaleratio=1)
fig_roc.update_xaxes(constrain='domain')
fig_roc.show()
print('Done!')
```
### Carga de datos y análisis exploratorio
Antes de entrenar el pipeline, es necesario cargar los datos. Existen diferentes opciones, entre estas:
- montar nuestra partición de Google Drive y leer un fichero desde esta.
- leer los datos desde un fichero en una carpeta local.
- leer los datos directamente de un URL.
Ejecute la siguiente casilla prestando atención a las instrucciones adicionales en los comentarios.
```
# descomente las siguientes 3 líneas para leer datos desde Google Drive, asumiendo que se trata de un fichero llamado review.csv localizado dentro de una carpeta llamada 'Datos' en su Google Drive
#from google.colab import drive
#drive.mount('/content/drive')
#path = '/content/drive/MyDrive/Datos/ejemplo_review_train.csv'
# descomente la siguiente línea para leer los datos desde un archivo local, por ejemplo, asumiendo que se encuentra dentro de un directorio llamado sample_data
#path = './sample_data/ejemplo_review_train.csv'
# descomente la siguiente línea para leer datos desde un URL
path = 'https://github.com/TeachingTextMining/TextClassification/raw/main/01-SA-Pipeline/sample_data/ejemplo_review_train.csv'
# leer los datos
data = pd.read_csv(path, sep=',')
print('Done!')
```
Una vez leídos los datos, ejecute la siguiente casilla para construir una gráfica que muestra la distribución de clases en el corpus.
```
text_col = 'Phrase' # columna del dataframe que contiene el texto (depende del formato de los datos)
class_col = 'Sentiment' # columna del dataframe que contiene la clase (depende del formato de los datos)
# obtener algunas estadísticas sobre los datos
categories = sorted(data[class_col].unique(), reverse=False)
hist= Counter(data[class_col])
print(f'Total de instancias -> {data.shape[0]}')
print(f'Distribución de clases -> {{item[0]:round(item[1]/len(data[class_col]), 3) for item in sorted(hist.items(), key=lambda x: x[0])}}')
print(f'Categorías -> {categories}')
print(f'Comentario de ejemplo -> {data[text_col][0]}')
print(f'Categoría del comentario -> {data[class_col][0]}')
fig = go.Figure(layout=go.Layout(height=400, width=600))
fig.add_trace(go.Bar(x=categories, y=[hist[cat] for cat in categories]))
fig.show()
print('Done!')
```
Finalmente, ejecute la siguiente casilla para crear los conjuntos de entrenamiento y validación que se utilizarán para entrenar y validar los modelos.
```
# obtener conjuntos de entrenamiento (90%) y validación (10%)
seed = 0 # fijar random_state para reproducibilidad
train, val = train_test_split(data, test_size=.1, stratify=data[class_col], random_state=seed)
print('Done!')
```
### Creación de un pipeline para la clasificación de textos
Para construir el pipeline, utilizaremos la clase Pipeline de sklean. Esta permite encadenar los diferentes pasos, por ejemplo, algoritmos de extracción de características y un clasificador. Por ejemplo, para obtener un pipeline que comprende CountVectorizer, seguido de TfidfTransformer y un Support Vector Machine como clasificador, se utilizaría esta sentencia:
~~~
Pipeline([
('dataVect', CountVectorizer(analyzer=english_stemmer)),
('tfidf', TfidfTransformer(smooth_idf=True, use_idf=True)),
(classifier, SVC(probability=True) )
])
~~~
Para tener mayor flexibilidad si se desean probar varios clasificadores, podría construirse el pipeline sin clasificador, incluyendo este con posterioridad. Este será el enfoque que seguiremos en la actividad.
Ejecute la siguiente casilla para definir una función que construye un pipeline con las características antes mencionadas.
```
def preprocess_pipeline():
return Pipeline([
('dataVect', CountVectorizer(analyzer=english_stemmer)),
('tfidf', TfidfTransformer(smooth_idf=True, use_idf=True)),
])
print('Done!')
```
### Entrenamiento del modelo
Ejecute la siguiente casilla que integra todas las funciones definidas para construir el pipeline, entrenarlo y guardarlo para su posterior uso.
```
# crear el pipeline (solo incluyendo los pasos de pre-procesamiento)
model = preprocess_pipeline()
# crear el clasificador y añadirlo al model. Puede probar diferentes clasificadores
# classifier = MultinomialNB()
# classifier = DecisionTreeClassifier()
classifier = SVC(probability=True)
model.steps.append(('classifier', classifier))
# obtener conjuntos de entrenamiento (90%) y validación (10%)
seed = 0 # fijar random_state para reproducibilidad
train, val = train_test_split(data, test_size=.1, stratify=data[class_col], random_state=seed)
# entrenar el modelo
model.fit(train[text_col], train[class_col])
# guardar el modelo
save_model(model)
print('Done!')
```
### Evaluación del modelo
Luego de entrenado el modelo, podemos evaluar su desempeño en los conjuntos de entrenamiento y validación.
Ejecute la siguiente casilla para evaluar el modelo en el conjunto de entrenamiento.
```
# predecir y evaluar el modelo en el conjunto de entrenamiento
print('==== Evaluación conjunto de entrenamiento ====')
data = train
true_labels = data[class_col]
m_pred = predict_model(model, data[text_col].to_list(), pref='m')
# el nombre de los campos dependerá de pref al llamar a predic_model y las clases. Ver comentarios en la definición de la función
evaluate_model(true_labels, m_pred['labels_m'], m_pred['scores_m_positive'], 'positive')
print('Done!')
```
Ejecute la siguiente casilla para evaluar el modelo en el conjunto de validación. Compare los resultados.
```
# predecir y evaluar el modelo en el conjunto de validación
print('==== Evaluación conjunto de validación ====')
data = val
true_labels = data[class_col]
m_pred = predict_model(model, data[text_col].to_list(), pref='m')
# el nombre de los campos dependerá de pref al llamar a predic_model y las clases. Ver comentarios en la definición de la función
evaluate_model(true_labels, m_pred['labels_m'], m_pred['scores_m_positive'], 'positive')
print('Done!')
```
## Predicción de nuevos datos
Una vez entrenado el modelo, podemos evaluar su rendimiento en datos no utilizados durante el entrenamiento o emplearlo para predecir nuevas instancias. En cualquier caso, se debe cuidar realizar los pasos de pre-procesamiento necesarios según el caso. En el ejemplo, utilizaremos la porción de prueba preparada inicialmente.
**Notar que**:
- se cargará el modelo previamente entrenado y guardado, estableciendo las configuraciones pertinentes.
- si disponemos de un modelo guardado, podremos ejecutar directamente esta parte del cuaderno. Sin embargo, será necesario al menos ejecutar previamente la sección [Instalación de librerías...](#sec:setup)
### Instanciar modelo pre-entrenado
Para predecir nuevas instancias es preciso cargar el modelo previamente entrenado. Esto dependerá del formato en el que se exportó el modelo, pero en general se requieren dos elementos: la estructura del modelo y los pesos.
Ejecute la siguiente casilla para cargar el modelo.
```
# cargar pipeline entrenado
model = load_model()
print('Done!')
```
### Predecir nuevos datos
Con el modelo cargado, es posible utilizarlo para analizar nuevos datos.
Ejecute las siguientes casillas para:
(a) categorizar un texto de muestra.
(b) cargar nuevos datos, categorizarlos y mostrar algunas estadísticas sobre el corpus.
```
# ejemplo de texto a clasificar en formato [text 1, text 2, ..., text n]
text = ['Brian De Palma\'s undeniable virtuosity can\'t really camouflage the fact that his plot here is a thinly disguised\
\"Psycho\" carbon copy, but he does provide a genuinely terrifying climax. His "Blow Out", made the next year, was an improvement.']
# predecir los nuevos datos.
m_pred = predict_model(model, text, pref='m')
# el nombre de los campos dependerá de pref al llamar a predic_model y las clases. Ver comentarios en la definición de la función
pred_labels = m_pred['labels_m'].values[0]
pred_proba = m_pred['scores_m_positive'].values[0]
print(f'La categoría del review es -> {pred_labels}')
print(f'El score asignado a la clase positiva es -> {pred_proba:.2f}')
print('Done!')
```
También podemos predecir nuevos datos cargados desde un fichero.
Ejecute la siguiente casilla, descomentando las instrucciones necesarias según sea el caso.
```
# descomente las siguientes 3 líneas para leer datos desde Google Drive, asumiendo que se trata de un fichero llamado review.csv localizado dentro de una carpeta llamada 'Datos' en su Google Drive
#from google.colab import drive
#drive.mount('/content/drive')
#path = '/content/drive/MyDrive/Datos/ejemplo_review_train.csv'
# descomente la siguiente línea para leer los datos desde un archivo local, por ejemplo, asumiendo que se encuentra dentro de un directorio llamado sample_data
#path = './sample_data/ejemplo_review_train.csv'
# descomente la siguiente línea para leer datos desde un URL
path = 'https://github.com/TeachingTextMining/TextClassification/raw/main/01-SA-Pipeline/sample_data/ejemplo_review_test.csv'
# leer los datos
new_data = pd.read_csv(path, sep=',')
print('Done!')
```
Ejecute la siguiente celda para predecir los datos y mostrar algunas estadísticas sobre el análisis realizado.
```
# predecir los datos de prueba
text_col = 'Phrase'
m_pred = predict_model(model, new_data[text_col].to_list(), pref='m')
pred_labels = m_pred['labels_m']
# obtener algunas estadísticas sobre la predicción en el conjunto de pruebas
categories = sorted(pred_labels.unique(), reverse=False)
hist = Counter(pred_labels.values)
fig = go.Figure(layout=go.Layout(height=400, width=600))
fig.add_trace(go.Bar(x=categories, y=[hist[cat] for cat in categories]))
fig.show()
print('Done!')
```
| true |
code
| 0.448306 | null | null | null | null |
|
Jeff's initial writeup -- 2019_01_21
## Comparing molecule loading using RDKit and OpenEye
It's really important that both RDKitToolkitWrapper and OpenEyeToolkitWrapper load the same file to equivalent OFFMol objects. If the ToolkitWrappers don't create the same OFFMol from a single file/external molecule representation, it's possible that the OpenForceField toolkit will assign the same molecule different parameters depending on whether OE or RDK is running on the backend(1). This notebook is designed to help us see which molecule formats can be reliably loaded using both toolkits.
The first test that is performed is loading from 3D. We have OpenEye load `MiniDrugBank_tripos.mol2`. RDKit can not load mol2, but can load SDF, so I've used openbabel(2) to convert `MiniDrugBank_tripos.mol2` to SDF (`MiniDrugBank.sdf`), and then we have RDKit load that.
### How do we compare whether two OFFMols are equivalent?
This is, surprisingly, an unresolved question. "Equivalent" for our purposes means "would have the same SMIRKS-based parameters applied, for any valid SMIRKS". Since we don't have an `offxml` file containing parameters for all valid SMIRKS (because there are infinity valid SMIRKS, and because we'd also need an infinitely large molecule test set to contain representatives of all those infinity substructures), I'd like to find some sort of test other than SMIRKS matching that will answer this question.
This notebook uses three comparison methods:
1. **graph isomorphism**: Convert the molecules to NetworkX graphs where nodes are atoms (described by element, is_aromatic, stereochemistry) and the edges are bonds (described by order, is_aromatic, stereochemistry). Then test to see if the graphs are isomorphic.
2. **SMILES comparison using OpenEye**: Convert each OFFMol to an OEMol, and then write them to canonical, isomeric, explicit hydrogen SMILES(3). Test for string equality.
3. **SMILES comparison using RDKit**: Convert each OFFMol to an RDMol, and then write them to canonical, isomeric, explicit hydrogen SMILES. Test for string equality.
_As a note for future efforts, it's possible that, since each SMILES is also a valid SMIRKS, we could test for equality between OFFMol_1 and OFFMol_2 by seeing if OFFMol_1's SMILES is found in a SMIRKS substructure search of OFFMol_2, and vice versa._
Each of these has some weaknesses.
* Graph isomorphism may be too strict -- eg. a toolkit may mess with the kekule structure around aromatic systems, selecting different resonance forms of bond networks. This would result in a chemically equivalent structure that fails an isomorphism test involving bond orders.
* SMILES mismatches are hard to debug. Are the original OFFMols really meaningfully different? Or is our `to_rdkit`. or `to_openeye` function not implemented correctly? Or is the mismatch due to some strange toolkit quirk or quiet sanitization that goes on?
### What if RDK and OE get different representations when loading from 3D?
This isn't the end of the world. We'd just remove SDF from RDKit's `ALLOWED_READ_FORMATS` list(4). RDKit's main input method would then just be SMILES. But actually we should ensure that...
### At a minimum, RDKit and OpenEye should be able to get the same OFFMol from the same SMILES
My initial thought here is that we could have both toolkits load molecules from a SMILES database. "I converted `MiniDrugBank_tripos.mol2` to SDF so RDKit could read it, why not convert it to SMILES too?".
**But conversion from 3D to SMILES requires either OpenEye or RDKit**, which relies on their 3D molecule interpretation being correct... which is what we're testing here in the first place!
So, I couldn't think of a clear resolution to this problem.
For background, Shuzhe Wang did some really good foundational work on toolkit molecule perception equivalence earlier in this project. Shuzhe's successful test of force field parameter application equivalence (5) used OE to load a test databse, convert the molecules to SMILES, and then had RDKit load those SMILES. It then tested whether the OE-loaded molecule and the RDKit-loaded molecule got identical force field parameters assigned. But this didn't test whether RDKit can load from 3D, just from SMILES. And not just any SMILES -- SMILES that came from OpenEye (including any sneaky sanitizaton that it could have done when loading from 3D). And since we didn't have a toolkit-independent molecule representation then (no OFFMols), he tested whether both molecules got the same force field parameters applied, which suffers from the "our current SMIRKS may not be fine-grained enough to catch all meaningful molecule differences" problem.
Shuzhe's approach does highlight one way to get a test database of SMILES -- Load a 3D database using OpenEyeToolkitWrapper, then write all the resulting OFFMols to SMILES, and then have RDKitToolkitWrapper read all the SMILES and create OFFMols, then test whether both sets of OFFMols are identical.
And, in case OE's molecule santiization is making us end up with unusually clean SMILES, we can do the same test in reverse -- that is, use RDKitToolkitWrapper to load a 3D SDF, write the resulting OFFMols to SMILES, and then have OpenEyeToolkitWrapper read the SMILES, and compare the resulting OFFMols.
## What this notebook does
#### This notebook creates four OFFMol test sets:
1. **`oe_mols_from 3d`**: The results of calling `OFFMol.from_file('MiniDrugBank_tripos.mol2', toolkit_registry=an_oe_toolkit_wrapper)`.
2. **`rdk_mols_from 3d`**: The results of calling `OFFMol.from_file('MiniDrugBank.sdf', toolkit_registry=a_rdk_toolkit_wrapper)`.
3. **`rdk_mols_from_smiles_from_oe_mols_from_3d`**: The result of taking `oe_mols_from_3d`, converting them all to SMILES using OpenEyeToolkitWrapper, then reading SMILES to OFFMols using RDKitToolkitWrapper.
4. **`oe_mols_from_smiles_from_rdk_mols_from_3d`**: The result of taking `rdk_mols_from_3d`, converting them all to SMILES using RDKitToolkitWrapper, then reading SMILES to OFFMols using OpenEyeToolkitWrapper.
#### This notebook then compares the OFFMol test sets using three methods (same as above):
1. Graph isomorphism
2. OFFMol.to_smiles() using OpenEyeToolkitWrapper
3. OFFMol.to_smiles using RDKitToolkitWrapper
## Results
When the notebook is run using the current codebase, the important outputs are as follows:
```
In comparing oe_mols_from_3d to rdk_mols_from_3d, I found 284 graph matches, 293 OE SMILES matches (26 comparisons errored), and 293 RDKit SMILES matches (7 comparisons errored) out of 346 molecules
```
This is the core test that we wanted to do (loading the same molecules from 3D), and these are pretty good results. We pass the strictest test (graph isomorphism) for 284 out of 346 molecules. We see the the SMILES tests are a little more forgiving, both giving 293/346 successes.
```
In comparing oe_mols_from_3d to rdk_mols_from_smiles_from_oe_mols_from_3d, I found 293 graph matches, 293 OE SMILES matches (26 comparisons errored), and 332 RDKit SMILES matches (0 comparisons errored) out of 365 molecules
```
```
In comparing oe_mols_from_smiles_from_rdk_mols_from_3d to rdk_mols_from_3d, I found 310 graph matches, 219 OE SMILES matches (0 comparisons errored), and 304 RDKit SMILES matches (7 comparisons errored) out of 319 molecules
```
## Conclusions
Based on this test, we can expect identical parameterization between RDKit and OpenEye ToolkitWrappers at least 82% (284/346) of the time. The real number is likely to be higher, as the SMILES comparisons are more realistic measures of identity. Also, this limit assumes infinitely specific SMIRKS.
Passing molecules **FROM** rdkit **TO** OE is troublesome largely because rdkit won't recognize stereo around trivalent nitrogens, whereas OE will. See discussion about "how much stereochemistry info do we want specified" here: https://github.com/openforcefield/openforcefield/issues/146
## Further work
There is low-hanging fruit that will improve reliability.
To continue debugging differences between OE and RDK, consider setting the "verbose" argument to `compare_mols_using_smiles` to True in the final cell of this workbook. Or, look at the molecule loading errors during dataset construction and add logic to catch those cases.
#### Footnotes
(1) Some molecule perception differences will be covered up by the fact that our SMIRKSes are somewhat coarse-grained currently (one SMIRKS can cover a lot of chemical space). But, this won't always be the case, as we may add finer-grained SMIRKS later. So, taking care of toolkit perception differences now can keep us from getting "surprised" in the future.
(2)`conda list` --> `openbabel 1!2.4.0 py37_2 omnia`
(3) `OFFMol.to_smiles()` actually operates by converting the OFFMol to an OEMol or RDMol (depending on which toolkit is available), and then uses the respective toolkit to create a SMILES. You can control which toolkit is used by instantialing an `openforcefield.utils.toolkits.OpenEyeToolkitWrapper` or `RDKitToolkitWrapper`, and passing it as the `toolkit_registry` argument to `to_smiles` (eg. `OFFMol.to_smiles(toolkit_registry=my_toolkit_wrapper)`)
(4) If they really wanted to load from SDF using RDKit, a determined OFF toolkit user could just make an RDMol manually from SDK (`Chem.MolSupplierFromFile()` or something like that), and then run the molecules through `RDKitToolkitWrapper.from_rdkit()` to get OFFMol. However, this would put the burden of correct chemical perception _on them_.
(5) https://github.com/openforcefield/openforcefield/blob/swang/examples/forcefield_modification/RDKitComparison.ipynb, search for `molecules =`
```
from openff.toolkit.utils.toolkits import RDKitToolkitWrapper, OpenEyeToolkitWrapper, UndefinedStereochemistryError
from openff.toolkit.utils import get_data_file_path
import difflib
OETKW = OpenEyeToolkitWrapper()
RDKTKW = RDKitToolkitWrapper()
```
### Load molecules from SDF using RDKit
```
from openff.toolkit.topology.molecule import Molecule
from rdkit import Chem
rdk_mols_from_3d = Molecule.from_file(get_data_file_path('molecules/MiniDrugBank.sdf'),
toolkit_registry = RDKTKW,
file_format='sdf',
allow_undefined_stereo=True)
# Known loading problems (numbers mean X: "DrugBank_X"):
# Pre-condition violations ("Stereo atoms should be specified...") for 3787 and 2684 are due to R-C=C=C-R motifs
# Sanitization errors:
# Nitro : 2799, 5415, 472, 794, 3739, 1570, 1802, 4865, 2465
# C#N : 3046, 3655, 1594, 6947, 2467
# C-N(=O)(C) : 6353
# Complicated aromatic situation with nitrogen?: 1659, 1661(?), 7049
# Unknown: 4346
```
### Load 3D molecules from Mol2 using OpenEye
```
# NBVAL_SKIP
from openff.toolkit.topology import Molecule
#molecules = Molecule.from_file(get_data_file_path('molecules/MiniDrugBank.sdf'),
oe_mols_from_3d = Molecule.from_file(get_data_file_path('molecules/MiniDrugBank_tripos.mol2'),
toolkit_registry = OETKW,
file_format='sdf',
allow_undefined_stereo=False)
```
### Convert each OE-derived OFFMol to SMILES, and then use RDKitToolkitWrapper to read the SMILES.
```
# NBVAL_SKIP
rdk_mols_from_smiles_from_oe_mols_from_3d = []
for oe_mol in oe_mols_from_3d:
if oe_mol is None:
continue
smiles = oe_mol.to_smiles(toolkit_registry=OETKW)
try:
new_mol = Molecule.from_smiles(smiles,
toolkit_registry=RDKTKW,
hydrogens_are_explicit=True
)
new_mol.name = oe_mol.name
rdk_mols_from_smiles_from_oe_mols_from_3d.append(new_mol)
except Exception as e:
print(smiles)
print(e)
print()
pass
```
### Convert each RDKit-derived OFFMol to SMILES, and then use OpeneyeToolkitWrapper to read the SMILES.
```
oe_mols_from_smiles_from_rdk_mols_from_3d = []
for rdk_mol in rdk_mols_from_3d:
try:
smiles = rdk_mol.to_smiles(toolkit_registry=RDKTKW)
new_mol = Molecule.from_smiles(smiles,
toolkit_registry=OETKW,
hydrogens_are_explicit=True
)
new_mol.name = rdk_mol.name
oe_mols_from_smiles_from_rdk_mols_from_3d.append(new_mol)
except UndefinedStereochemistryError as e:
print(smiles)
print(e)
print()
pass
```
### Define a few helper functions for molecule comparison
```
def print_smi_difference(mol_name,
smi_1, smi_2,
smi_1_label='OE: ',
smi_2_label='RDK:'):
print(mol_name)
print(smi_1_label, smi_1)
print(smi_2_label, smi_2)
differences = list(difflib.ndiff(smi_1, smi_2))
msg = ''
for i,s in enumerate(differences):
if s[0]==' ':
continue
elif s[0]=='-':
msg += u'Delete "{}" from position {}\n'.format(s[-1],i)
elif s[0]=='+':
msg += u'Add "{}" to position {}\n'.format(s[-1],i)
# Sometimes the diffs get really big. Skip printing in those cases
if msg.count('\n') < 5:
print(msg)
print()
def compare_mols_using_smiles(mol_1, mol_2,
toolkit_wrapper,
mol_1_label,
mol_2_label,
verbose=False):
mol_1_smi = mol_1.to_smiles(toolkit_registry=toolkit_wrapper)
mol_2_smi = mol_2.to_smiles(toolkit_registry=toolkit_wrapper)
if mol_1_smi == mol_2_smi:
return True
else:
if verbose:
print_smi_difference(mol_1.name,
mol_1_smi, mol_2_smi,
smi_1_label=mol_1_label,
smi_2_label=mol_2_label)
return False
def compare_mols_using_nx(mol_1, mol_2):
return mol_1 == mol_2
```
### And perform the actual comparisons
```
# NBVAL_SKIP
mol_sets_to_compare = ((('oe_mols_from_3d', oe_mols_from_3d),
('rdk_mols_from_3d', rdk_mols_from_3d)),
#(('oe_mols_from_smiles', oe_mols_from_smiles),
# ('rdk_mols_from_smiles', rdk_mols_from_smiles)),
(('oe_mols_from_3d', oe_mols_from_3d),
('rdk_mols_from_smiles_from_oe_mols_from_3d', rdk_mols_from_smiles_from_oe_mols_from_3d)),
(('oe_mols_from_smiles_from_rdk_mols_from_3d', oe_mols_from_smiles_from_rdk_mols_from_3d),
('rdk_mols_from_3d', rdk_mols_from_3d)),
)
for (set_1_name, mol_set_1), (set_2_name, mol_set_2) in mol_sets_to_compare:
set_1_name_to_mol = {mol.name:mol for mol in mol_set_1 if not(mol is None)}
set_2_name_to_mol = {mol.name:mol for mol in mol_set_2 if not(mol is None)}
names_in_common = set(set_1_name_to_mol.keys()) & set(set_2_name_to_mol.keys())
print()
print()
print()
print('There are {} molecules in the {} set'.format(len(mol_set_1), set_1_name))
print('There are {} molecules in the {} set'.format(len(mol_set_2), set_2_name))
print('These sets have {} molecules in common'.format(len(names_in_common)))
graph_matches = 0
rdk_smiles_matches = 0
oe_smiles_matches = 0
errored_graph_comparisons = 0
errored_rdk_smiles_comparisons = 0
errored_oe_smiles_comparisons = 0
for name in names_in_common:
set_1_mol = set_1_name_to_mol[name]
set_2_mol = set_2_name_to_mol[name]
nx_match = compare_mols_using_nx(set_1_mol, set_2_mol)
if nx_match:
graph_matches += 1
try:
rdk_smi_match = compare_mols_using_smiles(set_1_mol, set_2_mol,
RDKTKW,
'OE--(RDKTKW)-->SMILES: ','RDK--(RDKTKW)-->SMILES:',
verbose = False)
if rdk_smi_match:
rdk_smiles_matches += 1
except Exception as e:
errored_rdk_smiles_comparisons += 1
print(e)
try:
#if 1:
oe_smi_match = compare_mols_using_smiles(set_1_mol, set_2_mol,
OETKW,
'OE--(OETKW)-->SMILES: ','RDK--(OETKW)-->SMILES:',
verbose = False)
if oe_smi_match:
oe_smiles_matches += 1
except:
errored_oe_smiles_comparisons += 1
print("In comparing {} to {}, I found {} graph matches, {} OE SMILES matches ({} comparisons errored), and " \
"{} RDKit SMILES matches ({} comparisons errored) out of {} molecules".format(set_1_name,
set_2_name,
graph_matches,
rdk_smiles_matches,
errored_rdk_smiles_comparisons,
oe_smiles_matches,
errored_oe_smiles_comparisons,
len(names_in_common)))
```
| true |
code
| 0.224183 | null | null | null | null |
|
# logging
- 파이썬을 처음 배울 땐, 로그를 print문으로 남겼지만(이 당시에 이게 로그 개념인지도 몰랐음) 점점 서비스나 어플리케이션이 커지면 남기는 로그가 많아지고 관리도 어려워집니다
- 이를 위해 로그 관련 라이브러리들이 만들어졌습니다. 대표적으로 파이썬 내장 모듈인 logging이 있습니다
- 용도
- 현재 상태보기
- 버그 추적
- 로그 분석(빈도 확인)
## 로그 생성하기
```
import logging
import time
logging.basicConfig(level=logging.DEBUG)
logger = logging.getLogger("test")
```
### log level
- DEBUG : 상세한 정보가 필요시, 보통 디버깅이나 문제 분석시 사용
- INFO : 동작이 절차에 따라 진행되고 있는지 관찰할 때 사용
- WARNING : 어떤 문제가 조만간 발생할 조짐이 있을 경우 사용(디스크 용량 부족)
- ERROR : 프로그램에 문제가 발생해 기능 일부가 동작하지 않을 경우
- CRITICAL : 심각한 문제가 발생해 시스템이 정상적으로 동작할 수 없을 경우
```
logger.debug("debug message")
logger.info("info message {a}".format(a=1))
logger.warning("Warn message")
logger.error("error message")
logger.critical("critical!!!!")
dir(logger)
```
### 로그 생성 시간 추가하고 싶은 경우
```
mylogger = logging.getLogger("my")
mylogger.setLevel(logging.INFO)
formatter = logging.Formatter('%(asctime)s - %(name)s - %(levelname)s - %(message)s')
stream_hander = logging.StreamHandler()
stream_hander.setFormatter(formatter)
mylogger.addHandler(stream_hander)
file_handler = logging.FileHandler('my.log')
mylogger.addHandler(file_handler)
mylogger.info("server start")
```
### 로그 저장
```
logging.basicConfig(filename="test.log",
filemode='a',
level=logging.DEBUG)
```
# init
```
import logging
import optparse
LOGGING_LEVELS = {'critical': logging.CRITICAL,
'error': logging.ERROR,
'warning': logging.WARNING,
'info': logging.INFO,
'debug': logging.DEBUG}
def init():
parser = optparse.OptionParser()
parser.add_option('-l', '--logging-level', help='Logging level')
parser.add_option('-f', '--logging-file', help='Logging file name')
(options, args) = parser.parse_args()
logging_level = LOGGING_LEVELS.get(options.logging_level, logging.NOTSET)
logging.basicConfig(level=logging_level, filename=options.logging_file,
format='%(asctime)s %(levelname)s: %(message)s',
datefmt='%Y-%m-%d %H:%M:%S')
logging.debug("디버깅용 로그~~")
logging.info("도움이 되는 정보를 남겨요~")
logging.warning("주의해야되는곳!")
logging.error("에러!!!")
logging.critical("심각한 에러!!")
import logging
import logging.handlers
# 로거 인스턴스를 만든다
logger = logging.getLogger('mylogger')
# 포매터를 만든다
fomatter = logging.Formatter('[%(levelname)s|%(filename)s:%(lineno)s] %(asctime)s > %(message)s')
# 스트림과 파일로 로그를 출력하는 핸들러를 각각 만든다.
fileHandler = logging.FileHandler('./myLoggerTest.log')
streamHandler = logging.StreamHandler()
# 각 핸들러에 포매터를 지정한다.
fileHandler.setFormatter(fomatter)
streamHandler.setFormatter(fomatter)
# 로거 인스턴스에 스트림 핸들러와 파일핸들러를 붙인다.
logger.addHandler(fileHandler)
logger.addHandler(streamHandler)
# 로거 인스턴스로 로그를 찍는다.
logger.setLevel(logging.DEBUG)
logger.debug("===========================")
logger.info("TEST START")
logger.warning("스트림으로 로그가 남아요~")
logger.error("파일로도 남으니 안심이죠~!")
logger.critical("치명적인 버그는 꼭 파일로 남기기도 하고 메일로 발송하세요!")
logger.debug("===========================")
logger.info("TEST END!")
```
| true |
code
| 0.235746 | null | null | null | null |
|
# Anna KaRNNa
In this notebook, we'll build a character-wise RNN trained on Anna Karenina, one of my all-time favorite books. It'll be able to generate new text based on the text from the book.
This network is based off of Andrej Karpathy's [post on RNNs](http://karpathy.github.io/2015/05/21/rnn-effectiveness/) and [implementation in Torch](https://github.com/karpathy/char-rnn). Also, some information [here at r2rt](http://r2rt.com/recurrent-neural-networks-in-tensorflow-ii.html) and from [Sherjil Ozair](https://github.com/sherjilozair/char-rnn-tensorflow) on GitHub. Below is the general architecture of the character-wise RNN.
<img src="assets/charseq.jpeg" width="500">
```
import time
from collections import namedtuple
import numpy as np
import tensorflow as tf
```
First we'll load the text file and convert it into integers for our network to use. Here I'm creating a couple dictionaries to convert the characters to and from integers. Encoding the characters as integers makes it easier to use as input in the network.
```
with open('anna.txt', 'r') as f:
text=f.read()
vocab = sorted(set(text))
vocab_to_int = {c: i for i, c in enumerate(vocab)}
int_to_vocab = dict(enumerate(vocab))
encoded = np.array([vocab_to_int[c] for c in text], dtype=np.int32)
```
Let's check out the first 100 characters, make sure everything is peachy. According to the [American Book Review](http://americanbookreview.org/100bestlines.asp), this is the 6th best first line of a book ever.
```
text[:100]
```
And we can see the characters encoded as integers.
```
encoded[:100]
```
Since the network is working with individual characters, it's similar to a classification problem in which we are trying to predict the next character from the previous text. Here's how many 'classes' our network has to pick from.
```
len(vocab)
```
## Making training mini-batches
Here is where we'll make our mini-batches for training. Remember that we want our batches to be multiple sequences of some desired number of sequence steps. Considering a simple example, our batches would look like this:
<img src="assets/sequence_batching@1x.png" width=500px>
<br>
We start with our text encoded as integers in one long array in `encoded`. Let's create a function that will give us an iterator for our batches. I like using [generator functions](https://jeffknupp.com/blog/2013/04/07/improve-your-python-yield-and-generators-explained/) to do this. Then we can pass `encoded` into this function and get our batch generator.
The first thing we need to do is discard some of the text so we only have completely full batches. Each batch contains $N \times M$ characters, where $N$ is the batch size (the number of sequences) and $M$ is the number of steps. Then, to get the total number of batches, $K$, we can make from the array `arr`, you divide the length of `arr` by the number of characters per batch. Once you know the number of batches, you can get the total number of characters to keep from `arr`, $N * M * K$.
After that, we need to split `arr` into $N$ sequences. You can do this using `arr.reshape(size)` where `size` is a tuple containing the dimensions sizes of the reshaped array. We know we want $N$ sequences (`batch_size` below), let's make that the size of the first dimension. For the second dimension, you can use `-1` as a placeholder in the size, it'll fill up the array with the appropriate data for you. After this, you should have an array that is $N \times (M * K)$.
Now that we have this array, we can iterate through it to get our batches. The idea is each batch is a $N \times M$ window on the $N \times (M * K)$ array. For each subsequent batch, the window moves over by `n_steps`. We also want to create both the input and target arrays. Remember that the targets are the inputs shifted over one character.
The way I like to do this window is use `range` to take steps of size `n_steps` from $0$ to `arr.shape[1]`, the total number of steps in each sequence. That way, the integers you get from `range` always point to the start of a batch, and each window is `n_steps` wide.
> **Exercise:** Write the code for creating batches in the function below. The exercises in this notebook _will not be easy_. I've provided a notebook with solutions alongside this notebook. If you get stuck, checkout the solutions. The most important thing is that you don't copy and paste the code into here, **type out the solution code yourself.**
```
def get_batches(arr, batch_size, n_steps):
'''Create a generator that returns batches of size
batch_size x n_steps from arr.
Arguments
---------
arr :N*M*K: Array you want to make batches from
batch_size :N: Batch size, the number of sequences per batch
n_steps :M: Number of sequence steps per batch
n_batches :K: Total number of batches
'''
# Get the number of characters per batch and number of batches we can make
characters_per_batch = batch_size * n_steps
## 내 답
#n_batches = floor(len(arr) / characters_per_batch)
#floor, / 보다는 // 가 더 좋겠죠.
n_batches = len(arr) // characters_per_batch
# Keep only enough characters to make full batches
arr = arr[:characters_per_batch*n_batches]
# Reshape into batch_size rows
arr = arr.reshape((batch_size,-1))
for n in range(0, arr.shape[1], n_steps):
# The features
x = arr[:,n:n+n_steps] # 세로는 전부, 가로는 n ~ n+n_step까지
# The targets, shifted by one
y_temp = arr[:,n+1:n+n_steps+1]
y = np.zeros(x.shape, dtype = x.dtype)
y[:,:y_temp.shape[1]] = y_temp
yield x, y
```
Now I'll make my data sets and we can check out what's going on here. Here I'm going to use a batch size of 10 and 50 sequence steps.
```
batches = get_batches(encoded, 10, 50)
x, y = next(batches)
print('x\n', x[:10, :10])
print('\ny\n', y[:10, :10])
```
If you implemented `get_batches` correctly, the above output should look something like
```
x
[[55 63 69 22 6 76 45 5 16 35]
[ 5 69 1 5 12 52 6 5 56 52]
[48 29 12 61 35 35 8 64 76 78]
[12 5 24 39 45 29 12 56 5 63]
[ 5 29 6 5 29 78 28 5 78 29]
[ 5 13 6 5 36 69 78 35 52 12]
[63 76 12 5 18 52 1 76 5 58]
[34 5 73 39 6 5 12 52 36 5]
[ 6 5 29 78 12 79 6 61 5 59]
[ 5 78 69 29 24 5 6 52 5 63]]
y
[[63 69 22 6 76 45 5 16 35 35]
[69 1 5 12 52 6 5 56 52 29]
[29 12 61 35 35 8 64 76 78 28]
[ 5 24 39 45 29 12 56 5 63 29]
[29 6 5 29 78 28 5 78 29 45]
[13 6 5 36 69 78 35 52 12 43]
[76 12 5 18 52 1 76 5 58 52]
[ 5 73 39 6 5 12 52 36 5 78]
[ 5 29 78 12 79 6 61 5 59 63]
[78 69 29 24 5 6 52 5 63 76]]
```
although the exact numbers will be different. Check to make sure the data is shifted over one step for `y`.
## Building the model
Below is where you'll build the network. We'll break it up into parts so it's easier to reason about each bit. Then we can connect them up into the whole network.
<img src="assets/charRNN.png" width=500px>
### Inputs
First off we'll create our input placeholders. As usual we need placeholders for the training data and the targets. We'll also create a placeholder for dropout layers called `keep_prob`. This will be a scalar, that is a 0-D tensor. To make a scalar, you create a placeholder without giving it a size.
> **Exercise:** Create the input placeholders in the function below.
```
def build_inputs(batch_size, num_steps):
''' Define placeholders for inputs, targets, and dropout
Arguments
---------
batch_size: Batch size, number of sequences per batch
num_steps: Number of sequence steps in a batch
'''
# Declare placeholders we'll feed into the graph
inputs = tf.placeholder(tf.int32,shape=[batch_size,num_steps], name='inputs')
targets = tf.placeholder(tf.int32,shape=[batch_size,num_steps], name='targets')
# Keep probability placeholder for drop out layers
keep_prob = tf.placeholder(tf.float32, name='keep_prop')
return inputs, targets, keep_prob
```
### LSTM Cell
Here we will create the LSTM cell we'll use in the hidden layer. We'll use this cell as a building block for the RNN. So we aren't actually defining the RNN here, just the type of cell we'll use in the hidden layer.
We first create a basic LSTM cell with
```python
lstm = tf.contrib.rnn.BasicLSTMCell(num_units)
```
where `num_units` is the number of units in the hidden layers in the cell. Then we can add dropout by wrapping it with
```python
tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
```
You pass in a cell and it will automatically add dropout to the inputs or outputs. Finally, we can stack up the LSTM cells into layers with [`tf.contrib.rnn.MultiRNNCell`](https://www.tensorflow.org/versions/r1.0/api_docs/python/tf/contrib/rnn/MultiRNNCell). With this, you pass in a list of cells and it will send the output of one cell into the next cell. Previously with TensorFlow 1.0, you could do this
```python
tf.contrib.rnn.MultiRNNCell([cell]*num_layers)
```
This might look a little weird if you know Python well because this will create a list of the same `cell` object. However, TensorFlow 1.0 will create different weight matrices for all `cell` objects. But, starting with TensorFlow 1.1 you actually need to create new cell objects in the list. To get it to work in TensorFlow 1.1, it should look like
```python
def build_cell(num_units, keep_prob):
lstm = tf.contrib.rnn.BasicLSTMCell(num_units)
drop = tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
return drop
tf.contrib.rnn.MultiRNNCell([build_cell(num_units, keep_prob) for _ in range(num_layers)])
```
Even though this is actually multiple LSTM cells stacked on each other, you can treat the multiple layers as one cell.
We also need to create an initial cell state of all zeros. This can be done like so
```python
initial_state = cell.zero_state(batch_size, tf.float32)
```
Below, we implement the `build_lstm` function to create these LSTM cells and the initial state.
```
def build_lstm(lstm_size, num_layers, batch_size, keep_prob):
''' Build LSTM cell.
Arguments
---------
keep_prob: Scalar tensor (tf.placeholder) for the dropout keep probability
lstm_size: Size of the hidden layers in the LSTM cells
num_layers: Number of LSTM layers
batch_size: Batch size
'''
def build_cell(num_units, keep_prob):
### Build the LSTM Cell
# Use a basic LSTM cell
lstm = tf.contrib.rnn.BasicLSTMCell(num_units)
# Add dropout to the cell outputs
drop = tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob = keep_prob)
return drop
# Stack up multiple LSTM layers, for deep learning
cell = tf.contrib.rnn.MultiRNNCell([build_cell(lstm_size, keep_prob) for _ in range(num_layers)])
initial_state = cell.zero_state(batch_size, tf.float32)
return cell, initial_state
```
### RNN Output
Here we'll create the output layer. We need to connect the output of the RNN cells to a full connected layer with a softmax output. The softmax output gives us a probability distribution we can use to predict the next character, so we want this layer to have size $C$, the number of classes/characters we have in our text.
If our input has batch size $N$, number of steps $M$, and the hidden layer has $L$ hidden units, then the output is a 3D tensor with size $N \times M \times L$. The output of each LSTM cell has size $L$, we have $M$ of them, one for each sequence step, and we have $N$ sequences. So the total size is $N \times M \times L$.
We are using the same fully connected layer, the same weights, for each of the outputs. Then, to make things easier, we should reshape the outputs into a 2D tensor with shape $(M * N) \times L$. That is, one row for each sequence and step, where the values of each row are the output from the LSTM cells. We get the LSTM output as a list, `lstm_output`. First we need to concatenate this whole list into one array with [`tf.concat`](https://www.tensorflow.org/api_docs/python/tf/concat). Then, reshape it (with `tf.reshape`) to size $(M * N) \times L$.
One we have the outputs reshaped, we can do the matrix multiplication with the weights. We need to wrap the weight and bias variables in a variable scope with `tf.variable_scope(scope_name)` because there are weights being created in the LSTM cells. TensorFlow will throw an error if the weights created here have the same names as the weights created in the LSTM cells, which they will be default. To avoid this, we wrap the variables in a variable scope so we can give them unique names.
> **Exercise:** Implement the output layer in the function below.
```
def build_output(lstm_output, in_size, out_size):
''' Build a softmax layer, return the softmax output and logits.
Arguments
---------
lstm_output: List of output tensors from the LSTM layer
in_size: Size of the input tensor, for example, size of the LSTM cells
out_size: Size of this softmax layer
'''
# Reshape output so it's a bunch of rows, one row for each step for each sequence.
# Concatenate lstm_output over axis 1 (the columns)
seq_output = tf.concat(lstm_output,axis=1)
# Reshape seq_output to a 2D tensor with lstm_size columns
x = tf.reshape(seq_output,[-1,in_size])
# Connect the RNN outputs to a softmax layer
with tf.variable_scope('softmax'):
# Create the weight and bias variables here
softmax_w = tf.Variable(tf.truncated_normal((in_size, out_size), stddev=0.1))
softmax_b = tf.Variable(tf.zeros(out_size))
# Since output is a bunch of rows of RNN cell outputs, logits will be a bunch
# of rows of logit outputs, one for each step and sequence
logits = tf.matmul(x, softmax_w) + softmax_b
# Use softmax to get the probabilities for predicted characters
out = tf.nn.softmax(logits, name='predictions')
return out, logits
```
### Training loss
Next up is the training loss. We get the logits and targets and calculate the softmax cross-entropy loss. First we need to one-hot encode the targets, we're getting them as encoded characters. Then, reshape the one-hot targets so it's a 2D tensor with size $(M*N) \times C$ where $C$ is the number of classes/characters we have. Remember that we reshaped the LSTM outputs and ran them through a fully connected layer with $C$ units. So our logits will also have size $(M*N) \times C$.
Then we run the logits and targets through `tf.nn.softmax_cross_entropy_with_logits` and find the mean to get the loss.
>**Exercise:** Implement the loss calculation in the function below.
```
def build_loss(logits, targets, lstm_size, num_classes):
''' Calculate the loss from the logits and the targets.
Arguments
---------
logits: Logits from final fully connected layer
targets: Targets for supervised learning
lstm_size: Number of LSTM hidden units
num_classes: Number of classes in targets
'''
# One-hot encode targets and reshape to match logits, one row per sequence per step
y_one_hot = tf.one_hot(targets,num_classes)
y_reshaped = tf.reshape(y_one_hot,logits.get_shape())
# Softmax cross entropy loss
loss = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels = y_reshaped)
loss = tf.reduce_mean(loss)
return loss
```
### Optimizer
Here we build the optimizer. Normal RNNs have have issues gradients exploding and disappearing. LSTMs fix the disappearance problem, but the gradients can still grow without bound. To fix this, we can clip the gradients above some threshold. That is, if a gradient is larger than that threshold, we set it to the threshold. This will ensure the gradients never grow overly large. Then we use an AdamOptimizer for the learning step.
```
def build_optimizer(loss, learning_rate, grad_clip):
''' Build optmizer for training, using gradient clipping.
Arguments:
loss: Network loss
learning_rate: Learning rate for optimizer
'''
# Optimizer for training, using gradient clipping to control exploding gradients
tvars = tf.trainable_variables()
grads, _ = tf.clip_by_global_norm(tf.gradients(loss, tvars), grad_clip)
train_op = tf.train.AdamOptimizer(learning_rate)
optimizer = train_op.apply_gradients(zip(grads, tvars))
return optimizer
```
### Build the network
Now we can put all the pieces together and build a class for the network. To actually run data through the LSTM cells, we will use [`tf.nn.dynamic_rnn`](https://www.tensorflow.org/versions/r1.0/api_docs/python/tf/nn/dynamic_rnn). This function will pass the hidden and cell states across LSTM cells appropriately for us. It returns the outputs for each LSTM cell at each step for each sequence in the mini-batch. It also gives us the final LSTM state. We want to save this state as `final_state` so we can pass it to the first LSTM cell in the the next mini-batch run. For `tf.nn.dynamic_rnn`, we pass in the cell and initial state we get from `build_lstm`, as well as our input sequences. Also, we need to one-hot encode the inputs before going into the RNN.
> **Exercise:** Use the functions you've implemented previously and `tf.nn.dynamic_rnn` to build the network.
```
class CharRNN:
def __init__(self, num_classes, batch_size=64, num_steps=50,
lstm_size=128, num_layers=2, learning_rate=0.001,
grad_clip=5, sampling=False):
# When we're using this network for sampling later, we'll be passing in
# one character at a time, so providing an option for that
if sampling == True:
batch_size, num_steps = 1, 1
else:
batch_size, num_steps = batch_size, num_steps
tf.reset_default_graph()
# Build the input placeholder tensors
self.inputs, self.targets, self.keep_prob = build_inputs(batch_size, num_steps)
# Build the LSTM cell
cell, self.initial_state = build_lstm(lstm_size, num_layers, batch_size, self.keep_prob)
### Run the data through the RNN layers
# First, one-hot encode the input tokens
x_one_hot = tf.one_hot(self.inputs, num_classes)
# Run each sequence step through the RNN with tf.nn.dynamic_rnn
outputs, state = tf.nn.dynamic_rnn(
cell,
inputs=x_one_hot,
initial_state=self.initial_state
)
self.final_state = state
# Get softmax predictions and logits
self.prediction, self.logits = build_output(outputs, lstm_size, num_classes)
# Loss and optimizer (with gradient clipping)
self.loss = build_loss(self.logits, self.targets, lstm_size, num_classes)
self.optimizer = build_optimizer(self.loss, learning_rate, grad_clip)
```
## Hyperparameters
Here are the hyperparameters for the network.
* `batch_size` - Number of sequences running through the network in one pass.
* `num_steps` - Number of characters in the sequence the network is trained on. Larger is better typically, the network will learn more long range dependencies. But it takes longer to train. 100 is typically a good number here.
* `lstm_size` - The number of units in the hidden layers.
* `num_layers` - Number of hidden LSTM layers to use
* `learning_rate` - Learning rate for training
* `keep_prob` - The dropout keep probability when training. If you're network is overfitting, try decreasing this.
Here's some good advice from Andrej Karpathy on training the network. I'm going to copy it in here for your benefit, but also link to [where it originally came from](https://github.com/karpathy/char-rnn#tips-and-tricks).
> ## Tips and Tricks
>### Monitoring Validation Loss vs. Training Loss
>If you're somewhat new to Machine Learning or Neural Networks it can take a bit of expertise to get good models. The most important quantity to keep track of is the difference between your training loss (printed during training) and the validation loss (printed once in a while when the RNN is run on the validation data (by default every 1000 iterations)). In particular:
> - If your training loss is much lower than validation loss then this means the network might be **overfitting**. Solutions to this are to decrease your network size, or to increase dropout. For example you could try dropout of 0.5 and so on.
> - If your training/validation loss are about equal then your model is **underfitting**. Increase the size of your model (either number of layers or the raw number of neurons per layer)
> ### Approximate number of parameters
> The two most important parameters that control the model are `lstm_size` and `num_layers`. I would advise that you always use `num_layers` of either 2/3. The `lstm_size` can be adjusted based on how much data you have. The two important quantities to keep track of here are:
> - The number of parameters in your model. This is printed when you start training.
> - The size of your dataset. 1MB file is approximately 1 million characters.
>These two should be about the same order of magnitude. It's a little tricky to tell. Here are some examples:
> - I have a 100MB dataset and I'm using the default parameter settings (which currently print 150K parameters). My data size is significantly larger (100 mil >> 0.15 mil), so I expect to heavily underfit. I am thinking I can comfortably afford to make `lstm_size` larger.
> - I have a 10MB dataset and running a 10 million parameter model. I'm slightly nervous and I'm carefully monitoring my validation loss. If it's larger than my training loss then I may want to try to increase dropout a bit and see if that helps the validation loss.
> ### Best models strategy
>The winning strategy to obtaining very good models (if you have the compute time) is to always err on making the network larger (as large as you're willing to wait for it to compute) and then try different dropout values (between 0,1). Whatever model has the best validation performance (the loss, written in the checkpoint filename, low is good) is the one you should use in the end.
>It is very common in deep learning to run many different models with many different hyperparameter settings, and in the end take whatever checkpoint gave the best validation performance.
>By the way, the size of your training and validation splits are also parameters. Make sure you have a decent amount of data in your validation set or otherwise the validation performance will be noisy and not very informative.
```
batch_size = 10 # Sequences per batch
num_steps = 50 # Number of sequence steps per batch
lstm_size = 128 # Size of hidden layers in LSTMs
num_layers = 2 # Number of LSTM layers
learning_rate = 0.01 # Learning rate
keep_prob = 0.5 # Dropout keep probability
```
## Time for training
This is typical training code, passing inputs and targets into the network, then running the optimizer. Here we also get back the final LSTM state for the mini-batch. Then, we pass that state back into the network so the next batch can continue the state from the previous batch. And every so often (set by `save_every_n`) I save a checkpoint.
Here I'm saving checkpoints with the format
`i{iteration number}_l{# hidden layer units}.ckpt`
> **Exercise:** Set the hyperparameters above to train the network. Watch the training loss, it should be consistently dropping. Also, I highly advise running this on a GPU.
```
epochs = 20
# Print losses every N interations
print_every_n = 50
# Save every N iterations
save_every_n = 200
model = CharRNN(len(vocab), batch_size=batch_size, num_steps=num_steps,
lstm_size=lstm_size, num_layers=num_layers,
learning_rate=learning_rate)
saver = tf.train.Saver(max_to_keep=100)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
# Use the line below to load a checkpoint and resume training
#saver.restore(sess, 'checkpoints/______.ckpt')
counter = 0
for e in range(epochs):
# Train network
new_state = sess.run(model.initial_state)
loss = 0
for x, y in get_batches(encoded, batch_size, num_steps):
counter += 1
start = time.time()
feed = {model.inputs: x,
model.targets: y,
model.keep_prob: keep_prob,
model.initial_state: new_state}
batch_loss, new_state, _ = sess.run([model.loss,
model.final_state,
model.optimizer],
feed_dict=feed)
if (counter % print_every_n == 0):
end = time.time()
print('Epoch: {}/{}... '.format(e+1, epochs),
'Training Step: {}... '.format(counter),
'Training loss: {:.4f}... '.format(batch_loss),
'{:.4f} sec/batch'.format((end-start)))
if (counter % save_every_n == 0):
saver.save(sess, "checkpoints/i{}_l{}.ckpt".format(counter, lstm_size))
saver.save(sess, "checkpoints/i{}_l{}.ckpt".format(counter, lstm_size))
```
#### Saved checkpoints
Read up on saving and loading checkpoints here: https://www.tensorflow.org/programmers_guide/variables
```
tf.train.get_checkpoint_state('checkpoints')
```
## Sampling
Now that the network is trained, we'll can use it to generate new text. The idea is that we pass in a character, then the network will predict the next character. We can use the new one, to predict the next one. And we keep doing this to generate all new text. I also included some functionality to prime the network with some text by passing in a string and building up a state from that.
The network gives us predictions for each character. To reduce noise and make things a little less random, I'm going to only choose a new character from the top N most likely characters.
```
def pick_top_n(preds, vocab_size, top_n=5):
p = np.squeeze(preds)
p[np.argsort(p)[:-top_n]] = 0
p = p / np.sum(p)
c = np.random.choice(vocab_size, 1, p=p)[0]
return c
def sample(checkpoint, n_samples, lstm_size, vocab_size, prime="The "):
samples = [c for c in prime]
model = CharRNN(len(vocab), lstm_size=lstm_size, sampling=True)
saver = tf.train.Saver()
with tf.Session() as sess:
saver.restore(sess, checkpoint)
new_state = sess.run(model.initial_state)
for c in prime:
x = np.zeros((1, 1))
x[0,0] = vocab_to_int[c]
feed = {model.inputs: x,
model.keep_prob: 1.,
model.initial_state: new_state}
preds, new_state = sess.run([model.prediction, model.final_state],
feed_dict=feed)
c = pick_top_n(preds, len(vocab))
samples.append(int_to_vocab[c])
for i in range(n_samples):
x[0,0] = c
feed = {model.inputs: x,
model.keep_prob: 1.,
model.initial_state: new_state}
preds, new_state = sess.run([model.prediction, model.final_state],
feed_dict=feed)
c = pick_top_n(preds, len(vocab))
samples.append(int_to_vocab[c])
return ''.join(samples)
```
Here, pass in the path to a checkpoint and sample from the network.
```
tf.train.latest_checkpoint('checkpoints')
checkpoint = tf.train.latest_checkpoint('checkpoints')
samp = sample(checkpoint, 2000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i200_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i600_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i1200_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
```
| true |
code
| 0.718273 | null | null | null | null |
|
CT Reconstruction (ADMM Plug-and-Play Priors w/ BM3D, SVMBIR+CG)
================================================================
This example demonstrates the use of class
[admm.ADMM](../_autosummary/scico.optimize.rst#scico.optimize.ADMM) to
solve a tomographic reconstruction problem using the Plug-and-Play Priors
framework <cite data-cite="venkatakrishnan-2013-plugandplay2"/>, using BM3D
<cite data-cite="dabov-2008-image"/> as a denoiser and SVMBIR <cite data-cite="svmbir-2020"/> for
tomographic projection.
This version uses the data fidelity term as the ADMM f, and thus the
optimization with respect to the data fidelity uses CG rather than the
prox of the SVMBIRSquaredL2Loss functional.
```
import numpy as np
import jax
import matplotlib.pyplot as plt
import svmbir
from xdesign import Foam, discrete_phantom
import scico.numpy as snp
from scico import metric, plot
from scico.functional import BM3D, NonNegativeIndicator
from scico.linop import Diagonal, Identity
from scico.linop.radon_svmbir import SVMBIRSquaredL2Loss, TomographicProjector
from scico.optimize.admm import ADMM, LinearSubproblemSolver
from scico.util import device_info
plot.config_notebook_plotting()
```
Generate a ground truth image.
```
N = 256 # image size
density = 0.025 # attenuation density of the image
np.random.seed(1234)
x_gt = discrete_phantom(Foam(size_range=[0.05, 0.02], gap=0.02, porosity=0.3), size=N - 10)
x_gt = x_gt / np.max(x_gt) * density
x_gt = np.pad(x_gt, 5)
x_gt[x_gt < 0] = 0
```
Generate tomographic projector and sinogram.
```
num_angles = int(N / 2)
num_channels = N
angles = snp.linspace(0, snp.pi, num_angles, endpoint=False, dtype=snp.float32)
A = TomographicProjector(x_gt.shape, angles, num_channels)
sino = A @ x_gt
```
Impose Poisson noise on sinogram. Higher max_intensity means less noise.
```
max_intensity = 2000
expected_counts = max_intensity * np.exp(-sino)
noisy_counts = np.random.poisson(expected_counts).astype(np.float32)
noisy_counts[noisy_counts == 0] = 1 # deal with 0s
y = -np.log(noisy_counts / max_intensity)
```
Reconstruct using default prior of SVMBIR <cite data-cite="svmbir-2020"/>.
```
weights = svmbir.calc_weights(y, weight_type="transmission")
x_mrf = svmbir.recon(
np.array(y[:, np.newaxis]),
np.array(angles),
weights=weights[:, np.newaxis],
num_rows=N,
num_cols=N,
positivity=True,
verbose=0,
)[0]
```
Set up an ADMM solver.
```
y, x0, weights = jax.device_put([y, x_mrf, weights])
ρ = 15 # ADMM penalty parameter
σ = density * 0.18 # denoiser sigma
f = SVMBIRSquaredL2Loss(y=y, A=A, W=Diagonal(weights), scale=0.5)
g0 = σ * ρ * BM3D()
g1 = NonNegativeIndicator()
solver = ADMM(
f=f,
g_list=[g0, g1],
C_list=[Identity(x_mrf.shape), Identity(x_mrf.shape)],
rho_list=[ρ, ρ],
x0=x0,
maxiter=20,
subproblem_solver=LinearSubproblemSolver(cg_kwargs={"tol": 1e-4, "maxiter": 100}),
itstat_options={"display": True, "period": 1},
)
```
Run the solver.
```
print(f"Solving on {device_info()}\n")
x_bm3d = solver.solve()
hist = solver.itstat_object.history(transpose=True)
```
Show the recovered image.
```
norm = plot.matplotlib.colors.Normalize(vmin=-0.1 * density, vmax=1.2 * density)
fig, ax = plt.subplots(1, 3, figsize=[15, 5])
plot.imview(img=x_gt, title="Ground Truth Image", cbar=True, fig=fig, ax=ax[0], norm=norm)
plot.imview(
img=x_mrf,
title=f"MRF (PSNR: {metric.psnr(x_gt, x_mrf):.2f} dB)",
cbar=True,
fig=fig,
ax=ax[1],
norm=norm,
)
plot.imview(
img=x_bm3d,
title=f"BM3D (PSNR: {metric.psnr(x_gt, x_bm3d):.2f} dB)",
cbar=True,
fig=fig,
ax=ax[2],
norm=norm,
)
fig.show()
```
Plot convergence statistics.
```
plot.plot(
snp.vstack((hist.Prml_Rsdl, hist.Dual_Rsdl)).T,
ptyp="semilogy",
title="Residuals",
xlbl="Iteration",
lgnd=("Primal", "Dual"),
)
```
| true |
code
| 0.736303 | null | null | null | null |
|
# Magnetics - Directional derivatives, ASA and ASA2-PVD filtering
#### as part of worked filters in NFIS PROJECT - CPRM-UFPR
#### CPRM Intern researcher: Luizemara S. A. Szameitat (luizemara@gmail.com)
Notebook from https://github.com/lszam/cprm-nfis.
Last modified: Dec/2021
___
○ References:
Richard Blakely (1996). Potential Theory in Gravity & Magnetic Applications.
FORMATO DO GRID DE ENTRADA:
O dado precisa ser um array de duas dimensões, com nós das células nesta ordem: de oeste para leste, e de sul para norte.
```
import numpy as np
import scipy.fftpack
from math import radians, sin, cos, sqrt
import matplotlib.pyplot as plt
import seaborn as sb
```
##### Functions
```
def Kvalue(i, j, nx, ny, dkx, dky):
'''
Kvalue(i, j, nx, ny, dkx, dky)
adapted from Blakely (1996)
'''
nyqx = nx / 2 + 1
nyqy = ny / 2 + 1
kx = float()
ky = float()
if j <= nyqx:
kx = (j-1) * dkx
else:
kx = (j-nx-1) * dkx
if i <= nyqy:
ky = (i-1) * dky
else:
ky = (i-ny-1) * dky
return kx, ky
def go_filter(grid, filter_type, nx, ny, dkx, dky):
'''
Potential Field's filtering routines
'''
# FFT
gridfft = scipy.fftpack.fft2(grid)
# From matrix to vector
gridfft = np.reshape(gridfft, nx*ny)
# Creating complex vector
gridfft_filt = np.zeros(nx*ny).astype(complex)
# Filtering
if filter_type == 'dz1':
for j in range(1, ny+1):
for i in range(1, nx+1):
ij = (j-1) * nx + i
kx, ky = Kvalue(i, j, nx, ny, dkx, dky)
k = sqrt(kx**2 + ky**2)
gridfft_filt[ij-1] = gridfft[ij-1]*k**1 #filtering expression
elif filter_type == 'dy1':
for j in range(1, ny+1):
for i in range(1, nx+1):
ij = (j-1) * nx + i
kx, ky = Kvalue(i, j, nx, ny, dkx, dky)
k = kx
gridfft_filt[ij-1] = gridfft[ij-1]*k*complex(0, 1)
elif filter_type == 'dx1':
for j in range(1, ny+1):
for i in range(1, nx+1):
ij = (j-1) * nx + i
kx, ky = Kvalue(i, j, nx, ny, dkx, dky)
k = ky
gridfft_filt[ij-1] = gridfft[ij-1]*k*complex(0, 1)
else:
return print ('Not supported filter_type=', filter_type)
#Return to matrix
gridfft_filt = np.reshape(gridfft_filt, (ny, nx))
#iFFT
gridfft_filt = scipy.fftpack.ifft2(gridfft_filt)
grid_out = np.reshape(gridfft_filt.real, (ny, nx))
return grid_out
```
### Input data
```
# XYZ grid reading (CSV format, no header, no line numbers)
filename = 'https://raw.githubusercontent.com/lszam/cprm-nfis/main/data/pentanomaly.csv'
#reading csv columns - coordinates and physical property
csv_values = np.genfromtxt(filename, delimiter=",") #choose the delimiter
x = csv_values[:,0]
y = csv_values[:,1]
z = csv_values[:,2]
#Getting x and y values as lists
xnodes=[]
ynodes=[]
[xnodes.append(item) for item in x if not xnodes.count(item)]
[ynodes.append(item) for item in y if not ynodes.count(item)]
# Meshgrids of X and Y
xgrid, ygrid = np.meshgrid(xnodes, ynodes)
#Number of items in x and y directions
nx = np.size(xgrid,1)
ny = np.size(ygrid,0)
#Arranging the physical property into a matrix
Z = np.array(z) # data from list to array
grid_tfa = np.reshape(Z, (ny, nx))
dX, dY = np.abs(xnodes[0]-xnodes[1]), np.abs(ynodes[0]-ynodes[1]) # cell size
#Plot input data
plt.figure(figsize=(4, 4))
sb_plot2 = sb.heatmap(grid_tfa, cmap="Spectral", cbar_kws={'label': 'TFA(nT)'})
sb_plot2.invert_yaxis()
```
### Derivatives
```
π = np.pi
dkx = 2. * π / (nx * dX)
dky = 2. * π / (ny * dY)
# Filtering
gridX = go_filter(grid_tfa, 'dx1', nx, ny, dkx, dky)
gridY = go_filter(grid_tfa, 'dy1', nx, ny, dkx, dky)
gridZ = go_filter(grid_tfa, 'dz1', nx, ny, dkx, dky)
# Plot
plt.figure(figsize=(10.5, 3))
plt.subplot(1, 3, 1)
sb_plot1 = sb.heatmap(gridX, cmap="Spectral", cbar_kws={'label': 'DX nT/m'})
sb_plot1.invert_yaxis()
plt.subplot(1, 3, 2)
sb_plot2 = sb.heatmap(gridY, cmap="Spectral", cbar_kws={'label': 'DY nT/m'})
sb_plot2.invert_yaxis()
plt.subplot(1, 3, 3)
sb_plot3 = sb.heatmap(gridZ, cmap="Spectral", cbar_kws={'label': 'DZ nT/m'})
sb_plot3.invert_yaxis()
plt.tight_layout()
```
### ASA filter
```
# ASA filter
'''
Analytic signal amplitude (ASA)
'''
grid_asa = np.sqrt((gridX**2)+(gridY**2)+(gridZ**2))
# Plot
plt.figure(figsize=(4, 4))
sb_plot2 = sb.heatmap(grid_asa, cmap="Spectral", cbar_kws={'label': 'ASA'})
sb_plot2.invert_yaxis()
```
### Pseudo-vertical derivative of the squared ASA (ASA2-PVD)
```
grid_asa2pvd = go_filter(grid_asa**2, 'dz1', nx, ny, dkx, dky)
# Plot
plt.figure(figsize=(4, 4))
sb_plot2 = sb.heatmap(grid_asa2pvd, cmap="Spectral", cbar_kws={'label': 'ASA2-PVD'})
sb_plot2.invert_yaxis()
#Save results as txt file
grid_output = np.reshape(grid_asa2pvd, ny*nx)
np.savetxt(str('asa2pvd.xyz'),np.c_[x,y,grid_output])
```
| true |
code
| 0.421909 | null | null | null | null |
|
# Key Points for Review in this Section
- Hyperlinks in Markdown
- magic: ```!```, ```%%bash```, ```%%python``` and ```%%file```
- ```shift-tab``` to see help of function
- ```zip()```
- ```dict.get(key, otherwise)```
- immutability and identity -- box and things inside
- ```functions(*list)``` and ```function(**dict)```
- ```enumerarte(iterable, start)```
- lazy evaluation: ```range()``` and ```(x for x )```
- ```try``` and ```except```
# Crash course in Jupyter and Python
- Introduction to Jupyter
- Using Markdown
- Magic functions
- REPL
- Saving and exporting Jupyter notebooks
- Python
- Data types
- Operators
- Collections
- Functions and methods
- Control flow
- Loops, comprehension
- Packages and namespace
- Coding style
- Understanding error messages
- Getting help
## Class Repository
Course material will be posted here. Please make any personal modifications to a **copy** of the notebook to avoid merge conflicts.
https://github.com/cliburn/sta-663-2019.git
## Introduction to Jupyter
- [Official Jupyter docs](https://jupyter.readthedocs.io/en/latest/)
- User interface and kernels
- Notebook, editor, terminal
- Literate programming
- Code and markdown cells
- Menu and toolbar
- Key bindings
- Polyglot programming
```
%load_ext rpy2.ipython
import warnings
warnings.simplefilter('ignore', FutureWarning)
df = %R iris
df.head()
%%R -i df -o res
library(tidyverse)
res <- df %>% group_by(Species) %>% summarize_all(mean)
res
```
### Using Markdown
- What is markdown?
- Headers
- Formatting text
- Syntax-highlighted code
- Lists
- Hyperlinks and images
- LaTeX
See `Help | Markdown`
#### Hyperlinks
[I'm an inline-style link](https://www.google.com)
[I'm an inline-style link with title](https://www.google.com "Google's Homepage")
[I'm a reference-style link][Arbitrary case-insensitive reference text]
[I'm a relative reference to a repository file](../blob/master/LICENSE)
[You can use numbers for reference-style link definitions][1]
Or leave it empty and use the [link text itself].
URLs and URLs in angle brackets will automatically get turned into links.
http://www.example.com or <http://www.example.com> and sometimes
example.com (but not on Github, for example).
Some text to show that the reference links can follow later.
[arbitrary case-insensitive reference text]: https://www.mozilla.org
[1]: http://slashdot.org
[link text itself]: http://www.reddit.com
#### LaTex
using dollar for LaTex
$\alpha$
### Magic functions
- [List of magic functions](https://ipython.readthedocs.io/en/stable/interactive/magics.html)
- `%magic`
- Shell access
- Convenience functions
- Quick and dirty text files
```
%magic
! echo "hello world"
%%bash
echo "hello world"
%%python
print(1+2)
```
### REPL
- Read, Eval, Print, Loop
- Learn by experimentation
```
1 + 2
```
### Saving and exporting Jupyter notebooks
- The File menu item
- Save and Checkpoint
- Exporting
- Close and Halt
- Cleaning up with the Running tab
## Introduction to Python
- [Official Python docs](https://docs.python.org/3/)
- [Why Python?](https://insights.stackoverflow.com/trends?tags=python%2Cjavascript%2Cjava%2Cc%2B%2B%2Cr%2Cjulia-lang%2Cscala&utm_source=so-owned&utm_medium=blog&utm_campaign=gen-blog&utm_content=blog-link&utm_term=incredible-growth-python)
- General purpose language (web, databases, introductory programming classes)
- Language for scientific computation (physics, engineering, statistics, ML, AI)
- Human readable
- Interpreted
- Dynamic typing
- Strong typing
- Multi-paradigm
- Implementations (CPython, PyPy, Jython, IronPython)
### Data types
- boolean
- int, double, complex
- strings
- None
```
True, False
1, 2, 3
import numpy as np
np.pi, np.e
3 + 4j
'hello, world'
"hell's bells"
"""三轮车跑的快
上面坐个老太太
要五毛给一块
你说奇怪不奇怪"""
None
None is None
```
### Operators
- mathematical
- logical
- bitwise
- membership
- identity
- assignment and in-place operators
- operator precedence
#### Arithmetic
```
2 ** 3
11 / 3
11 // 3
11 % 3
```
#### Logical
```
True and False
True or False
not (True or False)
```
#### Relational
```
2 == 2, 2 == 3, 2 != 3, 2 < 3, 2 <= 3, 2 > 3, 2 >= 3
```
#### Bitwise
```
format(10, '04b')
format(7, '04b')
x = 10 & 7
x, format(x, '04b')
x = 10 | 7
x, format(x, '04b')
x = 10 ^ 7
x, format(x, '04b')
```
#### Membership
```
'hell' in 'hello'
3 in range(5), 7 in range(5)
'a' in dict(zip('abc', range(3)))
```
#### Identity
```
x = [2,3]
y = [2,3]
x == y, x is y
id(x), id(y)
x = 'hello'
y = 'hello'
x == y, x is y
id(x), id(y)
```
#### Assignment
```
x = 2
x = x + 2
x
x *= 2
x
```
### Collections
- Sequence containers - list, tuple
- Mapping containers - set, dict
- The [`collections`](https://docs.python.org/2/library/collections.html) module
#### Lists
```
xs = [1,2,3]
xs[0], xs[-1]
xs[1] = 9
xs
```
#### Tuples
```
ys = (1,2,3)
ys[0], ys[-1]
try:
ys[1] = 9
except TypeError as e:
print(e)
```
#### Sets
```
zs = [1,1,2,2,2,3,3,3,3]
set(zs)
```
#### Dictionaries
```
{'a': 0, 'b': 1, 'c': 2}
dict(a=0, b=1, c=2)
dict(zip('abc', range(3)))
list(zip([1, 2, 3], [4, 5, 6, 7], [8, 9, 10]))
d = {'a':1, 'b':2}
print(d.get('a'))
print(d.get('c', 0)) # using get is better than [] maybe
```
### Functions and methods
- Anatomy of a function
- Docstrings
- Class methods
```
list(range(10))
[item for item in dir() if not item.startswith('_')]
def f(a, b):
"""Do something with a and b.
Assume that the + and * operatores are defined for a and b.
"""
return 2*a + 3*b
f(2, 3)
f(3, 2)
f(b=3, a=2)
f(*(2,3))
f(**dict(a=2, b=3))
f('hello', 'world')
f([1,2,3], ['a', 'b', 'c'])
f((1, 2), ('a', 'b'))
print("sum() # shift-tab to see instructions")
```
### Control flow
- if and the ternary operator
- Checking conditions - what evaluates as true/false?
- if-elif-else
- while
- break, continue
- pass
```
if 1 + 1 == 2:
print("Phew!")
'vegan' if 1 + 1 == 2 else 'carnivore'
'vegan' if 1 + 1 == 3 else 'carnivore'
if 1+1 == 3:
print("oops")
else:
print("Phew!")
for grade in [94, 79, 81, 57]:
if grade > 90:
print('A')
elif grade > 80:
print('B')
elif grade > 70:
print('C')
else:
print('Are you in the right class?')
i = 10
while i > 0:
print(i)
i -= 1
for i in range(1, 10):
if i % 2 == 0:
continue
print(i)
for i in range(1, 10):
if i % 2 == 0:
break
print(i)
for i in range(1, 10):
if i % 2 == 0:
pass
else:
print(i)
```
### Loops and comprehensions
- for, range, enumerate
- lazy and eager evaluation
- list, set, dict comprehensions
- generator expression
```
for i in range(1,5):
print(i**2, end=',')
for i, x in enumerate(range(1,5)):
print(i, x**2)
for i, x in enumerate(range(1,5), start=10):
print(i, x**2)
range(5)
list(range(5))
```
#### Comprehensions
```
[x**3 % 3 for x in range(10)]
{x**3 % 3 for x in range(10)}
{k: v for k, v in enumerate('abcde')}
(x**3 for x in range(10))
list(x**3 for x in range(10))
```
### Packages and namespace
- Modules (file)
- Package (hierarchical modules)
- Namespace and naming conflicts
- Using `import`
- [Batteries included](https://docs.python.org/3/library/index.html)
```
%%file foo.py
def foo(x):
return f"And FOO you too, {x}"
import foo
foo.foo("Winnie the Pooh")
from foo import foo
foo("Winnie the Pooh")
import numpy as np
np.random.randint(0, 10, (5,5))
```
### Coding style
- [PEP 8 — the Style Guide for Python Code](https://pep8.org/)
- Many code editors can be used with linters to check if your code conforms to PEP 8 style guidelines.
- E.g. see [jupyter-autopep8](https://github.com/kenkoooo/jupyter-autopep8)
### Understanding error messages
- [Built-in exceptions](https://docs.python.org/3/library/exceptions.html)
```
try:
1 / 0
except ZeroDivisionError as e:
print(e)
```
### Getting help
- `?foo`, `foo?`, `help(foo)`
- Use a search engine
- Use `StackOverflow`
- Ask your TA
```
help(help)
```
| true |
code
| 0.746289 | null | null | null | null |
|
```
#hide
from fastai.vision.all import *
from utils import *
matplotlib.rc('image', cmap='Greys')
```
# Under the Hood: Training a Digit Classifier
## Pixels: The Foundations of Computer Vision
## Sidebar: Tenacity and Deep Learning
## End sidebar
```
path = untar_data(URLs.MNIST_SAMPLE)
#hide
Path.BASE_PATH = path
path.ls()
(path/'train').ls()
threes = (path/'train'/'3').ls().sorted()
sevens = (path/'train'/'7').ls().sorted()
threes
im3_path = threes[1]
im3 = Image.open(im3_path)
im3
array(im3)[4:10,4:10]
tensor(im3)[4:10,4:10]
im3_t = tensor(im3)
df = pd.DataFrame(im3_t[4:15,4:22])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')
```
## First Try: Pixel Similarity
```
seven_tensors = [tensor(Image.open(o)) for o in sevens]
three_tensors = [tensor(Image.open(o)) for o in threes]
len(three_tensors),len(seven_tensors)
show_image(three_tensors[1]);
stacked_sevens = torch.stack(seven_tensors).float()/255
stacked_threes = torch.stack(three_tensors).float()/255
stacked_threes.shape
len(stacked_threes.shape)
stacked_threes.ndim
mean3 = stacked_threes.mean(0)
show_image(mean3);
mean7 = stacked_sevens.mean(0)
show_image(mean7);
a_3 = stacked_threes[1]
show_image(a_3);
dist_3_abs = (a_3 - mean3).abs().mean()
dist_3_sqr = ((a_3 - mean3)**2).mean().sqrt()
dist_3_abs,dist_3_sqr
dist_7_abs = (a_3 - mean7).abs().mean()
dist_7_sqr = ((a_3 - mean7)**2).mean().sqrt()
dist_7_abs,dist_7_sqr
F.l1_loss(a_3.float(),mean7), F.mse_loss(a_3,mean7).sqrt()
```
### NumPy Arrays and PyTorch Tensors
```
data = [[1,2,3],[4,5,6]]
arr = array (data)
tns = tensor(data)
arr # numpy
tns # pytorch
tns[1]
tns[:,1]
tns[1,1:3]
tns+1
tns.type()
tns*1.5
```
## Computing Metrics Using Broadcasting
```
valid_3_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'3').ls()])
valid_3_tens = valid_3_tens.float()/255
valid_7_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'7').ls()])
valid_7_tens = valid_7_tens.float()/255
valid_3_tens.shape,valid_7_tens.shape
def mnist_distance(a,b): return (a-b).abs().mean((-1,-2))
mnist_distance(a_3, mean3)
valid_3_dist = mnist_distance(valid_3_tens, mean3)
valid_3_dist, valid_3_dist.shape
tensor([1,2,3]) + tensor([1,1,1])
(valid_3_tens-mean3).shape
def is_3(x): return mnist_distance(x,mean3) < mnist_distance(x,mean7)
is_3(a_3), is_3(a_3).float()
is_3(valid_3_tens)
accuracy_3s = is_3(valid_3_tens).float() .mean()
accuracy_7s = (1 - is_3(valid_7_tens).float()).mean()
accuracy_3s,accuracy_7s,(accuracy_3s+accuracy_7s)/2
```
## Stochastic Gradient Descent (SGD)
```
gv('''
init->predict->loss->gradient->step->stop
step->predict[label=repeat]
''')
def f(x): return x**2
plot_function(f, 'x', 'x**2')
plot_function(f, 'x', 'x**2')
plt.scatter(-1.5, f(-1.5), color='red');
```
### Calculating Gradients
```
xt = tensor(3.).requires_grad_()
yt = f(xt)
yt
yt.backward()
xt.grad
xt = tensor([3.,4.,10.]).requires_grad_()
xt
def f(x): return (x**2).sum()
yt = f(xt)
yt
yt.backward()
xt.grad
```
### Stepping With a Learning Rate
### An End-to-End SGD Example
```
time = torch.arange(0,20).float(); time
speed = torch.randn(20)*3 + 0.75*(time-9.5)**2 + 1
plt.scatter(time,speed);
def f(t, params):
a,b,c = params
return a*(t**2) + (b*t) + c
def mse(preds, targets): return ((preds-targets)**2).mean()
```
#### Step 1: Initialize the parameters
```
params = torch.randn(3).requires_grad_()
#hide
orig_params = params.clone()
```
#### Step 2: Calculate the predictions
```
preds = f(time, params)
def show_preds(preds, ax=None):
if ax is None: ax=plt.subplots()[1]
ax.scatter(time, speed)
ax.scatter(time, to_np(preds), color='red')
ax.set_ylim(-300,100)
show_preds(preds)
```
#### Step 3: Calculate the loss
```
loss = mse(preds, speed)
loss
```
#### Step 4: Calculate the gradients
```
loss.backward()
params.grad
params.grad * 1e-5
params
```
#### Step 5: Step the weights.
```
lr = 1e-5
params.data -= lr * params.grad.data
params.grad = None
preds = f(time,params)
mse(preds, speed)
show_preds(preds)
def apply_step(params, prn=True):
preds = f(time, params)
loss = mse(preds, speed)
loss.backward()
params.data -= lr * params.grad.data
params.grad = None
if prn: print(loss.item())
return preds
```
#### Step 6: Repeat the process
```
for i in range(10): apply_step(params)
#hide
params = orig_params.detach().requires_grad_()
_,axs = plt.subplots(1,4,figsize=(12,3))
for ax in axs: show_preds(apply_step(params, False), ax)
plt.tight_layout()
```
#### Step 7: stop
### Summarizing Gradient Descent
```
gv('''
init->predict->loss->gradient->step->stop
step->predict[label=repeat]
''')
```
## The MNIST Loss Function
```
train_x = torch.cat([stacked_threes, stacked_sevens]).view(-1, 28*28)
train_y = tensor([1]*len(threes) + [0]*len(sevens)).unsqueeze(1)
train_x.shape,train_y.shape
dset = list(zip(train_x,train_y))
x,y = dset[0]
x.shape,y
valid_x = torch.cat([valid_3_tens, valid_7_tens]).view(-1, 28*28)
valid_y = tensor([1]*len(valid_3_tens) + [0]*len(valid_7_tens)).unsqueeze(1)
valid_dset = list(zip(valid_x,valid_y))
def init_params(size, std=1.0): return (torch.randn(size)*std).requires_grad_()
weights = init_params((28*28,1))
bias = init_params(1)
(train_x[0]*weights.T).sum() + bias
def linear1(xb): return xb@weights + bias
preds = linear1(train_x)
preds
corrects = (preds>0.0).float() == train_y
corrects
corrects.float().mean().item()
weights[0] *= 1.0001
preds = linear1(train_x)
((preds>0.0).float() == train_y).float().mean().item()
trgts = tensor([1,0,1])
prds = tensor([0.9, 0.4, 0.2])
def mnist_loss(predictions, targets):
return torch.where(targets==1, 1-predictions, predictions).mean()
torch.where(trgts==1, 1-prds, prds)
mnist_loss(prds,trgts)
mnist_loss(tensor([0.9, 0.4, 0.8]),trgts)
```
### Sigmoid
```
def sigmoid(x): return 1/(1+torch.exp(-x))
plot_function(torch.sigmoid, title='Sigmoid', min=-4, max=4)
def mnist_loss(predictions, targets):
predictions = predictions.sigmoid()
return torch.where(targets==1, 1-predictions, predictions).mean()
```
### SGD and Mini-Batches
```
coll = range(15)
dl = DataLoader(coll, batch_size=5, shuffle=True)
list(dl)
ds = L(enumerate(string.ascii_lowercase))
ds
dl = DataLoader(ds, batch_size=6, shuffle=True)
list(dl)
```
## Putting It All Together
```
weights = init_params((28*28,1))
bias = init_params(1)
dl = DataLoader(dset, batch_size=256)
xb,yb = first(dl)
xb.shape,yb.shape
valid_dl = DataLoader(valid_dset, batch_size=256)
batch = train_x[:4]
batch.shape
preds = linear1(batch)
preds
loss = mnist_loss(preds, train_y[:4])
loss
loss.backward()
weights.grad.shape,weights.grad.mean(),bias.grad
def calc_grad(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
weights.grad.zero_()
bias.grad.zero_();
def train_epoch(model, lr, params):
for xb,yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_()
(preds>0.0).float() == train_y[:4]
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds>0.5) == yb
return correct.float().mean()
batch_accuracy(linear1(batch), train_y[:4])
def validate_epoch(model):
accs = [batch_accuracy(model(xb), yb) for xb,yb in valid_dl]
return round(torch.stack(accs).mean().item(), 4)
validate_epoch(linear1)
lr = 1.
params = weights,bias
train_epoch(linear1, lr, params)
validate_epoch(linear1)
for i in range(20):
train_epoch(linear1, lr, params)
print(validate_epoch(linear1), end=' ')
```
### Creating an Optimizer
```
linear_model = nn.Linear(28*28,1)
w,b = linear_model.parameters()
w.shape,b.shape
class BasicOptim:
def __init__(self,params,lr): self.params,self.lr = list(params),lr
def step(self, *args, **kwargs):
for p in self.params: p.data -= p.grad.data * self.lr
def zero_grad(self, *args, **kwargs):
for p in self.params: p.grad = None
opt = BasicOptim(linear_model.parameters(), lr)
def train_epoch(model):
for xb,yb in dl:
calc_grad(xb, yb, model)
opt.step()
opt.zero_grad()
validate_epoch(linear_model)
def train_model(model, epochs):
for i in range(epochs):
train_epoch(model)
print(validate_epoch(model), end=' ')
train_model(linear_model, 20)
linear_model = nn.Linear(28*28,1)
opt = SGD(linear_model.parameters(), lr)
train_model(linear_model, 20)
dls = DataLoaders(dl, valid_dl)
learn = Learner(dls, nn.Linear(28*28,1), opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)
learn.fit(10, lr=lr)
```
## Adding a Nonlinearity
```
def simple_net(xb):
res = xb@w1 + b1
res = res.max(tensor(0.0))
res = res@w2 + b2
return res
w1 = init_params((28*28,30))
b1 = init_params(30)
w2 = init_params((30,1))
b2 = init_params(1)
plot_function(F.relu)
simple_net = nn.Sequential(
nn.Linear(28*28,30),
nn.ReLU(),
nn.Linear(30,1)
)
learn = Learner(dls, simple_net, opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)
learn.fit(40, 0.1)
plt.plot(L(learn.recorder.values).itemgot(2));
learn.recorder.values[-1][2]
```
### Going Deeper
```
dls = ImageDataLoaders.from_folder(path)
learn = cnn_learner(dls, resnet18, pretrained=False,
loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(1, 0.1)
```
## Jargon Recap
## Questionnaire
1. How is a grayscale image represented on a computer? How about a color image?
1. How are the files and folders in the `MNIST_SAMPLE` dataset structured? Why?
1. Explain how the "pixel similarity" approach to classifying digits works.
1. What is a list comprehension? Create one now that selects odd numbers from a list and doubles them.
1. What is a "rank-3 tensor"?
1. What is the difference between tensor rank and shape? How do you get the rank from the shape?
1. What are RMSE and L1 norm?
1. How can you apply a calculation on thousands of numbers at once, many thousands of times faster than a Python loop?
1. Create a 3×3 tensor or array containing the numbers from 1 to 9. Double it. Select the bottom-right four numbers.
1. What is broadcasting?
1. Are metrics generally calculated using the training set, or the validation set? Why?
1. What is SGD?
1. Why does SGD use mini-batches?
1. What are the seven steps in SGD for machine learning?
1. How do we initialize the weights in a model?
1. What is "loss"?
1. Why can't we always use a high learning rate?
1. What is a "gradient"?
1. Do you need to know how to calculate gradients yourself?
1. Why can't we use accuracy as a loss function?
1. Draw the sigmoid function. What is special about its shape?
1. What is the difference between a loss function and a metric?
1. What is the function to calculate new weights using a learning rate?
1. What does the `DataLoader` class do?
1. Write pseudocode showing the basic steps taken in each epoch for SGD.
1. Create a function that, if passed two arguments `[1,2,3,4]` and `'abcd'`, returns `[(1, 'a'), (2, 'b'), (3, 'c'), (4, 'd')]`. What is special about that output data structure?
1. What does `view` do in PyTorch?
1. What are the "bias" parameters in a neural network? Why do we need them?
1. What does the `@` operator do in Python?
1. What does the `backward` method do?
1. Why do we have to zero the gradients?
1. What information do we have to pass to `Learner`?
1. Show Python or pseudocode for the basic steps of a training loop.
1. What is "ReLU"? Draw a plot of it for values from `-2` to `+2`.
1. What is an "activation function"?
1. What's the difference between `F.relu` and `nn.ReLU`?
1. The universal approximation theorem shows that any function can be approximated as closely as needed using just one nonlinearity. So why do we normally use more?
### Further Research
1. Create your own implementation of `Learner` from scratch, based on the training loop shown in this chapter.
1. Complete all the steps in this chapter using the full MNIST datasets (that is, for all digits, not just 3s and 7s). This is a significant project and will take you quite a bit of time to complete! You'll need to do some of your own research to figure out how to overcome some obstacles you'll meet on the way.
| true |
code
| 0.655749 | null | null | null | null |
|
# CNN with Bidirctional RNN - Char Classification
Using TensorFlow
## TODO
```
```
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
import tensorflow as tf
import tensorflow.contrib.seq2seq as seq2seq
import cv2
%matplotlib notebook
# Increase size of plots
plt.rcParams['figure.figsize'] = (9.0, 5.0)
# Helpers
from ocr.helpers import implt
from ocr.mlhelpers import TrainingPlot, DataSet
from ocr.imgtransform import coordinates_remap
from ocr.datahelpers import loadWordsData, correspondingShuffle
from ocr.tfhelpers import Graph, create_cell
tf.reset_default_graph()
sess = tf.InteractiveSession()
print("OpenCV: " + cv2.__version__)
print("Numpy: " + np.__version__)
print("TensorFlow: " + tf.__version__)
```
## Loading Images
```
images, _, gaplines = loadWordsData(['data/words/'],
loadGaplines=True)
```
## Settings
```
PAD = 0 # Value for PADding images
POS = 1 # Values of positive and negative label 0/-1
NEG = 0
POS_SPAN = 1 # Number of positive values around true position (5 is too high)
POS_WEIGHT = 10 # Weighting possitive values in loss counting
slider_size = (60, 30) # Height is set to 60 by data and width should be even
slider_step = 2 # Number of pixels slider moving
N_INPUT = 1800 # Size of sequence input vector will depend on CNN
num_buckets = 10
n_classes = 2 # Number of different outputs
rnn_layers = 4 # 4 - 2 - 256
rnn_residual_layers = 2 # HAVE TO be smaller than encoder_layers
rnn_units = 128
attention_size = 64
learning_rate = 1e-4 # 1e-4
dropout = 0.4 # Percentage of dopped out data
train_set = 0.8 # Percentage of training data
TRAIN_STEPS = 500000 # Number of training steps!
TEST_ITER = 150
LOSS_ITER = 50
SAVE_ITER = 2000
BATCH_SIZE = 32
# EPOCH = 2000 # "Number" of batches in epoch
```
## Dataset
```
# Shuffle data
images, gaplines = correspondingShuffle([images, gaplines])
for i in range(len(images)):
# Add border and offset gaplines - RUN ONLY ONCE
images[i] = cv2.copyMakeBorder(images[i],
0, 0, int(slider_size[1]/2), int(slider_size[1]/2),
cv2.BORDER_CONSTANT,
value=0)
gaplines[i] += int(slider_size[1] / 2)
# Image standardization same as tf.image.per_image_standardization
for i in range(len(images)):
images[i] = (images[i] - np.mean(images[i])) / max(np.std(images[i]), 1.0/math.sqrt(images[i].size))
# Split data on train and test dataset
div = int(train_set * len(images))
trainImages = images[0:div]
testImages = images[div:]
trainGaplines = gaplines[0:div]
testGaplines = gaplines[div:]
print("Training images:", div)
print("Testing images:", len(images) - div)
class BucketDataIterator():
""" Iterator for feeding seq2seq model during training """
def __init__(self,
images,
gaplines,
gap_span,
num_buckets=5,
slider=(60, 30),
slider_step=2,
imgprocess=lambda x: x,
train=True):
self.train = train
# self.slider = slider
# self.slider_step = slider_step
length = [(image.shape[1]-slider[1])//slider_step for image in images]
# Creating indices from gaplines
indices = gaplines - int(slider[1]/2)
indices = indices // slider_step
# Split images to sequence of vectors
# + targets seq of labels per image in images seq
images_seq = np.empty(len(images), dtype=object)
targets_seq = np.empty(len(images), dtype=object)
for i, img in enumerate(images):
images_seq[i] = [imgprocess(img[:, loc * slider_step: loc * slider_step + slider[1]].flatten())
for loc in range(length[i])]
targets_seq[i] = np.ones((length[i])) * NEG
for offset in range(gap_span):
ind = indices[i] + (-(offset % 2) * offset // 2) + ((1 - offset%2) * offset // 2)
if ind[0] < 0:
ind[0] = 0
if ind[-1] >= length[i]:
ind[-1] = length[i] - 1
targets_seq[i][ind] = POS
# Create pandas dataFrame and sort it by images seq lenght (length)
# in_length == out_length
self.dataFrame = pd.DataFrame({'length': length,
'images': images_seq,
'targets': targets_seq
}).sort_values('length').reset_index(drop=True)
bsize = int(len(images) / num_buckets)
self.num_buckets = num_buckets
# Create buckets by slicing parts by indexes
self.buckets = []
for bucket in range(num_buckets-1):
self.buckets.append(self.dataFrame.iloc[bucket * bsize: (bucket+1) * bsize])
self.buckets.append(self.dataFrame.iloc[(num_buckets-1) * bsize:])
self.buckets_size = [len(bucket) for bucket in self.buckets]
# cursor[i] will be the cursor for the ith bucket
self.cursor = np.array([0] * num_buckets)
self.bucket_order = np.random.permutation(num_buckets)
self.bucket_cursor = 0
self.shuffle()
print("Iterator created.")
def shuffle(self, idx=None):
""" Shuffle idx bucket or each bucket separately """
for i in [idx] if idx is not None else range(self.num_buckets):
self.buckets[i] = self.buckets[i].sample(frac=1).reset_index(drop=True)
self.cursor[i] = 0
def next_batch(self, batch_size):
"""
Creates next training batch of size: batch_size
Retruns: image seq, letter seq,
image seq lengths, letter seq lengths
"""
i_bucket = self.bucket_order[self.bucket_cursor]
# Increment cursor and shuffle in case of new round
self.bucket_cursor = (self.bucket_cursor + 1) % self.num_buckets
if self.bucket_cursor == 0:
self.bucket_order = np.random.permutation(self.num_buckets)
if self.cursor[i_bucket] + batch_size > self.buckets_size[i_bucket]:
self.shuffle(i_bucket)
# Handle too big batch sizes
if (batch_size > self.buckets_size[i_bucket]):
batch_size = self.buckets_size[i_bucket]
res = self.buckets[i_bucket].iloc[self.cursor[i_bucket]:
self.cursor[i_bucket]+batch_size]
self.cursor[i_bucket] += batch_size
# PAD input sequence and output
# Pad sequences with <PAD> to same length
max_length = max(res['length'])
input_seq = np.zeros((batch_size, max_length, N_INPUT), dtype=np.float32)
for i, img in enumerate(res['images']):
input_seq[i][:res['length'].values[i]] = img
input_seq = input_seq.swapaxes(0, 1)
# Need to pad according to the maximum length output sequence
targets = np.ones([batch_size, max_length], dtype=np.float32) * PAD
for i, target in enumerate(targets):
target[:res['length'].values[i]] = res['targets'].values[i]
return input_seq, targets, res['length'].values
def next_feed(self, size):
""" Create feed directly for model training """
(inputs_,
targets_,
length_) = self.next_batch(size)
return {
inputs: inputs_,
targets: targets_,
length: length_,
keep_prob: (1.0 - dropout) if self.train else 1.0
}
# Create iterator for feeding BiRNN
train_iterator = BucketDataIterator(trainImages,
trainGaplines,
POS_SPAN,
num_buckets,
slider_size,
slider_step,
train=True)
test_iterator = BucketDataIterator(testImages,
testGaplines,
POS_SPAN,
2,
slider_size,
slider_step,
train=False)
```
# Create classifier
## Inputs
```
# Input placehodlers
# N_INPUT -> size of vector representing one image in sequence
# Inputs shape (max_seq_length, batch_size, vec_size) - time major
inputs = tf.placeholder(shape=(None, None, N_INPUT),
dtype=tf.float32,
name='inputs')
length = tf.placeholder(shape=(None,),
dtype=tf.int32, # EDITED: tf.int32
name='length')
# required for training, not required for testing and application
targets = tf.placeholder(shape=(None, None),
dtype=tf.int64,
name='targets')
# Dropout value
keep_prob = tf.placeholder(tf.float32, name='keep_prob')
sequence_size, batch_size, _ = tf.unstack(tf.shape(inputs))
```
## Standardization + CNN
```
# Help functions for standard layers
def conv2d(x, W, name=None):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME', name=name)
def max_pool_2x2(x, name=None):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME', name=name)
# 1. Layer - Convulation variables
W_conv1 = tf.get_variable('W_conv1', shape=[5, 5, 1, 4],
initializer=tf.contrib.layers.xavier_initializer())
b_conv1 = tf.Variable(tf.constant(0.1, shape=[4]), name='b_conv1')
# 3. Layer - Convulation variables
W_conv2 = tf.get_variable('W_conv2', shape=[5, 5, 4, 8],
initializer=tf.contrib.layers.xavier_initializer())
b_conv2 = tf.Variable(tf.constant(0.1, shape=[8]), name='b_conv2')
def CNN(x):
# 1. Layer - Convulation
h_conv1 = tf.nn.relu(conv2d(x, W_conv1) + b_conv1, name='h_conv1')
# 2. Layer - Max Pool
h_pool1 = max_pool_2x2(h_conv1, name='h_pool1')
# 3. Layer - Convulation
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2, name='h_conv2')
# 4. Layer - Max Pool
return max_pool_2x2(h_conv2, name='h_pool2')
# Input images CNN
inpts = tf.map_fn(
lambda seq: tf.map_fn(
lambda img:
tf.reshape(
CNN(tf.reshape(img, [1, slider_size[0], slider_size[1], 1])), [-1]),
seq),
inputs,
dtype=tf.float32)
```
### Attention
```
# attention_states: size [batch_size, max_time, num_units]
attention_states = tf.transpose(inpts, [1, 0, 2])
# Create an attention mechanism
attention_mechanism = tf.contrib.seq2seq.LuongAttention(
rnn_units, attention_states,
memory_sequence_length=length)
final_cell = create_cell(rnn_units,
2*rnn_layers,
2*rnn_residual_layers,
is_dropout=True,
keep_prob=keep_prob)
final_cell = seq2seq.AttentionWrapper(
final_cell, attention_mechanism,
attention_layer_size=attention_size)
final_initial_state = final_cell.zero_state(batch_size, tf.float32)
attention_output, _ = tf.nn.dynamic_rnn(
cell=final_cell,
inputs=attention_states,
sequence_length=length,
# initial_state=final_initial_state,
dtype = tf.float32)
pred = tf.layers.dense(inputs=attention_output,
units=2,
name='pred')
prediction = tf.argmax(pred, axis=-1, name='prediction')
```
## Optimizer
```
# Define loss and optimizer
# loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=pred, labels=targets), name='loss')
weights = tf.multiply(targets, POS_WEIGHT) + 1
loss = tf.reduce_mean(tf.losses.sparse_softmax_cross_entropy(
logits=pred,
labels=targets,
weights=weights), name='loss')
train_step = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(loss, name='train_step')
# Evaluate model
correct_pred = tf.equal(prediction, targets)
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# accuracy = tf.reduce_mean(prediction * targets) # Testing for only zero predictions
```
## Training
```
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
# Creat plot for live stats ploting
trainPlot = TrainingPlot(TRAIN_STEPS, TEST_ITER, LOSS_ITER)
try:
for i_batch in range(TRAIN_STEPS):
fd = train_iterator.next_feed(BATCH_SIZE)
train_step.run(fd)
if i_batch % LOSS_ITER == 0:
# Plotting loss
tmpLoss = loss.eval(fd)
trainPlot.updateCost(tmpLoss, i_batch // LOSS_ITER)
if i_batch % TEST_ITER == 0:
# Plotting accuracy
fd_test = test_iterator.next_feed(BATCH_SIZE)
accTest = accuracy.eval(fd_test)
accTrain = accuracy.eval(fd)
trainPlot.updateAcc(accTest, accTrain, i_batch // TEST_ITER)
if i_batch % SAVE_ITER == 0:
saver.save(sess, 'models/gap-clas/A-RNN/model')
# if i_batch % EPOCH == 0:
# fd_test = test_iterator.next_feed(BATCH_SIZE)
# print('batch %r - loss: %r' % (i_batch, sess.run(loss, fd_test)))
# predict_, target_ = sess.run([pred, targets], fd_test)
# for i, (inp, pred) in enumerate(zip(target_, predict_)):
# print(' expected > {}'.format(inp))
# print(' predicted > {}'.format(pred))
# break
# print()
except KeyboardInterrupt:
saver.save(sess, 'models/gap-clas/A-RNN/model')
print('Training interrupted, model saved.')
fd_test = test_iterator.next_feed(2*BATCH_SIZE)
accTest = accuracy.eval(fd_test)
print("Training finished with accuracy:", accTest)
% matplotlib inline
num_examples = 5
# Shuffle test images
testImages = testImages[np.random.permutation(len(testImages))]
imgs = testImages[:num_examples]
# Split images to sequence of vectors
length = [(image.shape[1]-slider_size[1])//slider_step for image in imgs]
images_seq = np.empty(num_examples, dtype=object)
for i, img in enumerate(imgs):
images_seq[i] = np.array([img[:, loc * slider_step: loc * slider_step + slider_size[1]].flatten()
for loc in range(length[i])], dtype=np.float32)
# Create predictions using trained model
test_pred = []
for i, inpt in enumerate(images_seq):
inpt = np.reshape(inpt, (inpt.shape[0], 1, inpt.shape[1]))
img = imgs[i].copy()
# img = cv2.cvtColor(imgs[i].astype(np.float32), cv2.COLOR_GRAY2RGB)
pred = prediction.eval({'inputs:0': inpt,
'length:0': [len(inpt)],
'keep_prob:0': 1.0})
for pos, g in enumerate(pred[0]):
if g == 1:
cv2.line(img,
((int)(15 + pos*slider_step), 0),
((int)(15 + pos*slider_step), slider_size[0]),
1, 1)
implt(img, 'gray', t=str(i))
```
| true |
code
| 0.460835 | null | null | null | null |
|
## SIMPLE CONVOLUTIONAL NEURAL NETWORK
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
%matplotlib inline
print ("PACKAGES LOADED")
```
# LOAD MNIST
```
mnist = input_data.read_data_sets('data/', one_hot=True)
trainimg = mnist.train.images
trainlabel = mnist.train.labels
testimg = mnist.test.images
testlabel = mnist.test.labels
print ("MNIST ready")
```
# SELECT DEVICE TO BE USED
```
device_type = "/gpu:1"
```
# DEFINE CNN
```
with tf.device(device_type): # <= This is optional
n_input = 784
n_output = 10
weights = {
'wc1': tf.Variable(tf.random_normal([3, 3, 1, 64], stddev=0.1)),
'wd1': tf.Variable(tf.random_normal([14*14*64, n_output], stddev=0.1))
}
biases = {
'bc1': tf.Variable(tf.random_normal([64], stddev=0.1)),
'bd1': tf.Variable(tf.random_normal([n_output], stddev=0.1))
}
def conv_simple(_input, _w, _b):
# Reshape input
_input_r = tf.reshape(_input, shape=[-1, 28, 28, 1])
# Convolution
_conv1 = tf.nn.conv2d(_input_r, _w['wc1'], strides=[1, 1, 1, 1], padding='SAME')
# Add-bias
_conv2 = tf.nn.bias_add(_conv1, _b['bc1'])
# Pass ReLu
_conv3 = tf.nn.relu(_conv2)
# Max-pooling
_pool = tf.nn.max_pool(_conv3, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# Vectorize
_dense = tf.reshape(_pool, [-1, _w['wd1'].get_shape().as_list()[0]])
# Fully-connected layer
_out = tf.add(tf.matmul(_dense, _w['wd1']), _b['bd1'])
# Return everything
out = {
'input_r': _input_r, 'conv1': _conv1, 'conv2': _conv2, 'conv3': _conv3
, 'pool': _pool, 'dense': _dense, 'out': _out
}
return out
print ("CNN ready")
```
# DEFINE COMPUTATIONAL GRAPH
```
# tf Graph input
x = tf.placeholder(tf.float32, [None, n_input])
y = tf.placeholder(tf.float32, [None, n_output])
# Parameters
learning_rate = 0.001
training_epochs = 10
batch_size = 100
display_step = 1
# Functions!
with tf.device(device_type): # <= This is optional
_pred = conv_simple(x, weights, biases)['out']
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(_pred, y))
optm = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
_corr = tf.equal(tf.argmax(_pred,1), tf.argmax(y,1)) # Count corrects
accr = tf.reduce_mean(tf.cast(_corr, tf.float32)) # Accuracy
init = tf.initialize_all_variables()
# Saver
save_step = 1;
savedir = "nets/"
saver = tf.train.Saver(max_to_keep=3)
print ("Network Ready to Go!")
```
# OPTIMIZE
## DO TRAIN OR NOT
```
do_train = 1
sess = tf.Session(config=tf.ConfigProto(allow_soft_placement=True))
sess.run(init)
if do_train == 1:
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# Fit training using batch data
sess.run(optm, feed_dict={x: batch_xs, y: batch_ys})
# Compute average loss
avg_cost += sess.run(cost, feed_dict={x: batch_xs, y: batch_ys})/total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print ("Epoch: %03d/%03d cost: %.9f" % (epoch, training_epochs, avg_cost))
train_acc = sess.run(accr, feed_dict={x: batch_xs, y: batch_ys})
print (" Training accuracy: %.3f" % (train_acc))
test_acc = sess.run(accr, feed_dict={x: testimg, y: testlabel})
print (" Test accuracy: %.3f" % (test_acc))
# Save Net
if epoch % save_step == 0:
saver.save(sess, "nets/cnn_mnist_simple.ckpt-" + str(epoch))
print ("Optimization Finished.")
```
# RESTORE
```
if do_train == 0:
epoch = training_epochs-1
saver.restore(sess, "nets/cnn_mnist_simple.ckpt-" + str(epoch))
print ("NETWORK RESTORED")
```
# LET'S SEE HOW CNN WORKS
```
with tf.device(device_type):
conv_out = conv_simple(x, weights, biases)
input_r = sess.run(conv_out['input_r'], feed_dict={x: trainimg[0:1, :]})
conv1 = sess.run(conv_out['conv1'], feed_dict={x: trainimg[0:1, :]})
conv2 = sess.run(conv_out['conv2'], feed_dict={x: trainimg[0:1, :]})
conv3 = sess.run(conv_out['conv3'], feed_dict={x: trainimg[0:1, :]})
pool = sess.run(conv_out['pool'], feed_dict={x: trainimg[0:1, :]})
dense = sess.run(conv_out['dense'], feed_dict={x: trainimg[0:1, :]})
out = sess.run(conv_out['out'], feed_dict={x: trainimg[0:1, :]})
```
# Input
```
# Let's see 'input_r'
print ("Size of 'input_r' is %s" % (input_r.shape,))
label = np.argmax(trainlabel[0, :])
print ("Label is %d" % (label))
# Plot !
plt.matshow(input_r[0, :, :, 0], cmap=plt.get_cmap('gray'))
plt.title("Label of this image is " + str(label) + "")
plt.colorbar()
plt.show()
```
# Conv1 (convolution)
```
# Let's see 'conv1'
print ("Size of 'conv1' is %s" % (conv1.shape,))
# Plot !
for i in range(3):
plt.matshow(conv1[0, :, :, i], cmap=plt.get_cmap('gray'))
plt.title(str(i) + "th conv1")
plt.colorbar()
plt.show()
```
# Conv2 (+bias)
```
# Let's see 'conv2'
print ("Size of 'conv2' is %s" % (conv2.shape,))
# Plot !
for i in range(3):
plt.matshow(conv2[0, :, :, i], cmap=plt.get_cmap('gray'))
plt.title(str(i) + "th conv2")
plt.colorbar()
plt.show()
```
# Conv3 (ReLU)
```
# Let's see 'conv3'
print ("Size of 'conv3' is %s" % (conv3.shape,))
# Plot !
for i in range(3):
plt.matshow(conv3[0, :, :, i], cmap=plt.get_cmap('gray'))
plt.title(str(i) + "th conv3")
plt.colorbar()
plt.show()
```
# Pool (max_pool)
```
# Let's see 'pool'
print ("Size of 'pool' is %s" % (pool.shape,))
# Plot !
for i in range(3):
plt.matshow(pool[0, :, :, i], cmap=plt.get_cmap('gray'))
plt.title(str(i) + "th pool")
plt.colorbar()
plt.show()
```
# Dense
```
# Let's see 'dense'
print ("Size of 'dense' is %s" % (dense.shape,))
# Let's see 'out'
print ("Size of 'out' is %s" % (out.shape,))
```
# Convolution filters
```
# Let's see weight!
wc1 = sess.run(weights['wc1'])
print ("Size of 'wc1' is %s" % (wc1.shape,))
# Plot !
for i in range(3):
plt.matshow(wc1[:, :, 0, i], cmap=plt.get_cmap('gray'))
plt.title(str(i) + "th conv filter")
plt.colorbar()
plt.show()
```
| true |
code
| 0.62798 | null | null | null | null |
|
# Optimization with scipy.optimize
When we want to optimize something, we do not ofcourse need to start everything from scratch. It is good to know how algorithms work, but if the development of new algorithms is not the main point, then one can just use packages and libraries that have been premade.
In Python, there are multiple packages for optimization. At this lecture, we are goint to take a look at *scipy.optimize* package.
## Starting up
When we want to study a package in Python, we can import it..
```
from scipy.optimize import minimize
```
If we want to see the documentation, we can write the name of the package and two question marks and hit enter:
```
minimize??
```
## Optimization of multiple variables
Let us define again our friendly objective function:
```
def f_simple(x):
return (x[0] - 10.0)**2 + (x[1] + 5.0)**2+x[0]**2
```
### Method: `Nelder-Mead'
The documentation has the following to say:
<pre>
Method :ref:`Nelder-Mead <optimize.minimize-neldermead>` uses the
Simplex algorithm [1]_, [2]_. This algorithm has been successful
in many applications but other algorithms using the first and/or
second derivatives information might be preferred for their better
performances and robustness in general.
...
References
----------
.. [1] Nelder, J A, and R Mead. 1965. A Simplex Method for Function
Minimization. The Computer Journal 7: 308-13.
.. [2] Wright M H. 1996. Direct search methods: Once scorned, now
respectable, in Numerical Analysis 1995: Proceedings of the 1995
Dundee Biennial Conference in Numerical Analysis (Eds. D F
Griffiths and G A Watson). Addison Wesley Longman, Harlow, UK.
191-208.
</pre>
```
res = minimize(f_simple,[0,0],method='Nelder-Mead',
options={'disp': True})
print res.x
print type(res)
print res
print res.message
```
### Method: `CG`
The documentation has the following to say:
<pre>
Method :ref:`CG <optimize.minimize-cg>` uses a nonlinear conjugate
gradient algorithm by Polak and Ribiere, a variant of the
Fletcher-Reeves method described in [5]_ pp. 120-122. Only the
first derivatives are used.
...
References
----------
...
.. [5] Nocedal, J, and S J Wright. 2006. Numerical Optimization.
Springer New York.
</pre>
The Conjugate gradient method needs the gradient. The documentation has the following to say
<pre>
jac : bool or callable, optional
Jacobian (gradient) of objective function. Only for CG, BFGS,
Newton-CG, L-BFGS-B, TNC, SLSQP, dogleg, trust-ncg.
If `jac` is a Boolean and is True, `fun` is assumed to return the
gradient along with the objective function. If False, the
gradient will be estimated numerically.
`jac` can also be a callable returning the gradient of the
objective. In this case, it must accept the same arguments as `fun`.
</pre>
### Estimating the gradient numerically:
```
import numpy as np
res = minimize(f_simple, [0,0], method='CG', #Conjugate gradient method
options={'disp': True})
print res.x
```
### Giving the gradient with ad
```
import ad
res = minimize(f_simple, [0,0], method='CG', #Conjugate gradient method
options={'disp': True}, jac=ad.gh(f_simple)[0])
print res.x
```
### Method: `Newton-CG`
Newton-CG method uses a Newton-CG algorithm [5] pp. 168 (also known as the truncated Newton method). It uses a CG method to the compute the search direction. See also *TNC* method for a box-constrained minimization with a similar algorithm.
References
----------
.. [5] Nocedal, J, and S J Wright. 2006. Numerical Optimization.
Springer New York.
The Newton-CG algorithm needs the Jacobian and the Hessian. The documentation has the following to say:
<pre>
hess, hessp : callable, optional
Hessian (matrix of second-order derivatives) of objective function or
Hessian of objective function times an arbitrary vector p. Only for
Newton-CG, dogleg, trust-ncg.
Only one of `hessp` or `hess` needs to be given. If `hess` is
provided, then `hessp` will be ignored. If neither `hess` nor
`hessp` is provided, then the Hessian product will be approximated
using finite differences on `jac`. `hessp` must compute the Hessian
times an arbitrary vector.
</pre>
### Trying without reading the documentation
```
import numpy as np
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(f_simple, [0,0], method='Newton-CG', #Newton-CG method
options={'disp': True})
print res.x
```
### Giving the gradient
```
import ad
res = minimize(f_simple, [0,0], method='Newton-CG', #Newton-CG method
options={'disp': True},jac=ad.gh(f_simple)[0])
print res.x
```
### Giving also the hessian
```
import ad
res = minimize(f_simple, [0,0], method='Newton-CG', #Newton-CG method
options={'disp': True},jac=ad.gh(f_simple)[0],
hess=ad.gh(f_simple)[1])
print res.x
```
## Line search
```
def f_singlevar(x):
return 2+(1-x)**2
from scipy.optimize import minimize_scalar
minimize_scalar??
```
### Method: `Golden`
The documentation has the following to say:
<pre>
Method :ref:`Golden <optimize.minimize_scalar-golden>` uses the
golden section search technique. It uses analog of the bisection
method to decrease the bracketed interval. It is usually
preferable to use the *Brent* method.
</pre>
```
minimize_scalar(f_singlevar,method='golden',tol=0.00001)
```
### Method: `Brent`
The documentation has the following to say about the Brent method:
Method *Brent* uses Brent's algorithm to find a local minimum.
The algorithm uses inverse parabolic interpolation when possible to
speed up convergence of the golden section method.
```
minimize_scalar(f_singlevar,method='brent')
```
| true |
code
| 0.392715 | null | null | null | null |
|

# terrainbento model BasicRt steady-state solution
This model shows example usage of the BasicRt model from the TerrainBento package.
BasicRt modifies Basic by allowing for two lithologies:
$\frac{\partial \eta}{\partial t} = - K(\eta,\eta_C) Q^{1/2}S + D\nabla^2 \eta$
$K(\eta, \eta_C ) = w K_1 + (1 - w) K_2$
$w = \frac{1}{1+\exp \left( -\frac{(\eta -\eta_C )}{W_c}\right)}$
where $Q$ is the local stream discharge, $S$ is the local slope, $W_c$ is the contact-zone width, $K_1$ and $K_2$ are the erodibilities of the upper and lower lithologies, and $D$ is the regolith transport parameter. $w$ is a weight used to calculate the effective erodibility $K(\eta, \eta_C)$ based on the depth to the contact zone and the width of the contact zone.
Refer to [Barnhart et al. (2019)](https://www.geosci-model-dev.net/12/1267/2019/) for further explaination. For detailed information about creating a BasicRt model, see [the detailed documentation](https://terrainbento.readthedocs.io/en/latest/source/terrainbento.derived_models.model_basicRt.html).
This notebook (a) shows the initialization and running of this model, (b) saves a NetCDF file of the topography, which we will use to make an oblique Paraview image of the landscape, and (c) creates a slope-area plot at steady state.
```
# import required modules
from terrainbento import BasicRt, Clock, NotCoreNodeBaselevelHandler
from landlab.io.netcdf import write_netcdf
from landlab.values import random
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
from landlab import imshow_grid, RasterModelGrid
np.random.seed(4897)
#Ignore warnings
import warnings
warnings.filterwarnings('ignore')
# in this example we will create a grid, a clock, a boundary handler,
# and an output writer. We will then use these to construct the model.
grid = RasterModelGrid((25, 40), xy_spacing=40)
z = random(grid, "topographic__elevation", where="CORE_NODE")
contact = grid.add_zeros("node", "lithology_contact__elevation")
contact[grid.node_y > 500.0] = 10.
contact[grid.node_y <= 500.0] = -100000000.
clock = Clock(start=0, step=10, stop=1e7)
ncnblh = NotCoreNodeBaselevelHandler(grid,
modify_core_nodes=True,
lowering_rate=-0.001)
# the tolerance here is high, so that this can run on binder and for tests. (recommended value = 0.001 or lower).
tolerance = 20.0
# we can use an output writer to run until the model reaches steady state.
class run_to_steady(object):
def __init__(self, model):
self.model = model
self.last_z = self.model.z.copy()
self.tolerance = tolerance
def run_one_step(self):
if model.model_time > 0:
diff = (self.model.z[model.grid.core_nodes] -
self.last_z[model.grid.core_nodes])
if max(abs(diff)) <= self.tolerance:
self.model.clock.stop = model._model_time
print("Model reached steady state in " +
str(model._model_time) + " time units\n")
else:
self.last_z = self.model.z.copy()
if model._model_time <= self.model.clock.stop - self.model.output_interval:
self.model.clock.stop += self.model.output_interval
# initialize the model by passing the correct arguments and
# keyword arguments.
model = BasicRt(clock,
grid,
boundary_handlers={"NotCoreNodeBaselevelHandler": ncnblh},
output_interval=1e4,
save_first_timestep=True,
output_prefix="output/basicRt",
fields=["topographic__elevation"],
water_erodibility_lower=0.001,
water_erodibility_upper=0.01,
m_sp=0.5,
n_sp=1.0,
regolith_transport_parameter=0.1,
contact_zone__width=1.0,
output_writers={"class": [run_to_steady]})
# to run the model as specified, execute the following line:
model.run()
# MAKE SLOPE-AREA PLOT
# plot nodes that are not on the boundary or adjacent to it
core_not_boundary = np.array(
model.grid.node_has_boundary_neighbor(model.grid.core_nodes)) == False
plotting_nodes = model.grid.core_nodes[core_not_boundary]
upper_plotting_nodes = plotting_nodes[
model.grid.node_y[plotting_nodes] > 500.0]
lower_plotting_nodes = plotting_nodes[
model.grid.node_y[plotting_nodes] < 500.0]
# assign area_array and slope_array for ROCK
area_array_upper = model.grid.at_node["drainage_area"][upper_plotting_nodes]
slope_array_upper = model.grid.at_node["topographic__steepest_slope"][
upper_plotting_nodes]
# assign area_array and slope_array for TILL
area_array_lower = model.grid.at_node["drainage_area"][lower_plotting_nodes]
slope_array_lower = model.grid.at_node["topographic__steepest_slope"][
lower_plotting_nodes]
# instantiate figure and plot
fig = plt.figure(figsize=(6, 3.75))
slope_area = plt.subplot()
#plot the data for ROCK
slope_area.scatter(area_array_lower,
slope_array_lower,
marker="s",
edgecolor="0",
color="1",
label="Model BasicRt, Lower Layer")
#plot the data for TILL
slope_area.scatter(area_array_upper,
slope_array_upper,
color="k",
label="Model BasicRt, Upper Layer")
#make axes log and set limits
slope_area.set_xscale("log")
slope_area.set_yscale("log")
slope_area.set_xlim(9 * 10**1, 3 * 10**5)
slope_area.set_ylim(1e-5, 1e-1)
#set x and y labels
slope_area.set_xlabel(r"Drainage area [m$^2$]")
slope_area.set_ylabel("Channel slope [-]")
slope_area.legend(scatterpoints=1, prop={"size": 12})
slope_area.tick_params(axis="x", which="major", pad=7)
plt.show()
# # Save stack of all netcdfs for Paraview to use.
# model.save_to_xarray_dataset(filename="basicRt.nc",
# time_unit="years",
# reference_time="model start",
# space_unit="meters")
# remove temporary netcdfs
model.remove_output_netcdfs()
# make a plot of the final steady state topography
plt.figure()
imshow_grid(model.grid, "topographic__elevation",cmap ='terrain',
grid_units=("m", "m"),var_name="Elevation (m)")
plt.show()
```
## Challenge
Create a LEM with a hard bedrock layer underlying a soft cover in the eastern side of the domain or (extra challenge) as a square in the middle of the domain.
## Next Steps
- [Welcome page](../Welcome_to_TerrainBento.ipynb)
- There are three additional introductory tutorials:
1) [Introduction terrainbento](../example_usage/Introduction_to_terrainbento.ipynb)
2) [Introduction to boundary conditions in terrainbento](../example_usage/introduction_to_boundary_conditions.ipynb)
3) [Introduction to output writers in terrainbento](../example_usage/introduction_to_output_writers.ipynb).
- Five examples of steady state behavior in coupled process models can be found in the following notebooks:
1) [Basic](model_basic_steady_solution.ipynb) the simplest landscape evolution model in the terrainbento package.
2) [BasicVm](model_basic_var_m_steady_solution.ipynb) which permits the drainage area exponent to change
3) [BasicCh](model_basicCh_steady_solution.ipynb) which uses a non-linear hillslope erosion and transport law
4) [BasicVs](model_basicVs_steady_solution.ipynb) which uses variable source area hydrology
5) **This Notebook**: [BasisRt](model_basicRt_steady_solution.ipynb) which allows for two lithologies with different K values
6) [RealDEM](model_basic_realDEM.ipynb) Run the basic terrainbento model with a real DEM as initial condition.
| true |
code
| 0.783823 | null | null | null | null |
|
# 100 numpy exercises
This is a collection of exercises that have been collected in the numpy mailing list, on stack overflow and in the numpy documentation. The goal of this collection is to offer a quick reference for both old and new users but also to provide a set of exercises for those who teach.
If you find an error or think you've a better way to solve some of them, feel free to open an issue at <https://github.com/rougier/numpy-100>
#### 1. Import the numpy package under the name `np` (★☆☆)
```
import numpy as np
```
#### 2. Print the numpy version and the configuration (★☆☆)
```
print(np.__version__)
np.show_config()
```
#### 3. Create a null vector of size 10 (★☆☆)
```
Z = np.zeros(10)
print(Z)
```
#### 4. How to find the memory size of any array (★☆☆)
```
Z = np.zeros((10,10))
print("%d bytes" % (Z.size * Z.itemsize))
```
#### 5. How to get the documentation of the numpy add function from the command line? (★☆☆)
```
%run `python -c "import numpy; numpy.info(numpy.add)"`
```
#### 6. Create a null vector of size 10 but the fifth value which is 1 (★☆☆)
```
Z = np.zeros(10)
Z[4] = 1
print(Z)
```
#### 7. Create a vector with values ranging from 10 to 49 (★☆☆)
```
Z = np.arange(10,50)
print(Z)
```
#### 8. Reverse a vector (first element becomes last) (★☆☆)
```
Z = np.arange(50)
Z = Z[::-1]
print(Z)
```
#### 9. Create a 3x3 matrix with values ranging from 0 to 8 (★☆☆)
```
Z = np.arange(9).reshape(3,3)
print(Z)
```
#### 10. Find indices of non-zero elements from \[1,2,0,0,4,0\] (★☆☆)
```
nz = np.nonzero([1,2,0,0,4,0])
print(nz)
```
#### 11. Create a 3x3 identity matrix (★☆☆)
```
Z = np.eye(3)
print(Z)
```
#### 12. Create a 3x3x3 array with random values (★☆☆)
```
Z = np.random.random((3,3,3))
print(Z)
```
#### 13. Create a 10x10 array with random values and find the minimum and maximum values (★☆☆)
```
Z = np.random.random((10,10))
Zmin, Zmax = Z.min(), Z.max()
print(Zmin, Zmax)
```
#### 14. Create a random vector of size 30 and find the mean value (★☆☆)
```
Z = np.random.random(30)
m = Z.mean()
print(m)
```
#### 15. Create a 2d array with 1 on the border and 0 inside (★☆☆)
```
Z = np.ones((10,10))
Z[1:-1,1:-1] = 0
print(Z)
```
#### 16. How to add a border (filled with 0's) around an existing array? (★☆☆)
```
Z = np.ones((5,5))
Z = np.pad(Z, pad_width=1, mode='constant', constant_values=0)
print(Z)
```
#### 17. What is the result of the following expression? (★☆☆)
```
print(0 * np.nan)
print(np.nan == np.nan)
print(np.inf > np.nan)
print(np.nan - np.nan)
print(np.nan in set([np.nan]))
print(0.3 == 3 * 0.1)
```
#### 18. Create a 5x5 matrix with values 1,2,3,4 just below the diagonal (★☆☆)
```
Z = np.diag(1+np.arange(4),k=-1)
print(Z)
```
#### 19. Create a 8x8 matrix and fill it with a checkerboard pattern (★☆☆)
```
Z = np.zeros((8,8),dtype=int)
Z[1::2,::2] = 1
Z[::2,1::2] = 1
print(Z)
```
#### 20. Consider a (6,7,8) shape array, what is the index (x,y,z) of the 100th element?
```
print(np.unravel_index(100,(6,7,8)))
```
#### 21. Create a checkerboard 8x8 matrix using the tile function (★☆☆)
```
Z = np.tile( np.array([[0,1],[1,0]]), (4,4))
print(Z)
```
#### 22. Normalize a 5x5 random matrix (★☆☆)
```
Z = np.random.random((5,5))
Z = (Z - np.mean (Z)) / (np.std (Z))
print(Z)
```
#### 23. Create a custom dtype that describes a color as four unsigned bytes (RGBA) (★☆☆)
```
color = np.dtype([("r", np.ubyte, 1),
("g", np.ubyte, 1),
("b", np.ubyte, 1),
("a", np.ubyte, 1)])
```
#### 24. Multiply a 5x3 matrix by a 3x2 matrix (real matrix product) (★☆☆)
```
Z = np.dot(np.ones((5,3)), np.ones((3,2)))
print(Z)
# Alternative solution, in Python 3.5 and above
Z = np.ones((5,3)) @ np.ones((3,2))
```
#### 25. Given a 1D array, negate all elements which are between 3 and 8, in place. (★☆☆)
```
# Author: Evgeni Burovski
Z = np.arange(11)
Z[(3 < Z) & (Z <= 8)] *= -1
print(Z)
```
#### 26. What is the output of the following script? (★☆☆)
```
# Author: Jake VanderPlas
print(sum(range(5),-1))
from numpy import *
print(sum(range(5),-1))
```
#### 27. Consider an integer vector Z, which of these expressions are legal? (★☆☆)
```
Z**Z
2 << Z >> 2
Z <- Z
1j*Z
Z/1/1
Z<Z>Z
```
#### 28. What are the result of the following expressions?
```
print(np.array(0) / np.array(0))
print(np.array(0) // np.array(0))
print(np.array([np.nan]).astype(int).astype(float))
```
#### 29. How to round away from zero a float array ? (★☆☆)
```
# Author: Charles R Harris
Z = np.random.uniform(-10,+10,10)
print (np.copysign(np.ceil(np.abs(Z)), Z))
```
#### 30. How to find common values between two arrays? (★☆☆)
```
Z1 = np.random.randint(0,10,10)
Z2 = np.random.randint(0,10,10)
print(np.intersect1d(Z1,Z2))
```
#### 31. How to ignore all numpy warnings (not recommended)? (★☆☆)
```
# Suicide mode on
defaults = np.seterr(all="ignore")
Z = np.ones(1) / 0
# Back to sanity
_ = np.seterr(**defaults)
An equivalent way, with a context manager:
with np.errstate(divide='ignore'):
Z = np.ones(1) / 0
```
#### 32. Is the following expressions true? (★☆☆)
```
np.sqrt(-1) == np.emath.sqrt(-1)
```
#### 33. How to get the dates of yesterday, today and tomorrow? (★☆☆)
```
yesterday = np.datetime64('today', 'D') - np.timedelta64(1, 'D')
today = np.datetime64('today', 'D')
tomorrow = np.datetime64('today', 'D') + np.timedelta64(1, 'D')
```
#### 34. How to get all the dates corresponding to the month of July 2016? (★★☆)
```
Z = np.arange('2016-07', '2016-08', dtype='datetime64[D]')
print(Z)
```
#### 35. How to compute ((A+B)\*(-A/2)) in place (without copy)? (★★☆)
```
A = np.ones(3)*1
B = np.ones(3)*2
C = np.ones(3)*3
np.add(A,B,out=B)
np.divide(A,2,out=A)
np.negative(A,out=A)
np.multiply(A,B,out=A)
```
#### 36. Extract the integer part of a random array using 5 different methods (★★☆)
```
Z = np.random.uniform(0,10,10)
print (Z - Z%1)
print (np.floor(Z))
print (np.ceil(Z)-1)
print (Z.astype(int))
print (np.trunc(Z))
```
#### 37. Create a 5x5 matrix with row values ranging from 0 to 4 (★★☆)
```
Z = np.zeros((5,5))
Z += np.arange(5)
print(Z)
```
#### 38. Consider a generator function that generates 10 integers and use it to build an array (★☆☆)
```
def generate():
for x in range(10):
yield x
Z = np.fromiter(generate(),dtype=float,count=-1)
print(Z)
```
#### 39. Create a vector of size 10 with values ranging from 0 to 1, both excluded (★★☆)
```
Z = np.linspace(0,1,11,endpoint=False)[1:]
print(Z)
```
#### 40. Create a random vector of size 10 and sort it (★★☆)
```
Z = np.random.random(10)
Z.sort()
print(Z)
```
#### 41. How to sum a small array faster than np.sum? (★★☆)
```
# Author: Evgeni Burovski
Z = np.arange(10)
np.add.reduce(Z)
```
#### 42. Consider two random array A and B, check if they are equal (★★☆)
```
A = np.random.randint(0,2,5)
B = np.random.randint(0,2,5)
# Assuming identical shape of the arrays and a tolerance for the comparison of values
equal = np.allclose(A,B)
print(equal)
# Checking both the shape and the element values, no tolerance (values have to be exactly equal)
equal = np.array_equal(A,B)
print(equal)
```
#### 43. Make an array immutable (read-only) (★★☆)
```
Z = np.zeros(10)
Z.flags.writeable = False
Z[0] = 1
```
#### 44. Consider a random 10x2 matrix representing cartesian coordinates, convert them to polar coordinates (★★☆)
```
Z = np.random.random((10,2))
X,Y = Z[:,0], Z[:,1]
R = np.sqrt(X**2+Y**2)
T = np.arctan2(Y,X)
print(R)
print(T)
```
#### 45. Create random vector of size 10 and replace the maximum value by 0 (★★☆)
```
Z = np.random.random(10)
Z[Z.argmax()] = 0
print(Z)
```
#### 46. Create a structured array with `x` and `y` coordinates covering the \[0,1\]x\[0,1\] area (★★☆)
```
Z = np.zeros((5,5), [('x',float),('y',float)])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0,1,5),
np.linspace(0,1,5))
print(Z)
```
#### 47. Given two arrays, X and Y, construct the Cauchy matrix C (Cij =1/(xi - yj))
```
# Author: Evgeni Burovski
X = np.arange(8)
Y = X + 0.5
C = 1.0 / np.subtract.outer(X, Y)
print(np.linalg.det(C))
```
#### 48. Print the minimum and maximum representable value for each numpy scalar type (★★☆)
```
for dtype in [np.int8, np.int32, np.int64]:
print(np.iinfo(dtype).min)
print(np.iinfo(dtype).max)
for dtype in [np.float32, np.float64]:
print(np.finfo(dtype).min)
print(np.finfo(dtype).max)
print(np.finfo(dtype).eps)
```
#### 49. How to print all the values of an array? (★★☆)
```
np.set_printoptions(threshold=np.nan)
Z = np.zeros((16,16))
print(Z)
```
#### 50. How to find the closest value (to a given scalar) in a vector? (★★☆)
```
Z = np.arange(100)
v = np.random.uniform(0,100)
index = (np.abs(Z-v)).argmin()
print(Z[index])
```
#### 51. Create a structured array representing a position (x,y) and a color (r,g,b) (★★☆)
```
Z = np.zeros(10, [ ('position', [ ('x', float, 1),
('y', float, 1)]),
('color', [ ('r', float, 1),
('g', float, 1),
('b', float, 1)])])
print(Z)
```
#### 52. Consider a random vector with shape (100,2) representing coordinates, find point by point distances (★★☆)
```
Z = np.random.random((10,2))
X,Y = np.atleast_2d(Z[:,0], Z[:,1])
D = np.sqrt( (X-X.T)**2 + (Y-Y.T)**2)
print(D)
# Much faster with scipy
import scipy
# Thanks Gavin Heverly-Coulson (#issue 1)
import scipy.spatial
Z = np.random.random((10,2))
D = scipy.spatial.distance.cdist(Z,Z)
print(D)
```
#### 53. How to convert a float (32 bits) array into an integer (32 bits) in place?
```
Z = np.arange(10, dtype=np.float32)
Z = Z.astype(np.int32, copy=False)
print(Z)
```
#### 54. How to read the following file? (★★☆)
```
from io import StringIO
# Fake file
s = StringIO("""1, 2, 3, 4, 5\n
6, , , 7, 8\n
, , 9,10,11\n""")
Z = np.genfromtxt(s, delimiter=",", dtype=np.int)
print(Z)
```
#### 55. What is the equivalent of enumerate for numpy arrays? (★★☆)
```
Z = np.arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index])
```
#### 56. Generate a generic 2D Gaussian-like array (★★☆)
```
X, Y = np.meshgrid(np.linspace(-1,1,10), np.linspace(-1,1,10))
D = np.sqrt(X*X+Y*Y)
sigma, mu = 1.0, 0.0
G = np.exp(-( (D-mu)**2 / ( 2.0 * sigma**2 ) ) )
print(G)
```
#### 57. How to randomly place p elements in a 2D array? (★★☆)
```
# Author: Divakar
n = 10
p = 3
Z = np.zeros((n,n))
np.put(Z, np.random.choice(range(n*n), p, replace=False),1)
print(Z)
```
#### 58. Subtract the mean of each row of a matrix (★★☆)
```
# Author: Warren Weckesser
X = np.random.rand(5, 10)
# Recent versions of numpy
Y = X - X.mean(axis=1, keepdims=True)
# Older versions of numpy
Y = X - X.mean(axis=1).reshape(-1, 1)
print(Y)
```
#### 59. How to sort an array by the nth column? (★★☆)
```
# Author: Steve Tjoa
Z = np.random.randint(0,10,(3,3))
print(Z)
print(Z[Z[:,1].argsort()])
```
#### 60. How to tell if a given 2D array has null columns? (★★☆)
```
# Author: Warren Weckesser
Z = np.random.randint(0,3,(3,10))
print((~Z.any(axis=0)).any())
```
#### 61. Find the nearest value from a given value in an array (★★☆)
```
Z = np.random.uniform(0,1,10)
z = 0.5
m = Z.flat[np.abs(Z - z).argmin()]
print(m)
```
#### 62. Considering two arrays with shape (1,3) and (3,1), how to compute their sum using an iterator? (★★☆)
```
A = np.arange(3).reshape(3,1)
B = np.arange(3).reshape(1,3)
it = np.nditer([A,B,None])
for x,y,z in it: z[...] = x + y
print(it.operands[2])
```
#### 63. Create an array class that has a name attribute (★★☆)
```
class NamedArray(np.ndarray):
def __new__(cls, array, name="no name"):
obj = np.asarray(array).view(cls)
obj.name = name
return obj
def __array_finalize__(self, obj):
if obj is None: return
self.info = getattr(obj, 'name', "no name")
Z = NamedArray(np.arange(10), "range_10")
print (Z.name)
```
#### 64. Consider a given vector, how to add 1 to each element indexed by a second vector (be careful with repeated indices)? (★★★)
```
# Author: Brett Olsen
Z = np.ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z)
# Another solution
# Author: Bartosz Telenczuk
np.add.at(Z, I, 1)
print(Z)
```
#### 65. How to accumulate elements of a vector (X) to an array (F) based on an index list (I)? (★★★)
```
# Author: Alan G Isaac
X = [1,2,3,4,5,6]
I = [1,3,9,3,4,1]
F = np.bincount(I,X)
print(F)
```
#### 66. Considering a (w,h,3) image of (dtype=ubyte), compute the number of unique colors (★★★)
```
# Author: Nadav Horesh
w,h = 16,16
I = np.random.randint(0,2,(h,w,3)).astype(np.ubyte)
#Note that we should compute 256*256 first.
#Otherwise numpy will only promote F.dtype to 'uint16' and overfolw will occur
F = I[...,0]*(256*256) + I[...,1]*256 +I[...,2]
n = len(np.unique(F))
print(n)
```
#### 67. Considering a four dimensions array, how to get sum over the last two axis at once? (★★★)
```
A = np.random.randint(0,10,(3,4,3,4))
# solution by passing a tuple of axes (introduced in numpy 1.7.0)
sum = A.sum(axis=(-2,-1))
print(sum)
# solution by flattening the last two dimensions into one
# (useful for functions that don't accept tuples for axis argument)
sum = A.reshape(A.shape[:-2] + (-1,)).sum(axis=-1)
print(sum)
```
#### 68. Considering a one-dimensional vector D, how to compute means of subsets of D using a vector S of same size describing subset indices? (★★★)
```
# Author: Jaime Fernández del Río
D = np.random.uniform(0,1,100)
S = np.random.randint(0,10,100)
D_sums = np.bincount(S, weights=D)
D_counts = np.bincount(S)
D_means = D_sums / D_counts
print(D_means)
# Pandas solution as a reference due to more intuitive code
import pandas as pd
print(pd.Series(D).groupby(S).mean())
```
#### 69. How to get the diagonal of a dot product? (★★★)
```
# Author: Mathieu Blondel
A = np.random.uniform(0,1,(5,5))
B = np.random.uniform(0,1,(5,5))
# Slow version
np.diag(np.dot(A, B))
# Fast version
np.sum(A * B.T, axis=1)
# Faster version
np.einsum("ij,ji->i", A, B)
```
#### 70. Consider the vector \[1, 2, 3, 4, 5\], how to build a new vector with 3 consecutive zeros interleaved between each value? (★★★)
```
# Author: Warren Weckesser
Z = np.array([1,2,3,4,5])
nz = 3
Z0 = np.zeros(len(Z) + (len(Z)-1)*(nz))
Z0[::nz+1] = Z
print(Z0)
```
#### 71. Consider an array of dimension (5,5,3), how to mulitply it by an array with dimensions (5,5)? (★★★)
```
A = np.ones((5,5,3))
B = 2*np.ones((5,5))
print(A * B[:,:,None])
```
#### 72. How to swap two rows of an array? (★★★)
```
# Author: Eelco Hoogendoorn
A = np.arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A)
```
#### 73. Consider a set of 10 triplets describing 10 triangles (with shared vertices), find the set of unique line segments composing all the triangles (★★★)
```
# Author: Nicolas P. Rougier
faces = np.random.randint(0,100,(10,3))
F = np.roll(faces.repeat(2,axis=1),-1,axis=1)
F = F.reshape(len(F)*3,2)
F = np.sort(F,axis=1)
G = F.view( dtype=[('p0',F.dtype),('p1',F.dtype)] )
G = np.unique(G)
print(G)
```
#### 74. Given an array C that is a bincount, how to produce an array A such that np.bincount(A) == C? (★★★)
```
# Author: Jaime Fernández del Río
C = np.bincount([1,1,2,3,4,4,6])
A = np.repeat(np.arange(len(C)), C)
print(A)
```
#### 75. How to compute averages using a sliding window over an array? (★★★)
```
# Author: Jaime Fernández del Río
def moving_average(a, n=3) :
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
Z = np.arange(20)
print(moving_average(Z, n=3))
```
#### 76. Consider a one-dimensional array Z, build a two-dimensional array whose first row is (Z\[0\],Z\[1\],Z\[2\]) and each subsequent row is shifted by 1 (last row should be (Z\[-3\],Z\[-2\],Z\[-1\]) (★★★)
```
# Author: Joe Kington / Erik Rigtorp
from numpy.lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)
```
#### 77. How to negate a boolean, or to change the sign of a float inplace? (★★★)
```
# Author: Nathaniel J. Smith
Z = np.random.randint(0,2,100)
np.logical_not(Z, out=Z)
Z = np.random.uniform(-1.0,1.0,100)
np.negative(Z, out=Z)
```
#### 78. Consider 2 sets of points P0,P1 describing lines (2d) and a point p, how to compute distance from p to each line i (P0\[i\],P1\[i\])? (★★★)
```
def distance(P0, P1, p):
T = P1 - P0
L = (T**2).sum(axis=1)
U = -((P0[:,0]-p[...,0])*T[:,0] + (P0[:,1]-p[...,1])*T[:,1]) / L
U = U.reshape(len(U),1)
D = P0 + U*T - p
return np.sqrt((D**2).sum(axis=1))
P0 = np.random.uniform(-10,10,(10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10,10,( 1,2))
print(distance(P0, P1, p))
```
#### 79. Consider 2 sets of points P0,P1 describing lines (2d) and a set of points P, how to compute distance from each point j (P\[j\]) to each line i (P0\[i\],P1\[i\])? (★★★)
```
# Author: Italmassov Kuanysh
# based on distance function from previous question
P0 = np.random.uniform(-10, 10, (10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10, 10, (10,2))
print(np.array([distance(P0,P1,p_i) for p_i in p]))
```
#### 80. Consider an arbitrary array, write a function that extract a subpart with a fixed shape and centered on a given element (pad with a `fill` value when necessary) (★★★)
```
# Author: Nicolas Rougier
Z = np.random.randint(0,10,(10,10))
shape = (5,5)
fill = 0
position = (1,1)
R = np.ones(shape, dtype=Z.dtype)*fill
P = np.array(list(position)).astype(int)
Rs = np.array(list(R.shape)).astype(int)
Zs = np.array(list(Z.shape)).astype(int)
R_start = np.zeros((len(shape),)).astype(int)
R_stop = np.array(list(shape)).astype(int)
Z_start = (P-Rs//2)
Z_stop = (P+Rs//2)+Rs%2
R_start = (R_start - np.minimum(Z_start,0)).tolist()
Z_start = (np.maximum(Z_start,0)).tolist()
R_stop = np.maximum(R_start, (R_stop - np.maximum(Z_stop-Zs,0))).tolist()
Z_stop = (np.minimum(Z_stop,Zs)).tolist()
r = [slice(start,stop) for start,stop in zip(R_start,R_stop)]
z = [slice(start,stop) for start,stop in zip(Z_start,Z_stop)]
R[r] = Z[z]
print(Z)
print(R)
```
#### 81. Consider an array Z = \[1,2,3,4,5,6,7,8,9,10,11,12,13,14\], how to generate an array R = \[\[1,2,3,4\], \[2,3,4,5\], \[3,4,5,6\], ..., \[11,12,13,14\]\]? (★★★)
```
# Author: Stefan van der Walt
Z = np.arange(1,15,dtype=np.uint32)
R = stride_tricks.as_strided(Z,(11,4),(4,4))
print(R)
```
#### 82. Compute a matrix rank (★★★)
```
# Author: Stefan van der Walt
Z = np.random.uniform(0,1,(10,10))
U, S, V = np.linalg.svd(Z) # Singular Value Decomposition
rank = np.sum(S > 1e-10)
print(rank)
```
#### 83. How to find the most frequent value in an array?
```
Z = np.random.randint(0,10,50)
print(np.bincount(Z).argmax())
```
#### 84. Extract all the contiguous 3x3 blocks from a random 10x10 matrix (★★★)
```
# Author: Chris Barker
Z = np.random.randint(0,5,(10,10))
n = 3
i = 1 + (Z.shape[0]-3)
j = 1 + (Z.shape[1]-3)
C = stride_tricks.as_strided(Z, shape=(i, j, n, n), strides=Z.strides + Z.strides)
print(C)
```
#### 85. Create a 2D array subclass such that Z\[i,j\] == Z\[j,i\] (★★★)
```
# Author: Eric O. Lebigot
# Note: only works for 2d array and value setting using indices
class Symetric(np.ndarray):
def __setitem__(self, index, value):
i,j = index
super(Symetric, self).__setitem__((i,j), value)
super(Symetric, self).__setitem__((j,i), value)
def symetric(Z):
return np.asarray(Z + Z.T - np.diag(Z.diagonal())).view(Symetric)
S = symetric(np.random.randint(0,10,(5,5)))
S[2,3] = 42
print(S)
```
#### 86. Consider a set of p matrices wich shape (n,n) and a set of p vectors with shape (n,1). How to compute the sum of of the p matrix products at once? (result has shape (n,1)) (★★★)
```
# Author: Stefan van der Walt
p, n = 10, 20
M = np.ones((p,n,n))
V = np.ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector.
```
#### 87. Consider a 16x16 array, how to get the block-sum (block size is 4x4)? (★★★)
```
# Author: Robert Kern
Z = np.ones((16,16))
k = 4
S = np.add.reduceat(np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
np.arange(0, Z.shape[1], k), axis=1)
print(S)
```
#### 88. How to implement the Game of Life using numpy arrays? (★★★)
```
# Author: Nicolas Rougier
def iterate(Z):
# Count neighbours
N = (Z[0:-2,0:-2] + Z[0:-2,1:-1] + Z[0:-2,2:] +
Z[1:-1,0:-2] + Z[1:-1,2:] +
Z[2: ,0:-2] + Z[2: ,1:-1] + Z[2: ,2:])
# Apply rules
birth = (N==3) & (Z[1:-1,1:-1]==0)
survive = ((N==2) | (N==3)) & (Z[1:-1,1:-1]==1)
Z[...] = 0
Z[1:-1,1:-1][birth | survive] = 1
return Z
Z = np.random.randint(0,2,(50,50))
for i in range(100): Z = iterate(Z)
print(Z)
```
#### 89. How to get the n largest values of an array (★★★)
```
Z = np.arange(10000)
np.random.shuffle(Z)
n = 5
# Slow
print (Z[np.argsort(Z)[-n:]])
# Fast
print (Z[np.argpartition(-Z,n)[:n]])
```
#### 90. Given an arbitrary number of vectors, build the cartesian product (every combinations of every item) (★★★)
```
# Author: Stefan Van der Walt
def cartesian(arrays):
arrays = [np.asarray(a) for a in arrays]
shape = (len(x) for x in arrays)
ix = np.indices(shape, dtype=int)
ix = ix.reshape(len(arrays), -1).T
for n, arr in enumerate(arrays):
ix[:, n] = arrays[n][ix[:, n]]
return ix
print (cartesian(([1, 2, 3], [4, 5], [6, 7])))
```
#### 91. How to create a record array from a regular array? (★★★)
```
Z = np.array([("Hello", 2.5, 3),
("World", 3.6, 2)])
R = np.core.records.fromarrays(Z.T,
names='col1, col2, col3',
formats = 'S8, f8, i8')
print(R)
```
#### 92. Consider a large vector Z, compute Z to the power of 3 using 3 different methods (★★★)
```
# Author: Ryan G.
x = np.random.rand(5e7)
%timeit np.power(x,3)
%timeit x*x*x
%timeit np.einsum('i,i,i->i',x,x,x)
```
#### 93. Consider two arrays A and B of shape (8,3) and (2,2). How to find rows of A that contain elements of each row of B regardless of the order of the elements in B? (★★★)
```
# Author: Gabe Schwartz
A = np.random.randint(0,5,(8,3))
B = np.random.randint(0,5,(2,2))
C = (A[..., np.newaxis, np.newaxis] == B)
rows = np.where(C.any((3,1)).all(1))[0]
print(rows)
```
#### 94. Considering a 10x3 matrix, extract rows with unequal values (e.g. \[2,2,3\]) (★★★)
```
# Author: Robert Kern
Z = np.random.randint(0,5,(10,3))
print(Z)
# solution for arrays of all dtypes (including string arrays and record arrays)
E = np.all(Z[:,1:] == Z[:,:-1], axis=1)
U = Z[~E]
print(U)
# soluiton for numerical arrays only, will work for any number of columns in Z
U = Z[Z.max(axis=1) != Z.min(axis=1),:]
print(U)
```
#### 95. Convert a vector of ints into a matrix binary representation (★★★)
```
# Author: Warren Weckesser
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128])
B = ((I.reshape(-1,1) & (2**np.arange(8))) != 0).astype(int)
print(B[:,::-1])
# Author: Daniel T. McDonald
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))
```
#### 96. Given a two dimensional array, how to extract unique rows? (★★★)
```
# Author: Jaime Fernández del Río
Z = np.random.randint(0,2,(6,3))
T = np.ascontiguousarray(Z).view(np.dtype((np.void, Z.dtype.itemsize * Z.shape[1])))
_, idx = np.unique(T, return_index=True)
uZ = Z[idx]
print(uZ)
# Author: Andreas Kouzelis
# NumPy >= 1.13
uZ = np.unique(Z, axis=0)
print(uZ)
```
#### 97. Considering 2 vectors A & B, write the einsum equivalent of inner, outer, sum, and mul function (★★★)
```
# Author: Alex Riley
# Make sure to read: http://ajcr.net/Basic-guide-to-einsum/
A = np.random.uniform(0,1,10)
B = np.random.uniform(0,1,10)
np.einsum('i->', A) # np.sum(A)
np.einsum('i,i->i', A, B) # A * B
np.einsum('i,i', A, B) # np.inner(A, B)
np.einsum('i,j->ij', A, B) # np.outer(A, B)
```
#### 98. Considering a path described by two vectors (X,Y), how to sample it using equidistant samples (★★★)?
```
# Author: Bas Swinckels
phi = np.arange(0, 10*np.pi, 0.1)
a = 1
x = a*phi*np.cos(phi)
y = a*phi*np.sin(phi)
dr = (np.diff(x)**2 + np.diff(y)**2)**.5 # segment lengths
r = np.zeros_like(x)
r[1:] = np.cumsum(dr) # integrate path
r_int = np.linspace(0, r.max(), 200) # regular spaced path
x_int = np.interp(r_int, r, x) # integrate path
y_int = np.interp(r_int, r, y)
```
#### 99. Given an integer n and a 2D array X, select from X the rows which can be interpreted as draws from a multinomial distribution with n degrees, i.e., the rows which only contain integers and which sum to n. (★★★)
```
# Author: Evgeni Burovski
X = np.asarray([[1.0, 0.0, 3.0, 8.0],
[2.0, 0.0, 1.0, 1.0],
[1.5, 2.5, 1.0, 0.0]])
n = 4
M = np.logical_and.reduce(np.mod(X, 1) == 0, axis=-1)
M &= (X.sum(axis=-1) == n)
print(X[M])
```
#### 100. Compute bootstrapped 95% confidence intervals for the mean of a 1D array X (i.e., resample the elements of an array with replacement N times, compute the mean of each sample, and then compute percentiles over the means). (★★★)
```
# Author: Jessica B. Hamrick
X = np.random.randn(100) # random 1D array
N = 1000 # number of bootstrap samples
idx = np.random.randint(0, X.size, (N, X.size))
means = X[idx].mean(axis=1)
confint = np.percentile(means, [2.5, 97.5])
print(confint)
```
| true |
code
| 0.245695 | null | null | null | null |
|
## Spatial Adaptive Graph Neural Network for POI Graph Learning
In this tuorial, we will go through how to run the Spatial Adaptive Graph Neural Network (SA-GNN) to learn on the POI graph. If you are intersted in more details, please refer to the paper "Competitive analysis for points of interest".
```
import os
import pgl
import pickle
import pandas as pd
import numpy as np
from random import shuffle
import paddle
import paddle.nn as nn
import paddle.nn.functional as F
from sagnn import SpatialOrientedAGG, SpatialAttnProp
paddle.set_device('cpu')
```
### Load dataset and construct the POI graph
```
def load_dataset(file_path, dataset):
"""
1) Load the POI dataset from four files: edges file, two-dimensional coordinate file, POI feature file and label file.
2) Construct the PGL-based graph and return the pgl.Graph instance.
"""
edges = pd.read_table(os.path.join(file_path, '%s.edge' % dataset), header=None, sep=' ')
# ex, ey = np.array(edges[:][0]), np.array(edges[:][1])
edges = list(zip(edges[:][0],edges[:][1]))
coords = pd.read_table(os.path.join(file_path, '%s.coord' % dataset), header=None, sep=' ')
coords = np.array(coords)
feat_path = os.path.join(file_path, '%s.feat' % dataset) # pickle file
if os.path.exists(feat_path):
with open(feat_path, 'rb') as f:
features = pickle.load(f)
else:
features = np.eye(len(coords))
graph = pgl.Graph(edges, num_nodes=len(coords), node_feat={"feat": features, 'coord': coords})
ind_labels = pd.read_table(os.path.join(file_path, '%s.label' % dataset), header=None, sep=' ')
inds_1 = np.array(ind_labels)[:,0]
inds_2 = np.array(ind_labels)[:,1]
labels = np.array(ind_labels)[:,2:]
return graph, (inds_1, inds_2), labels
```
### Build the SA-GNN model for link prediction
```
class DenseLayer(nn.Layer):
def __init__(self, in_dim, out_dim, activation=F.relu, bias=True):
super(DenseLayer, self).__init__()
self.activation = activation
if not bias:
self.fc = nn.Linear(in_dim, out_dim, bias_attr=False)
else:
self.fc = nn.Linear(in_dim, out_dim)
def forward(self, input_feat):
return self.activation(self.fc(input_feat))
class SAGNNModel(nn.Layer):
def __init__(self, infeat_dim, hidden_dim=128, dense_dims=[128,128], num_heads=4, feat_drop=0.2, num_sectors=4, max_dist=0.1, grid_len=0.001, num_convs=1):
super(SAGNNModel, self).__init__()
self.num_convs = num_convs
self.agg_layers = nn.LayerList()
self.prop_layers = nn.LayerList()
in_dim = infeat_dim
for i in range(num_convs):
agg = SpatialOrientedAGG(in_dim, hidden_dim, num_sectors, transform=False, activation=None)
prop = SpatialAttnProp(hidden_dim, hidden_dim, num_heads, feat_drop, max_dist, grid_len, activation=None)
self.agg_layers.append(agg)
self.prop_layers.append(prop)
in_dim = num_heads * hidden_dim
self.mlp = nn.LayerList()
for hidden_dim in dense_dims:
self.mlp.append(DenseLayer(in_dim, hidden_dim, activation=F.relu))
in_dim = hidden_dim
self.output_layer = nn.Linear(2 * in_dim, 1)
def forward(self, graph, inds):
feat_h = graph.node_feat['feat']
for i in range(self.num_convs):
feat_h = self.agg_layers[i](graph, feat_h)
graph = graph.tensor()
feat_h = self.prop_layers[i](graph, feat_h)
for fc in self.mlp:
feat_h = fc(feat_h)
feat_h = paddle.concat([paddle.gather(feat_h, inds[0]), paddle.gather(feat_h, inds[1])], axis=-1)
output = F.sigmoid(self.output_layer(feat_h))
return output
```
Here we load a mock dataset for demonstration, you can load the full dataset as you want.
Note that all needed files should include:
1) one edge file (dataset.edge) for POI graph construction;
2) one coordinate file (dataset.coord) for POI position;
3) one label file (dataset.label) for training model;
4) one feature file (dataset.feat) for POI feature loading, which is optional. If there is no dataset.feat, the default POI feature is the one-hot vector.
```
graph, inds, labels = load_dataset('./data/', 'mock_poi')
ids = [i for i in range(len(labels))]
shuffle(ids)
train_num = int(0.6*len(labels))
train_inds = (inds[0][ids[:train_num]], inds[1][ids[:train_num]])
test_inds = (inds[0][ids[train_num:]], inds[1][ids[train_num:]])
train_labels = labels[ids[:train_num]]
test_labels = labels[ids[train_num:]]
print("dataset num: %s" % (len(labels)), "training num: %s" % (len(train_labels)))
infeat_dim = graph.node_feat['feat'].shape[0]
model = SAGNNModel(infeat_dim)
optim = paddle.optimizer.Adam(0.001, parameters=model.parameters())
```
### Strart training
```
def train(model, graph, inds, labels, optim):
model.train()
graph = graph.tensor()
inds = paddle.to_tensor(inds, 'int64')
labels = paddle.to_tensor(labels, 'float32')
preds = model(graph, inds)
bce_loss = paddle.nn.BCELoss()
loss = bce_loss(preds, labels)
loss.backward()
optim.step()
optim.clear_grad()
return loss.numpy()[0]
def evaluate(model, graph, inds, labels):
model.eval()
graph = graph.tensor()
inds = paddle.to_tensor(inds, 'int64')
labels = paddle.to_tensor(labels, 'float32')
preds = model(graph, inds)
bce_loss = paddle.nn.BCELoss()
loss = bce_loss(preds, labels)
return loss.numpy()[0], 1.0*np.sum(preds.numpy().astype(int) == labels.numpy().astype(int), axis=0) / len(labels)
for epoch_id in range(5):
train_loss = train(model, graph, train_inds, train_labels, optim)
print("epoch:%d train/loss:%s" % (epoch_id, train_loss))
test_loss, test_acc = evaluate(model, graph, test_inds, test_labels)
print("test loss: %s, test accuracy: %s" % (test_loss, test_acc))
```
| true |
code
| 0.710578 | null | null | null | null |
|
# Coding outside of Jupyter notebooks
To be able to run Python on your own computer, I recommend installing [Anaconda](https://www.continuum.io/downloads) which contains basic packages for you to be up and running.
While you are downloading things, also try the text editor [Atom](https://atom.io/).
We have used Jupyter notebooks in this class as a useful tool for integrating text and interactive, usable code. However, many people when real-life coding would not use Jupyter notebooks but would instead type code in text files and run them via a terminal window or in iPython. Many of you have done this before, perhaps analogously in Matlab by writing your code in a .m file and then running it in the Matlab GUI. Writing code in a separate file allows more heavy computations as well as allowing that code to be reused more easily than when it is written in a Jupyter notebook.
Later, we will demonstrate typing Python code in a .py file and then running it in an iPython window. First, a few of the other options...
# Google's Colaboratory
Google recently announced a partnership with Jupyter and have put out the Jupyter Notebook in their [own environment](https://colab.research.google.com/notebook). You can use it just like our in-class notebooks, share them through Google Drive, and even install packages. This may be the way of the future of teaching Python.
# Jupyter itself
The Jupyter project is becoming more and more sophisticated. The next project coming out is called [JupyterLab](https://towardsdatascience.com/jupyterlab-you-should-try-this-data-science-ui-for-jupyter-right-now-a799f8914bb3) and aims to more cleanly integrate modules that are already available in the server setup we have been using: notebooks, terminals, text editor, file hierarchy, etc. You can see a pre-alpha release image of it below:
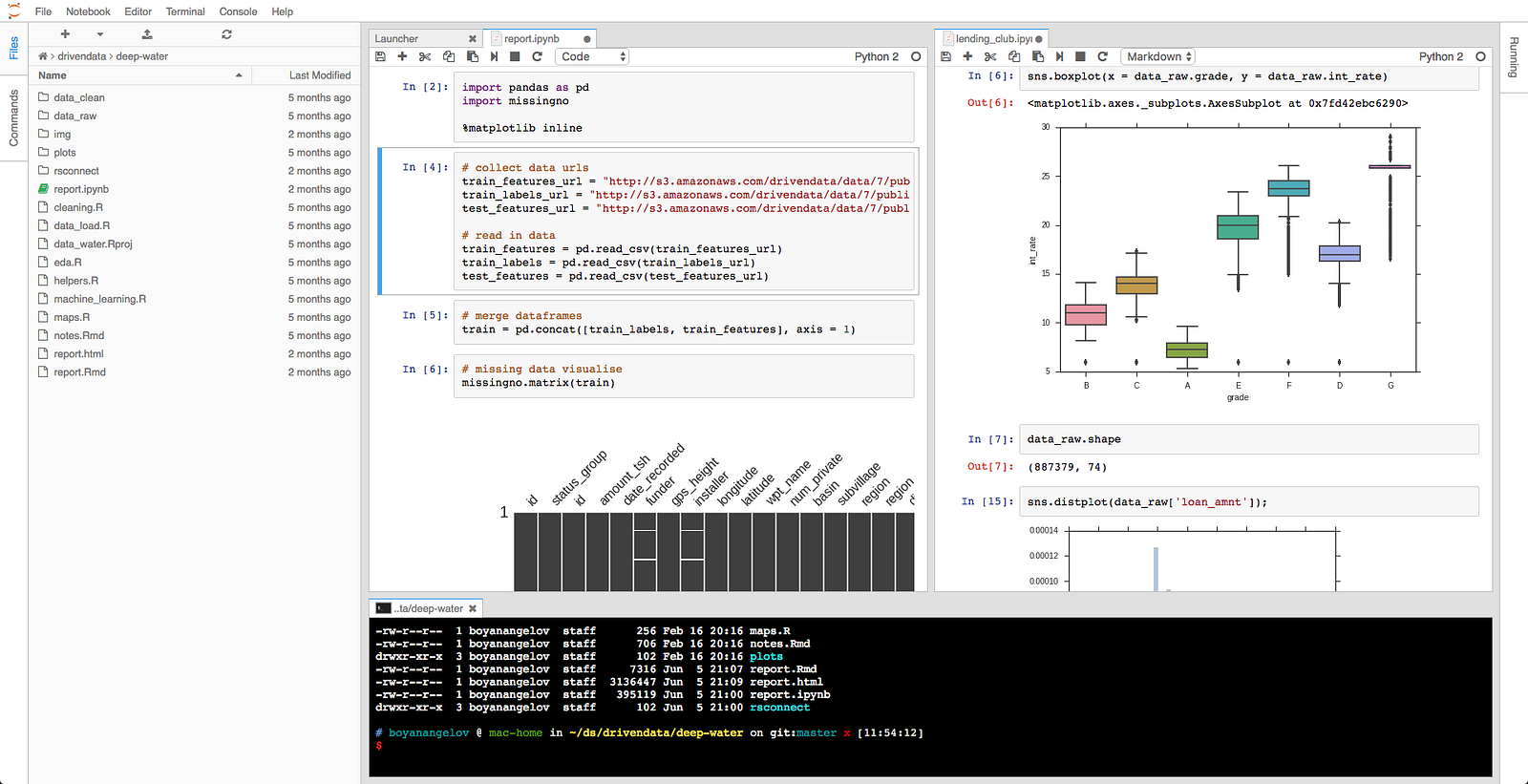
# MATLAB-like GUIs
Two options for using Python in a clickable, graphical user interface are [Spyder](https://pythonhosted.org/spyder/) and [Canopy](https://www.enthought.com/products/canopy/). Spyder is open source and Canopy is not, though the company that puts Canopy together (Enthought) does make a version available for free.
Both are shown below. They are generally similar from the perspective of what we've been using so far. They have a console for getting information when you run your code (equivalent to running a cell in your notebook), typing in your file, getting more information about code, having nice code syntax coloring, maybe being able to examine Python objects. Note that many of these features are being integrated in less formal GUI tools like this — you'll see even in the terminal window in iPython you have access to many nice features.


# Using iPython in a terminal window
Here we have code in our notebook:
```
import numpy as np
import matplotlib.pyplot as plt
# just for jupyter notebooks
%matplotlib inline
x = np.linspace(0, 10)
y = x**2
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y, 'k', lw=3)
```
Now let's switch to a terminal window and a text file...
## Open iPython
Get Anaconda downloaded and opened up on your machine if you want. Open a terminal window, or use the one that Anaconda opens, and type:
> ipython
Or, you can use redfish. On `redfish`:
Go to the home menu on redfish, on the right-hand-side under "New", choose "Terminal" to open a terminal window that is running on `redfish`. To run Python 3 in this terminal window, you'll need to use the command `ipython3` instead of `ipython`, due to the way the alias to the program is set up:
> ipython3
Note that we will use this syntax to mean that it is something to be typed in your terminal window/command prompt (or it is part of an exercise). To open ipython with some niceties added so that you don't have to import them by hand each time you open the program (numpy and matplotlib in particular), open it with
> ipython --pylab
Once you have done this, you'll see a series of text lines indicating that you are now in the program ipython. You can now type code as if you were in a code window in a Jupyter notebook (but without an ability to integrate text easily).
---
### *Exercise*
> Copy in the code to define `x` and `y` from above, then make the figure. If you haven't opened `ipython` with the option flag `--pylab`, you will need to still do the import statements, but not `%matplotlib inline` since that is only for notebooks.
> Notice how the figure appears as a separate window. Play with the figure window — you can change the size and properties of the plot using the GUI buttons, and you can zoom.
---
## Text editor
A typical coding set up is to have a terminal window with `ipython` running alongside a text window where you type your code. You can then go back and forth, trying things out in iPython, and keeping what works in the text window so that you finish with a working script, which can be run independently in the future. This is, of course, what you've been doing when you use Jupyter notebooks, except everything is combined into one place in that sort of setup. If you are familiar with Matlab, this is what you are used to when you have your Matlab window with your `*.m` text window alongside a "terminal window" where you can type things. (There is also a variable viewer included in Matlab.) This is also what you can do in a single program with Jupyterlab.
A good text editor should be able to highlight syntax – that is, use color and font style to differentiate between special key words and types for a given programming language. This is what has been happening in our Jupyter notebooks, when strings are colored red, for example. The editors will also key off typical behaviors in the language to try to be helpful, such as when in a Jupyter notebook if you write an `if` statement with a colon at the end and push `enter`, the next line will be automatically indented so that you can just start typing. These behaviors can be adjusted by changing user settings.
Some options are [TextMate](https://macromates.com/) for Mac, which costs money, and [Sublime Text](https://www.sublimetext.com/) which works on all operating systems and also costs money (after a free trial). For this class, we recommend using [Atom](https://atom.io/), which is free, works across operating systems, and integrates with GitHub since they wrote it.
So, go download Atom and start using it, unless you have a preferred alternative you want to use.
---
### *Exercise*: run a script
> If you are running python locally on your machine with Anaconda, copy and paste the code from above into a new text file in your text editor. Save it, then run the file in ipython with
> run [filename]
> If you are sticking with `redfish`, you can type out text in a text file from the home window (under New), and you can get most but not all functionality this way. Or you can try one of the GUIs.
---
## Package managing
The advantage of Anaconda is being able to really easily add packages, with
> conda install [packagename]
This will look for the Python package you want in the places known to conda. You may also tell it to look in another channel, which other people and groups can maintain. For example, `cartopy` is available through the `scitools channel`:
> conda install -c scitools cartopy
Sometimes, it is better or necessary to use `pip` to install packages, which links to the PyPI collections of packages that anyone can place there for other people to use. For example, you can get the `cmocean` colormaps package from [PyPI](https://pypi.python.org/pypi/cmocean) with
> pip install cmocean
## Running Jupyter notebooks on your own server
We've been running our notebooks on a TAMU server all semester. You can do this on your own machine pretty easily once you have Anaconda. There should be a place for you to double-click for it to open, or you can open a terminal window and type:
> jupyter notebook
This opens a window that should look familiar in your browser window. The difference is that instead of connecting to a remote server (on redfish), you are connecting to a local server on your own machine that you started running with the `jupyter notebook` command.
# Run a script
When you use the command `run` in iPython, parts of the code in that file are implemented as if they were written in the iPython window itself. Code that is outside of a function call will run: at 0 indentation level (import statements and maybe some variables definitions are common), but not any functions, though it will read the functions into your local variables so that they can be used. Code inside the line `if __name__ == '__main__':` will also be run. This syntax is available so that default run commands can be built into your script. This is often used to provide example or test code that can be easily run.
Note anytime you are accessing a saved file from iPython, you need to have at least one of the following be true:
* is in the same directory in your terminal window as the file;
* are referencing the file with either its full path or a relative path;
* have the path to your file be appended to the environmental variable PYTHONPATH.
---
### *Exercise*
> There is example code available to try at https://github.com/kthyng/python4geosciences/blob/master/data/optimal_interpolation.py. Copy this code into your text editor and save it to the same location on your computer as your iPython window is open.
> Within your iPython window, run optimal_interpolation.py with `run optimal_interpolation` (if you saved it in the same directory as your iPython window). Which part of the code actually runs? Why?
> Add some `print` statements into the script at 0 indentation as well as below the line `if __name__ == '__main__':` and see what comes through when you run the code. Can you access the class `oi_1d`?
---
# Importing your own code
The point of importing code is to be able to then use the functions and classes that you've written in other files. Importing your own code is just like importing `numpy` or any other package. You use the same syntax and you have the same ability to query the built-in methods.
> import numpy
or:
> import [your_code]
When you import a package, any code at the 0 indentation level will run; however, the code within `if __name__ == '__main__':` will not run.
When you are using a single script for analysis, you may just use `run` to use your code. However, as you build up complexity in your work, you'll probably want to make separate, independent code bases that can be called from subsequent code by importing them (again, just like us using the capabilities in `numpy`).
When you import a package, a `*.pyc` file is created which holds compiled code that is subsequently read when the package is again imported, in order to save time. When you are in a single session in iPython, that `*.pyc` will be used and not updated. If you have changed the code and want it to be updated, you either need to exit iPython and reopen it, or you need to `reload` the package. These is different syntax for this depending on the version of Python you are using, but we are using Python 3 (>3.4) so we will do the following:
**For >= Python3.4:**
import importlib
importlib.reload([code to reload])
---
### *Exercise*
> Import `optimal_interpolation.py`. Add a print statement with 0 indentation level in the code. Import the package again. Does the print statement run? Reload the package. How about now?
> What about if you run it instead of importing it?
### *Exercise*
> Write your own simple script with a function in it — your function should take at least one input (maybe several numbers) and return something (maybe a number that is the result of some calculation).
> Now, use your code in several ways. Run the code in ipython with
> run [filename]
> Make sure you have a __name__ definition for this (`if __name__ == '__main__':`, etc). Now import the code and use it:
> import [filename]
> Add a docstring to the top of the file and reload your package, then query the code. Do you see the docstring? Add a docstring to the function in the file, reload, and query. Do you see the docstring?
> You should have been able to run your code both ways: running it directly, and importing it, then using a function that is within the code.
---
# Unit testing
The idea of unit testing is to develop tests for your code as you develop it, so that you automatically know if it is working properly as you make changes. In fact, some coders prefer to write the unit tests first to drive the proper development of their code and to know when it is working. Of course, the quality of the testing is made up of the tests you include and aspects of your code that you test.
Here are some unit test [guidelines](http://docs.python-guide.org/en/latest/writing/tests/):
* Generally, you want to write unit tests that test one small aspect of your code functionality, as separately as possible from other parts of it. Then write many of these tests to cover all aspects of functionality.
* Make sure your unit tests run very quickly since you may end up with many of them
* Always run the full test suite before a coding session, and run it again after. This will give you more confidence that you did not break anything in the rest of the code.
* You can now run a program like [Travis CI](https://travis-ci.com/) through GitHub which runs your test suite before you push your code to your repository or merge a pull request.
* Use long and descriptive names for testing functions. The style guide here is slightly different than that of running code, where short names are often preferred. The reason is testing functions are never called explicitly. square() or even sqr() is ok in running code, but in testing code you would have names such as test_square_of_number_2(), test_square_negative_number(). These function names are displayed when a test fails, and should be as descriptive as possible.
* Include detailed docstrings and comments throughout your testing files since these may be read more than the original code.
How to set up a suite of unit tests:
1. make a `tests` directory in your code (or for simple code, just have your test file in the same directory);
1. make a new file to hold your tests, called `tests*.py` — it must start with "test" for it to be noticed by testing programs;
1. inside `tests*.py`, write a test function called `test_*()` — the testing programs look for functions with these names in particular and ignore other functions;
1. use functions like `assert` and `np.allclose` for numeric comparisons of function outputs and checking for output types.
1. run testing programs on your code. I recommend [nosetests](http://nose.readthedocs.org/en/latest/usage.html) or [pytest](http://pytest.org/latest/). You use these by running `nosetests` or `py.test` from the terminal window in the directory with your test code in it (or pointing to the directory). Next version will be `nose2`.
You can load files into Jupyter notebooks using the magic command `%load`. You can then run the code inside the notebook if you want (though the `import` statement will be an issue here), or just look at it.
```
# %load ../data/package.py
def add(x, y):
"""doc """
return x+y
print(add(1, 2))
if __name__ == '__main__':
print(add(1, 1))
# %load ../data/test.py
"""Test package.py"""
import package
import numpy as np
def test_add_12():
"""Test package with inputs 1, 2"""
assert package.add(1, 2) == np.sum([1, 2])
```
Now, run the test. We can do this by escaping to the terminal, or we can go to our terminal window and run it there.
Note: starting a line of code with "!" makes it from the terminal window. Some commands are so common that you don't need to use the "!" (like `ls`), but in general you need it.
```
!nosetests ../data/
```
---
### *Exercise*
> Start another file called `test*.py`. In it, write a test function, `test_*()`, that checks the accuracy of your original function in some way. Then run it with `nosetests`.
---
# PEP 0008
A [PEP](https://www.python.org/dev/peps/pep-0001/) is a Python Enhancement Proposal, describing ideas for design or processes to the Python community. The list of the PEPs is [available online](https://www.python.org/dev/peps/).
[PEP 0008](https://www.python.org/dev/peps/pep-0008/) is a set of style guidelines for writing good, clear, readable code, written with the assumption that code is read more often than it is written. These address questions such as, when a line of code is longer than one line, how should it be indented? And speaking of one line of code, how long should it be? Note than even in this document, they emphasize that these are guidelines and sometimes should be trumped by what has already been happening in a project or other considerations. But, generally, follow what they say here.
Here is a list of some style guidelines to follow, but check out the full guide for a wealth of good ideas:
* indent with spaces, not tabs
* indent with 4 spaces
* limit all lines to a maximum of 79 characters
* put a space after a comma
* avoid trailing whitespace anywhere
Note that you can tell your text editor to enforce pep8 style guidelines to help you learn. This is called a linter. I do this with a plug-in in Sublime Text. You can [get one](https://github.com/AtomLinter/linter-pep8) for Atom.
---
### *Exercise*
> Go back and clean up your code you've been writing so that it follows pep8 standards.
---
# Docstrings
Docstrings should be provided at the top of a code file for the whole package, and then for each function/class within the package.
## Overall style
Overall style for docstrings is given in [PEP 0257](https://www.python.org/dev/peps/pep-0257/), and includes the following guidelines:
* one liners: for really obvious functions. Keep the docstring completely on one line:
> def simple_function():
> """Simple functionality."""
* multiliners: Multi-line docstrings consist of a summary line just like a one-line docstring, followed by a blank line, followed by a more elaborate description. The summary line may be used by automatic indexing tools; it is important that it fits on one line and is separated from the rest of the docstring by a blank line. The summary line may be on the same line as the opening quotes or on the next line.
> def complex_function():
> """
> One liner describing overall.
>
> Now more involved description of inputs and outputs.
> Possibly usage example(s) too.
> """
## Styles for inputs/outputs
For the more involved description in the multi line docstring, there are several standards used. (These are summarized nicely in a [post](http://stackoverflow.com/questions/3898572/what-is-the-standard-python-docstring-format) on Stack Overflow; this list is copied from there.)
1. [reST](https://www.python.org/dev/peps/pep-0287/)
> def complex_function(param1, param2):
> """
> This is a reST style.
>
> :param param1: this is a first param
> :param param2: this is a second param
> :returns: this is a description of what is returned
> :raises keyError: raises an exception
> """
1. [Google](http://google.github.io/styleguide/pyguide.html#Python_Language_Rules)
> def complex_function(param1, param2):
> """
> This is an example of Google style.
>
> Args:
> param1: This is the first param.
> param2: This is a second param.
>
> Returns:
> This is a description of what is returned.
>
> Raises:
> KeyError: Raises an exception.
> """
1. [Numpydoc](https://github.com/numpy/numpy/blob/master/doc/HOWTO_DOCUMENT.rst.txt)
> def complex_function(first, second, third='value'):
> """
> Numpydoc format docstring.
>
> Parameters
> ----------
> first : array_like
> the 1st param name `first`
> second :
> the 2nd param
> third : {'value', 'other'}, optional
> the 3rd param, by default 'value'
>
> Returns
> -------
> string
> a value in a string
>
> Raises
> ------
> KeyError
> when a key error
> OtherError
> when an other error
> """
# Documentation generation
[Sphinx](http://www.sphinx-doc.org/en/stable/index.html) is a program that can be run to generate documentation for your project from your docstrings. You basically run the program and if you use the proper formatting in your docstrings, they will all be properly pulled out and presented nicely in a coherent way. There are various additions you can use with Sphinx in order to be able to write your docstrings in different formats (as shown above) and still have Sphinx be able to interpret them. For example, you can use [Napoleon](http://sphinxcontrib-napoleon.readthedocs.org/en/latest/) with Sphinx to be able to write using the Google style instead of reST, meaning that you can have much more readable docstrings and still get nicely-generated documentation out. Once you have generated this documentation, you can publish it using [Read the docs](https://readthedocs.org/). Here is documentation on readthedocs for a package that converts between colorspaces, [Colorspacious](https://colorspacious.readthedocs.org/en/latest/).
Another approach is to use Sphinx, but link it with [GitHub Pages](https://pages.github.com/), which is hosted directly from your GitHub repo page. Separately from documentation, I use GitHub Pages for [my own website](http://kristenthyng.com). I also use one for documentation for a package of mine, [cmocean](http://matplotlib.org/cmocean/) that provides colormaps for oceanography. To get this running, I followed instructions [online](http://gisellezeno.com/tutorials/sphinx-for-python-documentation.html). Note that GitHub pages is built using Jekyll but in this case we tell it not to use Jekyll and instead use Sphinx.
We can see that the docstrings in the code are nicely interpreted into documentation for the functions by comparing the [module docs](http://matplotlib.org/cmocean/cmocean.html#module-cmocean.tools) with the code below.
```
# %load https://raw.githubusercontent.com/matplotlib/cmocean/master/cmocean/tools.py
'''
Plot up stuff with colormaps.
'''
import numpy as np
import matplotlib as mpl
def print_colormaps(cmaps, N=256, returnrgb=True, savefiles=False):
'''Print colormaps in 256 RGB colors to text files.
:param returnrgb=False: Whether or not to return the rgb array. Only makes sense to do if print one colormaps' rgb.
'''
rgb = []
for cmap in cmaps:
rgbtemp = cmap(np.linspace(0, 1, N))[np.newaxis, :, :3][0]
if savefiles:
np.savetxt(cmap.name + '-rgb.txt', rgbtemp)
rgb.append(rgbtemp)
if returnrgb:
return rgb
def get_dict(cmap, N=256):
'''Change from rgb to dictionary that LinearSegmentedColormap expects.
Code from https://mycarta.wordpress.com/2014/04/25/convert-color-palettes-to-python-matplotlib-colormaps/
and http://nbviewer.ipython.org/github/kwinkunks/notebooks/blob/master/Matteo_colourmaps.ipynb
'''
x = np.linspace(0, 1, N) # position of sample n - ranges from 0 to 1
rgb = cmap(x)
# flip colormap to follow matplotlib standard
if rgb[0, :].sum() < rgb[-1, :].sum():
rgb = np.flipud(rgb)
b3 = rgb[:, 2] # value of blue at sample n
b2 = rgb[:, 2] # value of blue at sample n
# Setting up columns for tuples
g3 = rgb[:, 1]
g2 = rgb[:, 1]
r3 = rgb[:, 0]
r2 = rgb[:, 0]
# Creating tuples
R = list(zip(x, r2, r3))
G = list(zip(x, g2, g3))
B = list(zip(x, b2, b3))
# Creating dictionary
k = ['red', 'green', 'blue']
LinearL = dict(zip(k, [R, G, B]))
return LinearL
def cmap(rgbin, N=256):
'''Input an array of rgb values to generate a colormap.
:param rgbin: An [mx3] array, where m is the number of input color triplets which
are interpolated between to make the colormap that is returned. hex values
can be input instead, as [mx1] in single quotes with a #.
:param N=10: The number of levels to be interpolated to.
'''
# rgb inputs here
if not mpl.cbook.is_string_like(rgbin[0]):
# normalize to be out of 1 if out of 256 instead
if rgbin.max() > 1:
rgbin = rgbin/256.
cmap = mpl.colors.LinearSegmentedColormap.from_list('mycmap', rgbin, N=N)
return cmap
```
# Debugging
You can use the package [`pdb`](https://docs.python.org/3/library/pdb.html) while running your code to pause it intermittently and poke around to check variable values and understand what is going on.
A few key commands to get you started are:
* `pdb.set_trace()` pauses the code run at this location, then allows you to type in the iPython window. You can print statements or check variables shapes, etc. This is how you can dig into code.
* Once you have stopped your code at a trace, use:
* `n` to move to the next line;
* `s` to step into a function if that is the next line and you want to move into that function as opposed to just running the function;
* `c` to continue until there is another trace, the code ends, it reaches the end of a function, or an error occurs;
* `q` to quit out of the debugger, which will also quit out of the code being run.
---
### *Exercise*
> Use `pdb` to investigate variables after starting your code running.
---
# Make a package
To make a Python package that you want to be a bit more official because you plan to use it long-term, and/or you want to share it with other people and make it easy for them to use, you are going to want to get it on GitHub, provide documentation, and get it on PyPI (this is how you are able to then easily install it with `pip install [package_name]`). There are also a number of technical steps you'll need to do. More information about this sort of process is [available online](http://python-packaging.readthedocs.org/en/latest/minimal.html).
| true |
code
| 0.603757 | null | null | null | null |
|
# Example of physical analysis with IPython
```
%pylab inline
import numpy
import pandas
import root_numpy
folder = '/moosefs/notebook/datasets/Manchester_tutorial/'
```
## Reading simulation data
```
def load_data(filenames, preselection=None):
# not setting treename, it's detected automatically
data = root_numpy.root2array(filenames, selection=preselection)
return pandas.DataFrame(data)
sim_data = load_data(folder + 'PhaseSpaceSimulation.root', preselection=None)
```
Looking at data, taking first rows:
```
sim_data.head()
```
### Plotting some feature
```
# hist data will contain all information from histogram
hist_data = hist(sim_data.H1_PX, bins=40, range=[-100000, 100000])
```
## Adding interesting features
for each particle we compute it's P, PT and energy (under assumption this is Kaon)
```
def add_momenta_and_energy(dataframe, prefix, compute_energy=False):
"""Adding P, PT and У of particle with given prefix, say, 'H1_' """
pt_squared = dataframe[prefix + 'PX'] ** 2. + dataframe[prefix + 'PY'] ** 2.
dataframe[prefix + 'PT'] = numpy.sqrt(pt_squared)
p_squared = pt_squared + dataframe[prefix + 'PZ'] ** 2.
dataframe[prefix + 'P'] = numpy.sqrt(p_squared)
if compute_energy:
E_squared = p_squared + dataframe[prefix + 'M'] ** 2.
dataframe[prefix + 'E'] = numpy.sqrt(E_squared)
for prefix in ['H1_', 'H2_', 'H3_']:
# setting Kaon mass to each of particles:
sim_data[prefix + 'M'] = 493
add_momenta_and_energy(sim_data, prefix, compute_energy=True)
```
## Adding features of $B$
We are able to compute 4-momentum of B, given 4-momenta of produced particles
```
def add_B_features(data):
for axis in ['PX', 'PY', 'PZ', 'E']:
data['B_' + axis] = data['H1_' + axis] + data['H2_' + axis] + data['H3_' + axis]
add_momenta_and_energy(data, prefix='B_', compute_energy=False)
data['B_M'] = data.eval('(B_E ** 2 - B_PX ** 2 - B_PY ** 2 - B_PZ ** 2) ** 0.5')
add_B_features(sim_data)
```
looking at result (with added features)
```
sim_data.head()
_ = hist(sim_data['B_M'], range=[5260, 5280], bins=100)
```
# Dalitz plot
computing dalitz variables and checking that no resonances in simulation
```
def add_dalitz_variables(data):
"""function to add Dalitz variables, names of prudicts are H1, H2, H3"""
for i, j in [(1, 2), (1, 3), (2, 3)]:
momentum = pandas.DataFrame()
for axis in ['E', 'PX', 'PY', 'PZ']:
momentum[axis] = data['H{}_{}'.format(i, axis)] + data['H{}_{}'.format(j, axis)]
data['M_{}{}'.format(i,j)] = momentum.eval('(E ** 2 - PX ** 2 - PY ** 2 - PZ ** 2) ** 0.5')
add_dalitz_variables(sim_data)
scatter(sim_data.M_12, sim_data.M_13, alpha=0.05)
```
# Working with real data
## Preselection
```
preselection = """
H1_IPChi2 > 1 && H2_IPChi2 > 1 && H3_IPChi2 > 1
&& H1_IPChi2 + H2_IPChi2 + H3_IPChi2 > 500
&& B_VertexChi2 < 12
&& H1_ProbPi < 0.5 && H2_ProbPi < 0.5 && H3_ProbPi < 0.5
&& H1_ProbK > 0.9 && H2_ProbK > 0.9 && H3_ProbK > 0.9
&& !H1_isMuon
&& !H2_isMuon
&& !H3_isMuon
"""
preselection = preselection.replace('\n', '')
real_data = load_data([folder + 'B2HHH_MagnetDown.root', folder + 'B2HHH_MagnetUp.root'], preselection=preselection)
```
### adding features
```
for prefix in ['H1_', 'H2_', 'H3_']:
# setting Kaon mass:
real_data[prefix + 'M'] = 493
add_momenta_and_energy(real_data, prefix, compute_energy=True)
add_B_features(real_data)
_ = hist(real_data.B_M, bins=50)
```
### additional preselection
which uses added features
```
momentum_preselection = """
(H1_PT > 100) && (H2_PT > 100) && (H3_PT > 100)
&& (H1_PT + H2_PT + H3_PT > 4500)
&& H1_P > 1500 && H2_P > 1500 && H3_P > 1500
&& B_M > 5050 && B_M < 6300
"""
momentum_preselection = momentum_preselection.replace('\n', '').replace('&&', '&')
real_data = real_data.query(momentum_preselection)
_ = hist(real_data.B_M, bins=50)
```
## Adding Dalitz plot for real data
```
add_dalitz_variables(real_data)
# check that 2nd and 3rd particle have same sign
numpy.mean(real_data.H2_Charge * real_data.H3_Charge)
scatter(real_data['M_12'], real_data['M_13'], alpha=0.1)
xlabel('M_12'), ylabel('M_13')
show()
# lazy way for plots
real_data.plot('M_12', 'M_13', kind='scatter', alpha=0.1)
```
### Ordering dalitz variables
let's reorder particles so the first Dalitz variable is always greater
```
scatter(numpy.maximum(real_data['M_12'], real_data['M_13']),
numpy.minimum(real_data['M_12'], real_data['M_13']),
alpha=0.1)
xlabel('max(M12, M13)'), ylabel('min(M12, M13)')
show()
```
### Binned dalitz plot
let's plot the same in bins, as physicists like
```
hist2d(numpy.maximum(real_data['M_12'], real_data['M_13']),
numpy.minimum(real_data['M_12'], real_data['M_13']),
bins=8)
colorbar()
xlabel('max(M12, M13)'), ylabel('min(M12, M13)')
show()
```
## Looking at local CP-asimmetry
adding one more column
```
real_data['B_Charge'] = real_data.H1_Charge + real_data.H2_Charge + real_data.H3_Charge
hist(real_data.B_M[real_data.B_Charge == +1].values, bins=30, range=[5050, 5500], alpha=0.5)
hist(real_data.B_M[real_data.B_Charge == -1].values, bins=30, range=[5050, 5500], alpha=0.5)
pass
```
## Leaving only signal region in mass
```
signal_charge = real_data.query('B_M > 5200 & B_M < 5320').B_Charge
```
counting number of positively and negatively charged B particles
```
n_plus = numpy.sum(signal_charge == +1)
n_minus = numpy.sum(signal_charge == -1)
print n_plus, n_minus, n_plus - n_minus
print 'asymmetry = ', (n_plus - n_minus) / float(n_plus + n_minus)
```
### Estimating significance of deviation (approximately)
we will assume that $N_{+} + N_{-}$, and under null hypothesis each observation contains with $p=0.5$ positive or negative particle.
So, under these assumptions $N_{+}$ is distributed as binomial random variable.
```
# computing properties of n_plus according to H_0 hypothesis.
n_mean = len(signal_charge) * 0.5
n_std = numpy.sqrt(len(signal_charge) * 0.25)
print 'significance = ', (n_plus - n_mean) / n_std
```
# Subtracting background
using RooFit to fit mixture of exponential (bkg) and gaussian (signal) distributions.
Based on the fit, we estimate number of events in mass region
```
# Lots of ROOT imports for fitting and plotting
from rootpy import asrootpy, log
from rootpy.plotting import Hist, Canvas, set_style, get_style
from ROOT import (RooFit, RooRealVar, RooDataHist, RooArgList, RooArgSet,
RooAddPdf, TLatex, RooGaussian, RooExponential )
def compute_n_signal_by_fitting(data_for_fit):
"""
Computing the amount of signal with in region [x_min, x_max]
returns: canvas with fit, n_signal in mass region
"""
# fit limits
hmin, hmax = data_for_fit.min(), data_for_fit.max()
hist = Hist(100, hmin, hmax, drawstyle='EP')
root_numpy.fill_hist(hist, data_for_fit)
# Declare observable x
x = RooRealVar("x","x", hmin, hmax)
dh = RooDataHist("dh","dh", RooArgList(x), RooFit.Import(hist))
frame = x.frame(RooFit.Title("D^{0} mass"))
# this will show histogram data points on canvas
dh.plotOn(frame, RooFit.MarkerColor(2), RooFit.MarkerSize(0.9), RooFit.MarkerStyle(21))
# Signal PDF
mean = RooRealVar("mean", "mean", 5300, 0, 6000)
width = RooRealVar("width", "width", 10, 0, 100)
gauss = RooGaussian("gauss","gauss", x, mean, width)
# Background PDF
cc = RooRealVar("cc", "cc", -0.01, -100, 100)
exp = RooExponential("exp", "exp", x, cc)
# Combined model
d0_rate = RooRealVar("D0_rate", "rate of D0", 0.9, 0, 1)
model = RooAddPdf("model","exp+gauss",RooArgList(gauss, exp), RooArgList(d0_rate))
# Fitting model
result = asrootpy(model.fitTo(dh, RooFit.Save(True)))
mass = result.final_params['mean'].value
hwhm = result.final_params['width'].value
# this will show fit overlay on canvas
model.plotOn(frame, RooFit.Components("exp"), RooFit.LineStyle(3), RooFit.LineColor(3))
model.plotOn(frame, RooFit.LineColor(4))
# Draw all frames on a canvas
canvas = Canvas()
frame.GetXaxis().SetTitle("m_{K#pi#pi} [GeV]")
frame.GetXaxis().SetTitleOffset(1.2)
frame.Draw()
# Draw the mass and error label
label = TLatex(0.6, 0.8, "m = {0:.2f} #pm {1:.2f} GeV".format(mass, hwhm))
label.SetNDC()
label.Draw()
# Calculate the rate of background below the signal curve inside (x_min, x_max)
x_min, x_max = 5200, 5330
x.setRange(hmin, hmax)
bkg_total = exp.getNorm(RooArgSet(x))
sig_total = gauss.getNorm(RooArgSet(x))
x.setRange(x_min, x_max)
bkg_level = exp.getNorm(RooArgSet(x))
sig_level = gauss.getNorm(RooArgSet(x))
bkg_ratio = bkg_level / bkg_total
sig_ratio = sig_level / sig_total
n_elements = hist.GetEntries()
# TODO - normally get parameter form fit_result
sig_part = (d0_rate.getVal())
bck_part = (1 - d0_rate.getVal())
# estimating ratio of signal and background
bck_sig_ratio = (bkg_ratio * n_elements * bck_part) / (sig_ratio * n_elements * sig_part)
# n_events in (x_min, x_max)
n_events_in_mass_region = numpy.sum((data_for_fit > x_min) & (data_for_fit < x_max))
n_signal_in_mass_region = n_events_in_mass_region / (1. + bck_sig_ratio)
return canvas, n_signal_in_mass_region
B_mass_range = [5050, 5500]
mass_for_fitting_plus = real_data.query('(B_M > 5050) & (B_M < 5500) & (B_Charge == +1)').B_M
mass_for_fitting_minus = real_data.query('(B_M > 5050) & (B_M < 5500) & (B_Charge == -1)').B_M
canvas_plus, n_positive_signal = compute_n_signal_by_fitting(mass_for_fitting_plus)
canvas_plus
canvas_minus, n_negative_signal = compute_n_signal_by_fitting(mass_for_fitting_minus)
canvas_minus
```
## Computing asymmetry with subtracted background
```
print n_positive_signal, n_negative_signal
print (n_positive_signal - n_negative_signal) / (n_positive_signal + n_negative_signal)
n_mean = 0.5 * (n_positive_signal + n_negative_signal)
n_std = numpy.sqrt(0.25 * (n_positive_signal + n_negative_signal))
print (n_positive_signal - n_mean) / n_std
```
| true |
code
| 0.540499 | null | null | null | null |
|
# Seasonal Naive Approach
Benchmark model that simply forecasts the same value from the previous seasonal period.
```
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
matplotlib.rcParams['figure.figsize'] = (16, 9)
pd.options.display.max_columns = 999
```
## Load Dataset
```
df = pd.read_csv('../datasets/hourly-weather-wind_direction.csv', parse_dates=[0], index_col='DateTime')
print(df.shape)
df.head()
```
## Define Parameters
Make predictions for 24-hour period using a seasonality of 24-hours.
```
dataset_name = 'Hourly Weather Wind Direction'
dataset_abbr = 'HWD'
model_name = 'Naive'
context_length = 24
prediction_length = 24
```
## Define Error Metric
The seasonal variant of the mean absolute scaled error (MASE) will be used to evaluate the forecasts.
```
def calc_sMASE(training_series, testing_series, prediction_series, seasonality=prediction_length):
a = training_series.iloc[seasonality:].values
b = training_series.iloc[:-seasonality].values
if len(a) != 0:
d = np.sum(np.abs(a-b)) / len(a)
else:
return 1
errors = np.abs(testing_series - prediction_series)
return np.mean(errors) / d
```
## Evaluate Seasonal Naive Model
```
results = df.copy()
for i, col in enumerate(df.columns):
results['pred%s' % str(i+1)] = results[col].shift(context_length)
results.dropna(inplace=True)
sMASEs = []
for i, col in enumerate(df.columns):
sMASEs.append(calc_sMASE(results[col].iloc[-(context_length + prediction_length):-prediction_length],
results[col].iloc[-prediction_length:],
results['pred%s' % str(i+1)].iloc[-prediction_length:]))
fig, ax = plt.subplots()
ax.hist(sMASEs, bins=20)
ax.set_title('Distributions of sMASEs for {} dataset'.format(dataset_name))
ax.set_xlabel('sMASE')
ax.set_ylabel('Count');
sMASE = np.mean(sMASEs)
print("Overall sMASE: {:.4f}".format(sMASE))
```
Show some example forecasts.
```
fig, ax = plt.subplots(5, 2, sharex=True)
ax = ax.ravel()
for col in range(1, 11):
ax[col-1].plot(results.index[-prediction_length:], results['ts%s' % col].iloc[-prediction_length:],
label='Actual', c='k', linestyle='--', linewidth=1)
ax[col-1].plot(results.index[-prediction_length:], results['pred%s' % col].iloc[-prediction_length:],
label='Predicted', c='b')
fig.suptitle('{} Predictions'.format(dataset_name))
ax[0].legend();
```
Store the predictions and accuracy score for the Seasonal Naive Approach models.
```
import pickle
with open('{}-sMASE.pkl'.format(dataset_abbr), 'wb') as f:
pickle.dump(sMASE, f)
with open('../_results/{}/{}-results.pkl'.format(model_name, dataset_abbr), 'wb') as f:
pickle.dump(results.iloc[-prediction_length:], f)
```
| true |
code
| 0.477676 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.