prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Module 1: **Data Science - Basic Data Understanding**
Course website: [SHALA-2020](https://shala2020.github.io/)
Instructors: Sudhakar Kumar, Rishav Arjun, and Sahar Nasser
---
## Plotting mathematical functions
---
```
# Loading the libraries
import pandas as pd
import numpy as np
import seaborn as sns
import scipy.stats as stats
from matplotlib import pyplot as plt
from math import pi
# Refer to the official documentation of packages
x = np.arange(-pi, pi, 0.1)
y = np.sin(x)
plt.plot(x, y, 'o') # we can also try go/bo/ro/r- etc for changing the representation of the points (marker)
plt.plot(x,np.cos(x))
plt.legend(['sin', 'cos'])
plt.show()
```
---
## Plotting line plots
---
```
x = [1, 2, 3]
y = [1, 4, 9]
z = [10, 5, 0]
plt.plot(x, y)
# plt.plot(x, z)
# plt.title("test plot")
# plt.xlabel("x")
# plt.ylabel("y and z")
# plt.legend(["this is y", "this is z"])
plt.show()
```
---
## Visualizing data by loading dataframes
---
### Visualizing a sample data
```
# Slides
sample_data = pd.read_csv('sample_data.csv')
sample_data
#Pandas DataFrame is two-dimensional size-mutable, potentially heterogeneous tabular data structure
type(sample_data)
# type(sample_data['column_c'])
type(sample_data.column_c)
# extracting first element of the series
sample_data.column_c.iloc[0]
plt.plot(sample_data.column_a, sample_data.column_b, 'o')
plt.plot(sample_data.column_a, sample_data.column_c)
# Add titles and legend as described earlier
# plt.legend(["col_B", "col_C"])
plt.show()
```
### Visualizing data on the populations of countries
```
data = pd.read_csv('countries.csv')
# pd.set_option('display.max_rows', None)
# pd.set_option('display.max_columns', None)
data
# You can refer to the World Bank data for latest population (https://data.worldbank.org/).
# Compare the population growth in the US and China
data[data.country == 'United States']
us = data[data.country == 'United States']
china = data[data.country == 'China']
china
plt.plot(us.year, us.population)
# Observe the 1e8 on the Y-axis
# plt.plot(us.year, us.population / 10**6)
# plt.plot(china.year, china.population / 10**6)
# plt.legend(['United States', 'China'])
# plt.xlabel('year')
# plt.ylabel('population in million')
plt.show()
# Observe the population growth
us.population
us.population / us.population.iloc[0] * 100
# Find the percentage growth from the first year
plt.plot(us.year, us.population / us.population.iloc[0] * 100)
plt.plot(china.year, china.population / china.population.iloc[0] * 100)
plt.legend(['United States', 'China'])
plt.xlabel('year')
plt.ylabel('population growth (first year = 100)')
plt.show()
```
---
### Visualizing data on movies
---
```
movies = pd.read_csv('moviesData.csv')
pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)
movies.head()
movies.shape
# Plot a histogram of the object named runtime in movies.
# A histogram is a visual representation of the distribution of a dataset.
# It is used to plot the frequency of score occurrences in a continuous dataset.
# Observe the warning in the output
# Slide 9
plt.hist(movies.runtime)
movies.runtime.describe()
# observe that the count of runtime is one less than 600
print(movies.runtime.isna().sum())
movies = movies.dropna() # Drop the na datapoints
movies.shape
# One can also impute the values
# Assignment
print(movies.runtime.isna().sum())
plt.hist(movies.runtime, bins = 7, color='green', orientation='vertical')
# In the histogram there are 7 bins.
# Height of a bin represents the number of observations lying in that interval.
# https://matplotlib.org/3.2.1/api/_as_gen/matplotlib.pyplot.hist.html
plt.title("Distribution of movies' length")
plt.xlabel("Run time of movies")
plt.xlim(0,300)
movies.head()
# create a pie chart from the object genre in the movies data frame.
# A pie chart is a circular chart
# It is Divided into wedge-like sectors, illustrating proportion.
# The total value of the pie is always 100 percent.
# https://matplotlib.org/3.1.1/gallery/pie_and_polar_charts/pie_features.html
# Type of genre_counts
genre_counts = movies.genre.value_counts()
print(genre_counts)
plt.pie(genre_counts)
# plt.pie(genre_counts, labels=genre_counts)
# plt.pie(genre_counts, labels=genre_counts.index.tolist())
plt.show()
# Change the label of the pie chart
movies.head()
moviesSub = movies[0:10]
moviesSub.shape
# draw a bar chart of the object named imdb underscore rating in movies.
# A bar chart represents data in rectangular bars with length of the bar proportional to the value of the variable.
plt.bar(moviesSub.title, moviesSub.imdb_rating)
plt.xlabel('Movies title')
plt.title('imdb_rating')
# plt.xticks(rotation='vertical')
plt.ylim(0,10)
plt.show()
# Slide 10
plt.figure(figsize=(10,10))
# mask = np.zeros_like(movies.corr(), dtype=np.bool)
# mask[np.triu_indices_from(mask)] = True
sns.heatmap(movies.corr())
# vmin = -1, cmap='coolwarm', annot=True, mask = mask
# imdb underscore rating and audience underscore score.
# draw a scatter plot with these two objects by using plot function.
# Scatter plot is a graph in which the values of two variables are plotted along two axes.
# The pattern of the resulting points reveals the correlation.
plt.scatter(movies.imdb_rating, movies.audience_score, c='red')
# plt.scatter(movies.critics_score, movies.audience_score, c='red')
plt.xlim(0,11) # imdb varies from 0 to 10
plt.ylim(0,101) # audience varies from 0 to 100
plt.title('Scatter plot of imdb rating and audience score')
plt.show()
# Concept of correlation is needed here (intuition wise).
# Difference between auto-correlation (do not mix with correlation)
# Range, quartile, information in boxplot
# How to deal with outliers
plt.figure(figsize=(8,10))
movies['diff'] = movies['audience_score'] - movies['critics_score']
chart = sns.boxplot('genre', 'diff', data=movies)
chart.set_xticklabels(
chart.get_xticklabels(),
rotation=90,
horizontalalignment='right',
fontweight='light',
fontsize='x-large'
)
```
---
## Various distributions
---
---
### Bernoulli Distribution
---
Tossing a biased coin
```
probs = np.array([0.70, 0.3])
side = [0, 1]
plt.bar(side, probs)
plt.title('Bernoulli Distribution of a Biased Coin', fontsize=12)
plt.ylabel('Probability', fontsize=12)
plt.xlabel('Outcome', fontsize=12)
axes = plt.gca()
axes.set_ylim([0,1])
```
---
### Uniform Distribution
---
Rolling a dice
```
# Skewed pictorial representation
probs = [1/6]*6
side = [1,2,3,4,5,6]
s = pd.Series(probs,side)
#Set descriptions:
plt.title("Uniform Distribution",fontsize=16)
plt.ylabel('side', fontsize=16)
plt.xlabel('probability',fontsize=16)
#Set tick colors:
ax = plt.gca()
ax.tick_params(axis='x', colors='blue')
ax.tick_params(axis='y', colors='red')
ax.set_ylim([0,1])
#Plot the data:
s.plot(kind = 'bar')
plt.show()
```
---
### Binomial Distribution
---
Tossing a coin certain number of times
```
x = np.arange(0, 25)
prob = 0.2
p = 100 # shape parameter
binom = stats.binom.pmf(x,p, prob)
plt.plot(x, binom, '-o')
plt.xlabel('Random Variable', fontsize=12)
plt.ylabel('Probability', fontsize=12)
plt.title("Binomial Distribution")
```
---
### Gaussian Distribution
---
```
n = np.arange(-100, 100)
mean = 0
normal = stats.norm.pdf(n, mean, 20)
plt.plot(n, normal)
plt.xlabel('Random Variable', fontsize=12)
plt.ylabel('Probability', fontsize=12)
plt.title("Normal Distribution")
```
---
### Poisson Distribution
---
```
# n = number of events, lambd = expected number of events which can take place in a period
# The Poisson distribution is the discrete probability distribution of the number of events
# occurring in a given time period, given the average number of times the event occurs over that time period.
n = np.arange(0, 50)
for Lambda in range(0,10,2):
poisson = stats.poisson.pmf(n, Lambda)
plt.plot(n, poisson, '-o', label="λ = {:f}".format(Lambda))
plt.xlabel('Number of Events', fontsize=12)
plt.ylabel('Probability', fontsize=12)
plt.title("Poisson Distribution")
plt.legend()
```
---
### Exponential Distribution
---
```
Lambda = 0.5
x = np.arange(0, 15, 0.1)
y = Lambda*np.exp(-Lambda*x)
plt.plot(x,y, label="λ = {:f}".format(Lambda))
plt.xlabel('Random Variable', fontsize=12)
plt.ylabel('Probability', fontsize=12)
plt.title("Exponential Distribution")
plt.legend()
```
---
## References
* [Data Visualization with Python](https://www.youtube.com/watch?v=a9UrKTVEeZA)
* [Movies dataset](http://www2.stat.duke.edu/~mc301/data/movies.html)
---
| true |
code
| 0.628293 | null | null | null | null |
|
> This is one of the 100 recipes of the [IPython Cookbook](http://ipython-books.github.io/), the definitive guide to high-performance scientific computing and data science in Python.
# 4.7. Implementing an efficient rolling average algorithm with stride tricks
Stride tricks can be useful for local computations on arrays, when the computed value at a given position depends on the neighbor values. Examples include dynamical systems, filters, cellular automata, and so on. In this example, we will implement an efficient rolling average (a particular type of convolution-based linear filter) with NumPy stride tricks.
The idea is to start from a 1D vector, and make a "virtual" 2D array where each line is a shifted version of the previous line. When using stride tricks, this process does not involve any copy, so it is efficient.
```
import numpy as np
from numpy.lib.stride_tricks import as_strided
%precision 0
def id(x):
# This function returns the memory
# block address of an array.
return x.__array_interface__['data'][0]
n = 5; k = 2
a = np.linspace(1, n, n); aid = id(a)
```
Let's change the strides of `a` to add shifted rows.
```
as_strided(a, (k, n), (a.itemsize, a.itemsize))
id(a), id(as_strided(a, (k, n)))
```
The last value indicates an out-of-bounds problem: stride tricks can be dangerous as memory access is not checked. Here, we should take edge effects into account by limiting the shape of the array.
```
as_strided(a, (k, n - k + 1), (a.itemsize,)*2)
```
Let's apply this technique to calculate the rolling average of a random increasing signal.
First version using array copies.
```
def shift1(x, k):
return np.vstack([x[i:n-k+i+1] for i in range(k)])
```
Second version using stride tricks.
```
def shift2(x, k):
return as_strided(x, (k, n - k + 1), (8, 8))
b = shift1(a, k); b, id(b) == aid
c = shift2(a, k); c, id(c) == aid
```
Let's generate a signal.
```
n, k = 100, 10
t = np.linspace(0., 1., n)
x = t + .1 * np.random.randn(n)
```
We compute the signal rolling average by creating the shifted version of the signal, and averaging along the vertical dimension.
```
y = shift2(x, k)
x_avg = y.mean(axis=0)
```
Let's plot the signal and its averaged version.
```
%matplotlib inline
import matplotlib.pyplot as plt
f = plt.figure()
plt.plot(x[:-k+1], '-k');
plt.plot(x_avg, '-r');
```
### Benchmarks
Let's benchmark the first version (creation of the shifted array, and computation of the mean), which involves array copy.
```
%timeit shift1(x, k)
%%timeit y = shift1(x, k)
z = y.mean(axis=0)
```
And the second version, using stride tricks.
```
%timeit shift2(x, k)
%%timeit y = shift2(x, k)
z = y.mean(axis=0)
```
In the first version, most of the time is spent in the array copy, whereas in the stride trick version, most of the time is instead spent in the computation of the average.
> You'll find all the explanations, figures, references, and much more in the book (to be released later this summer).
> [IPython Cookbook](http://ipython-books.github.io/), by [Cyrille Rossant](http://cyrille.rossant.net), Packt Publishing, 2014 (500 pages).
| true |
code
| 0.50061 | null | null | null | null |
|
```
#hide
%load_ext autoreload
%autoreload 2
# default_exp latent_factor_fxns
```
# Latent Factor Functions
> This module contains the update and forecast functions to work with a latent factor DGLM. There are two sets of functions: The first works with the latent_factor class in PyBATS, which represents latent factors by a mean and a variance. The second set of functions relies on simulated values of a latent factor, which is a more precise but computationally slower method.
The default functions work with the `latent_factor` class, and are called automatically by `analysis`, `dglm.update`, `dglm.forecast_marginal`, and `dglm.forecast_path` when there are latent factors in the model.
To use simulated latent factor values, set the argument `analytic=False` in the `dglm` methods, and pass in the set of simulated values as `phi_samps`. It is not currently supported to use the simulated latent factor values within `analysis`.
```
#hide
#exporti
import numpy as np
from pybats_nbdev.forecast import forecast_path_copula_sim, forecast_path_copula_density_MC, forecast_aR, \
forecast_joint_copula_density_MC, forecast_joint_copula_sim
from pybats_nbdev.update import update_F
import multiprocessing
from functools import partial
```
## Moment-based latent factor analysis
```
#exporti
def update_F_lf(mod, phi, F=None):
if F is None:
if mod.nlf > 0:
mod.F[mod.ilf] = phi.reshape(mod.nlf, 1)
else:
if mod.nlf > 0:
F[mod.ilf] = phi.reshape(mod.nlf, 1)
return F
#export
def update_lf_analytic(mod, y = None, X = None, phi_mu = None, phi_sigma = None):
# If data is missing then skip discounting and updating, posterior = prior
if y is None or np.isnan(y):
mod.t += 1
mod.m = mod.a
mod.C = mod.R
# Get priors a, R for time t + 1 from the posteriors m, C
mod.a = mod.G @ mod.m
mod.R = mod.G @ mod.C @ mod.G.T
mod.R = (mod.R + mod.R.T)/2
mod.W = mod.get_W(X=X)
else:
update_F(mod, X)
# Put the mean of the latent factor phi_mu into the F vector
update_F_lf(mod, phi_mu)
# Mean and variance
ft, qt = mod.get_mean_and_var_lf(mod.F, mod.a, mod.R, phi_mu, phi_sigma, mod.ilf)
# if qt[0] < 0:
# print('correcting matrix')
# while qt<0:
# mod.R[np.diag_indices_from(mod.R)] += 0.001
# ft, qt = mod.get_mean_and_var_lf(mod.F, mod.a, mod.R, phi_mu, phi_sigma, mod.ilf)
# print(ft, qt)
# Choose conjugate prior, match mean and variance
# Initializing the optimization routine at 1,1 is important. At bad initializations, optimizer can shoot off to infinity.
mod.param1, mod.param2 = mod.get_conjugate_params(ft, qt, 1, 1)
if mod.param1 > 1E7:
print('Numerical instabilities appearing in params of ' + str(type(mod)))
# See time t observation y (which was passed into the update function)
mod.t += 1
# Update the conjugate parameters and get the implied ft* and qt*
mod.param1, mod.param2, ft_star, qt_star = mod.update_conjugate_params(y, mod.param1, mod.param2)
# Kalman filter update on the state vector (using Linear Bayes approximation)
mod.m = mod.a + mod.R @ mod.F * (ft_star - ft)/qt
mod.C = mod.R - mod.R @ mod.F @ mod.F.T @ mod.R * (1 - qt_star/qt)/qt
# Get priors a, R for time t + 1 from the posteriors m, C
mod.a = mod.G @ mod.m
mod.R = mod.G @ mod.C @ mod.G.T
mod.R = (mod.R + mod.R.T)/2
# Discount information in the time t + 1 prior
mod.W = mod.get_W(X=X)
mod.R = mod.R + mod.W
#export
def update_lf_analytic_dlm(mod, y=None, X=None, phi_mu = None, phi_sigma = None):
# If data is missing then skip discounting and updating, posterior = prior
if y is None or np.isnan(y):
mod.t += 1
mod.m = mod.a
mod.C = mod.R
# Get priors a, R for time t + 1 from the posteriors m, C
mod.a = mod.G @ mod.m
mod.R = mod.G @ mod.C @ mod.G.T
mod.R = (mod.R + mod.R.T) / 2
mod.W = mod.get_W(X=X)
else:
update_F(mod, X)
# Put the mean of the latent factor phi_mu into the F vector
update_F_lf(mod, phi_mu)
# Mean and variance
ft, qt = mod.get_mean_and_var_lf(mod.F, mod.a, mod.R, phi_mu, phi_sigma, mod.ilf)
mod.param1 = ft
mod.param2 = qt
# See time t observation y (which was passed into the update function)
mod.t += 1
# Update the parameters:
et = y - ft
# Adaptive coefficient vector
At = mod.R @ mod.F / qt
# Volatility estimate ratio
rt = (mod.n + et ** 2 / qt) / (mod.n + 1)
# Kalman filter update
mod.n = mod.n + 1
mod.s = mod.s * rt
mod.m = mod.a + At * et
mod.C = rt * (mod.R - qt * At @ At.T)
# mod.C = (mod.R - qt * At @ At.T)
# Get priors a, R for time t + 1 from the posteriors m, C
mod.a = mod.G @ mod.m
mod.R = mod.G @ mod.C @ mod.G.T
mod.R = (mod.R + mod.R.T) / 2
# Discount information
mod.W = mod.get_W(X=X)
mod.R = mod.R + mod.W
mod.n = mod.delVar * mod.n
#exporti
def get_mean_and_var_lf(self, F, a, R, phi_mu, phi_sigma, ilf):
p = len(ilf)
if p == 1:
extra_var = a[ilf] ** 2 * phi_sigma + a[ilf] * R[np.ix_(ilf, ilf)] * phi_sigma
else:
extra_var = a[ilf].T @ phi_sigma @ a[ilf] + np.trace(R[np.ix_(ilf, ilf)] @ phi_sigma)
return F.T @ a, (F.T @ R @ F + extra_var) / self.rho
#exporti
def get_mean_and_var_lf_dlm(F, a, R, phi_mu, phi_sigma, ilf, ct):
p = len(ilf)
if p == 1:
extra_var = a[ilf] ** 2 * phi_sigma + a[ilf]/ct * R[np.ix_(ilf, ilf)] * phi_sigma
else:
extra_var = a[ilf].T @ phi_sigma @ a[ilf]/ct + np.trace(R[np.ix_(ilf, ilf)] @ phi_sigma)
return F.T @ a, F.T @ R @ F + extra_var
#export
def forecast_marginal_lf_analytic(mod, k, X = None, phi_mu = None, phi_sigma = None, nsamps = 1, mean_only = False, state_mean_var = False):
# Plug in the correct F values
F = update_F(mod, X, F=mod.F.copy())
# Put the mean of the latent factor phi_mu into the F vector
F = update_F_lf(mod, phi_mu, F=F)
a, R = forecast_aR(mod, k)
# Mean and variance
ft, qt = mod.get_mean_and_var_lf(F, a, R, phi_mu, phi_sigma, mod.ilf)
if state_mean_var:
return ft, qt
# Choose conjugate prior, match mean and variance
param1, param2 = mod.get_conjugate_params(ft, qt, mod.param1, mod.param2)
if mean_only:
return mod.get_mean(param1, param2)
# Simulate from the forecast distribution
return mod.simulate(param1, param2, nsamps)
#export
def forecast_path_lf_copula(mod, k, X = None, phi_mu = None, phi_sigma = None, phi_psi = None, nsamps = 1, t_dist=False, y = None, nu=9, return_mu_cov=False):
lambda_mu = np.zeros([k])
lambda_cov = np.zeros([k, k])
F = np.copy(mod.F)
Flist = [None for x in range(k)]
Rlist = [None for x in range(k)]
alist = [None for x in range(k)]
for i in range(k):
# Get the marginal a, R
a, R = forecast_aR(mod, i+1)
alist[i] = a
Rlist[i] = R
# Plug in the correct F values
if mod.nregn > 0:
F = update_F(mod, X[i,:], F=F)
# if mod.nregn > 0:
# F[mod.iregn] = X[i,:].reshape(mod.nregn,1)
# Put the mean of the latent factor phi_mu into the F vector
F = update_F_lf(mod, phi_mu[i], F=F)
# if mod.nlf > 0:
# F[mod.ilf] = phi_mu[i].reshape(mod.nlf,1)
Flist[i] = np.copy(F)
# Find lambda mean and var
ft, qt = mod.get_mean_and_var_lf(F, a, R, phi_mu[i], phi_sigma[i], mod.ilf)
lambda_mu[i] = ft
lambda_cov[i,i] = qt
# Find covariances with previous lambda values
for j in range(i):
# Covariance matrix between the state vector at times j, k
cov_ij = np.linalg.matrix_power(mod.G, i-j) @ Rlist[j]
# Covariance between lambda at times j, i
# If phi_psi is none, we assume the latent factors phi at times t+i, t+j are independent of one another
if phi_psi is None:
lambda_cov[j,i] = lambda_cov[i,j] = Flist[j].T @ cov_ij @ Flist[i]
else:
lambda_cov[j,i] = lambda_cov[i,j] = Flist[j].T @ cov_ij @ Flist[i] + \
alist[i][mod.ilf].T @ phi_psi[i-1][:,:,j] @ alist[j][mod.ilf] + \
np.trace(cov_ij[np.ix_(mod.ilf, mod.ilf)] @ phi_psi[i-1][:,:,j])
if return_mu_cov:
return lambda_mu, lambda_cov
if y is not None:
return forecast_path_copula_density_MC(mod, y, lambda_mu, lambda_cov, t_dist, nu, nsamps)
else:
return forecast_path_copula_sim(mod, k, lambda_mu, lambda_cov, nsamps, t_dist, nu)
```
These functions are called automatically in PyBATS when working with a DGLM that has a latent factor component. The new arguments are:
- `phi_mu`: Mean vector of the latent factor. For `forecast_path_lf_copula`, it should be a list of `k` mean vectors.
- `phi_sigma`: Variance matrix of the latent factor. For `forecast_path_lf_copula`, it should be a list of `k` variance matrices.
The following extra arguments are only applicable to path forecasting with `forecast_path_lf_copula`:
- `phi_psi`: This is a list of `k-1` covariance matrices $cov(\phi_{t+k}, \phi_{t+j})$. Each element is a numpy array.
- `t_dist`: Boolean. By default, a Gaussian copula is used. If True, then a t-copula is used instead.
- `y`: Future path of observations y. If provided, output will be the forecast density of y.
- `nu`: Degrees of freedom for t-copula.
## Simulation-based latent factor analysis
```
#export
def update_lf_sample(mod, y = None, X = None, phi_samps = None, parallel=False):
"""
DGLM update function with samples of a latent factor.
$\phi_{samps}$ = Array of simulated values of a latent factor.
"""
# If data is missing then skip discounting and updating, posterior = prior
if y is None or np.isnan(y):
mod.t += 1
mod.m = mod.a
mod.C = mod.R
# Get priors a, R for time t + 1 from the posteriors m, C
mod.a = mod.G @ mod.m
mod.R = mod.G @ mod.C @ mod.G.T
mod.R = (mod.R + mod.R.T)/2
mod.W = mod.get_W(X=X)
else:
update_F(mod, X)
# Update m, C using a weighted average of the samples
if parallel:
f = partial(update_lf_sample_forwardfilt, mod, y, mod.F, mod.a, mod.R)
p = multiprocessing.Pool(10)
output = p.map(f, phi_samps)
p.close()
else:
output = map(lambda p: update_lf_sample_forwardfilt(mod, y, mod.F, mod.a, mod.R, p), phi_samps)
mlist, Clist, logliklist = list(map(list, zip(*output)))
w = (np.exp(logliklist) / np.sum(np.exp(logliklist))).reshape(-1,1,1)
mlist = np.array(mlist)
Clist = np.array(Clist)
mod.m = np.sum(mlist*w, axis=0)
mod.C = np.sum(Clist*w, axis=0) + np.cov((mlist).reshape(-1, mod.m.shape[0]), rowvar=False, aweights = w.reshape(-1))
# Add 1 to the time index
mod.t += 1
# Get priors a, R from the posteriors m, C
mod.a = mod.G @ mod.m
mod.R = mod.G @ mod.C @ mod.G.T
mod.R = (mod.R + mod.R.T)/2 # prevent rounding issues
# Discount information if observation is observed
mod.W = mod.get_W(X=X)
mod.R = mod.R + mod.W
#export
def update_lf_sample_forwardfilt(mod, y, F, a, R, phi):
F = update_F_lf(mod, phi, F=F)
# F[mod.ilf] = phi.reshape(-1,1)
ft, qt = mod.get_mean_and_var(F, a, R)
# get the conjugate prior parameters
param1, param2 = mod.get_conjugate_params(ft, qt, mod.param1, mod.param2)
# Get the log-likelihood of 'y' under these parameters
loglik = mod.loglik(y, param1, param2)
# Update to the conjugate posterior after observing 'y'
param1, param2, ft_star, qt_star = mod.update_conjugate_params(y, param1, param2)
# Kalman filter update on the state vector (using Linear Bayes approximation)
m = a + R @ F * (ft_star - ft)/qt
C = R - R @ F @ F.T @ R * (1 - qt_star/qt)/qt
return m, C, np.ravel(loglik)[0]
#export
def forecast_marginal_lf_sample(mod, k, X = None, phi_samps = None, mean_only = False):
# Plug in the correct F values
F = update_F(mod, X, F=mod.F.copy())
a, R = forecast_aR(mod, k)
# Simulate from the forecast distribution
return np.array(list(map(lambda p: lf_simulate_from_sample(mod, F, a, R, p), phi_samps))).reshape(-1)
#exporti
def lf_simulate_from_sample(mod, F, a, R, phi):
F = update_F_lf(mod, phi, F=F)
# F[mod.ilf] = phi.reshape(-1,1)
ft, qt = mod.get_mean_and_var(F, a, R)
# get the conjugate prior parameters
param1, param2 = mod.get_conjugate_params(ft, qt, mod.param1, mod.param2)
# Update to the conjugate posterior after observing 'y'
return mod.simulate(param1, param2, 1)
#export
def forecast_path_lf_sample(mod, k, X=None, phi_samps = None):
nsamps = len(phi_samps)
samps = np.zeros([nsamps, k])
F = np.copy(mod.F)
for n in range(nsamps):
param1 = mod.param1
param2 = mod.param2
a = np.copy(mod.a)
R = np.copy(mod.R)
for i in range(k):
# Plug in X values
if mod.nregn > 0:
F = update_F(mod, X[i, :], F=F)
# if mod.nregn > 0:
# F[mod.iregn] = X[i, :].reshape(mod.nregn, 1)
# Plug in phi sample
F = update_F_lf(mod, phi_samps[n][i], F=F)
# F[mod.ilf] = phi_samps[n][i].reshape(-1, 1)
# Get mean and variance
ft, qt = mod.get_mean_and_var(F, a, R)
# Choose conjugate prior, match mean and variance
param1, param2 = mod.get_conjugate_params(ft, qt, param1, param2)
# Simulate next observation
samps[n, i] = mod.simulate(param1, param2, nsamps=1)
# Update based on that observation
param1, param2, ft_star, qt_star = mod.update_conjugate_params(samps[n, i], param1, param2)
# Kalman filter update on the state vector (using Linear Bayes approximation)
m = a + R @ F * (ft_star - ft) / qt
C = R - R @ F @ F.T @ R * (1 - qt_star / qt) / qt
# Get priors a, R for the next time step
a = mod.G @ m
R = mod.G @ C @ mod.G.T
R = (R + R.T) / 2
# Discount information
if mod.discount_forecast:
R = R + mod.W
return samps
```
These functions can be called through `dglm.update`, `dglm.forecast_marginal`, and `dglm.forecast_path` by setting the argument `analytic=False`. They represent an alternative method of analysis by working with simulated values of the latent factor. The simulated values are passed into the function as an array `phi_samps`, where each row contains a simulated value of the latent factor.
This is a more accurate analysis method because it does not reduce the distribution of the latent factor down to its mean and variance. However, it is also more computationally demanding to work with the simulated values, so there is a trade-off between speed and accuracy.
## Multivariate forecasting with multiple DGLMs
```
#export
def forecast_joint_marginal_lf_copula(mod_list, k, X_list=None, phi_mu = None, phi_sigma = None,
nsamps=1, y=None, t_dist=False, nu=9, return_cov=False):
p = len(mod_list)
lambda_mu = np.zeros([p])
lambda_cov = np.zeros([p, p])
Flist = [None for x in range(p)]
Rlist = [None for x in range(p)]
alist = [None for x in range(p)]
if X_list is None:
X_list = [[] for i in range(p)]
for i, [X, mod] in enumerate(zip(X_list, mod_list)):
# Evolve to the prior at time t + k
a, R = forecast_aR(mod, k)
Rlist[i] = R
alist[i] = a[mod.ilf]
# Plug in the correct F values
if mod.nregn > 0:
F = update_F(mod, X, F=mod.F.copy())
else:
F = mod.F.copy()
# Put the mean of the latent factor phi_mu into the F vector
F = update_F_lf(mod, phi_mu, F=F)
Flist[i] = F
# Find lambda mean and var
ft, qt = mod.get_mean_and_var(F, a, R)
lambda_mu[i] = ft
lambda_cov[i, i] = qt
# Find covariances with lambda values from other models
for j in range(i):
# Covariance matrix between lambda from models i, j
if phi_sigma.ndim == 0:
lambda_cov[j, i] = lambda_cov[i, j] = np.squeeze(alist[i] * phi_sigma * alist[j])
else:
lambda_cov[j, i] = lambda_cov[i, j] = alist[i].T @ phi_sigma @ alist[j]
if return_cov:
return lambda_cov
if y is not None:
return forecast_joint_copula_density_MC(mod_list, y, lambda_mu, lambda_cov, t_dist, nu, nsamps)
else:
return forecast_joint_copula_sim(mod_list, lambda_mu, lambda_cov, nsamps, t_dist, nu)
```
`forecast_joint_marginal_lf_copula` is used to *recouple* a set of DGLMs which share the same latent factor. In other words, if the same latent factor is used in multiple models, then their forecasts will be correlated. This function allows for joint forecasting across these separated DGLMs.
A classic example comes from retail sales. The latent factor may represent an effect at the total store level - say, customer traffic based on the day-of-week. A separate DGLM models the sales of each individual item. To jointly forecast the sales of many items, the models can all be passed into `forecast_joint_marginal_lf_copula`, along with the latent factor mean and variance, to draw joint samples from the forecast distribution.
## Multivariate forecasting with multiple DCMMs
```
#export
def forecast_joint_marginal_lf_copula_dcmm(dcmm_list, k, X_list=None, phi_mu = None, phi_sigma = None,
nsamps=1, t_dist=False, nu=9, return_cov=False):
bern_list = [mod.bern_mod for mod in dcmm_list]
pois_list = [mod.pois_mod for mod in dcmm_list]
mod_list = [*bern_list, *pois_list]
p = len(mod_list)
lambda_mu = np.zeros([p])
lambda_cov = np.zeros([p, p])
Flist = [None for x in range(p)]
Rlist = [None for x in range(p)]
alist = [None for x in range(p)]
if X_list is None:
X_list = [[] for i in range(p)]
else:
X_list = [*X_list, *X_list]
for i, [X, mod] in enumerate(zip(X_list, mod_list)):
# Evolve to the prior at time t + k
a, R = forecast_aR(mod, k)
Rlist[i] = R
alist[i] = a[mod.ilf]
# Plug in the correct F values
if mod.nregn > 0:
F = update_F(mod, X, F=mod.F.copy())
else:
F = mod.F.copy()
# Put the mean of the latent factor phi_mu into the F vector
F = update_F_lf(mod, phi_mu, F=F)
Flist[i] = F
# Find lambda mean and var
ft, qt = mod.get_mean_and_var(F, a, R)
lambda_mu[i] = ft
lambda_cov[i, i] = qt
# Find covariances with lambda values from other models
for j in range(i):
# Covariance matrix between lambda from models i, j
if phi_sigma.ndim == 0:
lambda_cov[j, i] = lambda_cov[i, j] = np.squeeze(alist[i] * phi_sigma * alist[j])
else:
lambda_cov[j, i] = lambda_cov[i, j] = alist[i].T @ phi_sigma @ alist[j]
samps = forecast_joint_copula_sim(mod_list, lambda_mu, lambda_cov, nsamps, t_dist, nu)
bern_samps = samps[:,:len(bern_list)]
pois_samps = samps[:, len(bern_list):]
pois_samps += 1
samps = bern_samps * pois_samps
if return_cov:
return np.cov(samps.T)
return samps
```
`forecast_joint_marginal_lf_copula_dcmm` behaves similarly to `forecast_joint_marginal_lf_copula`, but for a set of related DCMMs instead of related DGLMs.
## DCMM forecast functions
```
#export
def forecast_marginal_lf_dcmm(mod, k, X=None, phi_mu=None, phi_sigma=None, nsamps=1, t_dist=False, nu=9, return_cov=False):
mod_list = [mod.bern_mod, mod.pois_mod]
lambda_mu = np.zeros(2)
lambda_cov = np.zeros([2,2])
a_lf_list=[]
for i, mod in enumerate(mod_list):
# Plug in the correct F values
F = update_F(mod, X, F=mod.F.copy())
# F = np.copy(mod.F)
# if mod.nregn > 0:
# F[mod.iregn] = X.reshape(mod.nregn,1)
# Put the mean of the latent factor phi_mu into the F vector
F = update_F_lf(mod, phi_mu, F=F)
# if mod.nlf > 0:
# F[mod.ilf] = phi_mu.reshape(mod.nlf,1)
a, R = forecast_aR(mod, k)
a_lf_list.append(a[mod.ilf])
# Mean and variance
ft, qt = mod.get_mean_and_var_lf(F, a, R, phi_mu, phi_sigma, mod.ilf)
lambda_mu[i] = ft
lambda_cov[i,i] = qt
lambda_cov[0,1] = lambda_cov[1,0] = a_lf_list[0].T @ phi_sigma @ a_lf_list[1]
samps = forecast_joint_copula_sim(mod_list, lambda_mu, lambda_cov, nsamps, t_dist, nu)
bern_samps = samps[:, 0]
pois_samps = samps[:, 1]
pois_samps += 1
samps = bern_samps * pois_samps
if return_cov:
return np.cov(samps.T)
return samps
#export
def forecast_path_lf_dcmm(mod, k, X=None, phi_mu=None, phi_sigma=None, phi_psi=None, nsamps=1, t_dist=False, nu=9, return_cov=False):
lambda_mu = np.zeros(k*2)
lambda_cov = np.zeros([k*2, k*2])
mucov_bern = forecast_path_lf_copula(mod.bern_mod, k, X, phi_mu, phi_sigma, phi_psi, return_mu_cov=True)
mucov_pois = forecast_path_lf_copula(mod.pois_mod, k, X, phi_mu, phi_sigma, phi_psi, return_mu_cov=True)
lambda_mu[:k] = mucov_bern[0]
lambda_mu[k:] = mucov_pois[0]
lambda_cov[:k,:k] = mucov_bern[1]
lambda_cov[k:,k:] = mucov_pois[1]
for i in range(k):
a_bern, R_bern = forecast_aR(mod.bern_mod, i+1)
for j in range(k):
a_pois, R_pois = forecast_aR(mod.pois_mod, j+1)
if i == j:
cov = float(a_bern[mod.bern_mod.ilf].T @ phi_sigma[i] @ a_pois[mod.pois_mod.ilf])
elif i > j:
cov = float(a_bern[mod.bern_mod.ilf].T @ phi_psi[i-1][j] @ a_pois[mod.pois_mod.ilf])
elif j > i:
cov = float(a_bern[mod.bern_mod.ilf].T @ phi_psi[j-1][i] @ a_pois[mod.pois_mod.ilf])
lambda_cov[i, j + k] = lambda_cov[j + k, i] = cov
mod_list = [*[mod.bern_mod]*k, *[mod.pois_mod]*k]
samps = forecast_joint_copula_sim(mod_list, lambda_mu, lambda_cov, nsamps, t_dist, nu)
bern_samps = samps[:, :k]
pois_samps = samps[:, k:]
pois_samps += 1
samps = bern_samps * pois_samps
if return_cov:
return np.cov(samps.T)
return samps
```
These functions are for marginal and path forecasting with a latent factor DCMM. They may be accessed as methods from `dcmm`.
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| true |
code
| 0.465145 | null | null | null | null |
|
# Investigate Web Application Firewall (WAF) Data </br>
**Author:** Vani Asawa <br/>
**Date:** December 2020 </br>
**Notebook Version:** 1.0 <br/>
**Python Version:** Python 3.6 <br/>
**Required Packages:** msticpy, pandas, kqlmagic <br/>
**Data Sources Required:** WAF data (AzureDiagnostics) <br/>
## What is the purpose of this Notebook?
Web Application Firewall (WAF) data records the monitored and blocked HTTP traffic to and from a web service.
Due to the large magnitudes of HTTP requests made to such services in any workspace, the data tends to be incredibly noisy, and hence may prevent an analyst from determining if there are any bad requests made to the servers, which could result in a potentially malicious attack.
This notebook analyses the blocked WAF Alerts and aim to surface any unusual HTTP requests made by the client IPs to the servers, using a variety of statistical techniques applied on several features of the WAF data, such as the Rule ID of the triggering event, the HTTP status code returned to the client from the alerts, and the contents of the request URIs themselves
## Overview
**[Distribution of WAF logs and blocked alerts over an extended time frame](#DistributionofWAF)**
1. Set an extended time frame to visualise the distribution of the logs/alerts on a bar graph
**[What is the distribution of WAF blocked alerts over Rule IDs, http-status codes, and client IP entities?](#DistOver_rID_http_ip)**
1. Set a time frame (recommended: time period of interest, after analysing the distribution of alerts in the extended time frame)
2. Pick a host entity to explore in further detail
3. Set x and y axes from the variables above, and view the number of alerts over the designate time frame.
**[Cluster the request URIs in WAF blocked alerts, based on TFIDF scores](#ClusterURIs)**
*Term frequency-inverse document frequency (TFIDF)* score is a numerical statistic of how important a variable is to a document. The value of the statistic is directly proportional to the variable's frequency in the document, and inversely proportional to the number of documents that contain the variable. More information about TFIDF can be found [here](https://www.researchgate.net/publication/326425709_Text_Mining_Use_of_TF-IDF_to_Examine_the_Relevance_of_Words_to_Documents)
In our analysis, the *variable* will be the 'split URIs' and 'rule IDs', while a single *document* is all the blocked alerts for a single client IP in the selected time frame. We will be assessing the relative importance of every single token of the split request URIs and the number of times a ruleID is triggered for our blocked alerts over multiple such 'documents'. We will be using these two sets of scores to cluster the request URIs, and obtain single/grouped sets of interesting (and potentially malicious) request URIs that were blocked by the WAF.
1. Compute TFIDF scores based on the following 2 approaches:
- Request URIs split on "/" against the client IP entities
- Number of blocked alerts for every Rule ID against the client IP entities
2. Visualising the TFIDF scores for both approaches
3. Performing DBScan Clustering + PCA to obtain the clustered and outlier request URIs for both approaches
4. KQL query to further examine the WAF logs and blocked alerts in the time frames with outlier request URIs**
## Using the Notebook
**Prerequisites**
- msticpy - install the latest using pip install --upgrade msticpy
- pandas- install using pip install pandas
- kqlmagic
**Running the Notebook**
The best way of using the notebook is as follows:
1. Individually run all of the cells up to the start of Section 1:
- Initialization and installation of libraries
- Authenticating to the workspace
- Setting notebook parameters
2. Default paramenters will allow the entire notebook to run from Section I using the 'Run Selected Cell and All Below' option under the Run tab. However, for added value, run the cells sequentially in any given section.
- At the beginning of each section, set the time parameters. It is recommended that the first and third section have a larger timeframe than the second and fourth sections.
- Wait for the cell to finish running, before proceeding
- Select the options from the widget boxes when displayed and proceed.
```
from pathlib import Path
import os
import sys
from pathlib import Path
from IPython.display import display, HTML
REQ_PYTHON_VER=(3, 6)
REQ_MSTICPY_VER=(1, 0, 0)
REQ_MP_EXTRAS = ["ml", "kql"]
update_nbcheck = (
"<p style='color: orange; text-align=left'>"
"<b>Warning: we needed to update '<i>utils/nb_check.py</i>'</b><br>"
"Please restart the kernel and re-run this cell."
"</p>"
)
display(HTML("<h3>Starting Notebook setup...</h3>"))
if Path("./utils/nb_check.py").is_file():
try:
from utils.nb_check import check_versions
except ImportError as err:
%xmode Minimal
!curl https://raw.githubusercontent.com/Azure/Azure-Sentinel-Notebooks/master/utils/nb_check.py > ./utils/nb_check.py 2>/dev/null
display(HTML(update_nbcheck))
if "check_versions" not in globals():
raise ImportError("Old version of nb_check.py detected - see instructions below.")
%xmode Verbose
check_versions(REQ_PYTHON_VER, REQ_MSTICPY_VER, REQ_MP_EXTRAS)
# If not using Azure Notebooks, install msticpy with
# !pip install msticpy
from msticpy.nbtools import nbinit
nbinit.init_notebook(
namespace=globals(),
additional_packages=["adjustText", "plotly"]
);
from ipywidgets import widgets
import plotly.graph_objects as go
import plotly.express as px
import re
from sklearn.feature_extraction.text import TfidfVectorizer
%matplotlib inline
from sklearn.cluster import KMeans
from sklearn import metrics
from sklearn.cluster import DBSCAN
from sklearn.decomposition import PCA
from adjustText import adjust_text
import itertools
import ipaddress
import traceback
pd.set_option('display.max_rows', 100)
pd.set_option('display.max_columns', 50)
pd.set_option('display.max_colwidth', 40)
pd.set_option('display.max_colwidth', None)
layout = widgets.Layout(width="50%", height="80px")
style = {"description_width": "200px"}
class color:
BOLD = '\033[1m'
END = '\033[0m'
# See if we have an Azure Sentinel Workspace defined in our config file.
# If not, let the user specify Workspace and Tenant IDs
ws_config = WorkspaceConfig()
if not ws_config.config_loaded:
ws_config.prompt_for_ws()
qry_prov = QueryProvider(data_environment="AzureSentinel")
print("done")
# Authenticate to Azure Sentinel workspace
qry_prov.connect(ws_config)
```
**Querying Function** : Accessing the results of the Kusto query as a pandas dataframe, and removing empty/null columns from the dataframe
```
def showQuery(query):
df = qry_prov.exec_query(query)
trimDF(df)
return df
def trimDF(df):
# Store names of columns with null values for all entries
empty_null_cols = [col for col in df.columns if df[col].isnull().all()]
# Store names of columns with empty string '' values for all entries
empty_str_cols = []
for col in df.columns:
try:
if ''.join(df[col].map(str)) == '':
empty_str_cols = empty_str_cols + [col]
except:
continue
df.drop(empty_null_cols + empty_str_cols, axis=1, inplace=True)
binIntervals = ['1m', '5m', '10m', '15m', '30m', '1h', '12h', '1d', '5d', '10d']
```
**Selecting a Host**
```
def queryHost(startTime, endTime):
query = '''
AzureDiagnostics
| where TimeGenerated between (datetime({startTime}).. datetime({endTime}))
| where Category == "ApplicationGatewayFirewallLog"
| where action_s == 'Blocked' or isempty(action_s)
| summarize AlertCountPerHost = count() by hostname_s, bin(timeStamp_t, {binInterval})
| render timechart
'''.format(startTime = startTime, endTime = endTime, binInterval = '1h')
return(query)
```
**Auto determine masking bits for clubbing IPs**
```
def maskBitsVal(uniqueIPLen):
if uniqueIPLen > 150:
return '/8'
elif uniqueIPLen > 40:
return '/16'
elif uniqueIPLen > 15:
return '/24'
return '/32'
```
## Section I: Distribution of WAF logs and blocked alerts over an extended time frame <a name="DistributionofWAF"></a>
Select an extended time frame to view the distribution of WAF logs and blocked alerts over all hosts.
```
query_times_1 = nbwidgets.QueryTime(units='day', max_before=30, before=-15, max_after=-1)
query_times_1.display()
categories = ['ApplicationGatewayAccessLog', 'ApplicationGatewayFirewallLog']
def viewLogs(category):
log_alert_query = '''
AzureDiagnostics
| where TimeGenerated between (datetime({startTime}).. datetime({endTime}))
| where Category == "{category}"
| where action_s == 'Blocked' or isempty(action_s)
| summarize NoOfAlerts= count() by bin(timeStamp_t, {binInterval})
| render timechart '''.format(startTime = query_times_1.start, endTime = query_times_1.end, category = category, binInterval = '1h')
%kql -query log_alert_query
rawDataQuery = """
AzureDiagnostics
| where TimeGenerated between (datetime({startTime}).. datetime({endTime}))
| where Category == '{category}'
| where action_s == 'Blocked' or isempty(action_s)
| take 15
""".format(startTime = query_times_1.start, endTime = query_times_1.end, category = category)
display(showQuery(rawDataQuery).head(5))
category = widgets.Select(options = categories, style = style, layout = layout, description = 'Choose logs/alerts: ')
display(category)
viewLogs(category = category.value)
```
## Section II: What is the distribution of blocked WAF alerts over Rule IDs, http-status codes, and client IP Entities? <a name="DistOver_rID_http_ip"></a>
Select a time frame of interest to view the distribution of WAF blocked alerts over all hosts.
*Recommended:* Analyse a shorter time frame than Section I for more detail
```
query_times_2 = nbwidgets.QueryTime(units='day', max_before=30, before=-10, max_after=-1)
query_times_2.display()
```
### Select a host entity
The following host entity will be used for the remainder of this section
```
query = queryHost(query_times_2.start, query_times_2.end)
%kql -query query
try:
df_host = showQuery(query)
list_hosts = set([x for x in df_host['hostname_s']])
df = df_host.groupby(['hostname_s']).agg({'AlertCountPerHost': sum}).rename(columns = {'AlertCountPerHost': 'Num_blocked_alerts'})
hosts = widgets.Select(options=list_hosts, style = style, layout = layout, value=df['Num_blocked_alerts'].idxmax(), description = 'Select Host: ')
display(df)
display(hosts)
except Exception as e:
print('Error: ' + e)
traceback.print_exc()
```
### Render visualisations of the distribution of blocked alerts for the selected host
We will be using balloon plots to visualise the number of WAF alerts over rule IDs, http-status codes, and client IP entities, for the selected host entity.
```
query_distribution = '''
AzureDiagnostics
| where TimeGenerated between (datetime({startTime}).. datetime({endTime}))
| where Category == "ApplicationGatewayFirewallLog"
| where hostname_s == "{host}"
| where action_s == 'Blocked' or isempty(action_s)
| join kind=leftouter ( AzureDiagnostics
| where TimeGenerated between (datetime({startTime}).. datetime({endTime}))
| where Category == "ApplicationGatewayAccessLog"
| summarize by requestUri_s, httpStatus_d
) on requestUri_s
| summarize NoOfAlerts = count(), make_set(requestUri_s), DistinctURIs = dcount(requestUri_s) by clientIp_s, ruleId_s, httpStatus_d1
'''.format(startTime = query_times_2.start, endTime = query_times_2.end, host = hosts.value)
try:
df_distribution = showQuery(query_distribution)
df_distribution.rename(columns = {'clientIp_s':'Ip Address', 'ruleId_s':'Rule ID', 'set_requestUri_s': 'Request Uris'}, inplace = True)
if 'httpStatus_d1' in df_distribution.columns:
df_distribution = df_distribution.sort_values(by=['httpStatus_d1'], ascending = True).reset_index(drop = True)
df_distribution.rename(columns = {'httpStatus_d1':'Http status'}, inplace = True)
df_distribution['Http status'] = 'h: ' + df_distribution['Http status'].astype(str)
maskBits = maskBitsVal(len(df_distribution['Ip Address'].unique()))
df_distribution['Ip Address'] = df_distribution['Ip Address'].apply(lambda x: ipaddress.IPv4Network(x + maskBits, strict = False))
df_distribution['Ip Address'], df_distribution['Rule ID'] = 'Ip ' + df_distribution['Ip Address'].astype(str), 'rID ' + df_distribution['Rule ID'].astype(str)
except Exception as e:
print('Error: ' + e)
traceback.print_exc()
options = ['Ip Address', 'Rule ID']
if 'Http status' in df_distribution.columns:
options += ['Http status']
def viewBalloonPlot(x_axis, y_axis, display_rawResult):
try:
df_balloon_plot = (df_distribution
.groupby([x_axis, y_axis], as_index=False)
.agg({'NoOfAlerts': sum, 'DistinctURIs': sum, 'Request Uris': list})
.reset_index(drop = True))
fig = px.scatter(df_balloon_plot, x=df_balloon_plot[x_axis], y = df_balloon_plot[y_axis],
size= np.log(1 + df_balloon_plot['NoOfAlerts'] ), color = 'NoOfAlerts',
hover_data=['NoOfAlerts', 'DistinctURIs'])
fig.update_layout(height = max(300, 30 * len(set(df_balloon_plot[y_axis]))), title_text='Alert Distribution for host ID '+ str(hosts.value))
fig.show()
if display_rawResult == 'Yes':
print('Top 5 raw results with the highest number of alerts: \n')
df_balloon_plot['Request Uris'] = [np.unique(list(itertools.chain(*row['Request Uris']))) for index, row in df_balloon_plot.iterrows() ]
df_balloon_plot['DistinctURIs'] = df_balloon_plot['Request Uris'].str.len()
display(df_balloon_plot[[y_axis, x_axis, 'NoOfAlerts','Request Uris', 'DistinctURIs']].sort_values(by='NoOfAlerts', ascending = False).head(5))
except ValueError:
print('ValueError: Choose distinct x and y axes')
except Exception as e:
print('Error: ' + e)
traceback.print_exc()
x_axis = widgets.Select(options = options, style = style, layout = layout, description = 'Select x-axis: ')
y_axis = widgets.Select(options = options, style = style, layout = layout, description = 'Select y-axis: ')
display_rawResult = widgets.Select(options = ['Yes', 'No'], description = 'Display raw results: ')
md("Select graph properties:", "bold")
display(x_axis)
display(y_axis)
display(display_rawResult)
viewBalloonPlot, x_axis = x_axis.value,
y_axis = y_axis.value, display_rawResult = display_rawResult.value)
display(w)
```
## Section III: Cluster the request URIs in blocked WAF Alerts, based on TFIDF scores <a name="ClusterURIs"></a>
Select the timeframe and host entity for this section of the notebook.
*Recommended*: Set a timeframe of >20 days
```
query_times_3 = nbwidgets.QueryTime(units='day', max_before=30, before=10, max_after=-1)
query_times_3.display()
df_host_2 = showQuery(queryHost(query_times_3.start, query_times_3.end))
df = df_host_2.groupby(['hostname_s']).agg({'AlertCountPerHost': sum}).rename(columns = {'AlertCountPerHost': 'Num_blocked_alerts'})
hosts_2 = widgets.Select(options=set([x for x in df_host_2['hostname_s']]), value=df['Num_blocked_alerts'].idxmax(), description = 'Select Host: ')
display(df)
display(hosts_2)
```
**Enter min_df and max_df value parameters**
*min_df*: The min_df variable is used to eliminate terms that do not appear very frequently in our data. A min_df value of 0.01 implies eliminating terms that apear in less than 1% of the data.
*max_df*: The max_df variable eliminates terms that appear very frequently in our data. A max_df value of 0.9 implies eliminating terms that appear in more than 90% of the data.
For more information about these parameters in the TFIDF vectorizer, please see [here](https://stackoverflow.com/questions/27697766/understanding-min-df-and-max-df-in-scikit-countvectorizer)
**Note:** In the case of errors running the code below for the two approaches (Request URIs split on "/" against the client IP entities OR Number of blocked alerts for every Rule ID against the client IPs), run the TFIDF vectoriser for ALL the data
If you would like to view the TFIDF scores for all the data, change the following code in the `tfidfScores` function:
`vectorizer = TfidfVectorizer(tokenizer=identity_tokenizer, lowercase=False, min_df = min_df_value, max_df = max_df_value) `
to
`vectorizer = TfidfVectorizer(tokenizer=identity_tokenizer, lowercase=False) `
```
min_df_widget = widgets.Text(style = style, layout = widgets.Layout(width="50%", height="30px"), description = 'Enter min_df: ', placeholder = '% or Integer or None', value = '0.01')
max_df_widget = widgets.Text(style = style, layout = widgets.Layout(width="50%", height="30px"), description = 'Enter max_df: ', placeholder = '% or Integer or None', value = '0.9')
display(min_df_widget)
display(max_df_widget)
try:
min_df_value = float(min_df_widget.value)
max_df_value = float(max_df_widget.value)
except Exception as e:
print('Error: ' + str(e))
traceback.print_exc()
def tfidfScores(df, tokenList = None):
def identity_tokenizer(text):
return text
vectorizer = TfidfVectorizer(tokenizer=identity_tokenizer, lowercase=False, min_df = min_df_value, max_df = max_df_value)
vectors = vectorizer.fit_transform(tokenList)
feature_names = vectorizer.get_feature_names()
dense = vectors.todense()
denselist = dense.tolist()
df_scores = pd.DataFrame(denselist, columns = feature_names)
multicol1 = pd.MultiIndex.from_tuples([('weight', str(j)) for j in df_scores.columns])
df_multiIndex = pd.DataFrame([list(df_scores.iloc[i]) for i in range(0, len(df_scores))], index=[df['Ip Address']], columns=multicol1)
return df_multiIndex
```
### Approach I: Compute TFIDF scores for split request URIs in the blocked WAF Alerts against client IP entities
```
query_URIs = '''
AzureDiagnostics
| where TimeGenerated between (datetime({startTime}).. datetime({endTime}))
| where Category == "ApplicationGatewayFirewallLog"
| where hostname_s startswith "{host}"
| where action_s == 'Blocked' or isempty(action_s)
| distinct clientIp_s, requestUri_s
| summarize make_list(requestUri_s) by clientIp_s
'''.format(startTime = query_times_3.start, endTime = query_times_3.end, host = hosts_2.value)
try:
df_URIs = showQuery(query_URIs)
df_URIs.rename(columns = {'clientIp_s':'Ip Address', 'list_requestUri_s': 'RequestUris'}, inplace = True)
viewData_splitUri = df_URIs.copy()
maskBits = maskBitsVal(len(viewData_splitUri['Ip Address'].unique()))
viewData_splitUri['Ip Address'] = viewData_splitUri['Ip Address'].apply(lambda x: ipaddress.IPv4Network(x + maskBits, strict = False))
viewData_splitUri.groupby(["Ip Address"], as_index=False).agg({'RequestUris': list})
tokenList = []
for index, row in viewData_splitUri.iterrows():
splitUris = re.split('/', ''.join(row['RequestUris']))
tokenList = tokenList + [splitUris]
df_splitUri_tfidf = tfidfScores(viewData_splitUri, tokenList)
except Exception as e:
print('Error: ' + str(e))
traceback.print_exc()
```
### Approach II: Computer TFIDF scores for volume of blocked WAF alerts for Rule Ids against the client IP entities
```
query_RuleIds = '''
AzureDiagnostics
| where TimeGenerated between (datetime({startTime}).. datetime({endTime}))
| where Category == "ApplicationGatewayFirewallLog"
| where hostname_s startswith "{host}"
| where action_s == 'Blocked'
| summarize alertCount = count(), make_set(requestUri_s) by clientIp_s, ruleId_s
'''.format(startTime = query_times_3.start, endTime = query_times_3.end, host = hosts_2.value)
try:
dfPrac = showQuery(query_RuleIds)
df_RuleIds = showQuery(query_RuleIds)
df_RuleIds.rename(columns = {'clientIp_s':'Ip Address', 'ruleId_s':'RuleId', 'set_requestUri_s': 'RequestUris'}, inplace = True)
maskBits = maskBitsVal(len(df_RuleIds['Ip Address'].unique()))
df_RuleIds['Ip Address'] = df_RuleIds['Ip Address'].apply(lambda x: ipaddress.IPv4Network(x + maskBits, strict = False))
viewData_ruleId = df_RuleIds.groupby(["Ip Address"], as_index=False).agg({'RuleId': list, 'alertCount': list, 'RequestUris': list})
tokenList = [sum([[s] * n for s, n in zip(viewData_ruleId['RuleId'][x], viewData_ruleId['alertCount'][x])], []) for x in range(0, len(viewData_ruleId))]
df_ruleId_tfidf = tfidfScores(viewData_ruleId, tokenList)
except Exception as e:
print('Error: ' + e)
traceback.print_exc()
```
### Visualisation of the TFIDF scores for both approaches
We will be using balloon plots to view the TFIDF scores for the two approaches
```
options = ['RuleId', 'SplitUris']
def visualiseTFIDF(TfidfCategory):
try:
max_category = 30
df = pd.DataFrame()
if TfidfCategory == 'RuleId': df = df_ruleId_tfidf.copy()
else:
df = df_splitUri_tfidf.copy()
df_tfidf = df.iloc[:, : max_category].stack().reset_index(drop = False).rename(columns = {'level_1':TfidfCategory, 'weight':'tfidf'})
df_tfidf['Ip Address'] = 'Ip ' + df_tfidf['Ip Address'].astype(str)
if 'RuleId' == TfidfCategory:
df_tfidf['RuleId'] = 'rID ' + df_tfidf['RuleId'].astype(str)
else:
df_tfidf['SplitUris'] = df_tfidf['SplitUris'].apply(lambda x: (x[0:20]+ '...') if len(x)> 20 else x)
fig = px.scatter(df_tfidf, x = df_tfidf[TfidfCategory], y = df_tfidf['Ip Address'],
size= np.log(1 + df_tfidf['tfidf']), color = df_tfidf['tfidf'],
hover_data=[df_tfidf['tfidf']])
fig.update_layout(height = max(800, 20 * len(set(df_tfidf[TfidfCategory]))), title_text= 'TFIDF distribution of ' + TfidfCategory + ' against client IPs', width = 1700)
fig.show()
except Exception as e:
print('Error: ' + e)
traceback.print_exc()
TfidfCategory = widgets.Select(options = options, style = style, layout = layout, description = 'TFIDF approach: ')
display(TfidfCategory)
visualiseTFIDF(TfidfCategory = TfidfCategory.value)
```
### DBSCAN Clustering and PCA of the request URIs for both approaches
DBSCAN is a non-parametric density-based spatial clustering algorithm, which groups together points that are "closely packed" together. Points which lie in low density regions are marked as outliers. For more information, please see [here](https://www.aaai.org/Papers/KDD/1996/KDD96-037.pdf). We use DBScan on our data in order to aggregate request URIs which are similar to each other, and surface unusual request URIs as outliers. The clustering uses the Tfidf scores data obtained for the rule ID and split URIs approaches respectively.
Select the eps and min_samples value for DBScan and n_components value for PCA below. More information about these parameters can be found [here](https://scikit-learn.org/stable/modules/generated/sklearn.cluster.dbscan.html) and [here](https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html).
**DBScan:**
*eps value:* Eps value is a measure of the distance below which two points are considered neighbors.
*min_samples:* The minimum number of neighbors that a point should have in order to be classified as a core point. The core point is included in the min_samples count.
**PCA:** PCA is a dimensionality reduction technique that compresses the multivariate data into principal components, which describe most of the variation in the original dataset. In our case, we are able to better visualise the clubbing of similar and outlier request URIs by visualising the first two Principal components.
*n_components:* Number of principal components
```
eps_widget = widgets.Text(style = style, layout = widgets.Layout(width="50%", height="30px"), description = 'DBSCAN - Enter eps value', value = '0.4')
min_samples_widget = widgets.IntSlider(style = style, layout = widgets.Layout(width="50%", height="30px"), description='DBSCAN - Enter min samples', start=1, end=15, step=1, value=5)
n_components_widget = widgets.IntSlider(style = style, layout = widgets.Layout(width="50%", height="30px"), description='PCA - Enter n_components', start=1, end=15, step=1, value=2)
display(eps_widget)
display(min_samples_widget)
display(n_components_widget)
def db_scan_clustering(data, eps = float(eps_widget.value)):
dbscan = DBSCAN(eps=eps, min_samples = int(min_samples.value))
dbscan.fit(data)
return dbscan.labels_
def principal_component_analysis(data, eps = float(eps_widget.value)):
while True:
try:
pca = PCA(n_components=int(n_components_widget.value))
pca.fit(data)
x_pca = pca.transform(data)
break
except:
continue
clusters = db_scan_clustering(data.values, eps)
label = list(range(0, len(data), 1))
plt.figure(figsize=(20,15))
scatter = plt.scatter(x_pca[:,0],x_pca[:,1],c = clusters,cmap='rainbow')
handles, labels = scatter.legend_elements(prop="colors", alpha=0.6)
plt.legend(handles, labels, loc="upper right", title="Clusters")
n = list(range(0, len(x_pca[:,0]), 1))
texts = []
for i, txt in enumerate(n):
texts.append(plt.text(x_pca[:,0][i], x_pca[:,1][i], txt))
adjust_text(texts)
plt.show()
options1 = ['RuleId', 'SplitUris']
def viewPCA(tfidfCategory):
df = df_splitUri_tfidf.copy()
viewData = viewData_splitUri.copy()
if tfidfCategory == 'RuleId':
df = df_ruleId_tfidf.copy()
viewData = viewData_ruleId.copy()
print(tfidfCategory + ' approach (Outliers + Clustered request URI data): \n')
while True:
try:
principal_component_analysis(df)
break
except:
continue
print(color.BOLD + 'Principal Component Analysis \n' + color.END)
tfidfCategory = widgets.Select(options = options1, style = style, layout = layout, description = 'TFIDF approach: ')
display(tfidfCategory)
viewPCA(tfidfCategory = tfidfCategory.value)
options1 = ['RuleId', 'SplitUris']
options2 = ['Outlier', 'Clustered']
def viewClusters(tfidfCategory, requestURIs):
try:
df = df_splitUri_tfidf.copy()
viewData = viewData_splitUri.copy()
if tfidfCategory == 'RuleId':
df = df_ruleId_tfidf.copy()
viewData = viewData_ruleId.copy()
clusters = db_scan_clustering(df.values)
print(requestURIs + ' URIs for ' + tfidfCategory+ ': \n')
clusterList = list(set(clusters))
try:
clusterList.remove(-1)
except:
print()
if requestURIs == 'Outlier':
clusterList = [-1]
if clusterList:
for k in clusterList:
print('Cluster ' + str(k))
display(viewData[viewData['Ip Address'].isin(df.index.get_level_values(0)[clusters == k])])
else:
print('No Data')
except Exception as e:
print('Error: ' + e)
traceback.print_exc()
print(color.BOLD + 'DBScan Clustering of the Request URIs \n' + color.END)
tfidfCategory = widgets.Select(options = options1, style = style, layout = layout, description = 'TFIDF approach: ')
requestURIs = widgets.Select(options = options2, style = style, layout = layout, description = 'Request URIs: ')
display(tfidfCategory)
display(requestURIs)
viewClusters, tfidfCategory = widgets.Select(options = options1, style = style, layout = layout, description = 'TFIDF approach: '), requestURIs = widgets.Select(options = options2, style = style, layout = layout, description = 'Request URIs: ') ))
```
### Kusto query to further examine the WAF logs and blocked alerts in the time frames with outlier request URIs
```
ipAddress = widgets.Text(style = style, layout = widgets.Layout(width="50%", height="30px"), description = 'IP address: ', placeholder = 'Enter masked IP address from the results above. Include masking bits.')
requestURI = widgets.Text(style = style, layout = widgets.Layout(width="50%", height="30px"), description = 'Request URI: ', placeholder = 'Enter request URI from the results above')
print(color.BOLD + '\nStart time: ' + color.END + str(query_times_3.start) + '\n')
print(color.BOLD + 'End time: ' + color.END + str(query_times_3.end) + '\n')
display(ipAddress)
display(requestURI)
try:
pd.set_option('display.max_colwidth', 20)
kql_query = '''
AzureDiagnostics
| where TimeGenerated between (datetime({startTime}).. datetime({endTime}))
| where Category == "{category}"
| where {hostname} startswith "{host}"
| where action_s == 'Blocked' or isempty(action_s)
| where {ip} startswith "{ipaddress}"
| extend originalRequestUriWithArgs_s = column_ifexists("originalRequestUriWithArgs_s", "")
| where requestUri_s contains {uri} or originalRequestUriWithArgs_s contains {uri}
| take 10
'''
cutOff = [1, 2, 3, 4]
intlist = [8, 16, 24, 32]
if ipAddress.value != '':
ipaddress = str(ipAddress.value).strip().split('/')[0]
maskBits = int(str(ipAddress.value).strip().split('/')[1])
ipaddress = '.'.join(ipaddress.split('.')[0:cutOff[intlist.index(maskBits)]])
else:
ipaddress = ''
print(color.BOLD + '\nStart time: ' + color.END + str(query_times_3.start) + '\n')
print(color.BOLD + 'End time: '+ color.END + str(query_times_3.end) + '\n')
print(color.BOLD + 'Ip Address entered: ' + color.END + str(ipAddress.value) + '\n')
print(color.BOLD + 'Request Uri entered: ' + color.END + str((requestURI.value).strip()) + '\n' )
category = 'ApplicationGatewayAccessLog'
ip_var = 'clientIP_s'
host_var = 'host_s'
uri = '\'' + (requestURI.value).strip() + '\''
kql_accessLogs = kql_query.format(hostname = host_var, startTime = query_times_3.start, endTime = query_times_3.end, host = hosts_2.value, category = category, ip = ip_var, ipaddress = ipaddress, uri = uri)
df_rawAccessKustoQuery = showQuery(kql_accessLogs)
print(category + ' (Raw) Data- \n')
display(df_rawAccessKustoQuery.head(10))
category = 'ApplicationGatewayFirewallLog'
ip_var = 'clientIp_s'
host_var = 'hostname_s'
uri = '@' + '\'' + (requestURI.value).strip() + '\''
kql_firewallLogs = kql_query.format(hostname = host_var, startTime = query_times_3.start, endTime = query_times_3.end, host = hosts_2.value, category = category, ip = ip_var, ipaddress = ipaddress, uri = uri,)
df_rawFirewallKustoQuery = showQuery(kql_firewallLogs)
print(category + ' (Alert) Data- \n')
display(df_rawFirewallKustoQuery.head(10))
pd.reset_option('max_colwidth')
except Exception as e:
print('Error: ' + str(e))
traceback.print_exc()
```
| true |
code
| 0.352257 | null | null | null | null |
|
# Transfer Learning experiments
```
import os
import torch
import mlflow
import numpy as np
from torch import nn
from torch import optim
from collections import OrderedDict
import torch.nn.functional as F
from torchvision import datasets, transforms, models
```
## Transfer Learning with DenseNet
### Loading data
```
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],[0.229, 0.224, 0.225])
])
test_transforms = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],[0.229, 0.224, 0.225])
])
# setting up data loaders
data_dir = os.path.join(os.pardir, 'data', 'Plant_leave_diseases_224')
train_data = datasets.ImageFolder(os.path.join(data_dir, 'train'), transform=train_transforms)
test_data = datasets.ImageFolder(os.path.join(data_dir, 'validation'), transform=test_transforms)
```
### Getting Resnet model
```
model = models.densenet121(pretrained=True)
# Freezing the paramiters of the layers we do not want to train
for parameters in model.parameters():
parameters.requires_grad = False
# Updating Classification layer
_inputs = model.classifier.in_features
model.classifier = nn.Sequential(OrderedDict([
('fc1', nn.Linear(_inputs, 500)),
('relu', nn.ReLU()),
('dropout', nn.Dropout(0.2)),
('fc2', nn.Linear(500, 39)),
('output', nn.LogSoftmax(dim=1))
]))
```
### Training
```
# Configs
config = {
'max_epochs': 200,
'learning_rate': 0.003,
'resolution': 224,
'name': 'densnet'
}
def train(model, train_loader, validation_loader, config, n_epochs=10, stopping_treshold=None):
if torch.cuda.is_available():
print('CUDA is available! Training on GPU ...')
model.cuda()
# Loss and optimizer setup
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=config['learning_rate'])
# Setting minimum validation loss to inf
validation_loss_minimum = np.Inf
train_loss_history = []
validation_loss_history = []
for epoch in range(1, n_epochs +1):
training_loss = 0.0
validation_loss = 0.0
# Training loop
training_accuracies = []
for X, y in train_loader:
# Moving data to gpu if using
if torch.cuda.is_available():
X, y = X.cuda(), y.cuda()
# clear the gradients of all optimized variables
optimizer.zero_grad()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(X)
# calculate the batch loss
loss = criterion(output, y)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
optimizer.step()
# update training loss
training_loss += loss.item()*X.size(0)
# calculating accuracy
ps = torch.exp(output)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == y.view(*top_class.shape)
training_accuracies.append(torch.mean(equals.type(torch.FloatTensor)).item())
# Validation Loop
with torch.no_grad():
accuracies = []
for X, y in validation_loader:
# Moving data to gpu if using
if torch.cuda.is_available():
X, y = X.cuda(), y.cuda()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(X)
# calculate the batch loss
loss = criterion(output, y)
# update validation loss
validation_loss += loss.item()*X.size(0)
# calculating accuracy
ps = torch.exp(output)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == y.view(*top_class.shape)
accuracies.append(torch.mean(equals.type(torch.FloatTensor)).item())
# Mean loss
mean_training_loss = training_loss/len(train_loader.sampler)
mean_validation_loss = validation_loss/len(validation_loader.sampler)
mean_train_accuracy = sum(training_accuracies)/len(training_accuracies)
mean_accuracy = sum(accuracies)/len(accuracies)
train_loss_history.append(mean_training_loss)
validation_loss_history.append(mean_validation_loss)
# Printing epoch stats
print(f'Epoch: {epoch}/{n_epochs}, ' +\
f'Training Loss: {mean_training_loss:.3f}, '+\
f'Train accuracy {mean_train_accuracy:.3f} ' +\
f'Validation Loss: {mean_validation_loss:.3f}, '+\
f'Validation accuracy {mean_accuracy:.3f}')
# logging with mlflow
if mlflow.active_run():
mlflow.log_metric('loss', mean_training_loss, step=epoch)
mlflow.log_metric('accuracy', mean_train_accuracy, step=epoch)
mlflow.log_metric('validation_accuracy', mean_accuracy, step=epoch)
mlflow.log_metric('validation_loss', mean_validation_loss, step=epoch)
# Testing for early stopping
if stopping_treshold:
if mean_validation_loss < validation_loss_minimum:
validation_loss_minimum = mean_validation_loss
print('New minimum validation loss (saving model)')
save_pth = os.path.join('models',f'{config["name"]}.pt')
torch.save(model.state_dict(), save_pth)
elif len([v for v in validation_loss_history[-stopping_treshold:] if v > validation_loss_minimum]) >= stopping_treshold:
print(f"Stopping early at epoch: {epoch}/{n_epochs}")
break
return train_loss_history, validation_loss_history
train_loader = torch.utils.data.DataLoader(train_data, batch_size=64, shuffle=True)
validation_loader = torch.utils.data.DataLoader(test_data, batch_size=64, shuffle=True)
mlflow.set_experiment("Plant Leaf Disease")
with mlflow.start_run():
mlflow.log_param('framework', 'pytorch')
mlflow.log_param('data_split', '90/10')
mlflow.log_param('type', 'DenseNet121')
mlflow.log_params(config)
train(model, train_loader, validation_loader, config, n_epochs=config['max_epochs'], stopping_treshold=15)
```
| true |
code
| 0.698265 | null | null | null | null |
|
## CNN WITH CLASSES FROM [HERE](https://github.com/hunkim/DeepLearningZeroToAll/blob/master/lab-10-6-mnist_nn_batchnorm.ipynb)
```
import os
import numpy as np
from scipy import ndimage
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow.contrib.slim as slim
from tensorflow.examples.tutorials.mnist import input_data
%matplotlib inline
print ("CURRENT TF VERSION IS [%s]" % (tf.__version__))
print ("PACKAGES LOADED")
```
## DEFINE MODEL CLASS WITH TF.LAYERS
```
class Model:
"""
# <EXAMPLE>
input_dim = 784
output_dim = 10
bn = Model('batchnorm', input_dim, output_dim, use_batchnorm=True)
"""
def __init__(self, name, input_dim, output_dim
, hidden_dims=[32, 32], use_batchnorm=True
, activation_fn=tf.nn.relu
, optimizer=tf.train.AdamOptimizer, lr=0.01):
with tf.variable_scope(name):
# SET PLACEHOLDERS
self.x = tf.placeholder(tf.float32, [None, input_dim], name='X')
self.y = tf.placeholder(tf.float32, [None, output_dim], name='Y')
self.istrain = tf.placeholder(tf.bool, name='IS_TRAIN')
# LOOP OVER HIDDEN LAYERS
net = self.x
for i, h_dim in enumerate(hidden_dims):
with tf.variable_scope('LAYER_{}'.format(i)):
# FULLY CONNECTED
net = tf.layers.dense(net, h_dim)
if use_batchnorm: # BATCH NORM
net = tf.layers.batch_normalization(net, training=self.istrain)
# ACTIVATION
net = activation_fn(net)
# FINAL FULLY CONNECTED LAYER
net = tf.contrib.layers.flatten(net)
net = tf.layers.dense(net, output_dim)
# DEFINE LOSS
self.loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(
logits=net, labels=self.y), name='LOSS')
# DEFINE OPTIMIZER
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS, scope=name)
with tf.control_dependencies(update_ops):
self.optm = optimizer(lr).minimize(self.loss)
# OTHERS
softmax = tf.nn.softmax(net, name='SOFTMAX')
self.corr = tf.equal(tf.argmax(softmax, 1), tf.argmax(self.y, 1))
self.accr = tf.reduce_mean(tf.cast(self.corr, tf.float32))
```
## DEFINE SOLVER CLASS
```
class Solver:
"""
# <EXAMPLE>
bn = Model('batchnorm', input_dim, output_dim, use_batchnorm=True)
sess = tf.InteractiveSession()
solver = Solver(sess, model)
# TRAIN
solver.train(x, y)
# EVALUATE
solver.evaluate(x, y, _batch_size=128)
"""
def __init__(self, _sess, _model):
self.model = _model
self.sess = _sess
# DEFINE TRAIN FUNCTION
def train(self, _x, _y):
feed = {
self.model.x: _x,
self.model.y: _y,
self.model.istrain: True
}
optm = self.model.optm
loss = self.model.loss
return self.sess.run([optm, loss], feed_dict=feed)
# DEFINE EVALUATE FUNCTION
def evaluate(self, _x, _y, _batch_size=None):
if _batch_size:
N = _x.shape[0]
total_loss = 0
total_accr = 0
for i in range(0, N, _batch_size):
x_batch = _x[i:i+_batch_size] # DON'T WORRY ABOUT OUT OF INDEX
y_batch = _y[i:i+_batch_size]
feed = {
self.model.x: x_batch,
self.model.y: y_batch,
self.model.istrain: False
}
loss = self.model.loss
accr = self.model.accr
step_loss, step_accr = self.sess.run([loss, accr], feed_dict=feed)
total_loss += step_loss * x_batch.shape[0]
total_accr += step_accr * x_batch.shape[0]
total_loss /= N
total_accr /= N
return total_loss, total_accr
else:
feed = {
self.model.x: _x,
self.model.y: _y,
self.model.istrain: False
}
loss = self.model.loss
accr = self.model.accr
return self.sess.run([loss, accr], feed_dict=feed)
```
## INSTANTIATE MODEL/SOLVER
```
tf.reset_default_graph()
sess = tf.InteractiveSession()
# CREATE TWO MODELS WITH AND WITHOUT BATCHNORM
input_dim = 784
output_dim = 10
bn = Model('BATCHNORM', input_dim, output_dim, hidden_dims=[128, 64], use_batchnorm=True)
nn = Model('NO_NORM', input_dim, output_dim, hidden_dims=[128, 64], use_batchnorm=False)
# CREATE TWO CORRESPONDING SOLVERS
bn_solver = Solver(sess, bn)
nn_solver = Solver(sess, nn)
print("MODELS AND SOLVERS READY")
```
## RUN
```
epoch_n = 10
batch_size = 32
mnist = input_data.read_data_sets("data/", one_hot=True)
tr_img = mnist.train.images
tr_label = mnist.train.labels
val_img = mnist.validation.images
val_label = mnist.validation.labels
# SAVE LOSSES AND ACCURACIES
tr_losses = []
tr_accrs = []
val_losses = []
val_accrs = []
# INITALIZE
sess.run(tf.global_variables_initializer())
# OPTIMIZE
for epoch in range(epoch_n):
# OPTIMIZE
for _ in range(mnist.train.num_examples//batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
_, bn_loss = bn_solver.train(X_batch, y_batch)
_, nn_loss = nn_solver.train(X_batch, y_batch)
# COMPUTE TRAIN LOSSES AND ACCUARACIES
b_train_loss, b_train_accr = bn_solver.evaluate(tr_img, tr_label, batch_size)
n_train_loss, n_train_accr = nn_solver.evaluate(tr_img, tr_label, batch_size)
# COMPUTE VALIDATION LOSSES AND ACCUARACIES
b_val_loss, b_val_accr = bn_solver.evaluate(val_img, val_label)
n_val_loss, n_val_accr = nn_solver.evaluate(val_img, val_label)
# SAVE THEM
tr_losses.append([b_train_loss, n_train_loss])
tr_accrs.append([b_train_accr, n_train_accr])
val_losses.append([b_val_loss, n_val_loss])
val_accrs.append([b_val_accr, n_val_accr])
# PRINT
print ("[%d/%d] [TRAIN] BATCHNORM: %.4f (%.4f) vs. NO-NORM: %.4f (%.4f)"
% (epoch, epoch_n, b_train_loss, b_train_accr, n_train_loss, n_train_accr))
print (" [VALIDATION] BATCHNORM: %.4f (%.4f) vs. NO-NORM: %.4f (%.4f)"
% (b_val_loss, b_val_accr, n_val_loss, n_val_accr))
print ("OPTIMIZATION FINISHED")
```
## COMPUTE TEST ACCURACY
```
b_test_loss, b_test_accr = bn_solver.evaluate(mnist.test.images, mnist.test.labels)
n_test_loss, n_test_accr = nn_solver.evaluate(mnist.test.images, mnist.test.labels)
print ("[TEST] BATCHNORM: %.4f (%.4f) vs. NO-NORM: %.4f (%.4f)"
% (b_test_loss, b_test_accr, n_test_loss, n_test_accr))
```
## PLOT COMPARISON
```
def plot_comp(val_list, ylim=None, title=None, loc=None):
bn = [i[0] for i in val_list]
nn = [i[1] for i in val_list]
plt.figure(figsize=(8, 5))
plt.plot(bn, label='With BN')
plt.plot(nn, label='Without BN')
if ylim:
plt.ylim(ylim)
if title:
plt.title(title)
plt.legend(loc=loc)
plt.grid('on')
plt.show()
```
## LOSSES
```
plot_comp(tr_losses, title="TRAINING LOSS")
plot_comp(val_losses, title="VALIDATION LOSS")
```
## ACCURACY
```
plot_comp(tr_accrs, title="TRAINING ACCURACY", loc=4)
plot_comp(val_accrs, title="VALIDATION ACCURACY", loc=4)
```
| true |
code
| 0.652906 | null | null | null | null |
|
Lambda School Data Science, Unit 2: Predictive Modeling
# Regression & Classification, Module 1
## Objectives
- Clean data & remove outliers
- Use scikit-learn for linear regression
- Organize & comment code
## Setup
#### If you're using [Anaconda](https://www.anaconda.com/distribution/) locally
Install required Python packages:
- [pandas-profiling](https://github.com/pandas-profiling/pandas-profiling), version >= 2.0
- [Plotly](https://plot.ly/python/getting-started/), version >= 4.0
```
conda install -c conda-forge pandas-profiling plotly
```
```
# If you're in Colab...
import os, sys
in_colab = 'google.colab' in sys.modules
if in_colab:
# Install required python packages:
# pandas-profiling, version >= 2.0
# plotly, version >= 4.0
!pip install --upgrade pandas-profiling plotly
# Pull files from Github repo
os.chdir('/content')
!git init .
!git remote add origin https://github.com/LambdaSchool/DS-Unit-2-Regression-Classification.git
!git pull origin master
# Change into directory for module
os.chdir('module1')
# Ignore this Numpy warning when using Plotly Express:
# FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead.
import warnings
warnings.filterwarnings(action='ignore', category=FutureWarning, module='numpy')
```
# Predict how much a NYC condo costs 🏠💸
[Amateurs & Experts Guess How Much a NYC Condo With a Private Terrace Costs](https://www.youtube.com/watch?v=JQCctBOgH9I)
> Real Estate Agent Leonard Steinberg just sold a pre-war condo in New York City's Tribeca neighborhood. We challenged three people - an apartment renter, an apartment owner and a real estate expert - to try to guess how much the apartment sold for. Leonard reveals more and more details to them as they refine their guesses.
The condo is 1,497 square feet.
Here are the final guesses:
- Apartment Renter: \$15 million
- Apartment Buyer: \$2.2 million
- Real Estate Expert: \$2.2 million
Let's see how we compare!
First, we need data:
- [Kaggle has NYC property sales data](https://www.kaggle.com/new-york-city/nyc-property-sales), but it's not up-to-date.
- The data comes from the [New York City Department of Finance](https://www1.nyc.gov/site/finance/taxes/property-rolling-sales-data.page). There's also a glossary of property sales terms and NYC Building Class Code Descriptions
- The data can also be found on the [NYC OpenData](https://data.cityofnewyork.us/browse?q=NYC%20calendar%20sales) portal.
## Clean data & remove outliers
```
import pandas as pd
import pandas_profiling
# Read New York City property sales data
df = pd.read_csv('../data/NYC_Citywide_Rolling_Calendar_Sales.csv')
# Change column names: replace spaces with underscores
df.columns = [col.replace(' ', '_') for col in df]
# Get Pandas Profiling Report
df.profile_report()
```
## Plot relationship between feature & target
- [Plotly Express](https://plot.ly/python/plotly-express/) examples
- [plotly_express.scatter](https://www.plotly.express/plotly_express/#plotly_express.scatter) docs
```
```
## Use scikit-learn for Linear Regression
#### Jake VanderPlas, [_Python Data Science Handbook_, Chapter 5.2: Introducing Scikit-Learn](https://jakevdp.github.io/PythonDataScienceHandbook/05.02-introducing-scikit-learn.html#Basics-of-the-API)
The best way to think about data within Scikit-Learn is in terms of tables of data.
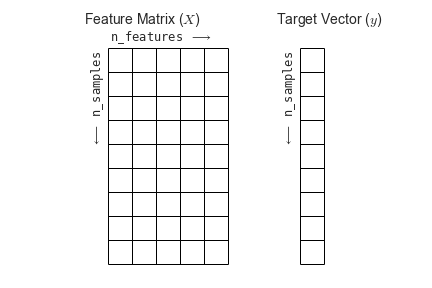
The features matrix is often stored in a variable named `X`. The features matrix is assumed to be two-dimensional, with shape `[n_samples, n_features]`, and is most often contained in a NumPy array or a Pandas `DataFrame`.
We also generally work with a label or target array, which by convention we will usually call `y`. The target array is usually one dimensional, with length `n_samples`, and is generally contained in a NumPy array or Pandas `Series`. The target array may have continuous numerical values, or discrete classes/labels.
The target array is the quantity we want to _predict from the data_: in statistical terms, it is the dependent variable.
Every machine learning algorithm in Scikit-Learn is implemented via the Estimator API, which provides a consistent interface for a wide range of machine learning applications.
Most commonly, the steps in using the Scikit-Learn estimator API are as follows:
1. Choose a class of model by importing the appropriate estimator class from Scikit-Learn.
2. Choose model hyperparameters by instantiating this class with desired values.
3. Arrange data into a features matrix and target vector following the discussion above.
4. Fit the model to your data by calling the `fit()` method of the model instance.
5. Apply the Model to new data: For supervised learning, often we predict labels for unknown data using the `predict()` method.
```
```
### Organize & comment code
```
```
# How'd we do? ...
| true |
code
| 0.678966 | null | null | null | null |
|
```
# Useful for debugging
%load_ext autoreload
%autoreload 2
# Nicer plotting
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
matplotlib.rcParams['figure.figsize'] = (8,4)
```
# Autophase and Autophase and Scale examples
```
from impact import Impact
import numpy as np
import os
ifile ='templates/lcls_injector/ImpactT.in'
# Make Impact object
I = Impact(ifile, verbose=True)
I.numprocs=1
```
# Phase and Scale the LCLS gun
```
from impact.autophase import autophase_and_scale
from pmd_beamphysics import single_particle
P0 = single_particle(pz=1e-15, z=1e-15)
autophase_and_scale(I, phase_ele_name='GUN', target=6e6, scale_range=(10e6, 100e6), initial_particles=P0, verbose=True)
# Check this:
I.verbose=False
PF = I.track(P0, s=0.15)
PF['mean_energy']
# Examine this process using the debug flag. This will return the function used for phasing and scaling.
ps_f, Itest = autophase_and_scale(I, phase_ele_name='GUN', target=6e6, initial_particles=P0, verbose=False,
debug = True)
# Phases to try
ptry = np.linspace(-100, 50, 30)
# scales to try
for sc in np.linspace(10e6, 100e6, 5):
res = np.array([ps_f(p, sc)/1e6 for p in ptry])
plt.plot(ptry, res, label=f'{sc/1e6:0.2f} MV')
plt.title('Final energy for various phases and scales')
plt.ylabel('Final energy (MeV)')
plt.xlabel('phase (deg)')
plt.legend()
# 3D plot
# Make data.
X = np.linspace(-100, 50, 10)
Y = np.linspace(10e6, 100e6, 10)
X, Y = np.meshgrid(X, Y)
@np.vectorize
def f(phase, scale):
return ps_f(phase, scale)
Z = f(X, Y)
# Plot the surface.
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Plot the surface.
surf = ax.plot_surface(X, Y/1e6, Z/1e6, cmap=matplotlib.cm.coolwarm,
linewidth=0, antialiased=True)
# Add a color bar which maps values to colors.
#fig.colorbar(surf, shrink=0.5, aspect=5)
ax.set_xlabel('phase (deg)')
ax.set_ylabel('scale (MV)')
ax.set_zlabel('Final energy (MeV)')
plt.show()
```
# Phase and scale LCLS linac sections
Linacs L0A and L0B are special, because they require 4 fieldmaps each to model the travelling wave structure. To tune these together, we need to add control groups
```
# Changes in phases
I.add_group('L0A', ele_names=['L0A_entrance', 'L0A_body_1', 'L0A_body_2', 'L0A_exit'], var_name='theta0_deg', attributes='theta0_deg')
I.add_group('L0B', ele_names=['L0B_entrance', 'L0B_body_1', 'L0B_body_2', 'L0B_exit'], var_name='theta0_deg', attributes='theta0_deg')
# Overall scaling, respecting the special factors.
I.add_group('L0A_scale', ele_names=['L0A_entrance', 'L0A_body_1', 'L0A_body_2', 'L0A_exit'],
var_name = 'rf_field_scale',
factors = [0.86571945106805, 1, 1, 0.86571945106805], # sin(k*d) with d = 3.5e-2 m
absolute=True)
# Overall scaling, respecting the special factors.
I.add_group('L0B_scale', ele_names=['L0B_entrance', 'L0B_body_1', 'L0B_body_2', 'L0B_exit'],
var_name = 'rf_field_scale',
factors = [0.86571945106805, 1, 1, 0.86571945106805], # sin(k*d) with d = 3.5e-2 m
absolute=True)
I['L0A_scale']['rf_field_scale'] = 30e6
#I['L0A_scale'].__dict__
# L0A to 64 MeV
res_L0A = autophase_and_scale(I, phase_ele_name='L0A', scale_ele_name='L0A_scale', target=64e6, scale_range=(10e6, 100e6), initial_particles=P0, verbose=True)
autophase_and_scale(I, phase_ele_name='L0B', scale_ele_name='L0B_scale', target=135e6, scale_range=(10e6, 100e6), initial_particles=P0, verbose=True)
I.track(P0, s=8.371612)['mean_energy']
plt.plot(I.stat('mean_z'), I.stat('mean_kinetic_energy')/1e6 + 0.511)
```
# Autophase without scaling
Just phasing is simpler.
```
from impact.autophase import autophase
ifile2 = 'templates/apex_gun/ImpactT.in'
I2 = Impact(ifile2, verbose=False)
autophase(I2, ele_name='APEX_GUN', initial_particles=P0, metric='mean_kinetic_energy', verbose=True)
phase_f, Itest = autophase(I2, ele_name='APEX_GUN', metric='mean_kinetic_energy', initial_particles=P0, debug = True)
# Phases to try
ptry = np.linspace(0, 360, 60)
energies = np.array([phase_f(p)/1e3 for p in ptry])
plt.plot(ptry, energies)
plt.ylim(0, 800)
plt.title('Final energy for various phases in the APEX gun')
plt.ylabel('Final kinetic energy (keV)')
plt.xlabel('phase (deg)')
```
# Autophase with alternative metric, and bunch tracking with space charge.
The above uses `mean_energy` as the metric to maximize. Alternatively, one might want to minimize energy spread. This is accomplished by passing `maximize=False` and `metric='sigma_pz'` or similar.
```
from distgen import Generator
ifile = 'templates/lcls_injector/ImpactT.in'
gfile = 'templates/lcls_injector/distgen.yaml'
G = Generator(gfile)
G['n_particle'] = 2000
G.run()
P0 = G.particles
%%time
I = Impact(ifile, initial_particles=P0, verbose=False)
I.stop = 0.16
I.numprocs=4
I.run()
phase_f, Itest = autophase(I, ele_name='GUN', metric='sigma_pz', maximize=False, initial_particles=P0, debug = True, verbose=True)
I.particles['final_particles'].plot('z', 'pz')
# Phases to try
ptry = np.linspace(290, 310, 20)
sigma_pzs = np.array([phase_f(p) for p in ptry])
plt.plot(ptry, sigma_pzs)
#plt.ylim(0, 800)
#plt.title('Final energy for various phases in the APEX gun')
#plt.ylabel('Final kinetic energy (keV)')
plt.xlabel('phase (deg)')
phase_f(293.5)
Itest.particles['final_particles'].plot('z', 'pz')
phase_f, Itest = autophase(I, ele_name='GUN', metric='sigma_pz',
maximize=False, initial_particles=P0, debug = True,
s_stop = 1.45,
verbose=True)
# Phases to try
ptry = np.linspace(270, 290, 30)
sigma_pzs = np.array([phase_f(p) for p in ptry])
plt.plot(ptry, sigma_pzs)
#plt.ylim(0, 800)
#plt.title('Final energy for various phases in the APEX gun')
#plt.ylabel('Final kinetic energy (keV)')
plt.xlabel('phase (deg)')
phase_f(280.0)
Itest.particles['final_particles'].plot('z', 'pz')
```
| true |
code
| 0.682759 | null | null | null | null |
|
# Introduction: Home Credit Default Risk Competition
This notebook is intended for those who are new to machine learning competitions or want a gentle introduction to the problem. I purposely avoid jumping into complicated models or joining together lots of data in order to show the basics of how to get started in machine learning! Any comments or suggestions are much appreciated.
In this notebook, we will take an initial look at the Home Credit default risk machine learning competition currently hosted on Kaggle. The objective of this competition is to use historical loan application data to predict whether or not an applicant will be able to repay a loan. This is a standard supervised classification task:
* __Supervised__: The labels are included in the training data and the goal is to train a model to learn to predict the labels from the features
* __Classification__: The label is a binary variable, 0 (will repay loan on time), 1 (will have difficulty repaying loan)
# Data
The data is provided by [Home Credit](http://www.homecredit.net/about-us.aspx), a service dedicated to provided lines of credit (loans) to the unbanked population. Predicting whether or not a client will repay a loan or have difficulty is a critical business need, and Home Credit is hosting this competition on Kaggle to see what sort of models the machine learning community can develop to help them in this task.
There are 7 different sources of data:
* application_train/application_test: the main training and testing data with information about each loan application at Home Credit. Every loan has its own row and is identified by the feature `SK_ID_CURR`. The training application data comes with the `TARGET` indicating 0: the loan was repaid or 1: the loan was not repaid.
* bureau: data concerning client's previous credits from other financial institutions. Each previous credit has its own row in bureau, but one loan in the application data can have multiple previous credits.
* bureau_balance: monthly data about the previous credits in bureau. Each row is one month of a previous credit, and a single previous credit can have multiple rows, one for each month of the credit length.
* previous_application: previous applications for loans at Home Credit of clients who have loans in the application data. Each current loan in the application data can have multiple previous loans. Each previous application has one row and is identified by the feature `SK_ID_PREV`.
* POS_CASH_BALANCE: monthly data about previous point of sale or cash loans clients have had with Home Credit. Each row is one month of a previous point of sale or cash loan, and a single previous loan can have many rows.
* credit_card_balance: monthly data about previous credit cards clients have had with Home Credit. Each row is one month of a credit card balance, and a single credit card can have many rows.
* installments_payment: payment history for previous loans at Home Credit. There is one row for every made payment and one row for every missed payment.
This diagram shows how all of the data is related:

Moreover, we are provided with the definitions of all the columns (in `HomeCredit_columns_description.csv`) and an example of the expected submission file.
In this notebook, we will stick to using only the main application training and testing data. Although if we want to have any hope of seriously competing, we need to use all the data, for now we will stick to one file which should be more manageable. This will let us establish a baseline that we can then improve upon. With these projects, it's best to build up an understanding of the problem a little at a time rather than diving all the way in and getting completely lost!
## Metric: ROC AUC
Once we have a grasp of the data (reading through the [column descriptions](https://www.kaggle.com/c/home-credit-default-risk/data) helps immensely), we need to understand the metric by which our submission is judged. In this case, it is a common classification metric known as the [Receiver Operating Characteristic Area Under the Curve (ROC AUC, also sometimes called AUROC)](https://stats.stackexchange.com/questions/132777/what-does-auc-stand-for-and-what-is-it).
The ROC AUC may sound intimidating, but it is relatively straightforward once you can get your head around the two individual concepts. The [Reciever Operating Characteristic (ROC) curve](https://en.wikipedia.org/wiki/Receiver_operating_characteristic) graphs the true positive rate versus the false positive rate:
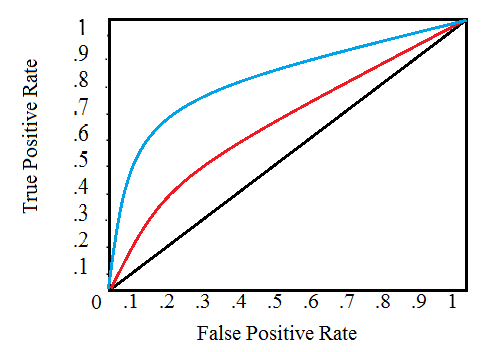
A single line on the graph indicates the curve for a single model, and movement along a line indicates changing the threshold used for classifying a positive instance. The threshold starts at 0 in the upper right to and goes to 1 in the lower left. A curve that is to the left and above another curve indicates a better model. For example, the blue model is better than the red model, which is better than the black diagonal line which indicates a naive random guessing model.
The [Area Under the Curve (AUC)](http://gim.unmc.edu/dxtests/roc3.htm) explains itself by its name! It is simply the area under the ROC curve. (This is the integral of the curve.) This metric is between 0 and 1 with a better model scoring higher. A model that simply guesses at random will have an ROC AUC of 0.5.
When we measure a classifier according to the ROC AUC, we do not generation 0 or 1 predictions, but rather a probability between 0 and 1. This may be confusing because we usually like to think in terms of accuracy, but when we get into problems with inbalanced classes (we will see this is the case), accuracy is not the best metric. For example, if I wanted to build a model that could detect terrorists with 99.9999% accuracy, I would simply make a model that predicted every single person was not a terrorist. Clearly, this would not be effective (the recall would be zero) and we use more advanced metrics such as ROC AUC or the [F1 score](https://en.wikipedia.org/wiki/F1_score) to more accurately reflect the performance of a classifier. A model with a high ROC AUC will also have a high accuracy, but the [ROC AUC is a better representation of model performance.](https://datascience.stackexchange.com/questions/806/advantages-of-auc-vs-standard-accuracy)
Not that we know the background of the data we are using and the metric to maximize, let's get into exploring the data. In this notebook, as mentioned previously, we will stick to the main data sources and simple models which we can build upon in future work.
__Follow-up Notebooks__
For those looking to keep working on this problem, I have a series of follow-up notebooks:
* [Manual Feature Engineering Part One](https://www.kaggle.com/willkoehrsen/introduction-to-manual-feature-engineering)
* [Manual Feature Engineering Part Two](https://www.kaggle.com/willkoehrsen/introduction-to-manual-feature-engineering-p2)
* [Introduction to Automated Feature Engineering](https://www.kaggle.com/willkoehrsen/automated-feature-engineering-basics)
* [Advanced Automated Feature Engineering](https://www.kaggle.com/willkoehrsen/tuning-automated-feature-engineering-exploratory)
* [Feature Selection](https://www.kaggle.com/willkoehrsen/introduction-to-feature-selection)
* [Intro to Model Tuning: Grid and Random Search](https://www.kaggle.com/willkoehrsen/intro-to-model-tuning-grid-and-random-search)
* [Automated Model Tuning](https://www.kaggle.com/willkoehrsen/automated-model-tuning)
* [Model Tuning Results](https://www.kaggle.com/willkoehrsen/model-tuning-results-random-vs-bayesian-opt/notebook)
__More references__
* [Credit Education](https://myscore.cibil.com/CreditView/creditEducation.page?enterprise=CIBIL&_ga=2.245893574.372615569.1603669858-164953316.1602941832&_gac=1.254345978.1602941832.CjwKCAjwrKr8BRB_EiwA7eFaplQtBsmINtLxLHOCalWYdx-uO20kyaj0AvRVD8WKNO4cj5mP7MoBTRoC6TEQAvD_BwE)
* [Credit Appraisal Methodology and Statndards](https://www.paisadukan.com/credit-assessment-methodology)
I'll add more notebooks as I finish them! Thanks for all the comments!
## Imports
We are using a typical data science stack: `numpy`, `pandas`, `sklearn`, `matplotlib`.
```
# numpy and pandas for data manipulation
import numpy as np
import pandas as pd
# sklearn preprocessing for dealing with categorical variables
from sklearn.preprocessing import LabelEncoder
# File system manangement
import os
# Suppress warnings
import warnings
warnings.filterwarnings('ignore')
# matplotlib and seaborn for plotting
import matplotlib.pyplot as plt
import seaborn as sns
import os
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_colwidth', -1)
pathToData = "C:\\Users\\Administrator\\OneDrive\\Documents\\home_credit_default_risk"
os.chdir(pathToData)
os.listdir()
app_train = pd.read_csv("application_train.csv")
app_test = pd.read_csv("application_test.csv.zip")
app_train.head()
app_train.shape # (307511, 122)
app_train.dtypes
col_desc = pd.read_csv("HomeCredit_columns_description.csv", encoding= 'unicode_escape')
col_desc.iloc[:122, 1:-1]
```
## Domain Knowledge Features
Some features generated through domain knowledge to help the algorithm:
* `CREDIT_INCOME_PERCENT`: the percentage of the credit amount relative to a client's income
* `ANNUITY_INCOME_PERCENT`: the percentage of the loan annuity relative to a client's income
* `CREDIT_TERM`: the length of the payment in months (since the annuity is the monthly amount due
* `DAYS_EMPLOYED_PERCENT`: the percentage of the days employed relative to the client's age
Again, thanks to Aguiar and [his great script](https://www.kaggle.com/jsaguiar/updated-0-792-lb-lightgbm-with-simple-features) for exploring these features.
```
app_train_domain = app_train.copy()
app_test_domain = app_test.copy()
app_train_domain['CREDIT_INCOME_PERCENT'] = app_train_domain['AMT_CREDIT'] / app_train_domain['AMT_INCOME_TOTAL']
app_train_domain['ANNUITY_INCOME_PERCENT'] = app_train_domain['AMT_ANNUITY'] / app_train_domain['AMT_INCOME_TOTAL']
app_train_domain['CREDIT_TERM'] = app_train_domain['AMT_ANNUITY'] / app_train_domain['AMT_CREDIT']
app_train_domain['DAYS_EMPLOYED_PERCENT'] = app_train_domain['DAYS_EMPLOYED'] / app_train_domain['DAYS_BIRTH']
app_test_domain['CREDIT_INCOME_PERCENT'] = app_test_domain['AMT_CREDIT'] / app_test_domain['AMT_INCOME_TOTAL']
app_test_domain['ANNUITY_INCOME_PERCENT'] = app_test_domain['AMT_ANNUITY'] / app_test_domain['AMT_INCOME_TOTAL']
app_test_domain['CREDIT_TERM'] = app_test_domain['AMT_ANNUITY'] / app_test_domain['AMT_CREDIT']
app_test_domain['DAYS_EMPLOYED_PERCENT'] = app_test_domain['DAYS_EMPLOYED'] / app_test_domain['DAYS_BIRTH']
pre_app = pd.read_csv("previous_application.csv.zip")
pre_app.shape # (1670214, 37)
pre_app.head()
pre_app.isnull().sum().sort_values(ascending = False)
col_desc.iloc[173:211, :]
```
## Read in Data
First, we can list all the available data files. There are a total of 9 files: 1 main file for training (with target) 1 main file for testing (without the target), 1 example submission file, and 6 other files containing additional information about each loan.
```
# List files available
print(os.listdir("../input/"))
# Training data
app_train = pd.read_csv('../input/application_train.csv')
print('Training data shape: ', app_train.shape)
app_train.head()
```
The training data has 307511 observations (each one a separate loan) and 122 features (variables) including the `TARGET` (the label we want to predict).
```
# Testing data features
app_test = pd.read_csv('../input/application_test.csv')
print('Testing data shape: ', app_test.shape)
app_test.head()
```
The test set is considerably smaller and lacks a `TARGET` column.
# Exploratory Data Analysis
Exploratory Data Analysis (EDA) is an open-ended process where we calculate statistics and make figures to find trends, anomalies, patterns, or relationships within the data. The goal of EDA is to learn what our data can tell us. It generally starts out with a high level overview, then narrows in to specific areas as we find intriguing areas of the data. The findings may be interesting in their own right, or they can be used to inform our modeling choices, such as by helping us decide which features to use.
## Examine the Distribution of the Target Column
The target is what we are asked to predict: either a 0 for the loan was repaid on time, or a 1 indicating the client had payment difficulties. We can first examine the number of loans falling into each category.
```
app_train['TARGET'].value_counts()
app_train['TARGET'].astype(int).plot.hist();
```
From this information, we see this is an [_imbalanced class problem_](http://www.chioka.in/class-imbalance-problem/). There are far more loans that were repaid on time than loans that were not repaid. Once we get into more sophisticated machine learning models, we can [weight the classes](http://xgboost.readthedocs.io/en/latest/parameter.html) by their representation in the data to reflect this imbalance.
## Examine Missing Values
Next we can look at the number and percentage of missing values in each column.
```
# Function to calculate missing values by column# Funct
def missing_values_table(df):
# Total missing values
mis_val = df.isnull().sum()
# Percentage of missing values
mis_val_percent = 100 * df.isnull().sum() / len(df)
# Make a table with the results
mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1)
# Rename the columns
mis_val_table_ren_columns = mis_val_table.rename(
columns = {0 : 'Missing Values', 1 : '% of Total Values'})
# Sort the table by percentage of missing descending
mis_val_table_ren_columns = mis_val_table_ren_columns[
mis_val_table_ren_columns.iloc[:,1] != 0].sort_values(
'% of Total Values', ascending=False).round(1)
# Print some summary information
print ("Your selected dataframe has " + str(df.shape[1]) + " columns.\n"
"There are " + str(mis_val_table_ren_columns.shape[0]) +
" columns that have missing values.")
# Return the dataframe with missing information
return mis_val_table_ren_columns
# Missing values statistics
missing_values = missing_values_table(app_train)
missing_values.head(20)
```
When it comes time to build our machine learning models, we will have to fill in these missing values (known as imputation). In later work, we will use models such as XGBoost that can [handle missing values with no need for imputation](https://stats.stackexchange.com/questions/235489/xgboost-can-handle-missing-data-in-the-forecasting-phase). Another option would be to drop columns with a high percentage of missing values, although it is impossible to know ahead of time if these columns will be helpful to our model. Therefore, we will keep all of the columns for now.
## Column Types
Let's look at the number of columns of each data type. `int64` and `float64` are numeric variables ([which can be either discrete or continuous](https://stats.stackexchange.com/questions/206/what-is-the-difference-between-discrete-data-and-continuous-data)). `object` columns contain strings and are [categorical features.](http://support.minitab.com/en-us/minitab-express/1/help-and-how-to/modeling-statistics/regression/supporting-topics/basics/what-are-categorical-discrete-and-continuous-variables/) .
```
# Number of each type of column
app_train.dtypes.value_counts()
```
Let's now look at the number of unique entries in each of the `object` (categorical) columns.
```
# Number of unique classes in each object column
app_train.select_dtypes('object').apply(pd.Series.nunique, axis = 0)
```
Most of the categorical variables have a relatively small number of unique entries. We will need to find a way to deal with these categorical variables!
## Encoding Categorical Variables
Before we go any further, we need to deal with pesky categorical variables. A machine learning model unfortunately cannot deal with categorical variables (except for some models such as [LightGBM](http://lightgbm.readthedocs.io/en/latest/Features.html)). Therefore, we have to find a way to encode (represent) these variables as numbers before handing them off to the model. There are two main ways to carry out this process:
* Label encoding: assign each unique category in a categorical variable with an integer. No new columns are created. An example is shown below
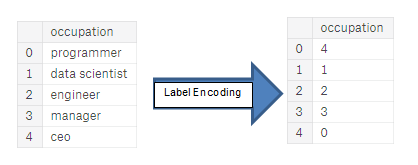
* One-hot encoding: create a new column for each unique category in a categorical variable. Each observation recieves a 1 in the column for its corresponding category and a 0 in all other new columns.
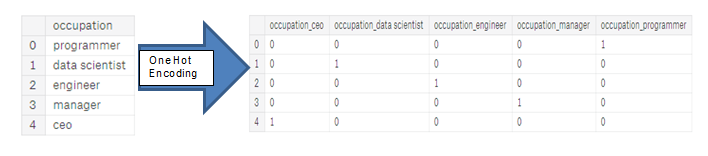
The problem with label encoding is that it gives the categories an arbitrary ordering. The value assigned to each of the categories is random and does not reflect any inherent aspect of the category. In the example above, programmer recieves a 4 and data scientist a 1, but if we did the same process again, the labels could be reversed or completely different. The actual assignment of the integers is arbitrary. Therefore, when we perform label encoding, the model might use the relative value of the feature (for example programmer = 4 and data scientist = 1) to assign weights which is not what we want. If we only have two unique values for a categorical variable (such as Male/Female), then label encoding is fine, but for more than 2 unique categories, one-hot encoding is the safe option.
There is some debate about the relative merits of these approaches, and some models can deal with label encoded categorical variables with no issues. [Here is a good Stack Overflow discussion](https://datascience.stackexchange.com/questions/9443/when-to-use-one-hot-encoding-vs-labelencoder-vs-dictvectorizor). I think (and this is just a personal opinion) for categorical variables with many classes, one-hot encoding is the safest approach because it does not impose arbitrary values to categories. The only downside to one-hot encoding is that the number of features (dimensions of the data) can explode with categorical variables with many categories. To deal with this, we can perform one-hot encoding followed by [PCA](http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf) or other [dimensionality reduction methods](https://www.analyticsvidhya.com/blog/2015/07/dimension-reduction-methods/) to reduce the number of dimensions (while still trying to preserve information).
In this notebook, we will use Label Encoding for any categorical variables with only 2 categories and One-Hot Encoding for any categorical variables with more than 2 categories. This process may need to change as we get further into the project, but for now, we will see where this gets us. (We will also not use any dimensionality reduction in this notebook but will explore in future iterations).
### Label Encoding and One-Hot Encoding
Let's implement the policy described above: for any categorical variable (`dtype == object`) with 2 unique categories, we will use label encoding, and for any categorical variable with more than 2 unique categories, we will use one-hot encoding.
For label encoding, we use the Scikit-Learn `LabelEncoder` and for one-hot encoding, the pandas `get_dummies(df)` function.
```
# Create a label encoder object
le = LabelEncoder()
le_count = 0
# Iterate through the columns
for col in app_train:
if app_train[col].dtype == 'object':
# If 2 or fewer unique categories
if len(list(app_train[col].unique())) <= 2:
# Train on the training data
le.fit(app_train[col])
# Transform both training and testing data
app_train[col] = le.transform(app_train[col])
app_test[col] = le.transform(app_test[col])
# Keep track of how many columns were label encoded
le_count += 1
print('%d columns were label encoded.' % le_count)
# one-hot encoding of categorical variables
app_train = pd.get_dummies(app_train)
app_test = pd.get_dummies(app_test)
print('Training Features shape: ', app_train.shape)
print('Testing Features shape: ', app_test.shape)
```
### Aligning Training and Testing Data
There need to be the same features (columns) in both the training and testing data. One-hot encoding has created more columns in the training data because there were some categorical variables with categories not represented in the testing data. To remove the columns in the training data that are not in the testing data, we need to `align` the dataframes. First we extract the target column from the training data (because this is not in the testing data but we need to keep this information). When we do the align, we must make sure to set `axis = 1` to align the dataframes based on the columns and not on the rows!
```
train_labels = app_train['TARGET']
# Align the training and testing data, keep only columns present in both dataframes
app_train, app_test = app_train.align(app_test, join = 'inner', axis = 1)
# Add the target back in
app_train['TARGET'] = train_labels
print('Training Features shape: ', app_train.shape)
print('Testing Features shape: ', app_test.shape)
```
The training and testing datasets now have the same features which is required for machine learning. The number of features has grown significantly due to one-hot encoding. At some point we probably will want to try [dimensionality reduction (removing features that are not relevant)](https://en.wikipedia.org/wiki/Dimensionality_reduction) to reduce the size of the datasets.
## Back to Exploratory Data Analysis
### Anomalies
One problem we always want to be on the lookout for when doing EDA is anomalies within the data. These may be due to mis-typed numbers, errors in measuring equipment, or they could be valid but extreme measurements. One way to support anomalies quantitatively is by looking at the statistics of a column using the `describe` method. The numbers in the `DAYS_BIRTH` column are negative because they are recorded relative to the current loan application. To see these stats in years, we can mutliple by -1 and divide by the number of days in a year:
```
(app_train['DAYS_BIRTH'] / -365).describe()
```
Those ages look reasonable. There are no outliers for the age on either the high or low end. How about the days of employment?
```
app_train['DAYS_EMPLOYED'].describe()
```
That doesn't look right! The maximum value (besides being positive) is about 1000 years!
```
app_train['DAYS_EMPLOYED'].plot.hist(title = 'Days Employment Histogram');
plt.xlabel('Days Employment');
```
Just out of curiousity, let's subset the anomalous clients and see if they tend to have higher or low rates of default than the rest of the clients.
```
anom = app_train[app_train['DAYS_EMPLOYED'] == 365243]
non_anom = app_train[app_train['DAYS_EMPLOYED'] != 365243]
print('The non-anomalies default on %0.2f%% of loans' % (100 * non_anom['TARGET'].mean()))
print('The anomalies default on %0.2f%% of loans' % (100 * anom['TARGET'].mean()))
print('There are %d anomalous days of employment' % len(anom))
```
Well that is extremely interesting! It turns out that the anomalies have a lower rate of default.
Handling the anomalies depends on the exact situation, with no set rules. One of the safest approaches is just to set the anomalies to a missing value and then have them filled in (using Imputation) before machine learning. In this case, since all the anomalies have the exact same value, we want to fill them in with the same value in case all of these loans share something in common. The anomalous values seem to have some importance, so we want to tell the machine learning model if we did in fact fill in these values. As a solution, we will fill in the anomalous values with not a number (`np.nan`) and then create a new boolean column indicating whether or not the value was anomalous.
```
# Create an anomalous flag column
app_train['DAYS_EMPLOYED_ANOM'] = app_train["DAYS_EMPLOYED"] == 365243
# Replace the anomalous values with nan
app_train['DAYS_EMPLOYED'].replace({365243: np.nan}, inplace = True)
app_train['DAYS_EMPLOYED'].plot.hist(title = 'Days Employment Histogram');
plt.xlabel('Days Employment');
```
The distribution looks to be much more in line with what we would expect, and we also have created a new column to tell the model that these values were originally anomalous (becuase we will have to fill in the nans with some value, probably the median of the column). The other columns with `DAYS` in the dataframe look to be about what we expect with no obvious outliers.
As an extremely important note, anything we do to the training data we also have to do to the testing data. Let's make sure to create the new column and fill in the existing column with `np.nan` in the testing data.
```
app_test['DAYS_EMPLOYED_ANOM'] = app_test["DAYS_EMPLOYED"] == 365243
app_test["DAYS_EMPLOYED"].replace({365243: np.nan}, inplace = True)
print('There are %d anomalies in the test data out of %d entries' % (app_test["DAYS_EMPLOYED_ANOM"].sum(), len(app_test)))
```
### Correlations
Now that we have dealt with the categorical variables and the outliers, let's continue with the EDA. One way to try and understand the data is by looking for correlations between the features and the target. We can calculate the Pearson correlation coefficient between every variable and the target using the `.corr` dataframe method.
The correlation coefficient is not the greatest method to represent "relevance" of a feature, but it does give us an idea of possible relationships within the data. Some [general interpretations of the absolute value of the correlation coefficent](http://www.statstutor.ac.uk/resources/uploaded/pearsons.pdf) are:
* .00-.19 “very weak”
* .20-.39 “weak”
* .40-.59 “moderate”
* .60-.79 “strong”
* .80-1.0 “very strong”
```
# Find correlations with the target and sort
correlations = app_train.corr()['TARGET'].sort_values()
# Display correlations
print('Most Positive Correlations:\n', correlations.tail(15))
print('\nMost Negative Correlations:\n', correlations.head(15))
```
Let's take a look at some of more significant correlations: the `DAYS_BIRTH` is the most positive correlation. (except for `TARGET` because the correlation of a variable with itself is always 1!) Looking at the documentation, `DAYS_BIRTH` is the age in days of the client at the time of the loan in negative days (for whatever reason!). The correlation is positive, but the value of this feature is actually negative, meaning that as the client gets older, they are less likely to default on their loan (ie the target == 0). That's a little confusing, so we will take the absolute value of the feature and then the correlation will be negative.
### Effect of Age on Repayment
```
# Find the correlation of the positive days since birth and target
app_train['DAYS_BIRTH'] = abs(app_train['DAYS_BIRTH'])
app_train['DAYS_BIRTH'].corr(app_train['TARGET'])
```
As the client gets older, there is a negative linear relationship with the target meaning that as clients get older, they tend to repay their loans on time more often.
Let's start looking at this variable. First, we can make a histogram of the age. We will put the x axis in years to make the plot a little more understandable.
```
# Set the style of plots
plt.style.use('fivethirtyeight')
# Plot the distribution of ages in years
plt.hist(app_train['DAYS_BIRTH'] / 365, edgecolor = 'k', bins = 25)
plt.title('Age of Client'); plt.xlabel('Age (years)'); plt.ylabel('Count');
```
By itself, the distribution of age does not tell us much other than that there are no outliers as all the ages are reasonable. To visualize the effect of the age on the target, we will next make a [kernel density estimation plot](https://en.wikipedia.org/wiki/Kernel_density_estimation) (KDE) colored by the value of the target. A [kernel density estimate plot shows the distribution of a single variable](https://chemicalstatistician.wordpress.com/2013/06/09/exploratory-data-analysis-kernel-density-estimation-in-r-on-ozone-pollution-data-in-new-york-and-ozonopolis/) and can be thought of as a smoothed histogram (it is created by computing a kernel, usually a Gaussian, at each data point and then averaging all the individual kernels to develop a single smooth curve). We will use the seaborn `kdeplot` for this graph.
```
plt.figure(figsize = (10, 8))
# KDE plot of loans that were repaid on time
sns.kdeplot(app_train.loc[app_train['TARGET'] == 0, 'DAYS_BIRTH'] / 365, label = 'target == 0')
# KDE plot of loans which were not repaid on time
sns.kdeplot(app_train.loc[app_train['TARGET'] == 1, 'DAYS_BIRTH'] / 365, label = 'target == 1')
# Labeling of plot
plt.xlabel('Age (years)'); plt.ylabel('Density'); plt.title('Distribution of Ages');
```
The target == 1 curve skews towards the younger end of the range. Although this is not a significant correlation (-0.07 correlation coefficient), this variable is likely going to be useful in a machine learning model because it does affect the target. Let's look at this relationship in another way: average failure to repay loans by age bracket.
To make this graph, first we `cut` the age category into bins of 5 years each. Then, for each bin, we calculate the average value of the target, which tells us the ratio of loans that were not repaid in each age category.
```
# Age information into a separate dataframe
age_data = app_train[['TARGET', 'DAYS_BIRTH']]
age_data['YEARS_BIRTH'] = age_data['DAYS_BIRTH'] / 365
# Bin the age data
age_data['YEARS_BINNED'] = pd.cut(age_data['YEARS_BIRTH'], bins = np.linspace(20, 70, num = 11))
age_data.head(10)
# Group by the bin and calculate averages
age_groups = age_data.groupby('YEARS_BINNED').mean()
age_groups
plt.figure(figsize = (8, 8))
# Graph the age bins and the average of the target as a bar plot
plt.bar(age_groups.index.astype(str), 100 * age_groups['TARGET'])
# Plot labeling
plt.xticks(rotation = 75); plt.xlabel('Age Group (years)'); plt.ylabel('Failure to Repay (%)')
plt.title('Failure to Repay by Age Group');
```
There is a clear trend: younger applicants are more likely to not repay the loan! The rate of failure to repay is above 10% for the youngest three age groups and beolow 5% for the oldest age group.
This is information that could be directly used by the bank: because younger clients are less likely to repay the loan, maybe they should be provided with more guidance or financial planning tips. This does not mean the bank should discriminate against younger clients, but it would be smart to take precautionary measures to help younger clients pay on time.
### Exterior Sources
The 3 variables with the strongest negative correlations with the target are `EXT_SOURCE_1`, `EXT_SOURCE_2`, and `EXT_SOURCE_3`.
According to the documentation, these features represent a "normalized score from external data source". I'm not sure what this exactly means, but it may be a cumulative sort of credit rating made using numerous sources of data.
Let's take a look at these variables.
First, we can show the correlations of the `EXT_SOURCE` features with the target and with each other.
```
# Extract the EXT_SOURCE variables and show correlations
ext_data = app_train[['TARGET', 'EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH']]
ext_data_corrs = ext_data.corr()
ext_data_corrs
plt.figure(figsize = (8, 6))
# Heatmap of correlations
sns.heatmap(ext_data_corrs, cmap = plt.cm.RdYlBu_r, vmin = -0.25, annot = True, vmax = 0.6)
plt.title('Correlation Heatmap');
```
All three `EXT_SOURCE` featureshave negative correlations with the target, indicating that as the value of the `EXT_SOURCE` increases, the client is more likely to repay the loan. We can also see that `DAYS_BIRTH` is positively correlated with `EXT_SOURCE_1` indicating that maybe one of the factors in this score is the client age.
Next we can look at the distribution of each of these features colored by the value of the target. This will let us visualize the effect of this variable on the target.
```
plt.figure(figsize = (10, 12))
# iterate through the sources
for i, source in enumerate(['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3']):
# create a new subplot for each source
plt.subplot(3, 1, i + 1)
# plot repaid loans
sns.kdeplot(app_train.loc[app_train['TARGET'] == 0, source], label = 'target == 0')
# plot loans that were not repaid
sns.kdeplot(app_train.loc[app_train['TARGET'] == 1, source], label = 'target == 1')
# Label the plots
plt.title('Distribution of %s by Target Value' % source)
plt.xlabel('%s' % source); plt.ylabel('Density');
plt.tight_layout(h_pad = 2.5)
```
`EXT_SOURCE_3` displays the greatest difference between the values of the target. We can clearly see that this feature has some relationship to the likelihood of an applicant to repay a loan. The relationship is not very strong (in fact they are all [considered very weak](http://www.statstutor.ac.uk/resources/uploaded/pearsons.pdf), but these variables will still be useful for a machine learning model to predict whether or not an applicant will repay a loan on time.
## Pairs Plot
As a final exploratory plot, we can make a pairs plot of the `EXT_SOURCE` variables and the `DAYS_BIRTH` variable. The [Pairs Plot](https://towardsdatascience.com/visualizing-data-with-pair-plots-in-python-f228cf529166) is a great exploration tool because it lets us see relationships between multiple pairs of variables as well as distributions of single variables. Here we are using the seaborn visualization library and the PairGrid function to create a Pairs Plot with scatterplots on the upper triangle, histograms on the diagonal, and 2D kernel density plots and correlation coefficients on the lower triangle.
If you don't understand this code, that's all right! Plotting in Python can be overly complex, and for anything beyond the simplest graphs, I usually find an existing implementation and adapt the code (don't repeat yourself)!
```
# Copy the data for plotting
plot_data = ext_data.drop(columns = ['DAYS_BIRTH']).copy()
# Add in the age of the client in years
plot_data['YEARS_BIRTH'] = age_data['YEARS_BIRTH']
# Drop na values and limit to first 100000 rows
plot_data = plot_data.dropna().loc[:100000, :]
# Function to calculate correlation coefficient between two columns
def corr_func(x, y, **kwargs):
r = np.corrcoef(x, y)[0][1]
ax = plt.gca()
ax.annotate("r = {:.2f}".format(r),
xy=(.2, .8), xycoords=ax.transAxes,
size = 20)
# Create the pairgrid object
grid = sns.PairGrid(data = plot_data, size = 3, diag_sharey=False,
hue = 'TARGET',
vars = [x for x in list(plot_data.columns) if x != 'TARGET'])
# Upper is a scatter plot
grid.map_upper(plt.scatter, alpha = 0.2)
# Diagonal is a histogram
grid.map_diag(sns.kdeplot)
# Bottom is density plot
grid.map_lower(sns.kdeplot, cmap = plt.cm.OrRd_r);
plt.suptitle('Ext Source and Age Features Pairs Plot', size = 32, y = 1.05);
```
In this plot, the red indicates loans that were not repaid and the blue are loans that are paid. We can see the different relationships within the data. There does appear to be a moderate positive linear relationship between the `EXT_SOURCE_1` and the `DAYS_BIRTH` (or equivalently `YEARS_BIRTH`), indicating that this feature may take into account the age of the client.
# Feature Engineering
Kaggle competitions are won by feature engineering: those win are those who can create the most useful features out of the data. (This is true for the most part as the winning models, at least for structured data, all tend to be variants on [gradient boosting](http://blog.kaggle.com/2017/01/23/a-kaggle-master-explains-gradient-boosting/)). This represents one of the patterns in machine learning: feature engineering has a greater return on investment than model building and hyperparameter tuning. [This is a great article on the subject)](https://www.featurelabs.com/blog/secret-to-data-science-success/). As Andrew Ng is fond of saying: "applied machine learning is basically feature engineering."
While choosing the right model and optimal settings are important, the model can only learn from the data it is given. Making sure this data is as relevant to the task as possible is the job of the data scientist (and maybe some [automated tools](https://docs.featuretools.com/getting_started/install.html) to help us out).
Feature engineering refers to a geneal process and can involve both feature construction: adding new features from the existing data, and feature selection: choosing only the most important features or other methods of dimensionality reduction. There are many techniques we can use to both create features and select features.
We will do a lot of feature engineering when we start using the other data sources, but in this notebook we will try only two simple feature construction methods:
* Polynomial features
* Domain knowledge features
## Polynomial Features
One simple feature construction method is called [polynomial features](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html). In this method, we make features that are powers of existing features as well as interaction terms between existing features. For example, we can create variables `EXT_SOURCE_1^2` and `EXT_SOURCE_2^2` and also variables such as `EXT_SOURCE_1` x `EXT_SOURCE_2`, `EXT_SOURCE_1` x `EXT_SOURCE_2^2`, `EXT_SOURCE_1^2` x `EXT_SOURCE_2^2`, and so on. These features that are a combination of multiple individual variables are called [interaction terms](https://en.wikipedia.org/wiki/Interaction_(statistics) because they capture the interactions between variables. In other words, while two variables by themselves may not have a strong influence on the target, combining them together into a single interaction variable might show a relationship with the target. [Interaction terms are commonly used in statistical models](https://www.theanalysisfactor.com/interpreting-interactions-in-regression/) to capture the effects of multiple variables, but I do not see them used as often in machine learning. Nonetheless, we can try out a few to see if they might help our model to predict whether or not a client will repay a loan.
Jake VanderPlas writes about [polynomial features in his excellent book Python for Data Science](https://jakevdp.github.io/PythonDataScienceHandbook/05.04-feature-engineering.html) for those who want more information.
In the following code, we create polynomial features using the `EXT_SOURCE` variables and the `DAYS_BIRTH` variable. [Scikit-Learn has a useful class called `PolynomialFeatures`](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html) that creates the polynomials and the interaction terms up to a specified degree. We can use a degree of 3 to see the results (when we are creating polynomial features, we want to avoid using too high of a degree, both because the number of features scales exponentially with the degree, and because we can run into [problems with overfitting](http://scikit-learn.org/stable/auto_examples/model_selection/plot_underfitting_overfitting.html#sphx-glr-auto-examples-model-selection-plot-underfitting-overfitting-py)).
```
# Make a new dataframe for polynomial features
poly_features = app_train[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH', 'TARGET']]
poly_features_test = app_test[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH']]
# imputer for handling missing values
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy = 'median')
poly_target = poly_features['TARGET']
poly_features = poly_features.drop(columns = ['TARGET'])
# Need to impute missing values
poly_features = imputer.fit_transform(poly_features)
poly_features_test = imputer.transform(poly_features_test)
from sklearn.preprocessing import PolynomialFeatures
# Create the polynomial object with specified degree
poly_transformer = PolynomialFeatures(degree = 3)
# Train the polynomial features
poly_transformer.fit(poly_features)
# Transform the features
poly_features = poly_transformer.transform(poly_features)
poly_features_test = poly_transformer.transform(poly_features_test)
print('Polynomial Features shape: ', poly_features.shape)
```
This creates a considerable number of new features. To get the names we have to use the polynomial features `get_feature_names` method.
```
poly_transformer.get_feature_names(input_features = ['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH'])[:15]
```
There are 35 features with individual features raised to powers up to degree 3 and interaction terms. Now, we can see whether any of these new features are correlated with the target.
```
# Create a dataframe of the features
poly_features = pd.DataFrame(poly_features,
columns = poly_transformer.get_feature_names(['EXT_SOURCE_1', 'EXT_SOURCE_2',
'EXT_SOURCE_3', 'DAYS_BIRTH']))
# Add in the target
poly_features['TARGET'] = poly_target
# Find the correlations with the target
poly_corrs = poly_features.corr()['TARGET'].sort_values()
# Display most negative and most positive
print(poly_corrs.head(10))
print(poly_corrs.tail(5))
```
Several of the new variables have a greater (in terms of absolute magnitude) correlation with the target than the original features. When we build machine learning models, we can try with and without these features to determine if they actually help the model learn.
We will add these features to a copy of the training and testing data and then evaluate models with and without the features. Many times in machine learning, the only way to know if an approach will work is to try it out!
```
# Put test features into dataframe
poly_features_test = pd.DataFrame(poly_features_test,
columns = poly_transformer.get_feature_names(['EXT_SOURCE_1', 'EXT_SOURCE_2',
'EXT_SOURCE_3', 'DAYS_BIRTH']))
# Merge polynomial features into training dataframe
poly_features['SK_ID_CURR'] = app_train['SK_ID_CURR']
app_train_poly = app_train.merge(poly_features, on = 'SK_ID_CURR', how = 'left')
# Merge polnomial features into testing dataframe
poly_features_test['SK_ID_CURR'] = app_test['SK_ID_CURR']
app_test_poly = app_test.merge(poly_features_test, on = 'SK_ID_CURR', how = 'left')
# Align the dataframes
app_train_poly, app_test_poly = app_train_poly.align(app_test_poly, join = 'inner', axis = 1)
# Print out the new shapes
print('Training data with polynomial features shape: ', app_train_poly.shape)
print('Testing data with polynomial features shape: ', app_test_poly.shape)
```
## Domain Knowledge Features
Maybe it's not entirely correct to call this "domain knowledge" because I'm not a credit expert, but perhaps we could call this "attempts at applying limited financial knowledge". In this frame of mind, we can make a couple features that attempt to capture what we think may be important for telling whether a client will default on a loan. Here I'm going to use five features that were inspired by [this script](https://www.kaggle.com/jsaguiar/updated-0-792-lb-lightgbm-with-simple-features) by Aguiar:
* `CREDIT_INCOME_PERCENT`: the percentage of the credit amount relative to a client's income
* `ANNUITY_INCOME_PERCENT`: the percentage of the loan annuity relative to a client's income
* `CREDIT_TERM`: the length of the payment in months (since the annuity is the monthly amount due
* `DAYS_EMPLOYED_PERCENT`: the percentage of the days employed relative to the client's age
Again, thanks to Aguiar and [his great script](https://www.kaggle.com/jsaguiar/updated-0-792-lb-lightgbm-with-simple-features) for exploring these features.
```
app_train_domain = app_train.copy()
app_test_domain = app_test.copy()
app_train_domain['CREDIT_INCOME_PERCENT'] = app_train_domain['AMT_CREDIT'] / app_train_domain['AMT_INCOME_TOTAL']
app_train_domain['ANNUITY_INCOME_PERCENT'] = app_train_domain['AMT_ANNUITY'] / app_train_domain['AMT_INCOME_TOTAL']
app_train_domain['CREDIT_TERM'] = app_train_domain['AMT_ANNUITY'] / app_train_domain['AMT_CREDIT']
app_train_domain['DAYS_EMPLOYED_PERCENT'] = app_train_domain['DAYS_EMPLOYED'] / app_train_domain['DAYS_BIRTH']
app_test_domain['CREDIT_INCOME_PERCENT'] = app_test_domain['AMT_CREDIT'] / app_test_domain['AMT_INCOME_TOTAL']
app_test_domain['ANNUITY_INCOME_PERCENT'] = app_test_domain['AMT_ANNUITY'] / app_test_domain['AMT_INCOME_TOTAL']
app_test_domain['CREDIT_TERM'] = app_test_domain['AMT_ANNUITY'] / app_test_domain['AMT_CREDIT']
app_test_domain['DAYS_EMPLOYED_PERCENT'] = app_test_domain['DAYS_EMPLOYED'] / app_test_domain['DAYS_BIRTH']
```
#### Visualize New Variables
We should explore these __domain knowledge__ variables visually in a graph. For all of these, we will make the same KDE plot colored by the value of the `TARGET`.
```
plt.figure(figsize = (12, 20))
# iterate through the new features
for i, feature in enumerate(['CREDIT_INCOME_PERCENT', 'ANNUITY_INCOME_PERCENT', 'CREDIT_TERM', 'DAYS_EMPLOYED_PERCENT']):
# create a new subplot for each source
plt.subplot(4, 1, i + 1)
# plot repaid loans
sns.kdeplot(app_train_domain.loc[app_train_domain['TARGET'] == 0, feature], label = 'target == 0')
# plot loans that were not repaid
sns.kdeplot(app_train_domain.loc[app_train_domain['TARGET'] == 1, feature], label = 'target == 1')
# Label the plots
plt.title('Distribution of %s by Target Value' % feature)
plt.xlabel('%s' % feature); plt.ylabel('Density');
plt.tight_layout(h_pad = 2.5)
```
It's hard to say ahead of time if these new features will be useful. The only way to tell for sure is to try them out!
# Baseline
For a naive baseline, we could guess the same value for all examples on the testing set. We are asked to predict the probability of not repaying the loan, so if we are entirely unsure, we would guess 0.5 for all observations on the test set. This will get us a Reciever Operating Characteristic Area Under the Curve (AUC ROC) of 0.5 in the competition ([random guessing on a classification task will score a 0.5](https://stats.stackexchange.com/questions/266387/can-auc-roc-be-between-0-0-5)).
Since we already know what score we are going to get, we don't really need to make a naive baseline guess. Let's use a slightly more sophisticated model for our actual baseline: Logistic Regression.
## Logistic Regression Implementation
Here I will focus on implementing the model rather than explaining the details, but for those who want to learn more about the theory of machine learning algorithms, I recommend both [An Introduction to Statistical Learning](http://www-bcf.usc.edu/~gareth/ISL/) and [Hands-On Machine Learning with Scikit-Learn and TensorFlow](http://shop.oreilly.com/product/0636920052289.do). Both of these books present the theory and also the code needed to make the models (in R and Python respectively). They both teach with the mindset that the best way to learn is by doing, and they are very effective!
To get a baseline, we will use all of the features after encoding the categorical variables. We will preprocess the data by filling in the missing values (imputation) and normalizing the range of the features (feature scaling). The following code performs both of these preprocessing steps.
```
from sklearn.preprocessing import MinMaxScaler, Imputer
# Drop the target from the training data
if 'TARGET' in app_train:
train = app_train.drop(columns = ['TARGET'])
else:
train = app_train.copy()
# Feature names
features = list(train.columns)
# Copy of the testing data
test = app_test.copy()
# Median imputation of missing values
imputer = Imputer(strategy = 'median')
# Scale each feature to 0-1
scaler = MinMaxScaler(feature_range = (0, 1))
# Fit on the training data
imputer.fit(train)
# Transform both training and testing data
train = imputer.transform(train)
test = imputer.transform(app_test)
# Repeat with the scaler
scaler.fit(train)
train = scaler.transform(train)
test = scaler.transform(test)
print('Training data shape: ', train.shape)
print('Testing data shape: ', test.shape)
```
We will use [`LogisticRegression`from Scikit-Learn](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html) for our first model. The only change we will make from the default model settings is to lower the [regularization parameter](http://scikit-learn.org/stable/modules/linear_model.html#logistic-regression), C, which controls the amount of overfitting (a lower value should decrease overfitting). This will get us slightly better results than the default `LogisticRegression`, but it still will set a low bar for any future models.
Here we use the familiar Scikit-Learn modeling syntax: we first create the model, then we train the model using `.fit` and then we make predictions on the testing data using `.predict_proba` (remember that we want probabilities and not a 0 or 1).
```
from sklearn.linear_model import LogisticRegression
# Make the model with the specified regularization parameter
log_reg = LogisticRegression(C = 0.0001)
# Train on the training data
log_reg.fit(train, train_labels)
```
Now that the model has been trained, we can use it to make predictions. We want to predict the probabilities of not paying a loan, so we use the model `predict.proba` method. This returns an m x 2 array where m is the number of observations. The first column is the probability of the target being 0 and the second column is the probability of the target being 1 (so for a single row, the two columns must sum to 1). We want the probability the loan is not repaid, so we will select the second column.
The following code makes the predictions and selects the correct column.
```
# Make predictions
# Make sure to select the second column only
log_reg_pred = log_reg.predict_proba(test)[:, 1]
```
The predictions must be in the format shown in the `sample_submission.csv` file, where there are only two columns: `SK_ID_CURR` and `TARGET`. We will create a dataframe in this format from the test set and the predictions called `submit`.
```
# Submission dataframe
submit = app_test[['SK_ID_CURR']]
submit['TARGET'] = log_reg_pred
submit.head()
```
The predictions represent a probability between 0 and 1 that the loan will not be repaid. If we were using these predictions to classify applicants, we could set a probability threshold for determining that a loan is risky.
```
# Save the submission to a csv file
submit.to_csv('log_reg_baseline.csv', index = False)
```
The submission has now been saved to the virtual environment in which our notebook is running. To access the submission, at the end of the notebook, we will hit the blue Commit & Run button at the upper right of the kernel. This runs the entire notebook and then lets us download any files that are created during the run.
Once we run the notebook, the files created are available in the Versions tab under the Output sub-tab. From here, the submission files can be submitted to the competition or downloaded. Since there are several models in this notebook, there will be multiple output files.
__The logistic regression baseline should score around 0.671 when submitted.__
## Improved Model: Random Forest
To try and beat the poor performance of our baseline, we can update the algorithm. Let's try using a Random Forest on the same training data to see how that affects performance. The Random Forest is a much more powerful model especially when we use hundreds of trees. We will use 100 trees in the random forest.
```
from sklearn.ensemble import RandomForestClassifier
# Make the random forest classifier
random_forest = RandomForestClassifier(n_estimators = 100, random_state = 50, verbose = 1, n_jobs = -1)
# Train on the training data
random_forest.fit(train, train_labels)
# Extract feature importances
feature_importance_values = random_forest.feature_importances_
feature_importances = pd.DataFrame({'feature': features, 'importance': feature_importance_values})
# Make predictions on the test data
predictions = random_forest.predict_proba(test)[:, 1]
# Make a submission dataframe
submit = app_test[['SK_ID_CURR']]
submit['TARGET'] = predictions
# Save the submission dataframe
submit.to_csv('random_forest_baseline.csv', index = False)
```
These predictions will also be available when we run the entire notebook.
__This model should score around 0.678 when submitted.__
### Make Predictions using Engineered Features
The only way to see if the Polynomial Features and Domain knowledge improved the model is to train a test a model on these features! We can then compare the submission performance to that for the model without these features to gauge the effect of our feature engineering.
```
poly_features_names = list(app_train_poly.columns)
# Impute the polynomial features
imputer = Imputer(strategy = 'median')
poly_features = imputer.fit_transform(app_train_poly)
poly_features_test = imputer.transform(app_test_poly)
# Scale the polynomial features
scaler = MinMaxScaler(feature_range = (0, 1))
poly_features = scaler.fit_transform(poly_features)
poly_features_test = scaler.transform(poly_features_test)
random_forest_poly = RandomForestClassifier(n_estimators = 100, random_state = 50, verbose = 1, n_jobs = -1)
# Train on the training data
random_forest_poly.fit(poly_features, train_labels)
# Make predictions on the test data
predictions = random_forest_poly.predict_proba(poly_features_test)[:, 1]
# Make a submission dataframe
submit = app_test[['SK_ID_CURR']]
submit['TARGET'] = predictions
# Save the submission dataframe
submit.to_csv('random_forest_baseline_engineered.csv', index = False)
```
This model scored 0.678 when submitted to the competition, exactly the same as that without the engineered features. Given these results, it does not appear that our feature construction helped in this case.
#### Testing Domain Features
Now we can test the domain features we made by hand.
```
app_train_domain = app_train_domain.drop(columns = 'TARGET')
domain_features_names = list(app_train_domain.columns)
# Impute the domainnomial features
imputer = Imputer(strategy = 'median')
domain_features = imputer.fit_transform(app_train_domain)
domain_features_test = imputer.transform(app_test_domain)
# Scale the domainnomial features
scaler = MinMaxScaler(feature_range = (0, 1))
domain_features = scaler.fit_transform(domain_features)
domain_features_test = scaler.transform(domain_features_test)
random_forest_domain = RandomForestClassifier(n_estimators = 100, random_state = 50, verbose = 1, n_jobs = -1)
# Train on the training data
random_forest_domain.fit(domain_features, train_labels)
# Extract feature importances
feature_importance_values_domain = random_forest_domain.feature_importances_
feature_importances_domain = pd.DataFrame({'feature': domain_features_names, 'importance': feature_importance_values_domain})
# Make predictions on the test data
predictions = random_forest_domain.predict_proba(domain_features_test)[:, 1]
# Make a submission dataframe
submit = app_test[['SK_ID_CURR']]
submit['TARGET'] = predictions
# Save the submission dataframe
submit.to_csv('random_forest_baseline_domain.csv', index = False)
```
This scores 0.679 when submitted which probably shows that the engineered features do not help in this model (however they do help in the Gradient Boosting Model at the end of the notebook).
In later notebooks, we will do more [feature engineering](https://docs.featuretools.com/index.html) by using the information from the other data sources. From experience, this will definitely help our model!
## Model Interpretation: Feature Importances
As a simple method to see which variables are the most relevant, we can look at the feature importances of the random forest. Given the correlations we saw in the exploratory data analysis, we should expect that the most important features are the `EXT_SOURCE` and the `DAYS_BIRTH`. We may use these feature importances as a method of dimensionality reduction in future work.
```
def plot_feature_importances(df):
"""
Plot importances returned by a model. This can work with any measure of
feature importance provided that higher importance is better.
Args:
df (dataframe): feature importances. Must have the features in a column
called `features` and the importances in a column called `importance
Returns:
shows a plot of the 15 most importance features
df (dataframe): feature importances sorted by importance (highest to lowest)
with a column for normalized importance
"""
# Sort features according to importance
df = df.sort_values('importance', ascending = False).reset_index()
# Normalize the feature importances to add up to one
df['importance_normalized'] = df['importance'] / df['importance'].sum()
# Make a horizontal bar chart of feature importances
plt.figure(figsize = (10, 6))
ax = plt.subplot()
# Need to reverse the index to plot most important on top
ax.barh(list(reversed(list(df.index[:15]))),
df['importance_normalized'].head(15),
align = 'center', edgecolor = 'k')
# Set the yticks and labels
ax.set_yticks(list(reversed(list(df.index[:15]))))
ax.set_yticklabels(df['feature'].head(15))
# Plot labeling
plt.xlabel('Normalized Importance'); plt.title('Feature Importances')
plt.show()
return df
# Show the feature importances for the default features
feature_importances_sorted = plot_feature_importances(feature_importances)
```
As expected, the most important features are those dealing with `EXT_SOURCE` and `DAYS_BIRTH`. We see that there are only a handful of features with a significant importance to the model, which suggests we may be able to drop many of the features without a decrease in performance (and we may even see an increase in performance.) Feature importances are not the most sophisticated method to interpret a model or perform dimensionality reduction, but they let us start to understand what factors our model takes into account when it makes predictions.
```
feature_importances_domain_sorted = plot_feature_importances(feature_importances_domain)
```
We see that all four of our hand-engineered features made it into the top 15 most important! This should give us confidence that our domain knowledge was at least partially on track.
# Conclusions
In this notebook, we saw how to get started with a Kaggle machine learning competition. We first made sure to understand the data, our task, and the metric by which our submissions will be judged. Then, we performed a fairly simple EDA to try and identify relationships, trends, or anomalies that may help our modeling. Along the way, we performed necessary preprocessing steps such as encoding categorical variables, imputing missing values, and scaling features to a range. Then, we constructed new features out of the existing data to see if doing so could help our model.
Once the data exploration, data preparation, and feature engineering was complete, we implemented a baseline model upon which we hope to improve. Then we built a second slightly more complicated model to beat our first score. We also carried out an experiment to determine the effect of adding the engineering variables.
We followed the general outline of a [machine learning project](https://towardsdatascience.com/a-complete-machine-learning-walk-through-in-python-part-one-c62152f39420):
1. Understand the problem and the data
2. Data cleaning and formatting (this was mostly done for us)
3. Exploratory Data Analysis
4. Baseline model
5. Improved model
6. Model interpretation (just a little)
Machine learning competitions do differ slightly from typical data science problems in that we are concerned only with achieving the best performance on a single metric and do not care about the interpretation. However, by attempting to understand how our models make decisions, we can try to improve them or examine the mistakes in order to correct the errors. In future notebooks we will look at incorporating more sources of data, building more complex models (by following the code of others), and improving our scores.
I hope this notebook was able to get you up and running in this machine learning competition and that you are now ready to go out on your own - with help from the community - and start working on some great problems!
__Running the notebook__: now that we are at the end of the notebook, you can hit the blue Commit & Run button to execute all the code at once. After the run is complete (this should take about 10 minutes), you can then access the files that were created by going to the versions tab and then the output sub-tab. The submission files can be directly submitted to the competition from this tab or they can be downloaded to a local machine and saved. The final part is to share the share the notebook: go to the settings tab and change the visibility to Public. This allows the entire world to see your work!
### Follow-up Notebooks
For those looking to keep working on this problem, I have a series of follow-up notebooks:
* [Manual Feature Engineering Part One](https://www.kaggle.com/willkoehrsen/introduction-to-manual-feature-engineering)
* [Manual Feature Engineering Part Two](https://www.kaggle.com/willkoehrsen/introduction-to-manual-feature-engineering-p2)
* [Introduction to Automated Feature Engineering](https://www.kaggle.com/willkoehrsen/automated-feature-engineering-basics)
* [Advanced Automated Feature Engineering](https://www.kaggle.com/willkoehrsen/tuning-automated-feature-engineering-exploratory)
* [Feature Selection](https://www.kaggle.com/willkoehrsen/introduction-to-feature-selection)
* [Intro to Model Tuning: Grid and Random Search](https://www.kaggle.com/willkoehrsen/intro-to-model-tuning-grid-and-random-search)
As always, I welcome feedback and constructive criticism. I write for Towards Data Science at https://medium.com/@williamkoehrsen/ and can be reached on Twitter at https://twitter.com/koehrsen_will
Will
# Just for Fun: Light Gradient Boosting Machine
Now (if you want, this part is entirely optional) we can step off the deep end and use a real machine learning model: the [gradient boosting machine](https://machinelearningmastery.com/gentle-introduction-gradient-boosting-algorithm-machine-learning/) using the [LightGBM library](http://lightgbm.readthedocs.io/en/latest/Quick-Start.html)! The Gradient Boosting Machine is currently the leading model for learning on structured datasets (especially on Kaggle) and we will probably need some form of this model to do well in the competition. Don't worry, even if this code looks intimidating, it's just a series of small steps that build up to a complete model. I added this code just to show what may be in store for this project, and because it gets us a slightly better score on the leaderboard. In future notebooks we will see how to work with more advanced models (which mostly means adapting existing code to make it work better), feature engineering, and feature selection. See you in the next notebook!
```
from sklearn.model_selection import KFold
from sklearn.metrics import roc_auc_score
import lightgbm as lgb
import gc
def model(features, test_features, encoding = 'ohe', n_folds = 5):
"""Train and test a light gradient boosting model using
cross validation.
Parameters
--------
features (pd.DataFrame):
dataframe of training features to use
for training a model. Must include the TARGET column.
test_features (pd.DataFrame):
dataframe of testing features to use
for making predictions with the model.
encoding (str, default = 'ohe'):
method for encoding categorical variables. Either 'ohe' for one-hot encoding or 'le' for integer label encoding
n_folds (int, default = 5): number of folds to use for cross validation
Return
--------
submission (pd.DataFrame):
dataframe with `SK_ID_CURR` and `TARGET` probabilities
predicted by the model.
feature_importances (pd.DataFrame):
dataframe with the feature importances from the model.
valid_metrics (pd.DataFrame):
dataframe with training and validation metrics (ROC AUC) for each fold and overall.
"""
# Extract the ids
train_ids = features['SK_ID_CURR']
test_ids = test_features['SK_ID_CURR']
# Extract the labels for training
labels = features['TARGET']
# Remove the ids and target
features = features.drop(columns = ['SK_ID_CURR', 'TARGET'])
test_features = test_features.drop(columns = ['SK_ID_CURR'])
# One Hot Encoding
if encoding == 'ohe':
features = pd.get_dummies(features)
test_features = pd.get_dummies(test_features)
# Align the dataframes by the columns
features, test_features = features.align(test_features, join = 'inner', axis = 1)
# No categorical indices to record
cat_indices = 'auto'
# Integer label encoding
elif encoding == 'le':
# Create a label encoder
label_encoder = LabelEncoder()
# List for storing categorical indices
cat_indices = []
# Iterate through each column
for i, col in enumerate(features):
if features[col].dtype == 'object':
# Map the categorical features to integers
features[col] = label_encoder.fit_transform(np.array(features[col].astype(str)).reshape((-1,)))
test_features[col] = label_encoder.transform(np.array(test_features[col].astype(str)).reshape((-1,)))
# Record the categorical indices
cat_indices.append(i)
# Catch error if label encoding scheme is not valid
else:
raise ValueError("Encoding must be either 'ohe' or 'le'")
print('Training Data Shape: ', features.shape)
print('Testing Data Shape: ', test_features.shape)
# Extract feature names
feature_names = list(features.columns)
# Convert to np arrays
features = np.array(features)
test_features = np.array(test_features)
# Create the kfold object
k_fold = KFold(n_splits = n_folds, shuffle = True, random_state = 50)
# Empty array for feature importances
feature_importance_values = np.zeros(len(feature_names))
# Empty array for test predictions
test_predictions = np.zeros(test_features.shape[0])
# Empty array for out of fold validation predictions
out_of_fold = np.zeros(features.shape[0])
# Lists for recording validation and training scores
valid_scores = []
train_scores = []
# Iterate through each fold
for train_indices, valid_indices in k_fold.split(features):
# Training data for the fold
train_features, train_labels = features[train_indices], labels[train_indices]
# Validation data for the fold
valid_features, valid_labels = features[valid_indices], labels[valid_indices]
# Create the model
model = lgb.LGBMClassifier(n_estimators=10000, objective = 'binary',
class_weight = 'balanced', learning_rate = 0.05,
reg_alpha = 0.1, reg_lambda = 0.1,
subsample = 0.8, n_jobs = -1, random_state = 50)
# Train the model
model.fit(train_features, train_labels, eval_metric = 'auc',
eval_set = [(valid_features, valid_labels), (train_features, train_labels)],
eval_names = ['valid', 'train'], categorical_feature = cat_indices,
early_stopping_rounds = 100, verbose = 200)
# Record the best iteration
best_iteration = model.best_iteration_
# Record the feature importances
feature_importance_values += model.feature_importances_ / k_fold.n_splits
# Make predictions
test_predictions += model.predict_proba(test_features, num_iteration = best_iteration)[:, 1] / k_fold.n_splits
# Record the out of fold predictions
out_of_fold[valid_indices] = model.predict_proba(valid_features, num_iteration = best_iteration)[:, 1]
# Record the best score
valid_score = model.best_score_['valid']['auc']
train_score = model.best_score_['train']['auc']
valid_scores.append(valid_score)
train_scores.append(train_score)
# Clean up memory
gc.enable()
del model, train_features, valid_features
gc.collect()
# Make the submission dataframe
submission = pd.DataFrame({'SK_ID_CURR': test_ids, 'TARGET': test_predictions})
# Make the feature importance dataframe
feature_importances = pd.DataFrame({'feature': feature_names, 'importance': feature_importance_values})
# Overall validation score
valid_auc = roc_auc_score(labels, out_of_fold)
# Add the overall scores to the metrics
valid_scores.append(valid_auc)
train_scores.append(np.mean(train_scores))
# Needed for creating dataframe of validation scores
fold_names = list(range(n_folds))
fold_names.append('overall')
# Dataframe of validation scores
metrics = pd.DataFrame({'fold': fold_names,
'train': train_scores,
'valid': valid_scores})
return submission, feature_importances, metrics
submission, fi, metrics = model(app_train, app_test)
print('Baseline metrics')
print(metrics)
fi_sorted = plot_feature_importances(fi)
submission.to_csv('baseline_lgb.csv', index = False)
```
This submission should score about 0.735 on the leaderboard. We will certainly best that in future work!
```
app_train_domain['TARGET'] = train_labels
# Test the domain knolwedge features
submission_domain, fi_domain, metrics_domain = model(app_train_domain, app_test_domain)
print('Baseline with domain knowledge features metrics')
print(metrics_domain)
fi_sorted = plot_feature_importances(fi_domain)
```
Again, we see tha some of our features made it into the most important. Going forward, we will need to think about whatother domain knowledge features may be useful for this problem (or we should consult someone who knows more about the financial industry!
```
submission_domain.to_csv('baseline_lgb_domain_features.csv', index = False)
```
This model scores about 0.754 when submitted to the public leaderboard indicating that the domain features do improve the performance! [Feature engineering](https://en.wikipedia.org/wiki/Feature_engineering) is going to be a critical part of this competition (as it is for all machine learning problems)!
| true |
code
| 0.368463 | null | null | null | null |
|
```
"""
You can run either this notebook locally (if you have all the dependencies and a GPU) or on Google Colab.
Instructions for setting up Colab are as follows:
1. Open a new Python 3 notebook.
2. Import this notebook from GitHub (File -> Upload Notebook -> "GITHUB" tab -> copy/paste GitHub URL)
3. Connect to an instance with a GPU (Runtime -> Change runtime type -> select "GPU" for hardware accelerator)
4. Run this cell to set up dependencies.
"""
## Install dependencies
!pip install wget
!pip install faiss-gpu
## Install NeMo
BRANCH = 'v1.0.2'
!python -m pip install git+https://github.com/NVIDIA/NeMo.git@$BRANCH#egg=nemo_toolkit[all]
import faiss
import torch
import wget
import os
import numpy as np
import pandas as pd
from omegaconf import OmegaConf
from pytorch_lightning import Trainer
from IPython.display import display
from tqdm import tqdm
from nemo.collections import nlp as nemo_nlp
from nemo.utils.exp_manager import exp_manager
```
## Entity Linking
#### Task Description
[Entity linking](https://en.wikipedia.org/wiki/Entity_linking) is the process of connecting concepts mentioned in natural language to their canonical forms stored in a knowledge base. For example, say a knowledge base contained the entity 'ID3452 influenza' and we wanted to process some natural language containing the sentence "The patient has flu like symptoms". An entity linking model would match the word 'flu' to the knowledge base entity 'ID3452 influenza', allowing for disambiguation and normalization of concepts referenced in text. Entity linking applications range from helping automate data ingestion to assisting in real time dialogue concept normalization. We will be focusing on entity linking in the medical domain for this demo, but the entity linking model, dataset, and training code within NVIDIA NeMo can be applied to other domains like finance and retail.
Within NeMo and this tutorial we use the entity linking approach described in Liu et. al's NAACL 2021 "[Self-alignment Pre-training for Biomedical Entity Representations](https://arxiv.org/abs/2010.11784v2)". The main idea behind this approach is to reshape an initial concept embedding space such that synonyms of the same concept are pulled closer together and unrelated concepts are pushed further apart. The concept embeddings from this reshaped space can then be used to build a knowledge base embedding index. This index stores concept IDs mapped to their respective concept embeddings in a format conducive to efficient nearest neighbor search. We can link query concepts to their canonical forms in the knowledge base by performing a nearest neighbor search- matching concept query embeddings to the most similar concepts embeddings in the knowledge base index.
In this tutorial we will be using the [faiss](https://github.com/facebookresearch/faiss) library to build our concept index.
#### Self Alignment Pretraining
Self-Alignment pretraining is a second stage pretraining of an existing encoder (called second stage because the encoder model can be further finetuned after this more general pretraining step). The dataset used during training consists of pairs of concept synonyms that map to the same ID. At each training iteration, we only select *hard* examples present in the mini batch to calculate the loss and update the model weights. In this context, a hard example is an example where a concept is closer to an unrelated concept in the mini batch than it is to the synonym concept it is paired with by some margin. I encourage you to take a look at [section 2 of the paper](https://arxiv.org/pdf/2010.11784.pdf) for a more formal and in depth description of how hard examples are selected.
We then use a [metric learning loss](https://openaccess.thecvf.com/content_CVPR_2019/papers/Wang_Multi-Similarity_Loss_With_General_Pair_Weighting_for_Deep_Metric_Learning_CVPR_2019_paper.pdf) calculated from the hard examples selected. This loss helps reshape the embedding space. The concept representation space is rearranged to be more suitable for entity matching via embedding cosine similarity.
Now that we have idea of what's going on, let's get started!
## Dataset Preprocessing
```
# Download data into project directory
PROJECT_DIR = "." #Change if you don't want the current directory to be the project dir
DATA_DIR = os.path.join(PROJECT_DIR, "tiny_example_data")
if not os.path.isdir(os.path.join(DATA_DIR)):
wget.download('https://dldata-public.s3.us-east-2.amazonaws.com/tiny_example_data.zip',
os.path.join(PROJECT_DIR, "tiny_example_data.zip"))
!unzip {PROJECT_DIR}/tiny_example_data.zip -d {PROJECT_DIR}
```
In this tutorial we will be using a tiny toy dataset to demonstrate how to use NeMo's entity linking model functionality. The dataset includes synonyms for 12 medical concepts. Entity phrases with the same ID are synonyms for the same concept. For example, "*chronic kidney failure*", "*gradual loss of kidney function*", and "*CKD*" are all synonyms of concept ID 5. Here's the dataset before preprocessing:
```
raw_data = pd.read_csv(os.path.join(DATA_DIR, "tiny_example_dev_data.csv"), names=["ID", "CONCEPT"], index_col=False)
print(raw_data)
```
We've already paired off the concepts for this dataset with the format `ID concept_synonym1 concept_synonym2`. Here are the first ten rows:
```
training_data = pd.read_table(os.path.join(DATA_DIR, "tiny_example_train_pairs.tsv"), names=["ID", "CONCEPT_SYN1", "CONCEPT_SYN2"], delimiter='\t')
print(training_data.head(10))
```
Use the [Unified Medical Language System (UMLS)](https://www.nlm.nih.gov/research/umls/index.html) dataset for full medical domain entity linking training. The data contains over 9 million entities and is a table of medical concepts with their corresponding concept IDs (CUI). After [requesting a free license and making a UMLS Terminology Services (UTS) account](https://www.nlm.nih.gov/research/umls/index.html), the [entire UMLS dataset](https://www.nlm.nih.gov/research/umls/licensedcontent/umlsknowledgesources.html) can be downloaded from the NIH's website. If you've cloned the NeMo repo you can run the data processing script located in `examples/nlp/entity_linking/data/umls_dataset_processing.py` on the full dataset. This script will take in the initial table of UMLS concepts and produce a .tsv file with each row formatted as `CUI\tconcept_synonym1\tconcept_synonym2`. Once the UMLS dataset .RRF file is downloaded, the script can be run from the `examples/nlp/entity_linking` directory like so:
```
python data/umls_dataset_processing.py
```
## Model Training
Second stage pretrain a BERT Base encoder on the self-alignment pretraining task (SAP) for improved entity linking. Using a GPU, the model should take 5 minutes or less to train on this example dataset and training progress will be output below the cell.
```
# Download config
wget.download("https://raw.githubusercontent.com/vadam5/NeMo/main/examples/nlp/entity_linking/conf/tiny_example_entity_linking_config.yaml",
os.path.join(PROJECT_DIR, "tiny_example_entity_linking_config.yaml"))
# Load in config file
cfg = OmegaConf.load(os.path.join(PROJECT_DIR, "tiny_example_entity_linking_config.yaml"))
# Set config file variables
cfg.project_dir = PROJECT_DIR
cfg.model.nemo_path = os.path.join(PROJECT_DIR, "tiny_example_sap_bert_model.nemo")
cfg.model.train_ds.data_file = os.path.join(DATA_DIR, "tiny_example_train_pairs.tsv")
cfg.model.validation_ds.data_file = os.path.join(DATA_DIR, "tiny_example_validation_pairs.tsv")
# Initialize the trainer and model
trainer = Trainer(**cfg.trainer)
exp_manager(trainer, cfg.get("exp_manager", None))
model = nemo_nlp.models.EntityLinkingModel(cfg=cfg.model, trainer=trainer)
# Train and save the model
trainer.fit(model)
model.save_to(cfg.model.nemo_path)
```
You can run the script at `examples/nlp/entity_linking/self_alignment_pretraining.py` to train a model on a larger dataset. Run
```
python self_alignment_pretraining.py project_dir=.
```
from the `examples/nlp/entity_linking` directory.
## Model Evaluation
Let's evaluate our freshly trained model and compare its performance with a BERT Base encoder that hasn't undergone self-alignment pretraining. We first need to restore our trained model and load our BERT Base Baseline model.
```
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# Restore second stage pretrained model
sap_model_cfg = cfg
sap_model_cfg.index.index_save_name = os.path.join(PROJECT_DIR, "tiny_example_entity_linking_index")
sap_model_cfg.index.index_ds.data_file = os.path.join(DATA_DIR, "tiny_example_index_data.tsv")
sap_model = nemo_nlp.models.EntityLinkingModel.restore_from(sap_model_cfg.model.nemo_path).to(device)
# Load original model
base_model_cfg = OmegaConf.load(os.path.join(PROJECT_DIR, "tiny_example_entity_linking_config.yaml"))
# Set train/val datasets to None to avoid loading datasets associated with training
base_model_cfg.model.train_ds = None
base_model_cfg.model.validation_ds = None
base_model_cfg.index.index_save_name = os.path.join(PROJECT_DIR, "base_model_index")
base_model_cfg.index.index_ds.data_file = os.path.join(DATA_DIR, "tiny_example_index_data.tsv")
base_model = nemo_nlp.models.EntityLinkingModel(base_model_cfg.model).to(device)
```
We are going evaluate our model on a nearest neighbor task using top 1 and top 5 accuracies as our metric. We will be using a tiny example test knowledge base and test queries. For this evaluation we are going to be comparing every test query with every concept vector in our test set knowledge base. We will rank each item in the knowledge base by its cosine similarity with the test query. We'll then compare the IDs of the predicted most similar test knowledge base concepts with our ground truth query IDs to calculate top 1 and top 5 accuracies. For this metric higher is better.
```
# Helper function to get data embeddings
def get_embeddings(model, dataloader):
embeddings, cids = [], []
with torch.no_grad():
for batch in tqdm(dataloader):
input_ids, token_type_ids, attention_mask, batch_cids = batch
batch_embeddings = model.forward(input_ids=input_ids.to(device),
token_type_ids=token_type_ids.to(device),
attention_mask=attention_mask.to(device))
# Accumulate index embeddings and their corresponding IDs
embeddings.extend(batch_embeddings.cpu().detach().numpy())
cids.extend(batch_cids)
return embeddings, cids
def evaluate(model, test_kb, test_queries, ks):
# Initialize knowledge base and query data loaders
test_kb_dataloader = model.setup_dataloader(test_kb, is_index_data=True)
test_query_dataloader = model.setup_dataloader(test_queries, is_index_data=True)
# Get knowledge base and query embeddings
test_kb_embs, test_kb_cids = get_embeddings(model, test_kb_dataloader)
test_query_embs, test_query_cids = get_embeddings(model, test_query_dataloader)
# Calculate the cosine distance between each query and knowledge base concept
score_matrix = np.matmul(np.array(test_query_embs), np.array(test_kb_embs).T)
accs = {k : 0 for k in ks}
# Compare the knowledge base IDs of the knowledge base entities with
# the smallest cosine distance from the query
for query_idx in tqdm(range(len(test_query_cids))):
query_emb = test_query_embs[query_idx]
query_cid = test_query_cids[query_idx]
query_scores = score_matrix[query_idx]
for k in ks:
topk_idxs = np.argpartition(query_scores, -k)[-k:]
topk_cids = [test_kb_cids[idx] for idx in topk_idxs]
# If the correct query ID is amoung the top k closest kb IDs
# the model correctly linked the entity
match = int(query_cid in topk_cids)
accs[k] += match
for k in ks:
accs[k] /= len(test_query_cids)
return accs
# Create configs for our test data
test_kb = OmegaConf.create({
"data_file": os.path.join(DATA_DIR, "tiny_example_test_kb.tsv"),
"max_seq_length": 128,
"batch_size": 10,
"shuffle": False,
})
test_queries = OmegaConf.create({
"data_file": os.path.join(DATA_DIR, "tiny_example_test_queries.tsv"),
"max_seq_length": 128,
"batch_size": 10,
"shuffle": False,
})
ks = [1, 5]
# Evaluate both models on our test data
base_accs = evaluate(base_model, test_kb, test_queries, ks)
base_accs["Model"] = "BERT Base Baseline"
sap_accs = evaluate(sap_model, test_kb, test_queries, ks)
sap_accs["Model"] = "BERT + SAP"
print("Top 1 and Top 5 Accuracy Comparison:")
results_df = pd.DataFrame([base_accs, sap_accs], columns=["Model", 1, 5])
results_df = results_df.style.set_properties(**{'text-align': 'left', }).set_table_styles([dict(selector='th', props=[('text-align', 'left')])])
display(results_df)
```
The purpose of this section was to show an example of evaluating your entity linking model. This evaluation set contains very little data, and no serious conclusions should be drawn about model performance. Top 1 accuracy should be between 0.7 and 1.0 for both models and top 5 accuracy should be between 0.8 and 1.0. When evaluating a model trained on a larger dataset, you can use a nearest neighbors index to speed up the evaluation time.
## Building an Index
To qualitatively observe the improvement we gain from the second stage pretraining, let's build two indices. One will be built with BERT base embeddings before self-alignment pretraining and one will be built with the model we just trained. Our knowledge base in this tutorial will be in the same domain and have some overlapping concepts as the training set. This data file is formatted as `ID\tconcept`.
The `EntityLinkingDataset` class can load the data used for training the entity linking encoder as well as for building the index if the `is_index_data` flag is set to true.
```
def build_index(cfg, model):
# Setup index dataset loader
index_dataloader = model.setup_dataloader(cfg.index.index_ds, is_index_data=True)
# Get index dataset embeddings
embeddings, _ = get_embeddings(model, index_dataloader)
# Train IVFFlat index using faiss
embeddings = np.array(embeddings)
quantizer = faiss.IndexFlatL2(cfg.index.dims)
index = faiss.IndexIVFFlat(quantizer, cfg.index.dims, cfg.index.nlist)
index = faiss.index_cpu_to_all_gpus(index)
index.train(embeddings)
# Add concept embeddings to index
for i in tqdm(range(0, embeddings.shape[0], cfg.index.index_batch_size)):
index.add(embeddings[i:i+cfg.index.index_batch_size])
# Save index
faiss.write_index(faiss.index_gpu_to_cpu(index), cfg.index.index_save_name)
build_index(sap_model_cfg, sap_model.to(device))
build_index(base_model_cfg, base_model.to(device))
```
## Entity Linking via Nearest Neighbor Search
Now it's time to query our indices! We are going to query both our index built with embeddings from BERT Base, and our index with embeddings built from the SAP BERT model we trained. Our sample query phrases will be "*high blood sugar*" and "*head pain*".
To query our indices, we first need to get the embedding of each query from the corresponding encoder model. We can then pass these query embeddings into the faiss index which will perform a nearest neighbor search, using cosine distance to compare the query embedding with embeddings present in the index. Once we get a list of knowledge base index concept IDs most closely matching our query, all that is left to do is map the IDs to a representative string describing the concept.
```
def query_index(cfg, model, index, queries, id2string):
# Get query embeddings from our entity linking encoder model
query_embs = get_query_embedding(queries, model).cpu().detach().numpy()
# Use query embedding to find closest concept embedding in knowledge base
distances, neighbors = index.search(query_embs, cfg.index.top_n)
# Get the canonical strings corresponding to the IDs of the query's nearest neighbors in the kb
neighbor_concepts = [[id2string[concept_id] for concept_id in query_neighbor] \
for query_neighbor in neighbors]
# Display most similar concepts in the knowledge base.
for query_idx in range(len(queries)):
print(f"\nThe most similar concepts to {queries[query_idx]} are:")
for cid, concept, dist in zip(neighbors[query_idx], neighbor_concepts[query_idx], distances[query_idx]):
print(cid, concept, 1 - dist)
def get_query_embedding(queries, model):
# Tokenize our queries
model_input = model.tokenizer(queries,
add_special_tokens = True,
padding = True,
truncation = True,
max_length = 512,
return_token_type_ids = True,
return_attention_mask = True)
# Pass tokenized input into model
query_emb = model.forward(input_ids=torch.LongTensor(model_input["input_ids"]).to(device),
token_type_ids=torch.LongTensor(model_input["token_type_ids"]).to(device),
attention_mask=torch.LongTensor(model_input["attention_mask"]).to(device))
return query_emb
# Load indices
sap_index = faiss.read_index(sap_model_cfg.index.index_save_name)
base_index = faiss.read_index(base_model_cfg.index.index_save_name)
# Map concept IDs to one canonical string
index_data = open(sap_model_cfg.index.index_ds.data_file, "r", encoding='utf-8-sig')
id2string = {}
for line in index_data:
cid, concept = line.split("\t")
id2string[int(cid) - 1] = concept.strip()
id2string
# Some sample queries
queries = ["high blood sugar", "head pain"]
# Query BERT Base
print("BERT Base output before Self Alignment Pretraining:")
query_index(base_model_cfg, base_model, base_index, queries, id2string)
print("\n" + "-" * 50 + "\n")
# Query SAP BERT
print("SAP BERT output after Self Alignment Pretraining:")
query_index(sap_model_cfg, sap_model, sap_index, queries, id2string)
print("\n" + "-" * 50 + "\n")
```
Even after only training on this tiny amount of data, the qualitative performance boost from self-alignment pretraining is visible. The baseline model links "*high blood sugar*" to the entity "*6 diabetes*" while our SAP BERT model accurately links "*high blood sugar*" to "*Hyperinsulinemia*". Similarly, "*head pain*" and "*Myocardial infraction*" are not the same concept, but "*head pain*" and "*Headache*" are.
For larger knowledge bases keeping the default embedding size might be too large and cause out of memory issues. You can apply PCA or some other dimensionality reduction method to your data to reduce its memory footprint. Code for creating a text file of all the UMLS entities in the correct format needed to build an index and creating a dictionary mapping concept ids to canonical concept strings can be found here `examples/nlp/entity_linking/data/umls_dataset_processing.py`.
The code for extracting knowledge base concept embeddings, training and applying a PCA transformation to the embeddings, building a faiss index and querying the index from the command line is located at `examples/nlp/entity_linking/build_index.py` and `examples/nlp/entity_linking/query_index.py`.
If you've cloned the NeMo repo, both of these steps can be run as follows on the command line from the `examples/nlp/entity_linking/` directory.
```
python data/umls_dataset_processing.py --index
python build_index.py --restore
python query_index.py --restore
```
By default the project directory will be "." but can be changed by adding the flag `--project_dir=<PATH>` after each of the above commands. Intermediate steps of the index building process are saved. In the occurrence of an error, previously completed steps do not need to be rerun.
## Command Recap
Here is a recap of the commands and steps to repeat this process on the full UMLS dataset.
1) Download the UMLS dataset file `MRCONSO.RRF` from the NIH website and place it in the `examples/nlp/entity_linking/data` directory.
2) Run the following commands from the `examples/nlp/entity_linking` directory
```
python data/umls_dataset_processing.py
python self_alignment_pretraining.py project_dir=.
python data/umls_dataset_processing.py --index
python build_index.py --restore
python query_index.py --restore
```
The model will take ~24hrs to train on two GPUs and ~48hrs to train on one GPU. By default the project directory will be "." but can be changed by adding the flag `--project_dir=<PATH>` after each of the above commands and changing `project_dir=<PATH>` in the `self_alignment_pretraining.py` command. If you change the project directory, you should also move the `MRCONOSO.RRF` file to a `data` sub directory within the one you've specified.
As mentioned in the introduction, entity linking within NVIDIA NeMo is not limited to the medical domain. The same data processing and training steps can be applied to a variety of domains and use cases. You can edit the datasets used as well as training and loss function hyperparameters within your config file to better suit your domain.
| true |
code
| 0.739904 | null | null | null | null |
|
# Inference and Validation
Now that you have a trained network, you can use it for making predictions. This is typically called **inference**, a term borrowed from statistics. However, neural networks have a tendency to perform *too well* on the training data and aren't able to generalize to data that hasn't been seen before. This is called **overfitting** and it impairs inference performance. To test for overfitting while training, we measure the performance on data not in the training set called the **validation** set. We avoid overfitting through regularization such as dropout while monitoring the validation performance during training. In this notebook, I'll show you how to do this in PyTorch.
As usual, let's start by loading the dataset through torchvision. You'll learn more about torchvision and loading data in a later part. This time we'll be taking advantage of the test set which you can get by setting `train=False` here:
```python
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
```
The test set contains images just like the training set. Typically you'll see 10-20% of the original dataset held out for testing and validation with the rest being used for training.
```
import torch
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
```
Here I'll create a model like normal, using the same one from my solution for part 4.
```
from torch import nn, optim
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
The goal of validation is to measure the model's performance on data that isn't part of the training set. Performance here is up to the developer to define though. Typically this is just accuracy, the percentage of classes the network predicted correctly. Other options are [precision and recall](https://en.wikipedia.org/wiki/Precision_and_recall#Definition_(classification_context)) and top-5 error rate. We'll focus on accuracy here. First I'll do a forward pass with one batch from the test set.
```
model = Classifier()
images, labels = next(iter(testloader))
# Get the class probabilities
ps = torch.exp(model(images))
# Make sure the shape is appropriate, we should get 10 class probabilities for 64 examples
print(ps.shape)
```
With the probabilities, we can get the most likely class using the `ps.topk` method. This returns the $k$ highest values. Since we just want the most likely class, we can use `ps.topk(1)`. This returns a tuple of the top-$k$ values and the top-$k$ indices. If the highest value is the fifth element, we'll get back 4 as the index.
```
top_p, top_class = ps.topk(1, dim=1)
# Look at the most likely classes for the first 10 examples
print(top_class[:10,:])
```
Now we can check if the predicted classes match the labels. This is simple to do by equating `top_class` and `labels`, but we have to be careful of the shapes. Here `top_class` is a 2D tensor with shape `(64, 1)` while `labels` is 1D with shape `(64)`. To get the equality to work out the way we want, `top_class` and `labels` must have the same shape.
If we do
```python
equals = top_class == labels
```
`equals` will have shape `(64, 64)`, try it yourself. What it's doing is comparing the one element in each row of `top_class` with each element in `labels` which returns 64 True/False boolean values for each row.
```
equals = top_class == labels.view(*top_class.shape)
```
Now we need to calculate the percentage of correct predictions. `equals` has binary values, either 0 or 1. This means that if we just sum up all the values and divide by the number of values, we get the percentage of correct predictions. This is the same operation as taking the mean, so we can get the accuracy with a call to `torch.mean`. If only it was that simple. If you try `torch.mean(equals)`, you'll get an error
```
RuntimeError: mean is not implemented for type torch.ByteTensor
```
This happens because `equals` has type `torch.ByteTensor` but `torch.mean` isn't implement for tensors with that type. So we'll need to convert `equals` to a float tensor. Note that when we take `torch.mean` it returns a scalar tensor, to get the actual value as a float we'll need to do `accuracy.item()`.
```
accuracy = torch.mean(equals.type(torch.FloatTensor))
print(f'Accuracy: {accuracy.item()*100}%')
```
The network is untrained so it's making random guesses and we should see an accuracy around 10%. Now let's train our network and include our validation pass so we can measure how well the network is performing on the test set. Since we're not updating our parameters in the validation pass, we can speed up the by turning off gradients using `torch.no_grad()`:
```python
# turn off gradients
with torch.no_grad():
# validation pass here
for images, labels in testloader:
...
```
>**Exercise:** Implement the validation loop below. You can largely copy and paste the code from above, but I suggest typing it in because writing it out yourself is essential for building the skill. In general you'll always learn more by typing it rather than copy-pasting.
```
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
epochs = 30
steps = 0
train_losses, test_losses = [], []
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
log_ps = model(images)
loss = criterion(log_ps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
test_loss = 0
accuracy = 0
# Turn off gradients for validation, saves memory and computations
with torch.no_grad():
for images, labels in testloader:
log_ps = model(images)
test_loss += criterion(log_ps, labels)
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(running_loss/len(trainloader)),
"Test Loss: {:.3f}.. ".format(test_loss/len(testloader)),
"Test Accuracy: {:.3f}".format(accuracy/len(testloader)))
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)
```
## Overfitting
If we look at the training and validation losses as we train the network, we can see a phenomenon known as overfitting.
<img src='assets/overfitting.png' width=450px>
The network learns the training set better and better, resulting in lower training losses. However, it starts having problems generalizing to data outside the training set leading to the validation loss increasing. The ultimate goal of any deep learning model is to make predictions on new data, so we should strive to get the lowest validation loss possible. One option is to use the version of the model with the lowest validation loss, here the one around 8-10 training epochs. This strategy is called *early-stopping*. In practice, you'd save the model frequently as you're training then later choose the model with the lowest validation loss.
The most common method to reduce overfitting (outside of early-stopping) is *dropout*, where we randomly drop input units. This forces the network to share information between weights, increasing it's ability to generalize to new data. Adding dropout in PyTorch is straightforward using the [`nn.Dropout`](https://pytorch.org/docs/stable/nn.html#torch.nn.Dropout) module.
```python
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# Dropout module with 0.2 drop probability
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
# Now with dropout
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output so no dropout here
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
During training we want to use dropout to prevent overfitting, but during inference we want to use the entire network. So, we need to turn off dropout during validation, testing, and whenever we're using the network to make predictions. To do this, you use `model.eval()`. This sets the model to evaluation mode where the dropout probability is 0. You can turn dropout back on by setting the model to train mode with `model.train()`. In general, the pattern for the validation loop will look like this, where you turn off gradients, set the model to evaluation mode, calculate the validation loss and metric, then set the model back to train mode.
```python
# turn off gradients
with torch.no_grad():
# set model to evaluation mode
model.eval()
# validation pass here
for images, labels in testloader:
...
# set model back to train mode
model.train()
```
> **Exercise:** Add dropout to your model and train it on Fashion-MNIST again. See if you can get a lower validation loss.
```
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# Dropout module with 0.2 drop probability
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
# Now with dropout
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output so no dropout here
x = F.log_softmax(self.fc4(x), dim=1)
return x
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
epochs = 30
steps = 0
train_losses, test_losses = [], []
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
log_ps = model(images)
loss = criterion(log_ps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
test_loss = 0
accuracy = 0
# Turn off gradients for validation, saves memory and computations
with torch.no_grad():
model.eval()
for images, labels in testloader:
log_ps = model(images)
test_loss += criterion(log_ps, labels)
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
model.train()
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(train_losses[-1]),
"Test Loss: {:.3f}.. ".format(test_losses[-1]),
"Test Accuracy: {:.3f}".format(accuracy/len(testloader)))
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)
```
## Inference
Now that the model is trained, we can use it for inference. We've done this before, but now we need to remember to set the model in inference mode with `model.eval()`. You'll also want to turn off autograd with the `torch.no_grad()` context.
```
# Import helper module (should be in the repo)
import helper
# Test out your network!
model.eval()
dataiter = iter(testloader)
images, labels = dataiter.next()
img = images[0]
# Convert 2D image to 1D vector
img = img.view(1, 784)
# Calculate the class probabilities (softmax) for img
with torch.no_grad():
output = model.forward(img)
ps = torch.exp(output)
# Plot the image and probabilities
helper.view_classify(img.view(1, 28, 28), ps, version='Fashion')
```
## Next Up!
In the next part, I'll show you how to save your trained models. In general, you won't want to train a model everytime you need it. Instead, you'll train once, save it, then load the model when you want to train more or use if for inference.
| true |
code
| 0.87925 | null | null | null | null |
|
# Demo for 2d DOT
```
import chainer
from chainer import Variable, optimizers, serializers, utils
from chainer import Link, Chain, ChainList
import chainer.functions as F
import chainer.links as L
from chainer import cuda
#import numpy as xp
gpu_device = 0
cuda.get_device(gpu_device).use()
import numpy as np
import cupy as xp
from model import *
import DOT
import sklearn.datasets
from matplotlib import pyplot as plt
%matplotlib inline
def show_three_figures(y, ty1, ty2, X_train, xmin, xmax, ymin, ymax):
plt.style.use('seaborn-darkgrid')
plt.figure(figsize=(20,5))
plt.subplot(1, 4, 1)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.title("Training samples", fontsize=20)
plt.scatter(X_train[:,:1], X_train[:,1:], alpha=0.5, color='gray', marker='o')
plt.subplot(1, 4, 2)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.title("Samples by G", fontsize=20)
y_d = y#.data
plt.scatter(y_d[:,:1], y_d[:,1:], alpha=0.5, color='blue', marker='o', label='y')
plt.subplot(1, 4, 3)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.title("DOT", fontsize=20)
y_d = ty1#.data
plt.scatter(y_d[:,:1], y_d[:,1:], alpha=0.5, color='red', marker='o', label='ty')
plt.subplot(1, 4, 4)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.title("Naive", fontsize=20)
y_d = ty2#.data
plt.scatter(y_d[:,:1], y_d[:,1:], alpha=0.5, color='red', marker='o', label='ty')
plt.show()
#### data generators are derived from https://github.com/lukovnikov/improved_wgan_training/blob/master/gan_toy.py
# Copyright (c) 2017 Ishaan Gulrajani
# Released under the MIT license
# https://github.com/lukovnikov/improved_wgan_training/blob/master/LICENSE
def prepare_swissroll_data(BATCH_SIZE=1000):
data = sklearn.datasets.make_swiss_roll(
n_samples=BATCH_SIZE,
noise=0.25
)[0]
data = data.astype('float32')[:, [0, 2]]
data /= 7.5 # stdev plus a little
return data
def prepare_25gaussian_data(BATCH_SIZE=1000):
dataset = []
for i in range(BATCH_SIZE//25):
for x in range(-2, 3):
for y in range(-2, 3):
point = np.random.randn(2)*0.05
point[0] += 2*x
point[1] += 2*y
dataset.append(point)
dataset = np.array(dataset, dtype=np.float32)
np.random.shuffle(dataset)
dataset /= 2.828 # stdev
return dataset
```
# 25 Gaussians
```
G = Generator(n_hidden=2, noize='uni', non_linear=F.leaky_relu, final=F.identity)
serializers.load_npz("trained_models/G_25gaussians_WGAN-GP.npz", G)
D = Discriminator(non_linear=F.leaky_relu, final=F.identity)
serializers.load_npz("trained_models/D_25gaussians_WGAN-GP.npz", D)
if gpu_device==0:
G.to_gpu()
D.to_gpu()
X_train = prepare_25gaussian_data(BATCH_SIZE=1000)
lcs = []
for i in range(10):
lcs.append(DOT.eff_K(G, D, 100).tolist())
K = xp.mean(xp.array(lcs))
K
Zy = G.make_hidden(1000)
y_xp = G(Zy).data
Opt = chainer.optimizers.Adam(0.01, beta1=0., beta2=0.9)
T = DOT.Transporter_in_target(G, D, K, Opt, y_xp, mode='dot')
DOT.discriminator_optimal_transport_from(y_xp, T, 100)
x_va = T.get_x_va().data
Opt = chainer.optimizers.Adam(0.01, beta1=0., beta2=0.9)
T = DOT.Transporter_in_target(G, D, K, Opt, y_xp, mode='naive')
DOT.discriminator_optimal_transport_from(y_xp, T, 100)
x_va2 = T.get_x_va().data
if gpu_device==0:
y_xp = cuda.to_cpu(y_xp)
x_va = cuda.to_cpu(x_va)
x_va2 = cuda.to_cpu(x_va2)
show_three_figures(y_xp, x_va, x_va2, X_train, -2,2,-2,2)
```
# Swissroll
```
G = Generator(n_hidden=2, noize='uni', non_linear=F.leaky_relu, final=F.identity)
serializers.load_npz("trained_models/G_swissroll_WGAN-GP.npz", G)
D = Discriminator(non_linear=F.leaky_relu, final=F.identity)
serializers.load_npz("trained_models/D_swissroll_WGAN-GP.npz", D)
if gpu_device==0:
G.to_gpu()
D.to_gpu()
X_train = prepare_swissroll_data(BATCH_SIZE=1000)
lcs = []
for i in range(10):
lcs.append(DOT.eff_K(G, D, 100).tolist())
K = xp.mean(xp.array(lcs))
K
Zy = G.make_hidden(1000)
y_xp = G(Zy).data
Opt = chainer.optimizers.Adam(0.01, beta1=0., beta2=0.9)
T = DOT.Transporter_in_target(G, D, K, Opt, y_xp, mode='dot')
DOT.discriminator_optimal_transport_from(y_xp, T, 100)
x_va = T.get_x_va().data
Opt = chainer.optimizers.Adam(0.01, beta1=0., beta2=0.9)
T = DOT.Transporter_in_target(G, D, K, Opt, y_xp, mode='naive')
DOT.discriminator_optimal_transport_from(y_xp, T, 100)
x_va2 = T.get_x_va().data
if gpu_device==0:
y_xp = cuda.to_cpu(y_xp)
x_va = cuda.to_cpu(x_va)
x_va2 = cuda.to_cpu(x_va2)
show_three_figures(y_xp, x_va, x_va2, X_train, -2,2.5,-2,2.5)
```
| true |
code
| 0.587707 | null | null | null | null |
|
```
import sys
sys.path.append('../../pyutils')
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import metrics
import utils
```
# Bernoulli Distribution
$$X \sim B(p)$$
$X$ is a single binary random variable.
Parameters:
- $p \in [0, 1]$: probability that X takes the value $1$
$$P(X=0) = 1-p$$
$$P(X=1) = p$$
$$P(X=x) = p^x(1-p)^{1-x}$$
$$\mathbb{E}[X] = p$$
$$\text{Var}(x) = p(1 - p)$$
```
N = 1000000
p = 0.4
x = (np.random.rand(N) < p).astype(np.int)
print('E[X]:', np.mean(x))
print('Var[X]:', np.var(x), p * (1-p))
```
# Binomial distribution
$$X \sim B(n, p)$$
$X$ is a single discrete value, corresponding to the number of successes when repeating $n$ independant Binomial experiments.
Parameters:
- $n$: number of trials
- $p \in [0, 1]$: success probability for each trial.
$p(X = k)$: $k$: number of successes.
$$\text{PMF: } f(k) = \binom{n}{k} p^k(1-p)^{n-k}$$
$$\mathbb{E}[X] = np$$
$$\text{Var}(X) = np(1 - p)$$
$$\binom{n}{k} = \frac{n!}{k!(n-k)!}$$
```
def rand_binomial(n, p):
data = (np.random.rand(n) < p).astype(np.int)
return np.sum(data)
N = 1000000
n = 7
p = 0.4
x = np.array([rand_binomial(n,p) for _ in range(N)])
print('E[X]:', np.mean(x), n*p)
print('Var[X]:', np.var(x), n*p * (1-p))
```
# Multinoulli (Categorical) Distribution
$X$ is a single discrete random variable with $k$ different states.
Parameters:
- $p_i$: probability that $x$ takes the value $i$: $\sum p_i = 1$, $p_i >= 0$
$$p(X=i) = p_i$$
# Multinomial distribution
$X$ is a discrete vector of size $k$, corresponding to the number of times each states it obtained when repeating $n$ independant Multinoulli experiments.
Parameters:
- $n$: number of trials
- $p_i$: probability of event $i$: $\sum p_i = 1$, $p_i >= 0$
$X$ discrete vector of size $K$: $X_i$: number of realisations of the event $i$.
$$\text{PMF: } f(x) = \binom{n}{x_1\text{...} x_k} \prod_{i=1}^K p_i^{x_i}$$
$$\mathbb{E}[X_i] = np_i$$
$$\text{Var}(X_i) = np_i(1 - p_i)$$
$$\text{Cov}(X_i, X_j) = -np_ip_j \space (i \neq j)$$
$$\binom{n}{k_1 \text{...} k_m}= \frac{n!}{\prod_{i=1}^m k_i!}$$
```
def rand_multinomial(p):
s = 0
p2 = np.empty(len(p))
for i in range(len(p)-1):
s += p[i]
p2[i] = s
p2[-1] = 1
u = np.random.rand()
k = 0
while u > p2[k]:
k += 1
return k
N = 1000000
x = np.empty(N).astype(np.int)
p = [0.1, 0.6, 0.3]
for i in range(N):
x[i] = rand_multinomial(p)
print('p[0]:', np.mean(x==0))
print('p[1]:', np.mean(x==1))
print('p[2]:', np.mean(x==2))
```
# Normal (Gaussian) distribution
$$X \sim \mathcal{N}(\mu, \sigma^2)$$
Parameters:
- $\mu$: mean
- $\sigma^2 \geq 0$: variance
$$\text{PDF: } f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \text{exp}(-\frac{(x - \mu)^2}{2\sigma^2})$$
$$\text{CDF: } F(x) = \frac{1}{2}[1 + \text{erf}(\frac{x - \mu}{\sigma \sqrt{2}})]$$
$$\mathbb{E}[X] = \mu$$
$$\text{Var}(X) = \sigma^2$$
$$ \text{erf}(x) = \frac{1}{\sqrt{\pi}} \int_{-x}^{x} e^{-t^2}dt$$
```
def normal_pdf(mu, v, x):
den = np.sqrt(2 * np.pi * v)
num = - (x - mu)**2 / (2*v)
return np.exp(num) / den
x = np.linspace(-3, 3, 1000)
plt.plot(x, normal_pdf(0, 0.5, x), c='r', label='N(0, 0.5)')
plt.plot(x, normal_pdf(0, 1, x), c='b', label='N(0, 1)')
plt.plot(x, normal_pdf(0, 1.5, x), c='y', label='N(0, 1,5)')
plt.plot(x, normal_pdf(2, 1, x), c='c', label='N(2, 1)')
plt.legend()
plt.show()
_box_muller = [None]
def norm_box_muller():
if _box_muller[0] is not None:
res = _box_muller[0]
_box_muller[0] = None
return res
u1, u2 = np.random.rand(2)
r = np.sqrt(-2*np.log(u1))
theta = 2*np.pi*u2
x = r * np.cos(theta)
y = r * np.sin(theta)
_box_muller[0] = x
return y
_marsagalia_polar = [None]
def norm_marsagalia_polar():
if _marsagalia_polar[0] is not None:
res = _marsagalia_polar[0]
_marsagalia_polar[0] = None
return res
while True:
x, y = 2 * np.random.rand(2) - 1
s = x**2 + y**2
if s < 1 and s>0:
break
f = np.sqrt((-2*np.log(s))/s)
a, b = x*f, y*f
_marsagalia_polar[0] = a
return b
N = 1000000
print('mu =', -1.3)
print('std =', 4.5)
x = np.random.randn(N) * 4.5 - 1.3
print('[NP] mu =', np.mean(x))
print('[NP] std =', np.std(x))
x = np.empty(N)
for i in range(N): x[i] = 4.5 * norm_box_muller() - 1.3
print('[BM] mu =', np.mean(x))
print('[BM] std =', np.std(x))
x = np.empty(N)
for i in range(N): x[i] = 4.5 * norm_marsagalia_polar() - 1.3
print('[MP] mu =', np.mean(x))
print('[MP] std =', np.std(x))
#Generate from gaussian using quantile function
import scipy.stats
def norm_cdf(x):
return 1/2 * (1 + scipy.special.erf(x / np.sqrt(2)))
def norm_quantile(x):
def f(v):
return norm_cdf(v) - x
return scipy.optimize.brentq(f, -10, 10)
def randn_qt(size):
u = np.random.rand(size)
x = np.array([norm_quantile(v) for v in u])
return x
v = 0.6
b1 = scipy.stats.norm.ppf(v)
b2 = norm_quantile(v)
print(b1)
print(b2)
print(metrics.tdist(b1, b2))
x = randn_qt(100000) * 4.5 - 1.3
print('[QT] mu =', np.mean(x))
print('[QT] std =', np.std(x))
```
# Multivariate Normal distribution
$$X \sim \mathcal{N}(\mu, \Sigma)$$
Parameters:
- $\mu \in \mathbb{R}^p$: mean
- $\Sigma \in \mathbb{R}^{p*p}$: covariance matrix (positive semi-definite)
$$\text{PDF: } f(x) = ((2\pi)^{p} \text{det}(\Sigma))^{-\frac{1}{2}} \exp(-\frac{1}{2} (x - \mu)^T \Sigma^{-1}(x-\mu))$$
$$\mathbb{E}[X] = \mu$$
$$\text{Var}(X) = \Sigma$$
```
rmu = np.array([0.5, -1.2, 4.6])
rsig = np.array([[0.4, 1.2, -1.8],[2.5,-2.8,-1.9],[-1.4,6.7,2.5]])
rsig = rsig.T @ rsig
N = 1000000
print('mu =', rmu)
print('sig=')
print(rsig)
X = np.random.multivariate_normal(rmu, rsig, size=N, check_valid='raise')
mu = np.mean(X, axis=0)
sig = 1/N * (X - mu.reshape(1,3)).T @ (X - mu.reshape(1,3))
print('[NP] mu =', mu)
print('[NP] sig=')
print(sig)
def normal_multivariate(mu, sig, size):
N = size
p = len(mu)
X = np.empty((N,p))
d, V = np.linalg.eig(sig)
Q = np.sqrt(d).reshape(1,p) * V
for i in range(N):
xn = np.random.randn(p)
X[i] = Q @ xn + mu
return X
X = normal_multivariate(rmu, rsig, size=N)
mu = np.mean(X, axis=0)
sig = 1/N * (X - mu.reshape(1,3)).T @ (X - mu.reshape(1,3))
print('mu =', mu)
print('sig=')
print(sig)
```
# Exponential distribution
X is a positive continuous variable with a sharp peak at $0$
Parameters:
- $\lambda \in \mathbb{R}$, $\lambda > 0$: rate or inverse scale
$$X \in [0, \infty[$$
$$\text{PDF: } f(x) = \lambda \exp(- \lambda x)$$
$$\text{CDF: } F(x) = 1 - \exp(- \lambda x)$$
$$\mathbb{E}[x] = \lambda^{-1}$$
$$\text{Var}(x) = \lambda^{-2}$$
```
def exponential_pdf(lbda, x):
return lbda * np.exp(-lbda * x)
x = np.linspace(0, 5, 1000)
plt.plot(x, exponential_pdf(.5, x), c='r', label='lambda = .5')
plt.plot(x, exponential_pdf(1, x), c='b', label='lambda = 1')
plt.plot(x, exponential_pdf(1.5, x), c='y', label='lambda = 1.5')
plt.legend()
plt.show()
```
# Laplace Distribution
$$X \sim \text{Laplace}(\mu;\gamma)$$
X is a continous variabe with a shark peak at $\mu$
Parameters:
- $\mu \in \mathbb{R}$: mean
- $\gamma \in \mathbb{R}$, $\gamma > 0$: scale
$$\text{PDF: } f(x) = \frac{1}{2 \gamma} \exp(-\frac{|x - \mu|}{\gamma})$$
$$\mathbb{E}[X] = \mu$$
$$\text{Var}(X) = 2\gamma^2$$
```
def laplace_pdf(mu, b, x):
den = 2 * b
num = - np.abs(x - mu) / b
return np.exp(num) / den
x = np.linspace(-3, 3, 1000)
plt.plot(x, laplace_pdf(0, 0.5, x), c='r', label='Laplace(0, 0.5)')
plt.plot(x, laplace_pdf(0, 1, x), c='b', label='Laplace(0, 1)')
plt.plot(x, laplace_pdf(0, 1.5, x), c='y', label='Laplace(0, 1,5)')
plt.plot(x, laplace_pdf(2, 1, x), c='c', label='Laplace(2, 1)')
plt.legend()
plt.show()
```
# Dirac Distribution
$X$ is a continous variable with a infitenely high peak at $\mu$, and $0$ everywhere.
Parameters:
- $\mu \in \mathbb{R}$: mean
$$\text{PDF}: f(x) = \delta(x - \mu)$$
with $\delta(x)$ the Dirac delta function, a function that is zero-valued everywhere except at $0$, and yet integrates to $1$.
# Empirical distribution
X define an empirical distribution of size $m$ (eg: dataset) over countinous variables
Parameters:
- datset $\{ x_1, \text{...}, x_m \}$
$$\text{PDF} f(x) = \frac{1}{m} \sum_{i=1}^m \delta(x - x_i)$$
The empirical distribution is the distribution when we sample data from a dataset.
This is the probability density that maximizes the likelihood of the training data.
# Beta distribution
$$X \sim \text{Beta}(\alpha, \beta)$$
Parameters:
- $\alpha \in \mathbb{R} > 0$
- $\beta \in \mathbb{R} > 0$
The parameter $x \in \mathbb{R}$ must bet in $[0,1]$
$$\text{PDF: } f(x) = \frac{x^{\alpha-1} (1-x)^{\beta - 1}}{B(\alpha,\beta)}$$
$$\text{where } B(\alpha,\beta) = \frac{\Gamma (\alpha) \Gamma(\beta)}{\Gamma (\alpha + \beta)}$$
$$\text{where } \Gamma(z) = \int_{0}^{+\infty} x^{z-1} e^{-x}dx$$
$$E[X] = \frac{\alpha}{\alpha + \beta}$$
$$\text{Var}(X) = \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$$
The beta distribution is the conjugate prior probability distribution of the bernoulli, bonomial, and geometric distributions.
It is usually used to describe prior knowledge concerning the probability of success of an event.
# Dirichlet distribution
$$X \sim \text{Dir}(\alpha)$$
Parameters:
$\alpha \in \mathbb{R}^K$, $K \geq 2$, $\alpha_k > 0$
Input: $x \in \mathbb{R}^K$, with $x_k \in [0,1]$, and $\sum_{k=1}^Kx_k=1$
$$\text{PDF: } \frac{1}{B(\alpha)} \prod_{i=1}^K x_i^{\alpha_i-1}$$
$$\text{where } B(\alpha) = \frac{\prod_{i=1}^K \Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^K\alpha_i)}$$
$$E[X_i] = \frac{\alpha_i}{\sum_{k=1}^K \alpha_k}$$
$$\text{Var}(X_i) = \frac{\alpha_i(\alpha_0 - \alpha_i)}{\alpha_0^2(\alpha_0 + 1)}$$
$$\text{where } \alpha_0 = \sum_{i=1}^K \alpha_i$$
The dirichlet distribution is a multivariate generalization of the beta distribution.
It's the conjugate prior probability distribution of the categorical and polynomial distribution.
# Mixture of distributions
A mixture distribution is made up of several components distributions.
On each trial, the choice of which component distribution generates the sample is determined by a multinoulli distribution:
$$P(x) = \sum_i P(c=i) P(x|c=i)$$
with $P(c)$ the multinoulli distribution, and $P(x|c=i)$ the PDF of the $i$-th component distribution.
$c$ is a latent variable.
A common type on mixture models is the Gaussian mixture, where each component is a multivariate normal distribution.
Each component may have a separate $\mu^{(i)}$ and $\Sigma^{(i)}$, or they may have some constraints (eg sharing, special form of covariance).
A gaussian mixture model is a universal approximator of disenties, given enough components.
```
def rand_gauss_mixture(means, stds, p):
c = np.random.choice(len(p), p=p)
x = np.random.randn() * stds[c] + means[c]
return x
means = np.array([-1, 1, 1])
stds = np.array([0.8, 1.3, 1.1])
p = np.array([0.4, 0.35, 0.25])
N = 100000
x = np.array([rand_gauss_mixture(means, stds, p) for _ in range(N)])
print('mu =', np.mean(x), means @ p)
print('std =', np.std(x), stds @ np.sqrt(p * (1-p)))
```
| true |
code
| 0.388618 | null | null | null | null |
|
### Gluon Implementation in Recurrent Neural Networks
```
import sys
sys.path.insert(0, '..')
import d2l
import math
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import loss as gloss, nn, rnn
import time
(corpus_indices, char_to_idx, idx_to_char,
vocab_size) = d2l.load_data_time_machine()
```
### Define the Model
```
num_hiddens = 256
rnn_layer = rnn.RNN(num_hiddens)
rnn_layer.initialize()
```
Then, we call the `rnn_layer`'s member function `begin_state` to return hidden state list for initialization. It has an element of the shape (number of hidden layers, batch size, number of hidden units).
```
batch_size = 2
state = rnn_layer.begin_state(batch_size=batch_size)
state[0].shape
```
### RNN Layer in Action
```
num_steps = 35
X = nd.random.uniform(shape=(num_steps, batch_size, vocab_size))
Y, state_new = rnn_layer(X, state)
print(X.shape, len(state), state[0].shape)
print(Y.shape, len(state_new), state_new[0].shape)
```
### RNN Block
```
# This class has been saved in the d2l package for future use.
class RNNModel(nn.Block):
def __init__(self, rnn_layer, vocab_size, **kwargs):
super(RNNModel, self).__init__(**kwargs)
self.rnn = rnn_layer
self.vocab_size = vocab_size
self.dense = nn.Dense(vocab_size)
def forward(self, inputs, state):
# Get the one-hot vector representation by transposing the input
# to (num_steps, batch_size).
X = nd.one_hot(inputs.T, self.vocab_size)
Y, state = self.rnn(X, state)
# The fully connected layer will first change the shape of Y to
# (num_steps * batch_size, num_hiddens).
# Its output shape is (num_steps * batch_size, vocab_size).
output = self.dense(Y.reshape((-1, Y.shape[-1])))
return output, state
def begin_state(self, *args, **kwargs):
return self.rnn.begin_state(*args, **kwargs)
```
### Prediction
```
def predict_rnn_gluon(prefix, num_chars, model, vocab_size, ctx, idx_to_char, char_to_idx):
# Use model's member function to initialize the hidden state.
state = model.begin_state(batch_size=1, ctx=ctx)
output = [char_to_idx[prefix[0]]]
for t in range(num_chars + len(prefix) - 1):
X = nd.array([output[-1]], ctx=ctx).reshape((1, 1))
(Y, state) = model(X, state)
# Forward computation does not require incoming model parameters.
if t < len(prefix) - 1:
output.append(char_to_idx[prefix[t + 1]])
else:
output.append(int(Y.argmax(axis=1).asscalar()))
return ''.join([idx_to_char[i] for i in output])
```
### Prediction with Garbage Parameters
```
ctx = d2l.try_gpu()
model = RNNModel(rnn_layer, vocab_size)
model.initialize(force_reinit=True, ctx=ctx)
predict_rnn_gluon('traveller', 10, model, vocab_size, ctx, idx_to_char,
char_to_idx)
```
Next, implement the training function. Its algorithm is the same as in the previous section, but only random sampling is used here to read the data.
```
# This function is saved in the d2l package for future use.
def train_and_predict_rnn_gluon(model, num_hiddens, vocab_size, ctx,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes):
loss = gloss.SoftmaxCrossEntropyLoss()
model.initialize(ctx=ctx, force_reinit=True, init=init.Normal(0.01))
trainer = gluon.Trainer(model.collect_params(), 'sgd',
{'learning_rate': lr, 'momentum': 0, 'wd': 0})
for epoch in range(num_epochs):
l_sum, n, start = 0.0, 0, time.time()
data_iter = d2l.data_iter_consecutive(
corpus_indices, batch_size, num_steps, ctx)
state = model.begin_state(batch_size=batch_size, ctx=ctx)
for X, Y in data_iter:
for s in state:
s.detach()
with autograd.record():
(output, state) = model(X, state)
y = Y.T.reshape((-1,))
l = loss(output, y).mean()
l.backward()
# Clip the gradient.
params = [p.data() for p in model.collect_params().values()]
d2l.grad_clipping(params, clipping_theta, ctx)
# Since the error has already taken the mean, the gradient does
# not need to be averaged.
trainer.step(1)
l_sum += l.asscalar() * y.size
n += y.size
if (epoch + 1) % pred_period == 0:
print('epoch %d, perplexity %f, time %.2f sec' % (
epoch + 1, math.exp(l_sum / n), time.time() - start))
for prefix in prefixes:
print(' -', predict_rnn_gluon(
prefix, pred_len, model, vocab_size, ctx, idx_to_char,
char_to_idx))
```
Train the model using the same hyper-parameters as previously.
```
num_epochs, batch_size, lr, clipping_theta = 200, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 50, 50, ['traveller', 'time traveller']
train_and_predict_rnn_gluon(model, num_hiddens, vocab_size, ctx,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)
```
| true |
code
| 0.696887 | null | null | null | null |
|
# bqplot https://github.com/bloomberg/bqplot
## A Jupyter - d3.js bridge
bqplot is a jupyter interactive widget library bringing d3.js visualization to the Jupyter notebook.
- Apache Licensed
bqplot implements the abstractions of Wilkinson’s “The Grammar of Graphics” as interactive Jupyter widgets.
bqplot provides both
- high-level plotting procedures with relevant defaults for common chart types,
- lower-level descriptions of data visualizations meant for complex interactive visualization dashboards and applications involving mouse interactions and user-provided Python callbacks.
**Installation:**
```bash
conda install -c conda-forge bqplot
```
```
from __future__ import print_function
from IPython.display import display
from ipywidgets import *
from traitlets import *
import numpy as np
import pandas as pd
import bqplot as bq
import datetime as dt
np.random.seed(0)
size = 100
y_data = np.cumsum(np.random.randn(size) * 100.0)
y_data_2 = np.cumsum(np.random.randn(size))
y_data_3 = np.cumsum(np.random.randn(size) * 100.)
x = np.linspace(0.0, 10.0, size)
price_data = pd.DataFrame(np.cumsum(np.random.randn(150, 2).dot([[0.5, 0.8], [0.8, 1.0]]), axis=0) + 100,
columns=['Security 1', 'Security 2'],
index=pd.date_range(start='01-01-2007', periods=150))
symbol = 'Security 1'
dates_all = price_data.index.values
final_prices = price_data[symbol].values.flatten()
```
# A simple plot with the pyplot API
```
from bqplot import pyplot as plt
plt.figure(1)
n = 100
plt.plot(np.linspace(0.0, 10.0, n), np.cumsum(np.random.randn(n)),
axes_options={'y': {'grid_lines': 'dashed'}})
plt.show()
```
### Scatter Plot
```
plt.figure(title='Scatter Plot with colors')
plt.scatter(y_data_2, y_data_3, color=y_data)
plt.show()
```
### Histogram
```
plt.figure()
plt.hist(y_data, colors=['OrangeRed'])
plt.show()
```
# Every component of the figure is an independent widget
```
xs = bq.LinearScale()
ys = bq.LinearScale()
x = np.arange(100)
y = np.cumsum(np.random.randn(2, 100), axis=1) #two random walks
line = bq.Lines(x=x, y=y, scales={'x': xs, 'y': ys}, colors=['red', 'green'])
xax = bq.Axis(scale=xs, label='x', grid_lines='solid')
yax = bq.Axis(scale=ys, orientation='vertical', tick_format='0.2f', label='y', grid_lines='solid')
fig = bq.Figure(marks=[line], axes=[xax, yax], animation_duration=1000)
display(fig)
# update data of the line mark
line.y = np.cumsum(np.random.randn(2, 100), axis=1)
xs = bq.LinearScale()
ys = bq.LinearScale()
x, y = np.random.rand(2, 20)
scatt = bq.Scatter(x=x, y=y, scales={'x': xs, 'y': ys}, default_colors=['blue'])
xax = bq.Axis(scale=xs, label='x', grid_lines='solid')
yax = bq.Axis(scale=ys, orientation='vertical', tick_format='0.2f', label='y', grid_lines='solid')
fig = bq.Figure(marks=[scatt], axes=[xax, yax], animation_duration=1000)
display(fig)
#data updates
scatt.x = np.random.rand(20) * 10
scatt.y = np.random.rand(20)
```
## The same holds for the attributes of scales, axes
```
xs.min = 4
xs.min = None
xax.label = 'Some label for the x axis'
```
## Use bqplot figures as input widgets
```
xs = bq.LinearScale()
ys = bq.LinearScale()
x = np.arange(100)
y = np.cumsum(np.random.randn(2, 100), axis=1) #two random walks
line = bq.Lines(x=x, y=y, scales={'x': xs, 'y': ys}, colors=['red', 'green'])
xax = bq.Axis(scale=xs, label='x', grid_lines='solid')
yax = bq.Axis(scale=ys, orientation='vertical', tick_format='0.2f', label='y', grid_lines='solid')
```
## Selections
```
def interval_change_callback(change):
db.value = str(change['new'])
intsel = bq.interacts.FastIntervalSelector(scale=xs, marks=[line])
intsel.observe(interval_change_callback, names=['selected'] )
db = widgets.Label()
db.value = str(intsel.selected)
display(db)
fig = bq.Figure(marks=[line], axes=[xax, yax], animation_duration=1000, interaction=intsel)
display(fig)
line.selected
```
# Handdraw
```
handdraw = bq.interacts.HandDraw(lines=line)
fig.interaction = handdraw
line.y[0]
```
# Moving points around
```
from bqplot import *
size = 100
np.random.seed(0)
x_data = range(size)
y_data = np.cumsum(np.random.randn(size) * 100.0)
## Enabling moving of points in scatter. Try to click and drag any of the points in the scatter and
## notice the line representing the mean of the data update
sc_x = LinearScale()
sc_y = LinearScale()
scat = Scatter(x=x_data[:10], y=y_data[:10], scales={'x': sc_x, 'y': sc_y}, default_colors=['blue'],
enable_move=True)
lin = Lines(scales={'x': sc_x, 'y': sc_y}, stroke_width=4, line_style='dashed', colors=['orange'])
m = Label(value='Mean is %s'%np.mean(scat.y))
def update_line(change):
with lin.hold_sync():
lin.x = [np.min(scat.x), np.max(scat.x)]
lin.y = [np.mean(scat.y), np.mean(scat.y)]
m.value='Mean is %s'%np.mean(scat.y)
update_line(None)
# update line on change of x or y of scatter
scat.observe(update_line, names='x')
scat.observe(update_line, names='y')
ax_x = Axis(scale=sc_x)
ax_y = Axis(scale=sc_y, tick_format='0.2f', orientation='vertical')
fig = Figure(marks=[scat, lin], axes=[ax_x, ax_y])
## In this case on drag, the line updates as you move the points.
with scat.hold_sync():
scat.enable_move = True
scat.update_on_move = True
scat.enable_add = False
display(m, fig)
```
| true |
code
| 0.759844 | null | null | null | null |
|
# Stochastic gradient descent (SGD)
SGD is an incremental gradient descent algorithm which modifies its weights, in an effort to reach a local minimum.
The cuML implementation takes only numpy arrays and cuDF datasets as inputs.
- In order to convert your dataset into a cuDF dataframe format please refer the [cuDF documentation](https://rapidsai.github.io/projects/cudf/en/latest/)
The SGD algorithm implemented in cuML can accept the following parameters:
1. `loss` : 'hinge', 'log', 'squared_loss' (default = 'squared_loss')
2. `penalty`: 'none', 'l1', 'l2', 'elasticnet' (default = 'none')
3. `alpha`: float (default = 0.0001)
4. `fit_intercept` : boolean (default = True)
5. `epochs` : int (default = 1000)
6. `tol` : float (default = 1e-3)
7. `shuffle` : boolean (default = True)
8. `eta0` : float (default = 0.0)
9. `power_t` : float (default = 0.5)
10. `learning_rate` : 'optimal', 'constant', 'invscaling', 'adaptive' (default = 'constant')
11. `n_iter_no_change` : int (default = 5)
For additional information on the SGD model please refer to the [cuML documentation](https://rapidsai.github.io/projects/cuml/en/latest/index.html)
- this setup may take a few minutes
- long output (output display removed)
```
!wget -nc https://github.com/rapidsai/notebooks-extended/raw/master/utils/rapids-colab.sh
!bash rapids-colab.sh
import sys, os
sys.path.append('/usr/local/lib/python3.6/site-packages/')
os.environ['NUMBAPRO_NVVM'] = '/usr/local/cuda/nvvm/lib64/libnvvm.so'
os.environ['NUMBAPRO_LIBDEVICE'] = '/usr/local/cuda/nvvm/libdevice/'
```
### Imports
```
import numpy as np
import pandas as pd
import cudf
from cuml.solvers import SGD as cumlSGD
from sklearn.linear_model import SGDRegressor
```
# Helper Functions
```
# check if the mortgage dataset is present and then extract the data from it, else just create a random dataset for sgd
import gzip
# change the path of the mortgage dataset if you have saved it in a different directory
def load_data(nrows, ncols, cached = 'data/mortgage.npy.gz'):
if os.path.exists(cached):
print('use mortgage data')
with gzip.open(cached) as f:
X = np.load(f)
# the 4th column is 'adj_remaining_months_to_maturity'
# used as the label
X = X[:,[i for i in range(X.shape[1]) if i!=4]]
y = X[:,4:5]
rindices = np.random.randint(0,X.shape[0]-1,nrows)
X = X[rindices,:ncols]
y = y[rindices]
else:
# create a random dataset
print('use random data')
X = np.random.rand(nrows,ncols)
y = np.random.randint(0,10,size=(nrows,1))
train_rows = int(nrows*0.8)
df_X_train = pd.DataFrame({'fea%d'%i:X[0:train_rows,i] for i in range(X.shape[1])})
df_X_test = pd.DataFrame({'fea%d'%i:X[train_rows:,i] for i in range(X.shape[1])})
df_y_train = pd.DataFrame({'fea%d'%i:y[0:train_rows,i] for i in range(y.shape[1])})
df_y_test = pd.DataFrame({'fea%d'%i:y[train_rows:,i] for i in range(y.shape[1])})
return df_X_train, df_X_test, df_y_train, df_y_test
# this function checks if the results obtained from two different methods (sklearn and cuml) are the same
from sklearn.metrics import mean_squared_error
def array_equal(a,b,threshold=2e-3,with_sign=True):
a = to_nparray(a).ravel()
b = to_nparray(b).ravel()
if with_sign == False:
a,b = np.abs(a),np.abs(b)
error = mean_squared_error(a,b)
res = error<threshold
return res
# the function converts a variable from ndarray or dataframe format to numpy array
def to_nparray(x):
if isinstance(x,np.ndarray) or isinstance(x,pd.DataFrame):
return np.array(x)
elif isinstance(x,np.float64):
return np.array([x])
elif isinstance(x,cudf.DataFrame) or isinstance(x,cudf.Series):
return x.to_pandas().values
return x
```
# Run tests
```
%%time
# nrows = number of samples
# ncols = number of features of each sample
nrows = 2**20
ncols = 399
# dataset is split into a ratio of 80:20,
# 80% is used as the training data and the remaining 20% is used as the test data
X_train, X_test, y_train, y_test = load_data(nrows,ncols)
y_train_ser = y_train['fea0']
print('training data',X_train.shape)
print('training label',y_train.shape)
print('testing data',X_test.shape)
print('testing label',y_test.shape)
```
Here we set the parameters usedby both libraries. You can change the number of iterations used by changing the `iterations` variable. Please note that making this too high can cause the functions to take a long time to complete.
```
#set parameters
learning_rate = 'adaptive'
datatype = np.float32
penalty = 'elasticnet'
loss = 'squared_loss'
iterations = 10
```
The `max_iter` parameter controls the maxixmum number of iterations the model can run for but it doesn’t guarantee that the model will definitely run for all those epochs, therefore the sklearn might run for less number of epochs than the cuML model
```
%%time
# use the sklearn SGD Regressor model to fit the dataset
sk_sgd = SGDRegressor(learning_rate=learning_rate, eta0=0.07,
max_iter=iterations, tol=0.0, fit_intercept=True,
penalty=penalty, loss=loss)
sk_sgd.fit(X_train, y_train_ser)
%%time
# test the model by predicting its results for the unseen test set
y_sk = sk_sgd.predict(X_test)
# calculate the Mean Squared Error for the model's predictions
error_sk = mean_squared_error(y_test,y_sk)
%%time
# convert the pandas dataframe to cuDF dataframe and series
X_cudf = cudf.DataFrame.from_pandas(X_train)
X_cudf_test = cudf.DataFrame.from_pandas(X_test)
y_cudf = cudf.Series(y_train_ser)
%%time
# fit the training data on cuML's implementation of SGD
cu_sgd = cumlSGD(learning_rate=learning_rate, eta0=0.07, epochs=iterations, #epochs == n_iter
batch_size=512,
tol=0.0, penalty=penalty, loss=loss)
cu_sgd.fit(X_cudf, y_cudf)
%%time
# test the model by predicting its values for the test set
y_pred = cu_sgd.predict(X_cudf_test)
y_pred = to_nparray(y_pred).ravel()
# calculate the Mean Squared Error for the model's predictions
error_cu = mean_squared_error(y_test,y_pred)
# print the MSE of the sklearn and cuML models to compare them
print("SKL MSE(y):")
print(error_sk)
print("CUML MSE(y):")
print(error_cu)
```
| true |
code
| 0.479626 | null | null | null | null |
|
# Unit 4: Neighborhood-based Collaborative Filtering for Rating Prediction
In this section we generate personalized recommendations for the first time. We exploit rating similarities among users and items to identify similar users and items that assist in finding the relevant items to recommend for each user.
This describes the fundamental idea behind Collaborative Filtering (CF) and using kNN is a neighborhood-based approach towards CF. In a later unit we will also have a look at model-based approaches.
This is also the first time we try to predict user ratings for unknown items using rating predictions to take the top-$N$ items with the highest rating predictions and recommend those to the user.
```
from collections import OrderedDict
import itertools
from typing import Dict, List, Tuple
import numpy as np
import pandas as pd
from recsys_training.data import Dataset
from recsys_training.evaluation import get_relevant_items
from recsys_training.utils import get_entity_sim
ml100k_ratings_filepath = '../../data/raw/ml-100k/u.data'
```
## Load Data
```
data = Dataset(ml100k_ratings_filepath)
data.rating_split(seed=42)
user_ratings = data.get_user_ratings()
```
The idea behind this recommender is to use item ratings of the $k$ most similar users (neighbors). We identify those _nearest neighbors_ with a similarity metric which we apply to the ratings both, root user and possible neighbor, have in common. Similarity thereby means having a similar opinion on movies.
The steps are as follows:
1. Compute user-user similarities (we use the Pearson Correlation Coefficient here, but feel free to try other similarity metrics)
2. For each user:
1. Get the k nearest neighbors along with their similarities
2. Collect the neighborhood item ratings and ignore those already rated by the root user
3. Item Rating Prediction: Compute the similarity-weighted sum of neighborhood item ratings
4. Recommendations: Get the $N$ items with the highest ratings that have a minimum rating count
### 1. User-User Similarities
```
sim_metric = 'pearson'
user_user_sims = {}
user_pairs = itertools.combinations(data.users, 2)
```
The following takes a few seconds to finish ...
```
for pair in user_pairs:
user_user_sims[pair] = get_entity_sim(pair[0], pair[1],
user_ratings,
sim_metric)
user_user_sims[(1,4)]
```
## 2. Computing Recommendations
### A. Implement Nearest Neighbors for a given user

**Task:** It's your turn again. Complete `get_k_nearest_neighbors` to return a sorted list of the $k$ nearest neighbors - identified by their id - for a given user, each along with its similarity.
```
def get_k_nearest_neighbors(user: int, k: int, user_user_sims: dict) -> List[Tuple[int, float]]:
neighbors = set(data.users)
neighbors.remove(user)
nearest_neighbors = dict()
for neighbor in neighbors:
sim = user_user_sims[tuple(sorted((user, neighbor)))][0]
if pd.notnull(sim):
nearest_neighbors[neighbor] = sim
nearest_neighbors = sorted(nearest_neighbors.items(),
key=lambda kv: kv[1],
reverse=True)
return nearest_neighbors[:k]
user_neighbors = get_k_nearest_neighbors(1, k=10, user_user_sims=user_user_sims)
user_neighbors
```
### B. Obtain the Neighborhood Ratings
**Task:** Now, use the nearest neighbors and get their ratings, but leave out the items our root user has already rated (known positives). Return a mapping from unknown item to a list of dicts with neighbor similarity and item rating.
```
def get_neighborhood_ratings(user, user_neighbors: List[Tuple[int, float]]) -> Dict[int, List[Dict[str, float]]]:
neighborhood_ratings = {}
for neighbor, sim in user_neighbors:
neighbor_ratings = user_ratings[neighbor].copy()
# collect neighbor ratings and items
for item, rating in neighbor_ratings.items():
add_item = {'sim': sim, 'rating': rating}
if item not in neighborhood_ratings.keys():
neighborhood_ratings[item] = [add_item]
else:
neighborhood_ratings[item].append(add_item)
# remove known items
known_items = list(user_ratings[user].keys())
for known_item in known_items:
neighborhood_ratings.pop(known_item, None)
return neighborhood_ratings
neighborhood_ratings = get_neighborhood_ratings(1, user_neighbors)
list(neighborhood_ratings.items())[:10]
```
### C. Compute Rating Predictions from Neighborhood Ratings

**Task:** In this step, we estimate ratings for the seed user based on the neighborhood ratings. We implement a similarity weighted average of neighbor ratings for that. Return a mapping from item to its prediction and the count of neighbor ratings received.
```
def compute_rating_pred(neighborhood_ratings: dict) -> dict:
rating_preds = dict()
for item, ratings in neighborhood_ratings.items():
if len(ratings) > 0:
sims = np.array([rating['sim'] for rating in ratings])
ratings = np.array([rating['rating'] for rating in ratings])
pred_rating = (sims * ratings).sum() / sims.sum()
count = len(sims)
rating_preds[item] = {'pred': pred_rating,
'count': count}
else:
rating_preds[item] = {'pred': None, 'count': 0}
return rating_preds
rating_preds = compute_rating_pred(neighborhood_ratings)
list(rating_preds.items())[:20]
```
### D. Compute the Top-$N$ Recommendation Items

**Task:** The last step takes the rating predictions and returns the $N$ highest predictions which have a minimum rating count, i.e. the number of neighbors from the neighborhood that rated this item.
```
def compute_top_n(rating_preds: dict, min_count: int, N: int) -> OrderedDict:
rating_preds = {key: val for (key, val) in rating_preds.items()
if val['count'] >= min_count}
# assuming more ratings mean higher confidence in the prediction
sorted_rating_preds = sorted(rating_preds.items(),
key=lambda kv: (kv[1]['pred'], kv[1]['count']),
reverse=True)
return OrderedDict(sorted_rating_preds[:N])
top_n_recs = compute_top_n(rating_preds, min_count=2, N=10)
top_n_recs
```
### Combine all steps in `get_recommendations`
```
def get_recommendations(user: int,
user_user_sims: dict,
k: int,
C: int,
N: int):
user_neighbors = get_k_nearest_neighbors(user, k=k, user_user_sims=user_user_sims)
neighborhood_ratings = get_neighborhood_ratings(user, user_neighbors)
rating_preds = compute_rating_pred(neighborhood_ratings)
top_n_recs = compute_top_n(rating_preds, min_count=C, N=N)
return top_n_recs
get_recommendations(1, user_user_sims, 10, 2, 10)
```
## Evaluation
Let's check the performance of the neighborhood- and user-based recommender for a neighborhood size of $k = 60$, minimum rating count of $C = 10$ and stay with $N = 10$ recommendations.
```
k = 60
C = 10
N = 10
relevant_items = get_relevant_items(data.test_ratings)
users = relevant_items.keys()
prec_at_N = dict.fromkeys(data.users)
for user in users:
recommendations = get_recommendations(user, user_user_sims, k, C, N)
recommendations = list(recommendations.keys())
hits = np.intersect1d(recommendations,
relevant_items[user])
prec_at_N[user] = len(hits)/N
np.mean([val for val in prec_at_N.values() if val is not None])
```
| true |
code
| 0.637962 | null | null | null | null |
|
```
BRANCH = 'v1.0.2'
"""
You can run either this notebook locally (if you have all the dependencies and a GPU) or on Google Colab.
Instructions for setting up Colab are as follows:
1. Open a new Python 3 notebook.
2. Import this notebook from GitHub (File -> Upload Notebook -> "GITHUB" tab -> copy/paste GitHub URL)
3. Connect to an instance with a GPU (Runtime -> Change runtime type -> select "GPU" for hardware accelerator)
4. Run this cell to set up dependencies.
"""
# If you're using Google Colab and not running locally, run this cell
# install NeMo
BRANCH = 'v1.0.2'
!python -m pip install git+https://github.com/NVIDIA/NeMo.git@$BRANCH#egg=nemo_toolkit[nlp]
import os
import wget
from nemo.collections import nlp as nemo_nlp
from nemo.collections import common as nemo_common
from omegaconf import OmegaConf
```
# Tokenizers Background
For Natural Language Processing, tokenization is an essential part of data preprocessing. It is the process of splitting a string into a list of tokens. One can think of token as parts like a word is a token in a sentence.
Depending on the application, different tokenizers are more suitable than others.
For example, a WordTokenizer that splits the string on any whitespace, would tokenize the following string
"My first program, Hello World." -> ["My", "first", "program,", "Hello", "World."]
To turn the tokens into numerical model input, the standard method is to use a vocabulary and one-hot vectors for [word embeddings](https://en.wikipedia.org/wiki/Word_embedding). If a token appears in the vocabulary, its index is returned, if not the index of the unknown token is returned to mitigate out-of-vocabulary (OOV).
# Tokenizers in NeMo
In NeMo, we support the most used tokenization algorithms. We offer a wrapper around [Hugging Faces's AutoTokenizer](https://huggingface.co/transformers/model_doc/auto.html#autotokenizer) - a factory class that gives access to all Hugging Face tokenizers. This includes particularly all BERT-like model tokenizers, such as BertTokenizer, AlbertTokenizer, RobertaTokenizer, GPT2Tokenizer. Apart from that, we also support other tokenizers such as WordTokenizer, CharTokenizer, and [Google's SentencePieceTokenizer](https://github.com/google/sentencepiece).
We make sure that all tokenizers are compatible with BERT-like models, e.g. BERT, Roberta, Albert, and Megatron. For that, we provide a high-level user API `get_tokenizer()`, which allows the user to instantiate a tokenizer model with only four input arguments:
* `tokenizer_name: str`
* `tokenizer_model: Optional[str] = None`
* `vocab_file: Optional[str] = None`
* `special_tokens: Optional[Dict[str, str]] = None`
Hugging Face and Megatron tokenizers (which uses Hugging Face underneath) can be automatically instantiated by only `tokenizer_name`, which downloads the corresponding `vocab_file` from the internet.
For SentencePieceTokenizer, WordTokenizer, and CharTokenizers `tokenizer_model` or/and `vocab_file` can be generated offline in advance using [`scripts/tokenizers/process_asr_text_tokenizer.py`](https://github.com/NVIDIA/NeMo/blob/main/scripts/process_asr_text_tokenizer.py)
The tokenizers in NeMo are designed to be used interchangeably, especially when
used in combination with a BERT-based model.
Let's take a look at the list of available tokenizers:
```
nemo_nlp.modules.get_tokenizer_list()
```
# Hugging Face AutoTokenizer
```
# instantiate tokenizer wrapper using pretrained model name only
tokenizer1 = nemo_nlp.modules.get_tokenizer(tokenizer_name="bert-base-cased")
# the wrapper has a reference to the original HuggingFace tokenizer
print(tokenizer1.tokenizer)
# check vocabulary (this can be very long)
print(tokenizer1.tokenizer.vocab)
# show all special tokens if it has any
print(tokenizer1.tokenizer.all_special_tokens)
# instantiate tokenizer using custom vocabulary
vocab_file = "myvocab.txt"
vocab = ["he", "llo", "world"]
with open(vocab_file, 'w') as vocab_fp:
vocab_fp.write("\n".join(vocab))
tokenizer2 = nemo_nlp.modules.get_tokenizer(tokenizer_name="bert-base-cased", vocab_file=vocab_file)
# Since we did not overwrite special tokens they should be the same as before
print(tokenizer1.tokenizer.all_special_tokens == tokenizer2.tokenizer.all_special_tokens )
```
## Adding Special tokens
We do not recommend overwriting special tokens for Hugging Face pretrained models,
since these are the commonly used default values.
If a user still wants to overwrite the special tokens, specify some of the following keys:
```
special_tokens_dict = {"unk_token": "<UNK>",
"sep_token": "<SEP>",
"pad_token": "<PAD>",
"bos_token": "<CLS>",
"mask_token": "<MASK>",
"eos_token": "<SEP>",
"cls_token": "<CLS>"}
tokenizer3 = nemo_nlp.modules.get_tokenizer(tokenizer_name="bert-base-cased",
vocab_file=vocab_file,
special_tokens=special_tokens_dict)
# print newly set special tokens
print(tokenizer3.tokenizer.all_special_tokens)
# the special tokens should be different from the previous special tokens
print(tokenizer3.tokenizer.all_special_tokens != tokenizer1.tokenizer.all_special_tokens )
```
Notice, that if you specify tokens that were not previously included in the tokenizer's vocabulary file, new tokens will be added to the vocabulary file. You will see a message like this:
`['<MASK>', '<CLS>', '<SEP>', '<PAD>', '<SEP>', '<CLS>', '<UNK>']
will be added to the vocabulary.
Please resize your model accordingly`
```
# A safer way to add special tokens is the following:
# define your model
pretrained_model_name = 'bert-base-uncased'
model = nemo_nlp.modules.get_lm_model(pretrained_model_name=pretrained_model_name)
# define pretrained tokenizer
tokenizer_default = nemo_nlp.modules.get_tokenizer(tokenizer_name=pretrained_model_name)
tokenizer_default.text_to_tokens('<MY_NEW_TOKEN> and another word')
```
As you can see in the above, the tokenizer splits `<MY_NEW_TOKEN>` into subtokens. Let's add this to the special tokens to make sure the tokenizer does not split this into subtokens.
```
special_tokens = {'bos_token': '<BOS>',
'cls_token': '<CSL>',
'additional_special_tokens': ['<MY_NEW_TOKEN>', '<ANOTHER_TOKEN>']}
tokenizer_default.add_special_tokens(special_tokens_dict=special_tokens)
# resize your model so that the embeddings for newly added tokens are updated during training/finetuning
model.resize_token_embeddings(tokenizer_default.vocab_size)
# let's make sure the tokenizer doesn't split our special tokens into subtokens
tokenizer_default.text_to_tokens('<MY_NEW_TOKEN> and another word')
```
Now, the model doesn't break down our special token into the subtokens.
## Megatron model tokenizer
```
# Megatron tokenizers are instances of the Hugging Face BertTokenizer.
tokenizer4 = nemo_nlp.modules.get_tokenizer(tokenizer_name="megatron-bert-cased")
```
# Train custom tokenizer model and vocabulary from text file
We use the [`scripts/tokenizers/process_asr_text_tokenizer.py`](https://github.com/NVIDIA/NeMo/blob/main/scripts/process_asr_text_tokenizer.py) script to create a custom tokenizer model with its own vocabulary from an input file
```
# download tokenizer script
script_file = "process_asr_text_tokenizer.py"
if not os.path.exists(script_file):
print('Downloading script file...')
wget.download(f'https://raw.githubusercontent.com/NVIDIA/NeMo/{BRANCH}/scripts/tokenizers/process_asr_text_tokenizer.py')
else:
print ('Script already exists')
# Let's prepare some small text data for the tokenizer
data_text = "NeMo is a toolkit for creating Conversational AI applications. \
NeMo toolkit makes it possible for researchers to easily compose complex neural network architectures \
for conversational AI using reusable components - Neural Modules. \
Neural Modules are conceptual blocks of neural networks that take typed inputs and produce typed outputs. \
Such modules typically represent data layers, encoders, decoders, language models, loss functions, or methods of combining activations. \
The toolkit comes with extendable collections of pre-built modules and ready-to-use models for automatic speech recognition (ASR), \
natural language processing (NLP) and text synthesis (TTS). \
Built for speed, NeMo can utilize NVIDIA's Tensor Cores and scale out training to multiple GPUs and multiple nodes."
# Write the text data into a file
data_file="data.txt"
with open(data_file, 'w') as data_fp:
data_fp.write(data_text)
# Some additional parameters for the tokenizer
# To tokenize at unigram, char or word boundary instead of using bpe, change --spe_type accordingly.
# More details see https://github.com/google/sentencepiece#train-sentencepiece-model
tokenizer_spe_type = "bpe" # <-- Can be `bpe`, `unigram`, `word` or `char`
vocab_size = 32
! python process_asr_text_tokenizer.py --data_file=$data_file --data_root=. --vocab_size=$vocab_size --tokenizer=spe --spe_type=$tokenizer_spe_type
# See created tokenizer model and vocabulary
spe_model_dir=f"tokenizer_spe_{tokenizer_spe_type}_v{vocab_size}"
! ls $spe_model_dir
```
# Use custom tokenizer for data preprocessing
## Example: SentencePiece for BPE
```
# initialize tokenizer with created tokenizer model, which inherently includes the vocabulary and specify optional special tokens
tokenizer_spe = nemo_nlp.modules.get_tokenizer(tokenizer_name="sentencepiece", tokenizer_model=spe_model_dir+"/tokenizer.model", special_tokens=special_tokens_dict)
# specified special tokens are added to the vocabuary
print(tokenizer_spe.vocab_size)
```
## Example: WordTokenizer from Vocabulary
```
# If you want to use a simple tokenizer like WordTokenizer without first generating the tokenizer.model first
# we provide the alternative class WordTokenizer or CharTokenizer that takes a user vocabulary as input
# initialize tokenizer with vocabulary and specify optional special tokens
tokenizer_word = nemo_nlp.modules.get_tokenizer(tokenizer_name="word", vocab_file=vocab_file, special_tokens=special_tokens_dict)
# specified special tokens are added to the vocabulary
print(tokenizer_word.vocab_size)
```
# Using any tokenizer to tokenize text into BERT compatible input
```
text="hello world"
# create tokens
tokenized = [tokenizer_word.bos_token] + tokenizer_word.text_to_tokens(text) + [tokenizer_word.eos_token]
print(tokenized)
# turn token into input_ids for a neural model, such as BERTModule
print(tokenizer_word.tokens_to_ids(tokenized))
```
| true |
code
| 0.622086 | null | null | null | null |
|
# Business and Data Understanding
## Airports Weather Data 2016
### Import Airports and their latitude/longitude. 10 US airports with the most weather related delays
```
from pyspark.sql import SQLContext
import numpy as np
from io import StringIO
import requests
import json
import pandas as pd
# @hidden_cell
# This function accesses a file in your Object Storage. The definition contains your credentials.
# You might want to remove those credentials before you share your notebook.
def get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375(container, filename):
"""This functions returns a StringIO object containing
the file content from Bluemix Object Storage."""
url1 = ''.join(['https://identity.open.softlayer.com', '/v3/auth/tokens'])
data = {'auth': {'identity': {'methods': ['password'],
'password': {'user': {'name': 'member_fa75ff3d05c0b00bdf62f0536608f1ca7c52af71','domain': {'id': 'daf5d7dceca34848ae07708c68826bb2'},
'password': 'ng[~3U24rFuL)UUm'}}}}}
headers1 = {'Content-Type': 'application/json'}
resp1 = requests.post(url=url1, data=json.dumps(data), headers=headers1)
resp1_body = resp1.json()
for e1 in resp1_body['token']['catalog']:
if(e1['type']=='object-store'):
for e2 in e1['endpoints']:
if(e2['interface']=='public'and e2['region']=='dallas'):
url2 = ''.join([e2['url'],'/', container, '/', filename])
s_subject_token = resp1.headers['x-subject-token']
headers2 = {'X-Auth-Token': s_subject_token, 'accept': 'application/json'}
resp2 = requests.get(url=url2, headers=headers2)
return StringIO(resp2.text)
airport_lat_long_data = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'airports lat long.csv'))
airport_lat_long_data.head()
airport_lat_long_data.dtypes
```
### Change column names for merging with weather data
```
airport_lat_long_data=airport_lat_long_data.rename(columns = {'Lat':'inputLatitude','Lon':'inputLongitude'})
airport_lat_long_data.head(1)
```
### Import weather data. Historical hourly weather data for 10 airports over the year 2016
```
weather_exported = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'weather_exported.csv'))
weather_exported.dtypes
weather_exported.head(2)
```
### Derive new date and hour columns
```
weather_exported['FL_DATE'] = weather_exported.DateHrLwt.str.slice(6, 10) + weather_exported.DateHrLwt.str.slice(0, 2) + weather_exported.DateHrLwt.str.slice(3, 5)
weather_exported['Hour'] = weather_exported.DateHrLwt.str.slice(11, 13)
weather_exported['Hour'] = weather_exported.Hour.astype('int')
weather_exported.head(1)
airports_weather_df = pd.merge(weather_exported, airport_lat_long_data, how='left', left_on=['inputLatitude','inputLongitude'], right_on = ['inputLatitude','inputLongitude'])
```
#### Drop columns that aren't features
```
airports_weather_df.drop(['SiteId','Latitude','Longitude','inputLatitude','inputLongitude','DateHrGmt','DateHrLwt','SurfaceDewpointTemperatureFahrenheit','SurfaceWetBulbTemperatureFahrenheit','RelativeHumidityPercent',
'SurfaceAirPressureMillibars','WindChillTemperatureFahrenheit','ApparentTemperatureFahrenheit','WindDirectionDegrees',
'DownwardSolarRadiationWsqm','DiffuseHorizontalRadiationWsqm','DirectNormalIrradianceWsqm','MslPressureMillibars',
'HeatIndexFahrenheit','PotentialEvapotranspirationMicrometersPerHour','TenToFortyLiquidSoilMoisturePercent',
'TenToFortySoilTemperatureFahrenheit','ZeroToTenLiquidSoilMoisturePercent','ZeroToTenSoilTemperatureFahrenheit'], axis=1,inplace='True')
airports_weather_df.head(1)
```
## Airports Flight Data 2016
### Retrieve historical flights data for all US airports over the year 2016
```
Jan2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Jan 2016 Flights.csv'))
Jan2016_df.head(1)
Feb2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Feb 2016 Flights.csv'))
Feb2016_df.head(1)
Mar2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Mar 2016 Flights.csv'))
Mar2016_df.head(1)
Apr2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Apr 2016 Flights.csv'))
Apr2016_df.head(1)
May2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'May 2016 Flights.csv'))
May2016_df.head(1)
Jun2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Jun 2016 Flights.csv'))
Jun2016_df.head(1)
Jul2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Jul 2016 Flights.csv'))
Jul2016_df.head(1)
Aug2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Aug 2016 Flights.csv'))
Aug2016_df.head(1)
Sep2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Sep 2016 Flights.csv'))
Sep2016_df.head(1)
Oct2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Oct 2016 Flights.csv'))
Oct2016_df.head(1)
Nov2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Nov 2016 Flights.csv'))
Nov2016_df.head(1)
Dec2016_df = pd.read_csv(get_object_storage_file_with_credentials_b12280b012b94907ad8decb8341d8375('FlightCancellation', 'Dec 2016 Flights.csv'))
Dec2016_df.head(1)
frames = [Jan2016_df, Feb2016_df, Mar2016_df, Apr2016_df, May2016_df, Jun2016_df, Jul2016_df, Aug2016_df, Sep2016_df, Oct2016_df,
Nov2016_df, Dec2016_df]
airport_flights_df = pd.concat(frames)
airport_flights_df.head(1)
airport_flights_df.shape
```
### Select 10 airports
```
airport_flights_df = airport_flights_df[(airport_flights_df.ORIGIN == "BOS") | (airport_flights_df.ORIGIN == "EWR") | (airport_flights_df.ORIGIN == "JFK") | (airport_flights_df.ORIGIN == "LGA") | (airport_flights_df.ORIGIN == "ORD") | (airport_flights_df.ORIGIN == "DEN") | (airport_flights_df.ORIGIN == "DFW") | (airport_flights_df.ORIGIN == "IAH") | (airport_flights_df.ORIGIN == "PHL") | (airport_flights_df.ORIGIN == "SFO")]
airport_flights_df = airport_flights_df[(airport_flights_df.DEST == "BOS") | (airport_flights_df.DEST == "EWR") | (airport_flights_df.DEST == "JFK") | (airport_flights_df.DEST == "LGA") | (airport_flights_df.DEST == "ORD") | (airport_flights_df.DEST == "DEN") | (airport_flights_df.DEST == "DFW") | (airport_flights_df.DEST == "IAH") | (airport_flights_df.DEST == "PHL") | (airport_flights_df.DEST == "SFO")]
airport_flights_df.shape
```
#### Derive the Hour from the scheduled departure time
```
airport_flights_df['Hour'] = airport_flights_df.CRS_DEP_TIME / 100
airport_flights_df['Hour'] = airport_flights_df.Hour.astype(int)
airport_flights_df.head(2)
```
#### Change FL_DATE format to match airport_weather_df FL_DATE format
```
airport_flights_df.FL_DATE = airport_flights_df.FL_DATE.str.replace('-', '')
airport_flights_df.head(1)
```
#### Drop columns that aren't needed as features
```
airport_flights_df.drop(['DEP_TIME','DEP_DELAY','TAXI_OUT','WHEELS_ON','TAXI_IN','ARR_TIME','ARR_DELAY','ACTUAL_ELAPSED_TIME',
'AIR_TIME','CARRIER_DELAY','WEATHER_DELAY','NAS_DELAY','SECURITY_DELAY','LATE_AIRCRAFT_DELAY', 'CRS_ELAPSED_TIME',
'CRS_DEP_TIME','CRS_ARR_TIME'], axis=1,inplace='True')
airport_flights_df.dtypes
airport_flights_df.shape
```
### Rename feature columns in the weather dataframe for merging with flight dataframe. This will add weather data for the ORIGIN airport
```
airports_weather_df.rename(columns={'Airport':'ORIGIN','SurfaceTemperatureFahrenheit':'O_SurfaceTemperatureFahrenheit',
'CloudCoveragePercent':'O_CloudCoveragePercent','WindSpeedMph':'O_WindSpeedMph',
'PrecipitationPreviousHourInches':'O_PrecipitationPreviousHourInches','SnowfallInches':'O_SnowfallInches',
'SurfaceWindGustsMph':'O_SurfaceWindGustsMph','SurfaceWaterRunOffMillimeters':'O_SurfaceWaterRunOffMillimeters'}, inplace=True)
airports_weather_df.dtypes
airports_weather_df.head(1)
flights_with_weather_df = pd.merge(airport_flights_df,airports_weather_df,on=['FL_DATE','Hour','ORIGIN'])
flights_with_weather_df.dtypes
flights_with_weather_df.shape
```
### Rename feature columns in the weather dataframe for merging with flight dataframe. This will add weather data for the DESTINATION airport
```
airports_weather_df.rename(columns={'ORIGIN':'DEST','O_SurfaceTemperatureFahrenheit':'D_SurfaceTemperatureFahrenheit',
'O_CloudCoveragePercent':'D_CloudCoveragePercent','O_WindSpeedMph':'D_WindSpeedMph',
'O_PrecipitationPreviousHourInches':'D_PrecipitationPreviousHourInches','O_SnowfallInches':'D_SnowfallInches',
'O_SurfaceWindGustsMph':'D_SurfaceWindGustsMph','O_SurfaceWaterRunOffMillimeters':'D_SurfaceWaterRunOffMillimeters'}, inplace=True)
airports_weather_df.dtypes
flights_with_weather_df = pd.merge(flights_with_weather_df,airports_weather_df,on=['FL_DATE','Hour','DEST'])
```
### Let's use pixiedust to see what it can do
```
import pixiedust
display(flights_with_weather_df)
```
# Data Preparation - first iteration
```
%matplotlib inline
flights_with_weather_df.CANCELLATION_CODE.value_counts(sort=False, dropna=False)
```
#### Clean up null values
```
flights_with_weather_df.isnull().sum()
```
#### Replace nulls with 0's
```
flights_with_weather_df['O_SurfaceWaterRunOffMillimeters'] = flights_with_weather_df['O_SurfaceWaterRunOffMillimeters'].replace(['$null$'], 0.000)
flights_with_weather_df['D_SurfaceWaterRunOffMillimeters'] = flights_with_weather_df['D_SurfaceWaterRunOffMillimeters'].replace(['$null$'], 0.000)
flights_with_weather_df['O_SurfaceWaterRunOffMillimeters'] = pd.to_numeric(flights_with_weather_df['O_SurfaceWaterRunOffMillimeters'], errors='coerce')
flights_with_weather_df['D_SurfaceWaterRunOffMillimeters'] = pd.to_numeric(flights_with_weather_df['D_SurfaceWaterRunOffMillimeters'], errors='coerce')
```
#### Filter out "non-weather" cancellations
```
calcel_code_list = ['A', 'C', 'D']
flights_with_weather_df = flights_with_weather_df.loc[~flights_with_weather_df['CANCELLATION_CODE'].isin(calcel_code_list)]
```
#### Drop columns not needed
```
flights_with_weather_df = flights_with_weather_df.drop(['FL_NUM','CANCELLATION_CODE'], axis=1)
```
#### The data is very imbalanced
```
flights_with_weather_df.CANCELLED.value_counts()
```
#### Install libraries to use SMOTE
```
! pip install imbalanced-learn
import pandas as pd
from sklearn import datasets, metrics
#from sklearn.cross_validation import train_test_split
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectFromModel
from sklearn.metrics import accuracy_score, roc_curve, roc_auc_score, f1_score
from sklearn.metrics import recall_score, precision_score, confusion_matrix
from sklearn.ensemble import RandomForestClassifier
#import balancing techniques
import imblearn
from imblearn.over_sampling import SMOTE
```
### Four feature columns will need to be converted
```
flights_with_weather_df.dtypes
```
#### Create features df and target
```
x = flights_with_weather_df
y = flights_with_weather_df['CANCELLED']
del x['CANCELLED']
print x.shape, y.shape
```
#### Run One Hot Encoding on the four string /object features
```
cols_to_transform = [ 'FL_DATE', 'UNIQUE_CARRIER', 'ORIGIN', 'DEST']
df_with_dummies = pd.get_dummies(x, columns = cols_to_transform )
```
#### One Hot Encoding expands the 4 feature columns into many more
```
print x.shape
print df_with_dummies.shape
```
### Creating the Training and Test Sets
ref: https://beckernick.github.io/oversampling-modeling/
```
training_features, test_features, training_target, test_target, = train_test_split(df_with_dummies, y, test_size=0.15, random_state=12)
print training_features.shape, test_features.shape
print training_target.shape, test_target.shape
```
#### Oversample only on the training data
```
x_train, x_val, y_train, y_val = train_test_split(training_features, training_target, test_size = .15, random_state=12)
sm = SMOTE(k=5, kind = 'regular', ratio='auto')
x_train_res, y_train_res = sm.fit_sample(x_train, y_train)
print training_target.value_counts(), np.bincount(y_train_res)
clf_rf = RandomForestClassifier(n_estimators=100, random_state=12)
clf_rf.fit(x_train_res, y_train_res)
```
Accuracy = (TP+TN) / (TP+TN+FP+FN)
Precision = TP / (TP+FP)
Recall = TP / (TP+FN)
```
print 'Validation Results'
print 'Accuracy: ', clf_rf.score(x_val, y_val)
print 'Precision:', precision_score(y_val, clf_rf.predict(x_val))
print 'Recall:', recall_score(y_val, clf_rf.predict(x_val))
print 'F1 score:', f1_score(y_val, clf_rf.predict(x_val),average='weighted')
print 'Confusion Matrix:\n', confusion_matrix(y_val, clf_rf.predict(x_val))
print '\nTest Results'
print 'Accuracy: ', clf_rf.score(test_features, test_target)
print 'Precision:', precision_score(test_target, clf_rf.predict(test_features))
print 'Recall: ', recall_score(test_target, clf_rf.predict(test_features))
print 'F1 score:', f1_score(test_target, clf_rf.predict(test_features),average='weighted')
print 'Confusion Matrix:\n', confusion_matrix(test_target, clf_rf.predict(test_features))
#!pip install --user ggplot
from ggplot import *
# from http://blog.yhat.com/posts/roc-curves.html
preds = clf_rf.predict_proba(test_features)[:,1]
fpr, tpr, _ = roc_curve(test_target, preds)
auc = metrics.auc(fpr,tpr)
df = pd.DataFrame(dict(fpr=fpr, tpr=tpr))
ggplot(df, aes(x='fpr', y='tpr')) +\
geom_line() +\
geom_abline(linetype='dashed') +\
ggtitle("ROC Curve w/ AUC=%s" % str(auc))
```
| true |
code
| 0.471041 | null | null | null | null |
|
## Importance Sampling and Particle filter
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.stats import poisson
```
## Importance Sampling and resampling
Before we dive into the vast universe of nonlinear filtering, let us take a step back and review importance sampling. The idea of importance is to empirically approximate a probability distribution, which we can evaluate but cannot directly sample from, by weighted samples from _another_ probability distribution.
As an example, let us consider a mysterious parabola-shaped probability function $p(x) = 3/4 * (1-x^2) $, defined on $x $ in $ [-1,1]$. We cannot sample from this distribution, but we can sample from the uniform distribution between -1 and 1. Let us now generate weighted samples to approximate the parabola distribution (algorithm 2)
```
# Approximate beta distribution with weighted samples from the uniform distribution
np.random.seed(42)
N = 1000
# draw samples from proposal
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
# compute weights
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
# normalize the weights such that they sum to 1
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
# histogram of original samples
fig, (ax1,ax2) = plt.subplots(2,1,figsize=(10,8))
fig.tight_layout()
ax1.hist(x)
ax1.set_title('Original samples')
# histogram of weighted samples, together with probability distribution
bins = np.linspace(-1, 1, int(np.sqrt(N)))
ax2.hist(x,weights=w,density = True,alpha=0.5)
xaxis = np.linspace(-1,1,50)
ax2.plot(xaxis,f(xaxis)/(4/3))
ax2.legend([r'$p(x)$','weighted histogram'])
ax2.set_title('Weighted samples')
plt.show()
```
Assume you don't want to store the weights for some reason, but want to have samples that represent the parabola distribution. In this case, you can use the resampling algorithm (algorithm 4) to generate equally weighted samples from the weight distribution:
```
def resample(x,w,N):
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
return x_r,w_r
#resample to produce equally weighted samples, which is equivalent to samples without the need for a weight
x_r,_ = resample(x,w,N)
# histogram of original samples
fig, ax2 = plt.subplots(1,1,figsize=(10,4))
fig.tight_layout()
# histogram of weighted samples
bins = np.linspace(-1, 1, int(np.sqrt(N)))
ax2.hist(x,weights=w,density = True,alpha=0.5)
ax2.hist(x_r,density = True,alpha=0.5)
xaxis = np.linspace(-1,1,50)
ax2.plot(xaxis,f(xaxis)/(4/3))
ax2.legend([r'$p(x)$','weighted histogram','resampled histogram'])
plt.show()
```
Note that even though the idea of resampling is intruguingly simple, it will increase the variance of the samples.
## Getting started with particle filters: Revisit the random walk
In order to compare the PF (and to benchmark it), let us use it on the simple random walk model that we have encountered in the KF section. We already have an optimal solution to this problem (the Kalman filter), and we will now compare the PF to this.
```
def KF1D_generateData(params):
x = np.zeros(params["T"]+1)
y = np.zeros(params["T"]+1)
# initialization
x[0] = np.random.normal(params["mu0"],np.sqrt(params["Sigma0"]))
y[0] = np.random.normal(params["H"] * x[0], np.sqrt(params["R"]))
for i in range(1,params["T"]+1):
x[i] = np.random.normal(params["F"] * x[i-1],np.sqrt(params["Q"]))
y[i] = np.random.normal(params["H"] * x[i], np.sqrt(params["R"]))
return x, y
def KF1D(y,params):
# %%%%%%%%%%%%%%% COPY CODE HERE %%%%%%%%%%%%%%%%%%%
return mu, Sigma
np.random.seed(42)
N = 2000
c = 0.5
params = {
"F": 1,
"Q": 1,
"H": 1,
"R": 10,
"mu0": 10,
"Sigma0": 2,
"T": 100
}
# generate the data
x, y = KF1D_generateData(params)
# compute the KF estimate
mu, Sigma = KF1D(y,params)
```
Let's code up the Boostrap Particle filter (Algorithm 5). You may use the resampling procedure that you have already defined above.
```
def BootstrapPF(y,N,c,params):
# initialization
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
# filtering recursion
for t in range(1,params["T"]+1):
# draw from proposal (transition density)
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
#compute weights
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
# normalize weights
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
# resample if necessary
# %%%%%%%%%%%%%%% ENTER CODE HERE %%%%%%%%%%%%%%%%%%%
return x, w
np.random.seed(42)
# compute the Bootstrap PF estimate
x_PF,w_PF = BootstrapPF(y,N,c,params)
# compute mean and variance
mu_PF = np.sum(w_PF * x_PF,1)
Sigma_PF = np.sum(w_PF * ((x_PF.T-mu_PF)**2).T,1)
# Plot the trajectory and the observations
# (assume no observation at y = 0 )
t = np.arange(params["T"]+1)
fig, (ax1,ax2) = plt.subplots(2,1,figsize=(10,8))
ax1.scatter(t[1:],y[1:],color='grey',facecolors='none')
ax1.scatter(t,x,color='black')
ax1.plot(t,mu,linewidth=2)
ax1.plot(t,mu_PF,'--',linewidth=2)
ax1.legend([r'$\mu_t$ (KF)',r'$\mu_t$ (PF)',r'$y_t$',r'$x_t$'])
ax1.grid(True)
ax1.set_xlim(0,params["T"])
ax1.set_title('Mean')
ax2.plot(t,Sigma)
ax2.plot(t,Sigma_PF)
ax2.set_xlim(0,params["T"])
ax2.set_title('Variance')
ax2.legend([r'$\Sigma_t$ (KF)',r'$\Sigma_t$ (PF)'])
plt.show()
```
## Nonlinear Gaussian models
Here, we consider a nonlinear filtering task, where the hidden state $X_t$ evolves according to a drift-diffusion with nonlinear drift function. Further, the observations $Y_t$ are linear and corrupted by Gaussian noise. Specifically, the generative model in terms of stochastic differential equations (SDE) reads:
\begin{eqnarray}
d X_t & = & \tilde{f}(X_t) \, dt + \sigma_x \, dW_t \\
d Z_t & = & \tilde{h}(X_t) \, dt + \sigma_y \, dV_t,
\end{eqnarray}
with $ \tilde{f}(x) = -4x(x^2-1) $ and $h(x) = x $.
Don't worry if you have never worked with SDE's before. It's actually nothing else than the dynamical system we looked at in the KF notebook, just written in a slightly weird way. Analogously, they can easily be discretized in time, and we can rewrite the model in terms of the following transition and emission probabilities:
\begin{eqnarray}
p(x_t | x_{t-1} ) & = & \mathcal{N} ( x_t ; f(x_{t-1}), Q) \\
p(y_t | x_{t} ) & = & \mathcal{N} ( z_t ; h(x_{t}) , R),
\end{eqnarray}
with
\begin{eqnarray}
f(x) & = & x + \tilde{f}(x) dt \\
Q & = & \sigma_x^2 dt \\
h(x) & = & \tilde{h}(x) dt \\
R & = & \sigma_y^2 / dt.
\end{eqnarray}
The observations $y_t$ can be considered a temporal derivative of the process $Z_t$ (don't tell the mathematicians I said that). Note that again the observation variance scales inversely with the time step: The smaller I make the time step, the less informative a single observation becomes. On the other hand, I also have more observations per time, so this prevents oversampling my observations and thus making the inference trivial.
This is a nonlinear model, and we cannot use the Kalman filter anymore. In other words: Whatever the particle filter is doing, we have to trust it...
```
def NLGauss_generateData(params):
# unpack some parameters for readibility
f = params["f"]
h = params["h"]
x = np.zeros(params["T"]+1)
y = np.zeros(params["T"]+1)
# initialization (draw from Gauss with mean mu0 and variance Sigma0)
x[0] = np.random.normal(params["mu0"],np.sqrt(params["Sigma0"]))
for t in range(1,params["T"]+1):
x[t] = np.random.normal( f(x[t-1]) , np.sqrt(params["Q"]) )
y[t] = np.random.normal(h(x[t]), np.sqrt(params["R"]) )
return x, y
np.random.seed(42)
N = 2000 # number of particles
c = 0.2 # resampling criterion
dt = 0.001
params = {
"f": lambda x: x-4*x*(x**2-1)*dt,
"Q": 2 * dt,
"h": lambda x: x,
"R": 0.1 / dt,
"mu0": 0,
"Sigma0": 1,
"T": int(5/dt),
}
x,y = NLGauss_generateData(params)
```
When you code the BPF, you can actually re-use a lot of the code from above.
```
def NLGauss_BPF(y,N,c,params):
# %%%%%%%%%%%%%%% COPY CODE HERE, ADJUST %%%%%%%%%%%%%%%%%%%
return x, w
np.random.seed(42)
x_PF,w_PF = NLGauss_BPF(y,N,c,params)
```
Let us now visualize the results:
```
# produces weighted histogram images
def histImage(x, bins, rang, w=0):
image = np.zeros((x.shape[0],bins))
if np.isscalar(w):
for i in range(x.shape[0]):
image[i,:] = np.histogram(x[i,:],bins,rang,density=True)[0]
else:
for i in range(x.shape[0]):
image[i,:] = np.histogram(x[i,:],bins,rang,weights=w[i,:],density=True)[0]
return image
T = params["T"]
plotrange = [0,T,-2.5,2.5]
t = np.arange(T+1)*dt
fig, (ax2) = plt.subplots(1,1,figsize=(10,6))
hist = np.transpose(histImage(x_PF,int(np.sqrt(N)),(-3,3),w=w_PF))
ax2.imshow(np.flipud(hist), cmap='Oranges', interpolation='nearest', extent=[0,T,-3,3],aspect='auto',vmax=0.7)
ax2.plot(t,x,color='xkcd:moss')
ax2.plot(t,np.average(x_PF,1,w_PF), linewidth=3,color = 'xkcd:azure')
ax2.axis(plotrange)
ax2.legend(['hidden state','BPF'],fontsize=16)
ax2.legend([r'$x_t$',r'$\mu_t$ (BPF)'])
plt.subplots_adjust(hspace=0.3)
plt.savefig('63 - particle filters - gauss.pdf')
plt.show()
```
## Nonlinear filtering with Poisson noise
As an alternative to Gaussian-type observation noise, we consider here point-process observations, with the intensity $ g(x_t)$ being a function of the latent state $x_t$.
\begin{eqnarray}
y_t &\sim & Poisson(g(x_t)).
\end{eqnarray}
As a concrete example, we consider a Gaussian-shaped rate function $ g(x) = g_0 \exp(\frac{x-m_o}{2 s_0^2}) dt $ for two sensors with peaks at $ m_0 = \pm 1 $ and width $ s_0 $ (i.e. conditionally independent two-dimensional observations).
The hidden dynamics is the same as in the previous example. If you want to draw the link to neuroscience, you might consider those "sensors" to be two place cells that fire with a higher rate once the animal (the latent state) is close to their respective place fields.
```
def NLPoisson_generateData(params):
# unpack some parameters for readibility
f = params["f"]
g = params["g"]
x = np.zeros(params["T"]+1)
y = np.zeros((params["T"]+1,2))
# initialization (draw from Gauss with mean mu0 and variance Sigma0)
x[0] = np.random.normal(params["mu0"],np.sqrt(params["Sigma0"]))
for t in range(1,params["T"]+1):
x[t] = np.random.normal( f(x[t-1]) , np.sqrt(params["Q"]) )
y[t] = np.random.poisson(g(x[t]))
return x, y
np.random.seed(42)
N = 2000
c = 0.2
dt = 0.001
g0 = 50
s0 = 0.05
m0 = np.array([-1,1])
params = {
"f": lambda x: x-4*x*(x**2-1)*dt,
"Q": 2 * dt,
"g": lambda x: g0 * np.transpose(np.exp( - np.array([x-m0[0],x-m0[1]])**2/(2 * s0**2) ))*dt,
"mu0": 0,
"Sigma0": 1,
"T": int(5/dt),
}
x,y = NLPoisson_generateData(params)
```
Same as before, just code up the BPF. Careful: The weighting step requires a bit of thinking...
```
def NLPoisson_BPF(y,N,c,params):
# %%%%%%%%%%%%%%% COPY CODE HERE, ADJUST %%%%%%%%%%%%%%%%%%%
return x, w
x_PF_PP,w_PF_PP = NLPoisson_BPF(y,N,c,params)
t_minus = np.where(y[:,0]>=1)[0]
t_plus = np.where(y[:,1]>=1)[0]
T = params["T"]*dt
t = np.arange(T/dt+1)*dt
plotrange = [0, T, -2.5, 2.5]
fig, (ax1,ax2) = plt.subplots(2,1,figsize=(7.5,8))
plt.subplots_adjust(hspace=0.5)
ax1.plot(t,x,color = 'xkcd:moss')
ax1.plot(t,np.average(x_PF_PP,1,w_PF_PP),color = 'xkcd:azure',linewidth=3)
for spikepos in t[np.where(y>=1)[0]]:
ax1.axvline(x=spikepos,linestyle='--',color = 'xkcd:light grey',linewidth=1)
ax1.scatter(t[t_plus],2.2*np.ones(t_plus.size),marker="^",c='xkcd:eggplant purple',s=100)
ax1.scatter(t[t_minus],-2.2*np.ones(t_minus.size),marker="v",c='xkcd:eggplant purple',s=100)
ax1.axis(plotrange)
ax1.legend(['hidden state','PF'],fontsize=16)
hist = np.transpose(histImage(x_PF_PP,int(np.sqrt(N)),(-3,3),w=w_PF_PP))
ax2.imshow(np.flipud(hist), cmap='Oranges', interpolation='nearest', extent=[0,T,-3,3],aspect='auto',vmax=0.7)
for spikepos in t[np.where(y>=1)[0]]:
ax2.axvline(x=spikepos,linestyle='--',color = 'xkcd:light grey',linewidth=1)
ax2.scatter(t[t_plus],2.2*np.ones(t_plus.size),marker="^",c='xkcd:eggplant purple',s=100)
ax2.scatter(t[t_minus],-2.2*np.ones(t_minus.size),marker="v",c='xkcd:eggplant purple',s=100)
ax2.plot(t,x,color='xkcd:moss')
ax2.plot(t,np.average(x_PF,1,w_PF), linewidth=3,color = 'xkcd:azure')
ax2.axis(plotrange)
plt.show()
```
| true |
code
| 0.662223 | null | null | null | null |
|
```
#default_exp test
#export
from fastcore.imports import *
from collections import Counter
from contextlib import redirect_stdout
from nbdev.showdoc import *
from fastcore.nb_imports import *
```
# Test
> Helper functions to quickly write tests in notebooks
## Simple test functions
We can check that code raises an exception when that's expected (`test_fail`). To test for equality or inequality (with different types of things) we define a simple function `test` that compares two object with a given `cmp` operator.
```
#export
def test_fail(f, msg='', contains='', args=None, kwargs=None):
args, kwargs = args or [], kwargs or {}
"Fails with `msg` unless `f()` raises an exception and (optionally) has `contains` in `e.args`"
try: f(*args, **kwargs)
except Exception as e:
assert not contains or contains in str(e)
return
assert False,f"Expected exception but none raised. {msg}"
def _fail(): raise Exception("foobar")
test_fail(_fail, contains="foo")
def _fail(): raise Exception()
test_fail(_fail)
```
We can also pass `args` and `kwargs` to function to check if it fails with special inputs.
```
def _fail_args(a):
if a == 5:
raise ValueError
test_fail(_fail_args, args=(5,))
test_fail(_fail_args, kwargs=dict(a=5))
#export
def test(a, b, cmp,cname=None):
"`assert` that `cmp(a,b)`; display inputs and `cname or cmp.__name__` if it fails"
if cname is None: cname=cmp.__name__
assert cmp(a,b),f"{cname}:\n{a}\n{b}"
test([1,2],[1,2], operator.eq)
test_fail(lambda: test([1,2],[1], operator.eq))
test([1,2],[1], operator.ne)
test_fail(lambda: test([1,2],[1,2], operator.ne))
show_doc(all_equal)
test(['abc'], ['abc'], all_equal)
show_doc(equals)
test([['abc'],['a']], [['abc'],['a']], equals)
#export
def nequals(a,b):
"Compares `a` and `b` for `not equals`"
return not equals(a,b)
test(['abc'], ['ab' ], nequals)
```
## test_eq test_ne, etc...
Just use `test_eq`/`test_ne` to test for `==`/`!=`. `test_eq_type` check things are equals and of the same type. We define them using `test`:
```
#export
def test_eq(a,b):
"`test` that `a==b`"
test(a,b,equals, '==')
test_eq([1,2],[1,2])
test_eq([1,2],map(int,[1,2]))
test_eq(array([1,2]),array([1,2]))
test_eq(array([1,2]),array([1,2]))
test_eq([array([1,2]),3],[array([1,2]),3])
test_eq(dict(a=1,b=2), dict(b=2,a=1))
test_fail(lambda: test_eq([1,2], 1), contains="==")
test_fail(lambda: test_eq(None, np.array([1,2])), contains="==")
test_eq({'a', 'b', 'c'}, {'c', 'a', 'b'})
#hide
import pandas as pd
import torch
df1 = pd.DataFrame(dict(a=[1,2],b=['a','b']))
df2 = pd.DataFrame(dict(a=[1,2],b=['a','b']))
df3 = pd.DataFrame(dict(a=[1,2],b=['a','c']))
test_eq(df1,df2)
test_eq(df1.a,df2.a)
test_fail(lambda: test_eq(df1,df3), contains='==')
class T(pd.Series): pass
test_eq(df1.iloc[0], T(df2.iloc[0]))
test_eq(torch.zeros(10), torch.zeros(10, dtype=torch.float64))
test_eq(torch.zeros(10), torch.ones(10)-1)
test_fail(lambda:test_eq(torch.zeros(10), torch.ones(1, 10)), contains='==')
test_eq(torch.zeros(3), [0,0,0])
#export
def test_eq_type(a,b):
"`test` that `a==b` and are same type"
test_eq(a,b)
test_eq(type(a),type(b))
if isinstance(a,(list,tuple)): test_eq(map(type,a),map(type,b))
test_eq_type(1,1)
test_fail(lambda: test_eq_type(1,1.))
test_eq_type([1,1],[1,1])
test_fail(lambda: test_eq_type([1,1],(1,1)))
test_fail(lambda: test_eq_type([1,1],[1,1.]))
#export
def test_ne(a,b):
"`test` that `a!=b`"
test(a,b,nequals,'!=')
test_ne([1,2],[1])
test_ne([1,2],[1,3])
test_ne(array([1,2]),array([1,1]))
test_ne(array([1,2]),array([1,1]))
test_ne([array([1,2]),3],[array([1,2])])
test_ne([3,4],array([3]))
test_ne([3,4],array([3,5]))
test_ne(dict(a=1,b=2), ['a', 'b'])
test_ne(['a', 'b'], dict(a=1,b=2))
#export
def is_close(a,b,eps=1e-5):
"Is `a` within `eps` of `b`"
if hasattr(a, '__array__') or hasattr(b,'__array__'):
return (abs(a-b)<eps).all()
if isinstance(a, (Iterable,Generator)) or isinstance(b, (Iterable,Generator)):
return all(abs(a_-b_)<eps for a_,b_ in zip(a,b))
return abs(a-b)<eps
#export
def test_close(a,b,eps=1e-5):
"`test` that `a` is within `eps` of `b`"
test(a,b,partial(is_close,eps=eps),'close')
test_close(1,1.001,eps=1e-2)
test_fail(lambda: test_close(1,1.001))
test_close([-0.001,1.001], [0.,1.], eps=1e-2)
test_close(np.array([-0.001,1.001]), np.array([0.,1.]), eps=1e-2)
test_close(array([-0.001,1.001]), array([0.,1.]), eps=1e-2)
#export
def test_is(a,b):
"`test` that `a is b`"
test(a,b,operator.is_, 'is')
test_fail(lambda: test_is([1], [1]))
a = [1]
test_is(a, a)
#export
def test_shuffled(a,b):
"`test` that `a` and `b` are shuffled versions of the same sequence of items"
test_ne(a, b)
test_eq(Counter(a), Counter(b))
a = list(range(50))
b = copy(a)
random.shuffle(b)
test_shuffled(a,b)
test_fail(lambda:test_shuffled(a,a))
a = 'abc'
b = 'abcabc'
test_fail(lambda:test_shuffled(a,b))
a = ['a', 42, True]
b = [42, True, 'a']
test_shuffled(a,b)
#export
def test_stdout(f, exp, regex=False):
"Test that `f` prints `exp` to stdout, optionally checking as `regex`"
s = io.StringIO()
with redirect_stdout(s): f()
if regex: assert re.search(exp, s.getvalue()) is not None
else: test_eq(s.getvalue(), f'{exp}\n' if len(exp) > 0 else '')
test_stdout(lambda: print('hi'), 'hi')
test_fail(lambda: test_stdout(lambda: print('hi'), 'ho'))
test_stdout(lambda: 1+1, '')
test_stdout(lambda: print('hi there!'), r'^hi.*!$', regex=True)
#export
def test_warns(f, show=False):
with warnings.catch_warnings(record=True) as w:
f()
test_ne(len(w), 0)
if show:
for e in w: print(f"{e.category}: {e.message}")
test_warns(lambda: warnings.warn("Oh no!"), {})
test_fail(lambda: test_warns(lambda: 2+2))
test_warns(lambda: warnings.warn("Oh no!"), show=True)
#export
TEST_IMAGE = 'images/puppy.jpg'
im = Image.open(TEST_IMAGE).resize((128,128)); im
#export
TEST_IMAGE_BW = 'images/mnist3.png'
im = Image.open(TEST_IMAGE_BW).resize((128,128)); im
#export
def test_fig_exists(ax):
"Test there is a figure displayed in `ax`"
assert ax and len(ax.figure.canvas.tostring_argb())
fig,ax = plt.subplots()
ax.imshow(array(im));
test_fig_exists(ax)
#export
class ExceptionExpected:
"Context manager that tests if an exception is raised"
def __init__(self, ex=Exception, regex=''): self.ex,self.regex = ex,regex
def __enter__(self): pass
def __exit__(self, type, value, traceback):
if not isinstance(value, self.ex) or (self.regex and not re.search(self.regex, f'{value.args}')):
raise TypeError(f"Expected {self.ex.__name__}({self.regex}) not raised.")
return True
def _tst_1(): assert False, "This is a test"
def _tst_2(): raise SyntaxError
with ExceptionExpected(): _tst_1()
with ExceptionExpected(ex=AssertionError, regex="This is a test"): _tst_1()
with ExceptionExpected(ex=SyntaxError): _tst_2()
```
`exception` is an abbreviation for `ExceptionExpected()`.
```
#export
exception = ExceptionExpected()
with exception: _tst_1()
#hide
def _f():
with ExceptionExpected(): 1
test_fail(partial(_f))
def _f():
with ExceptionExpected(SyntaxError): assert False
test_fail(partial(_f))
def _f():
with ExceptionExpected(AssertionError, "Yes"): assert False, "No"
test_fail(partial(_f))
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| true |
code
| 0.560072 | null | null | null | null |
|
# main function for decomposition
### Author: Yiming Fang
```
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.backends.cudnn as cudnn
from torch.optim.lr_scheduler import StepLR
import torchvision
import torchvision.transforms as transforms
from torchvision import models
import tensorly as tl
import tensorly
from itertools import chain
from tensorly.decomposition import parafac, partial_tucker
import os
import matplotlib.pyplot as plt
import numpy as np
import time
from nets import *
from decomp import *
# load data
def load_mnist():
print('==> Loading data..')
transform_train = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
transform_test = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
trainset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform_train)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True, num_workers=0)
testset = torchvision.datasets.MNIST(root='./data', train=False, download=True, transform=transform_test)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False, num_workers=0)
return trainloader, testloader
def load_cifar10():
print('==> Loading data..')
transform_train = transforms.Compose([
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
transform_test = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform_train)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True, num_workers=0)
testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform_test)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False, num_workers=0)
return trainloader, testloader
# ImageNet is no longer publically available
def load_imagenet():
print('==> Loading data..')
transform_train = transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.485, 0.456, 0.406), (0.229, 0.224, 0.225)),
])
transform_test = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize((0.485, 0.456, 0.406), (0.229, 0.224, 0.225)),
])
trainset = torchvision.datasets.ImageNet(root='./data', train=True, download=True, transform=transform_train)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True, num_workers=0)
testset = torchvision.datasets.ImageNet(root='./data', train=False, download=True, transform=transform_test)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False, num_workers=0)
return trainloader, testloader
def load_cifar100():
print('==> Loading data..')
transform_train = transforms.Compose([
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
transform_test = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
trainset = torchvision.datasets.CIFAR100(root='./data', train=True, download=True, transform=transform_train)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True, num_workers=0)
testset = torchvision.datasets.CIFAR100(root='./data', train=False, download=True, transform=transform_test)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False, num_workers=0)
return trainloader, testloader
# build model
def build(model, decomp='cp'):
print('==> Building model..')
tl.set_backend('pytorch')
full_net = model
full_net = full_net.to(device)
torch.save(full_net, 'models/model')
if decomp:
decompose(decomp)
net = torch.load("models/model").cuda()
print(net)
print('==> Done')
return net
# training
def train(epoch, train_acc, model):
print('\nEpoch: ', epoch)
model.train()
criterion = nn.CrossEntropyLoss()
train_loss = 0
correct = 0
total = 0
print('|', end='')
for batch_idx, (inputs, targets) in enumerate(trainloader):
inputs, targets = inputs.to(device), targets.to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, targets)
loss.backward()
optimizer.step()
train_loss += loss.item()
_, predicted = outputs.max(1)
total += targets.size(0)
correct += predicted.eq(targets).sum().item()
if batch_idx % 10 == 0:
print('=', end='')
print('|', 'Accuracy:', 100. * correct / total,'% ', correct, '/', total)
train_acc.append(correct / total)
return train_acc
# testing
def test(test_acc, model):
model.eval()
test_loss = 0
correct = 0
total = 0
criterion = nn.CrossEntropyLoss()
with torch.no_grad():
print('|', end='')
for batch_idx, (inputs, targets) in enumerate(testloader):
inputs, targets = inputs.to(device), targets.to(device)
outputs = model(inputs)
loss = criterion(outputs, targets)
test_loss += loss.item()
_, predicted = outputs.max(1)
total += targets.size(0)
correct += predicted.eq(targets).sum().item()
if batch_idx % 10 == 0:
print('=', end='')
acc = 100. * correct / total
print('|', 'Accuracy:', acc, '% ', correct, '/', total)
test_acc.append(correct / total)
return test_acc
# decompose
def decompose(decomp):
model = torch.load("models/model").cuda()
model.eval()
model.cpu()
for i, key in enumerate(model.features._modules.keys()):
if i >= len(model.features._modules.keys()) - 2:
break
conv_layer = model.features._modules[key]
if isinstance(conv_layer, torch.nn.modules.conv.Conv2d):
rank = max(conv_layer.weight.data.numpy().shape) // 10
if decomp == 'cp':
model.features._modules[key] = cp_decomposition_conv_layer(conv_layer, rank)
if decomp == 'tucker':
ranks = [int(np.ceil(conv_layer.weight.data.numpy().shape[0] / 3)),
int(np.ceil(conv_layer.weight.data.numpy().shape[1] / 3))]
model.features._modules[key] = tucker_decomposition_conv_layer(conv_layer, ranks)
if decomp == 'tt':
model.features._modules[key] = tt_decomposition_conv_layer(conv_layer, rank)
torch.save(model, 'models/model')
return model
# Run functions
def run_train(i, model):
train_acc = []
test_acc = []
for epoch in range(i):
s = time.time()
train_acc = train(epoch, train_acc, model)
test_acc = test(test_acc, model)
scheduler.step()
e = time.time()
print('This epoch took', e - s, 'seconds')
print('Current learning rate: ', scheduler.get_lr()[0])
print('Best training accuracy overall: ', max(test_acc))
return train_acc, test_acc
# main function
def run_all(dataset, decomp=None, iterations=100, rate=0.05):
global trainloader, testloader, device, optimizer, scheduler
# choose an appropriate learning rate
rate = rate
# choose dataset from (MNIST, CIFAR10, ImageNet)
if dataset == 'mnist':
trainloader, testloader = load_mnist()
model = Net()
if dataset == 'cifar10':
trainloader, testloader = load_cifar10()
model = VGG('VGG19')
if dataset == 'cifar100':
trainloader, testloader = load_cifar100()
model = VGG('VGG19')
# check GPU availability
device = 'cuda:0' if torch.cuda.is_available() else 'cpu'
# choose decomposition algorithm from (CP, Tucker, TT)
net = build(model, decomp)
optimizer = optim.SGD(net.parameters(), lr=rate, momentum=0.9, weight_decay=5e-4)
scheduler = StepLR(optimizer, step_size=5, gamma=0.9)
train_acc, test_acc = run_train(iterations, net)
if not decomp:
decomp = 'full'
filename = dataset + '_' + decomp
torch.save(net, 'models/' + filename)
np.save('curves/' + filename + '_train', train_acc)
np.save('curves/' + filename + '_test', test_acc)
%%time
run_all('mnist')
%%time
run_all('mnist', 'cp', rate=0.01)
%%time
run_all('mnist', 'tucker')
%%time
run_all('mnist', 'tt')
%%time
run_all('cifar10', iterations=200)
%%time
run_all('cifar10', 'tucker', iterations=200)
%%time
run_all('cifar100', 'tt', iterations=200)
```
| true |
code
| 0.69181 | null | null | null | null |
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Version Check
Plotly's python package is updated frequently. Run `pip install plotly --upgrade` to use the latest version.
```
import plotly
plotly.__version__
```
#### Basic Dot Plot
Dot plots show changes between two points in time or between two conditions.
```
import plotly.plotly as py
import plotly.graph_objs as go
trace1 = {"x": [72, 67, 73, 80, 76, 79, 84, 78, 86, 93, 94, 90, 92, 96, 94, 112],
"y": ["Brown", "NYU", "Notre Dame", "Cornell", "Tufts", "Yale",
"Dartmouth", "Chicago", "Columbia", "Duke", "Georgetown",
"Princeton", "U.Penn", "Stanford", "MIT", "Harvard"],
"marker": {"color": "pink", "size": 12},
"mode": "markers",
"name": "Women",
"type": "scatter"
}
trace2 = {"x": [92, 94, 100, 107, 112, 114, 114, 118, 119, 124, 131, 137, 141, 151, 152, 165],
"y": ["Brown", "NYU", "Notre Dame", "Cornell", "Tufts", "Yale",
"Dartmouth", "Chicago", "Columbia", "Duke", "Georgetown",
"Princeton", "U.Penn", "Stanford", "MIT", "Harvard"],
"marker": {"color": "blue", "size": 12},
"mode": "markers",
"name": "Men",
"type": "scatter",
}
data = [trace1, trace2]
layout = {"title": "Gender Earnings Disparity",
"xaxis": {"title": "Annual Salary (in thousands)", },
"yaxis": {"title": "School"}}
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filenmae='basic_dot-plot')
```
#### Styled Categorical Dot Plot
```
import plotly.plotly as py
import plotly.graph_objs as go
country = ['Switzerland (2011)', 'Chile (2013)', 'Japan (2014)',
'United States (2012)', 'Slovenia (2014)', 'Canada (2011)',
'Poland (2010)', 'Estonia (2015)', 'Luxembourg (2013)', 'Portugal (2011)']
voting_pop = [40, 45.7, 52, 53.6, 54.1, 54.2, 54.5, 54.7, 55.1, 56.6]
reg_voters = [49.1, 42, 52.7, 84.3, 51.7, 61.1, 55.3, 64.2, 91.1, 58.9]
trace0 = go.Scatter(
x=voting_pop,
y=country,
mode='markers',
name='Percent of estimated voting age population',
marker=dict(
color='rgba(156, 165, 196, 0.95)',
line=dict(
color='rgba(156, 165, 196, 1.0)',
width=1,
),
symbol='circle',
size=16,
)
)
trace1 = go.Scatter(
x=reg_voters,
y=country,
mode='markers',
name='Percent of estimated registered voters',
marker=dict(
color='rgba(204, 204, 204, 0.95)',
line=dict(
color='rgba(217, 217, 217, 1.0)',
width=1,
),
symbol='circle',
size=16,
)
)
data = [trace0, trace1]
layout = go.Layout(
title="Votes cast for ten lowest voting age population in OECD countries",
xaxis=dict(
showgrid=False,
showline=True,
linecolor='rgb(102, 102, 102)',
titlefont=dict(
color='rgb(204, 204, 204)'
),
tickfont=dict(
color='rgb(102, 102, 102)',
),
showticklabels=True,
dtick=10,
ticks='outside',
tickcolor='rgb(102, 102, 102)',
),
margin=dict(
l=140,
r=40,
b=50,
t=80
),
legend=dict(
font=dict(
size=10,
),
yanchor='middle',
xanchor='right',
),
width=800,
height=600,
paper_bgcolor='rgb(254, 247, 234)',
plot_bgcolor='rgb(254, 247, 234)',
hovermode='closest',
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='lowest-oecd-votes-cast')
```
### Reference
See https://plot.ly/python/reference/#scatter for more information and chart attribute options!
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'dot.ipynb', 'python/dot-plots/', 'Dot Plots',
'How to make dot plots in Python with Plotly.',
title = 'Python Dot Plots | plotly',
has_thumbnail='true', thumbnail='thumbnail/dot-plot.jpg',
language='python',
display_as='basic', order=3.1,
ipynb= '~notebook_demo/2')
```
| true |
code
| 0.623291 | null | null | null | null |
|
# High-performance simulations with TFF
This tutorial will describe how to setup high-performance simulations with TFF
in a variety of common scenarios.
TODO(b/134543154): Populate the content, some of the things to cover here:
- using GPUs in a single-machine setup,
- multi-machine setup on GCP/GKE, with and without TPUs,
- interfacing MapReduce-like backends,
- current limitations and when/how they will be relaxed.
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/federated/tutorials/simulations"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/federated/blob/master/docs/tutorials/simulations.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/federated/blob/master/docs/tutorials/simulations.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/federated/docs/tutorials/simulations.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
## Before we begin
First, make sure your notebook is connected to a backend that has the relevant
components (including gRPC dependencies for multi-machine scenarios) compiled.
Now, let's start by loading the MNIST example from the TFF website, and
declaring the Python function that will run a small experiment loop over
a group of 10 clients.
```
#@test {"skip": true}
!pip install --quiet --upgrade tensorflow-federated-nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
import collections
import time
import tensorflow as tf
import tensorflow_federated as tff
source, _ = tff.simulation.datasets.emnist.load_data()
def map_fn(example):
return collections.OrderedDict(
x=tf.reshape(example['pixels'], [-1, 784]), y=example['label'])
def client_data(n):
ds = source.create_tf_dataset_for_client(source.client_ids[n])
return ds.repeat(10).shuffle(500).batch(20).map(map_fn)
train_data = [client_data(n) for n in range(10)]
element_spec = train_data[0].element_spec
def model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.InputLayer(input_shape=(784,)),
tf.keras.layers.Dense(units=10, kernel_initializer='zeros'),
tf.keras.layers.Softmax(),
])
return tff.learning.from_keras_model(
model,
input_spec=element_spec,
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
trainer = tff.learning.build_federated_averaging_process(
model_fn, client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.02))
def evaluate(num_rounds=10):
state = trainer.initialize()
for _ in range(num_rounds):
t1 = time.time()
state, metrics = trainer.next(state, train_data)
t2 = time.time()
print('metrics {m}, round time {t:.2f} seconds'.format(
m=metrics, t=t2 - t1))
```
## Single-machine simulations
Now on by default.
```
evaluate()
```
## Multi-machine simulations on GCP/GKE, GPUs, TPUs, and beyond...
Coming very soon.
| true |
code
| 0.713419 | null | null | null | null |
|
```
import numpy as np
from keras.models import Model
from keras.layers import Input, Dense, RepeatVector
from keras.layers.merge import Add, Subtract, Multiply, Average, Maximum, Minimum, Concatenate, Dot
from keras import backend as K
import json
from collections import OrderedDict
def format_decimal(arr, places=6):
return [round(x * 10**places) / 10**places for x in arr]
DATA = OrderedDict()
```
**[merge.Multiply.0]**
```
random_seed = 100
data_in_shape = (6,)
layer_0 = Input(shape=data_in_shape)
layer_1a = Dense(2, activation='linear')(layer_0)
layer_1b = Dense(2, activation='linear')(layer_0)
layer_2 = Multiply()([layer_1a, layer_1b])
model = Model(inputs=layer_0, outputs=layer_2)
np.random.seed(random_seed)
data_in = np.expand_dims(2 * np.random.random(data_in_shape) - 1, axis=0)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(random_seed + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
result = model.predict(data_in)
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
DATA['merge.Multiply.0'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[merge.Multiply.1]**
```
random_seed = 100
data_in_shape = (6,)
layer_0 = Input(shape=data_in_shape)
layer_1a = Dense(2, activation='linear')(layer_0)
layer_1b = Dense(2, activation='linear')(layer_0)
layer_1c = Dense(2, activation='linear')(layer_0)
layer_2 = Multiply()([layer_1a, layer_1b, layer_1c])
model = Model(inputs=layer_0, outputs=layer_2)
np.random.seed(random_seed)
data_in = np.expand_dims(2 * np.random.random(data_in_shape) - 1, axis=0)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(random_seed + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
result = model.predict(data_in)
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
DATA['merge.Multiply.1'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[merge.Multiply.2]**
```
random_seed = 100
data_in_shape = (6,)
layer_0 = Input(shape=data_in_shape)
layer_1a = Dense(2, activation='linear')(layer_0)
layer_1b = Dense(2, activation='linear')(layer_0)
layer_1c = Dense(2, activation='linear')(layer_0)
layer_1d = Dense(2, activation='linear')(layer_0)
layer_2 = Multiply()([layer_1a, layer_1b, layer_1c, layer_1d])
model = Model(inputs=layer_0, outputs=layer_2)
np.random.seed(random_seed)
data_in = np.expand_dims(2 * np.random.random(data_in_shape) - 1, axis=0)
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(random_seed + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
result = model.predict(data_in)
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
DATA['merge.Multiply.2'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'weights': [{'data': format_decimal(w.ravel().tolist()), 'shape': w.shape} for w in weights],
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
### export for Keras.js tests
```
import os
filename = '../../../test/data/layers/merge/Multiply.json'
if not os.path.exists(os.path.dirname(filename)):
os.makedirs(os.path.dirname(filename))
with open(filename, 'w') as f:
json.dump(DATA, f)
print(json.dumps(DATA))
```
| true |
code
| 0.531878 | null | null | null | null |
|
# Noise Estimation using Correlation Methods
In this tutorial, we will demonstrate how to use 2-channel and 3-channel correlation methods,`kontrol.spectral.two_channel_correlation()` and `kontrol.spectral.three_channel_correlation()`, to estimate sensor self noise. Library reference is available [here](https://kontrol.readthedocs.io/en/latest/main_utilities.html#spectral-analysis-functions).
Description of this method is available in the baseline method section of [here](https://github.com/gw-vis/vis-commissioning-tex). We will also use notations in the document.
Let's say we have three sensors, with readouts $y_1(t)$, $y_2(t)$, and $y_3(t)$.
We place them in a position such that they sense a coherent signal
$x(t)=\Re\left(Ae^{\left(\sigma+i\omega_0e^{\gamma t}\right)t}\right)$,
where $i$ is the imaginary number, $A$ is $A$ is a real number, $\sigma$ and $\gamma$ are negative real numbers, and $\omega_0$ is a positive real number.
The first two sensors have dynamics
$H_1(s)=H_2(s)=\frac{s^2}{s^2+2\zeta\omega_ns+\omega_n^2}$,
where $\zeta>0$ and $\omega_n>0$, and the third sensor has dynamics
$H_3(s)=\frac{\omega_m}{s+\omega_m}$.
The sensors have noise dynamics
$N_i(s)=G_i(s)W_i(s)$,
where $i=1,2,3$, $W_i(s)$ is white noise with unit amplitude, and $G_i(s)$ is the noise dynamics of the sensors. Here, $W_i(s)$s are uncorrelated.
Let's say
$G_1(s)=G_2(s)=\frac{a_1}{s+\epsilon_1}$ and $G_3(s)=\frac{a_3}{(s+\epsilon_3)^2}$,
where $a_1$ and $a_3$ real number, $\epsilon_1$ and $\epsilon_3$ are real numbers, and $\epsilon_1\approx\epsilon_3\ll\omega_0$.
The readouts are then simply
$y_i(t) = \mathcal{L}^{-1}\left\{X(s)H_i(s) + N_i(s)\right\}$.
```
import control
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(123)
# Time axis and sampling frequency
fs = 128
t0 = 0
t_end = 512
t = np.arange(t0, t_end, 1/fs)
# The coherent signal
A = 1
sigma = -.01
gamma = -0.1
omega_0 = 10*2*np.pi
x = A*np.exp((sigma + 1j*omega_0*np.exp(gamma*t)) * t).real
# The sensor dynamics.
zeta = 1
omega_n = 1*2*np.pi
omega_m = 10
s = control.tf("s")
H1 = s**2 / (s**2 + 2*zeta*omega_n*s + omega_n**2)
H2 = H1
H3 = omega_m / (s+omega_m)
# Signals sensed by the sensors.
_, x1 = control.forced_response(sys=H1, T=t, U=x)
_, x2 = control.forced_response(sys=H2, T=t, U=x)
_, x3 = control.forced_response(sys=H3, T=t, U=x)
# The noises
w1 = np.random.normal(loc=0, scale=1, size=len(t))
w2 = np.random.normal(loc=0, scale=1, size=len(t))
w3 = np.random.normal(loc=0, scale=1, size=len(t))
a1 = 0.5
a3 =5
epsilon_1 = omega_0/100
epsilon_3 = omega_0/200
G1 = a1 / (s+epsilon_1)
G2 = G1
G3 = a3 / (s+epsilon_3)**2
_, n1 = control.forced_response(sys=G1, T=t, U=w1)
_, n2 = control.forced_response(sys=G2, T=t, U=w2)
_, n3 = control.forced_response(sys=G3, T=t, U=w3)
# The readouts
y1 = x1 + n1
y2 = x2 + n2
y3 = x3 + n3
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.plot(t, x, label="Coherent signal $x(t)$", lw=3)
plt.plot(t, y1, "--", label="Readout $y_1(t)$", lw=1)
plt.plot(t, y2, "--", label="Readout $y_2(t)$", lw=1)
plt.plot(t, y3, "k--", label="Readout $y_3(t)$", lw=1)
plt.legend(loc=0)
plt.ylabel("Ampitude (a.u.)")
plt.xlabel("Time (s)")
plt.subplot(122, title="Noises")
plt.plot(1,1) # just to shift the colors.
plt.plot(t, n1, label="noise in $y_1$")
plt.plot(t, n2, label="noise in $y_2$")
plt.plot(t, n3, "k", label="noise in $y_3$")
plt.legend(loc=0)
plt.ylabel("Ampitude (a.u.)")
plt.xlabel("Time (s)")
plt.show()
```
Let's plot the PSDs
```
import scipy.signal
f, P_x = scipy.signal.welch(x, fs=fs)
f, P_n1 = scipy.signal.welch(n1, fs=fs)
f, P_n2 = scipy.signal.welch(n2, fs=fs)
f, P_n3 = scipy.signal.welch(n3, fs=fs)
f, P_y1 = scipy.signal.welch(y1, fs=fs)
f, P_y2 = scipy.signal.welch(y2, fs=fs)
f, P_y3 = scipy.signal.welch(y3, fs=fs)
plt.figure(figsize=(10, 5))
plt.loglog(f, P_x, label="Signal $x(t)$", lw=3)
plt.loglog(f, P_n1, label="Noise $n_1(t)$", lw=3)
plt.loglog(f, P_n2, "--", label="Noise $n_2(t)$", lw=2)
plt.loglog(f, P_n3, label="Noise $n_3(t)$", lw=3)
plt.loglog(f, P_y1, "k--", label="Readout $y_1(t)$", lw=2)
plt.loglog(f, P_y2, "g-.", label="Readout $y_2(t)$", lw=2)
plt.loglog(f, P_y3, "b--", label="Readout $y_3(t)$", lw=2)
plt.legend(loc=0)
plt.grid(which="both")
plt.ylim(1e-9, 1e-1)
plt.xlim(0.5, 10)
plt.ylabel("Power spectral density (a.u./Hz)")
plt.xlabel("Frequency (Hz)")
plt.show()
```
## Two-channel method
Sensor 1 and sensor 2 has the same dynamics and noise PSD.
Let's see if we can predict the two noises using the two-channel correlation method.
Here, we will use Kontrol spectral analysis utilities.
```
import kontrol
# Use the time series directly.
P_n1_2channel = kontrol.spectral.two_channel_correlation(y1, y2, fs=fs)
P_n2_2channel = kontrol.spectral.two_channel_correlation(y2, y1, fs=fs)
# # Alternatively, use the PSD and coherence directly.
# _, coherence_12 = scipy.signal.coherence(y1, y2, fs=fs)
# _, coherence_21 = scipy.signal.coherence(y2, y1, fs=fs) # This is actually the same as coherence_12
# P_n1_2channel_coh = kontrol.spectral.two_channel_correlation(P_y1, P_y2, fs=fs, coherence=coherence_12)
# P_n2_2channel_coh = kontrol.spectral.two_channel_correlation(P_y2, P_y1, fs=fs, coherence=coherence_21)
# # Alternatively, use the PSD and cross power spectral density directly.
# _, cpsd_12 = scipy.signal.csd(y1, y2, fs=fs)
# _, cpsd_21 = scipy.signal.csd(y2, y1, fs=fs)
# P_n1_2channel_cpsd = kontrol.spectral.two_channel_correlation(P_y1, P_y2, fs=fs, cpsd=cpsd_12)
# P_n2_2channel_cpsd = kontrol.spectral.two_channel_correlation(P_y2, P_y1, fs=fs, cpsd=cpsd_21)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.loglog(f, P_n1, label="Sensor noise 1")
plt.loglog(f, P_n1_2channel, label="Predicted using 2-channel correlation method")
plt.legend(loc=0)
plt.grid(which="both")
plt.ylim(1e-7, 1e-3)
plt.xlim(0.5, 10)
plt.ylabel("Power spectral density (a.u./Hz)")
plt.xlabel("Frequency (Hz)")
plt.subplot(122)
plt.loglog(f, P_n2, label="Sensor noise 2")
plt.loglog(f, P_n2_2channel, label="Predicted using 2-channel correlation method")
plt.legend(loc=0)
plt.grid(which="both")
plt.ylim(1e-7, 1e-3)
plt.xlim(0.5, 10)
plt.ylabel("Power spectral density (a.u./Hz)")
plt.xlabel("Frequency (Hz)")
plt.show()
```
As can be seen, the 2-channnel method works perfectly in predicting the sensor noises using only the readouts.
Just curious to see what happens if we use sensor 3, which is not the same as sensor 1 and 2, instead.
```
P_n1_2channel_from_n3 = kontrol.spectral.two_channel_correlation(y1, y3, fs=fs)
P_n3_2channel_from_n1 = kontrol.spectral.two_channel_correlation(y3, y1, fs=fs)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.loglog(f, P_n1, label="Sensor noise 1")
plt.loglog(f, P_n1_2channel_from_n3, label="Predicted using 2-channel correlation method but with non-identical sensor")
plt.legend(loc=0)
plt.grid(which="both")
plt.ylim(1e-7, 1e-3)
plt.xlim(0.5, 10)
plt.ylabel("Power spectral density (a.u./Hz)")
plt.xlabel("Frequency (Hz)")
plt.subplot(122)
plt.loglog(f, P_n3, label="Sensor noise 3")
plt.loglog(f, P_n3_2channel_from_n1, label="Predicted using 2-channel correlation method but with non-identical sensor")
plt.legend(loc=0)
plt.grid(which="both")
# plt.ylim(1e-7, 1e-3)
plt.xlim(0.5, 10)
plt.ylabel("Power spectral density (a.u./Hz)")
plt.xlabel("Frequency (Hz)")
plt.show()
```
Interesting, somehow gets the sensor 3 noise more accurately than that of sensor 1. But it could be just a fluke.
## Three-channel correlation method
Now, let's compute the sensors noise using the three-channel method.
```
# Use time series directly
P_n1_3channel = kontrol.spectral.three_channel_correlation(y1, y2, y3, fs=fs)
P_n2_3channel = kontrol.spectral.three_channel_correlation(y2, y1, y3, fs=fs)
P_n3_3channel = kontrol.spectral.three_channel_correlation(y3, y1, y2, fs=fs)
# # Alternatively, use PSD and coherences
# _, coherence_12 = scipy.signal.coherence(y1, y2, fs=fs)
# _, coherence_13 = scipy.signal.coherence(y1, y3, fs=fs)
# _, coherence_21 = scipy.signal.coherence(y2, y1, fs=fs)
# _, coherence_23 = scipy.signal.coherence(y2, y3, fs=fs)
# _, coherence_31 = scipy.signal.coherence(y3, y1, fs=fs)
# _, coherence_32 = scipy.signal.coherence(y3, y2, fs=fs)
# n1_kwargs = {
# "coherence_13": coherence_13,
# "coherence_23": coherence_23,
# "coherence_21": coherence_21,
# }
# # Notice the changes.
# n2_kwargs = {
# "coherence_13": coherence_23,
# "coherence_23": coherence_13,
# "coherence_21": coherence_12,
# }
# n3_kwargs = {
# "coherence_13": coherence_32,
# "coherence_23": coherence_12,
# "coherence_21": coherence_13,
# }
# P_n1_3channel = kontrol.spectral.three_channel_correlation(P_y1, **n1_kwargs)
# P_n2_3channel = kontrol.spectral.three_channel_correlation(P_y2, **n2_kwargs)
# P_n3_3channel = kontrol.spectral.three_channel_correlation(P_y3, **n3_kwargs)
# # And Alternatively, use PSD and cross power spectral densities.
# _, cpsd_12 = scipy.signal.csd(y1, y2, fs=fs)
# _, cpsd_13 = scipy.signal.csd(y1, y3, fs=fs)
# _, cpsd_21 = scipy.signal.csd(y2, y1, fs=fs)
# _, cpsd_23 = scipy.signal.csd(y2, y3, fs=fs)
# _, cpsd_31 = scipy.signal.csd(y3, y1, fs=fs)
# _, cpsd_32 = scipy.signal.csd(y3, y2, fs=fs)
# n1_kwargs = {
# "cpsd_13": cpsd_13,
# "cpsd_23": cpsd_23,
# "cpsd_21": cpsd_21
# }
# n2_kwargs = {
# "cpsd_13": cpsd_23,
# "cpsd_23": cpsd_13,
# "cpsd_21": cpsd_12,
# }
# n3_kwargs = {
# "cpsd_13": cpsd_32,
# "cpsd_23": cpsd_12,
# "cpsd_21": cpsd_13
# }
# P_n1_3channel = kontrol.spectral.three_channel_correlation(P_y1, **n1_kwargs)
# P_n2_3channel = kontrol.spectral.three_channel_correlation(P_y2, **n2_kwargs)
# P_n3_3channel = kontrol.spectral.three_channel_correlation(P_y3, **n3_kwargs)
plt.figure(figsize=(15, 10))
plt.subplot(221)
plt.loglog(f, P_y1, label="Readout 1")
plt.loglog(f, P_n1, label="Sensor noise 1", lw=3)
plt.loglog(f, P_n1_2channel, "--", label="Predicted using 2-channel correlation method.", lw=2)
plt.loglog(f, P_n1_3channel, "k-.", label="Predicted using 3-channel correlation method.", lw=2, markersize=3)
plt.legend(loc=0)
plt.grid(which="both")
plt.ylim(1e-7, 1e-2)
plt.xlim(0.5, 10)
plt.ylabel("Power spectral density (a.u./Hz)")
plt.xlabel("Frequency (Hz)")
plt.subplot(222)
plt.loglog(f, P_y2, label="Readout 2",)
plt.loglog(f, P_n2, label="Sensor noise 2", lw=3)
plt.loglog(f, P_n2_2channel, "--", label="Predicted using 2-channel correlation method.", lw=2)
plt.loglog(f, P_n2_3channel, "k-.", label="Predicted using 3-channel correlation method.", lw=2, markersize=3)
plt.legend(loc=0)
plt.grid(which="both")
plt.ylim(1e-7, 1e-2)
plt.xlim(0.5, 10)
plt.ylabel("Power spectral density (a.u./Hz)")
plt.xlabel("Frequency (Hz)")
plt.subplot(223)
plt.loglog(f, P_y3, label="Readout 3")
plt.loglog(f, P_n3, label="Sensor noise 3", lw=3)
plt.loglog(f, P_n3_2channel_from_n1, "--", label="2-channel correlation method with sensor 1", lw=2)
plt.loglog(f, P_n3_3channel, "k-.", label="Predicted using 3-channel correlation method.", lw=2, markersize=3)
plt.legend(loc=0)
plt.grid(which="both")
plt.ylim(1e-9, 1e-1)
plt.xlim(0.5, 10)
plt.ylabel("Power spectral density (a.u./Hz)")
plt.xlabel("Frequency (Hz)")
# plt.loglog(f, P_n3)
# plt.loglog(f, np.abs(P_n3_3channel))
# plt.loglog(f, P_n3_3channel_coh)
plt.show()
```
| true |
code
| 0.726292 | null | null | null | null |
|
<img src="NotebookAddons/blackboard-banner.png" width="100%" />
<font face="Calibri">
<br>
<font size="5"> <b>Volcano Source Modeling Using InSAR</b> </font>
<br>
<font size="4"> <b> Franz J Meyer; University of Alaska Fairbanks </b> <br>
</font>
<img style="padding: 7px" src="NotebookAddons/UAFLogo_A_647.png" width="170" align="right" /> <font size="3"> This notebook will introduce you to the intersection between Radar Remote Sensing and Inverse Modeling. Radar Remote Sensing can provide us with geodetic observations of surface deformation. Inverse Modeling helps us understand the physical causes behind an observed deformation.
To illuminate the handoff from geodesy to geophysics, this notebook will show how to use InSAR observations to determine the most likely parameters of a volcanic magma source underneath Okmok volcano, Alaska. We will use a Mogi source model to describe the physics behind deformation at Okmok. We will again use our **Jupyter Notebook** framework implemented within the Amazon Web Services (AWS) cloud to work on this exercise. <br><br>
This notebook will introduce the following data analysis concepts:
- A Mogi Source Model describing volcanic source geometry and physics
- How to use the "grid search" method to perform a pseudo-inversion of a Mogi source model
- How to solve for the best fitting source parameters using modeling with InSAR data
</font>
<br>
<font size="3">To download, please select the following options in the main menu of the notebook interface:
<br>
<ol type="1">
<li><font color='rgba(200,0,0,0.2)'> <b> Save your notebook with all of its content</b></font> by selecting <i> File / Save and Checkpoint </i> </li>
<li><font color='rgba(200,0,0,0.2)'> <b>To export in Notebook format</b></font>, click on <i>File / Download as / Notebook (.ipynb)</i></li>
<li><font color='rgba(200,0,0,0.2)'> <b>To export in PDF format</b></font>, click on <i>File / Download as / PDF vs LaTeX (.pdf) </i></li>
</ol>
</font>
</font>
<hr>
<font face="Calibri" size="5" color="darkred"> <b>Important Note about JupyterHub</b> </font>
<br><br>
<font face="Calibri" size="3"> <b>Your JupyterHub server will automatically shutdown when left idle for more than 1 hour. Your notebooks will not be lost but you will have to restart their kernels and re-run them from the beginning. You will not be able to seamlessly continue running a partially run notebook.</b> </font>
```
%%javascript
var kernel = Jupyter.notebook.kernel;
var command = ["notebookUrl = ",
"'", window.location, "'" ].join('')
kernel.execute(command)
from IPython.display import Markdown
from IPython.display import display
user = !echo $JUPYTERHUB_USER
env = !echo $CONDA_PREFIX
if env[0] == '':
env[0] = 'Python 3 (base)'
if env[0] != '/home/jovyan/.local/envs/insar_analysis':
display(Markdown(f'<text style=color:red><strong>WARNING:</strong></text>'))
display(Markdown(f'<text style=color:red>This notebook should be run using the "insar_analysis" conda environment.</text>'))
display(Markdown(f'<text style=color:red>It is currently using the "{env[0].split("/")[-1]}" environment.</text>'))
display(Markdown(f'<text style=color:red>Select "insar_analysis" from the "Change Kernel" submenu of the "Kernel" menu.</text>'))
display(Markdown(f'<text style=color:red>If the "insar_analysis" environment is not present, use <a href="{notebookUrl.split("/user")[0]}/user/{user[0]}/notebooks/conda_environments/Create_OSL_Conda_Environments.ipynb"> Create_OSL_Conda_Environments.ipynb </a> to create it.</text>'))
display(Markdown(f'<text style=color:red>Note that you must restart your server after creating a new environment before it is usable by notebooks.</text>'))
```
<hr>
<font face="Calibri">
<font size="5"> <b> 0. Importing Relevant Python Packages </b> </font>
<font size="3"> First step in any notebook is to import the required Python libraries into the Jupyter environment. In this notebooks we use the following scientific libraries:
<ol type="1">
<li> <b><a href="http://www.numpy.org/" target="_blank">NumPy</a></b> is one of the principal packages for scientific applications of Python. It is intended for processing large multidimensional arrays. </li>
<li> <b><a href="https://matplotlib.org/index.html" target="_blank">Matplotlib</a></b> is a low-level library for creating two-dimensional diagrams and graphs. With its help, you can build diverse charts, from histograms and scatterplots to non-Cartesian coordinates graphs. </li>
</font>
<br>
<font face="Calibri" size="3">The first step is to <b>import all required python modules:</b></font>
```
%%capture
import os # for chdir, getcwd, path.basename, path.exists
import copy
%matplotlib inline
import matplotlib.pylab as plt # for add_subplot, cm.jet, colorbar, figure, grid, imshow, rcParams.update, savefig,
# set_bad, set_clim, set_title, set_xlabel, set_ylabel
import numpy as np # for arange, arctan, concatenate, cos, fromfile, isnan, ma.masked_value, min, pi, power, reshape,
# sqrt, square, sin, sum, tile, transpose, where, zeros
import asf_notebook as asfn
asfn.jupytertheme_matplotlib_format()
```
<hr>
<font face="Calibri">
<font size="5"> <b> 1. InSAR at Okmok Volcano, Alaska </b> </font>
<img style="padding: 7px" src="NotebookAddons/Lab6-OkmokdefoGPS.JPG" width="550" align="right" /><font size="3"> Okmok is one of the more active volcanoes in Alaska’s Aleutian Chain. Its last (known) eruption was in the summer of 2008. Okmok is interesting from an InSAR perspective as it inflates and deflates heavily as magma moves around in its magmatic source located roughly 2.5 km underneath the surface. To learn more about Okmok volcano and its eruptive history, please visit the very informative site of the <a href="https://avo.alaska.edu/volcanoes/activity.php?volcname=Okmok&eruptionid=604&page=basic" target="_blank">Alaska Volcano Observatory</a>.
This notebook uses a pair of C-band ERS-2 SAR images acquired on Aug 18, 2000 and Jul 19, 2002 to analyze the properties of a volcanic source that was responsible for an inflation of Okmok volcano of more than 3 cm near its summit. The figure to the right shows the Okmok surface deformation as measured by GPS data from field campaigns conducted in 2000 and 2002. The plots show that the deformation measured at the site is consistent with that created by an inflating point (Mogi) source.<br>
<b>The primary goal of the problem set is to estimate values for four unknown model parameters describing a source process beneath a volcano.</b> The notebook uses real InSAR data from Okmok volcano, so you should get some sense for how remote sensing can be used to infer physical processes at volcanoes. We will assume that the source can be modeled as an inflating point source (a so-called Mogi source; see <a href="https://radar.community.uaf.edu/files/2019/03/2019-Lecture14_UsingInSARinGeophysics.pdf" target="_blank">Lecture 14</a>) and will use a grid-search method for finding the source model parameters (3D source location and volume of magma influx) that best describe our InSAR-observed surface deformation.
</font>
</font>
<hr>
<font face="Calibri" size="5"> <b> 2. Download and Plot the Observed Deformation Map </b>
<font face="Calibri" size="4"> <b> 2.1 Download Data from AWS S3 Storage Bucket</b><br>
<font size="3"> We are using a deformation map created from C-band ERS-2 SAR images acquired on Aug 18, 2000 and Jul 19, 2002. The deformation map is <b>available to you on the Class AWS S3 data storage bucket:</b> </font>
<font face="Calibri" size="3"><b>Create a working directory for this analysis and change into it.</b></font>
```
path = "/home/jovyan/notebooks/SAR_Training/English/Master/data_InSAR_volcano_source_modeling"
asfn.new_directory(path)
os.chdir(path)
print(f"Current working directory: {os.getcwd()}")
```
<font face="Calibri" size="3"><b>Download the deformation map from the AWS-S3 bucket:</b></font>
```
deformation_map_path = 's3://asf-jupyter-data/E451_20000818_20020719.unw'
deformation_map = os.path.basename(deformation_map_path)
!aws --region=us-east-1 --no-sign-request s3 cp $deformation_map_path $deformation_map
```
<font face="Calibri" size="3"><b>Define some variables:</b></font>
```
sample = 1100
line = 980
posting = 40.0
half_wave = 28.3
```
<font face="Calibri" size="3"><b>Read the dataset into the notebook</b>, storing our observed deformation map in the variable <i>"observed_deformation_map"</i>: </font>
```
if asfn.path_exists(deformation_map):
with open (deformation_map, 'rb') as f:
coh = np.fromfile(f, dtype='>f', count=-1)
observed_deformation_map = np.reshape(coh, (line, sample))
```
<font face="Calibri" size="3"><b>Change the units to cm and replace all nans with 0</b></font>
```
observed_deformation_map = observed_deformation_map*half_wave/2.0/np.pi
where_are_NaNs = np.isnan(observed_deformation_map)
observed_deformation_map[where_are_NaNs] = 0
```
<font face="Calibri" size="3"> <b>Create a mask</b> that removes invalid samples (low coherence) from the deformation map: </font>
```
observed_deformation_map_m = np.ma.masked_where(observed_deformation_map==0, observed_deformation_map)
```
<hr>
<font face="Calibri" size="4"> <b> 2.2 Visualize The Deformation Map </b>
<font size="3"> We will visualize the deformation map both in units of [cm] and as a rewrapped interferogram.</font>
<br><br>
<font size="3"><b>Write a function that calculates the bounding box.</b></font>
```
def extents(vector_component):
delta = vector_component[1] - vector_component[0]
return [vector_component[0] - delta/2, vector_component[-1] + delta/2]
```
<font face="Calibri" size="3"><b>Create a directory in which to store the plots we are about to make, and move into it:</b></font>
```
os.chdir(path)
product_path = 'plots'
asfn.new_directory(product_path)
if asfn.path_exists(product_path) and os.getcwd() != f"{path}/{product_path}":
os.chdir(product_path)
print(f"Current working directory: {os.getcwd()}")
```
<font size="3"><b>Write a plotting function</b>:</font>
```
def plot_model(infile, line, sample, posting, output_filename=None, dpi=72):
# Calculate the bounding box
extent_xvec = extents((np.arange(1, sample*posting, posting)) / 1000)
extent_yvec = extents((np.arange(1, line*posting, posting)) / 1000)
extent_xy = extent_xvec + extent_yvec
plt.rcParams.update({'font.size': 14})
inwrapped = (infile/10 + np.pi) % (2*np.pi) - np.pi
cmap = copy.copy(plt.cm.get_cmap("jet"))
cmap.set_bad('white', 1.)
# Plot displacement
fig = plt.figure(figsize=(16, 8))
ax1 = fig.add_subplot(1, 2, 1)
im = ax1.imshow(infile, interpolation='nearest', cmap=cmap, extent=extent_xy, origin='upper')
cbar = ax1.figure.colorbar(im, ax=ax1, orientation='horizontal')
ax1.set_title("Displacement in look direction [mm]")
ax1.set_xlabel("Easting [km]")
ax1.set_ylabel("Northing [km]")
plt.grid()
# Plot interferogram
im.set_clim(-30, 30)
ax2 = fig.add_subplot(1, 2, 2)
im = ax2.imshow(inwrapped, interpolation='nearest', cmap=cmap, extent=extent_xy, origin='upper')
cbar = ax2.figure.colorbar(im, ax=ax2, orientation='horizontal')
ax2.set_title("Interferogram phase [rad]")
ax2.set_xlabel("Easting [km]")
ax2.set_ylabel("Northing [km]")
plt.grid()
if output_filename:
plt.savefig(output_filename, dpi=dpi)
```
<font face="Calibri" size="3">Call plot_model() to <b>plot our observed deformation map:</b> </font>
```
plot_model(observed_deformation_map_m, line, sample, posting, output_filename='Okmok-inflation-observation.png', dpi=200)
```
<hr>
<font face="Calibri" size="5"> <b> 3. The Mogi Source Model and InSAR</b>
<font face="Calibri" size="4"> <b> 3.1 The Mogi Equations</b><br>
<font size="3"> The Mogi model provides the 3D ground displacement, $u(x,y,z)$, due to an inflating source at location $(x_s,y_s,z_s)$ with volume change $V$:
\begin{equation}
u(x,y,z)=\frac{1}{\pi}(1-\nu)\cdot V\Big(\frac{x-x_s}{r(x,y,z)^3},\frac{y-y_s}{r(x,y,z)^3},\frac{z-z_s}{r(x,y,z)^3}\Big)
\end{equation}
<br>
\begin{equation}
r(x,y,z)=\sqrt{(x-x_s)^2+(y-y_s)^2+(z-z_s)^2}
\end{equation}
where $r$ is the distance from the Mogi source to $(x,y,z)$, and $\nu$ is the Poisson's ratio of the halfspace. The Poisson ratio describes how rocks react when put under stress (e.g., pressure). It is affected by temperature, the quantity of liquid to solid, and the composition of the soil material. <b>In our problem, we will assume that $\nu$ is fixed</b>.
</font>
<hr>
<font face="Calibri" size="4"> <b> 3.2 Projecting Mogi Deformation to InSAR Line-of-Sight</b><br>
<font size="3"> In our example, the $x$-axis points east, $y$ points north, and $z$ points up. However, in the code the input values for $z$ are assumed to be depth, such that the Mogi source is at depth $z_s > 0$. The observed interferogram is already corrected for the effect of topography, so the observations can be considered to be at $z = 0$.
<img style="padding: 7px" src="NotebookAddons/Lab6-LOSprojection.JPG" width="650" align="center" />
The satellite “sees” a projection of the 3D ground displacement, $u$, onto the look vector, $\hat{L}$, which points from the satellite to the target. Therefore, we are actually interested in the (signed magnitude of the) projection of $u$ onto $\hat{L}$ (right). This is given by
\begin{array}{lcl} proj_{\hat{L}}u & = & (u^T\hat{L})\hat{L} \\ u^T\hat{L} & = & u \cdot \hat{L} = |u||\hat{L}|cos(\alpha) = |u|cos(\alpha) \\ & = & u_x\hat{L}_x+ u_y\hat{L}_y + u_z\hat{L}_z \end{array}
where the look vector is given by $\hat{L}=(sin(l) \cdot cos(t), -sin(l) \cdot sin(t), -cos(l))$, where $l$ is the look angle measured from the nadir direction and $t$ is the satellite track angle measured clockwise from geographic north. All vectors are represented in an east-north-up basis.
Our forward model takes a Mogi source, $(x_s,y_s,z_s,V)$, and computes the look displacement at any given $(x, y, z)$ point. If we represent the <i>i</i>th point on our surface grid by $x_i = (x_i,y_i,z_i)$ the the displacement vector is $u_i = u(x_i, y_i, z_i)$, and the look displacement is
\begin{equation}
d_i = u_i \cdot \hat{L}
\end{equation}
<br>
<hr>
<font size="4"> <b> 3.3 Defining the Mogi Forward Model</b><br></font>
<font size="3">We can now represent the Mogi <i>forward problem</i> as
\begin{equation}
g(m) = d
\end{equation}
where $g(·)$ describes the forward model in the very first equation in this notebook, $m$ is the (unknown) Mogi model, and $d$ is the predicted interferogram. The following code cells calculate the Mogi forward model according to the equations given above:
</font>
<font face="Calibri" size="3"><b>Write a function to calculate a forward model for a Mogi source.</b> </font>
```
def calc_forward_model_mogi(n1, e1, depth, delta_volume, northing, easting, plook):
# This geophysical coefficient is needed to describe how pressure relates to volume change
displacement_coefficient = (1e6*delta_volume*3)/(np.pi*4)
# Calculating the horizontal distance from every point in the deformation map to the x/y source location
d_mat = np.sqrt(np.square(northing-n1) + np.square(easting-e1))
# denominator of displacement field for mogi source
tmp_hyp = np.power(np.square(d_mat) + np.square(depth),1.5)
# horizontal displacement
horizontal_displacement = displacement_coefficient * d_mat / tmp_hyp
# vertical displacement
vertical_displacement = displacement_coefficient * depth / tmp_hyp
# azimuthal angle
azimuth = np.arctan2((easting-e1), (northing-n1))
# compute north and east displacement from horizontal displacement and azimuth angle
east_displacement = np.sin(azimuth) * horizontal_displacement
north_displacement = np.cos(azimuth) * horizontal_displacement
# project displacement field onto look vector
temp = np.concatenate((east_displacement, north_displacement, vertical_displacement), axis=1)
delta_range = temp.dot(np.transpose([plook]))
delta_range = -1.0 * delta_range
return delta_range
```
<font face="Calibri" size="3"><b>Write a function to create simulated deformation data based on Mogi Source Model parameters:</b> </font>
```
def deformation_data_from_mogi(x, y, z, volume, iplot, imask):
# Organizing model parameters
bvc = [x, y, z, volume, 0, 0, 0, 0]
bvc = np.asarray(bvc, dtype=object)
bvc = np.transpose(bvc)
# Setting acquisition parameters
track = -13.3*np.pi / 180.0
look = 23.0*np.pi / 180.0
plook = [-np.sin(look)*np.cos(track), np.sin(look)*np.sin(track), np.cos(look)]
# Defining easting and northing vectors
northing = np.arange(0, (line)*posting, posting) / 1000
easting = np.arange(0, (sample)*posting, posting) / 1000
northing_mat = np.tile(northing, (sample, 1))
easting_mat = np.transpose(np.tile(easting, (line, 1)))
northing_vec = np.reshape(northing_mat, (line*sample, 1))
easting_vec = np.reshape(easting_mat, (line*sample, 1))
# Handing coordinates and model parameters over to the rngchg_mogi function
calc_range = calc_forward_model_mogi(bvc[1], bvc[0], bvc[2], bvc[3], northing_vec, easting_vec, plook)
# Reshaping surface deformation data derived via calc_forward_model_mogi()
surface_deformation = np.reshape(calc_range, (sample,line))
# return rotated surface deformation
return np.transpose(np.fliplr(surface_deformation))
```
<hr>
<font face="Calibri" size="4"> <b> 3.4 Plotting The Mogi Forward Model</b><br></font>
<font face="Calibri" size="3">The cell below plots several Mogi forward models by varying some of the four main Mogi modeling parameters $(x_s,y_s,z_s,V)$.
The examples below fix the <i>depth</i> parameter to $z_s = 2.58 km$ and the <i>volume</i> change parameter to $volume = 0.0034 km^3$. We then vary the <i>easting</i> and <i>northing</i> parameters $x_s$ and $y_s$ to demonstrate how the model predictions vary when model parameters are changed.</font>
<br><br>
<font face="Calibri" size="3"><b>Run the first example:</b> </font>
```
plt.rcParams.update({'font.size': 14})
extent_x = extents((np.arange(1, sample*posting, posting))/1000)
extent_y = extents((np.arange(1, line*posting, posting))/1000)
extent_xy = extent_x + extent_y
xs = np.arange(18, 24.2, 0.4)
ys = np.arange(20, 24.2, 0.4)
zs = 2.58;
volume = 0.0034;
xa = [0, 7, 15]
ya = [0 ,5, 10]
fig = plt.figure(figsize=(18, 18))
cmap = copy.copy(plt.cm.get_cmap("jet"))
subplot_index = 1
for k in xa:
for l in ya:
ax = fig.add_subplot(3, 3, subplot_index)
predicted_deformation_map = deformation_data_from_mogi(xs[k], ys[l], zs, volume, 0, 0)
predicted_deformation_map_m = np.ma.masked_where(observed_deformation_map==0, predicted_deformation_map)
im = ax.imshow(predicted_deformation_map_m, cmap=cmap, extent=extent_xy)
cbar = ax.figure.colorbar(im, ax=ax, orientation='horizontal')
plt.grid()
im.set_clim(-30, 30)
ax.plot(xs[k],ys[l], 'k*', markersize=25, markerfacecolor='w')
ax.set_title('Source: X=%4.2fkm; Y=%4.2fkm' % (xs[k], ys[l]))
ax.set_xlabel("Easting [km]")
ax.set_ylabel("Northing [km]")
subplot_index += 1
plt.savefig('Model-samples-3by3.png', dpi=200, transparent='false')
```
<hr>
<font face="Calibri" size="5"> <b> 4. Solving the [Pseudo]-Inverse Model</b><br></font>
<font face="Calibri" size="3"> The inverse problem seeks to determine the optimal parameters $(\hat{x_s},\hat{y_s},\hat{z_s},\hat{V})$ of the Mogi model $m$ by minimizing the <i>misfit</i> between predictions, $g(m)$, and observations $d^{obs}$ according to
\begin{equation}
\sum{\Big[g(m) - d^{obs}\Big]^2}
\end{equation}
This equation describes misfit using the <i>method of least-squares</i>, a standard approach to approximate the solution of an overdetermined equation system. We will use a <i>grid-search</i> approach to find the set of model parameters that minimize the the misfit function. The approach is composed of the following processing steps:
<ol>
<li>Loop through the mogi model parameters,</li>
<li>Calculate the forward model for each set of parameters,</li>
<li>Calculate the misfit $\sum{[g(m) - d^{obs}]^2}$, and</li>
<li>Find the parameter set that minimizes this misfit.</li>
</ol>
</font>
<hr>
<font face="Calibri" size="4"> <b> 4.1 Experimenting with Misfit</b></font>
<br><br>
<font face="Calibri" size="3">Let's <b>look at the misfit $\sum{[g(m) - d^{obs}]^2}$ for a number of different model parameter sets $(x_s,y_s,z_s,V)$:</b>
</font>
```
plt.rcParams.update({'font.size': 14})
extent_x = extents((np.arange(1, sample*posting, posting))/1000)
extent_y = extents((np.arange(1, line*posting, posting))/1000)
extent_xy = extent_x + extent_y
xs = np.arange(18, 24.2, 0.4)
ys = np.arange(20, 24.2, 0.4)
zs = 2.58;
volume = 0.0034;
xa = [0, 7, 15]
ya = [0 ,5, 10]
fig = plt.figure(figsize=(18, 18))
cmap = copy.copy(plt.cm.get_cmap("jet"))
subplot_index = 1
for k in xa:
for l in ya:
ax = fig.add_subplot(3, 3, subplot_index)
predicted_deformation_map = deformation_data_from_mogi(xs[k], ys[l], zs, volume, 0, 0)
predicted_deformation_map_m = np.ma.masked_where(observed_deformation_map==0, predicted_deformation_map)
im = ax.imshow(observed_deformation_map_m-predicted_deformation_map_m, cmap=cmap, extent=extent_xy)
cbar = ax.figure.colorbar(im, ax=ax, orientation='horizontal')
plt.grid()
im.set_clim(-30, 30)
ax.plot(xs[k], ys[l], 'k*', markersize=25, markerfacecolor='w')
ax.set_title('Source: X=%4.2fkm; Y=%4.2fkm' % (xs[k], ys[l]))
ax.set_xlabel("Easting [km]")
ax.set_ylabel("Northing [km]")
subplot_index += 1
plt.savefig('Misfit-samples-3by3.png', dpi=200, transparent='false')
```
<hr>
<font face="Calibri" size="4"> <b> 4.2 Running Grid-Search to Find Best Fitting Model Parameters $(\hat{x}_s,\hat{y}_s)$</b><br></font>
<font face="Calibri" size="3">The following code cell runs a grid-search approach to find the best fitting Mogi source parameters for the 2000-2002 deformation event at Okmok. To keep things simple, we will fix the depth $z_s$ and volume change $V$ parameters close to their "true" values and search only for the correct east/north source location ($x_s,y_s$).</font>
<br><br>
<font face="Calibri" size="3"><b>Write a script using the grid-search approach in Python:</b></font>
```
# FIX Z AND dV, SEARCH OVER X AND Y
# Setting up search parameters
xs = np.arange(19, 22.2, 0.2)
ys = np.arange(21, 23.2, 0.2)
zs = 2.58;
volume = 0.0034;
nx = xs.size
ny = ys.size
ng = nx * ny;
print(f"fixed z = {zs}km, dV = {volume}, searching over (x,y)")
misfit = np.zeros((nx, ny))
subplot_index = 0
# Commence grid-search for best model parameters
for k, xv in enumerate(xs):
for l, yv in enumerate(ys):
subplot_index += 1
predicted_deformation_map = deformation_data_from_mogi(xs[k], ys[l], zs, volume, 0, 0)
predicted_deformation_map_m = np.ma.masked_where(observed_deformation_map==0, predicted_deformation_map)
misfit[k,l] = np.sum(np.square(observed_deformation_map_m - predicted_deformation_map_m))
print(f"Source {subplot_index:3d}/{ng:3d} is x = {xs[k]:.2f} km, y = {ys[l]:.2f} km")
# Searching for the minimum in the misfit matrix
mmf = np.where(misfit == np.min(misfit))
print(f"\n----------------------------------------------------------------")
print('Best fitting Mogi Source located at: X = %5.2f km; Y = %5.2f km' % (xs[mmf[0]], ys[mmf[1]]))
print(f"----------------------------------------------------------------")
```
<hr>
<font face="Calibri" size="4"> <b> 4.3 Plot and Inspect the Misfit Function</b><br></font>
<font face="Calibri" size="3">The code cell below plots the misfit function ($\sum{[g(m) - d^{obs}]^2}$) describing the fit of different Mogi source parameterizations to the observed InSAR data. You should notice a clear minimum in the misfit plot at the location of the best fitting source location estimated above.
You may notice that, even for the best fitting solution, the misfit does not become zero. This could be due to other signals in the InSAR data (e.g., atmospheric effects or residual topography). Alternatively, it could also indicate that the observed deformation doesn't fully comply with Mogi theory.
</font>
<br><br>
<font face="Calibri" size="3"><b>Plot the misfit function ($\sum{[g(m) - d^{obs}]^2}$):</b></font>
```
plt.rcParams.update({'font.size': 18})
extent_xy = extents(xs) + extents(ys)
fig = plt.figure(figsize=(10, 10))
cmap = copy.copy(plt.cm.get_cmap("jet"))
ax1 = fig.add_subplot(1, 1 ,1)
im = ax1.imshow(np.transpose(misfit), origin='lower', cmap=cmap, extent=extent_xy)
# USE THIS COMMAND TO CHANGE COLOR SCALING: im.set_clim(-30, 30)
ax1.set_aspect('auto')
cbar = ax1.figure.colorbar(im, ax=ax1, orientation='horizontal')
ax1.plot(xs[mmf[0]], ys[mmf[1]], 'k*', markersize=25, markerfacecolor='w')
ax1.set_title("Misfit Function for Mogi-Source Approximation")
ax1.set_xlabel("Easting [km]")
ax1.set_ylabel("Northing [km]")
plt.savefig('Misfit-function.png', dpi=200, transparent='false')
```
<hr>
<font face="Calibri" size="4"> <b> 4.4 Plot Best-Fitting Mogi Forward Model and Compare to Observations</b><br></font>
<font face="Calibri" size="3">With the best-fitting model parameters defined, you can now analyze how well the model fits the InSAR-observed surface deformation. The best way to do that is to look at both the observed and predicted deformation maps and compare their spatial patterns. Additionally, we will also plot the residuals (<i>observed_deformation_map</i> - <i>observed_deformation_map</i>) to determine if there are additional signals in the data that are not modeled using Mogi theory.
</font>
<br><br>
<font face="Calibri" size="3"><b>Compare the observed and predicted deformation maps:</b></font>
```
# Calculate predicted deformation map for best-fitting Mogi parameters:
predicted_deformation_map = deformation_data_from_mogi(xs[mmf[0]], ys[mmf[1]], zs, volume, 0, 0)
# Mask the predicted deformation map to remove pixels incoherent in the observations:
predicted_deformation_map_m = np.ma.masked_where(observed_deformation_map==0, predicted_deformation_map)
# Plot observed deformation map
plot_model(observed_deformation_map_m, line, sample, posting)
# Plot simulated deformation map
plot_model(predicted_deformation_map_m, line, sample, posting)
plt.savefig('BestFittingMogiDefo.png', dpi=200, transparent='false')
# Plot simulated deformation map without mask applied
plot_model(predicted_deformation_map, line, sample, posting)
```
<font face="Calibri" size="3"><b>Determine if there are additional signals in the data that are not modeled using Mogi theory:</b></font>
```
# Plot residual between observed and predicted deformation maps
plot_model(observed_deformation_map_m-predicted_deformation_map_m, line, sample, posting)
plt.savefig('Residuals-ObsMinusMogi.png', dpi=200, transparent='false')
```
<font face="Calibri" size="2"> <i>InSAR_volcano_source_modeling.ipynb - Version 1.3.0 - April 2021 </i>
<br>
<b>Version Changes</b>
<ul>
<li>namespace asf_notebook</li>
</ul>
</font>
| true |
code
| 0.571408 | null | null | null | null |
|
# 19-05-16 Notes:

I was attempting to generate PDB files for my model's predictions (including sidechains), but I found out that my backbone reconstruction is poor to begin with. In this notebook, I'll use `prody` and `matplotlib` to try to root out the issue.
```
from prody import *
import sys
import numpy as np
import matplotlib.pyplot as plt
import torch
from glob import glob
sys.path.extend(['../transformer/'])
from Sidechains import SC_DATA
# from pylab import *
# %matplotlib inline
%matplotlib notebook
# %pylab
np.set_printoptions(suppress=True)
from numpy import sign, tile, concatenate, pi, cross, subtract, round, var
from numpy import ndarray, power, sqrt, array, zeros, arccos
RAD2DEG = 180 / pi
```
## Load true and predicted structures
```
true = parsePDB("1Y0M", chain="A").select('protein and name N CA C')
gen = parsePDB("../coords/0516a/1Y0M_A_l0.00.pdb")
# true = parsePDB("1h75", chain="A").select('protein and name N CA C')
# gen = parsePDB("../coords/0516a/1H75_A_l0.00.pdb")
true, gen
showProtein(true, gen)
```
## Do the dihedrals match the true structure?
```
def get_dihedral(coords1, coords2, coords3, coords4, radian=False):
"""Return the dihedral angle in degrees."""
a1 = coords2 - coords1
a2 = coords3 - coords2
a3 = coords4 - coords3
v1 = cross(a1, a2)
v1 = v1 / (v1 * v1).sum(-1)**0.5
v2 = cross(a2, a3)
v2 = v2 / (v2 * v2).sum(-1)**0.5
porm = sign((v1 * a3).sum(-1))
rad = arccos((v1*v2).sum(-1) / ((v1**2).sum(-1) * (v2**2).sum(-1))**0.5)
if radian:
return porm * rad
else:
return porm * rad * RAD2DEG
true.getNames()[:5], gen.getNames()[:5]
true.ca.getResnames()[:5], gen.ca.getResnames()[:5]
t_coords = true.getCoords()
g_coords = gen.getCoords()
i = 0
coords = ["N", "CA", "C"]*500
while i < len(true) - 3:
a, b, c, d = t_coords[i], t_coords[i+1], t_coords[i+2], t_coords[i+3]
w, x, y, z = g_coords[i], g_coords[i+1], g_coords[i+2], g_coords[i+3]
t_dihe = get_dihedral(a, b, c, d, radian=True)
g_dihe = get_dihedral(w, x, y, z, radian=True)
print(coords[i : (i+4)], t_dihe - g_dihe)
print(t_dihe, g_dihe)
i += 1
# Looking to see if using calcDihedral vs get_dihedral returns anything different
# i = 0
# coords = ["N", "CA", "C"]*500
# while i < len(true) - 3:
# a, b, c, d = true[i], true[i+1], true[i+2], true[i+3]
# w, x, y, z = gen[i], gen[i+1], gen[i+2], gen[i+3]
# t_dihe = calcDihedral(a, b, c, d, radian=True)
# g_dihe = calcDihedral(w, x, y, z, radian=True)
# d = t_dihe - g_dihe
# print(coords[i : (i+4)], d, d + 2 * pi, d + pi, d - pi)
# print(t_dihe, g_dihe)
# i += 1
list(true.getHierView())[0]
for tres, gres in zip(list(true.getHierView())[0].iterResidues(),
list(gen.getHierView())[0].iterResidues()):
try:
phi = calcPhi(tres, radian=True) - calcPhi(gres, radian=True)
gphi = calcPhi(gres, radian=True)
tphi = calcPhi(tres, radian=True)
except ValueError:
gphi = -999
phi = -999
tphi = -999
try:
psi = calcPsi(tres, radian=True) - calcPsi(gres, radian=True)
gpsi = calcPsi(gres, radian=True)
tpsi = calcPsi(tres, radian=True)
except ValueError:
gpsi = -999
psi = -999
tpsi = -999
try:
omega = calcOmega(tres, radian=True) - calcOmega(gres, radian=True)
gomega = calcOmega(gres, radian=True)
tomega = calcOmega(tres, radian=True)
except ValueError:
gomega = -999
omega = -999
tomega = -999
# print("{0}: {1:.2f} {2:.2f} {3:.2f}".format(tres, phi, psi, omega))
print("{0}: {1:.2f} {2:.2f} {3:.2f}".format(tres, tphi, tpsi, tomega))
import prody as pr
import sys
import numpy as np
import matplotlib.pyplot as plt
import torch
from glob import glob
sys.path.extend(['../transformer/'])
from Sidechains import SC_DATA
%matplotlib inline
SC_DATA["ARG"]
refs_fns = glob("../data/amino_acid_substructures/*.pdb")
refs = pr.parsePDB(refs_fns)
refs[0].getCoords(), refs[0].getNames()
```
| true |
code
| 0.4436 | null | null | null | null |
|
# PRMT-2324 Run top level table for first 2 weeks of August 2021
## Context
In our July data we saw a significant increase in GP2GP failures. We want to understand if these were blips, perhaps caused by something that happening during July, or whether these failures are continuing. We don’t want to wait until we have all August data to identify this as we are starting conversations with suppliers now.
```
import pandas as pd
import numpy as np
from datetime import datetime
transfer_file_location = "s3://prm-gp2gp-notebook-data-prod/PRMT-2324-2-weeks-august-data/transfers/v4/2021/8/transfers.parquet"
transfers_raw = pd.read_parquet(transfer_file_location)
transfers_raw.head()
# filter data to just include the first 2 weeks (15 days) of august
date_filter_bool = transfers_raw["date_requested"] < datetime(2021, 8, 16)
transfers_half_august = transfers_raw[date_filter_bool]
# Supplier data was only available from Feb/Mar 2021. Sending and requesting supplier values for all transfers before that are empty
# Dropping these columns to merge supplier data from ASID lookup files
transfers_half_august = transfers_half_august.drop(["sending_supplier", "requesting_supplier"], axis=1)
transfers = transfers_half_august.copy()
# Supplier name mapping
supplier_renaming = {
"EGTON MEDICAL INFORMATION SYSTEMS LTD (EMIS)":"EMIS",
"IN PRACTICE SYSTEMS LTD":"Vision",
"MICROTEST LTD":"Microtest",
"THE PHOENIX PARTNERSHIP":"TPP",
None: "Unknown"
}
# Generate ASID lookup that contains all the most recent entry for all ASIDs encountered
asid_file_location = "s3://prm-gp2gp-asid-lookup-preprod/2021/6/asidLookup.csv.gz"
asid_lookup = pd.read_csv(asid_file_location)
asid_lookup = asid_lookup.drop_duplicates().groupby("ASID").last().reset_index()
lookup = asid_lookup[["ASID", "MName"]]
transfers = transfers.merge(lookup, left_on='requesting_practice_asid',right_on='ASID',how='left')
transfers = transfers.rename({'MName': 'requesting_supplier', 'ASID': 'requesting_supplier_asid'}, axis=1)
transfers = transfers.merge(lookup, left_on='sending_practice_asid',right_on='ASID',how='left')
transfers = transfers.rename({'MName': 'sending_supplier', 'ASID': 'sending_supplier_asid'}, axis=1)
transfers["sending_supplier"] = transfers["sending_supplier"].replace(supplier_renaming.keys(), supplier_renaming.values())
transfers["requesting_supplier"] = transfers["requesting_supplier"].replace(supplier_renaming.keys(), supplier_renaming.values())
# Making the status to be more human readable here
transfers["status"] = transfers["status"].str.replace("_", " ").str.title()
import paths
import data
error_code_lookup_file = pd.read_csv(data.gp2gp_response_codes.path)
outcome_counts = transfers.fillna("N/A").groupby(by=["status", "failure_reason"]).agg({"conversation_id": "count"})
outcome_counts = outcome_counts.rename({"conversation_id": "Number of transfers", "failure_reason": "Failure Reason"}, axis=1)
outcome_counts["% of transfers"] = (outcome_counts["Number of transfers"] / outcome_counts["Number of transfers"].sum()).multiply(100)
outcome_counts.round(2)
transfers['month']=transfers['date_requested'].dt.to_period('M')
def convert_error_list_to_tuple(error_code_list, error_code_type):
return [(error_code_type, error_code) for error_code in set(error_code_list) if not np.isnan(error_code)]
def combine_error_codes(row):
sender_list = convert_error_list_to_tuple(row["sender_error_codes"], "Sender")
intermediate_list = convert_error_list_to_tuple(row["intermediate_error_codes"], "COPC")
final_list = convert_error_list_to_tuple(row["final_error_codes"], "Final")
full_error_code_list = sender_list + intermediate_list + final_list
if len(full_error_code_list) == 0:
return [("No Error Code", "No Error")]
else:
return full_error_code_list
transfers["all_error_codes"] = transfers.apply(combine_error_codes, axis=1)
def generate_high_level_table(transfers_sample):
# Break up lines by error code
transfers_split_by_error_code=transfers_sample.explode("all_error_codes")
# Create High level table
high_level_table=transfers_split_by_error_code.fillna("N/A").groupby(["requesting_supplier","sending_supplier","status","failure_reason","all_error_codes"]).agg({'conversation_id':'count'})
high_level_table=high_level_table.rename({'conversation_id':'Number of Transfers'},axis=1).reset_index()
# Count % of transfers
total_number_transfers = transfers_sample.shape[0]
high_level_table['% of Transfers']=(high_level_table['Number of Transfers']/total_number_transfers).multiply(100)
# Count by supplier pathway
supplier_pathway_counts = transfers_sample.fillna("Unknown").groupby(by=["sending_supplier", "requesting_supplier"]).agg({"conversation_id": "count"})['conversation_id']
high_level_table['% Supplier Pathway Transfers']=high_level_table.apply(lambda row: row['Number of Transfers']/supplier_pathway_counts.loc[(row['sending_supplier'],row['requesting_supplier'])],axis=1).multiply(100)
# Add in Paper Fallback columns
total_fallback = transfers_sample["failure_reason"].dropna().shape[0]
fallback_bool=high_level_table['status']!='Integrated On Time'
high_level_table.loc[fallback_bool,'% Paper Fallback']=(high_level_table['Number of Transfers']/total_fallback).multiply(100)
# % of error codes column
total_number_of_error_codes=transfers_split_by_error_code['all_error_codes'].value_counts().drop(('No Error Code','No Error')).sum()
error_code_bool=high_level_table['all_error_codes']!=('No Error Code', 'No Error')
high_level_table.loc[error_code_bool,'% of error codes']=(high_level_table['Number of Transfers']/total_number_of_error_codes).multiply(100)
# Adding columns to describe errors
high_level_table['error_type']=high_level_table['all_error_codes'].apply(lambda error_tuple: error_tuple[0])
high_level_table['error_code']=high_level_table['all_error_codes'].apply(lambda error_tuple: error_tuple[1])
high_level_table=high_level_table.merge(error_code_lookup_file[['ErrorCode','ResponseText']],left_on='error_code',right_on='ErrorCode',how='left')
# Select and re-order table
grouping_columns_order=['requesting_supplier','sending_supplier','status','failure_reason','error_type','ResponseText','error_code']
counting_columns_order=['Number of Transfers','% of Transfers','% Supplier Pathway Transfers','% Paper Fallback','% of error codes']
high_level_table=high_level_table[grouping_columns_order+counting_columns_order].sort_values(by='Number of Transfers',ascending=False)
return high_level_table
with pd.ExcelWriter("High Level Table First 2 weeks of August PRMT-2324.xlsx") as writer:
generate_high_level_table(transfers.copy()).to_excel(writer, sheet_name="All",index=False)
[generate_high_level_table(transfers[transfers['month']==month].copy()).to_excel(writer, sheet_name=str(month),index=False) for month in transfers['month'].unique()]
```
| true |
code
| 0.257345 | null | null | null | null |
|
# Model Evaluation and Refinement
---------------------------------
This notebook will discuss some techniques on how to evaluate models and a way to refine the Linear Regression Models.
After creating a model, it is vital to evaluate it for correctness and refine if necessary. There are various ways to do so.
We would be discussing some common ways to do so in here.
We would be trying to evaluate models that aim to predict the price of the car.
This is based on the IBM's Course on Data Analysis with Python.
We would be creating some simple models to demonstrate the techniques but they can be used on complex models.
First, let's do the necessary setup.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set(color_codes=True)
%matplotlib inline
```
Now, we will get the data.
```
path = 'https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DA0101EN-SkillsNetwork/labs/Data%20files/module_5_auto.csv'
df = pd.read_csv(path)
```
For our models, we would be using only the numeric data.
```
df=df._get_numeric_data()
df.head()
```
# Training and Testing
By training and testing, we refer to splitting your data into two componenets: one for training and another for testing.
This is a very important step since we can test our data pre-liminarily on 'unkown' values. The split generally depends on the problem but the test data tends to be between 10% to 30% of the total data.
First, let's create our X and y.
```
y = df['price']
```
For X, let's take everything except price.
```
X = df.drop('price', axis=1)
```
The next step is to split them into training and testing.
It's highly recommended to do so in a random manner.
To make our jobs easier, we would be using `train_test_split` from `model_selection` module in scikit-learn. To use the function, we pass in the X and y, the test size and a random_state variable. The `random_state` variable is used when applying the random function. This will allow us to reproduce the results.
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.10, random_state=1)
print("number of test samples :", X_test.shape[0])
print("number of training samples:",X_train.shape[0])
```
Let's create a simple linear regression model with horsepower as the predictor.
```
from sklearn.linear_model import LinearRegression
lre=LinearRegression()
lre.fit(X_train[['horsepower']], y_train)
```
# Evaluation with metrics
A good way to test the model is to use metrics. There are different metrics suitable for different situations. Let's classify them based on the problem type.
## Regression
Common metrics are R-squared and Root Mean Squared Error (RMSE).
* R-squared tells how close the data is to the linear regression line. It typically ranges from 0 to 1 with 1 being the highest; however it can be negative if the model is worse.
* RMSE (and other metrics such as MAE or MSE) give an account of the error. RMSE takes the root of the sum of error squares.
## Classification
Common metrics are Jaccard Index, Precision, Recall, and F1-Score.
* Jaccard Index tells us how 'accurate' the model. Essentially, the proportion of correctly predicted values. It is defined as the ratio of intersection (or the same values aka correct predictions) and union (all values).
* Precision talks about how precise your model is. That is, out of the predicted positive, how many of them are actual positives.
* Recall talks about how many of the Actual Positives our model captures via labeling them as Positive (True Positive)
* F1 Score is the harmonic mean of Precision and Recall. It's used when we need a balance between Precision and Recall. F1 Score might be a better measure to use if we need to seek a balance between Precision and Recall AND there is an uneven class distribution (large number of Actual Negatives). For example, if a positive means a terrorist and there a few positives, then we should use F1 Score because the cost of not capturing a terrorist is much higher than correctly identifying a civilian.
## Calculation
There are multiple ways to calculate them.
You can use the metrics in `sklearn.metrics.` You choose the desired metric function and pass in the true _y_ and predicted _y_. The function then returns back the metric.
We can also use the inherent `score` method built-in some of the objects by scikit-learn.
In `LinearRegression`, it calculates the R^2 on the test data:
```
lre.score(X_test[['horsepower']], y_test)
```
For the training data:
```
lre.score(X_train[['horsepower']], y_train)
```
This is not ideal at all. Furthermore, you might have realized that the scoring could depend heavily on the split too. For some splits, the metrics could be very different. For eg, if you change the random_state in the splitting to 0, the R-squared changes to around 0.74!
Furthermore, the dataset we have is not that large. We would need a better way to conduct tests.
This is where k-fold cross-validation comes in.
# K-Fold Cross-validation
From [Machine Learning Mastery](https://machinelearningmastery.com/k-fold-cross-validation/):
Cross-validation is a statistical method used to estimate the skill of machine learning models.
The general procedure is as follows:
* Shuffle the dataset randomly.
* Split the dataset into k groups
* For each unique group:
- Take the group as a hold out or test data set
- Take the remaining groups as a training data set
- Fit a model on the training set and evaluate it on the test set
- Retain the evaluation score and discard the model
* Summarize the skill of the model using the sample of model evaluation scores
As you can see, it is a very valuable and useful technique. Fortunately, sklearn has modules to makes our job easier.
To do cross-validation, we need to import the `cross_val_score` from `sklearn.model_selection`
```
from sklearn.model_selection import cross_val_score
from sklearn.metrics import r2_score
```
To use it, we would need to pass the _model_, _X_, _y_, and the number of folds as _cv_.
```
Rcross = cross_val_score(estimator=lre, X=X[['horsepower']], y=y, cv=4)
```
If we pass in nothing, the scorer would use the default scoring function of the estimator. The function returns an ndarray with each element containing the R-squared value for the fold run. We can see all the values by:
```
Rcross
```
## Getting the descriptive statistics
After getting the array, it's useful to calculate descriptive statistics such as the five number summary.
For the average and standard deviation. We can do just call the methods that are built-in:
```
print("The mean of the folds are", Rcross.mean(), "and the standard deviation is" , Rcross.std())
```
Here's a little hack to get the five number summary. We convert it to a panda series and then call the function describe on it.
```
pd.Series(Rcross).describe()
```
## Getting different metrics
If you want a different metric, simply pass on a string for it. To check what's available, we need to import `SCORERS` from `sklearn.metrics`.
Then we can use `SCORERS.keys`. Having it sorted is also helpful.
```
from sklearn.metrics import SCORERS
sorted(SCORERS.keys())
```
Here's how to get RMSE. Since the one here has negative, we need to multiple it by -1 to get the array of RMSEs.
```
-1 * cross_val_score(lre, X[['horsepower']], y, cv=4,
scoring='neg_root_mean_squared_error')
```
## Stratified K-Fold Cross Validation
Stratification is the process of rearranging the data as to ensure each fold is a good representative of the whole. For example in a binary classification problem where each class comprises 50% of the data, it is best to arrange the data such that in every fold, each class comprises around half the instances.
Stratified K-Fold is cross-validation object which is a variation of KFold that returns stratified folds. The folds are made by preserving the percentage of samples for each class.
## Script to use CV and get metric stats and graphs for different models
Here's a good quick find script to evaluate different models:
```python
# explore adaboost ensemble number of trees effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import AdaBoostClassifier
from matplotlib import pyplot
# get the dataset
def get_dataset():
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
return X, y
# get a list of models to evaluate
def get_models():
models = dict()
# define number of trees to consider
n_trees = [10, 50, 100, 500, 1000, 5000]
for n in n_trees:
models[str(n)] = AdaBoostClassifier(n_estimators=n)
return models
# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
# define the evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model and collect the results
scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
return scores
# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
# evaluate the model
scores = evaluate_model(model, X, y)
# store the results
results.append(scores)
names.append(name)
# summarize the performance along the way
print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()
```
Although this is specific for AdaBoostClassifier and generated dataset, it can be easily modified to use for different models and dataset by modifying get_models and get_dataset.
# Overfitting, Underfitting and Model Selection
The test data, sometimes referred to as the out of sample data, is a much better measure of how well your model performs in the real world. One reason for this is overfitting - when the model is overfitted or overspecific to the training data. It turns out these differences are more apparent in Multiple Linear Regression and Polynomial Regression so we will explore overfitting in that context.
Let's create Multiple linear regression objects and train the model using 'horsepower', 'curb-weight', 'engine-size' and 'highway-mpg' as features.
```
lr = LinearRegression()
lr.fit(X_train[['horsepower', 'curb-weight', 'engine-size', 'highway-mpg']],
y_train)
yhat_train = lr.predict(X_train[['horsepower', 'curb-weight', 'engine-size',
'highway-mpg']])
yhat_train[0:5]
yhat_test = lr.predict(X_test[['horsepower', 'curb-weight', 'engine-size',
'highway-mpg']])
yhat_test[0:5]
```
Let's perform some model evaluation using our training and testing data separately.
Let's examine the distribution of the predicted values of the training data.
```
plt.figure(figsize=(12, 10))
ax = sns.kdeplot(x=y)
sns.kdeplot(x=yhat_train, ax=ax)
ax.legend(['y', 'y_hat'], fontsize=14);
```
So far the model seems to be doing well in learning from the training dataset. But what happens when the model encounters new data from the testing dataset? When the model generates new values from the test data, we see the distribution of the predicted values is much different from the actual target values.
```
plt.figure(figsize=(12, 10))
ax = sns.kdeplot(x=y)
sns.kdeplot(x=yhat_test, ax=ax)
ax.legend(['y', 'y_hat'], fontsize=14);
```
Comparing the Figures, it is evident the distribution of the test data in Figure 1 is much better at fitting the data.
Let's see if polynomial regression also exhibits a drop in the prediction accuracy when analysing the test dataset.
```
from sklearn.preprocessing import PolynomialFeatures
```
Overfitting occurs when the model fits the noise, not the underlying process. Therefore when testing your model using the test-set, your model does not perform as well as it is modelling noise, not the underlying process that generated the relationship. Let's create a degree 5 polynomial model.
Let's use 55 percent of the data for training and the rest for testing:
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.45, random_state=0)
```
We will perform a degree 5 polynomial transformation on the feature 'horse power'
```
pr = PolynomialFeatures(degree=5)
X_train_pr = pr.fit_transform(X_train[['horsepower']])
X_test_pr = pr.fit_transform(X_test[['horsepower']])
pr
```
Now let's create a linear regression model "poly" and train it.
```
poly = LinearRegression()
poly.fit(X_train_pr, y_train)
```
We can see the output of our model using the method "predict." then assign the values to "yhat".
```
yhat = poly.predict(X_test_pr)
yhat[0:5]
```
Let's take the first five predicted values and compare it to the actual targets.
```
print("Predicted values:", yhat[0:4])
print("True values:", y_test[0:4].values)
```
To get a better idea, let's create a function to help us plot the data. We would be creating a function that will plot the training and testing values (aka real values) against the horsepower. Then the model's prediction for continous values in the lowest and highest horsepower.
Here's the function:
```
def PollyPlot(xtrain, xtest, y_train, y_test, lr,poly_transform):
width = 12
height = 10
plt.figure(figsize=(width, height))
#training data
#testing data
# lr: linear regression object
#poly_transform: polynomial transformation object
xmax=max([xtrain.values.max(), xtest.values.max()])
xmin=min([xtrain.values.min(), xtest.values.min()])
x=np.arange(xmin, xmax, 0.1)
plt.plot(xtrain, y_train, 'ro', label='Training Data')
plt.plot(xtest, y_test, 'go', label='Test Data')
plt.plot(x, lr.predict(poly_transform.fit_transform(x.reshape(-1, 1))), label='Predicted Function')
plt.ylim([-10000, 60000])
plt.ylabel('Price')
plt.legend()
```
Now, let's use the function.
```
PollyPlot(X_train[['horsepower']], X_test[['horsepower']], y_train, y_test, poly,pr)
```
Figur 4 A polynomial regression model, red dots represent training data, green dots represent test data, and the blue line represents the model prediction.
We see that the estimated function appears to track the data but around 200 horsepower, the function begins to diverge from the data points.
R^2 of the training data:
```
poly.score(X_train_pr, y_train)
```
R^2 of the test data:
```
poly.score(X_test_pr, y_test)
```
We see the R^2 for the training data is 0.5567 while the R^2 on the test data was -29.87. The lower the R^2, the worse the model, a Negative R^2 is a sign of overfitting.
Let's see how the R^2 changes on the test data for different order polynomials and plot the results:
```
Rsqu_test = []
order = [1, 2, 3, 4, 5]
for n in order:
pr = PolynomialFeatures(degree=n)
x_train_pr = pr.fit_transform(X_train[['horsepower']])
x_test_pr = pr.fit_transform(X_test[['horsepower']])
lr.fit(x_train_pr, y_train)
Rsqu_test.append(lr.score(x_test_pr, y_test))
print("The R-square values: ", Rsqu_test);
sns.lineplot(x=order, y=Rsqu_test, markers=True, marker='o')
plt.xlabel('order')
plt.ylabel('R^2')
plt.title('R^2 Using Test Data');
```
We see the R^2 gradually increases until an order three polynomial is used. Then the R^2 dramatically decreases at four.
So, what we can tell is that a model with a degree of 1 would be too loosely fitted (or underfitted) and a model of degree such as 5 would be too overfitted. Selecting the right method requires some experimentaion and getting the values.
# Hyperparameter Tuning
Often algorithms contain hyperparameters. For example, *alpha* in Ridge Regression, *kernel* in SVMs and so on. Sometimes, the choice of the hyperparemeters can be made easily from domain knowledge. Other times, it may not be that simple. For those, we may need to fit the model multiple times and fine tune it.
There are two main methods of doing it:
## Grid Search
A Grid Search performs an exhaustively generates candidates from a grid of parameter values specified. For example:
```python
param_grid = [
{'C': [1, 10, 100, 1000], 'kernel': ['linear']},
{'C': [1, 10, 100, 1000], 'gamma': [0.001, 0.0001], 'kernel': ['rbf']},
]
```
specifies that two grids should be explored: one with a linear kernel and C values in \[1, 10, 100, 1000\], and the second one with an RBF kernel, and the cross-product of C values ranging in \[1, 10, 100, 1000\] and gamma values in \[0.001, 0.0001\].
Here's an example:
```python
hyper_params = {'alpha': [0.0001, 0.001, 0.01, 0.1, 0, 1, 10, 100, 1000, 10000]}
grid = GridSearchCV(estimator=ridge, param_grid=hyper_params, scoring='r2', cv=4, n_jobs=-1)
grid.fit(X, y)
best_score = grid.best_score_
best_estimator = grid.best_estimator_
best_params = grid.best_params_
```
## Randomized Parameter Optimization
While using a grid of parameter settings is currently the most widely used method for parameter optimization, other search methods have more favourable properties. RandomizedSearchCV implements a randomized search over parameters, where each setting is sampled from a distribution over possible parameter values. This has two main benefits over an exhaustive search:
A budget can be chosen independent of the number of parameters and possible values.
Adding parameters that do not influence the performance does not decrease efficiency.
Specifying how parameters should be sampled is done using a dictionary, very similar to specifying parameters for GridSearchCV. Additionally, a computation budget, being the number of sampled candidates or sampling iterations, is specified using the n_iter parameter. For each parameter, either a distribution over possible values or a list of discrete choices (which will be sampled uniformly) can be specified:
```python
{'C': scipy.stats.expon(scale=100), 'gamma': scipy.stats.expon(scale=.1),
'kernel': ['rbf'], 'class_weight':['balanced', None]}
```
This example uses the scipy.stats module, which contains many useful distributions for sampling parameters, such as expon, gamma, uniform or randint.
In principle, any function can be passed that provides a rvs (random variate sample) method to sample a value. A call to the rvs function should provide independent random samples from possible parameter values on consecutive calls.
The usage (both calling and interpretation) is similar to GridSearchCV. Do take note that you should use continous distribution for continous variables.
# Author
By Abhinav Garg
| true |
code
| 0.516108 | null | null | null | null |
|
# Pilatus on a goniometer at ID28
Nguyen Thanh Tra who was post-doc at ESRF-ID28 enquired about a potential bug in pyFAI in October 2016: he calibrated 3 images taken with a Pilatus-1M detector at various detector angles: 0, 17 and 45 degrees.
While everything looked correct, in first approximation, one peak did not overlap properly with itself depending on the detector angle. This peak correspond to the peak in the angle of the detector, at 23.6° ...
This notebook will guide you through the calibration of the goniometer setup.
Let's first retrieve the images and initialize the environment:
```
%pylab nbagg
import os
#Nota: Set a proxy if you are befind a firewall
#os.environ["http_proxy"] = "http://proxy.company.fr:3128"
import fabio, pyFAI, os
print("Using pyFAI version:", pyFAI.version)
from os.path import basename
from pyFAI.gui import jupyter
from pyFAI.calibrant import get_calibrant
from silx.resources import ExternalResources
downloader = ExternalResources("thick", "http://www.silx.org/pub/pyFAI/testimages")
all_files = downloader.getdir("gonio_ID28.tar.bz2")
for afile in all_files:
print(basename(afile))
```
There are 3 images stored as CBF files and the associated control points as npt files.
```
images = [i for i in all_files if i.endswith("cbf")]
images.sort()
mask = None
fig, ax = subplots(1,3, figsize=(9,3))
for i, cbf in enumerate(images):
fimg = fabio.open(cbf)
jupyter.display(fimg.data, label=basename(cbf), ax=ax[i])
if mask is None:
mask = fimg.data<0
else:
mask |= fimg.data<0
numpy.save("mask.npy", mask)
```
To be able to calibrate the detector position, the calibrant used is LaB6 and the wavelength was 0.69681e-10m
```
wavelength=0.6968e-10
calibrant = get_calibrant("LaB6")
calibrant.wavelength = wavelength
print(calibrant)
detector = pyFAI.detector_factory("Pilatus1M")
# Define the function that extracts the angle from the filename:
def get_angle(basename):
"""Takes the basename (like det130_g45_0001.cbf ) and returns the angle of the detector"""
return float(os.path.basename((basename.split("_")[-2][1:])))
for afile in images:
print('filename', afile, "angle:",get_angle(afile))
#Define the transformation of the geometry as function of the goniometrer position.
# by default scale1 = pi/180 (convert deg to rad) and scale2 = 0.
from pyFAI.goniometer import GeometryTransformation, GoniometerRefinement, Goniometer
goniotrans2d = GeometryTransformation(param_names = ["dist", "poni1", "poni2",
"rot1", "rot2",
"scale1", "scale2"],
dist_expr="dist",
poni1_expr="poni1",
poni2_expr="poni2",
rot1_expr="scale1 * pos + rot1",
rot2_expr="scale2 * pos + rot2",
rot3_expr="0.0")
#Definition of the parameters start values and the bounds
param = {"dist":0.30,
"poni1":0.08,
"poni2":0.08,
"rot1":0,
"rot2":0,
"scale1": numpy.pi/180., # rot2 is in radians, while the motor position is in degrees
"scale2": 0
}
#Defines the bounds for some variables. We start with very strict bounds
bounds = {"dist": (0.25, 0.31),
"poni1": (0.07, 0.1),
"poni2": (0.07, 0.1),
"rot1": (-0.01, 0.01),
"rot2": (-0.01, 0.01),
"scale1": (numpy.pi/180., numpy.pi/180.), #strict bounds on the scale: we expect the gonio to be precise
"scale2": (0, 0) #strictly bound to 0
}
gonioref2d = GoniometerRefinement(param, #initial guess
bounds=bounds,
pos_function=get_angle,
trans_function=goniotrans2d,
detector=detector,
wavelength=wavelength)
print("Empty goniometer refinement object:")
print(gonioref2d)
# Populate with the images and the control points
for fn in images:
base = os.path.splitext(fn)[0]
bname = os.path.basename(base)
fimg = fabio.open(fn)
sg =gonioref2d.new_geometry(bname, image=fimg.data, metadata=bname,
control_points=base+".npt",
calibrant=calibrant)
print(sg.label, "Angle:", sg.get_position())
print("Filled refinement object:")
print(gonioref2d)
# Initial refinement of the goniometer model with 5 dof
gonioref2d.refine2()
# Remove constrains on the refinement:
gonioref2d.bounds=None
gonioref2d.refine2()
# Check the calibration on all 3 images
fig, ax = subplots(1, 3, figsize=(9, 3) )
for idx,lbl in enumerate(gonioref2d.single_geometries):
sg = gonioref2d.single_geometries[lbl]
if sg.control_points.get_labels():
sg.geometry_refinement.set_param(gonioref2d.get_ai(sg.get_position()).param)
jupyter.display(sg=sg, ax=ax[idx])
#Create a MultiGeometry integrator from the refined geometry:
angles = []
images = []
for sg in gonioref2d.single_geometries.values():
angles.append(sg.get_position())
images.append(sg.image)
multigeo = gonioref2d.get_mg(angles)
multigeo.radial_range=(0, 63)
print(multigeo)
# Integrate the whole set of images in a single run:
res_mg = multigeo.integrate1d(images, 10000)
ax = jupyter.plot1d(res_mg, label="multigeo")
for lbl, sg in gonioref2d.single_geometries.items():
ai = gonioref2d.get_ai(sg.get_position())
img = sg.image * ai.dist * ai.dist / ai.pixel1 / ai.pixel2
res = ai.integrate1d(img, 5000, unit="2th_deg", method="splitpixel")
ax.plot(*res, "--", label=lbl)
ax.legend()
#Let's focus on the inner most ring on the image taken at 45°:
#ax.set_xlim(21.5, 21.7)
ax.set_xlim(29.0, 29.2)
ax.set_ylim(0, 5e11)
```
On all three imges, the rings on the outer side of the detector are shifted in compatison with the average signal comming from the other two images.
This phenomenon could be related to volumetric absorption of the photon in the thickness of the detector.
To be able to investigate this phenomenon further, the goniometer geometry is saved in a JSON file:
```
gonioref2d.save("id28.json")
with open("id28.json") as f:
print(f.read())
```
## Peak profile
Let's plot the full-width at half maximum for every peak in the different intergated profiles:
```
#Peak profile
from scipy.interpolate import interp1d
from scipy.optimize import bisect
def calc_fwhm(integrate_result, calibrant):
"calculate the tth position and FWHM for each peak"
delta = integrate_result.intensity[1:] - integrate_result.intensity[:-1]
maxima = numpy.where(numpy.logical_and(delta[:-1]>0, delta[1:]<0))[0]
minima = numpy.where(numpy.logical_and(delta[:-1]<0, delta[1:]>0))[0]
maxima += 1
minima += 1
tth = []
FWHM = []
for tth_rad in calibrant.get_2th():
tth_deg = tth_rad*integrate_result.unit.scale
if (tth_deg<=integrate_result.radial[0]) or (tth_deg>=integrate_result.radial[-1]):
continue
idx_theo = abs(integrate_result.radial-tth_deg).argmin()
id0_max = abs(maxima-idx_theo).argmin()
id0_min = abs(minima-idx_theo).argmin()
I_max = integrate_result.intensity[maxima[id0_max]]
I_min = integrate_result.intensity[minima[id0_min]]
tth_maxi = integrate_result.radial[maxima[id0_max]]
I_thres = (I_max + I_min)/2.0
if minima[id0_min]>maxima[id0_max]:
if id0_min == 0:
min_lo = integrate_result.radial[0]
else:
min_lo = integrate_result.radial[minima[id0_min-1]]
min_hi = integrate_result.radial[minima[id0_min]]
else:
if id0_min == len(minima) -1:
min_hi = integrate_result.radial[-1]
else:
min_hi = integrate_result.radial[minima[id0_min+1]]
min_lo = integrate_result.radial[minima[id0_min]]
f = interp1d(integrate_result.radial, integrate_result.intensity-I_thres)
tth_lo = bisect(f, min_lo, tth_maxi)
tth_hi = bisect(f, tth_maxi, min_hi)
FWHM.append(tth_hi-tth_lo)
tth.append(tth_deg)
return tth, FWHM
fig, ax = subplots()
ax.plot(*calc_fwhm(res_mg, calibrant), "o", label="multi")
for lbl, sg in gonioref2d.single_geometries.items():
ai = gonioref2d.get_ai(sg.get_position())
img = sg.image * ai.dist * ai.dist / ai.pixel1 / ai.pixel2
res = ai.integrate1d(img, 5000, unit="2th_deg", method="splitpixel")
t,w = calc_fwhm(res, calibrant=calibrant)
ax.plot(t, w,"-o", label=lbl)
ax.set_title("Peak shape as function of the angle")
ax.set_xlabel(res_mg.unit.label)
ax.legend()
```
## Conclusion:
Can the FWHM and peak position be corrected using raytracing and deconvolution ?
| true |
code
| 0.468 | null | null | null | null |
|
# Building interactive plots using `bqplot` and `ipywidgets`
* `bqplot` is built on top of the `ipywidgets` framework
* `ipwidgets` and `bqplot` widgets can be seamlessly integrated to build interactive plots
* `bqplot` figure widgets can be stacked with UI controls available in `ipywidgets` by using `Layout` classes (Box, HBox, VBox) in `ipywidgets`
(Note that *only* `Figure` objects (not `Mark` objects) inherit from `DOMWidget` class and can be combined with other widgets from `ipywidgets`)
* Trait attributes of widgets can be linked using callbacks. Callbacks should be registered using the `observe` method
Please follow these links for detailed documentation on:
1. [Layout and Styling of Jupyter Widgets](https://ipywidgets.readthedocs.io/en/stable/examples/Widget%20Styling.html)
* [Linking Widgets](https://ipywidgets.readthedocs.io/en/stable/examples/Widget%20Events.html)
<br>Let's look at examples of linking plots with UI controls
```
import numpy as np
import ipywidgets as widgets
import bqplot.pyplot as plt
```
Update the plot on a button click
```
y = np.random.randn(100).cumsum() # simple random walk
# create a button
update_btn = widgets.Button(description="Update", button_style="success")
# create a figure widget
fig1 = plt.figure(animation_duration=750)
line = plt.plot(y)
# define an on_click function
def on_btn_click(btn):
# update the y attribute of line mark
line.y = np.random.randn(100).cumsum() # another random walk
# register the on_click function
update_btn.on_click(on_btn_click)
# stack button and figure using VBox
widgets.VBox([fig1, update_btn])
```
Let's look at an example where we link a plot to a dropdown menu
```
import pandas as pd
# create a dummy time series for 5 dummy stock tickers
dates = pd.date_range(start="20180101", end="20181231")
n = len(dates)
tickers = list("ABCDE")
prices = pd.DataFrame(np.random.randn(n, 5).cumsum(axis=0), columns=tickers)
# create a dropdown menu for tickers
dropdown = widgets.Dropdown(description="Ticker", options=tickers)
# create figure for plotting time series
current_ticker = dropdown.value
fig_title_tmpl = '"{}" Time Series' # string template for title of the figure
fig2 = plt.figure(title=fig_title_tmpl.format(current_ticker))
fig2.layout.width = "900px"
time_series = plt.plot(dates, prices[current_ticker])
plt.xlabel("Date")
plt.ylabel("Price")
# 1. create a callback which updates the plot when dropdown item is selected
def update_plot(*args):
selected_ticker = dropdown.value
# update the y attribute of the mark by selecting
# the column from the price data frame
time_series.y = prices[selected_ticker]
# update the title of the figure
fig2.title = fig_title_tmpl.format(selected_ticker)
# 2. register the callback by using the 'observe' method
dropdown.observe(update_plot, "value")
# stack the dropdown and fig widgets using VBox
widgets.VBox([dropdown, fig2])
```
Let's now create a scatter plot where we select X and Y data from the two dropdown menus
```
# create two dropdown menus for X and Y attributes of scatter
x_dropdown = widgets.Dropdown(description="X", options=tickers, value="A")
y_dropdown = widgets.Dropdown(description="Y", options=tickers, value="B")
# create figure for plotting the scatter
x_ticker = x_dropdown.value
y_ticker = y_dropdown.value
# set up fig_margin to allow space to display color bar
fig_margin = dict(top=20, bottom=40, left=60, right=80)
fig3 = plt.figure(animation_duration=1000, fig_margin=fig_margin)
# custom axis options for color data
axes_options = {"color": {"tick_format": "%m/%y", "side": "right", "num_ticks": 5}}
scatter = plt.scatter(
x=prices[x_ticker],
y=prices[y_ticker],
color=dates, # represent chronology using color scale
stroke="black",
colors=["red"],
default_size=32,
axes_options=axes_options,
)
plt.xlabel(x_ticker)
plt.ylabel(y_ticker)
# 1. create a callback which updates the plot when dropdown item is selected
def update_scatter(*args):
x_ticker = x_dropdown.value
y_ticker = y_dropdown.value
# update the x and y attributes of the mark by selecting
# the column from the price data frame
with scatter.hold_sync():
scatter.x = prices[x_ticker]
scatter.y = prices[y_ticker]
# update the title of the figure
plt.xlabel(x_ticker)
plt.ylabel(y_ticker)
# 2. register the callback by using the 'observe' method
x_dropdown.observe(update_scatter, "value")
y_dropdown.observe(update_scatter, "value")
# stack the dropdown and fig widgets using VBox
widgets.VBox([widgets.HBox([x_dropdown, y_dropdown]), fig3])
```
In the example below, we'll look at plots of trigonometic functions
```
funcs = dict(sin=np.sin, cos=np.cos, tan=np.tan, sinh=np.sinh, tanh=np.tanh)
dropdown = widgets.Dropdown(options=funcs, description="Function")
fig = plt.figure(title="sin(x)", animation_duration=1000)
# create x and y data attributes for the line chart
x = np.arange(-10, 10, 0.1)
y = np.sin(x)
line = plt.plot(x, y, "m")
def update_line(*args):
f = dropdown.value
fig.title = f"{f.__name__}(x)"
line.y = f(line.x)
dropdown.observe(update_line, "value")
widgets.VBox([dropdown, fig])
```
| true |
code
| 0.542621 | null | null | null | null |
|
# Pandas
<img src="https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/images/logo.png" width=150>
In this notebook, we'll learn the basics of data analysis with the Python Pandas library.
<img src="https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/images/pandas.png" width=500>
# Uploading the data
We're first going to get some data to play with. We're going to load the titanic dataset from the public link below.
```
import urllib
# Upload data from GitHub to notebook's local drive
url = "https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/data/titanic.csv"
response = urllib.request.urlopen(url)
html = response.read()
with open('titanic.csv', 'wb') as f:
f.write(html)
# Checking if the data was uploaded
!ls -l
```
# Loading the data
Now that we have some data to play with, let's load it into a Pandas dataframe. Pandas is a great Python library for data analysis.
```
import pandas as pd
# Read from CSV to Pandas DataFrame
df = pd.read_csv("titanic.csv", header=0)
# First five items
df.head()
```
These are the diferent features:
* pclass: class of travel
* name: full name of the passenger
* sex: gender
* age: numerical age
* sibsp: # of siblings/spouse aboard
* parch: number of parents/child aboard
* ticket: ticket number
* fare: cost of the ticket
* cabin: location of room
* emarked: port that the passenger embarked at (C - Cherbourg, S - Southampton, Q = Queenstown)
* survived: survial metric (0 - died, 1 - survived)
# Exploratory analysis
We're going to use the Pandas library and see how we can explore and process our data.
```
# Describe features
df.describe()
# Histograms
df["age"].hist()
# Unique values
df["embarked"].unique()
# Selecting data by feature
df["name"].head()
# Filtering
df[df["sex"]=="female"].head() # only the female data appears
# Sorting
df.sort_values("age", ascending=False).head()
# Grouping
survived_group = df.groupby("survived")
survived_group.mean()
# Selecting row
df.iloc[0, :] # iloc gets rows (or columns) at particular positions in the index (so it only takes integers)
# Selecting specific value
df.iloc[0, 1]
# Selecting by index
df.loc[0] # loc gets rows (or columns) with particular labels from the index
```
# Preprocessing
```
# Rows with at least one NaN value
df[pd.isnull(df).any(axis=1)].head() # specify axis=1 to look across rows rather than the default axis=0 for columns
# Drop rows with Nan values
df = df.dropna() # removes rows with any NaN values
df = df.reset_index() # reset's row indexes in case any rows were dropped
df.head()
# Dropping multiple columns
df = df.drop(["name", "cabin", "ticket"], axis=1) # we won't use text features for our initial basic models
df.head()
# Map feature values
df['sex'] = df['sex'].map( {'female': 0, 'male': 1} ).astype(int)
df["embarked"] = df['embarked'].dropna().map( {'S':0, 'C':1, 'Q':2} ).astype(int)
df.head()
```
# Feature engineering
```
# Lambda expressions to create new features
def get_family_size(sibsp, parch):
family_size = sibsp + parch
return family_size
df["family_size"] = df[["sibsp", "parch"]].apply(lambda x: get_family_size(x["sibsp"], x["parch"]), axis=1)
df.head()
# Reorganize headers
df = df[['pclass', 'sex', 'age', 'sibsp', 'parch', 'family_size', 'fare', 'embarked', 'survived']]
df.head()
```
# Saving data
```
# Saving dataframe to CSV
df.to_csv("processed_titanic.csv", index=False)
# See your saved file
!ls -l
```
| true |
code
| 0.391755 | null | null | null | null |
|
# Experiments on the COMPAS Dataset
Install ```AIF360``` with minimum requirements:
```
!pip install aif360
```
Install packages that we will use:
```
import numpy as np
import matplotlib.pyplot as plt
import pickle
from aif360.algorithms.preprocessing.optim_preproc_helpers.data_preproc_functions \
import load_preproc_data_compas
from aif360.algorithms.preprocessing.reweighing import Reweighing
from aif360.metrics import ClassificationMetric
from sklearn.preprocessing import StandardScaler
#from sklearn.linear_model import LogisticRegression
import torch
from torch.autograd import Variable
import torchvision.transforms as transforms
import torchvision.datasets as dsets
import torch.utils.data as Data
# These 2 functions will help us save and load objects
path = "/content/drive/My Drive/Colab Notebooks/Ethics/"
def save_obj(obj, name ):
with open(path+ name + '.pkl', 'wb') as f:
pickle.dump(obj, f, pickle.HIGHEST_PROTOCOL)
def load_obj(name ):
with open(path + name + '.pkl', 'rb') as f:
return pickle.load(f)
```
Define privileged and unprivileged groups:
```
privileged_groups = [{'race': 1}]
unprivileged_groups = [{'race': 0}]
```
Load COMPAS Dataset with 'race' as the sensitive attribute:
```
# COMPAS DATASET
compas_dataset_orig = load_preproc_data_compas(['race'])
```
Visualise Compas dataset with respect to the taget label ('Likelihood of reoffeding in 2 years'; Did recid(=1) or No recid(=0) and the sensitive attribute (race):
```
df = compas_dataset_orig.metadata['params']['df'].copy()
# Favored class == 1.0 (Caucasian)
# Number of Caucasian with no reicid (0.0)
caucasian_no_recid = sum(df[((df['race'] == 1.0))]['two_year_recid'] == 0.0)
# Number of Caucasian who did reicid (1.0)
caucasian_did_recid = sum(df[((df['race'] == 1.0))]['two_year_recid'] == 1.0)
# Number of non-Caucasian with no reicid (0.0)
non_caucasian_no_recid = sum(df[((df['race'] == 0.0))]['two_year_recid'] == 0.0)
# Number of non-Caucasian who did reicid (1.0)
non_caucasian_did_recid = sum(df[((df['race'] == 0.0))]['two_year_recid'] == 1.0)
print('Caucasian (Privilaged)')
print('No recid:', caucasian_no_recid,'\tDid recid:', caucasian_did_recid, 'Total:', caucasian_no_recid + caucasian_did_recid)
print('Non-Caucasian')
print('No recid:', non_caucasian_no_recid,'\tDid recid:', non_caucasian_did_recid, 'Total:', non_caucasian_no_recid + non_caucasian_did_recid)
print('\n\t\t\t\t\tTotal:', caucasian_no_recid + caucasian_did_recid + non_caucasian_no_recid + non_caucasian_did_recid)
# Plot a bar graph:
labels = ['Non-Caucasian', 'Caucasian']
did_recid = [non_caucasian_did_recid, caucasian_did_recid]
no_recid = [non_caucasian_no_recid, caucasian_no_recid]
x = np.arange(len(labels)) # the label locations
width = 0.4 # the width of the bars
fig, ax = plt.subplots(figsize=(7,5))
rects1 = ax.bar(x - width/2, did_recid, width, label='Did recid(=1)')
rects2 = ax.bar(x + width/2, no_recid, width, label='No recid(=0)')
ax.set_ylabel('Counts')
ax.set_title("Did/din't recid by race")
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
fig.tight_layout()
plt.show()
```
Split Dataset into training and test data:
```
train, test = compas_dataset_orig.split([0.7], shuffle=True)
# Preprocess data
scale_orig = StandardScaler()
X_train = scale_orig.fit_transform(train.features)
y_train = train.labels.ravel()
X_test = scale_orig.transform(test.features)
y_test = test.labels.ravel()
```
Create a Logistic Regression class with pytorch:
```
class LogisticRegression_torch(torch.nn.Module):
def __init__(self, input_dim, output_dim):
super(LogisticRegression_torch, self).__init__()
self.linear = torch.nn.Linear(input_dim, output_dim)
def forward(self, x):
outputs = torch.sigmoid(self.linear(x))
return outputs
GPU = True
device_idx = 0
if GPU:
device = torch.device("cuda:" + str(device_idx) if torch.cuda.is_available() else "cpu")
else:
device = torch.device("cpu")
BATCH_SIZE = 128
learning_rate = 0.0001
# Create a DataTensor
train_dataset = Data.TensorDataset(torch.tensor(X_train).float(), torch.Tensor(y_train).float())
if device == 0:
num_workers = 2
else:
num_workers = 0
# Data Loader
loader_train = Data.DataLoader(
dataset=train_dataset,
batch_size=BATCH_SIZE,
shuffle=True, num_workers=num_workers)
```
Train a LR-model for each regularization parameter $\lambda$ and test on the test set:
```
criterion = torch.nn.BCELoss(reduction='sum')
epochs = 20
accuracies = []
metrics = {}
lambdas = [0.0, 0.00001, 0.0001, 0.001, 0.01, 0.1, 0.2, 0.3, 0.5, 0.7, 0.9]
lambdas = np.concatenate((np.array(lambdas), np.linspace(1, 100, num=100)))
for reg_lambda in lambdas:
print('Lambda:', reg_lambda,'\n')
model = LogisticRegression_torch(X_train.shape[1], 1)
optimizer = torch.optim.SGD(model.parameters(), lr=0.0001)
for epoch in range(epochs):
train_loss = 0.0
for i, (x, y) in enumerate(loader_train):
# Converting inputs and labels to Variable
inputs = Variable(x.to(device))
labels = Variable(y.to(device))
# Clear gradient buffers because we don't want any gradient
# from previous epoch to carry forward, dont want to cummulate gradients
optimizer.zero_grad()
# get output from the model, given the inputs
outputs = model(inputs)
# Regularization
reg = 0
for param in model.parameters():
reg += 0.5 * (param ** 2).sum()
#reg += param.abs().sum()
# reg_lambda = 0
# get loss for the predicted output
loss = criterion(outputs.reshape(outputs.shape[0]), labels) + \
reg_lambda * reg
train_loss += loss.item()
# get gradients w.r.t to parameters
loss.backward()
# update parameters
optimizer.step()
if (epoch + 1) % 5 == 0:
print('epoch [{}/{}], Training loss:{:.6f}'.format(
epoch + 1,
epochs,
train_loss / len(loader_train.dataset)))
with torch.no_grad():
model.eval()
out = model(Variable(torch.Tensor(X_test).to(device))).detach().cpu()
pred = (out >= 0.5).int().numpy().squeeze()
accuracy = sum((y_test == pred))/len(y_test)
print('Accuracy: ', accuracy,'\n')
accuracies.append(accuracy)
test_pred = test.copy()
test_pred.labels = pred.reshape(-1,1)
metric = ClassificationMetric(test, test_pred,unprivileged_groups=unprivileged_groups, privileged_groups=privileged_groups)
metrics[reg_lambda] = {}
metrics[reg_lambda]['accuracy'] = accuracy
metrics[reg_lambda]['privilaged'] = metric.performance_measures(privileged=True)
metrics[reg_lambda]['unprivilaged'] = metric.performance_measures(privileged=False)
met = metric.binary_confusion_matrix(privileged=True)
PR_priv = (met['TP'] + met['FP']) / (met['TP'] + met['FP'] + met['TN'] + met['FN'])
metrics[reg_lambda]['privilaged']['PR'] = PR_priv
met = metric.binary_confusion_matrix(privileged=False)
PR_unpriv = (met['TP'] + met['FP']) / (met['TP'] + met['FP'] + met['TN'] + met['FN'])
metrics[reg_lambda]['unprivilaged']['PR'] = PR_unpriv
save_obj(metrics, 'metrics_compas')
```
Plot accuracy with respect to $\lambda$:
```
plt.plot(lambdas, accuracies)
plt.title('Accuracy of Logistic Regression on COMPAS dataset')
plt.xlabel('Reg-lambda')
plt.ylabel('Accuracy')
plt.ylim((0.6,0.7))
```
Plot TPR and NPR for each sensitive class with respect to $\lambda$:
```
TPR_priv = []
TPR_non_priv = []
TNR_priv = []
TNR_non_priv = []
for l in metrics:
TPR_priv.append(metrics[l]['privilaged']['TPR'])
TPR_non_priv.append(metrics[l]['unprivilaged']['TPR'])
TNR_priv.append(metrics[l]['privilaged']['TNR'])
TNR_non_priv.append(metrics[l]['unprivilaged']['TNR'])
fig, axs = plt.subplots(1, 2, figsize=(10,5))
fig.suptitle('Investigating Equalized Odds')
axs[0].plot(lambdas, TPR_non_priv)
axs[0].plot(lambdas, TPR_priv)
axs[0].set_title('TPR')
axs[0].set(xlabel='Reg-lambda', ylabel='TPR')
axs[0].legend(['Not Caucasian', 'Caucasian'])
axs[0].set(ylim=(0.3,1))
axs[1].plot(lambdas, TNR_non_priv)
axs[1].plot(lambdas, TNR_priv)
axs[1].set_title('TNR')
axs[1].set(xlabel='Reg-lambda', ylabel='TNR')
axs[1].legend(['Not Caucasian', 'Caucasian'])
axs[1].set(ylim=(0.2,0.9))
```
Plot positive and negative predictive parity for each sensitive class with respect to $\lambda$:
```
PPP_priv= []
PPP_non_priv= []
NPP_priv= []
NPP_non_priv = []
for l in metrics:
PPP_priv.append(metrics[l]['privilaged']['PPV'])
PPP_non_priv.append(metrics[l]['unprivilaged']['PPV'])
NPP_priv.append(metrics[l]['privilaged']['NPV'])
NPP_non_priv.append(metrics[l]['unprivilaged']['NPV'])
fig, axs = plt.subplots(1, 2, figsize=(10,5))
fig.suptitle('Investigating Predictive Parity')
axs[0].plot(lambdas, PPP_non_priv)
axs[0].plot(lambdas, PPP_priv)
axs[0].set_title('PPP')
axs[0].set(xlabel='Reg-lambda', ylabel='PPP')
axs[0].legend(['Not Caucasian', 'Caucasian'])
axs[0].set(ylim=(0.4,0.9))
axs[1].plot(lambdas, NPP_non_priv)
axs[1].plot(lambdas, NPP_priv)
axs[1].set_title('NPP')
axs[1].set(xlabel='Reg-lambda', ylabel='NPP')
axs[1].legend(['Not Caucasian', 'Caucasian'])
axs[1].set(ylim=(0,1))
```
Plot PR for each sensitive class with respect to $\lambda$:
```
PR_priv = []
PR_non_priv = []
ACC = []
for l in metrics:
PR_priv.append(metrics[l]['privilaged']['PR'])
PR_non_priv.append(metrics[l]['unprivilaged']['PR'])
ACC.append(metrics[l]['accuracy'])
fig, axs = plt.subplots(1, 2, figsize=(10,5))
axs[1].set_title('Investigating Demographic Parity')
axs[1].plot(lambdas, PR_non_priv)
axs[1].plot(lambdas, PR_priv)
axs[1].set(xlabel='Reg-lambda', ylabel='Positive Rate')
axs[1].legend(['Non-Caucasian', 'Caucasian'])
axs[1].set(ylim=(0,1))
axs[0].plot(lambdas, ACC)
axs[0].set_title('Accuracy')
axs[0].set(xlabel='Reg-lambda', ylabel = 'Accuracy')
axs[0].set(ylim=(0.6,0.7))
```
### Pre-processing by Reweighing:
```
RW = Reweighing(unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
train_rw = RW.fit_transform(train)
# Create a weights Tensor
weights = torch.FloatTensor(train_rw.instance_weights)
BATCH_SIZE = 32
learning_rate = 0.0001
# Data Tensor
# We now include the weights so that data will be reweighed during training
rw_train_dataset = Data.TensorDataset(torch.tensor(X_train).float(),
torch.Tensor(y_train).float(), weights)
# Data Loader
loader_train = Data.DataLoader(
dataset=rw_train_dataset,
batch_size=BATCH_SIZE,
shuffle=False, num_workers=num_workers)
```
Train a LR-model for each regularization parameter $\lambda$ and test on the test set:
```
epochs = 20
accuracies = []
metrics_rw = {}
lambdas = [0.0, 0.00001, 0.0001, 0.001, 0.01, 0.1, 0.2, 0.3, 0.5, 0.7, 0.9]
lambdas = np.concatenate((np.array(lambdas), np.linspace(1, 100, num=100)))
for reg_lambda in lambdas:
model = LogisticRegression_torch(X_train.shape[1], 1)
optimizer = torch.optim.SGD(model.parameters(), lr=0.0001)
for epoch in range(epochs):
train_loss = 0.0
for i, (x, y, w) in enumerate(loader_train):
# Converting inputs and labels to Variable
inputs = Variable(x.to(device))
labels = Variable(y.to(device))
# Clear gradient buffers because we don't want any gradient
# from previous epoch to carry forward, dont want to cummulate gradients
optimizer.zero_grad()
# get output from the model, given the inputs
outputs = model(inputs)
# Regularization
reg = 0
for param in model.parameters():
reg += 0.5 * (param ** 2).mean()
#reg += param.abs().sum()
# reg_lambda = 0
# criterion
criterion = torch.nn.BCELoss(weight=w, reduction='sum')
# get loss for the predicted output
loss = criterion(outputs.reshape(outputs.shape[0]), labels) + \
reg_lambda * reg
train_loss += loss.item()
# get gradients w.r.t to parameters
loss.backward()
# update parameters
optimizer.step()
if (epoch + 1) % 5 == 0:
print('epoch [{}/{}], Training loss:{:.6f}'.format(
epoch + 1,
epochs,
train_loss / len(loader_train.dataset)))
with torch.no_grad():
model.eval()
out = model(Variable(torch.Tensor(X_test).to(device))).detach().cpu()
pred = (out >= 0.5).int().numpy().squeeze()
accuracy = sum((y_test == pred))/len(y_test)
print('Accuracy: ', accuracy)
accuracies.append(accuracy)
test_pred = test.copy()
test_pred.labels = pred.reshape(-1,1)
metric_rew = ClassificationMetric(test, test_pred,unprivileged_groups=unprivileged_groups, privileged_groups=privileged_groups)
metrics_rw[reg_lambda] = {}
metrics_rw[reg_lambda]['accuracy'] = accuracy
metrics_rw[reg_lambda]['privilaged'] = metric_rew.performance_measures(privileged=True)
metrics_rw[reg_lambda]['unprivilaged'] = metric_rew.performance_measures(privileged=False)
met = metric_rew.binary_confusion_matrix(privileged=True)
PR_priv = (met['TP'] + met['FP']) / (met['TP'] + met['FP'] + met['TN'] + met['FN'])
metrics_rw[reg_lambda]['privilaged']['PR'] = PR_priv
met = metric_rew.binary_confusion_matrix(privileged=False)
PR_unpriv = (met['TP'] + met['FP']) / (met['TP'] + met['FP'] + met['TN'] + met['FN'])
metrics_rw[reg_lambda]['unprivilaged']['PR'] = PR_unpriv
save_obj(metrics, 'metrics_compas_rw')
```
Plot accuracy with respect to $\lambda$:
```
plt.plot(lambdas, accuracies)
plt.title('Accuracy of Logistic Regression on COMPAS dataset')
plt.xlabel('Reg-lambda')
plt.ylabel('Accuracy')
```
Plot TPR and NPR for each sensitive class with respect to $\lambda$:
```
TPR_priv_rw = []
TPR_non_priv_rw = []
TNR_priv_rw = []
TNR_non_priv_rw = []
for l in metrics_rw:
TPR_priv_rw.append(metrics_rw[l]['privilaged']['TPR'])
TPR_non_priv_rw.append(metrics_rw[l]['unprivilaged']['TPR'])
TNR_priv_rw.append(metrics_rw[l]['privilaged']['TNR'])
TNR_non_priv_rw.append(metrics_rw[l]['unprivilaged']['TNR'])
fig, axs = plt.subplots(1, 2, figsize=(10,5))
fig.suptitle('Investigating Equalized Odds')
axs[0].plot(lambdas, TPR_non_priv_rw)
axs[0].plot(lambdas, TPR_priv_rw)
axs[0].set_title('TPR')
axs[0].set(xlabel='Reg-lambda', ylabel='TPR')
axs[0].legend(['Non-Caucasian', 'Caucasian'])
axs[1].plot(lambdas, TNR_non_priv_rw)
axs[1].plot(lambdas, TNR_priv_rw)
axs[1].set_title('TNR')
axs[1].set(xlabel='Reg-lambda', ylabel='TNR')
axs[1].legend(['Non-Caucasian', 'Caucasian'])
axs[1].set(ylim=(0, 1))
```
Plot positive and negative predictive parity for each sensitive class with respect to $\lambda$:
```
PPP_priv_rw = []
PPP_non_priv_rw = []
NPP_priv_rw = []
NPP_non_priv_rw = []
for l in metrics_rw:
PPP_priv_rw.append(metrics_rw[l]['privilaged']['PPV'])
PPP_non_priv_rw.append(metrics_rw[l]['unprivilaged']['PPV'])
NPP_priv_rw.append(metrics_rw[l]['privilaged']['NPV'])
NPP_non_priv_rw.append(metrics_rw[l]['unprivilaged']['NPV'])
fig, axs = plt.subplots(1, 2, figsize=(10,5))
fig.suptitle('Investigating Predictive Parity')
axs[0].plot(lambdas, PPP_non_priv_rw)
axs[0].plot(lambdas, PPP_priv_rw)
axs[0].set_title('PPP')
axs[0].set(xlabel='Reg-lambda', ylabel='PPP')
axs[0].legend(['Non-Caucasian', 'Caucasian'])
axs[0].set(ylim=(0.4,0.8))
axs[1].plot(lambdas, NPP_non_priv_rw)
axs[1].plot(lambdas, NPP_priv_rw)
axs[1].set_title('NPP')
axs[1].set(xlabel='Reg-lambda', ylabel='NPP')
axs[1].legend(['Non-Caucasian', 'Caucasian'])
axs[1].set(ylim=(0.4,0.8))
```
Plot PR for each sensitive class with respect to $\lambda$:
```
PR_priv_rw = []
PR_non_priv_rw = []
ACC = []
for l in metrics_rw:
PR_priv_rw.append(metrics_rw[l]['privilaged']['PR'])
PR_non_priv_rw.append(metrics_rw[l]['unprivilaged']['PR'])
ACC.append(metrics_rw[l]['accuracy'])
fig, axs = plt.subplots(1, 2, figsize=(10,5))
axs[1].set_title('Investigating Demographic Parity')
axs[1].plot(lambdas, PR_non_priv_rw)
axs[1].plot(lambdas, PR_priv_rw)
axs[1].set(xlabel='Reg-lambda', ylabel='Positive Rate')
axs[1].legend(['Non-Caucasian', 'Caucasian'])
axs[0].plot(lambdas, ACC)
axs[0].set_title('Accuracy')
axs[0].set(xlabel='Reg-lambda', ylabel = 'Accuracy')
axs[0].set(ylim=(0.63,0.67))
with torch.no_grad():
model.eval()
out = model(Variable(torch.Tensor(X_test).to(device))).detach().cpu()
t = test.copy()
class1 = t.labels[t.features[:,1] == 0]
class2 = t.labels[t.features[:,1] == 1]
pred_class1 = out[t.features[:,1] == 0]
pred_class2 = out[t.features[:,1] == 1]
pip install scikitplot
from sklearn import svm, datasets
from sklearn import metrics
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
import matplotlib.pyplot as plt
fpr, tpr, _ = metrics.roc_curve(class1, pred_class1)
auc = metrics.roc_auc_score(class1, pred_class1)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
fpr, tpr, _ = metrics.roc_curve(class2, pred_class2)
auc = metrics.roc_auc_score(class2, pred_class2)
plt.plot(fpr,tpr,label="data 2, auc="+str(auc))
plt.legend()
plt.plot(np.linspace(0,1), np.linspace(0,1),'k--')
```
| true |
code
| 0.692798 | null | null | null | null |
|
# Temperature forecast for the general public (MAELSTROM-Yr dataset)
This dataset contains temperature weather forecast for the Nordic region, and are used to produce public weather forecasts on the weather app Yr (www.yr.no). The goal of the prediction task is to generate a deterministic temperature forecast together with an uncertainty range (10% to 90%) as shown here: https://www.yr.no/en/details/graph/5-18700/Norway/Oslo/Oslo/Oslo%20(Blindern).
The target field in the dataset is constructed using a high density network of citizen weather stations from [Netatmo](https://weathermap.netatmo.com/).
The current operational implementation uses a very simple regression model based on only a subset of the predictors available in the dataset. It is described in this article: https://journals.ametsoc.org/view/journals/bams/101/1/bams-d-18-0237.1.xml
## Prerequisites
To run the code in this notebook, you need the following packages:
`pip install climetlab climetlab_maelstrom_yr keras tensorflow numpy matplotlib`
## Loading the data
We can use climetlab to load the dataset into an xarray dataset. There will be several datasets available of different sizes: 300 MB (not available yet), 5GB, and 5TB (not available yet). The 5TB dataset contains the entire Nordic domain at 1x1 km resolution for all 60 hour leadtimes. The 5GB dataset contains only a subset of grid points (128x128) surrounding Oslo, Norway and only for leadtimes 6, 12, ..., 42 hours. All datasets contain the same input predictors and time period (4 years).
Currently, only "air_temperature" is available as the predictand parameter, however precipitation_amount will be added in the future.
The entire 5GB dataset will take a few minutes to load, since the data must be downloaded from europeanweather.cloud. Climetlab caches files locally, so files need not be when rerunning the code later. To only load a subset, add a dates argument to load_dataset, e.g. `dates=['2017-01-01', '2017-01-02']` or `dates=pandas.date_range(start="2017-01-01", end="2017-03-01", freq="1D")`.
```
import climetlab as cml
import pandas
cmlds = cml.load_dataset(
'maelstrom-yr',
size='5GB',
parameter='air_temperature',
)
ds = cmlds.to_xarray()
```
This dataset contains the following dimensions and variables
```
print(ds)
```
The dataset is mostly self explanatory. The `record` dimension represent different samples. The `predictor` variable contains all predictors stacked one after the other, including values for different leadtimes. The `target` variable contain target values.
### Plotting predictors and predictand (target)
```
import matplotlib.pyplot as plt
import numpy as np
names = ds["name_predictor"].values
names = np.array([''.join([qq.decode('utf-8') for qq in names[p, :]]) for p in range(names.shape[0])])
num_leadtimes = len(ds["leadtime"])
unique_predictor_names = np.unique(names)
print("Available predictors:", unique_predictor_names)
index_date = 0
target = ds["target"].values
plt.rcParams['figure.dpi'] = 100
plt.rcParams['figure.figsize'] = [10, 6]
for i, name in enumerate(unique_predictor_names):
plt.subplot(2, 4, i + 1)
index = np.where(names == name)[0][0]
plt.pcolormesh(ds["predictors"][index_date, :, :, index], shading="auto", rasterized=True)
plt.gca().set_aspect(1)
plt.title(name)
plt.subplot(2, 4, 8)
plt.pcolormesh(target[index_date, :, :, 0], shading="auto", rasterized=True)
plt.gca().set_aspect(1)
plt.title("Target")
```
## Example ML solution
### Normalizing the predictors
First we normalize the predictors, by subtractng the mean and dividing by the standard deviation:
```
raw_forecast = np.copy(ds["predictors"][:, :, :, 0:num_leadtimes])
predictors = np.copy(ds["predictors"].values)
num_predictors = predictors.shape[3]
for p in range(num_predictors):
predictors[:, :, :, p] -= np.nanmean(predictors[:, :, :, p])
predictors[:, :, :, p] /= np.nanstd(predictors[:, :, :, p])
```
### Defining the loss function
We use the quantile loss function, by scoring each of the three output quantiles of the model:
```
import keras
import tensorflow as tf
import keras.backend as K
global num_leadtimes
def quantile_loss_function(y_true, y_pred):
err0 = y_true - y_pred[:, :, :, 0:num_leadtimes]
err1 = y_true - y_pred[:, :, :, num_leadtimes:(2*num_leadtimes)]
err2 = y_true - y_pred[:, :, :, (2*num_leadtimes):(3*num_leadtimes)]
qtloss0 = (0.5 - tf.cast((err0 < 0), tf.float32)) * err0
qtloss1 = (0.1 - tf.cast((err1 < 0), tf.float32)) * err1
qtloss2 = (0.9 - tf.cast((err2 < 0), tf.float32)) * err2
return K.mean(qtloss0 + qtloss1 + qtloss2)
```
### Setting up the model
The model takes a gridded predictor set as input and outputs gridded fields for each leadtime and for three quantiles. The tempearture forecast on yr.no has both a deterministic best guess and a 10-90% confidence interval. We want the model to predict all three parameters simultaneously.
```
num_quantiles = 3
num_outputs = num_quantiles * num_leadtimes
model = keras.Sequential()
model.add(keras.layers.InputLayer(predictors.shape[1:]))
model.add(keras.layers.Dense(num_outputs))
model.compile(optimizer = tf.keras.optimizers.Adam(learning_rate = 1e-2), loss = quantile_loss_function)
model.summary()
```
### Training the model
We will split the dataset into a training and evaluation set, based on the record dimension.
```
Itrain = range(predictors.shape[0]//2)
Ieval = range(predictors.shape[0]//2, predictors.shape[0])
num_epochs = 50
batch_size = 4
model.fit(predictors[Itrain, ...], target[Itrain, ...], epochs=num_epochs, batch_size=batch_size)
```
### Predict output
```
output = model.predict(predictors[Ieval, ...])
```
## Model evaluation and visualization
### Evaluating the model
First, lets compare the mean absolute error of the raw forecast and the ML-forecast of the median
```
import numpy as np
print("Raw model MAE:", np.nanmean(np.abs(raw_forecast[Ieval, ...] - target[Ieval, ...])), "°C")
print("ML MAE:", np.nanmean(np.abs(output[:, :, :, 0:num_leadtimes] - target[Ieval, ...])), "°C")
```
Next, we can plot the MAE as a function of leadtime:
```
x = ds["leadtime"].astype(float) / 3600 / 1e9
plt.plot(x, [np.nanmean(np.abs(output[:, :, :, i] - target[Ieval, :, :, i])) for i in range(num_leadtimes)], 'ro-', lw=2, label="Model")
plt.plot(x, [np.nanmean(np.abs(raw_forecast[Ieval, :, :, i] - target[Ieval, :, :, i])) for i in range(num_leadtimes)], 'yo-', lw=2, label="Raw")
plt.legend()
plt.xlabel("Lead time (hours)")
plt.ylabel("Mean absolute error (°C)")
```
### Visualizing the results as timeseries
We can visualize the output as a timeseries. We will pick an example point (Oslo).
```
Y = 55
X = 55
plt.plot(x, output[0, Y, X, 0:num_leadtimes], 'r-', lw=2, label="Median")
plt.plot(x, raw_forecast[Ieval[0], Y, X, 0:num_leadtimes], 'y-', lw=2, label="Raw")
lower = output[0, Y, X,num_leadtimes:2*num_leadtimes]
upper = output[0, Y, X, 2*num_leadtimes:3*num_leadtimes]
plt.plot(x, lower, 'r--', lw=2, label="10%")
plt.plot(x, upper, 'r--', lw=2, label="90%")
xx = np.concatenate((x, x[::-1]))
plt.fill(np.concatenate((x, x[::-1])), np.concatenate((lower, upper[::-1])), color='r', alpha=0.2, linewidth=0)
plt.plot(x, target[Ieval[0], Y, X, :], 'bo-', lw=2, label="Target")
plt.legend()
plt.xlabel("Lead time (hours)")
plt.ylabel("Air temperature (°C)")
```
### Visualizing the results on a map
```
plt.subplot(1, 3, 1)
plt.pcolormesh(raw_forecast[Ieval[0], :, :, 0], rasterized=True)
plt.gca().set_aspect(1)
plt.title("Raw forecast")
plt.subplot(1, 3, 2)
plt.pcolormesh(output[0, :, :, 0], rasterized=True)
plt.gca().set_aspect(1)
plt.title("ML forecast")
plt.subplot(1, 3, 3)
plt.pcolormesh(target[Ieval[0], :, :, 0], rasterized=True)
plt.gca().set_aspect(1)
plt.title("Target (median)")
```
| true |
code
| 0.511046 | null | null | null | null |
|
# Compare Hankel and Fourier Transforms
This will compare the forward and inverse transforms for both Hankel and Fourier by either computing partial derivatives of solving a parital differential equation.
This notebook focuses on the Laplacian operator in the case of radial symmetry.
Consider two 2D circularly-symmetric functions $f(r)$ and $g(r)$ that are related by the following differential operator,
$$
g(r) = \nabla^2 f(r)
= \frac{1}{r} \frac{\partial}{\partial r} \left( r \frac{\partial f}{\partial r} \right)
$$
In this notebook we will consider two problems:
1. Given $f(r)$, compute the Laplacian to obtain $g(r)$
2. Given $g(r)$, invert the Laplacian to obtain $f(r)$
We can use the 1D Hankel (or 2D Fourier) transform to compute the Laplacian in three steps:
1. Compute the Forward Transform
$$
\mathcal{H}[f(r)] = \hat f(k)
$$
2. Differentiate in Spectral space
$$
\hat g(k) = - k^2 \hat f(k)
$$
3. Compute the Inverse Transform
$$
g(r) = \mathcal{H}^{-1} [\hat g(k)]
$$
This is easily done in two-dimensions using the Fast Fourier Transform (FFT) but one advantage of the Hankel transform is that we only have a one-dimensional transform.
## Import Relevant Libraries
```
# Import Libraries
import numpy as np # Numpy
from scipy.fftpack import fft2, ifft2, fftfreq, ifftn, fftn # Fourier
from hankel import HankelTransform, SymmetricFourierTransform # Hankel
from scipy.interpolate import InterpolatedUnivariateSpline as spline # Splines
import matplotlib.pyplot as plt # Plotting
import matplotlib as mpl
from os import path
%matplotlib inline
## Put the prefix to the figure directory here for your computer. If you don't want to save files, set to empty string, or None.
prefix = path.expanduser("~/Documents/Projects/HANKEL/laplacian_paper/Figures/")
```
## Standard Plot Aesthetics
```
mpl.rcParams['lines.linewidth'] = 2
mpl.rcParams['xtick.labelsize'] = 13
mpl.rcParams['ytick.labelsize'] = 13
mpl.rcParams['font.size'] = 15
mpl.rcParams['axes.titlesize'] = 14
```
## Define Sample Functions
We define the two functions
$$
f = e^{-r^2}
\quad \mbox{ and } \quad
g = 4 e^{-r^2} (r^2 - 1).
$$
It is easy to verify that they are related by the Laplacian operator.
```
# Define Gaussian
f = lambda r: np.exp(-r**2)
# Define Laplacian Gaussian function
g = lambda r: 4.0*np.exp(-r**2)*(r**2 - 1.0)
```
We can also define the FTs of these functions analytically, so we can compare our numerical results:
```
fhat = lambda x : np.pi*np.exp(-x**2/4.)
ghat = lambda x : -x**2*fhat(x)
# Make a plot of the sample functions
fig, ax = plt.subplots(1,2,figsize=(10,4))
r = np.linspace(0,10,128)
ax[0].plot(r, f(r), label=r"$f(r)$")
ax[0].plot(r, g(r), label=r'$g_2(r)$', ls="--")
ax[0].legend()
ax[0].set_xlabel(r"$r$")
ax[0].grid(True)
k = np.logspace(-2,2,128)
ax[1].plot(k, fhat(k), label=r"$\hat{f}_2(k)$")
ax[1].plot(k, ghat(k), label=r'$\hat{g}_2(k)$', ls="--")
ax[1].legend()
ax[1].set_xlabel(r"$k$")
ax[1].grid(True)
ax[1].set_xscale('log')
#plt.suptitle("Plot of Sample Functions")
if prefix:
plt.savefig(path.join(prefix,"sample_function.pdf"))
```
## Define Transformation Functions
```
def ft_transformation_2d(f,x, inverse=False):
xx,yy = np.meshgrid(x,x)
r = np.sqrt(xx**2 + yy**2)
# Appropriate k-space values
k = 2*np.pi*fftfreq(len(x),d=x[1]-x[0])
kx,ky = np.meshgrid(k,k)
K2 = kx**2+ky**2
# The transformation
if not inverse:
g2d = ifft2(-K2 * fft2(f(r)).real).real
else:
invK2 = 1./K2
invK2[np.isinf(invK2)] = 0.0
g2d = ifft2(-invK2 * fft2(f(r)).real).real
return x[len(x)//2:], g2d[len(x)//2,len(x)//2:]
def ht_transformation_nd(f,N_forward,h_forward,K,r,ndim=2, inverse=False, N_back=None, h_back=None,
ret_everything=False):
if N_back is None:
N_back = N_forward
if h_back is None:
h_back = h_forward
# Get transform of f
ht = SymmetricFourierTransform(ndim=ndim, N=N_forward, h=h_forward)
if ret_everything:
fhat, fhat_cumsum = ht.transform(f, K, ret_cumsum=True, ret_err=False)
else:
fhat = ht.transform(f, K, ret_err = False)
# Spectral derivative
if not inverse:
ghat = -K**2 * fhat
else:
ghat = -1./K**2 * fhat
# Transform back to physical space via spline
# The following should give best resulting splines for most kinds of functions
# Use log-space y if ghat is either all negative or all positive, otherwise linear-space
# Use order 1 because if we have to extrapolate, this is more stable.
# This will not be a good approximation for discontinuous functions... but they shouldn't arise.
if np.all(ghat<=1e-13):
g_ = spline(K[ghat<0],np.log(-ghat[ghat<0]),k=1)
ghat_spline = lambda x : -np.exp(g_(x))
elif np.all(ghat>=-1e-13):
g_ = spline(K[ghat>0],np.log(ghat[ghat>0]),k=1)
ghat_spline = lambda x : np.exp(g_(x))
else:
g_ = spline(K,ghat,k=1)
ghat_spline = g_
if N_back != N_forward or h_back != h_forward:
ht2 = SymmetricFourierTransform(ndim=ndim, N=N_back, h=h_back)
else:
ht2 = ht
if ret_everything:
g, g_cumsum = ht2.transform(ghat_spline, r, ret_err=False, inverse=True, ret_cumsum=True)
else:
g = ht2.transform(ghat_spline, r, ret_err=False, inverse=True)
if ret_everything:
return g, g_cumsum, fhat,fhat_cumsum, ghat, ht,ht2, ghat_spline
else:
return g
```
## Forward Laplacian
We can simply use the defined functions to determine the foward laplacian in each case. We just need to specify the grid.
```
L = 10.
N = 256
dr = L/N
x_ft = np.linspace(-L+dr/2,L-dr/2,2*N)
r_ht = np.linspace(dr/2,L-dr/2,N)
```
We also need to choose appropriate parameters for the forwards/backwards Hankel Transforms. To do this, we can use the ``get_h`` function in the ``hankel`` library:
```
from hankel import get_h
hback, res, Nback = get_h(ghat, nu=2, K=r_ht[::10], cls=SymmetricFourierTransform, atol=1e-8, rtol=1e-4, inverse=True)
K = np.logspace(-2, 2, N) # These values come from inspection of the plot above, which shows that ghat is ~zero outside these bounds
hforward, res, Nforward = get_h(f, nu=2, K=K[::50], cls=SymmetricFourierTransform, atol=1e-8, rtol=1e-4)
hforward, Nforward, hback, Nback
## FT
r_ft, g_ft = ft_transformation_2d(f,x_ft)
# Note: r_ft is equivalent to r_ht
## HT
g_ht = ht_transformation_nd(f,N_forward=Nforward, h_forward=hforward, N_back=Nback, h_back=hback, K = K, r = r_ht)
```
Now we plot the calculated functions against the analytic result:
```
fig, ax = plt.subplots(2,1, sharex=True,gridspec_kw={"hspace":0.08},figsize=(8,6))
ax[0].plot(r_ft,g_ft, label="Fourier Transform", lw=2)
ax[0].plot(r_ht, g_ht, label="Hankel Transform", lw=2, ls='--')
ax[0].plot(r_ht, g(r_ht), label = "$g_2(r)$", lw=2, ls = ':')
ax[0].legend(fontsize=15)
#ax[0].xaxis.set_ticks([])
ax[0].grid(True)
ax[0].set_ylabel(r"$\tilde{g}_2(r)$",fontsize=15)
ax[0].set_ylim(-4.2,1.2)
ax[1].plot(r_ft, np.abs(g_ft-g(r_ft)), lw=2)
ax[1].plot(r_ht, np.abs(g_ht-g(r_ht)),lw=2, ls='--')
#ax[1].set_ylim(-1,1)
ax[1].set_yscale('log')
#ax[1].set_yscale("symlog",linthreshy=1e-6)
ax[1].set_ylabel(r"$|\tilde{g}_2(r)-g_2(r)|$",fontsize=15)
ax[1].set_xlabel(r"$r$",fontsize=15)
ax[1].set_ylim(1e-15, 0.8)
plt.grid(True)
if prefix:
fig.savefig(path.join(prefix,"forward_laplacian.pdf"))
```
Timing for each calculation:
```
%timeit ft_transformation_2d(f,x_ft)
%timeit ht_transformation_nd(f,N_forward=Nforward, h_forward=hforward, N_back=Nback, h_back=hback, K = K, r = r_ht)
```
## Inverse Laplacian
We use the 1D Hankel (or 2D Fourier) transform to compute the Laplacian in three steps:
1. Compute the Forward Transform
$$
\mathcal{H}[g(r)] = \hat g(k)
$$
2. Differentiate in Spectral space
$$
\hat f(k) = - \frac{1}{k^2} \hat g(k)
$$
3. Compute the Inverse Transform
$$
f(r) = \mathcal{H}^{-1} [\hat f(k)]
$$
Again, we compute the relevant Hankel parameters:
```
hback, res, Nback = get_h(fhat, nu=2, K=r_ht[::10], cls=SymmetricFourierTransform, atol=1e-8, rtol=1e-4, inverse=True)
K = np.logspace(-2, 2, N) # These values come from inspection of the plot above, which shows that ghat is ~zero outside these bounds
hforward, res, Nforward = get_h(g, nu=2, K=K[::50], cls=SymmetricFourierTransform, atol=1e-8, rtol=1e-4)
hforward,Nforward,hback,Nback
## FT
r_ft, f_ft = ft_transformation_2d(g,x_ft, inverse=True)
# Note: r_ft is equivalent to r_ht
## HT
f_ht = ht_transformation_nd(g,N_forward=Nforward, h_forward=hforward,N_back=Nback, h_back=hback, K = K, r = r_ht, inverse=True)
fig, ax = plt.subplots(2,1, sharex=True,gridspec_kw={"hspace":0.08},figsize=(8,6))
#np.mean(f(r_ft)) - np.mean(f_ft)
ax[0].plot(r_ft,f_ft + f(r_ft)[-1] - f_ft[-1], label="Fourier Transform", lw=2)
ax[0].plot(r_ht, f_ht, label="Hankel Transform", lw=2, ls='--')
ax[0].plot(r_ht, f(r_ht), label = "$f(r)$", lw=2, ls = ':')
ax[0].legend()
ax[0].grid(True)
ax[0].set_ylabel(r"$\tilde{f}(r)$",fontsize=15)
ax[0].set_ylim(-0.2,1.2)
#ax[0].set_yscale('log')
ax[1].plot(r_ft, np.abs(f_ft + f(r_ft)[-1] - f_ft[-1] -f(r_ft)), lw=2)
ax[1].plot(r_ht, np.abs(f_ht -f(r_ht)),lw=2, ls='--')
ax[1].set_yscale('log')
ax[1].set_ylabel(r"$|\tilde{f}(r)-f(r)|$",fontsize=15)
ax[1].set_xlabel(r"$r$",fontsize=15)
ax[1].set_ylim(1e-19, 0.8)
plt.grid(True)
if prefix:
fig.savefig(path.join(prefix,"inverse_laplacian.pdf"))
%timeit ft_transformation_2d(g,x_ft, inverse=True)
%timeit ht_transformation_nd(g,N_forward=Nforward, h_forward=hforward,N_back=Nback, h_back=hback, K = K, r = r_ht, inverse=True)
```
## 3D Problem (Forward)
We need to define the FT function again, for 3D:
```
def ft_transformation_3d(f,x, inverse=False):
r = np.sqrt(np.sum(np.array(np.meshgrid(*([x]*3)))**2,axis=0))
# Appropriate k-space values
k = 2*np.pi*fftfreq(len(x),d=x[1]-x[0])
K2 = np.sum(np.array(np.meshgrid(*([k]*3)))**2,axis=0)
# The transformation
if not inverse:
g2d = ifftn(-K2 * fftn(f(r)).real).real
else:
invK2 = 1./K2
invK2[np.isinf(invK2)] = 0.0
g2d = ifftn(-invK2 * fftn(f(r)).real).real
return x[len(x)/2:], g2d[len(x)/2,len(x)/2, len(x)/2:]
```
We also need to define the 3D laplacian function:
```
g3 = lambda r: 4.0*np.exp(-r**2)*(r**2 - 1.5)
fhat_3d = lambda x : np.pi**(3./2)*np.exp(-x**2/4.)
ghat_3d = lambda x : -x**2*fhat_3d(x)
L = 10.
N = 128
dr = L/N
x_ft = np.linspace(-L+dr/2,L-dr/2,2*N)
r_ht = np.linspace(dr/2,L-dr/2,N)
```
Again, choose our resolution parameters
```
hback, res, Nback = get_h(ghat_3d, nu=3, K=r_ht[::10], cls=SymmetricFourierTransform, atol=1e-8, rtol=1e-4, inverse=True)
K = np.logspace(-2, 2, 2*N) # These values come from inspection of the plot above, which shows that ghat is ~zero outside these bounds
hforward, res, Nforward = get_h(f, nu=3, K=K[::50], cls=SymmetricFourierTransform, atol=1e-8, rtol=1e-4)
hforward, Nforward, hback, Nback
## FT
r_ft, g_ft = ft_transformation_3d(f,x_ft)
# Note: r_ft is equivalent to r_ht
## HT
K = np.logspace(-1.0,2.,N)
g_ht = ht_transformation_nd(f,N_forward=Nforward, h_forward=hforward, N_back=Nback, h_back=hback, K = K, r = r_ht, ndim=3)
fig, ax = plt.subplots(2,1, sharex=True,gridspec_kw={"hspace":0.08},figsize=(8,6))
ax[0].plot(r_ft,g_ft, label="Fourier Transform", lw=2)
ax[0].plot(r_ht, g_ht, label="Hankel Transform", lw=2, ls='--')
ax[0].plot(r_ht, g3(r_ht), label = "$g_3(r)$", lw=2, ls = ':')
ax[0].legend(fontsize=15)
#ax[0].xaxis.set_ticks([])
ax[0].grid(True)
ax[0].set_ylabel(r"$\tilde{g}_3(r)$",fontsize=15)
#ax[0].set_ylim(-4.2,1.2)
ax[1].plot(r_ft, np.abs(g_ft-g3(r_ft)), lw=2)
ax[1].plot(r_ht, np.abs(g_ht-g3(r_ht)),lw=2, ls='--')
ax[1].set_yscale('log')
ax[1].set_ylabel(r"$|\tilde{g}_3(r)-g_3(r)|$",fontsize=15)
ax[1].set_xlabel(r"$r$",fontsize=15)
plt.grid(True)
if prefix:
fig.savefig(path.join(prefix,"forward_laplacian_3D.pdf"))
%timeit ht_transformation_nd(f,N_forward=Nforward, h_forward=hforward, N_back=Nback, h_back=hback, K = K, r = r_ht, ndim=3)
%timeit ft_transformation_3d(f,x_ft)
```
## 3D Problem (Inverse)
```
hback, res, Nback = get_h(fhat_3d, nu=3, K=r_ht[::10], cls=SymmetricFourierTransform, atol=1e-8, rtol=1e-4, inverse=True)
K = np.logspace(-2, 2, N) # These values come from inspection of the plot above, which shows that ghat is ~zero outside these bounds
hforward, res, Nforward = get_h(g3, nu=3, K=K[::50], cls=SymmetricFourierTransform, atol=1e-8, rtol=1e-4)
hforward,Nforward,hback,Nback
## FT
r_ft, f_ft = ft_transformation_3d(g3,x_ft, inverse=True)
# Note: r_ft is equivalent to r_ht
## HT
f_ht = ht_transformation_nd(g3,ndim=3, N_forward=Nforward, h_forward=hforward,N_back=Nback, h_back=hback, K = K, r = r_ht, inverse=True)
fig, ax = plt.subplots(2,1, sharex=True,gridspec_kw={"hspace":0.08},figsize=(8,6))
#np.mean(f(r_ft)) - np.mean(f_ft)
ax[0].plot(r_ft, f_ft + f(r_ft)[-1] - f_ft[-1], label="Fourier Transform", lw=2)
ax[0].plot(r_ht, f_ht + f(r_ft)[-1] - f_ht[-1], label="Hankel Transform", lw=2, ls='--')
ax[0].plot(r_ht, f(r_ht), label = "$f(r)$", lw=2, ls = ':')
ax[0].legend()
ax[0].grid(True)
ax[0].set_ylabel(r"$\tilde{f}(r)$",fontsize=15)
ax[0].set_ylim(-0.2,1.2)
#ax[0].set_yscale('log')
ax[1].plot(r_ft, np.abs(f_ft + f(r_ft)[-1] - f_ft[-1] -f(r_ft)), lw=2)
ax[1].plot(r_ht, np.abs(f_ht + f(r_ft)[-1] - f_ht[-1] -f(r_ht)),lw=2, ls='--')
ax[1].set_yscale('log')
ax[1].set_ylabel(r"$|\tilde{f}(r)-f(r)|$",fontsize=15)
ax[1].set_xlabel(r"$r$",fontsize=15)
ax[1].set_ylim(1e-19, 0.8)
plt.grid(True)
if prefix:
fig.savefig(path.join(prefix,"inverse_laplacian_3d.pdf"))
```
| true |
code
| 0.647074 | null | null | null | null |
|
# Introduction to Chinook with Graphene
In the following exercise, we'll get a feeling for building and characterizing tight-binding models in chinook, in addition to some calculation of the associated ARPES intensity. I'll use graphene for this exercise.
I'll start by importing the requisite python libraries -- including the necessary chinook files. Numpy is the standard python numerics package.
```
import numpy as np
import chinook.build_lib as build_lib
import chinook.ARPES_lib as arpes_lib
import chinook.operator_library as op_lib
import chinook.orbital_plotting as oplot
```
Personally, I like to keep my model setup and my calculation execution in separate .py scripts. For the sake of code readability this helps a lot. For this Jupyter notebook though, I'm going to do things sort of linearly. It gets a bit cluttered, but will help with the flow. Have a look at the .py files saved on the same page as this notebook for the same exercises written in native python scripts.
To define a tight-binding model, I'll need four things: a lattice, an orbital basis, a Hamiltonian, and a momentum path of interest. We start with the lattice.
```
alatt = 2.46
interlayer = 100.0
avec = np.array([[-alatt/2,alatt*np.sqrt(3/4.),0.0],
[alatt/2,alatt*np.sqrt(3/4.),0.0],
[0.0,0.0,interlayer]])
```
Even though we are doing a 2D lattice, it's embedded in 3D space we live in. I've then defined an 'interlayer' distance, but this is fictitiously large so there will not be any 'interlayer' coupling. Next, we define our orbital basis:
```
spin_args = {'bool':False}
basis_positions = np.array([[0.0,0.0,0.0],
[0.0,alatt/np.sqrt(3.0),0.0]])
basis_args = {'atoms':[0,0],
'Z':{0:6},
'orbs':[["20","21x","21y","21z"],["20","21x","21y","21z"]],
'pos':basis_positions,
'spin':spin_args}
```
I'm going to ignore the spin-degree of freedom so I'm turning off the spin-switch. In other systems, these 'spin_args' allow for incorporation of spin-orbit coupling and magnetic ordering. The graphene lattice has two basis atoms per unit cell, and for now I'll include the full Carbon 2sp orbital space. This is a good point to clarify that most objects we define in chinook are generated using the 'dictionary' structure I've used here, where we use key-value pairs to define attributes in a user-readable fashion.
After the basis, I'll define my Hamiltonian. Following the introduction to Slater-Koster tight-binding, I define the relevant hoppings in the SK dictionary. The keys specify the atoms and orbitals associated with the hopping value. For example, '002211P' corresponds to the $V_{pp\pi}$ hopping between the 0$^{th}$ and 0$^{th}$ atom in our basis, coupling specifically the 2p (n=2, l=1) states.
```
SK = {"020":-8.81,"021":-0.44, #onsite energies
"002200S":-5.279, #nearest-neighbour Vssσ
"002201S":5.618, #nearest-neighbour Vspσ
"002211S":6.05,"002211P":-3.07} #nearest-neighbour Vppσ,Vppπ
hamiltonian_args = {'type':'SK',
'V':SK,
'avec':avec,
'cutoff':alatt*0.7,
'spin':spin_args}
```
Before building our model, the last thing I'll do is specify a k-path along which I want to find the band-structure.
```
G = np.array([0,0,0])
K = np.array([1./3,2./3,0])
M = np.array([0,0.5,0.0])
momentum_args= {'type':'F',
'avec':avec,
'grain':200,
'pts':[G,K,M,G],
'labels':['$\\Gamma$','K','M','$\\Gamma$']}
```
Finally then, I'll use the chinook.build_library to actually construct a tight-binding model for our use here
```
basis = build_lib.gen_basis(basis_args)
kpath = build_lib.gen_K(momentum_args)
TB = build_lib.gen_TB(basis,hamiltonian_args,kpath)
```
With this model so defined, I can now compute the eigenvalues along my k-path of interest:
```
TB.solve_H()
TB.plotting()
```
We see very nicely then the linear Dirac dispersion for which graphene is so famous, in addition the the sigma-bonding states at higher energies below $E_F$, composed of sp$_2$ hybrids, from which its mechanical strength is derived. Note also that I've chosen to n-dope my graphene, shifting the Dirac point below the chemical potential. Such a shift is routinely observed in graphene which is not free-standing, as typically used in ARPES experiments.
To understand the orbital composition more explicitly, I can compute the projection of the tight-binding eigenvectors onto the orbitals of my basis using the chinook.operator_library. Before doing so, I'll use a built-in method for the TB model object we've created to determine clearly, my orbital basis:
```
TB.print_basis_summary()
```
Clearly, orbitals [0,4] are 2s, [1,5] are 2p$_x$, [2,6] are 2p$_y$ and [3,7] are 2p$_z$. I'll use the op_lib.fatbs function to plot 'fat' bands for these basis combinations:
```
C2s = op_lib.fatbs([0,4],TB,Elims=(-30,15))
C2x = op_lib.fatbs([1,5],TB,Elims=(-30,15))
C2y = op_lib.fatbs([2,6],TB,Elims=(-30,15))
C2z = op_lib.fatbs([3,7],TB,Elims=(-30,15))
```
From these results, it's immediatedly obvious that if I am only concerned with the low-energy physics near the chemical potential (within $\pm$ 3 eV), then it is perfectly reasonable to adopt a model with only p$_z$ orbitals. I can actually redefine my model accordingly.
```
basis_args = {'atoms':[0,0],
'Z':{0:6},
'orbs':[["21z"],["21z"]],
'pos':basis_positions,
'spin':spin_args}
basis = build_lib.gen_basis(basis_args)
TB_pz = build_lib.gen_TB(basis,hamiltonian_args,kpath)
TB_pz.solve_H()
TB_pz.plotting()
```
The only difference in the above was that I redined the "orbs" argument for the basis definition, cutting out the "20", "21x", "21y" states. There is some redundancy left in this model, specifically I have defined additional hopping elements and onsite energies (for the 2s) which will not be used.
Let's shift our attention to ARPES. In ARPES experiments, one usually only sees one side of the Dirac cone. This is due to interference between the the two sublattice sites. To understand this, we can plot directly the tight-binding eigenvectors near the K-point. Since we defined our k-path with 200 points between each high-symmetry point, I'll plot the eigenvectors at the 190$^{th}$ k-point.
```
eigenvector1 = TB_pz.Evec[190,:,0]
eigenvector2 = TB_pz.Evec[190,:,1]
wfunction1 = oplot.wavefunction(basis=TB_pz.basis,vector=eigenvector1)
wfunction2 = oplot.wavefunction(basis=TB_pz.basis,vector=eigenvector2)
wplot1 = wfunction1.triangulate_wavefunction(20)
wplot2 = wfunction2.triangulate_wavefunction(20)
```
We see that the lower-energy state is the symmetric combination of sites $A$ and $B$, whereas the higher energy state is the antisymmetric combination. So we can anticipate that the symmetric state will produce constructive interference, whereas the antisymmetric will destructively interfere. Ok, let's continue with this model to calculate the ARPES spectra.
```
Kpt = np.array([1.702,0.0,0.0])
klimits = 0.1
Elimits = [-1.25,0.25]
Npoints = 100
arpes_args={'cube':{'X':[Kpt[0]-klimits,Kpt[0]+klimits,Npoints],
'Y':[Kpt[1]-klimits,Kpt[1]+klimits,Npoints],
'kz':Kpt[2],
'E':[Elimits[0],Elimits[1],1000]},
'SE':['poly',0.01,0,0.1], #Self-energy arguments (lineshape)
'hv': 21.2, # Photon energy (eV)
'pol':np.array([-1,0,1]), #light-polarization
'resolution':{'E':0.02,'k':0.005}, #energy, momentum resolution
'T':4.2} #Temperature (for Fermi distribution)
experiment = arpes_lib.experiment(TB_pz,arpes_args)
experiment.datacube()
Imap,Imap_resolution,axes = experiment.spectral(slice_select=('y',0))
Imap,Imap_resolution,axes = experiment.spectral(slice_select=('E',0))
Imap,Imap_resolution,axes = experiment.spectral(slice_select=('x',Kpt[0]))
```
I can also compare the result against what I would have with my larger basis size.
```
experiment_fullbasis = arpes_lib.experiment(TB,arpes_args)
experiment_fullbasis.datacube()
Imap,Imap_resolution,axes = experiment_fullbasis.spectral(slice_select=('x',Kpt[0]))
```
Perhaps unsurprisingly, the result is the same, as symmetries of the 2D lattice preclude hybridization of the Carbon 2p$_z$ orbitals with any of the other 2sp states.
# Manipulating the Hamiltonian
We can go beyond here and now start playing with our Hamiltonian. One possibility is to consider the effect of breaking inversion symmetry by imposing an onsite energy difference between the two Carbon sites. This is the familiar Semenoff mass proposed by UBC's Gordon Semenoff, as it modifies the massless Dirac dispersion near the K-point to become massive. I will define a simple helper function for this task:
```
def semenoff_mass(TB,mass):
Hnew = [[0,0,0,0,0,mass/2],
[1,1,0,0,0,-mass/2]]
TB.append_H(Hnew)
```
I can then call this function, acting on the pz-only model:
```
TB_semenoff = build_lib.gen_TB(basis,hamiltonian_args,kpath)
semenoff_mass(TB_semenoff,0.5)
TB_semenoff.Kobj = kpath
TB_semenoff.solve_H()
TB_semenoff.plotting()
```
By breaking inversion symmetry in the crystal, I have opened a gap at the K-point. The Dirac point need only be degenerate if both inversion and time reversal symmetries are preserved. Note that I have redefined my kpath to follow the same points as before, as the ARPES calculations impose the mesh of k-points used. Near the k-point, rather than have 'bonding' and 'anti-bonding' character, the Semenoff mass localizes the the wavefunction on one or the other sites. Printing the orbital wavefunction near K for the lower and upper states:
```
eigenvector1 = TB_semenoff.Evec[190,:,0]
eigenvector2 = TB_semenoff.Evec[190,:,1]
wfunction1 = oplot.wavefunction(basis=TB_semenoff.basis,vector=eigenvector1)
wfunction2 = oplot.wavefunction(basis=TB_semenoff.basis,vector=eigenvector2)
wplot1 = wfunction1.triangulate_wavefunction(20)
wplot2 = wfunction2.triangulate_wavefunction(20)
```
We see nicely that the eigenvector has been changed from before--while still resembling the symmetric and antisymmetric combinations we had above, now the charge distribution lies predominantly on one or the other site. Try changing the momentum point where you evaluate this, or increasing/decreasing the size of the mass term to observe its effect. I can compute the photoemission again, resulting in a gapped spectrum
```
experiment_semenoff = arpes_lib.experiment(TB_semenoff,arpes_args)
experiment_semenoff.datacube()
_ = experiment_semenoff.spectral(slice_select=('x',Kpt[0]))
_ = experiment_semenoff.spectral(slice_select=('w',-0.0))
```
In addition to the gap, we also see the modification of the eigenstate manifest in the redistribution of spectral weight on the Fermi surface, which no longer features the complete extinction of intensity on the inside the cone.
While the Semenoff mass does not break time-reversal symmetry, Duncan Haldane proposed a different form of perturbation which would have this effect. The Haldane model introduces a complex second-nearest neighbour hopping which has opposite sign on the two sublattice sites. I'll define again a function to introduce this perturbation:
```
def haldane_mass(TB,mass):
Hnew = []
vectors = [TB.avec[0],TB.avec[1],TB.avec[1]-TB.avec[0]]
for ii in range(2):
for jj in range(3):
Hnew.append([ii,ii,*vectors[jj],-(2*ii-1)*0.5j*mass])
Hnew.append([ii,ii,*(-vectors[jj]),(2*ii-1)*0.5j*mass])
TB.append_H(Hnew)
```
This function generates the simplest form of Haldane mass, with fixed phase. You can try modifying the above function to allow for arbitrary phase.
I'm going to define a separate tight-binding model for this perturbation, identical to the unperturbed p$_z$-only basis I used above. I'll then add a Haldane mass term which will result in roughly the same energy splitting as for the Semenoff mass.
```
TB_haldane = build_lib.gen_TB(basis,hamiltonian_args,kpath)
haldane_mass(TB_haldane,0.3)
TB_haldane.solve_H()
TB_haldane.plotting()
```
Evidently, we have effectively the same dispersion as before--breaking time-reversal symmetry now has the effect of gapping out the Dirac cone just as inversion symmetry breaking did.
Finally, I can of course also choose to add both a Haldane and a Semenoff mass. For a critically large Haldane mass, I enter a topologically non-trivial phase. In this case, it is useful to consider both inequivalent Dirac points in the unit cell. So I use a modified k-path here:
```
momentum_args= {'type':'F',
'avec':avec,
'grain':500,
'pts':[-1.5*K,-K,G,K,1.5*K],
'labels':["1.5K'","K'",'$\\Gamma$','K','1.5K']}
kpath_halsem = build_lib.gen_K(momentum_args)
TB_halsem = build_lib.gen_TB(basis,hamiltonian_args,kpath_halsem)
haldane_mass(TB_halsem,0.25/np.sqrt(3))
semenoff_mass(TB_halsem,0.25)
TB_halsem.solve_H()
TB_halsem.plotting(-1,0.5)
```
There we go, I've now broken both time-reversal and inversion symmetry, modifying the dispersion in a non-trivial way. While the $K$ and $K'$ points will be energetically inequivalent for arbitrary choices of $m_S$ and $m_H$, at $m_H$=$m_S/\sqrt{3}$ (as written in our formalism), the gap at $K$ closes. This can be contrast with the choice of Semenoff, and Haldane only, along this same path through both inequivalent k-points of the Brillouin zone.
```
TB_semenoff.Kobj = kpath_halsem
TB_haldane.Kobj = kpath_halsem
TB_semenoff.solve_H()
TB_haldane.solve_H()
TB_semenoff.plotting(-1,0.5)
TB_haldane.plotting(-1,0.5)
```
It is clear from this that the presence of either time-reversal or inversion symmetry preserve the energy-equivalence of the dispersion at $K$ and $K'$, and only by breaking both symmetries can we change this. Finally, we can compute the ARPES intensity for the system with critical Haldane and Semenoff masses at the $K$ and $K'$ points.
```
arpes_args['cube']['X'] =[-Kpt[0]-klimits,-Kpt[0]+klimits,500]
arpes_args['cube']['Y'] =[0,0,1]
arpes_args['cube']['E'] = [-1.5,0.25,1000]
experiment_halsem = arpes_lib.experiment(TB_halsem,arpes_args)
experiment_halsem.datacube()
_ = experiment_halsem.spectral(slice_select=('y',0),plot_bands=True)
arpes_args['cube']['X'] =[Kpt[0]-klimits,Kpt[0]+klimits,500]
experiment_halsem = arpes_lib.experiment(TB_halsem,arpes_args)
experiment_halsem.datacube()
_ = experiment_halsem.spectral(slice_select=('y',0),plot_bands=True)
```
| true |
code
| 0.346721 | null | null | null | null |
|
<img src="../../images/brownbear.png" width="400">
## A financial tool that can analyze and maximize investment portfolios on a risk adjusted basis
Description: This notebook is useful for examining potfolios comprised of stocks from the Dow Jones Industrial Average. Construct portfolios from the 30 stocks in the DJIA and examine the results of different weighting schemes.
```
%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;
}
# imports
import pandas as pd
import matplotlib.pyplot as plt
import brownbear as bb
# format price data
pd.options.display.float_format = '{:0.2f}'.format
# display all rows
pd.set_option('display.max_rows', None)
# do not truncate column names
pd.set_option('display.max_colwidth', None)
%matplotlib inline
# set size of inline plots
'''note: rcParams can't be in same cell as import matplotlib
or %matplotlib inline
%matplotlib notebook: will lead to interactive plots embedded within
the notebook, you can zoom and resize the figure
%matplotlib inline: only draw static images in the notebook
'''
plt.rcParams["figure.figsize"] = (10, 7)
```
### Some Globals
```
investment_universe = ['dow30-galaxy']
risk_free_rate = 0
annual_returns = '3 Yr'
vola = 'Vola'
ds_vola = 'DS Vola'
# Fetch Investment Options - all values annualized
df = bb.fetch(investment_universe, risk_free_rate, annual_returns, vola, ds_vola)
df
# add fundamental columns
df = bb.add_fundamental_columns(df)
df
# rank
rank = bb.rank(df, rank_by='Dividend Yield')
rank_filtered = rank
#rank_filtered = rank.loc[(rank['3 mo'] > 0) & rank['1 Yr'] > 0]
rank_filtered
```
### Sample Portfolios
Format 'Investment option': weight
```
# everything ranked
ranked_portfolio = {
'Title': 'Ranked Portfolio'
}
everything = list(rank_filtered['Investment Option'])[:20]
ranked_portfolio.update(dict.fromkeys(everything, 1/len(everything)))
# top 10
top10_portfolio = {
'Title': 'Top10 Portfolio'
}
top10 = list(rank['Investment Option'])[:10]
top10_portfolio.update(dict.fromkeys(top10, 1/len(top10)))
```
### Custom Portfolios
```
# My portfolio
my_portfolio = {
'Title': 'My Portfolio',
}
```
### Choose Portfolio Option
```
# Select one of the portfolios from above
portfolio_option = ranked_portfolio
# Make a copy so that the original portfolio is preserved
portfolio_option = portfolio_option.copy()
```
### Analysis Options
```
# Specify the weighting scheme. It will replace the weights specified in the portfolio
# You can also fix the weights on some Investent Options, Asset Classes, and Asset Subclasses
# while the others are automatically calculated.
# 'Equal' - will use equal weights.
# 'Sharpe Ratio' - will use proportionally weighted # allocations based on the percent
# of an investment option's sharpe ratio to the sum of all the sharpe ratios in the portfolio.
# 'Std Dev' - will use standard deviation adjusted weights
# 'Annual Returns' - will use return adjusted weights
# 'Vola' - will use volatility adjusted weights
# 'DS Vola' - will use downside volatility adjusted weights
# None: 'Investment Option' means use user specified weights
# 'Asset Class' means do not group by Asset Class
# 'Asset Subclass means do not group by Asset Subclass
weight_by = {
'Asset Class': {'weight_by': None},
'Asset Subclass': {'weight_by': 'Annual Returns'},
'Investment Option': {'weight_by': 'Equal'},
}
#weight_by = None
bb.DEBUG = False
# Analyze portfolio
annual_ret, std_dev, sharpe_ratio = \
bb.analyze(df, portfolio_option, weight_by)
# Display Results
summary = bb.summary(df, portfolio_option, annual_ret, std_dev, sharpe_ratio)
summary
# Show pie charts of investment and asset class weights
bb.show_pie_charts(df, portfolio_option, charts=['Investment Option', 'Asset Subclass'])
# Show exact weights
bb.print_portfolio(portfolio_option)
```
### Optimize Portfolio
```
# Run_portfolio_optimizer = True will run portfolio optimizer after portfolio analysis is complete
run_portfolio_optimizer = True
# Optimize sharpe ratio while specifying Annual Rate, Worst Typical Down Year,
# and Black Swan. Setting a constraint to None optimizes absolute Sharpe Ratio
# without regard to that constraint.
'''
constraints = {
'Annual Return': 12,
'Worst Typical Down Year': -5,
'Black Swan': None
}
'''
constraints = {
'Annual Return': 8,
'Worst Typical Down Year': None,
'Black Swan': -40
}
if run_portfolio_optimizer:
bb.optimizer(df, portfolio_option, constraints)
```
### Use Sharpe Ratio adjusted weights
Recommend that you also try using Sharpe Ratio adjusted weights and compare those results with the Optimized Portflio.
It tends to produce a higher Annual Return while keeping the allocations more balanced than the Optimizer. (See 'Analysis Options' section).
| true |
code
| 0.69125 | null | null | null | null |
|
```
import numpy as np
from scipy.io import loadmat
from sklearn.linear_model import LogisticRegression as LR
import matplotlib.pyplot as plt
%matplotlib inline
# Theano imports
import theano
theano.config.floatX = 'float32'
import theano.tensor as T
# Plotting utility
from utils import tile_raster_images as tri
```
# The dataset
The dataset is the mnist digits which is a common toy data set for testing machine learning methods on images. This is a subset of the mnist set which have also been shrunked in size. Let's load them and plot some. In addition to the images, there are also the labels: 0-9 or even-odd.
Load the data.
```
data = loadmat('small_mnist.mat')
# Training data (images, 0-9, even-odd)
# Images are stored in a (batch, x, y) array
# Labels are integers
train_im = data['train_im']
train_y = data['train_y'].ravel()
train_eo = data['train_eo'].ravel()
# Validation data (images, 0-9, even-odd)
# Same format as training data
valid_im = data['valid_im']
valid_y = data['valid_y'].ravel()
valid_eo = data['valid_eo'].ravel()
```
Plot 10 of the training images. Rerun this cell to plot new images.
```
im_size = train_im.shape[-1]
order = np.random.permutation(train_im.shape[0])
ims = tri(train_im[order[:10]].reshape((-1, im_size**2)), (im_size, im_size), (1, 10), (1,1))
plt.imshow(ims, cmap='gray', interpolation='nearest')
plt.axis('off')
print('Labels: {}'.format(train_y[order[:10]]))
print('Odd-Even: {}'.format(train_eo[order[:10]]))
```
## Baseline linear classifier
Before we spend our precious time setting up and training deep networks on the data, let's see how a simple linear classifier from sklearn can do.
```
# Create the classifier to do multinomial classification
linear_classifier = LR(solver='lbfgs', multi_class='multinomial', C=0.1)
# Train and evaluate the classifier
linear_classifier.fit(train_im.reshape(-1, im_size**2), train_y)
print('Training Error on (0-9): {}'.format(linear_classifier.score(train_im.reshape(-1, im_size**2), train_y)))
print('Validation Error on (0-9): {}'.format(linear_classifier.score(valid_im.reshape(-1, im_size**2), valid_y)))
```
Try training a linear classifier on the Even-Odd labels: train_eo!
# Using a Deep Nets library
If you're just starting off with deep nets and want to quickly try them on a dataset it is probably easiest to start with an existing library rather than writing your own. There are now a bunch of different libraries written for Python. We'll be using Keras which is designed to be easy to use. In matlab, there is the Neural Network Toolbox.
Keras documentation can be found here:
http://keras.io/
We'll do the next most complicated network comparer to linear regression: a two layer network!
```
# Import things from Keras Library
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers.convolutional import Convolution2D
from keras.regularizers import l2
from keras.optimizers import SGD, Adam, RMSprop
from keras.utils import np_utils
```
## Fully connected MLP
This is a simple network made from two layers. On the Keras documentation page, you can find other nonlinearities under "Core Layers".
You can add more layers, changes the layers, change the optimizer, or add dropout.
```
# Create the network!
mlp = Sequential()
# First fully connected layer
mlp.add(Dense(im_size**2/2, input_shape=(im_size**2,), W_regularizer=l2(0.001))) # number of hidden units, default is 100
mlp.add(Activation('tanh')) # nonlinearity
print('Shape after layer 1: {}'.format(mlp.output_shape))
# Second fully connected layer with softmax output
mlp.add(Dropout(0.0)) # dropout is currently turned off, you may need to train for more epochs if nonzero
mlp.add(Dense(10)) # number of targets, 10 for y, 2 for eo
mlp.add(Activation('softmax'))
# Adam is a simple optimizer, SGD has more parameters and is slower but may give better results
opt = Adam()
#opt = RMSprop()
#opt = SGD(lr=0.1, momentum=0.9, decay=0.0001, nesterov=True)
print('')
mlp.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
mlp.fit(train_im.reshape(-1, im_size**2), np_utils.to_categorical(train_y), nb_epoch=20, batch_size=100)
tr_score = mlp.evaluate(train_im.reshape(-1, im_size**2), np_utils.to_categorical(train_y), batch_size=100)
va_score = mlp.evaluate(valid_im.reshape(-1, im_size**2), np_utils.to_categorical(valid_y), batch_size=100)
print('')
print('Train loss: {}, train accuracy: {}'.format(*tr_score))
print('Validation loss: {}, validation accuracy: {}'.format(*va_score))
```
## Convolutional MLP
We can also have the first layer be a set of small filters which are convolved with the images.
Try different parameters and see what happens. (This network might be slow.)
```
# Create the network!
cnn = Sequential()
# First fully connected layer
cnn.add(Convolution2D(20, 5, 5, input_shape=(1, im_size, im_size), border_mode='valid', subsample=(2, 2)))
cnn.add(Activation('tanh')) # nonlinearity
print('Shape after layer 1: {}'.format(cnn.output_shape))
# Take outputs and turn them into a vector
cnn.add(Flatten())
print('Shape after flatten: {}'.format(cnn.output_shape))
# Fully connected layer
cnn.add(Dropout(0.0)) # dropout is currently turned off, you may need to train for more epochs if nonzero
cnn.add(Dense(100)) # number of targets, 10 for y, 2 for eo
cnn.add(Activation('tanh'))
# Second fully connected layer with softmax output
cnn.add(Dropout(0.0)) # dropout is currently turned off, you may need to train for more epochs if nonzero
cnn.add(Dense(10)) # number of targets, 10 for y, 2 for eo
cnn.add(Activation('softmax'))
# Adam is a simple optimizer, SGD has more parameters and is slower but may give better results
#opt = Adam()
#opt = RMSprop()
opt = SGD(lr=0.1, momentum=0.9, decay=0.0001, nesterov=True)
print('')
cnn.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
cnn.fit(train_im[:, np.newaxis, ...], np_utils.to_categorical(train_y), nb_epoch=20, batch_size=100)
tr_score = cnn.evaluate(train_im[:, np.newaxis, ...], np_utils.to_categorical(train_y), batch_size=100)
va_score = cnn.evaluate(valid_im[:, np.newaxis, ...], np_utils.to_categorical(valid_y), batch_size=100)
print('')
print('Train loss: {}, train accuracy: {}'.format(*tr_score))
print('Validation loss: {}, validation accuracy: {}'.format(*va_score))
```
# Visualizing the filters
## Linear classifier
```
W = linear_classifier.coef_
ims = tri(W, (im_size, im_size), (1, 10), (1,1))
plt.imshow(ims, cmap='gray', interpolation='nearest')
plt.axis('off')
```
## MLP
```
W = mlp.get_weights()[0].T
ims = tri(W, (im_size, im_size), (W.shape[0]//10, 10), (1,1))
plt.imshow(ims, cmap='gray', interpolation='nearest')
plt.axis('off')
```
## CNN
```
W = cnn.get_weights()[0]
ims = tri(W.reshape(-1, np.prod(W.shape[2:])), (W.shape[2], W.shape[3]), (W.shape[0]//10, 10), (1,1))
plt.imshow(ims, cmap='gray', interpolation='nearest')
plt.axis('off')
```
| true |
code
| 0.748496 | null | null | null | null |
|
# Using DALI in PyTorch
### Overview
This example shows how to use DALI in PyTorch.
This example uses CaffeReader.
See other [examples](../../index.rst) for details on how to use different data formats.
Let us start from defining some global constants
`DALI_EXTRA_PATH` environment variable should point to the place where data from [DALI extra repository](https://github.com/NVIDIA/DALI_extra) is downloaded. Please make sure that the proper release tag is checked out.
```
import os.path
test_data_root = os.environ['DALI_EXTRA_PATH']
# Caffe LMDB
lmdb_folder = os.path.join(test_data_root, 'db', 'lmdb')
N = 8 # number of GPUs
BATCH_SIZE = 128 # batch size per GPU
ITERATIONS = 32
IMAGE_SIZE = 3
```
Let us define a pipeline with a reader:
```
from nvidia.dali.pipeline import Pipeline
import nvidia.dali.ops as ops
import nvidia.dali.types as types
class CaffeReadPipeline(Pipeline):
def __init__(self, batch_size, num_threads, device_id, num_gpus):
super(CaffeReadPipeline, self).__init__(batch_size, num_threads, device_id)
self.input = ops.CaffeReader(path = lmdb_folder,
random_shuffle = True, shard_id = device_id, num_shards = num_gpus)
self.decode = ops.ImageDecoder(device = "mixed", output_type = types.RGB)
self.resize = ops.Resize(device = "gpu",
image_type = types.RGB,
interp_type = types.INTERP_LINEAR)
self.cmn = ops.CropMirrorNormalize(device = "gpu",
output_dtype = types.FLOAT,
crop = (227, 227),
image_type = types.RGB,
mean = [128., 128., 128.],
std = [1., 1., 1.])
self.uniform = ops.Uniform(range = (0.0, 1.0))
self.resize_rng = ops.Uniform(range = (256, 480))
def define_graph(self):
inputs, labels = self.input(name="Reader")
images = self.decode(inputs)
images = self.resize(images, resize_shorter = self.resize_rng())
output = self.cmn(images, crop_pos_x = self.uniform(),
crop_pos_y = self.uniform())
return (output, labels)
```
Let us create the pipeline and pass it to PyTorch generic iterator
```
from __future__ import print_function
import numpy as np
from nvidia.dali.plugin.pytorch import DALIGenericIterator
label_range = (0, 999)
pipes = [CaffeReadPipeline(batch_size=BATCH_SIZE, num_threads=2, device_id = device_id, num_gpus = N) for device_id in range(N)]
pipes[0].build()
dali_iter = DALIGenericIterator(pipes, ['data', 'label'], pipes[0].epoch_size("Reader"))
for i, data in enumerate(dali_iter):
if i >= ITERATIONS:
break
# Testing correctness of labels
for d in data:
label = d["label"]
image = d["data"]
## labels need to be integers
assert(np.equal(np.mod(label, 1), 0).all())
## labels need to be in range pipe_name[2]
assert((label >= label_range[0]).all())
assert((label <= label_range[1]).all())
print("OK")
```
| true |
code
| 0.51312 | null | null | null | null |
|
## Applying Neural Networks on Material Science dataset
The given dataset contains certain microstructurual properties like Yield Strength, Oxygen content, percentage of reheated microstructure and fraction of acicular ferrite. Since the number of features is just 4 and the dataset as only 59 datapoints, it is tough to obtain very high accuracy.
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
data = pd.read_csv('/Users/chiragbhattad/Downloads/DDP/Charpy Analysis/dataset.csv')
features = ['YS', 'O2', 'Reheated', 'ac_ferr']
target = ['T27J']
training_data = data[0:40]
test_data = data[40:60]
X_train = training_data[features]
Y_train = training_data[target]
X_test = test_data[features]
Y_test = test_data[target]
fig, ax = plt.subplots(nrows=1, ncols=1)
ax.set_facecolor('#FFEFD5')
plt.plot(range(40), Y_train, label = "Train Data")
plt.title('Training Dataset Temperatures')
plt.ylabel('Temperature')
plt.show()
fig, ax = plt.subplots(nrows=1, ncols=1)
ax.set_facecolor('#FFEFD5')
plt.plot(range(19), Y_test, label = "Test Data")
plt.title('Test Dataset Temperatures')
plt.ylabel('Temperature')
plt.show()
regr = linear_model.LinearRegression()
regr.fit(X_train, Y_train)
pred = regr.predict(X_test)
print('Coefficients: \n', regr.coef_)
print('Mean Squared Error: ', mean_squared_error(Y_test, pred))
print('Variance score:', r2_score(Y_test, pred))
plt.plot(range(19), Y_test, label = "Original Data")
plt.plot(range(19), pred, label = "Predicted Data")
plt.legend(loc='best')
plt.ylabel('Temperature')
plt.show()
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
import tensorflow as tf
scaler = MinMaxScaler()
X_train = scaler.fit_transform(training_data[features].as_matrix())
Y_train = scaler.fit_transform(training_data[target].as_matrix())
X_test = scaler.fit_transform(test_data[features].as_matrix())
Y_test = scaler.fit_transform(test_data[target].as_matrix())
Y_test
def neural_network(X_data, input_dim):
W_1 = tf.Variable(tf.random_uniform([input_dim,10]))
b_1 = tf.Variable(tf.zeros([10]))
layer_1 = tf.add(tf.matmul(X_data, W_1), b_1)
layer_1 = tf.nn.relu(layer_1)
W_2 = tf.Variable(tf.random_uniform([10,10]))
b_2 = tf.Variable(tf.zeros([10]))
layer_2 = tf.add(tf.matmul(layer_1, W_2), b_2)
layer_2 = tf.nn.relu(layer_2)
W_0 = tf.Variable(tf.random_uniform([10,1]))
b_0 = tf.Variable(tf.zeros([1]))
output = tf.add(tf.matmul(layer_2, W_0), b_0)
return output
xs = tf.placeholder("float")
ys = tf.placeholder("float")
output = neural_network(xs, 4)
cost = tf.reduce_mean(tf.square(output-ys))
train = tf.train.GradientDescentOptimizer(0.001).minimize(cost)
c_t = []
c_test = []
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
for i in range(100):
for j in range(X_train.shape[0]):
sess.run([cost,train], feed_dict = {xs:X_train[j,:].reshape(1,4), ys:Y_train[j]})
c_t.append(sess.run(cost, feed_dict={xs:X_train, ys: Y_train}))
c_test.append(sess.run(cost, feed_dict={xs: X_test, ys: Y_test}))
print('Epoch: ', i, 'Cost: ', c_t[i])
pred = sess.run(output, feed_dict = {xs:X_test})
print('Cost: ', sess.run(cost, feed_dict={xs: X_test, ys: pred}))
print(Y_test)
Y_test = Y_test.reshape(-1,1)
Y_test = scaler.inverse_transform(Y_test)
pred = pred.reshape(-1,1)
pred = scaler.inverse_transform(pred)
Y_test
fig, ax = plt.subplots(nrows=1, ncols=1)
ax.set_facecolor('#FFEFD5')
plt.plot(range(19), Y_test, label = "Original Data")
plt.plot(range(19), pred, label = "Predicted Data")
plt.title('Comparing original values with the model')
plt.legend(loc='best')
plt.ylabel('Temperature')
plt.show()
```
| true |
code
| 0.684686 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/NidhiChaurasia/LGMVIP-DataScience/blob/main/Stock_Prediction_Using_Linear_Regression_and_DecisionTree_Regression_Model.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Decision Tree is used in practical approaches of supervised learning.It can be used to solve both Regression and Classification tasks.It is a tree-structured classifier with three types of nodes.Decision tree builds regression or classification models in the form of a tree structure. It breaks down a dataset into smaller and smaller subsets while at the same time an associated decision tree is incrementally developed.Decision trees can handle both categorical and numerical data.
```
#Install the dependencies
import numpy as num
import pandas as pan
from sklearn.tree import DecisionTreeRegressor #Decision Trees in Machine Learning to Predict Stock Movements.A decision tree algorithm performs a set of recursive actions before it arrives at the end result and when you plot these actions on a screen, the visual looks like a big tree, hence the name 'Decision Tree'.
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as mat
plt.style.use('bmh')
#Load the data
from google.colab import files
uploaded = files.upload()
```
# The dataset comprises of Open, High, Low, Close Prices and Volume indicators (OHLCV).
```
#Store the data into a data frame
dataframe = pan.read_csv('NSE-TATAGLOBAL.csv')
dataframe.head(5)
#Get the number of trading days
dataframe.shape
#Visualize the close price data
mat.figure(figsize=(16,8))
mat.title('TATAGLOBAL')
mat.xlabel('Days')
mat.ylabel('Close Price USD ($)')
mat.plot(df['Close'])
mat.show()
#Get the close Price
dataframe = dataframe[['Close']]
dataframe.head(4)
#Create a variable to predict 'x' days out into the future
future_days = 25
#Create a new column (target) shifted 'x' units/days up
dataframe['Prediction'] = dataframe[['Close']].shift(-future_days)
dataframe.tail(4)
#Create the feature data set (X) and convert it to a numpy array and remove the last 'x' rows/days
X = num.array(dataframe.drop(['Prediction'],1))[:-future_days]
print(X)
#Create the target data set (y) and convert it to a numpy array and get all of the target values except the last 'x' rows/days
y = num.array(dataframe['Prediction'])[:-future_days]
print(y)
#Split the data into 75% training and 25% testing
x_train,x_test,y_train,y_test = train_test_split(X , y ,test_size = 0.25)
#Create the models
#Create the decision tree regressor model
tree = DecisionTreeRegressor().fit(x_train , y_train)
#Create the linear regression model
lr = LinearRegression().fit(x_train , y_train)
#Get the last 'x' rows of the feature data set
x_future = dataframe.drop(['Prediction'], 1)[:-future_days]
x_future = x_future.tail(future_days)
x_future = num.array(x_future)
x_future
#Show the model tree prediction
tree_prediction = tree.predict(x_future)
print(tree_prediction)
print()
#Show the model linear regression prediction
lr_prediction = lr.predict(x_future)
print(lr_prediction)
```
##Let's Visualize the data
```
predictions = tree_prediction #The regression decision trees take ordered values with continuous values.
valid = dataframe[X.shape[0]:]
valid['Predictions'] = predictions
mat.figure(figsize=(16,8))
mat.title('Stock Market Prediction Decision Tree Regression Model using sklearn')
mat.xlabel('Days')
mat.ylabel('Close Price USD ($)')
mat.plot(dataframe['Close'])
mat.plot(valid[['Close','Predictions']])
mat.legend(['Orig','Val','Pred'])
mat.show()
predictions = lr_prediction #Linear Model for Stock Price Prediction
valid = dataframe[X.shape[0]:]
valid['Predictions'] = predictions
mat.figure(figsize=(16,8))
mat.title('Stock Market Prediction Linear Regression Model')
mat.xlabel('Days')
mat.ylabel('Close Price USD ($)')
mat.plot(df['Close'])
mat.plot(valid[['Close','Predictions']])
mat.legend(['Orig','Val','Pred'])
mat.show()
```
| true |
code
| 0.636127 | null | null | null | null |
|
### Generative Adversarial Networks
Jay Urbain, Phd
Credits:
- https://github.com/eriklindernoren/Keras-GAN
- The network architecture has been found by, and optimized by, many contributors, including the authors of the DCGAN paper and people like Erik Linder-Norén, who’s excellent collection of GAN implementations called Keras GAN served as the basis of the code used here.
```
from keras.datasets import cifar10
from keras.layers import Input, Dense, Reshape, Flatten, Dropout
from keras.layers import BatchNormalization, Activation, ZeroPadding2D
from keras.layers.advanced_activations import LeakyReLU
from keras.layers.convolutional import UpSampling2D, Conv2D
from keras.models import Model
from keras.optimizers import Adam
import matplotlib
#matplotlib.use('Agg')
import matplotlib.pyplot as plt
import numpy as np
```
Run the following in the cell below:
from google.colab import drive
drive.mount('/content/gdrive')
```
from google.colab import drive
drive.mount('/content/gdrive')
#!mkdir '/content/gdrive/My Drive/Colab Notebooks/dcgan_cifar_images'
dcgan_cifar_images = '/content/gdrive/My Drive/Colab Notebooks/dcgan_cifar_images'
```
#### The CIFAR-10 dataset
The CIFAR-10 dataset consists of 60000 32x32 colour images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 test images.
The dataset is divided into five training batches and one test batch, each with 10000 images. The test batch contains exactly 1000 randomly-selected images from each class. The training batches contain the remaining images in random order, but some training batches may contain more images from one class than another. Between them, the training batches contain exactly 5000 images from each class.
Here are the classes in the dataset, as well as 10 random images from each:
airplane
automobile
bird
cat
deer
dog
frog
horse
ship
truck
```
from keras.datasets.cifar10 import load_data
# load the data - it returns 2 tuples of digits & labels - one for
# the train set & the other for the test set
(train_digits, train_labels), (test_digits, test_labels) = cifar10.load_data()
# display 14 random images from the training set
import numpy as np
np.random.seed(123)
rand_14 = np.random.randint(0, train_digits.shape[0],14)
sample_digits = train_digits[rand_14]
sample_labels = train_labels[rand_14]
# code to view the images
num_rows, num_cols = 2, 7
f, ax = plt.subplots(num_rows, num_cols, figsize=(12,5),
gridspec_kw={'wspace':0.03, 'hspace':0.01},
squeeze=True)
for r in range(num_rows):
for c in range(num_cols):
image_index = r * 7 + c
ax[r,c].axis("off")
ax[r,c].imshow(sample_digits[image_index], cmap='gray')
ax[r,c].set_title('No. %d' % sample_labels[image_index])
plt.show()
plt.close()
def load_data():
(X_train, _), (_, _) = cifar10.load_data()
#(X_train, y_train), (X_test, y_test) = cifar10.load_data()
X_train = (X_train.astype(np.float32) - 127.5) / 127.5
return X_train
X_train = load_data()
num_examples = np.shape(X_train)
print('Number of examples: ', num_examples)
def build_generator(noise_shape=(100,)):
input = Input(noise_shape)
x = Dense(128 * 8 * 8, activation="relu")(input)
x = Reshape((8, 8, 128))(x)
x = BatchNormalization(momentum=0.8)(x)
x = UpSampling2D()(x)
x = Conv2D(128, kernel_size=3, padding="same")(x)
x = Activation("relu")(x)
x = BatchNormalization(momentum=0.8)(x)
x = UpSampling2D()(x)
x = Conv2D(64, kernel_size=3, padding="same")(x)
x = Activation("relu")(x)
x = BatchNormalization(momentum=0.8)(x)
x = Conv2D(3, kernel_size=3, padding="same")(x)
out = Activation("tanh")(x)
model = Model(input, out)
print("-- Generator -- ")
model.summary()
return model
def build_discriminator(img_shape):
input = Input(img_shape)
x =Conv2D(32, kernel_size=3, strides=2, padding="same")(input)
x = LeakyReLU(alpha=0.2)(x)
x = Dropout(0.25)(x)
x = Conv2D(64, kernel_size=3, strides=2, padding="same")(x)
x = (LeakyReLU(alpha=0.2))(x)
x = Dropout(0.25)(x)
x = BatchNormalization(momentum=0.8)(x)
x = Conv2D(128, kernel_size=3, strides=2, padding="same")(x)
x = LeakyReLU(alpha=0.2)(x)
x = Dropout(0.25)(x)
x = BatchNormalization(momentum=0.8)(x)
x = Conv2D(256, kernel_size=3, strides=1, padding="same")(x)
x = LeakyReLU(alpha=0.2)(x)
x = Dropout(0.25)(x)
x = Flatten()(x)
out = Dense(1, activation='sigmoid')(x)
model = Model(input, out)
print("-- Discriminator -- ")
model.summary()
return model
def train(generator, discriminator, combined, epochs=2000, batch_size=128, save_interval=50):
X_train = load_data()
num_examples = X_train.shape[0]
num_batches = int(num_examples / float(batch_size))
print('Number of examples: ', num_examples)
print('Number of Batches: ', num_batches)
print('Number of epochs: ', epochs)
half_batch = int(batch_size / 2)
for epoch in range(epochs + 1):
print("Epoch: " + str(epoch))
for batch in range(num_batches):
print("Batch: " + str(batch) + "/" + str(num_batches))
# noise images for the batch
noise = np.random.normal(0, 1, (half_batch, 100))
fake_images = generator.predict(noise)
fake_labels = np.zeros((half_batch, 1))
# real images for batch
idx = np.random.randint(0, X_train.shape[0], half_batch)
real_images = X_train[idx]
real_labels = np.ones((half_batch, 1))
# Train the discriminator (real classified as ones and generated as zeros)
d_loss_real = discriminator.train_on_batch(real_images, real_labels)
d_loss_fake = discriminator.train_on_batch(fake_images, fake_labels)
d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)
noise = np.random.normal(0, 1, (batch_size, 100))
# Train the generator
g_loss = combined.train_on_batch(noise, np.ones((batch_size, 1)))
# Plot the progress
print("Epoch %d Batch %d/%d [D loss: %f, acc.: %.2f%%] [G loss: %f]" %
(epoch, batch, num_batches, d_loss[0], 100 * d_loss[1], g_loss))
if batch % 50 == 0:
save_imgs(generator, epoch, batch)
def save_imgs(generator, epoch, batch):
r, c = 5, 5
noise = np.random.normal(0, 1, (r * c, 100))
gen_imgs = generator.predict(noise)
# Rescale images 0 - 1
gen_imgs = 0.5 * gen_imgs + 0.5
fig, axs = plt.subplots(r, c)
cnt = 0
for i in range(r):
for j in range(c):
axs[i, j].imshow(gen_imgs[cnt, :, :, :])
axs[i, j].axis('off')
cnt += 1
fig.savefig(dcgan_cifar_images + "/mnist_%d_%d.png" % (epoch, batch))
plt.close()
def build_models():
gen_optimizer = Adam(lr=0.0002, beta_1=0.5)
disc_optimizer = Adam(lr=0.0002, beta_1=0.5)
discriminator = build_discriminator(img_shape=(32, 32, 3))
discriminator.compile(loss='binary_crossentropy',
optimizer=disc_optimizer,
metrics=['accuracy'])
generator = build_generator()
generator.compile(loss='binary_crossentropy', optimizer=gen_optimizer)
z = Input(shape=(100,))
img = generator(z)
discriminator.trainable = False
real = discriminator(img)
combined = Model(z, real)
combined.compile(loss='binary_crossentropy', optimizer=gen_optimizer)
return generator, discriminator, combined
def main():
generator, discriminator, combined = build_models()
train(generator, discriminator, combined,
epochs=100, batch_size=32, save_interval=1)
main()
```
| true |
code
| 0.856512 | null | null | null | null |
|
Earlier we trained a model to predict the ratings users would give to movies using a network with embeddings learned for each movie and user. Embeddings are powerful! But how do they actually work?
Previously, I claimed that embeddings capture the 'meaning' of the objects they represent, and discover useful latent structure. Let's put that to the test!
# Looking up embeddings
Let's load a model we trained earlier so we can investigate the embedding weights that it learned.
```
import os
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import tensorflow as tf
from tensorflow import keras
#_RM_
input_dir = '../input/movielens_preprocessed'
#_UNCOMMENT_
#input_dir = '../input/movielens-preprocessing'
#_RM_
model_dir = '.'
#_UNCOMMENT_
#model_dir = '../input/movielens-spiffy-model'
model_path = os.path.join(model_dir, 'movie_svd_model_32.h5')
model = keras.models.load_model(model_path)
```
The embedding weights are part of the model's internals, so we'll have to do a bit of digging around to access them. We'll grab the layer responsible for embedding movies, and use the `get_weights()` method to get its learned weights.
```
emb_layer = model.get_layer('movie_embedding')
(w,) = emb_layer.get_weights()
w.shape
```
Our weight matrix has 26,744 rows for that many movies. Each row is 32 numbers - the size of our movie embeddings.
Let's look at an example movie vector:
```
w[0]
```
What movie is this the embedding of? Let's load up our dataframe of movie metadata.
```
movies_path = os.path.join(input_dir, 'movie.csv')
movies_df = pd.read_csv(movies_path, index_col=0)
movies_df.head()
```
Of course, it's *Toy Story*! I should have recognized that vector anywhere.
Okay, I'm being facetious. It's hard to make anything of these vectors at this point. We never directed the model about how to use any particular embedding dimension. We left it alone to learn whatever representation it found useful.
So how do we check whether these representations are sane and coherent?
## Vector similarity
A simple way to test this is to look at how close or distant pairs of movies are in the embedding space. Embeddings can be thought of as a smart distance metric. If our embedding matrix is any good, it should map similar movies (like *Toy Story* and *Shrek*) to similar vectors.
```
i_toy_story = 0
i_shrek = movies_df.loc[
movies_df.title == 'Shrek',
'movieId'
].iloc[0]
toy_story_vec = w[i_toy_story]
shrek_vec = w[i_shrek]
print(
toy_story_vec,
shrek_vec,
sep='\n',
)
```
Comparing dimension-by-dimension, these look vaguely similar. If we wanted to assign a single number to their similarity, we could calculate the euclidean distance between these two vectors. (This is our conventional 'as the crow flies' notion of distance between two points. Easy to grok in 1, 2, or 3 dimensions. Mathematically, we can also extend it to 32 dimensions, though good luck visualizing it.)
```
from scipy.spatial import distance
distance.euclidean(toy_story_vec, shrek_vec)
```
How does this compare to a pair of movies that we would think of as very different?
```
i_exorcist = movies_df.loc[
movies_df.title == 'The Exorcist',
'movieId'
].iloc[0]
exorcist_vec = w[i_exorcist]
distance.euclidean(toy_story_vec, exorcist_vec)
```
As expected, much further apart.
## Cosine Distance
If you check out [the docs for the `scipy.spatial` module](https://docs.scipy.org/doc/scipy-0.14.0/reference/spatial.distance.html), you'll see there are actually a *lot* of different measures of distance that people use for different tasks.
When judging the similarity of embeddings, it's more common to use [cosine similarity](https://en.wikipedia.org/wiki/Cosine_similarity).
In brief, the cosine similarity of two vectors ranges from -1 to 1, and is a function of the *angle* between the vectors. If two vectors point in the same direction, their cosine similarity is 1. If they point in opposite directions, it's -1. If they're orthogonal (i.e. at right angles), their cosine similarity is 0.
Cosine distance is just defined as 1 minus the cosine similarity (and therefore ranges from 0 to 2).
Let's calculate a couple cosine distances between movie vectors:
```
print(
distance.cosine(toy_story_vec, shrek_vec),
distance.cosine(toy_story_vec, exorcist_vec),
sep='\n'
)
```
> **Aside:** *Why* is cosine distance commonly used when working with embeddings? The short answer, as with so many deep learning techniques, is "empirically, it works well". In the exercise coming up, you'll get to do a little hands-on investigation that digs into this question more deeply.
Which movies are most similar to *Toy Story*? Which movies fall right between *Psycho* and *Scream* in the embedding space? We could write a bunch of code to work out questions like this, but it'd be pretty tedious. Fortunately, there's already a library for exactly this sort of work: **Gensim**.
# Exploring embeddings with Gensim
I'll instantiate an instance of [`WordEmbeddingsKeyedVectors`](https://radimrehurek.com/gensim/models/keyedvectors.html#gensim.models.keyedvectors.WordEmbeddingsKeyedVectors) with our model's movie embeddings and the titles of the corresponding movies.
> Aside: You may notice that Gensim's docs and many of its class and method names refer to *word* embeddings. While the library is most frequently used in the text domain, we can use it to explore embeddings of any sort.
```
from gensim.models.keyedvectors import WordEmbeddingsKeyedVectors
# Limit to movies with at least this many ratings in the dataset
threshold = 100
mainstream_movies = movies_df[movies_df.n_ratings >= threshold].reset_index(drop=True)
movie_embedding_size = w.shape[1]
kv = WordEmbeddingsKeyedVectors(movie_embedding_size)
kv.add(
mainstream_movies['key'].values,
w[mainstream_movies.movieId]
)
```
Okay, so which movies are most similar to *Toy Story*?
```
kv.most_similar('Toy Story')
```
Wow, these are pretty great! It makes perfect sense that *Toy Story 2* is the most similar movie to *Toy Story*. And most of the rest are animated kids movies with a similar computer-animated style.
So it's learned something about 3-d animated kids flick, but maybe that was just a fluke. Let's look at the closest neighbours for a few more movies from a variety of genres:
```
#$HIDE_INPUT$
import textwrap
movies = ['Eyes Wide Shut', 'American Pie', 'Iron Man 3', 'West Side Story',
'Battleship Potemkin', 'Clueless'
]
def plot_most_similar(movie, ax, topn=5):
sim = kv.most_similar(movie, topn=topn)[::-1]
y = np.arange(len(sim))
w = [t[1] for t in sim]
ax.barh(y, w)
left = min(.6, min(w))
ax.set_xlim(right=1.0, left=left)
# Split long titles over multiple lines
labels = [textwrap.fill(t[0] , width=24)
for t in sim]
ax.set_yticks(y)
ax.set_yticklabels(labels)
ax.set_title(movie)
fig, axes = plt.subplots(3, 2, figsize=(15, 9))
for movie, ax in zip(movies, axes.flatten()):
plot_most_similar(movie, ax)
fig.tight_layout()
```
Artsy erotic dramas, raunchy sophomoric comedies, old-school musicals, superhero movies... our embeddings manage to nail a wide variety of cinematic niches!
# Semantic vector math
The [`most_similar`](https://radimrehurek.com/gensim/models/keyedvectors.html#gensim.models.keyedvectors.WordEmbeddingsKeyedVectors.most_similar) method optionally takes a second argument, `negative`. If we call `kv.most_similar(a, b)`, then instead of finding the vector closest to `a`, it will find the closest vector to `a - b`.
Why would you want to do that? It turns out that doing addition and subtraction of embedding vectors often gives surprisingly meaningful results. For example, how would you fill in the following equation?
Scream = Psycho + ________
*Scream* and *Psycho* are similar in that they're violent, scary movies somewhere on the border between Horror and Thriller. The biggest difference is that *Scream* has elements of comedy. So I'd say *Scream* is what you'd get if you combined *Psycho* with a comedy.
But we can actually ask Gensim to fill in the blank for us via vector math (after some rearranging):
________ = Scream - Psycho
```
kv.most_similar(
positive = ['Scream'],
negative = ['Psycho (1960)']
)
```
If you are familiar with these movies, you'll see that the missing ingredient that takes us from *Psycho* to *Scream* is comedy (and also late-90's-teen-movie-ness).
## Analogy solving
The SAT test which is used to get into American colleges and universities poses analogy questions like:
shower : deluge :: _____ : stare
(Read "shower is to deluge as ___ is to stare")
To solve this, we find the relationship between deluge and shower, and apply it to stare. A shower is a milder form of a deluge. What's a milder form of stare? A good answer here would be "glance", or "look".
It's kind of astounding that this works, but people have found that these can often be effectively solved by simple vector math on word embeddings. Can we solve movie analogies with our embeddings? Let's try. What about:
Brave : Cars 2 :: Pocahontas : _____
The answer is not clear. One interpretation would be that *Brave* is like *Cars 2*, except that the latter is aimed primarily at boys, and the former might be more appealing to girls, given its female protagonist. So maybe the answer should be, like *Pocahontas*, a mid-90's conventional animation kids movie, but more of a 'boy movie'. *Hercules*? *The Lion King*?
Let's ask our embeddings what they think.
In terms of vector math, we can frame this as...
Cars 2 = Brave + X
_____ = Pocahontas + X
Rearranging, we get:
____ = Pocahontas + (Cars 2 - Brave)
We can solve this by passing in two movies (*Pocahontas* and *Cars 2*) for the positive argument to `most_similar`, with *Brave* as the negative argument:
```
kv.most_similar(
['Pocahontas', 'Cars 2'],
negative = ['Brave']
)
```
This weakly fits our prediction: the 4 closest movies are indeed kids animated movies from the 90s. After that, the results are a bit more perplexing.
Is our model wrong, or were we? Another difference we failed to account for between *Cars 2* and *Brave* is that the former is a sequel, and the latter is not. 7/10 of our results are also sequels. This tells us something interesting about our learned embeddings (and, ultimately, about the problem of predicting movie preferences). "Sequelness" is an important property to our model - which suggests that some of the variance in our data is accounted for the fact that some people tend to like sequels more than others.
#$YOURTURN$
| true |
code
| 0.597784 | null | null | null | null |
|
```
# default_exp model_evaluation
```
# Model Evaluation 📈
```
#export
from tensorflow.keras.models import load_model
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import average_precision_score,precision_recall_curve
from funcsigs import signature
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
def show_loss_accurracy_plots(history):
"""Displays loss and accuracy plots for the input model history"""
acc = history['accuracy']
val_acc = history['val_accuracy']
loss = history['loss']
val_loss = history['val_loss']
epochs2 = range(len(acc))
plt.plot(epochs2, acc, 'b', label='Training')
plt.plot(epochs2, val_acc, 'r', label='Validation')
plt.title('Training and validation accuracy')
plt.ylabel('acc')
plt.xlabel('epoch')
plt.legend()
plt.figure()
plt.plot(epochs2, loss, 'b', label='Training')
plt.plot(epochs2, val_loss, 'r', label='Validation')
plt.title('Training and validation loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend()
plt.show()
```
## Loss Accuracy Plots
We want to see if we reach criticality
```
history = pd.read_csv('../08_test/history_training.csv')
show_loss_accurracy_plots(history)
# filepath changed from: 'alex-adapted-res-003/best_model.hdf5' for testing
path = '../08_test/best_model.hdf5'
# You must be using tensorflow 2.3 or greater
criticality_network_load = load_model(path) #<----- The Model
corpora_test_x = np.load('../08_test/corpora_test_x.npy')
target_test_y = np.load('../08_test/target_test_y.npy')
#export
def evaluate_model(criticality_network_load,corpora_test_x,target_test_y):
"""Displays the given model's: loss, accuracy, Average prcision-recall and AUC for the given data."""
score = criticality_network_load.evaluate(corpora_test_x, target_test_y, verbose=1)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
history_predict = criticality_network_load.predict(x=corpora_test_x)
history_predict
inferred_data = pd.DataFrame(history_predict,columns=list('AB'))
target_data = pd.DataFrame(target_test_y,columns=list('LN'))
data = target_data.join(inferred_data)
y_true = list(data['L'])
y_score= list(data['A'])
average_precision = average_precision_score(y_true, y_score)
print('Average precision-recall score: {0:0.2f}'.format(average_precision))
#ROC Curve (all our samples are balanced)
auc = roc_auc_score(y_true, y_score)
print('AUC: %.3f' % auc)
```
## Get Accuracy of Model
```
evaluate_model(criticality_network_load,corpora_test_x,target_test_y)
def clean_list(inp):
out = []
for i in inp:
out.append(i[0])
return out
def clean_input(inp):
return tuple(clean_list(inp.tolist()))
def summarize(inp):
total = 0
for i in inp:
# print(i)
total+=i
new = [total]
return new
```
# Shap Evaluations
```
from securereqnet.utils import Embeddings
import shap
model = criticality_network_load
```
## Get Reverse Embeddings Mapping
```
embeddings = Embeddings()
embed_path = '../data/word_embeddings-embed_size_100-epochs_100.csv'
embeddings_dict = embeddings.get_embeddings_dict(embed_path)
reverse_embeddings = {}
for key, value in embeddings_dict.items():
value = tuple(np.array(value, dtype='float32').tolist())
# print(value)
reverse_embeddings[value] = key
```
## Calculate Shap Values for 200 Images
We need a background of 400 to calculate these 200 points over
```
# select a set of background examples to take an expectation over
background = corpora_test_x[np.random.choice(corpora_test_x.shape[0], 400, replace=False)]
# explain predictions of the model on four images
e = shap.DeepExplainer(model, background)
# ...or pass tensors directly
# e = shap.DeepExplainer((model.layers[0].input, model.layers[-1].output), background)
shap_values = e.shap_values(corpora_test_x[0:200])
```
## Map Shap Values to Tokens
Using our reversed embeddings from earlier, we essentially undo the vectorization so we can map shap values to our tokens. Tokens are much more readable than vectors, and allow for easy human interpretation.
```
# map shap values to strings
# (shap, string)
shaps = []
for doc in range(shap_values[0].shape[0]):
for word in range(shap_values[0][doc].shape[0]):
# grab the word
try:
string = reverse_embeddings[clean_input(corpora_test_x[doc, word])]
shap_value = summarize(clean_list(shap_values[0][doc, word]))[0]
shaps.append((shap_value, string))
except KeyError as e:
pass
shaps = sorted(shaps, key = lambda x: abs(x[0]), reverse=True)
```
## Create Plot
Here we plot the top 25 shap values over the 200 data points and check their effects
```
import matplotlib.pyplot as plt
import math
import statistics
shap_vals = []
token = []
fig1 = plt.gcf()
data = {}
# Top 25 shap vals
uBound = 25
i = 0
while i < uBound:
if(i < len(shaps)):
curTok = shaps[i][1]
curShap = shaps[i][0]
if curTok in data.keys():
data[curTok].append(curShap)
uBound += 1
else:
data[curTok] = [curShap]
i += 1
# get the rest
for i in range(len(shaps)):
curTok = shaps[i][1]
curShap = shaps[i][0]
if curTok in data.keys():
data[curTok].append(curShap)
for key in data.keys():
for item in data[key]:
shap_vals.append(item)
token.append(key)
fig = plt.figure(figsize = (15, 10))
max_shap_val = max(shap_vals)
min_shap_val = min(shap_vals)
total_range = max_shap_val - min_shap_val
std_dev = statistics.stdev(shap_vals)
median = statistics.median(shap_vals)
mean = statistics.mean(shap_vals)
# define our gradient
# we want something less linear
redness = lambda x : math.sqrt(((x+abs(min_shap_val))/total_range) * 100) * 10 / 100
blueness = lambda x : 1 - redness(x)
# size as normal distribution
size = lambda x : 500 * math.ceil(100 * ((1/(std_dev*math.sqrt(math.pi))*math.e)**(-1*((x-mean)**2)/(2*std_dev**2)))) / 100 + 35
plt.xlabel("Shap Value")
plt.ylabel("token")
plt.title("Shap Visualization for 200 Issues")
plt.xlim([-1 * (max_shap_val + std_dev), max_shap_val + std_dev])
plt.gca().invert_yaxis()
# creating the bar plot
plt.scatter(shap_vals, token, c = [(redness(x), 0, blueness(x)) for x in shap_vals], marker='.', s = [size(x) for x in shap_vals])
plt.savefig("../images/shap_200_issues_alpha.png", transparent=False)
plt.show()
```
| true |
code
| 0.621282 | null | null | null | null |
|
<!--COURSE_INFORMATION-->
<img align="left" style="padding-right:10px;" src="https://user-images.githubusercontent.com/16768318/73986808-75b3ca00-4936-11ea-90f1-3a6c352766ce.png" width=10% >
<img align="right" style="padding-left:10px;" src="https://user-images.githubusercontent.com/16768318/73986811-764c6080-4936-11ea-9653-a3eacc47caed.png" width=10% >
**Bienvenidos!** Este *colab notebook* es parte del curso [**Introduccion a Google Earth Engine con Python**](https://github.com/csaybar/EarthEngineMasterGIS) desarrollado por el equipo [**MasterGIS**](https://www.mastergis.com/). Obten mas informacion del curso en este [**enlace**](https://www.mastergis.com/product/google-earth-engine/). El contenido del curso esta disponible en [**GitHub**](https://github.com/csaybar/EarthEngineMasterGIS) bajo licencia [**MIT**](https://opensource.org/licenses/MIT).
```
```
### **Ejercicio Resuelto: Mapa de Índice espectral - NDVI **
<img src="https://user-images.githubusercontent.com/60658810/112754764-28177800-8fa3-11eb-8952-a6aa210c259f.JPG" >
```
#Autenticar e iniciar Google Earth Engine
import ee
ee.Authenticate()
ee.Initialize()
#@title mapdisplay: Crea mapas interactivos usando folium
import folium
def mapdisplay(center, dicc, Tiles="OpensTreetMap",zoom_start=10):
'''
:param center: Center of the map (Latitude and Longitude).
:param dicc: Earth Engine Geometries or Tiles dictionary
:param Tiles: Mapbox Bright,Mapbox Control Room,Stamen Terrain,Stamen Toner,stamenwatercolor,cartodbpositron.
:zoom_start: Initial zoom level for the map.
:return: A folium.Map object.
'''
center = center[::-1]
mapViz = folium.Map(location=center,tiles=Tiles, zoom_start=zoom_start)
for k,v in dicc.items():
if ee.image.Image in [type(x) for x in v.values()]:
folium.TileLayer(
tiles = v["tile_fetcher"].url_format,
attr = 'Google Earth Engine',
overlay =True,
name = k
).add_to(mapViz)
else:
folium.GeoJson(
data = v,
name = k
).add_to(mapViz)
mapViz.add_child(folium.LayerControl())
return mapViz
```
### **1. Cargar datos vectoriales**
```
colombia = ee.FeatureCollection('users/sergioingeo/Colombia/Col')
colombia_img = colombia.draw(color = "000000", strokeWidth = 3, pointRadius = 3)
centroide = colombia.geometry().centroid().getInfo()['coordinates']
# Mostrar el ROI
mapdisplay(centroide,{'colombia':colombia_img.getMapId()},zoom_start= 6)
```
### **2. Cargar datos raster (Imagenes)**
```
#Colección de imagenes Landsat 8 "Surface Reflectance"
coleccion = ee.ImageCollection("LANDSAT/LC08/C01/T1_SR")\
.filterDate('2018-01-01', '2018-12-31')\
.filterBounds(colombia)\
.filterMetadata('CLOUD_COVER' ,'less_than',50)
```
### **3. Calculo del índice normalizado**
Utiliza .normalizedDifference para realizar este ejercicio
```
def ndvi(image):
return image.normalizedDifference([ 'B5' ,'B4']).rename('NDVI')
ndvi = coleccion.map(ndvi).mean().clip(colombia)
palette = [
'FFFFFF','CE7E45','DF923D','F18555','FCD163','998718',
'74A901','66A000','529400','3E8601','207401','056201',
'004C00','023801','012E01','011D01','011D01','011301']
NDVI= ndvi.getMapId({'min': 0, 'max': 1, 'palette':palette })
mapdisplay(centroide,{'NDVI':NDVI },zoom_start= 6)
```
### **4. Descargar los resultados (De Google Earth Engine a Google Drive)**
**ee.batch.Export.table.toDrive():** Guarda FeatureCollection como shapefile en Google Drive.
**ee.batch.Export.image.toDrive():** Guarda Images como GeoTIFF en Google Drive.
```
# Donde
# image: Es la imagén raster con la informacion del índice
# description: es el nombre que tendra el archivo en Google Drive.
# folder: es la carpeta que se creara en Google Drive.
# region: es el área que se exportará del producto creado.
# maxPixels: Aumenta o limita la cantidad máxima de pixels que pueden ser exportados.
# scale: El tamaño de los pixels de la imagén que serán exportados en metros.
task = ee.batch.Export.image.toDrive(
image= ndvi,
description='NDVI_Colombia',
folder='TareaMASTERGIS',
scale= 1000,
region = colombia.geometry(),
maxPixels = 1e13)
task.start()
from google.colab import drive
drive.mount('/content/drive')
#@title Mensage Final del curso
%%html
<marquee style='width: 30%; color: blue;'><b>MUCHAS GRACIAS ESPERO TE HAYAS DIVERTIDO TOMANDO ESTE CURSO :3 ... HASTA UNA PROXIMA OPORTUNIDAD</b></marquee>
```
### **¿Dudas con este Jupyer-Notebook?**
Estaremos felices de ayudarte!. Create una cuenta Github si es que no la tienes, luego detalla tu problema ampliamente en: https://github.com/csaybar/EarthEngineMasterGIS/issues
**Tienes que dar clic en el boton verde!**
<center>
<img src="https://user-images.githubusercontent.com/16768318/79680748-d5511000-81d8-11ea-9f89-44bd010adf69.png" width = 70%>
</center>
| true |
code
| 0.577078 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/clemencia/ML4PPGF_UERJ/blob/master/Amostragem_e_integracao_MC.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Amostragem de Monte Carlo pelo Método da Inversão
### Exemplo 1: ***A distribuição Exponencial por amostragem***
A PDF da exponencial é definida como:
\begin{equation*}
f(t) =
\begin{cases}
\frac{1}{\tau}e^{-t/\tau} \text{, se } t\geq 0 \\
0\text{, se } t<0
\end{cases}
\end{equation*}
Para essa distribuição a CDF é dada por
\begin{equation*}
F(t) = \int_{0}^t \frac{1}{\tau}e^{-t'/\tau} dt' = 1 - e^{-t/\tau}
\end{equation*}
Como sabemos, a função inversa da CDF, $F^{-1}(u)$, leva a uma variável aleatória uniforme. Sendo assim, ao inverter $u=F(t)$, obtemos
\begin{equation*}
u = 1 - e^{-t/\tau} \Rightarrow \boxed{ t = -\tau \ln{(1-u)} }
\end{equation*}
Histograma da amostragem da distribuição exponencial:
```
#@title
# Amostragem de MC de uma distribuição Exponencial pelo Método da Inversão
from numpy.random import random
from numpy import log
import matplotlib.pyplot as plt
plt.style.use('default') # para plots bonitinhos
# número de pontos
np=10000
# número de bins do histograma
nbins=200
# Vida média
tau=0.1
# Função CDF Inversa
def invCDF(u):
return -tau*log(1-u)
# Amostragem da CDF inversa, usando uma distribuição uniforme
sample = [invCDF(random()) for _ in range(np)]
# plotar a distribuição da CDF inversa com uma dist uniforme
plt.hist(sample,bins=nbins)
plt.suptitle("Amostragem da distribuição exponencial com "+str(np)+" pontos")
plt.show()
```
Histograma da amostragem da distribuição exponencial, com a pdf da exponencial sobreposta:
```
# MC Sampling an Exponential distribution by Invertion Method
import numpy as np
from numpy.random import random
from scipy.stats import expon
import matplotlib.pyplot as plt
plt.style.use('default') # para plots bonitinhos
# Inverse CDF function
#Como boa prática de Python, definimos todas as funções no começo do script!
def invCDF(u):
return -tau*np.log(u)
# lista com diferentes números de pontos
npts=[10, 100, 1000, 10000]
# número de bins dos histogramas
nbins = 100
# Vida Média
tau=0.1
# Cria uma figura que contém subplots sobrepostos (Histograma e Exponencial)
fig, ax = plt.subplots(len(npts), sharex=True)
ax[0].set_title('Distribuição Exponencial')
# cria um plot da distribuição exponencial
x = np.linspace(0,1,1000)
y = expon.pdf(x, scale=tau) # equivalente a y = (1/tau)*np.exp(-x/tau)
# Amostra de CDF inversa usando uma distribuição uniforme
for i in range(len(npts)):
sample = [invCDF(random()) for _ in range(npts[i])]
# cria um histograma com os dados de amostragem
ax[i].hist(sample,bins=nbins,density=1,label=str(npts[i])+" pts")
ax[i].plot(x,y,color='red',linewidth=1)
ax[i].legend(loc="upper right")
# show plot
plt.show()
```
### Exemplo 2: ***Criando uma distribuição de Breit-Wigner por amostragem***
A PDF da Breit-Wigner é definida cmo
\begin{equation*}
f(x) =\frac{2}{\pi}\frac{\Gamma}{4(x-a)^2+\Gamma^2}
\end{equation*}
Para essa distribuição a CDF é dada por
\begin{equation*}
F(x) = \frac{2}{\pi \Gamma} \int_{-\infty}^x \frac{\Gamma^2}{4(x'-a)^2+\Gamma^2} dx'
\end{equation*}
Para fazer a integração, faremos a mudança de variáveis $y=2(x-a)/\Gamma \Rightarrow dy=(2/\Gamma)dx$ , obtendo assim
\begin{align*}
F(x) &= \frac{1}{\pi} \int_{-\infty}^{2(x-a)/\Gamma } \frac{1}{y^2+1} dy = \frac{1}{\pi} \arctan{(y)}~\bigg|_{y=-\infty}^{y=2(x-a)/\Gamma} \\
&= \frac{ \arctan{\left( 2(x-a)/\Gamma \right)} }{\pi} +\frac{1}{2}
\end{align*}
Invertendo a CDF $u=F(x)$ , obtemos
\begin{align*}
F^{-1}(u) &= a+ \frac{\Gamma}{2} \tan{\left[ \pi \left( u - \frac{1}{2} \right) \right]}
\end{align*}
Plot do histograma de amostragem sobreposto com a PDF da Breit-Wigner
```
# MC Sampling an Exponential distribution by Invertion Method
import numpy as np
from numpy.random import random
import matplotlib.pyplot as plt
# função CDF Inversa
def invCDF(u, a, gamma):
return ( a+0.5*gamma*np.tan( np.pi*(u-0.5) ) )
# número de pontos
npts=10000
# número de bins do histograma
nbins=200
# parâmetros da Breit-Wigner (width and pole)
gamma=0.1
a=0
# amostragem da CDF inversa usando uma distribuição uniforme
sample = [invCDF(random(), a, gamma) for _ in range(npts)]
# criar a figura contendo os subplots sobrepostos (Histograma e B-W)
fig, ax = plt.subplots()
ax.set_title('Distribuição Breit-Wigner')
# criar um histograma com os dados
xmin=a-10*gamma
xmax=a+10*gamma
ax.hist(sample,bins=nbins,range=[xmin,xmax],density=1,label=str(npts)+" pts")
ax.legend(loc="upper right")
# criar um plot da distribuição B-W
x = np.linspace(xmin,xmax,1000)
y = 2/np.pi * gamma/( 4*(x-a)**2 + gamma**2 )
ax.plot(x,y,color='red',linewidth=1)
# show plot
plt.show()
```
## Amostragem de Monte Carlo pelo Método de Aceitação-Rejeição
### Exemplo 1: ***Amostragem da distribuição Gaussiana***
A PDF gaussiana é definida como
\begin{equation*}
f(x) = \frac{1}{ \sqrt{2\pi} \sigma } e^{-\frac{x^2}{2\sigma^2} }
\end{equation*}
Essa função tem uma CDF que não é expresa em termos de uma função elementar e é muito difícil encontrar sua inversa. Mas é bastante simples de se construir, usando o método de aceitação-rejeição.
```
# MC Sampling of a Gaussian distribution by Acceptance-Rejection Method
import numpy as np
from numpy.random import random
import matplotlib.pyplot as plt
from scipy.stats import norm
# number of points
npts=10000
# number of histogram bins
nbins=200
# Gaussian width and mean
sigma=3.0
mean=0
# Gaussian function definition
def gaussian(u):
return 1/(( 2*np.pi )**0.5*sigma)*np.exp( -(u-mean)**2/(2*sigma**2) )
# Sampling range
xmin=mean-10*sigma
xmax=mean+10*sigma
ymax=gaussian(mean)
# Accept or Reject the points
sample=[]
naccept=0
ntot=0
while naccept<npts:
ntot+=1
x=np.random.uniform(xmin,xmax) # x'
y=np.random.uniform(0,ymax) # y'
if y<gaussian(x):
sample.append(x)
naccept+=1
# Create a numpy array with the list of selected points
sample=np.array(sample)
# create a figure containing overlaid subplots (Histogram and Exponential)
fig, ax = plt.subplots()
ax.set_title('Gaussian Distribution')
# create a histogram with sampled data
ax.hist(sample,nbins,range=[xmin,xmax],density=1)
# create a plot of the exponential distribution
x = np.linspace(xmin,xmax,1000)
y = gaussian(x)
ax.plot(x,y,color='red',linewidth=1)
# show plot
plt.show()
print("Sampling Efficiency=",int(naccept/ntot*100),"%")
```
## Amostragem por rejeição eficiente (MC Importance Sampling)
**Problema 1**: Como usar a "importance sampling" para melhorar a eficiência de amostragem da Gaussiana? **Use o Método de Box-Muller como gerador de números aleatórios de uma Gaussiana**
**Problema 2**: Encontrar um algoritmo que gere uma variável aleatória x, distribuída de acordo com a seguinte PDF:
$f(x) = Ce^{-\lambda x}cos^2(kx)$
onde C é uma constante de normalização e $\lambda$ e $k$ são dois parâmetros conhecidos.
Podemos tomar a função $Ce^{-\lambda x}$ como a função "envelope" $g(x)$ e gerar números aleatórios de acordo com a distribuição exponencial, pelo ***método de inversão***. Em seguida, com o ***método de Aceitação-Rejeição***, aceitamos ou rejeitamos x de acordo com $cos^2kx$. A distribuição de probabilidade, sendo os dois processos independentes, é o produto das duas distribuições.
Para obter a variável aleatória $x$ da distribuição 'envelope' com o método da inversão, partimos da distribuição exponencial. A CDF da distribuição é dada por:
$\\$
$F(x) = \int_{0}^{x}g(x')dx' = \int_{0}^{x}Ce^{-\lambda x'} dx' = 1-e^{-\lambda x}$
$\\$
Invertendo $F(x)$, temos
$\\$
$u = 1 - e^{-\lambda x} \Rightarrow x = -log(1 - r)/\lambda$
$\\$
Em resumo, para obter a distribuição de $f(x)$ pelo método de "importance sampling":
1 - Gerar $r$ uniformemente entre [0,1[ ;
2 - Calcular $x = -log(1 - r)/\lambda$ ;
3 - Gerar $s$ uniformemente entre [0,1[ ;
4 - Se $s < cos^2kx$, guardar $x$, se não, retornar ao item 1.
```
# Amostragem de MC de uma distribuição Exponencial pelo Método da Inversão
import numpy as np
from numpy.random import random
from numpy import log
import matplotlib.pyplot as plt
plt.style.use('default') # para plots bonitinhos
# Função CDF Inversa
def invCDF(u, lamb):
return -log(1-u)/lamb
# Função da 'importance sampling'
def f(x, lamb, k):
return (1/np.pi)*np.exp(-lamb*x)*(np.cos(k*x))**2
# número de pontos
npts=10000
# número de bins do histograma
nbins=200
# Vida média
lamb=0.1
# k
k = 1
xmin=invCDF(0, lamb)
xmax=invCDF(.9999, lamb)
print(xmin, xmax)
# Amostra resultante do método de aceitação-rejeição
sample = []
naccept=0
ntot=0
while naccept<npts:
ntot+=1
s=np.random.uniform(0,1) # s
x=invCDF(np.random.uniform(0,1), lamb) # x
if s<f(x, lamb, k):
sample.append(x)
naccept+=1
# plotar a distribuição da CDF inversa com uma dist uniforme
plt.hist(sample,bins=nbins, range=[xmin, xmax], density=1,label=str(npts)+" pts")
#plotar a distribuição
x = np.linspace(xmin,xmax,nbins)
y = f(x, lamb, k)
plt.plot(x, y, color='red',linewidth=1)
plt.suptitle("Amostragem por rejeição eficiente")
plt.legend(loc="upper right")
plt.show()
print("eficiencia = {} %".format(naccept/ntot*100))
```
Distribuição de $f(x)$ pelo método de Aceitação-Rejeição
```
# Amostragem de MC de uma distribuição Exponencial pelo Método da Inversão
import numpy as np
from numpy.random import random
from numpy import log
import matplotlib.pyplot as plt
plt.style.use('default') # para plots bonitinhos
# Função
def f(x, lamb, k):
return (1/np.pi)*np.exp(-lamb*x)*(np.cos(k*x))**2
# número de pontos
npts=10000
# número de bins do histograma
nbins=200
# Vida média
lamb=0.1
# k
k = 1
xmin=0
xmax=40
print(xmin, xmax)
# Amostra resultante do método de aceitação-rejeição
sample = []
naccept=0
ntot=0
while naccept<npts:
ntot+=1
x=np.random.uniform(xmin,xmax) # s
y=np.random.uniform(0,1) # x
if y<f(x, lamb, k):
sample.append(x)
naccept+=1
# plotar a distribuição da CDF inversa com uma dist uniforme
plt.hist(sample,bins=nbins, range=[xmin, xmax], density=True,label=str(npts)+" pts")
#plotar a distribuição
x = np.linspace(xmin,xmax,nbins)
y = f(x, lamb, k)
plt.plot(x, y, color='red',linewidth=1)
plt.suptitle("Amostragem por aceitação-rejeição")
plt.legend(loc="upper right")
plt.show()
print("eficiencia = {} %".format(naccept/ntot*100))
```
Note que a eficiência do método de aceitação-rejeição é menor que a eficiência do método de "importance sampling".
### Exercício:
Nos exemplos de ***Amostragem por rejeição eficiente*** (Importance Sampling) acima, a constante $C$ de normalização da função $f(x)$ está determinada como $1/\pi$, o que não é correto. Implemente nos códigos acima a constante de normalização correta: $C=1/Z$ onde $Z=\int_{x_{min}}^{x_{max}}f(x)dx$ é a área da função em um dado intervalo.
| true |
code
| 0.601711 | null | null | null | null |
|
```
# default_exp batchbald
# hide
import blackhc.project.script
from nbdev.showdoc import *
```
# BatchBALD Algorithm
> Greedy algorithm and score computation
First, we will implement two helper classes to compute conditional entropies $H[y_i|w]$ and entropies $H[y_i]$.
Then, we will implement BatchBALD and BALD.
```
# exports
import math
from dataclasses import dataclass
from typing import List
import torch
from toma import toma
from tqdm.auto import tqdm
from batchbald_redux import joint_entropy
```
We are going to define a couple of sampled distributions to use for our testing our code.
$K=20$ means 20 inference samples.
```
K = 20
import numpy as np
def get_mixture_prob_dist(p1, p2, m):
return (1.0 - m) * np.asarray(p1) + m * np.asarray(p2)
p1 = [0.7, 0.1, 0.1, 0.1]
p2 = [0.3, 0.3, 0.2, 0.2]
y1_ws = [get_mixture_prob_dist(p1, p2, m) for m in np.linspace(0, 1, K)]
p1 = [0.1, 0.7, 0.1, 0.1]
p2 = [0.2, 0.3, 0.3, 0.2]
y2_ws = [get_mixture_prob_dist(p1, p2, m) for m in np.linspace(0, 1, K)]
p1 = [0.1, 0.1, 0.7, 0.1]
p2 = [0.2, 0.2, 0.3, 0.3]
y3_ws = [get_mixture_prob_dist(p1, p2, m) for m in np.linspace(0, 1, K)]
p1 = [0.1, 0.1, 0.1, 0.7]
p2 = [0.3, 0.2, 0.2, 0.3]
y4_ws = [get_mixture_prob_dist(p1, p2, m) for m in np.linspace(0, 1, K)]
def nested_to_tensor(l):
return torch.stack(list(map(torch.as_tensor, l)))
ys_ws = nested_to_tensor([y1_ws, y2_ws, y3_ws, y4_ws])
# hide
p = [0.25, 0.25, 0.25, 0.25]
yu_ws = [p for m in range(K)]
yus_ws = nested_to_tensor([yu_ws] * 4)
ys_ws.shape
```
## Conditional Entropies and Batched Entropies
To start with, we write two functions to compute the conditional entropy $H[y_i|w]$ and the entropy $H[y_i]$ for each input sample.
```
def compute_conditional_entropy(probs_N_K_C: torch.Tensor) -> torch.Tensor:
N, K, C = probs_N_K_C.shape
entropies_N = torch.empty(N, dtype=torch.double)
pbar = tqdm(total=N, desc="Conditional Entropy", leave=False)
@toma.execute.chunked(probs_N_K_C, 1024)
def compute(probs_n_K_C, start: int, end: int):
nats_n_K_C = probs_n_K_C * torch.log(probs_n_K_C)
nats_n_K_C[probs_n_K_C == 0] = 0.0
entropies_N[start:end].copy_(-torch.sum(nats_n_K_C, dim=(1, 2)) / K)
pbar.update(end - start)
pbar.close()
return entropies_N
def compute_entropy(probs_N_K_C: torch.Tensor) -> torch.Tensor:
N, K, C = probs_N_K_C.shape
entropies_N = torch.empty(N, dtype=torch.double)
pbar = tqdm(total=N, desc="Entropy", leave=False)
@toma.execute.chunked(probs_N_K_C, 1024)
def compute(probs_n_K_C, start: int, end: int):
mean_probs_n_C = probs_n_K_C.mean(dim=1)
nats_n_C = mean_probs_n_C * torch.log(mean_probs_n_C)
nats_n_C[mean_probs_n_C == 0] = 0.0
entropies_N[start:end].copy_(-torch.sum(nats_n_C, dim=1))
pbar.update(end - start)
pbar.close()
return entropies_N
# Make sure everything is computed correctly.
assert np.allclose(compute_conditional_entropy(yus_ws), [1.3863, 1.3863, 1.3863, 1.3863], atol=0.1)
assert np.allclose(compute_entropy(yus_ws), [1.3863, 1.3863, 1.3863, 1.3863], atol=0.1)
```
However, our neural networks usually use a `log_softmax` as final layer. To avoid having to call `.exp_()`, which is easy to miss and annoying to debug, we will instead use a version that uses `log_probs` instead of `probs`.
```
# exports
def compute_conditional_entropy(log_probs_N_K_C: torch.Tensor) -> torch.Tensor:
N, K, C = log_probs_N_K_C.shape
entropies_N = torch.empty(N, dtype=torch.double)
pbar = tqdm(total=N, desc="Conditional Entropy", leave=False)
@toma.execute.chunked(log_probs_N_K_C, 1024)
def compute(log_probs_n_K_C, start: int, end: int):
nats_n_K_C = log_probs_n_K_C * torch.exp(log_probs_n_K_C)
entropies_N[start:end].copy_(-torch.sum(nats_n_K_C, dim=(1, 2)) / K)
pbar.update(end - start)
pbar.close()
return entropies_N
def compute_entropy(log_probs_N_K_C: torch.Tensor) -> torch.Tensor:
N, K, C = log_probs_N_K_C.shape
entropies_N = torch.empty(N, dtype=torch.double)
pbar = tqdm(total=N, desc="Entropy", leave=False)
@toma.execute.chunked(log_probs_N_K_C, 1024)
def compute(log_probs_n_K_C, start: int, end: int):
mean_log_probs_n_C = torch.logsumexp(log_probs_n_K_C, dim=1) - math.log(K)
nats_n_C = mean_log_probs_n_C * torch.exp(mean_log_probs_n_C)
entropies_N[start:end].copy_(-torch.sum(nats_n_C, dim=1))
pbar.update(end - start)
pbar.close()
return entropies_N
# hide
# Make sure everything is computed correctly.
assert np.allclose(compute_conditional_entropy(yus_ws.log()), [1.3863, 1.3863, 1.3863, 1.3863], atol=0.1)
assert np.allclose(compute_entropy(yus_ws.log()), [1.3863, 1.3863, 1.3863, 1.3863], atol=0.1)
```
### Examples
```
conditional_entropies = compute_conditional_entropy(ys_ws.log())
print(conditional_entropies)
assert np.allclose(conditional_entropies, [1.2069, 1.2069, 1.2069, 1.2069], atol=0.01)
entropies = compute_entropy(ys_ws.log())
print(entropies)
assert np.allclose(entropies, [1.2376, 1.2376, 1.2376, 1.2376], atol=0.01)
```
## BatchBALD
To compute BatchBALD exactly for a candidate batch, we'd have to compute $I[(y_b)_B;w] = H[(y_b)_B] - H[(y_b)_B|w]$.
As the $y_b$ are independent given $w$, we can simplify $H[(y_b)_B|w] = \sum_b H[y_b|w]$.
Furthermore, we use a greedy algorithm to build up the candidate batch, so $y_1,\dots,y_{B-1}$ will stay fixed as we determine $y_{B}$. We compute
$H[(y_b)_{B-1}, y_i] - H[y_i|w]$ for each pool element $y_i$ and add the highest scorer as $y_{B}$.
We don't utilize the last optimization here in order to compute the actual scores.
### In the Paper

### Implementation
```
# exports
@dataclass
class CandidateBatch:
scores: List[float]
indices: List[int]
def get_batchbald_batch(
log_probs_N_K_C: torch.Tensor, batch_size: int, num_samples: int, dtype=None, device=None
) -> CandidateBatch:
N, K, C = log_probs_N_K_C.shape
batch_size = min(batch_size, N)
candidate_indices = []
candidate_scores = []
if batch_size == 0:
return CandidateBatch(candidate_scores, candidate_indices)
conditional_entropies_N = compute_conditional_entropy(log_probs_N_K_C)
batch_joint_entropy = joint_entropy.DynamicJointEntropy(
num_samples, batch_size - 1, K, C, dtype=dtype, device=device
)
# We always keep these on the CPU.
scores_N = torch.empty(N, dtype=torch.double, pin_memory=torch.cuda.is_available())
for i in tqdm(range(batch_size), desc="BatchBALD", leave=False):
if i > 0:
latest_index = candidate_indices[-1]
batch_joint_entropy.add_variables(log_probs_N_K_C[latest_index : latest_index + 1])
shared_conditinal_entropies = conditional_entropies_N[candidate_indices].sum()
batch_joint_entropy.compute_batch(log_probs_N_K_C, output_entropies_B=scores_N)
scores_N -= conditional_entropies_N + shared_conditinal_entropies
scores_N[candidate_indices] = -float("inf")
candidate_score, candidate_index = scores_N.max(dim=0)
candidate_indices.append(candidate_index.item())
candidate_scores.append(candidate_score.item())
return CandidateBatch(candidate_scores, candidate_indices)
```
### Example
```
get_batchbald_batch(ys_ws.log().double(), 4, 1000, dtype=torch.double)
```
## BALD
BALD is the same as BatchBALD, except that we evaluate points individually, by computing $I[y_i;w]$ for each, and then take the top $B$ scorers.
```
# exports
def get_bald_batch(log_probs_N_K_C: torch.Tensor, batch_size: int, dtype=None, device=None) -> CandidateBatch:
N, K, C = log_probs_N_K_C.shape
batch_size = min(batch_size, N)
candidate_indices = []
candidate_scores = []
scores_N = -compute_conditional_entropy(log_probs_N_K_C)
scores_N += compute_entropy(log_probs_N_K_C)
candiate_scores, candidate_indices = torch.topk(scores_N, batch_size)
return CandidateBatch(candiate_scores.tolist(), candidate_indices.tolist())
```
### Example
```
get_bald_batch(ys_ws.log().double(), 4)
```
| true |
code
| 0.684264 | null | null | null | null |
|
# Algorithms blind tasting wines
*In this study we present a simple application of Natural Language Processing to classifying grape types based on semi-professional text based description of a glass of wine. We build a classifier model with pipelines and test it through two different datasets. A part of one of the datasets was involved through the building of the concept while the other is a completely out of sample data source. We present classification results of 4 different grape types with an accuracy above 85% which is in our view quite remarkable concerning the simplicity of the model.*
**Important note: This is purely driven by sel-interest. None of the mentioned entities gave financial nor other type of support. Feel free to copy and distribute this work or give remarks or suggestions.**
Wine is one of the most popular alcohols that is being produced. Its production, selling and understanding has several thousands of years of expertise. A big industry has developed around producing the wine but also around describing it. The latter is very important since wine comes in different colour, taste, smell etc. It is important to describe these features of a bottle to customers because almost all of us enjoy different aspects of a glass of wine. The people who describe the wine are called wine experts or sommeliers [[1](#ch7)].
One has to be gifted with good genetics to be able to sense and identify numerous different smells and tastes and have enough lexical knowledge to map these features to his database of wine features. This way they can tell only from sampling a glass of wine what grape was used to make it, in which country was it made, what year and maybe some more. This is an amazing skill to have, but it requires years of practice (hopefully without getting drunk). There are schools, like the [Wine and Spirit Education Trust](https://www.wsetglobal.com/) [[2](#ch7)] where you can practice these skills and learn a framework to do blind tasting. They have their own terminology to describe certain wine features like: full-budied, oaky, dry, grassy etc. (see [[3](#ch7)] for a more complete list).
Would it be possible to create an algorithm that can identify the grape, the country or the year (vintage) of a wine based on professional description of wines? We think it would be possible, but it is certainly not an easy task and has many conditions to perform it. The very first issue is to find a reliable, complete and professional description of ten thousands of wines (or even more). The second issue is to create a natural language processing (NLP) model that is capable of extracting the relevent information from the descriptions and put them into an input format that a machine can handle and understand. The final issue is to find a classifier that can read the input and based on a set of optimizable parameters it can correctly tell us the target feature (in this study it will be the grape type) of the corresponding wine description.
In a previous study, called [Become a sommelier](https://diveki.github.io/projects/wine/wine.html) [[4](#ch7)], we explored the issue of collecting the data. We wrote a web scraping algorithm that collects wine descriptions from various online wine selling websites (please read that study for more details). This database contains roughly 2000 samples. These descriptions are more in a customer friendly style, rarely very detailed, in all together we could call them semi-professional descriptions, but written by experts. Later in our research we came accross a [Kaggle](https://www.kaggle.com/) [Wine Reviews](https://www.kaggle.com/zynicide/wine-reviews) [[5](#ch7)] by *zackthoutt*. He collected a similar database of wine descriptions from another source as we did and his database contains more than 100 thousand samples. This size of database starts to be in the usable range.
In another previous study, called [Application of TfIdf-vectorizer on wine data](https://diveki.github.io/projects/wine/tfidf.html) [[6](#ch7)] we established the concept of our model that extracts information from the wine description and turns it into a vectorized bag-of-words model. We used our own data set (and not the Kaggle one) to build up all the aspects of our model, that we will present here too, but for more details read the mentioned study. To make sure that our model do not get biased during the building process, we divided it into a train and a test set and we use the same concept here too. Basically we neglected any knowledge from the test set during the building process.
In this study we will combine the created NLP model with a classifier and test the model performance in different scenarios. We will show classification results on both databases separately and also show an example where the Kaggle database trains the constructed model and we test it on our database. We present hyperparameter optimization and kfold verification of the results too.
This study will step through the following topics:
1. [Loading data](#ch1)
2. [Model definition](#ch2)
2.1. [Stopwords](#ch2.1)
2.2. [POS tagging and Lemmatizing](#ch2.2)
2.3. [Label encoding](#ch2.3)
2.4. [Splitting data into train and test sets](#ch2.4)
2.5. [Defining selectors](#ch2.5)
2.6. [Defining data pre-processors](#ch2.6)
2.7. [Defining classiffiers](#ch2.7)
3. [Train and test the model](#ch3)
3.1. [Analysis of train predictions](#ch3.1)
3.2. [Analysis of test predictions](#ch3.2)
3.3. [Testing with different classifiers](#ch3.3)
3.4. [Hyperparameter tuning](#ch3.4)
4. [Classification of data from Kaggle](#ch4)
4.1. [Data formatting](#ch4.1)
4.2. [Classification](#ch4.2)
5. [Cross-data validation of the model](#ch5)
5.1. [Classifying more target features](#ch5.1)
6. [Conclusion](#ch6)
7. [References](#ch7)
<a id="ch1"></a>
# 1. Loading data
We start by loading all the required packages and data to solve the above described task. Most of the details about these steps are described in [Become a sommelier](https://diveki.github.io/projects/wine/wine.html) and [Application of Tfidf-vectorizer on wine data](https://diveki.github.io/projects/wine/tfidf.html).
We start by loading *pandas, numpy, re, scikit-learn* and *nltk* packages.
```
# importing packages
import pandas as pd
import re
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# sklearn packages
from sklearn import metrics
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_score, StratifiedKFold
from sklearn.pipeline import Pipeline, FeatureUnion
from sklearn.preprocessing import FunctionTransformer, StandardScaler
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.naive_bayes import MultinomialNB
from sklearn.dummy import DummyClassifier
from xgboost import XGBClassifier
# nltk packages
import nltk
from nltk import word_tokenize
from nltk.stem import WordNetLemmatizer
from nltk.corpus import stopwords
from string import punctuation
```
Then we load the wine data set that we scraped online. For the details about this data set see the Appendix of [Become a sommelier](https://diveki.github.io/projects/wine/wine.html).
```
filename = '../DataBase/5_grape_db.xlsx'
a0 = pd.read_excel(filename)
a0.head()
```
This data set contains all kinds of information about 5 grape types. We will use only 4 of the grape types, since the 5th does not have many samples. These 4 types are: *pinot noir, syrah* (red wines) and *chardonnay, sauvignon blanc* (white wines). By setting a limit to the minimum sample size we filter the input data.
```
result = a0['grape_variety']
limit = 40
## removing varieties that have only one member in the database
counts = nltk.Counter(result)
varieties = [key for key in counts if counts[key] > limit]
data_input = a0[a0['grape_variety'].isin(varieties)].reset_index()
data_input.head()
```
From this dataframe we will only use some of the features. The columns description and colour are the most important ones, but in the our first implementation we will add the Body feature as an input too. Let us see an example what does the code face in the descripiton column and extract reliable information in order to be able to classify grape types.
```
data_input.loc[1, 'description']
```
<a id="ch2"></a>
# 2. Model definition
As we showed in [Application of Tfidf-vectorizer on wine data](https://diveki.github.io/projects/wine/tfidf.html) in order to classify the grape types correctly, the processed input data for one grape should not correlate with other grape types. The applied model has to minimize this correlation. We did not perform an exact optimization process but rather added newer features to the model step-by-step and investigated what happens with the correlation. All the features presented here are the result of the mentioned study, so for details please go and read it. Some of the steps presented below are not discussed in that study, therefore we will elaborate them more.
Our model will be a very simple vectorized 1-gramm bag-of-words model. We will rely on term frequency - inverse document frequency (tf-idf) vectorization and some additional noise filters and word processors.
<a id="ch2.1"></a>
## 2.1. Stopwords
As you can see above, there are words in the description column that are certainly not adding any information about the grape type, like *with, and, by* etc. We can collect a list of these kind of words and call them stopwords. These will be filtered out from the text and not taken into account in the classification process. We will exploit the *nltk* package's stopwords and extend it with some words and punctuations defined by us.
```
# defining stopwords: using the one that comes with nltk + appending it with words seen from the above evaluation
stop_words = stopwords.words('english')
stop_append = ['.', ',', '`', '"', "'", '!', ';', 'wine', 'fruit', '%', 'flavour', 'aromas', 'palate']
stop_words1 = frozenset(stop_words + stop_append)
```
<a id="ch2.2"></a>
## 2.2. POS tagging and Lemmatizing
The text we want to analyse may contain the same word in different forms. A very simple example would be *cherry* and *cherries* the singular and plural version of the same word. Another example could be *good* and *better*. In their original form, these words are treated as separete ones by the code. To bring them to their common form we apply [lemmatization](https://en.wikipedia.org/wiki/Lemmatisation) [[7](#ch7)]. This is a very difficult task since it requires correct identification of the word (noun, verb etc.) type in the context. The latter is position tagging or POS tagging. We use *nltk*'s pos tagger, but as any other tagger this is not perfect neither.
The most information of a wine description is carried in its nouns and adjectives. Verbs and adverbs are rather common words to most of the wines. In our model we apply a filter that leaves nouns and adjectives in the text and removes anything else.
The POS tagging, lemmatizing and type selecting is carried out by the *LemmaTokenizer* class.
```
# list of word types (nouns and adjectives) to leave in the text
defTags = ['NN', 'NNS', 'NNP', 'NNPS', 'JJ', 'JJS', 'JJR']#, 'RB', 'RBS', 'RBR', 'VB', 'VBD', 'VBG', 'VBN', 'VBP', 'VBZ']
# functions to determine the type of a word
def is_noun(tag):
return tag in ['NN', 'NNS', 'NNP', 'NNPS']
def is_verb(tag):
return tag in ['VB', 'VBD', 'VBG', 'VBN', 'VBP', 'VBZ']
def is_adverb(tag):
return tag in ['RB', 'RBR', 'RBS']
def is_adjective(tag):
return tag in ['JJ', 'JJR', 'JJS']
# transform tag forms
def penn_to_wn(tag):
if is_adjective(tag):
return nltk.stem.wordnet.wordnet.ADJ
elif is_noun(tag):
return nltk.stem.wordnet.wordnet.NOUN
elif is_adverb(tag):
return nltk.stem.wordnet.wordnet.ADV
elif is_verb(tag):
return nltk.stem.wordnet.wordnet.VERB
return nltk.stem.wordnet.wordnet.NOUN
# lemmatizer + tokenizer (+ stemming) class
class LemmaTokenizer(object):
def __init__(self):
self.wnl = WordNetLemmatizer()
# we define (but not use) a stemming method, uncomment the last line in __call__ to get stemming tooo
self.stemmer = nltk.stem.SnowballStemmer('english')
def __call__(self, doc):
# pattern for numbers | words of length=2 | punctuations | words of length=1
pattern = re.compile(r'[0-9]+|\b[\w]{2,2}\b|[%.,_`!"&?\')({~@;:#}+-]+|\b[\w]{1,1}\b')
# tokenize document
doc_tok = word_tokenize(doc)
#filter out patterns from words
doc_tok = [pattern.sub('', x) for x in doc_tok]
# get rid of anything with length=1
doc_tok = [x for x in doc_tok if len(x) > 1]
# position tagging
doc_tagged = nltk.pos_tag(doc_tok)
# selecting nouns and adjectives
doc_tagged = [(t[0], t[1]) for t in doc_tagged if t[1] in defTags]
# preparing lemmatization
doc = [(t[0], penn_to_wn(t[1])) for t in doc_tagged]
# lemmatization
doc = [self.wnl.lemmatize(t[0], t[1]) for t in doc]
# uncomment if you want stemming as well
#doc = [self.stemmer.stem(x) for x in doc]
return doc
```
<a id="ch2.3"></a>
## 2.3. Label encoding
Although, we are mainly interested in classification by using text based description, from the database we can see that there are other, possible helpful features of the wine, that can help to classify. Such features are *body* and *colour*. Both of them are used by sommeliers to describe a wine. Colour can be easily observed while body is reflecting in a way the acidity of a wine.
These columns in the database are defined in text format, so we have to turn them into numbers so that the computer can understand them. Both of these features have discreate value, so we could just easily attach a number to them like: *red=1*, *rose=2*, *white=3*. This is called [label encoding](https://medium.com/@contactsunny/label-encoder-vs-one-hot-encoder-in-machine-learning-3fc273365621) [[8](#ch7)]. This would not be a disastrous approach, but the classifier might think there there is a trend like tendency between these categories (because of the increase in numbers), which is obviously false. Instead, sticking to the case of colours, we create three more columns (there are three colours), each representing one colour. Each column can take two values, 0 (if the wine does not have that feature) and 1 (if the wine has that feature). We do this for both the body and colour columns with the *pandas* get_dummies method.
The following cell prints an example of the modified data set that contains the encoded labels.
```
body_dummies = pd.get_dummies(data_input['Body']) # label encoding the Body column
colour_dummies = pd.get_dummies(data_input['colour']) # label encoding the colour column
# adding the body labels to the original dataset
data_input = data_input.merge(body_dummies, left_index=True, right_index=True)
# adding the colour labels to the original dataset
data_input = data_input.merge(colour_dummies, left_index=True, right_index=True)
data_input.head()
```
<a id="ch2.4"></a>
## 2.4. Splitting data into train and test sets
As we have already mentioned the analysis in [4,6](#ch7) were performed on a preselected train dataset from the whole database. We will use exactly the same train dataset to train our model. This is easy to do by setting the *random_state* argument to the same value as it was in those studies. Also, we only select the columns of description, labelled colours and labelled bodies. The *train_test_split* function will create train and test features and targets.
```
# split the data into train and test
combined_features = ['Body', 'description', 'full', 'light', 'medium', 'dry', 'red', 'rose', 'white']
target = 'grape_variety'
X_train, X_test, y_train, y_test = train_test_split(data_input[combined_features], data_input[target],
test_size=0.33, random_state=42)
X_train.head()
y_train.head()
```
<a id="ch2.5"></a>
## 2.5. Defining selectors
We will build up a [pipeline](https://medium.com/@yanhann10/a-brief-view-of-machine-learning-pipeline-in-python-5f50b941fca8) for this study. In a pipeline we chain together all kind of actions on the data into one stable flow. For example it combines data transformers (numerical normaliser) with data estimators (Naive Bayes classifier).
The input data has both text based and numerical features. They cannot be processed together by the classifier unless they are transformed into the same format, in this case numerical format. We aim to construct a pipeline that takes care of all these issues.
We define two classes where one of them will select the text based column from the input, the other will select the numerical input.
```
class TextSelector(BaseEstimator, TransformerMixin):
"""
Transformer to select a single column from the data frame to perform additional transformations on
Use on text columns in the data
"""
def __init__(self, key):
self.key = key
def fit(self, X, y=None, *parg, **kwarg):
return self
def transform(self, X):
# returns the input as a string
return X[self.key]
class NumberSelector(BaseEstimator, TransformerMixin):
"""
Transformer to select a single column from the data frame to perform additional transformations on
Use on numeric columns in the data
"""
def __init__(self, key):
self.key = key
def fit(self, X, y=None):
return self
def transform(self, X):
# returns the input as a dataframe
return X[[self.key]]
```
<a id="ch2.6"></a>
## 2.6. Defining data pre-processors and pipelines
As mentioned before, text based data cannot be used by the classifier. Therefore, we create a vectorizer that takes a string input and turns it into a vector of numbers.
We will use the [TfidfVectorizer](http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.TfidfVectorizer.html) with 1-grams of words, the predifined stopwords and LemmaTokenizer as helping tools. Tf-idf applies the bag-of-words concept, which creates a vocabulary (list of all the terms from the string) and maps a value to them. In the case of tf-idf this value is roughly the product of the term frequency (the number of times a term occured within the document string) and the inverse document frequency (the inverse of the the number of documents that this term is present). Basically, the first term emphasizes the terms that are frequent in one document while weighs down the terms that are frequent over several documents. The reason for the latter is that if a word is used in many documents it is unlikely that it has characteristic meaning to one topic. For more on this read the relevant sections in [Application of Tfidf-vectorizer on wine data](https://diveki.github.io/projects/wine/tfidf.html).
Let us define the vectorizer.
```
vec_tdidf = TfidfVectorizer(ngram_range=(1,1), stop_words=stop_words, analyzer='word',
norm='l2', tokenizer=LemmaTokenizer())
```
Now let us combine the text vectorizer with the text selector into one pipeline.
```
text = Pipeline([
('selector', TextSelector(key='description')),
('vectorizer', vec_tdidf)
])
```
Just as in the previous sell let us put the numeric selectors into pipelines too.
```
# pipelines of body features
full = Pipeline([
('selector', NumberSelector(key='full')),
])
medium = Pipeline([
('selector', NumberSelector(key='medium')),
])
light = Pipeline([
('selector', NumberSelector(key='light')),
])
dry = Pipeline([
('selector', NumberSelector(key='dry')),
])
#pipelines of colour features
red = Pipeline([
('selector', NumberSelector(key='red')),
])
rose = Pipeline([
('selector', NumberSelector(key='rose')),
])
white = Pipeline([
('selector', NumberSelector(key='white')),
])
```
Finally let us combine all these pipelines. Note, that to combine different features one has to use the [FeatureUnion](http://scikit-learn.org/stable/modules/generated/sklearn.pipeline.FeatureUnion.html) class. Now we have all methods of transformation and pre-processing put into one variable.
```
feats = FeatureUnion([('full', full),
('medium', medium),
('light', light),
('dry', dry),
('description', text),
('red', red),
('rose', rose),
('white', white)
])
```
<a id="ch2.7"></a>
## 2.7. Defining classiffiers
The last step in our pipeline is to define a classifier. Our first choice of classifier is the [Random Forest](https://en.wikipedia.org/wiki/Random_forest). It is an ensemble classifier of decision trees and it tends to be more accurate than a single decision tree classifier. It is very versatile in application and fit to determine which features are giving the most contribution to good prediction (although we will not use this feature here).
```
clf = RandomForestClassifier(random_state=42)
```
Now let us put this classifier in the pipeline to combine it with the feature union and then we are ready to go and do blind tasting.
```
pipe = Pipeline([('feats', feats),
('clf',clf)
])
```
<a id="ch3"></a>
# 3. Train and test the model
We have arrived to the point where we can train our model with the train data set. To do that we call the *fit* method of the *pipe* object. Since this database is not really big, this training does not take a lot of time, while you should keep in mind if you have millions of inputs, your training might take a considerable amount of time.
```
%timeit pipe.fit(X_train, y_train)
```
With the `%timeit` magic command you can measure how long does it take to run one line of code. In this case it took about 1 second to run it.
<a id="ch3.1"></a>
## 3.1. Analysis of train predictions
Now let us see the performance of this trained model. Let us first investigate how good the model is at classifying grape types in the train data set. This is actually a completely in-sample measurement. We expect it to be good.
We define a function to print out all kinds of statistics on the performance, since we will use this a lot.
```
def print_stats(preds, target, labels, sep='-', sep_len=40, fig_size=(10,8)):
print('Accuracy = %.3f' % metrics.accuracy_score(target, preds))
print(sep*sep_len)
print('Classification report:')
print(metrics.classification_report(target, preds))
print(sep*sep_len)
print('Confusion matrix')
cm=metrics.confusion_matrix(target, preds)
cm = cm / np.sum(cm, axis=1)[:,None]
sns.set(rc={'figure.figsize':fig_size})
sns.heatmap(cm,
xticklabels=labels,
yticklabels=labels,
annot=True, cmap = 'YlGnBu')
plt.pause(0.05)
```
We will print out the [accuracy](http://scikit-learn.org/stable/modules/model_evaluation.html#accuracy-score), the [classification report](http://scikit-learn.org/stable/modules/model_evaluation.html#classification-report) and the [confusion matrix](http://scikit-learn.org/stable/modules/model_evaluation.html#confusion-matrix).
Accuracy is the number of correctly predicted grape types divided by the total number of grapes.
Classification report is a concise way of presenting estimator performance through the following metrics: [precision](http://scikit-learn.org/stable/auto_examples/model_selection/plot_precision_recall.html), [recall](http://scikit-learn.org/stable/auto_examples/model_selection/plot_precision_recall.html), [f1-score](http://scikit-learn.org/stable/auto_examples/model_selection/plot_precision_recall.html) and the number of samples belonging to each target feature. A good classifier has a value close to 1 for both precision and recall and therefore for f1-score too.
Confusion matrix is again a simple way to present how many grape types were correctly identified (diagonal elements), while the off diagonal elemnts tell us how many samples were classified into another target type. Obviously, one would like to decrease the values of the off diagonal elements to get perfect classification. The vertical axis represents the true class of the target, why the horizontal axis shows the predicted value of the target.
```
#train stats
preds = pipe.predict(X_train)
print_stats(preds, y_train, pipe.classes_, fig_size=(7,4))
```
Well this model does a perfect job on the train data set. We kind of expect it to do, since it was trained on it. However we are still amazed that the vectorization of the text combined with body and colour description is capable to perfectly differentiate all the train input grape types. Let us turn now to the test set.
<a id="ch3.2"></a>
## 3.2. Analysis of test predictions
As we have mentioned earlier, this test data was never used with respect to the model. It is the first time that the model sees it. The target sample sizes are not big.
```
# test stats
preds = pipe.predict(X_test)
print_stats(y_test, preds, pipe.classes_)
```
The accuracy is 74%. We have expected to have false positive and false negative scores, but a surprising observation is that even though we explicitly tell the classifier what colour the wine has it is still able to confuse red with white wines and vice versa. In order to decide wether this result is rather good or bad, we establish a benchmark and also try out other classifiers.
<a id="ch3.3"></a>
## 3.3. Testing with different classifiers
First, we establish a reference classification outcome. We do it by creating a classifier that generates random predictions by respecting the training set target feature distribution (since not all the grape types are equally represented).
```
clf = DummyClassifier(strategy='stratified',random_state=42)
pipe = Pipeline([('feats', feats),
('clf',clf)
])
%timeit pipe.fit(X_train, y_train)
# test stats
preds = pipe.predict(X_test)
print_stats(y_test, preds, pipe.classes_)
```
Well a random stratified classifier achieves 29% accuracy. Our first try with the Random Forest classifier was clearly way better. Now let us look at one of the most used ensemble booster classifier, the XGBClassifier from [xgboost](https://xgboost.readthedocs.io/en/latest/python/python_api.html) package. Gradient boosting sequentially adds predictors and corrects previous models. The classifier fits the new model to new residuals of the previous prediction and then minimizes the loss when adding the latest prediction.
```
clf = XGBClassifier(random_state=42, n_jobs=1)
pipe = Pipeline([('feats', feats),
('clf',clf)
])
%timeit pipe.fit(X_train, y_train)
# test stats
preds = pipe.predict(X_test)
print_stats(y_test, preds, pipe.classes_)
```
Without any adjustment it improves the accuracy by 10% and all the other metrics compared to the Random Forest classifier. However, this is a slower method to apply.
One would say that let us stick to the XGBClassifier, but it turned out (we will not present it here, but you can check it by running the codes) when we go to the larger Kaggle data base, the difference between XGBClassifier and RandomForest classifier disappears (and actually the latter gives slightly better results by roughly 2%). This statement assumes default settings for both classifiers which does not give necessarily a good reference to compare the two classifiers.
Because of the above observations we will stick to the Random Forest classifier.
<a id="ch3.4"></a>
## 3.4. Hyperparameter tuning
There are a certain number of parameters that can be adjusted to improve the performance of a classifier. This is hyperparameter tuning. We will improve the Random Forest classifier by using a grid search techinque over the predefined parameter values and apply [cross validation](http://scikit-learn.org/stable/modules/cross_validation.html#cross-validation). All this can be done with the *GridSearchCV* class. Cross validation is basically a k-fold technique, where for example we split our data into $M$ equal pieces and assign the first $M-k$ to be the train set and the last $k$ set to be the test. In the next round we choose another *k* piece to be the test and the rest to be the train. We can repeat this several times and take statistics over the outcome. The train and test sets never overlap.
We have observed that by chosing the right amount of features (in our case the *max_features* argument) we can imporve the accuracy by a lot (above 80%). Below we will show how to obtimize the max_features and the number of estimators (the number of trees created in the Random Forest calculation process). We will use multiprocessing too (check if your operation system supports it). Also there are other parameters like, *max_depth* and *min_samples_leaf* that you can optimize if you uncomment them. We will perform 3 cross validations.
Obviously, the time for optimization increases with the number of parameters to optimize and the number of cross validation required. In the end one has to compromise between optimization time and best optimizer.
```
# classifier and pipeline definition
clf = RandomForestClassifier(random_state=42)
pipe = Pipeline([('feats', feats),
('clf',clf)
])
# definition of parameter grid to scan through
param_grid = {
#'clf__max_depth': [60, 100, 140],
'clf__max_features': ['log2', 'auto', None],
#'clf__min_samples_leaf': [5,10,50,100,200],
'clf__n_estimators': [100, 500, 1000]
}
# grid search cross validation instantiation
grid_search = GridSearchCV(estimator = pipe, param_grid = param_grid,
cv = 3, n_jobs = 1, verbose = 0)
#hyperparameter fitting
grid_search.fit(X_train, y_train)
```
Let us first see the accuracy measures on the test sets of the cross validation:
```
grid_search.cv_results_['mean_test_score']
```
There were 9 combinations of the input parameters, therefore there are 9 accuracies. All of them are above 80% meaning basically any pair of the input parameters would do a good job.
However let us check the best parameter combination:
```
grid_search.best_params_
```
Now that we have the best parameters, let us create a classifier with these inputs:
```
clf_opt=grid_search.best_estimator_
```
Let us verify the parameters this classifier use, just to make sure we really use what we intended:
```
clf_opt.named_steps['clf'].get_params()
```
Indeed, we have the right input parameters. Let us now train it and test it on our data set.
```
clf_opt.fit(X_train, y_train)
preds = clf_opt.predict(X_test)
print_stats(y_test, preds, clf_opt.classes_)
```
Our accuracy increased from 74% to 89%. We can see that the number of false positives and negatives has dropped a lot. Precision, recall and the f1-score are all close to 0.90. The cross wine colour misclassification has decreased too. This is a great improvement.
<a id="ch4"></a>
# 4. Classification of data from Kaggle
As we have already meantioned we came accross a [Kaggle](https://www.kaggle.com/) [Wine Reviews](https://www.kaggle.com/zynicide/wine-reviews) [[5](#ch7)] wine description database by *zackthoutt*. It is much larger than the database we constructed and comes from completely different source. Therefore, verifying if our classification process works even on this database would be an ideal out of sample test.
We will do 3 things. First, we apply the whole procedure we developed earlier on this database and hope to have good results. Second, we will use the Kaggle database as the train set to fit our model (since this is the larger set) and use our database as the test set. This would be a cross database check of our model which if it works proves the validity of the model. Finally, since the Kaggle database is huge we are not restricted to select only 4 or 5 grape types to classify. We will enlarge our target features, but not to the whole database.
First, we load the database and transform the relevant columns into the format we used earlier. Also notice, that this database has no explicit information on the body and the colour of the wine, therefore we will only use the description column. Plus, from literature we can add manually the colour of the wine, completing the input information.
We will not go through such a rigorous pre-processing of the description column as for our own database. We will accept it as it is (and drop any row with NAs). We pre-process the grape variety column with taking its lower case turning any shiraz into syrah.
```
filename = '../DataBase/winemag-data-130k-v2.csv'
# select the description and grape variety columns
kaggle = pd.read_csv(filename, usecols=['description', 'grape_variety'])
# transform the grape variety column into lower case strings
kaggle['grape_variety'] = kaggle['grape_variety'].str.lower()
kaggle['description'] = kaggle['description'].str.lower()
kaggle.head()
```
<a id="ch4.1"></a>
## 4.1. Data formatting
Below you can see a few steps of preprocessing.
```
# function to change any shiraz into syrah
def shiraz_filter(ss):
if ss == 'shiraz':
return 'syrah'
else:
return ss
kaggle['grape_variety'] = kaggle.apply(lambda row: shiraz_filter(row['grape_variety']), axis=1)
# drop any row that contains NAs
kaggle = kaggle.dropna()
# select the rows that contains the 4 grape names: chardonnay, syrah, pinot noir, sauvignon blanc
kaggle_input = kaggle[kaggle['grape_variety'].isin(varieties)].reset_index()
pd.unique(kaggle_input.grape_variety)
# define a colour dictionary that will be mapped into the databaes
colour_dict = {'pinot noir': 'red', 'syrah': 'red', 'chardonnay': 'white', 'sauvignon blanc': 'white'}
kaggle_input['colour'] = kaggle_input.apply(lambda row: colour_dict[row['grape_variety']], axis=1)
colour_dummies = pd.get_dummies(kaggle_input['colour'])
kaggle_input = kaggle_input.merge(colour_dummies, left_index=True, right_index=True)
```
Create the train and test sets.
```
# split the data into train and test
combined_features = ['description', 'white', 'red']
target = 'grape_variety'
X_train, X_test, y_train, y_test = train_test_split(kaggle_input[combined_features], kaggle_input[target],
test_size=0.33, random_state=42)
```
<a id="ch4.2"></a>
## 4.2. Classification
Let us create the corresponding pipeline with the colour features and the text vectorizer:
```
red = Pipeline([
('selector', NumberSelector(key='red')),
])
white = Pipeline([
('selector', NumberSelector(key='white')),
])
text = Pipeline([
('selector', TextSelector(key='description')),
('vectorizer', TfidfVectorizer(ngram_range=(1,1), stop_words=stop_words, analyzer='word',
norm='l2', tokenizer=LemmaTokenizer()))
])
feats = FeatureUnion([('description', text),
('red', red),
('white', white)
])
```
The database is fairly big, therefore doing hyperparameter optimization on it is rather memory intensive (in my case 4 GB RAM was not enough). Therefore, we present a classification first with the default setups then do a cross validation with the optimized parameters from the previous section (although they are related to another database).
```
# classifier and pipeline definition
clf = RandomForestClassifier(random_state=42)
pipe = Pipeline([('feats', feats),
('clf',clf)
])
pipe.fit(X_train, y_train)
preds = pipe.predict(X_test)
print_stats(y_test, preds, pipe.classes_)
# definition of parameter grid to scan through
#param_grid = {
# #'clf__max_depth': [60, 100, 140],
# 'clf__max_features': ['log2', 'auto', None],
# #'clf__min_samples_leaf': [5,10,50,100,200],
# 'clf__n_estimators': [100, 500, 1000]
#}
# grid search cross validation instantiation
#grid_search = GridSearchCV(estimator = pipe, param_grid = param_grid,
# cv = 3, n_jobs = 1, verbose = 0)
#hyperparameter fitting
#grid_search.fit(X_train, y_train)
#grid_search.cv_results_['mean_test_score']
```
Without refining the model we get an accuracy of 86.7%. False negatives are large for syrah and sauvignon blanc while false positives are large for pinot noir and chardonnay.
Now we apply the optimized parameters obtained from the previous section in a cross validational sense. Hopefully it will improve the accuracy in all folds.
```
clf = RandomForestClassifier(random_state=42, max_features='log2', n_estimators=1000)
pipe = Pipeline([('feats', feats),
('clf',clf)
])
### stratified training
from sklearn.model_selection import StratifiedKFold
skf = StratifiedKFold(n_splits=3)
sc_mean=[]
for train, test in skf.split(kaggle_input[combined_features], kaggle_input[target]):
pipe.fit(kaggle_input.loc[train,combined_features], kaggle_input.loc[train, target])
preds = pipe.predict(kaggle_input.loc[test,combined_features])
sc_mean.append(metrics.accuracy_score(kaggle_input.loc[test, target], preds))
print_stats(kaggle_input.loc[test, target], preds, pipe.classes_)
print('Mean: %s' % str(sum(sc_mean)/len(sc_mean)))
print('Standard deviation: %s' % str(np.std(np.array(sc_mean))))
```
Indeed, all 3 folds gave better accuracy than the default settings. Since we have only 3 folds we use t-statistics to infere a 95% level confidence interval for the mean of the accuracy: 0.868632 - 0.878568. Without optimization, the accuracy was 0.867, therefore we would infere that it is probable that the used parameters helped to imporve the accuracy. However, they did not helped to decrease the false positives for chardonnay and pinot noir.
We have to mention that the kaggle database has not been pre-processed as our own database therefore it may still contain things that causes false positives and negatives.
Let us see what happens if we train the model on one source of data set and test it on another source.
<a id="ch5"></a>
# 5. Cross-data validation of the model
Kaggle data will be trained, since it is much larger using the optimized input parameters, namely 1000 *n_estimators* and *log2 max_features*. To construct the pipeline we use the same steps as before.
```
# split the data into train and test
combined_features = ['description', 'white', 'red']
target = 'grape_variety'
red = Pipeline([
('selector', NumberSelector(key='red')),
])
white = Pipeline([
('selector', NumberSelector(key='white')),
])
text = Pipeline([
('selector', TextSelector(key='description')),
('vectorizer', TfidfVectorizer(ngram_range=(1,1), stop_words=stop_words, analyzer='word',
norm='l2', tokenizer=LemmaTokenizer()))
])
feats = FeatureUnion([('description', text),
('red', red),
('white', white)
])
clf = RandomForestClassifier(random_state=42, max_features='log2', n_estimators=1000, n_jobs=1)
pipe = Pipeline([('feats', feats),
('clf',clf)
])
# fit the entire kaggle data
pipe.fit(kaggle_input[combined_features], kaggle_input[target])
# test stats
preds = pipe.predict(data_input[combined_features])
print_stats(data_input[target], preds, pipe.classes_)
```
The accuracy out of sample has decreased to 72%. This is kind of expected. The train and test sets are coming from completely different sources and while the test set had some data cleaning the train dif not really. Besides these differences, the metrics are still quite good in the end.
<a id="ch5.1"></a>
## 5.1 Classifying more target features
Out of curiosity we will classify now more grape varieties only from the kaggle data set. We will subset the data set to contain single grape types which have more than 1000 samples.
```
# check how many grapes are in the sample
single_name = [name for name in kaggle.grape_variety if len(name.split())<=2]
# visually investigate what grapes got through the firs filter
count = nltk.FreqDist(single_name)
count.most_common(20)
```
As you can see there are many blends in the list and wines that do not detail the grape name. We will filter them out so that we have clean names.
```
limit=1000
# grape names to be filtered
filtered_name = ['red blend', 'portuguese red', 'white blend', 'sparkling blend', 'champagne blend',
'portuguese white', 'rosé']
selected_grapes = [key for key, value in count.items() if value > limit]
selected_grapes = [name for name in selected_grapes if name not in filtered_name]
selected_grapes
# select the rows that contains the 4 grape names: chardonnay, syrah, pinot noir, sauvignon blanc
kaggle_input = kaggle[kaggle['grape_variety'].isin(selected_grapes)].reset_index()
pd.unique(kaggle_input.grape_variety)
```
We end up with 18 grape types. For a human that is a lot to keep in memory all of these type's characteristics and be able to identify them.
Just as before, we construct a mapping between the grape type and its colour and complete the input with the colour of the wine.
```
# define a colour dictionary that will be mapped into the databaes
colour_dict = {'pinot noir': 'red', 'syrah': 'red', 'chardonnay': 'white', 'sauvignon blanc': 'white',
'pinot gris': 'white', 'riesling': 'white', 'gewürztraminer': 'white', 'cabernet sauvignon': 'red',
'malbec': 'red', 'merlot': 'red', 'gamay': 'red', 'sangiovese': 'red', 'cabernet franc': 'red',
'zinfandel': 'red', 'grüner veltliner': 'white', 'nebbiolo': 'red', 'pinot grigio': 'white',
'tempranillo': 'red'}
kaggle_input = kaggle_input.dropna()
kaggle_input['colour'] = kaggle_input.apply(lambda row: colour_dict[row['grape_variety']], axis=1)
colour_dummies = pd.get_dummies(kaggle_input['colour'])
kaggle_input = kaggle_input.merge(colour_dummies, left_index=True, right_index=True)
```
We select the colours and description as the input features and the grape variety as the target feature. Then we split the data into train and test sets while keeping the occurance ratio the same in both sets.
```
# split the data into train and test
combined_features = ['description', 'white', 'red']
target = 'grape_variety'
X_train, X_test, y_train, y_test = train_test_split(kaggle_input[combined_features], kaggle_input[target],
test_size=0.33, random_state=42, stratify=kaggle_input[target])
```
Finally, we define the pipeline of feature selection, vectorization and classification, fit the train set and investigate the test set.
```
red = Pipeline([
('selector', NumberSelector(key='red')),
])
white = Pipeline([
('selector', NumberSelector(key='white')),
])
text = Pipeline([
('selector', TextSelector(key='description')),
('vectorizer', TfidfVectorizer(ngram_range=(1,1), stop_words=stop_words, analyzer='word',
norm='l2', tokenizer=LemmaTokenizer()))
])
feats = FeatureUnion([('description', text),
('red', red),
('white', white)
])
# classifier and pipeline definition
clf = RandomForestClassifier(random_state=42, max_features='log2', n_estimators=1000)
pipe = Pipeline([('feats', feats),
('clf',clf)
])
pipe.fit(X_train, y_train)
preds = pipe.predict(X_test)
print_stats(y_test, preds, pipe.classes_, fig_size=(15,10))
```
It is quite remarkable that 18 grape types can be predicted from the description and colour of the wine with 70% accuracy. The precision is not performing well in general.
<a id="ch6"></a>
# 6. Conclusion
This study presented the construction of a classification model that is able to differentiate grape types based on the description of wine samples. After construction, the model is implemented on a smaller dataset that we collected, classification parameters are optimized and performance is improved. Because of the size of the dataset, we worked with only 4 grape types. Relying on the same principles we repeated the classification on a bigger data set and showed that the previously obtained optimized parameters are imporving the performance for this data set too. In both cases we managed to achieve a classification precision of above 85%. To show that this performance is not due to a mere luck and the choice of the data set, we performed a cross data set validation too, where the accuracy dropped to 72%. Finally, using the large data set, we predicted the grape types of 18 different grapes with an accuracy of 70% which is remarkable in terms of human measures.
If you have any question please feel free to contact me at [diveki@gmail.com](diveki@gmail.com). You can also fork this project from [my GitHub repository](https://github.com/diveki/WineSommelier) or you can take a sneaky look at [my GitHub Pages website](https://diveki.github.io). I am going to publish these results on [my Kaggle page](https://www.kaggle.com/diveki) to with some additional calculations.
Just as a bonus, the preludes for this report can be found [here](https://diveki.github.io/projects/wine/wine.html) and [here](https://diveki.github.io/projects/wine/tfidf.html).
<a id="ch7"></a>
# 7. References
1. https://en.wikipedia.org/wiki/Sommelier
2. Wine and Spirit Education Trust - https://www.wsetglobal.com/
3. Wine terminology list - https://www.cawineclub.com/wine-tasting-terms
4. Become a sommelier - https://diveki.github.io/projects/wine/wine.html
5. Kagge Wine Review - https://www.kaggle.com/zynicide/wine-reviews
6. Application of TfIdf-vectorizer on wine data - https://diveki.github.io/projects/wine/tfidf.html
7. Lemmatization - https://en.wikipedia.org/wiki/Lemmatisation
8. Label encoding - https://medium.com/@contactsunny/label-encoder-vs-one-hot-encoder-in-machine-learning-3fc273365621
| true |
code
| 0.531088 | null | null | null | null |
|
```
"""
You can run either this notebook locally (if you have all the dependencies and a GPU) or on Google Colab.
Instructions for setting up Colab are as follows:
1. Open a new Python 3 notebook.
2. Import this notebook from GitHub (File -> Upload Notebook -> "GITHUB" tab -> copy/paste GitHub URL)
3. Connect to an instance with a GPU (Runtime -> Change runtime type -> select "GPU" for hardware accelerator)
4. Run this cell to set up dependencies.
"""
# If you're using Google Colab and not running locally, run this cell.
import os
!pip install wget
!apt-get install sox
!git clone https://github.com/NVIDIA/NeMo.git
os.chdir('NeMo')
!bash reinstall.sh
!pip install unidecode
```
# **SPEAKER RECOGNITION**
Speaker Recognition (SR) is an broad research area which solves two major tasks: speaker identification (who is speaking?) and speaker verification (is the speaker who she claims to be?). In this work, we focmus on the far-field, text-independent speaker recognition when the identity of the speaker is based on how speech is spoken, not necessarily in what is being said. Typically such SR systems operate on unconstrained speech utterances,
which are converted into vectors of fixed length, called speaker embeddings. Speaker embeddings are also used in automatic speech recognition (ASR) and speech synthesis.
As the goal of most speaker related systems is to get good speaker level embeddings that could help distinguish from other speakers, we shall first train these embeddings in end-to-end manner optimizing the [QuatzNet](https://arxiv.org/abs/1910.10261) based encoder model on cross-entropy loss. We modify the original quartznet based decoder to get these fixed size embeddings irrespective of the length of the input audio. We employ mean and variance based statistics pooling method to grab these embeddings.
In this tutorial we shall first train these embeddings on speaker related datasets and then get speaker embeddings from a pretrained network for a new dataset. Since Google Colab has very slow read-write speeds, Please run this locally for training on [hi-mia](https://arxiv.org/abs/1912.01231).
We use the [get_hi-mia-data.py](https://github.com/NVIDIA/NeMo/blob/master/scripts/get_hi-mia_data.py) script to download the necessary files, extract them, also re-sample to 16Khz if any of these samples are not at 16Khz. We do also provide scripts to score these embeddings for a speaker-verification task like hi-mia dataset at the end.
```
data_dir = 'scripts/data/'
!mkdir $data_dir
# Download and process dataset. This will take a few moments...
!python scripts/get_hi-mia_data.py --data_root=$data_data
```
After download and conversion, your `data` folder should contain directories with manifest files as:
* `data/<set>/train.json`
* `data/<set>/dev.json`
* `data/<set>/{set}_all.json`
Also for each set we also create utt2spk files, these files later would be used in PLDA training.
Each line in manifest file describes a training sample - `audio_filepath` contains path to the wav file, `duration` it's duration in seconds, and `label` is the speaker class label:
`{"audio_filepath": "<absolute path to dataset>/data/train/SPEECHDATA/wav/SV0184/SV0184_6_04_N3430.wav", "duration": 1.22, "label": "SV0184"}`
`{"audio_filepath": "<absolute path to dataset>/data/train/SPEECHDATA/wav/SV0184/SV0184_5_03_F2037.wav", duration": 1.375, "label": "SV0184"}`
Import necessary packages
```
from ruamel.yaml import YAML
import nemo
import nemo.collections.asr as nemo_asr
import copy
from functools import partial
```
# Building Training and Evaluation DAGs with NeMo
Building a model using NeMo consists of
1. Instantiating the neural modules we need
2. specifying the DAG by linking them together.
In NeMo, the training and inference pipelines are managed by a NeuralModuleFactory, which takes care of checkpointing, callbacks, and logs, along with other details in training and inference. We set its log_dir argument to specify where our model logs and outputs will be written, and can set other training and inference settings in its constructor. For instance, if we were resuming training from a checkpoint, we would set the argument checkpoint_dir=`<path_to_checkpoint>`.
Along with logs in NeMo, you can optionally view the tensorboard logs with the create_tb_writer=True argument to the NeuralModuleFactory. By default all the tensorboard log files will be stored in {log_dir}/tensorboard, but you can change this with the tensorboard_dir argument. One can load tensorboard logs through tensorboard by running tensorboard --logdir=`<path_to_tensorboard dir>` in the terminal.
```
exp_name = 'quartznet3x2_hi-mia'
work_dir = './myExps/'
neural_factory = nemo.core.NeuralModuleFactory(
log_dir=work_dir+"/hi-mia_logdir/",
checkpoint_dir="./myExps/checkpoints/" + exp_name,
create_tb_writer=True,
random_seed=42,
tensorboard_dir=work_dir+'/tensorboard/',
)
```
Now that we have our neural module factory, we can specify our **neural modules and instantiate them**. Here, we load the parameters for each module from the configuration file.
```
logging = nemo.logging
yaml = YAML(typ="safe")
with open('examples/speaker_recognition/configs/quartznet_spkr_3x2x512_xvector.yaml') as f:
spkr_params = yaml.load(f)
sample_rate = spkr_params["sample_rate"]
time_length = spkr_params.get("time_length", 8)
logging.info("max time length considered for each file is {} sec".format(time_length))
```
Instantiating train data_layer using config arguments. `labels = None` automatically creates output labels from manifest files, if you would like to pass those speaker names you can use the labels option. So while instantiating eval data_layer, we can use pass labels to the class in order to match same the speaker output labels as we have in the training data layer. This comes in handy while training on multiple datasets with more than one manifest file.
```
train_dl_params = copy.deepcopy(spkr_params["AudioToSpeechLabelDataLayer"])
train_dl_params.update(spkr_params["AudioToSpeechLabelDataLayer"]["train"])
del train_dl_params["train"]
del train_dl_params["eval"]
batch_size=64
data_layer_train = nemo_asr.AudioToSpeechLabelDataLayer(
manifest_filepath=data_dir+'/train/train.json',
labels=None,
batch_size=batch_size,
time_length=time_length,
**train_dl_params,
)
eval_dl_params = copy.deepcopy(spkr_params["AudioToSpeechLabelDataLayer"])
eval_dl_params.update(spkr_params["AudioToSpeechLabelDataLayer"]["eval"])
del eval_dl_params["train"]
del eval_dl_params["eval"]
data_layer_eval = nemo_asr.AudioToSpeechLabelDataLayer(
manifest_filepath=data_dir+'/train/dev.json",
labels=data_layer_train.labels,
batch_size=batch_size,
time_length=time_length,
**eval_dl_params,
)
data_preprocessor = nemo_asr.AudioToMelSpectrogramPreprocessor(
sample_rate=sample_rate, **spkr_params["AudioToMelSpectrogramPreprocessor"],
)
encoder = nemo_asr.JasperEncoder(**spkr_params["JasperEncoder"],)
decoder = nemo_asr.JasperDecoderForSpkrClass(
feat_in=spkr_params["JasperEncoder"]["jasper"][-1]["filters"],
num_classes=data_layer_train.num_classes,
pool_mode=spkr_params["JasperDecoderForSpkrClass"]['pool_mode'],
emb_sizes=spkr_params["JasperDecoderForSpkrClass"]["emb_sizes"].split(","),
)
xent_loss = nemo_asr.CrossEntropyLossNM(weight=None)
```
The next step is to assemble our training DAG by specifying the inputs to each neural module.
```
audio_signal, audio_signal_len, label, label_len = data_layer_train()
processed_signal, processed_signal_len = data_preprocessor(input_signal=audio_signal, length=audio_signal_len)
encoded, encoded_len = encoder(audio_signal=processed_signal, length=processed_signal_len)
logits, _ = decoder(encoder_output=encoded)
loss = xent_loss(logits=logits, labels=label)
```
We would like to be able to evaluate our model on the dev set, as well, so let's set up the evaluation DAG.
Our evaluation DAG will reuse most of the parts of the training DAG with the exception of the data layer, since we are loading the evaluation data from a different file but evaluating on the same model. Note that if we were using data augmentation in training, we would also leave that out in the evaluation DAG.
```
audio_signal_test, audio_len_test, label_test, _ = data_layer_eval()
processed_signal_test, processed_len_test = data_preprocessor(
input_signal=audio_signal_test, length=audio_len_test
)
encoded_test, encoded_len_test = encoder(audio_signal=processed_signal_test, length=processed_len_test)
logits_test, _ = decoder(encoder_output=encoded_test)
loss_test = xent_loss(logits=logits_test, labels=label_test)
```
# Creating CallBacks
We would like to be able to monitor our model while it's training, so we use callbacks. In general, callbacks are functions that are called at specific intervals over the course of training or inference, such as at the start or end of every n iterations, epochs, etc. The callbacks we'll be using for this are the SimpleLossLoggerCallback, which reports the training loss (or another metric of your choosing, such as \% accuracy for speaker recognition tasks), and the EvaluatorCallback, which regularly evaluates the model on the dev set. Both of these callbacks require you to pass in the tensors to be evaluated--these would be the final outputs of the training and eval DAGs above.
Another useful callback is the CheckpointCallback, for saving checkpoints at set intervals. We create one here just to demonstrate how it works.
```
from nemo.collections.asr.helpers import (
monitor_classification_training_progress,
process_classification_evaluation_batch,
process_classification_evaluation_epoch,
)
from nemo.utils.lr_policies import CosineAnnealing
train_callback = nemo.core.SimpleLossLoggerCallback(
tensors=[loss, logits, label],
print_func=partial(monitor_classification_training_progress, eval_metric=[1]),
step_freq=1000,
get_tb_values=lambda x: [("train_loss", x[0])],
tb_writer=neural_factory.tb_writer,
)
callbacks = [train_callback]
chpt_callback = nemo.core.CheckpointCallback(
folder="./myExps/checkpoints/" + exp_name,
load_from_folder="./myExps/checkpoints/" + exp_name,
step_freq=1000,
)
callbacks.append(chpt_callback)
tagname = "hi-mia_dev"
eval_callback = nemo.core.EvaluatorCallback(
eval_tensors=[loss_test, logits_test, label_test],
user_iter_callback=partial(process_classification_evaluation_batch, top_k=1),
user_epochs_done_callback=partial(process_classification_evaluation_epoch, tag=tagname),
eval_step=1000, # How often we evaluate the model on the test set
tb_writer=neural_factory.tb_writer,
)
callbacks.append(eval_callback)
```
Now that we have our model and callbacks set up, how do we run it?
Once we create our neural factory and the callbacks for the information that we want to see, we can start training by simply calling the train function on the tensors we want to optimize and our callbacks! Since this notebook is for you to get started, by an4 as dataset is small it would quickly get higher accuracies. For better models use bigger datasets
```
# train model
num_epochs=25
N = len(data_layer_train)
steps_per_epoch = N // batch_size
logging.info("Number of steps per epoch {}".format(steps_per_epoch))
neural_factory.train(
tensors_to_optimize=[loss],
callbacks=callbacks,
lr_policy=CosineAnnealing(
num_epochs * steps_per_epoch, warmup_steps=0.1 * num_epochs * steps_per_epoch,
),
optimizer="novograd",
optimization_params={
"num_epochs": num_epochs,
"lr": 0.02,
"betas": (0.95, 0.5),
"weight_decay": 0.001,
"grad_norm_clip": None,
}
)
```
Now that we trained our embeddings, we shall extract these embeddings using our pretrained checkpoint present at `checkpoint_dir`. As we can see from the neural architecture, we extract the embeddings after the `emb1` layer.

Now use the test manifest to get the embeddings. As we saw before, let's create a new `data_layer` for test. Use previously instiated models and attach the DAGs
```
eval_dl_params = copy.deepcopy(spkr_params["AudioToSpeechLabelDataLayer"])
eval_dl_params.update(spkr_params["AudioToSpeechLabelDataLayer"]["eval"])
del eval_dl_params["train"]
del eval_dl_params["eval"]
eval_dl_params['shuffle'] = False # To grab the file names without changing data_layer
test_dataset = data_dir+'/test/test_all.json',
data_layer_test = nemo_asr.AudioToSpeechLabelDataLayer(
manifest_filepath=test_dataset,
labels=None,
batch_size=batch_size,
**eval_dl_params,
)
audio_signal_test, audio_len_test, label_test, _ = data_layer_test()
processed_signal_test, processed_len_test = data_preprocessor(
input_signal=audio_signal_test, length=audio_len_test)
encoded_test, _ = encoder(audio_signal=processed_signal_test, length=processed_len_test)
_, embeddings = decoder(encoder_output=encoded_test)
```
Now get the embeddings using neural_factor infer command, that just does forward pass of all our modules. And save our embeddings in `<work_dir>/embeddings`
```
import numpy as np
import json
eval_tensors = neural_factory.infer(tensors=[embeddings, label_test], checkpoint_dir="./myExps/checkpoints/" + exp_name)
inf_emb, inf_label = eval_tensors
whole_embs = []
whole_labels = []
manifest = open(test_dataset, 'r').readlines()
for line in manifest:
line = line.strip()
dic = json.loads(line)
filename = dic['audio_filepath'].split('/')[-1]
whole_labels.append(filename)
for idx in range(len(inf_label)):
whole_embs.extend(inf_emb[idx].numpy())
embedding_dir = './myExps/embeddings/'
if not os.path.exists(embedding_dir):
os.mkdir(embedding_dir)
filename = os.path.basename(test_dataset).split('.')[0]
name = embedding_dir + filename
np.save(name + '.npy', np.asarray(whole_embs))
np.save(name + '_labels.npy', np.asarray(whole_labels))
logging.info("Saved embedding files to {}".format(embedding_dir))
!ls $embedding_dir
```
# Cosine Similarity Scoring
Here we provide a script scoring on hi-mia whose trial file has structure `<speaker_name1> <speaker_name2> <target/nontarget>` . First copy the `trails_1m` file present in test folder to our embeddings directory
```
!cp $data_dir/test/trails_1m $embedding_dir/
```
the below command would output the EER% based on cosine similarity score
```
!python examples/speaker_recognition/hi-mia_eval.py --data_root $embedding_dir --emb $embedding_dir/test_all.npy --emb_labels $embedding_dir/test_all_labels.npy --emb_size 1024
```
# PLDA Backend
To finetune our speaker embeddings further, we used kaldi PLDA scripts to train PLDA and evaluate as well. so from this point going forward, please make sure you installed kaldi and was added to your path as KALDI_ROOT.
To train PLDA, we can either use dev set or training set. Let's use the training set embeddings to train PLDA and further use this trained PLDA model to score in test embeddings. in order to do that we should get embeddings for our training data as well. As similar to above steps, generate the train embeddings
```
test_dataset = data_dir+'/train/train.json',
data_layer_test = nemo_asr.AudioToSpeechLabelDataLayer(
manifest_filepath=test_dataset,
labels=None,
batch_size=batch_size,
**eval_dl_params,
)
audio_signal_test, audio_len_test, label_test, _ = data_layer_test()
processed_signal_test, processed_len_test = data_preprocessor(
input_signal=audio_signal_test, length=audio_len_test)
encoded_test, _ = encoder(audio_signal=processed_signal_test, length=processed_len_test)
_, embeddings = decoder(encoder_output=encoded_test)
eval_tensors = neural_factory.infer(tensors=[embeddings, label_test], checkpoint_dir="./myExps/checkpoints/" + exp_name)
inf_emb, inf_label = eval_tensors
whole_embs = []
whole_labels = []
manifest = open(test_dataset, 'r').readlines()
for line in manifest:
line = line.strip()
dic = json.loads(line)
filename = dic['audio_filepath'].split('/')[-1]
whole_labels.append(filename)
for idx in range(len(inf_label)):
whole_embs.extend(inf_emb[idx].numpy())
if not os.path.exists(embedding_dir):
os.mkdir(embedding_dir)
filename = os.path.basename(test_dataset).split('.')[0]
name = embedding_dir + filename
np.save(name + '.npy', np.asarray(whole_embs))
np.save(name + '_labels.npy', np.asarray(whole_labels))
logging.info("Saved embedding files to {}".format(embedding_dir))
```
As part of kaldi necessary files we need `utt2spk` \& `spk2utt` file to get ark file for PLDA training. to do that, copy the generated utt2spk file from `data_dir` train folder to create spk2utt file using
`utt2spk_to_spk2utt.pl $data_dir/train/utt2spk > $embedding_dir/spk2utt`
Then run the below python script to get EER score using PLDA backend scoring. This script does both data preparation for kaldi followed by PLDA scoring.
```
!python examples/speaker_recognition/kaldi_plda.py --root $embedding_dir --train_embs $embedding_dir/train.npy --train_labels $embedding_dir/train_labels.npy
--eval_embs $embedding_dir/all_embs_himia.npy --eval_labels $embedding_dir/all_ids_himia.npy --stage=1
```
Here `--stage = 1` trains PLDA model but if you already have a trained PLDA then you can directly evaluate on it by `--stage=2` option.
This should output an EER of 6.32% with minDCF: 0.455
# Performance Improvement
To improve your embeddings performance:
* Add more data and Train longer (100 epochs)
* Try adding the augmentation –see config file
* Use larger model
* Train on several GPUs and use mixed precision (on NVIDIA Volta and Turing GPUs)
* Start with pre-trained checkpoints
| true |
code
| 0.61422 | null | null | null | null |
|
# Data Cleaning and Preprocessing for Sentiment Analysis
> Copyright 2019 Dave Fernandes. All Rights Reserved.
>
> Licensed under the Apache License, Version 2.0 (the "License");
> you may not use this file except in compliance with the License.
> You may obtain a copy of the License at
>
> http://www.apache.org/licenses/LICENSE-2.0
>
> Unless required by applicable law or agreed to in writing, software
> distributed under the License is distributed on an "AS IS" BASIS,
> WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
> See the License for the specific language governing permissions and
> limitations under the License.
Data files can be downloaded from: https://www.kaggle.com/snap/amazon-fine-food-reviews/version/2
```
import numpy as np
import pandas as pd
import tensorflow as tf
import os
import re
import datetime
INPUT_DIR = './data'
OUTPUT_DIR = './data/TFRecords'
TRAIN_REVIEW = 'train_review'
TRAIN_SUMMARY = 'train_summary'
TRAIN_SCORES = 'train_scores'
TEST_REVIEW = 'test_review'
TEST_SUMMARY = 'test_summary'
TEST_SCORES = 'test_scores'
def txt_path(filename):
return os.path.join(INPUT_DIR, filename + '.txt')
def rec_path(filename):
return os.path.join(OUTPUT_DIR, filename + '.tfrec')
```
### Load and clean review content
```
REVIEWS_CSV = './data/amazon-fine-food-reviews/Reviews.csv'
reviews = pd.read_csv(REVIEWS_CSV)
print('Initial count:', reviews.shape)
reviews.drop(['Id', 'ProfileName', 'Time'], axis=1, inplace=True)
reviews.dropna(axis=0, inplace=True)
print('Has all data:', reviews.shape)
reviews.drop_duplicates(subset=['ProductId', 'UserId'], keep='first', inplace=True)
reviews.drop(['ProductId', 'UserId'], axis=1, inplace=True)
print('No duplicates:', reviews.shape)
```
### Balance the scores
- Scores at the extremes should be equally represented.
- Somewhat lower counts for middle scores is OK.
```
balanced = None
for score in range(1, 6):
score_group = reviews[reviews['Score'] == score]
if score == 1:
balanced = score_group
max_count = balanced.shape[0]
else:
if score_group.shape[0] > max_count:
score_group = score_group.sample(max_count)
balanced = pd.concat([balanced, score_group], axis=0)
del reviews
print(balanced.groupby('Score').size())
```
### Create test and train sets
```
TEST_FRACTION = 0.2
shuffled = balanced.sample(frac=1, axis=0)
del balanced
n = int(shuffled.shape[0] * TEST_FRACTION)
test_frame = shuffled[0:n]
train_frame = shuffled[n:-1]
del shuffled
print('Test:', test_frame.groupby('Score').size())
print('Train:', train_frame.groupby('Score').size())
# Save human-readable files
test_frame.to_csv('./data/test.csv', index=False)
train_frame.to_csv('./data/train.csv', index=False)
```
Save intermediate text files for processing into BERT feature vectors.
```
def write_column(column, file_path):
def clean_html(s):
clean_fn = re.compile('<.*?>')
return re.sub(clean_fn, '', s)
with open(file_path, 'w') as file:
text_list = column.apply(clean_html).values
for item in text_list:
file.write(item)
file.write('\n')
write_column(train_frame['Text'], txt_path(TRAIN_REVIEW))
write_column(train_frame['Summary'], txt_path(TRAIN_SUMMARY))
write_column(test_frame['Text'], txt_path(TEST_REVIEW))
write_column(test_frame['Summary'], txt_path(TEST_SUMMARY))
```
Save numerical columns in a TFRecord file.
```
def _int64_feature(value):
return tf.train.Feature(int64_list=tf.train.Int64List(value=[value]))
def _float_vector_feature(values):
return tf.train.Feature(float_list=tf.train.FloatList(value=values))
def _float_feature(value):
return _float_vector_feature([value])
def _bytes_feature(value):
return tf.train.Feature(bytes_list=tf.train.BytesList(value=[value]))
def _string_feature(value):
return _bytes_feature(value.encode('utf-8'))
def write_values(filename, data_frame):
with tf.python_io.TFRecordWriter(filename) as writer:
for index, row in data_frame.iterrows():
score = row['Score']
votes = row['HelpfulnessDenominator']
upvotes = row['HelpfulnessNumerator']
helpfulness = float(upvotes) / float(votes) if votes > 0 else 0.0
example = tf.train.Example(
features=tf.train.Features(
feature={
'score': _int64_feature(score),
'votes': _int64_feature(votes),
'helpfulness': _float_feature(helpfulness),
}))
writer.write(example.SerializeToString())
write_values(rec_path(TEST_SCORES), test_frame)
write_values(rec_path(TRAIN_SCORES), train_frame)
del test_frame
del train_frame
```
- First download the BERT model from: https://storage.googleapis.com/bert_models/2018_10_18/uncased_L-12_H-768_A-12.zip
- Unzip this file into the same directory as the `extract_features.py` script.
- Either run the feature extractor from the cell below; or,
- You can also run it from the command line: (you will have to repeat this for each of the 4 text files to be processed)
```
python extract_features.py \
--input_file=./data/train_text.txt \
--output_file=./data/train_text.tfrec \
--bert_model_dir=./uncased_L-12_H-768_A-12
```
- For running on a TPU, your files should be in Google Cloud Storage (`gs://my_bucket/filename`).
- And, add the following arguments to the above command:
```
--use_one_hot_embeddings=True
--tpu_name=<my_TPU_name>
--gcp_zone=<us-central1-b>
--gcp_project=<my_project_name>
```
- Finally, for the review files, allow text sequences to be processed (summary files can use the default 128):
```
--max_seq_length=512
```
This takes about 1 hour on an 8-core TPU. It will take a lot longer on GPU or CPU.
```
from extract_features import extract
MODEL_DIR = './uncased_L-12_H-768_A-12'
extract(input_file=txt_path(TEST_REVIEW), output_file=rec_path(TEST_REVIEW), bert_model_dir=MODEL_DIR, max_seq_length=512)
extract(input_file=txt_path(TEST_SUMMARY), output_file=rec_path(TEST_SUMMARY), bert_model_dir=MODEL_DIR)
extract(input_file=txt_path(TRAIN_REVIEW), output_file=rec_path(TRAIN_REVIEW), bert_model_dir=MODEL_DIR, max_seq_length=512)
extract(input_file=txt_path(TRAIN_SUMMARY), output_file=rec_path(TRAIN_SUMMARY), bert_model_dir=MODEL_DIR)
```
## Next
Run the `Regression.ipynb` notebook next...
| true |
code
| 0.391086 | null | null | null | null |
|
# tensorflow2.0教程-文本分类
我们将构建一个简单的文本分类器,并使用IMDB进行训练和测试
```
from __future__ import absolute_import, division, print_function
import tensorflow as tf
from tensorflow import keras
import numpy as np
print(tf.__version__)
```
## 1.IMDB数据集
下载
```
imdb=keras.datasets.imdb
(train_x, train_y), (test_x, text_y)=keras.datasets.imdb.load_data(num_words=10000)
```
了解IMDB数据
```
print("Training entries: {}, labels: {}".format(len(train_x), len(train_y)))
print(train_x[0])
print('len: ',len(train_x[0]), len(train_x[1]))
```
创建id和词的匹配字典
```
word_index = imdb.get_word_index()
word2id = {k:(v+3) for k, v in word_index.items()}
word2id['<PAD>'] = 0
word2id['<START>'] = 1
word2id['<UNK>'] = 2
word2id['<UNUSED>'] = 3
id2word = {v:k for k, v in word2id.items()}
def get_words(sent_ids):
return ' '.join([id2word.get(i, '?') for i in sent_ids])
sent = get_words(train_x[0])
print(sent)
```
## 2.准备数据
```
# 句子末尾padding
train_x = keras.preprocessing.sequence.pad_sequences(
train_x, value=word2id['<PAD>'],
padding='post', maxlen=256
)
test_x = keras.preprocessing.sequence.pad_sequences(
test_x, value=word2id['<PAD>'],
padding='post', maxlen=256
)
print(train_x[0])
print('len: ',len(train_x[0]), len(train_x[1]))
```
## 3.构建模型
```
import tensorflow.keras.layers as layers
vocab_size = 10000
model = keras.Sequential()
model.add(layers.Embedding(vocab_size, 16))
model.add(layers.GlobalAveragePooling1D())
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.summary()
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
```
## 4.模型训练与验证
```
x_val = train_x[:10000]
x_train = train_x[10000:]
y_val = train_y[:10000]
y_train = train_y[10000:]
history = model.fit(x_train,y_train,
epochs=40, batch_size=512,
validation_data=(x_val, y_val),
verbose=1)
result = model.evaluate(test_x, text_y)
print(result)
```
## 5.查看准确率时序图
```
import matplotlib.pyplot as plt
history_dict = history.history
history_dict.keys()
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
loss = history_dict['loss']
val_loss = history_dict['val_loss']
epochs = range(1, len(acc)+1)
plt.plot(epochs, loss, 'bo', label='train loss')
plt.plot(epochs, val_loss, 'b', label='val loss')
plt.title('Train and val loss')
plt.xlabel('Epochs')
plt.xlabel('loss')
plt.legend()
plt.show()
plt.clf() # clear figure
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
```
| true |
code
| 0.720294 | null | null | null | null |
|
# The atoms of computation
## Introduction
Programming a quantum computer is now something that anyone can do in the comfort of their own home. But what to create? What is a quantum program anyway? In fact, what is a quantum computer?
These questions can be answered by making comparisons to traditional digital computers. Unfortunately, most people don’t actually understand how traditional digital computers work either. On this page, we’ll look at the basic principles behind these traditional devices, and to help us transition over to quantum computing later on, we’ll do it using the same tools we'll use with quantum computers.
## Splitting information into bits
The first thing we need to know about is the idea of _bits_. These are designed to be the world’s simplest alphabet. With only two symbols, 0 and 1, we can represent any piece of information.
One example is numbers. You are probably used to representing a number through a [string](gloss:string) of the ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. In this string of digits, each digit represents how many times the number contains a certain [power](gloss:power) of ten. For example, when we write 213, we mean:
$$ 200+10+3 $$
or, expressed in a way that emphasizes the powers of ten
$$ (2×10^2)+(1×10^1)+(3×10^0) $$
Though we usually use this system based on the number 10, we can just as easily use one based on any other number. The binary number system, for example, is based on the number two. This means using the two characters 0 and 1 to express numbers as multiples of powers of two. For example, 213 becomes 11010101, since:
$$
\begin{aligned}
213 = & \phantom{+}(1×2^7)+(1×2^6)+(0×2^5)\\
& +(1×2^4)+(0×2^3)+(1×2^2)\\
& +(0×2^1)+(1×2^0) \\
\end{aligned}
$$
In this we are expressing numbers as multiples of 2, 4, 8, 16, 32, etc. instead of 10, 100, 1000, etc.
<!-- ::: q-block.binary -->
### Try it
q-binary
<!-- ::: -->
These strings of bits, known as binary strings, can be used to represent more than just numbers. For example, there is a way to represent any text using bits. For any letter, number, or punctuation mark you want to use, you can find a corresponding string of at most eight bits using [this table](https://www.ibm.com/docs/en/aix/7.2?topic=adapters-ascii-decimal-hexadecimal-octal-binary-conversion-table). Though these are quite arbitrary, this is a widely agreed-upon standard. In fact, it's what was used to transmit this article to you through the internet.
This is how all information is represented in conventional computers. Whether numbers, letters, images, or sound, it all exists in the form of binary strings.
Like our standard digital computers, quantum computers are based on this same basic idea. The main difference is that they use _qubits,_ an extension of the bit to [quantum mechanics](gloss:quantum-mechanics). In the rest of this textbook, we will explore what qubits are, what they can do, and how they do it. In this section, however, we are not talking about quantum at all. So, we just use qubits as if they were bits.
<!-- ::: q-block.exercise -->
### Quick quiz
<!-- ::: q-quiz(goal="intro-aoc-1") -->
<!-- ::: .question -->
If you have $n$ bits, how many different numbers could you write down?
<!-- ::: -->
<!-- ::: .option -->
1. $n$
<!-- ::: -->
<!-- ::: .option -->
2. $n^2$
<!-- ::: -->
<!-- ::: .option(correct) -->
3. $2^n$
<!-- ::: -->
<!-- ::: -->
<!-- ::: -->
## Circuit diagrams
We saw in the last page that a computation takes some input data and performs operations on this to produce some output data. With the quantum computers we’ll learn about in this textbook, this data will always be in the form of bits. Now we know what bits are, let’s see how we can manipulate them in order to turn the inputs we have into the outputs we need.
It’s often useful to represent this process in a diagram known as a _circuit diagram_. These diagrams have inputs on the left, outputs on the right, and operations represented by arcane symbols in between. These operations are called 'gates', mostly for historical reasons. Here's an example of what a circuit looks like for standard, bit-based computers. You aren't expected to understand what it does. It should simply give you an idea of what these circuits look like.

For quantum computers, we use the same basic idea but have different conventions for how to represent inputs, outputs, and the symbols used for operations. Here is the “quantum circuit” that represents the same process as above.

In the rest of this section, we will explain how to build quantum circuits. At the end, you'll know how to create the circuit above, what it does, and why it's useful.
## Creating circuits with Qiskit
To create a quantum circuit, we will import the <code>QuantumCircuit</code> class, and create a new <code>QuantumCircuit</code> object.
<!-- ::: q-block.reminder -->
### Reminder
<details>
<summary>Python basics (what’s all this about classes and objects?)</summary>
We know we can describe all information using a bunch of bits, which is how computers store and process everything, including quantum circuits! But it’s difficult for us humans to think about how we do this, and how we manipulate those bits to represent the circuits we want.
The <code>QuantumCircuit</code> class is a set of instructions for representing quantum circuits as bits. The line <code>qc = QuantumCircuit(4, 2)</code> in the cell below is a constructor, which tells Python to set aside some bits in your computer that we’ll use to represent a quantum circuit. When we want to refer to this quantum circuit (or rather, the bits that represent this quantum circuit) we’ll use the variable ‘<code>qc</code>’. We say ‘<code>qc</code>’ refers to a "<code>QuantumCircuit</code> object".
This allows us humans to think about quantum circuits at a high, abstract level; we can say things like “add an X-gate” and Qiskit will take care of what we need to do to the bits in our computer to reflect this change.
</details>
<!-- ::: -->
On creating a quantum circuit, we need to tell [Python](gloss:python) how many qubits our circuit should have, and we can optionally also tell it how many classical bits our circuit should have. We need classical bits to store the measurements of our qubits, the reason for this will become clear later in this course.
## Your first quantum circuit
In a circuit, we typically need to do three jobs: First, encode the input, then do some actual computation, and finally extract an output. For your first quantum circuit, we'll focus on the last of these jobs. We start by creating a quantum circuit with 3 qubits and 3 outputs.
```
from qiskit import QuantumCircuit
# Create quantum circuit with 3 qubits and 3 classical bits
# (we'll explain why we need the classical bits later)
qc = QuantumCircuit(3, 3)
qc.draw() # returns a drawing of the circuit
```
Finally the method <code>qc.draw()</code> creates a drawing of the circuit for us. Jupyter Notebooks evaluate the last line of a code cell and display it below the cell. Since <code>qc.draw()</code> [returns](gloss:return) a drawing, that’s what we’re seeing under the code. There are no gates in our circuit yet, so we just see some horizontal lines.
<!-- ::: q-block.reminder -->
### Reminder
<details>
<summary>Python basics (what’s a method?)</summary>
The <code>QuantumCircuit</code> class is a set of instructions for representing quantum circuits as bits, but when we want to change one of these circuits, we also need to know how to change the bits accordingly. In [Python](gloss:python), objects come with ‘methods’, which are sets of instructions for doing something with that object. In the cell above, the <code>.draw()</code> method looks at the circuit we’ve created and produces a human-readable drawing of that circuit.
</details>
<!-- ::: -->
Next, we need a way to tell our quantum computer to measure our qubits and record the results. To do this, we add a "measure" operation to our quantum circuit. We can do this with the `QuantumCircuit`'s `.measure()` method.
```
from qiskit import QuantumCircuit
qc = QuantumCircuit(3, 3)
# measure qubits 0, 1 & 2 to classical bits 0, 1 & 2 respectively
qc.measure([0,1,2], [0,1,2])
qc.draw()
```
Next, let's see what the results of running this circuit would be. To do this, we'll use a quantum simulator, which is a standard computer calculating what an ideal quantum computer would do. Because simulating a quantum computer is believed to be difficult for classical computers (the best algorithms we have grow exponentially with the number of qubits), these simulations are only possible for circuits with small numbers of qubits (up to ~30 qubits), or certain types of circuits for which we can use some tricks to speed up the simulation. Simulators are very useful tools for designing smaller quantum circuits.
Let's import Qiskit’s simulator (called Aer), and make a new simulator object.
```
from qiskit.providers.aer import AerSimulator
sim = AerSimulator() # make new simulator object
```
To do the simulation, we can use the simulators <code>.run()</code> method. This returns a "job", which contains information about the experiment, such as whether the experiment is running or completed, what backend we ran the experiment on, and importantly for us, what the results of the experiment are!
To get the results from the job, we use the results method, and the most popular way to view the results is as a dictionary of "counts".
```
job = sim.run(qc) # run the experiment
result = job.result() # get the results
result.get_counts() # interpret the results as a "counts" dictionary
```
The keys in counts dictionary are bit-strings, and the values are the number of times that bit-string was measured. Quantum computers can have randomness in their results, so it's common to repeat the circuit a few times. This circuit was repeated 1024 times, which is the default number of times to repeat a circuit in Qiskit. By convention, qubits always start in the state `0`, and since we are doing nothing to them before measurement, the results are always `0`.
### Encoding an input
Now let's look at how to encode a different binary string as an input. For this, we need what is known as a NOT gate. This is the most basic operation that you can do in a computer. It simply flips the bit value: 0 becomes 1 and 1 becomes 0. For qubits, we use a gate known as the _X-gate_ for this.
Below, we’ll create a new circuit dedicated to the job of encoding:
```
# Create quantum circuit with 3 qubits and 3 classical bits:
qc = QuantumCircuit(3, 3)
qc.x([0,1]) # Perform X-gates on qubits 0 & 1
qc.measure([0,1,2], [0,1,2])
qc.draw() # returns a drawing of the circuit
```
And let's simulate our circuit to see the results:
```
job = sim.run(qc) # run the experiment
result = job.result() # get the results
result.get_counts() # interpret the results as a "counts" dictionary
```
<!-- ::: q-block.exercise -->
### Quick quiz
<!-- ::: q-quiz(goal="intro-aoc-2") -->
<!-- ::: .question -->
What is the binary number `011` in decimal?
<!-- ::: -->
<!-- ::: .option -->
1. 5
<!-- ::: -->
<!-- ::: .option -->
2. 2
<!-- ::: -->
<!-- ::: .option(correct) -->
3. 3
<!-- ::: -->
<!-- ::: -->
Modify the code above to create a quantum circuit that encodes the numbers 6 and 4. Are the results what you'd expect?
<!-- ::: -->
Now we know how to encode information in a computer. The next step is to process it: To take an input that we have encoded, and turn it into an output that tells us something new.
## Creating an adder circuit
### Remembering how to add
To look at turning inputs into outputs, we need a problem to solve. Let’s do some basic maths. In primary school, you will have learned how to take large mathematical problems and break them down into manageable pieces. For example, how would you go about solving this addition problem?
<!-- ::: q-block -->
### Remembering how to add
<!-- ::: q-carousel -->
<!-- ::: div -->

How can we solve a problem like this? Click through this carousel to find out.
<!-- ::: -->
<!-- ::: div -->

One way is to do it digit by digit, from right to left. So we start with 3+4.
<!-- ::: -->
<!-- ::: div -->

And then 1+5.
<!-- ::: -->
<!-- ::: div -->

Then 2+8.
<!-- ::: -->
<!-- ::: div -->

Finally we have 9+1+1, and get our answer.
<!-- ::: -->
<!-- ::: -->
<!-- ::: -->
This may just be simple addition, but it demonstrates the principles behind all algorithms. Whether the algorithm is designed to solve mathematical problems or process text or images, we always break big tasks down into small and simple steps.
To run on a computer, algorithms need to be compiled down to the smallest and simplest steps possible. To see what these look like, let’s do the above addition problem again but in binary.
<!-- ::: q-block -->
### Adding binary numbers
<!-- ::: q-carousel -->
<!-- ::: div -->

Note that the second number has a bunch of extra 0s on the left. This just serves to make the two strings the same length.
<!-- ::: -->
<!-- ::: div -->

Our first task is to do the 1+0 for the column on the right. In binary, as in any number system, the answer is 1.
<!-- ::: -->
<!-- ::: div -->

We get the same result for the 0+1 of the second column.
<!-- ::: -->
<!-- ::: div -->

Next, we have 1+1. As you’ll surely be aware, 1+1=2. In binary, the number 2 is written 10, and so requires two bits. This means that we need to carry the 1, just as we would for the number 10 in decimal. The next column now requires us to calculate 1+1+1. This means adding three numbers together, so things are getting complicated for our computer.
<!-- ::: -->
<!-- ::: div -->

But we can still compile it down to simpler operations, and do it in a way that only ever requires us to add two bits together. For this, we can start with just the first two 1s.
<!-- ::: -->
<!-- ::: div -->

Now we need to add this 10 to the final 1 , which can be done using our usual method of going through the columns. The final answer is 11 (also known as 3).
<!-- ::: -->
<!-- ::: div -->

Now we can get back to the rest of the problem. With the answer of 11, we have another carry bit. So now we have another 1+1+1 to do. But we already know how to do that, so it’s not a big deal.
<!-- ::: -->
<!-- ::: div -->
In fact, everything left so far is something we already know how to do. This is because, if you break everything down into adding just two bits, there are only four possible things you’ll ever need to calculate. Here are the four basic sums (we’ll write all the answers with two bits to be consistent):

This is called a half adder. If our computer can implement this, and if it can chain many of them together, it can add anything.
<!-- ::: -->
<!-- ::: -->
<!-- ::: -->
### Adding with quantum circuits
Let's make our own half adder from a quantum circuit. This will include a part of the circuit that encodes the input, a part that executes the algorithm, and a part that extracts the result. The first part will need to be changed whenever we want to use a new input, but the rest will always remain the same.

The two bits we want to add are encoded in the qubits 0 and 1. The above example encodes a 1 in both these qubits, and so it seeks to find the solution of 1+1. The result will be a string of two bits, which we will read out from the qubits 2 and 3. All that remains is to fill in the actual program, which lives in the blank space in the middle.
The dashed lines in the image are just to distinguish the different parts of the circuit (although they can have more interesting uses too)
The basic operations of computing are known as logic gates. We’ve already used the NOT gate, but this is not enough to make our half adder. We could only use it to manually write out the answers. Since we want the computer to do the actual computing for us, we’ll need some more powerful gates.
To see what we need, let’s take another look at what our half adder needs to do.

The rightmost bit in all four of these answers is completely determined by whether the two bits we are adding are the same or different. So for 0+0 and 1+1, where the two bits are equal, the rightmost bit of the answer comes out 0. For 0+1 and 1+0, where we are adding different bit values, the rightmost bit is 1.
To get this part of our solution correct, we need something that can figure out whether two bits are different or not. Traditionally, in the study of digital computation, this is called an XOR gate.
<table>
<thead>
<tr>
<th>Input 1</th>
<th>Input 2</th>
<th>XOR Output</th>
</tr>
</thead>
<tbody>
<tr>
<td>0</td>
<td>0</td>
<td>0</td>
</tr>
<tr>
<td>0</td>
<td>1</td>
<td>1</td>
</tr>
<tr>
<td>1</td>
<td>0</td>
<td>1</td>
</tr>
<tr>
<td>1</td>
<td>1</td>
<td>0</td>
</tr>
</tbody>
</table>
In quantum computers, the job of the XOR gate is done by the ‘controlled-NOT gate’. Since that's quite a long name, we usually just call it the ‘CNOT’. In circuit diagrams, it is drawn as in the image below. This is applied to a pair of qubits. One acts as the control qubit (this is the one with the little dot). The other acts as the target qubit (with the big circle and cross - kind of like a target mark).

In Qiskit, we can use the `.cx()` method to add a CNOT to our circuit. We need to give the indices of the two qubits it acts on as arguments. Here's an example:
```
# Create quantum circuit with 2 qubits and 2 classical bits
qc = QuantumCircuit(2, 2)
qc.x(0)
qc.cx(0,1) # CNOT controlled by qubit 0 and targeting qubit 1
qc.measure([0,1], [0,1])
display(qc.draw()) # display a drawing of the circuit
job = sim.run(qc) # run the experiment
result = job.result() # get the results
# interpret the results as a "counts" dictionary
print("Result: ", result.get_counts())
```
For our half adder, we don’t want to overwrite one of our inputs. Instead, we want to write the result on a different pair of qubits. For this, we can use two CNOTs and write the output to a new qubit which we know will be in the state 0:

We are now halfway to a fully working half adder. We know how to calculate the rightmost output bit, so we just need to work out how to calculate the left output bit. If you look again at the four possible sums, you’ll notice that there is only one case for which this is 1 instead of 0: 1+1=10. It happens only when both the bits we are adding are 1.

To calculate this part of the output, we could just get our computer to look at whether both of the inputs are 1. If they are — and only if they are — we need to do a NOT gate on qubit 3. That will flip it to the required value of 1 for this case only, giving us the output we need.
For this, we need a new gate: like a CNOT but controlled on two qubits instead of just one. This will perform a NOT on the target qubit only when both controls are in state 1. This new gate is called the [Toffoli](gloss:toffoli) gate. For those of you who are familiar with Boolean logic gates, it is basically an AND gate.

In Qiskit, we can add this to a circuit using the `.ccx()` method. And there we have it! A circuit that can compute the famous mathematical problem of 1+1.
<!-- ::: q-block.exercise -->
### Try it
Arrange the blocks to create the code block that would produce the half-adder circuit above.
q-drag-and-drop-code(goal="intro-aoc-3")
.line from qiskit import QuantumCircuit
.line qc = QuantumCircuit(4, 2)
.line(group=0) qc.cx(0, 2)
.line(group=0) qc.cx(1, 2)
.line(group=0) qc.ccx(0, 1, 3)
.result-info
<!-- ::: -->
Great! Now we have our half adder, the next thing to do it to check that it works. To do this, we’ll create another circuit that encodes some input, applies the half adder, and extracts the output.
```
test_qc = QuantumCircuit(4, 2)
# First, our circuit should encode an input (here '11')
test_qc.x(0)
test_qc.x(1)
# Next, it should carry out the adder circuit we created
test_qc.cx(0,2)
test_qc.cx(1,2)
test_qc.ccx(0,1,3)
# Finally, we will measure the bottom two qubits to extract the output
test_qc.measure(2,0)
test_qc.measure(3,1)
test_qc.draw()
job = sim.run(test_qc) # run the experiment
result = job.result() # get the results
result.get_counts() # interpret the results as a “counts” dictionary
```
Here we can see that the result ‘10’ was measured 1024 times, and we didn’t measure any other result.
<!-- ::: q-block.exercise -->
### Exercise
Verify the half adder circuit works for all four possible inputs.
[Try in IBM Quantum Lab](https://quantum-computing.ibm.com/lab)
<!-- ::: -->
The half adder contains everything you need for addition. With the NOT, CNOT, and Toffoli gates, we can create programs that add any set of numbers of any size.
These three gates are enough to do everything else in computing too. In fact, we can even do without the CNOT. Additionally, the NOT gate is only really needed to create bits with value 1. The Toffoli gate is essentially the atom of mathematics. It is the simplest element, from which every other problem-solving technique can be compiled.
| true |
code
| 0.78315 | null | null | null | null |
|
<small><i>This notebook was put together by [Jake Vanderplas](http://www.vanderplas.com). Source and license info is on [GitHub](https://github.com/jakevdp/sklearn_tutorial/).</i></small>
# Density Estimation: Gaussian Mixture Models
Here we'll explore **Gaussian Mixture Models**, which is an unsupervised clustering & density estimation technique.
We'll start with our standard set of initial imports
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
plt.style.use('seaborn')
```
## Introducing Gaussian Mixture Models
We previously saw an example of K-Means, which is a clustering algorithm which is most often fit using an expectation-maximization approach.
Here we'll consider an extension to this which is suitable for both **clustering** and **density estimation**.
For example, imagine we have some one-dimensional data in a particular distribution:
```
np.random.seed(2)
x = np.concatenate([np.random.normal(0, 2, 2000),
np.random.normal(5, 5, 2000),
np.random.normal(3, 0.5, 600)])
plt.hist(x, 80, normed=True)
plt.xlim(-10, 20);
```
Gaussian mixture models will allow us to approximate this density:
```
from sklearn.mixture import GMM
X = x[:, np.newaxis]
clf = GMM(4, n_iter=500, random_state=3).fit(X)
xpdf = np.linspace(-10, 20, 1000)
density = np.exp(clf.score(xpdf[:, np.newaxis]))
plt.hist(x, 80, normed=True, alpha=0.5)
plt.plot(xpdf, density, '-r')
plt.xlim(-10, 20);
```
Note that this density is fit using a **mixture of Gaussians**, which we can examine by looking at the ``means_``, ``covars_``, and ``weights_`` attributes:
```
clf.means_
clf.covars_
clf.weights_
plt.hist(x, 80, normed=True, alpha=0.3)
plt.plot(xpdf, density, '-r')
for i in range(clf.n_components):
pdf = clf.weights_[i] * stats.norm(clf.means_[i, 0],
np.sqrt(clf.covars_[i, 0])).pdf(xpdf)
plt.fill(xpdf, pdf, facecolor='gray',
edgecolor='none', alpha=0.3)
plt.xlim(-10, 20);
```
These individual Gaussian distributions are fit using an expectation-maximization method, much as in K means, except that rather than explicit cluster assignment, the **posterior probability** is used to compute the weighted mean and covariance.
Somewhat surprisingly, this algorithm **provably** converges to the optimum (though the optimum is not necessarily global).
## How many Gaussians?
Given a model, we can use one of several means to evaluate how well it fits the data.
For example, there is the Aikaki Information Criterion (AIC) and the Bayesian Information Criterion (BIC)
```
print(clf.bic(X))
print(clf.aic(X))
```
Let's take a look at these as a function of the number of gaussians:
```
n_estimators = np.arange(1, 10)
clfs = [GMM(n, n_iter=1000).fit(X) for n in n_estimators]
bics = [clf.bic(X) for clf in clfs]
aics = [clf.aic(X) for clf in clfs]
plt.plot(n_estimators, bics, label='BIC')
plt.plot(n_estimators, aics, label='AIC')
plt.legend();
```
It appears that for both the AIC and BIC, 4 components is preferred.
## Example: GMM For Outlier Detection
GMM is what's known as a **Generative Model**: it's a probabilistic model from which a dataset can be generated.
One thing that generative models can be useful for is **outlier detection**: we can simply evaluate the likelihood of each point under the generative model; the points with a suitably low likelihood (where "suitable" is up to your own bias/variance preference) can be labeld outliers.
Let's take a look at this by defining a new dataset with some outliers:
```
np.random.seed(0)
# Add 20 outliers
true_outliers = np.sort(np.random.randint(0, len(x), 20))
y = x.copy()
y[true_outliers] += 50 * np.random.randn(20)
clf = GMM(4, n_iter=500, random_state=0).fit(y[:, np.newaxis])
xpdf = np.linspace(-10, 20, 1000)
density_noise = np.exp(clf.score(xpdf[:, np.newaxis]))
plt.hist(y, 80, normed=True, alpha=0.5)
plt.plot(xpdf, density_noise, '-r')
plt.xlim(-15, 30);
```
Now let's evaluate the log-likelihood of each point under the model, and plot these as a function of ``y``:
```
log_likelihood = clf.score_samples(y[:, np.newaxis])[0]
plt.plot(y, log_likelihood, '.k');
detected_outliers = np.where(log_likelihood < -9)[0]
print("true outliers:")
print(true_outliers)
print("\ndetected outliers:")
print(detected_outliers)
```
The algorithm misses a few of these points, which is to be expected (some of the "outliers" actually land in the middle of the distribution!)
Here are the outliers that were missed:
```
set(true_outliers) - set(detected_outliers)
```
And here are the non-outliers which were spuriously labeled outliers:
```
set(detected_outliers) - set(true_outliers)
```
Finally, we should note that although all of the above is done in one dimension, GMM does generalize to multiple dimensions, as we'll see in the breakout session.
## Other Density Estimators
The other main density estimator that you might find useful is *Kernel Density Estimation*, which is available via ``sklearn.neighbors.KernelDensity``. In some ways, this can be thought of as a generalization of GMM where there is a gaussian placed at the location of *every* training point!
```
from sklearn.neighbors import KernelDensity
kde = KernelDensity(0.15).fit(x[:, None])
density_kde = np.exp(kde.score_samples(xpdf[:, None]))
plt.hist(x, 80, density=True, alpha=0.5)
plt.plot(xpdf, density, '-b', label='GMM')
plt.plot(xpdf, density_kde, '-r', label='KDE')
plt.xlim(-10, 20)
plt.legend();
```
All of these density estimators can be viewed as **Generative models** of the data: that is, that is, the model tells us how more data can be created which fits the model.
| true |
code
| 0.675831 | null | null | null | null |
|
# Solving the heat equation
[AMath 586, Spring Quarter 2019](http://staff.washington.edu/rjl/classes/am586s2019/) at the University of Washington. For other notebooks, see [Index.ipynb](Index.ipynb) or the [Index of all notebooks on Github](https://github.com/rjleveque/amath586s2019/blob/master/notebooks/Index.ipynb).
Sample program to solve the heat equation with the Crank-Nicolson method.
We solve the heat equation $u_t = \kappa u_{xx}$ on the interval $0\leq x \leq 1$ with Dirichlet boundary conditions $u(0,t) = g_0(t)$ and $u(1,t) = g_1(t)$.
To test accuracy, we use cases where an exact solution to the heat equation for all $x$ is known. This `utrue` function is used to set initial conditions. It is also used in each time step to set boundary values on whatever finite interval we consider.
```
%pylab inline
from matplotlib import animation
from IPython.display import HTML
def make_animation(hs_input, hs_output, nplot=1):
"""
Plot every `nplot` frames of the solution and turn into
an animation.
"""
xfine = linspace(hs_input.ax,hs_input.bx,1001)
fig, ax = plt.subplots()
ax.set_xlim((hs_input.ax,hs_input.bx))
#ax.set_ylim((-0.2, 1.2))
ax.set_ylim((-1.2, 1.2))
line1, = ax.plot([], [], '+-', color='b', lw=2, label='computed')
line2, = ax.plot([], [], color='r', lw=1, label='true')
ax.legend()
title1 = ax.set_title('')
def init():
line1.set_data(hs_output.x_computed, hs_output.u_computed[:,0])
line2.set_data(xfine, hs_input.utrue(xfine, hs_input.t0))
title1.set_text('time t = %8.4f' % hs_input.t0)
return (line1,line2,title1)
def animate(n):
line1.set_data(hs_output.x_computed, hs_output.u_computed[:,n])
line2.set_data(xfine, hs_input.utrue(xfine, hs_output.t[n]))
title1.set_text('time t = %8.4f' % hs_output.t[n])
return (line1,line2,title1)
frames = range(0, len(hs_output.t), nplot) # which frames to plot
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=frames,
interval=200,
blit=True)
close('all') # so one last frame plot doesn't remain
return anim
class HeatSolutionInput(object):
def __init__(self):
# inputs:
self.t0 = 0.
self.tfinal = 1.
self.ax = 0.
self.bx = 1.
self.mx = 39.
self.utrue = None
self.kappa = 0.02
self.nsteps = 10
class HeatSolutionOutput(object):
def __init__(self):
# outputs:
self.h = None
self.dt = None
self.t = None
self.x_computed = None
self.u_computed = None
self.errors = None
```
## Forward Euler time stepping
```
def heat_FE(heat_solution_input):
"""
Solve u_t = kappa * u_{xx} on [ax,bx] with Dirichlet boundary conditions,
using centered differences in space and the Forward Euler method for time stepping,
with m interior points, taking nsteps time steps.
Input:
`heat_solution_input` should be on object of class `HeatSolutionInput`
specifying inputs.
Output:
an object of class `HeatSolutionOutput` with the solution and other info.
This routine can be embedded in a loop on m to test the accuracy.
Note: the vector x defined below is of length m+2 and includes both boundary points.
The vector uint is of length m and is only the interior points that we solve for,
by solving an m by m linear system each time step.
The vector u is of length m+2 and obtained by extending uint with the boundary values,
so that plotting (x,u) includes the boundary values.
"""
# unpack the inputs for brevity:
ax = heat_solution_input.ax
bx = heat_solution_input.bx
kappa = heat_solution_input.kappa
m = heat_solution_input.mx
utrue = heat_solution_input.utrue
t0 = heat_solution_input.t0
tfinal = heat_solution_input.tfinal
nsteps = heat_solution_input.nsteps
h = (bx-ax)/float(m+1) # h = delta x
x = linspace(ax,bx,m+2) # note x(1)=0 and x(m+2)=1
# u(1)=g0 and u(m+2)=g1 are known from BC's
dt = (tfinal - t0) / float(nsteps)
# initial conditions:
u0 = utrue(x,t0)
# initialize u and plot:
tn = 0
u = u0
t = empty((nsteps+1,), dtype=float)
errors = empty((nsteps+1,), dtype=float)
u_computed = empty((m+2,nsteps+1), dtype=float)
t[0] = tn
errors[0] = 0.
u_computed[:,0] = u0
# main time-stepping loop:
for n in range(1,nsteps+1):
tnp = tn + dt # = t_{n+1}
# indices of interior points as in integer numpy array:
jint = array(range(1,m+1), dtype=int)
# Then the numerical method can be written without a loop
# or matrix-vector multiply:
u[jint] = u[jint] + kappa * dt/h**2 * (u[jint-1] - 2*u[jint] + u[jint+1])
# evaluate true solution to get new boundary values at tnp:
g0np = utrue(ax,tnp)
g1np = utrue(bx,tnp)
# augment with boundary values:
u[0] = g0np
u[-1] = g1np
error = abs(u-utrue(x,tnp)).max() # max norm
t[n] = tnp
u_computed[:,n] = u
errors[n] = error
tn = tnp # for next time step
heat_solution_output = HeatSolutionOutput() # create object for output
heat_solution_output.dt = dt
heat_solution_output.h = h
heat_solution_output.t = t
heat_solution_output.x_computed = x
heat_solution_output.u_computed = u_computed
heat_solution_output.errors = errors
return heat_solution_output
```
## A smooth solution
We first use the decaying Gaussian
$$
u(x,t) = \frac{1}{\sqrt{4\beta\kappa t + 1}} \exp\left(\frac{-(x-x_0)^2}{4\kappa t + 1/\beta}\right).
$$
The initial data and boundary conditions are obtained by evaluating this function at $t=0$ or at $x=0$ or $x=1$. In particular, the initial conditions are simply
$$
u(x,0) = \eta(x) = \exp(-\beta(x-x_0)^2).
$$
```
beta = 150
x0 = 0.4
kappa = 0.02
utrue_gaussian = lambda x,t: exp(-(x-0.4)**2 / (4*kappa*t + 1./beta)) \
/ sqrt(4*beta*kappa*t+1.)
```
Recall that the forward Euler time stepping on the heat equation is only stable if the time step satisfies $k \leq 0.5h^2/\kappa$. However, for smooth solutions with very small components of the high wave number Fourier modes, it can take a long time for the instability to appear even if we take much larger $k$. Here's an example. Note that it is the highest wave number (the saw-tooth mode) that grows fastest and hence appears first...
```
t0 = 0.
tfinal = 4.
ax = 0.
bx = 1.
mx = 39
h = 1./((mx+1))
dt_stab = 0.5*h**2 / kappa
nsteps_stab = int(floor(tfinal-t0)/dt_stab) + 1
print('For stability, need to take at least %i time steps' % nsteps_stab)
heat_solution_input = HeatSolutionInput()
heat_solution_input.t0 = t0
heat_solution_input.tfinal = tfinal
heat_solution_input.ax = ax
heat_solution_input.bx = bx
heat_solution_input.mx = mx
heat_solution_input.utrue = utrue_gaussian
heat_solution_input.kappa = kappa
heat_solution_input.nsteps = 240
heat_solution_output = heat_FE(heat_solution_input)
error_tfinal = heat_solution_output.errors[-1] # last element
print('Using %i time steps' % heat_solution_input.nsteps)
print('Max-norm Error at t = %6.4f is %12.8f' % (heat_solution_input.tfinal, error_tfinal))
# make an animation of the results, plotting every 10th frame:
anim = make_animation(heat_solution_input, heat_solution_output, nplot=10)
HTML(anim.to_jshtml()) # or use the line below...
#HTML(anim.to_html5_video())
```
## Discontinous initial data
The instability is observed much more quickly if the initial data contains more high wave numbers, e.g. if it is discontinuous.
Consider the exact solution
$$
u(x,t) = \text{erf}\left(x/\sqrt{4\kappa t}\right)
$$
where erf is the *error function* defined as the integral of the Gaussian,
$$
\text{erf}(z) = \frac{2}{\pi} \int_0^z \exp(-t^2)\, dt.
$$
See e.g. https://en.wikipedia.org/wiki/Error_function.
As $t \rightarrow 0$, this approaches the discontinous function jumping from $-1$ for $x<0$ to $+1$ for $x>0$.
The error function is implemented in the `scipy.special` [library of special functions](https://docs.scipy.org/doc/scipy/reference/special.html).
```
kappa = 0.02
def utrue_erf(x,t):
from scipy.special import erf
if t==0:
return where(x>0, 1., -1.)
else:
return erf(x/sqrt(4*kappa*t))
t0 = 0.
tfinal = 2.
ax = -1.
bx = 1.
mx = 40
h = (bx-ax)/((mx+1))
dt_stab = 0.5*h**2 / kappa
nsteps_stab = int(floor(tfinal-t0)/dt_stab) + 1
print('For stability, need to take at least %i time steps' % nsteps_stab)
heat_solution_input = HeatSolutionInput()
heat_solution_input.t0 = t0
heat_solution_input.tfinal = tfinal
heat_solution_input.ax = ax
heat_solution_input.bx = bx
heat_solution_input.mx = mx
heat_solution_input.utrue = utrue_erf
heat_solution_input.kappa = kappa
heat_solution_input.nsteps = 32
heat_solution_output = heat_FE(heat_solution_input)
error_tfinal = heat_solution_output.errors[-1] # last element
print('Using %i time steps' % heat_solution_input.nsteps)
print('Max-norm Error at t = %6.4f is %12.8f' % (heat_solution_input.tfinal, error_tfinal))
anim = make_animation(heat_solution_input, heat_solution_output, nplot=1)
HTML(anim.to_jshtml())
```
## Crank-Nicolson method
This method uses the same centered difference spatial discretization with the Trapezoidal method for time stepping. That method is A-stable so this method is stable for any size time step (though not necessarily accurate).
Implementing this method requires solving a tridiagonal linear system in each time step, which we do using the [sparse matrix routines](https://docs.scipy.org/doc/scipy/reference/sparse.linalg.html) from `scipy.sparse.linalg`.
```
def heat_CN(heat_solution_input):
"""
Solve u_t = kappa * u_{xx} on [ax,bx] with Dirichlet boundary conditions,
using the Crank-Nicolson method with m interior points, taking nsteps
time steps.
Input:
`heat_solution_input` should be on object of class `HeatSolutionInput`
specifying inputs.
Output:
an object of class `HeatSolutionOutput` with the solution and other info.
Note: the vector x defined below is of length m+2 and includes both boundary points.
The vector uint is of length m and is only the interior points that we solve for,
by solving an m by m linear system each time step.
The vector u is of length m+2 and obtained by extending uint with the boundary values,
so that plotting (x,u) includes the boundary values.
"""
from scipy import sparse
from scipy.sparse.linalg import spsolve
# unpack the inputs for brevity:
ax = heat_solution_input.ax
bx = heat_solution_input.bx
kappa = heat_solution_input.kappa
m = heat_solution_input.mx
utrue = heat_solution_input.utrue
t0 = heat_solution_input.t0
tfinal = heat_solution_input.tfinal
nsteps = heat_solution_input.nsteps
h = (bx-ax)/float(m+1) # h = delta x
x = linspace(ax,bx,m+2) # note x(1)=0 and x(m+2)=1
# u(1)=g0 and u(m+2)=g1 are known from BC's
dt = tfinal / float(nsteps)
# initial conditions:
u0 = utrue(x,t0)
# Each time step we solve MOL system U' = AU + g using the Trapezoidal method
# set up matrices:
r = 0.5 * kappa* dt/(h**2)
em = ones(m)
em1 = ones(m-1)
A = sparse.diags([em1, -2*em, em1], [-1, 0, 1], shape=(m,m))
A1 = sparse.eye(m) - r * A
A2 = sparse.eye(m) + r * A
# initialize u and plot:
tn = 0
u = u0
t = empty((nsteps+1,), dtype=float)
errors = empty((nsteps+1,), dtype=float)
u_computed = empty((m+2,nsteps+1), dtype=float)
t[0] = tn
errors[0] = 0.
u_computed[:,0] = u0
# main time-stepping loop:
for n in range(1,nsteps+1):
tnp = tn + dt # = t_{n+1}
# boundary values u(0,t) and u(1,t) at times tn and tnp:
# boundary values are already set at time tn in array u:
g0n = u[0]
g1n = u[m+1]
# evaluate true solution to get new boundary values at tnp:
g0np = utrue(ax,tnp)
g1np = utrue(bx,tnp)
# compute right hand side for linear system:
uint = u[1:m+1] # interior points (unknowns)
rhs = A2.dot(uint) # sparse matrix-vector product A2 * uint
# fix-up right hand side using BC's (i.e. add vector g to A2*uint)
rhs[0] = rhs[0] + r*(g0n + g0np)
rhs[m-1] = rhs[m-1] + r*(g1n + g1np)
# solve linear system:
uint = spsolve(A1,rhs) # sparse solver
# augment with boundary values:
u = hstack([g0np, uint, g1np])
error = abs(u-utrue(x,tnp)).max() # max norm
t[n] = tnp
u_computed[:,n] = u
errors[n] = error
tn = tnp # for next time step
heat_solution_output = HeatSolutionOutput() # create object for output
heat_solution_output.dt = dt
heat_solution_output.h = h
heat_solution_output.t = t
heat_solution_output.x_computed = x
heat_solution_output.u_computed = u_computed
heat_solution_output.errors = errors
return heat_solution_output
```
## Test this with k = h:
With this method we can get a fine solution with only 40 steps (on a grid with 39 interior points). We only go out to time 1 but it would stay stable forever...
```
heat_solution_input = HeatSolutionInput()
heat_solution_input.t0 = 0.
heat_solution_input.tfinal = 1.
heat_solution_input.ax = 0.
heat_solution_input.bx = 1.
heat_solution_input.mx = 39
heat_solution_input.utrue = utrue_gaussian
heat_solution_input.kappa = kappa
heat_solution_input.nsteps = 40
heat_solution_output = heat_CN(heat_solution_input)
error_tfinal = heat_solution_output.errors[-1] # last element
print('dt = %6.4f' % heat_solution_output.dt)
print('Max-norm Error at t = %6.4f is %12.8f' % (heat_solution_input.tfinal, error_tfinal))
anim = make_animation(heat_solution_input, heat_solution_output)
HTML(anim.to_jshtml())
```
We can also plot how the max-norm error evolves with time:
```
plot(heat_solution_output.t,heat_solution_output.errors)
xlabel('time')
ylabel('max-norm error');
```
## Test for second-order accuracy
If dt and h are both reduced by 2, the error should go down by a factor 4 (for sufficiently small values).
Here we loop over a range of dt and h values, with dt = h in each solve.
```
nsteps_vals = [20,40,80,160,320] # values to test
E = empty(len(nsteps_vals))
# print table header:
print(" h dt error ratio estimated order")
for j,nsteps in enumerate(nsteps_vals):
heat_solution_input.nsteps = nsteps
heat_solution_input.mx = nsteps - 1
heat_solution_output = heat_CN(heat_solution_input)
E[j] = heat_solution_output.errors[-1] # last element
h = heat_solution_output.h
dt = heat_solution_output.dt
if j>0:
ratio = E[j-1] / E[j]
else:
ratio = nan
p = log(ratio)/log(2)
print("%8.6f %8.6f %12.8f %4.2f %4.2f" % (h, dt, E[j], ratio, p))
loglog(nsteps_vals, E, '-o')
title('Log-log plot of errors')
xlabel('nsteps')
ylabel('error')
```
## Observe oscillations if dt is too large
We know that Crank-Nicolson is stable for any time step, but the amplification factor approaches $-1$ as $k\lambda \rightarrow \infty$, so we expect high wavenumber modes to oscillate in time if we take the time step too large. This can be observed with the Gaussian initial data used here.
```
heat_solution_input.mx = 39
heat_solution_input.nsteps = 2
heat_solution_output = heat_CN(heat_solution_input)
error_tfinal = heat_solution_output.errors[-1] # last element
print('h = %6.4f, dt = %6.4f' % (heat_solution_output.h, heat_solution_output.dt))
print('Max-norm Error at t = %6.4f is %12.8f' % (heat_solution_input.tfinal, error_tfinal))
anim = make_animation(heat_solution_input, heat_solution_output)
HTML(anim.to_jshtml()) # or use the line below...
#HTML(anim.to_html5_video())
```
### Discontinous data
With a sufficiently small time step, Crank-Nicolson behaves well on the problem with discontinous data. Note that we use an even number of grid points `m = 40` so that they are symmetric about $x=0$. Try `m=39` and see how the asymmetry gives a larger error!
```
heat_solution_input = HeatSolutionInput()
heat_solution_input.t0 = 0.
heat_solution_input.tfinal = 1.5
heat_solution_input.ax = -1.
heat_solution_input.bx = 1.
heat_solution_input.mx = 40
heat_solution_input.utrue = utrue_erf
heat_solution_input.kappa = kappa
heat_solution_input.nsteps = 40
heat_solution_output = heat_CN(heat_solution_input)
error_tfinal = heat_solution_output.errors[-1] # last element
print('h = %6.4f, dt = %6.4f' % (heat_solution_output.h, heat_solution_output.dt))
print('Max-norm Error at t = %6.4f is %12.8f' % (heat_solution_input.tfinal, error_tfinal))
anim = make_animation(heat_solution_input, heat_solution_output)
HTML(anim.to_jshtml()) # or use the line below...
#HTML(anim.to_html5_video())
```
The issue with oscillations is more apparent with this discontinuous initial data. Taking a much larger time step on the same grid gives the results below. Note that the Crank-Nicolson method remains stable, but the saw-tooth mode is apparent near the interface if we try to step over the rapid transient behavior in this stiff problem.
```
heat_solution_input.nsteps = 3
heat_solution_output = heat_CN(heat_solution_input)
error_tfinal = heat_solution_output.errors[-1] # last element
print('h = %6.4f, dt = %6.4f' % (heat_solution_output.h, heat_solution_output.dt))
print('Max-norm Error at t = %6.4f is %12.8f' % (heat_solution_input.tfinal, error_tfinal))
anim = make_animation(heat_solution_input, heat_solution_output)
HTML(anim.to_jshtml()) # or use the line below...
#HTML(anim.to_html5_video())
```
An L-stable method like TR-BDF2 would do better in this case.
| true |
code
| 0.711143 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/satyajitghana/TSAI-DeepVision-EVA4.0/blob/master/05_CodingDrill/EVA4S5F9.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Import Libraries
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
```
## Data Transformations
We first start with defining our data transformations. We need to think what our data is and how can we augment it to correct represent images which it might not see otherwise.
```
# Train Phase transformations
train_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.RandomRotation((-7.0, 7.0), fill=(1,)),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
# Test Phase transformations
test_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
```
# Dataset and Creating Train/Test Split
```
train = datasets.MNIST('./data', train=True, download=True, transform=train_transforms)
test = datasets.MNIST('./data', train=False, download=True, transform=test_transforms)
```
# Dataloader Arguments & Test/Train Dataloaders
```
SEED = 1
# CUDA?
cuda = torch.cuda.is_available()
print("CUDA Available?", cuda)
# For reproducibility
torch.manual_seed(SEED)
if cuda:
torch.cuda.manual_seed(SEED)
# dataloader arguments - something you'll fetch these from cmdprmt
dataloader_args = dict(shuffle=True, batch_size=128, num_workers=4, pin_memory=True) if cuda else dict(shuffle=True, batch_size=64)
# train dataloader
train_loader = torch.utils.data.DataLoader(train, **dataloader_args)
# test dataloader
test_loader = torch.utils.data.DataLoader(test, **dataloader_args)
```
# The model
Let's start with the model we first saw
```
import torch.nn.functional as F
dropout_value = 0.1
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# Input Block
self.convblock1 = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=16, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
nn.BatchNorm2d(16),
nn.Dropout(dropout_value)
) # output_size = 26
# CONVOLUTION BLOCK 1
self.convblock2 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=32, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
nn.BatchNorm2d(32),
nn.Dropout(dropout_value)
) # output_size = 24
# TRANSITION BLOCK 1
self.convblock3 = nn.Sequential(
nn.Conv2d(in_channels=32, out_channels=10, kernel_size=(1, 1), padding=0, bias=False),
) # output_size = 24
self.pool1 = nn.MaxPool2d(2, 2) # output_size = 12
# CONVOLUTION BLOCK 2
self.convblock4 = nn.Sequential(
nn.Conv2d(in_channels=10, out_channels=16, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
nn.BatchNorm2d(16),
nn.Dropout(dropout_value)
) # output_size = 10
self.convblock5 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=16, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
nn.BatchNorm2d(16),
nn.Dropout(dropout_value)
) # output_size = 8
self.convblock6 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=16, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
nn.BatchNorm2d(16),
nn.Dropout(dropout_value)
) # output_size = 6
self.convblock7 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=16, kernel_size=(3, 3), padding=1, bias=False),
nn.ReLU(),
nn.BatchNorm2d(16),
nn.Dropout(dropout_value)
) # output_size = 6
# OUTPUT BLOCK
self.gap = nn.Sequential(
nn.AvgPool2d(kernel_size=6)
) # output_size = 1
self.convblock8 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=10, kernel_size=(1, 1), padding=0, bias=False),
# nn.BatchNorm2d(10),
# nn.ReLU(),
# nn.Dropout(dropout_value)
)
self.dropout = nn.Dropout(dropout_value)
def forward(self, x):
x = self.convblock1(x)
x = self.convblock2(x)
x = self.convblock3(x)
x = self.pool1(x)
x = self.convblock4(x)
x = self.convblock5(x)
x = self.convblock6(x)
x = self.convblock7(x)
x = self.gap(x)
x = self.convblock8(x)
x = x.view(-1, 10)
return F.log_softmax(x, dim=-1)
```
# Model Params
Can't emphasize on how important viewing Model Summary is.
Unfortunately, there is no in-built model visualizer, so we have to take external help
```
!pip install torchsummary
from torchsummary import summary
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
print(device)
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
```
# Training and Testing
All right, so we have 24M params, and that's too many, we know that. But the purpose of this notebook is to set things right for our future experiments.
Looking at logs can be boring, so we'll introduce **tqdm** progressbar to get cooler logs.
Let's write train and test functions
```
from tqdm import tqdm
train_losses = []
test_losses = []
train_acc = []
test_acc = []
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
correct = 0
processed = 0
for batch_idx, (data, target) in enumerate(pbar):
# get samples
data, target = data.to(device), target.to(device)
# Init
optimizer.zero_grad()
# In PyTorch, we need to set the gradients to zero before starting to do backpropragation because PyTorch accumulates the gradients on subsequent backward passes.
# Because of this, when you start your training loop, ideally you should zero out the gradients so that you do the parameter update correctly.
# Predict
y_pred = model(data)
# Calculate loss
loss = F.nll_loss(y_pred, target)
train_losses.append(loss)
# Backpropagation
loss.backward()
optimizer.step()
# Update pbar-tqdm
pred = y_pred.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
processed += len(data)
pbar.set_description(desc= f'Loss={loss.item()} Batch_id={batch_idx} Accuracy={100*correct/processed:0.2f}')
train_acc.append(100*correct/processed)
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
test_acc.append(100. * correct / len(test_loader.dataset))
from torch.optim.lr_scheduler import StepLR
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
# scheduler = StepLR(optimizer, step_size=6, gamma=0.1)
EPOCHS = 20
for epoch in range(EPOCHS):
print("EPOCH:", epoch)
train(model, device, train_loader, optimizer, epoch)
# scheduler.step()
test(model, device, test_loader)
```
| true |
code
| 0.919931 | null | null | null | null |
|
# ML 101
## Evaluation (Classification)
The metrics that you choose to evaluate your machine learning algorithms are very important.
Choice of metrics influences how the performance of machine learning algorithms is measured and compared. They influence how you weight the importance of different characteristics in the results and your ultimate choice of which algorithm to choose.
In this notebook we explored the following performance metrics using [Hold-out partition](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html):
1. Confusion Matrix
2. Accuracy
3. Precision
4. Recall
5. F1-score
6. MCC
7. ROC curve

```
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
from sklearn.metrics import matthews_corrcoef
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
def plot_decision_boundary(X, y, clf):
x_min, x_max = X[:, 0].min() - 2, X[:, 0].max() + 2
y_min, y_max = X[:, 1].min() - 2, X[:, 1].max() + 2
xx, yy = np.mgrid[x_min:x_max:.01, y_min:y_max:.01]
grid = np.c_[xx.ravel(), yy.ravel()]
probs = clf.predict_proba(grid)[:, 1].reshape(xx.shape)
f, ax = plt.subplots(figsize=(8, 6))
contour = ax.contourf(xx, yy, probs, 25, cmap="RdBu", vmin=0, vmax=1)
ax_c = f.colorbar(contour)
ax_c.set_label("$P(y = 1)$")
ax_c.set_ticks([0, .25, .5, .75, 1])
ax.scatter(X[:,0], X[:, 1], c=y, s=50, cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white", linewidth=1)
ax.set(aspect="equal", xlim=(x_min, x_max), ylim=(y_min, x_max), xlabel="$X_1$", ylabel="$X_2$")
plt.show()
```
## Hard Toy Dataset
```
# import dataset
df = pd.read_csv('https://media.githubusercontent.com/media/mariolpantunes/ml101/main/datasets/toy_dataset_01.csv')
# print the first rows of the dataset
df.head()
sns.relplot(x="X1", y="X2", hue="Y", data=df);
from sklearn.model_selection import train_test_split
X = df[['X1', 'X2']].to_numpy()
y = df['Y'].to_numpy()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=7, stratify=y)
g = sns.relplot(x=X_train[:,0], y=X_train[:,1], hue=y_train)
g.set(ylim=(-1, 6))
g.set(xlim=(-1, 6))
g = sns.relplot(x=X_test[:,0], y=X_test[:,1], hue=y_test)
g.set(ylim=(-1, 6))
g.set(xlim=(-1, 6))
```
### Logistic Regression
```
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression().fit(X_train, y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
### Naive Bayes
```
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB().fit(X_train,y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
### SVM
```
from sklearn.svm import SVC
clf = SVC(probability=True, kernel='rbf').fit(X_train,y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
### Neural Network
```
from sklearn.neural_network import MLPClassifier
clf = MLPClassifier(random_state=7, max_iter=5000).fit(X_train,y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
### KNN
```
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=7).fit(X_train,y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
### Decision Trees
```
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier().fit(X_train,y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
### Random Forest
```
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(random_state=0).fit(X_train,y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
### Gradient Boosting
```
from sklearn.ensemble import GradientBoostingClassifier
clf = GradientBoostingClassifier(random_state=0).fit(X_train,y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
### Voting Ensemble
```
from sklearn.ensemble import VotingClassifier
#c1 = LogisticRegression()
c2 = GaussianNB()
c3 = SVC(probability=True, kernel='rbf')
c4 = MLPClassifier(random_state=7, max_iter=5000)
c5 = KNeighborsClassifier(n_neighbors=7)
c6 = DecisionTreeClassifier()
c7 = RandomForestClassifier(random_state=42)
c8 = GradientBoostingClassifier(random_state=42)
clfs = [('nb', c2), ('svm', c3), ('nn', c4),
('knn', c5), ('dt', c6), ('rf', c7), ('gbc', c8)]
clf = VotingClassifier(clfs, voting='soft').fit(X_train,y_train)
plot_decision_boundary(X_train, y_train, clf)
plot_decision_boundary(X_test, y_test, clf)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True)
a = accuracy_score(y_test, y_pred)
p = precision_score(y_test, y_pred)
r = recall_score(y_test, y_pred)
f = f1_score(y_test, y_pred)
m = matthews_corrcoef(y_test, y_pred)
print(f'Acc {a}\nPre {p}\nRec {r}\nF1 {f}\nMCC {m}')
y_pred_proba = clf.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
| true |
code
| 0.655557 | null | null | null | null |
|
# E-news Express
## Import all the necessary libraries
```
import warnings
warnings.filterwarnings('ignore') # ignore warnings and do not display them
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%matplotlib inline
import seaborn as sns
```
## 1. Explore the dataset and extract insights using Exploratory Data Analysis. (10 Marks)
### Exploratory Data Analysis - Step by step approach
Typical Data exploration activity consists of the following steps:
1. Importing Data
2. Variable Identification
3. Variable Transformation/Feature Creation
4. Missing value detection
5. Univariate Analysis
6. Bivariate Analysis
### Reading the Data into a DataFrame
```
#read the dataset abtest.csv
data = pd.read_csv("abtest.csv")
```
### Data Overview
- View a few rows of the data frame.
- Check the shape and data types of the data frame. Add observations.
- Fix the data-types (if needed).
- Missing Value Check.
- Summary statistics from the data frame. Add observations.
```
# view a few rows of the data frame
data.head()
# check the number of rows and columns
data.shape
```
### Observation:
- The data frame has a 100 rows and 6 columns
```
# check data types
data.info()
# check if there are missing values
# return sum of missing values
data.isnull().sum().sum()
```
### Observation:
- There are no missing values in the data frame
```
# check memory usage before converting the object data types to category
memory_usage_before = data.memory_usage().sum()
print(memory_usage_before)
### Converting object data types to category.
### This will reduce memory size and also help in analysis
columns = ["group", "landing_page", "converted", "language_preferred"]
for column in columns:
data[column] = data[column].astype("category")
data.info()
# check memory usage after converting the object data types to category
memory_usage_after_conversion = data.memory_usage().sum()
print(memory_usage_after_conversion)
```
#### Observations:
- All columns that were have object data types are now category
- The memory usage has reduced from '4.8+ KB to 2.6 KB' as you can see and compare the memory usage before and after
```
# show statistical summary aof all columns in the data frame
data.describe(include='all').T
```
### Observation:
- The minimum and maximum time spent on the pages is 0.19 and 10.71 minutes respectively
- There are two groups of users.
- The converted users were a total of 54
- There are three unique values of languages preferred
### Let us find the values counts of each unique value in the given Series
```
# checking the value counts of each unique value in the "group" series
data["group"].value_counts()
```
#### Observation:
- There two equal groups of users
- The old landing page was served to 50 users(control)
- The new landing page was served to 50 users (treatment)
```
# checking the value counts of each unique value in the "landing page" series
data["landing_page"].value_counts()
```
#### Observations:
- There are two landing pages; new and old
- Each landing page has a total of 50 sampled users
```
# checking the value counts of each unique value in the "converted" series
data["converted"].value_counts()
```
#### Observations:
- There are two categories under converted; yes and no
- 54 users were converted and 46 users were not converted
```
# checking the value counts of each unique value in the "language_preferred" series
data["language_preferred"].value_counts()
```
#### Observations:
- There are three languages that users could choose; French, Spanish, English
- 34 users preferred French
- 34 users preferred Spanish
- and 32 users preferred English
```
# statistical summary of time spent on the pages
data["time_spent_on_the_page"].describe()
#create a subsetted dataframe for old landing page users
df_old = data[data["landing_page"]=="old"]
# statistical summary of time spent on the old page
df_old["time_spent_on_the_page"].describe()
# create a subsetted dataframe for new landing page users
df_new = data[data["landing_page"]=="new"]
# statistical summary of time spent on the new page
df_new["time_spent_on_the_page"].describe()
```
#### Observations:
Acoording to the statistical summary above:
- The maximum time spent on the new page is greater than the maximum time spent on the old page
- The average time spent on the new page is greater than the average time spent on the old page
- The minimum time spent on the new page is greater than the minimum time spent on the old page
### Univariate Analysis
```
# function to plot a boxplot and a histogram along the same scale.
def histogram_boxplot(data, feature, figsize=(12, 7), kde=False, bins=None):
"""
Boxplot and histogram combined
data: dataframe
feature: dataframe column
figsize: size of figure (default (12,7))
kde: whether to show the density curve (default False)
bins: number of bins for histogram (default None)
"""
f2, (ax_box2, ax_hist2) = plt.subplots(
nrows=2, # Number of rows of the subplot grid= 2
sharex=True, # x-axis will be shared among all subplots
gridspec_kw={"height_ratios": (0.25, 0.75)},
figsize=figsize,
) # creating the 2 subplots
sns.boxplot(
data=data, x=feature, ax=ax_box2, showmeans=True, color="violet"
) # boxplot will be created and a star will indicate the mean value of the column
sns.histplot(
data=data, x=feature, kde=kde, ax=ax_hist2, bins=bins, palette="winter"
) if bins else sns.histplot(
data=data, x=feature, kde=kde, ax=ax_hist2
) # For histogram
ax_hist2.axvline(
data[feature].mean(), color="green", linestyle="--"
) # Add mean to the histogram
ax_hist2.axvline(
data[feature].median(), color="black", linestyle="-"
) # Add median to the histogram
histogram_boxplot(df_old,"time_spent_on_the_page");
plt.xlabel("Time spent on old page");
histogram_boxplot(df_new,"time_spent_on_the_page")
plt.xlabel("Time spent on new page");
# function to create labeled barplots
def labeled_barplot(data, feature, perc=False, n=None):
"""
Barplot with percentage at the top
data: dataframe
feature: dataframe column
perc: whether to display percentages instead of count (default is False)
n: displays the top n category levels (default is None, i.e., display all levels)
"""
total = len(data[feature]) # length of the column
count = data[feature].nunique()
if n is None:
plt.figure(figsize=(count + 1, 5))
else:
plt.figure(figsize=(n + 1, 5))
plt.xticks(rotation=90, fontsize=15)
ax = sns.countplot(data=data, x=feature, palette="Paired", order=data[feature].value_counts().index[:n].sort_values())
for p in ax.patches:
if perc == True:
label = "{:.1f}%".format(100 * p.get_height() / total) # percentage of each class of the category
else:
label = p.get_height() # count of each level of the category
x = p.get_x() + p.get_width() / 2 # width of the plot
y = p.get_height() # height of the plot
ax.annotate(label, (x, y), ha="center", va="center", size=12, xytext=(0, 5), textcoords="offset points") # annotate the percentage
plt.show() # show the plot
# what percentage of users get converted after visiting the pages
labeled_barplot(data, "converted")
```
#### Observations:
The bar plot shows that 54% of the users get converted compared to 46% that don't get converted
- But our focus is where the most conversion rates occur, Is it on the new page or old page.
- Lets see that below
### Let us see the percentage of people that got converted on the different landing pages
1. Old page
```
# bar graph to show the percentage of people that visited the old page and got converted
labeled_barplot(df_old, "converted")
# bar graph to show the percentage of people that visited the new page and got converted
labeled_barplot(df_new, "converted")
```
#### Observations:
From the analysis above, the users who visited the new landing page got more converted.
```
# bar graph to show the percentage of users who preferred the different languages
labeled_barplot(data, "language_preferred")
```
#### Observations:
- Out of 100 sampled users; 34 prefer Spanish, 34 prefer French and 32 prefer English
```
# bar graph to show the percentage of users on the different pages
labeled_barplot(data, "landing_page")
```
### Observation:
- Like the objective states, 100 users were sampled and divided into two equal groups. The graph above proves this point as 50 users were served the old page and 50 users were served the new page
### Bivariate Analysis
### Landing page vs time pent on the page
```
sns.set(rc = {'figure.figsize':(10,8)}) # set size of the seaborn plots
sns.barplot(x="landing_page", y="time_spent_on_the_page", data=data);
```
### Observation:
- Users tend to spend more time on the new page as compared to the old page
### Converted users vs time spent on the page
```
sns.barplot(x="converted", y="time_spent_on_the_page", data=data);
```
### Observation:
- Users that got converted spent more time on the pages.
### Language preferred vs Converted status
```
sns.countplot(x="language_preferred", hue="converted", data=data);
```
### Observation:
- The ratio of users that got converted to that that did not get converted for English users is higher compared to other language users.
## 2. Do the users spend more time on the new landing page than the existing landing page? (10 Marks)
### Perform Visual Analysis
```
# visual analysis of the time spent on the new and old page
sns.boxplot(x = 'landing_page', y = 'time_spent_on_the_page', data = data);
```
### Step 1: Define the null and alternate hypotheses
Let $\mu_1, \mu_2$ be mean time users spend on the existing page and new page respectively.
We will test the null hypothesis
>$H_0:\mu_1=\mu_2$
against the alternate hypothesis
>$H_a:\mu_2>\mu_1$
### Step 2: Select Appropriate test
- one-tailed test
- two population means
- independent populations
NB: This is a T-test for independent populations.
### Step 3: Decide the significance level
- As provided in the problem statement, let us assume the significance level($\alpha$) = 0.05
### Step 4: Collect and prepare data
```
# Calculating standard deviation for time spend on new page
std_new_page = df_new["time_spent_on_the_page"].std()
print(round(std_new_page, 2))
# Calculating standard deviation for time spend on old page
std_old_page = df_old["time_spent_on_the_page"].std()
print(round(std_old_page,2))
```
#### Observation:
- The standard deviation of the time spent on the new page is different from that of the old page from the sample data.
- Hence the population deviations can not be assumed to be equal.
- This means we areto use the T-test for independent populations for unequal Standard deviations
### Step 5: Calculate the p-value
```
#import the required functions
from scipy.stats import ttest_ind
# find the p-value
test_stat, p_value = ttest_ind(df_new['time_spent_on_the_page'], df_old['time_spent_on_the_page'], equal_var = False, alternative = 'greater')
print('The p-value is ' + str(p_value))
```
### Step 6: Compare the p-value with $\alpha$
```
# print the whether p-value is greater or less than alpha
if p_value < 0.05:
print(" The p-value is less than the level of significance")
else:
print("The p-value is greater than the level of significance")
```
#### Observation:
The P-value is much less than $\alpha$
### Step 7: Draw inference
#### Observation:
Since the P-value is much less than the level of Significance, we reject the null hypothesis. Therefore we have enough statistical significance to conclude that users spend more time on the new landing page than the existing page.
## 3. Is the conversion rate (the proportion of users who visit the landing page and get converted) for the new page greater than the conversion rate for the old page? (10 Marks)
### Perform Visual analysis
```
# visual analysis of the proportion of users who visit the old landing page and get converted
labeled_barplot(df_old, "converted")
# visual analysis of the proportion of users who visit the new landing page and get converted
labeled_barplot(df_new, "converted")
```
### Step 1: Define the null and alternative hypothesis
Let $p_1,p_2$ be the proportions of users that visit the new page and old page and get converted respectively.
The manufacturer will test the null hypothesis
>$H_0:p_1 =p_2$
against the alternate hypothesis
>$H_a:p_1 > p_2$
### Step 2: Select Appropriate test
- Binomally distributed population
- One-tailed test
- two population proportions
- independent populations
NB: The appropriate test to be used will be the two-proportion Z-test
### Step 3: Decide the significance level
- As provided in the problem statement, let us assume the significance level($\alpha$) = 0.05
### Step 4: Collect and prepare data
```
# check for total number of users in each group
data["group"].value_counts()
# calculate the number of users that were served the new page and got converted
new_page_converted_users = df_new[df_new["converted"]=="yes"].value_counts()
print(len(new_page_converted_users))
# calculate the number of users that were served the old page and got converted
old_page_converted_users = df_old[df_old["converted"]=="yes"].value_counts()
print(len(old_page_converted_users))
```
### Insight:
- Each group of users has 50 people
- 33 users got converted when they visited the new page
- 21 users got converted when they visited the old page
### Step 5: Calculate the p-value
```
# import the required fuction
from statsmodels.stats.proportion import proportions_ztest
# set the count of converted users
converted_users = np.array([33, 21])
# set the sample sizes
sampled_users = np.array([50, 50])
# find the p-value
test_stat, p_value = proportions_ztest(converted_users, sampled_users)
print('The p-value is ' + str(p_value))
```
### Step 6: Compare the p-value with $\alpha$
```
# print the whether p-value is greater or less than alpha
if p_value < 0.05:
print(" The p-value is less than the level of significance")
else:
print("The p-value is greater than the level of significance")
```
### Step 7: Draw inference
As the p-value is less than the significance level 0.05, we reject the null hypothesis. Therefore, we have enough statistical significance to conclude that the conversion rate for the new page is greater than the conversion rate for the old page.
## 4. Is the conversion and preferred language are independent or related? (10 Marks)
### Perform Visual Analysis
```
# visual analysis of the coversion count depending on the language Preferences
sns.countplot(x="language_preferred", hue="converted", data=data);
```
### Step 1: Define null and alternative hypothesis
We will test the null hypothesis
>$H_0:$ Conversion is independent of preferred language .
against the alternate hypothesis
>$H_a:$ Conversion depends on preferred language.
### Step 2: Select appropriate test
- We are to test for independence
- The variables are categorical
- Number of observations in each category is greater than 5
NB: Therefore, the appropriate test for this problem is **Chi-Square Test for Independence**
### Step 3: Decide the significance level
- As provided in the problem statement, let us assume the significance level($\alpha$) = 0.05
### Step 4: Collect and prepare data
```
#preparing the contingency table
cont_table= pd.crosstab(data['language_preferred'],data['converted'])
cont_table
```
### Step 5: Calculate the p-value
```
from scipy.stats import chi2_contingency
chi, p_value, dof, expected = chi2_contingency(cont_table)
print('The p-value is ', p_value)
```
### Step 6: Compare the p-value with $\alpha$
```
# print the whether p-value is greater or less than alpha
if p_value < 0.05:
print(" The p-value is less than the level of significance")
else:
print("The p-value is greater than the level of significance")
```
### Step 7: Draw inference
#### Observation:
As the p-value is much greater than the significance level, we can not reject the null hypothesis. Hence, we do not have enough statistical significance to conclude that conversion depends on preferred language at 5% significance level.
## 5. Is the time spent on the new page same for the different language users? (10 Marks)
### Perform visual analysis
```
# print the mean of time spent on the new page by the different groups of users with different language preferences
print(df_new.groupby("language_preferred")["time_spent_on_the_page"].mean())
# plot the box plot of the time spent on the new page depending on language preferred
sns.boxplot(x= "language_preferred", y = 'time_spent_on_the_page' , data = df_new);
```
### Step 1: Define the null and alternative hypothesis
Let $\mu_1, \mu_2, \mu_3$ be the means of time spent on the new page by different language users; English, French, Spanish respectively
We will test the null hypothesis
>$H_0: \mu_1 = \mu_2 = \mu_3$
against the alternative hypothesis
>$H_a: $ In at least in one category of language, mean time spent on the new page is different
### Step 2: Decide the significance level
- As provided in the problem statement, let us assume the significance level($\alpha$) = 0.05
### Step 3: Select the appropriate test
- This problem concerns three population means, therefore we shall use One-way ANOVA test
- NB: Let us go ahead and test if the assumptions are satisfied for this test
### Testing for normality
#### Shapiro-Wilk’s test
We will test the null hypothesis
>$H_0:$ Time spent on the new page follows a normal distribution against
against the alternative hypothesis
>$H_a:$ Time spent on the new page does not follow a normal distribution
```
# Assumption 1: Normality
from scipy import stats
# find the p-value
w, p_value = stats.shapiro(df_new['time_spent_on_the_page'])
print('The p-value is', p_value)
```
Since p-value of the test is very large, we fail to reject the null hypothesis that the time spent on the new landing page follows the normal distribution.
### Testing for Equality of variances
#### Levene’s test
We will test the null hypothesis
>$H_0$: All the population variances are equal
against the alternative hypothesis
>$H_a$: At least one variance is different from the rest
### Prepare the data
```
# create a dataframe for users on the new page that prefer the English Language
df_new_english = df_new[df_new["language_preferred"]=="English"]
# create a dataframe for users on the new page that prefer the French Language
df_new_french = df_new[df_new["language_preferred"]=="French"]
# create a dataframe for users on the new page that prefer the Spanish Language
df_new_spanish = df_new[df_new["language_preferred"]=="Spanish"]
#Assumption 2: Homogeneity of Variance
from scipy.stats import levene
statistic, p_value = levene( df_new_english['time_spent_on_the_page'],
df_new_french['time_spent_on_the_page'],
df_new_spanish['time_spent_on_the_page'])
# find the p-value
print('The p-value is', p_value)
```
Since the p-value is large, we fail to reject the null hypothesis of equal of variances.
### Observations:
The assumptions for the One-way Anova test are satisfied according to the results of levene and shapiro tests. So we can go ahead with the test
### Step 4: Calculate the p-value
```
#import the required function
from scipy.stats import f_oneway
# perform one-way anova test
test_stat, p_value = f_oneway(df_new_english['time_spent_on_the_page'],
df_new_french['time_spent_on_the_page'],
df_new_spanish['time_spent_on_the_page'])
print('The p_value is ' + str(p_value))
```
### Step 5: Compare the p-value with $\alpha$
```
# print the whether p-value is greater or less than alpha
if p_value < 0.05:
print(" The p_value is less than the level of significance")
else:
print("The p_value is greater than the level of significance")
```
### Step 6: Draw inference
As the p-value is much greater than the level of significance, therefore we fail to reject the null hypothesis. We do not have enough statistical significance to conclude that the time spent on the new page is different for atleast one kind of language users at 5% significance level.
## Conclusion and Business Recommendations
- Basing on the analysis above, at 5% significance level, there is enough statistical significance to conclude that the conversion rate for the new page is greater than the conversion rate for the old page. This means that the new feature will be effective as the new page shows more effectiveness in gathering new subscribers.
- Something to also note, is that conversion is independent of the language preferred by the users.
- Also, Users spend more time on the new page but this time is independent of the language preferred by the users.
##### In conclusion therefore, the recommendation i give E-news Express is to go ahead with the new feature/new landing page designed by the design team as it shows effectiveness in gathering new subscibers.
| true |
code
| 0.612802 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
import grAdapt
from grAdapt.surrogate import NoModel, NoGradient
from grAdapt.optimizer import GradientDescentBisection, GradientDescent, Adam, AdamBisection, AMSGrad, AMSGradBisection
from grAdapt.models import Sequential
# data types
from grAdapt.space.datatype import Float
def sphere(x):
return np.sum(x**2)
bounds = [Float(-5, 5) for i in range(16)] # search space
```
## 1. Defining grAdapt Model
The gradients are estimated on the objective itself and exceed the number of function evaluations.
### 1.1 Gradient Descent
```
# Define surrogate
surrogate = NoModel()
# Define optimizer. Because the optimizer works on the surrogate, the surrogate must be passed.
optimizer = GradientDescent(surrogate=surrogate)
# Both are then passed to our sequential model.
model = Sequential(surrogate=surrogate, optimizer=optimizer)
# start optimizing
res = model.minimize(sphere, bounds, 100)
plt.plot(res['y'])
plt.ylabel('Loss')
plt.xlabel('No. of function evaluations')
plt.show()
print(res['y_sol'])
```
### 1.2 Gradient Descent Bisection
```
# Define surrogate
surrogate = NoModel()
# Define optimizer. Because the optimizer works on the surrogate, the surrogate must be passed.
optimizer = GradientDescentBisection(surrogate=surrogate)
# Both are then passed to our sequential model.
model = Sequential(surrogate=surrogate, optimizer=optimizer)
# start optimizing
res = model.minimize(sphere, bounds, 100)
plt.plot(res['y'])
plt.ylabel('Loss')
plt.xlabel('No. of function evaluations')
plt.show()
print(res['y_sol'])
```
### 1.3 Adam
```
# Define surrogate
surrogate = NoModel()
# Define optimizer. Because the optimizer works on the surrogate, the surrogate must be passed.
optimizer = Adam(surrogate=surrogate)
# Both are then passed to our sequential model.
model = Sequential(surrogate=surrogate, optimizer=optimizer)
# start optimizing
res = model.minimize(sphere, bounds, 100)
plt.plot(res['y'])
plt.ylabel('Loss')
plt.xlabel('No. of function evaluations')
plt.show()
print(res['y_sol'])
```
### 1.4 Adam Bisection
```
# Define surrogate
surrogate = NoModel()
# Define optimizer. Because the optimizer works on the surrogate, the surrogate must be passed.
optimizer = AdamBisection(surrogate=surrogate)
# Both are then passed to our sequential model.
model = Sequential(surrogate=surrogate, optimizer=optimizer)
# start optimizing
res = model.minimize(sphere, bounds, 100)
plt.plot(res['y'])
plt.ylabel('Loss')
plt.xlabel('No. of function evaluations')
plt.show()
print(res['y_sol'])
```
### 1.5 AMSGrad
```
# Define surrogate
surrogate = NoModel()
# Define optimizer. Because the optimizer works on the surrogate, the surrogate must be passed.
optimizer = AMSGrad(surrogate=surrogate)
# Both are then passed to our sequential model.
model = Sequential(surrogate=surrogate, optimizer=optimizer)
# start optimizing
res = model.minimize(sphere, bounds, 100)
plt.plot(res['y'])
plt.ylabel('Loss')
plt.xlabel('No. of function evaluations')
plt.show()
print(res['y_sol'])
```
### 1.6 AMSGrad Bisection
```
# Define surrogate
surrogate = NoModel()
# Define optimizer. Because the optimizer works on the surrogate, the surrogate must be passed.
optimizer = AMSGradBisection(surrogate=surrogate)
# Both are then passed to our sequential model.
model = Sequential(surrogate=surrogate, optimizer=optimizer)
# start optimizing
res = model.minimize(sphere, bounds, 100)
plt.plot(res['y'])
plt.ylabel('Loss')
plt.xlabel('No. of function evaluations')
plt.show()
print(res['y_sol'])
```
| true |
code
| 0.811956 | null | null | null | null |
|
## Домашнее задание по программированию.
## Производные. Частные производные. Градиент. Градиентный спуск.
Нам понадобится библиотека **numpy** - о ней было рассказано на первой лекции. Если ничего не помните, то можно обратиться к следующим ресурсам:
1. http://pyviy.blogspot.com/2009/09/numpy.html
2. https://pythonworld.ru/numpy (Часть 1, Часть 2)
```
import numpy as np
```
Отдельно напишем функцию, которая считает расстояние между двумя точками в произвольном пространстве. Математически это выглядит так $$dist(x, y) = \sum_{i=1}^{n}(x_{i} - y_{i})^{2}$$
```
def dist(x, y):
# Здесь мы можем обойтись без явного суммирования
# Если y и x - вектора из R^{n}, тогда
# y^{2} - x^{2} - тоже вектор из R^{n}
# (здесь x^{2}, y^{2} означает возведение в квадрат каждой из компонент вектора)
# Используя np.sum с атрибутом axis = 0 получим суммирование по столбцу
return np.sqrt(abs(np.sum(y ** 2 - x ** 2, axis = 0)))
```
Обычно пишут не универсальную функцию, которая принимает на вход функцию, минимум которой надо найти, и ее градиент, а явно задают эту функции внутри. Например, напишем функцию, которая будет находить точку минимума для функции многих переменных $$F(x, y) = x^{2} + y^{2}$$
```
def gradient_descent(starting_point,
learning_rate = None, iter_max = None,
precision = None, verbose = None, output = None):
f = lambda x: x[0] ** 2 + x[1] ** 2 # Обычная функция многих переменнных
# F(x, y) = x^2 + y^2
df_x = lambda x: 2 * x # Частная производная функции F по первой переменной
df_y = lambda y: 2 * y # Частная производная функции F по второй переменной
# Инициализация опциональных параметров
iter_num = 0
if learning_rate is None:
learning_rate = 0.001
if iter_max is None:
iter_max = 1e7
if precision is None:
precision = 1e-7
if verbose is None:
verbose = False
if output is None:
output = False
# Градиентный спуск
point = np.array([starting_point[0] - learning_rate * df_x(starting_point[0]),
starting_point[1] - learning_rate * df_y(starting_point[1])])
while dist(point, starting_point) > 1e-7 and iter_num < iter_max:
++iter_num
starting_point, point = np.array([
starting_point[0] - learning_rate * df_x(starting_point[0]),
starting_point[1] - learning_rate * df_y(starting_point[1])]),\
starting_point
if verbose:
print(starting_point, point)
if output:
return point, f(point)
else:
return np.round(point, 3), np.round(f(point), 3)
gradient_descent(np.array([2, -5]))
```
Вам необходимо написать функцию, которая будет находить минимум функции многих переменных $$F(x, y, z, t) = x^{4}y^{2} + z^{2}t^{2}$$
Указание - вам надо *немного* модифицировать предыдущую функцию.
```
def gradient_descent(starting_point,
learning_rate = None, iter_max = None,
precision = None, verbose = None, output = None):
f = lambda x: x[0] ** 4 * x[1] ** 2 + x[2] ** 2 * x[3] ** 2
df_x = lambda x: 4 * x[0] ** 3 * x[1] ** 2
df_y = lambda x: 2 * x[0] ** 4 * x[1]
df_z = lambda x: 2 * x[0] * x[1] ** 2
df_t = lambda x: 2 * x[0] ** 2 * x[1]
# Инициализация опциональных параметров
iter_num = 0
if learning_rate is None:
learning_rate = 0.001
if iter_max is None:
iter_max = 1e7
if precision is None:
precision = 1e-7
if verbose is None:
verbose = False
if output is None:
output = False
# Градиентный спуск
point = np.array([
starting_point[0] - learning_rate * df_x((starting_point[0], starting_point[1])),
starting_point[1] - learning_rate * df_y((starting_point[0], starting_point[1])),
starting_point[2] - learning_rate * df_z((starting_point[2], starting_point[3])),
starting_point[3] - learning_rate * df_t((starting_point[2], starting_point[3]))])
while dist(point, starting_point) > 1e-7 and iter_num < iter_max:
iter_num += 1
starting_point, point = np.array([
starting_point[0] - learning_rate * df_x((starting_point[0], starting_point[1])),
starting_point[1] - learning_rate * df_y((starting_point[0], starting_point[1])),
starting_point[2] - learning_rate * df_z((starting_point[2], starting_point[3])),
starting_point[3] - learning_rate * df_t((starting_point[2], starting_point[3]))]),\
starting_point
if verbose:
print(starting_point, point)
if output:
return point, f(point)
else:
return np.round(point, 3), np.round(f(point), 3)
gradient_descent(np.array([1, -1, 1, 1]),
learning_rate=0.1, iter_max=1000)
```
| true |
code
| 0.294583 | null | null | null | null |
|
# Pix2Pix implementation
* `Image-to-Image Translation with Conditional Adversarial Networks`, arXiv:1611.07004
* Phillip Isola, Jun-Yan Zhu, Tinghui Zhou, Alexei A. Efros
* This code is a modified version of [tensorflow pix2pix exmaple code](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/contrib/eager/python/examples/pix2pix/pix2pix_eager.ipynb).
* This code is implemented by only `tensorflow API` not `tf.keras`.
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os
import time
import numpy as np
import matplotlib.pyplot as plt
import PIL
from IPython.display import clear_output
# Import TensorFlow >= 1.10
import tensorflow as tf
slim = tf.contrib.slim
tf.logging.set_verbosity(tf.logging.INFO)
sess_config = tf.ConfigProto(gpu_options=tf.GPUOptions(allow_growth=True))
os.environ["CUDA_VISIBLE_DEVICES"]="0"
```
## Load the dataset
You can download this dataset and similar datasets from here. As mentioned in the paper we apply random jittering and mirroring to the training dataset.
* In random jittering, the image is resized to 286 x 286 and then randomly cropped to 256 x 256
* In random mirroring, the image is randomly flipped horizontally i.e left to right.
```
path_to_zip = tf.keras.utils.get_file('facades.tar.gz',
cache_subdir=os.path.abspath('.'),
origin='https://people.eecs.berkeley.edu/~tinghuiz/projects/pix2pix/datasets/facades.tar.gz',
extract=True)
PATH = os.path.join(os.path.dirname(path_to_zip), 'facades/')
train_dir = 'train/pix2pix/exp1/'
BUFFER_SIZE = 400
BATCH_SIZE = 1
IMG_WIDTH = 256
IMG_HEIGHT = 256
EPOCHS = 200
print_steps = 200
summary_steps = 400
save_epochs = 100
def load_image(image_file, is_train):
image = tf.read_file(image_file)
image = tf.image.decode_jpeg(image)
w = tf.shape(image)[1]
w = w // 2
real_image = image[:, :w, :]
input_image = image[:, w:, :]
input_image = tf.cast(input_image, tf.float32)
real_image = tf.cast(real_image, tf.float32)
if is_train:
# random jittering
# resizing to 286 x 286 x 3
input_image = tf.image.resize_images(input_image, [286, 286],
align_corners=True,
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
real_image = tf.image.resize_images(real_image, [286, 286],
align_corners=True,
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
# randomly cropping to 256 x 256 x 3
stacked_image = tf.stack([input_image, real_image], axis=0)
cropped_image = tf.random_crop(stacked_image, size=[2, IMG_HEIGHT, IMG_WIDTH, 3])
input_image, real_image = cropped_image[0], cropped_image[1]
if np.random.random() > 0.5:
# random mirroring
input_image = tf.image.flip_left_right(input_image)
real_image = tf.image.flip_left_right(real_image)
else:
input_image = tf.image.resize_images(input_image, size=[IMG_HEIGHT, IMG_WIDTH],
align_corners=True, method=2)
real_image = tf.image.resize_images(real_image, size=[IMG_HEIGHT, IMG_WIDTH],
align_corners=True, method=2)
# normalizing the images to [-1, 1]
input_image = (input_image / 127.5) - 1
real_image = (real_image / 127.5) - 1
return input_image, real_image
```
## Use tf.data to create batches, map(do preprocessing) and shuffle the dataset
```
train_dataset = tf.data.Dataset.list_files(PATH+'train/*.jpg')
train_dataset = train_dataset.shuffle(BUFFER_SIZE)
train_dataset = train_dataset.map(lambda x: load_image(x, True))
train_dataset = train_dataset.repeat(count=EPOCHS)
train_dataset = train_dataset.batch(1)
test_dataset = tf.data.Dataset.list_files(PATH+'test/*.jpg')
test_dataset = test_dataset.map(lambda x: load_image(x, False))
test_dataset = test_dataset.batch(1)
```
## Write the generator and discriminator models
* Generator
* The architecture of generator is a modified U-Net.
* Each block in the encoder is (Conv -> Batchnorm -> Leaky ReLU)
* Each block in the decoder is (Transposed Conv -> Batchnorm -> Dropout(applied to the first 3 blocks) -> ReLU)
* There are skip connections between the encoder and decoder (as in U-Net).
* Discriminator
* The Discriminator is a PatchGAN.
* Each block in the discriminator is (Conv -> BatchNorm -> Leaky ReLU)
* The shape of the output after the last layer is (batch_size, 30, 30, 1)
* Each 30x30 patch of the output classifies a 70x70 portion of the input image (such an architecture is called a PatchGAN).
* Discriminator receives 2 inputs.
* Input image and the target image, which it should classify as real.
* Input image and the generated image (output of generator), which it should classify as fake.
* We concatenate these 2 inputs together in the code (tf.concat([inp, tar], axis=-1))
* Shape of the input travelling through the generator and the discriminator is in the comments in the code.
To learn more about the architecture and the hyperparameters you can refer the paper.
```
class Generator(object):
def __init__(self, is_training=True, scope=None):
self.scope = scope
self.is_training = is_training
self.scope = scope
self.OUTPUT_CHANNELS = 3
self.batch_norm_params = {'is_training': self.is_training,
'scope': 'batch_norm'}
def upsample(self, x1, x2, num_outputs, apply_dropout=False, scope=None):
with tf.variable_scope(scope) as scope:
with slim.arg_scope([slim.conv2d_transpose],
kernel_size=[4, 4],
stride=[2, 2],
normalizer_fn=slim.batch_norm,
normalizer_params=self.batch_norm_params):
up = slim.conv2d_transpose(x1, num_outputs)
if apply_dropout:
up = slim.dropout(up, is_training=self.is_training)
output = tf.concat([up, x2], axis=-1)
return output
def __call__(self, x, reuse=False):
with tf.variable_scope('Generator/' + self.scope, reuse=reuse) as scope:
with slim.arg_scope([slim.conv2d],
kernel_size=[4, 4],
stride=[2, 2],
activation_fn=tf.nn.leaky_relu,
normalizer_fn=slim.batch_norm,
normalizer_params=self.batch_norm_params):
# Encoding part
self.down1 = slim.conv2d(x, 64, normalizer_fn=None, scope='down1')
self.down2 = slim.conv2d(self.down1, 128, scope='down2')
self.down3 = slim.conv2d(self.down2, 256, scope='down3')
self.down4 = slim.conv2d(self.down3, 512, scope='down4')
self.down5 = slim.conv2d(self.down4, 512, scope='down5')
self.down6 = slim.conv2d(self.down5, 512, scope='down6')
self.down7 = slim.conv2d(self.down6, 512, scope='down7')
self.down8 = slim.conv2d(self.down7, 512, scope='down8')
# Decoding part
self.up8 = self.upsample(self.down8, self.down7, 512, apply_dropout=True, scope='up8')
self.up7 = self.upsample(self.up8, self.down6, 512, apply_dropout=True, scope='up7')
self.up6 = self.upsample(self.up7, self.down5, 512, apply_dropout=True, scope='up6')
self.up5 = self.upsample(self.up6, self.down4, 512, scope='up5')
self.up4 = self.upsample(self.up5, self.down3, 256, scope='up4')
self.up3 = self.upsample(self.up4, self.down2, 128, scope='up3')
self.up2 = self.upsample(self.up3, self.down1, 64, scope='up2')
self.last = slim.conv2d_transpose(self.up2, self.OUTPUT_CHANNELS, [4, 4],
stride=[2, 2],
activation_fn=tf.nn.tanh,
scope='up1')
return self.last
class Discriminator(object):
def __init__(self, is_training=True, scope=None):
self.scope = scope
self.is_training = is_training
self.batch_norm_params = {'is_training': self.is_training,
'scope': 'batch_norm'}
def __call__(self, inputs, targets, reuse=False):
with tf.variable_scope('Discriminator/' + self.scope, reuse=reuse) as scope:
with slim.arg_scope([slim.conv2d],
kernel_size=[4, 4],
stride=[2, 2],
activation_fn=tf.nn.leaky_relu,
normalizer_fn=slim.batch_norm,
normalizer_params=self.batch_norm_params):
self.x = tf.concat([inputs, targets], axis=-1)
self.down1 = slim.conv2d(self.x, 64, normalizer_fn=None, scope='down1')
self.down2 = slim.conv2d(self.down1, 128, scope='down2')
self.down3 = slim.conv2d(self.down2, 256, scope='down3')
self.down3 = tf.pad(self.down3, tf.constant([[0, 0], [1, 1], [1, 1], [0, 0]]))
self.down4 = slim.conv2d(self.down3, 512, stride=1, padding='VALID', scope='down4')
self.down4 = tf.pad(self.down4, tf.constant([[0, 0], [1, 1], [1, 1], [0, 0]]))
self.last = slim.conv2d(self.down4, 512, stride=1, padding='VALID', activation_fn=None, scope='last')
return self.last
class Pix2Pix(object):
def __init__(self, mode, train_dataset, test_dataset):
assert mode in ["train", "translate"]
self.mode = mode
self.LAMBDA = 100
self.train_dataset = train_dataset
self.test_dataset = test_dataset
def build_images(self):
# tf.data.Iterator.from_string_handle의 output_shapes는 default = None이지만 꼭 값을 넣는 게 좋음
self.handle = tf.placeholder(tf.string, shape=[])
self.iterator = tf.data.Iterator.from_string_handle(self.handle,
self.train_dataset.output_types,
self.train_dataset.output_shapes)
self.input_image, self.target = self.iterator.get_next()
def discriminator_loss(self, disc_real_output, disc_generated_output):
real_loss = tf.losses.sigmoid_cross_entropy(multi_class_labels = tf.ones_like(disc_real_output),
logits = disc_real_output)
generated_loss = tf.losses.sigmoid_cross_entropy(multi_class_labels = tf.zeros_like(disc_generated_output),
logits = disc_generated_output)
total_disc_loss = real_loss + generated_loss
return total_disc_loss
def generator_loss(self, disc_generated_output, gen_output, target):
gan_loss = tf.losses.sigmoid_cross_entropy(multi_class_labels = tf.ones_like(disc_generated_output),
logits = disc_generated_output)
# mean absolute error
l1_loss = tf.reduce_mean(tf.abs(target - gen_output))
total_gen_loss = gan_loss + (self.LAMBDA * l1_loss)
return total_gen_loss
def build(self):
self.global_step = slim.get_or_create_global_step()
if self.mode == "translate":
pass
else:
self.build_images()
# Create generator and discriminator class
generator = Generator(is_training=True, scope='g')
discriminator = Discriminator(is_training=True, scope='d')
self.gen_output = generator(self.input_image)
self.disc_real_output = discriminator(self.input_image, self.target)
self.disc_generated_output = discriminator(self.input_image, self.gen_output, reuse=True)
self.gen_loss = self.generator_loss(self.disc_generated_output, self.gen_output, self.target)
self.disc_loss = self.discriminator_loss(self.disc_real_output, self.disc_generated_output)
self.g_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Generator')
self.d_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Discriminator')
print("complete model build.")
```
## Define the loss functions and the optimizer
* Discriminator loss
* The discriminator loss function takes 2 inputs; real images, generated images
* real_loss is a sigmoid cross entropy loss of the real images and an array of ones(since these are the real images)
* generated_loss is a sigmoid cross entropy loss of the generated images and an array of zeros(since these are the fake images)
* Then the total_loss is the sum of real_loss and the generated_loss
* Generator loss
* It is a sigmoid cross entropy loss of the generated images and an array of ones.
* The paper also includes L1 loss which is MAE (mean absolute error) between the generated image and the target image.
* This allows the generated image to become structurally similar to the target image.
* The formula to calculate the total generator loss = gan_loss + LAMBDA * l1_loss, where LAMBDA = 100. This value was decided by the authors of the paper.
## Checkpoints (Object-based saving)
```
#checkpoint_dir = './training_checkpoints'
#checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
#checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
# discriminator_optimizer=discriminator_optimizer,
# generator=generator,
# discriminator=discriminator)
```
## Training
* We start by iterating over the dataset
* The generator gets the input image and we get a generated output.
* The discriminator receives the input_image and the generated image as the first input. The second input is the input_image and the target_image.
* Next, we calculate the generator and the discriminator loss.
* Then, we calculate the gradients of loss with respect to both the generator and the discriminator variables(inputs) and apply those to the optimizer.
## Generate Images
* After training, its time to generate some images!
* We pass images from the test dataset to the generator.
* The generator will then translate the input image into the output we expect.
* Last step is to plot the predictions and voila!
```
def print_images(test_input, tar, prediction):
# the training=True is intentional here since
# we want the batch statistics while running the model
# on the test dataset. If we use training=False, we will get
# the accumulated statistics learned from the training dataset
# (which we don't want)
plt.figure(figsize=(15,15))
display_list = [test_input[0], tar[0], prediction[0]]
title = ['Input Image', 'Ground Truth', 'Predicted Image']
for i in range(3):
plt.subplot(1, 3, i+1)
plt.title(title[i])
# getting the pixel values between [0, 1] to plot it.
plt.imshow(display_list[i] * 0.5 + 0.5)
plt.axis('off')
plt.show()
model = Pix2Pix(mode="train", train_dataset=train_dataset, test_dataset=test_dataset)
model.build()
# show info for trainable variables
t_vars = tf.trainable_variables()
slim.model_analyzer.analyze_vars(t_vars, print_info=True)
opt_D = tf.train.AdamOptimizer(learning_rate=2e-4, beta1=0.5)
opt_G = tf.train.AdamOptimizer(learning_rate=2e-4, beta1=0.5)
with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS, scope='Discriminator')):
opt_D_op = opt_D.minimize(model.disc_loss, var_list=model.d_vars)
with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS, scope='Generator')):
opt_G_op = opt_G.minimize(model.gen_loss, global_step=model.global_step,
var_list=model.g_vars)
saver = tf.train.Saver(tf.global_variables(), max_to_keep=1000)
#with tf.Session(config=sess_config) as sess:
sess = tf.Session(config=sess_config)
sess.run(tf.global_variables_initializer())
tf.logging.info('Start Session.')
num_examples = 400
num_batches_per_epoch = int(num_examples / BATCH_SIZE)
#train_iterator = train_dataset.make_initializable_iterator()
train_iterator = train_dataset.make_one_shot_iterator()
train_handle = sess.run(train_iterator.string_handle())
test_iterator = test_dataset.make_initializable_iterator()
test_handle = sess.run(test_iterator.string_handle())
# save loss values for plot
loss_history = []
pre_epochs = 0
while True:
try:
start_time = time.time()
#for _ in range(k):
for _ in range(1):
_, loss_D = sess.run([opt_D_op, model.disc_loss],
feed_dict={model.handle: train_handle})
_, global_step_, loss_G = sess.run([opt_G_op,
model.global_step,
model.gen_loss],
feed_dict={model.handle: train_handle})
epochs = global_step_ * BATCH_SIZE / float(num_examples)
duration = time.time() - start_time
if global_step_ % print_steps == 0:
clear_output(wait=True)
examples_per_sec = BATCH_SIZE / float(duration)
print("Epochs: {:.2f} global_step: {} loss_D: {:.3f} loss_G: {:.3f} ({:.2f} examples/sec; {:.3f} sec/batch)".format(
epochs, global_step_, loss_D, loss_G, examples_per_sec, duration))
loss_history.append([epochs, loss_D, loss_G])
# print sample image
sess.run(test_iterator.initializer)
test_input, tar, prediction = sess.run([model.input_image, model.target, model.gen_output],
feed_dict={model.handle: test_handle})
print_images(test_input, tar, prediction)
# write summaries periodically
#if global_step_ % summary_steps == 0:
# summary_str = sess.run(summary_op)
# train_writer.add_summary(summary_str, global_step=global_step_)
# save model checkpoint periodically
if int(epochs) % save_epochs == 0 and pre_epochs != int(epochs):
tf.logging.info('Saving model with global step {} (= {} epochs) to disk.'.format(global_step_, int(epochs)))
saver.save(sess, train_dir + 'model.ckpt', global_step=global_step_)
pre_epochs = int(epochs)
except tf.errors.OutOfRangeError:
print("End of dataset") # ==> "End of dataset"
tf.logging.info('Saving model with global step {} (= {} epochs) to disk.'.format(global_step_, int(epochs)))
saver.save(sess, train_dir + 'model.ckpt', global_step=global_step_)
break
tf.logging.info('complete training...')
```
## Restore the latest checkpoint and test
```
# restoring the latest checkpoint in checkpoint_dir
#checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
```
## Testing on the entire test dataset
```
#with tf.Session(config=sess_config) as sess:
test_iterator = test_dataset.make_initializable_iterator()
test_handle = sess.run(test_iterator.string_handle())
sess.run(test_iterator.initializer)
test_input, tar, prediction = sess.run([model.input_image, model.target, model.gen_output],
feed_dict={model.handle: test_handle})
print_images(test_input, tar, prediction)
```
| true |
code
| 0.75944 | null | null | null | null |
|
## Probability distributions
Probability distribution is the backbone of uncertainty quantification.
Creating a probability distribution in `chaospy` is done by as follows:
```
import chaospy
normal = chaospy.Normal(mu=2, sigma=2)
normal
```
The distribution have a few methods that the user can used, which has names
and syntax very similar to that of
[scipy.stats](https://docs.scipy.org/doc/scipy/reference/stats.html). Below
some of these methods are demonstrated. For a full overview of the
distribution methods, see
[chaospy.Distribution](../../api/chaospy.Distribution.rst).
For an overview of available distributions, see then take a look at the
[collection listed in the reference](../../reference/distribution/collection.rst).
### (Pseudo-)random samples
The most important property a random variable has, is to create
(pseudo-)random samples. This can be created using
[chaospy.Distribution.sample()](../../api/chaospy.Distribution.sample.rst#chaospy.Distribution.sample):
```
samples = normal.sample(4, seed=1234)
samples
```
These can be used to create e.g. histograms:
```
from matplotlib import pyplot
pyplot.hist(normal.sample(10000, seed=1234), 30)
pyplot.show()
```
The input can be both be a integer, but also a sequence of integers. For
example:
```
normal.sample([2, 2], seed=1234)
```
### Random seed
Note that the `seed` parameters was passed to ensure reproducability. In
addition to having this flag, all `chaospy` distributions respects `numpy`'s
random seed. So the sample generation can also be done as follows:
```
import numpy
numpy.random.seed(1234)
normal.sample(4)
```
### Probability density function
The probability density function, is a function whose value at any given
sample in the sample space can be interpreted as providing a relative
likelihood that the value of the random variable would equal that sample.
This method is available through
[chaospy.Distribution.pdf()](../../api/chaospy.Distribution.pdf.rst):
```
normal.pdf([-2, 0, 2])
q_loc = numpy.linspace(-4, 8, 200)
pyplot.plot(q_loc, normal.pdf(q_loc))
pyplot.show()
```
### Cumulative probability function
the cumulative distribution function, defines the probability that a random
variables is at most the argument value provided. This method is available
through
[chaospy.Distribution.cdf()](../../api/chaospy.Distribution.cdf.rst):
```
normal.cdf([-2, 0, 2])
pyplot.plot(q_loc, normal.cdf(q_loc))
pyplot.show()
```
### Statistical moments
The moments of a random variable giving important descriptive information
about the variable reduced to single scalars. The raw moments is the building
blocks to build these descriptive statistics. The moments are available
through
[chaospy.Distribution.mom()](../../api/chaospy.Distribution.mom.rst):
```
normal.mom([0, 1, 2])
```
Not all random variables have raw moment variables, but for these variables
the raw moments are estimated using quadrature integration. This allows for
the moments to be available for all distributions. This approximation can
explicitly be evoked through
[chaospy.approximate_moment()](../../api/chaospy.approximate_moment.rst):
```
chaospy.approximate_moment(normal, [2])
```
See [quadrature integration](./quadrature_integration.ipynb) for more details on how this
is done in practice.
Central moments can be accessed through wrapper functions. The four first
central moments of our random variable are:
```
(chaospy.E(normal), chaospy.Var(normal),
chaospy.Skew(normal), chaospy.Kurt(normal))
```
See [descriptive statistics](./descriptive_statistics.ipynb) for details on
the functions extracting metrics of interest from random variables.
### Truncation
In the [collection of distributions](../../reference/distribution/collection.rst) some
distribution are truncated by default. However for those that are not, and
that is the majority of distributions, truncation can be invoiced using
[chaospy.Trunc()](../../api/chaospy.Trunc.rst). It supports one-sided
truncation:
```
normal_trunc = chaospy.Trunc(normal, upper=4)
pyplot.plot(q_loc, normal_trunc.pdf(q_loc))
pyplot.show()
```
and two-sided truncation:
```
normal_trunc2 = chaospy.Trunc(normal, lower=-1, upper=5)
pyplot.plot(q_loc, normal_trunc2.pdf(q_loc))
pyplot.show()
```
### Multivariate variables
`chaospy` also supports joint random variables. Some have their own
constructors defined in the
[collection of distributions](../../reference/distribution/collection.rst).
But more practical, multivariate variables can be constructed from univariate
ones through [chaospy.J](../../api/chaospy.J.rst):
```
normal_gamma = chaospy.J(chaospy.Normal(0, 1), chaospy.Gamma(1))
```
The multivariate variables have the same functionality as the univariate
ones, except that inputs and the outputs of the methods
[chaospy.Distribution.sample](../../api/chaospy.Distribution.sample.rst),
[chaospy.Distribution.pdf()](../../api/chaospy.Distribution.pdf.rst)
and
[chaospy.Distribution.cdf()](../../api/chaospy.Distribution.cdf.rst)
assumes an extra axis for dimensions. For example:
```
pyplot.rc("figure", figsize=[12, 4])
pyplot.subplot(131)
pyplot.title("random scatter")
pyplot.scatter(*normal_gamma.sample(1000, seed=1000), marker="x")
pyplot.subplot(132)
pyplot.title("probability density")
grid = numpy.mgrid[-3:3:100j, 0:4:100j]
pyplot.contourf(grid[0], grid[1], normal_gamma.pdf(grid), 50)
pyplot.subplot(133)
pyplot.title("cumulative distibution")
pyplot.contourf(grid[0], grid[1], normal_gamma.cdf(grid), 50)
pyplot.show()
```
### Rosenblatt transformation
One of the more sure-fire ways to create random variables, is to first
generate classical uniform samples and then use a inverse transformation to
map the sample to have the desired properties. In one-dimension, this mapping
is the inverse of the cumulative distribution function, and is available as
[chaospy.Distribution.ppf()](../../api/chaospy.Distribution.ppf.rst):
```
pyplot.subplot(121)
pyplot.title("standard uniform")
u_samples = chaospy.Uniform(0, 1).sample(10000, seed=1234)
pyplot.hist(u_samples, 30)
pyplot.subplot(122)
pyplot.title("transformed normal")
q_samples = normal.inv(u_samples)
pyplot.hist(q_samples, 30)
pyplot.show()
```
Note that `u_samples` and `q_samples` here consist of independently
identical distributed samples, the joint set `(u_samples, q_samples)` are
not. In fact, they are highly dependent by following the line of the normal
cumulative distribution function shape:
```
pyplot.subplot(121)
pyplot.title("coupled samples")
pyplot.scatter(q_samples, u_samples)
pyplot.subplot(122)
pyplot.title("normal cumulative distribution")
pyplot.plot(q_loc, normal.cdf(q_loc))
pyplot.show()
```
This idea also generalizes to the multivariate case. There the mapping
function is called an inverse Rosenblatt transformation $T^{-1}$, and is
defined in terms of conditional distribution functions:
$$
T^{-1}(q_0, q_1, q_2, \dots) =
\left[ F^{-1}_{Q_0}(q_0),
F^{-1}_{Q_1\mid Q_0}(q_1),
F^{-1}_{Q_2\mid Q_1,Q_0}(q_2), \dots \right]
$$
And likewise a forward Rosenblatt transformation is defined as:
$$
T(q_0, q_1, q_2, \dots) =
\left[ F_{Q_0}(q_0),
F_{Q_1\mid Q_0}(q_1),
F_{Q_2\mid Q_1,Q_0}(q_2), \dots \right]
$$
These functions can be used to map samples from standard multivariate uniform
distribution to a distribution of interest, and vise-versa.
In `chaospy` these methods are available through
[chaospy.Distribution.inv()](../../api/chaospy.Distribution.inv.rst)
and
[chaospy.Distribution.fwd()](../../api/chaospy.Distribution.fwd.rst):
```
pyplot.subplot(121)
pyplot.title("standard uniform")
uu_samples = chaospy.Uniform(0, 1).sample((2, 500), seed=1234)
pyplot.scatter(*uu_samples)
pyplot.subplot(122)
pyplot.title("transformed normal-gamma")
qq_samples = normal_gamma.inv(uu_samples)
pyplot.scatter(*qq_samples)
pyplot.show()
```
### User-defined distributions
The [collection of distributions](../../reference/distribution/collection.rst) contains a
lot of distributions, but if one needs something custom, `chaospy` allows for
the construction of user-defined distributions through
[chaospy.UserDistribution](../../api/chaospy.UserDistribution.rst).
These can be constructed by providing three functions: cumulative
distribution function, a lower bounds function, and a upper bounds function.
As an illustrative example, let us recreate the uniform distribution:
```
def cdf(x_loc, lo, up):
"""Cumulative distribution function."""
return (x_loc-lo)/(up-lo)
def lower(lo, up):
"""Lower bounds function."""
return lo
def upper(lo, up):
"""Upper bounds function."""
return up
```
The user-define distribution takes these functions, and a dictionary with the
parameter defaults as part of its initialization:
```
user_distribution = chaospy.UserDistribution(
cdf=cdf, lower=lower, upper=upper, parameters=dict(lo=-1, up=1))
```
The distribution can then be used in the same was as any other
[chaospy.Distribution](../../api/chaospy.Distribution.rst):
```
pyplot.subplot(131)
pyplot.title("binned random samples")
pyplot.hist(user_distribution.sample(10000), 30)
pyplot.subplot(132)
pyplot.title("probability density")
x_loc = numpy.linspace(-2, 2, 200)
pyplot.plot(x_loc, user_distribution.pdf(x_loc))
pyplot.subplot(133)
pyplot.title("cumulative distribution")
pyplot.plot(x_loc, user_distribution.cdf(x_loc))
pyplot.show()
```
Alternative, it is possible to define the same distribution using cumulative
distribution and point percentile function without the bounds:
```
def ppf(q_loc, lo, up):
"""Point percentile function."""
return q_loc*(up-lo)+lo
user_distribution = chaospy.UserDistribution(
cdf=cdf, ppf=ppf, parameters=dict(lo=-1, up=1))
```
In addition to the required fields, there are a few optional ones. These does
not provide new functionality, but allow for increased accuracy and/or lower
computational cost for the operations where they are used. These include raw
statistical moments which is used by
[chaospy.Distribution.mom()](../../api/chaospy.Distribution.rst):
```
def mom(k_loc, lo, up):
"""Raw statistical moment."""
return (up**(k_loc+1)-lo**(k_loc+1))/(k_loc+1)/(up-lo)
```
And three terms recurrence coefficients which is used by the method
[chaospy.Distribution.ttr()](../../api/chaospy.Distribution.ttr.rst)
to pass analytically to Stieltjes' method:
```
def ttr(k_loc, lo, up):
"""Three terms recurrence."""
return 0.5*up+0.5*lo, k_loc**2/(4*k_loc**2-1)*lo**2
```
What these coefficients are and why they are important are discussed in the
section [orthogonal polynomials](../polynomial/orthogonality.ipynb).
| true |
code
| 0.742475 | null | null | null | null |
|
# Matplotlib
## Introduction
- matplotlib is probably the single most used Python package for 2D-graphics
- it also provides good capablities to creade 3D-graphics
- quick way to visualize data from python in publication-quality
- for further information: https://matplotlib.org/
## Creating First Plots
### 1. Import pyplot package
- provides functions that makes matplotlib work like MATLAB
- object-oriented plotting
```
import matplotlib.pyplot as plt # import pyplot interface
```
### 3. Create [figure](https://matplotlib.org/api/figure_api.html) and [axes](https://matplotlib.org/api/_as_gen/matplotlib.figure.Figure.html)
```
fig = plt.figure() # a new figure window
ax = fig.add_subplot(1, 1, 1) # a new axes
plt.show(fig)
```
### 3. Create / [Plot data](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.plot.html) (sine)
```
import numpy as np
x = np.linspace(0,10,1000)
y = np.sin(x)
ax.plot(x,y, label = 'sine')
fig # this is required to re-display the figure
```
#### Customize Line Style
```
fig2 = plt.figure() # a new figure window
ax2 = fig2.add_subplot(1, 1, 1) # a new axes
x2 = np.linspace(0,10,50)
y2 = np.sin(x2)
ax2.plot(x2,y2, '-o', label = 'sine')
plt.show(fig2)
fig3 = plt.figure() # a new figure window
ax3 = fig3.add_subplot(1, 1, 1) # a new axes
x2 = np.linspace(0,10,50)
y2 = np.sin(x2)
ax3.plot(x2,y2, 'r-o', label = 'sine')
plt.show(fig3)
```
##### Line Colour
'r': red
'g': green
'b': blue
'c': cyan
'm': magenta
'y': yellow
'k': black
'w:': white
##### Line Style
'-': solid
'--': dashed
':': dotted
'-.': dot-dashed
'.': points
'o': filled circles
'^': filled triangles
### 4. Create / [Plot data](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.plot.html) (cosine)
```
y2 = np.cos(x)
ax.plot(x,y2, label = 'cosine')
fig
```
### 5. Create / [Plot data](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.plot.html) (3 * cosine) on second axes
```
ax_twin = ax.twinx()
y3 = 3 * np.cos(x+np.pi/4)
ax_twin.plot(x,y3, 'r',label = '3 * cosine')
fig
```
### 5. Set limits for [x](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.set_xlim.html)-/[y](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.set_ylim.html)-axis
```
ax.set_xlim(0,10)
ax.set_ylim(-1.5, 2.0)
fig
```
### 6. [Add legend](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.legend.html)
```
ax.legend()
fig
```
### 7. Add [x](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.set_xlabel.html)-/[y](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.set_ylabel.html)-label and [title](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.set_title.html)
```
ax.set_xlabel("$x$")
ax.set_ylabel("$\sin(x)$")
ax.set_title("I like $\pi$")
fig
```
### 7. [Add grid](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.grid.html)
```
ax.grid(True)
fig
```
### Excursion Subplots
- the command [fig.add_subplot](https://matplotlib.org/api/_as_gen/matplotlib.figure.Figure.html) divides the figures in grid with a certain number of axes
- syntax:
``` python
fig.add_subplot(rows, cols, num)
```
- rows = number of rows in the grid
- cols = number of columns in the grid
- num = number of the subplot to create (counting from left to right, top to bottom and indexed starting at 1)
```
fig = plt.figure()
for i in range(6):
ax = fig.add_subplot(2, 3, i + 1)
ax.set_title("Plot #%i" % i)
```
- the subplots are overlapping
- there are a few ways to fix it, i.e.:
```
fig.subplots_adjust(wspace=0.4, hspace=0.4)
fig
```
- ```wspace``` and ```hspace ``` determine the width and height between each plot
## 2. Various 2D Plotting
### [Histograms](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.hist.html)
```
x = np.random.normal(size=1000)
fig, ax = plt.subplots()
H = ax.hist(x, bins=50, alpha=0.5, histtype='stepfilled')
```
### [Pie Plot](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.pie.html)
```
fracs = [30, 15, 45, 10]
colors = ['b', 'g', 'r', 'w']
fig, ax = plt.subplots(figsize=(6, 6)) # make the plot square
pie = ax.pie(fracs, colors=colors, explode=(0, 0, 0.05, 0), shadow=True,
labels=['A', 'B', 'C', 'D'])
```
### [Errorbar Plots](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.errorbar.html)
```
x = np.linspace(0, 10, 30)
dy = 0.1
y = np.random.normal(np.sin(x),dy)
fig, ax = plt.subplots()
plt.errorbar(x, y, dy, fmt='.k')
```
### [Contour Plots (filled)](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.contourf.html)
```
x = np.linspace(0, 10, 50)
y = np.linspace(0, 20, 60)
z = np.cos(y[:, np.newaxis]) * np.sin(x)
fig, ax = plt.subplots()
# filled contours
im = ax.contourf(x, y, z, 100)
fig.colorbar(im, ax=ax)
```
### [Contour Plots (lines)](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.contour.html)
```
# contour lines
im2 = ax.contour(x, y, z, colors='k')
fig
```
## 3. [Various 3D Plotting](https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html)
```
# This is the 3D plotting toolkit
from mpl_toolkits.mplot3d import Axes3D
```
### [3D scatter Plot](https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html#scatter-plots)
```
fig = plt.figure()
ax = plt.axes(projection='3d')
z = np.linspace(0, 1, 100)
x = z * np.sin(20 * z)
y = z * np.cos(20 * z)
c = x + y
ax.scatter(x, y, z, c=c)
```
### [3D Line Plot](https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html#line-plots)
```
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot(x, y, z, '-b')
```
### [Surface Plot](https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html#surface-plots)
```
x = np.outer(np.linspace(-2, 2, 30), np.ones(30))
y = x.copy().T
z = np.cos(x ** 2 + y ** 2)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_surface(x, y, z, cmap=plt.cm.jet, rstride=1, cstride=1, linewidth=0)
```
| true |
code
| 0.675551 | null | null | null | null |
|
```
# default_exp custom_tf_training
```
# Custom Tensorflow Training
> Extending tf.keras for custom training functionality
```
# export
import os
from nbdev.showdoc import *
from fastcore.test import *
import tensorflow as tf
import sklearn
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
test_eq(sklearn.__version__ > "0.20", True)
test_eq(tf.__version__ > "2.0.0", True)
#hide
from nbdev.showdoc import *
TEMP_DIR = "tmp"
if not os.path.exists('tmp'):
os.makedirs('tmp')
```
### Custom Loss Functions
```
housing = sklearn.datasets.fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target.reshape(-1, 1), random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
X_test_scaled = scaler.transform(X_test)
def huber_fn(y_true, y_pred):
error = y_true - y_pred
is_small_error = tf.abs(error) < 1
squared_loss = tf.square(error) / 2
linear_loss = tf.abs(error) - 0.5
return tf.where(is_small_error, squared_loss, linear_loss)
plt.figure(figsize=(8, 3.5))
z = np.linspace(-4, 4, 200)
plt.plot(z, huber_fn(0, z), "b-", linewidth=2, label="huber($z$)")
plt.plot(z, z**2 / 2, "b:", linewidth=1, label=r"$\frac{1}{2}z^2$")
plt.plot([-1, -1], [0, huber_fn(0., -1.)], "r--")
plt.plot([1, 1], [0, huber_fn(0., 1.)], "r--")
plt.gca().axhline(y=0, color='k')
plt.gca().axvline(x=0, color='k')
plt.axis([-4, 4, 0, 4])
plt.grid(True)
plt.xlabel("$z$")
plt.legend(fontsize=14)
plt.title("Huber loss", fontsize=14)
plt.show()
input_shape = X_train.shape[1:]
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
tf.keras.layers.Dense(1),
])
model.compile(loss=huber_fn, optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
CUSTOM_MODEL = os.path.join(TEMP_DIR, "my_model_with_a_custom_loss.h5")
CUSTOM_MODEL_THRESHOLD = os.path.join(TEMP_DIR, "my_model_with_a_custom_loss_threshold.h5")
CUSTOM_MODEL_LOSS_CLASS = os.path.join(TEMP_DIR, "my_model_with_a_custom_loss_class.h5")
CUSTOM_MODEL_CUSTOM_PARTS = os.path.join(TEMP_DIR, "my_model_with_many_custom_parts.h5")
CUSTOM_MODEL_CUSTOM_PARTS_2 = os.path.join(TEMP_DIR, "my_model_with_many_custom_parts_2.h5")
model.save(CUSTOM_MODEL)
del model
model = tf.keras.models.load_model(CUSTOM_MODEL,
custom_objects={"huber_fn": huber_fn})
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
def create_huber(threshold=1.0):
def huber_fn(y_true, y_pred):
error = y_true - y_pred
is_small_error = tf.abs(error) < threshold
squared_loss = tf.square(error) / 2
linear_loss = threshold * tf.abs(error) - threshold**2 / 2
return tf.where(is_small_error, squared_loss, linear_loss)
return huber_fn
model.compile(loss=create_huber(2.0), optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.save(CUSTOM_MODEL_THRESHOLD)
del model
model = tf.keras.models.load_model(CUSTOM_MODEL_THRESHOLD,
custom_objects={"huber_fn": create_huber(2.0)})
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
class HuberLoss(tf.keras.losses.Loss):
def __init__(self, threshold=1.0, **kwargs):
self.threshold = threshold
super().__init__(**kwargs)
def call(self, y_true, y_pred):
error = y_true - y_pred
is_small_error = tf.abs(error) < self.threshold
squared_loss = tf.square(error) / 2
linear_loss = self.threshold * tf.abs(error) - self.threshold**2 / 2
return tf.where(is_small_error, squared_loss, linear_loss)
def get_config(self):
base_config = super().get_config()
return {**base_config, "threshold": self.threshold}
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
tf.keras.layers.Dense(1),
])
model.compile(loss=HuberLoss(2.), optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.save(CUSTOM_MODEL_LOSS_CLASS, save_format='h5')
# tf.saved_model.save(model, CUSTOM_MODEL_LOSS_CLASS)
# del model
# open issue: https://github.com/tensorflow/tensorflow/issues/25938
# model = tf.keras.models.load_model(CUSTOM_MODEL_LOSS_CLASS,
# {"HuberLoss": HuberLoss})
# model = tf.saved_model.load(CUSTOM_MODEL_LOSS_CLASS)
# related to : https://github.com/tensorflow/tensorflow/issues/25938
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
```
Notes
Saving tensorflow models with custom components is still very clunky.
* Saving loss classes of `tf.keras.losses.Loss` throws errors (related to: [this PR](https://github.com/tensorflow/tensorflow/issues/25938)
* `h5py` works most cases except for saving `tf.keras.losses.Loss` classes.
* Ideally would like to save all of this as a `SavedModel`, due to integreation with tensroflow serving.
### Custom Activation Functions, Initializers, Regularizers and Constants
```
def clear_keras_session():
tf.keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
clear_keras_session()
def my_softplus(z): # return value is just tf.nn.softplus(z)
return tf.math.log(tf.exp(z) + 1.0)
def my_glorot_initializer(shape, dtype=tf.float32):
stddev = tf.sqrt(2. / (shape[0] + shape[1]))
return tf.random.normal(shape, stddev=stddev, dtype=dtype)
def my_l1_regularizer(weights):
return tf.reduce_sum(tf.abs(0.01 * weights))
def my_positive_weights(weights): # return value is just tf.nn.relu(weights)
return tf.where(weights < 0., tf.zeros_like(weights), weights)
layer = tf.keras.layers.Dense(1, activation=my_softplus,
kernel_initializer=my_glorot_initializer,
kernel_regularizer=my_l1_regularizer,
kernel_constraint=my_positive_weights)
clear_keras_session()
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
tf.keras.layers.Dense(1, activation=my_softplus,
kernel_regularizer=my_l1_regularizer,
kernel_constraint=my_positive_weights,
kernel_initializer=my_glorot_initializer),
])
model.compile(loss="mse", optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.save(CUSTOM_MODEL_CUSTOM_PARTS)
del model
model = tf.keras.models.load_model(
CUSTOM_MODEL_CUSTOM_PARTS,
custom_objects={
"my_l1_regularizer": my_l1_regularizer,
"my_positive_weights": my_positive_weights,
"my_glorot_initializer": my_glorot_initializer,
"my_softplus": my_softplus,
})
class MyL1Regularizer(tf.keras.regularizers.Regularizer):
def __init__(self, factor):
self.factor = factor
def __call__(self, weights):
return tf.reduce_sum(tf.abs(self.factor * weights))
def get_config(self):
return {"factor": self.factor}
clear_keras_session()
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
tf.keras.layers.Dense(1, activation=my_softplus,
kernel_regularizer=MyL1Regularizer(0.01),
kernel_constraint=my_positive_weights,
kernel_initializer=my_glorot_initializer),
])
model.compile(loss="mse", optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.save(CUSTOM_MODEL_CUSTOM_PARTS_2)
model = tf.keras.models.load_model(
CUSTOM_MODEL_CUSTOM_PARTS_2,
custom_objects={
"MyL1Regularizer": MyL1Regularizer,
"my_positive_weights": my_positive_weights,
"my_glorot_initializer": my_glorot_initializer,
"my_softplus": my_softplus,
})
```
### Custom Metrics
### Custom Layers
### Custom Models
### Losses and Metrics Based on Model Internals
### Computing Gradients Using Autodiff
### Custom Training Loops
## References
* [Ch 12: Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow](https://github.com/ageron/handson-ml2/blob/master/12_custom_models_and_training_with_tensorflow.ipynb)
| true |
code
| 0.755406 | null | null | null | null |
|
<h3 style="text-align: center;"><b>Implementing Binomial Logistic Regression</b></h3>
<h5 style="text-align: center;">This notebook follows this wonderful tutorial by Nikhil Kumar: <a href="https://www.geeksforgeeks.org/understanding-logistic-regression/" target="_blank">https://www.geeksforgeeks.org/understanding-logistic-regression/</a><br></h5>
<h4 style="text-align: center;"><b>Note: most to all the description, code and some text is copied from GeeksToGeeks explanation mostly because its explained very well.</b></h4>
<h4 style="text-align: center;"><b>**To be honest I would recomend just following the GeeksToGeeks Tutorial. This notebook doesn't add anything much to that wonderful tutorial.</b></h4>
<h5 style="text-align: center;">Logistic regression is basically a supervised classification algorithm. In a classification problem, the target variable(or output), y, can take only discrete values for given set of features(or inputs), X.<br><br>Contrary to popular belief, logistic regression IS a regression model. The model builds a regression model to predict the probability that a given data entry belongs to the category numbered as “1”. Just like Linear regression assumes that the data follows a linear function, Logistic regression models the data using the sigmoid function.</h5>
$$ g(z) = \frac{1}{1 + e^{-z}} $$
<h5 style="text-align: center;">Logistic regression becomes a classification technique only when a decision threshold is brought into the picture. The setting of the threshold value is a very important aspect of Logistic regression and is dependent on the classification problem itself.<br>The decision for the value of the threshold value is majorly affected by the values of precision and recall. Ideally, we want both precision and recall to be 1, but this seldom is the case. In case of a Precision-Recall tradeoff we use the following arguments to decide upon the thresold:<ol><li>Low Precision/High Recall: In applications where we want to reduce the number of false negatives without necessarily reducing the number false positives, we choose a decision value which has a low value of Precision or high value of Recall. For example, in a cancer diagnosis application, we do not want any affected patient to be classified as not affected without giving much heed to if the patient is being wrongfully diagnosed with cancer. This is because, the absence of cancer can be detected by further medical diseases but the presence of the disease cannot be detected in an already rejected candidate.</li><li>High Precision/Low Recall: In applications where we want to reduce the number of false positives without necessarily reducing the number false negatives, we choose a decision value which has a high value of Precision or low value of Recall. For example, if we are classifying customers whether they will react positively or negatively to a personalised advertisement, we want to be absolutely sure that the customer will react positively to the advertisemnt because otherwise, a negative reaction can cause a loss potential sales from the customer.</li></ol></h5>
<h5 style="text-align: center;">Based on the number of categories, Logistic regression can be classified as:<ol><li>binomial: target variable can have only 2 possible types: “0” or “1” which may represent “win” vs “loss”, “pass” vs “fail”, “dead” vs “alive”, etc.</li><li>multinomial: target variable can have 3 or more possible types which are not ordered(i.e. types have no quantitative significance) like “disease A” vs “disease B” vs “disease C”.</li><li>ordinal: it deals with target variables with ordered categories. For example, a test score can be categorized as:“very poor”, “poor”, “good”, “very good”. Here, each category can be given a score like 0, 1, 2, 3.</li></ol></h5>
<h5 style="text-align: center;">Let the data be a p x n matrix, where p is the number of feature variables and n is the number of observations</h5>
$$ X = \begin{equation} \begin{bmatrix} 1 & x_{1,1} & \ldots & x_{1,p} \\ 1 & x_{2,1} & \ldots & x_{2,p} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n,1} & \ldots & x_{n,p} \end{bmatrix} \label{eq:aeqn} \end{equation} $$
<img src="https://latex.codecogs.com/gif.latex?x_i%20%3D%20%5Cbegin%7Bbmatrix%7D%201%5C%5C%20x_%7Bi1%7D%5C%5C%20x_%7Bi2%7D%5C%5C%20.%5C%5C%20.%5C%5C%20x_%7Bip%7D%5C%5C%20%5Cend%7Bbmatrix%7D" alt="">
$$ \text{Then } h(x_i) = \beta_0 + \beta_1x_{i,1} + \beta_2x_{i,2} + \ldots + \beta_px_{i,p}$$
$$ \text{Or can be } h(x_i) = \beta^Tx_i $$
$$ \text{The reason for taking } x_0 = 1 \text{is pretty clear now.
We needed to do a matrix product, but there was no
actual x_0 multiplied to } \beta_0 \text{in original hypothesis formula. So, we defined } x_0 = 1. $$
$$ \text{So } \begin{equation} h(x_i) = g(B^Tx_i) = \frac{1}{1 + e^{-\beta^Tx_i }} \end{equation} $$
<h5 style="text-align: center;">By the equation we know g(z) tends towards 1 as z -> ∞. And g(z) tends towards 0 as z -> -∞. Thus its always bounded between 0 and 1.</h5>
$$ \text{So for 2 labels (0 and 1) for } i^{th} $$
$$ P(y_i = 1|x_i;\beta) = h(x_i) $$
$$ P(y_i = 0|x_i;\beta) = 1 - h(x_i) $$
$$ \text{Or: } P(y_i|x_i;\beta) = (h(x_i))^{y_i}(1 - h(x_i))^{1 - y_i}$$
$$ \text{We also need likelihood which is: nothing but the probability of data(training examples), given a model and specific parameter values(here, }\beta \text{ ). It measures the support provided by the data for each possible value of the } \beta \text{. We obtain it by multiplying all } P(y_i|x_i) \text{ for given }\beta $$
$$ L(\beta) = \prod_{i=1}^{n} P(y_i|x_i;\beta) \text{ or } $$
$$ L(\beta) = \prod_{i=1}^{n} (h(x_i))^{y_i}(1 - h(x_i))^{1 - y_i} $$
$$ \text{For easier calculations: } l(\beta) = \log_{10}(L(\beta)) \text{ or }$$
$$ l(\beta) = \sum_{i=1}^{n}y_i\log_{10}(h(x_i)) + (1 - y_i)\log_{10}(1 - h(x_i)) $$
$$ \text{Cost Function: } J(\beta) = \sum_{i=1}^{n}-y_i\log_{10}(h(x_i)) - (1 - y_i)\log_{10}(1 - h(x_i)) $$
<h5 style="text-align: center;">Using Gradient Descent</h5>
$$ \frac{\partial J(\beta)}{\partial \beta_j} = (h(x) - y)x_j $$
```
"""
All code is from https://www.geeksforgeeks.org/understanding-logistic-regression/ by Nikhil Kumar
"""
import csv
import numpy as np
import matplotlib.pyplot as plt
def loadCSV(filename):
'''
function to load dataset
'''
with open(filename,"r") as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
for i in range(len(dataset)):
dataset[i] = [float(x) for x in dataset[i]]
return np.array(dataset)
def normalize(X):
'''
function to normalize feature matrix, X
'''
mins = np.min(X, axis = 0)
maxs = np.max(X, axis = 0)
rng = maxs - mins
norm_X = 1 - ((maxs - X)/rng)
return norm_X
def logistic_func(beta, X):
'''
logistic(sigmoid) function
'''
return 1.0/(1 + np.exp(-np.dot(X, beta.T)))
def log_gradient(beta, X, y):
'''
logistic gradient function
'''
return np.dot((logistic_func(beta, X) - y.reshape(X.shape[0], -1)).T, X)
def cost_func(beta, X, y):
'''
cost function, J
'''
y = np.squeeze(y)
final = -(y * np.log(logistic_func(beta, X))) - ((1 - y) * np.log(1 - logistic_func(beta, X)))
return np.mean(final)
def grad_desc(X, y, beta, lr=.01, converge_change=.001):
'''
gradient descent function
'''
cost = cost_func(beta, X, y)
change_cost = 1
num_iter = 1
while(change_cost > converge_change):
old_cost = cost
beta -= lr * log_gradient(beta, X, y)
cost = cost_func(beta, X, y)
change_cost = old_cost - cost
num_iter += 1
return beta, num_iter
def pred_values(beta, X):
'''
function to predict labels
'''
pred_prob = logistic_func(beta, X)
pred_value = np.where(pred_prob >= .5, 1, 0)
return np.squeeze(pred_value)
def plot_reg(X, y, beta):
'''
function to plot decision boundary
'''
# labelled observations
x_0 = X[np.where(y == 0.0)]
x_1 = X[np.where(y == 1.0)]
# plotting points with diff color for diff label
plt.scatter([x_0[:, 1]], [x_0[:, 2]], c='b', label='y = 0')
plt.scatter([x_1[:, 1]], [x_1[:, 2]], c='r', label='y = 1')
# plotting decision boundary
x1 = np.arange(0, 1, 0.1)
x2 = -(beta[0,0] + beta[0,1]*x1)/beta[0,2]
plt.plot(x1, x2, c='k', label='reg line')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
plt.show()
if __name__=='__main__':
dataset = loadCSV('Data\\binary_data.csv')
# normalizing feature matrix
X = normalize(dataset[:, :-1])
# stacking columns wth all ones in feature matrix
X = np.hstack((np.matrix(np.ones(X.shape[0])).T, X))
# response vector
y = dataset[:, -1]
# initial beta values
beta = np.matrix(np.zeros(X.shape[1]))
# beta values after running gradient descent
beta, num_iter = grad_desc(X, y, beta)
# estimated beta values and number of iterations
print("Estimated regression coefficients:", beta)
print("No. of iterations:", num_iter)
# predicted labels
y_pred = pred_values(beta, X)
# number of correctly predicted labels
print("Correctly predicted labels:", np.sum(y == y_pred))
# plotting regression line
plot_reg(X, y, beta)
from sklearn.linear_model import LogisticRegression
dataset = loadCSV('Data\\binary_data.csv')
X = normalize(dataset[:, :-1])
y = dataset[:, -1]
clf = LogisticRegression(random_state=0).fit(X, y)
print(clf.predict(X[:2, :]))
print(clf.predict_proba(X[:2, :]))
print(clf.score(X, y))
```
<h5 style="text-align: center;">Note: Gradient descent is one of the many way to estimate β Basically, these are more advanced algorithms which can be easily run in Python once you have defined your cost function and your gradients. These algorithms are:<ul><li>BFGS(Broyden–Fletcher–Goldfarb–Shanno algorithm)</li><li>L-BFGS(Like BFGS but uses limited memory)</li><li>Conjugate Gradient<li></ul></h5>
<h5 style="text-align: center;">Advantages/disadvantages of using any one of these algorithms over Gradient descent:</h5><h5 style="text-align: center;"><br>Advantages:<br><ul><li>Don’t need to pick learning rate</li><li>Often run faster (not always the case)</li><li>Can numerically approximate gradient for you (doesn’t always work out well)</li></ul><br>Disadvantages:<ul><li>More complex</li><li>More of a black box unless you learn the specifics</li></ul></h5>
```
"""
This part is from https://www.geeksforgeeks.org/ml-logistic-regression-using-python/
"""
from sklearn.model_selection import train_test_split
xtrain, xtest, ytrain, ytest = train_test_split(
X, y, test_size = 0.25, random_state = 0)
from sklearn.preprocessing import StandardScaler
sc_x = StandardScaler()
xtrain = sc_x.fit_transform(xtrain)
xtest = sc_x.transform(xtest)
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(xtrain, ytrain)
y_pred = classifier.predict(xtest)
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(ytest, y_pred)
print ("Confusion Matrix : \n", cm)
from sklearn.metrics import accuracy_score
print ("Accuracy : ", accuracy_score(ytest, y_pred))
from matplotlib.colors import ListedColormap
X_set, y_set = xtest, ytest
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1,
stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1,
stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(
np.array([X1.ravel(), X2.ravel()]).T).reshape(
X1.shape), alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Classifier (Test set)')
plt.legend()
plt.show()
```
| true |
code
| 0.726862 | null | null | null | null |
|
## This notebook will be focused on using gradient descent to solve simple linear regression and multivariate regression problems
Note: This notebook is for educational purposes as using normal equations would be a superior approach to solving the optimization problem for the datasets that I use in this notebook.
```
import numpy as np
from sklearn.linear_model import LinearRegression # Used for validation
from sklearn import datasets
import random
import matplotlib.pyplot as plt
import pandas as pd
import latex
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import time
from sklearn.metrics import mean_squared_error
```
### Initially this notebook will be focused on simple linear regression
```
# Will be using the diabetes dataset with a single predictor.
diabetes = datasets.load_diabetes()
X = diabetes.data[:, np.newaxis, 2]
y = diabetes.target
# Using sklearn's linear regression to determine the ideal output of my implementation
lr = LinearRegression()
lr.fit(X, y)
predictedVals = lr.predict(X)
print("R^2: " + str(lr.score(X, y)))
print("Coefs: " + str(lr.coef_))
print("Intercept: " + str(lr.intercept_))
# Mean squared error to compare to in the future
mean_squared_error(y, predictedVals)
plt.scatter(X, y)
plt.plot(X, predictedVals, color="black")
plt.title("Diabetes Linear Regression")
plt.xlabel("predictor")
plt.ylabel("y value")
plt.show()
```
### In order to implement gradient descent, we must have a cost function with incorporates the weight and bias terms
I will be experimenting with a numpy based implementation and a for loop implementation and seeing if there is any significant time difference in how long it takes for the functions to run. The numpy implementation is over 10x faster.
- N: number of observations, (mx<sub>i</sub> + b) is the prediction
$$MSE = \frac{1}{N}\sum_{i=1}^{n}(y_i - (mx_i + b))^2 $$
```
# Ensuring the shapes of the arrays are correct
# Note: if y is of the wrong shape, it messes up future equations which don't rely on for loops
y0 = y.shape[0]
x0 = X.shape[0]
y.shape = (y0,1)
X.shape = (x0,1)
# Cost function with numpy
def get_cost(X, y, weight, bias):
total_error = np.average((y-(X*weight+bias))**2)
# total_error = np.mean((y-(weight*X+bias))**2)
return total_error
# Cost function with a for loop
def cost_function(X, y, weight, bias):
total = len(X)
total_error = 0.0
for i in range(total):
total_error += (y[i] - (weight*X[i] + bias))**2
return total_error / total
# Testing the cost function implementation with random terms
weight = 3.1245
weight_arr = np.array([weight])
weight_arr.shape = (1,1)
bias = 0.0134
bias_arr = np.array(bias)
bias_arr.shape = (1,1)
start = time.clock()
parallel_cost = get_cost(X,y,weight_arr,bias_arr)
how_long = time.clock() - start
print("Took: ", how_long)
parallel_cost
start = time.clock()
normal_cost = cost_function(X,y,weight,bias)
how_long1 = time.clock() - start
print("Took: ", how_long1)
normal_cost
```
### Creating functions to update the weights and bias terms using gradient descent
Yet again, I will be comparing two implementations of an update_weight function, one using numpy and the other using a for loop to determine if there is a difference in performance. Within the update_weight for loop function, I will also be using the for loop implementation of mse.
$$ f(m,b) = \frac{1}{N}\sum_{i=1}^{n}(y_i-(mx_i-b))^2$$
$$ f^\prime(m,b) = \begin{split} & \frac{df}{dm} = \bigg[\frac{1}{N}\sum-2x_i(y_i-(mx_i+b))\bigg]
\\ & \frac{df}{db} = \bigg[\frac{1}{N}\sum-2(y_i-(mx_i+b))\bigg] \end{split} $$
```
# Updating the weights, without any normalization or optimization, using numpy
def update_weights(X, y, weight, bias, lr=0.01):
df_dm = (1/len(X)) * np.dot((-2*X).T, (y-(weight*X+bias)))
df_db = np.average(-2*(y-(weight*X+bias)))
weight = weight - (lr*df_dm)
bias = bias - (lr*df_db)
return weight,bias
def get_new_weights(X, y, weight, bias, learning_rate=0.01):
weight_deriv = 0
bias_deriv = 0
total = len(X)
for i in range(total):
# -2x(y - (mx + b))
weight_deriv += -2*X[i] * (y[i] - (weight*X[i] + bias))
# -2(y - (mx + b))
bias_deriv += -2*(y[i] - (weight*X[i] + bias))
weight -= (weight_deriv / total) * learning_rate
bias -= (bias_deriv / total) * learning_rate
return weight, bias
# Parameters set for parameter update function testing
# The numpy implementation was around 3x faster
weight = 10.2345
bias = 6.245
start = time.clock()
weight1,bias1 = update_weights(X, y, weight, bias)
took = time.clock() - start
print("Using Numpy: ")
print("Weight: {}, Bias: {}".format(weight1,bias1))
print("Took: ", took)
start = time.clock()
weight2,bias2 = get_new_weights(X, y, weight, bias)
took = time.clock() - start
print("Using For Loop: ")
print("Weight: {}, Bias: {}".format(weight2,bias2))
print("Took: ", took)
```
### Creating a optimization loop which will update the bias and weight parameters
I will be writing two training functions, one using the update_weight function that utilizes numpy and another that uses a simple for loop to update bias and weight terms. The numpy implementation is over 100x faster.
```
# Initializing weight and bias terms
Weight = 0
Bias = 0
# Training using the numpy update_weights function
def train_numpy(X, y, weight, bias, iters, lr=0.01):
cost = []
for i in range(iters):
weight, bias = update_weights(X, y, weight, bias, lr)
a_cost = get_cost(X, y, weight, bias)
cost.append(a_cost)
return cost, weight, bias
# Training using the for loop update_weights function
def train_for(X, y, weight, bias, iters, lr=0.01):
cost = []
for i in range(iters):
weight, bias = get_new_weights(X, y, weight, bias, lr)
a_cost = cost_function(X, y, weight, bias)
cost.append(a_cost)
return cost, weight, bias
# Not using the forloop made optimization around 3x faster
now_time = time.clock()
numpy_cost,numpy_weight,numpy_bias = train_numpy(X, y, Weight, Bias, 7000, 0.1)
took = time.clock() - now_time
print("Took: ", took)
print("Weight: {}, Bias: {}".format(numpy_weight, numpy_bias))
print("End cost: ", numpy_cost[-1])
now_time = time.clock()
for_cost,for_weight, for_bias = train_for(X, y, Weight, Bias, 7000, 0.1)
took = time.clock() - now_time
print("Took: ", took)
print("Weight: {}, Bias: {}".format(for_weight, for_bias))
print("End cost: ", for_cost[-1])
# For plotting cost against time
time_seq = [i for i in range(7000)]
# Although both implementations have similar end cost, the numpy implementation was over 100x faster
plt.figure(figsize=(22,7))
plt.subplot(1, 2, 1)
plt.plot(time_seq, numpy_cost)
plt.title("Cost vs Time Using Numpy")
plt.xlabel("Step Number")
plt.ylabel("Cost")
plt.subplot(1, 2, 2)
plt.plot(time_seq, for_cost)
plt.title("Cost vs Time Using For Loop")
plt.xlabel("Step Number")
plt.ylabel("Cost")
plt.tight_layout()
plt.show()
```
### Now getting the predictions to determine if my model matches the performance of the sklearn linear regression model
Overall, the cost function of my simple linear regression model closely matches that of the sklearn model and as such, I believe that my model is just as effective.
$$ Prediction = (mx_i + b) $$
```
X_list = list(X)
def get_predictions(X, weight, bias):
predictions = []
for i in range(len(X)):
pred = X[i] * weight + bias
predictions.append(pred)
return predictions
predictions = get_predictions(X_list, numpy_weight, numpy_bias)
predictions_arr = np.array(predictions)
# Ensuring predictions is the right shape
predictions_arr.shape = (442,1)
plt.scatter(X, y)
plt.plot(X, predictions_arr, color="black")
plt.title("Diabetes Linear Regression")
plt.xlabel("predictor")
plt.ylabel("y value")
plt.show()
```
## The next section of this notebook will be focused on mulivariate linear regression
Similar principles as earlier will be applied to this section of the notebook. Note that given the speed boost we saw earlier from using numpy and matrix algebra, all my new functions will be implementing these concepts.
```
# Getting a training set with multiple predictor variables
X2 = diabetes.data[:, np.newaxis, 2:5]
# Ensuring that the new X data is of the correct shape
X2.shape = (442,3)
# Getting a value to compare our model to
lr = LinearRegression()
lr.fit(X2, y)
predictedVals = lr.predict(X2)
print("R^2: " + str(lr.score(X2, y)))
print("Coefs: " + str(lr.coef_))
print("Intercept: " + str(lr.intercept_))
# Mean squared error to compare to in the future
mean_squared_error(y, predictedVals)
# Setting the new weights for multivariate regression
weight2 = np.array([[0],
[0],
[0]]) # corresponding with the three variables
bias2 = 0
# Ensuring shapes are correct
assert weight2.shape == (3,1)
assert X2.shape == (442,3)
assert y.shape == (442,1)
```
### Cost function for multivariate regression
$$ MSE = \frac{1}{2N}\sum_{i=1}^{n} (y_i - ((W_1x_1 + W_2x_2 + W_3x_3)+b))^2 $$
$$ \begin{split} & f^\prime(W_1) = -x_1(y-(W_1x_1 + W_2x_2 + W_3x_3+b)) \\
& f^\prime(W_2) = -x_2(y-(W_1x_1 + W_2x_2 + W_3x_3+b)) \\
& f^\prime(W_3) = -x_3(y-(W_1x_1 + W_2x_2 + W_3x_3+b)) \\
& f^\prime(Bias) = -(y-(W_1x_1 + W_2x_2 + W_3x_3+b) \end{split} $$
```
# Multivariate Cost function with numpy
def get_multi_cost(X, y, weight, bias):
total_error = (1/2) * np.average((y-(np.dot(X,weight)+bias))**2)
return total_error
# Testing the cost function
acost = get_multi_cost(X2, y, weight2, bias2)
acost
def update_multi_weights(X, y, weight, bias, lr=0.01):
"""
weight: shape (1,3)
X: shape(442,3)
y: shape(442,1)
output: shape(3,1)
"""
df_dm = (1/len(X)) * np.dot((-X.T), (y-(np.dot(X,weight)+bias)))
df_db = np.average(-(y-(np.dot(X,weight)+bias)))
weight = weight - (lr * df_dm)
bias = bias - (lr * df_db)
return weight,bias
weight2,bias2 = update_multi_weights(X2,y,weight2,0.1)
assert weight2.shape == (3,1)
weight2
# Training loop for multivariate regression
def train_multi(X, y, weight, bias, iters, lr=0.01):
cost = []
for i in range(iters):
weight,bias = update_multi_weights(X,y,weight,bias,lr)
a_cost = get_multi_cost(X, y, weight,bias)
cost.append(a_cost)
return cost, weight,bias
multi_weight = np.array([[0],[0],[0]])
multi_bias = 0
assert multi_weight.shape == (3,1)
cost,multi_weight,multi_bias = train_multi(X2, y, multi_weight, multi_bias, 17000, 0.1)
time_multi = [i for i in range(17000)]
plt.plot(time_multi, cost)
plt.title("Cost vs Time for Multivariate Regression")
plt.xlabel("Step Number")
plt.ylabel("Cost")
plt.show()
# These two cost values should be very similar
print("Final cost:", cost[-1]*2) # note - multiplied by 2 b/c my cost has an additional 1/2 factor
print("Should be around:", mean_squared_error(y, predictedVals))
# This is compared to [[780.74563174 393.19527108 52.90387802]]
multi_weight
# This is compared to [152.13348416]
multi_bias
```
### Finally, I will normalize my input data to see if it affects my cost in any way
$$ x_i = \frac{x_i - mean(X)}{max(X)-min(X)} $$
```
def normalize(X):
for feat in X.T:
mean = np.mean(feat)
rang = np.max(feat) - np.min(feat)
feat = (feat - mean) / rang
return X
# Getting the cost from using normalized data to see if there is any improvement
X2_norm = normalize(X2)
multi_bias = 0
multi_weight = np.array([[0],[0],[0]])
cost,multi_weight,multi_bias = train_multi(X2, y, multi_weight, multi_bias, 17000, 0.1)
# There is an insignificant difference from the normalization
print("Final cost:",cost[-1]*2)
```
| true |
code
| 0.599133 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
```
## Optimal Stopping Problem - [Secretary Problem](https://en.wikipedia.org/wiki/Secretary_problem)
- An administrator who wants to hire the best secretary out of n rankable applicants.
+ The applicants are interviewed one by one
+ Decision (hire/reject) must be made immediately after each interview.
+ Once rejected, an applicant cannot be recalled
- During the interview, the administrator can rank the applicants among all applicants interviewed so far, but is unaware of the quality of yet unseen applicants
- Optimal Stopping - Find the a strategy to hire the most optimal candidate(maximize the probability of selecting the best applicant)
## Solution
#### Observations
- Trade-off between sampling and exploiting
- If the sample size is small -> Not is enough info
- If the sample size is large -> Lot of info but waste many potential candidates
```
Sampling Exploiting
Candidates = x x x x x x o o o o o o o o o o o o o
```
#### Strategy
- n candidates
+ Sampling: sample size = r
+ Interview (r-1) first candidates and reject them all
+ Suppose X is the best candidate in (r-1)
+ Exploiting
+ Interview the rest if found a candidate i better than X -> hire
+ If no candidate better than X -> dont hire -> X is the global optimal candidate
- Find r to maximize the chance of hiring the best candidate
$$
\begin{align*}
P(r) &= \sum_{i=1}^{n}P(\text{applicant i is selected} \cap \text{applicant i is the best}) \\
&= \sum_{i=1}^{n}P(\text{applicant i is selected | applicant i is the best})*P(\text{applicant i is the best}) \\
&= \Bigg[\sum_{i=1}^{r-1}0+\sum_{i=r}^{n}P(\text{the best of the first i-1 applicants is in the first r-1 applicants | applicant i is the best})\Bigg]*\frac{1}{n} \\
&= \Bigg[\sum_{i=1}^{n}\frac{r-1}{i-1}\Bigg]*\frac{1}{n} \\
&= \frac{r-1}{n}\sum_{i=r}^{n}\frac{1}{i-1}
\end{align*}
$$
- If n is small the optimal value of r calculated as above
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|:----:|:---:|:---:|:-----:|:-----:|-------|-------|-------|-------|
| r | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 |
| P(r) | 0.5 | 0.5 | 0.458 | 0.433 | 0.428 | 0.414 | 0.410 | 0.406 |
- If n -> inf
$$P(x)=x\int_x^1\frac{1}{t}dt=-xln(x)$$
- P(x) -> 1/e ~ 0.368
- Optimal sampling size
```
r = n/e
```
```
# 1/e law of Optimal Strategy
def find_secrectary(candidates):
'''
Input: A list of candidates
Output:
sample_size: n/e ~ 36.8% candidates
idx_sample: index of the best candidate in sample set
idx_hired: index of the optimal hiring candidate (-1 if cant hire)
'''
N = len(candidates)
sample_size = (N/np.exp(1)).round().astype(int)
# Find the best candidate in sample set
idx_sample = 0;
for i in range(sample_size):
if candidates[i] > candidates[idx_sample]:
idx_sample = i
# Find the optimal candidate
idx_optimal = 0;
for i in range(sample_size, N):
if candidates[i] >= candidates[idx_sample]:
return sample_size, idx_sample, i
# Cant choose the optimal candidates
return sample_size, idx_sample, -1
```
## Test
```
def generate_test_set(n, a=30, b=100):
'''Generate n candidates
with normal distribution scores in range [a,b]
'''
# Generate normal distribution test
mu, sigma = a+(b-a)/2, (b-a)/8
candidates = np.random.normal(mu, sigma, n).round().astype(int)
# Shuffle the dataset
np.random.shuffle(candidates)
# Plot histogram
count, bins, ignored = plt.hist(candidates, 100, density=True)
plt.plot(
bins,
1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
linewidth=2, color='r')
plt.show();
return candidates
def test(n, isPrintList=True):
# Hire the optimal secretary
candidates = generate_test_set(n, 40, 100)
sample_size, idx_sample, idx_hired = find_secrectary(candidates)
# Find the global optimal
idx_globals = []
global_optimal = candidates.max()
for i in range(n):
if candidates[i] == global_optimal:
idx_globals.append(i)
# Print the list of candidate
if isPrintList:
print("List of candidates:")
print('\t', end='')
for i,candidate in enumerate(candidates):
print("[{}]{}".format(i, candidate), end=' ')
print('')
# Sampling
print("Sample candidates from [0] to [{}]".format(sample_size-1))
print("Best Sampling rejected candidate: [{}]{}".format(idx_sample, candidates[idx_sample]))
# Make hiring Decision
if idx_hired == -1:
print("Cant hire")
else:
print("Hired candidate: [{}]{}".format(idx_hired, candidates[idx_hired]))
# Global Optimal candidates
print("Global optimal candidates:",end=' ')
for idx in idx_globals:
print("[{}]{}".format(idx, candidates[idx]),end=' ')
test(10)
test(10)
test(20)
test(20)
test(100)
test(100)
test(1000, False)
test(1000, False)
test(int(1e6), False)
test(int(1e6), False)
```
| true |
code
| 0.54256 | null | null | null | null |
|
# Hands-on RL with Ray’s RLlib
## A beginner’s tutorial for working with multi-agent environments, models, and algorithms
<img src="images/pitfall.jpg" width=250> <img src="images/tesla.jpg" width=254> <img src="images/forklifts.jpg" width=169> <img src="images/robots.jpg" width=252> <img src="images/dota2.jpg" width=213>
### Overview
“Hands-on RL with Ray’s RLlib” is a beginners tutorial for working with reinforcement learning (RL) environments, models, and algorithms using Ray’s RLlib library. RLlib offers high scalability, a large list of algos to choose from (offline, model-based, model-free, etc..), support for TensorFlow and PyTorch, and a unified API for a variety of applications. This tutorial includes a brief introduction to provide an overview of concepts (e.g. why RL) before proceeding to RLlib (multi- and single-agent) environments, neural network models, hyperparameter tuning, debugging, student exercises, Q/A, and more. All code will be provided as .py files in a GitHub repo.
### Intended Audience
* Python programmers who want to get started with reinforcement learning and RLlib.
### Prerequisites
* Some Python programming experience.
* Some familiarity with machine learning.
* *Helpful, but not required:* Experience in reinforcement learning and Ray.
* *Helpful, but not required:* Experience with TensorFlow or PyTorch.
### Requirements/Dependencies
To get this very notebook up and running on your local machine, you can follow these steps here:
Install conda (https://www.anaconda.com/products/individual)
Then ...
#### Quick `conda` setup instructions (Linux):
```
$ conda create -n rllib python=3.8
$ conda activate rllib
$ pip install ray[rllib]
$ pip install tensorflow # <- either one works!
$ pip install torch # <- either one works!
$ pip install jupyterlab
```
#### Quick `conda` setup instructions (Mac):
```
$ conda create -n rllib python=3.8
$ conda activate rllib
$ pip install cmake "ray[rllib]"
$ pip install tensorflow # <- either one works!
$ pip install torch # <- either one works!
$ pip install jupyterlab
```
#### Quick `conda` setup instructions (Win10):
```
$ conda create -n rllib python=3.8
$ conda activate rllib
$ pip install ray[rllib]
$ pip install [tensorflow|torch] # <- either one works!
$ pip install jupyterlab
$ conda install pywin32
```
Also, for Win10 Atari support, we have to install atari_py from a different source (gym does not support Atari envs on Windows).
```
$ pip install git+https://github.com/Kojoley/atari-py.git
```
### Opening these tutorial files:
```
$ git clone https://github.com/sven1977/rllib_tutorials
$ cd rllib_tutorials
$ jupyter-lab
```
### Key Takeaways
* What is reinforcement learning and why RLlib?
* Core concepts of RLlib: Environments, Trainers, Policies, and Models.
* How to configure, hyperparameter-tune, and parallelize RLlib.
* RLlib debugging best practices.
### Tutorial Outline
1. RL and RLlib in a nutshell.
1. Defining an RL-solvable problem: Our first environment.
1. **Exercise No.1**: Environment loop.
(15min break)
1. Picking an algorithm and training our first RLlib Trainer.
1. Configurations and hyperparameters - Easy tuning with Ray Tune.
1. Fixing our experiment's config - Going multi-agent.
1. The "infinite laptop": Quick intro into how to use RLlib with Anyscale's product.
1. **Exercise No.2**: Run your own Ray RLlib+Tune experiment)
1. Neural network models - Provide your custom models using tf.keras or torch.nn.
(15min break)
1. Deeper dive into RLlib's parallelization architecture.
1. Specifying different compute resources and parallelization options through our config.
1. "Hacking in": Using callbacks to customize the RL loop and generate our own metrics.
1. **Exercise No.3**: Write your own custom callback.
1. "Hacking in (part II)" - Debugging with RLlib and PyCharm.
1. Checking on the "infinite laptop" - Did RLlib learn to solve the problem?
### Other Recommended Readings
* [Reinforcement Learning with RLlib in the Unity Game Engine](https://medium.com/distributed-computing-with-ray/reinforcement-learning-with-rllib-in-the-unity-game-engine-1a98080a7c0d)
<img src="images/unity3d_blog_post.png" width=400>
* [Attention Nets and More with RLlib's Trajectory View API](https://medium.com/distributed-computing-with-ray/attention-nets-and-more-with-rllibs-trajectory-view-api-d326339a6e65)
* [Intro to RLlib: Example Environments](https://medium.com/distributed-computing-with-ray/intro-to-rllib-example-environments-3a113f532c70)
## The RL cycle
<img src="images/rl-cycle.png" width=800>
### Coding/defining our "problem" via an RL environment.
We will use the following (adversarial) multi-agent environment
throughout this tutorial to demonstrate a large fraction of RLlib's
APIs, features, and customization options.
<img src="images/environment.png" width=800>
### A word or two on Spaces:
Spaces are used in ML to describe what possible/valid values inputs and outputs of a neural network can have.
RL environments also use them to describe what their valid observations and actions are.
Spaces are usually defined by their shape (e.g. 84x84x3 RGB images) and datatype (e.g. uint8 for RGB values between 0 and 255).
However, spaces could also be composed of other spaces (see Tuple or Dict spaces) or could be simply discrete with n fixed possible values
(represented by integers). For example, in our game, where each agent can only go up/down/left/right, the action space would be `Discrete(4)`
(no datatype, no shape needs to be defined here). Our observation space will be `MultiDiscrete([n, m])`, where n is the position of the agent observing and m is the position of the opposing agent, so if agent1 starts in the upper left corner and agent2 starts in the bottom right corner, agent1's observation would be: `[0, 63]` (in an 8 x 8 grid) and agent2's observation would be `[63, 0]`.
<img src="images/spaces.png" width=800>
```
# Let's code our multi-agent environment.
import gym
from gym.spaces import Discrete, MultiDiscrete
import numpy as np
import random
from ray.rllib.env.multi_agent_env import MultiAgentEnv
class MultiAgentArena(MultiAgentEnv):
def __init__(self, config=None):
config = config or {}
# Dimensions of the grid.
self.width = config.get("width", 10)
self.height = config.get("height", 10)
# End an episode after this many timesteps.
self.timestep_limit = config.get("ts", 100)
self.observation_space = MultiDiscrete([self.width * self.height,
self.width * self.height])
# 0=up, 1=right, 2=down, 3=left.
self.action_space = Discrete(4)
# Reset env.
self.reset()
def reset(self):
"""Returns initial observation of next(!) episode."""
# Row-major coords.
self.agent1_pos = [0, 0] # upper left corner
self.agent2_pos = [self.height - 1, self.width - 1] # lower bottom corner
# Accumulated rewards in this episode.
self.agent1_R = 0.0
self.agent2_R = 0.0
# Reset agent1's visited fields.
self.agent1_visited_fields = set([tuple(self.agent1_pos)])
# How many timesteps have we done in this episode.
self.timesteps = 0
# Return the initial observation in the new episode.
return self._get_obs()
def step(self, action: dict):
"""
Returns (next observation, rewards, dones, infos) after having taken the given actions.
e.g.
`action={"agent1": action_for_agent1, "agent2": action_for_agent2}`
"""
# increase our time steps counter by 1.
self.timesteps += 1
# An episode is "done" when we reach the time step limit.
is_done = self.timesteps >= self.timestep_limit
# Agent2 always moves first.
# events = [collision|agent1_new_field]
events = self._move(self.agent2_pos, action["agent2"], is_agent1=False)
events |= self._move(self.agent1_pos, action["agent1"], is_agent1=True)
# Useful for rendering.
self.collision = "collision" in events
# Get observations (based on new agent positions).
obs = self._get_obs()
# Determine rewards based on the collected events:
r1 = -1.0 if "collision" in events else 1.0 if "agent1_new_field" in events else -0.5
r2 = 1.0 if "collision" in events else -0.1
self.agent1_R += r1
self.agent2_R += r2
rewards = {
"agent1": r1,
"agent2": r2,
}
# Generate a `done` dict (per-agent and total).
dones = {
"agent1": is_done,
"agent2": is_done,
# special `__all__` key indicates that the episode is done for all agents.
"__all__": is_done,
}
return obs, rewards, dones, {} # <- info dict (not needed here).
def _get_obs(self):
"""
Returns obs dict (agent name to discrete-pos tuple) using each
agent's current x/y-positions.
"""
ag1_discrete_pos = self.agent1_pos[0] * self.width + \
(self.agent1_pos[1] % self.width)
ag2_discrete_pos = self.agent2_pos[0] * self.width + \
(self.agent2_pos[1] % self.width)
return {
"agent1": np.array([ag1_discrete_pos, ag2_discrete_pos]),
"agent2": np.array([ag2_discrete_pos, ag1_discrete_pos]),
}
def _move(self, coords, action, is_agent1):
"""
Moves an agent (agent1 iff is_agent1=True, else agent2) from `coords` (x/y) using the
given action (0=up, 1=right, etc..) and returns a resulting events dict:
Agent1: "new" when entering a new field. "bumped" when having been bumped into by agent2.
Agent2: "bumped" when bumping into agent1 (agent1 then gets -1.0).
"""
orig_coords = coords[:]
# Change the row: 0=up (-1), 2=down (+1)
coords[0] += -1 if action == 0 else 1 if action == 2 else 0
# Change the column: 1=right (+1), 3=left (-1)
coords[1] += 1 if action == 1 else -1 if action == 3 else 0
# Solve collisions.
# Make sure, we don't end up on the other agent's position.
# If yes, don't move (we are blocked).
if (is_agent1 and coords == self.agent2_pos) or (not is_agent1 and coords == self.agent1_pos):
coords[0], coords[1] = orig_coords
# Agent2 blocked agent1 (agent1 tried to run into agent2)
# OR Agent2 bumped into agent1 (agent2 tried to run into agent1)
return {"collision"}
# No agent blocking -> check walls.
if coords[0] < 0:
coords[0] = 0
elif coords[0] >= self.height:
coords[0] = self.height - 1
if coords[1] < 0:
coords[1] = 0
elif coords[1] >= self.width:
coords[1] = self.width - 1
# If agent1 -> "new" if new tile covered.
if is_agent1 and not tuple(coords) in self.agent1_visited_fields:
self.agent1_visited_fields.add(tuple(coords))
return {"agent1_new_field"}
# No new tile for agent1.
return set()
def render(self, mode=None):
print("_" * (self.width + 2))
for r in range(self.height):
print("|", end="")
for c in range(self.width):
field = r * self.width + c % self.width
if self.agent1_pos == [r, c]:
print("1", end="")
elif self.agent2_pos == [r, c]:
print("2", end="")
elif (r, c) in self.agent1_visited_fields:
print(".", end="")
else:
print(" ", end="")
print("|")
print("‾" * (self.width + 2))
print(f"{'!!Collision!!' if self.collision else ''}")
print("R1={: .1f}".format(self.agent1_R))
print("R2={: .1f}".format(self.agent2_R))
print()
env = MultiAgentArena()
obs = env.reset()
# Agent1 will move down, Agent2 moves up.
obs, rewards, dones, infos = env.step(action={"agent1": 2, "agent2": 0})
env.render()
print("Agent1's x/y position={}".format(env.agent1_pos))
print("Agent2's x/y position={}".format(env.agent2_pos))
print("Env timesteps={}".format(env.timesteps))
```
## Exercise No 1
<hr />
<img src="images/exercise1.png" width=400>
In the cell above, we performed a `reset()` and a single `step()` call. To walk through an entire episode, one would normally call `step()` repeatedly (with different actions) until the returned `done` dict has the "agent1" or "agent2" (or "__all__") key set to True. Your task is to write an "environment loop" that runs for exactly one episode using our `MultiAgentArena` class.
Follow these instructions here to get this done.
1. `reset` the already created (variable `env`) environment to get the first (initial) observation.
1. Enter an infinite while loop.
1. Compute the actions for "agent1" and "agent2" calling `DummyTrainer.compute_action([obs])` twice (once for each agent).
1. Put the results of the action computations into an action dict (`{"agent1": ..., "agent2": ...}`).
1. Pass this action dict into the env's `step()` method, just like it's done in the above cell (where we do a single `step()`).
1. Check the returned `dones` dict for True (yes, episode is terminated) and if True, break out of the loop.
**Good luck! :)**
```
class DummyTrainer:
"""Dummy Trainer class used in Exercise #1.
Use its `compute_action` method to get a new action for one of the agents,
given the agent's observation (a single discrete value encoding the field
the agent is currently in).
"""
def compute_action(self, single_agent_obs=None):
# Returns a random action for a single agent.
return np.random.randint(4) # Discrete(4) -> return rand int between 0 and 3 (incl. 3).
dummy_trainer = DummyTrainer()
# Check, whether it's working.
for _ in range(3):
# Get action for agent1 (providing agent1's and agent2's positions).
print("action_agent1={}".format(dummy_trainer.compute_action(np.array([0, 99]))))
# Get action for agent2 (providing agent2's and agent1's positions).
print("action_agent2={}".format(dummy_trainer.compute_action(np.array([99, 0]))))
print()
```
Write your solution code into this cell here:
```
# !LIVE CODING!
# Leave the following as-is. It'll help us with rendering the env in this very cell's output.
import time
from ipywidgets import Output
from IPython import display
import time
out = Output()
display.display(out)
with out:
# Solution to Exercise #1:
# Start coding here inside this `with`-block:
# 1) Reset the env.
# 2) Enter an infinite while loop (to step through the episode).
# 3) Calculate both agents' actions individually, using dummy_trainer.compute_action([individual agent's obs])
# 4) Compile the actions dict from both individual agents' actions.
# 5) Send the actions dict to the env's `step()` method to receive: obs, rewards, dones, info dicts
# 6) We'll do this together: Render the env.
# Don't write any code here (skip directly to 7).
out.clear_output(wait=True)
time.sleep(0.08)
env.render()
# 7) Check, whether the episde is done, if yes, break out of the while loop.
# 8) Run it! :)
```
------------------
## 15 min break :)
------------------
### And now for something completely different:
#### Plugging in RLlib!
```
import numpy as np
import pprint
import ray
# Start a new instance of Ray (when running this tutorial locally) or
# connect to an already running one (when running this tutorial through Anyscale).
ray.init() # Hear the engine humming? ;)
# In case you encounter the following error during our tutorial: `RuntimeError: Maybe you called ray.init twice by accident?`
# Try: `ray.shutdown() + ray.init()` or `ray.init(ignore_reinit_error=True)`
```
### Picking an RLlib algorithm - We'll use PPO throughout this tutorial (one-size-fits-all-kind-of-algo)
<img src="images/rllib_algos.png" width=800>
https://docs.ray.io/en/master/rllib-algorithms.html#available-algorithms-overview
```
# Import a Trainable (one of RLlib's built-in algorithms):
# We use the PPO algorithm here b/c its very flexible wrt its supported
# action spaces and model types and b/c it learns well almost any problem.
from ray.rllib.agents.ppo import PPOTrainer
# Specify a very simple config, defining our environment and some environment
# options (see environment.py).
config = {
"env": MultiAgentArena, # "my_env" <- if we previously have registered the env with `tune.register_env("[name]", lambda config: [returns env object])`.
"env_config": {
"config": {
"width": 10,
"height": 10,
"ts": 100,
},
},
# !PyTorch users!
#"framework": "torch", # If users have chosen to install torch instead of tf.
"create_env_on_driver": True,
}
# Instantiate the Trainer object using above config.
rllib_trainer = PPOTrainer(config=config)
rllib_trainer
```
### Ready to train with RLlib's PPO algorithm
That's it, we are ready to train.
Calling `Trainer.train()` will execute a single "training iteration".
One iteration for most algos involves:
1) sampling from the environment(s)
2) using the sampled data (observations, actions taken, rewards) to update the policy model (neural network), such that it would pick better actions in the future, leading to higher rewards.
Let's try it out:
```
results = rllib_trainer.train()
# Delete the config from the results for clarity.
# Only the stats will remain, then.
del results["config"]
# Pretty print the stats.
pprint.pprint(results)
```
### Going from single policy (RLlib's default) to multi-policy:
So far, our experiment has been ill-configured, because both
agents, which should behave differently due to their different
tasks and reward functions, learn the same policy: the "default_policy",
which RLlib always provides if you don't configure anything else.
Remember that RLlib does not know at Trainer setup time, how many and which agents
the environment will "produce". Agent control (adding agents, removing them, terminating
episodes for agents) is entirely in the Env's hands.
Let's fix our single policy problem and introduce the "multiagent" API.
<img src="images/from_single_agent_to_multi_agent.png" width=800>
In order to turn on RLlib's multi-agent functionality, we need two things:
1. A policy mapping function, mapping agent IDs (e.g. a string like "agent1", produced by the environment in the returned observation/rewards/dones-dicts) to a policy ID (another string, e.g. "policy1", which is under our control).
1. A policies definition dict, mapping policy IDs (e.g. "policy1") to 4-tuples consisting of 1) policy class (None for using the default class), 2) observation space, 3) action space, and 4) config overrides (empty dict for no overrides and using the Trainer's main config dict).
Let's take a closer look:
```
# Define the policies definition dict:
# Each policy in there is defined by its ID (key) mapping to a 4-tuple (value):
# - Policy class (None for using the "default" class, e.g. PPOTFPolicy for PPO+tf or PPOTorchPolicy for PPO+torch).
# - obs-space (we get this directly from our already created env object).
# - act-space (we get this directly from our already created env object).
# - config-overrides dict (leave empty for using the Trainer's config as-is)
policies = {
"policy1": (None, env.observation_space, env.action_space, {}),
"policy2": (None, env.observation_space, env.action_space, {"lr": 0.0002}),
}
# Note that now we won't have a "default_policy" anymore, just "policy1" and "policy2".
# Define an agent->policy mapping function.
# Which agents (defined by the environment) use which policies (defined by us)?
# The mapping here is M (agents) -> N (policies), where M >= N.
def policy_mapping_fn(agent_id: str):
# Make sure agent ID is valid.
assert agent_id in ["agent1", "agent2"], f"ERROR: invalid agent ID {agent_id}!"
# Map agent1 to policy1, and agent2 to policy2.
return "policy1" if agent_id == "agent1" else "policy2"
# We could - if we wanted - specify, which policies should be learnt (by default, RLlib learns all).
# Non-learnt policies will be frozen and not updated:
# policies_to_train = ["policy1", "policy2"]
# Adding the above to our config.
config.update({
"multiagent": {
"policies": policies,
"policy_mapping_fn": policy_mapping_fn,
# We'll leave this empty: Means, we train both policy1 and policy2.
# "policies_to_train": policies_to_train,
},
})
pprint.pprint(config)
print()
print(f"agent1 is now mapped to {policy_mapping_fn('agent1')}")
print(f"agent2 is now mapped to {policy_mapping_fn('agent2')}")
# Recreate our Trainer (we cannot just change the config on-the-fly).
rllib_trainer.stop()
# Using our updated (now multiagent!) config dict.
rllib_trainer = PPOTrainer(config=config)
rllib_trainer
```
Now that we are setup correctly with two policies as per our "multiagent" config, let's call `train()` on the new Trainer several times (what about 10 times?).
```
# Run `train()` n times. Repeatedly call `train()` now to see rewards increase.
# Move on once you see (agent1 + agent2) episode rewards of 10.0 or more.
for _ in range(10):
results = rllib_trainer.train()
print(f"Iteration={rllib_trainer.iteration}: R(\"return\")={results['episode_reward_mean']}")
# Do another loop, but this time, we will print out each policies' individual rewards.
for _ in range(10):
results = rllib_trainer.train()
r1 = results['policy_reward_mean']['policy1']
r2 = results['policy_reward_mean']['policy2']
r = r1 + r2
print(f"Iteration={rllib_trainer.iteration}: R(\"return\")={r} R1={r1} R2={r2}")
```
#### !OPTIONAL HACK! (<-- we will not do these during the tutorial, but feel free to try these cells by yourself)
Use the above solution of Exercise #1 and replace our `dummy_trainer` in that solution
with the now trained `rllib_trainer`. You should see a better performance of the two agents.
However, keep in mind that we are mostly training agent1 as we only trian a single policy and agent1
is the "easier" one to collect high rewards with.
#### !OPTIONAL HACK!
Feel free to play around with the following code in order to learn how RLlib - under the hood - calculates actions from the environment's observations using Policies and their model(s) inside our Trainer object):
```
# Let's actually "look inside" our Trainer to see what's in there.
from ray.rllib.utils.numpy import softmax
# To get to one of the policies inside the Trainer, use `Trainer.get_policy([policy ID])`:
policy = rllib_trainer.get_policy("policy1")
print(f"Our (only!) Policy right now is: {policy}")
# To get to the model inside any policy, do:
model = policy.model
#print(f"Our Policy's model is: {model}")
# Print out the policy's action and observation spaces.
print(f"Our Policy's observation space is: {policy.observation_space}")
print(f"Our Policy's action space is: {policy.action_space}")
# Produce a random obervation (B=1; batch of size 1).
obs = np.array([policy.observation_space.sample()])
# Alternatively for PyTorch:
#import torch
#obs = torch.from_numpy(obs)
# Get the action logits (as tf tensor).
# If you are using torch, you would get a torch tensor here.
logits, _ = model({"obs": obs})
logits
# Numpyize the tensor by running `logits` through the Policy's own tf.Session.
logits_np = policy.get_session().run(logits)
# For torch, you can simply do: `logits_np = logits.detach().cpu().numpy()`.
# Convert logits into action probabilities and remove the B=1.
action_probs = np.squeeze(softmax(logits_np))
# Sample an action, using the probabilities.
action = np.random.choice([0, 1, 2, 3], p=action_probs)
# Print out the action.
print(f"sampled action={action}")
```
### Saving and restoring a trained Trainer.
Currently, `rllib_trainer` is in an already trained state.
It holds optimized weights in its Policy's model that allow it to act
already somewhat smart in our environment when given an observation.
However, if we closed this notebook right now, all the effort would have been for nothing.
Let's therefore save the state of our trainer to disk for later!
```
# We use the `Trainer.save()` method to create a checkpoint.
checkpoint_file = rllib_trainer.save()
print(f"Trainer (at iteration {rllib_trainer.iteration} was saved in '{checkpoint_file}'!")
# Here is what a checkpoint directory contains:
print("The checkpoint directory contains the following files:")
import os
os.listdir(os.path.dirname(checkpoint_file))
```
### Restoring and evaluating a Trainer
In the following cell, we'll learn how to restore a saved Trainer from a checkpoint file.
We'll also evaluate a completely new Trainer (should act more or less randomly) vs an already trained one (the one we just restored from the created checkpoint file).
```
# Pretend, we wanted to pick up training from a previous run:
new_trainer = PPOTrainer(config=config)
# Evaluate the new trainer (this should yield random results).
results = new_trainer.evaluate()
print(f"Evaluating new trainer: R={results['evaluation']['episode_reward_mean']}")
# Restoring the trained state into the `new_trainer` object.
print(f"Before restoring: Trainer is at iteration={new_trainer.iteration}")
new_trainer.restore(checkpoint_file)
print(f"After restoring: Trainer is at iteration={new_trainer.iteration}")
# Evaluate again (this should yield results we saw after having trained our saved agent).
results = new_trainer.evaluate()
print(f"Evaluating restored trainer: R={results['evaluation']['episode_reward_mean']}")
```
In order to release all resources from a Trainer, you can use a Trainer's `stop()` method.
You should definitley run this cell as it frees resources that we'll need later in this tutorial, when we'll do parallel hyperparameter sweeps.
```
rllib_trainer.stop()
new_trainer.stop()
```
### Moving stuff to the professional level: RLlib in connection w/ Ray Tune
Running any experiments through Ray Tune is the recommended way of doing things with RLlib. If you look at our
<a href="https://github.com/ray-project/ray/tree/master/rllib/examples">examples scripts folder</a>, you will see that almost all of the scripts use Ray Tune to run the particular RLlib workload demonstrated in each script.
<img src="images/rllib_and_tune.png" width=400>
When setting up hyperparameter sweeps for Tune, we'll do this in our already familiar config dict.
So let's take a quick look at our PPO algo's default config to understand, which hyperparameters we may want to play around with:
```
# Configuration dicts and Ray Tune.
# Where are the default configuration dicts stored?
# PPO algorithm:
from ray.rllib.agents.ppo import DEFAULT_CONFIG as PPO_DEFAULT_CONFIG
print(f"PPO's default config is:")
pprint.pprint(PPO_DEFAULT_CONFIG)
# DQN algorithm:
#from ray.rllib.agents.dqn import DEFAULT_CONFIG as DQN_DEFAULT_CONFIG
#print(f"DQN's default config is:")
#pprint.pprint(DQN_DEFAULT_CONFIG)
# Common (all algorithms).
#from ray.rllib.agents.trainer import COMMON_CONFIG
#print(f"RLlib Trainer's default config is:")
#pprint.pprint(COMMON_CONFIG)
```
### Let's do a very simple grid-search over two learning rates with tune.run().
In particular, we will try the learning rates 0.00005 and 0.5 using `tune.grid_search([...])`
inside our config dict:
```
# Plugging in Ray Tune.
# Note that this is the recommended way to run any experiments with RLlib.
# Reasons:
# - Tune allows you to do hyperparameter tuning in a user-friendly way
# and at large scale!
# - Tune automatically allocates needed resources for the different
# hyperparam trials and experiment runs on a cluster.
from ray import tune
# Running stuff with tune, we can re-use the exact
# same config that we used when working with RLlib directly!
tune_config = config.copy()
# Let's add our first hyperparameter search via our config.
# How about we try two different learning rates? Let's say 0.00005 and 0.5 (ouch!).
tune_config["lr"] = tune.grid_search([0.0001, 0.5]) # <- 0.5? again: ouch!
tune_config["train_batch_size"] = tune.grid_search([3000, 4000])
# Now that we will run things "automatically" through tune, we have to
# define one or more stopping criteria.
# Tune will stop the run, once any single one of the criteria is matched (not all of them!).
stop = {
# Note that the keys used here can be anything present in the above `rllib_trainer.train()` output dict.
"training_iteration": 5,
"episode_reward_mean": 20.0,
}
# "PPO" is a registered name that points to RLlib's PPOTrainer.
# See `ray/rllib/agents/registry.py`
# Run a simple experiment until one of the stopping criteria is met.
tune.run(
"PPO",
config=tune_config,
stop=stop,
# Note that no trainers will be returned from this call here.
# Tune will create n Trainers internally, run them in parallel and destroy them at the end.
# However, you can ...
checkpoint_at_end=True, # ... create a checkpoint when done.
checkpoint_freq=10, # ... create a checkpoint every 10 training iterations.
)
```
### Why did we use 6 CPUs in the tune run above (3 CPUs per trial)?
PPO - by default - uses 2 "rollout" workers (`num_workers=2`). These are Ray Actors that have their own environment copy(ies) and step through those in parallel. On top of these two "rollout" workers, every Trainer in RLlib always also has a "local" worker, which - in case of PPO - handles the learning updates. This gives us 3 workers (2 rollout + 1 local learner), which require 3 CPUs.
## Exercise No 2
<hr />
Using the `tune_config` that we have built so far, let's run another `tune.run()`, but apply the following changes to our setup this time:
- Setup only 1 learning rate under the "lr" config key. Chose the (seemingly) best value from the run in the previous cell (the one that yielded the highest avg. reward).
- Setup only 1 train batch size under the "train_batch_size" config key. Chose the (seemingly) best value from the run in the previous cell (the one that yielded the highest avg. reward).
- Set `num_workers` to 5, which will allow us to run more environment "rollouts" in parallel and to collect training batches more quickly.
- Set the `num_envs_per_worker` config parameter to 5. This will clone our env on each rollout worker, and thus parallelize action computing forward passes through our neural networks.
Other than that, use the exact same args as in our `tune.run()` call in the previous cell.
**Good luck! :)**
```
# !LIVE CODING!
# Solution to Exercise #2
# Run for longer this time (100 iterations) and try to reach 40.0 reward (sum of both agents).
stop = {
"training_iteration": 180, # we have the 15min break now to run this many iterations
"episode_reward_mean": 60.0, # sum of both agents' rewards. Probably won't reach it, but we should try nevertheless :)
}
# tune_config.update({
# ???
# })
# analysis = tune.run(...)
```
------------------
## 15 min break :)
------------------
(while the above experiment is running (and hopefully learning))
## How do we extract any checkpoint from a trial of a tune.run?
```
# The previous tune.run (the one we did before the exercise) returned an Analysis object, from which we can access any checkpoint
# (given we set checkpoint_freq or checkpoint_at_end to reasonable values) like so:
print(analysis)
# Get all trials (we only have one).
trials = analysis.trials
# Assuming, the first trial was the best, we'd like to extract this trial's best checkpoint "":
best_checkpoint = analysis.get_best_checkpoint(trial=trials[0], metric="episode_reward_mean", mode="max")
print(f"Found best checkpoint for trial #2: {best_checkpoint}")
# Undo the grid-search config, which RLlib doesn't understand.
rllib_config = tune_config.copy()
rllib_config["lr"] = 0.00005
rllib_config["train_batch_size"] = 4000
# Restore a RLlib Trainer from the checkpoint.
new_trainer = PPOTrainer(config=rllib_config)
new_trainer.restore(best_checkpoint)
new_trainer
out = Output()
display.display(out)
with out:
obs = env.reset()
while True:
a1 = new_trainer.compute_action(obs["agent1"], policy_id="policy1")
a2 = new_trainer.compute_action(obs["agent2"], policy_id="policy2")
actions = {"agent1": a1, "agent2": a2}
obs, rewards, dones, _ = env.step(actions)
out.clear_output(wait=True)
env.render()
time.sleep(0.07)
if dones["agent1"] is True:
break
```
## Let's talk about customization options
### Deep Dive: How do we customize RLlib's RL loop?
RLlib offers a callbacks API that allows you to add custom behavior to
all major events during the environment sampling- and learning process.
**Our problem:** So far, we can only see standard stats, such as rewards, episode lengths, etc..
This does not give us enough insights sometimes into important questions, such as: How many times
have both agents collided? or How many times has agent1 discovered a new field?
In the following cell, we will create custom callback "hooks" that will allow us to
add these stats to the returned metrics dict, and which will therefore be displayed in tensorboard!
For that we will override RLlib's DefaultCallbacks class and implement the
`on_episode_start`, `on_episode_step`, and `on_episode_end` methods therein:
```
# Override the DefaultCallbacks with your own and implement any methods (hooks)
# that you need.
from ray.rllib.agents.callbacks import DefaultCallbacks
from ray.rllib.evaluation.episode import MultiAgentEpisode
class MyCallbacks(DefaultCallbacks):
def on_episode_start(self,
*,
worker,
base_env,
policies,
episode: MultiAgentEpisode,
env_index,
**kwargs):
# We will use the `MultiAgentEpisode` object being passed into
# all episode-related callbacks. It comes with a user_data property (dict),
# which we can write arbitrary data into.
# At the end of an episode, we'll transfer that data into the `hist_data`, and `custom_metrics`
# properties to make sure our custom data is displayed in TensorBoard.
# The episode is starting:
# Set per-episode object to capture, which states (observations)
# have been visited by agent1.
episode.user_data["new_fields_discovered"] = 0
# Set per-episode agent2-blocks counter (how many times has agent2 blocked agent1?).
episode.user_data["num_collisions"] = 0
def on_episode_step(self,
*,
worker,
base_env,
episode: MultiAgentEpisode,
env_index,
**kwargs):
# Get both rewards.
ag1_r = episode.prev_reward_for("agent1")
ag2_r = episode.prev_reward_for("agent2")
# Agent1 discovered a new field.
if ag1_r == 1.0:
episode.user_data["new_fields_discovered"] += 1
# Collision.
elif ag2_r == 1.0:
episode.user_data["num_collisions"] += 1
def on_episode_end(self,
*,
worker,
base_env,
policies,
episode: MultiAgentEpisode,
env_index,
**kwargs):
# Episode is done:
# Write scalar values (sum over rewards) to `custom_metrics` and
# time-series data (rewards per time step) to `hist_data`.
# Both will be visible then in TensorBoard.
episode.custom_metrics["new_fields_discovered"] = episode.user_data["new_fields_discovered"]
episode.custom_metrics["num_collisions"] = episode.user_data["num_collisions"]
# Setting up our config to point to our new custom callbacks class:
config = {
"env": MultiAgentArena,
"callbacks": MyCallbacks, # by default, this would point to `rllib.agents.callbacks.DefaultCallbacks`, which does nothing.
"num_workers": 5, # we know now: this speeds up things!
}
tune.run(
"PPO",
config=config,
stop={"training_iteration": 20},
checkpoint_at_end=True,
# If you'd like to restore the tune run from an existing checkpoint file, you can do the following:
#restore="/Users/sven/ray_results/PPO/PPO_MultiAgentArena_fd451_00000_0_2021-05-25_15-13-26/checkpoint_000010/checkpoint-10",
)
```
### Let's check tensorboard for the new custom metrics!
1. Head over to the Anyscale project view and click on the "TensorBoard" butten:
<img src="images/tensorboard_button.png" width=1000>
Alternatively - if you ran this locally on your own machine:
1. Head over to ~/ray_results/PPO/PPO_MultiAgentArena_[some key]_00000_0_[date]_[time]/
1. In that directory, you should see a `event.out....` file.
1. Run `tensorboard --logdir .` and head to https://localhost:6006
<img src="images/tensorboard.png" width=800>
### Deep Dive: Writing custom Models in tf or torch.
```
from ray.rllib.models.tf.tf_modelv2 import TFModelV2
from ray.rllib.models.torch.torch_modelv2 import TorchModelV2
from ray.rllib.utils.framework import try_import_tf, try_import_torch
tf1, tf, tf_version = try_import_tf()
torch, nn = try_import_torch()
# Custom Neural Network Models.
class MyKerasModel(TFModelV2):
"""Custom model for policy gradient algorithms."""
def __init__(self, obs_space, action_space, num_outputs, model_config,
name):
"""Build a simple [16, 16]-MLP (+ value branch)."""
super(MyKerasModel, self).__init__(obs_space, action_space,
num_outputs, model_config, name)
# Keras Input layer.
self.inputs = tf.keras.layers.Input(
shape=obs_space.shape, name="observations")
# Hidden layer (shared by action logits outputs and value output).
layer_1 = tf.keras.layers.Dense(
16,
name="layer1",
activation=tf.nn.relu)(self.inputs)
# Action logits output.
logits = tf.keras.layers.Dense(
num_outputs,
name="out",
activation=None)(layer_1)
# "Value"-branch (single node output).
# Used by several RLlib algorithms (e.g. PPO) to calculate an observation's value.
value_out = tf.keras.layers.Dense(
1,
name="value",
activation=None)(layer_1)
# The actual Keras model:
self.base_model = tf.keras.Model(self.inputs,
[logits, value_out])
def forward(self, input_dict, state, seq_lens):
"""Custom-define your forard pass logic here."""
# Pass inputs through our 2 layers and calculate the "value"
# of the observation and store it for when `value_function` is called.
logits, self.cur_value = self.base_model(input_dict["obs"])
return logits, state
def value_function(self):
"""Implement the value branch forward pass logic here:
We will just return the already calculated `self.cur_value`.
"""
assert self.cur_value is not None, "Must call `forward()` first!"
return tf.reshape(self.cur_value, [-1])
class MyTorchModel(TorchModelV2, nn.Module):
def __init__(self, obs_space, action_space, num_outputs, model_config,
name):
"""Build a simple [16, 16]-MLP (+ value branch)."""
TorchModelV2.__init__(self, obs_space, action_space, num_outputs,
model_config, name)
nn.Module.__init__(self)
self.device = torch.device("cuda"
if torch.cuda.is_available() else "cpu")
# Hidden layer (shared by action logits outputs and value output).
self.layer_1 = nn.Linear(obs_space.shape[0], 16).to(self.device)
# Action logits output.
self.layer_out = nn.Linear(16, num_outputs).to(self.device)
# "Value"-branch (single node output).
# Used by several RLlib algorithms (e.g. PPO) to calculate an observation's value.
self.value_branch = nn.Linear(16, 1).to(self.device)
self.cur_value = None
def forward(self, input_dict, state, seq_lens):
"""Custom-define your forard pass logic here."""
# Pass inputs through our 2 layers.
layer_1_out = self.layer_1(input_dict["obs"])
logits = self.layer_out(layer_1_out)
# Calculate the "value" of the observation and store it for
# when `value_function` is called.
self.cur_value = self.value_branch(layer_1_out).squeeze(1)
return logits, state
def value_function(self):
"""Implement the value branch forward pass logic here:
We will just return the already calculated `self.cur_value`.
"""
assert self.cur_value is not None, "Must call `forward()` first!"
return self.cur_value
# Do a quick test on the custom model classes.
test_model_tf = MyKerasModel(
obs_space=gym.spaces.Box(-1.0, 1.0, (2, )),
action_space=None,
num_outputs=2,
model_config={},
name="MyModel",
)
print("TF-output={}".format(test_model_tf({"obs": np.array([[0.5, 0.5]])})))
# For PyTorch, you can do:
#test_model_torch = MyTorchModel(
# obs_space=gym.spaces.Box(-1.0, 1.0, (2, )),
# action_space=None,
# num_outputs=2,
# model_config={},
# name="MyModel",
#)
#print("Torch-output={}".format(test_model_torch({"obs": torch.from_numpy(np.array([[0.5, 0.5]], dtype=np.float32))})))
# Set up our custom model and re-run the experiment.
config.update({
"model": {
"custom_model": MyKerasModel, # for torch users: "custom_model": MyTorchModel
"custom_model_config": {
#"layers": [128, 128],
},
},
})
tune.run(
"PPO",
config=config, # for torch users: config=dict(config, **{"framework": "torch"}),
stop={
"training_iteration": 5,
},
)
```
### Deep Dive: A closer look at RLlib's components
#### (Depending on time left and amount of questions having been accumulated :)
We already took a quick look inside an RLlib Trainer object and extracted its Policy(ies) and the Policy's model (neural network). Here is a much more detailed overview of what's inside a Trainer object.
At the core is the so-called `WorkerSet` sitting under `Trainer.workers`. A WorkerSet is a group of `RolloutWorker` (`rllib.evaluation.rollout_worker.py`) objects that always consists of a "local worker" (`Trainer.workers.local_worker()`) and n "remote workers" (`Trainer.workers.remote_workers()`).
<img src="images/rllib_structure.png" width=1000>
### Scaling RLlib
Scaling RLlib works by parallelizing the "jobs" that the remote `RolloutWorkers` do. In a vanilla RL algorithm, like PPO, DQN, and many others, the `@ray.remote` labeled RolloutWorkers in the figure above are responsible for interacting with one or more environments and thereby collecting experiences. Observations are produced by the environment, actions are then computed by the Policy(ies) copy located on the remote worker and sent to the environment in order to produce yet another observation. This cycle is repeated endlessly and only sometimes interrupted to send experience batches ("train batches") of a certain size to the "local worker". There these batches are used to call `Policy.learn_on_batch()`, which performs a loss calculation, followed by a model weights update, and a subsequent weights broadcast back to all the remote workers.
## Time for Q&A
...
## Thank you for listening and participating!
### Here are a couple of links that you may find useful.
- The <a href="https://github.com/sven1977/rllib_tutorials.git">github repo of this tutorial</a>.
- <a href="https://docs.ray.io/en/master/rllib.html">RLlib's documentation main page</a>.
- <a href="http://discuss.ray.io">Our discourse forum</a> to ask questions on Ray and its libraries.
- Our <a href="https://forms.gle/9TSdDYUgxYs8SA9e8">Slack channel</a> for interacting with other Ray RLlib users.
- The <a href="https://github.com/ray-project/ray/blob/master/rllib/examples/">RLlib examples scripts folder</a> with tons of examples on how to do different stuff with RLlib.
- A <a href="https://medium.com/distributed-computing-with-ray/reinforcement-learning-with-rllib-in-the-unity-game-engine-1a98080a7c0d">blog post on training with RLlib inside a Unity3D environment</a>.
| true |
code
| 0.785566 | null | null | null | null |
|
# DataCamp Certification Case Study
### Project Brief
A housing rental company has hired you for a new project. They are interested in developing an application to help people estimate the money they could earn renting out their living space.
The company has provided you with a dataset that includes details about each property rented, as well as the price charged per night. They want to avoid estimating prices that are more than 25 dollars off of the actual price, as this may discourage people.
You will need to present your findings to the head of rentals, who has no technical data science background.
The data you will use for this analysis can be accessed here: `"data/rentals.csv"`
```
import pandas as pd
import numpy as np
import re
import matplotlib.pyplot as plt
import plotly.express as px
import seaborn as sns
```
## I'M GOING TO USE THE MOST TYPICAL DATA SCIENCE PIPELINE. IT HAS 5 STEPS
## 1.Obtaining the data
## 2.Cleaning the data
## 3.Exploring and visualising the data
## 4.modelling the data
## 5.Interpreting the data
# 1.OBTAINING THE DATA
```
#reading the data into dataframe
df = pd.read_csv('./data/rentals.csv')
df.head()
#No of rows and columns in the dataframe
df.shape
```
# 2.CLEANING THE DATA
```
#checking if there are any null values
df.isna().sum()
```
Now we can see there are 12 null values in "bathrooms" and 4 null values in "bedrooms"
```
#dropping the null values
df.dropna(inplace=True)
df.isna().sum()
#checking the shape of the dataframe after dropping null values
df.shape
df.dtypes
#Now we change the datatype of column "price" from object to float64 using regular expression
df['price'] = df['price'].apply(lambda x: float(re.sub(r'\,|\$', '', x)))
#we dont need "id" because it makes no sense
df.drop(columns=['id'], inplace=True)
```
# 3A.EXPLORING THE DATA
```
# we want to explore every column of data and check what we need for our case study and rest can be dropped from the data
df.property_type.unique()
_ = pd.DataFrame([
df.property_type.value_counts(),
round(df.property_type.value_counts(1) * 100, 2)
], ).T
_.columns = ['count', 'percentage']
_
```
### anything less than 25 can be dropped and hotels, resorts and likewise should be dropped(according to our case study)
```
drop_list = [
'Bed and breakfast', 'Hostel', 'Guesthouse', 'Serviced apartment',
'Aparthotel', 'Guesthouse', 'Other', 'Bungalow', 'Hotel', 'Boutique hotel',
'Other', 'Resort', 'Resort', 'Cottage', 'Villa', 'Castle', 'Cabin',
'Tiny house', 'Earth house', 'Camper/RV', 'In-law', 'Hut', 'Dome house'
]
df = df[~df['property_type'].isin(drop_list)]
df.shape
df.property_type.unique()
df.room_type.unique()
_ = pd.DataFrame([
df.room_type.value_counts(),
round(df.room_type.value_counts(1) * 100, 2)
]).T
_.columns = ['count', 'percentage']
_
df=df[~df.room_type.eq('Entire home/apt')]
df.room_type.unique()
df.bathrooms.unique()
df[df['bathrooms']>5]
df.bedrooms.unique()
df[df['bedrooms']>4]
```
### Removal of Outlier
```
df.price.value_counts(bins=10)
before_removal= df.shape[0]
def find_outliers_IQR(data):
"""
Use Tukey's Method of outlier removal AKA InterQuartile-Range Rule
and return boolean series where True indicates it is an outlier.
- Calculates the range between the 75% and 25% quartiles
- Outliers fall outside upper and lower limits, using a treshold of 1.5*IQR the 75% and 25% quartiles.
IQR Range Calculation:
res = df.describe()
IQR = res['75%'] - res['25%']
lower_limit = res['25%'] - 1.5*IQR
upper_limit = res['75%'] + 1.5*IQR
Args:
data (Series,or ndarray): data to test for outliers.
Returns:
[boolean Series]: A True/False for each row use to slice outliers.
EXAMPLE USE:
>> idx_outs = find_outliers_df(df['AdjustedCompensation'])
>> good_data = df[~idx_outs].copy()
"""
df_b = data
res = df_b.describe()
IQR = res['75%'] - res['25%']
lower_limit = res['25%'] - 1.5 * IQR
upper_limit = res['75%'] + 1.5 * IQR
idx_outs = (df_b > upper_limit) | (df_b < lower_limit)
return idx_outs
df = df[~find_outliers_IQR(df.price)]
after_removal = df.shape[0]
data_loss = round(((after_removal - before_removal)/before_removal)*100,2)
print(data_loss)
df = df[~find_outliers_IQR(df.minimum_nights)]
def describe_dataframe(df: pd.DataFrame()):
"""Statistical description of the pandas.DataFrame."""
left = df.describe(include='all').round(2).T
right = pd.DataFrame(df.dtypes)
right.columns = ['dtype']
ret_df = pd.merge(left=left,
right=right,
left_index=True,
right_index=True)
na_df = pd.DataFrame(df.isna().sum())
na_df.columns = ['nulls']
ret_df = pd.merge(left=ret_df,
right=na_df,
left_index=True,
right_index=True)
ret_df.fillna('', inplace=True)
return ret_df
describe_dataframe(df)
df[df.minimum_nights>365]
#dropping properties that rents more than one year.
df = df[df.minimum_nights<=365]
df.head()
```
# 3B.VISUALISING THE DATA
```
sns.lmplot(x='bedrooms', y='price',data=df, scatter_kws={
"s": 8,
"color": 'silver'
},
line_kws={
'lw': 3,
'color': 'gold'
})
plt.xlabel("Bedrooms")
plt.ylabel("House Price")
plt.title("Bedrooms vs. Rent Price")
plt.show()
sns.lmplot(x='bathrooms', y='price',data=df)
plt.xlabel("bathrooms")
plt.ylabel("House Price")
plt.title("bathrooms vs. Rent Price")
plt.show()
sns.barplot(x='room_type', y='price',data=df)
plt.xlabel("room_type")
plt.ylabel("House Price")
plt.title("room_type vs. Rent Price")
plt.show()
def heatmap_of_features_correlation(df, annot_format='.1f'):
"""
Return a masked heatmap of the given DataFrame
Parameters:
===========
df = pandas.DataFrame object.
annot_format = str, for formatting; default: '.1f'
Example of `annot_format`:
--------------------------
.1e = scientific notation with 1 decimal point (standard form)
.2f = 2 decimal places
.3g = 3 significant figures
.4% = percentage with 4 decimal places
Note:
=====
Rounding error can happen if '.1f' is used.
"""
with plt.style.context('dark_background'):
plt.figure(figsize=(10, 10), facecolor='k')
mask = np.triu(np.ones_like(df.corr(), dtype=bool))
cmap = sns.diverging_palette(3, 3, as_cmap=True)
ax = sns.heatmap(df.corr(),
mask=mask,
cmap=cmap,
annot=True,
fmt=annot_format,
linecolor='k',
annot_kws={"size": 9},
square=True,
linewidths=.5,
cbar_kws={"shrink": .5})
plt.title(f'Features heatmap', fontdict={"size": 20})
plt.show()
return ax
return list(feature_corr)
def drop_features_based_on_correlation(df, threshold=0.75):
"""
Returns features with high collinearity.
Parameters:
===========
df = pandas.DataFrame; no default.
data to work on.
threshold = float; default: .75.
Cut off value of check of collinearity.
"""
# Set of all the names of correlated columns
feature_corr = set()
corr_matrix = df.corr()
for i in range(len(corr_matrix.columns)):
for j in range(i):
# absolute coeff value
if abs(corr_matrix.iloc[i, j]) > threshold:
# getting the name of column
colname = corr_matrix.columns[i]
feature_corr.add(colname)
if not feature_corr:
print(f'No multicollinearity detected at {threshold*100}% threshold.')
else:
return list(feature_corr)
heatmap_of_features_correlation(df)
drop_features_based_on_correlation(df)
```
### Train and Test split
```
X = df.drop(columns='price').copy()
y = df.price.copy()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=.8)
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder, MinMaxScaler, StandardScaler, RobustScaler
from sklearn.compose import ColumnTransformer
# isolating numerical cols
nume_col = list(X.select_dtypes('number').columns)
# isolating categorical cols
cate_col = list(X.select_dtypes('object').columns)
# pipeline for processing categorical features
pipe_cate = Pipeline([('ohe', OneHotEncoder(sparse=False, drop=None))])
# pipeline for processing numerical features
pipe_nume = Pipeline([('scaler', StandardScaler())])
# transformer
preprocessor = ColumnTransformer([('nume_feat', pipe_nume, nume_col),
('cate_feat', pipe_cate, cate_col)])
# creating dataframes
# X_train
X_train_pr = pd.DataFrame(preprocessor.fit_transform(X_train),
columns=nume_col +
list(preprocessor.named_transformers_['cate_feat'].
named_steps['ohe'].get_feature_names(cate_col)))
# X_test
X_test_pr = pd.DataFrame(preprocessor.transform(X_test),
columns=nume_col +
list(preprocessor.named_transformers_['cate_feat'].
named_steps['ohe'].get_feature_names(cate_col)))
X_train_pr
y_train
```
# 4.MODELLING THE DATA
### 1.DummyRegressor
```
from sklearn.dummy import DummyRegressor
from sklearn.metrics import mean_absolute_error, r2_score, mean_squared_error
dummy_regr = DummyRegressor(strategy="mean")
dummy_regr.fit(X_train_pr, y_train)
y_pred_dummy = dummy_regr.predict(X_test_pr)
print("MAE :", mean_absolute_error(y_test, y_pred_dummy))
print("r2 :", r2_score(y_test, y_pred_dummy))
```
### 2.LinearRegression
```
from sklearn.linear_model import LinearRegression
reg = LinearRegression(n_jobs=-1)
reg.fit(X_train_pr, y_train)
y_pred_reg = reg.predict(X_test_pr)
print("Coefs :\n", reg.coef_)
mae = (abs(y_test - y_pred_reg)).mean()
print("MAE :", mae)
print("r2 :", r2_score(y_test, y_pred_reg))
```
### 3.RandomForestRegressor
```
from sklearn.ensemble import RandomForestRegressor
def model_stat(y_test, y_pred):
print(' MAE:', mean_absolute_error(y_test, y_pred), '\n', 'MSE:',
mean_squared_error(y_test, y_pred), '\n', 'RMSE:',
np.sqrt(mean_squared_error(y_test, y_pred)), '\n', 'r2:',
r2_score(y_test, y_pred))
rf_reg = RandomForestRegressor(n_estimators=200,
criterion='mae',
n_jobs=-1)
rf_reg.fit(X_train_pr, y_train)
y_pred_rf = rf_reg.predict(X_test_pr)
model_stat(y_test, y_pred_rf)
```
### 4.GridSearch
```
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 200, stop = 1000, num = 5)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# # Maximum number of levels in tree
# max_depth = [int(x) for x in np.linspace(10, 60, num = 6)]
# max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 4]
# Method of selecting samples for training each tree
bootstrap = [True, False]
# oob_score=[True, False]
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
# 'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf,
# 'bootstrap': bootstrap,
# 'oob_score': oob_score
}
print(random_grid)
from sklearn.model_selection import RandomizedSearchCV
# Use the random grid to search for best hyperparameters
# First create the base model to tune
rf = RandomForestRegressor(criterion='mae')
# Random search of parameters, using 3 fold cross validation,
# search across 100 different combinations, and use all available cores
rf_random = RandomizedSearchCV(estimator=rf,
param_distributions=random_grid,
n_iter=50,
cv=2,
verbose=2,
scoring ='neg_mean_absolute_error',
random_state=42,
n_jobs=-1)
# Fit the random search model
rf_random.fit(X_train_pr, y_train)
print(rf_random.best_params_)
```
### 5.BestparameterswithRandomForestRegressor
```
rf_reg = RandomForestRegressor(n_estimators=1000,
criterion='mae',
min_samples_split=2,
min_samples_leaf=1,
max_features='sqrt',
max_depth=20,
bootstrap=False,
# oob_score=True,
n_jobs=-1)
rf_reg.fit(X_train_pr, y_train)
y_pred_rf = rf_reg.predict(X_test_pr)
model_stat(y_test, y_pred_rf)
sns.scatterplot(x=y_test, y=y_pred_rf)
sns.scatterplot(x=y_test, y=y_test)
rf_feat_imp = pd.DataFrame(rf_reg.feature_importances_, index=X_train_pr.columns)
rf_feat_imp.sort_values(by=0).plot(kind='barh', legend='', figsize=(10,15), title='Feature Importance', color = 'g')
plt.ylabel('Features')
plt.xlabel('Importance')
plt.show()
#SHAP (SHapley Additive exPlanations) is a game theoretic approach to explain the output of any machine learning model. It connects optimal credit allocation with local explanations using the classic Shapley values from game theory and their related extensions
import shap
shap.initjs()
explainer = shap.TreeExplainer(rf_reg)
shap_values = explainer.shap_values(X_test_pr)
with plt.style.context('seaborn-white'):
shap.summary_plot(shap_values, X_test_pr)
```
### 6.XGBRegressor
```
from xgboost import XGBRegressor, XGBRFRegressor
xgb_reg = XGBRegressor(learning_rate=0.1,
n_estimators=100,
# min_samples_split=2,
# min_samples_leaf=1,
# max_depth=3,
n_jobs=-1,
# subsample=1.0,
verbosity =1,
booster='gbtree',# gbtree, gblinear or dart
objective ='reg:squarederror',
random_state=2021)
xgb_reg.fit(X_train_pr, y_train)
y_pred_xgb = xgb_reg.predict(X_test_pr)
model_stat(y_test, y_pred_xgb)
```
### 7.SupportVectorMachine
```
from sklearn.svm import SVR
regressor = SVR(kernel = 'linear', C=1)
regressor.fit(X_train_pr, y_train)
y_pred_svr = regressor.predict(X_test_pr)
model_stat(y_test, y_pred_svr)
```
# 5.INTERPRETING THE DATA
### bEST MoDEL
### Among all the models tested, the "random forest model" produces the best results and has the smallest mean absolute error.
# CONCLUSION
#### 1. The location of your property does have an impact on rental income.
#### 2. In the near run, location is the most important factor in determining rental pricing.
#### 3. Condo owners might anticipate a boost in rental income.
#### 4. If your property is closer to the city's center, you can charge more.
# FUTURE WORK
#### 1. To assess quality, add demographic information to the model, such as area attractions, restaurants, income level, local transportation, year built information, or refurbishment information.
#### 2. Tweaking of hyperparameters
#### 3. Add Features of the house.
| true |
code
| 0.622 | null | null | null | null |
|
# Collaboration and Competition
### 1. Start the Environment
```
from unityagents import UnityEnvironment
import numpy as np
```
**_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Tennis.app"`
- **Windows** (x86): `"path/to/Tennis_Windows_x86/Tennis.exe"`
- **Windows** (x86_64): `"path/to/Tennis_Windows_x86_64/Tennis.exe"`
- **Linux** (x86): `"path/to/Tennis_Linux/Tennis.x86"`
- **Linux** (x86_64): `"path/to/Tennis_Linux/Tennis.x86_64"`
- **Linux** (x86, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86"`
- **Linux** (x86_64, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86_64"`
For instance, if you are using a Mac, then you downloaded `Tennis.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Tennis.app")
```
```
env = UnityEnvironment(file_name="./Tennis_Windows_x86_64/Tennis.exe")
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
In this environment, two agents control rackets to bounce a ball over a net. If an agent hits the ball over the net, it receives a reward of +0.1. If an agent lets a ball hit the ground or hits the ball out of bounds, it receives a reward of -0.01. Thus, the goal of each agent is to keep the ball in play.
The observation space consists of 8 variables corresponding to the position and velocity of the ball and racket. Two continuous actions are available, corresponding to movement toward (or away from) the net, and jumping.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents
num_agents = len(env_info.agents)
print('Number of agents:', num_agents)
# size of each action
action_size = brain.vector_action_space_size
print('Size of each action:', action_size)
# examine the state space
states = env_info.vector_observations
state_size = states.shape[1]
print('There are {} agents. Each observes a state with length: {}'.format(states.shape[0], state_size))
print('The state for the first agent looks like:', states[0])
```
### 3. Take Random Actions in the Environment
The cell below shows how to use the Python API to control the agents and receive feedback from the environment. Once this cell is executed, you will watch the agents' performance, if they select actions at random with each time step. A window should pop up that allows you to observe the agents.
```
# for i in range(1, 6): # play game for 5 episodes
# env_info = env.reset(train_mode=False)[brain_name] # reset the environment
# states = env_info.vector_observations # get the current state (for each agent)
# scores = np.zeros(num_agents) # initialize the score (for each agent)
# while True:
# actions = np.random.randn(num_agents, action_size) # select an action (for each agent)
# actions = np.clip(actions, -1, 1) # all actions between -1 and 1
# print('actions',actions )
# env_info = env.step(actions)[brain_name] # send all actions to tne environment
# next_states = env_info.vector_observations # get next state (for each agent)
# rewards = env_info.rewards # get reward (for each agent)
# dones = env_info.local_done # see if episode finished
# scores += env_info.rewards # update the score (for each agent)
# states = next_states # roll over states to next time step
# print('states',next_states )
# print('rewards',rewards )
# print('dones',dones )
# if np.any(dones): # exit loop if episode finished
# break
# print('Score (max over agents) from episode {}: {}'.format(i, np.max(scores)))
```
When finished, you can close the environment.
```
# env.close()
```
### 4. Training The Agents
```
from collections import deque
from itertools import count
import torch
import time
import matplotlib.pyplot as plt
from ddpg_agent import DDPGAgent
from ddpg_network import Actor, Critic
from multi_agent_ddpg import MADDPG
random_seed=5
meta_agent = MADDPG(num_agents=num_agents,state_size=state_size, action_size=action_size,random_seed=random_seed)
def train_maddpg(n_episodes=10000, max_t=1000):
avg_score = []
scores=[] # list containing scores from each episode
scores_window = deque(maxlen=100)
for i_episode in range(1, n_episodes+1):
env_info = env.reset(train_mode=True)[brain_name]
meta_agent.reset_agents()
states = env_info.vector_observations
score = np.zeros(num_agents)
for t in range(max_t):
actions = meta_agent.act(states, add_noise=True)
#Take action and observe reward and next state
env_info = env.step(actions)[brain_name] # send the actions to the environment
next_states = env_info.vector_observations # get the next states
rewards = env_info.rewards # get the rewards
dones = env_info.local_done # see if episode has finished
#Store experience tuple (s,a,s',r) in replay memory and learn from minibatch
meta_agent.step(states, actions, rewards, next_states, dones, i_episode)
states = next_states
score += rewards
if np.any(dones):
break
scores_window.append(np.max(score)) # episode score is max of the agents
scores.append(score) # save most recent score
avg_score= np.mean(scores_window)
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)), end="")
if i_episode%100==0:
print('\n Episode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)), end="")
meta_agent.save_checkpoint()
if avg_score>0.5:
print('\n Episode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)), end="")
print('Environment solved!')
meta_agent.save_checkpoint()
return scores,avg_score
return scores,avg_score
%%time
scores,avg_score = train_maddpg(10000,2000)
env.close()
#Save scores
np.save('MADDPG_scores.npy', np.array(scores))
# scores = np.load('MADDPG_scores.npy')
scores=np.asarray(scores)
plt.figure(figsize=(12,6))
plt.rc('font', size=20) # controls default text sizes
plt.rc('axes', titlesize=20) # fontsize of the axes title
plt.rc('axes', labelsize=20) # fontsize of the x and y labels
plt.rc('xtick', labelsize=20) # fontsize of the tick labels
plt.rc('ytick', labelsize=20) # fontsize of the tick labels
plt.rc('legend', fontsize=20) # legend fontsize
plt.rc('figure', titlesize=20) # fontsize of the figure title
plt.plot(scores[:,0],'b.')
plt.plot(scores[:,1],'r')
plt.plot(np.amax(scores,axis=1),'k')
plt.grid()
plt.xlabel('Episode')
plt.ylabel('Score')
plt.title('MADDPG')
plt.show()
```
| true |
code
| 0.580709 | null | null | null | null |
|
# Mutations with Grammars
In this notebook, we make a very short and simple introduction on how to use the `fuzzingbook` framework for grammar-based mutation – both for data and for code.
**Prerequisites**
* This chapter is meant to be self-contained.
## Defining Grammars
We define a grammar using standard Python data structures. Suppose we want to encode this grammar:
```
<start> ::= <expr>
<expr> ::= <term> + <expr> | <term> - <expr> | <term>
<term> ::= <term> * <factor> | <term> / <factor> | <factor>
<factor> ::= +<factor> | -<factor> | (<expr>) | <integer> | <integer>.<integer>
<integer> ::= <digit><integer> | <digit>
<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
```
```
import fuzzingbook_utils
from Grammars import syntax_diagram, is_valid_grammar, convert_ebnf_grammar, srange, crange
```
In Python, we encode this as a mapping (a dictionary) from nonterminal symbols to a list of possible expansions:
```
EXPR_GRAMMAR = {
"<start>":
["<expr>"],
"<expr>":
["<term> + <expr>", "<term> - <expr>", "<term>"],
"<term>":
["<factor> * <term>", "<factor> / <term>", "<factor>"],
"<factor>":
["+<factor>",
"-<factor>",
"(<expr>)",
"<integer>.<integer>",
"<integer>"],
"<integer>":
["<digit><integer>", "<digit>"],
"<digit>":
["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
}
assert is_valid_grammar(EXPR_GRAMMAR)
syntax_diagram(EXPR_GRAMMAR)
```
## Fuzzing with Grammars
We mostly use grammars for _fuzzing_, as in here:
```
from GrammarFuzzer import GrammarFuzzer
expr_fuzzer = GrammarFuzzer(EXPR_GRAMMAR)
for i in range(10):
print(expr_fuzzer.fuzz())
```
## Parsing with Grammars
We can parse a given input using a grammar:
```
expr_input = "2 + -2"
from Parser import EarleyParser, display_tree, tree_to_string
expr_parser = EarleyParser(EXPR_GRAMMAR)
expr_tree = list(expr_parser.parse(expr_input))[0]
display_tree(expr_tree)
```
Internally, each subtree is a pair of a node and a list of children (subtrees)
```
expr_tree
```
## Mutating a Tree
We define a simple mutator that traverses an AST to mutate it.
```
def swap_plus_minus(tree):
node, children = tree
if node == " + ":
node = " - "
elif node == " - ":
node = " + "
return node, children
def apply_mutator(tree, mutator):
node, children = mutator(tree)
return node, [apply_mutator(c, mutator) for c in children]
mutated_tree = apply_mutator(expr_tree, swap_plus_minus)
display_tree(mutated_tree)
```
## Unparsing the Mutated Tree
To unparse, we traverse the tree and look at all terminal symbols:
```
tree_to_string(mutated_tree)
```
## Lots of mutations
```
for i in range(10):
s = expr_fuzzer.fuzz()
s_tree = list(expr_parser.parse(s))[0]
s_mutated_tree = apply_mutator(s_tree, swap_plus_minus)
s_mutated = tree_to_string(s_mutated_tree)
print(' ' + s + '\n-> ' + s_mutated + '\n')
```
## Another Example: JSON
```
import string
CHARACTERS_WITHOUT_QUOTE = (string.digits
+ string.ascii_letters
+ string.punctuation.replace('"', '').replace('\\', '')
+ ' ')
JSON_EBNF_GRAMMAR = {
"<start>": ["<json>"],
"<json>": ["<element>"],
"<element>": ["<ws><value><ws>"],
"<value>": ["<object>", "<array>", "<string>", "<number>", "true", "false", "null"],
"<object>": ["{<ws>}", "{<members>}"],
"<members>": ["<member>(,<members>)*"],
"<member>": ["<ws><string><ws>:<element>"],
"<array>": ["[<ws>]", "[<elements>]"],
"<elements>": ["<element>(,<elements>)*"],
"<element>": ["<ws><value><ws>"],
"<string>": ['"' + "<characters>" + '"'],
"<characters>": ["<character>*"],
"<character>": srange(CHARACTERS_WITHOUT_QUOTE),
"<number>": ["<int><frac><exp>"],
"<int>": ["<digit>", "<onenine><digits>", "-<digits>", "-<onenine><digits>"],
"<digits>": ["<digit>+"],
"<digit>": ['0', "<onenine>"],
"<onenine>": crange('1', '9'),
"<frac>": ["", ".<digits>"],
"<exp>": ["", "E<sign><digits>", "e<sign><digits>"],
"<sign>": ["", '+', '-'],
"<ws>": ["( )*"]
}
assert is_valid_grammar(JSON_EBNF_GRAMMAR)
JSON_GRAMMAR = convert_ebnf_grammar(JSON_EBNF_GRAMMAR)
syntax_diagram(JSON_GRAMMAR)
json_input = '{"conference": "ICSE"}'
json_parser = EarleyParser(JSON_GRAMMAR)
json_tree = list(json_parser.parse(json_input))[0]
display_tree(json_tree)
def swap_venue(tree):
if tree_to_string(tree) == '"ICSE"':
tree = list(json_parser.parse('"ICST"'))[0]
return tree
mutated_tree = apply_mutator(json_tree, swap_venue)
tree_to_string(mutated_tree)
```
| true |
code
| 0.335848 | null | null | null | null |
|
### Nulltity Dataframe
- Use either .isnull() or .isna()
### Total missing values
- .sum()
### Percentage of missingness
- .mean() * 100
### Graphical analysis of missing data - missingno package
```python
import missingno as msno
msno.bar(data) # visualize completeness of the dataframe
msno.matrix(airquality) # describes the nullity in the dataset and appears blank wherever there are missing values
msno.matrix(data, freq='M') # monthwise missing data
msno.matrix(data.loc['May-1976':'Jul-1976'], freq='M') # fine tuning
```
### Analyzing missingness percentage
- Before jumping into treating missing data, it is essential to analyze the various factors surrounding missing data. The elementary step in analyzing the data is to analyze the amount of missingness, that is the number of values missing for a variable.
```
import pandas as pd
# Load the airquality dataset
airquality = pd.read_csv('./../data/air-quality.csv', parse_dates=['Date'], index_col='Date')
# Create a nullity DataFrame airquality_nullity
airquality_nullity = airquality.isnull()
print(airquality_nullity.head())
# Calculate total of missing values
missing_values_sum = airquality_nullity.sum()
print('Total Missing Values:\n', missing_values_sum)
# Calculate percentage of missing values
missing_values_percent = airquality_nullity.mean() * 100
print('Percentage of Missing Values:\n', missing_values_percent)
```
### Visualize missingness
```
# Import missingno as msno
import missingno as msno
import matplotlib.pyplot as plt
%matplotlib inline
# Plot amount of missingness
msno.bar(airquality)
# Display bar chart of missing values
# display("bar_chart.png")
# Plot nullity matrix of airquality
msno.matrix(airquality)
# Plot nullity matrix of airquality with frequency 'M'
msno.matrix(airquality, freq='M')
# Plot the sliced nullity matrix of airquality with frequency 'M'
msno.matrix(airquality.loc['May-1976':'Jul-1976'], freq='M')
```
## Mean , Median, Mode Imputation
```python
from sklearn.impute import SimpleImputer
diabetes_mean = diabetes.copy(deep=True)
mean_imputer = SimpleImputer(strategy='mean')
diabetes_mean.iloc[:,:] = mean_imputer.fit_transform(diabetes_mean)
# for median -> strategy='median' for mode -> strategy='most_frequent'
constant_imputer = SimpleImputer(strategy = 'constant', fill_value = 0)
```
### Visualizing imputations
```python
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 10))
nullity = diabetes['Serum_Insulin'].isnull()+diabetes['Glucose'].isnull()
imputations = {'Mean Imputation':diabetes_mean,
'Median Imputation':diabetes_median,
'Mode Imputation':diabetes_mode,
'Constant Imputation':, diabetes_constant}
for ax, df_key in zip(axes.flatten(), imputations):
# the flatten() method on axes flattens the axes array from (2,2) to (4,1)
# set 'colorbar=False' so that the color bar is not plotted
imputations[df_key].plot(x='Serum_Insulin', y='Glucose', kind='scatter', alpha=0.5, c=nullity, cmap='rainbow', ax=ax, colorbar=False, title=df_key)
```
- Observing the graph, there's a clear correlation between 'Serum_Insulin' and 'Glucose'. However the imputed values which are red just lie in a straight line as the imputed values do not vary against the other variable.
- **Therefore, we can conclude that mean, median and mode imputations only preserve these basic statistical features of the dataset but don't account for their correlations** .Moreover, this results in a bias in the dataset.
### Mean & median imputation
- Imputing missing values is the best method when you have large amounts of data to deal with. The simplest methods to impute missing values include filling in a constant or the mean of the variable or other basic statistical parameters like median and mode.
```
diabetes = pd.read_csv('./../data/pima-indians-diabetes data.csv')
diabetes.head()
from sklearn.impute import SimpleImputer
# Make a copy of diabetes
diabetes_mean = diabetes.copy(deep=True)
# Create mean imputer object
mean_imputer = SimpleImputer(strategy='mean')
# Impute mean values in the DataFrame diabetes_mean
diabetes_mean.iloc[:, :] = mean_imputer.fit_transform(diabetes_mean)
# Make a copy of diabetes
diabetes_median = diabetes.copy(deep=True)
# Create median imputer object
median_imputer = SimpleImputer(strategy='median')
# Impute median values in the DataFrame diabetes_median
diabetes_median.iloc[:, :] = median_imputer.fit_transform(diabetes_median)
```
### Mode and constant imputation
```
# Make a copy of diabetes
diabetes_mode = diabetes.copy(deep=True)
# Create mode imputer object
mode_imputer = SimpleImputer(strategy='most_frequent')
# Impute using most frequent value in the DataFrame mode_imputer
diabetes_mode.iloc[:, :] = mode_imputer.fit_transform(diabetes_mode)
# Make a copy of diabetes
diabetes_constant = diabetes.copy(deep=True)
# Create median imputer object
constant_imputer = SimpleImputer(strategy='constant', fill_value=0)
# Impute missing values to 0 in diabetes_constant
diabetes_constant.iloc[:, :] = constant_imputer.fit_transform(diabetes_constant)
```
### Visualize imputations
- Analyzing imputations and choosing the best one, is a task that requires lots of experimentation. It is important to make sure that our data does not become biased while imputing. We created 4 different imputations using mean, median, mode, and constant filling imputations.
- We'll create a scatterplot of the DataFrames we imputed previously. To achieve this, we'll create a dictionary of the DataFrames with the keys being their title.
```
import matplotlib.pyplot as plt
%matplotlib inline
# Set nrows and ncols to 2
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 10))
nullity = diabetes.Serum_Insulin.isnull()+diabetes.Glucose.isnull()
# Create a dictionary of imputations
imputations = {'Mean Imputation': diabetes_mean, 'Median Imputation': diabetes_median,
'Most Frequent Imputation': diabetes_mode, 'Constant Imputation': diabetes_constant}
# Loop over flattened axes and imputations
for ax, df_key in zip(axes.flatten(), imputations):
# Select and also set the title for a DataFrame
imputations[df_key].plot(x='Serum_Insulin', y='Glucose', kind='scatter',
alpha=0.5, c=nullity, cmap='rainbow', ax=ax,
colorbar=False, title=df_key)
plt.show()
```
- Notice how these imputations are portrayed as a straight line and don't adjust to the shape of the data
# Imputing using fancyimpute
- fancyimpute is a package containing several advanced imputation techniques that use machine learning algorithms to impute missing values.
- In mean, median, mode imputations only the respective column was utilized for computing and imputing missing values.
- In contrast, the advanced imputation techniques use other columns as well to predict the missing values and impute them. Think of it as fitting a ML model to predict the missing values in a column using the remaining columns.
- **KNN imputation** : find the most similar data points using all the non-missing features for a data point and calculates the average of these similar points to fill the missing feature. Here K specifies the number of similar or nearest points to consider.
```python
from fancyimpute import KNN
knn_imputer = KNN()
diabetes_knn = diabetes.copy(deep=True)
diabetes_knn.iloc[:,:] = knn_imputer.fit_transform(diabetes_knn)
```
#### Multiple Imputations by Chained Equations (MICE)
- Perform multiple regression over random sample of the data
- Take average of the multiple regression values
- Impute the missing feature value for the data point
- The MICE function is called 'IterativeImputer' in the fancyimpute package as it performs multiple imputations on the data.
```python
from fancyimpute import IterativeImputer
MICE_imputer = IterativeImputer()
diabetes_MICE = diabetes.copy(deep=True)
diabetes_MICE.iloc[:,:] = MICE_imputer.fit_transform(diabetes_MICE)
```
## KNN imputation
- **Datasets always have features which are correlated. Hence, it becomes important to consider them as a factor for imputing missing values**. Machine learning models use features in the DataFrame to find correlations and patterns and predict a selected feature.
- One of the simplest and most efficient models is the K Nearest Neighbors. It finds 'K' points most similar to the existing data points to impute missing values.
```
diabetes = pd.read_csv('./../data/pima-indians-diabetes data.csv')
diabetes.head()
diabetes.isnull().sum()
# Import KNN from fancyimpute
from fancyimpute import KNN
# Copy diabetes to diabetes_knn_imputed
diabetes_knn_imputed = diabetes.copy(deep=True)
# Initialize KNN
knn_imputer = KNN()
# Impute using fit_tranform on diabetes_knn_imputed
diabetes_knn_imputed.iloc[:, :] = knn_imputer.fit_transform(diabetes_knn_imputed)
diabetes_knn_imputed.isnull().sum()
```
# MICE imputation
- Here, we will use IterativeImputer or popularly called MICE for imputing missing values.The IterativeImputer performs multiple regressions on random samples of the data and aggregates for imputing the missing values.
```
diabetes = pd.read_csv('./../data/pima-indians-diabetes data.csv')
diabetes.head()
# Import IterativeImputer from fancyimpute
from fancyimpute import IterativeImputer
# Copy diabetes to diabetes_mice_imputed
diabetes_mice_imputed = diabetes.copy(deep=True)
# Initialize IterativeImputer
mice_imputer = IterativeImputer()
# Impute using fit_tranform on diabetes
diabetes_mice_imputed.iloc[:, :] = mice_imputer.fit_transform(diabetes)
diabetes_mice_imputed.isnull().sum()
```
## Imputing categorical values
- The complexity with categorical data is that they are usually strings. Hence imputations cannot be applied on them. The categorical values must first be converted or encoded to numeric values and then imputed.
- For converting categories to numeric values we need to encode the categories using ordinal encoder or one-hot encoder.
## Imputation techniques
- Simplest way is to just fill with most frequent category.
- Impute using statistical models like KNN
- Ordinal encoding cannot handle Nans, so skip Nans and then compute missing values.
### Ordinal Encoding
```python
from sklearn.preprocessing import OrdinalEncoder
# create Ordinal Encoder
ambience_ord_enc = OrdinalEncoder()
# select non-null values in ambience
ambience = users['ambience']
**ambience_not_null = ambience[ambience.notnull()]**
reshaped_vals = ambience_not_null.values.reshape(-1, 1)
# encode the non-null values of ambience
encoded_vals = ambience_ord_enc.fit_transform(reshaped_vals)
# replace the ambience column with ordinal values
users.loc[ambience.notnull(), 'ambience'] = np.squeeze(encoded_vals)
# generalized form for conversion by looping over the columns
# create a dictionary for ordinal encoders
ordinal_enc_dict = {}
# loop over columns to encode
for col_name in users:
# create ordinal encoder for the column
ordinal_enc_dict[col_name] = OrdinalEncoder()
# select the non-null values in the column
col = users[col_name]
col_not_null = col[col.notnull()]
reshaped_vals = col_not_null.values.reshape(-1, 1)
# encode the non-null values of the column
encoded_vals = ordinal_enc_dict[col_name].fit_transform(reshaped_vals)
# here we are also creating a unique encoder for each column and storing them using a dictionary 'ordinal_enc_dict'. This will help us to later convert them back to their respective categories
# imputing with KNN
users_KNN_imputed = users.copy(deep=True)
# create MICE imputer
KNN_imputer = KNN()
users_KNN_imputed.iloc[:,:] = np.round(KNN_imputer.fit_transform(imputed))
# last step is to convert back the ordinal values to its labels using the method **'inverse_transform'** with respective encoders and columns.
for col in imputed:
reshaped_col = imputed[col].values.reshape(-1, 1)
users_KNN_imputed[col] = ordinal_enc[col].inverse_transform(reshaped_col)
```
### Ordinal encoding of a categorical column
- Imputing categorical values involves a few additional steps over imputing numerical values. We need to first convert them to numerical values as statistical operations cannot be performed on strings.
```
users = pd.read_csv('./../data/')
from sklearn.preprocessing import OrdinalEncoder
# Create Ordinal encoder
ambience_ord_enc = OrdinalEncoder()
# Select non-null values of ambience column in users
ambience = users['ambience']
ambience_not_null = ambience[ambience.notnull()]
# Reshape ambience_not_null to shape (-1, 1)
reshaped_vals = ambience_not_null.values.reshape(-1, 1)
# Ordinally encode reshaped_vals
encoded_vals = ambience_ord_enc.fit_transform(reshaped_vals)
# Assign back encoded values to non-null values of ambience in users
users.loc[ambience.notnull(), 'ambience'] = np.squeeze(encoded_vals)
# Ordinal encoding of a DataFrame
# Create an empty dictionary ordinal_enc_dict
ordinal_enc_dict = {}
for col_name in users:
# Create Ordinal encoder for col
ordinal_enc_dict[col_name] = OrdinalEncoder()
col = users[col_name]
print(ordinal_enc_dict)
# Select non-null values of col
col_not_null = col[col.notnull()]
reshaped_vals = col_not_null.values.reshape(-1, 1)
encoded_vals = ordinal_enc_dict[col_name].fit_transform(reshaped_vals)
# Store the values to non-null values of the column in users
users.loc[col.notnull(), col_name] = np.squeeze(encoded_vals)
```
- Using this for loop, we're now able to automate encoding all categorical columns in the DataFrame!
```
# Create KNN imputer
KNN_imputer = KNN()
# Impute and round the users DataFrame
users.iloc[:, :] = np.round(KNN_imputer.fit_transform(users))
# Loop over the column names in users
for col_name in users:
# Reshape the data
reshaped = users[col_name].values.reshape(-1, 1)
# Perform inverse transform of the ordinally encoded columns
users[col_name] = ordinal_enc_dict[col_name].inverse_transform(reshaped)
```
- We're now able to convert categorical values to numerical ones, impute them using machine learning, and then re-convert them to categorical ones!
## Evaluation of different imputation techniques
- In Data Science, we usually impute missing data in order to improve model performance and decrease bias.
- Imputation with maximum machine learning model performance is selected.
- We can also use a simple linear regression on the various imputations we have done.
- **Another way to observe the imputation performance is to observe their density plots and see which one most resembles the shape of the original data**
- To perform linear regression we can use the statsmodels package as it produces various statistical summaries.
- Fit a linear model for statistical summary
- We can first create the complete case `diabetes_cc` by dropping the rows with missing values.
- This will be the baseline model to compare against other imputations.
```python
import statsmodels.api as sm
diabetes_cc = diabetes.dropna(how='any')
X = sm.add_constant(diabetes_cc.iloc[:, : -1])
y = diabetes_cc["Class"]
lm = sm.OLS(y,X).fit()
print(lm.summary())
```
#### R-squared and Coefficients
- While the R-sqaured measures the accuracy of the machine learning model, the coefficients explain the weights of different features in the data. The higher the R-squared the better the model.
- We can get the R-squared and coefficents using `lm.rsquared_adj` and `lm.params`
#### Fit linear model on different imputed Dataframes
```python
# mean imputation
X = sm.add_constant(diabetes_mean_imputed.iloc[:,:-1])
y = diabetes['Class']
lm_mean = sm.OLS(y, X).fit()
# KNN imputation
X = sm.add_constant(diabetes_knn_imputed.iloc[:,:-1])
lm_KNN = sm.OLS(y, X).fit()
# MICE Imputation
X = sm.add_constant(diabetes_mice_imputed.iloc[:,:-1])
lm_MICE = sm.OLS(y, X).fit()
```
#### Comparing R-squared of different imputations
```python
print(pd.DataFrame({'Complete':lm.rsquared_adj,
'Mean Imp':lm_mean.rsquared_adj,
'KNN Imp':lm_KNN.rsquared_adj,
'MICE Imp':lm_MICE.rsquared_adj},
index=['R_squared_adj']))
```
- We observe that the mean imputation has the least R-squared as it imputes the same mean value throughout the column.
- The complete case has the highest R-squared as half the rows with missing values have been dropped for fitting the linear model.
- We can similarly compare the coefficients of each of the imputations using the `.params` attribute
```python
print(pd.DataFrame({'Complete':lm.params,
'Mean Imp':lm_mean.params,
'KNN Imp':lm_KNN.params,
'MICE Imp':, lm_MICE.params}))
```
- We see that columns show that the imputed values add more weights to reinforce these features in the imputations.
#### Comparing density plots
- We can compare the density plots of the imputations to check which imputation most resembles the original dataset and does not introduce a bias.
```python
diabetes_cc['Skin_Fold'].plot(kind='kde', c='red', linewidth=3)
diabetes_mean_imputed['Skin_Fold'].plot(kind='kde')
diabetes_knn_imputed['Skin_Fold'].plot(kind='kde')
diabetes_mice_imputed['Skin_Fold'].plot(kind='kde')
labels = ['Baseline (complete case)', 'Mean Imputation', 'KNN Imputation', 'MICE Imputation']
plt.legend(labels)
plt.xlabel('Skin Fold')
```
- We observe that the mean imputation is completely out of shape as compared to the other imputations.
- The KNN and MICE imputations are much more identical to the base DataFrame with the peak of MICE imputation being slightly shifted.
### Analyze the summary of linear model
- Analyzing the performance of the different imputed models is one of the most significant tasks in dealing with missing data. It determines, the type of imputed DataFrame we can rely upon.
- For analysis, we can fit a linear regression model on the imputed DataFrame and check for various parameters that impact the selection of the imputation type.
```
diabetes_cc = pd.read_csv('./../data/pima-indians-diabetes data.csv')
diabetes_cc.head()
```
### Drop missing values : base line dataset
```
diabetes_cc.dropna(inplace=True)
diabetes_cc.reset_index(inplace = True, drop=True)
diabetes_cc.head()
print(diabetes_cc.shape)
diabetes_cc.isnull().sum()
import statsmodels.api as sm
# Add constant to X and set X & y values to fit linear model
X = sm.add_constant(diabetes_cc.iloc[:, : -1])
y = diabetes_cc["Class"]
lm = sm.OLS(y, X).fit()
# linear model for mean imputation
X = sm.add_constant(diabetes_mean.iloc[:,:-1])
y = diabetes_mean['Class']
lm_mean = sm.OLS(y, X).fit()
# linear model for KNN imputation
X = sm.add_constant(diabetes_knn_imputed.iloc[:,:-1])
y = diabetes_knn_imputed['Class']
lm_KNN = sm.OLS(y, X).fit()
# linear model for MICE imputation
X = sm.add_constant(diabetes_mice_imputed.iloc[:,:-1])
y = diabetes_mice_imputed['Class']
lm_MICE = sm.OLS(y, X).fit()
# Print summary of lm
print('\nSummary: ', lm.summary())
# Print R squared score of lm
print('\nAdjusted R-squared score: ', lm.rsquared_adj)
# Print the params of lm
print('\nCoefficcients:\n', lm.params)
```
## Comparing R-squared and coefficients : Numerical analysis
- During the analysis of imputed DataFrames on a linear model, the R-squared score which explains the accuracy and the coefficients which explains the model itself can act as some of the important characteristics to check for the quality of imputation.
```
# Store the Adj. R-squared scores of the linear models
r_squared = pd.DataFrame({'Complete Case': lm.rsquared_adj,
'Mean Imputation': lm_mean.rsquared_adj,
'KNN Imputation': lm_KNN.rsquared_adj,
'MICE Imputation': lm_MICE.rsquared_adj},
index=['Adj. R-squared'])
print(r_squared)
# Store the coefficients of the linear models
coeff = pd.DataFrame({'Complete Case': lm.params,
'Mean Imputation': lm_mean.params,
'KNN Imputation': lm_KNN.params,
'MICE Imputation': lm_MICE.params})
print(coeff)
r_squares = {'KNN Imputation': lm_KNN.rsquared_adj,
'Mean Imputation': lm_mean.rsquared_adj,
'MICE Imputation': lm_MICE.rsquared_adj}
# Select best R-squared
best_imputation = max(r_squares, key=r_squares.get)
print("The best imputation technique is: ", best_imputation)
```
### Comparing density plots : Graphical analysis
- The different imputations that we have performed earlier can be graphically compared with their density plots to realize which dataset has the most similar distribution compared to the original dataset. We will also be able to interpret which dataset has a biased imputation.
```
# Plot graphs of imputed DataFrames and the complete case
diabetes_cc['Skin_Fold'].plot(kind='kde', c='red', linewidth=3)
diabetes_mean['Skin_Fold'].plot(kind='kde')
diabetes_knn_imputed['Skin_Fold'].plot(kind='kde')
diabetes_mice_imputed['Skin_Fold'].plot(kind='kde')
# Create labels for the four DataFrames
labels = ['Baseline (Complete Case)', 'Mean Imputation', 'KNN Imputation', 'MICE Imputation']
plt.legend(labels)
# Set the x-label as Skin Fold
plt.xlabel('Skin_Fold')
plt.show()
```
| true |
code
| 0.632815 | null | null | null | null |
|
```
import pandas as pd
```
# Classification
We'll take a tour of the methods for classification in sklearn. First let's load a toy dataset to use:
```
from sklearn.datasets import load_breast_cancer
breast = load_breast_cancer()
```
Let's take a look
```
# Convert it to a dataframe for better visuals
df = pd.DataFrame(breast.data)
df.columns = breast.feature_names
df
```
And now look at the targets
```
print(breast.target_names)
breast.target
```
## Classification Trees
Using the scikit learn models is basically the same as in Julia's ScikitLearn.jl
```
from sklearn.tree import DecisionTreeClassifier
cart = DecisionTreeClassifier(max_depth=2, min_samples_leaf=140)
cart.fit(breast.data, breast.target)
```
Here's a helper function to plot the trees.
# Installing Graphviz (tedious)
## Windows
1. Download graphviz from https://graphviz.gitlab.io/_pages/Download/Download_windows.html
2. Install it by running the .msi file
3. Set the pat variable:
(a) Go to Control Panel > System and Security > System > Advanced System Settings > Environment Variables > Path > Edit
(b) Add 'C:\Program Files (x86)\Graphviz2.38\bin'
4. Run `conda install graphviz`
5. Run `conda install python-graphviz`
## macOS and Linux
1. Run `brew install graphviz` (install `brew` from https://docs.brew.sh/Installation if you don't have it)
2. Run `conda install graphviz`
3. Run `conda install python-graphviz`
```
import graphviz
import sklearn.tree
def visualize_tree(sktree):
dot_data = sklearn.tree.export_graphviz(sktree, out_file=None,
filled=True, rounded=True,
special_characters=False,
feature_names=df.columns)
return graphviz.Source(dot_data)
visualize_tree(cart)
```
We can get the label predictions with the `.predict` method
```
labels = cart.predict(breast.data)
labels
```
And similarly the predicted probabilities with `.predict_proba`
```
probs = cart.predict_proba(breast.data)
probs
```
Just like in Julia, the probabilities are returned for each class
```
probs.shape
```
We can extract the second column of the probs by slicing, just like how we did it in Julia
```
probs = cart.predict_proba(breast.data)[:,1]
probs
```
To evaluate the model, we can use functions from `sklearn.metrics`
```
from sklearn.metrics import roc_auc_score, accuracy_score, confusion_matrix
roc_auc_score(breast.target, probs)
accuracy_score(breast.target, labels)
confusion_matrix(breast.target, labels)
```
## Random Forests and Boosting
We use random forests and boosting in the same way as CART
```
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators=100)
forest.fit(breast.data, breast.target)
labels = forest.predict(breast.data)
probs = forest.predict_proba(breast.data)[:,1]
print(roc_auc_score(breast.target, probs))
print(accuracy_score(breast.target, labels))
confusion_matrix(breast.target, labels)
from sklearn.ensemble import GradientBoostingClassifier
boost = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1)
boost.fit(breast.data, breast.target)
labels = boost.predict(breast.data)
probs = boost.predict_proba(breast.data)[:,1]
print(roc_auc_score(breast.target, probs))
print(accuracy_score(breast.target, labels))
confusion_matrix(breast.target, labels)
```
## Logistic Regression
We can also access logistic regression from sklearn
```
from sklearn.linear_model import LogisticRegression
logit = LogisticRegression()
logit.fit(breast.data, breast.target)
labels = logit.predict(breast.data)
probs = logit.predict_proba(breast.data)[:,1]
print(roc_auc_score(breast.target, probs))
print(accuracy_score(breast.target, labels))
confusion_matrix(breast.target, labels)
```
The sklearn implementation has options for regularization in logistic regression. You can choose between L1 and L2 regularization:


Note that this regularization is adhoc and **not equivalent to robustness**. For a robust logistic regression, follow the approach from 15.680.
You control the regularization with the `penalty` and `C` hyperparameters. We can see that our model above used L2 regularization with $C=1$.
### Exercise
Try out unregularized logistic regression as well as L1 regularization. Which of the three options seems best? What if you try changing $C$?
```
# No regularization
logit = LogisticRegression(C=1e10)
logit.fit(breast.data, breast.target)
labels = logit.predict(breast.data)
probs = logit.predict_proba(breast.data)[:,1]
print(roc_auc_score(breast.target, probs))
print(accuracy_score(breast.target, labels))
confusion_matrix(breast.target, labels)
# L1 regularization
logit = LogisticRegression(C=100, penalty='l1')
logit.fit(breast.data, breast.target)
labels = logit.predict(breast.data)
probs = logit.predict_proba(breast.data)[:,1]
print(roc_auc_score(breast.target, probs))
print(accuracy_score(breast.target, labels))
confusion_matrix(breast.target, labels)
```
# Regression
Now let's take a look at regression in sklearn. Again we can start by loading up a dataset.
```
from sklearn.datasets import load_boston
boston = load_boston()
print(boston.DESCR)
```
Take a look at the X
```
df = pd.DataFrame(boston.data)
df.columns = boston.feature_names
df
boston.target
```
## Regression Trees
We use regression trees in the same way as classification
```
from sklearn.tree import DecisionTreeRegressor
cart = DecisionTreeRegressor(max_depth=2, min_samples_leaf=5)
cart.fit(boston.data, boston.target)
visualize_tree(cart)
```
Like for classification, we get the predicted labels out with the `.predict` method
```
preds = cart.predict(boston.data)
preds
```
There are functions provided by `sklearn.metrics` to evaluate the predictions
```
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
print(mean_absolute_error(boston.target, preds))
print(mean_squared_error(boston.target, preds))
print(r2_score(boston.target, preds))
```
## Random Forests and Boosting
Random forests and boosting for regression work the same as in classification, except we use the `Regressor` version rather than `Classifier`.
### Exercise
Test and compare the (in-sample) performance of random forests and boosting on the Boston data with some sensible parameters.
```
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=100)
forest.fit(boston.data, boston.target)
preds = forest.predict(boston.data)
print(mean_absolute_error(boston.target, preds))
print(mean_squared_error(boston.target, preds))
print(r2_score(boston.target, preds))
from sklearn.ensemble import GradientBoostingRegressor
boost = GradientBoostingRegressor(n_estimators=100, learning_rate=0.2)
boost.fit(boston.data, boston.target)
preds = boost.predict(boston.data)
print(mean_absolute_error(boston.target, preds))
print(mean_squared_error(boston.target, preds))
print(r2_score(boston.target, preds))
```
## Linear Regression Models
There are a large collection of linear regression models in sklearn. Let's start with a simple ordinary linear regression
```
from sklearn.linear_model import LinearRegression
linear = LinearRegression()
linear.fit(boston.data, boston.target)
preds = linear.predict(boston.data)
print(mean_absolute_error(boston.target, preds))
print(mean_squared_error(boston.target, preds))
print(r2_score(boston.target, preds))
```
We can also take a look at the betas:
```
linear.coef_
```
We can use regularized models as well. Here is ridge regression:
```
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=10)
ridge.fit(boston.data, boston.target)
preds = ridge.predict(boston.data)
print(mean_absolute_error(boston.target, preds))
print(mean_squared_error(boston.target, preds))
print(r2_score(boston.target, preds))
ridge.coef_
```
And here is lasso
```
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1)
lasso.fit(boston.data, boston.target)
preds = lasso.predict(boston.data)
print(mean_absolute_error(boston.target, preds))
print(mean_squared_error(boston.target, preds))
print(r2_score(boston.target, preds))
lasso.coef_
```
There are many other linear regression models available. See the [linear model documentation](http://scikit-learn.org/stable/modules/linear_model.html) for more.
### Exercise
The elastic net is another linear regression method that combines ridge and lasso regularization. Try running it on this dataset, referring to the documentation as needed to learn how to use it and control the hyperparameters.
```
from sklearn.linear_model import ElasticNet
net = ElasticNet(l1_ratio=0.3, alpha=1)
net.fit(boston.data, boston.target)
preds = net.predict(boston.data)
print(mean_absolute_error(boston.target, preds))
print(mean_squared_error(boston.target, preds))
print(r2_score(boston.target, preds))
net.coef_
```
| true |
code
| 0.589539 | null | null | null | null |
|
<h1 align="center"><font size="5">RECOMMENDATION SYSTEM WITH A RESTRICTED BOLTZMANN MACHINE</font></h1>
Welcome to the <b>Recommendation System with a Restricted Boltzmann Machine</b> notebook. In this notebook, we study and go over the usage of a Restricted Boltzmann Machine (RBM) in a Collaborative Filtering based recommendation system. This system is an algorithm that recommends items by trying to find users that are similar to each other based on their item ratings. By the end of this notebook, you should have a deeper understanding of how Restricted Boltzmann Machines are applied, and how to build one using TensorFlow.
<h2>Table of Contents</h2>
<ol>
<li><a href="#ref1">Acquiring the Data</a></li>
<li><a href="#ref2">Loading in the Data</a></li>
<li><a href="#ref3">The Restricted Boltzmann Machine model</a></li>
<li><a href="#ref4">Setting the Model's Parameters</a></li>
<li><a href="#ref5">Recommendation</a></li>
</ol>
<br>
<br>
<hr>
<a id="ref1"></a>
<h2>Acquiring the Data</h2>
To start, we need to download the data we are going to use for our system. The datasets we are going to use were acquired by <a href="http://grouplens.org/datasets/movielens/">GroupLens</a> and contain movies, users and movie ratings by these users.
After downloading the data, we will extract the datasets to a directory that is easily accessible.
```
!wget -c https://raw.githubusercontent.com/IBM/dl-learning-path-assets/main/unsupervised-deeplearning/data/ml-1m.zip -O moviedataset.zip
!unzip -o moviedataset.zip
```
With the datasets in place, let's now import the necessary libraries. We will be using <a href="https://www.tensorflow.org/">Tensorflow</a> and <a href="http://www.numpy.org/">Numpy</a> together to model and initialize our Restricted Boltzmann Machine and <a href="http://pandas.pydata.org/pandas-docs/stable/">Pandas</a> to manipulate our datasets. To import these libraries, run the code cell below.
```
#Tensorflow library. Used to implement machine learning models
import tensorflow as tf
#Numpy contains helpful functions for efficient mathematical calculations
import numpy as np
#Dataframe manipulation library
import pandas as pd
#Graph plotting library
import matplotlib.pyplot as plt
%matplotlib inline
```
<hr>
<a id="ref2"></a>
<h2>Loading in the Data</h2>
Let's begin by loading in our data with Pandas. The .dat files containing our data are similar to CSV files, but instead of using the ',' (comma) character to separate entries, it uses '::' (two colons) characters instead. To let Pandas know that it should separate data points at every '::', we have to specify the <code>sep='::'</code> parameter when calling the function.
Additionally, we also pass it the <code>header=None</code> parameter due to the fact that our files don't contain any headers.
Let's start with the movies.dat file and take a look at its structure:
```
#Loading in the movies dataset
movies_df = pd.read_csv('ml-1m/movies.dat', sep='::', header=None, engine='python')
movies_df.head()
```
We can do the same for the ratings.dat file:
```
#Loading in the ratings dataset
ratings_df = pd.read_csv('ml-1m/ratings.dat', sep='::', header=None, engine='python')
ratings_df.head()
```
So our <b>movies_df</b> variable contains a dataframe that stores a movie's unique ID number, title and genres, while our <b>ratings_df</b> variable stores a unique User ID number, a movie's ID that the user has watched, the user's rating to said movie and when the user rated that movie.
Let's now rename the columns in these dataframes so we can better convey their data more intuitively:
```
movies_df.columns = ['MovieID', 'Title', 'Genres']
movies_df.head()
```
And our final ratings_df:
```
ratings_df.columns = ['UserID', 'MovieID', 'Rating', 'Timestamp']
ratings_df.head()
```
<hr>
<a id="ref3"></a>
<h2>The Restricted Boltzmann Machine model</h2>
<img src="https://github.com/fawazsiddiqi/recommendation-system-with-a-Restricted-Boltzmann-Machine-using-tensorflow/blob/master/images/films.png?raw=true" width="300">
<br>
The Restricted Boltzmann Machine model has two layers of neurons, one of which is what we call a visible input layer and the other is called a hidden layer. The hidden layer is used to learn features from the information fed through the input layer. For our model, the input is going to contain X neurons, where X is the amount of movies in our dataset. Each of these neurons will possess a normalized rating value varying from 0 to 1, where 0 meaning that a user has not watched that movie and the closer the value is to 1, the more the user likes the movie that neuron's representing. These normalized values, of course, will be extracted and normalized from the ratings dataset.
After passing in the input, we train the RBM on it and have the hidden layer learn its features. These features are what we use to reconstruct the input, which in our case, will predict the ratings for movies that user hasn't watched, which is exactly what we can use to recommend movies!
We will now begin to format our dataset to follow the model's expected input.
<h3>Formatting the Data</h3>
First let's see how many movies we have and see if the movie ID's correspond with that value:
```
len(movies_df)
```
Now, we can start formatting the data into input for the RBM. We're going to store the normalized users ratings into as a matrix of user-rating called trX, and normalize the values.
```
user_rating_df = ratings_df.pivot(index='UserID', columns='MovieID', values='Rating')
user_rating_df.head()
```
Lets normalize it now:
```
norm_user_rating_df = user_rating_df.fillna(0) / 5.0
trX = norm_user_rating_df.values
trX[0:5]
```
<hr>
<a id="ref4"></a>
<h2>Setting the Model's Parameters</h2>
Next, let's start building our RBM with TensorFlow. We'll begin by first determining the number of neurons in the hidden layers and then creating placeholder variables for storing our visible layer biases, hidden layer biases and weights that connects the hidden layer with the visible layer. We will be arbitrarily setting the number of neurons in the hidden layers to 20. You can freely set this value to any number you want since each neuron in the hidden layer will end up learning a feature.
```
hiddenUnits = 20
visibleUnits = len(user_rating_df.columns)
vb = tf.Variable(tf.zeros([visibleUnits]), tf.float32) #Number of unique movies
hb = tf.Variable(tf.zeros([hiddenUnits]), tf.float32) #Number of features we're going to learn
W = tf.Variable(tf.zeros([visibleUnits, hiddenUnits]), tf.float32)
```
We then move on to creating the visible and hidden layer units and setting their activation functions. In this case, we will be using the <code>tf.sigmoid</code> and <code>tf.relu</code> functions as nonlinear activations since it is commonly used in RBM's.
```
v0 = tf.zeros([visibleUnits], tf.float32)
#testing to see if the matrix product works
tf.matmul([v0], W)
#Phase 1: Input Processing
#defining a function to return only the generated hidden states
def hidden_layer(v0_state, W, hb):
h0_prob = tf.nn.sigmoid(tf.matmul([v0_state], W) + hb) #probabilities of the hidden units
h0_state = tf.nn.relu(tf.sign(h0_prob - tf.random.uniform(tf.shape(h0_prob)))) #sample_h_given_X
return h0_state
#printing output of zeros input
h0 = hidden_layer(v0, W, hb)
print("first 15 hidden states: ", h0[0][0:15])
def reconstructed_output(h0_state, W, vb):
v1_prob = tf.nn.sigmoid(tf.matmul(h0_state, tf.transpose(W)) + vb)
v1_state = tf.nn.relu(tf.sign(v1_prob - tf.random.uniform(tf.shape(v1_prob)))) #sample_v_given_h
return v1_state[0]
v1 = reconstructed_output(h0, W, vb)
print("hidden state shape: ", h0.shape)
print("v0 state shape: ", v0.shape)
print("v1 state shape: ", v1.shape)
```
And set the error function, which in this case will be the Mean Absolute Error Function.
```
def error(v0_state, v1_state):
return tf.reduce_mean(tf.square(v0_state - v1_state))
err = tf.reduce_mean(tf.square(v0 - v1))
print("error" , err.numpy())
```
Now we train the RBM with 5 epochs with each epoch using a batchsize of 500, giving 12 batches. After training, we print out a graph with the error by epoch.
```
epochs = 5
batchsize = 500
errors = []
weights = []
K=1
alpha = 0.1
#creating datasets
train_ds = \
tf.data.Dataset.from_tensor_slices((np.float32(trX))).batch(batchsize)
#for i in range(epochs):
# for start, end in zip( range(0, len(trX), batchsize), range(batchsize, len(trX), batchsize)):
# batch = trX[start:end]
# cur_w = sess.run(update_w, feed_dict={v0: batch, W: prv_w, vb: prv_vb, hb: prv_hb})
# cur_vb = sess.run(update_vb, feed_dict={v0: batch, W: prv_w, vb: prv_vb, hb: prv_hb})
# cur_nb = sess.run(update_hb, feed_dict={v0: batch, W: prv_w, vb: prv_vb, hb: prv_hb})
# prv_w = cur_w
# prv_vb = cur_vb
# prv_hb = cur_hb
# errors.append(sess.run(err_sum, feed_dict={v0: trX, W: cur_w, vb: cur_vb, hb: cur_hb}))
# print (errors[-1])
v0_state=v0
for epoch in range(epochs):
batch_number = 0
for batch_x in train_ds:
for i_sample in range(len(batch_x)):
for k in range(K):
v0_state = batch_x[i_sample]
h0_state = hidden_layer(v0_state, W, hb)
v1_state = reconstructed_output(h0_state, W, vb)
h1_state = hidden_layer(v1_state, W, hb)
delta_W = tf.matmul(tf.transpose([v0_state]), h0_state) - tf.matmul(tf.transpose([v1_state]), h1_state)
W = W + alpha * delta_W
vb = vb + alpha * tf.reduce_mean(v0_state - v1_state, 0)
hb = hb + alpha * tf.reduce_mean(h0_state - h1_state, 0)
v0_state = v1_state
if i_sample == len(batch_x)-1:
err = error(batch_x[i_sample], v1_state)
errors.append(err)
weights.append(W)
print ( 'Epoch: %d' % (epoch + 1),
"batch #: %i " % batch_number, "of %i" % (len(trX)/batchsize),
"sample #: %i" % i_sample,
'reconstruction error: %f' % err)
batch_number += 1
plt.plot(errors)
plt.ylabel('Error')
plt.xlabel('Epoch')
plt.show()
```
<hr>
<a id="ref5"></a>
<h2>Recommendation</h2>
We can now predict movies that an arbitrarily selected user might like. This can be accomplished by feeding in the user's watched movie preferences into the RBM and then reconstructing the input. The values that the RBM gives us will attempt to estimate the user's preferences for movies that he hasn't watched based on the preferences of the users that the RBM was trained on.
Lets first select a <b>User ID</b> of our mock user:
```
mock_user_id = 215
#Selecting the input user
inputUser = trX[mock_user_id-1].reshape(1, -1)
inputUser = tf.convert_to_tensor(trX[mock_user_id-1],"float32")
v0 = inputUser
print(v0)
v0.shape
v0test = tf.zeros([visibleUnits], tf.float32)
v0test.shape
#Feeding in the user and reconstructing the input
hh0 = tf.nn.sigmoid(tf.matmul([v0], W) + hb)
vv1 = tf.nn.sigmoid(tf.matmul(hh0, tf.transpose(W)) + vb)
rec = vv1
tf.maximum(rec,1)
for i in vv1:
print(i)
```
We can then list the 20 most recommended movies for our mock user by sorting it by their scores given by our model.
```
scored_movies_df_mock = movies_df[movies_df['MovieID'].isin(user_rating_df.columns)]
scored_movies_df_mock = scored_movies_df_mock.assign(RecommendationScore = rec[0])
scored_movies_df_mock.sort_values(["RecommendationScore"], ascending=False).head(20)
```
So, how to recommend the movies that the user has not watched yet?
Now, we can find all the movies that our mock user has watched before:
```
movies_df_mock = ratings_df[ratings_df['UserID'] == mock_user_id]
movies_df_mock.head()
```
In the next cell, we merge all the movies that our mock users has watched with the predicted scores based on his historical data:
```
#Merging movies_df with ratings_df by MovieID
merged_df_mock = scored_movies_df_mock.merge(movies_df_mock, on='MovieID', how='outer')
```
lets sort it and take a look at the first 20 rows:
```
merged_df_mock.sort_values(["RecommendationScore"], ascending=False).head(20)
```
As you can see, there are some movies that user has not watched yet and has high score based on our model. So, we can recommend them to the user.
This is the end of the tutorial. If you want, you can try to change the parameters in the code -- adding more units to the hidden layer, changing the loss functions or maybe something else to see if it changes anything. Optimization settings can also be adjusted...the number of epochs, the size of K, and the batch size are all interesting numbers to explore.
Does the model perform better? Does it take longer to compute?
Thank you for reading this notebook. Hopefully, you now have a little more understanding of the RBM model, its applications and how it works with TensorFlow.
<hr>
## Want to learn more?
You can use __Watson Studio__ to run these notebooks faster with bigger datasets.__Watson Studio__ is IBM’s leading cloud solution for data scientists, built by data scientists. With Jupyter notebooks, RStudio, Apache Spark and popular libraries pre-packaged in the cloud, __Watson Studio__ enables data scientists to collaborate on their projects without having to install anything. Join the fast-growing community of __Watson Studio__ users today with a free account at [Watson Studio](http://ibm.biz/WatsonStudioRBM).This is the end of this lesson. Thank you for reading this notebook, and good luck on your studies.
### Thank you for completing this exercise!
Notebook created by: <a href = "https://ca.linkedin.com/in/saeedaghabozorgi">Saeed Aghabozorgi</a>, Gabriel Garcez Barros Sousa
Updated to TF 2.X by <a href="https://ca.linkedin.com/in/nilmeier"> Jerome Nilmeier</a><br />
Added to IBM Developer by <a href=https://www.linkedin.com/in/fawazsiddiqi/> Mohammad Fawaz Siddiqi </a> <br/>
<hr>
Copyright © 2020 [Cognitive Class](https://cocl.us/DX0108EN_CC). This notebook and its source code are released under the terms of the [MIT License](https://bigdatauniversity.com/mit-license/).
| true |
code
| 0.514827 | null | null | null | null |
|
# **Neural Word Embedding**
> **Word2Vec, Continuous Bag of Word (CBOW)**
> **Word2Vec, Skip-gram with negative sampling (SGNS)**
> **Main key point: Distributional Hypothesis**
> Goal: Predict the context words from a given word
# **How to implement SGNS Algorithm:**
1. Data preprocessing
2. Hyperparameters
3. Training Data
4. Model Fitting
5. Inference/Prediction the testing samples
### **Main Class**
```
from collections import defaultdict
import numpy as np
class word2vec():
def __init__(self):
self.n = hyperparameters['n']
self.learningrate = hyperparameters['learning_rate']
self.epochs = hyperparameters['epochs']
self.windowsize = hyperparameters['window_size']
def word2onehot(self, word):
word_vector = np.zeros(self.vocabulary_count)
word_index = self.word_index[word]
word_vector[word_index] = 1
return word_vector
def generate_training_data(self, setting, corpus):
word_counts = defaultdict(int)
# print(word_counts)
for row in corpus:
for token in row:
word_counts[token] +=1
#print(word_counts)
self.vocabulary_count = len(word_counts.keys())
#print(self.vocabulary_count)
self.words_list = list(word_counts.keys())
#print(self.words_list)
self.word_index = dict((word, i) for i, word in enumerate(self.words_list))
#print(self.word_index)
self.index_word = dict((i, word) for i, word in enumerate(self.words_list))
#print(self.index_word)
training_data = []
for sentence in corpus:
sentence_length = len(sentence)
for i , word in enumerate(sentence):
word_target = self.word2onehot(sentence[i])
#print(word_target)
word_context = []
for j in range(i - self.windowsize, i + self.windowsize + 1):
if j !=i and j <= sentence_length - 1 and j >= 0:
word_context.append(self.word2onehot(sentence[j]))
# print(word_context)
training_data.append([word_target, word_context])
return np.array(training_data)
def model_training(self, training_data):
self.w1 = np.random.uniform(-1, 1, (self.vocabulary_count, self.n))
self.w2 = np.random.uniform(-1, 1, (self.n, self.vocabulary_count))
for i in range(0, self.epochs):
# self.loss = 0
for word_target, word_context in training_data:
h, u, y_pred= self.forward_pass(word_target)
# print(y_pred)
def forward_pass(self, x):
h = np.dot(self.w1.T, x)
u = np.dot(self.w2.T, h)
y_pred= self.softmax(u)
return h, u, y_pred
def softmax(self, x):
e = np.exp(x - np.max(x))
return e / e.sum(axis=0)
def word_vector(self, word):
word_index = self.word_index[word]
word_vector = self.w1[word_index]
return word_vector
def similar_vectors(self, word, n):
vw1 = self.word_vector(word)
word_similar={}
for i in range(self.vocabulary_count):
vw2 = self.w1[i]
theta_nom= np.dot(vw1, vw2)
theta_denom = np.linalg.norm(vw1) * np.linalg.norm(vw2)
theta = theta_nom / theta_denom
# print(theta)
word = self.index_word[i]
word_similar[word] = theta
# {k: v for k, v in sorted(x.items(), key=lambda item: item[1])}
words_sorted = sorted(word_similar.items(), key=lambda ss: ss[1], reverse=True)
for word, similar in words_sorted[:n]:
print(word, similar)
```
### **1.Data PreProcessing**
```
# Define the mini corpus
document = "A combination of Machine Learning and Natural Language Processing works well"
# Tokenizing and build a vocabulary
corpus = [[]]
for token in document.split():
corpus[0].append(token.lower())
print(corpus)
```
### **2. Hyperparameters**
```
hyperparameters = {
'window_size': 2, #it covers two words left and two words right
'n': 11, # dimension of word embedding
'epochs': 40, # number of training epochs
'learning_rate': 0.01, # a coefficient for updating weights
}
```
### **3. Generate Training Data**
```
# we need to create one-hot vector based on our given corpus
# 1 [target(a)], [context(combination, of)] == [10000000000],[01000000000][00100000000]
# instance
w2v = word2vec()
training_data = w2v.generate_training_data(hyperparameters, corpus)
# print(training_data)
```
### **4. Model Training**
```
w2v.model_training(training_data)
```
### **5. Model Prediction**
```
vector = w2v.word_vector("works")
print(vector)
```
### **Finding Similar Words**
```
w2v.similar_vectors("works", 5)
```
| true |
code
| 0.486941 | null | null | null | null |
|
# Introduction to BioPython
```
# Load Biopython library & Functions
import Bio
from Bio import SeqIO
from Bio.Seq import Seq, MutableSeq
from Bio.Seq import transcribe, back_transcribe, translate, complement, reverse_complement
# Check Biopython version
Bio.__version__
```
## Sequence Operations
```
# Sequence
seq = Seq("GGACCTGGAACAGGCTGAACCCTTTATCCACCTCTCTCCAATTATACCTATCATCCTAACTTCTCAGTGGACCTAACAATCTTCTCCCTTCATCTAGCAGGAGTC")
# Alphabet
seq.alphabet
# Check type
type(seq.alphabet)
# Find sub-sequence: if TRUE <- SubSeq Position, else <- return -1
seq.find("ATC")
seq.find("ATGC")
# Number of `A`
seq.count("A")
# Number of `C`
seq.count("C")
# Number of `T`
seq.count("T")
# Number of `G`
seq.count("G")
# K-mer analysis, K = 2(AA)<--dimer
seq.count("AA")
# K-mer analysis, K = 3(AAA)<--trimer
seq.count("AAA")
# Count frequency of nucleotides
from collections import Counter
freq = Counter(seq)
print(freq)
# Reverse
print(f'RefSeq: {seq}')
rev = str(seq[::-1])
print(f'RevSeq: {rev}')
# Complement
print(f'RefSeq: {seq}')
com = seq.complement()
print(f'ComSeq: {com}')
# Reverse complement
print(f'RefSeq: {seq}')
rev_com = seq.reverse_complement()
print(f'RevCom: {rev_com}')
# Transcription(DNA ==> RNA)
print(f'DNA: {seq}')
rna = seq.transcribe()
print(f'RNA: {rna}')
# Back Transcription(RNA ==> DNA)
print(f'RNA: {rna}')
dna = rna.back_transcribe()
print(f'DNA: {dna}')
# Translation(DNA ==> Protein)
print(f'DNA: {seq}')
prt = seq.translate()
print(f'Protein: {prt}')
# Let's varify the protein with length property
len(seq)
# Make codons
len(seq) % 3
# Number of codons
len(seq) / 3
# Now varify the protein length
len(prt)
# Translation(DNA ==> Protein) Stop translation when found stop codon
print(f'DNA: {seq}')
prt = seq.translate(to_stop=True)
print(f'Protein: {prt}')
# Translation(DNA ==> Protein) for Mitochondrial DNA
print(f'DNA: {seq}')
prt = seq.translate(to_stop=True, table=2)
print(f'Protein: {prt}')
```
## Handling Files
```
for seq_record in SeqIO.parse("../data/den1.fasta", "fasta"):
ID = seq_record.id
seqs = seq_record.seq[:100]
rep = repr(seq_record)
length = len(seq_record)
# ID
print(ID)
# Sequence
print(seqs)
# Representation
print(rep)
# Length
print(length)
# Print the first nucleotide of each codon
seqs[0::3]
# Print the first codon position
seqs[1::3]
# Print the second codon position
seqs[2::3]
# Sequence Length Comparison
seq1 = Seq("TTGTGGCCGCTCAGATCAGGCAGTTTAGGCTTA")
seq2 = Seq("ATTTATAGAAATGTGGTTATTTCTTAAGCATGGC")
seq1 == seq2
# Mutable sequence
mut_seq = MutableSeq("TTGTGGCCGCTCAGATCAGGCAGTTTAGGCTTA")
print(f'MutSeq: {mut_seq}')
mut_seq[5] == "C"
print(mut_seq)
mut_seq.remove("T")
print(mut_seq)
mut_seq.reverse()
print(mut_seq)
!wget http://d28rh4a8wq0iu5.cloudfront.net/ads1/data/SRR835775_1.first1000.fastq
# Working with Fastq files
for record in SeqIO.parse("SRR835775_1.first1000.fastq", "fastq"):
print(record)
print(record.seq)
print(record.letter_annotations['phred_quality'])
quals = [record.letter_annotations['phred_quality'] for record in SeqIO.parse("SRR835775_1.first1000.fastq", "fastq")]
import matplotlib.pyplot as plt
plt.hist(quals, bins=10)
plt.title("Distribution of Phred Quality Score")
plt.xlabel("Base Position")
plt.ylabel("Phred Score")
plt.show()
sequences = [record.seq for record in SeqIO.parse("SRR835775_1.first1000.fastq", "fastq")]
sequences[:100]
```
| true |
code
| 0.608507 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/CcgAlberta/pygeostat/blob/master/examples/BoundaryModeling.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Boundary Modeling
The following notebook is comprised of 7 primary steps:
1. Initialize required packages, directories and parameters
2. Load and inspect the domain indicator data
3. Calculate and model the boundary indicator variogram
4. Calculate and model the Gaussian variogram that yields the indicator variogram when truncated
5. Model the distance function
6. Simulate boundary realizations, through truncation of simulated distance function deviates
7. Save project setting and clean the output files
## 1. Initialize required packages and parameters
```
import pygeostat as gs
import numpy as np
import os
import pandas as pd
import matplotlib.pyplot as plt
```
### Project settings
Load the previously set Matplotlib and Pygeostat settings.
```
#path to GSLIB executables
exe_dir="../pygeostat/executable/"
gs.Parameters['data.griddef'] = gs.GridDef('''
120 5.0 10.0
110 1205.0 10.0
1 0.5 1.0''')
gs.Parameters['data.catdict'] = {1: 'Inside', 0: 'Outside'}
# Data values
gs.Parameters['data.tmin'] = -998
gs.Parameters['data.null'] = -999
# Color map settings
gs.Parameters['plotting.cmap'] = 'bwr'
gs.Parameters['plotting.cmap_cat'] = 'bwr'
# Number of realizations
nreal = 100
gs.Parameters['data.nreal'] = nreal
# Parallel Processing threads
gs.Parameters['config.nprocess'] = 4
# Pot Style settings
gs.PlotStyle['legend.fontsize'] = 12
gs.PlotStyle['font.size'] = 11
```
### Directories
```
# Create the output directory
outdir = 'Output/'
gs.mkdir(outdir)
```
## 2. Load and Inspect the Boundary Data
Note that content in this section was explained in the introduction notebooks. Only new concepts are generally annotated in detail.
### Load the data and note its attributes
```
dat = gs.ExampleData('reservoir_boundary', cat='Domain Indicator')
dat.info
```
### Data content and summary statistics
```
print(dat.describe())
dat.head()
```
### Map of the indicator
```
gs.location_plot(dat)
```
## 3. Calculate and Model the Indicator Variogram
The indicator variogram is calculated and modeled, since this is required input to calculation of the Gaussian variogram model in the next section (used for distance function $df$ modeling).
### Apply the variogram object for convenience
Variogram calculation, modeling, plotting and checking are readily accomplished with the variogram object, although unprovided parameters are inferred.
```
# get the proportions
proportion = sum(dat['Domain Indicator'])/len(dat)
print('Proportion of inside data: %.3f'%(proportion))
variance = proportion - proportion**2
# Perform data spacing analysis
dat.spacing(n_nearest=1)
lag_length = dat['Data Spacing (m)'].values.mean()
print('average data spacing in XY plane: {:.3f} {}'.format(lag_length,
gs.Parameters['plotting.unit']))
mean_range = (np.ptp(dat[dat.x].values) + np.ptp(dat[dat.y].values)) * 0.5
n_lag = np.ceil((mean_range * 0.5) / lag_length)
lag_tol = lag_length * 0.6
var_calc = gs.Program(program=exe_dir+'varcalc')
parstr = """ Parameters for VARCALC
**********************
START OF PARAMETERS:
{file} -file with data
2 3 0 - columns for X, Y, Z coordinates
1 4 - number of variables,column numbers (position used for tail,head variables below)
{t_min} 1.0e21 - trimming limits
{n_directions} -number of directions
0.0 90 1000 0.0 22.5 1000 0.0 -Dir 01: azm,azmtol,bandhorz,dip,diptol,bandvert,tilt
{n_lag} {lag_length} {lag_tol} - number of lags,lag distance,lag tolerance
{output} -file for experimental variogram points output.
0 -legacy output (0=no, 1=write out gamv2004 format)
1 -run checks for common errors
1 -standardize sills? (0=no, 1=yes)
1 -number of variogram types
1 1 10 1 {variance} -tail variable, head variable, variogram type (and cutoff/category), sill
"""
n_directions = 1
varcalc_outfl = os.path.join(outdir, 'varcalc.out')
var_calc.run(parstr=parstr.format(file=dat.flname,
n_directions = n_directions,
t_min = gs.Parameters['data.tmin'],
n_lag=n_lag,
lag_length = lag_length,
lag_tol = lag_tol,
variance = variance,
output=varcalc_outfl),
liveoutput=True)
varfl = gs.DataFile(varcalc_outfl)
varfl.head()
var_model = gs.Program(program=exe_dir+'varmodel')
parstr = """ Parameters for VARMODEL
***********************
START OF PARAMETERS:
{varmodel_outfl} -file for modeled variogram points output
1 -number of directions to model points along
0.0 0.0 100 6 - azm, dip, npoints, point separation
2 0.05 -nst, nugget effect
1 ? 0.0 0.0 0.0 -it,cc,azm,dip,tilt (ang1,ang2,ang3)
? ? ? -a_hmax, a_hmin, a_vert (ranges)
1 ? 0.0 0.0 0.0 -it,cc,azm,dip,tilt (ang1,ang2,ang3)
? ? ? -a_hmax, a_hmin, a_vert (ranges)
1 100000 -fit model (0=no, 1=yes), maximum iterations
1.0 - variogram sill (can be fit, but not recommended in most cases)
1 - number of experimental files to use
{varcalc_outfl} - experimental output file 1
1 1 - # of variograms (<=0 for all), variogram #s
1 0 10 - # pairs weighting, inverse distance weighting, min pairs
0 10.0 - fix Hmax/Vert anis. (0=no, 1=yes)
0 1.0 - fix Hmin/Hmax anis. (0=no, 1=yes)
{varmodelfit_outfl} - file to save fit variogram model
"""
varmodel_outfl = os.path.join(outdir, 'varmodel.out')
varmodelfit_outfl = os.path.join(outdir, 'varmodelfit.out')
var_model.run(parstr=parstr.format(varmodel_outfl= varmodel_outfl,
varmodelfit_outfl = varmodelfit_outfl,
varcalc_outfl = varcalc_outfl), liveoutput=False, quiet=True)
varmdl = gs.DataFile(varmodel_outfl)
varmdl.head()
ax = gs.variogram_plot(varfl, index=1, color='b', grid=True, label = 'Indicator Variogram (Experimental)')
gs.variogram_plot(varmdl, index=1, ax=ax, color='b', experimental=False, label = 'Indicator Variogram (Model)')
_ = ax.legend(fontsize=12)
```
## 4. Calculate and model the Gaussian Variogram
The Gaussian variogram that yields the indicator variogram after truncation of a Gaussian random field is calculated. This Gaussian variogram is modeled and input to $df$ modeing.
#### Calculate the Gaussian variogram
The bigaus2 program applies the Gaussian integration method, given the indicator variogram and the proportion of the indicator.
```
bigaus2 = gs.Program(exe_dir+'bigaus2')
parstr = """ Parameters for BIGAUS2
**********************
START OF PARAMETERS:
1 -input mode (1) model or (2) variogram file
nofile.out -file for input variogram
{proportion} -threshold/proportion
2 -calculation mode (1) NS->Ind or (2) Ind->NS
{outfl} -file for output of variograms
1 -number of thresholds
{proportion} -threshold cdf values
1 {n_lag} -number of directions and lags
0 0.0 {lag_length} -azm(1), dip(1), lag(1)
{varstr}
"""
with open(varmodelfit_outfl, 'r') as f:
varmodel_ = f.readlines()
varstr = ''''''
for line in varmodel_:
varstr += line
pars = dict(proportion=proportion,
lag_length=lag_length,
n_lag=n_lag,
outfl= os.path.join(outdir, 'bigaus2.out'),
varstr=varstr)
bigaus2.run(parstr=parstr.format(**pars), nogetarg=True)
```
### Data manipulation to handle an odd data format
The bigaus2 program outputs an odd (legacyish) variogram format, which must be translated to the standard Variogram format.
```
# Read in the data before demonstrating its present form
expvargs = gs.readvarg(os.path.join(outdir, 'bigaus2.out'), 'all')
expvargs.head()
varclac_gaussian = gs.DataFile(data = varfl.data[:-1].copy(), flname=os.path.join(outdir,'gaussian_exp_variogram.out'))
varclac_gaussian['Lag Distance'] = expvargs['Distance']
varclac_gaussian['Variogram Value'] = expvargs['Value']
varclac_gaussian.write_file(varclac_gaussian.flname)
varclac_gaussian.head()
```
### Gaussian variogram modeling
This model is input to distance function estimation.
```
parstr = """ Parameters for VARMODEL
***********************
START OF PARAMETERS:
{varmodel_outfl} -file for modeled variogram points output
1 -number of directions to model points along
0.0 0.0 100 6 - azm, dip, npoints, point separation
2 0.01 -nst, nugget effect
3 ? 0.0 0.0 0.0 -it,cc,azm,dip,tilt (ang1,ang2,ang3)
? ? ? -a_hmax, a_hmin, a_vert (ranges)
3 ? 0.0 0.0 0.0 -it,cc,azm,dip,tilt (ang1,ang2,ang3)
? ? ? -a_hmax, a_hmin, a_vert (ranges)
1 100000 -fit model (0=no, 1=yes), maximum iterations
1.0 - variogram sill (can be fit, but not recommended in most cases)
1 - number of experimental files to use
{varcalc_outfl} - experimental output file 1
1 1 - # of variograms (<=0 for all), variogram #s
1 0 10 - # pairs weighting, inverse distance weighting, min pairs
0 10.0 - fix Hmax/Vert anis. (0=no, 1=yes)
0 1.0 - fix Hmin/Hmax anis. (0=no, 1=yes)
{varmodelfit_outfl} - file to save fit variogram model
"""
varmodel_outfl_g = os.path.join(outdir, 'varmodel_g.out')
varmodelfit_outfl_g = os.path.join(outdir, 'varmodelfit_g.out')
var_model.run(parstr=parstr.format(varmodel_outfl= varmodel_outfl_g,
varmodelfit_outfl = varmodelfit_outfl_g,
varcalc_outfl = varclac_gaussian.flname), liveoutput=True, quiet=False)
varmdl_g = gs.DataFile(varmodel_outfl_g)
varmdl_g.head()
fig, axes = plt.subplots(1, 2, figsize= (15,4))
ax = axes[0]
ax = gs.variogram_plot(varfl, index=1, ax=ax, color='b', grid=True, label = 'Indicator Variogram (Experimental)')
gs.variogram_plot(varmdl, index=1, ax=ax, color='b', experimental=False, label = 'Indicator Variogram (Model)')
_ = ax.legend(fontsize=12)
ax = axes[1]
gs.variogram_plot(varclac_gaussian, index=1, ax=ax, color='g', grid=True, label = 'Gaussian Variogram (Experimental)')
gs.variogram_plot(varmdl_g, index=1, ax=ax, color='g', experimental=False, label = 'Gaussian Variogram (Model)')
_ = ax.legend(fontsize=12)
```
## 5. Distance Function $df$ Modeling
The $df$ is calculated at the data locations, before being estimated at the grid locations. The $c$ parameter is applied to the $df$ calculation, defining the bandwidth of uncertainty that will be simulated in the next section.
### Determine the $c$ parameter
Normally the optimal $c$ would be calculated using a jackknife study, but it is simply provided here.
```
selected_c = 200
```
### Calculate the $df$ at the data locations
```
dfcalc = gs.Program(exe_dir+'dfcalc')
# Print the columns for populating the parameter file without variables
print(dat.columns)
parstr = """ Parameters for DFCalc
*********************
START OF PARAMETERS:
{datafl} -file with input data
1 2 3 0 4 -column for DH,X,Y,Z,Ind
1 -in code: indicator for inside domain
0.0 0.0 0.0 -angles for anisotropy ellipsoid
1.0 1.0 -first and second anisotropy ratios (typically <=1)
0 -proportion of drillholes to remove
696969 -random number seed
{c} -C
{outfl} -file for distance function output
'nofile.out' -file for excluded drillholes output
"""
pars = dict(datafl=dat.flname, c=selected_c,
outfl=os.path.join(outdir,'df_calc.out'))
dfcalc.run(parstr=parstr.format(**pars))
```
### Manipulate the $df$ data before plotting
A standard naming convention of the distance function variable is used for convenience in the workflow, motivating the manipulation.
```
# Load the data and note the abbreviated name of the distance function
dat_df = gs.DataFile(os.path.join(outdir,'df_calc.out'), notvariables='Ind', griddef=gs.Parameters['data.griddef'])
print('Initial distance Function variable name = ', dat_df.variables)
# Set a standard distance function name
dfvar = 'Distance Function'
dat_df.rename({dat_df.variables:dfvar})
print('Distance Function variable name = ', dat_df.variables)
# Set symmetric color limits for the distance function
df_vlim = (-350, 350)
gs.location_plot(dat_df, vlim=df_vlim, cbar_label='m')
```
### Estimate the $df$ across the grid
Kriging is performed with a large number of data to provide a smooth and conditionally unbiased estimate. Global kriging would also be appropriate.
```
kd3dn = gs.Program(exe_dir+'kt3dn')
varmodelfit_outfl_g
parstr = """ Parameters for KT3DN
********************
START OF PARAMETERS:
{input_file} -file with data
1 2 3 0 6 0 - columns for DH,X,Y,Z,var,sec var
-998.0 1.0e21 - trimming limits
0 -option: 0=grid, 1=cross, 2=jackknife
xvk.dat -file with jackknife data
1 2 0 3 0 - columns for X,Y,Z,vr and sec var
nofile.out -data spacing analysis output file (see note)
0 15.0 - number to search (0 for no dataspacing analysis, rec. 10 or 20) and composite length
0 100 0 -debugging level: 0,3,5,10; max data for GSKV;output total weight of each data?(0=no,1=yes)
{out_sum} -file for debugging output (see note)
{out_grid} -file for kriged output (see GSB note)
{gridstr}
1 1 1 -x,y and z block discretization
1 100 100 1 -min, max data for kriging,upper max for ASO,ASO incr
0 0 -max per octant, max per drillhole (0-> not used)
700.0 700.0 500.0 -maximum search radii
0.0 0.0 0.0 -angles for search ellipsoid
1 -0=SK,1=OK,2=LVM(resid),3=LVM((1-w)*m(u))),4=colo,5=exdrift,6=ICCK
0.0 0.6 0.8 1.6 - mean (if 0,4,5,6), corr. (if 4 or 6), var. reduction factor (if 4)
0 0 0 0 0 0 0 0 0 -drift: x,y,z,xx,yy,zz,xy,xz,zy
0 -0, variable; 1, estimate trend
extdrift.out -gridded file with drift/mean
4 - column number in gridded file
keyout.out -gridded file with keyout (see note)
0 1 - column (0 if no keyout) and value to keep
{varmodelstr}
"""
with open(varmodelfit_outfl_g, 'r') as f:
varmodel_ = f.readlines()
varstr = ''''''
for line in varmodel_:
varstr += line
pars = dict(input_file=os.path.join(outdir,'df_calc.out'),
out_grid=os.path.join(outdir,'kt3dn_df.out'),
out_sum=os.path.join(outdir,'kt3dn_sum.out'),
gridstr=gs.Parameters['data.griddef'], varmodelstr=varstr)
kd3dn.run(parstr=parstr.format(**pars))
```
### Manipulate and plot the $df$ estimate
pixelplt selects pointvar as the color of the overlain dat_df point data since its name matches the column name of est_df.
```
est_df = gs.DataFile(os.path.join(outdir,'kt3dn_df.out'))
# Drop the variance since we won't be using it,
# allowing for specification of the column to be avoided
est_df.drop('EstimationVariance')
# Rename to the standard distance function name for convenience
est_df.rename({est_df.variables:dfvar})
est_df.describe()
# Generate a figure object
fig, axes = gs.subplots(1, 2, figsize=(10, 8),cbar_mode='each',
axes_pad=0.8, cbar_pad=0.1)
# Location map of indicator data for comparison
gs.location_plot(dat, ax=axes[0])
# Map of distance function data and estimate
gs.slice_plot(est_df, pointdata=dat_df,
pointkws={'edgecolors':'k', 's':25},
cbar_label='Distance Function (m)', vlim=df_vlim, ax=axes[1])
```
## 6. Boundary Simulation
This section is subdivided into 4 sub-sections:
1. Boot starp a value between -c and c using a uniform distribution
2. Transform this Gaussian deviate into $df$ deviates with a range of $[−C, C]$
3. Add the $df$ deviates to the $df$ estimate, yielding a $df$ realization
4. Truncate the realization at $df=0$ , generating a realization of the domain indicator
```
# Required package for this calculation
from scipy.stats import norm
# Create a directory for the output
domaindir = os.path.join(outdir, 'Domains/')
gs.mkdir(domaindir)
for real in range(nreal):
# Transform the Gaussian deviates to probabilities
sim = np.random.rand()
# Transform the probabilities to distance function deviates
sim = 2 *selected_c * sim - selected_c
# Initialize the final realization as the distance function estimate
df = est_df[dfvar].values
idx = np.logical_and(est_df[dfvar].values>selected_c, est_df[dfvar].values<selected_c)
# Add the distance function deviates to the distance function estimate,
# yielding a distance function realization
df[idx] = df[idx] + sim
# If the distance function is greater than 0, the simulated indicator is 1
sim = (df <= 0).astype(int)
# Convert the Numpy array to a Pandas DataFrame, which is required
# for initializing a DataFile (aside from the demonstrated flname approach).
# The DataFile is then written out
sim = pd.DataFrame(data=sim, columns=[dat.cat])
sim = gs.DataFile(data=sim)
sim.write_file(domaindir+'real{}.out'.format(real+1))
```
### Plot the realizations
```
fig, axes = gs.subplots(2, 3, figsize=(15, 8), cbar_mode='single')
for real, ax in enumerate(axes):
sim = gs.DataFile(domaindir+'real{}.out'.format(real+1))
gs.slice_plot(sim, title='Realization {}'.format(real+1),
pointdata=dat,
pointkws={'edgecolors':'k', 's':25},
vlim=(0, 1), ax=ax)
```
## 7. Save project settings and clean the output directory
```
gs.Parameters.save('Parameters.json')
gs.rmdir(outdir) #command to delete generated data file
gs.rmfile('temp')
```
| true |
code
| 0.606615 | null | null | null | null |
|
# Sentiment Analysis, Part 2:
Machine Learning With Spark On Google Cloud
---------------
__[1. Introduction](#bullet1)__
__[2. Creating A GCP Hadoop Cluster ](#bullet2)__
__[3. Getting Data From An Atlas Cluter](#bullet3)__
__[4. Basic Models With Spark ML Pipelines](#bullet4)__
__[5. Stemming With Custom Transformers](#bullet5)__
__[6. N-Grams & Parameter Tunning Using A Grid Search](#bullet6)__
__[7. Conclusions](#bullet7)__
## Introduction <a class="anchor" id="bullet1"></a>
--------------
In the <a href="http://michael-harmon.com/blog/SentimentAnalysisP1.html">first part</a> of this two part blog post I went over the basics of ETL with PySpark and MongoDB. In this second part I will go over the actual machine learning aspects of sentiment analysis using <a href="https://spark.apache.org/docs/latest/ml-guide.html">SparkML</a> (aka MLlib, it seems the name is changing). Specifically, we'll be using <a href="https://spark.apache.org/docs/latest/ml-pipeline.html">ML Pipelines</a> and <a href="https://en.wikipedia.org/wiki/Logistic_regression">Logistic Regression</a> to build a basic linear classifier for sentiment analysis. Many people use Support Vector Machines (SVM) because they handle high dimensional data well (which NLP problems definitely are) and allow for the use of non-linear kernels. However, given the number of samples in our dataset and the fact Spark's <a href="https://spark.apache.org/docs/2.3.2/ml-classification-regression.html#linear-support-vector-machine">SVM</a> only supports linear Kernels (which have comparable performance to logistic regression) I decided to just stick with the simpler model, aka logistic regression.
After we build a baseline model for sentiment analysis, I'll introduce techniques to improve performance like removing stop words and using N-grams. I also introduce a custom Spark <a href="https://spark.apache.org/docs/1.6.2/ml-guide.html#transformers">Transformer</a> class that uses the <a href="https://www.nltk.org/">NLTK</a> to perform stemming. Lastly, we'll review <a href="https://spark.apache.org/docs/latest/ml-tuning.html">hyper-parameter tunning</a> with cross-validation to optimize our model. The point of this post *is not too build the best classifier on a huge dataset, but rather to show how to piece together advanced concepts using PySpark... and at the same time get reasonable results.*
That said we will continue to use the 1.6 million <a href="https://www.kaggle.com/kazanova/sentiment140">tweets</a> from Kaggle which I loaded into my <a href="https://www.mongodb.com/cloud/atlas">Atlas MongoDB</a> cluster with the Spark ETL job that was discussed in the previous <a href="http://michael-harmon.com/blog/SentimentAnalysisP1.html">post</a>. While 1.6 million tweets doesn't necessitate a distributed environment, using PySpark on this datset was a little too much for my whimpy 2013 Macbook Air and I needed to use a more powerful machine. Luckily <a href="https://cloud.google.com/">Google Cloud Platform</a> (GCP) gives everyone free credits to start using their platform and I was able to use Spark on a <a href="https://hadoop.apache.org/">Hadoop</a> cluster using <a href="https://cloud.google.com/dataproc/">dataproc</a> and <a href="https://cloud.google.com/datalab/">datalab</a>.
Let's get started!
## Creating A GCP Hadoop Cluster <a class="anchor" id="bullet2"></a>
---------
I have been using Hadoop and Spark for quite some time now, but have never spun up my own cluster and gained a new found respect for Hadoop admins. While Google does make the process easier, I still had to ask a friend for help to get things to work the way I wanted them to. Between getting the correct version of Python as well as the correct version of NLTK on both the driver and worker nodes, the correct MongoDB connection for PySpark 2.3.2 and the time it takes to spin up and spin down a cluster I was very much done configuting Hadoop clusters on my own. I want to say that made me a better person or at least a better data scientist, but I'm not so sure. :)
To start up the Hadoop cluster with two worker nodes (with the GCP free trial I could only use two worker nodes) I used the command below:

You can see dataproc image version, the string for the MongoDB connection, as well as the version of Python in the above commands. The bash scripts that I reference in my Google storage bucket for this project can be obtain from my repo <a href="https://github.com/mdh266/SentimentAnalysis/tree/master/GCP">here</a>. After the cluster is created we can ssh onto the master node by going to the console and clicking on "*Compute Engine*" tab. You will see a page like the one below:

We can ssh on the master node using the ssh tab to the right of the instance named **mikescluster-m**. The "-m" signifies it is the master node while the other instances have "-w" signifiying they are worker nodes. After connecting to the mater node you can see all the <a href="https://data-flair.training/blogs/top-hadoop-hdfs-commands-tutorial/">Hadoop commands</a> available:

We won't work on our Hadoop cluster through command line, but rather connect to the cluster through Jupyter notebooks using Google <a href="https://cloud.google.com/datalab/">datalab</a>. To do this involves creating an ssh-tunnel and proxy for Chrome, both of which I had no idea how to do, but luckily the same friend from before walked me through it. The bash scripts I used to do these last two procedures are located in my repo <a href="https://github.com/mdh266/SentimentAnalysis/tree/master/GCP">here</a>. After those steps were completed we can enter the address into our web browser to see the Jupyter notebooks,
http://mikescluster-m:8080
Note that the notebooks are running on the master node using port 8080 and that <a href="https://hadoop.apache.org/docs/current/hadoop-yarn/hadoop-yarn-site/YARN.html">YARN</a> can be seen from the same web address, but using port 8088. I'll come back to YARN a little later. Now that we have our Hadoop cluster up and running on Google Cloud we can talk about how to access our data.
## Getting The Dataset From An Atlas Cluster <a class="anchor" id="bullet3"></a>
---------
As I mentioned in the introduction I loaded the cleaned Twitter dataset into my Atlas MongoDB cluster as I discussed in the previous <a href="http://michael-harmon.com/blog/SentimentAnalysisP1.html">post</a>. In this post I won't go over the ETL process again, but will show how to connect PySpark to the Atlas cluster. One thing to highlight here is that in order to keep my collection within the memory limits of the free tier I had to store the data as strings instead of tokens as I showed in the previous post. (See the ETL job here <a href="https://github.com/mdh266/SentimentAnalysis/blob/master/ETL/BasicETL.py">here</a> for details) Therefore we'll do have to tokenize our strings again here.
The first step to connecting to the database is to create a connection url string that contains the cluster address, user info, password as well as database and collection name in the dictionary below:
```
mongo_conn = {"address" : "harmoncluster-xsarp.mongodb.net/",
"db_name" : "db_twitter",
"collection" : "tweets",
"user" : "",
"password" : ""}
url = "mongodb+srv://{user}:{password}@{address}{db_name}.{collection}".format(**mongo_conn)
```
Then we create a dataframe from the documents in the collection using the <code>spark.read</code> command, passing in the connection url as our option and specifying that we are using MongoDB as the format:
```
df = spark.read\
.format("com.mongodb.spark.sql.DefaultSource")\
.option("uri",url)\
.load()
```
At this point while the collection on the Atlas cluster has not been pulled to our Hadoop cluster yet, we would see an error if there was a mistake in our connection string. Additionally, at this point the dataframe allows us to see some metadata on the collection, i.e. the "schema",
```
df.printSchema()
```
You can see that each document has an <code>id</code>, <code>sentiment</code> and cleaneed tweet. Let's just pull the <code>tweet_clean</code> as well as `sentiment` fields and rename `sentiment` to `label`:
```
df2 = df.select("tweet_clean","sentiment")\
.withColumnRenamed("sentiment", "label")
```
Then let's split the dataframe into training and testing sets (using 80% of the data for training and 20% for testing) with a seed (1234),
```
train, test = df2.randomSplit([0.80, 0.20], 1234)
```
Now we can look at the number of tweets in the training set that have positive and negative sentiment. Note, since we will be using this dataframe many times below we will cache it to achieve better runtime performance.
```
train.cache()
train.groupby("label")\
.count()\
.show()
```
We can see that the two classes are well balanced, with over half a million positive and negative teets. We do the same for the testing set:
```
test.cache()
test.groupby("label")\
.count()\
.show()
```
Again, the classes are well balanced. This is great because we don't have to worry about dealing with imbalanced classes and *accuracy and ROC's area under the curve (AUC) are good metrics to see how well our models are performing.*
Now let's build our baseline model.
## Basic Models With Spark ML Pipelines <a class="anchor" id="bullet4"></a>
------------
In this section I'll go over how to build a basic logistic regression model using Spark <a href="https://spark.apache.org/docs/latest/ml-pipeline.html">ML Pipelines</a>. ML Pipelines are similar to <a href="https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html">Scikit-learn Pipelines</a>. We import the basic modules:
```
from pyspark.ml import Pipeline
from pyspark.ml.feature import Tokenizer, HashingTF, IDF
from pyspark.ml.classification import LogisticRegression
from pyspark.ml.evaluation import BinaryClassificationEvaluator
```
Next we instantiate our classification evalutor class and pass the label of the output column (the prediction column) from the model:
```
evaluator = BinaryClassificationEvaluator(rawPredictionCol="rawPrediction")
# get the name of the metric used
evaluator.getMetricName()
```
We'll be using the <a href="https://en.wikipedia.org/wiki/Bag-of-words_model">bag of words (BOW) model</a> to build features from tweets for our model. *In the bag-of-words model, a document (in this case tweet) is represented as "bag" or list of its words, disregarding grammar and ordering, but keeping the multiplicity of the words.* A two document example is:
- **D1:** Hi, I am Mike and I like Boston.
- **D2:** Boston is a city and people in Boston like the Red Sox.
From these two documents, a list, or 'bag-of-words' is constructed
bag = ['Hi', 'I', 'am', 'Mike', 'and', 'like', 'Boston', 'is',
'a', 'city, 'and', 'people', 'in', 'the', 'red', 'sox]
Notice how in our bag-of-words we have dropped repetitions of the words 'I', 'is' and 'Mike'. I will show how multiplicity of words enters into our model next.
After transforming the text (all documents) into a "bag of words" we generate a vector for each document that represents the number of times each word (or more generally token) in the BOW appears in the text. The order of entries in the BOW vector corresponds to the order of the entries in the bag-of-words list. For example, document D1 would have a vector,
[1, 2, 1, 1, 1, 1, 1, 0, 0, 0, 0 ,0, 0, 0, 0, 0]
while the second document, D2, would have the vector,
[0, 0, 0, 0, 0, 0, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1]
Each entry of the lists refers to frequency or count of the corresponding entry in the bag-of-words list. When we have a stacked collection of (row) vectors, or matrix, where each row corresponds to a document (vector), and each column corresponds to a word in the bag-of-words list, then this will be known as our **term-frequency ($\text{tf}$) [document matrix](https://en.wikipedia.org/wiki/Document-term_matrix)**. The general formula for an entry in the $\text{tf}$ matrix is,
$$\text{tf}(d,t) \, = \, f_{t,d}$$
where $f_{t,d}$ is the number of times the term $t$ occurs in document $d \in \mathcal{D}$, where $\mathcal{D}$ is our text corpus. We can create a term-frequency matrix using Spark's <a href="https://spark.apache.org/docs/latest/ml-features.html#tf-idf">HashingTF</a> class. To see the difference between HashingTF and <a href="https://spark.apache.org/docs/latest/ml-features.html#countvectorizer">CounterVectorizer</a> see this <a href="https://stackoverflow.com/questions/35205865/what-is-the-difference-between-hashingtf-and-countvectorizer-in-spark">stackoverflow post</a>.
Most often term-frequency alone is not a good measure of the importance of a word/term to a document's sentiment. Very common words like "the", "a", "to" are almost always the terms with the highest frequency in the text. Thus, having a high raw count of the number of times a term appears in a document does not necessarily mean that the corresponding word is more important to the sentiment of the document.
To circumvent the limination of term-frequency, we often normalize it by the **inverse document frequency (idf)**. This results in the **term frequency-inverse document frequency (tf-idf)** matrix. The *inverse document frequency is a measure of how much information the word provides, that is, whether the term is common or rare across all documents in the corpus*. We can give a formal defintion of the inverse-document-frequency by letting $\mathcal{D}$ be the corpus or the set of all documents and $N_{\mathcal{D}}$ is the number of documents in the corpus and $N_{t,D}$ be the number of documents that contain the term $t$ then,
$$idf(t,\mathcal{D}) \, = \, \log\left(\frac{N_{\mathcal{D}}}{1 + N_{t,\mathcal{D}}}\right) \, = \, - \log\left(\frac{1 + N_{t,\mathcal{D}}}{N_{\mathcal{D}}}\right) $$
The reason for the presence of the $1$ is for smoothing. Without it, if the term/word did not appear in any training documents, then its inverse-document-frequency would be $idf(t,\mathcal{D}) = \infty$. However, with the presense of the $1$ it will now have $idf(t,\mathcal{D}) = 0$.
Now we can formally define the term frequnecy-inverse document frequency as a normalized version of term-frequency,
$$\text{tf-idf}(t,d) \, = \, tf(t,d) \cdot idf(t,\mathcal{D}) $$
Like the term-frequency, the term frequency-inverse document frequency is a sparse matrix, where again, each row is a document in our training corpus ($\mathcal{D}$) and each column corresponds to a term/word in the bag-of-words list. The $\text{tf-idf}$ matrix can be constructed using the <a href="https://spark.apache.org/docs/latest/ml-features.html#tf-idf">SparkML IDF</a> class.
Now that we have gotten the definition of TF-IDF out of the way we can discuss the steps in building a basic pipeline. These include,
- tokenization
- creating term frequency
- creating term frequency inverse document frequency
- fitting a logistic regression model to the BOW created from the previous steps
This is all done (amazingly!) in the short few lines below:
```
# create tokens from tweets
tk = Tokenizer(inputCol= "tweet_clean", outputCol = "tokens")
# create term frequencies for each of the tokens
tf1 = HashingTF(inputCol="tokens", outputCol="rawFeatures", numFeatures=1e5)
# create tf-idf for each of the tokens
idf = IDF(inputCol="rawFeatures", outputCol="features", minDocFreq=2.0)
# create basic logistic regression model
lr = LogisticRegression(maxIter=20)
# create entire pipeline
basic_pipeline = Pipeline(stages=[tk, tf1, idf, lr])
```
The setting `numFeatures=1e5` means that our bag-of-words "vocabulary" contains 100,000 words (see above listed stackeroverflow comment for explanation of what this means). The filter `minDocFreq=2.0` requires that a word or token must appear a minimum of 2 documents to be counted as a feature (column). **This parameter can act as form a of regularization. Setting this value to larger integers increases the regularization by reducing the number of words we consider.** This helps to combat overfitting by eliminating words which occur very rarely so that they do not influence our model.
Now we can execute the entire pipleine of tokenization, feature extraction (tf-idf) and train the model all with the following command:
```
model1 = basic_pipeline.fit(train)
```
Once we have trained the pipeline model we can predict it's perfromance on the testing set using the <code>transform</code> method and the <code>evaluate</code> method of the evaluator object.
```
# predict on test set
predictions1 = model1.transform(test)
# get the performance on the test set
score1 = evaluator.evaluate(predictions1)
print("AUC SCORE: {}".format(score1))
```
We can also get the accuracy on the testing set. I couldn't really find any good documentation about how to do this without using the old MLlib (RDD based) library. What made this process even more confusing is that I had to use <a href="https://spark.apache.org/docs/2.3.2/mllib-evaluation-metrics.html">MulticlassMetrics</a> class to evualate the binary outcome ( the `BinaryClassificationMetrics` class only had area under the curve (AUC) and for ROC curve and AUC for Precision-Recall curve). The code snippet to get the accuracy on the testing set is:
```
predictedAndLabels = predictions1.select(["prediction","label"])\
.rdd.map(lambda r : (float(r[0]), float(r[1])))
from pyspark.mllib.evaluation import MulticlassMetrics
metrics = MulticlassMetrics(predictedAndLabels)
print("Test Set Accuracy: {}".format(metrics.accuracy))
```
A score of 0.885 for the AUC of the ROC curve and 81% accuracy is pretty good for Twitter sentiment analyis, but let's see if we can make any improvements using more techniques from natural language processing.
### Removing Stop Words
One trick people use as a prepocessing step in NLP is to remove stop words, i.e. common words that do not add any additional information into the model. Examples of stop words are: 'a', 'the', 'and', etc. We will remove stops from our tokens by using the <a href="https://spark.apache.org/docs/2.3.2/ml-features.html#stopwordsremover">StopWordsRemover</a> class. We import it below,
```
from pyspark.ml.feature import StopWordsRemover
```
Then instantiate a new StopWordsRemover object setting input column to be result of the tokenization procedure. Notice that the input column name for the HashingTF object is the same as the output column name for the StopWordRemover:
```
sw = StopWordsRemover(inputCol="tokens", outputCol="filtered")
tf2 = HashingTF(inputCol="filtered", outputCol="rawFeatures", numFeatures=1e5)
```
We can define our pipeline, train the new model and evaluate its performance on the testing set:
```
sw_pipleline = Pipeline(stages=[tk, sw, tf2, idf, lr])
model2 = stopwords_pipleline.fit(train)
predictions2 = model2.transform(test)
score2 = evaluator.evaluate(predictions2)
print("AUC SCORE: {}".format(score2))
```
Notice how easy it was to add a new stage to our ML Pipeline model!
We can see that the AUC for our ROC went down by a little over 1.5%. At first I was pretty puzzled by this and spent a lot of time trying to fix it only to learn that blindly removing stop words isn't always the best practice for sentiment analysis, especially when it comes to <a href="http://www.lrec-conf.org/proceedings/lrec2014/pdf/292_Paper.pdf">tweets</a>. Since removing stopped words gave our model worse performanace, we won't use it going forward. However, it's worthwhile to see examples of the words that were removed:
```
predictions2.select(["tweet_clean","tokens","filtered"]).show(5)
```
We can see that words like, 'a', 'and', 'was', and 'both' were removed. Removing stop words is more helpful for the case of <a href="http://michael-harmon.com/blog/NLP.html">document classification</a>, where often the class a document belongs to is determined by a few key words and removing stop words can help to understand what those key words are.
## Stemming With Customer Tranformers <a class="anchor" id="bullet5"></a>
------------
Another technique for preprocessing in NLP is stemming. We will use the Natural Language Tool Kit (<a href="https://www.nltk.org/">NLTK</a> ) with the Porter Stemmer for stemming. Stemming is the process of reducing words down to their root; for example from Wikipedia:
...the Porter algorithm reduces, argue, argued, argues, arguing, and argus all get reduced to the stem argu
Stemming is used as an approximate method for grouping words with a similar basic meaning together. For NLP and the bag-of-words model this reduces the dimension of our feature space since variations in words that would normally be counted seperately are reduced to one word that is counted collectively.
For some reason gcloud kept installing the wrong version of NLTK and inorder to get the correct version on both the driver and the workers I had to install within the notebook.
```
%sh
pip install -U nltk==3.4
```
Now we can import the NLTK to and check its version is correct.
```
import nltk
print(nltk.__version__)
from nltk.stem.porter import PorterStemmer
```
Before we dive into using NLTK with PySpark let's go over an example how stemming with the NLTK works on a simple sentence. First we instantiate the PorterStemmer object and tokenize a sentence:
```
stemmer = PorterStemmer()
tokens = "my feelings having studied all day".split(" ")
print("raw tokens: {}".format(tokens))
```
Then we can apply the stemmer's stem function to each token in the array:
```
tokens_stemmed = [stemmer.stem(token) for token in tokens]
print("clean tokens: {}".format(tokens_stemmed))
```
We can see that the word 'feelings' has been reduced to 'feel', 'having' to 'has' and 'studied' to 'studi'. I should note that stemming, like stop word removal, might not always be helpful in deciding the sentiment since the way a word is used might effect the sentiment.
Inorder to use the Porter stemmer within a ML Pipeline we must create a custom <a href="https://spark.apache.org/docs/latest/ml-pipeline.html#transformers">Transformer</a>. The Transformer class will allow us to apply non-Spark functions and transformations as stages within our ML Pipeline. We create a customer `PortersStemming` class which extends the PySpark's Transformer class, HasInputCol class and HasOutputCol class; see <a href="https://github.com/apache/spark/blob/master/python/pyspark/ml/param/shared.py">here</a> for these class definitions. This was also the first time I have used <a href="https://www.programiz.com/python-programming/multiple-inheritance">multiple inheritence</a> in Python which is pretty cool!
```
from pyspark import keyword_only
import pyspark.sql.functions as F
from pyspark.sql import DataFrame
from pyspark.sql.types import ArrayType, StringType
from pyspark.ml import Transformer
from pyspark.ml.param.shared import HasInputCol, HasOutputCol, Param
class PorterStemming(Transformer, HasInputCol, HasOutputCol):
"""
PosterStemming class using the NLTK Porter Stemmer
This comes from https://stackoverflow.com/questions/32331848/create-a-custom-transformer-in-pyspark-ml
Adapted to work with the Porter Stemmer from NLTK.
"""
@keyword_only
def __init__(self,
inputCol : str = None,
outputCol : str = None,
min_size : int = None):
"""
Constructor takes in the input column name, output column name,
plus the minimum legnth of a token (min_size)
"""
# call Transformer classes constructor since were extending it.
super(Transformer, self).__init__()
# set Parameter objects minimum token size
self.min_size = Param(self, "min_size", "")
self._setDefault(min_size=0)
# set the input keywork arguments
kwargs = self._input_kwargs
self.setParams(**kwargs)
# initialize Stemmer object
self.stemmer = PorterStemmer()
@keyword_only
def setParams(self,
inputCol : str = None,
outputCol : str = None,
min_size : int = None
) -> None:
"""
Function to set the keyword arguemnts
"""
kwargs = self._input_kwargs
return self._set(**kwargs)
def _stem_func(self, words : list) -> list:
"""
Stemmer function call that performs stemming on a
list of tokens in words and returns a list of tokens
that have meet the minimum length requiremnt.
"""
# We need a way to get min_size and cannot access it
# with self.min_size
min_size = self.getMinSize()
# stem that actual tokens by applying
# self.stemmer.stem function to each token in
# the words list
stemmed_words = map(self.stemmer.stem, words)
# now create the new list of tokens from
# stemmed_words by filtering out those
# that are not of legnth > min_size
filtered_words = filter(lambda x: len(x) > min_size, stemmed_words)
return list(filtered_words)
def _transform(self, df: DataFrame) -> DataFrame:
"""
Transform function is the method that is called in the
MLPipleline. We have to override this function for our own use
and have it call the _stem_func.
Notice how it takes in a type DataFrame and returns type Dataframe
"""
# Get the names of the input and output columns to use
out_col = self.getOutputCol()
in_col = self.getInputCol()
# create the stemming function UDF by wrapping the stemmer
# method function
stem_func_udf = F.udf(self._stem_func, ArrayType(StringType()))
# now apply that UDF to the column in the dataframe to return
# a new column that has the same list of words after being stemmed
df2 = df.withColumn(out_col, stem_func_udf(df[in_col]))
return df2
def setMinSize(self,value):
"""
This method sets the minimum size value
for the _paramMap dictionary.
"""
self._paramMap[self.min_size] = value
return self
def getMinSize(self) -> int:
"""
This method uses the parent classes (Transformer)
.getOrDefault method to get the minimum
size of a token.
"""
return self.getOrDefault(self.min_size)
```
After looking at the PySpark <a href="https://github.com/apache/spark/blob/master/python/pyspark/ml/base.py">source code</a> I learned that the Tranformer class is an <a href="https://docs.python.org/3/glossary.html#term-abstract-base-class">abstract base class</a> that specifically requires users to override the <code>_transform</code> method. After a lot of trial and error I found that the key steps to creating a custom transformer are:
- Creating a <code>Param</code> object (see <a href="https://github.com/apache/spark/blob/master/python/pyspark/ml/param/__init__.py">here</a> for class definition) for each paramster in the constructor that will hold the user defined parameter names, values and default values.
- Create the `_input_kwargs` member variable and set it.
- Write a new defintion for the <code>_transform</code> method that applies a customer transformation to the <code>inputCol</code> of the dataframe and returns the same dataframe with a new column named <code>outputCol</code> that is the result of the transformation defined in this code block.
I was also was curious about the <code>keyword_only</code> decorator and after <a href="http://spark.apache.org/docs/2.2.0/api/python/_modules/pyspark.html">digging deeper</a> found it is "a decorator that forces keyword arguments in the wrapped method and saves actual input keyword arguments in `_input_kwargs`."
### Stemming with the NLTK's PorterStemmer
Let's apply stemming to our problem without removing stop words to see if it improves the performance of our model.
```
stem2 = PorterStemming(inputCol="tokens", outputCol="stemmed")
```
We'll do things a little differently this time for the sake of runtime performance. Stemming is an expensive operation because it requires the use of a custom transformer. Anytime we introduce custom functions like UDFs or special Python functions outside of the SparkSQL functions we pay a runtime <a href="https://medium.com/teads-engineering/spark-performance-tuning-from-the-trenches-7cbde521cf60">penalty</a>. Therefore we want to be performing operations with custom functions as little as possible.
Since we will use stemming on multiple different models we will create new training and testing datasets that are already pre-stemmed. This avoids repeatedly having to tokenize and stem our datasets each time we train and test one of our models. We define a pipeline for creating the new datatset below,
```
stem_pipeline = Pipeline(stages= [tk, stem2]).fit(train)
```
Then we transform the training and testing set and cache them so they are in memory and can be used without having to recreate them,
```
train_stem = stem_pipeline.transform(train)\
.where(F.size(F.col("stemmed")) >= 1)
test_stem = stem_pipeline.transform(test)\
.where(F.size(F.col("stemmed")) >= 1)
# cache them to avoid running stemming
# each iteration in the grid search
train_stem.cache()
test_stem.cache()
```
Let's see some of the results of stemming the tweets:
```
test_stem.show(5)
```
We can see that the words 'baby' and 'beautiful' are reduced to 'babi' and 'beauti' respectively.
Let's now build our second pipeline (using TF-IDF and logistic regression) based off the pre-stemmed training dataset and test it on the pre-stemmed testing set.
```
# create the new pipline
idf = IDF(inputCol="rawFeatures", outputCol="features", minDocFreq=2.0)
lr = LogisticRegression(maxIter=20)
stemming_pipeline2 = Pipeline(stages= [tf3, idf, lr])
# fit and get predictions
model4 = stemming_pipeline2.fit(train_stem)
predictions4 = model4.transform(test_stem)
score4 = evaluator.evaluate(predictions4)
```
The AUC of the new model on the test set is,
```
print("AUC SCORE: {}".format(score4))
```
We can see that adding stemming degrades the AUC slightly compared to the baseline model, but *we'll keep using stemming in our future models since the jury's not out on whether it will improve future models*. One thing I will mention here is that I did try using stop word removal and stemming together, but this resulted in worse performance than just stop word removal alone.
As I mentioned previously, stemming using a customer Transformer is expensive. One way I could see that it is an expensive operation is by going to <a href="https://hadoop.apache.org/docs/current/hadoop-yarn/hadoop-yarn-site/YARN.html">YARN</a> (on our cluster this is the address: http://mikescluster-m:8088) shown below:

Then clicking on ApplicationMaster in the bottom right hand corner. This leads you to the <a href="https://jaceklaskowski.gitbooks.io/mastering-apache-spark/spark-webui.html">Spark Web UI </a>page:

Clicking on stages we can see the time and memory it takes for each stage in our pipelines (or more generally jobs). I used the Spark Web UI constantly to track the progress of my jobs and noticed that stemming caused the TF-IDF stages to take much longer than they did without it.
## N-Grams And Parameter Tunning With Cross Validation <a class="anchor" id="bullet6"></a>
--------------------
The last preprocessing technique we'll try to improve the predictive power of our model is to use N-grams. This technique is used to capture combinations of words that effect the sentiment of the document. For instance the sentence,
the food is not bad
is naturally assumed to have a positive sentiment, or atleast non-negative sentiment. After tokenizing the sentence we would have the list,
["the", "food", "is", "not", "bad"]
Using the normal bag-of-words with TF-IDF, our model would see the word 'bad' and most likely assume the that the sentence has negative sentiment. This is because the presence of the token 'bad' is usually associated with a negative sentiment. What our model fails to ascertain is that the presence of the word 'not' before 'bad' leads to the combination 'not bad' which normally coincides with a positive sentiment. In order to pick up these types of combinations of words we introduce n-grams. Bigrams combine consecutive pairs of words in our bag-of-words model. Using bigrams the previous example sentence would be,
[["the", "food"], ["food, "is"], ["is", "not"], ["not,"bad"]]
Using bigrams our model will see be the combination `["not", "bad"]` and be able to ascertain that sentiment of the sentence is postive. Bigrams use consecutive pairs of words to form tokens for our model, N-grams generalize this process to combine N consecutive words to form tokens for our bag-of-words model.
Another thing I should point out is that **while using bigrams introduces consecutive pairs of words in documents as tokens in the bag-of-words model the order of those bigrams in the document is not taken into consideration. Each tweet is reduced to a set of bigrams and the bag-of-words model treats those bigrams similar to categorial features/one-hot encoding.** The difference with bag-of-words and one-hot encoding being that instead of the value in each column for a token being 0 or 1 based on its presence in the tweet, the value is 0-N with N being how many times the token appears in the tweet.
### Basic model with bigrams
We import the NGram class from the features module and use bigrams (`n=2`) for our model,
```
from pyspark.ml.feature import NGram
bigram = NGram(inputCol="tokens", outputCol="bigrams", n=2)
```
Then we form a pipeline by first tokenizing the words in the sentence, forming bigrams, performing TF-IDF and then fitting the logistic regressionm model. One thing to note is that introducing bigrams means that our bag-of-words model has features that are based on pairs of word instead of individual words. Since the number of combinations of pairs of words is "larger" than the number of individual words we increase the number of features in our model to `200,000` instead of `100,000`.
We define the new pipeline, train, test and evaluate the model:
```
tf5 = HashingTF(inputCol="bigrams", outputCol="rawFeatures", numFeatures=2e5)
bigram_pipeline = Pipeline(stages= [tk, bigram, tf5, idf, lr])
model5 = bigram_pipeline.fit(train)
predictions5 = model5.transform(test)
score5 = evaluator.evaluate(predictions5)
print("AUC SCORE: {}".format(score5))
```
We can see that using bigrams provides an improvement to the basic model!
### Stemming with bigrams
While using stemming alone did not lead to an improvement over our baseline model, using stemming with bigrams might lead to an improvement. My reason for believing this is that while bigrams improve the performance of our model, they also increases the dimension of our problem. By introducing stemming we would reduce the number of variations of the word pairs, (the variance in our data) and also the reduce the dimension of our feature space.
We create our new pipeline on the pre-stemmed training and testing datasets as well as evaulate the model:
```
bigram2 = NGram(inputCol="stemmed", outputCol="bigrams", n=2)
tf6 = HashingTF(inputCol="bigrams", outputCol="rawFeatures", numFeatures=2e5)
idf = IDF(inputCol="rawFeatures", outputCol="features", minDocFreq=2.0)
lr = LogisticRegression(maxIter=20)
stem_bigram_pipeline = Pipeline(stages= [bigram2, tf6, idf, lr])
model6 = stem_bigram_pipeline.fit(train_stem)
predictions6 = model6.transform(test_stem)
score6 = evaluator.evaluate(predictions6)
print("AUC SCORE: {}".format(score))
```
We can see that using bigrams and stemming leads to not only an improvement over the baseline model, but also the bigram model! My intuition was right! :)
Let's take a look at examples of what each stage in the above pipeline did to the tweet:
```
predictions6.select(["tweet_clean","tokens","stemmed","bigrams"]).show(5)
```
### Parameter Tunning Using A Grid Search
Now let's try to improve the performance of the stemming-bigram model by tunning the hyperparameters in some of the stages in the pipeline. Tunning the hyperparameters in our model involves using a grid search which evaluates all hyperparameters we want to consider and returns the model with the best results. In order to get the best results from our model for out-of-sample performance we perform <a href="https://en.wikipedia.org/wiki/Cross-validation_(statistics)">cross-validation</a> within each of the parameter values in the grid search. Using cross validation within the grid search reduces the chances of overfitting our model and will hopefully give us the best performance on the test set.
In order to perform a grid search with cross validation we import the classes,
```
from pyspark.ml.tuning import CrossValidator, ParamGridBuilder
```
Then define the model pipeline,
```
bigram2 = NGram(inputCol="stemmed", outputCol="bigrams", n=2)
tf6 = HashingTF(inputCol="bigrams", outputCol="rawFeatures", numFeatures=2e5)
idf = IDF(inputCol="rawFeatures", outputCol="features")
lr = LogisticRegression(maxIter=20)
stem_bigram_pipeline = Pipeline(stages= [bigram2, tf6, idf, lr])
```
Next we declare the 'hyperparamter grid' we want to search over using the `ParamGridBuilder` class,
```
paramGrid = ParamGridBuilder() \
.addGrid(idf.minDocFreq, [2, 5]) \
.addGrid(lr.regParam, [0.0, 0.1]) \
.build()
```
This is a small grid because the training time on tiny 2-node Hadoop cluster is somewhat long. Again, the point of this blogpost is not to get the best performance possibles, but rather to show how the pieces of the SparkML library fit together. I will remark that these hyperparameter choices just seeing what level or regularization we want to apply in feature generation stage (`idf.minDocFreq`) and model fitting stage (`lr.regParam`) of our ML Pipeline.
Now lets's define the grid search with cross validation using the `CrossValidator` class,
```
crossval = CrossValidator(estimator = stem_bigram_pipeline,
estimatorParamMaps = paramGrid,
evaluator = BinaryClassificationEvaluator(),
numFolds = 3)
```
Notice for that we need
- the Spark ML Pipeline
- the parameter grid values
- the metric used to evulate the performance of the models
- the size of the fold's (k) in cross validation
While values of `k=5` or `k=10` are most often used in cross validation we have large sample size in our training set and the time it takes to train on the cluster is long so I chose a smaller value of 3. We could also have used the <code>TrainValidationSplit</code> class which only evaluates each parameter choice once instead of multiple times over each of the $K$ folds in <code>CrossValidator</code>. This estimator is not as expensive as cross validation,
but can produce less reliable results when dataset isn't large enough. See the <a href="https://spark.apache.org/docs/latest/ml-tuning.html#train-validation-split">documenation</a> for more infromation.
Now we can perform the grid search!
```
model = crossval.fit(train_stem)
```
Then make predictions on testing set to get the model performance,
```
predictions = model.transform(test_stem)
score = evaluator.evaluate(predictions)
print("AUC SCORE: {}".format(score))
```
Notice that while this result is better than baseline model, it is not as good as the stemmed-bigram model we first came up with. We could ostensibly try more parameter values and larger $k$ values to get a better score, but the performance of this model is good enough.
Next let's get the accuracy of the model on the testing set. We do this by first getting the best model from the grid search,
```
bestModel = model.bestModel
```
Then we can get the accuracy just as we did with the baseline model,
```
predictedAndLabels = predictions.select(["prediction","label"])\
.rdd.map(lambda r : (float(r[0]), float(r[1])))
metrics = MulticlassMetrics(predictedAndLabels)
print("Test Set Accuracy: {}".format(metrics.accuracy))
```
81.5% accuracy with a AUC of 0.891 is pretty good for Twitter sentiment analysis!
Let's now find out what the parameters from the gridsearch are that resulted in the best model. We can see the various stages in the model pipeline by using the `.stages` command:
```
bestModel.stages
```
Then within each stage we can get the hyperparameter value by passing the name to the `explainParam` method:
```
bestModel.stages[2].explainParam('minDocFreq')
bestModel.stages[-1].explainParam('regParam')
```
We can see that the best model came from a result of having `minDocFreq=5` and `regParam=0.1` in the IDF and Logistic Regression stage of our pipeline respectively.
The last thing we'll do is get an idea of the ROC curve for our best model. I could only do this for the training set by getting the logistic regression stages' summary:
```
summary = bestModel.stages[-1].summary
```
Then getting the True Postive Rate and False Positive Rate below and plotting them against one another:
```
import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
plt.plot([0, 1], [0, 1], 'r--')
plt.plot(summary.roc.select('FPR').collect(),
summary.roc.select('TPR').collect())
plt.xlabel('False Positive Rare')
plt.ylabel('True Positive Rate')
plt.title("ROC Curve")
plt.show()
```
## Conclusions <a class="anchor" id="bullet7"></a>
----------------------
In this two part blog post we went over how to perform Extract-Transform-Load (ETL) for NLP using Spark and MongoDB and then how to build a machine learning model for sentiment analysis using SparkML on the Google Cloud Platform (GCP). In this post we focused on creating a machine learning model using <a href="https://spark.apache.org/docs/latest/ml-pipeline.html">ML Pipelines</a> starting out with a basic model using TF-IDF and logistic regression. We added different stages to our ML Pipeline such as removing stop words, stemming and using bigrams to see which procedure would improve the predictive performance of our model. In the process we also went over how to write our own custom transformer in PySpark. Once we settled on using stemming and bigrams in our model we performed a grid search using cross validation to obtain a model that has a AUC of 0.891 in the ROC curve and 81.5% accuracy which is not too shabby! One thing I didn't go over that is valuable is how to persist the ML Pipeline model to use again later without having to retrain, for that see <a href="https://spark.apache.org/docs/latest/ml-pipeline.html#ml-persistence-saving-and-loading-pipelines">here</a>.
| true |
code
| 0.626952 | null | null | null | null |
|
### *** Names: [Insert Your Names Here]***
# Lab 4 - Plotting and Fitting with Hubble's Law
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
<div class=hw>
## Exercise 1
In the cell below, I have transcribed the data from Edwin Hubble's original 1928 paper "A relation between distance and radial velocity among extra-galactic nebulae", available [here](https://www.pnas.org/content/pnas/15/3/168.full.pdf).
a. Open the original paper. Use it and your knowledge of Python code to decipher what each line in the next two code cells is doing. Add a comment at the top of each line stating what it is doing and/or where in the paper it came from.
b. Create a scatter plot from Hubble's data. To make a scatterplot in python, you use the same plt.plot function that we used for line graphs last week except after the x and y arguments, you add a string describing the type of plotting symbol that you want. [Here](https://matplotlib.org/3.1.1/api/markers_api.html) is a list of plot symbols. Note that you can combine these with colors so, for example, 'go' is green circles and 'rx' is red xs. Give your plot a title and axis labels to match Hubble's original.
c. Write code that will print each entry in the list obj_list on its own line (you will need this for exercise 2, below).
```
NGC_nos = [6822,598,221,224,5457,4736,5194,4449,4214,
3031,3627,4826,5236,1068,5055,7331,4258,
4151,4382,4472,4486,4649]
obj_list = ['SMC', 'LMC']
for i in np.arange(len(NGC_nos)):
obj_list.append('NGC '+str(NGC_nos[i]))
dists = np.array([0.032,0.034,0.214,0.263,0.275,0.275,0.45,0.5,0.5,0.63,0.8,0.9,0.9,
0.9,0.9,1.0,1.1,1.1,1.4,1.7,2.0,2.0,2.0,2.0])#Mpc
vels = np.array([170.,290,-130,-70,-185,-220,200,290,270,200,300,-30,650,150,500,920,450,500,500,960,500,850,800,1000]) #km/sec
#plot goes here
#loop to print names goes here
```
<div class=hw>
## Exercise 2
Now, let's pull modern data for Hubble's galaxies. Copy and paste the list from Exercise 1c into the query form [here](http://ned.ipac.caltech.edu/forms/gmd.html). ***Before you click "Submit Query"***, scroll to the check boxes at the bottom of the page and make sure to check ***only*** the following:
* User Input Object Name
* Redshift
* Redshift Uncertainty
And in the bottom right panel:
* Metric Distance
* Mean
* Standard Deviation
* Number of measurements
Open the Macintosh application "TextEdit" and copy and paste the table into it. From the Format menu, select "make plain text" and then save it as cat.txt in the same folder as your Lab3 notebook.
The code cells below will "read in" the data using a python package called Pandas that we will learn about in great detail in the coming weeks. For now, just execute the cell below, which will create python lists stored in variables with descriptive names from your cat.txt file.
a)Describe in words at least two patterns that you note in the tabular data
b) Make a histogram for each of the following quantities: redshift, redshift_uncert, dist, and dist_uncert. All your plots should have axis labels, and for the histograms you should play around with the number of bins until you can justify your choice for this value. Discuss and compare the shapes of the distributions for each of the quantities in general, qualitative terms.
c) Plot the uncertainty in redshift as a function of redshift for these galaxies and the uncertainty in distance as a function of distance. What patterns do you notice, if any in the relationships between these quantities and their uncertainties?
```
import pandas
cols = ['Obj Name', 'Redshift', 'Redshift Uncert', 'Dist Mean (Mpc)', 'Dist Std Dev (Mpc)', 'Num Obs']
df = pandas.read_csv('cat.txt', delimiter ='|', skiprows=3, header = 0, names = cols, skipinitialspace=True)
redshift = df["Redshift"].tolist()
redshift_uncert = df["Redshift Uncert"].tolist()
dists2 = df["Dist Mean (Mpc)"].tolist()
dists2_uncert = df["Dist Std Dev (Mpc)"].tolist()
#display table (python "data frame" object)
df
```
***Answer to Part a***
```
#plots for part b - redshift
#plots for part b - redshift uncertainty
#plots for part b - distance
#plots for part b - distance uncertainty
```
***Part B explanation***
```
#part c scatter plot 1
#part c scatter plot 2
```
***Part C explanation***
<div class=hw>
## Exercise 3
The conversion between redshift (z) as provided in the database and recessional velocity as provided in Hubble's original paper is given by the formula below.
$$z=\sqrt{\frac{1+\beta}{1-\beta}}$$
where $\beta$=v/c. This formula can also be written as:
$$\beta=\frac{(z+1)^2-1}{(z+1)^2+1}$$
(a) Write a function with an appropriate docstring that applies this forumula to an input array. Your function should return an array of velocities in km/sec.
b) Apply your new function to your redshift and redshift uncertainty arrays here to translate them to "recessional velocities", as in Hubble's original plot
\* Note that technically we should do some more complicated error propagation here, and we will discuss this later in this class. Luckily though, this formula is roughly equivalent to z = v/c, which means that errors in z and v can be directly translated.
```
#part a here
#part b here
```
<div class=hw>
## Exercise 4
Make the following plots, with appropriate axis labels and titles.
a) A plot of the new data similar to the one you made in exercise 1, only with error bars. Use the function plt.errorbar and inflate the errors in the modern recessional velocities by a factor of 10, because they are actually so small for these very nearby galaxies with today's measurement techniques, that we can't even see them unless we
b) A plot showing both the new and old data overplotted, with different colors for each and a legend.
c) A plot showing Hubble's distances vs. the new distances, with a "
1 to 1" line overplotted
d) A plot showing Hubble's recessional velocities vs. the new velocities, with a "1 to 1" line overplotted
e) Discuss at least two trends that you see in the graphs and make a data-driven argument for how they might explain the discrepancy between the modern values and Hubble's. As always, your explanations need not be lengthy, but they should be ***clear and specific***.
```
#Plot a here
#Plot b here
#Plot c here
# Plot d here
```
***Part e explanations here***
***We will do the exercise below in class next week and you should not attempt it now. However, it builds directly on this lab, so take some time with your lab mates to think about how you will approach it, since you will only have one 50min class period in which to answer it.***
## In-Class Exercise for Next Week
Time for fitting! Use the lecture notes on Model fitting as a guide to help you.
a) Fit a linear model to Hubble's data and to the modern data. Make a plot showing both datasets and both fit lines. The plot should include a legend with both the points and the lines. The lines should be labeled in the legend with their equations.
b) Now, let's fit a linear model to the modern data that takes the error bars in the recessional velocities into account in the fit. The problem here though is that the uncertainties in redshifts/recessional velocities are VERY small for these galaxies. So small in fact that when you overplot error bars on the data points you can't even see them (you can do this to verify). So to demonstrate differences between weighted and unweighted fits here, let's inflate them by a factor of 50. Overplot both the unweighted and weighted lines together with the modern data (with y error bars) and an appropriate legend.
c) Discuss at least one trend or effect that you see in each graph. As always, your explanations need not be lengthy, but they should be ***clear, supported with references to the plot, and specific***.
d) We won't do fitting with x and y error bars, but you can easily make a plot that shows errors in both quantities using plt.errorbar. Do this using the TRUE errors in velocity and distance (not the inflated values), and use your plot to make an argument about whether the "Hubble's Law" line is a good fit to the data.
```
#import relevant modules here
#define a linear model function here
#calculate the values for your two fits here and print their values (to label lines)
#plot 1 goes here
#weighted fit goes here
#plot with error bars goes here
```
***Discuss trends or effects seen here***
```
#plot with x AND y errors goes here
from IPython.core.display import HTML
def css_styling():
styles = open("../../custom.css", "r").read()
return HTML(styles)
css_styling()
```
| true |
code
| 0.284092 | null | null | null | null |
|
```
!wget --no-check-certificate \
https://storage.googleapis.com/laurencemoroney-blog.appspot.com/horse-or-human.zip \
-O /tmp/horse-or-human.zip
```
The following python code will use the OS library to use Operating System libraries, giving you access to the file system, and the zipfile library allowing you to unzip the data.
```
import os
import zipfile
local_zip = '/tmp/horse-or-human.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('/tmp/horse-or-human')
zip_ref.close()
```
The contents of the .zip are extracted to the base directory `/tmp/horse-or-human`, which in turn each contain `horses` and `humans` subdirectories.
In short: The training set is the data that is used to tell the neural network model that 'this is what a horse looks like', 'this is what a human looks like' etc.
One thing to pay attention to in this sample: We do not explicitly label the images as horses or humans. If you remember with the handwriting example earlier, we had labelled 'this is a 1', 'this is a 7' etc. Later you'll see something called an ImageGenerator being used -- and this is coded to read images from subdirectories, and automatically label them from the name of that subdirectory. So, for example, you will have a 'training' directory containing a 'horses' directory and a 'humans' one. ImageGenerator will label the images appropriately for you, reducing a coding step.
Let's define each of these directories:
```
# Directory with our training horse pictures
train_horse_dir = os.path.join('/tmp/horse-or-human/horses')
# Directory with our training human pictures
train_human_dir = os.path.join('/tmp/horse-or-human/humans')
```
Now, let's see what the filenames look like in the `horses` and `humans` training directories:
```
train_horse_names = os.listdir(train_horse_dir)
print(train_horse_names[:10])
train_human_names = os.listdir(train_human_dir)
print(train_human_names[:10])
```
Let's find out the total number of horse and human images in the directories:
```
print('total training horse images:', len(os.listdir(train_horse_dir)))
print('total training human images:', len(os.listdir(train_human_dir)))
```
Now let's take a look at a few pictures to get a better sense of what they look like. First, configure the matplot parameters:
```
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
# Parameters for our graph; we'll output images in a 4x4 configuration
nrows = 4
ncols = 4
# Index for iterating over images
pic_index = 0
```
Now, display a batch of 8 horse and 8 human pictures. You can rerun the cell to see a fresh batch each time:
```
# Set up matplotlib fig, and size it to fit 4x4 pics
fig = plt.gcf()
fig.set_size_inches(ncols * 4, nrows * 4)
pic_index += 8
next_horse_pix = [os.path.join(train_horse_dir, fname)
for fname in train_horse_names[pic_index-8:pic_index]]
next_human_pix = [os.path.join(train_human_dir, fname)
for fname in train_human_names[pic_index-8:pic_index]]
for i, img_path in enumerate(next_horse_pix+next_human_pix):
# Set up subplot; subplot indices start at 1
sp = plt.subplot(nrows, ncols, i + 1)
sp.axis('Off') # Don't show axes (or gridlines)
img = mpimg.imread(img_path)
plt.imshow(img)
plt.show()
```
## Building a Small Model from Scratch
But before we continue, let's start defining the model:
Step 1 will be to import tensorflow.
```
import tensorflow as tf
```
We then add convolutional layers as in the previous example, and flatten the final result to feed into the densely connected layers.
Finally we add the densely connected layers.
Note that because we are facing a two-class classification problem, i.e. a *binary classification problem*, we will end our network with a [*sigmoid* activation](https://wikipedia.org/wiki/Sigmoid_function), so that the output of our network will be a single scalar between 0 and 1, encoding the probability that the current image is class 1 (as opposed to class 0).
```
model = tf.keras.models.Sequential([
# Note the input shape is the desired size of the image 300x300 with 3 bytes color
# This is the first convolution
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(300, 300, 3)),
tf.keras.layers.MaxPooling2D(2, 2),
# The second convolution
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The third convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The fourth convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The fifth convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# Flatten the results to feed into a DNN
tf.keras.layers.Flatten(),
# 512 neuron hidden layer
tf.keras.layers.Dense(512, activation='relu'),
# Only 1 output neuron. It will contain a value from 0-1 where 0 for 1 class ('horses') and 1 for the other ('humans')
tf.keras.layers.Dense(1, activation='sigmoid')
])
```
The model.summary() method call prints a summary of the NN
```
model.summary()
```
The "output shape" column shows how the size of your feature map evolves in each successive layer. The convolution layers reduce the size of the feature maps by a bit due to padding, and each pooling layer halves the dimensions.
Next, we'll configure the specifications for model training. We will train our model with the `binary_crossentropy` loss, because it's a binary classification problem and our final activation is a sigmoid. (For a refresher on loss metrics, see the [Machine Learning Crash Course](https://developers.google.com/machine-learning/crash-course/descending-into-ml/video-lecture).) We will use the `rmsprop` optimizer with a learning rate of `0.001`. During training, we will want to monitor classification accuracy.
**NOTE**: In this case, using the [RMSprop optimization algorithm](https://wikipedia.org/wiki/Stochastic_gradient_descent#RMSProp) is preferable to [stochastic gradient descent](https://developers.google.com/machine-learning/glossary/#SGD) (SGD), because RMSprop automates learning-rate tuning for us. (Other optimizers, such as [Adam](https://wikipedia.org/wiki/Stochastic_gradient_descent#Adam) and [Adagrad](https://developers.google.com/machine-learning/glossary/#AdaGrad), also automatically adapt the learning rate during training, and would work equally well here.)
```
from tensorflow.keras.optimizers import RMSprop
model.compile(loss='binary_crossentropy',
optimizer=RMSprop(lr=0.001),
metrics=['acc'])
```
### Data Preprocessing
Let's set up data generators that will read pictures in our source folders, convert them to `float32` tensors, and feed them (with their labels) to our network. We'll have one generator for the training images and one for the validation images. Our generators will yield batches of images of size 300x300 and their labels (binary).
As you may already know, data that goes into neural networks should usually be normalized in some way to make it more amenable to processing by the network. (It is uncommon to feed raw pixels into a convnet.) In our case, we will preprocess our images by normalizing the pixel values to be in the `[0, 1]` range (originally all values are in the `[0, 255]` range).
In Keras this can be done via the `keras.preprocessing.image.ImageDataGenerator` class using the `rescale` parameter. This `ImageDataGenerator` class allows you to instantiate generators of augmented image batches (and their labels) via `.flow(data, labels)` or `.flow_from_directory(directory)`. These generators can then be used with the Keras model methods that accept data generators as inputs: `fit_generator`, `evaluate_generator`, and `predict_generator`.
```
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(rescale=1/255)
# Flow training images in batches of 128 using train_datagen generator
train_generator = train_datagen.flow_from_directory(
'/tmp/horse-or-human/', # This is the source directory for training images
target_size=(300, 300), # All images will be resized to 150x150
batch_size=128,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
```
### Training
Let's train for 15 epochs -- this may take a few minutes to run.
Do note the values per epoch.
The Loss and Accuracy are a great indication of progress of training. It's making a guess as to the classification of the training data, and then measuring it against the known label, calculating the result. Accuracy is the portion of correct guesses.
```
history = model.fit_generator(
train_generator,
steps_per_epoch=8,
epochs=15,
verbose=1)
```
###Running the Model
Let's now take a look at actually running a prediction using the model. This code will allow you to choose 1 or more files from your file system, it will then upload them, and run them through the model, giving an indication of whether the object is a horse or a human.
```
import numpy as np
from google.colab import files
from keras.preprocessing import image
uploaded = files.upload()
for fn in uploaded.keys():
# predicting images
path = '/content/' + fn
img = image.load_img(path, target_size=(300, 300))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = model.predict(images, batch_size=10)
print(classes[0])
if classes[0]>0.5:
print(fn + " is a human")
else:
print(fn + " is a horse")
```
### Visualizing Intermediate Representations
To get a feel for what kind of features our convnet has learned, one fun thing to do is to visualize how an input gets transformed as it goes through the convnet.
Let's pick a random image from the training set, and then generate a figure where each row is the output of a layer, and each image in the row is a specific filter in that output feature map. Rerun this cell to generate intermediate representations for a variety of training images.
```
import numpy as np
import random
from tensorflow.keras.preprocessing.image import img_to_array, load_img
# Let's define a new Model that will take an image as input, and will output
# intermediate representations for all layers in the previous model after
# the first.
successive_outputs = [layer.output for layer in model.layers[1:]]
#visualization_model = Model(img_input, successive_outputs)
visualization_model = tf.keras.models.Model(inputs = model.input, outputs = successive_outputs)
# Let's prepare a random input image from the training set.
horse_img_files = [os.path.join(train_horse_dir, f) for f in train_horse_names]
human_img_files = [os.path.join(train_human_dir, f) for f in train_human_names]
img_path = random.choice(horse_img_files + human_img_files)
img = load_img(img_path, target_size=(300, 300)) # this is a PIL image
x = img_to_array(img) # Numpy array with shape (150, 150, 3)
x = x.reshape((1,) + x.shape) # Numpy array with shape (1, 150, 150, 3)
# Rescale by 1/255
x /= 255
# Let's run our image through our network, thus obtaining all
# intermediate representations for this image.
successive_feature_maps = visualization_model.predict(x)
# These are the names of the layers, so can have them as part of our plot
layer_names = [layer.name for layer in model.layers]
# Now let's display our representations
for layer_name, feature_map in zip(layer_names, successive_feature_maps):
if len(feature_map.shape) == 4:
# Just do this for the conv / maxpool layers, not the fully-connected layers
n_features = feature_map.shape[-1] # number of features in feature map
# The feature map has shape (1, size, size, n_features)
size = feature_map.shape[1]
# We will tile our images in this matrix
display_grid = np.zeros((size, size * n_features))
for i in range(n_features):
# Postprocess the feature to make it visually palatable
x = feature_map[0, :, :, i]
x -= x.mean()
x /= x.std()
x *= 64
x += 128
x = np.clip(x, 0, 255).astype('uint8')
# We'll tile each filter into this big horizontal grid
display_grid[:, i * size : (i + 1) * size] = x
# Display the grid
scale = 20. / n_features
plt.figure(figsize=(scale * n_features, scale))
plt.title(layer_name)
plt.grid(False)
plt.imshow(display_grid, aspect='auto', cmap='viridis')
```
As you can see we go from the raw pixels of the images to increasingly abstract and compact representations. The representations downstream start highlighting what the network pays attention to, and they show fewer and fewer features being "activated"; most are set to zero. This is called "sparsity." Representation sparsity is a key feature of deep learning.
These representations carry increasingly less information about the original pixels of the image, but increasingly refined information about the class of the image. You can think of a convnet (or a deep network in general) as an information distillation pipeline.
## Clean Up
Before running the next exercise, run the following cell to terminate the kernel and free memory resources:
```
import os, signal
os.kill(os.getpid(), signal.SIGKILL)
```
| true |
code
| 0.611498 | null | null | null | null |
|
#### Setup Notebook
```
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:80% !important; }</style>"))
# Put these at the top of every notebook, to get automatic reloading and inline plotting
%reload_ext autoreload
%autoreload 2
%matplotlib inline
```
# Predicting Price Movements of Cryptocurrencies - Using Convolutional Neural Networks to Classify 2D Images of Chart Data
```
# This file contains all the main external libs we'll use
from fastai.imports import *
from fastai.transforms import *
from fastai.conv_learner import *
from fastai.model import *
from fastai.dataset import *
from fastai.sgdr import *
from fastai.plots import *
# For downloading files
from IPython.display import FileLink, FileLinks
# For confusion matrix
from sklearn.metrics import confusion_matrix
PATH = 'data/btc/btcgraphs_cropped/'
!ls {PATH}
os.listdir(f'{PATH}train')
files = os.listdir(f'{PATH}train/DOWN')[:5]
files
img = plt.imread(f'{PATH}train/DOWN/{files[3]}')
print(f'{PATH}train/DOWN/{files[0]}')
print(f'{PATH}train/DOWN/{files[1]}')
plt.imshow(img)
FileLink(f'{PATH}train/DOWN/{files[3]}')
```
# The Steps to Follow
1. Enable data augmentation, and precompute=True
1. Use `lr_find()` to find highest learning rate where loss is still clearly improving
1. Train last layer from precomputed activations for 1-2 epochs
1. Train last layer with data augmentation (i.e. precompute=False) for 2-3 epochs with cycle_len=1
1. Unfreeze all layers
1. Set earlier layers to 3x-10x lower learning rate than next higher layer
1. Use `lr_find()` again
1. Train full network with cycle_mult=2 until over-fitting
## 0. Setup
```
arch = resnet34
sz = 480
batch_size = int(64)
```
## 1. Data Augmentation
**Not using data augmentation this time**
Starting without useing data augmentation because I don't think it makes sense for these graphs, we don't need to generalize to slightly different angles. All plots will always be straight on and square in the frame.
```
tfms = tfms_from_model(arch, sz)
data = ImageClassifierData.from_paths(PATH, bs=batch_size, tfms=tfms,
trn_name='train', val_name='valid')#, test_name='test')
```
## 2. Choose a Learning Rate
```
learn = ConvLearner.pretrained(arch, data, precompute=True)
learn.save('00_pretrained_480')
# learn.precompute = True
learn.load('00_pretrained_480')
lrf = learn.lr_find()
learn.sched.plot_lr()
learn.sched.plot()
learn.save('01_lr_found_480')
```
## 3. Train Last Layer
```
# learn.precompute = True
learn.load('01_lr_found_480')
learn.fit(1e-4, 1, cycle_save_name='01_weights')
learn.save("02_trained_once_480")
```
#### Accuracy
TODO
Do some tests on accuracy of training on single epoch
## 4. Train Last Layer with Data Augmentation
**Not actually using any augmentation, this is just a few more rounds of training**
```
# learn.precompute = True
learn.load("02_trained_once_480")
learn.precompute=False #I don't think this makes a difference without data augmentation
learn.fit(1e-4, 3, cycle_len=1, best_save_name="02_best_model", cycle_save_name='02_weights')
learn.save("03_trained_2x_480")
learn.load("trained_2_market_movement")
```
More accuracy test...
```
learn.unfreeze()
```
Using a relatively large learning rate to train the prvious layers because this data set is not very similar to ImageNet
```
lr = np.array([0.0001/9, 0.0001/3, 0.00001])
learn.fit(lr, 3, cycle_len=1, cycle_mult=2, \
best_save_name="03_best_model", cycle_save_name='03_weights')
learn.save("trained_3_market_movement")
learn.load("trained_3_market_movement")
```
# Look at Results
```
data.val_y
data.classes
# this gives prediction for validation set. Predictions are in log scale
log_preds = learn.predict()
log_preds.shape
log_preds[:10]
preds = np.argmax(log_preds, axis=1) # from log probabilities to 0 or 1
probs = np.exp(log_preds[:,1]) # pr(dog)
probs
probs[1]
def rand_by_mask(mask):
return np.random.choice(np.where(mask)[0], 4, replace=False)
def rand_by_correct(is_correct):
return rand_by_mask((preds == data.val_y)==is_correct)
def plot_val_with_title(idxs, title):
imgs = np.stack([data.val_ds[x][0] for x in idxs])
title_probs = [probs[x] for x in idxs]
print(title)
return plots(data.val_ds.denorm(imgs), rows=1, titles=title_probs)
def plots(ims, figsize=(12,6), rows=1, titles=None):
f = plt.figure(figsize=figsize)
for i in range(len(ims)):
sp = f.add_subplot(rows, len(ims)//rows, i+1)
sp.axis('Off')
if titles is not None: sp.set_title(titles[i], fontsize=16)
plt.imshow(ims[i])
def load_img_id(ds, idx):
return np.array(PIL.Image.open(PATH+ds.fnames[idx]))
def plot_val_with_title(idxs, title):
imgs = [load_img_id(data.val_ds,x) for x in idxs]
title_probs = [probs[x] for x in idxs]
print(title)
return plots(imgs, rows=1, titles=title_probs, figsize=(16,8))
plot_val_with_title(rand_by_correct(True), "Correctly classified")
def most_by_mask(mask, mult):
idxs = np.where(mask)[0]
return idxs[np.argsort(mult * probs[idxs])[:4]]
def most_by_correct(y, is_correct):
mult = -1 if (y==1)==is_correct else 1
return most_by_mask(((preds == data.val_y)==is_correct) & (data.val_y == y), mult)
plot_val_with_title(most_by_correct(0, True), "Most correct DOWN")
plot_val_with_title(most_by_correct(1, True), "Most correct UP")
plot_val_with_title(most_by_correct(0, False), "Most incorrect DOWN")
```
# Analyze Results
```
data.val_y
log_preds = learn.predict()
preds = np.argmax(log_preds, axis=1) # from log probabilities to 0 or 1
probs = np.exp(log_preds[:,1]) # pr(dog)
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(data.val_y, preds)
plot_confusion_matrix(cm, data.classes)
cm
(cm[0][0]+cm[1][1])/(np.sum(cm))
np.sum(cm)-(42313)
```
| true |
code
| 0.61115 | null | null | null | null |
|
# Photon-photon dispersion
This tutorial shows how to include photon-photon dispersion off of background photon fields in the ALP-photon propagation calculation. The relevance of photon dispersion for ALP calculations is discussed in [Dobrynina 2015](https://journals.aps.org/prd/abstract/10.1103/PhysRevD.91.083003). A background field adds to the dispersive part of the refractive index of the propagation medium $n = 1+\chi$. [Dobrynina 2015](https://journals.aps.org/prd/abstract/10.1103/PhysRevD.91.083003) show that at $z=0$, $\chi_{CMB} = 5.11\times10^{-43}$. Dispersion off the CMB is included by default, but other values of $\chi$ can be included manually.
First import what we will need:
```
from gammaALPs.core import Source, ALP, ModuleList
from gammaALPs.base import environs, transfer
import numpy as np
import matplotlib.pyplot as plt
from astropy import constants as c
from matplotlib.patheffects import withStroke
from astropy import units as u
import time
from scipy.interpolate import RectBivariateSpline as RBSpline
effect = dict(path_effects=[withStroke(foreground="w", linewidth=2)]) # used for plotting
```
$\chi$ is included in the code as a 2D spline function in energy and propagation distance. This means that the points at which $\chi$ is calculated at do not need to be exactly the same as the points used for the magnetic field. It is also possible to include $\chi$ as an array of size `(1)` if you want a constant value, or size `(len(EGeV),len(r))`, if you have calculated $\chi$ in the exact magnetic field domains you will be using.
## $\chi$ function
We will create a fake $\chi$ function which changes with distance and energy, and then see its effects on mixing in different environments.
```
EGeV = np.logspace(-5.,6.,1000)
chiCMB = transfer.chiCMB
chiCMB
```
$r$ will be in pc for the jets and kpc for the clusters and GMF.
```
rs = np.logspace(-2,5,200)
chis = 1.e9 * rs[np.newaxis,:]**-3 * chiCMB * EGeV[:,np.newaxis]**(1.5) + chiCMB
plt.loglog(rs,chis[0,:])
plt.loglog(rs,chis[500,:])
plt.loglog(rs,chis[-1,:])
plt.ylabel(r'$\chi$')
plt.xlabel('r [pc or kpc] or z')
```
Our $\chi$ changes with both energy and distance.
```
ee, rr = np.meshgrid(EGeV,rs,indexing='ij')
plt.pcolormesh(ee,rr,np.log10(chis),cmap=plt.get_cmap('coolwarm'),
shading='auto')
plt.colorbar(label=r"log($\chi$)")
plt.xscale('log')
plt.yscale('log')
plt.xlabel('E [GeV]')
plt.ylabel('r [pc or kpc]')
```
Make the spline function:
```
chispl = RBSpline(EGeV,rs,chis,kx=1,ky=1,s=0)
```
Now we can test it for a source. We will use 3C454.3 (see the individual environment tutorials for more details on each of the environments).
```
src = Source(z=0.859 , ra='22h53m57.7s', dec='+16d08m54s', bLorentz=60.) # 3C454.3
pin = np.diag((1.,1.,0.)) * 0.5
```
## Jet
First, let's test the `"Jet"` class:
```
ml = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
ml_chi = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
# other jet
gamma_min = 18.
```
Add the same jet module to each, including $\chi$ with the `chi` keyword for the second one.
```
ml.add_propagation("Jet",
0, # position of module counted from the source.
B0=0.32, # Jet field at r = R0 in G
r0=1., # distance from BH where B = B0 in pc
rgam=3.19e17 * u.cm.to('pc'), # distance of gamma-ray emitting region to BH
alpha=-1., # exponent of toroidal mangetic field (default: -1.)
psi=np.pi/4., # Angle between one photon polarization state and B field.
# Assumed constant over entire jet.
helical=True, # if True, use helical magnetic-field model from Clausen-Brown et al. (2011).
# In this case, the psi kwarg is treated is as the phi angle
# of the photon trajectory in the cylindrical jet coordinate system
equipartition=True, # if true, assume equipartition between electrons and the B field.
# This will overwrite the exponent of electron density beta = 2 * alpha
# and set n0 given the minimum electron lorentz factor set with gamma_min
gamma_min=gamma_min, # minimum lorentz factor of emitting electrons, only used if equipartition=True
gamma_max=np.exp(10.) * gamma_min, # maximum lorentz factor of emitting electrons,
# only used if equipartition=True
Rjet= 40., # maximum jet length in pc (default: 1000.)
n0=1e4, # normalization of electron density, overwritten if equipartition=True
beta=-2. # power-law index of electron density, overwritten if equipartition=True
)
ml_chi.add_propagation("Jet",
0, # position of module counted from the source.
B0=0.32, # Jet field at r = R0 in G
r0=1., # distance from BH where B = B0 in pc
rgam=3.19e17 * u.cm.to('pc'), # distance of gamma-ray emitting region to BH
alpha=-1., # exponent of toroidal mangetic field (default: -1.)
psi=np.pi/4., # Angle between one photon polarization state and B field.
# Assumed constant over entire jet.
helical=True, # if True, use helical magnetic-field model from Clausen-Brown et al. (2011).
# In this case, the psi kwarg is treated is as the phi angle
# of the photon trajectory in the cylindrical jet coordinate system
equipartition=True, # if true, assume equipartition between electrons and the B field.
# This will overwrite the exponent of electron density beta = 2 * alpha
# and set n0 given the minimum electron lorentz factor set with gamma_min
gamma_min=gamma_min, # minimum lorentz factor of emitting electrons, only used if equipartition=True
gamma_max=np.exp(10.) * gamma_min, # maximum lorentz factor of emitting electrons,
# only used if equipartition=True
Rjet= 40., # maximum jet length in pc (default: 1000.)
n0=1e4, # normalization of electron density, overwritten if equipartition=True
beta=-2., # power-law index of electron density, overwritten if equipartition=True
chi=chispl
)
```
Pick a mass and coupling where there is some mixing, and run the calculation for each.
```
ml.alp.m = 100.
ml.alp.g = 0.3
ml_chi.alp.m = 100.
ml_chi.alp.g = 0.3
px, py, pa = ml.run()
pgg = px + py
px_c, py_c, pa_c = ml_chi.run()
pgg_chi = px_c + py_c
for p in pgg:
plt.plot(ml.EGeV, p, label=r'$\chi_{CMB}$')
for p_c in pgg_chi:
plt.plot(ml_chi.EGeV, p_c, label=r'$\chi$-spline')
plt.grid(True, lw = 0.2)
plt.grid(True, which = 'minor', axis = 'y', lw = 0.2)
plt.xlabel('Energy (GeV)')
plt.ylabel(r'Photon survival probability')
plt.gca().set_xscale('log')
plt.annotate(r'$m_a = {0:.1f}\,\mathrm{{neV}}, g_{{a\gamma}}'
r' = {1:.2f} \times 10^{{-11}}\,\mathrm{{GeV}}^{{-1}}$'.format(ml.alp.m,ml.alp.g),
xy=(0.05,0.1),
size='large',
xycoords='axes fraction',
ha='left',
**effect)
plt.legend(loc='upper left')
```
The $P_{\gamma\gamma}$'s are quite different between the two cases. $\chi$ affects the mixing by lowering the high critical energy, $E_{crit}^{high}$, and so oftern reduces mixing at very high energies.
## Cluster
Now let's look at a cluster magnetic field, `"ICMGaussTurb"`. We can use the same $\chi$ array in $(E,r)$ but this time $r$ will be in kpc instead of pc.
```
# cluster
ml = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
ml_chi = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
ml.add_propagation("ICMGaussTurb",
0, # position of module counted from the source.
nsim=1, # number of random B-field realizations
B0=10., # rms of B field
n0=39., # normalization of electron density
n2=4.05, # second normalization of electron density, see Churazov et al. 2003, Eq. 4
r_abell=500., # extension of the cluster
r_core=80., # electron density parameter, see Churazov et al. 2003, Eq. 4
r_core2=280., # electron density parameter, see Churazov et al. 2003, Eq. 4
beta=1.2, # electron density parameter, see Churazov et al. 2003, Eq. 4
beta2=0.58, # electron density parameter, see Churazov et al. 2003, Eq. 4
eta=0.5, # scaling of B-field with electron denstiy
kL=0.18, # maximum turbulence scale in kpc^-1, taken from A2199 cool-core cluster, see Vacca et al. 2012
kH=9., # minimum turbulence scale, taken from A2199 cool-core cluster, see Vacca et al. 2012
q=-2.80, # turbulence spectral index, taken from A2199 cool-core cluster, see Vacca et al. 2012
seed=0 # random seed for reproducability, set to None for random seed.
)
ml_chi.add_propagation("ICMGaussTurb",
0, # position of module counted from the source.
nsim=1, # number of random B-field realizations
B0=10., # rms of B field
n0=39., # normalization of electron density
n2=4.05, # second normalization of electron density, see Churazov et al. 2003, Eq. 4
r_abell=500., # extension of the cluster
r_core=80., # electron density parameter, see Churazov et al. 2003, Eq. 4
r_core2=280., # electron density parameter, see Churazov et al. 2003, Eq. 4
beta=1.2, # electron density parameter, see Churazov et al. 2003, Eq. 4
beta2=0.58, # electron density parameter, see Churazov et al. 2003, Eq. 4
eta=0.5, # scaling of B-field with electron denstiy
kL=0.18, # maximum turbulence scale in kpc^-1, taken from A2199 cool-core cluster, see Vacca et al. 2012
kH=9., # minimum turbulence scale, taken from A2199 cool-core cluster, see Vacca et al. 2012
q=-2.80, # turbulence spectral index, taken from A2199 cool-core cluster, see Vacca et al. 2012
seed=0, # random seed for reproducability, set to None for random seed.
chi = chispl
)
ml.alp.m = 10.
ml.alp.g = 0.7
ml_chi.alp.m = 10.
ml_chi.alp.g = 0.7
px, py, pa = ml.run()
pgg = px + py
px_c, py_c, pa_c = ml_chi.run()
pgg_chi = px_c + py_c
for pi,p in enumerate(pgg):
if pi==0:
plt.plot(ml.EGeV, p, color=plt.cm.tab10(0.), alpha = 0.7, label=r'$\chi_{CMB}$')
else:
plt.plot(ml.EGeV, p, color=plt.cm.tab10(0.),alpha = 0.1)
for pi_c,p_c in enumerate(pgg_chi):
if pi_c==0:
plt.plot(ml_chi.EGeV, p_c, color=plt.cm.tab10(1), alpha = 0.7, label=r'$\chi$-spline')
else:
plt.plot(ml_chi.EGeV, p_c, color=plt.cm.tab10(1),alpha = 0.1)
plt.grid(True, lw = 0.2)
plt.grid(True, which = 'minor', axis = 'y', lw = 0.2)
plt.xlabel('Energy (GeV)')
plt.ylabel(r'Photon survival probability')
plt.gca().set_xscale('log')
plt.annotate(r'$m_a = {0:.1f}\,\mathrm{{neV}}, g_{{a\gamma}}'
r' = {1:.2f} \times 10^{{-11}}\,\mathrm{{GeV}}^{{-1}}$'.format(ml.alp.m,ml.alp.g),
xy=(0.05,0.1),
size='large',
xycoords='axes fraction',
ha='left',
**effect)
plt.legend(loc='upper left')
```
Again, including $\chi$ lowers the highest energy at which there is strong mixing.
## GMF
For the GMF:
```
# GMF
ml = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
ml_chi = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
ml.add_propagation("GMF",
0,
model='jansson12')
ml_chi.add_propagation("GMF",
0,
model='jansson12',
chi = chispl)
ml.alp.m = 1.
ml.alp.g = 3.
ml_chi.alp.m = 1.
ml_chi.alp.g = 3.
px, py, pa = ml.run()
pgg = px + py
px_c, py_c, pa_c = ml_chi.run()
pgg_chi = px_c + py_c
for p in pgg:
plt.plot(ml.EGeV, p, label=r'$\chi_{CMB}$')
for p_c in pgg_chi:
plt.plot(ml_chi.EGeV, p_c, label=r'$\chi$-spline')
plt.grid(True, lw = 0.2)
plt.grid(True, which = 'minor', axis = 'y', lw = 0.2)
plt.xlabel('Energy (GeV)')
plt.ylabel(r'Photon survival probability')
plt.gca().set_xscale('log')
plt.annotate(r'$m_a = {0:.1f}\,\mathrm{{neV}}, g_{{a\gamma}}'
r' = {1:.2f} \times 10^{{-11}}\,\mathrm{{GeV}}^{{-1}}$'.format(ml.alp.m,ml.alp.g),
xy=(0.05,0.1),
size='large',
xycoords='axes fraction',
ha='left',
**effect)
plt.legend(loc='upper left')
```
The effect is the same.
## IGMF
Mixing in the IGMF is slightly different. Far from pair-produciton energies, $\chi \propto \rho$ where $\rho$ is the energy density of the background field. The energy density of the CMB evolves with redshift as $\rho \propto T^4 \propto (1+z)^4$. Therefore, by default, mixing in the IGMF doesn't use a constant value of $\chi_{CMB}$, but rather uses $\chi(z)=\chi_{CMB}(1+z)^4$ where $\chi_{CMB} = 5.11\times10^{-43}$ as mentioned above and is calculated at $z=0$.
It is also possible to manually include a spline function for $\chi$ in the IGMF, but now the spline needs to be in energy and redshift instead of energy and distance:
```
zs = np.logspace(-1,np.log10(1.5),200)
chispl_z = RBSpline(EGeV,zs,chis,kx=1,ky=1,s=0)
# IGMF
ml = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
ml_chi = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
ml_chiz = ModuleList(ALP(m=1., g=2.), src, pin=pin, EGeV=EGeV, seed = 0)
```
For comparison we will also include a constant value of $\chi_{CMB}$. Any environment will accept a single value of chi in the form of `chi=np.array([chi])`.
```
ml.add_propagation("IGMF",
0, # position of module counted from the source.
nsim=1, # number of random B-field realizations
B0=1e-3, # B field strength in micro Gauss at z = 0
n0=1e-7, # normalization of electron density in cm^-3 at z = 0
L0=1e3, # coherence (cell) length in kpc at z = 0
eblmodel='dominguez', # EBL model
chi = np.array([chiCMB])
)
ml_chi.add_propagation("IGMF",
0, # position of module counted from the source.
nsim=1, # number of random B-field realizations
B0=1e-3, # B field strength in micro Gauss at z = 0
n0=1e-7, # normalization of electron density in cm^-3 at z = 0
L0=1e3, # coherence (cell) length in kpc at z = 0
eblmodel='dominguez', # EBL model
chi = chispl_z
)
ml_chiz.add_propagation("IGMF",
0, # position of module counted from the source.
nsim=1, # number of random B-field realizations
B0=1e-3, # B field strength in micro Gauss at z = 0
n0=1e-7, # normalization of electron density in cm^-3 at z = 0
L0=1e3, # coherence (cell) length in kpc at z = 0
eblmodel='dominguez' # EBL model
)
ml.alp.m = 0.1
ml.alp.g = 3.
ml_chi.alp.m = 0.1
ml_chi.alp.g = 3.
ml_chiz.alp.m = 0.1
ml_chiz.alp.g = 3.
px, py, pa = ml.run()
pgg = px + py
px_c, py_c, pa_c = ml_chi.run()
pgg_chi = px_c + py_c
px_cz, py_cz, pa_cz = ml_chiz.run()
pgg_chiz = px_cz + py_cz
for p in pgg:
plt.plot(ml.EGeV, p, label=r'$\chi_{CMB}$')
for p_cz in pgg_chiz:
plt.plot(ml_chiz.EGeV, p_cz, label=r'$\chi_{CMB} (1+z)^4$')
for p_c in pgg_chi:
plt.plot(ml_chi.EGeV, p_c, label=r'$\chi$-spline')
plt.grid(True, lw = 0.2)
plt.grid(True, which = 'minor', axis = 'y', lw = 0.2)
plt.xlabel('Energy (GeV)')
plt.ylabel(r'Photon survival probability')
plt.gca().set_xscale('log')
plt.annotate(r'$m_a = {0:.1f}\,\mathrm{{neV}}, g_{{a\gamma}}'
r' = {1:.2f} \times 10^{{-11}}\,\mathrm{{GeV}}^{{-1}}$'.format(ml.alp.m,ml.alp.g),
xy=(0.05,0.1),
size='large',
xycoords='axes fraction',
ha='left',
**effect)
plt.legend()
```
All three are different.
| true |
code
| 0.800546 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
%load_ext autoreload
%autoreload 2
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
```
# A Fundamental Property of Gaussians
A multivariate Gaussian is nothing more than a generalization of the univariate Gaussian.
We parameterize univariate Gaussians with a $\mu$ and $\sigma$, where $\mu$ and $\sigma$ are scalars.
A bivariate Gaussian is two univariate Gaussians that may also share a relationship to one another. We can jointly model both Gaussians by modelling not just how they vary independently, but also how they vary with one another.
```
mu1 = np.array(0)
mu2 = np.array(0)
sig11 = np.array(3)
sig12 = np.array(-2)
sig21 = np.array(-2)
sig22 = np.array(4)
mean = np.array([mu1, mu2])
cov = np.array([[sig11, sig12], [sig21, sig22]])
draws = np.random.multivariate_normal(mean, cov, size=1000)
plt.scatter(*draws.T)
```
One of the fundamental properties of Gaussians is that if you have a Multivariate Gaussian (e.g. a joint distribution of 2 or more Gaussian random variables), if we condition on any subset of Gaussians, the joint distribution of the rest of the Gaussians can be found analytically. There's a formula, and it's expressed in code below.
```
x1 = 0
mu_2g1 = mu2 + sig21 * 1 / sig11 * (x1 - mu1)
sig_2g1 = sig22 - sig21 * 1 / sig11 * sig12
mu_2g1, sig_2g1
```
Go ahead and play with the slider below.
```
from ipywidgets import interact, FloatSlider, IntSlider
@interact(x1=FloatSlider(min=-4, max=4, continuous_update=False))
def plot_conditional(x1):
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
axes[0].scatter(*draws.T)
axes[0].vlines(x=x1, ymin=draws[:, 1].min(), ymax=draws[:, 1].max(), color='red')
axes[0].hlines(y=0, xmin=draws[:, 0].min(), xmax=draws[:, 0].max(), color='black')
# Compute Conditional
mu_2g1 = mu2 + sig21 * 1 / sig11 * (x1 - mu1)
sig_2g1 = sig22 - sig21 * 1 / sig11 * sig12
x2_draws = np.random.normal(mu_2g1, sig_2g1, size=10000)
axes[1].hist(x2_draws, bins=100, color='red')
axes[1].vlines(x=0, ymin=0, ymax=400, color='black')
axes[1].set_xlim(-10, 10)
axes[1].set_ylim(0, 400)
```
# 2D $\mu$s
Take this into higher dimensions. Let's not compare two scalar $\mu$s, but now do two $\mu$s that are each a vector of 2 dimensions.
```
mu1 = np.array([0, 0])
mu2 = np.array([0, 0])
sig11 = np.array([[1, 0], [0, 1]])
sig12 = np.array([[2, 0], [0, 2]])
sig21 = sig12.T
sig22 = np.array([[0.8, 0], [0, 0.8]])
mean = np.array([mu1, mu2])
cov = np.array([[sig11, sig12], [sig21, sig22]])
# draws = np.random.multivariate_normal(mean, cov, size=1000)
# plt.scatter(*draws.T)
cov
x1 = np.array([0, -3])
mu_2g1 = mu2 + sig21 @ np.linalg.inv(sig11) @ (x1 - mu1)
sig_2g1 = sig22 - sig21 @ np.linalg.inv(sig11) @ sig12
sig_2g1, mu_2g1
```
# Implementing GP Prior
When we use a GP, we're essentially modelling the **outputs** as being described by a joint Gaussian distribution.
We would like to be able to specify the covariance matrix as a function of the distances between the inputs - regardless of whether the inputs are 1-D, 2-D, or more. That is the key to generalizing from 1D examples to the 2D examples commonly shown.
```
import seaborn as sns
n = 50
x_train = np.linspace(-5, 5, n).reshape(-1, 1)
# sns.heatmap(x_train - x_train.T, cmap='RdBu')
def sq_exp(x1, x2):
"""
Squared exponential kernel.
Assumes that x1 and x2 have the same shape.
"""
diff = x1 - x2.T
sqdiff = np.power(diff, 2)
return np.exp(-0.5 * sqdiff)
sns.heatmap(sq_exp(x_train, x_train), cmap='RdBu')
```
Draw from prior.
```
K = sq_exp(x_train, x_train)
eps = 1E-6 * np.eye(n) #
L = np.linalg.cholesky(K + eps)
f_prior = np.dot(L, np.random.normal(size=(n, 10)))
plt.plot(x_train, f_prior)
plt.show()
def true_function_1d(x):
x = x + 1E-10
return np.sin(x)
n = 200
x_samp = np.array([2, 18, -10, 10, -12, 12, -2, 5, -13, 6, -18, 8, -8, 0, 15]).reshape(-1, 1)
f_samp = true_function_1d(x_samp)
K_samp = sq_exp(x_samp, x_samp)
eps = 1E-6 * np.eye(len(x_samp))
L_samp = np.linalg.cholesky(K_samp + eps)
x_s = np.linspace(-20, 20, n).reshape(-1, 1)
K_ss = sq_exp(x_s, x_s)
K_s = sq_exp(x_samp, x_s)
mu_cond = K_s.T @ np.linalg.inv(K_samp) @ f_samp
sig_cond = K_ss - K_s.T @ np.linalg.inv(K_samp) @ K_s
f_posterior = np.random.multivariate_normal(mu_cond.flatten(), sig_cond, size=100)
for f in f_posterior:
plt.plot(x_s, f, color='grey', alpha=0.1)
plt.scatter(x_samp, f_samp)
plt.plot(x_s, true_function_1d(x_s))
plt.plot(x_s, mu_cond.flatten())
plt.show()
sig_cond.min()
sns.heatmap(sig_cond, cmap='RdBu')
```
We can rewrite extend this code to apply in two dimensions. Let's say that our data lived on a grid, rather than on a single dimension. A periodic function is applied on a 2D grid.
```
def true_function(x1, x2):
# return np.sin(x1**2 + x2**2) / (x1**2 + x2**2)
return np.sin(x1) + np.sin(x2)
```
# Prior
Let's sample a prior from a 2D plane.
```
sq_exp??
import numpy as np
import scipy
x1 = np.array([[2, 2], [2, 1], [1, 2], [1, 1]])
def sq_exp2d(x1, x2):
d = scipy.spatial.distance.cdist(x1, x2)
return np.exp(-0.5 * np.power(d, 2))
x1 = np.linspace(-5, 5, 20)
x2 = np.linspace(-5, 5, 20)
xx1, xx2 = np.meshgrid(x1, x2, sparse=True)
z = true_function(xx1, xx2)
h = plt.contourf(x1, x2, z)
plt.gca().set_aspect('equal')
plt.title('true function')
true_function(xx1, xx2).shape
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
z = true_function(xx1, xx2)
ax.plot_surface(xx1, xx2, z)
ax.set_title('true function')
plt.show()
```
We'll simulate sampling 5 starting points.
```
x_samp = np.array([[0, 3], [1, 2], [1, -5], [-2, -2], [-2, 2], [2, -2], [3, 5]])
f_samp = true_function(x_samp[:, 0], x_samp[:, 1])
K_samp = sq_exp2d(x_samp, x_samp)
eps = 1E-6 * np.eye(len(x_samp))
L_samp = np.linalg.cholesky(K_samp + eps)
n = 35
x_points = np.linspace(-5, 5, n).reshape(-1, 1)
xx1, xx2 = np.meshgrid(x_points, x_points, sparse=False)
x_spts = np.vstack([xx1.flatten(), xx2.flatten()])
K_ss = sq_exp2d(x_spts.T, x_spts.T)
K_s = sq_exp2d(x_samp, x_spts.T)
mu_cond = K_s.T @ np.linalg.inv(K_samp) @ f_samp.flatten()
sig_cond = K_ss - K_s.T @ np.linalg.inv(K_samp) @ K_s
n_samps = 1000
f_posterior = np.random.multivariate_normal(mu_cond, sig_cond, size=n_samps)
# for f in f_posterior:
# plt.plot(x_s, f, color='grey', alpha=0.1)
# plt.scatter(x_samp, f_samp)
# plt.plot(x_s, true_function(x_train))
# plt.plot(x_s, mu_cond.flatten())
f_posterior.reshape(n_samps, n, n).max(axis=0)
mu_cond.shape
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(xx1, xx2, mu_cond.reshape(n, n))
ax.set_title('mean')
plt.show()
lower, upper = np.percentile(f_posterior.reshape(n_samps, n, n), [2.5, 97.5], axis=0)
uncertainty = upper - lower
uncertainty.shape
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 5), sharex=True, sharey=True)
axes[0].contourf(xx1, xx2, uncertainty, levels=50)
axes[0].set_title('95% interval size')
axes[0].scatter(*x_samp.T, color='red')
axes[0].set_aspect('equal')
axes[0].set_ylim(-5, 5)
axes[0].set_xlim(-5, 5)
axes[1].contourf(xx1, xx2, true_function(xx1, xx2), levels=50)
axes[1].set_title('ground truth')
axes[1].scatter(*x_samp.T, color='red')
axes[1].set_aspect('equal')
axes[2].contourf(xx1, xx2, mu_cond.reshape(n, n), levels=50)
axes[2].set_title('mean')
axes[2].scatter(*x_samp.T, color='red')
axes[2].set_aspect('equal')
```
In the plot sabove, red dots mark where we have sampled points on the 2D grid.
The left plot shows the size of the 95% prediction interval at each point on the grid. We can see that we have the smallest uncertainty where we have sampled.
The middle plot shows ground truth, and the values where we have sampled data.
The right plot shows the value of the mean where we have sampled. It is evident that where we do not have better data, the function evaluations default to the mean function.
# Parting Thoughts
The key ingredient of a GP: A Kernel that can model "distance" of some kind between every pair of inputs. Thus, it isn't the number of dimensions that is limiting; it is the number of *data points that have been sampled* that is limiting! (Inversion of the matrix only depends on the data that we are conditioning on, and that is of order $O(n^3)$.)
```
x2_new, x1_new = np.where(uncertainty == uncertainty.max()) # row, then column, i.e. x2 then x1.
xx1_s, xx2_s = np.meshgrid(x_points, x_points, sparse=True)
xx1_s.flatten()[x1_new], xx2_s.flatten()[x2_new]
```
| true |
code
| 0.683842 | null | null | null | null |
|
# 7-11. 프로젝트 : 네이버 영화리뷰 감성분석 도전하기
이전 스텝까지는 영문 텍스트의 감정분석을 진행해 보았습니다. 그렇다면 이번에는 한국어 텍스트의 감정분석을 진행해 보면 어떨까요? 오늘 활용할 데이터셋은 네이버 영화의 댓글을 모아 구성된 Naver sentiment movie corpus입니다.
데이터 다운로드 없이 Cloud shell에서 해당 파일의 심볼릭 링크를 연결 해 주세요
### 평가기준
1. 다양한 방법으로 Text Classification 태스크를 성공적으로 구현하였다. (3가지 이상의 모델이 성공적으로 시도됨)
2. gensim을 활용하여 자체학습된 혹은 사전학습된 임베딩 레이어를 분석하였다. (gensim의 유사단어 찾기를 활용하여 자체학습한 임베딩과 사전학습 임베딩을 적절히 분석함)
3. 한국어 Word2Vec을 활용하여 가시적인 성능향상을 달성했다. (네이버 영화리뷰 데이터 감성분석 정확도를 85% 이상 달성함)
```
!pip install --upgrade gensim==3.8.3
```
### 1) 데이터 준비와 확인
```
import pandas as pd
import urllib.request
%matplotlib inline
import matplotlib.pyplot as plt
import re
from konlpy.tag import Okt
from tensorflow import keras
from tensorflow.keras.preprocessing.text import Tokenizer
import numpy as np
from tensorflow.keras.preprocessing.sequence import pad_sequences
from collections import Counter
# 데이터를 읽어봅시다.
train_data = pd.read_table('~/aiffel/sentiment_classification/data/ratings_train.txt')
test_data = pd.read_table('~/aiffel/sentiment_classification/data/ratings_test.txt')
train_data.head()
```
### 2) 데이터로더 구성
실습 때 다루었던 IMDB 데이터셋은 텍스트를 가공하여 imdb.data_loader() 메소드를 호출하면 숫자 인덱스로 변환된 텍스트와 word_to_index 딕셔너리까지 친절하게 제공합니다. 그러나 이번에 다루게 될 nsmc 데이터셋은 전혀 가공되지 않은 텍스트 파일로 이루어져 있습니다. 이것을 읽어서 imdb.data_loader()와 동일하게 동작하는 자신만의 data_loader를 만들어 보는 것으로 시작합니다. data_loader 안에서는 다음을 수행해야 합니다.
- 데이터의 중복 제거
- NaN 결측치 제거
- 한국어 토크나이저로 토큰화
- 불용어(Stopwords) 제거
- 사전word_to_index 구성
- 텍스트 스트링을 사전 인덱스 스트링으로 변환
- X_train, y_train, X_test, y_test, word_to_index 리턴
```
from konlpy.tag import Mecab
tokenizer = Mecab()
stopwords = ['의','가','이','은','들','는','좀','잘','걍','과','도','를','으로','자','에','와','한','하다']
def load_data(train_data, test_data, num_words=10000):
train_data.drop_duplicates(subset=['document'], inplace=True)
train_data = train_data.dropna(how = 'any')
test_data.drop_duplicates(subset=['document'], inplace=True)
test_data = test_data.dropna(how = 'any')
X_train = []
for sentence in train_data['document']:
temp_X = tokenizer.morphs(sentence) # 토큰화
temp_X = [word for word in temp_X if not word in stopwords] # 불용어 제거
X_train.append(temp_X)
X_test = []
for sentence in test_data['document']:
temp_X = tokenizer.morphs(sentence) # 토큰화
temp_X = [word for word in temp_X if not word in stopwords] # 불용어 제거
X_test.append(temp_X)
words = np.concatenate(X_train).tolist()
counter = Counter(words)
counter = counter.most_common(10000-4)
vocab = ['', '', '', ''] + [key for key, _ in counter]
word_to_index = {word:index for index, word in enumerate(vocab)}
def wordlist_to_indexlist(wordlist):
return [word_to_index[word] if word in word_to_index else word_to_index[''] for word in wordlist]
X_train = list(map(wordlist_to_indexlist, X_train))
X_test = list(map(wordlist_to_indexlist, X_test))
return X_train, np.array(list(train_data['label'])), X_test, np.array(list(test_data['label'])), word_to_index
X_train, y_train, X_test, y_test, word_to_index = load_data(train_data, test_data)
index_to_word = {index:word for word, index in word_to_index.items()}
# 문장 1개를 활용할 딕셔너리와 함께 주면, 단어 인덱스 리스트 벡터로 변환해 주는 함수입니다.
# 단, 모든 문장은 <BOS>로 시작하는 것으로 합니다.
def get_encoded_sentence(sentence, word_to_index):
return [word_to_index['<BOS>']]+[word_to_index[word] if word in word_to_index else word_to_index['<UNK>'] for word in sentence.split()]
# 여러 개의 문장 리스트를 한꺼번에 단어 인덱스 리스트 벡터로 encode해 주는 함수입니다.
def get_encoded_sentences(sentences, word_to_index):
return [get_encoded_sentence(sentence, word_to_index) for sentence in sentences]
# 숫자 벡터로 encode된 문장을 원래대로 decode하는 함수입니다.
def get_decoded_sentence(encoded_sentence, index_to_word):
return ' '.join(index_to_word[index] if index in index_to_word else '<UNK>' for index in encoded_sentence[1:]) #[1:]를 통해 <BOS>를 제외
# 여러 개의 숫자 벡터로 encode된 문장을 한꺼번에 원래대로 decode하는 함수입니다.
def get_decoded_sentences(encoded_sentences, index_to_word):
return [get_decoded_sentence(encoded_sentence, index_to_word) for encoded_sentence in encoded_sentences]
# encode가 정상적으로 decode 되는지 확인
print(X_train[0])
print(get_decoded_sentence(X_train[0], index_to_word))
print('라벨: ', y_train[0]) # 1번째 리뷰데이터의 라벨
```
#### 데이터셋에 PAD, BOS, UNK가 없다.
확인해 보면, 앞쪽에 있어야 할 PAD, BOS, UNK가 나타나지 않았음을 알 수 있다. 이들을 각각 index 0, 1, 2로 대응시켜 딕셔너리에 포함시킨다.
```
word_to_index
word_to_index["<PAD>"] = 0 # 패딩
word_to_index["<BOS>"] = 1 # 모든 문장의 시작
word_to_index["<UNK>"] = 2 # Unknown을 의미
index_to_word = {index:word for word, index in word_to_index.items()}
```
### 3) 모델구성을 위한 데이터 분석 및 가공
- 데이터셋 내 문장 길이 분포
- 적절한 최대 문장 길이 지정
= 문장 최대 길이 maxlen의 값 설정도 전체 모델 성능에 영향을 미치게 된다. 이 길이도 적절한 값을 찾기 위해서는 전체 데이터셋의 분포를 확인해 보는 것이 좋다.
- keras.preprocessing.sequence.pad_sequences 을 활용한 패딩 추가
```
# 데이터셋 내의 문장길이분포
print(X_train[0]) # 1번째 리뷰데이터
print('라벨: ', y_train[0]) # 1번째 리뷰데이터의 라벨
print('1번째 리뷰 문장 길이: ', len(X_train[0]))
print('2번째 리뷰 문장 길이: ', len(X_train[1]))
# 적절한 최대문장길이 지정
total_data_text = list(X_train) + list(X_test)
# 텍스트데이터 문장길이의 리스트를 생성한 후
num_tokens = [len(tokens) for tokens in total_data_text]
num_tokens = np.array(num_tokens)
# 문장길이의 평균값, 최대값, 표준편차를 계산
print('문장길이 평균 : ', np.mean(num_tokens))
print('문장길이 최대 : ', np.max(num_tokens))
print('문장길이 표준편차 : ', np.std(num_tokens))
# 예를들어, 최대 길이를 (평균 + 2*표준편차)로 한다면,
max_tokens = np.mean(num_tokens) + 2 * np.std(num_tokens)
maxlen = int(max_tokens)
print('pad_sequences maxlen : ', maxlen)
print('전체 문장의 {}%가 maxlen 설정값 이내에 포함됩니다. '.format(np.sum(num_tokens < max_tokens) / len(num_tokens)))
print('리뷰의 최대 길이 :',max(len(l) for l in X_train))
print('리뷰의 평균 길이 :',sum(map(len, X_train)) / len(X_train))
plt.hist([len(s) for s in X_train], bins=50)
plt.xlabel('length of samples')
plt.ylabel('number of samples')
plt.show()
```
##### 처음에 maxlen의 값을 높였을 때 전체 문장이 maxlen 설정값 이내에 포함되는 값이 클 수록 좋은 것이라고 생각했다.
##### 다만 문장길이가 너무 긴 이상치를 가진 데이터를 제거하고 학습하는 것이 더 효율적이라고 판단하여 maxlen을 int(평균 + 2*표준편차)로 지정하였다.
```
X_train = keras.preprocessing.sequence.pad_sequences(X_train,
value=word_to_index["<PAD>"],
padding='post',
maxlen=maxlen)
X_test = keras.preprocessing.sequence.pad_sequences(X_test,
value=word_to_index["<PAD>"],
padding='post',
maxlen=maxlen)
print(X_train.shape)
X_train[0]
# 훈련 데이터 앞쪽 50000개 까지 validation set으로 사용
X_val = X_train[:50000]
y_val = y_train[:50000]
# validation set을 제외한 나머지는 모두 훈련 데이터로 사용
partial_x_train = X_train[50000:]
partial_y_train = y_train[50000:]
print(partial_x_train.shape)
print(partial_y_train.shape)
print(X_val.shape)
print(y_val.shape)
```
### 4) 모델구성 및 validation set 구성
모델은 3가지 이상 다양하게 구성하여 실험해 보세요.
#### 1-D Conv
```
vocab_size = 10000 # 어휘 사전의 크기입니다(10개의 단어)
word_vector_dim = 16 # 단어 하나를 표현하는 임베딩 벡터의 차원 수입니다.
model = keras.Sequential()
model.add(keras.layers.Embedding(vocab_size, word_vector_dim, input_shape=(None,)))
model.add(keras.layers.Conv1D(16, 7, activation='relu'))
model.add(keras.layers.MaxPooling1D(5))
model.add(keras.layers.Conv1D(16, 7, activation='relu'))
model.add(keras.layers.GlobalMaxPooling1D())
model.add(keras.layers.Dense(8, activation='relu'))
model.add(keras.layers.Dense(1, activation='sigmoid')) # 최종 출력은 긍정/부정을 나타내는 1dim 입니다.
model.summary()
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
epochs = 10
history = model.fit(partial_x_train,
partial_y_train,
epochs=epochs,
batch_size=512,
validation_data=(X_val, y_val),
verbose=1)
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(history.history['loss'], marker='.', c='red', label='Train Loss')
plt.plot(history.history['val_loss'], marker='.', c='blue', label='Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(history.history['accuracy'], 'g--', label='Train accuracy')
plt.plot(history.history['val_accuracy'], 'k--', label='Validation accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim(0, 1)
plt.legend()
plt.show()
# 모델 평가
results = model.evaluate(X_test, y_test, verbose=2)
print(results)
```
#### LSTM
```
from tensorflow.keras.layers import Embedding, LSTM, Dense, Bidirectional, GRU
# Optimizer를 인수로 받는 train_model() 함수
def train_model(Optimizer, X_train, y_train, X_val, y_val):
model = keras.Sequential()
model.add(Embedding(input_dim=10000, output_dim=16))
model.add(LSTM(units=128))
model.add(Dense(units=1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer=Optimizer,
metrics=['accuracy'])
scores = model.fit(X_train, y_train, batch_size=512,
epochs=10,
validation_data=(X_val, y_val),
verbose=1)
return scores, model
RMSprop_score, RMSprop_model = train_model(Optimizer='RMSprop',
X_train=partial_x_train,
y_train=partial_y_train,
X_val=X_val,
y_val=y_val)
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(RMSprop_score.history['loss'], marker='.', c='red', label='Train Loss')
plt.plot(RMSprop_score.history['val_loss'], marker='.', c='blue', label='Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(RMSprop_score.history['accuracy'], 'g--', label='Train accuracy')
plt.plot(RMSprop_score.history['val_accuracy'], 'k--', label='Validation accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim(0, 1)
plt.legend()
plt.show()
# 모델 평가
results = RMSprop_model.evaluate(X_test, y_test, verbose=2)
print(results)
```
정확도를 85.10을 달성할 수 있었다.
#### Confusion Matrix
```
from sklearn.metrics import confusion_matrix
import seaborn as sns
plt.figure(figsize=(10, 7))
sns.set(font_scale=2)
y_test_pred = RMSprop_model.predict_classes(X_test)
c_matrix = confusion_matrix(y_test, y_test_pred)
ax = sns.heatmap(c_matrix, annot=True, xticklabels=['Negative Sentiment', 'Positive Sentiment'],
yticklabels=['Negative Sentiment', 'Positive Sentiment'], cbar=False, cmap='Blues', fmt='g')
ax.set_xlabel("Prediction")
ax.set_ylabel("Actual")
plt.show()
```
대부분의 예측은 맞았다. 틀린거는 negative 4568개, positive 2758개 였다.
```
false_negatives = [] # 예측은 부정. 실제로는 긍정적인 리뷰
false_positives = [] # 에측은 긍적. 실제로는 부정적인 리뷰
for i in range(len(y_test_pred)):
if y_test_pred[i][0] != y_test[i]:
if y_test[i] == 0: # FP: False Positive
false_positives.append(i)
else: # FN
false_negatives.append(i)
print(false_negatives[20])
print(false_negatives[30])
print(false_negatives[100])
# 실제로는 긍정적인 리뷰이지만 예측은 부정으로 한 케이스
string_1 = get_decoded_sentence(X_test[100], index_to_word).replace("<PAD>", "").strip()
string_2 = get_decoded_sentence(X_test[500], index_to_word).replace("<PAD>", "").strip()
string_3 = get_decoded_sentence(X_test[3000], index_to_word).replace("<PAD>", "").strip()
print(string_1)
print(string_2)
print(string_3)
print(false_positives[200])
print(false_positives[500])
print(false_positives[1500])
# 실제로는 부정적인 리뷰이지만 예측은 긍정으로 한 케이스
string_1 = get_decoded_sentence(X_test[1000], index_to_word).replace("<PAD>", "").strip()
string_2 = get_decoded_sentence(X_test[15000], index_to_word).replace("<PAD>", "").strip()
string_3 = get_decoded_sentence(X_test[30000], index_to_word).replace("<PAD>", "").strip()
print(string_1)
print(string_2)
print(string_3)
```
#### 딥러닝
```
vocab_size = 10000 # 어휘 사전의 크기입니다(10,000개의 단어)
word_vector_dim = 16 # 워드 벡터의 차원 수 (변경 가능한 하이퍼파라미터)
# model 설계 - 딥러닝 모델 코드를 직접 작성해 주세요.
model = keras.Sequential()
# [[YOUR CODE]]
model.add(keras.layers.Embedding(vocab_size, word_vector_dim, input_shape=(None,)))
model.add(keras.layers.Conv1D(16, 7, activation='relu'))
model.add(keras.layers.MaxPooling1D(5))
model.add(keras.layers.Conv1D(16, 7, activation='relu'))
model.add(keras.layers.GlobalMaxPooling1D())
model.add(keras.layers.Dense(8, activation='relu'))
model.add(keras.layers.Dense(8, activation='relu'))
model.add(keras.layers.Dense(1, activation='sigmoid')) # 최종 출력은 긍정/부정을 나타내는 1dim 입니다.
model.summary()
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
epochs=10 # 몇 epoch를 훈련하면 좋을지 결과를 보면서 바꾸어 봅시다.
history = model.fit(partial_x_train,
partial_y_train,
epochs=epochs,
batch_size=512,
validation_data=(X_val, y_val),
verbose=1)
results = model.evaluate(X_test, y_test, verbose=2)
print(results)
history_dict = history.history
print(history_dict.keys()) # epoch에 따른 그래프를 그려볼 수 있는 항목들
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
loss = history_dict['loss']
val_loss = history_dict['val_loss']
epochs = range(1, len(acc) + 1)
# "bo"는 "파란색 점"입니다
plt.plot(epochs, loss, 'bo', label='Training loss')
# b는 "파란 실선"입니다
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf() # 그림을 초기화합니다
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
```
#### Word2Vec
이전 스텝에서 라벨링 비용이 많이 드는 머신러닝 기반 감성분석의 비용을 절감하면서 정확도를 크게 향상시킬 수 있는 자연어처리 기법으로 단어의 특성을 저차원 벡터값으로 표현할 수 있는 워드 임베딩(word embedding) 기법이 있다는 언급을 한 바 있습니다.
우리는 이미 이전 스텝에서 워드 임베딩을 사용했습니다. 사용했던 model의 첫 번째 레이어는 바로 Embedding 레이어였습니다. 이 레이어는 우리가 가진 사전의 단어 개수 X 워드 벡터 사이즈만큼의 크기를 가진 학습 파라미터였습니다. 만약 우리의 감성분류 모델이 학습이 잘 되었다면, Embedding 레이어에 학습된 우리의 워드 벡터들도 의미 공간상에 유의미한 형태로 학습되었을 것입니다. 한번 확인해 봅시다.
## Embedding layer analysis
```
import os
import gensim
# genism = opensource library for the unsupervised learning and NLP
from gensim.models.keyedvectors import Word2VecKeyedVectors
from tensorflow.keras.initializers import Constant
embedding_layer = model.layers[0]
weights = embedding_layer.get_weights()[0]
print(weights.shape)
word2vec_file_path = os.getenv('HOME')+'/aiffel/EXP_07_sentiment_classification/word2vec.txt'
f = open(word2vec_file_path, 'w')
f.write('{} {}\n'.format(vocab_size-4, word_vector_dim))
vectors = model.get_weights()[0]
for i in range(4,vocab_size):
f.write('{} {}\n'.format(index_to_word[i], ' '.join(map(str, list(vectors[i, :])))))
f.close()
```
- 학습한 embedding parameter를 파일에 적어서 저장
- for문을 이용하여, 특수 문자를 제외한 단어 갯수 만큼의 워드 벡터를 파일에 기록
```
word_vectors = Word2VecKeyedVectors.load_word2vec_format(word2vec_file_path, binary=False)
word_vectors.similar_by_word("사랑")
```
- 파일에 기록된 embedding parameter를 이용하여, word vector로 활용
- 주어진 단어를 기준으로 유사한 단어, 유사도를 출력
- '사랑'이라는 단어를 기준으로 유사도를 확인해본 결과, 연관성이 없다고 봐도 무방할 정도의 단어들이 출력
- 해당 단어들의 유사도는 0.85 이상으로, 꽤 높은 유사도를 보여주고 있음
- 실제 유사한 단어가 아님에도 높은 유사도를 보이는 것은, 주어진 단어가 한글이기 때문에 gensim이 잘 작동하지 않는다고 판단됨
### 한국어 Word2Vec 임베딩 활용하여 성능개선
한국어 Word2Vec은 다음 경로에서 구할 수 있습니다.
- Pre-trained word vectors of 30+ languages (https://github.com/Kyubyong/wordvectors)
```
embedding_layer = model.layers[0]
weights = embedding_layer.get_weights()[0]
print(weights.shape) # shape: (vocab_size, embedding_dim)
import os
# 학습한 Embedding 파라미터를 파일에 써서 저장합니다.
word2vec_file_path = os.getenv('HOME')+'/aiffel/sentiment_classification/data/word2vec.txt'
f = open(word2vec_file_path, 'w')
f.write('{} {}\n'.format(vocab_size-4, word_vector_dim)) # 몇개의 벡터를 얼마 사이즈로 기재할지 타이틀을 씁니다.
# 단어 개수(에서 특수문자 4개는 제외하고)만큼의 워드 벡터를 파일에 기록합니다.
vectors = model.get_weights()[0]
for i in range(4,vocab_size):
f.write('{} {}\n'.format(index_to_word[i], ' '.join(map(str, list(vectors[i, :])))))
f.close()
from gensim.models.keyedvectors import Word2VecKeyedVectors
word_vectors = Word2VecKeyedVectors.load_word2vec_format(word2vec_file_path, binary=False)
vector = word_vectors['사랑']
vector
word_vectors.similar_by_word("재밌")
# 유사도를 분석!
from gensim.models import KeyedVectors
word2vec_path = os.getenv('HOME')+'/aiffel/EXP_07_sentiment_classification/word2vec/ko.tar.gz'
word2vec = KeyedVectors.load_word2vec_format(word2vec_path, binary=True, limit=1000000)
vector = word2vec['영화']
vector # 무려 300dim의 워드 벡터입니다.
```
| true |
code
| 0.216777 | null | null | null | null |
|
# Gather statistics about iterative point position & tagger precision estimation procedue
Perform $N_e$ experiments, in which data is simulated and used for the estimation procedure:
Simulate points $x_j$, tags $x_{ji} \sim N(x_j,\sigma_i^2)$ for N points ($j=1,...,N$) and $N_t$ taggers ($i=1,...,N_t$).
Peform the estimation procedure, and gather data after convergence:
1. The MSE for the estimation of $x_j$ (using the estimated sigmas, the real sigmas, and an equal-weight average)
2. The MSE for the estimation of $\sigma_i$
Gather data for different $N_t$, $\beta$.
```
import numpy as np
from numpy import linalg as LA
import matplotlib.pyplot as plt
import scipy
```
### Define functions that 1. Simulate the data 2. Run the estimation procedure
```
def simulate_data(N,Nt):
''' Simulate ground truth points, tagger properties, and tags
Args:
N (int): The number of ground truth points to simulate
Nt (ind): The number of taggers
Returns:
gt_pos: a (N,2) np.array with ground truth positions in 2D
sigma_sq: a length Nt np.array containing sigma**2 of tagger i in index i
clusters: length N array. clusters[i][0]: a list of taggers that tagged the i-th gt point,
clusters[i][1]: the tags generated for the i-th gt point
'''
L = 100 # gt points will be in [0,L]x[0,L]
# properties of taggers
# draw the values of the pi's from a uniform distribution in [0,1]
p = np.random.uniform(low=1, high=1, size=(Nt)) #p[i] is the detection probability of tagger i
sigma_sq = np.random.uniform(low=0.5, high=3, size=(Nt))**2 # sigma_sq[i] is the var of position tagged by tagger i
# draw ground truth position uniformly in [0,L] x [0,L]
gt_pos = np.random.uniform(low=0,high=L,size=(N,2))
# simulate tags for each of the clusters
clusters = [None]*N # if there are no tags for gt point k, clusters[k] will remain None
cluster_is_tagged = [False]*N # cluster_is_tagged[k]==True iff there is at least one tag for gt point k
for k in range(N):
is_tagged = [np.random.binomial(n=1,p=p[i]) for i in range(Nt)]
tagged_ind = np.where(is_tagged)[0]
# if no tags exist, don't save this cluster
if any(is_tagged):
#tagged_ind = list(range(Nt))
tags = np.zeros((len(tagged_ind),2))
for j,i in enumerate(tagged_ind): # loop over tags that exist
# draw position from normal distribution
tags[j,:] = np.random.multivariate_normal(mean=gt_pos[k,:],cov=sigma_sq[i]*np.identity(2))
clusters[k] = (tagged_ind, tags)
cluster_is_tagged[k] = True
# only worked with tagged points - through away the untagged ones
Neffective = sum(cluster_is_tagged) # the number of tagged gt points
if Neffective<N:
gt_pos = gt_pos[cluster_is_tagged,:]
clusters = np.array(clusters)
clusters = clusters[cluster_is_tagged]
return sigma_sq, gt_pos, clusters
# given sigma_sq_est, estimate the gt position
def update_pos(clusters, sigma_sq_est, N, beta=0):
# beta = regularization parameter to prevent weight divergence to infinity
gt_pos_est = np.zeros((N,2))
for k in range(N): # loop over clusters
tagged_ind, tags = clusters[k]
weights = np.expand_dims(1/(sigma_sq_est[tagged_ind]+beta), axis=-1)
gt_pos_est[k,:] = np.sum(tags*weights,axis=0) / np.sum(weights)
return gt_pos_est
def update_sigma_sq(clusters, gt_pos_est, N, Nt):
# given estimated positions, estimate sigma_sq[i]
# for each cluster, accumulate data for all tags that exist.
# keep count of how many points have from each, then divide
s = np.zeros(Nt) # s[i] = sum over (x-gt)**2 for tagger i (2D since have x,y)
count = np.zeros(Nt) # count[i] = number of data points for tagger i
for k in range(N): # loop over clusters
tagged_ind, tags = clusters[k]
gt_pos_est_k = gt_pos_est[k,:]
shifted_tags = tags - gt_pos_est_k
s[tagged_ind] += np.sum(shifted_tags**2, axis=1)
count[tagged_ind] += 2 # summed samples (each point gives 1 sample for x, 1 for y)
s = s / (count-1) # estimator of sigma squared
# lower bound possible s values:
#s_sq_min = 0.1
#s[s<s_sq_min] = s_sq_min
return s #sigma_sq_est
def estimate_positions_and_sigmas(N,Nt,clusters,beta):
''' Perform iterations to estimate the positions and sigmas.
Args:
clusters: length N array. clusters[i][0]: a list of taggers that tagged the i-th gt point,
clusters[i][1]: the tags generated for the i-th gt point
diff_thresh (float): a threshold for determining convergence
(small number below which can say the algorithm converged)
beta: regulrization parameter
Returns:
gt_pos_est, sigma_sq_est - estimates of gt positions, sigmas
'''
# set estimates to initial values
#p_est = 0.7*np.ones(Nt)
sigma_sq_est = 1*np.ones(Nt)
gt_pos_est = np.zeros((N,2))
diff_thresh = 1e-10
counter = 0
Nsteps_max= 1000 # if no convergence until reached, exit and display message
# perform first step of gt and sigma estimation
gt_pos_est_prev = gt_pos_est # save previous estimate
gt_pos_est = update_pos(clusters, sigma_sq_est, N, beta=beta)
sigma_sq_est = update_sigma_sq(clusters, gt_pos_est, N, Nt)
while LA.norm(gt_pos_est - gt_pos_est_prev)>diff_thresh:
gt_pos_est_prev = gt_pos_est
gt_pos_est = update_pos(clusters, sigma_sq_est, N, beta=beta)
sigma_sq_est = update_sigma_sq(clusters, gt_pos_est, N, Nt)
counter += 1
if counter==Nsteps_max:
print('Exited without converging after ' + str(Nsteps_max) + ' steps.')
break
#print(counter, LA.norm(gt_pos_est - gt_pos_est_prev))
#else:
#print('Converged after ', counter, ' steps.')
return gt_pos_est, sigma_sq_est
```
### Set parameters, initialize variables to collect results
```
#Ns = 1000 # number of repeats for each parameter value
Ns = 30
N = 2000 # number of points simulated in each instance
Nt = 3 # number of taggers
beta_list = np.arange(0,2,0.2)
#beta_list = np.array([0,0.25,0.5,0.75,1])
Nbeta = len(beta_list)
# beta = 1
# sigma_sq, gt_pos, clusters = simulate_data(N,Nt)
# gt_pos_est, sigma_sq_est = estimate_positions_and_sigmas(N,Nt,clusters,beta)
# collect stats
# initialize variables
min_sigma_sq = np.zeros((Ns,Nbeta))
pos_mse = np.zeros((Ns,Nbeta))
sigma_sq_mse = np.zeros((Ns,Nbeta))
pos_mse_real_sigma = np.zeros((Ns))
pos_mse_naive_average = np.zeros((Ns))
import time
t = time.time()
# for each instance of simulated data, perform the estimation with varying beta
for i in range(Ns):
sigma_sq, gt_pos, clusters = simulate_data(N,Nt) # simulate data
for j, beta in enumerate(beta_list):
gt_pos_est, sigma_sq_est = estimate_positions_and_sigmas(N,Nt,clusters,beta) # perform estimation
# collect stats about estimation result
min_sigma_sq[i,j] = min(sigma_sq_est)
SE_pos_est = np.sum((gt_pos_est - gt_pos)**2,axis=1)
pos_mse[i,j] = np.mean(SE_pos_est)
sigma_diff = sigma_sq - sigma_sq_est
sigma_sq_mse[i,j] = np.mean(sigma_diff**2)
# collect stats about instance of simulated data
gt_pos_est_real_s = update_pos(clusters, sigma_sq, N)
SE_real_s_est = np.sum((gt_pos_est_real_s - gt_pos)**2,axis=1)
pos_mse_real_sigma[i] = np.mean(SE_real_s_est)
gt_pos_est_equal_s = update_pos(clusters, np.ones(sigma_sq.shape), N)
SE_equal_s_est = np.sum((gt_pos_est_equal_s - gt_pos)**2,axis=1)
pos_mse_naive_average[i] = np.mean(SE_equal_s_est)
elapsed = time.time() - t
print(elapsed/60)
```
## plot results
```
mean_min_sigma = np.mean(min_sigma_sq, axis=0) # mean over instances, as function of beta
plt.plot(beta_list,mean_min_sigma,'.b')
plt.xlabel('$\\beta$',fontsize=16)
plt.ylabel('$min_i \hat{\sigma}_i$',fontsize=16);
plt.xticks(fontsize=14)
plt.yticks(fontsize=14);
from scipy import stats
mean_pos_mse = np.mean(pos_mse,axis=0) # mean over Ns simulated data instances
mean_pos_mse_real_sigma = np.mean(pos_mse_real_sigma)
mean_pos_mse_naive_average = np.mean(pos_mse_naive_average)
std_pos_mse = np.std(pos_mse,axis=0) # mean over Ns simulated data instances
std_pos_mse_real_sigma = np.std(pos_mse_real_sigma)
std_pos_mse_naive_average = np.std(pos_mse_naive_average)
sem_pos_mse = scipy.stats.sem(pos_mse,axis=0) # mean over Ns simulated data instances
sem_pos_mse_real_sigma = scipy.stats.sem(pos_mse_real_sigma)
sem_pos_mse_naive_average = scipy.stats.sem(pos_mse_naive_average)
plt.figure()
h = [None]*3
h[0], = plt.plot(beta_list,mean_pos_mse,'.--b')
h[1], = plt.plot(beta_list,np.ones(len(beta_list))*mean_pos_mse_real_sigma,'--g')
h[2], = plt.plot(beta_list,np.ones(len(beta_list))*mean_pos_mse_naive_average,'--r')
plt.fill_between(beta_list, mean_pos_mse - sem_pos_mse, mean_pos_mse + sem_pos_mse, color='blue', alpha=0.2)
#plt.errorbar(beta_list,mean_pos_mse,sem_pos_mse)
plt.fill_between(beta_list, np.ones(len(beta_list))*mean_pos_mse_real_sigma - np.ones(len(beta_list))*sem_pos_mse_real_sigma, np.ones(len(beta_list))*mean_pos_mse_real_sigma + np.ones(len(beta_list))*sem_pos_mse_real_sigma, color='green', alpha=0.2)
plt.fill_between(beta_list, np.ones(len(beta_list))*mean_pos_mse_naive_average - np.ones(len(beta_list))*sem_pos_mse_naive_average, np.ones(len(beta_list))*mean_pos_mse_naive_average + np.ones(len(beta_list))*sem_pos_mse_naive_average, color='red', alpha=0.2)
plt.xlabel('$\\beta$',fontsize=16)
plt.ylabel('MSE of $x_j$ estimate',fontsize=16);
plt.xticks(fontsize=14)
plt.yticks(fontsize=14);
plt.legend(h, ('est','real $\sigma_i$','naive'));
mean_sigma_sq_mse = np.mean(sigma_sq_mse, axis=0) # mean over instances, as function of beta
sem_sigma_sq_mse = scipy.stats.sem(sigma_sq_mse, axis=0) # mean over instances, as function of beta
#plt.plot(beta_list,mean_sigma_sq_mse,'.b')
plt.errorbar(beta_list,mean_sigma_sq_mse,sem_sigma_sq_mse,fmt='o')
plt.xlabel('$\\beta$',fontsize=16)
plt.ylabel('$MSE (\hat{\sigma}_i)$',fontsize=16);
plt.xticks(fontsize=14)
plt.yticks(fontsize=14);
```
| true |
code
| 0.69748 | null | null | null | null |
|
# SageMaker Tensorflow 컨테이너를 사용하여 하이퍼파라미터 튜닝하기
## [(원본)](https://github.com/awslabs/amazon-sagemaker-examples/tree/master/hyperparameter_tuning/tensorflow_mnist)
이 문서는 **SageMaker TensorFlow container**를 사용하여 [MNIST dataset](http://yann.lecun.com/exdb/mnist/)을 훈련시키기 위해 convolutional neural network 모델을 만드는 방법에 초점을 두고 있습니다.
이것은 하이퍼파라미터 튜닝을 활용하여 서로 다른 하이퍼파라미터를 조합하여 여러 훈련 Job을 실행함으로써 최상의 모델 훈련 결과를 제공하게 됩니다.
## 환경 설정
워크플로우를 시작하기 전에 몇가지 설정이 필요합니다.
1. 훈련 데이터셋과 모델 아티펙트가 저장될 s3버킷과 prefix를 지정합니다.
2. SageMaker가 s3와 같은 리소스를 접근할 수 있도록 실행 Role을 가져옵니다.
```
import sagemaker
bucket = '<My bucket name>'#sagemaker.Session().default_bucket() # we are using a default bucket here but you can change it to any bucket in your account
prefix = 'sagemaker/DEMO-hpo-tensorflow-high' # you can customize the prefix (subfolder) here
role = sagemaker.get_execution_role() # we are using the notebook instance role for training in this example
```
이제 필요한 Python 라이브러리를 import 합니다.
```
import boto3
from time import gmtime, strftime
from sagemaker.tensorflow import TensorFlow
from sagemaker.tuner import IntegerParameter, CategoricalParameter, ContinuousParameter, HyperparameterTuner
```
## MNIST 데이터셋 다운로드하기
```
import utils
from tensorflow.contrib.learn.python.learn.datasets import mnist
import tensorflow as tf
data_sets = mnist.read_data_sets('data', dtype=tf.uint8, reshape=False, validation_size=5000)
utils.convert_to(data_sets.train, 'train', 'data')
utils.convert_to(data_sets.validation, 'validation', 'data')
utils.convert_to(data_sets.test, 'test', 'data')
```
## 데이터 업로드하기
```sagemaker.Session.upload_data``` 함수를 이용하여 S3경로에 데이터셋을 업로드합니다. 해당 함수의 리턴값은 S3의 경로를 가르킵니다. 이 경로는 훈련 Job을 시작할 때 사용할 것입니다.
```
inputs = sagemaker.Session().upload_data(path='data', bucket=bucket, key_prefix=prefix+'/data/mnist')
print (inputs)
```
## 분산 훈련을 위한 스크립트 작성하기
다음은 네트워크 모델의 전체코드입니다.
```
!cat 'mnist.py'
```
이 스크립트는 [TensorFlow MNIST example](https://github.com/tensorflow/models/tree/master/official/mnist)를 수정한 것입니다.
이것은 훈련, 평가, 추론을 위해 사용되는```model_fn(features, labels, mode)`` 를 제공합니다.
### 일반적인 ```model_fn```
일반적인 **```model_fn```** 은 다음과 같은 패턴을 따릅니다.
1. [Neural network 정의](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L96)
- [Neural network에 ```features``` 적용](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L178)
- [```mode```가 ```PREDICT``` 이면 neural network에서 output 리턴](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L186)
- [Output과 ```labels```을 비교하는 loss fuction 계산](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L188)
- [Optimizer 생성 및 neural network 개선을 위한 loss function 최소화](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L193)
- [Output, optimizer, loss function 리턴](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L205)
### 분산 훈련에서의 ```model_fn``` 작성
분산 훈련이 일어나면, 동일한 neural network은 여러 훈련 인스턴스로 보내집니다. 개별 인스턴스는 데이터셋의 배치를 예측하고, loss를 계산하고 optimizer를 최소화합니다. 이 프로세스의 전체 루프를 **training step** 이라고 합니다.
#### training steps 동기화
A [global step](https://www.tensorflow.org/api_docs/python/tf/train/global_step)은 인스턴스 사이에 공유되는 전역 변수입니다.
그것은 분산 훈련에서 필요하기 때문에 Optimizer는 실행되는 중간에 **training steps** 의 수를 추척합니다.
```python
train_op = optimizer.minimize(loss, tf.train.get_or_create_global_step())
```
이것이 분산훈련을 위해 필요한 유일한 변경입니다!
## 하이퍼파라미터 튜닝 Job 설정
*참고: 아래의 기본 설정에서는 하이퍼파라미터 튜닝 Job이 완료하는데 30분이 소요될 수 있습니다.*
이제 다음 단계에 따라 SageMaker Python SDK를 사용하여 하이퍼파라미터 튜닝 Job을 설정합니다.
* TensorFlow 훈련 Job 설정을 위한 estimator 생성하기
* 튜닝하려는 하이퍼파라미터 범위 정의하기. 이 예제에서는 "learning_rate"를 튜닝함
* 최적화할 튜닝 Job의 목표 메트릭 정의하기
* 위의 설정과 튜닝 Resource Configuratin으로 하이퍼파라미터 Tuner 생성
SageMaker에서 단일 TensorFlow Job을 훈련하는 것과 유사하게, TensorFlow 스크립트, IAM role, (작업별)하드웨어 구성을 전달하는 TensorFlow estimator를 정의합니다.
```
estimator = TensorFlow(entry_point='mnist.py',
role=role,
framework_version='1.12.0',
training_steps=1000,
evaluation_steps=100,
train_instance_count=1,
train_instance_type='ml.m4.xlarge',
base_job_name='DEMO-hpo-tensorflow')
```
Once we've defined our estimator we can specify the hyperparameters we'd like to tune and their possible values. We have three different types of hyperparameters.
estimator를 정의하고 나면 튜닝하려는 하이퍼파라미터과 가능한 값을 지정할 수 있습니다. 하이퍼파라미터는 세 가지 유형이 있습니다.
- 범주형 파라미터는 이산형 셋(discrete set)에서 하나의 값을 가져야 합니다. 가능한 값 목록을 `CategoricalParameter(list)`으로 전달하여 정의합니다
- 연속형 파라미터는 `ContinuousParameter(min, max)` 에서 정의한 최소값과 최대값 사이의 실수 값을 가질 수 있습니다.
- 정수형 파라미터는 `IntegerParameter(min, max)`에서 정의한 최소값과 최대값 사이의 정수 값을 가질 수 있습니다.
*참고: 가능하면 값을 최소한의 restrictive type을 지정하는 것이 거의 항상 좋습니다. 예를 들면, learning rate는 연속값으로 0.01에서 0.2로 튜닝하는 것이 0.01, 0.1, 0.15 혹은 0.2의 범주형 파라미터로 튜닝하는 것보다 더 나은 결과를 얻을 수 있습니다.*
```
hyperparameter_ranges = {'learning_rate': ContinuousParameter(0.01, 0.02)}
```
다음으로 튜닝을 위한 목표 매트릭과 그것을 정의하기 위한 설정을 진행합니다. 이것은 훈련 Job이 CloudWatch 로그로부터 매트릭을 추출하는데 필요한 정규표현식(Regex)를 포함합니다. 이 경우, 스크립트는 loss값을 방출하고 목표 매트릭은 이를 목표 매트릭으로 사용할 것입니다. 또한 최상의 하이퍼파라미터 설정을 찾을 때, 목표 매트릭을 최소화하기 하이퍼파라미터를 튜닝하기 위해 objective_type은 'minimize'로 설정합니다. default로 objective_type은 'maximize' 설정됩니다.
```
objective_metric_name = 'loss'
objective_type = 'Minimize'
metric_definitions = [{'Name': 'loss',
'Regex': 'loss = ([0-9\\.]+)'}]
```
이제 `HyperparameterTuner` 객체를 생성할 것이고, 객체에 다음 값들이 전달됩니다.:
- 위에서 생성한 TensorFlow estimator
- 하이퍼파라미터 범위
- 목표 매트릭 이름 및 정의
- 총 훈련 Job의 갯수와 병렬적으로 실행할 훈련 Job의 수와 같은 튜닝 resource configurations
```
tuner = HyperparameterTuner(estimator,
objective_metric_name,
hyperparameter_ranges,
metric_definitions,
max_jobs=9,
max_parallel_jobs=3,
objective_type=objective_type)
```
## 하이퍼파라미터 튜닝 Job 시작하기
마지막으로 `.fit()`을 호출하고 훈련 및 테스트 데이터셋의 S3 경로를 전달함에 따라 하이퍼파라미터 훈련 Job을 시작할 수 있습니다.
하이퍼파라미터 튜닝 Job이 생성된 후, 다음 단계에서 진행 상태를 보기위해 위해 튜닝 Job을 describe 할 수있어야 합니다. SageMaker의 콘솔->Jobs으로 이동하여 하이퍼파라미터의 튜닝 Job의 진행상태를 확인할 수 있습니다.
```
tuner.fit(inputs)
```
하이퍼파라미터 튜닝 Job을 간단히 체크해하여 성공적으로 시작했는지 확인하시기 바랍니다.
```
boto3.client('sagemaker').describe_hyper_parameter_tuning_job(
HyperParameterTuningJobName=tuner.latest_tuning_job.job_name)['HyperParameterTuningJobStatus']
```
## 튜닝 Job 완료 후, 결과 분석하기
튜닝 Job 결과를 분석하기 위해 "HPO_Analyze_TuningJob_Results.ipynb" 예제를 참조하십시오.
## 최상의 모델 배포하기
이제 최상의 모델을 얻었으며, endpoint에서 배포할 수 있습니다. 모델을 배포하는 방법은 SageMaker sample notebook이나 SageMaker documentation을 참고하시기 바랍니다.
| true |
code
| 0.679923 | null | null | null | null |
|
<div style="width: 100%; overflow: hidden;">
<div style="width: 150px; float: left;"> <img src="data/D4Sci_logo_ball.png" alt="Data For Science, Inc" align="left" border="0"> </div>
<div style="float: left; margin-left: 10px;"> <h1>Graphs and Networks</h1>
<h2>Lesson II - Graph Properties</h2>
<p>Bruno Gonçalves<br/>
<a href="http://www.data4sci.com/">www.data4sci.com</a><br/>
@bgoncalves, @data4sci</p></div>
</div>
```
from collections import Counter
from pprint import pprint
import numpy as np
import matplotlib.pyplot as plt
import watermark
%load_ext watermark
%matplotlib inline
```
We start by print out the versions of the libraries we're using for future reference
```
%watermark -n -v -m -g -iv
```
Load default figure style
```
plt.style.use('./d4sci.mplstyle')
```
# Graph class
We now integrate our prefered graph representation into a class that we can build on. For now we provide it with just placeholders for our data
```
class Graph:
def __init__(self, directed=False):
self._nodes = {}
self._edges = {}
self._directed = directed
```
For ease of explanation, we will be adding methods to this class as we progress. To allow for this in a convenient way, we must declare a Python decorator that will be in charge of modifying the class as we implement further functionality
Understanding this function is not important for the scope of the lecture, but if you are curious, you cna find more information on [Decorators](https://www.python.org/dev/peps/pep-0318/) and [setattr](https://docs.python.org/3/library/functions.html#setattr) in the offical Python documentation
```
def add_method(cls):
def decorator(func):
setattr(cls, func.__name__, func)
return func
return decorator
```
We can already instanciate our skeleton class
```
G = Graph()
```
and verify that it has nothing hiding inside other than the default Python methods and the fields we defined
```
dir(G)
```
## Nodes
Now we add our first utility methors. *add_node* will be responsible for adding a single node to the Graph, while *add_nodes_from* will prove useful to add nodes in bulk. We can also add node attributes by passing keyword arguments to any of these two functions
```
@add_method(Graph)
def add_node(self, node, **kwargs):
self._nodes[node] = kwargs
@add_method(Graph)
def add_nodes_from(self, nodes, **kwargs):
for node in nodes:
if isinstance(node, tuple):
self._nodes[node[0]] = node[1:]
else:
self._nodes[node] = kwargs
@add_method(Graph)
def nodes(self):
return list(self._nodes.keys())
```
And we can now check that this added functionality is now available to our Graph
```
dir(G)
```
And that they work as promised
```
G.add_node("A", color="blue")
```
And naturally
```
G._nodes
```
Or, for a more complex example:
```
G.add_node("Z", color="green", size=14)
G._nodes
```
*add_nodes_from* treats the first parameter as an iterable. This means that we can pass a string and it will add a node for each character.
```
G.add_nodes_from("ABC", color='red')
G._nodes
```
Here it is important to note 2 things:
- Since add_nodes_from expects the first argument to be a list of nodes, it treated each character of the string as an individual node
- By adding the same node twice we overwrite the previous version.
# Edges
Now we add the equivalent functionality for edges.
```
@add_method(Graph)
def add_edge(self, node_i, node_j, **kwargs):
if node_i not in self._nodes:
self.add_node(node_i)
if node_j not in self._nodes:
self.add_node(node_j)
if node_i not in self._edges:
self._edges[node_i] = {}
if node_j not in self._edges[node_i]:
self._edges[node_i][node_j] = {}
self._edges[node_i][node_j] = kwargs
if not self._directed:
if node_j not in self._edges:
self._edges[node_j] = {}
if node_i not in self._edges[node_j]:
self._edges[node_j][node_i] = {}
self._edges[node_j][node_i] = kwargs
@add_method(Graph)
def add_edges_from(self, edges, **kwargs):
for edge in edges:
self.add_edge(*edge, **kwargs)
```
Before we proceed, let us create a new Graph object
```
G = Graph()
G._directed
```
And add the edges from the edge list we considered before
```
edge_list = [
('A', 'B'),
('A', 'C'),
('A', 'E'),
('B', 'C'),
('C', 'D'),
('C', 'E'),
('D', 'E')]
G.add_edges_from(edge_list)
```
And we can easily check that it looks correct, both for nodes and edges
```
G._nodes
G._edges
```
For Completeness, we add a function to return a list of all the edges and their attributes (if any)
```
@add_method(Graph)
def edges(self, node_i=None):
e = []
if node_i is None:
edges = self._edges
else:
edges = [node_i]
for node_i in edges:
for node_j in self._edges[node_i]:
e.append([node_i, node_j, self._edges[node_i][node_j]])
return e
```
So we recover the undirected version of the edge list we started with
```
G.edges()
```
## Graph properties
Now that we have a minimally functional Graph object, we can start implementing functionality to retrieve information about the Graph.
### Node information
Obtaining the number of nodes is simple enough:
```
@add_method(Graph)
def number_of_nodes(self):
return len(self._nodes)
```
So we confirm that we have 5 nodes as expected
```
G.number_of_nodes()
```
And to retrieve the degree of each node one must simply check the number of corresponding entries in the edge dictionary
```
@add_method(Graph)
def degrees(self):
deg = {}
for node in self._nodes:
if node in self._edges:
deg[node] = len(self._edges[node])
else:
deg[node] = 0
return deg
```
With the expected results
```
G.degrees()
```
### Edge Information
The number of edges is simply given by:
```
@add_method(Graph)
def number_of_edges(self):
n_edges = 0
for node_i in self._edges:
n_edges += len(self._edges[node_i])
# If the graph is undirected, don't double count the edges
if not self._directed:
n_edges /= 2
return n_edges
```
And so we find, as expected
```
G.number_of_edges()
```
We also add a conveniency method to check if the graph id directed
```
@add_method(Graph)
def is_directed(self):
return self._directed
G.is_directed()
```
### Weights
As we saw, each edge can potentially have a weight associated with it (it defaults to 1). We also provide a function to recover a dictionary mapping edges to weights
```
@add_method(Graph)
def weights(self, weight="weight"):
w = {}
for node_i in self._edges:
for node_j in self._edges[node_i]:
if weight in self._edges[node_i][node_j]:
w[(node_i, node_j)] = self._edges[node_i][node_j][weight]
else:
w[(node_i, node_j)] = 1
return w
```
As we didn't explicitly include any weight information in our graph, we find that all the weights are 1
```
G._edges['A']['B']['weight']=4
G._edges
G.weights()
```
### Topology and Correlations
One particularly useful property of a graph is the list of nearest neighbors of a given node. With our formulation, this is particularly simple to implement
```
@add_method(Graph)
def neighbours(self, node):
if node in self._edges:
return list(self._edges[node].keys())
else:
return []
```
So we find that node $C$ has as nearest neighbours nodes $A$, $B$, $D$, $E$
```
G.neighbours('C')
```
We are also intersted in the degree and weight distributions. Before we can compute them, we define a utility function to generate a probability distribution from a dictionary of values
```
@add_method(Graph)
def _build_distribution(data, normalize=True):
values = data.values()
dist = list(Counter(values).items())
dist.sort(key=lambda x:x[0])
dist = np.array(dist, dtype='float')
if normalize:
norm = dist.T[1].sum()
dist.T[1] /= norm
return dist
```
By default the probability distribution is normalized such that the sum of all values is 1. Using this utility function it is now easy to calculate the degree distribution
```
@add_method(Graph)
def degree_distribution(self, normalize=True):
deg = self.degrees()
dist = Graph._build_distribution(deg, normalize)
return dist
```
The degree distribution for our Graph is then:
```
G.degree_distribution(False)
```
Where we can see that we have 2 nodes of both degree 2 and 3 and 1 of degree 4.
Similarly, for the weight distribution
```
@add_method(Graph)
def weight_distribution(self, normalize=True):
deg = self.weights()
dist = Graph._build_distribution(deg, normalize)
return dist
```
And we naturally find that all of our edges have weight 1.
```
G.weight_distribution()
```
We now calculate the average degree of the nearest neighbours for each node.
```
@add_method(Graph)
def neighbour_degree(self):
knn = {}
deg = self.degrees()
for node_i in self._edges:
NN = self.neighbours(node_i)
total = [deg[node_j] for node_j in NN]
knn[node_i] = np.mean(total)
return knn
G.neighbour_degree()
```
And the distribution by degree:
```
@add_method(Graph)
def neighbour_degree_function(self):
knn = {}
count = {}
deg = self.degrees()
for node_i in self._edges:
NN = self.neighbours(node_i)
total = [deg[node_j] for node_j in NN]
curr_k = deg[node_i]
knn[curr_k] = knn.get(curr_k, 0) + np.mean(total)
count[curr_k] = count.get(curr_k, 0) + 1
for curr_k in knn:
knn[curr_k]/=count[curr_k]
knn = list(knn.items())
knn.sort(key=lambda x:x[0])
return np.array(knn)
```
From which we obtain:
```
G.neighbour_degree_function()
```
# Zachary Karate Club
J. Anthro. Res. 33, 452 (1977)
Let's now look at an empirical Graph
For convenience, we load the data from a file using numpy
```
edges = np.loadtxt('data/karate.txt')
edges[:10]
```
Now we can use the functions defined above to generate the corresponding graph
```
Karate = Graph()
Karate.add_edges_from(edges)
```
Our graph has 34 nodes
```
Karate.number_of_nodes()
```
And 78 edges
```
Karate.number_of_edges()
```
The degree distribution is:
```
Pk = Karate.degree_distribution()
Pk
```
Which we can plot easily
```
plt.plot(Pk.T[0], Pk.T[1])
plt.xlabel('k')
plt.ylabel('P[k]')
plt.gcf().set_size_inches(11, 8)
```
The average degree of the nearest neighbours as a function of the degree is:
```
knn = Karate.neighbour_degree_function()
```
Which we plot as well
```
plt.plot(knn.T[0], knn.T[1])
plt.xlabel('k')
plt.ylabel(r'$\langle K_{nn}[k] \rangle$')
plt.gcf().set_size_inches(11, 8)
```
Finally, before we proceed to the next nodebook, we save the current state of our Graph class. For this we use some Jupyter Notebook magic. It's not important to understand this, but you can read about it in the [Jupyter notebook](https://jupyter-notebook.readthedocs.io/en/stable/examples/Notebook/Importing%20Notebooks.html) documentation.
```
def export_class(path, filename):
import io
from nbformat import read
with io.open(path, 'r', encoding='utf-8') as f:
nb = read(f, 4)
fp = open(filename, "wt")
for cell in nb.cells:
if cell.cell_type == 'code':
first_line = cell.source.split('\n')[0]
if "class " in first_line or "add_method" in first_line:
print(cell.source, file=fp)
print("\n", file=fp)
elif "import" in first_line:
for line in cell.source.split('\n'):
if not line.startswith("%"):
print(line.strip(), file=fp)
print("\n", file=fp)
fp.close()
```
Suffice it to say, that after this line, we'll have a Python module called "Graph.py" containing all the methors in our Graph class
```
export_class('2. Graph Properties.ipynb', 'Graph.py')
```
<div style="width: 100%; overflow: hidden;">
<img src="data/D4Sci_logo_full.png" alt="Data For Science, Inc" align="center" border="0" width=300px>
</div>
| true |
code
| 0.634656 | null | null | null | null |
|
# Mean Field Theory
## Essence of Mean Field Approximation (MFA): replacing fluctuating terms by averages
Let us assume that each spin i independently of each other feels some average effect of a field:
$$H_i = -J\sum_{\delta} s_i s_{i+\delta} - h s_i = -\Big(J\sum_{\delta}s_{\delta} +h \Big) s_i$$
Each spin is experiencing a local field defined by its nearest neighours.
$$H_i = J\sum_{\delta}s_{\delta}+h$$
$$H^{eff}=\sum H_i s_i$$
> The difficulty with effective field is that $H_i$ depends on the instatnaous states of neighbouring spins of $s_i$ which flucutuate
We now make a dramaic approximations: replace the effective field by its mean field approximation where each spin is experiencing a field independent of others. The average magnetiszation per spin due to trasnlational invariance is same for every spin (in perioid cboundary conditions that is)
$$H^{MFA}_i = \langle H_i \rangle = J\sum_{\delta} \langle s_{\delta} \rangle+h = Jzm+h$$
- z=4 for 2D lattice
- z=6 for 3D lattice
**In MFA hamitlonian factors out into additive components**
Just like the exact case we had with J=0.
$$\boxed{m = tanh(\beta(Jzm+h))}$$
**The $h=0$ MFA case**
The equation can be solved in a self-consistent manner or graphically by finding intersection between:
- $m =tanh(x)$
- $x = \beta Jzm$
When the slope is equal to one it provides a dividing line between two behaviours.
$$k_B T_c =zJ$$
$$m = tanh \Big(\frac{Tc}{T} m \Big)$$
> **MFA shows phase transitio for 1D Ising model at finite $T=T_c$!**
```
import holoviews as hv
import ipywidgets as widgets
from ipywidgets import interact
import matplotlib.pyplot as plt
import numpy as np
import scipy as sp
@widgets.interact(T=(0.1,5), Tc=(0.1,5))
def mfa_ising1d_plot(T=1, Tc=1):
x = np.linspace(-3,3,1000)
f = lambda x: (T/Tc)*x
m = lambda x: np.tanh(x)
plt.plot(x,m(x), lw=3, alpha=0.9, color='green')
plt.plot(x,f(x),'--',color='black')
idx = np.argwhere(np.diff(np.sign(m(x) - f(x))))
plt.plot(x[idx], f(x)[idx], 'ro')
plt.legend(['m=tanh(x)', 'x'])
plt.ylim(-2,2)
plt.grid('True')
plt.xlabel('m',fontsize=16)
plt.ylabel(r'$tanh (\frac{Tc}{T} m )$',fontsize=16)
@widgets.interact(Tc_T=(0.1,5))
def mfa_ising1d_plot(Tc_T=1):
x = np.linspace(-1,1,200)
h = lambda x: np.arctanh(x) - Tc_T*x
plt.plot(h(x),x, lw=3, alpha=0.9, color='green')
plt.plot(x, np.zeros_like(x), lw=1, color='black')
plt.plot(np.zeros_like(x), x, lw=1, color='black')
plt.grid(True)
plt.ylabel('m',fontsize=16)
plt.xlabel('h',fontsize=16)
plt.ylim([-1,1])
plt.xlim([-1,1])
```
### Critical exponents
**A signature of phase transitions and critical phenomena is that there are universal power law behaviours near critical point**
$$m \sim |T-T_c |^{\beta}$$
$$c \sim |T-T_c|^{-\alpha}$$
$$\chi =\frac{\partial m}{\partial B} \sim |T-T_c|^{-\gamma}$$
**Correlation lengths $\xi$ diverge at critical points**
$$f(r=|j-k|) = \langle s_j s_k \rangle \sim r^{-d+2+\eta}e^{-r/\xi}$$
$$\xi \sim |T-T_c|^{-\nu}$$
### Mean field exponents
We can derive the value of critical exponent $\beta$ within mean field approximation by Taylor expanding the hyperbolic tangent
$$tanh(x) \approx x-\frac{1}{3}x^3+...$$
$$m = tanh(\beta J z m) \approx \beta J z m - \frac{1}{3} (\beta Jzm)^3$$
- One solution is obviously m = 0 which is the only solution above $T_c$
- Below $T_c$ the non-zero solution is found $m=\sqrt{3}\frac{T}{T_c} \Big(1-\frac{T}{T_c} \Big)^{1/2}+...$
- $\beta_{MFA}=1/2$
### Helmholtz Free energy
$$dF_{T, M} = -SdT + BdM $$
$$F = \int dF = F_0 + \int^{M}_0 B(M) dM$$
We will now make use of Mean field theory to approximate dependence of field on magnetization: $h(m) \approx m(1-T_c/T)+ 1/3 m^3$ which enables us to evaluate the integral above.
$$B(M) = aM +bM^3$$
$$F = F_0 + \frac{1}{2}aM^2 + \frac{1}{4} bM^4$$
Equilibirum is found by minimizing the free energy: $aM +bM^3 = 0$ with solutions M = 0 and $M=\pm (-a/b)^{1/2}$
- $T < T_c$ case we get $a<0$ and $M=\pm (-|a|/b)^{1/2} = \pm M_S$
- $T > T_c$ case we get $a>0$ and $M=0$
```
@widgets.interact(T=(400,800))
def HelmF(T=400):
Tc=631 # constnt for Ni
a = 882*(T/Tc-1)
b = 0.4734*T
M = np.linspace(-2,2,1000)
plt.plot(M, 0.5*a*M**2 + 0.25*b*M**4, lw=4, color='brown', label=f"T/Tc = {(T/Tc)}")
plt.grid(True)
plt.xlim([-2,2])
plt.ylim([-140,200])
plt.ylabel('$F(M)$')
plt.xlabel('$M$')
plt.legend()
```
### Problems
1. Use Transfer matrix method to solve general 1D Ising model with $h = 0$ (Do not simply copy the solution by setting h=0 but repeat the derivation :)
<br>
2. Find the free energy per particle $F/N$ in the limit $n\rightarrow \infty $ for both periodic bounary codnition conditions and free boundary cases.
3. Plot temperature dependence of heat capacity and free energy as a function for $(h=\neq, J\neq 0)$ $(h=0, J\neq 0)$ and $(h=\neq, J\neq \neq)$ cases of 1D Ising model. Coment on the observed behaviours.
4. Explain why heat capacity and magnetic susceptibility diverge at critical temperatures.
5. Explain why correlation functions diverge at a critical temperature
6. Explain why are there universal critical exponents.
7. Explain why the dimensionality and range of intereactions matters for existance and nature of phase transitions.
8. Using mean field approximation show that near critical temperature magnetization per spin goes as $m\sim (T_c-T)^{\beta}$ (critical exponent not to nbe confused with inverse $k_B T$) and find the value of \beta. Do the same for magnetic susceptibility $\chi \sim (T-T_c)^{-\gamma}$ and find the value of $\gamma$
9. Explain what is the nature of mean field theory approximation and why is predictions fail for low dimensionsal systems but consistently get better with higher dimensions?
10. Consider a 1D model given by the Hamiltonian:
$$H = -J\sum^{N}_{i=1} s_i s_{i+1} + D\sum^{N}_{i=1} s^2_i $$
where $J>1$, $D>1$ and $s_i =-1,0,+1$
- Assuming periodic boundary codnitions calcualte eigenvalues of the transfer matrix
- Obtain expresions for internal energy, entropy and free energy
- What is the ground state of this model (T=0) as a function of $d=D/J$ Obtain asymptotic form of the eigenvalues of the transfer matrix in the limit $T\rightarrow 0$ in the characteristic regimes of d (e.g consider differnet extereme cases)
| true |
code
| 0.557002 | null | null | null | null |
|
# Monte Carlo 2D Ising Model
Authors: Chris King, James Grant
This tutorial aims to help solidify your understanding of the theory underlying the Monte Carlo simulation technique by applying it to model the magnetic properties of a 2D material.
```
# import everything that we will need in this tutorial now
import numpy
import matplotlib.pyplot as plt
from inputs.Tut_2.sources.ising import IsingModel
from inputs.Tut_2.sources.isingdata import IsingModelData
```
## Introduction to Monte Carlo Methods:
Monte Carlo (MC) is the name given to the simulation technique that attempts to solve a problem by randomly sampling out of all of its possible outcomes ('configurational space')and obtaining a result based on numerical analysis of the sampling. MC is a stochastic method, which means that the final state of the system cannot be predicted precisely based on the initial state and parameters, but through numerical analysis, reproducible results can be obtained. This contrasts with other techniques like molecular dynamics, which are deterministic, where if you know the initial state and the inputs for the calculations, you can predict what the configuration of the system will be at any and all times thereafter. This distinction allows MC to be used in a variety of applications across the scientific community where deterministic techniques are ineffective or impossible to use, such as phase co-existence and criticality, adsorption, and development of solid-state defects [1].
Results from MC simulations are generally accurate and reliable, assuming that the technique has representatively sampled the distribution of possible configurations in the system ('configurational space'). In other words, if our sampling method returns the probability distribution we expect, then we know that are sampling method is reliable. In thermodynamic systems, the probability distribution of available states is given by the Boltzmann distribution:
$$W(\mathbf{r}) = \exp {\Bigl(\frac{E}{kT}\Bigr)}$$
where $W(\mathbf{r})$ is the probability of being in a state of energy, also known as the statistical weight, *E*, at temperature, *T*, and *k* is the Boltzmann constant. The ratio of Boltzmann distributions at two different energies, $E_2$ and $E_1$, is known as the Boltzmann factor:
$$\frac{W(\mathbf{r}_1)}{W(\mathbf{r}_2)} = \exp {\Bigl(\frac{E_2 -E_1}{kT}\Bigr)}$$
So if our sampling method yields the Boltzmann distribution, we know that our simulation accurately reflects real systems. There are many possible ways one can sample the configurational space of a simulated system, the intuitive case is simple random sampling in that we move randomly from one configuration to another. However, this process is only reliable in systems with a constant probability distribution of states as it does not take into account the respective weighting of a given configuration. For example, it can under-represent a small number of configurations who contribute significantly to the overall state of the system.
The concept of statistical weight is crucial in thermodynamics and describes how likely a particular configuration is of being observed out of a hypothetically *large* number of replicas of that system. For instance, consider the possible configurations of the gas molecules in this room, clearly, this system would have a high probability of being in a configuration where the gas molecules are evenly (on average) distributed throughout the volume of the room and so this configuration has a high weighting. Yet, there is a configuration where every gas molecule sits in one corner of the room, this configuration is highly unlikely to be seen and so its weighting is very low. The weight of a particular configuration is given by:
$$W(\mathbf{r}) = \frac{\exp {\Bigl(\frac{- E(\mathbf{r})}{kT}\Bigr)}}{\sum_{i} \exp {\Bigl(\frac{- E(\mathbf{r_{i}})}{kT}\Bigr)} }$$
where $E(\mathbf{r})$ is the energy of a configuration $\mathbf{r}$. In MC simulations, the statistical weight of moving from a configuration, $\mathbf{r_1}$, to a new configuration, $\mathbf{r_2}$, is:
$$W(\mathbf{r}_1 \rightarrow \mathbf{r}_2) = \frac{W(\mathbf{r_1})P(\mathbf{r}_1 \rightarrow \mathbf{r}_2)}{N}$$
where $W(\mathbf{r_1})$ is the weight associated with $\mathbf{r}$, $P(\mathbf{r}_1 \rightarrow \mathbf{r}_2)$ is the probability of moving from configuration $\mathbf{r}_1$ to $\mathbf{r}_2$ and *N* is the number of possible configurations. The corresponding weight of going from $\mathbf{r}_2$ back to $\mathbf{r}_1$ is:
$$W(\mathbf{r}_2 \rightarrow \mathbf{r}_1) = \frac{W(\mathbf{r_2})P(\mathbf{r}_2 \rightarrow \mathbf{r}_1)}{N}$$
<img src="images/Tut_2_images/weights.png" height='400' width='600'/>
<div style="text-align: center">**Figure 1:** The associated statistical weights of moving between two configurations, A and B.</div>
There are more sophisticated ways of sampling configurational space, such as the Metropolis Algorithm, which is one of the most widely used sampling schemes in MC simulations (including this one). First, it randomly selects a particle in the system and proposes a move to another configuration. It then calculates the new energy of the configuration and compares it with the energy of the previous configuration before the move was proposed. It then applies the following condition:
$$P_{\mathrm{acc}}(\mathbf{r}_1 \rightarrow \mathbf{r}_2) = \min(1, \exp \ \Bigl(- \frac{E(\mathbf{r}_2) - E(\mathbf{r}_1)}{kT}\Bigr) \ )$$
where $P_{\mathrm{acc}}(\mathbf{r}_1 \rightarrow \mathbf{r}_2)$ is the probability of accepting the move from the initial configuration, $\mathbf{r}_1$, with an energy, $E(\mathbf{r}_1)$, to the new configuration, $\mathbf{r}_2$, with an energy, $E(\mathbf{r}_2)$. The function min() means that the smallest value in the brackets is chosen. If the energy of the new configuration is less than that of the original, *i.e.* $E(\mathbf{r}_2) < E(\mathbf{r}_1)$, then $E(\mathbf{r}_2)-E(\mathbf{r}_1) < 0$ and so $\exp \ \Bigl(- \frac{E(\mathbf{r}_2) - E(\mathbf{r}_1)}{kT}\Bigr) \ > 1$ and so the move is accepted with $P_{\mathrm{acc}}(\mathbf{r}_1 \rightarrow \mathbf{r}_2) = 1$. If the new energy is greater than the energy of the original configuration, *i.e.* $E(\mathbf{r}_2) > E(\mathbf{r}_1)$, then $E(\mathbf{r}_2)-E(\mathbf{r}_1) > 0$ and so $\exp \ \Bigl(- \frac{E(\mathbf{r}_2) - E(\mathbf{r}_1)}{kT}\Bigr) \ > 1$ and the move is accepted with probability $P_{\mathrm{acc}}(\mathbf{r}_1 \rightarrow \mathbf{r}_2) = \exp \ \Bigl(- \frac{E(\mathbf{r}_2) - E(\mathbf{r}_1)}{kT}\Bigr) \ < 1$.
<img src="images/Tut_2_images/Metropolis_algorithm.png" />
<div style="text-align: center">**Figure 2:** Visual representation of the function of the Metropolis algorithm. Once one move outcome is complete, the algorithm repeats on the final configuration. </div>
Even if the proposed move leads to a higher-energy configuration, there is still a non-zero probability of it being accepted! Why should this be the case?
```
a = input()
```
What happens to the total number of accepted moves in a given simulation as we change the temperature? How might this affect the final outcome of your simulation?
```
b = input()
```
This defines the concept of detailed balance:
$$W(\mathbf{r}_1 \rightarrow \mathbf{r}_2)P_{\mathrm{acc}}(\mathbf{r}_1 \rightarrow \mathbf{r}_2) = W(\mathbf{r}_2 \rightarrow \mathbf{r}_1)P_{\mathrm{acc}}(\mathbf{r}_2 \rightarrow \mathbf{r}_1)$$
We can now obtain the required Boltzmann distribution from this condition by rearrangement:
$$\frac{W(\mathbf{r}_2 \rightarrow \mathbf{r}_1)}{W(\mathbf{r}_1 \rightarrow \mathbf{r}_2)} = \frac{P_{\mathrm{acc}}(\mathbf{r}_1 \rightarrow \mathbf{r}_2)}{P_{\mathrm{acc}}(\mathbf{r}_2 \rightarrow \mathbf{r}_1)} = exp \ {\Bigl(\frac{E_2 -E_1}{kT}\Bigr)}$$
This tells us that so long as we satisfy detailed balance, our system will be sampled according to the Boltzmann distribution and obey the rules of thermodynamics. Though it is important to note that the condition of detailed balance is *sufficient* but *not necessary* to ensure that are system accurately reflects thermodynamics, *i.e.* there are other simpler conditions one could employ that would ensure that our simulation obeys thermodynamics. For instance, one could ensure that *balance* is achieved from the system which simply states that moving from one state to another state is the same for any initial and final state pairing, *i.e.*:
$$\frac{\mathrm{d}W(\mathbf{r}_1)}{\mathrm{d}t} = 0$$
However, detailed balance also ensures equilibrium between all states such that the trajectory from one configuration to another via several steps has the same probability as the reverse trajectory. This ensures the reliability of the sampling method used without requiring additional corrections in the calculations.
<img src="images/Tut_2_images/detailed_balance2.png" height='700' width='700'/>
<div style="text-align: center">**Figure 3:** A visualisation of the difference between the condition of balance (left) and detailed balance (right) for a set of different configurations, A-H, in the configurational space of a system. </div>
Having discussed the concepts behind MC simulation methods, it is time to demonstrate how to apply them to a physical system. This tutorial will be centred on a MC simulation of the magnetic properties of solid materials.
## Ising Model of Magnetism
An application where MC is more effective than deterministic methods is simulating the magnetic behaviour of solid state materials.
Our simulation will be based on a 2D Ising model, which describes the macroscopic magnetic behaviour of a solid material as a result of the relative orientation of electron spins within the crystal lattice of a material. As you may recall, each electron has an intrinsic 'spin'. In simple terms, the spin of an electron can be thought of as a magnetic moment, with two possible orientations: 'up' and 'down'. This idea helps define two classes of magnetic materials: diamagnetic and paramagnetic.
Diamagnetic materials are made up of atoms/molecules without unpaired electrons, do not interact with external magnetic fields, making them non-magnetic. Paramagnetic materials contain unpaired electrons, exhibiting a net magnetic moment that can interact with external magnetic fields and give the material its magnetic properties. Figure 1 below shows an example of a paramagnetic material as a 2D lattice of colour-coded spins.
<img src="images/Tut_2_images/paramagnet_config.png" />
<div style="text-align: center">**Figure 4:** A 2D schematic of a paramagnetic material under an external magnetic field. Yellow indicates the spins that are aligned with the field and purple are spins that are anti-aligned. </div>
There is another type of magnetism observed known as ferromagnetism, where instead of a uniform alignment of spins as in paramagnetic materials, 'domains' of aligned spins form, bound by domains of oppositely aligned spins (see Figure 2). Ferromagnetic materials can show unique properties, such as being able to generate their own magnetic field (magnetisation) in the absence of an external magnetic field. These form the common magnets seen in real-world applications.
<img src="images/Tut_2_images/ferromagnet_cand2.png" />
<div style="text-align: center">**Figure 5:** A 2D schematic of a ferromagnetic material at $T < T_{c}$. Yellow and purple represent the two different spin orientations, 'up' and 'down', respectively. </div>
The main factor influencing whether a given atom's spin is aligned with its neighbours in a crystal, and hence what type of magnetism the material displays, is its exchange energy, *E*, which in the Ising model is given by:
$$E = -J \sum_{<i,j>} s_{i}s_{j}$$
where *J* is the coupling constant between adjacent atoms in a given material and $s_{i/j}$ is the spin of the particle in position i/j in the lattice, respectively. The <...> here mean the sum goes over the nearest neighbours of the atom in position (i,j), *i.e.* over the atoms at positions (i-1, j), (i+1, j), (i, j-1) and (i, j+1) only. The sign of *J* determines whether spin alignment (ferromagnetism) or anti-alignment (antiferromagnetism) is favourable.
The exchange energy can be thought of as an activation barrier for an atom to change its spin depending on the spins of its neighbours. This means that, like with any physical system with an energy barrier, spontaneous thermal fluctuations can overcome the barrier and cause some atoms/domains to flip their spin, with the likelihood of flipping a spin increasing as temperature increases. Therefore, ferromagnetic materials only show domains at temperatures under a specific critical, or Curie, temperature, $T_{c}$.
Above this point, ferromagnetic materials lose their ability to retain magnetisation because the thermal fluctuations are much larger than the energy required to switch a domain's alignment with respect to other domains. This results in a loss of the domain structure, and hence loss of magnetisation without an external field. It is for this reason that paramagnetism can be thought of as high-temperature ferromagnetism.
For more information on the Ising model, consult either [2] or [3].
The Metropolis algorithm is employed in these simulations, describe what constitutes a 'move' in the context of this system.
```
c = input()
```
Write an expression for the energy difference between the initial and final configurations, $E(\mathbf{r}_2) - E(\mathbf{r}_1)$, for the 2D Ising model.
```
d = input()
```
### Exercise 1)
The aim of this exercise is to familiarise yourself with running MC calculations on a simple 2D Ising model of a ferromagnetic material. The material is represented by a 64x64 2D lattice of points, each representing an atom with its own net spin. In this exercise, all atoms are spin-aligned. We will be running a MC simulation to look at how the overall spin alignment (magnetisation) and energy of the system evolves with both time and temperature.
First, we shall setup our intial simulation at a given temperature:
```
data = dlmonte.DLMonteData("")
```
Now let's run our first Monte Carlo simulation of the day!
```
# Run the initial simulation. Takes about a minute to complete
```
If you wish, you can look in your directory and see several new files have appeared. The nature of these files will be explained in detail next session.
Now that you have all the output data you could possibly need from this calculation, we shall proceed with extracting the time evolution of magnetisation and the distribution of the magnetisations over the course of the simulation.
```
# output data extraction and analysis into plots of magnetisation vs time and histogram of magnetisation distributions
T = 2.36
plt.figure()
plt.subplot(1,2,1)
plt.xlabel("Number of steps")
plt.ylabel("Magnetisation")
plt.title("Time evolution of magnetisation at T = {}".format(T))
plt.axis()
plt.plot(M_seq.dat, 'b-')
plt.savefig("inputs/Tut_2/main/{}/Mvst.png".format(T))
plt.subplot(1,2,2)
plt.xlabel("M")
plt.ylabel("P(M)")
plt.title("Distribution of magnetisations at T = {}".format(T))
plt.hist(M_seq.dat, bins=auto, normed=True, weights=None)
plt.savefig("inputs/Tut_2/main/{}/M_hist.png".format(T))
```
You will find several new files in your directory, but we will have used only on M_seq.dat and M_hist.dat in this exercise (we will get to the others later).
We shall now proceed to run the calculation at higher temperatures to obtain the temperature-dependence of the magnetisation. Repeat the simulation and analysis sections that you have done for this initial temperature with the other temperatures in the main directory.
Compare the evolution of magnetisation as the temperature changes and rationalise any observed trends using your knowledge of ferromagnetism. Do the results correspond to the Ising model?
```
e = input()
```
Compare the shapes of your magnetisation histograms as the temperature changes. What does this indicate is happening to your system as temperature changes? Does this behaviour support the Ising model and your magnetisation evolution data?
```
f = input()
```
Once you have done that, plot magnetisation vs temperature for the system. Comment on the shape of your graph and estimate the critical temperature, $T_{c}$, from it.
```
# collate all magnetisation-temperature data and plot it
plt.figure()
plt.xlabel("Temperature")
plt.ylabel("Average Magnetisation")
plt.title("Magnetisation vs Temperature")
#plt.axis()
plt.plot(x1, y1, 'b-')
plt.savefig("inputs/Tut_2/main/<M>vsT.png".format{T})
g = input()
```
For any square 2D Ising model where coupling along rows and along columns are equal, $T_{c}$ is given by:
$$T_{c} = \frac{2}{\ln(1+\sqrt{2})} \approx 2.269$$
Does your estimation of $T_{c}$ agree with that predicted by the above equation? Account for any observed discrepancies. How could you improve the accuracy of your estimated value for $T_{c}$?
```
h = input()
```
### Extension (optional):
You have seen what happens as the system is heated, but you can also look at the magnetisation upon cooling the system from a state above the critical temperature to a state below the critical temperature.
Go back to the beginning of Exercise 1 and now choose the inputs in ------- and plot the time-evolution of magnetisation.
How does this compare with the time evolution at $T>T_{c}$? Does this agree with the Ising model? If not, what do you think might be the problem with our simulation?
```
i = input()
```
### Exercise 2)
This exercise will demonstrate the stochastic nature of MC simulations as well as how the Metropolis algorithm produces reliable and accurate results for this simple 2D Ising model.
We have seen what happens when we start the simulations from a fixed starting configuration (all spins aligned), but what will happen when we start from a random configuration?
Go back the the beginning of Exercise 1 and repeat it for each temperature in the 'ranseed' folder, plotting the magnetisation vs. temperature once you have run all the simulations.
How do the results from this exercise compare with those of Exercise 1? What effect does the initial configuration have on the outcome of the simulation?
```
j = input()
```
### Extension (optional):
For one of the ranseed calculations, let us find out what the initial configuration was and use that as our fixed starting configuration and see how the results of both calculations compare. Using your current ranseed calculation, we will extract the initial configuration and set it as the starting configuration in the CONTROL file:
```
# pull out seeds, copy input files into a new directory, change ranseed to seeds in output
```
Now let's run this calculation:
```
# Run calculations here
```
We can compare the magnetisation data between the ranseed and this new simulation:
```
# plot both magentisations on the same graph
plt.figure()
plt.xlabel("Number of steps")
plt.ylabel("Magnetisation")
plt.title("Time evolution of magnetisation at T = {} for a randomly-generated initial state and the equivalent fixed initial state".format(T))
plt.axis()
plt.plot(x1, y1, 'b-', label='random', x2, y2, 'r-', label='fixed')
plt.legend()
plt.savefig("inputs/Tut_2/extensions/ranseed/Mvst_comparison.png")
```
What do you notice about the magnetisation evolution in the two calculations? Does this confirm that the stochastic nature of Monte Carlo methods can produce reliable results?
```
k = input()
```
## Conclusions:
Now that you have reached the end of this tutorial, you will hopefully have a better understanding of the Monte Carlo method and the motivation for its use. You have simulated the magnetic properties of a 2D material based on the Ising model and obtained:
- the temperature-dependence of magnetisation
- the evolution of magnetisation with time
- validation of the stochastic nature of Monte Carlo methods
In the next tutorial, you will be introduced to a general Monte Carlo program called DLMONTE and use it to model the thermal properties of a Lennard-Jones material.
## Extensions (optional):
### 1. Antiferromagnetism:
So far, you have looked at how the magnetic behaviour of a ferromagnetic system changes over time and temperature, but there is another possible type of magnetism called antiferromagnetism, where the sign of the coupling constant, *J*, changes sign. This means that it is now favourable for the spin of one atom to be opposed to the spin of its neighbours, resulting in a preferred 'checkerboard' pattern of magnetisation on the 2D lattice (see Figure 3). You can investigate the magnetic behaviour in this case using the 2D Ising model.
<img src="images/Tut_2_images/antiferromagnet.png" />
<div style="text-align: center">**Figure 6:** The most stable magnetic configuration of an antiferromagnetic material at $T < T_{c}$. </div>
Repeat Exercise 1 but this time using the inputs in the 'antiferromagnet' folder, plotting the temperature dependence of the magnetisation once you have run the simulation at each temperature.
Compare your results of the antiferromagnet with the ferromagnet. Rationalise any observed differences in terms of exchange energy and alignment of spins.
```
l = input()
```
## References:
[1] S. Mordechai (Editor), *Applications of Monte Carlo Method in Science and Engineering* [Online]. Available: https://www.intechopen.com/books/applications-of-monte-carlo-method-in-science-and-engineering
[2] J. V. Selinger, "Ising Model for Ferromagnetism" in *Introduction to the Theory of Soft Matter: From Ideal Gases to Liquid Crystals*. Cham: Springer International Publishing, 2016, pp. 7-24.
[3] N. J. Giordano, *Computational Physics*. Upper Saddle River, N.J.: Prentice Hall, 1997.
| true |
code
| 0.641085 | null | null | null | null |
|
# Overfitting and underfitting
The fundamental issue in machine learning is the tension between optimization and generalization. "Optimization" refers to the process of adjusting a model to get the best performance possible on the training data (the "learning" in "machine learning"), while "generalization" refers to how well the trained model would perform on data it has never seen before. The goal of the game is to get good generalization, of course, but you do not control generalization; you can only adjust the model based on its training data.
Note: in this notebook we will be using the IMDB test set as our validation set. It doesn't matter in this context.
```
from keras.datasets import imdb
import numpy as np
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
def vectorize_sequences(sequences, dimension=10000):
# Create an all-zero matrix of shape (len(sequences), dimension)
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1. # set specific indices of results[i] to 1s
return results
# Our vectorized training data
x_train = vectorize_sequences(train_data)
# Our vectorized test data
x_test = vectorize_sequences(test_data)
# Our vectorized labels
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
```
# Fighting overfitting
## Reducing the network's size
Unfortunately, there is no magical formula to determine what the right number of layers is, or what the right size for each layer is. You will have to evaluate an array of different architectures (on your validation set, not on your test set, of course) in order to find the right model size for your data. The general workflow to find an appropriate model size is to **start with relatively few layers and parameters, and start increasing the size of the layers or adding new layers until you see diminishing returns** with regard to the validation loss.
Let's try this on our movie review classification network. Our original network was as such:
```
from keras import models
from keras import layers
original_model = models.Sequential()
original_model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
original_model.add(layers.Dense(16, activation='relu'))
original_model.add(layers.Dense(1, activation='sigmoid'))
original_model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
```
Now let's try to replace it with this smaller network:
```
smaller_model = models.Sequential()
smaller_model.add(layers.Dense(4, activation='relu', input_shape=(10000,)))
smaller_model.add(layers.Dense(4, activation='relu'))
smaller_model.add(layers.Dense(1, activation='sigmoid'))
smaller_model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
```
### Comparison
Here's a comparison of the validation losses of the original network and the smaller network. The dots are the validation loss values of the smaller network, and the crosses are the initial network (remember: a lower validation loss signals a better model).
```
original_hist = original_model.fit(x_train, y_train,
epochs=20,
batch_size=512,
validation_data=(x_test, y_test))
smaller_model_hist = smaller_model.fit(x_train, y_train,
epochs=20,
batch_size=512,
validation_data=(x_test, y_test))
epochs = range(1, 21)
original_val_loss = original_hist.history['val_loss']
smaller_model_val_loss = smaller_model_hist.history['val_loss']
import matplotlib.pyplot as plt
# b+ is for "blue cross"
plt.plot(epochs, original_val_loss, 'b+', label='Original model')
# "bo" is for "blue dot"
plt.plot(epochs, smaller_model_val_loss, 'bo', label='Smaller model')
plt.xlabel('Epochs')
plt.ylabel('Validation loss')
plt.legend()
plt.show()
```
Now, for kicks, let's add to this benchmark a network that has much more capacity, far more than the problem would warrant:
```
bigger_model = models.Sequential()
bigger_model.add(layers.Dense(512, activation='relu', input_shape=(10000,)))
bigger_model.add(layers.Dense(512, activation='relu'))
bigger_model.add(layers.Dense(1, activation='sigmoid'))
bigger_model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
bigger_model_hist = bigger_model.fit(x_train, y_train,
epochs=20,
batch_size=512,
validation_data=(x_test, y_test))
```
Here's how the bigger network fares compared to the reference one. The dots are the validation loss values of the bigger network, and the crosses are the initial network.
```
bigger_model_val_loss = bigger_model_hist.history['val_loss']
plt.plot(epochs, original_val_loss, 'b+', label='Original model')
plt.plot(epochs, bigger_model_val_loss, 'bo', label='Bigger model')
plt.xlabel('Epochs')
plt.ylabel('Validation loss')
plt.legend()
plt.show()
```
Meanwhile, here are the training losses for our two networks:
```
original_train_loss = original_hist.history['loss']
bigger_model_train_loss = bigger_model_hist.history['loss']
plt.plot(epochs, original_train_loss, 'b+', label='Original model')
plt.plot(epochs, bigger_model_train_loss, 'bo', label='Bigger model')
plt.xlabel('Epochs')
plt.ylabel('Training loss')
plt.legend()
plt.show()
```
## Adding weight regularization
A "simple model" in this context is a model where the distribution of parameter values has less entropy (or a model with fewer parameters altogether, as we saw in the section above). Thus a common way to mitigate overfitting is to put constraints on the complexity of a network by forcing its weights to only take small values, which makes the distribution of weight values more "regular". This is called "weight regularization", and it is done by adding to the loss function of the network a cost associated with having large weights. This cost comes in two flavors:
- L1 regularization, where the cost added is proportional to the absolute value of the weights coefficients (i.e. to what is called the "L1 norm" of the weights).
- L2 regularization, where the cost added is proportional to the square of the value of the weights coefficients (i.e. to what is called the "L2 norm" of the weights). L2 regularization is also called weight decay in the context of neural networks. Don't let the different name confuse you: weight decay is mathematically the exact same as L2 regularization.
```
from keras import regularizers
l2_model = models.Sequential()
l2_model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
activation='relu', input_shape=(10000,)))
l2_model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
activation='relu'))
l2_model.add(layers.Dense(1, activation='sigmoid'))
l2_model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
```
Here's the impact of our L2 regularization penalty:
```
l2_model_hist = l2_model.fit(x_train, y_train,
epochs=20,
batch_size=512,
validation_data=(x_test, y_test))
l2_model_val_loss = l2_model_hist.history['val_loss']
plt.plot(epochs, original_val_loss, 'b+', label='Original model')
plt.plot(epochs, l2_model_val_loss, 'bo', label='L2-regularized model')
plt.xlabel('Epochs')
plt.ylabel('Validation loss')
plt.legend()
plt.show()
```
As alternatives to L2 regularization, you could use one of the following Keras weight regularizers:
```
from keras import regularizers
# L1 regularization
regularizers.l1(0.001)
# L1 and L2 regularization at the same time
regularizers.l1_l2(l1=0.001, l2=0.001)
```
## Adding dropout
Dropout is one of the most effective and most commonly used regularization techniques for neural networks, developed by Hinton and his students at the University of Toronto. Dropout, applied to a layer, consists of randomly "dropping out" (i.e. setting to zero) a number of output features of the layer during training. Let's say a given layer would normally have returned a vector [0.2, 0.5, 1.3, 0.8, 1.1] for a given input sample during training; after applying dropout, this vector will have a few zero entries distributed at random, e.g. [0, 0.5, 1.3, 0, 1.1]. The "dropout rate" is the fraction of the features that are being zeroed-out; it is usually set between 0.2 and 0.5. At test time, no units are dropped out, and instead the layer's output values are scaled down by a factor equal to the dropout rate, so as to balance for the fact that more units are active than at training time.
Consider a Numpy matrix containing the output of a layer, layer_output, of shape (batch_size, features). At training time, we would be zero-ing out at random a fraction of the values in the matrix:
At training time: we drop out 50% of the units in the output:
layer_output *= np.randint(0, high=2, size=layer_output.shape)
At test time:
layer_output *= 0.5
At training time:
layer_output *= np.randint(0, high=2, size=layer_output.shape)
Note that we are scaling *up* rather scaling *down* in this case:
layer_output /= 0.5
In Keras you can introduce dropout in a network via the Dropout layer, which gets applied to the output of layer right before it, e.g.:
model.add(layers.Dropout(0.5))
Let's add two Dropout layers in our IMDB network to see how well they do at reducing overfitting:
```
dpt_model = models.Sequential()
dpt_model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
dpt_model.add(layers.Dropout(0.5))
dpt_model.add(layers.Dense(16, activation='relu'))
dpt_model.add(layers.Dropout(0.5))
dpt_model.add(layers.Dense(1, activation='sigmoid'))
dpt_model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
dpt_model_hist = dpt_model.fit(x_train, y_train,
epochs=20,
batch_size=512,
validation_data=(x_test, y_test))
```
Let's plot the results:
```
dpt_model_val_loss = dpt_model_hist.history['val_loss']
plt.plot(epochs, original_val_loss, 'b+', label='Original model')
plt.plot(epochs, dpt_model_val_loss, 'bo', label='Dropout-regularized model')
plt.xlabel('Epochs')
plt.ylabel('Validation loss')
plt.legend()
plt.show()
```
## Conclusion
- The general workflow to find an appropriate model size is to start with relatively few layers and parameters, and start increasing the size of the layers or adding new layers until you see diminishing returns with regard to the validation loss.
Here the most common ways to prevent overfitting in neural networks:
- Getting more training data.
- Reducing the capacity of the network.
- Adding weight regularization.
- Adding dropout.
| true |
code
| 0.935494 | null | null | null | null |
|
# Bounding box using numpy
```
import numpy as np
from skimage import transform
import matplotlib.pyplot as plt
import cv2
def fill_oriented_bbox(img, fill_threshold=None, color=1):
_, contours, _ = cv2.findContours(img, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)
out = np.zeros_like(img, dtype=np.uint8)
for cnt in contours:
# Compute the oriented bounding box
rect = cv2.minAreaRect(cnt)
box = cv2.boxPoints(rect)
box = np.int0(box)
obbox = np.zeros_like(img, dtype=np.uint8)
cv2.fillPoly(obbox, [box], color)
if fill_threshold is not None:
# Fill the contour so we can compare it to the oriented bounding box later
cnt_fill = np.zeros_like(img, dtype=np.uint8)
cv2.fillPoly(cnt_fill, [cnt], color)
# Compare the areas and return the filled bounding box only if the ratio is lower than fill_threshold
if (np.sum(obbox) / np.sum(cnt_fill) < fill_threshold):
out = np.where(out > 0, out, obbox)
else:
out = np.where(out > 0, out, cnt_fill)
else:
out = np.where(out > 0, out, obbox)
return out
img1 = np.zeros((16,16))
img1[4:12,4:12] = 1
img1 = np.uint8(transform.rotate(img1, 0, order=0))
print("Test image:\n", img1)
obb = fill_oriented_bbox(img1)
print("OBBox:\n", obb)
plt.imshow(obb)
img1 = np.zeros((16,16))
img1[4:12,4:12] = 1.
img1[:4, 5] = 1.
img1 = np.uint8(transform.rotate(img1, -20, order=0) * 255)
print("Test image:\n", img1)
obb = fill_oriented_bbox(img1)
print("OBBox:\n", obb)
plt.imshow(obb)
img1 = np.zeros((16,16))
img1[4:12,4:12] = 1.
img1[:4, 5] = 1.
img1 = np.uint8(transform.rotate(img1, -20, order=0) * 255)
print("Test image:\n", img1)
obb = fill_oriented_bbox(img1, fill_threshold=1.5)
print("OBBox:\n", obb)
plt.imshow(obb)
img1 = np.zeros((16,16))
img1[4:12,4:12] = 1.
img1[:4, 5] = 1.
img1 = np.uint8(transform.rotate(img1, -20, order=0) * 255)
print("Test image:\n", img1)
obb = fill_oriented_bbox(img1, fill_threshold=1.2)
print("OBBox:\n", obb)
plt.imshow(obb)
img1 = np.zeros((16,16), dtype=np.uint8)
print("Test image:\n", img1)
obb = fill_oriented_bbox(img1)
print("OBBox:\n", obb)
plt.imshow(obb)
img1 = np.zeros((16,16), dtype=np.uint8)
img1[4:10, 4:10] = 1.
img1[9:14, 9:14] = 1.
print("Test image:\n", img1)
obb = fill_oriented_bbox(img1)
print("OBBox:\n", obb)
plt.imshow(obb)
img1 = np.zeros((16,16), dtype=np.uint8)
img1[4:10, 4:10] = 1.
img1[9:14, 9:14] = 1.
print("Test image:\n", img1)
obb = fill_oriented_bbox(img1, fill_threshold=1.2)
print("OBBox:\n", obb)
plt.imshow(obb)
img1 = np.zeros((16,16), dtype=np.uint8)
img1[4:7, 4:7] = 1.
img1[9:14, 9:14] = 1.
print("Test image:\n", img1)
obb = fill_oriented_bbox(img1)
print("OBBox:\n", obb)
plt.imshow(obb)
img1 = np.zeros((768,768))
img1[100:600,150:500] = 1.
img1 = np.uint8(transform.rotate(img1, -45, order=0) * 255)
%timeit fill_oriented_bbox(img1, fill_threshold=1.2)
```
| true |
code
| 0.465509 | null | null | null | null |
|
## 1. Welcome!
<p><img src="https://assets.datacamp.com/production/project_1170/img/office_cast.jpeg" alt="Markdown">.</p>
<p><strong>The Office!</strong> What started as a British mockumentary series about office culture in 2001 has since spawned ten other variants across the world, including an Israeli version (2010-13), a Hindi version (2019-), and even a French Canadian variant (2006-2007). Of all these iterations (including the original), the American series has been the longest-running, spanning 201 episodes over nine seasons.</p>
<p>In this notebook, we will take a look at a dataset of The Office episodes, and try to understand how the popularity and quality of the series varied over time. To do so, we will use the following dataset: <code>datasets/office_episodes.csv</code>, which was downloaded from Kaggle <a href="https://www.kaggle.com/nehaprabhavalkar/the-office-dataset">here</a>.</p>
<p>This dataset contains information on a variety of characteristics of each episode. In detail, these are:
<br></p>
<div style="background-color: #efebe4; color: #05192d; text-align:left; vertical-align: middle; padding: 15px 25px 15px 25px; line-height: 1.6;">
<div style="font-size:20px"><b>datasets/office_episodes.csv</b></div>
<ul>
<li><b>episode_number:</b> Canonical episode number.</li>
<li><b>season:</b> Season in which the episode appeared.</li>
<li><b>episode_title:</b> Title of the episode.</li>
<li><b>description:</b> Description of the episode.</li>
<li><b>ratings:</b> Average IMDB rating.</li>
<li><b>votes:</b> Number of votes.</li>
<li><b>viewership_mil:</b> Number of US viewers in millions.</li>
<li><b>duration:</b> Duration in number of minutes.</li>
<li><b>release_date:</b> Airdate.</li>
<li><b>guest_stars:</b> Guest stars in the episode (if any).</li>
<li><b>director:</b> Director of the episode.</li>
<li><b>writers:</b> Writers of the episode.</li>
<li><b>has_guests:</b> True/False column for whether the episode contained guest stars.</li>
<li><b>scaled_ratings:</b> The ratings scaled from 0 (worst-reviewed) to 1 (best-reviewed).</li>
</ul>
</div>
```
# import necessary libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# read the csv file
df = pd.read_csv('datasets/office_episodes.csv')
print(df.shape)
df.head(3)
```
# First Step:
```
# We need to create a scatter plot. The x-axis is episode number. The viewship (in millions) is y-axis
x_axis = df['episode_number']
y_axis = df['viewership_mil']
# A color scheme reflecting the scaled ratings
def color_change(score):
if score < 0.25:
return 'red'
elif 0.25 <= score < 0.5:
return 'orange'
elif 0.5 <= score < 0.75:
return 'lightgreen'
else:
return 'darkgreen'
color_scheme = df['scaled_ratings'].apply(color_change)
# size system, with guest appearances -> size equal to 250. Otherwise, 25
def mark_size(guest):
if guest is True:
return 250
return 25
size_system = df['has_guests'].apply(mark_size)
# initalize the matplotlib.pyplot fig
fig = plt.figure()
# Create the scatter plot
plt.scatter(x_axis, y_axis, c=color_scheme, s=size_system, marker='*')
# Plot with title 'Popularity, Quality, and Guest Appearances on the Office'
plt.title('Popularity, Quality, and Guest Appearances on the Office')
# Plot with xlabel "Episode Number"
plt.xlabel("Episode Number")
# plot with ylabel "Viewership (Millions)"
plt.ylabel('Viewership (Millions)')
# Setting the plot to become bigger
plt.rcParams['figure.figsize'] = [11, 7]
```
# Second Step:
```
# Select the rows which has_guests equal to True
df = df[df['has_guests'] == True]
# Using groupby function to aggreviate the guest_stars and calculate the sum of viewership
df = df.groupby(df['guest_stars']).sum()
# Select the viewship_mil column
guest_viewership = df['viewership_mil']
# Check the maximum value
max_view = max(np.array(guest_viewership))
# select the name which viewership equal to 22.91
popular_guest = guest_viewership[guest_viewership == 22.91]
top_star = popular_guest.index[0].split(',')[0]
top_star
```
| true |
code
| 0.556701 | null | null | null | null |
|
###### Content under Creative Commons Attribution license CC-BY 4.0, code under BSD 3-Clause License © 2019 by D. Koehn, notebook style sheet by L.A. Barba, N.C. Clementi
```
# Execute this cell to load the notebook's style sheet, then ignore it
from IPython.core.display import HTML
css_file = '../style/custom.css'
HTML(open(css_file, "r").read())
```
# Exercise: How to sail without wind
Imagine, the Bsc-students of the "Differential Equations in the Earth System" course are organizing a sailing trip in the Kiel Bay area and baltic sea. Unfortunately, the strong wind gusts predicted by the meteorologists, become not even a small breeze. Sometimes even physicists are not able to predict the future. We will learn why in the next lecture.
Fortunately, the oceanographers can deliver sea current data of the specified area. So how can the students sail without wind and stay on course? By letting their thoughts and boat drift and solving the simplest, uncoupled ordinary differential equation, I can imagine.
## Governing equations
The velocity vector field ${\bf{V}} = (v_x,v_y)^T$ is componentwise related to the spatial coordinates ${\bf{x}} = (x,y)^T$ by
\begin{equation}
v_x = \frac{dx}{dt},\; v_y = \frac{dy}{dt}
\end{equation}
To estimate the drift or **streamline** of our boat in the velocity vector field $\bf{V}$, starting from an initial position ${\bf{x_0}} = (x_0,y_0)^T$, we have to solve the uncoupled ordinary differential equations using the finite difference method introduced at the beginning of this class.
Approximating the temporal derivatives in eqs. (1) using the **backward FD operator**
\begin{equation}
\frac{df}{dt} \approx \frac{f(t)-f(t-dt)}{dt} \notag
\end{equation}
with the time sample interval $dt$ leads to
\begin{equation}
\begin{split}
v_x &= \frac{x(t)-x(t-dt)}{dt}\\
v_y &= \frac{y(t)-y(t-dt)}{dt}\\
\end{split}
\notag
\end{equation}
After solving for $x(t), y(t)$, we get the **explicit time integration scheme**:
\begin{equation}
\begin{split}
x(t) &= x(t-dt) + dt\; v_x\\
y(t) &= y(t-dt) + dt\; v_y\\
\end{split}
\notag
\end{equation}
and by introducing a temporal dicretization $t^n = n * dt$ with $n \in [0,1,...,nt]$, where $nt$ denotes the maximum time steps, the final FD code becomes:
\begin{equation}
\begin{split}
x^n &= x^{n-1} + dt\; v_x^{n-1}\\
y^n &= y^{n-1} + dt\; v_y^{n-1}\\
\end{split}
\end{equation}
These equations simply state, that we can extrapolate the next position of our boat $(x^{(n)},y^{(n)})^T$ in the velocity vector field based on the position at a previous time step $(x^{(n-1)},y^{(n-1)})^T$, the velocity field at this previous position $(v_x^{(n-1)},v_y^{(n-1)})^T$ and a predefined time step $dt$. Before implementing the FD scheme in Python, let 's try to find a simple velocity vector field ...
## Boring velocity vector field
We should start with a simple, boring velocity vector field, where we can easily predict the drift of the boat. Let's take - this:
\begin{equation}
{\bf{V}} = (y,-x)^T \notag
\end{equation}
and visualize it with Matplotlib using a `Streamplot`. First, we load all required libraries ...
```
# Import Libraries
# ----------------
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from pylab import rcParams
# Ignore Warning Messages
# -----------------------
import warnings
warnings.filterwarnings("ignore")
```
... and define the coordinates for the `Streamplot`:
```
dh = 50.
x1 = -1000.
x2 = 1000.
X, Y = np.meshgrid(np.arange(x1, x2, dh), np.arange(x1, x2, dh))
```
For more flexibility and avoid code redundances later on, we write a short function, which evaluates the velocity components $(v_x,v_y)^T$ at a given position $(x,y)^T$
```
# compute velocity components V = (vx,vy)^T at position x,y
def vel_xy(x,y):
vx = y / 1000.
vy = -x / 1000.
return vx, vy
```
After these preparations, we can plot the velocity vector field
```
# Define figure size
rcParams['figure.figsize'] = 8, 8
fig1, ax1 = plt.subplots()
# Define vector field components for coordinates X,Y
VX,VY = vel_xy(X,Y)
ax1.set_title(r'Plot of velocity vector field $V=(y,-x)^T$')
plt.axis('equal')
Q = ax1.streamplot(X,Y,VX,VY)
plt.xlabel('x [m]')
plt.ylabel('y [m]')
plt.savefig('Plot_vector_field_V_boring.pdf', bbox_inches='tight', format='pdf')
plt.show()
```
So the velocity vector field ${\bf{V}} = (y,-x)^T$ is simply a large vortex with zero velocity at the origin and linear increasing velocities with distance.
### Sailing in the boring vector field $V =(y,-x)^T$
Next, we want to predict our sailing course in this large vortex. Eventhough it is unrealistic, we assume, that such a large vortex exists in the [Kiel Fjord](https://en.wikipedia.org/wiki/Kieler_F%C3%B6rde#/media/File:Kiel_Luftaufnahme.JPG), maybe related to some suspicous, top secret activity in the Kiel military harbor.
##### Exercise 1
Complete the following Python code `sailing_boring`, to predict the sailing course in the boring velocity vector field $V =(y,-x)^T$. Most of the code is already implemented, you only have to add the FD solution of the uncoupled, ordinary differential equations (2):
```
def sailing_boring(tmax, dt, x0, y0):
# Compute number of time steps based on tmax and dt
nt = (int)(tmax/dt)
# vectors for storage of x, y positions
x = np.zeros(nt + 1)
y = np.zeros(nt + 1)
# define initial position
x[0] = x0
y[0] = y0
# start time stepping over time samples n
for n in range(1,nt + 1):
# compute velocity components at current position
vx, vy = vel_xy(x[n-1],y[n-1])
# compute new position using FD approximation of time derivative
# ADD FD SOLUTION OF THE UNCOUPLED, ORDINARY DIFFERENTIAL EQUATIONS (2) HERE!
x[n] =
y[n] =
# Define figure size
rcParams['figure.figsize'] = 8, 8
fig1, ax1 = plt.subplots()
# Define vector field components for Streamplot
VX,VY = vel_xy(X,Y)
ax1.set_title(r'Streamplot of vector field $V=(y,-x)^T$')
plt.axis('equal')
Q = ax1.streamplot(X,Y,VX,VY)
plt.plot(x,y,'r-',linewidth=3)
# mark initial and final position
plt.plot(x[0],y[0],'ro')
plt.plot(x[nt],y[nt],'go')
plt.xlabel('x [m]')
plt.ylabel('y [m]')
plt.savefig('sailing_boring.pdf', bbox_inches='tight', format='pdf')
plt.show()
```
##### Exercise 2
After completing the FD code `sailing_boring`, we can define some basic modelling parameters. How long do you want to sail, defined by the parameter $tmax [s]$. What time step $dt$ do you want to use? $dt=1.\;s$ should work for the first test of your FD code. To solve the problem you also have to define the initial position of your boat. Let's assume that ${\bf{x_{0}}}=(-900,0)^T$ is the location of some jetty on the western shore of the Kiel Fjord.
By executing the cell below (`SHIFT+ENTER`), the FD code `sailing_boring` should compute the course of the boat and plot it as red line on top of the `Streamplot`. Inital and final position are defined by a red and green dot, respectively.
What course would you expect, based on the `Streamplot`? Is it confirmed by your FD code solution? If not, there might be an error in your FD implementation.
```
# How long do you want to sail [s] ?
tmax = 1000
# Define time step dt
dt = 1.
# Define initial position
x0 = -900.
y0 = 0.
# Sail for tmax s in the boring vector field
sailing_boring(tmax, dt, x0, y0)
```
##### Exercise 3
At this point you might get an idea why the code is called `sailing_boring`. We start at the western shore of the Kiel Fjord, follow an enclosed streamline to the eastern shore and travel back to the initial position of the jetty - it 's a boring Kiel harbor tour.
How long will the boring tour actually take? Vary $tmax$ until the green dot of the final position coincides with the red dot of the initial position.
You also might think: why should I invest so much computation time into this boring tour.
Copy the cell above, below this text box and increase the time step $dt$ to 20 s. How does the new FD solution differ from the one above with $dt=1\; s$? Give a possible explanation.
### Sailing in the more exciting vector field $V=(cos((x+y)/500),sin((x-y)/500))^T$
Time to sail in a more complex and exciting velocity vector field, like this one:
\begin{equation}
V=(cos((x+y)/500),sin((x-y)/500))^T \notag
\end{equation}
As in the case of the boring vector field, we define a function to compute the velocity components for a given ${\bf{x}} = (x,y)^T$:
```
# define new vector field
def vel_xy_1(x,y):
vx = np.cos((x+y)/500)
vy = np.sin((x-y)/500)
return vx, vy
```
For the visualization of this more complex vector field, I recommend to use a `Quiver` instead of the `Streamplot`
```
# Define figure size
rcParams['figure.figsize'] = 8, 8
fig1, ax1 = plt.subplots()
# Define vector field components for coordinates X,Y
VX,VY = vel_xy_1(X,Y)
ax1.set_title(r'Plot of vector field $V=(cos((x+y)/500),sin((x-y)/500))^T$')
plt.axis('equal')
Q = ax1.quiver(X,Y,VX,VY)
plt.plot(392,392,'ro')
plt.xlabel('x [m]')
plt.ylabel('y [m]')
#plt.savefig('Plot_vector_field_V_exciting.pdf', bbox_inches='tight', format='pdf')
plt.show()
```
##### Exercise 4
Now, this velocity vector field looks more exciting, than the previous one. The red dot at ${\bf{x_{island}}}=(392,392)^T$ marks the location of an island you want to reach. To compute the course, we can recycle most parts of the `sailing_boring` code.
- Rename the code below from `sailing_boring` to `sailing_exciting`
- Add the FD solution of the uncoupled, ordinary differential equations (2) to the code
- Replace in the new `sailing_exciting` code the function calls of the boring velocity field `vel_xy` by the new exciting velocity field `vel_xy_1`
- Replace in `sailing_exciting` the `Streamplot` by a `Quiver` plot.
- Mark the position of the island by a red dot by inserting
```python
plt.plot(392,392,'ro')
```
below the `Quiver` plot in `sailing_exciting`
```
def sailing_boring(tmax, dt, x0, y0):
# Compute number of time steps
nt = (int)(tmax/dt)
# vectors for storage of x, y positions
x = np.zeros(nt + 1)
y = np.zeros(nt + 1)
# define initial position
x[0] = x0
y[0] = y0
# start time stepping
for n in range(1,nt + 1):
# compute velocity components at current position
vx, vy = vel_xy(x[n-1],y[n-1])
# compute new position using FD approximation of time derivative
# ADD FD SOLUTION OF THE UNCOUPLED, ORDINARY DIFFERENTIAL EQUATIONS (2) HERE!
x[n] =
y[n] =
# Define figure size
rcParams['figure.figsize'] = 8, 8
fig1, ax1 = plt.subplots()
# Define vector field components for quiver plot
VX,VY = vel_xy(X,Y)
ax1.set_title(r'Plot of vector field $V=(cos((x+y)/500),sin((x-y)/500))^T$')
plt.axis('equal')
Q = ax1.streamplot(X,Y,VX,VY)
plt.plot(x,y,'r-',linewidth=3)
# mark initial and final position
plt.plot(x[0],y[0],'ro')
plt.plot(x[nt],y[nt],'go')
print(x[nt],y[nt])
plt.xlabel('x [m]')
plt.ylabel('y [m]')
plt.savefig('sailing_exciting.pdf', bbox_inches='tight', format='pdf')
plt.show()
```
##### Exercise 5
Time to sail to the island. To make the problem more interesting, you have to find a course to the island from the north, south, east and west boundaries. In the four cells below the x0 and y0 coordinates of the given boundary is already defined. You only have to add and change the missing coordinate vector component until you reach the island. You might also have to modify $tmax$.
**Approach from the northern boundary**
```
# How long do you want to sail [s] ?
tmax = 1000
# Define time step dt
dt = 2.
# DEFINE INTIAL POSITION AT NORTHERN BOUNDARY HERE!
x0 =
y0 = 950.
# Sail for tmax s in the boring vector field
sailing_exciting(tmax, dt, x0, y0)
```
**Approach from the southern boundary**
```
# How long do you want to sail [s] ?
tmax = 1000
# Define time step dt
dt = 2.
# DEFINE INTIAL POSITION AT SOUTHERN BOUNDARY HERE!
x0 =
y0 = -980.
# Sail for tmax s in the boring vector field
sailing_exciting(tmax, dt, x0, y0)
```
**Approach from the western boundary**
```
# How long do you want to sail [s] ?
tmax = 1000
# Define time step dt
dt = 2.
# DEFINE INTIAL POSITION AT WESTERN BOUNDARY HERE!
x0 = -950.
y0 =
# Sail for tmax s in the boring vector field
sailing_exciting(tmax, dt, x0, y0)
```
**Approach from the eastern boundary**
```
# How long do you want to sail [s] ?
tmax = 1000
# Define time step dt
dt = 2.
# DEFINE INTIAL POSITION AT EASTERN BOUNDARY HERE!
x0 = 990.
y0 =
# Sail for tmax s in the boring vector field
sailing_exciting(tmax, dt, x0, y0)
```
##### Bonus Exercise
How do you reach the blue island in the vector plot below?
```
# Define figure size
rcParams['figure.figsize'] = 8, 8
fig1, ax1 = plt.subplots()
# Define vector field components for coordinates X,Y
VX,VY = vel_xy_1(X,Y)
ax1.set_title(r'Plot of vector field $V=(cos((x+y)/500),sin((x-y)/500))^T$')
plt.axis('equal')
Q = ax1.quiver(X,Y,VX,VY)
plt.plot(-392,-392,'bo')
plt.xlabel('x [m]')
plt.ylabel('y [m]')
plt.show()
```
## What we learned
- How to solve a simple system of ordinary differential equations by an explicit time integration scheme
- The long-term impact of small inaccuracies in time integration schemes by choosing a too large time step $dt$
- The solution to a problem is not only defined by a differential equation, but also by an initial condition
- How to sail without wind, by using flow data and numerical solutions of ordinary differential equations
| true |
code
| 0.620966 | null | null | null | null |
|
- Tensor board projection
- Visualizing loss and network on tensorboard
- Comments
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import mpld3
mpld3.enable_notebook()
from pylab import rcParams
rcParams['figure.figsize'] = 10, 10
import sys
import numpy as np
import random
import math
import tensorflow as tf
import matplotlib.pyplot as plt
sys.path.append("./../../Utils/")
from readWikiData import get_wikipedia_data
```
##### Get representation
```
sentences, word2idx, idx2word, _ = get_wikipedia_data(n_files=10, n_vocab=1000, by_paragraph=True)
def get_wiki_data_cbow(sentences, word2idx, window_size=5):
training_data = []
vocab_size = len(word2idx)
for sentence in sentences:
if len(sentence) < window_size * 2 + 1:
continue
for i in range(len(sentence)):
left_context = sentence[max(i-window_size, 0): i]
right_context = sentence[i+1:window_size + i + 1]
centre = sentence[i]
if len(left_context + right_context) < (2*window_size):
len_left = len(left_context)
len_right = len(right_context)
if len_left < len_right:
right_context = sentence[i+1 : window_size + i + 1 + (len_right - len_left)]
else:
left_context = sentence[max(i-window_size - (len_left - len_right), 0): i]
temp = left_context + right_context
if len(temp) < window_size * 2:
print sentence
print left_context
print right_context
print centre
break
training_data.append((tuple(temp), centre))
print training_data[:10]
training_data = list(set(training_data))
idx2word = {v:k for k, v in word2idx.iteritems()}
return len(word2idx), training_data, word2idx, idx2word
vocab_size, training_data, word2idx, idx2word = get_wiki_data_cbow(sentences, word2idx)
len(training_data)
training_data[:10]
```
##### Get batches
```
bucket_list = []
def getNextBatchCbow(bi_grams_, window_size=5, batch_size=10000):
global bucket_list
docs_ids_to_select = list(set(bi_grams_) - set(bucket_list))
if len(docs_ids_to_select) < batch_size:
bucket_list = []
docs_ids_to_select = bi_grams_
# Initialize two variables
train_X = np.ndarray(shape=(batch_size, window_size*2), dtype=np.int32)
train_label = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
# Get a random set of docs
random_docs = random.sample(docs_ids_to_select, batch_size)
bucket_list += random_docs
index = 0
# Iterate threw all the docs
for item in random_docs:
train_X[index] = item[0]
train_label[index] = item[1]
index += 1
return train_X, train_label
#getNextBatchCbow(training_data, 2)
```
##### Let's design the graph
```
def init_weight(Mi, Mo):
shape_sum = float(Mi + Mo)
return np.random.uniform(-np.sqrt(6/shape_sum),np.sqrt(6/shape_sum), [Mi, Mo])
embedding_size_w = 100
vocab_size = len(word2idx)
n_neg_samples = 20
learning_rate = 10e-5
epochs = 2
batch_size=10000
mu = 0.99
window_size = 5
# Define placeholders for training
train_X = tf.placeholder(tf.int32, shape=[batch_size, None])
train_label = tf.placeholder(tf.int32, shape=[batch_size, 1])
# Define matrix for doc_embedding and word_embedding
W1 = tf.Variable(init_weight(vocab_size, embedding_size_w), name="W1", dtype=tf.float32)
# Define weights for the output unit
W2 = tf.Variable(init_weight(vocab_size, embedding_size_w), name="W2", dtype=tf.float32)
biases = tf.Variable(tf.zeros(vocab_size))
print(train_X.get_shape(), train_label.get_shape(), W1.get_shape(), W2.get_shape())
embed = []
# generating a vector of size embedding_size_d
embed_w = tf.zeros([1, embedding_size_w], dtype=tf.float32)
# add all the word vecs in window_size
for j in range(window_size*2):
embed_w += tf.nn.embedding_lookup(W1, train_X[:, j])
#embed.append(embed_w)
#embed = tf.concat(1, embed)/(window_size*2)
embed = embed_w/(window_size*2)
print(embed.get_shape())
loss = tf.nn.sampled_softmax_loss(weights=W2, \
biases=biases, \
labels=train_label, \
inputs=embed, \
num_sampled=n_neg_samples, \
num_classes=vocab_size)
loss = tf.reduce_mean(loss)
#optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=mu).minimize(loss)
#optimizer = tf.train.AdagradOptimizer(learning_rate).minimize(loss)
global_step = tf.Variable(0, trainable=False)
starter_learning_rate = 0.01
learning_rate = tf.train.exponential_decay(starter_learning_rate, global_step,
1000, 0.96, staircase=True)
# Passing global_step to minimize() will increment it at each step.
optimizer = (
tf.train.MomentumOptimizer(learning_rate, momentum=mu).minimize(loss, global_step=global_step)
)
saver = tf.train.Saver()
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)
average_loss = 0
for step in range(epochs):
epoch_error = 0.0
temp_X , temp_labels = getNextBatchCbow(window_size=5, bi_grams_=training_data)
feed_dict = {train_X : temp_X, train_label : temp_labels}
op, l = sess.run([optimizer, loss],
feed_dict=feed_dict)
epoch_error += l
if step % 100 == 0:
print "Error at epoch : ", step, " = ", epoch_error
save_path = saver.save(sess, "./models/model_cbow_model.ckpt")
print("Model saved in file: %s" % save_path)
```
##### Embeddings
```
W1_embedding = None
W2_embedding = None
with tf.Session() as sess:
saver = tf.train.Saver()
# Restore variables from disk.
saver.restore(sess, "./models/model_cbow_model.ckpt")
print("Model restored.")
# Normalize word2vec
W1_embedding = W1.eval()
# Normalize word2vec
W2_embedding = W2.eval()
W1_embedding.shape
W2_embedding.shape
word2vec = np.mean([W1_embedding, W2_embedding], axis=0)
word2vec.shape
```
##### Projection of embeddings using t-SNE
```
idx2word = {v:k for k, v in word2idx.items()}
from sklearn.manifold import TSNE
model = TSNE()
Z = model.fit_transform(word2vec)
plt.scatter(Z[:,0], Z[:,1])
for i in xrange(len(idx2word)):
try:
plt.annotate(s=idx2word[i].encode("utf8"), xy=(Z[i,0], Z[i,1]))
except:
print "bad string:", idx2word[i]
plt.show()
```
| true |
code
| 0.459258 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Priyam145/MLprojects/blob/main/notebooks/LinearRegression_maths.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import numpy as np
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
import matplotlib.pyplot as plt
import seaborn as sns
fig, axs = plt.subplots(figsize=(10, 7))
fig.set_facecolor("white")
plt.scatter(X, y);
axs.set_xlabel('X')
axs.set_ylabel('y')
axs.set_xlim(xmin=0)
axs.set_ylim(ymin=0)
X_b = np.c_[np.ones((100, 1)), X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
X_b[:5]
theta_best
fig, axs = plt.subplots(figsize=(10, 7))
fig.set_facecolor("white")
plt.scatter(X, y);
plt.plot(X, X_b.dot(theta_best), color='red', label='Prediction line')
axs.set_xlabel('X')
axs.set_ylabel('y')
axs.set_xlim(xmin=0)
axs.set_ylim(ymin=0)
plt.legend();
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new] # add x0 = 1 to each instance
y_predict = X_new_b.dot(theta_best)
y_predict
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_
lin_reg.predict(X_new)
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
np.linalg.pinv(X_b).dot(y)
eta = 0.1
n_iterations = 1000
m = 100
fig, axs = plt.subplots(figsize=(15, 10))
fig.set_facecolor("white")
plt.scatter(X, y);
axs.set_xlabel(r'$X_1$')
axs.set_ylabel('y')
axs.set_xlim(xmin=0)
axs.set_ylim(ymin=0)
theta = np.random.randn(2, 1)
for iteration in range(n_iterations):
gradients = 2/m*X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
if iteration < 10:
plt.plot(X, X_b.dot(theta), label=f'iteration {iteration+1}')
axs.set_title('{eta}'.format(eta=r'$\eta = 0.1$'))
plt.legend();
theta
```
# Stochastic Gradient Descent
```
n_epochs = 50
t0, t1 = 5, 50 # learning schedule hyperparamters
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2, 1) # random initialization
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_b[random_index:random_index + 1]
yi = y[random_index:random_index + 1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
theta
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
```
# Mini-Batch Gradient Descent
# Polynomial Regression
```
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
fig, axs = plt.subplots(figsize=(15, 10))
fig.set_facecolor("white")
plt.scatter(X, y);
axs.set_xlabel(r'$X_1$')
axs.set_ylabel('y')
axs.set_xlim(xmin=-3)
axs.set_ylim(ymin=0);
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
X_poly[0]
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
fig, axs = plt.subplots(figsize=(15, 10))
fig.set_facecolor("white")
plt.scatter(X, y)
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
axs.set_xlabel(r'$X_1$')
axs.set_ylabel('y')
axs.set_xlim(xmin=-3)
axs.set_ylim(ymin=0);
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
fig, axs = plt.subplots(figsize=(10, 7))
fig.set_facecolor('white')
for style, width, degree in (("g-", 1, 300), ("b--", 2, 2), ("r-+", 2, 1)):
polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
std_scaler = StandardScaler()
lin_reg = LinearRegression()
polynomial_regression = Pipeline([
("poly_features", polybig_features),
("std_scaler", std_scaler),
("lin_reg", lin_reg),
])
polynomial_regression.fit(X, y)
y_newbig = polynomial_regression.predict(X_new)
plt.plot(X_new, y_newbig, style, label=str(degree), linewidth=width)
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
fig, axs = plt.subplots(figsize=(10, 7))
fig.set_facecolor('white')
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
train_errors, val_errors = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), 'r-+', linewidth=2, label='train')
plt.plot(np.sqrt(val_errors), 'b-', linewidth=3, label='val')
axs.set_xlabel('Training set size')
axs.set_ylabel('RMSE')
axs.set_xlim(xmin=0)
axs.set_ylim(ymin=0, ymax=3.0)
plt.legend()
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)
from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("lin_reg", LinearRegression())
])
plot_learning_curves(polynomial_regression, X, y)
```
# Ridge Regression
```
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver='cholesky')
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
sgd_reg = SGDRegressor(penalty='l2')
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
```
# Lasso Regression
```
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
lasso_reg = SGDRegressor(penalty='l1')
lasso_reg.fit(X, y.ravel())
lasso_reg.predict([[1.5]])
t1a, t1b, t2a, t2b = -1, 3, -1.5, 1.5
t1s = np.linspace(t1a, t1b, 500)
t2s = np.linspace(t2a, t2b, 500)
t1, t2 = np.meshgrid(t1s, t2s)
print(t1.shape)
T = np.c_[t1.ravel(), t2.ravel()]
Xr = np.array([[1, 1], [1, -1], [1, 0.5]])
yr = 2 * Xr[:, :1] + 0.5 * Xr[:, 1:]
J = (1/len(Xr) * np.sum((T.dot(Xr.T) - yr.T)**2, axis=1)).reshape(t1.shape)
N1 = np.linalg.norm(T, ord=1, axis=1).reshape(t1.shape)
N2 = np.linalg.norm(T, ord=2, axis=1).reshape(t1.shape)
t_min_idx = np.unravel_index(np.argmin(J), J.shape)
t1_min, t2_min = t1[t_min_idx], t2[t_min_idx]
t_init = np.array([[0.25], [-1]])
def bgd_path(theta, X, y, l1, l2, core = 1, eta = 0.05, n_iterations = 200):
path = [theta]
for iteration in range(n_iterations):
gradients = core * 2/len(X) * X.T.dot(X.dot(theta) - y) + l1 * np.sign(theta) + l2 * theta
theta = theta - eta * gradients
path.append(theta)
return np.array(path)
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(10.1, 8))
fig.set_facecolor('white')
for i, N, l1, l2, title in ((0, N1, 2., 0, "Lasso"), (1, N2, 0, 2., "Ridge")):
JR = J + l1 * N1 + l2 * 0.5 * N2**2
tr_min_idx = np.unravel_index(np.argmin(JR), JR.shape)
t1r_min, t2r_min = t1[tr_min_idx], t2[tr_min_idx]
levelsJ=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(J) - np.min(J)) + np.min(J)
levelsJR=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(JR) - np.min(JR)) + np.min(JR)
levelsN=np.linspace(0, np.max(N), 10)
path_J = bgd_path(t_init, Xr, yr, l1=0, l2=0)
path_JR = bgd_path(t_init, Xr, yr, l1, l2)
path_N = bgd_path(np.array([[2.0], [0.5]]), Xr, yr, np.sign(l1)/3, np.sign(l2), core=0)
ax = axes[i, 0]
ax.grid(True)
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.contourf(t1, t2, N / 2., levels=levelsN)
ax.plot(path_N[:, 0], path_N[:, 1], "y--")
ax.plot(0, 0, "ys")
ax.plot(t1_min, t2_min, "ys")
ax.set_title(r"$\ell_{}$ penalty".format(i + 1), fontsize=16)
ax.axis([t1a, t1b, t2a, t2b])
if i == 1:
ax.set_xlabel(r"$\theta_1$", fontsize=16)
ax.set_ylabel(r"$\theta_2$", fontsize=16, rotation=0)
ax = axes[i, 1]
ax.grid(True)
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.contourf(t1, t2, JR, levels=levelsJR, alpha=0.9)
ax.plot(path_JR[:, 0], path_JR[:, 1], "w-o")
ax.plot(path_N[:, 0], path_N[:, 1], "y--")
ax.plot(0, 0, "ys")
ax.plot(t1_min, t2_min, "ys")
ax.plot(t1r_min, t2r_min, "rs")
ax.set_title(title, fontsize=16)
ax.axis([t1a, t1b, t2a, t2b])
if i == 1:
ax.set_xlabel(r"$\theta_1$", fontsize=16)
plt.show()
```
# Elastic Net
```
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
```
# Early Stopping
```
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1)
X_train, X_val, y_train, y_val = train_test_split(X[:50], y[:50].ravel(), test_size=0.5, random_state=10)
```
## Early Stopping - Example Code:
```
from copy import deepcopy
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
("std_scaler", StandardScaler())
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train) # continues where it left off
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val, y_val_predict)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = deepcopy(sgd_reg)
```
## Early Stopping - Graph:
```
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
sgd_reg.fit(X_train_poly_scaled, y_train)
y_train_predict = sgd_reg.predict(X_train_poly_scaled)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
train_errors.append(mean_squared_error(y_train, y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])
fig, axs = plt.subplots(figsize=(10, 7))
fig.set_facecolor('white')
plt.annotate('Best model',
xy=(best_epoch, best_val_rmse),
xytext=(best_epoch, best_val_rmse + 1),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.05),
fontsize=16,
)
best_val_rmse -= 0.03 # just to make the graph look better
plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2)
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="Validation set")
plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="Training set")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("Epoch", fontsize=14)
plt.ylabel("RMSE", fontsize=14)
plt.show()
```
# Logistic Regression
```
t = np.linspace(-10, 10, 100)
sig = 1 / (1 + np.exp(-t))
fig, axs = plt.subplots(figsize=(15, 7))
fig.set_facecolor('white')
plt.plot([-10, 10], [0, 0], "k-")
plt.plot([-10, 10], [0.5, 0.5], "k:")
plt.plot([-10, 10], [1, 1], "k:")
plt.plot([0, 0], [-1.1, 1.1], "k-")
plt.plot(t, sig, "b-", linewidth=2, label=r"$\sigma(t) = \frac{1}{1 + e^{-t}}$")
plt.xlabel("t")
plt.legend(loc="upper left", fontsize=20)
plt.axis([-10, 10, -0.1, 1.1])
plt.show()
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
X = iris["data"][:, 3:] # petal width
y = (iris["target"] == 2).astype(np.int) # 1 if Iris virginica, else 0
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
fig, axs = plt.subplots(figsize=(10, 5))
fig.set_facecolor('white')
plt.plot(X_new, y_proba[:, 1], "g-", label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris virginica")
axs.set_xlim(xmin=0)
axs.set_ylim(ymin=0);
fig, axs = plt.subplots(figsize=(15, 7))
fig.set_facecolor('white')
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]
plt.plot(X[y==0], y[y==0], "bs")
plt.plot(X[y==1], y[y==1], "g^")
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
plt.text(decision_boundary+0.02, 0.15, "Decision boundary", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02])
plt.show()
log_reg.predict([[1.7], [1.5]])
```
# Softmax Regression
```
X = iris["data"][:, (2, 3)]
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10)
softmax_reg.fit(X, y)
softmax_reg.predict([[5, 2]])
softmax_reg.predict_proba([[5, 2]])
```
## Softmax Regression (Without scikit-learn):
```
import pandas as pd
iris_data = iris["data"]
iris_target = iris["target"]
iris_data[:5]
iris_target[:5]
np.unique(iris_target)
iris["target_names"]
```
### Adding bias to the data:
Every data will have a certain amount of bias i.e $x^{i}_0$ = 1, where $x^{i}_0$ = $0^{th}$ feature of $i^{th}$ instance of x
```
iris_data_with_bias = np.c_[np.ones((iris_data.shape[0], 1)), iris_data]
iris_data_with_bias[:5]
```
### Splitting the dataset into train and test without using Scikit-learn (train_test_split)
We will follow the general practice of splitting the dataset into 80% train and 20% test.
```
def train_test_split(X, y, test_ratio=0.2):
total_size = len(X)
random_indices = np.random.permutation(total_size)
train_size = int(total_size*(1 - test_ratio))
train = X[random_indices[:train_size]]
train_result = y[random_indices[:train_size]]
test = X[random_indices[train_size:]]
test_result = y[random_indices[train_size:]]
return train, train_result, test, test_result
iris_train, iris_train_result, iris_test, iris_test_result = train_test_split(iris_data_with_bias,
iris_target,
test_ratio=0.2)
print('training:', iris_train.shape,'training_result:', iris_train_result.shape )
print('train set:\n',iris_train[:5])
print('train result set:\n', iris_train_result[:5])
print('test:', iris_test.shape,'test_result:', iris_test_result.shape )
print('test set:\n',iris_test[:5])
print('test result set:\n', iris_test_result[:5])
```
### One-hot Encoding the train target set:
```
def one_hot_encoder(target):
encoded_target = np.zeros(shape=(target.size, np.unique(target).size))
encoded_target[np.arange(target.size), target] = 1
return encoded_target
encoded_target = one_hot_encoder(iris_train_result)
np.unique(encoded_target, axis=0)
```
### Fucntions for the Softmax scores and probabilities of training set:
```
def softmax_scores_func(data, theta):
return data.dot(theta)
def softmax_probability_func(softmax_scores):
return np.exp(softmax_scores)/np.sum(np.exp(softmax_scores), axis=1, keepdims=True)
```
### Finding Optimum $\vec{\theta}^{\,}_k$, where k $\epsilon$ (0, K), for K = no.of classes:
```
def optimum_theta(X, y, n_iterations, alpha, validation_ratio, n_validations, epsilon=1e-7):
best_accuracy = 0
best_theta = np.zeros(shape=(X.shape[1], np.unique(y).size))
best_validation = -1
for validation in range(n_validations):
X_train, y_train, X_valid, y_valid = train_test_split(X, y, test_ratio=validation_ratio)
n_classes = np.unique(y_train).size
softmax_theta = np.random.randn(X_train.shape[1], n_classes)
m = y_train.size
y_one_hot = one_hot_encoder(y_train)
y_valid_one_hot = one_hot_encoder(y_valid)
print('Validation : ', validation)
for iteration in range(n_iterations):
softmax_scores = softmax_scores_func(X_train, softmax_theta)
softmax_proba = softmax_probability_func(softmax_scores)
entropy_loss = -np.mean(np.sum(y_one_hot * np.log(softmax_proba + epsilon), axis=1))
loss = -np.mean(np.sum(y_one_hot * np.log(softmax_proba + epsilon), axis=1))
if iteration % 500 == 0:
print(iteration,' ', f'{loss:.5f}')
gradient = (1/m)*(X_train.T.dot(softmax_proba - y_one_hot))
softmax_theta = softmax_theta - alpha * gradient
y_predict = np.argmax(X_valid.dot(softmax_theta), axis=1)
accuracy = np.sum(y_predict == y_valid)/len(y_valid)
print(f'ACCURACY: {accuracy:.5f}')
if(accuracy > best_accuracy):
best_accuracy = accuracy
best_theta = softmax_theta
best_validation = validation
return best_theta, best_accuracy, best_validation
softmax_theta, validation_accuracy, validation = optimum_theta(iris_train, iris_train_result, n_iterations=5001, alpha=0.1, validation_ratio=0.4, n_validations=5)
print(softmax_theta)
print(validation_accuracy)
print(validation)
def predict(X, theta):
predictions = X.dot(theta)
return np.argmax(predictions, axis=1)
final_predictions = predict(iris_test, softmax_theta)
final_predictions[:5]
final_accuracy = np.sum(final_predictions == iris_test_result)/len(iris_test_result)
final_accuracy
```
### Adding Regularization to the $Optimum$ $Theta$ $Func.$
We will add $l_2$ loss to the model, hopefully it might help us achieve better result!
```
def optimum_theta(X, y, n_iterations, alpha, validation_ratio, n_validations, loss=True, reg_para=0.1, epsilon=1e-7):
best_accuracy = 0
best_theta = np.zeros(shape=(X.shape[1], np.unique(y).size))
best_validation = -1
# Handles all the loss parameters
loss_flag = int(loss)
for validation in range(n_validations):
X_train, y_train, X_valid, y_valid = train_test_split(X, y, test_ratio=validation_ratio)
n_classes = np.unique(y_train).size
softmax_theta = np.random.randn(X_train.shape[1], n_classes)
m = y_train.size
y_one_hot = one_hot_encoder(y_train)
y_valid_one_hot = one_hot_encoder(y_valid)
print('Validation : ', validation)
for iteration in range(n_iterations):
softmax_scores = softmax_scores_func(X_train, softmax_theta)
softmax_proba = softmax_probability_func(softmax_scores)
# Since, the total loss is a summation of two terms, we can separate them
entropy_loss = -np.mean(np.sum(y_one_hot * np.log(softmax_proba + epsilon), axis=1))
l2_loss = (loss_flag)*((1/2) * np.sum(np.square(softmax_theta[1:])))
total_loss = entropy_loss + reg_para * l2_loss
if iteration % 500 == 0:
print(iteration,' ', f'{total_loss:.5f}')
# Since, the total gradient is a summation of two terms, we can separate them
entropy_gradient = (1/m)*(X_train.T.dot(softmax_proba - y_one_hot))
l2_gradient = (loss_flag) * (np.r_[np.zeros([1, n_classes]), reg_para * softmax_theta[1:]])
softmax_theta = softmax_theta - alpha * (entropy_gradient + l2_gradient)
y_predict = np.argmax(X_valid.dot(softmax_theta), axis=1)
accuracy = np.sum(y_predict == y_valid)/len(y_valid)
print(f'ACCURACY: {accuracy:.5f}')
if(accuracy > best_accuracy):
best_accuracy = accuracy
best_theta = softmax_theta
best_validation = validation
return best_theta, best_accuracy, best_validation
softmax_theta, validation_accuracy, validation = optimum_theta(iris_train, iris_train_result, n_iterations=5001, alpha=0.1, validation_ratio=0.1, n_validations=5, loss=True)
print(softmax_theta)
print(validation_accuracy)
print(validation)
regularized_predictions = predict(iris_test, softmax_theta)
regularized_predictions[:5]
regularized_accuracy = np.mean(regularized_predictions == iris_test_result)
regularized_accuracy
```
The accuracy went down instead of going up, but we know the reason why.<br><br>
If you look at the loss values of each validation you will see that after a some iterations the loss values start to increase. This is because the model starts to overfit the data. And, hence as result our final accuracy goes down.<br><br>
*To solve this we will use ***EARLY-STOPPING*** Method*
### Adding Early-Stopping Method to $Regularized$ $Optimum$ $Theta$ $Func$.
```
def optimum_theta(X, y, n_iterations, alpha, validation_ratio, n_validations, loss=True, reg_para=0.1, epsilon=1e-7):
best_accuracy = 0
best_theta = np.zeros(shape=(X.shape[1], np.unique(y).size))
best_validation = -1
# Handles all the loss parameters
loss_flag = int(loss)
for validation in range(n_validations):
best_loss = np.infty
X_train, y_train, X_valid, y_valid = train_test_split(X, y)
n_classes = np.unique(y_train).size
softmax_theta = np.random.randn(X_train.shape[1], n_classes)
m = y_train.size
y_one_hot = one_hot_encoder(y_train)
y_valid_one_hot = one_hot_encoder(y_valid)
print('Validation : ', validation)
for iteration in range(n_iterations):
softmax_scores = softmax_scores_func(X_train, softmax_theta)
softmax_proba = softmax_probability_func(softmax_scores)
# Since, the total loss is a summation of two terms, we can separate them
entropy_loss = -np.mean(np.sum(y_one_hot * np.log(softmax_proba + epsilon), axis=1))
l2_loss = (loss_flag)*((1/2) * np.sum(np.square(softmax_theta[1:])))
total_loss = entropy_loss + reg_para * l2_loss
# Since, the total gradient is a summation of two terms, we can separate them
entropy_gradient = (1/m)*(X_train.T.dot(softmax_proba - y_one_hot))
l2_gradient = (loss_flag) * (np.r_[np.zeros([1, n_classes]), reg_para * softmax_theta[1:]])
softmax_theta = softmax_theta - alpha * (entropy_gradient + l2_gradient)
# Early-Stop condition
softmax_scores = softmax_scores_func(X_valid, softmax_theta)
softmax_proba = softmax_probability_func(softmax_scores)
entropy_loss = -(np.mean(np.sum(y_valid_one_hot * np.log(softmax_proba + epsilon), axis=1)))
l2_loss = (loss_flag)*((1/2)*np.sum(np.square(softmax_theta[1:])))
total_loss = entropy_loss + reg_para * l2_loss
if iteration % 500 == 0:
print(f'{iteration} -> {total_loss:.5f}')
if total_loss < best_loss:
best_loss = total_loss
else:
print(f'{iteration - 1} -> {best_loss:.5f} Best Loss!')
print(f'{iteration} -> {total_loss:.5f} Early Stopping!')
break
y_predict = np.argmax(X_valid.dot(softmax_theta), axis=1)
accuracy = np.sum(y_predict == y_valid)/len(y_valid)
print(f'ACCURACY: {accuracy:.5f}\n')
if(accuracy > best_accuracy):
best_accuracy = accuracy
best_theta = softmax_theta
best_validation = validation
return best_theta, best_accuracy, best_validation
softmax_theta, validation_accuracy, validation = optimum_theta(iris_train, iris_train_result, n_iterations=5001, alpha=0.07, validation_ratio=0.2, n_validations=5, loss=False, reg_para=0.1)
print(softmax_theta)
print(validation_accuracy)
print(validation)
early_stopping_predictions = predict(iris_test, softmax_theta)
early_stopping_predictions[:5]
early_stopping_accuracy = np.mean(early_stopping_predictions == iris_test_result)
early_stopping_accuracy
```
| true |
code
| 0.7237 | null | null | null | null |
|
```
import networkx as nx
import pandas as pd
import numpy as np
from statsmodels.distributions.empirical_distribution import ECDF
import matplotlib.pyplot as plt
from scipy.stats import poisson
import scipy.stats as stats
from scipy.spatial import distance
from dragsUtility import *
import json
import twitter
import numpy as np; np.random.seed(0)
import seaborn as sns; sns.set_theme()
df = pd.read_csv('Data/rutweet.csv')
graph = nx.from_pandas_edgelist(df, source="source", target="target", edge_attr="weight", create_using=nx.DiGraph)
```
# Preprocessing
Rimozione dei cappi
```
graph.remove_edges_from(nx.selfloop_edges(graph))
```
Cartoon Network
# Network info
```
print("Number of nodes {}".format(graph.order()))
print("Number of edges {}".format(graph.size()))
nx.is_directed_acyclic_graph(graph)
print("Density {}".format(nx.density(graph)))
```
## Degree Analysis
### In-Degree + Out-Degree = Degree
Media, mediana, deviazione standard, range interquartile, minimo e massimo sono dei buoni indici per riassumere la distribuzione.
```
degrees = list(dict(graph.degree(weight="weight")).values())
print('Mean degree: \t'+ str(np.mean(degrees)))
print('Standard deviation: ' + str(np.std(degrees)))
print('Median: ' + str(np.median(degrees)))
print('iqr: ' + str(np.quantile(degrees, 0.75) - np.quantile(degrees, 0.25)))
print('Min: ' + str(np.min(degrees)))
print('Max: ' + str(np.max(degrees)))
random_graph_erdos = nx.fast_gnp_random_graph(len(graph.nodes), nx.density(graph))
random_degrees = list(dict(random_graph_erdos.degree()).values())
cdf = ECDF(degrees)
x = np.unique(degrees)
y = cdf(x)
cdf_random = ECDF(random_degrees)
x_random = np.unique(random_degrees)
y_random = cdf_random(x_random)
fig_cdf_fb = plt.figure(figsize=(10,5))
axes = fig_cdf_fb.gca()
axes.set_xscale('log')
axes.set_yscale('log')
axes.loglog(x,1-y,marker='o',ms=8, linestyle='-', label = "Ru Net", color = "#61CAE2")
axes.loglog(x_random,1-y_random,marker='D',ms=10, linestyle='-', label="Random", color = "#EA63BD")
axes.legend()
axes.set_xlabel('Degree',size=20)
axes.set_ylabel('ECCDF', size = 20)
plt.savefig("Images/DegreeDistribution.png", dpi=1200, bbox_inches='tight')
plt.show()
```
### In-Degree
```
in_degrees_noitems = dict(graph.in_degree(weight='weight'))
in_degrees = list(in_degrees_noitems.values())
print('Mean degree: \t'+ str(np.mean(in_degrees)))
print('Standard deviation: ' + str(np.std(in_degrees)))
print('Median: ' + str(np.median(in_degrees)))
print('iqr: ' + str(np.quantile(in_degrees, 0.75) - np.quantile(in_degrees, 0.25)))
print('Min: ' + str(np.min(in_degrees)))
print('Max: ' + str(np.max(in_degrees)))
```
Il nodo con in-degree più alto è un partecipante?
```
pippo = dict(graph.in_degree(weight="weight"))
sortedPippo = {k: v for k, v in sorted(pippo.items(), key=lambda item: item[1], reverse=True)}
dragsUtility= DragsUtility()
dragsUtility.isaDrag(str(list(sortedPippo.keys())[0]))
random_digraph_erdos = nx.fast_gnp_random_graph(len(graph.nodes), nx.density(graph), directed=True)
random_in_degrees = list(dict(random_digraph_erdos.in_degree(weight="weight")).values())
cdf = ECDF(in_degrees)
x = np.unique(in_degrees)
y = cdf(x)
cdf_random = ECDF(random_in_degrees)
x_random = np.unique(random_in_degrees)
y_random = cdf_random(x_random)
fig_cdf_fb = plt.figure(figsize=(10,5))
axes = fig_cdf_fb.gca()
axes.set_xscale('log')
axes.set_yscale('log')
axes.loglog(x,1-y,marker='o',ms=8, linestyle='-', label = "Ru Net", color = "#61CAE2")
axes.loglog(x_random,1-y_random,marker='D',ms=10, linestyle='-', label="Random", color = "#EA63BD")
axes.legend()
axes.set_xlabel('In-Degree',size=20)
axes.set_ylabel('ECCDF', size = 20)
plt.savefig("Images/InDegreeDistribution.png", dpi=1200, bbox_inches='tight')
plt.show()
```
### Out-degree
```
out_degrees_dict = dict(graph.out_degree(weight="weight"))
out_degrees = list(out_degrees_dict.values())
print('Mean degree: \t'+ str(np.mean(out_degrees)))
print('Standard deviation: ' + str(np.std(out_degrees)))
print('Median: ' + str(np.median(out_degrees)))
print('iqr: ' + str(np.quantile(out_degrees, 0.75) - np.quantile(out_degrees, 0.25)))
print('Min: ' + str(np.min(out_degrees)))
print('Max: ' + str(np.max(out_degrees)))
random_out_degrees = list(dict(random_digraph_erdos.out_degree(weight="weight")).values())
cdf = ECDF(out_degrees)
x = np.unique(out_degrees)
y = cdf(x)
cdf_random = ECDF(random_out_degrees)
x_random = np.unique(random_out_degrees)
y_random = cdf_random(x_random)
fig_cdf_fb = plt.figure(figsize=(10,5))
axes = fig_cdf_fb.gca()
axes.set_xscale('log')
axes.set_yscale('log')
axes.loglog(x,1-y,marker='D',ms=8, linestyle='-', label = "Ru Net", color = "#61CAE2")
axes.loglog(x_random,1-y_random,marker='8',ms=10, linestyle='-', label="Random", color = "#EA63BD")
axes.legend()
axes.set_xlabel('Out-Degree',size=20)
axes.set_ylabel('ECCDF', size = 20)
plt.savefig("Images/OutDegreeDistribution.png", dpi=1200, bbox_inches='tight')
plt.show()
cdf_out = ECDF(out_degrees)
x_out = np.unique(out_degrees)
y_out = cdf_out(x_out)
cdf_in = ECDF(in_degrees)
x_in = np.unique(in_degrees)
y_in = cdf_in(x_in)
fig_cdf_fb = plt.figure(figsize=(10,5))
axes = fig_cdf_fb.gca()
axes.set_xscale('log')
axes.set_yscale('log')
axes.loglog(x_out,1-y_out,marker='o',ms=8, linestyle='-', label = "Out-degree", color = "#61CAE2")
axes.loglog(x_in,1-y_in,marker='o',ms=10, linestyle='-', label="In-degree", color = "#91D2BE")
axes.legend()
axes.set_xlabel('In-Out-Degree',size=20)
axes.set_ylabel('ECCDF', size = 20)
```
## Connectivity
```
nx.is_strongly_connected(graph),nx.is_weakly_connected(graph)
```
C'è una giant componenent?
```
components_strong = nx.strongly_connected_components(graph)
components_weak = nx.weakly_connected_components(graph)
component_list_strong = list(components_strong)
component_list_weak = list(components_weak)
```
Numero delle componenti connesse:
```
len(component_list_strong)
len(component_list_weak)
len_cc = [len(wcc) for wcc in component_list_weak]
counts = pd.Series(len_cc).value_counts().sort_index()
fig_gc = plt.figure(figsize=(8,4))
axes = fig_gc.gca()
axes.set_xscale('log')
axes.set_yscale('log')
axes.loglog(counts.index,counts.values,marker='o',ms=8, linestyle='None', color = "#EA63BD")
axes.set_xlabel('Weakly connected component size',size=20)
axes.set_ylabel('Count', size = 20)
plt.savefig("Images/ConnectedComponents.png", dpi=1200, bbox_inches='tight')
plt.show()
```
## Small World
```
sorted_components = sorted(component_list_weak, key = lambda x : len(x), reverse=True)
giant_component = graph.subgraph(sorted_components[0]).to_undirected()
# nx.diameter(giant_component)
```
E' 12 il diametro
## Transitivity
```
# global_clustering_coeff = nx.transitivity(graph.to_undirected())
# print("Coefficiente di Clustering globale: {}".format(global_clustering_coeff))
```
Coefficiente di Clustering globale: 0.0016440739612106675
```
# avg_local_clustering_coeff = nx.average_clustering(graph.to_undirected())
# avg_local_clustering_coeff0 = nx.average_clustering(graph.to_undirected(), count_zeros=False)
# print('Coefficiente di clustering locale medio: {}'.format(avg_local_clustering_coeff))
# print('Coefficiente di clustering locale medio >0 : {}'.format(avg_local_clustering_coeff0))
```
Coefficiente di clustering locale medio: 0.18450772763547055
Coefficiente di clustering locale medio >0 : 0.5825613071721611
## Reciprocity
```
print('Reciprocità: {}'.format(nx.overall_reciprocity(graph)))
```
Very low reciprocity is typical of an information network.
# Centrality
```
p99_indeg = np.percentile(in_degrees,99.9)
influencers_id = [(str(k),v) for k,v in in_degrees_noitems.items() if v>=p99_indeg]
bearer_token = json.load(open('application_keys.json'))['twitter']['bearer_token']
twitter_api = twitter.Twitter(auth=twitter.OAuth2(bearer_token=bearer_token))
in_deg_cen = nx.in_degree_centrality(graph)
out_deg_cen = nx.out_degree_centrality(graph)
influencers_username_centrality = [(twitter_api.users.show(user_id=k)['screen_name'],v,\
in_deg_cen[int(k)],out_degrees_dict[int(k)], out_deg_cen[int(k)], dragsUtility.isaDrag(str(k))) for (k,v) in influencers_id]
influencers_table = pd.DataFrame(influencers_username_centrality,\
columns=['user','in_degree','in_degree_centrality','out_degree','out_degree_centrality','isaCompetitor'])
influencers_table.set_index('user',inplace=True)
influencers_table.sort_values(by='in_degree_centrality',inplace=True,ascending=False)
influencers_table
influencers_table.to_csv('toTable/influencers.csv')
```
Tra gli influencer non ci sono tutti i partecipanti
```
ranking_by_degree_centrality = influencers_table.loc[influencers_table['isaCompetitor'] == True]
ranking_by_degree_centrality
len(ranking_by_degree_centrality)
contestant_degree = list(filter(lambda x: dragsUtility.isaDrag(str(x[0])),list(in_degrees_noitems.items())))
contestant_degree_centrality = [( dragsUtility.getInfoAboutQueenByID(str(k))["Name"] ,v,\
in_deg_cen[int(k)],out_degrees_dict[int(k)], out_deg_cen[int(k)]) for (k,v) in contestant_degree]
contestant_degree_table = pd.DataFrame(contestant_degree_centrality,\
columns=['contestant','in_degree','in_degree_centrality','out_degree','out_degree_centrality'])
contestant_degree_table.sort_values(by='in_degree_centrality',inplace=True,ascending=False)
contestant_degree_table
centrality_rankings = {}
centrality_rankings['in_degree_centrality'] = list(contestant_degree_table["contestant"])
```
**PageRank**
```
# pagerank = nx.pagerank(graph, alpha=0.9, weight="weight")
# pagerank2 = list(filter(lambda x: dragsUtility.isaDrag(str(x[0])), pagerank.items()))
# contestant_pagerank = [ (dragsUtility.getInfoAboutQueenByID(str(k))["Name"], v) for (k,v) in pagerank2]
# contestant_pagerank = list(sorted( contestant_pagerank,key=lambda x: x[1], reverse=True))
# centrality_rankings['pageRank'] = [ k for (k,v) in contestant_pagerank]
# centrality_rankings['pageRank']
```
**Betweenness Centrality**
```
# beetweeness = nx.betweenness_centrality(graph, weight="weight")
# beetweeness2 = list(filter(lambda x: dragsUtility.isaDrag(str(x[0])), beetweeness.items()))
# contestant_beetweeness = [ (dragsUtility.getInfoAboutQueenByID(str(k))["Name"], v) for (k,v) in beetweeness2]
# contestant_beetweeness = list(sorted( contestant_beetweeness,key=lambda x: x[1], reverse=True))
# centrality_rankings['betweenness_centrality'] = [ k for (k,v) in contestant_beetweeness]
# centrality_rankings['betweenness_centrality']
```
**Harmonic Centrality**
```
sources = list(filter(lambda x: dragsUtility.isaDrag(str(x)),list(graph.nodes)))
# harmonic = nx.harmonic_centrality(graph, nbunch=sources)
# harmonic2 = list(harmonic.items())
# contestant_harmonic = [ (dragsUtility.getInfoAboutQueenByID(str(k))["Name"], v) for (k,v) in harmonic2]
# contestant_harmonic = list(sorted( contestant_harmonic, key=lambda x: x[1], reverse=True))
# centrality_rankings['harmonic_centrality'] = [ k for (k,v) in contestant_harmonic]
# centrality_rankings['harmonic_centrality']
# harmonic_df = pd.DataFrame(contestant_harmonic, columns=["contestant", "harmonic_centrality"])
# harmonic_df.to_csv("harmonic_final.csv", index=False)
# import json
# with open('Data/rankings.json', 'w') as f:
# json.dump(centrality_rankings, f, indent=1)
centrality_table = pd.read_json('Data/rankings.json')
centrality_table["real_rank"] = dragsUtility.getRealRanking()
centrality_table = centrality_table[['real_rank', 'in_degree_centrality', 'pageRank', 'betweenness_centrality', 'harmonic_centrality']]
centrality_table
centrality_table = pd.read_json('Data/rankings.json')
centrality_table["real_rank"] = dragsUtility.getRealRanking()
centrality_table.to_csv("toTable/rankings.csv")
```
## Distanze delle classifiche
```
def get_distances(rank, real_rank):
tau, p_value = stats.kendalltau(rank, real_rank)
return {"kendall_tau": tau, "hamming": 1 - (distance.hamming(rank, real_rank))}
distance_json = {}
real_rank = dragsUtility.getRealRanking()
distance_json["in_degree_centrality"] = get_distances(list(centrality_table["in_degree_centrality"]), real_rank)
distance_json["pageRank"] = get_distances(list(centrality_table["pageRank"]), real_rank)
distance_json["betweenness_centrality"] = get_distances(list(centrality_table["betweenness_centrality"]), real_rank)
distance_json["harmonic_centrality"] = get_distances(list(centrality_table["harmonic_centrality"]), real_rank)
distance_json["DB"] = get_distances(dragsUtility.getDBRanking(), real_rank)
distance_json["age"] = get_distances(dragsUtility.getAgeRankig(), real_rank)
distance_json["real"] = get_distances(real_rank, real_rank)
distance_json
distance_table = pd.DataFrame.from_dict(distance_json, orient='index')
distance_table
distance_table.to_csv("toTable/distance.csv")
```
## Jaccard Similarity
```
def structural_equivalence_jaccard(graph, node1, node2):
neighbourn1, neighbourn2 = set(graph[node1].keys()),set(graph[node2].keys())
union = len(neighbourn1.union(neighbourn2))
inter = len(neighbourn1.intersection(neighbourn2))
return (inter/union) if (union > 0) else 0
sources = list(filter(lambda x: dragsUtility.isaDrag(str(x)),list(graph.nodes)))
similarity = [ tuple( ([dragsUtility.getInfoAboutQueenByID(str(node1))["Name"]] + [ structural_equivalence_jaccard(graph.to_undirected(), node1, node2) for node2 in sources ] )) \
for node1 in sources]
sources_names = [ dragsUtility.getInfoAboutQueenByID(str(drag))["Name"] for drag in sources]
data = pd.DataFrame(similarity, columns= ["contestant"] + sources_names)
data = data.set_index("contestant")
fig, ax = plt.subplots(figsize=(9,8))
ax = sns.heatmap(data, center = 0.45)
plt.savefig("Images/StructuralSimilarity.png", dpi=1200, bbox_inches='tight')
plt.show()
```
| true |
code
| 0.49408 | null | null | null | null |
|
```
# Helper libraries
import numpy as np
import matplotlib.pyplot as plt
# TensorFlow and tf.keras
import tensorflow as tf
from tensorflow import keras
```
### Train
More on model saving: https://www.tensorflow.org/alpha/guide/keras/saving_and_serializing
```
# %run 102_mnist_fashion.py --output outputs/102_mnist_fashion.h5 --epochs 10 --verbose 1
```
### Explore Data
```
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()
train_images = train_images / 255.0
test_images = test_images / 255.0
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()
```
### Evaluate Model
```
model = keras.models.load_model('outputs/102_mnist_fashion.h5')
# fix error: "OMP: Error #15: Initializing libiomp5.dylib, but found libiomp5.dylib already initialized."
import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'
predictions = model.predict(test_images)
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array[i], true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array[i], true_label[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
i = 0
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()
i = 12
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()
# Plot the first X test images, their predicted label, and the true label
# Color correct predictions in blue, incorrect predictions in red
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions, test_labels)
plt.show()
# Grab an image from the test dataset
img = test_images[0]
# Add the image to a batch where it's the only member.
img = (np.expand_dims(img, 0))
predictions_single = model.predict(img)
print(predictions_single)
plot_value_array(0, predictions_single, test_labels)
_ = plt.xticks(range(10), class_names, rotation=45)
```
| true |
code
| 0.70683 | null | null | null | null |
|
# Reproducible Data Analysis in Jupyter
*Jake VanderPlas, March 2017*
Jupyter notebooks provide a useful environment for interactive exploration of data. A common question, though, is how you can progress from this nonlinear, interactive, trial-and-error style of analysis to a more linear and reproducible analysis based on organized, well-tested code. This series of videos shows an example of how I approach reproducible data analysis within the Jupyter notebook.
Each video is approximately 5-8 minutes; the videos are
available in a [YouTube Playlist](https://www.youtube.com/playlist?list=PLYCpMb24GpOC704uO9svUrihl-HY1tTJJ).
Alternatively, below you can find the videos with some description and lists of relevant resources
```
# Quick utility to embed the videos below
from IPython.display import YouTubeVideo
def embed_video(index, playlist='PLYCpMb24GpOC704uO9svUrihl-HY1tTJJ'):
return YouTubeVideo('', index=index - 1, list=playlist, width=600, height=350)
```
## Part 1: Loading and Visualizing Data
*In this video, I introduce the dataset, and use the Jupyter notebook to download and visualize it.*
```
embed_video(1)
```
Relevant resources:
- [Fremont Bridge Bike Counter](http://www.seattle.gov/transportation/bikecounter_fremont.htm): the website where you can explore the data
- [A Whirlwind Tour of Python](https://github.com/jakevdp/WhirlwindTourOfPython): my book introducing the Python programming language, aimed at scientists and engineers.
- [Python Data Science Handbook](https://github.com/jakevdp/PythonDataScienceHandbook): my book introducing Python's data science tools, including an introduction to the IPython, Pandas, and Matplotlib tools used here.
## Part 2: Further Data Exploration
*In this video, I do some slightly more sophisticated visualization with the data, using matplotlib and pandas.*
```
embed_video(2)
```
Relevant Resources:
- [Pivot Tables Section](https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/03.09-Pivot-Tables.ipynb) from the Python Data Science Handbook
## Part 3: Version Control with Git & GitHub
*In this video, I set up a repository on GitHub and commit the notebook into version control.*
```
embed_video(3)
```
Relevant Resources:
- [Version Control With Git](https://swcarpentry.github.io/git-novice/): excellent novice-level tutorial from Software Carpentry
- [Github Guides](https://guides.github.com/): set of tutorials on using GitHub
- [The Whys and Hows of Licensing Scientific Code](http://www.astrobetter.com/blog/2014/03/10/the-whys-and-hows-of-licensing-scientific-code/): my 2014 blog post on AstroBetter
## Part 4: Working with Data and GitHub
*In this video, I refactor the data download script so that it only downloads the data when needed*
```
embed_video(4)
```
## Part 5: Creating a Python Package
*In this video, I move the data download utility into its own separate package*
```
embed_video(5)
```
Relevant Resources:
- [How To Package Your Python Code](https://python-packaging.readthedocs.io/): broad tutorial on Python packaging.
## Part 6: Unit Testing with PyTest
*In this video, I add unit tests for the data download utility*
```
embed_video(6)
```
Relevant resources:
- [Pytest Documentation](http://doc.pytest.org/)
- [Getting Started with Pytest](https://jacobian.org/writing/getting-started-with-pytest/): a nice tutorial by Jacob Kaplan-Moss
## Part 7: Refactoring for Speed
*In this video, I refactor the data download function to be a bit faster*
```
embed_video(7)
```
Relevant Resources:
- [Python ``strftime`` reference](http://strftime.org/)
- [Pandas Datetime Section](https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/03.11-Working-with-Time-Series.ipynb) from the Python Data Science Handbook
## Part 8: Debugging a Broken Function
*In this video, I discover that my refactoring has caused a bug. I debug it and fix it.*
```
embed_video(8)
```
## Part 8.5: Finding and Fixing a scikit-learn bug
*In this video, I discover a bug in the scikit-learn codebase, and go through the process of submitting a GitHub Pull Request fixing the bug*
```
embed_video(9)
```
## Part 9: Further Data Exploration: PCA and GMM
*In this video, I apply unsupervised learning techniques to the data to explore what we can learn from it*
```
embed_video(10)
```
Relevant Resources:
- [Principal Component Analysis In-Depth](https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.09-Principal-Component-Analysis.ipynb) from the Python Data Science Handbook
- [Gaussian Mixture Models In-Depth](https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.12-Gaussian-Mixtures.ipynb) from the Python Data Science Handbook
## Part 10: Cleaning-up the Notebook
*In this video, I clean-up the unsupervised learning analysis to make it more reproducible and presentable.*
```
embed_video(11)
```
Relevant Resources:
- [Learning Seattle's Work Habits from Bicycle Counts](https://jakevdp.github.io/blog/2015/07/23/learning-seattles-work-habits-from-bicycle-counts/): My 2015 blog post using Fremont Bridge data
| true |
code
| 0.454533 | null | null | null | null |
|
**Chapter 13 – Loading and Preprocessing Data with TensorFlow**
_This notebook contains all the sample code and solutions to the exercises in chapter 13._
<table align="left">
<td>
<a href="https://colab.research.google.com/github/ageron/handson-ml2/blob/master/13_loading_and_preprocessing_data.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
</td>
<td>
<a target="_blank" href="https://kaggle.com/kernels/welcome?src=https://github.com/ageron/handson-ml2/blob/add-kaggle-badge/13_loading_and_preprocessing_data.ipynb"><img src="https://kaggle.com/static/images/open-in-kaggle.svg" /></a>
</td>
</table>
# Setup
Đầu tiên hãy nhập một vài mô-đun thông dụng, đảm bảo rằng Matplotlib sẽ vẽ đồ thị ngay trong notebook, và chuẩn bị một hàm để lưu đồ thị. Ta cũng kiểm tra xem Python phiên bản từ 3.5 trở lên đã được cài đặt hay chưa (mặc dù Python 2.x vẫn có thể hoạt động, phiên bản này đã bị deprecated nên chúng tôi rất khuyến khích việc sử dụng Python 3), cũng như Scikit-Learn ≥ 0.20.
```
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Is this notebook running on Colab or Kaggle?
IS_COLAB = "google.colab" in sys.modules
IS_KAGGLE = "kaggle_secrets" in sys.modules
if IS_COLAB or IS_KAGGLE:
!pip install -q -U tfx==0.21.2
print("You can safely ignore the package incompatibility errors.")
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# TensorFlow ≥2.0 is required
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.0"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "data"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
```
## Datasets
```
X = tf.range(10)
dataset = tf.data.Dataset.from_tensor_slices(X)
dataset
```
Equivalently:
```
dataset = tf.data.Dataset.range(10)
for item in dataset:
print(item)
dataset = dataset.repeat(3).batch(7)
for item in dataset:
print(item)
dataset = dataset.map(lambda x: x * 2)
for item in dataset:
print(item)
#dataset = dataset.apply(tf.data.experimental.unbatch()) # Now deprecated
dataset = dataset.unbatch()
dataset = dataset.filter(lambda x: x < 10) # keep only items < 10
for item in dataset.take(3):
print(item)
tf.random.set_seed(42)
dataset = tf.data.Dataset.range(10).repeat(3)
dataset = dataset.shuffle(buffer_size=3, seed=42).batch(7)
for item in dataset:
print(item)
```
## Split the California dataset to multiple CSV files
Let's start by loading and preparing the California housing dataset. We first load it, then split it into a training set, a validation set and a test set, and finally we scale it:
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target.reshape(-1, 1), random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full, random_state=42)
scaler = StandardScaler()
scaler.fit(X_train)
X_mean = scaler.mean_
X_std = scaler.scale_
```
For a very large dataset that does not fit in memory, you will typically want to split it into many files first, then have TensorFlow read these files in parallel. To demonstrate this, let's start by splitting the housing dataset and save it to 20 CSV files:
```
def save_to_multiple_csv_files(data, name_prefix, header=None, n_parts=10):
housing_dir = os.path.join("datasets", "housing")
os.makedirs(housing_dir, exist_ok=True)
path_format = os.path.join(housing_dir, "my_{}_{:02d}.csv")
filepaths = []
m = len(data)
for file_idx, row_indices in enumerate(np.array_split(np.arange(m), n_parts)):
part_csv = path_format.format(name_prefix, file_idx)
filepaths.append(part_csv)
with open(part_csv, "wt", encoding="utf-8") as f:
if header is not None:
f.write(header)
f.write("\n")
for row_idx in row_indices:
f.write(",".join([repr(col) for col in data[row_idx]]))
f.write("\n")
return filepaths
train_data = np.c_[X_train, y_train]
valid_data = np.c_[X_valid, y_valid]
test_data = np.c_[X_test, y_test]
header_cols = housing.feature_names + ["MedianHouseValue"]
header = ",".join(header_cols)
train_filepaths = save_to_multiple_csv_files(train_data, "train", header, n_parts=20)
valid_filepaths = save_to_multiple_csv_files(valid_data, "valid", header, n_parts=10)
test_filepaths = save_to_multiple_csv_files(test_data, "test", header, n_parts=10)
```
Okay, now let's take a peek at the first few lines of one of these CSV files:
```
import pandas as pd
pd.read_csv(train_filepaths[0]).head()
```
Or in text mode:
```
with open(train_filepaths[0]) as f:
for i in range(5):
print(f.readline(), end="")
train_filepaths
```
## Building an Input Pipeline
```
filepath_dataset = tf.data.Dataset.list_files(train_filepaths, seed=42)
for filepath in filepath_dataset:
print(filepath)
n_readers = 5
dataset = filepath_dataset.interleave(
lambda filepath: tf.data.TextLineDataset(filepath).skip(1),
cycle_length=n_readers)
for line in dataset.take(5):
print(line.numpy())
```
Notice that field 4 is interpreted as a string.
```
record_defaults=[0, np.nan, tf.constant(np.nan, dtype=tf.float64), "Hello", tf.constant([])]
parsed_fields = tf.io.decode_csv('1,2,3,4,5', record_defaults)
parsed_fields
```
Notice that all missing fields are replaced with their default value, when provided:
```
parsed_fields = tf.io.decode_csv(',,,,5', record_defaults)
parsed_fields
```
The 5th field is compulsory (since we provided `tf.constant([])` as the "default value"), so we get an exception if we do not provide it:
```
try:
parsed_fields = tf.io.decode_csv(',,,,', record_defaults)
except tf.errors.InvalidArgumentError as ex:
print(ex)
```
The number of fields should match exactly the number of fields in the `record_defaults`:
```
try:
parsed_fields = tf.io.decode_csv('1,2,3,4,5,6,7', record_defaults)
except tf.errors.InvalidArgumentError as ex:
print(ex)
n_inputs = 8 # X_train.shape[-1]
@tf.function
def preprocess(line):
defs = [0.] * n_inputs + [tf.constant([], dtype=tf.float32)]
fields = tf.io.decode_csv(line, record_defaults=defs)
x = tf.stack(fields[:-1])
y = tf.stack(fields[-1:])
return (x - X_mean) / X_std, y
preprocess(b'4.2083,44.0,5.3232,0.9171,846.0,2.3370,37.47,-122.2,2.782')
def csv_reader_dataset(filepaths, repeat=1, n_readers=5,
n_read_threads=None, shuffle_buffer_size=10000,
n_parse_threads=5, batch_size=32):
dataset = tf.data.Dataset.list_files(filepaths).repeat(repeat)
dataset = dataset.interleave(
lambda filepath: tf.data.TextLineDataset(filepath).skip(1),
cycle_length=n_readers, num_parallel_calls=n_read_threads)
dataset = dataset.shuffle(shuffle_buffer_size)
dataset = dataset.map(preprocess, num_parallel_calls=n_parse_threads)
dataset = dataset.batch(batch_size)
return dataset.prefetch(1)
tf.random.set_seed(42)
train_set = csv_reader_dataset(train_filepaths, batch_size=3)
for X_batch, y_batch in train_set.take(2):
print("X =", X_batch)
print("y =", y_batch)
print()
train_set = csv_reader_dataset(train_filepaths, repeat=None)
valid_set = csv_reader_dataset(valid_filepaths)
test_set = csv_reader_dataset(test_filepaths)
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),
keras.layers.Dense(1),
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(learning_rate=1e-3))
batch_size = 32
model.fit(train_set, steps_per_epoch=len(X_train) // batch_size, epochs=10,
validation_data=valid_set)
model.evaluate(test_set, steps=len(X_test) // batch_size)
new_set = test_set.map(lambda X, y: X) # we could instead just pass test_set, Keras would ignore the labels
X_new = X_test
model.predict(new_set, steps=len(X_new) // batch_size)
optimizer = keras.optimizers.Nadam(learning_rate=0.01)
loss_fn = keras.losses.mean_squared_error
n_epochs = 5
batch_size = 32
n_steps_per_epoch = len(X_train) // batch_size
total_steps = n_epochs * n_steps_per_epoch
global_step = 0
for X_batch, y_batch in train_set.take(total_steps):
global_step += 1
print("\rGlobal step {}/{}".format(global_step, total_steps), end="")
with tf.GradientTape() as tape:
y_pred = model(X_batch)
main_loss = tf.reduce_mean(loss_fn(y_batch, y_pred))
loss = tf.add_n([main_loss] + model.losses)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
optimizer = keras.optimizers.Nadam(learning_rate=0.01)
loss_fn = keras.losses.mean_squared_error
@tf.function
def train(model, n_epochs, batch_size=32,
n_readers=5, n_read_threads=5, shuffle_buffer_size=10000, n_parse_threads=5):
train_set = csv_reader_dataset(train_filepaths, repeat=n_epochs, n_readers=n_readers,
n_read_threads=n_read_threads, shuffle_buffer_size=shuffle_buffer_size,
n_parse_threads=n_parse_threads, batch_size=batch_size)
for X_batch, y_batch in train_set:
with tf.GradientTape() as tape:
y_pred = model(X_batch)
main_loss = tf.reduce_mean(loss_fn(y_batch, y_pred))
loss = tf.add_n([main_loss] + model.losses)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
train(model, 5)
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
optimizer = keras.optimizers.Nadam(learning_rate=0.01)
loss_fn = keras.losses.mean_squared_error
@tf.function
def train(model, n_epochs, batch_size=32,
n_readers=5, n_read_threads=5, shuffle_buffer_size=10000, n_parse_threads=5):
train_set = csv_reader_dataset(train_filepaths, repeat=n_epochs, n_readers=n_readers,
n_read_threads=n_read_threads, shuffle_buffer_size=shuffle_buffer_size,
n_parse_threads=n_parse_threads, batch_size=batch_size)
n_steps_per_epoch = len(X_train) // batch_size
total_steps = n_epochs * n_steps_per_epoch
global_step = 0
for X_batch, y_batch in train_set.take(total_steps):
global_step += 1
if tf.equal(global_step % 100, 0):
tf.print("\rGlobal step", global_step, "/", total_steps)
with tf.GradientTape() as tape:
y_pred = model(X_batch)
main_loss = tf.reduce_mean(loss_fn(y_batch, y_pred))
loss = tf.add_n([main_loss] + model.losses)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
train(model, 5)
```
Here is a short description of each method in the `Dataset` class:
```
for m in dir(tf.data.Dataset):
if not (m.startswith("_") or m.endswith("_")):
func = getattr(tf.data.Dataset, m)
if hasattr(func, "__doc__"):
print("● {:21s}{}".format(m + "()", func.__doc__.split("\n")[0]))
```
## The `TFRecord` binary format
A TFRecord file is just a list of binary records. You can create one using a `tf.io.TFRecordWriter`:
```
with tf.io.TFRecordWriter("my_data.tfrecord") as f:
f.write(b"This is the first record")
f.write(b"And this is the second record")
```
And you can read it using a `tf.data.TFRecordDataset`:
```
filepaths = ["my_data.tfrecord"]
dataset = tf.data.TFRecordDataset(filepaths)
for item in dataset:
print(item)
```
You can read multiple TFRecord files with just one `TFRecordDataset`. By default it will read them one at a time, but if you set `num_parallel_reads=3`, it will read 3 at a time in parallel and interleave their records:
```
filepaths = ["my_test_{}.tfrecord".format(i) for i in range(5)]
for i, filepath in enumerate(filepaths):
with tf.io.TFRecordWriter(filepath) as f:
for j in range(3):
f.write("File {} record {}".format(i, j).encode("utf-8"))
dataset = tf.data.TFRecordDataset(filepaths, num_parallel_reads=3)
for item in dataset:
print(item)
options = tf.io.TFRecordOptions(compression_type="GZIP")
with tf.io.TFRecordWriter("my_compressed.tfrecord", options) as f:
f.write(b"This is the first record")
f.write(b"And this is the second record")
dataset = tf.data.TFRecordDataset(["my_compressed.tfrecord"],
compression_type="GZIP")
for item in dataset:
print(item)
```
### A Brief Intro to Protocol Buffers
For this section you need to [install protobuf](https://developers.google.com/protocol-buffers/docs/downloads). In general you will not have to do so when using TensorFlow, as it comes with functions to create and parse protocol buffers of type `tf.train.Example`, which are generally sufficient. However, in this section we will learn about protocol buffers by creating our own simple protobuf definition, so we need the protobuf compiler (`protoc`): we will use it to compile the protobuf definition to a Python module that we can then use in our code.
First let's write a simple protobuf definition:
```
%%writefile person.proto
syntax = "proto3";
message Person {
string name = 1;
int32 id = 2;
repeated string email = 3;
}
```
And let's compile it (the `--descriptor_set_out` and `--include_imports` options are only required for the `tf.io.decode_proto()` example below):
```
!protoc person.proto --python_out=. --descriptor_set_out=person.desc --include_imports
!ls person*
from person_pb2 import Person
person = Person(name="Al", id=123, email=["a@b.com"]) # create a Person
print(person) # display the Person
person.name # read a field
person.name = "Alice" # modify a field
person.email[0] # repeated fields can be accessed like arrays
person.email.append("c@d.com") # add an email address
s = person.SerializeToString() # serialize to a byte string
s
person2 = Person() # create a new Person
person2.ParseFromString(s) # parse the byte string (27 bytes)
person == person2 # now they are equal
```
#### Custom protobuf
In rare cases, you may want to parse a custom protobuf (like the one we just created) in TensorFlow. For this you can use the `tf.io.decode_proto()` function:
```
person_tf = tf.io.decode_proto(
bytes=s,
message_type="Person",
field_names=["name", "id", "email"],
output_types=[tf.string, tf.int32, tf.string],
descriptor_source="person.desc")
person_tf.values
```
For more details, see the [`tf.io.decode_proto()`](https://www.tensorflow.org/api_docs/python/tf/io/decode_proto) documentation.
### TensorFlow Protobufs
Here is the definition of the tf.train.Example protobuf:
```proto
syntax = "proto3";
message BytesList { repeated bytes value = 1; }
message FloatList { repeated float value = 1 [packed = true]; }
message Int64List { repeated int64 value = 1 [packed = true]; }
message Feature {
oneof kind {
BytesList bytes_list = 1;
FloatList float_list = 2;
Int64List int64_list = 3;
}
};
message Features { map<string, Feature> feature = 1; };
message Example { Features features = 1; };
```
**Warning**: in TensorFlow 2.0 and 2.1, there was a bug preventing `from tensorflow.train import X` so we work around it by writing `X = tf.train.X`. See https://github.com/tensorflow/tensorflow/issues/33289 for more details.
```
#from tensorflow.train import BytesList, FloatList, Int64List
#from tensorflow.train import Feature, Features, Example
BytesList = tf.train.BytesList
FloatList = tf.train.FloatList
Int64List = tf.train.Int64List
Feature = tf.train.Feature
Features = tf.train.Features
Example = tf.train.Example
person_example = Example(
features=Features(
feature={
"name": Feature(bytes_list=BytesList(value=[b"Alice"])),
"id": Feature(int64_list=Int64List(value=[123])),
"emails": Feature(bytes_list=BytesList(value=[b"a@b.com", b"c@d.com"]))
}))
with tf.io.TFRecordWriter("my_contacts.tfrecord") as f:
f.write(person_example.SerializeToString())
feature_description = {
"name": tf.io.FixedLenFeature([], tf.string, default_value=""),
"id": tf.io.FixedLenFeature([], tf.int64, default_value=0),
"emails": tf.io.VarLenFeature(tf.string),
}
for serialized_example in tf.data.TFRecordDataset(["my_contacts.tfrecord"]):
parsed_example = tf.io.parse_single_example(serialized_example,
feature_description)
parsed_example
parsed_example
parsed_example["emails"].values[0]
tf.sparse.to_dense(parsed_example["emails"], default_value=b"")
parsed_example["emails"].values
```
### Putting Images in TFRecords
```
from sklearn.datasets import load_sample_images
img = load_sample_images()["images"][0]
plt.imshow(img)
plt.axis("off")
plt.title("Original Image")
plt.show()
data = tf.io.encode_jpeg(img)
example_with_image = Example(features=Features(feature={
"image": Feature(bytes_list=BytesList(value=[data.numpy()]))}))
serialized_example = example_with_image.SerializeToString()
# then save to TFRecord
feature_description = { "image": tf.io.VarLenFeature(tf.string) }
example_with_image = tf.io.parse_single_example(serialized_example, feature_description)
decoded_img = tf.io.decode_jpeg(example_with_image["image"].values[0])
```
Or use `decode_image()` which supports BMP, GIF, JPEG and PNG formats:
```
decoded_img = tf.io.decode_image(example_with_image["image"].values[0])
plt.imshow(decoded_img)
plt.title("Decoded Image")
plt.axis("off")
plt.show()
```
### Putting Tensors and Sparse Tensors in TFRecords
Tensors can be serialized and parsed easily using `tf.io.serialize_tensor()` and `tf.io.parse_tensor()`:
```
t = tf.constant([[0., 1.], [2., 3.], [4., 5.]])
s = tf.io.serialize_tensor(t)
s
tf.io.parse_tensor(s, out_type=tf.float32)
serialized_sparse = tf.io.serialize_sparse(parsed_example["emails"])
serialized_sparse
BytesList(value=serialized_sparse.numpy())
dataset = tf.data.TFRecordDataset(["my_contacts.tfrecord"]).batch(10)
for serialized_examples in dataset:
parsed_examples = tf.io.parse_example(serialized_examples,
feature_description)
parsed_examples
```
## Handling Sequential Data Using `SequenceExample`
```proto
syntax = "proto3";
message FeatureList { repeated Feature feature = 1; };
message FeatureLists { map<string, FeatureList> feature_list = 1; };
message SequenceExample {
Features context = 1;
FeatureLists feature_lists = 2;
};
```
**Warning**: in TensorFlow 2.0 and 2.1, there was a bug preventing `from tensorflow.train import X` so we work around it by writing `X = tf.train.X`. See https://github.com/tensorflow/tensorflow/issues/33289 for more details.
```
#from tensorflow.train import FeatureList, FeatureLists, SequenceExample
FeatureList = tf.train.FeatureList
FeatureLists = tf.train.FeatureLists
SequenceExample = tf.train.SequenceExample
context = Features(feature={
"author_id": Feature(int64_list=Int64List(value=[123])),
"title": Feature(bytes_list=BytesList(value=[b"A", b"desert", b"place", b"."])),
"pub_date": Feature(int64_list=Int64List(value=[1623, 12, 25]))
})
content = [["When", "shall", "we", "three", "meet", "again", "?"],
["In", "thunder", ",", "lightning", ",", "or", "in", "rain", "?"]]
comments = [["When", "the", "hurlyburly", "'s", "done", "."],
["When", "the", "battle", "'s", "lost", "and", "won", "."]]
def words_to_feature(words):
return Feature(bytes_list=BytesList(value=[word.encode("utf-8")
for word in words]))
content_features = [words_to_feature(sentence) for sentence in content]
comments_features = [words_to_feature(comment) for comment in comments]
sequence_example = SequenceExample(
context=context,
feature_lists=FeatureLists(feature_list={
"content": FeatureList(feature=content_features),
"comments": FeatureList(feature=comments_features)
}))
sequence_example
serialized_sequence_example = sequence_example.SerializeToString()
context_feature_descriptions = {
"author_id": tf.io.FixedLenFeature([], tf.int64, default_value=0),
"title": tf.io.VarLenFeature(tf.string),
"pub_date": tf.io.FixedLenFeature([3], tf.int64, default_value=[0, 0, 0]),
}
sequence_feature_descriptions = {
"content": tf.io.VarLenFeature(tf.string),
"comments": tf.io.VarLenFeature(tf.string),
}
parsed_context, parsed_feature_lists = tf.io.parse_single_sequence_example(
serialized_sequence_example, context_feature_descriptions,
sequence_feature_descriptions)
parsed_context
parsed_context["title"].values
parsed_feature_lists
print(tf.RaggedTensor.from_sparse(parsed_feature_lists["content"]))
```
# The Features API
Let's use the variant of the California housing dataset that we used in Chapter 2, since it contains categorical features and missing values:
```
import os
import tarfile
import urllib.request
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
os.makedirs(housing_path, exist_ok=True)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
fetch_housing_data()
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
housing = load_housing_data()
housing.head()
housing_median_age = tf.feature_column.numeric_column("housing_median_age")
age_mean, age_std = X_mean[1], X_std[1] # The median age is column in 1
housing_median_age = tf.feature_column.numeric_column(
"housing_median_age", normalizer_fn=lambda x: (x - age_mean) / age_std)
median_income = tf.feature_column.numeric_column("median_income")
bucketized_income = tf.feature_column.bucketized_column(
median_income, boundaries=[1.5, 3., 4.5, 6.])
bucketized_income
ocean_prox_vocab = ['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN']
ocean_proximity = tf.feature_column.categorical_column_with_vocabulary_list(
"ocean_proximity", ocean_prox_vocab)
ocean_proximity
# Just an example, it's not used later on
city_hash = tf.feature_column.categorical_column_with_hash_bucket(
"city", hash_bucket_size=1000)
city_hash
bucketized_age = tf.feature_column.bucketized_column(
housing_median_age, boundaries=[-1., -0.5, 0., 0.5, 1.]) # age was scaled
age_and_ocean_proximity = tf.feature_column.crossed_column(
[bucketized_age, ocean_proximity], hash_bucket_size=100)
latitude = tf.feature_column.numeric_column("latitude")
longitude = tf.feature_column.numeric_column("longitude")
bucketized_latitude = tf.feature_column.bucketized_column(
latitude, boundaries=list(np.linspace(32., 42., 20 - 1)))
bucketized_longitude = tf.feature_column.bucketized_column(
longitude, boundaries=list(np.linspace(-125., -114., 20 - 1)))
location = tf.feature_column.crossed_column(
[bucketized_latitude, bucketized_longitude], hash_bucket_size=1000)
ocean_proximity_one_hot = tf.feature_column.indicator_column(ocean_proximity)
ocean_proximity_embed = tf.feature_column.embedding_column(ocean_proximity,
dimension=2)
```
## Using Feature Columns for Parsing
```
median_house_value = tf.feature_column.numeric_column("median_house_value")
columns = [housing_median_age, median_house_value]
feature_descriptions = tf.feature_column.make_parse_example_spec(columns)
feature_descriptions
with tf.io.TFRecordWriter("my_data_with_features.tfrecords") as f:
for x, y in zip(X_train[:, 1:2], y_train):
example = Example(features=Features(feature={
"housing_median_age": Feature(float_list=FloatList(value=[x])),
"median_house_value": Feature(float_list=FloatList(value=[y]))
}))
f.write(example.SerializeToString())
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
def parse_examples(serialized_examples):
examples = tf.io.parse_example(serialized_examples, feature_descriptions)
targets = examples.pop("median_house_value") # separate the targets
return examples, targets
batch_size = 32
dataset = tf.data.TFRecordDataset(["my_data_with_features.tfrecords"])
dataset = dataset.repeat().shuffle(10000).batch(batch_size).map(parse_examples)
```
**Warning**: the `DenseFeatures` layer currently does not work with the Functional API, see [TF issue #27416](https://github.com/tensorflow/tensorflow/issues/27416). Hopefully this will be resolved before the final release of TF 2.0.
```
columns_without_target = columns[:-1]
model = keras.models.Sequential([
keras.layers.DenseFeatures(feature_columns=columns_without_target),
keras.layers.Dense(1)
])
model.compile(loss="mse",
optimizer=keras.optimizers.SGD(learning_rate=1e-3),
metrics=["accuracy"])
model.fit(dataset, steps_per_epoch=len(X_train) // batch_size, epochs=5)
some_columns = [ocean_proximity_embed, bucketized_income]
dense_features = keras.layers.DenseFeatures(some_columns)
dense_features({
"ocean_proximity": [["NEAR OCEAN"], ["INLAND"], ["INLAND"]],
"median_income": [[3.], [7.2], [1.]]
})
```
# TF Transform
```
try:
import tensorflow_transform as tft
def preprocess(inputs): # inputs is a batch of input features
median_age = inputs["housing_median_age"]
ocean_proximity = inputs["ocean_proximity"]
standardized_age = tft.scale_to_z_score(median_age - tft.mean(median_age))
ocean_proximity_id = tft.compute_and_apply_vocabulary(ocean_proximity)
return {
"standardized_median_age": standardized_age,
"ocean_proximity_id": ocean_proximity_id
}
except ImportError:
print("TF Transform is not installed. Try running: pip3 install -U tensorflow-transform")
```
# TensorFlow Datasets
```
import tensorflow_datasets as tfds
datasets = tfds.load(name="mnist")
mnist_train, mnist_test = datasets["train"], datasets["test"]
print(tfds.list_builders())
plt.figure(figsize=(6,3))
mnist_train = mnist_train.repeat(5).batch(32).prefetch(1)
for item in mnist_train:
images = item["image"]
labels = item["label"]
for index in range(5):
plt.subplot(1, 5, index + 1)
image = images[index, ..., 0]
label = labels[index].numpy()
plt.imshow(image, cmap="binary")
plt.title(label)
plt.axis("off")
break # just showing part of the first batch
datasets = tfds.load(name="mnist")
mnist_train, mnist_test = datasets["train"], datasets["test"]
mnist_train = mnist_train.repeat(5).batch(32)
mnist_train = mnist_train.map(lambda items: (items["image"], items["label"]))
mnist_train = mnist_train.prefetch(1)
for images, labels in mnist_train.take(1):
print(images.shape)
print(labels.numpy())
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
datasets = tfds.load(name="mnist", batch_size=32, as_supervised=True)
mnist_train = datasets["train"].repeat().prefetch(1)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28, 1]),
keras.layers.Lambda(lambda images: tf.cast(images, tf.float32)),
keras.layers.Dense(10, activation="softmax")])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(learning_rate=1e-3),
metrics=["accuracy"])
model.fit(mnist_train, steps_per_epoch=60000 // 32, epochs=5)
```
# TensorFlow Hub
```
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
import tensorflow_hub as hub
hub_layer = hub.KerasLayer("https://tfhub.dev/google/nnlm-en-dim50/2",
output_shape=[50], input_shape=[], dtype=tf.string)
model = keras.Sequential()
model.add(hub_layer)
model.add(keras.layers.Dense(16, activation='relu'))
model.add(keras.layers.Dense(1, activation='sigmoid'))
model.summary()
sentences = tf.constant(["It was a great movie", "The actors were amazing"])
embeddings = hub_layer(sentences)
embeddings
```
# Exercises
## 1. to 8.
See Appendix A
## 9.
### a.
_Exercise: Load the Fashion MNIST dataset (introduced in Chapter 10); split it into a training set, a validation set, and a test set; shuffle the training set; and save each dataset to multiple TFRecord files. Each record should be a serialized `Example` protobuf with two features: the serialized image (use `tf.io.serialize_tensor()` to serialize each image), and the label. Note: for large images, you could use `tf.io.encode_jpeg()` instead. This would save a lot of space, but it would lose a bit of image quality._
```
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
train_set = tf.data.Dataset.from_tensor_slices((X_train, y_train)).shuffle(len(X_train))
valid_set = tf.data.Dataset.from_tensor_slices((X_valid, y_valid))
test_set = tf.data.Dataset.from_tensor_slices((X_test, y_test))
def create_example(image, label):
image_data = tf.io.serialize_tensor(image)
#image_data = tf.io.encode_jpeg(image[..., np.newaxis])
return Example(
features=Features(
feature={
"image": Feature(bytes_list=BytesList(value=[image_data.numpy()])),
"label": Feature(int64_list=Int64List(value=[label])),
}))
for image, label in valid_set.take(1):
print(create_example(image, label))
```
The following function saves a given dataset to a set of TFRecord files. The examples are written to the files in a round-robin fashion. To do this, we enumerate all the examples using the `dataset.enumerate()` method, and we compute `index % n_shards` to decide which file to write to. We use the standard `contextlib.ExitStack` class to make sure that all writers are properly closed whether or not an I/O error occurs while writing.
```
from contextlib import ExitStack
def write_tfrecords(name, dataset, n_shards=10):
paths = ["{}.tfrecord-{:05d}-of-{:05d}".format(name, index, n_shards)
for index in range(n_shards)]
with ExitStack() as stack:
writers = [stack.enter_context(tf.io.TFRecordWriter(path))
for path in paths]
for index, (image, label) in dataset.enumerate():
shard = index % n_shards
example = create_example(image, label)
writers[shard].write(example.SerializeToString())
return paths
train_filepaths = write_tfrecords("my_fashion_mnist.train", train_set)
valid_filepaths = write_tfrecords("my_fashion_mnist.valid", valid_set)
test_filepaths = write_tfrecords("my_fashion_mnist.test", test_set)
```
### b.
_Exercise: Then use tf.data to create an efficient dataset for each set. Finally, use a Keras model to train these datasets, including a preprocessing layer to standardize each input feature. Try to make the input pipeline as efficient as possible, using TensorBoard to visualize profiling data._
```
def preprocess(tfrecord):
feature_descriptions = {
"image": tf.io.FixedLenFeature([], tf.string, default_value=""),
"label": tf.io.FixedLenFeature([], tf.int64, default_value=-1)
}
example = tf.io.parse_single_example(tfrecord, feature_descriptions)
image = tf.io.parse_tensor(example["image"], out_type=tf.uint8)
#image = tf.io.decode_jpeg(example["image"])
image = tf.reshape(image, shape=[28, 28])
return image, example["label"]
def mnist_dataset(filepaths, n_read_threads=5, shuffle_buffer_size=None,
n_parse_threads=5, batch_size=32, cache=True):
dataset = tf.data.TFRecordDataset(filepaths,
num_parallel_reads=n_read_threads)
if cache:
dataset = dataset.cache()
if shuffle_buffer_size:
dataset = dataset.shuffle(shuffle_buffer_size)
dataset = dataset.map(preprocess, num_parallel_calls=n_parse_threads)
dataset = dataset.batch(batch_size)
return dataset.prefetch(1)
train_set = mnist_dataset(train_filepaths, shuffle_buffer_size=60000)
valid_set = mnist_dataset(valid_filepaths)
test_set = mnist_dataset(test_filepaths)
for X, y in train_set.take(1):
for i in range(5):
plt.subplot(1, 5, i + 1)
plt.imshow(X[i].numpy(), cmap="binary")
plt.axis("off")
plt.title(str(y[i].numpy()))
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
class Standardization(keras.layers.Layer):
def adapt(self, data_sample):
self.means_ = np.mean(data_sample, axis=0, keepdims=True)
self.stds_ = np.std(data_sample, axis=0, keepdims=True)
def call(self, inputs):
return (inputs - self.means_) / (self.stds_ + keras.backend.epsilon())
standardization = Standardization(input_shape=[28, 28])
# or perhaps soon:
#standardization = keras.layers.Normalization()
sample_image_batches = train_set.take(100).map(lambda image, label: image)
sample_images = np.concatenate(list(sample_image_batches.as_numpy_iterator()),
axis=0).astype(np.float32)
standardization.adapt(sample_images)
model = keras.models.Sequential([
standardization,
keras.layers.Flatten(),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer="nadam", metrics=["accuracy"])
from datetime import datetime
logs = os.path.join(os.curdir, "my_logs",
"run_" + datetime.now().strftime("%Y%m%d_%H%M%S"))
tensorboard_cb = tf.keras.callbacks.TensorBoard(
log_dir=logs, histogram_freq=1, profile_batch=10)
model.fit(train_set, epochs=5, validation_data=valid_set,
callbacks=[tensorboard_cb])
```
**Warning:** The profiling tab in TensorBoard works if you use TensorFlow 2.2+. You also need to make sure `tensorboard_plugin_profile` is installed (and restart Jupyter if necessary).
```
%load_ext tensorboard
%tensorboard --logdir=./my_logs --port=6006
```
## 10.
_Exercise: In this exercise you will download a dataset, split it, create a `tf.data.Dataset` to load it and preprocess it efficiently, then build and train a binary classification model containing an `Embedding` layer._
### a.
_Exercise: Download the [Large Movie Review Dataset](https://homl.info/imdb), which contains 50,000 movies reviews from the [Internet Movie Database](https://imdb.com/). The data is organized in two directories, `train` and `test`, each containing a `pos` subdirectory with 12,500 positive reviews and a `neg` subdirectory with 12,500 negative reviews. Each review is stored in a separate text file. There are other files and folders (including preprocessed bag-of-words), but we will ignore them in this exercise._
```
from pathlib import Path
DOWNLOAD_ROOT = "http://ai.stanford.edu/~amaas/data/sentiment/"
FILENAME = "aclImdb_v1.tar.gz"
filepath = keras.utils.get_file(FILENAME, DOWNLOAD_ROOT + FILENAME, extract=True)
path = Path(filepath).parent / "aclImdb"
path
for name, subdirs, files in os.walk(path):
indent = len(Path(name).parts) - len(path.parts)
print(" " * indent + Path(name).parts[-1] + os.sep)
for index, filename in enumerate(sorted(files)):
if index == 3:
print(" " * (indent + 1) + "...")
break
print(" " * (indent + 1) + filename)
def review_paths(dirpath):
return [str(path) for path in dirpath.glob("*.txt")]
train_pos = review_paths(path / "train" / "pos")
train_neg = review_paths(path / "train" / "neg")
test_valid_pos = review_paths(path / "test" / "pos")
test_valid_neg = review_paths(path / "test" / "neg")
len(train_pos), len(train_neg), len(test_valid_pos), len(test_valid_neg)
```
### b.
_Exercise: Split the test set into a validation set (15,000) and a test set (10,000)._
```
np.random.shuffle(test_valid_pos)
test_pos = test_valid_pos[:5000]
test_neg = test_valid_neg[:5000]
valid_pos = test_valid_pos[5000:]
valid_neg = test_valid_neg[5000:]
```
### c.
_Exercise: Use tf.data to create an efficient dataset for each set._
Since the dataset fits in memory, we can just load all the data using pure Python code and use `tf.data.Dataset.from_tensor_slices()`:
```
def imdb_dataset(filepaths_positive, filepaths_negative):
reviews = []
labels = []
for filepaths, label in ((filepaths_negative, 0), (filepaths_positive, 1)):
for filepath in filepaths:
with open(filepath) as review_file:
reviews.append(review_file.read())
labels.append(label)
return tf.data.Dataset.from_tensor_slices(
(tf.constant(reviews), tf.constant(labels)))
for X, y in imdb_dataset(train_pos, train_neg).take(3):
print(X)
print(y)
print()
%timeit -r1 for X, y in imdb_dataset(train_pos, train_neg).repeat(10): pass
```
It takes about 17 seconds to load the dataset and go through it 10 times.
But let's pretend the dataset does not fit in memory, just to make things more interesting. Luckily, each review fits on just one line (they use `<br />` to indicate line breaks), so we can read the reviews using a `TextLineDataset`. If they didn't we would have to preprocess the input files (e.g., converting them to TFRecords). For very large datasets, it would make sense to use a tool like Apache Beam for that.
```
def imdb_dataset(filepaths_positive, filepaths_negative, n_read_threads=5):
dataset_neg = tf.data.TextLineDataset(filepaths_negative,
num_parallel_reads=n_read_threads)
dataset_neg = dataset_neg.map(lambda review: (review, 0))
dataset_pos = tf.data.TextLineDataset(filepaths_positive,
num_parallel_reads=n_read_threads)
dataset_pos = dataset_pos.map(lambda review: (review, 1))
return tf.data.Dataset.concatenate(dataset_pos, dataset_neg)
%timeit -r1 for X, y in imdb_dataset(train_pos, train_neg).repeat(10): pass
```
Now it takes about 33 seconds to go through the dataset 10 times. That's much slower, essentially because the dataset is not cached in RAM, so it must be reloaded at each epoch. If you add `.cache()` just before `.repeat(10)`, you will see that this implementation will be about as fast as the previous one.
```
%timeit -r1 for X, y in imdb_dataset(train_pos, train_neg).cache().repeat(10): pass
batch_size = 32
train_set = imdb_dataset(train_pos, train_neg).shuffle(25000).batch(batch_size).prefetch(1)
valid_set = imdb_dataset(valid_pos, valid_neg).batch(batch_size).prefetch(1)
test_set = imdb_dataset(test_pos, test_neg).batch(batch_size).prefetch(1)
```
### d.
_Exercise: Create a binary classification model, using a `TextVectorization` layer to preprocess each review. If the `TextVectorization` layer is not yet available (or if you like a challenge), try to create your own custom preprocessing layer: you can use the functions in the `tf.strings` package, for example `lower()` to make everything lowercase, `regex_replace()` to replace punctuation with spaces, and `split()` to split words on spaces. You should use a lookup table to output word indices, which must be prepared in the `adapt()` method._
Let's first write a function to preprocess the reviews, cropping them to 300 characters, converting them to lower case, then replacing `<br />` and all non-letter characters to spaces, splitting the reviews into words, and finally padding or cropping each review so it ends up with exactly `n_words` tokens:
```
def preprocess(X_batch, n_words=50):
shape = tf.shape(X_batch) * tf.constant([1, 0]) + tf.constant([0, n_words])
Z = tf.strings.substr(X_batch, 0, 300)
Z = tf.strings.lower(Z)
Z = tf.strings.regex_replace(Z, b"<br\\s*/?>", b" ")
Z = tf.strings.regex_replace(Z, b"[^a-z]", b" ")
Z = tf.strings.split(Z)
return Z.to_tensor(shape=shape, default_value=b"<pad>")
X_example = tf.constant(["It's a great, great movie! I loved it.", "It was terrible, run away!!!"])
preprocess(X_example)
```
Now let's write a second utility function that will take a data sample with the same format as the output of the `preprocess()` function, and will output the list of the top `max_size` most frequent words, ensuring that the padding token is first:
```
from collections import Counter
def get_vocabulary(data_sample, max_size=1000):
preprocessed_reviews = preprocess(data_sample).numpy()
counter = Counter()
for words in preprocessed_reviews:
for word in words:
if word != b"<pad>":
counter[word] += 1
return [b"<pad>"] + [word for word, count in counter.most_common(max_size)]
get_vocabulary(X_example)
```
Now we are ready to create the `TextVectorization` layer. Its constructor just saves the hyperparameters (`max_vocabulary_size` and `n_oov_buckets`). The `adapt()` method computes the vocabulary using the `get_vocabulary()` function, then it builds a `StaticVocabularyTable` (see Chapter 16 for more details). The `call()` method preprocesses the reviews to get a padded list of words for each review, then it uses the `StaticVocabularyTable` to lookup the index of each word in the vocabulary:
```
class TextVectorization(keras.layers.Layer):
def __init__(self, max_vocabulary_size=1000, n_oov_buckets=100, dtype=tf.string, **kwargs):
super().__init__(dtype=dtype, **kwargs)
self.max_vocabulary_size = max_vocabulary_size
self.n_oov_buckets = n_oov_buckets
def adapt(self, data_sample):
self.vocab = get_vocabulary(data_sample, self.max_vocabulary_size)
words = tf.constant(self.vocab)
word_ids = tf.range(len(self.vocab), dtype=tf.int64)
vocab_init = tf.lookup.KeyValueTensorInitializer(words, word_ids)
self.table = tf.lookup.StaticVocabularyTable(vocab_init, self.n_oov_buckets)
def call(self, inputs):
preprocessed_inputs = preprocess(inputs)
return self.table.lookup(preprocessed_inputs)
```
Let's try it on our small `X_example` we defined earlier:
```
text_vectorization = TextVectorization()
text_vectorization.adapt(X_example)
text_vectorization(X_example)
```
Looks good! As you can see, each review was cleaned up and tokenized, then each word was encoded as its index in the vocabulary (all the 0s correspond to the `<pad>` tokens).
Now let's create another `TextVectorization` layer and let's adapt it to the full IMDB training set (if the training set did not fit in RAM, we could just use a smaller sample of the training set by calling `train_set.take(500)`):
```
max_vocabulary_size = 1000
n_oov_buckets = 100
sample_review_batches = train_set.map(lambda review, label: review)
sample_reviews = np.concatenate(list(sample_review_batches.as_numpy_iterator()),
axis=0)
text_vectorization = TextVectorization(max_vocabulary_size, n_oov_buckets,
input_shape=[])
text_vectorization.adapt(sample_reviews)
```
Let's run it on the same `X_example`, just to make sure the word IDs are larger now, since the vocabulary is bigger:
```
text_vectorization(X_example)
```
Good! Now let's take a look at the first 10 words in the vocabulary:
```
text_vectorization.vocab[:10]
```
These are the most common words in the reviews.
Now to build our model we will need to encode all these word IDs somehow. One approach is to create bags of words: for each review, and for each word in the vocabulary, we count the number of occurences of that word in the review. For example:
```
simple_example = tf.constant([[1, 3, 1, 0, 0], [2, 2, 0, 0, 0]])
tf.reduce_sum(tf.one_hot(simple_example, 4), axis=1)
```
The first review has 2 times the word 0, 2 times the word 1, 0 times the word 2, and 1 time the word 3, so its bag-of-words representation is `[2, 2, 0, 1]`. Similarly, the second review has 3 times the word 0, 0 times the word 1, and so on. Let's wrap this logic in a small custom layer, and let's test it. We'll drop the counts for the word 0, since this corresponds to the `<pad>` token, which we don't care about.
```
class BagOfWords(keras.layers.Layer):
def __init__(self, n_tokens, dtype=tf.int32, **kwargs):
super().__init__(dtype=dtype, **kwargs)
self.n_tokens = n_tokens
def call(self, inputs):
one_hot = tf.one_hot(inputs, self.n_tokens)
return tf.reduce_sum(one_hot, axis=1)[:, 1:]
```
Let's test it:
```
bag_of_words = BagOfWords(n_tokens=4)
bag_of_words(simple_example)
```
It works fine! Now let's create another `BagOfWord` with the right vocabulary size for our training set:
```
n_tokens = max_vocabulary_size + n_oov_buckets + 1 # add 1 for <pad>
bag_of_words = BagOfWords(n_tokens)
```
We're ready to train the model!
```
model = keras.models.Sequential([
text_vectorization,
bag_of_words,
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(1, activation="sigmoid"),
])
model.compile(loss="binary_crossentropy", optimizer="nadam",
metrics=["accuracy"])
model.fit(train_set, epochs=5, validation_data=valid_set)
```
We get about 73.5% accuracy on the validation set after just the first epoch, but after that the model makes no significant progress. We will do better in Chapter 16. For now the point is just to perform efficient preprocessing using `tf.data` and Keras preprocessing layers.
### e.
_Exercise: Add an `Embedding` layer and compute the mean embedding for each review, multiplied by the square root of the number of words (see Chapter 16). This rescaled mean embedding can then be passed to the rest of your model._
To compute the mean embedding for each review, and multiply it by the square root of the number of words in that review, we will need a little function. For each sentence, this function needs to compute $M \times \sqrt N$, where $M$ is the mean of all the word embeddings in the sentence (excluding padding tokens), and $N$ is the number of words in the sentence (also excluding padding tokens). We can rewrite $M$ as $\dfrac{S}{N}$, where $S$ is the sum of all word embeddings (it does not matter whether or not we include the padding tokens in this sum, since their representation is a zero vector). So the function must return $M \times \sqrt N = \dfrac{S}{N} \times \sqrt N = \dfrac{S}{\sqrt N \times \sqrt N} \times \sqrt N= \dfrac{S}{\sqrt N}$.
```
def compute_mean_embedding(inputs):
not_pad = tf.math.count_nonzero(inputs, axis=-1)
n_words = tf.math.count_nonzero(not_pad, axis=-1, keepdims=True)
sqrt_n_words = tf.math.sqrt(tf.cast(n_words, tf.float32))
return tf.reduce_sum(inputs, axis=1) / sqrt_n_words
another_example = tf.constant([[[1., 2., 3.], [4., 5., 0.], [0., 0., 0.]],
[[6., 0., 0.], [0., 0., 0.], [0., 0., 0.]]])
compute_mean_embedding(another_example)
```
Let's check that this is correct. The first review contains 2 words (the last token is a zero vector, which represents the `<pad>` token). Let's compute the mean embedding for these 2 words, and multiply the result by the square root of 2:
```
tf.reduce_mean(another_example[0:1, :2], axis=1) * tf.sqrt(2.)
```
Looks good! Now let's check the second review, which contains just one word (we ignore the two padding tokens):
```
tf.reduce_mean(another_example[1:2, :1], axis=1) * tf.sqrt(1.)
```
Perfect. Now we're ready to train our final model. It's the same as before, except we replaced the `BagOfWords` layer with an `Embedding` layer followed by a `Lambda` layer that calls the `compute_mean_embedding` layer:
```
embedding_size = 20
model = keras.models.Sequential([
text_vectorization,
keras.layers.Embedding(input_dim=n_tokens,
output_dim=embedding_size,
mask_zero=True), # <pad> tokens => zero vectors
keras.layers.Lambda(compute_mean_embedding),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(1, activation="sigmoid"),
])
```
### f.
_Exercise: Train the model and see what accuracy you get. Try to optimize your pipelines to make training as fast as possible._
```
model.compile(loss="binary_crossentropy", optimizer="nadam", metrics=["accuracy"])
model.fit(train_set, epochs=5, validation_data=valid_set)
```
The model is not better using embeddings (but we will do better in Chapter 16). The pipeline looks fast enough (we optimized it earlier).
### g.
_Exercise: Use TFDS to load the same dataset more easily: `tfds.load("imdb_reviews")`._
```
import tensorflow_datasets as tfds
datasets = tfds.load(name="imdb_reviews")
train_set, test_set = datasets["train"], datasets["test"]
for example in train_set.take(1):
print(example["text"])
print(example["label"])
```
| true |
code
| 0.520557 | null | null | null | null |
|
##### Let's change gears and talk about Game of thrones or shall I say Network of Thrones.
It is suprising right? What is the relationship between a fatansy TV show/novel and network science or python(it's not related to a dragon).

Andrew J. Beveridge, an associate professor of mathematics at Macalester College, and Jie Shan, an undergraduate created a network from the book A Storm of Swords by extracting relationships between characters to find out the most important characters in the book(or GoT).
The dataset is publicly available for the 5 books at https://github.com/mathbeveridge/asoiaf. This is an interaction network and were created by connecting two characters whenever their names (or nicknames) appeared within 15 words of one another in one of the books. The edge weight corresponds to the number of interactions.
Credits:
Blog: https://networkofthrones.wordpress.com
Math Horizons Article: https://www.maa.org/sites/default/files/pdf/Mathhorizons/NetworkofThrones%20%281%29.pdf
```
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
import community
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
book1 = pd.read_csv('data/asoiaf-book1-edges.csv')
book2 = pd.read_csv('data/asoiaf-book2-edges.csv')
book3 = pd.read_csv('data/asoiaf-book3-edges.csv')
book4 = pd.read_csv('data/asoiaf-book4-edges.csv')
book5 = pd.read_csv('data/asoiaf-book5-edges.csv')
G_book1 = nx.Graph()
G_book2 = nx.Graph()
G_book3 = nx.Graph()
G_book4 = nx.Graph()
G_book5 = nx.Graph()
for row in book1.iterrows():
G_book1.add_edge(row[1]['Source'], row[1]['Target'], weight=row[1]['weight'], book=row[1]['book'])
for row in book2.iterrows():
G_book2.add_edge(row[1]['Source'], row[1]['Target'], weight=row[1]['weight'], book=row[1]['book'])
for row in book3.iterrows():
G_book3.add_edge(row[1]['Source'], row[1]['Target'], weight=row[1]['weight'], book=row[1]['book'])
for row in book4.iterrows():
G_book4.add_edge(row[1]['Source'], row[1]['Target'], weight=row[1]['weight'], book=row[1]['book'])
for row in book5.iterrows():
G_book5.add_edge(row[1]['Source'], row[1]['Target'], weight=row[1]['weight'], book=row[1]['book'])
G_book1.edges(data=True)
```
### Finding the most important node i.e character in these networks.
We'll compare different centralities to find the importance of nodes in this network. There is no one right way of calaculating it, every approach has a different meaning. Let's start with degree centrality which is defined by degree of a node divided by a noramlising factor n-1 where n is the number of nodes.
```
list(G_book1.neighbors('Jaime-Lannister'))
```
##### nx.degree_centrality(graph) returns a dictionary where keys are the nodes and values are the corresponsing degree centrality. Let's find the five most important character according to degree centrality.
```
sorted(nx.degree_centrality(G_book1).items(), key=lambda x:x[1], reverse=True)[0:10]
# Plot a histogram of degree centrality
plt.hist(list(nx.degree_centrality(G_book4).values()))
plt.show()
```
### Exercise
Create a new centrality measure, weighted_degree_centrality(Graph, weight) which takes in Graph and the weight attribute and returns a weighted degree centrality dictionary. Weighted degree is calculated by summing the weight of the all edges of a node and normalise(divide) the weighted degree by the total weight of the graph(sum of weighted degrees of all nodes) and find the top five characters according to this measure.
```
def weighted_degree_centrality(G, weight):
result = dict()
total = 0
for node in G.nodes():
weight_degree = 0
for n in G.edges([node], data=True):
weight_degree += n[2]['weight']
result[node] = weight_degree
total += weight_degree
for node, value in result.items():
result[node] = value/total
return result
plt.hist(list(weighted_degree_centrality(G_book1, 'weight').values()))
plt.show()
sorted(weighted_degree_centrality(G_book1, 'weight').items(), key=lambda x:x[1], reverse=True)[0:10]
sum(list(weighted_degree_centrality(G_book1, 'weight').values()))
```
##### Betweeness centrality
From Wikipedia:
For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices such that either the number of edges that the path passes through (for unweighted graphs) or the sum of the weights of the edges (for weighted graphs) is minimized. The betweenness centrality for each vertex is the number of these shortest paths that pass through the vertex.
```
# unweighted
sorted(nx.betweenness_centrality(G_book1).items(), key=lambda x:x[1], reverse=True)[0:10]
sorted(nx.betweenness_centrality(G_book1, weight='weight').items(), key=lambda x:x[1], reverse=True)[0:10]
```
#### PageRank
The billion dollar algorithm, PageRank works by counting the number and quality of links to a page to determine a rough estimate of how important the website is. The underlying assumption is that more important websites are likely to receive more links from other websites.
```
# by default weight attribute in pagerank is weight, so we use weight=None to find the unweighted results
sorted(nx.pagerank_numpy(G_book1, weight=None).items(), key=lambda x:x[1], reverse=True)[0:10]
sorted(nx.pagerank_numpy(G_book1, weight='weight').items(), key=lambda x:x[1], reverse=True)[0:10]
```
### Is there a correlation between these techniques?
#### Exercise
Find the correlation between these three techniques.
```
cor = pd.DataFrame.from_records([nx.pagerank_numpy(G_book1, weight='weight'), nx.betweenness_centrality(G_book1, weight='weight'), weighted_degree_centrality(G_book1, 'weight')])
cor.T
```
#### What can we infer from this correlation matrix between these three methods?
```
cor.T.corr()
```
Till now we have been analysing only the first book, but what about the other 4 books? We can now look at the evolution of this character interaction network that adds temporality to this network.
```
evol = [weighted_degree_centrality(graph, 'weight') for graph in [G_book1, G_book2, G_book3, G_book4, G_book5]]
evol_df = pd.DataFrame.from_records(evol).fillna(0)
evol_df
pd.DataFrame.from_records(evol).max(axis=0).sort_values(ascending=False)[0:10]
```
##### Exercise
Plot the evolution of weighted degree centrality of the above mentioned characters over the 5 books, and repeat the same exercise for betweenness centrality.
```
evol_df[list(pd.DataFrame.from_records(evol).max(axis=0).sort_values(ascending=False)[0:10].index)].plot(figsize=(14,10))
plt.show()
evol = [nx.betweenness_centrality(graph, weight='weight') for graph in [G_book1, G_book2, G_book3, G_book4, G_book5]]
evol_df = pd.DataFrame.from_records(evol).fillna(0)
evol_df[list(pd.DataFrame.from_records(evol).max(axis=0).sort_values(ascending=False)[0:10].index)].plot(figsize=(14,10))
plt.show()
```
Where is Stannis Baratheon in degree centrality measure? Not even in top 10. Strange?
#### Communitty detection in Networks
A network is said to have community structure if the nodes of the network can be easily grouped into (potentially overlapping) sets of nodes such that each set of nodes is densely connected internally.
We will use louvain community detection algorithm to find the modules in our graph.
```
partition = community.best_partition(G_book1)
size = float(len(set(partition.values())))
pos = nx.spring_layout(G_book1)
count = 0.
for com in set(partition.values()) :
count = count + 1.
list_nodes = [nodes for nodes in partition.keys()
if partition[nodes] == com]
nx.draw_networkx_nodes(G_book1, pos, list_nodes, node_size = 20,
node_color = str(count / size))
nx.draw_networkx_edges(G_book1, pos, alpha=0.5)
plt.show()
d = {}
for character, par in partition.items():
if par in d:
d[par].append(character)
else:
d[par] = [character]
d
nx.draw(nx.subgraph(G_book1, d[1]))
nx.density(G_book1)
nx.density(nx.subgraph(G_book1, d[1]))
nx.density(nx.subgraph(G_book1, d[1]))/nx.density(G_book1)
```
#### Exercise
Find the most important node in the partitions according to pagerank, degree centrality and betweenness centrality of the nodes.
```
max_d = {}
page = nx.pagerank(G_book1)
for par in d:
temp = 0
for chars in d[par]:
if page[chars] > temp:
max_d[par] = chars
max_d
max_d = {}
page = nx.betweenness_centrality(G_book1)
for par in d:
temp = 0
for chars in d[par]:
if page[chars] > temp:
max_d[par] = chars
max_d
max_d = {}
page = nx.degree_centrality(G_book1)
for par in d:
temp = 0
for chars in d[par]:
if page[chars] > temp:
max_d[par] = chars
max_d
d[8]
```
| true |
code
| 0.362758 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.