prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# widgets.image_cleaner
fastai offers several widgets to support the workflow of a deep learning practitioner. The purpose of the widgets are to help you organize, clean, and prepare your data for your model. Widgets are separated by data type.
```
from fastai.vision import *
from fastai.widgets import DatasetFormatter, ImageCleaner
from fastai.gen_doc.nbdoc import show_doc
%reload_ext autoreload
%autoreload 2
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = create_cnn(data, models.resnet18, metrics=error_rate)
learn.fit_one_cycle(2)
learn.save('stage-1')
```
We create a databunch with all the data in the training set and no validation set (DatasetFormatter uses only the training set)
```
db = (ImageItemList.from_folder(path)
.no_split()
.label_from_folder()
.databunch())
learn = create_cnn(db, models.resnet18, metrics=[accuracy])
learn.load('stage-1');
show_doc(DatasetFormatter)
```
The [`DatasetFormatter`](/widgets.image_cleaner.html#DatasetFormatter) class prepares your image dataset for widgets by returning a formatted [`DatasetTfm`](/vision.data.html#DatasetTfm) based on the [`DatasetType`](/basic_data.html#DatasetType) specified. Use `from_toplosses` to grab the most problematic images directly from your learner. Optionally, you can restrict the formatted dataset returned to `n_imgs`.
```
show_doc(DatasetFormatter.from_similars)
from fastai.gen_doc.nbdoc import *
from fastai.widgets.image_cleaner import *
show_doc(DatasetFormatter.from_toplosses)
show_doc(ImageCleaner)
```
[`ImageCleaner`](/widgets.image_cleaner.html#ImageCleaner) is for cleaning up images that don't belong in your dataset. It renders images in a row and gives you the opportunity to delete the file from your file system. To use [`ImageCleaner`](/widgets.image_cleaner.html#ImageCleaner) we must first use `DatasetFormatter().from_toplosses` to get the suggested indices for misclassified images.
```
ds, idxs = DatasetFormatter().from_toplosses(learn)
ImageCleaner(ds, idxs, path)
```
[`ImageCleaner`](/widgets.image_cleaner.html#ImageCleaner) does not change anything on disk (neither labels or existence of images). Instead, it creates a 'cleaned.csv' file in your data path from which you need to load your new databunch for the files to changes to be applied.
```
df = pd.read_csv(path/'cleaned.csv', header='infer')
# We create a databunch from our csv. We include the data in the training set and we don't use a validation set (DatasetFormatter uses only the training set)
np.random.seed(42)
db = (ImageItemList.from_df(df, path)
.no_split()
.label_from_df()
.databunch(bs=64))
learn = create_cnn(db, models.resnet18, metrics=error_rate)
learn = learn.load('stage-1')
```
You can then use [`ImageCleaner`](/widgets.image_cleaner.html#ImageCleaner) again to find duplicates in the dataset. To do this, you can specify `duplicates=True` while calling ImageCleaner after getting the indices and dataset from `.from_similars`. Note that if you are using a layer's output which has dimensions [n_batches, n_features, 1, 1] then you don't need any pooling (this is the case with the last layer). The suggested use of `.from_similars()` with resnets is using the last layer and no pooling, like in the following cell.
```
ds, idxs = DatasetFormatter().from_similars(learn, layer_ls=[0,7,1], pool=None)
ImageCleaner(ds, idxs, path, duplicates=True)
```
## Methods
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
```
show_doc(ImageCleaner.make_dropdown_widget)
```
| true |
code
| 0.687761 | null | null | null | null |
|
# Harvesting Commonwealth Hansard
The proceedings of Australia's Commonwealth Parliament are recorded in Hansard, which is available online through the Parliamentary Library's ParlInfo database. [Results in ParlInfo](https://parlinfo.aph.gov.au/parlInfo/search/summary/summary.w3p;adv=yes;orderBy=_fragment_number,doc_date-rev;query=Dataset:hansardr,hansardr80;resCount=Default) are generated from well-structured XML files which can be downloaded individually from the web interface – one XML file for each sitting day. This notebook shows you how to download the XML files for large scale analysis. It's an updated version of the code I used to harvest Hansard in 2016.
**If you just want the data, a full harvest of the XML files for both houses between 1901–1980 and 1998–2005 [is available in this repository](https://github.com/wragge/hansard-xml). XML files are not currently available for 1981 to 1997. Open Australia provides access to [Hansard XML files from 2006 onwards](http://data.openaustralia.org.au/).**
The XML files are published on the Australian Parliament website [under a CC-BY-NC-ND licence](https://www.aph.gov.au/Help/Disclaimer_Privacy_Copyright#c).
## Method
When you search in ParlInfo, your results point to fragments within a day's procedings. Multiple fragments will be drawn from a single XML file, so there are many more results than there are files. The first step in harvesting the XML files is to work through the results for each year scraping links to the XML files from the HTML pages and discarding any duplicates. The `harvest_year()` function below does this. These lists of links are saved as CSV files – one for each house and year. You can view the CSV files in the `data` directory.
Once you have a list of XML urls for both houses across all years, you can simply use the urls to download the XML files.
## Import what we need
```
import re
import os
import time
import math
import requests
import requests_cache
import arrow
import pandas as pd
from tqdm.auto import tqdm
from bs4 import BeautifulSoup
from requests.adapters import HTTPAdapter
from requests.packages.urllib3.util.retry import Retry
s = requests_cache.CachedSession()
retries = Retry(total=5, backoff_factor=1, status_forcelist=[ 502, 503, 504 ])
s.mount('https://', HTTPAdapter(max_retries=retries))
s.mount('http://', HTTPAdapter(max_retries=retries))
```
## Set your output directory
This is where all the harvested data will go.
```
output_dir = 'data'
os.makedirs(output_dir, exist_ok=True)
```
## Define the base ParlInfo urls
These are the basic templates for searches in ParlInfo. Later on we'll insert a date range in the `query` slot to filter by year, and increment the `page` value to work through the complete set of results.
```
# Years you want to harvest
# Note that no XML files are available for the years 1981 to 1998, so harvests of this period will fail
START_YEAR = 1901
END_YEAR = 2005
URLS = {
'hofreps': (
'http://parlinfo.aph.gov.au/parlInfo/search/summary/summary.w3p;'
'adv=yes;orderBy=date-eLast;page={page};'
'query={query}%20Dataset%3Ahansardr,hansardr80;resCount=100'),
'senate': (
'http://parlinfo.aph.gov.au/parlInfo/search/summary/summary.w3p;'
'adv=yes;orderBy=date-eLast;page={page};'
'query={query}%20Dataset%3Ahansards,hansards80;resCount=100')
}
```
## Define some functions to do the work
```
def get_total_results(house, query):
'''
Get the total number of results in the search.
'''
# Insert query and page values into the ParlInfo url
url = URLS[house].format(query=query, page=0)
# Get the results page
response = s.get(url)
# Parse the HTML
soup = BeautifulSoup(response.text)
try:
# Find where the total results are given in the HTML
summary = soup.find('div', 'resultsSummary').contents[1].string
# Extract the number of results from the string
total = re.search(r'of (\d+)', summary).group(1)
except AttributeError:
total = 0
return int(total)
def get_xml_url(url):
'''
Extract the XML file url from an individual result.
'''
# Load the page for an individual result
response = s.get(url)
# Parse the HTML
soup = BeautifulSoup(response.text)
# Find the XML url by looking for a pattern in the href
try:
xml_url = soup.find('a', href=re.compile('toc_unixml'))['href']
except TypeError:
xml_url = None
if not response.from_cache:
time.sleep(1)
return xml_url
def harvest_year(house, year):
'''
Loop through a search by house and year, finding all the urls for XML files.
'''
# Format the start and end dates
start_date = '01%2F01%2F{}'.format(year)
end_date = '31%2F12%2F{}'.format(year)
# Prepare the query value using the start and end dates
query = 'Date%3A{}%20>>%20{}'.format(start_date, end_date)
# Get the total results
total_results = get_total_results(house, query)
xml_urls = []
dates = []
found_dates = []
if total_results > 0:
# Calculate the number of pages in the results set
num_pages = int(math.ceil(total_results / 100))
# Loop through the page range
for page in tqdm(range(0, num_pages + 1), desc=str(year), leave=False):
# Get the next page of results
url = URLS[house].format(query=query, page=page)
response = s.get(url)
# Parse the HTML
soup = BeautifulSoup(response.text)
# Find the list of results and loop through them
for result in tqdm(soup.find_all('div', 'resultContent'), leave=False):
# Try to identify the date
try:
date = re.search(r'Date: (\d{2}\/\d{2}\/\d{4})', result.find('div', 'sumMeta').get_text()).group(1)
date = arrow.get(date, 'DD/MM/YYYY').format('YYYY-MM-DD')
except AttributeError:
#There are some dodgy dates -- we'll just ignore them
date = None
# If there's a date, and we haven't seen it already, we'll grab the details
if date and date not in dates:
found_dates.append(date)
# Get the link to the individual result page
# This is where the XML file links live
result_link = result.find('div', 'sumLink').a['href']
# Get the XML file link from the individual record page
xml_url = get_xml_url(result_link)
if xml_url:
dates.append(date)
# Save dates and links
xml_urls.append({'date': date, 'url': 'https://parlinfo.aph.gov.au{}'.format(xml_url)})
if not response.from_cache:
time.sleep(1)
for f_date in list(set(found_dates)):
if f_date not in dates:
xml_urls.append({'date': f_date, 'url': ''})
return xml_urls
```
## Harvest all the XML file links
```
for house in ['hofreps', 'senate']:
for year in range(START_YEAR, END_YEAR + 1):
xml_urls = harvest_year(house, year)
df = pd.DataFrame(xml_urls)
df.to_csv(os.path.join(output_dir, '{}-{}-files.csv'.format(house, year)), index=False)
```
## Download all the XML files
This opens up each house/year list of file links and downloads the XML files. The directory structure is simple:
```
-- output directory ('data' by default)
-- hofreps
-- 1901
-- XML files...
```
```
for house in ['hofreps', 'senate']:
for year in range(START_YEAR, END_YEAR + 1):
output_path = os.path.join(output_dir, house, str(year))
os.makedirs(output_path, exist_ok=True)
df = pd.read_csv(os.path.join(output_dir, '{}-{}-files.csv'.format(house, year)))
for row in tqdm(df.itertuples(), desc=str(year), leave=False):
if pd.notnull(row.url):
filename = re.search(r'(?:%20)*([\w\(\)-]+?\.xml)', row.url).group(1)
# Some of the later files don't include the date in the filename so we'll add it.
if filename[:4] != str(year):
filename = f'{row.date}_{filename}'
filepath = os.path.join(output_path, filename)
if not os.path.exists(filepath):
response = s.get(row.url)
with open(filepath, 'w') as xml_file:
xml_file.write(response.text)
if not response.from_cache:
time.sleep(1)
```
## Summarise the data
This just merges all the house/year lists into one big list, adding columns for house and year. It saves the results as a CSV file. This will be useful to analyse things like the number of sitting days per year.
The fields in the CSV file are:
* `date` – date of sitting day in YYYY-MM-DD format
* `url` – url for XML file (where available)
* `year`
* `house` – 'hofreps' or 'senate'
Here's the results of my harvest from 1901 to 2005: [all-sitting-days.csv](data/all-sitting-days.csv)
```
df = pd.DataFrame()
for house in ['hofreps', 'senate']:
for year in range(START_YEAR, END_YEAR + 1):
year_df = pd.read_csv(os.path.join(output_dir, '{}-{}-files.csv'.format(house, year)))
year_df['year'] = year
year_df['house'] = house
df = df.append(year_df)
df.sort_values(by=['house', 'date'], inplace=True)
df.to_csv(os.path.join(output_dir, 'all-sitting-days.csv'), index=False)
```
## Zip up each year individually
For convenience you can zip up each year individually.
```
from shutil import make_archive
for house in ['hofreps', 'senate']:
xml_path = os.path.join(output_dir, house)
for year in [d for d in os.listdir(xml_path) if d.isnumeric()]:
year_path = os.path.join(xml_path, year)
make_archive(year_path, 'zip', year_path)
```
----
Created by [Tim Sherratt](https://timsherratt.org) for the [GLAM Workbench](https://glam-workbench.github.io/).
| true |
code
| 0.265238 | null | null | null | null |
|
# Enumerating BiCliques to Find Frequent Patterns
#### KDD 2019 Workshop
#### Authors
- Tom Drabas (Microsoft)
- Brad Rees (NVIDIA)
- Juan-Arturo Herrera-Ortiz (Microsoft)
#### Problem overview
From time to time PCs running Microsoft Windows fail: a program might crash or hang, or you experience a kernel crash leading to the famous blue screen (we do love those 'Something went wrong' messages as well...;)).
<img src="images/Windows_SomethingWentWrong.png" alt="Windows problems" width=380px class="center"/>
Well, when this happens it's not a good experience and we are truly interested in quickly finding out what might have gone wrong and/or at least what is common among the PCs that have failed.
## Import necessary modules
```
import cudf
import numpy
import azureml.core as aml
import time
```
## Load the data
The data prepared for this workshop will be available to download after the conference. We will share the link in the final notebook that will be available on RAPIDS github account.
### Data
The data we will be using in this workshop has been synthetically generate to showcase the type of scenarios we encounter in our work.
While running certain workloads, PCs might fail for one reason or another. We collect the information from both types of scenarios and enrich the observations with the metadata about each PC (hardware, software, failure logs etc.). This forms a dataset where each row represents a PC and the features column contains a list of all the metadata we want to mine to find frequent patterns about the population that has failed.
In this tutorial we will be representing this data in a form of a bi-partite graph. A bi-partite graph can be divided into two disconnected subgraphs (none of the vertices within the subgraphs are connected) with the edges connecting the vertices from one subgraph to the other. See the example below.
<img src="images/BiPartiteGraph_Example.png" alt="Bi-Partite graph example" width=200px class="center"/>
In order to operate on this type of data we convert the list-of-features per row to a COO (Coordinate list) format: each row represents an edge connection, the first column contains the source vertex, the second one contains the destination vertex, and the third column contains the failure flag (0 = success, 1 = failure).
```
!head -n 3 ../../../../data/fpm_graph/coo_fpm.csv
```
Now we can load the data into a RAPIDS DataFrame `cudf`. ***NOTE: This will take longer than if you were running this on your local machine since the data-store is separate from this running VM. Normally it would be almost instant.***
```
%%time
fpm_df = cudf.read_csv('../../../../data/fpm_graph/coo_fpm.csv', names=['src', 'dst', 'flag'])
import pandas as pd
%%time
fpm_pdf = pd.read_csv('../../../../data/fpm_graph/coo_fpm.csv', names=['src', 'dst', 'flag'])
```
Now that we have the data loaded let's check how big is our data.
```
%%time
shp = fpm_df.shape
print('Row cnt: {0}, col cnt: {1}'.format(*shp))
```
So, we have >41M records in our DataFrame. Let's see what it looks like:
```
print(fpm_df.head(10))
```
## Understand the data
Now that we have the data, let's explore it a bit.
### Overall failure rate
First, let's find out what is the overall failure rate. In general, we do not want to extract any patterns that are below the overall failure rate since the would not help us to understand anything about the phenomenon we're dealing with nor would help us pinpoint the actual problems.
```
%%time
print(fpm_df['flag'].sum() / float(fpm_df['flag'].count()))
```
So, the overall falure rate is 16.7%. However, you can see that running a `sum` and `count` reducers on 41M records took ~5-10ms.
### Device count
I didn't tell you how many devices we included in the dataset. Let's figure it out. Since the `src` column contains multiple edges per PC we need to count only the unique ids for this column.
```
%%time
print(fpm_df['src'].unique().count())
```
So, we have 755k devices in the dataset and it took only 1s to find this out!!!
### Distinct features count
Let's now check how many distinct meatadata features we included in the dataset
```
%%time
print(fpm_df['dst'].unique().count())
```
Now you can see it is a synthetic dataset ;) We have a universe of 15k distinct metadata features each PC can be comprised of.
### Degree distribution
Different PCs have different number of features: some have two CPUs or 4 GPUs (lucky...). Below we can quickly find how many features each PCs has.
```
%%time
degrees = fpm_df.groupby('src').agg({'dst': 'count'})
print(degrees)
print(
'On average PCs have {0:.2f} components. The one with the max numer has {1}.'
.format(
degrees['dst'].mean()
, degrees['dst'].max()
)
)
```
### Inspecting the distribution of degrees
We can very quickly calculate the deciles of degrees.
```
%%time
quantiles = degrees.quantile(q=[float(e) / 100 for e in range(0, 100, 10)])
print(quantiles.to_pandas())
```
Let's see how the distribution looks like.
```
%%time
buckets = degrees['dst'].value_counts().reset_index().to_pandas()
buckets.columns = ['Bucket', 'Count']
import matplotlib.pyplot as plt
%matplotlib inline
plt.bar(buckets['Bucket'], buckets['Count'])
```
## Mine the data and find the bi-cliques
In this part of the tutorial we will show you the prototype implementation of the iMBEA algorithm proposed in Zhang, Y et al. paper from 2014 titled _On finding bicliques in bipartite graphs: A novel algorithm and its application to the integration of diverse biological data types_ published in BMC bioinformatics 15 (110) URL: https://www.researchgate.net/profile/Michael_Langston/publication/261732723_On_finding_bicliques_in_bipartite_graphs_A_novel_algorithm_and_its_application_to_the_integration_of_diverse_biological_data_types/links/00b7d53a300726c5b3000000/On-finding-bicliques-in-bipartite-graphs-A-novel-algorithm-and-its-application-to-the-integration-of-diverse-biological-data-types.pdf
### Setup
First, we do some setting up.
```
from collections import OrderedDict
import numpy as np
# must be factor of 10
PART_SIZE = int(1000)
```
### Data partitioning
We partition the DataFrame into multiple parts to aid computations.
```
def _partition_data_by_feature(_df) :
#compute the number of sets
m = int(( _df['dst'].max() / PART_SIZE) + 1 )
_ui = [None] * (m + 1)
# Partition the data into a number of smaller DataFrame
s = 0
e = s + PART_SIZE
for i in range (m) :
_ui[i] = _df.query('dst >= @s and dst < @e')
s = e
e = e + PART_SIZE
return _ui, m
```
### Enumerating features
One of the key components of iMBEA algorithm is how it scans the graph starting from, in our case, from the most popular to the least popular feature. The `_count_features(...)` method below achieves exactly that and produces a sorted list of features ranked by their popularity.
```
def _count_features( _gdf, sort=True) :
aggs = OrderedDict()
aggs['dst'] = 'count'
c = fpm_df.groupby(['dst'], as_index=False).agg(aggs)
c = c.rename(columns={'dst':'count'})
c = c.reset_index()
if (sort) :
c = c.sort_values(by='count', ascending=False)
return c
print(_count_features(fpm_df))
```
### Fundamental methods
Below are some fundamental methods used iteratively by the final algorithm
#### `get_src_from_dst`
This method returns a DataFrame of all the source vertices that have the destination vertex `id` in their list of features.
```
# get all src vertices for a given dst
def get_src_from_dst( _gdf, id) :
_src_list = (_gdf.query('dst == @id'))
_src_list.drop_column('dst')
return _src_list
```
#### `get_all_features`
This method returns all the features that are connected to the vertices found in the `src_list_df`.
```
# get all the items used by the specified users
def get_all_feature(_gdf, src_list_df, N) :
c = [None] * N
for i in range(N) :
c[i] = src_list_df.merge(_gdf[i], on='src', how="inner")
return cudf.concat(c)
```
#### `is_same_as_last`
This method checks if the bi-clicque has already been enumerated.
```
def is_same_as_last(_old, _new) :
status = False
if (len(_old) == len(_new)) :
m = _old.merge(_new, on='src', how="left")
if m['src'].null_count == 0 :
status = True
return status
```
#### `update_results`
This is a util method that helps to (1) maintain a DataFrame with enumerated bi-cliques that contains some of the `src` and `dst` vertices, and (2) some basic information about these.
```
def update_results(m, f, key, b, s) :
"""
Input
* m = machines
* f = features
* key = cluster ID
* b = biclique answer
* s = stats answer
Returns
-------
B : cudf.DataFrame
A dataframe containing the list of machine and features. This is not the full
edge list to save space. Since it is a biclique, it is easy to recreate the edges
B['id'] - a cluster ID (this is a one up number - up to k)
B['vert'] - the vertex ID
B['type'] - 0 == machine, 1 == feature
S : cudf.DataFrame
A Pandas dataframe of statistics on the returned info.
This dataframe is (relatively small) of size k.
S['id'] - the cluster ID
S['total'] - total vertex count
S['machines'] - number of machine nodes
S['features'] - number of feature vertices
S['bad_ratio'] - the ratio of bad machine / total machines
"""
B = cudf.DataFrame()
S = cudf.DataFrame()
m_df = cudf.DataFrame()
m_df['vert'] = m['src'].astype(np.int32)
m_df['id'] = int(key)
m_df['type'] = int(0)
f_df = cudf.DataFrame()
f_df['vert'] = f['dst'].astype(np.int32)
f_df['id'] = int(key)
f_df['type'] = int(1)
if len(b) == 0 :
B = cudf.concat([m_df, f_df])
else :
B = cudf.concat([b, m_df, f_df])
# now update the stats
num_m = len(m_df)
num_f = len(f_df)
total = num_m# + num_f
num_bad = len(m.query('flag == 1'))
ratio = num_bad / total
# now stats
s_tmp = cudf.DataFrame()
s_tmp['id'] = key
s_tmp['total'] = total
s_tmp['machines'] = num_m
s_tmp['bad_machines'] = num_bad
s_tmp['features'] = num_f
s_tmp['bad_ratio'] = ratio
if len(s) == 0 :
S = s_tmp
else :
S = cudf.concat([s,s_tmp])
del m_df
del f_df
return B, S
```
#### `ms_find_maximal_bicliques`
This is the main loop for the algorithm. It iteratively scans the list of features and enumerates the bi-cliques.
```
def ms_find_maximal_bicliques(df, k,
offset=0,
max_iter=-1,
support=1.0,
min_features=1,
min_machines=10) :
"""
Find the top k maximal bicliques
Parameters
----------
df : cudf:DataFrame
A dataframe containing the bipartite graph edge list
Columns must be called 'src', 'dst', and 'flag'
k : int
The max number of bicliques to return
-1 mean all
offset : int
Returns
-------
B : cudf.DataFrame
A dataframe containing the list of machine and features. This is not the full
edge list to save space. Since it is a biclique, it is ease to recreate the edges
B['id'] - a cluster ID (this is a one up number - up to k)
B['vert'] - the vertex ID
B['type'] - 0 == machine, 1 == feature
S : cudf.DataFrame
A dataframe of statistics on the returned info.
This dataframe is (relatively small) of size k.
S['id'] - the cluster ID
S['total'] - total vertex count
S['machines'] - number of machine nodes
S['features'] - number of feature vertices
S['bad_ration'] - the ratio of bad machine / total machines
"""
x = [col for col in df.columns]
if 'src' not in x:
raise NameError('src column not found')
if 'dst' not in x:
raise NameError('dst column not found')
if 'flag' not in x:
raise NameError('flag column not found')
if support > 1.0 or support < 0.1:
raise NameError('support must be between 0.1 and 1.0')
# this removes a prep step that offset the values for CUDA process
if offset > 0 :
df['dst'] = df['dst'] - offset
# break the data into chunks to improve join/search performance
src_by_dst, num_parts = _partition_data_by_feature(df)
# Get a list of all the dst (features) sorted by degree
f_list = _count_features(df, True)
# create a dataframe for the answers
bicliques = cudf.DataFrame()
stats = cudf.DataFrame()
# create a dataframe to help prevent duplication of work
machine_old = cudf.DataFrame()
# create a dataframe for stats
stats = cudf.DataFrame()
answer_id = 0
iter_max = len(f_list)
if max_iter != -1 :
iter_max = max_iter
# Loop over all the features (dst) or until K is reached
for i in range(iter_max) :
# pop the next feature to process
feature = f_list['dst'][i]
degree = f_list['count'][i]
# compute the index to this item (which dataframe chunk is in)
idx = int(feature/PART_SIZE)
# get all machines that have this feature
machines = get_src_from_dst(src_by_dst[idx], feature)
# if this set of machines is the same as the last, skip this feature
if is_same_as_last(machine_old, machines) == False:
# now from those machines, hop out to the list of all the features
feature_list = get_all_feature(src_by_dst, machines, num_parts)
# summarize occurrences
ic = _count_features(feature_list, True)
goal = int(degree * support)
# only get dst nodes with the same degree
c = ic.query('count >= @goal')
# need more than X feature to make a biclique
if len(c) > min_features :
if len(machines) >= min_machines :
bicliques, stats = update_results(machines, c, answer_id, bicliques, stats)
answer_id = answer_id + 1
# end - if same
machine_old = machines
if k > -1:
if answer_id == k :
break
# end for loop
# All done, reset data
if offset > 0 :
df['dst'] = df['dst'] + offset
return bicliques, stats
```
### Finding bi-cliques
Now that we have a fundamental understanding how this works -- let's put it to action.
```
%%time
bicliques, stats = ms_find_maximal_bicliques(
df=fpm_df,
k=10,
offset=1000000,
max_iter=100,
support = 1.0,
min_features=3,
min_machines=100
)
```
It takes somewhere between <font size="10">10 to 15 seconds</font> to analyze <font size="10">>42M</font>edges and output the top 10 most important bicliques.
Let's see what we got. We enumerated 10 bicliques. The worst of them had a failure rate of over 97%.
```
print(stats)
```
Let's look at the one of the worst ones that affected the most machines: over 57k.
```
bicliques.query('id == 1 and type == 1')['vert'].sort_values().to_pandas()
```
If you change the `type` to `0` we could retrieve a sample list of PCs that fit this particular pattern/bi-clique: this is useful and sometimes helps us to further narrow down a problem by further scanning the logs from PCs.
| true |
code
| 0.528777 | null | null | null | null |
|
# LCLS Archiver restore
These examples show how single snapshots, and time series can be retreived from the archiver appliance.
Note that the times must always be in ISO 8601 format, UTC time (not local time).
```
%pylab --no-import-all inline
%config InlineBackend.figure_format = 'retina'
from lcls_live.archiver import lcls_archiver_restore
from lcls_live import data_dir
import json
import os
# This is the main function
?lcls_archiver_restore
```
## Optional: off-site setup
```
# Optional:
# Open an SSH tunnel in a terminal like:
# ssh -D 8080 <some user>@<some SLAC machine>
# And then set:
os.environ['http_proxy']='socks5h://localhost:8080'
os.environ['HTTPS_PROXY']='socks5h://localhost:8080'
os.environ['ALL_PROXY']='socks5h://localhost:8080'
```
# Restore known PVs
```
pvlist = [
'IRIS:LR20:130:MOTR_ANGLE',
'SOLN:IN20:121:BDES',
'QUAD:IN20:121:BDES',
'QUAD:IN20:122:BDES',
'ACCL:IN20:300:L0A_ADES',
'ACCL:IN20:300:L0A_PDES'
]
lcls_archiver_restore(pvlist, '2020-07-09T05:01:21.000000-07:00')
```
## Get snapshot from a large list
Same as above, but for processing large amounts of data
```
# Get list of PVs
fname = os.path.join(data_dir, 'classic/full_pvlist.json')
pvlist = json.load(open(fname))
pvlist[0:3]
# Simple filename naming
def snapshot_filename(isotime):
return 'epics_snapshot_'+isotime+'.json'
times = ['2018-03-06T15:21:15.000000-08:00']
lcls_archiver_restore(pvlist[0:10], times[0])
%%time
# Make multiple files
root = './data/'
for t in times:
newdata = lcls_archiver_restore(pvlist, t)
fname = os.path.join(root, snapshot_filename(t))
with open(fname, 'w') as f:
f.write(json.dumps(newdata))
print('Written:', fname)
```
# Get history of a single PV
This package also has a couple functions for getting the time history data of a pv.
The first, `lcls_archiver_history`, returns the raw data
```
from lcls_live.archiver import lcls_archiver_history, lcls_archiver_history_dataframe
t_start = '2020-07-09T05:01:15.000000-07:00'
t_end = '2020-07-09T05:03:00.000000-07:00'
secs, vals = lcls_archiver_history('SOLN:IN20:121:BDES', start=t_start, end=t_end)
secs[0:5], vals[0:5]
```
More convenient, is to format this as a pandas dataframe.
```
?lcls_archiver_history_dataframe
df1 = lcls_archiver_history_dataframe('YAGS:IN20:241:YRMS', start=t_start, end=t_end)
df1[0:5]
# Pandas has convenient plotting
df1.plot()
```
# Aligning the history of two PVs
The returned data will not necessarily be time-aligned. Here we will use Pandas' interpolate capabilities to fill in missing data.
```
import pandas as pd
# Try another PV. This one was smoothy scanned
df2 = lcls_archiver_history_dataframe('SOLN:IN20:121:BDES', start=t_start, end=t_end)
df2
df2.plot()
# Notice that some data are taken at the same time, others are not
df4 = pd.concat([df1, df2], axis=1)
df4
# This will fill in the missing values, and drop trailing NaNs
df5 = df4.interpolate().dropna()
df5
# make a plot
DF = df5[:-2] # The last two points are outside the main scan.
k1 = 'SOLN:IN20:121:BDES'
k2 = 'YAGS:IN20:241:YRMS'
plt.xlabel(k1)
plt.ylabel(k2)
plt.title(t_start+'\n to '+t_end)
plt.scatter(DF[k1], DF[k2], marker='.', color='black')
```
# This easily extends to a list
```
pvlist = ['SOLN:IN20:121:BDES', 'YAGS:IN20:241:XRMS', 'YAGS:IN20:241:YRMS']
dflist = []
for pvname in pvlist:
dflist.append(lcls_archiver_history_dataframe(pvname, start=t_start, end=t_end))
df6 = pd.concat(dflist, axis=1).interpolate().dropna()
df6
DF = df6[:-2] # Drop the last two that are unrelated to the scan
k1 = 'SOLN:IN20:121:BDES'
k2 = 'YAGS:IN20:241:XRMS'
k3 = 'YAGS:IN20:241:YRMS'
plt.xlabel(k1+' (kG-m)')
plt.ylabel('Measurement (um)')
plt.title(t_start+'\n to '+t_end)
X1 = DF[k1]
X2 = DF[k2]
X3 = DF[k3]
plt.scatter(X1, X2, marker='x', color='blue', label=k2)
plt.scatter(X1, X3, marker='x', color='green', label=k3)
plt.legend()
```
| true |
code
| 0.565419 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/jsedoc/ConceptorDebias/blob/master/Experiments/Conceptors/Gradient_Based_Conceptors.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import torch
import torch.nn.functional as F
from torch import nn, optim
import numpy as np
from numpy.linalg import inv
import matplotlib.pyplot as plt
%matplotlib inline
dtype = torch.float
device = torch.device('cuda:0')
torch.cuda.get_device_name(0)
```
# Gradient Approach To Conceptors
### Initializing Old Conceptors and Data
```
## Old Conceptors Implementations
def get_conceptor(x, alpha):
N = x.shape[1] - 1
cov = (x @ x.T)*(1/N)
return cov @ inv(cov + (1/alpha**2)*np.eye(x.shape[0]))
def improved_conceptor(X, alpha = 1):
N = X.shape[1]
means = np.mean(X, axis = 1)
stds = np.std(X,axis = 1)
X = X - means[:,None]
X = X / stds[:,None]
cov = (X @ X.T)*(1/N)
return cov @ inv(cov + (alpha**(-2))*np.eye(X.shape[0]))
## Generating Dataset
N = 100000
covariance = [[1,0.7],
[0.7,1]]
X = np.random.multivariate_normal([0,0],covariance,N).T
plt.title('Data Cloud')
plt.scatter(X[0],X[1], c = 'm')
plt.show()
print("\n")
## Checking Old Conceptors
alpha = 1
C = improved_conceptor(X, alpha)
print(C)
print(np.linalg.norm(X - C @ X)**2/N + np.linalg.norm(C)**2)
```
### Setup Gradient Based Conceptor
```
learning_rate = 0.1
x = torch.tensor(X.T, device = device, dtype = dtype)
y = x.clone().detach()
W = torch.rand(2,2, device = device, dtype = dtype, requires_grad = True)
for t in range(10001):
y_pred = x.mm(W)
l2_reg = W.norm(2).pow(2)
loss = (1/N)*(y_pred - y).pow(2).sum() + l2_reg
if(t%5000 == 0): print(t,': ', loss.item())
loss.backward()
with torch.no_grad():
W -= learning_rate *(1/(0.001*t+1)) * W.grad
W.grad.zero_()
print(W.data)
model = torch.nn.Sequential(torch.nn.Linear(2,2, bias = False))
model.cuda()
loss_fn = torch.nn.MSELoss(reduction = 'mean')
for t in range(15001):
y_pred = model(x)
# loss = loss_fn(y_pred,y)
l2_reg = None
for param in model.parameters():
if l2_reg is None:
l2_reg = param.norm(2).pow(2)
else:
l2_reg = l2_reg + param.norm(2)
loss = (1/N)*(y_pred - y).pow(2).sum() + l2_reg
if(t%5000 == 0): print(t,': ', loss.item())
model.zero_grad()
loss.backward()
with torch.no_grad():
for param in model.parameters():
param -= learning_rate*(1/(0.001*t+1)) * param.grad
for param in model.parameters():
print(param.data)
# optimizer = optim.SGD(net.parameters(),lr = 0.01, weight_decay = 1)
## NOT conceptor
notx = model(x).detach_()
noty = y.clone().detach()
notmodel = torch.nn.Sequential(torch.nn.Linear(2,2, bias = False))
notmodel.cuda()
learning_rate = 0.1
for t in range(15001):
y_pred = notmodel(notx)
loss = (1/N)*(y_pred - noty).pow(2).sum()
if(t%5000 == 0): print(t,': ', loss.item())
loss.backward()
with torch.no_grad():
for param in notmodel.parameters():
param -= learning_rate*(1/(0.001*t+1)) * param.grad
notmodel.zero_grad()
for param in notmodel.parameters():
print(param.data)
for param in notmodel.parameters():
for param2 in model.parameters():
print(param.mm(param2))
result = notmodel(x).detach().cpu()
plt.scatter(result[:,0],result[:,1])
plt.show()
```
### Nonlinear Conceptors Using Autoencoders (INCOMPLETE)
```
class Conceptor(nn.Module):
def __init__(self, size):
super(Conceptor, self).__init__()
self.fc1 = nn.Linear(size,2)
self.fc2 = nn.Linear(2,2)
self.fc3 = nn.Linear(2,size)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
conceptor = Conceptor(2)
conceptor.cuda()
learn_rate = 0.1
for t in range(3001):
pred_y = conceptor(x)
l2 = None
for param in conceptor.parameters():
if l2 is None:
l2 = param.norm(2).pow(2)
else:
l2 = l2 + param.norm(2).pow(2)
loss = (1/N)*(pred_y-y).pow(2).sum() + l2/100
if(t%300 == 0): print(t,': ', loss.item())
conceptor.zero_grad()
loss.backward()
with torch.no_grad():
for param in conceptor.parameters():
param -= learning_rate * param.grad
notC = Conceptor(2)
notC.cuda()
cX = conceptor(x).clone().detach()
for t in range(3001):
pred_y = notC(cX)
loss = (1/N)*(pred_y-y).pow(2).sum()
if(t%300 == 0): print(t,': ', loss.item())
notC.zero_grad()
loss.backward()
with torch.no_grad():
for param in notC.parameters():
param -= learning_rate * param.grad
test = np.random.multivariate_normal([0,0],[[1,0],
[0,1]],N)
test = torch.tensor(test, device = device, dtype = dtype)
testC = conceptor(test).detach().cpu()
plt.scatter(testC[:,0],testC[:,1], c = 'm')
plt.show()
original = xe.detach().cpu()
plt.scatter(original[:,0],original[:,1])
plt.show()
result = notC(x).detach().cpu()
plt.scatter(result[:,0],result[:,1])
plt.show()
what = original - result
plt.scatter(what[:,0],what[:,1])
plt.show()
```
| true |
code
| 0.793066 | null | null | null | null |
|
# DALI expressions and arithmetic operators
In this example, we will show simple examples how to use binary arithmetic operators in DALI Pipeline that allow for element-wise operations on tensors inside a pipeline. We will show available operators and examples of using constant and scalar inputs.
## Supported operators
DALI currently supports unary arithmetic operators: `+`, `-`; binary arithmetic operators: `+`, `-`, `*`, `/`, and `//`; comparison operators: `==`, `!=`, `<`, `<=`, `>`, `>=`; and bitwise binary operators: `&`, `|`, `^`. Binary operators can be used as an operation between two tensors, between a tensor and a scalar or a tensor and a constant. By tensor we consider the output of DALI operators (either regular ones or other arithmetic operators). Unary operators work only with Tensor inputs.
We will focus on binary arithmetic operators, Tensor, Constant and Scalar operands. The detailed type promotion rules for comparison and bitwise operators are covered in the **Supported operations** section of documentation as well as other examples.
### Prepare the test pipeline
First, we will prepare the helper code, so we can easily manipulate the types and values that will appear as tensors in the DALI pipeline.
We will be using numpy as source for the custom provided data and we also need to import several things from DALI needed to create Pipeline and use ExternalSource Operator.
```
import numpy as np
from nvidia.dali.pipeline import Pipeline
import nvidia.dali.ops as ops
import nvidia.dali.types as types
from nvidia.dali.types import Constant
```
### Defining the data
As we are dealing with binary operators, we need two inputs.
We will create a simple helper function that returns two batches of hardcoded data, stored as `np.int32`. In an actual scenario the data processed by DALI arithmetic operators would be tensors produced by other Operator containing some images, video sequences or other data.
You can experiment by changing those values or adjusting the `get_data()` function to use different input data. Keep in mind that shapes of both inputs need to match as those will be element-wise operations.
```
left_magic_values = [
[[42, 7, 0], [0, 0, 0]],
[[5, 10, 15], [10, 100, 1000]]
]
right_magic_values = [
[[3, 3, 3], [1, 3, 5]],
[[1, 5, 5], [1, 1, 1]]
]
batch_size = len(left_magic_values)
def convert_batch(batch):
return [np.int32(tensor) for tensor in batch]
def get_data():
return (convert_batch(left_magic_values), convert_batch(right_magic_values))
```
## Operating on tensors
### Defining the pipeline
The next step is to define our pipeline. The data will be obtained from `get_data` function and made available to the pipeline through `ExternalSource`.
Note, that we do not need to instantiate any additional operators, we can use regular Python arithmetic expressions on the results of other operators in the `define_graph` step.
Let's manipulate the source data by adding, multiplying and dividing it. `define_graph` will return both our data inputs and the result of applying arithmetic operations to them.
```
class ArithmeticPipeline(Pipeline):
def __init__(self, batch_size, num_threads, device_id):
super(ArithmeticPipeline, self).__init__(batch_size, num_threads, device_id)
self.source = ops.ExternalSource(get_data, num_outputs = 2)
def define_graph(self):
l, r = self.source()
sum_result = l + r
mul_result = l * r
div_result = l // r
return l, r, sum_result, mul_result, div_result
```
### Running the pipeline
Lets build and run our pipeline
```
pipe = ArithmeticPipeline(batch_size = batch_size, num_threads = 2, device_id = 0)
pipe.build()
out = pipe.run()
```
Now it's time to display the results:
```
def examine_output(pipe_out):
l = pipe_out[0].as_array()
r = pipe_out[1].as_array()
sum_out = pipe_out[2].as_array()
mul_out = pipe_out[3].as_array()
div_out = pipe_out[4].as_array()
print("{}\n+\n{}\n=\n{}\n\n".format(l, r, sum_out))
print("{}\n*\n{}\n=\n{}\n\n".format(l, r, mul_out))
print("{}\n//\n{}\n=\n{}\n\n".format(l, r, div_out))
examine_output(out)
```
As we can see the resulting tensors are obtained by applying the arithmetic operation between corresponding elements of its inputs.
The shapes of the arguments to arithmetic operators should match (with an exception for scalar tensor inputs that we will describe in the next section), otherwise we will get an error.
## Constant and scalar operands
Until now we considered only tensor inputs of matching shapes for inputs of arithmetic operators. DALI allows one of the operands to be a constant or a batch of scalars. They can appear on both sides of binary expressions.
## Constants
In `define_graph` step, constant operand for arithmetic operator can be: values of Python's `int` and `float` types used directly, or those values wrapped in `nvidia.dali.types.Constant`. Operation between tensor and constant results in the constant being broadcast to all elements of the tensor.
*Note: Currently all values of integral constants are passed internally to DALI as int32 and all values of floating point constants are passed to DALI as float32.*
The Python `int` values will be treated as `int32` and the `float` as `float32` in regard to type promotions.
The DALI `Constant` can be used to indicate other types. It accepts `DALIDataType` enum values as second argument and has convenience member functions like `.uint8()` or `.float32()` that can be used for conversions.
### Using the Constants
Let's adjust the Pipeline to utilize constants first.
```
class ArithmeticConstantsPipeline(Pipeline):
def __init__(self, batch_size, num_threads, device_id):
super(ArithmeticConstantsPipeline, self).__init__(batch_size, num_threads, device_id)
self.source = ops.ExternalSource(get_data, num_outputs = 2)
def define_graph(self):
l, r = self.source()
add_200 = l + 200
mul_075 = l * 0.75
sub_15 = Constant(15).float32() - r
return l, r, add_200, mul_075, sub_15
pipe = ArithmeticConstantsPipeline(batch_size = batch_size, num_threads = 2, device_id = 0)
pipe.build()
out = pipe.run()
```
Now it's time to display the results:
```
def examine_output(pipe_out):
l = pipe_out[0].as_array()
r = pipe_out[1].as_array()
add_200 = pipe_out[2].as_array()
mul_075 = pipe_out[3].as_array()
sub_15 = pipe_out[4].as_array()
print("{}\n+ 200 =\n{}\n\n".format(l, add_200))
print("{}\n* 0.75 =\n{}\n\n".format(l, mul_075))
print("15 -\n{}\n=\n{}\n\n".format(r, sub_15))
examine_output(out)
```
As we can see the constant value is used with all elements of all tensors in the batch.
## Dynamic scalars
It is sometimes useful to evaluate an expression with one argument being a tensor and the other being scalar. If the scalar value is constant thoughout the execution of the pipeline, `types.Cosntant` can be used. When dynamic scalar values are needed, they can be constructed as 0D tensors (with empty shape). If DALI encounters such a tensor, it will broadcast it to match the shape of the tensor argument. Note, that DALI operates on batches - and as such, the scalars are also supplied as batches, with each scalar operand being used with other operands at the same index in the batch.
### Using scalar tensors
We will use an `ExternalSource` to generate a sequence of numbers which will be then added to the tensor operands.
```
class ArithmeticScalarsPipeline(Pipeline):
def __init__(self, batch_size, num_threads, device_id):
super(ArithmeticScalarsPipeline, self).__init__(batch_size, num_threads, device_id)
# we only need one input
self.tensor_source = ops.ExternalSource(lambda: get_data()[0])
# a batch of scalars from 1 to batch_size
scalars = np.arange(1, batch_size + 1)
self.scalar_source = ops.ExternalSource(lambda: scalars)
def define_graph(self):
tensors = self.tensor_source()
scalars = self.scalar_source()
return tensors, scalars, tensors + scalars
```
Now it's time to build and run the Pipeline. It will allow to scale our input by some random numbers generated by the `Uniform` Operator.
```
pipe = ArithmeticScalarsPipeline(batch_size = batch_size, num_threads = 2, device_id = 0)
pipe.build()
out = pipe.run()
def examine_output(pipe_out):
t = pipe_out[0].as_array()
uni = pipe_out[1].as_array()
scaled = pipe_out[2].as_array()
print("{}\n+\n{}\n=\n{}".format(t, uni, scaled))
examine_output(out)
```
Notice how the first scalar in the batch (1) is added to all elements in the first tensor and the second scalar (2) to the second tensor.
| true |
code
| 0.541106 | null | null | null | null |
|
# Detailed execution time for cadCAD models
*Danilo Lessa Bernardineli*
---
This notebook shows how you can use metadata on PSUBs in order to do pre-processing on the simulations. We use two keys for flagging them: the `ignore` which indicates which PSUBs we want to skip, and the `debug`, which informs us what are the ones which we want to monitor the policies execution time.
```
from time import time
import logging
from functools import wraps
logging.basicConfig(level=logging.DEBUG)
def print_time(f):
"""
"""
@wraps(f)
def wrapper(*args, **kwargs):
# Current timestep
t = len(args[2])
t1 = time()
f_out = f(*args, **kwargs)
t2 = time()
text = f"{t}|{f.__name__} output (exec time: {t2 - t1:.2f}s): {f_out}"
logging.debug(text)
return f_out
return wrapper
```
## Dependences
```
%%capture
!pip install cadcad
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from cadCAD.configuration import Experiment
from cadCAD.configuration.utils import config_sim
from cadCAD.engine import ExecutionMode, ExecutionContext, Executor
```
## Definitions
### Initial conditions and parameters
```
initial_conditions = {
'prey_population': 100,
'predator_population': 15
}
params = {
"prey_birth_rate": [1.0],
"predator_birth_rate": [0.01],
"predator_death_const": [1.0],
"prey_death_const": [0.03],
"dt": [0.1] # Precision of the simulation. Lower is more accurate / slower
}
simulation_parameters = {
'N': 1,
'T': range(30),
'M': params
}
```
### Policies
```
def p_predator_births(params, step, sL, s):
dt = params['dt']
predator_population = s['predator_population']
prey_population = s['prey_population']
birth_fraction = params['predator_birth_rate'] + np.random.random() * 0.0002
births = birth_fraction * prey_population * predator_population * dt
return {'add_to_predator_population': births}
def p_prey_births(params, step, sL, s):
dt = params['dt']
population = s['prey_population']
birth_fraction = params['prey_birth_rate'] + np.random.random() * 0.1
births = birth_fraction * population * dt
return {'add_to_prey_population': births}
def p_predator_deaths(params, step, sL, s):
dt = params['dt']
population = s['predator_population']
death_rate = params['predator_death_const'] + np.random.random() * 0.005
deaths = death_rate * population * dt
return {'add_to_predator_population': -1.0 * deaths}
def p_prey_deaths(params, step, sL, s):
dt = params['dt']
death_rate = params['prey_death_const'] + np.random.random() * 0.1
prey_population = s['prey_population']
predator_population = s['predator_population']
deaths = death_rate * prey_population * predator_population * dt
return {'add_to_prey_population': -1.0 * deaths}
```
### State update functions
```
def s_prey_population(params, step, sL, s, _input):
y = 'prey_population'
x = s['prey_population'] + _input['add_to_prey_population']
return (y, x)
def s_predator_population(params, step, sL, s, _input):
y = 'predator_population'
x = s['predator_population'] + _input['add_to_predator_population']
return (y, x)
```
### State update blocks
```
partial_state_update_blocks = [
{
'label': 'Predator dynamics',
'ignore': False,
'debug': True,
'policies': {
'predator_births': p_predator_births,
'predator_deaths': p_predator_deaths
},
'variables': {
'predator_population': s_predator_population
}
},
{
'label': 'Prey dynamics',
'ignore': True,
'debug': True,
'policies': {
'prey_births': p_prey_births,
'prey_deaths': p_prey_deaths
},
'variables': {
'prey_population': s_prey_population
}
}
]
# Mantain only PSUBs which doesn't have the ignore flag
partial_state_update_blocks = [psub
for psub in partial_state_update_blocks
if psub.get('ignore', False) == False]
# Only check the execution time for the PSUBs with the debug flag
for psub in partial_state_update_blocks:
psub['policies'] = {label: print_time(f) for label, f in psub['policies'].items()}
```
### Configuration and Execution
```
sim_config = config_sim(simulation_parameters)
exp = Experiment()
exp.append_configs(sim_configs=sim_config,
initial_state=initial_conditions,
partial_state_update_blocks=partial_state_update_blocks)
from cadCAD import configs
exec_mode = ExecutionMode()
exec_context = ExecutionContext(exec_mode.local_mode)
executor = Executor(exec_context=exec_context, configs=configs)
(records, tensor_field, _) = executor.execute()
```
### Results
```
import plotly.express as px
df = pd.DataFrame(records)
fig = px.line(df,
x=df.prey_population,
y=df.predator_population,
color=df.run.astype(str))
fig.show()
```
| true |
code
| 0.531453 | null | null | null | null |
|
```
%matplotlib inline
```
# `scikit-learn` - Machine Learning in Python
[scikit-learn](http://scikit-learn.org) is a simple and efficient tool for data mining and data analysis. It is built on [NumPy](www.numpy.org), [SciPy](https://www.scipy.org/), and [matplotlib](https://matplotlib.org/). The following examples show some of `scikit-learn`'s power. For a complete list, go to the official homepage under [examples](http://scikit-learn.org/stable/auto_examples/index.html) or [tutorials](http://scikit-learn.org/stable/tutorial/index.html).
## Blind source separation using FastICA
This example of estimating sources from noisy data is adapted from [`plot_ica_blind_source_separation`](http://scikit-learn.org/stable/auto_examples/decomposition/plot_ica_blind_source_separation.html).
```
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from sklearn.decomposition import FastICA, PCA
# Generate sample data
n_samples = 2000
time = np.linspace(0, 8, n_samples)
s1 = np.sin(2 * time) # Signal 1: sinusoidal signal
s2 = np.sign(np.sin(3 * time)) # Signal 2: square signal
s3 = signal.sawtooth(2 * np.pi * time) # Signal 3: saw tooth signal
S = np.c_[s1, s2, s3]
S += 0.2 * np.random.normal(size=S.shape) # Add noise
S /= S.std(axis=0) # Standardize data
# Mix data
A = np.array([[1, 1, 1], [0.5, 2, 1.0], [1.5, 1.0, 2.0]]) # Mixing matrix
X = np.dot(S, A.T) # Generate observations
# Compute ICA
ica = FastICA(n_components=3)
S_ = ica.fit_transform(X) # Reconstruct signals
A_ = ica.mixing_ # Get estimated mixing matrix
# For comparison, compute PCA
pca = PCA(n_components=3)
H = pca.fit_transform(X) # Reconstruct signals based on orthogonal components
# Plot results
plt.figure(figsize=(12, 4))
models = [X, S, S_, H]
names = ['Observations (mixed signal)', 'True Sources',
'ICA recovered signals', 'PCA recovered signals']
colors = ['red', 'steelblue', 'orange']
for ii, (model, name) in enumerate(zip(models, names), 1):
plt.subplot(2, 2, ii)
plt.title(name)
for sig, color in zip(model.T, colors):
plt.plot(sig, color=color)
plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.46)
plt.show()
```
# Anomaly detection with Local Outlier Factor (LOF)
This example presents the Local Outlier Factor (LOF) estimator. The LOF algorithm is an unsupervised outlier detection method which computes the local density deviation of a given data point with respect to its neighbors. It considers as outlier samples that have a substantially lower density than their neighbors. This example is adapted from [`plot_lof`](http://scikit-learn.org/stable/auto_examples/neighbors/plot_lof.html).
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
# Generate train data
X = 0.3 * np.random.randn(100, 2)
# Generate some abnormal novel observations
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.r_[X + 2, X - 2, X_outliers]
# fit the model
clf = LocalOutlierFactor(n_neighbors=20)
y_pred = clf.fit_predict(X)
y_pred_outliers = y_pred[200:]
# Plot the level sets of the decision function
xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))
Z = clf._decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.title("Local Outlier Factor (LOF)")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)
a = plt.scatter(X[:200, 0], X[:200, 1], c='white', edgecolor='k', s=20)
b = plt.scatter(X[200:, 0], X[200:, 1], c='red', edgecolor='k', s=20)
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a, b], ["normal observations", "abnormal observations"], loc="upper left")
plt.show()
```
# SVM: Maximum margin separating hyperplane
Plot the maximum margin separating hyperplane within a two-class separable dataset using a Support Vector Machine classifier with a linear kernel. This example is adapted from [`plot_separating_hyperplane`](http://scikit-learn.org/stable/auto_examples/svm/plot_separating_hyperplane.html).
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
# we create 40 separable points
X, y = make_blobs(n_samples=40, centers=2, random_state=6)
# fit the model, don't regularize for illustration purposes
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
# plot the decision function
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
# plot decision boundary and margins
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none')
plt.show()
```
# `Scikit-Image` - Image processing in python
[scikit-image](http://scikit-image.org/) is a collection of algorithms for image processing and is based on [scikit-learn](http://scikit-learn.org). The following examples show some of `scikit-image`'s power. For a complete list, go to the official homepage under [examples](http://scikit-image.org/docs/stable/auto_examples/).
## Sliding window histogram
Histogram matching can be used for object detection in images. This example extracts a single coin from the `skimage.data.coins` image and uses histogram matching to attempt to locate it within the original image. This example is adapted from [`plot_windowed_histogram`](http://scikit-image.org/docs/stable/auto_examples/features_detection/plot_windowed_histogram.html).
```
from __future__ import division
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from skimage import data, transform
from skimage.util import img_as_ubyte
from skimage.morphology import disk
from skimage.filters import rank
def windowed_histogram_similarity(image, selem, reference_hist, n_bins):
# Compute normalized windowed histogram feature vector for each pixel
px_histograms = rank.windowed_histogram(image, selem, n_bins=n_bins)
# Reshape coin histogram to (1,1,N) for broadcast when we want to use it in
# arithmetic operations with the windowed histograms from the image
reference_hist = reference_hist.reshape((1, 1) + reference_hist.shape)
# Compute Chi squared distance metric: sum((X-Y)^2 / (X+Y));
# a measure of distance between histograms
X = px_histograms
Y = reference_hist
num = (X - Y) ** 2
denom = X + Y
denom[denom == 0] = np.infty
frac = num / denom
chi_sqr = 0.5 * np.sum(frac, axis=2)
# Generate a similarity measure. It needs to be low when distance is high
# and high when distance is low; taking the reciprocal will do this.
# Chi squared will always be >= 0, add small value to prevent divide by 0.
similarity = 1 / (chi_sqr + 1.0e-4)
return similarity
# Load the `skimage.data.coins` image
img = img_as_ubyte(data.coins())
# Quantize to 16 levels of greyscale; this way the output image will have a
# 16-dimensional feature vector per pixel
quantized_img = img // 16
# Select the coin from the 4th column, second row.
# Co-ordinate ordering: [x1,y1,x2,y2]
coin_coords = [184, 100, 228, 148] # 44 x 44 region
coin = quantized_img[coin_coords[1]:coin_coords[3],
coin_coords[0]:coin_coords[2]]
# Compute coin histogram and normalize
coin_hist, _ = np.histogram(coin.flatten(), bins=16, range=(0, 16))
coin_hist = coin_hist.astype(float) / np.sum(coin_hist)
# Compute a disk shaped mask that will define the shape of our sliding window
# Example coin is ~44px across, so make a disk 61px wide (2 * rad + 1) to be
# big enough for other coins too.
selem = disk(30)
# Compute the similarity across the complete image
similarity = windowed_histogram_similarity(quantized_img, selem, coin_hist,
coin_hist.shape[0])
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(12, 4))
axes[0].imshow(quantized_img, cmap='gray')
axes[0].set_title('Quantized image')
axes[0].axis('off')
axes[1].imshow(coin, cmap='gray')
axes[1].set_title('Coin from 2nd row, 4th column')
axes[1].axis('off')
axes[2].imshow(img, cmap='gray')
axes[2].imshow(similarity, cmap='hot', alpha=0.5)
axes[2].set_title('Original image with overlaid similarity')
axes[2].axis('off')
plt.tight_layout()
plt.show()
```
## Local Thresholding
If the image background is relatively uniform, then you can use a global threshold value as presented above. However, if there is large variation in the background intensity, adaptive thresholding (a.k.a. local or dynamic thresholding) may produce better results. This example is adapted from [`plot_thresholding`](http://scikit-image.org/docs/dev/auto_examples/xx_applications/plot_thresholding.html#local-thresholding).
```
from skimage.filters import threshold_otsu, threshold_local
image = data.page()
global_thresh = threshold_otsu(image)
binary_global = image > global_thresh
block_size = 35
adaptive_thresh = threshold_local(image, block_size, offset=10)
binary_adaptive = image > adaptive_thresh
fig, axes = plt.subplots(ncols=3, figsize=(16, 6))
ax = axes.ravel()
plt.gray()
ax[0].imshow(image)
ax[0].set_title('Original')
ax[1].imshow(binary_global)
ax[1].set_title('Global thresholding')
ax[2].imshow(binary_adaptive)
ax[2].set_title('Adaptive thresholding')
for a in ax:
a.axis('off')
plt.show()
```
## Finding local maxima
The peak_local_max function returns the coordinates of local peaks (maxima) in an image. A maximum filter is used for finding local maxima. This operation dilates the original image and merges neighboring local maxima closer than the size of the dilation. Locations, where the original image is equal to the dilated image, are returned as local maxima. This example is adapted from [`plot_peak_local_max`](http://scikit-image.org/docs/stable/auto_examples/segmentation/plot_peak_local_max.html).
```
from scipy import ndimage as ndi
import matplotlib.pyplot as plt
from skimage.feature import peak_local_max
from skimage import data, img_as_float
im = img_as_float(data.coins())
# image_max is the dilation of im with a 20*20 structuring element
# It is used within peak_local_max function
image_max = ndi.maximum_filter(im, size=20, mode='constant')
# Comparison between image_max and im to find the coordinates of local maxima
coordinates = peak_local_max(im, min_distance=20)
# display results
fig, axes = plt.subplots(1, 3, figsize=(12, 5), sharex=True, sharey=True,
subplot_kw={'adjustable': 'box'})
ax = axes.ravel()
ax[0].imshow(im, cmap=plt.cm.gray)
ax[0].axis('off')
ax[0].set_title('Original')
ax[1].imshow(image_max, cmap=plt.cm.gray)
ax[1].axis('off')
ax[1].set_title('Maximum filter')
ax[2].imshow(im, cmap=plt.cm.gray)
ax[2].autoscale(False)
ax[2].plot(coordinates[:, 1], coordinates[:, 0], 'r.')
ax[2].axis('off')
ax[2].set_title('Peak local max')
fig.tight_layout()
plt.show()
```
## Label image region
This example shows how to segment an image with image labeling. The following steps are applied:
1. Thresholding with automatic Otsu method
2. Close small holes with binary closing
3. Remove artifacts touching image border
4. Measure image regions to filter small objects
This example is adapted from [`plot_label`](http://scikit-image.org/docs/stable/auto_examples/segmentation/plot_label.html).
```
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from skimage import data
from skimage.filters import threshold_otsu
from skimage.segmentation import clear_border
from skimage.measure import label, regionprops
from skimage.morphology import closing, square
from skimage.color import label2rgb
image = data.coins()[50:-50, 50:-50]
# apply threshold
thresh = threshold_otsu(image)
bw = closing(image > thresh, square(3))
# remove artifacts connected to image border
cleared = clear_border(bw)
# label image regions
label_image = label(cleared)
image_label_overlay = label2rgb(label_image, image=image)
fig, ax = plt.subplots(figsize=(10, 6))
ax.imshow(image_label_overlay)
for region in regionprops(label_image):
# take regions with large enough areas
if region.area >= 100:
# draw rectangle around segmented coins
minr, minc, maxr, maxc = region.bbox
rect = mpatches.Rectangle((minc, minr), maxc - minc, maxr - minr,
fill=False, edgecolor='red', linewidth=2)
ax.add_patch(rect)
ax.set_axis_off()
plt.tight_layout()
plt.show()
```
| true |
code
| 0.815563 | null | null | null | null |
|
<a href="https://qworld.net" target="_blank" align="left"><img src="../qworld/images/header.jpg" align="left"></a>
$ \newcommand{\bra}[1]{\langle #1|} $
$ \newcommand{\ket}[1]{|#1\rangle} $
$ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
$ \newcommand{\dot}[2]{ #1 \cdot #2} $
$ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
$ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
$ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
$ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
$ \newcommand{\mypar}[1]{\left( #1 \right)} $
$ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
$ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
$ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
$ \newcommand{\onehalf}{\frac{1}{2}} $
$ \newcommand{\donehalf}{\dfrac{1}{2}} $
$ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
$ \newcommand{\vzero}{\myvector{1\\0}} $
$ \newcommand{\vone}{\myvector{0\\1}} $
$ \newcommand{\stateplus}{\myvector{ \sqrttwo \\ \sqrttwo } } $
$ \newcommand{\stateminus}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
$ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
$ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
$ \newcommand{\I}{ \mymatrix{rr}{1 & 0 \\ 0 & 1} } $
$ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
$ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
$ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
$ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
$ \newcommand{\pstate}[1]{ \lceil \mspace{-1mu} #1 \mspace{-1.5mu} \rfloor } $
$ \newcommand{\greenbit}[1] {\mathbf{{\color{green}#1}}} $
$ \newcommand{\bluebit}[1] {\mathbf{{\color{blue}#1}}} $
$ \newcommand{\redbit}[1] {\mathbf{{\color{red}#1}}} $
$ \newcommand{\brownbit}[1] {\mathbf{{\color{brown}#1}}} $
$ \newcommand{\blackbit}[1] {\mathbf{{\color{black}#1}}} $
<font style="font-size:28px;" align="left"><b><font color="blue"> Solutions for </font>Grover's Search: Implementation </b></font>
<br>
_prepared by Maksim Dimitrijev and Özlem Salehi_
<br><br>
<a id="task2"></a>
<h3>Task 2</h3>
Let $N=4$. Implement the query phase and check the unitary matrix for the query operator. Note that we are interested in the top-left $4 \times 4$ part of the matrix since the remaining parts are due to the ancilla qubit.
You are given a function $f$ and its corresponding quantum operator $U_f$. First run the following cell to load operator $U_f$. Then you can make queries to $f$ by applying the operator $U_f$ via the following command:
<pre>Uf(circuit,qreg).
```
%run quantum.py
```
Now use phase kickback to flip the sign of the marked element:
<ul>
<li>Set output qubit (qreg[2]) to $\ket{-}$ by applying X and H.</li>
<li>Apply operator $U_f$
<li>Set output qubit (qreg[2]) back.</li>
</ul>
(Can you guess the marked element by looking at the unitary matrix?)
<h3>Solution</h3>
```
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
qreg = QuantumRegister(3)
#No need to define classical register as we are not measuring
mycircuit = QuantumCircuit(qreg)
#set ancilla
mycircuit.x(qreg[2])
mycircuit.h(qreg[2])
Uf(mycircuit,qreg)
#set ancilla back
mycircuit.h(qreg[2])
mycircuit.x(qreg[2])
job = execute(mycircuit,Aer.get_backend('unitary_simulator'))
u=job.result().get_unitary(mycircuit,decimals=3)
#We are interested in the top-left 4x4 part
for i in range(4):
s=""
for j in range(4):
val = str(u[i][j].real)
while(len(val)<5): val = " "+val
s = s + val
print(s)
mycircuit.draw(output='mpl')
```
<a id="task3"></a>
<h3>Task 3</h3>
Let $N=4$. Implement the inversion operator and check whether you obtain the following matrix:
$\mymatrix{cccc}{-0.5 & 0.5 & 0.5 & 0.5 \\ 0.5 & -0.5 & 0.5 & 0.5 \\ 0.5 & 0.5 & -0.5 & 0.5 \\ 0.5 & 0.5 & 0.5 & -0.5}$.
<h3>Solution</h3>
```
def inversion(circuit,quantum_reg):
#step 1
circuit.h(quantum_reg[1])
circuit.h(quantum_reg[0])
#step 2
circuit.x(quantum_reg[1])
circuit.x(quantum_reg[0])
#step 3
circuit.ccx(quantum_reg[1],quantum_reg[0],quantum_reg[2])
#step 4
circuit.x(quantum_reg[1])
circuit.x(quantum_reg[0])
#step 5
circuit.x(quantum_reg[2])
#step 6
circuit.h(quantum_reg[1])
circuit.h(quantum_reg[0])
```
Below you can check the matrix of your inversion operator and how the circuit looks like. We are interested in top-left $4 \times 4$ part of the matrix, the remaining parts are because we used ancilla qubit.
```
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
qreg1 = QuantumRegister(3)
mycircuit1 = QuantumCircuit(qreg1)
#set ancilla qubit
mycircuit1.x(qreg1[2])
mycircuit1.h(qreg1[2])
inversion(mycircuit1,qreg1)
#set ancilla qubit back
mycircuit1.h(qreg1[2])
mycircuit1.x(qreg1[2])
job = execute(mycircuit1,Aer.get_backend('unitary_simulator'))
u=job.result().get_unitary(mycircuit1,decimals=3)
for i in range(4):
s=""
for j in range(4):
val = str(u[i][j].real)
while(len(val)<5): val = " "+val
s = s + val
print(s)
mycircuit1.draw(output='mpl')
```
<a id="task4"></a>
<h3>Task 4: Testing Grover's search</h3>
Now we are ready to test our operations and run Grover's search. Suppose that there are 4 elements in the list and try to find the marked element.
You are given the operator $U_f$. First run the following cell to load it. You can access it via <pre>Uf(circuit,qreg).</pre>
qreg[2] is the ancilla qubit and it is shared by the query and the inversion operators.
Which state do you observe the most?
```
%run quantum.py
```
<h3>Solution</h3>
```
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
qreg = QuantumRegister(3)
creg = ClassicalRegister(2)
mycircuit = QuantumCircuit(qreg,creg)
#Grover
#initial step - equal superposition
for i in range(2):
mycircuit.h(qreg[i])
#set ancilla
mycircuit.x(qreg[2])
mycircuit.h(qreg[2])
mycircuit.barrier()
#change the number of iterations
iterations=1
#Grover's iterations.
for i in range(iterations):
#query
Uf(mycircuit,qreg)
mycircuit.barrier()
#inversion
inversion(mycircuit,qreg)
mycircuit.barrier()
#set ancilla back
mycircuit.h(qreg[2])
mycircuit.x(qreg[2])
mycircuit.measure(qreg[0],creg[0])
mycircuit.measure(qreg[1],creg[1])
job = execute(mycircuit,Aer.get_backend('qasm_simulator'),shots=10000)
counts = job.result().get_counts(mycircuit)
# print the outcome
for outcome in counts:
print(outcome,"is observed",counts[outcome],"times")
mycircuit.draw(output='mpl')
```
<a id="task5"></a>
<h3>Task 5 (Optional, challenging)</h3>
Implement the inversion operation for $n=3$ ($N=8$). This time you will need 5 qubits - 3 for the operation, 1 for ancilla, and one more qubit to implement not gate controlled by three qubits.
In the implementation the ancilla qubit will be qubit 3, while qubits for control are 0, 1 and 2; qubit 4 is used for the multiple control operation. As a result you should obtain the following values in the top-left $8 \times 8$ entries:
$\mymatrix{cccccccc}{-0.75 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 \\ 0.25 & -0.75 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 \\ 0.25 & 0.25 & -0.75 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 \\ 0.25 & 0.25 & 0.25 & -0.75 & 0.25 & 0.25 & 0.25 & 0.25 \\ 0.25 & 0.25 & 0.25 & 0.25 & -0.75 & 0.25 & 0.25 & 0.25 \\ 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & -0.75 & 0.25 & 0.25 \\ 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & -0.75 & 0.25 \\ 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & -0.75}$.
<h3>Solution</h3>
```
def big_inversion(circuit,quantum_reg):
for i in range(3):
circuit.h(quantum_reg[i])
circuit.x(quantum_reg[i])
circuit.ccx(quantum_reg[1],quantum_reg[0],quantum_reg[4])
circuit.ccx(quantum_reg[2],quantum_reg[4],quantum_reg[3])
circuit.ccx(quantum_reg[1],quantum_reg[0],quantum_reg[4])
for i in range(3):
circuit.x(quantum_reg[i])
circuit.h(quantum_reg[i])
circuit.x(quantum_reg[3])
```
Below you can check the matrix of your inversion operator. We are interested in the top-left $8 \times 8$ part of the matrix, the remaining parts are because of additional qubits.
```
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
big_qreg2 = QuantumRegister(5)
big_mycircuit2 = QuantumCircuit(big_qreg2)
#set ancilla
big_mycircuit2.x(big_qreg2[3])
big_mycircuit2.h(big_qreg2[3])
big_inversion(big_mycircuit2,big_qreg2)
#set ancilla back
big_mycircuit2.h(big_qreg2[3])
big_mycircuit2.x(big_qreg2[3])
job = execute(big_mycircuit2,Aer.get_backend('unitary_simulator'))
u=job.result().get_unitary(big_mycircuit2,decimals=3)
for i in range(8):
s=""
for j in range(8):
val = str(u[i][j].real)
while(len(val)<6): val = " "+val
s = s + val
print(s)
```
<a id="task6"></a>
<h3>Task 6: Testing Grover's search for 8 elements (Optional, challenging)</h3>
Now we will test Grover's search on 8 elements.
You are given the operator $U_{f_8}$. First run the following cell to load it. You can access it via:
<pre>Uf_8(circuit,qreg)</pre>
Which state do you observe the most?
```
%run quantum.py
```
<h3>Solution</h3>
```
def big_inversion(circuit,quantum_reg):
for i in range(3):
circuit.h(quantum_reg[i])
circuit.x(quantum_reg[i])
circuit.ccx(quantum_reg[1],quantum_reg[0],quantum_reg[4])
circuit.ccx(quantum_reg[2],quantum_reg[4],quantum_reg[3])
circuit.ccx(quantum_reg[1],quantum_reg[0],quantum_reg[4])
for i in range(3):
circuit.x(quantum_reg[i])
circuit.h(quantum_reg[i])
circuit.x(quantum_reg[3])
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
qreg8 = QuantumRegister(5)
creg8 = ClassicalRegister(3)
mycircuit8 = QuantumCircuit(qreg8,creg8)
#set ancilla
mycircuit8.x(qreg8[3])
mycircuit8.h(qreg8[3])
#Grover
for i in range(3):
mycircuit8.h(qreg8[i])
mycircuit8.barrier()
#Try 1,2,6,12 8iterations of Grover
for i in range(2):
Uf_8(mycircuit8,qreg8)
mycircuit8.barrier()
big_inversion(mycircuit8,qreg8)
mycircuit8.barrier()
#set ancilla back
mycircuit8.h(qreg8[3])
mycircuit8.x(qreg8[3])
for i in range(3):
mycircuit8.measure(qreg8[i],creg8[i])
job = execute(mycircuit8,Aer.get_backend('qasm_simulator'),shots=10000)
counts8 = job.result().get_counts(mycircuit8)
# print the reverse of the outcome
for outcome in counts8:
print(outcome,"is observed",counts8[outcome],"times")
mycircuit8.draw(output='mpl')
```
<a id="task8"></a>
<h3>Task 8</h3>
Implement an oracle function which marks the element 00. Run Grover's search with the oracle you have implemented.
```
def oracle_00(circuit,qreg):
```
<h3>Solution</h3>
```
def oracle_00(circuit,qreg):
circuit.x(qreg[0])
circuit.x(qreg[1])
circuit.ccx(qreg[0],qreg[1],qreg[2])
circuit.x(qreg[0])
circuit.x(qreg[1])
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
qreg = QuantumRegister(3)
creg = ClassicalRegister(2)
mycircuit = QuantumCircuit(qreg,creg)
#Grover
#initial step - equal superposition
for i in range(2):
mycircuit.h(qreg[i])
#set ancilla
mycircuit.x(qreg[2])
mycircuit.h(qreg[2])
mycircuit.barrier()
#change the number of iterations
iterations=1
#Grover's iterations.
for i in range(iterations):
#query
oracle_00(mycircuit,qreg)
mycircuit.barrier()
#inversion
inversion(mycircuit,qreg)
mycircuit.barrier()
#set ancilla back
mycircuit.h(qreg[2])
mycircuit.x(qreg[2])
mycircuit.measure(qreg[0],creg[0])
mycircuit.measure(qreg[1],creg[1])
job = execute(mycircuit,Aer.get_backend('qasm_simulator'),shots=10000)
counts = job.result().get_counts(mycircuit)
# print the reverse of the outcome
for outcome in counts:
reverse_outcome = ''
for i in outcome:
reverse_outcome = i + reverse_outcome
print(reverse_outcome,"is observed",counts[outcome],"times")
mycircuit.draw(output='mpl')
```
| true |
code
| 0.480174 | null | null | null | null |
|
# 神经网络
## 全连接层
### 张量方式实现
```
import tensorflow as tf
from matplotlib import pyplot as plt
plt.rcParams['font.size'] = 16
plt.rcParams['font.family'] = ['STKaiti']
plt.rcParams['axes.unicode_minus'] = False
# 创建 W,b 张量
x = tf.random.normal([2,784])
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
# 线性变换
o1 = tf.matmul(x,w1) + b1
# 激活函数
o1 = tf.nn.relu(o1)
o1
```
### 层方式实现
```
x = tf.random.normal([4,28*28])
# 导入层模块
from tensorflow.keras import layers
# 创建全连接层,指定输出节点数和激活函数
fc = layers.Dense(512, activation=tf.nn.relu)
# 通过 fc 类实例完成一次全连接层的计算,返回输出张量
h1 = fc(x)
h1
```
上述通过一行代码即可以创建一层全连接层 fc, 并指定输出节点数为 512, 输入的节点数在fc(x)计算时自动获取, 并创建内部权值张量$W$和偏置张量$\mathbf{b}$。 我们可以通过类内部的成员名 kernel 和 bias 来获取权值张量$W$和偏置张量$\mathbf{b}$对象
```
# 获取 Dense 类的权值矩阵
fc.kernel
# 获取 Dense 类的偏置向量
fc.bias
# 待优化参数列表
fc.trainable_variables
# 返回所有参数列表
fc.variables
```
## 神经网络
### 张量方式实现
```
# 隐藏层 1 张量
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
# 隐藏层 2 张量
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
# 隐藏层 3 张量
w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1))
b3 = tf.Variable(tf.zeros([64]))
# 输出层张量
w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1))
b4 = tf.Variable(tf.zeros([10]))
with tf.GradientTape() as tape: # 梯度记录器
# x: [b, 28*28]
# 隐藏层 1 前向计算, [b, 28*28] => [b, 256]
h1 = x@w1 + tf.broadcast_to(b1, [x.shape[0], 256])
h1 = tf.nn.relu(h1)
# 隐藏层 2 前向计算, [b, 256] => [b, 128]
h2 = h1@w2 + b2
h2 = tf.nn.relu(h2)
# 隐藏层 3 前向计算, [b, 128] => [b, 64]
h3 = h2@w3 + b3
h3 = tf.nn.relu(h3)
# 输出层前向计算, [b, 64] => [b, 10]
h4 = h3@w4 + b4
```
### 层方式实现
```
# 导入常用网络层 layers
from tensorflow.keras import layers,Sequential
# 隐藏层 1
fc1 = layers.Dense(256, activation=tf.nn.relu)
# 隐藏层 2
fc2 = layers.Dense(128, activation=tf.nn.relu)
# 隐藏层 3
fc3 = layers.Dense(64, activation=tf.nn.relu)
# 输出层
fc4 = layers.Dense(10, activation=None)
x = tf.random.normal([4,28*28])
# 通过隐藏层 1 得到输出
h1 = fc1(x)
# 通过隐藏层 2 得到输出
h2 = fc2(h1)
# 通过隐藏层 3 得到输出
h3 = fc3(h2)
# 通过输出层得到网络输出
h4 = fc4(h3)
```
对于这种数据依次向前传播的网络, 也可以通过 Sequential 容器封装成一个网络大类对象,调用大类的前向计算函数一次即可完成所有层的前向计算,使用起来更加方便。
```
# 导入 Sequential 容器
from tensorflow.keras import layers,Sequential
# 通过 Sequential 容器封装为一个网络类
model = Sequential([
layers.Dense(256, activation=tf.nn.relu) , # 创建隐藏层 1
layers.Dense(128, activation=tf.nn.relu) , # 创建隐藏层 2
layers.Dense(64, activation=tf.nn.relu) , # 创建隐藏层 3
layers.Dense(10, activation=None) , # 创建输出层
])
out = model(x) # 前向计算得到输出
```
## 激活函数
### Sigmoid
$$\text{Sigmoid}(x) \triangleq \frac{1}{1 + e^{-x}}$$
```
# 构造-6~6 的输入向量
x = tf.linspace(-6.,6.,10)
x
# 通过 Sigmoid 函数
sigmoid_y = tf.nn.sigmoid(x)
sigmoid_y
def set_plt_ax():
# get current axis 获得坐标轴对象
ax = plt.gca()
ax.spines['right'].set_color('none')
# 将右边 上边的两条边颜色设置为空 其实就相当于抹掉这两条边
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
# 指定下边的边作为 x 轴,指定左边的边为 y 轴
ax.yaxis.set_ticks_position('left')
# 指定 data 设置的bottom(也就是指定的x轴)绑定到y轴的0这个点上
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
set_plt_ax()
plt.plot(x, sigmoid_y, color='C4', label='Sigmoid')
plt.xlim(-6, 6)
plt.ylim(0, 1)
plt.legend(loc=2)
plt.show()
```
### ReLU
$$\text{ReLU}(x) \triangleq \max(0, x)$$
```
# 通过 ReLU 激活函数
relu_y = tf.nn.relu(x)
relu_y
set_plt_ax()
plt.plot(x, relu_y, color='C4', label='ReLU')
plt.xlim(-6, 6)
plt.ylim(0, 6)
plt.legend(loc=2)
plt.show()
```
### LeakyReLU
$$\text{LeakyReLU}(x) \triangleq \left\{ \begin{array}{cc}
x \quad x \geqslant 0 \\
px \quad x < 0
\end{array} \right.$$
```
# 通过 LeakyReLU 激活函数
leakyrelu_y = tf.nn.leaky_relu(x, alpha=0.1)
leakyrelu_y
set_plt_ax()
plt.plot(x, leakyrelu_y, color='C4', label='LeakyReLU')
plt.xlim(-6, 6)
plt.ylim(-1, 6)
plt.legend(loc=2)
plt.show()
```
### Tanh
$$\tanh(x)=\frac{e^x-e^{-x}}{e^x + e^{-x}}= 2 \cdot \text{sigmoid}(2x) - 1$$
```
# 通过 tanh 激活函数
tanh_y = tf.nn.tanh(x)
tanh_y
set_plt_ax()
plt.plot(x, tanh_y, color='C4', label='Tanh')
plt.xlim(-6, 6)
plt.ylim(-1.5, 1.5)
plt.legend(loc=2)
plt.show()
```
## 输出层设计
### [0,1]区间,和为 1
$$Softmax(z_i) \triangleq \frac{e^{z_i}}{\sum_{j=1}^{d_{out}} e^{z_j}}$$
```
z = tf.constant([2.,1.,0.1])
# 通过 Softmax 函数
tf.nn.softmax(z)
# 构造输出层的输出
z = tf.random.normal([2,10])
# 构造真实值
y_onehot = tf.constant([1,3])
# one-hot 编码
y_onehot = tf.one_hot(y_onehot, depth=10)
# 输出层未使用 Softmax 函数,故 from_logits 设置为 True
# 这样 categorical_crossentropy 函数在计算损失函数前,会先内部调用 Softmax 函数
loss = tf.keras.losses.categorical_crossentropy(y_onehot,z,from_logits=True)
loss = tf.reduce_mean(loss) # 计算平均交叉熵损失
loss
# 创建 Softmax 与交叉熵计算类,输出层的输出 z 未使用 softmax
criteon = tf.keras.losses.CategoricalCrossentropy(from_logits=True)
loss = criteon(y_onehot,z) # 计算损失
loss
```
### [-1, 1]
```
x = tf.linspace(-6.,6.,10)
# tanh 激活函数
tf.tanh(x)
```
## 误差计算
### 均方差误差函数
$$\text{MSE}(y, o) \triangleq \frac{1}{d_{out}} \sum_{i=1}^{d_{out}}(y_i-o_i)^2$$
MSE 误差函数的值总是大于等于 0,当 MSE 函数达到最小值 0 时, 输出等于真实标签,此时神经网络的参数达到最优状态。
```
# 构造网络输出
o = tf.random.normal([2,10])
# 构造真实值
y_onehot = tf.constant([1,3])
y_onehot = tf.one_hot(y_onehot, depth=10)
# 计算均方差
loss = tf.keras.losses.MSE(y_onehot, o)
loss
# 计算 batch 均方差
loss = tf.reduce_mean(loss)
loss
# 创建 MSE 类
criteon = tf.keras.losses.MeanSquaredError()
# 计算 batch 均方差
loss = criteon(y_onehot,o)
loss
```
### 交叉熵误差函数
$$
\begin{aligned} H(p \| q)
&=D_{K L}(p \| q) \\
&=\sum_{j} y_{j} \log \left(\frac{y_j}{o_j}\right) \\
&= 1 \cdot \log \frac{1}{o_i}+ \sum_{j \neq i} 0 \cdot \log \left(\frac{0}{o_j}\right) \\
& =-\log o_{i}
\end{aligned}
$$
## 汽车油耗预测实战
```
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, losses
def load_dataset():
# 在线下载汽车效能数据集
dataset_path = keras.utils.get_file("auto-mpg.data",
"http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
# 效能(公里数每加仑),气缸数,排量,马力,重量
# 加速度,型号年份,产地
column_names = ['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values="?", comment='\t',
sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
return dataset
dataset = load_dataset()
# 查看部分数据
dataset.head()
def preprocess_dataset(dataset):
dataset = dataset.copy()
# 统计空白数据,并清除
dataset = dataset.dropna()
# 处理类别型数据,其中origin列代表了类别1,2,3,分布代表产地:美国、欧洲、日本
# 其弹出这一列
origin = dataset.pop('Origin')
# 根据origin列来写入新列
dataset['USA'] = (origin == 1) * 1.0
dataset['Europe'] = (origin == 2) * 1.0
dataset['Japan'] = (origin == 3) * 1.0
# 切分为训练集和测试集
train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)
return train_dataset, test_dataset
train_dataset, test_dataset = preprocess_dataset(dataset)
# 统计数据
sns_plot = sns.pairplot(train_dataset[["Cylinders", "Displacement", "Weight", "MPG"]], diag_kind="kde")
# 查看训练集的输入X的统计数据
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
def norm(x, train_stats):
"""
标准化数据
:param x:
:param train_stats: get_train_stats(train_dataset)
:return:
"""
return (x - train_stats['mean']) / train_stats['std']
# 移动MPG油耗效能这一列为真实标签Y
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
# 进行标准化
normed_train_data = norm(train_dataset, train_stats)
normed_test_data = norm(test_dataset, train_stats)
print(normed_train_data.shape,train_labels.shape)
print(normed_test_data.shape, test_labels.shape)
class Network(keras.Model):
# 回归网络
def __init__(self):
super(Network, self).__init__()
# 创建3个全连接层
self.fc1 = layers.Dense(64, activation='relu')
self.fc2 = layers.Dense(64, activation='relu')
self.fc3 = layers.Dense(1)
def call(self, inputs):
# 依次通过3个全连接层
x = self.fc1(inputs)
x = self.fc2(x)
x = self.fc3(x)
return x
def build_model():
# 创建网络
model = Network()
model.build(input_shape=(4, 9))
model.summary()
return model
model = build_model()
optimizer = tf.keras.optimizers.RMSprop(0.001)
train_db = tf.data.Dataset.from_tensor_slices((normed_train_data.values, train_labels.values))
train_db = train_db.shuffle(100).batch(32)
def train(model, train_db, optimizer, normed_test_data, test_labels):
train_mae_losses = []
test_mae_losses = []
for epoch in range(200):
for step, (x, y) in enumerate(train_db):
with tf.GradientTape() as tape:
out = model(x)
loss = tf.reduce_mean(losses.MSE(y, out))
mae_loss = tf.reduce_mean(losses.MAE(y, out))
if step % 10 == 0:
print(epoch, step, float(loss))
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
train_mae_losses.append(float(mae_loss))
out = model(tf.constant(normed_test_data.values))
test_mae_losses.append(tf.reduce_mean(losses.MAE(test_labels, out)))
return train_mae_losses, test_mae_losses
def plot(train_mae_losses, test_mae_losses):
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('MAE')
plt.plot(train_mae_losses, label='Train')
plt.plot(test_mae_losses, label='Test')
plt.legend()
# plt.ylim([0,10])
plt.legend()
plt.show()
train_mae_losses, test_mae_losses = train(model, train_db, optimizer, normed_test_data, test_labels)
plot(train_mae_losses, test_mae_losses)
```
| true |
code
| 0.638976 | null | null | null | null |
|
# "Namentliche Abstimmungen" in the Bundestag
> Parse and inspect "Namentliche Abstimmungen" (roll call votes) in the Bundestag (the federal German parliament)
[](https://mybinder.org/v2/gh/eschmidt42/bundestag/HEAD)
## Context
The German Parliament is so friendly to put all votes of all members into readable XLSX / XLS files (and PDFs ¯\\\_(ツ)\_/¯ ). Those files can be found here: https://www.bundestag.de/parlament/plenum/abstimmung/liste.
Furthermore, the organisation [abgeordnetenwatch](https://www.abgeordnetenwatch.de/) offers a great platform to get to know the individual politicians and their behavior as well as an [open API](https://www.abgeordnetenwatch.de/api) to request data.
## Purpose of this repo
The purpose of this repo is to help collect roll call votes from the parliament's site directly or via abgeordnetenwatch's API and make them available for analysis / modelling. This may be particularly interesting for the upcoming election in 2021. E.g., if you want to see what your local member of the parliament has been up to in terms of public roll call votes relative to the parties, or how individual parties agree in their votes, this dataset may be interesting for you.
Since the files on the bundestag website are stored in a way making it tricky to automatically crawl them, a bit of manual work is required to generate that dataset. But don't fret! Quite a few recent roll call votes (as of the publishing of this repo) are already prepared for you. But if older or more recent roll call votes are missing, convenience tools to reduce your manual effort are demonstrated below. An alternative route to get the same and more data (on politicians and local parliaments as well) is via the abgeordnetenwatch route.
For your inspiration, I have also included an analysis on how similar parties voted / how similar to parties individual MdBs votes and a small machine learning model which predicts the individual votes of parliament. Teaser: the "fraktionsszwang" seems to exist but is not absolute and the data shows 😁.
## How to install
`pip install bundestag`
## How to use
For detailed explanations see:
- parse data from bundestag.de $\rightarrow$ `nbs/00_html_parsing.ipynb`
- parse data from abgeordnetenwatch.de $\rightarrow$ `nbs/03_abgeordnetenwatch.ipynb`
- analyze party / abgeordneten similarity $\rightarrow$ `nbs/01_similarities.ipynb`
- cluster polls $\rightarrow$ `nbs/04_poll_clustering.ipynb`
- predict politician votes $\rightarrow$ `nbs/05_predicting_votes.ipynb`
For a short overview of the highlights see below.
### Setup
```
%load_ext autoreload
%autoreload 2
from bundestag import html_parsing as hp
from bundestag import similarity as sim
from bundestag.gui import MdBGUI, PartyGUI
from bundestag import abgeordnetenwatch as aw
from bundestag import poll_clustering as pc
from bundestag import vote_prediction as vp
from pathlib import Path
import pandas as pd
from fastai.tabular.all import *
```
### Part 1 - Party/Party similarities and Politician/Party similarities using bundestag.de data
**Loading the data**
If you have cloned the repo you should already have a `bundestag.de_votes.parquet` file in the root directory of the repo. If not feel free to download that file directly.
If you want to have a closer look at the preprocessing please check out `nbs/00_html_parsing.ipynb`.
```
df = pd.read_parquet(path='bundestag.de_votes.parquet')
df.head(3).T
```
Votes by party
```
%%time
party_votes = sim.get_votes_by_party(df)
sim.test_party_votes(party_votes)
```
Re-arranging `party_votes`
```
%%time
party_votes_pivoted = sim.pivot_party_votes_df(party_votes)
sim.test_party_votes_pivoted(party_votes_pivoted)
party_votes_pivoted.head()
```
**Similarity of a single politician with the parties**
Collecting the politicians votes
```
%%time
mdb = 'Peter Altmaier'
mdb_votes = sim.prepare_votes_of_mdb(df, mdb)
sim.test_votes_of_mdb(mdb_votes)
mdb_votes.head()
```
Comparing the politician against the parties
```
%%time
mdb_vs_parties = (sim.align_mdb_with_parties(mdb_votes, party_votes_pivoted)
.pipe(sim.compute_similarity, lsuffix='mdb', rsuffix='party'))
sim.test_mdb_vs_parties(mdb_vs_parties)
mdb_vs_parties.head(3).T
```
Plotting
```
sim.plot(mdb_vs_parties, title_overall=f'Overall similarity of {mdb} with all parties',
title_over_time=f'{mdb} vs time')
plt.tight_layout()
plt.show()
```

**Comparing one specific party against all others**
Collecting party votes
```
%%time
party = 'SPD'
partyA_vs_rest = (sim.align_party_with_all_parties(party_votes_pivoted, party)
.pipe(sim.compute_similarity, lsuffix='a', rsuffix='b'))
sim.test_partyA_vs_partyB(partyA_vs_rest)
partyA_vs_rest.head(3).T
```
Plotting
```
sim.plot(partyA_vs_rest, title_overall=f'Overall similarity of {party} with all parties',
title_over_time=f'{party} vs time', party_col='Fraktion/Gruppe_b')
plt.tight_layout()
plt.show()
```

**GUI to inspect similarities**
To make the above exploration more interactive, the class `MdBGUI` and `PartyGUI` was implemented to quickly go through the different parties and politicians
```
mdb = MdBGUI(df)
mdb.render()
party = PartyGUI(df)
party.render()
```
### Part 2 - predicting politician votes using abgeordnetenwatch data
The data used below was processed using `nbs/03_abgeordnetenwatch.ipynb`.
```
path = Path('./abgeordnetenwatch_data')
```
#### Clustering polls using Latent Dirichlet Allocation (LDA)
```
%%time
source_col = 'poll_title'
nlp_col = f'{source_col}_nlp_processed'
num_topics = 5 # number of topics / clusters to identify
st = pc.SpacyTransformer()
# load data and prepare text for modelling
df_polls_lda = (pd.read_parquet(path=path/'df_polls.parquet')
.assign(**{nlp_col: lambda x: st.clean_text(x, col=source_col)}))
# modelling clusters
st.fit(df_polls_lda[nlp_col].values, mode='lda', num_topics=num_topics)
# creating text features using fitted model
df_polls_lda, nlp_feature_cols = df_polls_lda.pipe(st.transform, col=nlp_col, return_new_cols=True)
# inspecting clusters
display(df_polls_lda.head(3).T)
pc.pca_plot_lda_topics(df_polls_lda, st, source_col, nlp_feature_cols)
```
#### Predicting votes
Loading data
```
df_all_votes = pd.read_parquet(path=path / 'df_all_votes.parquet')
df_mandates = pd.read_parquet(path=path / 'df_mandates.parquet')
df_polls = pd.read_parquet(path=path / 'df_polls.parquet')
```
Splitting data set into training and validation set. Splitting randomly here because it leads to an interesting result, albeit not very realistic for production.
```
splits = RandomSplitter(valid_pct=.2)(df_all_votes)
y_col = 'vote'
```
Training a neural net to predict `vote` based on embeddings for `poll_id` and `politician name`
```
%%time
to = TabularPandas(df_all_votes,
cat_names=['politician name', 'poll_id'], # columns in `df_all_votes` to treat as categorical
y_names=[y_col], # column to use as a target for the model in `learn`
procs=[Categorify], # processing of features
y_block=CategoryBlock, # how to treat `y_names`, here as categories
splits=splits) # how to split the data
dls = to.dataloaders(bs=512)
learn = tabular_learner(dls) # fastai function to set up a neural net for tabular data
lrs = learn.lr_find() # searches the learning rate
learn.fit_one_cycle(5, lrs.valley) # performs training using one-cycle hyperparameter schedule
```
**Predictions over unseen data**
Inspecting the predictions of the neural net over the validation set.
```
vp.plot_predictions(learn, df_all_votes, df_mandates, df_polls, splits,
n_worst_politicians=5)
```
Splitting our dataset randomly leads to a surprisingly good accuracy of ~88% over the validation set. The most reasonable explanation is that the model encountered polls and how most politicians voted for them already during training.
This can be interpreted as, if it is known how most politicians will vote during a poll, then the vote of the remaining politicians is highly predictable. Splitting the data set by `poll_id`, as can be done using `vp.poll_splitter` leads to random chance predictions. Anything else would be surprising as well since the only available information provided to the model is who is voting.
**Visualising learned embeddings**
Besides the actual prediction it also is interesting to inspect what the model actually learned. This can sometimes lead to [surprises](https://github.com/entron/entity-embedding-rossmann).
So let's look at the learned embeddings
```
embeddings = vp.get_embeddings(learn)
```
To make sense of the embeddings for `poll_id` as well as `politician name` we apply Principal Component Analysis (so one still kind of understands what distances mean) and project down to 2d.
Using the information which party was most strongly (% of their votes being "yes"), so its strongest proponent, we color code the individual polls.
```
vp.plot_poll_embeddings(df_all_votes, df_polls, embeddings, df_mandates=df_mandates)
```

The politician embeddings are color coded using the politician's party membership
```
vp.plot_politician_embeddings(df_all_votes, df_mandates, embeddings)
```

The politician embeddings may be the most surprising finding in its clarity. It seems we find for polls and politicians 2-3 clusters, but for politicians with a significant grouping of mandates associated with the government coalition. It seems we find one cluster for the government parties and one for the government opposition.
## To dos / contributing
Any contributions welcome. In the notebooks in `./nbs/` I've listed to dos here and there things which could be done.
**General to dos**:
- Check for discrepancies between bundestag.de and abgeordnetenwatch based data
- Make the clustering of polls and policitians interactive
- Extend the vote prediction model: currently, if the data is split by poll (which would be the realistic case when trying to predict votes of a new poll), the model is hardly better than chance. It would be interesting to see which information would help improve beyond chance.
- Extend the data processed from the stored json responses from abgeordnetenwatch (currently only using the bare minimum)
| true |
code
| 0.614018 | null | null | null | null |
|
```
# !pip install -q tf-nightly
import tensorflow as tf
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import os
import numpy as np
import matplotlib.pyplot as plt
print("Tensorflow Version: {}".format(tf.__version__))
print("GPU {} available.".format("is" if tf.config.experimental.list_physical_devices("GPU") else "not"))
```
# Data Preprocessing
This tutorial uses a filtered version of [Dags vs Cats](https://www.kaggle.com/c/dogs-vs-cats/data) dataset from kaggle.
```
_URL = 'https://storage.googleapis.com/mledu-datasets/cats_and_dogs_filtered.zip'
path_to_zip = tf.keras.utils.get_file("cats_and_dogs.zip", origin=_URL, extract=True)
PATH = os.path.join(os.path.dirname(path_to_zip), "cats_and_dogs_filtered")
PATH
!ls -al {PATH}
```
The data structure is below.
```text
cats_and_dogs_filtered
|- train +
|- cats +
|- xxx.jpg -
|- xxy.jpg -
|- dogs +
|- validation +
|- cats +
|- dogs +
|- vectorize.py
```
```
!ls -al {PATH}/train/cats | wc -l
train_dir = os.path.join(PATH, 'train')
validation_dir = os.path.join(PATH, 'validation')
train_cats_dir = os.path.join(train_dir, 'cats')
train_dogs_dir = os.path.join(train_dir, 'dogs')
validation_cats_dir = os.path.join(validation_dir, 'cats')
validation_dogs_dir = os.path.join(validation_dir, 'dogs')
```
Understand the dataset.
```
num_cats_tr = len(os.listdir(train_cats_dir))
num_dogs_tr = len(os.listdir(train_dogs_dir))
num_cats_val = len(os.listdir(validation_cats_dir))
num_dogs_val = len(os.listdir(validation_dogs_dir))
total_train = num_cats_tr + num_dogs_tr
total_val = num_cats_val + num_dogs_val
print("Train: cats {}, dogs {}.".format(num_cats_tr, num_dogs_tr))
print("Validation: cats {}, dogs {}".format(num_cats_val, num_dogs_val))
batch_size = 128
epochs = 15
IMG_HEIGHT = 150
IMG_WIDTH = 150
```
# Data Preparation
```
# normalize the image
train_img_generator = ImageDataGenerator(rescale=1./255.)
validation_img_generator = ImageDataGenerator(rescale=1./255.)
```
Load the data from the directory using the generators. (The parameter `directory` set here is the parent's path, not the category ones.)
```
train_data_gen = train_img_generator.flow_from_directory(
directory=train_dir, batch_size=batch_size, shuffle=True,
target_size=(IMG_HEIGHT, IMG_WIDTH), class_mode='binary')
val_data_gen = validation_img_generator.flow_from_directory(
directory=validation_dir, batch_size=batch_size,
target_size=(IMG_HEIGHT, IMG_WIDTH), class_mode='binary')
```
## Visualize the Training Images
```
sample_training_images, sample_training_labels = next(train_data_gen)
def plotImages(img_arr):
plt.figure(figsize=(10, 40))
for i in range(5):
plt.subplot(1, 5, i+1)
plt.imshow(img_arr[i])
plt.xticks([])
plt.yticks([])
plt.show()
plotImages(sample_training_images)
```
# Create the Model
```
def build_model():
def _model(inputs):
x = Conv2D(filters=16, kernel_size=(3, 3), padding='same', activation='elu')(inputs)
x = MaxPooling2D()(x)
x = Conv2D(filters=32, kernel_size=(3, 3), padding='same', activation='elu')(x)
x = MaxPooling2D()(x)
x = Conv2D(filters=64, kernel_size=(3, 3), padding='same', activation='elu')(x)
x = MaxPooling2D()(x)
x = Flatten()(x)
x = Dense(units=512, activation='elu')(x)
cls = Dense(units=1, activation='sigmoid')(x)
return cls
inputs = tf.keras.Input(shape=(IMG_HEIGHT, IMG_WIDTH, 3))
outputs = _model(inputs)
model = tf.keras.Model(inputs, outputs)
return model
model = build_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(),
optimizer=tf.keras.optimizers.Adam(),
metrics=[tf.keras.metrics.BinaryAccuracy()])
model.summary()
```
# Train the Model
```
history = model.fit(train_data_gen,
steps_per_epoch=total_train // batch_size,
epochs=epochs,
validation_data=val_data_gen,
validation_steps=total_val // batch_size)
```
# Visualize the Result
```
history.history.keys()
plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.plot(range(epochs), history.history['binary_accuracy'], label='Training Accuracy')
plt.plot(range(epochs), history.history['val_binary_accuracy'], label='Validation Accuracy')
plt.legend(loc='lower right')
plt.title('Accuracy')
plt.subplot(1, 2, 2)
plt.plot(range(epochs), history.history['loss'], label='Training Loss')
plt.plot(range(epochs), history.history['val_loss'], label='Validation Loss')
plt.legend(loc='lower right')
plt.title('Loss')
plt.show()
```
Let's look at what the wrong is and try to increase the overall performance of the model.
# Overfitting
The above result shows the overfitting of the model that can not perform well on the coming data. Here you can solve the overfitting using the data augmentation and adding a dropout.
# Data Augmentation
The goal is the model will never see the same image twice during training.
## Applying Horizontal Flip
```
image_gen = ImageDataGenerator(rescale=1./255., horizontal_flip=True)
train_data_gen = image_gen.flow_from_directory(
directory=train_dir, batch_size=batch_size, target_size=(IMG_HEIGHT, IMG_WIDTH),
shuffle=True)
augmented_images = [train_data_gen[0][0][0] for i in range(5)]
plotImages(augmented_images)
```
## Applying Randomly Rotations
```
image_gen = ImageDataGenerator(rescale=1./255., rotation_range=45)
train_data_gen = image_gen.flow_from_directory(
directory=train_dir, batch_size=batch_size, target_size=(IMG_HEIGHT, IMG_WIDTH),
shuffle=True
)
augmented_images = [train_data_gen[0][0][0] for _ in range(5)]
plotImages(augmented_images)
```
## Applying Zooming
```
# zoom range from 0 to 1 represents 0% to 100%
image_gen = ImageDataGenerator(rescale=1./255., zoom_range=0.5)
train_data_gen = image_gen.flow_from_directory(
directory=train_dir, batch_size=batch_size, target_size=(IMG_HEIGHT, IMG_WIDTH),
shuffle=True
)
augmented_images = [train_data_gen[0][0][0] for _ in range(5)]
plotImages(augmented_images)
```
## Combining Augmentation Methods
```
image_gen = ImageDataGenerator(
rescale=1./255.,
horizontal_flip=True,
rotation_range=45,
zoom_range=0.5,
width_shift_range=.15,
height_shift_range=.15)
train_data_gen = image_gen.flow_from_directory(
directory=train_dir, batch_size=batch_size, target_size=(IMG_HEIGHT, IMG_WIDTH),
shuffle=True, class_mode='binary')
augmented_images = [train_data_gen[0][0][0] for _ in range(5)]
plotImages(augmented_images)
```
## Creating a Validation Dataset Generator
Normally only the training dataset generator would be applied with the augmentation methods. On contrast, the validation dataset generator would not be augmented.
```
image_gen_val = ImageDataGenerator(rescale=1./255.)
val_data_gen = image_gen_val.flow_from_directory(
directory=validation_dir, batch_size=batch_size, target_size=(IMG_HEIGHT, IMG_WIDTH),
class_mode='binary')
```
# Dropout
The `dropout` is a form of regularization. It forces the model to use a small part of weights to do the prediction. When the dropout rate is set to 0.1, it means 10% output nodes are randomly set to zero (be dropped) in each epoch of training.
## A Model with the Dropout Layer
```
def build_model_dropout():
def _model(inputs):
x = Conv2D(filters=16, kernel_size=(3, 3), activation='elu',
padding='same')(inputs)
x = MaxPooling2D()(x)
# keras handles the dropout rate in training or inference phrase
x = Dropout(0.2)(x)
x = Conv2D(filters=32, kernel_size=(3, 3), activation='elu',
padding='same')(x)
x = MaxPooling2D()(x)
x = Conv2D(filters=64, kernel_size=(3, 3), activation='elu',
padding='same')(x)
x = MaxPooling2D()(x)
x = Dropout(0.2)(x)
x = Flatten()(x)
x = Dense(units=512, activation='elu')(x)
cls = Dense(units=1, activation='sigmoid')(x)
return cls
inputs = tf.keras.Input(shape=(IMG_HEIGHT, IMG_WIDTH, 3))
outputs = _model(inputs)
model = tf.keras.Model(inputs, outputs)
return model
model_new = build_model_dropout()
model_new.compile(loss=tf.keras.losses.BinaryCrossentropy(),
optimizer=tf.keras.optimizers.Adam(),
metrics=[tf.keras.metrics.BinaryAccuracy()])
model_new.summary()
```
## Train the Model
```
history = model_new.fit(train_data_gen,
steps_per_epoch=total_train // batch_size,
epochs=epochs,
validation_data=val_data_gen,
validation_steps=total_val // batch_size)
history.history.keys()
plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.plot(range(epochs), history.history['binary_accuracy'], label='Training')
plt.plot(range(epochs), history.history['val_binary_accuracy'], label='Validation')
plt.title('Accuracy')
plt.subplot(1, 2, 2)
plt.plot(range(epochs), history.history['loss'], label='Training')
plt.plot(range(epochs), history.history['val_loss'], label='Validation')
plt.title('Loss')
plt.show()
```
| true |
code
| 0.722429 | null | null | null | null |
|
```
# This cell is added by sphinx-gallery
!pip install mrsimulator --quiet
%matplotlib inline
import mrsimulator
print(f'You are using mrsimulator v{mrsimulator.__version__}')
```
# ¹¹⁹Sn MAS NMR of SnO
The following is a spinning sideband manifold fitting example for the 119Sn MAS NMR
of SnO. The dataset was acquired and shared by Altenhof `et al.` [#f1]_.
```
import csdmpy as cp
import matplotlib.pyplot as plt
from lmfit import Minimizer
from mrsimulator import Simulator, SpinSystem, Site, Coupling
from mrsimulator.methods import BlochDecaySpectrum
from mrsimulator import signal_processing as sp
from mrsimulator.utils import spectral_fitting as sf
from mrsimulator.utils import get_spectral_dimensions
```
## Import the dataset
```
filename = "https://sandbox.zenodo.org/record/814455/files/119Sn_SnO.csdf"
experiment = cp.load(filename)
# standard deviation of noise from the dataset
sigma = 0.6410905
# For spectral fitting, we only focus on the real part of the complex dataset
experiment = experiment.real
# Convert the coordinates along each dimension from Hz to ppm.
_ = [item.to("ppm", "nmr_frequency_ratio") for item in experiment.dimensions]
# plot of the dataset.
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
ax.plot(experiment, "k", alpha=0.5)
ax.set_xlim(-1200, 600)
plt.grid()
plt.tight_layout()
plt.show()
```
## Create a fitting model
**Guess model**
Create a guess list of spin systems. There are two spin systems present in this
example,
- 1) an uncoupled $^{119}\text{Sn}$ and
- 2) a coupled $^{119}\text{Sn}$-$^{117}\text{Sn}$ spin systems.
```
sn119 = Site(
isotope="119Sn",
isotropic_chemical_shift=-210,
shielding_symmetric={"zeta": 700, "eta": 0.1},
)
sn117 = Site(
isotope="117Sn",
isotropic_chemical_shift=0,
)
j_sn = Coupling(
site_index=[0, 1],
isotropic_j=8150.0,
)
sn117_abundance = 7.68 # in %
spin_systems = [
# uncoupled spin system
SpinSystem(sites=[sn119], abundance=100 - sn117_abundance),
# coupled spin systems
SpinSystem(sites=[sn119, sn117], couplings=[j_sn], abundance=sn117_abundance),
]
```
**Method**
```
# Get the spectral dimension parameters from the experiment.
spectral_dims = get_spectral_dimensions(experiment)
MAS = BlochDecaySpectrum(
channels=["119Sn"],
magnetic_flux_density=9.395, # in T
rotor_frequency=10000, # in Hz
spectral_dimensions=spectral_dims,
experiment=experiment, # add the measurement to the method.
)
# Optimize the script by pre-setting the transition pathways for each spin system from
# the method.
for sys in spin_systems:
sys.transition_pathways = MAS.get_transition_pathways(sys)
```
**Guess Spectrum**
```
# Simulation
# ----------
sim = Simulator(spin_systems=spin_systems, methods=[MAS])
sim.run()
# Post Simulation Processing
# --------------------------
processor = sp.SignalProcessor(
operations=[
sp.IFFT(),
sp.apodization.Exponential(FWHM="1500 Hz"),
sp.FFT(),
sp.Scale(factor=5000),
]
)
processed_data = processor.apply_operations(data=sim.methods[0].simulation).real
# Plot of the guess Spectrum
# --------------------------
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
ax.plot(experiment, "k", linewidth=1, label="Experiment")
ax.plot(processed_data, "r", alpha=0.75, linewidth=1, label="guess spectrum")
ax.set_xlim(-1200, 600)
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()
```
## Least-squares minimization with LMFIT
Use the :func:`~mrsimulator.utils.spectral_fitting.make_LMFIT_params` for a quick
setup of the fitting parameters.
```
params = sf.make_LMFIT_params(sim, processor, include={"rotor_frequency"})
# Remove the abundance parameters from params. Since the measurement detects 119Sn, we
# also remove the isotropic chemical shift parameter of 117Sn site from params. The
# 117Sn is the site at index 1 of the spin system at index 1.
params.pop("sys_0_abundance")
params.pop("sys_1_abundance")
params.pop("sys_1_site_1_isotropic_chemical_shift")
# Since the 119Sn site is shared between the two spin systems, we add constraints to the
# 119Sn site parameters from the spin system at index 1 to be the same as 119Sn site
# parameters from the spin system at index 0.
lst = [
"isotropic_chemical_shift",
"shielding_symmetric_zeta",
"shielding_symmetric_eta",
]
for item in lst:
params[f"sys_1_site_0_{item}"].expr = f"sys_0_site_0_{item}"
print(params.pretty_print(columns=["value", "min", "max", "vary", "expr"]))
```
**Solve the minimizer using LMFIT**
```
minner = Minimizer(sf.LMFIT_min_function, params, fcn_args=(sim, processor, sigma))
result = minner.minimize()
result
```
## The best fit solution
```
best_fit = sf.bestfit(sim, processor)[0]
residuals = sf.residuals(sim, processor)[0]
# Plot the spectrum
plt.figure(figsize=(4.25, 3.0))
ax = plt.subplot(projection="csdm")
ax.plot(experiment, "k", linewidth=1, label="Experiment")
ax.plot(best_fit, "r", alpha=0.75, linewidth=1, label="Best Fit")
ax.plot(residuals, alpha=0.75, linewidth=1, label="Residuals")
ax.set_xlim(-1200, 600)
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()
```
.. [#f1] Altenhof A. R., Jaroszewicz M. J., Lindquist A. W., Foster L. D. D.,
Veinberg S. L., and Schurko R. W. Practical Aspects of Recording Ultra-Wideline
NMR Patterns under Magic-Angle Spinning Conditions.
J. Phys. Chem. C. 2020, **124**, 27, 14730–14744
`DOI: 10.1021/acs.jpcc.0c04510 <https://doi.org/10.1021/acs.jpcc.0c04510>`_
| true |
code
| 0.779385 | null | null | null | null |
|
---
```
__authors__ = ["Tricia D Shepherd" , "Ryan C. Fortenberry", "Matthewy Kennedy", "C. David Sherril"]
__credits__ = ["Victor H. Chavez", "Lori Burns"]
__email__ = ["profshep@icloud.com", "r410@olemiss.edu"]
__copyright__ = "(c) 2008-2019, The Psi4Education Developers"
__license__ = "BSD-3-Clause"
__date__ = "2019-11-18"
```
---
## Introduction
The eigenfunctions solutions to the Schrödinger equation for a multielectron system depend on the coordinates of all electrons. The orbital approximation says that we can represent a many-electron eigenfunction in terms of individual electron orbitals, each of which depends only on the coordinates of a single electron. A *basis set* in this context is a set of *basis functions* used to approximate these orbitals. There are two general categories of basis sets: *minimal basis sets* that describe only occupied orbitals and *extended basis sets* that describe both occupied and unoccupied orbitals.
### Part A. What is the calculated Hartree Fock energy using a minimal basis set?
1. Import the required modules (**psi4** and **numpy**)
2. Define a Boron atom as a ```psi4.geometry``` object. Be mindful of the charge and spin multiplicity. For a neutral B atom, the atom can only be a doublet (1 unpaired electron).
3. Set psi4 options to select an **unrestricted** calculation (restricted calculation *won't* work with this electronic configuration).
4. Run a **Hartree-Fock** calculation using the basis set **STO-3G**, store both the energy and the wavefunction object. The energy will be given in atomic units.
5. Look at your results by printing them within a cell. It is possible to obtain information about the basis set from the wfn object. The number of basis functions can be accessed with: ```wfn.basiset().nbf()```
RESPONSE:
***
### Part B. How does the Hartree Fock energy depend on the trial basis set?
In computational chemistry, we focus on two types of functions: the Slater-type function and the Gaussian-type functions. Their most basic shape can be given by the following definitions.
$$ \Phi_{gaussian}(r) = 1.0 \cdot e^{-1.0 \cdot x^2} $$
and
$$ \Phi_{slater}(r) = 1.0 \cdot e^{-1.0 \cdot |x|} $$
Both functions can be visualized below:
```
import matplotlib.pyplot as plt
import numpy as np
r = np.linspace(0, 5, 100)
sto = 1.0 * np.exp(-np.abs(r))
gto = 1.0 * np.exp(-r**2)
fig, ax = plt.subplots(ncols=2, nrows=1)
p1 = ax[0]
p2 = ax[1]
fig.set_figheight(5)
fig.set_figwidth(15)
p1.plot(r, sto, lw=4, color="teal")
p1.plot(-r, sto, lw=4, color="teal")
p2.plot(r, gto, lw=4, color="salmon")
p2.plot(-r, gto, lw=4, color="salmon")
p1.title.set_text("Slater-type Orbital")
p2.title.set_text("Gaussian-type Orbital")
```
The STO is characterized by two features: 1) The peak at the nucleus and 2) the behavior far from the nucleus, which should tend to zero nice and smoothly. You can see that the GTO does not have those characteristics since the peak is smooth and the ends go to zero *too* quickly.
You may remember that the ground state eigenfunction of the Hydrogen atom with a spin equal to zero has the same shape as the STO. This is true not only for Hydrogen but for every atomistic system.
One may wonder then why are we not using STO in every calculation? The short answer is that we don't have the exact solution to each of the systems, and when it comes to handling approximations, the GTO are simply more efficient than the STO. Remember the theorem that states that the product of two Gaussians is also a Gaussian?
In the first part of the lab, we used the smallest basis set available STO-3G, where STO stands for *Slater-type orbital* which is approximated by the sum of *3 Gaussian functions*.
$$\phi^{STO-3G} = \sum_i^3 d_i \cdot C(\alpha_i) \cdot e^{-\alpha_i|r-R_A|^2} $$
Where the $\{ \alpha \}_i$ and $\{ d \}_i$ are the exponents and coefficients that define a basis set and are usually the components needed to create a basis set.
STO-3G is an example of a minimal basis set, *i.e.* it represents the orbitals of each occupied subshell with one basis function. While basis sets of the form STO-nG were popular in the 1980's, they are not widely used today. For the same reason that multiple Gaussian functions better approximate a Slater type orbital, multiple STO-nG functions are found more efficient to approximate atomic orbitals. In practice, inner shell (core) electrons are still described by a single STO-nG function and only valence electrons are expressed as the sum of STO-nG type functions.
You will see that the approximation performs really well. Look at the following example$^1$:
```
import matplotlib.pyplot as plt
def sto(r, coef, exp):
return coef * (2*exp/np.pi)**(3/4) * np.exp(-exp*(r)**2)
slater = (1/np.pi)**(0.5) * np.exp(-1.0*np.abs(r))
sto_1g = sto(r, 1.00, 0.270950)
sto_2g = sto(r, 0.67, 0.151623) + sto(r, 0.43, 0.851819)
sto_3g = sto(r, 0.44, 0.109818) + sto(r, 0.53, 0.405771) + sto(r, 0.154, 2.22766)
plt.figure(figsize=(15,5))
plt.plot(r, sto_1g, lw=4, c="c")
plt.plot(-r, sto_1g, label="STO-1G", lw=4, c="c")
plt.plot(r, sto_2g, lw=4, c="orchid")
plt.plot(-r, sto_2g, label="STO-2G", lw=4, c="orchid")
plt.plot(r, sto_3g, lw=4, c="gold" )
plt.plot(-r, sto_3g, label="STO-3G", lw=4, c="gold" )
plt.plot(r, slater, ls=":", lw=4, c="grey")
plt.plot(-r, slater, label="Slater-type function", ls=":", lw=4, c="grey")
plt.legend(fontsize=15)
plt.show()
```
We can clearly see that with the addition of each new Gaussian, our linear combination behaves more and more like a STO. Each of these Gaussians is commonly knon as *primitive*.
###### $^1$ Szabo, Attila, and Neil S. Ostlund. Modern quantum chemistry: introduction to advanced electronic structure theory. Courier Corporation, 2012.
___
To understand how to read each basis set, let's consider the next available basis set: 3-21G basis set. The number before the dash, "3" represents the 3 Gaussian primitives (i.e. a STO-"3"G) use to represent the inner shell electrons. The next two numbers represent the valence shell split into two sets of STO-nG functions--One with"2" Gaussian-type orbitals (GTOs) and one with "1" GTO. Let us see how this other basis set performs.
1. With the previously defined Boron atom. Run a new HF calculation using the basis set "3-21G".
2. Rationalize the number of basis functions used for the STO-3G and 3-21G calculations.
3. Compare the STO-3G and 3-21G HF energies. WHich basis set is more accurate? (Recall the variational principle states that for a given Hamiltonian operator, any trial wavefunction will have n average energy that is greater than or equal to the "true" corresponding ground state wavefunction. Because of this, the Hartree Fock energy is an upper bound to the ground state energy of a given molecule. )
RESPONSE:
***
### Part C. How can we improve the accuracy of the HF energy?
To make an even better approximation to our trial function, we may need to take into account the two following effects:
#### Polarization:
Accounts for the unequal distribution of electrons when two atoms approach each other. We can include these effects by adding STO's of higher orbital angular momentum, i.e., d-type functions are added to describe valence elctrons in 2p orbitals.
We can if there is presence of polarization functions with the use of asterisks:
* One asterisk (*) refers to polarization on heavy atoms.
* Two asterkisks (**) is used for polarization on Hydrogen (H-Bonding).
#### Difusse Functions:
These are useful for systems in an excited state, systems with low ionization potential, and systems with some significant negative charge attached.
The presence of diffuse functions is symbolized by the addition of a plus sign:
* One plus sign (+) adds diffuse functions on heavy atoms.
* Two plus signs (++) add diffuse functions on Hydrogen atoms.
***
Let us look at how the addition of these effects will improve our energy:
1. Repeat the boron atom energy calculation for each of the basis sets listed:
``['6-31G', '6-31+G', '6-31G*', '6-31+G*', '6-311G*', '6-311+G**', 'cc-pVDZ', 'cc-pVTZ']``
2. Using `print(f"")` statements, builld a table where for each basis you identify the type and number of STO-nG function used for the core and valence electrons.
3. For each basis, identify the type and number of STO-nG functions used for the core and valence electrons.
4. On the same table, specify wether polarized or difusse functions are included.
5. Record the total number of orbitals. For the Boron atom, which approximation (choice of basis set) is the most accurate? How does the accuracy relate to the number of basis functions used?
RESPONSE:
***
### Part D. How much "correlation energy" can we recover
At the Hartree Fock level of theory, each electron experiences an average potential field of all the other electrons. In essence, it is a "mean field" approach that neglects individual electron-electron interactions or "electron correlation". Thus, we define t he difference between the self-consistent field energy and the exact energy as the correlation energy. Two fundamentally different approaches to account for electron correlation effects are available by selecting a Correlation method: Moller Plesset (MP) Perturbation theory and Coupled Cluster (CC) theory.
1. Based on the calculated SCF energy for the *6-311+G** basis set, determine the value of the correlation energy for boron assuming an "experimental" energy of **-24.608 hartrees$^2$**
2. Using the same basis set, perform an energy calculation with MP2 and MP4.
(You may recover the MP2 energy from the MP4 calculation but you will have to look at the output file).
MP4 will require the use of the following options:
```psi4.set_options({"reference" :"rohf", "qc_module":"detci"})```
3. Using the same basis set, perform an energy calculation with CCSD and CCSD(T).
(You may recover the CCSD energy from the CCSD(T) calculation but you will have to look at the output file).
4. For each method, determine the percentage of the correlation energy recovered.
<br />
###### $^2$. H. S. Schaefer and F. Harris, (1968) Phys Rev. 167, 67
RESPONSE:
***
### Part E. Can we use DFT(B3LYP) to calculate the electron affinity of boron?
The electron affinity of atom A is the energy released for the process:
$$ A + e^{-} \rightarrow A^{-} $$
Or simply the energy difference between the anion and the neutral forms of an atom. These are reported in positive values:
$$ EA = - (E_{anion} - E_{neutral}) $$
It was reported$^3$ that the electron affinity of Boron at the B3LYP 6-311+G** level of theory is **-0.36 eV**. In comparison to the experimental value of **0.28 eV** this led to the assumption that B3LYP does not yield a reasonable electron affinity.
|
1. Define a Boron atom for two different configurations:
For the anion, set the charge to **-1**. Once we do that, the charge and spin multiplicity are no longer compatible. For 2 electrons in a set of *p* orbitals, the multiplicity can only be 3 (triplet state, unpaired spins) or 1 (singlet state, paired spins). Here, by Hund's rules, we expect the spins will remain unpaired, leading to a triplet. Run the calculation and record the energy for boron anion.
2. Calculate the electron affinity. Is this literature result consistent with your calculation? (Remember 1 hartree = 27.2116 eV)
3. Repeat the electron affinity calculation of boron, but this time, assume the anion is a singlet sate. Whata is the reason$^4$ for the reporte failure of the B3LYP method?
<br/>
###### $^3$C. W. Bauschlicher, (1998) Int. J. Quantum Chem. 66, 285
###### $^4$ B. S. Jursic, (1997) Int. J. Quantum Chem. 61, 93
RESPONSE:
| true |
code
| 0.635024 | null | null | null | null |
|
Utilities to visualize agent's trade execution and portfolio performance
Chapter 4, TensorFlow 2 Reinforcement Learning Cookbook | Praveen Palanisamy
```
import matplotlib
import matplotlib.pyplot as plt
import mplfinance as mpf
import numpy as np
import pandas as pd
from matplotlib import style
from mplfinance.original_flavor import candlestick_ohlc
style.use("seaborn-whitegrid")
class TradeVisualizer(object):
"""Visualizer for stock trades"""
def __init__(self, ticker, ticker_data_stream, title=None, skiprows=0):
self.ticker = ticker
# Stock/crypto market/exchange data stream. An offline file stream is used.
# Alternatively, a web
# API can be used to pull live data.
self.ohlcv_df = pd.read_csv(
ticker_data_stream, parse_dates=True, index_col="Date", skiprows=skiprows
).sort_values(by="Date")
if "USD" in self.ticker: # True for crypto-fiat currency pairs
# Use volume of the crypto currency for volume plot.
# A column with header="Volume" is required for default mpf plot.
# Remove "USD" from self.ticker string and clone the crypto volume column
self.ohlcv_df["Volume"] = self.ohlcv_df[
"Volume " + self.ticker[:-3] # e.g: "Volume BTC"
]
self.account_balances = np.zeros(len(self.ohlcv_df.index))
fig = plt.figure("TFRL-Cookbook", figsize=[12, 6])
fig.suptitle(title)
nrows, ncols = 6, 1
gs = fig.add_gridspec(nrows, ncols)
row, col = 0, 0
rowspan, colspan = 2, 1
# self.account_balance_ax = plt.subplot2grid((6, 1), (0, 0), rowspan=2, colspan=1)
self.account_balance_ax = fig.add_subplot(
gs[row : row + rowspan, col : col + colspan]
)
row, col = 2, 0
rowspan, colspan = 8, 1
self.price_ax = plt.subplot2grid(
(nrows, ncols),
(row, col),
rowspan=rowspan,
colspan=colspan,
sharex=self.account_balance_ax,
)
self.price_ax = fig.add_subplot(gs[row : row + rowspan, col : col + colspan])
plt.show(block=False)
self.viz_not_initialized = True
def _render_account_balance(self, current_step, account_balance, horizon):
self.account_balance_ax.clear()
date_range = self.ohlcv_df.index[current_step : current_step + len(horizon)]
self.account_balance_ax.plot_date(
date_range,
self.account_balances[horizon],
"-",
label="Account Balance ($)",
lw=1.0,
)
self.account_balance_ax.legend()
legend = self.account_balance_ax.legend(loc=2, ncol=2)
legend.get_frame().set_alpha(0.4)
last_date = self.ohlcv_df.index[current_step + len(horizon)].strftime(
"%Y-%m-%d"
)
last_date = matplotlib.dates.datestr2num(last_date)
last_account_balance = self.account_balances[current_step]
self.account_balance_ax.annotate(
"{0:.2f}".format(account_balance),
(last_date, last_account_balance),
xytext=(last_date, last_account_balance),
bbox=dict(boxstyle="round", fc="w", ec="k", lw=1),
color="black",
)
self.account_balance_ax.set_ylim(
min(self.account_balances[np.nonzero(self.account_balances)]) / 1.25,
max(self.account_balances) * 1.25,
)
plt.setp(self.account_balance_ax.get_xticklabels(), visible=False)
def render_image_observation(self, current_step, horizon):
window_start = max(current_step - horizon, 0)
step_range = range(window_start, current_step + 1)
date_range = self.ohlcv_df.index[current_step : current_step + len(step_range)]
stock_df = self.ohlcv_df[self.ohlcv_df.index.isin(date_range)]
if self.viz_not_initialized:
self.fig, self.axes = mpf.plot(
stock_df,
volume=True,
type="candle",
mav=2,
block=False,
returnfig=True,
style="charles",
tight_layout=True,
)
self.viz_not_initialized = False
else:
self.axes[0].clear()
self.axes[2].clear()
mpf.plot(
stock_df,
ax=self.axes[0],
volume=self.axes[2],
type="candle",
mav=2,
style="charles",
block=False,
tight_layout=True,
)
self.fig.canvas.set_window_title("TFRL-Cookbook")
self.fig.canvas.draw()
fig_data = np.frombuffer(self.fig.canvas.tostring_rgb(), dtype=np.uint8)
fig_data = fig_data.reshape(self.fig.canvas.get_width_height()[::-1] + (3,))
self.fig.set_size_inches(12, 6, forward=True)
self.axes[0].set_ylabel("Price ($)")
self.axes[0].yaxis.set_label_position("left")
self.axes[2].yaxis.set_label_position("left") # Volume
return fig_data
def _render_ohlc(self, current_step, dates, horizon):
self.price_ax.clear()
candlesticks = zip(
dates,
self.ohlcv_df["Open"].values[horizon],
self.ohlcv_df["Close"].values[horizon],
self.ohlcv_df["High"].values[horizon],
self.ohlcv_df["Low"].values[horizon],
)
candlestick_ohlc(
self.price_ax,
candlesticks,
width=np.timedelta64(1, "D"),
colorup="g",
colordown="r",
)
self.price_ax.set_ylabel(f"{self.ticker} Price ($)")
self.price_ax.tick_params(axis="y", pad=30)
last_date = self.ohlcv_df.index[current_step].strftime("%Y-%m-%d")
last_date = matplotlib.dates.datestr2num(last_date)
last_close = self.ohlcv_df["Close"].values[current_step]
last_high = self.ohlcv_df["High"].values[current_step]
self.price_ax.annotate(
"{0:.2f}".format(last_close),
(last_date, last_close),
xytext=(last_date, last_high),
bbox=dict(boxstyle="round", fc="w", ec="k", lw=1),
color="black",
)
plt.setp(self.price_ax.get_xticklabels(), visible=False)
def _render_trades(self, trades, horizon):
for trade in trades:
if trade["step"] in horizon:
date = self.ohlcv_df.index[trade["step"]].strftime("%Y-%m-%d")
date = matplotlib.dates.datestr2num(date)
high = self.ohlcv_df["High"].values[trade["step"]]
low = self.ohlcv_df["Low"].values[trade["step"]]
if trade["type"] == "buy":
high_low = low
color = "g"
arrow_style = "<|-"
else: # sell
high_low = high
color = "r"
arrow_style = "-|>"
proceeds = "{0:.2f}".format(trade["proceeds"])
self.price_ax.annotate(
f"{trade['type']} ${proceeds}".upper(),
(date, high_low),
xytext=(date, high_low),
color=color,
arrowprops=(
dict(
color=color,
arrowstyle=arrow_style,
connectionstyle="angle3",
)
),
)
def render(self, current_step, account_balance, trades, window_size=100):
self.account_balances[current_step] = account_balance
window_start = max(current_step - window_size, 0)
step_range = range(window_start, current_step + 1)
dates = self.ohlcv_df.index[step_range]
self._render_account_balance(current_step, account_balance, step_range)
self._render_ohlc(current_step, dates, step_range)
self._render_trades(trades, step_range)
"""
self.price_ax.set_xticklabels(
self.ohlcv_df.index[step_range], rotation=45, horizontalalignment="right",
)
"""
plt.grid()
plt.pause(0.001)
def close(self):
plt.close()
```
| true |
code
| 0.619874 | null | null | null | null |
|
# Downloading and saving CSV data files from the web
```
import urllib.request
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data'
csv_cont = urllib.request.urlopen(url)
csv_cont = csv_cont.read() # .decode('utf-8')
# saving the data to local drive
#with open('./datasets/wine_data.csv', 'wb') as out:
# out.write(csv_cont)
```
# Reading in a dataset from a CSV file
```
import numpy as np
# reading in all data into a NumPy array
all_data = np.loadtxt( "./datasets/wine_data.csv", delimiter=",", dtype=np.float64 )
# load class labels from column 1
y_wine = all_data[:,0]
# conversion of the class labels to integer-type array
y_wine = y_wine.astype(np.int64, copy=False)
# load the 14 features
X_wine = all_data[:,1:]
# printing some general information about the data
print('\ntotal number of samples (rows):', X_wine.shape[0])
print('total number of features (columns):', X_wine.shape[1])
# printing the 1st wine sample
float_formatter = lambda x: '{:.2f}'.format(x)
np.set_printoptions(formatter={'float_kind':float_formatter})
print('\n1st sample (i.e., 1st row):\nClass label: {:d}\n{:}\n'
.format(int(y_wine[0]), X_wine[0]))
# printing the rel.frequency of the class labels
print('Class label relative frequencies')
print('Class 1 samples: {:.2%}'.format(list(y_wine).count(1)/y_wine.shape[0]))
print('Class 2 samples: {:.2%}'.format(list(y_wine).count(2)/y_wine.shape[0]))
print('Class 3 samples: {:.2%}'.format(list(y_wine).count(3)/y_wine.shape[0]))
```
**Histograms** are a useful data to explore the distribution of each feature across the different classes. This could provide us with intuitive insights which features have a good and not-so-good inter-class separation. Below, we will plot a sample histogram for the "Alcohol content" feature for the three wine classes.
# Visualizating of a dataset with Histograms
```
first_fea = X_wine[:, 0]
print('minimum:', first_fea.min())
print('mean:', first_fea.mean())
print('Maximum:', first_fea.max())
%matplotlib inline
from matplotlib import pyplot as plt
from math import floor, ceil # for rounding up and down
# bin width of the histogram in steps of 0.15
#bins = np.arange(floor(min(X_wine[:,0])), ceil(max(X_wine[:,0])), 0.15)
bins = np.linspace(floor(min(X_wine[:,0])), ceil(max(X_wine[:,0])), 20)
labels = np.unique(y_wine)
plt.figure(figsize=(20,8))
# 我们可以下面的循环语句来plot直方图,不用这三个基本上重复的语句
#plt.hist(first_fea[y_wine == 1], bins, alpha = 0.3, color='red')
#plt.hist(first_fea[y_wine == 2], bins, alpha = 0.3, color='blue')
#plt.hist(first_fea[y_wine == 3], bins, alpha = 0.3, color='green')
# the order of the colors for each histogram
colors = ('blue', 'red', 'green')
for label, color in zip( labels, colors ):
plt.hist( first_fea[y_wine == label], bins=bins, alpha=0.3, color=color, label='class' + str(label) )
plt.title('Wine data set - Distribution of alocohol contents')
plt.xlabel('alcohol by volume', fontsize=14)
plt.ylabel('count', fontsize=14)
plt.legend(loc='upper right')
# 它返回的是数组的tuple,第一个数组是每个bin对应的值,第二个是bin的边界,因此第二个数组比第一个多1个元素
bin_value = np.histogram(first_fea, bins=bins)
# 找到最大的bin
max_bin = max(bin_value[0])
# 扩大y轴的范围
plt.ylim([0, max_bin*1.3])
plt.show()
```
# Visualizating of a dataset with Scatter plot
**Scatter plot** are useful for visualizing features in more than just one dimension, for example to get a feeling for the correlation between particular features.Below, we will create an example 2D-Scatter plot from the features "Alcohol content" and "Malic acid content".
```
second_fea = X_wine[:, 1]
print('minimum:', second_fea.min())
print('mean:', second_fea.mean())
print('Maximum:', second_fea.max())
plt.figure(figsize=(10,8))
markers = ('x', 'o', '^')
# 和上图的原理类似,只不过把hist替换成了scatter
for label,marker,color in zip( labels, markers, colors ):
plt.scatter( x=first_fea[y_wine == label],
y=second_fea[y_wine == label],
marker=marker, color=color,
alpha=0.7,
label='class' + str(label)
)
plt.title('Wine Dataset')
plt.xlabel('alcohol by volume in percent')
plt.ylabel('malic acid in g/l')
plt.legend(loc='upper right')
plt.show()
```
If we want to pack 3 different features into **one scatter plot at once**, we can also do the same thing in 3D.
```
third_fea = X_wine[:, 2]
print('minimum:', third_fea.min())
print('mean:', third_fea.mean())
print('Maximum:', third_fea.max())
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
for label, marker, color in zip( labels, markers, colors ):
ax.scatter( first_fea[y_wine == label],
second_fea[y_wine == label],
third_fea[y_wine == label],
marker=marker,
color=color,
s=40,
alpha=0.7,
label='class' + str(label)
)
ax.set_xlabel('alcohol by volume in percent')
ax.set_ylabel('malic acid in g/l')
ax.set_zlabel('ash content in g/l')
plt.title('Wine dataset')
plt.legend(loc='upper right')
plt.show()
```
# Splitting into training and test dataset
It is a typical procedure for machine learning and pattern classification tasks to split one dataset into two: a training dataset and a test dataset.
The training dataset is henceforth used to train our algorithms or classifier, and the test dataset is a way to validate the outcome quite objectively before we apply it to "new, real world data".
Here, we will split the dataset randomly so that 70% of the total dataset will become our training dataset, and 30% will become our test dataset, respectively.
```
from sklearn.cross_validation import train_test_split
# 加random_state的目的是reproducible
X_train, X_test, y_train, y_test = train_test_split(X_wine, y_wine, test_size=0.30, random_state=2016811)
```
# Standardization
Standardizing the features so that they are centered around 0 with a standard deviation of 1 is especially important if we are comparing measurements that have different units, e.g., in our "wine data" example, where the alcohol content is measured in volume percent, and the malic acid content in g/l.
```
from sklearn import preprocessing
# StandardScaler that implements the Transformer API to compute the mean and standard deviation on a training set
# so as to be able to later reapply the same transformation on the testing set.
std_scale = preprocessing.StandardScaler().fit(X_train)
X_train = std_scale.transform(X_train)
X_test = std_scale.transform(X_test)
f, ax = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(10,5))
# 和上面的图形一个原理,由于有重复的语句从而采用循环结构
for a, x_dat, y_lab in zip( ax, (X_train, X_test), (y_train, y_test) ):
for label, marker, color in zip( labels, markers, colors ):
a.scatter( x=x_dat[:,0][y_lab == label],
y=x_dat[:,1][y_lab == label],
marker=marker,
color=color,
alpha=0.7,
label='class' + str(label)
)
a.legend(loc='upper left')
ax[0].set_title('Training Dataset')
ax[1].set_title('Test Dataset')
f.text(0.5, 0.04, 'malic acid (standardized)', ha='center', va='center')
f.text(0.08, 0.5, 'alcohol (standardized)', ha='center', va='center', rotation='vertical')
plt.show()
```
# Min-Max scaling (Normalization)
In this approach, the data is scaled to a fixed range - usually 0 to 1.
The cost of having this bounded range - in contrast to standardization - is that we will end up with small standard deviations, for example in the case where outliers are present.
```
minmax_scale = preprocessing.MinMaxScaler(feature_range=(0, 1)).fit(X_train)
X_train_minmax = minmax_scale.transform(X_train)
X_test_minmax = minmax_scale.transform(X_test)
f, ax = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(10,5))
# 和上面的图形一个原理,由于有重复的语句从而采用循环结构
for a, x_dat, y_lab in zip( ax, (X_train_minmax, X_test_minmax), (y_train, y_test) ):
for label, marker, color in zip( labels, markers, colors ):
a.scatter( x=x_dat[:,0][y_lab == label],
y=x_dat[:,1][y_lab == label],
marker=marker,
color=color,
alpha=0.7,
label='class' + str(label)
)
a.legend(loc='upper left')
ax[0].set_title('Training Dataset')
ax[1].set_title('Test Dataset')
f.text(0.5, 0.04, 'malic acid (normalized)', ha='center', va='center')
f.text(0.08, 0.5, 'alcohol (normalized)', ha='center', va='center', rotation='vertical')
plt.show()
```
# Linear Transformation: Principal Component Analysis (PCA)
Here, our desired outcome of the principal component analysis is to project a feature space (our dataset consisting of n x d-dimensional samples) onto a smaller subspace that represents our data "well". A possible application would be a pattern classification task, where we want to reduce the computational costs and the error of parameter estimation by reducing the number of dimensions of our feature space by extracting a subspace that describes our data "best".
```
from sklearn.decomposition import PCA
pca_two_components = PCA(n_components = 2)
pca_train = pca_two_components.fit_transform(X_train)
plt.figure(figsize=(10,8))
for label,marker,color in zip( labels, markers, colors ):
plt.scatter( x=pca_train[:,0][y_train == label],
y=pca_train[:,1][y_train == label],
marker=marker,
color=color,
alpha=0.7,
label='class' + str(label)
)
plt.xlabel('vector 1')
plt.ylabel('vector 2')
plt.legend()
plt.title('Most significant singular vectors after linear transformation via PCA')
plt.show()
```
为了可视化的目的,上面我只保留了2个主成分。但是,在实际应用中,我们应该根据实际的情况来判断应该保留多少个主成分。下面的代码把n_components设置为None,因此,我们保留了所有的主成分,然后在打印出来,来分析一下我们应该怎样去保留主成分。
```
sklearn_pca = PCA(n_components=None)
sklearn_transf = sklearn_pca.fit_transform(X_train)
print(sklearn_pca.explained_variance_ratio_)
```
# Linear Transformation: Linear Discriminant Analysis
Principal Component Analysis (PCA) applied to this data identifies the combination of attributes (principal components, or directions in the feature space) that account for the most variance in the data.
Linear Discriminant Analysis (LDA) tries to identify attributes that account for the most variance between classes. In particular, LDA, in contrast to PCA, is a supervised method, using known class labels.
```
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda_two_components = LinearDiscriminantAnalysis(n_components = 2)
lda_train = lda_two_components.fit_transform(X_train, y_train)
plt.figure(figsize=(10,8))
for label,marker,color in zip( labels, markers, colors ):
plt.scatter( x=lda_train[:,0][y_train == label],
y=lda_train[:,1][y_train == label],
marker=marker,
color=color,
alpha=0.7,
label='class' + str(label)
)
plt.xlabel('vector 1')
plt.ylabel('vector 2')
plt.legend()
plt.title('Most significant singular vectors after linear transformation via LDA')
plt.show()
```
Linear Discriminant Analysis 不仅仅可以用于dimensionality reduction,它还可以作为分类器,详情请参考[Logistic Regression、Linear Discriminant Analysis、Shrinkage Methods(Ridge Regression and Lasso)](http://blog.csdn.net/xlinsist/article/details/52211334#t2)
| true |
code
| 0.619241 | null | null | null | null |
|
# Final Project Report Group 10
## <u> Insurance Cross Selling <u>
Ashwin Yenigalla. Natwar Koneru, Pratheep Raju, Rahul Narang
### <u> Data Dictionary <u>
The dataset is from Kaggle.com:
https://www.kaggle.com/anmolkumar/health-insurance-cross-sell-prediction
Unique ID Rows: 381109 values Data Features are as follows:
Attributes Count: There are 11 Attributes attached to each unique identifier. One is a Target Variable. Please find the included details below.
### <u> Introduction <u>
This project is focused on Vehicle Insurance cross sales by a health insurance company. <br>
The Health Insurance company guarantees compensation for damage to a person’s health, loss of life and any property loss incurred. They are now aimed at leveraging their repository of customer and prospect data to cross sell a vehicle insurance product. <br>
<br>
This is a continuous cycle that allows the company to follow the customer from more avenues. How to design a product that will win over most customers in this area is the business problem that we are trying to address. The case provides some data that has been generated from their beta market tests to develop an understanding of their customer responsiveness to the new vehicle insurance product based on certain identifying demographics. <br>
<br>
This case is being approached as a predictive analytics data mining problem. The steps we will follow to classify customers into viable candidates for cross-selling are based on the positive, or negative responses generated by their existing customers. A host of supervised and unsupervised classification algorithms will be trained on the data provided in this case study, treating their logged responses to the new vehicle insurance product as the target variable (yes/no to purchasing the product). The report below details the attributes of the dataset, feature engineering and data munging applied to the dataset and classification algorithms used in generating predictions to classify customers based on their responses.
Variable|Variable Description
:-----|:-----
ID|Unique ID for the customer
Gender|Gender of the customer
Age|Age of the customer
Driving License|0 for Customer that does not have a Driver’s License, <br>1 for Customer already has Driver’s License
Region Code|Unique code for the region of the customer
Previously Insured|1 for Customer already has previously opted for Vehicle Insurance, 0 for Customer that doesn't have pre-existing Vehicle Insurance coverage
Vehicle Age|Age of the Vehicle
Vehicle Damage|1 for Customer that damaged their vehicle in the past. 0 for Customer that did not damage their vehicle in the past.
Annual Premium|The amount customer would need to pay as premium in the year
Policy Sales Channel|Anonymized Code for the outbound sales channel connecting to the customer <br> i.e. Different Agents, Over Mail, Over Phone, In Person, etc.
Vintage |Number of Days, Customer has been associated with the company
Response|Target Variable. <br> 1 if the Customer shows a positive response to purchasing the insurance product, <br>0 for Customers who are not interested in purchasing this product
## <u> Exploratory Data Analysis [EDA] <u>
### To analyze the variables, some of the important libraries used in our project are numpy, pandas, matlotlib, seaborn sklearn.
### To know the dataset better, we need to know the relationship of variables with the target variable.
### Eliminating / dumping unnecessary variables is an important part of data cleaning.
### As part of our analysis, 'ID' does not play much significant role for better performance of algorithms in training and testing data set.
<br>
<br>
<br>
```
import numpy as np
import pandas as pd
# Packages for Ploting
import seaborn as sns
import matplotlib.pyplot as plt
import plotly.express as px
from sklearn.metrics import accuracy_score
# Importing the ML Algorithm Packages
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from xgboost import XGBClassifier
from sklearn.linear_model import LogisticRegression, RidgeClassifier
from sklearn.tree import DecisionTreeClassifier
# Importing the Matrics and Other Required Packages
from sklearn.metrics import plot_confusion_matrix
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix, accuracy_score
from sklearn.metrics import classification_report
from sklearn.utils import shuffle
import warnings
warnings.filterwarnings('ignore')
pd.set_option('display.max_columns', 300)
sns.set()
# Reading the Data from CSV File
df = pd.read_csv('train.csv')
# Copying the Main Data from csv to a New Varable DF1
df1 = df.copy()
df1 = df.drop(['id'],axis = 1)
# To Know the Type of Data
df.info()
# To get the Total Rows and Columns
df.shape
```
There are 381109 Rows and 12 Columns in the dataset
```
# Seeing if there are any Null Values
df.isnull().sum()
df_train = pd.read_csv('train.csv')
df1 = df_train.copy()
df1.Gender = df1.Gender.apply(lambda x: int(1) if x == 'Male' else int(0))
df1.Vehicle_Damage = df1.Vehicle_Damage.apply(lambda x: int(1) if x == 'Yes' else int(0))
df1.Vehicle_Age = df1.Vehicle_Damage.apply(lambda x: int(0) if x == 1.0 else (int(1) if x==1.5 else int(2)))
df1['Policy_Sales_Channel'] = df1['Policy_Sales_Channel'].astype(int)
df1['Region_Code'] = df1['Region_Code'].astype(int)
df1['Response'] = df1['Response'].astype(int)
df1['Vehicle_Age'] = df1['Vehicle_Age'].astype(int)
df1.describe()
df1.info()
```
## <u> Target Variable <u>
```
plt.plot
sns.countplot(df1['Response'])
plt.title("response plot (target variable)")
print( "Percentage of target class\n")
print(df1['Response'].value_counts()/len(df1)*100)
```
### The target variable is disproportionate and will affect the accuracy of the classification algorithm.
### The target variable needs to be rebalanced before we can proceed with our machine learning algorithm.
```
# DataFrame With All 1s in Response
df_once = df1[df1['Response'] == 1]
# DataFrame With All 0s Response
df_zeros = df1[df1['Response'] == 0]
# Takeing a random sample from df_zeros(0s) to a length of df_once(1s)
Zero_Resampling = df_zeros.sample(n = len(df_once))
# Concat(joining) df_once and Zero_Resampling
New_df = pd.concat([df_once,Zero_Resampling])
# Shuffleing the New_df
final_df = shuffle(New_df)
Responses_count = [len(final_df[final_df.Response == 1]),len(final_df[final_df.Response == 0])]
Responses_count
sns.countplot(df1['Response'])
plt.title("response plot (target variable)")
plt.show()
```
## <u> Gender Variable <u>
```
plt.figure(figsize = (13,5))
sns.countplot(df1['Gender'])
plt.show()
plt.figure(figsize=(13,5))
sns.countplot(df1['Gender'], hue = df1['Response'])
plt.title("Male and female responses")
plt.show()
```
## <u> Annual Premium Variable <u>
```
# Ploting a Distibution Plot for Annual_Premium
plt.figure(figsize=(10,5))
Annual_Premium_plot = sns.distplot(final_df.Annual_Premium)
sns.boxplot(final_df['Annual_Premium'])
```
### We are performing a log transform on Annual_premium since to remove the skewness and for better distribution
```
final_df['Log_Annual_Premium'] = np.log(final_df['Annual_Premium'])
final_df
sns.boxplot(final_df['Log_Annual_Premium'])
# Ploting a Distibution Plot for Annual_Premium
plt.figure(figsize=(10,5))
Annual_Premium_plot = sns.distplot(final_df.Log_Annual_Premium)
```
### We will examine the highest correlated attributes and eliminate attributes that are not contributing more to the information gain
```
corrmat = final_df.corr()
top_corr_features = corrmat.index
plt.figure(figsize=(20,20))
#plot heat map
g=sns.heatmap(final_df[top_corr_features].corr(),annot=True,cmap="RdYlGn")
def correlation(dataset, threshold):
col_corr = set()
corr_matrix = dataset.corr()
for i in range(len(corr_matrix.columns)):
for j in range(i):
if abs(corr_matrix.iloc[i, j]) > threshold:
colname = corr_matrix.columns[i]
col_corr.add(colname)
return col_corr
correlation(final_df, 0.6)
final_df = final_df.drop(['Vehicle_Damage'],axis = 1)
final_df = final_df.drop(['Annual_Premium'],axis = 1)
```
### We are removing Vehicle damage because it is highly correlated with two other attributes(vehicle_age and previously_insured) to avoid multicollinearity
```
corrmat = final_df.corr()
top_corr_features = corrmat.index
plt.figure(figsize=(20,20))
#plot heat map
g=sns.heatmap(final_df[top_corr_features].corr(),annot=True,cmap="RdYlGn")
final_df.head(10)
```
## <u> Previously Insured Variable <u>
```
sns.countplot('Previously_Insured', hue = 'Response',data = final_df)
```
### Train:Validate is 70:30 split
```
y = final_df.Response
X = final_df.drop(['Response'],axis = 1,inplace = False)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=12)
pipeline = {
'LogisticRegression': make_pipeline(StandardScaler(), LogisticRegression()),
'RidgeClassifier': make_pipeline(StandardScaler(), RidgeClassifier()),
'DecisionTreeClassifier': make_pipeline(StandardScaler(), DecisionTreeClassifier(random_state=0)),
'RandomForestClassifier': make_pipeline(StandardScaler(), RandomForestClassifier()),
'GradientBoostingClassifier': make_pipeline(StandardScaler(), GradientBoostingClassifier()),
'XGBClassifier': make_pipeline(StandardScaler(), XGBClassifier(verbosity=0)),
}
fit_model = {}
for algo,pipelines in pipeline.items():
model = pipelines.fit(X_train,y_train)
fit_model[algo] = model
score = []
names = []
dds = []
for algo,model in fit_model.items():
yhat = model.predict(X_test)
names.append(algo)
score.append(accuracy_score(y_test, yhat))
result= pd.DataFrame(names,columns = ['Name'])
result['Score'] = score
result
for names,value in pipeline.items():
model = value.fit(X_train,y_train)
preds = model.predict(X_test)
print(" ")
print(names)
print('-'*len(names))
print(' ')
print(classification_report(y_test, preds))
print(' ')
print('_'*55)
```
### XGBoost has the highest Classification Accuracy score among the classifiers listed above.
| true |
code
| 0.496826 | null | null | null | null |
|
# A/B test 2 - Loved journeys, control vs content similarity sorted list
This related links A/B test (ab2) was conducted from 26 Feb -5th March 2019.
The data used in this report are 27th Feb 2019 - 5th March because on 26th the split was not 50:50.
The test compared the existing related links (where available) to links generated using Google's universal sentence encoder V2. The first *500* words of all content in content store (clean_content.csv.gz) were encoded and cosine distance was used to find the nearest vector to each content vector. A maximum of 5 links were suggested and only links above a threshold of 0.15 were suggested.
## Import
```
import os
import pandas as pd
import numpy as np
import ast
import re
# z test
from statsmodels.stats.proportion import proportions_ztest
# bayesian bootstrap and vis
import matplotlib.pyplot as plt
import seaborn as sns
import bayesian_bootstrap.bootstrap as bb
from astropy.utils import NumpyRNGContext
# progress bar
from tqdm import tqdm, tqdm_notebook
from scipy import stats
from collections import Counter
import sys
sys.path.insert(0, '../../src' )
import analysis as analysis
# set up the style for our plots
sns.set(style='white', palette='colorblind', font_scale=1.3,
rc={'figure.figsize':(12,9),
"axes.facecolor": (0, 0, 0, 0)})
# instantiate progress bar goodness
tqdm.pandas(tqdm_notebook)
pd.set_option('max_colwidth',500)
# the number of bootstrap means used to generate a distribution
boot_reps = 10000
# alpha - false positive rate
alpha = 0.05
# number of tests
m = 4
# Correct alpha for multiple comparisons
alpha = alpha / m
# The Bonferroni correction can be used to adjust confidence intervals also.
# If one establishes m confidence intervals, and wishes to have an overall confidence level of 1-alpha,
# each individual confidence interval can be adjusted to the level of 1-(alpha/m).
# reproducible
seed = 1337
```
## File/dir locations
### Processed journey data
```
DATA_DIR = os.getenv("DATA_DIR")
filename = "full_sample_loved_947858.csv.gz"
filepath = os.path.join(
DATA_DIR, "sampled_journey", "20190227_20190305",
filename)
filepath
# read in processed sampled journey with just the cols we need for related links
df = pd.read_csv(filepath, sep ="\t", compression="gzip")
# convert from str to list
df['Event_cat_act_agg']= df['Event_cat_act_agg'].progress_apply(ast.literal_eval)
df['Page_Event_List'] = df['Page_Event_List'].progress_apply(ast.literal_eval)
df['Page_List'] = df['Page_List'].progress_apply(ast.literal_eval)
df['Page_List_Length'] = df['Page_List'].progress_apply(len)
# drop dodgy rows, where page variant is not A or B.
df = df.query('ABVariant in ["A", "B"]')
```
### Nav type of page lookup - is it a finding page? if not it's a thing page
```
filename = "document_types.csv.gz"
# created a metadata dir in the DATA_DIR to hold this data
filepath = os.path.join(
DATA_DIR, "metadata",
filename)
print(filepath)
df_finding_thing = pd.read_csv(filepath, sep="\t", compression="gzip")
df_finding_thing.head()
thing_page_paths = df_finding_thing[
df_finding_thing['is_finding']==0]['pagePath'].tolist()
finding_page_paths = df_finding_thing[
df_finding_thing['is_finding']==1]['pagePath'].tolist()
```
## Outliers
Some rows should be removed before analysis. For example rows with journey lengths of 500 or very high related link click rates. This process might have to happen once features have been created.
# Derive variables
## journey_click_rate
There is no difference in the proportion of journeys using at least one related link (journey_click_rate) between page variant A and page variant B.
\begin{equation*}
\frac{\text{total number of journeys including at least one click on a related link}}{\text{total number of journeys}}
\end{equation*}
```
# get the number of related links clicks per Sequence
df['Related Links Clicks per seq'] = df['Event_cat_act_agg'].map(analysis.sum_related_click_events)
# map across the Sequence variable, which includes pages and Events
# we want to pass all the list elements to a function one-by-one and then collect the output.
df["Has_Related"] = df["Related Links Clicks per seq"].map(analysis.is_related)
df['Related Links Clicks row total'] = df['Related Links Clicks per seq'] * df['Occurrences']
df.head(3)
```
## count of clicks on navigation elements
There is no statistically significant difference in the count of clicks on navigation elements per journey between page variant A and page variant B.
\begin{equation*}
{\text{total number of navigation element click events from content pages}}
\end{equation*}
### Related link counts
```
# get the total number of related links clicks for that row (clicks per sequence multiplied by occurrences)
df['Related Links Clicks row total'] = df['Related Links Clicks per seq'] * df['Occurrences']
```
### Navigation events
```
def count_nav_events(page_event_list):
"""Counts the number of nav events from a content page in a Page Event List."""
content_page_nav_events = 0
for pair in page_event_list:
if analysis.is_nav_event(pair[1]):
if pair[0] in thing_page_paths:
content_page_nav_events += 1
return content_page_nav_events
# needs finding_thing_df read in from document_types.csv.gz
df['Content_Page_Nav_Event_Count'] = df['Page_Event_List'].progress_map(count_nav_events)
def count_search_from_content(page_list):
search_from_content = 0
for i, page in enumerate(page_list):
if i > 0:
if '/search?q=' in page:
if page_list[i-1] in thing_page_paths:
search_from_content += 1
return search_from_content
df['Content_Search_Event_Count'] = df['Page_List'].progress_map(count_search_from_content)
# count of nav or search clicks
df['Content_Nav_or_Search_Count'] = df['Content_Page_Nav_Event_Count'] + df['Content_Search_Event_Count']
# occurrences is accounted for by the group by bit in our bayesian boot analysis function
df['Content_Nav_Search_Event_Sum_row_total'] = df['Content_Nav_or_Search_Count'] * df['Occurrences']
# required for journeys with no nav later
df['Has_No_Nav_Or_Search'] = df['Content_Nav_Search_Event_Sum_row_total'] == 0
```
## Temporary df file in case of crash
### Save
```
df.to_csv(os.path.join(
DATA_DIR,
"ab2_loved_temp.csv.gz"), sep="\t", compression="gzip", index=False)
```
### Frequentist statistics
#### Statistical significance
```
# help(proportions_ztest)
has_rel = analysis.z_prop(df, 'Has_Related')
has_rel
has_rel['p-value'] < alpha
```
#### Practical significance - uplift
```
# Due to multiple testing we used the Bonferroni correction for alpha
ci_low,ci_upp = analysis.zconf_interval_two_samples(has_rel['x_a'], has_rel['n_a'],
has_rel['x_b'], has_rel['n_b'], alpha = alpha)
print(' difference in proportions = {0:.2f}%'.format(100*(has_rel['p_b']-has_rel['p_a'])))
print(' % relative change in proportions = {0:.2f}%'.format(100*((has_rel['p_b']-has_rel['p_a'])/has_rel['p_a'])))
print(' 95% Confidence Interval = ( {0:.2f}% , {1:.2f}% )'
.format(100*ci_low, 100*ci_upp))
```
### Bayesian statistics
Based on [this](https://medium.com/@thibalbo/coding-bayesian-ab-tests-in-python-e89356b3f4bd) blog
To be developed, a Bayesian approach can provide a simpler interpretation.
### Bayesian bootstrap
```
analysis.compare_total_searches(df)
fig, ax = plt.subplots()
plot_df_B = df[df.ABVariant == "B"].groupby(
'Content_Nav_or_Search_Count').sum().iloc[:, 0]
plot_df_A = df[df.ABVariant == "A"].groupby(
'Content_Nav_or_Search_Count').sum().iloc[:, 0]
ax.set_yscale('log')
width =0.4
ax = plot_df_B.plot.bar(label='B', position=1, width=width)
ax = plot_df_A.plot.bar(label='A', color='salmon', position=0, width=width)
plt.title("Unloved journeys")
plt.ylabel("Log(number of journeys)")
plt.xlabel("Number of uses of search/nav elements in journey")
legend = plt.legend(frameon=True)
frame = legend.get_frame()
frame.set_facecolor('white')
plt.savefig('nav_counts_unloved_bar.png', dpi = 900, bbox_inches = 'tight')
a_bootstrap, b_bootstrap = analysis.bayesian_bootstrap_analysis(df, col_name='Content_Nav_or_Search_Count', boot_reps=boot_reps, seed = seed)
np.array(a_bootstrap).mean()
np.array(a_bootstrap).mean() - (0.05 * np.array(a_bootstrap).mean())
np.array(b_bootstrap).mean()
(1 - np.array(b_bootstrap).mean()/np.array(a_bootstrap).mean())*100
# ratio is vestigial but we keep it here for convenience
# it's actually a count but considers occurrences
ratio_stats = analysis.bb_hdi(a_bootstrap, b_bootstrap, alpha=alpha)
ratio_stats
ax = sns.distplot(b_bootstrap, label='B')
ax.errorbar(x=[ratio_stats['b_ci_low'], ratio_stats['b_ci_hi']], y=[2, 2], linewidth=5, c='teal', marker='o',
label='95% HDI B')
ax = sns.distplot(a_bootstrap, label='A', ax=ax, color='salmon')
ax.errorbar(x=[ratio_stats['a_ci_low'], ratio_stats['a_ci_hi']], y=[5, 5], linewidth=5, c='salmon', marker='o',
label='95% HDI A')
ax.set(xlabel='mean search/nav count per journey', ylabel='Density')
sns.despine()
legend = plt.legend(frameon=True, bbox_to_anchor=(0.75, 1), loc='best')
frame = legend.get_frame()
frame.set_facecolor('white')
plt.title("Unloved journeys")
plt.savefig('nav_counts_unloved.png', dpi = 900, bbox_inches = 'tight')
# calculate the posterior for the difference between A's and B's ratio
# ypa prefix is vestigial from blog post
ypa_diff = np.array(b_bootstrap) - np.array(a_bootstrap)
# get the hdi
ypa_diff_ci_low, ypa_diff_ci_hi = bb.highest_density_interval(ypa_diff)
# the mean of the posterior
print('mean:', ypa_diff.mean())
print('low ci:', ypa_diff_ci_low, '\nhigh ci:', ypa_diff_ci_hi)
ax = sns.distplot(ypa_diff)
ax.plot([ypa_diff_ci_low, ypa_diff_ci_hi], [0, 0], linewidth=10, c='k', marker='o',
label='95% HDI')
ax.set(xlabel='Content_Nav_or_Search_Count', ylabel='Density',
title='The difference between B\'s and A\'s mean counts times occurrences')
sns.despine()
legend = plt.legend(frameon=True)
frame = legend.get_frame()
frame.set_facecolor('white')
plt.show();
# We count the number of values greater than 0 and divide by the total number
# of observations
# which returns us the the proportion of values in the distribution that are
# greater than 0, could act a bit like a p-value
(ypa_diff > 0).sum() / ypa_diff.shape[0]
# We count the number of values less than 0 and divide by the total number
# of observations
# which returns us the the proportion of values in the distribution that are
# less than 0, could act a bit like a p-value
(ypa_diff < 0).sum() / ypa_diff.shape[0]
(ypa_diff>0).sum()
(ypa_diff<0).sum()
```
## proportion of journeys with a page sequence including content and related links only
There is no statistically significant difference in the proportion of journeys with a page sequence including content and related links only (including loops) between page variant A and page variant B
\begin{equation*}
\frac{\text{total number of journeys that only contain content pages and related links (i.e. no nav pages)}}{\text{total number of journeys}}
\end{equation*}
### Overall
```
# if (Content_Nav_Search_Event_Sum == 0) that's our success
# Has_No_Nav_Or_Search == 1 is a success
# the problem is symmetrical so doesn't matter too much
sum(df.Has_No_Nav_Or_Search * df.Occurrences) / df.Occurrences.sum()
sns.distplot(df.Content_Nav_or_Search_Count.values);
```
### Frequentist statistics
#### Statistical significance
```
nav = analysis.z_prop(df, 'Has_No_Nav_Or_Search')
nav
```
#### Practical significance - uplift
```
# Due to multiple testing we used the Bonferroni correction for alpha
ci_low,ci_upp = analysis.zconf_interval_two_samples(nav['x_a'], nav['n_a'],
nav['x_b'], nav['n_b'], alpha = alpha)
diff = 100*(nav['x_b']/nav['n_b']-nav['x_a']/nav['n_a'])
print(' difference in proportions = {0:.2f}%'.format(diff))
print(' 95% Confidence Interval = ( {0:.2f}% , {1:.2f}% )'
.format(100*ci_low, 100*ci_upp))
print("There was a {0: .2f}% relative change in the proportion of journeys not using search/nav elements".format(100 * ((nav['p_b']-nav['p_a'])/nav['p_a'])))
```
## Average Journey Length (number of page views)
There is no statistically significant difference in the average page list length of journeys (including loops) between page variant A and page variant B.
```
length_B = df[df.ABVariant == "B"].groupby(
'Page_List_Length').sum().iloc[:, 0]
lengthB_2 = length_B.reindex(np.arange(1, 501, 1), fill_value=0)
length_A = df[df.ABVariant == "A"].groupby(
'Page_List_Length').sum().iloc[:, 0]
lengthA_2 = length_A.reindex(np.arange(1, 501, 1), fill_value=0)
fig, ax = plt.subplots(figsize=(100, 30))
ax.set_yscale('log')
width = 0.4
ax = lengthB_2.plot.bar(label='B', position=1, width=width)
ax = lengthA_2.plot.bar(label='A', color='salmon', position=0, width=width)
plt.xlabel('length', fontsize=1)
legend = plt.legend(frameon=True)
frame = legend.get_frame()
frame.set_facecolor('white')
plt.show();
```
### Bayesian bootstrap for non-parametric hypotheses
```
# http://savvastjortjoglou.com/nfl-bayesian-bootstrap.html
# let's use mean journey length (could probably model parametrically but we use it for demonstration here)
# some journeys have length 500 and should probably be removed as they are liekely bots or other weirdness
#exclude journeys of longer than 500 as these could be automated traffic
df_short = df[df['Page_List_Length'] < 500]
print("The mean number of pages in an unloved journey is {0:.3f}".format(sum(df.Page_List_Length*df.Occurrences)/df.Occurrences.sum()))
# for reproducibility, set the seed within this context
a_bootstrap, b_bootstrap = analysis.bayesian_bootstrap_analysis(df, col_name='Page_List_Length', boot_reps=boot_reps, seed = seed)
a_bootstrap_short, b_bootstrap_short = analysis.bayesian_bootstrap_analysis(df_short, col_name='Page_List_Length', boot_reps=boot_reps, seed = seed)
np.array(a_bootstrap).mean()
np.array(b_bootstrap).mean()
print("There's a relative change in page length of {0:.2f}% from A to B".format((np.array(b_bootstrap).mean()-np.array(a_bootstrap).mean())/np.array(a_bootstrap).mean()*100))
print(np.array(a_bootstrap_short).mean())
print(np.array(b_bootstrap_short).mean())
# Calculate a 95% HDI
a_ci_low, a_ci_hi = bb.highest_density_interval(a_bootstrap)
print('low ci:', a_ci_low, '\nhigh ci:', a_ci_hi)
ax = sns.distplot(a_bootstrap, color='salmon')
ax.plot([a_ci_low, a_ci_hi], [0, 0], linewidth=10, c='k', marker='o',
label='95% HDI')
ax.set(xlabel='Journey Length', ylabel='Density', title='Page Variant A Mean Journey Length')
sns.despine()
plt.legend();
# Calculate a 95% HDI
b_ci_low, b_ci_hi = bb.highest_density_interval(b_bootstrap)
print('low ci:', b_ci_low, '\nhigh ci:', b_ci_hi)
ax = sns.distplot(b_bootstrap)
ax.plot([b_ci_low, b_ci_hi], [0, 0], linewidth=10, c='k', marker='o',
label='95% HDI')
ax.set(xlabel='Journey Length', ylabel='Density', title='Page Variant B Mean Journey Length')
sns.despine()
legend = plt.legend(frameon=True)
frame = legend.get_frame()
frame.set_facecolor('white')
plt.show();
ax = sns.distplot(b_bootstrap, label='B')
ax = sns.distplot(a_bootstrap, label='A', ax=ax, color='salmon')
ax.set(xlabel='Journey Length', ylabel='Density')
sns.despine()
legend = plt.legend(frameon=True)
frame = legend.get_frame()
frame.set_facecolor('white')
plt.title("Unloved journeys")
plt.savefig('journey_length_unloved.png', dpi = 900, bbox_inches = 'tight')
ax = sns.distplot(b_bootstrap_short, label='B')
ax = sns.distplot(a_bootstrap_short, label='A', ax=ax, color='salmon')
ax.set(xlabel='Journey Length', ylabel='Density')
sns.despine()
legend = plt.legend(frameon=True)
frame = legend.get_frame()
frame.set_facecolor('white')
plt.show();
```
We can also measure the uncertainty in the difference between the Page Variants's Journey Length by subtracting their posteriors.
```
# calculate the posterior for the difference between A's and B's YPA
ypa_diff = np.array(b_bootstrap) - np.array(a_bootstrap)
# get the hdi
ypa_diff_ci_low, ypa_diff_ci_hi = bb.highest_density_interval(ypa_diff)
# the mean of the posterior
ypa_diff.mean()
print('low ci:', ypa_diff_ci_low, '\nhigh ci:', ypa_diff_ci_hi)
ax = sns.distplot(ypa_diff)
ax.plot([ypa_diff_ci_low, ypa_diff_ci_hi], [0, 0], linewidth=10, c='k', marker='o',
label='95% HDI')
ax.set(xlabel='Journey Length', ylabel='Density',
title='The difference between B\'s and A\'s mean Journey Length')
sns.despine()
legend = plt.legend(frameon=True)
frame = legend.get_frame()
frame.set_facecolor('white')
plt.show();
```
We can actually calculate the probability that B's mean Journey Length was greater than A's mean Journey Length by measuring the proportion of values greater than 0 in the above distribution.
```
# We count the number of values greater than 0 and divide by the total number
# of observations
# which returns us the the proportion of values in the distribution that are
# greater than 0, could act a bit like a p-value
(ypa_diff > 0).sum() / ypa_diff.shape[0]
# We count the number of values greater than 0 and divide by the total number
# of observations
# which returns us the the proportion of values in the distribution that are
# greater than 0, could act a bit like a p-value
(ypa_diff < 0).sum() / ypa_diff.shape[0]
```
| true |
code
| 0.659707 | null | null | null | null |
|
# The Acrobot (v-1) Problem
Acrobot is a 2-link pendulum with only the second joint actuated.
Intitially, both links point downwards. The goal is to swing the
end-effector at a height at least the length of one link above the base.
Both links can swing freely and can pass by each other, i.e., they don't
collide when they have the same angle.
## States
The state consists of the sin() and cos() of the two rotational joint
angles and the joint angular velocities :
[cos(theta1) sin(theta1) cos(theta2) sin(theta2) thetaDot1 thetaDot2].
For the first link, an angle of 0 corresponds to the link pointing downwards.
The angle of the second link is relative to the angle of the first link.
An angle of 0 corresponds to having the same angle between the two links.
A state of [1, 0, 1, 0, ..., ...] means that both links point downwards.
## Actions
The action is either applying +1, 0 or -1 torque on the joint between
the two pendulum links.
FPS = 15
```
import gym
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
import torch
from utils.DQN_model import DQN_CNN
from PIL import Image
import time
import pickle
import random
from itertools import count
from utils.Schedule import LinearSchedule, ExponentialSchedule
from utils.Agent import AcrobotAgent, preprocess_frame
def calc_moving_average(lst, window_size=10):
'''
This function calculates the moving average of `lst` over
`window_size` samples.
Parameters:
arr: list (list)
window_size: size over which to average (int)
Returns:
mean_arr: array with the averages (np.array)
'''
assert len(lst) >= window_size
mean_arr = []
for j in range(1, window_size):
mean_arr.append(np.mean(lst[:j]))
i = 0
while i != (len(lst) - window_size + 1):
mean_arr.append(np.mean(lst[i : i + window_size]))
i += 1
return np.array(mean_arr)
def plot_rewards(episode_rewards, window_size=10, title=''):
'''
This function plots the rewards vs. episodes and the mean rewards vs. episodes.
The mean is taken over `windows_size` episodes.
Parameters:
episode_rewards: list of all the rewards (list)
'''
num_episodes = len(episode_rewards)
mean_rewards = calc_moving_average(episode_rewards, window_size)
plt.plot(list(range(num_episodes)), episode_rewards, label='rewards')
plt.plot(list(range(num_episodes)), mean_rewards, label='mean_rewards')
plt.title(title)
plt.xlabel('Episode')
plt.ylabel('Reward')
plt.legend()
plt.show()
# Play
def play_acrobot(env, agent, num_episodes=5):
'''
This function plays the Acrobot-v1 environment given an agent.
Parameters:
agent: the agent that holds the policy (AcrobotAgent)
num_episodes: number of episodes to play
'''
if agent.obs_represent == 'frame_seq':
print("Playing Acrobot-v1 with " , agent.name ,"agent using Frame Sequence")
start_time = time.time()
for episode in range(num_episodes):
episode_start_time = time.time()
env.reset()
last_obs = preprocess_frame(env, mode='atari', render=True)
episode_reward = 0
for t in count():
### Step the env and store the transition
# Store lastest observation in replay memory and last_idx can be used to store action, reward, done
last_idx = agent.replay_buffer.store_frame(last_obs)
# encode_recent_observation will take the latest observation
# that you pushed into the buffer and compute the corresponding
# input that should be given to a Q network by appending some
# previous frames.
recent_observation = agent.replay_buffer.encode_recent_observation()
action = agent.predict_action(recent_observation)
_ , reward, done, _ = env.step(action)
episode_reward += reward
# Store other info in replay memory
agent.replay_buffer.store_effect(last_idx, action, reward, done)
if done:
print("Episode: ", episode, " Done, Reward: ", episode_reward,
" Episode Time: %.2f secs" % (time.time() - episode_start_time))
break
last_obs = preprocess_frame(env, mode='atari', render=True)
env.close()
else:
# mode == 'frame diff'
print("Playing Acrobot-v1 with " , agent.name ,"agent using Frame Difference")
start_time = time.time()
for episode in range(num_episodes):
print("### Episode ", episode + 1, " ###")
episode_start_time = time.time()
env.reset()
last_obs = preprocess_frame(env, mode='control', render=True)
current_obs = preprocess_frame(env, mode='control', render=True)
state = current_obs - last_obs
episode_reward = 0
for t in count():
action = agent.predict_action(state)
_ , reward, done, _ = env.step(action)
episode_reward += reward
if done:
print("Episode: ", episode + 1, " Done, Reward: ",
episode_reward,
" Episode Time: %.2f secs" % (time.time() - episode_start_time))
break
last_obs = current_obs
current_obs = preprocess_frame(env, mode='control', render=True)
state = current_obs - last_obs
env.close()
exp_schedule = ExponentialSchedule(decay_rate=100)
lin_schedule = LinearSchedule(total_timesteps=1000)
gym.logger.set_level(40)
env = gym.make("Acrobot-v1")
agent = AcrobotAgent(env,
name='frame_seq_rep',
frame_history_len = 4,
exploration=lin_schedule,
steps_to_start_learn=10000,
target_update_freq=500,
learning_rate=0.00025,
clip_grads=True,
use_batch_norm=False)
mean_episode_reward = -float('nan')
best_mean_episode_reward = -float('inf')
last_obs = env.reset()
LOG_EVERY_N_STEPS = 5000
batch_size = 32 # 32
num_episodes = 100000
with open('./acrobot_agent_ckpt/frame_seq_training.status', 'rb') as fp:
training_status = pickle.load(fp)
mean_episode_reward = training_status['mean_episode_reward']
best_mean_episode_reward = training_status['best_mean_episode_reward']
episode_durations = training_status['episode_durations']
episodes_rewards = training_status['episodes_rewards']
total_steps = training_status['total_steps']
# episode_durations = []
# episodes_rewards = []
# total_steps = 0
start_time = time.time()
for episode in range(num_episodes):
episode_start_time = time.time()
env.reset()
last_obs = preprocess_frame(env, mode='atari', render=True)
episode_reward = 0
agent.episodes_seen += 1
for t in count():
agent.steps_count += 1
total_steps += 1
### Step the env and store the transition
# Store lastest observation in replay memory and last_idx can be used to store action, reward, done
last_idx = agent.replay_buffer.store_frame(last_obs)
# encode_recent_observation will take the latest observation
# that you pushed into the buffer and compute the corresponding
# input that should be given to a Q network by appending some
# previous frames.
recent_observation = agent.replay_buffer.encode_recent_observation()
action = agent.select_greedy_action(recent_observation, use_episode=True)
# Advance one step
_ , reward, done, _ = env.step(action)
episode_reward += reward
agent.replay_buffer.store_effect(last_idx, action, reward, done)
### Perform experience replay and train the network.
# Note that this is only done if the replay buffer contains enough samples
# for us to learn something useful -- until then, the model will not be
# initialized and random actions should be taken
agent.learn(batch_size)
### Log progress and keep track of statistics
if len(episodes_rewards) > 0:
mean_episode_reward = np.mean(episodes_rewards[-100:])
if len(episodes_rewards) > 100:
best_mean_episode_reward = max(best_mean_episode_reward, mean_episode_reward)
if total_steps % LOG_EVERY_N_STEPS == 0 and total_steps > agent.steps_to_start_learn:
print("Timestep %d" % (agent.steps_count,))
print("mean reward (100 episodes) %f" % mean_episode_reward)
print("best mean reward %f" % best_mean_episode_reward)
print("episodes %d" % len(episodes_rewards))
print("exploration value %f" % agent.epsilon)
total_time = time.time() - start_time
print("time since start %.2f seconds" % total_time)
training_status = {}
training_status['mean_episode_reward'] = mean_episode_reward
training_status['best_mean_episode_reward'] = best_mean_episode_reward
training_status['episode_durations'] = episode_durations
training_status['episodes_rewards'] = episodes_rewards
training_status['total_steps'] = total_steps
with open('./acrobot_agent_ckpt/frame_seq_training.status', 'wb') as fp:
pickle.dump(training_status, fp)
# Resets the environment when reaching an episode boundary.
if done:
episode_durations.append(t + 1)
episodes_rewards.append(episode_reward)
print("Episode: ", agent.episodes_seen, " Done, Reward: ", episode_reward,
" Step: ", agent.steps_count, " Episode Time: %.2f secs" % (time.time() - episode_start_time))
break
last_obs = preprocess_frame(env, mode='atari', render=True)
# print(last_obs)
print("Training Complete!")
env.close()
play_acrobot(env, agent, num_episodes=5)
plt.imshow(last_obs[:,:,0], cmap='gray')
with open('./acrobot_agent_ckpt/frame_seq_training.status', 'rb') as fp:
training_status = pickle.load(fp)
episodes_rewards = training_status['episodes_rewards']
plt.rcParams['figure.figsize'] = (20, 10)
plot_rewards(episodes_rewards, 100, title='Acrobot Frame Sequence')
# Frame Differenece
mean_episode_reward = -float('nan')
best_mean_episode_reward = -float('inf')
last_obs = env.reset()
LOG_EVERY_N_STEPS = 1000
batch_size = 128 # 32
num_episodes = 10000
agent = AcrobotAgent(env,
name='frame_diff',
exploration=lin_schedule,
steps_to_start_learn=2000,
target_update_freq=500,
learning_rate=0.003,
clip_grads=True,
use_batch_norm=True,
obs_represent='frame_diff')
with open('./acrobot_agent_ckpt/training.status', 'rb') as fp:
training_status = pickle.load(fp)
mean_episode_reward = training_status['mean_episode_reward']
best_mean_episode_reward = training_status['best_mean_episode_reward']
episode_durations = training_status['episode_durations']
episodes_rewards = training_status['episodes_rewards']
total_steps = training_status['total_steps']
# episode_durations = []
# episodes_rewards = []
# total_steps = 0
start_time = time.time()
for episode in range(num_episodes):
episode_start_time = time.time()
env.reset()
last_obs = preprocess_frame(env, mode='control', render=True)
current_obs = preprocess_frame(env, mode='control', render=True)
state = current_obs - last_obs
episode_reward = 0
agent.episodes_seen += 1
# agent.epsilon = agent.explore_schedule.value(agent.episodes_seen)
for t in count():
agent.steps_count += 1
total_steps += 1
### Step the env and store the transition
# Store lastest observation in replay memory and last_idx can be used to store action, reward, done
last_idx = agent.replay_buffer.store_frame(state)
# encode_recent_observation will take the latest observation
# that you pushed into the buffer and compute the corresponding
# input that should be given to a Q network by appending some
# previous frames.
recent_observation = agent.replay_buffer.encode_recent_observation()
action = agent.select_greedy_action(recent_observation, use_episode=True)
# Advance one step
_ , reward, done, _ = env.step(action)
episode_reward += reward
agent.replay_buffer.store_effect(last_idx, action, reward, done)
### Perform experience replay and train the network.
# Note that this is only done if the replay buffer contains enough samples
# for us to learn something useful -- until then, the model will not be
# initialized and random actions should be taken
agent.learn(batch_size)
### Log progress and keep track of statistics
if len(episodes_rewards) > 0:
mean_episode_reward = np.mean(episodes_rewards[-100:])
if len(episodes_rewards) > 100:
best_mean_episode_reward = max(best_mean_episode_reward, mean_episode_reward)
if total_steps % LOG_EVERY_N_STEPS == 0 and total_steps > agent.steps_to_start_learn:
print("Timestep %d" % (agent.steps_count,))
print("mean reward (100 episodes) %f" % mean_episode_reward)
print("best mean reward %f" % best_mean_episode_reward)
print("episodes %d" % len(episodes_rewards))
print("exploration value %f" % agent.epsilon)
total_time = time.time() - start_time
print("time since start %.2f seconds" % total_time)
training_status = {}
training_status['mean_episode_reward'] = mean_episode_reward
training_status['best_mean_episode_reward'] = best_mean_episode_reward
training_status['episode_durations'] = episode_durations
training_status['episodes_rewards'] = episodes_rewards
training_status['total_steps'] = total_steps
with open('./acrobot_agent_ckpt/frame_diff_training.status', 'wb') as fp:
pickle.dump(training_status, fp)
# Resets the environment when reaching an episode boundary.
if done:
episode_durations.append(t + 1)
episodes_rewards.append(episode_reward)
print("Episode: ", agent.episodes_seen, " Done, Reward: ",
episode_reward, " Step: ", agent.steps_count,
" Episode Time: %.2f secs" % (time.time() - episode_start_time))
break
last_obs = current_obs
current_obs = preprocess_frame(env, mode='control', render=True)
state = current_obs - last_obs
print("Training Complete!")
env.close()
agent.save_agent_state()
env.close()
plt.rcParams['figure.figsize'] = (15,15)
env.reset()
img = env.render(mode='rgb_array')
env.close()
img = np.reshape(img, [500, 500, 3]).astype(np.float32)
img = img[:, :, 0] * 0.299 + img[:, :, 1] * 0.587 + img[:, :, 2] * 0.114
# img = img[:, :, 0] * 0.5 + img[:, :, 1] * 0.4 + img[:, :, 2] * 0.1
img = Image.fromarray(img)
resized_screen = img.resize((84, 84), Image.BILINEAR)
resized_screen = np.array(resized_screen)
x_t_1 = np.reshape(resized_screen, [84, 84, 1])
x_t_1 = x_t.astype(np.uint8)
env.step(0)
img = env.render(mode='rgb_array')
env.close()
img = np.reshape(img, [500, 500, 3]).astype(np.float32)
# img = img[:, :, 0] * 0.299 + img[:, :, 1] * 0.587 + img[:, :, 2] * 0.114
img = img[:, :, 0] * 0.5 + img[:, :, 1] * 0.4 + img[:, :, 2] * 0.1
img = Image.fromarray(img)
resized_screen = img.resize((84, 84), Image.BILINEAR)
resized_screen = np.array(resized_screen)
x_t_1 = np.reshape(resized_screen, [84, 84, 1])
x_t_1 = x_t_1.astype(np.uint8)
env.step(1)
img = env.render(mode='rgb_array')
env.close()
img = np.reshape(img, [500, 500, 3]).astype(np.float32)
# img = img[:, :, 0] * 0.299 + img[:, :, 1] * 0.587 + img[:, :, 2] * 0.114
img = img[:, :, 0] * 0.7 + img[:, :, 1] * 0.2 + img[:, :, 2] * 0.1
img = Image.fromarray(img)
resized_screen = img.resize((84, 84), Image.BILINEAR)
resized_screen = np.array(resized_screen)
x_t_2 = np.reshape(resized_screen, [84, 84, 1])
x_t_2 = x_t_2.astype(np.uint8)
env.step(0)
img = env.render(mode='rgb_array')
env.close()
img = np.reshape(img, [500, 500, 3]).astype(np.float32)
# img = img[:, :, 0] * 0.299 + img[:, :, 1] * 0.587 + img[:, :, 2] * 0.114
img = img[:, :, 0] * 0.5 + img[:, :, 1] * 0.4 + img[:, :, 2] * 0.1
img[img < 150] = 0
img[img > 230] = 255
img = Image.fromarray(img)
resized_screen = img.resize((84, 84), Image.BILINEAR)
resized_screen = np.array(resized_screen)
x_t_3 = np.reshape(resized_screen, [84, 84, 1])
x_t_3 = x_t_3.astype(np.uint8)
env.step(0)
img = env.render(mode='rgb_array')
env.close()
img = np.reshape(img, [500, 500, 3]).astype(np.float32)
# img = img[:, :, 0] * 0.299 + img[:, :, 1] * 0.587 + img[:, :, 2] * 0.114
img = img[:, :, 0] * 0.9 + img[:, :, 1] * 0.05 + img[:, :, 2] * 0.05
img = Image.fromarray(img)
resized_screen = img.resize((84, 84), Image.BILINEAR)
resized_screen = np.array(resized_screen)
x_t_4 = np.reshape(resized_screen, [84, 84, 1])
x_t_4 = x_t_4.astype(np.uint8)
plt.subplot(2,2,1)
plt.imshow(np.uint8(x_t_1[:,:,0]),cmap='gray')
# plt.imshow(np.uint8(x_t_1[:,:,0]))
plt.subplot(2,2,2)
plt.imshow(np.uint8(x_t_2[:,:,0]),cmap='gray')
# plt.imshow(np.uint8(x_t_2[:,:,0]))
plt.subplot(2,2,3)
plt.imshow(np.uint8(x_t_3[:,:,0]),cmap='gray')
# plt.imshow(np.uint8(x_t_3[:,:,0]))
plt.subplot(2,2,4)
plt.imshow(np.uint8(x_t_4[:,:,0]),cmap='gray')
# plt.imshow(np.uint8(x_t_4[:,:,0]))
env.close()
with open('./acrobot_agent_ckpt/frame_diff_training.status', 'rb') as fp:
training_status = pickle.load(fp)
episodes_rewards = training_status['episodes_rewards']
plt.rcParams['figure.figsize'] = (20, 10)
plot_rewards(episodes_rewards, 100, title='Acrobot Frame Difference')
gym.logger.set_level(40)
env = gym.make("Acrobot-v1")
agent = AcrobotAgent(env, name='frame_diff', obs_represent='frame_diff', use_batch_norm=True)
play_acrobot(env, agent, num_episodes=10)
env.close()
```
| true |
code
| 0.641871 | null | null | null | null |
|
# py12box model usage
This notebook shows how to set up and run the AGAGE 12-box model.
## Model schematic
The model uses advection and diffusion parameters to mix gases between boxes. Box indices start at the northern-most box and are as shown in the following schematic:
<img src="box_model_schematic.png" alt="Box model schematic" style="display:block;margin-left:auto;margin-right:auto;width:20%"/>
## Model inputs
We will be using some synthetic inputs for CFC-11. Input files are in:
```data/example/CFC-11```
The location of this folder will depend on where you've installed py12box and your system. Perhaps the easiest place to view the contents is [in the repository](https://github.com/mrghg/py12box/tree/develop/py12box/data/example/CFC-11).
In this folder, you will see two files:
```CFC-11_emissions.csv```
```CFC-11_initial_conditions.csv```
As the names suggest, these contain the emissions, initial conditions and lifetimes.
### Emissions
The emissions file has four columns: ```year, box_1, box_2, box_3, box_4```.
The number of rows in this file determines the length of the box model simulation.
The ```year``` column should contain a decimal date (e.g. 2000.5 for ~June 2000), and can be monthly or annual resolution.
The other columns specify the emissions in Gg/yr in each surface box.
### Initial conditions
The initial conditions file can be used to specify the mole fraction in pmol/mol (~ppt) in each of the 12 boxes.
## How to run
Firstly import the ```Model``` class. This class contains all the input variables (emissions, initial conditions, etc., and run functions).
We are also importing the get_data helper function, only needed for this tutorial, to point to input data files.
```
# Import from this package
from py12box.model import Model
from py12box import get_data
# Import matplotlib for some plots
import matplotlib.pyplot as plt
```
The ```Model``` class takes two arguments, ```species``` and ```project_directory```. The latter is the location of the input files, here just redirecting to the "examples" folder.
The initialisation step may take a few seconds, mainly to compile the model.
```
# Initialise the model
mod = Model("CFC-11", get_data("example/CFC-11"))
```
Assuming this has compiled correctly, you can now check the model inputs by accessing elements of the model class. E.g. to see the emissions:
```
mod.emissions
```
In this case, the emissions should be a 4 x 12*n_years numpy array. If annual emissions were specified in the inputs, the annual mean emissions are repeated each month.
We can now run the model using:
```
# Run model
mod.run()
```
The primary outputs that you'll be interested in are ```mf``` for the mole fraction (pmol/mol) in each of the 12 boxes at each timestep.
Let's plot this up:
```
plt.plot(mod.time, mod.mf[:, 0])
plt.plot(mod.time, mod.mf[:, 3])
plt.ylabel("%s (pmol mol$^{-1}$)" % mod.species)
plt.xlabel("Year")
plt.show()
```
We can also view other outputs such as the burden and loss. Losses are contained in a dictionary, with keys:
- ```OH``` (tropospheric OH losses)
- ```Cl``` (losses via tropospheric chlorine)
- ```other``` (all other first order losses)
For CFC-11, the losses are primarily in the stratosphere, so are contained in ```other```:
```
plt.plot(mod.emissions.sum(axis = 1).cumsum())
plt.plot(mod.burden.sum(axis = 1))
plt.plot(mod.losses["other"].sum(axis = 1).cumsum())
```
Another useful output is the lifetime. This is broken down in a variety of ways. Here we'll plot the global lifetime:
```
plt.plot(mod.instantaneous_lifetimes["global_total"])
plt.ylabel("Global instantaneous lifetime (years)")
```
## Setting up your own model run
To create your own project, create a project folder (can be anywhere on your filesystem).
The folder must contain two files:
```<species>_emissions.csv```
```<species>_initial_conditions.csv```
To point to the new project, py12box will expect a pathlib.Path object, so make sure you import this first:
```
from pathlib import Path
new_model = Model("<SPECIES>", Path("path/to/project/folder"))
```
Once set up, you can run the model using:
```
new_model.run()
```
Note that you can modify any of the model inputs in memory by modifying the model class. E.g. to see what happens when you double the emissions:
```
new_model.emissions *= 2.
new_model.run()
```
## Changing lifetimes
If no user-defined lifetimes are passed to the model, it will use the values in ```data/inputs/species_info.csv```
However, you can start the model up with non-standard lifetimes using the following arguments to the ```Model``` class (all in years):
```lifetime_strat```: stratospheric lifetime
```lifetime_ocean```: lifetime with respect to ocean uptake
```lifetime_trop```: non-OH losses in the troposphere
e.g.:
```
new_model = Model("<SPECIES>", Path("path/to/project/folder"), lifetime_strat=100.)
```
To change the tropospheric OH lifetime, you need to modify the ```oh_a``` or ```oh_er``` attributes of the ```Model``` class.
To re-tune the lifetime of the model in-memory, you can use the ```tune_lifetime``` method of the ```Model``` class:
```
new_model.tune_lifetime(lifetime_strat=50., lifetime_ocean=1e12, lifetime_trop=1e12)
```
| true |
code
| 0.772959 | null | null | null | null |
|
# Windows Metadata Structure and Value Issues
This notebook shows a few examples of the varience that occurs and encumbers parsing windows metadata extracted and serialised via `Get-EventMetadata.ps1` into the file `.\Extracted\EventMetadata.json.zip`.
Below is the number of records in my sample metadata extract.
```
import os, zipfile, json, pandas as pd
if 'Windows Event Metadata' not in os.getcwd():
os.chdir('Windows Event Metadata')
json_import = json.load(zipfile.ZipFile('./Extracted/EventMetadata.json.zip', 'r').open('EventMetadata.json'))
df = pd.json_normalize(json_import)
n_records = len(df)
n_records
```
## Null vs empty lists for Keywords, Tasks, Opcodes and Levels
It's very common for some of the provider or message structure to not be used, e.g. Keywords. How these unused or undefined values are handled is highly inconsistent. Windows provider metadata has at least 3 variations for undefined metadata:
- Null value
- Empty list
- List which may contain a null value
## Null values
Keyword nodes for Providers can have null values or empty lists. As another example, the Keyword metadata for 'Microsoft-Windows-EtwCollector' is serialised as:
```json
{
{
"Name": "Microsoft-Windows-EtwCollector",
"Id": "9e5f9046-43c6-4f62-ba13-7b19896253ff",
"MessageFilePath": "C:\\WINDOWS\\system32\\ieetwcollectorres.dll",
"ResourceFilePath": "C:\\WINDOWS\\system32\\ieetwcollectorres.dll",
"ParameterFilePath": null,
"HelpLink": null,
"DisplayName": null,
"LogLinks": [],
"Levels": null,
"Opcodes": null,
"Keywords": null,
"Tasks": null,
"Events": null,
"ProviderName": "Microsoft-Windows-EtwCollector"
}
}
```
The listed summation results below per column label show a handful of Providers didn't use lists for Keywords, Tasks, and Opcodes, but instead were simply Null. E.g. 21 Providers had Null for Keywords.
```
df.isnull().sum()
```
## Empty lists
For providers, quite often empty lists indicate no keywords are defined. E.g. note the `"Keywords": []` for the Powershell provider (JSON object truncated for brevity).
```json
{
"Name": "PowerShell",
"Id": "00000000-0000-0000-0000-000000000000",
"MessageFilePath": "C:\\WINDOWS\\system32\\WindowsPowerShell\\v1.0\\pwrshmsg.dll",
"ResourceFilePath": null,
"ParameterFilePath": null,
"HelpLink": "https://go.microsoft.com/fwlink/events.asp?CoName=Microsoft%20Corporation&ProdName=Microsoft%c2%ae%20Windows%c2%ae%20Operating%20System&ProdVer=10.0.18362.1&FileName=pwrshmsg.dll&FileVer=10.0.18362.1",
"DisplayName": null,
"LogLinks": [
{
"LogName": "Windows PowerShell",
"IsImported": true,
"DisplayName": null
}
],
"Levels": [],
"Opcodes": [],
"Keywords": [],
"Tasks": [
{
"Name": "Engine Health\r\n",
"Value": 1,
"DisplayName": "Engine Health",
"EventGuid": "00000000-0000-0000-0000-000000000000"
},
{
"Name": "Command Health\r\n",
"Value": 2,
"DisplayName": "Command Health",
"EventGuid": "00000000-0000-0000-0000-000000000000"
}
]
}
```
E.g. Overall there were 684 empty list values in Keywords.
```
empty_counts = {}
for c in ['Keywords', 'Tasks', 'Opcodes', 'Levels']:
empty_counts.update(
{c: len(df[df[c].apply(lambda i: isinstance(i, list) and len(i) == 0)])}
)
empty_counts
```
## Null values in Keyword lists
### Event Keywords
For the Event metadata level, keywords can be defined as an empty list, but more often, they are serialised as a list usually with a null item regardless of how many other valid keywords are defined.
Keywords at the Provider metadata level don't seem to have nullfied name values (both 'DisplayName' and 'Name').
```
df_e = pd.json_normalize(json_import, record_path='Events', meta_prefix='Provider.', meta=['Id', 'Name'])
len(df_e)
```
Sometimes Keywords at the Event metadata level are empty lists, but not often. Only ~1200 used a null value.
```
len(df_e[df_e['Keywords'].apply(lambda i: isinstance(i, list) and len(i) == 0)])
```
As a sample of events using an empty keyword list object.
```
df_e[df_e['Keywords'].apply(lambda i: isinstance(i, list) and len(i) == 0)].head()
```
Most Keywords at the Event metadata level do seem to have at least one item with both 'DisplayName' and 'Name' as null.
```
def has_null_names(o):
if isinstance(o, list):
for i in o:
if i['Name'] == None and i['DisplayName'] == None:
return True
elif isinstance(o, dict):
return i['Name'] == None and i['DisplayName'] == None
return False
len(df_e[df_e['Keywords'].apply(has_null_names)])
```
And as a sample of the dual null keyword names
```
pd.options.display.max_colwidth = 100
df_e[df_e['Keywords'].apply(has_null_names)][['Id','Keywords','Description','LogLink.LogName','Provider.Name']].head()
```
With over 40,000 having the nullified keyword name present, it be interesting to observe the events that dont. E.g. for Keywords:
```
pandas.reset_option('display.max_colwidth')
df_e[df_e['Keywords'].apply(lambda k: not has_null_names(k))].head()
```
Unlike Keywords, Task, Opcode and Level objects were already flattened by `json_normalize()` into lables (as these are not nested in a list like Keywords). E.g a sample of nullified tasks.
```
df_e[df_e['Task.Name'].isnull() & df_e['Task.DisplayName'].isnull()][['Id','Task.Value','Task.Name','Task.DisplayName','Description','LogLink.LogName','Provider.Name']].head()
```
The nullified names for Tasks, Opcodes and Levels counted.
```
display_name_and_name_null_count = {}
for c in ['Level', 'Task', 'Opcode']:
display_name_and_name_null_count.update(
{c: len(df_e[df_e[f'{c}.Name'].isnull() & df_e[f'{c}.DisplayName'].isnull()])}
)
display_name_and_name_null_count
```
So while not being lists, the Task, Opcode and Level metadata for events is often nullfied. Even 3863 event ID had no level defined.
### Provider Keywords, Tasks, Opcodes and Levels
However, the Keyword metadata for Providers doens't include the nullfied name items like seen in the Event metadata.
```
has_null_names_in_list_counts = {}
for c in ['Keywords', 'Tasks', 'Opcodes', 'Levels']:
has_null_names_in_list_counts.update(
{c: len(df[df[c].apply(has_null_names)])}
)
has_null_names_in_list_counts
```
## Conclusion
Undefined Keywords, Tasks, Opcodes and Levels have widely divergent data structures. Sometimes it's a simple Null value and other times an empty list. But the metadata level of Provider vs Event also affects the structure used. Keyword lists are particularly awkward and often include special nullified value with a null 'DisplayName' and 'Names'. This nullfied value seems to be unecessarily included along with non-null defined keywords in the list.
| true |
code
| 0.297234 | null | null | null | null |
|
```
%load_ext autoreload
%autoreload 2
```
This notebook is a tentative overview of how we can use my custom library `neurgoo` to train ANNs.
Everything is written from scratch, directly utilizing `numpy`'s arrays and vectorizations.
`neurgoo`'s philosophy is to be as modular as possible, inspired from PyTorch's API design.
# Relevant Standard Imports
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.model_selection import train_test_split
from keras.datasets import mnist
import tensorflow as tf
from pprint import pprint
```
# Data Preprocessing
In this section we:
- load MNIST data
- normalize pixels to [0, 1] (dividing pixel values by 255)
- do train/val/test splits.
## Train/Val/Test splits
Since we're using data from keras module, it only returns
```
def load_data():
"""
This loader function encapsulates preprocessing as well as data splits
"""
(X_train, Y_train), (X_test, Y_test) = mnist.load_data()
Y_train = tf.keras.utils.to_categorical(Y_train)
Y_test = tf.keras.utils.to_categorical(Y_test)
h, w = X_train[0].shape
X_train = X_train.reshape((len(X_train), w*h))/255
X_test = X_test.reshape((len(X_test), w*h))/255
X_val, X_test, Y_val, Y_test = train_test_split(X_test, Y_test, test_size=0.5)
return (X_train, Y_train), (X_val, Y_val), (X_test, Y_test)
(X_train, Y_train), (X_val, Y_val), (X_test, Y_test) = load_data()
X_train.shape, Y_train.shape
X_val.shape, Y_val.shape
X_test.shape, Y_test.shape
```
# Custom Library implementation
Now, we're going to use my `neurgoo` library (see `neurgoo` packages).
There are mostly 5 components that are needed for training:
- layers (either linear or activation)
- models (encapsulate N number of layers into a container)
- losses (compute loss and gradient to find final dJ/dW)
- optimizers (perform weight update operation)
- trainers (encapsulate all the training loop into one single coherent method)
> See the report for more details on the architecture and implementation
## Import all the necessary stuff
Note: Please `pip install requirements.txt` first.
`neurgoo` can also be installed locally as:
- `pip install -e .`
- or `python setup.py install`
- or simple copy-paste the package `neurgoo` anywhere to use it.
### Layers
```
from neurgoo.layers.linear import Linear
from neurgoo.layers.activations import(
ReLU,
Sigmoid,
Softmax,
)
```
### Models
```
from neurgoo.models import DefaultNNModel
```
### Losses
```
from neurgoo.losses import (
BinaryCrossEntropyLoss,
CrossEntropyLossWithLogits,
HingeLoss,
MeanSquaredError,
)
```
### Optimizers
```
from neurgoo.optimizers import SGD
```
### Trainers
```
from neurgoo.trainers import DefaultModelTrainer
```
### Evaluators
```
from neurgoo.misc.eval import Evaluator
```
## Combine Components for training
Now we use available components to form one coherent trainer
### build model
We can add any number of layers.
Each `Linear` layer can take `in_features` number of inputs and gives `num_neurons` number of output.
Linear layer also has different initialization methods which we can access right after building the layer object.
(This is like a builder design pattern):
- `initialize_random()` initializes weights randomly
- `initialize_gaussian(variance=...)` initializes weights from a gaussian distribution with **mu** centered at 0 and variance supplied
Each layer's forward pass is done through `feed_forward(...)` method.
Each layer's backward pass is done through `backpropagate(...)` method.
### model 1
```
# a model with single hidden layer with 512 neurons
model = DefaultNNModel()
model.add_layer(
Linear(num_neurons=512, in_features=X_train.shape[1])\
.initialize_gaussian(variance=2/784)
)
model.add_layer(ReLU())
model.add_layer(Linear(num_neurons=10, in_features=512))
```
### model 2
```
# a model with single hidden layer with 128 neurons
model = DefaultNNModel()
model.add_layer(
Linear(num_neurons=128, in_features=X_train.shape[1])\
.initialize_gaussian(variance=2/784)
)
model.add_layer(ReLU())
model.add_layer(Linear(num_neurons=10, in_features=128))
```
### model 3
```
# a model with 2 hidden layers
model = DefaultNNModel()
model.add_layer(
Linear(num_neurons=256, in_features=X_train.shape[1])\
.initialize_gaussian(variance=2/784)
)
model.add_layer(ReLU())
model.add_layer(
Linear(num_neurons=128, in_features=256)\
.initialize_gaussian(variance=2/256)
)
model.add_layer(ReLU())
model.add_layer(Linear(num_neurons=10, in_features=128))
```
#### model 4
```
# a model with 2 hidden layers
model = DefaultNNModel()
model.add_layer(
Linear(num_neurons=512, in_features=X_train.shape[1]).initialize_gaussian()
)
model.add_layer(ReLU())
model.add_layer(
Linear(num_neurons=256, in_features=512).initialize_gaussian()
)
model.add_layer(ReLU())
model.add_layer(Linear(num_neurons=10, in_features=256))
print(model)
```
### build optimizer
```
params = model.params()
print(params)
optimizer = SGD(params=params, lr=0.001)
```
### build loss
```
# loss = CrossEntropyLossWithLogits()
loss = HingeLoss()
```
### build trainer
```
# helper component for evaluating the model
evaluator = Evaluator(num_classes=10)
trainer = DefaultModelTrainer(
model=model,
optimizer=optimizer,
evaluator=evaluator,
loss=loss,
debug=False,
)
```
## Start Training
We call `fit(...)` method of the trainer.The trainer takes in splitted data, number of epochs and batch_size.
Once the training is done, we get a ``dict`` that represents history of train/val/test for each epoch.
> Note: test is evaluated only when the whole training is complete, after the end of last epoch.
During training, several debug logs are also printed like:
- Information about number of epochs passed
- Train accuracy/loss
- Validation accuracy/loss
```
print(model[-1], loss)
history = trainer.fit(
X_train=X_train,
Y_train=Y_train,
X_val=X_val,
Y_val=Y_val,
X_test=X_test,
Y_test=Y_test,
nepochs=75,
batch_size=64,
)
```
### Understanding history
The history `dict` returned by the trainer consits of training history for train/val/test.
The `train` and `val` consists of list of `neurgoo.misc.eval.EvalData` objects. Each `EvalData` object can store:
- epoch
- loss
- accuracy
- precision (to be implemented)
- recall (to be implemented)
Unlike `train` and `val`, the `test` history is a single `EvalData` object, not a list which stores final evaluation data after the end of the training.
```
history["train"][:10]
history["val"][:10]
history["test"]
```
### Plot history
We use the plotting tools from neurgoo.
The `plot_history` is convenient helper that takes in the history dict and plots the metrics.
Since, we can plot train-vs-val losses and accuracies, the parameter `plot_type` controls what type of plot we want.
- `plot_type="loss"` for plotting losses
- `plot_type="accuracy"` for plotting accuracies
```
from neurgoo.misc.plot_utils import plot_history
plot_history(history, plot_type="loss")
plot_history(history, plot_type="accuracy")
```
# Inference Debug
Now that we have trained our model, we can do inference directly through its `predict(...)` method
which takes in X values and gives final output.
In this section we will do infernece on a random test data point.
The `plot_images` will plot image as well as the label assigned from target or got from predictions (np.argmax).
For the predicted Y values, we also add a probability text beside the label to debug the probabilities.
## Note
If we have the final layer as `neurgoo.layers.activations.Softmax`, we can get normalized probabilities directly from the prediction.
If we have usual `Linear` layer in the last, we won't have normalized probabilitites. So, we need to pass the prediction to a Softmax and then get the probabilities.
```
import random
def plot_images(X, Y, cols=5, title=""):
print(f"X.shape: {X.shape} | Y.shape: {Y.shape}")
_, axes = plt.subplots(nrows=1, ncols=cols, figsize=(10, 3))
n = int(X.shape[1]**0.5)
probs = Softmax()(Y)
for ax, img, t, p in zip(axes, X, Y, probs):
label = np.argmax(t)
prob = round(np.max(p), 3)
img = img.reshape((n, n))
ax.set_axis_off()
ax.imshow(img, cmap=plt.cm.gray_r, interpolation="nearest")
txt = f"{title}: {label}"
txt = f"{txt}({prob})" if "inf" in title.lower() else txt
ax.set_title(txt)
X_test.shape, Y_test.shape
model.eval_mode()
k = 7
for i in range(2):
indices_infer = random.choices(range(len(X_test)), k=k)
X_infer, Y_infer_target = X_test[indices_infer], Y_test[indices_infer]
# forward pass
predictions = model.predict(X_infer)
plot_images(X_infer, Y_infer_target, cols=k, title="Target")
plot_images(X_infer, predictions, cols=k, title="Inf")
```
# Observations
1) For visually similar numbers like 7 and 1, sometimes the model is less confidence while trying to predict for the number **7**. In such cases, we have relatively lower probabilities like `0.8`, `0.9`, etc. This can be mitigated if we "properly" trained the model with:
- better architecture
- more training time
- adding regularizations and dropout tricks
2) For unique images like `0, 5, 6`, we see high probilities as the model doesn't get "confused" much.
# Further Improvements to neurgoo
There's definitely more rooms for improvement in `neurgoo`. We could:
- implement `Dropout` and `BatchNorm` layers at `neurgoo.layers` using the base class `neurgoo._base.AbstractLayer`
- add regularization techniques
- implement better optimizers such as addition of Nesterov momentum, Adam optimizers, etc. This could be done by adding new optimizer components at `neurgoo.optimizers`, directly derived from `neurgoo._base.AbstractOptimizer`
- use automatic differentiation techniques [0] for computing accurate gradients.
# References and footnotes
- [0] - https://en.wikipedia.org/wiki/Automatic_differentiation
- [PyTorch Internals](http://blog.ezyang.com/2019/05/pytorch-internals/)
- [How Computational Graphs are Constructed in PyTorch](https://pytorch.org/blog/computational-graphs-constructed-in-pytorch/)
- [Why is the ReLU function not differentiable at x=0?](https://sebastianraschka.com/faq/docs/relu-derivative.html)
| true |
code
| 0.700652 | null | null | null | null |
|
# Sersic Profiles
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Setup" data-toc-modified-id="Setup-1"><span class="toc-item-num">1 </span>Setup</a></span></li><li><span><a href="#Sersic-parameter-fits" data-toc-modified-id="Sersic-parameter-fits-2"><span class="toc-item-num">2 </span>Sersic parameter fits</a></span></li><li><span><a href="#Timecourse-of-Sersic-profiles" data-toc-modified-id="Timecourse-of-Sersic-profiles-3"><span class="toc-item-num">3 </span>Timecourse of Sersic profiles</a></span><ul class="toc-item"><li><span><a href="#Half-mass-radius" data-toc-modified-id="Half-mass-radius-3.1"><span class="toc-item-num">3.1 </span>Half-mass radius</a></span></li><li><span><a href="#Sersic-parameter" data-toc-modified-id="Sersic-parameter-3.2"><span class="toc-item-num">3.2 </span>Sersic parameter</a></span></li></ul></li><li><span><a href="#Bulge-mass-profiles" data-toc-modified-id="Bulge-mass-profiles-4"><span class="toc-item-num">4 </span>Bulge mass profiles</a></span><ul class="toc-item"><li><span><a href="#MW,-3-timepoints" data-toc-modified-id="MW,-3-timepoints-4.1"><span class="toc-item-num">4.1 </span>MW, 3 timepoints</a></span></li><li><span><a href="#M31,-3-timepoints" data-toc-modified-id="M31,-3-timepoints-4.2"><span class="toc-item-num">4.2 </span>M31, 3 timepoints</a></span></li><li><span><a href="#MW-vs-M31,-two-timepoints" data-toc-modified-id="MW-vs-M31,-two-timepoints-4.3"><span class="toc-item-num">4.3 </span>MW vs M31, two timepoints</a></span></li></ul></li></ul></div>
## Setup
```
import numpy as np
import astropy.units as u
from scipy.optimize import curve_fit
# import plotting modules
import matplotlib.pyplot as plt
import matplotlib
from matplotlib import rcParams
%matplotlib inline
from galaxy.galaxy import Galaxy
from galaxy.galaxies import Galaxies
from galaxy.centerofmass import CenterOfMass
from galaxy.massprofile import MassProfile
from galaxy.timecourse import TimeCourse
def get_sersic(galname, snap, R):
mp = MassProfile(Galaxy(galname, snap, usesql=True))
Re_bulge, bulge_total, BulgeI = mp.bulge_Re(R)
n, err = mp.fit_sersic_n(R, Re_bulge, bulge_total, BulgeI)
return Re_bulge, n, err
tc = TimeCourse()
# Array of radii
R = np.arange(0.1, 30, 0.1) * u.kpc
```
## Sersic parameter fits
The next cell takes significant time to run so is commented out.
```
# with open('./sersic.txt', 'w') as f:
# f.write(f"# {'gal':>5s}{'snap':>8s}{'t':>8s}{'Re':>8s}{'n':>8s}{'err':>8s}\n")
# for galname in ('M31','MW'):
# print(galname)
# for snap in np.arange(0,802):
# t = tc.snap2time(snap)
# try:
# Re, n, err = get_sersic(galname, snap, R)
# with open('./sersic.txt', 'a') as f:
# f.write(f"{galname:>7s}{snap:8d}{t:8.3f}{Re.value:8.2f}{n:8.2f}{err:8.4f}\n")
# except ValueError:
# print(galname, snap)
```
## Timecourse of Sersic profiles
```
ser = np.genfromtxt('sersic_full.txt', names=True, skip_header=0,
dtype=[('gal', 'U3'), ('snap', '<i8'), ('t', '<f8'), ('Re', '<f8'),
('n', '<f8'), ('err', '<f8')])
MW = ser[ser['gal'] == 'MW']
M31 = ser[ser['gal'] == 'M31']
```
### Half-mass radius
```
fig = plt.figure(figsize=(8,5))
ax0 = plt.subplot()
# add the curves
n = 1 # plot every n'th time point
ax0.plot(MW['t'][::n], MW['Re'][::n], 'r-', lw=2, label='MW')
ax0.plot(M31['t'][::n], M31['Re'][::n], 'b:', lw=2, label='M31')
ax0.legend(fontsize='xx-large', shadow=True)
# Add axis labels
ax0.set_xlabel("time (Gyr)", fontsize=22)
ax0.set_ylabel("Re (kpc)", fontsize=22)
ax0.set_xlim(0,12)
ax0.set_ylim(0,6)
# ax0.set_title("Hernquist scale radius", fontsize=24)
#adjust tick label font size
label_size = 22
rcParams['xtick.labelsize'] = label_size
rcParams['ytick.labelsize'] = label_size
plt.tight_layout()
plt.savefig('sersic_Re.pdf', rasterized=True, dpi=350);
```
### Sersic parameter
```
fig = plt.figure(figsize=(8,5))
ax0 = plt.subplot()
# add the curves
n = 1 # plot every n'th time point
ax0.errorbar(MW['t'][::n], MW['n'][::n], yerr=MW['err'][::n], fmt='r-', lw=2, label='MW')
ax0.errorbar(M31['t'][::n], M31['n'][::n], yerr=M31['err'][::n], fmt='b:', lw=2, label='M31')
ax0.legend(fontsize='xx-large', shadow=True)
# Add axis labels
ax0.set_xlabel("time (Gyr)", fontsize=22)
ax0.set_ylabel("Sersic $n$", fontsize=22)
ax0.set_xlim(0,12)
ax0.set_ylim(5,7)
# ax0.set_title("Hernquist scale radius", fontsize=24)
#adjust tick label font size
label_size = 22
rcParams['xtick.labelsize'] = label_size
rcParams['ytick.labelsize'] = label_size
plt.tight_layout()
plt.savefig('sersic_n.pdf', rasterized=True, dpi=350);
```
## Bulge mass profiles
```
Re_bulge = {}
bulge_total = {}
BulgeI = {}
Sersic = {}
n = {}
for galname in ('MW','M31'):
for snap in (1, 335, 801):
key = f'{galname}_{snap:03}'
mp = MassProfile(Galaxy(galname, snap, usesql=True))
Re_bulge[key], bulge_total[key], BulgeI[key] = mp.bulge_Re(R)
n[key], _ = mp.fit_sersic_n(R, Re_bulge[key], bulge_total[key], BulgeI[key])
Sersic[key] = mp.sersic(R.value, Re_bulge[key].value, n[key], bulge_total[key])
```
### MW, 3 timepoints
```
fig = plt.figure(figsize=(8,8))
# subplots = (121, 122)
ax0 = plt.subplot()
galname = 'MW'
for snap in (1, 335, 801):
key = f'{galname}_{snap:03}'
t = tc.snap2time(snap)
# plot the bulge luminosity density as a proxy for surface brightness
ax0.semilogy(R, BulgeI[key], lw=2, label=f'Bulge Density, t={t:.2f} Gyr')
ax0.semilogy(R, Sersic[key], lw=3, ls=':',
label=f'Sersic n={n[key]:.2f}, Re={Re_bulge[key]:.1f}')
# Add axis labels
ax0.set_xlabel('Radius (kpc)', fontsize=22)
ax0.set_ylabel('Log(I) $L_\odot/kpc^2$', fontsize=22)
ax0.set_xlim(0,20)
#adjust tick label font size
label_size = 22
matplotlib.rcParams['xtick.labelsize'] = label_size
matplotlib.rcParams['ytick.labelsize'] = label_size
# add a legend with some customizations.
legend = ax0.legend(loc='upper right',fontsize='x-large');
```
### M31, 3 timepoints
```
fig = plt.figure(figsize=(8,8))
# subplots = (121, 122)
ax0 = plt.subplot()
galname = 'M31'
for snap in (1, 335, 801):
key = f'{galname}_{snap:03}'
t = tc.snap2time(snap)
# plot the bulge luminosity density as a proxy for surface brightness
ax0.semilogy(R, BulgeI[key], lw=2, label=f'Bulge Density, t={t:.2f} Gyr')
ax0.semilogy(R, Sersic[key], lw=3, ls=':',
label=f'Sersic n={n[key]:.2f}, Re={Re_bulge[key]:.1f}')
# Add axis labels
ax0.set_xlabel('Radius (kpc)', fontsize=22)
ax0.set_ylabel('Log(I) $L_\odot/kpc^2$', fontsize=22)
ax0.set_xlim(0,20)
#adjust tick label font size
label_size = 22
matplotlib.rcParams['xtick.labelsize'] = label_size
matplotlib.rcParams['ytick.labelsize'] = label_size
# add a legend with some customizations.
legend = ax0.legend(loc='upper right',fontsize='xx-large')
plt.tight_layout()
plt.savefig('MW_bulge_sersic.pdf', rasterized=True, dpi=350);
```
### MW vs M31, two timepoints
```
fig = plt.figure(figsize=(8,8))
# subplots = (121, 122)
ax0 = plt.subplot()
galname = 'MW'
for snap in (1, 801):
key = f'{galname}_{snap:03}'
t = tc.snap2time(snap)
# plot the bulge luminosity density as a proxy for surface brightness
ax0.semilogy(R, BulgeI[key], lw=2, label=f'MW, t={t:.2f} Gyr')
galname = 'M31'
for snap in (1, 801):
key = f'{galname}_{snap:03}'
t = tc.snap2time(snap)
# plot the bulge luminosity density as a proxy for surface brightness
ax0.semilogy(R, BulgeI[key], lw=2, ls=':', label=f'M31, t={t:.2f} Gyr')
# Add axis labels
ax0.set_xlabel('Radius (kpc)', fontsize=22)
ax0.set_ylabel('Log(I) $L_\odot/kpc^2$', fontsize=22)
ax0.set_xlim(0,20)
#adjust tick label font size
label_size = 22
matplotlib.rcParams['xtick.labelsize'] = label_size
matplotlib.rcParams['ytick.labelsize'] = label_size
# add a legend with some customizations.
legend = ax0.legend(loc='upper right',fontsize='xx-large')
plt.tight_layout()
plt.savefig('bulge_mp.pdf', rasterized=True, dpi=350);
```
| true |
code
| 0.555737 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/gtbook/robotics/blob/main/S36_vacuum_RL.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
%pip install -q -U gtbook
import numpy as np
import gtsam
import pandas as pd
import gtbook
import gtbook.display
from gtbook import vacuum
from gtbook.discrete import Variables
VARIABLES = Variables()
def pretty(obj):
return gtbook.display.pretty(obj, VARIABLES)
def show(obj, **kwargs):
return gtbook.display.show(obj, VARIABLES, **kwargs)
# From section 3.2:
N = 5
X = VARIABLES.discrete_series("X", range(1, N+1), vacuum.rooms)
A = VARIABLES.discrete_series("A", range(1, N), vacuum.action_space)
# From section 3.5:
conditional = gtsam.DiscreteConditional((2,5), [(0,5), (1,4)], vacuum.action_spec)
R = np.empty((5, 4, 5), float)
T = np.empty((5, 4, 5), float)
for assignment, value in conditional.enumerate():
x, a, y = assignment[0], assignment[1], assignment[2]
R[x, a, y] = 10.0 if y == vacuum.rooms.index("Living Room") else 0.0
T[x, a, y] = value
```
# Reinforcement Learning
> We will talk about model-based and model-free learning.
**This Section is still in draft mode and was released for adventurous spirits (and TAs) only.**
```
from gtbook.display import randomImages
from IPython.display import display
display(randomImages(3, 6, "steampunk", 1))
```
## Exploring to get Data
> Where we gather experience.
Let's adapt the `policy_rollout` code from the previous section to generate a whole lot of experiences of the form $(x,a,x',r)$.
```
def explore_randomly(x1, horizon=N):
"""Roll out states given a random policy, for given horizon."""
data = []
x = x1
for _ in range(1, horizon):
a = np.random.choice(4)
next_state_distribution = gtsam.DiscreteDistribution(X[1], T[x, a])
x_prime = next_state_distribution.sample()
data.append((x, a, x_prime, R[x, a, x_prime]))
x = x_prime
return data
```
Let us use it to create 499 experiences and show the first 10:
```
data = explore_randomly(vacuum.rooms.index("Living Room"), horizon=500)
print(data[:10])
```
## Model-based Reinforcement Learning
> Just count, then solve the MDP.
We can *estimate* the transition probabilities $T$ and reward table $R$ from the data, and then we can use the algorithms from before to calculate the value function and/or optimal policy.
The math is just a variant of what we saw in the learning section of the last chapter. The rewards is easiest:
$$
R(x,a,x') \approx \frac{1}{N(x,a,x')} \sum_{x,a,x'} r
$$
where $N(x,a,x')$ counts how many times an experience $(x,a,x')$ was recorded. The transition probabilities are a bit trickier:
$$
P(x'|x,a) \approx \frac{N(x,a,x)}{N(x,a)}
$$
where $N(x,a)=\sum_{x'} N(x,a,x')$ is the number of times we took action $a$ in a state $x$.
The code associated with that is fairly simple, modulo some numpy trickery to deal with division by zero and *broadcasting* the division:
```
R_sum = np.zeros((5, 4, 5), float)
T_count = np.zeros((5, 4, 5), float)
count = np.zeros((5, 4), int)
for x, a, x_prime, r in data:
R_sum[x, a, x_prime] += r
T_count[x, a, x_prime] += 1
R_estimate = np.divide(R_sum, T_count, where=T_count!=0)
xa_count = np.sum(T_count, axis=2)
T_estimate = T_count/np.expand_dims(xa_count, axis=-1)
```
Above `T_count` corresponds to $N(x,a,x')$, and the variable `xa_count` is $N(x,a)$. It is good to check the latter to see whether our experiences were more or less representative, i.e., visited all state-action pairs:
```
xa_count
```
This seems pretty good. If not, we can always gather more data, which we encourage you to experiment with.
We can compare the ground truth transition probabilities $T$ with the estimated transition probabilities $\hat{T}$, e.g., for the living room:
```
print(f"ground truth:\n{T[0]}")
print(f"estimate:\n{np.round(T_estimate[0],2)}")
```
Not bad. And for the rewards:
```
print(f"ground truth:\n{R[0]}")
print(f"estimate:\n{np.round(R_estimate[0],2)}")
```
In summary, learning in this context can simply be done by gathering lots of experiences, and estimating models for how the world behaves.
## Model-free Reinforcement Learning
> All you need is Q, la la la la.
A different, model-free approach is **Q_learning**. In the above we tried to *model* the world by trying estimate the (large) transition and reward tables. However, remember from the previous section that there is a much smaller table of Q-values $Q(x,a)$ that also allow us to act optimally, because we have
$$
\pi^*(x) = \arg \max_a Q^*(x,a)
$$
where the Q-values are defined as
$$
Q^*(x,a) \doteq \bar{R}(x,a) + \gamma \sum_{x'} P(x'|x, a) V^*(x')
$$
This begs the question whether we can simply learn the Q-values instead, which might be more *sample-efficient*, i.e., we would get more accurate values with less training data, as we have less quantities to estimate.
To do this, remember that the Bellman equation can be written as
$$
V^*(x) = \max_a Q^*(x,a)
$$
allowing us to rewrite the Q-values from above as
$$
Q^*(x,a) = \sum_{x'} P(x'|x, a) \{ R(x,a,x') + \gamma \max_{a'} Q^*(x',a') \}
$$
This gives us a way to estimate the Q-values, as we can approximate the above using a Monte Carlo estimate, summing over our experiences:
$$
Q^*(x,a) \approx \frac{1}{N(x,a)} \sum_{x,a,x'} R(x,a,x') + \gamma \max_{a'} Q^*(x',a')
$$
Unfortunately the estimate above *depends* on the optimal Q-values. Hence, the final Q-learning algorithm applies this estimate gradually, by "alpha-blending" between old and new estimates, which also averages over the reward:
$$
\hat{Q}(x,a) \leftarrow (1-\alpha) \hat{Q}(x,a) + \alpha \{R(x,a,x') + \gamma \max_{a'} \hat{Q}(x',a') \}
$$
In code:
```
alpha = 0.5 # learning rate
gamma = 0.9 # discount factor
Q = np.zeros((5, 4), float)
for x, a, x_prime, r in data:
old_Q_estimate = Q[x,a]
new_Q_estimate = r + gamma * np.max(Q[x_prime])
Q[x, a] = (1.0-alpha) * old_Q_estimate + alpha * new_Q_estimate
print(Q)
```
These values are not yet quite accurate, as you can ascertain yourself by changing the number of experiences above, but note that an optimal policy can be achieved before we even converge.
| true |
code
| 0.51501 | null | null | null | null |
|
# **Assignment - 2: Basic Data Understanding**
---
This assignment will get you familiarized with Python libraries and functions required for data visualization.
---
## Part 1 - Loading data
---
###Import the following libraries:
* ```numpy``` with an alias name ```np```,
* ```pandas``` with an alias name ```pd```,
* ```matplotlib.pyplot``` with an alias name ```plt```, and
* ```seaborn``` with an alias name ```sns```.
```
# Load the four libraries with their aliases
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
```
### Using the files ```train.csv``` and ```moviesData.csv```, peform the following:
* Load these file as ```pandas``` dataframes and store it in variables named ```df``` and ```movies``` respectively.
* Print the first ten rows of ```df```.
```
# Load the file as a dataframe
df = pd.read_csv("train.csv")
movies = pd.read_csv("moviesData.csv")
# Print the first ten rows of df
df.head(10)
```
### Using the dataframe ```df```, perform the following:
* Print the first five rows of the column ```MonthlyRate```.
* Find out the details of the column ```MonthlyRate``` like mean, maximum value, minimum value, etc.
```
# Print the first five rows of MonthlyRate
df["MonthlyRate"].head(5)
# Find the details of MonthlyRate
df["MonthlyRate"].describe()
```
---
## Part 2 - Cleaning and manipulating data
---
### Using the dataframe ```df```, peform the following:
* Check whether there are any missing values in ```df```.
* If yes, drop those values and print the size of ```df``` after dropping these.
```
# Check for missing values
df.isna()
# Drop the missing values
df.dropna()
# Print the size of df after dropping
df.shape
```
### Using the dataframe ```df```, peform the following:
* Add another column named ```MonthRateNew``` in ```df``` by subtracting the mean from ```MonthlyRate``` and dividing it by standard deviation.
```
# Add a column named MonthRateNew
df["MonthRateNew"] = (df["MonthlyRate"] - df["MonthlyRate"].mean()) / df["MonthlyRate"].std()
df
```
### Using the dataframe ```movies```, perform the following:
* Check whether there are any missing values in ```movies```.
* Find out the number of observations/rows having any of their features/columns missing.
* Drop the missing values and print the size of ```movies``` after dropping these.
* Instead of dropping the missing values, replace the missing values by their mean (or some suitable value).
```
# Check for missing values
movies.isna().sum()
# Replace the missing values
# You can use SimpleImputer of sklearn for this
# Drop the missing values
movies_new = movies.dropna()
movies_new.shape
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(missing_values=np.NaN, strategy="mean")
movies["runtime"] = imputer.fit_transform(movies[["runtime"]]).ravel()
movies["runtime"]
```
---
## Part 3 - Visualizing data
---
### Visualize the ```df``` by drawing the following plots:
* Plot a histogram of ```Age``` and find the range in which most people are there.
* Modify the histogram of ```Age``` by adding 30 bins.
* Draw a scatter plot between ```Age``` and ```Attrition``` and suitable labels to the axes. Find out whether people more than 50 years are more likely to leave the company. (```Attrition``` = 1 means people have left the company).
```
# Plot and modify the histogram of Age
plt.hist(df.Age)
df.hist(column="Age", bins=30, color="green", figsize=(10,10))
# Draw a scatter plot between Age and Attrition
plt.scatter(df.Age, df.Attrition, c="pink")
plt.xlim(10,70)
plt.ylim(0,1)
plt.title("Scatter Plot Example")
plt.show()
```
### Visualize the ```df``` by following the steps given below:
* Get a series containing counts of unique values of ```Attrition```.
* Draw a countplot for ```Attrition``` using ```sns.countplot()```.
### Visualize the ```df``` by following the steps given below:
* Draw a cross tabulation of ```Attrition``` and ```BusinessTravel``` as bar charts. Find which value of ```BusinessTravel``` has highest number of people.
```
# Get a series of counts of values of Attrition
# Draw a countplot for Attrition
# You may use countplot of seaborn for this
df.Attrition.value_counts()
sns.countplot(x="Attrition", data=df)
plt.ylim(0,1000)
plt.show()
# Draw a cross tab of Attritiona and BusinessTravel
# You may use crosstab of pandas for this
pd.crosstab(df.BusinessTravel, df.Attrition).plot(kind="bar")
plt.ylabel("Attrition")
```
### Visualize the ```df``` by drawing the following plot:
* Draw a stacked bar chart between ```Attrition``` and ```Gender``` columns.
```
# Draw a stacked bar chart between Attrition and Gender
new_df = pd.crosstab(df.Gender, df.Attrition)
new_df.plot(kind="bar", stacked=True)
plt.ylabel("Attrition")
```
### Visualize the ```df``` by drawing the following histogram:
* Draw a histogram of ```TotalWorkingYears``` with 30 bins.
* Draw a histogram of ```YearsAtCompany``` with 30 bins and find whether the values in ```YearsAtCompany``` are skewed.
```
# Draw a histogram of TotalWorkingYears with 30 bins
df.hist(column="TotalWorkingYears", bins=30, color="red")
plt.show()
# Draw a histogram of YearsAtCompany
df.hist(column="YearsAtCompany", figsize=(10,10), color="yellow")
```
### Visualize the ```df``` by drawing the following boxplot:
* Draw a boxplot of ```MonthlyIncome``` for each ```Department``` and report whether there is/are outlier(s).
```
# Draw a boxplot of MonthlyIncome for each Department and report outliers
sns.boxplot('Department', 'MonthlyIncome', data=df)
```
### Visualize the ```df``` by drawing the following piechart:
* Create a pie chart of the values in ```JobRole``` with suitable label and report which role has highest number of persons.
```
# Create a piechart of JobRole
# You will need to find the counts of unique values in JobRole.
number_of_roles = df.JobRole.value_counts()
number_of_roles
plt.pie(number_of_roles)
plt.pie(number_of_roles, labels=number_of_roles)
plt.pie(number_of_roles, labels=number_of_roles.index.tolist())
plt.show()
```
| true |
code
| 0.662278 | null | null | null | null |
|
Conditional Generative Adversarial Network
----------------------------------------
*Note: This example implements a GAN from scratch. The same model could be implemented much more easily with the `dc.models.GAN` class. See the MNIST GAN notebook for an example of using that class. It can still be useful to know how to implement a GAN from scratch for advanced situations that are beyond the scope of what the standard GAN class supports.*
A Generative Adversarial Network (GAN) is a type of generative model. It consists of two parts called the "generator" and the "discriminator". The generator takes random values as input and transforms them into an output that (hopefully) resembles the training data. The discriminator takes a set of samples as input and tries to distinguish the real training samples from the ones created by the generator. Both of them are trained together. The discriminator tries to get better and better at telling real from false data, while the generator tries to get better and better at fooling the discriminator.
A Conditional GAN (CGAN) allows additional inputs to the generator and discriminator that their output is conditioned on. For example, this might be a class label, and the GAN tries to learn how the data distribution varies between classes.
For this example, we will create a data distribution consisting of a set of ellipses in 2D, each with a random position, shape, and orientation. Each class corresponds to a different ellipse. Let's randomly generate the ellipses.
```
import deepchem as dc
import numpy as np
import tensorflow as tf
n_classes = 4
class_centers = np.random.uniform(-4, 4, (n_classes, 2))
class_transforms = []
for i in range(n_classes):
xscale = np.random.uniform(0.5, 2)
yscale = np.random.uniform(0.5, 2)
angle = np.random.uniform(0, np.pi)
m = [[xscale*np.cos(angle), -yscale*np.sin(angle)],
[xscale*np.sin(angle), yscale*np.cos(angle)]]
class_transforms.append(m)
class_transforms = np.array(class_transforms)
```
This function generates random data from the distribution. For each point it chooses a random class, then a random position in that class' ellipse.
```
def generate_data(n_points):
classes = np.random.randint(n_classes, size=n_points)
r = np.random.random(n_points)
angle = 2*np.pi*np.random.random(n_points)
points = (r*np.array([np.cos(angle), np.sin(angle)])).T
points = np.einsum('ijk,ik->ij', class_transforms[classes], points)
points += class_centers[classes]
return classes, points
```
Let's plot a bunch of random points drawn from this distribution to see what it looks like. Points are colored based on their class label.
```
%matplotlib inline
import matplotlib.pyplot as plot
classes, points = generate_data(1000)
plot.scatter(x=points[:,0], y=points[:,1], c=classes)
```
Now let's create the model for our CGAN.
```
import deepchem.models.tensorgraph.layers as layers
model = dc.models.TensorGraph(learning_rate=1e-4, use_queue=False)
# Inputs to the model
random_in = layers.Feature(shape=(None, 10)) # Random input to the generator
generator_classes = layers.Feature(shape=(None, n_classes)) # The classes of the generated samples
real_data_points = layers.Feature(shape=(None, 2)) # The training samples
real_data_classes = layers.Feature(shape=(None, n_classes)) # The classes of the training samples
is_real = layers.Weights(shape=(None, 1)) # Flags to distinguish real from generated samples
# The generator
gen_in = layers.Concat([random_in, generator_classes])
gen_dense1 = layers.Dense(30, in_layers=gen_in, activation_fn=tf.nn.relu)
gen_dense2 = layers.Dense(30, in_layers=gen_dense1, activation_fn=tf.nn.relu)
generator_points = layers.Dense(2, in_layers=gen_dense2)
model.add_output(generator_points)
# The discriminator
all_points = layers.Concat([generator_points, real_data_points], axis=0)
all_classes = layers.Concat([generator_classes, real_data_classes], axis=0)
discrim_in = layers.Concat([all_points, all_classes])
discrim_dense1 = layers.Dense(30, in_layers=discrim_in, activation_fn=tf.nn.relu)
discrim_dense2 = layers.Dense(30, in_layers=discrim_dense1, activation_fn=tf.nn.relu)
discrim_prob = layers.Dense(1, in_layers=discrim_dense2, activation_fn=tf.sigmoid)
```
We'll use different loss functions for training the generator and discriminator. The discriminator outputs its predictions in the form of a probability that each sample is a real sample (that is, that it came from the training set rather than the generator). Its loss consists of two terms. The first term tries to maximize the output probability for real data, and the second term tries to minimize the output probability for generated samples. The loss function for the generator is just a single term: it tries to maximize the discriminator's output probability for generated samples.
For each one, we create a "submodel" specifying a set of layers that will be optimized based on a loss function.
```
# Discriminator
discrim_real_data_loss = -layers.Log(discrim_prob+1e-10) * is_real
discrim_gen_data_loss = -layers.Log(1-discrim_prob+1e-10) * (1-is_real)
discrim_loss = layers.ReduceMean(discrim_real_data_loss + discrim_gen_data_loss)
discrim_submodel = model.create_submodel(layers=[discrim_dense1, discrim_dense2, discrim_prob], loss=discrim_loss)
# Generator
gen_loss = -layers.ReduceMean(layers.Log(discrim_prob+1e-10) * (1-is_real))
gen_submodel = model.create_submodel(layers=[gen_dense1, gen_dense2, generator_points], loss=gen_loss)
```
Now to fit the model. Here are some important points to notice about the code.
- We use `fit_generator()` to train only a single batch at a time, and we alternate between the discriminator and the generator. That way. both parts of the model improve together.
- We only train the generator half as often as the discriminator. On this particular model, that gives much better results. You will often need to adjust `(# of discriminator steps)/(# of generator steps)` to get good results on a given problem.
- We disable checkpointing by specifying `checkpoint_interval=0`. Since each call to `fit_generator()` includes only a single batch, it would otherwise save a checkpoint to disk after every batch, which would be very slow. If this were a real project and not just an example, we would want to occasionally call `model.save_checkpoint()` to write checkpoints at a reasonable interval.
```
batch_size = model.batch_size
discrim_error = []
gen_error = []
for step in range(20000):
classes, points = generate_data(batch_size)
class_flags = dc.metrics.to_one_hot(classes, n_classes)
feed_dict={random_in: np.random.random((batch_size, 10)),
generator_classes: class_flags,
real_data_points: points,
real_data_classes: class_flags,
is_real: np.concatenate([np.zeros((batch_size,1)), np.ones((batch_size,1))])}
discrim_error.append(model.fit_generator([feed_dict],
submodel=discrim_submodel,
checkpoint_interval=0))
if step%2 == 0:
gen_error.append(model.fit_generator([feed_dict],
submodel=gen_submodel,
checkpoint_interval=0))
if step%1000 == 999:
print(step, np.mean(discrim_error), np.mean(gen_error))
discrim_error = []
gen_error = []
```
Have the trained model generate some data, and see how well it matches the training distribution we plotted before.
```
classes, points = generate_data(1000)
feed_dict = {random_in: np.random.random((1000, 10)),
generator_classes: dc.metrics.to_one_hot(classes, n_classes)}
gen_points = model.predict_on_generator([feed_dict])
plot.scatter(x=gen_points[:,0], y=gen_points[:,1], c=classes)
```
| true |
code
| 0.539165 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/mashyko/Caffe2_Detectron2/blob/master/Caffe2_Quickload.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Tutorials Installation:
https://caffe2.ai/docs/tutorials.html
First download the tutorials source.
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/My Drive/
!git clone --recursive https://github.com/caffe2/tutorials caffe2_tutorials
# Model Quickload
This notebook will show you how to quickly load a pretrained SqueezeNet model and test it on images of your choice in four main steps.
1. Load the model
2. Format the input
3. Run the test
4. Process the results
The model used in this tutorial has been pretrained on the full 1000 class ImageNet dataset, and is downloaded from Caffe2's [Model Zoo](https://github.com/caffe2/caffe2/wiki/Model-Zoo). For an all around more in-depth tutorial on using pretrained models check out the [Loading Pretrained Models](https://github.com/caffe2/caffe2/blob/master/caffe2/python/tutorials/Loading_Pretrained_Models.ipynb) tutorial.
Before this script will work, you need to download the model and install it. You can do this by running:
```
sudo python -m caffe2.python.models.download -i squeezenet
```
Or make a folder named `squeezenet`, download each file listed below to it, and place it in the `/caffe2/python/models/` directory:
* [predict_net.pb](https://download.caffe2.ai/models/squeezenet/predict_net.pb)
* [init_net.pb](https://download.caffe2.ai/models/squeezenet/init_net.pb)
Notice, the helper function *parseResults* will translate the integer class label of the top result to an English label by searching through the [inference codes file](inference_codes.txt). If you want to really test the model's capabilities, pick a code from the file, find an image representing that code, and test the model with it!
```
from google.colab import drive
drive.mount('/content/drive')
!git clone --recursive https://github.com/caffe2/tutorials caffe2_tutorials
%cd /content/drive/My Drive/caffe2_tutorials
!pip3 install torch torchvision
!python -m caffe2.python.models.download -i squeezenet
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import numpy as np
import operator
# load up the caffe2 workspace
from caffe2.python import workspace
# choose your model here (use the downloader first)
from caffe2.python.models import squeezenet as mynet
# helper image processing functions
import helpers
##### Load the Model
# Load the pre-trained model
init_net = mynet.init_net
predict_net = mynet.predict_net
# Initialize the predictor with SqueezeNet's init_net and predict_net
p = workspace.Predictor(init_net, predict_net)
##### Select and format the input image
# use whatever image you want (urls work too)
# img = "https://upload.wikimedia.org/wikipedia/commons/a/ac/Pretzel.jpg"
img = "images/cat.jpg"
# img = "images/cowboy-hat.jpg"
# img = "images/cell-tower.jpg"
# img = "images/Ducreux.jpg"
# img = "images/pretzel.jpg"
# img = "images/orangutan.jpg"
# img = "images/aircraft-carrier.jpg"
#img = "images/flower.jpg"
# average mean to subtract from the image
mean = 128
# the size of images that the model was trained with
input_size = 227
# use the image helper to load the image and convert it to NCHW
img = helpers.loadToNCHW(img, mean, input_size)
##### Run the test
# submit the image to net and get a tensor of results
results = p.run({'data': img})
##### Process the results
# Quick way to get the top-1 prediction result
# Squeeze out the unnecessary axis. This returns a 1-D array of length 1000
preds = np.squeeze(results)
# Get the prediction and the confidence by finding the maximum value and index of maximum value in preds array
curr_pred, curr_conf = max(enumerate(preds), key=operator.itemgetter(1))
print("Top-1 Prediction: {}".format(curr_pred))
print("Top-1 Confidence: {}\n".format(curr_conf))
# Lookup our result from the inference list
response = helpers.parseResults(results)
print(response)
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
img=mpimg.imread('images/cat.jpg') #image to array
# show the original image
plt.figure()
plt.imshow(img)
plt.axis('on')
plt.title('Original image = RGB')
plt.show()
```
| true |
code
| 0.698497 | null | null | null | null |
|
# BERTを用いたテキスト分類
このノートブックでは、[BERT](https://arxiv.org/abs/1810.04805)を用いて分類器を構築します。BERTは事前学習済みのNLPのモデルであり、2018年にGoogleによって公開されました。データセットとしては、IMDBレビューデータセットを使います。
なお、学習には時間がかかるので、GPUを使うことを推奨します。
## 準備
### パッケージのインストール
```
!pip install tensorflow-text==2.6.0 tf-models-official==2.6.0
```
### インポート
```
import os
import re
import string
import numpy as np
import tensorflow as tf
import tensorflow_text as text
import tensorflow_datasets as tfds
import tensorflow_hub as hub
from official.nlp import optimization
```
### データセットの読み込み
```
train_data, validation_data, test_data = tfds.load(
name="imdb_reviews",
split=('train[:80%]', 'train[80%:]', 'test'),
as_supervised=True
)
```
## 前処理
前処理としては、以下の3つを行います。
- 小文字化
- HTMLタグの除去(`<br />`タグ)
- 句読点の除去
```
def preprocessing(input_data, label):
lowercase = tf.strings.lower(input_data)
stripped_html = tf.strings.regex_replace(lowercase, '<br />', ' ')
cleaned_html = tf.strings.regex_replace(
stripped_html,
'[%s]' % re.escape(string.punctuation),
''
)
return cleaned_html, label
AUTOTUNE = tf.data.AUTOTUNE
train_ds = train_data.batch(32).map(preprocessing).cache().prefetch(buffer_size=AUTOTUNE)
val_ds = validation_data.batch(32).map(preprocessing).cache().prefetch(buffer_size=AUTOTUNE)
test_ds = test_data.batch(32).map(preprocessing).cache().prefetch(buffer_size=AUTOTUNE)
```
## モデルの構築
今回は、[TensorFlow Hub](https://www.tensorflow.org/hub)を用いて、BERTを使ったモデルを構築します。TensorFlow Hubは、学習済みの機械学習モデルのリポジトリです。ここには、BERTを含む多数のモデルが公開されており、ファインチューニングすることで、素早くモデルを構築できます。BERT以外にも、以下のようなモデルが公開されています。
- ALBERT
- Electra
- Universal Sentence Encoder
それでは、TensorFlow Hubを使ってみましょう。
### 前処理モデル
テキストは、BERTへ入力される前に、数値トークンIDに変換される必要があります。TensorFlow Hubは、BERTモデルに対応する前処理モデルを提供しており、それを使うことで、テキストを変換できます。したがって、前処理のために長々とコードを書く必要はありません。以下のように、前処理モデルを指定して読み込むだけです。
```
tfhub_handle_preprocess = 'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3'
preprocess_model = hub.KerasLayer(tfhub_handle_preprocess)
```
前処理モデルの出力を確認してみましょう。
```
text_test = ['this is such an amazing movie!']
text_preprocessed = preprocess_model(text_test)
print(f'Keys : {list(text_preprocessed.keys())}')
print(f'Shape : {text_preprocessed["input_word_ids"].shape}')
print(f'Word Ids : {text_preprocessed["input_word_ids"][0, :12]}')
print(f'Input Mask : {text_preprocessed["input_mask"][0, :12]}')
print(f'Type Ids : {text_preprocessed["input_type_ids"][0, :12]}')
```
ご覧のとおり、前処理モデルは以下の3つの出力をします。
- input_words_id: 入力系列のトークンID
- input_mask: パディングされたトークンには0、それ以外は1
- input_type_ids: 入力セグメントのインデックス。複数の文を入力する場合に関係する。
その他、入力が128トークンに切り詰められていることがわかります。ちなみに、トークン数はオプション引数でカスタマイズできます。詳細は、[前処理モデルのドキュメント](https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3)をご覧ください。
### BERTモデル
モデルを構築する前に、BERTモデルの出力を確認してみましょう。
```
tfhub_handle_encoder = 'https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/3'
bert_model = hub.KerasLayer(tfhub_handle_encoder)
bert_results = bert_model(text_preprocessed)
print(f'Pooled Outputs Shape:{bert_results["pooled_output"].shape}')
print(f'Pooled Outputs Values:{bert_results["pooled_output"][0, :12]}')
print(f'Sequence Outputs Shape:{bert_results["sequence_output"].shape}')
print(f'Sequence Outputs Values:{bert_results["sequence_output"][0, :12]}')
```
`pooled_output`と`sequence_output`の説明は以下の通りです。
- pooled_output: 入力全体を表しているベクトルです。レビュー文全体の埋め込みと考えられます。今回のモデルの場合、形は`[batch_size, 768]`になります。上の例では入力は1つだけなので`[1, 768]`になります。
- sequence_output: 各入力トークンを表すベクトルです。各トークンの文脈を考慮した埋め込みと考えられます。形は、`[batch_size, seq_length, 768]`です。
今回は、レビューを分類すればいいので、`pooled_output`を使います。
### モデルの定義
```
def build_classifier_model():
text_input = tf.keras.layers.Input(shape=(), dtype=tf.string)
preprocessing_layer = hub.KerasLayer(tfhub_handle_preprocess)
encoder_inputs = preprocessing_layer(text_input)
encoder = hub.KerasLayer(tfhub_handle_encoder, trainable=True)
outputs = encoder(encoder_inputs)
net = outputs['pooled_output']
net = tf.keras.layers.Dropout(0.1)(net)
net = tf.keras.layers.Dense(1, activation='sigmoid')(net)
return tf.keras.Model(text_input, net)
```
## モデルの学習
```
model = build_classifier_model()
epochs = 2
steps_per_epoch = tf.data.experimental.cardinality(train_ds).numpy()
num_train_steps = steps_per_epoch * epochs
num_warmup_steps = int(0.1*num_train_steps)
init_lr = 3e-5
optimizer = optimization.create_optimizer(
init_lr=init_lr,
num_train_steps=num_train_steps,
num_warmup_steps=num_warmup_steps,
optimizer_type='adamw'
)
model.compile(
optimizer=optimizer,
loss='binary_crossentropy',
metrics=['acc']
)
model.fit(
train_ds,
validation_data=val_ds,
epochs=epochs,
)
loss, accuracy = model.evaluate(test_ds)
print(f'Loss: {loss}')
print(f'Accuracy: {accuracy}')
```
| true |
code
| 0.737752 | null | null | null | null |
|
# Demystifying Approximate Bayesian Computation
#### Brett Morris
### In this tutorial
We will write our own rejection sampling algorithm to approximate the posterior distributions for some fitting parameters.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import anderson_ksamp
from corner import corner
# The Anderson-Darling statistic often throws a harmless
# UserWarning which we will ignore in this example
# to avoid distractions:
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
```
### Generate a set of observations
First, let's generate a series of observations $y_\mathrm{obs}$, taken at times $x$. The observations will be drawn from one of two Gaussian distributions with a fixed standard deviation, separated by $3\sigma$ from one another. There will be a fraction $f$ of the total samples in the second mode of the distribution.
In the plots that follow, blue represents the observations or the true input parameters, and shades of gray or black represent samples from the posterior distributions.
```
# Set a random seed for reproducibility
np.random.seed(42)
# Standard deviation of both normal distributions
true_std = 1
# Mean of the first normal distribution
true_mean1 = np.pi
# Mean of the second normal distribution
true_mean2 = 3 * np.pi
# Fraction of samples in second mode: this
# algorithm works best when the fraction
# is between [0.2, 0.8]
true_fraction = 0.3
# Third number below is the number of samples to draw:
x = np.linspace(0, 1, 500)
# Generate a series of observations, drawn from
# two normal distributions:
y_obs = np.concatenate([true_mean1 + true_std * np.random.randn(int((1-true_fraction) * len(x))),
true_mean2 + true_std * np.random.randn(int(true_fraction * len(x)))])
# Plot the observations:
plt.hist(y_obs, bins=50, density=True, color='#4682b4',
histtype='step', lw=3)
plt.xlabel('$y_\mathrm{obs}$', fontsize=20)
ax = plt.gca()
ax2 = ax.twiny()
ax2.set_xlim(ax.get_xlim())
ax2.set_xticks([true_mean1, true_mean2])
ax2.set_xticklabels(['$\mu_1$', '$\mu_2$'], fontsize=20)
plt.show()
```
So how does one fit for the means and standard deviations of the bimodal distribution? Since this example is a mixture of normal distirbutions, one way is to use [Gaussian mixture models](https://dfm.io/posts/mixture-models/), but we're going to take a different approach, which we'll see is more general later.
## Approximate Bayesian Computation
For this particular dataset, it's easy to construct a model $\mathcal{M}$ which reproduces the observations $y_\mathcal{obs}$ – the model is simply the concatenation of two normal distributions $\mathcal{M} \sim \left[\mathcal{N} \left(\mu_1, \sigma, \textrm{size=(1-f)N}\right), \mathcal{N}\left(\mu_2, \sigma, \textrm{size=}fN\right)\right]$, where the `size` argument determines the number of samples to draw from the distribution, $N$ is the total number of draws, and $f$ is the fraction of draws in the second mode. One way to *approximate* the posterior distributions of $\theta = \{\mu_1, \mu_2, \sigma, f\}$ would be to propose new parameters $\theta^*$, and only keep a running list of the parameter combinations which produce a simulated dataset $y_\mathrm{sim}$ which very closely reproduces the observations $y_\mathrm{obs}$.
***
### Summary statistic: the Anderson-Darling statistic
In practice, this requires a *summary statistic*, which measures the "distance" between the simulated dataset $y_\mathrm{sim}$ and the observations $y_\mathrm{obs}$. In this example we need a metric which measures the probability that two randomly-drawn samples $y$ are drawn from the same distribution. One such metric is the [Anderson-Darling statistic](https://en.wikipedia.org/wiki/Anderson–Darling_test), which approaches a minimum near $A^2=-1.3$ for two sets $y$ that are drawn from indistinguishable distributions, and grows to $A^2 > 10^5$ for easily distinguishable distributions.
We can see how the Anderson-Darling statistic behaves in this simple example below:
```
n_samples = 10000
# Generate a bimodal distribution
a = np.concatenate([np.random.randn(n_samples),
3 + np.random.randn(n_samples//2)])
# Plot the bimodal distribution
fig, ax = plt.subplots(1, 2, figsize=(7, 3))
ax[0].hist(a, color='silver', range=[-4, 11], bins=50,
lw=2, histtype='stepfilled')
# For a set of bimodal distributions with varing means:
for mean in [0, 1.2, 5]:
# Generate a new bimodal distribution
c = mean + np.concatenate([np.random.randn(n_samples),
3 + np.random.randn(n_samples//2)])
# Measure, plot the Anderson-darling statistic
a2 = anderson_ksamp([a, c]).statistic
ax[0].hist(c, histtype='step', range=[-4, 11],
bins=50, lw=2)
ax[1].plot(mean, a2, 'o')
ax[0].set(xlabel='Samples', ylabel='Frequency')
ax[1].set(xlabel='Mean', ylabel='$A^2$')
fig.tight_layout()
```
In the figure above, we have a set of observations $y_\mathrm{obs}$ (left, gray) which we're comparing to the set of simulated observations $y_\mathrm{sim}$ (left, colors). The Anderson-Darling statistic $A^2$ is plotted for each pair of the observations and the simulations (right). You can see that the minimum of $A^2$ is near -1.3, and it grows very large when $y_\mathrm{obs}$ and $y_\mathrm{sim}$ distributions are significantly different.
In order to make our distance function approach zero when the Anderson-Darling statistic is at its minimum, we're going to rescale the outputs of the Anderson-Darling statistic a bit:
```
def distance(y_obs, y_sim):
"""
Our distance metric between the observations y_obs
and the simulation y_sim will be the Anderson-Darling
Statistic A^2 + 1.31, so that its minimum value is
approximately 0 and its maximum value is >10^5.
"""
return anderson_ksamp([y_sim, y_obs]).statistic + 1.31
```
***
### The rejection sampler
We're now have the ingredients we need to create a *rejection sampler*, which will follow this algorithm:
1. Perturb initial/previous parameters $\theta$ by a small amount to generate new trial parameters $\theta^*$
2. If the trial parameters $\theta^*$ are drawn from within the prior, continue, else return to (1)
3. Generate an example dataset $y_\mathrm{sim}$ using your model $\mathcal{M}$
4. Compute _distance_ between the simulated and observed datasets $\rho(y_\mathrm{obs}, y_\mathrm{sim})$
5. For some tolerance $h$, accept the step ($\theta^* = \theta$) if distance $\rho(y_\mathrm{obs}, y_\mathrm{sim}) \leq h$
6. Return to step (1)
In the limit $h \rightarrow 0$, the posterior samples are no longer an approximation.
```
def lnprior(theta):
"""
Define a prior probability, which simply requires
that -10 < mu_1, mu_2 < 20 and 0 < sigma < 10 and
0 < fraction < 1.
"""
mean1, mean2, std, fraction = theta
if -10 < mean1 < 20 and -10 < mean2 < 20 and 0 < std < 10 and 0 <= fraction <= 1:
return 0
return -np.inf
def propose_step(theta, scale):
"""
Propose new step: perturb the previous step
by adding random-normal values to the previous step
"""
return theta + scale * np.random.randn(len(theta))
def simulate_dataset(theta):
"""
Simulate a dataset by generating a bimodal distribution
with means mu_1, mu_2 and standard deviation sigma
"""
mean1, mean2, std, fraction = theta
return np.concatenate([mean1 + std * np.random.randn(int((1-fraction) * len(x))),
mean2 + std * np.random.randn(int(fraction * len(x)))])
def rejection_sampler(theta, h, n_steps, scale=0.1, quiet=False,
y_obs=y_obs, prior=lnprior,
simulate_y=simulate_dataset):
"""
Follow algorithm written above for a simple rejection sampler.
"""
# Some bookkeeping variables:
accepted_steps = 0
total_steps = 0
samples = np.zeros((n_steps, len(theta)))
printed = set()
while accepted_steps < n_steps:
# Make a simple "progress bar":
if not quiet:
if accepted_steps % 1000 == 0 and accepted_steps not in printed:
printed.add(accepted_steps)
print(f'Sample {accepted_steps} of {n_steps}')
# Propose a new step:
new_theta = propose_step(theta, scale)
# If proposed step is within prior:
if np.isfinite(prior(new_theta)):
# Generate a simulated dataset from new parameters
y_sim = simulate_y(new_theta)
# Compute distance between simulated dataset
# and the observations
dist = distance(y_obs, y_sim)
total_steps += 1
# If distance is less than tolerance `h`, accept step:
if dist <= h:
theta = new_theta
samples[accepted_steps, :] = new_theta
accepted_steps += 1
print(f'Acceptance rate: {accepted_steps/total_steps}')
return samples
```
We can now run our rejection sampler for a given value of the tolerance $h$.
```
# Initial step parameters for the mean and std:
theta = [true_mean1, true_mean2, true_std, true_fraction]
# Number of posterior samples to compute
n_steps = 5000
# `h` is the distance metric threshold for acceptance;
# try values of h between -0.5 and 5
h = 5
samples = rejection_sampler(theta, h, n_steps)
```
`samples` now contains `n_steps` approximate posterior samples. Let's make a corner plot which shows the results:
```
labels = ['$\mu_1$', '$\mu_2$', '$\sigma$', '$f$']
truths = [true_mean1, true_mean2, true_std, true_fraction]
corner(samples, truths=truths,
levels=[0.6], labels=labels,
show_titles=True);
```
You can experiment with the above example by changing the values of from $h=2$, for a more precise and more computationally expensive approximation to the posterior distribution, or to $h=10$ for a faster but less precise estimate of the posterior distribution.
In practice, a significant fraction of your effort when applying ABC is spent balancing the computational expense of a small $h$ with the precision you need on your posterior approximation.
We can see how the posterior distribution for the standard deviation $\sigma$ changes as we vary $h$, from a small value to a larger value:
```
samples_i = []
h_range = [3, 5, 8]
for h_i in h_range:
samples_i.append(rejection_sampler(truths, h_i, n_steps, quiet=True))
```
Let's plot the results:
```
fig, ax = plt.subplots(1, 4, figsize=(12, 3))
for s_i, h_i in zip(samples_i, h_range):
for j, axis in enumerate(ax):
axis.hist(s_i[len(s_i)//2:, j], histtype='step', lw=2,
label=f"h={h_i}", density=True,
bins=30)
axis.set_xlabel(labels[j])
axis.axvline(truths[j], ls='--', color='#4682b4')
ax[0].set_ylabel('Posterior PDF')
plt.legend()
plt.show()
```
In the plot above, blue histograms are for the smallest $h$, then orange, then green. You can see that the posterior distribution for the standard deviation is largest for the largest $h$, and converges to a narrower distribution centered on the correct value as $h$ decreases.
Now let's inspect how the simulated distributions look, generated using the posterior samples for our input parameters $\theta$:
```
props = dict(bins=25, range=[0, 12],
histtype='step', density=True)
for i in np.random.randint(0, len(samples_i), size=50):
plt.hist(simulate_dataset(samples_i[0][i, :]),
alpha=0.3, color='silver', **props)
plt.hist(y_obs, color='#4682b4', lw=3, **props)
plt.xlabel('$y_\mathrm{obs}, y_\mathrm{sim}$', fontsize=20)
plt.show()
```
The blue histogram is the set of observations $y_\mathrm{obs}$. Shown in silver are various draws from the simulated distributions with the parameters $\theta$ drawn randomly from the posterior distributions from the previous rejection sampling. You can see that the simulated (silver) histograms are "non-rejectable approximations" to the observations (blue).
***
## A non-Gaussian example
Now let's do an example where things are less Gaussian. Our data will be distributed with a _beta distribution_, according to
$$f(x; a,b) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1} (1 - x)^{\beta - 1},$$
where
$$B(\alpha, \beta) = \int_0^1 t^{\alpha - 1} (1 - t)^{\beta - 1} dt$$
This new distribution has positive parameters $\theta = \{\alpha, \beta\}$ which we can use ABC to infer:
```
from numpy.random import beta
np.random.seed(2019)
# The alpha and beta parameters are the tuning parameter
# for beta distributions.
true_a = 15
true_b = 2
y_obs_beta = beta(true_a, true_b, size=len(x));
plt.hist(y_obs_beta, density=True, histtype='step', color='#4682b4', lw=3)
plt.xlabel('$y_\mathrm{obs}$', fontsize=20)
plt.show()
```
In this example, we'll sample the logarithm of the $\alpha$ and $\beta$ parameters.
```
def lnprior_beta(theta):
lna, lnb = theta
if -100 < lna < 100 and -100 < lnb < 100:
return 0
return -np.inf
def simulate_dataset_beta(theta):
"""
Simulate a dataset by generating a bimodal distribution
with means mu_1, mu_2 and standard deviation sigma
"""
a, b = np.exp(theta)
return beta(a, b, size=len(x))
```
We'll keep the Anderson-Darling statistic as our summary statistic, which is non-parametric and agnostic about the distributions of the two samples it is comparing. We will swap in our new observations, prior, and simulation function, but nothing else changes in the rejection sampling algorithm:
```
# `h` is the distance metric threshold for acceptance;
# try values of h between 1 and 5
h = 1
samples = rejection_sampler([np.log(true_a), np.log(true_b)], h, n_steps,
y_obs=y_obs_beta,
prior=lnprior_beta,
simulate_y=simulate_dataset_beta)
labels_beta = [r'$\ln\alpha$', r'$\ln\beta$']
truths_beta = [np.log(true_a), np.log(true_b)]
corner(samples, labels=labels_beta,
truths=truths_beta,
levels=[0.6])
plt.show()
```
Let's see how random draws from the posterior distributions for $\alpha$ and $\beta$ compare with the observations:
```
props = dict(bins=25, range=[0.5, 1],
histtype='step', density=True)
for i in np.random.randint(0, len(samples), size=100):
lna, lnb = samples[i, :]
a = np.exp(lna)
b = np.exp(lnb)
plt.hist(beta(a, b, size=len(x)),
alpha=0.3, color='silver', **props)
plt.hist(y_obs_beta, color='#4682b4', lw=3, **props)
plt.xlabel('$y_\mathrm{obs}, y_\mathrm{sim}$', fontsize=20)
plt.show()
```
Again, the blue histogram is the set of observations $y_\mathrm{obs}$. Shown in silver are various draws from beta distributions with the parameters $\alpha$ and $\beta$ drawn randomly from the posterior distributions from the previous rejection sampling chain. You can see that the simulated (silver) histograms are "non-rejectable approximations" to the observations (blue).
| true |
code
| 0.795082 | null | null | null | null |
|
## Analysis of UK's Tradings for 2014 Trading Year
Task:
A country's economy depends, sometimes heavily, on its exports and imports. The United Nations Comtrade database provides data on global trade. It will be used to analyse the UK's imports and exports of milk and cream in 2015:
- How much does the UK export and import and is the balance positive (more exports than imports)?
- Which are the main trading partners, i.e. from/to which countries does the UK import/export the most?
- Which are the regular customers, i.e. which countries buy milk from the UK every month?
- Which countries does the UK both import from and export to?
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas import *
%matplotlib inline
data=pd.read_csv('comtrade_milk_uk_monthly_14.csv',dtype={'Commodity Code':str})
pd.options.display.max_columns=35
display(data.head(2))
data['Commodity Code'].value_counts()
data.describe().T
def milk_type(code):
if code=='0401':
return 'unprocessed'
if code=='0402':
return 'processed'
return 'unknown'
commodity= 'Milk and Cream'
data[commodity]=data['Commodity Code'].apply(milk_type)
data['Milk and Cream'].value_counts()
data_new=pd.DataFrame(data,columns=['Period','Partner','Milk and Cream','Trade Flow','Trade Value (US$)'])
data_new.tail(5)
```
## Question 1
### How much does the UK export and import and is the balance positive (more exports than imports)?
```
data_new['Trade Flow'].value_counts()
print(data_new.shape)
data_new.head()
# data_new.Partner.value_counts()
data_new=data_new[data_new['Partner']!='World']
data_new.shape
grouped_data=data_new.groupby("Trade Flow")
export_import=pd.DataFrame(grouped_data['Trade Value (US$)'].aggregate(sum))
export_import
difference=export_import['Trade Value (US$)'][0]-export_import['Trade Value (US$)'][1]
print(f'The difference between exports and imports is ${difference}')
```
We see here that there are more exports than imports worth $334766993
<b><i>Answer to question 1:</i><br>
Hence, the UK exports <i>$898651935 and imports $563884942</i> with a positive differnce of $334766993</b>
## Question 2
#### Which are the main trading partners, i.e. from/to which countries does the UK import/export the most?
##### Imports
```
imports=data_new[data_new['Trade Flow']=='Imports']
print(imports.shape)
imports.head()
grouped_import=imports.groupby('Partner')
grouped_import.head()
total_imports=grouped_import['Trade Value (US$)'].aggregate(sum).sort_values(inplace=False,ascending=False)
total_imports.head()
total_imports.head(8).plot(kind='barh')
plt.title("Top Countries Importing from the UK")
plt.xlabel("Amount in Billion Dollars")
plt.savefig("Top Countries Importing from the UK")
plt.show()
```
We see here that Ireland, France and Germany are the top three countries that import from the UK.
##### Exports
```
exports_data=data_new[data_new['Trade Flow']=="Exports"]
print(exports_data.shape)
exports_data.head()
grouped_export=exports_data.groupby("Partner")
total_exports=grouped_export['Trade Value (US$)'].aggregate(sum).sort_values(inplace=False,ascending=False)
total_exports.head()
total_exports.head(8).plot(kind='barh')
plt.title("UK's Exporting Destinations")
plt.xlabel("Amount in Billion Dollars")
plt.savefig("UK's Exporting Destinations")
plt.show()
```
Here, we see that UK's top three export destinations are Ireland, Algeria and The Netherlands.
## Question 3
### Which are the regular customers, i.e. which countries buy milk from the UK every month?
```
data['Period Desc.'].value_counts()
```
We see that there are 12 months listed in this data. So a regular customer buys the both products throughout the months.
```
def regular_customer(group):
return len(group)==24
grouped=exports_data.groupby('Partner')
regular=grouped.filter(regular_customer)
regular[(regular['Period']==201405)&(regular['Milk and Cream']=='unprocessed')]
percentage_volume=np.round((regular['Trade Value (US$)'].sum() / exports_data['Trade Value (US$)'].sum())*100)
print(f'The volume of trade that Uk gets from her exports is worth {percentage_volume}%')
```
We see here that any month and any commodity we take gives the same volume of trade.<br>
Also, we see that this trading volume is about 72%.
## Question 4
### Which countries does the UK both import from and export to?
We check here for where both countries exchange goods by using a pivot table
```
trading_countries=pivot_table(data_new, index=['Partner'],columns=['Trade Flow'],values='Trade Value (US$)',
aggfunc=sum)
print(trading_countries.shape)
trading_countries.head()
trading_countries.isnull().sum()
trading_countries.dropna(inplace=True)
print(trading_countries.shape)
trading_countries.head()
```
Here, we see that there are 25 countries where UK share mutual trading relationships.
## CONCLUSION
After analysing the data, we come to the following conclusions about 2014 of UK's trading year.
- The UK does well in her tradings as she records a positive difference of over $334 billion dollars.
- Ireland, France and Germany are the top three countries that import from the UK.
- UK's top three export destinations are Ireland, Algeria and The Netherlands.
- UK's trading volume is about 72%.
- UK shared mutual trading relationships with 25 countries in 2014 trading year.
| true |
code
| 0.320757 | null | null | null | null |
|
# Spark Lab
This lab will demonstrate how to perform web server log analysis with Spark. Log data is a very large, common data source and contains a rich set of information. It comes from many sources, such as web, file, and compute servers, application logs, user-generated content, and can be used for monitoring servers, improving business and customer intelligence, building recommendation systems, fraud detection, and much more. This lab will show you how to use Spark on real-world text-based production logs and fully harness the power of that data.
### Apache Web Server Log file format
The log files that we use for this assignment are in the [Apache Common Log Format (CLF)](http://httpd.apache.org/docs/1.3/logs.html#common) format. The log file entries produced in CLF will look something like this:
`127.0.0.1 - - [01/Aug/1995:00:00:01 -0400] "GET /images/launch-logo.gif HTTP/1.0" 200 1839`
Each part of this log entry is described below.
* **`127.0.0.1`:** this is the IP address (or host name, if available) of the client (remote host) which made the request to the server.
* **`-`:** the "hyphen" in the output indicates that the requested piece of information (user identity from remote machine) is not available.
* **`-`:** the "hyphen" in the output indicates that the requested piece of information (user identity from local logon) is not available.
* **`[01/Aug/1995:00:00:01 -0400]`:** the time that the server finished processing the request. The format is:
`[day/month/year:hour:minute:second timezone]`.
* **`"GET /images/launch-logo.gif HTTP/1.0"`:** this is the first line of the request string from the client. It consists of a three components: the request method (e.g., `GET`, `POST`, etc.), the endpoint, and the client protocol version.
* **`200`:** this is the status code that the server sends back to the client. This information is very valuable, because it reveals whether the request resulted in a successful response (codes beginning in 2), a redirection (codes beginning in 3), an error caused by the client (codes beginning in 4), or an error in the server (codes beginning in 5). The full list of possible status codes can be found in the HTTP specification ([RFC 2616](https://www.ietf.org/rfc/rfc2616.txt) section 10).
* **`1839`:** the last entry indicates the size of the object returned to the client, not including the response headers. If no content was returned to the client, this value will be "-" (or sometimes 0).
Using the CLF as defined above, we create a regular expression pattern to extract the nine fields of the log line. The function returns a pair consisting of a Row object and 1. If the log line fails to match the regular expression, the function returns a pair consisting of the log line string and 0. A '-' value in the content size field is cleaned up by substituting it with 0. The function converts the log line's date string into a `Cal` object using the given `parseApacheTime` function. We, then, create the primary RDD and we'll use in the rest of this assignment. We first load the text file and convert each line of the file into an element in an RDD. Next, we use `map(parseApacheLogLine)` to apply the parse function to each element and turn each line into a pair `Row` object. Finally, we cache the RDD in memory since we'll use it throughout this notebook. The log file is available at `data/apache/apache.log`.
```
import scala.util.matching
import org.apache.spark.rdd.RDD
case class Cal(year: Int, month: Int, day: Int, hour: Int, minute: Int, second: Int)
case class Row(host: String, clientID: String, userID: String, dateTime: Cal, method: String, endpoint: String,
protocol: String, responseCode: Int, contentSize: Long)
val month_map = Map("Jan" -> 1, "Feb" -> 2, "Mar" -> 3, "Apr" -> 4, "May" -> 5, "Jun" -> 6, "Jul" -> 7, "Aug" -> 8,
"Sep" -> 9, "Oct" -> 10, "Nov" -> 11, "Dec" -> 12)
//------------------------------------------------
// A regular expression pattern to extract fields from the log line
val APACHE_ACCESS_LOG_PATTERN = """^(\S+) (\S+) (\S+) \[([\w:/]+\s[+\-]\d{4})\] "(\S+) (\S+)\s*(\S*)\s*" (\d{3}) (\S+)""".r
//------------------------------------------------
def parseApacheTime(s: String): Cal = {
return Cal(s.substring(7, 11).toInt, month_map(s.substring(3, 6)), s.substring(0, 2).toInt,
s.substring(12, 14).toInt, s.substring(15, 17).toInt, s.substring(18, 20).toInt)
}
//------------------------------------------------
def parseApacheLogLine(logline: String): (Either[Row, String], Int) = {
val ret = APACHE_ACCESS_LOG_PATTERN.findAllIn(logline).matchData.toList
if (ret.isEmpty)
return (Right(logline), 0)
val r = ret(0)
val sizeField = r.group(9)
var size: Long = 0
if (sizeField != "-")
size = sizeField.toLong
return (Left(Row(r.group(1), r.group(2), r.group(3), parseApacheTime(r.group(4)), r.group(5), r.group(6),
r.group(7), r.group(8).toInt, size)), 1)
}
//------------------------------------------------
def parseLogs(): (RDD[(Either[Row, String], Int)], RDD[Row], RDD[String]) = {
val fileName = "data/apache/apache.log"
val parsedLogs = sc.textFile(fileName).map(parseApacheLogLine).cache()
val accessLogs = parsedLogs.filter(x => x._2 == 1).map(x => x._1.left.get)
val failedLogs = parsedLogs.filter(x => x._2 == 0).map(x => x._1.right.get)
val failedLogsCount = failedLogs.count()
if (failedLogsCount > 0) {
println(s"Number of invalid logline: $failedLogs.count()")
failedLogs.take(20).foreach(println)
}
println(s"Read $parsedLogs.count() lines, successfully parsed $accessLogs.count() lines, and failed to parse $failedLogs.count()")
return (parsedLogs, accessLogs, failedLogs)
}
val (parsedLogs, accessLogs, failedLogs) = parseLogs()
```
### Sample Analyses on the Web Server Log File
Let's compute some statistics about the sizes of content being returned by the web server. In particular, we'd like to know what are the average, minimum, and maximum content sizes. We can compute the statistics by applying a `map` to the `accessLogs` RDD. The given function to the `map` should extract the `contentSize` field from the RDD. The `map` produces a new RDD, called `contentSizes`, containing only the `contentSizes`. To compute the minimum and maximum statistics, we can use `min()` and `max()` functions on the new RDD. We can compute the average statistic by using the `reduce` function with a function that sums the two inputs, which represent two elements from the new RDD that are being reduced together. The result of the `reduce()` is the total content size from the log and it is to be divided by the number of requests as determined using the `count()` function on the new RDD. As the result of executing the following box, you should get the below result:
```
Content Size Avg: 17531, Min: 0, Max: 3421948
```
```
// Calculate statistics based on the content size.
val contentSizes = accessLogs.map(_.contentSize).cache()
println("Content Size Avg: " + contentSizes.sum()/contentSizes.count() + ", Min: " + contentSizes.min() + ", Max: " + contentSizes.max())
```
Next, lets look at the "response codes" that appear in the log. As with the content size analysis, first we create a new RDD that contains the `responseCode` field from the `accessLogs` RDD. The difference here is that we will use a *pair tuple* instead of just the field itself (i.e., (response code, 1)). Using a pair tuple consisting of the response code and 1 will let us count the number of of records with a particular response code. Using the new RDD `responseCodes`, we perform a `reduceByKey` function that applys a given function to each element, pairwise with the same key. Then, we cache the resulting RDD and create a list by using the `take` function. Once you run the code below, you should receive the following results:
```
Found 7 response codes
Response Code Counts: (404,6185) (200,940847) (304,79824) (500,2) (501,17) (302,16244) (403,58)
```
```
// extract the response code for each record and make pair of (response code, 1)
val responseCodes = accessLogs.map(x => (x.responseCode, 1))
// count the number of records for each key
val responseCodesCount = responseCodes.reduceByKey(_ + _).cache()
// take the first 100 records
val responseCodesCountList = responseCodesCount.take(100)
println("Found " + responseCodesCountList.length + " response codes")
print("Response Code Counts: ")
responseCodesCountList.foreach(x => print(x + " "))
```
Let's look at "hosts" that have accessed the server multiple times (e.g., more than 10 times). First we create a new RDD to keep the `host` field from the `accessLogs` RDD using a pair tuple consisting of the host and 1 (i.e., (host, 1)), which will let us count how many records were created by a particular host's request. Using the new RDD, we perform a `reduceByKey` function with a given function to add the two values. We then filter the result based on the count of accesses by each host (the second element of each pair) being greater than 10. Next, we extract the host name by performing a `map` to return the first element of each pair. Finally, we extract 20 elements from the resulting RDD. The result should be as below:
```
Any 20 hosts that have accessed more then 10 times:
ix-aug-ga1-13.ix.netcom.com
n1043347.ksc.nasa.gov
d02.as1.nisiq.net
192.112.22.82
anx3p4.trib.com
198.215.127.2
198.77.113.34
crc182.cac.washington.edu
telford-107.salford.ac.uk
universe6.barint.on.ca
gatekeeper.homecare.com
157.208.11.7
unknown.edsa.co.za
onyx.southwind.net
ppp-hck-2-12.ios.com
ix-lv5-04.ix.netcom.com
f-umbc7.umbc.edu
cs006p09.nam.micron.net
dd22-025.compuserve.com
hak-lin-kim.utm.edu
```
```
// extract the host field for each record and make pair of (host, 1)
val hosts = accessLogs.map(x => (x.da, 1))
// count the number of records for each key
val hostsCount = hosts.reduceByKey(_+_)
// keep the records with the count greater than 10
val hostMoreThan10 = hostsCount.filter(x => (x._2 > 10))
// take the first 100 records
val hostsPick20 = hostMoreThan10.map(_._1).take(20)
println("Any 20 hosts that have accessed more then 10 times: ")
hostsPick20.foreach(println)
```
For the final example, we'll look at the top endpoints (URIs) in the log. To determine them, we first create a new RDD to extract the `endpoint` field from the `accessLogs` RDD using a pair tuple consisting of the endpoint and 1 (i.e., (endpoint, 1)), which will let us count how many records were created by a particular host's request. Using the new RDD, we perform a `reduceByKey` to add the two values. We then extract the top 10 endpoints by performing a `takeOrdered` with a value of 10 and a function that multiplies the count (the second element of each pair) by -1 to create a sorted list with the top endpoints at the bottom. Here is the result:
```
Top ten endpoints:
(/images/NASA-logosmall.gif,59737)
(/images/KSC-logosmall.gif,50452)
(/images/MOSAIC-logosmall.gif,43890)
(/images/USA-logosmall.gif,43664)
(/images/WORLD-logosmall.gif,43277)
(/images/ksclogo-medium.gif,41336)
(/ksc.html,28582)
(/history/apollo/images/apollo-logo1.gif,26778)
(/images/launch-logo.gif,24755)
(/,20292)
```
```
// extract the endpoint for each record and make pair of (endpoint, 1)
val endpoints = accessLogs.map(x => (x.endpoint, 1))
// count the number of records for each key
val endpointCounts = endpoints.reduceByKey(_ + _)
// extract the top 10
val topEndpoints = endpointCounts.takeOrdered(10)(Ordering[Int].reverse.on(_._2))
println("Top ten endpoints: ")
topEndpoints.foreach(println)
```
### Analyzing Web Server Log File
What are the top ten endpoints which did not have return code 200? Create a sorted list containing top ten endpoints and the number of times that they were accessed with non-200 return code. Think about the steps that you need to perform to determine which endpoints did not have a 200 return code, how you will uniquely count those endpoints, and sort the list. You should receive the following result:
```
Top ten failed URLs:
(/images/NASA-logosmall.gif,8761)
(/images/KSC-logosmall.gif,7236)
(/images/MOSAIC-logosmall.gif,5197)
(/images/USA-logosmall.gif,5157)
(/images/WORLD-logosmall.gif,5020)
(/images/ksclogo-medium.gif,4728)
(/history/apollo/images/apollo-logo1.gif,2907)
(/images/launch-logo.gif,2811)
(/,2199)
(/images/ksclogosmall.gif,1622)
```
```
// keep the logs with error code not 200
val not200 = accessLogs.filter(x => x.responseCode != 200)
// make a pair of (x, 1)
val endpointCountPairTuple = not200.map(x => (x.endpoint, 1))
// count the number of records for each key x
val endpointSum = endpointCountPairTuple.reduceByKey(_+_)
// take the top 10
val topTenErrURLs = endpointSum.takeOrdered(10)(Ordering[Int].reverse.on(_._2))
println("Top ten failed URLs: ")
topTenErrURLs.foreach(println)
```
Let's count the number of unique hosts in the entire log. Think about the steps that you need to perform to count the number of different hosts in the log. The result should be as below:
```
Unique hosts: 54507
```
```
// extract the host field for each record
val hosts = accessLogs.map(x => x.host)
// keep the uniqe hosts
val uniqueHosts = hosts.distinct()
// count them
val uniqueHostCount = uniqueHosts.count()
println("Unique hosts: " + uniqueHostCount)
```
For an advanced exercise, let's determine the number of unique hosts in the entire log on a day-by-day basis. This computation will give us counts of the number of unique daily hosts. We'd like a list sorted by increasing day of the month, which includes the day of the month and the associated number of unique hosts for that day. Make sure you cache the resulting RDD `dailyHosts`, so that we can reuse it in the next exercise. Think about the steps that you need to perform to count the number of different hosts that make requests *each* day. Since the log only covers a single month, you can ignore the month. Here is the output you should receive:
```
Unique hosts per day:
(1,2582)
(3,3222)
(4,4190)
(5,2502)
(6,2537)
(7,4106)
(8,4406)
(9,4317)
(10,4523)
(11,4346)
(12,2864)
(13,2650)
(14,4454)
(15,4214)
(16,4340)
(17,4385)
(18,4168)
(19,2550)
(20,2560)
(21,4134)
(22,4456)
```
```
// make pairs of (day, host)
val dayToHostPairTuple = accessLogs.map(x => (x.dateTime.day, x.host))
// group by day
val dayGroupedHosts = dayToHostPairTuple.groupByKey()
// make pairs of (day, number of host in that day)
val dayHostCount = dayGroupedHosts.map(x => (x._1, x._2.toSet.size))
// sort by day
val dailyHosts = dayHostCount.sortByKey().cache()
// return the records as a list
val dailyHostsList = dailyHosts.take(30)
println("Unique hosts per day: ")
dailyHostsList.foreach(println)
```
Next, let's determine the average number of requests on a day-by-day basis. We'd like a list by increasing day of the month and the associated average number of requests per host for that day. Make sure you cache the resulting RDD `avgDailyReqPerHost` so that we can reuse it in the next exercise. To compute the average number of requests per host, get the total number of request across all hosts and divide that by the number of unique hosts. Since the log only covers a single month, you can skip checking for the month. Also to keep it simple, when calculating the approximate average use the integer value. The result should be as below:
```
Average number of daily requests per Hosts is:
(1,13)
(3,12)
(4,14)
(5,12)
(6,12)
(7,13)
(8,13)
(9,14)
(10,13)
(11,14)
(12,13)
(13,13)
(14,13)
(15,13)
(16,13)
(17,13)
(18,13)
(19,12)
(20,12)
(21,13)
(22,12)
```
```
// make pairs of (day, host)
val dayAndHostTuple = accessLogs.map(x => (x.dateTime.day, x.host))
// group by day
val groupedByDay = dayAndHostTuple.groupByKey()
// sort by day
val sortedByDay = groupedByDay.sortByKey()
// calculate the average request per day
val avgDailyReqPerHost = sortedByDay.map(x=>(x._1, x._2.size / x._2.toSet.size))
// return the records as a list
val avgDailyReqPerHostList = avgDailyReqPerHost.take(30)
println("Average number of daily requests per Hosts is: ")
avgDailyReqPerHostList.foreach(println)
```
### Exploring 404 Response Codes
Let's count the 404 response codes. Create a RDD containing only log records with a 404 response code. Make sure you `cache()` the RDD `badRecords` as we will use it in the rest of this exercise. How many 404 records are in the log? Here is the result:
```
Found 6185 404 URLs.
```
```
val badRecords = accessLogs.filter(x => x.responseCode == 404).cache()
println("Found " + badRecords.count() + " 404 URLs.")
```
Now, let's list the 404 response code records. Using the RDD containing only log records with a 404 response code that you cached in the previous part, print out a list up to 10 distinct endpoints that generate 404 errors - no endpoint should appear more than once in your list. You should receive the follwoing output as your result:
```
404 URLS:
/SHUTTLE/COUNTDOWN
/shuttle/missions/sts-71/images/www.acm.uiuc.edu/rml/Gifs
/shuttle/technology/stsnewsrof/stsref-toc.html
/de/systems.html
/ksc.htnl
/~pccomp/graphics/sinsght.gif
/PERSONS/NASA-CM.
/shuttle/missions/sts-1/sts-1-mission.html
/history/apollo/sa-1/sa-1-patch-small.gif
/images/sts-63-Imax
```
```
val badEndpoints = badRecords.map(x => x.endpoint)
val badUniqueEndpoints = badEndpoints.distinct()
val badUniqueEndpointsPick10 = badUniqueEndpoints.take(10)
println("404 URLS: ")
badUniqueEndpointsPick10.foreach(println)
```
Using the RDD containing only log records with a 404 response code that you cached before, print out a list of the top 10 endpoints that generate the most 404 errors. Remember, top endpoints should be in sorted order. The result would be as below:
```
Top ten 404 URLs:
(/pub/winvn/readme.txt,633)
(/pub/winvn/release.txt,494)
(/shuttle/missions/STS-69/mission-STS-69.html,431)
(/images/nasa-logo.gif,319)
(/elv/DELTA/uncons.htm,178)
(/shuttle/missions/sts-68/ksc-upclose.gif,156)
(/history/apollo/sa-1/sa-1-patch-small.gif,146)
(/images/crawlerway-logo.gif,120)
(/://spacelink.msfc.nasa.gov,117)
(/history/apollo/pad-abort-test-1/pad-abort-test-1-patch-small.gif,100)
```
```
val badEndpointsCountPairTuple = badRecords.map(x => (x.endpoint, 1))
val badEndpointsSum = badEndpointsCountPairTuple.reduceByKey(_+_)
val badEndpointsTop10 = badEndpointsSum.takeOrdered(10)(Ordering[Int].reverse.on[(String, Int)](_._2))
println("Top ten 404 URLs: ")
badEndpointsTop10.foreach(println)
```
Instead of looking at the endpoints that generated 404 errors, now let's look at the hosts that encountered 404 errors. Using the RDD containing only log records with a 404 response code that you cached before, print out a list of the top 10 hosts that generate the most 404 errors. Here is the result:
```
Top ten hosts that generated errors:
(piweba3y.prodigy.com,39)
(maz3.maz.net,39)
(gate.barr.com,38)
(m38-370-9.mit.edu,37)
(ts8-1.westwood.ts.ucla.edu,37)
(nexus.mlckew.edu.au,37)
(204.62.245.32,33)
(spica.sci.isas.ac.jp,27)
(163.206.104.34,27)
(www-d4.proxy.aol.com,26)
```
```
val errHostsCountPairTuple = badRecords.map(x => (x.host,1))
val errHostsSum = errHostsCountPairTuple.reduceByKey(_+_)
val errHostsTop10 = errHostsSum.takeOrdered(10)(Ordering[Int].reverse.on[(String, Int)](_._2))
println("Top ten hosts that generated errors: ")
errHostsTop10.foreach(println)
```
Let's explore the 404 records temporally. Break down the 404 requests by day and get the daily counts sorted by day as a list. Since the log only covers a single month, you can ignore the month in your checks. Cache the `errDateSorted` at the end. The output should be as below:
```
404 errors by day:
(1,243)
(3,303)
(4,346)
(5,234)
(6,372)
(7,532)
(8,381)
(9,279)
(10,314)
(11,263)
(12,195)
(13,216)
(14,287)
(15,326)
(16,258)
(17,269)
(18,255)
(19,207)
(20,312)
(21,305)
(22,288)
```
```
val errDateCountPairTuple = badRecords.map(x => (x.dateTime.day, 1))
val errDateSum = errDateCountPairTuple.reduceByKey(_+_)
val errDateSorted = errDateSum
val errByDate = errDateSorted.takeOrdered(30)
errDateSorted.cache()
println("404 errors by day: ")
errByDate.foreach(println)
```
Using the RDD `errDateSorted` you cached before, what are the top five days for 404 response codes and the corresponding counts of 404 response codes?
```
Top five dates for 404 requests: (7,532) (8,381) (6,372) (4,346) (15,326)
```
```
val topErrDate = errDateSorted.takeOrdered(5)(Ordering[Int].reverse.on[(Int, Int)](_._2))
print("Top five dates for 404 requests: ")
topErrDate.foreach(x => print(x + " "))
```
Using the RDD `badRecords` you cached before, and by hour of the day and in increasing order, create an RDD containing how many requests had a 404 return code for each hour of the day (midnight starts at 0).
```
Top hours for 404 requests:
(0,175)
(1,171)
(2,422)
(3,272)
(4,102)
(5,95)
(6,93)
(7,122)
(8,199)
(9,185)
(10,329)
(11,263)
(12,438)
(13,397)
(14,318)
(15,347)
(16,373)
(17,330)
(18,268)
(19,269)
(20,270)
(21,241)
(22,234)
(23,272)
```
```
val hourCountPairTuple = badRecords.map(x => (x.dateTime.hour, 1))
val hourRecordsSum = hourCountPairTuple.reduceByKey(_+_)
val hourRecordsSorted = hourRecordsSum.sortByKey()
val errHourList = hourRecordsSorted.collect()
println("Top hours for 404 requests: ")
errHourList.foreach(println)
```
| true |
code
| 0.341967 | null | null | null | null |
|
# Paper Figure Creation
- Created on a cloudly London Saturday morning, April 3rd 2021
- Revised versions of the figures
```
import climlab
import numpy as np
import xarray as xr
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
import xarray as xr
import pandas as pd
import cartopy.crs as ccrs
from cartopy.util import add_cyclic_point
from cartopy.mpl.ticker import LongitudeFormatter, LatitudeFormatter
from IPython.display import clear_output
import time
from mpl_toolkits.axes_grid1 import make_axes_locatable
import matplotlib.patches as patches
from matplotlib.colors import LogNorm
import matplotlib.colors
import matplotlib as mpl
```
# Fig. 1
```
values = xr.open_dataset('../../Data/CERES/clear_sky_ceres.nc')
landmask = xr.open_dataset('../../Data/Other/landsea.nc')
lats = values.lat.values
lons = values.lon.values
# Variables that you want to plot
plotvar1 = values.r2.values
# Adding a cyclic point to the two variables
# This removes a white line at lon = 0
lon_long = values.lon.values
plotvar_cyc1 = np.zeros((len(lats), len(lons)))
plotvar_cyc1, lon_long = add_cyclic_point(plotvar_cyc1, coord=lon_long)
for i in range(len(lats)):
for j in range(len(lons)):
plotvar_cyc1[i, j] = plotvar1[i, j]
plotvar_cyc1[:, len(lons)] = plotvar_cyc1[:, 0]
# Plotting
fig = plt.figure(figsize=(6, 2.7), constrained_layout=True)
width_vals = [2, 1]
gs = fig.add_gridspec(ncols=2, nrows=1, width_ratios=width_vals)
SIZE = 8
plt.rc('font', size=SIZE) # controls default text sizes
plt.rc('axes', titlesize=SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SIZE) # legend fontsize
plt.rc('figure', titlesize=SIZE) # fontsize of the figure title
# Upper left map
ax1 = fig.add_subplot(gs[0], projection=ccrs.PlateCarree())
ax1.coastlines()
ax1.set_title("a) Map of R$^2$ for Linear Fit of Monthly OLR to Monthly T$_S$")
C1 = ax1.pcolor(
lon_long, lats, plotvar_cyc1, transform=ccrs.PlateCarree(), cmap='RdYlGn', rasterized=True
)
ax1.set_xticks([-180, -90, 0, 90, 180], crs=ccrs.PlateCarree())
ax1.set_yticks([-90, 0, 90], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(number_format='.0f',
dateline_direction_label=True)
lat_formatter = LatitudeFormatter(number_format='.0f')
ax1.xaxis.set_major_formatter(lon_formatter)
ax1.yaxis.set_major_formatter(lat_formatter)
# Colourbars
cbar = fig.colorbar(
C1,
ax=ax1,
label=r"$R^2$",
fraction=0.1,
orientation="horizontal",
ticks=[0.001, 0.2, 0.4, 0.6, 0.8, 0.999]
)
cbar.ax.set_xticklabels(['0', '0.2', '0.4', '0.6', '0.8', '1'])
ax1.text(110, 70, 'a', horizontalalignment='center', verticalalignment='center', color='white',
fontsize=8, fontweight='bold', bbox={'facecolor': 'black', 'edgecolor': 'none', 'alpha': 0.5, 'pad': 5})
ax1.text(-110, -65, 'b', horizontalalignment='center', verticalalignment='center', color='white',
fontsize=8, fontweight='bold', bbox={'facecolor': 'black', 'edgecolor': 'none', 'alpha': 0.5, 'pad': 5})
ax1.text(27, -2, 'c', horizontalalignment='center', verticalalignment='center', color='white',
fontsize=8, fontweight='bold', bbox={'facecolor': 'black', 'edgecolor': 'none', 'alpha': 0.5, 'pad': 5})
ax1.text(0, -10, 'd', horizontalalignment='center', verticalalignment='center', color='white',
fontsize=8, fontweight='bold', bbox={'facecolor': 'black', 'edgecolor': 'none', 'alpha': 0.5, 'pad': 5})
ax1.text(80, 15, 'e', horizontalalignment='center', verticalalignment='center', color='white',
fontsize=8, fontweight='bold', bbox={'facecolor': 'black', 'edgecolor': 'none', 'alpha': 0.5, 'pad': 5})
# Upper right map
ax2 = fig.add_subplot(gs[1])
extra_tropics = list(np.arange(-90, -29, 1))
extra_tropics += list(np.arange(30, 91, 1))
tropics = list(np.arange(-30, 31, 1))
mask_sea_t = landmask.interp_like(values, method='nearest').sel(
lat=tropics).LSMASK.values == 0
mask_land_t = landmask.interp_like(
values, method='nearest').sel(lat=tropics).LSMASK.values == 1
mask_sea_et = landmask.interp_like(values, method='nearest').sel(
lat=extra_tropics).LSMASK.values == 0
mask_land_et = landmask.interp_like(values, method='nearest').sel(
lat=extra_tropics).LSMASK.values == 1
bnum = np.arange(-3, 5, 0.2)
lw = 2
ax2.hist(values.sel(lat=extra_tropics).grad.values[mask_land_et].flatten(
), bins=bnum, density=True, histtype='step', linewidth=lw, label='Extratropics:\nLand', color='C1')
ax2.hist(values.sel(lat=extra_tropics).grad.values[mask_sea_et].flatten(
), bins=bnum, density=True, histtype='step', linewidth=lw, label='Extratropics:\nOcean', color='C0')
ax2.hist(values.sel(lat=tropics).grad.values[mask_land_t].flatten(
), bins=bnum, density=True, histtype='step', linewidth=lw, label='Tropics:\nLand', color='red')
ax2.hist(values.sel(lat=tropics).grad.values[mask_sea_t].flatten(
), bins=bnum, density=True, histtype='step', linewidth=lw, label='Tropics:\nOcean', color='navy')
ax2.set_xlim(-3, 5)
ax2.set_title("b) Histogram of Slope $\partial$OLR/$\partial$T$_S$")
ax2.set_xlabel(r'Linear Slope $\partial$OLR/$\partial$T$_S$ (Wm$^{-2}$/K)')
ax2.set_ylabel('Probability Density')
ax2.legend(loc='upper left', handlelength=0.1)
ax1.set_anchor('N')
ax2.set_anchor('N')
path = "../../Figures/After first review/"
plt.savefig(path + 'Fig 1 CERES NEW.pdf',
bbox_inches='tight', dpi=300)
plt.close()
```
### Calculating Mean Values for the Figure Caption
```
area_factors = np.zeros_like(values.mean(dim='month').t2m.values)
lats = values.lat.values
lons = values.lon.values
for i in range(len(lats)):
area_factors[i, :] = np.cos(lats[i]*2*np.pi/360)
values['area_factors'] = (('lat', 'lon'), area_factors)
grad_area_scaled = np.zeros_like(values.mean(dim='month').t2m.values)
for i in range(len(lats)):
for j in range(len(lons)):
grad_area_scaled[i,j] = values.sel(lat=lats[i], lon=lons[j]).area_factors.values[()] * values.sel(lat=lats[i], lon=lons[j]).grad.values[()]
values['grad_area_scaled'] = (('lat', 'lon'), grad_area_scaled)
glbl = np.sum(values.grad_area_scaled.values.flatten()) / np.sum(values.area_factors.values.flatten())
print('Global area weighted mean is', glbl)
```
# Fig. 2
```
values_meas = xr.open_dataset('../../Data/CERES/clear_sky_ceres.nc')
lats = values_meas.lat.values
lons = values_meas.lon.values
fig = plt.figure(figsize=(6, 4.6), constrained_layout=True)
height_vals = [1, 4]
gs = fig.add_gridspec(ncols=5, nrows=2, height_ratios=height_vals)
month_list = np.arange(1, 13)
lc1 = "#7d7d7d"
cvals = [1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12.]
colors = ["#f1423f", "#f1613e", "#f79a33", "#feba28", "#efe720", "#b6d434",
"#00b34e", "#0098d1", "#0365b0", "#3e3f9b", "#83459b", "#bd2755"]
norm = plt.Normalize(min(cvals), max(cvals))
tuples = list(zip(map(norm, cvals), colors))
cmap_new = matplotlib.colors.LinearSegmentedColormap.from_list("", tuples)
SIZE = 8
plt.rc('font', size=SIZE) # controls default text sizes
plt.rc('axes', titlesize=SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SIZE) # legend fontsize
plt.rc('figure', titlesize=SIZE) # fontsize of the figure title
ax1 = fig.add_subplot(gs[0, 0])
ax2 = fig.add_subplot(gs[0, 1])
ax3 = fig.add_subplot(gs[0, 2])
ax4 = fig.add_subplot(gs[0, 3])
ax5 = fig.add_subplot(gs[0, 4])
top_axs = [ax1, ax2, ax3, ax4, ax5]
axs = fig.add_subplot(gs[1, :])
axs.scatter(
values_meas.sel(lat=lats[:-1]).t2m.values.flatten(),
values_meas.sel(lat=lats[:-1]).toa_lw_clr_c_mon.values.flatten(),
c=lc1,
s=1,
rasterized=True,
alpha=0.03
)
latvals = [70, -65, -2, -10, 15]
lonvals = [110, 250, 27, 0, 80]
titles = ['a) ', 'b) ', 'c) ', 'd) ', 'e) ']
style = "Simple, tail_width=0.3, head_width=3, head_length=3"
kw = dict(arrowstyle=style, color="k")
a1 = patches.FancyArrowPatch(
(284, 221), (259, 171), connectionstyle="arc3,rad=-0.3", **kw)
a2 = patches.FancyArrowPatch(
(274.5, 229), (271.5, 218), connectionstyle="arc3,rad=-0.3", **kw)
a3 = patches.FancyArrowPatch(
(297, 272), (297.7, 274.5), connectionstyle="arc3,rad=0.3", **kw)
a4 = patches.FancyArrowPatch(
(294.9, 294), (298, 294), connectionstyle="arc3,rad=0.4", **kw)
a5 = patches.FancyArrowPatch(
(301, 284), (297.5, 295), connectionstyle="arc3,rad=-0.4", **kw)
arrs = [a1, a2, a3, a4, a5]
for ind in range(len(latvals)):
latval = latvals[ind]
lonval = lonvals[ind]
i_raw = latval
j_raw = lonval
# Bottom loop plots
axs.plot(
values_meas.t2m.sel(lat=i_raw, lon=j_raw).values,
values_meas.toa_lw_clr_c_mon.sel(lat=i_raw, lon=j_raw).values,
c="k",
# label="Calculated OLR",
)
axs.plot(
values_meas.t2m.sel(lat=i_raw, lon=j_raw).values[0::11],
values_meas.toa_lw_clr_c_mon.sel(lat=i_raw, lon=j_raw).values[0::11],
c="k",
)
cplot = axs.scatter(
values_meas.t2m.sel(lat=i_raw, lon=j_raw).values,
values_meas.toa_lw_clr_c_mon.sel(lat=i_raw, lon=j_raw).values,
c=month_list,
cmap=cmap_new,
s=30,
)
axs.set_title('f$\,$)')
# Top plots
ax = top_axs[ind]
ax.plot(
values_meas.t2m.sel(lat=i_raw, lon=j_raw).values,
values_meas.toa_lw_clr_c_mon.sel(lat=i_raw, lon=j_raw).values,
c="k",
# label="Calculated OLR",
)
ax.plot(
values_meas.t2m.sel(lat=i_raw, lon=j_raw).values[0::11],
values_meas.toa_lw_clr_c_mon.sel(lat=i_raw, lon=j_raw).values[0::11],
c="k",
)
cplot = ax.scatter(
values_meas.t2m.sel(lat=i_raw, lon=j_raw).values,
values_meas.toa_lw_clr_c_mon.sel(lat=i_raw, lon=j_raw).values,
c=month_list,
cmap=cmap_new,
s=30,
)
ax.set_title(titles[ind]+str(i_raw)+', '+str(j_raw))
ax.add_patch(arrs[ind])
ax.margins(x=0.2,y=0.2)
ax3.set_xticks([296.5, 297.5])
top_axs[0].set_ylabel(r'OLR (Wm$^{-2}$)')
axs.set_xlabel(r'T$_s$ (K)')
axs.set_ylabel(r'OLR (Wm$^{-2}$)')
fig.suptitle('Latitude, Longitude')
cbar = fig.colorbar(
cplot,
ax=axs,
# label='Month',
fraction=0.1,
orientation="vertical",
aspect=40,
pad=0,
shrink=0.8,
ticks=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
)
cbar.ax.set_title(r'Month', y=1.02, x=2.5)
plt.savefig('../../Figures/After first review/Fig 2 CERES.pdf', format='pdf',
bbox_inches='tight', dpi=300)
plt.close()
```
# Fig. 3
```
# CERES
values_meas = xr.open_dataset('../../Data/CERES/clear_sky_ceres.nc')
# Offline calculations from cluster
values_calc = xr.open_dataset('../../Data/Cluster/clear_sky_calculated.nc')
lats = values_meas.lat.values
lons = values_meas.lon.values
plotvar = values_meas.hyst.values
lon_long = values_meas.lon.values
plotvar_cyc = np.zeros((len(lats), len(lons)))
plotvar_cyc, lon_long = add_cyclic_point(plotvar_cyc, coord=lon_long)
for i in range(len(lats)):
for j in range(len(lons)):
plotvar_cyc[i, j] = plotvar[i, j]
plotvar_cyc[:, len(lons)] = plotvar_cyc[:, 0]
fig = plt.figure(figsize=(6, 5.6), constrained_layout=True)
widths = [1, 1]
heights = [2, 0.9]
gs = fig.add_gridspec(
ncols=2, nrows=2, width_ratios=widths, height_ratios=heights)
SIZE = 8
plt.rc('font', size=SIZE) # controls default text sizes
plt.rc('axes', titlesize=SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SIZE) # legend fontsize
plt.rc('figure', titlesize=SIZE) # fontsize of the figure title
ax1 = fig.add_subplot(gs[0, :], projection=ccrs.PlateCarree())
ax1.coastlines()
C1 = ax1.pcolor(
lon_long, lats, plotvar_cyc, transform=ccrs.PlateCarree(), cmap='coolwarm', rasterized=True
)
C1.set_clim(vmin=-20, vmax=20)
ax1.set_title('a)')
ax1.set_xticks([-180, -90, 0, 90, 180], crs=ccrs.PlateCarree())
ax1.set_yticks([-90, 0, 90], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(number_format='.0f',
dateline_direction_label=True)
lat_formatter = LatitudeFormatter(number_format='.0f')
ax1.xaxis.set_major_formatter(lon_formatter)
ax1.yaxis.set_major_formatter(lat_formatter)
# Colourbars
fig.colorbar(
C1,
ax=ax1,
label="OLR Loopiness, $\mathcal{O}$ (Wm$^{-2}$)",
pad=-0.005,
aspect=40,
fraction=0.1,
# shrink=0.97,
orientation="horizontal",
)
xvals_l = values_meas.mean(
dim='month').toa_lw_clr_c_mon.values.flatten()
yvals_l = values_calc.mean(dim='month').olr_calc.values.flatten()
xvals_r = values_meas.mean(
dim='month').hyst.values.flatten()
yvals_r = values_calc.mean(dim='month').hyst.values.flatten()
# Bottom left plot
ax2 = fig.add_subplot(gs[1, 0])
hist1 = ax2.hist2d(xvals_l, yvals_l, 100, cmap='Greys',
norm=LogNorm(), vmin=0.2)
ax2.plot([np.amin(xvals_l), np.amax(xvals_l)], [np.amin(xvals_l), np.amax(
xvals_l)], c='C1', label='1:1 Line', linestyle='--', linewidth=2, rasterized=True)
ax2.set_xlabel(r'CERES (Wm$^{-2}$)')
ax2.set_ylabel(r'Offline Calculations (Wm$^{-2}$)')
ax2.set_title('b) Annual Mean OLR')
ax2.legend()
cbar1 = fig.colorbar(hist1[-1], ax=ax2, fraction=0, pad=-0.005, shrink=0.7, ticks=[1000, 100, 10, 1])
cbar1.ax.set_title(r'$\frac{\#}{(W m^{-2})^2}$', fontsize=10, y=1.15, x=4)
# Bottom right plot
ax3 = fig.add_subplot(gs[1, 1])
ax3.hist2d(xvals_r, yvals_r, 100, cmap='Greys', norm=LogNorm(), vmin=0.2)
ax3.plot([np.amin(xvals_r), np.amax(xvals_r)], [np.amin(xvals_r), np.amax(
xvals_r)], c='C1', label='1:1 Line', linestyle='--', linewidth=2, rasterized=True)
ax3.set_xlabel(r'CERES (Wm$^{-2}$)')
ax3.set_ylabel(r'Offline Calculations (Wm$^{-2}$)')
ax3.set_title("c) OLR Loopiness, $\mathcal{O}$")
ax3.legend()
cbar2 = fig.colorbar(hist1[-1], ax=ax3, fraction=0, pad=-0.005, shrink=0.7, ticks=[1000, 100, 10, 1])
cbar2.ax.set_title(r'$\frac{\#}{(W m^{-2})^2}$', fontsize=10, y=1.15, x=4)
plt.savefig('../../Figures/After first review/Fig 3 CERES.pdf',
format='pdf', bbox_inches='tight', dpi=300)
plt.close()
```
### Mean Absolute Error
```
xvals_l = values_meas.mean(
dim='month').toa_lw_clr_c_mon.values.flatten()
yvals_l = values_calc.mean(dim='month').olr_calc.values.flatten()
xvals_r = values_meas.mean(
dim='month').hyst.values.flatten()
yvals_r = values_calc.mean(dim='month').hyst.values.flatten()
diff_l = []
diff_r = []
for i in range(len(xvals_l)):
diff_l.append(np.abs(yvals_l[i]-xvals_l[i]))
diff_r.append(np.abs(yvals_r[i]-xvals_r[i]))
mae_l = np.mean(diff_l)
mae_r = np.mean(diff_r)
print('MAE Annual Mean:', mae_l)
print('MAE Loopiness :', mae_r)
```
### Calculating the Bias
```
# Calculate bias of cluster - CERES
bias = values_calc.hyst - values_meas.hyst
bias.mean(dim=('lat','lon')).values[()]
```
# Fig. 4
```
values_meas = xr.open_dataset('../../Data/CERES/clear_sky_ceres.nc')
values_meas_base = xr.open_dataset('../../Data/Cluster/Combined_data_ceres_base.nc')
values_meas_const_r = xr.open_dataset('../../Data/Cluster/clear_sky_calculated_const_rh.nc')
values_meas_const_t = xr.open_dataset('../../Data/Cluster/clear_sky_calculated_const_t.nc')
values_meas_atm = xr.open_dataset('../../Data/Cluster/data_atm.nc')
lats = values_meas.lat.values
lons = values_meas.lon.values
levels = values_meas_atm.level.values
month_val = 0
month_list = np.arange(1, 13, 1)
fig, axs = plt.subplots(nrows=4, ncols=3, figsize=(
6, 6), constrained_layout=True)
# Location, off of the coast of California (latitude value, longitude value)
lav = 32
lov = 237
month_list = np.arange(1, 13)
line_colour = "#7d7d7d"
SIZE = 8
plt.rc('font', size=SIZE) # controls default text sizes
plt.rc('axes', titlesize=SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SIZE) # legend fontsize
plt.rc('figure', titlesize=SIZE) # fontsize of the figure title
lcmap1 = mpl.cm.get_cmap('Blues')
lcmap2 = mpl.cm.get_cmap('Oranges')
lcmap3 = mpl.cm.get_cmap('Greens')
mean_t2m = np.mean(values_meas.sel(lat=lav, lon=lov).t2m.values)
for i in range(12):
lc1 = lcmap1(i/11)
lc2 = lcmap2(i/11)
a_val = 1 # * i/11
axs[0, 0].plot(
[j + (values_meas.sel(lat=lav, lon=lov).t2m.values[i] - mean_t2m)
for j in values_meas_atm.mean(dim="month").t.values],
levels,
c=lc1,
alpha=a_val,
)
axs[1, 0].plot(
values_meas_atm.sel(month=month_list[i]).t.values,
levels,
c=lc1,
alpha=a_val,
)
axs[2, 0].plot(
[j + (values_meas.sel(lat=lav, lon=lov).t2m.values[i] - mean_t2m)
for j in values_meas_atm.mean(dim="month").t.values],
levels,
c=lc1,
alpha=a_val,
)
axs[3, 0].plot(
values_meas_atm.sel(month=month_list[i]).t.values,
levels,
c=lc1,
alpha=a_val,
)
axs[2, 1].plot(
values_meas_atm.sel(month=month_list[i]).r.values,
levels,
c=lc2,
alpha=a_val,
)
axs[3, 1].plot(
values_meas_atm.sel(month=month_list[i]).r.values,
levels,
c=lc2,
alpha=a_val,
)
# Top two RH
axs[0, 1].plot(
values_meas_atm.mean(dim="month").r.values,
levels,
c=lcmap2(1.0),
)
axs[1, 1].plot(
values_meas_atm.mean(dim="month").r.values,
levels,
c=lcmap2(1.0),
)
# Base Case
axs[0, 2].plot(
values_meas_base.sel(lat=lav, lon=lov).ts.values,
values_meas_base.sel(lat=lav, lon=lov).olr_calc.values,
c=line_colour
)
axs[0, 2].plot(
values_meas_base.sel(lat=lav, lon=lov).ts.values[0::11],
values_meas_base.sel(lat=lav, lon=lov).olr_calc.values[0::11],
c=line_colour
)
axs[0, 2].scatter(
values_meas_base.sel(lat=lav, lon=lov).ts.values,
values_meas_base.sel(lat=lav, lon=lov).olr_calc.values,
c=month_list,
cmap=lcmap3,
s=30,
)
axs[0, 2].margins(x=0.2,y=0.2)
# Temperature Variation Only Case
axs[1, 2].plot(
values_meas_const_r.sel(lat=lav, lon=lov).ts.values,
values_meas_const_r.sel(lat=lav, lon=lov).olr_calc.values,
c=line_colour
)
axs[1, 2].plot(
values_meas_const_r.sel(lat=lav, lon=lov).ts.values[0::11],
values_meas_const_r.sel(lat=lav, lon=lov).olr_calc.values[0::11],
c=line_colour
)
axs[1, 2].scatter(
values_meas_const_r.sel(lat=lav, lon=lov).ts.values,
values_meas_const_r.sel(lat=lav, lon=lov).olr_calc.values,
c=month_list,
cmap=lcmap3,
s=30,
)
axs[1, 2].margins(x=0.2,y=0.2)
# Moisture Variation Only Case
axs[2, 2].plot(
values_meas_const_t.sel(lat=lav, lon=lov).ts.values,
values_meas_const_t.sel(lat=lav, lon=lov).olr_calc.values,
c=line_colour
)
axs[2, 2].plot(
values_meas_const_t.sel(lat=lav, lon=lov).ts.values[0::11],
values_meas_const_t.sel(lat=lav, lon=lov).olr_calc.values[0::11],
c=line_colour
)
axs[2, 2].scatter(
values_meas_const_t.sel(lat=lav, lon=lov).ts.values,
values_meas_const_t.sel(lat=lav, lon=lov).olr_calc.values,
c=month_list,
cmap=lcmap3,
s=30,
)
axs[2, 2].margins(x=0.2,y=0.2)
# Full Case
axs[3, 2].plot(
values_meas.sel(lat=lav, lon=lov).t2m.values,
values_meas.sel(lat=lav, lon=lov).toa_lw_clr_c_mon.values,
c=line_colour
)
axs[3, 2].plot(
values_meas.sel(lat=lav, lon=lov).t2m.values[0::11],
values_meas.sel(lat=lav, lon=lov).toa_lw_clr_c_mon.values[0::11],
c=line_colour
)
axs[3, 2].scatter(
values_meas.sel(lat=lav, lon=lov).t2m.values,
values_meas.sel(lat=lav, lon=lov).toa_lw_clr_c_mon.values,
c=month_list,
cmap=lcmap3,
s=30,
)
axs[3, 2].margins(x=0.2,y=0.2)
# Formatting
for i1 in range(3):
for i2 in range(4):
if i1 == 0:
axs[i2, i1].set_ylabel("Pressure (mBar)")
axs[0, 0].invert_yaxis()
axs[1, 0].invert_yaxis()
axs[2, 0].invert_yaxis()
axs[3, 0].invert_yaxis()
axs[0, 1].invert_yaxis()
axs[1, 1].invert_yaxis()
axs[2, 1].invert_yaxis()
axs[3, 1].invert_yaxis()
labels = ['']
axs[0,1].set_yticklabels(labels)
axs[1,1].set_yticklabels(labels)
axs[2,1].set_yticklabels(labels)
axs[3,1].set_yticklabels(labels)
axs[0,0].set_xticklabels(labels)
axs[1,0].set_xticklabels(labels)
axs[2,0].set_xticklabels(labels)
axs[0,1].set_xticklabels(labels)
axs[1,1].set_xticklabels(labels)
axs[2,1].set_xticklabels(labels)
axs[0,2].set_xticklabels(labels)
axs[1,2].set_xticklabels(labels)
axs[2,2].set_xticklabels(labels)
temp_ticks = [200, 230, 260, 290]
axs[0,0].set_xticks(temp_ticks)
axs[1,0].set_xticks(temp_ticks)
axs[2,0].set_xticks(temp_ticks)
axs[3,0].set_xticks(temp_ticks)
rh_ticks = [0, 30, 60, 90]
axs[0,1].set_xticks(rh_ticks)
axs[1,1].set_xticks(rh_ticks)
axs[2,1].set_xticks(rh_ticks)
axs[3,1].set_xticks(rh_ticks)
axs[0,2].yaxis.tick_right()
axs[1,2].yaxis.tick_right()
axs[2,2].yaxis.tick_right()
axs[3,2].yaxis.tick_right()
axs[0,2].yaxis.set_label_position("right")
axs[1,2].yaxis.set_label_position("right")
axs[2,2].yaxis.set_label_position("right")
axs[3,2].yaxis.set_label_position("right")
temp_xlim = axs[1,0].get_xlim()
axs[0,0].set_xlim(temp_xlim)
axs[1,0].set_xlim(temp_xlim)
axs[2,0].set_xlim(temp_xlim)
axs[3,0].set_xlim(temp_xlim)
rh_xlim = axs[2,1].get_xlim()
axs[0,1].set_xlim(rh_xlim)
axs[1,1].set_xlim(rh_xlim)
axs[2,1].set_xlim(rh_xlim)
axs[3,1].set_xlim(rh_xlim)
axs[0,2].set_ylabel('OLR (Wm$^{-2}$)', rotation=-90, labelpad=15)
axs[1,2].set_ylabel('OLR (Wm$^{-2}$)', rotation=-90, labelpad=15)
axs[2,2].set_ylabel('OLR (Wm$^{-2}$)', rotation=-90, labelpad=15)
axs[3,2].set_ylabel('OLR (Wm$^{-2}$)', rotation=-90, labelpad=15)
axs[3, 0].set_xlabel("Temperature (K)")
axs[3, 1].set_xlabel("Relative Humidity (%)")
axs[3, 2].set_xlabel('T$_s$ (K)')
xv = 1.55
yv = 1.08
fs = 8
axs[0,1].set_title('Base Case (Zero Loopiness)')
axs[1,1].set_title('Seasonal Temperature Variation Only')
axs[2,1].set_title('Seasonal Moisture Variation Only')
axs[3,1].set_title('Full Case (Full Loopiness)')
axs[0, 0].arrow(250, 550, 2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[0, 0].arrow(250, 550, -2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[2, 0].arrow(250, 550, 2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[2, 0].arrow(250, 550, -2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[1, 0].arrow(220, 350, 2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[1, 0].arrow(220, 350, -2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[1, 0].arrow(265, 850, 7.5, 0, head_width=40, head_length=2.5, fc='k')
axs[1, 0].arrow(265, 850, -7.5, 0, head_width=40, head_length=2.5, fc='k')
axs[3, 0].arrow(220, 350, 2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[3, 0].arrow(220, 350, -2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[3, 0].arrow(265, 850, 7.5, 0, head_width=40, head_length=2.5, fc='k')
axs[3, 0].arrow(265, 850, -7.5, 0, head_width=40, head_length=2.5, fc='k')
axs[2, 1].arrow(72, 830, 2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[2, 1].arrow(72, 830, -2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[2, 1].arrow(72, 250, 7.5, 0, head_width=40, head_length=2.5, fc='k')
axs[2, 1].arrow(72, 250, -7.5, 0, head_width=40, head_length=2.5, fc='k')
axs[3, 1].arrow(72, 830, 2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[3, 1].arrow(72, 830, -2.5, 0, head_width=40, head_length=2.5, fc='k')
axs[3, 1].arrow(72, 250, 7.5, 0, head_width=40, head_length=2.5, fc='k')
axs[3, 1].arrow(72, 250, -7.5, 0, head_width=40, head_length=2.5, fc='k')
plt.savefig('../../Figures/After first review/Fig 4 CERES.pdf',
bbox_inches='tight', format='pdf') # Save the figure
plt.close()
```
# Fig. 5
```
values_t = xr.open_dataset('../../Data/Cluster/clear_sky_calculated_const_t.nc')
values_r = xr.open_dataset('../../Data/Cluster/clear_sky_calculated_const_rh.nc')
lats = values_t.lat.values
lons = values_t.lon.values
# Variables that you want to plot
plotvar1 = values_r.hyst.values
plotvar2 = values_t.hyst.values
# Adding a cyclic point to the two variables
# This removes a white line at lon = 0
lon_long = values_r.lon.values
plotvar_cyc1 = np.zeros((len(lats), len(lons)))
plotvar_cyc1, lon_long = add_cyclic_point(plotvar_cyc1, coord=lon_long)
for i in range(len(lats)):
for j in range(len(lons)):
plotvar_cyc1[i, j] = plotvar1[i, j]
plotvar_cyc1[:, len(lons)] = plotvar_cyc1[:, 0]
lon_long = values_r.lon.values
plotvar_cyc2 = np.zeros((len(lats), len(lons)))
plotvar_cyc2, lon_long = add_cyclic_point(plotvar_cyc2, coord=lon_long)
for i in range(len(lats)):
for j in range(len(lons)):
plotvar_cyc2[i, j] = plotvar2[i, j]
plotvar_cyc2[:, len(lons)] = plotvar_cyc2[:, 0]
# Plotting
fig = plt.figure(figsize=(6, 2.4), constrained_layout=True)
gs = fig.add_gridspec(ncols=2, nrows=1)
SIZE = 8
plt.rc('font', size=SIZE) # controls default text sizes
plt.rc('axes', titlesize=SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SIZE) # legend fontsize
plt.rc('figure', titlesize=SIZE) # fontsize of the figure title
# Left map
ax1 = fig.add_subplot(gs[0], projection=ccrs.PlateCarree())
ax1.coastlines()
C1 = ax1.pcolor(
lon_long, lats, plotvar_cyc1, transform=ccrs.PlateCarree(), cmap='coolwarm', rasterized=True
)
C1.set_clim(vmin=-20, vmax=20)
ax1.set_title("a) Temperature Variation Only")
ax1.set_xticks([-180, -90, 0, 90, 180], crs=ccrs.PlateCarree())
ax1.set_yticks([-90, 0, 90], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(number_format='.0f',
dateline_direction_label=True)
lat_formatter = LatitudeFormatter(number_format='.0f')
ax1.xaxis.set_major_formatter(lon_formatter)
ax1.yaxis.set_major_formatter(lat_formatter)
# Colourbars
fig.colorbar(
C1,
ax=ax1,
label="OLR Loopiness, $\mathcal{O}$ (Wm$^{-2}$)",
pad=0,
aspect=20,
fraction=0.1,
# shrink=0.95,
orientation="horizontal",
)
# Right map
ax2 = fig.add_subplot(gs[1], projection=ccrs.PlateCarree())
ax2.coastlines()
C2 = ax2.pcolor(
lon_long, lats, plotvar_cyc2, transform=ccrs.PlateCarree(), cmap='coolwarm', rasterized=True
)
C2.set_clim(vmin=-20, vmax=20)
ax2.set_title("b) Moisture Variation Only")
ax2.set_xticks([-180, -90, 0, 90, 180], crs=ccrs.PlateCarree())
ax2.set_yticks([-90, 0, 90], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(number_format='.0f',
dateline_direction_label=True)
lat_formatter = LatitudeFormatter(number_format='.0f')
ax2.xaxis.set_major_formatter(lon_formatter)
ax2.yaxis.set_major_formatter(lat_formatter)
# Colourbars
fig.colorbar(
C2,
ax=ax2,
label="OLR Loopiness, $\mathcal{O}$ (Wm$^{-2}$)",
pad=0,
aspect=20,
fraction=0.1,
# shrink=0.95,
orientation="horizontal",
)
plt.savefig('../../Figures/After first review/Fig 5 CERES.pdf',
format='pdf', dpi=300, bbox_inches='tight')
plt.close()
```
# Fig. 6
```
values_as = xr.open_dataset('../../Data/CERES/all_sky_ceres.nc')
values_cs = xr.open_dataset('../../Data/CERES/clear_sky_ceres.nc')
lats = values_cs.lat.values
lons = values_cs.lon.values
# Variables that you want to plot
plotvar1 = values_cs.hyst_over_olr_range.values
plotvar2 = values_as.hyst_over_olr_range.values
# Adding a cyclic point to the two variables
# This removes a white line at lon = 0
lon_long = values_cs.lon.values
plotvar_cyc1 = np.zeros((len(lats), len(lons)))
plotvar_cyc1, lon_long = add_cyclic_point(plotvar_cyc1, coord=lon_long)
for i in range(len(lats)):
for j in range(len(lons)):
plotvar_cyc1[i, j] = plotvar1[i, j]
plotvar_cyc1[:, len(lons)] = plotvar_cyc1[:, 0]
lon_long = values_cs.lon.values
plotvar_cyc2 = np.zeros((len(lats), len(lons)))
plotvar_cyc2, lon_long = add_cyclic_point(plotvar_cyc2, coord=lon_long)
for i in range(len(lats)):
for j in range(len(lons)):
plotvar_cyc2[i, j] = plotvar2[i, j]
plotvar_cyc2[:, len(lons)] = plotvar_cyc2[:, 0]
# Plotting
fig = plt.figure(figsize=(6, 2.4), constrained_layout=True)
gs = fig.add_gridspec(ncols=2, nrows=1)
SIZE = 8
plt.rc('font', size=SIZE) # controls default text sizes
plt.rc('axes', titlesize=SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SIZE) # legend fontsize
plt.rc('figure', titlesize=SIZE) # fontsize of the figure title
# Left map
ax1 = fig.add_subplot(gs[0], projection=ccrs.PlateCarree())
ax1.coastlines()
C1 = ax1.pcolor(
lon_long, lats, plotvar_cyc1, transform=ccrs.PlateCarree(), cmap='coolwarm', rasterized=True
)
C1.set_clim(vmin=-100, vmax=100)
ax1.set_title("a) Clear Sky")
ax1.set_xticks([-180, -90, 0, 90, 180], crs=ccrs.PlateCarree())
ax1.set_yticks([-90, 0, 90], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(number_format='.0f',
dateline_direction_label=True)
lat_formatter = LatitudeFormatter(number_format='.0f')
ax1.xaxis.set_major_formatter(lon_formatter)
ax1.yaxis.set_major_formatter(lat_formatter)
# Colourbars
cbar1 = fig.colorbar(
C1,
ax=ax1,
label=" $\mathcal{O}$ / OLR Range (%)",
pad=0,
aspect=20,
fraction=0.1,
# shrink=0.95,
orientation="horizontal",
)
cbar1.ax.set_xticklabels(
['-100%', '-50%', '0%', '50%', '100%'])
# Right map
ax2 = fig.add_subplot(gs[1], projection=ccrs.PlateCarree())
ax2.coastlines()
C2 = ax2.pcolor(
lon_long, lats, plotvar_cyc2, transform=ccrs.PlateCarree(), cmap='coolwarm', rasterized=True
)
C2.set_clim(vmin=-100, vmax=100)
ax2.set_title("b) All Sky")
ax2.set_xticks([-180, -90, 0, 90, 180], crs=ccrs.PlateCarree())
ax2.set_yticks([-90, 0, 90], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(number_format='.0f',
dateline_direction_label=True)
lat_formatter = LatitudeFormatter(number_format='.0f')
ax2.xaxis.set_major_formatter(lon_formatter)
ax2.yaxis.set_major_formatter(lat_formatter)
# Colourbars
cbar2 = fig.colorbar(
C2,
ax=ax2,
label="$\mathcal{O}$ / OLR Range (%)",
pad=0,
aspect=20,
fraction=0.1,
# shrink=0.95,
orientation="horizontal",
)
cbar2.ax.set_xticklabels(
['-100%', '-50%', '0%', '50%', '100%'])
plt.savefig('../../Figures/After first review/Fig 6 CERES.pdf',
format='pdf', dpi=300, bbox_inches='tight')
plt.close()
```
### Global normalised values
```
area_factors = np.zeros_like(values_cs.mean(dim='month').t2m.values)
lats = values_cs.lat.values
lons = values_cs.lon.values
for i in range(len(lats)):
area_factors[i, :] = np.cos(lats[i]*2*np.pi/360)
values_cs['area_factors'] = (('lat', 'lon'), area_factors)
hyst_over_olr_area_scaled_cs = np.zeros_like(values_cs.mean(dim='month').t2m.values)
hyst_over_olr_area_scaled_as = np.zeros_like(values_as.mean(dim='month').t2m.values)
for i in range(len(lats)):
for j in range(len(lons)):
hyst_over_olr_area_scaled_cs[i,j] = values_cs.sel(lat=lats[i], lon=lons[j]).area_factors.values[()] * np.abs(values_cs.sel(lat=lats[i], lon=lons[j]).hyst_over_olr_range.values[()])
hyst_over_olr_area_scaled_as[i,j] = values_cs.sel(lat=lats[i], lon=lons[j]).area_factors.values[()] * np.abs(values_as.sel(lat=lats[i], lon=lons[j]).hyst_over_olr_range.values[()])
values_cs['hyst_over_olr_area_scaled'] = (('lat', 'lon'), hyst_over_olr_area_scaled_cs)
values_as['hyst_over_olr_area_scaled'] = (('lat', 'lon'), hyst_over_olr_area_scaled_as)
glbl_cs = np.sum(values_cs.hyst_over_olr_area_scaled.values.flatten()) / np.sum(values_cs.area_factors.values.flatten())
glbl_as = np.sum(values_as.hyst_over_olr_area_scaled.values.flatten()) / np.sum(values_cs.area_factors.values.flatten())
print('Global area weighted clear sky mean is', '%.2f' % glbl_cs, '%')
print('Global area weighted all sky mean is', '%.2f' % glbl_as, '%')
```
# Supplementary Information
```
# ERA5
values_meas_era5 = xr.open_dataset('../../Data/Other/values_meas_dir_int_hyst.nc')
# CERES
values_meas_ceres = xr.open_dataset('../../Data/CERES/clear_sky_ceres.nc')
lats = values_meas_ceres.lat.values
lons = values_meas_ceres.lon.values
plotvar1 = values_meas_era5.directional_int_hyst.values
plotvar2 = values_meas_ceres.hyst.values
lon_long1 = values_meas_era5.lon.values
plotvar_cyc1 = np.zeros((len(lats), len(lons)))
plotvar_cyc1, lon_long1 = add_cyclic_point(plotvar_cyc1, coord=lon_long1)
for i in range(len(lats)):
for j in range(len(lons)):
plotvar_cyc1[i, j] = plotvar1[i, j]
plotvar_cyc1[:, len(lons)] = plotvar_cyc1[:, 0]
lon_long2 = values_meas_ceres.lon.values
plotvar_cyc2 = np.zeros((len(lats), len(lons)))
plotvar_cyc2, lon_long2 = add_cyclic_point(plotvar_cyc2, coord=lon_long2)
for i in range(len(lats)):
for j in range(len(lons)):
plotvar_cyc2[i, j] = plotvar2[i, j]
plotvar_cyc2[:, len(lons)] = plotvar_cyc2[:, 0]
fig = plt.figure(figsize=(6, 7), constrained_layout=True)
gs = fig.add_gridspec(
ncols=1, nrows=2)
SIZE = 8
plt.rc('font', size=SIZE) # controls default text sizes
plt.rc('axes', titlesize=SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SIZE) # legend fontsize
plt.rc('figure', titlesize=SIZE) # fontsize of the figure title
ax1 = fig.add_subplot(gs[0], projection=ccrs.PlateCarree())
ax1.coastlines()
C1 = ax1.pcolor(
lon_long1, lats, plotvar_cyc1, transform=ccrs.PlateCarree(), cmap='coolwarm', rasterized=True
)
C1.set_clim(vmin=-20, vmax=20)
ax1.set_title('a) ERA5')
ax1.set_xticks([-180, -90, 0, 90, 180], crs=ccrs.PlateCarree())
ax1.set_yticks([-90, 0, 90], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(number_format='.0f',
dateline_direction_label=True)
lat_formatter = LatitudeFormatter(number_format='.0f')
ax1.xaxis.set_major_formatter(lon_formatter)
ax1.yaxis.set_major_formatter(lat_formatter)
ax2 = fig.add_subplot(gs[1], projection=ccrs.PlateCarree())
ax2.coastlines()
C2 = ax2.pcolor(
lon_long2, lats, plotvar_cyc2, transform=ccrs.PlateCarree(), cmap='coolwarm', rasterized=True
)
C2.set_clim(vmin=-20, vmax=20)
ax2.set_title('b) CERES')
ax2.set_xticks([-180, -90, 0, 90, 180], crs=ccrs.PlateCarree())
ax2.set_yticks([-90, 0, 90], crs=ccrs.PlateCarree())
lon_formatter = LongitudeFormatter(number_format='.0f',
dateline_direction_label=True)
lat_formatter = LatitudeFormatter(number_format='.0f')
ax2.xaxis.set_major_formatter(lon_formatter)
ax2.yaxis.set_major_formatter(lat_formatter)
# Colourbar
fig.colorbar(
C2,
ax=ax2,
label="OLR Loopiness, $\mathcal{O}$ (Wm$^{-2}$)",
pad=-0.005,
aspect=40,
fraction=0.1,
# shrink=0.97,
orientation="horizontal",
)
plt.savefig('../../Figures/After first review/SI.pdf',
format='pdf', bbox_inches='tight', dpi=300)
plt.close()
```
| true |
code
| 0.642012 | null | null | null | null |
|
# 2A.data - Matplotlib
Tutoriel sur [matplotlib](https://matplotlib.org/).
```
from jyquickhelper import add_notebook_menu
add_notebook_menu()
```
*Aparté*
Les librairies de visualisation en python se sont beaucoup développées ([10 plotting librairies](http://www.xavierdupre.fr/app/jupytalk/helpsphinx/2016/pydata2016.html)).
La référence reste [matplotlib](http://matplotlib.org/), et la plupart sont pensées pour être intégrées à ses objets (c'est par exemple le cas de [seaborn](https://stanford.edu/~mwaskom/software/seaborn/introduction.html), [mpld3](http://mpld3.github.io/), [plotly](https://plot.ly/) et [bokeh](http://bokeh.pydata.org/en/latest/)). Il est donc utile de commencer par se familiariser avec matplotlib.
Pour reprendre les termes de ses développeurs : *"matplotlib is a python 2D plotting library which produces publication quality figures in a variety of hardcopy formats and interactive environments across platforms. matplotlib can be used in python scripts, the python and ipython shell (ala MatLab or mathematica), web application servers, and six graphical user interface toolkits."*
La structure sous-jacente de matplotlib est très générale et personnalisable (gestion de l'interface utilisateur, possibilité d'intégration dans des applications web, etc.). Heureusement, il n'est pas nécessaire de maîtriser l'ensemble de ces méthodes pour produire un graphe (il existe pas moins de 2840 pages de [documentation](http://matplotlib.org/Matplotlib.pdf)). Pour générer des graphes et les modifier, il suffit de passer par l'interface [pyplot]().
L'interface pyplot est inspirée de celle de MATLAB. Ceux qui la connaissent s'y retrouveront rapidement.
Pour résumer :
- matplotlib - accès "low level" à la librairie de visualisation. Utile si vous souhaitez créer votre propre librairie de visualisation python ou faire des choses très custom.
- matplotlib.pyplot - interface proche de celle de Matplab pour produire vos graphes
- pylab - matplotlib.pyplot + numpy
```
#Pour intégrer les graphes à votre notebook, il suffit de faire
%matplotlib inline
#ou alors
%pylab inline
#pylab charge également numpy. C'est la commande du calcul scientifique python.
```
La structure des objets décrits par l'API est très hiérarchique, comme illustré par ce schéma :
- "Figure" contient l'ensemble de la représentation visuelle. C'est par exemple grâce à cette méta-structure que l'on peut facilement ajouter un titre à une représentation qui contiendrait plusieurs graphes ;
- "Axes" (ou "Subplots") décrit l'ensemble contenant un ou pusieurs graphes (correspond à l'objet subplot et aux méthodes add_subplot)
- "Axis" correspond aux axes d'un graphique (ou instance de subplot) donné.
<img src="http://matplotlib.org/_images/fig_map.png" />
Une dernière remarque d'ordre général : [pyplot est une machine à état](https://en.wikipedia.org/wiki/Matplotlib).
Cela implique que les méthodes pour tracer un graphe ou éditer un label s'appliquent par défaut au dernier état en cours (dernière instance de subplot ou dernière instance d'axe par exemple).
Conséquence : il faut concevoir ses codes comme une séquence d'instructions (par exemple, il ne faut pas séparer les instructions qui se rapportent au même graphique dans deux cellules différentes du Notebook).
### Figures et Subplots
```
from matplotlib import pyplot as plt
plt.figure(figsize=(10,8))
plt.subplot(111) # Méthode subplot : pour définir les graphiques appartenant à l'objet figure, ici 1 X 1, indice 1
#plt.subplot(1,1,1) fonctionne aussi
#attention, il est nécessaire de conserver toutes les instructions d'un même graphique dans le même bloc
#pas besoin de plt.show() dans un notebook, sinon c'est nécessaire
```
Un graphique (très) simple avec l'instruction plot.
```
from numpy import random
import numpy as np
import pandas as p
plt.figure(figsize=(10,8))
plt.subplot(111)
plt.plot([random.random_sample(1) for i in range(5)])
#Il est possible de passer des listes, des arrays de numpy, des Series et des Dataframes de pandas
plt.plot(np.array([random.random_sample(1) for i in range(5)]))
plt.plot(p.DataFrame(np.array([random.random_sample(1) for i in range(5)])))
#pour afficher plusieurs courbes, il suffit de cumuler les instructions plt.plot
#plt.show()
```
Pour faire plusieurs sous graphes, il suffit de modifier les valeurs des paramètres de l'objet subplot.
```
fig = plt.figure(figsize=(15,10))
ax1 = fig.add_subplot(2,2,1) #modifie l'objet fig et créé une nouvelle instance de subplot, appelée ax1
#vous verrez souvent la convention ax comme instance de subplot : c'est parce que l'on parle aussi d'objet "Axe"
#à ne pas confondre avec l'objet "Axis"
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,3)
```
Si aucune instance d'axes n'est précisée, la méthode plot est appliquée à la dernière instance créée.
```
from numpy.random import randn
fig = plt.figure(figsize=(10,8))
ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,3)
plt.plot(randn(50).cumsum(),'k--')
# plt.show()
from numpy.random import randn
fig = plt.figure(figsize=(15,10))
ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,3)
# On peut compléter les instances de sous graphiques par leur contenu.
# Au passage, quelques autres exemples de graphes
ax1.hist(randn(100),bins=20,color='k',alpha=0.3)
ax2.scatter(np.arange(30),np.arange(30)+3*randn(30))
ax3.plot(randn(50).cumsum(),'k--')
```
Pour explorer l'ensemble des catégories de graphiques possibles : [Gallery](http://matplotlib.org/gallery.html). Les plus utiles pour l'analyse de données : [scatter](http://matplotlib.org/examples/lines_bars_and_markers/scatter_with_legend.html), [scatterhist](http://matplotlib.org/examples/axes_grid/scatter_hist.html), [barchart](http://matplotlib.org/examples/pylab_examples/barchart_demo.html), [stackplot](http://matplotlib.org/examples/pylab_examples/stackplot_demo.html), [histogram](http://matplotlib.org/examples/statistics/histogram_demo_features.html), [cumulative distribution function](http://matplotlib.org/examples/statistics/histogram_demo_cumulative.html), [boxplot](http://matplotlib.org/examples/statistics/boxplot_vs_violin_demo.html), , [radarchart](http://matplotlib.org/examples/api/radar_chart.html).
### Ajuster les espaces entre les graphes
```
fig,axes = plt.subplots(2,2,sharex=True,sharey=True)
# Sharex et sharey portent bien leurs noms : si True, ils indiquent que les sous-graphiques
# ont des axes paramétrés de la même manière
for i in range(2):
for j in range(2):
axes[i,j].hist(randn(500),bins=50,color='k',alpha=0.5)
# L'objet "axes" est un 2darray, simple à indicer et parcourir avec une boucle
print(type(axes))
# N'h'ésitez pas à faire varier les paramètres qui vous posent question. Par exemple, à quoi sert alpha ?
plt.subplots_adjust(wspace=0,hspace=0)
# Cette dernière méthode permet de supprimer les espaces entres les sous graphes.
```
Pas d'autres choix que de paramétrer à la main pour corriger les chiffres qui se superposent.
### Couleurs, Marqueurs et styles de ligne
MatplotLib offre la possibilité d'adopter deux types d'écriture : chaîne de caractère condensée ou paramétrage explicite via un système clé-valeur.
```
from numpy.random import randn
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(111)
ax1.plot(randn(50).cumsum(),color='g',marker='o',linestyle='dashed')
# plt.show()
from numpy.random import randn
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(111)
ax1.plot(randn(50).cumsum(),'og--') #l'ordre des paramètres n'importe pas
```
Plus de détails dans la documentation sur l'API de matplotlib pour paramétrer la
<a href="http://matplotlib.org/api/colors_api.html">
couleur
</a>
, les
<a href="http://matplotlib.org/api/markers_api.html">
markers
</a>
, et le
<a href="http://matplotlib.org/api/lines_api.html#matplotlib.lines.Line2D.set_linestyle">
style des lignes
</a>
. MatplotLib est compatible avec plusieurs standards de couleur :
- sous forme d'une lettre : 'b' = blue (bleu), 'g' = green (vert), 'r' = red (rouge), 'c' = cyan (cyan), 'm' = magenta (magenta), 'y' = yellow (jaune), 'k' = black (noir), 'w' = white (blanc).
- sous forme d'un nombre entre 0 et 1 entre quotes qui indique le niveau de gris : par exemple '0.70' ('1' = blanc, '0' = noir).
- sous forme d'un nom : par exemple 'red'.
- sous forme html avec les niveaux respectifs de rouge (R), vert (G) et bleu (B) : '#ffee00'. Voici un site pratique pour récupérer une couleur en [RGB hexadécimal](http://www.proftnj.com/RGB3.htm).
- sous forme d'un triplet de valeurs entre 0 et 1 avec les niveaux de R, G et B : (0.2, 0.9, 0.1).
```
from numpy.random import randn
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(1,1,1)
#avec la norme RGB
ax1.plot(randn(50).cumsum(),color='#D0BBFF',marker='o',linestyle='-.')
ax1.plot(randn(50).cumsum(),color=(0.8156862745098039, 0.7333333333333333, 1.0),marker='o',linestyle='-.')
```
### Ticks labels et legendes
3 méthodes clés :
- xlim() : pour délimiter l'étendue des valeurs de l'axe
- xticks() : pour passer les graduations sur l'axe
- xticklabels() : pour passer les labels
Pour l'axe des ordonnées c'est ylim, yticks, yticklabels.
Pour récupérer les valeurs fixées :
- plt.xlim() ou plt.get_xlim()
- plt.xticks() ou plt.get_xticks()
- plt.xticklabels() ou plt.get_xticklabels()
Pour fixer ces valeurs :
- plt.xlim([start,end]) ou plt.set_xlim([start,end])
- plt.xticks(my_ticks_list) ou plt.get_xticks(my_ticks_list)
- plt.xticklabels(my_labels_list) ou plt.get_xticklabels(my_labels_list)
Si vous voulez customiser les axes de plusieurs sous graphiques, passez par une [instance de axis](http://matplotlib.org/users/artists.html) et non subplot.
```
from numpy.random import randn
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(1,1,1)
serie1=randn(50).cumsum()
serie2=randn(50).cumsum()
serie3=randn(50).cumsum()
ax1.plot(serie1,color='#33CCFF',marker='o',linestyle='-.',label='un')
ax1.plot(serie2,color='#FF33CC',marker='o',linestyle='-.',label='deux')
ax1.plot(serie3,color='#FFCC99',marker='o',linestyle='-.',label='trois')
#sur le graphe précédent, pour raccourcir le range
ax1.set_xlim([0,21])
ax1.set_ylim([-20,20])
#faire un ticks avec un pas de 2 (au lieu de 5)
ax1.set_xticks(range(0,21,2))
#changer le label sur la graduation
ax1.set_xticklabels(["j +" + str(l) for l in range(0,21,2)])
ax1.set_xlabel('Durée après le traitement')
ax1.legend(loc='best')
#permet de choisir l'endroit le plus vide
```
### Inclusion d'annotation et de texte, titre et libellé des axes
```
from numpy.random import randn
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(1,1,1)
ax1.plot(serie1,color='#33CCFF',marker='o',linestyle='-.',label='un')
ax1.plot(serie2,color='#FF33CC',marker='o',linestyle='-.',label='deux')
ax1.plot(serie3,color='#FFCC99',marker='o',linestyle='-.',label='trois')
ax1.set_xlim([0,21])
ax1.set_ylim([-20,20])
ax1.set_xticks(range(0,21,2))
ax1.set_xticklabels(["j +" + str(l) for l in range(0,21,2)])
ax1.set_xlabel('Durée après le traitement')
ax1.annotate("You're here", xy=(7, 7), #point de départ de la flèche
xytext=(10, 10), #position du texte
arrowprops=dict(facecolor='#000000', shrink=0.10),
)
ax1.legend(loc='best')
plt.xlabel("Libellé de l'axe des abscisses")
plt.ylabel("Libellé de l'axe des ordonnées")
plt.title("Une idée de titre ?")
plt.text(5, -10, r'$\mu=100,\ \sigma=15$')
# plt.show()
```
### matplotlib et le style
Il est possible de définir son propre style. Cette possibilité est intéressante si vous faîtes régulièrement les mêmes graphes et voulez définir des templates (plutôt que de copier/coller toujours les mêmes lignes de code). Tout est décrit dans [style_sheets](http://matplotlib.org/users/style_sheets.html).
```
from numpy.random import randn
#pour que la définition du style soit seulement dans cette cellule notebook
with plt.style.context('ggplot'):
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(1,1,1)
ax1.plot(serie1,color='#33CCFF',marker='o',linestyle='-.',label='un')
ax1.plot(serie2,color='#FF33CC',marker='o',linestyle='-.',label='deux')
ax1.plot(serie3,color='#FFCC99',marker='o',linestyle='-.',label='trois')
ax1.set_xlim([0,21])
ax1.set_ylim([-20,20])
ax1.set_xticks(range(0,21,2))
ax1.set_xticklabels(["j +" + str(l) for l in range(0,21,2)])
ax1.set_xlabel('Durée après le traitement')
ax1.annotate("You're here", xy=(7, 7), #point de départ de la flèche
xytext=(10, 10), #position du texte
arrowprops=dict(facecolor='#000000', shrink=0.10),
)
ax1.legend(loc='best')
plt.xlabel("Libellé de l'axe des abscisses")
plt.ylabel("Libellé de l'axe des ordonnées")
plt.title("Une idée de titre ?")
plt.text(5, -10, r'$\mu=100,\ \sigma=15$')
#plt.show()
import numpy as np
import matplotlib.pyplot as plt
print("De nombreux autres styles sont disponibles, pick up your choice! ", plt.style.available)
with plt.style.context('dark_background'):
plt.plot(serie1, 'r-o')
# plt.show()
```
Comme suggéré dans le nom des styles disponibles dans matplotlib, la librairie seaborn, qui est une sorte de surcouche de matplotlib, est un moyen très pratique d'accéder à des styles pensés et adaptés pour la mise en valeur de pattern dans les données.
Voici quelques exemples, toujours sur la même série de données. Je vous invite également à explorer les [palettes de couleurs](https://stanford.edu/~mwaskom/software/seaborn/tutorial/color_palettes.html).
```
#on peut remarquer que le style ggplot est resté.
import seaborn as sns
#5 styles disponibles
#sns.set_style("whitegrid")
#sns.set_style("darkgrid")
#sns.set_style("white")
#sns.set_style("dark")
#sns.set_style("ticks")
#si vous voulez définir un style temporairement
with sns.axes_style("ticks"):
fig = plt.figure(figsize(8,6))
ax1 = fig.add_subplot(1,1,1)
plt.plot(serie1)
```
En dehors du style et des couleurs, Seaborn a mis l'accent sur :
- les graphes de distribution ([univariés](https://stanford.edu/~mwaskom/software/seaborn/examples/distplot_options.html#distplot-options) / [bivariés](https://stanford.edu/~mwaskom/software/seaborn/examples/joint_kde.html#joint-kde)). Particulièrement utiles et pratiques : les [pairwiseplot](https://stanford.edu/~mwaskom/software/seaborn/tutorial/distributions.html#visualizing-pairwise-relationships-in-a-dataset)
- les graphes de [régression](https://stanford.edu/~mwaskom/software/seaborn/tutorial/regression.html)
- les graphes de [variables catégorielles](https://stanford.edu/~mwaskom/software/seaborn/tutorial/categorical.html)
- les [heatmap](https://stanford.edu/~mwaskom/software/seaborn/examples/heatmap_annotation.html) sur les matrices de données
Seaborn ce sont des graphes pensés pour l'analyse de données et la présentation de rapports à des collègues ou clients. C'est peut-être un peu moins customisable que matplotlib mais vous avez le temps avant de vous sentir limités dans les possibilités.
# Matplotlib et pandas, intéractions avec seaborn
Comme vu précédemment, matplotlib permet de manipuler et de représenter sous forme de graphes toutes sortes d'objets : listes, arrays numpy, Series et DataFrame pandas. Inversement, pandas a prévu des méthodes qui intègrent les objets matplotlib les plus utiles pour le tracé de graphiques. Nous allons tester un peu l'intégration [pandas/matplotlib](http://pandas.pydata.org/pandas-docs/stable/visualization.html). D'une amanière générale, tout un [écosystème](http://pandas.pydata.org/pandas-docs/stable/ecosystem.html#ecosystem-visualization) de visualisation s'est développé autour de pandas. Nous allons tester les différentes librairies évoquées. Télécharger les données de l'exercice 4 du TD sur pandas et disponible sur le site de l'INSEE [Naissances, décès et mariages de 1998 à 2013](https://www.insee.fr/fr/statistiques/2407910?sommaire=2117120#titre-bloc-3).
```
import urllib.request
import zipfile
def download_and_save(name, root_url):
if root_url == 'xd':
from pyensae.datasource import download_data
download_data(name)
else:
response = urllib.request.urlopen(root_url+name)
with open(name, "wb") as outfile:
outfile.write(response.read())
def unzip(name):
with zipfile.ZipFile(name, "r") as z:
z.extractall(".")
filenames = ["etatcivil2012_mar2012_dbase.zip",
"etatcivil2012_nais2012_dbase.zip",
"etatcivil2012_dec2012_dbase.zip", ]
# Une copie des fichiers a été postée sur le site www.xavierdupre.fr
# pour tester le notebook plus facilement.
root_url = 'xd' # http://telechargement.insee.fr/fichiersdetail/etatcivil2012/dbase/'
for filename in filenames:
download_and_save(filename, root_url)
unzip(filename)
print("Download of {}: DONE!".format(filename))
```
Penser à installer le module [dbfread](https://github.com/olemb/dbfread/) si ce n'est pas fait.
```
import pandas
try:
from dbfread import DBF
use_dbfread = True
except ImportError as e :
use_dbfread = False
if use_dbfread:
print("use of dbfread")
def dBase2df(dbase_filename):
table = DBF(dbase_filename, load=True, encoding="cp437")
return pandas.DataFrame(table.records)
df = dBase2df('mar2012.dbf')
#df.to_csv("mar2012.txt", sep="\t", encoding="utf8", index=False)
else :
print("use of zipped version")
import pyensae.datasource
data = pyensae.datasource.download_data("mar2012.zip")
df = pandas.read_csv(data[0], sep="\t", encoding="utf8", low_memory = False)
df.shape, df.columns
```
Dictionnaire des variables.
```
vardf = dBase2df("varlist_mariages.dbf")
print(vardf.shape, vardf.columns)
vardf
```
Représentez l'age des femmes en fonction de celui des hommes au moment du mariage.
```
#Calcul de l'age (au moment du mariage)
df.head()
#conversion des années en entiers
for c in ['AMAR','ANAISF','ANAISH']:
df[c]=df[c].apply(lambda x: int(x))
#calcul de l'age
df['AGEF'] = df['AMAR'] - df['ANAISF']
df['AGEH'] = df['AMAR'] - df['ANAISH']
```
Le module pandas a prévu un [wrapper](http://pandas.pydata.org/pandas-docs/stable/visualization.html) matplotlib
```
#version pandas : df.plot()
#deux possibilités : l'option kind dans df.plot()
df.plot(x='AGEH',y='AGEF',kind='scatter')
#ou la méthode scatter()
#df.plot.scatter(x='AGEH',y='AGEF')
#ensemble des graphiques disponibles dans la méthode plot de pandas : df.plot.<TAB>
#version matplotlib
from matplotlib import pyplot as plt
plt.style.use('seaborn-whitegrid')
fig = plt.figure(figsize(8.5,5))
ax = fig.add_subplot(1,1,1)
ax.scatter(df['AGEH'],df['AGEF'], color="#3333FF", edgecolors='#FFFFFF')
plt.xlabel('AGEH')
plt.ylabel('AGEH')
#Si vous voulez les deux graphes en 1, il suffit de reprendre la structure de matplotlib
#(notamment l'objet subplot) et de voir comment il peut etre appelé dans
#chaque méthode de tracé (df.plot de pandas et sns.plot de searborn)
from matplotlib import pyplot as plt
plt.style.use('seaborn-whitegrid')
fig = plt.figure(figsize(8.5,5))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
ax1.scatter(df['AGEH'],df['AGEF'], color="#3333FF", edgecolors='#FFFFFF')
df.plot(x='AGEH',y='AGEF',kind='scatter',ax=ax2)
plt.xlabel('AGEH')
plt.ylabel('AGEH')
```
### Exercice 1 : analyser l'âge des hommes en fonction de l'âge des femmes
Ajoutez un titre, changez le style du graphe, faites varier les couleurs (avec un camaïeu), faites une [heatmap](https://en.wikipedia.org/wiki/Heat_map) avec le wrapper pandas [hexbin](http://pandas.pydata.org/pandas-docs/stable/visualization.html#visualization-hexbin) et avec [seaborn](https://stanford.edu/~mwaskom/software/seaborn/generated/seaborn.heatmap.html).
```
df.plot.hexbin(x='AGEH', y='AGEF', gridsize=100)
```
Avec seaborn
```
import seaborn as sns
sns.set_style('white')
sns.set_context('paper')
#il faut crééer la matrice AGEH x AGEF
df['nb']=1
df[['AGEH','AGEF']]
df["nb"] = 1
#pour utiliser heatmap, il faut mettre df au frmat wide (au lieu de long) => df.pivot(...)
matrice = df[['nb','AGEH','AGEF']].groupby(['AGEH','AGEF'],as_index=False).count()
matrice=matrice.pivot('AGEH','AGEF','nb')
matrice=matrice.sort_index(axis=0,ascending=False)
fig = plt.figure(figsize(8.5,5))
ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,3)
df.plot.hexbin(x='AGEH', y='AGEF', gridsize=100, ax=ax1)
cmap=sns.blend_palette(["#CCFFFF", "#006666"], as_cmap=True)
#Dans tous les graphes qui prévoient une fonction cmap vous pourrez intégrer votre propre palette de couleur
sns.heatmap(matrice,annot=False, xticklabels=10,yticklabels=10,cmap=cmap,ax=ax2)
sample = df.sample(100)
sns.kdeplot(sample['AGEH'],sample['AGEF'],cmap=cmap,ax=ax3)
```
Seaborn est bien pensé pour les [couleurs](https://seaborn.pydata.org/tutorial/color_palettes.html). Vous pouvez intégrer des palettes convergentes, divergentes. Essayez de faire un camaïeu entre deux couleurs au fur et à mesure de l'age, pour faire ressortir les contrastes.
### Exercice 2 : représentez la répartition de la différence d'âge de couples mariés
```
df["differenceHF"] = df["ANAISH"] - df["ANAISF"]
df["nb"] = 1
dist = df[["nb","differenceHF"]].groupby("differenceHF", as_index=False).count()
dist.tail()
#version pandas
import seaborn as sns
sns.set_style('whitegrid')
sns.set_context('paper')
fig = plt.figure(figsize(8.5,5))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
df["differenceHF"].hist(figsize=(16,6), bins=50, ax=ax1)
ax1.set_title('Graphique avec pandas', fontsize=15)
sns.distplot(df["differenceHF"], kde=True,ax=ax2)
#regardez ce que donne l'option kde
ax2.set_title('Graphique avec seaborn', fontsize=15)
```
### Exercice 3 : analyser le nombre de mariages par département
```
df["nb"] = 1
dep = df[["DEPMAR","nb"]].groupby("DEPMAR", as_index=False).sum().sort_values("nb",ascending=False)
ax = dep.plot(kind = "bar", figsize=(18,6))
ax.set_xlabel("départements", fontsize=16)
ax.set_title("nombre de mariages par départements", fontsize=16)
ax.legend().set_visible(False) # on supprime la légende
# on change la taille de police de certains labels
for i,tick in enumerate(ax.xaxis.get_major_ticks()):
if i > 10 :
tick.label.set_fontsize(8)
```
# Exercice 4 : répartition du nombre de mariages par jour
```
df["nb"] = 1
dissem = df[["JSEMAINE","nb"]].groupby("JSEMAINE",as_index=False).sum()
total = dissem["nb"].sum()
repsem = dissem.cumsum()
repsem["nb"] /= total
sns.set_style('whitegrid')
ax = dissem["nb"].plot(kind="bar")
repsem["nb"].plot(ax=ax, secondary_y=True)
ax.set_title("Distribution des mariages par jour de la semaine",fontsize=16)
df.head()
```
# Graphes intéractifs : bokeh, altair, bqplot
Pour faire simple, il est possible d'introduire du JavaScript dans l'application web locale créée par jupyter. C'est ce que fait D3.js. Les librairies interactives comme [bokeh](http://bokeh.pydata.org/en/latest/) ou [altair](https://altair-viz.github.io/) ont associé le design de [matplotlib](https://matplotlib.org/) avec des librairies javascript comme [vega-lite](https://vega.github.io/vega-lite/). L'exemple suivant utilise [bokeh](http://bokeh.pydata.org/en/latest/).
```
from bokeh.plotting import figure, show, output_notebook
output_notebook()
fig = figure()
sample = df.sample(500)
fig.scatter(sample['AGEH'],sample['AGEF'])
fig.xaxis.axis_label = 'AGEH'
fig.yaxis.axis_label = 'AGEH'
show(fig)
```
La page [callbacks](https://bokeh.pydata.org/en/latest/docs/user_guide/interaction/callbacks.html) montre comment utiliser les interactions utilisateurs. Seul inconvénient, il faut connaître le javascript.
```
from bokeh.plotting import figure, output_file, show
from bokeh.models import ColumnDataSource, HoverTool, CustomJS
# define some points and a little graph between them
x = [2, 3, 5, 6, 8, 7]
y = [6, 4, 3, 8, 7, 5]
links = {
0: [1, 2],
1: [0, 3, 4],
2: [0, 5],
3: [1, 4],
4: [1, 3],
5: [2, 3, 4]
}
p = figure(plot_width=400, plot_height=400, tools="", toolbar_location=None, title='Hover over points')
source = ColumnDataSource({'x0': [], 'y0': [], 'x1': [], 'y1': []})
sr = p.segment(x0='x0', y0='y0', x1='x1', y1='y1', color='olive', alpha=0.6, line_width=3, source=source, )
cr = p.circle(x, y, color='olive', size=30, alpha=0.4, hover_color='olive', hover_alpha=1.0)
# Add a hover tool, that sets the link data for a hovered circle
code = """
var links = %s;
var data = {'x0': [], 'y0': [], 'x1': [], 'y1': []};
var cdata = circle.data;
var indices = cb_data.index['1d'].indices;
for (i=0; i < indices.length; i++) {
ind0 = indices[i]
for (j=0; j < links[ind0].length; j++) {
ind1 = links[ind0][j];
data['x0'].push(cdata.x[ind0]);
data['y0'].push(cdata.y[ind0]);
data['x1'].push(cdata.x[ind1]);
data['y1'].push(cdata.y[ind1]);
}
}
segment.data = data;
""" % links
callback = CustomJS(args={'circle': cr.data_source, 'segment': sr.data_source}, code=code)
p.add_tools(HoverTool(tooltips=None, callback=callback, renderers=[cr]))
show(p)
```
Le module [bqplot](https://github.com/bloomberg/bqplot/blob/master/examples/Interactions/Mark%20Interactions.ipynb) permet de définir des *callbacks* en Python. L'inconvénient est que cela ne fonction que depuis un notebook et il vaut mieux ne pas trop mélanger les librairies javascripts qui ne peuvent pas toujours fonctionner ensemble.
# Plotly
- Plotly: https://plot.ly/python/
- Doc: https://plot.ly/python/reference/
- Colors: http://www.cssportal.com/css3-rgba-generator/
```
import pandas as pd
import numpy as np
```
# Creation dataframe
```
indx = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
value1 = [0,1,2,3,4,5,6,7,8,9]
value2 = [1,5,2,3,7,5,1,8,9,1]
df = {'indx': indx, 'value1': value1, 'value2': value2}
df = pd.DataFrame(df)
df['rate1'] = df.value1 / 100
df['rate2'] = df.value2 / 100
df = df.set_index('indx')
df.head()
```
# Bars and Scatter
```
# installer plotly
import plotly.plotly as py
import os
from pyquickhelper.loghelper import get_password
user = get_password("plotly", "ensae_teaching_cs,login")
pwd = get_password("plotly", "ensae_teaching_cs,pwd")
try:
py.sign_in(user, pwd)
except Exception as e:
print(e)
import plotly
from plotly.graph_objs import Bar, Scatter, Figure, Layout
import plotly.plotly as py
import plotly.graph_objs as go
# BARS
trace1 = go.Bar(
x = df.index,
y = df.value1,
name='Value1', # Bar legend
#orientation = 'h',
marker = dict( # Colors
color = 'rgba(237, 74, 51, 0.6)',
line = dict(
color = 'rgba(237, 74, 51, 0.6)',
width = 3)
))
trace2 = go.Bar(
x = df.index,
y = df.value2,
name='Value 2',
#orientation = 'h', # Uncomment to have horizontal bars
marker = dict(
color = 'rgba(0, 74, 240, 0.4)',
line = dict(
color = 'rgba(0, 74, 240, 0.4)',
width = 3)
))
# SCATTER
trace3 = go.Scatter(
x = df.index,
y = df.rate1,
name='Rate',
yaxis='y2', # Define 2 axis
marker = dict( # Colors
color = 'rgba(187, 0, 0, 1)',
))
trace4 = go.Scatter(
x = df.index,
y = df.rate2,
name='Rate2',
yaxis='y2', # To have a 2nd axis
marker = dict( # Colors
color = 'rgba(0, 74, 240, 0.4)',
))
data = [trace2, trace1, trace3, trace4]
layout = go.Layout(
title='Stack bars and scatter',
barmode ='stack', # Take value 'stack' or 'group'
xaxis=dict(
autorange=True,
showgrid=False,
zeroline=False,
showline=True,
autotick=True,
ticks='',
showticklabels=True
),
yaxis=dict( # Params 1st axis
#range=[0,1200000], # Set range
autorange=True,
showgrid=False,
zeroline=False,
showline=True,
autotick=True,
ticks='',
showticklabels=True
),
yaxis2=dict( # Params 2nd axis
overlaying='y',
autorange=True,
showgrid=False,
zeroline=False,
showline=True,
autotick=True,
ticks='',
side='right'
))
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='marker-h-bar')
trace5 = go.Scatter(
x = ['h', 'h'],
y = [0,0.09],
yaxis='y2', # Define 2 axis
showlegend = False, # Hiding legend for this trace
marker = dict( # Colors
color = 'rgba(46, 138, 24, 1)',
)
)
from plotly import tools
import plotly.plotly as py
import plotly.graph_objs as go
fig = tools.make_subplots(rows=1, cols=2)
# 1st subplot
fig.append_trace(trace1, 1, 1)
fig.append_trace(trace2, 1, 1)
# 2nd subplot
fig.append_trace(trace3, 1, 2)
fig.append_trace(trace4, 1, 2)
fig.append_trace(trace5, 1, 2) # Vertical line here
fig['layout'].update(height=600, width=1000, title='Two in One & Vertical line')
py.iplot(fig, filename='make-subplots')
```
### Exercice : représenter le nombre de mariages par département avec plotly ou tout autre librairie javascript
[Bokeh](https://bokeh.pydata.org/en/latest/), [altair](https://altair-viz.github.io/), ...
| true |
code
| 0.264881 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/ShreyasJothish/ai-platform/blob/master/tasks/methodology/word-embeddings/Word_Embeddings.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Word Embeddings using Word2Vec.
### Procedure
1) I shall be working with [Fake News data](https://www.kaggle.com/mrisdal/fake-news) from Kaggle as an example for Word Embedding.
This data set has sufficient data containing documents to train the model on.
2) Clean/Tokenize the documents in the data set.
3) Vectorize the model using Word2Vec and explore the results like finding most similar words, finding similarity and differences.
[gensim](https://radimrehurek.com/gensim/) package is used for Word2Vec functionality.
```
# Basic imports
import pandas as pd
import numpy as np
!pip install -U gensim
import gensim
```
### Downloading Kaggle data set
1. You'll have to sign up for Kaggle and [authorize](https://github.com/Kaggle/kaggle-api#api-credentials) the API.
2. Specify the path for accessing the kaggle.json file. For Colab we can store the kaggle.json on Google Drive.
3. Download Fake News Data.
4. The data is present in compressed form this needs to be unzipped.
```
!pip install kaggle
from google.colab import drive
drive.mount('/content/drive')
%env KAGGLE_CONFIG_DIR=/content/drive/My Drive/
!kaggle datasets download -d mrisdal/fake-news
!unzip fake-news.zip
df = pd.read_csv("fake.csv")
df['title_text'] = df['title'] + df ['text']
df.drop(columns=['uuid', 'ord_in_thread', 'author', 'published', 'title', 'text',
'language', 'crawled', 'site_url', 'country', 'domain_rank',
'thread_title', 'spam_score', 'main_img_url', 'replies_count',
'participants_count', 'likes', 'comments', 'shares', 'type'], inplace=True)
df.dropna(inplace=True)
df.title_text = df.title_text.str.lower()
```
### Data cleaning
1. The information related to document is contained in **title** and **text** columns. So I shall be using only these two columns.
2. Turn a document into clean tokens.
3. Build the model using gensim.
```
df.head()
import string
def clean_doc(doc):
# split into tokens by white space
tokens = doc.split()
# remove punctuation from each token
table = str.maketrans('', '', string.punctuation)
tokens = [w.translate(table) for w in tokens]
# remove remaining tokens that are not alphabetic
tokens = [word for word in tokens if word.isalpha()]
tokens = [word for word in tokens if len(word) > 1]
return tokens
df['cleaned'] = df.title_text.apply(clean_doc)
print(df.shape)
df.head()
from gensim.models import Word2Vec
w2v = Word2Vec(df.cleaned, min_count=20, window=3, size=300, negative=20)
words = list(w2v.wv.vocab)
print(f'Vocabulary Size: {len(words)}')
```
### Verification
Explore the results like finding most similar words, finding similarity and differences.
```
w2v.wv.most_similar('trump', topn=15)
w2v.wv.most_similar(positive=["fbi"], topn=15)
w2v.wv.doesnt_match(['fbi', 'cat', 'nypd'])
w2v.wv.similarity("fbi","nypd")
w2v.wv.similarity("fbi","trump")
```
| true |
code
| 0.316283 | null | null | null | null |
|
## Classes for callback implementors
```
from fastai.gen_doc.nbdoc import *
from fastai.callback import *
from fastai.basics import *
```
fastai provides a powerful *callback* system, which is documented on the [`callbacks`](/callbacks.html#callbacks) page; look on that page if you're just looking for how to use existing callbacks. If you want to create your own, you'll need to use the classes discussed below.
A key motivation for the callback system is that additional functionality can be entirely implemented in a single callback, so that it's easily read. By using this trick, we will have different methods categorized in different callbacks where we will find clearly stated all the interventions the method makes in training. For instance in the [`LRFinder`](/callbacks.lr_finder.html#LRFinder) callback, on top of running the fit function with exponentially growing LRs, it needs to handle some preparation and clean-up, and all this code can be in the same callback so we know exactly what it is doing and where to look if we need to change something.
In addition, it allows our [`fit`](/basic_train.html#fit) function to be very clean and simple, yet still easily extended. So far in implementing a number of recent papers, we haven't yet come across any situation where we had to modify our training loop source code - we've been able to use callbacks every time.
```
show_doc(Callback)
```
To create a new type of callback, you'll need to inherit from this class, and implement one or more methods as required for your purposes. Perhaps the easiest way to get started is to look at the source code for some of the pre-defined fastai callbacks. You might be surprised at how simple they are! For instance, here is the **entire** source code for [`GradientClipping`](/train.html#GradientClipping):
```python
@dataclass
class GradientClipping(LearnerCallback):
clip:float
def on_backward_end(self, **kwargs):
if self.clip:
nn.utils.clip_grad_norm_(self.learn.model.parameters(), self.clip)
```
You generally want your custom callback constructor to take a [`Learner`](/basic_train.html#Learner) parameter, e.g.:
```python
@dataclass
class MyCallback(Callback):
learn:Learner
```
Note that this allows the callback user to just pass your callback name to `callback_fns` when constructing their [`Learner`](/basic_train.html#Learner), since that always passes `self` when constructing callbacks from `callback_fns`. In addition, by passing the learner, this callback will have access to everything: e.g all the inputs/outputs as they are calculated, the losses, and also the data loaders, the optimizer, etc. At any time:
- Changing self.learn.data.train_dl or self.data.valid_dl will change them inside the fit function (we just need to pass the [`DataBunch`](/basic_data.html#DataBunch) object to the fit function and not data.train_dl/data.valid_dl)
- Changing self.learn.opt.opt (We have an [`OptimWrapper`](/callback.html#OptimWrapper) on top of the actual optimizer) will change it inside the fit function.
- Changing self.learn.data or self.learn.opt directly WILL NOT change the data or the optimizer inside the fit function.
In any of the callbacks you can unpack in the kwargs:
- `n_epochs`, contains the number of epochs the training will take in total
- `epoch`, contains the number of the current
- `iteration`, contains the number of iterations done since the beginning of training
- `num_batch`, contains the number of the batch we're at in the dataloader
- `last_input`, contains the last input that got through the model (eventually updated by a callback)
- `last_target`, contains the last target that gor through the model (eventually updated by a callback)
- `last_output`, contains the last output spitted by the model (eventually updated by a callback)
- `last_loss`, contains the last loss computed (eventually updated by a callback)
- `smooth_loss`, contains the smoothed version of the loss
- `last_metrics`, contains the last validation loss and metrics computed
- `pbar`, the progress bar
- [`train`](/train.html#train), flag to know if we're in training mode or not
### Methods your subclass can implement
All of these methods are optional; your subclass can handle as many or as few as you require.
```
show_doc(Callback.on_train_begin)
```
Here we can initiliaze anything we need.
The optimizer has now been initialized. We can change any hyper-parameters by typing, for instance:
```
self.opt.lr = new_lr
self.opt.mom = new_mom
self.opt.wd = new_wd
self.opt.beta = new_beta
```
```
show_doc(Callback.on_epoch_begin)
```
This is not technically required since we have `on_train_begin` for epoch 0 and `on_epoch_end` for all the other epochs,
yet it makes writing code that needs to be done at the beginning of every epoch easy and more readable.
```
show_doc(Callback.on_batch_begin)
```
Here is the perfect place to prepare everything before the model is called.
Example: change the values of the hyperparameters (if we don't do it on_batch_end instead)
If we return something, that will be the new value for `xb`,`yb`.
```
show_doc(Callback.on_loss_begin)
```
Here is the place to run some code that needs to be executed after the output has been computed but before the
loss computation.
Example: putting the output back in FP32 when training in mixed precision.
If we return something, that will be the new value for the output.
```
show_doc(Callback.on_backward_begin)
```
Here is the place to run some code that needs to be executed after the loss has been computed but before the gradient computation.
Example: `reg_fn` in RNNs.
If we return something, that will be the new value for loss. Since the recorder is always called first,
it will have the raw loss.
```
show_doc(Callback.on_backward_end)
```
Here is the place to run some code that needs to be executed after the gradients have been computed but
before the optimizer is called.
```
show_doc(Callback.on_step_end)
```
Here is the place to run some code that needs to be executed after the optimizer step but before the gradients
are zeroed
```
show_doc(Callback.on_batch_end)
```
Here is the place to run some code that needs to be executed after a batch is fully done.
Example: change the values of the hyperparameters (if we don't do it on_batch_begin instead)
If we return true, the current epoch is interrupted (example: lr_finder stops the training when the loss explodes)
```
show_doc(Callback.on_epoch_end)
```
Here is the place to run some code that needs to be executed at the end of an epoch.
Example: Save the model if we have a new best validation loss/metric.
If we return true, the training stops (example: early stopping)
```
show_doc(Callback.on_train_end)
```
Here is the place to tidy everything. It's always executed even if there was an error during the training loop,
and has an extra kwarg named exception to check if there was an exception or not.
Examples: save log_files, load best model found during training
```
show_doc(Callback.get_state)
```
This is used internally when trying to export a [`Learner`](/basic_train.html#Learner). You won't need to subclass this function but you can add attribute names to the lists `exclude` or `not_min`of the [`Callback`](/callback.html#Callback) you are designing. Attributes in `exclude` are never saved, attributes in `not_min` only if `minimal=False`.
## Annealing functions
The following functions provide different annealing schedules. You probably won't need to call them directly, but would instead use them as part of a callback. Here's what each one looks like:
```
annealings = "NO LINEAR COS EXP POLY".split()
fns = [annealing_no, annealing_linear, annealing_cos, annealing_exp, annealing_poly(0.8)]
for fn, t in zip(fns, annealings):
plt.plot(np.arange(0, 100), [fn(2, 1e-2, o)
for o in np.linspace(0.01,1,100)], label=t)
plt.legend();
show_doc(annealing_cos)
show_doc(annealing_exp)
show_doc(annealing_linear)
show_doc(annealing_no)
show_doc(annealing_poly)
show_doc(CallbackHandler)
```
You probably won't need to use this class yourself. It's used by fastai to combine all the callbacks together and call any relevant callback functions for each training stage. The methods below simply call the equivalent method in each callback function in [`self.callbacks`](/callbacks.html#callbacks).
```
show_doc(CallbackHandler.on_backward_begin)
show_doc(CallbackHandler.on_backward_end)
show_doc(CallbackHandler.on_batch_begin)
show_doc(CallbackHandler.on_batch_end)
show_doc(CallbackHandler.on_epoch_begin)
show_doc(CallbackHandler.on_epoch_end)
show_doc(CallbackHandler.on_loss_begin)
show_doc(CallbackHandler.on_step_end)
show_doc(CallbackHandler.on_train_begin)
show_doc(CallbackHandler.on_train_end)
show_doc(CallbackHandler.set_dl)
show_doc(OptimWrapper)
```
This is a convenience class that provides a consistent API for getting and setting optimizer hyperparameters. For instance, for [`optim.Adam`](https://pytorch.org/docs/stable/optim.html#torch.optim.Adam) the momentum parameter is actually `betas[0]`, whereas for [`optim.SGD`](https://pytorch.org/docs/stable/optim.html#torch.optim.SGD) it's simply `momentum`. As another example, the details of handling weight decay depend on whether you are using `true_wd` or the traditional L2 regularization approach.
This class also handles setting different WD and LR for each layer group, for discriminative layer training.
```
show_doc(OptimWrapper.clear)
show_doc(OptimWrapper.create)
show_doc(OptimWrapper.new)
show_doc(OptimWrapper.read_defaults)
show_doc(OptimWrapper.read_val)
show_doc(OptimWrapper.set_val)
show_doc(OptimWrapper.step)
show_doc(OptimWrapper.zero_grad)
show_doc(SmoothenValue)
```
Used for smoothing loss in [`Recorder`](/basic_train.html#Recorder).
```
show_doc(SmoothenValue.add_value)
show_doc(Stepper)
```
Used for creating annealing schedules, mainly for [`OneCycleScheduler`](/callbacks.one_cycle.html#OneCycleScheduler).
```
show_doc(Stepper.step)
show_doc(AverageMetric)
```
See the documentation on [`metrics`](/metrics.html#metrics) for more information.
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(AverageMetric.on_epoch_begin)
show_doc(AverageMetric.on_batch_end)
show_doc(AverageMetric.on_epoch_end)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.915432 | null | null | null | null |
|
What is PyTorch?
================
It’s a Python-based scientific computing package targeted at two sets of
audiences:
- A replacement for NumPy to use the power of GPUs
- a deep learning research platform that provides maximum flexibility
and speed
Getting Started
---------------
Tensors
^^^^^^^
Tensors are similar to NumPy’s ndarrays, with the addition being that
Tensors can also be used on a GPU to accelerate computing.
** Here are some high frequency operations you should get used to **
```
import cv2
import numpy as np
%matplotlib inline
#The line above is necesary to show Matplotlib's plots inside a Jupyter Notebook
from matplotlib import pyplot as plt
from __future__ import print_function
import torch
```
### Construct a 5x3 matrix, uninitialized using [torch.empty]()
```
x = torch.empty(5, 3)
print(x)
# other examples
torch.normal(0,1,[2,2])
torch.randperm(10)
torch.linspace(1,10,10)
```
### Print out the size of a tensor.
you will be doing this frequently if developing/debuggin a neural network
```
x.size()
```
### Construct a matrix filled zeros and of dtype floating point 16. Here is a link to available [types](https://pytorch.org/docs/stable/tensor_attributes.html#torch.torch.dtype)
Can you change long to floating point16 below
<details>
<summary>Hint</summary>
<p> torch.zeros(5, 3, dtype=torch.float16) </p></details>
```
x = torch.zeros(5, 3, dtype=torch.long)
print(x)
```
### Element operations
examples of element operations

do an element wise add of A and B
```
A = torch.rand(5, 3)
B = torch.rand(5, 3)
print(A)
print(B)
print(A + B)
```
### Alternate method using torch.add
```
# more than one way to do it [operator overloading]
orch.add(A, B)
A.add(B)
```
### Addition: providing an output tensor as argument
```
result = torch.empty(5, 3)
torch.add(A, B, out=result)
print(result)
```
### Addition: in-place
```
#### adds x to y
B.add_(A)
print(B)
```
<div class="alert alert-info"><h4>Note</h4><p>Any operation that mutates a tensor in-place is post-fixed with an ``_``.
For example: ``x.copy_(y)``, ``x.t_()``, will change ``x``.</p></div>
### Linear Alg operations - Matrix Multiply Example

```
a = torch.randint(4,(2,3))
b = torch.randint(4,(3,2))
print(a)
print(b)
# all equivalent!
# 2x3 @ 3x2 ~ 2x2
a.mm(b)
torch.matmul(a,b)
torch.mm(a,b)
a.T.mm(a)
```
### Create a onehot vector
```
batch_size = 5
nb_digits = 10
# Dummy input that HAS to be 2D for the scatter (you can use view(-1,1) if needed)
y = torch.LongTensor(batch_size,1).random_() % nb_digits
# One hot encoding buffer that you create out of the loop and just keep reusing
y_onehot = torch.FloatTensor(batch_size, nb_digits)
# In your for loop
y_onehot.zero_()
y_onehot.scatter_(1, y, 1)
print(y)
print(y_onehot)
```
### Use argmax to grab the index of the highest value
```
A = torch.rand(3,4,5)
print(A)
A.argmax(dim=2)
```
### Aggregation over a dimension
```
x = torch.ones([2,3,4])
# inplace multiply a selected column
x[0,:,0].mul_(30)
x
#Suppose the shape of the input is (m, n, k)
#If dim=0 is specified, the shape of the output is (1, n, k) or (n, k)
#If dim=1 is specified, the shape of the output is (m, 1, k) or (m, k)
#If dim=2 is specified, the shape of the output is (m, n, 1) or (m, n)
x.sum(dim=1)
```
### Broadcasting
```
x = torch.ones([10,10])
y = torch.linspace(1,10,10)
print(x.size())
print(y.size())
z = x + y
### Masking
mask = z>4
print(mask.size())
mask
# Apply mask, but observe dim change
new =z[z>4]
print(new.size())
new
```
### You can use standard NumPy-like indexing with all bells and whistles!
Example Grab the middle column of A (index = 1)
```
A = torch.rand(3,3)
print(A)
print(A[:, 1])
```
### Resizing: If you want to resize/reshape tensor, you can use ``torch.view``:
```
x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1, 8) # the size -1 is inferred from other dimensions
print(x.size(), y.size(), z.size())
```
### If you have a one element tensor, use ``.item()`` to get the value as a
Python number
```
x = torch.randn(1)
print(x)
print(x.item())
```
**Read later:**
100+ Tensor operations, including transposing, indexing, slicing,
mathematical operations, linear algebra, random numbers, etc.,
are described
`here <http://pytorch.org/docs/torch>`_.
NumPy Bridge
------------
Converting a Torch Tensor to a NumPy array and vice versa is a breeze.
The Torch Tensor and NumPy array will share their underlying memory
locations, and changing one will change the other.
### Converting a Torch Tensor to a NumPy Array
```
a = torch.ones(5)
print(a)
b = a.numpy()
print(b)
```
### See how the numpy array changed in value.
```
a.add_(1)
print(a)
print(b)
```
Converting NumPy Array to Torch Tensor
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
See how changing the np array changed the Torch Tensor automatically
```
import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
print(a)
print(b)
```
All the Tensors on the CPU except a CharTensor support converting to
NumPy and back.
CUDA Tensors
------------
Tensors can be moved onto any device using the ``.to`` method.
```
# let us run this cell only if CUDA is available
# We will use ``torch.device`` objects to move tensors in and out of GPU
x = torch.rand(2,2,2)
if torch.cuda.is_available():
device = torch.device("cuda") # a CUDA device object
y = torch.ones_like(x, device=device) # directly create a tensor on GPU
x = x.to(device) # or just use strings ``.to("cuda")``
z = x + y
print(z)
print(z.to("cpu", torch.double)) # ``.to`` can also change dtype together!
```
### ND Tensors
When working with neural networks, you are always dealing with multidimensional arrays. Here are some quick tricks
#### Assume A is a 32x32 RGB image
```
## 3D Tensors
import torch
A = torch.rand(32,32,3)
plt.imshow(A)
```
### Slicing Tensors - grab 'RED' dimension
```
red_data = A[:,:,0] #0 represents the first channel of RGB
red_data.size()
```
### Swap the RGB dimension and make the tensor a 3x32x32 tensor
```
A_rgb_first = A.permute(2,0,1)
print(A_rgb_first.size())
```
### Add a BatchSize to our Image Tensor
Usually you need to do this to run inference on your trained model
```
Anew = A.unsqueeze(0)
print(Anew.size())
```
### Drop the tensor dimension.
sometimes like in the example above, you might have a tensor with on of the dimensions equal to one. Use **squeeze()** to drop that dimension>
```
print(Anew.squeeze(0).size())
```
| true |
code
| 0.635505 | null | null | null | null |
|
# Aim of this notebook
* To construct the singular curve of universal type to finalize the solution of the optimal control problem
# Preamble
```
from sympy import *
init_printing(use_latex='mathjax')
# Plotting
%matplotlib inline
## Make inline plots raster graphics
from IPython.display import set_matplotlib_formats
## Import modules for plotting and data analysis
import matplotlib.pyplot as plt
from matplotlib import gridspec,rc,colors
import matplotlib.ticker as plticker
## Parameters for seaborn plots
import seaborn as sns
sns.set(style='white',font_scale=1.25,
rc={"xtick.major.size": 6, "ytick.major.size": 6,
'text.usetex': False, 'font.family': 'serif', 'font.serif': ['Times']})
import pandas as pd
pd.set_option('mode.chained_assignment',None)
import numpy as np
from scipy.optimize import fsolve, root
from scipy.integrate import ode
backend = 'dopri5'
import warnings
# Timer
import time
from copy import deepcopy
from itertools import cycle
palette_size = 10;
clrs = sns.color_palette("Reds",palette_size)
iclrs = cycle(clrs) # iterated colors
# Suppress warnings
import warnings
warnings.filterwarnings("ignore")
```
# Parameter values
* Birth rate and const of downregulation are defined below in order to fit some experim. data
```
d = .13 # death rate
α = .3 # low equilibrium point at expression of the main pathway (high equilibrium is at one)
θ = .45 # threshold value for the expression of the main pathway
κ = 40 # robustness parameter
```
* Symbolic variables - the list insludes μ & μbar, because they will be varied later
```
σ, φ0, φ, x, μ, μbar = symbols('sigma, phi0, phi, x, mu, mubar')
```
* Main functions
```
A = 1-σ*(1-θ)
Eminus = (α*A-θ)**2/2
ΔE = A*(1-α)*((1+α)*A/2-θ)
ΔEf = lambdify(σ,ΔE)
```
* Birth rate and cost of downregulation
```
b = (0.1*(exp(κ*(ΔEf(1)))+1)-0.14*(exp(κ*ΔEf(0))+1))/(exp(κ*ΔEf(1))-exp(κ*ΔEf(0))) # birth rate
χ = 1-(0.14*(exp(κ*ΔEf(0))+1)-b*exp(κ*ΔEf(0)))/b
b, χ
c_relative = 0.2
c = c_relative*(b-d)/b+(1-c_relative)*χ/(exp(κ*ΔEf(0))+1) # cost of resistance
c
```
* Hamiltonian *H* and a part of it ρ that includes the control variable σ
```
h = b*(χ/(exp(κ*ΔE)+1)*(1-x)+c*x)
H = -φ0 + φ*(b*(χ/(exp(κ*ΔE)+1)-c)*x*(1-x)+μ*(1-x)/(exp(κ*ΔE)+1)-μbar*exp(-κ*Eminus)*x) + h
ρ = (φ*(b*χ*x+μ)+b*χ)/(exp(κ*ΔE)+1)*(1-x)-φ*μbar*exp(-κ*Eminus)*x
H, ρ
```
* Same but for no treatment (σ = 0)
```
h0 = h.subs(σ,0)
H0 = H.subs(σ,0)
ρ0 = ρ.subs(σ,0)
H0, ρ0
```
* Machinery: definition of the Poisson brackets
```
PoissonBrackets = lambda H1, H2: diff(H1,x)*diff(H2,φ)-diff(H1,φ)*diff(H2,x)
```
* Necessary functions and defining the right hand side of dynamical equations
```
ρf = lambdify((x,φ,σ,μ,μbar),ρ)
ρ0f = lambdify((x,φ,μ,μbar),ρ0)
dxdτ = lambdify((x,φ,σ,μ,μbar),-diff(H,φ))
dφdτ = lambdify((x,φ,σ,μ,μbar),diff(H,x))
dVdτ = lambdify((x,σ),h)
dρdσ = lambdify((σ,x,φ,μ,μbar),diff(ρ,σ))
dδρdτ = lambdify((x,φ,σ,μ,μbar),-PoissonBrackets(ρ0-ρ,H))
def ode_rhs(t,state,μ,μbar):
x, φ, V, δρ = state
σs = [0,1]
if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
σstar = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
else:
σstar = 1.;
if ρf(x,φ,σstar,μ,μbar) < ρ0f(x,φ,μ,μbar):
sgm = 0
else:
sgm = σstar
return [dxdτ(x,φ,sgm,μ,μbar),dφdτ(x,φ,sgm,μ,μbar),dVdτ(x,sgm),dδρdτ(x,φ,σstar,μ,μbar)]
def get_primary_field(name, experiment,μ,μbar):
solutions = {}
solver = ode(ode_rhs).set_integrator(backend)
τ0 = experiment['τ0']
tms = np.linspace(τ0,experiment['T_end'],1e3+1)
for x0 in experiment['x0']:
δρ0 = ρ0.subs(x,x0).subs(φ,0)-ρ.subs(x,x0).subs(φ,0).subs(σ,1.)
solver.set_initial_value([x0,0,0,δρ0],0.).set_f_params(μ,μbar)
sol = []; k = 0;
while (solver.t < experiment['T_end']) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[k])
sol.append([solver.t]+list(solver.y))
k += 1
solutions[x0] = {'solution': sol}
for x0, entry in solutions.items():
entry['τ'] = [entry['solution'][j][0] for j in range(len(entry['solution']))]
entry['x'] = [entry['solution'][j][1] for j in range(len(entry['solution']))]
entry['φ'] = [entry['solution'][j][2] for j in range(len(entry['solution']))]
entry['V'] = [entry['solution'][j][3] for j in range(len(entry['solution']))]
entry['δρ'] = [entry['solution'][j][4] for j in range(len(entry['solution']))]
return solutions
def get_δρ_value(tme,x0,μ,μbar):
solver = ode(ode_rhs).set_integrator(backend)
δρ0 = ρ0.subs(x,x0).subs(φ,0)-ρ.subs(x,x0).subs(φ,0).subs(σ,1.)
solver.set_initial_value([x0,0,0,δρ0],0.).set_f_params(μ,μbar)
while (solver.t < tme) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tme)
sol = [solver.t]+list(solver.y)
return solver.y[3]
def get_δρ_ending(params,μ,μbar):
tme, x0 = params
solver = ode(ode_rhs).set_integrator(backend)
δρ0 = ρ0.subs(x,x0).subs(φ,0)-ρ.subs(x,x0).subs(φ,0).subs(σ,1.)
solver.set_initial_value([x0,0,0,δρ0],0.).set_f_params(μ,μbar)
δτ = 1.0e-8; tms = [tme,tme+δτ]
_k = 0; sol = []
while (_k<len(tms)):# and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[_k])
sol.append(solver.y)
_k += 1
#print(sol)
return(sol[0][3],(sol[1][3]-sol[0][3])/δτ)
def get_state(tme,x0,μ,μbar):
solver = ode(ode_rhs).set_integrator(backend)
δρ0 = ρ0.subs(x,x0).subs(φ,0)-ρ.subs(x,x0).subs(φ,0).subs(σ,1.)
solver.set_initial_value([x0,0,0,δρ0],0.).set_f_params(μ,μbar)
δτ = 1.0e-8; tms = [tme,tme+δτ]
_k = 0; sol = []
while (solver.t < tms[-1]) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[_k])
sol.append(solver.y)
_k += 1
return(list(sol[0])+[(sol[1][3]-sol[0][3])/δτ])
```
# Machinery for the universal line
* To find the universal singular curve we need to define two parameters
```
γ0 = PoissonBrackets(PoissonBrackets(H,H0),H)
γ1 = PoissonBrackets(PoissonBrackets(H0,H),H0)
```
* The dynamics
```
dxdτSingExpr = -(γ0*diff(H0,φ)+γ1*diff(H,φ))/(γ0+γ1)
dφdτSingExpr = (γ0*diff(H0,x)+γ1*diff(H,x))/(γ0+γ1)
dVdτSingExpr = (γ0*h0+γ1*h)/(γ0+γ1)
σSingExpr = γ1*σ/(γ0+γ1)
```
* Machinery for Python: lambdify the functions above
```
dxdτSing = lambdify((x,φ,σ,μ,μbar),dxdτSingExpr)
dφdτSing = lambdify((x,φ,σ,μ,μbar),dφdτSingExpr)
dVdτSing = lambdify((x,φ,σ,μ,μbar),dVdτSingExpr)
σSing = lambdify((x,φ,σ,μ,μbar),σSingExpr)
def ode_rhs_Sing(t,state,μ,μbar):
x, φ, V = state
if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
σstar = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
else:
σstar = 1.;
#print([σstar,σSing(x,φ,σstar,μ,μbar)])
return [dxdτSing(x,φ,σstar,μ,μbar),dφdτSing(x,φ,σstar,μ,μbar),dVdτSing(x,φ,σstar,μ,μbar)]
# def ode_rhs_Sing(t,state,μ,μbar):
# x, φ, V = state
# if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
# σstar = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
# else:
# σstar = 1.;
# σTrav = fsolve(lambda σ: dxdτ(x,φ,σ,μ,μbar)-dxdτSing(x,φ,σstar,μ,μbar),.6)[0]
# print([σstar,σTrav])
# return [dxdτSing(x,φ,σstar,μ,μbar),dφdτSing(x,φ,σstar,μ,μbar),dVdτ(x,σTrav)]
def get_universal_curve(end_point,tmax,Nsteps,μ,μbar):
tms = np.linspace(end_point[0],tmax,Nsteps);
solver = ode(ode_rhs_Sing).set_integrator(backend)
solver.set_initial_value(end_point[1:4],end_point[0]).set_f_params(μ,μbar)
_k = 0; sol = []
while (solver.t < tms[-1]):
solver.integrate(tms[_k])
sol.append([solver.t]+list(solver.y))
_k += 1
return sol
def get_σ_universal(tme,end_point,μ,μbar):
δτ = 1.0e-8; tms = [tme,tme+δτ]
solver = ode(ode_rhs_Sing).set_integrator(backend)
solver.set_initial_value(end_point[1:4],end_point[0]).set_f_params(μ,μbar)
_k = 0; sol = []
while (solver.t < tme+δτ):
solver.integrate(tms[_k])
sol.append([solver.t]+list(solver.y))
_k += 1
x, φ = sol[0][:2]
sgm = fsolve(lambda σ: dxdτ(x,φ,σ,μ,μbar)-(sol[1][0]-sol[0][0])/δτ,θ/2)[0]
return sgm
def get_state_universal(tme,end_point,μ,μbar):
solver = ode(ode_rhs_Sing).set_integrator(backend)
solver.set_initial_value(end_point[1:4],end_point[0]).set_f_params(μ,μbar)
solver.integrate(tme)
return [solver.t]+list(solver.y)
def ode_rhs_with_σstar(t,state,μ,μbar):
x, φ, V = state
if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
σ = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
else:
σ = 1.;
return [dxdτ(x,φ,σ,μ,μbar),dφdτ(x,φ,σ,μ,μbar),dVdτ(x,σ)]
def ode_rhs_with_given_σ(t,state,σ,μ,μbar):
x, φ, V = state
return [dxdτ(x,φ,σ,μ,μbar),dφdτ(x,φ,σ,μ,μbar),dVdτ(x,σ)]
def get_trajectory_with_σstar(starting_point,tmax,Nsteps,μ,μbar):
tms = np.linspace(starting_point[0],tmax,Nsteps)
solver = ode(ode_rhs_with_σstar).set_integrator(backend)
solver.set_initial_value(starting_point[1:],starting_point[0]).set_f_params(μ,μbar)
sol = []; _k = 0;
while solver.t < max(tms) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[_k])
sol.append([solver.t]+list(solver.y))
_k += 1
return sol
def get_trajectory_with_given_σ(starting_point,tmax,Nsteps,σ,μ,μbar):
tms = np.linspace(starting_point[0],tmax,100)
solver = ode(ode_rhs_with_given_σ).set_integrator(backend)
solver.set_initial_value(starting_point[1:],starting_point[0]).set_f_params(σ,μ,μbar)
sol = []; _k = 0;
while solver.t < max(tms) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[_k])
sol.append([solver.t]+list(solver.y))
_k += 1
return sol
def get_state_with_σstar(tme,starting_point,μ,μbar):
solver = ode(ode_rhs_with_σstar).set_integrator(backend)
solver.set_initial_value(starting_point[1:4],starting_point[0]).set_f_params(μ,μbar)
solver.integrate(tme)
return [solver.t]+list(solver.y)
def get_finalizing_point_from_universal_curve(tme,tmx,end_point,μ,μbar):
unv_point = get_state_universal(tme,end_point,μ,μbar)
return get_state_with_σstar(tmx,unv_point,μ,μbar)[1]
```
# Field of optimal trajectories as the solution of the Bellman equation
* μ & μbar are varied by *T* and *T*bar ($\mu=1/T$ and $\bar\mu=1/\bar{T}$)
```
tmx = 180.
end_switching_curve = {'t': 24., 'x': .9/.8}
# for Τ, Τbar in zip([28]*5,[14,21,28,35,60]):
for Τ, Τbar in zip([28],[60]):
μ = 1./Τ; μbar = 1./Τbar
print("Parameters: μ = %.5f, μbar = %.5f"%(μ,μbar))
end_switching_curve['t'], end_switching_curve['x'] = root(get_δρ_ending,(end_switching_curve['t'],end_switching_curve['x']),args=(μ,μbar)).x
end_point = [end_switching_curve['t']]+get_state(end_switching_curve['t'],end_switching_curve['x'],μ,μbar)
print("Ending point for the switching line: τ = %.1f days, x = %.1f%%" % (end_point[0], end_point[1]*100))
print("Checking the solution - should give zero values: ")
print(get_δρ_ending([end_switching_curve['t'],end_switching_curve['x']],μ,μbar))
print("* Constructing the primary field")
experiments = {
'sol1': { 'T_end': tmx, 'τ0': 0., 'x0': list(np.linspace(0,end_switching_curve['x']-(1e-3),10))+list(np.linspace(end_switching_curve['x']+(1e-6),1.,10)) } }
primary_field = []
for name, values in experiments.items():
primary_field.append(get_primary_field(name,values,μ,μbar))
print("* Constructing the switching curve")
switching_curve = []
x0s = np.linspace(end_switching_curve['x'],1,21); _y = end_switching_curve['t']
for x0 in x0s:
tme = fsolve(get_δρ_value,_y,args=(x0,μ,μbar))[0]
if (tme>0):
switching_curve = switching_curve+[[tme,get_state(tme,x0,μ,μbar)[0]]]
_y = tme
print("* Constructing the universal curve")
universal_curve = get_universal_curve(end_point,tmx,25,μ,μbar)
print("* Finding the last characteristic")
#time0 = time.time()
# tuniv = fsolve(get_finalizing_point_from_universal_curve,tmx-40.,args=(tmx,end_point,μ,μbar,))[0]
tuniv = root(get_finalizing_point_from_universal_curve,tmx-40,args=(tmx,end_point,μ,μbar)).x
print(tuniv)
#print("The proccess to find the last characteristic took %0.1f minutes" % ((time.time()-time0)/60.))
univ_point = get_state_universal(tuniv,end_point,μ,μbar)
print("The last point on the universal line:")
print(univ_point)
last_trajectory = get_trajectory_with_σstar(univ_point,tmx,50,μ,μbar)
print("Final state:")
final_state = get_state_with_σstar(tmx,univ_point,μ,μbar)
print(final_state)
print("Fold-change in tumor size: %.2f"%(exp((b-d)*tmx-final_state[-1])))
# Plotting
plt.rcParams['figure.figsize'] = (6.75, 4)
_k = 0
for solutions in primary_field:
for x0, entry in solutions.items():
plt.plot(entry['τ'], entry['x'], 'k-', linewidth=.9, color=clrs[_k%palette_size])
_k += 1
plt.plot([x[0] for x in switching_curve],[x[1] for x in switching_curve],linewidth=2,color="red")
plt.plot([end_point[0]],[end_point[1]],marker='o',color="red")
plt.plot([x[0] for x in universal_curve],[x[1] for x in universal_curve],linewidth=2,color="red")
plt.plot([x[0] for x in last_trajectory],[x[1] for x in last_trajectory],linewidth=.9,color="black")
plt.xlim([0,tmx]); plt.ylim([0,1]);
plt.xlabel("time, days"); plt.ylabel("fraction of resistant cells")
plt.show()
print()
import csv
from numpy.linalg import norm
File = open("../figures/draft/sensitivity_mu-high_cost.csv", 'w')
File.write("T,Tbar,mu,mubar,sw_start_x,sw_end_t,sw_end_x,univ_point_t,univ_point_x,outcome,err_sw_t,err_sw_x\n")
writer = csv.writer(File,lineterminator='\n')
end_switching_curve0 = {'t': 40.36, 'x': .92}
end_switching_curve_prev_t = end_switching_curve0['t']
tuniv = tmx-30.
Ts = np.arange(40,3,-1) #Τbars;
Τbars = np.arange(40,3,-1) #np.arange(120,1,-1) #need to change here if more
for Τ in Ts:
μ = 1./Τ
end_switching_curve = deepcopy(end_switching_curve0)
for Τbar in Τbars:
μbar = 1./Τbar
print("* Parameters: T = %.1f, Tbar = %.1f (μ = %.5f, μbar = %.5f)"%(Τ,Τbar,μ,μbar))
success = False; err = 1.
while (not success)|(norm(err)>1e-6):
end_switching_curve = {'t': 2*end_switching_curve['t']-end_switching_curve_prev_t-.001,
'x': end_switching_curve['x']-0.002}
sol = root(get_δρ_ending,(end_switching_curve['t'],end_switching_curve['x']),args=(μ,μbar))
end_switching_curve_prev_t = end_switching_curve['t']
end_switching_curve_prev_x = end_switching_curve['x']
end_switching_curve['t'], end_switching_curve['x'] = sol.x
success = sol.success
err = get_δρ_ending([end_switching_curve['t'],end_switching_curve['x']],μ,μbar)
if (not success):
print("! Trying again...", sol.message)
elif (norm(err)>1e-6):
print("! Trying again... Convergence is not sufficient")
else:
end_point = [end_switching_curve['t']]+get_state(end_switching_curve['t'],end_switching_curve['x'],μ,μbar)
print("Ending point: t = %.2f, x = %.2f%%"%(end_switching_curve['t'],100*end_switching_curve['x'])," Checking the solution:",err)
universal_curve = get_universal_curve(end_point,tmx,25,μ,μbar)
tuniv = root(get_finalizing_point_from_universal_curve,tuniv,args=(tmx,end_point,μ,μbar)).x
err_tuniv = get_finalizing_point_from_universal_curve(tuniv,tmx,end_point,μ,μbar)
univ_point = get_state_universal(tuniv,end_point,μ,μbar)
print("tuniv = %.2f"%tuniv,"xuniv = %.2f%%"%(100*univ_point[1])," Checking the solution: ",err_tuniv)
final_state = get_state_with_σstar(tmx,univ_point,μ,μbar)
outcome = exp((b-d)*tmx-final_state[-1])
print("Fold-change in tumor size: %.2f"%(outcome))
output = [Τ,Τbar,μ,μbar,end_switching_curve['x'],end_point[0],end_point[1]]+list(univ_point[0:2])+[outcome]+list(err)+[err_tuniv]
writer.writerow(output)
if (Τbar==Τ):
end_switching_curve0 = deepcopy(end_switching_curve)
File.close()
```
| true |
code
| 0.285565 | null | null | null | null |
|
# Shor's Algorithm for Factorization of Integers
Given a large number $N$, say with at least 100 digits, how can we find a factor of $N$? There are several famous classical algorithms, and [Wikipedia](https://en.wikipedia.org/wiki/Integer_factorization) contains an exhaustive list of these algorithms. The best known algorithm for huge integers is the _general field sieve_ algorithm, which has a runtime of $\exp(O(\ln N)^{1/3}(\ln\ln N)^{2/3})$.
Factorization is definitely a hard problem, but it is not known whether it can be solved in $\text{poly}(n)$ time (where $n = \lceil\log_2 N\rceil$). It is widely assumed that Factorization is not in $P$, and this is the base of cryptographic protocols such as RSA that are in use today.
Shor's algorithm provides a fast quantum solution to the factoring problem (in time polynomial in the number of input bits), and we shall see in this tutorial how exactly it finds factors of composite numbers.
## Part I: Reduction of Factorization to Order-finding
Let us start by picking an $x$ uniformly at random from $\{2,\ldots, N-1\}$. The [Euclidean Algorithm](http://www-math.ucdenver.edu/~wcherowi/courses/m5410/exeucalg.html) is able to determine $\text{gcd}(x,N)$ efficiently. If $\text{gcd}(x,N)\neq 1$, we were lucky and already find a factor of $N$! Otherwise, there's more work left...
Let $r\ge 1$ be the smallest integer (known as the *order*) such that $x^r\equiv 1 \mod N$. If $r$ is even, we know that
$$ (x^{r/2}-1)(x^{r/2}+1)\equiv 0 \mod N,$$
implying $\text{gcd}(x^{r/2}-1, N)$ or $\text{gcd}(x^{r/2}+1, N)$ will give a factor $d$ of $N$. We can then run the same order-finding algorithm recursively on $N/d$.
Thus, if we have an efficient way of calculating $r = A(x,N)$, the order of $x$ modulo $N$, we can solve the factorization problem as follows:
> factorize($N$):
> + pick $x$ uniformly at random from $\{2,\ldots,N-1\}$.
> + if $d = \text{gcd}(x,N)\neq 1$, return $d$ as a factor and run _factorize($N/d$)_.
> + else:
> - let $r = A(x,N)$.
> - if $r$ is even, $\text{gcd}(x^{r/2}-1, N)$ or $\text{gcd}(x^{r/2}+1, N)$ will give a factor $d$. return $d$ and run _factorize($N/d$)_.
> - else pick another $x$ uniformly at random and repeat.
## Part II: Finding the order
In order to compute the value of $r = A(x,n)$, we shall first require a unitary operator $U_x$ such that
$$U_x\lvert j\rangle_t \lvert k\rangle_n = \lvert j\rangle_t \lvert k\oplus (x^j\mbox{ mod } N)\rangle_n.$$
Then, we consider the following circuit with Register 1 of $t$ qubits and Register 2 of $n$ qubits:
<img src="./img/104_shor_ckt.png" alt="shor-circuit" width="600"/>
Here $n=\lceil \log_2N\rceil$ and $t=\lceil 2\log_2 N\rceil$ in general. The choice of $t$ can be simplified to $t=n=\lceil \log_2N\rceil$ if $r=A(x,n)$ is a power of $2$. We shall consider this special case first.
### Case 1: Order is a power of 2
Then, after the initialization we obtain the state
$$\varphi_1 = \frac 1{\sqrt{2^t}}\sum_{j=0}^{2^t-1}\lvert j\rangle \lvert 0\rangle,$$
And therefore,
$$\varphi_2 = U_x\varphi_1 = \frac 1{\sqrt{2^t}}\sum_{j=0}^{2^t-1}\lvert j\rangle \lvert x^j\mbox{ mod }N\rangle.$$
$\varphi_2$ could be thought of as an encoding of all $x^j\mbox{ mod }N$ calculated for each integer $j<2^t$, and we would be interested in finding the smallest $j$ for which $x^j\mbox{ mod }N=1$.
For simplicity of calculations, we first measure the second register. Note that as every $j$ can be written as
$$ j = ar+b, \mbox{ where }0\le a < 2^t/r \mbox{ and } 0\le b <r,$$
we can then write $\varphi_2$ as the following double sum:
$$\varphi_2 = \frac 1{\sqrt{2^t}}\sum_{b=0}^{r-1}\sum_{a=0}^{2^t/r -1}\lvert ar+b\rangle\lvert x^{ar+b}\mbox{ mod }N\rangle.$$
Note that $x^{ar+b}\mbox{ mod }N = x^b\mbox{ mod }N$. Also, recall that $2^t/r$ is an integer since $r$ is a power of $2$ in this case. Thus, we can finally write
$$\varphi_2 = \frac 1{\sqrt{2^t}}\sum_{b=0}^{r-1}\sum_{a=0}^{2^t/r -1}\lvert ar+b\rangle\lvert x^{b}\mbox{ mod }N\rangle.$$
Now we measure the second register. Each choice $x^0, \ldots, x^{r-1}$ are equally probably to be measured. Say the output of the measurement is $x^{b_0}$, then $\varphi_2$ ends up in the following state:
$$\varphi_3 = \frac{\sqrt r}{\sqrt{2^t}}\sum_{a=0}^{2^t/r - 1} \lvert ar+b_0\rangle \lvert x^{b_0}\mbox{ mod }N \rangle.$$
Now the only uncertainty is in the first register, and if measured, we'll see a probability of $r/2^t$ of each state $\lvert ar+b_0\rangle, 0\le a<2^t/r$ to be measured. Finally, we apply inverse QFT on the first register. Recall that we already covered the action of $\mbox{QFT}$ and $\mbox{QFT}^\dagger$, and this lets us compute the final quantum state of the circuit as follows:
$$
\begin{aligned}\varphi_4 &= \frac{\sqrt{r}}{\sqrt{2^t}} \sum_{a=0}^{2^t/r-1}\left[\frac1{\sqrt{2^t}}\sum_{j=0}^{2^t-1}\exp\left(\frac{-2\pi i j(ar+b_0)}{2^r}\right)\lvert j\rangle \right]\lvert x^{b_0}\mbox{ mod }N \rangle\\
& = \frac1{\sqrt r}\left[\sum_{j=0}^{2^t-1}\left(\frac r{2^t}\sum_{a=0}^{2^t/r-1}\exp\left(\frac{-2\pi ija}{2^t/r}\right) \right)\exp\left(\frac{-2\pi ijb_0}{2^t}\right)\lvert j\rangle\right]\lvert x^{b_0}\mbox{ mod }N \rangle\end{aligned}.$$
Using the Fourier identity $\frac 1N\sum_{j=0}^{N-1} \exp(2\pi ijk/N) = 1$ if $k$ is a multiple of $N$ and $0$ otherwise, we see that the expression in the inner parentheses is $0$ most of the time. Only when $j$ is a multiple of $2^t/r$, we obtain a nonzero expression. Thus,
$$\varphi_4 = \frac 1{\sqrt r}\sum_{k=0}^{r-1}\exp\left(\frac{-2\pi ikb_0}r\right) \lvert k2^t/r\rangle \lvert x^{b_0}\mbox{ mod }N\rangle.$$
The measurement outcomes from measuring $\varphi_4$ therefore are $k2^t/r$, for $0\le k \le r-1$.
Let us now measure $\varphi_4$. We now do the following steps with the outcome $B = k_02^t/r$.
+ If the outcome $B$ is $0$, then we obtain no information about $r$, and will run our circuit again.
+ If we $B = k_02^t/r$ for some $0 < k_0\le r-1$, compute $k_0/r = B/2^t$. We then know that the denominator of $B/2^t$ _divides_ $r$.
- Let $r_1$ be the denominator. If $x^{r_1}\mbox{ mod }N = 1$, $r_1$ is the order, and we can stop.
- Otherwise, Let $r_2 = r/r_1$. Note that $r_2$ is the order of $x^{r_1}$, and we run the algorithm again to find the order of $x^{r_1}$. We apply the algorithm recursively until we find the entire order $r$.
This is the full description of Shor's algorithm. Although technical, it's an efficient algorithm with clear basic steps. For now, we postpone the discussion of Case 2 to a later section.
### Implementation of Shor's Algorithm for Case 1
Let us now implement Shor's Algorithm to factorize $N=15$. We choose $15$ since the orders of the numbers $\{1,2,4,7,8,11,13,14\}$ which are less than $15$ and coprime to $15$ are all $2$ or $4$, leading to an ideal circuit for us.
Recall that we need $t=4$ qubits in the first register and $n=4$ qubits in the second register!
We shall now focus on finding the order of $7$ modulo $15$.
### Implementing $U_x$
One of the main challenges in implementing Shor's algorithm is to create the circuit $U_x$ using physical gates. We take the implementation for $x^b\mbox{ mod }N$ for $N=15$ from [Markov-Saeedi](https://arxiv.org/pdf/1202.6614.pdf).
```
# Install blueqat!
# !pip install blueqat
# Import libraries
from blueqat import Circuit
import numpy as np
# Recall QFT dagger from our previous tutorial
def apply_qft_dagger(circuit: Circuit(), qubits):
num_qubits = len(qubits)
# Reverse the order of qubits at the end
for i in range(int(num_qubits/2)):
circuit.swap(qubits[i],qubits[num_qubits-i-1])
for i in range(num_qubits):
for j in range(i):
circuit.cphase(-np.pi/(2 ** (j-i)))[qubits[j],qubits[i]]
circuit.h[qubits[i]]
# Implementation of U_x as a black box. More details can be found in the previously mentioned paper.
def apply_U_7_mod15(circuit: Circuit(), qubits):
assert len(qubits) == 8, 'Must have 8 qubits as input.'
circuit.x[qubits[7]]
circuit.ccx[qubits[0],qubits[6],qubits[7]]
circuit.ccx[qubits[0],qubits[7],qubits[6]]
circuit.ccx[qubits[0],qubits[6],qubits[7]]
circuit.ccx[qubits[0],qubits[5],qubits[6]]
circuit.ccx[qubits[0],qubits[6],qubits[5]]
circuit.ccx[qubits[0],qubits[5],qubits[6]]
circuit.ccx[qubits[0],qubits[4],qubits[5]]
circuit.ccx[qubits[0],qubits[5],qubits[4]]
circuit.ccx[qubits[0],qubits[4],qubits[5]]
circuit.cx[qubits[0],qubits[4]]
circuit.cx[qubits[0],qubits[5]]
circuit.cx[qubits[0],qubits[6]]
circuit.cx[qubits[0],qubits[7]]
circuit.ccx[qubits[1],qubits[6],qubits[7]]
circuit.ccx[qubits[1],qubits[7],qubits[6]]
circuit.ccx[qubits[1],qubits[6],qubits[7]]
circuit.ccx[qubits[1],qubits[5],qubits[6]]
circuit.ccx[qubits[1],qubits[6],qubits[5]]
circuit.ccx[qubits[1],qubits[5],qubits[6]]
circuit.ccx[qubits[1],qubits[4],qubits[5]]
circuit.ccx[qubits[1],qubits[5],qubits[4]]
circuit.ccx[qubits[1],qubits[4],qubits[5]]
circuit.cx[qubits[1],qubits[4]]
circuit.cx[qubits[1],qubits[5]]
circuit.cx[qubits[1],qubits[6]]
circuit.cx[qubits[1],qubits[7]]
circuit.ccx[qubits[1],qubits[6],qubits[7]]
circuit.ccx[qubits[1],qubits[7],qubits[6]]
circuit.ccx[qubits[1],qubits[6],qubits[7]]
circuit.ccx[qubits[1],qubits[5],qubits[6]]
circuit.ccx[qubits[1],qubits[6],qubits[5]]
circuit.ccx[qubits[1],qubits[5],qubits[6]]
circuit.ccx[qubits[1],qubits[4],qubits[5]]
circuit.ccx[qubits[1],qubits[5],qubits[4]]
circuit.ccx[qubits[1],qubits[4],qubits[5]]
circuit.cx[qubits[1],qubits[4]]
circuit.cx[qubits[1],qubits[5]]
circuit.cx[qubits[1],qubits[6]]
circuit.cx[qubits[1],qubits[7]]
circuit.ccx[qubits[2],qubits[6],qubits[7]]
circuit.ccx[qubits[2],qubits[7],qubits[6]]
circuit.ccx[qubits[2],qubits[6],qubits[7]]
circuit.ccx[qubits[2],qubits[5],qubits[6]]
circuit.ccx[qubits[2],qubits[6],qubits[5]]
circuit.ccx[qubits[2],qubits[5],qubits[6]]
circuit.ccx[qubits[2],qubits[4],qubits[5]]
circuit.ccx[qubits[2],qubits[5],qubits[4]]
circuit.ccx[qubits[2],qubits[4],qubits[5]]
circuit.cx[qubits[2],qubits[4]]
circuit.cx[qubits[2],qubits[5]]
circuit.cx[qubits[2],qubits[6]]
circuit.cx[qubits[2],qubits[7]]
circuit.ccx[qubits[2],qubits[6],qubits[7]]
circuit.ccx[qubits[2],qubits[7],qubits[6]]
circuit.ccx[qubits[2],qubits[6],qubits[7]]
circuit.ccx[qubits[2],qubits[5],qubits[6]]
circuit.ccx[qubits[2],qubits[6],qubits[5]]
circuit.ccx[qubits[2],qubits[5],qubits[6]]
circuit.ccx[qubits[2],qubits[4],qubits[5]]
circuit.ccx[qubits[2],qubits[5],qubits[4]]
circuit.ccx[qubits[2],qubits[4],qubits[5]]
circuit.cx[qubits[2],qubits[4]]
circuit.cx[qubits[2],qubits[5]]
circuit.cx[qubits[2],qubits[6]]
circuit.cx[qubits[2],qubits[7]]
circuit.ccx[qubits[2],qubits[6],qubits[7]]
circuit.ccx[qubits[2],qubits[7],qubits[6]]
circuit.ccx[qubits[2],qubits[6],qubits[7]]
circuit.ccx[qubits[2],qubits[5],qubits[6]]
circuit.ccx[qubits[2],qubits[6],qubits[5]]
circuit.ccx[qubits[2],qubits[5],qubits[6]]
circuit.ccx[qubits[2],qubits[4],qubits[5]]
circuit.ccx[qubits[2],qubits[5],qubits[4]]
circuit.ccx[qubits[2],qubits[4],qubits[5]]
circuit.cx[qubits[2],qubits[4]]
circuit.cx[qubits[2],qubits[5]]
circuit.cx[qubits[2],qubits[6]]
circuit.cx[qubits[2],qubits[7]]
circuit.ccx[qubits[2],qubits[6],qubits[7]]
circuit.ccx[qubits[2],qubits[7],qubits[6]]
circuit.ccx[qubits[2],qubits[6],qubits[7]]
circuit.ccx[qubits[2],qubits[5],qubits[6]]
circuit.ccx[qubits[2],qubits[6],qubits[5]]
circuit.ccx[qubits[2],qubits[5],qubits[6]]
circuit.ccx[qubits[2],qubits[4],qubits[5]]
circuit.ccx[qubits[2],qubits[5],qubits[4]]
circuit.ccx[qubits[2],qubits[4],qubits[5]]
circuit.cx[qubits[2],qubits[4]]
circuit.cx[qubits[2],qubits[5]]
circuit.cx[qubits[2],qubits[6]]
circuit.cx[qubits[2],qubits[7]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[7],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[4]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.cx[qubits[3],qubits[4]]
circuit.cx[qubits[3],qubits[5]]
circuit.cx[qubits[3],qubits[6]]
circuit.cx[qubits[3],qubits[7]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[7],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[4]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.cx[qubits[3],qubits[4]]
circuit.cx[qubits[3],qubits[5]]
circuit.cx[qubits[3],qubits[6]]
circuit.cx[qubits[3],qubits[7]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[7],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[4]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.cx[qubits[3],qubits[4]]
circuit.cx[qubits[3],qubits[5]]
circuit.cx[qubits[3],qubits[6]]
circuit.cx[qubits[3],qubits[7]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[7],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[4]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.cx[qubits[3],qubits[4]]
circuit.cx[qubits[3],qubits[5]]
circuit.cx[qubits[3],qubits[6]]
circuit.cx[qubits[3],qubits[7]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[7],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[4]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.cx[qubits[3],qubits[4]]
circuit.cx[qubits[3],qubits[5]]
circuit.cx[qubits[3],qubits[6]]
circuit.cx[qubits[3],qubits[7]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[7],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[4]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.cx[qubits[3],qubits[4]]
circuit.cx[qubits[3],qubits[5]]
circuit.cx[qubits[3],qubits[6]]
circuit.cx[qubits[3],qubits[7]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[7],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[4]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.cx[qubits[3],qubits[4]]
circuit.cx[qubits[3],qubits[5]]
circuit.cx[qubits[3],qubits[6]]
circuit.cx[qubits[3],qubits[7]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[7],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[7]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[6],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[6]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.ccx[qubits[3],qubits[5],qubits[4]]
circuit.ccx[qubits[3],qubits[4],qubits[5]]
circuit.cx[qubits[3],qubits[4]]
circuit.cx[qubits[3],qubits[5]]
circuit.cx[qubits[3],qubits[6]]
circuit.cx[qubits[3],qubits[7]]
# Now we build the Shor Circuit!
circuit = Circuit(8)
register1 = list(range(4))
register2 = list(range(4,8))
qubits = register1+register2
for i in register1:
circuit.h[i]
apply_U_7_mod15(circuit, qubits)
apply_qft_dagger(circuit, register1)
# Run and measure the outcome from first register.
# In the theory we measure the second register first to reduce complexity of calculations.
# But that is unnecessary for the final outcome.
circuit.m[0:4].run(shots=10000)
```
The states that have been amplified are $\lvert 0000\rangle, \lvert 0100\rangle, \lvert 1000\rangle, \lvert 1100\rangle$. These represent $0,4,8,12$ in decimal. Hence,
$k_0/r = B/16$ can take values $0, \frac 14, \frac 12, \frac 34$, leading to guesses $1,2$ or $4$ for the order. It is clear that $7^1, 7^2$ are not $1 \mbox{ mod }15$, and therefore we end up at $4$ being the order of $7$ modulo $15$!
### Case 2: What if order isn't a power of 2?
If not, recall that we chose $t$ such that $N^2\le 2^t < 2N^2$ (equivalent to saying $t=\lceil2 \log_2 N\rceil$). We now work out an example of Shor's Algorithm for $N=21$, and demonstrate the generalization. Let us select $x=2$, coprime with $N$.
Then, we observe that
$$\begin{aligned}\varphi_1 &= \frac 1{\sqrt{512}}\sum_{j=0}^{512}\lvert j\rangle \lvert 0\rangle, \\
\varphi_2 & = \frac 1{\sqrt{512}}\sum_{j=0}^{512}\lvert j\rangle \lvert 2^j\mbox{ mod }N\rangle \\
& = \frac 1{\sqrt{512}}\left[\psi_0\lvert 1\rangle + \psi_1\lvert 2\rangle + \psi_2\lvert 4\rangle + \psi_3\lvert 8\rangle + \psi_{4}\lvert 16\rangle + \psi_{5}\lvert 11\rangle\right],\end{aligned}$$
Where $\psi_0 = \lvert 0\rangle + \lvert 6\rangle + \cdots + \lvert 510\rangle$ is the superposition of all states $0\mbox{ mod }6$, $\psi_1$ those of $1\mbox{ mod }6$, etc.
Now suppose we measure $4$ in the second register, then
$$\varphi_3 = \frac1{\sqrt{86}} \sum_{a=0}^{85} \lvert 6a+2\rangle,$$
Implying
$$\varphi_4 = \frac 1{\sqrt{512}}\sum_{j=0}^{511}\left[\left(\frac{1}{\sqrt{86}}\sum_{a=0}^{85}\exp(\frac{-2\pi i \cdot 6 j a}{512})\right)\exp(\frac{-2\pi i\cdot 2j}{512})\lvert j\rangle\right]\lvert 2\rangle.$$
Then, the probability of measuring state $j$ is
$$P(j) = \frac{1}{512\cdot 86}\left\lvert\sum_{a=0}^{85}\exp(\frac{-2\pi i \cdot 6 j a}{512})\right\rvert^2.$$
Let's plot $P(j)$ versus $j$.
```
import matplotlib.pyplot as plt
N = 512
P = []
for j in range (N):
s = 0
for a in range(86):
theta = -2*np.pi*6*j*a/float(512)
s += complex(np.cos(theta), np.sin(theta))
P.append((s.real **2 + s.imag ** 2)/float(86*512))
# print(P)
# the histogram of the data
plt.plot(range(N),P)
plt.xlim(0,N)
plt.xlabel('j')
plt.ylabel('P(j)')
plt.show()
```
We see 5 peaks achieved at the following points:
```
peaks = [i for i in range(N) if P[i] > 0.05]
print(peaks)
```
If we measure $0$, we are out of luck, and have to re-run the algorithm. Suppose instead we measure $B=85$. Then, $\frac B{512}=\frac{85}{512}$, and we are supposed to figure out $r$ from here. Note that $\frac{85}{512}$ is a rational approximation of $\frac{k_0}{r}$, and so we can use the method of partial fractions to figure out $r$!
We do this as follows:
```
import pandas as pd
import fractions
rows = []
for i in peaks:
f = fractions.Fraction(i/512).limit_denominator(15)
rows.append([i, f.denominator])
print(pd.DataFrame(rows, columns=["Peak", "Guess for r"]))
```
If we guess $r=6$, we're good as that is the order of $2$ modulo $21$! However, if we stumble upon $2$ or $3$, we can easily check that $2^2$ and $2^3$ are not $1\mbox{ mod }21$, and continue running the algorithm recursively to find the order of $2^2$ or $2^3$, respectively.
## Conclusion
This gives us a complete picture of how Shor's algorithm works.
We make one final remark, that the more qubits $t$ that we reserve in the first register, the better the accuracy of the algorithm becomes due to higher peaks.
## Further Reading and References
1. [Prof. Bernhard Ömer's Webpage](http://tph.tuwien.ac.at/~oemer/doc/quprog/node18.html)
2. [Markov-Saeedi: "Constant-Optimized Quantum Circuits for Modular Multiplication and Exponentiation"](https://arxiv.org/pdf/1202.6614.pdf)
3. [Quirk Circuit for Shor's Algorithm](tinyurl.com/8awfhrkd)
4. [Wikipedia page on Shor's Algorithm](https://en.wikipedia.org/wiki/Shor%27s_algorithm)
5. [IBM Composer Guide on Shor's Algorithm (in qiskit)](https://quantum-computing.ibm.com/composer/docs/iqx/guide/shors-algorithm)
| true |
code
| 0.519156 | null | null | null | null |
|
# fastai and the New DataBlock API
> A quick glance at the new top-level api
- toc: true
- badges: true
- comments: true
- image: images/chart-preview.png
- category: DataBlock
---
This blog is also a Jupyter notebook available to run from the top down. There will be code snippets that you can then run in any environment. In this section I will be posting what version of `fastai2` and `fastcore` I am currently running at the time of writing this:
* `fastai2`: 0.0.13
* `fastcore`: 0.1.15
---
## What is the `DataBlock` API?
The `DataBlock` API is certainly nothing new to `fastai`. It was here in a lesser form in the previous version, and the start of an *idea*. This idea was: "How do we let the users of the `fastai` library build `DataLoaders` in a way that is simple enough that someone with minimal coding knowledge could get the hang of it, but be advanced enough to allow for exploration." The old version was a struggle to do this from a high-level API standpoint, as you were very limited in what you could do: variables must be passed in a particular order, the error checking wasn't very explanatory (to those unaccustomed to debugging issues), and while the general idea seemed to flow, sometimes it didn't quite work well enough. For our first example, we'll look at the Pets dataset and compare it from `fastai` version 1 to `fastai` version 2
The `DataBlock` itself is built on "building blocks", think of them as legos. (For more information see [fastai: A Layered API for Deep Learning](https://arxiv.org/abs/2002.04688)) They can go in any order but together they'll always build something. Our lego bricks go by these general names:
* `blocks`
* `get_items`
* `get_x`/`get_y`
* `getters`
* `splitter`
* `item_tfms`
* `batch_tfms`
We'll be exploring each one more closely throughout this series, so we won't hit on all of them today
## Importing from the library
The library itself is still split up into modules, similar to the first version where we have Vision, Text, and Tabular. To import from these libraries, we'll be calling their `.all` files. Our example problem for today will involve Computer Vision so we will call from the `.vision` library
```
from fastai2.vision.all import *
```
## Pets
Pets is a dataset in which you try to identify one of 37 different species of cats and dogs. To get the dataset, we're going to use functions very familiar to those that used fastai version 1. We'll use `untar_data` to grab the dataset we want. In our case, the Pets dataset lives in `URLs.PETS`
```
URLs.PETS
path = untar_data(URLs.PETS)
```
### Looking at the dataset
When starting to look at adapting the API for a particular problem, we need to know just *how* the data is stored. We have an image problem here so we can use the `get_image_files` function to go grab all the file locations of our images and we can look at the data!
```
fnames = get_image_files(path/'images')
```
To investigate how the files are named and where they are located, let's look at the first one:
```
fnames[0]
```
Now as `get_image_files` grabs the filename of our `x` for us, we don't need to include our `get_x` here (which defaults to `None`) as we just want to use this filepath! Now onto our file paths and how they relate to our labels. If we look at our returned path, this particular image has the class of **pug**.
Where do I see that?
**Here**:
Path('/root/.fastai/data/oxford-iiit-pet/images/**pug**_119.jpg')
All the images follow this same format, and we can use a [Regular Expression](https://www.rexegg.com/): to get it out. In our case, it would look something like so:
```
pat = r'([^/]+)_\d+.*$'
```
How do we know it worked? Let's apply it to the first file path real quick with `re.search` where we pass in the pattern followed by an item to try and find a match in the first group (set of matches) with a Regular Expression
```
re.search(pat, str(fnames[0])).group(1)
```
We have our label! So what parts do we have so far? We know how to grab our items (`get_items` and `get_x`), our labels (`get_y`), what's left? Well, we'll want some way to split our data and our data augmentation. Let's focus on the prior.
### Splitting and Augmentation
Any time we train a model, the data must be split between a training and validation dataset. The general idea is that the training dataset is what the model adjusts and fits its weights to, while the validation set is for us to understand how the model is performing. `fastai2` has a family of split functions to look at that will slowly get covered throughout these blogs. For today we'll randomly split our data so 80% goes into our training set and 20% goes into the validation. We can utilize `RandomSplitter` to do so by passing in a percentage to split by, and optionally a seed as well to get the same validation split on multiple runs
```
splitter = RandomSplitter(valid_pct=0.2, seed=42)
```
How is this splitter applied? The splitter itself is a function that we can then apply over some set of data or numbers (an array). It works off of indexes. What does that look like? Let's see:
```
splitter(fnames)
```
That doesn't look like filenames! Correct, instead its the **location** in our list of filenames and what group it belongs to. What this special looking list (or `L`) also tells us is how many *items* are in each list. In this example, the first (which is our training data) has 5,912 samples and the second (which is our validation) contains 1,478 samples.
Now let's move onto the augmentation. As noted earlier, there are two kinds: `item_tfms` and `batch_tfms`. Each do what it sounds like: an item transform is applied on an individual item basis, and a batch transform is applied over each batch of data. The role of the item transform is to prepare everything for a batch level (and to apply any specific item transformations you need), and the batch transform is to further apply any augmentations on the batch level efficently (normalization of your data also happens on a batch level). One of the **biggest** differences between the two though is *where* each is done. Item transforms are done on the **CPU** while batch transforms are performed on the **GPU**.
Now that we know this, let's build a basic transformation pipeline that looks something like so:
1. Resize our images to a fixed size (224x224 pixels)
2. After they are batched together, choose a quick basic augmentation function
3. Normalize all of our image data
Let's build it!
```
item_tfms = [Resize(224, method='crop')]
batch_tfms=[*aug_transforms(size=256), Normalize.from_stats(*imagenet_stats)]
```
Woah, woah, woah, what in the world is this `aug_transforms` thing you just showed me I hear you ask? It runs a series of augmentations similar to the `get_transforms()` from version 1. The entire list is quite exhaustive and we'll discuss it in a later blog, but for now know we can pass in an image size to resize our images to (we'll make our images a bit larger, doing 256x256).
Alright, we know how we want to get our data, how to label it, split it, and augment it, what's left? That `block` bit I mentioned before.
### The `Block`
`Block`'s are used to help nest transforms inside of pre-defined problem domains.
Lazy-man's explaination?
If it's an image problem I can tell the library to use `Pillow` without explicitly saying it, or if we have a Bounding Box problem I can tell the DataBlock to expect two coordinates for boxes and to apply the transforms for points, again without explicitly saying these transforms.
What will we use today? Well let's think about our problem: we are using an image for our `x`, and our labels (or `y`'s) are some category. Is there blocks for this? Yes! And they're labeled `ImageBlock` and `CategoryBlock`! Remember how I said it just "made more sense?" This is a direct example. Let's define them:
```
blocks = (ImageBlock, CategoryBlock)
```
## Now let's build this `DataBlock` thing already!
Alright we have all the pieces now, let's see how they fit together. We'll all wrap them up in a nice little package of a `DataBlock`. Think of the `DataBlock` as a list of instructions to do when we're building batches and our `DataLoaders`. It doesn't need any items explicitly to be done, and instead is a blueprint of how to operate. We define it like so:
```
block = DataBlock(blocks=blocks,
get_items=get_image_files,
get_y=RegexLabeller(pat),
splitter=splitter,
item_tfms=item_tfms,
batch_tfms=batch_tfms)
```
Once we have our `DataBlock`, we can build some `DataLoaders` off of it. To do so we simply pass in a source for our data that our `DataBlock` would be expecting, specifically our `get_x` and `get_y`, so we'll follow the same idea we did above to get our filenames and pass in a path to the folder we want to use along with a batch size:
```
dls = block.dataloaders(path, bs=64)
```
While it's a bit long, you can understand why we had to define everything the way that we did. If you're used to how fastai v1 looked with the `ImageDataBunch.from_x`, well this is stil here too:
```
dls = ImageDataLoaders.from_name_re(path, fnames, pat, item_tfms=item_tfms,
batch_tfms=batch_tfms, bs=64)
```
I'm personally a much larger fan of the first example, and if you're planning on using the library quite a bit you should get used to it more as well! This blog series will be focusing on that nomenclature specifically. To make sure everything looks okay and we like our augmentation we can show a batch of images from our `DataLoader`. It's as simple as:
```
dls.show_batch()
```
## Fitting a Model
Now from here everything looks and behaves exactly how it did in `fastai` version 1:
1. Define a `Learner`
2. Find a learning rate
3. Fit
We'll quickly see that `fastai2` has a quick function for transfer learning problems like we are doing, but first let's build the `Learner`. This will use `cnn_learner`, as we are doing transfer learning, and we'll tell the function to use a `resnet34` architecture with accuracy metrics
```
learn = cnn_learner(dls, resnet34, metrics=accuracy)
```
Now normally we would do `learn.lr_find()` and find a learning rate, but with the new library, we now have a `fine_tune()` function we can use instead specifically designed for transfer learning scenarios. It runs a specified number of epochs (the number of times we fully go through the dataset) on a frozen model (where all but the last layer's weights are not trainable) and then the last few will be on an unfrozen model (where all weights are trainable again). When just passing in one set of epochs, like below, it will run frozen for one and unfrozen for the rest. Let's try it!
```
learn.fine_tune(3)
```
As we can see we did pretty goood just with this default! Generally when the accuracy is this high, we want to turn instead to `error_rate` for our metric, as this would show ~6.5% and is a better comparison when it gets very fine tuned.
But that's it for this first introduction! We looked at how the Pets dataset can be loaded into the new high-level `DataBlock` API, and what it's built with. In the next blog we will be exploring more variations with the `DataBlock` as we get more and more creative. Thanks for reading!
| true |
code
| 0.643329 | null | null | null | null |
|
# Learning Curves and Bias-Variance Tradeoff
In practice, much of the task of machine learning involves selecting algorithms,
parameters, and sets of data to optimize the results of the method. All of these
things can affect the quality of the results, but it’s not always clear which is
best. For example, if your results have an error that’s larger than you hoped,
you might imagine that increasing the training set size will always lead to better
results. But this is not the case! Below, we’ll explore the reasons for this.
Much of the material in this section was adapted from Andrew Ng’s excellent set
of machine learning video lectures. See http://www.ml-class.org.
In this section we’ll work with an extremely simple learning model: polynomial
regression. This simply fits a polynomial of degree d to the data: if d = 1,
then it is simple linear regression.
First we'll ensure that we're in pylab mode, with figures being displayed inline:
```
%pylab inline
```
Polynomial regression can be done with the functions ``polyfit``
and ``polyval``, available in ``numpy``. For example:
```
import numpy as np
np.random.seed(42)
x = np.random.random(20)
y = np.sin(2 * x)
p = np.polyfit(x, y, 1) # fit a 1st-degree polynomial (i.e. a line) to the data
print p # slope and intercept
x_new = np.random.random(3)
y_new = np.polyval(p, x_new) # evaluate the polynomial at x_new
print abs(np.sin(x_new) - y_new)
```
Using a 1st-degree polynomial fit (that is, fitting a straight line to x and y),
we predicted the value of y for a new input. This prediction has an absolute
error of about 0.2 for the few test points which we tried. We can visualize
the fit with the following function:
```
import pylab as pl
def plot_fit(x, y, p):
xfit = np.linspace(0, 1, 1000)
yfit = np.polyval(p, xfit)
pl.scatter(x, y, c='k')
pl.plot(xfit, yfit)
pl.xlabel('x')
pl.ylabel('y')
plot_fit(x, y, p)
```
When the error of predicted results is larger than desired,
there are a few courses of action that can be taken:
1. Increase the number of training points N. This might give us a
training set with more coverage, and lead to greater accuracy.
2. Increase the degree d of the polynomial. This might allow us to
more closely fit the training data, and lead to a better result
3. Add more features. If we were to, for example, perform a linear
regression using $x$, $\sqrt{x}$, $x^{-1}$, or other functions, we might
hit on a functional form which can better be mapped to the value of y.
The best course to take will vary from situation to situation, and from
problem to problem. In this situation, number 2 and 3 may be useful, but
number 1 will certainly not help: our model does not intrinsically fit the
data very well. In machine learning terms, we say that it has high bias
and that the data is *under-fit*. The ability to quickly figure out how
to tune and improve your model is what separates good machine learning
practitioners from the bad ones. In this section we’ll discuss some tools
that can help determine which course is most likely to lead to good results.
## Bias, Variance, Overfitting, and Underfitting
We’ll work with a simple example. Imagine that you would like to build
an algorithm which will predict the price of a house given its size.
Naively, we’d expect that the cost of a house grows as the size increases,
but there are many other factors which can contribute. Imagine we approach
this problem with the polynomial regression discussed above. We can tune
the degree $d$ to try to get the best fit.
First let's define some utility functions:
```
def test_func(x, err=0.5):
return np.random.normal(10 - 1. / (x + 0.1), err)
def compute_error(x, y, p):
yfit = np.polyval(p, x)
return np.sqrt(np.mean((y - yfit) ** 2))
```
Run the following code to produce an example plot:
```
N = 8
np.random.seed(42)
x = 10 ** np.linspace(-2, 0, N)
y = test_func(x)
xfit = np.linspace(-0.2, 1.2, 1000)
titles = ['d = 1 (under-fit)', 'd = 2', 'd = 6 (over-fit)']
degrees = [1, 2, 6]
pl.figure(figsize = (9, 3.5))
pl.subplots_adjust(left = 0.06, right=0.98,
bottom=0.15, top=0.85,
wspace=0.05)
for i, d in enumerate(degrees):
pl.subplot(131 + i, xticks=[], yticks=[])
pl.scatter(x, y, marker='x', c='k', s=50)
p = np.polyfit(x, y, d)
yfit = np.polyval(p, xfit)
pl.plot(xfit, yfit, '-b')
pl.xlim(-0.2, 1.2)
pl.ylim(0, 12)
pl.xlabel('house size')
if i == 0:
pl.ylabel('price')
pl.title(titles[i])
```
In the above figure, we see fits for three different values of $d$.
For $d = 1$, the data is under-fit. This means that the model is too
simplistic: no straight line will ever be a good fit to this data. In
this case, we say that the model suffers from high bias. The model
itself is biased, and this will be reflected in the fact that the data
is poorly fit. At the other extreme, for $d = 6$ the data is over-fit.
This means that the model has too many free parameters (6 in this case)
which can be adjusted to perfectly fit the training data. If we add a
new point to this plot, though, chances are it will be very far from
the curve representing the degree-6 fit. In this case, we say that the
model suffers from high variance. The reason for this label is that if
any of the input points are varied slightly, it could result in an
extremely different model.
In the middle, for $d = 2$, we have found a good mid-point. It fits
the data fairly well, and does not suffer from the bias and variance
problems seen in the figures on either side. What we would like is a
way to quantitatively identify bias and variance, and optimize the
metaparameters (in this case, the polynomial degree d) in order to
determine the best algorithm. This can be done through a process
called cross-validation.
## Cross-validation and Testing
Let's start by defining a new dataset which we can use to explore
cross-validation. We will use a simple x vs. y regression estimator
for ease of visualization, but the concepts also readily apply to
more complicated datasets and models.
```
Ntrain = 100
Ncrossval = 100
Ntest = 50
error = 1.0
# randomly sample the data
np.random.seed(0)
x = np.random.random(Ntrain + Ncrossval + Ntest)
y = test_func(x, error)
# select training set
# data is already random, so we can just choose a slice.
xtrain = x[:Ntrain]
ytrain = y[:Ntrain]
# select cross-validation set
xcrossval = x[Ntrain:Ntrain + Ncrossval]
ycrossval = y[Ntrain:Ntrain + Ncrossval]
# select test set
xtest = x[Ntrain:-Ntest]
ytest = y[Ntrain:-Ntest]
pl.scatter(xtrain, ytrain, color='red')
pl.scatter(xcrossval, ycrossval, color='blue')
```
In order to quantify the effects of bias and variance and construct
the best possible estimator, we will split our training data into
three parts: a *training set*, a *cross-validation set*, and a
*test set*. As a general rule, the training set should be about
60% of the samples, and the cross-validation and test sets should
be about 20% each.
The general idea is as follows. The model parameters (in our case,
the coefficients of the polynomials) are learned using the training
set as above. The error is evaluated on the cross-validation set,
and the meta-parameters (in our case, the degree of the polynomial)
are adjusted so that this cross-validation error is minimized.
Finally, the labels are predicted for the test set. These labels
are used to evaluate how well the algorithm can be expected to
perform on unlabeled data.
Why do we need both a cross-validation set and a test set? Many
machine learning practitioners use the same set of data as both
a cross-validation set and a test set. This is not the best approach,
for the same reasons we outlined above. Just as the parameters can
be over-fit to the training data, the meta-parameters can be over-fit
to the cross-validation data. For this reason, the minimal
cross-validation error tends to under-estimate the error expected
on a new set of data.
The cross-validation error of our polynomial classifier can be visualized by plotting the error as a function of the polynomial degree d. We can do this as follows. This will spit out warnings about "poorly conditioned" polynomials: that is OK for now.
```
degrees = np.arange(1, 21)
train_err = np.zeros(len(degrees))
crossval_err = np.zeros(len(degrees))
test_err = np.zeros(len(degrees))
for i, d in enumerate(degrees):
p = np.polyfit(xtrain, ytrain, d)
train_err[i] = compute_error(xtrain, ytrain, p)
crossval_err[i] = compute_error(xcrossval, ycrossval, p)
pl.figure()
pl.title('Error for 100 Training Points')
pl.plot(degrees, crossval_err, lw=2, label = 'cross-validation error')
pl.plot(degrees, train_err, lw=2, label = 'training error')
pl.plot([0, 20], [error, error], '--k', label='intrinsic error')
pl.legend()
pl.xlabel('degree of fit')
pl.ylabel('rms error')
```
This figure compactly shows the reason that cross-validation is
important. On the left side of the plot, we have very low-degree
polynomial, which under-fits the data. This leads to a very high
error for both the training set and the cross-validation set. On
the far right side of the plot, we have a very high degree
polynomial, which over-fits the data. This can be seen in the fact
that the training error is very low, while the cross-validation
error is very high. Plotted for comparison is the intrinsic error
(this is the scatter artificially added to the data: click on the
above image to see the source code). For this toy dataset,
error = 1.0 is the best we can hope to attain. Choosing $d=6$ in
this case gets us very close to the optimal error.
The astute reader will realize that something is amiss here: in
the above plot, $d = 6$ gives the best results. But in the previous
plot, we found that $d = 6$ vastly over-fits the data. What’s going
on here? The difference is the **number of training points** used.
In the previous example, there were only eight training points.
In this example, we have 100. As a general rule of thumb, the more
training points used, the more complicated model can be used.
But how can you determine for a given model whether more training
points will be helpful? A useful diagnostic for this are learning curves.
## Learning Curves
A learning curve is a plot of the training and cross-validation
error as a function of the number of training points. Note that
when we train on a small subset of the training data, the training
error is computed using this subset, not the full training set.
These plots can give a quantitative view into how beneficial it
will be to add training samples.
```
# suppress warnings from Polyfit
import warnings
warnings.filterwarnings('ignore', message='Polyfit*')
def plot_learning_curve(d):
sizes = np.linspace(2, Ntrain, 50).astype(int)
train_err = np.zeros(sizes.shape)
crossval_err = np.zeros(sizes.shape)
for i, size in enumerate(sizes):
p = np.polyfit(xtrain[:size], ytrain[:size], d)
crossval_err[i] = compute_error(xcrossval, ycrossval, p)
train_err[i] = compute_error(xtrain[:size], ytrain[:size], p)
fig = pl.figure()
pl.plot(sizes, crossval_err, lw=2, label='cross-val error')
pl.plot(sizes, train_err, lw=2, label='training error')
pl.plot([0, Ntrain], [error, error], '--k', label='intrinsic error')
pl.xlabel('traning set size')
pl.ylabel('rms error')
pl.legend(loc = 0)
pl.ylim(0, 4)
pl.xlim(0, 99)
pl.title('d = %i' % d)
plot_learning_curve(d=1)
```
Here we show the learning curve for $d = 1$. From the above
discussion, we know that $d = 1$ is a high-bias estimator which
under-fits the data. This is indicated by the fact that both the
training and cross-validation errors are very high. If this is
the case, adding more training data will not help matters: both
lines have converged to a relatively high error.
```
plot_learning_curve(d=20)
```
Here we show the learning curve for $d = 20$. From the above
discussion, we know that $d = 20$ is a high-variance estimator
which over-fits the data. This is indicated by the fact that the
training error is much less than the cross-validation error. As
we add more samples to this training set, the training error will
continue to climb, while the cross-validation error will continue
to decrease, until they meet in the middle. In this case, our
intrinsic error was set to 1.0, and we can infer that adding more
data will allow the estimator to very closely match the best
possible cross-validation error.
```
plot_learning_curve(d=6)
```
For our $d=6$ case, we see that we have more training data than we need.
This is not a problem (especially if the algorithm scales well with large $N$),
but if our data were expensive to obtain or if the training scales unfavorably
with $N$, we could have used a diagram like this to determine this and stop
once we had recorded 40-50 training samples.
## Summary
We’ve seen above that an under-performing algorithm can be due
to two possible situations: high bias (under-fitting) and high
variance (over-fitting). In order to evaluate our algorithm, we
set aside a portion of our training data for cross-validation.
Using the technique of learning curves, we can train on progressively
larger subsets of the data, evaluating the training error and
cross-validation error to determine whether our algorithm has
high variance or high bias. But what do we do with this information?
#### High Bias
If our algorithm shows high bias, the following actions might help:
- **Add more features**. In our example of predicting home prices,
it may be helpful to make use of information such as the neighborhood
the house is in, the year the house was built, the size of the lot, etc.
Adding these features to the training and test sets can improve
a high-bias estimator
- **Use a more sophisticated model**. Adding complexity to the model can
help improve on bias. For a polynomial fit, this can be accomplished
by increasing the degree d. Each learning technique has its own
methods of adding complexity.
- **Use fewer samples**. Though this will not improve the classification,
a high-bias algorithm can attain nearly the same error with a smaller
training sample. For algorithms which are computationally expensive,
reducing the training sample size can lead to very large improvements
in speed.
- **Decrease regularization**. Regularization is a technique used to impose
simplicity in some machine learning models, by adding a penalty term that
depends on the characteristics of the parameters. If a model has high bias,
decreasing the effect of regularization can lead to better results.
#### High Variance
If our algorithm shows high variance, the following actions might help:
- **Use fewer features**. Using a feature selection technique may be
useful, and decrease the over-fitting of the estimator.
- **Use more training samples**. Adding training samples can reduce
the effect of over-fitting, and lead to improvements in a high
variance estimator.
- **Increase Regularization**. Regularization is designed to prevent
over-fitting. In a high-variance model, increasing regularization
can lead to better results.
These choices become very important in real-world situations. For example,
due to limited telescope time, astronomers must seek a balance between
observing a large number of objects, and observing a large number of
features for each object. Determining which is more important for a
particular learning task can inform the observing strategy that the
astronomer employs. In a later exercise, we will explore the use of
learning curves for the photometric redshift problem.
| true |
code
| 0.717643 | null | null | null | null |
|
# First and Second order random walks
First and second order random walks are a node-sampling mechanism that can be employed in a large number of algorithms. In this notebook we will shortly show how to use Ensmallen to sample a large number of random walks from big graphs.
To install the GraPE library run:
```
pip install grape
```
To install the Ensmallen module exclusively, which may be useful when the TensorFlow dependency causes problems, do run:
```
pip install ensmallen
! pip install -q ensmallen
```
## Retrieving a graph to run the sampling on
In this tutorial we will run examples on the [Homo Sapiens graph from STRING](https://string-db.org/cgi/organisms). If you want to load a graph from an edge list, just follow the examples provided from the Loading a Graph in Ensmallen tutorial.
```
from ensmallen.datasets.string import HomoSapiens
```
Retrieving and loading the graph
```
graph = HomoSapiens()
# We also create a version of the graph without edge weights
unweighted_graph = graph.remove_edge_weights()
```
We compute the graph report:
```
graph
```
and the unweighted graph report:
```
unweighted_graph
```
## Random walks are heavily parallelized
All the algorithms to sample random walks provided by Ensmallen are heavily parallelized. Therefore, their execution on instances with a large amount amount of threads will lead to (obviously) better time performance. This notebook is being executed on a COLAB instance with only 2 core; therefore the performance will not be as good as they could be even on your notebook, or your cellphone (Ensmallen can run on Android phones).
```
from multiprocessing import cpu_count
cpu_count()
```
## Unweighted first-order random walks
Computation of first-order random walks ignoring the edge weights. In the following examples random walks are computed (on unweighted and weighted graphs) by either invoking method *random_walks* or method *complete_walks*.
*random_walks* automatically chooses between exact and sampled random walks; use this method if you want to let *Grape* to chose the best option.
*complete_walks* is the method used to compute exact walks.
```
%%time
unweighted_graph.random_walks(
# We want random walks with length 100
walk_length=32,
# We want to get random walks starting from 1000 random nodes
quantity=1000,
# We want 2 iterations from each node
iterations=2
)
%%time
unweighted_graph.complete_walks(
# We want random walks with length 100
walk_length=100,
# We want 2 iterations from each node
iterations=2
)
```
## Weighted first-order random walks
Computation of first-order random walks, biased using the edge weights.
```
%%time
graph.random_walks(
# We want random walks with length 100
walk_length=100,
# We want to get random walks starting from 1000 random nodes
quantity=1000,
# We want 2 iterations from each node
iterations=2
)
```
Similarly, to get random walks from all of the nodes in the graph it is possible to use:
```
%%time
graph.complete_walks(
# We want random walks with length 100
walk_length=100,
# We want 2 iterations from each node
iterations=2
)
```
## Second-order random walks
In the following we show the computation of second-order random walks, that is random walks that use [Node2Vec parameters](https://arxiv.org/abs/1607.00653) to bias the random walk towards a BFS or a DFS.
```
%%time
graph.random_walks(
# We want random walks with length 100
walk_length=32,
# We want to get random walks starting from 1000 random nodes
quantity=1000,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
)
%%time
unweighted_graph.random_walks(
# We want random walks with length 100
walk_length=32,
# We want to get random walks starting from 1000 random nodes
quantity=1000,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
)
%%time
graph.complete_walks(
# We want random walks with length 100
walk_length=32,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
)
%%time
unweighted_graph.complete_walks(
# We want random walks with length 100
walk_length=32,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
)
```
## Approximated second-order random walks
When working on graphs where some nodes have an extremely high node degree, *d* (e.g. *d > 50000*), the computation of the transition weights can be a bottleneck. In those use-cases approximated random walks can help make the computation considerably faster, by randomly subsampling each node's neighbourhood to a maximum number, provided by the user. In the considered graph, the highest node degree id *d $\approx$ 7000*.
In the GraPE paper we show experiments comparing the edge-prediction performance of a model trained on graph embeddings obtained by the Skipgram model when using either exact random walks, or random walks obtained by with significant subsampling of the nodes (maximum node degree clipped at 10). The comparative evaluation shows no decrease in performance.
```
%%time
graph.random_walks(
# We want random walks with length 100
walk_length=32,
# We want to get random walks starting from 1000 random nodes
quantity=1000,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
# We will subsample the neighbours of the nodes
# dynamically to 100.
max_neighbours=100
)
%%time
graph.complete_walks(
# We want random walks with length 100
walk_length=32,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
# We will subsample the neighbours of the nodes
# dynamically to 100.
max_neighbours=100
)
```
## Enabling the speedups
Ensmallen provides numerous speed-ups based on time-memory tradeoffs, which allow faster computation. Automatic Speed-up can be enabled by simply seeting a semaphor:
```
graph.enable()
```
### Weighted first order random walks with speedups
The first order random walks have about an order of magnitude speed increase.
```
%%time
graph.random_walks(
# We want random walks with length 100
walk_length=100,
# We want to get random walks starting from 1000 random nodes
quantity=1000,
# We want 10 iterations from each node
iterations=2
)
%%time
graph.complete_walks(
# We want random walks with length 100
walk_length=100,
# We want 10 iterations from each node
iterations=2
)
```
### Second order random walks with speedups
```
%%time
graph.random_walks(
# We want random walks with length 100
walk_length=32,
# We want to get random walks starting from 1000 random nodes
quantity=1000,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
)
%%time
graph.complete_walks(
# We want random walks with length 100
walk_length=32,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
)
```
## Approximated second-order random walks with speedups
```
%%time
graph.random_walks(
# We want random walks with length 100
walk_length=32,
# We want to get random walks starting from 1000 random nodes
quantity=1000,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
# We will subsample the neighbours of the nodes
# dynamically to 100.
max_neighbours=100
)
%%time
graph.complete_walks(
# We want random walks with length 100
walk_length=32,
# We want 2 iterations from each node
iterations=2,
return_weight=2.0,
explore_weight=2.0,
# We will subsample the neighbours of the nodes
# dynamically to 100.
max_neighbours=100
)
```
| true |
code
| 0.796915 | null | null | null | null |
|
<a href="https://practicalai.me"><img src="https://raw.githubusercontent.com/practicalAI/images/master/images/rounded_logo.png" width="100" align="left" hspace="20px" vspace="20px"></a>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/nn.png" width="200" vspace="10px" align="right">
<div align="left">
<h1>Multilayer Perceptron (MLP)</h1>
In this lesson, we will explore multilayer perceptrons (MLPs) which are a basic type of neural network. We will implement them using Tensorflow with Keras.</div>
<table align="center">
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/rounded_logo.png" width="25"><a target="_blank" href="https://practicalai.me"> View on practicalAI</a>
</td>
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/colab_logo.png" width="25"><a target="_blank" href="https://colab.research.google.com/github/practicalAI/practicalAI/blob/master/notebooks/06_Multilayer_Perceptron.ipynb"> Run in Google Colab</a>
</td>
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/github_logo.png" width="22"><a target="_blank" href="https://github.com/practicalAI/practicalAI/blob/master/notebooks/basic_ml/06_Multilayer_Perceptron.ipynb"> View code on GitHub</a>
</td>
</table>
# Overview
* **Objective:** Predict the probability of class $y$ given the inputs $X$. Non-linearity is introduced to model the complex, non-linear data.
* **Advantages:**
* Can model non-linear patterns in the data really well.
* **Disadvantages:**
* Overfits easily.
* Computationally intensive as network increases in size.
* Not easily interpretable.
* **Miscellaneous:** Future neural network architectures that we'll see use the MLP as a modular unit for feed forward operations (affine transformation (XW) followed by a non-linear operation).
Our goal is to learn a model 𝑦̂ that models 𝑦 given 𝑋 . You'll notice that neural networks are just extensions of the generalized linear methods we've seen so far but with non-linear activation functions since our data will be highly non-linear.
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/nn.png" width="550">
$z_1 = XW_1$
$a_1 = f(z_1)$
$z_2 = a_1W_2$
$\hat{y} = softmax(z_2)$ # classification
* $X$ = inputs | $\in \mathbb{R}^{NXD}$ ($D$ is the number of features)
* $W_1$ = 1st layer weights | $\in \mathbb{R}^{DXH}$ ($H$ is the number of hidden units in layer 1)
* $z_1$ = outputs from first layer $\in \mathbb{R}^{NXH}$
* $f$ = non-linear activation function
*nn $a_1$ = activation applied first layer's outputs | $\in \mathbb{R}^{NXH}$
* $W_2$ = 2nd layer weights | $\in \mathbb{R}^{HXC}$ ($C$ is the number of classes)
* $z_2$ = outputs from second layer $\in \mathbb{R}^{NXH}$
* $\hat{y}$ = prediction | $\in \mathbb{R}^{NXC}$ ($N$ is the number of samples)
**Note**: We're going to leave out the bias terms $\beta$ to avoid further crowding the backpropagation calculations.
### Training
1. Randomly initialize the model's weights $W$ (we'll cover more effective initialization strategies later in this lesson).
2. Feed inputs $X$ into the model to do the forward pass and receive the probabilities.
* $z_1 = XW_1$
* $a_1 = f(z_1)$
* $z_2 = a_1W_2$
* $\hat{y} = softmax(z_2)$
3. Compare the predictions $\hat{y}$ (ex. [0.3, 0.3, 0.4]]) with the actual target values $y$ (ex. class 2 would look like [0, 0, 1]) with the objective (cost) function to determine loss $J$. A common objective function for classification tasks is cross-entropy loss.
* $J(\theta) = - \sum_i y_i ln (\hat{y_i}) $
* Since each input maps to exactly one class, our cross-entropy loss simplifies to:
* $J(\theta) = - \sum_i ln(\hat{y_i}) = - \sum_i ln (\frac{e^{X_iW_y}}{\sum_j e^{X_iW}}) $
4. Calculate the gradient of loss $J(\theta)$ w.r.t to the model weights.
* $\frac{\partial{J}}{\partial{W_{2j}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}0 - e^{a_1W_{2y}}e^{a_1W_{2j}}a_1}{(\sum_j e^{a_1W})^2} = \frac{a_1e^{a_1W_{2j}}}{\sum_j e^{a_1W}} = a_1\hat{y}$
* $\frac{\partial{J}}{\partial{W_{2y}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}a_1 - e^{a_1W_{2y}}e^{a_1W_{2y}}a_1}{(\sum_j e^{a_1W})^2} = \frac{1}{\hat{y}}(a_1\hat{y} - a_1\hat{y}^2) = a_1(\hat{y}-1)$
* $ \frac{\partial{J}}{\partial{W_1}} = \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{a_2}} \frac{\partial{a_2}}{\partial{z_2}} \frac{\partial{z_2}}{\partial{W_1}} = W_2(\partial{scores})(\partial{ReLU})X $
5. Update the weights $W$ using a small learning rate $\alpha$. The updates will penalize the probabiltiy for the incorrect classes (j) and encourage a higher probability for the correct class (y).
* $W_i = W_i - \alpha\frac{\partial{J}}{\partial{W_i}}$
6. Repeat steps 2 - 4 until model performs well.
# Set up
```
# Use TensorFlow 2.x
%tensorflow_version 2.x
import os
import numpy as np
import tensorflow as tf
# Arguments
SEED = 1234
SHUFFLE = True
DATA_FILE = "spiral.csv"
INPUT_DIM = 2
NUM_CLASSES = 3
NUM_SAMPLES_PER_CLASS = 500
TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15
NUM_EPOCHS = 10
BATCH_SIZE = 32
HIDDEN_DIM = 100
LEARNING_RATE = 1e-2
# Set seed for reproducibility
np.random.seed(SEED)
tf.random.set_seed(SEED)
```
# Data
Download non-linear spiral data for a classification task.
```
import matplotlib.pyplot as plt
import pandas as pd
import urllib
# Upload data from GitHub to notebook's local drive
url = "https://raw.githubusercontent.com/practicalAI/practicalAI/master/data/spiral.csv"
response = urllib.request.urlopen(url)
html = response.read()
with open(DATA_FILE, 'wb') as fp:
fp.write(html)
# Load data
df = pd.read_csv(DATA_FILE, header=0)
X = df[['X1', 'X2']].values
y = df['color'].values
df.head(5)
print ("X: ", np.shape(X))
print ("y: ", np.shape(y))
# Visualize data
plt.title("Generated non-linear data")
colors = {'c1': 'red', 'c2': 'yellow', 'c3': 'blue'}
plt.scatter(X[:, 0], X[:, 1], c=[colors[_y] for _y in y], edgecolors='k', s=25)
plt.show()
```
# Split data
```
import collections
import json
from sklearn.model_selection import train_test_split
```
### Components
```
def train_val_test_split(X, y, val_size, test_size, shuffle):
"""Split data into train/val/test datasets.
"""
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=test_size, stratify=y, shuffle=shuffle)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=val_size, stratify=y_train, shuffle=shuffle)
return X_train, X_val, X_test, y_train, y_val, y_test
```
### Operations
```
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, val_size=VAL_SIZE, test_size=TEST_SIZE, shuffle=SHUFFLE)
class_counts = dict(collections.Counter(y))
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"X_train[0]: {X_train[0]}")
print (f"y_train[0]: {y_train[0]}")
print (f"Classes: {class_counts}")
```
# Label encoder
```
import json
from sklearn.preprocessing import LabelEncoder
# Output vectorizer
y_tokenizer = LabelEncoder()
# Fit on train data
y_tokenizer = y_tokenizer.fit(y_train)
classes = list(y_tokenizer.classes_)
print (f"classes: {classes}")
# Convert labels to tokens
print (f"y_train[0]: {y_train[0]}")
y_train = y_tokenizer.transform(y_train)
y_val = y_tokenizer.transform(y_val)
y_test = y_tokenizer.transform(y_test)
print (f"y_train[0]: {y_train[0]}")
# Class weights
counts = collections.Counter(y_train)
class_weights = {_class: 1.0/count for _class, count in counts.items()}
print (f"class counts: {counts},\nclass weights: {class_weights}")
```
# Standardize data
We need to standardize our data (zero mean and unit variance) in order to optimize quickly. We're only going to standardize the inputs X because out outputs y are class values.
```
from sklearn.preprocessing import StandardScaler
# Standardize the data (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
# Apply scaler on training and test data (don't standardize outputs for classification)
standardized_X_train = X_scaler.transform(X_train)
standardized_X_val = X_scaler.transform(X_val)
standardized_X_test = X_scaler.transform(X_test)
# Check
print (f"standardized_X_train: mean: {np.mean(standardized_X_train, axis=0)[0]}, std: {np.std(standardized_X_train, axis=0)[0]}")
print (f"standardized_X_val: mean: {np.mean(standardized_X_val, axis=0)[0]}, std: {np.std(standardized_X_val, axis=0)[0]}")
print (f"standardized_X_test: mean: {np.mean(standardized_X_test, axis=0)[0]}, std: {np.std(standardized_X_test, axis=0)[0]}")
```
# Linear model
Before we get to our neural network, we're going to implement a generalized linear model (logistic regression) first to see why linear models won't suffice for our dataset. We will use Tensorflow with Keras to do this.
```
import itertools
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Input
from tensorflow.keras.losses import SparseCategoricalCrossentropy
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
```
### Components
```
# Linear model
class LogisticClassifier(Model):
def __init__(self, hidden_dim, num_classes):
super(LogisticClassifier, self).__init__()
self.fc1 = Dense(units=hidden_dim, activation='linear') # linear = no activation function
self.fc2 = Dense(units=num_classes, activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
def plot_confusion_matrix(y_true, y_pred, classes, cmap=plt.cm.Blues):
"""Plot a confusion matrix using ground truth and predictions."""
# Confusion matrix
cm = confusion_matrix(y_true, y_pred)
cm_norm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
# Figure
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(cm, cmap=plt.cm.Blues)
fig.colorbar(cax)
# Axis
plt.title("Confusion matrix")
plt.ylabel("True label")
plt.xlabel("Predicted label")
ax.set_xticklabels([''] + classes)
ax.set_yticklabels([''] + classes)
ax.xaxis.set_label_position('bottom')
ax.xaxis.tick_bottom()
# Values
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, f"{cm[i, j]:d} ({cm_norm[i, j]*100:.1f}%)",
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
# Display
plt.show()
def plot_multiclass_decision_boundary(model, X, y, savefig_fp=None):
"""Plot the multiclass decision boundary for a model that accepts 2D inputs.
Arguments:
model {function} -- trained model with function model.predict(x_in).
X {numpy.ndarray} -- 2D inputs with shape (N, 2).
y {numpy.ndarray} -- 1D outputs with shape (N,).
"""
# Axis boundaries
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101),
np.linspace(y_min, y_max, 101))
# Create predictions
x_in = np.c_[xx.ravel(), yy.ravel()]
y_pred = model.predict(x_in)
y_pred = np.argmax(y_pred, axis=1).reshape(xx.shape)
# Plot decision boundary
plt.contourf(xx, yy, y_pred, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
# Plot
if savefig_fp:
plt.savefig(savefig_fp, format='png')
```
### Operations
```
# Initialize the model
model = LogisticClassifier(hidden_dim=HIDDEN_DIM,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
model.compile(optimizer=Adam(lr=LEARNING_RATE),
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Metrics
plot_confusion_matrix(y_test, pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
# Activation functions
Using the generalized linear method (logistic regression) yielded poor results because of the non-linearity present in our data. We need to use an activation function that can allow our model to learn and map the non-linearity in our data. There are many different options so let's explore a few.
```
from tensorflow.keras.activations import relu
from tensorflow.keras.activations import sigmoid
from tensorflow.keras.activations import tanh
# Fig size
plt.figure(figsize=(12,3))
# Data
x = np.arange(-5., 5., 0.1)
# Sigmoid activation (constrain a value between 0 and 1.)
plt.subplot(1, 3, 1)
plt.title("Sigmoid activation")
y = sigmoid(x)
plt.plot(x, y)
# Tanh activation (constrain a value between -1 and 1.)
plt.subplot(1, 3, 2)
y = tanh(x)
plt.title("Tanh activation")
plt.plot(x, y)
# Relu (clip the negative values to 0)
plt.subplot(1, 3, 3)
y = relu(x)
plt.title("ReLU activation")
plt.plot(x, y)
# Show plots
plt.show()
```
The ReLU activation function ($max(0,z)$) is by far the most widely used activation function for neural networks. But as you can see, each activation function has its own constraints so there are circumstances where you'll want to use different ones. For example, if we need to constrain our outputs between 0 and 1, then the sigmoid activation is the best choice.
<img width="45" src="http://bestanimations.com/HomeOffice/Lights/Bulbs/animated-light-bulb-gif-29.gif" align="left" vspace="20px" hspace="10px">
In some cases, using a ReLU activation function may not be sufficient. For instance, when the outputs from our neurons are mostly negative, the activation function will produce zeros. This effectively creates a "dying ReLU" and a recovery is unlikely. To mitigate this effect, we could lower the learning rate or use [alternative ReLU activations](https://medium.com/tinymind/a-practical-guide-to-relu-b83ca804f1f7), ex. leaky ReLU or parametric ReLU (PReLU), which have a small slope for negative neuron outputs.
# From scratch
Now let's create our multilayer perceptron (MLP) which is going to be exactly like the logistic regression model but with the activation function to map the non-linearity in our data. Before we use TensorFlow 2.0 + Keras we will implement our neural network from scratch using NumPy so we can:
1. Absorb the fundamental concepts by implementing from scratch
2. Appreciate the level of abstraction TensorFlow provides
<div align="left">
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/lightbulb.gif" width="45px" align="left" hspace="10px">
</div>
It's normal to find the math and code in this section slightly complex. You can still read each of the steps to build intuition for when we implement this using TensorFlow + Keras.
```
print (f"X: {standardized_X_train.shape}")
print (f"y: {y_train.shape}")
```
Our goal is to learn a model 𝑦̂ that models 𝑦 given 𝑋 . You'll notice that neural networks are just extensions of the generalized linear methods we've seen so far but with non-linear activation functions since our data will be highly non-linear.
$z_1 = XW_1$
$a_1 = f(z_1)$
$z_2 = a_1W_2$
$\hat{y} = softmax(z_2)$ # classification
* $X$ = inputs | $\in \mathbb{R}^{NXD}$ ($D$ is the number of features)
* $W_1$ = 1st layer weights | $\in \mathbb{R}^{DXH}$ ($H$ is the number of hidden units in layer 1)
* $z_1$ = outputs from first layer $\in \mathbb{R}^{NXH}$
* $f$ = non-linear activation function
* $a_1$ = activation applied first layer's outputs | $\in \mathbb{R}^{NXH}$
* $W_2$ = 2nd layer weights | $\in \mathbb{R}^{HXC}$ ($C$ is the number of classes)
* $z_2$ = outputs from second layer $\in \mathbb{R}^{NXH}$
* $\hat{y}$ = prediction | $\in \mathbb{R}^{NXC}$ ($N$ is the number of samples)
1. Randomly initialize the model's weights $W$ (we'll cover more effective initialization strategies later in this lesson).
```
# Initialize first layer's weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
print (f"W1: {W1.shape}")
print (f"b1: {b1.shape}")
```
2. Feed inputs $X$ into the model to do the forward pass and receive the probabilities.
First we pass the inputs into the first layer.
* $z_1 = XW_1$
```
# z1 = [NX2] · [2X100] + [1X100] = [NX100]
z1 = np.dot(standardized_X_train, W1) + b1
print (f"z1: {z1.shape}")
```
Next we apply the non-linear activation function, ReLU ($max(0,z)$) in this case.
* $a_1 = f(z_1)$
```
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
print (f"a_1: {a1.shape}")
```
We pass the activations to the second layer to get our logits.
* $z_2 = a_1W_2$
```
# Initialize second layer's weights
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
print (f"W2: {W2.shape}")
print (f"b2: {b2.shape}")
# z2 = logits = [NX100] · [100X3] + [1X3] = [NX3]
logits = np.dot(a1, W2) + b2
print (f"logits: {logits.shape}")
print (f"sample: {logits[0]}")
```
We'll apply the softmax function to normalize the logits and btain class probabilities.
* $\hat{y} = softmax(z_2)$
```
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
print (f"y_hat: {y_hat.shape}")
print (f"sample: {y_hat[0]}")
```
3. Compare the predictions $\hat{y}$ (ex. [0.3, 0.3, 0.4]]) with the actual target values $y$ (ex. class 2 would look like [0, 0, 1]) with the objective (cost) function to determine loss $J$. A common objective function for classification tasks is cross-entropy loss.
* $J(\theta) = - \sum_i ln(\hat{y_i}) = - \sum_i ln (\frac{e^{X_iW_y}}{\sum_j e^{X_iW}}) $
```
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
```
4. Calculate the gradient of loss $J(\theta)$ w.r.t to the model weights.
The gradient of the loss w.r.t to W2 is the same as the gradients from logistic regression since $\hat{y} = softmax(z_2)$.
* $\frac{\partial{J}}{\partial{W_{2j}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}0 - e^{a_1W_{2y}}e^{a_1W_{2j}}a_1}{(\sum_j e^{a_1W})^2} = \frac{a_1e^{a_1W_{2j}}}{\sum_j e^{a_1W}} = a_1\hat{y}$
* $\frac{\partial{J}}{\partial{W_{2y}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}a_1 - e^{a_1W_{2y}}e^{a_1W_{2y}}a_1}{(\sum_j e^{a_1W})^2} = \frac{1}{\hat{y}}(a_1\hat{y} - a_1\hat{y}^2) = a_1(\hat{y}-1)$
The gradient of the loss w.r.t W1 is a bit trickier since we have to backpropagate through two sets of weights.
* $ \frac{\partial{J}}{\partial{W_1}} = \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{a_1}} \frac{\partial{a_1}}{\partial{z_1}} \frac{\partial{z_1}}{\partial{W_1}} = W_2(\partial{scores})(\partial{ReLU})X $
```
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(standardized_X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)
```
5. Update the weights $W$ using a small learning rate $\alpha$. The updates will penalize the probabiltiy for the incorrect classes (j) and encourage a higher probability for the correct class (y).
* $W_i = W_i - \alpha\frac{\partial{J}}{\partial{W_i}}$
```
# Update weights
W1 += -LEARNING_RATE * dW1
b1 += -LEARNING_RATE * db1
W2 += -LEARNING_RATE * dW2
b2 += -LEARNING_RATE * db2
```
6. Repeat steps 2 - 4 until model performs well.
```
# Initialize random weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
# Training loop
for epoch_num in range(1000):
# First layer forward pass [NX2] · [2X100] = [NX100]
z1 = np.dot(standardized_X_train, W1) + b1
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
# z2 = logits = [NX100] · [100X3] = [NX3]
logits = np.dot(a1, W2) + b2
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
# show progress
if epoch_num%100 == 0:
# Accuracy
y_pred = np.argmax(logits, axis=1)
accuracy = np.mean(np.equal(y_train, y_pred))
print (f"Epoch: {epoch_num}, loss: {loss:.3f}, accuracy: {accuracy:.3f}")
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(standardized_X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)
# Update weights
W1 += -1e0 * dW1
b1 += -1e0 * db1
W2 += -1e0 * dW2
b2 += -1e0 * db2
class MLPFromScratch():
def predict(self, x):
z1 = np.dot(x, W1) + b1
a1 = np.maximum(0, z1)
logits = np.dot(a1, W2) + b2
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
return y_hat
# Evaluation
model = MLPFromScratch()
logits_train = model.predict(standardized_X_train)
pred_train = np.argmax(logits_train, axis=1)
logits_test = model.predict(standardized_X_test)
pred_test = np.argmax(logits_test, axis=1)
# Training and test accuracy
train_acc = np.mean(np.equal(y_train, pred_train))
test_acc = np.mean(np.equal(y_test, pred_test))
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
Credit for the plotting functions and the intuition behind all this is due to [CS231n](http://cs231n.github.io/neural-networks-case-study/), one of the best courses for machine learning. Now let's implement the MLP with TensorFlow + Keras.
# TensorFlow + Keras
### Components
```
# MLP
class MLP(Model):
def __init__(self, hidden_dim, num_classes):
super(MLP, self).__init__()
self.fc1 = Dense(units=hidden_dim, activation='relu') # replaced linear with relu
self.fc2 = Dense(units=num_classes, activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
### Operations
```
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
optimizer = Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer,
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Metrics
plot_confusion_matrix(y_test, pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
# Inference
```
# Inputs for inference
X_infer = pd.DataFrame([{'X1': 0.1, 'X2': 0.1}])
X_infer.head()
# Standardize
standardized_X_infer = X_scaler.transform(X_infer)
print (standardized_X_infer)
# Predict
y_infer = model.predict(standardized_X_infer)
_class = np.argmax(y_infer)
print (f"The probability that you have a class {classes[_class]} is {y_infer[0][_class]*100.0:.0f}%")
```
# Initializing weights
So far we have been initializing weights with small random values and this isn't optimal for convergence during training. The objective is to have weights that are able to produce outputs that follow a similar distribution across all neurons. We can do this by enforcing weights to have unit variance prior the affine and non-linear operations.
<img width="45" src="http://bestanimations.com/HomeOffice/Lights/Bulbs/animated-light-bulb-gif-29.gif" align="left" vspace="20px" hspace="10px">
A popular method is to apply [xavier initialization](http://andyljones.tumblr.com/post/110998971763/an-explanation-of-xavier-initialization), which essentially initializes the weights to allow the signal from the data to reach deep into the network. You may be wondering why we don't do this for every forward pass and that's a great question. We'll look at more advanced strategies that help with optimization like batch/layer normalization, etc. in future lessons. Meanwhile you can check out other initializers [here](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/initializers).
```
from tensorflow.keras.initializers import glorot_normal
# MLP
class MLP(Model):
def __init__(self, hidden_dim, num_classes):
super(MLP, self).__init__()
xavier_initializer = glorot_normal() # xavier glorot initiailization
self.fc1 = Dense(units=hidden_dim,
kernel_initializer=xavier_initializer,
activation='relu')
self.fc2 = Dense(units=num_classes,
activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
# Dropout
A great technique to overcome overfitting is to increase the size of your data but this isn't always an option. Fortuntely, there are methods like regularization and dropout that can help create a more robust model.
Dropout is a technique (used only during training) that allows us to zero the outputs of neurons. We do this for `dropout_p`% of the total neurons in each layer and it changes every batch. Dropout prevents units from co-adapting too much to the data and acts as a sampling strategy since we drop a different set of neurons each time.
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/dropout.png" width="350">
* [Dropout: A Simple Way to Prevent Neural Networks from
Overfitting](http://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf)
```
from tensorflow.keras.layers import Dropout
from tensorflow.keras.regularizers import l2
```
### Components
```
# MLP
class MLP(Model):
def __init__(self, hidden_dim, lambda_l2, dropout_p, num_classes):
super(MLP, self).__init__()
self.fc1 = Dense(units=hidden_dim,
kernel_regularizer=l2(lambda_l2), # adding L2 regularization
activation='relu')
self.dropout = Dropout(rate=dropout_p)
self.fc2 = Dense(units=num_classes,
activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
if training:
z = self.dropout(z, training=training) # adding dropout
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
### Operations
```
# Arguments
DROPOUT_P = 0.1 # % of the neurons that are dropped each pass
LAMBDA_L2 = 1e-4 # L2 regularization
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
lambda_l2=LAMBDA_L2,
dropout_p=DROPOUT_P,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
```
# Overfitting
Though neural networks are great at capturing non-linear relationships they are highly susceptible to overfitting to the training data and failing to generalize on test data. Just take a look at the example below where we generate completely random data and are able to fit a model with [$2*N*C + D$](https://arxiv.org/abs/1611.03530) hidden units. The training performance is good (~70%) but the overfitting leads to very poor test performance. We'll be covering strategies to tackle overfitting in future lessons.
```
# Arguments
NUM_EPOCHS = 500
NUM_SAMPLES_PER_CLASS = 50
LEARNING_RATE = 1e-1
HIDDEN_DIM = 2 * NUM_SAMPLES_PER_CLASS * NUM_CLASSES + INPUT_DIM # 2*N*C + D
# Generate random data
X = np.random.rand(NUM_SAMPLES_PER_CLASS * NUM_CLASSES, INPUT_DIM)
y = np.array([[i]*NUM_SAMPLES_PER_CLASS for i in range(NUM_CLASSES)]).reshape(-1)
print ("X: ", format(np.shape(X)))
print ("y: ", format(np.shape(y)))
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X, y, val_size=VAL_SIZE, test_size=TEST_SIZE, shuffle=SHUFFLE)
print ("X_train:", X_train.shape)
print ("y_train:", y_train.shape)
print ("X_val:", X_val.shape)
print ("y_val:", y_val.shape)
print ("X_test:", X_test.shape)
print ("y_test:", y_test.shape)
# Standardize the inputs (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
# Apply scaler on training and test data (don't standardize outputs for classification)
standardized_X_train = X_scaler.transform(X_train)
standardized_X_val = X_scaler.transform(X_val)
standardized_X_test = X_scaler.transform(X_test)
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
lambda_l2=0.0,
dropout_p=0.0,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
optimizer = Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer,
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Classification report
plot_confusion_matrix(y_true=y_test, y_pred=pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
It's important that we experiment, starting with simple models that underfit (high bias) and improve it towards a good fit. Starting with simple models (linear/logistic regression) let's us catch errors without the added complexity of more sophisticated models (neural networks).
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/fit.png" width="700">
---
<div align="center">
Subscribe to our <a href="https://practicalai.me/#newsletter">newsletter</a> and follow us on social media to get the latest updates!
<a class="ai-header-badge" target="_blank" href="https://github.com/practicalAI/practicalAI">
<img src="https://img.shields.io/github/stars/practicalAI/practicalAI.svg?style=social&label=Star"></a>
<a class="ai-header-badge" target="_blank" href="https://www.linkedin.com/company/madewithml">
<img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a class="ai-header-badge" target="_blank" href="https://twitter.com/madewithml">
<img src="https://img.shields.io/twitter/follow/madewithml.svg?label=Follow&style=social">
</a>
</div>
</div>
| true |
code
| 0.788807 | null | null | null | null |
|
# Policy Gradient (PG)
Referências:
- [Schulman, John. _Optimizing Expectations_: From Deep Reinforcement Learning to Stochastic Computation Graphs](https://www2.eecs.berkeley.edu/Pubs/TechRpts/2016/EECS-2016-217.html).
- [Spinning Up](https://spinningup.openai.com/en/latest/spinningup/rl_intro3.html)
# Conceito
Em todos os métodos que vimos até agora (Monte Carlo, TD/Q-Learning, ...), o agente aprende uma função de valor $V(s | \theta)$ ou $Q(s,a | \theta)$, onde $\theta$ são os parâmetros/pesos do modelo. O agente então segue uma política ($\varepsilon$-)gulosa, (quase-)deterministica, derivada da função de valor. Esses métodos são todos aproximações de programação dinâmica e encontram a política ótima de maneira indireta.
Um método alternativo é estimar as políticas ótimas diretamente, ou seja, estimar os parâmetros ótimos $\theta$ para a política $\pi(a | s, \theta)$.
Os métodos que utilizam gradientes para realizar essa tarefa são chamados de Policy Gradient.
No caso de DQN, nós estimávamos a qualidade de uma ação usando bootstrap e minizávamos o erro entre o agente e esse $Q_{\mathrm{bootstrap}}$. Em PG, a situação é um pouco diferente, porque não é tão simples estimar diretamente algum "$\pi_{\mathrm{bootstrap}}$". Ao invés disso, utilizamos _gradient ascent_ para maximizar alguma função objetivo, como:
- $J_0(\theta) = V^{\pi_\theta}(s_0)$ (valor do estado inicial)
- $J_{\mathrm{mean}V}(\theta) = E_{s|\theta}\left[V^{\pi_\theta}(s)\right]$ (valor médio)
- $J_{\mathrm{mean}\mathcal{R}}(\theta) = E_{s,a|\theta}\left[\mathcal{R}_s^a\right]$ (recompensa média)
- $J_{\mathrm{mean}G}(\theta) = E_{\tau|\theta}\left[G_\tau\right]$ (retorno médio por episódio)
O algoritmo de PG então se reduz a:
$$\theta_{k+1} = \theta_k + \alpha \nabla_\theta J(\theta_k),$$
onde $\alpha$ é a taxa de aprendizado. Só falta um detalhe bem importante nessa equação: como calcular o gradiente de $J$.
Obs: O resto dessa explicação, assim como a tese de referência, assume que a função objetivo é $J(\theta) = J_{\mathrm{mean}G}(\theta)$, ou seja, queremos maximizar o retorno médio por episódio.
## Teorema de Policy Gradient
Definida a nossa função objetivo $J$, precisamos encontrar seu gradiente para então aplicar o gradiente ascendente. Para qualquer uma das funções objetivo especificadas acima, o gradiente de $J$ é dado por:
$$\nabla_\theta J(\theta) = E_{\tau|\theta}\left[\sum_{t=0}^\infty Q(s_t,a_t|\theta) \nabla_\theta \log\pi(a_t|s_t,\theta)\right].$$
A demonstração do teorema encontra-se no [Apêndice](#apendice) deste notebook.
## REINFORCE
**REINFORCE**, o algoritmo mais simples de PG, é obtido ao utilizar a função objetivo do retorno médio por episódio ($J_{\mathrm{mean}G}(\theta) = E_{\tau|\theta}\left[G_\tau\right]$) para avaliar nosso agente. Neste caso, o gradiente da nossa função objetivo poderia ser estimado por:
\begin{align*}
\nabla_\theta J(\theta) &= E_{\tau|\theta}\left[\sum_{t=0}^\infty Q(s_t,a_t|\theta) \nabla_\theta \log\pi(a_t|s_t,\theta)\right] \\
&\approx \sum_{t=0}^T G_t \nabla_\theta \log\pi(a_t|s_t,\theta)
\end{align*}
Dessa forma, seu algoritmo é dado por:

Note que esse algoritmo é on-policy, pois o cálculo do gradiente depende da distribuição de estados e ações e é válido apenas para a política que gerou essa distribuição.
## REINFORCE com Baseline
Uma extensão dessa ideia é utilizar reinforce com baselines. Nesse método, ao invés de $G_t$, utilizamos a função vantagem (_advantage_) $A = G_t - V(s_t)$, que indica a qualidade de uma ação-estado em relação à qualidade média daquele estado. Para isso, é necessário treinar uma função de valor $V(s)$. O uso da vantagem reduz a variância do modelo e melhora significantemente sua convergência.
O algoritmo fica:

## Imports
```
import gym
import math
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions.categorical import Categorical
```
## Rede Neural
```
def logits_net(in_dim, out_dim):
return nn.Sequential(nn.Linear(in_dim, 64),
nn.ReLU(),
nn.Linear(64, 64),
nn.ReLU(),
nn.Linear(64, out_dim))
def value_net(in_dim):
return nn.Sequential(nn.Linear(in_dim, 32),
nn.ReLU(),
nn.Linear(32, 16),
nn.ReLU(),
nn.Linear(16, 1))
```
## Buffer PG
```
class PGBuffer:
"""
Armazena as experiências que serão utilizadas para treinar o agente de PG.
"""
def __init__(self, observation_space, max_length, gamma=1):
self.gamma = gamma
self.max_length = max_length
self.states = np.zeros((max_length, *observation_space.shape), dtype=np.float32)
self.actions = np.zeros(max_length, dtype=np.int32)
self.rewards = np.zeros(max_length, dtype=np.float32)
self.size = 0
def update(self, state, action, reward):
self.states[self.size] = state
self.actions[self.size] = action
self.rewards[self.size] = reward
self.size += 1
def clear(self):
self.states[:] = 0
self.actions[:] = 0
self.rewards[:] = 0
self.size = 0
def get_returns(self):
discounted_rewards = self.gamma**np.arange(self.max_length) * self.rewards
return discounted_rewards[::-1].cumsum()[::-1].copy()
def __len__(self):
return self.size
```
## Agente PG
```
class PGAgent:
"""
Uma classe que cria um agente PG.
"""
def __init__(self,
observation_space,
action_space,
max_length,
baseline=True,
gamma=0.99,
policy_lr=3e-4,
baseline_lr=3e-4):
"""
Inicializa o agente com os parâmetros dados
"""
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.gamma = gamma
self.action_space = action_space
self.memory = PGBuffer(observation_space, max_length, gamma=gamma)
self.policy_logit = logits_net(observation_space.shape[0], action_space.n).to(self.device)
self.policy_optimizer = optim.Adam(self.policy_logit.parameters(), lr=policy_lr)
if baseline:
self.baseline = value_net(observation_space.shape[0]).to(self.device)
self.baseline_optimizer = optim.Adam(self.baseline.parameters(), lr=baseline_lr)
else:
self.baseline = None
def policy(self, state):
if not torch.is_tensor(state):
state = torch.FloatTensor(state).to(self.device)
p = Categorical(logits=self.policy_logit(state))
return p
def act(self, state):
return self.policy(state).sample().item()
def logp(self, state, action):
action = torch.IntTensor(action).to(self.device)
return self.policy(state).log_prob(action)
def remember(self, state, action, reward):
self.memory.update(state, action, reward)
def is_full(self):
return len(self.memory) == self.memory.max_length
def train(self):
size = len(self.memory)
returns = self.memory.get_returns()[:size]
states = torch.FloatTensor(self.memory.states[:size]).to(self.device)
actions = self.memory.actions[:size]
logps = self.logp(states, actions)
advantages = torch.FloatTensor(returns).to(self.device)
if self.baseline:
v = self.baseline(states).flatten()
advantages -= v.detach()
baseline_loss = F.smooth_l1_loss(v, torch.FloatTensor(returns).to(self.device))
self.baseline_optimizer.zero_grad()
baseline_loss.backward(retain_graph=True)
torch.nn.utils.clip_grad_norm_(self.baseline.parameters(), 1)
self.baseline_optimizer.step()
policy_loss = -(advantages * logps).sum()
self.policy_optimizer.zero_grad()
policy_loss.backward()
self.policy_optimizer.step()
self.memory.clear()
return policy_loss.item(), (baseline_loss.item() if self.baseline else 0)
```
### Definição de parâmetros
```
env_name = 'CartPole-v1'
env = gym.make(env_name)
GAMMA = .999
MAX_LENGTH = 1000
POLICY_LR = 1e-3
BASELINE = True
BASELINE_LR = 4e-4
TRAIN_TIME = 100_000
```
### Criando o agente
```
agent = PGAgent(env.observation_space,
env.action_space,
max_length=MAX_LENGTH,
baseline=BASELINE,
policy_lr=POLICY_LR,
baseline_lr=BASELINE_LR,
gamma=GAMMA)
```
## Treinamento
```
def train(agent, env, total_timesteps):
total_reward = 0
episode_returns = []
avg_returns = []
state = env.reset()
timestep = 0
episode = 0
pl = 0
bl = 0
while timestep < total_timesteps:
action = agent.act(state)
next_state, reward, done, _ = env.step(action)
agent.remember(state, action, reward)
timestep += 1
total_reward += reward
if done:
episode_returns.append(total_reward)
avg_returns.append(np.mean(episode_returns[-10:]))
episode += 1
next_state = env.reset()
pl, bl = agent.train()
total_reward *= 1 - done
state = next_state
ratio = np.ceil(100 * timestep / total_timesteps)
avg_return = avg_returns[-1] if avg_returns else np.nan
print(f'\r[{ratio:3.0f}%] '
f'timestep = {timestep}/{total_timesteps}, '
f'episode = {episode:3d}, '
f'avg_return = {avg_returns[-1] if avg_returns else 0 :10.4f}, '
f'policy_loss={pl:9.4f}, '
f'baseline_loss={bl:9.4f}', end='')
print()
if len(agent.memory) > 0:
agent.train()
return episode_returns, avg_returns
returns, avg_returns = train(agent, env, TRAIN_TIME)
plt.plot(returns, label='Retorno')
plt.plot(avg_returns, label='Retorno médio')
plt.xlabel('episode')
plt.ylabel('return')
plt.legend()
plt.show()
```
## Testando nosso Agente
```
def evaluate(agent, env, episodes=10):
total_reward = 0
episode_returns = []
episode = 0
state = env.reset()
while episode < episodes:
action = agent.act(state)
next_state, reward, done, _ = env.step(action)
total_reward += reward
if done:
episode_returns.append(total_reward)
episode += 1
next_state = env.reset()
total_reward *= 1 - done
state = next_state
ratio = np.ceil(100 * episode / episodes)
print(f"\r[{ratio:3.0f}%] episode = {episode:3d}, avg_return = {np.mean(episode_returns) if episode_returns else 0:10.4f}", end="")
return np.mean(episode_returns)
evaluate(agent, env, 10)
```
## Variância
```
episodes = []
returns = []
avg_returns = []
for _ in range(5):
agent_ = PGAgent(env.observation_space,
env.action_space,
max_length=MAX_LENGTH,
baseline=True,
policy_lr=POLICY_LR,
baseline_lr=BASELINE_LR,
gamma=GAMMA)
x, y = train(agent_, env, TRAIN_TIME)
returns += x
avg_returns += y
episodes += list(range(len(x)))
import pandas as pd
import seaborn as sns
df = pd.DataFrame({'episodes': episodes, 'returns': returns, 'avg_returns': avg_returns})
melted = df.melt(id_vars=['episodes'], value_vars=['returns', 'avg_returns'])
sns.lineplot(x='episodes', y='value', hue='variable', data=melted, ci='sd')
episodes = []
returns = []
avg_returns = []
for _ in range(5):
agent_ = PGAgent(env.observation_space,
env.action_space,
max_length=MAX_LENGTH,
baseline=False,
policy_lr=POLICY_LR,
baseline_lr=BASELINE_LR,
gamma=GAMMA)
x, y = train(agent_, env, TRAIN_TIME)
returns += x
avg_returns += y
episodes += list(range(len(x)))
import pandas as pd
import seaborn as sns
df = pd.DataFrame({'episodes': episodes, 'returns': returns, 'avg_returns': avg_returns})
melted = df.melt(id_vars=['episodes'], value_vars=['returns', 'avg_returns'])
sns.lineplot(x='episodes', y='value', hue='variable', data=melted, ci='sd')
```
<a id="apendice"></a>
# Apêndice
## A probabilidade de uma trajetória
Algo que será bem útil é o cálculo da probabilidade de uma trajetória $\tau = (s_0,a_0,s_1,a_1,\dots)$. Se a distribuição inicial de estados é dada por $\mu(s) = $ _prob. do estado inicial ser_ $s$, temos:
$$p(\tau|\theta) = \mu(s_0) \pi(a_0|s_0,\theta) p(s_1|s_0,a_0) \pi(a_1|s_1,\theta)\cdots.$$
Tomando o log dessa expressão, obtemos:
\begin{align*}
\log p(\tau|\theta) &= \log \mu(s_0) + \log\pi(a_0|s_0,\theta) + \log p(s_1|s_0,a_0) + \log \pi(a_1|s_1,\theta) + \cdots = \\
&= \log \mu(s_0) + \sum_{t=0}^\infty \left[\log \pi(a_t|s_t,\theta) + \log p(s_{t+1} | s_t, a_t)\right]
\end{align*}
Como os únicos termos que dependem de $\theta$ na última expressão são os termos da forma $\log \pi(a_t|s_t,\theta)$, temos por fim:
$$\nabla \log p(\tau|\theta) = \sum_{t=0}^\infty \nabla \log \pi(a_t|s_t,\theta)$$
## O gradiente de _J_
Do cálculo, sabemos que:
$$\frac{d}{dx} \log x = \frac1x \implies \frac{d}{dx} \log g(x) = \frac{1}{g(x)} g'(x).$$
Em cálculo multivariável, vale analogamente:
$$\nabla \log g(\theta) = \frac{1}{g(\theta)} \nabla g(\theta), \quad \text{ou seja}, \quad \nabla g(\theta) = g(\theta) \nabla \log g(\theta).$$
A função objetivo pode ser escrita em forma integral como:
$$J(\theta) = E_{\tau|\theta}\left[G_\tau\right] = \int_\tau p(\tau|\theta) G_\tau d\tau$$
O gradiente de $J$ fica então:
\begin{align*}
\nabla J(\theta) &= \nabla_\theta \int_\tau p(\tau|\theta) \cdot G_\tau d\tau \\
&= \int G_\tau \cdot \nabla_\theta p(\tau|\theta) d\tau \\
&= \int G_\tau \cdot p(\tau|\theta) \nabla_\theta \log p(\tau|\theta) d\tau \\
&= \int p(\tau|\theta) \cdot G_\tau \nabla_\theta \log p(\tau|\theta) d\tau \\
&= E_{\tau|\theta}\left[G_\tau \nabla_\theta \log p(\tau|\theta)\right] \\
&= E_{\tau|\theta}\left[G_\tau \sum_{t=0}^\infty \nabla_\theta \log \pi(a_t|s_t,\theta)\right]
\end{align*}
### Demonstração do Teorema de Policy Gradient
A demonstração completa e rigorosa pode ser vista no material de referência e, em particular, [nesse material extra](https://spinningup.openai.com/en/latest/spinningup/extra_pg_proof1.html) do Spinning Up. Aqui será passada apenas a ideia básica. Primeiramente, podemos reescrever o gradiente de $J$ como:
$$\nabla_\theta J(\theta) = E_{\tau|\theta}\left[\sum_{t=0}^\infty G_\tau \nabla_\theta \log \pi(a_t|s_t,\theta)\right].$$
Note que para qualquer instante $t=t_i$, essa fórmula considera o retorno total a partir do instante $t=0$, o que é um pouco contra-intuitivo. Final, o agente deveria considerar apenas as recompensas futuras ($t \ge t_i$) ao decidir qual ação tomar. Essa intuição pode ser confirmada matemáticamente, de forma que:
\begin{align*}
\nabla_\theta J(\theta) &= E_{\tau|\theta}\left[\sum_{t=0}^T G_{\tau}^{t:\infty} \nabla_\theta \log \pi(a_t|s_t,\theta)\right] \\
&= E_{\tau|\theta}\left[\sum_{t=0}^T Q(s_t,a_t|\theta) \nabla_\theta \log \pi(a_t|s_t,\theta)\right]
\end{align*}
Note que assumimos que o episódio tem uma duração máxima $T$ e que a distribuição de estados é estacionária (i.e. $s_t,a_t$ tem a mesma distribuição que $a,t$).
| true |
code
| 0.808294 | null | null | null | null |
|
# Assignment 3 - Practical Deep Learning Workshop
#### In this task we will work with the dataset of the Home depot product search relevance competition.
#### Some background:
In this competition, Home Depot is asking to help them improve their customers' shopping experience by developing a model that can accurately predict the relevance of search results.
Search relevancy is an implicit measure Home Depot uses to gauge how quickly they can get customers to the right products.
This data set contains a number of products and real customer search terms from Home Depot's website. The challenge is to predict a relevance score for the provided combinations of search terms and products. To create the ground truth labels, Home Depot has crowdsourced the search/product pairs to multiple human raters.
The relevance is a number between 1 (not relevant) to 3 (highly relevant). For example, a search for "AA battery" would be considered highly relevant to a pack of size AA batteries (relevance = 3), mildly relevant to a cordless drill battery (relevance = 2), and not relevant to a snow shovel (relevance = 1).
Each pair was evaluated by at least three human raters. The provided relevance scores are the average value of the ratings. There are three additional things to know about the ratings:
• The specific instructions given to the raters is provided in relevance_instructions.docx.
• Raters did not have access to the attributes.
• Raters had access to product images, while the competition does not include images.
#### Out task here is to predict the relevance for each pair listed in the test set. The test set contains both seen and unseen search terms.
```
from sklearn.feature_extraction.text import CountVectorizer
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.models import Model, Sequential
from keras.layers import * # Dense, Embedding, LSTM
from sklearn.model_selection import train_test_split
from keras.utils.np_utils import to_categorical
from keras.regularizers import l2
import re
import pandas as pd
import numpy as np
import datetime
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
%matplotlib inline
from google.colab import drive
drive.mount('/content/gdrive')
```
#### First of all, we'll take a look at the data in each dataset of the input:
train.csv is the training set, contains products, searches, and relevance scores.
```
train = pd.read_csv('/content/gdrive/My Drive/Colab Notebooks/input/train.csv',encoding='latin1')
train.head()
```
test.csv is the test set, contains products and searches. We will need to predict the relevance for these pairs.
```
test = pd.read_csv('/content/gdrive/My Drive/Colab Notebooks/input/test.csv',encoding='latin1')
test.head()
```
product_descriptions.csv contains a text description of each product. We may join this table to the training or test set via the product_uid.
```
product_descriptions = pd.read_csv('/content/gdrive/My Drive/Colab Notebooks/input/product_descriptions.csv',encoding='latin1')
product_descriptions.head()
```
attributes.csv provides extended information about a subset of the products (typically representing detailed technical specifications). Not every product will have attributes.
```
attributes = pd.read_csv('/content/gdrive/My Drive/Colab Notebooks/input/attributes.csv',encoding='latin1')
attributes.head()
```
Data fields:
- id - a unique Id field which represents a (search_term, product_uid) pair
- product_uid - an id for the products
- product_title - the product title
- product_description - the text description of the product (may contain HTML content)
- search_term - the search query
- relevance - the average of the relevance ratings for a given id
- name - an attribute name
- value - the attribute's value
## Preprocessing the data
We would like to have the products' corresponding product description, so we will merge the train and test datasets with the product_description table.
Note: in order to decrease the dimensionality of the text, we will lower the characters.
```
mergedTrain = pd.merge(train, product_descriptions, how='inner', on='product_uid')
mergedTrain.search_term = mergedTrain.search_term.apply(lambda x: x.lower())
mergedTrain.product_description = mergedTrain.product_description.apply(lambda x: x.lower())
mergedTrain.head()
mergedTest= pd.merge(test, product_descriptions, how='inner', on='product_uid')
mergedTest.search_term = mergedTest.search_term.apply(lambda x: x.lower())
mergedTest.product_description = mergedTest.product_description.apply(lambda x: x.lower())
mergedTest.head()
```
We convert the product_description and search_term attributes' values to lists of characters.
```
search_term_chars = []
product_description_chars = []
search_term_chars = mergedTrain.search_term.apply(lambda x: search_term_chars + list(x))
product_description_chars = mergedTrain.product_description.apply(lambda x: product_description_chars + list(x))
search_term_chars = [item for sublist in search_term_chars for item in sublist]
product_description_chars = [item for sublist in product_description_chars for item in sublist]
```
And then, translate the characters to a unique integer values. We create two dictionaries (one for search_term and another for product_description), containing the pairs of characters and their uniquie values.
```
search_term_char_set = sorted(set(search_term_chars))
product_description_char_set = sorted(set(product_description_chars))
# translate from character to number, it's enumerator
search_term_char_to_int = dict((c, i) for i, c in enumerate(search_term_char_set))
search_term_int_to_char = dict((i, c) for i, c in enumerate(search_term_char_set))
product_description_char_to_int = dict((c, i) for i, c in enumerate(product_description_char_set))
product_description_int_to_char = dict((i, c) for i, c in enumerate(product_description_char_set))
# summarize the loaded data
n_chars = len(search_term_chars)
n_vocab = len(search_term_char_set)
print("search_term Total Characters: ", n_chars)
print("search_term Total Vocab: ", n_vocab)
n_chars2 = len(product_description_chars)
n_vocab2 = len(product_description_char_set)
print("product_description Total Characters: ", n_chars2)
print("product_description Total Vocab: ", n_vocab2)
mergedTrain.search_term = mergedTrain.search_term.apply(lambda x: list(x))
mergedTrain.product_description = mergedTrain.product_description.apply(lambda x: list(x))
mergedTrain.head()
```
We would like to turn the search_term and the product_description into sequences of unique integers.
```
def createData(char_to_int, char_arr):
#seq_length = 100
dataX = []
for i in range(0,len(char_arr)):
dataX.append(char_to_int[char_arr[i]])
return np.asarray(dataX)
mergedTrain.search_term = mergedTrain.search_term.apply(lambda x: createData(search_term_char_to_int, x))
mergedTrain.product_description = mergedTrain.product_description.apply(lambda x: createData(product_description_char_to_int, x))
mergedTrain.head()
```
## The target value - relevance
Each pair was evaluated by at least three human raters. The provided relevance scores are the average value of the ratings. Thus, we would like to see the number of unique values, between 1 and 3. There are 13 unique relevance values in the data sample. We could address the problem as a classification problem, but we want to address the distance from the maximum relevance value, so we will treat this as a regression problem.
```
plt.hist(np.unique(mergedTrain.relevance.values),density=True, histtype='bar')
plt.show()
np.unique(mergedTrain.relevance.values).size
```
In order to predict the relevance values we need to preprocess the values, and change the range from 1 - 3, to 0 - 1. We want to see the maximum length of each column - the search_term and product_description. We try to limit the char sequences to 75 chars as in the same manner as characters, the lengths of the sequences must be the same in order to unite the data in specified part of the network to enable predictions based on both of these inputs. We also want to see the max sizes of sequences in each column to find the optimal value that will get enough data from both of the columns.
```
from sklearn import preprocessing
target = mergedTrain['relevance'].values
min_max_scaler = preprocessing.MinMaxScaler()
Y = min_max_scaler.fit_transform(target.reshape(-1, 1))
Y[:5]
X1 = mergedTrain['search_term'].values
X2 = mergedTrain['product_description'].values
search_terms_lens = []
for element in mergedTrain['search_term'].values:
search_terms_lens.append(len(element))
product_description_lens = []
for element in mergedTrain['product_description'].values:
product_description_lens.append(len(element))
max_length1 = max(search_terms_lens)
max_length2 = max(product_description_lens)
```
After trying a few options, we choose the maximum lenght of the sequences to be 75 integers, in order to yield better results. Sequences that are shorter, will be padded in order to meet this lenght.
```
max_length = 75
def padding(seq, length):
ans = []
for i in range(0,min(len(seq),length)):
ans.append(seq[i])
if len(seq) <= length:
for i in range(0,length-len(seq)):
ans.append(0)
return ans
X1 = np.asarray([padding(x,max_length) for x in X1])
X2 = np.asarray([padding(x,max_length) for x in X2])
X1 = X1.reshape(X1.shape[0],X1.shape[1],1)
X2 = X2.reshape(X2.shape[0],X2.shape[1],1)
X1 = X1.astype(np.float32)
X2 = X2.astype(np.float32)
print(X1.shape)
print(X2.shape)
```
This is the input that we insert into the model.
## Building the model
We create a siamese model
################## ADDDDDDDDDDD
```
st_input = Input(shape=(max_length,1), name='st_input',dtype='float32')
pd_input = Input(shape=(max_length,1), name='pd_input',dtype='float32')
def createModel():
model = Sequential()
model.add(LSTM(40))
model.add(Dense(64, activation='relu'))
return model
from keras.optimizers import Adadelta
st_model = createModel()
pd_model = createModel()
def createSiameseModel(model1,model2,customLoss):
out = Lambda(function=lambda x: K.exp(-K.sum(K.abs(x[0]-x[1]), axis=1, keepdims=True)),
output_shape=lambda x: (x[0][0], 1),
name='prediction')([model1(st_input), model2(pd_input)])
siamese_net = Model(input=[st_input,pd_input],output=[out])
siamese_net.compile(loss=customLoss,optimizer=Adadelta(lr=1.0, rho=0.95,clipnorm=1.20))
return siamese_net
siamese_net1 = createSiameseModel(st_model,pd_model,'mse')
siamese_net2 = createSiameseModel(st_model,pd_model,'mae')
st_model.summary()
siamese_net1.summary()
```
We have a good amount of trainable parameters.
```
X1_train,X1_val,X2_train,X2_val,Y_train, Y_val = train_test_split(X1,X2,Y,test_size = 0.2)
```
We split the data into train and validation/test sets. We choose the validation to be 20% of the entire data.
We save the model weights that are best, in order to use them later for feature extraction without the need to train the model again.
```
from keras.callbacks import *
path = 'gdrive/My Drive/Colab Notebooks'
def set_callbacks(description='run1',patience=15,tb_base_logdir='./logs/'):
cp = ModelCheckpoint(path + '/best_model_weights_char.h5'.format(description),save_best_only=True)
rlop = ReduceLROnPlateau(patience=5)
cb = [cp,rlop]
return cb
```
### Here we train the model:
```
start = time.time()
history = siamese_net1.fit([X1_train,X2_train],Y_train,batch_size=1024, epochs=5, verbose=1, validation_data=([X1_val,X2_val],Y_val), callbacks=set_callbacks())
end = time.time()
total_time = end - start
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()
val_preds = siamese_net1.predict([X1_val,X2_val])
train_preds = siamese_net1.predict([X1_train,X2_train])
plt.hist(val_preds,density=True, histtype='bar')
plt.show()
plt.hist(Y_val,density=True, histtype='bar')
plt.show()
```
We can see that the model predicted values around the average mark.
```
resultsTable = pd.DataFrame(columns=['model','runtime','TrainRMSE','ValRMSE','TestRMSE','TrainMAE','ValMAE','TestMAE'])
def addToTable(modelName,runtime,train_rmse,val_rmse,test_rmse,train_mae,val_mae,test_mae):
return resultsTable.append({'model': modelName,'runtime': runtime,'TrainRMSE': train_rmse,'ValRMSE': val_rmse,
'TrainMAE': test_rmse,'TrainMAE': train_mae,'ValMAE' :val_mae,'TestMAE': test_mae},ignore_index=True)
```
Lets run the model on the test samples, in order to do that we need to repeat the preprocessing and normalization process on the test data set.
```
search_term_chars2 = []
product_description_chars2 = []
search_term_chars2 = mergedTest.search_term.apply(lambda x: search_term_chars2 + list(x))
product_description_chars2 = mergedTest.product_description.apply(lambda x: product_description_chars2 + list(x))
search_term_chars2 = [item for sublist in search_term_chars2 for item in sublist]
product_description_chars2 = [item for sublist in product_description_chars2 for item in sublist]
search_term_char_set2 = sorted(set(search_term_chars2))
product_description_char_set2 = sorted(set(product_description_chars2))
# translate from character to number, it's enumerator
search_term_char_to_int2 = dict((c, i) for i, c in enumerate(search_term_char_set2))
search_term_int_to_char2 = dict((i, c) for i, c in enumerate(search_term_char_set2))
product_description_char_to_int2 = dict((c, i) for i, c in enumerate(product_description_char_set2))
product_description_int_to_char2 = dict((i, c) for i, c in enumerate(product_description_char_set2))
mergedTest.search_term = mergedTest.search_term.apply(lambda x: list(x))
mergedTest.product_description = mergedTest.product_description.apply(lambda x: list(x))
mergedTest.search_term = mergedTest.search_term.apply(lambda x: createData(search_term_char_to_int2, x))
mergedTest.product_description = mergedTest.product_description.apply(lambda x: createData(product_description_char_to_int2, x))
mergedTest.head()
X1_test = mergedTest.search_term.values
X2_test = mergedTest.product_description.values
X1_test = np.asarray([padding(x,max_length) for x in X1_test])
X2_test = np.asarray([padding(x,max_length) for x in X2_test])
X1_test = X1_test.reshape(X1_test.shape[0],X1_test.shape[1],1)
X2_test = X2_test.reshape(X2_test.shape[0],X2_test.shape[1],1)
test_preds = siamese_net1.predict([X1_test,X2_test])
from sklearn.metrics import mean_absolute_error as mae
from sklearn.metrics import mean_squared_error as mse
resultsTable = addToTable('CHAR_SiameseNetwork',total_time,mse(train_preds,Y_train),mse(val_preds,Y_val),'-',mae(train_preds,Y_train),mae(val_preds,Y_val),'-')
resultsTable
```
We calculated the RMSE and the MAE between the prediction and the true value in each one of the training, validation and test parts of the dataset.
* Note: We could not find the true results of the test data samples, so we could not calculate the MAE and RMSE on these samples.
## ML Benchmark
Lets create a benchmark model to compare the results of our model and the benchmark. We do a similiar character embedding process like in our model, but this time we will use the sklearn Vectorizer to do this process. The benchmark model that we will use is the Random Forest Regressor.
```
mergedTrain2 = pd.merge(train, product_descriptions, how='inner', on='product_uid')
mergedTrain2.head()
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(encoding='latin-1', analyzer='char')
vectorizer.fit(mergedTrain2['search_term'])
mltrain_x, mlval_x, mltrain_y, mlval_y = train_test_split(mergedTrain2['search_term'].values,mergedTrain2['relevance'].values, test_size = 0.2)
train_x_count = vectorizer.transform(mltrain_x)
val_x_count = vectorizer.transform(mlval_x)
from sklearn import model_selection, preprocessing, linear_model, naive_bayes, metrics, svm,ensemble
ml = ensemble.RandomForestRegressor()
start_time = time.time()
ml.fit(train_x_count, mltrain_y)
end_time = time.time()
total_time = end_time - start_time
ml_train_preds = ml.predict(train_x_count)
ml_val_preds = ml.predict(val_x_count)
print(ml_val_preds.shape)
resultsTable = addToTable('CHAR_RandomForestBenchmark',total_time,mse(ml_train_preds,mltrain_y),mse(ml_val_preds,mlval_y),'-',mae(ml_train_preds,mltrain_y),mae(ml_val_preds,mlval_y),'-')
resultsTable
plt.hist(ml_val_preds,density=True, histtype='bar')
plt.show()
plt.hist(mlval_y,density=True, histtype='bar')
plt.show()
```
The benchmark model performed better than our siamese model. This shows us that our model is not achieving the desired scores to see good enough results.
Here are some possible ways to improve the model:
* The model is still not tuned with the correct parameters in the intermediate layers. Finding the most percise values for the LSTM node number or the number of outputs in the Dense layer. We tried higher values but it looked like the model was overfitted when it handles large number of LSTM nodes.
* There might be some imbalance in the data when we pad the search_term and the product_description, the search_term sequences are a lot shorter than the product_description, so we need to chose the right amount of characters in each sequence or change the value that we pad with in the padding function, currently its 0.
## Feature Extraction
We want to check how the feature extarction abilities of the model compare by taking out the last layers outputs - the processed search_term and product_description inputs and concatinate that to feed to a ML model to see the RMSE and MAE of the ML models with the features from our network.
The machine learning we use are the Random Forest model and the Linear Regression model from sklearn.
```
fe_st_input = Input(shape=(max_length,1), name='st_input',dtype='float32')
fe_pd_input = Input(shape=(max_length,1), name='pd_input',dtype='float32')
input_layer1 = siamese_net1.layers[0].input[0]
input_layer2 = siamese_net1.layers[1].input[0]
fe_st_model = createModel()
fe_pd_model = createModel()
output_layer1 = siamese_net1.layers[3].get_output_at(0)
output_layer2 = siamese_net1.layers[3].get_output_at(1)
output_fn = K.function([st_input, pd_input], [output_layer1, output_layer2])
def extractFeatures(model1,model2,customLoss):
out = concatenate([model1(fe_st_input), model2(fe_pd_input)])
siamese_net = Model(input=[fe_st_input,fe_pd_input],output=[out])
siamese_net.load_weights(path + '/best_model_weights_char.h5')
siamese_net.compile(loss=customLoss,optimizer=Adadelta(lr=1.0, rho=0.95,clipnorm=1.20))
return siamese_net
fe_model = extractFeatures(fe_st_model,fe_pd_model,'mse')
fe_train_features = fe_model.predict([X1_train,X2_train])
fe_val_features = fe_model.predict([X1_val,X2_val])
fe_test_features = fe_model.predict([X1_test,X2_test])
randomForest = ensemble.RandomForestRegressor()
start_time = time.time()
randomForest.fit(fe_train_features, Y_train)
end_time = time.time()
total_time = end_time - start_time
fe_train_preds = randomForest.predict(fe_train_features)
fe_val_preds = randomForest.predict(fe_val_features)
resultsTable = addToTable('FE_RandomForest_CHAR',total_time,mse(fe_train_preds,Y_train),mse(fe_val_preds,Y_val),'-',mae(fe_train_preds,Y_train),mae(fe_val_preds,Y_val),'-')
linear = linear_model.LinearRegression()
start_time = time.time()
linear.fit(fe_train_features, Y_train)
end_time = time.time()
total_time = end_time - start_time
fe_train_preds2= linear.predict(fe_train_features)
fe_val_preds2 = linear.predict(fe_val_features)
resultsTable = addToTable('FE_LinearRegression_CHAR',total_time,mse(fe_train_preds2,Y_train),mse(fe_val_preds2,Y_val),'-',mae(fe_train_preds2,Y_train),mae(fe_val_preds2,Y_val),'-')
resultsTable
```
We see that the feature extraction ML models had pretty much the same performance as the siamese network, This means that the inaccuarcy of our model is in the feature extraction phase, maybe by making the improvements listed above we might acheive a better score.
# Word Level Embedding
We want to repeat the process but this time we want to do the embedding on a word level. every word instead of every character (as in the last part) will get a unique value in a sequence of values that will be fed to a similiar siamese network and will be checked in the same manner as the character embedding.
## Data Preprocessing
Similiarly we find the amount of unique words that are available for each of the search_term and product_description samples and create dictionaries for each one of them to converts the texts to unique value sequences for the model to train and predict on.
```
mergedTrain = pd.merge(train, product_descriptions, how='inner', on='product_uid')
mergedTrain.search_term = mergedTrain.search_term.apply(lambda x: x.lower())
mergedTrain.product_description = mergedTrain.product_description.apply(lambda x: x.lower())
mergedTrain.head()
mergedTest= pd.merge(test, product_descriptions, how='inner', on='product_uid')
mergedTest.search_term = mergedTest.search_term.apply(lambda x: x.lower())
mergedTest.product_description = mergedTest.product_description.apply(lambda x: x.lower())
mergedTest.head()
import nltk
nltk.download('punkt')
from nltk.tokenize import word_tokenize
st_words = []
for term in mergedTrain.search_term.values:
for word in word_tokenize(term):
st_words.append(word)
st_word_set = sorted(set(st_words))
st_dict = dict((c, i) for i, c in enumerate(st_word_set))
pd_words = []
for term in mergedTrain.product_description.values:
for word in word_tokenize(term):
pd_words.append(word)
pd_word_set = sorted(set(pd_words))
pd_dict = dict((c, i) for i, c in enumerate(pd_word_set))
st_words2 = []
for term in mergedTest.search_term.values:
for word in word_tokenize(term):
st_words2.append(word)
st_word_set2 = sorted(set(st_words2))
st_dict2 = dict((c, i) for i, c in enumerate(st_word_set2))
pd_words2 = []
for term in mergedTest.product_description.values:
for word in word_tokenize(term):
pd_words2.append(word)
pd_word_set2 = sorted(set(pd_words2))
pd_dict2 = dict((c, i) for i, c in enumerate(pd_word_set2))
mergedTrain.search_term = mergedTrain.search_term.apply(lambda x: createData(st_dict, word_tokenize(x)))
mergedTrain.product_description = mergedTrain.product_description.apply(lambda x: createData(pd_dict, word_tokenize(x)))
mergedTrain.head()
mergedTest.search_term = mergedTest.search_term.apply(lambda x: createData(st_dict2, word_tokenize(x)))
mergedTest.product_description = mergedTest.product_description.apply(lambda x: createData(pd_dict2, word_tokenize(x)))
mergedTest.head()
```
## Data Normalization
We normalize the target relevance to be in the 0 - 1 range, like in the first part. We try to limit the word sequences to 50 words as in the same manner as characters.
```
target = mergedTrain['relevance'].values
min_max_scaler = preprocessing.MinMaxScaler()
Y = min_max_scaler.fit_transform(target.reshape(-1, 1))
Y[:5]
X1 = mergedTrain['search_term'].values
X2 = mergedTrain['product_description'].values
search_terms_lens = []
for element in mergedTrain['search_term'].values:
search_terms_lens.append(len(element))
product_description_lens = []
for element in mergedTrain['product_description'].values:
product_description_lens.append(len(element))
max_length1 = max(search_terms_lens)
max_length2 = max(product_description_lens)
max_length = 50
def padding(seq, length):
ans = []
for i in range(0,min(len(seq),length)):
ans.append(seq[i])
if len(seq) <= length:
for i in range(0,length-len(seq)):
ans.append(0)
return ans
X1 = np.asarray([padding(x,max_length) for x in X1])
X2 = np.asarray([padding(x,max_length) for x in X2])
X1 = X1.reshape(X1.shape[0],X1.shape[1],1)
X2 = X2.reshape(X2.shape[0],X2.shape[1],1)
X1_test = mergedTest.search_term.values
X2_test = mergedTest.product_description.values
X1_test = np.asarray([padding(x,max_length) for x in X1_test])
X2_test = np.asarray([padding(x,max_length) for x in X2_test])
X1_test = X1_test.reshape(X1_test.shape[0],X1_test.shape[1],1)
X2_test = X2_test.reshape(X2_test.shape[0],X2_test.shape[1],1)
```
## Model Fitting + Predictions
The model is created in the same manner as in the first part. the only difference is that the input now are embedded word sequences of the data samples.
```
def set_callbacks2(description='run1',patience=15,tb_base_logdir='./logs/'):
cp = ModelCheckpoint(path + '/best_model_weights_word.h5'.format(description),save_best_only=True)
rlop = ReduceLROnPlateau(patience=5)
cb = [cp,rlop]
return cb
st_input = Input(shape=(max_length,1), name='st_input')
pd_input = Input(shape=(max_length,1), name='pd_input')
def createModel():
model = Sequential()
model.add(LSTM(60))
model.add(Dense(140, activation='relu'))
return model
st_model3 = createModel()
pd_model3 = createModel()
def createSiameseModel(model1,model2,customLoss):
out = Lambda(function=lambda x: K.exp(-K.sum(K.abs(x[0]-x[1]), axis=1, keepdims=True)),
output_shape=lambda x: (x[0][0], 1),
name='prediction')([model1(st_input), model2(pd_input)])
siamese_net = Model(input=[st_input,pd_input],output=[out])
siamese_net.compile(loss=customLoss,optimizer=Adadelta(lr=1.0, rho=0.95,clipnorm=1.20))
return siamese_net
siamese_net3 = createSiameseModel(st_model3,pd_model3,'mse')
siamese_net4 = createSiameseModel(st_model3,pd_model3,'mae')
siamese_net3.summary()
X1_train,X1_val,X2_train,X2_val,Y_train, Y_val = train_test_split(X1,X2,Y,test_size = 0.2)
start = time.time()
history3 = siamese_net3.fit([X1_train,X2_train],Y_train,batch_size=1024, epochs=5, verbose=1, validation_data=([X1_val,X2_val],Y_val), callbacks=set_callbacks2())
end = time.time()
total_time = end - start
val_preds = siamese_net3.predict([X1_val,X2_val])
train_preds = siamese_net3.predict([X1_train,X2_train])
test_preds = siamese_net3.predict([X1_test,X2_test])
plt.plot(history3.history['loss'], label='train')
plt.plot(history3.history['val_loss'], label='test')
plt.legend()
plt.show()
plt.hist(val_preds,density=True, histtype='bar')
plt.show()
plt.hist(Y_val,density=True, histtype='bar')
plt.show()
resultsTable = addToTable('WORD_SiameseNetwork',total_time,mse(train_preds,Y_train),mse(val_preds,Y_val),'-',mae(train_preds,Y_train),mae(val_preds,Y_val),'-')
resultsTable
```
The word model outperformed the char model only by a little bit.
## Feature Extraction - Word Level
Again, we want to check our feature extraction capabilites of the word model by feeding the features that the model finds to classic ML models to see their performance with the processed data that our model creates during the learning phase.
```
fe_st_input = Input(shape=(max_length,1), name='st_input',dtype='float32')
fe_pd_input = Input(shape=(max_length,1), name='pd_input',dtype='float32')
input_layer1 = siamese_net1.layers[0].input[0]
input_layer2 = siamese_net1.layers[1].input[0]
fe_st_model = createModel()
fe_pd_model = createModel()
output_layer1 = siamese_net1.layers[3].get_output_at(0)
output_layer2 = siamese_net1.layers[3].get_output_at(1)
output_fn = K.function([st_input, pd_input], [output_layer1, output_layer2])
def extractFeatures(model1,model2,customLoss):
out = concatenate([model1(fe_st_input), model2(fe_pd_input)])
siamese_net = Model(input=[fe_st_input,fe_pd_input],output=[out])
siamese_net.load_weights(path + '/best_model_weights_word.h5')
siamese_net.compile(loss=customLoss,optimizer=Adadelta(lr=1.0, rho=0.95,clipnorm=1.20))
return siamese_net
fe_model = extractFeatures(fe_st_model,fe_pd_model,'mse')
fe_train_features = fe_model.predict([X1_train,X2_train])
fe_val_features = fe_model.predict([X1_val,X2_val])
fe_test_features = fe_model.predict([X1_test,X2_test])
randomForest2 = ensemble.RandomForestRegressor()
start_time = time.time()
randomForest2.fit(fe_train_features, Y_train)
end_time = time.time()
total_time = end_time - start_time
fe_train_preds = randomForest2.predict(fe_train_features)
fe_val_preds = randomForest2.predict(fe_val_features)
resultsTable = addToTable('FE_RandomForest_WORD',total_time,mse(fe_train_preds,Y_train),mse(fe_val_preds,Y_val),'-',mae(fe_train_preds,Y_train),mae(fe_val_preds,Y_val),'-')
linear2 = linear_model.LinearRegression()
start_time = time.time()
linear2.fit(fe_train_features, Y_train)
end_time = time.time()
total_time = end_time - start_time
fe_train_preds2= linear2.predict(fe_train_features)
fe_val_preds2 = linear2.predict(fe_val_features)
resultsTable = addToTable('FE_LinearRegression_WORD',total_time,mse(fe_train_preds2,Y_train),mse(fe_val_preds2,Y_val),'-',mae(fe_train_preds2,Y_train),mae(fe_val_preds2,Y_val),'-')
resultsTable
```
## Test results submission
```
subans = test_preds.reshape(test_preds.shape[0])
subans = min_max_scaler.inverse_transform(subans.reshape(1, -1))
subans = subans.reshape(subans.shape[1])
subans
sub = pd.read_csv("/content/gdrive/My Drive/Colab Notebooks/input/sample_submission.csv")
sub.reset_index(drop = True)
print(sub.relevance.values.shape)
sub['relevance'] = subans
sub.to_csv(path + '/sub.csv')
```
# Summary
| true |
code
| 0.525308 | null | null | null | null |
|
# Word2Vec for Text Classification
In this short notebook, we will see an example of how to use a pre-trained Word2vec model for doing feature extraction and performing text classification.
We will use the sentiment labelled sentences dataset from UCI repository
http://archive.ics.uci.edu/ml/datasets/Sentiment+Labelled+Sentences
The dataset consists of 1500 positive, and 1500 negative sentiment sentences from Amazon, Yelp, IMDB. Let us first combine all the three separate data files into one using the following unix command:
```cat amazon_cells_labelled.txt imdb_labelled.txt yelp_labelled.txt > sentiment_sentences.txt```
For a pre-trained embedding model, we will use the Google News vectors.
https://drive.google.com/file/d/0B7XkCwpI5KDYNlNUTTlSS21pQmM
Let us get started!
```
# To install only the requirements of this notebook, uncomment the lines below and run this cell
# ===========================
!pip install numpy==1.19.5
!pip install pandas==1.1.5
!pip install gensim==3.8.3
!pip install wget==3.2
!pip install nltk==3.5
!pip install scikit-learn==0.21.3
# ===========================
# To install the requirements for the entire chapter, uncomment the lines below and run this cell
# ===========================
# try:
# import google.colab
# !curl https://raw.githubusercontent.com/practical-nlp/practical-nlp/master/Ch4/ch4-requirements.txt | xargs -n 1 -L 1 pip install
# except ModuleNotFoundError:
# !pip install -r "ch4-requirements.txt"
# ===========================
#basic imports
import warnings
warnings.filterwarnings('ignore')
import os
import wget
import gzip
import shutil
from time import time
#pre-processing imports
import nltk
nltk.download('stopwords')
nltk.download('punkt')
from nltk.tokenize import word_tokenize
from nltk.corpus import stopwords
from string import punctuation
#imports related to modeling
import numpy as np
from gensim.models import Word2Vec, KeyedVectors
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
try:
from google.colab import files
# upload 'amazon_cells_labelled.txt', 'imdb_labelled.txt' and 'yelp_labelled.txt' present in "sentiment labelled sentences" folder
uploaded = files.upload()
!mkdir DATAPATH
!mv -t DATAPATH amazon_cells_labelled.txt imdb_labelled.txt yelp_labelled.txt
!cat DATAPATH/amazon_cells_labelled.txt DATAPATH/imdb_labelled.txt DATAPATH/yelp_labelled.txt > DATAPATH/sentiment_sentences.txt
except ModuleNotFoundError:
fil = 'sentiment_sentences.txt'
if not os.path.exists("Data/sentiment_sentences.txt"):
file = open(os.path.join(path, fil), 'w')
file.close()
# combined the three files to make sentiment_sentences.txt
filenames = ['amazon_cells_labelled.txt', 'imdb_labelled.txt', 'yelp_labelled.txt']
with open('Data/sentiment_sentences.txt', 'w') as outfile:
for fname in filenames:
with open('Data/sentiment labelled sentences/' + fname) as infile:
outfile.write(infile.read())
print("File created")
else:
print("File already exists")
#Load the pre-trained word2vec model and the dataset
try:
from google.colab import files
data_path= "DATAPATH"
!wget -P DATAPATH https://s3.amazonaws.com/dl4j-distribution/GoogleNews-vectors-negative300.bin.gz
!gunzip DATAPATH/GoogleNews-vectors-negative300.bin.gz
path_to_model = 'DATAPATH/GoogleNews-vectors-negative300.bin'
training_data_path = "DATAPATH/sentiment_sentences.txt"
except ModuleNotFoundError:
data_path= "Data"
if not os.path.exists('GoogleNews-vectors-negative300.bin'):
if not os.path.exists('../Ch2/GoogleNews-vectors-negative300.bin'):
if not os.path.exists('../Ch3/GoogleNews-vectors-negative300.bin'):
wget.download("https://s3.amazonaws.com/dl4j-distribution/GoogleNews-vectors-negative300.bin.gz")
with gzip.open('GoogleNews-vectors-negative300.bin.gz', 'rb') as f_in:
with open('GoogleNews-vectors-negative300.bin', 'wb') as f_out:
shutil.copyfileobj(f_in, f_out)
path_to_model = 'GoogleNews-vectors-negative300.bin'
else:
path_to_model = '../Ch3/GoogleNews-vectors-negative300.bin'
else:
path_to_model = '../Ch2/GoogleNews-vectors-negative300.bin'
else:
path_to_model = 'GoogleNews-vectors-negative300.bin'
training_data_path = os.path.join(data_path, "sentiment_sentences.txt")
#Load W2V model. This will take some time.
%time w2v_model = KeyedVectors.load_word2vec_format(path_to_model, binary=True)
print('done loading Word2Vec')
#Read text data, cats.
#the file path consists of tab separated sentences and cats.
texts = []
cats = []
fh = open(training_data_path)
for line in fh:
text, sentiment = line.split("\t")
texts.append(text)
cats.append(sentiment)
#Inspect the model
word2vec_vocab = w2v_model.vocab.keys()
word2vec_vocab_lower = [item.lower() for item in word2vec_vocab]
print(len(word2vec_vocab))
#Inspect the dataset
print(len(cats), len(texts))
print(texts[1])
print(cats[1])
#preprocess the text.
def preprocess_corpus(texts):
mystopwords = set(stopwords.words("english"))
def remove_stops_digits(tokens):
#Nested function that lowercases, removes stopwords and digits from a list of tokens
return [token.lower() for token in tokens if token.lower() not in mystopwords and not token.isdigit()
and token not in punctuation]
#This return statement below uses the above function to process twitter tokenizer output further.
return [remove_stops_digits(word_tokenize(text)) for text in texts]
texts_processed = preprocess_corpus(texts)
print(len(cats), len(texts_processed))
print(texts_processed[1])
print(cats[1])
# Creating a feature vector by averaging all embeddings for all sentences
def embedding_feats(list_of_lists):
DIMENSION = 300
zero_vector = np.zeros(DIMENSION)
feats = []
for tokens in list_of_lists:
feat_for_this = np.zeros(DIMENSION)
count_for_this = 0 + 1e-5 # to avoid divide-by-zero
for token in tokens:
if token in w2v_model:
feat_for_this += w2v_model[token]
count_for_this +=1
if(count_for_this!=0):
feats.append(feat_for_this/count_for_this)
else:
feats.append(zero_vector)
return feats
train_vectors = embedding_feats(texts_processed)
print(len(train_vectors))
#Take any classifier (LogisticRegression here, and train/test it like before.
classifier = LogisticRegression(random_state=1234)
train_data, test_data, train_cats, test_cats = train_test_split(train_vectors, cats)
classifier.fit(train_data, train_cats)
print("Accuracy: ", classifier.score(test_data, test_cats))
preds = classifier.predict(test_data)
print(classification_report(test_cats, preds))
```
Not bad. With little efforts we got 81% accuracy. Thats a great starting model to have!!
| true |
code
| 0.656988 | null | null | null | null |
|
<h2>Grover's Search: One Qubit Representation</h2>
[Watch Lecture](https://youtu.be/VwzshIQsDBA)
The execution of Grover's search algorithm can be simulated on the unit circle.
Throughout the computation, the amplitudes of the marked (or unmarked) elements never differ from each other. Therefore, we can group the elements as marked and unmarked elements.
As the length of the list is 1, we can represent the list as an unit vector on the unit circle where the vertical line represents the marked elements and horizantal line represents the unmarked elements.
### Example: N = 8 with 3 marked elements
Suppose that the 3rd, 4th, and 7th elements are marked. We can use three qubits and we can associate each element with one of basis states:
$$ \myarray{|c|c|}{
\hline element & state \\ \hline
1st & \ket{000} \\ \hline
2nd & \ket{001} \\ \hline
\mathbf{3rd} & \mathbf{\ket{010}} \\ \hline
\mathbf{4th} & \mathbf{\ket{011}} \\ \hline
5th & \ket{100} \\ \hline
6th & \ket{101} \\ \hline
\mathbf{7th} & \mathbf{\ket{110}} \\ \hline
8th & \ket{111} \\ \hline
} $$
Grover's search algorithm starts in the following quantum state:
$$ \ket{u} = H\ket{0} \otimes H \ket{0} \otimes H \ket{0} = H^{\otimes 3} \ket{000} $$
$$ \ket{u} = \mypar{ \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1} } \otimes
\mypar{ \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1} } \otimes
\mypar{ \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1} } $$
$$ \ket{u} = \frac{1}{2\sqrt{2}} \ket{000} + \frac{1}{2\sqrt{2}} \ket{001} + \frac{1}{2\sqrt{2}} \ket{010} + \frac{1}{2\sqrt{2}} \ket{011} + \frac{1}{2\sqrt{2}} \ket{100} + \frac{1}{2\sqrt{2}} \ket{101} + \frac{1}{2\sqrt{2}} \ket{110} + \frac{1}{2\sqrt{2}} \ket{111}. $$
We group them as unmarked and marked elements:
$$ \ket{u} = \frac{1}{2\sqrt{2}} \big( \ket{000} + \ket{001} + \ket{100} + \ket{101} + \ket{111} \big) + \frac{1}{2\sqrt{2}} \big(\mathbf{ \ket{010} + \ket{011} + \ket{110} } \big) $$
or as vectors
$$ \ket{u} = \ket{u_{unmarked}} + \ket{u_{marked}} = \frac{1}{2\sqrt{2}} \myvector{1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1} + \frac{1}{2\sqrt{2}} \myvector{0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0} $$
#### Orthogonality of $ \ket{u_{unmarked}} $ and $ \ket{u_{marked}} $
It is clear that the quantum states $ \ket{u_{unmarked}} $ and $ \ket{u_{marked}} $ are orthogonal each other, i.e., $ \ket{u_{unmarked}} \perp \ket{u_{marked}} $.
On the unit circle, the state $ \ket{0} $ and $ \ket{1} $ are orthogonal to each other, and so, we can represent (map) $ \ket{u} = \ket{u_{unmarked}} + \ket{u_{marked}} $ on the unit circle as
$$ \ket{u} \rightarrow \alpha \ket{0} + \beta \ket{1} $$
or by re-naming the basis states
$$ \ket{u} \rightarrow \alpha \ket{unmarked} + \beta \ket{marked}. $$
#### How can we determine the amplitudes of the states $ \ket{0} $ and $ \ket{1} $ based on the amplitudes of the marked and unmarked elements?
We can rewrite $ \ket{u} $ as follows:
$$ \ket{u} = \ket{u_{unmarked}} + \ket{u_{marked}} = \frac{\sqrt{5}}{2\sqrt{2}} \myvector{\frac{1}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \\ 0 \\ \frac{1}{\sqrt{5}} } + \frac{\sqrt{3}}{2\sqrt{2}} \myvector{0 \\ 0 \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{3}} \\ 0} $$
Here both vectors have unit length and so we can replaces them with the states $ \ket{unmarked} $ and $ \ket{marked} $, respectively. Thus, the coefficients of the vectors are *the amplitudes* we are looking for:
$$ \ket{u} \rightarrow \frac{\sqrt{5}}{2\sqrt{2}} \ket{unmarked} + \frac{\sqrt{3}}{2\sqrt{2}} \ket{marked} $$.
We draw the obtained unit circle by using python below.
```
%run qlatvia.py
draw_qubit_grover()
draw_quantum_state((5/8)**0.5,(3/8)**0.5,"|u>")
```
#### The amplitudes of states $ \ket{marked} $ and $ \ket{unmarked} $ during the computation
Remark that, after each phase of Grover's algorithm, the states $ \ket{marked} $ and $ \ket{unmarked} $ do not change (see also below).
Any quantum state during the computation of Grover's algorithm can be represented, for some $ a,b $, as
$$ \ket{u_j} = \ket{u_{j,unmarked}} + \ket{u_{j,marked}} = \myvector{ a \\ a \\ 0 \\ 0 \\ a \\ a \\ 0 \\ a } + \myvector{0 \\ 0 \\b \\ b \\ 0 \\ 0 \\ b \\ 0} =
a \sqrt{5} \myvector{\frac{1}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \\ 0 \\ \frac{1}{\sqrt{5}} } + b \sqrt{3} \myvector{0 \\ 0 \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{3}} \\ 0} = a\sqrt{5} ~ \ket{unmarked} + b\sqrt{3} ~ \ket{marked}.
$$
As a generic rule:
For $ N $ elements with $ k $ marked ones, if the amplitudes of an unmarked and a marked elements are $ a $ and $ b $, respectively, then the quantum state can be represented as
$$ a\sqrt{N-k} ~ \ket{unmarked} + b \sqrt{k} ~ \ket{marked}. $$
## Visualization of Grover's Search algorithm
In this section, we execute Grover's search algorithm by using the modified game explained in notebook [Inversion About the Mean](B80_Inversion_About_the_Mean.ipynb).
You may use your functions *oracle* and *inversion* in [Task 2](B80_Inversion_About_the_Mean.ipynb#task2) in the same notebook.
*For simplicity, we assume that the first element is always marked and the last element is always unmarked.*
<h3> Task 1 </h3>
Execute Grover's search algorithm for 5 steps where $ N = 16 $ and the first element is marked.
Draw all quantum states on the unit circle during the execution.
Print the angle of each state in degree (use $\sin^{-1}$), and check whether there is any pattern for the oracle and inversion operators?
Is there any pattern for each step of Grover's algorithm?
```
def query(elements=[1],marked_elements=[0]):
for i in marked_elements:
elements[i] = -1 * elements[i]
return elements
def inversion (elements=[1]):
# summation of all values
summation = 0
for i in range(len(elements)):
summation += elements[i]
# mean of all values
mean = summation / len(elements)
# reflection over mean
for i in range(len(elements)):
value = elements[i]
new_value = mean - (elements[i]-mean)
elements[i] = new_value
return elements
from math import asin, pi
# initial values
iteration = 5
N = 16
marked_elements = [0]
k = len(marked_elements)
elements = []
states_on_unit_circle= []
# initial quantum state
for i in range(N):
elements.append(1/N**0.5)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,"0"])
# Execute Grover's search algorithm for $iteration steps
for step in range(iteration):
# query
elements = query(elements,marked_elements)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,str(step)+"''"])
# inversion
elements = inversion(elements)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,str(step+1)])
# draw all states
%run qlatvia.py
draw_qubit_grover()
for state in states_on_unit_circle:
draw_quantum_state(state[0],state[1],state[2])
# print the angles
print("angles in degree")
for state in states_on_unit_circle:
print(asin(state[1])/pi*180)
```
#### Observations
The operator oracle is a reflection over the $x$-axis.
The operator inversion is a reflection over the initial state.
If the angle of the first state $ \theta $, then each step of Grover's algorithm is a rotation with angle $ 2 \theta $.
<hr>
<h3> Task 2 </h3>
In Task 1, after which step the probability of observing a marked element is the highest?
As can be verified from the angles, after the third step, the probability of observing a marking element is the highest.
<h3> Task 3 </h3>
We have a list of size $ N = 128 $. We iterate Grover's search algorithm 10 steps.
Visually determine (i.e., Tasks 1 & 2) the good number of iterations if the number of marked elements is 1, 2, 4, or 8. (The quantum state on the unit circle should be close to the $y$-axis.)
```
def query(elements=[1],marked_elements=[0]):
for i in marked_elements:
elements[i] = -1 * elements[i]
return elements
def inversion (elements=[1]):
# summation of all values
summation = 0
for i in range(len(elements)):
summation += elements[i]
# mean of all values
mean = summation / len(elements)
# reflection over mean
for i in range(len(elements)):
value = elements[i]
new_value = mean - (elements[i]-mean)
elements[i] = new_value
return elements
from math import asin, pi
# initial values
iteration = 10
N = 128
# try each case one by one
marked_elements = [0]
#marked_elements = [0,1]
#marked_elements = [0,1,2,3]
#marked_elements = [0,1,2,3,4,5,6,7]
k = len(marked_elements)
elements = []
states_on_unit_circle= []
# initial quantum state
for i in range(N):
elements.append(1/N**0.5)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,"0"])
# Execute Grover's search algorithm for $iteration steps
for step in range(iteration):
# query
elements = query(elements,marked_elements)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,str(step)+"''"])
# inversion
elements = inversion(elements)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,str(step+1)])
# draw all states
%run qlatvia.py
draw_qubit_grover()
for state in states_on_unit_circle:
draw_quantum_state(state[0],state[1],state[2])
# print the angles
print("angles in degree")
for state in states_on_unit_circle:
print(asin(state[1])/pi*180)
```
#### Observations
The good number of iterations
- For $ k = 1 $, $ 8 $ iterations
- For $ k = 2 $, $ 6 $ iterations
- For $ k = 4 $, $ 4 $ iterations
- For $ k = 8 $, $ 3 $ or $ 9 $ iterations
<hr>
<h3> Task 4 </h3>
We have a list of size $ N = 256 $. We iterate Grover's search algorithm 20 (or 10) steps.
Visually determine (i.e., Tasks 1 & 2) the good number of iterations if the number of marked elements is 1, 2, 4, or 8. (The quantum state on the unit circle should be close to the $y$-axis.)
```
def query(elements=[1],marked_elements=[0]):
for i in marked_elements:
elements[i] = -1 * elements[i]
return elements
def inversion (elements=[1]):
# summation of all values
summation = 0
for i in range(len(elements)):
summation += elements[i]
# mean of all values
mean = summation / len(elements)
# reflection over mean
for i in range(len(elements)):
value = elements[i]
new_value = mean - (elements[i]-mean)
elements[i] = new_value
return elements
from math import asin, pi
# initial values
iteration = 20
#iteration = 10
N = 256
# try each case one by one
marked_elements = [0]
#marked_elements = [0,1]
#marked_elements = [0,1,2,3]
#marked_elements = [0,1,2,3,4,5,6,7]
k = len(marked_elements)
elements = []
states_on_unit_circle= []
# initial quantum state
for i in range(N):
elements.append(1/N**0.5)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,"0"])
# Execute Grover's search algorithm for $iteration steps
for step in range(iteration):
# query
elements = query(elements,marked_elements)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,str(step)+"''"])
# inversion
elements = inversion(elements)
x = elements[N-1] * ((N-k)**0.5)
y = elements[0] * (k**0.5)
states_on_unit_circle.append([x,y,str(step+1)])
# draw all states
%run qlatvia.py
draw_qubit_grover()
for state in states_on_unit_circle:
draw_quantum_state(state[0],state[1],state[2])
# print the angles
print("angles in degree")
for state in states_on_unit_circle:
print(asin(state[1])/pi*180)
```
#### Observations
The good number of iterations
- For $ k = 1 $, $ 12 $ iterations
- For $ k = 2 $, $ 8 $ iterations
- For $ k = 4 $, $ 6 $ iterations
- For $ k = 8 $, $ 4 $ iterations
## More on Grover's search algorithm
The idea behind on Grover's search algorithm is that
<ul>
<li> the amplitudes of the marked (less frequent) elements can be quickly amplified, </li>
<li> and so the probability of observing one of the marked elements quickly approches to 1.</li>
</ul>
For "quick" amplification, we iteratively apply two reflections to our quantum states.
The first reflection is a clockwise rotation, and the second reflection is a counterclockwise rotation.
The second reflection always rotates $ 2 \theta $ degree more than the first reflection, where the $ \theta $ is the angle of this initial state on the unit circle.
Therefore, the quantum state is rotated by $ 2 \theta $ in counter-clockwise direction after two reflections.
As an example, we consider the rotation on the unit circle with angle $ \frac{\pi}{8} $ that starts in $ \ket{0} $.
<ul>
<li> After every 4 rotations, we visit states $ \ket{1} $, $ -\ket{0} $, $ -\ket{1} $, again $ \ket{0} $, and so on. </li>
<li> Remark that the probability of observing the state $ \ket{1} $ oscillates between 0 and 1 while rotating. </li>
</ul>
Similarly, when iterating Grover's search algorithm, we should be careful when to stop.
<ul>
<li> Because, after hitting a maximum value, these amplitudes start to quickly decrease, and after hitting a minimum value, they are amplified again, and so on.</li>
</ul>
### Mathematical derivation of the reflection by inversion (optional)
_(You will see a similar but alternative derivation in the next notebook.)_
It is clear that query operators reflects the quantum state on the unit circle over $ x $-axis.
On the other hand, inversion operator reflects the quantum state on the unit circle over the line defined by the initial state, say $ \ket{u} $. This fact is not so obvious and we present here how to derive it. ($ \bra{u} $ is the conjugate transpose of the vector $ \ket{u} $.)
The initial quantum state is $ \ket{u} = \myvector{\frac{1}{\sqrt{N}} \\ \vdots \\ \frac{1}{\sqrt{N}}}$ and the inversion is a linear operator and represened by the matrix:
$$ D = 2 \mymatrix{ccc}{
\frac{1}{N} & \cdots & \frac{1}{N} \\
\vdots & \ddots & \vdots \\
\frac{1}{N} & \cdots & \frac{1}{N} \\
}
- I . $$
Since $ \ket{u} \bra{u} = \mymatrix{ccc}{
\frac{1}{N} & \cdots & \frac{1}{N} \\
\vdots & \ddots & \vdots \\
\frac{1}{N} & \cdots & \frac{1}{N} \\
} $, we can represent $ D $ in terms of $ \ket{u} $ as $ D = 2 \ket{u} \bra{u} - I$.
Let our current quantum state be $a \ket{u} + b \ket{u^\perp}$, where $\ket{u^\perp}$ denotes the state, which is orthogonal (perpendicular) to $\ket{u}$. After appling $D$ to our current quantum state, we obtain
$$D \big(a \ket{u} + b \ket{u^\perp}\big) = \big(2 \ket{u} \bra{u} - I \big) \big(a \ket{u} + b \ket{u^\perp} \big) = a \big(2 \ket{u} \bra{u} \ket{u} - \ket{u} \big) + b \big(2 \ket{u} \bra{u} \ket{u^\perp} - \ket{u^\perp} \big). $$
To simplify this equation, we use the following two facts:
<ul>
<li>$\bra{u} \ket{u} = 1$, because the inner product of a quantum state gives its length square, which is equal to 1;</li>
<li>$\bra{u} \ket{u^\perp} = 0$, because the states are orthogonal to each other.</li>
</ul>
$$ a \big( 2 \ket{u} \bra{u} \ket{u} - \ket{u} \big) + b \big( 2 \ket{u} \bra{u} \ket{u^\perp} - \ket{u^\perp} \big) = a \big( 2 \ket{u} - \ket{u} \big) + b \big( 2 \ket{u} \cdot 0 - \ket{u^\perp} \big) = a \ket{u} - b \ket{u^\perp}. $$
As $D (a \ket{u} + b \ket{u^\perp}) = a \ket{u} - b \ket{u^\perp}$, we conclude that $D$ is a reflection over axis formed by the state $\ket{u}$.
<h3> The number of iterations </h3>
If there is a single marked element in a list of size $ N $, then $ \pi \dfrac{\sqrt{N}}{4} $ iterations can give the marked element with high probability.
If there are $k$ marked elements, then it is better to iterate $ \pi \dfrac{\sqrt{\frac{N}{k}}}{4} $ times.
If $k$ is unknown, then we can execute the algorithm with different iterations. One way of doing this is to iterate the algorithm
$$ \pi \dfrac{\sqrt{\frac{N}{1}}}{4}, \pi \dfrac{\sqrt{\frac{N}{2}}}{4}, \pi \dfrac{\sqrt{\frac{N}{4}}}{4}, \pi \dfrac{\sqrt{\frac{N}{8}}}{4}, \ldots $$ times.
The total number of iterations will still be proportional to $ \pi \dfrac{\sqrt{N}}{4} $: $ O \Big( \pi \dfrac{\sqrt{N}}{4} \Big) $.
| true |
code
| 0.358493 | null | null | null | null |
|
# What is Survival Analysis?
[Survival analysis](https://en.wikipedia.org/wiki/Survival_analysis) is used to study the **time** until some **event** of interest (often referred to as **death**) occurs. Time could be measured in years, months, weeks, days, etc. The event could be anything of interest. It could be an actual death, a birth, a Pokemon Go server crash, etc. In this post we are interested in how long drafted NFL players are in the league, so the event of interest will be the retirement of drafted NFL players. The duration of time leading up to the event of interest can be called the **survival time**. In our case, the survival time is the number of years that a player was active in the league (according to [Pro Football Reference](http://www.pro-football-reference.com/)).
Some of the players in this analysis are still active players (e.g. Aaron Rodgers, Eli Manning, etc.), so we haven't observed their retirement (the event of interest). Those players are considered **censored**. While we have some information about their career length (or survival time), we don't know the full length of their career. This specific type of censorship, one in which we do not observe end of the survival time, is called **right-censorship**. The methods developed in the field of survival analysis were created in order to deal with the issue of censored data. In this post we will use one such method, called the [Kaplan-Meier estimator](https://en.wikipedia.org/wiki/Kaplan%E2%80%93Meier_estimator), to estimate the survival function and construct the survival curve for an NFL career.
## A brief comment on the data used
I used the draft data scraped from my [previous post](http://savvastjortjoglou.com/nfl-draft.html). The duration of a player's career is just the difference between "To" value from the [PFR draft table](http://www.pro-football-reference.com/years/2015/draft.htm) and the year the player was drafted. Players were considered active, if there name was in bold. However there are may be some players who are retired that PFR still considers active (e.g. Mike Kafka). You can check out how I prepared the data in [this Jupyter notebook](https://github.com/savvastj/nfl_survival_analysis/blob/master/Data_Prep.ipynb). Let me know if you see any issues/mistakes I've made.
# What is the Survival Function?
The [survival function](https://en.wikipedia.org/wiki/Survival_function), $S(t)$, of a population is defined as follows:
$$S(t) = Pr(T > t)$$
Capital $T$ is a [random variable](https://www.khanacademy.org/math/probability/random-variables-topic/random-variables-prob-dist/v/random-variables) that represents a subject's survival time. In our case $T$ represents an NFL player's career length. Lower case $t$ represents a specific time of interest for $T$. In our analysis the $t$ represents a specific number of years played. In other words the survival function just gives us the probability that someone survives longer than (or at least as long as) a specified value of time, $t$. So in the context of our analysis, $S(3)$ will provide us the probability that an NFL career lasts longer than 3 years.
# What is the Kaplan-Meier estimator?
To estimate the survival function of NFL players we will use the Kaplan-Meier estimator. The Kaplan-Meier estimator is defined by the following product (from the [`lifelines` documentation](https://lifelines.readthedocs.io/en/latest/Intro%20to%20lifelines.html#estimating-the-survival-function-using-kaplan-meier)):
$$\hat{S}(t) = \prod_{t_i \lt t} \frac{n_i - d_i}{n_i}$$
where $d_i$ are the number of death events at time $t$ and $n_i$ is the number of subjects at risk of death just prior to time $t$.
We will walk through a simple example in a bit in order to get a better understanding of the above definition.
# Estimating the Survival Function of NFL Players
To estimate the survival function of NFL players we will be using the [`lifelines` library](https://lifelines.readthedocs.io/en/latest/index.html). It provides a user friendly interface for survival analyis using Python. Lets get started by importing what we need and reading in the data.
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from lifelines import KaplanMeierFitter
draft_df = pd.read_csv("data/nfl_survival_analysis_data.csv")
# set some plotting aesthetics, similar to ggplot
sns.set(palette = "colorblind", font_scale = 1.35,
rc = {"figure.figsize": (12,9), "axes.facecolor": ".92"})
draft_df.head()
```
The columns of interest for our analysis are the *Duration* and *Retired* columns. The *Duration* column represents the number of years a player played in the NFL. The *Retired* column represents whether the player retired from the NFL or not. 1 indicates that he is retired, while 0 indicates that he is still an active player.
To calculate the Kaplan-Meier estimate we will need to create a `KaplanMeierFitter` object.
```
kmf = KaplanMeierFitter()
```
We can then fit the data by calling the `KaplanMeierFitter`s `fit` method.
```
# The 1st arg accepts an array or pd.Series of individual survival times
# The 2nd arg accepts an array or pd.Series that indicates if the event
# interest (or death) occured.
kmf.fit(durations = draft_df.Duration,
event_observed = draft_df.Retired)
```
After fitting our data we can access the event table that contains a bunch of information regarding the subjects (the NFL players) at each time period.
```
kmf.event_table
```
The *removed* column contains the number of observations removed during that time period, whether due to death (the value in the *observed* column) or censorship. So the *removed* column is just the sum of the *observed* and *censorship* columns. The *entrance* column tells us whether any new subjects entered the population at that time period. Since all the players we are studying start at $time = 0$ (the moment they were drafted), the *entrance* value is 15,592 at that time and 0 for all other times.
The *at_risk* column contains the number of subjects that are still alive during a given time. The value for *at_risk* at $time = 0$, is just equal to the *entrance* value. For the remaining time periods, the *at_risk* value is equal to the difference between the time previous period's *at_risk* value and *removed* value, plus the current period's *entrance* value. For example for $time = 1$, the number of subject's *at risk* is 10,995 which is equal to 15,592 (the previous *at_risk* value) - 4,597 (the previous *removed* value) + 0 (the current period's *entrance* value).
Since we have access to the survival table we can calculate the survival probability at different times "by hand."
Let us take a look at the definition of the Kaplan-Meier Estimate again:
$$\hat{S}(t) = \prod_{t_i \lt t} \frac{n_i - d_i}{n_i}$$
where $d_i$ are the number of death events at time $t$ and $n_i$ is the number of subjects at risk of death just prior to time $t$.
What the above essentially tells us is that the value of the survival function for time $t$, is the product of the survival probabilities for all individual time periods leading up to time $t$.
We can define the survival probability for an individual time period as follows:
$$S_t = \frac{\substack{\text{Number of subjects} \\ \text{at risk at the start}} - \substack{\text{Number of subjects} \\ \text{that died}}}{\substack{\text{Number of subjects} \\ \text{at risk at the start}}}$$
**NOTE** the number of deaths in the above formula does not include the number of censored observations.
Lets walk through a simple example and calculate the the probability that an NFL career lasts longer than 2 years. First we calculate the individual survival probabilities for $t = 0$, $t = 1$, and $t = 2$.
Here's the calculation for the survival probability time for $t = 0$:
$$S_0 = \frac{\substack{\text{Number of players at risk at the start} \\ \text{(i.e. Number of players drafted)}} - \substack{\text{Number of players} \\ \text{that immediately failed}}}{\substack{\text{Number of players at risk at the start} \\ \text{(i.e. Number of players drafted)}}} = \frac{15,592 - 4,504}{15,592} = \frac{11,088}{15,592} \approx 0.711$$
And the code for the calculation:
```
# get the values for time = 0 from the survival table
event_at_0 = kmf.event_table.iloc[0, :]
# now calculate the survival probability for t = 0
surv_for_0 = (event_at_0.at_risk - event_at_0.observed) / event_at_0.at_risk
surv_for_0
```
What the above means is that about 71.1% of players drafted make it on to the field.
Now the individual survival probability for $t = 1$:
$$S_1 = \frac{\substack{\text{Number of players} \\ \text{that survive the draft}} - \substack{\text{Number of players} \\ \text{that failed in the 1st year}}}{\substack{\text{Number of players} \\ \text{that survive the draft}}} = \frac{10,995 - 1,076}{10,995} = \frac{9,919}{10,995} \approx 0.902$$
```
# Calculate the survival probability for t = 1
event_at_1 = kmf.event_table.iloc[1, :]
surv_for_1 = (event_at_1.at_risk - event_at_1.observed) / event_at_1.at_risk
surv_for_1
```
The value for $S_1$ represents the conditional probability that if a player does not immediately fail once drafted, then he has a 90.2% chance of playing 1 year of football.
Below is the calculation for $S_2$:
$$S_2 = \frac{\substack{\text{Number of players that survive the} \\ \text{1st year and are entering the 2nd year}} - \substack{\text{Number of players} \\ \text{that failed in the 2nd year}}}{\substack{\text{Number of players that survive the} \\ \text{1st year and are entering the 2nd year}}} = \frac{9,685 - 1,176}{9,685} = \frac{8,509}{9,685} \approx 0.879$$
```
# Calculate the survival probability for t = 2
event_at_2 = kmf.event_table.iloc[2, :]
surv_for_2 = (event_at_2.at_risk - event_at_2.observed) / event_at_2.at_risk
surv_for_2
```
$S_2$ also represents a conditional probability. It is the probability that a player plays in their 2nd year given that he did not retire after his 1st year. This ends up being about 87.9%.
Finally to calculate the probability that an NFL career will last more than 2 years, we just multiply the three individual survival probabilities:
$$S(2) = S_0 \times S_1 \times S_2 = \frac{11,088}{15,592} \times \frac{9,919}{10,995} \times \frac{8,509}{9,685} \approx 0.564$$
```
# The probability that an NFL player has a career longer than 2 years
surv_after_2 = surv_for_0 * surv_for_1 * surv_for_2
surv_after_2
```
So we see that drafted players have about a 56.4% chance of making it past their 2nd year, or having a career as long as 2 years. Hopefully going through that short example gives you a better idea of how the Kaplan-Meier estimator works.
Our `KaplanMeierFitter` object has already done all of the above calculations for us. We can get the survival probability after a given time by simply using the `predict` method. So to get the value for $S(2)$ we just pass in 2 into the `predict` method.
```
kmf.predict(2)
```
That's pretty close to the value we calculated by hand. (I'm not sure why they aren't exactly the same. Possibly a rounding issue? If you do know why please let me know).
The `predict` method can also handle an array of numbers, returning an array of probabilities.
```
# The survival probabilities of NFL players after 1, 3, 5, and 10 yrs played
kmf.predict([1,3,5,10])
```
To get the full list of estimated probabilities from our `KaplanMeierFitter`, access the `survival_function_` attribute.
```
kmf.survival_function_
```
The `median_` attribute also provides us the number of years where on average 50% of players are out of the league.
```
kmf.median_
```
## Plotting the Kaplan-Meier Estimate
Plotting the Kaplan-Meier estimate (along with its confidence intervals) is pretty straightfoward. All we need to do is call the `plot` method.
```
# plot the KM estimate
kmf.plot()
# Add title and y-axis label
plt.title("The Kaplan-Meier Estimate for Drafted NFL Players\n(1967-2015)")
plt.ylabel("Probability a Player is Still Active")
plt.show()
```
The first thing thing that you should notice is that the Kaplan-Meier estimate is a step function. Each horizontal line represents the probability that a player is still active after a given time $t$. For example, when $t = 0$, the probability that a player is still active after that point is about 71%.
### Plotting the Kaplan-Meier Estimate by Position
Before we plot the career lengths by position, lets clean up some of the data. We will merge and drop some of the player positions in order to make the plotting a bit more manageable.
```
draft_df.Pos.unique() # check out all the different positions
draft_df.Pos.value_counts() # get a count for each position
# Relabel/Merge some of the positions
# Set all HBs to RB
draft_df.loc[draft_df.Pos == "HB", "Pos"] = "RB"
# Set all Safeties and Cornernbacks to DBs
draft_df.loc[draft_df.Pos.isin(["SS", "FS", "S", "CB"]), "Pos"] = "DB"
# Set all types of Linebackers to LB
draft_df.loc[draft_df.Pos.isin(["OLB", "ILB"]), "Pos"] = "LB"
# drop players from the following positions [FL, E, WB, KR, LS, OL]
# get the row indices for players with undesired postions
idx = draft_df.Pos.isin(["FL", "E", "WB", "KR", "LS", "DL", "OL"])
# keep the players that don't have the above positions
draft_df_2 = draft_df.loc[~idx, :]
# check the number of positions in order to decide
# on the plotting grid dimiensions
len(draft_df_2.Pos.unique())
```
Now that we have the data organized, lets plot the Kaplan-Meier estimate for each position. I've commented the code below to walk you through the process of plotting each position in a 5x3 plotting grid.
```
# create a new KMF object
kmf_by_pos = KaplanMeierFitter()
duration = draft_df_2.Duration
observed = draft_df_2.Retired
# Set the order that the positions will be plotted
positions = ["QB", "RB", "WR",
"TE", "T", "G",
"C", "DE", "DT",
"NT", "LB", "DB",
"FB", "K", "P"]
# Set up the the 5x3 plotting grid by creating figure and axes objects
# Set sharey to True so that each row of plots share the left most y-axis labels
fig, axes = plt.subplots(nrows = 5, ncols = 3, sharey = True,
figsize=(12,15))
# flatten() creates a 1-D array of the individual axes (or subplots)
# that we will plot on in our grid
# We zip together the two 1-D arrays containing the positions and axes
# so we can iterate over each postion and plot its KM estimate onto
# its respective axes
for pos, ax in zip(positions, axes.flatten()):
# get indices for players with the matching position label
idx = draft_df_2.Pos == pos
# fit the kmf for the those players
kmf_by_pos.fit(duration[idx], observed[idx])
# plot the KM estimate for that position on its respective axes
kmf_by_pos.plot(ax=ax, legend=False)
# place text indicating the median for the position
# the xy-coord passed in represents the fractional value for each axis
# for example (.5, .5) places text at the center of the plot
ax.annotate("Median = {:.0f} yrs".format(kmf_by_pos.median_), xy = (.47, .85),
xycoords = "axes fraction")
# get rid the default "timeline" x-axis label set by kmf.plot()
ax.set_xlabel("")
# label each plot by its position
ax.set_title(pos)
# set a common x and y axis across all plots
ax.set_xlim(0,25)
ax.set_ylim(0,1)
# tighten up the padding for the subplots
fig.tight_layout()
# https://stackoverflow.com/questions/16150819/common-xlabel-ylabel-for-matplotlib-subplots
# set a common x-axis label
fig.text(0.5, -0.01, "Timeline (Years)", ha="center")
# set a common y-axis label
fig.text(-0.01, 0.5, "Probability That a Player is Still Active",
va="center", rotation="vertical")
# add the title for the whole plot
fig.suptitle("Survival Curve for each NFL Position\n(Players Drafted from 1967-2015)",
fontsize=20)
# add some padding between the title and the rest of the plot to avoid overlap
fig.subplots_adjust(top=0.92)
plt.show()
```
## Checking the Conditional Survival Time
Another interesting attribute in our `KaplanMeierFitter` is the `conditional_time_to_event_`. It is a `DataFrame` that contains the estimated median remaining lifetime, conditioned on surviving up to time $t$. So from the table below we see that if a player is in the league for 1 year, their expected remaining career length is 5 years. Please note that some of the conditional survival times for later time values are a bit funky due to the smaller sample sizes of those time periods.
```
kmf._conditional_time_to_event_()
```
# Resources
Here are the resources I used to help write up this post and learn about survival analysis:
## Papers, Articles, and Documentation
- [The `lifelines` documentation](https://lifelines.readthedocs.io/en/latest/index.html)
- [The PDF to the original paper by Kapalan and Meier](http://www.csee.wvu.edu/~xinl/library/papers/math/statistics/kaplan.pdf)
- [Survival Analysis: A Self Learning Text](https://www.amazon.com/Survival-Analysis-Self-Learning-Statistics-Biology/dp/1441966455)
- [A Practical Guide to Understanding Kaplan-Meier Curves](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3932959/)
- [Understanding survival analysis: Kaplan-Meier estimate](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3059453/)
- [What is Survival Analysis (PDF)](https://www.cscu.cornell.edu/news/statnews/stnews78.pdf)
- [A short article by Kaplan](http://www.garfield.library.upenn.edu/classics1983/A1983QS51100001.pdf)
## Videos
- [Lifelines: Survival Analysis in Python](https://www.youtube.com/watch?v=XQfxndJH4UA), by Cameron Davidson-Pilon (the creator of the `lifelines` library)
- [Survival Analysis in Python and R](https://www.youtube.com/watch?v=fli-yE5grtY), by Linda Uruchurtu
As always you can find my code and data on [github](https://github.com/savvastj/nfl_survival_analysis). Please let me know if you see any mistakes/issues or have any suggestions on improving this post.
| true |
code
| 0.775573 | null | null | null | null |
|
<i>Copyright (c) Microsoft Corporation.</i>
<i>Licensed under the MIT License.</i>
# ARIMA: Autoregressive Integrated Moving Average
This notebook provides an example of how to train an ARIMA model to generate point forecasts of product sales in retail. We will train an ARIMA based model on the Orange Juice dataset.
An ARIMA, which stands for AutoRegressive Integrated Moving Average, model can be created using an `ARIMA(p,d,q)` model within `statsmodels` library. In this notebook, we will be using an alternative library `pmdarima`, which allows us to automatically search for optimal ARIMA parameters, within a specified range. More specifically, we will be using `auto_arima` function within `pmdarima` to automatically discover the optimal parameters for an ARIMA model. This function wraps `ARIMA` and `SARIMAX` models of `statsmodels` library, that correspond to non-seasonal and seasonal model space, respectively.
In an ARIMA model there are 3 parameters that are used to help model the major aspects of a times series: seasonality, trend, and noise. These parameters are:
- **p** is the parameter associated with the auto-regressive aspect of the model, which incorporates past values.
- **d** is the parameter associated with the integrated part of the model, which effects the amount of differencing to apply to a time series.
- **q** is the parameter associated with the moving average part of the model.,
If our data has a seasonal component, we use a seasonal ARIMA model or `ARIMA(p,d,q)(P,D,Q)m`. In that case, we have an additional set of parameters: `P`, `D`, and `Q` which describe the autoregressive, differencing, and moving average terms for the seasonal part of the ARIMA model, and `m` refers to the number of periods in each season.
We provide a [quick-start ARIMA example](../00_quick_start/auto_arima_forecasting.ipynb), in which we explain the process of using ARIMA model to forecast a single time series, and analyze the model performance. Please take a look at this notebook for more information.
In this notebook, we will train an ARIMA model on multiple splits (round) of the train/test data.
## Global Settings and Imports
```
import os
import sys
import math
import warnings
import itertools
import numpy as np
import pandas as pd
import scrapbook as sb
from datetime import datetime
from pmdarima.arima import auto_arima
from fclib.common.utils import git_repo_path, module_exists
from fclib.common.plot import plot_predictions_with_history
from fclib.evaluation.evaluation_utils import MAPE
from fclib.dataset.ojdata import download_ojdata, split_train_test, complete_and_fill_df
pd.options.display.float_format = "{:,.2f}".format
np.set_printoptions(precision=2)
warnings.filterwarnings("ignore")
print("System version: {}".format(sys.version))
```
## Parameters
Next, we define global settings related to the model. We will use historical weekly sales data only, without any covariate features to train the ARIMA model. The model parameter ranges are provided in params. These are later used by the `auto_arima()` function to search the space for the optimal set of parameters. To increase the space of models to search over, increase the `max_p` and `max_q` parameters.
> NOTE: Our data does not show a strong seasonal component (as demonstrated in data exploration example notebook), so we will not be searching over the seasonal ARIMA models. To learn more about the seasonal ARIMA models, please take a look at the quick start ARIMA notebook, referenced above in the introduction.
```
# Use False if you've already downloaded and split the data
DOWNLOAD_SPLIT_DATA = True
# Data directory
DATA_DIR = os.path.join(git_repo_path(), "ojdata")
# Forecasting settings
N_SPLITS = 5
HORIZON = 2
GAP = 2
FIRST_WEEK = 40
LAST_WEEK = 156
# Parameters of ARIMA model
params = {
"seasonal": False,
"start_p": 0,
"start_q": 0,
"max_p": 5,
"max_q": 5,
}
# Run notebook on a subset of stores (to reduce the run time)
STORE_SUBSET = True
```
## Data Preparation
We need to download the Orange Juice data and split it into training and test sets. By default, the following cell will download and spit the data. If you've already done so, you may skip this part by switching `DOWNLOAD_SPLIT_DATA` to `False`.
We store the training data and test data using dataframes. The training data includes `train_df` and `aux_df` with `train_df` containing the historical sales up to week 135 (the time we make forecasts) and `aux_df` containing price/promotion information up until week 138. Here we assume that future price and promotion information up to a certain number of weeks ahead is predetermined and known. In our example, we will be using historical sales only, and will not be using the `aux_df` data. The test data is stored in `test_df` which contains the sales of each product in week 137 and 138. Assuming the current week is week 135, our goal is to forecast the sales in week 137 and 138 using the training data. There is a one-week gap between the current week and the first target week of forecasting as we want to leave time for planning inventory in practice.
The setting of the forecast problem are defined in `fclib.dataset.ojdata.split_train_test` function. We can change this setting (e.g., modify the horizon of the forecast or the range of the historical data) by passing different parameters to this functions. Below, we split the data into `n_splits=N_SPLITS` splits, using the forecasting settings listed above in the *Parameters* section.
```
if DOWNLOAD_SPLIT_DATA:
download_ojdata(DATA_DIR)
train_df_list, test_df_list, _ = split_train_test(
DATA_DIR,
n_splits=N_SPLITS,
horizon=HORIZON,
gap=GAP,
first_week=FIRST_WEEK,
last_week=LAST_WEEK,
write_csv=True,
)
print("Finished data downloading and splitting.")
```
To create training data and test data for multi-round forecasting, we pass a number greater than `1` to `n_splits` parameter in `split_train_test()` function. Note that the forecasting periods we generate in each test round are **non-overlapping**. This allows us to evaluate the forecasting model on multiple rounds of data, and get a more robust estimate of our model's performance.
For visual demonstration, this is what the time series splits would look like for `N_SPLITS = 5`, and using other settings as above:

### Process training data
Our time series data is not complete, since we have missing sales for some stores/products and weeks. We will fill in those missing values by propagating the last valid observation forward to next available value. We will define functions for data frame processing, then use these functions within a loop that loops over each forecasting rounds.
Note that our time series are grouped by `store` and `brand`, while `week` represents a time step, and `logmove` represents the value to predict.
```
def process_training_df(train_df):
"""Process training data frame."""
train_df = train_df[["store", "brand", "week", "logmove"]]
store_list = train_df["store"].unique()
brand_list = train_df["brand"].unique()
train_week_list = range(FIRST_WEEK, max(train_df.week))
train_filled = complete_and_fill_df(train_df, stores=store_list, brands=brand_list, weeks=train_week_list)
return train_filled
```
### Process test data
Let's now process the test data. Note that, in addition to filling out missing values, we also convert unit sales from logarithmic scale to the counts. We will do model training on the log scale, due to improved performance, however, we will transfrom the test data back into the unit scale (counts) by applying `math.exp()`, so that we can evaluate the performance on the unit scale.
```
def process_test_df(test_df):
"""Process test data frame."""
test_df["actuals"] = test_df.logmove.apply(lambda x: round(math.exp(x)))
test_df = test_df[["store", "brand", "week", "actuals"]]
store_list = test_df["store"].unique()
brand_list = test_df["brand"].unique()
test_week_list = range(min(test_df.week), max(test_df.week) + 1)
test_filled = complete_and_fill_df(test_df, stores=store_list, brands=brand_list, weeks=test_week_list)
return test_filled
```
## Model training
Now let's run model training across all the stores and brands, and across all rounds. We will re-run the same code to automatically search for the best parameters, simply wrapped in a for loop iterating over stores and brands.
We will use [Ray](https://ray.readthedocs.io/en/latest/#) to distribute the computation to the cores available on your machine if Ray is installed. Otherwise, we will train the models for different stores, brands, and rounds sequentially. By the time we develop this example, Ray only supports Linux and MacOS. Thus, sequential training will be used on Windows. In the cells below, we first define a function that trains an ARIMA model for a specific store-brand-round. Then, we use the following to leverage Ray:
- `ray.init()` will start all the relevant Ray processes
- we define a function to run an ARIMA model on a single brand and single store. To turn this function into a function that can be executed remotely, we declare the function with the ` @ray.remote` decorator.
- `ray.get()` collects the results, and `ray.shutdown()` will stop Ray.
It will take around 4.5 minutes to run the below cell for 5 rounds on a machine with 4 cores and about 2.7 minutes on a machine with 6 cores. To speed up the execution, we model only a subset of twenty stores in each round. To change this behavior, and run ARIMA modeling over *all stores and brands*, switch the boolean indicator `STORE_SUBSET` to `False` under the *Parameters* section on top.
```
def train_store_brand(train, test, store, brand, split):
train_ts = train.loc[(train.store == store) & (train.brand == brand)]
train_ts = np.array(train_ts["logmove"])
model = auto_arima(
train_ts,
seasonal=params["seasonal"],
start_p=params["start_p"],
start_q=params["start_q"],
max_p=params["max_p"],
max_q=params["max_q"],
stepwise=True,
error_action="ignore",
)
model.fit(train_ts)
preds = model.predict(n_periods=GAP + HORIZON - 1)
predictions = np.round(np.exp(preds[-HORIZON:]))
test_week_list = range(min(test.week), max(test.week) + 1)
pred_df = pd.DataFrame(
{"predictions": predictions, "store": store, "brand": brand, "week": test_week_list, "round": split + 1,}
)
test_ts = test.loc[(test.store == store) & (test.brand == brand)]
return pd.merge(pred_df, test_ts, on=["store", "brand", "week"], how="left")
%%time
if module_exists("ray"):
print("Ray is available. Parallel training will be used. \n")
import ray
import logging
# Initialize Ray
print("Initializing Ray...")
address_info = ray.init(log_to_driver=False, logging_level=logging.ERROR)
print("Address information about the processes started by Ray:")
print(address_info, "\n")
@ray.remote
def ray_train_store_brand(train, test, store, brand, split):
return train_store_brand(train, test, store, brand, split)
# Create an empty df to store predictions
result_df = pd.DataFrame(None, columns=["predictions", "store", "brand", "week", "round", "actuals"])
for r in range(N_SPLITS):
print(f"{datetime.now().time()} --- Round " + str(r + 1) + " ---")
# Process training data set
train_df = train_df_list[r].reset_index()
train_filled = process_training_df(train_df)
# Process test data set
test_df = test_df_list[r].reset_index()
test_filled = process_test_df(test_df)
store_list = train_filled["store"].unique()
brand_list = train_filled["brand"].unique()
if STORE_SUBSET:
store_list = store_list[0:20]
# persist input data into Ray shared memory
train_filled_id = ray.put(train_filled)
test_filled_id = ray.put(test_filled)
# train for each store/brand
print("Training ARIMA model ...")
results = [
ray_train_store_brand.remote(train_filled_id, test_filled_id, store, brand, r)
for store, brand in itertools.product(store_list, brand_list)
]
result_round = pd.concat(ray.get(results), ignore_index=True)
result_df = result_df.append(result_round, ignore_index=True)
# Stop Ray
ray.shutdown()
```
If Ray is not installed, we will train all the models sequentially as follows. The training time could be several times longer compared with training the models in parallel with Ray.
```
%%time
if not module_exists("ray"):
print("Ray is not available. Sequential training will be used. \n")
from tqdm import tqdm
# CHANGE to False to model across all stores
subset_stores = True
# Create an empty df to store predictions
result_df = pd.DataFrame(None, columns=["predictions", "store", "brand", "week", "actuals", "round"])
for r in tqdm(range(N_SPLITS)):
print("-------- Round " + str(r + 1) + " --------")
# Process training data set
train_df = train_df_list[r].reset_index()
train_filled = process_training_df(train_df)
# Process test data set
test_df = test_df_list[r].reset_index()
test_filled = process_test_df(test_df)
print("Training ARIMA model ...")
store_list = train_filled["store"].unique()
brand_list = train_filled["brand"].unique()
if subset_stores:
store_list = store_list[0:10]
for store, brand in itertools.product(store_list, brand_list):
combined_df = train_store_brand(train_filled, test_filled, store, brand, r)
result_df = result_df.append(combined_df, ignore_index=True)
```
Note that since `auto_arima` model makes consecutive forecasts from the last time point, we want to forecast the next `n_periods = GAP + HORIZON - 1` points, so that we can account for the GAP, as described in the data setup.
## Model evaluation
To evaluate the model, we will use *mean absolute percentage error* or [MAPE](https://en.wikipedia.org/wiki/Mean_absolute_percentage_error).
```
mape_r = result_df.groupby("round").apply(lambda x: MAPE(x.predictions, x.actuals) * 100)
print("MAPE values for each forecasting round:")
print(mape_r)
metric_value = MAPE(result_df.predictions, result_df.actuals) * 100
sb.glue("MAPE", metric_value)
print(f"Overall MAPE is {metric_value:.2f} %")
```
The resulting MAPE value is relatively high. As `auto_arima` searches a restricted space of the models, defined by the range of `p` and `q` parameters, we often might not find an optimal model for each time series. In addition, when building a model for a large number of time series, it is often difficult to examine each model individually, which would usually help us improve an ARIMA model. Please refer to the [quick start ARIMA notebook](../00_quick_start/auto_arima_forecasting.ipynb) for a more comprehensive evaluation of a single ARIMA model.
Now let's plot a few examples of forecasted results.
```
num_samples = 6
min_week = 140
sales = pd.read_csv(os.path.join(DATA_DIR, "yx.csv"))
sales["move"] = sales.logmove.apply(lambda x: round(math.exp(x)) if x > 0 else 0)
result_df["move"] = result_df.predictions
plot_predictions_with_history(
result_df,
sales,
grain1_unique_vals=store_list,
grain2_unique_vals=brand_list,
time_col_name="week",
target_col_name="move",
grain1_name="store",
grain2_name="brand",
min_timestep=min_week,
num_samples=num_samples,
predict_at_timestep=145,
line_at_predict_time=False,
title="Prediction results for a few sample time series",
x_label="week",
y_label="unit sales",
random_seed=2,
)
```
## Additional Reading
\[1\] Rob J Hyndman and George Athanasopoulos. 2018. Forecasting: Principles and Practice. Chapter 8 ARIMA models: https://otexts.com/fpp2/arima.html <br>
\[2\] Modern Parallel and Distributed Python: A Quick Tutorial on Ray: https://rise.cs.berkeley.edu/blog/modern-parallel-and-distributed-python-a-quick-tutorial-on-ray/ <br>
| true |
code
| 0.483039 | null | null | null | null |
|
# Cross-Validation and the Test Set
In the last lecture, we saw how keeping some data hidden from our model could help us to get a clearer understanding of whether or not the model was overfitting. This time, we'll introduce a common automated framework for handling this task, called **cross-validation**. We'll also incorporate a designated **test set**, which we won't touch until the very end of our analysis to get an overall view of the performance of our model.
```
import numpy as np
from matplotlib import pyplot as plt
import pandas as pd
# assumes that you have run the function retrieve_data()
# from "Introduction to ML in Practice" in ML_3.ipynb
titanic = pd.read_csv("data.csv")
titanic
```
We are again going to use the `train_test_split` function to divide our data in two. This time, however, we are not going to be using the holdout data to determine the model complexity. Instead, we are going to hide the holdout data until the very end of our analysis. We'll use a different technique for handling the model complexity.
```
from sklearn.model_selection import train_test_split
np.random.seed(1234) # for reproducibility
train, test = train_test_split(titanic, test_size = 0.2) # hold out 20% of data
```
We again need to clean our data:
```
from sklearn import preprocessing
def prep_titanic_data(data_df):
df = data_df.copy()
le = preprocessing.LabelEncoder()
df['Sex'] = le.fit_transform(df['Sex'])
df = df.drop(['Name'], axis = 1)
X = df.drop(['Survived'], axis = 1).values
y = df['Survived'].values
return(X, y)
X_train, y_train = prep_titanic_data(train)
X_test, y_test = prep_titanic_data(test)
```
## K-fold Cross-Validation
The idea of k-fold cross validation is to take a small piece of our training data, say 10%, and use that as a mini test set. We train the model on the remaining 90%, and then evaluate on the 10%. We then take a *different* 10%, train on the remaining 90%, and so on. We do this many times, and finally average the results to get an overall average picture of how the model might be expected to perform on the real test set. Cross-validation is a highly efficient tool for estimating the optimal complexity of a model.
<figure class="image" style="width:100%">
<img src="https://scikit-learn.org/stable/_images/grid_search_cross_validation.png" alt="Illustration of k-fold cross validation. The training data is sequentially partitioned into 'folds', each of which is used as mini-testing data exactly once. The image shows five-fold validation, with four boxes of training data and one box of testing data. The diagram then indicates a final evaluation against additional testing data not used in cross-validation." width="600px">
<br>
<caption><i>K-fold cross-validation. Source: scikit-learn docs.</i></caption>
</figure>
The good folks at `scikit-learn` have implemented a function called `cross_val_score` which automates this entire process. It repeatedly selects holdout data; trains the model; and scores the model against the holdout data. While exceptions apply, you can often use `cross_val_score` as a plug-and-play replacement for `model.fit()` and `model.score()` during your model selection phase.
```
from sklearn.model_selection import cross_val_score
from sklearn import tree
# make a model
T = tree.DecisionTreeClassifier(max_depth = 3)
# 10-fold cross validation: hold out 10%, train on the 90%, repeat 10 times.
cv_scores = cross_val_score(T, X_train, y_train, cv=10)
cv_scores
cv_scores.mean()
fig, ax = plt.subplots(1)
best_score = 0
for d in range(1,30):
T = tree.DecisionTreeClassifier(max_depth = d)
cv_score = cross_val_score(T, X_train, y_train, cv=10).mean()
ax.scatter(d, cv_score, color = "black")
if cv_score > best_score:
best_depth = d
best_score = cv_score
l = ax.set(title = "Best Depth : " + str(best_depth),
xlabel = "Depth",
ylabel = "CV Score")
```
Now that we have a reasonable estimate of the optimal depth, we can try evaluating against the unseen testing data.
```
T = tree.DecisionTreeClassifier(max_depth = best_depth)
T.fit(X_train, y_train)
T.score(X_test, y_test)
```
Great! We even got slightly higher accuracy on the test set than we did in validation, although this is rare.
# Machine Learning Workflow: The Big Picture
We now have all of the elements that we need to execute the core machine learning workflow. At a high-level, here's what should go into a machine task:
1. Separate out the test set from your data.
2. Clean and prepare your data if needed. It is best practice to clean your training and test data separately. It's convenient to write a function for this.
3. Identify a set of candidate models (e.g. decision trees with depth up to 30, logistic models with between 1 and 3 variables, etc).
4. Use a validation technique (k-fold cross-validation is usually sufficient) to estimate how your models will perform on the unseen test data. Select the best model as measured by validation.
5. Finally, score the best model against the test set and report the result.
Of course, this isn't all there is to data science -- you still need to do exploratory analysis; interpret your model; etc. etc.
We'll discuss model interpretation further in a coming lecture.
| true |
code
| 0.55929 | null | null | null | null |
|
# stockmanager
stockmanager has the following main modules:
- Ticker: a class to retrieve price, company info of a ticker.
- visualization: a set of visualization functions, e.g. plot_price()
- Portfolio: a class
```
from stockmanager import Ticker, Portfolio, plot_price
# For debugging:
import matplotlib.pyplot as plt
import numpy as np
import mplfinance as mpf
msft = Ticker('MSFT')
price = msft.get_price(period='1mo', interval='1d')
plot_price(price, backend='matplotlib', mav=[2,5], title=msft.name, type='ohlc')
fig.update_layout(title={'text': msft.name,
'xanchor': 'auto'},
yaxis_title='Price', xaxis=dict(tickangle=-90))
fig.show()
plot_price(price, type='line')
plot(price, type='candle', mav=5)
plot(price, type='line')
import chart_studio.plotly as py
import plotly.figure_factory as ff
import pandas as pd
price
import chart_studio.plotly as py
import plotly.graph_objects as go
data = [go.Bar(x=price.Close,
y=price.index)]
# py.offline.iplot(data, filename='jupyter-basic_bar')
import plotly
print(plotly.__version__)
import plotly.express as px
def plotly():
fig = px.line(price, x=price.index, y="Close", title='Price')
fig.show()
plotly()
plot(price, type='line')
import plotly.graph_objects as go
def price_plot_with_plotly(price):
"""Use plotly to plot the stock data
Parameters
----------
price : pd.DataFrame
price data frame
"""
show_hours = True
if show_hours:
pstr = [p.strftime("%y-%m-%d (%H:%M:%S)") for p in price.index.to_list()]
else:
pstr = [p.strftime("%y-%m-%d") for p in price.index.to_list()]
fig = go.Figure()
fig.add_trace(go.Scatter(x=pstr, y=price.Close,
line=dict(color='royalblue')))
fig.update_layout(title='Stock Price Chart',
yaxis_title='Price',
xaxis = dict(tickangle=-90))
fig.show()
price_plot_with_plotly(price)
def price_plot_with_plotly(price):
"""Use plotly to plot the stock data
Parameters
----------
price : pd.DataFrame
price data frame
"""
show_hours = True
has_ohlc, ohlc = get_ohlc(price)
if show_hours:
pstr = [p.strftime("%y-%m-%d (%H:%M:%S)") for p in price.index.to_list()]
else:
pstr = [p.strftime("%y-%m-%d") for p in price.index.to_list()]
fig = go.Figure()
fig.add_trace(go.Candlestick(x=pstr,
open=ohlc[0],
high=ohlc[1],
low=ohlc[2],
close=ohlc[3]))
fig.update_layout(title='Stock Price Chart',
yaxis_title='Price',
xaxis = dict(tickangle=-90))
fig.show()
price_plot_with_plotly(price)
```
| true |
code
| 0.714404 | null | null | null | null |
|
# Lista 01 - EDA + Visualização
```
# -*- coding: utf 8
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
plt.style.use('seaborn-colorblind')
plt.ion()
```
# Exercício 01:
Em determinadas épocas do ano a venda de certos produtos sofre um aumento significativo. Um exemplo disso, são as vendas de sorvete que aumentam bastante no verão. Além do sorvete, outros itens como protetor solar e vestuário de banho podem ganhar maior atenção durante essa época do ano enquanto outros produtos podem não ser tão valorizados. Neste primeiro exercício, implemente a função abaixo que recebe quatro listas e cria um dataframe das quatro. A primeira lista será o índice do seu dataframe. A última, o nome das colunas.
Por exemplo, ao passar:
```python
ice_cream = [3000, 2600, 1400, 1500, 1200, 500, 300, 400, 700, 600, 800, 1900]
sunglasses = [1000, 800, 100, 70, 50, 190, 60, 50, 100, 120, 130, 900]
coats = [10, 20, 80, 120, 100, 500, 900, 780, 360, 100, 120, 20]
labels = ["Jan", "Fev", "Mar", "Abr", "Mai", "Jun", "Jul", "Ago", "Set", "Out", "Nov", "Dez"]
names = ["icecream", "sunglasses", "coats"]
cria_df(labels, ice_cream, sunglasses, coats, names)
```
A tabela deve ser da forma:
```
icecream sunglasses coats
------------------------------------
Jan 3000 1000 10
Fev 2600 800 20
... ... ... ...
Dez 1900 900 20
```
__Dica__
Usar `list(zip(colunas))`. Ou, montar um dicionário na mão.
```
def cria_df(labels, coluna1, coluna2, coluna3, names):
total = list(zip(coluna1, coluna2, coluna3))
resultado = pd.DataFrame(data=total, columns=names, index=labels)
return resultado
ice_cream = [3000, 2600, 1400, 1500, 1200, 500, 300, 400, 700, 600, 800, 1900]
sunglasses = [1000, 800, 100, 70, 50, 190, 60, 50, 100, 120, 130, 900]
coats = [10, 20, 80, 120, 100, 500, 900, 780, 360, 100, 120, 20]
labels = ["Jan", "Fev", "Mar", "Abr", "Mai", "Jun", "Jul", "Ago", "Set", "Out", "Nov", "Dez"]
names = ["icecream", "sunglasses", "coats"]
df = cria_df(labels, ice_cream, sunglasses, coats, names)
df
```
# Exercício 02:
Agora, crie uma função que recebe seu dataframe e crie um gráfico de linhas mostrando a evolução das vendas dos produtos ao longo dos meses em porcentagem. Ou seja, um gráfico relacionando a porcentagem de produtos vendidos naquele mês em relação ao ano como um todo para as vendas de sorvetes, óculos de sol e casacos.
Seu gráfico deve parecer com o plot abaixo:
```
# Note as duas linhas de código abaixo não é a resposta!!! Estou apenas mostrando a imagem que espero!
from IPython.display import Image
Image('plot1.png')
x = [i for i in range(0, len(labels))]
y = df.values / np.array(df.sum())
data = pd.DataFrame(data=y, columns=names, index=labels)
grafico = data.plot(title="Sales", linewidth=3)
grafico.set_ylabel("% sold")
plt.xticks(x, labels)
grafico
```
# Exercício 03:
Utilizando os mesmos dados do exercício anterior, crie uma função que faz um scatter plot entre **icecream** e as outras duas colunas..
__Dicas:__
1. "_Correlação não é o mesmo que causalidade!_"
1. Abaixo novamente mostramos exemplos de figuras que você pode gerar.
```
Image('plot2.png')
Image('plot3.png')
#Exemplo:
ice_cream = [3000, 2600, 1400, 1500, 1200, 500, 300, 400, 700, 600, 800, 1900]
sunglasses = [1000, 800, 100, 70, 50, 190, 60, 50, 100, 120, 130, 900]
coats = [10, 20, 80, 120, 100, 500, 900, 780, 360, 100, 120, 20]
labels = ["Jan", "Fev", "Mar", "Abr", "Mai", "Jun", "Jul", "Ago", "Set", "Out", "Nov", "Dez"]
def scatter(df):
for column in df:
if column != 'icecream':
df.plot(x='icecream', y=column, style='o', legend=False)
plt.ylabel(column)
scatter(df)
```
# Exercício 04:
Agora vamos trabalhar com dados reais. Na mesma pasta deste notebook, encontra-se um `json` com os dados do site http://www.capitaldoscandidatos.info/. Sua tarefa será usar funções como `groupby` e `hist` para analisar tais dados. Diferente das perguntas anteriores, não vamos mais pedir para que você implemente funções. Ou seja, pode trabalhar diretamente nas células do Jupyter estilo um cientista de dados.
Sua primeira tarefa será indicar os 10 partidos que em média mais lucraram depois da primeira eleição. Ou seja, a diferença de patrimônio entre 2014 (eleição 1) e 2018 (eleição 2). Assim, a célula de solução (abaixo, depois da célula que carrega os dados), deve criar uma variável `resposta`. A mesma é uma série pandas com os top 10 partidos que mais lucraram em média. **A resposta tem que ser um pd.Series, ou seja, uma única coluna!**
__Dicas__
Não necessariamente para este trabalho, mas é sempre bom lembrar:
1. Você já aprendeu a programar e quando estiver repetindo muito chamadas, é um bom sinal que deve criar um função.
2. Notebooks não são IDEs, use para trabalho exploratório.
```
df = pd.read_json('capital.json')
ax = df.groupby('sigla_partido')[['patrimonio_eleicao_1', 'patrimonio_eleicao_2']].sum()
ax = ax.patrimonio_eleicao_2.sub(ax.patrimonio_eleicao_1).to_frame('resposta').sort_values(by='resposta', ascending=False)
resposta = ax.head(10).T.squeeze()
resposta
```
Plote sua resposta abaixo!
```
resposta.plot.bar()
```
# Exercício 05:
Por fim, plote o histograma dos valores acima (lucro entre eleições) para todos os partidos. Brinque com valores diferentes do número de bins e interprete os dados. Para que a correção funcione, use a chamada da seguinte forma. Brinque também com variações de histograma normalizado ou não.
```
df = pd.read_json('capital.json') # carregando os dados +1 vez, caso tenha alterado.
ax.hist(bins=20)
```
| true |
code
| 0.213541 | null | null | null | null |
|
# Process specifications
Dynamically adjusting parameters in a process to meet a specification is critical in designing a production process, and even more so when its under uncertaintly. BioSTEAM groups process specifications into two categories: analytical specifications, and numerical specifications. As the name suggests, an analytical specification is directly solved within a single loop of a system. A numerical specification, on the other hand, is solved numerically by rerunning a unit operation or even by reconverging a recycle system. The following real world examples will explain this in detail.
## Analytical specifications
### Denature ethanol fuel in a bioethanol process
Vary the amount of denaturant to add according to the flow of bioethanol. The final bioethanol product must be 2 wt. % denaturant:
```
from biosteam import settings, Chemical, Stream, units, main_flowsheet
# First name a new flowsheet
main_flowsheet.set_flowsheet('mix_ethanol_with_denaturant')
# Set the thermodynamic property package.
# In an actual process, much more chemicals
# would be defined, but here we keep it short.
settings.set_thermo(['Water', 'Ethanol', 'Octane'])
# Assume 40 million gal ethanol produced a year
# with 330 operating days
dehydrated_ethanol = Stream('dehydrated_ethanol', T=340,
Water=0.1, Ethanol=99.9, units='kg/hr')
operating_days_per_year = 330
dehydrated_ethanol.F_vol = 40e6 / operating_days_per_year
denaturant = Stream('denaturant', Octane=1)
M1 = units.Mixer('M1', ins=(dehydrated_ethanol, denaturant), outs='denatured_ethanol')
# Create the specification function.
@M1.add_specification
def adjust_denaturant_flow():
denaturant_over_ethanol_flow = 0.02 / 0.98 # A mass ratio
denaturant.imass['Octane'] = denaturant_over_ethanol_flow * dehydrated_ethanol.F_mass
M1.run() # Run mass and energy balance
# Simulate, and check results.
M1.simulate()
M1.show(composition=True, flow='kg/hr')
```
All specifications are in the unit's specification list:
```
M1.specification
```
### Preparing corn slurry in a conventional dry-grind process
The solids content of a corn slurry fed to a conventional dry-grind corn ethanol plant is typically about 32 wt. %. Adjust the flow rate of water mixed with the milled corn for such that the slurry is 32 wt. %:
```
# First name a new flowsheet
main_flowsheet.set_flowsheet('corn_slurry_example')
# Create a general chemicals to represent the
# components of corn.
Starch = Chemical.blank('Starch', phase='s')
Fiber = Chemical.blank('Fiber', phase='s')
Oil = Chemical('Oil', search_ID='Oleic_acid')
Water = Chemical('Water')
# The exact properties are not important for
# the example, so just assume its like water at
# 25 C and 1 atm.
Starch.default()
Fiber.default()
# Set the thermodynamic property package.
# In an actual process, much more chemicals
# would be defined, but here we keep it short.
settings.set_thermo([Starch, Oil, Fiber, Water])
# A typical dry grind process may produce
# 40 million gal of ethanol a year with a
# yield of 2.7 gal ethanol per bushel of corn.
corn_flow_per_year = 40e6 / 2.7 # In bushels
days_per_year = 365
operating_days_per_year = 330
corn_flow_per_day = corn_flow_per_year * days_per_year / operating_days_per_year
# The corn kernel iscomposed of starch (62%), protein and fiber (19%),
# water (15%), and oil (4%).
corn_feed = Stream('corn_feed',
Starch=62, Fiber=19, Water=15, Oil=4, units='kg/hr')
corn_feed.set_total_flow(corn_flow_per_day, units='bu/day')
# Water that will be mixed with the milled corn to create the slurry.
slurry_water = Stream('slurry_water', Water=1)
M1 = units.Mixer('M1', ins=(slurry_water, corn_feed), outs='slurry')
@M1.add_specification
def adjust_water_flow():
F_mass_moisture = corn_feed.imass['Water']
F_mass_solids = corn_feed.F_mass - F_mass_moisture
slurry_water.F_mass = F_mass_solids * (1 - 0.32) / 0.32 - F_mass_moisture
M1._run() # Run mass and energy balance
# Simulate, and check results.
M1.simulate()
M1.show(flow='kg/hr', composition=True)
```
## Numerical specifications
### Flash design specification
Let's say we have a mixture of water, ethanol and propanol and we would like to evaporate 50% of the liquid by mass (not by mol). We can solve this problem numerically by testing whether the specification is met at a given temperature:
```
# First name a new flowsheet
main_flowsheet.set_flowsheet('flash_specification_example')
# Set the thermodynamic property package.
# In an actual process, much more chemicals
# would be defined, but here we keep it short.
settings.set_thermo(['Water', 'Ethanol', 'Propanol'])
# Feed stream
mixture = Stream('mixture', T=340,
Water=1000, Ethanol=1000, Propanol=1000,
units='kg/hr')
# Create a flash vessel
F1 = units.Flash('F1',
ins=mixture,
outs=('vapor', 'liquid'),
T=373, P=101325)
# Set a numerical specification which solves the objective function when called.
@F1.add_bounded_numerical_specification(x0=351.39, x1=373.15, xtol=1e-6)
def f(x):
# Objective function where f(x) = 0 at a
# vapor fraction of 50 wt. %.
F1.T = x
F1._run() # IMPORTANT: This runs the mass and energy balance at the new conditions
feed = F1.ins[0]
vapor = F1.outs[0]
V = vapor.F_mass / feed.F_mass
return V - 0.5
# Now create the system, simulate, and check results.
system = main_flowsheet.create_system()
system.simulate()
system.diagram()
print('vapor mass fraction: ', format(F1.outs[0].F_mass / mixture.F_mass, '.0%'))
```
| true |
code
| 0.675096 | null | null | null | null |
|
```
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc3 as pm
%load_ext watermark
az.style.use('arviz-darkgrid')
```
# Sequential Monte Carlo - Approximate Bayesian Computation
Approximate Bayesian Computation methods (also called likelihood free inference methods), are a group of techniques developed for inferring posterior distributions in cases where the likelihood function is intractable or costly to evaluate. This does not mean that the likelihood function is not part of the analysis, rather that it is not directly evaluated.
ABC comes useful when modelling complex phenomena in certain fields of study, like systems biology. Such models often contain unobservable random quantities, which make the likelihood function hard to specify, but data can be simulated from the model.
These methods follow a general form:
1- Sample a parameter $\theta^*$ from a prior/proposal distribution $\pi(\theta)$.
2- Simulate a data set $y^*$ using a function that takes $\theta$ and returns a data set of the same dimensions as the observed data set $y_0$ (simulator).
3- Compare the simulated dataset $y^*$ with the experimental data set $y_0$ using a distance function $d$ and a tolerance threshold $\epsilon$.
In some cases a distance function is computed between two summary statistics $d(S(y_0), S(y^*))$, avoiding the issue of computing distances for entire datasets.
As a result we obtain a sample of parameters from a distribution $\pi(\theta | d(y_0, y^*)) \leqslant \epsilon$.
If $\epsilon$ is sufficiently small this distribution will be a good approximation of the posterior distribution $\pi(\theta | y_0)$.
[Sequential monte carlo](https://docs.pymc.io/notebooks/SMC2_gaussians.html?highlight=smc) ABC is a method that iteratively morphs the prior into a posterior by propagating the sampled parameters through a series of proposal distributions $\phi(\theta^{(i)})$, weighting the accepted parameters $\theta^{(i)}$ like:
$$ w^{(i)} \propto \frac{\pi(\theta^{(i)})}{\phi(\theta^{(i)})} $$
It combines the advantages of traditional SMC, i.e. ability to sample from distributions with multiple peaks, but without the need for evaluating the likelihood function.
_(Lintusaari, 2016), (Toni, T., 2008), (Nuñez, Prangle, 2015)_
# A trivial example
Estimating the mean and standard deviation of normal data
```
data = np.random.normal(loc=0, scale=1, size=1000)
def normal_sim(a, b):
return np.random.normal(a, b, 1000)
with pm.Model() as example:
a = pm.Normal("a", mu=0, sd=5)
b = pm.HalfNormal("b", sd=1)
s = pm.Simulator("s", normal_sim, params=(a, b), observed=np.sort(data))
trace_example = pm.sample_smc(kernel="ABC", sum_stat="sorted")
az.plot_trace(trace_example);
az.summary(trace_example)
_, ax = plt.subplots(figsize=(10, 4))
az.plot_kde(data, label="True data", ax=ax, plot_kwargs={"color": "C2"})
az.plot_kde(normal_sim(trace_example["a"].mean(), trace_example["b"].mean()), ax=ax)
for i in np.random.randint(0, 500, 25):
az.plot_kde(
normal_sim(trace_example["a"][i], trace_example["b"][i]),
ax=ax,
plot_kwargs={"zorder": 0, "alpha": 0.2},
)
ax.legend();
```
# Lotka–Volterra
In this example we will try to find parameters for the Lotka-Volterra equations. A common biological competition model for describing how the number of individuals of each species changes when there is a predator/prey interaction (A Biologist’s Guide to Mathematical Modeling in Ecology and Evolution,Otto and Day, 2007). For example, rabbits and foxes. Given an initial population number for each species, the integration of this ordinary differential equations (ODE) describes curves for the progression of both populations. This ODE’s takes four parameters:
* a is the natural growing rate of rabbits, when there’s no fox.
* b is the natural dying rate of rabbits, due to predation.
* c is the natural dying rate of fox, when there’s no rabbit.
* d is the factor describing how many caught rabbits let create a new fox.
This example is based on the Scipy Lokta-Volterra Tutorial.
```
from scipy.integrate import odeint
```
First we will generate data using known parameters.
```
# Definition of parameters
a = 1.0
b = 0.1
c = 1.5
d = 0.75
# initial population of rabbits and foxes
X0 = [10.0, 5.0]
# size of data
size = 100
# time lapse
time = 15
t = np.linspace(0, time, size)
# Lotka - Volterra equation
def dX_dt(X, t, a, b, c, d):
""" Return the growth rate of fox and rabbit populations. """
return np.array([a * X[0] - b * X[0] * X[1], -c * X[1] + d * b * X[0] * X[1]])
```
This model is based on a simulator, a function that returns data in the same dimensions as the observed data. In this case, the function solves the ODE.
```
# simulator function
def competition_model(a, b):
return odeint(dX_dt, y0=X0, t=t, rtol=0.1, args=(a, b, c, d))
```
Using the simulator function we will obtain a dataset with some noise added, for using it as observed data.
```
# function for generating noisy data to be used as observed data.
def add_noise(a, b, c, d):
noise = np.random.normal(size=(size, 2))
simulated = competition_model(a, b)
simulated += noise
indexes = np.sort(np.random.randint(low=0, high=size, size=size))
return simulated[indexes]
# plotting observed data.
observed = add_noise(a, b, c, d)
_, ax = plt.subplots(figsize=(12, 4))
ax.plot(observed[:, 0], "x", label="prey")
ax.plot(observed[:, 1], "x", label="predator")
ax.set_xlabel("time")
ax.set_ylabel("population")
ax.set_title("Observed data")
ax.legend();
```
On this model, instead of specifyng a likelihood function, we use `pm.Simulator()`, a "container" that stores the simulator function and the observed data. During sampling, samples from a and b priors will be passed to the simulator function.
```
with pm.Model() as model:
a = pm.Normal("a", mu=1, sd=5)
b = pm.Normal("b", mu=1, sd=5)
simulator = pm.Simulator(
"simulator", competition_model, params=(a, b), observed=observed
)
trace = pm.sample_smc(kernel="ABC", epsilon=20)
az.plot_trace(trace);
az.plot_posterior(trace);
# plot results
_, ax = plt.subplots(figsize=(14, 6))
ax.plot(observed[:, 0], "x", label="prey", c="C0")
ax.plot(observed[:, 1], "x", label="predator", c="C1")
ax.plot(competition_model(trace["a"].mean(), trace["b"].mean()), linewidth=2.5)
for i in np.random.randint(0, size, 75):
ax.plot(
competition_model(trace["a"][i], trace["b"][i])[:, 0],
alpha=0.1,
c="C2",
zorder=0,
)
ax.plot(
competition_model(trace["a"][i], trace["b"][i])[:, 1],
alpha=0.1,
c="C3",
zorder=0,
)
ax.set_xlabel("time")
ax.set_ylabel("population")
ax.legend();
%watermark -n -u -v -iv -w
```
| true |
code
| 0.693849 | null | null | null | null |
|
# Suave demo notebook: BAO basis on a periodic box
Hello! In this notebook we'll show you how to use suave, an implementation of the Continuous-Function Estimator, with a basis based on the standard baryon acoustic oscillation (BAO) fitting function.
```
import os
import numpy as np
import matplotlib.pyplot as plt
import Corrfunc
from Corrfunc.io import read_lognormal_catalog
from Corrfunc.theory.DDsmu import DDsmu
from Corrfunc.theory.xi import xi
from Corrfunc.utils import evaluate_xi
from Corrfunc.utils import trr_analytic
from Corrfunc.bases import bao_bases
from colossus.cosmology import cosmology
import matplotlib
from matplotlib import pylab
%config InlineBackend.figure_format = 'retina'
matplotlib.rcParams['figure.dpi'] = 80
textsize = 'x-large'
params = {'legend.fontsize': 'x-large',
'figure.figsize': (10, 8),
'axes.labelsize': textsize,
'axes.titlesize': textsize,
'xtick.labelsize': textsize,
'ytick.labelsize': textsize}
pylab.rcParams.update(params)
plt.ion()
```
## Load in data
We'll demonstrate with a low-density lognormal simulation box, which we've included with the code. We'll show here the box with 3e-4 ($h^{-1}$Mpc)$^{-3}$, but if you're only running with a single thread, you will want to run this notebook with the 1e-4 ($h^{-1}$Mpc)$^{-3}$ box for speed. (The code is extremely parallel, so when you're running for real, you'll definitely want to bump up the number of threads.)
```
x, y, z = read_lognormal_catalog(n='2e-4')
boxsize = 750.0
nd = len(x)
print("Number of data points:",nd)
```
We don't need a random catalog for this example, as we'll use a periodic box such that we can calculate the random-random (and data-random) term analytically.
## Construct BAO basis
We will use a basis that is based on the standard BAO fitting function. It starts from the correlation function for a given cosmology, with the freedom for a scale shift using a scale dilation parameter $\alpha$. It includes a term that is the derivative of the correlation function with respect to $\alpha$, linearizing around this value. There are also nuisance parameter terms. For a full explanation, see [our paper](https://arxiv.org/abs/2011.01836).
To construct the BAO basis, we'll need to choose the r-range, as well as the redshift and bias. We can also select the cosmology, using the Colossus package. Note that we can also use a custom cosmology; see the [Colossus docs](https://bitbucket.org/bdiemer/colossus/src/master/).
We also select our initial guess for the scale dilation parameter $\alpha_\mathrm{guess}$. A value of 1.0 means that we will not shift the correlation function, so let's start there. We also choose $k_0$, the initial magnitude of the partial derivative term.
```
rmin = 40
rmax = 150
cosmo = cosmology.setCosmology('planck15')
redshift = 1.0
bias = 2.0
alpha_guess = 1.0
k0 = 0.1
projfn = 'bao_basis.dat'
bases = bao_bases(rmin, rmax, projfn, cosmo_base=cosmo, alpha_guess=alpha_guess, k0=k0,
ncont=2000, redshift=0.0, bias=1.0)
```
Plotting the bases, we see that the dark green basis is the correlation function for the given cosmology (and redshift and bias). It depends on the scale shift `alpha_guess` parameter; the default `alpha_guess=1.0`, meaning no shift.
The next-darkest green is the derivative with respect to the base cosmology. It depends on the dalpha and k0 parameters (we have just used the defaults here).
The other bases are nuisances parameters to marginalize over the broadband shape of the correlation function. We can also set the initial magnitudes of these by passing the `k1`, `k2`, and `k3` parameters.
```
plt.figure(figsize=(8,5))
bao_base_colors = ['#41ab5d', '#74c476', '#a1d99b', '#005a32', '#238b45'] #from https://colorbrewer2.org/#type=sequential&scheme=Greens&n=8, last 5 out of 8
bao_base_names = [r'$\frac{k_1}{s^2}$', r'$\frac{k_2}{s}$', r'$k_3$',
r'$\xi^\mathrm{mod}(\alpha_\mathrm{guess} s)$',
r'$k_0 \frac{\mathrm{d} \xi^\mathrm{mod}(\alpha_\mathrm{guess} s)}{\mathrm{d} \alpha}$']
r = bases[:,0]
base_vals = bases[:,1:]
for i in range(base_vals.shape[1]):
plt.plot(r, base_vals[:,i], label=bao_base_names[i], color=bao_base_colors[i])
plt.legend()
plt.xlim(rmin, rmax)
plt.ylim(-0.0025, 0.01)
plt.xlabel(r'separation $r$ ($h^{-1}\,$Mpc)')
plt.ylabel('BAO basis functions $f_k(r)$')
```
## Suave with a BAO basis
We set the suave parameters. The BAO basis we created is a file with a set of basis values at each separation r, so we use `proj_type=generalr`. We are also assuming a periodic box. We want the 3D correlation function, so we can use `DDsmu` with a single giant mu bin.
```
nthreads = 4
# Need to give a dummy r_edges for compatibility with standard Corrfunc.
# But we will use this later to compute the standard xi, so give something reasonable.
r_edges = np.linspace(rmin, rmax, 15)
mumax = 1.0
nmubins = 1
periodic = True
proj_type = 'generalr'
ncomponents = base_vals.shape[1]
dd_res_bao, dd_bao, _ = DDsmu(1, nthreads, r_edges, mumax, nmubins, x, y, z,
boxsize=boxsize, periodic=periodic, proj_type=proj_type,
ncomponents=ncomponents, projfn=projfn)
```
Because we are working with a periodic box, we can compute the v_RR and T_RR terms analytically. From those we can compute the amplitudes. Note that we are using Landy-Szalay here, but the v_DR term is equal to the v_RR term for a periodic box, so we don't need to compute it and the LS numerator reduces to v_DD - v_RR.
```
volume = boxsize**3
rr_ana_bao, trr_ana_bao = trr_analytic(rmin, rmax, nd, volume, ncomponents, proj_type, projfn=projfn)
numerator = dd_bao - rr_ana_bao
amps_ana_bao = np.linalg.solve(trr_ana_bao, numerator) # Use linalg.solve instead of actually computing inverse!
```
We can then evaluate the correlation function using these amplitudes at any set of r values:
```
r_fine = np.linspace(rmin, rmax, 2000)
xi_ana_bao = evaluate_xi(amps_ana_bao, r_fine, proj_type, projfn=projfn)
```
Let's also compute the standard correlation function for comparison:
```
xi_res = xi(boxsize, nthreads, r_edges, x, y, z, output_ravg=True)
r_avg, xi_standard = xi_res['ravg'], xi_res['xi']
```
And plot the results:
```
plt.figure(figsize=(8,5))
plt.plot(r_fine, xi_ana_bao, color='green', label='BAO basis')
plt.plot(r_avg, xi_standard, marker='o', ls='None', color='grey', label='Standard estimator')
plt.xlim(rmin, rmax)
plt.xlabel(r'r ($h^{-1}$Mpc)')
plt.ylabel(r'$\xi$(r)')
plt.legend()
```
Voila, a nice, continuous, well-motivated correlation function!
## Recovering the scale dilation parameter $\alpha$
We can read the estimated value of $\alpha$ directly from our amplitudes. The amplitude of the derivative term (let's call it C) is the amount that we need to shift $\alpha$ from our initial guess $\alpha_\mathrm{guess}$, moderated by $k_0$. Explicitly,
$$ \hat{\alpha} = \alpha_\mathrm{guess} + C \, k_0 $$
```
C = amps_ana_bao[4]
alpha_est = alpha_guess + C*k0
print(f"alpha_est = {alpha_est:.4f}")
```
So we found that the best fit to the data is not the initial cosmology, but that correlation function shifted by this factor.
This is a pretty signficant shift, so the right thing to do is perform an iterative procedure to converge on the best-fit alpha. To do this, the next time around we pass `alpha_guess = alpha_est`. Then we'll get a new value for `alpha_est`, and can repeat the process until some criterion is reached (e.g. the fractional change between `alpha_est` for subsequent iterations dips below some threshold). See [our paper](https://arxiv.org/abs/2011.01836) for details.
Finally, remember to clean up the basis function file:
```
os.remove(projfn)
```
| true |
code
| 0.656025 | null | null | null | null |
|
**Sustainable Software Development, block course, March 2021**
*Scientific Software Center, Institute for Scientific Computing, Dr. Inga Ulusoy*
# Analysis of the data
Imagine you perform a "measurement" of some type and obtain "scientific data". You know what your data represents, but you have only a vague idea how different features in the data are connected, and what information you can extract from the data.
You would start first with going through the data, making sure your data set is complete and that the result is reasonable. Imagine this already happened.
In the next step, you would inspect your data more closely and try to identify structures. That is the step that we are focusing on in this unit.
In the `data` folder, you will find several data files (`*.t` and `*.dat`). These are data files generated through some "new approach" that hasn't been used in your lab before. No previous analysis software exists, and you are going to establish a protocol for this "new approach" and "publish your results".
The data can be grouped into two categories:
1. data to be analyzed using statistical methods;
2. data to be analyzed using numerical methods.
In your hypothetical lab, you are an "expert" in one particular "method", and your co-worker is an "expert" in the other. Combined these two methods will lead to much more impactful results than if only one of you analyzed the data. Now, the task in this course is to be solved collaboratively with your team member working on one of the analysis approaches, and you working on the other. You will both implement functionality into the same piece of "software", but do so collaboratively through git.
As you do not know yet which analysis is most meaningful for your data, and how to implement it, you will start with a jupyter notebook. You and your team member will work on the same notebook that will be part of a github repository for your project. This is the task for today. Discuss with your team members who will work on the statistical and who on the numerical analysis.
## Step 1
Generate a github repository with the relevant files.
## Step 2
Clone the repository to your local machine.
## Step 3
Start working on task 1 for your analysis approach.
## Step 4
Create your own branch of the repository and commit your changes to your branch; push to the remote repository.
## Step 5
Open a `pull request` so your team member can review your implementation. Likewise, your team member will ask you to review theirs.
## Step 6
Merge the changes in your branch into `main`. Resolve conflicts.
## Step 7
Repeat working on task; committing and pushing to your previously generated branch or a new branch; open a pull request; merge with main; until you have finished all the tasks in your analysis approach. Delete obsolete branches.
# Start of the analysis notebook
**Author : Hannah Weiser**
*Date : 2022/03/01*
*Affiliation : Heidelberg University, Institute of Geography, 3DGeo group*
Place the required modules in the top, followed by required constants and global functions.
```
# required modules
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import display
sns.set_theme(style="darkgrid")
# constants and global functions
# filepaths:
expec = "../data/expec.t"
npop = "../data/npop.t"
npop_corr = "npop_corr.csv"
table = "../data/table.dat"
euclid = "euclid.csv"
# reading of the data files
```
# Statistical analysis
Find correlations in the data sets. Analyse the data statistically and plot your results.
Here we would want to do everything with pandas and leave the data in a dataframe. The files that are relevant to you are `expect.t`, `npop.t` and `table.dat`.
### Task 1: Read in expec.t and plot relevant data
```
# read and plot expec.t
df_expec = pd.read_csv(expec, sep=" ", skipinitialspace=True)
display(df_expec)
```
We can discard the entries norm, \<x>, and \<y> as these are mostly constant.
```
# explore variance of entries to find a suitable threshold
df_expec.var()
# eliminate columns based on the variance:
# if the variance of the values
# in a column is below a given threshold, that column is discarded
var_thresh = 0.0001
df_expec_clean = df_expec.loc[:, (df_expec.var() >= var_thresh)]
display(df_expec_clean)
```
### Task 2: Create plots of the relevant data and save as .pdf.
```
# create plots
fig, axs = plt.subplots(2)
fig.suptitle("Exploring the data")
axs[0].plot(df_expec_clean["time"], df_expec_clean["<z>"])
axs[0].set_ylabel("z")
axs[1].plot(df_expec_clean["time"], df_expec_clean["<H>"])
axs[1].set_ylabel("H")
plt.xlabel("Time")
plt.savefig("expec.pdf")
```
### Task 3: Read in file `npop.t` and analyze correlations in the data
```
# read in npop.t
df_npop = pd.read_csv(npop, sep=" ", skipinitialspace=True)
df_npop
# explore variance of entries to find a suitable filtering threshold
df_npop.var()
# discard all columns with variance below a set threshold
# - we can consider them as constant
var_thresh = 0.00001
df_npop_clean = df_npop.loc[:, (df_npop.var() >= var_thresh)]
display(df_npop_clean)
```
Plot the remaining columns. Seaborn prefers "long format" (one column for all measurement values, one column to indicate the type) as input, whereas the cvs is in "wide format" (one column per measurement type).
```
# plot ideally with seaborn
df_npop_melted = df_npop_clean.melt("time", var_name="columns", value_name="values")
g = sns.relplot(x="time", y="values", hue="columns", data=df_npop_melted, kind="line")
g.set(title="All columns in one plot")
plt.savefig("npop.pdf")
sns.relplot(x="time", y="MO3", data=df_npop_clean, kind="line")
sns.relplot(x="time", y="MO4", data=df_npop_clean, kind="line")
sns.relplot(x="time", y="MO6", data=df_npop_clean, kind="line")
sns.relplot(x="time", y="MO11", data=df_npop_clean, kind="line")
sns.relplot(x="time", y="MO12", data=df_npop_clean, kind="line")
sns.relplot(x="time", y="MO14", data=df_npop_clean, kind="line")
```
## Quantify the pairwise correlation in the data
- negative correlation: y values decrease for increasing x - large values of one feature correspond to small values of the other feature
- weak or no correlation: no trend observable, association between two features is hardly observable
- positive correlation: y values increase for decreasing x - small values of one feature correspond to small values of the other feature
Remember that correlation does not indicate causation - the reason that two features are associated can lie in their dependence on same factors.
Correlate the value pairs using Pearson's $r$. Pearson's $r$ is a measure of the linear relationship between features:
$r = \frac{\sum_i(x_i − \bar{x})(y_i − \bar{y})}{\sqrt{\sum_i(x_i − \bar{x})^2 \sum_i(y_i − \bar{y})^2}}$
Here, $\bar{x}$ and $\bar{y}$ indicate mean values. $i$ runs over the whole data set. For a positive correlation, $r$ is positive, and negative for a negative correlation, with minimum and maximum values of -1 and 1, indicating a perfectly linear relationship. Weakly or not correlated features are characterized by $r$-values close to 0.
Other measures of correlation that can be used are Spearman's rank (value pairs follow monotonic function) or Kendall's $\tau$ (measures ordinal association), but they do not apply here. You can also define measures yourself.
```
# print the correlation matrix
df_npop_clean.corr()
```
The diagonal values tell us that each value is perfectly correlated with itself. We are not interested in the diagonal values and also not in the correlation with time. We also need to get rid of redundant entries. Finally, we need to find the value pairs that exhibit the highest linear correlation. We still want to know if it is positive or negative correlation, so we cannot get rid of the sign.
```
# get rid of time column, lower triangular and diagonal entries of the
# correlation matrix
# sort the remaing values according to their absolute value, but keep the sign
r = df_npop_clean.corr()
r_ut = r.where((np.triu(np.ones(r.shape)).astype(bool)) & (r != 1.0))
r_ut.pop("time")
display(r_ut)
sorted_r = r_ut.unstack().dropna().sort_values()
display(sorted_r)
```
Note that the entries in the left column are not repeated if they do not change from the row above (so the fourth feature pair is MO3 and MO6).
### Task 4: Print the resulting data to a file
```
# write to file
sorted_r.to_csv(npop_corr, header=False)
```
### Task 5: Calculate the Euclidean distance (L2 norm) for the vectors in `table.dat`
The Euclidean distance measures the distance between to objects that are not points:
$d(p,q) = \sqrt{\left(p-q\right)^2}$
In this case, consider each of the columns in table.dat as a vector in Euclidean space, where column $r(x)$ and column $v(x)$ denote a pair of vectors that should be compared, as well as $r(y)$ and $v(y)$, and r(z) and v(z).
(Background: These are dipole moment components in different gauges, the length and velocity gauge.)
```
# read in table.dat - I suggest reading it as a numpy array
# replace the NaNs by zero
tab = np.genfromtxt(table, names=True, autostrip=True, dtype=None)
# using loadtxt, bc nan_to_num did not work with np.genfromtxt()
tab = np.loadtxt(table, skiprows=1)
tab = np.nan_to_num(tab)
```
Now calculate how different the vectors in column 2 are from column 3, column 4 from column 5, and column 6 from column 7.
```
# calculate the Euclidean distance
def euclid_dist(a, b):
return np.sqrt((a - b) ** 2)
dist_x = euclid_dist(tab[:, 2], tab[:, 3])
dist_y = euclid_dist(tab[:, 4], tab[:, 5])
dist_z = euclid_dist(tab[:, 6], tab[:, 7])
# plot the result and save to a .pdf
fig, axs = plt.subplots(1, 3, sharey=True, tight_layout=True)
n_bins = 15
# we are not plotting the full range, because we have many Zeros,
# which we want to exclude, and some very large outliers
axs[0].hist(dist_x, bins=n_bins, range=[0.00001, 1])
axs[0].set_title("$r(x)$ - $v(x)$")
axs[1].hist(dist_y, bins=n_bins, range=[0.00001, 1])
axs[1].set_title("$r(y)$ - $v(y)$")
axs[2].hist(dist_z, bins=n_bins, range=[0.00001, 1])
axs[2].set_title("$r(z)$ - $v(z)$")
fig.suptitle("Histograms of Euclidean distances")
plt.savefig("euclid.pdf")
# print the result to a file
d = {"dist_x": dist_x, "dist_y": dist_y, "dist_z": dist_z}
df_euclid = pd.DataFrame(data=d)
df_euclid.to_csv(euclid, index=False)
```
# Numerical analysis
Analyze the data using autocorrelation functions and discrete Fourier transforms. Plot your results.
```
# define some global functions
path_efield = "../data/efield.t"
```
### Task 1: Read in `efield.t` and Fourier-transform relevant columns
```
tmp = []
with open(path_efield) as f:
for line in f:
tmp.append(line.strip().split())
efield = np.array(tmp)
display(efield)
# read and plot efield.t
t = efield[1:, 0].astype("float64") # drop first row (time)
y = efield[1:, 2].astype("float64") # drop first row (y)
plt.plot(t, y)
plt.show()
```
Here we are interested in column 2 since the others are constant.
```
# discard the columns with variance below threshold
# - these are considered constant
thold = 0
efield_c = efield[
:,
np.var(
efield[
1:,
].astype("float64"),
0,
)
> thold,
]
display(efield_c)
# discrete Fourier transform of the remaining column:
# You only need the real frequencies
fft = np.fft.fft(efield_c[1:, 1].astype("float64"))
fftfreq = np.fft.fftfreq(fft.size, 0.1)
plt.plot(fftfreq, fft.real, fftfreq, fft.imag)
plt.show()
```
### Task 2: Generate a plot of your results to be saved as pdf.
```
# plot your results
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(25, 9))
plt.rcParams["font.size"] = "25"
fig.suptitle("Task 1 results")
ax1.plot(t, y)
ax1.set_title("Electric field")
ax2.plot(fftfreq, fft.real)
ax2.set_title("Fourier transform")
plt.savefig("task1_res.pdf")
```
### Task 3: Calculate the autocorrelation function from nstate_i.t
The autocorrelation function measures how correlated subsequent vectors are with an initial vector; ie.
$\Psi_{corr} = \langle \Psi(t=0) | \Psi(t) \rangle = \int_0^{tfin} \Psi(0)^* \Psi(t) dt$
Since we are in a numerical representation, the integral can be replaced with a sum; and the given vectors are already normalized.
```
# read in as numpy array
path_nstate = "../data/nstate_i.t"
nstate = np.loadtxt(path_nstate, skiprows=1)
# shape (101,481)
# store the time column (column 0) in a vector and drop from array
time = nstate[:, 0] # (101,)
time_vector = time[:, np.newaxis] # (101, 1)
nstate_notime = nstate[:, 1:] # (101, 480)
# correct the data representation: this is in fact a complex matrix
# the real part of each matrix column is contained in
# numpy array column 0, 2, 4, 6, ...
# the imaginary part of each matrix column is contained in
# numpy array column 1, 3, 5, 7, ...
# convert the array that was read as dtype=float into a dtype=complex array
# thought: nstate_compl has half no. of columns compared to nstate_notime
# for even numbers incl zero
# nstate_compl = []
nstate_compl = np.empty((101,))
# print(nstate_compl.shape)
for i in range(0, nstate_notime.shape[1], 2):
real = np.asarray(nstate_notime[:, i])
imag = np.asarray(nstate_notime[:, i + 1])
# complex = np.vectorize(complex)(real, imag)
mycomplex = real + 1j * imag
nstate_compl = np.column_stack((nstate_compl, mycomplex))
nstate_compl = nstate_compl[:, 1:] # shape (101, 240)
# complex = np.vectorize(complex, otypes=[np.float64])(real, imag)
# or
# complex = real + 1j*imag
len(nstate_compl)
# for the autocorrelation function, we want the overlap between the first
# vector at time 0 and all
# subsequent vectors at later times - the sum of the product of initial and
# subsequent vectors for each time step
# Def. Autocorrelation: correlation of a signal with a delayed copy of itself as a function of delay
# ACF represents how similar a value is to a previous value within a time series
# acf = np.zeros(len(nstate_compl[0]), dtype=complex)
# for i in range(0, len(nstate_compl[0])):
# acf[i] = np.sum(nstate_compl[:, 0] * np.conjugate(nstate_compl[:, i]))
acf = np.zeros(len(nstate_compl), dtype=complex)
for i in range(0, len(nstate_compl)):
acf[i] = np.sum(nstate_compl[0, :] * np.conjugate(nstate_compl[i, :]))
print(acf)
plt.plot(abs(acf**2))
plt.show()
```
### Task 4: Generate a plot of your results to be saved as pdf.
```
# plot the autocorrelation function - real, imaginary and absolute part
plt.plot(abs(acf**2), label="absolute")
plt.plot(acf.real**2, label="real")
plt.plot(acf.imag**2, label="imaginary")
plt.legend()
plt.show()
plt.savefig("task3_res.pdf")
```
### Task 5: Discrete Fourier transform of the autocorrelation function
```
# discrete Fourier-transform the autocorrelation function
# - now we need all frequency components,
# also the negative ones
```
### Task 6: Generate a plot of your results to be saved as pdf.
```
# plot the power spectrum (abs**2)
```
| true |
code
| 0.642629 | null | null | null | null |
|
# Implementing Simple Linear regression
Python implementation of the linear regression exercise from Andrew Ng's course: Machine Learning on coursera.
Exercise 1
Source notebooks:
[1][1]
[2][2]
[3][3]
[4][4]
[1]:https://github.com/kaleko/CourseraML/blob/a815ac95ba3d863b7531926b1edcdb4f5dd0eb6b/ex1/ex1.ipynb
[2]:http://nbviewer.jupyter.org/github/jdwittenauer/ipython-notebooks/blob/master/notebooks/ml/ML-Exercise1.ipynb
[3]:http://nbviewer.jupyter.org/github/JWarmenhoven/Machine-Learning/blob/master/notebooks/Programming%20Exercise%201%20-%20Linear%20Regression.ipynb
[4]:http://nbviewer.jupyter.org/github/JWarmenhoven/Machine-Learning/blob/master/notebooks/Programming%20Exercise%201%20-%20Linear%20Regression.ipynb
```
import os
import math as m
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline
data_path = '/Users/User/Desktop/Computer_Science/stanford_ml/machine-learning-ex1/ex1'
os.chdir(data_path)
```
# Loading data set and formating data
```
#Reading data file and shape
data = pd.read_csv('ex1data1.txt', header = None)
m,n = data.shape
#Initializing X and Y according to shape and converting to numpy arrays
X = data.iloc[:,0:n-1].values
y = data.iloc[:,n-1:n].values
#Adding the columns of 1s to X
X = np.concatenate((np.ones((m,1)),X), axis = 1)
#Initializing theta
theta = np.zeros((n,1),dtype = 'int8')
```
## Plotting the data
```
plt.scatter(X[:,1], y, s=30, c='r', marker='x', linewidths=1)
plt.xlabel('Population of City in 10,000s')
plt.ylabel('Profit in $10,000s');
```
# Cost Function computation
$J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2 $
$J(\theta) = \frac{1}{2m}(X\theta - y)^T(X\theta - y) $ (vectorized version)
## Gradient descent computation
$\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{m}X^T(X\theta - y) $
```
theta = np.zeros((n,1),dtype = 'int8')
def cost_function(X,y,theta):
#Initialisation of useful values
m = np.size(y)
J = 0
#Hypothesis function in vectorized form
h = np.dot(X,theta)
#Cost function in vectorized form
J = float((1./(2*m)) * np.dot((h - y).T, (h - y)));
return J;
def gradient_descent(X,y,theta,alpha = 0.0005,num_iters=1000):
#Initialisation of useful values
m = np.size(y)
J_history = np.zeros(num_iters)
J_vec = [] #Used to plot the cost function convergence
thetahistory = [] #Used for three d plot of convergence
for i in range(num_iters):
#Hypothesis function
h = np.dot(X,theta)
#Calculating the grad function in vectorized form
theta = theta - alpha * (1/m)* (X.T.dot(h-y))
J_history[i] = cost_function(X,y,theta)
#Calculate the cost for each iteration(used to plot convergence)
J_vec.append(cost_function(X,y,theta))
thetahistory.append(list(theta[:,0]))
return theta,J_history,J_vec, thetahistory;
def grad_descent_loop(X,y,theta,alpha = 0.015,num_iters=1000):
#Initialisation of useful values
m = np.size(y)
theta0 = 0
theta1 = 0
h = 0
for _ in range(num_iters):
grad0,grad1 = 0,0
for i in range(m):
h = theta0 + theta1 * X[:,1][i]
grad0 += (h - y[i])
grad1 += (h - y[i]) * X[:,1][i]
#Calculating the grad function in vectorized form
theta0 = theta0 - alpha * (1./m)* grad0
theta1 = theta1 - alpha * (1./m)* grad1
return np.array([theta0, theta1])
grad_descent_loop(X, y,theta)
```
## Run gradient descent
```
theta_calc , Cost_J, J_vec,thetahistory = gradient_descent(X, y,theta)
theta_calc
#gradient_descent(X,y,theta,alpha = 0.0005,num_iters=1000):
```
## Plot convergence
```
def plot_convergence(jvec):
plt.figure(figsize=(10,6))
plt.plot(range(len(jvec)),jvec)
plt.grid(True)
plt.title("Convergence of Cost Function")
plt.xlabel("Iteration number")
plt.ylabel("Cost function")
plot_convergence(J_vec)
```
## Fit regression line to data
Prediction = $h_\theta(x)=\theta_0 + \theta_1x$
```
def prediction(X,theta):
y_pred = theta[0] + theta[1] * X[:,1]
return y_pred;
#Calculating prediction
y_pred = X @ theta_calc
#Plotting figure
plt.figure(figsize=(10,6))
plt.plot(X[:,1],y[:,0],'rx',markersize=10,label='Training Data')
plt.plot(X[:,1],y_pred,'b-', label = 'Prediction h(x) = %0.2f + %0.2fx'%(theta_calc[0],theta_calc[1]))
plt.title('Data vs Linear regression prediction')
plt.xlabel('Population of City in 10,000s')
plt.ylabel('Profit in $10,000s');
plt.xlim(4.9)
plt.grid()
plt.legend()
```
## Visualizing the cost minimization path of gradient descent
Source: https://github.com/kaleko/CourseraML/blob/a815ac95ba3d863b7531926b1edcdb4f5dd0eb6b/ex1/ex1.ipynb
```
theta_calc , Cost_J, J_vec,thetahistory = gradient_descent(X, y,np.array([0,0]).reshape(-1,1), alpha = .0005, num_iters = 10000 )
theta_calc
#gradient_descent(X,y,theta,alpha = 0.0005,num_iters=1000):
#Import necessary matplotlib tools for 3d plots
from mpl_toolkits.mplot3d import axes3d, Axes3D
from matplotlib import cm
import itertools
fig = plt.figure(figsize=(12,12))
ax = fig.gca(projection='3d')
xvals = np.arange(-10,10,.5)
yvals = np.arange(-4,4,.1)
myxs, myys, myzs = [], [], []
for david in xvals:
for kaleko in yvals:
myxs.append(david)
myys.append(kaleko)
myzs.append(cost_function(X,y,np.array([[david], [kaleko]])))
scat = ax.scatter(myxs,myys,myzs,c=np.abs(myzs),cmap='jet')
plt.xlabel(r'$\theta_0$',fontsize=30)
plt.ylabel(r'$\theta_1$',fontsize=30)
plt.title('Cost (Minimization Path Shown in Blue)',fontsize=20)
plt.plot([x[0] for x in thetahistory],[x[1] for x in thetahistory],J_vec,'bo-')
ax.view_init(45, 0)
plt.show()
```
| true |
code
| 0.558929 | null | null | null | null |
|
# PRMS v6 BMI coupling - runtime interaction demo
* This demonstration will illustrate how the coupled surface-, soil-, groundwater-, and streamflow-BMIs can be interacted with at runtime.
* Some initial setup including matching an HRU polygon shapefile with order of HRUs in input file
* Visualizing results by mapping onto geopandas dataframe
* Using web-based data-services to drive climate forcing
* User controled forcing to inspect HRU response
* Note there are several python files with helper functions associated with this notebook.
* helper.py - has plotting functions
* gridmet.py / helpers.py - contains functions for the Gridmet data service. More information about Gridmet can be found here: http://www.climatologylab.org/gridmet.html In particular we use the netcdf subsetting service found here: http://thredds.northwestknowledge.net:8080/thredds/reacch_climate_MET_aggregated_catalog.html
* Demonstration based on the model devloped for Pipestem Creek Watershed in the Prairie Pothole region of North Dakota.

Hay, L, Norton, P, Viger, R, Markstrom, S, Regan, RS, Vanderhoof, M. Modelling surface‐water depression storage in a Prairie Pothole Region. Hydrological Processes. 2018; 32: 462– 479. https://doi.org/10.1002/hyp.11416
```
%matplotlib inline
import numpy as np
from pymt.models import PRMSSurface, PRMSSoil, PRMSGroundwater, PRMSStreamflow
from pathlib import Path
import geopandas as gpd
import pandas as pd
from gridmet import Gridmet
import matplotlib.pyplot as plt
import matplotlib
import datetime as dt
import helper
# # If using locally set path HRU and streamsegment shapefiles from data download in README
# hru_shp = '../GIS/nhru_10U.shp'
# hru_strmseg = '../GIS/nsegment_10U.shp'
# # set path to Gridmet weights file for mapping Gridmet gridded data to HRU
# weight_file = '../GIS/weights.csv'
# If using notebook in CSDMS JupyterHub. See README for instruction on where to
# get the data and uncomment out the following lines
hru_shp = '/opt/data/GIS/nhru_10U.shp'
hru_strmseg = '/opt/data/GIS/nsegment_10U.shp'
# set path to Gridmet weights file for mapping Gridmet gridded data to HRU
weight_file = '/opt/data/GIS/weights.csv'
```
### Set inputfiles for each of the 4 BMI and instantiate.
```
run_dir = '../prms/pipestem'
config_surf= 'control_surface.simple1'
config_soil = 'control_soil.simple1'
config_gw = 'control_groundwater.simple1'
config_sf = 'control_streamflow.simple1'
print(Path(run_dir).exists())
print((Path(run_dir) / config_surf).exists())
print((Path(run_dir) / config_soil).exists())
print((Path(run_dir) / config_gw).exists())
print((Path(run_dir) / config_sf).exists())
msurf = PRMSSurface()
msoil = PRMSSoil()
mgw = PRMSGroundwater()
msf = PRMSStreamflow()
print(msurf.name, msoil.name, mgw.name, msf.name)
```
### Initialize the BMIs
```
msurf.initialize(config_surf, run_dir)
msoil.initialize(config_soil, run_dir)
mgw.initialize(config_gw, run_dir)
msf.initialize(config_sf, run_dir)
```
---
### Open shapefile for the pipestem HRUs and stream segments and make sure the order in geopandas dataframe match the order from model components so they can be easily maps. Shapefiles are used for spatial plots of the prms6 variables.
- get_gdf and get_gdf_stream can be found in helper.py
---
```
gdf_ps = helper.get_gdf(hru_shp, msurf)
# print(gdf_ps.head())
gdf_streams = helper.get_gdf_streams(hru_strmseg, msurf)
# print(gdf_streams.head())
```
---
### Open climate driver data used by PRMS and plot the first days data and after one year of model time look for significant precipitation even to view.
---
```
clim_file = Path('../prms/pipestem/daymet.nc')
#plot climate and return clim_file as xarray object
clim = helper.plot_climate2(clim_file, gdf_ps, msurf)
# plot cumulative sum to find precipitation event
cum_sum = clim.cumsum(dim='time')
cum_sum.prcp.isel(hru=1)[365:485].plot()
```
---
## Get some model time information
---
```
# Get time information from the model.
print(msurf.get_value('nowtime'))
# print(msoil.var['nowtime'].data)
print(f'Start time: {msurf.start_time}')
print(f'End time: {msurf.end_time}')
print(f'Current time : {msurf.time}')
```
---
## Functions to couple Surface, Soil, Groundwater, and Streamflow BMIs
___
```
soil_input_cond_vars = ['soil_rechr_chg', 'soil_moist_chg']
surf2soil_vars = ['hru_ppt', 'hru_area_perv', 'hru_frac_perv', 'dprst_evap_hru',
'dprst_seep_hru', 'infil', 'sroff','potet', 'hru_intcpevap',
'snow_evap', 'snowcov_area', 'soil_rechr', 'soil_rechr_max',
'soil_moist', 'soil_moist_max', 'hru_impervevap' ,
'srunoff_updated_soil','transp_on']
soil2surf_vars = ['infil', 'sroff', 'soil_rechr', 'soil_moist']
surf2gw_vars = ['pkwater_equiv', 'dprst_seep_hru', 'dprst_stor_hru', 'hru_intcpstor',
'hru_impervstor', 'sroff']
soil2gw_vars = ['soil_moist_tot', 'soil_to_gw', 'ssr_to_gw', 'ssres_flow']
surf2sf_vars = ['potet', 'swrad', 'sroff']
soil2sf_vars = ['ssres_flow']
gw2sf_vars = ['gwres_flow']
def soilinput(msurf, msoil, exch_vars, cond_vars, dprst_flag, imperv_flag):
for var in exch_vars:
msoil.set_value(var, msurf.get_value(var))
if dprst_flag in [1, 3] or imperv_flag in [1, 3]:
for var in cond_vars:
msoil.set_value(var, msurf.get_value(var))
def soil2surface(msoil, msurf, exch_vars):
for var in exch_vars:
msurf.set_value(var, msoil.get_value(var))
def gwinput(msurf, msoil, mgw, surf_vars, soil_vars):
for var in surf_vars:
mgw.set_value(var, msurf.get_value(var))
for var in soil_vars:
mgw.set_value(var, msoil.get_value(var))
def sfinput(msurf, msoil, mgw, msf, surf_vars, soil_vars, gw_vars):
for var in surf_vars:
msf.set_value(var, msurf.get_value(var))
for var in soil_vars:
msf.set_value(var, msoil.get_value(var))
for var in gw_vars:
msf.set_value(var, mgw.get_value(var))
dprst_flag = msoil.get_value('dyn_dprst_flag')
imperv_flag = msoil.get_value('dyn_imperv_flag')
def update_coupled(msurf, msoil, mgw, msf, dprst_flag, imperv_flag):
msurf.update()
soilinput(msurf, msoil, surf2soil_vars, soil_input_cond_vars, dprst_flag, imperv_flag)
msoil.update()
soil2surface(msoil, msurf, soil2surf_vars)
gwinput(msurf, msoil, mgw, surf2gw_vars, soil2gw_vars)
mgw.update()
sfinput(msurf, msoil, mgw, msf, surf2sf_vars, soil2sf_vars, gw2sf_vars)
msf.update()
```
---
Run for 1-year plus 90 days just prior to preciptation event in cumulative plot above
---
```
for time in range(455):
update_coupled(msurf, msoil, mgw, msf, dprst_flag, imperv_flag)
```
---
Run for 7-days and plot results
---
```
for i in range(7):
update_coupled(msurf, msoil, mgw, msf, dprst_flag, imperv_flag)
ptime = msurf.var['nowtime'].data
timesel = dt.datetime(ptime[0], ptime[1], ptime[2])
print(f'Model time: {msurf.time}, Date: {timesel}')
helper.example_plot_strm(clim, gdf_ps, gdf_streams, msurf, msoil, mgw, msf, i, timesel)
# helper.example_plot(clim, gdf_ps, msurf, msoil, i, timesel)
for i in range(19):
update_coupled(msurf, msoil, mgw, msf, dprst_flag, imperv_flag)
ptime = msurf.var['nowtime'].data
timesel = dt.datetime(ptime[0], ptime[1], ptime[2])
print(f'Model time: {msurf.time}, Date: {timesel}')
```
### Drive climate forcing with web-based data services - here Gridmet
* Pull Gridmet data from web-service for specified period and map to HRUs
```
# initialize Gridmet data service
gmdata = Gridmet("1981-04-26", end_date="1981-05-04", hrumap=True, hru_id=msurf.get_value('nhm_id'), wght_file=weight_file)
for i in np.arange(7):
msurf.set_value('hru_ppt', (gmdata.precip.data[i,:]*.0393701).astype(np.float32))
msurf.set_value('tmax', ((gmdata.tmax.data[i,:]*(9./5.))+32.0).astype(np.float32))
msurf.set_value('tmin', ((gmdata.tmin.data[i,:]*(9./5.))+32.0).astype(np.float32))
# print(gmdata.precip[i,:]*.0393701)
# print((gmdata.tmax[i,:]*(9/5))+32.0)
# print((gmdata.tmin[i,:]*(9/5))+32.0)
update_coupled(msurf, msoil, mgw, msf, dprst_flag, imperv_flag)
ptime = msurf.var['nowtime'].data
timesel = dt.datetime(ptime[0], ptime[1], ptime[2])
print(f'Model time: {msurf.time}, Date: {timesel}')
# print(gmdata.precip.data[i,:]*.0393701)
helper.example_plot_strm(clim, gdf_ps, gdf_streams, msurf, msoil, mgw, msf, i, timesel)
```
---
In the next cell the precipitation, normally read from the netCDF file is overridden with user defined values. Here we kick one HRU with a large amount of precipitation, 3", and view the response
---
```
for i in range(14):
if i == 0:
grid_id = msurf.var_grid('hru_ppt')
var_type = msurf.var_type('hru_ppt')
grid_size = msurf.grid_node_count(grid_id)
ppt_override = np.zeros(shape = (grid_size), dtype=var_type)
ppt_override[0] = 3.0
msurf.set_value('hru_ppt', ppt_override)
update_coupled(msurf, msoil, mgw, msf, dprst_flag, imperv_flag)
ptime = msurf.var['nowtime'].data
timesel = dt.datetime(ptime[0], ptime[1], ptime[2])
print(f'Model time: {msurf.time}, Date: {timesel}')
helper.example_plot_strm(clim, gdf_ps, gdf_streams, msurf, msoil, mgw, msf, i, timesel)
```
View response at individual HRUs by reading the netCDF output files.
```
t_hru = 0
t_seg = 0
start_date = msoil.time-14
end_date = msoil.time
print(start_date, end_date)
import xarray as xr
surface_file = Path('../prms/pipestem/output/summary_surf_daily.nc')
soil_file = Path('../prms/pipestem/output/summary_soil_daily.nc')
gw_file = Path('../prms/pipestem/output/summary_gw_daily.nc')
strm_file = Path('../prms/pipestem/output/summary_streamflow_daily.nc')
dsurf = xr.open_dataset(surface_file, decode_times=False)
dsoil = xr.open_dataset(soil_file, decode_times=False)
dgw = xr.open_dataset(gw_file, decode_times=False)
dsf = xr.open_dataset(strm_file, decode_times=False)
fig, ax = plt.subplots(ncols=5, figsize=(12,4))
helper.bmi_prms6_value_plot(dsoil, t_hru, 'soil_moist_tot', 'surface-bmi', start_date, end_date, ax[0])
helper.bmi_prms6_value_plot(dsurf, t_hru, 'sroff', 'surface-bmi', start_date, end_date, ax[1])
helper.bmi_prms6_value_plot(dsoil, t_hru, 'ssres_flow', 'soil-bmi', start_date, end_date, ax[2])
helper.bmi_prms6_value_plot(dgw, t_hru, 'gwres_flow', 'groundwater-bmi', start_date, end_date, ax[3])
helper.bmi_prms6_value_plot(dsf, t_seg, 'seg_outflow', 'streamflow-bmi', start_date, end_date, ax[4])
plt.tight_layout()
plt.show()
```
Finalize the BMIs and shut down
```
msurf.finalize()
msoil.finalize()
mgw.finalize()
msf.finalize()
```
| true |
code
| 0.227963 | null | null | null | null |
|
```
%load_ext autoreload
%autoreload 2
```
> **How to run this notebook (command-line)?**
1. Install the `ReinventCommunity` environment:
`conda env create -f environment.yml`
2. Activate the environment:
`conda activate ReinventCommunity`
3. Execute `jupyter`:
`jupyter notebook`
4. Copy the link to a browser
# `REINVENT` score transformation notebook
This notebook serves two purposes: **(a)** to explain, what is meant by *score transformation* in the context of `REINVENT` and how to use it and **(b)** to serve as a way to find the proper transfomation parameters for a new or updated component.
### Background
As described in the Reinforcement Learning notebook in this repository, `REINVENT` uses different components in its scoring functions, which can be freely combined to generate a composite score for a compound. Each component returns a partial score between '0' and '1' and a selected functional form (either a product or a sum) produces the final composite score (again, a number between '0' and '1'). The following lines are an excerpt of an actual run that illustrates this:
```
INFO
Step 0 Fraction valid SMILES: 99.2 Score: 0.1583 Time elapsed: 0 Time left: 0.0
Agent Prior Target Score SMILES
-29.25 -29.25 -0.60 0.22 n1c(CN2CCOCC2)cnc2[nH]c3c(cc(C)c(C)c3)c12
-27.63 -27.63 -27.63 0.00 C1N(Cc2ccccc2)C(=O)c2cccc(N3C(=O)c4ccc(C(O)=O)cc4C3=O)c2C1
-40.76 -40.76 -14.11 0.21 C(NC(c1csnn1)=O)(c1ccc(-c2cc(Cl)cc(F)c2-c2nnn(C)n2)o1)(C)CC
Regression model Matching substructure Custom alerts QED Score
0.3370678424835205 0.5 1.0 0.78943
0.3446018993854522 1.0 0.0 0.64563
0.3945346176624298 0.5 1.0 0.46391
```
Each component (e.g. the `QED Score`) produces a partial score which is combined into `Score` (see product functional below).

For this to work, we need to ensure, that all components return a meaningful value from the interval [0,1], on top of which values closer to '1' must mean "better" as we are always trying to maximize the composite score. However, most components will not naturally comply with this requirements. In those cases, we can define a transformation (effectively the application of a mathematical function with given parameters) to the "raw" score returned by the component before feeding it into the scoring function.
First, let's load up everything we need:
```
# load the dependencies and classes used
%run code/score_transformation_code.py
# set plotting parameters
small = 12
med = 16
large = 22
params = {"axes.titlesize": large,
"legend.fontsize": med,
"figure.figsize": (16, 10),
"axes.labelsize": med,
"axes.titlesize": med,
"xtick.labelsize": med,
"ytick.labelsize": med,
"figure.titlesize": large}
plt.rcParams.update(params)
plt.style.use("seaborn-whitegrid")
sns.set_style("white")
%matplotlib inline
# set up Enums and factory
tt_enum = TransformationTypeEnum()
csp_enum = ComponentSpecificParametersEnum()
factory = TransformationFactory()
```
### Example
The following example simulates the incorporation of a new (fictious) component. Let us assume, we have run 10 compounds through this component and got the following values:
```
-12.4, -9.0, 1.3, 2.3, 0.7, -4.2, -0.3, -7.7, -9.9, 3.3
```
From your experience, you do consider a value above 0.3 to be very interesting and anything below -3 as completely useless. Thus we will choose a `sigmoid` transformation and adapt the parameters to reflect that. To get a nice curve in a plot which helps us deciding whether we are on the right track, we will define a range of values from -10 to 5 in a list.
```
# specify a list of dummy input values
values_list = np.arange(-10, 5, 0.25).tolist()
# set up the parameters
specific_parameters = {csp_enum.TRANSFORMATION: True,
csp_enum.LOW: -2,
csp_enum.HIGH: 1.25,
csp_enum.K: 0.17,
csp_enum.TRANSFORMATION_TYPE: tt_enum.SIGMOID}
transform_function = factory.get_transformation_function(specific_parameters)
transformed_scores = transform_function(predictions=values_list,
parameters=specific_parameters)
# render the curve
render_curve(title="Sigmoid transformation function", x=values_list, y=transformed_scores)
# check, whether the transformation does what we expect
input_values = [-12.4, -9.0, 1.3, 2.3, 0.7, -4.2, -0.3, -7.7, -9.9, 3.3]
output_values = transform_function(predictions=input_values,
parameters=specific_parameters)
print(input_values)
print([round(x, 1) for x in output_values])
```
As you can see, we have found a transformation that satisfies our needs in this case. It is important, that there is a smooth transition (so do not set parameter `K` to very high values), so that the "trail" can be picked up. You can play around with the parameters to see the effect on the curve and the output values. The parameters can be directly set in the `REINVENT` configuration file.
### All transformations
Of course, sometimes you will need other transformations than a `sigmoid` one, so below is a complete list of all transformations available at the moment.
```
# sigmoid transformation
# ---------
values_list = np.arange(-30, 20, 0.25).tolist()
specific_parameters = {csp_enum.TRANSFORMATION: True,
csp_enum.LOW: -25,
csp_enum.HIGH: 10,
csp_enum.K: 0.4505,
csp_enum.TRANSFORMATION_TYPE: tt_enum.SIGMOID}
transform_function = factory.get_transformation_function(specific_parameters)
transformed_scores = transform_function(predictions=values_list,
parameters=specific_parameters)
# render the curve
render_curve(title="Sigmoid transformation function", x=values_list, y=transformed_scores)
# reverse sigmoid transformation
# ---------
values_list = np.arange(-30, 20, 0.25).tolist()
specific_parameters = {csp_enum.TRANSFORMATION: True,
csp_enum.LOW: -20,
csp_enum.HIGH: -5,
csp_enum.K: 0.2,
csp_enum.TRANSFORMATION_TYPE: tt_enum.REVERSE_SIGMOID}
transform_function = factory.get_transformation_function(specific_parameters)
transformed_scores = transform_function(predictions=values_list,
parameters=specific_parameters)
# render the curve
render_curve(title="Reverse sigmoid transformation", x=values_list, y=transformed_scores)
# double sigmoid
# ---------
values_list = np.arange(-20, 20, 0.25).tolist()
specific_parameters = {csp_enum.TRANSFORMATION: True,
csp_enum.LOW: -10,
csp_enum.HIGH: 3,
csp_enum.COEF_DIV: 500,
csp_enum.COEF_SI: 250,
csp_enum.COEF_SE: 250,
csp_enum.TRANSFORMATION_TYPE: tt_enum.DOUBLE_SIGMOID}
transform_function = factory.get_transformation_function(specific_parameters)
transformed_scores = transform_function(predictions=values_list,
parameters=specific_parameters)
# render the curve
render_curve(title="Double-sigmoid transformation function", x=values_list, y=transformed_scores)
# step
# ---------
values_list = np.arange(-20, 20, 0.25).tolist()
specific_parameters = {csp_enum.TRANSFORMATION: True,
csp_enum.LOW: -10,
csp_enum.HIGH: 3,
csp_enum.TRANSFORMATION_TYPE: tt_enum.STEP}
transform_function = factory.get_transformation_function(specific_parameters)
transformed_scores = transform_function(predictions=values_list,
parameters=specific_parameters)
# render the curve
render_curve(title="Step transformation function", x=values_list, y=transformed_scores)
# right step
# ---------
values_list = np.arange(-20, 20, 0.25).tolist()
specific_parameters = {csp_enum.TRANSFORMATION: True,
csp_enum.LOW: -10,
csp_enum.TRANSFORMATION_TYPE: tt_enum.RIGHT_STEP}
transform_function = factory.get_transformation_function(specific_parameters)
transformed_scores = transform_function(predictions=values_list,
parameters=specific_parameters)
# render the curve
render_curve(title="Right step transformation function", x=values_list, y=transformed_scores)
```
There is also a `no_transformation` type, which does not change the input values at all.
| true |
code
| 0.665954 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/RSNA/AI-Deep-Learning-Lab-2021/blob/main/sessions/object-detection-seg/segmentation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Overview
In this tutorial we will explore how to create a contract-expanding fully convolutional neural network (CNN) for segmentation of pneumonia (lung infection) from chest radiographs, the most common imaging modality used to screen for pulmonary disease. For any patient with suspected lung infection, including viral penumonia such as as COVID-19, the initial imaging exam of choice is a chest radiograph.
## Workshop Links
Use the following link to access materials from this workshop: https://github.com/peterchang77/dl_tutor/tree/master/workshops
*Tutorials*
* Introduction to Tensorflow 2.0 and Keras: https://bit.ly/2VSYaop
* CNN for pneumonia classification: https://bit.ly/2D9ZBrX
* CNN for pneumonia segmentation: https://bit.ly/2VQMWk9 (**current tutorial**)
# Environment
The following lines of code will configure your Google Colab environment for this tutorial.
### Enable GPU runtime
Use the following instructions to switch the default Colab instance into a GPU-enabled runtime:
```
Runtime > Change runtime type > Hardware accelerator > GPU
```
### Jarvis library
In this notebook we will Jarvis, a custom Python package to facilitate data science and deep learning for healthcare. Among other things, this library will be used for low-level data management, stratification and visualization of high-dimensional medical data.
```
# --- Install Jarvis library
% pip install jarvis-md
```
### Imports
Use the following lines to import any needed libraries:
```
import numpy as np, pandas as pd
from tensorflow import losses, optimizers
from tensorflow.keras import Input, Model, models, layers, metrics
from jarvis.train import datasets, custom
from jarvis.utils.display import imshow
```
# Data
The data used in this tutorial will consist of (frontal projection) chest radiographs from a subset of the RSNA / Kaggle pneumonia challenge (https://www.kaggle.com/c/rsna-pneumonia-detection-challenge). From the complete cohort, a random subset of 1,000 exams will be used for training and evaluation.
### Download
The custom `datasets.download(...)` method can be used to download a local copy of the dataset. By default the dataset will be archived at `/data/raw/xr_pna`; as needed an alternate location may be specified using `datasets.download(name=..., path=...)`.
```
# --- Download dataset
datasets.download(name='xr/pna-512')
```
### Python generators
Once the dataset is downloaded locally, Python generators to iterate through the dataset can be easily prepared using the `datasets.prepare(...)` method:
```
# --- Prepare generators
gen_train, gen_valid, client = datasets.prepare(name='xr/pna-512', keyword='seg-512')
```
The created generators, `gen_train` and `gen_valid`, are designed to yield two variables per iteration: `xs` and `ys`. Both `xs` and `ys` each represent a dictionary of NumPy arrays containing model input(s) and output(s) for a single *batch* of training. The use of Python generators provides a generic interface for data input for a number of machine learning libraries including Tensorflow 2.0 / Keras.
Note that any valid Python iterable method can be used to loop through the generators indefinitely. For example the Python built-in `next(...)` method will yield the next batch of data:
```
# --- Yield one example
xs, ys = next(gen_train)
```
### Data exploration
To help facilitate algorithm design, each original chest radiograph has been resampled to a uniform `(512, 512)` matrix. Overall, the dataset comprises a total of `1,000` 2D images: a total of `500` negaative exams and `500` positive exams.
### `xs` dictionary
The `xs` dictionary contains a single batch of model inputs:
1. `dat`: input chest radiograph resampled to `(1, 512, 512, 1)` matrix shape
```
# --- Print keys
for key, arr in xs.items():
print('xs key: {} | shape = {}'.format(key.ljust(8), arr.shape))
```
### `ys` dictionary
The `ys` dictionary contains a single batch of model outputs:
1. `pna`: output segmentation mask for pneumonia equal in size to the input `(1, 512, 512, 1)` matrix shape
* 0 = pixels negative for pneumonia
* 1 = pixels positive for pneumonia
```
# --- Print keys
for key, arr in ys.items():
print('ys key: {} | shape = {}'.format(key.ljust(8), arr.shape))
```
### Visualization
Use the following lines of code to visualize a single input image and mask using the `imshow(...)` method:
```
# --- Show labels
xs, ys = next(gen_train)
imshow(xs['dat'][0], ys['pna'][0], radius=3)
```
Use the following lines of code to visualize an N x N mosaic of all images and masks in the current batch using the `imshow(...)` method:
```
# --- Show "montage" of all images
xs, ys = next(gen_train)
imshow(xs['dat'], ys['pna'], figsize=(12, 12), radius=3)
```
### Model inputs
For every input in `xs`, a corresponding `Input(...)` variable can be created and returned in a `inputs` dictionary for ease of model development:
```
# --- Create model inputs
inputs = client.get_inputs(Input)
```
In this example, the equivalent Python code to generate `inputs` would be:
```python
inputs = {}
inputs['dat'] = Input(shape=(1, 512, 512, 1))
```
# U-Net Architecture
The **U-Net** architecture is a common fully-convolutional neural network used to perform instance segmentation. The network topology comprises of symmetric contracting and expanding arms to map an original input image to an output segmentation mask that appoximates the size of the original image:
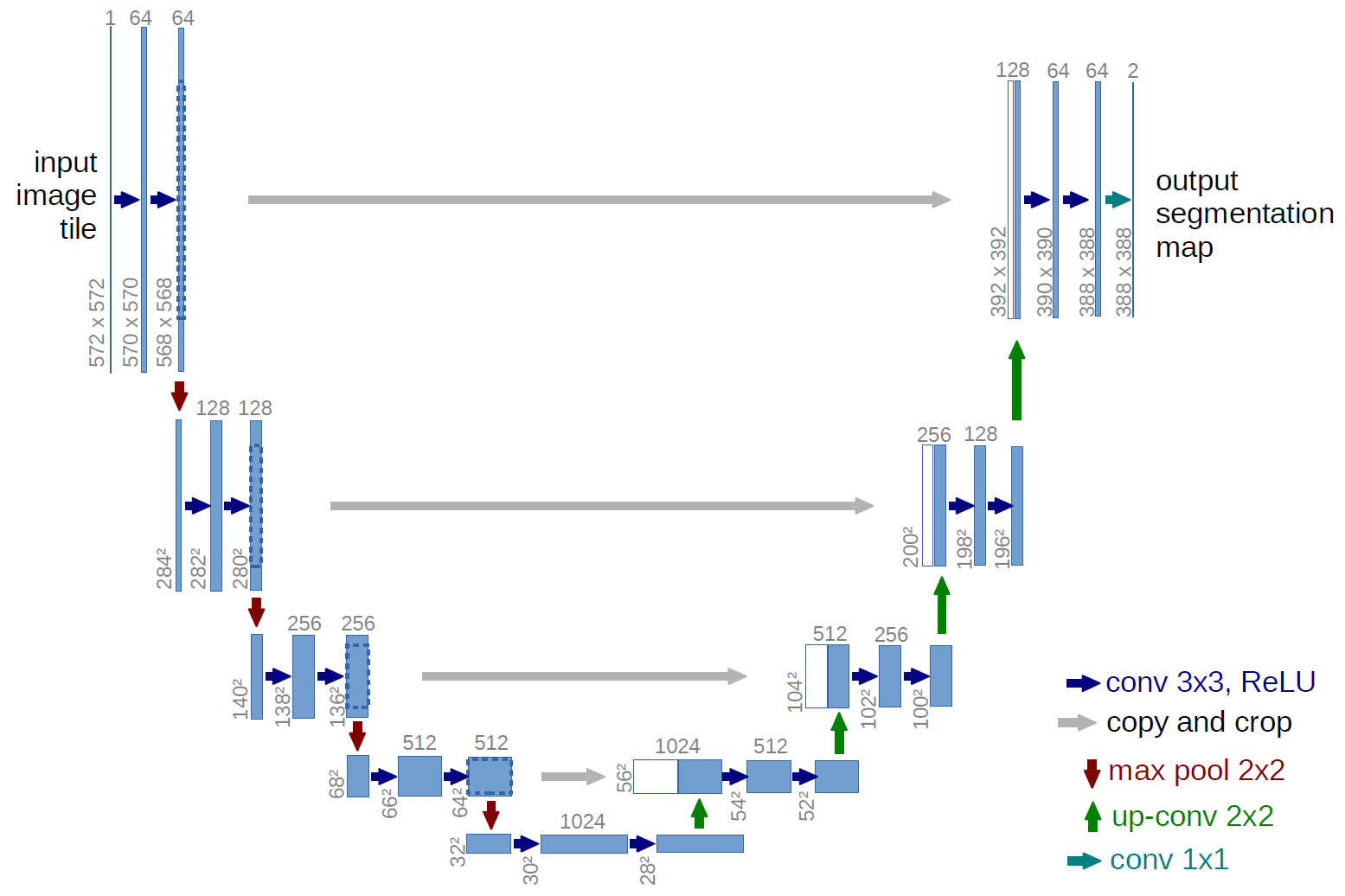
# Contracting Layers
The contracting layers of a U-Net architecture are essentially identical to a standard feed-forward CNN. Compared to the original architecture above, several key modifications will be made for ease of implementation and to optimize for medical imaging tasks including:
* same padding (vs. valid padding)
* strided convoltions (vs. max-pooling)
* smaller filters (channel depths)
Let us start by defining the contracting layer architecture below:
```
# --- Define kwargs dictionary
kwargs = {
'kernel_size': (1, 3, 3),
'padding': 'same'}
# --- Define lambda functions
conv = lambda x, filters, strides : layers.Conv3D(filters=filters, strides=strides, **kwargs)(x)
norm = lambda x : layers.BatchNormalization()(x)
relu = lambda x : layers.ReLU()(x)
# --- Define stride-1, stride-2 blocks
conv1 = lambda filters, x : relu(norm(conv(x, filters, strides=1)))
conv2 = lambda filters, x : relu(norm(conv(x, filters, strides=(1, 2, 2))))
```
Using these lambda functions, let us define a simple 9-layer contracting network topology with a total a four subsample (stride-2 convolution) operations:
```
# --- Define contracting layers
l1 = conv1(16, inputs['dat'])
l2 = conv1(32, conv2(32, l1))
l3 = conv1(48, conv2(48, l2))
l4 = conv1(64, conv2(64, l3))
l5 = conv1(80, conv2(80, l4))
```
**Checkpoint**: What is the shape of the `l5` feature map?
```
```
# Expanding Layers
The expanding layers are simply implemented by reversing the operations found in the contract layers above. Specifically, each subsample operation is now replaced by a **convolutional transpose**. Due to the use of **same** padding, defining a transpose operation with the exact same parameters as a strided convolution will ensure that layers in the expanding pathway will exactly match the shape of the corresponding contracting layer.
### Convolutional transpose
Let us start by defining an additional lambda function for the convolutional transpose:
```
# --- Define single transpose
tran = lambda x, filters, strides : layers.Conv3DTranspose(filters=filters, strides=strides, **kwargs)(x)
# --- Define transpose block
tran2 = lambda filters, x : relu(norm(tran(x, filters, strides=(1, 2, 2))))
```
Carefully compare these functions to the single `conv` operations as well as the `conv1` and `conv2` blocks above. Notice that they share the exact same configurations.
Let us now apply the first convolutional transpose block to the `l5` feature map:
```
# --- Define expanding layers
l6 = tran2(64, l5)
```
**Checkpoint**: What is the shape of the `l6` feature map?
### Concatenation
The first connection in this specific U-Net derived architecture is a link between the `l4` and the `l6` layers:
```
l1 -------------------> l9
\ /
l2 -------------> l8
\ /
l3 -------> l7
\ /
l4 -> l6
\ /
l5
```
To mediate the first connection between contracting and expanding layers, we must ensure that `l4` and `l6` match in feature map size (the number of filters / channel depth *do not* necessarily). Using the `same` padding as above should ensure that this is the case and thus simplifies the connection operation:
```
# --- Ensure shapes match
print(l4.shape)
print(l6.shape)
# --- Concatenate
concat = lambda a, b : layers.Concatenate()([a, b])
concat(l4, l6)
```
Note that since `l4` and `l6` are **exactly the same shape** (including matching channel depth), what additional operation could be used here instead of a concatenation?
### Full expansion
Alternate the use of `conv1` and `tran2` blocks to build the remainder of the expanding pathway:
```
# --- Define expanding layers
l7 = tran2(48, conv1(64, concat(l4, l6)))
l8 = tran2(32, conv1(48, concat(l3, l7)))
l9 = tran2(16, conv1(32, concat(l2, l8)))
l10 = conv1(16, l9)
```
# Logits
The last convolution projects the `l10` feature map into a total of just `n` feature maps, one for each possible class prediction. In this 2-class prediction task, a total of `2` feature maps will be needed. Recall that these feature maps essentially act as a set of **logit scores** for each voxel location throughout the image. As with a standard CNN architecture, **do not** use an activation here in the final convolution:
```
# --- Create logits
logits = {}
logits['pna'] = layers.Conv3D(filters=2, name='pna', **kwargs)(l10)
```
# Model
Let us first create our model:
```
# --- Create model
model = Model(inputs=inputs, outputs=logits)
```
### Custom Dice score metric
The metric of choice for tracking performance of a medical image segmentation algorithm is the **Dice score**. The Dice score is not a default metric built in the Tensorflow library, however a custom metric is available for your convenience as part of the `jarvis-md` package. It is invoked using the `custom.dsc(cls=...)` call, where the argument `cls` refers to the number of *non-zero* classes to track (e.g. the background Dice score is typically not tracked). In this exercise, it will be important to track the performance of segmentation for **pneumonia** (class = 1) only, thus set the `cls` argument to `1`.
```
# --- Compile model
model.compile(
optimizer=optimizers.Adam(learning_rate=2e-4),
loss={'pna': losses.SparseCategoricalCrossentropy(from_logits=True)},
metrics={'pna': custom.dsc(cls=1)},
experimental_run_tf_function=False)
```
# Model Training
### In-Memory Data
The following line of code will load all training data into RAM memory. This strategy can be effective for increasing speed of training for small to medium-sized datasets.
```
# --- Load data into memory
client.load_data_in_memory()
```
### Training
Once the model has been compiled and the data prepared (via a generator), training can be invoked using the `model.fit(...)` method. Ensure that both the training and validation data generators are used. In this particular example, we are defining arbitrary epochs of 100 steps each. Training will proceed for 8 epochs in total. Validation statistics will be assess every fourth epoch. As needed, tune these arugments as need.
```
model.fit(
x=gen_train,
steps_per_epoch=100,
epochs=8,
validation_data=gen_valid,
validation_steps=100,
validation_freq=4)
```
# Evaluation
To test the trained model, the following steps are required:
* load data
* use `model.predict(...)` to obtain logit scores
* use `np.argmax(...)` to obtain prediction
* compare prediction with ground-truth
Recall that the generator used to train the model simply iterates through the dataset randomly. For model evaluation, the cohort must instead be loaded manually in an orderly way. For this tutorial, we will create new **test mode** data generators, which will simply load each example individually once for testing.
```
# --- Create validation generator
test_train, test_valid = client.create_generators(test=True)
```
### Dice score
While the Dice score metric for Tensorflow has been provided already, an implementation must still be used to manually calculate the performance during validation. Use the following code cell block to implement:
```
def dice(y_true, y_pred, c=1, epsilon=1):
"""
Method to calculate the Dice score coefficient for given class
:params
(np.ndarray) y_true : ground-truth label
(np.ndarray) y_pred : predicted logits scores
(int) c : class to calculate DSC on
"""
assert y_true.ndim == y_pred.ndim
true = y_true[..., 0] == c
pred = np.argmax(y_pred, axis=-1) == c
A = np.count_nonzero(true & pred) * 2
B = np.count_nonzero(true) + np.count_nonzero(pred) + epsilon
return A / B
```
Use the following lines of code to loop through the test set generator and run model prediction on each example:
```
# --- Test model
dsc = []
for x, y in test_valid:
if y['pna'].any():
# --- Predict
logits = model.predict(x['dat'])
if type(logits) is dict:
logits = logits['pna']
# --- Argmax
dsc.append(dice(y['pna'][0], logits[0], c=1))
dsc = np.array(dsc)
```
Use the following lines of code to calculate validataion cohort performance:
```
# --- Calculate accuracy
print('{}: {:0.5f}'.format('Mean Dice'.ljust(20), np.mean(dsc)))
print('{}: {:0.5f}'.format('Median Dice'.ljust(20), np.median(dsc)))
print('{}: {:0.5f}'.format('25th-centile Dice'.ljust(20), np.percentile(dsc, 25)))
print('{}: {:0.5f}'.format('74th-centile Dice'.ljust(20), np.percentile(dsc, 75)))
```
## Saving and Loading a Model
After a model has been successfully trained, it can be saved and/or loaded by simply using the `model.save()` and `models.load_model()` methods.
```
# --- Serialize a model
model.save('./cnn.hdf5')
# --- Load a serialized model
del model
model = models.load_model('./cnn.hdf5', compile=False)
```
| true |
code
| 0.816662 | null | null | null | null |
|
# Class Session 2
## Comparing running times for enumerating neighbors of all vertices in a graph (with different graph data structures)
In this notebook we will measure the running time for enumerating the neighbor vertices for three different data structures for representing an undirected graph:
- adjacency matrix
- adjacency list
- edge list
Let's assume that each vertex is labeled with a unique integer number. So if there are N vertices, the vertices are labeled 0, 2, 3, 4, ..., N-1.
First, we will import all of the Python modules that we will need for this exercise:
note how we assign a short name, "np" to the numpy module. This will save typing.
```
import numpy as np
import igraph
import timeit
import itertools
```
Now, define a function that returns the index numbers of the neighbors of a vertex i, when the
graph is stored in adjacency matrix format. So your function will accept as an input a NxN numpy matrix. The function should return a list (of index numbers of the neighbors).
```
def enumerate_matrix(gmat, i):
return np.nonzero(gmat[i,:])[1].tolist()
```
Define a function that enumerates the neighbors of a vertex i, when the
graph is stored in adjacency list format (a list of lists). The function should return a list (of index numbers of the neighbors).
```
def enumerate_adj_list(adj_list, i):
return adj_list[i]
```
Define a function that enumerates the neighbors of a vertex i, when the
graph is stored in edge-list format (a numpy array of length-two-lists); use `numpy.where` and `numpy.unique`. The function should return a list (of index numbers of the neighbors).
```
def enumerate_edge_list(edge_list, i):
inds1 = np.where(edge_list[:,0] == i)[0]
elems1 = edge_list[inds1, 1].tolist()
inds2 = np.where(edge_list[:,1] == i)[0]
elems2 = edge_list[inds2, 0].tolist()
return np.unique(elems1 + elems2).tolist()
```
In this notebook, we are going to create some random networks. We'll use the Barabasi-Albert method, which has two parameters, *n* and *m* (where *n* > *m*). (For more information on the Barabasi-Albert model, see http://barabasi.com/f/622.pdf). In `igraph`, the `igraph.Graph.Barabasi` method will generate a single connected undirected graph with *n* vertices and where the total number *E* of edges is:
E = nm - (m^2 / 2) - m/2
Let's plot a Barabasi-Albert graph generated using *n*=5 and *m*=3:
```
igraph.drawing.plot(igraph.Graph.Barabasi(5,3), bbox=[0,0,200,200])
```
Now we need to write a simulation funtion that generates random graphs and enumerates all neighbors of each vertex in the graph (while computing running time), for each of three different graph data structures (adjacency matrix, adjacency list, and edge list). The function's sole argument "n" is the number of vertices.
It returns a length-three list containing the average running time for enumerating the neighbor vertices of a vertex in the graph.
```
def do_sim_ms(n):
retlist = []
nrep = 10
nsubrep = 10
# this is (sort of) a Python way of doing the R function "replicate":
for _ in itertools.repeat(None, nrep):
# make a random undirected graph with fixed (average) vertex degree = 5
g = igraph.Graph.Barabasi(n, 5)
# get the graph in three different representations
g_matrix = np.matrix(g.get_adjacency().data)
g_adj_list = g.get_adjlist()
g_edge_list = np.array(g.get_edgelist())
start_time = timeit.default_timer()
for _ in itertools.repeat(None, nsubrep):
for i in range(0, n):
enumerate_matrix(g_matrix, i)
matrix_elapsed = timeit.default_timer() - start_time
start_time = timeit.default_timer()
for _ in itertools.repeat(None, nsubrep):
for i in range(0, n):
enumerate_adj_list(g_adj_list, i)
adjlist_elapsed = timeit.default_timer() - start_time
start_time = timeit.default_timer()
for _ in itertools.repeat(None, nsubrep):
for i in range(0, n):
enumerate_edge_list(g_edge_list, i)
edgelist_elapsed = timeit.default_timer() - start_time
retlist.append([matrix_elapsed, adjlist_elapsed, edgelist_elapsed])
resarray = 1000 * np.mean(np.array(retlist), axis=0)/n
resdict = {'adjacency matrix': resarray[0],
'adjacency list': resarray[1],
'edge list': resarray[2]}
# average over replicates and then
# divide by n so that the running time results are on a per-vertex basis
return resdict
```
A simulation with 1000 vertices clearly shows that adjacency list is fastest:
```
do_sim_ms(1000)
```
Now let's quadruple "n". We see the expected behavior, with the running time for the adjacency-matrix and edge-list formats going up when we increase "n", but there is hardly any change in the running time for the graph stored in adjacency list format:
```
do_sim_ms(4000)
```
| true |
code
| 0.365103 | null | null | null | null |
|
# An example of the Nonlinear inference with multiple latent functions.
This notebook briefly shows an example for an inverse problem where multiple latent functions to be infered.
*Keisuke Fujii 3rd Oct. 2016*
## Synthetic observation
Consider we observe a cylindrical transparent mediam with multiple ($N$) lines-of-sight, as shown below.
<img src=figs/abel_inversion.png width=240pt>
<img src=figs/los_theta.png width=180pt>
The local emission intensity $a(r)$, local flow velocity $v(r)$, and local temperature $\sigma(r)$ are functions of radius $r$.,
The local spectrum $\\mathbf{y}_{i,j}$ from $i$-th shell with radius $r_i$ measured with the $j$-th sight line can be written as,
$$
\mathbf{y}_{i,j} = \frac{a(r_i)}{\sqrt{2\pi}\sigma_i}\exp\left[
\frac{(\lambda-\lambda_0 v_i/c \cos\theta_{i,j})^2}{2\sigma_i^2}
\right]
+ \mathbf{e}_i
$$
where $\theta_{i,j}$ is an angle between the $i$-th shell and $j$-th sight line.
$\mathbf{e}$ is i.i.d. Gaussian noise.
## Non-linear model and transform
We assume $\log \mathbf{a}$, $\mathbf{v}$, $\log \mathbf{\sigma}$ follow Gaussian process,
with the identical kernel $\mathrm{K_a}$, $\mathrm{K_v}$, $\mathrm{K_\sigma}$, respecvitvely.
In this notebook, we infer $\mathbf{a},\mathbf{v},\mathbf{\sigma},$ by
1. Stochastic approximation of the variational Gaussian process.
2. Markov Chain Monte-Carlo (MCMC) method.
## Import several libraries including GPinv
```
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import tensorflow as tf
import sys
# In ../testing/ dir, we prepared a small script for generating the above matrix A
sys.path.append('../testing/')
import make_LosMatrix
# Import GPinv
import GPinv
```
## Synthetic signals
Here, we make a synthetic measurement.
The synthetic signal $\mathrm{y}$ is simulated from the grand truth solution $g_true$ and random gaussian noise.
```
n = 30 # radial coordinate
N = 40 # number of cite lines
# radial coordinate
r = np.linspace(0, 1., n)
# synthetic latent function
a = np.exp(-(r-0.3)*(r-0.3)/0.1) + np.exp(-(r+0.3)*(r+0.3)/0.1)
v = 3.*np.exp(-(r-0.6)*(r-0.6)/0.05)*(r-0.6)
sigma = 1.*np.exp(-(r-0.0)*(r-0.0)/0.3) + 0.2
# plotting the latent function
plt.figure(figsize=(4,3))
plt.plot(r, a, label='a')
plt.plot(r, v, label='v')
plt.plot(r, sigma, label='$\sigma$')
plt.plot([0,1], [0,0], '--k')
plt.xlabel('r')
plt.legend()
```
### Prepare the synthetic signal.
```
# los height
z = np.linspace(-0.9,0.9, N)
# Los-matrix
A = make_LosMatrix.make_LosMatrix(r, z)
cosTheta = make_LosMatrix.make_cosTheta(r,z)
print(A.shape, cosTheta.shape)
# Wavelength coordinate
# number of coordinate
m = 50
# coordinate
lam = np.linspace(-3,3,50)
# true (synthetic) signals.
f_true = np.zeros((m, N, n))
for i in range(N):
for j in range(n):
f_true[:,i,j] = a[j] / (np.sqrt(2*np.pi)*sigma[j]) * np.exp(-0.5*((lam-v[j]*cosTheta[i,j])/sigma[j])**2)
# synthetic observation
y_syn = np.zeros((m,N))
for i in range(N):
for j in range(n):
y_syn[:,i] += A[i,j] * f_true[:,i,j]
y_syn+=np.random.randn(m,N)*0.02
# plot
plt.figure(figsize=(5,3))
for i in range(0,N,2):
plt.plot(lam, y_syn[:,i]+0.05*i, '-+', ms=2)
plt.xlabel('lam')
plt.ylabel('signal')
```
# Inference
In order to carry out an inference, a custom **likelihood**, which calculates $p(\mathbf{Y}|\mathbf{f})$ with given $\mathbf{f}$, must be prepared according to the problem.
The method to be implemented is **logp(f,Y)** method, that calculates log-likelihood for data **Y** with given **f**
```
class SpecAbelLikelihood(GPinv.likelihoods.Likelihood):
def __init__(self, Amat, cosTheta, lam):
GPinv.likelihoods.Likelihood.__init__(self)
# Amat, cosTheta shape [m,n]
self.Amat = GPinv.param.DataHolder(Amat)
self.cosT = GPinv.param.DataHolder(cosTheta)
# lam [k,1]
self.lam = GPinv.param.DataHolder(lam.reshape(-1,1))
self.variance = GPinv.param.Param(np.ones(1), GPinv.transforms.positive)
def sample_F(self, F):
"""
:param tf.tensor F: sized [N,n,R]
:return tf.tensor Transformed F: sized [N,k,m]
where N is number of samples to approximate integration.
n is number of radial coordinate,
R is number of latent functions (a, sigma, v),
k is number of wavelength points
m is number of citelines.
"""
N = tf.shape(F)[0]
n = tf.shape(F)[1]
k = tf.shape(self.lam)[0]
m = tf.shape(self.Amat)[0]
# latent functions
a, s, v = tf.unpack(F, axis=-1, num=3) # shape [N,n]
# map a and s by exp
a = tf.exp(a)
s = tf.exp(s)
# Tile latent functions to be sized [N,k,m,n]
a = tf.tile(tf.expand_dims(tf.expand_dims(a, 1),-2), [1,k,m,1])
s = tf.tile(tf.expand_dims(tf.expand_dims(s, 1),-2), [1,k,m,1])
v = tf.tile(tf.expand_dims(tf.expand_dims(v, 1),-2), [1,k,m,1])
Amat = tf.tile(tf.expand_dims(tf.expand_dims(self.Amat,0), 0), [N,k,1,1])
cosT = tf.tile(tf.expand_dims(tf.expand_dims(self.cosT,0), 0), [N,k,1,1])
lam = tf.tile(tf.expand_dims(tf.expand_dims(self.lam, 0),-1), [N,1,m,n])
# Latent spectrum at wavelength k, radial position n, cite line m
f = a / (np.sqrt(2*np.pi)*s) * tf.exp(-0.5*tf.square((lam - v * cosTheta)/s))
# Latent spectrum at wavelength k, cite line m, [N,k,m]
Af = tf.reduce_sum(Amat * f, 3)
return Af
def logp(self, F, Y):
"""
:param tf.tensor Y: sized [k,m]
:return tf.tensor : tensor containing logp values.
"""
# Expand Y to shape [N,k,m]
f_samples = self.sample_F(F)
Y = tf.tile(tf.expand_dims(Y, 0), [tf.shape(f_samples)[0],1,1])
return GPinv.densities.gaussian(f_samples, Y, self.variance)
lik = SpecAbelLikelihood(A, cosTheta, lam)
```
### Kernel
The statistical property is interpreted in Gaussian Process kernel.
Since $a$ and $s$ are cylindrically symmetric functions,
we adopt **RBF_csym** kernel for $\mathbf{K}_a$ and $\mathbf{K}_s$ with **same** lengthscale.
Since $v$ is a cylindrically anti-symmetric functions, we adopt **RBF_casym** kernel for $\mathbf{K}_v$.
```
# kernel for a and s
kern_as = GPinv.kernels.RBF_csym(1, 2)
kern_as.lengthscales = 0.3
# kernel for v
kern_v = GPinv.kernels.RBF_casym(1, 1)
kern_v.lengthscales = 0.3
# Stacked kernel
kern = GPinv.kernels.Stack([kern_as, kern_v])
```
### MeanFunction
To make $a$ and $s$ scale invariant, we added the constant mean_function for them.
We adopt a zero mean for $v$
```
# mean for a and s
mean_as = GPinv.mean_functions.Constant(2, c=np.ones(2)*(-2))
# mean for v
mean_v = GPinv.mean_functions.Zero(1)
# Stacked mean
mean = GPinv.mean_functions.Stack([mean_as, mean_v])
```
## Variational inference by StVGP
In StVGP, we evaluate the posterior $p(\mathbf{f}|\mathbf{y},\theta)$ by approximating as a multivariate Gaussian distribution.
The hyperparameters are obtained at the maximum of the evidence lower bound (ELBO) $p(\mathbf{y}|\theta)$.
```
model_stvgp = GPinv.stvgp.StVGP(r.reshape(-1,1), y_syn,
kern = kern, mean_function = mean,likelihood=lik,
num_latent=3, num_samples=5)
```
## Draw the initial estimate.
```
# Data Y should scatter around the transform F of the GP function f.
sample_F = model_stvgp.sample_F(100)
plt.figure(figsize=(5,3))
# initial estimate
for s in sample_F:
for i in range(0,N,2):
plt.plot(lam, s[:,i]+0.05*i, '-k',lw=1, alpha=0.1)
# observation
for i in range(0,N,2):
plt.plot(lam, y_syn[:,i]+0.05*i, '-o', ms=2)
# plot
plt.xlabel('lam')
plt.ylabel('signal')
```
Although the initial estimate does not seem good, we start from here.
## Iteration
```
# This function visualizes the iteration.
from IPython import display
logf = []
def logger(x):
if (logger.i % 10) == 0:
obj = -model_stvgp._objective(x)[0]
logf.append(obj)
# display
if (logger.i % 100) ==0:
plt.clf()
plt.plot(logf, '--ko', markersize=3, linewidth=1)
plt.ylabel('ELBO')
plt.xlabel('iteration')
display.display(plt.gcf())
display.clear_output(wait=True)
logger.i+=1
logger.i = 1
import time
# start time
start_time = time.time()
plt.figure(figsize=(6,3))
# Rough optimization by scipy.minimize
model_stvgp.optimize()
# Final optimization by tf.train
trainer = tf.train.AdamOptimizer(learning_rate=0.003)
_= model_stvgp.optimize(trainer, maxiter=5000, callback=logger)
display.clear_output(wait=True)
print('Ellapsed Time is', time.time()-start_time, ' (s)')
```
## Plot the result
## Latent function
```
r_new = np.linspace(0.,1., 30)
plt.figure(figsize=(10,3))
# --- StVGP ---
f_pred, f_var = model_stvgp.predict_f(r_new.reshape(-1,1))
f_plus = f_pred + 2.*np.sqrt(f_var)
f_minus = f_pred - 2.*np.sqrt(f_var)
# --- observed and grand truth ---
plt.subplot(1,3,1)
plt.fill_between(r_new, np.exp(f_plus[:,0]), np.exp(f_minus[:,0]), alpha=0.2)
plt.plot(r_new, np.exp(f_pred[:,0]), label='StVGP',lw=1.5)
plt.plot(r, a, '-k', label='true',lw=1.5)
plt.xlabel('$r$: Radial coordinate')
plt.ylabel('$a$: Emissivity')
plt.subplot(1,3,2)
plt.fill_between(r_new, f_plus[:,2], f_minus[:,2], alpha=0.2)
plt.plot(r_new, f_pred[:,2], label='StVGP',lw=1.5)
plt.plot(r, v, '-k', label='true',lw=1.5)
plt.xlabel('$r$: Radial coordinate')
plt.ylabel('$v$: Velocity')
plt.subplot(1,3,3)
plt.fill_between(r_new, np.exp(f_plus[:,1]), np.exp(f_minus[:,1]), alpha=0.2)
plt.plot(r_new, np.exp(f_pred[:,1]), label='StVGP',lw=1.5)
plt.plot(r, sigma, '-k', label='true',lw=1.5)
plt.xlabel('$r$: Radial coordinate')
plt.ylabel('$\sigma$: Temperature')
plt.tight_layout()
```
## Transformed functions
```
# Data Y should scatter around the transform F of the GP function f.
sample_F = model_stvgp.sample_F(100)
plt.figure(figsize=(5,3))
# initial estimate
for s in sample_F:
for i in range(0,N,2):
plt.plot(lam, s[:,i]+0.05*i, '-k', lw=1, alpha=0.1)
# observation
for i in range(0,N,2):
plt.plot(lam, y_syn[:,i]+0.05*i, '-o', ms=2)
plt.xlabel('lam')
plt.ylabel('signal')
```
| true |
code
| 0.598312 | null | null | null | null |
|
# Effect of learning rate
In this notebook, we will discuss the impact of learning rate, which will determine step size and change the distance from initialzation to the solution, which contributes to breaking the NTK regime.
```
import torch
from torch import optim, nn
from torchvision import datasets, transforms
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt
import copy
import os
import random
from models import train_ntk
os.environ["CUDA_VISIBLE_DEVICES"] = "3"
# training parameters
batch_size = 128
transform = transforms.Compose([
transforms.ToTensor()
])
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('data', train=True, download=True, transform=transform),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('data', train=False, download=True, transform=transform),
batch_size=batch_size, shuffle=True)
h_dim = 5000
train_epoch = 100
alpha_set = [h_dim**(0.1*k) for k in range(11)]
alpha = alpha_set[5]
srr1,saa1,sll1 = train_ntk(train_loader, test_loader,h_dim,alpha,train_epoch,1)
srr2,saa2,sll2 = train_ntk(train_loader, test_loader,h_dim,alpha,train_epoch,.1)
srr3,saa3,sll3 = train_ntk(train_loader, test_loader,h_dim,alpha,train_epoch,.01)
```
## Plot
According to the notebook, a large learning rate will directly break the NTK regime. Since all the proof are approximating the gradient flow (infinite small learning rate), a large step makes the parameter get out of the initialization neighborhood.
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("whitegrid")
from scipy.ndimage.filters import gaussian_filter1d
plt.plot(np.arange(train_epoch)+1,100*gaussian_filter1d(np.array(saa1)[:,0],3),label = r'NN, $\eta = 1$')
plt.plot(np.arange(train_epoch)+1,100*gaussian_filter1d(np.array(saa2)[:,0],3),label = r'NN, $\eta = 0.1$')
plt.plot(np.arange(train_epoch)+1,100*gaussian_filter1d(np.array(saa3)[:,0],3),label = r'NN, $\eta = 0.01$')
plt.plot(np.arange(train_epoch)+1,100*gaussian_filter1d(np.array(saa1)[:,1],3),linestyle='dashed',label = r'NTK, $\eta = 1$')
plt.plot(np.arange(train_epoch)+1,100*gaussian_filter1d(np.array(saa2)[:,1],3),linestyle='dashed',label = r'NTK, $\eta = 0.1$')
plt.plot(np.arange(train_epoch)+1,100*gaussian_filter1d(np.array(saa3)[:,1],3,),linestyle='dashed',label = r'NTK, $\eta = 0.01$')
#plt.plot(np.arange(50)+1,np.array(srr4)[:,0],label = r'$\alpha = m^{0.7}$')
plt.legend()
plt.ylabel(r'accuracy (%)',fontsize=15)
plt.xlabel('epoch',fontsize=15)
#plt.ylim([0.8,0.99])
#plt.yscale('log')
plt.legend(fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("whitegrid")
plt.plot(np.arange(train_epoch)+1,np.array(srr1)[:,0],label = r'$\eta = 1$')
plt.plot(np.arange(train_epoch)+1,np.array(srr2)[:,0],label = r'$\eta = 0.1$')
plt.plot(np.arange(train_epoch)+1,np.array(srr3)[:,0],label = r'$\eta = 0.01$')
plt.legend(fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=11)
plt.ylabel(r'${\Vert \theta-\tilde{\theta} \Vert}$',fontsize=11)
plt.xlabel('epoch',fontsize=15)
#plt.ylim([0.1,10])
plt.yscale('log')
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("whitegrid")
plt.plot(np.arange(train_epoch)+1,np.array(srr1)[:,1],label = r'$\eta = 1$')
plt.plot(np.arange(train_epoch)+1,np.array(srr2)[:,1],label = r'$\eta = 0.1$')
plt.plot(np.arange(train_epoch)+1,np.array(srr3)[:,1],label = r'$\eta = 0.01$')
plt.legend(fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=11)
plt.ylabel(r'${\Vert u-\tilde{u} \Vert}$',fontsize=11)
plt.xlabel('epoch',fontsize=15)
plt.ylim([0.8,100])
plt.yscale('log')
```
| true |
code
| 0.730097 | null | null | null | null |
|
## Day 3: Cells in Silicon
Welcome to Day 3! Today, we start with our discussion with the Hodgkin Huxley Neurons and how we can simulate them in python using Tensorflow and Numerical Integration.
### What is the Hodgkin Huxley Neuron Model?
(Modified from Neuronal Dynamics, EPFL)
Hodgkin and Huxley performed many experiments on the giant axon of the squid and found three different types of ion currents - sodium, potassium, and a leak current. They found that specific voltage-dependent ion channels, for sodium and for potassium, control the flow of those ions through the cell membrane from different electrophysiology studies involving phamacological blocking of ion channels. The leak current essentially takes care of other channel types which are not described explicitly.
<img src="cd.png" alt="cd.png" width="600"/>
The Hodgkin-Huxley model of neurons can easily be understood with the help of a circuit diagram. The semipermeable cell membrane separates the interior of the cell from the extracellular liquid and acts as a capacitor. If an input current I(t) is injected into the cell, it may add further charge on the capacitor, or leak through the channels in the cell membrane. Because of active ion transport through the cell membrane, the ion concentration inside the cell is different from that in the extracellular liquid. The Nernst potential generated by the difference in ion concentration is represented by a battery.
Let us now translate the above considerations into mathematical equations. The conservation of electric charge on a piece of membrane implies that the applied current $I(t)$ may be split in a capacitive current $I_C$ which charges the capacitor $C_m = 1 \mu F/cm^2$ and further components $I_k$ which pass through the ion channels. Thus $I(t) = I_C(t) + \sum_kI_k(t)$ where the sum runs over all ion channels.
In the standard Hodgkin-Huxley model, there are only three types of channel: a Sodium channel, a Potassium channel and an unspecific leakage channel. From the definition of a capacitance $C_m=\frac{q}{u}$, $I_C=C_m\frac{du}{dt}$ where $q$ is a charge and $u$ the voltage across the capacitor. Thus the model becomes:
$$C_m\frac{du}{dt}=−I_{Na}(t)−I_{K}(t)−I_{L}(𝑡)+I(t)$$
In biological terms, $u$ is the voltage across the membrane. Hogkin and Huxley found the Na and K ion currents to be dependent on the voltage and of the form given below:
$$I_{Na} = g_{Na}m^3h(u−E_{Na})$$
$$I_K = g_Kn^4(u−E_K)$$
$$I_L = g_L(u−E_L)$$
where $E_{Na}=50\ mV$, $E_K = -95\ mV$ and $E_L=-55\ mV$ are the reversal potentials; $g_{Na} = 100\ \mu S/cm^2$, $g_K = 10\ \mu S/cm^2$ and $g_L = 0.15\ \mu S/cm^2$ are the channel conductances; and m,h, and n are gating variables that follow the dynamics given by:
$$\frac{dm}{dt} = - \frac{1}{\tau_m}(m-m_0)$$
$$\frac{dh}{dt} = - \frac{1}{\tau_h}(h-h_0)$$
$$\frac{dn}{dt} = - \frac{1}{\tau_n}(n-n_0)$$
where $\tau_m$, $\tau_h$ and $\tau_n$ are voltage dependent time constants and $m_0$, $h_0$ and $n_0$ are voltage dependent asymptotic gating values. These functions are empirically determined for different types of neurons.
<img src="dyn.png" alt="dyn.png" width="800"/>
#### Recalling the Generalized TensorFlow Integrator
On day 2, we had created a RK4 based numerical integrator. We recall the implementation of the Integrator.
```
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
%matplotlib inline
def tf_check_type(t, y0): # Ensure Input is Correct
if not (y0.dtype.is_floating and t.dtype.is_floating):
raise TypeError('Error in Datatype')
class _Tf_Integrator():
def integrate(self, func, y0, t):
time_delta_grid = t[1:] - t[:-1]
def scan_func(y, t_dt):
t, dt = t_dt
dy = self._step_func(func,t,dt,y) # Make code more modular.
return y + dy
y = tf.scan(scan_func, (t[:-1], time_delta_grid),y0)
return tf.concat([[y0], y], axis=0)
def _step_func(self, func, t, dt, y):
k1 = func(y, t)
half_step = t + dt / 2
dt_cast = tf.cast(dt, y.dtype) # Failsafe
k2 = func(y + dt_cast * k1 / 2, half_step)
k3 = func(y + dt_cast * k2 / 2, half_step)
k4 = func(y + dt_cast * k3, t + dt)
return tf.add_n([k1, 2 * k2, 2 * k3, k4]) * (dt_cast / 6)
def odeint(func, y0, t):
t = tf.convert_to_tensor(t, preferred_dtype=tf.float64, name='t')
y0 = tf.convert_to_tensor(y0, name='y0')
tf_check_type(y0,t)
return _Tf_Integrator().integrate(func,y0,t)
```
#### Implementing the Dynamical Function for an Hodkin Huxley Neuron
Recall, a simple Hodgkin Huxley Neuron has a 4 main dynamical variables:
$V = Membrane\ Potential$
$m = Sodium\ Activation\ Gating\ Variable$
$h = Sodium\ Inactivation\ Gating\ Variable$
$n = Potassium\ Channel\ Gating\ Variable$
And the dynamics are given by:
$$C_m\frac{dV}{dt} = I_{injected} - I_{Na} - I_K - I_L$$
$$\frac{dm}{dt} = - \frac{1}{\tau_m}(m-m_0)$$
$$\frac{dh}{dt} = - \frac{1}{\tau_h}(h-h_0)$$
$$\frac{dn}{dt} = - \frac{1}{\tau_n}(n-n_0)$$
where the values of $\tau_m$, $\tau_h$, $\tau_n$, $m_0$, $h_0$, $n_0$ are given from the equations mentioned earlier.
##### Step 1: Defining Parameters of the Neuron
```
C_m = 1 # Membrane Capacitance
g_K = 10
E_K = -95
g_Na = 100
E_Na = 50
g_L = 0.15
E_L = -55
```
##### Step 2: Defining functions that calculate $\tau_m$, $\tau_h$, $\tau_n$, $m_0$, $h_0$, $n_0$
Note: Always use Tensorflow functions for all mathematical operations.
For our Hodgkin Huxley Model, we will determine the values of $\tau_m$, $\tau_h$, $\tau_n$, $m_0$, $h_0$, $n_0$ by the following equations:
<img src="eqns1.png" alt="eqns1.png" width="600"/>
```
def K_prop(V):
T = 22
phi = 3.0**((T-36.0)/10)
V_ = V-(-50)
alpha_n = 0.02*(15.0 - V_)/(tf.exp((15.0 - V_)/5.0) - 1.0)
beta_n = 0.5*tf.exp((10.0 - V_)/40.0)
t_n = 1.0/((alpha_n+beta_n)*phi)
n_0 = alpha_n/(alpha_n+beta_n)
return n_0, t_n
def Na_prop(V):
T = 22
phi = 3.0**((T-36)/10)
V_ = V-(-50)
alpha_m = 0.32*(13.0 - V_)/(tf.exp((13.0 - V_)/4.0) - 1.0)
beta_m = 0.28*(V_ - 40.0)/(tf.exp((V_ - 40.0)/5.0) - 1.0)
alpha_h = 0.128*tf.exp((17.0 - V_)/18.0)
beta_h = 4.0/(tf.exp((40.0 - V_)/5.0) + 1.0)
t_m = 1.0/((alpha_m+beta_m)*phi)
t_h = 1.0/((alpha_h+beta_h)*phi)
m_0 = alpha_m/(alpha_m+beta_m)
h_0 = alpha_h/(alpha_h+beta_h)
return m_0, t_m, h_0, t_h
```
##### Step 3: Defining function that calculate Neuronal currents
<img src="eqns2.png" alt="eqns2.png" width="600"/>
```
def I_K(V, n):
return g_K * n**4 * (V - E_K)
def I_Na(V, m, h):
return g_Na * m**3 * h * (V - E_Na)
def I_L(V):
return g_L * (V - E_L)
```
##### Step 4: Define the function dX/dt where X is the State Vector
```
def dXdt(X, t):
V = X[0:1]
m = X[1:2]
h = X[2:3]
n = X[3:4]
dVdt = (5 - I_Na(V, m, h) - I_K(V, n) - I_L(V)) / C_m
# Here the current injection I_injected = 5 uA
m0,tm,h0,th = Na_prop(V)
n0,tn = K_prop(V)
dmdt = - (1.0/tm)*(m-m0)
dhdt = - (1.0/th)*(h-h0)
dndt = - (1.0/tn)*(n-n0)
out = tf.concat([dVdt,dmdt,dhdt,dndt],0)
return out
```
##### Step 5: Define Initial Condition and Integrate
```
y0 = tf.constant([-71,0,0,0], dtype=tf.float64)
epsilon = 0.01
t = np.arange(0,200,epsilon)
state = odeint(dXdt,y0,t)
with tf.Session() as sess:
state = sess.run(state)
```
##### Step 6: Plot Output
```
plt.style.use('seaborn-colorblind')
plt.style.use('seaborn-ticks')
ax = plt.subplot(111)
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
ax.grid(color='#DDDDDD', linestyle='--', linewidth=0.3)
plt.plot(t,state.T[0,:])
plt.xlabel("Time (in ms)")
plt.ylabel("Voltage (in mV)")
fig = plt.gcf()
fig.savefig("fig4.eps",format='eps')
plt.show()
```
#### Simulating Multiple Independent HH Neurons at the Same Time
Although, simulating a Single Hodgkin-Huxley Neuron is possible in TensorFlow, the real ability of tensorflow can be seen only when a large number of simultaneous diffential equations are to be solved at the the same time. Let's try to simulate 20 independent HH neurons with different input currents and characterise the firing rates.
##### Methods of Parallelization
TensorFlow has the intrinsic ability to speed up any and all Tensor computations using available multi-cores, and GPU/TPU setups. There are two major parts of the code where TensorFlow can help us really speed up the computation:
1. **RK4 Steps:** Since the TensorFlow implementation of the Integrator utilizes Tensor calculations, TensorFlow will automatically speed it up.
2. **Functional Evaluations:** Looking at Dynamical Equations that describe the neuronal dynamics, its easy to notice that all simple HH Neurons share the same or atleast similar dynamical equations but will vary only in the values of parameters. We can exploit this to speed up the computations.
Say $\vec{X}=[V,m,n,h]$ is the state vector of a single neuron and its dynamics are defined using parameters $C_m,g_K,...E_L$ equations of the form: $$\frac{d\vec{X}}{dt} = [f_1(\vec{X},C_m,g_K,...E_L),f_2(\vec{X},C_m,g_K,...E_L)...f_m(\vec{X},C_m,g_K,...E_L)]$$ We have to somehow convert these to a form in which all evaluations are done as vector calculations and NOT scalar calculations.
So, what we need for a system of n neurons is to have a method to evaluate the updation of $\mathbf{X}=[\vec{X_1},\vec{X_2}...\vec{X_n}]$ where $\vec{X_i}=[V_1,m_1,n_1,h_1]$ is the state vector of the $i$th neuron. Now there is a simple trick that allows us to maximize the parallel processing. Each neuron represented by $\vec{X_i}$ has a distinct set of parameters and differential equations.
Now, despite the parameters being different, the functional forms of the updation is similar for the same state variable for different neurons. Thus, the trick is to reorganize $\mathbf{X}$ as $\mathbf{X'}=[(V_1,V_2,...V_n),(m_1,m_2,...m_n),(h_1,h_2,...h_n),(n_1,n_2,...n_n)]=[\vec{V},\vec{m},\vec{h},\vec{n}]$. And the parameters as $\vec{C_m},\vec{g_K}$ and so on.
Now that we know the trick, what is the benefit? Earlier, each state variable (say $V_i$) had a DE of the form: $$\frac{dV_i}{dt}=f(V_i,m_i,h_i,n_i,C_{m_i},g_{K_i}...)$$ This is now easily parallelizable using a vector computation of a form: $$\frac{d\vec{V}}{dt}=f(\vec{V},\vec{m},\vec{h},\vec{n},\vec{C_m},\vec{g_K}...)$$
Thus we can do the calculations as:
$$\frac{d\mathbf{X'}}{dt}= \Big[\frac{d\vec{V}}{dt},\frac{d\vec{m}}{dt},\frac{d\vec{h}}{dt},\frac{d\vec{n}}{dt}\Big]$$
```
n_n = 20 # number of simultaneous neurons to simulate
# parameters will now become n_n-vectors
C_m = [1.0]*n_n
g_K = [10.0]*n_n
E_K = [-95.0]*n_n
g_Na = [100]*n_n
E_Na = [50]*n_n
g_L = [0.15]*n_n
E_L = [-55.0]*n_n
def K_prop(V):
T = 22
phi = 3.0**((T-36.0)/10)
V_ = V-(-50)
alpha_n = 0.02*(15.0 - V_)/(tf.exp((15.0 - V_)/5.0) - 1.0)
beta_n = 0.5*tf.exp((10.0 - V_)/40.0)
t_n = 1.0/((alpha_n+beta_n)*phi)
n_0 = alpha_n/(alpha_n+beta_n)
return n_0, t_n
def Na_prop(V):
T = 22
phi = 3.0**((T-36)/10)
V_ = V-(-50)
alpha_m = 0.32*(13.0 - V_)/(tf.exp((13.0 - V_)/4.0) - 1.0)
beta_m = 0.28*(V_ - 40.0)/(tf.exp((V_ - 40.0)/5.0) - 1.0)
alpha_h = 0.128*tf.exp((17.0 - V_)/18.0)
beta_h = 4.0/(tf.exp((40.0 - V_)/5.0) + 1.0)
t_m = 1.0/((alpha_m+beta_m)*phi)
t_h = 1.0/((alpha_h+beta_h)*phi)
m_0 = alpha_m/(alpha_m+beta_m)
h_0 = alpha_h/(alpha_h+beta_h)
return m_0, t_m, h_0, t_h
def I_K(V, n):
return g_K * n**4 * (V - E_K)
def I_Na(V, m, h):
return g_Na * m**3 * h * (V - E_Na)
def I_L(V):
return g_L * (V - E_L)
def dXdt(X, t):
V = X[:1*n_n] # First n_n values are Membrane Voltage
m = X[1*n_n:2*n_n] # Next n_n values are Sodium Activation Gating Variables
h = X[2*n_n:3*n_n] # Next n_n values are Sodium Inactivation Gating Variables
n = X[3*n_n:] # Last n_n values are Potassium Gating Variables
dVdt = (np.linspace(0,10,n_n) - I_Na(V, m, h) - I_K(V, n) -I_L(V)) / C_m
# Input current is linearly varied between 0 and 10
m0,tm,h0,th = Na_prop(V)
n0,tn = K_prop(V)
dmdt = - (1.0/tm)*(m-m0)
dhdt = - (1.0/th)*(h-h0)
dndt = - (1.0/tn)*(n-n0)
out = tf.concat([dVdt,dmdt,dhdt,dndt],0)
return out
y0 = tf.constant([-71]*n_n+[0,0,0]*n_n, dtype=tf.float64)
epsilon = 0.01
t = np.arange(0,200,epsilon)
state = odeint(dXdt,y0,t)
with tf.Session() as sess:
state = sess.run(state)
plt.style.use('seaborn-colorblind')
plt.style.use('seaborn-ticks')
plt.figure(figsize=(12,17))
for i in range(20):
ax = plt.subplot(10,2,i+1)
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
ax.grid(color='#DDDDDD', linestyle='--', linewidth=0.3)
plt.plot(t,state[:,i])
plt.title("Injected Current = {:0.1f}".format(i/2))
plt.ylim([-90,60])
plt.xlabel("Time (in ms)")
plt.ylabel("Voltage (in mV)")
plt.tight_layout()
fig = plt.gcf()
fig.savefig("fig5.eps",format='eps')
plt.show()
```
#### Quantifying the Firing Rates against Input Current
One way to quantify the firing rate is to perform a fourier analysis and find peak frequency, but an easier way to find the rate is to see how many times it crosses a threshold say 0 mV in a given time, here it is for 200ms = 0.2s, and find the rate.
```
plt.style.use('seaborn-colorblind')
plt.style.use('seaborn-ticks')
ax = plt.subplot(111)
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
ax.grid(color='#DDDDDD', linestyle='--', linewidth=0.3)
plt.plot(np.linspace(0,10,20),np.bitwise_and(state[:-1,:20]<0,state[1:,:20]>0).sum(axis=0)/0.2,"o")
# plt.plot(np.linspace(0,10,20),np.bitwise_and(state[:-1,:20]<0,state[1:,:20]>0).sum(axis=0)/0.2,":")
plt.xlabel("Injected Current(mA)")
plt.ylabel("Firing Rate (Hz)")
fig = plt.gcf()
fig.savefig("fig6.eps",format='eps')
plt.show()
```
| true |
code
| 0.554591 | null | null | null | null |
|
# Styling
*New in version 0.17.1*
<span style="color: red">*Provisional: This is a new feature and still under development. We'll be adding features and possibly making breaking changes in future releases. We'd love to hear your feedback.*</span>
This document is written as a Jupyter Notebook, and can be viewed or downloaded [here](http://nbviewer.ipython.org/github/pandas-dev/pandas/blob/master/doc/source/style.ipynb).
You can apply **conditional formatting**, the visual styling of a DataFrame
depending on the data within, by using the ``DataFrame.style`` property.
This is a property that returns a ``Styler`` object, which has
useful methods for formatting and displaying DataFrames.
The styling is accomplished using CSS.
You write "style functions" that take scalars, `DataFrame`s or `Series`, and return *like-indexed* DataFrames or Series with CSS `"attribute: value"` pairs for the values.
These functions can be incrementally passed to the `Styler` which collects the styles before rendering.
## Building Styles
Pass your style functions into one of the following methods:
- ``Styler.applymap``: elementwise
- ``Styler.apply``: column-/row-/table-wise
Both of those methods take a function (and some other keyword arguments) and applies your function to the DataFrame in a certain way.
`Styler.applymap` works through the DataFrame elementwise.
`Styler.apply` passes each column or row into your DataFrame one-at-a-time or the entire table at once, depending on the `axis` keyword argument.
For columnwise use `axis=0`, rowwise use `axis=1`, and for the entire table at once use `axis=None`.
For `Styler.applymap` your function should take a scalar and return a single string with the CSS attribute-value pair.
For `Styler.apply` your function should take a Series or DataFrame (depending on the axis parameter), and return a Series or DataFrame with an identical shape where each value is a string with a CSS attribute-value pair.
Let's see some examples.
```
import matplotlib.pyplot
# We have this here to trigger matplotlib's font cache stuff.
# This cell is hidden from the output
import pandas as pd
import numpy as np
np.random.seed(24)
df = pd.DataFrame({'A': np.linspace(1, 10, 10)})
df = pd.concat([df, pd.DataFrame(np.random.randn(10, 4), columns=list('BCDE'))],
axis=1)
df.iloc[0, 2] = np.nan
```
Here's a boring example of rendering a DataFrame, without any (visible) styles:
```
df.style
```
*Note*: The `DataFrame.style` attribute is a property that returns a `Styler` object. `Styler` has a `_repr_html_` method defined on it so they are rendered automatically. If you want the actual HTML back for further processing or for writing to file call the `.render()` method which returns a string.
The above output looks very similar to the standard DataFrame HTML representation. But we've done some work behind the scenes to attach CSS classes to each cell. We can view these by calling the `.render` method.
```
df.style.highlight_null().render().split('\n')[:10]
```
The `row0_col2` is the identifier for that particular cell. We've also prepended each row/column identifier with a UUID unique to each DataFrame so that the style from one doesn't collide with the styling from another within the same notebook or page (you can set the `uuid` if you'd like to tie together the styling of two DataFrames).
When writing style functions, you take care of producing the CSS attribute / value pairs you want. Pandas matches those up with the CSS classes that identify each cell.
Let's write a simple style function that will color negative numbers red and positive numbers black.
```
def color_negative_red(val):
"""
Takes a scalar and returns a string with
the css property `'color: red'` for negative
strings, black otherwise.
"""
color = 'red' if val < 0 else 'black'
return 'color: %s' % color
```
In this case, the cell's style depends only on it's own value.
That means we should use the `Styler.applymap` method which works elementwise.
```
s = df.style.applymap(color_negative_red)
s
```
Notice the similarity with the standard `df.applymap`, which operates on DataFrames elementwise. We want you to be able to reuse your existing knowledge of how to interact with DataFrames.
Notice also that our function returned a string containing the CSS attribute and value, separated by a colon just like in a `<style>` tag. This will be a common theme.
Finally, the input shapes matched. `Styler.applymap` calls the function on each scalar input, and the function returns a scalar output.
Now suppose you wanted to highlight the maximum value in each column.
We can't use `.applymap` anymore since that operated elementwise.
Instead, we'll turn to `.apply` which operates columnwise (or rowwise using the `axis` keyword). Later on we'll see that something like `highlight_max` is already defined on `Styler` so you wouldn't need to write this yourself.
```
def highlight_max(s):
'''
highlight the maximum in a Series yellow.
'''
is_max = s == s.max()
return ['background-color: yellow' if v else '' for v in is_max]
df.style.apply(highlight_max)
```
In this case the input is a `Series`, one column at a time.
Notice that the output shape of `highlight_max` matches the input shape, an array with `len(s)` items.
We encourage you to use method chains to build up a style piecewise, before finally rending at the end of the chain.
```
df.style.\
applymap(color_negative_red).\
apply(highlight_max)
```
Above we used `Styler.apply` to pass in each column one at a time.
<span style="background-color: #DEDEBE">*Debugging Tip*: If you're having trouble writing your style function, try just passing it into <code style="background-color: #DEDEBE">DataFrame.apply</code>. Internally, <code style="background-color: #DEDEBE">Styler.apply</code> uses <code style="background-color: #DEDEBE">DataFrame.apply</code> so the result should be the same.</span>
What if you wanted to highlight just the maximum value in the entire table?
Use `.apply(function, axis=None)` to indicate that your function wants the entire table, not one column or row at a time. Let's try that next.
We'll rewrite our `highlight-max` to handle either Series (from `.apply(axis=0 or 1)`) or DataFrames (from `.apply(axis=None)`). We'll also allow the color to be adjustable, to demonstrate that `.apply`, and `.applymap` pass along keyword arguments.
```
def highlight_max(data, color='yellow'):
'''
highlight the maximum in a Series or DataFrame
'''
attr = 'background-color: {}'.format(color)
if data.ndim == 1: # Series from .apply(axis=0) or axis=1
is_max = data == data.max()
return [attr if v else '' for v in is_max]
else: # from .apply(axis=None)
is_max = data == data.max().max()
return pd.DataFrame(np.where(is_max, attr, ''),
index=data.index, columns=data.columns)
```
When using ``Styler.apply(func, axis=None)``, the function must return a DataFrame with the same index and column labels.
```
df.style.apply(highlight_max, color='darkorange', axis=None)
```
### Building Styles Summary
Style functions should return strings with one or more CSS `attribute: value` delimited by semicolons. Use
- `Styler.applymap(func)` for elementwise styles
- `Styler.apply(func, axis=0)` for columnwise styles
- `Styler.apply(func, axis=1)` for rowwise styles
- `Styler.apply(func, axis=None)` for tablewise styles
And crucially the input and output shapes of `func` must match. If `x` is the input then ``func(x).shape == x.shape``.
## Finer Control: Slicing
Both `Styler.apply`, and `Styler.applymap` accept a `subset` keyword.
This allows you to apply styles to specific rows or columns, without having to code that logic into your `style` function.
The value passed to `subset` behaves simlar to slicing a DataFrame.
- A scalar is treated as a column label
- A list (or series or numpy array)
- A tuple is treated as `(row_indexer, column_indexer)`
Consider using `pd.IndexSlice` to construct the tuple for the last one.
```
df.style.apply(highlight_max, subset=['B', 'C', 'D'])
```
For row and column slicing, any valid indexer to `.loc` will work.
```
df.style.applymap(color_negative_red,
subset=pd.IndexSlice[2:5, ['B', 'D']])
```
Only label-based slicing is supported right now, not positional.
If your style function uses a `subset` or `axis` keyword argument, consider wrapping your function in a `functools.partial`, partialing out that keyword.
```python
my_func2 = functools.partial(my_func, subset=42)
```
## Finer Control: Display Values
We distinguish the *display* value from the *actual* value in `Styler`.
To control the display value, the text is printed in each cell, use `Styler.format`. Cells can be formatted according to a [format spec string](https://docs.python.org/3/library/string.html#format-specification-mini-language) or a callable that takes a single value and returns a string.
```
df.style.format("{:.2%}")
```
Use a dictionary to format specific columns.
```
df.style.format({'B': "{:0<4.0f}", 'D': '{:+.2f}'})
```
Or pass in a callable (or dictionary of callables) for more flexible handling.
```
df.style.format({"B": lambda x: "±{:.2f}".format(abs(x))})
```
## Builtin Styles
Finally, we expect certain styling functions to be common enough that we've included a few "built-in" to the `Styler`, so you don't have to write them yourself.
```
df.style.highlight_null(null_color='red')
```
You can create "heatmaps" with the `background_gradient` method. These require matplotlib, and we'll use [Seaborn](http://stanford.edu/~mwaskom/software/seaborn/) to get a nice colormap.
```
import seaborn as sns
cm = sns.light_palette("green", as_cmap=True)
s = df.style.background_gradient(cmap=cm)
s
```
`Styler.background_gradient` takes the keyword arguments `low` and `high`. Roughly speaking these extend the range of your data by `low` and `high` percent so that when we convert the colors, the colormap's entire range isn't used. This is useful so that you can actually read the text still.
```
# Uses the full color range
df.loc[:4].style.background_gradient(cmap='viridis')
# Compress the color range
(df.loc[:4]
.style
.background_gradient(cmap='viridis', low=.5, high=0)
.highlight_null('red'))
```
There's also `.highlight_min` and `.highlight_max`.
```
df.style.highlight_max(axis=0)
```
Use `Styler.set_properties` when the style doesn't actually depend on the values.
```
df.style.set_properties(**{'background-color': 'black',
'color': 'lawngreen',
'border-color': 'white'})
```
### Bar charts
You can include "bar charts" in your DataFrame.
```
df.style.bar(subset=['A', 'B'], color='#d65f5f')
```
New in version 0.20.0 is the ability to customize further the bar chart: You can now have the `df.style.bar` be centered on zero or midpoint value (in addition to the already existing way of having the min value at the left side of the cell), and you can pass a list of `[color_negative, color_positive]`.
Here's how you can change the above with the new `align='mid'` option:
```
df.style.bar(subset=['A', 'B'], align='mid', color=['#d65f5f', '#5fba7d'])
```
The following example aims to give a highlight of the behavior of the new align options:
```
import pandas as pd
from IPython.display import HTML
# Test series
test1 = pd.Series([-100,-60,-30,-20], name='All Negative')
test2 = pd.Series([10,20,50,100], name='All Positive')
test3 = pd.Series([-10,-5,0,90], name='Both Pos and Neg')
head = """
<table>
<thead>
<th>Align</th>
<th>All Negative</th>
<th>All Positive</th>
<th>Both Neg and Pos</th>
</thead>
</tbody>
"""
aligns = ['left','zero','mid']
for align in aligns:
row = "<tr><th>{}</th>".format(align)
for serie in [test1,test2,test3]:
s = serie.copy()
s.name=''
row += "<td>{}</td>".format(s.to_frame().style.bar(align=align,
color=['#d65f5f', '#5fba7d'],
width=100).render()) #testn['width']
row += '</tr>'
head += row
head+= """
</tbody>
</table>"""
HTML(head)
```
## Sharing Styles
Say you have a lovely style built up for a DataFrame, and now you want to apply the same style to a second DataFrame. Export the style with `df1.style.export`, and import it on the second DataFrame with `df1.style.set`
```
df2 = -df
style1 = df.style.applymap(color_negative_red)
style1
style2 = df2.style
style2.use(style1.export())
style2
```
Notice that you're able share the styles even though they're data aware. The styles are re-evaluated on the new DataFrame they've been `use`d upon.
## Other Options
You've seen a few methods for data-driven styling.
`Styler` also provides a few other options for styles that don't depend on the data.
- precision
- captions
- table-wide styles
- hiding the index or columns
Each of these can be specified in two ways:
- A keyword argument to `Styler.__init__`
- A call to one of the `.set_` or `.hide_` methods, e.g. `.set_caption` or `.hide_columns`
The best method to use depends on the context. Use the `Styler` constructor when building many styled DataFrames that should all share the same properties. For interactive use, the`.set_` and `.hide_` methods are more convenient.
### Precision
You can control the precision of floats using pandas' regular `display.precision` option.
```
with pd.option_context('display.precision', 2):
html = (df.style
.applymap(color_negative_red)
.apply(highlight_max))
html
```
Or through a `set_precision` method.
```
df.style\
.applymap(color_negative_red)\
.apply(highlight_max)\
.set_precision(2)
```
Setting the precision only affects the printed number; the full-precision values are always passed to your style functions. You can always use `df.round(2).style` if you'd prefer to round from the start.
### Captions
Regular table captions can be added in a few ways.
```
df.style.set_caption('Colormaps, with a caption.')\
.background_gradient(cmap=cm)
```
### Table Styles
The next option you have are "table styles".
These are styles that apply to the table as a whole, but don't look at the data.
Certain sytlings, including pseudo-selectors like `:hover` can only be used this way.
```
from IPython.display import HTML
def hover(hover_color="#ffff99"):
return dict(selector="tr:hover",
props=[("background-color", "%s" % hover_color)])
styles = [
hover(),
dict(selector="th", props=[("font-size", "150%"),
("text-align", "center")]),
dict(selector="caption", props=[("caption-side", "bottom")])
]
html = (df.style.set_table_styles(styles)
.set_caption("Hover to highlight."))
html
```
`table_styles` should be a list of dictionaries.
Each dictionary should have the `selector` and `props` keys.
The value for `selector` should be a valid CSS selector.
Recall that all the styles are already attached to an `id`, unique to
each `Styler`. This selector is in addition to that `id`.
The value for `props` should be a list of tuples of `('attribute', 'value')`.
`table_styles` are extremely flexible, but not as fun to type out by hand.
We hope to collect some useful ones either in pandas, or preferable in a new package that [builds on top](#Extensibility) the tools here.
### Hiding the Index or Columns
The index can be hidden from rendering by calling `Styler.hide_index`. Columns can be hidden from rendering by calling `Styler.hide_columns` and passing in the name of a column, or a slice of columns.
```
df.style.hide_index()
df.style.hide_columns(['C','D'])
```
### CSS Classes
Certain CSS classes are attached to cells.
- Index and Column names include `index_name` and `level<k>` where `k` is its level in a MultiIndex
- Index label cells include
+ `row_heading`
+ `row<n>` where `n` is the numeric position of the row
+ `level<k>` where `k` is the level in a MultiIndex
- Column label cells include
+ `col_heading`
+ `col<n>` where `n` is the numeric position of the column
+ `level<k>` where `k` is the level in a MultiIndex
- Blank cells include `blank`
- Data cells include `data`
### Limitations
- DataFrame only `(use Series.to_frame().style)`
- The index and columns must be unique
- No large repr, and performance isn't great; this is intended for summary DataFrames
- You can only style the *values*, not the index or columns
- You can only apply styles, you can't insert new HTML entities
Some of these will be addressed in the future.
### Terms
- Style function: a function that's passed into `Styler.apply` or `Styler.applymap` and returns values like `'css attribute: value'`
- Builtin style functions: style functions that are methods on `Styler`
- table style: a dictionary with the two keys `selector` and `props`. `selector` is the CSS selector that `props` will apply to. `props` is a list of `(attribute, value)` tuples. A list of table styles passed into `Styler`.
## Fun stuff
Here are a few interesting examples.
`Styler` interacts pretty well with widgets. If you're viewing this online instead of running the notebook yourself, you're missing out on interactively adjusting the color palette.
```
from IPython.html import widgets
@widgets.interact
def f(h_neg=(0, 359, 1), h_pos=(0, 359), s=(0., 99.9), l=(0., 99.9)):
return df.style.background_gradient(
cmap=sns.palettes.diverging_palette(h_neg=h_neg, h_pos=h_pos, s=s, l=l,
as_cmap=True)
)
def magnify():
return [dict(selector="th",
props=[("font-size", "4pt")]),
dict(selector="td",
props=[('padding', "0em 0em")]),
dict(selector="th:hover",
props=[("font-size", "12pt")]),
dict(selector="tr:hover td:hover",
props=[('max-width', '200px'),
('font-size', '12pt')])
]
np.random.seed(25)
cmap = cmap=sns.diverging_palette(5, 250, as_cmap=True)
bigdf = pd.DataFrame(np.random.randn(20, 25)).cumsum()
bigdf.style.background_gradient(cmap, axis=1)\
.set_properties(**{'max-width': '80px', 'font-size': '1pt'})\
.set_caption("Hover to magnify")\
.set_precision(2)\
.set_table_styles(magnify())
```
## Export to Excel
*New in version 0.20.0*
<span style="color: red">*Experimental: This is a new feature and still under development. We'll be adding features and possibly making breaking changes in future releases. We'd love to hear your feedback.*</span>
Some support is available for exporting styled `DataFrames` to Excel worksheets using the `OpenPyXL` or `XlsxWriter` engines. CSS2.2 properties handled include:
- `background-color`
- `border-style`, `border-width`, `border-color` and their {`top`, `right`, `bottom`, `left` variants}
- `color`
- `font-family`
- `font-style`
- `font-weight`
- `text-align`
- `text-decoration`
- `vertical-align`
- `white-space: nowrap`
Only CSS2 named colors and hex colors of the form `#rgb` or `#rrggbb` are currently supported.
```
df.style.\
applymap(color_negative_red).\
apply(highlight_max).\
to_excel('styled.xlsx', engine='openpyxl')
```
A screenshot of the output:

## Extensibility
The core of pandas is, and will remain, its "high-performance, easy-to-use data structures".
With that in mind, we hope that `DataFrame.style` accomplishes two goals
- Provide an API that is pleasing to use interactively and is "good enough" for many tasks
- Provide the foundations for dedicated libraries to build on
If you build a great library on top of this, let us know and we'll [link](http://pandas.pydata.org/pandas-docs/stable/ecosystem.html) to it.
### Subclassing
If the default template doesn't quite suit your needs, you can subclass Styler and extend or override the template.
We'll show an example of extending the default template to insert a custom header before each table.
```
from jinja2 import Environment, ChoiceLoader, FileSystemLoader
from IPython.display import HTML
from pandas.io.formats.style import Styler
%mkdir templates
```
This next cell writes the custom template.
We extend the template `html.tpl`, which comes with pandas.
```
%%file templates/myhtml.tpl
{% extends "html.tpl" %}
{% block table %}
<h1>{{ table_title|default("My Table") }}</h1>
{{ super() }}
{% endblock table %}
```
Now that we've created a template, we need to set up a subclass of ``Styler`` that
knows about it.
```
class MyStyler(Styler):
env = Environment(
loader=ChoiceLoader([
FileSystemLoader("templates"), # contains ours
Styler.loader, # the default
])
)
template = env.get_template("myhtml.tpl")
```
Notice that we include the original loader in our environment's loader.
That's because we extend the original template, so the Jinja environment needs
to be able to find it.
Now we can use that custom styler. It's `__init__` takes a DataFrame.
```
MyStyler(df)
```
Our custom template accepts a `table_title` keyword. We can provide the value in the `.render` method.
```
HTML(MyStyler(df).render(table_title="Extending Example"))
```
For convenience, we provide the `Styler.from_custom_template` method that does the same as the custom subclass.
```
EasyStyler = Styler.from_custom_template("templates", "myhtml.tpl")
EasyStyler(df)
```
Here's the template structure:
```
with open("template_structure.html") as f:
structure = f.read()
HTML(structure)
```
See the template in the [GitHub repo](https://github.com/pandas-dev/pandas) for more details.
```
# Hack to get the same style in the notebook as the
# main site. This is hidden in the docs.
from IPython.display import HTML
with open("themes/nature_with_gtoc/static/nature.css_t") as f:
css = f.read()
HTML('<style>{}</style>'.format(css))
```
| true |
code
| 0.534673 | null | null | null | null |
|
## Engineering Rare Categories
Rare values are categories within a categorical variable that are present only in a small percentage of the observations. There is no rule of thumb to determine how small is a small percentage, but typically, any value below 5 % can be considered rare.
As we discussed in section 3 of the course, Infrequent labels are so few, that it is hard to derive reliable information from them. But more importantly, if you remember from section 3, infrequent labels tend to appear only on train set or only on the test set:
- If only on the train set, they may cause over-fitting
- If only on the test set, our machine learning model will not know how to score them
Therefore, to avoid this behaviour, we tend to group those into a new category called 'Rare' or 'Other'.
Rare labels can appear in low or highly cardinal variables. There is no rule of thumb to determine how many different labels are considered high cardinality. It depend as well on how many observations there are in the dataset. In a dataset with 1,000 observations, 100 labels may seem a lot, whereas in a dataset with 100,000 observations it may not be so high.
Highly cardinal variables tend to have many infrequent or rare categories, whereas low cardinal variables, may have only 1 or 2 rare labels.
### Note the following:
**Note that grouping infrequent labels or categories under a new category called 'Rare' or 'Other' is the common practice in machine learning for business.**
- Grouping categories into rare for variables that show low cardinality may or may not improve model performance, however, we tend to re-group them into a new category to smooth model deployment.
- Grouping categories into rare for variables with high cardinality, tends to improve model performance as well.
## In this demo:
We will learn how to re-group rare labels under a new category called rare, and compare the implications of this encoding in variables with:
- One predominant category
- A small number of categories
- High cardinality
For this demo, we will use the House Sale dataset. We will re-group variables using pandas an feature-engine.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# to split the datasets
from sklearn.model_selection import train_test_split
pd.set_option('display.max_columns', None) # to display the total number columns present in the dataset
```
## House Sale Price dataset
```
# let's load the house price dataset
data = pd.read_csv('../houseprice.csv')
data.head()
```
### Important
The identification of rare labels should be done using only the training set, and then propagated to the test set. Rare labels should be identified in the training set only. In practice, what we will do is identify **non-rare labels**, and then any other label, either in the train or the test or future live data that is not in that list of **non-rare** labels, will be re=grouped into the new category.
For example, let's imagine that we have in the training set the variable 'city' with the labels 'London', 'Manchester' and 'Yorkshire'. 'Yorkshire' is present in less than 5% of the observations so we decide to re-group it in a new category called 'Rare'.
In the test set, we should also replace 'Yorkshire' by 'Rare', regardless of the percentage of observations for 'Yorkshire' in the test set. In addition, if in the test set we find the category 'Milton Keynes', that was not present in the training set, we should also replace that category by 'Rare'. On other words, all categories present in test set, not present in the list of **non-rare** categories derived from the training set, should be treated as rare values and re-grouped into 'Rare'.
```
# let's divide into train and test set
X_train, X_test, y_train, y_test = train_test_split(
data.drop(labels=['SalePrice'], axis=1), # predictors
data.SalePrice, # target
test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
```
## Variables with one dominant category
```
# let's explore a few examples in which variables have only a few categories, say less than 3
for col in X_train.columns:
if X_train[col].dtypes == 'O': # if the variable is categorical
if X_train[col].nunique() < 3: # if the variable has less than 3 categories
# print percentage of observations per category
print(X_train.groupby(col)[col].count() / len(X_train))
print()
```
### Conclusion
The 3 variables above, Street, Utilities and CentralAir, show one dominating category which accounts for more than 93-99% of the observations. Re-grouping the rare label in this situation does not make any sense. We could determine if these variables are useful with exploratory analysis, or any feature selection algorithm, or drop the variables altogether.
## Variables with few categories
```
# the columns in the below list have only 4 different labels
cols = ['MasVnrType', 'ExterQual', 'BsmtCond']
for col in cols:
print(X_train.groupby(col)[col].count() / len(X_train)) # frequency
print()
```
The variables above have only 4 categories, and in all three cases, there is at least one category that is infrequent, that is, that is present in less than 5% of the observations.
When the variable has only a few categories, then perhaps it makes no sense to re-categorise the rare labels into something else.
For example the first variable MasVnrType shows only 1 rare label, BrkCmn. Thus, re-categorising it into a new label will leave the variable in the same situation.
The second variable ExterQual, contains 2 rare labels Ex and Fa, we could group these 2 into a new label called 'Rare'.
The third variable BsmtCond contains 3 rare labels, Fa, Gd and Po, so we could group these 3 under the new label 'Rare'.
## Variable with high cardinality
```
# let's explore examples in which variables have several categories, say more than 10
multi_cat_cols = []
for col in X_train.columns:
if X_train[col].dtypes =='O': # if variable is categorical
if X_train[col].nunique() > 10: # and has more than 10 categories
multi_cat_cols.append(col) # add to the list
print(X_train.groupby(col)[col].count()/ len(X_train)) # and print the percentage of observations within each category
print()
```
We can see that many categories are rare in the 3 categorical variables printed above. In fact, we can plot them using the same code we learned in the lecture on rare labels in section 3:
```
for col in ['Neighborhood', 'Exterior1st', 'Exterior2nd']:
temp_df = pd.Series(X_train[col].value_counts() / len(X_train) )
# make plot with the above percentages
fig = temp_df.sort_values(ascending=False).plot.bar()
fig.set_xlabel(col)
# add a line at 5 % to flag the threshold for rare categories
fig.axhline(y=0.05, color='red')
fig.set_ylabel('Percentage of houses')
plt.show()
```
## Re-grouping rare labels with pandas
```
def find_non_rare_labels(df, variable, tolerance):
temp = df.groupby([variable])[variable].count() / len(df)
non_rare = [x for x in temp.loc[temp>tolerance].index.values]
return non_rare
# non rare labels
find_non_rare_labels(X_train, 'Neighborhood', 0.05)
# rare labels
[x for x in X_train['Neighborhood'].unique(
) if x not in find_non_rare_labels(X_train, 'Neighborhood', 0.05)]
def rare_encoding(X_train, X_test, variable, tolerance):
X_train = X_train.copy()
X_test = X_test.copy()
# find the most frequent category
frequent_cat = find_non_rare_labels(X_train, variable, tolerance)
# re-group rare labels
X_train[variable] = np.where(X_train[variable].isin(
frequent_cat), X_train[variable], 'Rare')
X_test[variable] = np.where(X_test[variable].isin(
frequent_cat), X_test[variable], 'Rare')
return X_train, X_test
for variable in ['Neighborhood', 'Exterior1st', 'Exterior2nd']:
X_train, X_test = rare_encoding(X_train, X_test, variable, 0.05)
for col in ['Neighborhood', 'Exterior1st', 'Exterior2nd']:
temp_df = pd.Series(X_train[col].value_counts() / len(X_train) )
# make plot with the above percentages
fig = temp_df.sort_values(ascending=False).plot.bar()
fig.set_xlabel(col)
# add a line at 5 % to flag the threshold for rare categories
fig.axhline(y=0.05, color='red')
fig.set_ylabel('Percentage of houses')
plt.show()
```
And now let's encode the low cardinal variables.
```
for variable in ['MasVnrType', 'ExterQual', 'BsmtCond']:
X_train, X_test = rare_encoding(X_train, X_test, variable, 0.05)
for col in ['MasVnrType', 'ExterQual', 'BsmtCond']:
temp_df = pd.Series(X_train[col].value_counts() / len(X_train) )
# make plot with the above percentages
fig = temp_df.sort_values(ascending=False).plot.bar()
fig.set_xlabel(col)
# add a line at 5 % to flag the threshold for rare categories
fig.axhline(y=0.05, color='red')
fig.set_ylabel('Percentage of houses')
plt.show()
```
## Encoding Rare Labels with Feature-Engine
```
from feature_engine.categorical_encoders import RareLabelCategoricalEncoder
# let's divide into train and test set
X_train, X_test, y_train, y_test = train_test_split(
data.drop(labels=['SalePrice'], axis=1), # predictors
data.SalePrice, # target
test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
# Rare value encoder
rare_encoder = RareLabelCategoricalEncoder(
tol=0.05, # minimal percentage to be considered non-rare
n_categories=4, # minimal number of categories the variable should have to re-cgroup rare categories
variables=['Neighborhood', 'Exterior1st', 'Exterior2nd',
'MasVnrType', 'ExterQual', 'BsmtCond'] # variables to re-group
)
rare_encoder.fit(X_train.fillna('Missing'))
```
Note how the encoder is warning us that the variable **ExterQual** contains less than 4 categories, and thus, categories will not be regrouped under Rare, even if the percentage of observations is less than 0.05.
```
rare_encoder.variables
# the encoder_dict_ is a dictionary of variable: frequent labels pair
rare_encoder.encoder_dict_
X_train = rare_encoder.transform(X_train.fillna('Missing'))
X_test = rare_encoder.transform(X_test.fillna('Missing'))
```
| true |
code
| 0.660337 | null | null | null | null |
|
# K-Nearest Neighbors Algorithm
* Last class, we introduced the probabilistic generative classifier.
* As discussed, the probabilistic generative classifier requires us to assume a parametric form for each class (e.g., each class is represented by a multi-variate Gaussian distribution, etc..). Because of this, the probabilistic generative classifier is a *parametric* approach
* Parametric approaches have the drawback that the functional parametric form needs to be decided/assumed in advance and, if chosen poorly, might be a poor model of the distribution that generates the data resulting in poor performance.
* Non-parametric methods are those that do not assume a particular generating distribution for the data. The $K$-nearest neighbors algorithm is one example of a non-parametric classifier.
* Nearest neighbor methods compare a test point to the $k$ nearest training data points and then estimate an output value based on the desired/true output values of the $k$ nearest training points
* Essentially, there is no ''training'' other than storing the training data points and their desired outputs
* In test, you need to: (1) determine which $k$ training data points are closest to the test point; and (2) determine the output value for the test point
* In order to find the $k$ nearest neighbors in the training data, you need to define a *similarity measure* or a *dissimilarity measure*. The most common dissimilarity measure is Euclidean distance.
* Euclidean distance: $d_E = \sqrt{\left(\mathbf{x}_1-\mathbf{x}_2\right)^T\left(\mathbf{x}_1-\mathbf{x}_2\right)}$
* City block distance: $d_C = \sum_{i=1}^d \left| x_{1i} - x_{2i} \right|$
* Mahalanobis distance: $\left(\mathbf{x}_1-\mathbf{x}_2\right)^T\Sigma^{-1}\left(\mathbf{x}_1-\mathbf{x}_2\right)$
* Geodesic distance
* Cosine angle similarity: $\cos \theta = \frac{\mathbf{x}_1^T\mathbf{x}_2}{\left\|\mathbf{x}_1\right\|_2^2\left\|\mathbf{x}_2\right\|_2^2}$
* and many more...
* If you are doing classification, once you find the $k$ nearest neighbors to your test point in the training data, then you can determine the class label of your test point using (most commonly) *majority vote*
* If there are ties, they can be broken randomly or using schemes like applying the label of the closest data point in the neighborhood
* Of course, there are MANY modifications you can make to this. A common one is to weight the votes of each of the nearest neighbors by their distance/similarity measure value. If they are closer, they get more weight.
```
# Reference for some code: http://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_moons, make_circles, make_classification
from sklearn import neighbors
%matplotlib inline
#figure params
h = .02 # step size in the mesh
figure = plt.figure(figsize=(17, 9))
#set up classifiers
n_neighbors = 3
classifiers = []
classifiers.append(neighbors.KNeighborsClassifier(n_neighbors, weights='uniform'))
classifiers.append(neighbors.KNeighborsClassifier(n_neighbors, weights='distance'))
names = ['K-NN_Uniform', 'K-NN_Weighted']
#Put together datasets
n_samples = 300
X, y = make_classification(n_samples, n_features=2, n_redundant=0, n_informative=2,
random_state=0, n_clusters_per_class=1)
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_separable = (X, y)
datasets = [make_moons(n_samples, noise=0.3, random_state=0),
make_circles(n_samples, noise=0.2, factor=0.5, random_state=1),
linearly_separable]
i = 1
# iterate over datasets
for X, y in datasets:
# preprocess dataset, split into training and test part
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.8) #split into train/test folds
#set up meshgrid for figure
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# just plot the dataset first
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
# Plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
# and testing points
ax.scatter(X_test[:, 0], X_test[:, 1], marker='+', c=y_test, cmap=cm_bright, alpha=0.6)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
i += 1
# iterate over classifiers
for name, clf in zip(names, classifiers):
ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)
# Plot also the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
# and testing points
ax.scatter(X_test[:, 0], X_test[:, 1], marker='+', c=y_test, cmap=cm_bright,
alpha=0.4)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(name)
ax.text(xx.max() - .3, yy.min() + .3, ('%.2f' % score).lstrip('0'),
size=15, horizontalalignment='right')
i += 1
figure.subplots_adjust(left=.02, right=.98)
plt.show()
```
# Error and Evaluation Metrics
* A key step in machine learning algorithm development and testing is determining a good error and evaluation metric.
* Evaluation metrics help us to estimate how well our model is trained and it is important to pick a metric that matches our overall goal for the system.
* Some common evaluation metrics include precision, recall, receiver operating curves, and confusion matrices.
### Classification Accuracy and Error
* Classification accuracy is defined as the number of correctly classified samples divided by all samples:
\begin{equation}
\text{accuracy} = \frac{N_{cor}}{N}
\end{equation}
where $N_{cor}$ is the number of correct classified samples and $N$ is the total number of samples.
* Classification error is defined as the number of incorrectly classified samples divided by all samples:
\begin{equation}
\text{error} = \frac{N_{mis}}{N}
\end{equation}
where $N_{mis}$ is the number of misclassified samples and $N$ is the total number of samples.
* Suppose there is a 3-class classification problem, in which we would like to classify each training sample (a fish) to one of the three classes (A = salmon or B = sea bass or C = cod).
* Let's assume there are 150 samples, including 50 salmon, 50 sea bass and 50 cod. Suppose our model misclassifies 3 salmon, 2 sea bass and 4 cod.
* Prediction accuracy of our binary classification model is calculated as:
\begin{equation}
\text{accuracy} = \frac{47+48+46}{50+50+50} = \frac{47}{50}
\end{equation}
* Prediction error is calculated as:
\begin{equation}
\text{error} = \frac{N_{mis}}{N} = \frac{3+2+4}{50+50+50} = \frac{3}{50}
\end{equation}
### Confusion Matrices
* A confusion matrix summarizes the classification accuracy across several classes. It shows the ways in which our classification model is confused when it makes predictions, allowing visualization of the performance of our algorithm. Generally, each row represents the instances of an actual class while each column represents the instances in a predicted class.
* If our classifier is trained to distinguish between salmon, sea bass and cod, then we can summarize the prediction result in the confusion matrix as follows:
| Actual/Predicted | Salmon | Sea bass | Cod |
| --- | --- | --- | --- |
| Salmon | 47 | 2 | 1 |
| Sea Bass | 2 | 48 | 0 |
| Cod | 0 | 0 | 50 |
* In this confusion matrix, of the 50 actual salmon, the classifier predicted that 2 are sea bass, 1 is cod incorrectly and 47 are labeled salmon correctly. All correct predictions are located in the diagonal of the table. So it is easy to visually inspect the table for prediction errors, as they will be represented by values outside the diagonal.
### TP, FP, TN, and FN
* True positive (TP): correctly predicting event values
* False positive (FP): incorrectly calling non-events as an event
* True negative (TN): correctly predicting non-event values
* False negative (FN): incorrectly labeling events as non-event
* Precision is also called positive predictive value.
\begin{equation}
\text{Precision} = \frac{\text{TP}}{\text{TP}+\text{FP}}
\end{equation}
* Recall is also called true positive rate, probability of detection
\begin{equation}
\text{Recall} = \frac{\text{TP}}{\text{TP}+\text{FN}}
\end{equation}
* Fall-out is also called false positive rate, probability of false alarm.
\begin{equation}
\text{Fall-out} = \frac{\text{FP}}{\text{N}}= \frac{\text{FP}}{\text{FP}+\text{TN}}
\end{equation}
* *Consider the salmon/non-salmon classification problem, what are the TP, FP, TN, FN values?*
| Actual/Predicted | Salmon | Non-Salmon |
| --- | --- | --- |
| Salmon | 47 | 3 |
| Non-Salmon | 2 | 98 |
### ROC curves
* The Receiver Operating Characteristic (ROC) curve is a plot between the true positive rate (TPR) and the false positive rate (FPR), where the TPR is defined on the $x$-axis and FPR is defined on the $y$-axis.
* $TPR = TP/(TP+FN)$ is defined as ratio between true positive prediction and all real positive samples. The definition used for $FPR$ in a ROC curve is often problem dependent. For example, for detection of targets in an area, FPR may be defined as the ratio between the number of false alarms per unit area ($FA/m^2$). In another example, if you have a set number of images and you are looking for targets in these collection of images, FPR may be defined as the number of false alarms per image. In some cases, it may make the most sense to simply use the Fall-out or false positive rate.
* Given a binary classifier and its threshold, the (x,y) coordinates of ROC space can be calculated from all the prediction result. You trace out a ROC curve by varying the threshold to get all of the points on the ROC.
* The diagonal between (0,0) and (1,1) separates the ROC space into two areas, which are left up area and right bottom area. The points above the diagonal represent good classification (better than random guess) which below the diagonal represent bad classification (worse than random guess).
* *What is the perfect prediction point in a ROC curve?*
### MSE and MAE
* *Mean Square Error* (MSE) is the average of the squared error between prediction and actual observation.
* For each sample $\mathbf{x}_i$, the prediction value is $y_i$ and the actual output is $d_i$. The MSE is
\begin{equation}
MSE = \sum_{i=1}^n \frac{(d_i - y_i)^2}{n}
\end{equation}
* *Root Mean Square Error* (RMSE) is simply the square root the MSE.
\begin{equation}
RMSE = \sqrt{MSE}
\end{equation}
* *Mean Absolute Error* (MAE) is the average of the absolute error.
\begin{equation}
MAE = \frac{1}{n} \sum_{i=1}^n \lvert d_i - y_i \rvert
\end{equation}
| true |
code
| 0.673339 | null | null | null | null |
|
# K Nearest Neighbors Classifiers
So far we've covered learning via probability (naive Bayes) and learning via errors (regression). Here we'll cover learning via similarity. This means we look for the datapoints that are most similar to the observation we are trying to predict.
#### What type of model is k-nearest neighbors algorithm (k-NN)?
A supervised, classification, nonparametric, instance-based model.
Supervised
----
You have to have labeled data. Each points belong to a group.
Your new point will be classfied into other existing groups.
Parametric vs Nonparametric Models
-----
Parametric: Make an assumption about form of the function of the data
Nonparametric: Do __not__ make an assumption about the functional form.
Instance-based
---------
Uses only the actual observed data to classify. There is no model!
<center><img src="images/knn2.png" width="50%"/></center>
Let's start by the simplest example: **Nearest Neighbor**.
## Nearest Neighbor
Let's use this example: classifying a song as either "rock" or "jazz". For this data we have measures of duration in seconds and loudness in loudness units (we're not going to be using decibels since that isn't a linear measure, which would create some problems we'll get into later).
```
import numpy as np
import scipy
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
music = pd.DataFrame()
# Some data to play with.
music['duration'] = [184, 134, 243, 186, 122, 197, 294, 382, 102, 264,
205, 110, 307, 110, 397, 153, 190, 192, 210, 403,
164, 198, 204, 253, 234, 190, 182, 401, 376, 102]
music['loudness'] = [18, 34, 43, 36, 22, 9, 29, 22, 10, 24,
20, 10, 17, 51, 7, 13, 19, 12, 21, 22,
16, 18, 4, 23, 34, 19, 14, 11, 37, 42]
# We know whether the songs in our training data are jazz or not.
music['jazz'] = [ 1, 0, 0, 0, 1, 1, 0, 1, 1, 0,
0, 1, 1, 0, 1, 1, 0, 1, 1, 1,
1, 1, 1, 1, 0, 0, 1, 1, 0, 0]
music.head()
# Look at our data.
plt.scatter(
music[music['jazz'] == 1].duration,
music[music['jazz'] == 1].loudness,
color='red'
)
plt.scatter(
music[music['jazz'] == 0].duration,
music[music['jazz'] == 0].loudness,
color='blue'
)
plt.legend(['Jazz', 'Rock'])
plt.title('Jazz and Rock Characteristics')
plt.xlabel('Duration')
plt.ylabel('Loudness')
plt.show()
```
The simplest form of a similarity model is the Nearest Neighbor model. This works quite simply: when trying to predict an observation, we find the closest (or _nearest_) known observation in our training data and use that value to make our prediction. Here we'll use the model as a classifier, the outcome of interest will be a category.
To find which observation is "nearest" we need some kind of way to measure distance. Typically we use _Euclidean distance_, the standard distance measure that you're familiar with from geometry. With one observation in n-dimensions $(x_1, x_2, ...,x_n)$ and the other $(w_1, w_2,...,w_n)$:
$$ \sqrt{(x_1-w_1)^2 + (x_2-w_2)^2+...+(x_n-w_n)^2} $$
## Other distance functions:
1-norm distance, aka City Block (Manhattan) distance
------
<center><img src="images/1_norm_1.svg" width="35%"/></center>
<center><img src="images/1_norm_2.jpg" width="35%"/></center>
2-norm distance, aka Eculidian (as the crow flies)
-----
<center><img src="images/2_norm_1.svg" width="35%"/></center>
<center><img src="images/2_norm_2.jpg" width="35%"/></center>
p-norm distance, aka Minkowski distance of order p
-----
Generalization notion of normed vector space distance.
When p = 1, Manhattan distance
When p = 2, Euclidean distance
<center><img src="images/p_norm.svg" width="35%"/></center>
You can technically define any distance measure you want, and there are times where this customization may be valuable. As a general standard, however, we'll use Euclidean distance.
Now that we have a distance measure from each point in our training data to the point we're trying to predict the model can find the datapoint with the smallest distance and then apply that category to our prediction.
Let's try running this model, using the SKLearn package.
```
from sklearn.neighbors import KNeighborsClassifier
neighbors = KNeighborsClassifier(n_neighbors=3)
X = music[['loudness', 'duration']]
Y = music.jazz
neighbors.fit(X,Y)
neighbors.predict_proba([[30, 160]])
## Predict for a song with 24 loudness that's 190 seconds long.
neighbors.predict([[30, 160]])
```
It's as simple as that. Looks like our model is predicting that 24 loudness, 190 second long song is _not_ jazz. All it takes to train the model is a dataframe of independent variables and a dataframe of dependent outcomes.
You'll note that for this example, we used the `KNeighborsClassifier` method from SKLearn. This is because Nearest Neighbor is a simplification of K-Nearest Neighbors. The jump, however, isn't that far.
## K-Nearest Neighbors
<center><img src="images/knn1.png" width="50%"/></center>
**K-Nearest Neighbors** (or "**KNN**") is the logical extension of Nearest Neighbor. Instead of looking at just the single nearest datapoint to predict an outcome, we look at several of the nearest neighbors, with $k$ representing the number of neighbors we choose to look at. Each of the $k$ neighbors gets to vote on what the predicted outcome should be.
This does a couple of valuable things. Firstly, it smooths out the predictions. If only one neighbor gets to influence the outcome, the model explicitly overfits to the training data. Any single outlier can create pockets of one category prediction surrounded by a sea of the other category.
This also means instead of just predicting classes, we get implicit probabilities. If each of the $k$ neighbors gets a vote on the outcome, then the probability of the test example being from any given class $i$ is:
$$ \frac{votes_i}{k} $$
And this applies for all classes present in the training set. Our example only has two classes, but this model can accommodate as many classes as the data set necessitates. To come up with a classifier prediction it simply takes the class for which that fraction is maximized.
Let's expand our initial nearest neighbors model from above to a KNN with a $k$ of 5.
```
neighbors = KNeighborsClassifier(n_neighbors=5)
X = music[['loudness', 'duration']]
Y = music.jazz
neighbors.fit(X,Y)
## Predict for a 24 loudness, 190 seconds long song.
print(neighbors.predict([[24, 190]]))
print(neighbors.predict_proba([[24, 190]]))
```
### predict vs predict_proba
If there are say 3 classes (say -1, 0, 1), predict will give "to which class the data point belongs to" i.e. either (-1 or 0 or 1). Predict_proba will give the probability that the data point belongs to each of the classes, like (0.2, 0.7, 0.1).
In general, we can say that the "predict" function is a class decision function, where as the predict_proba is a more general form of predicting the probability for each of the classes.
Now our test prediction has changed. In using the five nearest neighbors it appears that there were two votes for rock and three for jazz, so it was classified as a jazz song. This is different than our simpler Nearest Neighbors model. While the closest observation was in fact rock, there are more jazz songs in the nearest $k$ neighbors than rock.
We can visualize our decision bounds with something called a _mesh_. This allows us to generate a prediction over the whole space. Read the code below and make sure you can pull out what the individual lines do, consulting the documentation for unfamiliar methods if necessary.
## Normalization & Weighing
It can be a more obvious challenge if you were dealing with something where the relative scales are strikingly different. For example, if you were looking at buildings and you have height in floors and square footage, you'd have a model that would really only care about square footage since distance in that dimension would be a far greater number of units than the number of floors.
Turn all the values to be between 0 and 1 or -1 to 1 (same thing)
There is one more thing to address when talking about distance, and that is weighting. In the vanilla version of KNN, all k of the closest observations are given equal votes on what the outcome of our test observation should be. When the data is densely populated that isn't necessarily a problem.
However, sometimes the k nearest observations are not all similarly close to the test. In that case it may be useful to weight by distance. Functionally this will weight by the inverse of distance, so that closer datapoints (with a low distance) have a higher weight than further ones.
```
import numpy as np
# Our data. Converting from data frames to arrays for the mesh.
X = np.array(X)
Y = np.array(Y)
# Mesh size.
h = 4.0
# Plot the decision boundary. We assign a color to each point in the mesh.
x_min = X[:, 0].min() - .5
x_max = X[:, 0].max() + .5
y_min = X[:, 1].min() - .5
y_max = X[:, 1].max() + .5
xx, yy = np.meshgrid(
np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h)
)
Z = neighbors.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot.
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(6, 4))
plt.set_cmap(plt.cm.Paired)
plt.pcolormesh(xx, yy, Z)
# Add the training points to the plot.
plt.scatter(X[:, 0], X[:, 1], c=Y)
plt.xlabel('Loudness')
plt.ylabel('Duration')
plt.title('Mesh visualization')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()
```
Looking at the visualization above, any new point that fell within a blue area would be predicted to be jazz, and any point that fell within a brown area would be predicted to be rock.
The boundaries above are strangly jagged here, and we'll get into that in more detail in the next lesson.
Also note that the visualization isn't completely continuous. There are an infinite number of points in this space, and we can't calculate the value for each one. That's where the mesh comes in. We set our mesh size (`h = 4.0`) to 4.0 above, which means we calculate the value for each point in a grid where the points are spaced 4.0 away from each other.
You can make the mesh size smaller to get a more continuous visualization, but at the cost of a more computationally demanding calculation. In the cell below, recreate the plot above with a mesh size of `10.0`. Then reduce the mesh size until you get a plot that looks good but still renders in a reasonable amount of time. When do you get a visualization that looks acceptably continuous? When do you start to get a noticeable delay?
```
from sklearn.neighbors import KNeighborsClassifier
from scipy import stats
neighbors = KNeighborsClassifier(n_neighbors=5, weights='distance')
# Our input data frame will be the z-scores this time instead of raw data.
# zscoring it is normalizing it
X = pd.DataFrame({
'loudness': stats.zscore(music.loudness),
'duration': stats.zscore(music.duration)
})
# Fit our model.
Y = music.jazz
neighbors.fit(X, Y)
# Arrays, not data frames, for the mesh.
X = np.array(X)
Y = np.array(Y)
# Mesh size.
h = .01
# Plot the decision boundary. We assign a color to each point in the mesh.
x_min = X[:,0].min() - .5
x_max = X[:,0].max() + .5
y_min = X[:,1].min() - .5
y_max = X[:,1].max() + .5
xx, yy = np.meshgrid(
np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h)
)
Z = neighbors.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(6, 4))
plt.set_cmap(plt.cm.Paired)
plt.pcolormesh(xx, yy, Z)
# Add the training points to the plot.
plt.scatter(X[:, 0], X[:, 1], c=Y)
plt.xlabel('Loudness')
plt.ylabel('Duration')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()
```
| true |
code
| 0.644029 | null | null | null | null |
|
# Autobatching log-densities example
This notebook demonstrates a simple Bayesian inference example where autobatching makes user code easier to write, easier to read, and less likely to include bugs.
Inspired by a notebook by @davmre.
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import functools
import itertools
import re
import sys
import time
from matplotlib.pyplot import *
import jax
from jax import lax
from jax import numpy as np
from jax import scipy
from jax import random
import numpy as onp
import scipy as oscipy
```
# Generate a fake binary classification dataset
```
onp.random.seed(10009)
num_features = 10
num_points = 100
true_beta = onp.random.randn(num_features).astype(np.float32)
all_x = onp.random.randn(num_points, num_features).astype(np.float32)
y = (onp.random.rand(num_points) < oscipy.special.expit(all_x.dot(true_beta))).astype(np.int32)
y
```
# Write the log-joint function for the model
We'll write a non-batched version, a manually batched version, and an autobatched version.
## Non-batched
```
def log_joint(beta):
result = 0.
# Note that no `axis` parameter is provided to `np.sum`.
result = result + np.sum(scipy.stats.norm.logpdf(beta, loc=0., scale=1.))
result = result + np.sum(-np.log(1 + np.exp(-(2*y-1) * np.dot(all_x, beta))))
return result
log_joint(onp.random.randn(num_features))
# This doesn't work, because we didn't write `log_prob()` to handle batching.
batch_size = 10
batched_test_beta = onp.random.randn(batch_size, num_features)
log_joint(onp.random.randn(batch_size, num_features))
```
## Manually batched
```
def batched_log_joint(beta):
result = 0.
# Here (and below) `sum` needs an `axis` parameter. At best, forgetting to set axis
# or setting it incorrectly yields an error; at worst, it silently changes the
# semantics of the model.
result = result + np.sum(scipy.stats.norm.logpdf(beta, loc=0., scale=1.),
axis=-1)
# Note the multiple transposes. Getting this right is not rocket science,
# but it's also not totally mindless. (I didn't get it right on the first
# try.)
result = result + np.sum(-np.log(1 + np.exp(-(2*y-1) * np.dot(all_x, beta.T).T)),
axis=-1)
return result
batch_size = 10
batched_test_beta = onp.random.randn(batch_size, num_features)
batched_log_joint(batched_test_beta)
```
## Autobatched with vmap
It just works.
```
vmap_batched_log_joint = jax.vmap(log_joint)
vmap_batched_log_joint(batched_test_beta)
```
# Self-contained variational inference example
A little code is copied from above.
## Set up the (batched) log-joint function
```
@jax.jit
def log_joint(beta):
result = 0.
# Note that no `axis` parameter is provided to `np.sum`.
result = result + np.sum(scipy.stats.norm.logpdf(beta, loc=0., scale=10.))
result = result + np.sum(-np.log(1 + np.exp(-(2*y-1) * np.dot(all_x, beta))))
return result
batched_log_joint = jax.jit(jax.vmap(log_joint))
```
## Define the ELBO and its gradient
```
def elbo(beta_loc, beta_log_scale, epsilon):
beta_sample = beta_loc + np.exp(beta_log_scale) * epsilon
return np.mean(batched_log_joint(beta_sample), 0) + np.sum(beta_log_scale - 0.5 * onp.log(2*onp.pi))
elbo = jax.jit(elbo, static_argnums=(2, 3))
elbo_val_and_grad = jax.jit(jax.value_and_grad(elbo, argnums=(0, 1)))
```
## Optimize the ELBO using SGD
```
def normal_sample(key, shape):
"""Convenience function for quasi-stateful RNG."""
new_key, sub_key = random.split(key)
return new_key, random.normal(sub_key, shape)
normal_sample = jax.jit(normal_sample, static_argnums=(1,))
key = random.PRNGKey(10003)
beta_loc = np.zeros(num_features, np.float32)
beta_log_scale = np.zeros(num_features, np.float32)
step_size = 0.01
batch_size = 128
epsilon_shape = (batch_size, num_features)
for i in range(1000):
key, epsilon = normal_sample(key, epsilon_shape)
elbo_val, (beta_loc_grad, beta_log_scale_grad) = elbo_val_and_grad(
beta_loc, beta_log_scale, epsilon)
beta_loc += step_size * beta_loc_grad
beta_log_scale += step_size * beta_log_scale_grad
if i % 10 == 0:
print('{}\t{}'.format(i, elbo_val))
```
## Display the results
Coverage isn't quite as good as we might like, but it's not bad, and nobody said variational inference was exact.
```
figure(figsize=(7, 7))
plot(true_beta, beta_loc, '.', label='Approximated Posterior Means')
plot(true_beta, beta_loc + 2*np.exp(beta_log_scale), 'r.', label='Approximated Posterior $2\sigma$ Error Bars')
plot(true_beta, beta_loc - 2*np.exp(beta_log_scale), 'r.')
plot_scale = 3
plot([-plot_scale, plot_scale], [-plot_scale, plot_scale], 'k')
xlabel('True beta')
ylabel('Estimated beta')
legend(loc='best')
```
| true |
code
| 0.890247 | null | null | null | null |
|
**Chapter 5 – Support Vector Machines**
_This notebook contains all the sample code and solutions to the exercises in chapter 5._
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/ageron/handson-ml/blob/master/05_support_vector_machines.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
</table>
**Warning**: this is the code for the 1st edition of the book. Please visit https://github.com/ageron/handson-ml2 for the 2nd edition code, with up-to-date notebooks using the latest library versions.
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "svm"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
```
# Large margin classification
The next few code cells generate the first figures in chapter 5. The first actual code sample comes after:
```
from sklearn.svm import SVC
from sklearn import datasets
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
# SVM Classifier model
svm_clf = SVC(kernel="linear", C=float("inf"))
svm_clf.fit(X, y)
# Bad models
x0 = np.linspace(0, 5.5, 200)
pred_1 = 5*x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 * x0 + 0.5
def plot_svc_decision_boundary(svm_clf, xmin, xmax):
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# At the decision boundary, w0*x0 + w1*x1 + b = 0
# => x1 = -w0/w1 * x0 - b/w1
x0 = np.linspace(xmin, xmax, 200)
decision_boundary = -w[0]/w[1] * x0 - b/w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
svs = svm_clf.support_vectors_
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
plt.plot(x0, decision_boundary, "k-", linewidth=2)
plt.plot(x0, gutter_up, "k--", linewidth=2)
plt.plot(x0, gutter_down, "k--", linewidth=2)
plt.figure(figsize=(12,2.7))
plt.subplot(121)
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "m-", linewidth=2)
plt.plot(x0, pred_3, "r-", linewidth=2)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 5.5, 0, 2])
plt.subplot(122)
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([0, 5.5, 0, 2])
save_fig("large_margin_classification_plot")
plt.show()
```
# Sensitivity to feature scales
```
Xs = np.array([[1, 50], [5, 20], [3, 80], [5, 60]]).astype(np.float64)
ys = np.array([0, 0, 1, 1])
svm_clf = SVC(kernel="linear", C=100)
svm_clf.fit(Xs, ys)
plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(Xs[:, 0][ys==1], Xs[:, 1][ys==1], "bo")
plt.plot(Xs[:, 0][ys==0], Xs[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, 0, 6)
plt.xlabel("$x_0$", fontsize=20)
plt.ylabel("$x_1$ ", fontsize=20, rotation=0)
plt.title("Unscaled", fontsize=16)
plt.axis([0, 6, 0, 90])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(Xs)
svm_clf.fit(X_scaled, ys)
plt.subplot(122)
plt.plot(X_scaled[:, 0][ys==1], X_scaled[:, 1][ys==1], "bo")
plt.plot(X_scaled[:, 0][ys==0], X_scaled[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, -2, 2)
plt.xlabel("$x_0$", fontsize=20)
plt.title("Scaled", fontsize=16)
plt.axis([-2, 2, -2, 2])
save_fig("sensitivity_to_feature_scales_plot")
```
# Sensitivity to outliers
```
X_outliers = np.array([[3.4, 1.3], [3.2, 0.8]])
y_outliers = np.array([0, 0])
Xo1 = np.concatenate([X, X_outliers[:1]], axis=0)
yo1 = np.concatenate([y, y_outliers[:1]], axis=0)
Xo2 = np.concatenate([X, X_outliers[1:]], axis=0)
yo2 = np.concatenate([y, y_outliers[1:]], axis=0)
svm_clf2 = SVC(kernel="linear", C=10**9)
svm_clf2.fit(Xo2, yo2)
plt.figure(figsize=(12,2.7))
plt.subplot(121)
plt.plot(Xo1[:, 0][yo1==1], Xo1[:, 1][yo1==1], "bs")
plt.plot(Xo1[:, 0][yo1==0], Xo1[:, 1][yo1==0], "yo")
plt.text(0.3, 1.0, "Impossible!", fontsize=24, color="red")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.annotate("Outlier",
xy=(X_outliers[0][0], X_outliers[0][1]),
xytext=(2.5, 1.7),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=16,
)
plt.axis([0, 5.5, 0, 2])
plt.subplot(122)
plt.plot(Xo2[:, 0][yo2==1], Xo2[:, 1][yo2==1], "bs")
plt.plot(Xo2[:, 0][yo2==0], Xo2[:, 1][yo2==0], "yo")
plot_svc_decision_boundary(svm_clf2, 0, 5.5)
plt.xlabel("Petal length", fontsize=14)
plt.annotate("Outlier",
xy=(X_outliers[1][0], X_outliers[1][1]),
xytext=(3.2, 0.08),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=16,
)
plt.axis([0, 5.5, 0, 2])
save_fig("sensitivity_to_outliers_plot")
plt.show()
```
# Large margin *vs* margin violations
This is the first code example in chapter 5:
```
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica
svm_clf = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge", random_state=42)),
])
svm_clf.fit(X, y)
svm_clf.predict([[5.5, 1.7]])
```
Now let's generate the graph comparing different regularization settings:
```
scaler = StandardScaler()
svm_clf1 = LinearSVC(C=1, loss="hinge", random_state=42)
svm_clf2 = LinearSVC(C=100, loss="hinge", random_state=42)
scaled_svm_clf1 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf1),
])
scaled_svm_clf2 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf2),
])
scaled_svm_clf1.fit(X, y)
scaled_svm_clf2.fit(X, y)
# Convert to unscaled parameters
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])
# Find support vectors (LinearSVC does not do this automatically)
t = y * 2 - 1
support_vectors_idx1 = (t * (X.dot(w1) + b1) < 1).ravel()
support_vectors_idx2 = (t * (X.dot(w2) + b2) < 1).ravel()
svm_clf1.support_vectors_ = X[support_vectors_idx1]
svm_clf2.support_vectors_ = X[support_vectors_idx2]
plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris-Versicolor")
plot_svc_decision_boundary(svm_clf1, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])
plt.subplot(122)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])
save_fig("regularization_plot")
```
# Non-linear classification
```
X1D = np.linspace(-4, 4, 9).reshape(-1, 1)
X2D = np.c_[X1D, X1D**2]
y = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.plot(X1D[:, 0][y==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][y==1], np.zeros(5), "g^")
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r"$x_1$", fontsize=20)
plt.axis([-4.5, 4.5, -0.2, 0.2])
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(X2D[:, 0][y==0], X2D[:, 1][y==0], "bs")
plt.plot(X2D[:, 0][y==1], X2D[:, 1][y==1], "g^")
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plt.gca().get_yaxis().set_ticks([0, 4, 8, 12, 16])
plt.plot([-4.5, 4.5], [6.5, 6.5], "r--", linewidth=3)
plt.axis([-4.5, 4.5, -1, 17])
plt.subplots_adjust(right=1)
save_fig("higher_dimensions_plot", tight_layout=False)
plt.show()
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
def plot_dataset(X, y, axes):
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.axis(axes)
plt.grid(True, which='both')
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
])
polynomial_svm_clf.fit(X, y)
def plot_predictions(clf, axes):
x0s = np.linspace(axes[0], axes[1], 100)
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(x0s, x1s)
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
save_fig("moons_polynomial_svc_plot")
plt.show()
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
poly_kernel_svm_clf.fit(X, y)
poly100_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
poly100_kernel_svm_clf.fit(X, y)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)
plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)
save_fig("moons_kernelized_polynomial_svc_plot")
plt.show()
def gaussian_rbf(x, landmark, gamma):
return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1)**2)
gamma = 0.3
x1s = np.linspace(-4.5, 4.5, 200).reshape(-1, 1)
x2s = gaussian_rbf(x1s, -2, gamma)
x3s = gaussian_rbf(x1s, 1, gamma)
XK = np.c_[gaussian_rbf(X1D, -2, gamma), gaussian_rbf(X1D, 1, gamma)]
yk = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.scatter(x=[-2, 1], y=[0, 0], s=150, alpha=0.5, c="red")
plt.plot(X1D[:, 0][yk==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][yk==1], np.zeros(5), "g^")
plt.plot(x1s, x2s, "g--")
plt.plot(x1s, x3s, "b:")
plt.gca().get_yaxis().set_ticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"Similarity", fontsize=14)
plt.annotate(r'$\mathbf{x}$',
xy=(X1D[3, 0], 0),
xytext=(-0.5, 0.20),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18,
)
plt.text(-2, 0.9, "$x_2$", ha="center", fontsize=20)
plt.text(1, 0.9, "$x_3$", ha="center", fontsize=20)
plt.axis([-4.5, 4.5, -0.1, 1.1])
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(XK[:, 0][yk==0], XK[:, 1][yk==0], "bs")
plt.plot(XK[:, 0][yk==1], XK[:, 1][yk==1], "g^")
plt.xlabel(r"$x_2$", fontsize=20)
plt.ylabel(r"$x_3$ ", fontsize=20, rotation=0)
plt.annotate(r'$\phi\left(\mathbf{x}\right)$',
xy=(XK[3, 0], XK[3, 1]),
xytext=(0.65, 0.50),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18,
)
plt.plot([-0.1, 1.1], [0.57, -0.1], "r--", linewidth=3)
plt.axis([-0.1, 1.1, -0.1, 1.1])
plt.subplots_adjust(right=1)
save_fig("kernel_method_plot")
plt.show()
x1_example = X1D[3, 0]
for landmark in (-2, 1):
k = gaussian_rbf(np.array([[x1_example]]), np.array([[landmark]]), gamma)
print("Phi({}, {}) = {}".format(x1_example, landmark, k))
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)
from sklearn.svm import SVC
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)
svm_clfs = []
for gamma, C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
])
rbf_kernel_svm_clf.fit(X, y)
svm_clfs.append(rbf_kernel_svm_clf)
plt.figure(figsize=(11, 7))
for i, svm_clf in enumerate(svm_clfs):
plt.subplot(221 + i)
plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
gamma, C = hyperparams[i]
plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
save_fig("moons_rbf_svc_plot")
plt.show()
```
# Regression
```
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1)).ravel()
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5, random_state=42)
svm_reg.fit(X, y)
svm_reg1 = LinearSVR(epsilon=1.5, random_state=42)
svm_reg2 = LinearSVR(epsilon=0.5, random_state=42)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)
def find_support_vectors(svm_reg, X, y):
y_pred = svm_reg.predict(X)
off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
return np.argwhere(off_margin)
svm_reg1.support_ = find_support_vectors(svm_reg1, X, y)
svm_reg2.support_ = find_support_vectors(svm_reg2, X, y)
eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])
def plot_svm_regression(svm_reg, X, y, axes):
x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
y_pred = svm_reg.predict(x1s)
plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
plt.plot(X, y, "bo")
plt.xlabel(r"$x_1$", fontsize=18)
plt.legend(loc="upper left", fontsize=18)
plt.axis(axes)
plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_reg1, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
#plt.plot([eps_x1, eps_x1], [eps_y_pred, eps_y_pred - svm_reg1.epsilon], "k-", linewidth=2)
plt.annotate(
'', xy=(eps_x1, eps_y_pred), xycoords='data',
xytext=(eps_x1, eps_y_pred - svm_reg1.epsilon),
textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
)
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.subplot(122)
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)
save_fig("svm_regression_plot")
plt.show()
np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()
```
**Warning**: the default value of `gamma` will change from `'auto'` to `'scale'` in version 0.22 to better account for unscaled features. To preserve the same results as in the book, we explicitly set it to `'auto'`, but you should probably just use the default in your own code.
```
from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="auto")
svm_poly_reg.fit(X, y)
from sklearn.svm import SVR
svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="auto")
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1, gamma="auto")
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)
plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.subplot(122)
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)
save_fig("svm_with_polynomial_kernel_plot")
plt.show()
```
# Under the hood
```
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica
from mpl_toolkits.mplot3d import Axes3D
def plot_3D_decision_function(ax, w, b, x1_lim=[4, 6], x2_lim=[0.8, 2.8]):
x1_in_bounds = (X[:, 0] > x1_lim[0]) & (X[:, 0] < x1_lim[1])
X_crop = X[x1_in_bounds]
y_crop = y[x1_in_bounds]
x1s = np.linspace(x1_lim[0], x1_lim[1], 20)
x2s = np.linspace(x2_lim[0], x2_lim[1], 20)
x1, x2 = np.meshgrid(x1s, x2s)
xs = np.c_[x1.ravel(), x2.ravel()]
df = (xs.dot(w) + b).reshape(x1.shape)
m = 1 / np.linalg.norm(w)
boundary_x2s = -x1s*(w[0]/w[1])-b/w[1]
margin_x2s_1 = -x1s*(w[0]/w[1])-(b-1)/w[1]
margin_x2s_2 = -x1s*(w[0]/w[1])-(b+1)/w[1]
ax.plot_surface(x1s, x2, np.zeros_like(x1),
color="b", alpha=0.2, cstride=100, rstride=100)
ax.plot(x1s, boundary_x2s, 0, "k-", linewidth=2, label=r"$h=0$")
ax.plot(x1s, margin_x2s_1, 0, "k--", linewidth=2, label=r"$h=\pm 1$")
ax.plot(x1s, margin_x2s_2, 0, "k--", linewidth=2)
ax.plot(X_crop[:, 0][y_crop==1], X_crop[:, 1][y_crop==1], 0, "g^")
ax.plot_wireframe(x1, x2, df, alpha=0.3, color="k")
ax.plot(X_crop[:, 0][y_crop==0], X_crop[:, 1][y_crop==0], 0, "bs")
ax.axis(x1_lim + x2_lim)
ax.text(4.5, 2.5, 3.8, "Decision function $h$", fontsize=15)
ax.set_xlabel(r"Petal length", fontsize=15)
ax.set_ylabel(r"Petal width", fontsize=15)
ax.set_zlabel(r"$h = \mathbf{w}^T \mathbf{x} + b$", fontsize=18)
ax.legend(loc="upper left", fontsize=16)
fig = plt.figure(figsize=(11, 6))
ax1 = fig.add_subplot(111, projection='3d')
plot_3D_decision_function(ax1, w=svm_clf2.coef_[0], b=svm_clf2.intercept_[0])
#save_fig("iris_3D_plot")
plt.show()
```
# Small weight vector results in a large margin
```
def plot_2D_decision_function(w, b, ylabel=True, x1_lim=[-3, 3]):
x1 = np.linspace(x1_lim[0], x1_lim[1], 200)
y = w * x1 + b
m = 1 / w
plt.plot(x1, y)
plt.plot(x1_lim, [1, 1], "k:")
plt.plot(x1_lim, [-1, -1], "k:")
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot([m, m], [0, 1], "k--")
plt.plot([-m, -m], [0, -1], "k--")
plt.plot([-m, m], [0, 0], "k-o", linewidth=3)
plt.axis(x1_lim + [-2, 2])
plt.xlabel(r"$x_1$", fontsize=16)
if ylabel:
plt.ylabel(r"$w_1 x_1$ ", rotation=0, fontsize=16)
plt.title(r"$w_1 = {}$".format(w), fontsize=16)
plt.figure(figsize=(12, 3.2))
plt.subplot(121)
plot_2D_decision_function(1, 0)
plt.subplot(122)
plot_2D_decision_function(0.5, 0, ylabel=False)
save_fig("small_w_large_margin_plot")
plt.show()
from sklearn.svm import SVC
from sklearn import datasets
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica
svm_clf = SVC(kernel="linear", C=1)
svm_clf.fit(X, y)
svm_clf.predict([[5.3, 1.3]])
```
# Hinge loss
```
t = np.linspace(-2, 4, 200)
h = np.where(1 - t < 0, 0, 1 - t) # max(0, 1-t)
plt.figure(figsize=(5,2.8))
plt.plot(t, h, "b-", linewidth=2, label="$max(0, 1 - t)$")
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.yticks(np.arange(-1, 2.5, 1))
plt.xlabel("$t$", fontsize=16)
plt.axis([-2, 4, -1, 2.5])
plt.legend(loc="upper right", fontsize=16)
save_fig("hinge_plot")
plt.show()
```
# Extra material
## Training time
```
X, y = make_moons(n_samples=1000, noise=0.4, random_state=42)
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
import time
tol = 0.1
tols = []
times = []
for i in range(10):
svm_clf = SVC(kernel="poly", gamma=3, C=10, tol=tol, verbose=1)
t1 = time.time()
svm_clf.fit(X, y)
t2 = time.time()
times.append(t2-t1)
tols.append(tol)
print(i, tol, t2-t1)
tol /= 10
plt.semilogx(tols, times)
```
## Linear SVM classifier implementation using Batch Gradient Descent
```
# Training set
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64).reshape(-1, 1) # Iris-Virginica
from sklearn.base import BaseEstimator
class MyLinearSVC(BaseEstimator):
def __init__(self, C=1, eta0=1, eta_d=10000, n_epochs=1000, random_state=None):
self.C = C
self.eta0 = eta0
self.n_epochs = n_epochs
self.random_state = random_state
self.eta_d = eta_d
def eta(self, epoch):
return self.eta0 / (epoch + self.eta_d)
def fit(self, X, y):
# Random initialization
if self.random_state:
np.random.seed(self.random_state)
w = np.random.randn(X.shape[1], 1) # n feature weights
b = 0
m = len(X)
t = y * 2 - 1 # -1 if t==0, +1 if t==1
X_t = X * t
self.Js=[]
# Training
for epoch in range(self.n_epochs):
support_vectors_idx = (X_t.dot(w) + t * b < 1).ravel()
X_t_sv = X_t[support_vectors_idx]
t_sv = t[support_vectors_idx]
J = 1/2 * np.sum(w * w) + self.C * (np.sum(1 - X_t_sv.dot(w)) - b * np.sum(t_sv))
self.Js.append(J)
w_gradient_vector = w - self.C * np.sum(X_t_sv, axis=0).reshape(-1, 1)
b_derivative = -C * np.sum(t_sv)
w = w - self.eta(epoch) * w_gradient_vector
b = b - self.eta(epoch) * b_derivative
self.intercept_ = np.array([b])
self.coef_ = np.array([w])
support_vectors_idx = (X_t.dot(w) + t * b < 1).ravel()
self.support_vectors_ = X[support_vectors_idx]
return self
def decision_function(self, X):
return X.dot(self.coef_[0]) + self.intercept_[0]
def predict(self, X):
return (self.decision_function(X) >= 0).astype(np.float64)
C=2
svm_clf = MyLinearSVC(C=C, eta0 = 10, eta_d = 1000, n_epochs=60000, random_state=2)
svm_clf.fit(X, y)
svm_clf.predict(np.array([[5, 2], [4, 1]]))
plt.plot(range(svm_clf.n_epochs), svm_clf.Js)
plt.axis([0, svm_clf.n_epochs, 0, 100])
print(svm_clf.intercept_, svm_clf.coef_)
svm_clf2 = SVC(kernel="linear", C=C)
svm_clf2.fit(X, y.ravel())
print(svm_clf2.intercept_, svm_clf2.coef_)
yr = y.ravel()
plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(X[:, 0][yr==1], X[:, 1][yr==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][yr==0], X[:, 1][yr==0], "bs", label="Not Iris-Virginica")
plot_svc_decision_boundary(svm_clf, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.title("MyLinearSVC", fontsize=14)
plt.axis([4, 6, 0.8, 2.8])
plt.subplot(122)
plt.plot(X[:, 0][yr==1], X[:, 1][yr==1], "g^")
plt.plot(X[:, 0][yr==0], X[:, 1][yr==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.title("SVC", fontsize=14)
plt.axis([4, 6, 0.8, 2.8])
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(loss="hinge", alpha = 0.017, max_iter = 50, tol=-np.infty, random_state=42)
sgd_clf.fit(X, y.ravel())
m = len(X)
t = y * 2 - 1 # -1 if t==0, +1 if t==1
X_b = np.c_[np.ones((m, 1)), X] # Add bias input x0=1
X_b_t = X_b * t
sgd_theta = np.r_[sgd_clf.intercept_[0], sgd_clf.coef_[0]]
print(sgd_theta)
support_vectors_idx = (X_b_t.dot(sgd_theta) < 1).ravel()
sgd_clf.support_vectors_ = X[support_vectors_idx]
sgd_clf.C = C
plt.figure(figsize=(5.5,3.2))
plt.plot(X[:, 0][yr==1], X[:, 1][yr==1], "g^")
plt.plot(X[:, 0][yr==0], X[:, 1][yr==0], "bs")
plot_svc_decision_boundary(sgd_clf, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.title("SGDClassifier", fontsize=14)
plt.axis([4, 6, 0.8, 2.8])
```
# Exercise solutions
## 1. to 7.
See appendix A.
# 8.
_Exercise: train a `LinearSVC` on a linearly separable dataset. Then train an `SVC` and a `SGDClassifier` on the same dataset. See if you can get them to produce roughly the same model._
Let's use the Iris dataset: the Iris Setosa and Iris Versicolor classes are linearly separable.
```
from sklearn import datasets
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
from sklearn.svm import SVC, LinearSVC
from sklearn.linear_model import SGDClassifier
from sklearn.preprocessing import StandardScaler
C = 5
alpha = 1 / (C * len(X))
lin_clf = LinearSVC(loss="hinge", C=C, random_state=42)
svm_clf = SVC(kernel="linear", C=C)
sgd_clf = SGDClassifier(loss="hinge", learning_rate="constant", eta0=0.001, alpha=alpha,
max_iter=100000, tol=-np.infty, random_state=42)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
lin_clf.fit(X_scaled, y)
svm_clf.fit(X_scaled, y)
sgd_clf.fit(X_scaled, y)
print("LinearSVC: ", lin_clf.intercept_, lin_clf.coef_)
print("SVC: ", svm_clf.intercept_, svm_clf.coef_)
print("SGDClassifier(alpha={:.5f}):".format(sgd_clf.alpha), sgd_clf.intercept_, sgd_clf.coef_)
```
Let's plot the decision boundaries of these three models:
```
# Compute the slope and bias of each decision boundary
w1 = -lin_clf.coef_[0, 0]/lin_clf.coef_[0, 1]
b1 = -lin_clf.intercept_[0]/lin_clf.coef_[0, 1]
w2 = -svm_clf.coef_[0, 0]/svm_clf.coef_[0, 1]
b2 = -svm_clf.intercept_[0]/svm_clf.coef_[0, 1]
w3 = -sgd_clf.coef_[0, 0]/sgd_clf.coef_[0, 1]
b3 = -sgd_clf.intercept_[0]/sgd_clf.coef_[0, 1]
# Transform the decision boundary lines back to the original scale
line1 = scaler.inverse_transform([[-10, -10 * w1 + b1], [10, 10 * w1 + b1]])
line2 = scaler.inverse_transform([[-10, -10 * w2 + b2], [10, 10 * w2 + b2]])
line3 = scaler.inverse_transform([[-10, -10 * w3 + b3], [10, 10 * w3 + b3]])
# Plot all three decision boundaries
plt.figure(figsize=(11, 4))
plt.plot(line1[:, 0], line1[:, 1], "k:", label="LinearSVC")
plt.plot(line2[:, 0], line2[:, 1], "b--", linewidth=2, label="SVC")
plt.plot(line3[:, 0], line3[:, 1], "r-", label="SGDClassifier")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs") # label="Iris-Versicolor"
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo") # label="Iris-Setosa"
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper center", fontsize=14)
plt.axis([0, 5.5, 0, 2])
plt.show()
```
Close enough!
# 9.
_Exercise: train an SVM classifier on the MNIST dataset. Since SVM classifiers are binary classifiers, you will need to use one-versus-all to classify all 10 digits. You may want to tune the hyperparameters using small validation sets to speed up the process. What accuracy can you reach?_
First, let's load the dataset and split it into a training set and a test set. We could use `train_test_split()` but people usually just take the first 60,000 instances for the training set, and the last 10,000 instances for the test set (this makes it possible to compare your model's performance with others):
```
try:
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, cache=True, as_frame=False)
except ImportError:
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original')
X = mnist["data"]
y = mnist["target"]
X_train = X[:60000]
y_train = y[:60000]
X_test = X[60000:]
y_test = y[60000:]
```
Many training algorithms are sensitive to the order of the training instances, so it's generally good practice to shuffle them first:
```
np.random.seed(42)
rnd_idx = np.random.permutation(60000)
X_train = X_train[rnd_idx]
y_train = y_train[rnd_idx]
```
Let's start simple, with a linear SVM classifier. It will automatically use the One-vs-All (also called One-vs-the-Rest, OvR) strategy, so there's nothing special we need to do. Easy!
```
lin_clf = LinearSVC(random_state=42)
lin_clf.fit(X_train, y_train)
```
Let's make predictions on the training set and measure the accuracy (we don't want to measure it on the test set yet, since we have not selected and trained the final model yet):
```
from sklearn.metrics import accuracy_score
y_pred = lin_clf.predict(X_train)
accuracy_score(y_train, y_pred)
```
Wow, 86% accuracy on MNIST is a really bad performance. This linear model is certainly too simple for MNIST, but perhaps we just needed to scale the data first:
```
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float32))
X_test_scaled = scaler.transform(X_test.astype(np.float32))
lin_clf = LinearSVC(random_state=42)
lin_clf.fit(X_train_scaled, y_train)
y_pred = lin_clf.predict(X_train_scaled)
accuracy_score(y_train, y_pred)
```
That's much better (we cut the error rate in two), but still not great at all for MNIST. If we want to use an SVM, we will have to use a kernel. Let's try an `SVC` with an RBF kernel (the default).
**Warning**: if you are using Scikit-Learn ≤ 0.19, the `SVC` class will use the One-vs-One (OvO) strategy by default, so you must explicitly set `decision_function_shape="ovr"` if you want to use the OvR strategy instead (OvR is the default since 0.19).
```
svm_clf = SVC(decision_function_shape="ovr", gamma="auto")
svm_clf.fit(X_train_scaled[:10000], y_train[:10000])
y_pred = svm_clf.predict(X_train_scaled)
accuracy_score(y_train, y_pred)
```
That's promising, we get better performance even though we trained the model on 6 times less data. Let's tune the hyperparameters by doing a randomized search with cross validation. We will do this on a small dataset just to speed up the process:
```
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import reciprocal, uniform
param_distributions = {"gamma": reciprocal(0.001, 0.1), "C": uniform(1, 10)}
rnd_search_cv = RandomizedSearchCV(svm_clf, param_distributions, n_iter=10, verbose=2, cv=3)
rnd_search_cv.fit(X_train_scaled[:1000], y_train[:1000])
rnd_search_cv.best_estimator_
rnd_search_cv.best_score_
```
This looks pretty low but remember we only trained the model on 1,000 instances. Let's retrain the best estimator on the whole training set (run this at night, it will take hours):
```
rnd_search_cv.best_estimator_.fit(X_train_scaled, y_train)
y_pred = rnd_search_cv.best_estimator_.predict(X_train_scaled)
accuracy_score(y_train, y_pred)
```
Ah, this looks good! Let's select this model. Now we can test it on the test set:
```
y_pred = rnd_search_cv.best_estimator_.predict(X_test_scaled)
accuracy_score(y_test, y_pred)
```
Not too bad, but apparently the model is overfitting slightly. It's tempting to tweak the hyperparameters a bit more (e.g. decreasing `C` and/or `gamma`), but we would run the risk of overfitting the test set. Other people have found that the hyperparameters `C=5` and `gamma=0.005` yield even better performance (over 98% accuracy). By running the randomized search for longer and on a larger part of the training set, you may be able to find this as well.
## 10.
_Exercise: train an SVM regressor on the California housing dataset._
Let's load the dataset using Scikit-Learn's `fetch_california_housing()` function:
```
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
X = housing["data"]
y = housing["target"]
```
Split it into a training set and a test set:
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
```
Don't forget to scale the data:
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
```
Let's train a simple `LinearSVR` first:
```
from sklearn.svm import LinearSVR
lin_svr = LinearSVR(random_state=42)
lin_svr.fit(X_train_scaled, y_train)
```
Let's see how it performs on the training set:
```
from sklearn.metrics import mean_squared_error
y_pred = lin_svr.predict(X_train_scaled)
mse = mean_squared_error(y_train, y_pred)
mse
```
Let's look at the RMSE:
```
np.sqrt(mse)
```
In this training set, the targets are tens of thousands of dollars. The RMSE gives a rough idea of the kind of error you should expect (with a higher weight for large errors): so with this model we can expect errors somewhere around $10,000. Not great. Let's see if we can do better with an RBF Kernel. We will use randomized search with cross validation to find the appropriate hyperparameter values for `C` and `gamma`:
```
from sklearn.svm import SVR
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import reciprocal, uniform
param_distributions = {"gamma": reciprocal(0.001, 0.1), "C": uniform(1, 10)}
rnd_search_cv = RandomizedSearchCV(SVR(), param_distributions, n_iter=10, verbose=2, cv=3, random_state=42)
rnd_search_cv.fit(X_train_scaled, y_train)
rnd_search_cv.best_estimator_
```
Now let's measure the RMSE on the training set:
```
y_pred = rnd_search_cv.best_estimator_.predict(X_train_scaled)
mse = mean_squared_error(y_train, y_pred)
np.sqrt(mse)
```
Looks much better than the linear model. Let's select this model and evaluate it on the test set:
```
y_pred = rnd_search_cv.best_estimator_.predict(X_test_scaled)
mse = mean_squared_error(y_test, y_pred)
np.sqrt(mse)
```
| true |
code
| 0.581481 | null | null | null | null |
|
## Coming soon in `numba` 0.34
You can install the release candidate as of 07/09/2017 from the `numba` conda channel
```
conda install -c numba numba
```
```
import numpy
from numba import njit
```
Define some reasonably expensive operation in a function.
```
def do_trig(x, y):
z = numpy.sin(x**2) + numpy.cos(y)
return z
```
We can start with 1000 x 1000 arrays
```
x = numpy.random.random((1000, 1000))
y = numpy.random.random((1000, 1000))
%timeit do_trig(x, y)
```
Now let's `jit` this function. What do we expect to get out of this? Probably nothing, honestly. As we've seen, `numpy` is pretty good at what it does.
```
do_trig_jit = njit()(do_trig)
%timeit do_trig_jit(x, y)
```
Maybe a _hair_ slower than the bare `numpy` version. So yeah, no improvement.
### BUT
Starting in version 0.34, with help from the Intel Parallel Accelerator team, you can now pass a `parallel` keyword argument to `jit` and `njit`.
Like this:
```
do_trig_jit_par = njit(parallel=True)(do_trig)
```
How do we think this will run?
```
%timeit do_trig_jit_par(x, y)
```
Not bad -- around a 3x speedup for a single line?
And what if we unroll the array operations like we've seen before? Does that help us out?
```
@njit
def do_trig(x, y):
z = numpy.empty_like(x)
for i in range(x.shape[0]):
for j in range(x.shape[1]):
z[i, j] = numpy.sin(x[i, j]**2) + numpy.cos(y[i, j])
return z
%timeit do_trig(x, y)
```
Hmm, that's actually a hair faster than before. Cool!
Now let's parallelize it!
```
@njit(parallel=True)
def do_trig(x, y):
z = numpy.empty_like(x)
for i in range(x.shape[0]):
for j in range(x.shape[1]):
z[i, j] = numpy.sin(x[i, j]**2) + numpy.cos(y[i, j])
return z
%timeit do_trig(x, y)
```
What happened?
Well, automatic parallelization is a _pretty hard_ problem. (This is a massive understatement).
Basically, parallel `jit` is "limited" to working on array operations, so in this case, unrolling loops will hurt you.
Blarg.
### FAQ that I just made up
- Why didn't you tell us about this before?
It is brand new. The numba team is great, but have a really bad habit of releasing new features 5-10 days before I run a tutorial.
- Is regular `jit` just dead now?
It honestly might be. I've only started playing around with it but I haven't seen any speed _hits_ for using it when there are no array operations to operate on.
- Is all of that stuff about `vectorize` just useless now?
Short answer: no. Long answer: Let's check it out!
```
from numba import vectorize
import math
```
Recall that we define the function as if it operates on scalars, then apply the vectorize decorator.
```
@vectorize
def do_trig_vec(x, y):
z = math.sin(x**2) + math.cos(y)
return z
%timeit do_trig_vec(x, y)
```
A little faster, but roughly equivalent to the base `numpy` and `jit` versions. Now let's type our inputs and run it in `parallel`
```
@vectorize('float64(float64, float64)', target='parallel')
def do_trig_vec_par(x, y):
z = math.sin(x**2) + math.cos(y)
return z
%timeit do_trig_vec_par(x, y)
```
Yowza! So yeah, `vectorize` is still the best performer when you have element-wise operations, but if you have a big mess of stuff that you just want to speed up, then parallel `jit` is an awesome and easy way to try to boost performance.
```
a = x
b = y
c = numpy.random.random((a.shape))
%%timeit
b**2 - 4 * a * c
def discrim(a, b, c):
return b**2 - 4 * a * c
discrim_vec = vectorize()(discrim)
%timeit discrim_vec(a, b, c)
discrim_vec_par = vectorize('float64(float64, float64, float64)', target='parallel')(discrim)
%timeit discrim_vec_par(a, b, c)
discrim_jit = njit()(discrim)
%timeit discrim_jit(a, b, c)
discrim_jit_par = njit(parallel=True)(discrim)
%timeit discrim_jit_par(a, b, c)
```
| true |
code
| 0.419262 | null | null | null | null |
|
# Deming Regression
-------------------------------
This function shows how to use TensorFlow to solve linear Deming regression.
$y = Ax + b$
We will use the iris data, specifically:
y = Sepal Length and x = Petal Width.
Demming regression is also called total least squares, in which we minimize the shortest distance from the predicted line and the actual (x,y) points.
If least squares linear regression minimizes the vertical distance to the line, Deming regression minimizes the total distance to the line. This type of regression minimizes the error in the y values and the x values. See the below figure for a comparison.
<img src="../images/05_demming_vs_linear_reg.png" width="512">
To implement this in TensorFlow, we start by loading the necessary libraries.
```
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
ops.reset_default_graph()
```
Start a computational graph session:
```
sess = tf.Session()
```
We load the iris data.
```
# Load the data
# iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data]) # Petal Width
y_vals = np.array([y[0] for y in iris.data]) # Sepal Length
```
Next we declare the batch size, model placeholders, model variables, and model operations.
```
# Declare batch size
batch_size = 125
# Initialize placeholders
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# Create variables for linear regression
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
# Declare model operations
model_output = tf.add(tf.matmul(x_data, A), b)
```
For the demming loss, we want to compute:
$$ \frac{\left| A \cdot x + b - y \right|}{\sqrt{A^{2} + 1}} $$
Which will give us the shortest distance between a point (x,y) and the predicted line, $A \cdot x + b$.
```
# Declare Demming loss function
demming_numerator = tf.abs(tf.subtract(tf.add(tf.matmul(x_data, A), b), y_target))
demming_denominator = tf.sqrt(tf.add(tf.square(A),1))
loss = tf.reduce_mean(tf.truediv(demming_numerator, demming_denominator))
```
Next we declare the optimization function and initialize all model variables.
```
# Declare optimizer
my_opt = tf.train.GradientDescentOptimizer(0.25)
train_step = my_opt.minimize(loss)
# Initialize variables
init = tf.global_variables_initializer()
sess.run(init)
```
Now we train our Demming regression for 250 iterations.
```
# Training loop
loss_vec = []
for i in range(1500):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(temp_loss)
if (i+1)%100==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))
```
Retrieve the optimal coefficients (slope and intercept).
```
# Get the optimal coefficients
[slope] = sess.run(A)
[y_intercept] = sess.run(b)
# Get best fit line
best_fit = []
for i in x_vals:
best_fit.append(slope*i+y_intercept)
```
Here is matplotlib code to plot the best fit Demming regression line and the Demming Loss.
```
# Plot the result
plt.plot(x_vals, y_vals, 'o', label='Data Points')
plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)
plt.legend(loc='upper left')
plt.title('Sepal Length vs Pedal Width')
plt.xlabel('Pedal Width')
plt.ylabel('Sepal Length')
plt.show()
# Plot loss over time
plt.plot(loss_vec, 'k-')
plt.title('Demming Loss per Generation')
plt.xlabel('Iteration')
plt.ylabel('Demming Loss')
plt.show()
```
tested; Gopal
| true |
code
| 0.655915 | null | null | null | null |
|
# Finding the maximum value of 2d function
Given equation:
\begin{align}
f(x, y) = 2xy + 2x - x^2 -2y^2
\end{align}
### Implementation of needed functions:
```
# Importing dependency functions and packages
from random import random
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D, get_test_data
from matplotlib import cm
import numpy as np
%matplotlib notebook
# function
def f(x, y):
return 2*x*y + 2*x - x**2 - 2*y**2
# random search algorithm
def random_search(f, n, xl, xu, yl, yu):
# generate lists of random x and y values
x_cand = [xl + (xu - xl)*random() for _ in range(n)]
y_cand = [yl + (yu - yl)*random() for _ in range(n)]
# calculate appropriate to x and y values function values
poss_max = [f(x, y) for x, y in zip(x_cand, y_cand)]
# finding index of maximum value (argmax)
max_val = max(poss_max)
max_indexes = [i for i, j in enumerate(poss_max) if j == max_val]
# return maximum value of function and its parameters x, y
return max_val, x_cand[max_indexes[0]], y_cand[max_indexes[0]]
# simple rms error function
def rms_error(x_ref, y_ref, x, y):
return np.sqrt(((x_ref - x)/x_ref)**2 + ((y_ref - y)/y_ref)**2)
```
The problem is in guessing limits of parameters (x, y) for random number generation. The smaller limits are, the bigger accuracy we will get. Let's visualize function and judge from there.
```
fig = plt.figure(figsize=plt.figaspect(0.5))
ax = fig.add_subplot(1, 1, 1, projection='3d')
x = np.arange(-100, 100, 5)
y = np.arange(-100, 100, 5)
x, y = np.meshgrid(x, y)
z = f(x, y)
surf = ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
fig.colorbar(surf, shrink=0.5, aspect=10)
plt.show()
```
From above 3D plot it is seen that solution lies between -50 and 50 for both parameters x, y.
```
f_ref, x_ref, y_ref = random_search(f, 10000000, -50, 50, -50, 50)
print('Using 10000000 random points and ranges between -50 and 50, it is found that maximum value of given function is:', f_ref)
```
The roots found using random search method using 10 million points and considered as reference roots and as ideal. This is done in order to determine root-mean-square error somehow and find dependency of error to number of random points. Since reference roots are found using 10 million random points, it is more accurate than roots found below for error plotting reasons.
```
error_list = []
for n in np.logspace(1, 6, num=20):
_, x, y = random_search(f, int(n), -50, 50, -50, 50)
error_list += [rms_error(x_ref, y_ref, x, y)]
plt.semilogx(np.logspace(1, 6, num=20), error_list, '-')
plt.grid(which='both')
plt.xlabel('Number of random points')
plt.ylabel('RMS error of x and y roots')
plt.show()
```
From error vs #of_points plot it is seen that line have linear dependency on number of random points (Exponential shape on log-scale). This confirms the fact that x and y values are generated uniformly and increased number of random points also increases accuracy linearly, distributing on 2d space equally.
| true |
code
| 0.578924 | null | null | null | null |
|
# Medical Image Analysis workshop - IT-IST
## Image Filtering (edge preserving denoising, smoothing, etc.), Resampling and Segmentation
Lets load the image saved in previous notebook and view it.
```
import SimpleITK as sitk
import itk
import itkwidgets as itkw
from ipywidgets import interactive
import ipywidgets as widgets
import numpy as np
image_itk = itk.imread('./cT1wNeuro.nrrd')
image_sitk = sitk.ReadImage('./cT1wNeuro.nrrd')
itkw.view(image_itk, cmap='Grayscale', mode='x')
```
## Filters
### Curvature Anisotropic Diffusion Filter
The Curvature Anisotropic Diffusion Filter ([Documentation SimpleITK](https://itk.org/SimpleITKDoxygen/html/classitk_1_1simple_1_1CurvatureAnisotropicDiffusionImageFilter.html)) is widely used in medical images to denoise your image while preserving the edges.
Note 1: ITK/SimpleITK often poses restriction into the pixel/voxel type to execute some operations. In this case we can use the Cast Image filter to convert our image of type short into float. Be careful when performing the cast operation from higher to lower pixel/voxel types (rescaling may be required)
Note 2: There are several types of Anisotropic Diffusion Filters and another commonly used is the Gradient Anisotropic Diffusion filter (an example of that may be found on the Extras notebook).
```
image_sitk_float = sitk.Cast(image_sitk, sitk.sitkFloat32)
smooth_cadf_sitk = sitk.CurvatureAnisotropicDiffusion(image_sitk_float)
itkw.view(smooth_cadf_sitk, cmap='Grayscale', mode='x')
```
As previously mentioned, ITK is more verbose than SimpleITK but it more customizable and offers additional filters.
The same result that was achieved by with three lines requires the following in ITK
```
castImageFilter = itk.CastImageFilter[image_itk, itk.Image[itk.F,3]].New(image_itk)
castImageFilter.Update()
image_itk_float = castImageFilter.GetOutput()
curv_ani_dif_filter = itk.CurvatureAnisotropicDiffusionImageFilter[image_itk_float, itk.Image[itk.F,3]].New(image_itk_float)
curv_ani_dif_filter.Update()
smooth_cadf = curv_ani_dif_filter.GetOutput()
itkw.view(smooth_cadf, cmap='Grayscale', mode='x')
```
### Median Filter
[Documentation SimpleITK](https://itk.org/SimpleITKDoxygen/html/classitk_1_1simple_1_1MedianImageFilter.html)
```
# median_filter = sitk.MedianImageFilter()
# median_filter.SetRadius(2) # In pixels/voxels
# median_image = median_filter.Execute(image_sitk_float)
median_image = sitk.Median(image_sitk_float, [2, 2, 2])
itkw.view(median_image, cmap='Grayscale', mode='x')
```
### Sobel Filter
[Documentation SimpleITK](https://itk.org/SimpleITKDoxygen/html/classitk_1_1simple_1_1SobelEdgeDetectionImageFilter.html)
```
sobel_edge_image = sitk.SobelEdgeDetection(image_sitk_float)
itkw.view(sobel_edge_image, cmap='Grayscale', mode='x')
```
### Laplacian Sharpening Image Filter
[Documentation SimpleITK](https://itk.org/SimpleITKDoxygen/html/classitk_1_1simple_1_1LaplacianSharpeningImageFilter.html)
```
laplacian_sharped_image = sitk.LaplacianSharpening(image_sitk_float)
itkw.view(laplacian_sharped_image, cmap='Grayscale', mode='x')
```
You can also compare two images using the following command
```
itkw.checkerboard(median_image, laplacian_sharped_image, cmap='Grayscale', mode='x', pattern=5)
```
## Resampling an Image
This image is isotropic with voxels of size 1mm x 1mm x 1mm. Often images come with different voxel sizes, and depending on the analysis we may have to normalize the voxel size accross the dataset.
So lets learn how to change the voxel spacing/size from 1mm x 1mm x 1mm to 1.5mm x 2mm x 3mm.
```
resample = sitk.ResampleImageFilter()
resample.SetInterpolator = sitk.sitkBSpline
resample.SetOutputDirection(image_sitk_float.GetDirection())
resample.SetOutputOrigin(image_sitk_float.GetOrigin())
new_spacing = [1.5, 2, 5]
resample.SetOutputSpacing(new_spacing)
orig_size = np.array(image_sitk_float.GetSize(), dtype=np.int)
orig_spacing = np.array(image_sitk_float.GetSpacing(), dtype=np.float)
new_size = orig_size * (orig_spacing / new_spacing)
new_size = np.ceil(new_size).astype(np.int) # Image dimensions are in integers
new_size = [int(s) for s in new_size]
resample.SetSize(new_size)
resampled_image = resample.Execute(image_sitk_float)
print('Resample image spacing:', list(resampled_image.GetSpacing()))
print('Resample image size:', list(resampled_image.GetSize()))
print('Original image spacing:', list(image_sitk_float.GetSpacing()))
print('Original image size:', list(image_sitk_float.GetSize()))
```
## Segmentation Filters
Another common task on the medical image domain is the segmentation.
In this example we will work with a different image.
```
image_brainT1 = sitk.ReadImage('./brain_T1.nii.gz')
image_brainT1_mask_float = sitk.ReadImage('./brain_T1_mask.nii.gz')
# it is possible to force reading an image with a specific pixel/voxel type
image_brainT1_mask_uc = sitk.ReadImage('./brain_T1_mask.nii.gz', sitk.sitkUInt8)
itkw.view(image_brainT1, cmap='Grayscale', mode='z')
```
It is possible to observe that for this case we also have a binary mask corresponding to the brain.
Using the multiply filter we can obtain an image with just the brain.
```
brain_image = sitk.Multiply(image_brainT1, image_brainT1_mask_float)# image_atlas * image_atlas_mask
itkw.view(brain_image, cmap='Grayscale', mode='z')
```
NOTE: show multiplication by using *
### Thresholding Filters
#### Binary Threshold with lower and upper threshold
[Documentation SimpleITK](https://itk.org/SimpleITKDoxygen/html/classitk_1_1simple_1_1BinaryThresholdImageFilter.html)
```
binary_mask = sitk.BinaryThreshold(brain_image, lowerThreshold=300, upperThreshold=600, insideValue=1, outsideValue=0)
itkw.view(binary_mask, cmap='Grayscale', mode='z')
```
#### Interactively discretize your image using Otsu Multiple Threshold method
[Documentation SimpleITK](https://itk.org/SimpleITKDoxygen/html/classitk_1_1simple_1_1OtsuMultipleThresholdsImageFilter.html)
In this example you can see how to use SimpleITK and ipywidgets interactively change parameters of a filter (Otsu Multiple Thresholds) and check the results immediately!!
```
from ipywidgets import interactive
import ipywidgets as widgets
viewer_int = itkw.view(brain_image, cmap='Grayscale', mode='z', annotations=False)
# Create an itk smoother filter object. By re-using the object, output memory-reallocation is avoided
otsu_filter = sitk.OtsuMultipleThresholdsImageFilter() # [brain_image, itk.Image[itk.F,3]].New(brain_image)
otsu_filter.SetNumberOfHistogramBins(64)
def otsu_and_view(thresholds=2):
otsu_filter.SetNumberOfThresholds(thresholds)
# Execute and Update the image used in the viewer
viewer_int.image = otsu_filter.Execute(brain_image)
slider = interactive(otsu_and_view, thresholds=(1, 5, 1))
widgets.VBox([viewer_int, slider])
```
### Region Growing Filters
[Documentation SimpleITK](https://itk.org/SimpleITKDoxygen/html/classitk_1_1simple_1_1ConfidenceConnectedImageFilter.html)
These are a type filters that require a seed point to perform the segmentation. We will try to segment the white matter using the Confidence Connected algorithm but other implementations like the Connected Threshold and the Neighborhood Connected.
```
confidence_connected_filter = sitk.ConfidenceConnectedImageFilter()
confidence_connected_filter.SetMultiplier(1.80)
confidence_connected_filter.SetSeed([30, 61, 77])
confidence_connected_filter.SetNumberOfIterations( 10 );
confidence_connected_filter.SetReplaceValue( 255 );
confidence_connected_filter.SetInitialNeighborhoodRadius( 3 );
white_matter_image = confidence_connected_filter.Execute(brain_image)
itkw.view(white_matter_image, cmap='Grayscale', mode='z')
```
This segmentation is far from perfect. If we go back to the image, it is possible to observe that this MRI image was affected by bias field inhomogeneity. This artifact affects the performance of segmentation filters.
## Filtering MRI bias field inhomogeneity
<img src="bias_field_example.jpeg"> [Image Source](http://digitool.library.mcgill.ca/webclient/StreamGate?folder_id=0&dvs=1579874409466~728)
### N4 Bias Field Correction Image Filter
[Documentation SimpleITK](https://itk.org/SimpleITKDoxygen/html/classitk_1_1simple_1_1N4BiasFieldCorrectionImageFilter.html)
```
bias_field_filter = sitk.N4BiasFieldCorrectionImageFilter()
bias_field_filter.SetNumberOfControlPoints([4,4,4])
bias_corrected_image = bias_field_filter.Execute(sitk.Cast(brain_image,sitk.sitkFloat32), image_brainT1_mask_uc)
itkw.checkerboard(bias_corrected_image, brain_image, cmap='Grayscale', mode='z', pattern=4)
```
#### Let's now try to segment the white matter again using the same filter and parameters
```
confidence_connected_filter = sitk.ConfidenceConnectedImageFilter()
# confidence_connected_filter.SetInput(bias_corrected_image)
confidence_connected_filter.SetSeed([30, 61, 77])
confidence_connected_filter.SetMultiplier( 1.80 );
confidence_connected_filter.SetNumberOfIterations( 10 );
confidence_connected_filter.SetReplaceValue( 255 );
confidence_connected_filter.SetInitialNeighborhoodRadius( 3 );
white_matter_mask = confidence_connected_filter.Execute(bias_corrected_image)
itkw.view(white_matter_mask, cmap='Grayscale', mode='z')
```
#### Checkboard of Brain Image <-> White Matter Segmentation
```
white_matter_mask_float = sitk.Cast(white_matter_mask, sitk.sitkFloat32) * 5 ## * 5 -> bring the mask to an intensity ~ of the image
itkw.checkerboard(white_matter_mask_float, image_brainT1, cmap='Grayscale', mode='z', pattern=6)
```
## More Advanced Segmentation Filters
### Bayesian Classifier Image Filter Segmentation
This filter
This filter does not exist in SimpleITK, only in ITK. Using the numpy (python scientific computing package providing powerful N-dimensional array object) interface of both libraries we will recreate the bias field corrected simple itk images as an itk image.
The conversion of SimpleITK image to and ITK image will be your first exercise.
#### Exercise #1
Convert the bias_corrected_image, which is a SimpleITK image object to ITK image object called bias_corrected_itk_image.
##### Tips (functions required):
- sitk.GetArrayFromImage() - converts the SimpleITK image into a numpy array (physical properties of image like spacing, origin and direction are lost)
- itk.GetImageFromArray() - converts the numpy array into a SimpleITK image (physical properties of image like spacing, origin and direction are set to default values)
- bias_corrected_image.GetOrigin() - get SimpleITK image world coordinates origin vector
- bias_corrected_image.GetSpacing() - get SimpleITK image spacing vector
- bias_corrected_image.GetDirection() - get SimpleITK image direction vector
- bias_corrected_itk_image.SetOrigin(<vector_correct_origin>) - set the correct world coordinates origin using the values prodived in the vector
- bias_corrected_itk_image.SetSpacing(<vector_correct_spacing>) - set the correct spacing using the values prodived in the vector
- Set direction is a little bit trickier so here is the example of the code that you can use:
```python
# The interface for the direction is a little trickier
np_dir_vnl = itk.vnl_matrix_from_array(np.array(original_direction).reshape(3,3))
DirectionType = type(bias_corrected_itk_image.GetDirection())
direction = DirectionType(np_dir_vnl)
bias_corrected_itk_image.SetDirection(direction)
```
```
## use this code box to write your solution
bias_corrected_np_image = sitk.GetArrayFromImage(bias_corrected_image)
original_spacing = bias_corrected_image.GetSpacing()
original_origin = bias_corrected_image.GetOrigin()
original_direction = bias_corrected_image.GetDirection()
bias_corrected_itk_image = itk.GetImageFromArray(bias_corrected_np_image)
bias_corrected_itk_image.SetSpacing(original_spacing)
bias_corrected_itk_image.SetOrigin(original_origin)
# The interface for the direction is a little trickier
np_dir_vnl = itk.vnl_matrix_from_array(np.array(original_direction).reshape(3,3))
DirectionType = type(bias_corrected_itk_image.GetDirection())
direction = DirectionType(np_dir_vnl)
bias_corrected_itk_image.SetDirection(direction)
itkw.view(bias_corrected_itk_image, cmap='Grayscale', mode='z')
# The goal of this filter is to generate a membership image that indicates the membership of each pixel to each class.
# These membership images are fed as input to the Bayesian classifier filter.
# BayesianClassifierInitializationImageFilter runs K-means on the image to determine k Gaussian density functions centered
# around 'n' pixel intensity values. This is equivalent to generate Gaussian mixture model for the input image.
instance = itk.BayesianClassifierInitializationImageFilter[bias_corrected_itk_image, itk.F].New(bias_corrected_itk_image)
instance.SetNumberOfClasses(5)
instance.Update()
# The output to this filter is an itk::VectorImage that represents pixel memberships to 'n' classes.
image_bayesian_class = instance.GetOutput()
# Performs Bayesian Classification on an image using the membership Vector Image obtained by the itk.BayesianClassifierInitializationImageFilter.
bc = itk.BayesianClassifierImageFilter[image_bayesian_class, itk.SS, itk.F, itk.F].New(image_bayesian_class)
bc.Update()
labelled_bayesian = bc.GetOutput()
itkw.view(labelled_bayesian, cmap='Grayscale', mode='z')
```
### Gaussian Misture Models (GMMs) Segmentation
To execute this we will make use of the interface ITK <-> numpy and use scikit-learn use Gaussian Mixture Models (GMMs) to perform the segmentation.
We will start by getting some statistics of the image using the segmentation labels.
These will be used in the GMM.
```
import sklearn
from sklearn.mixture import GaussianMixture
## Copy of itk.Image to numpy.ndarray
np_copy = itk.array_from_image(bias_corrected_itk_image)
np_mask_copy = itk.array_from_image(labelled_bayesian)
middle_slice = int(np.floor(np_copy.shape[0]/2))
gmm = GaussianMixture(n_components = 4)
## Fit the GMM on a single slice of the MRI data
data = np_copy[middle_slice]
gmm.fit(np.reshape(data, (data.size, 1)))
## Classify the all images according to the GMM
for j in range(2):
im = np_copy[j]
cls = gmm.predict(im.reshape((im.size, 1)))
seg = np.zeros(np_copy[0].shape)
seg = cls.reshape(np_copy[0].shape)
np_mask_copy[j] = seg
## Copy of numpy.ndarray to itk.Image
mask_itk = itk.image_from_array(np_mask_copy)
## The conversion itk -> numpy -> itk will change axis orientation. Correct it with the following filter
flipFilter = itk.FlipImageFilter[itk.Image.SS3].New()
flipFilter.SetInput(mask_itk)
flipAxes = (False, True, False)
flipFilter.SetFlipAxes(flipAxes)
flipFilter.Update()
corrected_mask = flipFilter.GetOutput()
itkw.view(corrected_mask, cmap='Grayscale', mode='z')
```
#### Save mask for next notebook on Quantification
```
write_filter = itk.ImageFileWriter[labelled_bayesian].New(labelled_bayesian)
write_filter.SetFileName('bayesian_mask.nii.gz')
write_filter.Update()
```
| true |
code
| 0.471284 | null | null | null | null |
|
# Compound representation learning and property prediction
In this tuorial, we will go through how to run a Graph Neural Network (GNN) model for compound property prediction. In particular, we will demonstrate how to pretrain and finetune the model in the downstream tasks. If you are intersted in more details, please refer to the README for "[info graph](https://github.com/PaddlePaddle/PaddleHelix/apps/pretrained_compound/info_graph)" and "[pretrained GNN](https://github.com/PaddlePaddle/PaddleHelix/apps/pretrained_compound/pretrain_gnns)".
# Part I: Pretraining
In this part, we will show how to pretrain a compound GNN model. The pretraining skills here are adapted from the work of pretrain gnns, including attribute masking, context prediction and supervised pretraining.
Visit `pretrain_attrmask.py` and `pretrain_supervised.py` for more details.
```
import os
import numpy as np
import sys
sys.path.insert(0, os.getcwd() + "/..")
os.chdir("../apps/pretrained_compound/pretrain_gnns")
```
The Pahelix framework is build upon PaddlePaddle, which is a deep learning framework.
```
import paddle
import paddle.nn as nn
import pgl
from pahelix.model_zoo.pretrain_gnns_model import PretrainGNNModel, AttrmaskModel
from pahelix.datasets.zinc_dataset import load_zinc_dataset
from pahelix.utils.splitters import RandomSplitter
from pahelix.featurizers.pretrain_gnn_featurizer import AttrmaskTransformFn, AttrmaskCollateFn
from pahelix.utils import load_json_config
```
## Load configurations
Here, we use `compound_encoder_config`,`model_config` to hold the compound encoder and model configurations. `PretrainGNNModel` is the basic GNN Model used in pretrain gnns,`AttrmaskModel` is an unsupervised pretraining model which randomly masks the atom type of a node and then tries to predict the masked atom type. In the meanwhile, we use the Adam optimizer and set the learning rate to be 0.001.
```
compound_encoder_config = load_json_config("model_configs/pregnn_paper.json")
model_config = load_json_config("model_configs/pre_Attrmask.json")
compound_encoder = PretrainGNNModel(compound_encoder_config)
model = AttrmaskModel(model_config, compound_encoder)
opt = paddle.optimizer.Adam(0.001, parameters=model.parameters())
```
## Dataset loading and feature extraction
### Download the dataset using wget
First, we need to download a small dataset for this demo. If you do not have `wget` on your machine, you could also
copy the url below into your web browser to download the data. But remember to copy the data manually to the
path "../apps/pretrained_compound/pretrain_gnns/".
```
### Download a toy dataset for demonstration:
!wget "https://baidu-nlp.bj.bcebos.com/PaddleHelix%2Fdatasets%2Fcompound_datasets%2Fchem_dataset_small.tgz" --no-check-certificate
!tar -zxf "PaddleHelix%2Fdatasets%2Fcompound_datasets%2Fchem_dataset_small.tgz"
!ls "./chem_dataset_small"
### Download the full dataset as you want:
# !wget "http://snap.stanford.edu/gnn-pretrain/data/chem_dataset.zip" --no-check-certificate
# !unzip "chem_dataset.zip"
# !ls "./chem_dataset"
```
### Load the dataset and generate features
The Zinc dataset is used as the pretraining dataset.Here we use a toy dataset for demonstration,you can load the full dataset as you want.
`AttrmaskTransformFn` is used along with `AttrmaskModel`.It is used to generate features. The original features are processed into features available on the network, such as smiles strings into node and edge features.
```
### Load the first 1000 of the toy dataset for speed up
dataset = load_zinc_dataset("./chem_dataset_small/zinc_standard_agent/")
dataset = dataset[:1000]
print("dataset num: %s" % (len(dataset)))
transform_fn = AttrmaskTransformFn()
dataset.transform(transform_fn, num_workers=2)
```
## Start train
Now we train the attrmask model for 2 epochs for demostration purposes. Here we use `AttrmaskTransformFn` to aggregate multiple samples into a mini-batch.And the data loading process is accelerated with 4 processors.Then the pretrained model is saved to "./model/pretrain_attrmask", which will serve as the initial model of the downstream tasks.
```
def train(model, dataset, collate_fn, opt):
data_gen = dataset.get_data_loader(
batch_size=128,
num_workers=4,
shuffle=True,
collate_fn=collate_fn)
list_loss = []
model.train()
for graphs, masked_node_indice, masked_node_label in data_gen:
graphs = graphs.tensor()
masked_node_indice = paddle.to_tensor(masked_node_indice, 'int64')
masked_node_label = paddle.to_tensor(masked_node_label, 'int64')
loss = model(graphs, masked_node_indice, masked_node_label)
loss.backward()
opt.step()
opt.clear_grad()
list_loss.append(loss.numpy())
return np.mean(list_loss)
collate_fn = AttrmaskCollateFn(
atom_names=compound_encoder_config['atom_names'],
bond_names=compound_encoder_config['bond_names'],
mask_ratio=0.15)
for epoch_id in range(2):
train_loss = train(model, dataset, collate_fn, opt)
print("epoch:%d train/loss:%s" % (epoch_id, train_loss))
paddle.save(compound_encoder.state_dict(),
'./model/pretrain_attrmask/compound_encoder.pdparams')
```
The above is about the pretraining steps,you can adjust as needed.
# Part II: Downstream finetuning
Below we will introduce how to use the pretrained model for the finetuning of downstream tasks.
Visit `finetune.py` for more details.
```
from pahelix.utils.splitters import \
RandomSplitter, IndexSplitter, ScaffoldSplitter
from pahelix.datasets import *
from src.model import DownstreamModel
from src.featurizer import DownstreamTransformFn, DownstreamCollateFn
from src.utils import calc_rocauc_score, exempt_parameters
```
The downstream datasets are usually small and have different tasks. For example, the BBBP dataset is used for the predictions of the Blood-brain barrier permeability. The Tox21 dataset is used for the predictions of toxicity of compounds. Here we use the Tox21 dataset for demonstrations.
```
task_names = get_default_tox21_task_names()
print(task_names)
```
## Load configurations
Here, we use `compound_encoder_config` and `model_config` to hold the model configurations. Note that the configurations of the model architecture should align with that of the pretraining model, otherwise the loading will fail.
`DownstreamModel` is an supervised GNN model which predicts the tasks shown in `task_names`. Meanwhile, we use BCEloss as the criterion,Adam optimizer and set the lr to be 0.001.
```
compound_encoder_config = load_json_config("model_configs/pregnn_paper.json")
model_config = load_json_config("model_configs/down_linear.json")
model_config['num_tasks'] = len(task_names)
compound_encoder = PretrainGNNModel(compound_encoder_config)
model = DownstreamModel(model_config, compound_encoder)
criterion = nn.BCELoss(reduction='none')
opt = paddle.optimizer.Adam(0.001, parameters=model.parameters())
```
## Load pretrained models
Load the pretrained model in the pretraining phase. Here we load the model "pretrain_attrmask" as an example.
```
compound_encoder.set_state_dict(paddle.load('./model/pretrain_attrmask/compound_encoder.pdparams'))
```
## Dataset loading and feature extraction
`DownstreamTransformFn` is used along with `DownstreamModel`.It is used to generate features. The original features are processed into features available on the network, such as smiles strings into node and edge features.
The Tox21 dataset is used as the downstream dataset and we use `ScaffoldSplitter` to split the dataset into train/valid/test set. `ScaffoldSplitter` will firstly order the compounds according to Bemis-Murcko scaffold, then take the first `frac_train` proportion as the train set, the next `frac_valid` proportion as the valid set and the rest as the test set. `ScaffoldSplitter` can better evaluate the generalization ability of the model on out-of-distribution samples. Note that other splitters like `RandomSplitter`, `RandomScaffoldSplitter` and `IndexSplitter` is also available.
```
### Load the toy dataset:
dataset = load_tox21_dataset("./chem_dataset_small/tox21", task_names)
### Load the full dataset:
# dataset = load_tox21_dataset("./chem_dataset/tox21", task_names)
dataset.transform(DownstreamTransformFn(), num_workers=4)
# splitter = RandomSplitter()
splitter = ScaffoldSplitter()
train_dataset, valid_dataset, test_dataset = splitter.split(
dataset, frac_train=0.8, frac_valid=0.1, frac_test=0.1)
print("Train/Valid/Test num: %s/%s/%s" % (
len(train_dataset), len(valid_dataset), len(test_dataset)))
```
## Start train
Now we train the attrmask model for 4 epochs for demostration purposes.Here we use `DownstreamCollateFn` to aggregate multiple samples data into a mini-batch. Since each downstream task will contain more than one sub-task, the performance of the model is evaluated by the average roc-auc on all sub-tasks.
```
def train(model, train_dataset, collate_fn, criterion, opt):
data_gen = train_dataset.get_data_loader(
batch_size=128,
num_workers=4,
shuffle=True,
collate_fn=collate_fn)
list_loss = []
model.train()
for graphs, valids, labels in data_gen:
graphs = graphs.tensor()
labels = paddle.to_tensor(labels, 'float32')
valids = paddle.to_tensor(valids, 'float32')
preds = model(graphs)
loss = criterion(preds, labels)
loss = paddle.sum(loss * valids) / paddle.sum(valids)
loss.backward()
opt.step()
opt.clear_grad()
list_loss.append(loss.numpy())
return np.mean(list_loss)
def evaluate(model, test_dataset, collate_fn):
data_gen = test_dataset.get_data_loader(
batch_size=128,
num_workers=4,
shuffle=False,
collate_fn=collate_fn)
total_pred = []
total_label = []
total_valid = []
model.eval()
for graphs, valids, labels in data_gen:
graphs = graphs.tensor()
labels = paddle.to_tensor(labels, 'float32')
valids = paddle.to_tensor(valids, 'float32')
preds = model(graphs)
total_pred.append(preds.numpy())
total_valid.append(valids.numpy())
total_label.append(labels.numpy())
total_pred = np.concatenate(total_pred, 0)
total_label = np.concatenate(total_label, 0)
total_valid = np.concatenate(total_valid, 0)
return calc_rocauc_score(total_label, total_pred, total_valid)
collate_fn = DownstreamCollateFn(
atom_names=compound_encoder_config['atom_names'],
bond_names=compound_encoder_config['bond_names'])
for epoch_id in range(4):
train_loss = train(model, train_dataset, collate_fn, criterion, opt)
val_auc = evaluate(model, valid_dataset, collate_fn)
test_auc = evaluate(model, test_dataset, collate_fn)
print("epoch:%s train/loss:%s" % (epoch_id, train_loss))
print("epoch:%s val/auc:%s" % (epoch_id, val_auc))
print("epoch:%s test/auc:%s" % (epoch_id, test_auc))
paddle.save(model.state_dict(), './model/tox21/model.pdparams')
```
# Part III: Downstream Inference
In this part, we will briefly introduce how to use the trained downstream model to do inference on the given SMILES sequences.
## Load configurations
This part is the basically the same as the part II.
```
compound_encoder_config = load_json_config("model_configs/pregnn_paper.json")
model_config = load_json_config("model_configs/down_linear.json")
model_config['num_tasks'] = len(task_names)
compound_encoder = PretrainGNNModel(compound_encoder_config)
model = DownstreamModel(model_config, compound_encoder)
```
## Load finetuned models
Load the finetuned model from part II.
```
model.set_state_dict(paddle.load('./model/tox21/model.pdparams'))
```
## Start Inference
Do inference on the given SMILES sequence. We use directly call `DownstreamTransformFn` and `DownstreamCollateFn` to convert the raw SMILES sequence to the model input.
Using Tox21 dataset as an example, our finetuned downstream model can make predictions over 12 sub-tasks on Tox21.
```
SMILES="O=C1c2ccccc2C(=O)C1c1ccc2cc(S(=O)(=O)[O-])cc(S(=O)(=O)[O-])c2n1"
transform_fn = DownstreamTransformFn(is_inference=True)
collate_fn = DownstreamCollateFn(
atom_names=compound_encoder_config['atom_names'],
bond_names=compound_encoder_config['bond_names'],
is_inference=True)
graph = collate_fn([transform_fn({'smiles': SMILES})])
preds = model(graph.tensor()).numpy()[0]
print('SMILES:%s' % SMILES)
print('Predictions:')
for name, prob in zip(task_names, preds):
print(" %s:\t%s" % (name, prob))
```
| true |
code
| 0.563978 | null | null | null | null |
|
# Elliptical Trap Simulation
```
import numpy as np
import matplotlib.pyplot as plt
import src.analysis as src
from multiprocessing import Process, Queue
import pandas as pd
import time
from tqdm import tqdm
plt.gcf().subplots_adjust(bottom=0.15)
%load_ext autoreload
%autoreload 2
```
### 10 Particles
```
conf = src.config()
cutoff = 500
conf["directory"] = "elliptical_10_interacting"
conf["threads"] = 12
conf["numPart"] = 10
conf["numDim"] = 3
conf["numSteps"] = 2**20 + cutoff
conf["stepLength"] = 0.5
conf["importanceSampling"] = 1
conf["alpha"] = 0.5
conf["a"] = 0.0043
conf["InitialState"] = "HardshellInitial"
conf["Wavefunction"] = "EllipticalHardshellWavefunction"
conf["Hamiltonian"] = "EllipticalOscillator"
```
#### Gradient decent
```
mu = 0.01
for i in range(5):
src.runner(conf)
localEnergies, _, psiGrad, acceptanceRate = src.readData(conf)
gradient = src.calculateGradient(localEnergies, psiGrad)
conf["alpha"] -= mu*gradient
print(f"gradient: {gradient:.5f}. alpha: {conf['alpha']:.5f}. acceptance rate: {acceptanceRate[0]:.5f}.")
```
#### Using optimal alpha
```
conf["numSteps"] = 2**20 + cutoff
conf["alpha"] = 0.49752
src.runner(conf, verbose = True)
localEnergies, _, psiGrad, acceptanceRate = src.readData(conf, cutoff, readPos = False)
localEnergies = np.concatenate(localEnergies)
bins = np.linspace(0, 3, 200)
densityInteracting_10 = src.densityParallel(conf, bins)/conf["numSteps"]
conf["directory"] = "elliptical_10_noninteracting"
conf["a"] = 0
src.runner(conf, verbose = True)
bins = np.linspace(0, 3, 200)
densityNonInteracting = src.densityParallel(conf, bins)/conf["numSteps"]
```
#### Estimation of energy and uncertainty
```
E = np.mean(localEnergies)
Var = src.blocking(localEnergies, 18)
plt.plot(Var)
plt.show()
print(f"<E> = {E} +- {np.sqrt(Var[9])}")
```
#### Radial onebody density
```
fig = plt.figure()
plt.plot(bins, densityNonInteracting)
plt.plot(bins, densityInteracting_10, "--")
plt.xlabel("R")
plt.ylabel("number of particles per R")
plt.grid()
plt.show()
fig.savefig("figures/density10.pdf", bbox_inches = "tight")
```
### 50 particles
```
conf = src.config()
cutoff = 2000
conf["threads"] = 12
conf["numPart"] = 50
conf["numDim"] = 3
conf["numSteps"] = 2**20 + cutoff
conf["stepLength"] = 0.5
conf["importanceSampling"] = 1
conf["alpha"] = 0.49752
conf["a"] = 0.0043
conf["InitialState"] = "HardshellInitial"
conf["Wavefunction"] = "EllipticalHardshellWavefunction"
conf["Hamiltonian"] = "EllipticalOscillator"
mu = 0.001
for i in range(5):
src.runner(conf)
localEnergies, _, psiGrad, acceptanceRate = src.readData(conf, cutoff, readPos = False)
gradient = src.calculateGradient(localEnergies, psiGrad)
conf["alpha"] -= mu*gradient
print(f"gradient: {gradient:.5f}. alpha: {conf['alpha']:.5f}. acceptance rate: {acceptanceRate[0]:.5f}.")
```
#### Using optimal alpha
```
conf["directory"] = "elliptical_50_interacting"
conf["alpha"] = 0.48903
src.runner(conf, verbose = True)
localEnergies, _, psiGrad, acceptanceRate = src.readData(conf, cutoff, readPos = False)
localEnergies = np.concatenate(localEnergies)
bins = np.linspace(0, 3, 200)
conf["threads"] = 6 #downscale, to avoid using too much memory
densityInteracting_50 = src.densityParallel(conf, bins)/conf["numSteps"]
conf["directory"] = "elliptical_50_noninteracting"
conf["alpha"] = 0.48903
conf["a"] = 0
src.runner(conf, verbose = True)
bins = np.linspace(0, 3, 200)
densityNonInteracting = src.densityParallel(conf, bins)/conf["numSteps"]
```
#### Estimation of energy and uncertainty
```
E = np.mean(localEnergies)
Var = src.blocking(localEnergies, 18)
plt.plot(Var)
plt.show()
print(f"<E> = {E} +- {np.sqrt(Var[13])}")
```
#### Radial onebody density
```
fig = plt.figure()
plt.plot(bins, densityNonInteracting)
plt.plot(bins, densityInteracting_50, "--")
plt.xlabel("R")
plt.ylabel("number of particles per R")
plt.grid()
plt.show()
fig.savefig("figures/density50.pdf", bbox_inches = "tight")
```
### 100 Particles
```
conf = src.config()
cutoff = 2000
conf["threads"] = 12
conf["numPart"] = 100
conf["numDim"] = 3
conf["numSteps"] = 2**20 + cutoff
conf["stepLength"] = 0.5
conf["importanceSampling"] = 1
conf["alpha"] = 0.48903
conf["a"] = 0.0043
conf["InitialState"] = "HardshellInitial"
conf["Wavefunction"] = "EllipticalHardshellWavefunction"
conf["Hamiltonian"] = "EllipticalOscillator"
mu = 0.001
for i in range(5):
src.runner(conf)
localEnergies, _, psiGrad, acceptanceRate = src.readData(conf, cutoff, readPos = False)
gradient = src.calculateGradient(localEnergies, psiGrad)
conf["alpha"] -= mu*gradient
print(f"gradient: {gradient:.5f}. alpha: {conf['alpha']:.5f}. acceptance rate: {acceptanceRate[0]:.5f}.")
```
#### Using optimal alpha
```
conf["directory"] = "elliptical_100_interacting"
conf["alpha"] = 0.48160
src.runner(conf, verbose = True)
localEnergies, _, psiGrad, acceptanceRate = src.readData(conf, cutoff, readPos = False)
localEnergies = np.concatenate(localEnergies)
bins = np.linspace(0, 3, 200)
conf["threads"] = 3 #downscale, to avoid using too much memory
densityInteracting_100 = src.densityParallel(conf, bins)/conf["numSteps"]
conf["directory"] = "elliptical_100_noninteracting"
conf["alpha"] = 0.48160
conf["a"] = 0
src.runner(conf, verbose = True)
bins = np.linspace(0, 3, 200)
densityNonInteracting = src.densityParallel(conf, bins)/conf["numSteps"]
```
#### Estiamtion of Energy and Uncertainty
```
E = np.mean(localEnergies)
Var = src.blocking(localEnergies, 18)
plt.plot(Var)
print(f"<E> = {E} +- {np.sqrt(Var[15])}")
```
#### Radial Onebody Density
```
fig = plt.figure()
plt.plot(bins, densityNonInteracting)
plt.plot(bins, densityInteracting_100, "--")
plt.xlabel("R")
plt.ylabel("number of particles per R")
plt.grid()
plt.show()
fig.savefig("figures/density100.pdf", bbox_inches = "tight")
fig = plt.figure()
plt.plot(bins, densityNonInteracting/10)
plt.plot(bins, densityInteracting_10/10)
plt.plot(bins, densityInteracting_50/50)
plt.plot(bins, densityInteracting_100/100)
plt.xlabel("R")
plt.ylabel("scaled number of particles per R")
plt.legend(["Non-interacting", "10 particles", "50 particles", "100 particles"])
plt.grid()
plt.show()
fig.savefig("figures/density_all.pdf", bbox_inches = "tight")
```
| true |
code
| 0.63077 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#largest-number-of-fans-and-blotches" data-toc-modified-id="largest-number-of-fans-and-blotches-1"><span class="toc-item-num">1 </span>largest number of fans and blotches</a></span></li><li><span><a href="#parameter_scan" data-toc-modified-id="parameter_scan-2"><span class="toc-item-num">2 </span>parameter_scan</a></span></li><li><span><a href="#pipeline-examples" data-toc-modified-id="pipeline-examples-3"><span class="toc-item-num">3 </span>pipeline examples</a></span></li><li><span><a href="#ROIs-map" data-toc-modified-id="ROIs-map-4"><span class="toc-item-num">4 </span>ROIs map</a></span></li></ul></div>
```
from planet4 import plotting, catalog_production
rm = catalog_production.ReleaseManager('v1.0b4')
fans = rm.read_fan_file()
blotches = rm.read_blotch_file()
cols = ['angle', 'distance', 'tile_id', 'marking_id',
'obsid', 'spread',
'l_s', 'map_scale', 'north_azimuth',
'PlanetographicLatitude',
'PositiveEast360Longitude']
fans.head()
fans[cols].rename(dict(PlanetographicLatitude='Latitude',
PositiveEast360Longitude='Longitude'),
axis=1).head()
fans.columns
fan_counts = fans.groupby('tile_id').size()
blotch_counts = blotches.groupby('tile_id').size()
ids = fan_counts[fan_counts > 4][fan_counts < 10].index
pure_fans = list(set(ids) - set(blotches.tile_id))
len(ids)
len(pure_fans)
rm.savefolder
%matplotlib ipympl
plt.close('all')
from ipywidgets import interact
id_ = pure_fans[51]
def do_plot(i):
id_ = pure_fans[i]
plotting.plot_image_id_pipeline(id_, datapath=rm.savefolder, via_obsid=False,
save=True, figsize=(8,4),
saveroot='/Users/klay6683/Dropbox/src/p4_paper1/figures')
interact(do_plot, i=48)
from planet4 import markings
def do_plot(i=0):
plt.close('all')
fig, ax = plt.subplots()
markings.ImageID(pure_fans[i]).show_subframe(ax=ax)
ax.set_title(pure_fans[i])
interact(do_plot, i=(0,len(pure_fans),1))
markings.ImageID('6n3').image_name
from planet4 import markings
markings.ImageID(pure_fans[15]).image_name
plotting.plot_raw_fans(id_)
plotting.plot_finals(id_, datapath=rm.savefolder)
```
# largest number of fans and blotches
```
g_id = fans.groupby('tile_id')
g_id.size().sort_values(ascending=False).head()
blotches.groupby('tile_id').size().sort_values(ascending=False).head()
plotting.plot_finals('6mr', datapath=rm.savefolder)
plotting.plot_finals('7t9', datapath=rm.savefolder)
```
# parameter_scan
```
from planet4 import dbscan
db = dbscan.DBScanner()
import seaborn as sns
sns.set_context('paper')
db.parameter_scan(id_, 'fan', [0.13, 0.2], [10, 20, 30], size_to_scan='small')
```
# pipeline examples
```
plotting.plot_image_id_pipeline('bk7', datapath=rm.savefolder, via_obsid=False,
save=True, figsize=(8,4), do_title=False,
saveroot='/Users/klay6683/Dropbox/src/p4_paper1/figures')
plotting.plot_image_id_pipeline('ops', datapath=rm.savefolder, via_obsid=False,
save=True, figsize=(8,4), do_title=False,
saveroot='/Users/klay6683/Dropbox/src/p4_paper1/figures')
plotting.plot_image_id_pipeline('b0t', datapath=rm.savefolder, via_obsid=False,
save=True, figsize=(8,4), do_title=False,
saveroot='/Users/klay6683/Dropbox/src/p4_paper1/figures')
```
# ROIs map
```
from astropy.table import Table
tab = Table.read('/Users/klay6683/Dropbox/src/p4_paper1/rois_table.tex')
rois = tab.to_pandas()
rois.drop(0, inplace=True)
rois.head()
rois.columns = ['Latitude', 'Longitude', 'Informal Name', '# Images (MY29)', '# Images (MY30)']
rois.head()
rois.to_csv('/Users/klay6683/Dropbox/data/planet4/p4_analysis/rois.csv')
```
| true |
code
| 0.468791 | null | null | null | null |
|
# Politics and Social Sciences - Session 5 and 6
In this notebook we are going to look into the results of US presidential elections and test the Benford's law.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#Read the data
url = 'https://raw.githubusercontent.com/warwickdatasciencesociety/beginners-python/master/session-six/subject_questions/data/president_county_candidate.csv'
votes_df = pd.read_csv(url)
votes_df.head()
```
The above table (technically a dataframe) contains the results of US presidential elections grouped by each state, county and candidate. From this data set we extract two lists of numbers:
`biden_votes` - a list of total votes for Biden. Each number represents the total number of votes for Biden in a county
`trump_votes` - a list of total votes for Trump. Each number represents the total number of votes for Biden in a county
```
biden_votes = votes_df[votes_df['candidate'] == 'Joe Biden'].total_votes.to_list()
trump_votes = votes_df[votes_df['candidate'] == 'Donald Trump'].total_votes.to_list()
```
## Benford's law
The law of anomalous numbers, or the first-digit law, is an observation about the frequency distribution of leading digits in many real-life sets of numerical data. The law states that in many naturally occurring collections of numbers, the leading digit is likely to be small. In sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time.
[<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/4/46/Rozklad_benforda.svg/2560px-Rozklad_benforda.svg.png">](http://google.com.au/)
We would like to test if the 2020 elections data follows the Benford's distribution. The first step is to write a function which given a number returns its first digit. Define this funciton as `get_first_digit()`
```
def get_first_digit(x):
return int(str(x)[0])
```
Now we need to write another function `count_first_digits()` which will calculate the distribution of first digits.
The input for this function is a list of integers $[x_1, x_2, ....., x_n]$ The function should return a new list $[y_0, y_1, ..., y_9]$ such that for each $i\in{0, 1, ..., 9}$, $y_i$ is the count of $x's$ such that the first digit of $x$ is equal to $i$.
Example input: $ x = [123, 2343, 6535, 123, 456, 678]$
Expected output: $ y = [0, 2, 1, 0, 0, 0, 6, 0, 0, 0]$
In the input list there are 2 numbers whose first digit is 6, therefore $y[6] = 2$
**HINT**: define a counter list of length 10 with every entry initially set to 0. Iterate through the input list and for each number in this list find its first digit and then increase the corresponding value in the counter list by one.
```
def count_first_digits(votes_ls):
digit_counter = [0 for i in range(0,10)]
for x in votes_ls:
first_digit = get_first_digit(x)
digit_counter[first_digit] += 1
return digit_counter
```
Use the `count_first_digits()` function to calculate the distribution of first digits for Biden and Trump votes. The Benford's law does not take into considaration 0's hence, truncate the lists to delete the first entry (which corresponds to the number of 0 votes for a candidate)
```
biden_1digits_count = count_first_digits(biden_votes)[1:]
trump_1digits_count = count_first_digits(trump_votes)[1:]
```
Create a function `calculate_percentages` which given a list of numbers returns a new list whose entries are the values of the input list divided by the total sum of the input list's entries and multiplied by 100. Apply this function to the `biden_1digits_count` and `trump_1digits_count`.
```
def calculate_percentages(ls):
sum_ls = sum(ls)
percentage_ls = []
for i in range(0,len(ls)):
percentage_ls.append(ls[i]/sum_ls * 100)
return percentage_ls
biden_1digits_pc = calculate_percentages(biden_1digits_count)
trump_1digits_pc = calculate_percentages(biden_1digits_count)
```
Run the cell below to generate the plots for distribution of first digits of Biden's and Trump's votes and compare it against the theoretical Benfords law distribution.
```
from math import log10
# generate theoretical Benfords distribution
benford = [log10(1 + 1/i)*100 for i in range(1, 10)]
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (20,10))
ax1.bar(x = list(range(1,10)), height = biden_1digits_pc, color = 'C0')
ax2.bar(x = list(range(1,10)), height = trump_1digits_pc, color = 'C3')
ax3.bar(x = list(range(1,10)), height = benford, color = 'C2')
ax1.set_title("Distribution of counts of first digits \n for Biden's votes per county")
ax2.set_title("Distribution of counts of first digits \n for Trump's votes per county")
ax3.set_title("Theoretical distribution of first digits \n according to Benford's law")
ax1.set_xticks(list(range(1,10)))
ax2.set_xticks(list(range(1,10)))
ax3.set_xticks(list(range(1,10)))
fig.show()
```
By visual inspection of the distribution plots we could suspect that the first digits law is applies. (To make this statement more rigorous we should run statistical tests to reject or confirm our hypothesis).
## Second-digit Benford's law
Walter Mebane, a political scientist and statistician at the University of Michigan, was the first to apply the **second-digit** Benford's law-test in election forensics. Such analyses are considered a simple, though not foolproof, method of identifying irregularities in election results and helping to detect electoral fraud.
In analogy to the previous exercise we would like to inspect now the distribution of second digits in the election results. Start by writing a function which given a number (you may assume that it has more than than 1 digit) returns its second digit. Define this funciton as `get_second_digit()`
```
def get_second_digit(x):
return int(str(x)[1])
```
Similarily as before define a function `count_first_digits()`.
**HINT** before applying the `get_second_digit()` function you need to make sure that the number which is currently under consideration is at least 10. If not, then this number should be omitted in the calculations. (Make use of the control flow statements)
```
def count_first_digits(votes_ls):
digit_counter = [0 for i in range(0,10)]
for x in votes_ls:
if x < 10:
continue
else:
second_digit = get_second_digit(x)
digit_counter[second_digit] += 1
return digit_counter
```
Use the `count_second_digits()` function to calculate the distribution of first digits for Biden and Trump votes. (There is no need to disregard 0's in the case of second digits case). Next apply the `calculate_percentages` functions the newly created lists.
```
trump_2digits_count = count_first_digits(trump_votes)
biden_2digits_count = count_first_digits(biden_votes)
biden_2digits_pc = calculate_percentages(biden_2digits_count)
trump_2digits_pc = calculate_percentages(trump_2digits_count)
```
Run the cell below to generate the plots for distribution of second digits for Biden's and Trump's votes.
```
#theoretical distribution of Benford second digits
benford_2 = [12, 11.4, 10.9, 10.4, 10.0, 9.7, 9.3, 9.0, 8.8, 8.5]
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (20,10))
ax1.bar(x = list(range(0,10)), height = biden_2digits_pc, color = 'C0')
ax2.bar(x = list(range(0,10)), height = trump_2digits_pc, color = 'C3')
ax3.bar(x = list(range(0,10)), height = benford_2, color = 'C2')
ax1.set_title("Distribution of counts of second digits \n for Biden's votes per county")
ax2.set_title("Distribution of counts of second digits \n for Trump's votes per county")
ax3.set_title("Theoretical distribution of second digits \n according to Benford's law")
ax1.set_xticks(list(range(0,10)))
ax2.set_xticks(list(range(0,10)))
ax3.set_xticks(list(range(0,10)))
fig.show()
```
The distributions still seem to be fairly similar to the theoretical distribution of second digits according to Benford's law. The two tests did not produce any striking results, there are no signs of irregularity in the officially declared vote counts.
| true |
code
| 0.507263 | null | null | null | null |
|
# Introduction
## Getting started with Jupyter notebooks
The majority of your work in this course will be done using Jupyter notebooks so we will here introduce some of the basics of the notebook system. If you are already comfortable using notebooks or just would rather get on with some coding feel free to [skip straight to the exercises below](#Exercises).
*Note: Jupyter notebooks are also known as IPython notebooks. The Jupyter system now supports languages other than Python [hence the name was changed to make it more language agnostic](https://ipython.org/#jupyter-and-the-future-of-ipython) however IPython notebook is still commonly used.*
### Jupyter basics: the server, dashboard and kernels
In launching this notebook you will have already come across two of the other key components of the Jupyter system - the notebook *server* and *dashboard* interface.
We began by starting a notebook server instance in the terminal by running
```
jupyter notebook
```
This will have begun printing a series of log messages to terminal output similar to
```
$ jupyter notebook
[I 08:58:24.417 NotebookApp] Serving notebooks from local directory: ~/mlpractical
[I 08:58:24.417 NotebookApp] 0 active kernels
[I 08:58:24.417 NotebookApp] The Jupyter Notebook is running at: http://localhost:8888/
```
The last message included here indicates the URL the application is being served at. The default behaviour of the `jupyter notebook` command is to open a tab in a web browser pointing to this address after the server has started up. The server can be launched without opening a browser window by running `jupyter notebook --no-browser`. This can be useful for example when running a notebook server on a remote machine over SSH. Descriptions of various other command options can be found by displaying the command help page using
```
juptyer notebook --help
```
While the notebook server is running it will continue printing log messages to terminal it was started from. Unless you detach the process from the terminal session you will need to keep the session open to keep the notebook server alive. If you want to close down a running server instance from the terminal you can use `Ctrl+C` - this will bring up a confirmation message asking you to confirm you wish to shut the server down. You can either enter `y` or skip the confirmation by hitting `Ctrl+C` again.
When the notebook application first opens in your browser you are taken to the notebook *dashboard*. This will appear something like this
<img src='res/jupyter-dashboard.png' />
The dashboard above is showing the `Files` tab, a list of files in the directory the notebook server was launched from. We can navigate in to a sub-directory by clicking on a directory name and back up to the parent directory by clicking the `..` link. An important point to note is that the top-most level that you will be able to navigate to is the directory you run the server from. This is a security feature and generally you should try to limit the access the server has by launching it in the highest level directory which gives you access to all the files you need to work with.
As well as allowing you to launch existing notebooks, the `Files` tab of the dashboard also allows new notebooks to be created using the `New` drop-down on the right. It can also perform basic file-management tasks such as renaming and deleting files (select a file by checking the box alongside it to bring up a context menu toolbar).
In addition to opening notebook files, we can also edit text files such as `.py` source files, directly in the browser by opening them from the dashboard. The in-built text-editor is less-featured than a full IDE but is useful for quick edits of source files and previewing data files.
The `Running` tab of the dashboard gives a list of the currently running notebook instances. This can be useful to keep track of which notebooks are still running and to shutdown (or reopen) old notebook processes when the corresponding tab has been closed.
### The notebook interface
The top of your notebook window should appear something like this:
<img src='res/jupyter-notebook-interface.png' />
The name of the current notebook is displayed at the top of the page and can be edited by clicking on the text of the name. Displayed alongside this is an indication of the last manual *checkpoint* of the notebook file. On-going changes are auto-saved at regular intervals; the check-point mechanism is mainly meant as a way to recover an earlier version of a notebook after making unwanted changes. Note the default system only currently supports storing a single previous checkpoint despite the `Revert to checkpoint` dropdown under the `File` menu perhaps suggesting otherwise.
As well as having options to save and revert to checkpoints, the `File` menu also allows new notebooks to be created in same directory as the current notebook, a copy of the current notebook to be made and the ability to export the current notebook to various formats.
The `Edit` menu contains standard clipboard functions as well as options for reorganising notebook *cells*. Cells are the basic units of notebooks, and can contain formatted text like the one you are reading at the moment or runnable code as we will see below. The `Edit` and `Insert` drop down menus offer various options for moving cells around the notebook, merging and splitting cells and inserting new ones, while the `Cell` menu allow running of code cells and changing cell types.
The `Kernel` menu offers some useful commands for managing the Python process (kernel) running in the notebook. In particular it provides options for interrupting a busy kernel (useful for example if you realise you have set a slow code cell running with incorrect parameters) and to restart the current kernel. This will cause all variables currently defined in the workspace to be lost but may be necessary to get the kernel back to a consistent state after polluting the namespace with lots of global variables or when trying to run code from an updated module and `reload` is failing to work.
To the far right of the menu toolbar is a kernel status indicator. When a dark filled circle is shown this means the kernel is currently busy and any further code cell run commands will be queued to happen after the currently running cell has completed. An open status circle indicates the kernel is currently idle.
The final row of the top notebook interface is the notebook toolbar which contains shortcut buttons to some common commands such as clipboard actions and cell / kernel management. If you are interested in learning more about the notebook user interface you may wish to run through the `User Interface Tour` under the `Help` menu drop down.
### Markdown cells: easy text formatting
This entire introduction has been written in what is termed a *Markdown* cell of a notebook. [Markdown](https://en.wikipedia.org/wiki/Markdown) is a lightweight markup language intended to be readable in plain-text. As you may wish to use Markdown cells to keep your own formatted notes in notebooks, a small sampling of the formatting syntax available is below (escaped mark-up on top and corresponding rendered output below that); there are many much more extensive syntax guides - for example [this cheatsheet](https://github.com/adam-p/markdown-here/wiki/Markdown-Cheatsheet).
---
```
## Level 2 heading
### Level 3 heading
*Italicised* and **bold** text.
* bulleted
* lists
and
1. enumerated
2. lists
Inline maths $y = mx + c$ using [MathJax](https://www.mathjax.org/) as well as display style
$$ ax^2 + bx + c = 0 \qquad \Rightarrow \qquad x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
```
---
## Level 2 heading
### Level 3 heading
*Italicised* and **bold** text.
* bulleted
* lists
and
1. enumerated
2. lists
Inline maths $y = mx + c$ using [MathJax]() as well as display maths
$$ ax^2 + bx + c = 0 \qquad \Rightarrow \qquad x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
---
We can also directly use HTML tags in Markdown cells to embed rich content such as images and videos.
---
```
<img src="http://placehold.it/350x150" />
```
---
<img src="http://placehold.it/350x150" />
---
### Code cells: in browser code execution
Up to now we have not seen any runnable code. An example of a executable code cell is below. To run it first click on the cell so that it is highlighted, then either click the <i class="fa-step-forward fa"></i> button on the notebook toolbar, go to `Cell > Run Cells` or use the keyboard shortcut `Ctrl+Enter`.
```
from __future__ import print_function
import sys
print('Hello world!')
print('Alarming hello!', file=sys.stderr)
print('Hello again!')
'And again!'
```
This example shows the three main components of a code cell.
The most obvious is the input area. This (unsuprisingly) is used to enter the code to be run which will be automatically syntax highlighted.
To the immediate left of the input area is the execution indicator / counter. Before a code cell is first run this will display `In [ ]:`. After the cell is run this is updated to `In [n]:` where `n` is a number corresponding to the current execution counter which is incremented whenever any code cell in the notebook is run. This can therefore be used to keep track of the relative order in which cells were last run. There is no fundamental requirement to run cells in the order they are organised in the notebook, though things will usually be more readable if you keep things in roughly in order!
Immediately below the input area is the output area. This shows any output produced by the code in the cell. This is dealt with a little bit confusingly in the current Jupyter version. At the top any output to [`stdout`](https://en.wikipedia.org/wiki/Standard_streams#Standard_output_.28stdout.29) is displayed. Immediately below that output to [`stderr`](https://en.wikipedia.org/wiki/Standard_streams#Standard_error_.28stderr.29) is displayed. All of the output to `stdout` is displayed together even if there has been output to `stderr` between as shown by the suprising ordering in the output here.
The final part of the output area is the *display* area. By default this will just display the returned output of the last Python statement as would usually be the case in a (I)Python interpreter run in a terminal. What is displayed for a particular object is by default determined by its special `__repr__` method e.g. for a string it is just the quote enclosed value of the string itself.
### Useful keyboard shortcuts
There are a wealth of keyboard shortcuts available in the notebook interface. For an exhaustive list see the `Keyboard Shortcuts` option under the `Help` menu. We will cover a few of those we find most useful below.
Shortcuts come in two flavours: those applicable in *command mode*, active when no cell is currently being edited and indicated by a blue highlight around the current cell; those applicable in *edit mode* when the content of a cell is being edited, indicated by a green current cell highlight.
In edit mode of a code cell, two of the more generically useful keyboard shortcuts are offered by the `Tab` key.
* Pressing `Tab` a single time while editing code will bring up suggested completions of what you have typed so far. This is done in a scope aware manner so for example typing `a` + `[Tab]` in a code cell will come up with a list of objects beginning with `a` in the current global namespace, while typing `np.a` + `[Tab]` (assuming `import numpy as np` has been run already) will bring up a list of objects in the root NumPy namespace beginning with `a`.
* Pressing `Shift+Tab` once immediately after opening parenthesis of a function or method will cause a tool-tip to appear with the function signature (including argument names and defaults) and its docstring. Pressing `Shift+Tab` twice in succession will cause an expanded version of the same tooltip to appear, useful for longer docstrings. Pressing `Shift+Tab` four times in succession will cause the information to be instead displayed in a pager docked to bottom of the notebook interface which stays attached even when making further edits to the code cell and so can be useful for keeping documentation visible when editing e.g. to help remember the name of arguments to a function and their purposes.
A series of useful shortcuts available in both command and edit mode are `[modifier]+Enter` where `[modifier]` is one of `Ctrl` (run selected cell), `Shift` (run selected cell and select next) or `Alt` (run selected cell and insert a new cell after).
A useful command mode shortcut to know about is the ability to toggle line numbers on and off for a cell by pressing `L` which can be useful when trying to diagnose stack traces printed when an exception is raised or when referring someone else to a section of code.
### Magics
There are a range of *magic* commands in IPython notebooks, than provide helpful tools outside of the usual Python syntax. A full list of the inbuilt magic commands is given [here](http://ipython.readthedocs.io/en/stable/interactive/magics.html), however three that are particularly useful for this course:
* [`%%timeit`](http://ipython.readthedocs.io/en/stable/interactive/magics.html?highlight=matplotlib#magic-timeit) Put at the beginning of a cell to time its execution and print the resulting timing statistics.
* [`%precision`](http://ipython.readthedocs.io/en/stable/interactive/magics.html?highlight=matplotlib#magic-precision) Set the precision for pretty printing of floating point values and NumPy arrays.
* [`%debug`](http://ipython.readthedocs.io/en/stable/interactive/magics.html?highlight=matplotlib#magic-debug) Activates the interactive debugger in a cell. Run after an exception has been occured to help diagnose the issue.
### Plotting with `matplotlib`
When setting up your environment one of the dependencies we asked you to install was `matplotlib`. This is an extensive plotting and data visualisation library which is tightly integrated with NumPy and Jupyter notebooks.
When using `matplotlib` in a notebook you should first run the [magic command](http://ipython.readthedocs.io/en/stable/interactive/magics.html?highlight=matplotlib)
```
%matplotlib inline
```
This will cause all plots to be automatically displayed as images in the output area of the cell they are created in. Below we give a toy example of plotting two sinusoids using `matplotlib` to show case some of the basic plot options. To see the output produced select the cell and then run it.
```
# use the matplotlib magic to specify to display plots inline in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# generate a pair of sinusoids
x = np.linspace(0., 2. * np.pi, 100)
y1 = np.sin(x)
y2 = np.cos(x)
# produce a new figure object with a defined (width, height) in inches
fig = plt.figure(figsize=(8, 4))
# add a single axis to the figure
ax = fig.add_subplot(111)
# plot the two sinusoidal traces on the axis, adjusting the line width
# and adding LaTeX legend labels
ax.plot(x, y1, linewidth=2, label=r'$\sin(x)$')
ax.plot(x, y2, linewidth=2, label=r'$\cos(x)$')
# set the axis labels
ax.set_xlabel('$x$', fontsize=16)
ax.set_ylabel('$y$', fontsize=16)
# force the legend to be displayed
ax.legend()
# adjust the limits of the horizontal axis
ax.set_xlim(0., 2. * np.pi)
# make a grid be displayed in the axis background
ax.grid('on')
```
# Exercises
Today's exercises are meant to allow you to get some initial familiarisation with the `mlp` package and how data is provided to the learning functions. Next week onwards, we will follow with the material covered in lectures.
If you are new to Python and/or NumPy and are struggling to complete the exercises, you may find going through [this Stanford University tutorial](http://cs231n.github.io/python-numpy-tutorial/) by [Justin Johnson](http://cs.stanford.edu/people/jcjohns/) first helps. There is also a derived Jupyter notebook by [Volodymyr Kuleshov](http://web.stanford.edu/~kuleshov/) and [Isaac Caswell](https://symsys.stanford.edu/viewing/symsysaffiliate/21335) which you can download [from here](https://github.com/kuleshov/cs228-material/raw/master/tutorials/python/cs228-python-tutorial.ipynb) - if you save this in to your `mlpractical/notebooks` directory you should be able to open the notebook from the dashboard to run the examples.
## Data providers
Open (in the browser) the [`mlp.data_providers`](../../edit/mlp/data_providers.py) module. Have a look through the code and comments, then follow to the exercises.
### Exercise 1
The `MNISTDataProvider` iterates over input images and target classes (digit IDs) from the [MNIST database of handwritten digit images](http://yann.lecun.com/exdb/mnist/), a common supervised learning benchmark task. Using the data provider and `matplotlib` we can for example iterate over the first couple of images in the dataset and display them using the following code:
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import mlp.data_providers as data_providers
def show_single_image(img, fig_size=(2, 2)):
fig = plt.figure(figsize=fig_size)
ax = fig.add_subplot(111)
ax.imshow(img, cmap='Greys')
ax.axis('off')
plt.show()
return fig, ax
# An example for a single MNIST image
mnist_dp = data_providers.MNISTDataProvider(
which_set='valid', batch_size=1, max_num_batches=2, shuffle_order=True)
for inputs, target in mnist_dp:
show_single_image(inputs.reshape((28, 28)))
print('Image target: {0}'.format(target))
```
Generally we will want to deal with batches of multiple images i.e. `batch_size > 1`. As a first task:
* Using MNISTDataProvider, write code that iterates over the first 5 minibatches of size 100 data-points.
* Display each batch of MNIST digits in a $10\times10$ grid of images.
**Notes**:
* Images are returned from the provider as tuples of numpy arrays `(inputs, targets)`. The `inputs` matrix has shape `(batch_size, input_dim)` while the `targets` array is of shape `(batch_size,)`, where `batch_size` is the number of data points in a single batch and `input_dim` is dimensionality of the input features.
* Each input data-point (image) is stored as a 784 dimensional vector of pixel intensities normalised to $[0, 1]$ from inital integer values in $[0, 255]$. However, the original spatial domain is two dimensional, so before plotting you will need to reshape the one dimensional input arrays in to two dimensional arrays 2D (MNIST images have the same height and width dimensions).
```
def show_batch_of_images(img_batch, fig_size=(3, 3)):
fig = plt.figure(figsize=fig_size)
batch_size, im_height, im_width = img_batch.shape
# calculate no. columns per grid row to give square grid
grid_size = int(batch_size**0.5)
# intialise empty array to tile image grid into
tiled = np.empty((im_height * grid_size,
im_width * batch_size // grid_size))
# iterate over images in batch + indexes within batch
for i, img in enumerate(img_batch):
# calculate grid row and column indices
r, c = i % grid_size, i // grid_size
tiled[r * im_height:(r + 1) * im_height,
c * im_height:(c + 1) * im_height] = img
ax = fig.add_subplot(111)
ax.imshow(tiled, cmap='Greys')
ax.axis('off')
fig.tight_layout()
plt.show()
return fig, ax
batch_size = 100
num_batches = 5
mnist_dp = data_providers.MNISTDataProvider(
which_set='valid', batch_size=batch_size,
max_num_batches=num_batches, shuffle_order=True)
for inputs, target in mnist_dp:
# reshape inputs from batch of vectors to batch of 2D arrays (images)
_ = show_batch_of_images(inputs.reshape((batch_size, 28, 28)))
```
### Exercise 2
`MNISTDataProvider` as `targets` currently returns a vector of integers, each element in this vector represents an the integer ID of the class the corresponding data-point represents.
For training of neural networks a 1-of-K representation of multi-class targets is more useful. Instead of representing class identity by an integer ID, for each data point a vector of length equal to the number of classes is created, will all elements zero except for the element corresponding to the class ID.
For instance, given a batch of 5 integer targets `[2, 2, 0, 1, 0]` and assuming there are 3 different classes
the corresponding 1-of-K encoded targets would be
```
[[0, 0, 1],
[0, 0, 1],
[1, 0, 0],
[0, 1, 0],
[1, 0, 0]]
```
* Implement the `to_one_of_k` method of `MNISTDataProvider` class.
* Uncomment the overloaded `next` method, so the raw targets are converted to 1-of-K coding.
* Test your code by running the the cell below.
```
mnist_dp = data_providers.MNISTDataProvider(
which_set='valid', batch_size=5, max_num_batches=5, shuffle_order=False)
for inputs, targets in mnist_dp:
assert np.all(targets.sum(-1) == 1.)
assert np.all(targets >= 0.)
assert np.all(targets <= 1.)
print(targets)
```
### Exercise 3
Here you will write your own data provider `MetOfficeDataProvider` that wraps [weather data for south Scotland](http://www.metoffice.gov.uk/hadobs/hadukp/data/daily/HadSSP_daily_qc.txt). A previous version of this data has been stored in `data` directory for your convenience and skeleton code for the class provided in `mlp/data_providers.py`.
The data is organised in the text file as a table, with the first two columns indexing the year and month of the readings and the following 31 columns giving daily precipitation values for the corresponding month. As not all months have 31 days some of entries correspond to non-existing days. These values are indicated by a non-physical value of `-99.9`.
* You should read all of the data from the file ([`np.loadtxt`](http://docs.scipy.org/doc/numpy/reference/generated/numpy.loadtxt.html) may be useful for this) and then filter out the `-99.9` values and collapse the table to a one-dimensional array corresponding to a sequence of daily measurements for the whole period data is available for. [NumPy's boolean indexing feature](http://docs.scipy.org/doc/numpy/user/basics.indexing.html#boolean-or-mask-index-arrays) could be helpful here.
* A common initial preprocessing step in machine learning tasks is to normalise data so that it has zero mean and a standard deviation of one. Normalise the data sequence so that its overall mean is zero and standard deviation one.
* Each data point in the data provider should correspond to a window of length specified in the `__init__` method as `window_size` of this contiguous data sequence, with the model inputs being the first `window_size - 1` elements of the window and the target output being the last element of the window. For example if the original data sequence was `[1, 2, 3, 4, 5, 6]` and `window_size=3` then `input, target` pairs iterated over by the data provider should be
```
[1, 2], 3
[4, 5], 6
```
* **Extension**: Have the data provider instead overlapping windows of the sequence so that more training data instances are produced. For example for the sequence `[1, 2, 3, 4, 5, 6]` the corresponding `input, target` pairs would be
```
[1, 2], 3
[2, 3], 4
[3, 4], 5
[4, 5], 6
```
* Test your code by running the cell below.
```
batch_size = 3
for window_size in [2, 5, 10]:
met_dp = data_providers.MetOfficeDataProvider(
window_size=window_size, batch_size=batch_size,
max_num_batches=1, shuffle_order=False)
fig = plt.figure(figsize=(6, 3))
ax = fig.add_subplot(111)
ax.set_title('Window size {0}'.format(window_size))
ax.set_xlabel('Day in window')
ax.set_ylabel('Normalised reading')
# iterate over data provider batches checking size and plotting
for inputs, targets in met_dp:
assert inputs.shape == (batch_size, window_size - 1)
assert targets.shape == (batch_size, )
ax.plot(np.c_[inputs, targets].T, '.-')
ax.plot([window_size - 1] * batch_size, targets, 'ko')
```
| true |
code
| 0.805173 | null | null | null | null |
|
# Classificador Naive Bayes
Francisco Aparecido Rodrigues, francisco@icmc.usp.br.<br>
Universidade de São Paulo, São Carlos, Brasil.<br>
https://sites.icmc.usp.br/francisco <br>
Copyright: Creative Commons
<hr>
No classificador Naive Bayes, podemos assumir que os atributos são normalmente distribuídos.
```
import random
random.seed(42) # define the seed (important to reproduce the results)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#data = pd.read_csv('data/vertebralcolumn-3C.csv', header=(0))
data = pd.read_csv('data/Iris.csv', header=(0))
data = data.dropna(axis='rows') #remove NaN
# armazena os nomes das classes
classes = np.array(pd.unique(data[data.columns[-1]]), dtype=str)
print("Número de linhas e colunas na matriz de atributos:", data.shape)
attributes = list(data.columns)
data.head(10)
data = data.to_numpy()
nrow,ncol = data.shape
y = data[:,-1]
X = data[:,0:ncol-1]
```
Selecionando os conjuntos de treinamento e teste.
```
from sklearn.model_selection import train_test_split
p = 0.7 # fracao de elementos no conjunto de treinamento
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size = p, random_state = 42)
```
### Classificação: implementação do método
Inicialmente, definimos uma função para calcular a densidade de probabilidade conjunta: $$p(\vec{x}|C_i) = \prod_{j=1}^d p(x_j|C_i), \quad i=1,\ldots, k$$
onde $C_i$ são as classes. Se a distribuição for normal, temos que cada atributo $X_j$ tem a seguinte função densidade de probabilidade associada, para cada classe:
$$
p(x_j|C_i) = \frac{1}{\sqrt{2\pi\sigma_{C_i}}}\exp \left[ -\frac{1}{2}\left( \frac{x_j-\mu_{C_i}}{\sigma_{C_i}}\right)^2 \right], \quad i=1,2,\ldots, k.
$$
Assim, definimos uma função para calcular a função de verossimilhança.
```
def likelyhood(y, Z):
def gaussian(x, mu, sig):
return np.exp(-np.power(x - mu, 2.) / (2 * np.power(sig, 2.)))
prob = 1
for j in np.arange(0, Z.shape[1]):
m = np.mean(Z[:,j])
s = np.std(Z[:,j])
prob = prob*gaussian(y[j], m, s)
return prob
```
A seguir, realizamos a estimação para cada classe:
```
P = pd.DataFrame(data=np.zeros((X_test.shape[0], len(classes))), columns = classes)
for i in np.arange(0, len(classes)):
elements = tuple(np.where(y_train == classes[i]))
Z = X_train[elements,:][0]
for j in np.arange(0,X_test.shape[0]):
x = X_test[j,:]
pj = likelyhood(x,Z)
P[classes[i]][j] = pj*len(elements)/X_train.shape[0]
```
Para as observações no conjunto de teste, a probabilidade pertencer a cada classe:
```
P.head(10)
from sklearn.metrics import accuracy_score
y_pred = []
for i in np.arange(0, P.shape[0]):
c = np.argmax(np.array(P.iloc[[i]]))
y_pred.append(P.columns[c])
y_pred = np.array(y_pred, dtype=str)
score = accuracy_score(y_pred, y_test)
print('Accuracy:', score)
```
### Classificação: usando a biblioteca scikit-learn
Podemos realizar a classificação usando a função disponível na biblioteca scikit-learn.
```
from sklearn.naive_bayes import GaussianNB
from sklearn import metrics
model = GaussianNB()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
score = accuracy_score(y_pred, y_test)
print('Accuracy:', score)
```
Outra maneira de efetuarmos a classificação é assumirmos que os atributos possuem distribuição diferente da normal.
Uma possibilidade é assumirmos que os dados possuem distribuição de Bernoulli.
```
from sklearn.naive_bayes import BernoulliNB
model = BernoulliNB()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
score = accuracy_score(y_pred, y_test)
print('Accuracy:', score)
```
Código completo.
```
import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
random.seed(42)
data = pd.read_csv('data/Iris.csv', header=(0))
classes = np.array(pd.unique(data[data.columns[-1]]), dtype=str)
# Converte para matriz e vetor do numpy
data = data.to_numpy()
nrow,ncol = data.shape
y = data[:,-1]
X = data[:,0:ncol-1]
# Transforma os dados para terem media igual a zero e variancia igual a 1
#scaler = StandardScaler().fit(X)
#X = scaler.transform(X)
# Seleciona os conjuntos de treinamento e teste
p = 0.8 # fraction of elements in the test set
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size = p, random_state = 42)
# ajusta o classificador Naive-Bayes de acordo com os dados
model = GaussianNB()
model.fit(X_train, y_train)
# realiza a predicao
y_pred = model.predict(X_test)
# calcula a acuracia
score = accuracy_score(y_pred, y_test)
print('Acuracia:', score)
```
## Região de decisão
Selecionando dois atributos, podemos visualizar a região de decisão. Para graficar a região de separação, precisamos instalar a bibliteca mlxtend: http://rasbt.github.io/mlxtend/installation/<br>
Pode ser usado: conda install -c conda-forge mlxtend
Para o classificador Naive Bayes:
```
from mlxtend.plotting import plot_decision_regions
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
import sklearn.datasets as skdata
from matplotlib import pyplot
from pandas import DataFrame
# Gera os dados em duas dimensões
n_samples = 100 # número de observações
# centro dos grupos
centers = [(-4, 0), (0, 0), (3, 3)]
X, y = skdata.make_blobs(n_samples=100, n_features=2, cluster_std=1.0, centers=centers,
shuffle=False, random_state=42)
# monta a matrix de atributos
d = np.column_stack((X,np.transpose(y)))
# converte para o formato dataframe do Pandas
data = DataFrame(data = d, columns=['X1', 'X2', 'y'])
features_names = ['X1', 'X2']
class_labels = np.unique(y)
from mlxtend.plotting import plot_decision_regions
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
# mostra os dados e colori de acordo com as classes
colors = ['red', 'blue', 'green', 'black']
aux = 0
for c in class_labels:
ind = np.where(y == c)
plt.scatter(X[ind,0][0], X[ind,1][0], color = colors[aux], label = c)
aux = aux + 1
plt.legend()
plt.show()
# Training a classifier
model = GaussianNB()
model.fit(X, y)
# Plotting decision regions
plot_decision_regions(X, y, clf=model, legend=2)
plt.xlabel('X1')
plt.ylabel('X2')
plt.title('Decision Regions')
plt.show()
```
### Exercícios de fixação
1 - Repita todos os passos acima para a base de dados BreastCancer.
2 - Considere a base vertebralcolumn-3C e compare o classificadores: Naive Bayes, Classificador Bayesiano paramétrico e o classiificador Bayesiano não-paramétrico.
3 - Considerando a base de dados Vehicle, projete os dados em duas dimensões usando PCA e mostre as regiões de separação como feito acima.
4 - Faça a classificação dos dados gerados artificialmente com o código abaixo. Compare os resultados para os métodos Naive Bayes, Classificador Bayesiano paramétrico e o classiificador Bayesiano não-paramétrico.
```
from sklearn import datasets
plt.figure(figsize=(6,4))
n_samples = 1000
data = datasets.make_moons(n_samples=n_samples, noise=.05)
X = data[0]
y = data[1]
plt.scatter(X[:,0], X[:,1], c=y, cmap='viridis', s=50, alpha=0.7)
plt.show(True)
```
5 - Encontre a região de separação dos dados do exercício anterior usando o método Naive Bayes.
6 - (Facultativo) Escolha outras distribuições de probabilidade e implemente um algoritmo Naive Bayes geral. Ou seja, o algoritmo faz a classificação usando várias distribuições e obtém o melhor resultado, mostrando também qual a distribuição mais adequada.
7 - (Para pensar) É possível implementar o Naive Bayes heterogêneo, ou seja, com diferentes distribuições para cada atributo?
8 - (Desafio) Gere dados com diferentes níveis de correlação entre as variáveis e verifique se a perfomance do algoritmo muda com a correlação.
## Código completo
```
import random
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
random.seed(42)
data = pd.read_csv('data/Iris.csv', header=(0))
# classes: setosa, virginica e versicolor
classes = pd.unique(data[data.columns[-1]])
classes = np.array(classes, dtype=str)
# converte para matrizes do numpy
data = data.to_numpy()
nrow,ncol = data.shape
y = data[:,-1]
X = data[:,0:ncol-1]
# Seleciona o conjunto de teste e treinamento
p = 0.7
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size = p)
# funcao para calcular a verossimilhanca
def likelyhood(y, Z):
def gaussian(x, mu, sig):
return np.exp(-np.power(x - mu, 2.) / (2 * np.power(sig, 2.)))
prob = 1
for j in np.arange(0, Z.shape[1]):
m = np.mean(Z[:,j])
s = np.std(Z[:,j])
prob = prob*gaussian(y[j], m, s)
return prob
# matriz que armazena o produto da verossimilhanca pela priori
P = pd.DataFrame(data=np.zeros((X_test.shape[0], len(classes))), columns = classes)
for i in np.arange(0, len(classes)):
elements = tuple(np.where(y_train == classes[i]))
Z = X_train[elements,:][0]
for j in np.arange(0,X_test.shape[0]):
x = X_test[j,:]
pj = likelyhood(x,Z) #verossimilhanca
pc = len(elements)/X_train.shape[0] # priori
P[classes[i]][j] = pj*pc
# realiza a classificao seguindo a regra de Bayes
y_pred = []
for i in np.arange(0, P.shape[0]):
c = np.argmax(np.array(P.iloc[[i]]))
y_pred.append(P.columns[c])
y_pred = np.array(y_pred, dtype=str)
# calcula a acuracia na classificacao
score = accuracy_score(y_pred, y_test)
print('Accuracy:', score)
```
| true |
code
| 0.503479 | null | null | null | null |
|
# Wordle Notebook
This notebook is primarily intended as a coding demonstration of Python and Pandas for the filtering and processing of a set of string data. On a secondary basis, it also serves to simply the daily filtering and sorting of wordle-style puzzles, such as those found at https://www.nytimes.com/games/wordle/index.html
For the Python and Pandas coder, the example code includes:
1. Pulling text data out of a URL into a dataframe
2. Dynamic .assign statements using dictionaries
3. Method chaining filtering with Pandas
4. Logging statements within a method chain
5. Dynamically creating a variety of regex statements using list comprehensions, lambdas, and reduce
```
import pandas as pd
import re
import logging
from functools import reduce
logging.basicConfig(format='%(asctime)s %(message)s', datefmt='%m/%d/%Y %I:%M:%S %p', level=logging.INFO)
df = pd.read_csv(
'https://raw.githubusercontent.com/tabatkins/wordle-list/main/words',
header=None,
names=['words']
)
df = df.assign(**{f'l{i+1}' : eval(f'lambda x: x.words.str[{i}]') for i in range(0,5)})
def pipe_logger(val, label):
logging.info(f'{label} : {val}')
return val
```
## Find today's word
```
# tries is a list of tuples, each containing 5 letters
# the first tuple is the submitted word
# the second tuple contains matches
# - Lower case = Yellow match
# - Upper case = Green match
tries = [
#'-----', '-----'
('takes', ' '),
# ('chino', ' n '),
]
# Generate remaining candidates out of the tries list of tuples
candidates = (
df
[
# match words not containing letters that failed matches
~df.words.str.contains(
pipe_logger(
''.join(
[r'['] +
[
re.sub(
'\.',
'',
reduce(
# iterate over the mask, replacing each space with the letter in word a
lambda a, b: ''.join([re.sub(' ', a[i], b[i]) for i in range(0,5)]),
[
t[0],
# create a mask for removing characters
re.sub('[A-Za-z]','.',t[1])
]
)
)
# iterate over tuples
for t in tries
] +
[']']
),
'Unmatched Regex',
),
regex=True,
)
# match words containing successful letter placement
& df.words.str.contains(
pipe_logger(
# create a regular expression to find exact matches
re.sub(
' ',
'.',
# reduce the list of successful letter finds to a single word
reduce(
# iterate over the letter, replacing spaces in word a with the letter in word b
lambda a, b: ''.join([re.sub(' ', b[i], a[i]) for i in range(0,5)]),
# select the Capital letters from the successful tries
[re.sub('[a-z]',' ',t[1]) for t in tries]
)
),
'Successful Placement Regex',
),
case=False,
regex=True
)
# match words that must contain characters but placement is unknown
& df.words.str.contains(
pipe_logger(
''.join(
['^'] +
[f'(?=.*{i}.*)' for i in set(sorted(''.join([re.sub('[A-Z ]','',t[1]) for t in tries])))] +
['.*$']
),
'Unknown Placement',
),
regex=True,
)
# match words that do not have incorrect placment of characters
& df.words.str.contains(
pipe_logger(
''.join([
# replace empty characters sets with '.'
re.sub(
r'\[\^\]',
r'.',
# drop spaces and build simple regex character set for 'not'
'[^' + re.sub(' ','',t) + ']'
)
for t in
# split list by every word attempt
re.findall(
'.' * len(tries),
# merge into a single string of characters
''.join(
# take the nth character from each incorrect placement result
[re.sub('[A-Z]',' ',t[1])[i] for i in range(0,5) for t in tries]
)
)
]),
'Incorrect Placement',
),
regex=True,
)
]
)
logging.info(f'Possible Candidates : {candidates.shape[0]}')
display(candidates)
# Calculate letter frequencies in remaining candidate words
freq = (
pd.concat(
[
candidates.l1.value_counts(),
candidates.l2.value_counts(),
candidates.l3.value_counts(),
candidates.l4.value_counts(),
candidates.l5.value_counts(),
],
axis = 1
)
.fillna(0)
.astype('int')
)
freq['total'] = freq.sum(axis=1)
display(freq.sort_values('total', ascending=False))
```
| true |
code
| 0.391464 | null | null | null | null |
|
```
# default_exp core
```
# Utility functions
> A set of utility functions used throughout the library.
```
# export
import torch
import torch.nn.functional as F
import collections
import numpy as np
```
## General utils
```
# exports
def flatten_dict(nested, sep='/'):
"""Flatten dictionary and concatenate nested keys with separator."""
def rec(nest, prefix, into):
for k, v in nest.items():
if sep in k:
raise ValueError(f"separator '{sep}' not allowed to be in key '{k}'")
if isinstance(v, collections.Mapping):
rec(v, prefix + k + sep, into)
else:
into[prefix + k] = v
flat = {}
rec(nested, '', flat)
return flat
def stack_dicts(stats_dicts):
"""Stack the values of a dict."""
results = dict()
for k in stats_dicts[0]:
stats_list = [torch.flatten(d[k]) for d in stats_dicts]
results[k] = torch.stack(stats_list)
return results
def add_suffix(input_dict, suffix):
"""Add suffix to dict keys."""
return dict((k + suffix, v) for k,v in input_dict.items())
```
## Torch utils
```
# exports
def pad_to_size(tensor, size, dim=1, padding=50256):
"""Pad tensor to size."""
t_size = tensor.size()[dim]
if t_size==size:
return tensor
else:
return torch.nn.functional.pad(tensor, (0,size-t_size), 'constant', padding)
def logprobs_from_logits(logits, labels):
"""
See: https://github.com/pytorch/pytorch/issues/563#issuecomment-330103591
"""
logp = F.log_softmax(logits, dim=2)
logpy = torch.gather(logp, 2, labels.unsqueeze(2)).squeeze(-1)
return logpy
def whiten(values, shift_mean=True):
"""Whiten values."""
mean, var = torch.mean(values), torch.var(values)
whitened = (values - mean) * torch.rsqrt(var + 1e-8)
if not shift_mean:
whitened += mean
return whitened
def clip_by_value(x, tensor_min, tensor_max):
"""
Tensor extenstion to torch.clamp
https://github.com/pytorch/pytorch/issues/2793#issuecomment-428784713
"""
clipped = torch.max(torch.min(x, tensor_max), tensor_min)
return clipped
def entropy_from_logits(logits):
"""Calculate entropy from logits."""
pd = torch.nn.functional.softmax(logits, dim=-1)
entropy = torch.logsumexp(logits, axis=-1) - torch.sum(pd*logits, axis=-1)
return entropy
def average_torch_dicts(list_of_dicts):
"""Average values of a list of dicts wiht torch tensors."""
average_dict = dict()
for key in list_of_dicts[0].keys():
average_dict[key] = torch.mean(torch.stack([d[key] for d in list_of_dicts]), axis=0)
return average_dict
def stats_to_np(stats_dict):
"""Cast all torch.tensors in dict to numpy arrays."""
new_dict = dict()
for k, v in stats_dict.items():
if isinstance(v, torch.Tensor):
new_dict[k] = v.detach().cpu().numpy()
else:
new_dict[k] = v
if np.isscalar(new_dict[k]):
new_dict[k] = float(new_dict[k])
return new_dict
```
## BERT utils
```
# exports
def build_bert_batch_from_txt(text_list, tokenizer, device):
"""Create token id and attention mask tensors from text list for BERT classification."""
# tokenize
tensors = [tokenizer.encode(txt, return_tensors="pt").to(device) for txt in text_list]
# find max length to pad to
max_len = max([t.size()[1] for t in tensors])
# get padded tensors and attention masks
# (attention masks make bert ignore padding)
padded_tensors = []
attention_masks = []
for tensor in tensors:
attention_mask = torch.ones(tensor.size(), device=device)
padded_tensors.append(pad_to_size(tensor, max_len, padding=0))
attention_masks.append(pad_to_size(attention_mask, max_len, padding=0))
# stack all tensors
padded_tensors = torch.cat(padded_tensors)
attention_masks = torch.cat(attention_masks)
return padded_tensors, attention_masks
```
| true |
code
| 0.770335 | null | null | null | null |
|
# Exploratory data analysis (EDA)
## Iris Flower dataset
* A simple dataset to learn the basics.
* 3 flowers of Iris species.
* 1936 by Ronald Fisher.
* Objective: Classify a new flower as belonging to one of the 3 classes given the 4 features.
```
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams.update({'font.size': 22})
```
## Reading the data with pandas
```
try:
iris = pd.read_csv("iris.csv") # iris is a pandas dataframe
except FileNotFoundError:
import requests
r = requests.get("https://raw.githubusercontent.com/aviralchharia/EDA-on-Iris-dataset/master/iris.csv.txt")
with open("iris.csv",'wb') as f:
f.write(r.content)
iris = pd.read_csv("iris.csv")
# iris
# iris.columns
# iris.head(2)
# iris.tail(2)
# iris.count()
# iris.shape
# iris.describe() # stats on features
# iris["species"].count() # counts all values
# iris["species"].value_counts() # counts distinct values - balanced data or not??
# iris.groupby(by="species").size()
# iris.groupby(by="species").mean() # mean of each col with distinct value of "species"
# iris.groupby(by="species").std()
# iris.groupby(by="species").count()
```
## 2-D Scatter Plot
```
#2-D scatter plot:
iris.plot(kind='scatter', x='sepal_length', y='sepal_width') ;
plt.show()
sns.FacetGrid(iris, hue="species", height=4)
# 2-D Scatter plot with color-coding for each flower type/class.
sns.set_style("whitegrid")
sns.FacetGrid(iris, hue="species", height=4) \
.map(plt.scatter, "sepal_length", "sepal_width") \
.add_legend()
plt.show()
```
**Observation(s):**
1. Using sepal_length and sepal_width features, we can distinguish Setosa flowers from others.
2. Seperating Versicolor from Viginica is much harder as they have considerable overlap.
## 3D Scatter plot
## Pair-plot
```
# pairwise scatter plot: Pair-Plot
plt.close();
sns.set_style("whitegrid");
sns.pairplot(iris, hue="species", height=5);
plt.show()
# NOTE: the diagonal elements are PDFs for each feature. PDFs are expalined below.
```
**Observations**
1. petal_length and petal_width are the most useful features to identify various flower types.
2. While Setosa can be easily identified (linearly seperable), Virnica and Versicolor have some overlap (almost linearly seperable).
3. We can find "lines" and "if-else" conditions to build a simple model to classify the flower types.
**Disadvantages**
- Can be used when number of features is not too large.
- Cannot visualize higher dimensional patterns in 3-D and 4-D.
- Only possible to view 2D patterns.
# Probability Density Function and Histogram
When the number of samples is too large, scatter plot is not good, instead we use PDF
```
# 1-D scatter plot of petal-length
import numpy as np
iris_setosa = iris.loc[iris["species"] == "setosa"]
iris_virginica = iris.loc[iris["species"] == "virginica"]
iris_versicolor = iris.loc[iris["species"] == "versicolor"]
#print(iris_setosa["petal_length"])
plt.plot(iris_setosa["petal_length"], np.zeros_like(iris_setosa['petal_length']), 'o')
plt.plot(iris_versicolor["petal_length"], np.zeros_like(iris_versicolor['petal_length']), 'o')
plt.plot(iris_virginica["petal_length"], np.zeros_like(iris_virginica['petal_length']), 'o')
plt.show()
# Disadvantages of 1-D scatter plot: Very hard to make sense as points are overlapping a lot.
sns.FacetGrid(iris, hue="species", height=5) \
.map(sns.distplot, "petal_length") \
.add_legend();
plt.show();
# map: petal_length, petal_width, sepal_length, sepal_width
# y[b] = (no of points falling in bin b)/((total no of points) * bin_width)
# pdf and not pmf
# Histograms and Probability Density Functions (PDF) using KDE
# Disadv of PDF: Can we say what percentage of versicolor points have a petal_length of less than 5?
# Do some of these plots look like a bell-curve you studied in under-grad?
# Gaussian/Normal distribution
# Need for Cumulative Distribution Function (CDF)
# We can visually see what percentage of versicolor flowers have a petal_length of less than 5?
#Plot CDF of petal_length
for species in ["setosa", "virginica", 'versicolor']:
data = iris.loc[iris["species"] == species]
counts, bin_edges = np.histogram(data['petal_length'], bins=10,
density = True)
pdf = counts
cdf = np.cumsum(pdf)
# plt.figure()
plt.plot(bin_edges[1:], pdf, label='pdf '+species)
plt.plot(bin_edges[1:], cdf, label='CDF '+species)
plt.legend(loc=(1.04,0))
plt.show()
```
| true |
code
| 0.62309 | null | null | null | null |
|
## 00:56:22 - Language model from scratch
* Going to learn how a recurrent neural network works.
## 00:56:52 - Question: are there model interpretabilty tools for language models?
* There are some, but won't be covered in this part of the course.
## 00:58:11 - Preparing the dataset: tokenisation and numericalisation
* Jeremy created a dataset called human numbers that contains first 10k numbers written out in English.
* Seems very few people create datasets, even though it's not particularly hard.
```
from fastai.text.all import *
from fastcore.foundation import L
path = untar_data(URLs.HUMAN_NUMBERS)
Path.BASE_PATH = path
path.ls()
lines = L()
with open(path/'train.txt') as f:
lines += L(*f.readlines())
with open(path/'valid.txt') as f:
lines += L(*f.readlines())
lines
```
* Concat them together and put a dot between them for tokenising.
```
text = ' . '.join([l.strip() for l in lines])
text[:100]
```
* Tokenise by splitting on spaces:
```
tokens = L(text.split(' '))
tokens[100:110]
```
* Create a vocab by getting unique tokens:
```
vocab = L(tokens).unique()
vocab, len(vocab)
```
* Convert tokens into numbers by looking up index of each word:
```
word2idx = {w: i for i,w in enumerate(vocab)}
nums = L(word2idx[i] for i in tokens)
tokens, nums
```
* That gives us a small easy dataset for building a language model.
## 01:01:31 - Language model from scratch
* Create a independent and dependent pair: first 3 words are input, next is dependent.
```
L((tokens[i:i+3], tokens[i+3]) for i in range(0, len(tokens)-4, 3))
```
* Same thing numericalised:
```
seqs = L((tensor(nums[i:i+3]), nums[i+3]) for i in range(0, len(nums)-4, 3))
seqs
```
* Can batch those with a `DataLoader` object
* Take first 80% as training, last 20% as validation.
```
bs = 64
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[:cut], bs=64, shuffle=False)
```
## 01:03:35 - Simple Language model
* 3 layer neural network.
* One linear layer that is reused 3 times.
* Each time the result is added to the embedding.
```
class LMModel(Module):
def __init__(self, vocab_sz, n_hidden):
self.input2hidden = nn.Embedding(vocab_sz, n_hidden)
self.hidden2hidden = nn.Linear(n_hidden, n_hidden)
self.hidden2output = nn.Linear(n_hidden, vocab_sz)
def forward(self, x):
hidden = self.input2hidden(x[:,0])
hidden = F.relu(self.hidden2hidden(hidden))
hidden = hidden + self.input2hidden(x[:,1])
hidden = F.relu(self.hidden2hidden(hidden))
hidden = hidden + self.input2hidden(x[:,2])
hidden = F.relu(self.hidden2hidden(hidden))
return self.hidden2output(hidden)
```
## 01:04:49 - Question: can you speed up fine-tuning the NLP model?
* Do something else while you wait or leave overnight.
## 01:05:44 - Simple Language model cont.
* 2 interesting happening:
* Some of the inputs are being fed into later layers, instead of just the first.
* The model is reusing hidden state throughout layers.
```
learn = Learner(dls, LMModel(len(vocab), 64), loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(4, 1e-3)
```
* We can find out if that accuracy is good by making a simple model that predicts most common token:
```
c = Counter(tokens[cut:])
mc = c.most_common(5)
mc
mc[0][1]/len(tokens[cut:])
```
## 01:14:41 - Recurrent neural network
* We can refactor in Python using a for loop.
* Note that `hidden = 0` is being broadcast into the hidden state.
```
class LMModel2(Module):
def __init__(self, vocab_sz, n_hidden):
self.input2hidden = nn.Embedding(vocab_sz, n_hidden)
self.hidden2hidden = nn.Linear(n_hidden, n_hidden)
self.hidden2output = nn.Linear(n_hidden, vocab_sz)
def forward(self, x):
hidden = 0.
for i in range(3):
hidden = hidden + self.input2hidden(x[:,i])
hidden = F.relu(self.hidden2hidden(hidden))
return self.hidden2output(hidden)
learn = Learner(dls, LMModel2(len(vocab), 64), loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(4, 1e-3)
```
* That's what a Recurrent Neural Network is!
## 01:18:39 - Improving the RNN
* Note that we're setting the previous state to 0.
* However, the hidden state from sequence to sequence contains useful information.
* We can rewrite to maintain state of RNN.
```
class LMModel3(Module):
def __init__(self, vocab_sz, n_hidden):
self.input2hidden = nn.Embedding(vocab_sz, n_hidden)
self.hidden2hidden = nn.Linear(n_hidden, n_hidden)
self.hidden2output = nn.Linear(n_hidden, vocab_sz)
self.hidden = 0.
def forward(self, x):
for i in range(3):
self.hidden = self.hidden + self.input2hidden(x[:,i])
self.hidden = F.relu(self.hidden2hidden(self.hidden))
output = self.hidden2output(self.hidden)
self.hidden = self.hidden.detach()
return output
def reset(self):
self.h = 0.
```
## 01:19:41 - Back propagation through time
* Note that we called `self.hidden.detach()` each forward pass to ensure we're not back propogating through all the previous forward passes.
* Known as Back propagation through time (BPTT)
## 01:22:19 - Ordered sequences and callbacks
* Samples must be seen in correct order - each batch needs to connect to previous batch.
* At the start of each epoch, we need to call reset.
```
def group_chunks(ds, bs):
m = len(ds) // bs
new_ds = L()
for i in range(m):
new_ds += L(ds[i + m*j] for j in range(bs))
return new_ds
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(
group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False
)
```
* At start of epoch, we call `reset`
* Last thing to add is little tweak of training model via a`Callback` called `ModelReseter`
```
from fastai.callback.rnn import ModelResetter
learn = Learner(dls, LMModel3(len(vocab), 64), loss_func=F.cross_entropy, metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(10, 3e-3)
```
* Training is doing a lot better now.
## 01:25:00 - Creating more signal
* Instead of putting output stage outside the loop, can put it in the loop.
* After every hidden state, we get a prediction.
* Can we change the data so dependant variable has each of the three words after each three input words.
```
sl = 16
seqs = L((tensor(nums[i:i+sl]), tensor(nums[i+1:i+sl+1]))
for i in range(0, len(nums) - sl - 1, sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False)
[L(vocab[o] for o in s) for s in seqs[0]]
```
* We can modify the model to return a list of outputs.
```
class LMModel4(Module):
def __init__(self, vocab_sz, n_hidden):
self.input2hidden = nn.Embedding(vocab_sz, n_hidden)
self.hidden2hidden = nn.Linear(n_hidden, n_hidden)
self.hidden2output = nn.Linear(n_hidden, vocab_sz)
self.hidden = 0.
def forward(self, x):
outputs = []
for i in range(sl):
self.hidden = self.hidden + self.input2hidden(x[:,i])
self.hidden = F.relu(self.hidden2hidden(self.hidden))
outputs.append(self.hidden2output(self.hidden))
self.hidden = self.hidden.detach()
return torch.stack(outputs, dim=1)
def reset(self):
self.h = 0.
```
* We have to write a custom loss function to flatten the outputs:
```
def loss_func(inp, targ):
return F.cross_entropy(inp.view(-1, len(vocab)), targ.view(-1))
learn = Learner(dls, LMModel4(len(vocab), 64), loss_func=loss_func, metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)
```
## 01:28:29 - Multilayer RNN
* Even though the RNN seemed to have a lot of layers, each layer is sharing the same weight matrix.
* Not that much better than a simple linear model.
* A multilayer RNN can stake multiple linear layers within the for loop.
* PyTorch provides the `nn.RNN` class for creating multilayers RNNs.
```
class LMModel5(Module):
def __init__(self, vocab_sz, n_hidden, n_layers):
self.input2hidden = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.RNN(n_hidden, n_hidden, n_layers, batch_first=True)
self.hidden2output = nn.Linear(n_hidden, vocab_sz)
self.hidden = torch.zeros(n_layers, bs, n_hidden)
def forward(self, x):
res, h = self.rnn(self.input2hidden(x), self.hidden)
self.hidden = h.detach()
return self.hidden2output(res)
def reset(self):
self.hidden.zero_()
learn = Learner(dls, LMModel5(len(vocab), 64, 2), loss_func=loss_func, metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)
```
* The model seems to be doing worse. Validation loss appears to be really bad now.
## 01:32:39 - Exploding and vanishing gradients
* Very deep models can be hard to train due to exploding or vanishing gradients.
* Doing a lot of matrix multiplications across layers can give you very big or very small results.
* This can also cause gradients to grow.
* This is because numbers in a computer aren't stored precisely: they're stored as floating point numbers.
* Really big or small numbers become very close together and differences become practically 0.
* Lots of ways to deal with this:
* Batch norm.
* Smart initialisation.
* One simple technique is to use an RNN architecture called LSTM.
## 01:36:29 - LSTM
* Designed such that there's mini neural networks that decide how much previous state should be kept or discarded.
* Main detail: can replace matrix multiplication with LSTMCell sequence below:
```
class LSTMCell(nn.Module):
def __init__(self, num_inputs, num_hidden):
self.forget_gate = nn.Linear(num_inputs + num_hidden, num_hidden)
self.input_gate = nn.Linear(num_inputs + num_hidden, num_hidden)
self.cell_gate = nn.Linear(num_inputs + num_hidden, num_hidden)
self.output_gate = nn.Linear(num_inputs + num_hidden, num_hidden)
def forward(self, input, state):
h, c = state
h = torch.stack([h, input], dim=1)
forget = torch.sigmoid(self.forget_gate(h))
c = c * forget
inp = torch.sigmoid(self.input_gate(h))
cell = torch.tanh(self.cell_gate(h))
c = c + inp * cell
outgate = torch.sigmoid(self.output_gate(h))
h = outgate * torch.tanh(c)
return h, (h, c)
```
* RNN that uses LSTMCell is called `LSTM`
```
class LMModel6(Module):
def __init__(self, vocab_sz, n_hidden, n_layers):
self.input2hidden = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.hidden2output = nn.Linear(n_hidden, vocab_sz)
self.hidden = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
def forward(self, x):
res, h = self.rnn(self.input2hidden(x), self.hidden)
self.hidden = [h_.detach() for h_ in h]
return self.hidden2output(res)
def reset(self):
for h in self.hidden:
h.zero_()
learn = Learner(dls, LMModel6(len(vocab), 64, 2), loss_func=loss_func, metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 1e-2)
```
## 01:40:00 - Questions
* Can we use regularisation to make RNN params close to identity matrix?
* Will look at regularisation approaches.
* Can you check if activations are exploding or vanishing?
* Yes. You can output activations of each layer with print statements.
## 01:42:23 - Regularisation using Dropout
* Dropout is basically deleting activations at random.
* By removing activations at random, no single activations can become too "overspecialised"
* Dropout implementation:
```
class Dropout(nn.Module):
def __init__(self, p):
self.p = p
def forward(self, x):
if not self.training:
return x
mask = x.new(*x.shape).bernoulli_(1-p)
return x * mask.div_(1-p)
```
* A bermoulli random variable is a bunch of 1 and 0s with `1-p` probability of getting a 1.
* By multipying that by our input, we end up removing some layers.
## 01:47:16 - AR and TAR regularisation
* Jeremy has only seen in RNNs.
* AR (for activation regularisation)
* Similar to Weight Decay.
* Rather than adding a multiplier * sum of squares * weights.
* We add multiplier * sum of squares * activations.
* TAR (for temporal activation regularisation).
* TAR is used to calculate the difference of activations between each layer.
## 01:49:09 - Weight tying
* Since predicting the next word is about converting activations to English words.
* An embedding is about converting words to activations.
* Hypothesis: since they're roughly the same idea, can't they use the same weight matrix?
* Yes! This appears to work in practice.
```
class LMModel7(Module):
def __init__(self, vocab_sz, n_hidden, n_layers, p):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.drop = nn.Dropout(p)
self.h_o = nn.Linear(n_hidden, vocab_sz)
# This new line of code ensures that the weights of the embedding will always be the same as linear weights.
self.h_o.weight = self.i_h.weight
self.h = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
def forward(self, x):
raw, h = self.rnn(self.i_h(x), self.h)
out = self.drop(raw)
self.h = [h_.detach() for h_ in h]
return self.h_o(out), raw, out
def reset(self):
for h in self.h:
h.zero_()
```
## 01:51:00 - TextLearner
* We pass in `RNNRegularizer` callback:
```
learn = Learner(
dls,
LMModel7(len(vocab), 64, 2, 0.5),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=[ModelResetter, RNNRegularizer(alpha=2, beta=1)])
```
* Or use the `TextLearner` which passes it for us:
```
learn = TextLearner(
dls,
LMModel7(len(vocab), 64, 2, 0.5),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy
)
learn.fit_one_cycle(15, 1e-2, wd=0.1)
```
* We've now reproduced everything in AWD LSTM, which was state of the art a few years ago.
## 01:52:48 - Conclusions
* Go idea to connect with other people in your community or forum who are along the learning journey.
| true |
code
| 0.713063 | null | null | null | null |
|
# Stock Value Prediction
In this Notebook, we will create the actual prediction system, by testing various approaches and accuracy against multiple time-horizons (target_days variable).
First we will load all libraries:
```
import pandas as pd
import numpy as np
import sys, os
from datetime import datetime
sys.path.insert(1, '..')
import recommender as rcmd
from matplotlib import pyplot as plt
import seaborn as sns
%matplotlib inline
# classification approaches
import tensorflow as tf
from sklearn.linear_model import LogisticRegression
from sklearn.multioutput import MultiOutputClassifier
from sklearn.mixture import GaussianMixture
from sklearn.svm import SVC
# regression approaches
from sklearn.linear_model import LinearRegression
# data handling and scoring
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import recall_score, precision_score, f1_score, mean_squared_error
```
Next, we create the input data pipelines for stock and statement data. Therefore we will have to split data into training and test sets. There are two options for doing that:
* Splitting the list of symbols
* Splitting the results list of training stock datapoints
We will use the first option in order ensure a clear split (since the generate data has overlapping time frames, the second options would generate data that might have been seen by the system beforehand).
```
# create cache object
cache = rcmd.stocks.Cache()
# load list of all available stocks and sample sub-list
stocks = cache.list_data('stock')
def train_test_data(back, ahead, xlim, split=0.3, count=2000, stocks=stocks, cache=cache):
'''Generetes a train test split'''
sample = np.random.choice(list(stocks.keys()), 2000)
# split the stock data
count_train = int((1-split) * count)
sample_train = sample[:count_train]
sample_test = sample[count_train:]
# generate sample data
df_train = rcmd.learning.preprocess.create_dataset(sample_train, stocks, cache, back, ahead, xlim)
df_test = rcmd.learning.preprocess.create_dataset(sample_test, stocks, cache, back, ahead, xlim)
return df_train, df_test
df_train, df_test = train_test_data(10, 22, (-.5, .5), split=0.2, count=4000)
print(df_train.shape)
df_train.head()
# shortcut: store / load created datasets
df_train.to_csv('../data/train.csv')
df_test.to_csv('../data/test.csv')
# load data
#df_train = pd.read_csv('../data/train.csv')
#df_test = pd.read_csv('../data/test.csv')
```
Now that we have loaded and split the data, we have to divide it into input and output data:
```
def divide_data(df, xlim, balance_mode=None, balance_weight=1):
'''Splits the data into 3 sets: input, ouput_classify, output_regression.
Note that this function will also sample the data if choosen to create a more balanced dataset. Options are:
`under`: Undersamples the data (takes lowest data sample and )
`over`: Oversamples data to the highest number of possible samples
`over_under`: takes the mean count and samples in both directions
Args:
df (DataFrame): DF to contain all relevant data
xlim (tuple): tuple of integers used to clip and scale regression values to a range of 0 to 1
balance_mode (str): Defines the balance mode of the data (options: 'over_under', 'under', 'over')
balance_weight (float): Defines how much the calculate sample count is weighted in comparision to the actual count (should be between 0 and 1)
Returns:
df_X: DataFrame with input values
df_y_cls: DataFrame with classification labels
df_y_reg: DataFrame with regression values
'''
# sample the data correctly
if balance_mode is not None:
if balance_mode == 'over_under':
# find median
num_samples = df['target_cat'].value_counts().median().astype('int')
elif balance_mode == 'over':
# find highest number
num_samples = df['target_cat'].value_counts().max()
elif balance_mode == 'under':
# find minimal number
num_samples = df['target_cat'].value_counts().min()
else:
raise ValueError('Unkown sample mode: {}'.format(balance_mode))
# sample categories
dfs = []
for cat in df['target_cat'].unique():
df_tmp = df[df['target_cat'] == cat]
cur_samples = int(balance_weight * num_samples + (1-balance_weight) * df_tmp.shape[0])
sample = df_tmp.sample(cur_samples, replace=cur_samples > df_tmp.shape[0])
dfs.append(sample)
# concat and shuffle the rows
df = pd.concat(dfs, axis=0).sample(frac=1)
# remove all target cols
df_X = df.drop(['target', 'target_cat', 'norm_price', 'symbol'], axis=1)
# convert to dummy classes
df_y_cls = pd.get_dummies(df['target_cat'], prefix='cat', dummy_na=False)
# clip values and scale to vals
df_y_reg = np.divide( np.subtract( df['target'].clip(xlim[0], xlim[1]), xlim[0] ), (xlim[1] - xlim[0]) )
return df, df_X, df_y_cls, df_y_reg
df_train_bm, X_train, y_ctrain, y_rtrain = divide_data(df_train, (-.5, .5), balance_mode='over_under', balance_weight=0.9)
df_test_bm, X_test, y_ctest, y_rtest = divide_data(df_test, (-.5, .5))
print(pd.concat([y_ctrain.sum(axis=0), y_ctest.sum(axis=0)], axis=1))
```
Before we create the actual prediction systems, we will have to define metrics, how we want to measure the success of the systems.
As we have two approaches (classification and regression) we will use two types metrics:
* Precision, Recall & Accuracy
* RMSE
```
def _metric_classifier(y_true, y_pred, avg=None):
p = precision_score(y_true, y_pred, average=avg)
r = recall_score(y_true, y_pred, average=avg)
f1 = f1_score(y_true, y_pred, average=avg)
return f1, p, r
def score_classifier(y_true, y_pred):
'''Calculates the relevant scores for a classifer and outputs. This should show predicitions per class.'''
f1, p, r = _metric_classifier(y_true, y_pred, avg='micro')
print("Model Performance: F1={:.4f} (P={:.4f} / R={:.4f})".format(f1, p, r))
# list scores of single classes
for i, c in enumerate(y_true.columns):
sf1, sp, sr = _metric_classifier(y_true.iloc[:, i], y_pred[:, i], avg='binary')
print(" {:10} F1={:.4f} (P={:.4f} / R={:.4f})".format(c + ":", sf1, sp, sr))
def score_regression(y_true, y_pred):
mse = mean_squared_error(y_true, y_pred)
print("Model Performance: MSE={:.4f}".format(mse))
```
## Classification
The first step is to create a baseline for both approaches (classification and regression). In case of regression our target value will be `target` and for classification it will be `target_cat` (which we might convert into a one-hot vector along the way).
Lets start with the simpler form of classification:
```
y_ctrain.sum(axis=0)
# scale input data to improve convergance (Note: scaler has to be used for other input data as well)
scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.transform(X_test)
# train element
classifier = MultiOutputClassifier(LogisticRegression(max_iter=500, solver='lbfgs'))
classifier.fit(X_train_std, y_ctrain)
# predict data
y_pred = classifier.predict(X_test_std)
score_classifier(y_ctest, y_pred)
```
We can see a strong bias in the system for `cat_3`, which also has the highest number of training samples. Future work might include oversampling or more target datapoint selection to reduce these biases.
Next, support vector machines:
```
classifier_svm = MultiOutputClassifier(SVC())
classifier_svm.fit(X_train_std, y_ctrain)
y_pred_svm = classifier_svm.predict(X_test_std)
score_classifier(y_ctest, y_pred_svm)
```
We can see the results improve
```
class TestCallback(tf.keras.callbacks.Callback):
def __init__(self, data=X_test_std):
self.data = data
def on_epoch_end(self, epoch, logs={}):
loss, acc = self.model.evaluate(self.data, df_test_bm['target_cat'].to_numpy(), verbose=0)
print('\nTesting loss: {}, acc: {}\n'.format(loss, acc))
# simple feed forward network
print(X_train.shape)
print(df_train.shape)
classifier_ffn = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(X_train_std.shape[1],)),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(256, activation=tf.nn.relu),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(y_ctrain.shape[1], activation=tf.nn.softmax)
])
classifier_ffn.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
classifier_ffn.fit(X_train.to_numpy(), df_train_bm['target_cat'].to_numpy(), epochs=100, callbacks=[TestCallback()])
y_pred_ffn = classifier_ffn.predict(X_test.to_numpy())
y_pred_ffn = pd.get_dummies(y_pred_ffn.argmax(axis=1))
print(y_pred_ffn.sum(axis=0))
score_classifier(y_ctest, y_pred_ffn.to_numpy())
```
It is noteworthy that the output of the model in the test data resembles the input distribution. Lets try to improve generalization with a more complex model
```
act = tf.keras.layers.PReLU
classifier_ffn = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(X_train_std.shape[1],)),
tf.keras.layers.Dense(32), act(),
tf.keras.layers.Dense(64), act(),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Dense(128), act(),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(256), act(),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.4),
tf.keras.layers.Dense(128), act(),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(64), act(),
tf.keras.layers.Dense(y_ctrain.shape[1], activation=tf.nn.softmax)
])
classifier_ffn.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
classifier_ffn.fit(X_train.to_numpy(), df_train_bm['target_cat'].to_numpy(), epochs=200, callbacks=[TestCallback(X_test.to_numpy())])
y_pred_ffn = classifier_ffn.predict(X_test.to_numpy())
print(y_pred_ffn)
y_pred_ffn = pd.get_dummies(y_pred_ffn.argmax(axis=1))
print(y_pred_ffn.sum(axis=0))
score_classifier(y_ctest, y_pred_ffn.to_numpy())
# save the model
classifier_ffn.save('../data/keras-model.h5')
```
## Regression
The other possible option is regression. We will test a linear regression against neural networks based on RMSE score to see how the predictions hold.
```
reg = LinearRegression()
reg.fit(X_train.iloc[:, :7].to_numpy(), y_rtrain)
y_pred_reg = reg.predict(X_test.iloc[:, :7].to_numpy())
score_regression(y_rtest, y_pred_reg)
```
Now the neural Network
```
classifier_reg = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(X_train_std.shape[1],)),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(256, activation=tf.nn.relu),
tf.keras.layers.Dense(256, activation=tf.nn.relu),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(1)
])
opt = tf.keras.optimizers.SGD(learning_rate=0.00000001, nesterov=False)
classifier_reg.compile(optimizer=opt, loss='mean_squared_error', metrics=['accuracy'])
classifier_reg.fit(X_train.to_numpy(), y_rtrain.to_numpy(), epochs=20)
y_pred_reg = classifier_reg.predict(X_test.to_numpy())
score_regression(y_rtest, y_pred_reg)
y_pred_reg
y_pred_reg.shape
y_pred_ffn = classifier_ffn.predict(X_test.to_numpy())
print(y_pred_ffn)
```
| true |
code
| 0.65946 | null | null | null | null |
|
# Representing Qubit States
You now know something about bits, and about how our familiar digital computers work. All the complex variables, objects and data structures used in modern software are basically all just big piles of bits. Those of us who work on quantum computing call these *classical variables.* The computers that use them, like the one you are using to read this article, we call *classical computers*.
In quantum computers, our basic variable is the _qubit:_ a quantum variant of the bit. These have exactly the same restrictions as normal bits do: they can store only a single binary piece of information, and can only ever give us an output of `0` or `1`. However, they can also be manipulated in ways that can only be described by quantum mechanics. This gives us new gates to play with, allowing us to find new ways to design algorithms.
To fully understand these new gates, we first need understand how to write down qubit states. For this we will use the mathematics of vectors, matrices and complex numbers. Though we will introduce these concepts as we go, it would be best if you are comfortable with them already. If you need a more in-depth explanation or refresher, you can find a guide [here](../ch-prerequisites/linear_algebra.html).
## Contents
1. [Classical vs Quantum Bits](#cvsq)
1.1 [Statevectors](#statevectors)
1.2 [Qubit Notation](#notation)
1.3 [Exploring Qubits with Qiskit](#exploring-qubits)
2. [The Rules of Measurement](#rules-measurement)
2.1 [A Very Important Rule](#important-rule)
2.2 [The Implications of this Rule](#implications)
3. [The Bloch Sphere](#bloch-sphere)
3.1 [Describing the Restricted Qubit State](#bloch-sphere-1)
3.2 [Visually Representing a Qubit State](#bloch-sphere-2)
## 1. Classical vs Quantum Bits <a id="cvsq"></a>
### 1.1 Statevectors<a id="statevectors"></a>
In quantum physics we use _statevectors_ to describe the state of our system. Say we wanted to describe the position of a car along a track, this is a classical system so we could use a number $x$:

$$ x=4 $$
Alternatively, we could instead use a collection of numbers in a vector called a _statevector._ Each element in the statevector contains the probability of finding the car in a certain place:

$$
|x\rangle = \begin{bmatrix} 0\\ \vdots \\ 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}
\begin{matrix} \\ \\ \\ \leftarrow \\ \\ \\ \\ \end{matrix}
\begin{matrix} \\ \\ \text{Probability of} \\ \text{car being at} \\ \text{position 4} \\ \\ \\ \end{matrix}
$$
This isn’t limited to position, we could also keep a statevector of all the possible speeds the car could have, and all the possible colours the car could be. With classical systems (like the car example above), this is a silly thing to do as it requires keeping huge vectors when we only really need one number. But as we will see in this chapter, statevectors happen to be a very good way of keeping track of quantum systems, including quantum computers.
### 1.2 Qubit Notation <a id="notation"></a>
Classical bits always have a completely well-defined state: they are either `0` or `1` at every point during a computation. There is no more detail we can add to the state of a bit than this. So to write down the state of a of classical bit (`c`), we can just use these two binary values. For example:
c = 0
This restriction is lifted for quantum bits. Whether we get a `0` or a `1` from a qubit only needs to be well-defined when a measurement is made to extract an output. At that point, it must commit to one of these two options. At all other times, its state will be something more complex than can be captured by a simple binary value.
To see how to describe these, we can first focus on the two simplest cases. As we saw in the last section, it is possible to prepare a qubit in a state for which it definitely gives the outcome `0` when measured.
We need a name for this state. Let's be unimaginative and call it $0$ . Similarly, there exists a qubit state that is certain to output a `1`. We'll call this $1$. These two states are completely mutually exclusive. Either the qubit definitely outputs a ```0```, or it definitely outputs a ```1```. There is no overlap. One way to represent this with mathematics is to use two orthogonal vectors.
$$
|0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \, \, \, \, |1\rangle =\begin{bmatrix} 0 \\ 1 \end{bmatrix}.
$$
This is a lot of notation to take in all at once. First, let's unpack the weird $|$ and $\rangle$. Their job is essentially just to remind us that we are talking about the vectors that represent qubit states labelled $0$ and $1$. This helps us distinguish them from things like the bit values ```0``` and ```1``` or the numbers 0 and 1. It is part of the bra-ket notation, introduced by Dirac.
If you are not familiar with vectors, you can essentially just think of them as lists of numbers which we manipulate using certain rules. If you are familiar with vectors from your high school physics classes, you'll know that these rules make vectors well-suited for describing quantities with a magnitude and a direction. For example, the velocity of an object is described perfectly with a vector. However, the way we use vectors for quantum states is slightly different to this, so don't hold on too hard to your previous intuition. It's time to do something new!
With vectors we can describe more complex states than just $|0\rangle$ and $|1\rangle$. For example, consider the vector
$$
|q_0\rangle = \begin{bmatrix} \tfrac{1}{\sqrt{2}} \\ \tfrac{i}{\sqrt{2}} \end{bmatrix} .
$$
To understand what this state means, we'll need to use the mathematical rules for manipulating vectors. Specifically, we'll need to understand how to add vectors together and how to multiply them by scalars.
<p>
<details>
<summary>Reminder: Matrix Addition and Multiplication by Scalars (Click here to expand)</summary>
<p>To add two vectors, we add their elements together:
$$|a\rangle = \begin{bmatrix}a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix}, \quad
|b\rangle = \begin{bmatrix}b_0 \\ b_1 \\ \vdots \\ b_n \end{bmatrix}$$
$$|a\rangle + |b\rangle = \begin{bmatrix}a_0 + b_0 \\ a_1 + b_1 \\ \vdots \\ a_n + b_n \end{bmatrix} $$
</p>
<p>And to multiply a vector by a scalar, we multiply each element by the scalar:
$$x|a\rangle = \begin{bmatrix}x \times a_0 \\ x \times a_1 \\ \vdots \\ x \times a_n \end{bmatrix}$$
</p>
<p>These two rules are used to rewrite the vector $|q_0\rangle$ (as shown above):
$$
\begin{aligned}
|q_0\rangle & = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle \\
& = \tfrac{1}{\sqrt{2}}\begin{bmatrix}1\\0\end{bmatrix} + \tfrac{i}{\sqrt{2}}\begin{bmatrix}0\\1\end{bmatrix}\\
& = \begin{bmatrix}\tfrac{1}{\sqrt{2}}\\0\end{bmatrix} + \begin{bmatrix}0\\\tfrac{i}{\sqrt{2}}\end{bmatrix}\\
& = \begin{bmatrix}\tfrac{1}{\sqrt{2}} \\ \tfrac{i}{\sqrt{2}} \end{bmatrix}\\
\end{aligned}
$$
</details>
</p>
<p>
<details>
<summary>Reminder: Orthonormal Bases (Click here to expand)</summary>
<p>
It was stated before that the two vectors $|0\rangle$ and $|1\rangle$ are orthonormal, this means they are both <i>orthogonal</i> and <i>normalised</i>. Orthogonal means the vectors are at right angles:
</p><p><img src="images/basis.svg"></p>
<p>And normalised means their magnitudes (length of the arrow) is equal to 1. The two vectors $|0\rangle$ and $|1\rangle$ are <i>linearly independent</i>, which means we cannot describe $|0\rangle$ in terms of $|1\rangle$, and vice versa. However, using both the vectors $|0\rangle$ and $|1\rangle$, and our rules of addition and multiplication by scalars, we can describe all possible vectors in 2D space:
</p><p><img src="images/basis2.svg"></p>
<p>Because the vectors $|0\rangle$ and $|1\rangle$ are linearly independent, and can be used to describe any vector in 2D space using vector addition and scalar multiplication, we say the vectors $|0\rangle$ and $|1\rangle$ form a <i>basis</i>. In this case, since they are both orthogonal and normalised, we call it an <i>orthonormal basis</i>.
</details>
</p>
Since the states $|0\rangle$ and $|1\rangle$ form an orthonormal basis, we can represent any 2D vector with a combination of these two states. This allows us to write the state of our qubit in the alternative form:
$$ |q_0\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle $$
This vector, $|q_0\rangle$ is called the qubit's _statevector,_ it tells us everything we could possibly know about this qubit. For now, we are only able to draw a few simple conclusions about this particular example of a statevector: it is not entirely $|0\rangle$ and not entirely $|1\rangle$. Instead, it is described by a linear combination of the two. In quantum mechanics, we typically describe linear combinations such as this using the word 'superposition'.
Though our example state $|q_0\rangle$ can be expressed as a superposition of $|0\rangle$ and $|1\rangle$, it is no less a definite and well-defined qubit state than they are. To see this, we can begin to explore how a qubit can be manipulated.
### 1.3 Exploring Qubits with Qiskit <a id="exploring-qubits"></a>
First, we need to import all the tools we will need:
```
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi
```
In Qiskit, we use the `QuantumCircuit` object to store our circuits, this is essentially a list of the quantum gates in our circuit and the qubits they are applied to.
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
```
In our quantum circuits, our qubits always start out in the state $|0\rangle$. We can use the `initialize()` method to transform this into any state. We give `initialize()` the vector we want in the form of a list, and tell it which qubit(s) we want to initialise in this state:
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
initial_state = [0,1] # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
qc.draw() # Let's view our circuit
```
We can then use one of Qiskit’s simulators to view the resulting state of our qubit. To begin with we will use the statevector simulator, but we will explain the different simulators and their uses later.
```
backend = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
```
To get the results from our circuit, we use `execute` to run our circuit, giving the circuit and the backend as arguments. We then use `.result()` to get the result of this:
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
initial_state = [0,1] # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
result = execute(qc,backend).result() # Do the simulation, returning the result
```
from `result`, we can then get the final statevector using `.get_statevector()`:
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
initial_state = [0,1] # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
result = execute(qc,backend).result() # Do the simulation, returning the result
out_state = result.get_statevector()
print(out_state) # Display the output state vector
```
**Note:** Python uses `j` to represent $i$ in complex numbers. We see a vector with two complex elements: `0.+0.j` = 0, and `1.+0.j` = 1.
Let’s now measure our qubit as we would in a real quantum computer and see the result:
```
qc.measure_all()
qc.draw()
```
This time, instead of the statevector we will get the counts for the `0` and `1` results using `.get_counts()`:
```
result = execute(qc,backend).result()
counts = result.get_counts()
plot_histogram(counts)
```
We can see that we (unsurprisingly) have a 100% chance of measuring $|1\rangle$. This time, let’s instead put our qubit into a superposition and see what happens. We will use the state $|q_0\rangle$ from earlier in this section:
$$ |q_0\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle $$
We need to add these amplitudes to a python list. To add a complex amplitude we use `complex`, giving the real and imaginary parts as arguments:
```
initial_state = [1/sqrt(2), 1j/sqrt(2)] # Define state |q>
```
And we then repeat the steps for initialising the qubit as before:
```
qc = QuantumCircuit(1) # Must redefine qc
qc.initialize(initial_state, 0) # Initialise the 0th qubit in the state `initial_state`
state = execute(qc,backend).result().get_statevector() # Execute the circuit
print(state) # Print the result
results = execute(qc,backend).result().get_counts()
plot_histogram(results)
```
We can see we have equal probability of measuring either $|0\rangle$ or $|1\rangle$. To explain this, we need to talk about measurement.
## 2. The Rules of Measurement <a id="rules-measurement"></a>
### 2.1 A Very Important Rule <a id="important-rule"></a>
There is a simple rule for measurement. To find the probability of measuring a state $|\psi \rangle$ in the state $|x\rangle$ we do:
$$p(|x\rangle) = | \langle \psi| x \rangle|^2$$
The symbols $\langle$ and $|$ tell us $\langle \psi |$ is a row vector. In quantum mechanics we call the column vectors _kets_ and the row vectors _bras._ Together they make up _bra-ket_ notation. Any ket $|a\rangle$ has a corresponding bra $\langle a|$, and we convert between them using the conjugate transpose.
<details>
<summary>Reminder: The Inner Product (Click here to expand)</summary>
<p>There are different ways to multiply vectors, here we use the <i>inner product</i>. The inner product is a generalisation of the <i>dot product</i> which you may already be familiar with. In this guide, we use the inner product between a bra (row vector) and a ket (column vector), and it follows this rule:
$$\langle a| = \begin{bmatrix}a_0^*, & a_1^*, & \dots & a_n^* \end{bmatrix}, \quad
|b\rangle = \begin{bmatrix}b_0 \\ b_1 \\ \vdots \\ b_n \end{bmatrix}$$
$$\langle a|b\rangle = a_0^* b_0 + a_1^* b_1 \dots a_n^* b_n$$
</p>
<p>We can see that the inner product of two vectors always gives us a scalar. A useful thing to remember is that the inner product of two orthogonal vectors is 0, for example if we have the orthogonal vectors $|0\rangle$ and $|1\rangle$:
$$\langle1|0\rangle = \begin{bmatrix} 0 , & 1\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} = 0$$
</p>
<p>Additionally, remember that the vectors $|0\rangle$ and $|1\rangle$ are also normalised (magnitudes are equal to 1):
$$
\begin{aligned}
\langle0|0\rangle & = \begin{bmatrix} 1 , & 0\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} = 1 \\
\langle1|1\rangle & = \begin{bmatrix} 0 , & 1\end{bmatrix}\begin{bmatrix}0 \\ 1\end{bmatrix} = 1
\end{aligned}
$$
</p>
</details>
In the equation above, $|x\rangle$ can be any qubit state. To find the probability of measuring $|x\rangle$, we take the inner product of $|x\rangle$ and the state we are measuring (in this case $|\psi\rangle$), then square the magnitude. This may seem a little convoluted, but it will soon become second nature.
If we look at the state $|q_0\rangle$ from before, we can see the probability of measuring $|0\rangle$ is indeed $0.5$:
$$
\begin{aligned}
|q_0\rangle & = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle \\
\langle q_0| & = \tfrac{1}{\sqrt{2}}\langle0| - \tfrac{i}{\sqrt{2}}\langle 1| \\
\langle q_0| 0 \rangle & = \tfrac{1}{\sqrt{2}}\langle 0|0\rangle - \tfrac{i}{\sqrt{2}}\langle 1|0\rangle \\
\langle q_0| 0 \rangle & = \tfrac{1}{\sqrt{2}}\cdot 1 - \tfrac{i}{\sqrt{2}} \cdot 0\\
\langle q_0| 0 \rangle & = \tfrac{1}{\sqrt{2}}\\
|\langle q_0| 0 \rangle|^2 & = \tfrac{1}{2}
\end{aligned}
$$
You should verify the probability of measuring $|1\rangle$ as an exercise.
This rule governs how we get information out of quantum states. It is therefore very important for everything we do in quantum computation. It also immediately implies several important facts.
### 2.2 The Implications of this Rule <a id="implications"></a>
### #1 Normalisation
The rule shows us that amplitudes are related to probabilities. If we want the probabilities to add up to 1 (which they should!), we need to ensure that the statevector is properly normalized. Specifically, we need the magnitude of the state vector to be 1.
$$ \langle\psi|\psi\rangle = 1 \\ $$
Thus if:
$$ |\psi\rangle = \alpha|0\rangle + \beta|1\rangle $$
Then:
$$ \sqrt{|\alpha|^2 + |\beta|^2} = 1 $$
This explains the factors of $\sqrt{2}$ you have seen throughout this chapter. In fact, if we try to give `initialize()` a vector that isn’t normalised, it will give us an error:
```
vector = [1,1]
qc.initialize(vector, 0)
```
#### Quick Exercise
1. Create a state vector that will give a $1/3$ probability of measuring $|0\rangle$.
2. Create a different state vector that will give the same measurement probabilities.
3. Verify that the probability of measuring $|1\rangle$ for these two states is $2/3$.
You can check your answer in the widget below (you can use 'pi' and 'sqrt' in the vector):
```
# Run the code in this cell to interact with the widget
from qiskit_textbook.widgets import state_vector_exercise
state_vector_exercise(target=1/3)
```
### #2 Alternative measurement
The measurement rule gives us the probability $p(|x\rangle)$ that a state $|\psi\rangle$ is measured as $|x\rangle$. Nowhere does it tell us that $|x\rangle$ can only be either $|0\rangle$ or $|1\rangle$.
The measurements we have considered so far are in fact only one of an infinite number of possible ways to measure a qubit. For any orthogonal pair of states, we can define a measurement that would cause a qubit to choose between the two.
This possibility will be explored more in the next section. For now, just bear in mind that $|x\rangle$ is not limited to being simply $|0\rangle$ or $|1\rangle$.
### #3 Global Phase
We know that measuring the state $|1\rangle$ will give us the output `1` with certainty. But we are also able to write down states such as
$$\begin{bmatrix}0 \\ i\end{bmatrix} = i|1\rangle.$$
To see how this behaves, we apply the measurement rule.
$$ |\langle x| (i|1\rangle) |^2 = | i \langle x|1\rangle|^2 = |\langle x|1\rangle|^2 $$
Here we find that the factor of $i$ disappears once we take the magnitude of the complex number. This effect is completely independent of the measured state $|x\rangle$. It does not matter what measurement we are considering, the probabilities for the state $i|1\rangle$ are identical to those for $|1\rangle$. Since measurements are the only way we can extract any information from a qubit, this implies that these two states are equivalent in all ways that are physically relevant.
More generally, we refer to any overall factor $\gamma$ on a state for which $|\gamma|=1$ as a 'global phase'. States that differ only by a global phase are physically indistinguishable.
$$ |\langle x| ( \gamma |a\rangle) |^2 = | \gamma \langle x|a\rangle|^2 = |\langle x|a\rangle|^2 $$
Note that this is distinct from the phase difference _between_ terms in a superposition, which is known as the 'relative phase'. This becomes relevant once we consider different types of measurement and multiple qubits.
### #4 The Observer Effect
We know that the amplitudes contain information about the probability of us finding the qubit in a specific state, but once we have measured the qubit, we know with certainty what the state of the qubit is. For example, if we measure a qubit in the state:
$$ |q\rangle = \alpha|0\rangle + \beta|1\rangle$$
And find it in the state $|0\rangle$, if we measure again, there is a 100% chance of finding the qubit in the state $|0\rangle$. This means the act of measuring _changes_ the state of our qubits.
$$ |q\rangle = \begin{bmatrix} \alpha \\ \beta \end{bmatrix} \xrightarrow{\text{Measure }|0\rangle} |q\rangle = |0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$$
We sometimes refer to this as _collapsing_ the state of the qubit. It is a potent effect, and so one that must be used wisely. For example, were we to constantly measure each of our qubits to keep track of their value at each point in a computation, they would always simply be in a well-defined state of either $|0\rangle$ or $|1\rangle$. As such, they would be no different from classical bits and our computation could be easily replaced by a classical computation. To acheive truly quantum computation we must allow the qubits to explore more complex states. Measurements are therefore only used when we need to extract an output. This means that we often place the all measurements at the end of our quantum circuit.
We can demonstrate this using Qiskit’s statevector simulator. Let's initialise a qubit in superposition:
```
qc = QuantumCircuit(1) # Redefine qc
initial_state = [0.+1.j/sqrt(2),1/sqrt(2)+0.j]
qc.initialize(initial_state, 0)
qc.draw()
```
This should initialise our qubit in the state:
$$ |q\rangle = \tfrac{i}{\sqrt{2}}|0\rangle + \tfrac{1}{\sqrt{2}}|1\rangle $$
We can verify this using the simulator:
```
state = execute(qc, backend).result().get_statevector()
print("Qubit State = " + str(state))
```
We can see here the qubit is initialised in the state `[0.+0.70710678j 0.70710678+0.j]`, which is the state we expected.
Let’s now measure this qubit:
```
qc.measure_all()
qc.draw()
```
When we simulate this entire circuit, we can see that one of the amplitudes is _always_ 0:
```
state = execute(qc, backend).result().get_statevector()
print("State of Measured Qubit = " + str(state))
```
You can re-run this cell a few times to reinitialise the qubit and measure it again. You will notice that either outcome is equally probable, but that the state of the qubit is never a superposition of $|0\rangle$ and $|1\rangle$. Somewhat interestingly, the global phase on the state $|0\rangle$ survives, but since this is global phase, we can never measure it on a real quantum computer.
### A Note about Quantum Simulators
We can see that writing down a qubit’s state requires keeping track of two complex numbers, but when using a real quantum computer we will only ever receive a yes-or-no (`0` or `1`) answer for each qubit. The output of a 10-qubit quantum computer will look like this:
`0110111110`
Just 10 bits, no superposition or complex amplitudes. When using a real quantum computer, we cannot see the states of our qubits mid-computation, as this would destroy them! This behaviour is not ideal for learning, so Qiskit provides different quantum simulators: The `qasm_simulator` behaves as if you are interacting with a real quantum computer, and will not allow you to use `.get_statevector()`. Alternatively, `statevector_simulator`, (which we have been using in this chapter) does allow peeking at the quantum states before measurement, as we have seen.
## 3. The Bloch Sphere <a id="bloch-sphere"></a>
### 3.1 Describing the Restricted Qubit State <a id="bloch-sphere-1"></a>
We saw earlier in this chapter that the general state of a qubit ($|q\rangle$) is:
$$
|q\rangle = \alpha|0\rangle + \beta|1\rangle
$$
$$
\alpha, \beta \in \mathbb{C}
$$
(The second line tells us $\alpha$ and $\beta$ are complex numbers). The first two implications in section 2 tell us that we cannot differentiate between some of these states. This means we can be more specific in our description of the qubit.
Firstly, since we cannot measure global phase, we can only measure the difference in phase between the states $|0\rangle$ and $|1\rangle$. Instead of having $\alpha$ and $\beta$ be complex, we can confine them to the real numbers and add a term to tell us the relative phase between them:
$$
|q\rangle = \alpha|0\rangle + e^{i\phi}\beta|1\rangle
$$
$$
\alpha, \beta, \phi \in \mathbb{R}
$$
Finally, since the qubit state must be normalised, i.e.
$$
\sqrt{\alpha^2 + \beta^2} = 1
$$
we can use the trigonometric identity:
$$
\sqrt{\sin^2{x} + \cos^2{x}} = 1
$$
to describe the real $\alpha$ and $\beta$ in terms of one variable, $\theta$:
$$
\alpha = \cos{\tfrac{\theta}{2}}, \quad \beta=\sin{\tfrac{\theta}{2}}
$$
From this we can describe the state of any qubit using the two variables $\phi$ and $\theta$:
$$
|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle
$$
$$
\theta, \phi \in \mathbb{R}
$$
### 3.2 Visually Representing a Qubit State <a id="bloch-sphere-2"></a>
We want to plot our general qubit state:
$$
|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle
$$
If we interpret $\theta$ and $\phi$ as spherical co-ordinates ($r = 1$, since the magnitude of the qubit state is $1$), we can plot any qubit state on the surface of a sphere, known as the _Bloch sphere._
Below we have plotted a qubit in the state $|{+}\rangle$. In this case, $\theta = \pi/2$ and $\phi = 0$.
(Qiskit has a function to plot a bloch sphere, `plot_bloch_vector()`, but at the time of writing it only takes cartesian coordinates. We have included a function that does the conversion automatically).
```
from qiskit_textbook.widgets import plot_bloch_vector_spherical
coords = [pi/2,0,1] # [Theta, Phi, Radius]
plot_bloch_vector_spherical(coords) # Bloch Vector with spherical coordinates
```
#### Warning!
When first learning about qubit states, it's easy to confuse the qubits _statevector_ with its _Bloch vector_. Remember the statevector is the vector disucssed in [1.1](#notation), that holds the amplitudes for the two states our qubit can be in. The Bloch vector is a visualisation tool that maps the 2D, complex statevector onto real, 3D space.
#### Quick Exercise
Use `plot_bloch_vector()` or `plot_bloch_sphere_spherical()` to plot a qubit in the states:
1. $|0\rangle$
2. $|1\rangle$
3. $\tfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$
4. $\tfrac{1}{\sqrt{2}}(|0\rangle - i|1\rangle)$
5. $\tfrac{1}{\sqrt{2}}\begin{bmatrix}i\\1\end{bmatrix}$
We have also included below a widget that converts from spherical co-ordinates to cartesian, for use with `plot_bloch_vector()`:
```
from qiskit_textbook.widgets import bloch_calc
bloch_calc()
import qiskit
qiskit.__qiskit_version__
```
| true |
code
| 0.823453 | null | null | null | null |
|
# <font color="#0000cd">SSDの中身が意味プなのでがんばって解剖してみたい件</font>
***
## <font color="#4169e1">non maximum suppressionの実装</font>
1. Conjugate Contours : coords
座標をもとにバウンディングボックスを結合する
2. Conjugate Contours : areas
面積の重複が閾値を超えたら削除する
3. non maximum suppression : Python
Pythonでのnon maximum suppressionの実装
4. non maximum suppression : tensorflow
tensorflowで実装されているnon maximum suppression
## 1. Conjugate Contours : coords
```
import datetime
import cv2
import numpy as np
import matplotlib.pyplot as plt
% matplotlib inline
contours = [
[782, 363, 53, 31], [752, 360, 58, 18], [800, 600, 100, 125], [779, 349, 20, 10],
[816, 294, 77, 52], [1042, 247, 139, 91], [1079, 171, 84, 132], [1141, 161, 67, 62],
[488, 126, 44, 43], [702, 121, 50, 48], [721, 108, 59, 64], [606, 90, 21, 31],
[896, 75, 1, 1], [897, 70, 1, 1], [590, 30, 24, 27], [616, 17, 94, 94], [349, 0, 666, 652]]
fig = plt.figure(figsize=(8,6))
plt.xlim(200, 1400)
plt.ylim(-100, 800)
ax = fig.add_subplot(111)
for i in contours:
rect = plt.Rectangle((i[0],i[1]),i[2],i[3], fill=False)
ax.add_patch(rect)
plt.show()
def draw_image(contours):
old=datetime.datetime.now()
fig = plt.figure(figsize=(8,6))
plt.xlim(200, 1400)
plt.ylim(-100, 800)
ax = fig.add_subplot(111)
for i in contours:
rect = plt.Rectangle((i[0],i[1]),i[2],i[3], fill=False)
ax.add_patch(rect)
for i in conjugate_contours(contours):
rect = plt.Rectangle((i[0],i[1]),i[2],i[3], fill=False, edgecolor='#ff0000')
#rect = plt.Rectangle((i[0],i[1]),i[2]-i[0],i[3]-i[1], fill=False, edgecolor='#ff0000')
ax.add_patch(rect)
print('-------------------------------------------------------')
print('・cost time : ',(datetime.datetime.now()-old))
print('-------------------------------------------------------')
return plt.show()
def conjugate_contours(contours):
# 固定座標のインデックス, 無限ループを終えるための変数を設定
index = 0
stop = 0
while (index < len(contours) and stop < 5):
# 比較座標は固定座標の右隣からスタート
step = 1
# 一周したらリセット(最後がFalseで終了)
if index + 1 == len(contours):
index = 0
stop += 1
while (index + step < len(contours)):
# 固定座標
xmin = contours[index][0]
ymin = contours[index][1]
xmax = contours[index][2] + xmin
ymax = contours[index][3] + ymin
# 比較座標
cxmin = contours[index + step][0]
cymin = contours[index + step][1]
cxmax = contours[index + step][2] + cxmin
cymax = contours[index + step][3] + cymin
# AがBを含む、もしくはAがBに含まれる場合
if (xmin <= cxmin <= xmax or xmin <= cxmax <= xmax or cxmin <= xmin <= cxmax or cxmin <= xmax <= cxmax)\
and (ymin <= cymin <= ymax or ymin <= cymax <= ymax or cymin <= ymin <= cymax or cymin <= ymax <= cymax):
# 統合された座標
nxmin = min(xmin, cxmin)
nymin = min(ymin, cymin)
nxmax = max(xmax, cxmax)
nymax = max(ymax, cymax)
# 固定座標を統合座標で更新
contours[index] = [nxmin, nymin, nxmax-nxmin, nymax-nymin]
# 比較座標を削除
contours.pop(index + step)
# 一周したらリセット(最後がTrueで終了)
if step == 1 and index + step == len(contours):
index = 0
step = 1
# どちらにも含まれない場合、比較座標を1つずらす
else:
step += 1
# 重なるboxがなくなったら固定座標を1つずらす
else:
index += 1
return contours
draw_image(contours)
```
## 2. Conjugate Contours : areas
```
def non_max_suppression_slow(boxes, overlapThresh):
# if there are no boxes, return an empty list
if len(boxes) == 0:
return []
# initialize the list of picked indexes
pick = []
# grab the coordinates of the bounding boxes
x1 = boxes[:,0] # xmin
y1 = boxes[:,1] # ymin
x2 = boxes[:,2] # xmax
y2 = boxes[:,3] # ymax
# compute the area of the bounding boxes and sort the bounding
# boxes by the bottom-right y-coordinate of the bounding box
area = (x2 - x1 + 1) * (y2 - y1 + 1)
idxs = np.argsort(y2) # ymaxの値を昇順, [0, 2, 1]
print('idxs', idxs)
# keep looping while some indexes still remain in the indexes
# list
while len(idxs) > 0:
# grab the last index in the indexes list, add the index
# value to the list of picked indexes, then initialize
# the suppression list (i.e. indexes that will be deleted)
# using the last index
last = len(idxs) - 1 # index of biggest ymax in sort boxes
i = idxs[last] # index of biggest ymax in boxes
pick.append(i) # pick = [1]
suppress = [last] # suppress = [2]
# loop over all indexes in the indexes list
for pos in range(0, last): # last = 2
# grab the current index
j = idxs[pos]
# find the largest (x, y) coordinates for the start of
# the bounding box and the smallest (x, y) coordinates
# for the end of the bounding box
xx1 = max(x1[i], x1[j])
yy1 = max(y1[i], y1[j])
xx2 = min(x2[i], x2[j])
yy2 = min(y2[i], y2[j])
# compute the width and height of the bounding box
w = max(0, xx2 - xx1 + 1) # 接触していなければ0
h = max(0, yy2 - yy1 + 1)
# compute the ratio of overlap between the computed
# bounding box and the bounding box in the area list
overlap = float(w * h) / area[j]
# if there is sufficient overlap, suppress the
# current bounding box
if overlap > overlapThresh:
suppress.append(pos)
# delete all indexes from the index list that are in the
# suppression list
idxs = np.delete(idxs, suppress)
# return only the bounding boxes that were picked
return boxes[pick]
images = [
("audrey.jpg", np.array([
(120, 10, 1120, 810),
(240, 100, 1390, 1100),
(300, 250, 1100, 1000)]))]
for (imagePath, boundingBoxes) in images:
# originalのbounding boxを描画(左図)
image = cv2.imread("audrey.jpg")
plt.figure(figsize=(16, 8))
plt.subplot(1, 2, 1)
plt.imshow(image)
#plt.axis('off')
currentAxis = plt.gca()
for xmin, ymin, xmax, ymax in boundingBoxes:
coords = (xmin, ymin), xmax - xmin +1, ymax - ymin +1
currentAxis.add_patch(plt.Rectangle(*coords, fill=False, edgecolor='#ff0000', linewidth=2))
print('original : ', coords)
# after non maximum suppressionのbounding boxを描画(右図)
plt.subplot(1, 2, 2)
plt.imshow(image)
#plt.axis('off')
currentAxis = plt.gca()
old=datetime.datetime.now()
pick = non_max_suppression_slow(boundingBoxes, 0.3)
print('-------------------------------------------------------')
print('・cost time : ',(datetime.datetime.now()-old))
print('-------------------------------------------------------')
for xmin, ymin, xmax, ymax in pick:
coords = (xmin, ymin), xmax - xmin +1, ymax - ymin +1
currentAxis.add_patch(plt.Rectangle(*coords, fill=False, edgecolor='#00ff00', linewidth=2))
print('after nms : ', coords)
```
## 3. non maximum suppression : Python
```
coords = [[187, 82, 337, 317],[150, 67, 305, 282],[246, 121, 368, 304]]
bounding_boxes = [[187, 82, 337-187, 317-82],[150, 67, 305-150, 282-67],[246, 121, 368-246, 304-121]]
confidence_score = [0.9, 0.75, 0.8]
fig = plt.figure(figsize=(8,6))
plt.xlim(0, 400)
plt.ylim(0, 400)
ax = fig.add_subplot(111)
for label, i in enumerate(bounding_boxes):
# rect = plt.Rectangle((i[0],i[1]),i[2],i[3], fill=False)
coords = (i[0], i[1]), i[2], i[3]
plt.gca().add_patch(plt.Rectangle(*coords, fill=False, edgecolor='#FF0000', linewidth=2))
plt.gca().text(i[0], i[1]+i[3], str(confidence_score[label]), bbox={'facecolor':'#FF0000', 'alpha':0.5})
#ax.add_patch(rect)
plt.show()
def nms(bounding_boxes, score, threshold):
# If no bounding boxes, return empty list
if len(bounding_boxes) == 0:
return [], [] # picked boxes, picked scores
# coordinates of bounding boxes
start_x = bounding_boxes[:, 0]
start_y = bounding_boxes[:, 1]
end_x = bounding_boxes[:, 2]
end_y = bounding_boxes[:, 3]
# Picked bounding boxes
picked_boxes = []
picked_score = []
intersection_areas = []
# Compute areas of bounding boxes
areas = (end_x - start_x + 1) * (end_y - start_y + 1)
# Sort by confidence score of bounding boxes
order = np.argsort(score)
# Iterate bounding boxes
while order.size > 0:
# The index of largest confidence score
index = order[-1]
# Pick the bounding box with largest confidence score
picked_boxes.append(bounding_boxes[index])
picked_score.append(confidence_score[index])
# Compute ordinates of intersection-over-union(IOU)
x1 = np.maximum(start_x[index], start_x[order[:-1]])
x2 = np.minimum(end_x[index], end_x[order[:-1]])
y1 = np.maximum(start_y[index], start_y[order[:-1]])
y2 = np.minimum(end_y[index], end_y[order[:-1]])
intersection_areas.append([x1, y1, x2, y2])
# Compute areas of intersection-over-union
w = np.maximum(0.0, x2 - x1 + 1)
h = np.maximum(0.0, y2 - y1 + 1)
intersection = w * h
# Compute the ratio between intersection and union
ratio = intersection / (areas[index] + areas[order[:-1]] - intersection)
left = np.where(ratio < threshold)
order = order[left]
return picked_boxes, picked_score, intersection_areas
bounding_boxes =np.asarray([[187, 82, 337, 317],[150, 67, 305, 282],[246, 121, 368, 304]],dtype=np.float32)
confidence_score = np.asarray([0.9, 0.75, 0.8],dtype=np.float32)
# IoU threshold
threshold = 0.5
old=datetime.datetime.now()
picked_boxes, picked_score, intersection_areas = nms(bounding_boxes, confidence_score, threshold)
print('-------------------------------------------------------')
print('・cost time : ',(datetime.datetime.now()-old))
print('-------------------------------------------------------')
#print('nms : ', picked_boxes,picked_score)
fig = plt.figure(figsize=(8,6))
plt.xlim(0, 400)
plt.ylim(0, 400)
#ax1 = fig.add_subplot(121)
#ax2 = fig.add_subplot(122)
for label, i in enumerate(bounding_boxes):
# rect = plt.Rectangle((i[0],i[1]),i[2],i[3], fill=False)
coords = (i[0], i[1]), i[2]-i[0]+1, i[3]-i[1]+1
inter_xmin = intersection_areas[0][0][0]
inter_ymin = intersection_areas[0][1][0]
inter_xmax = intersection_areas[0][2][0]
inter_ymax = intersection_areas[0][3][0]
inter_coords = (inter_xmin, inter_ymin), inter_xmax-inter_xmin+1, inter_ymax-inter_ymin+1
plt.gca().add_patch(plt.Rectangle(*coords, fill=False, edgecolor='#FF0000', linewidth=2))
#plt.gca().add_patch(plt.Rectangle(*inter_coords, fill=True, facecolor={'facecolor':'#FF0000','alpha':0.5}, edgecolor='#FF0000', linewidth=0))
plt.gca().text(i[0], i[3], str(confidence_score[label]), bbox={'facecolor':'#FF0000', 'alpha':0.5})
#ax.add_patch(rect)
#plt.show()
fig = plt.figure(figsize=(8,6))
plt.xlim(0, 400)
plt.ylim(0, 400)
#plt.subplot(1,2,2)
for label, i in enumerate(picked_boxes):
rect = plt.Rectangle((i[0],i[1]),i[2],i[3], fill=False)
coords = (i[0], i[1]), i[2]-i[0]+1, i[3]-i[1]+1
plt.gca().add_patch(plt.Rectangle(*coords, fill=False, edgecolor='#FF0000', linewidth=2))
plt.gca().text(i[0], i[3], str(picked_score[label]), bbox={'facecolor':'#FF0000', 'alpha':0.5})
#ax.add_patch(rect)
#plt.subplot(1,2,2)
#plt.show()
#print(intersection_areas)
#print(intersection_areas[0][0])
```
## 4. non maximum suppression : tensorflow
Predictionsとして数千のバウンディングボックスの座標が出力される
→max_output_sizeとして定めた値まで減らす
```
# non maximum suppression : Python
print(picked_boxes, picked_score)
import tensorflow as tf
threshold = 0.5
with tf.Session() as sess:
for i in range(3): # forなしだと、nms.eval()がエラー、expected an indented block
old=datetime.datetime.now()
nms = tf.image.non_max_suppression(bounding_boxes,confidence_score, max_output_size=5, iou_threshold=threshold)
print('-------------------------------------------------------')
print('・cost time : ',(datetime.datetime.now()-old)) # .microseconds
print('・face detected : ', len(nms.eval()))
for index, value in enumerate(nms.eval()): # nms.eval() → インデックスを返す
rect = bounding_boxes[value]
print('・value : ', value)
print('・rect : ', rect)
```
# <font color="#4169e1">感想</font>
***
・tensorflow作ったひとすごい
・SSD作ったひともすごい
・車輪の再発明も勉強になるから悪くない
・1つ1つ処理せずに行列でまとめて処理したほうが確かにスーパー早い
・nmsしてもmax_output_sizeを200とかにしてるから画面がバウンディングボックスで埋まる
・テスト画像にオードリーヘップバーンを使うとテンション上がる
・引き続きSSDを解明していきたい
| true |
code
| 0.411111 | null | null | null | null |
|
# Direct Search Optimiser Example
The Direct Search Optimiser module is used to optimise the thresholds of an existing set of rules, given a labelled dataset, using Direct Search-type Optimisation algorithms.
## Requirements
To run, you'll need the following:
* A rule set stored in the standard Iguanas lambda expression format, along with the keyword arguments for each lambda expression (more information on how to do this later)
* A labelled dataset containing the features present in the rule set.
----
### Import packages
```
from iguanas.rule_optimisation import DirectSearchOptimiser
from iguanas.rules import Rules
from iguanas.rule_application import RuleApplier
from iguanas.metrics.classification import FScore
import pandas as pd
from sklearn.model_selection import train_test_split
```
### Read in data
Firstly, we need to read in the raw data containing the features and the fraud label:
```
data = pd.read_csv(
'dummy_data/dummy_pipeline_output_data.csv',
index_col='eid'
)
```
Then we need to split out the dataset into the features (`X`) and the target column (`y`):
```
fraud_column = 'sim_is_fraud'
X = data.drop(fraud_column, axis=1)
y = data[fraud_column]
```
Finally, we can split the features and target column into training and test sets:
```
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
test_size=0.33,
random_state=0
)
```
## Read in the rules
In this example, we'll read in the rule conditions from a pickle file, where they are stored in the standard Iguanas string format. However, you can use any Iguanas-ready rule format - see the example notebook in the `rules` module.
```
import pickle
with open('dummy_data/rule_strings.pkl', 'rb') as f:
rule_strings = pickle.load(f)
```
Now we can instantiate the `Rules` class with these rules:
```
rules = Rules(rule_strings=rule_strings)
```
We now need to convert the rules into the standard Iguanas lambda expression format. This format allows new threshold values to be injected into the rule condition before being evaluated - this is how the Bayesian Optimiser finds the optimal threshold values:
```
rule_lambdas = rules.as_rule_lambdas(
as_numpy=False,
with_kwargs=True
)
```
By converting the rule conditions to the standard Iguanas lambda expression format, we also generate a dictionary which gives the keyword arguments to each lambda expression (this dictionary is saved as the class attribute `lambda_kwargs`). Using these keyword arguments as inputs to the lambda expressions will convert them into the standard Iguanas string format.
----
## Optimise rules
### Set up class parameters
Now we can set our class parameters for the Direct Search Optimiser.
Here we're using the F1 score as the optimisation function (you can choose a different function from the `metrics` module or create your own - see the `classification.ipynb` example notebook in the `metrics` module).
**Note that if you're using the FScore, Precision or Recall score as the optimisation function, use the *FScore*, *Precision* or *Recall* classes in the *metrics.classification* module rather than the same functions from Sklearn's *metrics* module, as the former are ~100 times faster on larger datasets.**
We're also using the `Nelder-Mead` algorithm, which often benefits from setting the optional `initial_simplex` parameter. This is set through the `options` keyword argument. Here, we'll generate the initial simplex of each rule using the `create_initial_simplexes` method (but you can create your own if required).
**Please see the class docstring for more information on each parameter.**
```
f1 = FScore(beta=1)
initial_simplexes = DirectSearchOptimiser.create_initial_simplexes(
X=X_train,
lambda_kwargs=rules.lambda_kwargs,
shape='Minimum-based'
)
params = {
'rule_lambdas': rule_lambdas,
'lambda_kwargs': rules.lambda_kwargs,
'metric': f1.fit,
'method': 'Nelder-Mead',
'options': initial_simplexes,
'verbose': 1,
}
```
### Instantiate class and run fit method
Once the parameters have been set, we can run the `fit` method to optimise the rules.
```
ro = DirectSearchOptimiser(**params)
X_rules = ro.fit(
X=X_train,
y=y_train,
sample_weight=None
)
```
### Outputs
The `fit` method returns a dataframe giving the binary columns of the optimised + unoptimisable (but applicable) rules as applied to the training dataset. See the `Attributes` section in the class docstring for a description of each attribute generated:
```
X_rules.head()
ro.opt_rule_performances
```
----
## Apply rules to a separate dataset
Use the `transform` method to apply the optimised rules to a separate dataset:
```
X_rules_test = ro.transform(X=X_test)
```
### Outputs
The `transform` method returns a dataframe giving the binary columns of the rules as applied to the given dataset:
```
X_rules_test.head()
```
---
## Plotting the performance uplift
We can visualise the performance uplift of the optimised rules using the `plot_performance_uplift` and `plot_performance_uplift_distribution` methods:
* `plot_performance_uplift`: Generates a scatterplot showing the performance of each rule before and after optimisation.
* `plot_performance_uplift_distribution`: Generates a boxplot showing the distribution of performance uplifts (original rules vs optimised rules).
### On the training set
To visualise the uplift on the training set, we can use the class attributes `orig_rule_performances` and `opt_rule_performances` in the plotting methods, as these were generated as part of the optimisation process:
```
ro.plot_performance_uplift(
orig_rule_performances=ro.orig_rule_performances,
opt_rule_performances=ro.opt_rule_performances,
figsize=(10, 5)
)
ro.plot_performance_uplift_distribution(
orig_rule_performances=ro.orig_rule_performances,
opt_rule_performances=ro.opt_rule_performances,
figsize=(3, 7)
)
```
### On the test set
To visualise the uplift on the test set, we first need to generate the `orig_rule_performances` and `opt_rule_performances` parameters used in the plotting methods as these aren't created as part of the optimisation process. To do this, we need to apply both the original rules and the optimised rules to the test set.
**Note:** before we apply the original rules, we need to remove those that either have no optimisable conditions, have zero variance features or have features that are missing in `X_train`:
```
# Original rules
rules_to_exclude = ro.rule_names_missing_features + ro.rule_names_no_opt_conditions + ro.rule_names_zero_var_features
rules.filter_rules(exclude=rules_to_exclude)
orig_X_rules = rules.transform(X_test)
orig_f1s = f1.fit(orig_X_rules, y_test)
orig_rule_performances_test = dict(zip(orig_X_rules.columns.tolist(), orig_f1s))
# Optimised rules
opt_X_rules = ro.transform(X_test)
opt_f1s = f1.fit(opt_X_rules, y_test)
opt_rule_performances_test = dict(zip(opt_X_rules.columns.tolist(), opt_f1s))
ro.plot_performance_uplift(
orig_rule_performances=orig_rule_performances_test,
opt_rule_performances=opt_rule_performances_test,
figsize=(10, 5)
)
ro.plot_performance_uplift_distribution(
orig_rule_performances=orig_rule_performances_test,
opt_rule_performances=opt_rule_performances_test,
figsize=(3, 7)
)
```
----
| true |
code
| 0.632786 | null | null | null | null |
|
# Name
Batch prediction using Cloud Machine Learning Engine
# Label
Cloud Storage, Cloud ML Engine, Kubeflow, Pipeline, Component
# Summary
A Kubeflow Pipeline component to submit a batch prediction job against a deployed model on Cloud ML Engine.
# Details
## Intended use
Use the component to run a batch prediction job against a deployed model on Cloud ML Engine. The prediction output is stored in a Cloud Storage bucket.
## Runtime arguments
| Argument | Description | Optional | Data type | Accepted values | Default |
|--------------------|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|----------|--------------|-----------------|---------|
| project_id | The ID of the Google Cloud Platform (GCP) project of the job. | No | GCPProjectID | | |
| model_path | The path to the model. It can be one of the following:<br/> <ul> <li>projects/[PROJECT_ID]/models/[MODEL_ID]</li> <li>projects/[PROJECT_ID]/models/[MODEL_ID]/versions/[VERSION_ID]</li> <li>The path to a Cloud Storage location containing a model file.</li> </ul> | No | GCSPath | | |
| input_paths | The path to the Cloud Storage location containing the input data files. It can contain wildcards, for example, `gs://foo/*.csv` | No | List | GCSPath | |
| input_data_format | The format of the input data files. See [REST Resource: projects.jobs](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#DataFormat) for more details. | No | String | DataFormat | |
| output_path | The path to the Cloud Storage location for the output data. | No | GCSPath | | |
| region | The Compute Engine region where the prediction job is run. | No | GCPRegion | | |
| output_data_format | The format of the output data files. See [REST Resource: projects.jobs](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#DataFormat) for more details. | Yes | String | DataFormat | JSON |
| prediction_input | The JSON input parameters to create a prediction job. See [PredictionInput](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#PredictionInput) for more information. | Yes | Dict | | None |
| job_id_prefix | The prefix of the generated job id. | Yes | String | | None |
| wait_interval | The number of seconds to wait in case the operation has a long run time. | Yes | | | 30 |
## Input data schema
The component accepts the following as input:
* A trained model: It can be a model file in Cloud Storage, a deployed model, or a version in Cloud ML Engine. Specify the path to the model in the `model_path `runtime argument.
* Input data: The data used to make predictions against the trained model. The data can be in [multiple formats](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#DataFormat). The data path is specified by `input_paths` and the format is specified by `input_data_format`.
## Output
Name | Description | Type
:--- | :---------- | :---
job_id | The ID of the created batch job. | String
output_path | The output path of the batch prediction job | GCSPath
## Cautions & requirements
To use the component, you must:
* Set up a cloud environment by following this [guide](https://cloud.google.com/ml-engine/docs/tensorflow/getting-started-training-prediction#setup).
* Run the component under a secret [Kubeflow user service account](https://www.kubeflow.org/docs/started/getting-started-gke/#gcp-service-accounts) in a Kubeflow cluster. For example:
```python
mlengine_predict_op(...).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
* Grant the following types of access to the Kubeflow user service account:
* Read access to the Cloud Storage buckets which contains the input data.
* Write access to the Cloud Storage bucket of the output directory.
## Detailed description
Follow these steps to use the component in a pipeline:
1. Install the Kubeflow Pipeline SDK:
```
%%capture --no-stderr
KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.14/kfp.tar.gz'
!pip3 install $KFP_PACKAGE --upgrade
```
2. Load the component using KFP SDK
```
import kfp.components as comp
mlengine_batch_predict_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/e7a021ed1da6b0ff21f7ba30422decbdcdda0c20/components/gcp/ml_engine/batch_predict/component.yaml')
help(mlengine_batch_predict_op)
```
### Sample Code
Note: The following sample code works in an IPython notebook or directly in Python code.
In this sample, you batch predict against a pre-built trained model from `gs://ml-pipeline-playground/samples/ml_engine/census/trained_model/` and use the test data from `gs://ml-pipeline-playground/samples/ml_engine/census/test.json`.
#### Inspect the test data
```
!gsutil cat gs://ml-pipeline-playground/samples/ml_engine/census/test.json
```
#### Set sample parameters
```
# Required Parameters
PROJECT_ID = '<Please put your project ID here>'
GCS_WORKING_DIR = 'gs://<Please put your GCS path here>' # No ending slash
# Optional Parameters
EXPERIMENT_NAME = 'CLOUDML - Batch Predict'
OUTPUT_GCS_PATH = GCS_WORKING_DIR + '/batch_predict/output/'
```
#### Example pipeline that uses the component
```
import kfp.dsl as dsl
import kfp.gcp as gcp
import json
@dsl.pipeline(
name='CloudML batch predict pipeline',
description='CloudML batch predict pipeline'
)
def pipeline(
project_id = PROJECT_ID,
model_path = 'gs://ml-pipeline-playground/samples/ml_engine/census/trained_model/',
input_paths = '["gs://ml-pipeline-playground/samples/ml_engine/census/test.json"]',
input_data_format = 'JSON',
output_path = OUTPUT_GCS_PATH,
region = 'us-central1',
output_data_format='',
prediction_input = json.dumps({
'runtimeVersion': '1.10'
}),
job_id_prefix='',
wait_interval='30'):
mlengine_batch_predict_op(
project_id=project_id,
model_path=model_path,
input_paths=input_paths,
input_data_format=input_data_format,
output_path=output_path,
region=region,
output_data_format=output_data_format,
prediction_input=prediction_input,
job_id_prefix=job_id_prefix,
wait_interval=wait_interval).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
#### Compile the pipeline
```
pipeline_func = pipeline
pipeline_filename = pipeline_func.__name__ + '.zip'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
```
#### Submit the pipeline for execution
```
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
```
#### Inspect prediction results
```
OUTPUT_FILES_PATTERN = OUTPUT_GCS_PATH + '*'
!gsutil cat OUTPUT_FILES_PATTERN
```
## References
* [Component python code](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/component_sdk/python/kfp_component/google/ml_engine/_batch_predict.py)
* [Component docker file](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/Dockerfile)
* [Sample notebook](https://github.com/kubeflow/pipelines/blob/master/components/gcp/ml_engine/batch_predict/sample.ipynb)
* [Cloud Machine Learning Engine job REST API](https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs)
## License
By deploying or using this software you agree to comply with the [AI Hub Terms of Service](https://aihub.cloud.google.com/u/0/aihub-tos) and the [Google APIs Terms of Service](https://developers.google.com/terms/). To the extent of a direct conflict of terms, the AI Hub Terms of Service will control.
| true |
code
| 0.723132 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/yohanesnuwara/mem/blob/master/altmann2010_poroelasticity.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import numpy as np
import matplotlib.pyplot as plt
import scipy
```
Radius to reservoir from wellbore ranging from 0 to 500 m, in a sandstone reservoir
```
r = np.arange(0, 5010, 10) # radius, m
year = 1
t = year * (3.154E+7) # time, seconds in year
# knowns from Altmann paper
Kd = 12 # drained bulk modulus, GPa
Kg = 40 # grain bulk modulus, GPa
G = 5.5 # shear modulus, GPa
Kf = 2 # fluid bulk modulus, GPa
rhof = 1000 # fluid density, kg/m3
poro = 0.167 # porosity of sandstone
g = 9.8 # gravitational acceleration, m/s2
kf = 0.1E-6 # hydraulic conductivity, m/s
# Gassmann fluid substitution, according to Altmann
Ku = (Kg + (Kd * (poro * (Kg / Kf) - poro - 1))) / (1 - poro - (Kd / Kg) + (poro * (Kg / Kf)))
print('The undrained (saturated) bulk modulus:', Ku, 'GPa')
# Biot-Willis coeff
alpha = 1 - (Kd / Kg)
print('The Biot-Willis coefficient:', alpha)
# Lame parameter lambda
lame_lambda = Kd - (2 * G / 3)
# undrained Lame parameter lambda
lame_lambda_u = Ku - (2 * G / 3)
# stress path defined by Engelder & Fischer (1994), assume infinite reservoir
v = lame_lambda / (3 * Kd - lame_lambda)
sp = alpha * ((1 - 2 * v) / (1 - v))
print('Stress path at infinite time and infinite reservoir:', sp, '\n')
# diffusivity
k = kf / (g * rhof)
numerator = (lame_lambda_u - lame_lambda) * (lame_lambda + 2 * G)
denominator = (alpha**2) * (lame_lambda_u + 2 * G)
c = k * ((numerator / denominator) * 1E+9) # GPa to Pa, multiply by 1E+9
print('Diffusivity:', c, 'm2/s')
# boltzmann variable (dimensionless)
boltz = r / np.sqrt(c * t)
# error function
errf = scipy.special.erf(0.5 * boltz)
errfc = 1 - errf
g_func = errf - ((1 / np.sqrt(np.pi)) * boltz * np.exp(-0.25 * (boltz**2)))
# spatio-temporal radial stress path
A = (2 * alpha * G) / (lame_lambda + 2 * G)
B = 1 + ( ((2 / boltz**2) * g_func) / (errfc) )
stress_path_radial = A * B
# plot stress path
plt.figure(figsize=(10,7))
p1 = plt.plot(r, stress_path_radial, color='blue')
p2 = plt.plot([0, max(r)], [sp, sp], '--', color='red')
plt.legend((p1[0], p2[0]), (['Spatio-temporal stress path (Altmann et al, 2010)', 'Stress path at infinite (Engelder and Fischer, 1994)']))
plt.title('Reservoir Stress Path', size=20, pad=10)
plt.xlabel('Radius from wellbore (m)', size=15)
plt.ylabel('$\Delta \sigma_r / \Delta P$', size=15)
plt.xlim(0, max(r))
plt.ylim(0, 1.5)
```
| true |
code
| 0.600305 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/predicthq/phq-data-science-docs/blob/master/features-api/features-api.ipynb" target="_blank"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Features API
The Features API provides features for ML Models across all types of demand causal factors, including attended events and non-attended events.
It allows you to go straight to feature-importance testing and improving your models rather than having to worry about first building a data lake and then aggregating the data.
Features API is new and features will be expanded and added to over time. The endpoint currently supports:
* PHQ Attendance features (for attendance based events)
* PHQ Rank features (for scheduled, non-attendance based events)
* PHQ Viewership features (for viewership based events)
This notebook will guide you through how to use the Features API.
- [Setup](#setup)
- [Getting Started](#getting-started)
- [PHQ Attendance](#phq-attendance)
- [PHQ Rank](#phq-rank)
- [Academic Events](#academic-events)
- [Wide Data ranges](#wide-data-ranges)
- [Exploring the data](#exploring-the-data)
- [Concert trends for San Francisco vs Oakland](#concert)
- [Exploring TV Viewership with the Feature API](#tv-viewership)
- [Retrieving Multiple Locations](#multiple-locations)
- [List of lat/lon](#lat-lon)
- [Multiple Categories](#multiple-categories)
<a id='setup'></a>
# Setup
If using Google Colab uncomment the following code block.
```
# %%capture
# !git clone https://github.com/predicthq/phq-data-science-docs.git
# %cd phq-data-science-docs/features-api
# !pip install aiohttp==3.7.4.post0 asyncio==3.4.3 backoff==1.10.0 bleach==3.3.0 calmap==0.0.9 iso8601==0.1.14 matplotlib==3.4.2 numpy==1.20.3 pandas==1.2.4 seaborn==0.11.1 uvloop==0.15.2
```
### Requirements
If running locally, configure the required dependencies in your Python environment by using the [requirements.txt](https://github.com/predicthq/phq-data-science-docs/blob/master/features-api/requirements.txt) file which is shared alongside the notebook.
These requirements can be installed by running the command `pip install -r requirements.txt`
```
import requests
import json
```
<a id='getting-started'></a>
## Getting Started
### Access Token
You will need an access token that has the `events` scope. The following link will guide you through setting up an access token: [https://docs.predicthq.com/guides/quickstart/](https://docs.predicthq.com/guides/quickstart/)
### Basic Concepts
Every request to the API must specify which features are needed. Throughout the notebook you will become familiar with the naming convention for features, and we will talk about features by name.
Each request must specify a date range and location (that applies to all features in that request).
Certain groups of features support additional filtering/parameters.
Results are at the daily level.
Each request can currently fetch up to 90 days worth - for longer date ranges, multiple requests must be made and we have some examples of how to do that in this notebook. There is no pagination in this API.
```
# Paste your access token here
ACCESS_TOKEN = '<TOKEN>'
headers = {
'Content-Type': 'application/json',
'Accept': 'application/json',
'Authorization': f'Bearer {ACCESS_TOKEN}'
}
url = 'https://api.predicthq.com/v1/features'
```
<a id='phq-attendance'></a>
## PHQ Attendance
This group of features is based on PHQ Attendance. The following features are supported:
- `phq_attendance_sports`
- `phq_attendance_conferences`
- `phq_attendance_expos`
- `phq_attendance_concerts`
- `phq_attendance_festivals`
- `phq_attendance_performing_arts`
- `phq_attendance_community`
- `phq_attendance_academic_graduation`
- `phq_attendance_academic_social`
Each of these features includes stats. You define which stats you need (or don't define any and receive the default set of stats). Supported stats are:
- `sum` (included in default set of stats)
- `count` (included in default set of stats)
- `min`
- `max`
- `avg`
- `median`
- `std_dev`
These features also support filtering by PHQ Rank as you'll see in the example below.
```
payload = {
'active': {
'gte': '2019-11-28',
'lte': '2019-11-30'
},
'location': {
'place_id': [5224323, 5811704, 4887398]
},
'phq_attendance_concerts': True,
'phq_attendance_sports': {
'stats': ['count', 'std_dev', 'median'],
'phq_rank': {
'gt': 50
}
}
}
response = requests.request('POST', url, headers=headers, json=payload)
print(json.dumps(response.json(), indent=4))
```
### Example with a lat/lon
The location filter supports Place IDs and lat/lon with a radius.
```
payload = {
'active': {
'gte': '2019-11-28',
'lte': '2019-11-30'
},
'location': {
'geo': {
'lat': 47.62064,
'lon': -117.40401,
'radius': '50km'
}
},
'phq_attendance_concerts': True,
'phq_attendance_sports': {
'stats': ['count', 'std_dev', 'median'],
'phq_rank': {
'gt': 50
}
}
}
response = requests.request('POST', url, headers=headers, json=payload)
print(json.dumps(response.json(), indent=4))
```
<a id='phq-rank'></a>
## PHQ Rank
This group of features is based on PHQ Rank for non-attendance based events (mostly scheduled non-attendance based). The following features are supported:
- `phq_rank_public_holidays`
- `phq_rank_school_holidays`
- `phq_rank_observances`
- `phq_rank_politics`
- `phq_rank_daylight_savings`
- `phq_rank_health_warnings`
- `phq_rank_academic_session`
- `phq_rank_academic_exam`
- `phq_rank_academic_holiday`
Results are broken down by PHQ Rank Level (1 to 5). Rank Levels are groupings of Rank and are grouped as follows:
- 1 = between 0 and 20
- 2 = between 21 and 40
- 3 = between 41 and 60
- 4 = between 61 and 80
- 5 = between 81 and 100
Additional filtering for PHQ Rank features is not currently supported.
```
payload = {
'active': {
'gte': '2019-11-28',
'lte': '2019-11-30'
},
'location': {
'place_id': [5224323, 5811704, 4887398]
},
'phq_rank_school_holidays': True,
'phq_rank_public_holidays': True,
'phq_rank_health_warnings': True
}
response = requests.request('POST', url, headers=headers, json=payload)
print(json.dumps(response.json(), indent=4))
```
## Academic Events
Academic events are slightly different in that they contain both attended and non-attended events. You may have noted above that there are features in PHQ Attendance and PHQ Rank for academic events.
There are 5 different academic types - namely:
- `graduation`
- `social`
- `academic-session`
- `exam`
- `holiday`
The types `graduation` and `social` are attendance based events which (as noted earlier) means we have the following PHQ Attendance features:
- `phq_attendance_academic_graduation`
- `phq_attendance_academic_social`
The types `academic-session`, `exam` and `holiday` are non-attendace based events which means we have the following PHQ Rank features:
- `phq_rank_academic_session`
- `phq_rank_academic_exam`
- `phq_rank_academic_holiday`
<a id='wide-data-ranges'></a>
# Wide Date Ranges
As mentioned earlier, the API currently supports a date range of up to 90 days. In order to fetch data across a wider range, multiple requests must be made. Here is an example using asyncio that fetches a few years worth of data in parallel.
There are a few functions we'll define first.
```
import asyncio
import aiohttp
import uvloop
import iso8601
import backoff
from datetime import timedelta
asyncio.set_event_loop(uvloop.new_event_loop())
query = {
'location': {
'place_id': [5391959] # 5391959 = San Francisco
},
'phq_attendance_concerts': {
'stats': ['count', 'std_dev', 'median', 'avg'],
'phq_rank': {
'gt': 60
}
},
'phq_attendance_sports': {
'stats': ['count', 'std_dev', 'median'],
'phq_rank': {
'gt': 50
}
},
'phq_attendance_community': {
'stats': ['count', 'std_dev', 'median'],
'phq_rank': {
'gt': 50
}
},
'phq_attendance_conferences': {
'stats': ['count', 'std_dev', 'median'],
'phq_rank': {
'gt': 50
}
},
'phq_rank_public_holidays': True,
'phq_attendance_academic_graduation': True
}
format_date = lambda x: x.strftime('%Y-%m-%d')
parse_date = lambda x: iso8601.parse_date(x)
# The API has rate limits so failed requests should be retried automatically
@backoff.on_exception(backoff.expo, (aiohttp.ClientError), max_time=60)
async def get(
session: aiohttp.ClientSession,
query: dict,
start: str,
end: str,
**kwargs ) -> dict:
payload = {
'active': {
'gte': start,
'lte': end
},
**query
}
resp = await session.request('POST', url=url, headers=headers, raise_for_status=True, json=payload, **kwargs)
data = await resp.json()
return data
async def gather_with_concurrency(n, *tasks):
semaphore = asyncio.Semaphore(n)
async def sem_task(task):
async with semaphore:
return await task
return await asyncio.gather(*(sem_task(task) for task in tasks))
async def gather_stats(query: dict, start_date: str, end_date: str, **kwargs):
date_ranges = []
start_date = parse_date(start_date)
end_date = parse_date(end_date)
start_ref = start_date
while start_ref + timedelta(days=90) < end_date:
date_ranges.append({'start': format_date(start_ref),
'end': format_date(start_ref + timedelta(days=90))})
start_ref = start_ref + timedelta(days=91)
date_ranges.append({'start': format_date(start_ref),
'end': format_date(end_date)})
async with aiohttp.ClientSession() as session:
tasks = []
for date_range in date_ranges:
tasks.append(
get(
session=session,
query=query,
start=date_range['start'],
end=date_range['end'], **kwargs))
responses = await gather_with_concurrency(5, *tasks)
results = []
for response in responses:
results.extend(response['results'])
return results
```
If using Google Colab uncomment the following code block to fix broken async functionality.
This is as a result of how Google implemented notebooks and are running their async event loop.
Google Colab's Tornado 5.0 (Currently running 5.1.x) update bricked asyncio functionalities after the addition of its own asyncio event loop.
Thus, for any asyncio functionality to run on Google Colab Notebook you cannot invoke a `run_until_complete()` or `await`, since the loop you will receive from `asyncio.get_event_loop()` will be active and throw the exception seen.
JupterHub/JupyterLab had the same issue but have since fixed this, which is why you can easily just `await` the resolution, processing and response of an async call with the await keyword.
So we need to `"monkey patch"` the running event loop on Google Colab to hijack the event loop to allow us to issue tasks to be scheduled!
```
# import asyncio
# import nest_asyncio
# nest_asyncio.apply()
# def awaitx(x): return asyncio.get_event_loop().run_until_complete(x)
# responses = awaitx(gather_stats(
# query=query,
# start_date='2016-01-01',
# end_date='2021-12-31'))
# len(responses)
```
## Use the following code block only if running locally in JupyterHub or JupyterLab
```
responses = await gather_stats(
query=query,
start_date='2016-01-01',
end_date='2021-12-31')
len(responses)
print(json.dumps(responses[0], indent=4))
```
<a id='exploring-the-data'></a>
# Exploring the Data
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import os
import calmap
import warnings
# To display more columns and with a larger width in the DataFrame
pd.set_option('display.max_columns', None)
pd.options.display.max_colwidth = 100
```
<a id='concert'></a>
## Concert Trends for San Francisco vs Oakland
```
# IDs are from https://www.geonames.org/
sf_id = 5391959
oak_id = 5378538
# San Francisco
query = {
'location': {
'place_id': [sf_id]
},
'phq_attendance_concerts': {
'stats': ['count', 'sum', 'median']
},
'phq_attendance_festivals': {
'stats': ['count', 'sum', 'median']
}
}
```
If running on Google Colab uncomment following block to obtain results.
```
# import asyncio
# import nest_asyncio
# nest_asyncio.apply()
# def awaitx(x): return asyncio.get_event_loop().run_until_complete(x)
# sf_responses = awaitx(gather_stats(
# query=query,
# start_date='2016-01-01',
# end_date='2021-04-01'))
```
If running locally or within JupyterHub/JupyterLab use this block instead to obtain results.
```
sf_responses = await gather_stats(
query=query,
start_date='2016-01-01',
end_date='2021-04-01')
# Oakland
query = {
'location': {
'place_id': [oak_id]
},
'phq_attendance_concerts': {'stats': ['count', 'sum', 'median'], },
'phq_attendance_festivals': {'stats': ['count', 'sum', 'median'], },
}
```
If running on Google Colab uncomment following block to obtain results.
```
# import asyncio
# import nest_asyncio
# nest_asyncio.apply()
# def awaitx(x): return asyncio.get_event_loop().run_until_complete(x)
# oak_responses = awaitx(gather_stats(
# query=query,
# start_date='2016-01-01',
# end_date='2021-04-01'))
```
If running locally or within JupyterHub/JupyterLab use this block instead to obtain results.
```
oak_responses = await gather_stats(
query=query,
start_date='2016-01-01',
end_date='2021-04-01')
sf_df = pd.DataFrame.from_dict(sf_responses)
oak_df = pd.DataFrame.from_dict(oak_responses)
sf_df.head()
```
Reshaping the responses into tabular form
```
FIELDS = ['sum', 'count', 'median']
def parse_element(response: dict, fields: list) -> np.array:
"""
Extracts the feature fields from a dictionary into an array
"""
blank_response = np.zeros(shape=(len(fields)))
if isinstance(response, dict):
if not 'stats' in response: return blank_response
stats = response['stats']
if stats['count'] == 0: return blank_response
return np.array([stats[field] for field in fields])
def add_flat_features(df: pd.DataFrame, column: str,
feature_name: str, fields: list) -> pd.DataFrame:
"""
Adds features into dataframe
"""
list_feature = df[column].apply(parse_element, fields=fields)
fts = pd.DataFrame(list_feature.to_list(), columns=fields)
fts.columns = [f'{feature_name}_{col}' for col in fts.columns]
return df.join(fts)
sf_flat = add_flat_features(sf_df, 'phq_attendance_concerts', 'concerts', fields=FIELDS)
sf_flat = add_flat_features(sf_flat, 'phq_attendance_festivals', 'festivals', fields=FIELDS)
oak_flat = add_flat_features(oak_df, 'phq_attendance_concerts', 'concerts', fields=FIELDS)
oak_flat = add_flat_features(oak_flat, 'phq_attendance_festivals', 'festivals', fields=FIELDS)
sf_flat['date'] = pd.to_datetime(sf_flat['date'])
oak_flat['date'] = pd.to_datetime(oak_flat['date'])
sf_flat.head(2)
oak_flat.head(2)
def truncate_to_month(date_col):
return date_col - pd.Timedelta('1 day') * (date_col.dt.day - 1)
sf_flat['month'] = truncate_to_month(sf_flat['date'])
oak_flat['month'] = truncate_to_month(oak_flat['date'])
agg_dict = {'concerts_sum': 'sum',
'concerts_count': 'sum',
'concerts_median': 'median',
'festivals_sum': 'sum',
'festivals_count': 'sum',
'festivals_median': 'median',}
sf_monthly = (sf_flat
.groupby('month')
.agg(agg_dict)
)
oak_monthly = (oak_flat
.groupby('month')
.agg(agg_dict)
)
sf_monthly.columns = [f'{col}_sf' for col in sf_monthly.columns]
oak_monthly.columns = [f'{col}_oak' for col in oak_monthly.columns]
both_monthly = sf_monthly.join(oak_monthly).reset_index()
both_monthly.head()
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
both_monthly['month'] = pd.to_datetime(both_monthly['month'])
sns.lineplot(data=both_monthly[['month', 'concerts_count_sf',
'concerts_count_oak']], ax=ax)
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
ticks = [item.get_text() for item in ax.get_xticklabels()]
plt.xticks(rotation=90);
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
sns.lineplot(data=both_monthly[['month', 'concerts_sum_sf',
'concerts_sum_oak']], ax=ax)
# plt.xticks(both_monthly['month'])
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
plt.xticks(rotation=90);
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
sns.lineplot(data=both_monthly[['month', 'concerts_median_sf',
'concerts_median_oak']], ax=ax)
# plt.xticks(both_monthly['month'])
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
plt.xticks(rotation=90);
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
sns.lineplot(data=both_monthly[['month', 'festivals_count_sf',
'festivals_count_oak']], ax=ax)
# plt.xticks(both_monthly['month'])
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
plt.xticks(rotation=90);
```
<a id='tv-viewership'></a>
## Exploring TV Viewership with the Features API
This group of features is based on PHQ Viewership. The following features are some examples that are supported:
- `phq_viewership_sports_american_football` (viewership across all supported American Football leagues)
- `phq_viewership_sports_american_football_nfl` (viewership for NFL)
- `phq_viewership_sports_baseball` (viewership across all supported Baseball leagues)
- `phq_viewership_sports_soccer_mls` (viewership for MLS)
- `phq_viewership_sports_basketball` (viewership across all supported Basketball leagues)
- `phq_viewership_sports_basketball_nba` (viewership for NBA)
- `phq_viewership_sports_ice_hockey_nhl` (viewership for NHL)
The full list of available viewership feature fields are in our documentation [here](https://docs.predicthq.com/resources/features/#viewership-based-feature-fields).
For this section we will demonstrate how to apply the Features API to explore the viewership for two different sports. For one example we will be comparing viewership for all supported American Football leagues in San Francisco against viewership for all supported American Football leagues in Oakland. The second example we will be comparing viewership for all supported Basketball leagues in San Francisco against viewership for all supported Basketball leagues in Oakland.
```
# San Francisco
query = {
'location': {
'place_id': [sf_id]
},
'phq_viewership_sports_american_football': {
'stats': ['count', 'sum', 'median'],
},
'phq_viewership_sports_basketball': {
'stats': ['count', 'sum', 'median'],
},
}
```
If running on Google Colab uncomment the following block to obtain results.
```
# import asyncio
# import nest_asyncio
# nest_asyncio.apply()
# def awaitx(x): return asyncio.get_event_loop().run_until_complete(x)
# sf_responses = awaitx(gather_stats(
# query=query,
# start_date='2020-01-01',
# end_date='2020-12-31'))
```
If running locally or within JupyterHub/JupyterLab use this block instead to obtain results.
```
sf_responses = await gather_stats(
query=query,
start_date='2020-01-01',
end_date='2020-12-31')
sf_df = pd.DataFrame.from_dict(sf_responses)
sf_df.head()
# Oakland
query = {
'location': {
'place_id': [oak_id]
},
'phq_viewership_sports_american_football': {
'stats': ['count', 'sum', 'median'],
},
'phq_viewership_sports_basketball': {
'stats': ['count', 'sum', 'median'],
},
}
```
If running on Google Colab uncomment the following block to obtain results.
```
# import asyncio
# import nest_asyncio
# nest_asyncio.apply()
# def awaitx(x): return asyncio.get_event_loop().run_until_complete(x)
# oak_responses = awaitx(gather_stats(
# query=query,
# start_date='2020-01-01',
# end_date='2020-12-31'))
```
If running locally or within JupyterHub/JupyterLab use this block instead to obtain results.
```
oak_responses = await gather_stats(
query=query,
start_date='2020-01-01',
end_date='2020-12-31')
oak_df = pd.DataFrame.from_dict(oak_responses)
oak_df.head()
sf_view_flat = add_flat_features(sf_df, 'phq_viewership_sports_american_football', 'american_football', fields=FIELDS)
sf_view_flat = add_flat_features(sf_view_flat, 'phq_viewership_sports_basketball', 'basketball', fields=FIELDS)
oak_view_flat = add_flat_features(oak_df, 'phq_viewership_sports_american_football', 'american_football', fields=FIELDS)
oak_view_flat = add_flat_features(oak_view_flat, 'phq_viewership_sports_basketball', 'basketball', fields=FIELDS)
sf_view_flat['date'] = pd.to_datetime(sf_view_flat['date'])
oak_view_flat['date'] = pd.to_datetime(oak_view_flat['date'])
sf_view_flat['month'] = truncate_to_month(sf_view_flat['date'])
oak_view_flat['month'] = truncate_to_month(oak_view_flat['date'])
sf_view_flat.head()
oak_view_flat.head()
```
Reshaping the responses into tabular form
```
agg_dict = {'american_football_sum': 'sum',
'american_football_count': 'sum',
'american_football_median': 'median',
'basketball_sum': 'sum',
'basketball_count': 'sum',
'basketball_median': 'median',}
sf_monthly = (sf_view_flat
.groupby('month')
.agg(agg_dict)
)
oak_monthly = (oak_view_flat
.groupby('month')
.agg(agg_dict)
)
sf_monthly.columns = [f'{col}_sf' for col in sf_monthly.columns]
oak_monthly.columns = [f'{col}_oak' for col in oak_monthly.columns]
both_monthly = sf_monthly.join(oak_monthly).reset_index()
both_monthly.head()
```
The results of viewership between San Francisco and Oakland for All American Football are graphed below.
```
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
both_monthly['month'] = pd.to_datetime(both_monthly['month'])
sns.lineplot(data=both_monthly[['month', 'american_football_count_sf',
'american_football_count_oak']], ax=ax)
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
ticks = [item.get_text() for item in ax.get_xticklabels()]
plt.xticks(rotation=90);
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
both_monthly['month'] = pd.to_datetime(both_monthly['month'])
sns.lineplot(data=both_monthly[['month', 'american_football_sum_sf',
'american_football_sum_oak']], ax=ax)
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
ticks = [item.get_text() for item in ax.get_xticklabels()]
plt.xticks(rotation=90);
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
both_monthly['month'] = pd.to_datetime(both_monthly['month'])
sns.lineplot(data=both_monthly[['month', 'american_football_median_sf',
'american_football_median_oak']], ax=ax)
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
ticks = [item.get_text() for item in ax.get_xticklabels()]
plt.xticks(rotation=90);
```
The results for viewership between San Francisco and Oakland for All Basketball are graphed below.
```
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
both_monthly['month'] = pd.to_datetime(both_monthly['month'])
sns.lineplot(data=both_monthly[['month', 'basketball_count_sf',
'basketball_count_oak']], ax=ax)
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
ticks = [item.get_text() for item in ax.get_xticklabels()]
plt.xticks(rotation=90);
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
both_monthly['month'] = pd.to_datetime(both_monthly['month'])
sns.lineplot(data=both_monthly[['month', 'basketball_sum_sf',
'basketball_sum_oak']], ax=ax)
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
ticks = [item.get_text() for item in ax.get_xticklabels()]
plt.xticks(rotation=90);
with warnings.catch_warnings():
warnings.simplefilter('ignore')
fig, ax = plt.subplots()
both_monthly['month'] = pd.to_datetime(both_monthly['month'])
sns.lineplot(data=both_monthly[['month', 'basketball_median_sf',
'basketball_median_oak']], ax=ax)
ax.set_xticklabels(both_monthly['month'].dt.strftime('%Y-%m'))
ticks = [item.get_text() for item in ax.get_xticklabels()]
plt.xticks(rotation=90);
```
<a id='multiple-locations'></a>
### Retrieving Multiple Locations
You can specify multiple locations in a single request and the results for all specified locations will be aggregated together as in the example below.
```
query = {
'location': {
'place_id': [sf_id, oak_id]
},
'phq_attendance_concerts': {
'stats': ['count', 'sum', 'median']
},
'phq_attendance_festivals': {
'stats': ['count', 'sum', 'median']
}
}
```
If running on Google Colab uncomment following block to obtain results.
```
# import asyncio
# import nest_asyncio
# nest_asyncio.apply()
# def awaitx(x): return asyncio.get_event_loop().run_until_complete(x)
# both_responses = awaitx(gather_stats(
# query=query,
# start_date='2016-01-01',
# end_date='2021-04-01'))
```
If running locally or within JupyterHub/JupyterLab use this block instead to obtain results.
```
both_responses = await gather_stats(
query=query,
start_date='2016-01-01',
end_date='2021-04-01')
pd.DataFrame.from_dict(both_responses).head(5)
```
<a id='lat-lon'></a>
## List of lat/lon
You might need to fetch data for a wide date range as well as a large number of different locations. This example loads a list of lat/lon from a CSV file and fetches data for each of them.
```
examples = pd.read_csv('./data/lat_lon_examples.csv').sample(50)
examples.head(5)
# Check number of locations
len(examples)
query_f = lambda lat, long: {
'location': {
'geo': {
'lat': float(lat),
'lon': float(long),
'radius': '10km'
}
},
'phq_attendance_sports': {
'stats': ['count', 'avg'],
'phq_rank': {
'gt': 50
}
},
"phq_attendance_concerts": {
'stats': ['count', 'avg'],
'phq_rank': {
'gt': 50
}
},
}
async def pull_one_lat_long(city, lat, long):
response = await gather_stats(
query=query_f(lat, long),
start_date='2016-01-01',
end_date='2021-04-01')
return {city: response}
import time
start_time = time.time()
all_locations = []
for ix , row in examples.iterrows():
all_locations += [pull_one_lat_long(row['City'],
row['Latitude'],
row['Longitude'])]
```
If running on Google Colab uncomment following block to obtain results.
```
# import asyncio
# import nest_asyncio
# nest_asyncio.apply()
# def awaitx(x): return asyncio.get_event_loop().run_until_complete(x)
# # This might take a few seconds
# all_results = awaitx(gather_with_concurrency(5, *all_locations))
```
If running locally or within JupyterHub/JupyterLab use this block instead to obtain results.
```
# This might take a few seconds
all_results = await gather_with_concurrency(5, *all_locations)
end_time = time.time()
taken = (time.time() - start_time)
print(f"{taken}s processing time")
features_list = [
"phq_attendance_sports",
"phq_attendance_concerts"
]
all_counts = [val[key]['stats']['count'] for place_data in all_results
for place_name, data in place_data.items() for val in data for key in features_list]
print(
f"Features analysed for {sum(all_counts)} events across 21 quarters or ~1920 days for 2 different categories ")
FIELDS = ['count', 'avg']
all_locs = []
for city in all_results:
one_loc = pd.DataFrame(list(city.values())[0])
one_loc = add_flat_features(one_loc, 'phq_attendance_sports',
'sports', FIELDS)
one_loc.drop(['phq_attendance_sports'],
axis=1, inplace=True)
one_loc['City'] = list(city.keys())[0]
all_locs.append(one_loc)
cities = pd.concat(all_locs)
cities.pivot_table(index='date', columns='City', values='sports_avg')
```
<a id='multiple-categories'></a>
## Multiple Categories
For San Francisco
```
FIELDS = ['sum', 'count']
query = {
'location': {
'place_id': [sf_id]
},
'phq_attendance_concerts': {
'stats': FIELDS
},
'phq_attendance_community': {
'stats': FIELDS
},
'phq_attendance_conferences': {
'stats': FIELDS
},
'phq_attendance_expos': {
'stats': FIELDS
},
'phq_attendance_performing_arts': {
'stats': FIELDS
},
'phq_attendance_sports': {
'stats': FIELDS
},
'phq_attendance_festivals': {
'stats': FIELDS
},
'phq_rank_public_holidays': True,
'phq_rank_school_holidays': True,
'phq_rank_observances': True
}
```
If running on Google Colab uncomment following block to obtain results.
```
# import asyncio
# import nest_asyncio
# nest_asyncio.apply()
# def awaitx(x): return asyncio.get_event_loop().run_until_complete(x)
# sf_mlt_responses = awaitx(gather_stats(
# query=query,
# start_date='2016-01-01',
# end_date='2021-04-01'))
```
If running locally or within JupyterHub/JupyterLab use this block instead to obtain results.
```
sf_mlt_responses = await gather_stats(
query=query,
start_date='2016-01-01',
end_date='2021-04-01')
```
Parse Rank Columns
```
def parse_rank_column(col):
rank_levels = col.apply(lambda x: x['rank_levels'])
max_values = []
for row in rank_levels:
not_null = {k: v for k, v in row.items() if v>0}
if not_null:
max_values.append(int(max(not_null)))
else:
# all values were zero
max_values.append(0)
return max_values
holidays_att = pd.DataFrame.from_dict(sf_mlt_responses)
holidays_att['public-holiday'] = \
parse_rank_column(holidays_att['phq_rank_public_holidays'])
holidays_att['public-holiday'] = \
parse_rank_column(holidays_att['phq_rank_public_holidays'])
holidats_pa = add_flat_features(holidays_att, 'phq_attendance_performing_arts',
'performing_arts', FIELDS)
holidats_pa = add_flat_features(holidats_pa, 'phq_attendance_concerts',
'concerts', FIELDS)
holidats_pa = add_flat_features(holidats_pa, 'phq_attendance_community',
'community', FIELDS)
holidats_pa = add_flat_features(holidats_pa, 'phq_attendance_conferences',
'conferences', FIELDS)
holidats_pa = add_flat_features(holidats_pa, 'phq_attendance_expos',
'expos', FIELDS)
holidats_pa = add_flat_features(holidats_pa, 'phq_attendance_festivals',
'festivals', FIELDS)
holidats_pa = add_flat_features(holidats_pa, 'phq_attendance_sports',
'sports', FIELDS)
holidats_pa.set_index('date', inplace=True)
holidats_pa.index = pd.to_datetime(holidats_pa.index)
(holidats_pa
.groupby('public-holiday')
.agg({'conferences_sum': 'median',
'community_sum': 'median',
'conferences_count': 'median',
'community_count': 'median',
}
)
)
```
Visualize in a Calendar
```
for category in ['performing-arts', 'conferences']:
feature = category.replace('-','_')+'_count'
fig, ax = calmap.calendarplot(holidats_pa[feature], cmap="YlGn")
fig.set_size_inches(18, 15)
fig.colorbar(ax[0].get_children()[1], ax=ax.ravel().tolist())
_ = fig.suptitle(f"Number of {category} per day in calmap")
```
| true |
code
| 0.295141 | null | null | null | null |
|
# Using the PyTorch JIT Compiler with Pyro
This tutorial shows how to use the PyTorch [jit compiler](https://pytorch.org/docs/master/jit.html) in Pyro models.
#### Summary:
- You can use compiled functions in Pyro models.
- You cannot use pyro primitives inside compiled functions.
- If your model has static structure, you can use a `Jit*` version of an `ELBO` algorithm, e.g.
```diff
- Trace_ELBO()
+ JitTrace_ELBO()
```
- The [HMC](http://docs.pyro.ai/en/dev/mcmc.html#pyro.infer.mcmc.HMC) and [NUTS](http://docs.pyro.ai/en/dev/mcmc.html#pyro.infer.mcmc.NUTS) classes accept `jit_compile=True` kwarg.
- Models should input all tensors as `*args` and all non-tensors as `**kwargs`.
- Each different value of `**kwargs` triggers a separate compilation.
- Use `**kwargs` to specify all variation in structure (e.g. time series length).
- To ignore jit warnings in safe code blocks, use `with pyro.util.ignore_jit_warnings():`.
- To ignore all jit warnings in `HMC` or `NUTS`, pass `ignore_jit_warnings=True`.
#### Table of contents
- [Introduction](#Introduction)
- [A simple model](#A-simple-model)
- [Varying structure](#Varying-structure)
```
import os
import torch
import pyro
import pyro.distributions as dist
from torch.distributions import constraints
from pyro import poutine
from pyro.distributions.util import broadcast_shape
from pyro.infer import Trace_ELBO, JitTrace_ELBO, TraceEnum_ELBO, JitTraceEnum_ELBO, SVI
from pyro.infer.mcmc import MCMC, NUTS
from pyro.infer.autoguide import AutoDiagonalNormal
from pyro.optim import Adam
smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('1.7.0')
```
## Introduction
PyTorch 1.0 includes a [jit compiler](https://pytorch.org/docs/master/jit.html) to speed up models. You can think of compilation as a "static mode", whereas PyTorch usually operates in "eager mode".
Pyro supports the jit compiler in two ways. First you can use compiled functions inside Pyro models (but those functions cannot contain Pyro primitives). Second, you can use Pyro's jit inference algorithms to compile entire inference steps; in static models this can reduce the Python overhead of Pyro models and speed up inference.
The rest of this tutorial focuses on Pyro's jitted inference algorithms: [JitTrace_ELBO](http://docs.pyro.ai/en/dev/inference_algos.html#pyro.infer.trace_elbo.JitTrace_ELBO), [JitTraceGraph_ELBO](http://docs.pyro.ai/en/dev/inference_algos.html#pyro.infer.tracegraph_elbo.JitTraceGraph_ELBO), [JitTraceEnum_ELBO](http://docs.pyro.ai/en/dev/inference_algos.html#pyro.infer.traceenum_elbo.JitTraceEnum_ELBO), [JitMeanField_ELBO](http://docs.pyro.ai/en/dev/inference_algos.html#pyro.infer.trace_mean_field_elbo.JitTraceMeanField_ELBO), [HMC(jit_compile=True)](http://docs.pyro.ai/en/dev/mcmc.html#pyro.infer.mcmc.HMC), and [NUTS(jit_compile=True)](http://docs.pyro.ai/en/dev/mcmc.html#pyro.infer.mcmc.NUTS). For further reading, see the [examples/](https://github.com/pyro-ppl/pyro/tree/dev/examples) directory, where most examples include a `--jit` option to run in compiled mode.
## A simple model
Let's start with a simple Gaussian model and an [autoguide](http://docs.pyro.ai/en/dev/infer.autoguide.html).
```
def model(data):
loc = pyro.sample("loc", dist.Normal(0., 10.))
scale = pyro.sample("scale", dist.LogNormal(0., 3.))
with pyro.plate("data", data.size(0)):
pyro.sample("obs", dist.Normal(loc, scale), obs=data)
guide = AutoDiagonalNormal(model)
data = dist.Normal(0.5, 2.).sample((100,))
```
First let's run as usual with an SVI object and `Trace_ELBO`.
```
%%time
pyro.clear_param_store()
elbo = Trace_ELBO()
svi = SVI(model, guide, Adam({'lr': 0.01}), elbo)
for i in range(2 if smoke_test else 1000):
svi.step(data)
```
Next to run with a jit compiled inference, we simply replace
```diff
- elbo = Trace_ELBO()
+ elbo = JitTrace_ELBO()
```
Also note that the `AutoDiagonalNormal` guide behaves a little differently on its first invocation (it runs the model to produce a prototype trace), and we don't want to record this warmup behavior when compiling. Thus we call the `guide(data)` once to initialize, then run the compiled SVI,
```
%%time
pyro.clear_param_store()
guide(data) # Do any lazy initialization before compiling.
elbo = JitTrace_ELBO()
svi = SVI(model, guide, Adam({'lr': 0.01}), elbo)
for i in range(2 if smoke_test else 1000):
svi.step(data)
```
Notice that we have a more than 2x speedup for this small model.
Let us now use the same model, but we will instead use MCMC to generate samples from the model's posterior. We will use the No-U-Turn(NUTS) sampler.
```
%%time
nuts_kernel = NUTS(model)
pyro.set_rng_seed(1)
mcmc_run = MCMC(nuts_kernel, num_samples=100).run(data)
```
We can compile the potential energy computation in NUTS using the `jit_compile=True` argument to the NUTS kernel. We also silence JIT warnings due to the presence of tensor constants in the model by using `ignore_jit_warnings=True`.
```
%%time
nuts_kernel = NUTS(model, jit_compile=True, ignore_jit_warnings=True)
pyro.set_rng_seed(1)
mcmc_run = MCMC(nuts_kernel, num_samples=100).run(data)
```
We notice a significant increase in sampling throughput when JIT compilation is enabled.
## Varying structure
Time series models often run on datasets of multiple time series with different lengths. To accomodate varying structure like this, Pyro requires models to separate all model inputs into tensors and non-tensors.$^\dagger$
- Non-tensor inputs should be passed as `**kwargs` to the model and guide. These can determine model structure, so that a model is compiled for each value of the passed `**kwargs`.
- Tensor inputs should be passed as `*args`. These must not determine model structure. However `len(args)` may determine model structure (as is used e.g. in semisupervised models).
To illustrate this with a time series model, we will pass in a sequence of observations as a tensor `arg` and the sequence length as a non-tensor `kwarg`:
```
def model(sequence, num_sequences, length, state_dim=16):
# This is a Gaussian HMM model.
with pyro.plate("states", state_dim):
trans = pyro.sample("trans", dist.Dirichlet(0.5 * torch.ones(state_dim)))
emit_loc = pyro.sample("emit_loc", dist.Normal(0., 10.))
emit_scale = pyro.sample("emit_scale", dist.LogNormal(0., 3.))
# We're doing manual data subsampling, so we need to scale to actual data size.
with poutine.scale(scale=num_sequences):
# We'll use enumeration inference over the hidden x.
x = 0
for t in pyro.markov(range(length)):
x = pyro.sample("x_{}".format(t), dist.Categorical(trans[x]),
infer={"enumerate": "parallel"})
pyro.sample("y_{}".format(t), dist.Normal(emit_loc[x], emit_scale),
obs=sequence[t])
guide = AutoDiagonalNormal(poutine.block(model, expose=["trans", "emit_scale", "emit_loc"]))
# This is fake data of different lengths.
lengths = [24] * 50 + [48] * 20 + [72] * 5
sequences = [torch.randn(length) for length in lengths]
```
Now lets' run SVI as usual.
```
%%time
pyro.clear_param_store()
elbo = TraceEnum_ELBO(max_plate_nesting=1)
svi = SVI(model, guide, Adam({'lr': 0.01}), elbo)
for i in range(1 if smoke_test else 10):
for sequence in sequences:
svi.step(sequence, # tensor args
num_sequences=len(sequences), length=len(sequence)) # non-tensor args
```
Again we'll simply swap in a `Jit*` implementation
```diff
- elbo = TraceEnum_ELBO(max_plate_nesting=1)
+ elbo = JitTraceEnum_ELBO(max_plate_nesting=1)
```
Note that we are manually specifying the `max_plate_nesting` arg. Usually Pyro can figure this out automatically by running the model once on the first invocation; however to avoid this extra work when we run the compiler on the first step, we pass this in manually.
```
%%time
pyro.clear_param_store()
# Do any lazy initialization before compiling.
guide(sequences[0], num_sequences=len(sequences), length=len(sequences[0]))
elbo = JitTraceEnum_ELBO(max_plate_nesting=1)
svi = SVI(model, guide, Adam({'lr': 0.01}), elbo)
for i in range(1 if smoke_test else 10):
for sequence in sequences:
svi.step(sequence, # tensor args
num_sequences=len(sequences), length=len(sequence)) # non-tensor args
```
Again we see more than 2x speedup. Note that since there were three different sequence lengths, compilation was triggered three times.
$^\dagger$ Note this section is only valid for SVI, and HMC/NUTS assume fixed model arguments.
| true |
code
| 0.809671 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/josephineHonore/AIF360/blob/master/colab_examples/colab_workshop_adversarial_debiasing.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Colab Setup
This section configures your environment to be able to run this notebook on Google Colab. Before you run this notebook, make sure you are running in a python 3 environment. You can change your runtime environment by choosing
> Runtime > Change runtime type
in the menu.
```
!python --version
# This notebook runs in Tensorflow 1.x. Soon will default be 2.x in Colab.
%tensorflow_version 1.x
!pip install -q -U \
aif360==0.2.2 \
tqdm==4.38.0 \
tensorflow==1.15 \
numpy==1.17.4 \
matplotlib==3.1.1 \
pandas==0.25.3 \
scipy==1.3.2 \
scikit-learn==0.21.3 \
cvxpy==1.0.25 \
scs==2.1.0 \
numba==0.42.0 \
networkx==2.4 \
imgaug==0.2.6 \
BlackBoxAuditing==0.1.54 \
lime==0.1.1.36 \
adversarial-robustness-toolbox==1.0.1
```
## Notes
- The above pip command is created using AIF360's [requirements.txt](https://github.com/josephineHonore/AIF360/blob/master/requirements.txt). At the moment, the job to update these libraries is manual.
- The original notebook uses Markdown to display formated text. Currently this is [unsupported](https://github.com/googlecolab/colabtools/issues/322) in Colab.
- The tensorflow dependency is not needed for all other notebooks.
- We have changed TensorFlow's logging level to `ERROR`, just after the import of the library, to limit the amount of logging shown to the user.
- We have added code to fix the random seeds for reproducibility
```
def printb(text):
"""Auxiliar function to print in bold.
Compensates for bug in Colab that doesn't show Markdown(diplay('text'))
"""
print('\x1b[1;30m'+text+'\x1b[0m')
```
# Start of Original Notebook
#### This notebook demonstrates the use of adversarial debiasing algorithm to learn a fair classifier.
Adversarial debiasing [1] is an in-processing technique that learns a classifier to maximize prediction accuracy and simultaneously reduce an adversary's ability to determine the protected attribute from the predictions. This approach leads to a fair classifier as the predictions cannot carry any group discrimination information that the adversary can exploit. We will see how to use this algorithm for learning models with and without fairness constraints and apply them on the Adult dataset.
```
%matplotlib inline
# Load all necessary packages
import sys
sys.path.append("../")
from aif360.datasets import BinaryLabelDataset
from aif360.datasets import AdultDataset, GermanDataset, CompasDataset
from aif360.metrics import BinaryLabelDatasetMetric
from aif360.metrics import ClassificationMetric
from aif360.metrics.utils import compute_boolean_conditioning_vector
from aif360.algorithms.preprocessing.optim_preproc_helpers.data_preproc_functions import load_preproc_data_adult, load_preproc_data_compas, load_preproc_data_german
from aif360.algorithms.inprocessing.adversarial_debiasing import AdversarialDebiasing
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler, MaxAbsScaler
from sklearn.metrics import accuracy_score
from IPython.display import Markdown, display
import matplotlib.pyplot as plt
import tensorflow as tf
tf.compat.v1.logging.set_verbosity(tf.logging.ERROR)
SEED = 42
```
#### Load dataset and set options
```
# Get the dataset and split into train and test
dataset_orig = load_preproc_data_adult()
privileged_groups = [{'sex': 1}]
unprivileged_groups = [{'sex': 0}]
dataset_orig_train, dataset_orig_test = dataset_orig.split([0.7], shuffle=True, seed=SEED)
# print out some labels, names, etc.
#display(Markdown("#### Training Dataset shape"))
printb('#### Training Dataset shape')
print(dataset_orig_train.features.shape)
#display(Markdown("#### Favorable and unfavorable labels"))
printb("#### Favorable and unfavorable labels")
print(dataset_orig_train.favorable_label, dataset_orig_train.unfavorable_label)
#display(Markdown("#### Protected attribute names"))
printb("#### Protected attribute names")
print(dataset_orig_train.protected_attribute_names)
#display(Markdown("#### Privileged and unprivileged protected attribute values"))
printb("#### Privileged and unprivileged protected attribute values")
print(dataset_orig_train.privileged_protected_attributes,
dataset_orig_train.unprivileged_protected_attributes)
#display(Markdown("#### Dataset feature names"))
printb("#### Dataset feature names")
print(dataset_orig_train.feature_names)
```
#### Metric for original training data
```
# Metric for the original dataset
metric_orig_train = BinaryLabelDatasetMetric(dataset_orig_train,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
#display(Markdown("#### Original training dataset"))
printb("#### Original training dataset")
print("Train set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_orig_train.mean_difference())
metric_orig_test = BinaryLabelDatasetMetric(dataset_orig_test,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
print("Test set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_orig_test.mean_difference())
min_max_scaler = MaxAbsScaler()
dataset_orig_train.features = min_max_scaler.fit_transform(dataset_orig_train.features)
dataset_orig_test.features = min_max_scaler.transform(dataset_orig_test.features)
metric_scaled_train = BinaryLabelDatasetMetric(dataset_orig_train,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
#display(Markdown("#### Scaled dataset - Verify that the scaling does not affect the group label statistics"))
printb("#### Scaled dataset - Verify that the scaling does not affect the group label statistics")
print("Train set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_scaled_train.mean_difference())
metric_scaled_test = BinaryLabelDatasetMetric(dataset_orig_test,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
print("Test set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_scaled_test.mean_difference())
```
### Learn plan classifier without debiasing
```
# Load post-processing algorithm that equalizes the odds
# Learn parameters with debias set to False
sess = tf.Session()
tf.set_random_seed(SEED)
plain_model = AdversarialDebiasing(privileged_groups = privileged_groups,
unprivileged_groups = unprivileged_groups,
scope_name='plain_classifier',
debias=False,
sess=sess,
seed=SEED)
plain_model.fit(dataset_orig_train)
# Apply the plain model to test data
dataset_nodebiasing_train = plain_model.predict(dataset_orig_train)
dataset_nodebiasing_test = plain_model.predict(dataset_orig_test)
# Metrics for the dataset from plain model (without debiasing)
#display(Markdown("#### Plain model - without debiasing - dataset metrics"))
printb("#### Plain model - without debiasing - dataset metrics")
metric_dataset_nodebiasing_train = BinaryLabelDatasetMetric(dataset_nodebiasing_train,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
print("Train set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_dataset_nodebiasing_train.mean_difference())
metric_dataset_nodebiasing_test = BinaryLabelDatasetMetric(dataset_nodebiasing_test,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
print("Test set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_dataset_nodebiasing_test.mean_difference())
#display(Markdown("#### Plain model - without debiasing - classification metrics"))
printb("#### Plain model - without debiasing - classification metrics")
classified_metric_nodebiasing_test = ClassificationMetric(dataset_orig_test,
dataset_nodebiasing_test,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
print("Test set: Classification accuracy = %f" % classified_metric_nodebiasing_test.accuracy())
TPR = classified_metric_nodebiasing_test.true_positive_rate()
TNR = classified_metric_nodebiasing_test.true_negative_rate()
bal_acc_nodebiasing_test = 0.5*(TPR+TNR)
print("Test set: Balanced classification accuracy = %f" % bal_acc_nodebiasing_test)
print("Test set: Disparate impact = %f" % classified_metric_nodebiasing_test.disparate_impact())
print("Test set: Equal opportunity difference = %f" % classified_metric_nodebiasing_test.equal_opportunity_difference())
print("Test set: Average odds difference = %f" % classified_metric_nodebiasing_test.average_odds_difference())
print("Test set: Theil_index = %f" % classified_metric_nodebiasing_test.theil_index())
```
### Apply in-processing algorithm based on adversarial learning
```
sess.close()
tf.reset_default_graph()
sess = tf.Session()
tf.set_random_seed(SEED)
# Learn parameters with debias set to True
debiased_model = AdversarialDebiasing(privileged_groups = privileged_groups,
unprivileged_groups = unprivileged_groups,
scope_name='debiased_classifier',
debias=True,
sess=sess,
seed=SEED)
debiased_model.fit(dataset_orig_train)
# Apply the plain model to test data
dataset_debiasing_train = debiased_model.predict(dataset_orig_train)
dataset_debiasing_test = debiased_model.predict(dataset_orig_test)
# Metrics for the dataset from plain model (without debiasing)
#display(Markdown("#### Plain model - without debiasing - dataset metrics"))
printb("#### Plain model - without debiasing - dataset metrics")
print("Train set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_dataset_nodebiasing_train.mean_difference())
print("Test set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_dataset_nodebiasing_test.mean_difference())
# Metrics for the dataset from model with debiasing
#display(Markdown("#### Model - with debiasing - dataset metrics"))
printb("#### Model - with debiasing - dataset metrics")
metric_dataset_debiasing_train = BinaryLabelDatasetMetric(dataset_debiasing_train,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
print("Train set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_dataset_debiasing_train.mean_difference())
metric_dataset_debiasing_test = BinaryLabelDatasetMetric(dataset_debiasing_test,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
print("Test set: Difference in mean outcomes between unprivileged and privileged groups = %f" % metric_dataset_debiasing_test.mean_difference())
#display(Markdown("#### Plain model - without debiasing - classification metrics"))
printb("#### Plain model - without debiasing - classification metrics")
print("Test set: Classification accuracy = %f" % classified_metric_nodebiasing_test.accuracy())
TPR = classified_metric_nodebiasing_test.true_positive_rate()
TNR = classified_metric_nodebiasing_test.true_negative_rate()
bal_acc_nodebiasing_test = 0.5*(TPR+TNR)
print("Test set: Balanced classification accuracy = %f" % bal_acc_nodebiasing_test)
print("Test set: Disparate impact = %f" % classified_metric_nodebiasing_test.disparate_impact())
print("Test set: Equal opportunity difference = %f" % classified_metric_nodebiasing_test.equal_opportunity_difference())
print("Test set: Average odds difference = %f" % classified_metric_nodebiasing_test.average_odds_difference())
print("Test set: Theil_index = %f" % classified_metric_nodebiasing_test.theil_index())
#display(Markdown("#### Model - with debiasing - classification metrics"))
printb("#### Model - with debiasing - classification metrics")
classified_metric_debiasing_test = ClassificationMetric(dataset_orig_test,
dataset_debiasing_test,
unprivileged_groups=unprivileged_groups,
privileged_groups=privileged_groups)
print("Test set: Classification accuracy = %f" % classified_metric_debiasing_test.accuracy())
TPR = classified_metric_debiasing_test.true_positive_rate()
TNR = classified_metric_debiasing_test.true_negative_rate()
bal_acc_debiasing_test = 0.5*(TPR+TNR)
print("Test set: Balanced classification accuracy = %f" % bal_acc_debiasing_test)
print("Test set: Disparate impact = %f" % classified_metric_debiasing_test.disparate_impact())
print("Test set: Equal opportunity difference = %f" % classified_metric_debiasing_test.equal_opportunity_difference())
print("Test set: Average odds difference = %f" % classified_metric_debiasing_test.average_odds_difference())
print("Test set: Theil_index = %f" % classified_metric_debiasing_test.theil_index())
```
References:
[1] B. H. Zhang, B. Lemoine, and M. Mitchell, "Mitigating UnwantedBiases with Adversarial Learning,"
AAAI/ACM Conference on Artificial Intelligence, Ethics, and Society, 2018.
# Exploring the results
Let's take a deeper look at the previous results.
```
#@title Code to define `print_table` function to show results in tabular format
from IPython.display import HTML, display
def print_table(headers,data,caption=""):
"""
Prints a table given headers and data
Inputs:
- headers: a list of N headers
- data: a list of N-element lists containing the data to display
- caption: a string describing the data
Outputs:
- A HTML display of the table
Example:
caption = "A caption"
headers = ["row","title 1", "title 2"]
data = [["first row", 1, 2], ["second row", 2, 3]]
print_table(headers,data,caption)
A Caption
-----------------------------------
| row | title 1 | title 2 |
-----------------------------------
| first row | 1 | 2 |
-----------------------------------
| second row | 2 | 3 |
-----------------------------------
"""
display(HTML(
'<table border="1"><caption>{0}</caption><tr>{1}</tr><tr>{2}</tr></table>'.format(
caption,
'<th>{}</th>'.format('</th><th>'.join(line for line in headers)),
'</tr><tr>'.join(
'<td>{}</td>'.format(
'</td><td>'.join(
str(_) for _ in row)) for row in data))
))
table = [["Train set",metric_dataset_nodebiasing_train.mean_difference(),metric_dataset_debiasing_train.mean_difference()],
["Test set",metric_dataset_nodebiasing_test.mean_difference(),metric_dataset_debiasing_test.mean_difference()]]
headers = ['Statistical parity difference','Without debiasing','With debiasing']
caption = "Difference in mean outcomes between unprivileged and privileged groups"
print_table(headers,table,caption)
```
We observe a big reduction in the statistical parity difference by training with Adversarial learning debias mitigation.
Let's look at the result of this technique by evaluating other fairness metrics.
```
metrics_final = [["Accuracy", "%f" % classified_metric_nodebiasing_test.accuracy(), "%f" % classified_metric_debiasing_test.accuracy()],
["Balanced classification accuracy","%f" % bal_acc_nodebiasing_test, "%f" % bal_acc_debiasing_test],
["Disparate impact","%f" % classified_metric_nodebiasing_test.disparate_impact(), "%f" % classified_metric_debiasing_test.disparate_impact()],
["Equal opportunity difference", "%f" % classified_metric_nodebiasing_test.equal_opportunity_difference(), "%f" % classified_metric_debiasing_test.equal_opportunity_difference()],
["Average odds difference", "%f" % classified_metric_nodebiasing_test.average_odds_difference(), "%f" % classified_metric_debiasing_test.average_odds_difference()],
["Theil_index", "%f" % classified_metric_nodebiasing_test.theil_index(), "%f" % classified_metric_debiasing_test.theil_index()]]
headers_final = ["Classification metric", "Without debiasing","With debiasing"]
caption_final = "Difference in model performance by using Adversarial Learning mitigation"
print_table(headers_final, metrics_final, caption_final)
```
It is hard to remember the definition and the ideal expected value for each metric. We can use [explainers](https://aif360.readthedocs.io/en/latest/modules/explainers.html#) to explain each metric. There are two kind of flavours: TEXT and JSON. The JSON explainers provide structured explanations that can be used to present information to the users. Here are some examples.
```
#@title Define `format_json` function for pretty print of JSON explainers
import json
from collections import OrderedDict
def format_json(json_str):
return json.dumps(json.loads(json_str, object_pairs_hook=OrderedDict), indent=2)
from aif360.explainers import MetricJSONExplainer
# Define explainers for the metrics with and without debiasing
ex_nondebias_test = MetricJSONExplainer(classified_metric_nodebiasing_test)
ex_debias_test = MetricJSONExplainer(classified_metric_debiasing_test)
```
Now let's print the explainers for the metrics we used above. Make sure you read the whole text.
```
printb("Nondebiasing")
print(format_json(ex_nondebias_test.accuracy()))
printb("Debiasing")
print(format_json(ex_debias_test.accuracy()))
printb("Nondebiasing")
print(format_json(ex_nondebias_test.disparate_impact()))
printb("Debiasing")
print(format_json(ex_debias_test.disparate_impact()))
printb("Nondebiasing")
print(format_json(ex_nondebias_test.equal_opportunity_difference()))
printb("Debiasing")
print(format_json(ex_debias_test.equal_opportunity_difference()))
printb("Nondebiasing")
print(format_json(ex_nondebias_test.average_odds_difference()))
printb("Debiasing")
print(format_json(ex_debias_test.average_odds_difference()))
printb("Nondebiasing")
print(format_json(ex_nondebias_test.theil_index()))
printb("Debiasing")
print(format_json(ex_debias_test.theil_index()))
```
# Excercises and questions
Let's make sure you understand what you just did while working on this notebook.
1. Rerun this notebook with `race` as the protected attribute. How different are the results on the fairness metrics?
2. What does the `Adversarial Debiasing` technique do?
3. What kind of classifier is this technique using? What hyperparameters could you tune?
4. Can I use the current implementation to optimize for several protected attributes?
| true |
code
| 0.522507 | null | null | null | null |
|
# General Structured Output Models with Shogun Machine Learning Toolbox
#### Shell Hu (GitHub ID: [hushell](https://github.com/hushell))
#### Thanks Patrick Pletscher and Fernando J. Iglesias García for taking time to help me finish the project! Shoguners = awesome! Me = grateful!
## Introduction
This notebook illustrates the training of a <a href="http://en.wikipedia.org/wiki/Factor_graph">factor graph</a> model using <a href="http://en.wikipedia.org/wiki/Structured_support_vector_machine">structured SVM</a> in Shogun. We begin by giving a brief outline of factor graphs and <a href="http://en.wikipedia.org/wiki/Structured_prediction">structured output learning</a> followed by the corresponding API in Shogun. Finally, we test the scalability by performing an experiment on a real <a href="http://en.wikipedia.org/wiki/Optical_character_recognition">OCR</a> data set for <a href="http://en.wikipedia.org/wiki/Handwriting_recognition">handwritten character recognition</a>.
### Factor Graph
A factor graph explicitly represents the factorization of an undirected graphical model in terms of a set of factors (potentials), each of which is defined on a clique in the original graph [1]. For example, a MRF distribution can be factorized as
$$
P(\mathbf{y}) = \frac{1}{Z} \prod_{F \in \mathcal{F}} \theta_F(\mathbf{y}_F),
$$
where $F$ is the factor index, $\theta_F(\mathbf{y}_F)$ is the energy with respect to assignment $\mathbf{y}_F$. In this demo, we focus only on table representation of factors. Namely, each factor holds an energy table $\theta_F$, which can be viewed as an unnormalized CPD. According to different factorizations, there are different types of factors. Usually we assume the Markovian property is held, that is, factors have the same parameterization if they belong to the same type, no matter how location or time changes. In addition, we have parameter free factor type, but nothing to learn for such kinds of types. More detailed implementation will be explained later.
### Structured Prediction
Structured prediction typically involves an input $\mathbf{x}$ (can be structured) and a structured output $\mathbf{y}$. A joint feature map $\Phi(\mathbf{x},\mathbf{y})$ is defined to incorporate structure information into the labels, such as chains, trees or general graphs. In general, the linear parameterization will be used to give the prediction rule. We leave the kernelized version for future work.
$$
\hat{\mathbf{y}} = \underset{\mathbf{y} \in \mathcal{Y}}{\operatorname{argmax}} \langle \mathbf{w}, \Phi(\mathbf{x},\mathbf{y}) \rangle
$$
where $\Phi(\mathbf{x},\mathbf{y})$ is the feature vector by mapping local factor features to corresponding locations in terms of $\mathbf{y}$, and $\mathbf{w}$ is the global parameter vector. In factor graph model, parameters are associated with a set of factor types. So $\mathbf{w}$ is a collection of local parameters.
The parameters are learned by regularized risk minimization, where the risk defined by user provided loss function $\Delta(\mathbf{y},\mathbf{\hat{y}})$ is usually non-convex and non-differentiable, e.g. the Hamming loss. So the empirical risk is defined in terms of the surrogate hinge loss $H_i(\mathbf{w}) = \max_{\mathbf{y} \in \mathcal{Y}} \Delta(\mathbf{y}_i,\mathbf{y}) - \langle \mathbf{w}, \Psi_i(\mathbf{y}) \rangle $, which is an upper bound of the user defined loss. Here $\Psi_i(\mathbf{y}) = \Phi(\mathbf{x}_i,\mathbf{y}_i) - \Phi(\mathbf{x}_i,\mathbf{y})$. The training objective is given by
$$
\min_{\mathbf{w}} \frac{\lambda}{2} ||\mathbf{w}||^2 + \frac{1}{N} \sum_{i=1}^N H_i(\mathbf{w}).
$$
In Shogun's factor graph model, the corresponding implemented functions are:
- <a href="http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CStructuredModel.html#a15bd99e15bbf0daa8a727d03dbbf4bcd">FactorGraphModel::get_joint_feature_vector()</a> $\longleftrightarrow \Phi(\mathbf{x}_i,\mathbf{y})$
- <a href="http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CFactorGraphModel.html#a36665cfdd7ea2dfcc9b3c590947fe67f">FactorGraphModel::argmax()</a> $\longleftrightarrow H_i(\mathbf{w})$
- <a href="http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CFactorGraphModel.html#a17dac99e933f447db92482a6dce8489b">FactorGraphModel::delta_loss()</a> $\longleftrightarrow \Delta(\mathbf{y}_i,\mathbf{y})$
## Experiment: OCR
### Show Data
First of all, we load the OCR data from a prepared mat file. The raw data can be downloaded from <a href="http://www.seas.upenn.edu/~taskar/ocr/">http://www.seas.upenn.edu/~taskar/ocr/</a>. It has 6876 handwritten words with an average length of 8 letters from 150 different persons. Each letter is rasterized into a binary image of size 16 by 8 pixels. Thus, each $\mathbf{y}$ is a chain, and each node has 26 possible states denoting ${a,\cdots,z}$.
```
%pylab inline
%matplotlib inline
import os
SHOGUN_DATA_DIR=os.getenv('SHOGUN_DATA_DIR', '../../../data')
import numpy as np
import scipy.io
dataset = scipy.io.loadmat(os.path.join(SHOGUN_DATA_DIR, 'ocr/ocr_taskar.mat'))
# patterns for training
p_tr = dataset['patterns_train']
# patterns for testing
p_ts = dataset['patterns_test']
# labels for training
l_tr = dataset['labels_train']
# labels for testing
l_ts = dataset['labels_test']
# feature dimension
n_dims = p_tr[0,0].shape[0]
# number of states
n_stats = 26
# number of training samples
n_tr_samples = p_tr.shape[1]
# number of testing samples
n_ts_samples = p_ts.shape[1]
```
Few examples of the handwritten words are shown below. Note that the first capitalized letter has been removed.
```
import matplotlib.pyplot as plt
def show_word(patterns, index):
"""show a word with padding"""
plt.rc('image', cmap='binary')
letters = patterns[0,index][:128,:]
n_letters = letters.shape[1]
for l in range(n_letters):
lett = np.transpose(np.reshape(letters[:,l], (8,16)))
lett = np.hstack((np.zeros((16,1)), lett, np.zeros((16,1))))
lett = np.vstack((np.zeros((1,10)), lett, np.zeros((1,10))))
subplot(1,n_letters,l+1)
imshow(lett)
plt.xticks(())
plt.yticks(())
plt.tight_layout()
show_word(p_tr, 174)
show_word(p_tr, 471)
show_word(p_tr, 57)
```
### Define Factor Types and Build Factor Graphs
Let's define 4 factor types, such that a word will be able to be modeled as a chain graph.
- The unary factor type will be used to define unary potentials that capture the appearance likelihoods of each letter. In our case, each letter has $16 \times 8$ pixels, thus there are $(16 \times 8 + 1) \times 26$ parameters. Here the additional bits in the parameter vector are bias terms. One for each state.
- The pairwise factor type will be used to define pairwise potentials between each pair of letters. This type in fact gives the Potts potentials. There are $26 \times 26$ parameters.
- The bias factor type for the first letter is a compensation factor type, since the interaction is one-sided. So there are $26$ parameters to be learned.
- The bias factor type for the last letter, which has the same intuition as the last item. There are also $26$ parameters.
Putting all parameters together, the global parameter vector $\mathbf{w}$ has length $4082$.
```
from shogun import TableFactorType
# unary, type_id = 0
cards_u = np.array([n_stats], np.int32)
w_gt_u = np.zeros(n_stats*n_dims)
fac_type_u = TableFactorType(0, cards_u, w_gt_u)
# pairwise, type_id = 1
cards = np.array([n_stats,n_stats], np.int32)
w_gt = np.zeros(n_stats*n_stats)
fac_type = TableFactorType(1, cards, w_gt)
# first bias, type_id = 2
cards_s = np.array([n_stats], np.int32)
w_gt_s = np.zeros(n_stats)
fac_type_s = TableFactorType(2, cards_s, w_gt_s)
# last bias, type_id = 3
cards_t = np.array([n_stats], np.int32)
w_gt_t = np.zeros(n_stats)
fac_type_t = TableFactorType(3, cards_t, w_gt_t)
# all initial parameters
w_all = [w_gt_u,w_gt,w_gt_s,w_gt_t]
# all factor types
ftype_all = [fac_type_u,fac_type,fac_type_s,fac_type_t]
```
Next, we write a function to construct the factor graphs and prepare labels for training. For each factor graph instance, the structure is a chain but the number of nodes and edges depend on the number of letters, where unary factors will be added for each letter, pairwise factors will be added for each pair of neighboring letters. Besides, the first and last letter will get an additional bias factor respectively.
```
def prepare_data(x, y, ftype, num_samples):
"""prepare FactorGraphFeatures and FactorGraphLabels """
from shogun import Factor, TableFactorType, FactorGraph
from shogun import FactorGraphObservation, FactorGraphLabels, FactorGraphFeatures
samples = FactorGraphFeatures(num_samples)
labels = FactorGraphLabels(num_samples)
for i in range(num_samples):
n_vars = x[0,i].shape[1]
data = x[0,i].astype(np.float64)
vc = np.array([n_stats]*n_vars, np.int32)
fg = FactorGraph(vc)
# add unary factors
for v in range(n_vars):
datau = data[:,v]
vindu = np.array([v], np.int32)
facu = Factor(ftype[0], vindu, datau)
fg.add_factor(facu)
# add pairwise factors
for e in range(n_vars-1):
datap = np.array([1.0])
vindp = np.array([e,e+1], np.int32)
facp = Factor(ftype[1], vindp, datap)
fg.add_factor(facp)
# add bias factor to first letter
datas = np.array([1.0])
vinds = np.array([0], np.int32)
facs = Factor(ftype[2], vinds, datas)
fg.add_factor(facs)
# add bias factor to last letter
datat = np.array([1.0])
vindt = np.array([n_vars-1], np.int32)
fact = Factor(ftype[3], vindt, datat)
fg.add_factor(fact)
# add factor graph
samples.add_sample(fg)
# add corresponding label
states_gt = y[0,i].astype(np.int32)
states_gt = states_gt[0,:]; # mat to vector
loss_weights = np.array([1.0/n_vars]*n_vars)
fg_obs = FactorGraphObservation(states_gt, loss_weights)
labels.add_label(fg_obs)
return samples, labels
# prepare training pairs (factor graph, node states)
n_tr_samples = 350 # choose a subset of training data to avoid time out on buildbot
samples, labels = prepare_data(p_tr, l_tr, ftype_all, n_tr_samples)
```
An example of graph structure is visualized as below, from which you may have a better sense how a factor graph being built. Note that different colors are used to represent different factor types.
```
try:
import networkx as nx # pip install networkx
except ImportError:
import pip
pip.main(['install', '--user', 'networkx'])
import networkx as nx
import matplotlib.pyplot as plt
# create a graph
G = nx.Graph()
node_pos = {}
# add variable nodes, assuming there are 3 letters
G.add_nodes_from(['v0','v1','v2'])
for i in range(3):
node_pos['v%d' % i] = (2*i,1)
# add factor nodes
G.add_nodes_from(['F0','F1','F2','F01','F12','Fs','Ft'])
for i in range(3):
node_pos['F%d' % i] = (2*i,1.006)
for i in range(2):
node_pos['F%d%d' % (i,i+1)] = (2*i+1,1)
node_pos['Fs'] = (-1,1)
node_pos['Ft'] = (5,1)
# add edges to connect variable nodes and factor nodes
G.add_edges_from([('v%d' % i,'F%d' % i) for i in range(3)])
G.add_edges_from([('v%d' % i,'F%d%d' % (i,i+1)) for i in range(2)])
G.add_edges_from([('v%d' % (i+1),'F%d%d' % (i,i+1)) for i in range(2)])
G.add_edges_from([('v0','Fs'),('v2','Ft')])
# draw graph
fig, ax = plt.subplots(figsize=(6,2))
nx.draw_networkx_nodes(G,node_pos,nodelist=['v0','v1','v2'],node_color='white',node_size=700,ax=ax)
nx.draw_networkx_nodes(G,node_pos,nodelist=['F0','F1','F2'],node_color='yellow',node_shape='s',node_size=300,ax=ax)
nx.draw_networkx_nodes(G,node_pos,nodelist=['F01','F12'],node_color='blue',node_shape='s',node_size=300,ax=ax)
nx.draw_networkx_nodes(G,node_pos,nodelist=['Fs'],node_color='green',node_shape='s',node_size=300,ax=ax)
nx.draw_networkx_nodes(G,node_pos,nodelist=['Ft'],node_color='purple',node_shape='s',node_size=300,ax=ax)
nx.draw_networkx_edges(G,node_pos,alpha=0.7)
plt.axis('off')
plt.tight_layout()
```
### Training
Now we can create the factor graph model and start training. We will use the tree max-product belief propagation to do MAP inference.
```
from shogun import FactorGraphModel, TREE_MAX_PROD
# create model and register factor types
model = FactorGraphModel(samples, labels, TREE_MAX_PROD)
model.add_factor_type(ftype_all[0])
model.add_factor_type(ftype_all[1])
model.add_factor_type(ftype_all[2])
model.add_factor_type(ftype_all[3])
```
In Shogun, we implemented several batch solvers and online solvers. Let's first try to train the model using a batch solver. We choose the dual bundle method solver (<a href="http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CDualLibQPBMSOSVM.html">DualLibQPBMSOSVM</a>) [2], since in practice it is slightly faster than the primal n-slack cutting plane solver (<a a href="http://www.shogun-toolbox.org/doc/en/latest/PrimalMosekSOSVM_8h.html">PrimalMosekSOSVM</a>) [3]. However, it still will take a while until convergence. Briefly, in each iteration, a gradually tighter piece-wise linear lower bound of the objective function will be constructed by adding more cutting planes (most violated constraints), then the approximate QP will be solved. Finding a cutting plane involves calling the max oracle $H_i(\mathbf{w})$ and in average $N$ calls are required in an iteration. This is basically why the training is time consuming.
```
from shogun import DualLibQPBMSOSVM
from shogun import BmrmStatistics
import pickle
import time
# create bundle method SOSVM, there are few variants can be chosen
# BMRM, Proximal Point BMRM, Proximal Point P-BMRM, NCBM
# usually the default one i.e. BMRM is good enough
# lambda is set to 1e-2
bmrm = DualLibQPBMSOSVM(model, labels, 0.01)
bmrm.put('m_TolAbs', 20.0)
bmrm.put('verbose', True)
bmrm.set_store_train_info(True)
# train
t0 = time.time()
bmrm.train()
t1 = time.time()
w_bmrm = bmrm.get_real_vector('m_w')
print("BMRM took", t1 - t0, "seconds.")
```
Let's check the duality gap to see if the training has converged. We aim at minimizing the primal problem while maximizing the dual problem. By the weak duality theorem, the optimal value of the primal problem is always greater than or equal to dual problem. Thus, we could expect the duality gap will decrease during the time. A relative small and stable duality gap may indicate the convergence. In fact, the gap doesn't have to become zero, since we know it is not far away from the local minima.
```
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12,4))
primal_bmrm = bmrm.get_helper().get_real_vector('primal')
dual_bmrm = bmrm.get_result().get_hist_Fd_vector()
len_iter = min(primal_bmrm.size, dual_bmrm.size)
primal_bmrm = primal_bmrm[1:len_iter]
dual_bmrm = dual_bmrm[1:len_iter]
# plot duality gaps
xs = range(dual_bmrm.size)
axes[0].plot(xs, (primal_bmrm-dual_bmrm), label='duality gap')
axes[0].set_xlabel('iteration')
axes[0].set_ylabel('duality gap')
axes[0].legend(loc=1)
axes[0].set_title('duality gaps');
axes[0].grid(True)
# plot primal and dual values
xs = range(dual_bmrm.size-1)
axes[1].plot(xs, primal_bmrm[1:], label='primal')
axes[1].plot(xs, dual_bmrm[1:], label='dual')
axes[1].set_xlabel('iteration')
axes[1].set_ylabel('objective')
axes[1].legend(loc=1)
axes[1].set_title('primal vs dual');
axes[1].grid(True)
```
There are other statitics may also be helpful to check if the solution is good or not, such as the number of cutting planes, from which we may have a sense how tight the piece-wise lower bound is. In general, the number of cutting planes should be much less than the dimension of the parameter vector.
```
# statistics
bmrm_stats = bmrm.get_result()
nCP = bmrm_stats.nCP
nzA = bmrm_stats.nzA
print('number of cutting planes: %d' % nCP)
print('number of active cutting planes: %d' % nzA)
```
In our case, we have 101 active cutting planes, which is much less than 4082, i.e. the number of parameters. We could expect a good model by looking at these statistics. Now come to the online solvers. Unlike the cutting plane algorithms re-optimizes over all the previously added dual variables, an online solver will update the solution based on a single point. This difference results in a faster convergence rate, i.e. less oracle calls, please refer to Table 1 in [4] for more detail. Here, we use the stochastic subgradient descent (<a href="http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CStochasticSOSVM.html">StochasticSOSVM</a>) to compare with the BMRM algorithm shown before.
```
from shogun import StochasticSOSVM
# the 3rd parameter is do_weighted_averaging, by turning this on,
# a possibly faster convergence rate may be achieved.
# the 4th parameter controls outputs of verbose training information
sgd = StochasticSOSVM(model, labels, True, True)
sgd.put('num_iter', 100)
sgd.put('lambda', 0.01)
# train
t0 = time.time()
sgd.train()
t1 = time.time()
w_sgd = sgd.get_real_vector('m_w')
print("SGD took", t1 - t0, "seconds.")
```
We compare the SGD and BMRM in terms of the primal objectives versus effective passes. We first plot the training progress (until both algorithms converge) and then zoom in to check the first 100 passes. In order to make a fair comparison, we set the regularization constant to 1e-2 for both algorithms.
```
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12,4))
primal_sgd = sgd.get_helper().get_real_vector('primal')
xs = range(dual_bmrm.size-1)
axes[0].plot(xs, primal_bmrm[1:], label='BMRM')
axes[0].plot(range(99), primal_sgd[1:100], label='SGD')
axes[0].set_xlabel('effecitve passes')
axes[0].set_ylabel('primal objective')
axes[0].set_title('whole training progress')
axes[0].legend(loc=1)
axes[0].grid(True)
axes[1].plot(range(99), primal_bmrm[1:100], label='BMRM')
axes[1].plot(range(99), primal_sgd[1:100], label='SGD')
axes[1].set_xlabel('effecitve passes')
axes[1].set_ylabel('primal objective')
axes[1].set_title('first 100 effective passes')
axes[1].legend(loc=1)
axes[1].grid(True)
```
As is shown above, the SGD solver uses less oracle calls to get to converge. Note that the timing is 2 times slower than they actually need, since there are additional computations of primal objective and training error in each pass. The training errors of both algorithms for each pass are shown in below.
```
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12,4))
terr_bmrm = bmrm.get_helper().get_real_vector('train_error')
terr_sgd = sgd.get_helper().get_real_vector('train_error')
xs = range(terr_bmrm.size-1)
axes[0].plot(xs, terr_bmrm[1:], label='BMRM')
axes[0].plot(range(99), terr_sgd[1:100], label='SGD')
axes[0].set_xlabel('effecitve passes')
axes[0].set_ylabel('training error')
axes[0].set_title('whole training progress')
axes[0].legend(loc=1)
axes[0].grid(True)
axes[1].plot(range(99), terr_bmrm[1:100], label='BMRM')
axes[1].plot(range(99), terr_sgd[1:100], label='SGD')
axes[1].set_xlabel('effecitve passes')
axes[1].set_ylabel('training error')
axes[1].set_title('first 100 effective passes')
axes[1].legend(loc=1)
axes[1].grid(True)
```
Interestingly, the training errors of SGD solver are lower than BMRM's in first 100 passes, but in the end the BMRM solver obtains a better training performance. A probable explanation is that BMRM uses very limited number of cutting planes at beginning, which form a poor approximation of the objective function. As the number of cutting planes increasing, we got a tighter piecewise lower bound, thus improve the performance. In addition, we would like to show the pairwise weights, which may learn important co-occurrances of letters. The hinton diagram is a wonderful tool for visualizing 2D data, in which positive and negative values are represented by white and black squares, respectively, and the size of each square represents the magnitude of each value. In our case, a smaller number i.e. a large black square indicates the two letters tend to coincide.
```
def hinton(matrix, max_weight=None, ax=None):
"""Draw Hinton diagram for visualizing a weight matrix."""
ax = ax if ax is not None else plt.gca()
if not max_weight:
max_weight = 2**np.ceil(np.log(np.abs(matrix).max())/np.log(2))
ax.patch.set_facecolor('gray')
ax.set_aspect('equal', 'box')
ax.xaxis.set_major_locator(plt.NullLocator())
ax.yaxis.set_major_locator(plt.NullLocator())
for (x,y),w in np.ndenumerate(matrix):
color = 'white' if w > 0 else 'black'
size = np.sqrt(np.abs(w))
rect = plt.Rectangle([x - size / 2, y - size / 2], size, size,
facecolor=color, edgecolor=color)
ax.add_patch(rect)
ax.autoscale_view()
ax.invert_yaxis()
# get pairwise parameters, also accessible from
# w[n_dims*n_stats:n_dims*n_stats+n_stats*n_stats]
model.w_to_fparams(w_sgd) # update factor parameters
w_p = ftype_all[1].get_w()
w_p = np.reshape(w_p,(n_stats,n_stats))
hinton(w_p)
```
### Inference
Next, we show how to do inference with the learned model parameters for a given data point.
```
# get testing data
samples_ts, labels_ts = prepare_data(p_ts, l_ts, ftype_all, n_ts_samples)
from shogun import FactorGraphFeatures, FactorGraphObservation, TREE_MAX_PROD, MAPInference
# get a factor graph instance from test data
fg0 = samples_ts.get_sample(100)
fg0.compute_energies()
fg0.connect_components()
# create a MAP inference using tree max-product
infer_met = MAPInference(fg0, TREE_MAX_PROD)
infer_met.inference()
# get inference results
y_pred = infer_met.get_structured_outputs()
y_truth = FactorGraphObservation.obtain_from_generic(labels_ts.get_label(100))
print(y_pred.get_data())
print(y_truth.get_data())
```
### Evaluation
In the end, we check average training error and average testing error. The evaluation can be done by two methods. We can either use the apply() function in the structured output machine or use the <a href="http://www.shogun-toolbox.org/doc/en/latest/classshogun_1_1CSOSVMHelper.html">SOSVMHelper</a>.
```
from shogun import SOSVMHelper
# training error of BMRM method
bmrm.put('m_w', w_bmrm)
model.w_to_fparams(w_bmrm)
lbs_bmrm = bmrm.apply()
acc_loss = 0.0
ave_loss = 0.0
for i in range(n_tr_samples):
y_pred = lbs_bmrm.get_label(i)
y_truth = labels.get_label(i)
acc_loss = acc_loss + model.delta_loss(y_truth, y_pred)
ave_loss = acc_loss / n_tr_samples
print('BMRM: Average training error is %.4f' % ave_loss)
# training error of stochastic method
print('SGD: Average training error is %.4f' % SOSVMHelper.average_loss(w_sgd, model))
# testing error
bmrm.set_features(samples_ts)
bmrm.set_labels(labels_ts)
lbs_bmrm_ts = bmrm.apply()
acc_loss = 0.0
ave_loss_ts = 0.0
for i in range(n_ts_samples):
y_pred = lbs_bmrm_ts.get_label(i)
y_truth = labels_ts.get_label(i)
acc_loss = acc_loss + model.delta_loss(y_truth, y_pred)
ave_loss_ts = acc_loss / n_ts_samples
print('BMRM: Average testing error is %.4f' % ave_loss_ts)
# testing error of stochastic method
print('SGD: Average testing error is %.4f' % SOSVMHelper.average_loss(sgd.get_real_vector('m_w'), model))
```
## References
[1] Kschischang, F. R., B. J. Frey, and H.-A. Loeliger, Factor graphs and the sum-product algorithm, IEEE Transactions on Information Theory 2001.
[2] Teo, C.H., Vishwanathan, S.V.N, Smola, A. and Quoc, V.Le, Bundle Methods for Regularized Risk Minimization, JMLR 2010.
[3] Tsochantaridis, I., Hofmann, T., Joachims, T., Altun, Y., Support Vector Machine Learning for Interdependent and Structured Ouput Spaces, ICML 2004.
[4] Lacoste-Julien, S., Jaggi, M., Schmidt, M., Pletscher, P., Block-Coordinate Frank-Wolfe Optimization for Structural SVMs, ICML 2013.
| true |
code
| 0.599427 | null | null | null | null |
|
<img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# Remotive - Get jobs from categories
<a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/Remotive/Remotive_Get_jobs_from_categories.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
**Tags:** #remotive #jobs #csv #snippet #opendata #dataframe
**Author:** [Sanjeet Attili](https://www.linkedin.com/in/sanjeet-attili-760bab190/)
With this notebook, you will be able to get jobs offer from Remotive:
- **URL:** Job offer url.
- **TITLE:** Job title.
- **COMPANY:** Company name.
- **PUBLICATION_DATE:** Date of publication.
## Input
### Import libraries
```
import pandas as pd
import requests
import time
from datetime import datetime
```
### Setup Remotive
#### Get categories from Remotive
```
def get_remotejob_categories():
req_url = f"https://remotive.io/api/remote-jobs/categories"
res = requests.get(req_url)
try:
res.raise_for_status()
except requests.HTTPError as e:
return e
res_json = res.json()
# Get categories
jobs = res_json.get('jobs')
return pd.DataFrame(jobs)
df_categories = get_remotejob_categories()
df_categories
```
#### Enter your parameters
```
categories = ['data'] # Pick the list of categories in columns "slug"
date_from = - 10 # Choose date difference in days from now => must be negative
```
### Variables
```
csv_output = "REMOTIVE_JOBS.csv"
```
## Model
### Get all jobs posted after timestamp_date
All jobs posted after the date from will be fetched.<br>
In summary, we can set the value, in seconds, of 'search_data_from' to fetch all jobs posted since this duration
```
REMOTIVE_DATETIME = "%Y-%m-%dT%H:%M:%S"
NAAS_DATETIME = "%Y-%m-%d %H:%M:%S"
def get_remotive_jobs_since(jobs, date):
ret = []
for job in jobs:
publication_date = datetime.strptime(job['publication_date'], REMOTIVE_DATETIME).timestamp()
if publication_date > date:
ret.append({
'URL': job['url'],
'TITLE': job['title'],
'COMPANY': job['company_name'],
'PUBLICATION_DATE': datetime.fromtimestamp(publication_date).strftime(NAAS_DATETIME)
})
return ret
def get_category_jobs_since(category, date, limit):
url = f"https://remotive.io/api/remote-jobs?category={category}&limit={limit}"
res = requests.get(url)
if res.json()['jobs']:
publication_date = datetime.strptime(res.json()['jobs'][-1]['publication_date'], REMOTIVE_DATETIME).timestamp()
if len(res.json()['jobs']) < limit or date > publication_date:
print(f"Jobs from catgory {category} fetched ✅")
return get_remotive_jobs_since(res.json()['jobs'], date)
else:
return get_category_jobs_since(category, date, limit + 5)
return []
def get_jobs_since(categories: list,
date_from: int):
if date_from >= 0:
return("'date_from' must be negative. Please update your parameter.")
# Transform datefrom int to
search_jobs_from = date_from * 24 * 60 * 60 # days in seconds
timestamp_date = time.time() + search_jobs_from
jobs = []
for category in categories:
jobs += get_category_jobs_since(category, timestamp_date, 5)
print(f'- All job since {datetime.fromtimestamp(timestamp_date)} have been fetched:', len(jobs))
return pd.DataFrame(jobs)
df_jobs = get_jobs_since(categories, date_from=date_from)
df_jobs.head(5)
```
## Output
### Save dataframe in csv
```
df_jobs.to_csv(csv_output, index=False)
```
| true |
code
| 0.427935 | null | null | null | null |
|
## Model explainability
Explainability is the extent to which a model can be explained in human terms. Interpretability is the extent to which you can explain the outcome of a model after a change in input parameters. Often times we are working with black box models, which only show the prediction and not the steps that led up to that decision. Explainability methods uncover vulnerabilities in models and are able to offer a broader insight as to how differing inputs change the outcome.
We'll start by loading the data and splitting the data into training and test sets.
```
import pandas as pd
import shap
from sklearn import model_selection
import numpy as np
import pickle
from alibi.explainers import CEM, KernelShap
import warnings
warnings.filterwarnings("ignore")
pt_info_clean = pd.read_csv("../data/processed/pt_info_clean.csv")
train, test = model_selection.train_test_split(pt_info_clean, random_state=43)
```
We'll translate the pandas data frame into numpy arrays in order to agree with the necessary inputs for our explainability methods.
```
x_train = np.asarray(train.iloc[:,2:train.shape[1]])
x_test = np.asarray(test.iloc[:,2:train.shape[1]])
y_train = np.asarray(train['mrsa_positive'])
y_test = np.asarray(test['mrsa_positive'])
```
Next, we'll import our logistic regression model from before, fit it to the data, and generate predictions. Note: we could use either model here since the methods are model agnostic.
```
# loading model
filename = '../models/logistic_model.sav'
model = pickle.load(open(filename, 'rb'))
# fit model
model.fit(x_train, y_train)
# generate predictions
y_preds = model.predict(x_test)
```
Our model has now made a classification prediction for each of the test data points. However, we don't have much intuition as to how the model chose to classify these values. Explainability methods exist to offer ways to explore the decision making process of black-box models such as this one. Let's see if we can figure out why this prediction was made.
```
def class_names(idx):
if idx > 0:
print('MRSA+')
else:
print('MRSA-')
```
We'll start by looking at one singular patient and why they were classified the way they were. This is called looking at a _local explanation_.
```
predict_fn = lambda x: model.predict_proba(x) # input needs the prediction
# probabilites for each class
shape_ = (1,) + x_train.shape[1:] # dimension of one row, in this case, one patient
feature_names = list(test.columns[2:])
mode = 'PN'
```
## SHAP
One type of explainability method is [SHAP](https://christophm.github.io/interpretable-ml-book/shap.html), or SHapley Additive exPlanations, where a local prediction is explained by displaying each feature's contribution to the prediction. The output of a SHAP method is a linear model created for a particular instance. We'll use the [Alibi](https://github.com/SeldonIO/alibi) library again to use [KernelSHAP](https://docs.seldon.io/projects/alibi/en/latest/methods/KernelSHAP.html), which is used as a black-box SHAP method for an arbitrary classification model.
```
shap_explainer = KernelShap(predict_fn)
shap_explainer.fit(x_train)
shap_explanation = shap_explainer.explain(x_test, l1_reg=False)
```
## Visualizations
After initializing the explainers, we can look at both global and local explanation methods. We'll use a `force_plot` visualization to better understand the local linear model generated by SHAP. This plot shows which features contributed to making the prediction, and to what extent they moved the prediction from the base value (output of model if no inputs are given) to the output value for that instance.
```
shap.initjs()
idx = 0
instance = test.iloc[idx,2:test.shape[1]] # shape of the instance to be explained
class_idx = y_preds[idx].astype(int) # predicted class
feature_names = list(test.columns[2:])
shap.force_plot(
shap_explainer.expected_value[class_idx],
shap_explanation.shap_values[class_idx][idx, :],
instance,
feature_names = feature_names,
text_rotation=15,
matplotlib=True
)
```
Note that this is a local explanation. Other instances will have different weights for each feature, so we cannot generalize this output to the whole model. We can see from the plot that the ethnicity and location of admission features had the biggest influence on the model's decision to classify this instance. We could look at other explainability methods such as [counterfactuals](https://christophm.github.io/interpretable-ml-book/counterfactual.html) to find out what changes to the input would create the correct classification.
We see what influenced this instance the most, but what about the overall model? SHAP also offers global explanations, which can be viewed best by a `summary_plot`.
```
shap.summary_plot(shap_explanation.shap_values[idx],
test.iloc[:,2:test.shape[1]],
feature_names = feature_names)
```
This plot shows the total sum of each feature's SHAP value for each of the instances in `x_test` with a class `0` (MRSA negative). Features with the highest impact are at the top of the plot. This model has the highest valued features being `ethnicity_HISPANIC/LATINO - PUERTO RICAN`, `gender_F`, and `ethnicity_WHITE`; with the prescence of these values, the model is more likely to predict class `0`. This outcome definitely raises questions in terms of model bias or input bias: what does the underlying population look like that ethnicity and gender are driving features of this function? We would probably expect diagnoses to be more important, but it could be that there are a vast amount of diagnoses for any one to be heavily weighted. If this model was going into production, we would probably want to take a step back and do more research to ensure our model is able to generalize well to all patients.
# Conclusion
In the end, **explainers are not built to fix problems in models, but rather expose them.** Understanding how black-box models make decisions before launching them into production helps ensure transparency and avoid unconscious bias.
## Contrastive Explanation Methods
There's a variety of explainability methods that supply local or global explanations for how a model is making certain classification decisions; we'll use a library called [Alibi](https://github.com/SeldonIO/alibi) in order to create some of these methods. [Contrastive explanation methods](https://arxiv.org/abs/1802.07623), or CEMs, focus on explaining instances in terms of pertinent positives and pertinent negatives. **Pertinent positives** refer to features that should be minimally and sufficiently present to predict the same class as on the original instance. (e.g. if all people who contract MRSA are between the ages 35 and 55). **Pertinent negatives**, on the other hand, identify what features should be minimally and necessarily absent from the instance to be explained in order to maintain the original prediction class (e.g. NO people with respiratory distress contracted MRSA).
Alibi offers black-box explanations for models, which means all that the CEM needs is a predict function for the model. This gives us the flexibility to input nearly any model without having to rewrite any code to initialize the CEM. The only edit we have done is change ```predict``` to ```predict_proba```, which gives the output of the probability of each possible predicted class rather than the prediction itself.
```
cem = CEM(predict_fn,
mode = mode, # either PN or PP
shape = shape_) # instance shape
idx = 0
X = x_test[idx].reshape((1,) + x_test[idx].shape)
cem.fit(x_train, no_info_type='median') # we need to define what feature values contain the least
# info wrt predictions
# here we will naively assume that the feature-wise median
# contains no info
cem_explanation = cem.explain(X, verbose=False)
columns = pd.Series(feature_names)
pn_df = pd.DataFrame(cem_explanation.PN,
columns = columns)
pn_df.loc[:, (pn_df < 0).any(axis=0)]
print('Actual class: ')
class_names(y_test[idx])
print('Model prediction for patient: ')
class_names(model.predict(X))
```
| true |
code
| 0.458167 | null | null | null | null |
|
# Week 10 - Programming Paradigms
## Learning Objectives
* List popular programming paradigms
* Demonstrate object oriented programming
* Compare procedural programming and object oriented programming
* Apply object oriented programming to solve sample problems
Computer programs and the elements they contain can be built in a variety of different ways. Several different styles, or paradigms, exist with differing popularity and usefulness for different tasks.
Some programming languages are designed to support a particular paradigm, while other languages support several different paradigms.
Three of the most commonly used paradigms are:
* Procedural
* Object oriented
* Functional
Python supports each of these paradigms.
## Procedural
You may not have realized it but the procedural programming paradigm is probably the approach you are currently taking with your programs.
Programs and functions are simply a series of steps to be performed.
For example:
```
primes = []
i = 2
while len(primes) < 25:
for p in primes:
if i % p == 0:
break
else:
primes.append(i)
i += 1
print(primes)
```
## Functional
Functional programming is based on the evaluation of mathematical functions. This is a more restricted form of function than you may have used previously - mutable data and changing state is avoided. This makes understanding how a program will behave more straightforward.
Python does support functional programming although it is not as widely used as procedural and object oriented programming. Some languages better known for supporting functional programming include Lisp, Clojure, Erlang, and Haskell.
### Functions - Mathematical vs subroutines
In the general sense, functions can be thought of as simply wrappers around blocks of code. In this sense they can also be thought of as subroutines. Importantly they can be written to fetch data and change the program state independently of the function arguments.
In functional programming the output of a function should depend solely on the function arguments.
There is an extensive howto in the [python documentation](https://docs.python.org/3.5/howto/functional.html).
[This presentation from PyCon US 2013](https://www.youtube.com/watch?v=Ta1bAMOMFOI) is also worth watching.
[This presentation from PyGotham 2014](https://www.youtube.com/watch?v=yW0cK3IxlHc) covers decorators specifically.
### List and generator comprehensions
```
def square(val):
print(val)
return val ** 2
squared_numbers = [square(i) for i in range(5)]
print('Squared from list:')
print(squared_numbers)
squared_numbers = (square(i) for i in range(5))
print('Squared from iterable:')
print(squared_numbers)
```
### Generators
```
def squared_numbers(num):
for i in range(num):
yield i ** 2
print('This is only printed after all the numbers output have been consumed')
print(squared_numbers(5))
for i in squared_numbers(5):
print(i)
import functools
def plus(val, n):
return val + n
f = functools.partial(plus, 5)
f(5)
```
### Decorators
```
def decorator(inner):
def inner_decorator():
print('before')
inner()
print('after')
return inner_decorator
def decorated():
print('decorated')
f = decorator(decorated)
f()
@decorator
def decorated():
print('decorated')
decorated()
import time
@functools.lru_cache()
def slow_compute(n):
time.sleep(1)
print(n)
start = time.time()
slow_compute(1)
print('First time function runs with these arguments takes ', time.time() - start)
start = time.time()
slow_compute(1)
print('Second time function runs with these arguments takes ', time.time() - start)
start = time.time()
slow_compute(2)
print('Changing the arguments causes slow_compute to be run again and takes ', time.time() - start)
```
## Object oriented
Object oriented programming is a paradigm that combines data with code into objects. The code can interact with and modify the data in an object. A program will be separated out into a number of different objects that interact with each other.
Object oriented programming is a widely used paradigm and a variety of different languages support it including Python, C++, Java, PHP, Ruby, and many others.
Each of these languages use slightly different syntax but the underlying design choices will be the same in each language.
Objects __are__ things, their names often recognise this and are nouns. These might be physical things like a chair, or concepts like a number.
While procedural programs make use of global information, object oriented design forgoes this global knowledge in favor of local knowledge. Objects contain information and can __do__ things. The information they contain are in attributes. The things they can do are in their methods (similar to functions, but attached to the object).
Finally, to achieve the objective of the program objects must interact.
We will look at the python syntax for creating objects later, first let's explore how objects might work in various scenarios.
## Designing Object Oriented Programs
These are the simple building blocks for classes and objects. Just as with the other programming constructs available in python, although the language is relatively simple if used effectively they are very powerful.
[Learn Python the Hard Way](http://learnpythonthehardway.org/book/ex43.html) has a very good description of how to design a program using the object oriented programming paradigm. The linked exercise particularly is worth reading.
The best place to start is describing the problem. What are you trying to do? What are the items involved?
### Example 1: A Laboratory Inventory
I would like to keep track of all the __items__ in the __laboratory__ so I can easily find them the next time I need them. Both __equipment__ and __consumables__ would be tracked. We have multiple __rooms__, and items can be on __shelves__, in __refrigerators__, in __freezers__, etc. Items can also be in __boxes__ containing other items in all these places.
The words in __bold__ would all be good ideas to turn into classes. Now we know some of the classes we will need we can start to think about what each of these classes should do, what the methods will be. Let's consider the consumables class:
For consumables we will need to manage their use so there should be an initial quantity and a quantity remaining that is updated every time we use some. We want to make sure that temperature sensitive consumables are always stored at the correct temperature, and that flammables are stored in a flammables cabinet etc.
The consumable class will need a number of attributes:
* Initial quantity
* Current quantity
* Storage temperature
* Flammability
The consumable class will need methods to:
* Update the quantity remaining
* Check for improper storage?
The consumable class might interact with the shelf, refrigerator, freezer, and/or box classes.
Reading back through our description of consumables there is reference to a flammables cabinet that was not mentioned in our initial description of the problem. This is an iterative design process so we should go back and add a flammables cabinet class.
### Exercise: A Chart
We have used matplotlib several times now to generate charts. If we were to create a charting library ourselves what are the objects we would use?
I would like to plot some data on a chart. The data, as a series of points and lines, would be placed on a set of x-y axes that are numbered and labeled to accurately describe the data. There should be a grid so that values can be easily read from the chart.
What are the classes you would use to create this plot?
Pick one class and describe the methods it would have, and the other classes it might interact with.
### Exercise 2: A Cookbook
A system to manage different recipes, with their ingredients, equipment needed and instructions. Recipes should be scalable to different numbers of servings with the amount of ingredients adjusted appropriately and viewable in metric and imperial units. Nutritional information should be tracked.
What are the classes you would use to create this system?
Pick one class and describe the methods it would have, and the other classes it might interact with.
[Building Skills in Object Oriented Design](http://www.itmaybeahack.com/homepage/books/oodesign.html) is a good resource to learn more about this process.
## Syntax
Now let's look at the syntax we use to work with objects in python.
There is a tutorial in the [python documentation](https://docs.python.org/3.5/tutorial/classes.html).
Before we use an object in our program we must first define it. Just as we define a function with the *def* keyword, we use *class* to define a class. What is a class? Think of it as the template, or blueprint from which our objects will be made.
Remember that in addition to code, objects can also contain data that can change so we may have many different instances of an object. Although each may contain different data they are all formed from the same class definition.
As an example:
```
class Person(object):
"""A class definition for a person. The following attributes are supported:
Attributes:
name: A string representing the person's name.
age: An integer representing the person's age."""
mammal = True
def __init__(self, name, age):
"""Return a Person object with name and age set to the values supplied"""
self.name = name
self.age = age
person1 = Person('Alice', 25)
person2 = Person('Bob', 30)
print(person1, person2)
```
There is a lot happening above.
__class Person(object):__ The *class* keyword begins the definition of our class. Here, we are naming the class *Person*. Next, *(object)* means that this class will inherit from the object class. This is not strictly necessary but is generally good practice. Inheritance will be discussed in greater depth next week. Finally, just as for a function definition we finish with a *colon*.
__"""Documentation"""__ Next, a docstring provides important notes on usage.
__mammal = True__ This is a class attribute. This is useful for defining data that our objects will need that is the same for all instances.
**def __init__(self, name, age):** This is a method definition. The *def* keyword is used just as for functions. The first parameter here is *self* which refers to the object this method will be part of. The double underscores around the method name signify that this is a special method. In this case the \_\_init\_\_ method is called when the object is first instantiated.
__self.name = name__ A common reason to define an \_\_init\_\_ method is to set instance attributes. In this class, name and age are set to the values supplied.
That is all there is to this class definition. Next, we create two instances of this class. The values supplied will be passed to the \_\_init\_\_ method.
Printing these objects don't provide a useful description of what they are. We can improve on this with another special method.
```
class Person(object):
"""A class definition for a person. The following attributes are supported:
Attributes:
name: A string representing the person's name.
age: An integer representing the person's age."""
mammal = True
def __init__(self, name, age):
"""Return a Person object with name and age set to the values supplied"""
self.name = name
self.age = age
def __str__(self):
return '{0} who is {1} years old.'.format(self.name, self.age)
person1 = Person('Alice', 25)
person2 = Person('Bob', 30)
print(person1, person2)
```
[There are many more special methods](https://docs.python.org/3.5/reference/datamodel.html#special-method-names).
Before we go on a note of caution is needed for class attributes. Do you remember the strange fibonacci sequence function from our first class?
```
def next_fibonacci(status=[]):
if len(status) < 2:
status.append(1)
return 1
status.append(status[-2] + status[-1])
return status[-1]
print(next_fibonacci(), next_fibonacci(), next_fibonacci(), next_fibonacci(), next_fibonacci(), next_fibonacci())
```
The same issue can happen with classes, only this is a much more common source of bugs.
If only using strings and numbers the behaviour will likely be much as you expect. However, if using a list, dictionary, or other similar type you may get a surprise.
```
class Person(object):
"""A class definition for a person. The following attributes are supported:
Attributes:
name: A string representing the person's name.
age: An integer representing the person's age."""
friends = []
def __init__(self, name, age):
"""Return a Person object with name and age set to the values supplied"""
self.name = name
self.age = age
def __str__(self):
return '{0} who is {1} years old'.format(self.name, self.age)
person1 = Person('Alice', 25)
person2 = Person('Bob', 30)
person1.friends.append('Charlie')
person2.friends.append('Danielle')
print(person1.friends, person2.friends)
```
Both of our objects point to the same instance of the list type so adding a new friend to either object shows up in both.
The solution to this is creating our *friends* attribute only at instantiation of the object. This can be done by creating it in the \_\_init\_\_ method.
```
class Person(object):
"""A class definition for a person. The following attributes are supported:
Attributes:
name: A string representing the person's name.
age: An integer representing the person's age."""
def __init__(self, name, age):
"""Return a Person object with name and age set to the values supplied"""
self.name = name
self.age = age
self.friends = []
def __str__(self):
return '{0} who is {1} years old'.format(self.name, self.age)
person1 = Person('Alice', 25)
person2 = Person('Bob', 30)
person1.friends.append('Charlie')
person2.friends.append('Danielle')
print(person1.friends, person2.friends)
```
Objects have their own namespace, although we have created variables called name, age, and friends they can only be accessed in the context of the object.
```
print('This works:', person1.friends)
print('This does not work:', friends)
```
We are not limited to special methods when creating classes. Standard functions, or in this context methods, are an integral part of object oriented programming. Their definition is identical to special methods and functions outside of classes.
```
class Person(object):
"""A class definition for a person. The following attributes are supported:
Attributes:
name: A string representing the person's name.
age: An integer representing the person's age."""
def __init__(self, name, age):
"""Return a Person object with name and age set to the values supplied"""
self.name = name
self.age = age
self.friends = []
def __str__(self):
"""Return a string representation of the object"""
return '{0} who is {1} years old'.format(self.name, self.age)
def add_friend(self, friend):
"""Add a friend"""
self.friends.append(friend)
person1 = Person('Alice', 25)
person2 = Person('Bob', 30)
person1.add_friend('Charlie')
person2.add_friend('Danielle')
print(person1.friends, person2.friends)
```
### Private vs Public
Some programming languages support hiding methods and attributes in an object. This can be useful to simplify the public interface someone using the class will see while still breaking up components into manageable blocks 'under-the-hood'. We will discuss designing the public interface in detail in future classes.
Python does not support private variables beyond convention. Names prefixed with a underscore are assumed to be private. This means they may be changed without warning between different versions of the package. For public attributes/methods this is highly discouraged.
### Glossary
__Class__: Our definition, or template, for an object.
__Object__: An instance of a class.
__Method__: A function that belongs to an object
__Attribute__: A characteristic of an object, these can be data attributes and methods.
# Assignments
1. Send in your final project ideas / contact me for suggestions if you don't have an idea. Email would be better for this than okpy. You don't need a polished idea, the intention is to start a conversation at this stage.
2. Considering exercise 2, list out the main classes. Pick two and list out the attributes and methods they will need. Treat this as a first, very rough, pass just as we did during class.
3. For one of the classes convert your list of attributes and methods to actual code. Provide a very short description of each method as a docstring.
**Assignment 1 should be emailed, and assignments 2 and 3 submitted through okpy.**
### Exercise 2: A Cookbook
A system to manage different recipes, with their ingredients, equipment needed and instructions. Recipes should be scalable to different numbers of servings with the amount of ingredients adjusted appropriately and viewable in metric and imperial units. Nutritional information should be tracked.
What are the classes you would use to create this system?
Pick one class and describe the methods it would have, and the other classes it might interact with.
| true |
code
| 0.388879 | null | null | null | null |
|
# Navigation
---
Congratulations for completing the first project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893)! In this notebook, you will learn how to control an agent in a more challenging environment, where it can learn directly from raw pixels! **Note that this exercise is optional!**
### 1. Start the Environment
We begin by importing some necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
```
from unityagents import UnityEnvironment
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/VisualBanana.app"`
- **Windows** (x86): `"path/to/VisualBanana_Windows_x86/Banana.exe"`
- **Windows** (x86_64): `"path/to/VisualBanana_Windows_x86_64/Banana.exe"`
- **Linux** (x86): `"path/to/VisualBanana_Linux/Banana.x86"`
- **Linux** (x86_64): `"path/to/VisualBanana_Linux/Banana.x86_64"`
- **Linux** (x86, headless): `"path/to/VisualBanana_Linux_NoVis/Banana.x86"`
- **Linux** (x86_64, headless): `"path/to/VisualBanana_Linux_NoVis/Banana.x86_64"`
For instance, if you are using a Mac, then you downloaded `VisualBanana.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="VisualBanana.app")
```
```
#env = UnityEnvironment(file_name="VisualBanana_Linux/Banana.x86_64")
env = UnityEnvironment(file_name="VisualBanana_Windows_x86_64/Banana.exe")
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
The simulation contains a single agent that navigates a large environment. At each time step, it has four actions at its disposal:
- `0` - walk forward
- `1` - walk backward
- `2` - turn left
- `3` - turn right
The environment state is an array of raw pixels with shape `(1, 84, 84, 3)`. *Note that this code differs from the notebook for the project, where we are grabbing **`visual_observations`** (the raw pixels) instead of **`vector_observations`**.* A reward of `+1` is provided for collecting a yellow banana, and a reward of `-1` is provided for collecting a blue banana.
Run the code cell below to print some information about the environment.
```
from PIL import Image, ImageEnhance
def crop(state):
return state[:,42:,:,:]
def enhance_contrast(image_array):
image = Image.fromarray(np.squeeze(np.uint8(image_array * 255)))
image = ImageEnhance.Brightness(image).enhance(1.5)
image = ImageEnhance.Contrast(image).enhance(2.)
image_array = np.expand_dims(np.array(image) / 255, axis=0)
return image_array
def convert_rgb_to_grayscale(image):
return np.expand_dims(np.dot(image[...,:3], [0.2989, 0.5870, 0.1140]), axis=3)
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents in the environment
print('Number of agents:', len(env_info.agents))
# number of actions
action_size = brain.vector_action_space_size
print('Number of actions:', action_size)
# examine the state space
state = env_info.visual_observations[0]
print('States look like:')
plt.imshow(np.squeeze(state))
#plt.show()
state_size = crop(state).shape
print('States have shape:', state.shape)
# crop
print('Cropped state look like:')
cropped_state = crop(state)
print('States have shape:', cropped_state.shape)
plt.imshow(np.squeeze(cropped_state))
plt.show()
# convert to grayscale
print('Grayscale state look like:')
grayscale_image = convert_rgb_to_grayscale(enhance_contrast(cropped_state))
plt.imshow(np.squeeze(grayscale_image), cmap='gray')
plt.show()
```
### 3. Implement an Agent
I extended `dqn_agent.py` by a parameter called `use_cnn`. If this parameter is set to `True` then the agent uses the neural network architecture with convolutional layers in `cnn_model.py` to map visual states to action values.
### 4. Train the Agent
```
from IPython.display import clear_output
from matplotlib import pyplot as plt
%matplotlib notebook
def init_plot():
fig,ax = plt.subplots(1,1)
ax.grid(True)
ax.set_xlabel('Episode #')
return fig, ax
def live_plot(fig, ax, data_dict, figsize=(7,5), title=''):
if ax.lines:
for line in ax.lines:
line.set_xdata(list(range(len(data_dict[line.get_label()]))))
line.set_ydata(data_dict[line.get_label()])
ax.set_xlim(0, len(data_dict[line.get_label()]))
else:
for label,data in data_dict.items():
line, = ax.plot(data)
line.set_label(label)
ax.legend()
ax.set_ylim(-5, 20)
fig.canvas.draw()
def preprocess(state):
return convert_rgb_to_grayscale(enhance_contrast(crop(state)))
import time
import torch
from collections import defaultdict, deque
from dqn_agent import Agent
def remove_actions_move_backward_and_turn_right(action):
# remove action 1 "walk backward" from actions
if action > 0:
# walk forward: action 0 --> 0
# turn left: action 1 --> 2
# turn right: action 2 --> 3
action += 1
return action
def train(agent, n_episodes=1400, eps_start=1.0, eps_end=0.01, eps_decay=0.995, episodes_per_print=100):
"""
Params
======
n_episodes (int): maximum number of training episodes
eps_start (float): starting value of epsilon, for epsilon-greedy action selection
eps_end (float): minimum value of epsilon
eps_decay (float): multiplicative factor (per episode) for decreasing epsilon
"""
scores = defaultdict(list) # list containing scores from each episode and average scores
scores_window = deque(maxlen=100) # last 100 scores
eps = eps_start # initialize epsilon
fig,ax = init_plot()
for i_episode in range(1, n_episodes+1):
episode_start = time.time()
# reset environment and score
env_info = env.reset(train_mode=True)[brain_name]
state = preprocess(env_info.visual_observations[0])
score = 0
# run for 1 episode
while True:
action = agent.act(state, eps)
env_info = env.step(remove_actions_move_backward_and_turn_right(action).astype(int))[brain_name]
next_state = preprocess(env_info.visual_observations[0])
reward = env_info.rewards[0]
done = env_info.local_done[0]
agent.step(state, action, reward, next_state - state, done)
# update score and state
score += reward
state = next_state
if done:
break
# save score
scores_window.append(score)
scores["score"].append(score)
scores["average score"].append(np.mean(scores_window))
# decrease epsilon
eps = max(eps_end, eps_decay*eps)
# print current performance
live_plot(fig, ax, scores)
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)), end="")
if i_episode % episodes_per_print == 0:
print('\rEpisode {}\tAverage Score: {:.2f} \tDuration: {:.6f} Min'.format(i_episode,
np.mean(scores_window),
(time.time() - episode_start) / 60. * episodes_per_print
))
torch.save(agent.qnetwork_local.state_dict(), 'pixels_checkpoint.pth')
return scores
# remove action 1 "walk backward" and action 3 "turn right" from actions
action_size -= 1
agent = Agent(np.prod(state_size), action_size, seed=0, buffer_size=10000, batch_size=16, lr=0.0003,
scheduler_step_size=3000, scheduler_gamma=0.9, use_cnn=True)
scores = train(agent, eps_start=1.0, eps_end=0.1, eps_decay=0.999)
import torch
from dqn_agent import Agent
agent = Agent(state_size, action_size, seed=0, use_cnn=True)
# load the weights from file
agent.qnetwork_local.load_state_dict(torch.load('pixels_checkpoint.pth'))
# reset environment and score
env_info = env.reset(train_mode=False)[brain_name]
state = preprocess(env_info.visual_observations[0])
score = 0
# run for one episode
while True:
action = agent.act(state, eps=0.)
env_info = env.step(remove_actions_move_backward_and_turn_right(action.astype(int)))[brain_name]
next_state = preprocess(env_info.visual_observations[0])
reward = env_info.rewards[0]
done = env_info.local_done[0]
score += reward
state = next_state
if done:
break
print("Score: {}".format(score))
#env.close()
```
| true |
code
| 0.568296 | null | null | null | null |
|
```
%matplotlib inline
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from scipy import optimize
import optunity
```
# Search space
```
# range of possible lengths
L = np.linspace(0.01,3,200)
# physical angles for each length
theta_max = np.rad2deg(np.arctan(0.8/L))
theta_min = np.rad2deg(np.arctan(0.1/L))
def theta(beta, M1, gamma):
# function of the compressible flow theta-beta-Mach function to get theta
# constraints of the function to avoid angles outside range
if np.rad2deg(beta) < 0:
return 10
elif np.rad2deg(beta) > 90:
return 10
else:
# negative sign is used to minime the function
return -np.arctan(2*(M1**2*(np.sin(beta))**2-1)/((np.tan(beta))*(M1**2*(gamma+np.cos(2*beta))+2)))
# case boundary conditions
M1 = 2
gamma = 1.4
# minimum possible angle for detached oblique shock waves
minimum = optimize.fmin(theta, np.deg2rad(20), args=(M1, gamma))
detached = -np.rad2deg(theta(minimum[0],M1,gamma))
print('Detached oblique shock waves will occur if theta > %.4f deg' %detached)
def Lmin(x):
# difference between detached shock wave angle and the minimum geometrical angle for each x
# created to compute the length where maximum physical angle mets minimum geometrical angle
if x > 0.1:
return np.abs(detached - np.rad2deg(np.arctan(0.1/x)))
else:
return np.inf
minimum_L = optimize.fmin(Lmin, 0.25)
print('The length where minimum geometrical theta angle intersects maximum physical angle is %.4f' %minimum_L)
```
```
fig, ax = plt.subplots(1, figsize=(15,10))
ax.plot(L,theta_max,'b',linewidth=3,label=r'$\theta_{max} - geom$')
ax.plot(L,theta_min,'r',linewidth=3,label=r'$\theta_{min} - geom$')
ax.plot([0,3.0],[detached,detached],'k',linewidth=3,label=r'$\theta_{max} - phys$')
ax.plot([2.5,2.5],[0,45],'g',linewidth=3,label=r'$L_{max}$')
ax.set_xlim([L.min(),L.max()])
ax.set_ylim([1,45])
ax.fill_between(L,detached*np.ones(len(L)),color='k',alpha=0.2, label='Search space')
ax.fill_between(L,100*np.ones(len(L)),theta_max,color='w')
ax.fill_between(L,theta_min,color='w')
ax.fill_between([2.5,3.0],[45,45],color='w')
ax.set_xlabel('Length $L$ ($m$)',fontsize=30)
ax.set_ylabel(r'Angle $\theta$ ($deg$)',fontsize=30)
ax.legend(fontsize=28, loc='best', bbox_to_anchor=(1.02,0.7))
ax.tick_params(axis = 'both', labelsize = 28)
ax.set_title('Search space', fontsize = 40)
# plt.savefig('./SearchSpace.png', bbox_inches='tight')
```
# First population definition
```
def constraint(L,theta):
''' Function to test the length and angle constraints
INPUTS:
L: array with possible lengths
theta: array with possible angles theta
OUTPUTS:
boolMat: boolean matrix with 1 for the non valid points (constrained)'''
# space preallocation for boolean matrix
boolMat = np.zeros([len(L)])
# fill the boolean matrix
for i in range(len(L)):
# maximum allowable length
if L[i] > 2.5:
boolMat[i] = True
# angle for detached shock wave
elif theta[i] > detached:
boolMat[i] = True
# upper geometrical angle limit
elif L[i]*np.tan(np.deg2rad(theta[i])) > 0.8:
boolMat[i] = True
# lower geometrical angle limit
elif L[i]*np.tan(np.deg2rad(theta[i])) < 0.1:
boolMat[i] = True
else:
boolMat[i] = False
return boolMat
# get the limits of the x and y components of each individual
x_low = L[np.argwhere(theta_min < detached)[0][0]]
x_high = 2.5
y_low = theta_min[np.argwhere(L > 2.5)[0][0]]
y_high = detached
# Sobol sampling initialization
x1, x2 = zip(*optunity.solvers.Sobol.i4_sobol_generate(2, 128, int(np.sqrt(128))))
sobol = np.vstack(((x_high - x_low) * np.array([x1]) + x_low,
(y_high - y_low) * np.array([x2]) + y_low)).T
# unconstraint the Sobol initialization
while sum(constraint(sobol[:,0], sobol[:,1])) != 0:
boolMat = constraint(sobol[:,0], sobol[:,1])
for i in np.argwhere(boolMat == True):
sobol[i] = np.array([x_low+np.random.rand(1)*(x_high-x_low),y_low+np.random.rand(1)*(y_high-y_low)]).T
fig, ax = plt.subplots(1, figsize=(20,10))
ax.plot(L,theta_max,'b',linewidth=3,label=r'$\theta_{max}$ (geom)')
ax.plot(L,theta_min,'r',linewidth=3,label=r'$\theta_{min}$ (geom)')
ax.plot([0,3.0],[detached,detached],'k',linewidth=3,label=r'$\theta_{max}$ (phys)')
ax.plot([2.5,2.5],[0,45],'g',linewidth=3,label=r'$L_{max}$')
ax.set_xlim([L.min(),L.max()])
ax.set_ylim([0,45])
ax.fill_between(L,detached*np.ones(len(L)),color='k',alpha=0.3)
ax.fill_between(L,100*np.ones(len(L)),theta_max,color='w')
ax.fill_between(L,theta_min,color='w')
ax.fill_between([2.5,3.0],[45,45],color='w')
ax.set_xlabel('Parameter $L$',fontsize=16)
ax.set_ylabel(r'Parameter $\theta$',fontsize=18)
ax.tick_params(axis = 'both', labelsize = 14)
ax.set_title('Search space and first population (Sobol initialization)', fontsize = 22)
ax.plot(sobol[:,0],sobol[:,1],'k.',markersize=10,label='Population')
ax.legend(fontsize=16, loc='best')
```
| true |
code
| 0.653182 | null | null | null | null |
|
```
# Useful for debugging
%load_ext autoreload
%autoreload 2
# Nicer plotting
import matplotlib
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
matplotlib.rcParams['figure.figsize'] = (8,4)
```
# Movie example using write_beam
Here we insert write_beam elements into an existing lattice, run, save the beams to an h5 file, and plot using openPMD-beamphysics tools
```
from impact import Impact
from distgen import Generator
import numpy as np
import matplotlib.pyplot as plt
import os
IMPACT_IN = 'templates/apex_gun/ImpactT.in'
DISTGEN_IN = 'templates/apex_gun/distgen.yaml'
os.path.exists(IMPACT_IN)
G = Generator(DISTGEN_IN)
G['n_particle'] = 10000
G.run()
P0 = G.particles
P0.plot('x', 'y')
# Make Impact object
I = Impact(IMPACT_IN, initial_particles = P0, verbose=True)
# Change some things
I.header['Nx'] = 32
I.header['Ny'] = 32
I.header['Nz'] = 32
I.header['Dt'] = 1e-13
I.total_charge = P0['charge']
# Change stop location
I.stop = 0.1
# Make new write_beam elements and add them to the lattice.
from impact.lattice import new_write_beam
# Make a list of s
for s in np.linspace(0.001, 0.1, 98):
ele = new_write_beam(s=s, ref_eles=I.lattice) # ref_eles will ensure that there are no naming conflicts
I.add_ele(ele)
I.timeout = 1000
I.run()
len(I.particles)
```
# Plot
```
from bokeh.plotting import show, figure, output_notebook
from bokeh.layouts import column, row
from bokeh.models import ColumnDataSource
from bokeh import palettes, colors
pal = palettes.Viridis[256]
white=colors.named.white
pal = list(pal)
pal[0] = white # replace 0 with white
pal = tuple(pal)
output_notebook(verbose=False, hide_banner=True)
import os
# Prepare histogram function
PL = I.particles
ilist = []
for k in PL:
if k.startswith('write_beam_'):
ilist.append(int(k.strip('write_beam_')))
def bin_particles(i, key1='x', key2='y', bins=40):
P = I.particles[f'write_beam_{i}']
return np.histogram2d(P[key1], P[key2], weights=P.weight, bins=bins)
bin_particles(100)
# Prepare a datasource for Bokeh
def bin_bunch_datasource_h5(i, key1, key2, bins=20, nice=True, liveOnly=True, liveStatus=1):
H, xedges, yedges = bin_particles(i, key1, key2, bins=bins)
xmin = min(xedges)
xmax = max(xedges)
ymin = min(yedges)
ymax = max(yedges)
#if nice:
# f1 = nice_phase_space_factor[component1]
# f2 = nice_phase_space_factor[component2]
# xlabel = nice_phase_space_label[component1]
# ylabel = nice_phase_space_label[component2]
# xmin *= f1
# xmax *= f1
# ymin *= f2
# ymax *= f2
#else:
# xlabel = component1
# ylabel = component2
# Form datasource
dat = {'image':[H.transpose()], 'xmin':[xmin], 'ymin':[ymin], 'dw':[xmax-xmin], 'dh':[ymax-ymin]}
dat['xmax'] = [xmax]
dat['ymax'] = [ymax]
ds = ColumnDataSource(data=dat)
return ds
ds = bin_bunch_datasource_h5(100, 'x', 'y')
plot = figure(#x_range=[xmin,xmax], y_range=[ymin,ymax],
# x_axis_label = xlabel, y_axis_label = ylabel,
plot_width=500, plot_height=500)
plot.image(image='image', x='xmin', y='ymin', dw='dw', dh='dh', source=ds,palette=pal)
show(plot)
```
# Interactive
```
from bokeh.models.widgets import Slider
from bokeh import palettes, colors
# interactive
def myapp2(doc):
bunches = ilist
doc.bunchi = bunches[0]
doc.component1 = 'z'
doc.component2 = 'x'
doc.xlabel = doc.component1
doc.ylabel = doc.component2
doc.bins = 100
#doc.range = FULLRANGE
ds = bin_bunch_datasource_h5(doc.bunchi, doc.component1, doc.component2,bins=doc.bins)
def refresh():
ds.data = dict(bin_bunch_datasource_h5(doc.bunchi, doc.component1, doc.component2,bins=doc.bins).data )
# Default plot
plot = figure(title='',
x_axis_label = doc.xlabel, y_axis_label = doc.ylabel,
plot_width=500, plot_height=500)
plot.image(image='image', x='xmin', y='ymin', dw='dw', dh='dh', source=ds, palette=pal)
def slider_handler(attr, old, new):
doc.bunchi = bunches[new]
refresh()
slider = Slider(start=0, end=len(bunches)-1, value=0, step=1, title='x')
slider.on_change('value', slider_handler)
# Add plot to end
doc.add_root(column(slider, plot))
show(myapp2)# , notebook_url=remote_jupyter_proxy_url)
# If there are multiple
import os
os.environ['BOKEH_ALLOW_WS_ORIGIN'] = 'localhost:8888'
%%time
I.archive()
```
| true |
code
| 0.549882 | null | null | null | null |
|
# Семинар 6 - Введение в простые модели ML
Дополнительно понадобятся следующие библиотеки. Раскомментируйте код, чтобы установить их.
```
# !pip install -U scikit-learn
# !pip install pandas
```
# Метрики
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, mean_squared_error
from sklearn.datasets import load_digits
from sklearn.linear_model import LinearRegression
import warnings
warnings.simplefilter('ignore')
plt.style.use('seaborn')
%matplotlib inline
```
Зададим истинные и "предсказанные" метки для того, чтобы посмотреть на точность предсказаний.
```
y_pred = [0, 1, 1, 0, 0, 1, 0, 3]
y_true = [0, 1, 2, 0, 1, 2, 3, 4]
```
## Accuracy
```
accuracy_score(y_true, y_pred)
```
## Precision
```
precision_score(y_true, y_pred, average=None)
```
## Recall
```
recall_score(y_true, y_pred, average=None)
```
## F1_score
```
f1_score(y_true, y_pred, average=None)
```
# KNN
## Загрузим данные
```
data = load_digits()
print(data['DESCR'])
img = data.data[56].reshape(8, 8)
print(data.target[56])
plt.imshow(img)
plt.show()
X, y = data.data, data.target
print('В датасете {} объектов и {} признака'.format(X.shape[0], X.shape[1]))
```
### Посмотрим на объекты:
```
i = np.random.randint(0, X.shape[0])
print('Class name: {}'.format(y[i]))
print(X[i].reshape(8,8))
X[i]
plt.imshow(X[i].reshape(8,8), cmap='gray_r')
plt.show()
```
Посмотрим на баланс классов:
```
counts = np.unique(y, return_counts=True)
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.bar(counts[0], counts[1])
plt.show()
```
Разделим выборку на две части: обучающую и тестовую
```
X_train, X_test, y_train, y_test = train_test_split(X, y,
train_size=0.5,
test_size=0.5,
shuffle=True,
random_state=18)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
```
## Метод ближайших соседей
Зададим классификатор:
```
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
knn_predictons = knn.predict(X_test)
preds = pd.DataFrame(y_test, columns=['True'])
preds['knn_pred'] = knn_predictons
preds.head(200).T
```
Посмотрим долю правильных ответов:
```
accuracy_score(y_test, knn_predictons)
```
## Поиск оптимальных параметров
```
from sklearn.model_selection import GridSearchCV
n = np.linspace(1, 21, 21, dtype=int)
n
kNN_cv = KNeighborsClassifier(n_neighbors=5)
params = {
'metric':['minkowski', 'manhattan'],
'n_neighbors': n,
}
gcv = GridSearchCV(kNN_cv, param_grid=params, cv=5, scoring='accuracy')
gcv.fit(X_train, y_train)
gcv.get_params()
def print_cv_results(a, len_gs, params, param_r, param_sep):
d = len(params['param_grid'][param_sep])
ar = np.array(a).reshape(d, len_gs).T
df = pd.DataFrame(ar)
pen_par = params['param_grid'][param_sep]
c_par = params['param_grid'][param_r]
if type(c_par) != list:
c_par = c_par.tolist()
columns_mapper = dict(zip(range(0, len(pen_par)), pen_par))
row_mapper = dict(zip(range(0, len(c_par)), c_par))
df.rename(columns=columns_mapper, index=row_mapper, inplace=True)
plot = df.plot(title='Mean accuracy rating', grid=True)
plot.set_xlabel(param_r, fontsize=13)
plot.set_ylabel('acc', rotation=0, fontsize=13, labelpad=15)
plt.show()
gcv.get_params()
print_cv_results(gcv.cv_results_['mean_test_score'],
21, gcv.get_params(), 'n_neighbors','metric')
gcv.best_params_
print('Лучший скор %.4f' % gcv.best_score_)
print('при метрике %(metric)s и %(n_neighbors)s соседей' % gcv.best_params_)
```
### Что получится на тесте?
```
accuracy_score(y_test, gcv.predict(X_test))
gcv_preds = pd.DataFrame(gcv.predict(X_test), columns=['kNN'])
gcv_preds['True'] = y_test
gcv_preds
```
Посмотрим на те цифры, которые "путает" наш классификатор
```
gcv_preds[gcv_preds['True'] != gcv_preds['kNN']]
```
# Линейные модели
## Постановка задачи

Где линейная модель - это: $$ \hat{y} = f(x) = \theta_0*1 + \theta_1*x_1 + ... + \theta_n*x_n = \theta^T*X$$
Сгенерируем исскуственные данные, на основе функции:
$$f(x) = 4x+5$$
```
def lin_function(x):
return 4 * x + 5
x_true = np.array([-2, 2])
y_true = lin_function(x_true)
plt.plot(x_true, y_true, linewidth=1)
plt.show()
n = 100
x = np.random.rand(n, 1) * 4 - 2
e = np.random.rand(n, 1) * 4 - 2
y = lin_function(x) + e
plt.scatter(x, y, color='g')
plt.plot(x_true, y_true, linewidth=1)
plt.show()
```
## Метрики
Mean Absoulte Error:
$$MAE = \frac1N \sum_{i = 1}^N|f(x_i) - y_i| = \frac1N \sum_{i = 1}^N|\hat y_i - y_i| = \frac1N || \hat Y - Y||_1$$
Mean Sqared Error:
$$MSE = \frac1N \sum_{i = 1}^N(f(x_i) - y_i)^2 = \frac1N \sum_{i = 1}^N(\hat y_i - y_i)^2 = \frac1N ||\hat Y - Y||_2$$
## Аналитический метод поиска минимума по MSE
$$MSE -> min $$
$$MSE = \frac1N \sum_{i = 1}^N(\hat y_i - y_i)^2 = \frac1N \sum_{i = 1}^N(\theta_i * x_i - y_i)^2 = \frac1N ||X \theta - Y||_2 = \frac1N (X\theta - Y)^T*(X\theta - Y) $$
$$ \frac{d}{d\theta}[\frac1N (X\theta - Y)^T*(X\theta - Y)] = \frac1N \frac{d}{d\theta}[Y^TY - 2Y^TX\theta+\theta^TX^TX\theta] $$
$$\hat \theta = \bigl(X^T \cdot X \bigr)^{-1} \cdot X^T \cdot y $$
```
x_matrix = np.hstack([np.ones((n, 1)), x])
%%time
# найдем аналитическое решение
thetha_matrix = np.linalg.inv(x_matrix.T.dot(x_matrix)).dot(x_matrix.T).dot(y)
```
Обратите внимание на время работы
```
thetha_matrix.T[0].tolist()
print("Свободный член: {[0][0]:.7}".format(thetha_matrix.T))
print("Коэфициент: {[0][1]:.7}".format(thetha_matrix.T))
%%time
lr = LinearRegression()
lr.fit(x,y);
print("Свободный член: {:.7}".format(lr.intercept_[0]))
print("Коэфициент: {:.7}".format(lr.coef_[0][0]))
plt.scatter(x, y, color='g')
plt.scatter(x, lr.predict(x), color='r')
plt.plot(x_true, y_true, linewidth=1)
plt.show()
```
## Градиентный спуск
$$\theta^{(t+1)} = \theta^{(t)} - lr\cdot \nabla MSE(\theta^{(t)}),$$
где $lr$ — длина шага градиентного спуска (learning rate).
$$\nabla MSE(\theta)= \frac{2}{N} X^T \cdot \bigl(X \cdot \theta - Y \bigr) $$
```
def animate_solutions(iter_solutions):
fig, ax = plt.subplots(figsize=(6.4 * 1, 4.8 * 1))
def update(idx):
_theta = iter_solutions[idx]
ax.clear()
ax.scatter(x, y, color='g', label='Выборка')
ax.plot(x_true, y_true, linewidth=1, label='Исходная зависимость')
ax.plot(x_true, x_true * _theta[1] + _theta[0], linewidth=1, color='r', label='Предсказанная зависимость')
ax.legend(loc='upper left', fontsize=13)
fps = 3
ani = animation.FuncAnimation(fig, update, len(iter_solutions), interval=100 / fps)
return ani
%%time
lr = 0.1 # шаг обучения
n_iterations = 150 # количество итераций
theta = np.random.randn(2,1) # начальная инициализация
iter_solutions = [theta]
for iteration in range(n_iterations):
gradients = 2 / n * x_matrix.T @ (x_matrix @ theta - y)
theta = theta - lr * gradients
iter_solutions.append(theta)
# изобразим результаты численного решения
plt.figure(figsize=(6.4 * 1, 4.8 * 1))
plt.scatter(x, y, color='g', label='Выборка')
plt.plot(x_true, y_true, linewidth=1, label='Исходная зависимость')
plt.plot(x_true, x_true * theta[1] + theta[0], linewidth=1, color='r', label='Предсказанная зависимость')
plt.legend(loc='upper left', fontsize=13)
plt.show()
ani = animate_solutions(iter_solutions)
HTML(ani.to_html5_video())
```
| true |
code
| 0.55911 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.