prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Batch Scoring on IBM Cloud Pak for Data (ICP4D)
We are going to use this notebook to create and/or run a batch scoring job against a model that has previously been created and deployed to the Watson Machine Learning (WML) instance on Cloud Pak for Data (CP4D).
## 1.0 Install required packages
There are a couple of Python packages we will use in this notebook. First we make sure the Watson Machine Learning client v3 is removed (its not installed by default) and then install/upgrade the v4 version of the client (this package is installed by default on CP4D).
- WML Client: https://wml-api-pyclient-dev-v4.mybluemix.net/#repository
```
!pip uninstall watson-machine-learning-client -y
!pip install --user watson-machine-learning-client-v4==1.0.99 --upgrade | tail -n 1
import json
from watson_machine_learning_client import WatsonMachineLearningAPIClient
```
## 2.0 Create Batch Deployment Job
### 2.1 Instantiate Watson Machine Learning Client
To interact with the local Watson Machine Learning instance, we will be using the Python SDK.
<font color=red>**<< UPDATE THE VARIABLES BELOW >>**</font>
<font color='red'>Replace the `username` and `password` values of `************` with your Cloud Pak for Data `username` and `password`. The value for `url` should match the `url` for your Cloud Pak for Data cluster, which you can get from the browser address bar (be sure to include the 'https://'.</font> The credentials should look something like this (these are example values, not the ones you will use):
`
wml_credentials = {
"url": "https://zen.clusterid.us-south.containers.appdomain.cloud",
"username": "cp4duser",
"password" : "cp4dpass",
"instance_id": "wml_local",
"version" : "2.5.0"
}
`
#### NOTE: Make sure that there is no trailing forward slash `/` in the `url`
```
# Be sure to update these credentials before running the cell.
wml_credentials = {
"url": "******",
"username": "******",
"password" : "*****",
"instance_id": "wml_local",
"version" : "2.5.0"
}
wml_client = WatsonMachineLearningAPIClient(wml_credentials)
wml_client.spaces.list()
```
### 2.2 Find Deployment Space
We will try to find the `GUID` for the deployment space you want to use and set it as the default space for the client.
<font color=red>**<< UPDATE THE VARIABLES BELOW >>**</font>
- Update with the value with the name of the deployment space where you have created the batch deployment (one of the values in the output from the cell above).
```
# Be sure to update the name of the space with the one you want to use.
DEPLOYMENT_SPACE_NAME = 'INSERT-YOUR-DEPLOYMENT-SPACE-NAME-HERE'
all_spaces = wml_client.spaces.get_details()['resources']
space_id = None
for space in all_spaces:
if space['entity']['name'] == DEPLOYMENT_SPACE_NAME:
space_id = space["metadata"]["guid"]
print("\nDeployment Space GUID: ", space_id)
if space_id is None:
print("WARNING: Your space does not exist. Create a deployment space before proceeding.")
# We could programmatically create the space.
#space_id = wml_client.spaces.store(meta_props={wml_client.spaces.ConfigurationMetaNames.NAME: space_name})["metadata"]["guid"]
# Now set the default space to the GUID for your deployment space. If this is successful, you will see a 'SUCCESS' message.
wml_client.set.default_space(space_id)
# These are the models and deployments we currently have in our deployment space.
wml_client.repository.list_models()
wml_client.deployments.list()
```
### 2.3 Find Batch Deployment
We will try to find the batch deployment which was created.
<font color=red>**<< UPDATE THE VARIABLES BELOW >>**</font>
- Update with the name of the batch deployment.
```
DEPLOYMENT_NAME = 'INSERT-YOUR-BATCH-DEPLOYMENT-NAME-HERE'
wml_deployments = wml_client.deployments.get_details()
deployment_uid = None
deployment_details = None
for deployment in wml_deployments['resources']:
if DEPLOYMENT_NAME == deployment['entity']['name']:
deployment_uid = deployment['metadata']['guid']
deployment_details = deployment
#print(json.dumps(deployment_details, indent=3))
break
print("Deployment id: {}".format(deployment_uid))
wml_client.deployments.get_details(deployment_uid)
```
### 2.4 Get Batch Test Data
We will load some data to run the batch predictions.
```
import pandas as pd
from project_lib import Project
project = Project.access()
batch_set = pd.read_csv(project.get_file('Telco-Customer-Churn-SmallBatchSet.csv'))
batch_set = batch_set.drop('customerID', axis=1)
batch_set.head()
```
### 2.5 Create Job
We can now use the information about the deployment and the test data to create a new job against our batch deployment. We submit the data as inline payload and want the results (i.e predictions) stored in a CSV file.
```
import time
timestr = time.strftime("%Y%m%d_%H%M%S")
job_payload = {
wml_client.deployments.ScoringMetaNames.INPUT_DATA: [{
'fields': batch_set.columns.values.tolist(),
'values': batch_set.values.tolist()
}],
wml_client.deployments.ScoringMetaNames.OUTPUT_DATA_REFERENCE: {
"type": "data_asset",
"connection": {},
"location": {
"name": "batchres_{}_{}.csv".format(timestr,deployment_uid),
"description": "results"
}
}
}
job = wml_client.deployments.create_job(deployment_id=deployment_uid, meta_props=job_payload)
job_uid = wml_client.deployments.get_job_uid(job)
print('Job uid = {}'.format(job_uid))
wml_client.deployments.list_jobs()
```
## 3.0 Monitor Batch Job Status
The batch job is an async operation. We can use the identifier to track its progress. Below we will just poll until the job completes (or fails).
```
def poll_async_job(client, job_uid):
import time
while True:
job_status = client.deployments.get_job_status(job_uid)
print(job_status)
state = job_status['state']
if state == 'completed' or 'fail' in state:
return client.deployments.get_job_details(job_uid)
time.sleep(5)
job_details = poll_async_job(wml_client, job_uid)
wml_client.deployments.list_jobs()
```
### 3.1 Check Results
With the job complete, we can see the predictions.
```
wml_client.deployments.get_job_details()
print(json.dumps(job_details, indent=2))
```
## Congratulations, you have created and submitted a job for batch scoring !
| true |
code
| 0.299649 | null | null | null | null |
|
<a href="https://www.pieriandata.com"><img src="../Pierian_Data_Logo.PNG"></a>
<strong><center>Copyright by Pierian Data Inc.</center></strong>
<strong><center>Created by Jose Marcial Portilla.</center></strong>
# Convolutional Neural Networks for Image Classification
```
import pandas as pd
import numpy as np
from tensorflow.keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
```
## Visualizing the Image Data
```
import matplotlib.pyplot as plt
%matplotlib inline
x_train.shape
single_image = x_train[0]
single_image
single_image.shape
plt.imshow(single_image)
```
# PreProcessing Data
We first need to make sure the labels will be understandable by our CNN.
## Labels
```
y_train
y_test
```
Hmmm, looks like our labels are literally categories of numbers. We need to translate this to be "one hot encoded" so our CNN can understand, otherwise it will think this is some sort of regression problem on a continuous axis. Luckily , Keras has an easy to use function for this:
```
from tensorflow.keras.utils import to_categorical
y_train.shape
y_example = to_categorical(y_train)
y_example
y_example.shape
y_example[0]
y_cat_test = to_categorical(y_test,10)
y_cat_train = to_categorical(y_train,10)
```
### Processing X Data
We should normalize the X data
```
single_image.max()
single_image.min()
x_train = x_train/255
x_test = x_test/255
scaled_single = x_train[0]
scaled_single.max()
plt.imshow(scaled_single)
```
## Reshaping the Data
Right now our data is 60,000 images stored in 28 by 28 pixel array formation.
This is correct for a CNN, but we need to add one more dimension to show we're dealing with 1 RGB channel (since technically the images are in black and white, only showing values from 0-255 on a single channel), an color image would have 3 dimensions.
```
x_train.shape
x_test.shape
```
Reshape to include channel dimension (in this case, 1 channel)
```
x_train = x_train.reshape(60000, 28, 28, 1)
x_train.shape
x_test = x_test.reshape(10000,28,28,1)
x_test.shape
```
# Training the Model
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, MaxPool2D, Flatten
model = Sequential()
# CONVOLUTIONAL LAYER
model.add(Conv2D(filters=32, kernel_size=(4,4),input_shape=(28, 28, 1), activation='relu',))
# POOLING LAYER
model.add(MaxPool2D(pool_size=(2, 2)))
# FLATTEN IMAGES FROM 28 by 28 to 764 BEFORE FINAL LAYER
model.add(Flatten())
# 128 NEURONS IN DENSE HIDDEN LAYER (YOU CAN CHANGE THIS NUMBER OF NEURONS)
model.add(Dense(128, activation='relu'))
# LAST LAYER IS THE CLASSIFIER, THUS 10 POSSIBLE CLASSES
model.add(Dense(10, activation='softmax'))
# https://keras.io/metrics/
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy']) # we can add in additional metrics https://keras.io/metrics/
model.summary()
from tensorflow.keras.callbacks import EarlyStopping
early_stop = EarlyStopping(monitor='val_loss',patience=2)
```
## Train the Model
```
model.fit(x_train,y_cat_train,epochs=10,validation_data=(x_test,y_cat_test),callbacks=[early_stop])
```
## Evaluate the Model
```
model.metrics_names
losses = pd.DataFrame(model.history.history)
losses.head()
losses[['accuracy','val_accuracy']].plot()
losses[['loss','val_loss']].plot()
print(model.metrics_names)
print(model.evaluate(x_test,y_cat_test,verbose=0))
from sklearn.metrics import classification_report,confusion_matrix
predictions = model.predict_classes(x_test)
y_cat_test.shape
y_cat_test[0]
predictions[0]
y_test
print(classification_report(y_test,predictions))
confusion_matrix(y_test,predictions)
import seaborn as sns
plt.figure(figsize=(10,6))
sns.heatmap(confusion_matrix(y_test,predictions),annot=True)
# https://github.com/matplotlib/matplotlib/issues/14751
```
# Predicting a given image
```
my_number = x_test[0]
plt.imshow(my_number.reshape(28,28))
# SHAPE --> (num_images,width,height,color_channels)
model.predict_classes(my_number.reshape(1,28,28,1))
```
Looks like the CNN performed quite well!
| true |
code
| 0.680574 | null | null | null | null |
|
# Augmentations in NLP
Data Augmentation techniques in NLP show substantial improvements on datasets with less than 500 observations, as illustrated by the original paper.
https://arxiv.org/abs/1901.11196
The Paper Considered here is EDA: Easy Data Augmentation Techniques for Boosting Performance on Text Classification Tasks
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# You can write up to 5GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
```
# ***Simple Data Augmentatons Techniques* are:**
1. SR : Synonym Replacement
2. RD : Random Deletion
3. RS : Random Swap
4. RI : Random Insertion
```
data = pd.read_csv('../input/tweet-sentiment-extraction/train.csv')
data.head()
list_to_drop = ['textID','selected_text','sentiment']
data.drop(list_to_drop,axis=1,inplace=True)
data.head()
print(f"Total number of examples to be used is : {len(data)}")
```
# 1. Synonym Replacement :
Synonym replacement is a technique in which we replace a word by one of its synonyms
For identifying relevent Synonyms we use WordNet
The get_synonyms funtion will return pre-processed list of synonyms of given word
Now we will replace the words with synonyms
```
from nltk.corpus import stopwords
stop_words = []
for w in stopwords.words('english'):
stop_words.append(w)
print(stop_words)
import random
from nltk.corpus import wordnet
def get_synonyms(word):
synonyms = set()
for syn in wordnet.synsets(word):
for l in syn.lemmas():
synonym = l.name().replace("_", " ").replace("-", " ").lower()
synonym = "".join([char for char in synonym if char in ' qwertyuiopasdfghjklzxcvbnm'])
synonyms.add(synonym)
if word in synonyms:
synonyms.remove(word)
return list(synonyms)
def synonym_replacement(words, n):
words = words.split()
new_words = words.copy()
random_word_list = list(set([word for word in words if word not in stop_words]))
random.shuffle(random_word_list)
num_replaced = 0
for random_word in random_word_list:
synonyms = get_synonyms(random_word)
if len(synonyms) >= 1:
synonym = random.choice(list(synonyms))
new_words = [synonym if word == random_word else word for word in new_words]
num_replaced += 1
if num_replaced >= n: #only replace up to n words
break
sentence = ' '.join(new_words)
return sentence
print(f" Example of Synonym Replacement: {synonym_replacement('The quick brown fox jumps over the lazy dog',4)}")
```
To Get Larger Diversity of Sentences we could try replacing 1,2 3, .. Words in the given sentence.
Now lets get an example from out dataset and try augmenting it so that we could create 3 additional sentences per tweet
```
trial_sent = data['text'][25]
print(trial_sent)
# Create 3 Augmented Sentences per data
for n in range(3):
print(f" Example of Synonym Replacement: {synonym_replacement(trial_sent,n)}")
```
Now we are able to augment this Data :)
You can create New colums for the Same text-id in our tweet - sentiment Dataset
# 2.Random Deletion (RD)
In Random Deletion, we randomly delete a word if a uniformly generated number between 0 and 1 is smaller than a pre-defined threshold. This allows for a random deletion of some words of the sentence.
```
def random_deletion(words, p):
words = words.split()
#obviously, if there's only one word, don't delete it
if len(words) == 1:
return words
#randomly delete words with probability p
new_words = []
for word in words:
r = random.uniform(0, 1)
if r > p:
new_words.append(word)
#if you end up deleting all words, just return a random word
if len(new_words) == 0:
rand_int = random.randint(0, len(words)-1)
return [words[rand_int]]
sentence = ' '.join(new_words)
return sentence
```
Lets test out this Augmentation with our test_sample
```
print(random_deletion(trial_sent,0.2))
print(random_deletion(trial_sent,0.3))
print(random_deletion(trial_sent,0.4))
```
This Could help us in reducing Overfitting and may help to imporve our Model Accuracy
# 3. Random Swap (RS)
In Random Swap, we randomly swap the order of two words in a sentence.
```
def swap_word(new_words):
random_idx_1 = random.randint(0, len(new_words)-1)
random_idx_2 = random_idx_1
counter = 0
while random_idx_2 == random_idx_1:
random_idx_2 = random.randint(0, len(new_words)-1)
counter += 1
if counter > 3:
return new_words
new_words[random_idx_1], new_words[random_idx_2] = new_words[random_idx_2], new_words[random_idx_1]
return new_words
def random_swap(words, n):
words = words.split()
new_words = words.copy()
# n is the number of words to be swapped
for _ in range(n):
new_words = swap_word(new_words)
sentence = ' '.join(new_words)
return sentence
print(random_swap(trial_sent,1))
print(random_swap(trial_sent,2))
print(random_swap(trial_sent,3))
```
This Random Swapping will help to make our models robust and may inturn help in text classification.
High order of swapping may downgrade the model
There is a high chance to loose semantics of language so be careful while using this augmentaion.
# 4. Random Insertion (RI)
Finally, in Random Insertion, we randomly insert synonyms of a word at a random position.
Data augmentation
operations should not change the true label of
a sentence, as that would introduce unnecessary
noise into the data. Inserting a synonym of a word
in a sentence, opposed to a random word, is more
likely to be relevant to the context and retain the
original label of the sentence.
```
def random_insertion(words, n):
words = words.split()
new_words = words.copy()
for _ in range(n):
add_word(new_words)
sentence = ' '.join(new_words)
return sentence
def add_word(new_words):
synonyms = []
counter = 0
while len(synonyms) < 1:
random_word = new_words[random.randint(0, len(new_words)-1)]
synonyms = get_synonyms(random_word)
counter += 1
if counter >= 10:
return
random_synonym = synonyms[0]
random_idx = random.randint(0, len(new_words)-1)
new_words.insert(random_idx, random_synonym)
print(random_insertion(trial_sent,1))
print(random_insertion(trial_sent,2))
print(random_insertion(trial_sent,3))
def aug(sent,n,p):
print(f" Original Sentence : {sent}")
print(f" SR Augmented Sentence : {synonym_replacement(sent,n)}")
print(f" RD Augmented Sentence : {random_deletion(sent,p)}")
print(f" RS Augmented Sentence : {random_swap(sent,n)}")
print(f" RI Augmented Sentence : {random_insertion(sent,n)}")
aug(trial_sent,4,0.3)
```
| true |
code
| 0.382199 | null | null | null | null |
|
# Variational Quantum Regression
$$
\newcommand{\ket}[1]{\left|{#1}\right\rangle}
\newcommand{\bra}[1]{\left\langle{#1}\right|}
\newcommand{\braket}[2]{\left\langle{#1}\middle|{#2}\right\rangle}
$$
## Introduction
Here we create a protocol for linear regression which can exploit the properties of a quantum computer. For this problem, we assume that we have two data sets, x and y, where x is the independent data and y is the dependent data. There are N data points in each data set. We first want to fit this data to the following equation:
$$y = ax + b$$
and then we will include higher powers of x. First, we will theoretically explore this proposed algorithm, and then we will tweak the code slightly so that it can be run on a real quantum computer. This algorithm has no known advantage over the most widely-used classical algorithm ([Least Squares Method](https://doi.org/10.1016/j.proeng.2012.09.545)), but does nicely demonstrate the different elements of variational quantum algorithms.
## Variational Quantum Computing
Variational quantum computing exploits the advantages of both classical computing and quantum computing. In a very general sense, we propose an initial solution to a problem, called an ansatz. In our case our ansatz will be an ansatz parametrised by a and b. We then prepare our qubits (the quantum equivalent of bits on a normal computer) and test how good the ansatz is, using the quantum computer. Testing the ansatz equates to minimising a cost function. We feed the result of this cost function back to the classical computer, and use some classical optimisers to improve on our ansatz, i.e. our initial guesses for a and b. We repeat this process until the ansatz is good enough within some tolerance.

## Translate to Quantum Domain
We now need to explore how we will translate the data set, y, onto a quantum computer. Let us think of y as a length N vector. The easiest way to encode this data set onto a quantum computer is by initialising qubits in the state $\ket{y}$, where
$$\ket{y} = \frac{1}{C_y}\vec{y}$$
and $C_y$ is a normalisation factor.
Now we propose a trial solution, or ansatz, which is parametrised by a and b, as follows:
$$\ket{\Phi} = \frac{1}{C_{\Phi}}(a\vec{x} + b)$$
where $C_{\Phi}$ is again a normalisation factor.
Due to the definition of the tensor product and the fact that the general statevector of a single qubit is a vector of length 2, $n$ qubits can encode length-$2^n$ vectors.
### Cost Function
Our proposed cost function, which we wish to minimise is equal to
$$C_P = \big(1 - \braket{y}{\Phi}\big)^2$$
This computes the normalised fidelity (similarity) of $\ket{y}$ and $\ket{\Phi}$. We see that if $\ket{y}$ and $\ket{\Phi}$ are equal, our cost function will equal 0, otherwise it will be greater than 0. Thus, we need to compute this cost function with our quantum hardware, and couple it with classical minimising algorithms.
### Computing Inner Products on a Quantum Computer
It is clear we now need a quantum algorithm for computing inner products. Let us go through the theory of computing the inner product $\braket{x}{y}$ here, which will be translated to quantum hardware in a couple of sections.
Firstly, assume we have a state:
$$ \ket{\phi} = \frac{1}{\sqrt{2}}\big(\ket{0}\ket{x} + \ket{1}\ket{y}\big) $$
where we want to find the inner product, $\braket{x}{y}$. Applying a Hadamard gate on the first qubit, we find:
$$ \ket{\tilde{\phi}} = \frac{1}{2}\Big(\ket{0}\big(\ket{x}+\ket{y}\big) + \ket{1}\big(\ket{x}-\ket{y}\big)\Big) $$
This means that the probability to measure the first qubit as $\ket{0}$ in the computational basis equals:
$$ P(0) = \frac{1}{2}\Big(1+Re\big[\braket{x}{y}\big]\Big) $$
This follows because:
$$
\begin{aligned}
P(0) &= \Big|\bra{0}\otimes\mathbb{1}\ket{\tilde{\phi}}\Big|^2 \\
&= \frac{1}{4}\Big|\ket{x}+\ket{y}\Big|^2 \\
&= \frac{1}{4}\big(\braket{x}{x}+\braket{x}{y}+\braket{y}{x}+\braket{y}{y}\big) \\
&= \frac{1}{4}\Big(2 + 2 Re\big[\braket{x}{y}\big]\Big) \\
&= \frac{1}{2}\Big(1+Re\big[\braket{x}{y}\big]\Big)
\end{aligned}
$$
After a simple rearrangement, we see that
$$Re\big[\braket{x}{y}\big] = 2P(0) - 1$$
It follows from a similar logic that if we apply a phase rotation on our initial state:
$$ \ket{\phi} = \frac{1}{\sqrt{2}}\big(\ket{0}\ket{x} -i \ket{1}\ket{y}\big) $$
then the probability of the same measurement:
$$ P(0) = \frac{1}{2}\Big(1+Im\big[\braket{x}{y}\big]\Big) $$
We can then combine both probabilities to find the true $\braket{x}{y}$. For this work, we assume that our states are fully real, and so just need the first measurement.
## Code Implementation - Theoretical Approach
It should be noted here that qiskit orders its qubits with the last qubit corresponding to the left of the tensor product. For this run through, we are computing the inner product of length-8 vectors. Thus, we require 4 qubits ($8 + 8 = 16 = 2^4$) to encode the state:
$$
\begin{aligned}
\ket{\phi} &= \frac{1}{\sqrt{2}}(\ket{0}\ket{x} + \ket{1}\ket{y}) \\ &= \frac{1}{\sqrt{2}}\left(\begin{bmatrix}1\\0\end{bmatrix}\otimes\begin{bmatrix}x_1\\x_2\\\vdots\\x_n \end{bmatrix} +\begin{bmatrix}0\\1\end{bmatrix}\otimes\begin{bmatrix}y_1\\y_2\\\vdots\\y_n \end{bmatrix} \right) \\
&= \frac{1}{\sqrt{2}}\left(\begin{bmatrix}x_1\\x_2\\\vdots\\x_n \\y_1\\y_2\\\vdots\\y_n \end{bmatrix} \right)
\end{aligned}
$$
Finally, in order to measure the probability of measuring the bottom (leftmost) qubit as $\ket{0}$ in the computational basis, we can find the exact theoretical value by finding the resultant statevector and summing up the amplitude squared of the first $2^{n-1}$ entries (i.e. half of them). On a real quantum computer, we would just have to perform the actual measurement many times over, and compute the probability that way. We will show the theoretical approach in practice first.
```
# importing necessary packages
import qiskit
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit import Aer, execute
import math
import random
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
```
Now, let's draw the required diagram for theoretically computing the inner product of any two states. Note that the only difference between this circuit diagram and the real, practical diagram for actually running on a quantum computer is that we do not measure the left-most qubit in the computational basis. Again, note that the left-most qubit corresponds to the bottom qubit.
```
x = np.arange(0,8,1) # define some vectors x and y
y = x
N = len(x)
nqubits = math.ceil(np.log2(N)) # compute how many qubits needed to encode either x or y
xnorm = np.linalg.norm(x) # normalise vectors x and y
ynorm = np.linalg.norm(y)
x = x/xnorm
y = y/ynorm
circ = QuantumCircuit(nqubits+1) # create circuit
vec = np.concatenate((x,y))/np.sqrt(2) # concatenate x and y as above, with renormalisation
circ.initialize(vec, range(nqubits+1))
circ.h(nqubits) # apply hadamard to bottom qubit
circ.draw() # draw the circuit
```
Now let's build a function around this circuit, so that we can theoretically compute the inner product between any two normalised vectors.
```
#Creates a quantum circuit to calculate the inner product between two normalised vectors
def inner_prod(vec1, vec2):
#first check lengths are equal
if len(vec1) != len(vec2):
raise ValueError('Lengths of states are not equal')
circ = QuantumCircuit(nqubits+1)
vec = np.concatenate((vec1,vec2))/np.sqrt(2)
circ.initialize(vec, range(nqubits+1))
circ.h(nqubits)
backend = Aer.get_backend('statevector_simulator')
job = execute(circ, backend, backend_options = {"zero_threshold": 1e-20})
result = job.result()
o = np.real(result.get_statevector(circ))
m_sum = 0
for l in range(N):
m_sum += o[l]**2
return 2*m_sum-1
x = np.arange(0,8,1)
y = x
N = len(x)
nqubits = math.ceil(np.log2(N))
xnorm = np.linalg.norm(x)
ynorm = np.linalg.norm(y)
x = x/xnorm
y = y/ynorm
print("x: ", x)
print()
print("y: ", y)
print()
print("The inner product of x and y equals: ", inner_prod(x,y))
```
Now, let's build a function to compute the cost function associated with any choice of a and b. We have set up x and y such that the correct parameters are (a,b) = (1,0).
```
#Implements the entire cost function by feeding the ansatz to the quantum circuit which computes inner products
def calculate_cost_function(parameters):
a, b = parameters
ansatz = a*x + b # compute ansatz
ansatzNorm = np.linalg.norm(ansatz) # normalise ansatz
ansatz = ansatz/ansatzNorm
y_ansatz = ansatzNorm/ynorm * inner_prod(y,ansatz) # use quantum circuit to test ansatz
# note the normalisation factors
return (1-y_ansatz)**2
x = np.arange(0,8,1)
y = x
N = len(x)
nqubits = math.ceil(np.log2(N))
ynorm = np.linalg.norm(y)
y = y/ynorm
a = 1.0
b = 1.0
print("Cost function for a =", a, "and b =", b, "equals:", calculate_cost_function([a,b]))
```
Now putting everything together and using a classical optimiser from the scipy library, we get the full code.
```
#first set up the data sets x and y
x = np.arange(0,8,1)
y = x # + [random.uniform(-1,1) for p in range(8)] # can add noise here
N = len(x)
nqubits = math.ceil(np.log2(N))
ynorm = np.linalg.norm(y) # normalise the y data set
y = y/ynorm
x0 = [0.5,0.5] # initial guess for a and b
#now use different classical optimisers to see which one works best
out = minimize(calculate_cost_function, x0=x0, method="BFGS", options={'maxiter':200}, tol=1e-6)
out1 = minimize(calculate_cost_function, x0=x0, method="COBYLA", options={'maxiter':200}, tol=1e-6)
out2 = minimize(calculate_cost_function, x0=x0, method="Nelder-Mead", options={'maxiter':200}, tol=1e-6)
out3 = minimize(calculate_cost_function, x0=x0, method="CG", options={'maxiter':200}, tol=1e-6)
out4 = minimize(calculate_cost_function, x0=x0, method="trust-constr", options={'maxiter':200}, tol=1e-6)
out_a1 = out1['x'][0]
out_b1 = out1['x'][1]
out_a = out['x'][0]
out_b = out['x'][1]
out_a2 = out2['x'][0]
out_b2 = out2['x'][1]
out_a3 = out3['x'][0]
out_b3 = out3['x'][1]
out_a4 = out4['x'][0]
out_b4 = out4['x'][1]
plt.scatter(x,y*ynorm)
xfit = np.linspace(min(x), max(x), 100)
plt.plot(xfit, out_a*xfit+out_b, label='BFGS')
plt.plot(xfit, out_a1*xfit+out_b1, label='COBYLA')
plt.plot(xfit, out_a2*xfit+out_b2, label='Nelder-Mead')
plt.plot(xfit, out_a3*xfit+out_b3, label='CG')
plt.plot(xfit, out_a4*xfit+out_b4, label='trust-constr')
plt.legend()
plt.title("y = x")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
```
## Code Implementation - Practical Approach
In order to modify the above slightly so that it can be run on a real quantum computer, we simply have to modify the `inner_prod` function. Instead of theoretically extracting the probabilility of measuring a 0 on the leftmost qubit in the computational basis, we must actually measure this qubit a number of times and calculate the probability from these samples. Our new circuit can be created as follows, which is identical to the theoretical circuit, but we just add a measurement, and hence need a classical bit.
```
x = np.arange(0,8,1) # define some vectors x and y
y = x
N = len(x)
nqubits = math.ceil(np.log2(N)) # compute how many qubits needed to encode either x or y
xnorm = np.linalg.norm(x) # normalise vectors x and y
ynorm = np.linalg.norm(y)
x = x/xnorm
y = y/ynorm
circ = QuantumCircuit(nqubits+1,1) # create circuit
vec = np.concatenate((x,y))/np.sqrt(2) # concatenate x and y as above, with renormalisation
circ.initialize(vec, range(nqubits+1))
circ.h(nqubits) # apply hadamard to bottom qubit
circ.measure(nqubits,0) # measure bottom qubit in computational basis
circ.draw() # draw the circuit
```
Now, we can build a new inner_prod function around this circuit, using a different simulator from qiskit.
```
#Creates quantum circuit which calculates the inner product between two normalised vectors
def inner_prod(vec1, vec2):
#first check lengths are equal
if len(vec1) != len(vec2):
raise ValueError('Lengths of states are not equal')
circ = QuantumCircuit(nqubits+1,1)
vec = np.concatenate((vec1,vec2))/np.sqrt(2)
circ.initialize(vec, range(nqubits+1))
circ.h(nqubits)
circ.measure(nqubits,0)
backend = Aer.get_backend('qasm_simulator')
job = execute(circ, backend, shots=20000)
result = job.result()
outputstate = result.get_counts(circ)
if ('0' in outputstate.keys()):
m_sum = float(outputstate["0"])/20000
else:
m_sum = 0
return 2*m_sum-1
x = np.arange(0,8,1)
y = x
N = len(x)
nqubits = math.ceil(np.log2(N))
xnorm = np.linalg.norm(x)
ynorm = np.linalg.norm(y)
x = x/xnorm
y = y/ynorm
print("x: ", x)
print()
print("y: ", y)
print()
print("The inner product of x and y equals: ", inner_prod(x,y))
```
Our cost function calculation is the same as before, but we now just use this new method for computing the inner product, so the full code can be run as follows.
```
#first set up the data sets x and y
x = np.arange(0,8,1)
y = x # + [random.uniform(-1,1) for p in range(8)] # can add noise here
N = len(x)
nqubits = math.ceil(np.log2(N))
ynorm = np.linalg.norm(y) # normalise y data set
y = y/ynorm
x0 = [0.5,0.5] # initial guess for a and b
#now use different classical optimisers to see which one works best
out = minimize(calculate_cost_function, x0=x0, method="BFGS", options={'maxiter':200}, tol=1e-6)
out1 = minimize(calculate_cost_function, x0=x0, method="COBYLA", options={'maxiter':200}, tol=1e-6)
out2 = minimize(calculate_cost_function, x0=x0, method="Nelder-Mead", options={'maxiter':200}, tol=1e-6)
out3 = minimize(calculate_cost_function, x0=x0, method="CG", options={'maxiter':200}, tol=1e-6)
out4 = minimize(calculate_cost_function, x0=x0, method="trust-constr", options={'maxiter':200}, tol=1e-6)
out_a1 = out1['x'][0]
out_b1 = out1['x'][1]
out_a = out['x'][0]
out_b = out['x'][1]
out_a2 = out2['x'][0]
out_b2 = out2['x'][1]
out_a3 = out3['x'][0]
out_b3 = out3['x'][1]
out_a4 = out4['x'][0]
out_b4 = out4['x'][1]
plt.scatter(x,y*ynorm)
xfit = np.linspace(min(x), max(x), 100)
plt.plot(xfit, out_a*xfit+out_b, label='BFGS')
plt.plot(xfit, out_a1*xfit+out_b1, label='COBYLA')
plt.plot(xfit, out_a2*xfit+out_b2, label='Nelder-Mead')
plt.plot(xfit, out_a3*xfit+out_b3, label='CG')
plt.plot(xfit, out_a4*xfit+out_b4, label='trust-constr')
plt.legend()
plt.title("y = x")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
```
## Extending to Higher Order Fits
We can also extend to fitting to quadratic, cubic, and higher order polynomials. The code remains relatively unchanged, but will update the cost function slightly. We can of course use either the theoretical or practical method for computing the inner products in the following cost function. We are now fitting to an n$^{th}$-order polynomial:
$$y = a_0+ a_1 x + a_2 x^2 + \dots + a_n x^n$$
```
# New cost function calculation, allowing for higher order polynomials
# Implements the entire cost function by feeding the ansatz to the quantum circuit which computes inner products
def calculate_cost_function_n(parameters):
ansatz = parameters[0] # compute ansatz
for i in range(1,len(parameters)):
ansatz += parameters[i] * x**i
ansatzNorm = np.linalg.norm(ansatz) # normalise ansatz
ansatz = ansatz/ansatzNorm
y_ansatz = ansatzNorm/ynorm * inner_prod(y,ansatz) # use quantum circuit to test ansatz
# note the normalisation factors
return (1-y_ansatz)**2
#first set up the data sets x and y
x = np.arange(0,8,1)
y = (2*x-1)**3 + [random.uniform(-1,1) for p in range(8)]
N = len(x)
nqubits = math.ceil(np.log2(N))
ynorm = np.linalg.norm(y) #normalise y data set
y = y/ynorm
order = 3
x0 = [random.uniform(0,2) for p in range(order+1)] #random initial guess for a and b
#now use different classical optimisers to see which one works best
out = minimize(calculate_cost_function_n, x0=x0, method="BFGS", options={'maxiter':200}, tol=1e-6)
out1 = minimize(calculate_cost_function_n, x0=x0, method="COBYLA", options={'maxiter':200}, tol=1e-6)
out2 = minimize(calculate_cost_function_n, x0=x0, method="Nelder-Mead", options={'maxiter':200}, tol=1e-6)
out3 = minimize(calculate_cost_function_n, x0=x0, method="CG", options={'maxiter':200}, tol=1e-6)
out4 = minimize(calculate_cost_function_n, x0=x0, method="trust-constr", options={'maxiter':200}, tol=1e-6)
class_fit = np.polyfit(x,y*ynorm,order)
class_fit = class_fit[::-1]
xfit = np.linspace(min(x), max(x), 100)
def return_fits(xfit):
c_fit = np.zeros(100)
q_fit = np.zeros(100)
q_fit1 = np.zeros(100)
q_fit2 = np.zeros(100)
q_fit3 = np.zeros(100)
q_fit4 = np.zeros(100)
for i in range(order+1):
c_fit += xfit**i*class_fit[i]
q_fit += xfit**i*out['x'][i]
q_fit1 += xfit**i*out1['x'][i]
q_fit2 += xfit**i*out2['x'][i]
q_fit3 += xfit**i*out3['x'][i]
q_fit4 += xfit**i*out4['x'][i]
return c_fit, q_fit, q_fit1, q_fit2, q_fit3, q_fit4
c_fit, q_fit, q_fit1, q_fit2, q_fit3, q_fit4 = return_fits(xfit)
plt.scatter(x,y*ynorm)
xfit = np.linspace(min(x), max(x), 100)
plt.plot(xfit, c_fit, label='Classical')
plt.plot(xfit, q_fit, label='BFGS')
plt.plot(xfit, q_fit1, label='COBYLA')
plt.plot(xfit, q_fit2, label='Nelder-Mead')
plt.plot(xfit, q_fit3, label='CG')
plt.plot(xfit, q_fit4, label='trust-constr')
plt.legend()
plt.title("$y = (2x-1)^3$ + Random Perturbation")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
```
## Acknowledgements
I would like to thank Dr. Lee O'Riordan for his supervision and guidance on this work. The work was mainly inspired by work presented in the research paper "Variational Quantum Linear Solver: A Hybrid Algorithm for Linear Systems", written by Carlos Bravo-Prieto, Ryan LaRose, M. Cerezo, Yiğit Subaşı, Lukasz Cincio, and Patrick J. Coles, which is available at this [link](https://arxiv.org/abs/1909.05820). I would also like to thank the Irish Centre for High End Computing for allowing me to access the national HPC infrastructure, Kay.
| true |
code
| 0.634911 | null | null | null | null |
|
```
import cupy as cp
import cusignal
from scipy import signal
import numpy as np
```
### Generate Sinusodial Signals with N Carriers
**On CPU where**:
* fs = sample rate of signal
* freq = list of carrier frequencies
* N = number of points in signal
```
def cpu_gen_signal(fs, freq, N):
T = 1/fs
sig = 0
x = np.linspace(0.0, N*(1.0/fs), N)
for f in freq:
sig += np.cos(f*2*cp.pi*x)
return sig
def cpu_gen_ensemble(fs, N, num_sig):
sig_ensemble = np.zeros((int(num_sig), int(N)))
for i in range(int(num_sig)):
# random number of carriers in random locations for each signal
freq = 1e6 * np.random.randint(1, 10, np.random.randint(1,5))
sig_ensemble[i,:] = cpu_gen_signal(fs, freq, N)
return sig_ensemble
```
**On GPU**
Please note, first run of GPU functions includes setting up memory and 'pre-warming' the GPU. For accurate performance and benchmarking each cell is typically run multiple times.
```
def gpu_gen_signal(fs, freq, N):
T = 1/fs
sig = 0
x = cp.linspace(0.0, N*(1.0/fs), N)
for f in freq:
sig += cp.cos(f*2*cp.pi*x)
return sig
# Storing num carriers for deep learning prediction -- We're even HURTING ourself here with benchmarks!
def gpu_gen_ensemble(fs, N, num_sig):
sig_ensemble = cp.zeros((int(num_sig), int(N)))
num_carriers = cp.zeros(int(num_sig))
for i in range(int(num_sig)):
# random number of carriers in random locations for each signal
num_carrier = int(cp.random.randint(1,5))
freq = 1e6 * cp.random.randint(1, 10, num_carrier)
sig_ensemble[i,:] = gpu_gen_signal(fs, freq, N)
num_carriers[i] = num_carrier
return sig_ensemble, num_carriers
```
Generate a bunch of different signals with arbitrary carrier frequencies. Allow user to select number of signals, sample frequency of the ensemble, and number of points in the signal
```
#10MHz
fs = 10e6
# Overwrite
num_sig = 2000
N = 2**15
# Change sample rate so N=2^16
up = 2
down = 1
cpu_ensemble = cpu_gen_ensemble(fs, N, num_sig)
[gpu_ensemble, num_carriers] = gpu_gen_ensemble(fs, N, num_sig)
```
### Resample Ensemble - Use Polyphase Resampler to upsample by 2
**On CPU**
```
%%time
resample_cpu_ensemble = signal.resample_poly(cpu_ensemble, up, down, axis=1, window='flattop')
```
**On GPU**
```
%%time
resample_gpu_ensemble = cusignal.resample_poly(gpu_ensemble, up, down, axis=1, window='flattop')
```
### Run Periodogram with Flattop Filter over Each Row of Ensemble
**On CPU**
```
%%time
cf, cPxx_den = signal.periodogram(resample_cpu_ensemble, fs, 'flattop', scaling='spectrum', axis=1)
```
**On GPU**
```
%%time
gf, gPxx_den = cusignal.periodogram(resample_gpu_ensemble, fs, 'flattop', scaling='spectrum', axis=1)
```
### Visualize Output
**On CPU**
```
%matplotlib inline
import matplotlib.pyplot as plt
plt.semilogy(cf, cPxx_den[0,:])
plt.show()
```
**On GPU**
```
import matplotlib.pyplot as plt
plt.semilogy(cp.asnumpy(gf), cp.asnumpy(gPxx_den[0,:]))
plt.show()
```
### Move to PyTorch to try to 'predict' number of carriers in signal
```
# Uncomment the line below to ensure PyTorch is installed.
# PyTorch is intentionally excluded from our Docker images due to its size.
# Alternatively, the docker image can be run with the following variable:
# docker run -e EXTRA_CONDA_PACKAGES="-c pytorch pytorch"...
#!conda install -y -c pytorch pytorch
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import torch.nn.functional as F
device = torch.device("cuda:0")
#90 percent of dataset for training
training_idx_max = int(0.9*gPxx_den.shape[0])
gPxx_den = gPxx_den.astype(cp.float32)
num_carriers = num_carriers.astype(cp.int64)
# Zero copy memory from cupy to DLPack to Torch
x = torch.as_tensor(gPxx_den[0:training_idx_max,:], device=device)
y = torch.as_tensor(num_carriers[0:training_idx_max], device=device)
# Test
x_t = torch.as_tensor(gPxx_den[training_idx_max:gPxx_den.shape[0],:], device=device)
y_t = torch.as_tensor(num_carriers[training_idx_max:gPxx_den.shape[0]], device=device)
# Number of possible carriers
output_size = 10
epochs = 75
batch_size = 10
learning_rate = 1e-2
class Network(nn.Module):
def __init__(self):
super(Network, self).__init__()
self.l1 = nn.Linear(x.shape[1], 1500)
self.relu = nn.ReLU()
self.l3 = nn.Linear(1500, 750)
self.relu = nn.ReLU()
self.l5 = nn.Linear(750, output_size)
def forward(self, x):
x = self.l1(x)
x = self.relu(x)
x = self.l3(x)
x = self.relu(x)
x = self.l5(x)
return F.log_softmax(x, dim=1)
net = Network().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate, momentum=0.5)
loss_log = []
for e in range(epochs):
for i in range(0, x.shape[0], batch_size):
x_mini = x[i:i + batch_size]
y_mini = y[i:i + batch_size]
x_var = Variable(x_mini)
y_var = Variable(y_mini)
optimizer.zero_grad()
net_out = net(x_var)
loss = F.nll_loss(net_out, y_var)
loss.backward()
optimizer.step()
if i % 100 == 0:
loss_log.append(loss.data)
print('Epoch: {} - Loss: {:.6f}'.format(e, loss.data))
```
**Measure Inference Accuracy on Test Set**
```
test_loss = 0
correct = 0
for i in range(x_t.shape[0]):
pred = net(x_t[i,:].expand(1,-1)).argmax()
correct += pred.eq(y_t[i].view_as(pred)).sum().item()
print('Accuracy: ', 100. * correct / x_t.shape[0])
```
**Save Model**
```
checkpoint = {'net': Network(),
'state_dict': net.state_dict(),
'optimizer': optimizer.state_dict()}
torch.save(checkpoint,"E2E_sig_proc.pt")
```
**Load Model**
```
checkpoint = torch.load('E2E_sig_proc.pt')
checkpoint.keys()
```
**Generate New Signal and Look at Inferencing Power**
```
num_carrier = 2
freq = 1e6 * cp.random.randint(1, 10, num_carrier)
sig = gpu_gen_signal(fs, freq, N)
r_sig = cusignal.resample_poly(sig, up, down, window='flattop')
f, Pxx = cusignal.periodogram(r_sig, fs, 'flattop', scaling='spectrum')
x = torch.as_tensor(Pxx.astype(cp.float32), device=device)
pred_num_carrier = net(x.expand(1,-1)).argmax().item()
print(pred_num_carrier)
```
| true |
code
| 0.708855 | null | null | null | null |
|
# Node elevations and edge grades
Author: [Geoff Boeing](https://geoffboeing.com/)
- [Overview of OSMnx](http://geoffboeing.com/2016/11/osmnx-python-street-networks/)
- [GitHub repo](https://github.com/gboeing/osmnx)
- [Examples, demos, tutorials](https://github.com/gboeing/osmnx-examples)
- [Documentation](https://osmnx.readthedocs.io/en/stable/)
- [Journal article/citation](http://geoffboeing.com/publications/osmnx-complex-street-networks/)
OSMnx allows you to automatically add elevation attributes to your graph's nodes with the `elevation` module, using either local raster files or the Google Maps Elevation API as the elevation data source. If you use the Google API, you will need an API key. Once your nodes have elevation values, OSMnx can automatically calculate your edges' grades (inclines).
```
import sys
import numpy as np
import osmnx as ox
import pandas as pd
%matplotlib inline
ox.__version__
```
## Elevation from local raster file(s)
OSMnx can attach elevations to graph nodes using either a single raster file or a list of raster files. The latter creates a virtual raster VRT composed of the rasters at those filepaths. By default, it uses all available CPUs but you can configure this with an argument.
```
address = "600 Montgomery St, San Francisco, California, USA"
G = ox.graph_from_address(address=address, dist=500, dist_type="bbox", network_type="bike")
# add node elevations from a single raster file
# some nodes will be null because the single file does not cover the graph's extents
raster_path = "./input_data/elevation1.tif"
G = ox.elevation.add_node_elevations_raster(G, raster_path, cpus=1)
# add node elevations from multiple raster files
# no nulls should remain
raster_paths = ["./input_data/elevation1.tif", "./input_data/elevation2.tif"]
G = ox.elevation.add_node_elevations_raster(G, raster_paths)
assert not np.isnan(np.array(G.nodes(data="elevation"))[:, 1]).any()
# add edge grades and their absolute values
G = ox.elevation.add_edge_grades(G, add_absolute=True)
```
## Elevation from Google Maps Elevation API
You will need a Google Maps Elevation [API key](https://developers.google.com/maps/documentation/elevation/start). Consider your API usage limits. OSMnx rounds coordinates to 5 decimal places (approx 1 meter) to fit 350 locations in a batch. Note that there is some spatial inaccuracy given Google's dataset's resolution. For example, in San Francisco (where the resolution is 19 meters) a couple of edges in hilly parks have a 50+ percent grade because Google assigns one of their nodes the elevation of a hill adjacent to the street.
```
# replace this with your own API key!
try:
from keys import google_elevation_api_key
except ImportError:
sys.exit() # you need an API key to proceed
# get the street network for san francisco
place = "San Francisco"
place_query = {"city": "San Francisco", "state": "California", "country": "USA"}
G = ox.graph_from_place(place_query, network_type="drive")
# add elevation to each of the nodes, using the google elevation API, then calculate edge grades
G = ox.elevation.add_node_elevations_google(G, api_key=google_elevation_api_key)
G = ox.elevation.add_edge_grades(G)
```
## Calculate some summary stats
Use an undirected representation of the network so we don't overcount two-way streets (because they have reciprocal edges pointing in each direction). We use the absolute value of edge grade because we're interested in steepness, not directionality.
```
# calculate the edges' absolute grades (and drop any infinite/null values)
grades = pd.Series([d["grade_abs"] for _, _, d in ox.get_undirected(G).edges(data=True)])
grades = grades.replace([np.inf, -np.inf], np.nan).dropna()
avg_grade = np.mean(grades)
print("Average street grade in {} is {:.1f}%".format(place, avg_grade * 100))
med_grade = np.median(grades)
print("Median street grade in {} is {:.1f}%".format(place, med_grade * 100))
```
## Plot the nodes by elevation
Plot them colored from low (violet) to high (yellow).
```
# get one color for each node, by elevation, then plot the network
nc = ox.plot.get_node_colors_by_attr(G, "elevation", cmap="plasma")
fig, ax = ox.plot_graph(G, node_color=nc, node_size=5, edge_color="#333333", bgcolor="k")
```
## Plot the edges by grade
Grade is the ratio of elevation change to edge length. Plot edges colored from low/flat (violet) to high/steep (yellow).
```
# get a color for each edge, by grade, then plot the network
ec = ox.plot.get_edge_colors_by_attr(G, "grade_abs", cmap="plasma", num_bins=5, equal_size=True)
fig, ax = ox.plot_graph(G, edge_color=ec, edge_linewidth=0.5, node_size=0, bgcolor="k")
```
## Calculate shortest paths, considering grade impedance
This example approximates the route of "The Wiggle" in San Francisco.
```
# select an origin and destination node and a bounding box around them
origin = ox.distance.nearest_nodes(G, -122.426, 37.77)
destination = ox.distance.nearest_nodes(G, -122.441, 37.773)
bbox = ox.utils_geo.bbox_from_point((37.772, -122.434), dist=1500)
# define some edge impedance function here
def impedance(length, grade):
penalty = grade ** 2
return length * penalty
# add impedance and elevation rise values to each edge in the projected graph
# use absolute value of grade in impedance function if you want to avoid uphill and downhill
for _, _, _, data in G.edges(keys=True, data=True):
data["impedance"] = impedance(data["length"], data["grade_abs"])
data["rise"] = data["length"] * data["grade"]
```
#### First find the shortest path that minimizes *trip distance*:
```
route_by_length = ox.shortest_path(G, origin, destination, weight="length")
fig, ax = ox.plot_graph_route(G, route_by_length, bbox=bbox, node_size=0)
```
#### Now find the shortest path that avoids slopes by minimizing *impedance* (function of length and grade):
```
route_by_impedance = ox.shortest_path(G, origin, destination, weight="impedance")
fig, ax = ox.plot_graph_route(G, route_by_impedance, bbox=bbox, node_size=0)
```
#### Print some summary stats about these two routes:
```
def print_route_stats(route):
route_grades = ox.utils_graph.get_route_edge_attributes(G, route, "grade_abs")
msg = "The average grade is {:.1f}% and the max is {:.1f}%"
print(msg.format(np.mean(route_grades) * 100, np.max(route_grades) * 100))
route_rises = ox.utils_graph.get_route_edge_attributes(G, route, "rise")
ascent = np.sum([rise for rise in route_rises if rise >= 0])
descent = np.sum([rise for rise in route_rises if rise < 0])
msg = "Total elevation change is {:.1f} meters: {:.0f} meter ascent and {:.0f} meter descent"
print(msg.format(np.sum(route_rises), ascent, abs(descent)))
route_lengths = ox.utils_graph.get_route_edge_attributes(G, route, "length")
print("Total trip distance: {:,.0f} meters".format(np.sum(route_lengths)))
# stats of route minimizing length
print_route_stats(route_by_length)
# stats of route minimizing impedance (function of length and grade)
print_route_stats(route_by_impedance)
```
So, we decreased the average slope along the route from a 5% grade to a 2% grade. The total elevation change is obviously (approximately, due to rounding) the same with either route, but using our impedance function we decrease the total ascent from 69 meters to 40 meters (but the trip distance increases from 1.9 km to 2.6 km).
| true |
code
| 0.613208 | null | null | null | null |
|
# [ATM 623: Climate Modeling](../index.ipynb)
[Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html), University at Albany
# Lecture 7: Elementary greenhouse models
## Warning: content out of date and not maintained
You really should be looking at [The Climate Laboratory book](https://brian-rose.github.io/ClimateLaboratoryBook) by Brian Rose, where all the same content (and more!) is kept up to date.
***Here you are likely to find broken links and broken code.***
### About these notes:
This document uses the interactive [`Jupyter notebook`](https://jupyter.org) format. The notes can be accessed in several different ways:
- The interactive notebooks are hosted on `github` at https://github.com/brian-rose/ClimateModeling_courseware
- The latest versions can be viewed as static web pages [rendered on nbviewer](http://nbviewer.ipython.org/github/brian-rose/ClimateModeling_courseware/blob/master/index.ipynb)
- A complete snapshot of the notes as of May 2017 (end of spring semester) are [available on Brian's website](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2017/Notes/index.html).
[Also here is a legacy version from 2015](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/Notes/index.html).
Many of these notes make use of the `climlab` package, available at https://github.com/brian-rose/climlab
```
# Ensure compatibility with Python 2 and 3
from __future__ import print_function, division
```
## Contents
1. [A single layer atmosphere](#section1)
2. [Introducing the two-layer grey gas model](#section2)
3. [Tuning the grey gas model to observations](#section3)
4. [Level of emission](#section4)
5. [Radiative forcing in the 2-layer grey gas model](#section5)
6. [Radiative equilibrium in the 2-layer grey gas model](#section6)
7. [Summary](#section7)
____________
<a id='section1'></a>
## 1. A single layer atmosphere
____________
We will make our first attempt at quantifying the greenhouse effect in the simplest possible greenhouse model: a single layer of atmosphere that is able to absorb and emit longwave radiation.
<img src='../images/1layerAtm_sketch.png'>
### Assumptions
- Atmosphere is a single layer of air at temperature $T_a$
- Atmosphere is **completely transparent to shortwave** solar radiation.
- The **surface** absorbs shortwave radiation $(1-\alpha) Q$
- Atmosphere is **completely opaque to infrared** radiation
- Both surface and atmosphere emit radiation as **blackbodies** ($\sigma T_s^4, \sigma T_a^4$)
- Atmosphere radiates **equally up and down** ($\sigma T_a^4$)
- There are no other heat transfer mechanisms
We can now use the concept of energy balance to ask what the temperature need to be in order to balance the energy budgets at the surface and the atmosphere, i.e. the **radiative equilibrium temperatures**.
### Energy balance at the surface
\begin{align}
\text{energy in} &= \text{energy out} \\
(1-\alpha) Q + \sigma T_a^4 &= \sigma T_s^4 \\
\end{align}
The presence of the atmosphere above means there is an additional source term: downwelling infrared radiation from the atmosphere.
We call this the **back radiation**.
### Energy balance for the atmosphere
\begin{align}
\text{energy in} &= \text{energy out} \\
\sigma T_s^4 &= A\uparrow + A\downarrow = 2 \sigma T_a^4 \\
\end{align}
which means that
$$ T_s = 2^\frac{1}{4} T_a \approx 1.2 T_a $$
So we have just determined that, in order to have a purely **radiative equilibrium**, we must have $T_s > T_a$.
*The surface must be warmer than the atmosphere.*
### Solve for the radiative equilibrium surface temperature
Now plug this into the surface equation to find
$$ \frac{1}{2} \sigma T_s^4 = (1-\alpha) Q $$
and use the definition of the emission temperature $T_e$ to write
$$ (1-\alpha) Q = \sigma T_e^4 $$
*In fact, in this model, $T_e$ is identical to the atmospheric temperature $T_a$, since all the OLR originates from this layer.*
Solve for the surface temperature:
$$ T_s = 2^\frac{1}{4} T_e $$
Putting in observed numbers, $T_e = 255$ K gives a surface temperature of
$$T_s = 303 ~\text{K}$$
This model is one small step closer to reality: surface is warmer than atmosphere, emissions to space generated in the atmosphere, atmosphere heated from below and helping to keep surface warm.
BUT our model now overpredicts the surface temperature by about 15ºC (or K).
Ideas about why?
Basically we just need to read our **list of assumptions** above and realize that none of them are very good approximations:
- Atmosphere absorbs some solar radiation.
- Atmosphere is NOT a perfect absorber of longwave radiation
- Absorption and emission varies strongly with wavelength *(atmosphere does not behave like a blackbody)*.
- Emissions are not determined by a single temperature $T_a$ but by the detailed *vertical profile* of air temperture.
- Energy is redistributed in the vertical by a variety of dynamical transport mechanisms (e.g. convection and boundary layer turbulence).
____________
<a id='section2'></a>
## 2. Introducing the two-layer grey gas model
____________
Let's generalize the above model just a little bit to build a slighly more realistic model of longwave radiative transfer.
We will address two shortcomings of our single-layer model:
1. No vertical structure
2. 100% longwave opacity
Relaxing these two assumptions gives us what turns out to be a very useful prototype model for **understanding how the greenhouse effect works**.
### Assumptions
- The atmosphere is **transparent to shortwave radiation** (still)
- Divide the atmosphere up into **two layers of equal mass** (the dividing line is thus at 500 hPa pressure level)
- Each layer **absorbs only a fraction $\epsilon$ ** of whatever longwave radiation is incident upon it.
- We will call the fraction $\epsilon$ the **absorptivity** of the layer.
- Assume $\epsilon$ is the same in each layer
This is called the **grey gas** model, where grey here means the emission and absorption have no spectral dependence.
We can think of this model informally as a "leaky greenhouse".
Note that the assumption that $\epsilon$ is the same in each layer is appropriate if the absorption is actually carried out by a gas that is **well-mixed** in the atmosphere.
Out of our two most important absorbers:
- CO$_2$ is well mixed
- H$_2$O is not (mostly confined to lower troposphere due to strong temperature dependence of the saturation vapor pressure).
But we will ignore this aspect of reality for now.
In order to build our model, we need to introduce one additional piece of physics known as **Kirchoff's Law**:
$$ \text{absorptivity} = \text{emissivity} $$
So if a layer of atmosphere at temperature $T$ absorbs a fraction $\epsilon$ of incident longwave radiation, it must emit
$$ \epsilon ~\sigma ~T^4 $$
both up and down.
### A sketch of the radiative fluxes in the 2-layer atmosphere
<img src='../images/2layerAtm_sketch.png'>
- Surface temperature is $T_s$
- Atm. temperatures are $T_0, T_1$ where $T_0$ is closest to the surface.
- absorptivity of atm layers is $\epsilon$
- Surface emission is $\sigma T_s^4$
- Atm emission is $\epsilon \sigma T_0^4, \epsilon \sigma T_1^4$ (up and down)
- Absorptivity = emissivity for atmospheric layers
- a fraction $(1-\epsilon)$ of the longwave beam is **transmitted** through each layer
### A fun aside: symbolic math with the `sympy` package
This two-layer grey gas model is simple enough that we can work out all the details algebraically. There are three temperatures to keep track of $(T_s, T_0, T_1)$, so we will have 3x3 matrix equations.
We all know how to work these things out with pencil and paper. But it can be tedious and error-prone.
Symbolic math software lets us use the computer to automate a lot of tedious algebra.
The [sympy](http://www.sympy.org/en/index.html) package is a powerful open-source symbolic math library that is well-integrated into the scientific Python ecosystem.
```
import sympy
# Allow sympy to produce nice looking equations as output
sympy.init_printing()
# Define some symbols for mathematical quantities
# Assume all quantities are positive (which will help simplify some expressions)
epsilon, T_e, T_s, T_0, T_1, sigma = \
sympy.symbols('epsilon, T_e, T_s, T_0, T_1, sigma', positive=True)
# So far we have just defined some symbols, e.g.
T_s
# We have hard-coded the assumption that the temperature is positive
sympy.ask(T_s>0)
```
### Longwave emissions
Let's denote the emissions from each layer as
\begin{align}
E_s &= \sigma T_s^4 \\
E_0 &= \epsilon \sigma T_0^4 \\
E_1 &= \epsilon \sigma T_1^4
\end{align}
recognizing that $E_0$ and $E_1$ contribute to **both** the upwelling and downwelling beams.
```
# Define these operations as sympy symbols
# And display as a column vector:
E_s = sigma*T_s**4
E_0 = epsilon*sigma*T_0**4
E_1 = epsilon*sigma*T_1**4
E = sympy.Matrix([E_s, E_0, E_1])
E
```
### Shortwave radiation
Since we have assumed the atmosphere is transparent to shortwave, the incident beam $Q$ passes unchanged from the top to the surface, where a fraction $\alpha$ is reflected upward out to space.
```
# Define some new symbols for shortwave radiation
Q, alpha = sympy.symbols('Q, alpha', positive=True)
# Create a dictionary to hold our numerical values
tuned = {}
tuned[Q] = 341.3 # global mean insolation in W/m2
tuned[alpha] = 101.9/Q.subs(tuned) # observed planetary albedo
tuned[sigma] = 5.67E-8 # Stefan-Boltzmann constant in W/m2/K4
tuned
# Numerical value for emission temperature
#T_e.subs(tuned)
```
### Upwelling beam
Let $U$ be the upwelling flux of longwave radiation.
The upward flux from the surface to layer 0 is
$$ U_0 = E_s $$
(just the emission from the suface).
```
U_0 = E_s
U_0
```
Following this beam upward, we can write the upward flux from layer 0 to layer 1 as the sum of the transmitted component that originated below layer 0 and the new emissions from layer 0:
$$ U_1 = (1-\epsilon) U_0 + E_0 $$
```
U_1 = (1-epsilon)*U_0 + E_0
U_1
```
Continuing to follow the same beam, the upwelling flux above layer 1 is
$$ U_2 = (1-\epsilon) U_1 + E_1 $$
```
U_2 = (1-epsilon) * U_1 + E_1
```
Since there is no more atmosphere above layer 1, this upwelling flux is our Outgoing Longwave Radiation for this model:
$$ OLR = U_2 $$
```
U_2
```
The three terms in the above expression represent the **contributions to the total OLR that originate from each of the three levels**.
Let's code this up explicitly for future reference:
```
# Define the contributions to OLR originating from each level
OLR_s = (1-epsilon)**2 *sigma*T_s**4
OLR_0 = epsilon*(1-epsilon)*sigma*T_0**4
OLR_1 = epsilon*sigma*T_1**4
OLR = OLR_s + OLR_0 + OLR_1
print( 'The expression for OLR is')
OLR
```
### Downwelling beam
Let $D$ be the downwelling longwave beam. Since there is no longwave radiation coming in from space, we begin with
```
fromspace = 0
D_2 = fromspace
```
Between layer 1 and layer 0 the beam contains emissions from layer 1:
$$ D_1 = (1-\epsilon)D_2 + E_1 = E_1 $$
```
D_1 = (1-epsilon)*D_2 + E_1
D_1
```
Finally between layer 0 and the surface the beam contains a transmitted component and the emissions from layer 0:
$$ D_0 = (1-\epsilon) D_1 + E_0 = \epsilon(1-\epsilon) \sigma T_1^4 + \epsilon \sigma T_0^4$$
```
D_0 = (1-epsilon)*D_1 + E_0
D_0
```
This $D_0$ is what we call the **back radiation**, i.e. the longwave radiation from the atmosphere to the surface.
____________
<a id='section3'></a>
## 3. Tuning the grey gas model to observations
____________
In building our new model we have introduced exactly one parameter, the absorptivity $\epsilon$. We need to choose a value for $\epsilon$.
We will tune our model so that it **reproduces the observed global mean OLR** given **observed global mean temperatures**.
To get appropriate temperatures for $T_s, T_0, T_1$, let's revisit the [global, annual mean lapse rate plot from NCEP Reanalysis data](Lecture06 -- Radiation.ipynb) from the previous lecture.
### Temperatures
First, we set
$$T_s = 288 \text{ K} $$
From the lapse rate plot, an average temperature for the layer between 1000 and 500 hPa is
$$ T_0 = 275 \text{ K}$$
Defining an average temperature for the layer between 500 and 0 hPa is more ambiguous because of the lapse rate reversal at the tropopause. We will choose
$$ T_1 = 230 \text{ K}$$
From the graph, this is approximately the observed global mean temperature at 275 hPa or about 10 km.
```
# add to our dictionary of values:
tuned[T_s] = 288.
tuned[T_0] = 275.
tuned[T_1] = 230.
tuned
```
### OLR
From the [observed global energy budget](Lecture01 -- Planetary energy budget.ipynb) we set
$$ OLR = 238.5 \text{ W m}^{-2} $$
### Solving for $\epsilon$
We wrote down the expression for OLR as a function of temperatures and absorptivity in our model above.
We just need to equate this to the observed value and solve a **quadratic equation** for $\epsilon$.
This is where the real power of the symbolic math toolkit comes in.
Subsitute in the numerical values we are interested in:
```
# the .subs() method for a sympy symbol means
# substitute values in the expression using the supplied dictionary
# Here we use observed values of Ts, T0, T1
OLR2 = OLR.subs(tuned)
OLR2
```
We have a quadratic equation for $\epsilon$.
Now use the `sympy.solve` function to solve the quadratic:
```
# The sympy.solve method takes an expression equal to zero
# So in this case we subtract the tuned value of OLR from our expression
eps_solution = sympy.solve(OLR2 - 238.5, epsilon)
eps_solution
```
There are two roots, but the second one is unphysical since we must have $0 < \epsilon < 1$.
Just for fun, here is a simple of example of *filtering a list* using powerful Python *list comprehension* syntax:
```
# Give me only the roots that are between zero and 1!
list_result = [eps for eps in eps_solution if 0<eps<1]
print( list_result)
# The result is a list with a single element.
# We need to slice the list to get just the number:
eps_tuned = list_result[0]
print( eps_tuned)
```
We conclude that our tuned value is
$$ \epsilon = 0.586 $$
This is the absorptivity that guarantees that our model reproduces the observed OLR given the observed tempertures.
```
tuned[epsilon] = eps_tuned
tuned
```
____________
<a id='section4'></a>
## 4. Level of emission
____________
Even in this very simple greenhouse model, there is **no single level** at which the OLR is generated.
The three terms in our formula for OLR tell us the contributions from each level.
```
OLRterms = sympy.Matrix([OLR_s, OLR_0, OLR_1])
OLRterms
```
Now evaluate these expressions for our tuned temperature and absorptivity:
```
OLRtuned = OLRterms.subs(tuned)
OLRtuned
```
So we are getting about 67 W m$^{-2}$ from the surface, 79 W m$^{-2}$ from layer 0, and 93 W m$^{-2}$ from the top layer.
In terms of fractional contributions to the total OLR, we have (limiting the output to two decimal places):
```
sympy.N(OLRtuned / 239., 2)
```
Notice that the largest single contribution is coming from the top layer. This is in spite of the fact that the emissions from this layer are weak, because it is so cold.
Comparing to observations, the actual contribution to OLR from the surface is about 22 W m$^{-2}$ (or about 9% of the total), not 67 W m$^{-2}$. So we certainly don't have all the details worked out yet!
As we will see later, to really understand what sets that observed 22 W m$^{-2}$, we will need to start thinking about the spectral dependence of the longwave absorptivity.
____________
<a id='section5'></a>
## 5. Radiative forcing in the 2-layer grey gas model
____________
Adding some extra greenhouse absorbers will mean that a greater fraction of incident longwave radiation is absorbed in each layer.
Thus **$\epsilon$ must increase** as we add greenhouse gases.
Suppose we have $\epsilon$ initially, and the absorptivity increases to $\epsilon_2 = \epsilon + \delta_\epsilon$.
Suppose further that this increase happens **abruptly** so that there is no time for the temperatures to respond to this change. **We hold the temperatures fixed** in the column and ask how the radiative fluxes change.
**Do you expect the OLR to increase or decrease?**
Let's use our two-layer leaky greenhouse model to investigate the answer.
The components of the OLR before the perturbation are
```
OLRterms
```
After the perturbation we have
```
delta_epsilon = sympy.symbols('delta_epsilon')
OLRterms_pert = OLRterms.subs(epsilon, epsilon+delta_epsilon)
OLRterms_pert
```
Let's take the difference
```
deltaOLR = OLRterms_pert - OLRterms
deltaOLR
```
To make things simpler, we will neglect the terms in $\delta_\epsilon^2$. This is perfectly reasonably because we are dealing with **small perturbations** where $\delta_\epsilon << \epsilon$.
Telling `sympy` to set the quadratic terms to zero gives us
```
deltaOLR_linear = sympy.expand(deltaOLR).subs(delta_epsilon**2, 0)
deltaOLR_linear
```
Recall that the three terms are the contributions to the OLR from the three different levels. In this case, the **changes** in those contributions after adding more absorbers.
Now let's divide through by $\delta_\epsilon$ to get the normalized change in OLR per unit change in absorptivity:
```
deltaOLR_per_deltaepsilon = \
sympy.simplify(deltaOLR_linear / delta_epsilon)
deltaOLR_per_deltaepsilon
```
Now look at the **sign** of each term. Recall that $0 < \epsilon < 1$. **Which terms in the OLR go up and which go down?**
**THIS IS VERY IMPORTANT, SO STOP AND THINK ABOUT IT.**
The contribution from the **surface** must **decrease**, while the contribution from the **top layer** must **increase**.
**When we add absorbers, the average level of emission goes up!**
### "Radiative forcing" is the change in radiative flux at TOA after adding absorbers
In this model, only the longwave flux can change, so we define the radiative forcing as
$$ R = - \delta OLR $$
(with the minus sign so that $R$ is positive when the climate system is gaining extra energy).
We just worked out that whenever we add some extra absorbers, the emissions to space (on average) will originate from higher levels in the atmosphere.
What does this mean for OLR? Will it increase or decrease?
To get the answer, we just have to sum up the three contributions we wrote above:
```
R = -sum(deltaOLR_per_deltaepsilon)
R
```
Is this a positive or negative number? The key point is this:
**It depends on the temperatures, i.e. on the lapse rate.**
### Greenhouse effect for an isothermal atmosphere
Stop and think about this question:
If the **surface and atmosphere are all at the same temperature**, does the OLR go up or down when $\epsilon$ increases (i.e. we add more absorbers)?
Understanding this question is key to understanding how the greenhouse effect works.
#### Let's solve the isothermal case
We will just set $T_s = T_0 = T_1$ in the above expression for the radiative forcing.
```
R.subs([(T_0, T_s), (T_1, T_s)])
```
which then simplifies to
```
sympy.simplify(R.subs([(T_0, T_s), (T_1, T_s)]))
```
#### The answer is zero
For an isothermal atmosphere, there is **no change** in OLR when we add extra greenhouse absorbers. Hence, no radiative forcing and no greenhouse effect.
Why?
The level of emission still must go up. But since the temperature at the upper level is the **same** as everywhere else, the emissions are exactly the same.
### The radiative forcing (change in OLR) depends on the lapse rate!
For a more realistic example of radiative forcing due to an increase in greenhouse absorbers, we can substitute in our tuned values for temperature and $\epsilon$.
We'll express the answer in W m$^{-2}$ for a 1% increase in $\epsilon$.
The three components of the OLR change are
```
deltaOLR_per_deltaepsilon.subs(tuned) * 0.01
```
And the net radiative forcing is
```
R.subs(tuned) * 0.01
```
So in our example, **the OLR decreases by 2.2 W m$^{-2}$**, or equivalently, the radiative forcing is +2.2 W m$^{-2}$.
What we have just calculated is this:
*Given the observed lapse rates, a small increase in absorbers will cause a small decrease in OLR.*
The greenhouse effect thus gets stronger, and energy will begin to accumulate in the system -- which will eventually cause temperatures to increase as the system adjusts to a new equilibrium.
____________
<a id='section6'></a>
## 6. Radiative equilibrium in the 2-layer grey gas model
____________
In the previous section we:
- made no assumptions about the processes that actually set the temperatures.
- used the model to calculate radiative fluxes, **given observed temperatures**.
- stressed the importance of knowing the lapse rates in order to know how an increase in emission level would affect the OLR, and thus determine the radiative forcing.
A key question in climate dynamics is therefore this:
**What sets the lapse rate?**
It turns out that lots of different physical processes contribute to setting the lapse rate.
Understanding how these processes acts together and how they change as the climate changes is one of the key reasons for which we need more complex climate models.
For now, we will use our prototype greenhouse model to do the most basic lapse rate calculation: the **radiative equilibrium temperature**.
We assume that
- the only exchange of energy between layers is longwave radiation
- equilibrium is achieved when the **net radiative flux convergence** in each layer is zero.
### Compute the radiative flux convergence
First, the **net upwelling flux** is just the difference between flux up and flux down:
```
# Upwelling and downwelling beams as matrices
U = sympy.Matrix([U_0, U_1, U_2])
D = sympy.Matrix([D_0, D_1, D_2])
# Net flux, positive up
F = U-D
F
```
#### Net absorption is the flux convergence in each layer
(difference between what's coming in the bottom and what's going out the top of each layer)
```
# define a vector of absorbed radiation -- same size as emissions
A = E.copy()
# absorbed radiation at surface
A[0] = F[0]
# Compute the convergence
for n in range(2):
A[n+1] = -(F[n+1]-F[n])
A
```
#### Radiative equilibrium means net absorption is ZERO in the atmosphere
The only other heat source is the **shortwave heating** at the **surface**.
In matrix form, here is the system of equations to be solved:
```
radeq = sympy.Equality(A, sympy.Matrix([(1-alpha)*Q, 0, 0]))
radeq
```
Just as we did for the 1-layer model, it is helpful to rewrite this system using the definition of the **emission temperture** $T_e$
$$ (1-\alpha) Q = \sigma T_e^4 $$
```
radeq2 = radeq.subs([((1-alpha)*Q, sigma*T_e**4)])
radeq2
```
In this form we can see that we actually have a **linear system** of equations for a set of variables $T_s^4, T_0^4, T_1^4$.
We can solve this matrix problem to get these as functions of $T_e^4$.
```
# Solve for radiative equilibrium
fourthpower = sympy.solve(radeq2, [T_s**4, T_1**4, T_0**4])
fourthpower
```
This produces a dictionary of solutions for the fourth power of the temperatures!
A little manipulation gets us the solutions for temperatures that we want:
```
# need the symbolic fourth root operation
from sympy.simplify.simplify import nthroot
fourthpower_list = [fourthpower[key] for key in [T_s**4, T_0**4, T_1**4]]
solution = sympy.Matrix([nthroot(item,4) for item in fourthpower_list])
# Display result as matrix equation!
T = sympy.Matrix([T_s, T_0, T_1])
sympy.Equality(T, solution)
```
In more familiar notation, the radiative equilibrium solution is thus
\begin{align}
T_s &= T_e \left( \frac{2+\epsilon}{2-\epsilon} \right)^{1/4} \\
T_0 &= T_e \left( \frac{1+\epsilon}{2-\epsilon} \right)^{1/4} \\
T_1 &= T_e \left( \frac{ 1}{2 - \epsilon} \right)^{1/4}
\end{align}
Plugging in the tuned value $\epsilon = 0.586$ gives
```
Tsolution = solution.subs(tuned)
# Display result as matrix equation!
sympy.Equality(T, Tsolution)
```
Now we just need to know the Earth's emission temperature $T_e$!
(Which we already know is about 255 K)
```
# Here's how to calculate T_e from the observed values
sympy.solve(((1-alpha)*Q - sigma*T_e**4).subs(tuned), T_e)
# Need to unpack the list
Te_value = sympy.solve(((1-alpha)*Q - sigma*T_e**4).subs(tuned), T_e)[0]
Te_value
```
#### Now we finally get our solution for radiative equilibrium
```
# Output 4 significant digits
Trad = sympy.N(Tsolution.subs([(T_e, Te_value)]), 4)
sympy.Equality(T, Trad)
```
Compare these to the values we derived from the **observed lapse rates**:
```
sympy.Equality(T, T.subs(tuned))
```
The **radiative equilibrium** solution is substantially **warmer at the surface** and **colder in the lower troposphere** than reality.
This is a very general feature of radiative equilibrium, and we will see it again very soon in this course.
____________
<a id='section7'></a>
## 7. Summary
____________
## Key physical lessons
- Putting a **layer of longwave absorbers** above the surface keeps the **surface substantially warmer**, because of the **backradiation** from the atmosphere (greenhouse effect).
- The **grey gas** model assumes that each layer absorbs and emits a fraction $\epsilon$ of its blackbody value, independent of wavelength.
- With **incomplete absorption** ($\epsilon < 1$), there are contributions to the OLR from every level and the surface (there is no single **level of emission**)
- Adding more absorbers means that **contributions to the OLR** from **upper levels** go **up**, while contributions from the surface go **down**.
- This upward shift in the weighting of different levels is what we mean when we say the **level of emission goes up**.
- The **radiative forcing** caused by an increase in absorbers **depends on the lapse rate**.
- For an **isothermal atmosphere** the radiative forcing is zero and there is **no greenhouse effect**
- The radiative forcing is positive for our atmosphere **because tropospheric temperatures tends to decrease with height**.
- Pure **radiative equilibrium** produces a **warm surface** and **cold lower troposphere**.
- This is unrealistic, and suggests that crucial heat transfer mechanisms are missing from our model.
### And on the Python side...
Did we need `sympy` to work all this out? No, of course not. We could have solved the 3x3 matrix problems by hand. But computer algebra can be very useful and save you a lot of time and error, so it's good to invest some effort into learning how to use it.
Hopefully these notes provide a useful starting point.
### A follow-up assignment
You are now ready to tackle [Assignment 5](../Assignments/Assignment05 -- Radiative forcing in a grey radiation atmosphere.ipynb), where you are asked to extend this grey-gas analysis to many layers.
For more than a few layers, the analytical approach we used here is no longer very useful. You will code up a numerical solution to calculate OLR given temperatures and absorptivity, and look at how the lapse rate determines radiative forcing for a given increase in absorptivity.
<div class="alert alert-success">
[Back to ATM 623 notebook home](../index.ipynb)
</div>
____________
## Version information
____________
```
%load_ext version_information
%version_information sympy
```
____________
## Credits
The author of this notebook is [Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html), University at Albany.
It was developed in support of [ATM 623: Climate Modeling](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/), a graduate-level course in the [Department of Atmospheric and Envionmental Sciences](http://www.albany.edu/atmos/index.php)
Development of these notes and the [climlab software](https://github.com/brian-rose/climlab) is partially supported by the National Science Foundation under award AGS-1455071 to Brian Rose. Any opinions, findings, conclusions or recommendations expressed here are mine and do not necessarily reflect the views of the National Science Foundation.
____________
| true |
code
| 0.664241 | null | null | null | null |
|
## Model 1: Policy simulation
The objective of this model-based simulation is to analyse the impact of policy, technology, and commodity changes on consumer price inflation in selected countries. The simulation environment is learnt from real data, after which simulations using synthetic data are used to do policy analysis by manipulating a number of selected variables such as government debt, cellular subscription, gdp growth, and real interest rates in the synthetic data. A secondary purpose of the simulation model is to identify and map the interactions between world-level and country-level indicator variables.
#### Features
------------
Multivariate human and technological development indicator timeseries
1. aggregated across nations using hand-crafted rules.
2. raw, collected on a per-country level.
#### Labels
----------
Consumer price inflation levels for the following countries:
* Singapore
* Switzerland
* Netherlands
* Japan
* France
* United States
* China
* India
* Brazil
* Colombia
* Indonesia
* Senegal
* Ghana
#### Training
------------
Training is done on a feature - single country basis.
### Load and prepare the data
```
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
from tensorflow import keras
%matplotlib inline
warnings.filterwarnings('ignore')
pd.options.display.float_format = '{:20,.4f}'.format
sns.set_style("whitegrid")
sns.set_palette("colorblind")
country = 'Colombia'
country_labels = ['Brazil', 'China', 'Colombia', 'France', 'Ghana', 'India', 'Indonesia', 'Japan', 'Netherlands',
'Senegal', 'Singapore', 'Switzerland', 'United States']
assert country in country_labels
```
#### Load and combine the features and labels
```
features_df = pd.read_csv('features/m_one/world_aggregate.csv', sep=';', header=0)
labels_df = pd.read_csv('features/m_one/labels_interpolated.csv', sep=';', header=0)
features_df.head()
labels_df.head()
combined_df = pd.concat([features_df, labels_df.drop(columns=['date'])], axis=1)
combined_df.head()
fig, ax = plt.subplots(figsize=(15,7))
[sns.lineplot(x='date', y=c, markers=True, ax=ax, label=c, data=combined_df) for c in list(filter(lambda x: x not in ['Brazil', 'Indonesia', 'Ghana'], country_labels))]
xticks=ax.xaxis.get_major_ticks()
for i in range(len(xticks)):
if i % 12 == 1:
xticks[i].set_visible(True)
else:
xticks[i].set_visible(False)
ax.set_xticklabels(combined_df['date'], rotation=45);
combined_df.columns
```
### Prepare the country features
```
base_feature_df = combined_df[['bank capital to assets ratio', 'bank nonperforming loans', 'cereal yield',
'energy imports', 'food exports', 'high-tech exports', 'inflation',
'lending interest rate', 'life expectancy', 'population density', 'real interest rate',
'broad money', 'exports of goods and services', 'gross domestic savings',
'high-tech value added', 'household consumption expenditure',
'imports of goods and services', 'listed companies', 'manufacturing value added',
'r and d spend', 'services trade', 'trade', 'government debt service',
'government interest payments external debt', 'government tax revenue', 'birth deaths',
'broadband subscriptions', 'electricity access', 'co2 emissions',
'electricity consumption', 'mobile subscriptions', 'newborns', 'overweight',
'rural population', 'unemployed', 'urban population', 'workers', country]]
base_feature_df.to_csv('features/m_one/combined_%s.csv' % country.lower(), sep=',', index=False)
base_feature_df['label'] = base_feature_df[country].shift(periods=1)
base_df = base_feature_df.drop(country, axis=1).fillna(0.00);
num_obs = len(base_df)
num_cols = len(base_df.columns)
num_features = len(base_df.columns) - 1
```
### Model iterations
---------------------
### Exploration 1
**Multivariate LSTM** fitted on the real data, see https://machinelearningmastery.com/multivariate-time-series-forecasting-lstms-keras/
- Activation function: Leaky ReLU.
- Loss function: mean squared error.
- Optimizer: adam.
- Num observations source dataset: 684 (using lagshift, 1960-2016 inclusive monthly)
- Num sequences (@ sequence length 6): 116.
- Batch size: 4-8 sequences (although `size=48` would lead to more stable training)
```
from keras import Sequential
from keras.layers import LSTM, Dense, LeakyReLU
from keras.optimizers import Adam
from sklearn.metrics import mean_squared_error
lstm_params = {
'sequence_length': 4,
'batch_size': 8,
'num_epochs': 600,
'num_units': 128,
'lrelu_alpha': 0.3
}
```
#### LSTM features
```
features = []
labels = []
for i in range(int(num_obs / lstm_params['sequence_length'])):
labels_df = base_df['label']
labels.append(labels_df[i:(i+lstm_params['sequence_length'])].values[-1:])
features.append(base_df[i:(i+lstm_params['sequence_length'])].values)
lstm_train_X = np.asarray(features[0:100])
lstm_train_X = lstm_train_X.reshape((lstm_train_X.shape[0], lstm_params['sequence_length'], num_cols))
lstm_train_y = np.asarray(labels[0:100])
lstm_train_y = lstm_train_y.reshape((lstm_train_y.shape[0]))
lstm_test_X = np.asarray(features[100:])
lstm_test_X = lstm_test_X.reshape((lstm_test_X.shape[0], lstm_params['sequence_length'], num_cols))
lstm_test_y = np.asarray(labels[100:])
lstm_test_y = lstm_test_y.reshape((lstm_test_y.shape[0]))
X = np.asarray(features)
X = X.reshape((X.shape[0], lstm_params['sequence_length'], num_cols))
y = np.asarray(labels)
y = y.reshape((y.shape[0], 1))
print('X: %s, y: %s' % (X.shape, y.shape))
```
#### Model: LSTM
```
model = Sequential()
model.add(LSTM(lstm_params['num_units'], input_shape=(lstm_params['sequence_length'], num_cols)))
model.add(Dense(1, activation=LeakyReLU(alpha=lstm_params['lrelu_alpha'])))
model.compile(loss='mse', optimizer='adam')
model.summary()
train_run = model.fit(lstm_train_X, lstm_train_y, epochs=lstm_params['num_epochs'], batch_size=lstm_params['batch_size'])
plt.plot(train_run.history['loss'], label='train')
plt.legend()
plt.show()
```
##### Evaluate model performance
```
model.evaluate(lstm_test_X, lstm_test_y)
yhat = model.predict(lstm_test_X)
plt.figure(figsize=(15,7))
plt.plot(lstm_test_y, label='observed')
plt.plot(yhat, label='predicted')
plt.legend()
plt.title('Observed versus predicted values for consumer price inflation in %s' % country)
plt.show()
print('rmse: %s\nmean observed: %s\nmean predicted: %s' % (np.sqrt(mean_squared_error(lstm_test_y, yhat)),
np.mean(lstm_test_y), np.mean(yhat)))
```
## Exploration 2
--------------------
**GAN** to generate training data, **LSTM** trained on generated data validated on the real data.
### Conditional GAN for policy-constrained timeseries generation
See https://arxiv.org/pdf/1706.02633.pdf.
```
from keras.models import Sequential, Model
from keras.layers import Input
from keras.optimizers import Adam
from sklearn.metrics import mean_squared_error
gan_df = base_df
gan_df.shape
gan_cols = gan_df.shape[1]
gan_params = {
'num_epochs': 1500,
'save_interval': 100,
'sequence_length': 6,
'num_variables': gan_cols,
'batch_size': 64,
'lr': 0.0001
}
generator_params = {
'noise_sigma': 0.3,
'lstm_units': 128,
'lstm_dropout': 0.4,
'gru_units': 64,
'lr': 0.0001
}
discriminator_params = {
'bi_lstm_units': 256,
'dropout_rate': 0.4,
'lr': 0.0001
}
```
#### GAN input sequences
The collated World Bank and IMF data used as input for the data generator and to validate the model trained on generated data.
```
gan_features = []
gan_labels = []
for i in range(int(num_obs / gan_params['sequence_length'])):
gan_labels_df = gan_df['label']
gan_labels.append(gan_labels_df[i:(i+gan_params['sequence_length'])].values[-1:])
gan_features.append(gan_df[i:(i+gan_params['sequence_length'])].values)
real = np.asarray(gan_features)
real = real.reshape((real.shape[0], gan_params['sequence_length'], gan_cols))
real.shape
```
#### Generator
```
from keras.layers import GaussianNoise, LSTM, Dropout, BatchNormalization, Dense, LocallyConnected2D, GRU, Reshape
def build_encoder(params):
gshape = params['sequence_length'], params['num_variables']
inputs = Input(shape=(gshape))
e = Sequential(name='encoder')
e.add(LSTM(params['lstm_units'], input_shape=(gshape), return_sequences=True))
e.add(Dropout(params['lstm_dropout']))
e.add(GaussianNoise(stddev=params['noise_sigma']))
e.add(BatchNormalization(axis=2, momentum=0.8, epsilon=0.01))
e.add(Dense(params['num_variables'], activation='relu'))
e.summary()
return Model(inputs, e(inputs))
encoder = build_encoder({**gan_params, **generator_params})
def build_generator(params):
gshape = params['sequence_length'], params['num_variables']
inputs = Input(shape=(gshape))
g = Sequential(name='generator')
g.add(GRU(params['gru_units'], input_shape=(gshape), return_sequences=True))
g.add(Dense(params['num_variables'], activation='softmax'))
g.add(Reshape(target_shape=(gshape)))
g.summary()
return Model(inputs, g(inputs))
generator = build_generator({**gan_params, **generator_params})
```
#### Discriminator
```
from keras.layers import Bidirectional, LSTM, Dense, concatenate, Flatten
def build_discriminator(params):
dshape = params['sequence_length'], params['num_variables']
batch_shape = params['batch_size'], params['sequence_length'], params['num_variables']
real = Input(shape=(dshape))
generated = Input(shape=(dshape))
inputs = concatenate([generated, real], axis=1)
d = Sequential(name='discriminator')
d.add(Bidirectional(LSTM(params['bi_lstm_units']), batch_input_shape=(batch_shape)))
d.add(Dropout(params['dropout_rate']))
d.add(Dense(1, activation='sigmoid'))
d.summary()
return Model([generated, real], d(inputs))
discriminator = build_discriminator({**gan_params, **discriminator_params})
discriminator.compile(loss='binary_crossentropy', optimizer=Adam(lr=discriminator_params['lr']), metrics=['accuracy'])
```
#### GAN
Bidirectional generative adversarial network, viz https://arxiv.org/abs/1605.09782.
```
def build_gan(encoder, generator, discriminator, params):
ganshape = params['sequence_length'], params['num_variables']
discriminator.trainable = False
noise = Input(shape=(ganshape))
generated = generator(noise)
data = Input(shape=(ganshape))
encoded = encoder(data)
fake = discriminator([noise, generated])
real = discriminator([encoded, data])
gan = Model([noise, data], [fake, real], name='gan')
gan.summary()
return gan
gan = build_gan(encoder, generator, discriminator, gan_params)
gan.compile(loss=['kullback_leibler_divergence', 'kullback_leibler_divergence'], optimizer=Adam(lr=generator_params['lr']), metrics=['mse', 'mse'])
%%time
def train_gan(real, batch_size, params):
g_metrics = []
d_real_metrics = []
d_synth_metrics = []
reals = np.ones(batch_size)
synths = np.zeros(batch_size)
for i in range(params['num_epochs']):
# create input of real and synthetic data
random_index = np.random.randint(0, len(real) - batch_size)
half_real = real[random_index:int(random_index + batch_size)]
half_synth = np.random.normal(-1.0, 1.0, size=[batch_size, params['sequence_length'], real.shape[2]])
# apply generator and encoder
generated = generator.predict(half_synth)
encoded = encoder.predict(half_real)
# train discriminator
d_real = discriminator.train_on_batch([encoded, half_real], reals)
d_synth = discriminator.train_on_batch([half_synth, generated], synths)
# train gan
gen_ = gan.train_on_batch([half_synth, half_real], [reals, synths])
if i % 100 == 0:
print('Epoch %s losses: discriminator real: %.4f%%, discriminator synth: %.4f%%, generator: %.4f%%' %
(i, d_real[0], d_synth[0], gen_[0]))
d_real_metrics.append(d_real)
d_synth_metrics.append(d_synth)
g_metrics.append(gen_)
return d_real_metrics, d_synth_metrics, g_metrics
d_r_metrics, d_s_metrics, g_metrics = train_gan(real, gan_params['batch_size'], gan_params)
plt.figure(figsize=(15,7))
plt.plot([metrics[0] for metrics in d_r_metrics], label='discriminator loss on reals')
plt.plot([metrics[0] for metrics in d_s_metrics], label='discriminator loss on synths')
plt.plot([metrics[0] for metrics in g_metrics], label='generator loss')
plt.legend()
plt.title('GAN losses')
plt.show()
plt.figure(figsize=(15,7))
plt.plot([metrics[1] for metrics in d_r_metrics], label='discriminator accuracy reals')
plt.plot([metrics[1] for metrics in d_s_metrics], label='discriminator accuracy synths')
plt.plot([metrics[1] for metrics in g_metrics], label='generator mean average error')
plt.legend()
plt.title('GAN performance metrics')
plt.show()
generated_y = generator.predict(np.random.rand(num_obs, gan_params['sequence_length'], gan_cols))[:,-1,-1]
gan_y = gan_df['label'].values
plt.figure(figsize=(15,7))
plt.plot(gan_y, label='observed cpi')
plt.plot(generated_y, label='gan-generated cpi')
plt.legend()
plt.title('Observed versus GAN-generated values for consumer price inflation in %s' % country)
plt.show()
print('rmse: %s\nmean observed: %s\nmean generated: %s' % (np.sqrt(mean_squared_error(gan_y, generated_y)),
np.mean(gan_y), np.mean(generated_y)))
```
## Simulation 1
Question: what happens to consumer price inflation in the long run if the government decides to borrow more money?
##### Simulation parameters
- central government debt
- time horizon
##### Environment variables
- world economy: selected generated macroeconomic indicators
- country economy: selected generated country-level indicators
- hybrid: interaction country x world
## Exploration 3
--------------------
**Sequence transformer network** to generate training data, **LSTM** trained on generated data validated on the real data. See https://arxiv.org/abs/1808.06725
| true |
code
| 0.591074 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/camminady/sPYnning/blob/master/visworld_colab.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!pip install randomcolor
import randomcolor # see: https://pypi.org/project/randomcolor/
!pip install gif
import gif # see https://github.com/maxhumber/gif
!pip install reverse_geocoder
import reverse_geocoder as rg # see ttps://pypi.org/project/reverse_geocoder/
import numpy as np
# plotting
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import cm, colors
# 3d
!sudo apt-get install libgeos-dev
!sudo pip3 install https://github.com/matplotlib/basemap/archive/master.zip
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
# everything below is used to color the globe
from mpl_toolkits.basemap import Basemap
import json
import requests
from numpy import loadtxt, degrees, arcsin, arctan2, sort, unique
from mpl_toolkits.basemap import Basemap
import reverse_geocoder as rg
import randomcolor
def domino(lol):
# Takes a list (length n) of lists (length 2)
# and returns a list of indices order,
# such that lol[order[i]] and lol[order[i+1]]
# have at least one element in common.
# If that is not possible, multiple
# domino chains will be created.
# This works in a greedy way.
n = len(lol)
order = [0] # Greedy
link = lol[0][-1]
links = [lol[0][0],lol[0][1]]
while len(order)<n:
for i in [j for j in range(n) if not j in order]:
if link in lol[i]: # They connect
order.append(i) # Save the id of the "stone"
link = lol[i][0] if not(lol[i][0]==link) else lol[i][1] # The new link is the other element
links.append(link)
break
return order,links[:-1]
def getpatches(color,quadrature):
xyz,neighbours,triangles = quadrature["xyz"], quadrature["neighbours"], quadrature["triangles"]
nq = len(color)
patches = []
for center in range(nq):
lol = [] # list of lists
for i in neighbours[center,:]:
if i>-1:
lol.append(list(sort(triangles[i,triangles[i,:] != center])))
order,links = domino(lol)
neighx = [xyz[j,0] for j in links]
neighy = [xyz[j,1] for j in links]
neighz = [xyz[j,2] for j in links]
# Get the actual hexagon that surrounds a center point
x = []
y = []
z = []
for i in range(len(order)):
x.append((xyz[center,0]+neighx[i]) / 2)
x.append((xyz[center,0]+neighx[i]+neighx[(i+1)%len(order)])/3)
y.append((xyz[center,1]+neighy[i]) / 2)
y.append((xyz[center,1]+neighy[i]+neighy[(i+1)%len(order)])/3)
z.append((xyz[center,2]+neighz[i]) / 2)
z.append((xyz[center,2]+neighz[i]+neighz[(i+1)%len(order)])/3)
verts = [list(zip(x,y,z))]
patches.append(verts[0])
return patches
def getquadrature(nq):
prefix ="https://raw.githubusercontent.com/camminady/sPYnning/master/"
quadrature = {}
quadrature["nq"] = nq
quadrature["xyz"] = loadtxt(f"{prefix}quadrature/{nq}/points.txt")
quadrature["weights"] = loadtxt(f"{prefix}quadrature/{nq}/weights.txt")
quadrature["neighbours"] = loadtxt(f"{prefix}quadrature/{nq}/neighbours.txt",dtype=int)-1 # julia starts at 1
quadrature["triangles"] = loadtxt(f"{prefix}quadrature/{nq}/triangles.txt",dtype=int)-1 # julia starts at 1
# Also convert to latitute, longitude
quadrature["lat"] = degrees(arcsin(quadrature["xyz"][:,2]/1))
quadrature["lon"] = degrees(arctan2(quadrature["xyz"][:,1], quadrature["xyz"][:,0]))
return quadrature
def color_land(quadrature):
bm = Basemap()
colors = []
for i,(ypt, xpt) in enumerate(zip(quadrature["lat"],quadrature["lon"])):
land = (bm.is_land(xpt,ypt))
colors.append("tab:green" if land else "tab:blue")
return colors
def color_country(quadrature):
# uses reverse_geocoder
results = rg.search([(la,lo) for la,lo in zip(quadrature["lat"],quadrature["lon"])]) # default mode = 2
countries = []
for i in range(len(results)):
c = results[i]["cc"]
countries.append(c)
nunique = len(unique(countries))
raco = randomcolor.RandomColor()
randomcolors = raco.generate(luminosity="dark", count=nunique) # options: https://github.com/kevinwuhoo/randomcolor-py
colordict = dict(zip(unique(countries),randomcolors))
colorland = color_land(quadrature) # so we can color the ocean also in "tab:blue"
colorcountries = [colordict[country] if colorland[i]!="tab:blue" else "tab:blue" for i,country in enumerate(countries) ]
return colorcountries
@gif.frame
def myplot(color,quadrature, filename, angle=30):
patches = getpatches(color,quadrature) # Get the hexagons
fig = plt.figure(figsize=plt.figaspect(1)*2,constrained_layout=False)
ax = fig.gca(projection='3d')
# Visualize each hexagon, that is given in "color". A color is computed
# for the center of the hexagon and then applied for the full hexagon
ax.add_collection3d(Poly3DCollection(patches,facecolor = color,linewidth=0.1,edgecolor=color))
# Some styling
l = 0.6
plt.axis("off")
ax.set_xlim([-l,l]), ax.set_ylim([-l,l]),ax.set_zlim([-l,l])
ax.set_xticks([]), ax.set_yticks([]), ax.set_zticks([])
ax.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
ax.w_yaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
ax.w_zaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
for spine in ax.spines.values():
spine.set_visible(False)
plt.tight_layout()
ax.view_init(30, angle)
fig.savefig(filename)
# pick the number of cells on the globe from this list
# [92, 492, 1212, 2252, 3612, 5292, 7292, 9612, 12252, 15212]
nq = 2252
quadrature = getquadrature(nq)
# plot the earth
colors = color_land(quadrature)
myplot(colors,quadrature,"earth.png")
# higher resolution to plot countries
nq = 7292
quadrature = getquadrature(nq)
colors = color_country(quadrature)
myplot(colors,quadrature,"earth_country.png")
# creating a gif
nq = 7292
quadrature = getquadrature(nq)
colors = color_land(quadrature)
frames = []
nframes = 20 # the more, the slower
for i,angle in enumerate(np.linspace(0,360,nframes)[:-1]):
print(i,end=",")
frames.append(myplot(colors,quadrature,"tmp.png",angle=angle))
gif.save(frames,"spinning_earth.gif")
```
| true |
code
| 0.421671 | null | null | null | null |
|
## Image classification vs Object detection vs Image segmentation
<img src="https://media.discordapp.net/attachments/763819251249184789/857822034045567016/image.png">
<br><br>
## Image annotation: assigning labels
<br>
## Popular datasets: ImageNet, COCO, Google Open Images
## Tensorflow hub has pre-train models
## Sliding window approch for object detection (Single Shot MultiBox Detector)
- ### Keep on sliding a smaller window on the test image until find a match
- ### Trial and error to find the right window size
- ### Cons: too much calculation & bounding box shape maybe not accurate
## *Therefore there are faster algorithms:*
## R CNN (Retina-Net) --> Fast R CNN --> Faster R CNN --> YOLO (you only look once)
# YOLO
<img src="https://media.discordapp.net/attachments/763819251249184789/857843667619676190/image.png?width=1845&height=1182" width=700>
<br>
- ### Divide a image to multiple grid cells (usually 19 x 19)
- ### An Object is in a specific cell only when the center coords of the box lie in that cell
- ### Eliminates the bounding boxes using IoU (Intersection over Union: Overlapping area) to get the highest possibility one
- ### Duplicate step # 3 until only 1 bounding box left (Non max supression)
- ### If multiple objects belongs to one cell, we concatenate ancher boxes together (2 vector of size 8 --> 1 vector of size 16)
<br>
### X_train: <br>
image<br><br>
### y_train:
| Name | Explanation |
|:---:|:---:|
| P | Probability of a object in the image |
| Bx | Center of box X coord |
| By | Center of box Y coord |
| Bw | Width |
| Bh | Height |
| C1 | Is the object belongs to class 1? |
| C2 | Is the object belongs to class 2? |
```
# A simple YOLO v5 demo
import cv2
import pathlib
import numpy as np
from PIL import Image
from yolov5 import YOLOv5
from matplotlib import pyplot as plt
%matplotlib inline
# set model params
model_path = f"{os.path.dirname(os.path.abspath('__file__'))}/yolov5/weights/yolov5s.pt" # it automatically downloads yolov5s model to given path
device = "cuda" # or "cpu"
# init yolov5 model
yolov5 = YOLOv5(model_path, device)
# load images
image1 = 'https://github.com/ultralytics/yolov5/raw/master/data/images/zidane.jpg'
image2 = 'https://github.com/ultralytics/yolov5/blob/master/data/images/bus.jpg'
# perform inference
results = yolov5.predict(image1)
# perform inference with larger input size
results = yolov5.predict(image1, size=1280)
# perform inference with test time augmentation
results = yolov5.predict(image1, augment=True)
# perform inference on multiple images
# results = yolov5.predict([image1, image2], size=1280, augment=True)
# parse results
predictions = results.pred[0]
boxes = predictions[:, :4] # x1, x2, y1, y2
scores = predictions[:, 4]
categories = predictions[:, 5]
# show detection bounding boxes on image
# plt.imshow(np.reshape(results.imgs, (720, 1280, 3))), results.pred
def plot_one_box(x, im, color=(128, 128, 128), label=None, line_thickness=3):
# Plots one bounding box on image 'im' using OpenCV
assert im.data.contiguous, 'Image not contiguous. Apply np.ascontiguousarray(im) to plot_on_box() input image.'
tl = line_thickness or round(0.002 * (im.shape[0] + im.shape[1]) / 2) + 1 # line/font thickness
c1, c2 = (int(x[0]), int(x[1])), (int(x[2]), int(x[3]))
cv2.rectangle(im, c1, c2, color, thickness=tl, lineType=cv2.LINE_AA)
if label:
tf = max(tl - 1, 1) # font thickness
t_size = cv2.getTextSize(label, 0, fontScale=tl / 3, thickness=tf)[0]
c2 = c1[0] + t_size[0], c1[1] - t_size[1] - 3
cv2.rectangle(im, c1, c2, color, -1, cv2.LINE_AA) # filled
cv2.putText(im, label, (c1[0], c1[1] - 2), 0, tl / 3, [225, 255, 255], thickness=tf, lineType=cv2.LINE_AA)
class Colors:
# Ultralytics color palette https://ultralytics.com/
def __init__(self):
# hex = matplotlib.colors.TABLEAU_COLORS.values()
hex = ('FF3838', 'FF9D97', 'FF701F', 'FFB21D', 'CFD231', '48F90A', '92CC17', '3DDB86', '1A9334', '00D4BB',
'2C99A8', '00C2FF', '344593', '6473FF', '0018EC', '8438FF', '520085', 'CB38FF', 'FF95C8', 'FF37C7')
self.palette = [self.hex2rgb('#' + c) for c in hex]
self.n = len(self.palette)
def __call__(self, i, bgr=False):
c = self.palette[int(i) % self.n]
return (c[2], c[1], c[0]) if bgr else c
@staticmethod
def hex2rgb(h): # rgb order (PIL)
return tuple(int(h[1 + i:1 + i + 2], 16) for i in (0, 2, 4))
colors = Colors()
for i, (im, pred) in enumerate(zip(results.imgs, results.pred)):
str = f'image {i + 1}/{len(results.pred)}: {im.shape[0]}x{im.shape[1]} '
if pred is not None:
for c in pred[:, -1].unique():
n = (pred[:, -1] == c).sum() # detections per class
str += f"{n} {results.names[int(c)]}{'s' * (n > 1)}, " # add to string
for *box, conf, cls in pred: # xyxy, confidence, class
label = f'{results.names[int(cls)]} {conf:.2f}'
plot_one_box(box, im, label=label, color=colors(cls))
im = Image.fromarray(im.astype(np.uint8)) if isinstance(im, np.ndarray) else im # from np
plt.imshow(im)
```
| true |
code
| 0.675417 | null | null | null | null |
|
# Modeling and Simulation in Python
Chapter 6
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import functions from the modsim.py module
from modsim import *
from pandas import read_html
```
### Code from the previous chapter
```
filename = 'data/World_population_estimates.html'
tables = read_html(filename, header=0, index_col=0, decimal='M')
table2 = tables[2]
table2.columns = ['census', 'prb', 'un', 'maddison',
'hyde', 'tanton', 'biraben', 'mj',
'thomlinson', 'durand', 'clark']
un = table2.un / 1e9
un.head()
census = table2.census / 1e9
census.head()
t_0 = get_first_label(census)
t_end = get_last_label(census)
elapsed_time = t_end - t_0
p_0 = get_first_value(census)
p_end = get_last_value(census)
total_growth = p_end - p_0
annual_growth = total_growth / elapsed_time
```
### System objects
We can rewrite the code from the previous chapter using system objects.
```
system = System(t_0=t_0,
t_end=t_end,
p_0=p_0,
annual_growth=annual_growth)
```
And we can encapsulate the code that runs the model in a function.
```
def run_simulation1(system):
"""Runs the constant growth model.
system: System object
returns: TimeSeries
"""
results = TimeSeries()
results[system.t_0] = system.p_0
for t in linrange(system.t_0, system.t_end):
results[t+1] = results[t] + system.annual_growth
return results
```
We can also encapsulate the code that plots the results.
```
def plot_results(census, un, timeseries, title):
"""Plot the estimates and the model.
census: TimeSeries of population estimates
un: TimeSeries of population estimates
timeseries: TimeSeries of simulation results
title: string
"""
plot(census, ':', label='US Census')
plot(un, '--', label='UN DESA')
plot(timeseries, color='gray', label='model')
decorate(xlabel='Year',
ylabel='World population (billion)',
title=title)
```
Here's how we run it.
```
results = run_simulation1(system)
plot_results(census, un, results, 'Constant growth model')
```
## Proportional growth
Here's a more realistic model where the number of births and deaths is proportional to the current population.
```
def run_simulation2(system):
"""Run a model with proportional birth and death.
system: System object
returns: TimeSeries
"""
results = TimeSeries()
results[system.t_0] = system.p_0
for t in linrange(system.t_0, system.t_end):
births = system.birth_rate * results[t]
deaths = system.death_rate * results[t]
results[t+1] = results[t] + births - deaths
return results
```
I picked a death rate that seemed reasonable and then adjusted the birth rate to fit the data.
```
system.death_rate = 0.01
system.birth_rate = 0.027
```
Here's what it looks like.
```
results = run_simulation2(system)
plot_results(census, un, results, 'Proportional model')
savefig('figs/chap03-fig03.pdf')
```
The model fits the data pretty well for the first 20 years, but not so well after that.
### Factoring out the update function
`run_simulation1` and `run_simulation2` are nearly identical except the body of the loop. So we can factor that part out into a function.
```
def update_func1(pop, t, system):
"""Compute the population next year.
pop: current population
t: current year
system: system object containing parameters of the model
returns: population next year
"""
births = system.birth_rate * pop
deaths = system.death_rate * pop
return pop + births - deaths
```
The name `update_func` refers to a function object.
```
update_func1
```
Which we can confirm by checking its type.
```
type(update_func1)
```
`run_simulation` takes the update function as a parameter and calls it just like any other function.
```
def run_simulation(system, update_func):
"""Simulate the system using any update function.
system: System object
update_func: function that computes the population next year
returns: TimeSeries
"""
results = TimeSeries()
results[system.t_0] = system.p_0
for t in linrange(system.t_0, system.t_end):
results[t+1] = update_func(results[t], t, system)
return results
```
Here's how we use it.
```
t_0 = get_first_label(census)
t_end = get_last_label(census)
p_0 = census[t_0]
system = System(t_0=t_0,
t_end=t_end,
p_0=p_0,
birth_rate=0.027,
death_rate=0.01)
results = run_simulation(system, update_func1)
plot_results(census, un, results, 'Proportional model, factored')
```
Remember not to put parentheses after `update_func1`. What happens if you try?
**Exercise:** When you run `run_simulation`, it runs `update_func1` once for each year between `t_0` and `t_end`. To see that for yourself, add a print statement at the beginning of `update_func1` that prints the values of `t` and `pop`, then run `run_simulation` again.
### Combining birth and death
Since births and deaths get added up, we don't have to compute them separately. We can combine the birth and death rates into a single net growth rate.
```
def update_func2(pop, t, system):
"""Compute the population next year.
pop: current population
t: current year
system: system object containing parameters of the model
returns: population next year
"""
net_growth = system.alpha * pop
return pop + net_growth
```
Here's how it works:
```
system.alpha = system.birth_rate - system.death_rate
results = run_simulation(system, update_func2)
plot_results(census, un, results, 'Proportional model, combined birth and death')
```
### Exercises
**Exercise:** Maybe the reason the proportional model doesn't work very well is that the growth rate, `alpha`, is changing over time. So let's try a model with different growth rates before and after 1980 (as an arbitrary choice).
Write an update function that takes `pop`, `t`, and `system` as parameters. The system object, `system`, should contain two parameters: the growth rate before 1980, `alpha1`, and the growth rate after 1980, `alpha2`. It should use `t` to determine which growth rate to use. Note: Don't forget the `return` statement.
Test your function by calling it directly, then pass it to `run_simulation`. Plot the results. Adjust the parameters `alpha1` and `alpha2` to fit the data as well as you can.
```
# Solution goes here
# Solution goes here
```
| true |
code
| 0.737321 | null | null | null | null |
|
# Hierarchical Live sellers
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.style as style
from datetime import datetime as dt
style.use('ggplot')
#importando dataset e dropando colunas vazias e sem informação útil
dataset = pd.read_csv("Live.csv").drop(columns = {'status_id','Column1','Column2','Column3','Column4'})
#transformando pra datetime
dataset['status_published'] = dataset['status_published'].astype(str).str.replace("/","-")
dataset['status_published'] = pd.to_datetime(dataset['status_published'])
dataset['day'] = dataset['status_published'].dt.weekday #adiciona o dia da semana
#dataset['month'] = dataset['status_published'].dt.month #adiciona o mes
dataset['hour'] = dataset['status_published'].dt.hour #adiciona a hora
dataset['minute'] = dataset['status_published'].dt.minute #adiciona os minutos
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
#transformando as labels em atributos numéricos
dataset['status_type'] = encoder.fit_transform(dataset['status_type'])
#dropando a coluna antiga, pois já adicionamos a mesma numerizada
dataset = dataset.drop(columns = {'status_published'})
dataset.head()
#função para fazer o nome das colunas.
def column_name(name, df):
result = []
for i in range(len(df.columns)):
result.append(name + str(i))
return result
from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder(sparse=False)
day = pd.DataFrame(ohe.fit_transform(dataset.iloc[:,10:11].values),index = dataset.index).drop(columns = {0})
day.columns = column_name("day",day)
day.shape
hour = pd.DataFrame(ohe.fit_transform(dataset.iloc[:,11:12].values)).drop(columns = {0})
hour.columns = column_name("hour",hour)
hour.shape
minute = pd.DataFrame(ohe.fit_transform(dataset.iloc[:,12:13].values)).drop(columns = {0})
minute.columns = column_name("minute",minute)
minute.shape
dataset = dataset.drop(columns = {'hour','day','minute'})
dataset = dataset.join(hour).join(day).join(minute)
dataset.head()
```
Faremos o PCA para ajudar na visualização dos dados e reduzin a dimensionalidade
```
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X = pca.fit_transform(dataset)
explained_variance = pca.explained_variance_ratio_
explained_variance.sum()
```
Com 2 componentes conseguimos ficar com 0.99 de variância
# Hierárquico (single linkage)
```
import scipy.cluster.hierarchy as sch
dendrogram = sch.dendrogram(sch.linkage(X, method = 'single'))
plt.title('Dendrogram')
plt.xlabel('Axis')
plt.ylabel('Euclidean distances')
plt.show()
```
Tem-se dois clusters, visto que a maior linha vertical sem interrupções de linhas horizontais é a azul, que divide em dois clusters, o vermelho e o verde. A figura está anexada para melhor análise.
```
from sklearn.cluster import AgglomerativeClustering
hc = AgglomerativeClustering(n_clusters = 2, affinity = 'euclidean', linkage = 'single')
y_hc = hc.fit_predict(X)
pd.Series(hc.labels_).value_counts()
```
De fato, mesmo tendo uma quantidade menor de instâncias no segundo cluster, se aumentassemos o número de clusters até 4 teríamos a seguinte distribuição:
```
hc_hipotesis = AgglomerativeClustering(n_clusters = 4, affinity = 'euclidean', linkage = 'single')
y_hc_hipotesis = hc_hipotesis.fit_predict(X)
pd.Series(hc_hipotesis.labels_).value_counts()
```
Vamos agora plotar o resultado do nosso cluster.
```
import collections, numpy
collections.Counter(y_hc) #Número de elementos em cada cluster
#plot do gráfico com clusters
plt.scatter(X[y_hc == 0, 0], X[y_hc == 0, 1], s = 50, c = 'red', label = 'Cluster 0')
plt.scatter(X[y_hc == 1, 0], X[y_hc == 1, 1], s = 20, c = 'blue', label = 'Cluster 1')
plt.xlabel('PC2')
plt.ylabel('PC1')
plt.legend()
plt.show()
```
# Hierárquico (complete linkage)
```
import scipy.cluster.hierarchy as sch
dendrogram = sch.dendrogram(sch.linkage(X, method = 'complete'))
plt.title('Dendrogram')
plt.xlabel('Axis')
plt.ylabel('Euclidean distances')
plt.show()
```
Nesse caso, devido à ao espaçamento maior no dendograma, podemos ver que a escolha entre 2 e 3 clusters torna-se a mais adequada.
```
from sklearn.cluster import AgglomerativeClustering
hc_link = AgglomerativeClustering(n_clusters = 3, affinity = 'euclidean', linkage = 'complete')
y_hc_link = hc_link.fit_predict(X)
pd.Series(hc_link.labels_).value_counts()
```
Podemos ver que ao adicionarmos um cluster a mais, diferentemente do single linked, ele criou um novo cluster com 104 instâncias
```
plt.scatter(X[y_hc_link == 1, 0], X[y_hc_link == 1, 1], s = 50, c = 'red', label = 'Cluster 0')
plt.scatter(X[y_hc_link == 0, 0], X[y_hc_link == 0, 1], s = 30, c = 'green', label = 'Cluster 1')
plt.scatter(X[y_hc_link == 2, 0], X[y_hc_link == 2, 1], s = 20, c = 'blue', label = 'Cluster 2')
plt.xlabel('PC2')
plt.ylabel('PC1')
plt.legend()
plt.show()
```
# Normalizando os dados e tentando novamente
```
X
from sklearn.preprocessing import StandardScaler, MinMaxScaler
#limitando os valores ao intervalo -1 a 1
scaler = MinMaxScaler(feature_range=(-1,1))
X_scaled = scaler.fit_transform(X)
X_scaled
```
# Hierárquico (single linkage scaled)
```
import scipy.cluster.hierarchy as sch
dendrogram = sch.dendrogram(sch.linkage(X_scaled, method = 'single'))
plt.title('Dendrogram')
plt.xlabel('Axis')
plt.ylabel('Euclidean distances')
plt.show()
```
Tem-se dois clusters,ao dar um zoom na imagem fica mais perceptível
```
from sklearn.cluster import AgglomerativeClustering
hc_single_scaled = AgglomerativeClustering(n_clusters = 2, affinity = 'euclidean', linkage = 'single')
y_hc_single_scaled = hc_single_scaled.fit_predict(X_scaled)
pd.Series(hc_single_scaled.labels_).value_counts()
#plt.scatter(X[:,0], X[:,1], c=hc.labels_, cmap='rainbow')
plt.scatter(X_scaled[y_hc_single_scaled == 1, 0], X_scaled[y_hc_single_scaled == 1, 1], s = 50, c = 'red', label = 'Cluster 0')
plt.scatter(X_scaled[y_hc_single_scaled == 0, 0], X_scaled[y_hc_single_scaled == 0, 1], s = 20, c = 'blue', label = 'Cluster 1')
plt.xlabel('PC2')
plt.ylabel('PC1')
plt.legend()
plt.show()
```
# Hierárquico (complete linkage)
```
import scipy.cluster.hierarchy as sch
dendrogram = sch.dendrogram(sch.linkage(X_scaled, method = 'complete'))
plt.title('Dendrogram')
plt.xlabel('Axis')
plt.ylabel('Euclidean distances')
plt.show()
```
É possível ter de 2 a 3 clusters de acordo com o dendograma
```
from sklearn.cluster import AgglomerativeClustering
hc_link_complete_scaled = AgglomerativeClustering(n_clusters = 3, affinity = 'euclidean', linkage = 'complete')
y_hc_link_complete_scaled = hc_link_complete_scaled.fit_predict(X_scaled)
pd.Series(hc_link_complete_scaled.labels_).value_counts()
```
se rodarmos com 2 clusters ele junta o primeiro com o segunda e deixa o 0 que só tem 12 e se adicionarmos um a mais ele divide o de 12 em 7 e 5, o que acaba sendo, possivelmente muito específico
```
plt.scatter(X_scaled[y_hc_link_complete_scaled == 0, 0], X_scaled[y_hc_link_complete_scaled == 0, 1], s = 50, c = 'red', label = 'Cluster 0')
plt.scatter(X_scaled[y_hc_link_complete_scaled == 1, 0], X_scaled[y_hc_link_complete_scaled == 1, 1], s = 20, c = 'blue', label = 'Cluster 1')
plt.scatter(X_scaled[y_hc_link_complete_scaled == 2, 0], X_scaled[y_hc_link_complete_scaled == 2, 1], s = 20, c = 'green', label = 'Cluster 2')
plt.xlabel('PC2')
plt.ylabel('PC1')
plt.legend()
plt.show()
```
# Comparando
```
#single linkage sem normalização
pd.Series(hc.labels_).value_counts()
#single linkage com normalização
pd.Series(hc_single_scaled.labels_).value_counts()
```
No single linkage houveram poucas mudanças, embora o dendograma tenha mudado, a distribuição de clusters indicada por ele permaneceu a mesma, ao passo que o número de instâncias também.
```
#complete linkage sem normalização
pd.Series(hc_link.labels_).value_counts()
#complete linkage com normalização
pd.Series(hc_link_complete_scaled.labels_).value_counts()
```
No complete linkage vemos uma mudança tanto no dendograma quanto na distribuição das instâncias nos clusters. Embora tenha permanecido o mesmo número de clusters após a normalização, os valores em cada um foram alterados
| true |
code
| 0.537163 | null | null | null | null |
|
This notebook is an analysis of predictive accuracy in relative free energy calculations from the Schrödinger JACS dataset:
> Wang, L., Wu, Y., Deng, Y., Kim, B., Pierce, L., Krilov, G., ... & Romero, D. L. (2015). Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. Journal of the American Chemical Society, 137(7), 2695-2703.
http://doi.org/10.1021/ja512751q
```
%matplotlib inline
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pylab as plt
def read_ddGs
# Read the Excel sheet
df = pd.read_excel('ja512751q_si_003.xlsx', sheet_name='dG')
# Delete rows with summary statistics
rows_to_drop = list()
for i, row in df.iterrows():
if str(df.loc[i,'Ligand']) == 'nan':
rows_to_drop.append(i)
print('dropping rows: {}'.format(rows_to_drop))
df = df.drop(index=rows_to_drop);
# Populate 'system' field for each entry
system = df.loc[0,'Systems']
for i, row in df.iterrows():
if str(df.loc[i,'Systems']) == 'nan':
df.loc[i, "Systems"] = system
else:
system = df.loc[i, "Systems"]
def bootstrap_sign_prediction(DeltaG_predicted, DeltaG_experimental, threshold, ci=0.95, nbootstrap = 1000):
"""Compute mean and confidence intervals for predicting correct sign.
Parameters
----------
DeltaG_predicted : numpy array with dimensions (Nligands,)
Predicted free energies (kcal/mol)
DeltaG_experimental : numpy array with dimensions (Nligands,)
Experimental free energies (kcal/mol)
threshold : float
Threshold in free energy (kcal/mol)
ci : float, optional, default=0.95
Interval for CI
nbootstrap : int, optional. default=10000
Number of bootstrap samples
Returns
-------
mean : float
The mean statistic for the whole dataset
stderr : float
The standard error
low, high : float
Low and high ends of CI
"""
def compute_fraction(DeltaG_predicted, DeltaG_experimental, threshold):
# Compute all differences
N = len(DeltaG_predicted)
DDG_predicted = np.zeros([N*(N-1)], np.float64)
DDG_experimental = np.zeros([N*(N-1)], np.float64)
index = 0
for i in range(N):
for j in range(N):
if i != j:
DDG_predicted[index] = (DeltaG_predicted[j] - DeltaG_predicted[i])
DDG_experimental[index] = (DeltaG_experimental[j] - DeltaG_experimental[i])
index += 1
indices = np.where(np.abs(DDG_predicted) > threshold)[0]
return np.sum(np.sign(DDG_predicted[indices]) == np.sign(DDG_experimental[indices])) / float(len(indices))
N_ligands = len(DeltaG_predicted)
fraction_n = np.zeros([nbootstrap], np.float64)
for replicate in range(nbootstrap):
bootstrapped_sample = np.random.choice(np.arange(N_ligands), size=[N_ligands])
fraction_n[replicate] = compute_fraction(DeltaG_predicted[bootstrapped_sample], DeltaG_experimental[bootstrapped_sample], threshold)
fraction_n = np.sort(fraction_n)
fraction = compute_fraction(DeltaG_predicted, DeltaG_experimental, threshold)
dfraction = np.std(fraction_n)
low_frac = (1.0-ci)/2.0
high_frac = 1.0 - low_frac
fraction_low = fraction_n[int(np.floor(nbootstrap*low_frac))]
fraction_high = fraction_n[int(np.ceil(nbootstrap*high_frac))]
return fraction, dfraction, fraction_low, fraction_high
# Collect data by system
def plot_data(system, rows):
DeltaG_experimental = rows['Exp. dG'].values
DeltaG_predicted = rows['Pred. dG'].values
plt.xlabel('threshold (kcal/mol)');
plt.ylabel('P(correct sign)');
Nligands = len(DeltaG_experimental)
print(system, Nligands)
[min_threshold, max_threshold] = [0, 2]
thresholds = np.linspace(min_threshold, max_threshold, 20)
fractions = thresholds * 0.0
dfractions = thresholds * 0.0
fractions_low = thresholds * 0.0
fractions_high = thresholds * 0.0
for index, threshold in enumerate(thresholds):
fractions[index], dfractions[index], fractions_low[index], fractions_high[index] = bootstrap_sign_prediction(DeltaG_predicted, DeltaG_experimental, threshold)
plt.fill_between(thresholds, fractions_low, fractions_high, alpha=0.5)
plt.plot(thresholds, fractions, 'ko');
#plt.plot(thresholds, fractions_low, 'k-')
#plt.plot(thresholds, fractions_high, 'k-')
plt.title('{} (N = {})'.format(system, Nligands));
plt.xlim(min_threshold, max_threshold);
plt.ylim(0, 1);
systems = df['Systems'].unique()
nsystems = len(systems)
nx = int(np.ceil(np.sqrt(nsystems)))
ny = int(np.ceil(np.sqrt(nsystems)))
fig = plt.figure(figsize=[12,12])
for plot_index, system in enumerate(systems):
plt.subplot(ny, nx, plot_index+1)
rows = df.query("Systems == '{}'".format(system))
plot_data(system, rows)
plt.subplot(ny, nx, nsystems+1)
system = 'all'
plot_data(df)
fig.tight_layout()
fig.savefig('jacs-fraction-analysis.pdf');
```
| true |
code
| 0.692018 | null | null | null | null |
|
# Inference and Validation
```
import torch
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/',
download=True,
train=True,
transform=transform)
trainloader = torch.utils.data.DataLoader(trainset,
batch_size=64,
shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/',
download=True,
train=False,
transform=transform)
testloader = torch.utils.data.DataLoader(testset,
batch_size=64,
shuffle=True)
# Create a model
from torch import nn, optim
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
The goal of validation is to measure the model's performance on data that isn't part of the training set. There many options like accuracy, precision an recall, top-5 error rate an so on.
```
model = Classifier()
images, labels = next(iter(testloader))
# Get the class probabilities
ps = torch.exp(model(images))
# we should get 10 class probabilities for 64 examples
print(ps.shape)
```
With the probabilities, we can get the most likely class using the `ps.topk` method. This returns the $k$ highest values. Since we just want the most likely class, we can use `ps.topk(1)`. This returns a tuple of the top-$k$ values and the top-$k$ indices. If the highest value is the fifth element, we'll get back 4 as the index.
```
top_p, top_class = ps.topk(1, dim=1)
# look at the most likely classes for the first
# 10 examples
print(top_class[:10,:])
```
Now we can check if the predicted classes match the labels. This is simple to do by equating `top_class` and `labels`, but we have to be careful of the shapes. Here `top_class` is a 2D tensor with shape `(64, 1)` while `labels` is 1D with shape `(64)`. To get the equality to work out the way we want, `top_class` and `labels` must have the same shape.
If we do
```python
equals = top_class == labels
```
`equals` will have shape `(64, 64)`, try it yourself. What it's doing is comparing the one element in each row of `top_class` with each element in `labels` which returns 64 True/False boolean values for each row.
```
#equals = top_class == labels
equals = top_class == labels.view(*top_class.shape)
print(equals.shape)
print(equals)
```
Now we need to calculate the percentage of correct predictions. `equals` has binary values, either 0 or 1. This means that if we just sum up all the values and divide by the number of values, we get the percentage of correct predictions. This is the same operation as taking the mean, so we can get the accuracy with a call to `torch.mean`. If only it was that simple. If you try `torch.mean(equals)`, you'll get an error
```
RuntimeError: mean is not implemented for type torch.ByteTensor
```
This happens because `equals` has type `torch.ByteTensor` but `torch.mean` isn't implement for tensors with that type. So we'll need to convert `equals` to a float tensor. Note that when we take `torch.mean` it returns a scalar tensor, to get the actual value as a float we'll need to do `accuracy.item()`.
```
equals.shape
equals
```
Now we need to calculate the percentage of correct predictions.
But first we need to convert them to floats.
```
accuracy = torch.mean(equals.type(torch.FloatTensor))
print(f'Accuracy: {accuracy.item()*100}%')
accuracy
```
**Exercise**
Implement the validation loop below and print out the total accuracy after the loop.
```
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(),
lr=0.003)
epochs = 30
steps = 0
train_losses, test_losses = [], []
for epoch in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
log_ps = model(images)
loss = criterion(log_ps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
test_loss = 0
val_accuracy = 0
# Implement the validation pass and
# print out the validation accuracy
with torch.no_grad():
for images, labels in testloader:
log_ps = model(images)
test_loss += criterion(log_ps, labels)
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
val_accuracy += torch.mean(equals.type(torch.FloatTensor))
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(epoch+1, epochs),
"Training Loss: {:.3f}.. ".format(running_loss/len(trainloader)),
"Test Loss: {:.3f}.. ".format(test_loss/len(testloader)),
"Test Accuracy: {:.3f}".format(val_accuracy/len(testloader))
)
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training Loss')
plt.plot(test_losses, label='Test Loss')
plt.legend(frameon=False)
```
# Overfitting
The most common method to reduce overfitting is dropout, where we randomly drop input units. This forces the network to share information between weights, increasing it's ability to generalize to new data.
We need to turn off dropout during validation, testing and whenever we're using the network to make predictions.
**Exercise**
Add dropout to your model and train it on Fasion-MNIST again. Try to get a lower validation loss or higher accuracy.
```
import torch.nn.functional as F
from torch import nn, optim
# Define the model with dropout
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# Dropout module with 0.2 drop probability
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
# with dropout
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output, so no dropout here
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
During training we want to use dropout to prevent overfitting, but during inference we want to use the entire network. So, we need to turn off dropout during validation, testing, and whenever we're using the network to make predictions. To do this, you use model.eval(). This sets the model to evaluation mode where the dropout probability is 0. You can turn dropout back on by setting the model to train mode with model.train(). In general, the pattern for the validation loop will look like this, where you turn off gradients, set the model to evaluation mode, calculate the validation loss and metric, then set the model back to train mode.
```python
# turn off gradients
with torch.no_grad():
# set model to evaluation mode
model.eval()
# validation pass here
for images, labels in testloader:
...
# set model back to train mode
model.train()
```
```
# Train the model with dropout, and monitor
# the training process with the validation loss
# and accuracy
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
epochs = 3
steps = 0
train_losses, test_losses = [], []
for epoch in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
logps = model(images)
loss = criterion(logps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
val_accuracy = 0
test_loss = 0
with torch.no_grad():
model.eval()
for images, labels in testloader:
logps = model(images)
loss = criterion(logps, labels)
test_loss += loss
ps = torch.exp(logps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
val_accuracy += torch.mean(equals.type(torch.FloatTensor))
model.train()
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch {}/{}".format(epoch+1, epochs),
"Training Loss.. {}".format(running_loss/len(trainloader)),
"Testing Loss.. {}".format(test_loss/len(testloader)),
"Validation Accuracy.. {}".format(val_accuracy/len(testloader)))
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)
```
# Inference
We need to set the model in inference mode with *model.eval()*.
```
import helper
model.eval()
dataiter = iter(testloader)
images, labels = dataiter.next()
img = images[0]
# Convert 2D image to 1D vector
img = img.view(1, 784)
# Calculate the class probabilities
with torch.no_grad():
output = model.forward(img)
ps = torch.exp(output)
# Plot the image and probabilities
helper.view_classify(img.view(1, 28, 28),
ps,
version='Fashion')
```
| true |
code
| 0.863075 | null | null | null | null |
|
# Reinforcement Learning
В этом задании постараемся разобраться в проблеме обучения с подкреплением, реализуем алгоритм REINFORCE и научим агента с помощью этого алгоритма играть в игру Cartpole.
Установим и импортируем необходимые библиотеки, а также вспомогательные функции для визуализации игры агента.
```
!pip install gym pandas torch matplotlib pyvirtualdisplay > /dev/null 2>&1
!apt-get install -y xvfb python-opengl ffmpeg x11-utils > /dev/null 2>&1
from IPython.display import clear_output, HTML
from IPython import display as ipythondisplay
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import glob
import time
import io
import base64
import gym
from gym.wrappers import Monitor
import torch
import collections
import pandas as pd
from torch import nn
from torch.optim import Adam
from torch.distributions import Categorical
from pyvirtualdisplay import Display
display = Display(visible=0, size=(1400, 900))
display.start()
"""
Utility functions to enable video recording of gym environment and displaying it
To enable video, just do "env = wrap_env(env)""
"""
def show_video():
mp4list = glob.glob('video/*.mp4')
if len(mp4list) > 0:
mp4 = mp4list[0]
video = io.open(mp4, 'r+b').read()
encoded = base64.b64encode(video)
ipythondisplay.display(HTML(data='''<video alt="test" autoplay
loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>'''.format(encoded.decode('ascii'))))
else:
print("Could not find video")
def wrap_env(env):
env = Monitor(env, './video', force=True)
return env
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu') #позволяет перенести тензор на GPU, если он доступен в системе
```
## OpenAI Gym
[OpenAI Gym](https://gym.openai.com) это набор сред для разработки и сравнения алгоритмов обучения с подкреплением.
OpenAI Gym предоставляет простой и универсальный API ко многим средам с разными свойствами, как простым так и сложным:
* Классические задачи управления и игрушечные примеры, которые можно найти в учебниках и на которых демонстрируется работа алгоритмов обучения с подкреплением (одна из этих сред используется в этом задании)
* Игры Atari (оказали огромное влияние на достижения в обучении с подкреплением в последние годы)
* 2D и 3D среды для контроля роботов в симуляции (используют проприетарный движок [Mojuco](http://www.mujoco.org))
Рассмотрим, как устроена среда [CartPole-v0](https://gym.openai.com/envs/CartPole-v0), с которой мы будем работать.
Для этого создадим среду и выведем ее описание.
```
env = gym.make("CartPole-v0")
print(env.env.__doc__)
```
Из этого описания мы можем узнать, как устроены пространства состояний и действий в этой среды, какие награды получаются на каждом шаге, а также, что нам необходимо сделать, чтобы научиться "решать" эту среду, а именно достич средней награды больше 195.0 или больше за 100 последовательных запусков агента в этой среде. Именно такого агента мы и попробуем создать и обучить.
Но для начала напишем вспомогательную функцию, которая будет принимать на вход среду, агента и число эпизодов, и возвращать среднюю награду за 100 эпизодов. С помощью этой функции мы сможем протестировать, насколько хорошо обучился наш агент, а также визуализировать его поведение в среде.
```
def test_agent(env, agent=None, n_episodes=100):
"""Runs agent for n_episodes in environment and calclates mean reward.
Args:
env: The environment for agent to play in
agent: The agent to play with. Defaults to None -
in this case random agent is used.
n_episodes: Number of episodes to play. Defaults to 100.
Returns:
Mean reward for 100 episodes.
"""
total_reward = []
for episode in range(n_episodes):
episode_reward = 0
observation = env.reset()
t = 0
while True:
if agent:
with torch.no_grad():
probs = agent(torch.FloatTensor(observation).to(device))
dist = Categorical(probs)
action = dist.sample().item()
else:
action = env.action_space.sample()
observation, reward, done, info = env.step(action)
episode_reward += reward
t += 1
if done:
print("Episode {} finished after {} timesteps".format(episode+1, t+1))
break
total_reward.append(episode_reward)
env.close()
return np.mean(total_reward)
```
Протестируем и визуализируем случайного агента (параметр ```agent=False```).
```
test_agent(env, agent=False, n_episodes=100)
```
Как видно, наш случайный агент выступает не очень хорошо и в среднем может удержать шест всего около 20 шагов.
Напишем функцию для визуализации агента и посмотрим на случайного агента.
```
def agent_viz(env="CartPole-v0", agent=None):
"""Visualizes agent play in the given environment.
Args:
env: The environment for agent to play in. Defaults to CartPole-v0.
agent: The agent to play with. Defaults to None -
in this case random agent is used.
Returns:
Nothing is returned. Visualization is created and can be showed
with show_video() function.
"""
env = wrap_env(gym.make(env))
observation = env.reset()
while True:
env.render()
if agent:
with torch.no_grad():
probs = agent(torch.FloatTensor(observation).to(device))
dist = Categorical(probs)
action = dist.sample().item()
else:
action = env.action_space.sample()
observation, reward, done, info = env.step(action)
if done:
break
env.close()
agent_viz()
show_video()
```
Попробуем применить обучение с подкреплением и алгоритм REINFORCE для того, чтобы в среднем за 100 эпиздов мы держали шест не менее 195 шагов.
## REINFORCE
Вспомним, что из себя представляет алгоритм REINFORCE (Sutton & Barto) <img src="//i.imgur.com/bnASTrY.png" width="700">
1. Инициализуем политику (в качестве политики мы будем использовать глубокую нейронную сеть).
2. "Играем" в среде эпизод, используя нашу политику, или несколько (мы будем использовать последний вариант) и собираем данные о состояниях, действиях и полученных наградах.
3. Для каждого состояния в собранных эпизодах вычисляем сумму дисконтированных наград, полученных из этого состояния, а также логорифм правдоподобия предпринятого действия в этом состоянии для нашей политики.
4. Обновляем параметры нашей политики по формуле на схеме.
### Политика
Наша политика должна принимать на вход состояние среды, а на выходе выдавать распределение по действиям, которые мы можем осуществлять в среде.
**Задание:** Создать класс нейронной сети со следующей архитектурой ```Linear -> ReLU -> Linear -> Softmax```. Параметрами инициализации должны служить размерности пространства состояний, пространства действий и размер скрытого слоя.
```
class Policy(nn.Module):
"""Policy to be used by agent.
Attributes:
state_size: Dimention of the state space of the environment.
act_size: Dimention of the action space of the environment.
hidden_size: Dimention of the hidden state of the agent's policy.
"""
# TO DO
```
### Оценка правдоподобия и расчет суммы дисконтированных наград
**Задание:** Напишем вспомогательная функцию, которая принимает на вход политику, батч траекторий и фактор дисконтирования, и должна вернуть следующие величины:
* правдоподобие действия на каждом шаге на траектории посчитанные для всего батча;
* дисконтированные суммы наград (reward-to-go) из каждого состояния среды на траектории посчитанные для всего батча;
**Hint**: Представим батч траекторий как ```list```, в котром также хранится ```list``` для каждой траектории, в котором каждый шаг хранится, как ```namedtuple```:
```transition = collections.namedtuple("transition", ["state", "action", "reward"])```
```
def process_traj_batch(policy, batch, discount):
"""Computes log probabilities for each action
and rewards-to-go for each state in the batch of trajectories.
Args:
policy: Policy of the agent.
batch (list of list of collections.namedtuple): Batch of trajectories.
discount (float): Discount factor for rewards-to-go calculation.
Returns:
log_probs (list of torch.FloatTensor): List of log probabilities for
each action in the batch of trajectories.
returns (list of rewards-to-go): List of rewards-to-go for
each state in the batch of trajectories.
"""
# TO DO
return log_probs, returns
```
Ваша реализация функции должна проходить следующий тест.
```
def test_process_traj_batch(process_traj_batch):
transition = collections.namedtuple("transition", ["state", "action", "reward"])
class HelperPolicy(nn.Module):
def __init__(self):
super(HelperPolicy, self).__init__()
self.act = nn.Sequential(
nn.Linear(4, 2),
nn.Softmax(dim=0),
)
def forward(self, x):
return self.act(x)
policy = HelperPolicy()
for name, param in policy.named_parameters():
if name == "act.0.weight":
param.data = torch.tensor([[1.7492, -0.2471, 0.3310, 1.1494],
[0.6171, -0.6026, 0.5025, -0.3196]])
else:
param.data = torch.tensor([0.0262, 0.1882])
batch = [
[
transition(state=torch.tensor([ 0.0462, -0.0018, 0.0372, 0.0063]), action=torch.tensor(0), reward=1.0),
transition(state=torch.tensor([ 0.0462, -0.1975, 0.0373, 0.3105]), action=torch.tensor(1), reward=1.0),
transition(state=torch.tensor([ 0.0422, -0.0029, 0.0435, 0.0298]), action=torch.tensor(0), reward=1.0),
transition(state=torch.tensor([ 0.0422, -0.1986, 0.0441, 0.3359]), action=torch.tensor(0), reward=1.0),
],
[
transition(state=torch.tensor([ 0.0382, -0.3943, 0.0508, 0.6421]), action=torch.tensor(1), reward=1.0),
transition(state=torch.tensor([ 0.0303, -0.2000, 0.0637, 0.3659]), action=torch.tensor(1), reward=1.0),
transition(state=torch.tensor([ 0.0263, -0.0058, 0.0710, 0.0939]), action=torch.tensor(1), reward=1.0),
transition(state=torch.tensor([ 0.0262, 0.1882, 0.0729, -0.1755]), action=torch.tensor(0), reward=1.0)
]
]
log_probs, returns = process_traj_batch(policy, batch, 0.9)
assert sum(log_probs).item() == -6.3940582275390625, "Log probabilities calculation is incorrect!!!"
assert sum(returns) == 18.098, "Log probabilities calculation is incorrect!!!"
print("Correct!")
test_process_traj_batch(process_traj_batch)
```
### Вспомогательные функции и гиперпараметры
Функция для расчета скользящего среднего - ее мы будем использовать для визуализации наград по эпизодам.
```
moving_average = lambda x, **kw: pd.DataFrame({'x':np.asarray(x)}).x.ewm(**kw).mean().values
```
Определим также гиперпараметры.
```
STATE_SIZE = env.observation_space.shape[0] # размерность пространства состояний среды
ACT_SIZE = env.action_space.n # размерность пространства действий среды
HIDDEN_SIZE = 256 # размер скрытого слоя для политики
NUM_EPISODES = 1000 # количество эпиздов, которые будут сыграны для обучения
DISCOUNT = 0.99 # фактор дисконтирования
TRAIN_EVERY = 20
```
Инициализуем политику и алгоритм оптимизации - мы будем использовать Adam c праметрами по умолчанию.
```
policy = Policy(STATE_SIZE, ACT_SIZE, HIDDEN_SIZE).to(device)
optimizer = Adam(policy.parameters())
transition = collections.namedtuple("transition", ["state", "action", "reward"])
```
### Основной цикл обучения
Теперь, когда мы опредлели вспомогательные функции, то нам следует написать основной цикл обучения агент.
В цикле должно происходить следующее:
1. Играем количество эпизодов, определенное в гиперпараметре ```NUM_EPISODES```.
2. В каждом эпизоде сохраняем информацию о шагах на траектории - состояние, действие и награду.
3. В конце каждого эпизода сохраняем вышеуказанную информацию о траектории.
4. Периодически обучаемся на собранных эпизодах каждые ```TRAIN_EVERY``` эпизодов:
4.1. Считаем для собранного батча для каждого шага на трактории правдоподобие и сумму дисконтированных наград.
4.2. Обновляем параметры политики агента по формуле, приведенной на схеме.
**Задание:** Реализовать алгоритм обучения, описанный на схеме и в тексте выше. Шаблон кода алгоритма представлен ниже. При этом следует сохранять сумму ревордов для каждого эпизода в переменную ```returns_history```. Алгоритму потребуется около 1000 эпизодов игры, для того чтобы научиться играть в игру (если после 1000 эпизодов агент играет немного хуже, чем для победы в игре, попробуйте обучать его немного дольше или установите критерий останова - когда средняя награда за 100 последних эпизодов превышает значение в ```env.spec.reward_threshold``` )
```
returns_history = []
traj_batch = []
for i in range(NUM_EPISODES):
# TO DO
returns_history.append(rewards)
traj_batch.append(traj)
if i % TRAIN_EVERY:
log_probs, returns = process_traj_batch(policy, traj_batch, DISCOUNT)
loss = -(torch.stack(log_probs) * torch.FloatTensor(returns).to(device)).sum()
optimizer.zero_grad()
loss.backward()
optimizer.step()
traj_batch = []
if i % 10:
clear_output(True)
plt.figure(figsize=[12, 6])
plt.title('Returns'); plt.grid()
plt.scatter(np.arange(len(returns_history)), returns_history, alpha=0.1)
plt.plot(moving_average(returns_history, span=10, min_periods=10))
plt.show()
```
Протестируем обученного агента.
```
test_agent(env, agent=policy, n_episodes=100)
```
Обученный агент должен приближаться к искомому значению средней награды за 100 эпизодов 195.
Визуализируем обученного агента.
```
agent_viz(agent=policy)
show_video()
```
Как видно, агент выучил довольно хорошую стратегию для игры и способен долго удерживать шест.
### REINFORCE with baselines (Опционально)
В лекциях вы слышали, что при расчете градиентов для обновления параметров политики агента мы можем вычесть из суммы дисконтированных наград ```baseline``` для уменьшения дисперсии градиентов и ускорения сходимости обучения - такой алгоритм называется REINFORCE with baselines. В качестве ```baseline``` мы можем использовать другую нейронную сеть, которая будет оценивать сумму дисконтированных наград из данного состояния *V(s)*.
Схема алгоритма REINFORCE with baselines (Sutton & Barto) <img src="//i.imgur.com/j3BcbHP.png" width="700">
**Задание**: Включите в уже разработанный алгоритм вторую нейронную сеть для оценки суммы дисконтированных наград *V(s)*. Используйте разницу между фактической суммой дисконтированных наград и оценкой в формуле функции потерь политики. В качестве функции потерь для *V(s)* используйте ```MSELoss```. Оцените скорость сходимости нового алгоритма.
| true |
code
| 0.530905 | null | null | null | null |
|
# Agregando funciones no lineales a las capas
> Transformaciones no lineales para mejorar las predicciones de nuestras redes
Algunas de las transformaciones no lineales más comunes en una red neuronal son la funcion ```sigmoide```, ```tanh``` y ```ReLU```
Para agregar estas funciones debemos agregar los siguientes metodos a la clase ```Tensor```
```
def sigmoid(self):
if (self.autograd):
return Tensor(1/(1+np.exp(-self.data)),
autograd=True,
creators=[self],
creation_op='sigmoid')
return Tensor(1/(1+np.exp(-self.data)))
def tanh(self):
if (self.autograd):
return Tensor(np.tanh(self.data),
autograd=True,
creators=[self],
creation_op='tanh')
return Tensor(1/(1+np.exp(-self.data)))
def relu(self):
ones_and_zeros = self.data > 0
if (self.autograd):
return Tensor(self.data * ones_and_zeros,
autograd=True,
creators=[self],
creation_op='relu')
return Tensor(self.data * ones_and_zeros)
```
Y las siguientes condiciones al metodo ```backward()``` de la clase Tensor
```
if (self.creation_op == 'sigmoid'):
ones = Tensor(np.ones_like(self.grad.data))
self.creators[0].backward(self.grad * (self * (ones - self)))
if (self.creation_op == 'tanh'):
ones = Tensor(np.ones_like(self.grad.data))
self.creators[0].backward(self.grad * (ones - (self * self)))
if (self.creation_op == 'relu'):
mask = Tensor(self.data > 0)
self.creators[0].backward(self.grad * mask)
```
```
import numpy as np
class Tensor(object):
def __init__(self, data,
autograd=False,
creators=None,
creation_op=None,
id=None):
'''
Inicializa un tensor utilizando numpy
@data: una lista de numeros
@creators: lista de tensores que participarion en la creacion de un nuevo tensor
@creators_op: la operacion utilizada para combinar los tensores en el nuevo tensor
@autograd: determina si se realizara backprop o no sobre el tensor
@id: identificador del tensor, para poder dar seguimiento a los hijos y padres del mismo
'''
self.data = np.array(data)
self.creation_op = creation_op
self.creators = creators
self.grad = None
self.autograd = autograd
self.children = {}
# se asigna un id al tensor
if (id is None):
id = np.random.randint(0, 100000)
self.id = id
# se hace un seguimiento de cuantos hijos tiene un tensor
# si los creadores no es none
if (creators is not None):
# para cada tensor padre
for c in creators:
# se verifica si el tensor padre posee el id del tensor hijo
# en caso de no estar, agrega el id del tensor hijo al tensor padre
if (self.id not in c.children):
c.children[self.id] = 1
# si el tensor ya se encuentra entre los hijos del padre
# y vuelve a aparece, se incrementa en uno
# la cantidad de apariciones del tensor hijo
else:
c.children[self.id] += 1
def all_children_grads_accounted_for(self):
'''
Verifica si un tensor ha recibido la cantidad
correcta de gradientes por cada uno de sus hijos
'''
# print('tensor id:', self.id)
for id, cnt in self.children.items():
if (cnt != 0):
return False
return True
def backward(self, grad, grad_origin=None):
'''
Funcion que propaga recursivamente el gradiente a los creators o padres del tensor
@grad: gradiente
@grad_orign
'''
if (self.autograd):
if grad is None:
grad = Tensor(np.ones_like(self.data))
if (grad_origin is not None):
# Verifica para asegurar si se puede hacer retropropagacion
if (self.children[grad_origin.id] == 0):
raise Exception("No se puede retropropagar mas de una vez")
# o si se está esperando un gradiente, en dicho caso se decrementa
else:
# el contador para ese hijo
self.children[grad_origin.id] -= 1
# acumula el gradiente de multiples hijos
if (self.grad is None):
self.grad = grad
else:
self.grad += grad
if (self.creators is not None and
(self.all_children_grads_accounted_for() or grad_origin is None)):
if (self.creation_op == 'neg'):
self.creators[0].backward(self.grad.__neg__())
if (self.creation_op == 'add'):
# al recibir self.grad, empieza a realizar backprop
self.creators[0].backward(self.grad, grad_origin=self)
self.creators[1].backward(self.grad, grad_origin=self)
if (self.creation_op == "sub"):
self.creators[0].backward(Tensor(self.grad.data), self)
self.creators[1].backward(Tensor(self.grad.__neg__().data), self)
if (self.creation_op == "mul"):
new = self.grad * self.creators[1]
self.creators[0].backward(new, self)
new = self.grad * self.creators[0]
self.creators[1].backward(new, self)
if (self.creation_op == "mm"):
layer = self.creators[0] # activaciones => layer
weights = self.creators[1] # pesos = weights
# c0 = self.creators[0] # activaciones => layer
# c1 = self.creators[1] # pesos = weights
# new = self.grad.mm(c1.transpose()) # grad = delta => delta x weights.T
new = Tensor.mm(self.grad, weights.transpose()) # grad = delta => delta x weights.T
layer.backward(new)
# c0.backward(new)
# new = self.grad.transpose().mm(c0).transpose() # (delta.T x layer).T = layer.T x delta
new = Tensor.mm(layer.transpose(), self.grad) # layer.T x delta
weights.backward(new)
# c1.backward(new)
if (self.creation_op == "transpose"):
self.creators[0].backward(self.grad.transpose())
if ("sum" in self.creation_op):
dim = int(self.creation_op.split("_")[1])
self.creators[0].backward(self.grad.expand(dim, self.creators[0].data.shape[dim]))
if ("expand" in self.creation_op):
dim = int(self.creation_op.split("_")[1])
self.creators[0].backward(self.grad.sum(dim))
if (self.creation_op == "sigmoid"):
ones = Tensor(np.ones_like(self.grad.data))
self.creators[0].backward(self.grad * (self * (ones - self)))
if (self.creation_op == "tanh"):
ones = Tensor(np.ones_like(self.grad.data))
self.creators[0].backward(self.grad * (ones - (self * self)))
if (self.creation_op == 'relu'):
mask = Tensor(self.data > 0)
self.creators[0].backward(self.grad * mask)
def __neg__(self):
if (self.autograd):
return Tensor(self.data * -1,
autograd=True,
creators=[self],
creation_op='neg')
return Tensor(self.data * -1)
def __add__(self, other):
'''
@other: un Tensor
'''
if (self.autograd and other.autograd):
return Tensor(self.data + other.data,
autograd=True,
creators=[self, other],
creation_op='add')
return Tensor(self.data + other.data)
def __sub__(self, other):
'''
@other: un Tensor
'''
if (self.autograd and other.autograd):
return Tensor(self.data - other.data,
autograd=True,
creators=[self, other],
creation_op='sub')
return Tensor(self.data - other.data)
def __mul__(self, other):
'''
@other: un Tensor
'''
if (self.autograd and other.autograd):
return Tensor(self.data * other.data,
autograd=True,
creators=[self, other],
creation_op="mul")
return Tensor(self.data * other.data)
def sum(self, dim):
'''
Suma atravez de dimensiones, si tenemos una matriz 2x3 y
aplicamos sum(0) sumara todos los valores de las filas
dando como resultado un vector 1x3, en cambio si se aplica
sum(1) el resultado es un vector 2x1
@dim: dimension para la suma
'''
if (self.autograd):
return Tensor(self.data.sum(dim),
autograd=True,
creators=[self],
creation_op="sum_" + str(dim))
return Tensor(self.data.sum(dim))
def expand(self, dim, copies):
'''
Se utiliza para retropropagar a traves de una suma sum().
Copia datos a lo largo de una dimension
'''
trans_cmd = list(range(0, len(self.data.shape)))
trans_cmd.insert(dim, len(self.data.shape))
new_data = self.data.repeat(copies).reshape(list(self.data.shape) + [copies]).transpose(trans_cmd)
if (self.autograd):
return Tensor(new_data,
autograd=True,
creators=[self],
creation_op="expand_" + str(dim))
return Tensor(new_data)
def transpose(self):
if (self.autograd):
return Tensor(self.data.transpose(),
autograd=True,
creators=[self],
creation_op="transpose")
return Tensor(self.data.transpose())
def mm(self, x):
if (self.autograd):
return Tensor(self.data.dot(x.data),
autograd=True,
creators=[self, x],
creation_op="mm")
return Tensor(self.data.dot(x.data))
def sigmoid(self):
if (self.autograd):
return Tensor(1/(1+np.exp(-self.data)),
autograd=True,
creators=[self],creation_op='sigmoid')
return Tensor(1/(1+np.exp(-self.data)))
def tanh(self):
if (self.autograd):
return Tensor(np.tanh(self.data),
autograd=True,
creators=[self],
creation_op='tanh')
return Tensor(np.tanh(self.data))
def relu(self):
ones_and_zeros = self.data > 0
if (self.autograd):
return Tensor(self.data * ones_and_zeros,
autograd=True,
creators=[self],
creation_op='relu')
return Tensor(self.data * ones_and_zeros)
def __repr__(self):
return str(self.data.__repr__())
def __str__(self):
return str(self.data.__str__())
class SGD(object):
def __init__(self, parameters, alpha=0.1):
self.parameters = parameters
self.alpha = alpha
def zero(self):
for p in self.parameters:
p.grad.data *= 0
def step(self, zero=True):
for p in self.parameters:
p.data = p.data - (self.alpha * p.grad.data)
if(zero):
p.grad.data *= 0
class Layer(object):
def __init__(self):
self.parameters = list()
def get_parameters(self):
return self.parameters
class Linear(Layer):
def __init__(self, n_inputs, n_outputs):
super().__init__()
W = np.random.randn(n_inputs, n_outputs) * np.sqrt(2.0 / (n_inputs))
self.weight = Tensor(W, autograd=True)
self.bias = Tensor(np.zeros(n_outputs), autograd=True)
self.parameters.append(self.weight)
self.parameters.append(self.bias)
def forward(self, input):
return Tensor.mm(input, self.weight) + self.bias.expand(0, len(input.data))
class Sequential(Layer):
def __init__(self, layers=list()):
super().__init__()
self.layers = layers
def add(self, layer):
self.layers.append(layer)
def forward(self, input):
for layer in self.layers:
input = layer.forward(input)
return input
def get_parameters(self):
params = list()
for l in self.layers:
params += l.get_parameters()
return params
class Tanh(Layer):
def __init__(self):
super().__init__()
def forward(self, input):
return input.tanh()
class Sigmoid(Layer):
def __init__(self):
super().__init__()
def forward(self, input):
return input.sigmoid()
class Relu(Layer):
def __init__(self):
super().__init__()
def forward(self, input):
return input.relu()
class MSELoss(Layer):
def __init__(self):
super().__init__()
def forward(self, pred, target):
return ((pred - target) * (pred - target)).sum(0)
```
## Una red neuronal contransformaciones no lineales
```
np.random.seed(0)
data = Tensor(np.array([[0,0],[0,1],[1,0],[1,1]]), autograd=True) # (4,2)
target = Tensor(np.array([[0],[1],[0],[1]]), autograd=True) # (4,1)
model = Sequential([Linear(2,3),
Tanh(),
Linear(3,1),
Sigmoid()])
criterion = MSELoss()
# optim = SGD(model.get_parameters(), alpha=0.05) # Lineal
optim = SGD(model.get_parameters(), alpha=1) # Tanh, Sigmoid
for i in range(10):
# Predecir
pred = model.forward(data)
# Comparar
loss = criterion.forward(pred, target)
# Aprender
loss.backward(Tensor(np.ones_like(loss.data)))
optim.step()
print(loss)
```
## Aprendiendo XOR
```
np.random.seed(0)
data = Tensor(np.array([[0,0],[0,1],[1,0],[1,1]]), autograd=True) # (4,2)
target = Tensor(np.array([[0],[1],[1],[0]]), autograd=True) # (4,1)
model = Sequential([Linear(2,3),
Tanh(),
Linear(3,1),
Sigmoid()])
criterion = MSELoss()
# optim = SGD(model.get_parameters(), alpha=0.05) # Lineal
optim = SGD(model.get_parameters(), alpha=1) # Tanh, Sigmoid
for i in range(10):
# Predecir
pred = model.forward(data)
# Comparar
loss = criterion.forward(pred, target)
# Aprender
loss.backward(Tensor(np.ones_like(loss.data)))
optim.step()
if (i%1 == 0):
print(loss)
```
| true |
code
| 0.393764 | null | null | null | null |
|
# Convolutional Neural Networks
CNNs are a twist on the neural network concept designed specifically to process data with spatial relationships. In the deep neural networks we've seen so far every node is always connected to every other node in the subsequent layer. While spatial relationships CAN be captured, as we've seen with out results on MNIST, the networks were not explicitly built with the assumption that spatial relationships definitely exist. Artificial neural networks are perfectly appropriate for data where the relationships are not spatial.
But, for data such as images, it seems crazy to ignore the spatial relationships! For the vast majority of image data, neighboring pixels combined with each other tell us much more than combining the pixels in opposite corners or the image. CNN's rely on the assumption that our data has spatial relationships, and they have produced state-of-the-art results especially in image processing and computer vision.
The fundamental unit of a CNN is a "convolution":

> Image Source: https://github.com/PetarV-/TikZ/tree/master/2D%20Convolution
The key component of the convolution is called the kernel, which is a matrix. K in the image above. The kernel has a shape, 3x3 in this example, but we can define the for each convolution. We "slide" the kernel across every 3x3 section of the image performing item-by-item multiplication, for example in the above image the 4 highlighted in green is produced by taking the values highlighted in red, multiplying the values in the same position in the kernel, and summing the result of those multiplications. Specifically:
```
position: [0,0] [0,1] [0,2] [1,0] [1,1] [1,2] [2,0] [2,1] [2,2]
operation: (1*1) + (0*0) + (0*1) + (1*0) + (1*1) + (0*0) + (1*1) + (1*0) + (1*1) == 4
```
This value is (optionally, but typically) then passed through a non-linearity like ReLU or Sigmoid before it is passed to the next layer.
> Side note: In the literature, you'll discover that in a "true" convolution the kernel is inverted prior to the multiply+sum operation, and that this operation without the inversion is actually called "cross correlation" by most mathematicians. This matters in some contexts but we typically ignore it in deep learning because the values of the kernel are the things that are fine tuned, and storing them as "pre-inverted" matrixes is computationally efficent compared to inverting the kernel repeatedly.
Here is a helpful animation to visualize convolutions:

> Image source: https://towardsdatascience.com/types-of-convolutions-in-deep-learning-717013397f4d
A convolutional layer has a few important properties:
* **Number of kernels** -- this is similar to the number of nodes in an ANN
* Each kernel will be separately trained on the input data.
* Each kernel will produce an output layer, sometimes called a feature map.
* These feature maps are used as input to the next layer.
* **Kernel size** -- these are almost always 3x3 or 5x5.
* Bigger kernels are more computationally expensive.
* Bigger kernals have a wider "field of view" which can be helpful.
* Dialted convolutions can capture a wider field of view at a lower computational cost (see additional resources).
* **Padding** -- notice above that a convolution produces a smaller output layer than the input layer by 1 pixel in each direction. Padding the input (typically with 0 values) allows the convolution to produce an output with the same size as the input.
* Downsampling to smaller sizes isn't always bad.
* It reduces the computational costs at the next layer.
* If we don't pad, it limits the possible depth of the network esp. for small inputs
* Padding tends to preserve information at the borders. If your images have important features on the edges, padding can improve performance
* **Stride** -- in the above we "slide" the kernel over by 1 pixel at every step. Increasing the stride increases the amount we slide by.
* Stride is typically set to 1.
* Higher values reduce the amount of information captured.
* Higher values are more computationally efficent, as fewer values are combined per convolution.
One last important concept before we build a CNN: pooling. Pooling is a tactic used to decrease the resolution of our feature maps, and it is largely an issue of computational efficency. There are 2 popular kinds, max pooling and average pooling. Pooling layers use a window size, say 2x2, and take either the max or average value within each window to produce the output layer. The windows are almost always square, and the stride size is almost always set to the size of the window:

> Image source: https://cs231n.github.io/convolutional-networks/
It is worth noting that pooling has fallen out of favor in a lot of modern architectures. Many machine learning practitioners have started downsampling through convolutions with larger stride sizes instead of pooling.
### Building Our First CNN
Let's use Keras to build a CNN now.
```
# Setting up MNST, this should look familiar:
import numpy as np
from matplotlib import pyplot as plt
from keras.datasets import fashion_mnist
from keras.models import Sequential
from keras.layers import Dense, MaxPooling2D, Conv2D, Flatten, Dropout
from keras.utils import to_categorical
# For examining results
from sklearn.metrics import confusion_matrix
import seaborn as sn
num_classes = 10
image_size = 784
(training_images, training_labels), (test_images, test_labels) = fashion_mnist.load_data()
training_data = training_images.reshape(training_images.shape[0], image_size)
test_data = test_images.reshape(test_images.shape[0], image_size)
training_labels = to_categorical(training_labels, num_classes)
test_labels = to_categorical(test_labels, num_classes)
conv_training_data = training_images.reshape(60000, 28, 28, 1)
conv_test_data = test_images.reshape(10000, 28, 28, 1)
def plot_training_history(history, model, eval_images=False):
figure = plt.figure()
plt.subplot(1, 2, 1)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['training', 'validation'], loc='best')
plt.tight_layout()
plt.subplot(1, 2, 2)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['training', 'validation'], loc='best')
plt.tight_layout()
figure.tight_layout()
plt.show()
if eval_images:
loss, accuracy = model.evaluate(conv_test_data, test_labels, verbose=False)
else:
loss, accuracy = model.evaluate(test_data, test_labels, verbose=False)
print(f'Test loss: {loss:.3}')
print(f'Test accuracy: {accuracy:.3}')
```
This time, we're using a new dataset called "Fashion MNIST". Like the handwritten digits dataset, this is a set of grayscale images each 28 by 28 pixels. However, the subject of these images is very different from the handwritten digits dataset. Instead, these are images of fashion objects. Let's take a look at some:
```
# Lets visualize the first 100 images from the dataset
for i in range(100):
ax = plt.subplot(10, 10, i+1)
ax.axis('off')
plt.imshow(training_images[i], cmap='Greys')
i = 0 # So we can look at one at a time...
# So we can see the label
label_map = {
0: 'T-shirt/top',
1: 'Trouser',
2: 'Pullover',
3: 'Dress',
4: 'Coat',
5: 'Sandal',
6: 'Shirt',
7: 'Sneaker',
8: 'Bag',
9: 'Ankle boot'
}
label = np.argmax(training_labels[i])
plt.title(label_map[label])
plt.imshow(training_images[i], cmap='Greys')
i += 1
```
Once again, there are 10 classes of image:
0 T-shirt/top
1 Trouser
2 Pullover
3 Dress
4 Coat
5 Sandal
6 Shirt
7 Sneaker
8 Bag
9 Ankle boot
As you might guess, this is a bigger challenge than the handwritten digits. Firstly, at 28 by 28 pixels much more fidelity is lost in this dataset compared to the digits dataset. Secondly, more pixels matter. In the digits dataset, we rarely care about the weight of the pixel, more or less what matters is if it's white or something else—we mostly cared about the edges between where someone had drawn and where they had not. Now internal differences in grayscale intensity are more informative, and comprise a larger amount of the image.
Let's quickly verify that a standard ANN that worked well in the context of MNIST fails in Fashion MNIST:
```
# Recall from the Optimizers section that we were able to get 97+ test accuracy with this network:
model = Sequential()
model.add(Dense(units=64, activation='relu', input_shape=(image_size,)))
model.add(Dense(units=64, activation='relu'))
model.add(Dense(units=64, activation='relu'))
model.add(Dense(units=64, activation='relu'))
model.add(Dense(units=64, activation='relu'))
model.add(Dense(units=64, activation='relu'))
model.add(Dense(units=num_classes, activation='softmax'))
# nadam performed best, as did categorical cross entropy in our previous experiments...
model.compile(optimizer='nadam', loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(training_data, training_labels, batch_size=128, epochs=10, verbose=False, validation_split=.1)
plot_training_history(history, model)
```
Not bad, but not nearly as good as we were able to achieve with regular MNIST. Plus some overfitting concerns are showing themselves in the chart...
```
# The model is still sequentail, nothing new here.
model = Sequential()
# add model layers. The first parameter is the number of filters to make at each layer.
# Meaning here the result of the first layer is 64 different "feature maps" or "activation maps"
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu', padding='same', input_shape=(28,28,1)))
model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', padding='same',))
model.add(Flatten())
model.add(Dense(num_classes, activation='softmax'))
# Lets fit it with identical parameters and see what happens...
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
# OOPS! Previously, we flattened our training data, but now we INTEND on having 2D input data.
# training_data => 784 long vector
# training_images => 28 x 28 matrix
# Plus one small caveat: we have to indicate the number of color channels explicitly as a dimension...
history = model.fit(conv_training_data, training_labels, batch_size=128, epochs=3, verbose=True, validation_split=.1)
plot_training_history(history, model, eval_images=True)
# When did our evaluator do poorly?
predictions = model.predict(conv_test_data)
cm = confusion_matrix(np.argmax(predictions, axis=1), np.argmax(test_labels, axis=1))
plt.figure(figsize = (15, 15))
name_labels = [
'T-shirt/top',
'Trouser',
'Pullover',
'Dress',
'Coat',
'Sandal',
'Shirt',
'Sneaker',
'Bag',
'Ankle boot'
]
sn.heatmap(cm, annot=True, xticklabels=name_labels, yticklabels=name_labels)
plt.show()
# Lets make a few small changes and see what happens...
model = Sequential()
# Note, fewer filters and a bigger kernel, plus a pooling layer
model.add(Conv2D(32, kernel_size=(5, 5), activation='relu', padding='same', input_shape=(28,28,1)))
model.add(MaxPooling2D(pool_size=(2, 2)))
# Note, more filters and a pooling
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu', padding='same'))
model.add(MaxPooling2D(pool_size=(2, 2)))
# 2 dense layers with dropout before the final.
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(num_classes, activation='softmax'))
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(conv_training_data, training_labels, batch_size=128, epochs=5, verbose=True, validation_split=.1)
plot_training_history(history, model, eval_images=True)
predictions = model.predict(conv_test_data)
cm = confusion_matrix(np.argmax(predictions, axis=1), np.argmax(test_labels, axis=1))
plt.figure(figsize = (15, 15))
sn.heatmap(cm, annot=True, xticklabels=name_labels, yticklabels=name_labels)
plt.show()
```
90% is pretty respectible, especially considering how speedy training was, and given that we didn't apply any data augmentation. [Some state of the art networks get around 93-95% accuracy](https://github.com/zalandoresearch/fashion-mnist). It's also worth noting that we only really fail on comparing pullovers to coats, and tops to t-shirts.
```
# Lets get rid of pooling and try using striding to do the downsampling instead.
model = Sequential()
model.add(Conv2D(32, kernel_size=(5, 5), strides=(2,2), activation='relu', padding='same', input_shape=(28,28,1)))
model.add(Conv2D(64, kernel_size=(3, 3), strides=(2,2), activation='relu', padding='same'))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dropout(rate=0.2))
model.add(Dense(num_classes, activation='softmax'))
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(conv_training_data, training_labels, batch_size=128, epochs=5, verbose=True, validation_split=.1)
plot_training_history(history, model, eval_images=True)
predictions = model.predict(conv_test_data)
cm = confusion_matrix(np.argmax(predictions, axis=1), np.argmax(test_labels, axis=1))
plt.figure(figsize = (15, 15))
sn.heatmap(cm, annot=True, xticklabels=name_labels, yticklabels=name_labels)
plt.show()
# Sweet, faster and similar performance, looks a bit at risk for overfitting.
# Lets try one more:
model = Sequential()
# Downsample on the first layer via strides.
model.add(Conv2D(32, kernel_size=(5, 5), strides=(2,2), activation='relu', padding='same', input_shape=(28,28,1)))
# Once downsampled, don't down sample further (strides back to (1,1))
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu', padding='same'))
model.add(Flatten())
# NOTE, because we're downsampling much less I reduced the number of nodes in this layer.
# keeping it at 256 explodes the total parameter count and slows down learning a lot.
model.add(Dense(64, activation='relu'))
model.add(Dropout(rate=0.2))
model.add(Dense(num_classes, activation='softmax'))
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(conv_training_data, training_labels, batch_size=128, epochs=5, verbose=True, validation_split=.1)
plot_training_history(history, model, eval_images=True)
# Pretty similar results. This would be a good place to apply data augmentation or collect a bit more data.
# We could continue to experiment with different models and probably find some small improvements as well.
# Plus, these models might all improve some if we kept training. They are overfitting a bit, but validation
# Scores are still rising by the end.
```
| true |
code
| 0.722564 | null | null | null | null |
|
# Lasso and Ridge Regression
**Lasso regression:** It is a type of linear regression that uses shrinkage. Shrinkage is where data values are shrunk towards a central point, like the mean.
<hr>
**Ridge Regression:** It is a way to create a predictive and explonatory model when the number of predictor variables in a set exceeds the number of observations, or when a data set has multicollinearity (correlations between predictor variables).
<hr>
- With this brief knowledge of Lasso and Ridge, in this notebook we are going to predict the Height of the person given the age.
**Dataset can be directly downloaded from <a href="https://archive.org/download/ages-and-heights/AgesAndHeights.pkl">here</a>.**
## Importing Libraries
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
from sklearn.preprocessing import MinMaxScaler
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
```
## Importing Dataset
```
!wget 'https://archive.org/download/ages-and-heights/AgesAndHeights.pkl'
raw_data = pd.read_pickle(
'AgesAndHeights.pkl'
) # Dataset Link: https://archive.org/download/ages-and-heights/AgesAndHeights.pkl
raw_data
raw_data.describe()
raw_data.info()
```
## Data Visualisation
```
sns.histplot(raw_data['Age'])
plt.show()
sns.histplot(raw_data['Height'], kde=False, bins=10)
plt.show()
```
## Data Preprocessing
```
cleaned = raw_data[raw_data['Age'] > 0]
cleaned.shape
# 7 Columns in the Dataset where the Age was less than 0, which is pretty unobvious.
sns.histplot(cleaned['Age'], kde=True)
plt.show()
cleaned.describe()
cleaned.info()
sns.scatterplot(cleaned['Age'],
cleaned['Height'],
label='Age, Height')
plt.title('Age VS Height', color='blue')
plt.xlabel('Age', color='green')
plt.ylabel('Height', color='green')
plt.legend()
plt.show()
```
**Scaling the Data in the range of (0, 1) to fit the model easily.**
```
scaler = MinMaxScaler()
cleaned_data = pd.DataFrame(scaler.fit_transform(cleaned))
cleaned_data.columns = ['Age', 'Height']
cleaned_data
```
## Model Building
```
age = cleaned_data['Age']
height = cleaned_data['Height']
```
### Lasso
```
model_l = Lasso()
X = cleaned_data[['Age']]
y = cleaned_data[['Height']]
model_l.fit(X, y)
```
#### Lasso - Predict
```
np.float64(model_l.predict([[16]]) * 100)
```
### Ridge
```
model_r = Ridge()
model_r.fit(X, y)
```
#### Ridge - Predict
```
np.float64(model_r.predict([[16]]) * 10)
```
### With and Without Regularisation
Use `ML Algorithms` to build and train the model. Here, `Simple Linear Regression` is used. Before that let's create a necessary environment to build the model.
Actual -> $y = \alpha + \beta x + \epsilon$
True -> $\hat{y} = \alpha + \beta x$
```
# random parameter values
parameters = {'alpha': 40, 'beta': 4}
# y_hat using formulas mentioned above
def y_hat(age, params):
alpha = params['alpha']
beta = params['beta']
return alpha + beta * age
age = int(input('Enter age: '))
y_hat(age, parameters)
# learning better parameters for optimum result (using Regularisation)
def learn_parameters(data, params):
x, y = data['Age'], data['Height']
x_bar, y_bar = x.mean(), y.mean()
x, y = x.to_numpy(), y.to_numpy()
beta = sum(((x - x_bar) * (y - y_bar)) / sum((x - x_bar)**2))
alpha = y_bar - beta * x_bar
params['alpha'] = alpha
params['beta'] = beta
# new parameters derived from 'learn_parameters' function
new_parameter = {'alpha': -2, 'beta': 1000}
learn_parameters(cleaned, new_parameter)
new_parameter
# general untrained predictions
spaced_ages = list(range(19))
spaced_untrained_predictions = [y_hat(x, parameters) for x in spaced_ages]
print(spaced_untrained_predictions)
# Untrained Predictions
ages = cleaned_data[['Age']] * 17.887852
heights = cleaned_data[['Height']] * 68.170414
plt.scatter(ages, heights, label='Raw Data')
plt.plot(spaced_ages,
spaced_untrained_predictions,
label='Untrained Predictions',
color='green')
plt.title('Height VS Age')
plt.xlabel('Age[Years]')
plt.ylabel('Height[Inches]')
plt.legend()
plt.show()
# Trained Predictions
spaced_trained_predictions = [y_hat(x, new_parameter) for x in spaced_ages]
print('Trained Predicted Values: ',spaced_trained_predictions)
plt.scatter(ages,heights, label='Raw Data')
plt.plot(spaced_ages, spaced_untrained_predictions, label = 'Untrained Predictions', color = 'green')
plt.plot(spaced_ages, spaced_trained_predictions, label = 'Trained Predictions', color = 'red')
plt.title('Height VS Age')
plt.xlabel('Age[Years]')
plt.ylabel('Height[Inches]')
plt.legend()
plt.show()
# We can see that the result is not optimal but has changed significantly from a normal Linear Regression Type Model
```
# Summary
_Input (Age):_ 16
| **Model Name** | **Results** |
| :------------: | :---------- |
| Lasso | 42.3622 |
| Ridge | 128.0477 |
- We can see from the above plot how a normal Linear Regression performs and how a Linear Regression with either L1 or L2 norm Regularisations improves the predictions.
- From the above table, we can conclude that Ridge model out performs Lasso by a huge margin and point to be **noted**, that it is the case with this dataset, which may prove wrong for a different Dataset.
- It also satisfies the definition of Lasso and Ridge Regression, mentioned at the start of the notebook.
**P.S.** It always cannot be the case that Regularisation Model outperforms Linear Regression in all cases. It happens in almost all cases but in some exceptional cases it is the vice versa.
| true |
code
| 0.624236 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Plot parameters
sns.set()
%pylab inline
pylab.rcParams['figure.figsize'] = (4, 4)
plt.rcParams['xtick.major.size'] = 0
plt.rcParams['ytick.major.size'] = 0
# Avoid inaccurate floating values (for inverse matrices in dot product for instance)
# See https://stackoverflow.com/questions/24537791/numpy-matrix-inversion-rounding-errors
np.set_printoptions(suppress=True)
%%html
<style>
.pquote {
text-align: left;
margin: 40px 0 40px auto;
width: 70%;
font-size: 1.5em;
font-style: italic;
display: block;
line-height: 1.3em;
color: #5a75a7;
font-weight: 600;
border-left: 5px solid rgba(90, 117, 167, .1);
padding-left: 6px;
}
.notes {
font-style: italic;
display: block;
margin: 40px 10%;
}
</style>
```
$$
\newcommand\bs[1]{\boldsymbol{#1}}
\newcommand\norm[1]{\left\lVert#1\right\rVert}
$$
<span class='notes'>
This content is part of a series following the chapter 2 on linear algebra from the [Deep Learning Book](http://www.deeplearningbook.org/) by Goodfellow, I., Bengio, Y., and Courville, A. (2016). It aims to provide intuitions/drawings/python code on mathematical theories and is constructed as my understanding of these concepts. You can check the syllabus in the [introduction post](https://hadrienj.github.io/posts/Deep-Learning-Book-Series-Introduction/).
</span>
# Introduction
The [2.4](https://hadrienj.github.io/posts/Deep-Learning-Book-Series-2.4-Linear-Dependence-and-Span/) was heavy but this one is light. We will however see an important concept for machine learning and deep learning. The norm is what is generally used to evaluate the error of a model. For instance it is used to calculate the error between the output of a neural network and what is expected (the actual label or value). You can think of the norm as the length of a vector. It is a function that maps a vector to a positive value. Different functions can be used and we will see few examples.
# 2.5 Norms
Norms are any functions that are characterized by the following properties:
1- Norms are non-negative values. If you think of the norms as a length, you easily see why it can't be negative.
2- Norms are $0$ if and only if the vector is a zero vector
3- Norms respect the triangle inequity. See bellow.
4- $\norm{\bs{k}\cdot \bs{u}}=\norm{\bs{k}}\cdot\norm{\bs{u}}$. The norm of a vector multiplied by a scalar is equal to the absolute value of this scalar multiplied by the norm of the vector.
It is usually written with two horizontal bars: $\norm{\bs{x}}$
# The triangle inequity
The norm of the sum of some vectors is less than or equal the sum of the norms of these vectors.
$$
\norm{\bs{u}+\bs{v}} \leq \norm{\bs{u}}+\norm{\bs{v}}
$$
### Example 1.
$$
\bs{u}=
\begin{bmatrix}
1 & 6
\end{bmatrix}
$$
and
$$
\bs{v}=
\begin{bmatrix}
4 & 2
\end{bmatrix}
$$
$$
\norm{\bs{u}+\bs{v}} = \sqrt{(1+4)^2+(6+2)^2} = \sqrt{89} \approx 9.43
$$
$$
\norm{\bs{u}}+\norm{\bs{v}} = \sqrt{1^2+6^2}+\sqrt{4^2+2^2} = \sqrt{37}+\sqrt{20} \approx 10.55
$$
Let's check these results:
```
u = np.array([1, 6])
u
v = np.array([4, 2])
v
u+v
np.linalg.norm(u+v)
np.linalg.norm(u)+np.linalg.norm(v)
u = [0,0,1,6]
v = [0,0,4,2]
u_bis = [1,6,v[2],v[3]]
w = [0,0,5,8]
plt.quiver([u[0], u_bis[0], w[0]],
[u[1], u_bis[1], w[1]],
[u[2], u_bis[2], w[2]],
[u[3], u_bis[3], w[3]],
angles='xy', scale_units='xy', scale=1, color=sns.color_palette())
# plt.rc('text', usetex=True)
plt.xlim(-2, 6)
plt.ylim(-2, 9)
plt.axvline(x=0, color='grey')
plt.axhline(y=0, color='grey')
plt.text(-1, 3.5, r'$||\vec{u}||$', color=sns.color_palette()[0], size=20)
plt.text(2.5, 7.5, r'$||\vec{v}||$', color=sns.color_palette()[1], size=20)
plt.text(2, 2, r'$||\vec{u}+\vec{v}||$', color=sns.color_palette()[2], size=20)
plt.show()
plt.close()
```
<span class='pquote'>
Geometrically, this simply means that the shortest path between two points is a line
</span>
# P-norms: general rules
Here is the recipe to get the $p$-norm of a vector:
1. Calculate the absolute value of each element
2. Take the power $p$ of these absolute values
3. Sum all these powered absolute values
4. Take the power $\frac{1}{p}$ of this result
This is more condensly expressed with the formula:
$$
\norm{\bs{x}}_p=(\sum_i|\bs{x}_i|^p)^{1/p}
$$
This will be clear with examples using these widely used $p$-norms.
# The $L^0$ norm
All positive values will get you a $1$ if you calculate its power $0$ except $0$ that will get you another $0$. Therefore this norm corresponds to the number of non-zero elements in the vector. It is not really a norm because if you multiply the vector by $\alpha$, this number is the same (rule 4 above).
# The $L^1$ norm
$p=1$ so this norm is simply the sum of the absolute values:
$$
\norm{\bs{x}}_1=\sum_{i} |\bs{x}_i|
$$
# The Euclidean norm ($L^2$ norm)
The Euclidean norm is the $p$-norm with $p=2$. This may be the more used norm with the squared $L^2$ norm.
$$
\norm{\bs{x}}_2=(\sum_i \bs{x}_i^2)^{1/2}\Leftrightarrow \sqrt{\sum_i \bs{x}_i^2}
$$
Let's see an example of this norm:
### Example 2.
Graphically, the Euclidean norm corresponds to the length of the vector from the origin to the point obtained by linear combination (like applying Pythagorean theorem).
$$
\bs{u}=
\begin{bmatrix}
3 \\\\
4
\end{bmatrix}
$$
$$
\begin{align*}
\norm{\bs{u}}_2 &=\sqrt{|3|^2+|4|^2}\\\\
&=\sqrt{25}\\\\
&=5
\end{align*}
$$
So the $L^2$ norm is $5$.
The $L^2$ norm can be calculated with the `linalg.norm` function from numpy. We can check the result:
```
np.linalg.norm([3, 4])
```
Here is the graphical representation of the vectors:
```
u = [0,0,3,4]
plt.quiver([u[0]],
[u[1]],
[u[2]],
[u[3]],
angles='xy', scale_units='xy', scale=1)
plt.xlim(-2, 4)
plt.ylim(-2, 5)
plt.axvline(x=0, color='grey')
plt.axhline(y=0, color='grey')
plt.annotate('', xy = (3.2, 0), xytext = (3.2, 4),
arrowprops=dict(edgecolor='black', arrowstyle = '<->'))
plt.annotate('', xy = (0, -0.2), xytext = (3, -0.2),
arrowprops=dict(edgecolor='black', arrowstyle = '<->'))
plt.text(1, 2.5, r'$\vec{u}$', size=18)
plt.text(3.3, 2, r'$\vec{u}_y$', size=18)
plt.text(1.5, -1, r'$\vec{u}_x$', size=18)
plt.show()
plt.close()
```
In this case, the vector is in a 2-dimensional space but this stands also for more dimensions.
$$
u=
\begin{bmatrix}
u_1\\\\
u_2\\\\
\cdots \\\\
u_n
\end{bmatrix}
$$
$$
||u||_2 = \sqrt{u_1^2+u_2^2+\cdots+u_n^2}
$$
# The squared Euclidean norm (squared $L^2$ norm)
$$
\sum_i|\bs{x}_i|^2
$$
The squared $L^2$ norm is convenient because it removes the square root and we end up with the simple sum of every squared values of the vector.
The squared Euclidean norm is widely used in machine learning partly because it can be calculated with the vector operation $\bs{x}^\text{T}\bs{x}$. There can be performance gain due to the optimization See [here](https://softwareengineering.stackexchange.com/questions/312445/why-does-expressing-calculations-as-matrix-multiplications-make-them-faster) and [here](https://www.quora.com/What-makes-vector-operations-faster-than-for-loops) for more details.
### Example 3.
$$
\bs{x}=
\begin{bmatrix}
2 \\\\
5 \\\\
3 \\\\
3
\end{bmatrix}
$$
$$
\bs{x}^\text{T}=
\begin{bmatrix}
2 & 5 & 3 & 3
\end{bmatrix}
$$
$$
\begin{align*}
\bs{x}^\text{T}\bs{x}&=
\begin{bmatrix}
2 & 5 & 3 & 3
\end{bmatrix} \times
\begin{bmatrix}
2 \\\\
5 \\\\
3 \\\\
3
\end{bmatrix}\\\\
&= 2\times 2 + 5\times 5 + 3\times 3 + 3\times 3= 47
\end{align*}
$$
```
x = np.array([[2], [5], [3], [3]])
x
euclideanNorm = x.T.dot(x)
euclideanNorm
np.linalg.norm(x)**2
```
It works!
## Derivative of the squared $L^2$ norm
Another advantage of the squared $L^2$ norm is that its partial derivative is easily computed:
$$
u=
\begin{bmatrix}
u_1\\\\
u_2\\\\
\cdots \\\\
u_n
\end{bmatrix}
$$
$$
\norm{u}_2 = u_1^2+u_2^2+\cdots+u_n^2
$$
$$
\begin{cases}
\dfrac{d\norm{u}_2}{du_1} = 2u_1\\\\
\dfrac{d\norm{u}_2}{du_2} = 2u_2\\\\
\cdots\\\\
\dfrac{d\norm{u}_2}{du_n} = 2u_n
\end{cases}
$$
## Derivative of the $L^2$ norm
In the case of the $L^2$ norm, the derivative is more complicated and takes every elements of the vector into account:
$$
\norm{u}_2 = \sqrt{(u_1^2+u_2^2+\cdots+u_n^2)} = (u_1^2+u_2^2+\cdots+u_n^2)^{\frac{1}{2}}
$$
$$
\begin{align*}
\dfrac{d\norm{u}_2}{du_1} &=
\dfrac{1}{2}(u_1^2+u_2^2+\cdots+u_n^2)^{\frac{1}{2}-1}\cdot
\dfrac{d}{du_1}(u_1^2+u_2^2+\cdots+u_n^2)\\\\
&=\dfrac{1}{2}(u_1^2+u_2^2+\cdots+u_n^2)^{-\frac{1}{2}}\cdot
\dfrac{d}{du_1}(u_1^2+u_2^2+\cdots+u_n^2)\\\\
&=\dfrac{1}{2}\cdot\dfrac{1}{(u_1^2+u_2^2+\cdots+u_n^2)^{\frac{1}{2}}}\cdot
\dfrac{d}{du_1}(u_1^2+u_2^2+\cdots+u_n^2)\\\\
&=\dfrac{1}{2}\cdot\dfrac{1}{(u_1^2+u_2^2+\cdots+u_n^2)^{\frac{1}{2}}}\cdot
2\cdot u_1\\\\
&=\dfrac{u_1}{\sqrt{(u_1^2+u_2^2+\cdots+u_n^2)}}\\\\
\end{align*}
$$
$$
\begin{cases}
\dfrac{d\norm{u}_2}{du_1} = \dfrac{u_1}{\sqrt{(u_1^2+u_2^2+\cdots+u_n^2)}}\\\\
\dfrac{d\norm{u}_2}{du_2} = \dfrac{u_2}{\sqrt{(u_1^2+u_2^2+\cdots+u_n^2)}}\\\\
\cdots\\\\
\dfrac{d\norm{u}_2}{du_n} = \dfrac{u_n}{\sqrt{(u_1^2+u_2^2+\cdots+u_n^2)}}\\\\
\end{cases}
$$
One problem of the squared $L^2$ norm is that it hardly discriminates between 0 and small values because the increase of the function is slow.
We can see this by graphically comparing the squared $L^2$ norm with the $L^2$ norm. The $z$-axis corresponds to the norm and the $x$- and $y$-axis correspond to two parameters. The same thing is true with more than 2 dimensions but it would be hard to visualize it.
$L^2$ norm:
<img src="images/L2Norm.png" alt="L2Norm" width="500">
Squared $L^2$ norm:
<img src="images/squaredL2Norm.png" alt="squaredL2Norm" width="500">
$L^1$ norm:
<img src="images/L1Norm.png" alt="L1Norm" width="500">
These plots are done with the help of this [website](https://academo.org/demos/3d-surface-plotter/). Go and plot these norms if you need to move them in order to catch their shape.
# The max norm
It is the $L^\infty$ norm and corresponds to the absolute value of the greatest element of the vector.
$$
\norm{\bs{x}}_\infty = \max\limits_i|x_i|
$$
# Matrix norms: the Frobenius norm
$$
\norm{\bs{A}}_F=\sqrt{\sum_{i,j}A^2_{i,j}}
$$
This is equivalent to take the $L^2$ norm of the matrix after flattening.
The same Numpy function can be use:
```
A = np.array([[1, 2], [6, 4], [3, 2]])
A
np.linalg.norm(A)
```
# Expression of the dot product with norms
$$
\bs{x}^\text{T}\bs{y} = \norm{\bs{x}}_2\cdot\norm{\bs{y}}_2\cos\theta
$$
### Example 4.
$$
\bs{x}=
\begin{bmatrix}
0 \\\\
2
\end{bmatrix}
$$
and
$$
\bs{y}=
\begin{bmatrix}
2 \\\\
2
\end{bmatrix}
$$
```
x = [0,0,0,2]
y = [0,0,2,2]
plt.xlim(-2, 4)
plt.ylim(-2, 5)
plt.axvline(x=0, color='grey', zorder=0)
plt.axhline(y=0, color='grey', zorder=0)
plt.quiver([x[0], y[0]],
[x[1], y[1]],
[x[2], y[2]],
[x[3], y[3]],
angles='xy', scale_units='xy', scale=1)
plt.text(-0.5, 1, r'$\vec{x}$', size=18)
plt.text(1.5, 0.5, r'$\vec{y}$', size=18)
plt.show()
plt.close()
```
We took this example for its simplicity. As we can see, the angle $\theta$ is equal to 45°.
$$
\bs{x^\text{T}y}=
\begin{bmatrix}
0 & 2
\end{bmatrix} \cdot
\begin{bmatrix}
2 \\\\
2
\end{bmatrix} =
0\times2+2\times2 = 4
$$
and
$$
\norm{\bs{x}}_2=\sqrt{0^2+2^2}=\sqrt{4}=2
$$
$$
\norm{\bs{y}}_2=\sqrt{2^2+2^2}=\sqrt{8}
$$
$$
2\times\sqrt{8}\times cos(45)=4
$$
Here are the operations using numpy:
```
# Note: np.cos take the angle in radian
np.cos(np.deg2rad(45))*2*np.sqrt(8)
```
<span class='notes'>
Feel free to drop me an email or a comment. The syllabus of this series can be found [in the introduction post](https://hadrienj.github.io/posts/Deep-Learning-Book-Series-Introduction/). All the notebooks can be found on [Github](https://github.com/hadrienj/deepLearningBook-Notes).
</span>
# References
- https://en.wikipedia.org/wiki/Norm_(mathematics)
- [3D plots](https://academo.org/demos/3d-surface-plotter/)
| true |
code
| 0.644505 | null | null | null | null |
|
```
import os
import numpy as np
from matplotlib import pyplot as plt, colors, lines
```
## Generate plots for Adaptive *k*-NN on Random Subspaces and Tiny ImageNet
This code expects the output from the `Adaptive k-NN Subspaces Tiny ImageNet` notebook, so be sure to run that first.
```
plt.rc('text', usetex=True)
plt.rcParams['figure.figsize'] = [3.25, 2.5]
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.family'] = 'Times New Roman'
plt.rcParams['font.size'] = 8
plt.rcParams['axes.titlesize'] = 'small'
plt.rcParams['axes.titlepad'] = 3
plt.rcParams['xtick.labelsize'] = 'x-small'
plt.rcParams['ytick.labelsize'] = plt.rcParams['xtick.labelsize']
plt.rcParams['legend.fontsize'] = 6
plt.rcParams['legend.handlelength'] = 1.5
plt.rcParams['lines.markersize'] = 4
plt.rcParams['lines.linewidth'] = 0.7
plt.rcParams['axes.linewidth'] = 0.6
plt.rcParams['grid.linewidth'] = 0.6
plt.rcParams['xtick.major.width'] = 0.6
plt.rcParams['xtick.minor.width'] = 0.4
plt.rcParams['ytick.major.width'] = plt.rcParams['xtick.major.width']
plt.rcParams['ytick.minor.width'] = plt.rcParams['xtick.minor.width']
color_cycle = ['#003366', '#800000']
res_npz = np.load(os.path.join('results', 'tiny_imagenet_subspaces.npz'))
res_tiny_imagenet_np=res_npz['res_tiny_imagenet_np']
res_subspace_np=res_npz['res_subspace_np']
n=res_npz['n']
m=res_npz['m']
ps=res_npz['ps']
k=res_npz['k']
h=res_npz['h']
delta=res_npz['delta']
n_trials=res_npz['n_trials']
which_alpha=res_npz['which_alpha']
alpha_cs=res_npz['alpha_cs']
alpha_cs_ti=res_npz['alpha_cs_ti']
def plot_twin_ax_with_quartiles(ax, title, recovered_frac, n_iter_frac, alpha_cs, legend=True, left=True, bottom=True, right=True):
y_recover = np.median(recovered_frac, axis=0)
y_recover_1q = np.percentile(recovered_frac, 25, axis=0)
y_recover_3q = np.percentile(recovered_frac, 75, axis=0)
y_n_iter = np.median(n_iter_frac, axis=0)
y_n_iter_1q = np.percentile(n_iter_frac, 25, axis=0)
y_n_iter_3q = np.percentile(n_iter_frac, 75, axis=0)
ax_r = ax.twinx()
ax.fill_between(alpha_cs, y_recover_1q, y_recover_3q, facecolor=color_cycle[0], alpha=0.3)
ax.semilogx(alpha_cs, y_recover, c=color_cycle[0], label='top $k$ fraction')
ax.set_ylim(-0.1, 1.1)
ax.set_yticks(np.linspace(0, 1, 6))
#ax.set_ylabel('Fraction of top $k$ found')
#ax.set_xlabel(r'$C_\alpha$')
if legend:
solid_legend = ax.legend(loc='upper left')
ax.set_title(title)
ax.grid(axis='x')
ax.grid(which='minor', axis='x', alpha=0.2)
ax.set_zorder(ax_r.get_zorder() + 1)
ax.patch.set_visible(False)
ax.tick_params(axis='both', which='both', left=left, labelleft=left, bottom=bottom, labelbottom=bottom)
ax_r.fill_between(alpha_cs, y_n_iter_1q, y_n_iter_3q, facecolor=color_cycle[1], alpha=0.3)
ax_r.loglog(alpha_cs, y_n_iter, '--', c=color_cycle[1])
ax_r.set_yscale('log')
ax_r.set_ylim(1e-4 * 10**(1/3), 10**(1/3))
#ax_r.set_ylabel('\#iters / mn')
if legend:
dashed_plt, = ax.plot([], [], '--', c=color_cycle[1])
ax.legend((dashed_plt,), ('\#iters / mn',), loc='lower right')
ax.add_artist(solid_legend)
ax_r.grid(True)
ax_r.grid(which='minor', alpha=0.2)
ax_r.tick_params(axis='both', which='both', right=right, labelright=right)
fig, axes = plt.subplots(2, 2)
for i in range(3):
plot_twin_ax_with_quartiles(axes.ravel()[i], '$p = %g$' % ps[i],
res_subspace_np[:, i, 0, 0, 0, 0, 0, :, 0] / k,
res_subspace_np[:, i, 0, 0, 0, 0, 0, :, 1] / n / m,
alpha_cs, legend=False, left=i % 2 == 0, bottom=True, right=i % 2 == 1)
plot_twin_ax_with_quartiles(axes[1, 1], 'Tiny ImageNet',
res_tiny_imagenet_np[:, 0, 0, 0, 0, 0, :, 0] / k,
res_tiny_imagenet_np[:, 0, 0, 0, 0, 0, :, 1] / n / m,
alpha_cs_ti, legend=False, left=False)
plt.tight_layout(pad=1.7, h_pad=0.2, w_pad=0.2)
# add legend to axis labels
left_solid_line = lines.Line2D([0.017]*2, [0.375, 0.425], color=color_cycle[0], transform=fig.transFigure, figure=fig)
right_dashed_line = lines.Line2D([0.985]*2, [0.265, 0.315], linestyle='--', color=color_cycle[1], transform=fig.transFigure, figure=fig)
fig.lines.extend([left_solid_line, right_dashed_line])
fig.canvas.draw()
fig.text(0.5, 0.965, r'Effect of varying $C_\alpha$', ha='center', va='center', size='large')
fig.text(0.017, 0.5, 'Recall', ha='center', va='center', rotation='vertical')
fig.text(0.5, 0.015, r'$C_\alpha$', ha='center', va='center')
fig.text(0.985, 0.5, r'\#iterations / $mn$', ha='center', va='center', rotation='vertical')
plt.savefig(os.path.join('results', 'tiny_imagenet_subspaces.pdf'))
plt.show()
```
| true |
code
| 0.625753 | null | null | null | null |
|
# Introduction to Deep Learning with PyTorch
In this notebook, you'll get introduced to [PyTorch](http://pytorch.org/), a framework for building and training neural networks. PyTorch in a lot of ways behaves like the arrays you love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with Python and the Numpy/Scipy stack compared to TensorFlow and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
# use fastai venv to run since pytorch installed
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
# activation(3.2)
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1,5))
# True weights for our data, random normal variables again
weights = torch.randn((1,5))
# and a true bias term
bias = torch.randn((1, 1))
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
```
## Calculate the output of this network using the weights and bias tensors
weights.shape
activation(torch.sum(features * weights ) + bias)
```
You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second column. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), and [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
weights.shape
## Calculate the output of this network using matrix multiplication
activation(torch.mm(features, weights.view(5,1))+bias)
```
### Stack them up!
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
features
features.shape
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
W1
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
W2
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
B1
B2
```
> **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
## Your solution here
H1 = activation((torch.mm(features, W1))+B1)
y = activation(torch.mm(H1,W2)+B2)
H1
y
```
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
a = np.random.rand(4,3)
a
b = torch.from_numpy(a)
b
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place, underscore means in place operation
b.mul_(2)
# Numpy array matches new values from Tensor
a
```
| true |
code
| 0.629888 | null | null | null | null |
|
# 1. Introduction
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from prml.preprocess import PolynomialFeature
from prml.linear import (
LinearRegression,
RidgeRegression,
BayesianRegression
)
np.random.seed(1234)
```
## 1.1. Example: Polynomial Curve Fitting
```
def create_toy_data(func, sample_size, std):
x = np.linspace(0, 1, sample_size)
t = func(x) + np.random.normal(scale=std, size=x.shape)
return x, t
def func(x):
return np.sin(2 * np.pi * x)
x_train, y_train = create_toy_data(func, 10, 0.25)
x_test = np.linspace(0, 1, 100)
y_test = func(x_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.legend()
plt.show()
for i, degree in enumerate([0, 1, 3, 9]):
plt.subplot(2, 2, i + 1)
feature = PolynomialFeature(degree)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = LinearRegression()
model.fit(X_train, y_train)
y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="fitting")
plt.ylim(-1.5, 1.5)
plt.annotate("M={}".format(degree), xy=(-0.15, 1))
plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.show()
def rmse(a, b):
return np.sqrt(np.mean(np.square(a - b)))
training_errors = []
test_errors = []
for i in range(10):
feature = PolynomialFeature(i)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = LinearRegression()
model.fit(X_train, y_train)
y = model.predict(X_test)
training_errors.append(rmse(model.predict(X_train), y_train))
test_errors.append(rmse(model.predict(X_test), y_test + np.random.normal(scale=0.25, size=len(y_test))))
plt.plot(training_errors, 'o-', mfc="none", mec="b", ms=10, c="b", label="Training")
plt.plot(test_errors, 'o-', mfc="none", mec="r", ms=10, c="r", label="Test")
plt.legend()
plt.xlabel("degree")
plt.ylabel("RMSE")
plt.show()
```
#### Regularization
```
feature = PolynomialFeature(9)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = RidgeRegression(alpha=1e-3)
model.fit(X_train, y_train)
y = model.predict(X_test)
y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="fitting")
plt.ylim(-1.5, 1.5)
plt.legend()
plt.annotate("M=9", xy=(-0.15, 1))
plt.show()
```
### 1.2.6 Bayesian curve fitting
```
model = BayesianRegression(alpha=2e-3, beta=2)
model.fit(X_train, y_train)
y, y_err = model.predict(X_test, return_std=True)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="mean")
plt.fill_between(x_test, y - y_err, y + y_err, color="pink", label="std.", alpha=0.5)
plt.xlim(-0.1, 1.1)
plt.ylim(-1.5, 1.5)
plt.annotate("M=9", xy=(0.8, 1))
plt.legend(bbox_to_anchor=(1.05, 1.), loc=2, borderaxespad=0.)
plt.show()
```
| true |
code
| 0.705522 | null | null | null | null |
|
# Prediction models for Project1
This notebook explores the following models:
* MeanModel - Predicts mean value for all future values
* LastDayModel - Predicts the same values like last day (given as futures)
Table of contents:
* Load model and create training and test datasets
* Evaluate Mean model
* Evaluate LastDayModel
* Explore error
```
import datetime
import calendar
import pprint
import json
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['figure.figsize'] = 12, 4
```
# Load project
```
project_folder = '../../datasets/radon-small/'
with open(project_folder + 'project.json', 'r') as file:
project = json.load(file)
pprint.pprint(project)
print('Flow1')
flow = pd.read_csv(project_folder + 'flow1.csv', parse_dates=['time'])
flow = flow[(flow.time >= project['start-date']) & (flow.time < project['end-date'])]
print(flow.info())
flow.head()
```
## Create train and test dataset
Dataset consists of the following features:
* Vector of last 24h data
and target value:
* Vector of next 24 predictions
```
flow['day'] = flow.time.map(pd.Timestamp.date)
flow['hour'] = flow.time.map(pd.Timestamp.time)
target = flow.pivot(index='day', columns='hour', values='flow')
target = target.fillna(0)
features = target.shift()
# Skip first days as they are 0.0 anyway
target = target[datetime.date(2013, 9, 13):]
features = features[datetime.date(2013, 9, 13):]
# Now lets create train and test dataset on given split day
split_day = datetime.date(2016, 11, 11)
X_train = features[:split_day].values
Y_train = target[:split_day].values
X_test = features[split_day:].values
Y_test = target[split_day:].values
X_test.shape
```
## Helper functions
Helper functions for building training and test sets and calculating score
```
class PredictionModel:
def fit(self, X, Y):
pass
def predict(self, X):
pass
def mae(y_hat, y):
"""
Calculate Mean Absolute Error
"""
return np.sum(np.absolute(y_hat-y), axis=1)/y.shape[0]
def evaluate_model(model):
"""
Evaluate model on all days starting from split_day.
Returns 90th percentile error as model score
"""
model.fit(X_train, Y_train)
costs = mae(model.predict(X_test), Y_test)
return np.percentile(costs, 90), costs
```
# Models
## ConstantMeanModel
Calculate mean from all datapoint in the training set.
Ignore features and predict constant value (equal to this mean) for all predicted values
```
class ConstantMeanModel(PredictionModel):
def __init__(self):
self.mu = 0
def fit(self, X, y):
self.mu = np.mean(y)
def predict(self, X):
return np.ones(X.shape) * self.mu
score, costs = evaluate_model(ConstantMeanModel())
print('ConstantMeanModel score: {:.2f}'.format(score))
```
## Last day model
Here our model will predict the same values like they were in the previos day
```
class LastDayModel(PredictionModel):
def fit(self, X, y):
pass
def predict(self, X):
return X.copy()
score, costs = evaluate_model(LastDayModel())
print('LastDayModel score: {:.2f}'.format(score))
```
### Explore errors
Check the biggest errors for Last day model:
```
df = pd.Series(costs, target[split_day:].index)
df.plot()
plt.show()
df = pd.DataFrame({'day': target[split_day:].index, 'cost': costs})
df['weekday'] = df['day'].apply(lambda x: calendar.day_name[x.weekday()])
df_sorted = df.sort_values(by=['cost'], ascending=False)
df_sorted.head(10)
```
#### Explore daily flow
The biggest error is at 2017-06-23 (Friday) (and in the next day)
```
def plot_days(start_day, end_day, show_prediction=True):
df = flow[(flow.time >= start_day) & (flow.time <= end_day)].set_index('time').flow
plt.plot(df)
# df.plot()
if show_prediction:
plt.plot(df.shift(288))
plt.show()
plot_days('2017-06-20', '2017-06-25')
```
This can probably be atributed to anomaly in data reading.
Or some problems in the network (kind of congestions)
Lets check week 2017-05-01 (Monday)
```
plot_days('2017-04-28', '2017-05-8')
```
Given flow in those days, it is not suprising that the model is not working here
| true |
code
| 0.635958 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Raw-data-stats" data-toc-modified-id="Raw-data-stats-1"><span class="toc-item-num">1 </span>Raw data stats</a></span></li><li><span><a href="#Read-in-data" data-toc-modified-id="Read-in-data-2"><span class="toc-item-num">2 </span>Read in data</a></span><ul class="toc-item"><li><span><a href="#Produce-latex-table" data-toc-modified-id="Produce-latex-table-2.1"><span class="toc-item-num">2.1 </span>Produce latex table</a></span></li><li><span><a href="#Add-region" data-toc-modified-id="Add-region-2.2"><span class="toc-item-num">2.2 </span>Add region</a></span></li></ul></li><li><span><a href="#Calculate-number-of-empty-tiles" data-toc-modified-id="Calculate-number-of-empty-tiles-3"><span class="toc-item-num">3 </span>Calculate number of empty tiles</a></span><ul class="toc-item"><li><span><a href="#Create-sample-to-check-what's-empty" data-toc-modified-id="Create-sample-to-check-what's-empty-3.1"><span class="toc-item-num">3.1 </span>Create sample to check what's empty</a></span></li></ul></li><li><span><a href="#highest-number-of-markings-per-tile" data-toc-modified-id="highest-number-of-markings-per-tile-4"><span class="toc-item-num">4 </span>highest number of markings per tile</a></span></li><li><span><a href="#Convert-distance-to-meters" data-toc-modified-id="Convert-distance-to-meters-5"><span class="toc-item-num">5 </span>Convert distance to meters</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Reduction-of-number-of-fan-markings-to-finals" data-toc-modified-id="Reduction-of-number-of-fan-markings-to-finals-5.0.1"><span class="toc-item-num">5.0.1 </span>Reduction of number of fan markings to finals</a></span></li></ul></li></ul></li><li><span><a href="#Length-stats" data-toc-modified-id="Length-stats-6"><span class="toc-item-num">6 </span>Length stats</a></span><ul class="toc-item"><li><span><a href="#Blotch-sizes" data-toc-modified-id="Blotch-sizes-6.1"><span class="toc-item-num">6.1 </span>Blotch sizes</a></span></li><li><span><a href="#Longest-fans" data-toc-modified-id="Longest-fans-6.2"><span class="toc-item-num">6.2 </span>Longest fans</a></span></li></ul></li><li><span><a href="#North-azimuths" data-toc-modified-id="North-azimuths-7"><span class="toc-item-num">7 </span>North azimuths</a></span></li><li><span><a href="#User-stats" data-toc-modified-id="User-stats-8"><span class="toc-item-num">8 </span>User stats</a></span></li><li><span><a href="#pipeline-output-examples" data-toc-modified-id="pipeline-output-examples-9"><span class="toc-item-num">9 </span>pipeline output examples</a></span></li></ul></div>
```
%matplotlib ipympl
import seaborn as sns
sns.set()
sns.set_context('paper')
sns.set_palette('colorblind')
from planet4 import io, stats, markings, plotting, region_data
from planet4.catalog_production import ReleaseManager
fans = pd.read_csv("/Users/klay6683/Dropbox/data/planet4/p4_analysis/P4_catalog_v1.0/P4_catalog_v1.0_L1C_cut_0.5_fan_meta_merged.csv")
blotch = pd.read_csv("/Users/klay6683/Dropbox/data/planet4/p4_analysis/P4_catalog_v1.0/P4_catalog_v1.0_L1C_cut_0.5_blotch_meta_merged.csv")
pd.set_option("display.max_columns", 150)
fans.head()
fans.l_s.head().values[0]
group_blotch = blotch.groupby("obsid")
type(group_blotch)
counts = group_blotch.marking_id.count()
counts.head()
counts.plot(c='r')
plt.figure()
counts.hist()
counts.max()
counts.min()
fans.head()
plt.figure(constrained_layout=True)
counts[:20].plot.bar()
plt.figure()
counts[:10].plot(use_index=True)
plt.figure()
counts[:10]
grouped = fans.groupby("obsid")
grouped.tile_id.nunique().sort_values(ascending=False).head()
%matplotlib inline
from planet4.markings import ImageID
p4id = ImageID('7t9')
p4id.image_name
p4id.plot_fans()
filtered = fans[fans.tile_id=='APF0000cia']
filtered.shape
p4id.plot_fans(data=filtered)
```
# Raw data stats
```
import dask.dataframe as dd
db = io.DBManager()
db.dbname
df = dd.read_hdf(db.dbname, 'df')
df.columns
grp = df.groupby(['user_name'])
s = grp.classification_id.nunique().compute().sort_values(ascending=False).head(5)
s
```
# Read in data
```
rm = ReleaseManager('v1.0')
db = io.DBManager()
data = db.get_all()
fans = pd.read_csv(rm.fan_merged)
fans.shape
fans.columns
from planet4.stats import define_season_column
define_season_column(fans)
fans.columns
season2 = fans[fans.season==2]
season2.shape
img223 = fans.query("image_name=='ESP_012265_0950'")
img223.shape
plt.figure()
img223.angle.hist()
fans.season.dtype
meta = pd.read_csv(rm.metadata_path, dtype='str')
cols_to_merge = ['OBSERVATION_ID',
'SOLAR_LONGITUDE', 'north_azimuth', 'map_scale']
fans = fans.merge(meta[cols_to_merge], left_on='obsid', right_on='OBSERVATION_ID')
fans.drop(rm.DROP_FOR_FANS, axis=1, inplace=True)
fans.image_x.head()
ground['image_x'] = pd.to_numeric(ground.image_x)
ground['image_y'] = pd.to_numeric(ground.image_y)
fans_new = fans.merge(ground[rm.COLS_TO_MERGE], on=['obsid', 'image_x', 'image_y'])
fans_new.shape
fans.shape
s = pd.to_numeric(ground.BodyFixedCoordinateX)
s.head()
s.round(decimals=4)
blotches = rm.read_blotch_file().assign(marking='blotch')
fans = rm.read_fan_file().assign(marking='fan')
combined = pd.concat([blotches, fans], ignore_index=True)
blotches.head()
```
## Produce latex table
```
fans.columns
cols1 = fans.columns[:13]
print(cols1)
cols2 = fans.columns[13:-4]
print(cols2)
cols3 = fans.columns[-4:-1]
cols3
fanshead1 = fans[cols1].head(10)
fanshead2 = fans[cols2].head(10)
fanshead3 = fans[cols3].head(10)
with open("fan_table1.tex", 'w') as f:
f.write(fanshead1.to_latex())
with open("fan_table2.tex", 'w') as f:
f.write(fanshead2.to_latex())
with open("fan_table3.tex", 'w') as f:
f.write(fanshead3.to_latex())
```
## Add region
Adding a region identifier, immensely helpful in automatically plotting stuff across regions.
```
for Reg in region_data.regions:
reg = Reg()
print(reg.name)
combined.loc[combined.obsid.isin(reg.all_obsids), 'region'] = reg.name
fans.loc[fans.obsid.isin(reg.all_obsids), 'region']= reg.name
blotches.loc[blotches.obsid.isin(reg.all_obsids), 'region'] = reg.name
```
# Calculate number of empty tiles
```
tiles_marked = combined.tile_id.unique()
db = io.DBManager()
input_tiles = db.image_ids
input_tiles.shape[0]
n_empty = input_tiles.shape[0] - tiles_marked.shape[0]
n_empty
n_empty / input_tiles.shape[0]
empty_tiles = list(set(input_tiles) - set(tiles_marked))
all_data = db.get_all()
all_data.set_index('image_id', inplace=True)
empty_data = all_data.loc[empty_tiles]
meta = pd.read_csv(rm.metadata_path)
meta.head()
empty_tile_numbers = empty_data.reset_index().groupby('image_name')[['x_tile', 'y_tile']].max()
empty_tile_numbers['total'] = empty_tile_numbers.x_tile*empty_tile_numbers.y_tile
empty_tile_numbers.head()
n_empty_per_obsid = empty_data.reset_index().groupby('image_name').image_id.nunique()
n_empty_per_obsid = n_empty_per_obsid.to_frame()
n_empty_per_obsid.columns = ['n']
df = n_empty_per_obsid
df = df.join(empty_tile_numbers.total)
df = df.assign(ratio=df.n/df.total)
df = df.join(meta.set_index('OBSERVATION_ID'))
df['scaled_n'] = df.n / df.map_scale / df.map_scale
import seaborn as sns
sns.set_context('notebook')
df.plot(kind='scatter', y='ratio', x='SOLAR_LONGITUDE')
ax = plt.gca()
ax.set_ylabel('Fraction of empty tiles per HiRISE image')
ax.set_xlabel('Solar Longitude [$^\circ$]')
ax.set_title("Distribution of empty tiles vs time")
plt.savefig("/Users/klay6683/Dropbox/src/p4_paper1/figures/empty_data_vs_ls.pdf")
df[df.ratio > 0.8]
```
## Create sample to check what's empty
```
sample = np.random.choice(empty_tiles, 200)
cd plots
from tqdm import tqdm
for image_id in tqdm(sample):
fig, ax = plt.subplots(ncols=2)
plotting.plot_raw_fans(image_id, ax=ax[0])
plotting.plot_raw_blotches(image_id, ax=ax[1])
fig.savefig(f"empty_tiles/{image_id}_input_markings.png", dpi=150)
plt.close('all')
```
# highest number of markings per tile
```
fans_per_tile = fans.groupby('tile_id').size().sort_values(ascending=False)
fans_per_tile.head()
blotches_per_tile = blotches.groupby('tile_id').size().sort_values(ascending=False)
blotches_per_tile.head()
print(fans_per_tile.median())
blotches_per_tile.median()
plt.close('all')
by_image_id = combined.groupby(['marking', 'tile_id']).size()
by_image_id.name = 'Markings per tile'
by_image_id = by_image_id.reset_index()
by_image_id.columns
g = sns.FacetGrid(by_image_id, col="marking", aspect=1.2)
bins = np.arange(0, 280, 5)
g.map(sns.distplot, 'Markings per tile', kde=False, bins=bins, hist_kws={'log':True})
plt.savefig('/Users/klay6683/Dropbox/src/p4_paper1/figures/number_distributions.pdf', dpi=150)
blotches_per_tile.median()
from planet4 import plotting
# %load -n plotting.plot_finals_with_input
def plot_finals_with_input(id_, datapath=None, horizontal=True, scope='planet4'):
imgid = markings.ImageID(id_, scope=scope)
pm = io.PathManager(id_=id_, datapath=datapath)
if horizontal is True:
kwargs = {'ncols': 2}
else:
kwargs = {'nrows': 2}
fig, ax = plt.subplots(figsize=(4,5), **kwargs)
ax[0].set_title(imgid.imgid, fontsize=8)
imgid.show_subframe(ax=ax[0])
for marking in ['fan', 'blotch']:
try:
df = getattr(pm, f"final_{marking}df")
except:
continue
else:
data = df[df.image_id == imgid.imgid]
imgid.plot_markings(marking, data, ax=ax[1])
fig.subplots_adjust(top=0.95,bottom=0, left=0, right=1, hspace=0.01, wspace=0.01)
fig.savefig(f"/Users/klay6683/Dropbox/src/p4_paper1/figures/{imgid.imgid}_final.png",
dpi=150)
plot_finals_with_input('7t9', rm.savefolder, horizontal=False)
markings.ImageID('7t9').image_name
```
# Convert distance to meters
```
fans['distance_m'] = fans.distance*fans.map_scale
blotches['radius_1_m'] = blotches.radius_1*blotches.map_scale
blotches['radius_2_m'] = blotches.radius_2*blotches.map_scale
```
### Reduction of number of fan markings to finals
```
n_fan_in = 2792963
fans.shape[0]
fans.shape[0] / n_fan_in
```
# Length stats
Percentage of fan markings below 100 m:
```
import scipy
scipy.stats.percentileofscore(fans.distance_m, 100)
```
Cumulative histogram of fan lengths
```
def add_percentage_line(ax, meters, column):
y = scipy.stats.percentileofscore(column, meters)
ax.axhline(y/100, linestyle='dashed', color='black', lw=1)
ax.axvline(meters, linestyle='dashed', color='black', lw=1)
ax.text(meters, y/100, f"{y/100:0.2f}")
plt.close('all')
fans.distance_m.max()
bins = np.arange(0,380, 5)
fig, ax = plt.subplots(figsize=(8,3), ncols=2, sharey=False)
sns.distplot(fans.distance_m, bins=bins, kde=False,
hist_kws={'cumulative':False,'normed':True, 'log':True},
axlabel='Fan length [m]', ax=ax[0])
sns.distplot(fans.distance_m, bins=bins, kde=False, hist_kws={'cumulative':True,'normed':True},
axlabel='Fan length [m]', ax=ax[1])
ax[0].set_title("Normalized Log-Histogram of fan lengths ")
ax[1].set_title("Cumulative normalized histogram of fan lengths")
ax[1].set_ylabel("Fraction of fans with given length")
add_percentage_line(ax[1], 100, fans.distance_m)
add_percentage_line(ax[1], 50, fans.distance_m)
fig.tight_layout()
fig.savefig("/Users/klay6683/Dropbox/src/p4_paper1/figures/fan_lengths_histos.pdf",
dpi=150, bbox_inches='tight')
fans.query('distance_m>350')[['distance_m', 'obsid', 'l_s']]
fans.distance_m.describe()
```
In words, the mean length of fans is {{f"{fans.distance_m.describe()['mean']:.1f}"}} m, while the median is
{{f"{fans.distance_m.describe()['50%']:.1f}"}} m.
```
fans.replace("Manhattan_Frontinella", "Manhattan_\nFrontinella", inplace=True)
fig, ax = plt.subplots()
sns.boxplot(y="region", x="distance_m", data=fans, ax=ax,
fliersize=3)
ax.set_title("Fan lengths in different ROIs")
fig.tight_layout()
fig.savefig("/Users/klay6683/Dropbox/src/p4_paper1/figures/fan_lengths_vs_regions.pdf",
dpi=150, bbox_inches='tight')
```
## Blotch sizes
```
plt.figure()
cols = ['radius_1','radius_2']
sns.distplot(blotches[cols], kde=False, bins=np.arange(2.0,50.),
color=['r','g'], label=cols)
plt.legend()
plt.figure()
cols = ['radius_1_m','radius_2_m']
sns.distplot(blotches[cols], kde=False, bins=np.arange(2.0,50.),
color=['r','g'], label=cols)
plt.legend()
fig, ax = plt.subplots(figsize=(8,4))
sns.distplot(blotches.radius_2_m, bins=500, kde=False, hist_kws={'cumulative':True,'normed':True},
axlabel='Blotch radius_1 [m]', ax=ax)
ax.set_title("Cumulative normalized histogram for blotch lengths")
ax.set_ylabel("Fraction of blotches with given radius_1")
add_percentage_line(ax, 30, blotches.radius_2_m)
add_percentage_line(ax, 10, blotches.radius_2_m)
import scipy
scipy.stats.percentileofscore(blotches.radius_2_m, 30)
plt.close('all')
```
## Longest fans
```
fans.query('distance_m > 350')[
'distance_m distance obsid image_x image_y tile_id'.split()].sort_values(
by='distance_m')
from planet4 import plotting
plotting.plot_finals('de3', datapath=rm.catalog)
plt.gca().set_title('APF0000de3')
plotting.plot_image_id_pipeline('de3', datapath=rm.catalog, via_obsid=False, figsize=(12,8))
from planet4 import region_data
from planet4 import stats
stats.define_season_column(fans)
stats.define_season_column(blotches)
fans.season.value_counts()
fans.query('season==2').distance_m.median()
fans.query('season==3').distance_m.median()
from planet4 import region_data
for region in ['Manhattan2', 'Giza','Ithaca']:
print(region)
obj = getattr(region_data, region)
for s in ['season2','season3']:
print(s)
obsids = getattr(obj, s)
print(fans[fans.obsid.isin(obsids)].distance_m.median())
db = io.DBManager()
all_data = db.get_all()
image_names = db.image_names
g_all = all_data.groupby('image_id')
g_all.size().sort_values().head()
fans.columns
cols_to_drop = ['path', 'image_name', 'binning', 'LineResolution', 'SampleResolution', 'Line', 'Sample']
fans.drop(cols_to_drop, axis=1, inplace=True, errors='ignore')
fans.columns
fans.iloc[1]
```
# North azimuths
```
s = """ESP\_011296\_0975 & -82.197 & 225.253 & 178.8 & 2008-12-23 & 17:08 & 91 \\
ESP\_011341\_0980 & -81.797 & 76.13 & 180.8 & 2008-12-27 & 17:06 & 126 \\
ESP\_011348\_0950 & -85.043 & 259.094 & 181.1 & 2008-12-27 & 18:01 & 91 \\
ESP\_011350\_0945 & -85.216 & 181.415 & 181.2 & 2008-12-27 & 16:29 & 126 \\
ESP\_011351\_0945 & -85.216 & 181.548 & 181.2 & 2008-12-27 & 18:18 & 91 \\
ESP\_011370\_0980 & -81.925 & 4.813 & 182.1 & 2008-12-29 & 17:08 & 126 \\
ESP\_011394\_0935 & -86.392 & 99.068 & 183.1 & 2008-12-31 & 19:04 & 72 \\
ESP\_011403\_0945 & -85.239 & 181.038 & 183.5 & 2009-01-01 & 16:56 & 164 \\
ESP\_011404\_0945 & -85.236 & 181.105 & 183.6 & 2009-01-01 & 18:45 & 91 \\
ESP\_011406\_0945 & -85.409 & 103.924 & 183.7 & 2009-01-01 & 17:15 & 126 \\
ESP\_011407\_0945 & -85.407 & 103.983 & 183.7 & 2009-01-01 & 19:04 & 91 \\
ESP\_011408\_0930 & -87.019 & 86.559 & 183.8 & 2009-01-01 & 19:43 & 59 \\
ESP\_011413\_0970 & -82.699 & 273.129 & 184.0 & 2009-01-01 & 17:17 & 108 \\
ESP\_011420\_0930 & -87.009 & 127.317 & 184.3 & 2009-01-02 & 20:16 & 54 \\
ESP\_011422\_0930 & -87.041 & 72.356 & 184.4 & 2009-01-02 & 20:15 & 54 \\
ESP\_011431\_0930 & -86.842 & 178.244 & 184.8 & 2009-01-03 & 19:41 & 54 \\
ESP\_011447\_0950 & -84.805 & 65.713 & 185.5 & 2009-01-04 & 17:19 & 218 \\
ESP\_011448\_0950 & -84.806 & 65.772 & 185.6 & 2009-01-04 & 19:09 & 59 \\"""
lines = s.split(' \\')
s.replace('\\', '')
obsids = [line.split('&')[0].strip().replace('\\','') for line in lines][:-1]
meta = pd.read_csv(rm.metadata_path)
meta.query('obsid in @obsids').sort_values(by='obsid').
blotches.groupby('obsid').north_azimuth.nunique()
```
# User stats
```
db = io.DBManager()
db.dbname = '/Users/klay6683/local_data/planet4/2018-02-11_planet_four_classifications_queryable_cleaned_seasons2and3.h5'
with pd.HDFStore(str(db.dbname)) as store:
user_names = store.select_column('df', 'user_name').unique()
user_names.shape
user_names[:10]
not_logged = [i for i in user_names if i.startswith('not-logged-in')]
logged = list(set(user_names) - set(not_logged))
len(logged)
len(not_logged)
not_logged[:20]
df = db.get_all()
df[df.marking=='fan'].shape
df[df.marking=='blotch'].shape
df[df.marking=='interesting'].shape
n_class_by_user = df.groupby('user_name').classification_id.nunique()
n_class_by_user.describe()
logged_users = df.user_name[~df.user_name.str.startswith("not-logged-in")].unique()
logged_users.shape
not_logged = list(set(df.user_name.unique()) - set(logged_users))
len(not_logged)
n_class_by_user[not_logged].describe()
n_class_by_user[logged_users].describe()
n_class_by_user[n_class_by_user>50].shape[0]/n_class_by_user.shape[0]
n_class_by_user.shape
```
# pipeline output examples
```
pm = io.PathManager('any', datapath=rm.savefolder)
cols1 = pm.fandf.columns[:8]
cols2 = pm.fandf.columns[8:-2]
cols3 = pm.fandf.columns[-2:]
print(pm.fandf[cols1].to_latex())
print(pm.fandf[cols2].to_latex())
print(pm.fandf[cols3].to_latex())
df = pm.fnotchdf.head(4)
cols1 = df.columns[:6]
cols2 = df.columns[6:14]
cols3 = df.columns[14:]
for i in [1,2,3]:
print(df[eval(f"cols{i}")].to_latex())
```
| true |
code
| 0.461684 | null | null | null | null |
|
# Tutorial
We will solve the following problem using a computer to estimate the expected
probabilities:
```{admonition} Problem
An experiment consists of selecting a token from a bag and spinning a coin. The
bag contains 5 red tokens and 7 blue tokens. A token is selected at random from
the bag, its colour is noted and then the token is returned to the bag.
When a red token is selected, a biased coin with probability $\frac{2}{3}$
of landing heads is spun.
When a blue token is selected a fair coin is spun.
1. What is the probability of picking a red token?
2. What is the probability of obtaining Heads?
3. If a heads is obtained, what is the probability of having selected a red
token.
```
We will use the `random` library from the Python standard library to do this.
First we start off by building a Python **tuple** to represent the bag with the
tokens. We assign this to a variable `bag`:
```
bag = (
"Red",
"Red",
"Red",
"Red",
"Red",
"Blue",
"Blue",
"Blue",
"Blue",
"Blue",
"Blue",
"Blue",
)
bag
```
```{attention}
We are there using the circular brackets `()` and the quotation marks
`"`. Those are important and cannot be omitted. The choice of brackets `()` as
opposed to `{}` or `[]` is in fact important as it instructs Python to do
different things (we will learn about this later). You can use `"` or `'`
interchangeably.
```
Instead of writing every entry out we can create a Python **list** which allows
for us to carry out some basic algebra on the items. Here we essentially:
- Create a list with 5 `"Red"`s.
- Create a list with 7 `"Blue"`s.
- Combine both lists:
```
bag = ["Red"] * 5 + ["Blue"] * 7
bag
```
Now to sample from that we use the `random` library which has a `choice`
command:
```
import random
random.choice(bag)
```
If we run this many times we will not always get the same outcome:
```
random.choice(bag)
```
```{attention}
The `bag` variable is unchanged:
```
```
bag
```
In order to answer the first question (what is the probability of picking a red
token) we want to repeat this many times.
We do this by defining a Python function (which is akin to a mathematical
function) that allows us to repeat code:
```
def pick_a_token(container):
"""
A function to randomly sample from a `container`.
"""
return random.choice(container)
```
We can then call this function, passing our `bag` to it as the `container` from
which to pick:
```
pick_a_token(container=bag)
pick_a_token(container=bag)
```
In order to simulate the probability of picking a red token we need to repeat
this not once or twice but tens of thousands of times. We will do this using
something called a "list comprehension" which is akin to the mathematical
notation we use all the time to create sets:
$$
S_1 = \{f(x)\text{ for }x\text{ in }S_2\}
$$
```
number_of_repetitions = 10000
samples = [pick_a_token(container=bag) for repetition in range(number_of_repetitions)]
samples
```
We can confirm that we have the correct number of samples:
```
len(samples)
```
```{attention}
`len` is the Python tool to get the length of a given Python iterable.
```
Using this we can now use `==` (double `=`) to check how many of those samples are `Red`:
```
sum(token == "Red" for token in samples) / number_of_repetitions
```
We have sampled probability of around .41. The theoretic value is $\frac{5}{5 +
7}$:
```
5 / (5 + 7)
```
To answer the second question (What is the probability of obtaining Heads?) we
need to make use of another Python tool: an `if` statement. This will allow us
to write a function that does precisely what is described in the problem:
- Choose a token;
- Set the probability of flipping a given coin;
- Select that coin.
```{attention}
For the second random selection (flipping a coin) we will not choose from a list
but instead select a random number between 0 and 1.
```
```
import random
def sample_experiment(bag):
"""
This samples a token from a given bag and then
selects a coin with a given probability.
If the sampled token is red then the probability
of selecting heads is 2/3 otherwise it is 1/2.
This function returns both the selected token
and the coin face.
"""
selected_token = pick_a_token(container=bag)
if selected_token == "Red":
probability_of_selecting_heads = 2 / 3
else:
probability_of_selecting_heads = 1 / 2
if random.random() < probability_of_selecting_heads:
coin = "Heads"
else:
coin = "Tails"
return selected_token, coin
```
Using this we can sample according to the problem description:
```
sample_experiment(bag=bag)
sample_experiment(bag=bag)
```
We can now find out the probability of selecting heads by carrying out a large
number of repetitions and checking which ones have a coin that is heads:
```
samples = [sample_experiment(bag=bag) for repetition in range(number_of_repetitions)]
sum(coin == "Heads" for token, coin in samples) / number_of_repetitions
```
We can compute this theoretically as well, the expected probability is:
```
import sympy as sym
sym.S(5) / (12) * sym.S(2) / 3 + sym.S(7) / (12) * sym.S(1) / 2
41 / 72
```
We can also use our samples to calculate the conditional probability that a
token was read if the coin is heads. This is done again using the list
comprehension notation but including an `if` statement which allows us to
emulate the mathematical notation:
$$
S_3 = \{x \in S_1 | \text{ if some property of \(x\) holds}\}
$$
```
samples_with_heads = [(token, coin) for token, coin in samples if coin == "Heads"]
sum(token == "Red" for token, coin in samples_with_heads) / len(samples_with_heads)
```
Using Bayes' theorem this is given theoretically by:
$$
P(\text{Red}|\text{Heads}) = \frac{P(\text{Heads} | \text{Red})P(\text{Red})}{P(\text{Heads})}
$$
```
(sym.S(2) / 3 * sym.S(5) / 12) / (sym.S(41) / 72)
20 / 41
```
```{important}
In this tutorial we have
- Randomly sampled from an iterable.
- Randomly sampled a number between 0 and 1.
- Written a function to represent a random experiment.
- Created a list using list comprehensions.
- Counted outcomes of random experiments.
```
| true |
code
| 0.717618 | null | null | null | null |
|
# Thinking in tensors, writing in PyTorch
A hands-on course by [Piotr Migdał](https://p.migdal.pl) (2019).
<a href="https://colab.research.google.com/github/stared/thinking-in-tensors-writing-in-pytorch/blob/master/5%20Nonlinear%20regression.ipynb" target="_parent">
<img src="https://colab.research.google.com/assets/colab-badge.svg"/>
</a>
## Notebook 5: Non-linear regression
Very **Work in Progress**

### Exercise
Which of the following can be described by linear regression:
* without any modifications,
* by after rescaling *x* or *y*,
* cannot be described by linear regression?
**TODO**
* Prepare examples
* 1d function with nonlinearities (by hand and automatically)
* More advanced
**Datasets to consider**
* https://en.wikipedia.org/wiki/Flight_airspeed_record
**TODO later**
* livelossplot `plot_extrema` error
* drawing a plot
* consider using [hiddenlayer](https://github.com/waleedka/hiddenlayer)
```
%matplotlib inline
from matplotlib import pyplot as plt
import torch
from torch import nn
from torch import tensor
from livelossplot import PlotLosses
X = torch.linspace(-2., 2., 30).unsqueeze(1)
Y = torch.cat([torch.zeros(10), torch.linspace(0., 1., 10), 1. + torch.zeros(10)], dim=0)
plt.plot(X.squeeze().numpy(), Y.numpy(), 'r.')
linear_model = nn.Linear(in_features=1, out_features=1)
def train(X, Y, model, loss_function, optim, num_epochs):
loss_history = []
def extra_plot(*args):
plt.plot(X.squeeze(1).numpy(), Y.numpy(), 'r.', label="Ground truth")
plt.plot(X.squeeze(1).numpy(), model(X).detach().numpy(), '-', label="Model")
plt.title("Prediction")
plt.legend(loc='lower right')
liveloss = PlotLosses(extra_plots=[extra_plot], plot_extrema=False)
for epoch in range(num_epochs):
epoch_loss = 0.0
Y_pred = model(X)
loss = loss_function(Y_pred, Y)
loss.backward()
optim.step()
optim.zero_grad()
liveloss.update({
'loss': loss.data.item(),
})
liveloss.draw()
```
## Linear model
$$y = a x + b$$
```
class Linear(nn.Module):
def __init__(self):
super().__init__()
self.layer_weights = nn.Parameter(torch.randn(1, 1))
self.layer_bias = nn.Parameter(torch.randn(1))
def forward(self, x):
return x.matmul(self.layer_weights).add(self.layer_bias).squeeze()
linear_model = Linear()
optim = torch.optim.SGD(linear_model.parameters(), lr=0.03)
loss_function = nn.MSELoss()
list(linear_model.parameters())
linear_model(X)
train(X, Y, linear_model, loss_function, optim, num_epochs=50)
```
## Nonlinear
$$ x \mapsto h \mapsto y$$
```
class Nonlinear(nn.Module):
def __init__(self, hidden_size=2):
super().__init__()
self.layer_1_weights = nn.Parameter(torch.randn(1, hidden_size))
self.layer_1_bias = nn.Parameter(torch.randn(hidden_size))
self.layer_2_weights = nn.Parameter(torch.randn(hidden_size, 1) )
self.layer_2_bias = nn.Parameter(torch.randn(1))
def forward(self, x):
x = x.matmul(self.layer_1_weights).add(self.layer_1_bias)
x = x.relu()
x = x.matmul(self.layer_2_weights).add(self.layer_2_bias)
return x.squeeze()
def nonrandom_init(self):
self.layer_1_weights.data = tensor([[1.1, 0.8]])
self.layer_1_bias.data = tensor([0.5 , -0.7])
self.layer_2_weights.data = tensor([[0.3], [-0.7]])
self.layer_2_bias.data = tensor([0.2])
nonlinear_model = Nonlinear(hidden_size=2)
nonlinear_model.nonrandom_init()
optim = torch.optim.SGD(nonlinear_model.parameters(), lr=0.2)
# optim = torch.optim.Adam(nonlinear_model.parameters(), lr=0.1)
loss_function = nn.MSELoss()
train(X, Y, nonlinear_model, loss_function, optim, num_epochs=200)
```
## Other shapes and activations
```
Y_sin = (2 * X).sin()
plt.plot(X.squeeze().numpy(), Y_sin.numpy(), 'r.')
# warning:
# for 1-d problems it rarely works (often gets stuck in some local minimum)
nonlinear_model = Nonlinear(hidden_size=10)
optim = torch.optim.Adam(nonlinear_model.parameters(), lr=0.01)
loss_function = nn.MSELoss()
train(X, Y_sin, nonlinear_model, loss_function, optim, num_epochs=100)
class NonlinearSigmoid2(nn.Module):
def __init__(self, hidden_size=2):
super().__init__()
self.layer_1_weights = nn.Parameter(torch.randn(1, hidden_size))
self.layer_1_bias = nn.Parameter(torch.randn(hidden_size))
self.layer_2_weights = nn.Parameter(torch.randn(hidden_size, 1))
self.layer_2_bias = nn.Parameter(torch.randn(1))
def forward(self, x):
x = x.matmul(self.layer_1_weights).add(self.layer_1_bias)
x = x.sigmoid()
x = x.matmul(self.layer_2_weights).add(self.layer_2_bias)
x = x.sigmoid()
return x.squeeze()
X1 = torch.linspace(-2., 2., 30).unsqueeze(1)
Y1 = torch.cat([torch.zeros(10), 1. + torch.zeros(10), torch.zeros(10)], dim=0)
plt.plot(X1.squeeze().numpy(), Y1.numpy(), 'r.')
nonlinear_model = NonlinearSigmoid2(hidden_size=2)
# optim = torch.optim.SGD(nonlinear_model.parameters(), lr=0.1)
optim = torch.optim.Adam(nonlinear_model.parameters(), lr=0.1)
loss_function = nn.MSELoss()
train(X1, Y1, nonlinear_model, loss_function, optim, num_epochs=100)
```
## Nonlinear model - by hand
```
my_nonlinear_model = Nonlinear(hidden_size=2)
my_nonlinear_model.layer_1_weights.data = tensor([[1. , 1.]])
my_nonlinear_model.layer_1_bias.data = tensor([1. , -1.])
X.matmul(my_nonlinear_model.layer_1_weights).add(my_nonlinear_model.layer_1_bias).relu()
my_nonlinear_model.layer_2_weights.data = tensor([[0.5], [-0.5]])
my_nonlinear_model.layer_2_bias.data = tensor([0.])
my_nonlinear_model(X)
plt.plot(X.squeeze(1).numpy(), Y.numpy(), 'r.')
plt.plot(X.squeeze(1).numpy(), my_nonlinear_model(X).detach().numpy(), '-')
```
| true |
code
| 0.861567 | null | null | null | null |
|
<a id='python-by-example'></a>
<div id="qe-notebook-header" align="right" style="text-align:right;">
<a href="https://quantecon.org/" title="quantecon.org">
<img style="width:250px;display:inline;" width="250px" src="https://assets.quantecon.org/img/qe-menubar-logo.svg" alt="QuantEcon">
</a>
</div>
# An Introductory Example
<a id='index-0'></a>
## Contents
- [An Introductory Example](#An-Introductory-Example)
- [Overview](#Overview)
- [The Task: Plotting a White Noise Process](#The-Task:-Plotting-a-White-Noise-Process)
- [Version 1](#Version-1)
- [Alternative Implementations](#Alternative-Implementations)
- [Another Application](#Another-Application)
- [Exercises](#Exercises)
- [Solutions](#Solutions)
## Overview
We’re now ready to start learning the Python language itself.
In this lecture, we will write and then pick apart small Python programs.
The objective is to introduce you to basic Python syntax and data structures.
Deeper concepts will be covered in later lectures.
You should have read the [lecture](https://python-programming.quantecon.org/getting_started.html) on getting started with Python before beginning this one.
## The Task: Plotting a White Noise Process
Suppose we want to simulate and plot the white noise
process $ \epsilon_0, \epsilon_1, \ldots, \epsilon_T $, where each draw $ \epsilon_t $ is independent standard normal.
In other words, we want to generate figures that look something like this:
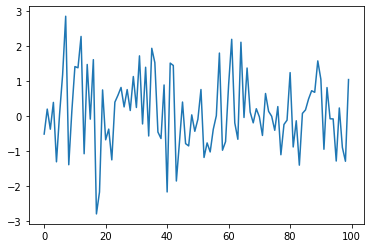
(Here $ t $ is on the horizontal axis and $ \epsilon_t $ is on the
vertical axis.)
We’ll do this in several different ways, each time learning something more
about Python.
We run the following command first, which helps ensure that plots appear in the
notebook if you run it on your own machine.
```
%matplotlib inline
```
## Version 1
<a id='ourfirstprog'></a>
Here are a few lines of code that perform the task we set
```
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10,6)
ϵ_values = np.random.randn(100)
plt.plot(ϵ_values)
plt.show()
```
Let’s break this program down and see how it works.
<a id='import'></a>
### Imports
The first two lines of the program import functionality from external code
libraries.
The first line imports [NumPy](https://python-programming.quantecon.org/numpy.html), a favorite Python package for tasks like
- working with arrays (vectors and matrices)
- common mathematical functions like `cos` and `sqrt`
- generating random numbers
- linear algebra, etc.
After `import numpy as np` we have access to these attributes via the syntax `np.attribute`.
Here’s two more examples
```
np.sqrt(4)
np.log(4)
```
We could also use the following syntax:
```
import numpy
numpy.sqrt(4)
```
But the former method (using the short name `np`) is convenient and more standard.
#### Why So Many Imports?
Python programs typically require several import statements.
The reason is that the core language is deliberately kept small, so that it’s easy to learn and maintain.
When you want to do something interesting with Python, you almost always need
to import additional functionality.
#### Packages
<a id='index-1'></a>
As stated above, NumPy is a Python *package*.
Packages are used by developers to organize code they wish to share.
In fact, a package is just a directory containing
1. files with Python code — called **modules** in Python speak
1. possibly some compiled code that can be accessed by Python (e.g., functions compiled from C or FORTRAN code)
1. a file called `__init__.py` that specifies what will be executed when we type `import package_name`
In fact, you can find and explore the directory for NumPy on your computer
easily enough if you look around.
On this machine, it’s located in
```ipython
anaconda3/lib/python3.7/site-packages/numpy
```
#### Subpackages
<a id='index-2'></a>
Consider the line `ϵ_values = np.random.randn(100)`.
Here `np` refers to the package NumPy, while `random` is a **subpackage** of NumPy.
Subpackages are just packages that are subdirectories of another package.
### Importing Names Directly
Recall this code that we saw above
```
import numpy as np
np.sqrt(4)
```
Here’s another way to access NumPy’s square root function
```
from numpy import sqrt
sqrt(4)
```
This is also fine.
The advantage is less typing if we use `sqrt` often in our code.
The disadvantage is that, in a long program, these two lines might be
separated by many other lines.
Then it’s harder for readers to know where `sqrt` came from, should they wish to.
### Random Draws
Returning to our program that plots white noise, the remaining three lines
after the import statements are
```
ϵ_values = np.random.randn(100)
plt.plot(ϵ_values)
plt.show()
```
The first line generates 100 (quasi) independent standard normals and stores
them in `ϵ_values`.
The next two lines genererate the plot.
We can and will look at various ways to configure and improve this plot below.
## Alternative Implementations
Let’s try writing some alternative versions of [our first program](#ourfirstprog), which plotted IID draws from the normal distribution.
The programs below are less efficient than the original one, and hence
somewhat artificial.
But they do help us illustrate some important Python syntax and semantics in a familiar setting.
### A Version with a For Loop
Here’s a version that illustrates `for` loops and Python lists.
<a id='firstloopprog'></a>
```
ts_length = 100
ϵ_values = [] # empty list
for i in range(ts_length):
e = np.random.randn()
ϵ_values.append(e)
plt.plot(ϵ_values)
plt.show()
```
In brief,
- The first line sets the desired length of the time series.
- The next line creates an empty *list* called `ϵ_values` that will store the $ \epsilon_t $ values as we generate them.
- The statement `# empty list` is a *comment*, and is ignored by Python’s interpreter.
- The next three lines are the `for` loop, which repeatedly draws a new random number $ \epsilon_t $ and appends it to the end of the list `ϵ_values`.
- The last two lines generate the plot and display it to the user.
Let’s study some parts of this program in more detail.
<a id='lists-ref'></a>
### Lists
<a id='index-3'></a>
Consider the statement `ϵ_values = []`, which creates an empty list.
Lists are a *native Python data structure* used to group a collection of objects.
For example, try
```
x = [10, 'foo', False]
type(x)
```
The first element of `x` is an [integer](https://en.wikipedia.org/wiki/Integer_%28computer_science%29), the next is a [string](https://en.wikipedia.org/wiki/String_%28computer_science%29), and the third is a [Boolean value](https://en.wikipedia.org/wiki/Boolean_data_type).
When adding a value to a list, we can use the syntax `list_name.append(some_value)`
```
x
x.append(2.5)
x
```
Here `append()` is what’s called a *method*, which is a function “attached to” an object—in this case, the list `x`.
We’ll learn all about methods later on, but just to give you some idea,
- Python objects such as lists, strings, etc. all have methods that are used to manipulate the data contained in the object.
- String objects have [string methods](https://docs.python.org/3/library/stdtypes.html#string-methods), list objects have [list methods](https://docs.python.org/3/tutorial/datastructures.html#more-on-lists), etc.
Another useful list method is `pop()`
```
x
x.pop()
x
```
Lists in Python are zero-based (as in C, Java or Go), so the first element is referenced by `x[0]`
```
x[0] # first element of x
x[1] # second element of x
```
### The For Loop
<a id='index-4'></a>
Now let’s consider the `for` loop from [the program above](#firstloopprog), which was
```
for i in range(ts_length):
e = np.random.randn()
ϵ_values.append(e)
```
Python executes the two indented lines `ts_length` times before moving on.
These two lines are called a `code block`, since they comprise the “block” of code that we are looping over.
Unlike most other languages, Python knows the extent of the code block *only from indentation*.
In our program, indentation decreases after line `ϵ_values.append(e)`, telling Python that this line marks the lower limit of the code block.
More on indentation below—for now, let’s look at another example of a `for` loop
```
animals = ['dog', 'cat', 'bird']
for animal in animals:
print("The plural of " + animal + " is " + animal + "s")
```
This example helps to clarify how the `for` loop works: When we execute a
loop of the form
```python3
for variable_name in sequence:
<code block>
```
The Python interpreter performs the following:
- For each element of the `sequence`, it “binds” the name `variable_name` to that element and then executes the code block.
The `sequence` object can in fact be a very general object, as we’ll see
soon enough.
### A Comment on Indentation
<a id='index-5'></a>
In discussing the `for` loop, we explained that the code blocks being looped over are delimited by indentation.
In fact, in Python, **all** code blocks (i.e., those occurring inside loops, if clauses, function definitions, etc.) are delimited by indentation.
Thus, unlike most other languages, whitespace in Python code affects the output of the program.
Once you get used to it, this is a good thing: It
- forces clean, consistent indentation, improving readability
- removes clutter, such as the brackets or end statements used in other languages
On the other hand, it takes a bit of care to get right, so please remember:
- The line before the start of a code block always ends in a colon
- `for i in range(10):`
- `if x > y:`
- `while x < 100:`
- etc., etc.
- All lines in a code block **must have the same amount of indentation**.
- The Python standard is 4 spaces, and that’s what you should use.
### While Loops
<a id='index-6'></a>
The `for` loop is the most common technique for iteration in Python.
But, for the purpose of illustration, let’s modify [the program above](#firstloopprog) to use a `while` loop instead.
<a id='whileloopprog'></a>
```
ts_length = 100
ϵ_values = []
i = 0
while i < ts_length:
e = np.random.randn()
ϵ_values.append(e)
i = i + 1
plt.plot(ϵ_values)
plt.show()
```
Note that
- the code block for the `while` loop is again delimited only by indentation
- the statement `i = i + 1` can be replaced by `i += 1`
## Another Application
Let’s do one more application before we turn to exercises.
In this application, we plot the balance of a bank account over time.
There are no withdraws over the time period, the last date of which is denoted
by $ T $.
The initial balance is $ b_0 $ and the interest rate is $ r $.
The balance updates from period $ t $ to $ t+1 $ according to $ b_{t+1} = (1 + r) b_t $.
In the code below, we generate and plot the sequence $ b_0, b_1, \ldots, b_T $.
Instead of using a Python list to store this sequence, we will use a NumPy
array.
```
r = 0.025 # interest rate
T = 50 # end date
b = np.empty(T+1) # an empty NumPy array, to store all b_t
b[0] = 10 # initial balance
for t in range(T):
b[t+1] = (1 + r) * b[t]
plt.plot(b, label='bank balance')
plt.legend()
plt.show()
```
The statement `b = np.empty(T+1)` allocates storage in memory for `T+1`
(floating point) numbers.
These numbers are filled in by the `for` loop.
Allocating memory at the start is more efficient than using a Python list and
`append`, since the latter must repeatedly ask for storage space from the
operating system.
Notice that we added a legend to the plot — a feature you will be asked to
use in the exercises.
## Exercises
Now we turn to exercises. It is important that you complete them before
continuing, since they present new concepts we will need.
### Exercise 1
Your first task is to simulate and plot the correlated time series
$$
x_{t+1} = \alpha \, x_t + \epsilon_{t+1}
\quad \text{where} \quad
x_0 = 0
\quad \text{and} \quad t = 0,\ldots,T
$$
The sequence of shocks $ \{\epsilon_t\} $ is assumed to be IID and standard normal.
In your solution, restrict your import statements to
```
import numpy as np
import matplotlib.pyplot as plt
```
Set $ T=200 $ and $ \alpha = 0.9 $.
### Exercise 2
Starting with your solution to exercise 2, plot three simulated time series,
one for each of the cases $ \alpha=0 $, $ \alpha=0.8 $ and $ \alpha=0.98 $.
Use a `for` loop to step through the $ \alpha $ values.
If you can, add a legend, to help distinguish between the three time series.
Hints:
- If you call the `plot()` function multiple times before calling `show()`, all of the lines you produce will end up on the same figure.
- For the legend, noted that the expression `'foo' + str(42)` evaluates to `'foo42'`.
### Exercise 3
Similar to the previous exercises, plot the time series
$$
x_{t+1} = \alpha \, |x_t| + \epsilon_{t+1}
\quad \text{where} \quad
x_0 = 0
\quad \text{and} \quad t = 0,\ldots,T
$$
Use $ T=200 $, $ \alpha = 0.9 $ and $ \{\epsilon_t\} $ as before.
Search online for a function that can be used to compute the absolute value $ |x_t| $.
### Exercise 4
One important aspect of essentially all programming languages is branching and
conditions.
In Python, conditions are usually implemented with if–else syntax.
Here’s an example, that prints -1 for each negative number in an array and 1
for each nonnegative number
```
numbers = [-9, 2.3, -11, 0]
for x in numbers:
if x < 0:
print(-1)
else:
print(1)
```
Now, write a new solution to Exercise 3 that does not use an existing function
to compute the absolute value.
Replace this existing function with an if–else condition.
<a id='pbe-ex3'></a>
### Exercise 5
Here’s a harder exercise, that takes some thought and planning.
The task is to compute an approximation to $ \pi $ using [Monte Carlo](https://en.wikipedia.org/wiki/Monte_Carlo_method).
Use no imports besides
```
import numpy as np
```
Your hints are as follows:
- If $ U $ is a bivariate uniform random variable on the unit square $ (0, 1)^2 $, then the probability that $ U $ lies in a subset $ B $ of $ (0,1)^2 $ is equal to the area of $ B $.
- If $ U_1,\ldots,U_n $ are IID copies of $ U $, then, as $ n $ gets large, the fraction that falls in $ B $, converges to the probability of landing in $ B $.
- For a circle, $ area = \pi * radius^2 $.
## Solutions
### Exercise 1
Here’s one solution.
```
α = 0.9
T = 200
x = np.empty(T+1)
x[0] = 0
for t in range(T):
x[t+1] = α * x[t] + np.random.randn()
plt.plot(x)
plt.show()
```
### Exercise 2
```
α_values = [0.0, 0.8, 0.98]
T = 200
x = np.empty(T+1)
for α in α_values:
x[0] = 0
for t in range(T):
x[t+1] = α * x[t] + np.random.randn()
plt.plot(x, label=f'$\\alpha = {α}$')
plt.legend()
plt.show()
```
### Exercise 3
Here’s one solution:
```
α = 0.9
T = 200
x = np.empty(T+1)
x[0] = 0
for t in range(T):
x[t+1] = α * np.abs(x[t]) + np.random.randn()
plt.plot(x)
plt.show()
```
### Exercise 4
Here’s one way:
```
α = 0.9
T = 200
x = np.empty(T+1)
x[0] = 0
for t in range(T):
if x[t] < 0:
abs_x = - x[t]
else:
abs_x = x[t]
x[t+1] = α * abs_x + np.random.randn()
plt.plot(x)
plt.show()
```
Here’s a shorter way to write the same thing:
```
α = 0.9
T = 200
x = np.empty(T+1)
x[0] = 0
for t in range(T):
abs_x = - x[t] if x[t] < 0 else x[t]
x[t+1] = α * abs_x + np.random.randn()
plt.plot(x)
plt.show()
```
### Exercise 5
Consider the circle of diameter 1 embedded in the unit square.
Let $ A $ be its area and let $ r=1/2 $ be its radius.
If we know $ \pi $ then we can compute $ A $ via
$ A = \pi r^2 $.
But here the point is to compute $ \pi $, which we can do by
$ \pi = A / r^2 $.
Summary: If we can estimate the area of a circle with diameter 1, then dividing
by $ r^2 = (1/2)^2 = 1/4 $ gives an estimate of $ \pi $.
We estimate the area by sampling bivariate uniforms and looking at the
fraction that falls into the circle.
```
n = 100000
count = 0
for i in range(n):
u, v = np.random.uniform(), np.random.uniform()
d = np.sqrt((u - 0.5)**2 + (v - 0.5)**2)
if d < 0.5:
count += 1
area_estimate = count / n
print(area_estimate * 4) # dividing by radius**2
```
| true |
code
| 0.613005 | null | null | null | null |
|
## Introduction of Fairness Workflow Tutorial
## (Dataset/Model Bias Check and Mitigation by Reweighing)
### Table of contents :
* [1 Introduction](#1.-Introduction)
* [2. Data preparation](#2.-Data-preparation)
* [3. Data fairness](#3.-Data-fairness)
* [Data bias checking](#3.1-Bias-Detection)
* [Data mitigation](#3.2-Bias-mitigation)
* [Data-Fairness-comparison](#3.3-Data-Fairness-comparison)
* [4. Model fairness on different ML models](#4.-Model-Fairness---on-different-ML-models)
* [5. Summary](#Summary)
## 1. Introduction
Welcome!
With the proliferation of ML and AI across diverse set of real world problems, there is strong need to keep an eye on explainability and fairness of the impact of ML-AI techniques. This tutorial is one such attempt, offering glimpse into the world of fairness.
We will walk you through an interesting case study in this tutorial. The aim is to familiarize you with one of the primary problem statements in Responsible AI: `Bias Detection and Mitigation`.
Bias is one of the basic problems which plagues datasets and ML models. After all, ML models are only as good as the data they see.
Before we go into detailed explanation, we would like to give a sneak peak of the steps involved in the bias detection and mitigation process.
As illustrated in the picture, one must first prepare the data for analysis, detect bias, mitigate bias and observe the effect of bias mitigation objectively with data fairness and model fairness metrics.
```
# Preparation
!git clone https://github.com/sony/nnabla-examples.git
%cd nnabla-examples/responsible_ai/gender_bias_mitigation
import cv2
from google.colab.patches import cv2_imshow
img = cv2.imread('images/xai-bias-mitigation-workflow.png')
cv2_imshow(img)
```
### 1.1 Sources of bias :
There are many types of bias in data, which can exist in many shapes and forms, some of which may lead to unfairness [1].
Following are some examples of sources which introduce bias in datasets:
__Insufficient data :__
There may not be sufficient data overall or for some minority groups in the training data.<br>
__Data collection practice :__
Bad data collection practices could introduce bias even for large datasets. For example, high proportion of missing values for few features in some groups - indication of incomplete representation of these groups in the dataset.<br>
__Historical bias :__
Significant difference in the target distribution for different groups could also be present due to underlying human prejudices.
### 1.2 Bias detection :
There are multiple definitions of fairness and bias. Depending on the use case, appropriate fairness definition must be chosen to decide the criterion to detect bias in the model predictions.
<br>
### 1.3 Bias mitigation :
There are three different approaches of bias-reduction intervention in the ML pipelines:
1. Pre-processing
2. In-processing
3. Post-processing
In this tutorial, we will see how to identify bias in [German credit dataset ](https://archive.ics.uci.edu/ml/datasets/Statlog+%28German+Credit+Data%29)[7] and mitigate it with a `pre-processing algorithm (reweighing)`.<br>
### 1.4 German credit dataset :
[German Credit dataset](https://archive.ics.uci.edu/ml/datasets/Statlog+%28German+Credit+Data%29) has classification of people into good/bad credit categories. It has 1000 instances and 20 features.
In this dataset, one may observe age/gender playing significant role in the prediction of credit risk label. Instances with one gender may be favored and other gender[s] may be discriminated against by ML models.
So, we must be aware of the following: <br>
* Training dataset may not be representative of the true population across age/gender groups
* Even if it is representative of the population, it is not fair to base any decision on applicant's age/gender
Let us get our hands dirty with the dataset. We shall determine presence of such biases in this dataset, try using a preprocessing algorithm to mitigate the bias and then evaluate model and data fairness.
```
import sys
import copy
import pandas as pd # for tabular data
import matplotlib.pyplot as plt # to plot charts
import seaborn as sns # to make pretty charts
import numpy as np # for math
# # sklearn to work with ML models, splitting the train-test data as well as imported metrics
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from xgboost import XGBClassifier
sys.path.append('../responsible-ai/gender-bias-mitigation/')
from utils import *
%matplotlib inline
```
## 2. Data preparation
#### Load dataset
First, let’s load [dataset](https://archive.ics.uci.edu/ml/machine-learning-databases/statlog/german/german.data). Column names as listed in [`german.doc`](https://archive.ics.uci.edu/ml/machine-learning-databases/statlog/german/german.doc)
```
filepath = r'https://archive.ics.uci.edu/ml/machine-learning-databases/statlog/german/german.data'
dataframe = load_dataset(filepath)
dataframe.head()
```
Interesting! The dataframe has discrete numerical values and some encoded representations.
Let us quickly sift through features/attributes in this dataset.
##### Number of attributes/features :
This dataset has a total of 20 (7 numerical + 13 categorical) attributes/features.
##### [Categorical attributes/features](https://en.wikipedia.org/wiki/Categorical_variable):
13 categorical features: 'status', 'credit_history', 'purpose', 'savings', 'employment', 'personal_status', 'other_debtors', 'property', 'installment_plans', 'housing', 'skill_level', 'telephone', 'foreign_worker' <br>
##### Numerical attributes/features :
Seven numerical features: 'month', 'credit_amount', 'investment_as_income_percentage', 'residence_since', 'age', 'number_of_credits' and 'people_liable_for'. <br>
##### [Target variable](https://en.wikipedia.org/wiki/Dependent_and_independent_variables#:~:text=Known%20values%20for%20the%20target,but%20not%20in%20unsupervised%20learning.) :
Credit coloumn represents target variable in this dataset. It has classification of good or bad credit label (good credit = 1, bad credit= 2). <br>
#### Nomenclature and properties relevant to Bias Detection and mitigation
Allow us to introduce some terms related to `bias detection and mitigation` in the context of dataset now.
##### Favourable & Unfavourable class :
Target values which are considered to be positive(good) may be called favourable class. The opposite may be called unfavourable class.
##### Protected attributes :
An attribute that partitions a population into groups with parity. Examples include race, gender, caste, and religion. Protected attributes are not universal, but are application specific [protected attributes](https://www.fairwork.gov.au/employee-entitlements/protections-at-work/protection-from-discrimination-at-work). Age and gender are the protected attributes in this dataset. <br>
##### Privileged class & Unprivileged class :
* Class in the protected attribute with majority is called privileged class.
* The opposite is called unprivileged class.<br>
#### Dataset specific preprocessing
Data preprocessing in machine learning is a crucial step that helps enhance the quality of data to promote the extraction of meaningful insights from the data.
For now let us specify the data specific preprocessing arguments to enhance the quality of data, for Ex: what is favourable & unfavourable labels, Protected attributes, privileged & unprivileged class ...etc to process the dataset.
```
# To keep it simple, in this tutorial, we shall try to determine whether there is gender bias in the dataset
# and mitigate that.
protected_attribute_names = ['gender']
privileged_classes = [['male']]
# derive the gender attribute from personal_status (you can refer the german.doc)
status_map = {'A91': 'male', 'A93': 'male', 'A94': 'male',
'A92': 'female', 'A95': 'female'}
dataframe['gender'] = dataframe['personal_status'].replace(status_map)
# target variable
label_name = 'credit'
favorable_label = 1.0 # good credit
unfavorable_label = 0.0 # bad credit
categorical_features = ['status', 'credit_history', 'purpose',
'savings', 'employment', 'other_debtors', 'property',
'installment_plans', 'housing', 'skill_level', 'telephone',
'foreign_worker']
features_to_drop = ['personal_status']
# dataset specific preprocessing
dataframe = preprocess_dataset(dataframe, label_name, protected_attribute_names,
privileged_classes, favorable_class=favorable_label,
categorical_features=categorical_features,
features_to_drop=features_to_drop)
dataframe.head()
```
Split the preprocessed data set into train and test data i.e,how well does the trained model perform on unseen data (test data)?
```
train = dataframe.sample(frac=0.7, random_state=0)
test = dataframe.drop(train.index)
```
## 3. Data fairness
### 3.1 Bias Detection
Before creating ML models, one must first analyze and check for biases in dataset, as mentioned [earlier](#1.2-Bias-detection-:). In this tutorial, we will aim to achieve `Statistical Parity`. Statistical parity is achieved when all segments of protected class (e.g. gender/age) have equal rates of positive outcome.
#### 3.1.1 Statistical parity difference
`Statistical Parity` is checked by computing `Statistical Parity Difference (SPD)`. SPD is the difference between the rate of favorable outcomes received by unprivileged group compared to privileged group. Negative value indicates less favorable outcomes for unprivileged groups.
Please look at the code below to get mathematical idea of SPD. It is ok to skip through follow sections and come back later if you want to understand from holistic perspective:
```
# return `True` if the corresponding row satisfies the `condition` and `False` otherwise
def get_condition_vector(X, feature_names, condition=None):
if condition is None:
return np.ones(X.shape[0], dtype=bool)
overall_cond = np.zeros(X.shape[0], dtype=bool)
for group in condition:
group_cond = np.ones(X.shape[0], dtype=bool)
for name, val in group.items():
index = feature_names.index(name)
group_cond = np.logical_and(group_cond, X[:, index] == val)
overall_cond = np.logical_or(overall_cond, group_cond)
return overall_cond
```
##### Compute the number of positives
```
def get_num_pos_neg(X, y, w, feature_names, label, condition=None):
"""
Returns number of optionally conditioned positives/negatives
"""
y = y.ravel()
cond_vec = get_condition_vector(X, feature_names, condition=condition)
return np.sum(w[np.logical_and(y == label, cond_vec)], dtype=np.float64)
```
##### Compute the number of instances
```
def get_num_instances(X, w, feature_names, condition=None):
cond_vec = get_condition_vector(X, feature_names, condition)
return np.sum(w[cond_vec], dtype=np.float64)
```
##### Compute the rate of favourable result for a given condition
```
# Compute the base rate, :`Pr(Y = 1) = P/(P+N)
# Compute the persentage of favourable result for a given condition
def get_base_rate(X, y, w, feature_names, label, condition=None):
return (get_num_pos_neg(X, y, w, feature_names, label, condition=condition)
/ get_num_instances(X, w, feature_names, condition=condition))
```
##### Compute fairness in training data
For computing the fairness of the data using SPD, we need to specify and get some of the key inputs. So, let us specify what are privileged & unprivileged groups, Protected attributes, and instance weights to be considered in the train data set.
```
# target value
labels_train = train[label_name].values.copy()
# protected attributes
df_prot = train.loc[:, protected_attribute_names]
protected_attributes = df_prot.values.copy()
privileged_groups = [{'gender': 1}]
unprivileged_groups = [{'gender': 0}]
# equal weights for all classes by default in the train dataset
instance_weights = np.ones_like(train.index, dtype=np.float64)
```
now let's compute the fairness of data with respect to protected attribute
```
positive_privileged = get_base_rate(protected_attributes, labels_train, instance_weights,
protected_attribute_names,
favorable_label, privileged_groups)
positive_unprivileged = get_base_rate(protected_attributes, labels_train, instance_weights,
protected_attribute_names,
favorable_label, unprivileged_groups)
```
Let's look at favorable results for privileged & unprivileged groups in terms of statistical parity difference.
```
x = ["positive_privileged", "positive_unprivileged"]
y = [positive_privileged, positive_unprivileged]
plt.barh(x, y, color=['green', 'blue'])
for index, value in enumerate(y):
plt.text(value, index, str(round(value, 2)), fontweight='bold')
plt.text(0.2, 0.5, "Statistical parity difference : " + str(
round((positive_unprivileged - positive_privileged), 3)),
bbox=dict(facecolor='white', alpha=0.4), fontweight='bold')
plt.title("Statistical parity difference", fontweight='bold')
plt.show()
```
Privileged group gets 10.8% more positive outcomes in the training dataset. This is `Bias`. Such Bias must be mitigated.
```
def statistical_parity_difference(X, y, w, feature_names, label, privileged_groups,
unprivileged_groups):
"""
Compute difference in the metric between unprivileged and privileged groups.
"""
positive_privileged = get_base_rate(X, y, w, feature_names, label, privileged_groups)
positive_unprivileged = get_base_rate(X, y, w, feature_names, label, unprivileged_groups)
return (positive_unprivileged - positive_privileged)
```
Let's store the fairnes of data in a variable
```
original = statistical_parity_difference(protected_attributes,
labels_train, instance_weights,
protected_attribute_names, favorable_label,
privileged_groups, unprivileged_groups)
```
#### 3.1.2 Analyze bias in the dataset
Let's understand how bias occurred in the dataset with respect to protected attribute.
First, let's calculate the frequency count for categories of protected attributes in the training dataset.
```
# get the only privileged condition vector for the given protected attributes
# Values are `True` for the privileged values else 'False'
privileged_cond = get_condition_vector(
protected_attributes,
protected_attribute_names,
condition=privileged_groups)
# Get the only unprivileged condition vector for the given protected attributes
# Values are `True` for the unprivileged values else 'False)
unprivileged_cond = get_condition_vector(
protected_attributes,
protected_attribute_names,
condition=unprivileged_groups)
# get the favorable(postive outcome) condition vector
# Values are `True` for the favorable values else 'False'
favorable_cond = labels_train.ravel() == favorable_label
# get the unfavorable condition vector
# Values are `True` for the unfavorable values else 'False'
unfavorable_cond = labels_train.ravel() == unfavorable_label
# combination of label and privileged/unprivileged groups
# Postive outcome for privileged group
privileged_favorable_cond = np.logical_and(favorable_cond, privileged_cond)
# Negative outcome for privileged group
privileged_unfavorable_cond = np.logical_and(unfavorable_cond, privileged_cond)
# Postive outcome for unprivileged group
unprivileged_favorable_cond = np.logical_and(favorable_cond, unprivileged_cond)
# Negative outcome for unprivileged group
unprivileged_unfavorable_cond = np.logical_and(unfavorable_cond, unprivileged_cond)
```
We need total number of instances, privileged, unprivileged, favorable outcomes, etc..
```
instance_count = train.shape[0]
privileged_count = np.sum(privileged_cond, dtype=np.float64)
unprivileged_count = np.sum(unprivileged_cond, dtype=np.float64)
favourable_count = np.sum(favorable_cond, dtype=np.float64)
unfavourable_count = np.sum(unfavorable_cond, dtype=np.float64)
privileged_favourable_count = np.sum(privileged_favorable_cond, dtype=np.float64)
privileged_unfavourable_count = np.sum(privileged_unfavorable_cond, dtype=np.float64)
unprivileged_favourable_count = np.sum(unprivileged_favorable_cond, dtype=np.float64)
unprivileged_unfavourable_count = np.sum(unprivileged_unfavorable_cond, dtype=np.float64)
```
Now, let us analyze above variables and see how the frequency of count is distributed for protected attribute.
```
x = ["privileged_favourable_count", "privileged_unfavourable_count",
"unprivileged_favourable_count", "unprivileged_unfavourable_count"]
y = [privileged_favourable_count, privileged_unfavourable_count, unprivileged_favourable_count,
unprivileged_unfavourable_count]
plt.barh(x, y, color=['blue', 'green', 'orange', 'brown'])
for index, value in enumerate(y):
plt.text(value, index,
str(value), fontweight='bold')
plt.show()
```
##### Privileged and unprivileged group outcomes
```
labels_privileged = ['male - rated good', 'male - rated bad']
sz_privileged = [privileged_favourable_count, privileged_unfavourable_count]
labels_unprivileged = ['female - rated good', 'female - rated bad']
sz_unpriveleged = [unprivileged_favourable_count, unprivileged_unfavourable_count]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 15))
ax1.pie(sz_privileged, labels=labels_privileged, autopct='%1.1f%%', shadow=True)
ax1.title.set_text('Privileged class outcomes')
ax2.pie(sz_unpriveleged, labels=labels_unprivileged, autopct='%1.1f%%', shadow=True)
ax2.title.set_text('Unprivileged class outcomes')
plt.show()
```
Male is the privileged group with 73.5% favourable outcome and 26.5% unfavourable outcome.
Female is the unprivileged group with a 62.7% favourable outcome and 37.3% unfavourable outcome. <br>
So, there is bias against the unprivileged group (privileged group gets 10.8% more positive outcomes).
There may have been insufficient data for certain groups (gender attribute) at the feature (column) level resulting in an incomplete representation of these groups in the dataset. So, we could try to mitigate such bias using a pre-processing mitigation technique.
### 3.2 Bias mitigation
Pre-processing describes the set of data preparation and feature engineering steps before application of machine learning algorithms. Sampling, reweighing and suppression are examples of pre-processing bias mitigation techniques proposed in academic literature[2]. In this tutorial, we will focus on reweighing [3] technique that assigns weights to instances.
#### 3.2.1 Reweighing algorithm
This approach assigns different weights to the examples based on the categories in protected attribute and outcomes such that bias is removed from the training dataset. Weights are based on frequency counts. But this technique is designed to work only with classifiers that can handle row-level weights.
#### Compute the reweighing weights (Equations)
***
1. Privileged group with the favourable outcome : $W_\text{privileged favourable} = \displaystyle\frac{\#\{\text{favourable}\} \times \#\{\text{privileged}\}}{\#\{\text{all}\} \times \#\{\text{privileged favourable}\}}$ <br>
2. Privileged group with the unfavourable outcome : $W_\text{privileged unfavourable} = \displaystyle\frac{\#\{\text{unfavourable}\} \times \#\{\text{prvileged}\}}{\#\{\text{all}\} \times \#\{\text{prvileged unfavourable}\}}$ <br>
3. Unprivileged group with the favourable outcome : $W_\text{unprivileged favourable} = \displaystyle\frac{\#\{\text{favourable}\} \times \#\{\text{unprvileged}\}}{\#\{\text{all}\} \times \#\{\text{unprivileged favourable}\}}$ <br>
4. Unprivileged group with the unfavourable outcome : $W_\text{unprivileged unfavourable} = \displaystyle\frac{\#\{\text{unfavourable}\} \times \#\{\text{unprivileged}\}}{\#\{\text{all}\} \times \#\{\text{unprivileged unfavourable}\}}$ <br>
***
```
# reweighing weights
weight_privileged_favourable = favourable_count * privileged_count / (instance_count * privileged_favourable_count)
weight_privileged_unfavourable = unfavourable_count * privileged_count / (instance_count * privileged_unfavourable_count)
weight_unprivileged_favourable = favourable_count * unprivileged_count / (instance_count * unprivileged_favourable_count)
weight_unprivileged_unfavourable = unfavourable_count * unprivileged_count / (instance_count * unprivileged_unfavourable_count)
transformed_instance_weights = copy.deepcopy(instance_weights)
transformed_instance_weights[privileged_favorable_cond] *= weight_privileged_favourable
transformed_instance_weights[privileged_unfavorable_cond] *= weight_privileged_unfavourable
transformed_instance_weights[unprivileged_favorable_cond] *= weight_unprivileged_favourable
transformed_instance_weights[unprivileged_unfavorable_cond] *= weight_unprivileged_unfavourable
```
Now that we have transformed instance_weights from reweighing algorithm, we can check how effective it is in removing bias by calculating the same metric(statistical parity difference) again.
```
mitigated = statistical_parity_difference(protected_attributes,
labels_train, transformed_instance_weights,
protected_attribute_names, favorable_label,
privileged_groups, unprivileged_groups)
```
### 3.3 Data Fairness comparison
```
plt.figure(facecolor='#FFFFFF', figsize=(4, 4))
plt.ylim([-0.6, 0.6])
plt.axhline(y=0.0, color='r', linestyle='-')
plt.bar(["Original", "Mitigated"], [original, mitigated], color=["blue", "green"])
plt.ylabel("statistical parity")
plt.title("Before vs After Bias Mitigation", fontsize=15)
y = [original, mitigated]
for index, value in enumerate(y):
if value < 0:
plt.text(index, value - 0.1,
str(round(value, 3)), fontweight='bold', color='red',
bbox=dict(facecolor='red', alpha=0.4))
else:
plt.text(index, value + 0.1,
str(round(value, 3)), fontweight='bold', color='red',
bbox=dict(facecolor='red', alpha=0.4))
plt.grid(None, axis="y")
plt.show()
```
Reweighing algorithm has been very effective since statistical_parity_difference is zero. So we went from a 10.8% advantage for the privileged group to equality in terms of positive outcome.
Now that we have both original and bias mitigated data, let's evaluate model fairness before and after bias mitigation.
## 4. Model Fairness - on different ML models
Model Fairness is a relatively new field in Machine Learning,
Since predictive ML models have started making their way into the industry including sensitive medical, insurance and banking sectors, it has become prudent to implement strategies to ensure the fairness of those models to check discriminative behavior during predictions. Several definitions have been proposed [4][5][6] to evaluate model fairness.
In this tutorial, we will implement statistical parity (demographical parity) strategy to evaluate model fairness and detect any discriminative behavior during the prediction.
#### Statistical parity (Demographic parity)
As discussed in [sec. 3.1.1](#3.1.1-Statistical-parity-difference), statistical parity states that the each segment of a protected class (e.g. gender) should receive the positive outcome at equal rates (the outcome is independent of a protected class). For example, the probability of getting admission to a college must be independent of gender. Let us assume the prediction of a machine learning model (Ŷ) to be independent of protected class A.
$P(Ŷ | A=a) = P(Ŷ | A=a’)$, <br>
where a and a' are different sensitive attribute values (for example, gender male vs gender female).
##### Compute fairness of the different ML models
To compute model fairness (SPD), let us specify privileged & unprivileged groups, protected attributes and instance weights to be considered in the test data set.
```
# protected attribute
df_prot_test = test.loc[:, protected_attribute_names]
protected_attributes_test = df_prot_test.values.copy()
privileged_groups = [{'gender': 1}]
unprivileged_groups = [{'gender': 0}]
# equal weights for all classes by default in the testing dataset
instance_weights_test = np.ones_like(test.index, dtype=np.float64)
```
Well, before training any ML model we need to standardize our dataset, when all numerical variables are scaled to a common range in the dataset, machine learning algorithms converge faster. So, we do scaling with the standardization technique in this tutorial.
```
# split the features and labels for both train and test data
feature_names = [n for n in train.columns if n not in label_name]
X_train, X_test, Y_train, Y_test = train[feature_names].values.copy(), test[
feature_names].values.copy(), train[label_name].values.copy(), test[label_name].values.copy()
# standardize the inputs
scale_orig = StandardScaler()
X_train = scale_orig.fit_transform(X_train)
X_test = scale_orig.fit_transform(X_test)
```
It is important to compare fairness and performance of multiple different machine learning algorithms before and after bias mitigation. We shall do that for Logistic Regression, Decision Trees, Random Forest classifier, XG Boost and SVM in this tutorial.
```
# prepare list of models
models = []
models.append(('LR', LogisticRegression()))
models.append(('DT', DecisionTreeClassifier(random_state=0)))
models.append(('RF', RandomForestClassifier(random_state=4)))
models.append(('XGB', XGBClassifier(use_label_encoder=False, eval_metric='mlogloss')))
models.append(('SVM', SVC()))
```
let's compute the Performance & Model Fairness before after bias mitigation on the above models
```
ml_models = []
base_accuracy_ml_models = []
base_fariness_ml_models = []
bias_mitigated_accuracy_ml_models = []
bias_mitigated_fairness_ml_models = []
for name, model in models:
# evaluate the base model
base_accuracy, base_predicted = train_model_and_get_test_results(model, X_train, Y_train,
X_test, Y_test,
sample_weight=instance_weights)
# compute SPD for base model
base_fairness = statistical_parity_difference(protected_attributes_test,
base_predicted, instance_weights_test,
protected_attribute_names, favorable_label,
privileged_groups, unprivileged_groups)
# evaluate the mitigated model
bias_mitigated_accuracy, bias_mitigated_predicted = train_model_and_get_test_results(model,
X_train,
Y_train,
X_test,
Y_test,
sample_weight=transformed_instance_weights)
# compute SPD for mitigated model
bias_mitigated_fairness = statistical_parity_difference(protected_attributes_test,
bias_mitigated_predicted,
instance_weights_test,
protected_attribute_names,
favorable_label,
privileged_groups, unprivileged_groups)
ml_models.append(name)
base_accuracy_ml_models.append(base_accuracy)
base_fariness_ml_models.append(base_fairness)
bias_mitigated_accuracy_ml_models.append(bias_mitigated_accuracy)
bias_mitigated_fairness_ml_models.append(bias_mitigated_fairness)
```
##### Graphical Comparison of fairness & performance
```
visualize_model_comparison(ml_models, base_fariness_ml_models, bias_mitigated_fairness_ml_models,
base_accuracy_ml_models, bias_mitigated_accuracy_ml_models)
```
Fig. a is comparison of fairness for different models. X-axis has names of ML models while Y-axis represents SPD.
Fig. b is comparison of model accuracy. X-axis has names of ML models while Y-axis represents model accuracy.
It can be observed that the classifiers learned on the bias mitigated data produce less discriminatory results (fairness improved) as compared to the biased data; For ex., in Fig (a) before bias mitigation, `LR` classifies the future data objects with `-0.25` discrimination ( more positive outcomes for the privileged group i.e., the model is biased against the unprivileged group). After application of the `Reweighing` algorithm on the training dataset, the discrimination goes down to `-0.14`. Though there is bias in favor of the privileged group after reweighing, it is much lesser and keeps the ML practitioner informed about the amount of bias in order to make calculated decisions. Besides, it can be observed in Fig.(b), there is no significant drop in the accuracy/performance for any algorithm after bias mitigation. This is good and it makes strong case for `Bias Detection and Mitigation`.
Well, let us visualize the detailed flow of everything we learned in this tutorial:
```
from google.colab.patches import cv2_imshow
img2 = cv2.imread('images/xai-bias-mitigation.png')
cv2_imshow(img2)
```
In short, we can summarize the procedure in the following 4 steps:
1. Prepare the data for analysis
2. Detect bias in the data set
3. Mitigate bias in the data set
4. Observe the fairness of the model before and after bias mitigation
### Summary
In this tutorial, we have tried to give a gentle introduction to gender bias detection and mitigation to enthusiasts of Responsible AI. Although there are many ways to detect and mitigate bias, we have only illustrated one simple way to detect bias and mitigate it with `Reweighing` algorithm in this tutorial. We plan to create and open-source tutorials illustrating other ways of bias detection and mitigation in the future.
### References
[1] [Ninareh Mehrabi, Fred Morstatter, Nripsuta Saxena, Kristina Lerman, Aram Galstyan. A Survey on Bias and Fairness in Machine Learning. arXiv:1908.09635
](https://arxiv.org/abs/1908.09635)
[2] Kamiran F, Calders T (2009a) Classifying without discriminating. In: Proceedings of IEEE IC4 international conference on computer, Control & Communication. IEEE press<br>
[3] [Kamiran, Faisal and Calders, Toon. Data preprocessing techniques for classification without discrimination](https://link.springer.com/content/pdf/10.1007%2Fs10115-011-0463-8.pdf). Knowledge and Information Systems, 33(1):1–33, 2012<br>
[4] Hardt, M., Price, E., and Srebro, N. (2016). “Equality of opportunity in supervised learning,” in Advances in Neural Information Processing Systems, eds D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett (Barcelona: Curran Associates, Inc.), 3315–3323.<br>
[5] Chouldechova, A. (2017). Fair prediction with disparate impact: a study of bias in recidivism prediction instruments. Big Data 5, 153–163. doi: 10.1089/big.2016.0047<br>
[6] Zafar, M. B., Valera, I., Gomez Rodriguez, M., and Gummadi, K. P. (2017a). “Fairness beyond disparate treatment & disparate impact: Learning classification without disparate mistreatment,” in Proceedings of the 26th International Conference on World Wide Web (Perth: International World Wide Web Conferences Steering Committee), 1171–1180. doi: 10.1145/3038912.3052660<br>
[7] https://archive.ics.uci.edu/ml/datasets/Statlog+%28German+Credit+Data%29 <br>
| true |
code
| 0.732823 | null | null | null | null |
|
<img src="img/saturn_logo.png" width="300" />
# Introduction to Dask
Before we get into too much complexity, let's talk about the essentials of Dask.
## What is Dask?
Dask is an open-source framework that enables parallelization of Python code. This can be applied to all kinds of Python use cases, not just machine learning. Dask is designed to work well on single-machine setups and on multi-machine clusters. You can use Dask with pandas, NumPy, scikit-learn, and other Python libraries - for our purposes, we'll focus on how you might use it with PyTorch. If you want to learn more about the other areas where Dask can be useful, there's a [great website explaining all of that](https://dask.org/).
## Why Parallelize?
For our use case, there are a couple of areas where Dask parallelization might be useful for making our work faster and better.
* Loading and handling large datasets (especially if they are too large to hold in memory)
* Running time or computation heavy tasks at the same time, quickly
## Delaying Tasks
Delaying a task with Dask can queue up a set of transformations or calculations so that it's ready to run later, in parallel. This is what's known as "lazy" evaluation - it won't evaluate the requested computations until explicitly told to. This differs from other kinds of functions, which compute instantly upon being called. Many very common and handy functions are ported to be native in Dask, which means they will be lazy (delayed computation) without you ever having to even ask.
However, sometimes you will have complicated custom code that is written in pandas, scikit-learn, or even base python, that isn't natively available in Dask. Other times, you may just not have the time or energy to refactor your code into Dask, if edits are needed to take advantage of native Dask elements.
If this is the case, you can decorate your functions with `@dask.delayed`, which will manually establish that the function should be lazy, and not evaluate until you tell it. You'd tell it with the processes `.compute()` or `.persist()`, described in the next section. We'll use `@dask.delayed` several times in this workshop to make PyTorch tasks easily parallelized.
### Example 1
```
def exponent(x, y):
'''Define a basic function.'''
return x ** y
# Function returns result immediately when called
exponent(4, 5)
import dask
@dask.delayed
def lazy_exponent(x, y):
'''Define a lazily evaluating function'''
return x ** y
# Function returns a delayed object, not computation
lazy_exponent(4, 5)
# This will now return the computation
lazy_exponent(4,5).compute()
```
### Example 2
We can take this knowledge and expand it - because our lazy function returns an object, we can assign it and then chain it together in different ways later.
Here we return a delayed value from the first function, and call it x. Then we pass x to the function a second time, and call it y. Finally, we multiply x and y to produce z.
```
x = lazy_exponent(4, 5)
y = lazy_exponent(x, 2)
z = x * y
z
z.visualize(rankdir="LR")
z.compute()
```
***
## Persist vs Compute
How should we instruct our computer to run the computations we have queued up lazily? We have two choices: `.persist()` and `.compute()`.
First, remember we have several machines working for us right now. We have our Jupyter instance right here running on one, and then our cluster of worker machines also.
### Compute
If we use `.compute()`, we are asking Dask to take all the computations and adjustments to the data that we have queued up, and run them, and bring it all to the surface here, in Jupyter.
That means if it was distributed we want to convert it into a local object here and now. If it's a Dask Dataframe, when we call `.compute()`, we're saying "Run the transformations we've queued, and convert this into a pandas dataframe immediately."
### Persist
If we use `.persist()`, we are asking Dask to take all the computations and adjustments to the data that we have queued up, and run them, but then the object is going to remain distributed and will live on the cluster, not on the Jupyter instance.
So when we do this with a Dask Dataframe, we are telling our cluster "Run the transformations we've queued, and leave this as a distributed Dask Dataframe."
So, if you want to process all the delayed tasks you've applied to a Dask object, either of these methods will do it. The difference is where your object will live at the end.
***
### Example: Distributed Data Objects
When we use a Dask Dataframe object, we can see the effect of `.persist()` and `.compute()` in practice.
```
import dask
import dask.dataframe as dd
df = dask.datasets.timeseries()
df.npartitions
```
So our Dask Dataframe has 30 partitions. So, if we run some computations on this dataframe, we still have an object that has a number of partitions attribute, and we can check it. We'll filter it, then do some summary statistics with a groupby.
```
df2 = df[df.y > 0]
df3 = df2.groupby('name').x.std()
print(type(df3))
df3.npartitions
```
Now, we have reduced the object down to a Series, rather than a dataframe, so it changes the partition number.
We can `repartition` the Series, if we want to!
```
df4 = df3.repartition(npartitions=3)
df4.npartitions
```
What will happen if we use `.persist()` or `.compute()` on these objects?
As we can see below, `df4` is a Dask Series with 161 queued tasks and 3 partitions. We can run our two different computation commands on the same object and see the different results.
```
df4
%%time
df4.persist()
```
So, what changed when we ran .persist()? Notice that we went from 161 tasks at the bottom of the screen, to just 3. That indicates that there's one task for each partition.
Now, let's try .compute().
```
%%time
df4.compute().head()
```
We get back a pandas Series, not a Dask object at all.
***
## Submit to Cluster
To make this all work in a distributed fashion, we need to understand how we send instructions to our cluster. When we use the `@dask.delayed` decorator, we queue up some work and put it in a list, ready to be run. So how do we send it to the workers and explain what we want them to do?
We use the `distributed` module from Dask to make this work. We connect to our cluster (as you saw in [Notebook 1](01-getting-started.ipynb)), and then we'll use some commands to send instructions.
```
from dask_saturn import SaturnCluster
from dask.distributed import Client
cluster = SaturnCluster()
client = Client(cluster)
from dask_saturn.core import describe_sizes
describe_sizes()
```
## Sending Tasks
Now we have created the object `client`. This is the handle we'll use to connect with our cluster, for whatever commands we want to send! We will use a few processes to do this communication: `.submit()` and `.map()`.
* `.submit()` lets us send one task to the cluster, to be run once on whatever worker is free.
* `.map()` lets us send lots of tasks, which will be disseminated to workers in the most efficient way.
There's also `.run()` which you can use to send one task to EVERY worker on the cluster simultaneously. This is only used for small utility tasks, however - like installing a library or collecting diagnostics.
### map Example
For example, you can use `.map()` in this way:
`futures = client.map(function, list_of_inputs)`
This takes our function, maps it over all the inputs, and then these tasks are distributed to the cluster workers. Note: they still won't actually compute yet!
Let's try an example. Recall our `lazy_exponent` function from earlier. We are going to alter it so that it accepts its inputs as a single list, then we can use it with `.map()`.
```
@dask.delayed
def lazy_exponent(args):
x,y = args
'''Define a lazily evaluating function'''
return x ** y
inputs = [[1,2], [3,4], [5,6]]
example_future = client.map(lazy_exponent, inputs)
```
***
## Processing Results
We have one more step before we use .compute(), which is .gather(). This creates one more instruction to be included in this big delayed job we're establishing: retrieving the results from all of our jobs. It's going to sit tight as well until we finally say .compute().
### gather Example
```
futures_gathered = client.gather(example_future)
```
It may help to think of all the work as instructions in a list. We have so far told our cluster: "map our delayed function over this list of inputs, and pass the resulting tasks to the workers", "Gather up the results of those tasks, and bring them back". But the one thing we haven't said is "Ok, now begin to process all these instructions"! That's what `.compute()` will do. For us this looks like:
```
futures_computed = client.compute(futures_gathered, sync=False)
```
We can investigate the results, and use a small list comprehension to return them for later use.
```
futures_computed
futures_computed[0].result()
results = [x.result() for x in futures_computed]
results
```
Now we have the background knowledge we need to move on to running PyTorch jobs!
* If you want to do inference, go to [Notebook 3](03-single-inference.ipynb).
* If you want to do training/transfer learning, go to [Notebook 5](05-transfer-prepro.ipynb).
### Helpful reference links:
* https://distributed.dask.org/en/latest/client.html
* https://distributed.dask.org/en/latest/manage-computation.html
| true |
code
| 0.720577 | null | null | null | null |
|
```
import matplotlib.pyplot as plt
import numpy as np
import pickle
from skimage.segmentation import slic
import scipy.ndimage
import scipy.spatial
import torch
from torchvision import datasets
import sys
sys.path.append("../")
from chebygin import ChebyGIN
from extract_superpixels import process_image
from graphdata import comput_adjacency_matrix_images
from train_test import load_save_noise
from utils import list_to_torch, data_to_device, normalize_zero_one
```
# MNIST-75sp
```
data_dir = '../data'
checkpoints_dir = '../checkpoints'
device = 'cuda'
# Load images using standard PyTorch Dataset
data = datasets.MNIST(data_dir, train=False, download=True)
images = data.test_data.numpy()
targets = data.test_labels
# mean and std computed for superpixel features
# features are 3 pixel intensities and 2 coordinates (x,y)
# 3 pixel intensities because we replicate mean pixel value 3 times to test on colored MNIST images
mn = torch.tensor([0.11225057, 0.11225057, 0.11225057, 0.44206527, 0.43950436]).view(1, 1, -1)
sd = torch.tensor([0.2721889, 0.2721889, 0.2721889, 0.2987583, 0.30080357]).view(1, 1, -1)
class SuperpixelArgs():
def __init__(self):
self.n_sp = 75
self.compactness = 0.25
self.split = 'test'
self.dataset = 'mnist'
img_size = images.shape[1]
noises = load_save_noise('../data/mnist_75sp_noise.pt', (images.shape[0], 75))
color_noises = load_save_noise('../data/mnist_75sp_color_noise.pt', (images.shape[0], 75, 3))
n_images = images.shape[0]
noise_levels = np.array([0.4, 0.6])
def acc(pred):
return torch.mean((torch.stack(pred) == targets[:len(pred)]).float()).item() * 100
# This function takes a single 28x28 MNIST image, model object, and std of noise added to node features,
# performs all necessary preprocessing (including superpixels extraction) and returns predictions
def test(model, img, index, noise_std, colornoise_std, show_img=False):
sp_intensity, sp_coord, sp_order, superpixels = process_image((img, 0, 0, SuperpixelArgs(), False, False))
#assert np.
if show_img:
sz = img.shape
plt.figure(figsize=(20,5))
plt.subplot(141)
plt.imshow(img / 255., cmap='gray')
plt.title('Input MNIST image')
img_sp = np.zeros((sz[0], sz[1]))
img_noise = np.zeros((sz[0], sz[1], 3))
img_color_noise = np.zeros((sz[0], sz[1], 3))
for sp_intens, sp_index in zip(sp_intensity, sp_order):
mask = superpixels == sp_index
x = (sp_intens - mn[0, 0, 0].item()) / sd[0, 0, 0].item()
img_sp[mask] = x
img_noise[mask] = x + noises[index, sp_index] * noise_std
img_color_noise[mask] = x + color_noises[index, sp_index] * colornoise_std
plt.subplot(142)
plt.imshow(normalize_zero_one(img_sp), cmap='gray')
plt.title('Superpixels of the image')
plt.subplot(143)
plt.imshow(normalize_zero_one(img_noise), cmap='gray')
plt.title('Noisy superpixels')
plt.subplot(144)
plt.imshow(normalize_zero_one(img_color_noise))
plt.title('Noisy and colored superpixels')
plt.show()
sp_coord = sp_coord / img_size
N_nodes = sp_intensity.shape[0]
mask = torch.ones(1, N_nodes, dtype=torch.uint8)
x = (torch.from_numpy(np.pad(np.concatenate((sp_intensity, sp_coord), axis=1),
((0, 0), (2, 0)), 'edge')).unsqueeze(0) - mn) / sd
A = torch.from_numpy(comput_adjacency_matrix_images(sp_coord)).float().unsqueeze(0)
y, other_outputs = model(data_to_device([x, A, mask, -1, {'N_nodes': torch.zeros(1, 1) + N_nodes}],
device))
y_clean = torch.argmax(y).data.cpu()
alpha_clean = other_outputs['alpha'][0].data.cpu() if 'alpha' in other_outputs else []
x_noise = x.clone()
x_noise[:, :, :3] += noises[index, :N_nodes].unsqueeze(0).unsqueeze(2) * noise_std
y, other_outputs = model(data_to_device([x_noise, A, mask, -1, {'N_nodes': torch.zeros(1, 1) + N_nodes}],
device))
y_noise = torch.argmax(y).data.cpu()
alpha_noise = other_outputs['alpha'][0].data.cpu() if 'alpha' in other_outputs else []
x_noise = x.clone()
x_noise[:, :, :3] += color_noises[index, :N_nodes] * colornoise_std
y, other_outputs = model(data_to_device([x_noise, A, mask, -1, {'N_nodes': torch.zeros(1, 1) + N_nodes}],
device))
y_colornoise = torch.argmax(y).data.cpu()
alpha_color_noise = other_outputs['alpha'][0].data.cpu() if 'alpha' in other_outputs else []
return y_clean, y_noise, y_colornoise, alpha_clean, alpha_noise, alpha_color_noise
# This function returns predictions for the entire clean and noise test sets
def get_predictions(model_path):
state = torch.load(model_path)
args = state['args']
model = ChebyGIN(in_features=5,
out_features=10,
filters=args.filters,
K=args.filter_scale,
n_hidden=args.n_hidden,
aggregation=args.aggregation,
dropout=args.dropout,
readout=args.readout,
pool=args.pool,
pool_arch=args.pool_arch)
model.load_state_dict(state['state_dict'])
model = model.eval().to(device)
#print(model)
# Get predictions
pred, pred_noise, pred_colornoise = [], [], []
alpha, alpha_noise, alpha_colornoise = [], [], []
for index, img in enumerate(images):
y = test(model, img, index, noise_levels[0], noise_levels[1], index == 0)
pred.append(y[0])
pred_noise.append(y[1])
pred_colornoise.append(y[2])
alpha.append(y[3])
alpha_noise.append(y[4])
alpha_colornoise.append(y[5])
if len(pred) % 1000 == 0:
print('{}/{}, acc clean={:.2f}%, acc noise={:.2f}%, acc color noise={:.2f}%'.format(len(pred),
n_images,
acc(pred),
acc(pred_noise),
acc(pred_colornoise)))
return pred, pred_noise, pred_colornoise, alpha, alpha_noise, alpha_colornoise
```
## Global pooling model
```
pred = get_predictions('%s/checkpoint_mnist-75sp_820601_epoch30_seed0000111.pth.tar' % checkpoints_dir)
```
## Visualize heat maps
```
with open('../checkpoints/mnist-75sp_alpha_WS_test_seed111_orig.pkl', 'rb') as f:
global_pool_attn_orig = pickle.load(f)
with open('../checkpoints/mnist-75sp_alpha_WS_test_seed111_noisy.pkl', 'rb') as f:
global_pool_attn_noise = pickle.load(f)
with open('../checkpoints/mnist-75sp_alpha_WS_test_seed111_noisy-c.pkl', 'rb') as f:
global_pool_attn_colornoise = pickle.load(f)
# Load precomputed superpixels to have the order of superpixels consistent with those in global_pool_attn_orig
with open('../data/mnist_75sp_test.pkl', 'rb') as f:
test_data = pickle.load(f)[1]
with open('../data/mnist_75sp_test_superpixels.pkl', 'rb') as f:
test_superpixels = pickle.load(f)
# Get ids of the first test sample for labels from 0 to 9
ind = []
labels_added = set()
for i, lbl in enumerate(data.test_labels.numpy()):
if lbl not in labels_added:
ind.append(i)
labels_added.add(lbl)
ind_sorted = []
for i in np.argsort(data.test_labels):
if i in ind:
ind_sorted.append(i)
sz = data.test_data.shape
images_sp, images_noise, images_color_noise, images_heat, images_heat_noise, images_heat_noise_color = [], [], [], [], [], []
for i in ind_sorted:
# sp_intensity, sp_coord, sp_order, superpixels = process_image((images[i], 0, 0, SuperpixelArgs(), False, False))
sp_intensity, sp_coord, sp_order = test_data[i]
superpixels = test_superpixels[i]
n_sp = sp_intensity.shape[0]
noise, color_noise = noises[i, :n_sp], color_noises[i, :n_sp]
img = np.zeros((sz[1], sz[1]))
img_noise = np.zeros((sz[1], sz[1], 3))
img_color_noise = np.zeros((sz[1], sz[1], 3))
img_heat = np.zeros((sz[1], sz[1]))
img_heat_noise = np.zeros((sz[1], sz[1]))
img_heat_noise_color = np.zeros((sz[1], sz[1]))
for j, (sp_intens, sp_index) in enumerate(zip(sp_intensity, sp_order)):
mask = superpixels == sp_index
x = (sp_intens - mn[0, 0, 0].item()) / sd[0, 0, 0].item()
img[mask] = x
img_noise[mask] = x + noise[sp_index] * noise_levels[0]
img_color_noise[mask] = x + color_noise[sp_index] * noise_levels[1]
img_heat[mask] = global_pool_attn_orig[i][j]
img_heat_noise[mask] = global_pool_attn_noise[i][j]
img_heat_noise_color[mask] = global_pool_attn_colornoise[i][j]
images_sp.append(img)
images_noise.append(img_noise)
images_color_noise.append(img_color_noise)
images_heat.append(img_heat)
images_heat_noise.append(img_heat_noise)
images_heat_noise_color.append(img_heat_noise_color)
for fig_id, img_set in enumerate([images_sp, images_noise, images_color_noise,
images_heat, images_heat_noise, images_heat_noise_color]):
fig = plt.figure(figsize=(15, 6))
n_cols = 5
n_rows = 2
for i in range(n_rows):
for j in range(n_cols):
index = i*n_cols + j
ax = fig.add_subplot(n_rows, n_cols, index + 1)
if fig_id in [0]:
ax.imshow(img_set[index], cmap='gray')
else:
ax.imshow(normalize_zero_one(img_set[index]))
ax.axis('off')
plt.subplots_adjust(hspace=0.1, wspace=0.1)
plt.show()
```
## Models with attention
```
# General function to visualize attention coefficients alpha for models with attention
def visualize(alpha, alpha_noise, alpha_colornoise):
# Get ids of the first test sample for labels from 0 to 9
ind = []
labels_added = set()
for i, lbl in enumerate(data.test_labels.numpy()):
if lbl not in labels_added:
ind.append(i)
labels_added.add(lbl)
ind_sorted = []
for i in np.argsort(data.test_labels):
if i in ind:
ind_sorted.append(i)
sz = data.test_data.shape
images_sp, images_noise, images_color_noise, images_attn, images_attn_noise, images_attn_noise_color = [], [], [], [], [], []
for i in ind_sorted:
sp_intensity, sp_coord, sp_order, superpixels = process_image((images[i], 0, 0, SuperpixelArgs(), False, False))
n_sp = sp_intensity.shape[0]
noise, color_noise = noises[i, :n_sp], color_noises[i, :n_sp]
img = np.zeros((sz[1], sz[1]))
img_noise = np.zeros((sz[1], sz[1], 3))
img_color_noise = np.zeros((sz[1], sz[1], 3))
img_attn = np.zeros((sz[1], sz[1]))
img_attn_noise = np.zeros((sz[1], sz[1]))
img_attn_noise_color = np.zeros((sz[1], sz[1]))
for sp_intens, sp_index in zip(sp_intensity, sp_order):
mask = superpixels == sp_index
x = (sp_intens - mn[0, 0, 0].item()) / sd[0, 0, 0].item()
img[mask] = x
img_noise[mask] = x + noise[sp_index] * noise_levels[0]
img_color_noise[mask] = x + color_noise[sp_index] * noise_levels[1]
img_attn[mask] = alpha[i][0, sp_index].item()
img_attn_noise[mask] = alpha_noise[i][0, sp_index].item()
img_attn_noise_color[mask] = alpha_colornoise[i][0, sp_index].item()
images_sp.append(img)
images_noise.append(img_noise)
images_color_noise.append(img_color_noise)
images_attn.append(img_attn)
images_attn_noise.append(img_attn_noise)
images_attn_noise_color.append(img_attn_noise_color)
for fig_id, img_set in enumerate([images_sp, images_noise, images_color_noise,
images_attn, images_attn_noise, images_attn_noise_color]):
fig = plt.figure(figsize=(15, 6))
n_cols = 5
n_rows = 2
for i in range(n_rows):
for j in range(n_cols):
index = i*n_cols + j
ax = fig.add_subplot(n_rows, n_cols, index + 1)
if fig_id in [0]:
ax.imshow(img_set[index], cmap='gray')
else:
ax.imshow(normalize_zero_one(img_set[index]))
ax.axis('off')
plt.subplots_adjust(hspace=0.1, wspace=0.1)
plt.show()
```
## Weakly-supervised attention model
```
pred, pred_noise, pred_colornoise, alpha, alpha_noise, alpha_colornoise = get_predictions('%s/checkpoint_mnist-75sp_065802_epoch30_seed0000111.pth.tar' % checkpoints_dir)
visualize(alpha, alpha_noise, alpha_colornoise)
```
## Unsupervised attention model
```
pred, pred_noise, pred_colornoise, alpha, alpha_noise, alpha_colornoise = get_predictions('%s/checkpoint_mnist-75sp_330394_epoch30_seed0000111.pth.tar' % checkpoints_dir)
visualize(alpha, alpha_noise, alpha_colornoise)
```
## Supervised attention model
```
pred, pred_noise, pred_colornoise, alpha, alpha_noise, alpha_colornoise = get_predictions('%s/checkpoint_mnist-75sp_139255_epoch30_seed0000111.pth.tar' % checkpoints_dir)
visualize(alpha, alpha_noise, alpha_colornoise)
```
| true |
code
| 0.66647 | null | null | null | null |
|
For network data visualization we can use a number of libraries. Here we'll use [networkX](https://networkx.github.io/documentation/networkx-2.4/install.html).
```
! pip3 install networkx
! pip3 install pytest
import networkx as nx
! ls ../facebook_large/
import pandas as pd
target = pd.read_csv('../facebook_large/musae_facebook_target.csv')
edges = pd.read_csv('../facebook_large/musae_facebook_edges.csv')
target.shape
edges.shape
! cat ../facebook_large/README.txt
edges.head(5)
target.head(10)
```
So, we have undirected edges `(n1 <-> n2)` stored as a tuple `(n1, n2)`, and the nodes have `3` columns, out of which `facebook_id` and `page_name` should be anonymized and not used for clustering/classification.
Let's use `networkX` to visualize this graph, and look at some histograms to get an idea of the data (like class imbalance, etc.)
```
import matplotlib.pyplot as plt
%matplotlib inline
target['page_type'].hist()
# Note: there's some node imbalance but not that much
# visualizing the degree histogram will also give us an insight into the graph
from collections import Counter
degree_sequence = sorted([d for n, d in G.degree()], reverse=True)
degree_count = Counter(degree_sequence)
deg, cnt = zip(*degree_count.items())
fig, ax = plt.subplots(figsize=(20, 10))
plt.bar(deg, cnt, width=0.80, color="b")
plt.title("Degree Histogram")
plt.ylabel("Count")
plt.xlabel("Degree")
plt.xlim(0, 200)
plt.show()
# create an empty nx Graph
G = nx.Graph()
# add all nodes to the graph, with page_type as the node attribute
for it, cat in zip(target['id'], target['page_type']):
G.add_node(it, page_type=cat)
# add all edges, no edge attributes required rn
for n1, n2 in zip(edges['id_1'], edges['id_2']):
G.add_edge(n1, n2)
# nx.draw(G, with_labels=True)
# Note: Viewing such a huge graph will take a lot of time to process
# so it's better to save the huge graph into a file, and visualize a subgraph instead
from matplotlib import pylab
def save_graph(graph, file_name):
plt.figure(num=None, figsize=(20, 20), dpi=80)
plt.axis('off')
fig = plt.figure(1)
pos = nx.spring_layout(graph)
nx.draw_networkx_nodes(graph,pos)
nx.draw_networkx_edges(graph,pos)
nx.draw_networkx_labels(graph,pos)
cut = 1.00
xmax = cut * max(xx for xx, yy in pos.values())
ymax = cut * max(yy for xx, yy in pos.values())
plt.xlim(0, xmax)
plt.ylim(0, ymax)
plt.savefig(file_name, bbox_inches="tight")
pylab.close()
del fig
SG = G.subgraph(nodes=[0, 1, 22208, 22271, 234])
nx.draw(SG, with_labels = True)
# Note that it is a very sparse graph (~0.0006 density)
save_graph(G, 'page-page.pdf')
# Note: this will take a lot of time to run
```
| true |
code
| 0.527134 | null | null | null | null |
|
# NEST by Example - An Introduction to the Neural Simulation Tool NEST Version 2.12.0
# Introduction
NEST is a simulator for networks of point neurons, that is, neuron
models that collapse the morphology (geometry) of dendrites, axons,
and somata into either a single compartment or a small number of
compartments <cite data-cite="Gewaltig2007">(Gewaltig and Diesmann, 2007)</cite>. This simplification is useful for
questions about the dynamics of large neuronal networks with complex
connectivity. In this text, we give a practical introduction to neural
simulations with NEST. We describe how network models are defined and
simulated, how simulations can be run in parallel, using multiple
cores or computer clusters, and how parts of a model can be
randomized.
The development of NEST started in 1994 under the name SYNOD to
investigate the dynamics of a large cortex model, using
integrate-and-fire neurons <cite data-cite="SYNOD">(Diesmann et al., 1995)</cite>. At that time the only
available simulators were NEURON <cite data-cite="Hine:1997(1179)">(Hines and Carnevale, 1997)</cite> and GENESIS <cite data-cite="Bower95a">(Bower and Beeman, 1995)</cite>
, both focusing on morphologically detailed neuron
models, often using data from microscopic reconstructions.
Since then, the simulator has been under constant development. In
2001, the Neural Simulation Technology Initiative was founded to
disseminate our knowledge of neural simulation technology. The
continuing research of the member institutions into algorithms for the
simulation of large spiking networks has resulted in a number of
influential publications. The algorithms and techniques developed are
not only implemented in the NEST simulator, but have also found their
way into other prominent simulation projects, most notably the NEURON
simulator (for the Blue Brain Project: <cite data-cite="Migliore06_119">Migliore et al., 2006</cite>) and
IBM's C2 simulator <cite data-cite="Ananthanarayanan09">(Ananthanarayanan et al. 2009)</cite>.
Today, in 2017, there are several simulators for large spiking
networks to choose from <cite data-cite="Brette2007">(Brette et al., 2007)</cite>, but NEST remains the
best established simulator with the the largest developer
networks to choose from.
A NEST simulation consists of three main components:
* **Nodes** are all neurons, devices, and also
sub-networks. Nodes have a dynamic state that changes over time and
that can be influenced by incoming *events*.
* **Events** are pieces of information of a particular
type. The most common event is the spike-event. Other event types
are voltage events and current events.
* **Connections** are communication channels between
nodes. Only if one node is connected to another node, can they
exchange events. Connections are weighted, directed, and specific to
one event type. Directed means that events can flow only in one
direction. The node that sends the event is called *source* and
the node that receives the event is called *target*. The weight
determines how strongly an event will influence the target node. A
second parameter, the *delay*, determines how long an event
needs to travel from source to target.
In the next sections, we will illustrate how to use NEST, using
examples with increasing complexity. Each of the examples is
self-contained.
# First steps
We begin by starting Python. For interactive sessions, we here use
the IPython shell <cite data-cite="Pere:2007(21)">(Pérez and Granger, 2007)</cite>. It is convenient,
because you can edit the command line and access previously typed
commands using the up and down keys. However, all examples in this
chapter work equally well without IPython. For data analysis and
visualization, we also recommend the Python packages Matplotlib
<cite data-cite="Hunt:2007(90)">(Hunter, 2007)</cite> and NumPy <cite data-cite="Olip:Guid">(Oliphant, 2006)</cite>.
Our first simulation investigates the response of one
integrate-and-fire neuron to an alternating current and Poisson spike
trains from an excitatory and an inhibitory source. We record the
membrane potential of the neuron to observe how the stimuli influence
the neuron.
In this model, we inject a sine current with a frequency of 2 Hz and
an amplitude of 100 pA into a neuron. At the same time, the neuron
receives random spiking input from two sources known as Poisson
generators. One Poisson generator represents a large population of
excitatory neurons and the other a population of inhibitory
neurons. The rate for each Poisson generator is set as the product of
the assumed number of synapses per target neuron received from the
population and the average firing rate of the source neurons.
The small network is simulated for 1000 milliseconds, after which the
time course of the membrane potential during this period is plotted. For this, we use the `pylab` plotting routines of Python's Matplotlib package.
The Python code for this small model is shown below.
```
%matplotlib inline
import nest
import nest.voltage_trace
nest.ResetKernel()
neuron = nest.Create('iaf_psc_alpha')
sine = nest.Create('ac_generator', 1,
{'amplitude': 100.0,
'frequency': 2.0})
noise = nest.Create('poisson_generator', 2,
[{'rate': 70000.0},
{'rate': 20000.0}])
voltmeter = nest.Create('voltmeter', 1,
{'withgid': True})
nest.Connect(sine, neuron)
nest.Connect(voltmeter, neuron)
nest.Connect(noise[:1], neuron, syn_spec={'weight': 1.0, 'delay': 1.0})
nest.Connect(noise[1:], neuron, syn_spec={'weight': -1.0, 'delay': 1.0})
nest.Simulate(1000.0)
nest.voltage_trace.from_device(voltmeter);
```
We will now go through the simulation script and explain the
individual steps. The first two lines `import` the modules `nest` and its sub-module `voltage_trace`. The `nest` module must be imported in every interactive session
and in every Python script in which you wish to use NEST. NEST is a
C++ library that provides a simulation kernel, many neuron and synapse
models, and the simulation language interpreter SLI. The library which
links the NEST simulation language interpreter to the Python
interpreter is called PyNEST <cite data-cite="Eppler09_12">(Eppler et al. 2009)</cite>.
Importing `nest` as shown above puts all NEST commands in
the *namespace* `nest`. Consequently, all commands must
be prefixed with the name of this namespace.
Next we use the command `Create`
to produce one node of the type `iaf_psc_alpha`. As you see in subsequent lines, `Create` is used for all node types.
The first argument, `'iaf_psc_alpha'`, is a string, denoting
the type of node that you want to create.
The second parameter of `Create` is an integer representing
the number of nodes you want to create. Thus, whether you want one neuron
or 100,000, you only need to call `Create` once.
`nest.Models()` provides a list of all available node and
connection models.
The third parameter is either a dictionary or a list of dictionaries,
specifying the parameter settings for the created nodes. If only one
dictionary is given, the same parameters are used for all created
nodes. If an array of dictionaries is given, they are used in order
and their number must match the number of created nodes. This variant
of `Create` is to set the parameters
for the Poisson noise generator, the sine generator (for the
alternating current), and the voltmeter. All parameters of a model
that are not set explicitly are initialized with default values. You
can display them with
`nest.GetDefaults(model_name)`.
Note that only the first
parameter of `Create` is mandatory.
`Create` returns a list of integers, the global
identifiers (or GID for short) of each node created. The GIDs are
assigned in the order in which nodes are created. The first node is
assigned GID 1, the second node GID 2, and so on.
After creating the neuron, sine and noise generators, and voltmeter, we connect the nodes. First we connect the sine generator and the voltmeter
to the neuron. The command `Connect` takes two or more
arguments. The first argument is a list of source nodes. The second
argument is a list of target nodes. `Connect` iterates these
two lists and connects the corresponding pairs.
A node appears in the source position of `Connect` if it sends events
to the target node. In our example, the sine generator is in the
source position because it injects an alternating current into the
neuron. The voltmeter is in the source position because it polls the
membrane potential of the neuron. Other devices may be in the target
position, e.g., the spike detector which receives spike events from a
neuron. If in doubt about the order, consult the documentation of the
respective nodes using NEST's help system. For example, to read the
documentation of the ac\_generator you can type
`nest.help('ac_generator')`.
Dismiss the help by typing `q`.
Next, we use the command `Connect` with the
`syn_spec` parameter to connect the
two Poisson generators to the neuron. In this example the synapse
specification `syn_spec` provides only weight and delay
values, in this case $\pm 1$ pA input current amplitude and $1$ ms
delay. We will see more advanced uses of `syn_spec` below.
After connecting the nodes, the network is ready. We call the NEST function `Simulate` which runs the
network for 1000 milliseconds. The function returns after the
simulation is finished. Then, function `voltage_trace` is
called to plot the membrane potential of the neuron. If you are
running the script for the first time, you may have to tell Python to display
the figure by typing `pylab.show()`.
If you want to inspect how your network looks so far, you can print
it using the command `PrintNetwork()`:
```
nest.PrintNetwork(2)
```
The input argument here is the depth to print to. Output from this function will be in the terminal, and you should get
```
+-[0] root dim=[5]
|
+-[1] iaf_psc_alpha
+-[2] ac_generator
+-[3]...[4] poisson_generator
+-[5] voltmeter
```
If you run the example a second time, NEST will leave the existing
nodes intact and will create a second instance for each node. To start
a new NEST session without leaving Python, you can call
`nest.ResetKernel()`. This function will erase the existing
network so that you can start from scratch.
# Example 1: A sparsely connected recurrent network
Next we discuss a model of activity dynamics in a local cortical
network proposed by <cite data-cite="Brunel00">Brunel (2000)</cite>. We only describe those parts of
the model which are necessary to understand its NEST
implementation. Please refer to the original paper for further details.
The local cortical network consists of two neuron populations: a
population of $N_E$ excitatory neurons and a population of $N_I$
inhibitory neurons. To mimic the cortical ratio of 80% excitatory neurons
and 20% inhibitory neurons, we assume that $N_E=$ 8000 and $N_I=$ 2000. Thus,
our local network has a total of 10,000 neurons.
For both the excitatory and the inhibitory population, we use the same
integrate-and-fire neuron model with current-based synapses. Incoming
excitatory and inhibitory spikes displace the membrane potential $V_m$
by $J_{E}$ and $J_I$, respectively. If $V_m$ reaches the threshold
value $V_{\text{th}}$, the membrane potential is reset to $V_{\text{reset}}$,
a spike is sent with delay $D=$ 1.5 ms to all post-synaptic
neurons, and the neuron remains refractory for $\tau_{\text{rp}}=$ 2.0 ms.
The neurons are mutually connected with a probability of
10%. Specifically, each neuron receives input from $C_{E}= 0.1 \cdot N_{E}$ excitatory and $C_I=0.1\cdot N_{I}$ inhibitory neurons (see figure below). The inhibitory synaptic weights
$J_I$ are chosen with respect to the excitatory synaptic weights $J_E$
such that
$J_I = -g \cdot J_E$,
with $g=$ 5.0 in this example.
<table class="image">
<caption align="bottom">Sketch of the network model proposed by <cite data-cite="Brunel00">Brunel (2000)</cite>. The network consists of three populations: $N_E$ excitatory neurons (circle labelled E), $N_I$ inhibitory neurons (circle labelled I), and a population of identical, independent Poisson processes (PGs) representing activity from outside the network. Arrows represent connections between the network nodes. Triangular arrow-heads represent excitatory and round arrow-heads represent inhibitory connections. The numbers at the start and end of each arrow indicate the multiplicity of the connection.</caption>
<tr><td><img src="figures/brunel_detailed_external_single2.jpg" alt="Brunel detailed network"/></td></tr>
</table>
In addition to the sparse recurrent inputs from within the local
network, each neuron receives randomly timed excitatory input, mimicking
the input from the rest of cortex. The random input is modelled as $C_E$
independent and identically distributed Poisson processes with rate
$\nu_{\text{ext}}$, or equivalently, by a single Poisson process with rate
$C_E \cdot \nu_{\text{ext}}$. Here, we set $\nu_{\text{ext}}$ to twice the
rate $\nu_{\text{th}}$ that is needed to drive a neuron to threshold
asymptotically. The details of the model are summarized in the tables below.
In the resulting plot you should see a raster plot of 50
excitatory neurons during the first 300 ms of simulated time. Time is
shown along the x-axis, neuron ID along the y-axis. At $t=0$, all
neurons are in the same state $V_m=0$ and hence there is no spiking
activity. The external stimulus rapidly drives the membrane potentials
towards the threshold. Due to the random nature of the external
stimulus, not all the neurons reach the threshold at the same
time. After a few milliseconds, the neurons start to spike irregularly at
roughly 40 spikes/s. In the original paper, this network
state is called the *asynchronous irregular state* <cite data-cite="Brunel00">(Brunel, 2000)</cite>.
### Summary of the network model
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-header{vertical-align:top}
.tg .tg-yw4l{vertical-align:top}
</style>
<table class="tg" width=90%>
<tr>
<th class="tg-header" style="font-weight:bold;background-color:#000000;color:#ffffff;" colspan="2">A: Model Summary<br></th>
</tr>
<tr>
<td class="tg-yw4l">Populations</td>
<td class="tg-yw4l">Three: excitatory, inhibitory, external input</td>
</tr>
<tr>
<td class="tg-yw4l">Topology</td>
<td class="tg-yw4l">—</td>
</tr>
<tr>
<td class="tg-yw4l">Connectivity</td>
<td class="tg-yw4l">Random convergent connections with probability $P=0.1$ and fixed in-degree of $C_E=P N_E$ and $C_I=P N_I$.</td>
</tr>
<tr>
<td class="tg-yw4l">Neuron model</td>
<td class="tg-yw4l">Leaky integrate-and-fire, fixed voltage threshold, fixed absolute refractory time (voltage clamp).</td>
</tr>
<tr>
<td class="tg-yw4l">Channel models</td>
<td class="tg-yw4l">—</td>
</tr>
<tr>
<td class="tg-yw4l">Synapse model</td>
<td class="tg-yw4l">$\delta$-current inputs (discontinuous,voltage jumps)</td>
</tr>
<tr>
<td class="tg-yw4l">Plasticity</td>
<td class="tg-yw4l">—</td>
</tr>
<tr>
<td class="tg-yw4l">Input</td>
<td class="tg-yw4l">Independent fixed-rate Poisson spike trains to all neurons</td>
</tr>
<tr>
<td class="tg-yw4l">Measurements</td>
<td class="tg-yw4l">Spike activity</td>
</tr>
</table>
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-iuc6{font-weight:bold}
.tg .tg-yw4l{vertical-align:top}
</style>
<table class="tg" width=90%>
<tr>
<th class="tg" style="font-weight:bold;background-color:#000000;color:#ffffff;" colspan="3">B: Populations<br></th>
</tr>
<tr>
<td class="tg-iuc6">**Name**</td>
<td class="tg-iuc6">**Elements**</td>
<td class="tg-iuc6">**Size**</td>
</tr>
<tr>
<td class="tg-031e">nodes_E</td>
<td class="tg-031e">`iaf_psc_delta` neuron<br></td>
<td class="tg-yw4l">$N_{\text{E}} = 4N_{\text{I}}$</td>
</tr>
<tr>
<td class="tg-031e">nodes_I</td>
<td class="tg-031e">`iaf_psc_delta` neuron<br></td>
<td class="tg-yw4l">$N_{\text{I}}$</td>
</tr>
<tr>
<td class="tg-yw4l">noise</td>
<td class="tg-yw4l">Poisson generator<br></td>
<td class="tg-yw4l">1</td>
</tr>
</table>
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-e3zv{font-weight:bold}
.tg .tg-hgcj{font-weight:bold;text-align:center}
.tg .tg-9hbo{font-weight:bold;vertical-align:top}
.tg .tg-yw4l{vertical-align:top}
</style>
<table class="tg" width=90%>
<tr>
<th class="tg" style="font-weight:bold;background-color:#000000;color:#ffffff;" colspan="4" >C: Connectivity<br></th>
</tr>
<tr>
<td class="tg-e3zv">**Name**</td>
<td class="tg-e3zv">**Source**</td>
<td class="tg-9hbo">**Target**</td>
<td class="tg-9hbo">**Pattern**</td>
</tr>
<tr>
<td class="tg-031e">EE</td>
<td class="tg-031e">nodes_E<br></td>
<td class="tg-yw4l">nodes_E<br></td>
<td class="tg-yw4l">Random convergent $C_{\text{E}}\rightarrow 1$, weight $J$, delay $D$</td>
</tr>
<tr>
<td class="tg-031e">IE<br></td>
<td class="tg-031e">nodes_E<br></td>
<td class="tg-yw4l">nodes_I<br></td>
<td class="tg-yw4l">Random convergent $C_{\text{E}}\rightarrow 1$, weight $J$, delay $D$</td>
</tr>
<tr>
<td class="tg-yw4l">EI</td>
<td class="tg-yw4l">nodes_I</td>
<td class="tg-yw4l">nodes_E</td>
<td class="tg-yw4l">Random convergent $C_{\text{I}}\rightarrow 1$, weight $-gJ$, delay $D$</td>
</tr>
<tr>
<td class="tg-yw4l">II</td>
<td class="tg-yw4l">nodes_I</td>
<td class="tg-yw4l">nodes_I</td>
<td class="tg-yw4l">Random convergent $C_{\text{I}}\rightarrow 1$, weight $-gJ$, delay $D$</td>
</tr>
<tr>
<td class="tg-yw4l">Ext</td>
<td class="tg-yw4l">noise</td>
<td class="tg-yw4l">nodes_E $\cup$ nodes_I</td>
<td class="tg-yw4l">Divergent $1 \rightarrow N_{\text{E}} + N_{\text{I}}$, weight $J$, delay $D$</td>
</tr>
</table>
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-e3zv{font-weight:bold}
.tg .tg-hgcj{font-weight:bold;text-align:center}
.tg .tg-yw4l{vertical-align:top}
</style>
<table class="tg" width=90%>
<tr>
<th class="tg" style="font-weight:bold;background-color:#000000;color:#ffffff;" colspan="2">D: Neuron and Synapse Model<br></th>
</tr>
<tr>
<td class="tg-031e">**Name**</td>
<td class="tg-031e">`iaf_psc_delta` neuron<br></td>
</tr>
<tr>
<td class="tg-031e">**Type**<br></td>
<td class="tg-031e">Leaky integrate- and-fire, $\delta$-current input</td>
</tr>
<tr>
<td class="tg-031e">**Sub-threshold dynamics**<br></td>
<td class="tg-031e">\begin{equation*}
\begin{array}{rll}
\tau_m \dot{V}_m(t) = & -V_m(t) + R_m I(t) &\text{if not refractory}\; (t > t^*+\tau_{\text{rp}}) \\[1ex]
V_m(t) = & V_{\text{r}} & \text{while refractory}\; (t^*<t\leq t^*+\tau_{\text{rp}}) \\[2ex]
I(t) = & {\frac{\tau_m}{R_m} \sum_{\tilde{t}} w
\delta(t-(\tilde{t}+D))}
\end{array}
\end{equation*}<br></td>
</tr>
<tr>
<td class="tg-yw4l">**Spiking**<br></td>
<td class="tg-yw4l">If $V_m(t-)<V_{\theta} \wedge V_m(t+)\geq V_{\theta}$<br> 1. set $t^* = t$<br> 2. emit spike with time-stamp $t^*$<br></td>
</tr>
</table>
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-e3zv{font-weight:bold}
.tg .tg-hgcj{font-weight:bold;text-align:center}
</style>
<table class="tg" width=90%>
<tr>
<th class="tg" style="font-weight:bold;background-color:#000000;color:#ffffff;" colspan="2">E: Input<br></th>
</tr>
<tr>
<td class="tg-031e">**Type**<br></td>
<td class="tg-031e">**Description**<br></td>
</tr>
<tr>
<td class="tg-031e">Poisson generator<br></td>
<td class="tg-031e">Fixed rate $\nu_{\text{ext}} \cdot C_{\text{E}}$, one generator providing independent input to each target neuron</td>
</tr>
</table>
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-e3zv{font-weight:bold}
.tg .tg-hgcj{font-weight:bold;text-align:center}
</style>
<table class="tg" width=90%>
<tr>
<th class="tg" style="font-weight:bold;background-color:#000000;color:#ffffff;" colspan="2">F: Measurements<br></th>
</tr>
<tr>
<td class="tg-031e" colspan="2">Spike activity as raster plots, rates and ''global frequencies'', no details given</td>
</tr>
</table>
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-yw4l{vertical-align:top;}
</style>
<table class="tg" width=90%>
<tr>
<th class="tg" style="font-weight:bold;background-color:#000000;color:#ffffff;" colspan="2">G: Network Parameters<br></th>
</tr>
<tr>
<td class="tg-yw4l" style="border-right-style:hidden">**Parameter**</td>
<td class="tg-yw4l" style="text-align:right;">**Value**<br></td>
</tr>
<tr>
<td class="tg-yw4l" style="border-right-style:hidden">Number of excitatory neurons $N_E$</td>
<td class="tg-yw4l" style="text-align:right;">8000</td>
</tr>
<tr>
<td class="tg-yw4l" style="border-right-style:hidden;border-top-style:hidden">Number of inhibitory neurons $N_I$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">2000</td>
</tr>
<tr>
<td class="tg-yw4l" style="border-right-style:hidden;border-top-style:hidden">Excitatory synapses per neuron $C_E$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">800</td>
</tr>
<tr>
<td class="tg-yw4l" style="border-right-style:hidden;border-top-style:hidden">Inhibitory synapses per neuron $C_I$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">200</td>
</tr>
<tr>
</tr>
</table>
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-e3zv{font-weight:bold}
.tg .tg-hgcj{font-weight:bold;text-align:center}
.tg .tg-yw4l{vertical-align:top}
</style>
<table class="tg" width=90%>
<tr>
<th class="tg" style="font-weight:bold;background-color:#000000;color:#ffffff;" colspan="2">H: Neuron Parameters<br></th>
</tr>
<tr>
<td class="tg-031e" style="border-right-style:hidden">**Parameter**</td>
<td class="tg-031e" style="text-align:right;">**Value**<br></td>
</tr>
<tr>
<td class="tg-yw4l" style="border-right-style:hidden">Membrane time constant $\tau_m$</td>
<td class="tg-yw4l" style="text-align:right;">20 ms</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Refractory period $\tau_{\text{rp}}$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">2 ms</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Firing threshold $V_{\text{th}}$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">20 mV</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Membrane capacitance $C_m$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">1 pF</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Resting potential $V_E$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">0 mV</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Reset potential $V_{\text{reset}}$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">10 mV</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Excitatory PSP amplitude $J_E$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">0.1 mV</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Inhibitory PSP amplitude $J_I$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">-0.5 mV</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Synaptic delay $D$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">1.5 ms</td>
</tr>
<tr>
<td class="tg-yw4l"style="border-right-style:hidden;border-top-style:hidden">Background rate $\eta$</td>
<td class="tg-yw4l" style="text-align:right;border-top-style:hidden;">2.0</td>
</tr>
<tr>
</tr>
</table>
## NEST Implementation
We now show how this model is implemented in NEST. Along the way, we
explain the required steps and NEST commands in more detail so that
you can apply them to your own models.
### Preparations
The first three lines import NEST, a NEST module for raster plots, and
the plotting package `pylab`. We then assign the various model
parameters to variables.
```
import nest
import nest.raster_plot
import pylab
nest.ResetKernel()
g = 5.0
eta = 2.0
delay = 1.5
tau_m = 20.0
V_th = 20.0
N_E = 8000
N_I = 2000
N_neurons = N_E + N_I
C_E = int(N_E / 10)
C_I = int(N_I / 10)
J_E = 0.1
J_I = -g * J_E
nu_ex = eta * V_th / (J_E * C_E * tau_m)
p_rate = 1000.0 * nu_ex * C_E
```
In the second to last line, we compute the firing rate
`nu_ex` ($\nu_{\text{ext}}$) of a neuron in the external population. We define
`nu_ex` as the product of a constant `eta` times
the threshold rate $\nu_{\text{th}}$, i.e. the steady state firing
rate which is needed to bring a neuron to threshold. The value of the
scaling constant is defined with `eta`.
In the final line, we compute the combined input rate due to the
external population. With $C_E$ incoming synapses per neuron, the total rate is
simply the product `nu_ex*C_E`. The factor 1000.0 in the
product changes the units from spikes per ms to spikes per second.
Next, we prepare the simulation kernel of NEST
```
nest.SetKernelStatus({'print_time': True})
```
The command `SetKernelStatus`
modifies parameters of the simulation kernel. The argument is a Python
dictionary with *key*:*value* pairs. Here, we set the NEST
kernel to print the progress of the simulation time during simulation. Note that the progress is output only to the terminal.
### Creating neurons and devices
As a rule of thumb, we recommend that you create all elements in your
network, i.e., neurons, stimulating devices and recording devices
first, before creating any connections.
```
nest.SetDefaults('iaf_psc_delta',
{'C_m': 1.0,
'tau_m': tau_m,
't_ref': 2.0,
'E_L': 0.0,
'V_th': V_th,
'V_reset': 10.0})
```
Here we change the parameters of the neuron model we want to use from the
built-in values to the defaults for our investigation.
`SetDefaults` expects two parameters. The first is a string,
naming the model for which the default parameters should be
changed. Our neuron model for this simulation is the simplest
integrate-and-fire model in NEST's repertoire:
`'iaf_psc_delta'`. The second parameter is a dictionary with
parameters and their new values, entries separated by commas. All
parameter values are taken from Brunel's paper <cite data-cite="Brunel00">(Brunel, 2000)</cite> and we
insert them directly for brevity. Only the membrane time constant
`tau_m` and the threshold potential `V_th` are
read from variables, because these values are needed in several places.
```
nodes = nest.Create('iaf_psc_delta', N_neurons)
nodes_E = nodes[:N_E]
nodes_I = nodes[N_E:]
noise = nest.Create('poisson_generator', 1, {'rate': p_rate})
nest.SetDefaults('spike_detector', {'to_file': True})
spikes = nest.Create('spike_detector', 2,
[{'label': 'brunel-py-ex'},
{'label': 'brunel-py-in'}])
spikes_E = spikes[:1]
spikes_I = spikes[1:]
```
As before we create the neurons with `Create`, which returns a list of the global IDs which
are consecutive numbers from 1 to `N_neurons`.
We split this range into excitatory and inhibitory neurons. We then select the first `N_E`
elements from the list `nodes` and assign them to the
variable `nodes_E`. This list now holds the GIDs of the
excitatory neurons.
Similarly, in the next line, we assign the range from position
`N_E` to the end of the list to the variable
`nodes_I`. This list now holds the GIDs of all inhibitory
neurons. The selection is carried out using standard Python list commands. You
may want to consult the Python documentation for more details.
Next, we create and connect the external population and some devices
to measure the spiking activity in the network.
We create a device known as a
`poisson_generator`, which produces a spike train governed
by a Poisson process at a given rate. We use the third parameter of
`Create` to initialize the rate of the Poisson process to
the population rate `p_rate` which we have previously computed.
If a Poisson generator is connected to $n$ targets, it generates $n$
independent and identically distributed spike trains. Thus, we only
need one generator to model an entire population of randomly firing
neurons.
To observe how the neurons in the recurrent network respond to the
random spikes from the external population, we create two spike detectors.
By default, spike detectors record to memory but not to file. We override this default behaviour to also record
to file. Then we create one detector for the
excitatory neurons and one for the inhibitory neurons.
The default file names are automatically generated from the device type and
its global ID. We use the third argument of `Create` to give each
spike detector a `'label'`, which will be part of the name of the
output file written by the detector. Since two devices are created, we supply
a list of dictionaries.
In the second to last line, we store the GID of the first spike
detector in a one-element list and assign it to the variable
`spikes_E`. In the next line, we do the same for the second
spike detector that is dedicated to the inhibitory population.
### Connecting the network
Once all network elements are in place, we connect them.
```
nest.CopyModel('static_synapse_hom_w',
'excitatory',
{'weight': J_E,
'delay': delay})
nest.Connect(nodes_E, nodes,
{'rule': 'fixed_indegree',
'indegree': C_E},
'excitatory')
nest.CopyModel('static_synapse_hom_w',
'inhibitory',
{'weight': J_I,
'delay':delay})
nest.Connect(nodes_I, nodes,
{'rule': 'fixed_indegree',
'indegree': C_I},
'inhibitory')
```
We create a new connection
type `'excitatory'` by copying the built-in connection type
`'static_synapse_hom_w'` while changing its default values
for *weight* and *delay*. The command `CopyModel`
expects either two or three arguments: the name of an existing neuron
or synapse model, the name of the new model, and optionally a
dictionary with the new default values of the new model.
The connection type `'static_synapse_hom_w'` uses the same
values of weight for all synapses. This saves memory for
networks in which these values are identical for all connections. Later (in 'Randomness in NEST') we will use a different connection model to
implement randomized weights and delays.
Having created and parameterized an appropriate synapse model, we draw
the incoming excitatory connections for each neuron. The function
`Connect` expects four arguments: a list of
source nodes, a list of target nodes, a connection rule, and a synapse
specification. Some connection rules, in particular
`'one_to_one'` and `'all_to_all'` require no
parameters and can be specified as strings. All other connection rules
must be specified as a dictionary, which at least must contain the key
`'rule'` specifying a connection rule;
`nest.ConnectionRules()` shows all connection rules. The
remaining dictionary entries depend on the particular rule. We use the
`'fixed_indegree'` rule, which creates exactly
`indegree` connections to each target neuron; in previous
versions of NEST, this connectivity was provided by
`RandomConvergentConnect`.
The final argument specifies the synapse model to be used, here the
`'excitatory'` model we defined previously.
In the final lines we
repeat the same steps for the inhibitory connections: we create a new
connection type and draw the incoming inhibitory connections for all neurons.
```
nest.Connect(noise, nodes, syn_spec='excitatory')
N_rec = 50
nest.Connect(nodes_E[:N_rec], spikes_E)
nest.Connect(nodes_I[:N_rec], spikes_I)
```
Here we use `Connect` to
connect the Poisson generator to all nodes of the local network. Since
these connections are excitatory, we use the `'excitatory'`
connection type. Finally, we connect a subset of excitatory and
inhibitory neurons to the spike detectors to record from them. If no connection rule
is given, `Connect` connects all sources to all targets (`all_to_all` rule),
i.e., the noise generator is connected to all neurons
(previously `DivergentConnect`), while in the second to last line, all recorded
excitatory neurons are connected to the `spikes_E` spike detector
(previously `ConvergentConnect`).
Our network consists of 10,000 neurons, all of which have the same
activity statistics due to the random connectivity. Thus, it suffices
to record from a representative sample of neurons, rather than from
the entire network. Here, we choose to record from 50 neurons and
assign this number to the variable `N_rec`. We then connect
the first 50 excitatory neurons to their spike detector. Again, we use
standard Python list operations to select `N_rec` neurons
from the list of all excitatory nodes. Alternatively, we could select
50 neurons at random, but since the neuron order has no meaning in
this model, the two approaches would yield qualitatively the same
results. Finally, we repeat this step for the inhibitory neurons.
### Simulating the network
Now everything is set up and we can run the simulation.
```
simtime = 300
nest.Simulate(simtime)
ex_events, in_events = nest.GetStatus(spikes, 'n_events')
events_to_rate = 1000. / simtime / N_rec
rate_ex = ex_events * events_to_rate
print('Excitatory rate: {:.2f} Hz'.format(rate_ex))
rate_in = in_events * events_to_rate
print('Inhibitory rate: {:.2f} Hz'.format(rate_in))
nest.raster_plot.from_device(spikes_E, hist=True);
```
First we select a simulation time of
300 milliseconds and assign it to a variable. Next, we call the NEST
command `Simulate` to run the simulation for 300 ms. During
simulation, the Poisson generators send spikes into the network
and cause the neurons to fire. The spike detectors receive spikes
from the neurons and write them to a file and to memory.
When the function returns, the simulation time has progressed by
300 ms. You can call `Simulate` as often as you like and
with different arguments. NEST will resume the simulation at the point
where it was last stopped. Thus, you can partition your simulation time
into small epochs to regularly inspect the progress of your model.
After the simulation is finished, we compute the firing rate of the
excitatory neurons and the inhibitory
neurons. Finally, we call the NEST
function `raster_plot` to produce the raster plot. `raster_plot` has two
modes. `raster_plot.from_device` expects the global ID of a
spike detector. `raster_plot.from_file` expects the name of
a data file. This is useful to plot data without repeating a
simulation.
# Parallel simulation
Large network models often require too much time or computer memory to
be conveniently simulated on a single computer. For example, if we increase the number of
neurons in the previous model to 100,000, there will be a total of
$10^9$ connections, which won't fit into the memory of most computers.
Similarly, if we use plastic synapses (see Example 3: plastic networks) and run the model for minutes or hours of
simulated time, the execution times become uncomfortably long.
To address this issue, NEST has two modes of parallelization:
multi-threading and distribution. Multi-threaded and distributed
simulation can be used in isolation or in combination <cite data-cite="Ples:2007(672)">(Plesser et al., 2007)</cite>
, and both modes allow you to connect and run
networks more quickly than in the serial case.
Multi-threading means that NEST uses all
available processors or cores of the computer. Today, most desktop
computers and even laptops have at least two processing cores. Thus,
you can use NEST's multi-threaded mode to make your simulations
execute more quickly whilst still maintaining the convenience of
interactive sessions. Since a given computer has a fixed memory size,
multi-threaded simulation can only reduce execution times. It cannot
solve the problem that large models exhaust the computer's memory.
Distribution means that NEST uses
many computers in a network or computer cluster. Since each computer
contributes memory, distributed simulation allows you to simulate
models that are too large for a single computer. However, in
distributed mode it is not currently possible to use NEST
interactively.
In most cases, writing a simulation script to be run in parallel is as
easy as writing one to be executed on a single processor. Only minimal
changes are required, as described below, and you can ignore the fact
that the simulation is actually executed by more than one core or
computer. However, in some cases your knowledge about the distributed
nature of the simulation can help you improve efficiency even
further. For example, in the distributed mode, all computers execute
the same simulation script. We can improve performance if the
script running on a specific computer only tries to execute commands
relating to nodes that are represented on the
same computer. An example of this technique is shown below in Example 2.
To switch NEST into
multi-threaded mode, you only have to add one line to your simulation
script:
```
nest.ResetKernel()
n = 4 # number of threads
nest.SetKernelStatus({'local_num_threads': n})
```
Here, `n` is the number of threads you want to use. It is
important that you set the number of threads *before* you create
any nodes. If you try to change the number of threads after nodes were
created, NEST will issue an error.
A good choice for the number of threads is the number of cores or
processors on your computer. If your processor supports
hyperthreading, you can select an even higher number of threads.
The distributed mode of NEST is particularly useful for large simulations
for which not only the processing speed, but also the memory of a single
computer are insufficient. The distributed mode of NEST uses the
Message Passing Interface <cite data-cite="MPI2009">(MPI Forum, 2009)</cite>, a library that must be
installed on your computer network when you install NEST. For details,
please refer to NEST documentation at [www.nest-simulator.org](http://www.nest-simulator.org/documentation/).
The distributed mode of NEST is also easy to use. All you need to do
is start NEST with the MPI command `mpirun`:
`mpirun -np m python script.py`
where `m` is the number of MPI processes that should be
started. One sensible choice for `m` is the total number of
cores available on the cluster. Another reasonable choice is the
number of physically distinct machines, utilizing their cores through
multithreading as described above. This can be useful on clusters of
multi-core computers.
In NEST, processes and threads are both mapped to *virtual processes* <cite data-cite="Ples:2007(672)">(Plesser et al. 2007)</cite> . If a
simulation is started with `m` MPI processes and
`n` threads on each process, then there are
`m`$\times$`n` virtual processes. You can obtain
the number of virtual processes in a simulation with
```
nest.GetKernelStatus('total_num_virtual_procs')
```
The virtual process concept is reflected in the labelling of output
files. For example, the data files for the excitatory spikes produced
by the network discussed here follow the form
`brunel-py-ex-x-y.gdf`, where `x` is the ID of the
data recording node and `y` is the ID of the virtual
process.
# Randomness in NEST
NEST has built-in random number sources that can be used for tasks
such as randomizing spike trains or network connectivity. In this
section, we discuss some of the issues related to the use of random
numbers in parallel simulations. In example 2, we illustrate how to randomize
parameters in a network.
Let us first consider the case that a simulation script does not
explicitly generate random numbers. In this case, NEST produces
identical simulation results for a given number of virtual processes,
irrespective of how the virtual processes are partitioned into threads
and MPI processes. The only difference between the output of two
simulations with different configurations of threads and processes
resulting in the same number of virtual processes is the result of
query commands such as `GetStatus`. These commands
gather data over threads on the local machine, but not over remote
machines.
In the case that random numbers are explicitly generated in the
simulation script, more care must be taken to produce results that are
independent of the parallel configuration. Consider, for example, a
simulation where two threads have to draw a random number from a
single random number generator. Since only one thread can access the
random number generator at a time, the outcome of the simulation will
depend on the access order.
Ideally, all random numbers in a simulation should come from a single
source. In a serial simulation this is trivial to implement, but in
parallel simulations this would require shipping a large number of
random numbers from a central random number generator (RNG) to all
processes. This is impractical. Therefore, NEST uses one independent
random number generator on each
virtual process. Not all random number generators can be used in
parallel simulations, because many cannot reliably produce
uncorrelated parallel streams. Fortunately, recent years have seen
great progress in RNG research and there is a range of random number
generators that can be used with great fidelity in parallel
applications.
Based on this knowledge, each virtual process (VP) in NEST has its own
RNG. Numbers from these RNGs are used to
* choose random connections
* create random spike trains (e.g., `poisson_generator`)
or random currents
(e.g., `noise_generator`).
In order to randomize model parameters in a PyNEST script, it is
convenient to use the random number generators provided by
NumPy. To ensure consistent results for a given number
of virtual processes, each virtual process should use a separate
Python RNG. Thus, in a simulation running on $N_{vp}$ virtual processes,
there should be $2N_{vp}+1$ RNGs in total:
* the global NEST RNG;
* one RNG per VP in NEST;
* one RNG per VP in Python.
We need to provide separate seed values for each of these generators.
Modern random number generators work equally well for all seed
values. We thus suggest the following approach to choosing seeds: For
each simulation run, choose a master seed $msd$ and seed the RNGs
with seeds $msd$, $msd+1$, $\dots$ $msd+2N_{vp}$. Any two master seeds must
differ by at least $2N_{vp}+1$ to avoid correlations between simulations.
By default, NEST uses Knuth's lagged Fibonacci RNG, which has the nice
property that each seed value provides a different sequence of
some $2^{70}$ random numbers <cite data-cite="Knut:Art(2)(1998)">(Knuth, 1998, Ch. 3.6)</cite>. Python
uses the Mersenne Twister MT19937 generator <cite data-cite="Mats:1998(3)">(Matsumoto and Nishimura, 1998)</cite>,
which provides no explicit guarantees, but given the enormous state
space of this generator it appears astronomically unlikely that
neighbouring integer seeds would yield overlapping number
sequences. For a recent overview of RNGs, see <cite data-cite="Lecu:2007(22)">L'Ecuyer and Simard (2007)</cite>. For general introductions to random number
generation, see <cite data-cite="Gent:Rand(2003)">Gentle (2003)</cite>, <cite data-cite="Knut:Art(2)(1998)">Knuth (1998, Ch. 3)</cite> or <cite data-cite="Ples:2010(399)">Plesser (2010)</cite>.
# Example 2: Randomizing neurons and synapses
Let us now consider how to randomize some neuron and synapse
parameters in the sparsely connected network model introduced in Example 1. We shall
* explicitly seed the random number generators;
* randomize the initial membrane potential of all neurons;
* randomize the weights of the recurrent excitatory connections.
We begin by setting up the parameters
```
import numpy
import nest
nest.ResetKernel()
# Network parameters. These are given in Brunel (2000) J.Comp.Neuro.
g = 5.0 # Ratio of IPSP to EPSP amplitude: J_I/J_E
eta = 2.0 # rate of external population in multiples of threshold rate
delay = 1.5 # synaptic delay in ms
tau_m = 20.0 # Membrane time constant in mV
V_th = 20.0 # Spike threshold in mV
N_E = 8000
N_I = 2000
N_neurons = N_E + N_I
C_E = int(N_E / 10) # number of excitatory synapses per neuron
C_I = int(N_I / 10) # number of inhibitory synapses per neuron
J_E = 0.1
J_I = -g * J_E
nu_ex = eta * V_th / (J_E * C_E * tau_m) # rate of an external neuron in ms^-1
p_rate = 1000.0 * nu_ex * C_E # rate of the external population in s^-1
# Set parameters of the NEST simulation kernel
nest.SetKernelStatus({'print_time': True,
'local_num_threads': 2})
```
So far the code is similar to Example 1, but now we insert code to seed the
random number generators:
```
# Create and seed RNGs
msd = 1000 # master seed
n_vp = nest.GetKernelStatus('total_num_virtual_procs')
msdrange1 = range(msd, msd + n_vp)
pyrngs = [numpy.random.RandomState(s) for s in msdrange1]
msdrange2 = range(msd + n_vp + 1, msd + 1 + 2 * n_vp)
nest.SetKernelStatus({'grng_seed': msd + n_vp,
'rng_seeds': msdrange2})
```
We first define the master seed `msd` and then obtain the number of
virtual processes `n_vp`. Then we create a list of `n_vp` NumPy random number generators
with seeds `msd`, `msd+1`, $\dots$
`msd+n_vp-1`. The next two lines set new seeds for the
built-in NEST RNGs: the global RNG is seeded with
`msd+n_vp`, the per-virtual-process RNGs with
`msd+n_vp+1`, $\dots$, `msd+2*n_vp`. Note that the
seeds for the per-virtual-process RNGs must always be passed as a
list, even in a serial simulation.
Then we create the nodes
```
nest.SetDefaults('iaf_psc_delta',
{'C_m': 1.0,
'tau_m': tau_m,
't_ref': 2.0,
'E_L': 0.0,
'V_th': V_th,
'V_reset': 10.0})
nodes = nest.Create('iaf_psc_delta', N_neurons)
nodes_E = nodes[:N_E]
nodes_I = nodes[N_E:]
noise = nest.Create('poisson_generator', 1, {'rate': p_rate})
spikes = nest.Create('spike_detector', 2,
[{'label': 'brunel-py-ex'},
{'label': 'brunel-py-in'}])
spikes_E = spikes[:1]
spikes_I = spikes[1:]
```
After creating the neurons as before, we insert the following code to randomize the membrane potential
of all neurons:
```
node_info = nest.GetStatus(nodes)
local_nodes = [(ni['global_id'], ni['vp'])
for ni in node_info if ni['local']]
for gid, vp in local_nodes:
nest.SetStatus([gid], {'V_m': pyrngs[vp].uniform(-V_th, V_th)})
```
In this code, we meet the concept of *local* nodes for the first
time (Plesser et al. 2007). In serial and multi-threaded
simulations, all nodes are local. In an MPI-based simulation with $m$
MPI processes, each MPI process represents and is responsible for
updating (approximately) $1/m$-th of all nodes—these are the local
nodes for each process. We obtain status
information for each node; for local nodes, this will be full information,
for non-local nodes this will only be minimal information. We then use a list
comprehension to create
a list of `gid` and `vp` tuples for all local
nodes. The `for`-loop then iterates over this list and draws
for each node a membrane potential value uniformly distributed in
$[-V_{\text{th}}, V_{\text{th}})$, i.e., $[-20\text{mV},
20\text{mV})$. We draw the initial membrane potential for each node
from the NumPy RNG assigned to the virtual process `vp`
responsible for updating that node.
As the next step, we create excitatory recurrent connections with the
same connection rule as in the original script, but with randomized
weights.
```
nest.CopyModel('static_synapse', 'excitatory')
nest.Connect(nodes_E, nodes,
{'rule': 'fixed_indegree',
'indegree': C_E},
{'model': 'excitatory',
'delay': delay,
'weight': {'distribution': 'uniform',
'low': 0.5 * J_E,
'high': 1.5 * J_E}})
```
The first difference to the original is that we base the excitatory
synapse model on the built-in `static_synapse` model instead
of `static_synapse_hom_w`, as the latter implies equal
weights for all synapses. The second difference is that we randomize
the initial weights. To this end, we have replaced the simple synapse
specification `'excitatory'` with a subsequent synapse specification
dictionary. Such
a dictionary must always contain the key `'model'` providing
the synapse model to use. In addition, we specify a fixed delay, and a
distribution from which to draw the weights, here a uniform
distribution over $[J_E/2, 3J_E/2)$. NEST will automatically use the
correct random number generator for each weight.
To see all available random distributions, please run
`nest.sli_run('rdevdict info')`. To access documentation for
an individual distribution, run, e.g., `nest.help('rdevdict::binomial')`.
These distributions can be
used for all parameters of a synapse.
We then make the rest of the connections.
```
nest.CopyModel('static_synapse_hom_w',
'inhibitory',
{'weight': J_I,
'delay': delay})
nest.Connect(nodes_I, nodes,
{'rule': 'fixed_indegree',
'indegree': C_I},
'inhibitory')
# connect one noise generator to all neurons
nest.CopyModel('static_synapse_hom_w',
'excitatory_input',
{'weight': J_E,
'delay': delay})
nest.Connect(noise, nodes, syn_spec='excitatory_input')
# connect all recorded E/I neurons to the respective detector
N_rec = 50 # Number of neurons to record from
nest.Connect(nodes_E[:N_rec], spikes_E)
nest.Connect(nodes_I[:N_rec], spikes_I)
```
Before starting our simulation, we want to visualize the randomized
initial membrane potentials and weights. To this end, we insert the
following code just before we start the simulation:
```
pylab.figure(figsize=(12,3))
pylab.subplot(121)
V_E = nest.GetStatus(nodes_E[:N_rec], 'V_m')
pylab.hist(V_E, bins=10)
pylab.xlabel('Membrane potential V_m [mV]')
pylab.title('Initial distribution of membrane potentials')
pylab.subplot(122)
ex_conns = nest.GetConnections(nodes_E[:N_rec],
synapse_model='excitatory')
w = nest.GetStatus(ex_conns, 'weight')
pylab.hist(w, bins=100)
pylab.xlabel('Synaptic weight [pA]')
pylab.title(
'Distribution of synaptic weights ({:d} synapses)'.format(len(w)));
```
Here, `nest.GetStatus` retrieves the membrane potentials of all 50
recorded neurons. The data is then displayed as a histogram with 10
bins.
The function `nest.GetConnections` here finds
all connections that
* have one of the 50 recorded excitatory neurons as source;
* have any local node as target;
* and are of type `excitatory`.
Next, we then use `GetStatus()` to
obtain the weights of these connections. Running the script in a
single MPI process, we record approximately 50,000 weights, which we
display in a histogram with 100 bins.
Note that the code above
will return complete results only when run in a single MPI
process. Otherwise, only data from local neurons or connections with
local targets will be obtained. It is currently not possible to
collect recorded data across MPI processes in NEST. In distributed
simulations, you should thus let recording devices write data to files
and collect the data after the simulation is complete.
Comparing the
raster plot from the simulation with randomized initial membrane
potentials with the same plot for the
original network reveals that the
membrane potential randomization has prevented the synchronous onset
of activity in the network.
We now run the simulation.
```
simtime = 300. # how long shall we simulate [ms]
nest.Simulate(simtime)
```
As a final point, we make a slight improvement to the rate computation of the original
script. Spike detectors count only spikes from neurons on the local
MPI process. Thus, the original computation is correct only for a
single MPI process. To obtain meaningful results when simulating
on several MPI processes, we count how many of the `N_rec`
recorded nodes are local and use that number to compute the rates:
```
events = nest.GetStatus(spikes, 'n_events')
N_rec_local_E = sum(nest.GetStatus(nodes_E[:N_rec], 'local'))
rate_ex = events[0] / simtime * 1000.0 / N_rec_local_E
print('Excitatory rate : {:.2f} Hz'.format(rate_ex))
N_rec_local_I = sum(nest.GetStatus(nodes_I[:N_rec], 'local'))
rate_in = events[1] / simtime * 1000.0 / N_rec_local_I
print('Inhibitory rate : {:.2f} Hz'.format(rate_in))
```
Each MPI process then reports the rate of activity of its locally
recorded nodes.
# Example 3: Plastic Networks
NEST provides synapse models with a variety of short-term and
long-term dynamics. To illustrate this, we extend the sparsely
connected network introduced in Example 1 with
randomized synaptic weights as described in section 'Randomness in NEST' to incorporate spike-timing-dependent plasticity <cite data-cite="Bi98">(Bi and Poo, 1998)</cite> at its recurrent excitatory-excitatory synapses.
We create all nodes and randomize their initial membrane potentials
as before. We then generate a plastic synapse model for the excitatory-excitatory
connections and a static synapse model for the excitatory-inhibitory
connections:
```
nest.ResetKernel()
# Synaptic parameters
STDP_alpha = 2.02 # relative strength of STDP depression w.r.t potentiation
STDP_Wmax = 3 * J_E # maximum weight of plastic synapse
# Simulation parameters
N_vp = 8 # number of virtual processes to use
base_seed = 10000 # increase in intervals of at least 2*n_vp+1
N_rec = 50 # Number of neurons to record from
data2file = True # whether to record data to file
simtime = 300. # how long shall we simulate [ms]
# Set parameters of the NEST simulation kernel
nest.SetKernelStatus({'print_time': True,
'local_num_threads': 2})
# Create and seed RNGs
ms = 1000 # master seed
n_vp = nest.GetKernelStatus('total_num_virtual_procs')
pyrngs = [numpy.random.RandomState(s) for s in range(ms, ms + n_vp)]
nest.SetKernelStatus({'grng_seed': ms + n_vp,
'rng_seeds': range(ms + n_vp + 1, ms + 1 + 2 * n_vp)})
# Create nodes -------------------------------------------------
nest.SetDefaults('iaf_psc_delta',
{'C_m': 1.0,
'tau_m': tau_m,
't_ref': 2.0,
'E_L': 0.0,
'V_th': V_th,
'V_reset': 10.0})
nodes = nest.Create('iaf_psc_delta', N_neurons)
nodes_E = nodes[:N_E]
nodes_I = nodes[N_E:]
noise = nest.Create('poisson_generator', 1, {'rate': p_rate})
spikes = nest.Create('spike_detector', 2,
[{'label': 'brunel_py_ex'},
{'label': 'brunel_py_in'}])
spikes_E = spikes[:1]
spikes_I = spikes[1:]
# randomize membrane potential
node_info = nest.GetStatus(nodes, ['global_id', 'vp', 'local'])
local_nodes = [(gid, vp) for gid, vp, islocal in node_info if islocal]
for gid, vp in local_nodes:
nest.SetStatus([gid], {'V_m': pyrngs[vp].uniform(-V_th, V_th)})
nest.CopyModel('stdp_synapse_hom',
'excitatory_plastic',
{'alpha': STDP_alpha,
'Wmax': STDP_Wmax})
nest.CopyModel('static_synapse', 'excitatory_static')
```
Here, we set the parameters `alpha` and `Wmax` of
the synapse model but use the default settings for all its other
parameters. The `_hom` suffix in the synapse model name
indicates that all plasticity parameters such as `alpha` and
`Wmax` are shared by all synapses of this model.
We again use `nest.Connect` to create connections with
randomized weights:
```
nest.Connect(nodes_E, nodes_E,
{'rule': 'fixed_indegree',
'indegree': C_E},
{'model': 'excitatory_plastic',
'delay': delay,
'weight': {'distribution': 'uniform',
'low': 0.5 * J_E,
'high': 1.5 * J_E}})
nest.Connect(nodes_E, nodes_I,
{'rule': 'fixed_indegree',
'indegree': C_E},
{'model': 'excitatory_static',
'delay': delay,
'weight': {'distribution': 'uniform',
'low': 0.5 * J_E,
'high': 1.5 * J_E}})
nest.CopyModel('static_synapse',
'inhibitory',
{'weight': J_I,
'delay': delay})
nest.Connect(nodes_I, nodes,
{'rule': 'fixed_indegree',
'indegree': C_I},
'inhibitory')
# connect noise generator to all neurons
nest.CopyModel('static_synapse_hom_w',
'excitatory_input',
{'weight': J_E,
'delay': delay})
nest.Connect(noise, nodes, syn_spec='excitatory_input')
# connect all recorded E/I neurons to the respective detector
nest.Connect(nodes_E[:N_rec], spikes_E)
nest.Connect(nodes_I[:N_rec], spikes_I)
# Simulate -----------------------------------------------------
# Visualization of initial membrane potential and initial weight
# distribution only if we run on single MPI process
if nest.NumProcesses() == 1:
pylab.figure(figsize=(12,3))
# membrane potential
V_E = nest.GetStatus(nodes_E[:N_rec], 'V_m')
V_I = nest.GetStatus(nodes_I[:N_rec], 'V_m')
pylab.subplot(121)
pylab.hist([V_E, V_I], bins=10)
pylab.xlabel('Membrane potential V_m [mV]')
pylab.legend(('Excitatory', 'Inibitory'))
pylab.title('Initial distribution of membrane potentials')
pylab.draw()
# weight of excitatory connections
w = nest.GetStatus(nest.GetConnections(nodes_E[:N_rec],
synapse_model='excitatory_plastic'),
'weight')
pylab.subplot(122)
pylab.hist(w, bins=100)
pylab.xlabel('Synaptic weight w [pA]')
pylab.title('Initial distribution of excitatory synaptic weights')
pylab.draw()
else:
print('Multiple MPI processes, skipping graphical output')
nest.Simulate(simtime)
events = nest.GetStatus(spikes, 'n_events')
# Before we compute the rates, we need to know how many of the recorded
# neurons are on the local MPI process
N_rec_local_E = sum(nest.GetStatus(nodes_E[:N_rec], 'local'))
rate_ex = events[0] / simtime * 1000.0 / N_rec_local_E
print('Excitatory rate : {:.2f} Hz'.format(rate_ex))
N_rec_local_I = sum(nest.GetStatus(nodes_I[:N_rec], 'local'))
rate_in = events[1] / simtime * 1000.0 / N_rec_local_I
print('Inhibitory rate : {:.2f} Hz'.format(rate_in))
```
After a period of simulation, we can access the plastic synaptic
weights for analysis:
```
if nest.NumProcesses() == 1:
nest.raster_plot.from_device(spikes_E, hist=True)
# weight of excitatory connections
w = nest.GetStatus(nest.GetConnections(nodes_E[:N_rec],
synapse_model='excitatory_plastic'),
'weight')
pylab.figure(figsize=(12,4))
pylab.hist(w, bins=100)
pylab.xlabel('Synaptic weight [pA]')
# pylab.savefig('../figures/rand_plas_w.eps')
# pylab.show()
else:
print('Multiple MPI processes, skipping graphical output')
```
Plotting a histogram of the synaptic weights reveals that the initial
uniform distribution has begun to soften, as we can see in the plots resulting from the simulation above. Simulation for a longer period
results in an approximately Gaussian distribution of weights.
# Example 4: Classes and Automatization Techniques
Running the examples line for line is possible in interactive sessions, but if you want to run a
simulation several times, possibly with different parameters, it is
more practical to write a script that can be loaded from Python.
Python offers a number of mechanisms to structure and organize not
only your simulations, but also your simulation data. The first step
is to re-write a model as a *class*. In Python, and other
object-oriented languages, a class is a data structure which groups
data and functions into a single entity. In our case, data are the
different parameters of a model, and functions are what you can do with
a model.
Classes allow you to solve various common problems in simulations:
* **Parameter sets** Classes are data structures and so are
ideally suited to hold the parameter set for a model. Class inheritance
allows you to modify one, a few, or all parameters while maintaining
the relation to the original model.
* **Model variations** Often, we want to change minor aspects of
a model. For example, in one version we have homogeneous connections
and in another we want randomized weights. Again, we can use class
inheritance to express both cases while maintaining the conceptual
relation between the models.
* **Data management** Often, we run simulations with different
parameters or other variations and forget to record which data file
belonged to which simulation. Python's class mechanisms provide a
simple solution.
We organize the model from Example 1 into a class,
by realizing that each simulation has five steps which can be factored
into separate functions:
1. Define all independent parameters of the model. Independent
parameters are those that have concrete values which do not depend
on any other parameter. For example, in the Brunel model, the
parameter $g$ is an independent parameter.
2. Compute all dependent parameters of the model. These are all
parameters or variables that have to be computed from other
quantities (e.g., the total number of neurons).
3. Create all nodes (neurons, devices, etc.)
4. Connect the nodes.
5. Simulate the model.
We translate these steps into a simple class layout that will fit
most models:
```
class Model(object):
"""Model description."""
# Define all independent variables.
def __init__(self):
"""Initialize the simulation, set up data directory"""
def calibrate(self):
"""Compute all dependent variables"""
def build(self):
"""Create all nodes"""
def connect(self):
"""Connect all nodes"""
def run(self, simtime):
"""Build, connect, and simulate the model"""
```
In the following, we illustrate how to fit the model from Example 1 into this scaffold. The complete and commented
listing can be found in your NEST distribution.
```
class Brunel2000(object):
"""
Implementation of the sparsely connected random network,
described by Brunel (2000) J. Comp. Neurosci.
Parameters are chosen for the asynchronous irregular
state (AI).
"""
g = 5.0
eta = 2.0
delay = 1.5
tau_m = 20.0
V_th = 20.0
N_E = 8000
N_I = 2000
J_E = 0.1
N_rec = 50
threads = 2 # Number of threads for parallel simulation
built = False # True, if build() was called
connected = False # True, if connect() was called
# more definitions follow...
def __init__(self):
"""
Initialize an object of this class.
"""
self.name = self.__class__.__name__
self.data_path = self.name + '/'
nest.ResetKernel()
if not os.path.exists(self.data_path):
os.makedirs(self.data_path)
print("Writing data to: " + self.data_path)
nest.SetKernelStatus({'data_path': self.data_path})
def calibrate(self):
"""
Compute all parameter dependent variables of the
model.
"""
self.N_neurons = self.N_E + self.N_I
self.C_E = self.N_E / 10
self.C_I = self.N_I / 10
self.J_I = -self.g * self.J_E
self.nu_ex = self.eta * self.V_th / (self.J_E * self.C_E * self.tau_m)
self.p_rate = 1000.0 * self.nu_ex * self.C_E
nest.SetKernelStatus({"print_time": True,
"local_num_threads": self.threads})
nest.SetDefaults("iaf_psc_delta",
{"C_m": 1.0,
"tau_m": self.tau_m,
"t_ref": 2.0,
"E_L": 0.0,
"V_th": self.V_th,
"V_reset": 10.0})
def build(self):
"""
Create all nodes, used in the model.
"""
if self.built:
return
self.calibrate()
# remaining code to create nodes
self.built = True
def connect(self):
"""
Connect all nodes in the model.
"""
if self.connected:
return
if not self.built:
self.build()
# remaining connection code
self.connected = True
def run(self, simtime=300):
"""
Simulate the model for simtime milliseconds and print the
firing rates of the network during this period.
"""
if not self.connected:
self.connect()
nest.Simulate(simtime)
# more code, e.g., to compute and print rates
```
A Python class is defined by the keyword `class` followed by
the class name, `Brunel2000` in this example. The parameter
`object` indicates that our class is a subclass of a general
Python Object. After the colon, we can supply a documentation string,
encased in triple quotes, which will be printed if we type
`help(Brunel2000)`. After the documentation string, we
define all independent parameters of the model as well as some global
variables for our simulation. We also introduce two Boolean variables
`built` and `connected` to ensure that the
functions `build()` and `connect()` are executed
exactly once.
Next, we define the class functions. Each function has at least the
parameter `self`, which is a reference to the
current class object. It is used to access the functions and
variables of the object.
The first function from the code above is also the first one that is called for
every class object. It has the somewhat cryptic name
`__init__()`. `__init__()` is automatically called by Python whenever a
new object of a class is created and before any other class function
is called. We use it to initialize the NEST simulation kernel and to
set up a directory where the simulation data will be stored.
The general idea is this: each simulation with a specific parameter
set gets its own Python class. We can then use the class name to
define the name of a data directory where all simulation data are
stored.
In Python it is possible to read out the name of a class from an
object. This is done with `self.name=self.__class__.__name__`. Don't worry
about the many underscores, they tell us that these names are provided
by Python. In the next line, we assign the class name plus a trailing
slash to the new object variable `data_path`. Note how all
class variables are prefixed with `self`.
Next we reset the NEST simulation kernel to remove any leftovers from
previous simulations, using `nest.ResetKernel()`.
The following two lines use functions from the Python library
`os` which provides functions related to the operating
system. In the `if`-test we check whether a directory
with the same name as the class already exists. If not, we create a
new directory with this name. Finally, we set the data path property
of the simulation kernel. All recording devices use this location to
store their data. This does not mean that this directory is
automatically used for any other Python output functions. However,
since we have stored the data path in an object variable, we can use
it whenever we want to write data to file.
The other class functions are quite straightforward.
`Brunel2000.build()` accumulates all commands that
relate to creating nodes. The only addition is a piece of code that
checks whether the nodes were already created. The last line in this function sets the variable
`self.built` to `True` so that other functions
know that all nodes were created.
In function `Brunel2000.connect()` we first ensure that all nodes are
created before we attempt to draw any connection. Again, the last line sets a variable, telling other functions that the
connections were drawn successfully.
`Brunel2000.built` and `Brunel2000.connected` are
state variables that help you to make dependencies between functions
explicit and to enforce an order in which certain functions are
called.
The main function `Brunel2000.run()` uses both
state variables to build and connect the network.
In order to use the class we have to create an object of the class (after loading the file with the class
definition, if it is in another file):
```
import os
net = Brunel2000()
net.run(500)
```
Finally, we demonstrate how to use Python's class inheritance to
express different parameter configurations and versions of a model.
In the following listing, we derive a new class that simulates a
network where excitation and inhibition are exactly balanced,
i.e. $g=4$:
```
class Brunel_balanced(Brunel2000):
"""
Exact balance of excitation and inhibition
"""
g = 4
```
Class `Brunel_balanced` is defined with class
`Brunel2000` as parameter. This means the new class inherits
all parameters and functions from class `Brunel2000`. Then,
we redefine the value of the parameter `g`. When we create
an object of this class, it will create its new data directory.
We can use the same mechanism to implement an alternative version of the
model. For example, instead of re-implementing the model with
randomized connection weights, we can use inheritance to change just the way
nodes are connected:
```
class Brunel_randomized(Brunel2000):
"""
Like Brunel2000, but with randomized connection weights.
"""
def connect(self):
"""
Connect nodes with randomized weights.
"""
# Code for randomized connections follows
```
Thus, using inheritance, we can easily keep track of different
parameter sets and model versions and their associated simulation
data. Moreover, since we keep all alternative versions, we also have a
simple versioning system that only depends on Python features, rather
than on third party tools or libraries.
The full implementation of the model using classes can be found in the
examples directory of your NEST distribution.
# How to continue from here
In this chapter we have presented a step-by-step introduction to NEST,
using concrete examples. The simulation scripts and more examples are
part of the examples included in the NEST distribution.
Information about individual PyNEST functions can be obtained with
Python's `help()` function (in iPython it suffices to append `?` to the function). For example:
```
help(nest.Connect)
```
To learn more about NEST's node and synapse types, you can access
NEST's help system. NEST's online help still
uses a lot of syntax of SLI, NEST's native simulation language. However,
the general information is also valid for PyNEST.
Help and advice can also be found on NEST's user mailing list where
developers and users exchange their experience, problems, and ideas.
And finally, we encourage you to visit the web site of the NEST
Initiative at [www.nest-initiative.org](http://www.nest-initiative.org "NEST initiative").
# Acknowledgements
AM partially funded by BMBF grant 01GQ0420 to BCCN Freiburg, Helmholtz
Alliance on Systems Biology (Germany), Neurex, and the Junior
Professor Program of Baden-Württemberg. HEP partially supported by
RCN grant 178892/V30 eNeuro. HEP and MOG were partially supported by EU
grant FP7-269921 (BrainScaleS).
# References
Rajagopal Ananthanarayanan, Steven K. Esser, Horst D. Simon, and Dharmendra S. Modha. The cat is out of the bag: Cortical simulations with 109 neurons and 1013 synapses. In Supercomputing 09: Proceedings of the ACM/IEEE SC2009 Conference on High Performance Networking and Computing,
Portland, OR, 2009.
G.-q. Bi and M.-m. Poo. Synaptic modifications in cultured hippocampal neurons: Dependence on spike
timing, synaptic strength, and postsynaptic cell type. Journal Neurosci, 18:10464–10472, 1998.
James M. Bower and David Beeman. The Book of GENESIS: Exploring realistic neural models with the
GEneral NEural SImulation System. TELOS, Springer-Verlag-Verlag, New York, 1995.
R. Brette, M. Rudolph, T. Carnevale, M. Hines, D. Beeman, J.M. Bower, M. Diesmann, A. Morrison,
P.H. Goodman, F.C. Harris, and Others. Simulation of networks of spiking neurons: A review of
tools and strategies. Journal of computational neuroscience, 23(3):349398, 2007. URL http://www.springerlink.com/index/C2J0350168Q03671.pdf.
Nicolas Brunel. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons.
Journal Comput Neurosci, 8(3):183–208, 2000.
M. Diesmann, M.-O. Gewaltig, and A. Aertsen. SYNOD: an environment for neural systems simulations.
Language interface and tutorial. Technical Report GC-AA-/95-3, Weizmann Institute of Science, The
Grodetsky Center for Research of Higher Brain Functions, Israel, May 1995.
J. M. Eppler, M. Helias, E. Muller, M. Diesmann, and M. Gewaltig. PyNEST: a convenient interface to
the NEST simulator. Front. Neuroinform., 2:12, 2009.
James E. Gentle. Random Number Generation and Monte Carlo Methods. Springer Science+Business
Media, New York, second edition, 2003.
Marc-Oliver Gewaltig and Markus Diesmann. NEST (Neural Simulation Tool). In Eugene Izhikevich, ed-
itor, Scholarpedia Encyclopedia of Computational Neuroscience, page 11204. Eugene Izhikevich, 2007.
URL http://www.scholarpedia.org/article/NEST\_(Neural\_Simulation\_Tool).
Marc-Oliver Gewaltig, Abigail Morrison, and Hans Ekkehard Plesser. NEST by example: An introduction
to the neural simulation tool NEST. In Nicolas Le Novère, editor, Computational Systems Neurobiology, chapter 18, pages 533–558. Springer Science+Business Media, Dordrecht, 2012.
M. L. Hines and N. T. Carnevale. The NEURON simulation environment. Neural Comput, 9:1179–1209,
1997.
John D. Hunter. Matplotlib: A 2d graphics environment. Computing In Science & Engineering, 9(3):
90–95, May-Jun 2007.
D. E. Knuth. The Art of Computer Programming, volume 2. Addison-Wesley, Reading, MA, third
edition, 1998.
P. L’Ecuyer and R. Simard. TestU01: A C library for empirical testing of random number generators.
ACM Transactions on Mathematical Software, 33:22, 2007. URL http://www.iro.umontreal.ca/~simardr/testu01/tu01.html. Article 22, 40 pages.
M. Matsumoto and T. Nishimura. Mersenne twister: A 623-dimensonally equidistributed uniform pseu-
dorandom number generator. ACM Trans Model Comput Simul, 8:3–30, 1998.
M. Migliore, C. Cannia, W. W. Lytton, H. Markram, and M.L. Hines. Parallel network simulations with
NEURON. Journal Comput Neurosci, 21(2):119–223, 2006.
MPI Forum. MPI: A message-passing interface standard. Technical report, University of Ten-
nessee, Knoxville, TN, USA, September 2009. URL http://www.mpi-forum.org/docs/mpi-2.2/mpi22-report.pdf.
Travis E. Oliphant. Guide to NumPy. Trelgol Publishing (Online), 2006. URL http://www.tramy.us/numpybook.pdf.
Fernando Pérez and Brian E. Granger. Ipython: A system for interactive scientific computing. Computing in Science and Engineering, 9:21–29, 2007. ISSN 1521-9615.
H. E. Plesser, J. M. Eppler, A. Morrison, M. Diesmann, and M.-O. Gewaltig. Efficient parallel simulation of large-scale neuronal networks on clusters of multiprocessor computers. In A.-M. Kermarrec, L. Bougé and T. Priol, editors, Euro-Par 2007: Parallel Processing, volume 4641 of Lecture Notes inComputer Science, pages 672–681, Berlin, 2007. Springer-Verlag.
Hans Ekkehard Plesser. Generating random numbers. In Sonja Grün and Stefan Rotter, editors, Analysis of Parallel Spike Trains, Springer Series in Computational Neuroscience, chapter 19, pages 399–411.
Springer, New York, 2010.
| true |
code
| 0.391988 | null | null | null | null |
|
To Queue or Not to Queue
=====================
In this notebook we look at the relative performance of a single queue vs multiple queues
using the [Simpy](https://simpy.readthedocs.io/en/latest/) framework as well as exploring various
common load balancing algorithms and their performance in M/G/k systems.
First we establish a baseline simulator which can simulate arbitrary latency distributions and
generative processes.
```
# %load src/request_simulator.py
import random
from collections import namedtuple
import numpy as np
import simpy
LatencyDatum = namedtuple(
'LatencyDatum',
('t_queued', 't_processing', 't_total')
)
class RequestSimulator(object):
""" Simulates a M/G/k process common in request processing (computing)
:param worker_desc: A tuple of (count, capacity) to construct workers with
:param local_balancer: A function which takes the current request number
and the list of workers and returns the index of the worker to send the
next request to
:param latency_fn: A function which takes the curent
request number and the worker that was assigned by the load balancer
amd returns the number of milliseconds a request took to process
:param number_of_requests: The number of requests to run through the
simulator
:param request_per_s: The rate of requests per second.
"""
def __init__(
self, worker_desc, load_balancer, latency_fn,
number_of_requests, request_per_s):
self.worker_desc = worker_desc
self.load_balancer = load_balancer
self.latency_fn = latency_fn
self.number_of_requests = int(number_of_requests)
self.request_interval_ms = 1. / (request_per_s / 1000.)
self.data = []
def simulate(self):
# Setup and start the simulation
random.seed(1)
np.random.seed(1)
self.env = simpy.Environment()
count, cap = self.worker_desc
self.workers = []
for i in range(count):
worker = simpy.Resource(self.env, capacity=cap)
worker.zone = "abc"[i % 3]
self.workers.append(worker)
self.env.process(self.generate_requests())
self.env.run()
def generate_requests(self):
for i in range(self.number_of_requests):
idx = self.load_balancer(i, self.workers)
worker = self.workers[idx]
response = self.process_request(
i, worker,
)
self.env.process(response)
# Exponential inter-arrival times == Poisson
arrival_interval = random.expovariate(
1.0 / self.request_interval_ms
)
yield self.env.timeout(arrival_interval)
def process_request(self, request_id, worker):
""" Request arrives, possibly queues, and then processes"""
t_arrive = self.env.now
with worker.request() as req:
yield req
t_start = self.env.now
t_queued = t_start - t_arrive
# Let the operation take w.e. amount of time the latency
# function tells us to
yield self.env.timeout(self.latency_fn(request_id, worker))
t_done = self.env.now
t_processing = t_done - t_start
t_total_response = t_done - t_arrive
datum = LatencyDatum(t_queued, t_processing, t_total_response)
self.data.append(datum)
def run_simulation(
worker_desc, load_balancer, num_requests, request_per_s, latency_fn):
simulator = RequestSimulator(
worker_desc, load_balancer, latency_fn,
num_requests, request_per_s
)
simulator.simulate()
return simulator.data
# %load src/lb_policies.py
import random
import numpy as np
def queue_size(resource):
return resource.count + len(resource.queue)
def random_lb(request_num, workers):
return random.randint(0, len(workers) - 1)
def rr_lb(request_num, workers):
return request_num % len(workers)
def choice_two_lb(request_num, workers):
r1, r2 = np.random.choice(range(len(workers)), 2, replace=False)
r1 = random_lb(request_num, workers)
r2 = random_lb(request_num, workers)
if queue_size(workers[r1]) < queue_size(workers[r2]):
return r1
return r2
def _zone(request):
return "abc"[request % 3]
def choice_n_weighted(n):
def lb(request_num, workers):
choices = np.random.choice(range(len(workers)), n, replace=False)
result = []
for idx, w in enumerate(choices):
weight = 1.0;
if _zone(request_num) == workers[w].zone:
weight *= 1.0
else:
weight *= 4.0
result.append((w, weight * (1 + queue_size(workers[w]))))
result = sorted(result, key=lambda x:x[1])
return result[0][0]
return lb
def choice_two_adjacent_lb(request_num, workers):
r1 = random_lb(request_num, workers)
if r1 + 2 >= len(workers):
r2 = r1 - 1
r3 = r1 - 2
else:
r2 = r1 + 1
r3 = r1 + 2
iq = [(queue_size(workers[i]), i) for i in (r1, r2, r3)]
return (sorted(iq)[0][1])
def shortest_queue_lb(request_num, workers):
idx = 0
for i in range(len(workers)):
if queue_size(workers[i]) < queue_size(workers[idx]):
idx = i
return idx
# %load src/latency_distributions.py
import random
import numpy as np
def zone(request):
return "abc"[request % 3]
def service(mean, slow, shape, slow_freq, slow_count):
scale = mean - mean / shape
scale_slow = slow - slow / shape
def latency(request, worker):
base = ((np.random.pareto(shape) + 1) * scale)
if (zone(request) != worker.zone):
base += 0.8
if (request % slow_freq) < slow_count:
add_l = ((np.random.pareto(shape) + 1) * scale_slow)
else:
add_l = 0
return base + add_l
return latency
def pareto(mean, shape):
# mean = scale * shape / (shape - 1)
# solve for scale given mean and shape (aka skew)
scale = mean - mean / shape
def latency(request, worker):
return ((np.random.pareto(shape) + 1) * scale)
return latency
def expon(mean):
def latency(request, worker):
return random.expovariate(1.0 / mean)
return latency
```
Simulation of Single vs Multiple Queues
================================
Here we explore the effects of having N queues that handle 1/N the load (aka "Frequency Division Multiplexing",
aka `FDM`) vs a single queue distributing out to N servers (aka M/M/k queue aka `MMk`). We confirm the theoretical results that can be obtained using the closed form solutions for `E[T]_MMk` and `E[T]_FDM` via
a simulation.
In particular M/M/k queues have a closed form solution for the mean response time given the probability of queueing (and we know if requests queued)
```
E[T]_MMk = (1 / λ) * Pq * ρ / (1-ρ) + 1 / μ
Where
λ = the arrival rate (hertz)
Pq = the probability of a request queueing
ρ = the system load aka λ / (k * μ)
μ = the average response time (hertz)
```
Frequency division multiplexing (multiple queues) also has a closed form solution:
```
E[T]_FDM = (k / (k * μ - λ))
```
```
# Simulate the various choices
NUM_REQUESTS = 60000
QPS = 18000
AVG_RESPONSE_MS = 0.4
SERVERS = 10
multiple_queues_latency = []
for i in range(SERVERS):
multiple_queues_latency.extend([
i[2] for i in run_simulation((1, 1), rr_lb, NUM_REQUESTS/SERVERS, QPS/SERVERS, expon(AVG_RESPONSE_MS))
])
single_queue = [
i for i in run_simulation((1, SERVERS), rr_lb, NUM_REQUESTS, QPS, expon(AVG_RESPONSE_MS))
]
single_queue_latency = [i[2] for i in single_queue]
Pq = sum([i[0] > 0 for i in single_queue]) / float(NUM_REQUESTS)
# MMk have a closed for mean given the probability of queueing (and we know if requests queued)
# E[T]_MMk = (1 / λ) * Pq * ρ / (1-ρ) + 1 / μ
# Where
# λ = the arrival rate (hertz)
# Pq = the probability of a request queueing
# ρ = the system load aka λ / (k * μ)
# μ = the average response time (hertz)
mu_MMk = (1.0 / AVG_RESPONSE_MS) * 1000
lambda_MMk = QPS
rho_MMk = lambda_MMk / (SERVERS * mu_MMk)
expected_MMk_mean_s = (1 / (lambda_MMk)) * Pq * (rho_MMk / (1-rho_MMk)) + 1 / mu_MMk
expected_MMk_mean_ms = expected_MMk_mean_s * 1000.0
# Frequency-division multiplexing also has a closed form for mean
# E[T]_FDM = (k / (k * μ - λ))
expected_FDM_mean_ms = (SERVERS / (SERVERS * mu_MMk - lambda_MMk)) * 1000.0
print("Theory Results")
print("--------------")
print("Pq = {0:4.2f}".format(Pq))
print("E[T]_FDM = {0:4.2f}".format(expected_FDM_mean_ms))
print("E[T]_MMk = {0:4.2f}".format(expected_MMk_mean_ms))
# And now the simulation
queueing_options = {
'Multiple Queues': multiple_queues_latency,
'Single Queue': single_queue_latency,
}
print()
print("Simulation results")
print("------------------")
hdr = "{0:16} | {1:>7} | {2:>7} | {3:>7} | {4:>7} | {5:>7} | {6:>7} |".format(
"Strategy", "mean", "var", "p50", "p95", "p99", "p99.9")
print(hdr)
for opt in sorted(queueing_options.keys()):
mean = np.mean(queueing_options[opt])
var = np.var(queueing_options[opt])
percentiles = np.percentile(queueing_options[opt], [50, 95, 99, 99.9])
print ("{0:16} | {1:7.2f} | {2:7.2f} | {3:7.2f} | {4:7.2f} | {5:>7.2f} | {6:7.2f} |".format(
opt, mean, var, percentiles[0], percentiles[1], percentiles[2],
percentiles[3]
))
import numpy as np
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
import matplotlib.style as style
style.use('seaborn-pastel')
def color_bplot(bp, edge_color, fill_color):
for element in ['boxes', 'whiskers', 'fliers', 'means', 'medians', 'caps']:
plt.setp(bp[element], color=edge_color)
for box in bp['boxes']:
box.set_facecolor(fill_color)
fig1, ax = plt.subplots(figsize=(12,3))
opts = sorted(queueing_options.keys())
data = [queueing_options[i] for i in opts]
flier = dict(markerfacecolor='r', marker='.')
bplot1 = ax.boxplot(data,whis=[1,99],showfliers=True,flierprops=flier, labels=opts,
patch_artist=True, vert=False)
color_bplot(bplot1, 'black', 'lightblue')
plt.title("Response Time Distribution \n[{0} QPS @ {1}ms avg with {2} servers]".format(
QPS, AVG_RESPONSE_MS, SERVERS)
)
plt.minorticks_on()
plt.grid(which='major', linestyle=':', linewidth='0.4', color='black')
# Customize the minor grid
plt.grid(which='minor', linestyle=':', linewidth='0.4', color='black')
plt.xlabel('Response Time (ms)')
plt.show()
from multiprocessing import Pool
def run_multiple_simulations(simulation_args):
with Pool(12) as p:
results = p.starmap(run_simulation, simulation_args)
return results
# Should overload 10 servers with 0.4ms avg response time at 25k
qps_range = [i*1000 for i in range(1, 21)]
multi = []
num_requests = 100000
# Can't pickle inner functions apparently...
def expon_avg(request, worker):
return random.expovariate(1.0 / AVG_RESPONSE_MS)
print("Multi Queues")
args = []
for qps in qps_range:
args.clear()
multiple_queues_latency = []
for i in range(SERVERS):
args.append(
((1, 1), rr_lb, num_requests/SERVERS, qps/SERVERS, expon_avg)
)
for d in run_multiple_simulations(args):
multiple_queues_latency.extend([i.t_total for i in d])
print('({0:>4.2f} -> {1:>4.2f})'.format(qps, np.mean(multiple_queues_latency)), end=', '),
percentiles = np.percentile(multiple_queues_latency, [10, 50, 90])
multi.append(percentiles)
single = []
args.clear()
for qps in qps_range:
args.append(
((1, SERVERS), rr_lb, num_requests, qps, expon_avg)
)
print("\nSingle Queue")
for idx, results in enumerate(run_multiple_simulations(args)):
d = [i.t_total for i in results]
print('({0:>4.2f} -> {1:>4.2f})'.format(qps_range[idx], np.mean(d)), end=', ')
percentiles = np.percentile(d, [25, 50, 75])
single.append(percentiles)
import matplotlib.gridspec as gridspec
fig = plt.figure(figsize=(14, 5))
gs = gridspec.GridSpec(1, 2, hspace=0.1, wspace=0.1)
plt.suptitle("Response Time Distribution, {0}ms avg response time with {1} servers".format(
AVG_RESPONSE_MS, SERVERS), fontsize=14
)
ax1 = plt.subplot(gs[0, 0])
ax1.plot(qps_range, [m[1] for m in multi], '.b-', label='Multi-Queue median')
ax1.fill_between(qps_range, [m[0] for m in multi], [m[2] for m in multi], alpha=0.4,
label='Multi-Queue IQR', edgecolor='black')
ax1.set_title('Multi-Queue Performance')
ax1.minorticks_on()
ax1.grid(which='major', linestyle=':', linewidth='0.4', color='black')
ax1.grid(which='minor', linestyle=':', linewidth='0.4', color='black')
ax1.set_xlabel('QPS (req / s)')
ax1.set_ylabel('Response Time (ms)')
ax1.legend(loc='upper left')
ax2 = plt.subplot(gs[0, 1], sharey=ax1)
ax2.plot(qps_range, [m[1] for m in single], '.g-', label='Single-Queue median')
ax2.fill_between(qps_range, [m[0] for m in single], [m[2] for m in single], alpha=0.4,
label='Single-Queue IQR', color='lightgreen', edgecolor='black')
ax2.set_title('Single-Queue Performance')
ax2.minorticks_on()
ax2.grid(which='major', linestyle=':', linewidth='0.4', color='black')
ax2.grid(which='minor', linestyle=':', linewidth='0.4', color='black')
ax2.set_xlabel('QPS (req / s)')
ax2.legend(loc='upper left')
plt.show()
```
Multiple Queues: Load Balancing
===========================
Now we look at the affects of choosing different load balancing algorithms on the multiple queue approach:
1. Random Load Balancer: This strategy chooses a server at random
2. Join Shortest Queue: This strategy chooses the shortest queue to ensure load balancing
3. Two adjacent: Somewhat of a variant of "choice of two" where you randomly pick two servers
and take the shortest queue between them; modified to only allow neighbors
```
multiple_queues_latency = []
for i in range(SERVERS):
multiple_queues_latency.extend([
i[2] for i in run_simulation((1, 1), rr_lb, NUM_REQUESTS/SERVERS,
request_per_s=QPS/SERVERS, latency_fn=expon(AVG_RESPONSE_MS))
])
random_queue_latency = [
i[2] for i in run_simulation((SERVERS, 1), random_lb, NUM_REQUESTS, QPS, expon(AVG_RESPONSE_MS))
]
join_shorted_queue_latency = [
i[2] for i in run_simulation((SERVERS, 1), shortest_queue_lb, NUM_REQUESTS, QPS, expon(AVG_RESPONSE_MS))
]
two_adjacent_latency = [
i[2] for i in run_simulation((SERVERS, 1), choice_two_adjacent_lb, NUM_REQUESTS, QPS, expon(AVG_RESPONSE_MS))
]
# And now the simulation
all_queueing_options = {
'Multiple Queues': multiple_queues_latency,
'Single Queue': single_queue_latency,
'LB: Join Shortest': join_shorted_queue_latency,
'LB: Best of Two Adj': two_adjacent_latency,
'LB: Random': random_queue_latency
}
print()
print("Simulation results")
print("------------------")
hdr = "{0:20} | {1:>7} | {2:>7} | {3:>7} | {4:>7} | {5:>7} | {6:>7} ".format(
"Strategy", "mean", "var", "p50", "p95", "p99", "p99.9")
print(hdr)
for opt in sorted(all_queueing_options.keys()):
mean = np.mean(all_queueing_options[opt])
var = np.var(all_queueing_options[opt])
percentiles = np.percentile(all_queueing_options[opt], [50, 95, 99, 99.9])
print ("{0:20} | {1:7.2f} | {2:7.2f} | {3:7.2f} | {4:7.2f} | {5:>7.2f} | {6:7.2f} |".format(
opt, mean, var, percentiles[0], percentiles[1], percentiles[2],
percentiles[3]
))
fig1, ax = plt.subplots(figsize=(12,4))
opts = sorted(all_queueing_options.keys())
data = [all_queueing_options[i] for i in opts]
bplot1 = ax.boxplot(data, whis=[1,99],showfliers=True,flierprops=flier, labels=opts,
patch_artist=True, vert=False)
color_bplot(bplot1, 'black', 'lightblue')
plt.title("Response Time Distribution \n[{0} QPS @ {1}ms avg with {2} servers]".format(
QPS, AVG_RESPONSE_MS, SERVERS)
)
plt.minorticks_on()
plt.grid(which='major', linestyle=':', linewidth='0.4', color='black')
plt.grid(which='minor', linestyle=':', linewidth='0.4', color='black')
plt.xlabel('Response Time (ms)')
plt.show()
```
Simulation of M/G/k queues
======================
Now we look at M/G/k queues over multiple different load balancing choices.
We explore:
* Join Shorted Queue (JSK): The request is dispatched to the shortest queue
* M/G/k (MGk): A single queue is maintained and workers take requests as they are free
* Choice of two (choice_two): Two random workers are chosen, and then the request goes to the shorter queue
* Random (random): A random queue is chosen
* Round-robin (roundrobin): The requests are dispatched to one queue after the other
```
lb_algos = {
'choice-of-two': choice_two_lb,
'random': random_lb,
'round-robin': rr_lb,
'shortest-queue': shortest_queue_lb,
'weighted-choice-8': choice_n_weighted(8),
}
SERVERS = 16
QPS = 8000
# Every 1000 requests have 10 that are slow (simulating a GC pause)
latency = service(AVG_RESPONSE_MS, 20, 2, 1000, 10)
lbs = {
k : [i[2] for i in run_simulation((SERVERS, 1), v, NUM_REQUESTS, QPS, latency)]
for (k, v) in lb_algos.items()
}
lbs['MGk'] = [
i[2] for i in run_simulation((1, SERVERS), rr_lb, NUM_REQUESTS, QPS, latency)]
#lbs['join-idle'] = [
# i[2] for i in run_simulation((1, SERVERS), rr_lb, NUM_REQUESTS, QPS,
# lambda request: 0.1 + pareto(AVG_RESPONSE_MS, 2)(request))
#]
types = sorted(lbs.keys())
hdr = "{0:20} | {1:>7} | {2:>7} | {3:>7} | {4:>7} | {5:>7} | {6:>7} ".format(
"Strategy", "mean", "var", "p50", "p95", "p99", "p99.9")
print(hdr)
print("-"*len(hdr))
for lb in types:
mean = np.mean(lbs[lb])
var = np.var(lbs[lb])
percentiles = np.percentile(lbs[lb], [50, 95, 99, 99.9])
print ("{0:20} | {1:7.1f} | {2:7.1f} | {3:7.1f} | {4:7.1f} | {5:>7.1f} | {6:7.1f} |".format(
lb, mean, var, percentiles[0], percentiles[1], percentiles[2],
percentiles[3]
))
fig1, ax = plt.subplots(figsize=(20,10))
diamond = dict(markerfacecolor='r', marker='D')
data = [lbs[i] for i in types]
bplot1 = ax.boxplot(data, whis=[10,90],showfliers=False,flierprops=flier, labels=types,
patch_artist=True, vert=False)
color_bplot(bplot1, 'black', 'lightblue')
plt.title('Response Distribution M/G Process ({0} QPS @ {1}ms avg with {2} servers):'.format(
QPS, AVG_RESPONSE_MS, SERVERS)
)
plt.minorticks_on()
plt.grid(which='major', linestyle=':', linewidth='0.4', color='black')
plt.grid(which='minor', linestyle=':', linewidth='0.4', color='black')
plt.xlabel('Response Time (ms)')
plt.show()
```
| true |
code
| 0.602062 | null | null | null | null |
|
# Machine Learning and Statistics for Physicists
Material for a [UC Irvine](https://uci.edu/) course offered by the [Department of Physics and Astronomy](https://www.physics.uci.edu/).
Content is maintained on [github](github.com/dkirkby/MachineLearningStatistics) and distributed under a [BSD3 license](https://opensource.org/licenses/BSD-3-Clause).
[Table of contents](Contents.ipynb)
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
import pandas as pd
import scipy.stats
```
## Bayesian Statistics
### Types of Probability
We construct a probability space by assigning a numerical probability in the range $[0,1]$ to sets of outcomes (events) in some space.
When outcomes are the result of an uncertain but **repeatable** process, probabilities can always be measured to arbitrary accuracy by simply observing many repetitions of the process and calculating the frequency at which each event occurs. These **frequentist probabilities** have an appealing objective reality to them.
**DISCUSS:** How might you assign a frequentist probability to statements like:
- The electron spin is 1/2.
- The Higgs mass is between 124 and 126 GeV.
- The fraction of dark energy in the universe today is between 68% and 70%.
- The superconductor Hg-1223 has a critical temperature above 130K.
You cannot (if we assume that these are universal constants), since that would require a measurable process whose outcomes had different values for a universal constant.
The inevitable conclusion is that the statements we are most interested in cannot be assigned frequentist probabilities.
However, if we allow probabilities to also measure your subjective "degree of belief" in a statement, then we can use the full machinery of probability theory to discuss more interesting statements. These are called **Bayesian probabiilities**.
Roughly speaking, the choice is between:
- **frequentist statistics:** objective probabilities of uninteresting statements.
- **Bayesian statistics:** subjective probabilities of interesting statements.
---
### Bayesian Joint Probability
Bayesian statistics starts from a joint probability distribution
$$
P(D, \Theta_M, M)
$$
over data features $D$, model parameters $\Theta_M$ and hyperparameters $M$. The subscript on $\Theta_M$ is to remind us that, in general, the set of parameters being used depends on the hyperparameters (e.g., increasing `n_components` adds parameters for the new components). We will sometimes refer to the pair $(\Theta_M, M)$ as the **model**.
This joint probability implies that model parameters and hyperparameters are random variables, which in turn means that they label possible outcomes in our underlying probability space.
For a concrete example, consider the possible outcomes necessary to discuss the statement "*the electron spin is 1/2*", which must be labeled by the following random variables:
- $D$: the measured electron spin for an outcome, $S_z = 0, \pm 1/2, \pm 1, \pm 3/2, \ldots$
- $\Theta_M$: the total electron spin for an outcome, $S = 0, 1/2, 1, 3/2, \ldots$
- $M$: whether the electron is a boson or a fermion for an outcome.
A table of random-variable values for possible outcomes would then look like:
| $M$ | $\Theta_M$ | $D$ |
| ---- |----------- | --- |
| boson | 0 | 0 |
| fermion | 1/2 | -1/2 |
| fermion | 1/2 | +1/2 |
| boson | 1 | -1 |
| boson | 1 | 0 |
| boson | 1 | +1 |
| ... | ... | ... |
Only two of these outcomes occur in our universe, but a Bayesian approach requires us to broaden the sample space from "*all possible outcomes*" to "*all possible outcomes in all possible universes*".
### Likelihood
The **likelihood** ${\cal L}_M(\Theta_M, D)$ is a function of model parameters $\Theta_M$ (given hyperparameters $M$) and data features $D$, and measures the probability (density) of observing the data given the model. For example, a Gaussian mixture model has the likelihood function:
$$
{\cal L}_M\left(\mathbf{\Theta}_M, \vec{x} \right) = \sum_{k=1}^{K}\, \omega_k G(\vec{x} ; \vec{\mu}_k, C_k) \; ,
$$
with parameters
$$
\begin{aligned}
\mathbf{\Theta}_M = \big\{
&\omega_1, \omega_2, \ldots, \omega_K, \\
&\vec{\mu}_1, \vec{\mu}_2, \ldots, \vec{\mu}_K, \\
&C_1, C_2, \ldots, C_K \big\}
\end{aligned}
$$
and hyperparameter $K$. Note that the likelihood must be normalized over the data for any values of the (fixed) parameters and hyperparameters. However, it is not normalized over the parameters or hyperparameters.
The likelihood function plays a central role in both frequentist and Bayesian statistics, but is used and interpreted differently. We will focus on the Bayesian perspective, where $\Theta_M$ and $M$ are considered random variables and the likelihood function is associated with the conditional probability
$$
{\cal L}_M\left(\Theta_M, D \right) = P(D\mid \Theta_M, M)
$$
of observing features $D$ given the model $(\Theta_M, M)$.
### Bayesian Inference
Once we associated the likelihood with a conditional probability, we can apply the earlier rules (2 & 3) of probability calculus to derive the generalized Bayes' rule:
$$
P(\Theta_M\mid D, M) = \frac{P(D\mid \Theta_M, M)\,P(\Theta_M\mid M)}{P(D\mid M)}
$$
Each term above has a name and measures a different probability:
1. **Posterior:** $P(\Theta_M\mid D, M)$ is the probability of the parameter values $\Theta_M$ given the data and the choice of hyperparameters.
2. **Likelihood:** $P(D\mid \Theta_M, M)$ is the probability of the data given the model.
3. **Prior:** $P(\Theta_M\mid M)$ is the probability of the model parameters given the hyperparameters and *marginalized over all possible data*.
4. **Evidence:** $P(D\mid M)$ is the probability of the data given the hyperparameters and *marginalized over all possible parameter values given the hyperparameters*.
In typical inference problems, the posterior (1) is what we really care about and the likelihood (2) is what we know how to calculate. The prior (3) is where we must quantify our subjective "degree of belief" in different possible universes.
What about the evidence (4)? Using the earlier rule (5) of probability calculus, we discover that (4) can be calculated from (2) and (3):
$$
P(D\mid M) = \int d\Theta_M' P(D\mid \Theta_M', M)\, P(\Theta_M'\mid M) \; .
$$
Note that this result is not surprising since the denominator must normalize the ratio to yield a probability (density). When the set of possible parameter values is discrete, $\Theta_M \in \{ \Theta_{M,1}, \Theta_{M,2}, \ldots\}$, the normalization integral reduces to a sum:
$$
P(D\mid M) \rightarrow \sum_k\, P(D\mid \Theta_{M,k}, M)\, P(\Theta_{M,k}\mid M) \; .
$$
The generalized Bayes' rule above assumes fixed values of any hyperparameters (since $M$ is on the RHS of all 4 terms), but a complete inference also requires us to consider different hyperparameter settings. We will defer this (harder) **model selection** problem until later.

**EXERCISE:** Suppose that you meet someone for the first time at your next conference and they are wearing an "England" t-shirt. Estimate the probability that they are English by:
- Defining the data $D$ and model $\Theta_M$ assuming, for simplicity, that there are no hyperparameters.
- Assigning the relevant likelihoods and prior probabilities (terms 2 and 3 above).
- Calculating the resulting LHS of the generalized Baye's rule above.
Solution:
- Define the data $D$ as the observation that the person is wearing an "England" t-shirt.
- Define the model to have a single parameter, the person's nationality $\Theta \in \{ \text{English}, \text{!English}\}$.
- We don't need to specify a full likelihood function over all possible data since we only have a single datum. Instead, it is sufficient to assign the likelihood probabilities:
$$
P(D\mid \text{English}) = 0.4 \quad , \quad P(D\mid \text{!English}) = 0.1
$$
- Assign the prior probabilities for attendees at the conference:
$$
P(\text{English}) = 0.2 \quad , \quad P(\text{!English}) = 0.8
$$
- We can now calculate:
$$
\begin{aligned}
P(\text{English}\mid D) &= \frac{P(D\mid \text{English})\, P(\text{English})}
{P(D\mid \text{English})\, P(\text{English}) + P(D\mid \text{!English})\, P(\text{!English})} \\
&= \frac{0.4\times 0.2}{0.4\times 0.2 + 0.1\times 0.8} \\
&= 0.5 \; .
\end{aligned}
$$
Note that we calculate the evidence $P(D)$ using a sum rather than integral, because $\Theta$ is discrete.
You probably assigned different probabilities, since these are subjective assessments where reasonable people can disagree. However, by allowing some subjectivity we are able to make a precise statement under some (subjective) assumptions.
Note that the likelihood probabilities do not sum to one since the likelihood is normalized over the data, not the model, unlike the prior probabilities which do sum to one.
A simple example like this can be represented graphically in the 2D space of joint probability $P(D, \Theta)$:

---
The generalized Bayes' rule can be viewed as a learning rule that updates our knowledge as new information becomes available:

The implied timeline motivates the *posterior* and *prior* terminology, although there is no requirement that the prior be based on data collected before the "new" data.
Bayesian inference problems can be tricky to get right, even when they sound straightforward, so it is important to clearly spell out what you know or assume, and what you wish to learn:
1. List the possible models, i.e., your hypotheses.
2. Assign a prior probability to each model.
3. Define the likelihood of each possible observation $D$ for each model.
4. Apply Bayes' rule to learn from new data and update your prior.
For problems with a finite number of possible models and observations, the calculations required are simple arithmetic but quickly get cumbersome. A helper function lets you hide the arithmetic and focus on the logic:
```
def learn(prior, likelihood, D):
# Calculate the Bayes' rule numerator for each model.
prob = {M: prior[M] * likelihood(D, M) for M in prior}
# Calculate the Bayes' rule denominator.
norm = sum(prob.values())
# Return the posterior probabilities for each model.
return {M: prob[M] / norm for M in prob}
```
For example, the problem above becomes:
```
prior = {'English': 0.2, '!English': 0.8}
def likelihood(D, M):
if M == 'English':
return 0.4 if D == 't-shirt' else 0.6
else:
return 0.1 if D == 't-shirt' else 0.9
learn(prior, likelihood, D='t-shirt')
```
Note that the (posterior) output from one learning update can be the (prior) input to the next update. For example, how should we update our knowledge if the person wears an "England" t-shirt the next day also?
```
post1 = learn(prior, likelihood, 't-shirt')
post2 = learn(post1, likelihood, 't-shirt')
print(post2)
```
The `mls` package includes a function `Learn` for these calculations that allows multiple updates with one call and displays the learning process as a pandas table:
```
from mls import Learn
Learn(prior, likelihood, 't-shirt', 't-shirt')
```

https://commons.wikimedia.org/wiki/File:Dice_(typical_role_playing_game_dice).jpg
**EXERCISE:** Suppose someone rolls 6, 4, 5 on a dice without telling you whether it has 4, 6, 8, 12, or 20 sides.
- What is your intuition about the true number of sides based on the rolls?
- Identify the models (hypotheses) and data in this problem.
- Define your priors assuming that each model is equally likely.
- Define a likelihood function assuming that each dice is fair.
- Use the `Learn` function to estimate the posterior probability for the number of sides after each roll.
We can be sure the dice is not 4-sided (because of the rolls > 4) and guess that it is unlikely to be 12 or 20 sided (since the largest roll is a 6).
The models in this problem correspond to the number of sides on the dice: 4, 6, 8, 12, 20.
The data in this problem are the dice rolls: 6, 4, 5.
Define the prior assuming that each model is equally likely:
```
prior = {4: 0.2, 6: 0.2, 8: 0.2, 12: 0.2, 20: 0.2}
```
Define the likelihood assuming that each dice is fair:
```
def likelihood(D, M):
if D <= M:
return 1.0 / M
else:
return 0.0
```
Finally, put the pieces together to estimate the posterior probability of each model after each roll:
```
Learn(prior, likelihood, 6, 4, 5)
```
Somewhat surprisingly, this toy problem has a practical application with historical significance!
Imagine a factory that has made $N$ items, each with a serial number 1 - $N$. If you randomly select items and read their serial numbers, the problem of estimating $N$ is analogous to our dice problem, but with many more models to consider. This approach was successfully used in World-War II by the Allied Forces to [estimate the production rate of German tanks](https://en.wikipedia.org/wiki/German_tank_problem) at a time when most academic statisticians rejected Bayesian methods.
For more historical perspective on the development of Bayesian methods (and many obstacles along the way), read the entertaining book [The Theory That Would Not Die](https://www.amazon.com/Theory-That-Would-Not-Die/dp/0300188226).
---
The discrete examples above can be solved exactly, but this is not true in general. The challenge is to calculate the evidence, $P(D\mid M$), in the Bayes' rule denominator, as the marginalization integral:
$$
P(D\mid M) = \int d\Theta_M' P(D\mid \Theta_M', M)\, P(\Theta_M'\mid M) \; .
$$
With careful choices of the prior and likelihood function, this integral can be performed analytically. However, for most practical work, an approximate numerical approach is required. Popular methods include **Markov-Chain Monte Carlo** and **Variational Inference**, which we will meet soon.
### What Priors Should I Use?
The choice of priors is necessarily subjective and sometimes contentious, but keep the following general guidelines in mind:
- Inferences on data from an informative experiment are not very sensitive to your choice of priors.
- If your (posterior) results are sensitive to your choice of priors you need more (or better) data.
For a visual demonstration of these guidelines, the following function performs exact inference for a common task: you make a number of observations and count how many pass some predefined test, and want to infer the fraction $0\le \theta\le 1$ that pass. This applies to questions like:
- What fraction of galaxies contain a supermassive black hole?
- What fraction of Higgs candidate decays are due to background?
- What fraction of of my nanowires are superconducting?
- What fraction of my plasma shots are unstable?
For our prior, $P(\theta)$, we use the [beta distribution](https://en.wikipedia.org/wiki/Beta_distribution) which is specified by hyperparameters $a$ and $b$:
$$
P(\theta\mid a, b) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\, \theta^{a-1} \left(1 - \theta\right)^{b-1} \; ,
$$
where $\Gamma$ is the [gamma function](https://en.wikipedia.org/wiki/Gamma_function) related to the factorial $\Gamma(n) = (n-1)!$ This function provides the prior (or posterior) corresponding to previous (or updated) measurements of a binomial process with $a + b - 2$ trials with $a - 1$ passing (and therefore $b - 1$ not passing).
```
def binomial_learn(prior_a, prior_b, n_obs, n_pass):
theta = np.linspace(0, 1, 100)
# Calculate and plot the prior on theta.
prior = scipy.stats.beta(prior_a, prior_b)
plt.fill_between(theta, prior.pdf(theta), alpha=0.25)
plt.plot(theta, prior.pdf(theta), label='Prior')
# Calculate and plot the likelihood of the fixed data given any theta.
likelihood = scipy.stats.binom.pmf(n_pass, n_obs, theta)
plt.plot(theta, likelihood, 'k:', label='Likelihood')
# Calculate and plot the posterior on theta given the observed data.
posterior = scipy.stats.beta(prior_a + n_pass, prior_b + n_obs - n_pass)
plt.fill_between(theta, posterior.pdf(theta), alpha=0.25)
plt.plot(theta, posterior.pdf(theta), label='Posterior')
# Plot cosmetics.
plt.legend(bbox_to_anchor=(0., 1.02, 1., .102), loc=3,
ncol=3, mode="expand", borderaxespad=0., fontsize='large')
plt.ylim(0, None)
plt.xlim(theta[0], theta[-1])
plt.xlabel('Pass fraction $\\theta$')
```
**EXERCISE:**
**Q1:** Think of a question in your research area where this inference problem applies.
**Q2:** Infer $\theta$ from 2 observations with 1 passing, using hyperparameters $(a=1,b=1)$.
- Explain why the posterior is reasonable given the observed data.
- What values of $\theta$ are absolutely ruled out by this data? Does this make sense?
- How are the three quantities plotted normalized?
**Q3:** Infer $\theta$ from the same 2 observations with 1 passing, using instead $(a=5,b=10)$.
- Is the posterior still reasonable given the observed data? Explain your reasoning.
- How might you choose between these two subjective priors?
**Q4:** Use each of the priors above with different data: 100 trials with 60 passing.
- How does the relative importance of the prior and likelihood change with better data?
- Why are the likelihood values so much smaller now?
```
binomial_learn(1, 1, 2, 1)
```
- The posterior peaks at the mean observed pass rate, 1/2, which is reasonable. It is very broad because we have only made two observations.
- Values of 0 and 1 are absolutely ruled out, which makes sense since we have already observed 1 pass and 1 no pass.
- The prior and posterior are probability densities normalized over $\theta$, so their area in the plot is 1. The likelihood is normalized over all possible data, so does not have area of 1 in this plot.
```
binomial_learn(5, 10, 2, 1)
```
- The posterior now peaks away from the mean observed pass rate of 1/2. This is reasonable if we believe our prior information since, with relatively uninformative data, Bayes' rule tells us that it should dominate our knowledge of $\theta$. On the other hand, if we cannot justify why this prior is more believable than the earlier flat prior, then we must conclude that the value of $\theta$ is unknown and that our data has not helped.
- If a previous experiment with $13=(a-1)+(b-1)$ observations found $4=a-1$ passing, then our new prior would be very reasonable. However, if this process has never been observed and we have no theoretical prejudice, then the original flat prior would be reasonable.
```
binomial_learn(1, 1, 100, 60)
binomial_learn(5, 10, 100, 60)
```
- With more data, the prior has much less influence. This is always the regime you want to be in.
- The likelihood values are larger because there are many more possible outcomes (pass or not) with more observations, so any one outcome becomes relatively less likely. (Recall that the likelihood is normalized over data outcomes, not $\theta$).
---
You are hopefully convinced now that your choice of priors is mostly a non issue, since inference with good data is relatively insensitive to your choice. However, you still need to make a choice, so here are some practical guidelines:
- A "missing" prior, $P(\Theta\mid M) = 1$, is still a prior but not necessarily a "natural" choice or a "safe default". It is often not even normalizable, although you can finesse this problem with good enough data.
- The prior on a parameter you care about (does it appear in your paper's abstract?) should usually summarize previous measurements, assuming that you trust them but you are doing a better experiment. In this case, your likelihood measures the information provided by your data alone, and the posterior provides the new "world average".
- The prior on a **nuisance parameter** (which you need for technical reasons but are not interesting in measuring) should be set conservatively (restrict as little as possible, to minimize the influence on the posterior) and in different ways (compare posteriors with different priors to estimate systematic uncertainty).
- If you really have no information on which to base a prior, learn about [uninformative priors](https://en.wikipedia.org/wiki/Prior_probability#Uninformative_priors), but don't be fooled by their apparent objectivity.
- If being able to calculate your evidence integral analytically is especially important, look into [conjugate priors](https://en.wikipedia.org/wiki/Conjugate_prior), but don't be surprised if this forces you to adopt an oversimplified model. The binomial example above is one of the rare cases where this works out.
- Always state your priors (in your code, papers, talks, etc), even when they don't matter much.
### Graphical Models
We started above with the Bayesian joint probability:
$$
P(D, \Theta_M, M)
$$
When the individual data features, parameters and hyperparameters are all written out, this often ends up being a very high-dimensional function.
In the most general case, the joint probability requires a huge volume of data to estimate (recall our earlier discussion of [dimensionality reduction](Dimensionality.ipynb)). However, many problems can be (approximately) described by a joint probability that is simplified by assuming that some random variables are mutually independent.
Graphical models are a convenient visualization of the assumed direct dependencies between random variables. For example, suppose we have two parameters $(\alpha, \beta)$ and no hyperparameters, then the joint probability $P(D, \alpha, \beta)$ can be expanded into a product of conditionals different ways using the rules of probability calculus, e.g.
$$
P(D, \alpha, \beta) = P(D,\beta\mid \alpha)\, P(\alpha) = P(D\mid \alpha,\beta)\, P(\beta\mid \alpha)\, P(\alpha) \; .
$$
or, equally well as,
$$
P(D, \alpha, \beta) = P(D,\alpha\mid \beta)\, P(\beta) = P(D\mid \alpha,\beta)\, P(\alpha\mid \beta)\, P(\beta) \; ,
$$
The corresponding diagrams are:


The way to read these diagrams is that a node labeled with $X$ represents a (multiplicative) factor $P(X\mid\ldots)$ in the joint probability, where $\ldots$ lists other nodes whose arrows feed into this node (in any order, thanks to probability calculus Rule-1). A shaded node indicates a random variable that is directly observed (i.e., data) while non-shaded nodes represent (unobserved) latent random variables.
These diagrams both describe a fully general joint probability with two parameters. The rules for building a fully general joint probability with any number of parameters are:
- Pick an (arbitrary) ordering of the parameters.
- The first parameter's node has arrows pointing to all other nodes (including the data).
- The n-th parameter's node has arrows pointing to all later parameter nodes and the data.
With $n$ parameters, there are then $n!$ possible diagrams and the number of potential dependencies grows rapidly with $n$.
To mitigate this factorial growth, we seek pairs of random variables that should not depend on each other. For example, in the two parameter case:


Notice how each diagram tells a different story. For example, the first diagram tells us that the data can be predicted knowing only $\beta$, but that our prior knowledge of $\beta$ depends on $\alpha$. In effect, then, simplifying a joint probability involves drawing a diagram that tells a suitable story for your data and models.
**EXERCISE:** Consider observing someone throwing a ball and measuring how far away it lands to infer the strength of gravity:
- Our data is the measured range $r$.
- Our parameters are the ball's initial speed $v$ and angle $\phi$, and the strength of gravity $g$.
- Our hyperparameters are the ball's diameter $d$ and the wind speed $w$.
Draw one example of a fully general diagram of this inference's joint probability $P(r, v, \phi, g, d, w)$.
Suppose the thrower always throws as hard as they can, then adjusts the angle according to the wind. Draw a diagram to represent the direct dependencies in this simpler joint probability.
Write down the posterior we are interested in for this inference problem.


The posterior we are most likely interested in for this inference is
$$
P(g\mid r) \; ,
$$
but a more explicit posterior would be:
$$
P(g\mid r, v, \phi, d, w) \; .
$$
The difference between is these is that we marginalized over the "nuisance" parameters $v, \phi, d, w$ in the first case.
---
The arrows in these diagrams define the direction of conditional dependencies. They often mirror a causal influence in the underlying physical system, but this is not necessary. Probabilistic diagrams with directed edges are known as **Bayesian networks** or **belief networks**.
It is also possible to draw diagrams where nodes are connected symmetrically, without a specified direction. These are known as **Markov random fields** or **Markov networks** and appropriate when dependencies flow in both directions or in an unknown direction. You can read more about these [here](https://en.wikipedia.org/wiki/Markov_random_field).
| true |
code
| 0.7526 | null | null | null | null |
|
# Custom widgets in a notebook
The notebook explore a couple of ways to interact with the user and modifies the output based on these interactions. This is inspired from the examples from [ipwidgets](http://ipywidgets.readthedocs.io/).
```
from jyquickhelper import add_notebook_menu
add_notebook_menu()
```
## List of widgets
[Widget List](https://ipywidgets.readthedocs.io/en/latest/examples/Widget%20List.html)
```
import ipywidgets
import datetime
obj = ipywidgets.DatePicker(
description='Pick a Date',
disabled=False,
value=datetime.datetime.now(),
)
obj
obj.value
```
## Events
```
from IPython.display import display
button = ipywidgets.Button(description="Click Me!")
display(button)
def on_button_clicked(b):
print("Button clicked.")
button.on_click(on_button_clicked)
int_range = ipywidgets.IntSlider()
display(int_range)
def on_value_change(change):
print(change['new'])
int_range.observe(on_value_change, names='value')
```
## matplotlib
```
%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx
def random_lobster(n, m, k, p):
return nx.random_lobster(n, p, p / m)
def powerlaw_cluster(n, m, k, p):
return nx.powerlaw_cluster_graph(n, m, p)
def erdos_renyi(n, m, k, p):
return nx.erdos_renyi_graph(n, p)
def newman_watts_strogatz(n, m, k, p):
return nx.newman_watts_strogatz_graph(n, k, p)
def plot_random_graph(n, m, k, p, generator):
g = generator(n, m, k, p)
nx.draw(g)
plt.show()
ipywidgets.interact(plot_random_graph, n=(2,30), m=(1,10), k=(1,10), p=(0.0, 1.0, 0.001),
generator={
'lobster': random_lobster,
'power law': powerlaw_cluster,
'Newman-Watts-Strogatz': newman_watts_strogatz,
'Erdős-Rényi': erdos_renyi,
});
```
## Custom widget - text
[Building a Custom Widget - Hello World](http://ipywidgets.readthedocs.io/en/latest/examples/Widget%20Custom.html).
```
import ipywidgets as widgets
from traitlets import Unicode, validate
class HelloWidget(widgets.DOMWidget):
_view_name = Unicode('HelloView').tag(sync=True)
_view_module = Unicode('hello').tag(sync=True)
_view_module_version = Unicode('0.1.0').tag(sync=True)
value = Unicode('Hello World! - ').tag(sync=True)
%%javascript
require.undef('hello');
define('hello', ["@jupyter-widgets/base"], function(widgets) {
var HelloView = widgets.DOMWidgetView.extend({
render: function() {
this.value_changed();
this.model.on('change:value', this.value_changed, this);
},
value_changed: function() {
this.el.textContent = this.model.get('value');
},
});
return {
HelloView : HelloView
};
});
w = HelloWidget()
w
w.value = 'changed the value'
```
## Custom widget - html - svg - events
See [Low Level Widget Tutorial](http://ipywidgets.readthedocs.io/en/latest/examples/Widget%20Low%20Level.html), [CircleView](https://github.com/paul-shannon/notebooks/blob/master/study/CircleView.ipynb). The following example links a custom widget and a sliding bar which defines the radius of circle to draw. See [Linking two similar widgets](http://ipywidgets.readthedocs.io/en/latest/examples/Widget%20Basics.html#Linking-two-similar-widgets). The information (circles, radius) is declared in a python class *CircleWidget* and available in the javascript code in two places: the widget (``this.model``) and the view itself (used to connect event to it). Finally, a link is added between two values: value from the first widget (sliding bar) and radius from the second widget (*CircleWidget*).
```
%%javascript
require.config({
paths: {
d3: '//cdnjs.cloudflare.com/ajax/libs/d3/3.4.8/d3.min'
},
});
import ipywidgets
from traitlets import Int, Unicode, Tuple, CInt, Dict, validate
class CircleWidget(ipywidgets.DOMWidget):
_view_name = Unicode('CircleView').tag(sync=True)
_view_module = Unicode('circle').tag(sync=True)
radius = Int(100).tag(sync=True)
circles = Tuple().tag(sync=True)
width = Int().tag(sync=True)
height = Int().tag(sync=True)
radius = Int().tag(sync=True)
def __init__(self, **kwargs):
super(ipywidgets.DOMWidget, self).__init__(**kwargs)
self.width = kwargs.get('width', 500)
self.height = kwargs.get('height', 100)
self.radius = 1
def drawCircle(self, x, y, fillColor="white", borderColor="black"):
newCircle = {"x": x, "y": y, "radius": self.radius * 10, "fillColor": fillColor, "borderColor": borderColor}
self.circles = self.circles + (newCircle,)
%%javascript
"use strict";
require.undef('circle');
define('circle', ["@jupyter-widgets/base", "d3"], function(widgets, d3) {
var CircleView = widgets.DOMWidgetView.extend({
initialize: function() {
console.log("---- initialize, this:");
console.log(this);
this.circles = [];
this.radius = 1;
},
createDiv: function(){
var width = this.model.get('width');
var height = this.model.get('height');
var divstyle = $("<div id='d3DemoDiv' style='border:1px solid red; height: " +
height + "px; width: " + width + "px'>");
return(divstyle);
},
createCanvas: function(){
var width = this.model.get('width');
var height = this.model.get('height');
var radius = this.model.get('radius');
console.log("--SIZE--", width, 'x', height, " radius", radius);
var svg = d3.select("#d3DemoDiv")
.append("svg")
.attr("id", "svg").attr("width", width).attr("height", height);
this.svg = svg;
var circleView = this;
svg.on('click', function() {
var coords = d3.mouse(this);
//debugger;
var radius = circleView.radius;
console.log('--MOUSE--', coords, " radius:", radius);
var newCircle = {x: coords[0], y: coords[1], radius: 10 * radius,
borderColor: "black", fillColor: "beige"};
circleView.circles.push(newCircle);
circleView.drawCircle(newCircle);
//debugger;
circleView.model.set("circles", JSON.stringify(circleView.circles));
circleView.touch();
});
},
drawCircle: function(obj){
this.svg.append("circle")
.style("stroke", "gray")
.style("fill", "white")
.attr("r", obj.radius)
.attr("cx", obj.x)
.attr("cy", obj.y)
.on("mouseover", function(){d3.select(this).style("fill", "aliceblue");})
.on("mouseout", function(){d3.select(this).style("fill", "white");});
},
render: function() {
this.$el.append(this.createDiv());
this.listenTo(this.model, 'change:circles', this._circles_changed, this);
this.listenTo(this.model, 'change:radius', this._radius_changed, this);
var circleView = this;
function myFunc(){
circleView.createCanvas()
};
setTimeout(myFunc, 500);
},
_circles_changed: function() {
var circles = this.model.get("circles");
var newCircle = circles[circles.length-1];
console.log('--DRAW--', this.circles);
this.circles.push(newCircle);
console.log('--LENGTH--', circles.length, " == ", circles.length);
this.drawCircle(newCircle);
},
_radius_changed: function() {
console.log('--RADIUS--', this.radius, this.model.get('radius'));
this.radius = this.model.get('radius');
}
});
return {
CircleView : CircleView
};
});
cw = CircleWidget(width=500, height=100)
scale = ipywidgets.IntSlider(1, 0, 10)
box = widgets.VBox([scale, cw])
mylink = ipywidgets.jslink((cw, 'radius'), (scale, 'value'))
box
cw.drawCircle(x=30, y=30)
scale.value = 2
cw.drawCircle(x=60, y=30)
```
| true |
code
| 0.318886 | null | null | null | null |
|
# Huggingface SageMaker-SDK - BERT Japanese NER example
1. [Introduction](#Introduction)
2. [Development Environment and Permissions](#Development-Environment-and-Permissions)
1. [Installation](#Installation)
2. [Permissions](#Permissions)
3. [Uploading data to sagemaker_session_bucket](#Uploading-data-to-sagemaker_session_bucket)
3. [Fine-tuning & starting Sagemaker Training Job](#Fine-tuning-\&-starting-Sagemaker-Training-Job)
1. [Creating an Estimator and start a training job](#Creating-an-Estimator-and-start-a-training-job)
2. [Estimator Parameters](#Estimator-Parameters)
3. [Download fine-tuned model from s3](#Download-fine-tuned-model-from-s3)
4. [Named Entity Recognition on Local](#Named-Entity-Recognition-on-Local)
4. [_Coming soon_:Push model to the Hugging Face hub](#Push-model-to-the-Hugging-Face-hub)
# Introduction
このnotebookは書籍:[BERTによる自然言語処理入門 Transformersを使った実践プログラミング](https://www.ohmsha.co.jp/book/9784274227264/)の[固有表現抽出(Named Entity Recognition)](https://github.com/stockmarkteam/bert-book/blob/master/Chapter8.ipynb)をAmazon SageMakerで動作する様に変更を加えたものです。
データは[ストックマーク株式会社](https://stockmark.co.jp/)さんで作成された[Wikipediaを用いた日本語の固有表現抽出データセット](https://github.com/stockmarkteam/ner-wikipedia-dataset)を使用します。
このデモでは、AmazonSageMakerのHuggingFace Estimatorを使用してSageMakerのトレーニングジョブを実行します。
_**NOTE: このデモは、SagemakerNotebookインスタンスで動作検証しています**_
# Development Environment and Permissions
## Installation
このNotebookはSageMakerの`conda_pytorch_p36`カーネルを利用しています。
日本語処理のため、`transformers`ではなく`transformers[ja]`をインスールします。
**_Note: このnotebook上で推論テストを行う場合、(バージョンが古い場合は)pytorchのバージョンアップが必要になります。_**
```
# localで推論のテストを行う場合(CPU)
!pip install torch==1.7.1
# localで推論のテストを行う場合(GPU)
#!pip install torch==1.7.1+cu110 torchvision==0.8.2+cu110 torchaudio==0.7.2 -f https://download.pytorch.org/whl/torch_stable.html
!pip install "sagemaker>=2.31.0" "transformers[ja]==4.6.1" "datasets[s3]==1.6.2" --upgrade
```
## Permissions
ローカル環境でSagemakerを使用する場合はSagemakerに必要な権限を持つIAMロールにアクセスする必要があります。[こちら](https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-roles.html)を参照してください
```
import sagemaker
sess = sagemaker.Session()
# sagemaker session bucket -> used for uploading data, models and logs
# sagemaker will automatically create this bucket if it not exists
sagemaker_session_bucket=None
if sagemaker_session_bucket is None and sess is not None:
# set to default bucket if a bucket name is not given
sagemaker_session_bucket = sess.default_bucket()
role = sagemaker.get_execution_role()
sess = sagemaker.Session(default_bucket=sagemaker_session_bucket)
print(f"sagemaker role arn: {role}")
print(f"sagemaker bucket: {sess.default_bucket()}")
print(f"sagemaker session region: {sess.boto_region_name}")
```
# データの準備
[ストックマーク株式会社](https://stockmark.co.jp/)さんで作成された[Wikipediaを用いた日本語の固有表現抽出データセット](https://github.com/stockmarkteam/ner-wikipedia-dataset)をダウンロードします。
```
!git clone --branch v2.0 https://github.com/stockmarkteam/ner-wikipedia-dataset
import json
# データのロード
dataset = json.load(open('ner-wikipedia-dataset/ner.json','r'))
```
データの形式は以下のようになっています
```
dataset[0:5]
# https://github.com/stockmarkteam/bert-book/blob/master/Chapter8.ipynb
import unicodedata
# 固有表現のタイプとIDを対応付る辞書
type_id_dict = {
"人名": 1,
"法人名": 2,
"政治的組織名": 3,
"その他の組織名": 4,
"地名": 5,
"施設名": 6,
"製品名": 7,
"イベント名": 8
}
# カテゴリーをラベルに変更、文字列の正規化する。
for sample in dataset:
sample['text'] = unicodedata.normalize('NFKC', sample['text'])
for e in sample["entities"]:
e['type_id'] = type_id_dict[e['type']]
del e['type']
dataset[0:5]
import random
# データセットの分割
random.seed(42)
random.shuffle(dataset)
n = len(dataset)
n_train = int(n*0.6)
n_val = int(n*0.2)
dataset_train = dataset[:n_train]
dataset_val = dataset[n_train:n_train+n_val]
dataset_test = dataset[n_train+n_val:]
# https://github.com/stockmarkteam/bert-book/blob/master/Chapter8.ipynb
def create_dataset(tokenizer, dataset, max_length):
"""
データセットをデータローダに入力できる形に整形。
"""
input_ids = []
token_type_ids = []
attention_mask = []
labels= []
for sample in dataset:
text = sample['text']
entities = sample['entities']
encoding = tokenizer.encode_plus_tagged(
text, entities, max_length=max_length
)
input_ids.append(encoding['input_ids'])
token_type_ids.append(encoding['token_type_ids'])
attention_mask.append(encoding['attention_mask'])
labels.append(encoding['labels'])
d = {
"input_ids": input_ids,
"token_type_ids": token_type_ids,
"attention_mask": attention_mask,
"labels": labels
}
return d
# https://github.com/stockmarkteam/bert-book/blob/master/Chapter8.ipynb
from transformers import BertJapaneseTokenizer
class NER_tokenizer_BIO(BertJapaneseTokenizer):
# 初期化時に固有表現のカテゴリーの数`num_entity_type`を
# 受け入れるようにする。
def __init__(self, *args, **kwargs):
self.num_entity_type = kwargs.pop('num_entity_type')
super().__init__(*args, **kwargs)
def encode_plus_tagged(self, text, entities, max_length):
"""
文章とそれに含まれる固有表現が与えられた時に、
符号化とラベル列の作成を行う。
"""
# 固有表現の前後でtextを分割し、それぞれのラベルをつけておく。
splitted = [] # 分割後の文字列を追加していく
position = 0
for entity in entities:
start = entity['span'][0]
end = entity['span'][1]
label = entity['type_id']
splitted.append({'text':text[position:start], 'label':0})
splitted.append({'text':text[start:end], 'label':label})
position = end
splitted.append({'text': text[position:], 'label':0})
splitted = [ s for s in splitted if s['text'] ]
# 分割されたそれぞれの文章をトークン化し、ラベルをつける。
tokens = [] # トークンを追加していく
labels = [] # ラベルを追加していく
for s in splitted:
tokens_splitted = tokenizer.tokenize(s['text'])
label = s['label']
if label > 0: # 固有表現
# まずトークン全てにI-タグを付与
labels_splitted = \
[ label + self.num_entity_type ] * len(tokens_splitted)
# 先頭のトークンをB-タグにする
labels_splitted[0] = label
else: # それ以外
labels_splitted = [0] * len(tokens_splitted)
tokens.extend(tokens_splitted)
labels.extend(labels_splitted)
# 符号化を行いBERTに入力できる形式にする。
input_ids = tokenizer.convert_tokens_to_ids(tokens)
encoding = tokenizer.prepare_for_model(
input_ids,
max_length=max_length,
padding='max_length',
truncation=True
)
# ラベルに特殊トークンを追加
labels = [0] + labels[:max_length-2] + [0]
labels = labels + [0]*( max_length - len(labels) )
encoding['labels'] = labels
return encoding
def encode_plus_untagged(
self, text, max_length=None, return_tensors=None
):
"""
文章をトークン化し、それぞれのトークンの文章中の位置も特定しておく。
IO法のトークナイザのencode_plus_untaggedと同じ
"""
# 文章のトークン化を行い、
# それぞれのトークンと文章中の文字列を対応づける。
tokens = [] # トークンを追加していく。
tokens_original = [] # トークンに対応する文章中の文字列を追加していく。
words = self.word_tokenizer.tokenize(text) # MeCabで単語に分割
for word in words:
# 単語をサブワードに分割
tokens_word = self.subword_tokenizer.tokenize(word)
tokens.extend(tokens_word)
if tokens_word[0] == '[UNK]': # 未知語への対応
tokens_original.append(word)
else:
tokens_original.extend([
token.replace('##','') for token in tokens_word
])
# 各トークンの文章中での位置を調べる。(空白の位置を考慮する)
position = 0
spans = [] # トークンの位置を追加していく。
for token in tokens_original:
l = len(token)
while 1:
if token != text[position:position+l]:
position += 1
else:
spans.append([position, position+l])
position += l
break
# 符号化を行いBERTに入力できる形式にする。
input_ids = tokenizer.convert_tokens_to_ids(tokens)
encoding = tokenizer.prepare_for_model(
input_ids,
max_length=max_length,
padding='max_length' if max_length else False,
truncation=True if max_length else False
)
sequence_length = len(encoding['input_ids'])
# 特殊トークン[CLS]に対するダミーのspanを追加。
spans = [[-1, -1]] + spans[:sequence_length-2]
# 特殊トークン[SEP]、[PAD]に対するダミーのspanを追加。
spans = spans + [[-1, -1]] * ( sequence_length - len(spans) )
# 必要に応じてtorch.Tensorにする。
if return_tensors == 'pt':
encoding = { k: torch.tensor([v]) for k, v in encoding.items() }
return encoding, spans
@staticmethod
def Viterbi(scores_bert, num_entity_type, penalty=10000):
"""
Viterbiアルゴリズムで最適解を求める。
"""
m = 2*num_entity_type + 1
penalty_matrix = np.zeros([m, m])
for i in range(m):
for j in range(1+num_entity_type, m):
if not ( (i == j) or (i+num_entity_type == j) ):
penalty_matrix[i,j] = penalty
path = [ [i] for i in range(m) ]
scores_path = scores_bert[0] - penalty_matrix[0,:]
scores_bert = scores_bert[1:]
for scores in scores_bert:
assert len(scores) == 2*num_entity_type + 1
score_matrix = np.array(scores_path).reshape(-1,1) \
+ np.array(scores).reshape(1,-1) \
- penalty_matrix
scores_path = score_matrix.max(axis=0)
argmax = score_matrix.argmax(axis=0)
path_new = []
for i, idx in enumerate(argmax):
path_new.append( path[idx] + [i] )
path = path_new
labels_optimal = path[np.argmax(scores_path)]
return labels_optimal
def convert_bert_output_to_entities(self, text, scores, spans):
"""
文章、分類スコア、各トークンの位置から固有表現を得る。
分類スコアはサイズが(系列長、ラベル数)の2次元配列
"""
assert len(spans) == len(scores)
num_entity_type = self.num_entity_type
# 特殊トークンに対応する部分を取り除く
scores = [score for score, span in zip(scores, spans) if span[0]!=-1]
spans = [span for span in spans if span[0]!=-1]
# Viterbiアルゴリズムでラベルの予測値を決める。
labels = self.Viterbi(scores, num_entity_type)
# 同じラベルが連続するトークンをまとめて、固有表現を抽出する。
entities = []
for label, group \
in itertools.groupby(enumerate(labels), key=lambda x: x[1]):
group = list(group)
start = spans[group[0][0]][0]
end = spans[group[-1][0]][1]
if label != 0: # 固有表現であれば
if 1 <= label <= num_entity_type:
# ラベルが`B-`ならば、新しいentityを追加
entity = {
"name": text[start:end],
"span": [start, end],
"type_id": label
}
entities.append(entity)
else:
# ラベルが`I-`ならば、直近のentityを更新
entity['span'][1] = end
entity['name'] = text[entity['span'][0]:entity['span'][1]]
return entities
tokenizer_name = 'cl-tohoku/bert-base-japanese-whole-word-masking'
# トークナイザのロード
# 固有表現のカテゴリーの数`num_entity_type`を入力に入れる必要がある。
tokenizer = NER_tokenizer_BIO.from_pretrained(tokenizer_name, num_entity_type=8)
# データセットの作成
max_length = 128
dataset_train = create_dataset(
tokenizer,
dataset_train,
max_length
)
dataset_val = create_dataset(
tokenizer,
dataset_val,
max_length
)
import datasets
dataset_train = datasets.Dataset.from_dict(dataset_train)
dataset_val = datasets.Dataset.from_dict(dataset_val)
dataset_train
dataset_val
# set format for pytorch
dataset_train.set_format('torch', columns=['input_ids', 'attention_mask', 'token_type_ids', 'labels'])
dataset_val.set_format('torch', columns=['input_ids', 'attention_mask', 'token_type_ids', 'labels'])
dataset_train[0]
```
## Uploading data to `sagemaker_session_bucket`
S3へデータをアップロードします。
```
import botocore
from datasets.filesystems import S3FileSystem
s3_prefix = 'samples/datasets/ner-wikipedia-dataset-bio'
s3 = S3FileSystem()
# save train_dataset to s3
training_input_path = f's3://{sess.default_bucket()}/{s3_prefix}/train'
dataset_train.save_to_disk(training_input_path, fs=s3)
# save test_dataset to s3
test_input_path = f's3://{sess.default_bucket()}/{s3_prefix}/test'
dataset_val.save_to_disk(test_input_path, fs=s3)
# 以下のpathにdatasetがuploadされました
print(training_input_path)
print(test_input_path)
```
# Fine-tuning & starting Sagemaker Training Job
`HuggingFace`のトレーニングジョブを作成するためには`HuggingFace` Estimatorが必要になります。
Estimatorは、エンドツーエンドのAmazonSageMakerトレーニングおよびデプロイタスクを処理します。 Estimatorで、どのFine-tuningスクリプトを`entry_point`として使用するか、どの`instance_type`を使用するか、どの`hyperparameters`を渡すかなどを定義します。
```python
huggingface_estimator = HuggingFace(
entry_point='train.py',
source_dir='./scripts',
base_job_name='huggingface-sdk-extension',
instance_type='ml.p3.2xlarge',
instance_count=1,
transformers_version='4.4',
pytorch_version='1.6',
py_version='py36',
role=role,
hyperparameters={
'epochs': 1,
'train_batch_size': 32,
'model_name':'distilbert-base-uncased'
}
)
```
SageMakerトレーニングジョブを作成すると、SageMakerは`huggingface`コンテナを実行するために必要なec2インスタンスの起動と管理を行います。
Fine-tuningスクリプト`train.py`をアップロードし、`sagemaker_session_bucket`からコンテナ内の`/opt/ml/input/data`にデータをダウンロードして、トレーニングジョブを実行します。
```python
/opt/conda/bin/python train.py --epochs 1 --model_name distilbert-base-uncased --train_batch_size 32
```
`HuggingFace estimator`で定義した`hyperparameters`は、名前付き引数として渡されます。
またSagemakerは、次のようなさまざまな環境変数を通じて、トレーニング環境に関する有用なプロパティを提供しています。
* `SM_MODEL_DIR`:トレーニングジョブがモデルアーティファクトを書き込むパスを表す文字列。トレーニング後、このディレクトリのアーティファクトはモデルホスティングのためにS3にアップロードされます。
* `SM_NUM_GPUS`:ホストで使用可能なGPUの数を表す整数。
* `SM_CHANNEL_XXXX`:指定されたチャネルの入力データを含むディレクトリへのパスを表す文字列。たとえば、HuggingFace estimatorのfit呼び出しで`train`と`test`という名前の2つの入力チャネルを指定すると、環境変数`SM_CHANNEL_TRAIN`と`SM_CHANNEL_TEST`が設定されます。
このトレーニングジョブをローカル環境で実行するには、`instance_type='local'`、GPUの場合は`instance_type='local_gpu'`で定義できます。
**_Note:これはSageMaker Studio内では機能しません_**
```
# トレーニングジョブで実行されるコード
!pygmentize ./scripts/train.py
from sagemaker.huggingface import HuggingFace
num_entity_type = 8
num_labels = 2*num_entity_type+1
# hyperparameters, which are passed into the training job
hyperparameters={
'epochs': 5,
'train_batch_size': 32,
'eval_batch_size': 256,
'learning_rate' : 1e-5,
'model_name':'cl-tohoku/bert-base-japanese-whole-word-masking',
'output_dir':'/opt/ml/checkpoints',
'num_labels': num_labels,
}
# s3 uri where our checkpoints will be uploaded during training
job_name = "bert-ner-bio"
#checkpoint_s3_uri = f's3://{sess.default_bucket()}/{job_name}/checkpoints'
```
# Creating an Estimator and start a training job
```
huggingface_estimator = HuggingFace(
entry_point='train.py',
source_dir='./scripts',
instance_type='ml.p3.2xlarge',
instance_count=1,
base_job_name=job_name,
#checkpoint_s3_uri=checkpoint_s3_uri,
#use_spot_instances=True,
#max_wait=7200, # This should be equal to or greater than max_run in seconds'
#max_run=3600, # expected max run in seconds
role=role,
transformers_version='4.6',
pytorch_version='1.7',
py_version='py36',
hyperparameters=hyperparameters,
)
# starting the train job with our uploaded datasets as input
huggingface_estimator.fit({'train': training_input_path, 'test': test_input_path})
# ml.p3.2xlarge, 5 epochでの実行時間の目安
#Training seconds: 558
#Billable seconds: 558
```
# Estimator Parameters
```
# container image used for training job
print(f"container image used for training job: \n{huggingface_estimator.image_uri}\n")
# s3 uri where the trained model is located
print(f"s3 uri where the trained model is located: \n{huggingface_estimator.model_data}\n")
# latest training job name for this estimator
print(f"latest training job name for this estimator: \n{huggingface_estimator.latest_training_job.name}\n")
# access the logs of the training job
huggingface_estimator.sagemaker_session.logs_for_job(huggingface_estimator.latest_training_job.name)
```
# Download-fine-tuned-model-from-s3
```
import os
OUTPUT_DIR = './output/'
if not os.path.exists(OUTPUT_DIR):
os.makedirs(OUTPUT_DIR)
from sagemaker.s3 import S3Downloader
# 学習したモデルのダウンロード
S3Downloader.download(
s3_uri=huggingface_estimator.model_data, # s3 uri where the trained model is located
local_path='.', # local path where *.targ.gz is saved
sagemaker_session=sess # sagemaker session used for training the model
)
# OUTPUT_DIRに解凍します
!tar -zxvf model.tar.gz -C output
```
## Named Entity Recognition on Local
```
from transformers import AutoModelForTokenClassification
tokenizer_name = 'cl-tohoku/bert-base-japanese-whole-word-masking'
tokenizer = NER_tokenizer_BIO.from_pretrained(tokenizer_name, num_entity_type=8)
model = AutoModelForTokenClassification.from_pretrained('./output')
# model = model.cuda() # GPUで推論する場合
# https://github.com/stockmarkteam/bert-book/blob/master/Chapter8.ipynb
import itertools
import numpy as np
from tqdm import tqdm
import torch
original_text=[]
entities_list = [] # 正解の固有表現を追加していく
entities_predicted_list = [] # 抽出された固有表現を追加していく
for sample in tqdm(dataset_test):
text = sample['text']
original_text.append(text)
encoding, spans = tokenizer.encode_plus_untagged(
text, return_tensors='pt'
)
#encoding = { k: v.cuda() for k, v in encoding.items() } # GPUで推論する場合
with torch.no_grad():
output = model(**encoding)
scores = output.logits
scores = scores[0].cpu().numpy().tolist()
# 分類スコアを固有表現に変換する
entities_predicted = tokenizer.convert_bert_output_to_entities(
text, scores, spans
)
entities_list.append(sample['entities'])
entities_predicted_list.append( entities_predicted )
print("テキスト: ", original_text[0])
print("正解: ", entities_list[0])
print("抽出: ", entities_predicted_list[0])
```
# Evaluate NER model
```
# https://github.com/stockmarkteam/bert-book/blob/master/Chapter8.ipynb
def evaluate_model(entities_list, entities_predicted_list, type_id=None):
"""
正解と予測を比較し、モデルの固有表現抽出の性能を評価する。
type_idがNoneのときは、全ての固有表現のタイプに対して評価する。
type_idが整数を指定すると、その固有表現のタイプのIDに対して評価を行う。
"""
num_entities = 0 # 固有表現(正解)の個数
num_predictions = 0 # BERTにより予測された固有表現の個数
num_correct = 0 # BERTにより予測のうち正解であった固有表現の数
# それぞれの文章で予測と正解を比較。
# 予測は文章中の位置とタイプIDが一致すれば正解とみなす。
for entities, entities_predicted in zip(entities_list, entities_predicted_list):
if type_id:
entities = [ e for e in entities if e['type_id'] == type_id ]
entities_predicted = [
e for e in entities_predicted if e['type_id'] == type_id
]
get_span_type = lambda e: (e['span'][0], e['span'][1], e['type_id'])
set_entities = set(get_span_type(e) for e in entities)
set_entities_predicted = set(get_span_type(e) for e in entities_predicted)
num_entities += len(entities)
num_predictions += len(entities_predicted)
num_correct += len( set_entities & set_entities_predicted )
# 指標を計算
precision = num_correct/num_predictions # 適合率
recall = num_correct/num_entities # 再現率
f_value = 2*precision*recall/(precision+recall) # F値
result = {
'num_entities': num_entities,
'num_predictions': num_predictions,
'num_correct': num_correct,
'precision': precision,
'recall': recall,
'f_value': f_value
}
return result
print(evaluate_model(entities_list, entities_predicted_list))
```
| true |
code
| 0.578091 | null | null | null | null |
|
```
# Select the TensorFlow 2.0 runtime
%tensorflow_version 2.x
# Install Weights and Biases (WnB)
#!pip install wandb
# Primary imports
import tensorflow as tf
import numpy as np
import wandb
# Load the FashionMNIST dataset, scale the pixel values
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
X_train = X_train/255.
X_test = X_test/255.
X_train.shape, X_test.shape, y_train.shape, y_test.shape
# Define the labels of the dataset
CLASSES=["T-shirt/top","Trouser","Pullover","Dress","Coat",
"Sandal","Shirt","Sneaker","Bag","Ankle boot"]
# Change the pixel values to float32 and reshape input data
X_train = X_train.astype("float32").reshape(-1, 28, 28, 1)
X_test = X_test.astype("float32").reshape(-1, 28, 28, 1)
y_train.shape, y_test.shape
# TensorFlow imports
from tensorflow.keras.models import *
from tensorflow.keras.layers import *
# Define utility function for building a basic shallow Convnet
def get_training_model():
model = Sequential()
model.add(Conv2D(16, (5, 5), activation="relu",
input_shape=(28, 28,1)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(32, (5, 5), activation="relu"))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(128, activation="relu"))
model.add(Dense(len(CLASSES), activation="softmax"))
return model
# Define loass function and optimizer
loss_func = tf.keras.losses.SparseCategoricalCrossentropy()
#optimizer = tf.keras.optimizers.Adam()
optimizer_adam = tf.keras.optimizers.Adam()
optimizer_adadelta = tf.keras.optimizers.Adadelta()
train_loss_adam = tf.keras.metrics.Mean(name="train_loss")
valid_loss_adam = tf.keras.metrics.Mean(name="test_loss")
# Specify the performance metric
train_acc_adam= tf.keras.metrics.SparseCategoricalAccuracy(name="train_acc")
valid_acc_adam = tf.keras.metrics.SparseCategoricalAccuracy(name="valid_acc")
# Batches of 64
train_ds = tf.data.Dataset.from_tensor_slices((X_train, y_train)).batch(64)
test_ds = tf.data.Dataset.from_tensor_slices((X_test, y_test)).batch(64)
# Train the model
@tf.function
def model_train_adam(features, labels):
# Define the GradientTape context
with tf.GradientTape() as tape:
# Get the probabilities
predictions = model(features)
# Calculate the loss
loss = loss_func(labels, predictions)
# Get the gradients
gradients = tape.gradient(loss, model.trainable_variables)
# Update the weights
#optimizer.apply_gradients(zip(gradients, model.trainable_variables))
optimizer_adam.apply_gradients(zip(gradients, model.trainable_variables))
# Update the loss and accuracy
train_loss_adam(loss)
train_acc_adam(labels, predictions)
# Validating the model
# Validating the model
@tf.function
def model_validate(features, labels):
predictions = model(features)
v_loss = loss_func(labels, predictions)
valid_loss(v_loss)
valid_acc(labels, predictions)
@tf.function
def model_validate_adam(features, labels):
predictions = model(features)
v_loss = loss_func(labels, predictions)
valid_acc_adam(v_loss)
valid_acc_adam(labels, predictions)
@tf.function
def model_validate_adadelta(features, labels):
predictions = model(features)
v_loss = loss_func(labels, predictions)
valid_acc_adadelta(v_loss)
valid_acc_adadelta(labels, predictions)
# A shallow Convnet
model = get_training_model()
# Grab random images from the test and make predictions using
# the model *while it is training* and log them using WnB
def get_sample_predictions():
predictions = []
images = []
random_indices = np.random.choice(X_test.shape[0], 25)
for index in random_indices:
image = X_test[index].reshape(1, 28, 28, 1)
prediction = np.argmax(model(image).numpy(), axis=1)
prediction = CLASSES[int(prediction)]
images.append(image)
predictions.append(prediction)
wandb.log({"predictions": [wandb.Image(image, caption=prediction)
for (image, prediction) in zip(images, predictions)]})
# Train the model for 5 epochs
for epoch in range(10):
# Run the model through train and test sets respectively
for (features, labels) in train_ds:
model_train_adam(features, labels)
model_train_adadelta(features, labels)
for test_features, test_labels in test_ds:
model_validate_adam(test_features, test_labels)
model_validate_adadelta(test_features, test_labels)
# Grab the results
(loss_adadelta, acc_adadelta) = train_loss_adadelta.result(), train_acc_adadelta.result()
(val_loss_adadelta, val_acc_adadelta) = valid_loss_adadelta.result(), valid_acc_adadelta.result()
# Clear the current state of the metrics
train_loss_adadelta.reset_states(), train_acc_adadelta.reset_states()
valid_loss_adadelta.reset_states(), valid_acc_adadelta.reset_states()
# Local logging
template = "Epoch {}, loss: {:.3f}, acc: {:.3f}, val_loss: {:.3f}, val_acc: {:.3f}"
print (template.format(epoch+1,
loss_adadelta,
acc_adadelta,
val_loss_adadelta,
val_acc_adadelta))
# Logging with WnB
wandb.log({"train_loss_adadelta": loss_adadelta.numpy(),
"train_accuracy_adadelta": acc_adadelta.numpy(),
"val_loss_adadelta": val_loss_adadelta.numpy(),
"val_accuracy_adadelta": val_acc_adadelta.numpy()
})
# adam
# Grab the results
(loss_adam, acc_adam) = train_loss_adam.result(), train_acc_adam.result()
(val_loss_adam, val_acc_adam) = valid_loss_adam.result(), valid_acc_adam.result()
# Clear the current state of the metrics
train_loss_adam.reset_states(), train_acc_adam.reset_states()
valid_loss_adam.reset_states(), valid_acc_adam.reset_states()
# Local logging
template = "Epoch {}, loss: {:.3f}, acc: {:.3f}, val_loss: {:.3f}, val_acc: {:.3f}"
print (template.format(epoch+1,
loss_adam,
acc_adam,
val_loss_adam,
val_acc_adam))
# Logging with WnB
wandb.log({"train_loss_adadelta": loss_adam.numpy(),
"train_accuracy_adadelta": acc_adam.numpy(),
"val_loss_adadelta": val_loss_adam.numpy(),
"val_accuracy_adadelta": val_acc_adam.numpy()
})
get_sample_predictions()
```
| true |
code
| 0.711656 | null | null | null | null |
|
# 2017 August Duplicate Bug Detection
[**Find more on wiki**](https://wiki.nvidia.com/itappdev/index.php/Duplicate_Detection)
[**Demo Link**](http://qlan-vm-1.client.nvidia.com:8080/)
## Walk through of the Algorithm
<img src="imgsrc/Diagram.png">
## 1. Data Cleaning - SenteceParser Python 3
Available on Perforce and [Github](https://github.com/lanking520/NVBugsLib)
### Core Feature
- NLTK: remove stopwords and do stemming
- BeautifulSoup: Remove Html Tags
- General Regex: clean up white spaces and other symbols
### Other Functions:
- NVBugs Specific Cleaner for Synopsis, Description and Comments
- Counting Vectorizer embedded
- Auto-merge Column
```
def readfile(self, filepath, filetype, encod ='ISO-8859-1', header =None):
logger.info('Start reading File')
if not os.path.isfile(filepath):
logger.error("File Not Exist!")
sys.exit()
if filetype == 'csv':
df = pd.read_csv(filepath, encoding=encod, header =header)
elif filetype == 'json':
df = pd.read_json(filepath, encoding=encod, lines=True)
elif filetype == 'xlsx':
df = pd.read_excel(filepath, encoding=encod, header =header)
else:
logger.error("Extension Type not Accepted!")
sys.exit()
def processtext(self, column, removeSymbol = True, remove_stopwords=False, stemming=False):
logger.info("Start Data Cleaning...")
self.data[column] = self.data[column].str.replace(r'[\n\r\t]+', ' ')
# Remove URLs
self.data[column] = self.data[column].str.replace(self.regex_str[3],' ')
tempcol = self.data[column].values.tolist()
stops = set(stopwords.words("english"))
# This part takes a lot of times
printProgressBar(0, len(tempcol), prefix='Progress:', suffix='Complete', length=50)
for i in range(len(tempcol)):
row = BeautifulSoup(tempcol[i],'html.parser').get_text()
if removeSymbol:
row = re.sub('[^a-zA-Z0-9]', ' ', row)
words = row.split()
if remove_stopwords:
words = [w for w in words if not w in stops and not w.replace('.', '', 1).isdigit()]
row = ' '.join(words)
tempcol[i] = row.lower()
printProgressBar(i+1, len(tempcol), prefix='Progress:', suffix='Complete', length=50)
print("\n")
return tempcol
```
### Process by each line or Process by column
```
from SentenceParserPython3 import SentenceParser as SP
test = SP(20)
sample_text = "I @#$@have a @#$@#$@#%dog @#%@$^#$()_+%at home"
test.processline(sample_text, True, True)
```
## 2. Word Embedding
### 2.1 TF-IDF
**Term Frequency** denoted by tf, is the number of occurrencesof a term t in the document D.
**Inverse Document Frequency** of a term t, denoted by idf is log(N/df), where N is the total number of documents in thespace. So, it reduces the weight when a term occurs manytimes in a document, or in other words a word with rareoccurrences has more weight.
TF-IDF = Term Frequency * Inverse Document Frequency<br>
Inverse Document Frequency = log(N/df)
** Vocabulary size: 10000-100000 is the range used in this project **
Note: TF-IDF will brings Sparse Matrix back to reduce the memory use. Sparse Matrix is supported by K-Means. Sometimes we need to tranform it into dense when we actually use it to do the calculation
```
from sklearn.feature_extraction.text import TfidfVectorizer
def TFIDF(text, size):
print("Using TFIDF Doing data cleaning...")
vectorizer = TfidfVectorizer(stop_words='english', analyzer='word', strip_accents='unicode', max_features=size)
X = vectorizer.fit_transform(text)
return vectorizer, X
```
### Let's Translate one
REF: BugID 200235622
```
import pickle
from sklearn.externals import joblib
vectorizer = joblib.load('model/MSD2016NowTFIDF.pkl')
sample = 'GFE Share Telemetry item for OSC Hotkey Toggle'
result = vectorizer.transform([sample])
result.toarray()
```
### 2.2 Other Word Vectorization Tool
- Hashing Vectorization
- Word2Vec
- Infersent (Facebook)
- Skip-Thought
```
from gensim.models import word2vec
def W2V(text, size):
sentences = []
for idx in range(len(text)):
sentences.append(text[idx].split())
num_features = size
min_word_count = 20
num_workers = 4
context = 10
downsampling = 1e-3
model_name = "./model/w2vec.model"
model = word2vec.Word2Vec(sentences, workers=num_workers, \
size=num_features, min_count = min_word_count, \
window = context, sample = downsampling)
model.init_sims(replace=True)
return model
def Word2VecEmbed(text, model, num_features):
worddict = {}
for key in model.wv.vocab.keys():
worddict[key] = model.wv.word_vec(key)
X = []
for idx in range(len(text)):
words = text[idx].split()
counter = 0
temprow = np.zeros(num_features)
for word in words:
if word in worddict:
counter += 1
temprow += worddict[word]
if counter != 0:
X.append(temprow/counter)
else:
X.append(temprow)
X = np.array(X)
return X
```
## 3. Linear PCA
**Principal component analysis (PCA)** is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components (or sometimes, principal modes of variation). The number of principal components is less than or equal to the smaller of the number of original variables or the number of observations. This transformation is defined in such a way that the first principal component has the largest possible variance (that is, accounts for as much of the variability in the data as possible), and each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components. The resulting vectors are an uncorrelated orthogonal basis set. PCA is sensitive to the relative scaling of the original variables.
### TruncatedSVD
Dimensionality reduction using truncated SVD (aka LSA).
This transformer performs linear dimensionality reduction by means of truncated singular value decomposition (SVD). Contrary to PCA, this estimator does not center the data before computing the singular value decomposition. This means it can work with scipy.sparse matrices efficiently.
### Dimension Reduction
In our model, we reduce the dimension from 100000 to 6000 and keep **77%** of Variance
```
from sklearn.decomposition import TruncatedSVD
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import Normalizer
def DRN(X, DRN_size):
print("Performing dimensionality reduction using LSA")
svd = TruncatedSVD(DRN_size)
normalizer = Normalizer(copy=False)
lsa = make_pipeline(svd, normalizer)
X = lsa.fit_transform(X)
explained_variance = svd.explained_variance_ratio_.sum()
print("Explained variance of the SVD step: {}%".format( int(explained_variance * 100)))
return svd, X
```
## 4. Clustering
**clustering** is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense or another) to each other than to those in other groups (clusters). It is a main task of exploratory data mining, and a common technique for statistical data analysis, used in many fields, including machine learning, pattern recognition, image analysis, information retrieval, bioinformatics, data compression, and computer graphics.
### 4.1 KMeans Clustering
The current Algorithm we are using is the General KM without Mini-Batches. Mini-Batches are not working as well as the normal K-Means in our dataset.
### 4.2 "Yinyang" K-means and K-nn using NVIDIA CUDA
K-means implementation is based on ["Yinyang K-Means: A Drop-In Replacement
of the Classic K-Means with Consistent Speedup"](https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/ding15.pdf).
While it introduces some overhead and many conditional clauses
which are bad for CUDA, it still shows 1.6-2x speedup against the Lloyd
algorithm. K-nearest neighbors employ the same triangle inequality idea and
require precalculated centroids and cluster assignments, similar to the flattened
ball tree.
| Benchmarks | sklearn KMeans | KMeansRex | KMeansRex OpenMP | Serban | kmcuda | kmcuda 2 GPUs |
|---------------------------|----------------|-----------|------------------|--------|--------|---------------|
| speed | 1x | 4.5x | 8.2x | 15.5x | 17.8x | 29.8x |
| memory | 1x | 2x | 2x | 0.6x | 0.6x | 0.6x |
```
from sklearn.cluster import KMeans
def kmtrain(X, num_clusters):
km = KMeans(n_clusters=num_clusters, init='k-means++', max_iter=100, n_init=1, verbose=1)
print("Clustering sparse data with %s" % km)
km.fit(X)
return km
from libKMCUDA import kmeans_cuda
def cudatrain(X, num_clusters):
centroids, assignments = kmeans_cuda(X, num_clusters, verbosity=1, yinyang_t=0, seed=3)
return centroids, assignments
```
# Verfication
### Check the Assignment Match the Actual ones
```
correct = 0.0
assignment = []
printProgressBar(0, X.shape[0], prefix='Progress:', suffix='Complete', length=50)
for idx, item in enumerate(X):
center = np.squeeze(np.sum(np.square(item - centroid), axis =1)).argsort()[0]
if assign[idx] == center:
correct +=1.0
assignment.append(center)
printProgressBar(idx, X.shape[0], prefix='Progress:', suffix='Complete'+' Acc:' + str(correct/(idx+1)), length=50)
```
### See the Distribution based on the assignment
```
count = np.bincount(assignment)
count
```
### Filtering the Duplicate bug set to remove non-existed duplicated bugs
```
verifier = pd.read_csv('DuplicateBugs.csv',header=None)
verifier = verifier.as_matrix()
available = []
printProgressBar(0, verifier.shape[0], prefix='Progress:', suffix='Complete', length=50)
for idx, row in enumerate(verifier):
if not np.isnan(row).any():
leftcomp = df.loc[df["BugId"]==int(row[0])]
rightcomp = df.loc[df["BugId"]==int(row[1])]
if (not leftcomp.empty) and (not rightcomp.empty):
available.append([leftcomp.index[0], rightcomp.index[0]])
printProgressBar(idx, verifier.shape[0], prefix='Progress:', suffix='Complete', length=50)
temp = np.array(available)
```
### Test the Duplicated Bug set are inside of the top 3 cluster and top 5 recommendation
```
correctrow = 0
correctdist = []
vectorizer = joblib.load(root+divname+'TFIDF.pkl')
X = vectorizer.transform(text)
printProgressBar(0, temp.shape[0], prefix='Progress:', suffix='Complete', length=50)
for idx, row in enumerate(temp):
clusterset = np.squeeze(np.sum(np.square(real_center - X[row[0]].toarray()),axis=1)).argsort()[0:3]
dist = []
for cluster in clusterset:
dataset = wholeX[np.array((df["cluster"] == cluster).tolist())]
for datarow in dataset:
dist.append(np.sum(np.square(datarow.toarray() - wholeX[row[0]].toarray())))
dist = np.array(dist)
smalldist = np.sum(np.square(wholeX[row[1]].toarray() - wholeX[row[0]].toarray()))
sorteddist = np.sort(dist)
if sorteddist.shape[0] <= 5 or smalldist <= sorteddist[5]:
correctrow += 1
correctdist.append(smalldist)
printProgressBar(idx, temp.shape[0], prefix='Progress:', suffix='Complete', length=50)
print("Accuracy: "+ str(1.0*correctrow/temp.shape[0]))
```
# Prediction
```
def bugidgetter(df, cluster, loc):
bigset = df.loc[df['cluster'] == cluster]
return bigset.iloc[[loc],:]["BugId"].tolist()[0]
def bugindata(df, bugid):
return not df.loc[df["BugId"]==int(bugid)].empty
def predict(text, topkclusters, topktopics):
bugiddist = []
row = vectorizer.transform([text])
clusterset = np.squeeze(np.sum(np.square(real_center - row.toarray()),axis=1)).argsort()[0:topkclusters]
dist = []
print(clusterset)
for cluster in clusterset:
dataset = X[np.array((df["cluster"] == cluster).tolist())]
for idx, datarow in enumerate(dataset):
dist.append([np.sum(np.square(datarow.toarray() - row.toarray())), cluster, idx])
dist = np.array(dist)
topk = dist[dist[:,0].argsort()][0:topktopics]
# print(topk)
for idx, row in enumerate(topk):
bugiddist.append({'BugId':bugidgetter(df, row[1],row[2]), 'Distance': row[0]})
return bugiddist
```
| true |
code
| 0.229492 | null | null | null | null |
|
# Stellargraph example: GraphSAGE on the CORA citation network
Import NetworkX and stellar:
```
import networkx as nx
import pandas as pd
import os
import stellargraph as sg
from stellargraph.mapper import GraphSAGENodeGenerator
from stellargraph.layer import GraphSAGE
from tensorflow.keras import layers, optimizers, losses, metrics, Model
from sklearn import preprocessing, feature_extraction, model_selection
```
### Loading the CORA network
**Downloading the CORA dataset:**
The dataset used in this demo can be downloaded from [here](https://linqs-data.soe.ucsc.edu/public/lbc/cora.tgz).
The following is the description of the dataset:
> The Cora dataset consists of 2708 scientific publications classified into one of seven classes.
> The citation network consists of 5429 links. Each publication in the dataset is described by a
> 0/1-valued word vector indicating the absence/presence of the corresponding word from the dictionary.
> The dictionary consists of 1433 unique words. The README file in the dataset provides more details.
Download and unzip the cora.tgz file to a location on your computer and set the `data_dir` variable to
point to the location of the dataset (the directory containing "cora.cites" and "cora.content").
```
data_dir = os.path.expanduser("~/data/cora")
```
Load the graph from edgelist (in `cited-paper` <- `citing-paper` order)
```
edgelist = pd.read_csv(os.path.join(data_dir, "cora.cites"), sep='\t', header=None, names=["target", "source"])
edgelist["label"] = "cites"
Gnx = nx.from_pandas_edgelist(edgelist, edge_attr="label")
nx.set_node_attributes(Gnx, "paper", "label")
```
Load the features and subject for the nodes
```
feature_names = ["w_{}".format(ii) for ii in range(1433)]
column_names = feature_names + ["subject"]
node_data = pd.read_csv(os.path.join(data_dir, "cora.content"), sep='\t', header=None, names=column_names)
```
We aim to train a graph-ML model that will predict the "subject" attribute on the nodes. These subjects are one of 7 categories:
```
set(node_data["subject"])
```
### Splitting the data
For machine learning we want to take a subset of the nodes for training, and use the rest for testing. We'll use scikit-learn again to do this
```
train_data, test_data = model_selection.train_test_split(node_data, train_size=0.1, test_size=None, stratify=node_data['subject'])
```
Note using stratified sampling gives the following counts:
```
from collections import Counter
Counter(train_data['subject'])
```
The training set has class imbalance that might need to be compensated, e.g., via using a weighted cross-entropy loss in model training, with class weights inversely proportional to class support. However, we will ignore the class imbalance in this example, for simplicity.
### Converting to numeric arrays
For our categorical target, we will use one-hot vectors that will be fed into a soft-max Keras layer during training. To do this conversion ...
```
target_encoding = feature_extraction.DictVectorizer(sparse=False)
train_targets = target_encoding.fit_transform(train_data[["subject"]].to_dict('records'))
test_targets = target_encoding.transform(test_data[["subject"]].to_dict('records'))
```
We now do the same for the node attributes we want to use to predict the subject. These are the feature vectors that the Keras model will use as input. The CORA dataset contains attributes 'w_x' that correspond to words found in that publication. If a word occurs more than once in a publication the relevant attribute will be set to one, otherwise it will be zero.
```
node_features = node_data[feature_names]
```
## Creating the GraphSAGE model in Keras
Now create a StellarGraph object from the NetworkX graph and the node features and targets. It is StellarGraph objects that we use in this library to perform machine learning tasks on.
```
G = sg.StellarGraph(Gnx, node_features=node_features)
print(G.info())
```
To feed data from the graph to the Keras model we need a data generator that feeds data from the graph to the model. The generators are specialized to the model and the learning task so we choose the `GraphSAGENodeGenerator` as we are predicting node attributes with a GraphSAGE model.
We need two other parameters, the `batch_size` to use for training and the number of nodes to sample at each level of the model. Here we choose a two-level model with 10 nodes sampled in the first layer, and 5 in the second.
```
batch_size = 50; num_samples = [10, 5]
```
A `GraphSAGENodeGenerator` object is required to send the node features in sampled subgraphs to Keras
```
generator = GraphSAGENodeGenerator(G, batch_size, num_samples)
```
Using the `generator.flow()` method, we can create iterators over nodes that should be used to train, validate, or evaluate the model. For training we use only the training nodes returned from our splitter and the target values. The `shuffle=True` argument is given to the `flow` method to improve training.
```
train_gen = generator.flow(train_data.index, train_targets, shuffle=True)
```
Now we can specify our machine learning model, we need a few more parameters for this:
* the `layer_sizes` is a list of hidden feature sizes of each layer in the model. In this example we use 32-dimensional hidden node features at each layer.
* The `bias` and `dropout` are internal parameters of the model.
```
graphsage_model = GraphSAGE(
layer_sizes=[32, 32],
generator=generator,
bias=True,
dropout=0.5,
)
```
Now we create a model to predict the 7 categories using Keras softmax layers.
```
x_inp, x_out = graphsage_model.build()
prediction = layers.Dense(units=train_targets.shape[1], activation="softmax")(x_out)
```
### Training the model
Now let's create the actual Keras model with the graph inputs `x_inp` provided by the `graph_model` and outputs being the predictions from the softmax layer
```
model = Model(inputs=x_inp, outputs=prediction)
model.compile(
optimizer=optimizers.Adam(lr=0.005),
loss=losses.categorical_crossentropy,
metrics=["acc"],
)
```
Train the model, keeping track of its loss and accuracy on the training set, and its generalisation performance on the test set (we need to create another generator over the test data for this)
```
test_gen = generator.flow(test_data.index, test_targets)
history = model.fit_generator(
train_gen,
epochs=20,
validation_data=test_gen,
verbose=2,
shuffle=False
)
import matplotlib.pyplot as plt
%matplotlib inline
def plot_history(history):
metrics = sorted(history.history.keys())
metrics = metrics[:len(metrics)//2]
for m in metrics:
# summarize history for metric m
plt.plot(history.history[m])
plt.plot(history.history['val_' + m])
plt.title(m)
plt.ylabel(m)
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='best')
plt.show()
plot_history(history)
```
Now we have trained the model we can evaluate on the test set.
```
test_metrics = model.evaluate_generator(test_gen)
print("\nTest Set Metrics:")
for name, val in zip(model.metrics_names, test_metrics):
print("\t{}: {:0.4f}".format(name, val))
```
### Making predictions with the model
Now let's get the predictions themselves for all nodes using another node iterator:
```
all_nodes = node_data.index
all_mapper = generator.flow(all_nodes)
all_predictions = model.predict_generator(all_mapper)
```
These predictions will be the output of the softmax layer, so to get final categories we'll use the `inverse_transform` method of our target attribute specifcation to turn these values back to the original categories
```
node_predictions = target_encoding.inverse_transform(all_predictions)
```
Let's have a look at a few:
```
results = pd.DataFrame(node_predictions, index=all_nodes).idxmax(axis=1)
df = pd.DataFrame({"Predicted": results, "True": node_data['subject']})
df.head(10)
```
Add the predictions to the graph, and save as graphml, e.g. for visualisation in [Gephi](https://gephi.org)
```
for nid, pred, true in zip(df.index, df["Predicted"], df["True"]):
Gnx.nodes[nid]["subject"] = true
Gnx.nodes[nid]["PREDICTED_subject"] = pred.split("=")[-1]
```
Also add isTrain and isCorrect node attributes:
```
for nid in train_data.index:
Gnx.nodes[nid]["isTrain"] = True
for nid in test_data.index:
Gnx.nodes[nid]["isTrain"] = False
for nid in Gnx.nodes():
Gnx.nodes[nid]["isCorrect"] = Gnx.nodes[nid]["subject"] == Gnx.nodes[nid]["PREDICTED_subject"]
```
Save in GraphML format
```
pred_fname = "pred_n={}.graphml".format(num_samples)
nx.write_graphml(Gnx, os.path.join(data_dir,pred_fname))
```
## Node embeddings
Evaluate node embeddings as activations of the output of graphsage layer stack, and visualise them, coloring nodes by their subject label.
The GraphSAGE embeddings are the output of the GraphSAGE layers, namely the `x_out` variable. Let's create a new model with the same inputs as we used previously `x_inp` but now the output is the embeddings rather than the predicted class. Additionally note that the weights trained previously are kept in the new model.
```
embedding_model = Model(inputs=x_inp, outputs=x_out)
emb = embedding_model.predict_generator(all_mapper)
emb.shape
```
Project the embeddings to 2d using either TSNE or PCA transform, and visualise, coloring nodes by their subject label
```
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
import pandas as pd
import numpy as np
X = emb
y = np.argmax(target_encoding.transform(node_data[["subject"]].to_dict('records')), axis=1)
if X.shape[1] > 2:
transform = TSNE #PCA
trans = transform(n_components=2)
emb_transformed = pd.DataFrame(trans.fit_transform(X), index=node_data.index)
emb_transformed['label'] = y
else:
emb_transformed = pd.DataFrame(X, index=node_data.index)
emb_transformed = emb_transformed.rename(columns = {'0':0, '1':1})
emb_transformed['label'] = y
alpha = 0.7
fig, ax = plt.subplots(figsize=(7,7))
ax.scatter(emb_transformed[0], emb_transformed[1], c=emb_transformed['label'].astype("category"),
cmap="jet", alpha=alpha)
ax.set(aspect="equal", xlabel="$X_1$", ylabel="$X_2$")
plt.title('{} visualization of GraphSAGE embeddings for cora dataset'.format(transform.__name__))
plt.show()
```
| true |
code
| 0.665044 | null | null | null | null |
|
```
try:
from openmdao.utils.notebook_utils import notebook_mode
except ImportError:
!python -m pip install openmdao[notebooks]
from openmdao.utils.assert_utils import assert_near_equal
import os
if os.path.exists('cases.sql'):
os.remove('cases.sql')
```
# Driver Recording
A CaseRecorder is commonly attached to the problem’s Driver in order to gain insight into the convergence of the model as the driver finds a solution. By default, a recorder attached to a driver will record the design variables, constraints and objectives.
The driver recorder is capable of capturing any values from any part of the model, not just the design variables, constraints, and objectives.
```
import openmdao.api as om
om.show_options_table("openmdao.core.driver.Driver", recording_options=True)
```
```{note}
Note that the `excludes` option takes precedence over the `includes` option.
```
## Driver Recording Example
In the example below, we first run a case while recording at the driver level. Then, we examine the objective, constraint, and design variable values at the last recorded case. Lastly, we print the full contents of the last case, including outputs from the problem that are not design variables, constraints, or objectives.
Specifically, `y1` and `y2` are some of those intermediate outputs that are recorded due to the use of:
`driver.recording_options['includes'] = ['*']`
```
from openmdao.utils.notebook_utils import get_code
from myst_nb import glue
glue("code_src89", get_code("openmdao.test_suite.components.sellar.SellarDerivatives"), display=False)
```
:::{Admonition} `SellarDerivatives` class definition
:class: dropdown
{glue:}`code_src89`
:::
```
import openmdao.api as om
from openmdao.test_suite.components.sellar import SellarDerivatives
import numpy as np
prob = om.Problem(model=SellarDerivatives())
model = prob.model
model.add_design_var('z', lower=np.array([-10.0, 0.0]),
upper=np.array([10.0, 10.0]))
model.add_design_var('x', lower=0.0, upper=10.0)
model.add_objective('obj')
model.add_constraint('con1', upper=0.0)
model.add_constraint('con2', upper=0.0)
driver = prob.driver = om.ScipyOptimizeDriver(optimizer='SLSQP', tol=1e-9)
driver.recording_options['includes'] = ['*']
driver.recording_options['record_objectives'] = True
driver.recording_options['record_constraints'] = True
driver.recording_options['record_desvars'] = True
driver.recording_options['record_inputs'] = True
driver.recording_options['record_outputs'] = True
driver.recording_options['record_residuals'] = True
recorder = om.SqliteRecorder("cases.sql")
driver.add_recorder(recorder)
prob.setup()
prob.run_driver()
prob.cleanup()
cr = om.CaseReader("cases.sql")
driver_cases = cr.list_cases('driver')
assert len(driver_cases) == 7
last_case = cr.get_case(driver_cases[-1])
print(last_case)
last_case.get_objectives()
assert_near_equal(last_case.get_objectives()['obj'], 3.18339395, tolerance=1e-8)
last_case.get_design_vars()
design_vars = last_case.get_design_vars()
assert_near_equal(design_vars['x'], 0., tolerance=1e-8)
assert_near_equal(design_vars['z'][0], 1.97763888, tolerance=1e-8)
last_case.get_constraints()
constraints = last_case.get_constraints()
assert_near_equal(constraints['con1'], 0, tolerance=1e-8)
assert_near_equal(constraints['con2'], -20.24472223, tolerance=1e-8)
last_case.inputs['obj_cmp.x']
assert_near_equal(last_case.inputs['obj_cmp.x'], 0, tolerance=1e-8)
last_case.outputs['z']
assert_near_equal(last_case.outputs['z'][0], 1.97763888, tolerance=1e-8)
assert_near_equal(last_case.outputs['z'][1], 0, tolerance=1e-8)
last_case.residuals['obj']
assert_near_equal(last_case.residuals['obj'], 0, tolerance=1e-8)
last_case['y1']
assert_near_equal(last_case['y1'], 3.16, tolerance=1e-8)
```
| true |
code
| 0.607256 | null | null | null | null |
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import my_utils as my_utils
635 - 243
1027 - 635
```
## prepare test data
```
row_test = pd.read_csv('./1962_to_1963.csv')
# row_test = pd.read_excel('./normalized_bs.xlsx')
row_test[row_data.day > 635].head()
test_data = row_test[['id', 'day', 'bs', 'Tmin0', 'rainfall', 'x', 'y', 'h']]
test_data = test_data[test_data.day > 635]
test_data = test_data[test_data.day < 1027]
test_tensor = to_tensor(test_data)
(test_Y, test_X_1, test_X_2, test_X_3) = preprocess2(test_tensor)
```
## prepare data
```
row_data = pd.read_csv('./1961_to_1962.csv')
# row_data = pd.read_excel('./normalized_bs.xlsx')
print('columns: {}'.format(row_data.columns))
row_data.head()
# 1962.06 - 1963.06のデータ。冬のピークをみたいので
data = row_data[['id', 'day', 'bs', 'Tmin0', 'rainfall', 'x', 'y', 'h']]
data = data[data.day > 243]
data = data[data.day < 635]
len(data[data.id == 82])
data[data.id == 82].mean()
def to_tensor(pd_data):
dayMin = pd_data.day.min()
dayMax = pd_data.day.max()
stations = pd_data.id.unique()
column_num = len(pd_data.columns)
result = np.empty((0, len(stations), 8), float)
for day in range(dayMin, dayMax):
mat = np.empty((0, column_num), float)
data_on_day = pd_data[pd_data.day == day] # その日のデータのみ
for stat_id in stations:
# もし、あるstationのデータがあったら
station_data = data_on_day[data_on_day.id == stat_id]
if not station_data.empty:
mat = np.append(mat, station_data.as_matrix(), axis = 0)
else: # なかったら、0詰め
stat_pos = pd_data[pd_data.id == stat_id]
means = stat_pos.mean()
stat_pos = stat_pos[0: 1].as_matrix()[0]
mat = np.append(mat, np.array([[stat_id, day, means[2], means[3], means[4], stat_pos[5], stat_pos[6], stat_pos[7]]], float), axis = 0)
result = np.append(result, mat.reshape(1, len(stations), column_num), axis = 0)
return result
tensor_data = to_tensor(data)
print('tensor shape: (days, stations, variables) = {}'.format(tensor_data.shape))
print('variables: {}'.format(data.columns))
```
### Our Model
$$BS^t = F(T_{min}, ~R, ~G(BS^{t-1}, ~P))$$
ただし、
$$F: Regression Model, G: Diffusion Term$$
$$T_{min}: Minimum ~Temparature ~at ~the ~time, ~R: Rainfall, ~BS^t: Black Smog[\mu g] ~at~ t, ~P: Position ~of ~Station$$
また、
$$F: Multi~ Regression$$
$$G(BS^{t-1}, ~P)|_i = \sum_j{\frac{BS^(t-1)_j - BS^(t-1)_i}{dist(P_{ij})^2}}$$
とする。
### Caculate necesary data
Gを計算する
```
def preprocess(tensor):
shape_1 = tensor.shape[0] # days
shape_2 = tensor.shape[1] # stations
shape_3 = tensor.shape[2] # variables
Y = np.empty((0, shape_2, 1), float) # bs
X = np.empty((0, shape_2, 3), float) # Tmin0, rainfall, Dist
for t in range(1, shape_1):
mat_Y = tensor[t, :, 2] # bs^t
mat_X = np.empty((0, 3), float)
for s in range(shape_2):
dist = 0
for s_j in range(shape_2):
if s != s_j:
diff_ij = tensor[t - 1, s, 2] - tensor[t - 1, s_j, 2]
dist_ij = tensor[t - 1, s, 5:] - tensor[t - 1, s_j, 5:]
dist_ij = np.dot(dist_ij, dist_ij)
dist += diff_ij / dist_ij
mat_X = np.append(mat_X, np.array([tensor[t, s, 3], tensor[t, s, 4], dist]).reshape((1, 3)), axis=0) # Tmin, rainfall, Dist
Y = np.append(Y, mat_Y.reshape(1, shape_2, 1), axis=0)
X = np.append(X, mat_X.reshape(1, shape_2, 3), axis=0)
return (Y, X)
def preprocess2(tensor):
shape_1 = tensor.shape[0] # days
shape_2 = tensor.shape[1] # stations
shape_3 = tensor.shape[2] # variables
Y = tensor[:, :, 2].T # bs
X_1 = tensor[:, :, 3].T # Tmin0
X_2 = tensor[:, :, 4].T # rainfall
X_3 = [] # Dist
print(shape_1, shape_2, shape_3)
print(tensor)
for t in range(1, shape_1+1):
mat_X = []
for s in range(shape_2):
dist = 0
for s_j in range(shape_2):
if s != s_j:
diff_ij = tensor[t - 1, s_j, 2] - tensor[t - 1, s, 2]
dist_ij = tensor[t - 1, s_j, 5:] - tensor[t - 1, s, 5:]
dist_ij = np.dot(dist_ij, dist_ij)
dist += diff_ij / dist_ij
mat_X.append(dist)
X_3.append(mat_X)
X_3 = np.array(X_3).T
return (Y, X_1, X_2, X_3)
test_row_data = pd.read_csv('./test.csv')
test_tensor = to_tensor(test_row_data)
(yyy, xx1, xx2, xx3) = preprocess2(test_tensor)
xx3
tensor_data[:, :, 2].T.shape
# (train_Y, train_X) = preprocess(tensor_data)
(train_Y, train_X_1, train_X_2, train_X_3) = preprocess2(tensor_data)
train_Y[5, 0]
train_X_1[5, 0]
train_X_2[5, 0]
train_X_3[5, 0]
train_Y[0, 5, :]
train_X[0, 5, :]
print('shape Y: {}, shape X: {}'.format(train_Y.shape, train_X.shape))
print(train_Y.shape, train_X_1.shape, train_X_2.shape, train_X_3.shape)
```
### Let's 回帰分析
```
import tensorflow as tf
station_n = 321
tf.reset_default_graph()
Y_data = tf.placeholder(tf.float32, shape=[station_n, None], name='Y_data')
X_1 = tf.placeholder(tf.float32, shape=[station_n, None], name='X_1_data')
X_2 = tf.placeholder(tf.float32, shape=[station_n, None], name='X_2_data')
X_3 = tf.placeholder(tf.float32, shape=[station_n, None], name='X_3_data')
a_1 = tf.Variable(1.)
a_2 = tf.Variable(1.)
a_3 = tf.Variable(1.)
b_1 = tf.Variable(1.)
Y = a_1 * X_1 + a_2 * X_2 + b_1
# Y = a_1 * X_1 + a_2 * X_2 + a_3 * X_3 + b_1
# Y = a_1 * X_1 + a_2 * X_3 + b_1
Loss = tf.reduce_sum(tf.square(Y - Y_data)) # squared error
optimizer = tf.train.AdagradOptimizer(0.25)
trainer = optimizer.minimize(Loss)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for i in range(10000):
_trainer, _loss = sess.run([trainer, Loss], feed_dict={'Y_data:0': train_Y, 'X_1_data:0': train_X_1, 'X_2_data:0': train_X_2, 'X_3_data:0': train_X_3})
if i % 500 == 0:
_test_loss = sess.run([Loss], feed_dict={'Y_data:0': test_Y, 'X_1_data:0': test_X_1, 'X_2_data:0': test_X_2, 'X_3_data:0': test_X_3})
print('iterate: {}, loss: {}, test loss: {}'.format(i, _loss, _test_loss))
for i in range(1000):
_trainer, _loss = sess.run([trainer, Loss], feed_dict={'Y_data:0': train_Y, 'X_1_data:0': train_X_1, 'X_2_data:0': train_X_2, 'X_3_data:0': train_X_3})
if i % 100 == 0:
print('iterate: {}, loss: {}'.format(i, _loss))
sess.run([a_1, a_2, a_3, b_1])
predict = sess.run(Y, feed_dict={'X_1_data:0': train_X_1, 'X_2_data:0': train_X_2, 'X_3_data:0': train_X_3})
predict_test = sess.run(Y, feed_dict={'X_1_data:0': test_X_1, 'X_2_data:0': test_X_2, 'X_3_data:0': test_X_3})
1 - np.sum(np.square(train_Y - predict)) / np.sum(np.square(train_Y - np.mean(train_Y)))
1 - np.sum(np.square(test_Y - predict_test)) / np.sum(np.square(test_Y - np.mean(test_Y)))
np.max(teY)
test_pd = pd.DataFrame(data=predict_test)
test_pd = pd.DataFrame(data=predict_test)
test_pd = test_pd[test_pd < 9999]
test_pd = test_pd[test_pd > -9999]
test_pd = test_pd.fillna(method='ffill')
np.sum(np.square(test_Y - test_pd.as_matrix()))
1 - np.sum(np.square(test_Y -test_pd.as_matrix())) / np.sum(np.square(test_Y - np.mean(test_Y)))
np.sum(np.square(test_Y - predict_test))
predict.shape
for i in range(110, 115):
plt.plot(train_Y[i])
plt.plot(predict[i])
plt.show()
for i in range(110, 115):
plt.plot(test_Y[i])
plt.plot(predict_test[i])
plt.show()
train_X.shape
train_Y.shape
testA_array = np.array([[[1], [2], [3]]])
testA_array.shape
testA = tf.constant(np.array([[[1], [2], [3]]]))
import seaborn as sns
normalized_data = pd.read_excel('./normalized_bs.xlsx')
normalized_data = normalized_data[['day', 'bs', 'Tmin0', 'rainfall']]
normalized_data.head()
sns.pairplot(normalized_data)
```
| true |
code
| 0.224565 | null | null | null | null |
|
# [LEGALST-190] Lab 3/20: TF-IDF and Classification
This lab will cover the term frequency-inverse document frequency method, and classification algorithms in machine learning.
Estimated Lab time: 30 minutes
```
# Dependencies
from datascience import *
import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction import DictVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.stop_words import ENGLISH_STOP_WORDS
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.metrics import confusion_matrix
from sklearn import svm
import matplotlib.pyplot as plt
from sklearn.naive_bayes import MultinomialNB
import itertools
import seaborn as sn
%matplotlib inline
```
# The Data
For this lab, we'll use a dataset that was drawn from a Kaggle collection of questions posed on stackexchange (a website/forum where people ask and answer questions about statistics, programming etc.)
The data has the following features:
- "Id": The Id number for the question
- "Body": The text of the answer
- "Tag": Whether the question was tagged as dealing with python, xml, java, json, or android
```
stack_data = pd.read_csv('data/stackexchange.csv', encoding='latin-1')
stack_data.head(5)
```
# Section 1: TF-IDF Vectorizer
The term frequency-inverse document frequency (tf-idf) vectorizer is a statistic that measures similarity within and across documents. Term frequency refers to the number of times a term shows up within a document. Inverse document frequency is the logarithmically scaled inverse fraction of the documents that contains the word, and penalizes words that occur frequently. Tf-idf multiplies these two measures together.
#### Question 1: Why is tf-idf a potentially more attractive vectorizer than the standard count vectorizer?
Let's get started! First, extract the "Body" column into its own numpy array called "text_list"
```
# Extract Text Data
text_list = stack_data['Body']
```
Next, initialize a term frequency-inverse document frequency (tf-idf) vectorizer. Check out the documentation to fill in the arguments: http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.TfidfVectorizer.html
```
tf = TfidfVectorizer(analyzer='word',
ngram_range=(1,3),
min_df = 0,
stop_words = 'english')
```
Next, use the "fit_transform" method to take in the list of documents, and convert them into a document term matrix. Use "geat_feature_names()" and "len" to calculate how many features this generates.
```
tfidf_matrix = tf.fit_transform(text_list)
feature_names = tf.get_feature_names()
len(feature_names)
```
#### Question 2: The dimensionality explodes quickly. Why might this be a problem as you use more data?
Calculate the tf-idf scores for the first document in the corpus. Do the following:
1. Use ".todense()" to turn the tfidf matrix into a dense matrix (get rid of the sparsity)
2. Create an object for th document by calling the 0th index of the dense matrix, converting it to a list. Try something like: document = dense[0].tolist()[0]
3. Calculate the phrase scores by using the "zip" command to iterate from 0 to the length of the document, retraining scores greater than 0.
4. Sort the scores using the "sorted" command
5. Print the top 20 scores
```
dense = tfidf_matrix.todense()
document = dense[0].tolist()[0]
phrase_scores = [pair for pair in zip(range(0, len(document)), document) if pair[1] > 0]
sorted_phrase_scores = sorted(phrase_scores, key=lambda t: t[1] * -1)
for phrase, score in [(feature_names[word_id], score) for (word_id, score) in sorted_phrase_scores][:20]:
print('{0: <20} {1}'.format(phrase, score))
```
# Section 2: Classification Algorithms
One of the main tasks in supervised machine learning is classification. In this case, we will develop algorithms that will predict a question's tag based on the text of its answer.
The first step is to split our data into training, validation, and test sets.
```
# Training, Validation, Test Sets
# X
X = stack_data['Body']
tf = TfidfVectorizer(analyzer='word',
ngram_range=(1,3),
min_df = 0,
stop_words = 'english')
tfidf_matrix = tf.fit_transform(X)
#y
y = stack_data['Tag']
# Train/Test Split
X_train, X_test, y_train, y_test = train_test_split(tfidf_matrix, y,
train_size = .80,
test_size = .20)
# Train/Validation Split
X_train, X_validate, y_train, y_validate = train_test_split(X_train, y_train,
train_size = .75,
test_size = .25)
```
## Naive Bayes
Naive Bayes classifers classify observations by making the assumption that features are all independent of one another. Do the following:
1. Initialize a Naive Bayes classifier method with "MultinomialNB()"
2. Fit the model on your training data
3. Predict on the validation data and store the predictions
4. Use "np.mean" to calculate how correct the classier was on average
5. Calcualte the confusion matrix using "confusion_matrix," providing the true values first and the predicted values second.
```
nb = MultinomialNB()
nb_model = nb.fit(X_train, y_train)
nb_pred = nb_model.predict(X_validate)
np.mean(nb_pred == y_validate)
nb_cf_matrix = confusion_matrix(y_validate, nb_pred)
```
Let's plot the confusion matrix! Use the following code from the "seaborn" package to make a heatmap out of the matrix.
```
nb_df_cm = pd.DataFrame(nb_cf_matrix, range(5),
range(5))
nb_df_cm = nb_df_cm.rename(index=str, columns={0: "python", 1: "xml", 2: "java", 3: "json", 4: "android"})
nb_df_cm.index = ['python', 'xml', 'java', 'json', 'android']
plt.figure(figsize = (10,7))
sn.set(font_scale=1.4)#for label size
sn.heatmap(nb_df_cm,
annot=True,
annot_kws={"size": 16})
plt.title("Naive Bayes Confusion Matrix")
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
plt.show()
```
#### Question 3: Do you notice any patterns? Are there any patterns in misclassification that are worrisome?
## Multinomial Logistic Regression
Next, let's try multinomial logistic regression! Follow the same steps as with Naive Bayes, and plot the confusion matrix.
```
logreg = linear_model.LogisticRegression(solver = "newton-cg", multi_class = 'multinomial')
log_model = logreg.fit(X_train, y_train)
log_pred = log_model.predict(X_validate)
np.mean(log_pred == y_validate)
log_cf_matrix = confusion_matrix(y_validate, log_pred)
log_df_cm = pd.DataFrame(log_cf_matrix, range(5),
range(5))
log_df_cm = log_df_cm.rename(index=str, columns={0: "python", 1: "xml", 2: "java", 3: "json", 4: "android"})
log_df_cm.index = ['python', 'xml', 'java', 'json', 'android']
plt.figure(figsize = (10,7))
sn.set(font_scale=1.4)#for label size
sn.heatmap(log_df_cm,
annot=True,
annot_kws={"size": 16})
plt.title("Multinomial Logistic Regression Confusion Matrix")
plt.xlabel("Predicted Label")
plt.ylabel("True Labels")
plt.show()
```
## SVM
Now do the same for a Support Vector Machine.
```
svm = svm.LinearSVC()
svm_model = svm.fit(X_train, y_train)
svm_pred = svm_model.predict(X_validate)
np.mean(svm_pred == y_validate)
svm_cf_matrix = confusion_matrix(y_validate, svm_pred)
svm_df_cm = pd.DataFrame(svm_cf_matrix, range(5),
range(5))
svm_df_cm = svm_df_cm.rename(index=str, columns={0: "python", 1: "xml", 2: "java", 3: "json", 4: "android"})
svm_df_cm.index = ['python', 'xml', 'java', 'json', 'android']
plt.figure(figsize = (10,7))
sn.set(font_scale=1.4)#for label size
sn.heatmap(svm_df_cm,
annot=True,
annot_kws={"size": 16})
plt.title("Multinomial Logistic Regression Confusion Matrix")
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
plt.show()
```
#### Question 4: How did each of the classifiers do? Which one would you prefer the most?
## Test Final Classifier
Choose your best classifier and use it to predict on the test set. Report the mean accuracy and confusion matrix.
```
svm_test_pred = svm_model.predict(X_test)
np.mean(svm_test_pred == y_test)
svm_cf_matrix = confusion_matrix(y_test, svm_test_pred)
svm_df_cm = pd.DataFrame(svm_cf_matrix, range(5),
range(5))
svm_df_cm = svm_df_cm.rename(index=str, columns={0: "python", 1: "xml", 2: "java", 3: "json", 4: "android"})
svm_df_cm.index = ['python', 'xml', 'java', 'json', 'android']
plt.figure(figsize = (10,7))
sn.set(font_scale=1.4)#for label size
sn.heatmap(svm_df_cm,
annot=True,
annot_kws={"size": 16})
plt.title("Multinomial Logistic Regression Confusion Matrix")
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
plt.show()
```
| true |
code
| 0.606528 | null | null | null | null |
|
<center><img src='../../img/ai4eo_logos.jpg' alt='Logos AI4EO MOOC' width='80%'></img></center>
<hr>
<br>
<a href='https://www.futurelearn.com/courses/artificial-intelligence-for-earth-monitoring/1/steps/1280514' target='_blank'><< Back to FutureLearn</a><br>
# 3B - Tile-based classification using Sentinel-2 L1C and EuroSAT data - Functions
<i>by Nicolò Taggio, Planetek Italia S.r.l., Bari, Italy</i>
<hr>
### <a id='from_folder_to_stack'></a> `from_folder_to_stack`
```
'''
function name:
from_folder_to_stack
description:
This function transform the .SAFE file into three different arrays (10m, 20m and 60m).
Input:
safe_path: the path of the .SAFE file;
data_bands_20m: if True, the function computes stack using Sentinel2 band with 20m of pixel resolution (default=True);
data_bands_60m: if True, the function computes stack using Sentinel2 band with 60m of pixel resolution (default=True);
Output:
stack_10m: stack with the following S2L1C bands (B02,B03,B04,B08)
stack_20m: stack with the following S2L1C bands (B05,B06,B07,B11,B12,B8A)
stack_60m: stack with the following S2L1C bands (B01,B09,B10)
'''
def from_folder_to_stack(
safe_path,
data_bands_20m=True,
data_bands_60m=True,
):
level_folder_name_list = glob.glob(safe_path + 'GRANULE/*')
level_folder_name = level_folder_name_list[0]
if level_folder_name.find("L2A") < 0:
safe_path = [level_folder_name + '/IMG_DATA/']
else:
safe_path_10m = level_folder_name + '/IMG_DATA/R10m/'
safe_path = [safe_path_10m]
text_files = []
for i in range(0,len(safe_path)):
print("[AI4EO_MOOC]_log: Loading .jp2 images in %s" % (safe_path[i]))
text_files_tmp = [f for f in os.listdir(safe_path[i]) if f.endswith('.jp2')]
text_files.append(text_files_tmp)
lst_stack_60m=[]
lst_code_60m =[]
lst_stack_20m=[]
lst_code_20m =[]
lst_stack_10m=[]
lst_code_10m =[]
for i in range(0,len(safe_path)):
print("[AI4EO_MOOC]_log: Reading .jp2 files in %s" % (safe_path[i]))
for name in range(0, len(text_files[i])):
text_files_tmp = text_files[i]
if data_bands_60m == True:
cond_60m = ( (text_files_tmp[name].find("B01") > 0) or (text_files_tmp[name].find("B09") > 0)
or (text_files_tmp[name].find("B10") > 0))
if cond_60m:
print("[AI4EO_MOOC]_log: Using .jp2 image: %s" % text_files_tmp[name])
lst_stack_60m.append(gdal_array.LoadFile(safe_path[i] + text_files_tmp[name]))
lst_code_60m.append(text_files_tmp[name][24:26])
if data_bands_20m == True:
cond_20m = (text_files_tmp[name].find("B05") > 0) or (text_files_tmp[name].find("B06") > 0) or (
text_files_tmp[name].find("B07") > 0) or (text_files_tmp[name].find("B11") > 0) or (
text_files_tmp[name].find("B12") > 0) or (text_files_tmp[name].find("B8A") > 0)
cond_60m_L2 = (text_files_tmp[name].find("B05_60m") < 0) and (text_files_tmp[name].find("B06_60m") < 0) and (
text_files_tmp[name].find("B07_60m") < 0) and (text_files_tmp[name].find("B11_60m") < 0) and (
text_files_tmp[name].find("B12_60m") < 0) and (text_files_tmp[name].find("B8A_60m") < 0)
cond_20m_tot = cond_20m and cond_60m_L2
if cond_20m_tot:
print("[AI4EO_MOOC]_log: Using .jp2 image: %s" % text_files_tmp[name])
lst_stack_20m.append(gdal_array.LoadFile(safe_path[i] + text_files_tmp[name]))
lst_code_20m.append(text_files_tmp[name][24:26])
else:
stack_20m = 0
cond_10m = (text_files_tmp[name].find("B02") > 0) or (text_files_tmp[name].find("B03") > 0) or (
text_files_tmp[name].find("B04") > 0) or (text_files_tmp[name].find("B08") > 0)
cond_20m_L2 = (text_files_tmp[name].find("B02_20m") < 0) and (text_files_tmp[name].find("B03_20m") < 0) and (
text_files_tmp[name].find("B04_20m") < 0) and (text_files_tmp[name].find("B08_20m") < 0)
cond_60m_L2 = (text_files_tmp[name].find("B02_60m") < 0) and(text_files_tmp[name].find("B03_60m") < 0) and(
text_files_tmp[name].find("B04_60m") < 0) and (text_files_tmp[name].find("B08_60m") < 0)
cond_10m_tot = cond_10m and cond_20m_L2 and cond_60m_L2
if cond_10m_tot:
print("[AI4EO_MOOC]_log: Using .jp2 image: %s" % text_files_tmp[name])
lst_stack_10m.append(gdal_array.LoadFile(safe_path[i] + text_files_tmp[name]))
lst_code_10m.append(text_files_tmp[name][24:26])
stack_10m=np.asarray(lst_stack_10m)
sorted_list_10m = ['02','03','04','08']
print('[AI4EO_MOOC]_log: Sorting stack 10m...')
stack_10m_final_sorted = stack_sort(stack_10m, lst_code_10m, sorted_list_10m)
stack_20m=np.asarray(lst_stack_20m)
sorted_list_20m = ['05','06','07','11','12','8A']
print('[AI4EO_MOOC]_log: Sorting stack 20m...')
stack_20m_final_sorted = stack_sort(stack_20m, lst_code_20m, sorted_list_20m)
stack_60m=np.asarray(lst_stack_60m)
sorted_list_60m = ['01','09','10']
print('[AI4EO_MOOC]_log: Sorting stack 60m...')
stack_60m_final_sorted = stack_sort(stack_60m, lst_code_60m, sorted_list_60m)
return stack_10m_final_sorted, stack_20m_final_sorted, stack_60m_final_sorted
```
<br>
### <a id='stack_sort'></a>`stack_sort`
```
def stack_sort(stack_in, lst_code, sorted_list):
b,r,c = stack_in.shape
stack_sorted = np.zeros((r,c,b), dtype=np.uint16)
len_list_bands = len(lst_code)
c = np.zeros((len_list_bands),dtype=np.uint8)
count = 0
count_sort = 0
while count_sort != len_list_bands:
if lst_code[count] == sorted_list[count_sort]:
c[count_sort] = count
count_sort = count_sort + 1
count = 0
else:
count = count + 1
print('[AI4EO_MOOC]_log: sorted list:', sorted_list)
print('[AI4EO_MOOC]_log: bands:', c)
for i in range(0, len_list_bands):
stack_sorted[:,:,i]=stack_in[c[i],:,:]
return stack_sorted
```
<br>
### <a id='resample_3d'></a>`resample_3d`
```
'''
function name:
resample_3d
description:
Wrapper of ndimage zoom. Bilinear interpolation for resampling array
Input:
stack: array to be resampled;
row10m: the expected row;
col10m: the expected col;
rate: the rate of the tranformation;
Output:
stack_10m: resampled array
'''
def resample_3d(
stack,
row10m,
col10m,
rate):
row, col, bands = stack.shape
print("[AI4EO_MOOC]_log: Array shape (%d,%d,%d)" % (row, col, bands))
stack_10m = np.zeros((row10m, col10m, bands),dtype=np.uint16)
print("[AI4EO_MOOC]_log: Resize array bands from (%d,%d,%d) to (%d,%d,%d)" % (
row, col, bands, row10m, col10m, bands))
for i in range(0, bands):
stack_10m[:, :, i] = ndimage.zoom(stack[:, :,i], rate)
del (stack)
return stack_10m
```
<br>
### <a id='sentinel2_format'></a>`sentinel2_format`
```
'''
function name:
sentinel2_format
description:
This function transform the multistack into sentinel2 format array with bands in the right position for AI model.
Input:
total_stack: array that is the concatenation of stack10, stack_20mTo10m and stack_60mTo10m,;
Output:
sentinel2: sentinel2 format array
'''
def sentinel2_format(
total_stack):
row_tot, col_tot, bands_tot = total_stack.shape
sentinel2 = np.zeros((row_tot, col_tot,bands_tot),dtype=np.uint16)
print("[AI4EO_MOOC]_log: Creating total stack with following bands list:")
print("[AI4EO_MOOC]_log: Band 1 – Coastal aerosol")
print("[AI4EO_MOOC]_log: Band 2 – Blue")
print("[AI4EO_MOOC]_log: Band 3 – Green")
print("[AI4EO_MOOC]_log: Band 4 – Red")
print("[AI4EO_MOOC]_log: Band 5 – Vegetation red edge")
print("[AI4EO_MOOC]_log: Band 6 – Vegetation red edge")
print("[AI4EO_MOOC]_log: Band 7 – Vegetation red edge")
print("[AI4EO_MOOC]_log: Band 8 – NIR")
print("[AI4EO_MOOC]_log: Band 8A – Narrow NIR")
print("[AI4EO_MOOC]_log: Band 9 – Water vapour")
print("[AI4EO_MOOC]_log: Band 10 – SWIR – Cirrus")
print("[AI4EO_MOOC]_log: Band 11 – SWIR")
print("[AI4EO_MOOC]_log: Band 12 – SWIR")
sentinel2[:, :, 0] = total_stack[:, :, 10]
sentinel2[:, :, 1] = total_stack[:, :, 0]
sentinel2[:, :, 2] = total_stack[:, :, 1]
sentinel2[:, :, 3] = total_stack[:, :, 2]
sentinel2[:, :, 4] = total_stack[:, :, 4]
sentinel2[:, :, 5] = total_stack[:, :, 5]
sentinel2[:, :, 6] = total_stack[:, :, 6]
sentinel2[:, :, 7] = total_stack[:, :, 3]
sentinel2[:, :, 8] = total_stack[:, :, 9]
sentinel2[:, :, 9] = total_stack[:, :,11]
sentinel2[:, :,10] = total_stack[:, :,12]
sentinel2[:, :,11] = total_stack[:, :, 7]
sentinel2[:, :,12] = total_stack[:, :, 8]
del (total_stack)
return sentinel2
```
<br>
## `sliding`
```
'''
Function_name:
sliding
description:
Input:
shape: the target shape
window_size: the shape of the window
step_size:
fixed
Output:
windows:
'''
def sliding(shape, window_size, step_size=None, fixed=True):
h, w = shape
if step_size:
h_step = step_size
w_step = step_size
else:
h_step = window_size
w_step = window_size
h_wind = window_size
w_wind = window_size
windows = []
for y in range(0, h, h_step):
for x in range(0, w, w_step):
h_min = min(h_wind, h - y)
w_min = min(w_wind, w - x)
if fixed:
if h_min < h_wind or w_min < w_wind:
continue
window = (x, y, w_min, h_min)
windows.append(window)
return windows
```
<br>
<a href='https://www.futurelearn.com/courses/artificial-intelligence-for-earth-monitoring/1/steps/1280514' target='_blank'><< Back to FutureLearn</a><br>
<hr>
<img src='../../img/copernicus_logo.png' alt='Copernicus logo' align='left' width='20%'></img>
Course developed for <a href='https://www.eumetsat.int/' target='_blank'> EUMETSAT</a>, <a href='https://www.ecmwf.int/' target='_blank'> ECMWF</a> and <a href='https://www.mercator-ocean.fr/en/' target='_blank'> Mercator Ocean International</a> in support of the <a href='https://www.copernicus.eu/en' target='_blank'> EU's Copernicus Programme</a> and the <a href='https://wekeo.eu/' target='_blank'> WEkEO platform</a>.
| true |
code
| 0.23568 | null | null | null | null |
|
# MNIST distributed training
The **SageMaker Python SDK** helps you deploy your models for training and hosting in optimized, productions ready containers in SageMaker. The SageMaker Python SDK is easy to use, modular, extensible and compatible with TensorFlow and MXNet. This tutorial focuses on how to create a convolutional neural network model to train the [MNIST dataset](http://yann.lecun.com/exdb/mnist/) using **TensorFlow distributed training**.
### Set up the environment
```
import os
import sagemaker
from sagemaker import get_execution_role
sagemaker_session = sagemaker.Session()
role = get_execution_role()
```
### Download the MNIST dataset
```
import utils
from tensorflow.contrib.learn.python.learn.datasets import mnist
import tensorflow as tf
data_sets = mnist.read_data_sets('data', dtype=tf.uint8, reshape=False, validation_size=5000)
utils.convert_to(data_sets.train, 'train', 'data')
utils.convert_to(data_sets.validation, 'validation', 'data')
utils.convert_to(data_sets.test, 'test', 'data')
```
### Upload the data
We use the ```sagemaker.Session.upload_data``` function to upload our datasets to an S3 location. The return value inputs identifies the location -- we will use this later when we start the training job.
```
inputs = sagemaker_session.upload_data(path='data', key_prefix='data/DEMO-mnist')
```
# Construct a script for distributed training
Here is the full code for the network model:
```
!cat 'mnist.py'
```
The script here is and adaptation of the [TensorFlow MNIST example](https://github.com/tensorflow/models/tree/master/official/mnist). It provides a ```model_fn(features, labels, mode)```, which is used for training, evaluation and inference.
## A regular ```model_fn```
A regular **```model_fn```** follows the pattern:
1. [defines a neural network](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L96)
- [applies the ```features``` in the neural network](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L178)
- [if the ```mode``` is ```PREDICT```, returns the output from the neural network](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L186)
- [calculates the loss function comparing the output with the ```labels```](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L188)
- [creates an optimizer and minimizes the loss function to improve the neural network](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L193)
- [returns the output, optimizer and loss function](https://github.com/tensorflow/models/blob/master/official/mnist/mnist.py#L205)
## Writing a ```model_fn``` for distributed training
When distributed training happens, the same neural network will be sent to the multiple training instances. Each instance will predict a batch of the dataset, calculate loss and minimize the optimizer. One entire loop of this process is called **training step**.
### Syncronizing training steps
A [global step](https://www.tensorflow.org/api_docs/python/tf/train/global_step) is a global variable shared between the instances. It's necessary for distributed training, so the optimizer will keep track of the number of **training steps** between runs:
```python
train_op = optimizer.minimize(loss, tf.train.get_or_create_global_step())
```
That is the only required change for distributed training!
## Create a training job using the sagemaker.TensorFlow estimator
```
from sagemaker.tensorflow import TensorFlow
mnist_estimator = TensorFlow(entry_point='mnist.py',
role=role,
framework_version='1.12.0',
training_steps=1000,
evaluation_steps=100,
train_instance_count=2,
train_instance_type='ml.c4.xlarge')
mnist_estimator.fit(inputs)
```
The **```fit```** method will create a training job in two **ml.c4.xlarge** instances. The logs above will show the instances doing training, evaluation, and incrementing the number of **training steps**.
In the end of the training, the training job will generate a saved model for TF serving.
# Deploy the trained model to prepare for predictions
The deploy() method creates an endpoint which serves prediction requests in real-time.
```
mnist_predictor = mnist_estimator.deploy(initial_instance_count=1,
instance_type='ml.m4.xlarge')
```
# Invoking the endpoint
```
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
for i in range(10):
data = mnist.test.images[i].tolist()
tensor_proto = tf.make_tensor_proto(values=np.asarray(data), shape=[1, len(data)], dtype=tf.float32)
predict_response = mnist_predictor.predict(tensor_proto)
print("========================================")
label = np.argmax(mnist.test.labels[i])
print("label is {}".format(label))
prediction = predict_response['outputs']['classes']['int64_val'][0]
print("prediction is {}".format(prediction))
```
# Deleting the endpoint
```
sagemaker.Session().delete_endpoint(mnist_predictor.endpoint)
```
| true |
code
| 0.704008 | null | null | null | null |
|
# Configuring analyzers for the MSMARCO Document dataset
Before we start tuning queries and other index parameters, we wanted to first show a very simple iteration on the standard analyzers. In the MS MARCO Document dataset we have three fields: `url`, `title` and `body`. We tried just couple very small improvements, mostly to stopword lists, to see what would happen to our baseline queries. We now have two indices to play with:
- `msmarco-doument.defaults` with some default analyzers
- `url`: standard
- `title`: english
- `body`: english
- `msmarco-document` with customized analyzers
- `url`: english with URL-specific stopword list
- `title`: english with question-specfic stopword list
- `body`: english with question-specfic stopword list
The stopword lists have been changed:
1. Since the MS MARCO query dataset is all questions, it makes sense to add a few extra stop words like: who, what, when where, why, how
1. URLs in addition have some other words that don't really need to be searched on: http, https, www, com, edu
More details can be found in the index settings in `conf`.
```
%load_ext autoreload
%autoreload 2
import importlib
import os
import sys
from elasticsearch import Elasticsearch
# project library
sys.path.insert(0, os.path.abspath('..'))
import qopt
importlib.reload(qopt)
from qopt.notebooks import evaluate_mrr100_dev
# use a local Elasticsearch or Cloud instance (https://cloud.elastic.co/)
es = Elasticsearch('http://localhost:9200')
# set the parallelization parameter `max_concurrent_searches` for the Rank Evaluation API calls
max_concurrent_searches = 10
```
## Comparisons
The following runs a series of comparisons between the baseline default index `msmarco-document.default` and the custom index `msmarco-document`. We use multiple query types just to confirm that we make improvements across all of them.
### Query: combined per-field `match`es
```
def combined_matches(index):
evaluate_mrr100_dev(es, max_concurrent_searches, index, 'combined_matches', params={})
%%time
combined_matches('msmarco-document.defaults')
%%time
combined_matches('msmarco-document')
```
### Query: `multi_match` `cross_fields`
```
def multi_match_cross_fields(index):
evaluate_mrr100_dev(es, max_concurrent_searches, index,
template_id='cross_fields',
params={
'operator': 'OR',
'minimum_should_match': 50, # in percent/%
'tie_breaker': 0.0,
'url|boost': 1.0,
'title|boost': 1.0,
'body|boost': 1.0,
})
%%time
multi_match_cross_fields('msmarco-document.defaults')
%%time
multi_match_cross_fields('msmarco-document')
```
### Query: `multi_match` `best_fields`
```
def multi_match_best_fields(index):
evaluate_mrr100_dev(es, max_concurrent_searches, index,
template_id='best_fields',
params={
'tie_breaker': 0.0,
'url|boost': 1.0,
'title|boost': 1.0,
'body|boost': 1.0,
})
%%time
multi_match_best_fields('msmarco-document.defaults')
%%time
multi_match_best_fields('msmarco-document')
```
## Conclusion
As you can see, there's a measurable and consistent improvement with just some minor changes to the default analyzers. All other notebooks that follow will use the custom analyzers including for their baseline measurements.
| true |
code
| 0.452536 | null | null | null | null |
|
# Objective
In this notebook we will:
+ load and merge data from different sources (in this case, data source is filesystem.)
+ preprocess data
+ create features
+ visualize feature distributions across the classes
+ write down our observations about the data
```
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
male_df = pd.read_csv("../data/male.csv")
female_df = pd.read_csv("../data/female.csv")
male_df.head()
female_df.head()
#join these two dataframes into one
df = male_df.append(female_df)
#drop 'race' column as it is 'indian' for all
df = df.drop('race',axis=1)
#let's checkout head
df.head()
#let's checkout the tail
df.tail()
# Preprocessing
```
We want to predict the gender from the first name, because the surname doesn't say anything significant about Indian
names because Indian women generally adopt their husband's surname after marriage.
Also, it is a custom for many names to have prefixes like "Shri"/"Sri"/"Mr" for Men and "Smt"/"Ms."/"Miss." for women.
Let's validate that hypothesis and remove them.
```
df.describe()
df.info()
df.shape
```
the count of name and gender doesn't match. There must be some null values for name. Let's remove those.
```
df = df[~df.name.isnull()]
df.info()
```
there could be duplicate names. Let's find out and remove them.
```
fig,ax = plt.subplots(figsize=(12,7))
ax = df.name.value_counts().head(10).plot(kind='bar')
ax.set_xlabel('names')
ax.set_ylabel('frequency');
df = df.drop_duplicates('name')
df.shape
# our dataset almost reduced by half !
# let's remove special characters from the names. Some names might have been written in non-ASCII encodings.
# We need to remove those as well.
import re
import string
def remove_punctuation_and_numbers(x):
x = x.lower()
x = re.sub(r'[^\x00-\x7f]', r'', x)
# Removing (replacing with empty spaces actually) all the punctuations
x = re.sub("[" + string.punctuation + "]", "", x)
x = re.sub(r'[0-9]+',r'',x)
x = x.strip()
return x
df['name'] = df['name'].apply(remove_punctuation_and_numbers)
df.name.value_counts().head()
#let's remove names having less than 2 characters
df = df[df.name.str.len() > 2]
df.name.value_counts().head()
#let's see our class distribution
df.gender.value_counts()
#let's extract prefix/firstnames from the names
df['firstname'] = df.name.apply(lambda x: x.strip().split(" ")[0])
df.firstname.value_counts().head(10)
```
In India,
+ married women use the prefix *smt* or *Shrimati*,*Mrs*
+ unmarried women use *ku*, *kum* or *kumari*
+ *mohd* or *md* as the prefix for Muslim Men.
+ mr./kumar/kr/sri/shree/shriman/sh is a honorific for men
some more prefixes not present in the top 10 list above are:
```
df[df.firstname=='mr'].shape
df[df.firstname=='kumar'].shape
df[df.firstname=='kr'].shape
df[df.firstname=='miss'].shape
df[df.firstname=='mrs'].shape
df[df.firstname=='kum'].shape
df[df.firstname=='sri'].shape
df[df.firstname=='shri'].shape
df[df.firstname=='sh'].shape
df[df.firstname=='shree'].shape
df[df.firstname=='shrimati'].shape
df[df.name.str.startswith('su shree')].shape #edge case, sushri/su shree/kumari is used for unmarried Indian women, similar to Miss.
df[df.firstname == 'sushri'].shape
prefix = ['mr','kumar','kr','ku','kum','kumari','km',
'miss','mrs','mohd','md',
'sri','shri','sh','smt','shree','shrimati','su','sushri']
```
These prefixes can actually be used as a feature for our model. However, we won't use it in this iteration. We want to build a model based on just the name( without prefix or suffix/surname)
```
df.head()
# keep those names whose firstname is not a prefix
df_wo_prefix = df[~df.firstname.isin(prefix)]
df_wo_prefix.head()
df_wo_prefix.firstname.value_counts().head()
df_wo_prefix.shape
# drop duplicates from firstname column
df_wo_prefix = df_wo_prefix.drop_duplicates('firstname')
df_wo_prefix.head()
df_wo_prefix.shape
df_wo_prefix.firstname.value_counts().head()
# class distribution now
df_wo_prefix.gender.value_counts()
#drop name column
df_wo_prefix = df_wo_prefix.drop('name',axis=1)
df_wo_prefix.head()
# this is the final dataset we will be working with, let's save it to file
df_wo_prefix.to_csv('../data/names_processed.csv',index=False)
def extract_features(name):
name = name.lower() #making sure that the name is in lower case
features= {
'first_1':name[0],
'first_2':name[:2],
'first_3':name[:3],
'last_2':name[-2:],
'last_1': name[-1],
'length': len(name)
}
return features
extract_features('amit')
features = (df_wo_prefix
.firstname
.apply(extract_features)
.values
.tolist())
features_df = pd.DataFrame(features)
features_df.head()
# let's append our gender column here
features_df['gender'] = df_wo_prefix['gender'].values
features_df.head()
# let's analyse the features now.
# Question: how does the length of names differ between male and female?
freq = features_df['length'].value_counts() # frequency of lengths
fig,ax = plt.subplots(figsize=(12,7))
ax = freq.plot(kind='bar');
ax.set_xlabel('name length');
ax.set_ylabel('frequency');
```
Majority of name lengths lie between 5-7 characters. By name, we refer to 'firstname' here and will be referred to as same henceforth.
```
male_name_lengths = features_df.loc[features_df.gender=='m','length']
male_name_lengths_freq = male_name_lengths.value_counts()
male_name_lengths_freq
female_name_lengths = features_df.loc[features_df.gender=='f','length']
female_name_lengths_freq = female_name_lengths.value_counts()
female_name_lengths_freq
length_freq_long = (features_df
.groupby(['gender','length'])['length']
.agg({'length': 'count'})
.rename(columns={'gender':'gender','length':'freq'})
.reset_index())
length_freq_long.head()
length_freq_wide = length_freq_long.pivot(index='length',columns='gender',values='freq')
length_freq_wide = length_freq_wide.fillna(0)
length_freq_wide = length_freq_wide.astype('int')
length_freq_wide
fig,ax = plt.subplots(figsize=(12,6))
ax = length_freq_wide.plot(kind='bar',ax=ax)
ax.set_ylabel('frequency');
length_freq_wide.m.mean(),length_freq_wide.m.std()
length_freq_wide.f.mean(),length_freq_wide.f.std()
```
So does gender and name lengths have any relationship?
## Hypothesis
H0 : gender and name lengths are independent
Ha : gender and name lenghts are dependent
## significance level
For this test, let's keep the significance level as 0.05
```
from scipy.stats.mstats import normaltest
print('m: ',normaltest(length_freq_wide.m))
print('f: ',normaltest(length_freq_wide.f))
```
the p-value for both male and female name lengths are much less than the Chi-Square test statistics, hence null hypothesis is rejected.
**This means that there's a relationship between name length and gender.**
| true |
code
| 0.481271 | null | null | null | null |
|
# eICU Collaborative Research Database
# Notebook 4: Summary statistics
This notebook shows how summary statistics can be computed for a patient cohort using the `tableone` package. Usage instructions for tableone are at: https://pypi.org/project/tableone/
## Load libraries and connect to the database
```
# Import libraries
import numpy as np
import os
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.path as path
# Make pandas dataframes prettier
from IPython.display import display, HTML
# Access data using Google BigQuery.
from google.colab import auth
from google.cloud import bigquery
# authenticate
auth.authenticate_user()
# Set up environment variables
project_id='tdothealthhack-team'
os.environ["GOOGLE_CLOUD_PROJECT"]=project_id
# Helper function to read data from BigQuery into a DataFrame.
def run_query(query):
return pd.io.gbq.read_gbq(query, project_id=project_id, dialect="standard")
```
## Install and load the `tableone` package
The tableone package can be used to compute summary statistics for a patient cohort. Unlike the previous packages, it is not installed by default in Colab, so will need to install it first.
```
!pip install tableone
# Import the tableone class
from tableone import TableOne
```
## Load the patient cohort
In this example, we will load all data from the patient data, and link it to APACHE data to provide richer summary information.
```
# Link the patient and apachepatientresult tables on patientunitstayid
# using an inner join.
query = """
SELECT p.unitadmitsource, p.gender, p.age, p.ethnicity, p.admissionweight,
p.unittype, p.unitstaytype, a.acutephysiologyscore,
a.apachescore, a.actualiculos, a.actualhospitalmortality,
a.unabridgedunitlos, a.unabridgedhosplos
FROM `physionet-data.eicu_crd_demo.patient` p
INNER JOIN `physionet-data.eicu_crd_demo.apachepatientresult` a
ON p.patientunitstayid = a.patientunitstayid
WHERE apacheversion LIKE 'IVa'
"""
cohort = run_query(query)
cohort.head()
```
## Calculate summary statistics
Before summarizing the data, we will need to convert the ages to numerical values.
```
cohort['agenum'] = pd.to_numeric(cohort['age'], errors='coerce')
columns = ['unitadmitsource', 'gender', 'agenum', 'ethnicity',
'admissionweight','unittype','unitstaytype',
'acutephysiologyscore','apachescore','actualiculos',
'unabridgedunitlos','unabridgedhosplos']
TableOne(cohort, columns=columns, labels={'agenum': 'age'},
groupby='actualhospitalmortality',
label_suffix=True, limit=4)
```
## Questions
- Are the severity of illness measures higher in the survival or non-survival group?
- What issues suggest that some of the summary statistics might be misleading?
- How might you address these issues?
## Visualizing the data
Plotting the distribution of each variable by group level via histograms, kernel density estimates and boxplots is a crucial component to data analysis pipelines. Vizualisation is often is the only way to detect problematic variables in many real-life scenarios. We'll review a couple of the variables.
```
# Plot distributions to review possible multimodality
cohort[['acutephysiologyscore','agenum']].dropna().plot.kde(figsize=[12,8])
plt.legend(['APS Score', 'Age (years)'])
plt.xlim([-30,250])
```
## Questions
- Do the plots change your view on how these variable should be reported?
| true |
code
| 0.600013 | null | null | null | null |
|
# Ler a informação de um catálogo a partir de um arquivo texto e fazer gráficos de alguns parâmetros
## Autores
Adrian Price-Whelan, Kelle Cruz, Stephanie T. Douglas
## Tradução
Ricardo Ogando, Micaele Vitória
## Objetivos do aprendizado
* Ler um arquivo ASCII usando o `astropy.io`
* Converter entre representações de componentes de coordenadas usando o `astropy.coordinates` (de horas para graus)
* Fazer um gráfico do céu com projeção esférica usando o `matplotlib`
## Palavras-chave
arquivo entrada/saída, coordenadas, tabelas, unidades, gráficos de dispersão, matplotlib
## Sumário
Esse tutorial demonstra o uso do `astropy.io.ascii` para ler dados em ASCII, `astropy.coordinates` e `astropy.units` para converter Ascenção Reta (AR) (como um ângulo sexagesimal) para graus decimais, e `matplotlib` para fazer um diagrama cor-magnitude e localizações no céu em uma projeção Mollweide.
```
!wget https://raw.githubusercontent.com/astropy/astropy-tutorials/main/tutorials/notebooks/plot-catalog/Young-Objects-Compilation.csv
!wget https://raw.githubusercontent.com/astropy/astropy-tutorials/main/tutorials/notebooks/plot-catalog/simple_table.csv
!pwd
!rm Young-Objects-Compilation.csv.1
!cat simple_table.csv
import numpy as np
# Set up matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
```
Astropy provê funcionalidade para ler e manipular dados tabulares através do subpacote `astropy.table`. Um conjunto adicional de ferramentas para ler e escrever dados no formato ASCII, são dadas no subpacote `astropy.io.ascii`, mas usa fundamentalmente as classes e métodos implementadas no `astropy.table`.
Vamos começar importando o subpacote `ascii`:
```
from astropy.io import ascii
```
Em muitos casos, é suficiente usar a função `ascii.read('filename')`
como uma caixa preta para ler dados de arquivos com texto em formato de tabela.
Por padrão, essa função vai tentar descobrir como o seu dado está formatado/delimitado (por default, `guess=True`). Por exemplo, se o seu dado se parece com o a seguir:
# name,ra,dec
BLG100,17:51:00.0,-29:59:48
BLG101,17:53:40.2,-29:49:52
BLG102,17:56:20.2,-29:30:51
BLG103,17:56:20.2,-30:06:22
...
(veja o _simple_table.csv_)
`ascii.read()` vai retornar um objeto `Table`:
```
ascii.read("simple_table.csv")
tbl = ascii.read("simple_table.csv")
print(tbl)
```
Os nomes no cabeçalho são extraídos do topo do arquivo, e o delimitador é inferido a partir do resto do arquivo -- incrível!!!!
Podemos acessar as colunas diretamente usando seus nomes como 'chaves' da tabela:
```
tbl["ra"]
tbl[-1]
```
If we want to then convert the first RA (as a sexagesimal angle) to
decimal degrees, for example, we can pluck out the first (0th) item in
the column and use the `coordinates` subpackage to parse the string:
```
import astropy.coordinates as coord
import astropy.units as u
first_row = tbl[0] # get the first (0th) row
ra = coord.Angle(first_row["ra"], unit=u.hour) # create an Angle object
ra.degree # convert to degrees
```
Qual é a conta que o astropy está fazendo por você
```
17*15+(51/60)*15
```
Now let's look at a case where this breaks, and we have to specify some
more options to the `read()` function. Our data may look a bit messier::
,,,,2MASS Photometry,,,,,,WISE Photometry,,,,,,,,Spectra,,,,Astrometry,,,,,,,,,,,
Name,Designation,RA,Dec,Jmag,J_unc,Hmag,H_unc,Kmag,K_unc,W1,W1_unc,W2,W2_unc,W3,W3_unc,W4,W4_unc,Spectral Type,Spectra (FITS),Opt Spec Refs,NIR Spec Refs,pm_ra (mas),pm_ra_unc,pm_dec (mas),pm_dec_unc,pi (mas),pi_unc,radial velocity (km/s),rv_unc,Astrometry Refs,Discovery Refs,Group/Age,Note
,00 04 02.84 -64 10 35.6,1.01201,-64.18,15.79,0.07,14.83,0.07,14.01,0.05,13.37,0.03,12.94,0.03,12.18,0.24,9.16,null,L1γ,,Kirkpatrick et al. 2010,,,,,,,,,,,Kirkpatrick et al. 2010,,
PC 0025+04,00 27 41.97 +05 03 41.7,6.92489,5.06,16.19,0.09,15.29,0.10,14.96,0.12,14.62,0.04,14.14,0.05,12.24,null,8.89,null,M9.5β,,Mould et al. 1994,,0.0105,0.0004,-0.0008,0.0003,,,,,Faherty et al. 2009,Schneider et al. 1991,,,00 32 55.84 -44 05 05.8,8.23267,-44.08,14.78,0.04,13.86,0.03,13.27,0.04,12.82,0.03,12.49,0.03,11.73,0.19,9.29,null,L0γ,,Cruz et al. 2009,,0.1178,0.0043,-0.0916,0.0043,38.4,4.8,,,Faherty et al. 2012,Reid et al. 2008,,
...
(see _Young-Objects-Compilation.csv_)
If we try to just use `ascii.read()` on this data, it fails to parse the names out and the column names become `col` followed by the number of the column:
```
tbl = ascii.read("Young-Objects-Compilation.csv")
tbl.colnames
tbl
```
What happened? The column names are just `col1`, `col2`, etc., the
default names if `ascii.read()` is unable to parse out column
names. We know it failed to read the column names, but also notice
that the first row of data are strings -- something else went wrong!
```
tbl[0]
```
A few things are causing problems here. First, there are two header
lines in the file and the header lines are not denoted by comment
characters. The first line is actually some meta data that we don't
care about, so we want to skip it. We can get around this problem by
specifying the `header_start` keyword to the `ascii.read()` function.
This keyword argument specifies the index of the row in the text file
to read the column names from:
```
tbl = ascii.read("Young-Objects-Compilation.csv", header_start=1)
tbl.colnames
```
Great! Now the columns have the correct names, but there is still a
problem: all of the columns have string data types, and the column
names are still included as a row in the table. This is because by
default the data are assumed to start on the second row (index=1).
We can specify `data_start=2` to tell the reader that the data in
this file actually start on the 3rd (index=2) row:
```
tbl = ascii.read("Young-Objects-Compilation.csv", header_start=1, data_start=2)
```
Some of the columns have missing data, for example, some of the `RA` values are missing (denoted by -- when printed):
```
print(tbl['RA'])
```
This is called a __Masked column__ because some missing values are
masked out upon display. If we want to use this numeric data, we have
to tell `astropy` what to fill the missing values with. We can do this
with the `.filled()` method. For example, to fill all of the missing
values with `NaN`'s:
```
tbl['RA'].filled(np.nan)
```
Let's recap what we've done so far, then make some plots with the
data. Our data file has an extra line above the column names, so we
use the `header_start` keyword to tell it to start from line 1 instead
of line 0 (remember Python is 0-indexed!). We then used had to specify
that the data starts on line 2 using the `data_start`
keyword. Finally, we note some columns have missing values.
```
data = ascii.read("Young-Objects-Compilation.csv", header_start=1, data_start=2)
```
Now that we have our data loaded, let's plot a color-magnitude diagram.
Here we simply make a scatter plot of the J-K color on the x-axis
against the J magnitude on the y-axis. We use a trick to flip the
y-axis `plt.ylim(reversed(plt.ylim()))`. Called with no arguments,
`plt.ylim()` will return a tuple with the axis bounds,
e.g. (0,10). Calling the function _with_ arguments will set the limits
of the axis, so we simply set the limits to be the reverse of whatever they
were before. Using this `pylab`-style plotting is convenient for
making quick plots and interactive use, but is not great if you need
more control over your figures.
```
plt.scatter(data["Jmag"] - data["Kmag"], data["Jmag"]) # plot J-K vs. J
plt.ylim(reversed(plt.ylim())) # flip the y-axis
plt.xlabel("$J-K_s$", fontsize=20)
plt.ylabel("$J$", fontsize=20)
```
As a final example, we will plot the angular positions from the
catalog on a 2D projection of the sky. Instead of using `pylab`-style
plotting, we'll take a more object-oriented approach. We'll start by
creating a `Figure` object and adding a single subplot to the
figure. We can specify a projection with the `projection` keyword; in
this example we will use a Mollweide projection. Unfortunately, it is
highly non-trivial to make the matplotlib projection defined this way
follow the celestial convention of longitude/RA increasing to the left.
The axis object, `ax`, knows to expect angular coordinate
values. An important fact is that it expects the values to be in
_radians_, and it expects the azimuthal angle values to be between
(-180º,180º). This is (currently) not customizable, so we have to
coerce our RA data to conform to these rules! `astropy` provides a
coordinate class for handling angular values, `astropy.coordinates.Angle`.
We can convert our column of RA values to radians, and wrap the
angle bounds using this class.
```
ra = coord.Angle(data['RA'].filled(np.nan)*u.degree)
ra = ra.wrap_at(180*u.degree)
dec = coord.Angle(data['Dec'].filled(np.nan)*u.degree)
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection="mollweide")
ax.scatter(ra.radian, dec.radian)
```
By default, matplotlib will add degree tick labels, so let's change the
horizontal (x) tick labels to be in units of hours, and display a grid:
```
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection="mollweide")
ax.scatter(ra.radian, dec.radian)
ax.set_xticklabels(['14h','16h','18h','20h','22h','0h','2h','4h','6h','8h','10h'])
ax.grid(True)
```
We can save this figure as a PDF using the `savefig` function:
```
fig.savefig("map.pdf")
```
## Exercises
Make the map figures as just above, but color the points by the `'Kmag'` column of the table.
```
```
Try making the maps again, but with each of the following projections: `aitoff`, `hammer`, `lambert`, and `None` (which is the same as not giving any projection). Do any of them make the data seem easier to understand?
```
```
| true |
code
| 0.603465 | null | null | null | null |
|
# Introduction to Classification.
Notebook version: 2.1 (Oct 19, 2018)
Author: Jesús Cid Sueiro (jcid@tsc.uc3m.es)
Jerónimo Arenas García (jarenas@tsc.uc3m.es)
Changes: v.1.0 - First version. Extracted from a former notebook on K-NN
v.2.0 - Adapted to Python 3.0 (backcompatible with Python 2.7)
v.2.1 - Minor corrections affecting the notation and assumptions
```
from __future__ import print_function
# To visualize plots in the notebook
%matplotlib inline
# Import some libraries that will be necessary for working with data and displaying plots
import csv # To read csv files
import random
import matplotlib.pyplot as plt
import numpy as np
from scipy import spatial
from sklearn import neighbors, datasets
```
## 1. The Classification problem
In a generic classification problem, we are given an observation vector ${\bf x}\in \mathbb{R}^N$ which is known to belong to one and only one *category* or *class*, $y$, in the set ${\mathcal Y} = \{0, 1, \ldots, M-1\}$. The goal of a classifier system is to predict the value of $y$ based on ${\bf x}$.
To design the classifier, we are given a collection of labelled observations ${\mathcal D} = \{({\bf x}^{(k)}, y^{(k)})\}_{k=0}^{K-1}$ where, for each observation ${\bf x}^{(k)}$, the value of its true category, $y^{(k)}$, is known.
### 1.1 Binary Classification
We will focus in binary classification problems, where the label set is binary, ${\mathcal Y} = \{0, 1\}$. Despite its simplicity, this is the most frequent case.
Many multi-class classification problems are usually solved by decomposing them into a collection of binary problems.
### 1.2. The i.i.d. assumption.
The classification algorithms, as many other machine learning algorithms, are based on two major underlying hypothesis:
- All samples in dataset ${\mathcal D}$ have been generated by the same distribution $p_{{\bf X}, Y}({\bf x}, y)$.
- For any test data, the tuple formed by the input sample and its unknown class, $({\bf x}, y)$, is an independent outcome of the *same* distribution.
These two assumptions are essential to have some guarantees that a classifier design based on ${\mathcal D}$ has a good perfomance when applied to new input samples. Note that, despite assuming the existence of an underlying distribution, such distribution is unknown: otherwise, we could ignore ${\mathcal D}$ and apply classic decision theory to find the optimal predictor based on $p_{{\bf X}, Y}({\bf x}, y)$.
## 2. A simple classification problem: the Iris dataset
(Iris dataset presentation is based on this <a href=http://machinelearningmastery.com/tutorial-to-implement-k-nearest-neighbors-in-python-from-scratch/> Tutorial </a> by <a href=http://machinelearningmastery.com/about/> Jason Brownlee</a>)
As an illustration, consider the <a href = http://archive.ics.uci.edu/ml/datasets/Iris> Iris dataset </a>, taken from the <a href=http://archive.ics.uci.edu/ml/> UCI Machine Learning repository </a>. Quoted from the dataset description:
> This is perhaps the best known database to be found in the pattern recognition literature. The data set contains 3 classes of 50 instances each, where each class refers to a type of iris plant. [...] One class is linearly separable from the other 2; the latter are NOT linearly separable from each other.
The *class* is the species, which is one of *setosa*, *versicolor* or *virginica*. Each instance contains 4 measurements of given flowers: sepal length, sepal width, petal length and petal width, all in centimeters.
```
# Taken from Jason Brownlee notebook.
with open('datasets/iris.data', 'r') as csvfile:
lines = csv.reader(csvfile)
for row in lines:
print(','.join(row))
```
Next, we will split the data into a training dataset, that will be used to learn the classification model, and a test dataset that we can use to evaluate its the accuracy.
We first need to convert the flower measures that were loaded as strings into numbers that we can work with. Next we need to split the data set **randomly** into train and datasets. A ratio of 67/33 for train/test will be used.
The code fragment below defines a function `loadDataset` that loads the data in a CSV with the provided filename and splits it randomly into train and test datasets using the provided split ratio.
```
# Adapted from a notebook by Jason Brownlee
def loadDataset(filename, split):
xTrain = []
cTrain = []
xTest = []
cTest = []
with open(filename, 'r') as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
for i in range(len(dataset)-1):
for y in range(4):
dataset[i][y] = float(dataset[i][y])
item = dataset[i]
if random.random() < split:
xTrain.append(item[0:-1])
cTrain.append(item[-1])
else:
xTest.append(item[0:-1])
cTest.append(item[-1])
return xTrain, cTrain, xTest, cTest
```
We can use this function to get a data split. Note that, because of the way samples are assigned to the train or test datasets, the number of samples in each partition will differ if you run the code several times.
```
xTrain_all, cTrain_all, xTest_all, cTest_all = loadDataset('./datasets/iris.data', 0.67)
nTrain_all = len(xTrain_all)
nTest_all = len(xTest_all)
print('Train:', str(nTrain_all))
print('Test:', str(nTest_all))
```
To get some intuition about this four dimensional dataset we can plot 2-dimensional projections taking only two variables each time.
```
i = 2 # Try 0,1,2,3
j = 3 # Try 0,1,2,3 with j!=i
# Take coordinates for each class separately
xiSe = [xTrain_all[n][i] for n in range(nTrain_all) if cTrain_all[n]=='Iris-setosa']
xjSe = [xTrain_all[n][j] for n in range(nTrain_all) if cTrain_all[n]=='Iris-setosa']
xiVe = [xTrain_all[n][i] for n in range(nTrain_all) if cTrain_all[n]=='Iris-versicolor']
xjVe = [xTrain_all[n][j] for n in range(nTrain_all) if cTrain_all[n]=='Iris-versicolor']
xiVi = [xTrain_all[n][i] for n in range(nTrain_all) if cTrain_all[n]=='Iris-virginica']
xjVi = [xTrain_all[n][j] for n in range(nTrain_all) if cTrain_all[n]=='Iris-virginica']
plt.plot(xiSe, xjSe,'bx', label='Setosa')
plt.plot(xiVe, xjVe,'r.', label='Versicolor')
plt.plot(xiVi, xjVi,'g+', label='Virginica')
plt.xlabel('$x_' + str(i) + '$')
plt.ylabel('$x_' + str(j) + '$')
plt.legend(loc='best')
plt.show()
```
In the following, we will design a classifier to separate classes "Versicolor" and "Virginica" using $x_0$ and $x_1$ only. To do so, we build a training set with samples from these categories, and a bynary label $y^{(k)} = 1$ for samples in class "Virginica", and $0$ for "Versicolor" data.
```
# Select two classes
c0 = 'Iris-versicolor'
c1 = 'Iris-virginica'
# Select two coordinates
ind = [0, 1]
# Take training test
X_tr = np.array([[xTrain_all[n][i] for i in ind] for n in range(nTrain_all)
if cTrain_all[n]==c0 or cTrain_all[n]==c1])
C_tr = [cTrain_all[n] for n in range(nTrain_all)
if cTrain_all[n]==c0 or cTrain_all[n]==c1]
Y_tr = np.array([int(c==c1) for c in C_tr])
n_tr = len(X_tr)
# Take test set
X_tst = np.array([[xTest_all[n][i] for i in ind] for n in range(nTest_all)
if cTest_all[n]==c0 or cTest_all[n]==c1])
C_tst = [cTest_all[n] for n in range(nTest_all)
if cTest_all[n]==c0 or cTest_all[n]==c1]
Y_tst = np.array([int(c==c1) for c in C_tst])
n_tst = len(X_tst)
# Separate components of x into different arrays (just for the plots)
x0c0 = [X_tr[n][0] for n in range(n_tr) if Y_tr[n]==0]
x1c0 = [X_tr[n][1] for n in range(n_tr) if Y_tr[n]==0]
x0c1 = [X_tr[n][0] for n in range(n_tr) if Y_tr[n]==1]
x1c1 = [X_tr[n][1] for n in range(n_tr) if Y_tr[n]==1]
# Scatterplot.
labels = {'Iris-setosa': 'Setosa',
'Iris-versicolor': 'Versicolor',
'Iris-virginica': 'Virginica'}
plt.plot(x0c0, x1c0,'r.', label=labels[c0])
plt.plot(x0c1, x1c1,'g+', label=labels[c1])
plt.xlabel('$x_' + str(ind[0]) + '$')
plt.ylabel('$x_' + str(ind[1]) + '$')
plt.legend(loc='best')
plt.show()
```
## 3. A Baseline Classifier: Maximum A Priori.
For the selected data set, we have two clases and a dataset with the following class proportions:
```
print('Class 0 (' + c0 + '): ' + str(n_tr - sum(Y_tr)) + ' samples')
print('Class 1 (' + c1 + '): ' + str(sum(Y_tr)) + ' samples')
```
The maximum a priori classifier assigns any sample ${\bf x}$ to the most frequent class in the training set. Therefore, the class prediction $y$ for any sample ${\bf x}$ is
```
y = int(2*sum(Y_tr) > n_tr)
print('y = ' + str(y) + ' (' + (c1 if y==1 else c0) + ')')
```
The error rate for this baseline classifier is:
```
# Training and test error arrays
E_tr = (Y_tr != y)
E_tst = (Y_tst != y)
# Error rates
pe_tr = float(sum(E_tr)) / n_tr
pe_tst = float(sum(E_tst)) / n_tst
print('Pe(train):', str(pe_tr))
print('Pe(test):', str(pe_tst))
```
The error rate of the baseline classifier is a simple benchmark for classification. Since the maximum a priori decision is independent on the observation, ${\bf x}$, any classifier based on ${\bf x}$ should have a better (or, at least, not worse) performance than the baseline classifier.
## 3. Parametric vs non-parametric classification.
Most classification algorithms can be fitted to one of two categories:
1. Parametric classifiers: to classify any input sample ${\bf x}$, the classifier applies some function $f_{\bf w}({\bf x})$ which depends on some parameters ${\bf w}$. The training dataset is used to estimate ${\bf w}$. Once the parameter has been estimated, the training data is no longer needed to classify new inputs.
2. Non-parametric classifiers: the classifier decision for any input ${\bf x}$ depend on the training data in a direct manner. The training data must be preserve to classify new data.
| true |
code
| 0.332292 | null | null | null | null |
|
Per a recent request somebody posted on Twitter, I thought it'd be fun to write a quick scraper for the [biorxiv](http://biorxiv.org/), an excellent new tool for posting pre-prints of articles before they're locked down with a publisher embargo.
A big benefit of open science is the ability to use modern technologies (like web scraping) to make new use of data that would originally be unavailable to the public. One simple example of this is information and metadata about published articles. While we're not going to dive too deeply here, maybe this will serve as inspiration for somebody else interested in scraping the web.
First we'll do a few imports. We'll rely heavily on the `requests` and `BeautifulSoup` packages, which together make an excellent one-two punch for doing web scraping. We coud use something like `scrapy`, but that seems a little overkill for this small project.
```
import requests
import pandas as pd
import seaborn as sns
import numpy as np
from bs4 import BeautifulSoup as bs
import matplotlib.pyplot as plt
from tqdm import tqdm
%matplotlib inline
```
From a quick look at the biorxiv we can see that its search API works in a pretty simple manner. I tried typing in a simple search query and got something like this:
`http://biorxiv.org/search/neuroscience%20numresults%3A100%20sort%3Arelevance-rank`
Here we can see that the term you search for comes just after `/search/`, and parameters for the search, like `numresults`. The keyword/value pairs are separated by a `%3A` character, which corresponds to `:` (see [this site](http://www.degraeve.com/reference/urlencoding.php) for a reference of url encoding characters), and these key/value pairs are separated by `%20`, which corresponds to a space.
So, let's do a simple scrape and see what the results look like. We'll query the biorxiv API to see what kind of structure the result will have.
```
n_results = 20
url = "http://biorxiv.org/search/neuroscience%20numresults%3A{}".format(
n_results)
resp = requests.post(url)
# I'm not going to print this because it messes up the HTML rendering
# But you get the idea...probably better to look in Chrome anyway ;)
# text = bs(resp.text)
```
If we search through the result, you may notice that search results are organized into a list (denoted by `li` for each item). Inside each item is information about the article's title (in a `div` of class `highwire-cite-title`) and author information (in a `div` of calss `highwire-cite-authors`).
Let's use this information to ask three questions:
1. How has the rate of publications for a term changed over the years
1. Who's been publishing under that term.
1. What kinds of things are people publishing?
For each, we'll simply use the phrase "neuroscience", although you could use whatever you like.
To set up this query, we'll need to use another part of the biorxiv API, the `limit_from` paramter. This lets us constrain the search to a specific month of the year. That way we can see the monthly submissions going back several years.
We'll loop through years / months, and pull out the author and title information. We'll do this with two dataframes, one for authors, one for articles.
```
# Define the URL and start/stop years
stt_year = 2012
stp_year = 2016
search_term = "neuroscience"
url_base = "http://biorxiv.org/search/{}".format(search_term)
url_params = "%20limit_from%3A{0}-{1}-01%20limit_to%3A{0}-{2}-01%20numresults%3A100%20format_result%3Astandard"
url = url_base + url_params
# Now we'll do the scraping...
all_articles = []
all_authors = []
for yr in tqdm(range(stt_year, stp_year + 1)):
for mn in range(1, 12):
# Populate the fields with our current query and post it
this_url = url.format(yr, mn, mn + 1)
resp = requests.post(this_url)
html = bs(resp.text)
# Collect the articles in the result in a list
articles = html.find_all('li', attrs={'class': 'search-result'})
for article in articles:
# Pull the title, if it's empty then skip it
title = article.find('span', attrs={'class': 'highwire-cite-title'})
if title is None:
continue
title = title.text.strip()
# Collect year / month / title information
all_articles.append([yr, mn, title])
# Now collect author information
authors = article.find_all('span', attrs={'class': 'highwire-citation-author'})
for author in authors:
all_authors.append((author.text, title))
# We'll collect these into DataFrames for subsequent use
authors = pd.DataFrame(all_authors, columns=['name', 'title'])
articles = pd.DataFrame(all_articles, columns=['year', 'month', 'title'])
```
To make things easier to cross-reference, we'll add an `id` column that's unique for each title. This way we can more simply join the dataframes to do cool things:
```
# Define a dictionary of title: ID mappings
unique_ids = {title: ii for ii, title in enumerate(articles['title'].unique())}
articles['id'] = [unique_ids[title] for title in articles['title']]
authors['id'] = [unique_ids[title] for title in authors['title']]
```
Now, we can easily join these two dataframes together if we so wish:
```
pd.merge(articles, authors, on=['id', 'title']).head()
```
# Question 1: How has the published articles rate changed?
This one is pretty easy to ask. Since we have both year / month data about each article, we can plot the number or articles for each group of time. To do this, let's first turn these numbers into an actual "datetime" object. This let's us do some clever plotting magic with pandas
```
# Add a "date" column
dates = [pd.datetime(yr, mn, day=1)
for yr, mn in articles[['year', 'month']].values]
articles['date'] = dates
# Now drop the year / month columns because they're redundant
articles = articles.drop(['year', 'month'], axis=1)
```
Now, we can simply group by month, sum the number of results, and plot this over time:
```
monthly = articles.groupby('date').count()['title'].to_frame()
ax = monthly['title'].plot()
ax.set_title('Articles published per month for term\n{}'.format(search_term))
```
We can also plot the cumulative number of papers published:
```
cumulative = np.cumsum(monthly.values)
monthly['cumulative'] = cumulative
# Now plot cumulative totals
ax = monthly['cumulative'].plot()
ax.set_title('Cumulative number of papers matching term \n{}'.format(search_term))
ax.set_ylabel('Number of Papers')
```
# Question 2: Which author uses pre-prints the most?
For this one, we can use the "authors" dataframe. We'll group by author name, and count the number of publications per author:
```
# Group by author and count the number of items
author_counts = authors.groupby('name').count()['title'].to_frame('count')
# We'll take the top 30 authors
author_counts = author_counts.sort_values('count', ascending=False)
author_counts = author_counts.iloc[:30].reset_index()
```
We'll use some `pandas` magical gugu to get this one done. Who is the greatest pre-print neuroscientist of them all?
```
# So we can plot w/ pretty colors
cmap = plt.cm.viridis
colors = cmap(author_counts['count'].values / float(author_counts['count'].max()))
# Make the plot
fig, ax = plt.subplots(figsize=(10, 5))
ax = author_counts.plot.bar('name', 'count', color=colors, ax=ax)
_ = plt.setp(ax.get_xticklabels(), rotation=45, ha='right')
```
Rather than saying congratulations to #1 etc here, I'll just take this space to say that all of these researchers are awesome for helping push scientific publishing technologies into the 21st century ;)
# Question 3: What topics are covered in the titles?
For this one we'll use a super floofy answer, but maybe it'll give us something pretty. We'll use the wordcloud module, which implements `fit` and `predict` methods similar to scikit-learn. We can train it on the words in the titles, and then create a pretty word cloud using these words.
To do this, we'll use the `wordcloud` module along with `sklearn`'s stop words (which are also useful for text analysis, incidentally)
```
import wordcloud as wc
from sklearn.feature_extraction.text import ENGLISH_STOP_WORDS
# We'll collect the titles and turn them into one giant string
titles = articles['title'].values
titles = ' '.join(titles)
# Then define stop words to use...we'll include some "typical" brain words
our_stop_words = list(ENGLISH_STOP_WORDS) + ['brain', 'neural']
```
Now, generating a word cloud is as easy as a call to `generate_from_text`. Then we can output in whatever format we like
```
# This function takes a buch of dummy arguments and returns random colors
def color_func(word=None, font_size=None, position=None,
orientation=None, font_path=None, random_state=None):
rand = np.clip(np.random.rand(), .2, None)
cols = np.array(plt.cm.rainbow(rand)[:3])
cols = cols * 255
return 'rgb({:.0f}, {:.0f}, {:.0f})'.format(*cols)
# Fit the cloud
cloud = wc.WordCloud(stopwords=our_stop_words,
color_func=color_func)
cloud.generate_from_text(titles)
# Now make a pretty picture
im = cloud.to_array()
fig, ax = plt.subplots()
ax.imshow(im, cmap=plt.cm.viridis)
ax.set_axis_off()
```
Looks like those cognitive neuroscience folks are leading the charge towards pre-print servers. Hopefully in the coming years we'll see increased adoption from the systems and cellular fields as well.
# Wrapup
Here we played with just a few questions that you can ask with some simple web scraping and the useful tools in python. There's a lot more that you could do with it, but I'll leave that up to readers to figure out for themselves :)
| true |
code
| 0.580233 | null | null | null | null |
|
# Chebychev polynomial and spline approximantion of various functions
**Randall Romero Aguilar, PhD**
This demo is based on the original Matlab demo accompanying the <a href="https://mitpress.mit.edu/books/applied-computational-economics-and-finance">Computational Economics and Finance</a> 2001 textbook by Mario Miranda and Paul Fackler.
Original (Matlab) CompEcon file: **demapp05.m**
Running this file requires the Python version of CompEcon. This can be installed with pip by running
!pip install compecon --upgrade
<i>Last updated: 2021-Oct-01</i>
<hr>
## About
Demonstrates Chebychev polynomial, cubic spline, and linear spline approximation for the following functions
\begin{align}
y &= 1 + x + 2x^2 - 3x^3 \\
y &= \exp(-x) \\
y &= \frac{1}{1+25x^2} \\
y &= \sqrt{|x|}
\end{align}
## Initial tasks
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from compecon import BasisChebyshev, BasisSpline, nodeunif
```
### Functions to be approximated
```
funcs = [lambda x: 1 + x + 2 * x ** 2 - 3 * x ** 3,
lambda x: np.exp(-x),
lambda x: 1 / ( 1 + 25 * x ** 2),
lambda x: np.sqrt(np.abs(x))]
fst = ['$y = 1 + x + 2x^2 - 3x^3$', '$y = \exp(-x)$',
'$y = 1/(1+25x^2)$', '$y = \sqrt{|x|}$']
```
Set degree of approximation and endpoints of approximation interval
```
n = 7 # degree of approximation
a = -1 # left endpoint
b = 1 # right endpoint
```
Construct uniform grid for error ploting
```
x = np.linspace(a, b, 2001)
def subfig(f, title):
# Construct interpolants
C = BasisChebyshev(n, a, b, f=f)
S = BasisSpline(n, a, b, f=f)
L = BasisSpline(n, a, b, k=1, f=f)
data = pd.DataFrame({
'actual': f(x),
'Chebyshev': C(x),
'Cubic Spline': S(x),
'Linear Spline': L(x)},
index = x)
fig1, axs = plt.subplots(2,2, figsize=[12,6], sharex=True, sharey=True)
fig1.suptitle(title)
data.plot(ax=axs, subplots=True)
errors = data[['Chebyshev', 'Cubic Spline']].subtract(data['actual'], axis=0)
fig2, ax = plt.subplots(figsize=[12,3])
fig2.suptitle("Approximation Error")
errors.plot(ax=ax)
```
## Polynomial
$y = 1 + x + 2x^2 - 3x^3$
```
subfig(lambda x: 1 + x + 2*x**2 - 3*x**3, '$y = 1 + x + 2x^2 - 3x^3$')
```
## Exponential
$y = \exp(-x)$
```
subfig(lambda x: np.exp(-x),'$y = \exp(-x)$')
```
## Rational
$y = 1/(1+25x^2)$
```
subfig(lambda x: 1 / ( 1 + 25 * x ** 2),'$y = 1/(1+25x^2)$')
```
## Kinky
$y = \sqrt{|x|}$
```
subfig(lambda x: np.sqrt(np.abs(x)), '$y = \sqrt{|x|}$')
```
| true |
code
| 0.592077 | null | null | null | null |
|
```
Copyright 2021 IBM Corporation
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
```
# Logistic Regression on MNIST8M Dataset
## Background
The MNIST database of handwritten digits has a training set of 60,000 examples, and a test set of 10,000 examples. It is a subset of a larger set available from NIST. The digits have been size-normalized and centered in a fixed-size image. It is a good database for people who want to try learning techniques and pattern recognition methods on real-world data while spending minimal efforts on preprocessing and formatting.
## Source
We use an inflated version of the dataset (`mnist8m`) from the paper:
Gaëlle Loosli, Stéphane Canu and Léon Bottou: *Training Invariant Support Vector Machines using Selective Sampling*, in [Large Scale Kernel Machines](https://leon.bottou.org/papers/lskm-2007), Léon Bottou, Olivier Chapelle, Dennis DeCoste, and Jason Weston editors, 301–320, MIT Press, Cambridge, MA., 2007.
We download the pre-processed dataset from the [LIBSVM dataset repository](https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/).
## Goal
The goal of this notebook is to illustrate how Snap ML can accelerate training of a logistic regression model on this dataset.
## Code
```
cd ../../
CACHE_DIR='cache-dir'
import numpy as np
import time
from datasets import Mnist8m
from sklearn.linear_model import LogisticRegression
from snapml import LogisticRegression as SnapLogisticRegression
from sklearn.metrics import accuracy_score as score
dataset = Mnist8m(cache_dir=CACHE_DIR)
X_train, X_test, y_train, y_test = dataset.get_train_test_split()
print("Number of examples: %d" % (X_train.shape[0]))
print("Number of features: %d" % (X_train.shape[1]))
print("Number of classes: %d" % (len(np.unique(y_train))))
model = LogisticRegression(fit_intercept=False, n_jobs=4, multi_class='ovr')
t0 = time.time()
model.fit(X_train, y_train)
t_fit_sklearn = time.time()-t0
score_sklearn = score(y_test, model.predict(X_test))
print("Training time (sklearn): %6.2f seconds" % (t_fit_sklearn))
print("Accuracy score (sklearn): %.4f" % (score_sklearn))
model = SnapLogisticRegression(fit_intercept=False, n_jobs=4)
t0 = time.time()
model.fit(X_train, y_train)
t_fit_snapml = time.time()-t0
score_snapml = score(y_test, model.predict(X_test))
print("Training time (snapml): %6.2f seconds" % (t_fit_snapml))
print("Accuracy score (snapml): %.4f" % (score_snapml))
speed_up = t_fit_sklearn/t_fit_snapml
score_diff = (score_snapml-score_sklearn)/score_sklearn
print("Speed-up: %.1f x" % (speed_up))
print("Relative diff. in score: %.4f" % (score_diff))
```
## Disclaimer
Performance results always depend on the hardware and software environment.
Information regarding the environment that was used to run this notebook are provided below:
```
import utils
environment = utils.get_environment()
for k,v in environment.items():
print("%15s: %s" % (k, v))
```
## Record Statistics
Finally, we record the enviroment and performance statistics for analysis outside of this standalone notebook.
```
import scrapbook as sb
sb.glue("result", {
'dataset': dataset.name,
'n_examples_train': X_train.shape[0],
'n_examples_test': X_test.shape[0],
'n_features': X_train.shape[1],
'n_classes': len(np.unique(y_train)),
'model': type(model).__name__,
'score': score.__name__,
't_fit_sklearn': t_fit_sklearn,
'score_sklearn': score_sklearn,
't_fit_snapml': t_fit_snapml,
'score_snapml': score_snapml,
'score_diff': score_diff,
'speed_up': speed_up,
**environment,
})
```
| true |
code
| 0.844601 | null | null | null | null |
|
## Example 1 - Common Driver
Here we investigate the statistical association between summer precipitation (JJA mean) in Denmark (DK) and the Mediterranean (MED). A standard correlation test shows them to be negatively correlated (r = -0.24). However, this association is not causal but is due to both regions being affected by the position of the North Atlantic storm tracks, as described by the North Atlantic Oscillation (NAO) index.
<img src="../images/ex1.png" width="500" height="600">
### References / Notes
1. Mediterranean region as described in http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.368.3679&rep=rep1&type=pdf
## Imports
```
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import os
import iris
import iris.quickplot as qplt
import statsmodels.api as sm
from scipy import signal
from scipy import stats
```
### Step 1) Load the data + Extract regions of interest
```
precip = iris.load_cube('../sample_data/precip_jja.nc', 'Monthly Mean of Precipitation Rate')
nao = iris.load_cube('../sample_data/nao_jja.nc', 'nao')
```
#### Extract regions of interest:
#### Mediterranean (MED)
```
med = precip.intersection(longitude=(10.0, 30.0), latitude=(36, 41.0))
qplt.pcolormesh(med[0])
plt.gca().coastlines()
```
#### Denmark (DK)
```
dk = precip.intersection(longitude=(2, 15), latitude=(50, 60))
qplt.pcolormesh(dk[0])
plt.gca().coastlines()
```
#### Create regional means
```
def areal_mean(cube):
grid_areas = iris.analysis.cartography.area_weights(cube)
cube = cube.collapsed(['longitude', 'latitude'], iris.analysis.MEAN, weights=grid_areas)
return cube
# Areal mean
med = areal_mean(med)
dk = areal_mean(dk)
```
### Step 2) Plotting + Data Processing
```
fig = plt.figure(figsize=(8, 8))
plt.subplot(311)
qplt.plot(nao)
plt.title('NAO')
plt.subplot(312)
qplt.plot(med)
plt.title('Med precip')
plt.subplot(313)
qplt.plot(dk)
plt.title('Denmark precip')
plt.tight_layout()
```
#### Standardize the data (zero mean, unit variance)
```
NAO = (nao - np.mean(nao.data))/np.std(nao.data)
MED = (med - np.mean(med.data))/np.std(med.data)
DK = (dk - np.mean(dk.data))/np.std(dk.data)
```
#### Detrend
```
NAO = signal.detrend(NAO.data)
MED = signal.detrend(MED.data)
DK = signal.detrend(DK.data)
```
### Step 3) Data analysis
```
#==========================================================
# Calculate the Pearson Correlation of MED and DK
#==========================================================
X = DK[:]
Y = MED[:]
r_dk_med, p_dk_med = stats.pearsonr(X, Y)
print(" The correlation of DK and MED is ", round(r_dk_med,2))
print(" p-value is ", round(p_dk_med, 2))
#==================================================================================
# Condtion out the effect of NAO
# here this is done by calculating the partial correlation of DK and MED conditiona on NAO
# alternatively, one could also just regress DK on on MED and NAO
#==================================================================================
# 1) regress MED on NAO
X = NAO[:]
Y = MED[:]
model = sm.OLS(Y,X)
results = model.fit()
res_med = results.resid
# 2) regress DK on NAO
X = NAO[:]
Y = DK[:]
model = sm.OLS(Y,X)
results = model.fit()
res_dk = results.resid
# 3) correlate the residuals (= partial correlation)
par_corr, p = stats.pearsonr(res_dk, res_med)
print(" The partial correlation of DK and MED (cond on NAO) is ", round(par_corr, 2))
#=====================================================
# Determine the causal effect from NAO --> MED
#=====================================================
Y = MED[:]
X = NAO[:]
model = sm.OLS(Y,X)
results = model.fit()
ce_nao_med = results.params[0]
print("The causal effect of NAO on MED is ", round(ce_nao_med,2))
#=====================================================
# Determine the causal effect from NAO --> DK
#=====================================================
Y = DK[:]
X = NAO[:]
model = sm.OLS(Y,X)
results = model.fit()
ce_nao_dk = results.params[0]
print("The effect of NAO on DK is ", round(ce_nao_dk,2))
#=====================================================
# Path tracing rule:
#=====================================================
exp_corr_dk_med = ce_nao_med * ce_nao_dk
print("The expected correlation of MED and DK is ", round(exp_corr_dk_med,2))
print("The actual correlation of MED and DK is ", round(r_dk_med, 2))
```
### Conclusions
There is a spurious correlation of MED and DK due to the influence of the common driver NAO. If one controls for NAO the correlation is shown to be negligible.
| true |
code
| 0.553988 | null | null | null | null |
|
```
## https://pytorch.org/tutorials/intermediate/reinforcement_q_learning.html - original tutorial
```
## Packages
```
import gym
import math
import random
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple
from itertools import count
from PIL import Image
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision.transforms as T
```
## Task
- The agent has to decide between two actions - moving the cart left or right - so that the pole attached to it stays upright.
- As the agent observes the current state of the environment and chooses an action, the environment transitions to a new state, and also returns a reward that indicates the consequences of the action. In this task, the environment terminates if the pole falls over too far.
```
env = gym.make('CartPole-v0').unwrapped
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
from IPython import display
plt.ion()
# if gpu is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
## Replay memory
- We’ll be using experience replay memory for training our DQN. It stores the transitions that the agent observes, allowing us to reuse this data later. By sampling from it randomly, the transitions that build up a batch are decorrelated.
It has been shown that this greatly stabilizes and improves the DQN training procedure.
```
Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))
class ReplayMemory(object):
def __init__(self, capacity):
self.capacity = capacity
self.memory = []
self.position = 0
def push(self, *args):
"""Saves a transition."""
if len(self.memory) < self.capacity:
self.memory.append(None)
self.memory[self.position] = Transition(*args)
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)
```
## Q-network
- Our model will be a convolutional neural network that takes in the difference between the current and previous screen patches. It has two outputs, representing Q(s,left) and Q(s,right) (where s is the input to the network).
In effect, the network is trying to predict the quality of taking each action given the current input.
```
class DQN(nn.Module):
def __init__(self):
super(DQN, self).__init__()
self.conv1 = nn.Conv2d(3, 16, kernel_size=5, stride=2)
self.bn1 = nn.BatchNorm2d(16)
self.conv2 = nn.Conv2d(16, 32, kernel_size=5, stride=2)
self.bn2 = nn.BatchNorm2d(32)
self.conv3 = nn.Conv2d(32, 32, kernel_size=5, stride=2)
self.bn3 = nn.BatchNorm2d(32)
self.head = nn.Linear(6336, 2)
def forward(self, x):
x = F.relu(self.bn1(self.conv1(x)))
x = F.relu(self.bn2(self.conv2(x)))
x = F.relu(self.bn3(self.conv3(x)))
return self.head(x.view(x.size(0), -1))
```
## Utilities
```
resize = T.Compose([T.ToPILImage(),
T.Resize(100, interpolation=Image.CUBIC),
T.ToTensor()])
# This is based on the code from gym.
screen_width = 600
def get_cart_location():
world_width = env.x_threshold * 2
scale = screen_width / world_width
return int(env.state[0] * scale + screen_width / 2.0) # MIDDLE OF CART
def get_screen():
screen = env.render(mode='rgb_array').transpose((2, 0, 1)) # transpose into torch order (CHW)
# Strip off the top and bottom of the screen
screen = screen[:, 160:320]
view_width = 320
cart_location = get_cart_location()
if cart_location < view_width // 2:
slice_range = slice(view_width)
elif cart_location > (screen_width - view_width // 2):
slice_range = slice(-view_width, None)
else:
slice_range = slice(cart_location - view_width // 2,
cart_location + view_width // 2)
# Strip off the edges, so that we have a square image centered on a cart
screen = screen[:, :, slice_range]
# Convert to float, rescare, convert to torch tensor
# (this doesn't require a copy)
screen = np.ascontiguousarray(screen, dtype=np.float32) / 255
screen = torch.from_numpy(screen)
# Resize, and add a batch dimension (BCHW)
return resize(screen).unsqueeze(0).to(device)
env.reset()
plt.figure()
plt.imshow(get_screen().cpu().squeeze(0).permute(1, 2, 0).numpy(), interpolation='none')
plt.title('Example extracted screen')
plt.show()
```
## TRAINING
```
BATCH_SIZE = 256
GAMMA = 0.999
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 200
TARGET_UPDATE = 10
policy_net = DQN().to(device)
target_net = DQN().to(device)
target_net.load_state_dict(policy_net.state_dict())
target_net.eval()
optimizer = optim.Adam(policy_net.parameters())
memory = ReplayMemory(20000)
steps_done = 0
def select_action(state):
global steps_done
sample = random.random()
eps_threshold = EPS_END + (EPS_START - EPS_END) * math.exp(-1. * steps_done / EPS_DECAY)
steps_done += 1
if sample > eps_threshold:
with torch.no_grad():
return policy_net(state).max(1)[1].view(1, 1)
else:
return torch.tensor([[random.randrange(2)]], device=device, dtype=torch.long)
episode_durations = []
def plot_durations():
plt.figure(2)
plt.clf()
durations_t = torch.tensor(episode_durations, dtype=torch.float)
plt.title('Training...')
plt.xlabel('Episode')
plt.ylabel('Duration')
plt.plot(durations_t.numpy())
# Take 100 episode averages and plot them too
if len(durations_t) >= 100:
means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
means = torch.cat((torch.zeros(99), means))
plt.plot(means.numpy())
plt.pause(0.001) # pause a bit so that plots are updated
if is_ipython:
display.clear_output(wait=True)
display.display(plt.gcf())
```
## Training loop
```
def optimize_model():
if len(memory) < BATCH_SIZE:
return
transitions = memory.sample(BATCH_SIZE)
# Transpose the batch (see http://stackoverflow.com/a/19343/3343043 for
# detailed explanation).
batch = Transition(*zip(*transitions))
# Compute a mask of non-final states and concatenate the batch elements
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,
batch.next_state)), device=device, dtype=torch.uint8)
non_final_next_states = torch.cat([s for s in batch.next_state
if s is not None])
state_batch = torch.cat(batch.state)
action_batch = torch.cat(batch.action)
reward_batch = torch.cat(batch.reward)
# Compute Q(s_t, a) - the model computes Q(s_t), then we select the
# columns of actions taken
state_action_values = policy_net(state_batch).gather(1, action_batch)
# Compute V(s_{t+1}) for all next states.
next_state_values = torch.zeros(BATCH_SIZE, device=device)
next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0].detach()
# Compute the expected Q values
expected_state_action_values = (next_state_values * GAMMA) + reward_batch
# Compute Huber loss
loss = F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1))
# Optimize the model
optimizer.zero_grad()
loss.backward()
for param in policy_net.parameters():
param.grad.data.clamp_(-1, 1)
optimizer.step()
```
- Below, you can find the main training loop. At the beginning we reset the environment and initialize the state Tensor.
Then, we sample an action, execute it, observe the next screen and the reward (always 1), and optimize our model once.
When the episode ends (our model fails), we restart the loop.
```
num_episodes = 1000
for i_episode in range(num_episodes):
# Initialize the environment and state
env.reset()
last_screen = get_screen()
current_screen = get_screen()
state = current_screen - last_screen
for t in count():
# Select and perform an action
action = select_action(state)
_, reward, done, _ = env.step(action.item())
reward = torch.tensor([reward], device=device)
# Observe new state
last_screen = current_screen
current_screen = get_screen()
if not done:
next_state = current_screen - last_screen
else:
next_state = None
# Store the transition in memory
memory.push(state, action, next_state, reward)
# Move to the next state
state = next_state
# Perform one step of the optimization (on the target network)
optimize_model()
if done:
episode_durations.append(t + 1)
plot_durations()
break
# Update the target network
if i_episode % TARGET_UPDATE == 0:
target_net.load_state_dict(policy_net.state_dict())
print('Complete')
env.render()
env.close()
plt.ioff()
plt.show()
```
| true |
code
| 0.924005 | null | null | null | null |
|
# StreamingPhish
------
**Author**: Wes Connell <a href="https://twitter.com/wesleyraptor">@wesleyraptor</a>
This notebook is a subset of the streamingphish command-line tool and is focused exclusively on describing the process of going from raw data to a trained predictive model. If you've never trained a predictive model before, hopefully you find this notebook to be useful.
We'll walk through each step in the machine learning lifecycle for developing a predictive model that examines a fully-qualified domain name (i.e. 'help.github.com') and predicts it as either phishing or not phishing. I've loosely defined these steps as follows:
1. Load training data.
2. Define features to extract from raw data.
3. Compute the features.
4. Train the classifier.
5. Explore classifier performance metrics.
6. Test the classifier against new data.
## 1. Load Training Data
The data necessary for training (~5K phishing domains, and ~5K non-phishing domains) has already been curated. Calling this function loads the domain names from disk and returns them in a list. The function also returns the labels for the data, which is mandatory for supervised learning (0 = not phishing, 1 = phishing).
Note that the ~10K total training samples are a subset of what the streamingphish CLI tool uses. This notebook is for demonstration purposes and I wanted to keep the feature extraction time to a few seconds (vs a minute or longer).
```
import os
import random
def load_training_data():
"""
Load the phishing domains and benign domains from disk into python lists
NOTE: I'm using a smaller set of samples than from the CLI tool so the feature extraction is quicker.
@return training_data: dictionary where keys are domain names and values
are labels (0 = benign, 1 = phishing).
"""
training_data = {}
benign_path = "/opt/streamingphish/training_data/benign/"
for root, dirs, files in os.walk(benign_path):
files = [f for f in files if not f[0] == "."]
for f in files:
with open(os.path.join(root, f)) as infile:
for item in infile.readlines():
# Safeguard to prevent adding duplicate data to training set.
if item not in training_data:
training_data[item.strip('\n')] = 0
phishing_path = "/opt/streamingphish/training_data/malicious/"
for root, dirs, files in os.walk(phishing_path):
files = [f for f in files if not f[0] == "."]
for f in files:
with open(os.path.join(root, f)) as infile:
for item in infile.readlines():
# Safeguard to prevent adding duplicate data to training set.
if item not in training_data:
training_data[item.strip('\n')] = 1
print("[+] Completed.")
print("\t - Not phishing domains: {}".format(sum(x == 0 for x in training_data.values())))
print("\t - Phishing domains: {}".format(sum(x == 1 for x in training_data.values())))
return training_data
training_data = load_training_data()
```
## 2. Define and Compute Features From Data
Next step is to identify characteristics/features in the data that we think will be effective in distinguishing between the two classes (phishing and not phishing). As humans, we tend to prefer practically significant features (i.e. is 'paypal' in the subdomain?), but it's important to also consider statistically significant features that may not be obvious (i.e. measuring the standard deviation for number of subdomains across the entire population).
The features identified in this research are spatial features, meaning each domain name is evaluated independently. The benefit is that the feature extraction is pretty simple (no need to focus on time intervals). Other implementations of machine learning for enterprise information security tend to be far more complex (multiple data sources, temporal features, sophisticated algorithms, etc).
Features can either be categorical or continuous - this prototype uses a mix of both. Generally speaking, continuous features can be measured (number of dashes in a FQDN), whereas categorical features are more of a boolean expression (is the top-level domain 'co.uk'? is the top-level domain 'bid'? is the top-level domain 'com'?). The features from this prototype are as follows:
- [Categorical] Top-level domain (TLD).
- [Categorical] Targeted phishing brand presence in subdomain.
- [Categorical] Targeted phishing brand presence in domain.
- [Categorical] 1:1 keyword match of common phishing words.
- [Continuous] Domain entropy (randomness).
- [Categorical] Levenshtein distance of 1 to common phishing words (word similarity).
- [Continuous] Number of periods.
- [Continuous] Number of dashes.
We're merely defining the features we want to extract in the code snippet below (we'll actually invoke this method a few steps down the road).
```
import os
import math
import re
from collections import Counter, OrderedDict
from Levenshtein import distance
import tldextract
import pandas as pd
import numpy as np
FEATURE_PATHS = {
'targeted_brands_dir': '/opt/streamingphish/training_data/targeted_brands/',
'keywords_dir': '/opt/streamingphish/training_data/keywords/',
'fqdn_keywords_dir': '/opt/streamingphish/training_data/fqdn_keywords/',
'similarity_words_dir': '/opt/streamingphish/training_data/similarity_words/',
'tld_dir': '/opt/streamingphish/training_data/tlds/'
}
class PhishFeatures:
"""
Library of functions that extract features from FQDNs. Each of those functions returns
a dictionary with feature names and their corresponding values, i.e.:
{
'num_dashes': 0,
'paypal_kw_present': 1,
'alexa_25k_domain': 0,
'entropy': 0
}
"""
def __init__(self):
"""
Loads keywords, phishing words, and targeted brands used by other functions in this class.
Args:
data_config (dictionary): Contains paths to files on disk needed for training.
"""
self._brands = self._load_from_directory(FEATURE_PATHS['targeted_brands_dir'])
self._keywords = self._load_from_directory(FEATURE_PATHS['keywords_dir'])
self._fqdn_keywords = self._load_from_directory(FEATURE_PATHS['fqdn_keywords_dir'])
self._similarity_words = self._load_from_directory(FEATURE_PATHS['similarity_words_dir'])
self._tlds = self._load_from_directory(FEATURE_PATHS['tld_dir'])
@staticmethod
def _remove_common_hosts(fqdn):
"""
Takes a FQDN, removes common hosts prepended to it in the subdomain, and returns it.
Args:
fqdn (string): FQDN from certstream.
Returns:
fqdn (string): FQDN with common benign hosts removed (these hosts have no bearing
on malicious/benign determination).
"""
try:
first_host = fqdn.split(".")[0]
except IndexError:
# In the event the FQDN doesn't have any periods?
# This would only happen in manual mode.
return fqdn
if first_host == "*":
fqdn = fqdn[2:]
elif first_host == "www":
fqdn = fqdn[4:]
elif first_host == "mail":
fqdn = fqdn[5:]
elif first_host == "cpanel":
fqdn = fqdn[7:]
elif first_host == "webmail":
fqdn = fqdn[8:]
elif first_host == "webdisk":
fqdn = fqdn[8:]
elif first_host == "autodiscover":
fqdn = fqdn[13:]
return fqdn
@staticmethod
def _fqdn_parts(fqdn):
"""
Break apart domain parts and return a dictionary representing the individual attributes
like subdomain, domain, and tld.
Args:
fqdn (string): FQDN being analyzed.
Returns:
result (dictionary): Each part of the fqdn, i.e. subdomain, domain, domain + tld
"""
parts = tldextract.extract(fqdn)
result = {}
result['subdomain'] = parts.subdomain
result['domain'] = parts.domain
result['tld'] = parts.suffix
return result
@staticmethod
def _load_from_directory(path):
"""
Read all text files from a directory on disk, creates list, and returns.
Args:
path (string): Path to directory on disk, i.e. '/opt/streamingphish/keywords/'
Returns:
values (list): Values from all text files in the supplied directory.
"""
values = []
# Load brand names from all the text files in the provided folder.
for root, _, files in os.walk(path):
files = [f for f in files if not f[0] == "."]
for f in files:
with open(os.path.join(root, f)) as infile:
for item in infile.readlines():
values.append(item.strip('\n'))
return values
def compute_features(self, fqdns, values_only=True):
"""
Calls all the methods in this class that begin with '_fe_'. Not sure how pythonic
this is, but I wanted dynamic functions so those can be written without having
to manually define them here. Shooting for how python's unittest module works,
there's a chance this is a python crime.
Args:
fqdns (list): fqdns to compute features for.
values_only (boolean, optional): Instead computes a np array w/ values only
and returns that instead of a list of dictionaries (reduces perf overhead).
Returns:
result (dict): 'values' will always be returned - list of feature values of
each FQDN being analyzed. Optional key included is 'names', which is the
feature vector and will be returned if values_only=True.
"""
result = {}
# Raw features are a list of dictionaries, where keys = feature names and
# values = feature values.
features = []
for fqdn in fqdns:
sample = self._fqdn_parts(fqdn=fqdn)
sample['fqdn'] = self._remove_common_hosts(fqdn=fqdn)
sample['fqdn_words'] = re.split('\W+', fqdn)
analysis = OrderedDict()
for item in dir(self):
if item.startswith('_fe_'):
method = getattr(self, item)
result = method(sample)
analysis = {**analysis, **result}
# Must sort dictionary by key before adding.
analysis = OrderedDict(sorted(analysis.items()))
features.append(analysis)
# Split out keys and values from list of dictionaries. Keys = feature names, and
# values = feature values.
result = {}
result['values'] = []
for item in features:
result['values'].append(np.fromiter(item.values(), dtype=float))
if not values_only:
# Take the dictionary keys from the first item - this is the feature vector.
result['names'] = list(features[0].keys())
return result
def _fe_extract_tld(self, sample):
"""
Check if TLD is in a list of ~30 TLDs indicative of phishing / not phishing. Originally,
this was a categorical feature extended via get_dummies / one hot encoding, but it was
adding too many unnecessary features to the feature vector resulting in a large tax
performance wise.
Args:
sample (dictionary): Info about the sample being analyzed i.e. subdomain, tld, fqdn
Returns:
result (dictionary): Keys are feature names, values are feature scores.
"""
result = OrderedDict()
for item in self._tlds:
result["tld_{}".format(item)] = 1 if item == sample['tld'] else 0
return result
def _fe_brand_presence(self, sample):
"""
Checks for brands targeted by phishing in subdomain (likely phishing) and in domain
+ TLD (not phishing).
Args:
sample (dictionary): Info about the sample being analyzed i.e. subdomain, tld, fqdn
Retuns:
result (dictionary): Keys are feature names, values are feature scores.
"""
result = OrderedDict()
for item in self._brands:
result["{}_brand_subdomain".format(item)] = 1 if item in sample['subdomain'] else 0
result["{}_brand_domain".format(item)] = 1 if item in sample['domain'] else 0
return result
def _fe_keyword_match(self, sample):
"""
Look for presence of keywords anywhere in the FQDN i.e. 'account' would match on
'dswaccounting.tk'.
Args:
sample (dictionary): Info about the sample being analyzed i.e. subdomain, tld, fqdn
Returns:
result (dictionary): Keys are feature names, values are feature scores.
"""
result = OrderedDict()
for item in self._keywords:
result[item + "_kw"] = 1 if item in sample['fqdn'] else 0
return result
def _fe_keyword_match_fqdn_words(self, sample):
"""
Compare FQDN words (previous regex on special characters) against a list of common
phishing keywords, look for exact match on those words. Probably more decisive
in identifying phishing domains.
Args:
sample (dictionary): Info about the sample being analyzed i.e. subdomain, tld, fqdn
Returns:
result (dictionary): Keys are feature names, values are feature scores.
"""
result = OrderedDict()
for item in self._fqdn_keywords:
result[item + "_kw_fqdn_words"] = 1 if item in sample['fqdn_words'] else 0
return result
@staticmethod
def _fe_compute_domain_entropy(sample):
"""
Takes domain name from FQDN and computes entropy (randomness, repeated characters, etc).
Args:
sample (dictionary): Info about the sample being analyzed i.e. subdomain, tld, fqdn
Returns:
result (dictionary): Keys are feature names, values are feature scores.
"""
# Compute entropy of domain.
result = OrderedDict()
p, lns = Counter(sample['domain']), float(len(sample['domain']))
entropy = -sum(count / lns * math.log(count / lns, 2) for count in list(p.values()))
result['entropy'] = entropy
return result
def _fe_check_phishing_similarity_words(self, sample):
"""
Takes a list of words from the FQDN (split by special characters) and checks them
for similarity against words commonly disguised as phishing words. This method only
searches for a distance of 1.
i.e. 'pavpal' = 1 for 'paypal', 'verifycation' = 1 for 'verification',
'app1eid' = 1 for 'appleid'.
Args:
sample (dictionary): Info about the sample being analyzed i.e. subdomain, tld, fqdn
Returns:
result (dictionary): Keys are feature names, values are feature scores.
"""
result = OrderedDict()
for key in self._similarity_words:
result[key + "_lev_1"] = 0
for word in sample['fqdn_words']:
if distance(word, key) == 1:
result[key + "_lev_1"] = 1
return result
@staticmethod
def _fe_number_of_dashes(sample):
"""
Compute the number of dashes - several could be a sign of URL padding, etc.
Args:
sample (dictionary): Info about the sample being analyzed i.e. subdomain, tld, fqdn
Returns:
result (dictionary): Keys are feature names, values are feature scores.
"""
result = OrderedDict()
result['num_dashes'] = 0 if "xn--" in sample['fqdn'] else sample['fqdn'].count("-")
return result
@staticmethod
def _fe_number_of_periods(sample):
"""
Compute number of periods - several subdomains could be indicative of a phishing domain.
Args:
sample (dictionary): Info about the sample being analyzed i.e. subdomain, tld, fqdn
Returns:
result (dictionary): Keys are feature names, values are feature scores.
"""
result = OrderedDict()
result['num_periods'] = sample['fqdn'].count(".")
return result
```
# 3. Compute the Features
Let's create an instance of the `Features` class and invoke the `compute_features()` method. This method returns a list of numbers representing each domain in our training set. The position of each number is very important because it aligns to a single feature from the feature vector, for example:
|Sample | TLD |
|----------------|-------|
|espn.com | com |
|torproject.org | org |
|notphishing.tk | tk |
|Sample |TLD_com |TLD_org |TLD_tk |
|----------------|----------|------------|-----------|
|espn.com |1.0 |0.0 |0.0 |
|torproject.org |0.0 |1.0 |0.0 |
|notphishing.tk |0.0 |0.0 |1.0 |
We also save the feature vector to a variable named `feature_vector` because we'll use it shortly to visually depict the names of the features that have the highest coefficients (i.e. significantly impact the prediction score returned by the classifier).
```
# Compute features.
print("[*] Computing features...")
f = PhishFeatures()
training_features = f.compute_features(training_data.keys(), values_only=False)
feature_vector = training_features['names']
print("[+] Features computed for the {} samples in the training set.".format(len(training_features['values'])))
```
# 4. Train the Classifier
So far we've transformed the raw training data (['espn.com', 'api.twitter.com', 'apppleid-suspended.activity.apple.com.490548678792.tk']) into features that describe the data and also created the feature vector. Now we'll run through the remaining routines to train a classifier:
1. Assign the labels (0 = benign, 1 = phishing) from the training samples to an array. We got the labels when we read in the training data from text files in step 1.
2. Split the data into a training set and a test set (helps evaluate model performance like overfitting, accuracy, etc).
3. Train a classifier using the Logistic Regression algorithm.
**NOTE**: If this were anything beyond a simple prototype, I would evaluate multiple algorithms, multiple parameters for said algorithms, features for down-selection, and multiple folds for cross validation. Feel free to explore these concepts on your own - they are currently out of scope.
```
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# Assign the labels (0s and 1s) to a numpy array.
labels = np.fromiter(training_data.values(), dtype=np.float)
print("[+] Assigned the labels to a numpy array.")
# Split the data into a training set and a test set.
X_train, X_test, y_train, y_test = train_test_split(training_features['values'], labels, random_state=5)
print("[+] Split the data into a training set and test set.")
# Insert silver bullet / black magic / david blaine / unicorn one-liner here :)
classifier = LogisticRegression(C=10).fit(X_train, y_train)
print("[+] Completed training the classifier: {}".format(classifier))
```
# 5. Explore Classifier Performance Metrics
This section could be a book by itself. To keep this brief, we'll briefly touch on a few metrics we can use to evaluate performance:
<h4>Accuracy Against Training and Test Sets:</h4> Since we have labeled data, we can run the features from each sample from our training set through the classifier and see if it predicts the right label. That's what the scores here represent. We can identify things like overfitting and underfitting (which can be attributed to any number of things, as we're in control of several independent variables like the algorithm, parameters, feature vector, training data, etc).
```
# See how well it performs against training and test sets.
print("Accuracy on training set: {:.3f}".format(classifier.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(classifier.score(X_test, y_test)))
```
<h4>Logistic Regression Coefficient Weights:</h4> This is the 'secret sauce' of supervised machine learning. Based on the training data, their respective labels, and the feature vector we generated, the algorithm determined the most optimal weights for each feature. The chart below depicts the features that were deemed to be most significant by the algorithm. The presence or absence of these features in domains that we evaluate **significantly** impacts the score returned by the trained classifier.
```
import mglearn
%matplotlib inline
import matplotlib.pyplot as plt
print("Number of features: {}".format(len(feature_vector)))
# Visualize the most important coefficients from the LogisticRegression model.
coef = classifier.coef_
mglearn.tools.visualize_coefficients(coef, feature_vector, n_top_features=10)
```
<h4>Precision / Recall:</h4> Precision shows how often the classifier is right when it cries wolf. Recall shows how many fish (no pun intended) the classifier caught out of all the fish in the pond. By default, the classifier assumes a malicious threshold of 0.5 on a scale of 0 to 1. This chart (and the subsequent TPR vs FPR chart) shows how these metrics change when increasing or decreasing the malicious threshold.<br>
```
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(y_test, classifier.predict_proba(X_test)[:, 1])
close_zero = np.argmin(np.abs(thresholds - 0.5))
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10, label="threshold 0.5", fillstyle="none",
c='k', mew=2)
plt.plot(precision, recall, label="precision recall curve")
plt.xlabel("Precision")
plt.ylabel("Recall")
plt.legend(loc="best")
print("Precision: {:.3f}\nRecall: {:.3f}\nThreshold: {:.3f}".format(precision[close_zero], recall[close_zero], thresholds[close_zero]))
```
<h4>True Positive Rate (TPR) / False Positive Rate (FPR):</h4> Basically a summary of misclassifications from the classifier against the test set.<br>
```
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_test, classifier.predict_proba(X_test)[:, 1])
plt.plot(fpr, tpr, label="ROC Curve")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
close_zero = np.argmin(np.abs(thresholds - 0.5))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10, label="threshold 0.5", fillstyle="none", c="k",
mew=2)
plt.legend(loc=4)
print("TPR: {:.3f}\nFPR: {:.3f}\nThreshold: {:.3f}".format(tpr[close_zero], fpr[close_zero],
thresholds[close_zero]))
```
<h4>Classification Report:</h4> Shows a lot of the same metrics plus the f1-score (combination of precision and recall) as well as support (shows possible class imbalance from the training set.<br>
```
from sklearn.metrics import classification_report
predictions = classifier.predict_proba(X_test)[:, 1] > 0.5
print(classification_report(y_test, predictions, target_names=['Not Phishing', 'Phishing']))
```
<h4>Confusion Matrix:</h4> Also depicts misclassifications against the test dataset.
```
# Confusion matrix.
from sklearn.metrics import confusion_matrix
confusion = confusion_matrix(y_test, predictions)
print("Confusion matrix:\n{}".format(confusion))
# A prettier way to see the same data.
scores_image = mglearn.tools.heatmap(
confusion_matrix(y_test, predictions), xlabel="Predicted Label", ylabel="True Label",
xticklabels=["Not Phishing", "Phishing"],
yticklabels=["Not Phishing", "Phishing"],
cmap=plt.cm.gray_r, fmt="%d")
plt.title("Confusion Matrix")
plt.gca().invert_yaxis()
```
# 6. Test Classifier Against New Data
The metrics look great. The code snippet below shows how you can transform a list of any FQDNs you'd like, extract features, reindex the features against the feature vector from training, and make a prediction.
```
phish = PhishFeatures() # We need the compute_features() method to evaluate new data.
LABEL_MAP = {0: "Not Phishing", 1: "Phishing"}
example_domains = [
"paypal.com",
"apple.com",
"patternex.com",
"support-apple.xyz",
"paypall.com",
"pavpal-verify.com"
]
# Compute features, and also note we need to provide the feature vector from when we
# trained the model earlier in this notebook.
features = phish.compute_features(example_domains)
prediction = classifier.predict_proba(features['values'])[:, 1] > 0.5
prediction_scores = classifier.predict_proba(features['values'])[:, 1]
for domain, classification, score in zip(example_domains, prediction, prediction_scores):
print("[{}]\t{}\t{:.3f}".format(LABEL_MAP[classification], domain, score))
```
<div style="float: center; margin: 10px 10px 10px 10px"><img src="../images/fishwordgraph.png"></div>
| true |
code
| 0.695338 | null | null | null | null |
|
# Compare trained NPEs accuracy as a function of $N_{\rm train}$
```
import numpy as np
from scipy import stats
from sedflow import obs as Obs
from sedflow import train as Train
from IPython.display import IFrame
# --- plotting ---
import corner as DFM
import matplotlib as mpl
import matplotlib.pyplot as plt
#mpl.use('PDF')
#mpl.rcParams['text.usetex'] = True
mpl.rcParams['font.family'] = 'serif'
mpl.rcParams['axes.linewidth'] = 1.5
mpl.rcParams['axes.xmargin'] = 1
mpl.rcParams['xtick.labelsize'] = 'x-large'
mpl.rcParams['xtick.major.size'] = 5
mpl.rcParams['xtick.major.width'] = 1.5
mpl.rcParams['ytick.labelsize'] = 'x-large'
mpl.rcParams['ytick.major.size'] = 5
mpl.rcParams['ytick.major.width'] = 1.5
mpl.rcParams['legend.frameon'] = False
import torch
import torch.nn as nn
import torch.nn.functional as F
from sbi import utils as Ut
from sbi import inference as Inference
```
# Load test data
```
# x = theta_sps
# y = [u, g, r, i, z, sigma_u, sigma_g, sigma_r, sigma_i, sigma_z, z]
x_test, y_test = Train.load_data('test', version=1, sample='flow', params='thetas_unt')
x_test[:,6] = np.log10(x_test[:,6])
x_test[:,7] = np.log10(x_test[:,7])
```
# calculate KS test p-value for trained `SEDflow` models
```
prior_low = [7, 0., 0., 0., 0., 1e-2, np.log10(4.5e-5), np.log10(4.5e-5), 0, 0., -2.]
prior_high = [12.5, 1., 1., 1., 1., 13.27, np.log10(1.5e-2), np.log10(1.5e-2), 3., 3., 1.]
lower_bounds = torch.tensor(prior_low)
upper_bounds = torch.tensor(prior_high)
prior = Ut.BoxUniform(low=lower_bounds, high=upper_bounds, device='cpu')
def pps(anpe_samples, ntest=100, nmcmc=10000):
''' given npe, calculate pp for ntest test data
'''
pp_thetas, rank_thetas = [], []
for igal in np.arange(ntest):
_mcmc_anpe = anpe_samples[igal]
pp_theta, rank_theta = [], []
for itheta in range(_mcmc_anpe.shape[1]):
pp_theta.append(stats.percentileofscore(_mcmc_anpe[:,itheta], x_test[igal,itheta])/100.)
rank_theta.append(np.sum(np.array(_mcmc_anpe[:,itheta]) < x_test[igal,itheta]))
pp_thetas.append(pp_theta)
rank_thetas.append(rank_theta)
pp_thetas = np.array(pp_thetas)
rank_thetas = np.array(rank_thetas)
return pp_thetas, rank_thetas
# architectures
archs = ['500x10.0', '500x10.1', '500x10.2', '500x10.3', '500x10.4']
nhidden = [500 for arch in archs]
nblocks = [10 for arch in archs]
ks_pvalues, ks_tot_pvalues = [], []
for i in range(len(archs)):
anpe_samples = np.load('/scratch/network/chhahn/sedflow/anpe_thetaunt_magsigz.toy.%s.samples.npy' % archs[i])
_pp, _rank = pps(anpe_samples, ntest=1000, nmcmc=10000)
ks_p = []
for ii in range(_pp.shape[1]):
_, _ks_p = stats.kstest(_pp[ii], 'uniform')
ks_p.append(_ks_p)
ks_pvalues.append(np.array(ks_p))
_, _ks_tot_p = stats.kstest(_pp.flatten(), 'uniform')
ks_tot_pvalues.append(_ks_tot_p)
print(archs[i], _ks_tot_p)
ks_all_p_nt, ks_tot_p_nt = [], []
for ntrain in [500000, 200000, 100000, 50000]:
anpe_samples = np.load('/scratch/network/chhahn/sedflow/anpe_thetaunt_magsigz.toy.ntrain%i.%s.samples.npy' % (ntrain, archs[i]))
_pp_nt, _rank_nt = pps(anpe_samples, ntest=1000, nmcmc=10000)
ks_p_nt = []
for ii in range(_pp_nt.shape[1]):
_, _ks_p = stats.kstest(_pp_nt[ii], 'uniform')
ks_p_nt.append(_ks_p)
ks_all_p_nt.append(ks_p_nt)
_, _ks_tot_p_nt = stats.kstest(_pp_nt.flatten(), 'uniform')
print('ntrain%i.%s' % (ntrain, archs[i]), _ks_tot_p_nt)
ks_tot_p_nt.append(_ks_tot_p_nt)
ks_all_p_nt = np.array(ks_all_p_nt)
ks_tot_p_nt = np.array(ks_tot_p_nt)
print(ks_tot_p_nt)
theta_lbls = [r'$\log M_*$', r"$\beta'_1$", r"$\beta'_2$", r"$\beta'_3$", r'$f_{\rm burst}$', r'$t_{\rm burst}$', r'$\log \gamma_1$', r'$\log \gamma_2$', r'$\tau_1$', r'$\tau_2$', r'$n_{\rm dust}$']
fig = plt.figure(figsize=(18,8))
sub = fig.add_subplot(121)
for itheta in range(_pp.shape[1]):
sub.plot([1e6, 500000, 200000, 100000, 50000], np.array([ks_p[itheta]] + list(ks_all_p_nt[:,itheta]))/ks_p[itheta], label=theta_lbls[itheta])
sub.legend(loc='upper left', fontsize=20)
sub.set_xlim(1.1e6, 5e4)
sub.set_yscale('log')
sub = fig.add_subplot(122)
print(_ks_tot_p)
print(ks_tot_p_nt)
print(np.array([_ks_tot_p] + list(ks_tot_p_nt))/_ks_tot_p)
sub.plot([1e6, 500000, 200000, 100000, 50000], np.array([_ks_tot_p] + list(ks_tot_p_nt))/_ks_tot_p)
sub.set_xlim(1.1e6, 5e4)
sub.set_yscale('log')
plt.show()
```
| true |
code
| 0.483161 | null | null | null | null |
|
# High-Order Example
[](https://mybinder.org/v2/gh/teseoch/fem-intro/master?filepath=fem-intro-high-order.ipynb)

Run it with binder!
```
import numpy as np
import scipy.sparse as spr
from scipy.sparse.linalg import spsolve
import plotly.graph_objects as go
```
As in the linear case, the domain is $\Omega = [0, 1]$, which we discretize with $n_{el}$ segments (or elements) $s_i$.
Now we also create the high-order nodes.
Note that we append them at the end.
```
#domain
omega = np.array([0, 1])
#number of bases and elements
n_el = 10
#Regular nodes, as before
s = np.linspace(omega[0], omega[1], num=n_el+1)
# s = np.cumsum(np.random.rand(n_elements+1))
s = (s-s[0])/(s[-1]-s[0])
# we now pick the order
order = 3
nodes = s
#more bases
n_bases = n_el + 1 + n_el*(order-1)
#create the nodes for the plots
for e in range(n_el):
#For every segment, we create order + 1 new high-order nodes
tmp = np.linspace(s[e], s[e+1], num=order+1)
#exclude the first and last since they already exists
tmp = tmp[1:-1]
#and append at the end of nodes
nodes = np.append(nodes, tmp)
```
Plot, in orange the high-order nodes, in blue the linear nodes.
```
go.Figure(data=[
go.Scatter(x=s, y=np.zeros(s.shape), mode='lines+markers'),
go.Scatter(x=nodes[n_el+1:], y=np.zeros(nodes.shape), mode='markers')
])
```
# Local bases
As in the linear case, we define the **reference element** $\hat s= [0, 1]$, a segment of unit length.
On each element we now have `order+1` (e.g., 2 for linear, 3 for quadratic) **non-zero** local bases.
We define their "piece" on $\hat s$.
It is important to respect the order of the nodes: the first 2 bases are always for the endpoints, and the others are ordered left to right.
Definition of linear bases, same as before
```
def hat_phi_1_0(x):
return 1-x
def hat_phi_1_1(x):
return x
```
Definition of quadratic bases
```
def hat_phi_2_0(x):
return 2*(x-0.5)*(x-1)
def hat_phi_2_1(x):
return 2*(x-0)*(x-0.5)
def hat_phi_2_2(x):
return -4*(x-0.5)**2+1
```
Definition of cubic bases
```
def hat_phi_3_0(x):
return -9/2*(x-1/3)*(x-2/3)*(x-1)
def hat_phi_3_1(x):
return 9/2*(x-0)*(x-1/3)*(x-2/3)
def hat_phi_3_2(x):
return 27/2*(x-0)*(x-2/3)*(x-1)
def hat_phi_3_3(x):
return -27/2*(x-0)*(x-1/3)*(x-1)
```
Utility function to return the list of functions
```
def hat_phis(order):
if order == 1:
return [hat_phi_1_0, hat_phi_1_1]
elif order == 2:
return [hat_phi_2_0, hat_phi_2_1, hat_phi_2_2]
elif order == 3:
return [hat_phi_3_0, hat_phi_3_1, hat_phi_3_2, hat_phi_3_3]
```
We can now plot the `order+1` local bases, same code as before.
Note that the first two bases correspond to the end-points, and the others are ordered.
```
x = np.linspace(0, 1)
data = []
tmp = hat_phis(order)
for o in range(order+1):
data.append(go.Scatter(x=x, y=tmp[o](x), mode='lines', name="$\hat\phi_{}$".format(o)))
go.Figure(data=data)
```
We use `sympy` to compute the gradients of the local bases.
```
import sympy as sp
xsym = sp.Symbol('x')
def grad_hat_phis(order):
#For linear we need to get the correct size
if order == 1:
return [lambda x : -np.ones(x.shape), lambda x : np.ones(x.shape)]
res = []
tmp = hat_phis(order)
for fun in tmp:
res.append(sp.lambdify(xsym, fun(xsym).diff(xsym)))
return res
```
Plotting gradients
```
x = np.linspace(0, 1)
data = []
tmp = grad_hat_phis(order)
for o in range(order+1):
data.append(go.Scatter(x=x, y=tmp[o](x), mode='lines', name="$\hat\phi_{}$".format(o)))
go.Figure(data=data)
```
# Basis construction
This code is exacly as before.
The only difficulty is the local to global mapping:
- the first 2 nodes are always the same
$$g_e^0 = e \qquad\mathrm{and}\qquad g_e^1=g+1$$
- the others are
$$g_e^i = n_{el} + e (\mathrm{order}-1) + i.$$
```
elements = []
for e in range(n_el):
el = {}
el["n_bases"] = order+1
#2 bases
el["phi"] = hat_phis(order)
el["grad_phi"] = grad_hat_phis(order)
#local to global mapping
high_order_nodes = list(range(n_el + 1 + e*(order-1), n_el + e*(order-1) + order))
el["loc_2_glob"] = [e, e+1] + high_order_nodes
#geometric mapping
el["gmapping"] = lambda x, e=e : s[e] + x*(s[e+1]-s[e])
el["grad_gmapping"] = lambda x : (s[e+1]-s[e])
elements.append(el)
```
We define a function to interpolate the vector $\vec{u}$ using the local to global, geometric mapping, and local bases to interpolate the data, as before.
```
def interpolate(u):
uinterp = np.array([])
x = np.array([])
xhat = np.linspace(0, 1)
for e in range(n_el):
el = elements[e]
uloc = np.zeros(xhat.shape)
for i in range(el["n_bases"]):
glob_node = el["loc_2_glob"][i]
loc_base = el["phi"][i]
uloc += u[glob_node] * loc_base(xhat)
uinterp = np.append(uinterp, uloc)
x = np.append(x, el["gmapping"](xhat))
return x, uinterp
```
We can generate a random vector $\vec{u}$ and use the previous function. This will interpolate all nodes.
```
u = np.random.rand(n_bases)
x, uinterp = interpolate(u)
go.Figure(data=[
go.Scatter(x=x, y=uinterp, mode='lines'),
go.Scatter(x=nodes, y=u, mode='markers'),
])
```
# Assembly
We are now ready the assemble the global stiffness matrix, which is exacly as before.
```
import quadpy
scheme = quadpy.line_segment.gauss_patterson(5)
rows = []
cols = []
vals = []
for e in range(n_el):
el = elements[e]
for i in range(el["n_bases"]):
for j in range(el["n_bases"]):
val = scheme.integrate(
lambda x:
el["grad_phi"][i](x) * el["grad_phi"][j](x) / el["grad_gmapping"](x),
[0.0, 1.0])
rows.append(el["loc_2_glob"][i])
cols.append(el["loc_2_glob"][j])
vals.append(val)
rows = np.array(rows)
cols = np.array(cols)
vals = np.array(vals)
L = spr.coo_matrix((vals, (rows, cols)))
L = spr.csr_matrix(L)
```
We set the rows `0` and `n_el` to identity for the boundary conditions.
```
for bc in [0, n_el]:
_, nnz = L[bc,:].nonzero()
for j in nnz:
if j != bc:
L[bc, j] = 0.0
L[bc, bc] = 1.0
```
We set the right-hand side to zero, and set the two boundary conditions to 1 and 4.
```
f = np.zeros((n_bases, 1))
f[0] = 1
f[n_el] = 4
```
We now solve $L\vec{u}=f$ for $\vec{u}$.
```
u = spsolve(L, f)
```
We now plot the solution. We expect a line, independently of `order`!
```
x, uinterp = interpolate(u)
go.Figure(data=[
go.Scatter(x=x, y=uinterp, mode='lines', name="solution"),
go.Scatter(x=nodes, y=u, mode='markers', name="$u$"),
])
```
# Mass Matrix
This is exactly as before!
```
rows = []
cols = []
vals = []
for e in range(n_el):
el = elements[e]
for i in range(el["n_bases"]):
for j in range(el["n_bases"]):
val = scheme.integrate(
lambda x:
el["phi"][i](x) * el["phi"][j](x) * el["grad_gmapping"](x),
[0.0, 1.0])
rows.append(el["loc_2_glob"][i])
cols.append(el["loc_2_glob"][j])
vals.append(val)
rows = np.array(rows)
cols = np.array(cols)
vals = np.array(vals)
M = spr.coo_matrix((vals, (rows, cols)))
M = spr.csr_matrix(M)
```
Now we set $\vec{f}=4$ and zero boundary conditions.
```
f = 4*np.ones((n_bases, 1))
f = M*f
f[0] = 0
f[n_el] = 0
```
We now solve $L\vec{u}=M\vec{f}$ for $\vec{u}$
```
u = spsolve(L, f)
x, uinterp = interpolate(u)
go.Figure(data=[
go.Scatter(x=x, y=uinterp, mode='lines', name="solution"),
go.Scatter(x=nodes, y=u, mode='markers', name="$u$"),
])
```
| true |
code
| 0.238129 | null | null | null | null |
|
# **Amazon Lookout for Equipment** - SDK Tutorial
#### Temporary cell to be executed until module is published on PyPI:
```
!pip install --quiet --use-feature=in-tree-build ..
```
## Initialization
---
### Imports
```
import boto3
import matplotlib.pyplot as plt
import matplotlib.ticker as mtick
import numpy as np
import os
import pandas as pd
import sagemaker
import sys
from lookoutequipment import plot, dataset, model, evaluation, scheduler
```
### Parameters
<span style="color: white; background-color: OrangeRed; padding: 0px 15px 0px 15px; border-radius: 20px;">**Note:** Update the value of the **bucket** and **prefix** variables below **before** running the following cell</span>
Make sure the IAM role used to run your notebook has access to the chosen bucket.
```
bucket = '<<YOUR-BUCKET>>'
prefix = '<<YOUR_PREFIX>>/' # Keep the trailing slash at the end
plt.style.use('Solarize_Light2')
plt.rcParams['lines.linewidth'] = 0.5
```
### Dataset preparation
```
data = dataset.load_dataset(dataset_name='expander', target_dir='expander-data')
dataset.upload_dataset('expander-data', bucket, prefix)
```
## Role definition
---
Before you can run this notebook (for instance, from a SageMaker environment), you will need:
* To allow SageMaker to run Lookout for Equipment API calls
* To allow Amazon Lookout for Equipment to access your training data (located in the bucket and prefix defined in the previous cell)
### Authorizing SageMaker to make Lookout for Equipment calls
You need to ensure that this notebook instance has an IAM role which allows it to call the Amazon Lookout for Equipment APIs:
1. In your IAM console, look for the SageMaker execution role endorsed by your notebook instance (a role with a name like `AmazonSageMaker-ExecutionRole-yyyymmddTHHMMSS`)
2. On the `Permissions` tab, click on `Attach policies`
3. In the Filter policies search field, look for `AmazonLookoutEquipmentFullAccess`, tick the checkbox next to it and click on `Attach policy`
4. Browse to the `Trust relationship` tab for this role, click on the `Edit trust relationship` button and fill in the following policy. You may already have a trust relationship in place for this role, in this case, just add the **"lookoutequipment.amazonaws.com"** in the service list:
```json
{
"Version": "2012-10-17",
"Statement": [
{
"Effect": "Allow",
"Principal": {
"Service": [
"sagemaker.amazonaws.com",
// ... Other services
"lookoutequipment.amazonaws.com"
]
},
"Action": "sts:AssumeRole"
}
]
}
```
5. Click on `Update the Trust Policy`: your SageMaker notebook instance can now call the Lookout for Equipment APIs
### Give access to your S3 data to Lookout for Equipment
When Lookout for Equipment will run, it will try to access your S3 data at several occasions:
* When ingesting the training data
* At training time when accessing the label data
* At inference time to run the input data and output the results
To enable these access, you need to create a role that Lookout for Equipment can endorse by following these steps:
1. Log in again to your [**IAM console**](https://console.aws.amazon.com/iamv2/home)
2. On the left menu bar click on `Roles` and then on the `Create role` button located at the top right
3. On the create role screen, selected `AWS Service` as the type of trusted entity
4. In the following section (`Choose a use case`), locate `SageMaker` and click on the service name. Not all AWS services appear in these ready to configure use cases and this is why we are using SageMaker as the baseline for our new role. In the next steps, we will adjust the role created to configure it specifically for Amazon Lookout for Equipment.
5. Click on the `Next` button until you reach the last step (`Review`): give a name and a description to your role (for instance `LookoutEquipmentS3AccessRole`)
6. Click on `Create role`: your role is created and you are brought back to the list of existing role
7. In the search bar, search for the role you just created and choose it from the returned result to see a summary of your role
8. At the top of your screen, you will see a role ARN field: **copy this ARN and paste it in the following cell, replacing the `<<YOUR_ROLE_ARN>>` string below**
9. Click on the cross at the far right of the `AmazonSageMakerFullAccess` managed policy to remove this permission for this role as we don't need it.
10. Click on `Add inline policy` and then on the `JSON` tab. Then fill in the policy with the following document (update the name of the bucket with the one you created earlier):
```json
{
"Version": "2012-10-17",
"Statement": [
{
"Effect": "Allow",
"Action": [
"s3:ListBucket",
"s3:GetObject"
],
"Resource": [
"arn:aws:s3:::<<YOUR-BUCKET>>/*",
"arn:aws:s3:::<<YOUR-BUCKET>>"
]
}
]
}
```
10. Give a name to your policy (for instance: `LookoutEquipmentS3AccessPolicy`) and click on `Create policy`.
11. On the `Trust relationships` tab, choose `Edit trust relationship`.
12. Under policy document, replace the whole policy by the following document and click on the `Update Trust Policy` button on the bottom right:
```json
{
"Version": "2012-10-17",
"Statement": [
{
"Sid": "",
"Effect": "Allow",
"Principal": {
"Service": "lookoutequipment.amazonaws.com"
},
"Action": "sts:AssumeRole"
}
]
}
```
And you're done! When Amazon Lookout for Equipment will try to read the datasets you just uploaded in S3, it will request permissions from IAM by using the role we just created:
1. The **trust policy** allows Lookout for Equipment to assume this role.
2. The **inline policy** specifies that Lookout for Equipment is authorized to list and access the objects in the S3 bucket you created earlier.
<span style="color: white; background-color: OrangeRed; padding: 0px 15px 0px 15px; border-radius: 20px;">Don't forget to update the **role_arn** variable below with the ARN of the role you just create **before** running the following cell</span>
```
role_arn = '<<YOUR_ROLE_ARN>>'
```
## Lookout for Equipment end-to-end walkthrough
---
### Dataset creation and data ingestion
```
lookout_dataset = dataset.LookoutEquipmentDataset(
dataset_name='my_dataset',
access_role_arn=role_arn,
component_root_dir=f's3://{bucket}/{prefix}training-data'
)
lookout_dataset.create()
response = lookout_dataset.ingest_data(bucket, prefix + 'training-data/', wait=True)
```
### Building an anomaly detection model
#### Model training
```
lookout_model = model.LookoutEquipmentModel(model_name='my_model',
dataset_name='my_dataset')
lookout_model.set_time_periods(data['evaluation_start'],
data['evaluation_end'],
data['training_start'],
data['training_end'])
lookout_model.set_label_data(bucket=bucket,
prefix=prefix + 'label-data/',
access_role_arn=role_arn)
lookout_model.set_target_sampling_rate(sampling_rate='PT5M')
response = lookout_model.train()
lookout_model.poll_model_training(sleep_time=300)
```
#### Trained model evaluation overview
```
LookoutDiagnostics = evaluation.LookoutEquipmentAnalysis(model_name='my_model', tags_df=data['data'])
predicted_ranges = LookoutDiagnostics.get_predictions()
labels_fname = os.path.join('expander-data', 'labels.csv')
labeled_range = LookoutDiagnostics.get_labels(labels_fname)
TSViz = plot.TimeSeriesVisualization(timeseries_df=data['data'], data_format='tabular')
TSViz.add_signal(['signal-028'])
TSViz.add_labels(labeled_range)
TSViz.add_predictions([predicted_ranges])
TSViz.add_train_test_split(data['evaluation_start'])
TSViz.add_rolling_average(60*24)
TSViz.legend_format = {'loc': 'upper left', 'framealpha': 0.4, 'ncol': 3}
fig, axis = TSViz.plot()
```
### Scheduling inferences
#### Preparing inferencing data
```
dataset.prepare_inference_data(
root_dir='expander-data',
sample_data_dict=data,
bucket=bucket,
prefix=prefix,
start_date='2015-11-21 04:00:00',
num_sequences=12
)
```
#### Configuring and starting a scheduler
```
lookout_scheduler = scheduler.LookoutEquipmentScheduler(
scheduler_name='my_scheduler',
model_name='my_model'
)
scheduler_params = {
'input_bucket': bucket,
'input_prefix': prefix + 'inference-data/input/',
'output_bucket': bucket,
'output_prefix': prefix + 'inference-data/output/',
'role_arn': role_arn,
'upload_frequency': 'PT5M',
'delay_offset': None,
'timezone_offset': '+00:00',
'component_delimiter': '_',
'timestamp_format': 'yyyyMMddHHmmss'
}
lookout_scheduler.set_parameters(**scheduler_params)
response = lookout_scheduler.create()
```
#### Post-processing the inference results
```
results_df = lookout_scheduler.get_predictions()
results_df.head()
event_details = pd.DataFrame(results_df.iloc[0, 1:]).reset_index()
fig, ax = plot.plot_event_barh(event_details, fig_width=12)
```
| true |
code
| 0.604837 | null | null | null | null |
|
# *Density Matrices and Path Integrals*
`Doruk Efe Gökmen -- 14/08/2018 -- Ankara`
## Stationary states of the quantum harmonic oscillator
The 1-dimensional (1D) quantum mechanical harmonic oscillator with characteristic frequency $\omega$ is described by the same potential energy as its classical counterpart acting on a mass $m$: $V(x)=\frac{1}{2}m\omega^2x^2$. The physical structure of the allowed states subjected to this potential is governed by the time independent Schrödinger equation (TISE) $\mathcal{H}\psi=\left(-\frac{\hbar^2}{2m}\frac{\text{d}^2}{\text{d}x^2}+\frac{1}{2}m\omega^2x^2\right)\psi=E\psi$, where $E$ is an energy eigenvalue. Note that here we have taken $\hbar=1$, $m=1$, $\omega=1$ for simplicity. The stationary states $\psi_n(x)$ (Hermite polynomials) and the corresponding energy eigenvalues $E_n$ are calculated by the following program.
```
%pylab inline
import math, pylab
n_states = 20 #number of stationary states to be plotted
grid_x = [i * 0.1 for i in range(-50, 51)] #define the x-grid
psi = {} #intialise the list of stationary states
for x in grid_x:
psi[x] = [math.exp(-x ** 2 / 2.0) / math.pi ** 0.25] # ground state
psi[x].append(math.sqrt(2.0) * x * psi[x][0]) # first excited state
# other excited states (through Hermite polynomial recursion relations):
for n in range(2, n_states):
psi[x].append(math.sqrt(2.0 / n) * x * psi[x][n - 1] -
math.sqrt((n - 1.0) / n) * psi[x][n - 2])
# graphics output
for n in range(n_states):
shifted_psi = [psi[x][n] + n for x in grid_x] # vertical shift
pylab.plot(grid_x, shifted_psi)
pylab.title('Harmonic oscillator wavefunctions')
pylab.xlabel('$x$', fontsize=16)
pylab.ylabel('$\psi_n(x)$ (shifted)', fontsize=16)
pylab.xlim(-5.0, 5.0)
pylab.savefig('plot-harmonic_wavefunction.png')
pylab.show()
```
The following section checks whether the above results are correct (normalisation, ortanormality and TISE). TISE condition is verified by a discrete appoximation of the second derivative.
```
import math
def orthonormality_check(n, m):
integral_n_m = sum(psi[n][i] * psi[m][i] for i in range(nx)) * dx
return integral_n_m
nx = 1000
L = 10.0
dx = L / (nx - 1)
x = [- L / 2.0 + i * dx for i in range(nx)]
n_states = 4
psi = [[math.exp(-x[i] ** 2 / 2.0) / math.pi ** 0.25 for i in range(nx)]]
psi.append([math.sqrt(2.0) * x[i] * psi[0][i] for i in range(nx)])
for n in range(2, n_states):
psi.append([math.sqrt(2.0 / n) * x[i] * psi[n - 1][i] - \
math.sqrt((n - 1.0) / n) * psi[n - 2][i] for i in range(nx)])
n = n_states - 1
print 'checking energy level', n
#discrete approximation for the second derivative
H_psi = [0.0] + [(- 0.5 * (psi[n][i + 1] - 2.0 * psi[n][i] + psi[n][i - 1]) /
dx ** 2 + 0.5 * x[i] ** 2 * psi[n][i]) for i in range(1, nx - 1)]
for i in range(1, nx - 1):
print n, x[i], H_psi[i] / psi[n][i]
import math, pylab
nx = 300 # nx is even, to avoid division by zero
L = 10.0
dx = L / (nx - 1)
x = [- L / 2.0 + i * dx for i in range(nx)]
# construct wavefunctions:
n_states = 4
psi = [[math.exp(-x[i] ** 2 / 2.0) / math.pi ** 0.25 for i in range(nx)]] # ground state
psi.append([math.sqrt(2.0) * x[i] * psi[0][i] for i in range(nx)]) # first excited state
for n in range(2, n_states):
psi.append([math.sqrt(2.0 / n) * x[i] * psi[n - 1][i] - \
math.sqrt((n - 1.0) / n) * psi[n - 2][i] for i in range(nx)])
# local energy check:
H_psi_over_psi = []
for n in range(n_states):
H_psi = [(- 0.5 * (psi[n][i + 1] - 2.0 * psi[n][i] + psi[n][i - 1])
/ dx ** 2 + 0.5 * x[i] ** 2 * psi[n][i]) for i in range(1, nx - 1)]
H_psi_over_psi.append([H_psi[i] / psi[n][i+1] for i in range(nx - 2)])
# graphics output:
for n in range(n_states):
pylab.plot(x[1:-1], [n + 0.5 for i in x[1:-1]], 'k--', lw=1.5)
pylab.plot(x[1:-1], H_psi_over_psi[n], '-', lw=1.5)
pylab.xlabel('$x$', fontsize=18)
pylab.ylabel('$H \psi_%i(x)/\psi_%i(x)$' % (n, n), fontsize=18)
pylab.xlim(x[0], x[-1])
pylab.ylim(n, n + 1)
pylab.title('Schroedinger equation check (local energy)')
#pylab.savefig('plot-check_schroedinger_energy-%i.png' % n)
pylab.show()
```
## Quantum statistical mechanics - Density matrices
In a thermal ensemble, the probability of being in $n$th energy eigenstate is given by the Boltzmann factor $\pi(n)\propto e^{-\beta E_n}$, where $\beta=\frac{1}{k_BT}$. Hence, e.g the probability $\pi(x,n)$ to be in state $n$ and in position $x$ is proportional to $e^{-\beta E_n}|\psi_n(x)|^2$.
We can consider the diagonal density matrix $\rho(x,x,\beta)=\sum_n e^{\beta E_n}\psi_n(x)\psi_n^*(x)$, which is the probability $\pi(x)$ of being at position $x$. This is a special case of the more general density matrix $\rho(x,x',\beta)=\sum_n e^{\beta E_n}\psi_n(x)\psi_n^*(x')$, which is the central object of quantum statistical mechanics. The partition function is given by $Z(\beta)=\text{Tr}\rho_u=\int_{-\infty}^\infty \rho_u(x,x,\beta)\text{d}x$, where $\rho_u=e^{-\beta \mathcal{H}}$ is the unnormalised density matrix. It follows that $\rho(\beta)=\frac{e^{-\beta\mathcal{H}}}{\text{Tr}(e^{-\beta\mathcal{H}})}$.
Properties of the density matrix:
* *The convolution property*: $\int \rho(x,x',\beta_1) \rho(x',x'',\beta_2) \text{d}x' = \int \text{d}x' \sum_{n,m} \psi_n(x)e^{-\beta_1 E_n} \psi_n^*(x')\psi_m(x')e^{-\beta_2 E_m}\psi_m^*(x'')$ $ = \sum_{n,m} \psi_n(x)e^{-\beta_1 E_n} \int \text{d}x' \psi_n^*(x')\psi_m(x')e^{-\beta_2 E_m}\psi_m^*(x'') = \sum_n \psi_n(x)e^{-(\beta_1+\beta_2)E_n}\psi_n^*(x'')=\rho(x,x'',\beta_1+\beta_2)$ $\implies \boxed{ \int \rho(x,x',\beta) \rho(x',x'',\beta) \text{d}x' = \rho(x,x'',2\beta)}$ (note that in the discrete case, this is just matrix squaring). **So, if we have the density matrix at temperature $T=k_B/\beta$ this equation allows us to compute the density matrix at temperature $T/2$**.
* *The free density matrix* for a system of infinte size is $\rho^\text{free}(x,x',\beta)=\frac{1}{\sqrt{2\pi\beta}}\exp{\left[-\frac{(x-x')^2}{2\beta}\right]}$. Notice that in the high temperature limit ($\beta\rightarrow 0$) the density matrix becomes classical: $\rho^\text{free}\rightarrow \delta(x-x')$. The quantum system exihibits its peculiar properties more visibly at low temperatures.
* *High temperature limit and the Trotter decomposition*. In general any Hamiltonian can be written as $\mathcal{H}=\mathcal{H}^\text{free}+V(x)$. At high temperatures ($\beta\rightarrow 0$) we can approximate the density matrix as $\rho(x,x',\beta)=e^{-\beta V(x)/2}\rho^\text{free}e^{-\beta V(x')/2}$ (Trotter expansion). Hence an explicit expression for the density matrix is available without solving the Schrödinger (or more preciesly Liouville) equation for any potential.
Getting the density matrix for the harmonic oscillator at high temperatures by the Trotter decomposition.
```
%pylab inline
import math, pylab
# density matrix for a free particle (exact)
def funct_rho_free(x, xp, beta):
return (math.exp(-(x - xp) ** 2 / (2.0 * beta)) /
math.sqrt(2.0 * math.pi * beta))
beta = 0.1
nx = 300
L = 10.0
x = [-L / 2.0 + i * L / float(nx - 1) for i in range(nx)]
rho_free, rho_harm = [], []
for i in range(nx):
rho_free.append([funct_rho_free(x[i], x[j], beta) for j in range(nx)])
rho_harm.append([rho_free[i][j] * math.exp(- beta * x[i] ** 2 / 4.0 -
beta * x[j] ** 2 / 4.0) for j in range(nx)])
# graphics output (free particle)
pylab.imshow(rho_free, extent=[0.0, L, 0.0, L], origin='lower')
pylab.xlabel('$x$', fontsize=16)
pylab.ylabel('$x\'$', fontsize=16)
pylab.colorbar()
pylab.title('$\\beta$=%s (free)' % beta)
pylab.savefig('plot-trotter-free.png')
pylab.show()
# graphics output (harmonic potential)
pylab.imshow(rho_harm, extent=[0.0, L, 0.0, L], origin='lower')
pylab.xlabel('$x$', fontsize=16)
pylab.ylabel('$x\'$', fontsize=16)
pylab.colorbar()
pylab.title('$\\beta$=%s (harmonic)' % beta)
pylab.savefig('plot-trotter-harmonic.png')
```
So, at high temperature, the density matrix is given by a simple correction to the free density matrix as seen above. Taking $\rho^\text{free}$ as a starting point, by the convolution property we can obtain the density matrix at low temperatures too, hence leading to a convenient numerical scheme through matrix squaring. The following section contains an implementation of this.
```
import math, numpy, pylab
#matrix squaring and convolution to calculate the density matrix at any temperature.
# Free off-diagonal density matrix
def rho_free(x, xp, beta):
return (math.exp(-(x - xp) ** 2 / (2.0 * beta)) /
math.sqrt(2.0 * math.pi * beta))
# Harmonic density matrix in the Trotter approximation (returns the full matrix)
def rho_harmonic_trotter(grid, beta):
return numpy.array([[rho_free(x, xp, beta) * \
numpy.exp(-0.5 * beta * 0.5 * (x ** 2 + xp ** 2)) \
for x in grid] for xp in grid])
#construct the position grid
x_max = 5.0 #maximum position value on the grid
nx = 100 #number of grid elements
dx = 2.0 * x_max / (nx - 1) #the grid spacing
x = [i * dx for i in range(-(nx - 1) / 2, nx / 2 + 1)] #the position grid
beta_tmp = 2.0 ** (-8) # initial value of beta (power of 2)
beta = 2.0 ** 0 # actual value of beta (power of 2)
rho = rho_harmonic_trotter(x, beta_tmp) # density matrix at initial beta
#reduce the temperature in log_2 steps by the convolution property (matrix squaring)
#and get the updated density matrix rho
while beta_tmp < beta:
rho = numpy.dot(rho, rho) #matrix squaring is implemented by the dot product in numpy
rho *= dx #multiply by the position differential since we are in the position representation
beta_tmp *= 2.0 #reduce the temperute by a factor of 2
# graphics output
pylab.imshow(rho, extent=[-x_max, x_max, -x_max, x_max], origin='lower')
pylab.colorbar()
pylab.title('$\\beta = 2^{%i}$' % math.log(beta, 2))
pylab.xlabel('$x$', fontsize=18)
pylab.ylabel('$x\'$', fontsize=18)
pylab.savefig('plot-harmonic-rho.png')
```
### $\rho^\text{free}$ with periodic boundary conditions
Free density matrix in periodic boundary conditions (periodic box of size $L$) can be obtained by the *Poisson sum rule?* by $\rho^\text{per}(x,x',\beta)=\frac{1}{L}\sum^\infty_{n=-\infty}e^{i\frac{2\pi n (x-x')}{L}}e^{-\beta\frac{2\pi^2 n^2}{L^2}}=\sum^\infty_{w=-\infty}\rho^\text{free}(x,x'+wL,\beta)$, where $w$ is the *winding number* (that is the winding around the box of size L). The diagonal stripe is a manifestation of the fact that the system is translation invariant, i.e. $\rho^\text{free}(x,x',\beta)$ is a function of $x-x'$.
```
import math, cmath, pylab
ntot = 21 # odd number
beta = 1.0 #inverse temperature
nx = 100 #number of grid elements
L = 10.0 #length of the system
x = [i * L / float(nx - 1) for i in range(nx)] #position grid
rho_complex = []
for i in range(nx):
rho_complex.append([sum(
math.exp(- 2.0 * beta * (math.pi * n / L) ** 2) *
cmath.exp(1j * 2.0 * n * math.pi * (x[i] - x[j]) / L) / L
for n in range(-(ntot - 1) / 2, (ntot + 1) / 2))
for j in range(nx)]) #append the i'th line to the density matrix
#(j loop is for constructing the line)
rho_real = [[rho_complex[i][j].real for i in range(nx)] for j in range(nx)]
# graphics output
pylab.imshow(rho_real, extent=[0.0, L, 0.0, L], origin='lower')
pylab.colorbar()
pylab.title('$\\beta$=%s (complex exp)' % beta)
pylab.xlabel('$x$', fontsize=16)
pylab.ylabel('$x\'$', fontsize=16)
pylab.savefig('plot-periodic-complex.png')
```
## Path integrals - Quantum Monte Carlo
### Path integral representation of the kernel
The kernel $K$ is the matrix element of the unitary time evolution operator $U(t_i-t_f)=e^{-i/\hbar(t_f-t_i)\mathcal{H}}$ in the position representation: $K(x_i,x_f;t_f-t_i)=\langle x_f \left| U(t_f-t_i) \right| x_i \rangle$. We can write $K(x_i,x_f;t_f-t_i)=\langle x_f \left| U^N((t_f-t_i)/N) \right| x_i \rangle$, that is, divide the time interval $[t_i,t_f]$ into $N$ equal intervals $[t_k,t_{k+1}]$ of length $\epsilon$, where $\epsilon=t_{k+1}-t_k=(t_f-t_i)/N$.
Then we can insert $N-1$ resolutions of identity ($\int_{-\infty}^\infty \text{d} x_k \left|x_k\rangle\langle x_k\right|$) to obtain
$K(x_i,x_f;t_f-t_i)= \left[\Pi_{k=1}^{N-1}\int_{-\infty}^\infty dx_k \right] \left[\Pi_{k=0}^{N-1} K(x_i,x_f;\epsilon = (t_f-t_i)/N)\right]$,
where $x_f=x_N$ and $x_i=x_0$. In the continuous limit, we would have
$K(x_i,x_f;t_f-t_i)= \lim_{N\rightarrow\infty} \left[\Pi_{k=1}^{N-1}\int_{-\infty}^\infty dx_k \right] \left[\Pi_{k=0}^{N-1} K(x_i,x_f;\epsilon = (t_f-t_i)/N)\right]$. (A)
Let us now consider the limit $\epsilon\rightarrow 0$ ($N\rightarrow \infty$) to obtain the short time kernel $K(x_i,x_f;\epsilon)$ and thereby switching from discrete to the continuous limit. It is known that for small $\epsilon$ the Trotter formula implies that to a very good approximation
$K(x_i,x_f;\epsilon = (t_f-t_i)/N) \simeq \langle x_{k+1} \left| e^{-i(\hbar\epsilon T} e^{-i/\hbar \epsilon V} \right| x_k\rangle$,
which becomes exact as $\epsilon\rightarrow 0$. If we insert resolution of identity $\int \text{d}p_k \left| p_k \rangle\langle p_k \right|$, we get
$K(x_i,x_f;\epsilon) = \int_{-\infty}^\infty \text{d}p_k \langle x_{k+1} \left| e^{-i(\hbar\epsilon T} \left| p_k \rangle\langle p_k \right| e^{-i/\hbar \epsilon V} \right| x_k\rangle = \int_{-\infty}^\infty \text{d}p_k \langle x_{k+1} \left| p_k \rangle\langle p_k \right| x_k\rangle e^{-i/\hbar \epsilon \left(\frac{p_k}{2m} + V(x)\right)}$
$\implies K(x_i,x_f;\epsilon) = \frac{1}{2\pi \hbar}\int_{-\infty}^\infty \text{d}p_k e^{i/\hbar \epsilon \left[p_k\frac{x_{k+1}-x_k}{\epsilon}-\mathcal{H}(p_k,x_k) \right]}$. (B)
Hence, inserting (B) into (A) we get
$K(x_i,x_f;t_f-t_i) = \lim_{N\rightarrow \infty}\left[\Pi_{k=1}^{N-1}\int_{-\infty}^\infty dx_k \right] \left \{ \Pi_{k=0}^{N-1} \int_{-\infty}^\infty \text{d}p_k e^{i/\hbar \epsilon \left[p_k\frac{x_{k+1}-x_k}{\epsilon}-\mathcal{H}(p_k,x_k) \right]} \right\}$. (C)
We can simplify the exponent of the integrand in the limiting case $N\rightarrow \infty$,
$\lim_{N\rightarrow \infty} \epsilon \sum_{k=0}^{N-1}\left[p_k\frac{x_{k+1}-x_k}{\epsilon}-\mathcal{H}(p_k,x_k) \right] =\int_{t_1}^{t_2}\text{d}t[p(t)\dot{x}(t)-\mathcal{H}[p(t),x(t)]]$
$=\int_{t_1}^{t_2}\text{d}t \mathcal{L}[x(t),\dot{x}(t)] = \mathcal{S}[x(t);t_f,t_i]$, (D)
where $\mathcal{L}[x(t),\dot{x}(t)] = \frac{m}{2}\dot{x}(t)^2-V[x(t)]$ is the Lagrangian and $\mathcal{S}[x(t);t_f,t_i]$ is the action between times $t_f$ and $t_i$.
Furthermore we can introduce the following notation for the integrals over *paths*:
$\lim_{N\rightarrow \infty}\left(\Pi_{k=1}^{N-1} \int_{-\infty}^\infty \text{d}x_k\right)=\int_{x(t_i)=x_i}^{x(t_f)=x_f}\mathcal{D}[x(t)]$, (E.1)
$\lim_{N\rightarrow \infty}\left(\Pi_{k=1}^{N-1}\int_{-\infty}^\infty\frac{\text{d}p_k}{2\pi\hbar}\right) =\int \mathcal{D}\left[\frac{p(t)}{2\pi\hbar}\right]$. (E.2)
Using (D) and (E) in (C), we get the path integral representation of the kernel
$K(x_i,x_f;t_f-t_i)= \int_{x(t_i)=x_i}^{x(t_f)=x_f}\mathcal{D}[x(t)] \int \mathcal{D}\left[\frac{p(t)}{2\pi\hbar}\right] e^{i/\hbar \mathcal{S}[x(t)]}$
$\implies \boxed{K(x_i,x_f;t_f-t_i)= \mathcal{N} \int_{x(t_i)=x_i}^{x(t_f)=x_f}\mathcal{D}[x(t)] e^{i/\hbar \mathcal{S}[x(t)]}}$, (F)
where $\mathcal{N}$ is the normalisation factor.
Here we see that each path has a phase proportional to the action. The equation (F) implies that we sum over all paths, which in fact interfere with one another. The true quantum mechanical amplitude is determined by the constructive and destructive interferences between these paths. For example, actions that are very large compared to $\hbar$, lead to very different phases even between nearby paths that differ only slightly, and that causes destructive interference between them. Only in the extremely close vicinity of the classical path $\bar x(t)$, where the action changes little when the phase varies, will neighbouring paths contirbute to the interference constructively. This leads to a classical deterministic path $\bar x(t)$, and this is why the classical approximation is valid when the action is very large compared to $\hbar$. Hence we see how the classical laws of motion arise from quantum mechanics.
### Path integral representation of the partition function
**Heuristic derivation of the discrete case:** Recall the convolution property of the density matrix, we can apply it repeatedly:
$\rho(x_0,x_2,\beta) = \int \rho(x_0,x_2,\beta/2) \rho(x_2,x_1,\beta/2) \text{d}x_2 = \int \int \int \rho(x_0,x_3,\beta/4) \rho(x_3, x_2,\beta/4) \rho(x_2,x_4,\beta/4) \rho(x_4,x_1 ,\beta/4) \text{d}x_2 \text{d}x_3 \text{d}x_4 = \cdots $
In other words: $\rho(x_0,x_N,\beta) = \int\int \cdots \int \text{d}x_1 \text{d}x_2 \cdots \text{d}x_{N-1}\rho(x_0,x_1,\beta/N)\rho(x_1,x_2,\beta/N)\cdots\rho(x_{N-1},x_N,\beta/N)$. The variables $x_k$ in this integral is called a *path*. We can imagine the variable $x_k$ to be at position $x_k$ at given slice $k\beta/N$ of an imaginary time variable $\tau$ that goes from $0$ to $\beta$ in steps of $\Delta\tau=\beta/N$. Density matrices and partition functions can thus be expressed as multiple integrals over path variables, which are none other than the path integrals that were introduced in the previous subsection.
Given the unnormalised density matrix $\rho_u$, the discrete partition $Z_d(\beta)$ function can be written as a path integral for all ***closed*** paths (because of the trace property), i.e., paths with the same beginning and end points ($x_0=x_N$), over a “time” interval $−i\hbar\beta$.
$Z_d(\beta)= \text{Tr}(e^{-\beta \mathcal{H}}) = \text{Tr}(\rho_u(x_0,x_N,\beta) )=\int \text{d}x_0 \rho_u (x_0,x_N=x_0,\beta) $ $ = \int \int\int \cdots \int \text{d}x_0 \text{d}x_1 \text{d}x_2 \cdots \text{d}x_{N-1}\rho_u(x_0,x_1,\beta/N)\rho_u(x_1,x_2,\beta/N)\cdots\rho_u(x_{N-1},x_N,\beta/N)\rho_u(x_{N-1},x_0,\beta/N)$.
The integrand is the probabilistic weight $\Phi\left[\{x_i\}\right]$ of the discrete path consisting of points $\{x_i\}$. The continuous case can be obtained by taking the limit $N\rightarrow \infty$. By defining
$\Phi[x(\tau)] = \lim_{N\rightarrow \infty} \rho_u(x_0,x_1,\beta/N)\cdots \rho_u(x_{N-1},x_N,\beta/N)$, (G)
(note that this is the probability weight of a particular continuous path), and by using (E.1), we can express the continuous partition function $Z(\beta)$ as
$Z(\beta) = \int_{x(0)}^{x(\hbar \beta)=x(0)}\mathcal{D}[x(\tau)] \Phi[x(\tau)]$. (H)
But what is $\Phi[x(\tau)]$?
**Derivation of the continuous case:** Again we start from $Z(\beta)= \text{Tr}(e^{-\beta \mathcal{H}})$. The main point of the argument that follows is the operational resemblance between the unitary time evolution operator $U(t)=e^{-(i/\hbar) t\mathcal{H}}$ and the unnormalised density matrix $e^{-\beta \mathcal{H}}$: the former is used to define the kernel which reads $K(x,x';t)=\langle x \left| e^{-(i/\hbar) t\mathcal{H}} \right| x' \rangle$; and the latter is used in defining the density matrix which reads $\rho(x,x';\beta)=\langle x \left| e^{-\beta \mathcal{H}} \right| x' \rangle$. If we regard $\beta$ as the analytic continuation of the real time $t$ to the imaginary values: $t\rightarrow i \tau \rightarrow i \hbar \beta$, and $t=t_i-t_f$, we get the cousin of the partition function that lives in the imaginary spacetime (i.e. Euclidian rather than Minkowskian)
$Z\left[\beta\rightarrow -\frac{i}{\hbar}(t_f-t_i)\right]=\text{Tr}\left[U(t_f-t_i)\right]=\int_{-\infty}^\infty \text{d}x \langle x \left| U(t_f-t_i) \right| x \rangle$
$=\int_{-\infty}^\infty \text{d}x K(x,x;t_f-t_i)$
$=\int_{-\infty}^\infty \text{d}x \mathcal{N} \int_{x(t_i)=x}^{x(t_f)=x}\mathcal{D}[x(t)] e^{i/\hbar \int_{t_i}^{t_f}\text{d}t \mathcal{L}[x(t),\dot{x}(t)]} $ (using (F))
$=\mathcal{N} \int_{x(t_f)=x(t_i)}\mathcal{D}[x(t)] e^{i/\hbar \int_{t_i}^{t_f}\text{d}t \mathcal{L}[x(t),\dot{x}(t)]} = \mathcal{N} \int_{x(t_f)=x(t_i)}\mathcal{D}[x(t)] e^{i/\hbar \int_{t_i}^{t_f}\text{d}t \left[\frac{m}{2}\dot{x}(t)^2-V[x(t)]\right]}$,
which means that one is integrating not over all paths but over all *closed* paths (loops) at $x$. We are now ready to get the path integral representation of the real partition function by making the transformations $t\rightarrow i\tau$ so that $t_i\rightarrow 0$ and $t_f\rightarrow -i\hbar \beta$ (also note that $\dot{x(t)}=\frac{\partial x(t)}{\partial t}\rightarrow -i \frac{\partial x(\tau)} {\partial \tau} = -i x'(\tau) \implies \dot{x}(t)^2 \rightarrow -x'(\tau)^2$):
$\implies Z(\beta)=\mathcal{N} \int_{x(\hbar \beta)=x(0)}\mathcal{D}[x(\tau)] e^{-\frac{1}{\hbar} \int_{0}^{\beta \hbar}\text{d}\tau\left( \frac{m}{2}x'(\tau)^2+V[x(\tau)]\right)}$
$\implies \boxed{ Z(\beta)=\mathcal{N} \int_{x(\hbar \beta)=x(0)}\mathcal{D}[x(\tau)] e^{-\frac{1}{\hbar} \int_{0}^{\beta \hbar}\text{d}\tau \mathcal{H}[p(\tau),x(\tau)]} }$. (I)
Notice that by comparing (H) and (I) we get an expression for the probabilistic weight $\Phi[x(\tau)]$ of a particular path $x(\tau)$, that is
$\Phi[x(\tau)] = \lim_{N\rightarrow \infty} \rho_u(x_0,x_1;\beta/N)\cdots \rho_u(x_{N-1},x_N;\beta/N) = \exp{\left\{ e^{-\frac{1}{\hbar} \int_{0}^{\beta \hbar}\text{d}\tau \mathcal{H}[p(\tau),x(\tau)]}\right\}}$ (J), which is very intuitive, considering the definition of the unnormalised density matrix $\rho_u$. This is an intriguing result, since we were able to obtain the complete statistical description of a quantum mechanical system without the appearance of complex numbers.
Because of this reason, using (J) it is easy to see why some paths contribute very little to the path integral: those are paths for which the exponent is very large due to high energy, and thus the integrand is negligibly small. *Furthermore, it is unnecessary to consider whether or not nearby paths cancel each other's contributions, for in the present case they do not interfere (since no complex numbers involved) i.e. all contributions add together with some being large and others small.*
#### Path integral Monte Carlo
In the algorithm, so called the *naïve path integral (Markov-chain) Monte Carlo*, we move from one path configuration consisting of $\{x_i\}$ to another one consisting of $\{x'_i\}$ by choosing a single position $x_k$ and by making a little displacement $\Delta x$ that can be positive or negative. We compute the weight before ($\Phi[\{x_i\}]$) this move and after ($\Phi[\{x'_i\}]$) the move and accept the move with the Metropolis acceptance rate (reject with certainty if the new weight is greater than the old one, smaller the new weight is, the higher the acceptance rate). Defining $\epsilon \equiv \beta/N$, we can approximate $\Phi[\{x_i\}]$ by making a Trotter decomposition *only around the point $x_k$*:
$\Phi\left[\{x_i\}\right]\approx \cdots \rho^\text{free}(x_{k-1},x_k;\epsilon) e^{-\frac{1}{2}\epsilon V(x_k)} e^{-\frac{1}{2}\epsilon V(x_k)} \rho^\text{free}(x_{k},x_{k+1};\epsilon)\cdots$.
Therefore, the acceptance ratio $\frac{\Phi\left[\{x'_i\}\right]}{\Phi\left[\{x_i\}\right]}$ can be approximated as
$\frac{\Phi\left[\{x'_i\}\right]}{\Phi\left[\{x_i\}\right]}\approx\frac{\rho^\text{free}(x_{k-1},x'_k;\epsilon) e^{-\epsilon V(x'_k)}\rho^\text{free}(x'_k,x_{k+1};\epsilon)}{\rho^\text{free}(x_{k-1},x_k;\epsilon) e^{-\epsilon V(x_k)} \rho^\text{free}(x_k,x_{k+1};\epsilon)}$.
This is implemented in the following program.
```
%pylab qt
import math, random, pylab, os
# Exact quantum position distribution:
def p_quant(x, beta):
p_q = sqrt(tanh(beta / 2.0) / pi) * exp(- x**2.0 * tanh(beta / 2.0))
return p_q
def rho_free(x, y, beta): # free off-diagonal density matrix
return math.exp(-(x - y) ** 2 / (2.0 * beta))
output_dir = 'snapshots_naive_harmonic_path'
if not os.path.exists(output_dir): os.makedirs(output_dir)
fig = pylab.figure(figsize=(6, 10))
def show_path(x, k, x_old, Accepted, hist_data, step, fig):
pylab.clf()
path = x + [x[0]] #Final position is the same as the initial position.
#Note that this notation appends the first element of x as a new element to x
y_axis = range(len(x) + 1) #construct the imaginary time axis
ax = fig.add_subplot(2, 1, 1)
#Plot the paths
if Accepted:
old_path = x[:] #save the updated path as the old path
old_path[k] = x_old #revert the update to get the actual old path
old_path = old_path + [old_path[0]] #final position is the initial position
ax.plot(old_path, y_axis, 'ko--', label='old path')
if not Accepted and step !=0:
old_path = x[:]
old_path[k] = x_old
old_path = old_path + [old_path[0]]
ax.plot(old_path, y_axis, 'ro-', label='rejection', linewidth=3)
ax.plot(path, y_axis, 'bo-', label='new path') #plot the new path
ax.legend()
ax.set_xlim(-2.5, 2.5)
ax.set_ylabel('$\\tau$', fontsize=14)
ax.set_title('Naive path integral Monte Carlo, step %i' % step)
ax.grid()
#Plot the histogram
ax = fig.add_subplot(2, 1, 2)
x = [a / 10.0 for a in range(-100, 100)]
y = [p_quant(a, beta) for a in x]
ax.plot(x, y, c='gray', linewidth=1.0, label='Exact quantum distribution')
ax.hist(hist_data, 10, histtype='step', normed = 'True', label='Path integral Monte Carlo') #histogram of the sample
ax.set_title('Position distribution at $T=%.2f$' % T)
ax.set_xlim(-2.5, 2.5) #restrict the range over which the histogram is shown
ax.set_xlabel('$x$', fontsize = 14)
ax.set_ylabel('$\pi(x)=e^{-\\beta E_n}|\psi_n(x)|^2$', fontsize = 14)
ax.legend(fontsize = 6)
ax.grid()
pylab.pause(0.2)
pylab.savefig(output_dir + '/snapshot_%05i.png' % step)
beta = 4.0 # inverse temperature
T = 1 / beta
N = 8 # number of (imagimary time) slices
dtau = beta / N
delta = 1.0 # maximum displacement on one slice
n_steps = 4 # number of Monte Carlo steps
hist_data = []
x = [random.uniform(-1.0, 1.0) for k in range(N)] # initial path (a position for each time)
show_path(x, 0, 0.0, False, hist_data, 0, fig) #show the initial path
for step in range(n_steps):
#print 'step',step
k = random.randint(0, N - 1) # randomly choose slice
knext, kprev = (k + 1) % N, (k - 1) % N # next/previous slices
x_old = x[k]
x_new = x[k] + random.uniform(-delta, delta) # new position at slice k
#calculate the weight before and after the move
old_weight = (rho_free(x[knext], x_old, dtau) *
rho_free(x_old, x[kprev], dtau) *
math.exp(-0.5 * dtau * x_old ** 2))
new_weight = (rho_free(x[knext], x_new, dtau) *
rho_free(x_new, x[kprev], dtau) *
math.exp(-0.5 * dtau * x_new ** 2))
if random.uniform(0.0, 1.0) < new_weight / old_weight: #accept with metropolis acceptance rate
x[k] = x_new
Accepted = True
else:
Accepted = False
show_path(x, k, x_old, Accepted, hist_data, step + 1, fig)
hist_data.append(x[k])
```

Note that the above program is very slow, as it takes very long to explore all of the available phase space.
## Unitary time evolution
Taking advantage of the Fourier transforms, the Trotter decomposition can also be used to efficiently simulate the unitary time evolution of a wavefunction as demonstrated by the following algorithm.
```
%pylab qt
import numpy, pylab, os
#Define the direct and inverse Fourier transformations:
def fourier_x_to_p(phi_x, dx):
phi_p = [(phi_x * numpy.exp(-1j * p * grid_x)).sum() * dx for p in grid_p]
return numpy.array(phi_p)
def fourier_p_to_x(phi_p, dp):
phi_x = [(phi_p * numpy.exp(1j * x * grid_p)).sum() * dp for x in grid_x]
return numpy.array(phi_x) / (2.0 * numpy.pi)
#The time evolution algorithm (using the Trotter decomposition)
def time_step_evolution(psi0, potential, grid_x, grid_p, dx, dp, delta_t):
psi0 = numpy.exp(-1j * potential * delta_t / 2.0) * psi0 #potential part of U (multiplicative)
psi0 = fourier_x_to_p(psi0, dx) #pass to the momentum space to apply the kinetic energy part
psi0 = numpy.exp(-1j * grid_p ** 2 * delta_t / 2.0) * psi0 #kinetic part of U (multiplicative)
psi0 = fourier_p_to_x(psi0, dp) #return to the position space
psi0 = numpy.exp(-1j * potential * delta_t / 2.0) * psi0 #potential part of U (multiplicative)
return psi0
#Potential function (barrier potential to demonstrate tunneling):
def funct_potential(x):
if x < -8.0: return (x + 8.0) ** 2 #barrier on the left hand side
elif x <= -1.0: return 0.0 #0 potential in between the left wall and the bump barrier
elif x < 1.0: return numpy.exp(-1.0 / (1.0 - x ** 2)) / numpy.exp(-1.0) #gaussian bump barrier
else: return 0.0 #0 potential elsewhere
#movie output of the time evolution
output_dir = 'snapshots_time_evolution'
if not os.path.exists(output_dir): os.makedirs(output_dir)
def show(x, psi, pot, time, timestep):
pylab.clf()
pylab.plot(x, psi, 'g', linewidth = 2.0, label = '$|\psi(x)|^2$') #plot wf in green colour
pylab.xlim(-10, 15)
pylab.ylim(-0.1, 1.15)
pylab.plot(x, pot, 'k', linewidth = 2.0, label = '$V(x)$') #plot potential in black colour
pylab.xlabel('$x$', fontsize = 20)
pylab.title('time = %s' % time)
pylab.legend(loc=1)
pylab.savefig(output_dir + '/snapshot_%05i.png' % timestep)
timestep += 1 #updtate the current time step
pylab.pause(0.1)
pylab.show()
steps = 800 #total number of position (momentum) steps
x_min = -12.0 #minimum position (momentum)
x_max = 40.0 #maximum position (momentum)
grid_x = numpy.linspace(x_min, x_max, steps) #position grid
grid_p = numpy.linspace(x_min, x_max, steps) #momentum grid
dx = grid_x[1] - grid_x[0] #position step
dp = grid_p[1] - grid_p[0] #momentum step
delta_t = 0.05 #time step width
t_max = 16.0 #maximum time
potential = [funct_potential(x) for x in grid_x] #save the potential on the position grid
potential = numpy.array(potential)
# initial state:
x0 = -8.0 #centre location
sigma = .5 #width of the gaussian
psi = numpy.exp(-(grid_x - x0) ** 2 / (2.0 * sigma ** 2) ) #initial state is a gaussian
psi /= numpy.sqrt( sigma * numpy.sqrt( numpy.pi ) ) #normalisation
# time evolution
time = 0.0 #initialise the time
timestep = 0 #initialise the current timestep
while time < t_max:
if timestep % 1 == 0:
show(grid_x, numpy.absolute(psi) ** 2.0, potential, time, timestep) #plot the wavefunction
#print time
time += delta_t #update the current time
timestep += 1 #update the current timestep
psi = time_step_evolution(psi, potential, grid_x, grid_p, dx, dp, delta_t) #update the wf
```

## Harmonic and anharmonic oscillators
### Harmonic oscillator
#### Markov-chain sampling by Metropolis acceptance using exact stationary states (Hermite polynomials)
Probability distribution at $T=0$ is $|\psi_0(x)|^2$. We can easily develop a Monte Carlo scheme for this system, because the stationary states of the harmonic oscillator are known, i.e. Hermite polynomials. In the following section, we obtain this distribution for $0$ temperature and finite temperatures by using the Markov-chain Monte Carlo algorithms implementing the Metropolis acceptance rate.
```
import random, math, pylab
from math import *
def psi_0_sq(x):
psi = exp(- x ** 2.0 / 2.0) / pi ** (1.0 / 4.0)
return abs(psi) ** 2.0
xx = 0.0
delta = 0.1
hist_data = []
for k in range(1000000):
x_new = xx + random.uniform(-delta, delta)
if random.uniform(0.0, 1.0) < psi_0_sq(x_new) / psi_0_sq(xx):
xx = x_new
hist_data.append(xx)
#print x
pylab.hist(hist_data, 500, normed = 'True', label='Markov-chain sampling') #histogram of the sample
x = [a / 10.0 for a in range(-30, 30)]
y = [psi_0_sq(a) for a in x]
pylab.plot(x, y, c='red', linewidth=2.0, label='Exact quantum')
pylab.title('Position distribution at $T=0$', fontsize = 13)
pylab.xlabel('$x$', fontsize = 15)
pylab.ylabel('$\pi(x)=|\psi_0(x)|^2$', fontsize = 15)
pylab.legend()
pylab.savefig('plot_T0_prob.png')
pylab.show()
```
Probability distribution at a finite temperature is given by $e^{-\beta E_n}|\psi_n(x)|^2$, where $\beta=1/T$.
```
import random, math, pylab
from math import *
# Energy eigenstates of the harmonic oscillator
def psi_n_sq(x, n):
if n == -1:
return 0.0
else:
psi = [math.exp(-x ** 2 / 2.0) / math.pi ** 0.25]
psi.append(math.sqrt(2.0) * x * psi[0]) #save the wf's in a vector "psi"
for k in range(2, n + 1):
psi.append(math.sqrt(2.0 / k) * x * psi[k - 1] -
math.sqrt((k - 1.0) / k) * psi[k - 2]) #Hermite polynomial recursion relations
return psi[n] ** 2
# Energy eigenvalues of the harmonic oscillator
def E(n):
E = n + 1.0 / 2.0
return E
# Markov-chain Monte Carlo algorithm:
def markov_prob(beta, n_trials):
# Energy move:
xx = 0.0
delta = 0.1
n = 0
hist_data_n = []
hist_data_x = []
for l in range(1000000):
if xx == 0.0:
xx += 0.00001 #avoid division by 0
m = n + random.choice([1,-1]) #take a random energy step
if m >= 0 and random.uniform(0.0, 1.0) \
< psi_n_sq(xx, m) / psi_n_sq(xx, n) * exp(-beta * (E(m) - E(n))):
n = m
hist_data_n.append(n)
# Position move:
x_new = xx + random.uniform(-delta, delta) #take a random position step
if random.uniform(0.0, 1.0) < psi_n_sq(x_new, n) / psi_n_sq(xx, n):
xx = x_new
hist_data_x.append(xx)
return hist_data_x, hist_data_n
#Exact quantum position distribution
def p_quant(x, beta):
p_q = sqrt(tanh(beta / 2.0) / pi) * exp(- x**2.0 * tanh(beta / 2.0))
return p_q
#Exact classical position distribution
def p_class(x, beta):
p_c = sqrt(beta / (2.0 * pi)) * exp(- beta * x**2.0 / 2.0)
return p_c
#Run the algorithm for different values of temperature:
n_trials = 10000
for beta in [0.2, 1.0, 5.0]:
B = beta
T = 1 / beta
hist_data_x, hist_data_n = markov_prob(beta, n_trials)
pylab.hist(hist_data_x, 500, normed = 'True', label='Markov-chain sampling') #position histogram of the sample
x = [a / 10.0 for a in range(-100, 100)]
y1 = [p_quant(a, beta) for a in x]
y2 = [p_class(a, beta) for a in x]
pylab.plot(x, y1, c='red', linewidth=4.0, label='exact quantum')
pylab.plot(x, y2, c='green', linewidth=2.0, label='exact classical')
pylab.title('Position distribution at $T=$%.2f' % T, fontsize = 13)
pylab.xlabel('$x$', fontsize = 15)
pylab.ylabel('$\pi(x)=e^{-\\beta E_n}|\psi_n(x)|^2$', fontsize = 15)
pylab.xlim([-7,7])
pylab.legend()
pylab.savefig('plot_T_%.2f_prob.png' % T)
pylab.show()
pylab.hist(hist_data_n, 100, normed = 'True') #energy histogram of the sample
pylab.title('Energy distribution at $T=$%.2f' % T, fontsize = 13)
pylab.xlabel('$n$', fontsize = 15)
pylab.ylabel('$\pi(n)$', fontsize = 15)
pylab.legend()
pylab.grid()
pylab.savefig('plot_T_%.2f_energy.png' % T)
pylab.show()
```
One can see that at high temperatures e.g $T=5$, the position distributions are almost the same. Hence the classical harmonic oscillator is a very good approximation for the quantum harmonic oscillator at high temperatures. The quantum behaviour becomes more prominent at low temperatures (eventually only the ground state is available for a sufficiently low thermal energy), especially below $T=0.2$, as one can see from the above figures.
Here we also got an histogram for the energy ($n$) distribution. The result indicates that the values of $n$ are distributed according to a Poisson distribution?
#### Trotter decomposition (convolution) and path integral monte carlo simulation
On the other hand, we can still obtain the position distributions even if we do not a priori have the analytic stationary states at our disposal. That is, we can approximate the density matrix at high temperatures by the Trotter decomposition and then take advantage of the convolution property to obtain the density matrix at successively reduced temperatures. This is implemented in the following algorithm.
```
%pylab inline
import math, numpy, pylab
from numpy import *
# Free off-diagonal density matrix:
def rho_free(x, xp, beta):
return (math.exp(-(x - xp) ** 2 / (2.0 * beta)) /
math.sqrt(2.0 * math.pi * beta))
# Harmonic density matrix in the Trotter approximation (returns the full matrix):
def rho_harmonic_trotter(grid, beta):
return numpy.array([[rho_free(x, xp, beta) * \
numpy.exp(-0.5 * beta * 0.5 * (x ** 2 + xp ** 2)) \
for x in grid] for xp in grid])
# Exact quantum position distribution:
def p_quant(x, beta):
p_q = sqrt(tanh(beta / 2.0) / pi) * exp(- x**2.0 * tanh(beta / 2.0))
return p_q
# Construct the position grid:
x_max = 5 #maximum position value
nx = 100 #number of elements on the x grid
dx = 2.0 * x_max / (nx - 1) #position differential
x = [i * dx for i in range(-(nx - 1) / 2, nx / 2 + 1)] #position grid
beta_tmp = 2.0 ** (-5) # initial (low) value of beta (power of 2) (high temperature)
beta = 2.0 ** 2 # actual value of beta (power of 2)
rho = rho_harmonic_trotter(x, beta_tmp) # density matrix at initial (low) beta (Trotter decomp.)
# Reduce the temperature by the convolution property (matrix squaring):
while beta_tmp < beta:
rho = numpy.dot(rho, rho) #matrix squaring (convolution)
rho *= dx #also multiply by the differential since we are in position representation
beta_tmp *= 2.0 #reduce the temperature by a factor of 2
#print 'beta: %s -> %s' % (beta_tmp / 2.0, beta_tmp)
# Output position distribution pi(x) at the final beta onto a file:
Z = sum(rho[j, j] for j in range(nx + 1)) * dx #partition function (to normalise)
pi_of_x = [rho[j, j] / Z for j in range(nx + 1)] #the diagonal element of the density matrix
f = open('data_harm_matrixsquaring_beta' + str(beta) + '.dat', 'w')
for j in range(nx + 1):
f.write(str(x[j]) + ' ' + str(rho[j, j] / Z) + '\n')
f.close()
# Plot the obtained final position distribution:
T = 1 / beta
x = linspace(-x_max, x_max, nx+1)
y1 = [p_quant(a, beta) for a in x]
pylab.plot(x, pi_of_x, c='red', linewidth=4.0, label='matrix squaring')
pylab.plot(x, y1, c='green', linewidth=2.0, label='exact quantum')
pylab.title('Position distribution at $T=$%.2f' % T, fontsize = 13)
pylab.xlabel('$x$', fontsize = 15)
pylab.xlim([-2,2])
pylab.ylabel('$\pi(x)=e^{-\\beta E_n}|\psi_n(x)|^2$', fontsize = 15)
pylab.legend()
pylab.grid()
pylab.savefig('plot_T_%.2f_prob_matrix_squaring.png' % T)
pylab.show()
```
Path integral Monte Carlo method is implemented in the following program.
```
%pylab inline
import math, random, pylab
def rho_free(x, y, beta): # free off-diagonal density matrix
return math.exp(-(x - y) ** 2 / (2.0 * beta))
def read_file(filename):
list_x = []
list_y = []
with open(filename) as f:
for line in f:
x, y = line.split()
list_x.append(float(x))
list_y.append(float(y))
f.close()
return list_x, list_y
beta = 4.0
T = 1 / beta
N = 10 # number of slices
dtau = beta / N
delta = 1.0 # maximum displacement on one slice
n_steps = 1000000 # number of Monte Carlo steps
x = [0.0] * N # initial path
hist_data = []
for step in range(n_steps):
k = random.randint(0, N - 1) # random slice
knext, kprev = (k + 1) % N, (k - 1) % N # next/previous slices
x_new = x[k] + random.uniform(-delta, delta) # new position at slice k
old_weight = (rho_free(x[knext], x[k], dtau) *
rho_free(x[k], x[kprev], dtau) *
math.exp(-0.5 * dtau * x[k] ** 2))
new_weight = (rho_free(x[knext], x_new, dtau) *
rho_free(x_new, x[kprev], dtau) *
math.exp(-0.5 * dtau * x_new ** 2))
if random.uniform(0.0, 1.0) < new_weight / old_weight:
x[k] = x_new
if step % 10 == 0:
hist_data.append(x[0])
# Figure output:
list_x, list_y = read_file('data_harm_matrixsquaring_beta' + str(beta) + '.dat')
pylab.plot(list_x, list_y, c='red', linewidth=4.0, label='path integral Monte Carlo')
pylab.hist(hist_data, 100, normed = 'True', label='matrix squaring') #histogram of the sample
pylab.title('Position distribution at $T=%.2f$' % T, fontsize = 13)
pylab.xlim(-2.0, 2.0) #restrict the range over which the histogram is shown
pylab.xlabel('$x$', fontsize = 15)
pylab.ylabel('$\pi(x)=e^{-\\beta E_n}|\psi_n(x)|^2$', fontsize = 15)
pylab.legend()
pylab.savefig('plot_T_%.2f_prob_path_int.png' % T)
pylab.show()
```
### Anharmonic oscillator
Our anharmonic oscillator is described by the potential $V_a(x)=\frac{x^2}{2}+\gamma_{cubic}x^3 + \gamma_{quartic}x^4$, where the coefficients $\gamma_{cubic}, \gamma_{quartic}$ are small. We consider the case $-\gamma_{cubic}=\gamma_{quartic}>0$.
#### Trotter decomposition
When the cubic and quartic parameters are rather small, the anharmonic potential is similar to the harmonic one. In this case, there exists a perturbative expression for the energy levels $E_n(\gamma_{cubic}, \gamma_{quartic})$ of the anharmonic oscillator. This expression (that is too complicated for us to derive, see e.g. Landau Lifshitz: "Quantum Mechanics (vol 3)", exercise 3 of chap 38) allows us to compute the partition function $\sum_n \exp(-\beta E_n)$ for small $\gamma_{cubic}$ and $\gamma_{quartic}$ (this is the meaning of the word "perturbative"), but it becomes totally wrong at larger values of the parameters.
```
import math, numpy, pylab
from numpy import *
# Define the anharmonic (quartic) potential
def V_anharmonic(x, gamma, kappa):
V = x**2 / 2 + gamma * x**3 + kappa * x**4
return V
# Free off-diagonal density matrix:
def rho_free(x, xp, beta):
return (math.exp(-(x - xp) ** 2 / (2.0 * beta)) /
math.sqrt(2.0 * math.pi * beta))
# Harmonic density matrix in the Trotter approximation (returns the full matrix):
def rho_anharmonic_trotter(grid, beta):
return numpy.array([[rho_free(x, xp, beta) * \
numpy.exp(-0.5 * beta * (V_anharmonic(x, -g, g) + V_anharmonic(xp, -g, g))) \
for x in grid] for xp in grid])
# Exact harmonic oscillator quantum position distribution:
def p_quant(x, beta):
p_q = sqrt(tanh(beta / 2.0) / pi) * exp(- x**2.0 * tanh(beta / 2.0))
return p_q
# Perturbative energy levels
def Energy_pert(n, cubic, quartic):
return n + 0.5 - 15.0 / 4.0 * cubic **2 * (n ** 2 + n + 11.0 / 30.0) \
+ 3.0 / 2.0 * quartic * (n ** 2 + n + 1.0 / 2.0)
# Partition function obtained using perturbative energies
def Z_pert(cubic, quartic, beta, n_max):
Z = sum(math.exp(-beta * Energy_pert(n, cubic, quartic)) for n in range(n_max + 1))
return Z
# Construct the position grid:
x_max = 5 #maximum position value
nx = 100 #number of elements on the x grid
dx = 2.0 * x_max / (nx - 1) #position differential
x = [i * dx for i in range(-(nx - 1) / 2, nx / 2 + 1)] #position grid
beta_tmp = 2.0 ** (-5) # initial (low) value of beta (power of 2) (high temperature)
beta = 2.0 ** 1 # actual value of beta (power of 2)
#g = 1.0 #-cubic and quartic coefficient
for g in [0.001, 0.01, 0.1, 0.2, 0.3, 0.4, 0.5]:
Z_p = Z_pert(-g, g, beta, 15)
rho = rho_anharmonic_trotter(x, beta_tmp) # density matrix at initial (low) beta (Trotter decomp.)
# Reduce the temperature by the convolution property (matrix squaring):
while beta_tmp < beta:
rho = numpy.dot(rho, rho) #matrix squaring (convolution)
rho *= dx #also multiply by the differential since we are in position representation
beta_tmp *= 2.0 #reduce the temperature by a factor of 2
#print 'beta: %s -> %s' % (beta_tmp / 2.0, beta_tmp)
# Output position distribution pi(x) at the final beta onto a file:
Z = sum(rho[j, j] for j in range(nx + 1)) * dx #partition function
pi_of_x = [rho[j, j] / Z for j in range(nx + 1)] #the diagonal element of the density matrix
f = open('data_anharm_matrixsquaring_beta' + str(beta) + '.dat', 'w')
for j in range(nx + 1):
f.write(str(x[j]) + ' ' + str(rho[j, j] / Z) + '\n')
f.close()
# Plot the obtained final position distribution:
T = 1 / beta
x = linspace(-x_max, x_max, nx+1)
y2 = [V_anharmonic(a, -g, g) for a in x]
y1 = [p_quant(a, beta) for a in x]
pylab.plot(x, y2, c='gray', linewidth=2.0, label='Anharmonic potential')
pylab.plot(x, y1, c='green', linewidth=2.0, label='Harmonic exact quantum')
pylab.plot(x, pi_of_x, c='red', linewidth=4.0, label='Anharmonic matrix squaring')
pylab.ylim(0,1)
pylab.xlim(-2,2)
pylab.title('Anharmonic oscillator position distribution at $T=$%.2f' % T, fontsize = 13)
pylab.xlabel('$x$', fontsize = 15)
pylab.ylabel('$\pi(x)$', fontsize = 15)
pylab.legend()
pylab.grid()
pylab.savefig('plot_T_%.2f_anharm_g_%.1f_prob_matrix_squaring.png' % (T,g))
pylab.show()
print 'g =', g, 'Perturbative partition function:', Z_p, 'Monte Carlo partition function', Z
```
#### Path integral Monte Carlo
```
%pylab inline
import math, random, pylab
# Define the anharmonic (quartic) potential
def V_anharmonic(x, gamma, kappa):
V = x**2 / 2 + gamma * x**3 + kappa * x**4
return V
def rho_free(x, y, beta): # free off-diagonal density matrix
return math.exp(-(x - y) ** 2 / (2.0 * beta))
def read_file(filename):
list_x = []
list_y = []
with open(filename) as f:
for line in f:
x, y = line.split()
list_x.append(float(x))
list_y.append(float(y))
f.close()
return list_x, list_y
beta = 4.0
g = 1.0 #-cubic and quartic coefficients
T = 1 / beta
N = 16 # number of imaginary times slices
dtau = beta / N
delta = 1.0 # maximum displacement on one slice
n_steps = 1000000 # number of Monte Carlo steps
x = [0.0] * N # initial path
hist_data = []
for step in range(n_steps):
k = random.randint(0, N - 1) # random slice
knext, kprev = (k + 1) % N, (k - 1) % N # next/previous slices
x_new = x[k] + random.uniform(-delta, delta) # new position at slice k
old_weight = (rho_free(x[knext], x[k], dtau) *
rho_free(x[k], x[kprev], dtau) *
math.exp(-dtau * V_anharmonic(x[k], -g, g)))
new_weight = (rho_free(x[knext], x_new, dtau) *
rho_free(x_new, x[kprev], dtau) *
math.exp(-dtau * V_anharmonic(x_new ,-g, g)))
if random.uniform(0.0, 1.0) < new_weight / old_weight:
x[k] = x_new
if step % 10 == 0:
hist_data.append(x[0])
# Figure output:
list_x, list_y = read_file('data_anharm_matrixsquaring_beta' + str(beta) + '.dat')
v = [V_anharmonic(a, -g, g) for a in list_x]
pylab.plot(list_x, v, c='gray', linewidth=2.0, label='Anharmonic potential')
pylab.plot(list_x, list_y, c='red', linewidth=4.0, label='path integral Monte Carlo')
pylab.hist(hist_data, 100, normed = 'True', label='matrix squaring') #histogram of the sample
pylab.ylim(0,1)
pylab.xlim(-2,2)
pylab.title('Position distribution at $T=%.2f$, $\gamma_{cubic}=%.2f$, $\gamma_{quartic}=%.2f$' % (T,-g,g), fontsize = 13)
pylab.xlim(-2.0, 2.0) #restrict the range over which the histogram is shown
pylab.xlabel('$x$', fontsize = 15)
pylab.ylabel('$\pi(x)$', fontsize = 15)
pylab.legend()
pylab.savefig('plot_T_%.2f_anharm_g_%.1f_prob_path_int.png' % (T,g))
pylab.show()
```
| true |
code
| 0.506469 | null | null | null | null |
|
```
# Copyright (c) Facebook, Inc. and its affiliates. All rights reserved.
```
# Absolute camera orientation given set of relative camera pairs
This tutorial showcases the `cameras`, `transforms` and `so3` API.
The problem we deal with is defined as follows:
Given an optical system of $N$ cameras with extrinsics $\{g_1, ..., g_N | g_i \in SE(3)\}$, and a set of relative camera positions $\{g_{ij} | g_{ij}\in SE(3)\}$ that map between coordinate frames of randomly selected pairs of cameras $(i, j)$, we search for the absolute extrinsic parameters $\{g_1, ..., g_N\}$ that are consistent with the relative camera motions.
More formally:
$$
g_1, ..., g_N =
{\arg \min}_{g_1, ..., g_N} \sum_{g_{ij}} d(g_{ij}, g_i^{-1} g_j),
$$,
where $d(g_i, g_j)$ is a suitable metric that compares the extrinsics of cameras $g_i$ and $g_j$.
Visually, the problem can be described as follows. The picture below depicts the situation at the beginning of our optimization. The ground truth cameras are plotted in purple while the randomly initialized estimated cameras are plotted in orange:

Our optimization seeks to align the estimated (orange) cameras with the ground truth (purple) cameras, by minimizing the discrepancies between pairs of relative cameras. Thus, the solution to the problem should look as follows:
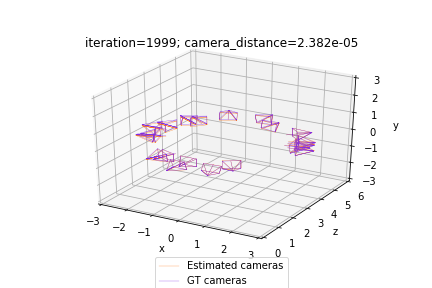
In practice, the camera extrinsics $g_{ij}$ and $g_i$ are represented using objects from the `SfMPerspectiveCameras` class initialized with the corresponding rotation and translation matrices `R_absolute` and `T_absolute` that define the extrinsic parameters $g = (R, T); R \in SO(3); T \in \mathbb{R}^3$. In order to ensure that `R_absolute` is a valid rotation matrix, we represent it using an exponential map (implemented with `so3_exp_map`) of the axis-angle representation of the rotation `log_R_absolute`.
Note that the solution to this problem could only be recovered up to an unknown global rigid transformation $g_{glob} \in SE(3)$. Thus, for simplicity, we assume knowledge of the absolute extrinsics of the first camera $g_0$. We set $g_0$ as a trivial camera $g_0 = (I, \vec{0})$.
## 0. Install and Import Modules
Ensure `torch` and `torchvision` are installed. If `pytorch3d` is not installed, install it using the following cell:
```
import os
import sys
import torch
need_pytorch3d=False
try:
import pytorch3d
except ModuleNotFoundError:
need_pytorch3d=True
if need_pytorch3d:
if torch.__version__.startswith("1.9") and sys.platform.startswith("linux"):
# We try to install PyTorch3D via a released wheel.
version_str="".join([
f"py3{sys.version_info.minor}_cu",
torch.version.cuda.replace(".",""),
f"_pyt{torch.__version__[0:5:2]}"
])
!pip install pytorch3d -f https://dl.fbaipublicfiles.com/pytorch3d/packaging/wheels/{version_str}/download.html
else:
# We try to install PyTorch3D from source.
!curl -LO https://github.com/NVIDIA/cub/archive/1.10.0.tar.gz
!tar xzf 1.10.0.tar.gz
os.environ["CUB_HOME"] = os.getcwd() + "/cub-1.10.0"
!pip install 'git+https://github.com/facebookresearch/pytorch3d.git@stable'
# imports
import torch
from pytorch3d.transforms.so3 import (
so3_exp_map,
so3_relative_angle,
)
from pytorch3d.renderer.cameras import (
SfMPerspectiveCameras,
)
# add path for demo utils
import sys
import os
sys.path.append(os.path.abspath(''))
# set for reproducibility
torch.manual_seed(42)
if torch.cuda.is_available():
device = torch.device("cuda:0")
else:
device = torch.device("cpu")
print("WARNING: CPU only, this will be slow!")
```
If using **Google Colab**, fetch the utils file for plotting the camera scene, and the ground truth camera positions:
```
!wget https://raw.githubusercontent.com/facebookresearch/pytorch3d/main/docs/tutorials/utils/camera_visualization.py
from camera_visualization import plot_camera_scene
!mkdir data
!wget -P data https://raw.githubusercontent.com/facebookresearch/pytorch3d/main/docs/tutorials/data/camera_graph.pth
```
OR if running **locally** uncomment and run the following cell:
```
# from utils import plot_camera_scene
```
## 1. Set up Cameras and load ground truth positions
```
# load the SE3 graph of relative/absolute camera positions
camera_graph_file = './data/camera_graph.pth'
(R_absolute_gt, T_absolute_gt), \
(R_relative, T_relative), \
relative_edges = \
torch.load(camera_graph_file)
# create the relative cameras
cameras_relative = SfMPerspectiveCameras(
R = R_relative.to(device),
T = T_relative.to(device),
device = device,
)
# create the absolute ground truth cameras
cameras_absolute_gt = SfMPerspectiveCameras(
R = R_absolute_gt.to(device),
T = T_absolute_gt.to(device),
device = device,
)
# the number of absolute camera positions
N = R_absolute_gt.shape[0]
```
## 2. Define optimization functions
### Relative cameras and camera distance
We now define two functions crucial for the optimization.
**`calc_camera_distance`** compares a pair of cameras. This function is important as it defines the loss that we are minimizing. The method utilizes the `so3_relative_angle` function from the SO3 API.
**`get_relative_camera`** computes the parameters of a relative camera that maps between a pair of absolute cameras. Here we utilize the `compose` and `inverse` class methods from the PyTorch3D Transforms API.
```
def calc_camera_distance(cam_1, cam_2):
"""
Calculates the divergence of a batch of pairs of cameras cam_1, cam_2.
The distance is composed of the cosine of the relative angle between
the rotation components of the camera extrinsics and the l2 distance
between the translation vectors.
"""
# rotation distance
R_distance = (1.-so3_relative_angle(cam_1.R, cam_2.R, cos_angle=True)).mean()
# translation distance
T_distance = ((cam_1.T - cam_2.T)**2).sum(1).mean()
# the final distance is the sum
return R_distance + T_distance
def get_relative_camera(cams, edges):
"""
For each pair of indices (i,j) in "edges" generate a camera
that maps from the coordinates of the camera cams[i] to
the coordinates of the camera cams[j]
"""
# first generate the world-to-view Transform3d objects of each
# camera pair (i, j) according to the edges argument
trans_i, trans_j = [
SfMPerspectiveCameras(
R = cams.R[edges[:, i]],
T = cams.T[edges[:, i]],
device = device,
).get_world_to_view_transform()
for i in (0, 1)
]
# compose the relative transformation as g_i^{-1} g_j
trans_rel = trans_i.inverse().compose(trans_j)
# generate a camera from the relative transform
matrix_rel = trans_rel.get_matrix()
cams_relative = SfMPerspectiveCameras(
R = matrix_rel[:, :3, :3],
T = matrix_rel[:, 3, :3],
device = device,
)
return cams_relative
```
## 3. Optimization
Finally, we start the optimization of the absolute cameras.
We use SGD with momentum and optimize over `log_R_absolute` and `T_absolute`.
As mentioned earlier, `log_R_absolute` is the axis angle representation of the rotation part of our absolute cameras. We can obtain the 3x3 rotation matrix `R_absolute` that corresponds to `log_R_absolute` with:
`R_absolute = so3_exp_map(log_R_absolute)`
```
# initialize the absolute log-rotations/translations with random entries
log_R_absolute_init = torch.randn(N, 3, dtype=torch.float32, device=device)
T_absolute_init = torch.randn(N, 3, dtype=torch.float32, device=device)
# furthermore, we know that the first camera is a trivial one
# (see the description above)
log_R_absolute_init[0, :] = 0.
T_absolute_init[0, :] = 0.
# instantiate a copy of the initialization of log_R / T
log_R_absolute = log_R_absolute_init.clone().detach()
log_R_absolute.requires_grad = True
T_absolute = T_absolute_init.clone().detach()
T_absolute.requires_grad = True
# the mask the specifies which cameras are going to be optimized
# (since we know the first camera is already correct,
# we only optimize over the 2nd-to-last cameras)
camera_mask = torch.ones(N, 1, dtype=torch.float32, device=device)
camera_mask[0] = 0.
# init the optimizer
optimizer = torch.optim.SGD([log_R_absolute, T_absolute], lr=.1, momentum=0.9)
# run the optimization
n_iter = 2000 # fix the number of iterations
for it in range(n_iter):
# re-init the optimizer gradients
optimizer.zero_grad()
# compute the absolute camera rotations as
# an exponential map of the logarithms (=axis-angles)
# of the absolute rotations
R_absolute = so3_exp_map(log_R_absolute * camera_mask)
# get the current absolute cameras
cameras_absolute = SfMPerspectiveCameras(
R = R_absolute,
T = T_absolute * camera_mask,
device = device,
)
# compute the relative cameras as a composition of the absolute cameras
cameras_relative_composed = \
get_relative_camera(cameras_absolute, relative_edges)
# compare the composed cameras with the ground truth relative cameras
# camera_distance corresponds to $d$ from the description
camera_distance = \
calc_camera_distance(cameras_relative_composed, cameras_relative)
# our loss function is the camera_distance
camera_distance.backward()
# apply the gradients
optimizer.step()
# plot and print status message
if it % 200==0 or it==n_iter-1:
status = 'iteration=%3d; camera_distance=%1.3e' % (it, camera_distance)
plot_camera_scene(cameras_absolute, cameras_absolute_gt, status)
print('Optimization finished.')
```
## 4. Conclusion
In this tutorial we learnt how to initialize a batch of SfM Cameras, set up loss functions for bundle adjustment, and run an optimization loop.
| true |
code
| 0.635166 | null | null | null | null |
|
# Introduction
## Motivation
This notebook follows up `model_options.ipynb`.
The key difference is that we filter using the category distance metric (see `bin/wp-get-links` for details), rather than relying solely on the regression to pick relevant articles. Thus, we want to decide what an appropriate category distance threshold is.
Our hope is that by adding this filter, we can now finalize the regression algorithm selection and configuration.
## Summary
(You may want to read this section last, as it refers to the full analysis below.)
### Q1. Which algorithm?
In `model_options`, we boiled down the selection to three choices:
1. Lasso, normalized, positive, auto 𝛼 (LA_NPA)
2. Elastic net, normalized, positive, auto 𝛼, auto 𝜌 (EN_NPAA)
3. Elastic net, normalized, positive, auto 𝛼, manual 𝜌 = ½ (EN_NPAM)
The results below suggest three conclusions:
1. LA_NPA vs. EN_NPAA:
* EN_NPAA has (probably insignificantly) better RMSE.
* Forecasts look almost identical.
* EN_NPAA chooses a more reasonable-feeling number of articles.
* EN_NPAA is more principled (lasso vs. elastic net).
2. EN_NPAM vs. EN_NPAA:
* EN_NPAA has better RMSE.
* Forecasts look almost identical, except EN_NPAM has some spikes in the 2014–2015 season, which probably accounts for the RMSE difference.
* EN_NPAA chooses fewer articles, though EN_NPAM does not feel excessive.
* EN_NPAA is more principles (manual 𝜌 vs. auto).
On balance, **EN_NPAA seems the best choice**, based on principles and article quantity rather than results, which are nearly the same across the board.
### Q2. What distance threshold?
Observations for EN_NPAA at distance threshold 1, 2, 3:
* d = 2 is where RMSE reaches its minimum, and it stays more or less the same all the way through d = 8.
* d = 2 and 3 have nearly identical-looking predictions.
* d = 2 and 3 have very similar articles and coefficient ranking. Of the 10 and 13 articles respectively, 9 are shared and in almost the same order.
These suggests that the actual models for d = 2..8 are very similar. Further:
* d = 2 or 3 does not have the spikes in 3rd season that d = 1 does. This suggests that the larger number of articles gives a more robust model.
* d = 2 or 3 matches the overall shape of the outbreak better than d = 1, though the latter gets the peak intensity more correct in the 1st season.
Finally, examining the article counts in `COUNTS` and `COUNTS_CUM`, d = 2 would give very small input sets in some of the sparser cases, while d = 3 seems safer (e.g., "es+Infecciones por clamidias" and "he+שעלת"). On the other hand, Arabic seems to have a shallower category structure, and d = 3 would capture most articles.
On balance, **d = 3 seems the better choice**. It performs as well as d = 2, without catching irrelevant articles, and d = 2 seems too few articles in several cases. The Arabic situation is a bit of an unknown, as none of us speak Arabic, but erring on the side of too many articles seems less risky than clearly too few.
### Q3. What value of 𝜌?
In both this notebook and `model_options`, every auto-selected 𝜌 has been 0.9, i.e., mostly lasso. Thus, we will **fix 𝜌 = 0.9** for performance reasons.
### Conclusion
We select **EN_NPAM with 𝜌 = 0.9**.
# Preamble
## Imports
```
%matplotlib inline
import collections
import gzip
import pickle
import os
import urllib.parse
import numpy as np
import matplotlib as plt
import pandas as pd
import sklearn as sk
import sklearn.linear_model
DATA_PATH = os.environ['WEIRD_AL_YANKOVIC']
plt.rcParams['figure.figsize'] = (12, 4)
```
## Load, preprocess, and clean data
Load and preprocess the truth spreadsheet.
```
truth = pd.read_excel(DATA_PATH + '/truth.xlsx', index_col=0)
TRUTH_FLU = truth.loc[:,'us+influenza'] # pull Series
TRUTH_FLU.index = TRUTH_FLU.index.to_period('W-SAT')
TRUTH_FLU.head()
```
Load the Wikipedia link data. We convert percent-encoded URLs to Unicode strings for convenience of display.
```
def unquote(url):
(lang, url) = url.split('+', 1)
url = urllib.parse.unquote(url)
url = url.replace('_', ' ')
return (lang + '+' + url)
raw_graph = pickle.load(gzip.open(DATA_PATH + '/articles/wiki-graph.pkl.gz'))
GRAPH = dict()
for root in raw_graph.keys():
unroot = unquote(root)
GRAPH[unroot] = { unquote(a): d for (a, d) in raw_graph[root].items() }
```
Load all the time series. Most of the 4,299 identified articles were in the data set.
Note that in contrast to `model_options`, we do not remove any time series by the fraction that they are zero. The results seem good anyway. This filter also may not apply well to the main experiment, because the training periods are often not long enough to make it meaningful.
```
TS_ALL = pd.read_csv(DATA_PATH + '/tsv/forecasting_W-SAT.norm.tsv',
sep='\t', index_col=0, parse_dates=True)
TS_ALL.index = TS_ALL.index.to_period('W-SAT')
TS_ALL.rename(columns=lambda x: unquote(x[:-5]), inplace=True)
len(TS_ALL.columns)
(TS_ALL, TRUTH_FLU) = TS_ALL.align(TRUTH_FLU, axis=0, join='inner')
TRUTH_FLU.plot()
TS_ALL.iloc[:,:5].plot()
```
## Summarize distance from root
Number of articles by distance from each root.
```
COUNTS = pd.DataFrame(columns=range(1,9), index=sorted(GRAPH.keys()))
COUNTS.fillna(0, inplace=True)
for (root, leaves) in GRAPH.items():
for (leaf, dist) in leaves.items():
COUNTS[dist][root] += 1
COUNTS
```
Number of articles of at most the given distance.
```
COUNTS_CUM = COUNTS.cumsum(axis=1)
COUNTS_CUM
```
# Parameter sweep
Return the set of articles with maximum category distance from a given root.
```
def articles_dist(root, dist):
return { a for (a, d) in GRAPH[root].items() if d <= dist }
```
Return time series for articles with a maximum category distance from the given root.
```
def select_by_distance(root, d):
keep_cols = articles_dist(root, d)
return TS_ALL.filter(items=keep_cols, axis=1)
select_by_distance('en+Influenza', 1).head()
```
Fit function. The core is the same as the `model_options` one, with non-constant training series set and a richer summary.
```
def fit(root, train_week_ct, d, alg, plot=True):
ts_all = select_by_distance(root, d)
ts_train = ts_all.iloc[:train_week_ct,:]
truth_train = TRUTH_FLU.iloc[:train_week_ct]
m = alg.fit(ts_train, truth_train)
m.input_ct = len(ts_all.columns)
pred = m.predict(ts_all)
pred_s = pd.Series(pred, index=TRUTH_FLU.index)
m.r = TRUTH_FLU.corr(pred_s)
m.rmse = ((TRUTH_FLU - pred_s)**2).mean()
m.nonzero = np.count_nonzero(m.coef_)
if (not hasattr(m, 'l1_ratio_')):
m.l1_ratio_ = -1
# this is just a line to show how long the training period is
train_period = TRUTH_FLU.iloc[:train_week_ct].copy(True)
train_period[:] = 0
if (plot):
pd.DataFrame({'truth': TRUTH_FLU,
'prediction': pred,
'training pd': train_period}).plot(ylim=(-1,9))
sumry = pd.DataFrame({'coefs': m.coef_,
'coefs_abs': np.abs(m.coef_)},
index=ts_all.columns)
sumry.sort_values(by='coefs_abs', ascending=False, inplace=True)
sumry = sumry.loc[:, 'coefs']
for a in ('intercept_', 'alpha_', 'l1_ratio_', 'nonzero', 'rmse', 'r', 'input_ct'):
try:
sumry = pd.Series([getattr(m, a)], index=[a]).append(sumry)
except AttributeError:
pass
return (m, pred, sumry)
```
Which 𝛼 and 𝜌 to explore? Same as `model_options`.
```
ALPHAS = np.logspace(-15, 2, 25)
RHOS = np.linspace(0.1, 0.9, 9)
```
Try all distance filters and summarize the result in a table.
```
def fit_summary(root, label, train_week_ct, alg, **kwargs):
result = pd.DataFrame(columns=[[label] * 4,
['input_ct', 'rmse', 'rho', 'nonzero']],
index=range(1, 9))
preds = dict()
for d in range(1, 9):
(m, preds[d], sumry) = fit(root, train_week_ct, d, alg(**kwargs), plot=False)
result.loc[d,:] = (m.input_ct, m.rmse, m.l1_ratio_, m.nonzero)
return (result, preds)
```
## Lasso, normalized, positive, auto 𝛼
```
la_npa = fit_summary('en+Influenza', 'la_npa', 104, sk.linear_model.LassoCV,
normalize=True, positive=True, alphas=ALPHAS,
max_iter=1e5, selection='random', n_jobs=-1)
la_npa[0]
(m, _, s) = fit('en+Influenza', 104, 1,
sk.linear_model.LassoCV(normalize=True, positive=True, alphas=ALPHAS,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
(m, _, s) = fit('en+Influenza', 104, 2,
sk.linear_model.LassoCV(normalize=True, positive=True, alphas=ALPHAS,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
(m, _, s) = fit('en+Influenza', 104, 3,
sk.linear_model.LassoCV(normalize=True, positive=True, alphas=ALPHAS,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
```
## Elastic net, normalized, positive, auto 𝛼, auto 𝜌
```
en_npaa = fit_summary('en+Influenza', 'en_npaa', 104, sk.linear_model.ElasticNetCV,
normalize=True, positive=True, alphas=ALPHAS, l1_ratio=RHOS,
max_iter=1e5, selection='random', n_jobs=-1)
en_npaa[0]
(m, _, s) = fit('en+Influenza', 104, 1,
sk.linear_model.ElasticNetCV(normalize=True, positive=True,
alphas=ALPHAS, l1_ratio=RHOS,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
(m, _, s) = fit('en+Influenza', 104, 2,
sk.linear_model.ElasticNetCV(normalize=True, positive=True,
alphas=ALPHAS, l1_ratio=RHOS,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
(m, _, s) = fit('en+Influenza', 104, 3,
sk.linear_model.ElasticNetCV(normalize=True, positive=True,
alphas=ALPHAS, l1_ratio=RHOS,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
```
## Elastic net, normalized, positive, auto 𝛼, manual 𝜌 = ½
```
en_npam = fit_summary('en+Influenza', 'en_npam', 104, sk.linear_model.ElasticNetCV,
normalize=True, positive=True, alphas=ALPHAS, l1_ratio=0.5,
max_iter=1e5, selection='random', n_jobs=-1)
en_npam[0]
(m, _, s) = fit('en+Influenza', 104, 1,
sk.linear_model.ElasticNetCV(normalize=True, positive=True,
alphas=ALPHAS, l1_ratio=0.5,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
(m, _, s) = fit('en+Influenza', 104, 2,
sk.linear_model.ElasticNetCV(normalize=True, positive=True,
alphas=ALPHAS, l1_ratio=0.5,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
(m, _, s) = fit('en+Influenza', 104, 3,
sk.linear_model.ElasticNetCV(normalize=True, positive=True,
alphas=ALPHAS, l1_ratio=0.5,
max_iter=1e5, selection='random', n_jobs=-1))
s.head(27)
```
## Summary
All the result tables next to one another.
```
pd.concat([la_npa[0], en_npaa[0], en_npam[0]], axis=1)
```
Plot the predictions by distance filter next to one another.
```
def plot(data, ds):
for d in ds:
D = collections.OrderedDict([('truth', TRUTH_FLU)])
D[d] = data[1][d]
pd.DataFrame(D).plot(figsize=(12,3))
plot(la_npa, range(1, 4))
plot(en_npaa, range(1, 4))
plot(en_npam, range(1, 4))
```
| true |
code
| 0.470068 | null | null | null | null |
|
# Linear Elasticity in 2D for 3 Phases
## Introduction
This example provides a demonstration of using PyMKS to compute the linear strain field for a three-phase composite material. It demonstrates how to generate data for delta microstructures and then use this data to calibrate the first order MKS influence coefficients. The calibrated influence coefficients are used to predict the strain response for a random microstructure and the results are compared with those from finite element. Finally, the influence coefficients are scaled up and the MKS results are again compared with the finite element data for a large problem.
PyMKS uses the finite element tool [SfePy](http://sfepy.org) to generate both the strain fields to fit the MKS model and the verification data to evaluate the MKS model's accuracy.
### Elastostatics Equations and Boundary Conditions
The governing equations for elasticostaics and the boundary conditions used in this example are the same as those provided in the [Linear Elastic in 2D](elasticity_2D.html) example.
Note that an inappropriate boundary condition is used in this example because current version of SfePy is unable to implement a periodic plus displacement boundary condition. This leads to some issues near the edges of the domain and introduces errors into the resizing of the coefficients. We are working to fix this issue, but note that the problem is not with the MKS regression itself, but with the calibration data used. The finite element package ABAQUS includes the displaced periodic boundary condition and can be used to calibrate the MKS regression correctly.
## Modeling with MKS
### Calibration Data and Delta Microstructures
The first order MKS influence coefficients are all that is needed to compute a strain field of a random microstructure as long as the ratio between the elastic moduli (also known as the contrast) is less than 1.5. If this condition is met we can expect a mean absolute error of 2% or less when comparing the MKS results with those computed using finite element methods [1].
Because we are using distinct phases and the contrast is low enough to only need the first-order coefficients, delta microstructures and their strain fields are all that we need to calibrate the first-order influence coefficients [2].
Here we use the `make_delta_microstructure` function from `pymks.datasets` to create the delta microstructures needed to calibrate the first-order influence coefficients for a two-phase microstructure. The `make_delta_microstructure` function uses SfePy to generate the data.
```
#PYTEST_VALIDATE_IGNORE_OUTPUT
import pymks
%matplotlib inline
%load_ext autoreload
%autoreload 2
import numpy as np
import matplotlib.pyplot as plt
from pymks.tools import draw_microstructures
from pymks.datasets import make_delta_microstructures
n = 21
n_phases = 3
X_delta = make_delta_microstructures(n_phases=n_phases, size=(n, n))
```
Let's take a look at a few of the delta microstructures by importing `draw_microstructures` from `pymks.tools`.
```
draw_microstructures(X_delta[::2])
```
Using delta microstructures for the calibration of the first-order influence coefficients is essentially the same, as using a unit [impulse response](http://en.wikipedia.org/wiki/Impulse_response) to find the kernel of a system in signal processing. Any given delta microstructure is composed of only two phases with the center cell having an alternative phase from the remainder of the domain. The number of delta microstructures that are needed to calibrated the first-order coefficients is $N(N-1)$ where $N$ is the number of phases, therefore in this example we need 6 delta microstructures.
### Generating Calibration Data
The `make_elasticFEstrain_delta` function from `pymks.datasets` provides an easy interface to generate delta microstructures and their strain fields, which can then be used for calibration of the influence coefficients. The function calls the `ElasticFESimulation` class to compute the strain fields.
In this example, lets look at a three phase microstructure with elastic moduli values of 80, 100 and 120 and Poisson's ratio values all equal to 0.3. Let's also set the macroscopic imposed strain equal to 0.02. All of these parameters used in the simulation must be passed into the `make_elasticFEstrain_delta` function. The number of Poisson's ratio values and elastic moduli values indicates the number of phases. Note that `make_elasticFEstrain_delta` does not take a number of samples argument as the number of samples to calibrate the MKS is fixed by the number of phases.
```
from pymks.datasets import make_elastic_FE_strain_delta
from pymks.tools import draw_microstructure_strain
elastic_modulus = (80, 100, 120)
poissons_ratio = (0.3, 0.3, 0.3)
macro_strain = 0.02
size = (n, n)
X_delta, strains_delta = make_elastic_FE_strain_delta(elastic_modulus=elastic_modulus,
poissons_ratio=poissons_ratio,
size=size, macro_strain=macro_strain)
```
Let's take a look at one of the delta microstructures and the $\varepsilon_{xx}$ strain field.
```
draw_microstructure_strain(X_delta[0], strains_delta[0])
```
Because `slice(None)` (the default slice operator in Python, equivalent to array[:]) was passed in to the `make_elasticFEstrain_delta` function as the argument for `strain_index`, the function returns all the strain fields. Let's also take a look at the $\varepsilon_{yy}$ and $\varepsilon_{xy}$ strain fields.
### Calibrating First-Order Influence Coefficients
Now that we have the delta microstructures and their strain fields, we will calibrate the influence coefficients by creating an instance of the `MKSLocalizatoinModel` class. Because we are going to calibrate the influence coefficients with delta microstructures, we can create an instance of `PrimitiveBasis` with `n_states` equal to 3, and use it to create an instance of `MKSLocalizationModel`. The delta microstructures and their strain fields will then be passed to the `fit` method.
```
from pymks import MKSLocalizationModel
from pymks import PrimitiveBasis
p_basis =PrimitiveBasis(n_states=3, domain=[0, 2])
model = MKSLocalizationModel(basis=p_basis)
```
Now, pass the delta microstructures and their strain fields into the `fit` method to calibrate the first-order influence coefficients.
```
model.fit(X_delta, strains_delta)
```
That's it, the influence coefficient have been calibrated. Let's take a look at them.
```
from pymks.tools import draw_coeff
draw_coeff(model.coef_)
```
The influence coefficients for $l=0$ and $l = 1$ have a Gaussian-like shape, while the influence coefficients for $l=2$ are constant-valued. The constant-valued influence coefficients may seem superfluous, but are equally as important. They are equivalent to the constant term in multiple linear regression with [categorical variables](http://en.wikipedia.org/wiki/Dummy_variable_%28statistics%29).
### Predict of the Strain Field for a Random Microstructure
Let's now use our instance of the `MKSLocalizationModel` class with calibrated influence coefficients to compute the strain field for a random two-phase microstructure and compare it with the results from a finite element simulation.
The `make_elasticFEstrain_random` function from `pymks.datasets` is an easy way to generate a random microstructure and its strain field results from finite element analysis.
```
from pymks.datasets import make_elastic_FE_strain_random
np.random.seed(101)
X, strain = make_elastic_FE_strain_random(n_samples=1, elastic_modulus=elastic_modulus,
poissons_ratio=poissons_ratio, size=size,
macro_strain=macro_strain)
draw_microstructure_strain(X[0] , strain[0])
```
**Note that the calibrated influence coefficients can only be used to reproduce the simulation with the same boundary conditions that they were calibrated with.**
Now, to get the strain field from the `MKSLocalizationModel`, just pass the same microstructure to the `predict` method.
```
strain_pred = model.predict(X)
```
Finally let's compare the results from finite element simulation and the MKS model.
```
from pymks.tools import draw_strains_compare
draw_strains_compare(strain[0], strain_pred[0])
```
Let's plot the difference between the two strain fields.
```
from pymks.tools import draw_differences
draw_differences([strain[0] - strain_pred[0]], ['Finite Element - MKS'])
```
The MKS model is able to capture the strain field for the random microstructure after being calibrated with delta microstructures.
## Resizing the Coefficeints to use on Larger Microstructures
The influence coefficients that were calibrated on a smaller microstructure can be used to predict the strain field on a larger microstructure though spectral interpolation [3], but accuracy of the MKS model drops slightly. To demonstrate how this is done, let's generate a new larger random microstructure and its strain field.
```
m = 3 * n
size = (m, m)
print(size)
X, strain = make_elastic_FE_strain_random(n_samples=1, elastic_modulus=elastic_modulus,
poissons_ratio=poissons_ratio, size=size,
macro_strain=macro_strain)
draw_microstructure_strain(X[0] , strain[0])
```
The influence coefficients that have already been calibrated on a $n$ by $n$ delta microstructures, need to be resized to match the shape of the new larger $m$ by $m$ microstructure that we want to compute the strain field for. This can be done by passing the shape of the new larger microstructure into the `resize_coeff` method.
```
model.resize_coeff(X[0].shape)
```
Let's now take a look that ther resized influence coefficients.
```
draw_coeff(model.coef_)
```
Because the coefficients have been resized, they will no longer work for our original $n$ by $n$ sized microstructures they were calibrated on, but they can now be used on the $m$ by $m$ microstructures. Just like before, just pass the microstructure as the argument of the `predict` method to get the strain field.
```
strain_pred = model.predict(X)
draw_strains_compare(strain[0], strain_pred[0])
```
Again, let's plot the difference between the two strain fields.
```
draw_differences([strain[0] - strain_pred[0]], ['Finite Element - MKS'])
```
As you can see, the results from the strain field computed with the resized influence coefficients is not as accurate as they were before they were resized. This decrease in accuracy is expected when using spectral interpolation [4].
## References
[1] Binci M., Fullwood D., Kalidindi S.R., A new spectral framework for establishing localization relationships for elastic behavior of composites and their calibration to finite-element models. Acta Materialia, 2008. 56 (10) p. 2272-2282 [doi:10.1016/j.actamat.2008.01.017](http://dx.doi.org/10.1016/j.actamat.2008.01.017).
[2] Landi, G., S.R. Niezgoda, S.R. Kalidindi, Multi-scale modeling of elastic response of three-dimensional voxel-based microstructure datasets using novel DFT-based knowledge systems. Acta Materialia, 2009. 58 (7): p. 2716-2725 [doi:10.1016/j.actamat.2010.01.007](http://dx.doi.org/10.1016/j.actamat.2010.01.007).
[3] Marko, K., Kalidindi S.R., Fullwood D., Computationally efficient database and spectral interpolation for fully plastic Taylor-type crystal plasticity calculations of face-centered cubic polycrystals. International Journal of Plasticity 24 (2008) 1264–1276 [doi:10.1016/j.ijplas.2007.12.002](http://dx.doi.org/10.1016/j.ijplas.2007.12.002).
[4] Marko, K. Al-Harbi H. F. , Kalidindi S.R., Crystal plasticity simulations using discrete Fourier transforms. Acta Materialia 57 (2009) 1777–1784 [doi:10.1016/j.actamat.2008.12.017](http://dx.doi.org/10.1016/j.actamat.2008.12.017).
| true |
code
| 0.614278 | null | null | null | null |
|
# Short-Circuit Calculation according to IEC 60909
pandapower supports short-circuit calculations with the method of equivalent voltage source at the fault location according to IEC 60909. The pandapower short-circuit calculation supports the following elements:
- sgen (as motor or as full converter generator)
- gen (as synchronous generator)
- ext_grid
- line
- trafo
- trafo3w
- impedance
with the correction factors as defined in IEC 60909. Loads and shunts are neglected as per standard. The pandapower switch model is fully integrated into the short-circuit calculation.
The following short-circuit currents can be calculated:
- ikss (Initial symmetrical short-circuit current)
- ip (short-circuit current peak)
- ith (equivalent thermal short-circuit current)
either as
- symmetrical three-phase or
- asymmetrical two-phase
short circuit current. Calculations are available for meshed as well as for radial networks. ip and ith are only implemented for short circuits far from synchronous generators.
The results for all elements and different short-circuit currents are tested against commercial software to ensure that correction factors are correctly applied.
### Example Network
Here is a little example on how to use the short-circuit calculation. First, we create a simple open ring network with 4 buses, that are connected by one transformer and two lines with one open sectioning point. The network is fed by an external grid connection at bus 1:
<img src="shortcircuit/example_network_sc.png">
```
import pandapower as pp
import pandapower.shortcircuit as sc
def ring_network():
net = pp.create_empty_network()
b1 = pp.create_bus(net, 220)
b2 = pp.create_bus(net, 110)
b3 = pp.create_bus(net, 110)
b4 = pp.create_bus(net, 110)
pp.create_ext_grid(net, b1, s_sc_max_mva=100., s_sc_min_mva=80., rx_min=0.20, rx_max=0.35)
pp.create_transformer(net, b1, b2, "100 MVA 220/110 kV")
pp.create_line(net, b2, b3, std_type="N2XS(FL)2Y 1x120 RM/35 64/110 kV" , length_km=15.)
l2 = pp.create_line(net, b3, b4, std_type="N2XS(FL)2Y 1x120 RM/35 64/110 kV" , length_km=12.)
pp.create_line(net, b4, b2, std_type="N2XS(FL)2Y 1x120 RM/35 64/110 kV" , length_km=10.)
pp.create_switch(net, b4, l2, closed=False, et="l")
return net
```
## Symmetric Short-Circuit Calculation
### Maximum Short Circuit Currents
Now, we load the network and calculate the maximum short-circuit currents with the calc_sc function:
```
net = ring_network()
sc.calc_sc(net, case="max", ip=True, ith=True)
net.res_bus_sc
```
where ikss is the initial short-circuit current, ip is the peak short-circuit current and ith is the thermal equivalent current.
For branches, the results are defined as the maximum current flows through that occurs for a fault at any bus in the network. The results are available seperately for lines:
```
net.res_line_sc
```
and transformers:
```
net.res_trafo_sc
```
### Minimum Short Circuit Currents
Minimum short-circuits can be calculated in the same way. However, we need to specify the end temperature of the lines after a fault as per standard first:
```
net = ring_network()
net.line["endtemp_degree"] = 80
sc.calc_sc(net, case="min", ith=True, ip=True)
net.res_bus_sc
```
The branch results are now the minimum current flows through each branch:
```
net.res_line_sc
net.res_trafo_sc
```
### Asynchronous Motors
Asynchronous motors can be specified by creating a static generator of type "motor". For the short circuit impedance, an R/X ratio "rx" as well as the ratio between nominal current and short circuit current "k" has to be specified:
```
net = ring_network()
pp.create_sgen(net, 2, p_kw=0, sn_kva=500, k=1.2, rx=7., type="motor")
net
```
If we run the short-circuit calculation again, we can see that the currents increased due to the contribution of the inverteres to the short-circuit currents.
```
sc.calc_sc(net, case="max", ith=True, ip=True)
net.res_bus_sc
```
### Synchronous Generators
Synchronous generators can also be considered in the short-circuit calculation with the gen element. According to the standard, the rated cosine(phi) "cos_phi", rated voltage "vn_kv", rated apparent power "sn_kva" and subtransient resistance "rdss" and reactance "xdss" are necessary to calculate the short circuit impedance:
```
net = ring_network()
pp.create_gen(net, 2, p_kw=0, vm_pu=1.0, cos_phi=0.8, vn_kv=22, sn_kva=5e3, xdss=0.2, rdss=0.005)
net
```
and run the short-circuit calculation again:
```
sc.calc_sc(net, case="max", ith=True, ip=True)
net.res_bus_sc
```
Once again, the short-circuit current increases due to the contribution of the generator. As can be seen in the warning, the values for peak and thermal equivalent short-circuit current will only be accurate for faults far from generators.
## Meshed Networks
The correction factors for aperiodic and thermal currents differ between meshed and radial networks. pandapower includes a meshing detection that automatically detects the meshing for each short-circuit location. Alternatively, the topology can be set to "radial" or "meshed" to circumvent the check and save calculation time.
We load the radial network and close the open sectioning point to get a closed ring network:
```
net = ring_network()
net.switch.closed = True
sc.calc_sc(net, topology="auto", ip=True, ith=True)
net.res_bus_sc
```
the network is automatically detected to be meshed and application factors are applied. This can be validated by setting the topology to radial and comparing the results:
```
sc.calc_sc(net, topology="radial", ip=True, ith=True)
net.res_bus_sc
```
If we look at the line results, we can see that the line currents are significantly smaller than the bus currents:
```
sc.calc_sc(net, topology="auto", ip=True, ith=True)
net.res_line_sc
```
this is because the short-circuit current is split up on both paths of the ring, which is correctly considered by pandapower.
## Fault Impedance
It is also possible to specify a fault impedance in the short-circuit calculationn:
```
net = ring_network()
sc.calc_sc(net, topology="radial", ip=True, ith=True, r_fault_ohm=1., x_fault_ohm=2.)
```
which of course decreases the short-circuit currents:
```
net.res_bus_sc
```
## Asymetrical Two-Phase Short-Circuit Calculation
All calculations above can be carried out for a two-phase short-circuit current in the same way by specifying "2ph" in the fault parameter:
```
net = ring_network()
sc.calc_sc(net, fault="2ph", ip=True, ith=True)
net.res_bus_sc
```
Two phase short-circuits are often used for minimum short-circuit calculations:
```
net = ring_network()
net.line["endtemp_degree"] = 150
sc.calc_sc(net, fault="2ph", case="min", ip=True, ith=True)
net.res_bus_sc
```
| true |
code
| 0.210523 | null | null | null | null |
|
# Matplotlib example (https://matplotlib.org/gallery/index.html)
```
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot([1,2,3,4])
plt.show()
# to save
# plt.savefig('test_nb.png')
```
# Pandas examples (https://pandas.pydata.org/pandas-docs/stable/visualization.html)
```
import pandas as pd
import numpy as np
ts = pd.Series(np.random.randn(1000), index=pd.date_range('1/1/2000', periods=1000))
df = pd.DataFrame(np.random.randn(1000, 4), index=ts.index, columns=list('ABCD'))
df.cumsum().plot()
# new figure
plt.figure()
df.diff().hist(color='k', alpha=0.5, bins=50)
```
# Seaborn examples (https://seaborn.pydata.org/examples/index.html)
```
# Joint distributions
import seaborn as sns
sns.set(style="ticks")
rs = np.random.RandomState(11)
x = rs.gamma(2, size=1000)
y = -.5 * x + rs.normal(size=1000)
sns.jointplot(x, y, kind="hex", color="#4CB391")
# Multiple linear regression
sns.set()
# Load the iris dataset
iris = sns.load_dataset("iris")
# Plot sepal with as a function of sepal_length across days
g = sns.lmplot(x="sepal_length", y="sepal_width", hue="species",
truncate=True, height=5, data=iris)
# Use more informative axis labels than are provided by default
g.set_axis_labels("Sepal length (mm)", "Sepal width (mm)")
```
# Cartopy examples (https://scitools.org.uk/cartopy/docs/latest/gallery/index.html)
```
import cartopy.crs as ccrs
from cartopy.examples.arrows import sample_data
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(1, 1, 1, projection=ccrs.PlateCarree())
ax.set_extent([-90, 75, 10, 85], crs=ccrs.PlateCarree())
ax.coastlines()
x, y, u, v, vector_crs = sample_data(shape=(80, 100))
magnitude = (u ** 2 + v ** 2) ** 0.5
ax.streamplot(x, y, u, v, transform=vector_crs,
linewidth=2, density=2, color=magnitude)
plt.show()
import matplotlib.patches as mpatches
import shapely.geometry as sgeom
import cartopy.io.shapereader as shpreader
fig = plt.figure()
ax = fig.add_axes([0, 0, 1, 1], projection=ccrs.LambertConformal())
ax.set_extent([-125, -66.5, 20, 50], ccrs.Geodetic())
shapename = 'admin_1_states_provinces_lakes_shp'
states_shp = shpreader.natural_earth(resolution='110m',
category='cultural', name=shapename)
# Hurricane Katrina lons and lats
lons = [-75.1, -75.7, -76.2, -76.5, -76.9, -77.7, -78.4, -79.0,
-79.6, -80.1, -80.3, -81.3, -82.0, -82.6, -83.3, -84.0,
-84.7, -85.3, -85.9, -86.7, -87.7, -88.6, -89.2, -89.6,
-89.6, -89.6, -89.6, -89.6, -89.1, -88.6, -88.0, -87.0,
-85.3, -82.9]
lats = [23.1, 23.4, 23.8, 24.5, 25.4, 26.0, 26.1, 26.2, 26.2, 26.0,
25.9, 25.4, 25.1, 24.9, 24.6, 24.4, 24.4, 24.5, 24.8, 25.2,
25.7, 26.3, 27.2, 28.2, 29.3, 29.5, 30.2, 31.1, 32.6, 34.1,
35.6, 37.0, 38.6, 40.1]
# to get the effect of having just the states without a map "background" turn off the outline and background patches
ax.background_patch.set_visible(False)
ax.outline_patch.set_visible(False)
ax.set_title('US States which intersect the track of '
'Hurricane Katrina (2005)')
# turn the lons and lats into a shapely LineString
track = sgeom.LineString(zip(lons, lats))
# buffer the linestring by two degrees (note: this is a non-physical
# distance)
track_buffer = track.buffer(2)
for state in shpreader.Reader(states_shp).geometries():
# pick a default color for the land with a black outline,
# this will change if the storm intersects with our track
facecolor = [0.9375, 0.9375, 0.859375]
edgecolor = 'black'
if state.intersects(track):
facecolor = 'red'
elif state.intersects(track_buffer):
facecolor = '#FF7E00'
ax.add_geometries([state], ccrs.PlateCarree(),
facecolor=facecolor, edgecolor=edgecolor)
ax.add_geometries([track_buffer], ccrs.PlateCarree(),
facecolor='#C8A2C8', alpha=0.5)
ax.add_geometries([track], ccrs.PlateCarree(),
facecolor='none', edgecolor='k')
# make two proxy artists to add to a legend
direct_hit = mpatches.Rectangle((0, 0), 1, 1, facecolor="red")
within_2_deg = mpatches.Rectangle((0, 0), 1, 1, facecolor="#FF7E00")
labels = ['State directly intersects\nwith track',
'State is within \n2 degrees of track']
ax.legend([direct_hit, within_2_deg], labels,
loc='lower left', bbox_to_anchor=(0.025, -0.1), fancybox=True)
plt.show()
```
# Xarray examples (http://xarray.pydata.org/en/stable/plotting.html)
```
import xarray as xr
airtemps = xr.tutorial.load_dataset('air_temperature')
airtemps
# Convert to celsius
air = airtemps.air - 273.15
# copy attributes to get nice figure labels and change Kelvin to Celsius
air.attrs = airtemps.air.attrs
air.attrs['units'] = 'deg C'
air.sel(lat=50, lon=225).plot()
fig, axes = plt.subplots(ncols=2)
air.sel(lat=50, lon=225).plot(ax=axes[0])
air.sel(lat=50, lon=225).plot.hist(ax=axes[1])
plt.tight_layout()
plt.show()
air.sel(time='2013-09-03T00:00:00').plot()
# Faceting
# Plot evey 250th point
air.isel(time=slice(0, 365 * 4, 250)).plot(x='lon', y='lat', col='time', col_wrap=3)
# Overlay data on cartopy map
ax = plt.axes(projection=ccrs.Orthographic(-80, 35))
air.isel(time=0).plot.contourf(ax=ax, transform=ccrs.PlateCarree());
ax.set_global(); ax.coastlines();
```
| true |
code
| 0.612136 | null | null | null | null |
|
# Averaging Example
Example system of
$$
\begin{gather*}
\ddot{x} + \epsilon \left( x^2 + \dot{x}^2 - 4 \right) \dot{x} + x = 0.
\end{gather*}
$$
For this problem, $h(x,\dot{x}) = x^2 + \dot{x}^2 - 4$ where $\epsilon \ll 1$. The if we assume the solution for x to be
$$
\begin{gather*}
x(t) = a\cos(t + \phi) = a \cos\theta
\end{gather*}
$$
we have
$$
\begin{align*}
h(x,\dot{x}) &= \left(a^2\cos^2\theta + a^2\sin^2\theta - 4\right)\left(-a\sin\theta\right)\\
&= -a^3\cos^2\theta\sin\theta - a^3\sin^3\theta + 4a\sin\theta.
\end{align*}
$$
From the averaging equations we know that
\begin{align*}
\dot{a} &= \dfrac{\epsilon}{2\pi}\int_0^{2\pi}{\left( -a^3\cos^2\theta\sin\theta - a^3\sin^3\theta + 4a\sin\theta \right)\sin\theta}{d\theta}\\
&= \dfrac{\epsilon}{2\pi}\int_{0}^{2\pi}{\left( -a^3\cos^2\theta\sin^2\theta - a^3\sin^4\theta + 4a\sin^2\theta \right)}{d\theta}
\end{align*}
since
\begin{gather*}
\int_{0}^{2\pi}{\cos^2\theta\sin^2\theta}{d\theta} = \dfrac{\pi}{4}\\
\int_{0}^{2\pi}{\sin^2\theta}{d\theta} = \pi\\
\int_{0}^{2\pi}{\sin^4\theta}{d\theta} = \dfrac{3\pi}{4}
\end{gather*}
we have
\begin{align*}
\dot{a} = 2\epsilon a - \dfrac{\epsilon}{2}a^3 + O(\epsilon^2).
\end{align*}
To solve this analytically, let $b = a^{-2}$, then
\begin{gather*}
\dot{b} = -2a^{-3}\dot{a} \phantom{-} \longrightarrow \phantom{-} \dot{a} = -\dfrac{1}{2}a^3b.
\end{gather*}
If we plug this back into the nonlinear ODE we get
\begin{gather*}
-\dfrac{1}{2}a^3\dot{b} - 2\epsilon a = -\dfrac{\epsilon}{2}a^3\\
\therefore \dot{b} + 4\epsilon b = \epsilon.
\end{gather*}
This nonhomogeneous linear ODE can be solved by
$$
\begin{align*}
b(t) &= e^{\int{-4\epsilon t}{dt}}\left[ \int{\epsilon e^{\int{4\epsilon t}{dt}}}{dt} + C \right]\\
&= \dfrac{1}{4} + Ce^{-4\epsilon t}.
\end{align*}
$$
If we apply the initial condition of $a(0) = a_0$ we get
\begin{gather*}
b(t) = \dfrac{1}{4} + \left( \dfrac{1}{a_0^2} - \dfrac{1}{4} \right)e^{-4\epsilon t}.
\end{gather*}
And therefore,
\begin{gather*}
a(t) = \sqrt{\dfrac{1}{\dfrac{1}{4} + \left( \dfrac{1}{a_0^2} - \dfrac{1}{4} \right)e^{-4\epsilon t}}} + O(\epsilon^2).
\end{gather*}
Additionally,
\begin{align*}
\dot{\phi} &= \dfrac{\epsilon}{2\pi}\int_{0}^{2\pi}{\left(-a^3\cos^2\theta\sin\theta - a^3\sin^3\theta + 4a\sin\theta \right)\cos\theta}{d\theta}\\
&= \dfrac{\epsilon}{2\pi}\int_{0}^{2\pi}{\left(-a^3\cos^3\theta\sin\theta - a^3\cos\theta\sin^3\theta + 4a\cos\theta\sin\theta \right)}{d\theta}\\
&= 0
\end{align*}
and thus,
\begin{gather*}
\phi(t) = \phi_0 + O(\epsilon^2).
\end{gather*}
Finally, we have the following approximated expression
\begin{gather*}
x(t) = \sqrt{\dfrac{1}{\dfrac{1}{4} + \left( \dfrac{1}{a_0^2} - \dfrac{1}{4} \right)e^{-4\epsilon t}}}\cos\left( t + \phi_0 \right) + O(\epsilon^2).
\end{gather*}
If we assume, $\dot{x} = 0$
\begin{gather*}
0 = -a_0\sin\phi_0\\
\therefore \phi_0 = 0.
\end{gather*}
Hence,
\begin{gather*}
{x(t) = \sqrt{\dfrac{1}{\dfrac{1}{4} + \left( \dfrac{1}{a_0^2} - \dfrac{1}{4} \right)e^{-4\epsilon t}}}\cos\left( t \right) + O(\epsilon^2).}
\end{gather*}
Since $\omega = 1$ for this approximation, the period $T$ of the limit cycle is
\begin{gather*}
{T = \dfrac{2\pi}{\omega} = 2\pi.}
\end{gather*}
```
# We plot the phase plane of this system to check the limit cycle
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp, DOP853
from typing import List
# System
def nlsys(t, x, epsilon):
return [x[1], -epsilon*(x[0]**2 + x[1]**2 - 4)*x[1] - x[0]]
def solve_diffeq(func, t, tspan, ic, parameters={}, algorithm='DOP853', stepsize=np.inf):
return solve_ivp(fun=func, t_span=tspan, t_eval=t, y0=ic, method=algorithm,
args=tuple(parameters.values()), atol=1e-8, rtol=1e-5, max_step=stepsize)
def phasePlane(x1, x2, func, params):
X1, X2 = np.meshgrid(x1, x2) # create grid
u, v = np.zeros(X1.shape), np.zeros(X2.shape)
NI, NJ = X1.shape
for i in range(NI):
for j in range(NJ):
x = X1[i, j]
y = X2[i, j]
dx = func(0, (x, y), *params.values()) # compute values on grid
u[i, j] = dx[0]
v[i, j] = dx[1]
M = np.hypot(u, v)
u /= M
v /= M
return X1, X2, u, v, M
def DEplot(sys: object, tspan: tuple, x0: List[List[float]],
x: np.ndarray, y: np.ndarray, params: dict):
if len(tspan) != 3:
raise Exception('tspan should be tuple of size 3: (min, max, number of points).')
# Set up the figure the way we want it to look
plt.figure(figsize=(12, 9))
X1, X2, dx1, dx2, M = phasePlane(
x, y, sys, params
)
# Quiver plot
plt.quiver(X1, X2, dx1, dx2, M, scale=None, pivot='mid')
plt.grid()
if tspan[0] < 0:
t1 = np.linspace(0, tspan[0], tspan[2])
t2 = np.linspace(0, tspan[1], tspan[2])
if min(tspan) < 0:
t_span1 = (np.max(t1), np.min(t1))
else:
t_span1 = (np.min(t1), np.max(t1))
t_span2 = (np.min(t2), np.max(t2))
for x0i in x0:
sol1 = solve_diffeq(sys, t1, t_span1, x0i, params)
plt.plot(sol1.y[0, :], sol1.y[1, :], '-r')
sol2 = solve_diffeq(sys, t2, t_span2, x0i, params)
plt.plot(sol2.y[0, :], sol2.y[1, :], '-r')
else:
t = np.linspace(tspan[0], tspan[1], tspan[2])
t_span = (np.min(t), np.max(t))
for x0i in x0:
sol = solve_diffeq(sys, t, t_span, x0i, params)
plt.plot(sol.y[0, :], sol.y[1, :], '-r')
plt.xlim([np.min(x), np.max(x)])
plt.ylim([np.min(y), np.max(y)])
plt.show()
x10 = np.arange(0, 10, 1)
x20 = np.arange(0, 10, 1)
x0 = np.stack((x10, x20), axis=-1)
p = {'epsilon': 0.001}
x1 = np.linspace(-5, 5, 20)
x2 = np.linspace(-5, 5, 20)
DEplot(nlsys, (-8, 8, 1000), x0, x1, x2, p)
# Compare the approximation to the actual solution
# let a = 2
tmax = 2
tmin = 30
tspan = np.linspace(tmin, tmax, 1000)
# ODE solver solution
sol = solve_diffeq(nlsys, tspan, (tmin, tmax), [2, 0], p)
# Approximation
def nlsys_averaging(t, a, e):
return np.sqrt(1 / (0.25 + (1/a**2 - 0.25) * np.exp(-4*e*t))) * np.cos(t)
approx = nlsys_averaging(tspan, 2, 0.001)
plt.figure(figsize=(12, 9))
plt.plot(tspan, sol.y[0, :])
plt.plot(tspan, approx)
plt.grid(True)
plt.xlabel('$t$')
plt.ylabel('$x$')
plt.show()
```
| true |
code
| 0.676206 | null | null | null | null |
|
## 2.3 Combination Matrix over undirected network
### 2.3.1 Weight
We now associate each edge with a positive weight. This weight is used to scale information following over the associated edge.
For a given topology, we define $w_{ij}$, the weight to scale information flowing from agent $j$ to agent $i$, as follows:
\begin{align}\label{wij}
w_{ij}
\begin{cases}
> 0 & \mbox{if $(j,i) \in \mathcal{E}$, or $i=j$;} \\
= 0 & \mbox{otherwise.}
\end{cases}
\end{align}
### 2.3.2 Combination matrix and a fundamental assumption
We further define the combination matrix $W = [w_{ij}]_{i,j=1}^{n} \in \mathbb{R}^{n\times n}$ to stack all weights into a matrix. Such matrix $W$ will characterize the sparsity and connectivity of the underlying network topology. Throughout this section, we assume the combination matrix $W$ satisfies the following important assumption.
> **Assumption 1 (Doubly stochastic)** We assume $W$ is a doubly stochastic matrix, i.e.,
$W \mathbf{1} = \mathbf{1}$ and $\mathbf{1}^T W = \mathbf{1}^T$.
The above assumption essentially implies that both the row sum and the column sum of matrix $W$ are $1$, i.e., $\sum_{j=1}^n w_{ij} = 1$ and $\sum_{i=1}^n w_{ij} = 1$. This assumption indicates that each agent is taking a wighted local average in this neighborhood, and it is fundamental to guarantee that average consensus will converge to the global average $\bar{x}$ asymtotically.
### 2.3.3 Combination matrix over the undirected network
In a undirected network, the edges $(i,j)$ and $(j,i)$ will appear in a pari-wise manner. Undirected network is very common in nature. In a [random geometric graph](https://networkx.org/documentation/stable/auto_examples/drawing/plot_random_geometric_graph.html), two agents $i$ and $j$ within a certain distance are regarded neighbors. Apparently, both edges $(i,j)$ and $(j,i)$ exist for this scenario. Given a undirected network topology, there are many rules that can help generate combination matrix satisfying Assumption 1. The most well-known rule is the Metropolis-Hastings rule \[Refs\]:
> **Metropolis-Hastings rule.** Providing a undirected and connected topology $\mathcal{G}$, we select $w_{ij}$ as
>
>\begin{align}
\hspace{-3mm} w_{ij}=
\begin{cases}
\begin{array}{ll}\displaystyle
\hspace{-2mm}\frac{1}{1 + \max\{d_i, d_j \}},& \mbox{if $j \in \mathcal{N}(i)$}, \\
\hspace{-2mm}\displaystyle 1 - \sum_{j\in \mathcal{N}(i)}w_{ij}, & \mbox{if $i = j$},\\
\hspace{-2mm}0,& \mbox{if $j \notin \mathcal{N}(i)$ and $j\neq i$}.
\end{array}
\end{cases}
\end{align}
>
> where $d_i = |\mathcal{N}(i)|$ (the number of incoming neighbors of agent $k$). It is easy to verify such $W$ is always doubly-stochastic.
The other popular approaches can be found in Table 14.1 of reference \[Refs\].
#### 2.3.3.1 Example I: Commonly-used topology and associated combination matrix
In BlueFog, we support various commonly-used undirected topologies such as ring, star, 2D-mesh, fully-connected graph, hierarchical graph, etc. One can organize his clusters into any of these topopology easily with the function ```bluefog.common.topology_util```, see the deatil in the [user manual](https://bluefog-lib.github.io/bluefog/topo_api.html?highlight=topology#module-bluefog.common.topology_util). In addition, BlueFog also provides the associated combination matrix for these topologies. These matrices are guaranteed to be symmetric and doubly stochas
**Note:** The reader not familiar with how to run BlueFog in ipython notebook environment is encouraged to read Sec. \[HelloWorld section\] first.
- **A: Test whether BlueFog works normally (the same steps as illustrated in Sec. 2.1)**
In the following code, you should be able to see the id of your CPUs. We use 8 CPUs to conduct the following experiment.
```
import numpy as np
import bluefog.torch as bf
import torch
import networkx as nx # nx will be used for network topology creating and plotting
from bluefog.common import topology_util
import matplotlib.pyplot as plt
%matplotlib inline
import ipyparallel as ipp
np.set_printoptions(precision=3, suppress=True, linewidth=200)
rc = ipp.Client(profile="bluefog")
rc.ids
%%px
import numpy as np
import bluefog.torch as bf
import torch
from bluefog.common import topology_util
import networkx as nx
bf.init()
```
- **B: Undirected Ring topology and associated combination matrix**
We now construct a ring topology. Note that to plot the topology, we have to pull the topology information from the agent to the Jupyter engine. That is why we have to use ```dview.pull```. In the following code, ```bf.size()``` will return the size of the network.
```
# Generate topology.
# Plot figure
%px G = topology_util.RingGraph(bf.size())
dview = rc[:]
G_0 = dview.pull("G", block=True, targets=0)
nx.draw_circular(G_0)
```
When the topology is generated through BlueFog utilities (such as ```RingGraph()```, ```ExponentialTwoGraph()```, ```MeshGrid2DGraph()``` and others in the [user manual](https://bluefog-lib.github.io/bluefog/topo_api.html?highlight=topology#module-bluefog.common.topology_util)), the associated combination matrix is provided automatically.
Now we examine the self weight and neighbor weights of each agent in the ring topology. To this end, we can use ```GetRecvWeights()``` to get these information. In the following code, ```bf.rank()``` will return the label of that agent. Note that all agents will run the following code in parallel (One can see that from the magic command ```%%px```).
```
%%px
self_weight, neighbor_weights = topology_util.GetRecvWeights(G, bf.rank())
```
Now we examine the self weight and neighbor weights of agent $0$.
```
%%px
if bf.rank() == 0:
print("self weights: {}\n".format(self_weight))
print("neighbor weights:")
for k, v in neighbor_weights.items():
print("neighbor id:{}, weight:{}".format(k, v))
```
We can even construct the combination matrix $W$ and examine its property. To this end, we will pull the weights of each agent into the Jupyter engine and then construct the combination matrix. The method to pull information from agent is
```dview.pull(information_to_pull, targets=agent_idx)```
It should be noted that ```agent_idx``` is not the rank of each agent. Instead, it is essentially the order that the engine collects information from each agent. We need to establish a mapping between rank and agent_idx.
```
network_size = dview.pull("bf.size()", block=True, targets=0)
agentID_to_rank = {}
for idx in range(network_size):
agentID_to_rank[idx] = dview.pull("bf.rank()", block=True, targets=idx)
for k, v in agentID_to_rank.items():
print("id:{}, rank:{}".format(k, v))
```
Now we construct the combination matrix $W$.
```
W = np.zeros((network_size, network_size))
for idx in range(network_size):
self_weight = dview.pull("self_weight", block=True, targets=idx)
neighbor_weights = dview.pull("neighbor_weights", block=True, targets=idx)
W[agentID_to_rank[idx], agentID_to_rank[idx]] = self_weight
for k, v in neighbor_weights.items():
W[agentID_to_rank[idx], k] = v
print("The matrix W is:")
print(W)
# check the row sum and column sum
print("\nRow sum of W is:", np.sum(W, axis=1))
print("Col sum of W is:", np.sum(W, axis=0))
if np.sum(W, axis=1).all() and np.sum(W, axis=0).all():
print("The above W is doubly stochastic.")
```
- **I-C: Undirected Star topology and associated combination matrix**
We can follow the above codes to draw the star topology and its associated combination matrix
```
# Generate topology.
# Plot figure
%px G = topology_util.StarGraph(bf.size())
G_0 = dview.pull("G", block=True, targets=0)
nx.draw_circular(G_0)
%%px
self_weight, neighbor_weights = topology_util.GetRecvWeights(G, bf.rank())
network_size = dview.pull("bf.size()", block=True, targets=0)
W = np.zeros((network_size, network_size))
for idx in range(network_size):
self_weight = dview.pull("self_weight", block=True, targets=idx)
neighbor_weights = dview.pull("neighbor_weights", block=True, targets=idx)
W[agentID_to_rank[idx], agentID_to_rank[idx]] = self_weight
for k, v in neighbor_weights.items():
W[agentID_to_rank[idx], k] = v
print("The matrix W is:")
print(W)
# check the row sum and column sum
print("\nRow sum of W is:", np.sum(W, axis=1))
print("Col sum of W is:", np.sum(W, axis=0))
if np.sum(W, axis=1).all() and np.sum(W, axis=0).all():
print("The above W is doubly stochastic.")
```
- **I-D: Undirected 2D-Mesh topology and associated combination matrix**
```
# Generate topology.
# Plot figure
%px G = topology_util.MeshGrid2DGraph(bf.size())
G_0 = dview.pull("G", block=True, targets=0)
nx.draw_spring(G_0)
%%px
self_weight, neighbor_weights = topology_util.GetRecvWeights(G, bf.rank())
network_size = dview.pull("bf.size()", block=True, targets=0)
W = np.zeros((network_size, network_size))
for idx in range(network_size):
self_weight = dview.pull("self_weight", block=True, targets=idx)
neighbor_weights = dview.pull("neighbor_weights", block=True, targets=idx)
W[agentID_to_rank[idx], agentID_to_rank[idx]] = self_weight
for k, v in neighbor_weights.items():
W[agentID_to_rank[idx], k] = v
print("The matrix W is:")
print(W)
# check the row sum and column sum
print("\nRow sum of W is:", np.sum(W, axis=1))
print("Col sum of W is:", np.sum(W, axis=0))
if np.sum(W, axis=1).all() and np.sum(W, axis=0).all():
print("The above W is doubly stochastic.")
```
- **I-E: Undirected 2D-Mesh topology and associated combination matrix**
```
# Generate topology.
# Plot figure
%px G = topology_util.FullyConnectedGraph(bf.size())
G_0 = dview.pull("G", block=True, targets=0)
nx.draw_circular(G_0)
%%px
self_weight, neighbor_weights = topology_util.GetRecvWeights(G, bf.rank())
network_size = dview.pull("bf.size()", block=True, targets=0)
W = np.zeros((network_size, network_size))
for idx in range(network_size):
self_weight = dview.pull("self_weight", block=True, targets=idx)
neighbor_weights = dview.pull("neighbor_weights", block=True, targets=idx)
W[agentID_to_rank[idx], agentID_to_rank[idx]] = self_weight
for k, v in neighbor_weights.items():
W[agentID_to_rank[idx], k] = v
print("The matrix W is:")
print(W)
# check the row sum and column sum
print("\nRow sum of W is:", np.sum(W, axis=1))
print("Col sum of W is:", np.sum(W, axis=0))
if np.sum(W, axis=1).all() and np.sum(W, axis=0).all():
print("The above W is doubly stochastic.")
```
The readers are encourged to test other topologies and examine their associated combination matrix. Check the topology related utility function in [user manual](https://bluefog-lib.github.io/bluefog/topo_api.html?highlight=topology#module-bluefog.common.topology_util).
#### 2.3.3.2 Example II: Set up your own topology
There also exist scenarios in which you want to organize the agents into your own magic topologies. In this example, we will show how to produce the combination matrix via the Metropolis-Hastings rule and generate the network topology that can be imported to BlueFog utilities.
Before we generate the combination matrix, you have to prepare an [adjacency matrix](https://en.wikipedia.org/wiki/Adjacency_matrix) of your topology. Since the topology is undirected, the adjacency matrix should be symmetric.
```
def gen_comb_matrix_via_MH(A):
"""Generate combinational matrix via Metropolis-Hastings rule
Args:
A: numpy 2D array with dims (n,n) representing adjacency matirx.
Returns:
A combination matrix W: numpy 2D array with dims (n,n).
"""
# the adjacency matrix must be symmetric
assert np.linalg.norm(A - A.T) < 1e-6
# make sure the diagonal elements of A are 0
n, _ = A.shape
for i in range(n):
A[i, i] = 0
# compute the degree of each agent
d = np.sum(A, axis=1)
# identify the neighbor of each agent
neighbors = {}
for i in range(n):
neighbors[i] = set()
for j in range(n):
if A[i, j] == 1:
neighbors[i].add(j)
# generate W via M-H rule
W = np.zeros((n, n))
for i in range(n):
for j in neighbors[i]:
W[i, j] = 1 / (1 + np.maximum(d[i], d[j]))
W_row_sum = np.sum(W, axis=1)
for i in range(n):
W[i, i] = 1 - W_row_sum[i]
return W
```
Random geometric graph is one of the undirected graph that nutrally appears in many application. It is constructed by randomly placing $n$ nodes in some metric space (according to a specified probability distribution) and connecting two nodes by a link if and only if their distance is in a given range $r$.
Random geometric graph is not provided in BlueFog. In the following codes, we will show how to generate the combination matrix of random geometric graph via Metropolis-Hastings rule, and how to import the topology, and the combination matrix into BlueFog to facilitate the downstream average consensus and decentralized optimization algorithms.
test the correctedness of the above function. To this end, we define a new network topology: we randomly generate the 2D coordinates of $n$ agents within a $1 \times 1$ square. If the distance between two nodes are within $r$, they are regarded as neighbors. We call such network topology as distance-decided network.
The following functioin will return the adjacency matrix of the random geometric graph.
```
def gen_random_geometric_topology(num_agents, r):
"""Generate random geometric topology.
Args:
num_agents: the number of agents in the network.
r: two agents within the distance 'r' are regarded as neighbors.
"""
# Generate n random 2D coordinates within a 1*1 square
agents = {}
for i in range(num_agents):
agents[i] = np.random.rand(2, 1)
A = np.zeros((num_agents, num_agents))
for i in range(num_agents):
for j in range(i + 1, num_agents):
dist = np.linalg.norm(agents[i] - agents[j])
if dist < r:
A[i, j] = 1
A[j, i] = 1
return A
```
Now we use the above utility function to generate a random distance-decided network. One can adjust parameter ```r``` to manipulate the density of the network topology.
```
np.random.seed(seed=2021)
num_nodes = len(rc.ids)
A = gen_random_geometric_topology(num_agents=num_nodes, r=0.5)
print("The adjacency matrix of the generated network is:")
print(A)
print("\n")
print("The associated combination matrix is:")
W = gen_comb_matrix_via_MH(A)
print(W)
# test whether it is symmetric and doubly stochastic
print("\n")
if np.linalg.norm(W - W.T) == 0:
print("W is symmetric.")
if np.sum(W, axis=0).all() == 1 and np.sum(W, axis=1).all() == 1:
print("W is doubly stochastic.")
# generate topology from W
G = nx.from_numpy_array(W, create_using=nx.DiGraph)
# draw topology
nx.draw_spring(G)
```
Given $W$ generated from the M-H rule, next we organize the agents into the above topology with ```set_topology(G)```. We further examine whether the agents' associated combination matrix is consistent with the above generated ombination matrix $W$.
```
dview.push({"W": W}, block=True)
%%px
G = nx.from_numpy_array(W, create_using=nx.DiGraph)
bf.set_topology(G)
topology = bf.load_topology()
self_weight, neighbor_weights = topology_util.GetRecvWeights(topology, bf.rank())
network_size = dview.pull("bf.size()", block=True, targets=0)
W = np.zeros((network_size, network_size))
for idx in range(network_size):
self_weight = dview.pull("self_weight", block=True, targets=idx)
neighbor_weights = dview.pull("neighbor_weights", block=True, targets=idx)
W[agentID_to_rank[idx], agentID_to_rank[idx]] = self_weight
for k, v in neighbor_weights.items():
W[agentID_to_rank[idx], k] = v
print("The matrix W is:")
print(W)
# check the row sum and column sum
print("\nRow sum of W is:", np.sum(W, axis=1))
print("Col sum of W is:", np.sum(W, axis=0))
if np.sum(W, axis=1).all() and np.sum(W, axis=0).all():
print("The above W is doubly stochastic.")
```
It is observed that the agents' associated combination matrix is consistent with the above generated associated combination matrix.
| true |
code
| 0.689123 | null | null | null | null |
|
# Lecture 11 - Gaussian Process Regression
## Objectives
+ to do regression using a GP
+ to find the hyperparameters of the GP by maximizing the (marginal) likelihood
+ to use GP regression for uncertainty propagation
## Readings
+ Please read [this](http://www.kyb.mpg.de/fileadmin/user_upload/files/publications/pdfs/pdf2903.pdf) OR watch [this video lecture](http://videolectures.net/mlss03_rasmussen_gp/?q=MLSS).
+ [Section 5.4 in GP for ML textbook](http://www.gaussianprocess.org/gpml/chapters/RW5.pdf).
+ See slides for theory.
## Example
The purpose of this example is to demonstrate Gaussian process regression. To motivate the need let us introduce a toy uncertainty quantification example:
> We have developed an "amazing code" that models an extremely important physical phenomenon. The code works with a single input paramete $x$ and responds with a single value $y=f(x)$. A physicist, who is an expert in the field, tells us that $x$ must be somewhere between 0 and 1. Therefore, we treat it as uncertain and we assign to it a uniform probability density:
$$
p(x) = \mathcal{U}(x|0,1).
$$
Our engineers tell us that it is vitally important to learn about the average behavior of $y$. Furthermore, they believe that a value of $y$ greater than $1.2$ signifies a catastrophic failure. Therefore, we wish to compute:
1. the variance of $y$:
$$
v_y = \mathbb{V}[f(x)] = \int\left(f(x) - \mathbb{E}[f(x)]\right)^2p(x)dx,
$$
2. and the probability of failure:
$$
p_{\mbox{fail}} = P[y > 1.2] = \int\mathcal{X}_{[1.2,+\infty)}(f(x))p(x)dx,
$$
where $\mathcal{X}_A$ is the characteristic function of the set A, i.e., $\mathcal{X}_A(x) = 1$ if $x\in A$ and $\mathcal{X}_A(x) = 0$ otherwise.
Unfortunately, our boss is not very happy with our performance. He is going to shut down the project unless we have an answer in ten days. However, a single simulation takes a day... We can only do 10 simulations! What do we do?
Here is the "amazing code"...
```
import numpy as np
# Here is an amazing code:
solver = lambda(x): -np.cos(np.pi * x) + np.sin(4. * np.pi * x)
# It accepts just one input parameter that varies between 0 and 1.
```
### Part 1 - Learning About GP Regression
This demonstrates how do do Gaussian process regression.
```
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn
import cPickle as pickle
import GPy
# Ensure reproducibility
np.random.seed(1345678)
# Select the number of simulations you want to perform:
num_sim = 10
# Generate the input data (needs to be column matrix)
X = np.random.rand(num_sim, 1)
# Evaluate our amazing code at these points:
Y = solver(X)
# Pick a covariance function
k = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.)
# Construct the GP regression model
m = GPy.models.GPRegression(X, Y, k)
# That's it. Print some details about the model:
print m
# Now we would like to make some predictions
# Namely, we wish to predict at this dense set of points:
X_p = np.linspace(0, 1., 100)[:, None]
# We can make predictions as follows
Y_p, V_p = m.predict(X_p) # Y_p = mean prediction, V_p = predictive variance
# Here is the standard deviation:
S_p = np.sqrt(V_p)
# Lower predictive bound
Y_l = Y_p - 2. * S_p
# Upper predictive bound
Y_u = Y_p + 2. * S_p
# Plot the results
fig, ax = plt.subplots()
ax.plot(X_p, Y_p, label='Predictive mean')
ax.fill_between(X_p.flatten(), Y_l.flatten(), Y_u.flatten(), alpha=0.25, label='Predictive error bars')
ax.plot(X, Y, 'kx', markeredgewidth=2, label='Observed data')
# Write the model to a file
print '> writing model to file: surrogate.pcl'
#with open('surrogate.pcl', 'wb') as fd:
# pickle.dump(m, fd)
```
#### Questions
1. The fit looks pretty bad. Why do you think that is? Are our prior assumptions about the parameters of the GP compatible with reality?
2. Ok. We know that our code is deterministic but the GP thinks that there is noise there. Let’s fix this. Go to line 40 and type:
```
m.likelihood.variance = 0
```
This tells the GP that the observations have no noise. Rerun the code. Is the fit better?
3. The previous question was not supposed to work. Why do you think it failed? It
can be fixed by making the variance something small, e.g., make it 1e-6 instead of exactly zero. Rerun the code. Is the fit now any better?
4. We are not quite there. The length scale we are using is 1. Perhaps our function is not that smooth. Try to pick a more reasonable value for the length scale and rerun the code. What do you think is a good value?
5. Repeat 3 for the variance parameter of the SE covariance function.
6. That’s too painful and not very scientific. The proper way to find the parameters is to maximize the likelihood. Undo the modifications you made so far and type ```m.optimize()``` after the model definition.
This maximizes the marginal likelihood of your model using the BFGS algorithm and honoring any constraints. Rerun the examples. What are the parameters that the algorithm finds? Do they make sense? How do the results look like?
7. Based on the results you obtained in 5, we decide to ask our boss for one more
day. We believe that doing one more simulation will greatly reduce error in our predictions. At which input point you think we should make this simulation? You can augement the input data by typing:
```
X = np.vstack([X, [[0.7]]])
```
where, of course, you should replace “0.7” with the point you think is the best. This just appends a new input point to the existing X. Rerun the example. What fit do you get now?
8. If you are this fast, try repeating 5-6 with a less smooth covariance function, e.g.,
the Matern32. What do you observe? Is the prediction uncertainty larger or smaller?
| true |
code
| 0.668826 | null | null | null | null |
|
# SEIR-Campus Examples
This file illustrates some of the examples from the corresponding paper on the SEIR-Courses package. Many of the function here call on classes inside the SEIR-Courses package. We encourage you to look inside the package and explore!
The data file that comes in the examples, publicdata.data, is based on course network published by Weeden and Cornwell at https://osf.io/6kuet/. Course names, as well as some student demographic information, and varsity athlete ids have been assigned randomly and are not accurate representations of student demographics and varsity athletics at Cornell University.
```
from datetime import datetime, timedelta
from PySeirCampus import *
```
### Load the data for the simulations.
```
holiday_list = [(2020, 10, 14)]
holidays = set(datetime(*h) for h in holiday_list)
semester = Semester('publicdata.data', holidays)
```
### Run a first simulation!
```
parameters = Parameters(reps = 10)
run_repetitions(semester, parameters)
```
### Example when no one self reports/shows symptoms.
```
parameters = Parameters(reps = 10)
parameters.infection_duration = BasicInfectionDuration(1 / 3.5, 1 / 4.5)
run_repetitions(semester, parameters)
```
### Example of infection testing
```
parameters = Parameters(reps = 10)
parameters.intervention_policy = IpWeekdayTesting(semester)
run_repetitions(semester, parameters)
```
### Example with Contact Tracing and Quarantines
```
parameters = Parameters(reps = 10)
parameters.contact_tracing = BasicContactTracing(14)
run_repetitions(semester, parameters)
```
### Example with hybrid classes
```
semester_alt_hybrid = make_alternate_hybrid(semester)
parameters = Parameters(reps = 10)
run_repetitions(semester_alt_hybrid, parameters)
```
### Building social groups.
For proper randomization, these groups should be recreated for each simulation repetition using the preprocess feature in the parameters. However, this can add significant time to the computations.
First, consider generating random clusters of students each day.
```
settings = ClusterSettings(
start_date = min(semester.meeting_dates), end_date = max(semester.meeting_dates),
weekday_group_count = 280, weekday_group_size = 10, weekday_group_time = 120,
weekend_group_count = 210, weekend_group_size = 20, weekend_group_time = 180)
def groups_random(semester):
clusters = make_randomized_clusters(semester.students, settings)
return make_from_clusters(semester, clusters)
parameters = Parameters(reps = 10)
parameters.preprocess = groups_random
run_repetitions(semester, parameters)
```
Next, consider when some students form pairs.
```
def pairing(semester):
clusters, _ = make_social_groups_pairs(semester, 0.25, interaction_time = 1200,
weighted=False)
return make_from_clusters(semester, clusters)
parameters = Parameters(reps = 10)
parameters.preprocess = pairing
run_repetitions(semester, parameters)
```
Next, we consider social interactions among varsity athletes. In the first case, we assume that new social clusters are formed within teams each day.
```
def groups_varsity(semester):
clusters, processed = make_social_groups_varsity(semester, 6, 240, 6, 240)
return make_from_clusters(semester, clusters)
parameters = Parameters(reps = 10)
parameters.preprocess = groups_varsity
run_repetitions(semester, parameters)
```
Finally, we consider varsity teams again but assume that the athletes keep socialization within the same cluster of people each day.
```
def groups_static_varsity(semester):
clusters, processed = make_social_groups_varsity_static(semester, 6, 240)
return make_from_clusters(semester, clusters)
parameters = Parameters(reps = 10)
parameters.preprocess = groups_static_varsity
run_repetitions(semester, parameters)
```
## Other ways to explore
Here are some other ideas for how to play around with the simulations!
Try changing the infection rate. Here we retry the first simulation, but with 10% lower infection rate.
```
def test_infection_sensitivity(semester, delta):
parameters = Parameters(reps = 10)
parameters.rate *= (1 + delta)
run_repetitions(semester, parameters)
test_infection_sensitivity(semester, -0.10)
```
Suppose that the percentage of students that are asymptomatic is now 50% instead of 75%.
```
def test_asymptomatic(semester, ratio):
parameters = Parameters(reps = 10)
parameters.infection_duration = VariedResponse(1 / 3.5, 1 / 4.5, 1 / 2, ratio)
run_repetitions(semester, parameters)
test_asymptomatic(semester, 0.5)
```
Eliminate external sources of exposure.
```
def test_outsideclass(semester, increase_factor):
parameters = Parameters(reps = 10)
parameters.daily_spontaneous_prob *= increase_factor
run_repetitions(semester, parameters)
test_outsideclass(semester, 0)
```
Change the number of initial infections from 10 to 0 (reasonable if arrival testing is conducted).
```
def test_initialconditions(semester, initial_change):
parameters = Parameters(reps = 10)
parameters.initial_exposure *= initial_change
run_repetitions(semester, parameters)
test_initialconditions(semester, 0)
```
Test students once per week, on Sunday.
```
def test_test_onceperweek(semester, weekday = 0):
parameters = Parameters(reps = 10)
parameters.intervention_policy = IpWeeklyTesting(semester, weekday = weekday)
run_repetitions(semester, parameters)
test_test_onceperweek(semester, weekday = 6)
```
Test students one per week, on Monday.
```
test_test_onceperweek(semester, weekday = 0)
```
| true |
code
| 0.594669 | null | null | null | null |
|
### Telecom Customer Churn Prediction
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.ticker as mtick
import matplotlib.pyplot as plt
```
### Reading the data
The dataset contains the following information:
1- Customers who left within the last month – the column is called Churn
2- Services that each customer has signed up for – phone, multiple lines, internet, online security, online backup, device protection, tech support, and streaming TV and movies
3- Customer account information – how long they’ve been a customer, contract, payment method, paperless billing, monthly charges, and total charges
4- Demographic info about customers – gender, age range, and if they have partners and dependents
```
telecom_data = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')
telecom_data.head().T
```
### Checking the missing values from dataset
```
telecom_data.dtypes
telecom_data.shape
# Converting Total Charges to a numerical data type.
telecom_data.TotalCharges = pd.to_numeric(telecom_data.TotalCharges, errors='coerce')
telecom_data.isnull().sum()
### 11 missing values were found for the TotalCharges and will be removed from our dataset
#Removing missing values
telecom_data.dropna(inplace = True)
#Remove customer IDs from the data set
df2 = telecom_data.set_index('customerID')
#Convertin the predictor variable in a binary numeric variable
df2['Churn'].replace(to_replace='Yes', value=1, inplace=True)
df2['Churn'].replace(to_replace='No', value=0, inplace=True)
#Let's convert all the categorical variables into dummy variables
df_dummies = pd.get_dummies(df2)
df_dummies.head()
df2.head()
## Evaluating the correlation of "Churn" with other variables
plt.figure(figsize=(15,8))
df_dummies.corr()['Churn'].sort_values(ascending = False).plot(kind = 'bar')
```
As it is depicted, month to month contract, online security, and techsupport seem to be highly correlated values with high possibility of churn. tenure and two years contract are negatively correlated with churn.
### Evaluating the Churn Rate
```
colors = ['g','r']
ax = (telecom_data['Churn'].value_counts()*100.0 /len(telecom_data)).plot(kind='bar',
stacked = True,
rot = 0,
color = colors)
ax.yaxis.set_major_formatter(mtick.PercentFormatter())
ax.set_ylabel('% Customers')
ax.set_xlabel('Churn')
ax.set_title('Churn Rate')
# create a list to collect the plt.patches data
totals = []
# find the values and append to list
for i in ax.patches:
totals.append(i.get_width())
# set individual bar lables using above list
total = sum(totals)
for i in ax.patches:
# get_width pulls left or right; get_y pushes up or down
ax.text(i.get_x()+.15, i.get_height()-4.0, \
str(round((i.get_height()/total), 1))+'%',
fontsize=12,
color='white',
weight = 'bold')
```
Here, we can see almost 74% of customers stayed with the company and 27% of customers churned.
### Churn by Contract Type
As shown in the correlation plot, customer with monthly plan, have a high potential of churning
```
contract_churn = telecom_data.groupby(['Contract','Churn']).size().unstack()
ax = (contract_churn.T*100.0 / contract_churn.T.sum()).T.plot(kind='bar',
width = 0.3,
stacked = True,
rot = 0,
figsize = (8,6),
color = colors)
ax.yaxis.set_major_formatter(mtick.PercentFormatter())
ax.legend(loc='best',prop={'size':12},title = 'Churn')
ax.set_ylabel('% Customers')
ax.set_title('Churn by Contract Type')
# Code to add the data labels on the stacked bar chart
for p in ax.patches:
width, height = p.get_width(), p.get_height()
x, y = p.get_xy()
ax.annotate('{:.0f}%'.format(height), (p.get_x()+.25*width, p.get_y()+.4*height),
color = 'white',
weight = 'bold')
```
### Churn by Monthly Charges
In this part, we can see customer with higher monthly charges, have more tend to churn.
```
ax = sns.kdeplot(telecom_data.MonthlyCharges[(telecom_data["Churn"] == 'No') ],
color="Red", shade = True)
ax = sns.kdeplot(telecom_data.MonthlyCharges[(telecom_data["Churn"] == 'Yes') ],
ax =ax, color="Blue", shade= True)
ax.legend(["Not Churn","Churn"],loc='upper right')
ax.set_ylabel('Density')
ax.set_xlabel('Monthly Charges')
ax.set_title('Distribution of monthly charges by churn')
```
## Applying Machine Learning Algorithms
### Logestic Regression
```
# We will use the data frame where we had created dummy variables
y = df_dummies['Churn'].values
X = df_dummies.drop(columns = ['Churn'])
# Scaling all the variables to a range of 0 to 1
from sklearn.preprocessing import MinMaxScaler
features = X.columns.values
scaler = MinMaxScaler(feature_range = (0,1))
scaler.fit(X)
X = pd.DataFrame(scaler.transform(X), index= df_dummies.index)
X.columns = features
X.head()
# Create Train & Test Data
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
# Running logistic regression model
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
result = model.fit(X_train, y_train)
from sklearn import metrics
prediction_test = model.predict(X_test)
# Print the prediction accuracy
print (metrics.accuracy_score(y_test, prediction_test))
# To get the weights of all the variables
weights = pd.Series(model.coef_[0],
index=X.columns.values)
weights.sort_values(ascending = False)
```
From Logestic Regression model we can understand having two years contract, and internet service DSL reduces the churn rate. Also, tenure and two years contract have the least churn rate.
On the other hand, total charges, monthly contract, and internet service fiber optic have the highest churn rate from the logestic regression model.
### Random Forest
```
from sklearn.ensemble import RandomForestClassifier
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
model_rf = RandomForestClassifier(n_estimators=1000 , oob_score = True, n_jobs = -1,
random_state =50, max_features = "auto",
max_leaf_nodes = 30)
model_rf.fit(X_train, y_train)
# Make predictions
prediction_test = model_rf.predict(X_test)
print (metrics.accuracy_score(y_test, prediction_test))
importances = model_rf.feature_importances_
weights = pd.Series(importances,
index=X.columns.values)
weights.sort_values()[-10:].plot(kind = 'barh')
```
Based on the Random Forest model, monthly contract, tenure, and total charges are considered as the most important factors for churning.
### Support Vecor Machine (SVM)
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=99)
from sklearn.svm import SVC
model.svm = SVC(kernel='linear')
model.svm.fit(X_train,y_train)
preds = model.svm.predict(X_test)
metrics.accuracy_score(y_test, preds)
```
Suport vector machine shows better performance in terms of accuracy compare to Logestic Regression and Random Forest models.
```
Churn_pred = preds[preds==1]
Churn_X_test = X_test[preds==1]
print("Number of customers predicted to be churner is:", Churn_X_test.shape[0], " out of ", X_test.shape[0])
Churn_X_test.head()
```
This is the list of target customers, who haven't churned but are likely to.
## Confusion matrix definition
```
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
```
## Compute confusion matrix for SVM
```
from sklearn.metrics import confusion_matrix
import itertools
cnf_matrix = confusion_matrix(y_test, preds)
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
class_names = ['Not churned','churned']
plot_confusion_matrix(cnf_matrix, classes=class_names,
title='Confusion matrix, without normalization')
# Plot normalized confusion matrix
#plt.figure()
#plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True,
# title='Normalized confusion matrix')
#plt.show()
```
In the first column, confusion matrix predicted 1,117 customer with not churned label. Out of this number, 953 customer predicted with true label and did not churned and 164 customer predicted with false label and churned.
Similarly, in the second column, confusion matrix predicted 290 customers with churned label. Out of this number, 201 customer predicted with true label and churned and 89 customers predicted with flase label and did not churned.
## Applying Artificial Intelligence Methods
### Here we use Keras library with TensorFlow backend to run Deep Neural Network model.
```
from keras import backend as K
from keras.models import Sequential
from keras.layers import Dense, LSTM, Dropout, TimeDistributed, Bidirectional
from keras.layers.convolutional import Conv1D, MaxPooling1D
from keras.regularizers import l1, l2, l1_l2
from keras.callbacks import EarlyStopping, ReduceLROnPlateau, ModelCheckpoint
X_train.shape
```
### Designing the Model
```
model = Sequential()
model.add(Dense(10, input_dim=X_train.shape[1], kernel_initializer='normal', activation= 'relu'))
model.add(Dense(1, kernel_initializer='normal', activation= 'sigmoid'))
model.summary()
```
### Compiling the Model and Fit It
```
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
checkpointer = ModelCheckpoint(filepath="weights.hdf5", verbose=0, save_best_only=True)
history = model.fit(X_train, y_train, epochs=3000, batch_size=100, validation_split=.30, verbose=0,callbacks=[checkpointer])
model.load_weights('weights.hdf5')
```
### summarize history
```
# list all data in history
print(history.history.keys())
# summarize history for accuracy
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
### Evaluating the Model
```
prediction_test_Dense= model.predict_classes(X_test)
cm = confusion_matrix(y_test, prediction_test_Dense)
# Plot non-normalized confusion matrix
plt.figure()
class_names = ['Not churned','churned']
plot_confusion_matrix(cm, classes=class_names,
title='Confusion matrix, without normalization')
print('''In the first column, confusion matrix predicted''',(cm[0,0]+cm[1,0]),'''customer with not churned label.
Out of this number,''' ,(cm[0,0]),'''customers were predicted with true label and did not churned
and''' ,(cm[1,0]),'''customers were predicted with false label and churned.''')
print('''Similarly, in the second column, confusion matrix predicted''' ,(cm[0,1]+cm[1,1]),'''customers with churned label.
Out of this number,''' ,(cm[1,1]),'''customers were predicted with true label
and churned and''' ,(cm[0,1]),'''customers were predicted with flase label and did not churned.''')
```
## Analyse time to churn based on features
```
##Using lifeline features
import lifelines
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
T = telecom_data['tenure']
#Convertin the predictor variable in a binary numeric variable
telecom_data['Churn'].replace(to_replace='Yes', value=1, inplace=True)
telecom_data['Churn'].replace(to_replace='No', value=0, inplace=True)
E = telecom_data['Churn']
kmf.fit(T, event_observed=E)
```
### Plot Survival
```
kmf.survival_function_.plot()
plt.title('Survival function of Telecom customers');
max_life = T.max()
ax = plt.subplot(111)
telecom_data['MultipleLines'].replace(to_replace='Yes', value='MultipleLines', inplace=True)
telecom_data['MultipleLines'].replace(to_replace='No', value='SingleLine', inplace=True)
feature_columns = ['InternetService', 'gender', 'Contract', 'PaymentMethod', 'MultipleLines']
for feature in feature_columns:
feature_types = telecom_data[feature].unique()
for i,feature_type in enumerate(feature_types):
ix = telecom_data[feature] == feature_type
kmf.fit( T[ix], E[ix], label=feature_type)
kmf.plot(ax=ax, legend=True, figsize=(12,6))
plt.title(feature_type)
plt.xlim(0, max_life)
if i==0:
plt.ylabel(feature+ 'to churn after $n$ months')
plt.tight_layout()
```
This plot shows month-to-month contract and electronic check have very high potential of churn, while two years contract and no phone service are mostly staying with company for longer periods.
| true |
code
| 0.615926 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
```
# Implementing activation functions with numpy
## Sigmoid
```
x = np.arange(-10,10,0.1)
z = 1/(1 + np.exp(-x))
plt.figure(figsize=(20, 10))
plt.plot(x, z, label = 'sigmoid function', lw=5)
plt.axvline(lw=0.5, c='black')
plt.axhline(lw=0.5, c='black')
plt.box(on=None)
plt.legend()
plt.show()
```
## Tanh
```
x = np.arange(-10,10,0.1)
z = (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))
plt.figure(figsize=(20, 10))
plt.plot(x, z, label = 'Tanh function', lw=5)
plt.axvline(lw=0.5, c='black')
plt.axhline(lw=0.5, c='black')
plt.box(on=None)
plt.legend()
plt.show()
```
## Relu
```
x = np.arange(-10,10,0.1)
z = np.maximum(0, x)
plt.figure(figsize=(20, 10))
plt.plot(x, z, label = 'ReLU function', lw=5)
plt.axvline(lw=0.5, c='black')
plt.axhline(lw=0.5, c='black')
plt.box(on=None)
plt.legend()
plt.show()
```
## Leaky ReLU
```
x = np.arange(-10,10,0.1)
z = np.maximum(0.1*x, x)
plt.figure(figsize=(20, 10))
plt.plot(x, z, label = 'LReLU function', lw=5)
plt.axvline(lw=0.5, c='black')
plt.axhline(lw=0.5, c='black')
plt.box(on=None)
plt.legend()
plt.show()
```
## ELU
```
x1 = np.arange(-10,0,0.1)
x2 = np.arange(0,10,0.1)
alpha = 1.67326324
z1 = alpha * (np.exp(x1) - 1)
z2 = x2
plt.figure(figsize=(20, 10))
plt.plot(np.append(x1, x2), np.append(z1, z2), label = 'ELU function', lw=5)
plt.axvline(lw=0.5, c='black')
plt.axhline(lw=0.5, c='black')
plt.box(on=None)
plt.legend()
plt.show()
```
## SELU
```
x1 = np.arange(-10,0,0.1)
x2 = np.arange(0,10,0.1)
alpha = 1.67326324
scale = 1.05070098
z1 = scale * alpha * (np.exp(x1) - 1)
z2 = scale * x2
plt.figure(figsize=(20, 10))
plt.plot(np.append(x1, x2), np.append(z1, z2), label = 'SELU function', lw=5)
plt.axvline(lw=0.5, c='black')
plt.axhline(lw=0.5, c='black')
plt.box(on=None)
plt.legend()
plt.show()
```
## Swish
```
x = np.arange(-10,10,0.1)
z = x * (1/(1 + np.exp(-x)))
plt.figure(figsize=(20, 10))
plt.plot(x, z, label = 'Swish function', lw=5)
plt.axvline(lw=0.5, c='black')
plt.axhline(lw=0.5, c='black')
plt.box(on=None)
plt.legend()
plt.show()
```
## Chapter 11
```
import numpy as np
import tensorflow as tf
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
import pandas as pd
X,y = load_iris(return_X_y=True)
y = pd.get_dummies(y).values
y
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)
X_train, X_valid, y_train, y_valid = train_test_split(X_train, y_train, test_size=0.2)
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, activation="relu", input_shape=X_train.shape[1:]),
tf.keras.layers.Dense(10, kernel_initializer="he_normal"),
tf.keras.layers.LeakyReLU(alpha=0.2),
tf.keras.layers.Dense(10, activation="selu", kernel_initializer="lecun_normal"),
tf.keras.layers.Dense(3, activation="softmax")
])
model.compile(loss="categorical_crossentropy", optimizer="sgd", metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))
model.summary()
train, test = tf.keras.datasets.mnist.load_data()
X_train, y_train = train
X_test, y_test = test
model2 = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation="softmax")
])
model2.summary()
[(var.name, var.trainable) for var in model2.layers[1].variables]
[(var.name, var.trainable) for var in model2.layers[2].variables]
```
| true |
code
| 0.63168 | null | null | null | null |
|
<img src="https://raw.githubusercontent.com/google/jax/main/images/jax_logo_250px.png" width="300" height="300" align="center"/><br>
I hope you all enjoyed the first JAX tutorial where we discussed **DeviceArray** and some other fundamental concepts in detail. This is the fifth tutorial in this series, and today we will discuss another important concept specific to JAX. If you haven't looked at the previous tutorials, I highly suggest going through them once. Here are the links:
1. [TF_JAX_Tutorials - Part 1](https://www.kaggle.com/aakashnain/tf-jax-tutorials-part1)
2. [TF_JAX_Tutorials - Part 2](https://www.kaggle.com/aakashnain/tf-jax-tutorials-part2)
3. [TF_JAX_Tutorials - Part 3](https://www.kaggle.com/aakashnain/tf-jax-tutorials-part3)
4. [TF_JAX_Tutorials - Part 4 (JAX and DeviceArray)](https://www.kaggle.com/aakashnain/tf-jax-tutorials-part-4-jax-and-devicearray)
Without any further delay, let's jump in and talk about **pure functions** along with code examples
# Pure Functions
According to [Wikipedia](https://en.wikipedia.org/wiki/Pure_function), a function is pure if:
1. The function returns the same values when invoked with the same inputs
2. There are no side effects observed on a function call
Although the definition looks pretty simple, without examples it can be hard to comprehend and it can sound very vague (especially to the beginners). The first point is clear, but what does a **`side-effect`** mean? What constitutes or is marked as a side effect? What can you do to avoid side effects?
Though I can state all the things here and you can try to "fit" them in your head to make sure that you aren't writing anything that has a side effect, I prefer taking examples so that everyone can understand the "why" part in an easier way. So, let's take a few examples and see some common mistakes that can create side effects
```
import numpy as np
import jax
import jax.numpy as jnp
from jax import grad
from jax import jit
from jax import lax
from jax import random
%config IPCompleter.use_jedi = False
```
# Case 1 : Globals
```
# A global variable
counter = 5
def add_global_value(x):
"""
A function that relies on the global variable `counter` for
doing some computation.
"""
return x + counter
x = 2
# We will `JIT` the function so that it runs as a JAX transformed
# function and not like a normal python function
y = jit(add_global_value)(x)
print("Global variable value: ", counter)
print(f"First call to the function with input {x} with global variable value {counter} returned {y}")
# Someone updated the global value later in the code
counter = 10
# Call the function again
y = jit(add_global_value)(x)
print("\nGlobal variable changed value: ", counter)
print(f"Second call to the function with input {x} with global variable value {counter} returned {y}")
```
Wait...What??? What just happened?
When you `jit` your function, JAX tracing kicks in. On the first call, the results would be as expected, but on the subsequent function calls you will get the **`cached`** results unless:
1. The type of the argument has changed or
2. The shape of the argument has changed
Let's see it in action
```
# Change the type of the argument passed to the function
# In this case we will change int to float (2 -> 2.0)
x = 2.0
y = jit(add_global_value)(x)
print(f"Third call to the function with input {x} with global variable value {counter} returned {y}")
# Change the shape of the argument
x = jnp.array([2])
# Changing global variable value again
counter = 15
# Call the function again
y = jit(add_global_value)(x)
print(f"Third call to the function with input {x} with global variable value {counter} returned {y}")
```
What if I don't `jit` my function in the first place? ¯\_(ツ)_/¯ <br>
Let's take an example of that as well. We are in no hurry!
```
def apply_sin_to_global():
return jnp.sin(jnp.pi / counter)
y = apply_sin_to_global()
print("Global variable value: ", counter)
print(f"First call to the function with global variable value {counter} returned {y}")
# Change the global value again
counter = 90
y = apply_sin_to_global()
print("\nGlobal variable value: ", counter)
print(f"Second call to the function with global variable value {counter} returned {y}")
```
*`Hooraaayy! Problem solved! You can use JIT, I won't!`* If you are thinking in this direction, then it's time to remember two things:
1. We are using JAX so that we can transform our native Python code to make it run **faster**
2. We can achieve 1) if we compile (using it loosely here) the code so that it can run on **XLA**, the compiler used by JAX
Hence, avoid using `globals` in your computation because globals introduce **impurity**
# Case 2: Iterators
We will take a very simple example to see the side effect. We will add numbers from `0 to 5` but in two different ways:
1. Passing an actual array of numbers to a function
2. Passing an **`iterator`** object to the same function
```
# A function that takes an actual array object
# and add all the elements present in it
def add_elements(array, start, end, initial_value=0):
res = 0
def loop_fn(i, val):
return val + array[i]
return lax.fori_loop(start, end, loop_fn, initial_value)
# Define an array object
array = jnp.arange(5)
print("Array: ", array)
print("Adding all the array elements gives: ", add_elements(array, 0, len(array), 0))
# Redefining the same function but this time it takes an
# iterator object as an input
def add_elements(iterator, start, end, initial_value=0):
res = 0
def loop_fn(i, val):
return val + next(iterator)
return lax.fori_loop(start, end, loop_fn, initial_value)
# Define an iterator
iterator = iter(np.arange(5))
print("\n\nIterator: ", iterator)
print("Adding all the elements gives: ", add_elements(iterator, 0, 5, 0))
```
Why the result turned out to be zero in the second case?<br>
This is because an `iterator` introduces an **external state** to retrieve the next value.
# Case 3: IO
Let's take one more example, a very **unusual** one that can turn your functions impure.
```
def return_as_it_is(x):
"""Returns the same element doing nothing. A function that isn't
using `globals` or any `iterator`
"""
print(f"I have received the value")
return x
# First call to the function
print(f"Value returned on first call: {jit(return_as_it_is)(2)}\n")
# Second call to the fucntion with different value
print(f"Value returned on second call: {jit(return_as_it_is)(4)}")
```
Did you notice that? The statement **`I have received the value`** didn't get printed on the subsequent call. <br>
At this point, most people would literally say `Well, this is insane! I am not using globals, no iterators, nothing at all and there is still a side effect? How is that even possible?`
The thing is that your function is still **dependent** on an external state. The **print** statement! It is using the standard output stream to print. What if the stream isn't available on the subsequent calls for whatsoever reason? That will violate the first principle of "returning the same thing" when called with the same inputs.
In a nutshell, to keep function pure, don't use anything that depends on an **external state**. The word **external** is important because you can use stateful objects internally and still keep the functions pure. Let's take an example of this as well
# Pure functions with stateful objects
```
# Function that uses stateful objects but internally and is still pure
def pure_function_with_stateful_obejcts(array):
array_dict = {}
for i in range(len(array)):
array_dict[i] = array[i] + 10
return array_dict
array = jnp.arange(5)
# First call to the function
print(f"Value returned on first call: {jit(pure_function_with_stateful_obejcts)(array)}")
# Second call to the fucntion with different value
print(f"\nValue returned on second call: {jit(pure_function_with_stateful_obejcts)(array)}")
```
So, to keep things **pure**, remember not to use anything inside a function that depends on any **external state**, including the IO as well. If you do that, transforming the function would give you unexpected results, and you would end up wasting a lot of time debugging your code when the transformed function returns a cached result, which is ironical because pure functions are easy to debug
# Why pure functions?
A natural question that comes to mind is that why JAX uses pure functions in the first place? No other framework like TensorFlow, PyTorch, mxnet, etc uses it. <br>
Another thing that you must be thinking right is probably this: Using pure functions is such a headache, I never have to deal with these nuances in TF/Torch.
Well, if you are thinking that, you aren't alone but before jumping to any conclusion, consider the advantages of relying on pure functions.
### 1. Easy to debug
The fact that a function is pure implies that you don't need to look beyond the scope of the pure function. All you need to focus on is the arguments, the logic inside the function, and the returned value. That's it! Same inputs => Same outputs
### 2. Easy to parallelize
Let's say you have three functions A, B, and C and there is a computation involved like this one:<br>
<div style="font-style: italic; text-align: center;">
`res = A(x) + B(y) + C(z)` <br>
</div>
Because all the functions are pure, you don't have to worry about the dependency on an external state or a shared state. There is no dependency between A, B, and C in terms of how are they executed. Each function receives some argument and returns the same output. Hence you can easily offload the computation to many threads, cores, devices, etc. The only thing that the compiler has to ensure that the results of all the functions (A, b, and C in this case) are available before item assignment
### 3. Caching or Memoization
We saw in the above examples that once we compile a pure function, the function will return a cached result on the subsequent calls. We can cache the results of the transformed functions to make the whole program a lot faster
### 4. Functional Composition
When functions are pure, you can `chain` them to solve complex things in a much easier way. For example, in JAX you will see these patterns very often:
<div style="font-style: italic; text-align: center;">
jit(vmap(grad(..)))
</div>
### 5. Referential transparency
An expression is called referentially transparent if it can be replaced with its corresponding value (and vice-versa) without changing the program's behavior. This can only be achieved when the function is pure. It is especially helpful when doing algebra (which is all we do in ML). For example, consider the expression<br>
<div style="font-style: italic; text-align: center;">
x = 5 <br>
y = 5 <br>
z = x + y <br>
</div>
Now you can replace `x + y` with `z` anywhere in your code, considering the value of `z` is coming from a pure function
That's it for Part-5! We will look into other building blocks in the next few chapters, and then we will dive into building neural networks in JAX!
**References:**<br>
1. https://jax.readthedocs.io/en/latest/
2. https://alvinalexander.com/scala/fp-book/benefits-of-pure-functions/
3. https://www.sitepoint.com/what-is-referential-transparency/#referentialtransparencyinmaths
| true |
code
| 0.593079 | null | null | null | null |
|
# RadiusNeighborsClassifier with Scale & Quantile Transformer
This Code template is for the Classification task using a simple Radius Neighbor Classifier with separate feature scaling using Scale pipelining Quantile Transformer which is a feature transformation technique. It implements learning based on the number of neighbors within a fixed radius r of each training point, where r is a floating-point value specified by the user.
### Required Packages
```
!pip install imblearn
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from imblearn.over_sampling import RandomOverSampler
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import LabelEncoder,scale,QuantileTransformer
from sklearn.model_selection import train_test_split
from sklearn.neighbors import RadiusNeighborsClassifier
from sklearn.metrics import classification_report,plot_confusion_matrix
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X = df[features]
Y = df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
#### Distribution Of Target Variable
```
plt.figure(figsize = (10,6))
se.countplot(Y)
```
### Data Rescaling
<Code>scale</Code> standardizes a dataset along any axis. It standardizes features by removing the mean and scaling to unit variance.
scale is similar to <Code>StandardScaler</Code> in terms of feature transformation, but unlike StandardScaler, it lacks Transformer API i.e., it does not have <Code>fit_transform</Code>, <Code>transform</Code> and other related methods.
```
X_Scaled = scale(X)
X_Scaled=pd.DataFrame(X_Scaled,columns=X.columns)
X_Scaled.head()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X_Scaled,Y,test_size=0.2,random_state=123)
```
#### Handling Target Imbalance
The challenge of working with imbalanced datasets is that most machine learning techniques will ignore, and in turn have poor performance on, the minority class, although typically it is performance on the minority class that is most important.
One approach to addressing imbalanced datasets is to oversample the minority class. The simplest approach involves duplicating examples in the minority class.We will perform overspampling using imblearn library.
```
x_train,y_train = RandomOverSampler(random_state=123).fit_resample(x_train, y_train)
```
### Feature Transformation
QuantileTransformer transforms features using quantiles information.
This method transforms the features to follow a uniform or a normal distribution. Therefore, for a given feature, this transformation tends to spread out the most frequent values. It also reduces the impact of (marginal) outliers: this is therefore a robust preprocessing scheme.The transformation is applied on each feature independently.
##### For more information on QuantileTransformer [ click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.QuantileTransformer.html)
### Model
RadiusNeighborsClassifier implements learning based on the number of neighbors within a fixed radius of each training point, where is a floating-point value specified by the user.
In cases where the data is not uniformly sampled, radius-based neighbors classification can be a better choice.
Refer [API](https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.RadiusNeighborsClassifier.html) for parameters
```
# Build Model here
# Change outlier_label as per specific use-case
model=make_pipeline(QuantileTransformer(),RadiusNeighborsClassifier(n_jobs=-1, outlier_label='most_frequent'))
model.fit(x_train,y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
#### Confusion Matrix
A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
```
plot_confusion_matrix(model,x_test,y_test,cmap=plt.cm.Blues)
```
#### Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
* **where**:
- Precision:- Accuracy of positive predictions.
- Recall:- Fraction of positives that were correctly identified.
- f1-score:- percent of positive predictions were correct
- support:- Support is the number of actual occurrences of the class in the specified dataset.
```
print(classification_report(y_test,model.predict(x_test)))
```
#### Creator: Ganapathi Thota , Github: [Profile](https://github.com/Shikiz)
| true |
code
| 0.326876 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/florentPoux/point-cloud-processing/blob/main/Point_cloud_data_sub_sampling_with_Python.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Created by Florent Poux. Licence MIT
* To reuse in your project, please cite the article accessible here:
[To Medium Article](https://towardsdatascience.com/how-to-automate-lidar-point-cloud-processing-with-python-a027454a536c)
* Have fun with this notebook that you can very simply run (ctrl+Enter) !
* The first time thought, it will ask you to get a key for it to be able to acces your Google drive folders if you want to work all remotely.
* Simply accept, and then change the input path by the folder path containing your data, on Google Drive.
Enjoy!
# Step 1: Setting up the environment
```
#This code snippet allows to use data directly from your Google drives files.
#If you want to use a shared folder, just add the folder to your drive
from google.colab import drive
drive.mount('/content/gdrive')
```
# Step 2: Load and prepare the data
```
#https://pythonhosted.org/laspy/
!pip install laspy
#libraries used
import numpy as np
import laspy as lp
#create paths and load data
input_path="gdrive/My Drive/10-MEDIUM/DATA/Point Cloud Sample/"
output_path="gdrive/My Drive/10-MEDIUM/DATA/Point Cloud Sample/"
#Load the file
dataname="NZ19_Wellington"
point_cloud=lp.file.File(input_path+dataname+".las", mode="r")
#store coordinates in "points", and colors in "colors" variable
points = np.vstack((point_cloud.x, point_cloud.y, point_cloud.z)).transpose()
colors = np.vstack((point_cloud.red, point_cloud.green, point_cloud.blue)).transpose()
```
# Step 3: Choose a sub-sampling strategy
## 1- Point Cloud Decimation
```
#The decimation strategy, by setting a decimation factor
factor=160
decimated_points = points[::factor]
#decimated_colors = colors[::factor]
len(decimated_points)
```
## 2 - Point Cloud voxel grid
```
# Initialize the number of voxels to create to fill the space including every point
voxel_size=6
nb_vox=np.ceil((np.max(points, axis=0) - np.min(points, axis=0))/voxel_size)
#nb_vox.astype(int) #this gives you the number of voxels per axis
# Compute the non empty voxels and keep a trace of indexes that we can relate to points in order to store points later on.
# Also Sum and count the points in each voxel.
non_empty_voxel_keys, inverse, nb_pts_per_voxel= np.unique(((points - np.min(points, axis=0)) // voxel_size).astype(int), axis=0, return_inverse=True, return_counts=True)
idx_pts_vox_sorted=np.argsort(inverse)
#len(non_empty_voxel_keys) # if you need to display how many no-empty voxels you have
#Here, we loop over non_empty_voxel_keys numpy array to
# > Store voxel indices as keys in a dictionnary
# > Store the related points as the value of each key
# > Compute each voxel barycenter and add it to a list
# > Compute each voxel closest point to the barycenter and add it to a list
voxel_grid={}
grid_barycenter,grid_candidate_center=[],[]
last_seen=0
for idx,vox in enumerate(non_empty_voxel_keys):
voxel_grid[tuple(vox)]=points[idx_pts_vox_sorted[last_seen:last_seen+nb_pts_per_voxel[idx]]]
grid_barycenter.append(np.mean(voxel_grid[tuple(vox)],axis=0))
grid_candidate_center.append(voxel_grid[tuple(vox)][np.linalg.norm(voxel_grid[tuple(vox)]-np.mean(voxel_grid[tuple(vox)],axis=0),axis=1).argmin()])
last_seen+=nb_pts_per_voxel[idx]
```
# Step 4: Vizualise and export the results
```
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
ax = plt.axes(projection='3d')
ax.scatter(decimated_points[:,0], decimated_points[:,1], decimated_points[:,2], c = decimated_colors/65535, s=0.01)
plt.show()
%timeit np.savetxt(output_path+dataname+"_voxel-best_point_%s.xyz" % (voxel_size), grid_candidate_center, delimiter=";", fmt="%s")
```
# Step 5 - Automate with functions
```
#Define a function that takes as input an array of points, and a voxel size expressed in meters. It returns the sampled point cloud
def grid_subsampling(points, voxel_size):
nb_vox=np.ceil((np.max(points, axis=0) - np.min(points, axis=0))/voxel_size)
non_empty_voxel_keys, inverse, nb_pts_per_voxel= np.unique(((points - np.min(points, axis=0)) // voxel_size).astype(int), axis=0, return_inverse=True, return_counts=True)
idx_pts_vox_sorted=np.argsort(inverse)
voxel_grid={}
grid_barycenter,grid_candidate_center=[],[]
last_seen=0
for idx,vox in enumerate(non_empty_voxel_keys):
voxel_grid[tuple(vox)]=points[idx_pts_vox_sorted[last_seen:last_seen+nb_pts_per_voxel[idx]]]
grid_barycenter.append(np.mean(voxel_grid[tuple(vox)],axis=0))
grid_candidate_center.append(voxel_grid[tuple(vox)][np.linalg.norm(voxel_grid[tuple(vox)]-np.mean(voxel_grid[tuple(vox)],axis=0),axis=1).argmin()])
last_seen+=nb_pts_per_voxel[idx]
return subsampled_points
#Execute the function, and store the results in the grid_sampled_point_cloud variable
grid_sampled_point_cloud variable = grid_subsampling(point_cloud, 6)
#Save the variable to an ASCII file to open in a 3D Software
%timeit np.savetxt(output_path+dataname+"_sampled.xyz", grid_sampled_point_cloud variable, delimiter=";", fmt="%s")
```
| true |
code
| 0.541591 | null | null | null | null |
|
# Time-series prediction (temperature from weather stations)
Companion to [(Time series prediction, end-to-end)](./sinewaves.ipynb), except on a real dataset.
```
# change these to try this notebook out
BUCKET = 'cloud-training-demos-ml'
PROJECT = 'cloud-training-demos'
REGION = 'us-central1'
import os
os.environ['BUCKET'] = BUCKET
os.environ['PROJECT'] = PROJECT
os.environ['REGION'] = REGION
%%datalab project set -p $PROJECT
```
# Data exploration and cleanup
The data are temperature data from US weather stations. This is a public dataset from NOAA.
```
import numpy as np
import seaborn as sns
import pandas as pd
import tensorflow as tf
import google.datalab.bigquery as bq
from __future__ import print_function
def query_to_dataframe(year):
query="""
SELECT
stationid, date,
MIN(tmin) AS tmin,
MAX(tmax) AS tmax,
IF (MOD(ABS(FARM_FINGERPRINT(stationid)), 10) < 7, True, False) AS is_train
FROM (
SELECT
wx.id as stationid,
wx.date as date,
CONCAT(wx.id, " ", CAST(wx.date AS STRING)) AS recordid,
IF (wx.element = 'TMIN', wx.value/10, NULL) AS tmin,
IF (wx.element = 'TMAX', wx.value/10, NULL) AS tmax
FROM
`bigquery-public-data.ghcn_d.ghcnd_{}` AS wx
WHERE STARTS_WITH(id, 'USW000')
)
GROUP BY
stationid, date
""".format(year)
df = bq.Query(query).execute().result().to_dataframe()
return df
df = query_to_dataframe(2016)
df.head()
df.describe()
```
Unfortunately, there are missing observations on some days.
```
df.isnull().sum()
```
One way to fix this is to do a pivot table and then replace the nulls by filling it with nearest valid neighbor
```
def cleanup_nulls(df, variablename):
df2 = df.pivot_table(variablename, 'date', 'stationid', fill_value=np.nan)
print('Before: {} null values'.format(df2.isnull().sum().sum()))
df2.fillna(method='ffill', inplace=True)
df2.fillna(method='bfill', inplace=True)
df2.dropna(axis=1, inplace=True)
print('After: {} null values'.format(df2.isnull().sum().sum()))
return df2
traindf = cleanup_nulls(df[df['is_train']], 'tmin')
traindf.head()
seq = traindf.iloc[:,0]
print('{} values in the sequence'.format(len(seq)))
ax = sns.tsplot(seq)
ax.set(xlabel='day-number', ylabel='temperature');
seq.to_string(index=False).replace('\n', ',')
# Save the data to disk in such a way that each time series is on a single line
# save to sharded files, one for each year
# This takes about 15 minutes
import shutil, os
shutil.rmtree('data/temperature', ignore_errors=True)
os.makedirs('data/temperature')
def to_csv(indf, filename):
df = cleanup_nulls(indf, 'tmin')
print('Writing {} sequences to {}'.format(len(df.columns), filename))
with open(filename, 'w') as ofp:
for i in xrange(0, len(df.columns)):
if i%10 == 0:
print('{}'.format(i), end='...')
seq = df.iloc[:365,i] # chop to 365 days to avoid leap-year problems ...
line = seq.to_string(index=False, header=False).replace('\n', ',')
ofp.write(line + '\n')
print('Done')
for year in xrange(2000, 2017):
print('Querying data for {} ... hang on'.format(year))
df = query_to_dataframe(year)
to_csv(df[df['is_train']], 'data/temperature/train-{}.csv'.format(year))
to_csv(df[~df['is_train']], 'data/temperature/eval-{}.csv'.format(year))
%bash
head -1 data/temperature/eval-2004.csv | tr ',' ' ' | wc
head -1 data/temperature/eval-2005.csv | tr ',' ' ' | wc
wc -l data/temperature/train*.csv
wc -l data/temperature/eval*.csv
%bash
gsutil -m rm -rf gs://${BUCKET}/temperature/*
gsutil -m cp data/temperature/*.csv gs://${BUCKET}/temperature
```
Our CSV file sequences consist of 365 values. For training, each instance's 0~364 numbers are inputs, and 365th is truth.
# Model
This is the same model as [(Time series prediction, end-to-end)](./sinewaves.ipynb)
```
%bash
#for MODEL in dnn; do
for MODEL in cnn dnn lstm lstm2 lstmN; do
OUTDIR=gs://${BUCKET}/temperature/$MODEL
JOBNAME=temperature_${MODEL}_$(date -u +%y%m%d_%H%M%S)
REGION=us-central1
gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=trainer.task \
--package-path=${PWD}/sinemodel/trainer \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC_GPU \
--runtime-version=1.2 \
-- \
--train_data_paths="gs://${BUCKET}/temperature/train*.csv" \
--eval_data_paths="gs://${BUCKET}/temperature/eval*.csv" \
--output_dir=$OUTDIR \
--train_steps=5000 --sequence_length=365 --model=$MODEL
done
```
## Results
When I ran it, these were the RMSEs that I got for different models:
| Model | # of steps | Minutes | RMSE |
| --- | ----| --- | --- | --- |
| dnn | 5000 | 19 min | 9.82 |
| cnn | 5000 | 22 min | 6.68 |
| lstm | 5000 | 41 min | 3.15 |
| lstm2 | 5000 | 107 min | 3.91 |
| lstmN | 5000 | 107 min | 11.5 |
As you can see, on real-world time-series data, LSTMs can really shine, but the highly tuned version for the synthetic data doesn't work as well on a similiar, but different problem. Instead, we'll probably have to retune ...
<p>
## Next steps
This is likely not the best way to formulate this problem. A better method to work with this data would be to pull out arbitrary, shorter sequences (say of length 20) from the input sequences. This would be akin to image augmentation in that we would get arbitrary subsets, and would allow us to predict the sequence based on just the last 20 values instead of requiring a whole year. It would also avoid the problem that currently, we are training only for Dec. 30/31.
Feature engineering would also help. For example, we might also add a climatological average (average temperature at this location over the last 10 years on this date) as one of the inputs. I'll leave both these improvements as exercises for the reader :)
Copyright 2017 Google Inc. Licensed under the Apache License, Version 2.0 (the \"License\"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an \"AS IS\" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.226848 | null | null | null | null |
|
# [ATM 623: Climate Modeling](../index.ipynb)
[Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html), University at Albany
# Lecture 3: Climate sensitivity and feedback
Tuesday February 3 and Thursday February 5, 2015
### About these notes:
This document uses the interactive [`IPython notebook`](http://ipython.org/notebook.html) format (now also called [`Jupyter`](https://jupyter.org)). The notes can be accessed in several different ways:
- The interactive notebooks are hosted on `github` at https://github.com/brian-rose/ClimateModeling_courseware
- The latest versions can be viewed as static web pages [rendered on nbviewer](http://nbviewer.ipython.org/github/brian-rose/ClimateModeling_courseware/blob/master/index.ipynb)
- A complete snapshot of the notes as of May 2015 (end of spring semester) are [available on Brian's website](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/Notes/index.html).
Many of these notes make use of the `climlab` package, available at https://github.com/brian-rose/climlab
## Contents
1. [The feedback concept](#section1)
2. [Climate feedback: some definitions](#section2)
3. [Calculating $\lambda$ for the zero-dimensional EBM](#section3)
4. [Climate sensitivity](#section4)
5. [Feedbacks diagnosed from complex climate models](#section5)
6. [Feedback analysis of the zero-dimensional model with variable albedo](#section6)
## Preamble
- Questions and discussion about the previous take-home assignment on
- zero-dimensional EBM
- exponential relaxation
- timestepping the model to equilibrium
- multiple equilibria with ice albedo feedback
- Reading assigment:
- Everyone needs to read through Chapters 1 and 2 of "The Climate Modelling Primer (4th ed)"
- It is now on reserve at the Science Library
- Read it ASAP, but definitely before the mid-term exam
- Discuss the use of IPython notebook
____________
<a id='section1'></a>
## 1. The feedback concept
____________
A concept borrowed from electrical engineering. You have all probably heard or used the term before, but we’ll try take a more precise approach today.
A feedback occurs when a portion of the output from the action of a system is added to the input and subsequently alters the output:
```
from IPython.display import Image
Image(filename='../images/feedback_sketch.png', width=500)
```
The result of a loop system can either be amplification or dampening of the process, depending on the sign of the gain in the loop.
We will call amplifying feedbacks **positive** and damping feedbacks **negative**.
We can think of the “process” here as the entire climate system, which contains many examples of both positive and negative feedback.
### Two classic examples:
#### Water vapor feedback
The capacity of the atmosphere to hold water vapor (saturation specific humidity) increases exponentially with temperature. Warming is thus accompanied by moistening (more water vapor), which leads to more warming due to the enhanced water vapor greenhouse effect.
**Positive or negative feedback?**
#### Ice-albedo feedback
Colder temperatures lead to expansion of the areas covered by ice and snow, which tend to be more reflective than water and vegetation. This causes a reduction in the absorbed solar radiation, which leads to more cooling.
**Positive or negative feedback?**
*Make sure it’s clear that the sign of the feedback is the same whether we are talking about warming or cooling.*
_____________
<a id='section2'></a>
## 2. Climate feedback: some definitions
____________
Let’s go back to the concept of the **planetary energy budget**:
$$C \frac{d T_s}{dt} = F_{TOA} $$
where
$$ F_{TOA} = (1-\alpha) Q - \sigma T_e^4$$
is the **net downward energy flux** at the top of the atmosphere.
So for example when the planet is in equilibrium, we have $d/dt = 0$, or solar energy in = longwave emissions out
Let’s imagine we force the climate to change by adding some extra energy to the system, perhaps due to an increase in greenhouse gases, or a decrease in reflective aerosols. Call this extra energy a **radiative forcing**, denoted by $R$ in W m$^{-2}$.
The climate change will be governed by
$$C \frac{d \Delta T_s}{dt} = R + \Delta F_{TOA}$$
where $\Delta T_s$ is the change in global mean surface temperature. This budget accounts for two kinds of changes to $T_s$:
- due to the radiative forcing: $R$
- due to resulting changes in radiative processes (internal to the climate system): $\Delta F_{TOA}$
### The feedback factor: a linearization of the perturbation energy budget
The **key assumption** in climate feedback analysis is that *changes in radiative flux are proportional to surface temperature changes*:
$$ \Delta F_{TOA} = \lambda \Delta T_s $$
where $\lambda$ is a constant of proportionality, with units of W m$^{-2}$ K$^{-1}$.
Mathematically, we are assuming that the changes are sufficiently small that we can linearize the budget about the equilibrium state (as we did explicitly in our previous analysis of the zero-dimensional EBM).
Using a first-order Taylor Series expansion, a generic definition for $\lambda$ is thus
$$ \lambda = \frac{\partial}{\partial T_s} \bigg( \Delta F_{TOA} \bigg) $$
The budget for the perturbation temperature then becomes
$$ C \frac{d \Delta T}{dt} = R + \lambda \Delta T_s $$
We will call $\lambda$ the **climate feedback parameter**.
A key question for which we need climate models is this:
*How much warming do we expect for a given radiative forcing?*
Or more explicitly, how much warming if we double atmospheric CO$_2$ concentration (which it turns out produces a radiative forcing of roughly 4 W m$^{-2}$, as we will see later).
Given sufficient time, the system will reach its new equilibrium temperature, at which point
$$\frac{d \Delta T_s}{dt} = 0$$
And the perturbation budget is thus
$$ 0 = R + \lambda \Delta T_s $$
or
$$ \Delta T_s = - \frac{R}{\lambda}$$
where $R$ is the forcing in W m$^{-2}$ and $\lambda$ is the feedback in W m$^{-2}$ K$^{-1}$.
Notice that we have NOT invoked a specific model for the radiative emissions (yet). This is a very general concept that we can apply to ANY climate model.
We have defined things here such that **$\lambda > 0$ for a positive feedback, $\lambda < 0$ for a negative feedback**. That’s convenient!
### Decomposing the feedback into additive components
Another thing to note: we can decompose the total climate feedback into **additive components** due to different processes:
$$ \lambda = \lambda_0 + \lambda_1 + \lambda_2 + ... = \sum_{i=0}^n \lambda_i$$
This is possible because of our assumption of linear dependence on $\Delta T_s$.
We might decompose the net climate feedbacks into, for example
- longwave and shortwave processes
- cloud and non-cloud processes
These individual feedback processes may be positive or negative. This is very powerful, because we can **measure the relative importance of different feedback processes** simply by comparing their $\lambda_i$ values.
Let’s reserve the symbol $\lambda$ to mean the overall or net climate feedback, and use subscripts to denote specific feedback processes.
QUESTION: what is the sign of $\lambda$?
Could there be energy balance for a planet with a positive λ? Think about your experiences timestepping the energy budget equation.
_____________
<a id='section3'></a>
## 3. Calculating $\lambda$ for the zero-dimensional EBM
____________
Our prototype climate model is the **zero-dimensional EBM**
$$C \frac{d T_s}{dt}=(1-α)Q-σ(\beta T_s )^4$$
where $\beta$ is a parameter measuring the proportionality between surface temperature and emission temperature. From observations we estimate
$$ \beta = 255 / 288 = 0.885$$
We now add a radiative forcing to the model:
$$C \frac{d T_s}{dt}=(1-α)Q-σ(\beta T_s )^4 + R $$
We saw in the previous lecture that we can **linearize** the model about a reference temperature $\overline{T_s}$ using a first-order Taylor expansion to get
$$C \frac{d \Delta T_s}{d t} = R + \lambda \Delta T_s$$
with the constant of proportionality
$$\lambda = -\Big(4 \sigma \beta^4 \overline{T_s}^3 \Big)$$
which, according to the terminology we have just introduced above, is the net climate feedback for this model.
Evaluating $\lambda$ at the observed global mean temperature of 288 K and using our tuned value of $\beta$ gives
$$ \lambda = -3.3 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1} $$
Note that we are treating the albedo $\alpha$ as fixed in this model. We will generalize to variable albedo below.
### What does this mean?
It means that, for every W m$^{-2}$ of excess energy we put into our system, our model predicts that the surface temperature must increase by $-1/ \lambda = 0.3$ K in order to re-establish planetary energy balance.
This model only represents a **single feedback process**: the increase in longwave emission to space with surface warming.
This is called the **Planck feedback** because it is fundamentally due to the Planck blackbody radiation law (warmer temperatures = higher emission).
Here and henceforth we will denote this feedback by $\lambda_0$. To be clear, we are saying that *for this particular climate model*
$$ \lambda = \lambda_0 = -\Big(4 \sigma \beta^4 \overline{T_s}^3 \Big) $$
### Every climate model has a Planck feedback
The Planck feedback is the most basic and universal climate feedback, and is present in every climate model. It is simply an expression of the fact that a warm planet radiates more to space than a cold planet.
As we will see, our estimate of $\lambda_0 = -3.3 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1} $ is essentially the same as the Planck feedback diagnosed from complex GCMs. Unlike our simple zero-dimensional model, however, most other climate models (and the real climate system) have other radiative processes, such that $\lambda \ne \lambda_0$.
________________
<a id='section4'></a>
## 4. Climate sensitivity
____________
Let’s now define another important term:
**Equilibrium Climate Sensitivity (ECS)**: the global mean surface warming necessary to *balance the planetary energy budget* after a *doubling* of atmospheric CO2.
We will denote this temperature as $\Delta T_{2\times CO_2}$
ECS is an important number. A major goal of climate modeling is to provide better estimates of ECS and its uncertainty.
Let's estimate ECS for our zero-dimensional model. We know that the warming for any given radiative forcing $R$ is
$$ \Delta T_s = - \frac{R}{\lambda}$$
To calculate $\Delta T_{2\times CO_2}$ we need to know the radiative forcing from doubling CO$_2$, which we will denote $R_{2\times CO_2}$. We will spend some time looking at this quantity later in the semester. For now, let's just take a reasonable value
$$ R_{2\times CO_2} \approx 4 ~\text{W} ~\text{m}^{-2} $$
Our estimate of ECS follows directly:
$$ \Delta T_{2\times CO_2} = - \frac{R_{2\times CO_2}}{\lambda} = - \frac{4 ~\text{W} ~\text{m}^{-2}}{-3.3 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1}} = 1.2 ~\text{K} $$
### Is this a good estimate?
**What are the current best estimates for ECS?**
Latest IPCC report AR5 gives a likely range of **1.5 to 4.5 K**.
(there is lots of uncertainty in these numbers – we will definitely come back to this question)
So our simplest of simple climate models is apparently **underestimating climate sensitivity**.
Let’s assume that the true value is $\Delta T_{2\times CO_2} = 3 ~\text{K}$ (middle of the range).
This implies that the true net feedback is
$$ \lambda = -\frac{R_{2\times CO_2}}{\Delta T_{2\times CO_2}} = -\frac{4 ~\text{W} ~\text{m}^{-2}}{3 ~\text{K}} = -1.3 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1} $$
We can then deduce the total of the “missing” feedbacks:
$$ \lambda = \lambda_0 + \sum_{i=1}^n \lambda_i $$
$$ -1.3 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1} = -3.3 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1} + \sum_{i=1}^n \lambda_i $$
$$ \sum_{i=1}^n \lambda_i = +2.0 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1} $$
The *net effect of all the processes not included* in our simple model is a **positive feedback**, which acts to **increase the equilibrium climate sensitivity**. Our model is not going to give accurate predictions of global warming because it does not account for these positive feedbacks.
(This does not mean the feedback associated with every missing process is positive! Just that the linear sum of all the missing feedbacks is positive!)
This is consistent with our discussion above. We started our feedback discussion with two examples (water vapor and albedo feedback) which are both positive, and both absent from our model!
We've already seen (in homework exercise) a simple way to add an albedo feedback into the zero-dimensional model. We will analyze this version of the model below. But first, let's take a look at the feedbacks as diagnosed from current GCMs.
____________
<a id='section5'></a>
## 5. Feedbacks diagnosed from complex climate models
____________
### Data from the IPCC AR5
This figure is reproduced from the recent IPCC AR5 report. It shows the feedbacks diagnosed from the various models that contributed to the assessment.
(Later in the term we will discuss how the feedback diagnosis is actually done)
See below for complete citation information.
```
feedback_ar5 = 'http://www.climatechange2013.org/images/figures/WGI_AR5_Fig9-43.jpg'
Image(url=feedback_ar5, width=800)
```
**Figure 9.43** | (a) Strengths of individual feedbacks for CMIP3 and CMIP5 models (left and right columns of symbols) for Planck (P), water vapour (WV), clouds (C), albedo (A), lapse rate (LR), combination of water vapour and lapse rate (WV+LR) and sum of all feedbacks except Planck (ALL), from Soden and Held (2006) and Vial et al. (2013), following Soden et al. (2008). CMIP5 feedbacks are derived from CMIP5 simulations for abrupt fourfold increases in CO2 concentrations (4 × CO2). (b) ECS obtained using regression techniques by Andrews et al. (2012) against ECS estimated from the ratio of CO2 ERF to the sum of all feedbacks. The CO2 ERF is one-half the 4 × CO2 forcings from Andrews et al. (2012), and the total feedback (ALL + Planck) is from Vial et al. (2013).
*Figure caption reproduced from the AR5 WG1 report*
Legend:
- P: Planck feedback
- WV: Water vapor feedback
- LR: Lapse rate feedback
- WV+LR: combined water vapor plus lapse rate feedback
- C: cloud feedback
- A: surface albedo feedback
- ALL: sum of all feedback except Plank, i.e. ALL = WV+LR+C+A
Things to note:
- The models all agree strongly on the Planck feedback.
- The Planck feedback is about $\lambda_0 = -3.3 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1} $ just like our above estimate.
- The water vapor feedback is strongly positive in every model.
- The lapse rate feedback is something we will study later. It is slightly negative.
- For reasons we will discuss later, the best way to measure the water vapor feedback is to combine it with lapse rate feedback.
- Models agree strongly on the combined water vapor plus lapse rate feedback.
- The albedo feedback is slightly positive but rather small globally.
- By far the largest spread across the models occurs in the cloud feedback.
- Global cloud feedback ranges from slighly negative to strongly positive across the models.
- Most of the spread in the total feedback is due to the spread in the cloud feedback.
- Therefore, most of the spread in the ECS across the models is due to the spread in the cloud feedback.
- Our estimate of $+2.0 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1}$ for all the missing processes is consistent with the GCM ensemble.
### Citation
This is Figure 9.43 from Chapter 9 of the IPCC AR5 Working Group 1 report.
The report and images can be found online at
<http://www.climatechange2013.org/report/full-report/>
The full citation is:
Flato, G., J. Marotzke, B. Abiodun, P. Braconnot, S.C. Chou, W. Collins, P. Cox, F. Driouech, S. Emori, V. Eyring, C. Forest, P. Gleckler, E. Guilyardi, C. Jakob, V. Kattsov, C. Reason and M. Rummukainen, 2013: Evaluation of Climate Models. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker, T.F., D. Qin, G.-K. Plattner, M. Tignor, S.K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P.M. Midgley (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp. 741–866, doi:10.1017/CBO9781107415324.020
____________
<a id='section6'></a>
## 6. Feedback analysis of the zero-dimensional model with variable albedo
____________
### The model
In the recent homework you were asked to include a new process in the zero-dimensional EBM: a temperature-dependent albedo.
We used the following formulae:
$$C \frac{dT_s}{dt} =(1-\alpha)Q - \sigma (\beta T_s)^4 + R$$
$$ \alpha(T_s) = \left\{ \begin{array}{ccc}
\alpha_i & & T_s \le T_i \\
\alpha_o + (\alpha_i-\alpha_o) \frac{(T_s-T_o)^2}{(T_i-T_o)^2} & & T_i < T_s < T_o \\
\alpha_o & & T_s \ge T_o \end{array} \right\}$$
with the following parameters:
- $R$ is a radiative forcing in W m$^{-2}$
- $C = 4\times 10^8$ J m$^{-2}$ K$^{-1}$ is a heat capacity for the atmosphere-ocean column
- $\alpha$ is the global mean planetary albedo
- $\sigma = 5.67 \times 10^{-8}$ W m$^{-2}$ K$^{-4}$ is the Stefan-Boltzmann constant
- $\beta=0.885$ is our parameter for the proportionality between surface temperature and emission temperature
- $Q = 341.3$ W m$^{-2}$ is the global-mean incoming solar radiation.
- $\alpha_o = 0.289$ is the albedo of a warm, ice-free planet
- $\alpha_i = 0.7$ is the albedo of a very cold, completely ice-covered planet
- $T_o = 293$ K is the threshold temperature above which our model assumes the planet is ice-free
- $T_i = 260$ K is the threshold temperature below which our model assumes the planet is completely ice covered.
As you discovered in the homework, this model has **multiple equilibria**. For the parameters listed above, there are three equilibria. The warm (present-day) solution and the completely ice-covered solution are both stable equilibria. There is an intermediate solution that is an unstable equilibrium.
### Feedback analysis
In this model, the albedo is not fixed but depends on temperature. Therefore it will change in response to an initial warming or cooling. A feedback!
The net climate feedback in this model is now
$$ \lambda = \lambda_0 + \lambda_\alpha $$
where we are denoting the albedo contribution as $\lambda_\alpha$.
The Planck feedback is unchanged: $\lambda_0 = -3.3 ~\text{W} ~\text{m}^{-2} ~\text{K}^{-1} $
To calculate $\lambda_\alpha$ we need to **linearize the albedo function**. Like any other linearization, we use a Taylor expansion and must take a first derivative:
$$ \Delta F_{TOA} = \lambda \Delta T_s = \big(\lambda_0 + \lambda_\alpha \big) \Delta T_s$$
$$ \lambda_0 = -\Big(4 \sigma \beta^4 \overline{T_s}^3 \Big)$$
$$ \lambda_\alpha = \frac{d}{d T_s} \Big( (1-\alpha)Q \Big) = - Q \frac{d \alpha}{d T_s} $$
Using the above definition for the albedo function, we get
$$ \lambda_\alpha = -Q ~\left\{ \begin{array}{ccc}
0 & & T_s \le T_i \\
2 (\alpha_i-\alpha_o) \frac{(T_s-T_o)}{(T_i-T_o)^2} & & T_i < T < T_o \\
0 & & T_s \ge T_o \end{array} \right\}$$
Notice that the feedback we have just calculated in **not constant** but depends on the state of the climate system (i.e. the surface temperature).
### Coding up the model in Python
This largely repeats what I asked you to do in your homework.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def albedo(T, alpha_o = 0.289, alpha_i = 0.7, To = 293., Ti = 260.):
alb1 = alpha_o + (alpha_i-alpha_o)*(T-To)**2 / (Ti - To)**2
alb2 = np.where(T>Ti, alb1, alpha_i)
alb3 = np.where(T<To, alb2, alpha_o)
return alb3
def ASR(T, Q=341.3):
alpha = albedo(T)
return Q * (1-alpha)
def OLR(T, sigma=5.67E-8, beta=0.885):
return sigma * (beta*T)**4
def Ftoa(T):
return ASR(T) - OLR(T)
T = np.linspace(220., 300., 100)
plt.plot(T, albedo(T))
plt.xlabel('Temperature (K)')
plt.ylabel('albedo')
plt.ylim(0,1)
plt.title('Albedo as a function of global mean temperature')
```
### Graphical solution: TOA fluxes as functions of temperature
```
plt.plot(T, OLR(T), label='OLR')
plt.plot(T, ASR(T), label='ASR')
plt.plot(T, Ftoa(T), label='Ftoa')
plt.xlabel('Surface temperature (K)')
plt.ylabel('TOA flux (W m$^{-2}$)')
plt.grid()
plt.legend(loc='upper left')
```
### Numerical solution to get the three equilibrium temperatures
```
# Use numerical root-finding to get the equilibria
from scipy.optimize import brentq
# brentq is a root-finding function
# Need to give it a function and two end-points
# It will look for a zero of the function between those end-points
Teq1 = brentq(Ftoa, 280., 300.)
Teq2 = brentq(Ftoa, 260., 280.)
Teq3 = brentq(Ftoa, 200., 260.)
print Teq1, Teq2, Teq3
```
### Feedback analysis in the neighborhood of each equilibrium
```
def lambda_0(T, beta=0.885, sigma=5.67E-8):
return -4 * sigma * beta**4 * T**3
def lambda_alpha(T, Q=341.3, alpha_o = 0.289, alpha_i = 0.7,
To = 293., Ti = 260.):
lam1 = 2*(alpha_i-alpha_o)*(T-To) / (Ti - To)**2
lam2 = np.where(T>Ti, lam1, 0.)
lam3 = np.where(T<To, lam2, 0.)
return -Q * lam3
```
Here we will loop through each equilibrium temperature and compute the feedback factors for those temperatures.
This code also shows an example of how to do nicely formated numerical output with the `print` function. The format string `%.1f` means floating point number rounded to one decimal place.
```
for Teq in (Teq1, Teq2, Teq3):
print 'Equilibrium temperature: %.1f K' % Teq
print ' Planck feedback: %.1f W/m2/K' % lambda_0(Teq)
print ' Albedo feedback: %.1f W/m2/K' % lambda_alpha(Teq)
print ' Net feedback: %.1f W/m2/K' %(lambda_0(Teq) + lambda_alpha(Teq))
```
### Results of the feedback analysis
- The Planck feedback is always negative, but gets a bit weaker in absolute value at very cold temperatures.
- The albedo feedback in this model depends strongly on the state of the system.
- At the intermediate solution $T_s = 273.9$ K, the albedo feedback is strongly positive.
- The **net feedback is positive** at this intermediate temperature.
- The **net feedback is negative** at the warm and cold temperatures.
### What does a **positive** net feedback mean?
Recall from our analytical solutions of the linearized model that the temperature will evolve according to
$$\Delta T_s(t) = \Delta T_s(0) \exp \bigg(-\frac{t}{\tau} \bigg)$$
with the timescale given by
$$ \tau = \frac{C}{-\lambda} $$
In the vicinity of $T_s = 273.9$ K we find that $\lambda > 0$ due to the very strong albedo feedback. Thus $\tau < 0$ in this case, and we are dealing with **exponential growth** of the temperature anomaly rather than exponential decay.
In other words, if the global mean temperature is close to (but not exactly) this value:
```
print Teq2
```
the climate system will rapidly warm up OR cool down. The temperature will NOT remain close to $T_s = 273.9$ K. This is an example of an **unstable equilibrium**.
The final state of the system after a perturbation will be one of the **stable equilibria**:
```
print Teq1, Teq3
```
Hopefully this is consistent with what you found numerically in the homework.
<div class="alert alert-success">
[Back to ATM 623 notebook home](../index.ipynb)
</div>
____________
## Version information
____________
```
%install_ext http://raw.github.com/jrjohansson/version_information/master/version_information.py
%load_ext version_information
%version_information numpy, climlab
```
____________
## Credits
The author of this notebook is [Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html), University at Albany.
It was developed in support of [ATM 623: Climate Modeling](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/), a graduate-level course in the [Department of Atmospheric and Envionmental Sciences](http://www.albany.edu/atmos/index.php), offered in Spring 2015.
____________
| true |
code
| 0.627495 | null | null | null | null |
|
```
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
import seaborn as sns
from scipy.stats import skew
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
from sklearn.model_selection import RepeatedKFold
from sklearn.model_selection import cross_val_score
from google.colab import drive
!pip install tikzplotlib
import tikzplotlib
```
* Station Code: Código único para cada lugar
* Locations: Nome do rio e para onde flui
* State: O estado em que o rio está fluindo
* Temp: Valor médio de temperatura
* DO: Valor médio de oxigênio dissolvido
* PH: Valor médio de pH
* Conductivity: Valor médio de condutividade
* BOD: Valor médio da demanda bioquímica de oxigênio
* NITRATE_N_NITRITE_N: Valor médio de nitrato-n e nitrito-n
* FECAL_COLIFORM: Valor médio de coliformes fecais
* TOTAL_COLIFORM: Valor médio de coliformes totais
```
path ="/content/waterquality.csv"
dados = pd.read_csv(path,sep=',', engine='python')
dados.head()
```
**Pré-processamento**
Verifica-se a presença ou não de dados faltantes. Realiza também uma normalização dos dados em relação a média e o desvio padrão em virtude da ordem de grandeza dos dados.
```
dados =dados.drop(['STATION CODE', 'LOCATIONS','STATE'], axis=1)
dados.isnull().sum()
```
Verifica-se a presença de dados faltantes, opta-se por preencher com a o último registro válido
```
dadostratados = dados.fillna(method='bfill')
dadostratados.isnull().sum()
variaveis = ['TEMP','DO','pH','CONDUCTIVITY','BOD','NITRATE_N_NITRITE_N','FECAL_COLIFORM','TOTAL_COLIFORM']
dadostratados.head()
```
Seja $X_i$ um preditor do dataset, $\mu_i$ e $\sigma_i$ a média e o desvio padrão desse respectivo preditor, realiza-se a seguinte normalização:
$$
X^{*}_i=\frac{X_i-\mu_i}{\sigma_i}
$$
```
dadostratados = (dadostratados - dadostratados.mean())/dadostratados.std()
plt.figure(figsize=(10, 10))
corr = dadostratados.corr()
_ = sns.heatmap(corr, annot=True )
```
Verifica-se a baixa correlação entre a BOD e os seguintes preditores: temperatura, pH e condutividade.Então em virtude da sua pouca colacaboração para a construção do modelo opta-se por não considerá-los.
```
variaveis = ['DO','BOD','NITRATE_N_NITRITE_N','FECAL_COLIFORM','TOTAL_COLIFORM']
dadostratados =dadostratados.drop(['pH', 'TEMP','CONDUCTIVITY'], axis=1)
plt.figure(figsize=(10, 10))
corr = dadostratados.corr()
_ = sns.heatmap(corr, annot=True )
dadostratados
```
## Métricas de avaliação e validação
Uma métrica qualitativa de avaliação do desempenho é o erro quadrático médio (MSE) é dado pela soma dos erros ao quadrado dividido pelo total de amostras
\begin{equation}
MSE = \frac{1}{N}\sum_{i=1}^{N}\left ( y_i-\hat{y}_i \right )^2
\end{equation}
Tirando a raíz quadrada do $MSE$ defini-se o $RMSE$ :
\begin{equation}
RMSE = \sqrt{\frac{1}{N}\sum_{i=1}^{N}\left ( y_i-\hat{y}_i \right )^2}
\end{equation}
O $RMSE$ mede a performace do modelo, o $R^2$ representa a proporção da variância para uma variável dependente que é explicada por uma variável independente em um modelo de regressão, o qual é difinido pela da seguinte forma:
\begin{equation}
R^2 =1 -\frac{RSS}{TSS}
\end{equation}
onde $RSS= \sum_{i=1}^{N}(y_i-\hat{y}_i)^2$, que pode ser interpretado como uma medida dispersão dos dados gerados pelo em relação aos originais e $TSS = \sum_{i=1}^{N}\left ( y_i -\bar{y}\right )$, que mede a variância em relação a saída.
## Regressão linear por mínimos quadrados
A regressão linear é uma abordagem muito simples para o aprendizado supervisionado. É uma abordagem muito simples para prever uma resposta quantitativa de uma saída $Y$ no
tendo como base em uma única variável preditora de entrada $X$. é preciso que exista uma relação aproximadamente linear entre $X$ e $Y$:
\begin{equation}
Y \approx \beta_0+\beta_1X_1+\beta_1X_1+...+\beta_NX_N
\end{equation}
Onde $\beta_0$,$\beta_1$,...,$\beta_N$ são constantes desconhecidas a seren determinadas no processo, . Os dados são utilizados para estimar os coeficientes. $\hat{\beta}_0$ , $\hat{\beta}_1$,...,$\hat{\beta}_1$, que serão utilizados para determinar o nosso estimados $\hat{y}$. Nesse processo existe a presença de um erro irredutível, o objetivo consiste em minimizar a soma dos erros quadrados:
\begin{equation}
J\left ( \beta_0,\beta_1,..,\beta_N \right ) = \sum_{i=1}^{N}e_i^2 = \sum_{i=1}^{N}\left ( y_i-\hat{\beta}_0-\hat{\beta}_1x_i \right )^2
\end{equation}
Igualando a derivada a função custo a zero, determina-se as coeficientes do modelo,
\begin{equation}
\frac{\partial J}{\partial \beta_n} =0
\end{equation}
Obtem-se um sistema de equações com $N$ incógnitas.
```
from sklearn import linear_model
from sklearn.metrics import mean_absolute_error
X = dadostratados.drop(['BOD'], axis=1)
Y = dadostratados['BOD']
X_train, X_test, y_train, y_test = train_test_split( X, Y, test_size=0.30, random_state=42)
regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)
cv = RepeatedKFold(n_splits=10, n_repeats=5, random_state=1)
RMSE = cross_val_score(regr, X_train, y_train,scoring = 'neg_mean_squared_error',cv=cv, n_jobs=-1)
RMSE = np.sqrt(-RMSE.mean())
'RMSE treino',RMSE
cv = RepeatedKFold(n_splits=5, n_repeats=5, random_state=1)
RMSE = cross_val_score(regr, X_test, y_test,scoring = 'neg_mean_squared_error',cv=cv, n_jobs=-1)
RMSE = np.sqrt(-RMSE.mean())
'RMSE teste',RMSE
r2_score(y_train, regr.predict(X_train))
r2_score(y_test, regr.predict(X_test))
y_pred = np.array(regr.predict(X_test))
plt.scatter(y_test,y_pred,color='black')
plt.xlabel('Real')
plt.ylabel('Estimado')
tikzplotlib.save("real_estimado_regrlinear.pgf")
```
## Modelos penalizados- Ridge Regression
Os coeficientes produzidos pela regressão de mínimos quadrados ordinários são imparciais e, este modelo também tem a variância mais baixa. Dado que o $MSE$ consiste em uma combinação de variância e bias, é possível gerar modelos com MSEs menores, faz com que estimativas dos parâmetros obitidos sejam tendenciosas. O normal que ocorra um pequeno aumento no viés inplique em uma queda considerável na variância, produzindo um $MSE$ menor do que os coeficientes de regressão de mínimos quadrados. Uma consequência das grandes correlações entre as variâncias do preditor é que a variância pode se tornar muito grande.
Uma possível solução seria penalizar a soma dos erros quadráticos. No presente estudo utilizou-se a Ridge regression, a qual adiciona uma penalidade na soma do parâmetro de regressão quadrado:
\begin{equation}
RSS_{L2} = \sum_{i=1}^{N}\left ( y_i -\hat{y}_i\right )+\lambda\sum_{j=1}^{N}\beta^2_j
\end{equation}
Este método reduz as estimativas para 0 à medida que a penalidade $\lambda$ torna-se grande.Ao penalizar o moelo, realiza-se uma compensação entre a variância e o viés do modelo.
```
from sklearn.linear_model import Ridge
def ridge(x, y,alpha,preditor):
X_train,X_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=42)
rr = Ridge(alpha=alpha)
rr.fit(X_train, y_train)
cv = RepeatedKFold(n_splits=10, n_repeats=5, random_state=1)
RMSE = cross_val_score(rr, X_train, y_train,scoring = 'neg_mean_squared_error',cv=cv, n_jobs=-1)
RMSE = np.sqrt(-RMSE.mean())
return RMSE
RMSEval = []
lambdas = [ ]
l2 = []
alpha = np.linspace(0.01,300,10)
for j in range(0,1):
for i in range(0,10):
RMSEval.append(ridge(dadostratados.drop(['BOD'], axis=1), dadostratados['BOD'].values.reshape(-1, 1),alpha[i],variaveis[0]))
lambdas.append(alpha[i])
print(round(min(RMSEval),4), lambdas[RMSEval.index(min(RMSEval))])
l2.append(lambdas[RMSEval.index(min(RMSEval))])
print('ideal lambda:',l2)
plt.plot(alpha,RMSEval,color='black')
plt.xlabel('$\lambda$')
plt.ylabel('$RMSE$')
tikzplotlib.save("rmsexlambda.pgf")
x=dadostratados.drop(['BOD'], axis=1)
y= dadostratados['BOD'].values.reshape(-1, 1)
X_train,X_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=42)
rr = Ridge(alpha=l2)
rr.fit(X_train, y_train)
y_pred = np.array(rr.predict(X_test))
plt.scatter(y_test,y_pred,color='black')
plt.xlabel('Real')
plt.ylabel('Estimado')
tikzplotlib.save("real_estimado_ridge.pgf")
cv = RepeatedKFold(n_splits=10, n_repeats=5, random_state=1)
RMSE = cross_val_score(rr, X_train, y_train,scoring = 'neg_mean_squared_error',cv=cv, n_jobs=-1)
RMSE = np.sqrt(-RMSE.mean())
'RMSE treino',RMSE
cv = RepeatedKFold(n_splits=10, n_repeats=5, random_state=1)
RMSE = cross_val_score(rr, X_test, y_test,scoring = 'neg_mean_squared_error',cv=cv, n_jobs=-1)
RMSE = np.sqrt(-RMSE.mean())
'RMSE treino',RMSE
r2_score(y_train, rr.predict(X_train))
r2_score(y_test, rr.predict(X_test))
```
# Regressão por Minimos Quadrados Parciais - PLS
```
from sklearn import model_selection
from sklearn.cross_decomposition import PLSRegression, PLSSVD
X = dadostratados.drop(['BOD'], axis=1).astype('float64')
y= dadostratados['BOD']
X_train, X_test , y_train, y_test = model_selection.train_test_split(X, y, test_size=0.3, random_state=1)
from sklearn.preprocessing import scale
n = len(X_train)
kf_10 = RepeatedKFold(n_splits=5, n_repeats=5, random_state=1)
rmse = []
for i in np.arange(1,4):
pls = PLSRegression(n_components=i)
score = model_selection.cross_val_score(pls, scale(X_train), y_train, cv=kf_10, scoring='neg_mean_squared_error').mean()
rmse.append(np.sqrt(-score))
plt.plot(np.arange(1, 4), np.array(rmse), '-x',color='black')
plt.xlabel(' N° de componentes principais')
plt.ylabel('RMSE')
tikzplotlib.save("pls.pgf")
pls = PLSRegression(n_components=3)
cv = RepeatedKFold(n_splits=10, n_repeats=5, random_state=1)
RMSE = cross_val_score(pls, X_train, y_train,scoring = 'neg_mean_squared_error',cv=cv, n_jobs=-1)
RMSE = np.sqrt(-RMSE.mean())
'RMSE treino',RMSE
cv = RepeatedKFold(n_splits=10, n_repeats=5, random_state=1)
RMSE = cross_val_score(pls, X_test, y_test,scoring = 'neg_mean_squared_error',cv=cv, n_jobs=-1)
RMSE = np.sqrt(-RMSE.mean())
'RMSE treino',RMSE
pls.fit(X, Y)
y_pred = pls.predict(X)
r2_score(y_train, pls.predict(X_train))
r2_score(y_test, pls.predict(X_test))
y_pred =pls.predict(X_test)
plt.scatter(y_test,y_pred,color='black')
plt.xlabel('Real')
plt.ylabel('Estimado')
tikzplotlib.save("real_estimado_pls.pgf")
```
#Rede neural
```
X = dadostratados.drop(['BOD'], axis=1)
Y = dadostratados['BOD']
X_train, X_test, y_train, y_test = train_test_split( X, Y, test_size=0.30, random_state=42)
from sklearn.neural_network import MLPRegressor
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
regr = MLPRegressor(random_state=42, max_iter=5000).fit(X_train, y_train)
mean_absolute_error(y_test, regr.predict(X_test))
r2_score(y_test, regr.predict(X_test))
y_pred =regr.predict(X_test)
plt.scatter(y_test,y_pred,color='black')
plt.xlabel('Real')
plt.ylabel('Estimado')
tikzplotlib.save("real_estimado_mlp.pgf")
cv = RepeatedKFold(n_splits=10, n_repeats=5, random_state=1)
RMSE = cross_val_score(regr, X_train, y_train,scoring = 'neg_mean_squared_error',cv=cv, n_jobs=-1)
RMSE = np.sqrt(-RMSE.mean())
'RMSE treino',RMSE
```
| true |
code
| 0.485844 | null | null | null | null |
|
### x lines of Python
# Reading and writing LAS files
This notebook goes with [the Agile blog post](https://agilescientific.com/blog/2017/10/23/x-lines-of-python-load-curves-from-las) of 23 October.
Set up a `conda` environment with:
conda create -n welly python=3.6 matplotlib=2.0 scipy pandas
You'll need `welly` in your environment:
conda install tqdm # Should happen automatically but doesn't
pip install welly
This will also install the latest versions of `striplog` and `lasio`.
```
import welly
ls ../data/*.LAS
```
### 1. Load the LAS file with `lasio`
```
import lasio
l = lasio.read('../data/P-129.LAS') # Line 1.
```
That's it! But the object itself doesn't tell us much — it's really just a container:
```
l
```
### 2. Look at the WELL section of the header
```
l.header['Well'] # Line 2.
```
You can go in and find the KB if you know what to look for:
```
l.header['Parameter']['EKB']
```
### 3. Look at the curve data
The curves are all present one big NumPy array:
```
l.data
```
Or we can go after a single curve object:
```
l.curves.GR # Line 3.
```
And there's a shortcut to its data:
```
l['GR'] # Line 4.
```
...so it's easy to make a plot against depth:
```
import matplotlib.pyplot as plt
plt.figure(figsize=(15,3))
plt.plot(l['DEPT'], l['GR'])
plt.show()
```
### 4. Inspect the curves as a `pandas` dataframe
```
l.df().head() # Line 5.
```
### 5. Load the LAS file with `welly`
```
from welly import Well
w = Well.from_las('../data/P-129.LAS') # Line 6.
```
`welly` Wells know how to display some basics:
```
w
```
And the `Well` object also has `lasio`'s access to a pandas DataFrame:
```
w.df().head()
```
### 6. Look at `welly`'s Curve object
Like the `Well`, a `Curve` object can report a bit about itself:
```
gr = w.data['GR'] # Line 7.
gr
```
One important thing about Curves is that each one knows its own depths — they are stored as a property called `basis`. (It's not actually stored, but computed on demand from the start depth, the sample interval (which must be constant for the whole curve) and the number of samples in the object.)
```
gr.basis
```
### 7. Plot part of a curve
We'll grab the interval from 300 m to 1000 m and plot it.
```
gr.to_basis(start=300, stop=1000).plot() # Line 8.
```
### 8. Smooth a curve
Curve objects are, fundamentally, NumPy arrays. But they have some extra tricks. We've already seen `Curve.plot()`.
Using the `Curve.smooth()` method, we can easily smooth a curve, eg by 15 m (passing `samples=True` would smooth by 15 samples):
```
sm = gr.smooth(window_length=15, samples=False) # Line 9.
sm.plot()
```
### 9. Export a set of curves as a matrix
You can get at all the data through the lasio `l.data` object:
```
print("Data shape: {}".format(w.las.data.shape))
w.las.data
```
But we might want to do some other things, such as specify which curves you want (optionally using aliases like GR1, GRC, NGC, etc for GR), resample the data, or specify a start and stop depth — `welly` can do all this stuff. This method is also wrapped by `Project.data_as_matrix()` which is nice because it ensures that all the wells are exported at the same sample interval.
Here are the curves in this well:
```
w.data.keys()
keys=['CALI', 'DT', 'DTS', 'RHOB', 'SP']
w.plot(tracks=['TVD']+keys)
X, basis = w.data_as_matrix(keys=keys, start=275, stop=1850, step=0.5, return_basis=True)
w.data['CALI'].shape
```
So CALI had 12,718 points in it... since we downsampled to 0.5 m and removed the top and tail, we should have substantially fewer points:
```
X.shape
plt.figure(figsize=(15,3))
plt.plot(X.T[0])
plt.show()
```
### 10+. BONUS: fix the lat, lon
OK, we're definitely going to go over our budget on this one.
Did you notice that the location of the well did not get loaded properly?
```
w.location
```
Let's look at some of the header:
# LAS format log file from PETREL
# Project units are specified as depth units
#==================================================================
~Version information
VERS. 2.0:
WRAP. YES:
#==================================================================
~WELL INFORMATION
#MNEM.UNIT DATA DESCRIPTION
#---- ------ -------------- -----------------------------
STRT .M 1.0668 :START DEPTH
STOP .M 1939.13760 :STOP DEPTH
STEP .M 0.15240 :STEP
NULL . -999.25 :NULL VALUE
COMP . Elmworth Energy Corporation :COMPANY
WELL . Kennetcook #2 :WELL
FLD . Windsor Block :FIELD
LOC . Lat = 45* 12' 34.237" N :LOCATION
PROV . Nova Scotia :PROVINCE
UWI. Long = 63* 45'24.460 W :UNIQUE WELL ID
LIC . P-129 :LICENSE NUMBER
CTRY . CA :COUNTRY (WWW code)
DATE. 10-Oct-2007 :LOG DATE {DD-MMM-YYYY}
SRVC . Schlumberger :SERVICE COMPANY
LATI .DEG :LATITUDE
LONG .DEG :LONGITUDE
GDAT . :GeoDetic Datum
SECT . 45.20 Deg N :Section
RANG . PD 176 :Range
TOWN . 63.75 Deg W :Township
Look at **LOC** and **UWI**. There are two problems:
1. These items are in the wrong place. (Notice **LATI** and **LONG** are empty.)
2. The items are malformed, with lots of extraneous characters.
We can fix this in two steps:
1. Remap the header items to fix the first problem.
2. Parse the items to fix the second one.
We'll define these in reverse because the remapping uses the transforming function.
```
import re
def transform_ll(text):
"""
Parses malformed lat and lon so they load properly.
"""
def callback(match):
d = match.group(1).strip()
m = match.group(2).strip()
s = match.group(3).strip()
c = match.group(4).strip()
if c.lower() in ('w', 's') and d[0] != '-':
d = '-' + d
return ' '.join([d, m, s])
pattern = re.compile(r""".+?([-0-9]+?).? ?([0-9]+?).? ?([\.0-9]+?).? +?([NESW])""", re.I)
text = pattern.sub(callback, text)
return welly.utils.dms2dd([float(i) for i in text.split()])
```
Make sure that works!
```
print(transform_ll("""Lat = 45* 12' 34.237" N"""))
remap = {
'LATI': 'LOC', # Use LOC for the parameter LATI.
'LONG': 'UWI', # Use UWI for the parameter LONG.
'LOC': None, # Use nothing for the parameter SECT.
'SECT': None, # Use nothing for the parameter SECT.
'RANG': None, # Use nothing for the parameter RANG.
'TOWN': None, # Use nothing for the parameter TOWN.
}
funcs = {
'LATI': transform_ll, # Pass LATI through this function before loading.
'LONG': transform_ll, # Pass LONG through it too.
'UWI': lambda x: "No UWI, fix this!"
}
w = Well.from_las('../data/P-129.LAS', remap=remap, funcs=funcs)
w.location.latitude, w.location.longitude
w.uwi
```
Let's just hope the mess is the same mess in every well. (LOL, no-one's that lucky.)
<hr>
**© 2017 [agilescientific.com](https://www.agilescientific.com/) and licensed [CC-BY 4.0](https://creativecommons.org/licenses/by/4.0/)**
| true |
code
| 0.364424 | null | null | null | null |
|
# Nodes
From the [Interface](basic_interfaces.ipynb) tutorial, you learned that interfaces are the core pieces of Nipype that run the code of your desire. But to streamline your analysis and to execute multiple interfaces in a sensible order, you have to put them in something that we call a ``Node``.
In Nipype, a node is an object that executes a certain function. This function can be anything from a Nipype interface to a user-specified function or an external script. Each node consists of a name, an interface category and at least one input field, and at least one output field.
Following is a simple node from the `utility` interface, with the name `name_of_node`, the input field `IN` and the output field `OUT`:

Once you connect multiple nodes to each other, you create a directed graph. In Nipype we call such graphs either workflows or pipelines. Directed connections can only be established from an output field (below `node1_out`) of a node to an input field (below `node2_in`) of another node.

This is all there is to Nipype. Connecting specific nodes with certain functions to other specific nodes with other functions. So let us now take a closer look at the different kind of nodes that exist and see when they should be used.
## Example of a simple node
First, let us take a look at a simple stand-alone node. In general, a node consists of the following elements:
nodename = Nodetype(interface_function(), name='labelname')
- **nodename**: Variable name of the node in the python environment.
- **Nodetype**: Type of node to be created. This can be a `Node`, `MapNode` or `JoinNode`.
- **interface_function**: Function the node should execute. Can be user specific or coming from an `Interface`.
- **labelname**: Label name of the node in the workflow environment (defines the name of the working directory)
Let us take a look at an example: For this, we need the `Node` module from Nipype, as well as the `Function` module. The second only serves a support function for this example. It isn't a prerequisite for a `Node`.
```
# Import Node and Function module
from nipype import Node, Function
# Create a small example function
def add_two(x_input):
return x_input + 2
# Create Node
addtwo = Node(Function(input_names=["x_input"],
output_names=["val_output"],
function=add_two),
name='add_node')
```
As specified before, `addtwo` is the **nodename**, `Node` is the **Nodetype**, `Function(...)` is the **interface_function** and `add_node` is the **labelname** of the this node. In this particular case, we created an artificial input field, called `x_input`, an artificial output field called `val_output` and specified that this node should run the function `add_two()`.
But before we can run this node, we need to declare the value of the input field `x_input`:
```
addtwo.inputs.x_input = 4
```
After all input fields are specified, we can run the node with `run()`:
```
addtwo.run()
temp_res = addtwo.run()
temp_res.outputs
```
And what is the output of this node?
```
addtwo.result.outputs
```
## Example of a neuroimaging node
Let's get back to the BET example from the [Interface](basic_interfaces.ipynb) tutorial. The only thing that differs from this example, is that we will put the ``BET()`` constructor inside a ``Node`` and give it a name.
```
# Import BET from the FSL interface
from nipype.interfaces.fsl import BET
# Import the Node module
from nipype import Node
# Create Node
bet = Node(BET(frac=0.3), name='bet_node')
```
In the [Interface](basic_interfaces.ipynb) tutorial, we were able to specify the input file with the ``in_file`` parameter. This works exactly the same way in this case, where the interface is in a node. The only thing that we have to be careful about when we use a node is to specify where this node should be executed. This is only relevant for when we execute a node by itself, but not when we use them in a [Workflow](basic_workflow.ipynb).
```
in_file = '/data/ds000114/sub-01/ses-test/anat/sub-01_ses-test_T1w.nii.gz'
# Specify node inputs
bet.inputs.in_file = in_file
bet.inputs.out_file = '/output/node_T1w_bet.nii.gz'
res = bet.run()
```
As we know from the [Interface](basic_interfaces.ipynb) tutorial, the skull stripped output is stored under ``res.outputs.out_file``. So let's take a look at the before and the after:
```
from nilearn.plotting import plot_anat
%matplotlib inline
import matplotlib.pyplot as plt
plot_anat(in_file, title='BET input', cut_coords=(10,10,10),
display_mode='ortho', dim=-1, draw_cross=False, annotate=False);
plot_anat(res.outputs.out_file, title='BET output', cut_coords=(10,10,10),
display_mode='ortho', dim=-1, draw_cross=False, annotate=False);
```
### Exercise 1
Define a `Node` for `IsotropicSmooth` (from `fsl`). Run the node for T1 image for one of the subjects.
```
# write your solution here
# Import the Node module
from nipype import Node
# Import IsotropicSmooth from the FSL interface
from nipype.interfaces.fsl import IsotropicSmooth
# Define a node
smooth_node = Node(IsotropicSmooth(), name="smoothing")
smooth_node.inputs.in_file = '/data/ds000114/sub-01/ses-test/anat/sub-01_ses-test_T1w.nii.gz'
smooth_node.inputs.fwhm = 4
smooth_node.inputs.out_file = '/output/node_T1w_smooth.nii.gz'
smooth_res = smooth_node.run()
```
### Exercise 2
Plot the original image and the image after smoothing.
```
# write your solution here
from nilearn.plotting import plot_anat
%pylab inline
plot_anat(smooth_node.inputs.in_file, title='smooth input', cut_coords=(10,10,10),
display_mode='ortho', dim=-1, draw_cross=False, annotate=False);
plot_anat(smooth_res.outputs.out_file, title='smooth output', cut_coords=(10,10,10),
display_mode='ortho', dim=-1, draw_cross=False, annotate=False);
```
| true |
code
| 0.551695 | null | null | null | null |
|
(2.1.0)=
# 2.1.0 Download ORACC JSON Files
Each public [ORACC](http://oracc.org) project has a `zip` file that contains a collection of JSON files, which provide data on lemmatizations, transliterations, catalog data, indexes, etc. The `zip` file can be found at `http://oracc.museum.upenn.edu/[PROJECT]/json/[PROJECT].zip`, where `[PROJECT]` is to be replaced with the project abbreviation. For sub-projects the address is `http://oracc.museum.upenn.edu/[PROECT]/[SUBPROJECT]/json/[PROJECT]-[SUBPROJECT].zip`
:::{note}
For instance http://oracc.museum.upenn.edu/etcsri/json/etcsri.zip or, for a subproject http://oracc.museum.upenn.edu/cams/gkab/json/cams-gkab.zip.
:::
One may download these files by hand (simply type the address in your browser), or use the code in the current notebook. The notebook will create a directory `jsonzip` and copy the file to that directory - all further scripts will expect the `zip` files to reside in `jsonzip`.
:::{note}
One may also use the function `oracc_download()` in the `utils` module. See below ([2.1.0.5](2.1.0.5)) for instructions on how to use the `utils` module.
:::
```{figure} ../images/mocci_banner.jpg
:scale: 50%
:figclass: margin
```
Some [ORACC](http://oracc.org) projects are maintained by the Munich Open-access Cuneiform Corpus Initiative ([MOCCI](https://www.en.ag.geschichte.uni-muenchen.de/research/mocci/index.html)). This includes, for example, Official Inscriptions of the Middle East in Antiquity ([OIMEA](http://oracc.org/oimea)) and, Archival Texts of the Middle East in Antiquity ([ATMEA](http://oracc.org/atmea)) and various other projects and sub-projects. In theory, project data are copied from the Munich server to the Philadelphia ORACC server (and v.v.), but in order to get the most recent data set it is sometimes advisable to request the `zip` files directly from the Munich server. The address is `http://oracc.ub.uni-muenchen.de/[PROJECT]/[SUBPROJECT]/json/[PROJECT]-[SUBPROJECT].zip`.
:::{note}
The function `oracc_download()` in the `utils` module will try the various servers to find the project(s) of your choice.
:::
After downloading the JSON `zip` file you may unzip it to inspect its contents but there is no necessity to do so. For larger projects unzipping may result in hundreds or even thousands of files; the scripts will always read the data directly from the `zip` file.
## 2.1.0.0. Import Packages
* requests: for communicating with a server over the internet
* tqdm: for creating progress bars
* os: for basic Operating System operations (such as creating a directory)
* ipywidgets: for user interface (input project names to be downloaded)
```
import requests
from tqdm.auto import tqdm
import os
import ipywidgets as widgets
```
## 2.1.0.1. Create Download Directory
Create a directory called `jsonzip`. If the directory already exists, do nothing.
```
os.makedirs("jsonzip", exist_ok = True)
```
## 2.1.0.2 Input a List of Project Abbreviations
Enter one or more project abbreviations to download their JSON zip files. The project names are separated by commas. Note that subprojects must be given explicitly, they are not automatically included in the main project. For instance:
* saao/saa01, aemw/alalakh/idrimi, rimanum
```
projects = widgets.Textarea(
placeholder='Type project names, separated by commas',
description='Projects:',
)
projects
```
## 2.1.0.3 Split the List of Projects
Lower case the list of projects and split it to create a list of project names.
```
project_list = projects.value.lower().split(',') # split at each comma and make a list called `project_list`
project_list = [project.strip() for project in project_list] # strip spaces left and right of each entry
```
## 2.1.0.4 Download the ZIP files
For larger projects (such as [DCCLT](http://oracc.org/dcclt)) the `zip` file may be 25Mb or more. Downloading may take some time and it may be necessary to chunk the downloading process. The `iter_content()` function in the `requests` library takes care of that.
In order to show a progress bar (with `tqdm`) we need to know how large the file to be downloaded is (this value is is then fed to the `total` parameter). The http protocol provides a key `content-length` in the headers (a dictionary) that indicates file length. Not all servers provide this field - if `content-length` is not avalaible it is set to 0. With the `total` value of 0 `tqdm` will show a bar and will count the number of chunks received, but it will not indicate the degree of progress.
```
CHUNK = 1024
for project in project_list:
proj = project.replace('/', '-')
url = f"http://oracc.museum.upenn.edu/json/{proj}.zip"
file = f'jsonzip/{proj}.zip'
with requests.get(url, stream=True) as request:
if request.status_code == 200: # meaning that the file exists
total_size = int(request.headers.get('content-length', 0))
tqdm.write(f'Saving {url} as {file}')
t=tqdm(total=total_size, unit='B', unit_scale=True, desc = project)
with open(file, 'wb') as f:
for c in request.iter_content(chunk_size=CHUNK):
t.update(len(c))
f.write(c)
else:
tqdm.write(f"WARNING: {url} does not exist.")
```
(2.1.0.5)=
## 2.1.0.5 Downloading with the utils Module
In the chapters 3-6, downloading of [ORACC](http://oracc.org) data will be done with the `oracc_download()` function in the module `utils` that can be found in the `utils` directory. The following code illustrates how to use that function.
The function `oracc_download()` takes a list of project names as its first argument. Replace the line
```python
projects = ["dcclt", "saao/saa01"]
```
with the list of projects (and sub-projects) of your choice.
The second (optional) argument is `server`; possible values are "penn" (default; try the Penn server first) and "lmu" (try the Munich server first). The `oracc_download()` function returns a cleaned list of projects with duplicates and non-existing projects removed.
```
import os
import sys
util_dir = os.path.abspath('../utils') # When necessary, adapt the path to the utils directory.
sys.path.append(util_dir)
import utils
directories = ["jsonzip"]
os.makedirs("jsonzip", exist_ok = True)
projects = ["dcclt", "saao/saa01"] # or any list of ORACC projects
utils.oracc_download(projects, server="penn")
```
| true |
code
| 0.72812 | null | null | null | null |
|
Nineth exercice: non-Cartesian MR image reconstruction
=============================================
In this tutorial we will reconstruct an MRI image from radial undersampled kspace measurements. Let us denote $\Omega$ the undersampling mask, the under-sampled Fourier transform now reads $F_{\Omega}$.
Import neuroimaging data
--------------------------------------
We use the toy datasets available in pysap, more specifically a 2D brain slice and the radial under-sampling scheme. We compare zero-order image reconstruction with Compressed sensing reconstructions (analysis vs synthesis formulation) using the FISTA algorithm for the synthesis formulation and the Condat-Vu algorithm for the analysis formulation.
We remind that the synthesis formulation reads (minimization in the sparsifying domain):
$$
\widehat{z} = \text{arg}\,\min_{z\in C^n_\Psi} \frac{1}{2} \|y - F_\Omega \Psi^*z \|_2^2 + \lambda \|z\|_1
$$
and the image solution is given by $\widehat{x} = \Psi^*\widehat{z}$. For an orthonormal wavelet transform,
we have $n_\Psi=n$ while for a frame we may have $n_\Psi > n$.
while the analysis formulation consists in minimizing the following cost function (min. in the image domain):
$$
\widehat{x} = \text{arg}\,\min_{x\in C^n} \frac{1}{2} \|y - F_\Omega x\|_2^2 + \lambda \|\Psi x\|_1 \,.
$$
- Author: Chaithya G R & Philippe Ciuciu
- Date: 01/06/2021
- Target: ATSI MSc students, Paris-Saclay University
```
# Package import
from mri.operators import NonCartesianFFT, WaveletN, WaveletUD2
from mri.operators.utils import convert_locations_to_mask, \
gridded_inverse_fourier_transform_nd
from mri.reconstructors import SingleChannelReconstructor
import pysap
from pysap.data import get_sample_data
# Third party import
from modopt.math.metrics import ssim
from modopt.opt.linear import Identity
from modopt.opt.proximity import SparseThreshold
import numpy as np
import matplotlib.pyplot as plt
```
Loading input data
---------------------------
```
image = get_sample_data('2d-mri')
radial_mask = get_sample_data("mri-radial-samples")
kspace_loc = radial_mask.data
mask = pysap.Image(data=convert_locations_to_mask(kspace_loc, image.shape))
plt.figure()
plt.imshow(image, cmap='gray')
plt.figure()
plt.imshow(mask, cmap='gray')
plt.show()
```
Generate the kspace
-------------------
From the 2D brain slice and the acquisition mask, we retrospectively
undersample the k-space using a cartesian acquisition mask
We then reconstruct the zero order solution as a baseline
Get the locations of the kspace samples
```
fourier_op = NonCartesianFFT(samples=kspace_loc, shape=image.shape,
implementation='cpu')
kspace_obs = fourier_op.op(image.data)
```
Gridded solution
```
grid_space = np.linspace(-0.5, 0.5, num=image.shape[0])
grid2D = np.meshgrid(grid_space, grid_space)
grid_soln = gridded_inverse_fourier_transform_nd(kspace_loc, kspace_obs,
tuple(grid2D), 'linear')
plt.imshow(np.abs(grid_soln), cmap='gray')
# Calculate SSIM
base_ssim = ssim(grid_soln, image)
plt.title('Gridded Solution\nSSIM = ' + str(base_ssim))
plt.show()
```
FISTA optimization
------------------
We now want to refine the zero order solution using a FISTA optimization.
The cost function is set to Proximity Cost + Gradient Cost
```
linear_op = WaveletN(wavelet_name="sym8", nb_scales=4)
regularizer_op = SparseThreshold(Identity(), 6 * 1e-7, thresh_type="soft")
```
# Generate operators
```
reconstructor = SingleChannelReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
verbose=1,
)
```
Synthesis formulation: FISTA optimization
------------------------------------------------------------
We now want to refine the zero order solution using a FISTA optimization.
The cost function is set to Proximity Cost + Gradient Cost
```
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='fista',
num_iterations=200,
)
image_rec = pysap.Image(data=np.abs(x_final))
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
recon_ssim = ssim(image_rec, image)
plt.title('FISTA Reconstruction\nSSIM = ' + str(recon_ssim))
plt.show()
```
## POGM reconstruction
```
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='pogm',
num_iterations=200,
)
image_rec = pysap.Image(data=np.abs(x_final))
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
recon_ssim = ssim(image_rec, image)
plt.title('POGM Reconstruction\nSSIM = ' + str(recon_ssim))
plt.show()
```
Analysis formulation: Condat-Vu reconstruction
---------------------------------------------------------------------
```
#linear_op = WaveletN(wavelet_name="sym8", nb_scales=4)
linear_op = WaveletUD2(
wavelet_id=24,
nb_scale=4,
)
reconstructor = SingleChannelReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='analysis',
verbose=1,
)
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='condatvu',
num_iterations=200,
)
image_rec = pysap.Image(data=np.abs(x_final))
plt.imshow(np.abs(image_rec), cmap='gray')
recon_ssim = ssim(image_rec, image)
plt.title('Condat-Vu Reconstruction\nSSIM = ' + str(recon_ssim))
plt.show()
```
| true |
code
| 0.756796 | null | null | null | null |
|
# Cloud APIs for Computer Vision: Up and Running in 15 Minutes
This code is part of [Chapter 8- Cloud APIs for Computer Vision: Up and Running in 15 Minutes ](https://learning.oreilly.com/library/view/practical-deep-learning/9781492034858/ch08.html).
## Get MSCOCO validation image ids with legible text
We will develop a dataset of images from the MSCOCO dataset that contain at least a single instance of legible text and are in the validation split.
In order to do this, we first need to download `cocotext.v2.json` from https://bgshih.github.io/cocotext/.
```
!wget -nc -q -O tmp.zip https://github.com/bgshih/cocotext/releases/download/dl/cocotext.v2.zip && unzip -n tmp.zip && rm tmp.zip
```
Let's verify that the file has been downloaded and that it exists.
```
import os
os.path.isfile('./cocotext.v2.json')
```
We also need to download the `coco_text.py` file from the COCO-Text repository from http://vision.cornell.edu/se3/coco-text/
```
!wget -nc https://raw.githubusercontent.com/bgshih/coco-text/master/coco_text.py
import coco_text
# Load the COCO text json file
ct = coco_text.COCO_Text('./cocotext.v2.json')
# Find the total number of images in validation set
print(len(ct.val))
```
Add the paths to the `train2014` directory downloaded from the [MSCOCO website](http://cocodataset.org/#download).
```
path = <PATH_TO_IMAGES> # Please update with local absolute path to train2014
os.path.exists(path)
```
Get all images containing at least one instance of legible text
```
image_ids = ct.getImgIds(imgIds=ct.val, catIds=[('legibility', 'legible')])
```
Find total number of validation images which have legible text
```
print(len(image_ids))
```
In the data we downloaded, make sure all the image IDs exist.
```
def filename_from_image_id(image_id):
return "COCO_train2014_000000" + str(image_id) + ".jpg"
final_image_ids = []
for each in image_ids:
filename = filename_from_image_id(each)
if os.path.exists(path + filename):
final_image_ids.append(each)
print(len(final_image_ids))
```
Make a folder where all the temporary data files can be stored
```
!mkdir data-may-2020
!mkdir data-may-2020/legible-images
```
Save a list of the image ids of the validation images
```
with open('./data-may-2020/val-image-ids-final.csv', 'w') as f:
f.write("\n".join(str(image_id) for image_id in final_image_ids))
```
Move these images to a separate folder for future use.
```
from shutil import copy2
for each in final_image_ids:
filename = filename_from_image_id(each)
if os.path.exists(path + filename):
copy2(path + filename, './data-may-2020/legible-images/')
```
| true |
code
| 0.275422 | null | null | null | null |
|
# Fleet Predictive Maintenance: Part 2. Data Preparation with Data Wrangler
1. [Architecure](0_usecase_and_architecture_predmaint.ipynb#0_Architecture)
1. [Data Prep: Processing Job from Data Wrangler Output](./1_dataprep_dw_job_predmaint.ipynb)
1. [Data Prep: Featurization](./2_dataprep_predmaint.ipynb)
1. [Train, Tune and Predict using Batch Transform](./3_train_tune_predict_predmaint.ipynb.ipynb)
## SageMaker Data Wrangler Job Notebook
This notebook uses the Data Wrangler .flow file to submit a SageMaker Data Wrangler Job
with the following steps:
* Push Data Wrangler .flow file to S3
* Parse the .flow file inputs, and create the argument dictionary to submit to a boto client
* Submit the ProcessingJob arguments and wait for Job completion
Optionally, the notebook also gives an example of starting a SageMaker XGBoost TrainingJob using
the newly processed data.
```
# SageMaker Python SDK version 2.x is required
import pkg_resources
import subprocess
import sys
original_version = pkg_resources.get_distribution("sagemaker").version
_ = subprocess.check_call([sys.executable, "-m", "pip", "install", "sagemaker==2.20.0"])
import json
import os
import time
import uuid
import boto3
import sagemaker
```
## Parameters
The following lists configurable parameters that are used throughout this notebook.
```
# S3 bucket for saving processing job outputs
# Feel free to specify a different bucket here if you wish.
sess = sagemaker.Session()
bucket = sess.default_bucket()
prefix = "data_wrangler_flows"
flow_id = f"{time.strftime('%d-%H-%M-%S', time.gmtime())}-{str(uuid.uuid4())[:8]}"
flow_name = f"flow-{flow_id}"
flow_uri = f"s3://{bucket}/{prefix}/{flow_name}.flow"
flow_file_name = "dw_flow/prm.flow"
iam_role = sagemaker.get_execution_role()
container_uri = (
"415577184552.dkr.ecr.us-east-2.amazonaws.com/sagemaker-data-wrangler-container:1.2.1"
)
# Processing Job Resources Configurations
# Data wrangler processing job only supports 1 instance.
instance_count = 1
instance_type = "ml.m5.4xlarge"
# Processing Job Path URI Information
output_prefix = f"export-{flow_name}/output"
output_path = f"s3://{bucket}/{output_prefix}"
output_name = "ff586e7b-a02d-472b-91d4-da3dd05d7a30.default"
processing_job_name = f"data-wrangler-flow-processing-{flow_id}"
processing_dir = "/opt/ml/processing"
# Modify the variable below to specify the content type to be used for writing each output
# Currently supported options are 'CSV' or 'PARQUET', and default to 'CSV'
output_content_type = "CSV"
# URL to use for sagemaker client.
# If this is None, boto will automatically construct the appropriate URL to use
# when communicating with sagemaker.
sagemaker_endpoint_url = None
```
__For this demo, the following cell has been added to the generated code from the Data Wrangler export. The changes are needed to update the S3 bucket in the .flow file to match your S3 location as well as make sure we have the right container URI depending on your region.__
```
from demo_helpers import update_dw_s3uri, get_dw_container_for_region
# update the flow file to change the s3 location to our bucket
update_dw_s3uri(flow_file_name)
# get the Data Wrangler container associated with our region
region = boto3.Session().region_name
container_uri = get_dw_container_for_region(region)
dw_output_path_prm = output_path
print(
f"Storing dw_output_path_prm = {dw_output_path_prm} for use in next notebook 2_fleet_predmaint.ipynb"
)
%store dw_output_path_prm
```
## Push Flow to S3
Use the following cell to upload the Data Wrangler .flow file to Amazon S3 so that
it can be used as an input to the processing job.
```
# Load .flow file
with open(flow_file_name) as f:
flow = json.load(f)
# Upload to S3
s3_client = boto3.client("s3")
s3_client.upload_file(flow_file_name, bucket, f"{prefix}/{flow_name}.flow")
print(f"Data Wrangler Flow notebook uploaded to {flow_uri}")
```
## Create Processing Job arguments
This notebook submits a Processing Job using the Sagmaker Python SDK. Below, utility methods are
defined for creating Processing Job Inputs for the following sources: S3, Athena, and Redshift.
```
from sagemaker.processing import ProcessingInput, ProcessingOutput
from sagemaker.dataset_definition.inputs import (
AthenaDatasetDefinition,
DatasetDefinition,
RedshiftDatasetDefinition,
)
def create_flow_notebook_processing_input(base_dir, flow_s3_uri):
return ProcessingInput(
source=flow_s3_uri,
destination=f"{base_dir}/flow",
input_name="flow",
s3_data_type="S3Prefix",
s3_input_mode="File",
s3_data_distribution_type="FullyReplicated",
)
def create_s3_processing_input(s3_dataset_definition, name, base_dir):
return ProcessingInput(
source=s3_dataset_definition["s3ExecutionContext"]["s3Uri"],
destination=f"{base_dir}/{name}",
input_name=name,
s3_data_type="S3Prefix",
s3_input_mode="File",
s3_data_distribution_type="FullyReplicated",
)
def create_athena_processing_input(athena_dataset_defintion, name, base_dir):
return ProcessingInput(
input_name=name,
dataset_definition=DatasetDefinition(
local_path=f"{base_dir}/{name}",
athena_dataset_definition=AthenaDatasetDefinition(
catalog=athena_dataset_defintion["catalogName"],
database=athena_dataset_defintion["databaseName"],
query_string=athena_dataset_defintion["queryString"],
output_s3_uri=athena_dataset_defintion["s3OutputLocation"] + f"{name}/",
output_format=athena_dataset_defintion["outputFormat"].upper(),
),
),
)
def create_redshift_processing_input(redshift_dataset_defintion, name, base_dir):
return ProcessingInput(
input_name=name,
dataset_definition=DatasetDefinition(
local_path=f"{base_dir}/{name}",
redshift_dataset_definition=RedshiftDatasetDefinition(
cluster_id=redshift_dataset_defintion["clusterIdentifier"],
database=redshift_dataset_defintion["database"],
db_user=redshift_dataset_defintion["dbUser"],
query_string=redshift_dataset_defintion["queryString"],
cluster_role_arn=redshift_dataset_defintion["unloadIamRole"],
output_s3_uri=redshift_dataset_defintion["s3OutputLocation"] + f"{name}/",
output_format=redshift_dataset_defintion["outputFormat"].upper(),
),
),
)
def create_processing_inputs(processing_dir, flow, flow_uri):
"""Helper function for creating processing inputs
:param flow: loaded data wrangler flow notebook
:param flow_uri: S3 URI of the data wrangler flow notebook
"""
processing_inputs = []
flow_processing_input = create_flow_notebook_processing_input(processing_dir, flow_uri)
processing_inputs.append(flow_processing_input)
for node in flow["nodes"]:
if "dataset_definition" in node["parameters"]:
data_def = node["parameters"]["dataset_definition"]
name = data_def["name"]
source_type = data_def["datasetSourceType"]
if source_type == "S3":
processing_inputs.append(create_s3_processing_input(data_def, name, processing_dir))
elif source_type == "Athena":
processing_inputs.append(
create_athena_processing_input(data_def, name, processing_dir)
)
elif source_type == "Redshift":
processing_inputs.append(
create_redshift_processing_input(data_def, name, processing_dir)
)
else:
raise ValueError(f"{source_type} is not supported for Data Wrangler Processing.")
return processing_inputs
def create_processing_output(output_name, output_path, processing_dir):
return ProcessingOutput(
output_name=output_name,
source=os.path.join(processing_dir, "output"),
destination=output_path,
s3_upload_mode="EndOfJob",
)
def create_container_arguments(output_name, output_content_type):
output_config = {output_name: {"content_type": output_content_type}}
return [f"--output-config '{json.dumps(output_config)}'"]
```
## Start ProcessingJob
Now, the Processing Job is submitted using the Processor from the Sagemaker SDK.
Logs are turned off, but can be turned on for debugging purposes.
```
%%time
from sagemaker.processing import Processor
processor = Processor(
role=iam_role,
image_uri=container_uri,
instance_count=instance_count,
instance_type=instance_type,
sagemaker_session=sess,
)
processor.run(
inputs=create_processing_inputs(processing_dir, flow, flow_uri),
outputs=[create_processing_output(output_name, output_path, processing_dir)],
arguments=create_container_arguments(output_name, output_content_type),
wait=True,
logs=False,
job_name=processing_job_name,
)
```
## Kick off SageMaker Training Job (Optional)
Data Wrangler is a SageMaker tool for processing data to be used for Machine Learning. Now that
the data has been processed, users will want to train a model using the data. The following shows
an example of doing so using a popular algorithm XGBoost.
It is important to note that the following XGBoost objective ['binary', 'regression',
'multiclass'], hyperparameters, or content_type may not be suitable for the output data, and will
require changes to train a proper model. Furthermore, for CSV training, the algorithm assumes that
the target variable is in the first column. For more information on SageMaker XGBoost, please see
https://docs.aws.amazon.com/sagemaker/latest/dg/xgboost.html.
### Find Training Data path
The below demonstrates how to recursively search the output directory to find the data location.
```
s3_client = boto3.client("s3")
list_response = s3_client.list_objects_v2(Bucket=bucket, Prefix=output_prefix)
training_path = None
for content in list_response["Contents"]:
if "_SUCCESS" not in content["Key"]:
training_path = content["Key"]
print(training_path)
```
Next, the Training Job hyperparameters are set. For more information on XGBoost Hyperparameters,
see https://xgboost.readthedocs.io/en/latest/parameter.html.
```
region = boto3.Session().region_name
container = sagemaker.image_uris.retrieve("xgboost", region, "1.2-1")
hyperparameters = {
"max_depth": "5",
"objective": "reg:squarederror",
"num_round": "10",
}
train_content_type = (
"application/x-parquet" if output_content_type.upper() == "PARQUET" else "text/csv"
)
train_input = sagemaker.inputs.TrainingInput(
s3_data=f"s3://{bucket}/{training_path}",
content_type=train_content_type,
)
```
The TrainingJob configurations are set using the SageMaker Python SDK Estimator, and which is fit
using the training data from the ProcessingJob that was run earlier.
```
estimator = sagemaker.estimator.Estimator(
container,
iam_role,
hyperparameters=hyperparameters,
instance_count=1,
instance_type="ml.m5.2xlarge",
)
estimator.fit({"train": train_input})
```
### Cleanup
Uncomment the following code cell to revert the SageMaker Python SDK to the original version used
before running this notebook. This notebook upgrades the SageMaker Python SDK to 2.x, which may
cause other example notebooks to break. To learn more about the changes introduced in the
SageMaker Python SDK 2.x update, see
[Use Version 2.x of the SageMaker Python SDK.](https://sagemaker.readthedocs.io/en/stable/v2.html).
```
# _ = subprocess.check_call(
# [sys.executable, "-m", "pip", "install", f"sagemaker=={original_version}"]
# )
```
| true |
code
| 0.433682 | null | null | null | null |
|
# Purpose
This notebook's purpose is to sift through all of the hospital chargemasters and metadata generated via the work already done in [this wonderful repo](https://github.com/vsoch/hospital-chargemaster) (from which I forked my repo). This is where the data engineering for Phase II of this project occurs. For more information on what Phase II is, please see [the README](README.md) for this project. Results from the explorations done in this notebook will be incorporated into a single cleaning script within the repo.
Based upon the originating repo's own README, there's at least some data collection that still needs to be done for completeness (e.g. [data from hospitalpriceindex.com](https://search.hospitalpriceindex.com/hospital/Barnes-Jewish-Hospital/5359?page=1) has to be scraped but they're denying IP addresses that try to do so). However, that is beyond the current scope of this work.
# Background
*Assume everything in this cell is quoted directly from the originating repo README, albeit with some extra content removed for the purposes of streamlining. Anything in italics like this should be assumed to be editorial additions by me.*
**From the original README:**
## Get List of Hospital Pages
We have compiled a list of hospitals and links in the [hospitals.tsv](hospitals.tsv)
file, generated via the [0.get_hospitals.py](0.get_hospitals.py) script *which pulls these data from [a Quartz article](https://qz.com/1518545/price-lists-for-the-115-biggest-us-hospitals-new-transparency-law/) detailing ~115 hospital URLs from which the authors were able to find chargemasters in one form or another*.
The file includes the following variables, separated by tabs:
- **hospital_name** is the human friendly name
- **hospital_url** is the human friendly URL, typically the page that includes a link to the data.
- **hospital_id** is the unique identifier for the hospital, the hospital name, in lowercase, with spaces replaced with `-`
## Organize Data
Each hospital has records kept in a subfolder in the [data](data) folder. Specifically,
each subfolder is named according to the hospital name (made all lowercase, with spaces
replaced with `-`). If a subfolder begins with an underscore, it means that I wasn't
able to find the charge list on the hospital site (and maybe you can help?)
Within that folder, you will find:
- `scrape.py`: A script to scrape the data
- `browser.py`: If we need to interact with a browser, we use selenium to do this.
- `latest`: a folder with the last scraped (latest data files)
- `YYYY-MM-DD` folders, where each folder includes:
- `records.json` the complete list of records scraped for a particular data
- `*.csv` or `*.xlsx` or `*.json`: the scraped data files.
## Parsing
This is likely one of the hardest steps. I wanted to see the extent to which I could
create a simple parser that would generate a single TSV (tab separted value) file
per hospital, with minimally an identifier for a charge, and a price in dollars. If
provided, I would also include a description and code:
- **charge_code**
- **price**
- **description**
- **hospital_id**
- **filename**
Each of these parsers is also in the hospital subfolder, and named as "parser.py." The parser would output a data-latest.tsv file at the top level of the folder, along with a dated (by year `data-<year>.tsv`). At some point
I realized that there were different kinds of charges, including inpatient, outpatient, DRG (diagnostic related group) and others called
"standard" or "average." I then went back and added an additional column
to the data:
- **charge_type** can be one of standard, average, inpatient, outpatient, drg, or (if more detail is supplied) insured, uninsured, pharmacy, or supply. This is not a gold standard labeling but a best effort. If not specified, I labeled as standard, because this would be a good assumption.
# Exploring the Chargemaster Data
OK, I think I have a handle on this, let's take a look at the chargemaster data from @vsoch's repo.
```
#Make sure any changes to custom packages can be reflected immediately
#in the notebook without kernel restart
import autoreload
%load_ext autoreload
%autoreload 2
```
## Reading in the Tabulated Data
OK, there are **a lot** of files to plow through here! And @vsoch was kind enough to try and compile them whenever appropriate in the various hospital/site-specific folders within `data` as `data-latest[-n].tsv` (`-n` indicates that, if the file gets above 100 MB, it's split into `data-latest-1.tsv`, `data-latest-2.tsv`, etc. to avoid going over the GitHub per-file size limit).
Let's try to parse all of these TSV files into a single coherent DataFrame for analysis purposes! The entire `data` folder set is less than 4 GB, and I'm confident that more than half of that is individual XLSX/CSV files, so I think this should be something we can hold in memory easily enough.
...still, we'll use some tricks (e.g. making the sub-dataframes as a generator instead of a list) to ensure optimal memory usage, just to be safe.
```
import pandas as pd
# Search through the data/hospital-id folders for data-latest[-n].tsv files
# so you can concatenate them into a single DataFrame
from glob import glob, iglob
def load_data(filepath='data/*/data-latest*.tsv'):
'''
Re-constitute the DataFrame after doing work outside of the DataFrame in memory,
such as correcting and re-running a parser.
Inputs
------
filepath: str. Provides an explicit or wildcard-based filepath for all
data files that should be concatenated together
Outputs
-------
Returns a single pandas DataFrame that contains all data from the files
specified by filepath
'''
# Setup the full dataframe using iterators/generators to save on memory
all_files = iglob(filepath)
individual_dfs = (pd.read_csv(f, delimiter = '\t',
low_memory = False,
thousands = ',') for f in all_files)
return pd.concat(individual_dfs, ignore_index=True)
df = load_data()
df.info(memory_usage = 'deep', verbose = True, null_counts = True)
df.head()
df.tail()
```
## Checking and Cleaning Columns
Since these datasets were all put together by individual parsing scripts that parsed through a bunch of non-standardized data files from different sources, there's almost guaranteed to be leakage of values from one column to another and so on. So we're going to check each column for anomalies and correct them as we go before proceeding any further.
```
df.columns
```
### Filename
Since the values in this column come internally from the project data collection process, I expect that this column will be clean and orderly...right?
```
print(f"There are {df['filename'].nunique()} unique values in this column\n")
df['filename'].value_counts()
```
OK, nothing stands out as problematic here. Since every filename should end with `.file_extension`, let's do a quick check that nothing violates that rule.
```
# Check how many values match the structure of ".letters" at the end
df['filename'].str.contains(r'\.[a-z]+$', case=False).sum() / len(df['filename'].dropna())
```
Interesting, so a few values don't match. Let's see what they are.
```
# Return values that don't match what we're expecting
df.loc[~df['filename'].str.contains(r'\.[a-z]+$', case=False),
'filename']
```
**Oy vay, looks like we found some anomalies!** These entries clearly have had their `hospital_id` values leak into their `filename` column. We'll need to repair the parser once we're sure we know which one(s) are the problem.
```
df.loc[~df['filename'].str.contains(r'\.[a-z]+$', case=False),
'filename'].value_counts()
df[~df['filename'].str.contains(r'\.[a-z]+$', case=False)].head()
```
**Yup, it's all of the data from the `geisinger-medical-center` data folder.** I'll take a look at the parser and correct it then re-import then DataFrame and see if it's improved at all.
```
df = load_data()
# Is it fixed? Shouldn't return any values
df.loc[~df['filename'].str.contains(r'\.[a-z]+$', case=False),
'filename'].value_counts()
```
**That did the trick!** At this point, we can be sure that all of the entries in the `filename` column have file extensions, which seems like a reasonable data check. Onwards!
### Hospital ID
Again, since these data are essentially internal to this project, I'm thinking that this one will be good to go already or require minimal cleaning. Here's hoping...
Note that it's my intent to convert these into more human-readable names once I've cleaned them up so that they'll be able to match with the Centers for Medicare and Medicaid (CMS) hospital names and can then be mapped to standardized hospital identifiers.
```
print(f"There are {df['hospital_id'].nunique()} unique values in this column\n")
df['hospital_id'].value_counts()
```
**OK, it looks like I'll need to correct some parser issues here too.**
* At first I thought I could use the names of the folders in the `data/` folder for the project as the gold standard of `hospital_id` values, but there's only 115 of those and possibly twice as many `hospital_id` values (correcting for the erroneous ones we're seeing here). The Geisinger Medical Center ones alone all are within the `geisinger-medical-center` folder even though there are actually 7-8 unique `hospital_id` values.
* Let's start by looking for values that don't have at least one hyphen with letters on either side of it.
* After correcting for these, we can also look to see if any low-value-count anomalies remain and go from there.
```
# Find hospital_id values that don't have at least one hyphen with letters on either side of it
df.dropna(subset=['hospital_id']).loc[~df['hospital_id'].dropna().
str.contains(r'[a-z]+-[a-z]+',
case=False),
'hospital_id'].value_counts()
```
Interesting. A few things to note:
1. 'x0020' seems to be the space character for some text encodings
2. It looks like the vast majority of these are hospital names that never translated into `hospital_id` values for some reason, with some instances of `description` or `charge_code` values also leaking into these.
3. Quick review of many of these indicates they are hospital names (or stems of names) of hospitals from the `advent-health/` directory, which has a single parser. So if I can correct that one, I may make substantial progress in one fell swoop!
Since we know that the only (hopefully) fully cleaned column is `filename`, we'll have to use that as our guide. I'll first focus on the parsers for those hospitals I can identify and see if those are easy fixes and hopefully by clearing away that clutter we can correct the vast majority of the problem children here. I'll then tackle what remains individually. And at the end of it all, I'll also need too look at how to correct the records that have `hospital_id == np.nan`.
#### Correct Parsers Wherein `hospital_id == hospital name`
```
df.loc[df['hospital_id'] == 'Heartland']
df.dropna(subset=['hospital_id']).loc[df['hospital_id'].dropna().str.startswith('adventhealth'),
'hospital_id'].value_counts()
```
**Interesting! It looks like the majority of the data files for advent health don't have proper IDs in the database.** Likely this means there's some common thread in the parser that, when corrected, will cause a lot of my `hospital_id` problems to evaporate. Or at least I hope so!
**It looks like the parser was taking the raw hospital IDs from the data files (the capitalized and space-delimited names) and not modifying them.** So I simply modified them to be all lowercase and replace spaces with hyphens. Let's see how that goes!
...this is going to take a while, given the sheer amount of data being parsed. In the meantime, let's address the hospitals that *aren't* Advent Health.
```
df.loc[df['hospital_id'] == 'Stanislaus Surgical Hospital']
```
Based upon a quick search of the `data/` folder, it looks like the Stanislaus entries are probably coming from the `california-pacific-medical-center-r.k.-davies-medical-center/` and `st.-luke’s-hospital-(san-francisco)` folders, the `chargemaster-2019.xlsx` and `chargemaster-2019.json` files, resp.
```
# Take a look at St. Luke's first - stealing code from parse.py to make this simple
import codecs, json
filename = "data/st.-luke’s-hospital-(san-francisco)/latest/chargemaster-2019.json"
with codecs.open(filename, "r", encoding='utf-8-sig', errors='ignore') as filey:
content = json.loads(filey.read())
names = set()
for row in content['CDM']:
if 'HOSPITAL_NAME' in row:
names.add(row['HOSPITAL_NAME'])
print(names)
```
**Alrighty, it's pretty clear that Stanislaus is in this dataset.** Let's check the other one too.
Fun fact, for some reason CPMC-RKDMC has both a JSON and an XLSX file! The parser only pays attention to the XLSX file though, so that's all we'll worry about too (likely one is just a different file format version of the other).
```
# Now for CPMC-RKDMC
filename = "data/california-pacific-medical-center-\
r.k.-davies-medical-center/latest/chargemaster-2019.xlsx"
temp = pd.read_excel(filename)
temp.dropna(subset=['HOSPITAL_NAME'])[temp['HOSPITAL_NAME'].dropna().str.contains('Stanislaus')]
for row in temp.iterrows():
print(row)
break
temp.head()
temp.loc[0:2,'HOSPITAL_NAME'].astype(str).str.lower().str.replace(" ", "-")
temp.loc[0:2]
temp[['FACILITY', 'CMS_PROV_ID']] = temp[['HOSPITAL_NAME', 'SERVICE_SETTING']]
temp.loc[0:2]
```
Yup, this is one of them too! OK, now we know what hospital data folders we're looking at (who was this Stanislaus person anyhow? Quite the surgical philanthropist...). The problem here is that each of these chargemasters covers data for multiple hospitals, making it so that the `records.json` URI isn't terribly useful.
What I'm going to do instead is modify them so that the hospital names extracted are of a similar format to all other hospital IDs in our dataset.
```
# Find hospital_id values that don't have at least one hyphen with letters on either side of it
df = load_data()
df.dropna(subset=['hospital_id']).loc[~df['hospital_id'].dropna().
str.contains(r'[a-z]+-[a-z]+',
case=False),
'hospital_id'].value_counts()
```
**Very nice! By fixing those few parsers, we reduced the number of problem IDs from more than 350 to only a little more than 100!** There's still a ways to go, but I'm hopeful. Let's take a look at that `baptist` entry...
#### Correct Parsers and Data for Remaining Problem IDs
#### Correct Records Wherein `hospital_id == np.nan`
Note that, from my experience parsing the Stanislaus Surgical Hospital data, these NaN values could be coming from the parsing process itself, even when it's properly done (e.g. source chargemaster doesn't have actually hospital names to pull for some rows for some reason, not that one column got confused with another).
#### Hospital ID -> Hospital Name
Now I'll convert this cleaned up column of "IDs" that are actually just the hospital names with hyphens instead of spaces into regular hospital names so that I can match them to CMS records and combine the CMS hospital data in seamlessly.
Ultimately, what I'll do is create names based upon the mapping of URIs to names in the individual `results.json` files in `data/<hospital group>/latest/`
### Price
As this should be a continuous variable (maybe with some commas or dollar signs to pull out, but otherwise just float values), determining what are reasonable values for this column and what are anomalous should be easy...ish.
### Charge Type
I think these are again internally-derived labels for this project (that are also totally valid categories of charges mind you) and, as such, likely to not have too many values to contend with, making cleaning them pretty seamless (I hope).
### Charge Code
This one will be tough. There's theoretically nothing limiting a hospital from making its own random charge code mappings, alphanumeric values being fair game. Likely there will be a few oddballs that stand out as being problematic, but I may not be able to catch all of the problems in this one.
That all being said, this isn't a critical field to begin with, and hopefully most corrections in the earlier columns will correct most of the problems in this one. My priority will be to find any entries in this column that are clearly meant to be in the other columns (especially `description`) so that I can rely on them at this column's expense.
### Description
This one is the trickiest and the most important. It can theoretically have any value and will be what I need to aggregate on in order to find trends in prices across hospitals. Hopefully by fixing all of the other columns prior to this one I'll have minimized the cleaning to be done here.
## Optimize the DataFrame
This dataframe is quite large (almost 4GB in memory!) and that's likely to cause all sorts of problems when it comes time tofilepathnalysis. So we'll need to make sure we understand the nature of each column's data and then optimize for it (after potentially correcting for things like strings that are actually numbers).
To start with, let's check out the nature of the data in each column:
1. How often do charge codes exist?
2. We'll check, but likely that description exists for most
3. Other than decimal numbers, what values are in price?
4. What are all of the different charge type values, and which ones can we filter out (e.g. drg)?
* Do charge codes get embedded in descriptions a lot, like what we see in df.tail()? Or is this something that is only present for non-standard charge_type?
```
# In case you need to reinitialize df after experimenting...
#Make sure any changes to custom packages can be reflected immediately
#in the notebook without kernel restart
import autoreload
%load_ext autoreload
%autoreload 2
import pandas as pd
import numpy as np
df = pd.read_csv('data/all_hospitals-latest.csv', index_col = 0, low_memory = False)
# First, let's get a better handle on unique values, so we can figure out what fields make
# sense as categoricals and what ones definitely don't
unique_vals = pd.DataFrame(df.nunique()).rename(columns = {0: 'number of unique values'})
unique_vals['fraction of all values'] = round(unique_vals['number of unique values'] / len(df), 2)
unique_vals['data type'] = df.dtypes
# Assumes strings are involved if feature should be categorical,
# although may not be true for numerically-coded categoricals
unique_vals['make categorical?'] = (unique_vals['fraction of all values'] < 0.5) \
& (unique_vals['data type'] == 'object')
unique_vals
df['description'].value_counts()
df['hospital_id'].value_counts()
```
**Interesting. There are so many records with repeat information that we can change the dtype of pretty much all of them to be categorical.** Here's what we're going to do:
1. `charge_code`, `price`, and `description`: I'm not going to convert these to categoricals
* `charge_code` and `description`: while from a data perspective these would likely be better handled in memory by making anything categorical that has so few unique values that the count of them is less than 50% of the count of all rows, it doesn't make sense to make these fields categoricals, as that implies they are drawing from a common data reference. That's simply not the case.
* Given that two different hospitals can have the charge code `1001` refer to two totally different procedures/consumables, there's no reason to add confusion by treating these in the dataset like they have the same meaning.
* The same logic goes for the description field (although that one has me scratching my head a bit, as I'd expect it to be a bit more free text in nature and thus not likely to have repeated values)
* `price`: this should be a continuous variable, not a categorical one!
2. `hospital_id`, `filename`, and `charge_type`: these are classic examples of categorical variables and we should convert them.
* That being said, it's pretty clear from a very brief look at the unique values in the `hospital_id` field that something is fishy here and that likely some of the parsers have failed to work properly. So it looks like we'll need to parse each column separately and make corrections before proceeding further.
### Categorically Annoying
```
# Make categorical columns where appropriate
cat_cols = ['hospital_id', 'filename', 'charge_type']
for col in cat_cols:
df.loc[:, col] = df.loc[:, col].astype('category')
df['charge_type'].cat.categories
df.info(memory_usage = 'deep', verbose = True, null_counts = True)
```
**Nice! We cut the memory usage in half!** OK, on to less obvious optimizing!
### Description and Charge Code Fields
```
# What do our missing values look like? How sparse are these data?
missing = pd.DataFrame(df.isnull().sum()).rename(columns = {0: 'total missing'})
missing['percent missing'] = round(missing['total missing'] / len(df),2)
missing.sort_values('total missing', ascending = False)
missing
```
**Looks like we have description text for all but 12% of the data.** Not bad.
```
# How often do charge codes exist?
df['charge_code'].describe()
df['charge_code'].value_counts()
```
**Quite a few different charge codes, with lots of different possible values.** Given that charge codes are likely a somewhat-random "unique" identifiers (air quotes because I'm suspicious of any large entity's data management practices until that suspicion is proven unwarranted). Nothing to see here.
*OK, let's get to the meat of it, the thing that's actually most interesting (arguably): the price!*
### The Price Column, AKA The Super Important Yet Extremely Messy Column
```
# Separate out only the price rows that are non-numeric
df['price'].dropna().apply(type).value_counts()
```
**So about half of the non-null prices are `str` type.** Now we need to figure out what those strings actually are.
```
# Look at only string prices
df.loc[df['price'].apply(type) == str,'price']
```
**Huh, how odd. These strings all look like regular old float values.** Why is pandas importing them as strings? Let's force the column to be float type and then we'll see how our missing values change (since we can force non-numeric strings to be `NaN`)
```
# Convert price to be float type, then see if missing['total_missing'] changes
missing_price_initial = missing.loc['price','total missing']
delta = pd.to_numeric(df['price'], errors = 'coerce').isnull().sum() - missing_price_initial
delta
```
**OK, so we see about 300K of the 4.67M string values become `NaN` when we do this numeric conversion. That's not ideal.** Looks like we're losing a lot of data with this conversion, is there a better way? Or should we just consider this an acceptable loss?
```
# How to filter so we can see a sample of the ~300K true non-float strings in price
# so we can get an idea as to how to deal with them?
# Show only the prices that are null after numeric conversion
df.loc[pd.to_numeric(df['price'], errors = 'coerce').isnull(), 'price']
```
**Ah, I see the issues here! We've got commas making numbers look like they're not numbers, and this weird ' - ' string that must be a certain hospitals equivalent of `null`.** Let's correct for these!
The `null` string is one space, following by a hyphen and three spaces.
```
# Set ' - ' to proper NaN
import numpy as np
df['price'].replace(' - ', np.nan, inplace = True)
# What are the values that contain commas?
df.loc[df['price'].str.contains(r'\d,\d', na = False), 'price']
```
**Oh goodie, there are *ranges* of dollar amounts that we have to worry about!** Fantastic, just fantastic. These hospitals sure don't like making this easy, do they?
Here's the plan:
1. Strip dollar signs from all of these strings. They're superfluous and just make things complicated
2. Split strings on the string ' - '
3. Remove commas and cast results as float values
* Any rows with `NaN` for the second split column are just regular comma-in-the-thousands-place numbers. Leave them alone for the moment
* Any with non-null values in the second column: take the average of the two columns and overwrite the first column with the average. This midpoint value will be considered the useful estimate of the cost
4. Push the first column values (now overwritten in the case of ranges of values to be the midpoints) back into their places in the `price` column and continue hunting for edge cases
```
# Replace effectively null prices with np.nan
df.loc[df['price'] == '-', 'price'] = np.nan
def remove_silly_chars(row):
'''
It is assumed that this will be used as part of a Series.apply() call.
Takes in an element of a pandas Series that should be a string representation
of a price or a range of prices and spits back the string without any thousands
separators (e.g. commas) or dollar signs. If it detects that there's a range of
prices being provided (e.g. $1.00 - $2.00), it returns the midpoint of the range.
Parameters
----------
row: str. The string representation of a price or range of prices.
Returns
-------
float. The price (or midpoint price if a range was given in row)
'''
# Replace '$', ',', and '-' with empty strings, splitting on the hyphen
price_strings = row.replace('$','').replace(',','').split('-')
# Strip leading and trailing whitespace from list of split strings
# and take the average of the different prices from the original range,
# returning it as a float value
# If ValueError raised, assume there were invalid characters and
# set to np.nan
try:
return pd.Series([float(i.strip()) for i in price_strings]).mean()
except ValueError:
return np.nan
# When only digits + commas + $, convert to only digits
# Also take average if multiple value range provided in string
ix = df['price'].str.contains(r'\d,\d|\$\d', na=False, case=False)
df.loc[ix, 'price'] = df.loc[ix,'price'].apply(remove_silly_chars)
```
**OK, now that we've cleaned up a lot of those strings so that they can be proper floats, how many bad strings are we left with?** When we ran this check prior to the `$` and `,` cleaning process, we had about 300K records coming up as null after the numeric conversion that weren't null previously. What does it look like now?
```
# Convert price to be float type, then see if missing['total_missing'] changes
missing_price_initial = missing.loc['price','total missing']
delta = pd.to_numeric(df['price'], errors = 'coerce').isnull().sum() - missing_price_initial
delta
```
**SIGH. Now we're done to 200K, but that's not awesome.** At this point, I'm fine with it. We'll lose about 2.1% of these that may not appropriately be null (although most probably should be), but anything else I've tried to pare it down further actually makes things worse, so I say we're good now!
```
# Coerce any obvious float strings to floats
df.loc[:, 'price'] = pd.to_numeric(df['price'], errors = 'coerce')
df.info(memory_usage = 'deep', verbose = True, null_counts = True)
df['price'].describe()
```
**Ah nuts, looks like we have some unreasonable ranges on these data.** If I had to guess, likely these are issues with non-price floats being inserted into the `price` column incorrectly by individual hospital chargemaster parsers. Let's take a quick look at these data, identify the outliers, and see if we can fix them (and what the magnitude of the problem is).
```
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
g = sns.distplot(df['price'].dropna(), kde = False)
g.axes.set_yscale('log')
```
**WHOA. The x-axis goes up to \\$10B USD?!** I'm going to assume that this is unreasonable...
In fact, looks like we have a non-trivial amount of data above \\$1B! That's ludicrous. Let's take a closer look in the \\$1M to \\$10B scale.
```
df.loc[(df['price'] >= 1E6) & (df['price'] <= 1E10), 'price'].describe()
g = sns.distplot(df.loc[(df['price'] >= 1E6) & (df['price'] <= 1E10), 'price'].dropna(),
kde=False)
g.axes.set_yscale('log')
df.loc[(df['price'] >= 1E6) & (df['price'] <= 1E10), 'hospital_id'].value_counts()
```
**OK, so it's pretty clear to me here that we have a problem hospital here (foothill-presbyterian-hospital).** For simplicity's sake, we may just need to drop them from the dataset, but I'll take a look at their data and see if a fix is possible (I think it's a matter of switching the `price` and `charge_code` column data).
For the other hospitals, the counts are so low that we can probably parse those out manually to make sure they aren't nonsensical.
**TO DO**
1. See if it's reasonable to switch `price` and `charge_code` data for foothill hospital. If it is, do so. If there's a problem, drop them from dataset.
2. Check out the other hospitals in this price range and see if there are persistent problems with their `price` data too that need to be corrected.
3. Look at how many records have `hospital_id` without any hyphens, like the last one in the list above. Clearly there's a problem with those...
4. Once you're satisfied that the data are clean, script up an `import_data` file and start up a new analysis-focused Jupyter notebook.
* Subset by `charge_type == standard`
* Cluster based on `description` similarity, and assume those are similar procedures/consumables
* Figure out if there's a way to validate this
* Do some analyses on price spreads and trends among the different clusters/procedures/consumables
* Anything cool that can be predicted??
| true |
code
| 0.432782 | null | null | null | null |
|
# Import
```
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter('runs/lenet')
```
# Load data
```
# Prepare data transformator
transform = transforms.Compose(
[
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
]
)
# Load train set
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4, shuffle=True)
# Load test set
testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4, shuffle=False)
# Prepare class labels
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
```
# Show sample
```
# function to show an image
def imshow(img, convert_gpu=False):
img = img / 2 + 0.5 # unnormalize
if convert_gpu:
img = img.cpu()
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
# show some test images
dataiter = iter(testloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join(f'{classes[labels[j]]}' for j in range(4)))
```
# Build architecture
```
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
# Prepare layers
def forward(self, x):
# Connect layers
return x
net = LeNet()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
```
# GPU
```
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
if device.type == 'cuda':
net.to(device)
print('GPU Activated')
```
# Train
```
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader):
# get the inputs; data is a list of [inputs, labels]
if device.type == 'cuda':
inputs, labels = data[0].to(device), data[1].to(device)
else:
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward
outputs = net(inputs)
loss = criterion(outputs, labels)
# backward
loss.backward()
# optimize
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print(f'epoch: {epoch + 1} batches: {i + 1} loss: {running_loss / 2000:.3f}')
writer.add_scalar('train loss', running_loss / 2000, epoch * len(trainloader) + i)
running_loss = 0.0
print('Finished Training')
```
# Testing
```
correct = 0
total = 0
with torch.no_grad():
for i, data in enumerate(testloader):
# get the inputs; data is a list of [inputs, labels]
if device.type == 'cuda':
images, labels = data[0].to(device), data[1].to(device)
else:
images, labels = data
# get outputs
outputs = net(images)
# gather which class had highest prediction score
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
# Show prediction for 1st batch
if i == 0:
imshow(torchvision.utils.make_grid(images), device.type == 'cuda')
print('GroundTruth: ', ' '.join(f'{classes[labels[j]]}' for j in range(4)))
print('Predicted: ', ' '.join(f'{classes[predicted[j]]}' for j in range(4)))
print(f'Accuracy of the network on the 10000 test images: {100 * correct / total} %')
```
| true |
code
| 0.781268 | null | null | null | null |
|
# Vietnam
## Table of contents
1. [General Geography](#1)<br>
1.1 [Soil Resources](#11)<br>
1.2 [Road and Railway Network](#12)<br>
2. [Poverty in Vietnam](#2)<br>
2.1 [The percentage of malnourished children under 5 in 2018 by locality](#21)<br>
2.2 [Proportion of poor households by region from 1998 to 2016 ](#22)<br>
3. [Vietnam Economy](#3)<br>
3.1 [Employment](#31)<br>
3.2 [The Aquaculture Production from 2013 to 2018 by Provinces](#32)<br>
3.3 [Various sources of income by provinces in 2018](#33)<br>
I. [Important Notes](#333)<br>
II. [References](#666)<br>
```
import json
import pandas as pd
import numpy as np
import plotly.express as px
import plotly.graph_objects as go
import geopandas as gpd
import shapely.geometry
from ipywidgets import widgets
# Plot in browser
import plotly.io as pio
pio.renderers.default = 'browser'
from codes.auxiliary import convert_id_map
from codes.plot import *
```
## 1. General Geography <a id="1"></a>
### 1.1 Soil Resources <a id="11"></a>
Dataset of soil types of Vietnam is a geospatial polygon data which is based on FAO classification
[Source](https://data.opendevelopmentmekong.net/dataset/soil-types-in-vietnam)
```
soil_geo = json.load(open('geodata/soilmap_vietnam.geojson',"r"))
# split unique soil type
imap = convert_id_map(soil_geo, 'Type', 'faosoil')
map_keys = imap.keys()
soil_list = []
soil_dict = {}
for key in map_keys:
soil_type = key.split("sols")[0]
soil_type +="sols"
if key not in soil_dict.keys():
soil_dict[key] = soil_type
if soil_type not in soil_list:
soil_list.append(soil_type)
# Soilmap Dataframe
soil_pd = gpd.read_file('geodata/soilmap_vietnam.geojson')
# soil_pd = soil_pd.iloc[:,0:4]
soil_pd["Soil_type"] = soil_pd['Type'].map(soil_dict)
# Plotting soil map
fig = px.choropleth_mapbox(
soil_pd,
geojson=soil_geo,
color = "Soil_type",
color_discrete_sequence=px.colors.qualitative.Light24,
locations = "gid",
featureidkey="properties.gid",
mapbox_style = "carto-positron",
center = {"lat": 16, "lon": 106},
zoom = 5,
title = "Soil Map"
)
fig.update_layout(margin={"r":0,"t":0,"l":0,"b":0})
fig.show()
```
<img src="figures/soilmap.png" alt="drawing" style="width:950px;"/>
### 1.2 Road and Railway network <a id="12"></a>
A geospatial dataset containing polylines of transportation network in Vietnam. It contains the railways, the principal roads and the secondary roads.
[Source](https://data.opendevelopmentmekong.net/dataset/giao-thng-vit-nam)
```
# open a zipped shapefile with the zip:// pseudo-protocol
transport_df = gpd.read_file("geodata/transport.zip")
lats = []
lons = []
names = []
for feature, name in zip(transport_df.geometry, transport_df.Name):
if isinstance(feature, shapely.geometry.linestring.LineString):
linestrings = [feature]
elif isinstance(feature, shapely.geometry.multilinestring.MultiLineString):
linestrings = feature.geoms
else:
continue
for linestring in linestrings:
x, y = linestring.xy
lats = np.append(lats, y)
lons = np.append(lons, x)
names = np.append(names, [name]*len(y))
lats = np.append(lats, None)
lons = np.append(lons, None)
names = np.append(names, None)
fig = px.line_mapbox(lat=lats, lon=lons, hover_name=names,
mapbox_style="stamen-terrain", zoom=4.5, center={"lat": 16, "lon": 106})
fig.show()
```
<img src="figures/South_railway_road.png" alt="drawing" style="width:950px;"/>
## 2. Poverty In Vietnam <a id="2"></a>
### 2.1. The percentage of malnourished children under 5 in 2018 by locality <a id="21"></a>
The attributes include the total weight, hight and weight based on height.
```
# Malnutrition data
malnutrition_children_vn_2018 = pd.read_csv("geodata/malnutrition_children_vn_2018.csv")
#Vietnam map
vietnam_geo = json.load(open("geodata/vietnam_state.geojson","r"))
# Plotting
fig = px.choropleth_mapbox(
malnutrition_children_vn_2018,
locations = 'Code',
featureidkey="properties.Code",
geojson = vietnam_geo,
color = 'Wei_Hei',
hover_name = "Name",
mapbox_style = "carto-positron",
center = {"lat": 16,"lon": 106},
zoom = 4.5,
title = "malnourished children under 5 in 2018 by locality in Vietnam ",
)
fig.update_geos(fitbounds = "locations", visible=False)
fig.show()
```
<img src="figures/Malnutrion_children_2018.png" alt="drawing" style="width:950px;"/>
### 2.2 Proportion of poor households by region from 1998 to 2016 <a id="22"></a>
The dataset includes le pourcentage of poor households by region in Vietnam from 1998 to 2016. The standard of poor households for this period based on the average income per person per month of households is updated according to the consumer price index as follows: In 2010, VND 400,000 for rural areas and VND 500,000 for urban areas; Similarly, in 2013 it was VND 570,000 and VND 710,000; in 2014, VND 605,000 dong and VND 750,000; in 2015, there were VND 615,000 and VND 760,000 dong; In 2016, VND 630,000 and VND 780,000 respectively.
```
# Import the Vietnam map by region data (error geojson file)
vnregion_geo = json.load(open("geodata/poverty_rate_1998_2016.geojson", "r",encoding='utf-8'))
# Import aquaculture_production csv
poverty_rate_1998_2016 = pd.read_csv("geodata/poverty_rate_1998_2016.csv")
cols = sorted(poverty_rate_1998_2016.columns[3:], reverse=False)
for i, y in enumerate(cols):
poverty = "Poverty" + y
poverty_rate_1998_2016[poverty] = poverty_rate_1998_2016[y]
# Convert wide to long format
poverty = poverty_rate_1998_2016.drop(cols, axis=1)
final_poverty = pd.wide_to_long(poverty,"Poverty", i=['Name_EN','Name_VI','id'], j= "year")
final_poverty.reset_index(inplace=True)
```
### Choropleth map using GeoJSON
```
input_year ='1998' #1998 2002 2004 2006 2008 2010 2011 2012 2013 2014 2015 2016
fig = px.choropleth_mapbox(
poverty_rate_1998_2016,
locations = 'id',
geojson = vnregion_geo,
featureidkey="properties.id",
color = "Poverty" + input_year ,
color_continuous_scale="Viridis",
range_color=(0, 65),
hover_name = "Name_EN",
# hover_data = ["Poverty_percentage" + input_year],
mapbox_style = "carto-positron",
center = {"lat": 17,"lon": 106},
zoom = 4.5,
title = "Proportion of poor households by region in Vietnam "+ input_year,
)
fig.update_geos(fitbounds = "locations", visible=False)
fig.show()
```
<img src="figures/poverty_rate_1998_2016.png" alt="drawing" style="width:950px;"/>
### Animated figures with GeoJSON, Plotly Express
```
fig = px.choropleth(
final_poverty,
locations = 'id',
featureidkey="properties.id",
animation_frame = "year",
geojson = vnregion_geo,
color = "Poverty",
color_continuous_scale="Viridis",
range_color=(0, 65),
hover_name = "Name_EN",
# hover_data = ['Poverty_percentage'],
title = "Proportion of poor households by region in Vietnam from 1998 to 2016",
)
fig.update_geos(fitbounds = "locations", visible=False)
fig.show()
```
## 3. Vietnam Economy <a id="3"></a>
### 3.1 Employment <a id="31"></a>
[Source](https://www.gso.gov.vn/en/employment/)
```
# Import csv
trained_employee = pd.read_csv("geodata/trained_employee15_vn.csv")
labor_force = pd.read_csv("geodata/labor_force_vn.csv")
```
<img src="figures/Percent_employ15.png" alt="drawing" style="width:950px;"/>
#### Labour force at 15 years of age and above by province
```
title31 = "Labour force at 15 years of age and above by province from 2010 to 2018"
plot_animation_frame_vietnamstate(labor_force,vietnam_geo,"labor_force", title31)
```
#### Percentage of employed workers at 15 years of age and above among population by province
```
title32 = "Percentage of employed workers at 15 years of age and above among population by province from 2010 to 2018"
plot_animation_frame_vietnamstate(trained_employee,vietnam_geo,"percentage", title32)
```
### 3.2 The Aquaculture Production from 2013 to 2018 by Provinces <a id="32"></a>
Published by: Open Development Vietnam The data provides information on Vietnam's aquaculture production from 2013 to 2018. The aquaculture in Vietnam includes: farmed fish production, farmed shrimp production and other aquatic products. Aquaculture production is divided by province and city.
```
# import the Vietnam map by provinces data
vietnam_geo = json.load(open("geodata/vietnam_state.geojson", "r"))
# Convert map properties/
state_id_map = convert_id_map(vietnam_geo, "Name", "Code")
# Import aquaculture_production csv
df = pd.read_csv("geodata/aquaculture_production_2013__2018.csv")
years = ['2013','2014','2015','2016','2017','2018']
for i, y in enumerate(years):
scale = 'Production_Scale'+ y
prod = 'Production' + y
df[scale] = np.log10(df[y])
df[prod] = df[y]
# Convert wide to long format
prod = df.drop(years, axis=1)
final_prod = pd.wide_to_long(prod, stubnames=['Production_Scale','Production'], i=['Name','Code'], j="year")
final_prod.reset_index(inplace=True)
```
### Choropleth map using GeoJSON
```
input_year = '2018'
fig = px.choropleth_mapbox(
df,
geojson = vietnam_geo,
locations ="Code",
color = "Production_Scale" + input_year,
range_color=(2, 6),
hover_name = "Name",
featureidkey = "properties.Code",
hover_data = ['Production'+ input_year],
mapbox_style="carto-positron",
center={"lat": 16, "lon": 106},
zoom=4.5,
title ="The Aquaculture Production of Vietnam by Province in " + input_year
)
fig.update_geos(fitbounds ="locations", visible=False)
fig.show()
```
<img src="figures/Aqua_prod_2013.png" alt="drawing" style="width:950px;"/>
### Animated figures with GeoJSON, Plotly Express
```
title33 = "The Aquaculture Production of Vietnam from 2013 to 2018 by Province"
plot_animation_frame_vietnamstate(final_prod, vietnam_geo, "Production_Scale", title33)
```
## 3.3 Various sources of income by provinces in 2018 <a id="33"></a>
The data provide the information on per capita in come by province in 2018 in Vietnam. The total income per month includes the salary, the income from agriculture, forestry, aquaculture and non-agriculture, non-forestry, non-aquaculture and from other income. The income unit is in thousands vnd
[Source](https://data.opendevelopmentmekong.net/dataset/per-capita-income-by-province-in-2018-in-vietnam)
```
# Import csv and geojson
income_df = pd.read_csv("geodata/thunhapbinhquan.csv")
categories = sorted(income_df.columns[3:])
#Vietnam map
vietnam_geo = json.load(open("geodata/vietnam_state.geojson","r"))
```
<img src="figures/Wage_agri_by_province.png" alt="drawing" style="width:950px;"/>
```
trace = go.Choroplethmapbox(
geojson = vietnam_geo,
featureidkey='properties.Code',
locations = income_df["Code"],
z=income_df.loc[0:, 'income_total_average'],
hovertext = 'Province: ' + income_df.Name_EN,
colorscale ='viridis',
marker_opacity=0.9,
marker_line_width=0.9,
showscale=True
)
lyt = dict(title='Income by provinces',
height = 700,
mapbox_style = "white-bg",
mapbox_zoom = 4,
mapbox_center = {"lat": 17,"lon": 106})
fig = go.FigureWidget(data=[trace], layout=lyt)
# Add dropdowns
## 'Income' dropdown
cat_options = ['total_average', 'salary', 'agri', 'non_agri', 'others']
category = widgets.Dropdown(options=cat_options,
value='total_average',
description='Category')
# Add Submit button
submit = widgets.Button(description='Submit',
disabled=False,
button_style='info',
icon='check')
def submit_event_handler(args):
if category.value in cat_options:
new_data = income_df.loc[0:, 'income_' + str(category.value)]
with fig.batch_update():
fig.data[0].z = new_data
fig.layout.title = ' '.join(['Income ',str(category.value), ' in 2018'])
submit.on_click(submit_event_handler)
container = widgets.HBox([category, submit])
widgets.VBox([container, fig])
```
## Important Notes <a id="333"></a>
## Reference <a id="666"></a>
For additional information and attributes for creating bubble charts in Plotly see: https://plotly.com/python/bubble-charts/.
For more documentation on creating animations with Plotly, see https://plotly.com/python/animations.
| true |
code
| 0.459622 | null | null | null | null |
|
# 02 - Ensembling: Bagging, Boosting and Ensemble
<div class="alert alert-block alert-success">
<b>Version:</b> v0.1 <b>Date:</b> 2020-06-09
在这个Notebook中,记录了`Randomforest` `XGBoost` 以及模型组合的实现策略。
</div>
<div class="alert alert-block alert-info">
<b>💡:</b>
- **环境依赖**: Fastai v2 (0.0.18), XGBoost(1.1.1), sklearn
- **数据集**:[ADULT_SAMPLE](http://files.fast.ai/data/examples/adult_sample.tgz)
</div>
<div class="alert alert-block alert-danger">
<b>注意📌:</b>
本文档中只是各个算法的初步测试,非最佳实践.
</div>
## 数据准备
```
from fastai2.tabular.all import *
```
Let's first build our `TabularPandas` object:
```
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
df.head()
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['age', 'fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
y_names = 'salary'
y_block = CategoryBlock()
splits = RandomSplitter()(range_of(df))
to = TabularPandas(df, procs=procs, cat_names=cat_names, cont_names=cont_names,
y_names=y_names, y_block=y_block, splits=splits)
X_train,y_train = to.train.xs.values,to.train.ys.values.squeeze()
X_valid,y_valid = to.valid.xs.values,to.valid.ys.values.squeeze()
features = to.x_names
```
# XGBoost
* Gradient Boosting
* [Documentation](https://xgboost.readthedocs.io/en/latest/)
```
import xgboost as xgb
xgb.__version__
model = xgb.XGBClassifier(n_estimators = 100, max_depth=8, learning_rate=0.1, subsample=0.5)
```
And now we can fit our classifier:
```
xgb_model = model.fit(X_train, y_train)
```
And we'll grab the raw probabilities from our test data:
```
xgb_preds = xgb_model.predict_proba(X_valid)
xgb_preds
```
And check it's accuracy
```
accuracy(tensor(xgb_preds), tensor(y_valid))
```
We can even plot the importance
```
from xgboost import plot_importance
plot_importance(xgb_model).set_yticklabels(list(features))
```
## `fastai2` 中的`Tabular Learner`
```
dls = to.dataloaders()
learn = tabular_learner(dls, layers=[200,100], metrics=accuracy)
learn.fit(5, 1e-2)
```
As we can see, our neural network has 83.84%, slighlty higher than the GBT
Now we'll grab predictions
```
nn_preds = learn.get_preds()[0]
nn_preds
```
Let's check to see if our feature importance changed at all
```
class PermutationImportance():
"Calculate and plot the permutation importance"
def __init__(self, learn:Learner, df=None, bs=None):
"Initialize with a test dataframe, a learner, and a metric"
self.learn = learn
self.df = df if df is not None else None
bs = bs if bs is not None else learn.dls.bs
self.dl = learn.dls.test_dl(self.df, bs=bs) if self.df is not None else learn.dls[1]
self.x_names = learn.dls.x_names.filter(lambda x: '_na' not in x)
self.na = learn.dls.x_names.filter(lambda x: '_na' in x)
self.y = dls.y_names
self.results = self.calc_feat_importance()
self.plot_importance(self.ord_dic_to_df(self.results))
def measure_col(self, name:str):
"Measures change after column shuffle"
col = [name]
if f'{name}_na' in self.na: col.append(name)
orig = self.dl.items[col].values
perm = np.random.permutation(len(orig))
self.dl.items[col] = self.dl.items[col].values[perm]
metric = learn.validate(dl=self.dl)[1]
self.dl.items[col] = orig
return metric
def calc_feat_importance(self):
"Calculates permutation importance by shuffling a column on a percentage scale"
print('Getting base error')
base_error = self.learn.validate(dl=self.dl)[1]
self.importance = {}
pbar = progress_bar(self.x_names)
print('Calculating Permutation Importance')
for col in pbar:
self.importance[col] = self.measure_col(col)
for key, value in self.importance.items():
self.importance[key] = (base_error-value)/base_error #this can be adjusted
return OrderedDict(sorted(self.importance.items(), key=lambda kv: kv[1], reverse=True))
def ord_dic_to_df(self, dict:OrderedDict):
return pd.DataFrame([[k, v] for k, v in dict.items()], columns=['feature', 'importance'])
def plot_importance(self, df:pd.DataFrame, limit=20, asc=False, **kwargs):
"Plot importance with an optional limit to how many variables shown"
df_copy = df.copy()
df_copy['feature'] = df_copy['feature'].str.slice(0,25)
df_copy = df_copy.sort_values(by='importance', ascending=asc)[:limit].sort_values(by='importance', ascending=not(asc))
ax = df_copy.plot.barh(x='feature', y='importance', sort_columns=True, **kwargs)
for p in ax.patches:
ax.annotate(f'{p.get_width():.4f}', ((p.get_width() * 1.005), p.get_y() * 1.005))
imp = PermutationImportance(learn)
```
And it did! Is that bad? No, it's actually what we want. If they utilized the same things, we'd expect very similar results. We're bringing in other models to hope that they can provide a different outlook to how they're utilizing the features (hopefully differently)
## 组合两个模型
And perform our ensembling! To do so we'll average our predictions to gather (take the sum and divide by 2)
```
avgs = (nn_preds + xgb_preds) / 2
avgs
```
And now we'll take the argmax to get our predictions:
```
argmax = avgs.argmax(dim=1)
argmax
```
How do we know if it worked? Let's grade our predictions:
```
y_valid
accuracy(tensor(nn_preds), tensor(y_valid))
accuracy(tensor(xgb_preds), tensor(y_valid))
accuracy(tensor(avgs), tensor(y_valid))
```
As you can see we scored a bit higher!
## Random Forests
Let's also try with Random Forests
```
from sklearn.ensemble import RandomForestClassifier
tree = RandomForestClassifier(n_estimators=100,max_features=0.5,min_samples_leaf=5)
```
Now let's fit
```
tree.fit(X_train, y_train);
```
Now, we are not going to use the default importances. Why? Read up here:
[Beware Default Random Forest Importances](https://explained.ai/rf-importance/) by Terence Parr, Kerem Turgutlu, Christopher Csiszar, and Jeremy Howard
Instead, based on their recommendations we'll be utilizing their `rfpimp` package
```
#!pip install rfpimp
from rfpimp import *
imp = importances(tree, to.valid.xs, to.valid.ys)
plot_importances(imp)
```
Which as we can see, was also very different.
Now we can get our raw probabilities:
```
forest_preds = tree.predict_proba(X_valid)
forest_preds
```
And now we can add it to our ensemble:
```
accuracy(tensor(forest_preds),tensor(y_valid))
avgs = (nn_preds + xgb_preds + forest_preds) / 3
accuracy(tensor(avgs), tensor(y_valid))
```
As we can see, it didn't quite work how we wanted to. But that is okay, the goal was to experiment!
| true |
code
| 0.716857 | null | null | null | null |
|
# Pretrained Transformers as Universal Computation Engines Demo
This is a demo notebook illustrating creating a Frozen Pretrained Transformer (FPT) and training on the Bit XOR task, which converges within a couple minutes.
arXiv: https://arxiv.org/pdf/2103.05247.pdf
Github: https://github.com/kzl/universal-computation
```
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
from transformers.models.gpt2.modeling_gpt2 import GPT2Model
```
## Creating the dataset
For this demo, we'll look at calculating the elementwise XOR between two randomly generated bitstrings.
If you want to play more with the model, feel free to try larger $n$, although it will take longer to train.
```
def generate_example(n):
bits = np.random.randint(low=0, high=2, size=(2, n))
xor = np.logical_xor(bits[0], bits[1]).astype(np.long)
return bits.reshape((2*n)), xor
n = 5
bits, xor = generate_example(n)
print(' String 1:', bits[:n])
print(' String 2:', bits[n:])
print('Output XOR:', xor)
```
## Creating the frozen pretrained transformer
We simply wrap a pretrained GPT-2 model with linear input and output layers, then freeze the weights of the self-attention and feedforward layers.
You can also see what happens using a randomly initialized model instead.
```
if torch.cuda.is_available():
device = 'cuda'
else:
device = 'cpu'
gpt2 = GPT2Model.from_pretrained('gpt2') # loads a pretrained GPT-2 base model
in_layer = nn.Embedding(2, 768) # map bit to GPT-2 embedding dim of 768
out_layer = nn.Linear(768, 2) # predict logits
for name, param in gpt2.named_parameters():
# freeze all parameters except the layernorm and positional embeddings
if 'ln' in name or 'wpe' in name:
param.requires_grad = True
else:
param.requires_grad = False
```
## Training loop
We train the model with stochastic gradient descent on the Bit XOR task.
The model should converge within 5000 samples.
```
params = list(gpt2.parameters()) + list(in_layer.parameters()) + list(out_layer.parameters())
optimizer = torch.optim.Adam(params)
loss_fn = nn.CrossEntropyLoss()
for layer in (gpt2, in_layer, out_layer):
layer.to(device=device)
layer.train()
accuracies = [0]
while sum(accuracies[-50:]) / len(accuracies[-50:]) < .99:
x, y = generate_example(n)
x = torch.from_numpy(x).to(device=device, dtype=torch.long)
y = torch.from_numpy(y).to(device=device, dtype=torch.long)
embeddings = in_layer(x.reshape(1, -1))
hidden_state = gpt2(inputs_embeds=embeddings).last_hidden_state[:,n:]
logits = out_layer(hidden_state)[0]
loss = loss_fn(logits, y)
accuracies.append((logits.argmax(dim=-1) == y).float().mean().item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
if len(accuracies) % 500 == 0:
accuracy = sum(accuracies[-50:]) / len(accuracies[-50:])
print(f'Samples: {len(accuracies)}, Accuracy: {accuracy}')
print(f'Final accuracy: {sum(accuracies[-50:]) / len(accuracies[-50:])}')
```
## Visualizing attention map
We can visualize the attention map of the first layer: the model learns to attend to the relevant bits for each element in the XOR operation.
Note the two consistent diagonal lines for output tokens 5-9 across samples, denoting each position of either string (the pattern is stronger if the model is allowed to train longer or evaluated on more samples).
```
for layer in (gpt2, in_layer, out_layer):
layer.eval()
bits, xor = generate_example(n)
with torch.no_grad():
x = torch.from_numpy(bits).to(device=device, dtype=torch.long)
embeddings = in_layer(x)
transformer_outputs = gpt2(
inputs_embeds=embeddings,
return_dict=True,
output_attentions=True,
)
logits = out_layer(transformer_outputs.last_hidden_state[n:])
predictions = logits.argmax(dim=-1).cpu().numpy()
print(' String 1:', bits[:n])
print(' String 2:', bits[n:])
print('Prediction:', predictions)
print('Output XOR:', xor)
attentions = transformer_outputs.attentions[0][0] # first layer, first in batch
mean_attentions = attentions.mean(dim=0) # take the mean over heads
mean_attentions = mean_attentions.cpu().numpy()
plt.xlabel('Input Tokens', size=16)
plt.xticks(range(10), bits)
plt.ylabel('Output Tokens', size=16)
plt.yticks(range(10), ['*'] * 5 + list(predictions))
plt.imshow(mean_attentions)
```
## Sanity check
As a sanity check, we can see that the model could solve this task without needing to finetune the self-attention layers! The XOR was computed using only the connections already present in GPT-2.
```
fresh_gpt2 = GPT2Model.from_pretrained('gpt2')
gpt2.to(device='cpu')
gpt2_state_dict = gpt2.state_dict()
for name, param in fresh_gpt2.named_parameters():
if 'attn' in name or 'mlp' in name:
new_param = gpt2_state_dict[name]
if torch.abs(param.data - new_param.data).sum() > 1e-8:
print(f'{name} was modified')
else:
print(f'{name} is unchanged')
```
| true |
code
| 0.641843 | null | null | null | null |
|
# An agent-based model of social support
*Joël Foramitti, 10.02.2022*
This notebook introduces a simple agent-based model to explore the propagation of social support through a population.
```
import agentpy as ap
import networkx as nx
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme()
```
The agents of the model have one variable `support` which indicates their support for a particular cause.
At every time-step, an agent interacts with their friends as well as some random encounters.
The higher the perceived support amongst their encounters, the higher the likelyhood that the agent will also support the cause.
```
class Individual(ap.Agent):
def setup(self):
# Initiate a variable support
# 0 indicates no support, 1 indicates support
self.support = 0
def adapt_support(self):
# Perceive average support amongst friends and random encounters
random_encounters = self.model.agents.random(self.p.random_encounters)
all_encounters = self.friends + random_encounters
perceived_support = sum(all_encounters.support) / len(all_encounters)
# Adapt own support based on random chance and perceived support
random_draw = self.model.random.random() # Draw between 0 and 1
self.support = 1 if random_draw < perceived_support else 0
```
At the start of the simulation, the model initiates a population of agents, defines a random network of friendships between these agents, and chooses a random share of agents to be the initial supporters of the cause.
At every simulation step, agents change their support and the share of supporters is recorded.
At the end of the model, the cause is designated a success if all agents support it.
```
class SupportModel(ap.Model):
def setup(self):
# Initiating agents
self.agents = ap.AgentList(self, self.p.n_agents, Individual)
# Setting up friendships
graph = nx.watts_strogatz_graph(
self.p.n_agents,
self.p.n_friends,
self.p.network_randomness)
self.network = self.agents.network = ap.Network(self, graph=graph)
self.network.add_agents(self.agents, self.network.nodes)
for a in self.agents:
a.friends = self.network.neighbors(a).to_list()
# Setting up initial supporters
initial_supporters = int(self.p.initial_support * self.p.n_agents)
for a in self.agents.random(initial_supporters):
a.support = 1
def step(self):
# Let every agent adapt their support
self.agents.adapt_support()
def update(self):
# Record the share of supporters at each time-step
self.supporter_share = sum(self.agents.support) / self.p.n_agents
self.record('supporter_share')
def end(self):
# Report the success of the social movement
# at the end of the simulation
self.success = 1 if self.supporter_share == 1 else 0
self.model.report('success')
```
For the generation of the network graph, we will use the [Watts-Strogatz model](https://en.wikipedia.org/wiki/Watts%E2%80%93Strogatz_model). This is an algorithm that generates a regular network were every agent will have the same amount of connections, and then introduces a certain amount of randomness to change some of these connections. A network where most agents are not neighbors, but where it is easy to reach every other agent in a small number of steps, is called a [small-world network](https://en.wikipedia.org/wiki/Small-world_network).
<img src="networks.png" alt="drawing" width="600"/>
## A single-run simulation
```
parameters = {
'steps': 100,
'n_agents': 100,
'n_friends': 2,
'network_randomness': 0.5,
'initial_support': 0.5,
'random_encounters': 1
}
model = SupportModel(parameters)
results = model.run()
success = 'Yes' if model.success else 'No'
print(f'Success: {success}')
ax = results.variables.SupportModel.plot()
```
## A multi-run experiment
```
sample_parameters = {
'steps': 100,
'n_agents': 100,
'n_friends': 2,
'network_randomness': 0.5,
'initial_support': ap.Range(0, 1),
'random_encounters': 1
}
sample = ap.Sample(sample_parameters, n=50)
exp = ap.Experiment(SupportModel, sample, iterations=50)
results = exp.run()
ax = sns.lineplot(
data=results.arrange_reporters(),
x='initial_support',
y='success'
)
ax.set_xlabel('Initial share of supporters')
ax.set_ylabel('Chances of success');
```
## Questions for discussion
- What happens under different parameter values?
- How does this model compare to real-world dynamics?
- What false conclusions could be made from this model?
- How could the model be improved or extended?
| true |
code
| 0.556701 | null | null | null | null |
|
# Density Tree for N-dimensional data and labels
The code below implements a **density** tree for non-labelled data.
## Libraries
First, some libraries are loaded and global figure settings are made for exporting.
```
import numpy as np
import matplotlib.pyplot as plt
import os
from IPython.core.display import Image, display
# Custom Libraries
from density_tree.density_forest import *
from density_tree.density_tree_create import *
from density_tree.density_tree_traverse import *
from density_tree.create_data import *
from density_tree.helpers import *
from density_tree.plots import *
```
# Generate Data
First, let's generate some unlabelled data:
```
dimensions = 2
nclusters = 5
covariance = 10
npoints = 100
minRange = 10
maxRange = 100
dataset = create_data(nclusters, dimensions, covariance, npoints, minrange=minRange, maxrange=maxRange,
labelled=False, random_flip=True, nonlinearities=True)
if dimensions == 2:
fig, ax = plt.subplots(1, 1)
fig.set_size_inches(8,6)
plot_data(dataset, "Unlabelled data", ax, labels=False)
plt.savefig("../Figures/unlabelled-data.pdf", bbox_inches='tight', pad_inches=0)
plt.show()
```
#### Create single Density Tree
```
import warnings
warnings.filterwarnings("ignore")
root = create_density_tree(dataset, dimensions=dimensions, clusters=nclusters)
def get_values_preorder(node, cut_dims, cut_vals):
cut_dims.append(node.split_dimension)
cut_vals.append(node.split_value)
if node.left is not None:
get_values_preorder(node.left, cut_dims, cut_vals)
if node.right is not None:
get_values_preorder(node.right, cut_dims, cut_vals)
return cut_vals, cut_dims
cut_vals, cut_dims = get_values_preorder(root, [], [])
cut_vals = np.asarray(cut_vals).astype(float)
cut_dims = np.asarray(cut_dims).astype(int)
x_split = cut_vals[cut_dims == 0]
y_split = cut_vals[cut_dims == 1]
if dimensions == 2:
fig, ax = plt.subplots(1, 1)
plot_data(dataset, "Training data after splitting", ax, labels=False, lines_x=x_split, lines_y=y_split,
minrange=minRange, maxrange=maxRange, covariance=covariance)
%clear
plt.show()
print(cut_dims, cut_vals)
```
# Printing the Tree
```
print(covs[0])
def tree_visualize(root):
tree_string = ""
tree_string = print_density_tree_latex(root, tree_string)
os.system("cd ../Figures; rm main.tex; more main_pt1.tex >> density-tree.tex; echo '' >> density-tree.tex;")
os.system("cd ../Figures; echo '" + tree_string + "' >> density-tree.tex; more main_pt2.tex >> density-tree.tex;")
os.system("cd ../Figures; /Library/TeX/texbin/pdflatex density-tree.tex; convert -density 300 -trim density-tree.pdf -quality 100 density-tree.png")
os.system("cd ../Figures; rm *.aux *.log")
display(Image('../Figures/density-tree.png', retina=True))
tree_visualize(root)
```
#### Showing all Clusters Covariances
```
covs, means = get_clusters(root, [], [])
if dimensions == 2:
fig, ax = plt.subplots(1, 1)
fig.set_size_inches(8,6)
plot_data(dataset, "Unlabelled data", ax, labels=False, covs=covs, means=means,
minrange = minRange, maxrange = maxRange, covariance=covariance)
plt.savefig("../Figures/unlabelled-data-cov.pdf", bbox_inches='tight', pad_inches=0)
plt.show()
print(cut_dims, cut_vals)
```
#### Descend tree (predict "label")
```
# for all points
probas = []
probas_other = []
for d in dataset:
# descend tree
d_mean, d_cov, d_pct = descend_density_tree(d,root)
# probability for this point to be from this distribution
probas.append(multivariate_normal.pdf(d, d_mean, d_cov)*d_pct)
for i in range(5):
probas_other.append(multivariate_normal.pdf(d, means[i], covs[i])*d_pct)
print("Probability to come from the leaf node cluster: %.5f%%" % np.mean(probas))
print("Probability to come from an arbitrary cluster: %.5f%%" % np.mean(probas_other))
```
#### Density Forest
```
root_nodes = density_forest_create(dataset, dimensions, nclusters, 100, .3, -1)
probas = density_forest_traverse(dataset, root_nodes)
# mean probability of all points to belong to the cluster in the root node
print(np.mean(probas))
```
| true |
code
| 0.647436 | null | null | null | null |
|
Tensor RTに変換された学習済みモデルをつかって自動走行します。
```
import torch
import torchvision
CATEGORIES = ['apex']
device = torch.device('cuda')
model = torchvision.models.resnet18(pretrained=False)
model.fc = torch.nn.Linear(512, 2 * len(CATEGORIES))
model = model.cuda().eval().half()
```
Tensor RT形式のモデルを読み込む。
```
import torch
from torch2trt import TRTModule
model_trt = TRTModule()
model_trt.load_state_dict(torch.load('road_following_model_trt.pth'))
```
racecarクラスをインスタンス化する
```
from jetracer.nvidia_racecar import NvidiaRacecar
type = "TT02"
car = NvidiaRacecar(type)
```
カメラの起動のためにカメラを制御するnvargus-daemonの再起動。
```
!echo jetson | sudo -S systemctl restart nvargus-daemon
```
カメラクラスをインスタンス化する。
```
from jetcam.csi_camera import CSICamera
camera = CSICamera(width=224, height=224, capture_fps=40)
```
最後に、JetRacerを下に置き、下記セルを実行します。
* 車の左右にうまく回らない場合は、`STEERING_GAIN` を小さいくする
* ターンがうまくいかない場合は、`STEERING_GAIN`を大きくする
* 車が左に傾く場合は、`STEERING_BIAS`を値を-0.05ぐらいづつマイナスにする
* 車が右に傾く場合は、`STEERING_BIAS`を値を+0.05ぐらいづつプラスにする
|値|意味|
|:--|:--|
|st_gain|ハンドルの曲がる比率を調整(推論開始ボタンを押したタイミングで反映)|
|st_offset|ハンドルの初期位置を調整(推論開始ボタンを押したタイミングで反映)|
```
import ipywidgets.widgets as widgets
from IPython.display import display
from utils import preprocess
import numpy as np
import threading
import traitlets
import time
throttle_slider = widgets.FloatSlider(description='throttle', min=-1.0, max=1.0, step=0.01, value=0.0, orientation='vertical')
steering_gain = widgets.BoundedFloatText(description='st_gain',min=-1.0, max=1.0, step=0.01, value=-0.65)
steering_offset = widgets.BoundedFloatText(description='st_offset',min=-1.0, max=1.0, step=0.01, value=0)
check_button = widgets.Button(description='ハンドルのチェック')
run_button = widgets.Button(description='推論開始')
stop_button = widgets.Button(description='推論停止')
log_widget = widgets.Textarea(description='ログ')
result_widget = widgets.FloatText(description='推論から導いたXの値')
def live():
global running, count
log_widget.value = "live"
count = 0
while running:
count = count + 1
log_widget.value = str(count) + "回目の推論"
image = camera.read()
image = preprocess(image).half()
output = model_trt(image).detach().cpu().numpy().flatten()
x = float(output[0])
steering_value = x * car.steering_gain + car.steering_offset
result_widget.value = steering_value
car.steering = steering_value
def run(c):
global running, execute_thread, start_time
log_widget.value = "run"
running = True
execute_thread = threading.Thread(target=live)
execute_thread.start()
start_time = time.time()
def stop(c):
global running, execute_thread, start_time, count
end_time = time.time() - start_time
fps = count/int(end_time)
log_widget.value = "FPS: " + str(fps) + "(1秒あたりの推論実行回数)"
running = False
execute_thread.stop()
def check(c):
global running, execute_thread, start_time, count
end_time = time.time() - start_time
fps = count/int(end_time)
log_widget.value = "チェック用に推論を停止します。FPS: " + str(fps) + "(1秒あたりの推論実行回数)"
running = False
count = 0
log_widget.value = "car.steering:1"
car.steering = 1
time.sleep(1)
car.steering = -1
time.sleep(1)
car.steering = 0
run_button.on_click(run)
stop_button.on_click(stop)
check_button.on_click(check)
# create a horizontal box container to place the sliders next to eachother
run_widget = widgets.VBox([
widgets.HBox([throttle_slider, steering_gain,steering_offset,check_button]),
widgets.HBox([run_button, stop_button]),
result_widget,
log_widget
])
throttle_link = traitlets.link((throttle_slider, 'value'), (car, 'throttle'))
steering_gain_link = traitlets.link((steering_gain, 'value'), (car, 'steering_gain'))
steering_offset_link = traitlets.link((steering_offset, 'value'), (car, 'steering_offset'))
# display the container in this cell's output
display(run_widget)
```
| true |
code
| 0.593109 | null | null | null | null |
|
# Build Experiment from tf.layers model
Embeds a 3 layer FCN model to predict MNIST handwritten digits in a Tensorflow Experiment. The model is built using the __tf.layers__ API, and wrapped in a custom Estimator, which is then wrapped inside an Experiment.
```
from __future__ import division, print_function
from tensorflow.contrib.learn.python.learn.estimators import model_fn as model_fn_lib
import matplotlib.pyplot as plt
import numpy as np
import os
import shutil
import tensorflow as tf
DATA_DIR = "../../data"
TRAIN_FILE = os.path.join(DATA_DIR, "mnist_train.csv")
TEST_FILE = os.path.join(DATA_DIR, "mnist_test.csv")
MODEL_DIR = os.path.join(DATA_DIR, "expt-learn-model")
NUM_FEATURES = 784
NUM_CLASSES = 10
NUM_STEPS = 100
LEARNING_RATE = 1e-3
BATCH_SIZE = 128
tf.logging.set_verbosity(tf.logging.INFO)
```
## Prepare Data
```
def parse_file(filename):
xdata, ydata = [], []
fin = open(filename, "rb")
i = 0
for line in fin:
if i % 10000 == 0:
print("{:s}: {:d} lines read".format(
os.path.basename(filename), i))
cols = line.strip().split(",")
ydata.append(int(cols[0]))
xdata.append([float(x) / 255. for x in cols[1:]])
i += 1
fin.close()
print("{:s}: {:d} lines read".format(os.path.basename(filename), i))
y = np.array(ydata, dtype=np.float32)
X = np.array(xdata, dtype=np.float32)
return X, y
Xtrain, ytrain = parse_file(TRAIN_FILE)
Xtest, ytest = parse_file(TEST_FILE)
print(Xtrain.shape, ytrain.shape, Xtest.shape, ytest.shape)
```
The train_input_fn and test_input_fn below are equivalent to using the full batches. There is some information on [building batch oriented input functions](http://blog.mdda.net/ai/2017/02/25/estimator-input-fn), but I was unable to make it work. Commented out block is adapted from a Keras data generator, but that does not work either.
```
def train_input_fn():
return tf.constant(Xtrain), tf.constant(ytrain)
def test_input_fn():
return tf.constant(Xtest), tf.constant(ytest)
# def batch_input_fn(X, y, batch_size=BATCH_SIZE,
# num_epochs=NUM_STEPS):
# for e in range(num_epochs):
# num_recs = X.shape[0]
# sids = np.random.permutation(np.arange(num_recs))
# num_batches = num_recs // batch_size
# for bid in range(num_batches):
# sids_b = sids[bid * batch_size : (bid + 1) * batch_size]
# X_b = np.zeros((batch_size, NUM_FEATURES))
# y_b = np.zeros((batch_size,))
# for i in range(batch_size):
# X_b[i] = X[sids_b[i]]
# y_b[i] = y[sids_b[i]]
# yield tf.constant(X_b, dtype=tf.float32), \
# tf.constant(y_b, dtype=tf.float32)
# def train_input_fn():
# return batch_input_fn(Xtrain, ytrain, BATCH_SIZE).next()
# def test_input_fn():
# return batch_input_fn(Xtest, ytest, BATCH_SIZE).next()
```
## Define Model Function
Estimator expects a model_fn function that has all the information about the model, the loss function, etc.
```
def model_fn(features, labels, mode):
# define model
in_training = (mode == tf.contrib.learn.ModeKeys.TRAIN)
fc1 = tf.layers.dense(inputs=features, units=512,
activation=tf.nn.relu, name="fc1")
fc1_dropout = tf.layers.dropout(inputs=fc1, rate=0.2,
training=in_training,
name="fc1_dropout")
fc2 = tf.layers.dense(inputs=fc1_dropout, units=256,
activation=tf.nn.relu, name="fc2")
fc2_dropout = tf.layers.dropout(inputs=fc2, rate=0.2,
training=in_training,
name="fc2_dropout")
logits = tf.layers.dense(inputs=fc2_dropout, units=NUM_CLASSES,
name="logits")
# loss (for TRAIN and EVAL)
loss = None
if mode != tf.contrib.learn.ModeKeys.INFER:
onehot_labels = tf.one_hot(indices=tf.cast(labels, tf.int32),
depth=NUM_CLASSES)
loss = tf.losses.softmax_cross_entropy(
onehot_labels=onehot_labels, logits=logits)
# optimizer (TRAIN only)
train_op = None
if mode == tf.contrib.learn.ModeKeys.TRAIN:
train_op = tf.contrib.layers.optimize_loss(
loss=loss,
global_step=tf.contrib.framework.get_global_step(),
learning_rate=LEARNING_RATE,
optimizer="Adam")
# predictions
predictions = {
"classes" : tf.argmax(input=logits, axis=1),
"probabilities": tf.nn.softmax(logits, name="softmax_tensor")}
# additional metrics
accuracy = tf.metrics.accuracy(labels, predictions["classes"])
eval_metric_ops = { "accuracy": accuracy }
# logging variables to tensorboard
tf.summary.scalar("loss", loss)
tf.summary.scalar("accuracy", accuracy[0] / accuracy[1])
summary_op = tf.summary.merge_all()
tb_logger = tf.contrib.learn.monitors.SummarySaver(summary_op,
save_steps=10)
return model_fn_lib.ModelFnOps(mode=mode,
predictions=predictions,
loss=loss,
train_op=train_op,
eval_metric_ops=eval_metric_ops)
```
## Define Estimator
```
shutil.rmtree(MODEL_DIR, ignore_errors=True)
estimator = tf.contrib.learn.Estimator(model_fn=model_fn,
model_dir=MODEL_DIR,
config=tf.contrib.learn.RunConfig(save_checkpoints_secs=30000))
```
## Train Estimator
Using the parameters x, y and batch are deprecated and the warnings say to use the input_fn instead. However, using that results in very slow fit and evaluate. The solution is to use batch oriented input_fns. The commented portions will be opened up once I figure out how to make the batch oriented input_fns work.
```
estimator.fit(x=Xtrain, y=ytrain,
batch_size=BATCH_SIZE,
steps=NUM_STEPS)
# estimator.fit(input_fn=train_input_fn, steps=NUM_STEPS)
```
## Evaluate Estimator
```
results = estimator.evaluate(x=Xtest, y=ytest)
# results = estimator.evaluate(input_fn=test_input_fn)
print(results)
```
## alternatively...
## Define Experiment
A model is wrapped in an Estimator, which is then wrapped in an Experiment. Once you have an Experiment, you can run this in a distributed manner on CPU or GPU.
```
NUM_STEPS = 20
def experiment_fn(run_config, params):
feature_cols = [tf.contrib.layers.real_valued_column("",
dimension=NUM_FEATURES)]
estimator = tf.contrib.learn.Estimator(model_fn=model_fn,
model_dir=MODEL_DIR)
return tf.contrib.learn.Experiment(
estimator=estimator,
train_input_fn=train_input_fn,
train_steps=NUM_STEPS,
eval_input_fn=test_input_fn)
```
## Run Experiment
```
shutil.rmtree(MODEL_DIR, ignore_errors=True)
tf.contrib.learn.learn_runner.run(experiment_fn,
run_config=tf.contrib.learn.RunConfig(
model_dir=MODEL_DIR))
```
| true |
code
| 0.589953 | null | null | null | null |
|

created by Fernando Perez ( https://www.youtube.com/watch?v=g8xQRI3E8r8 )

# Prerequisites2 : Python Data Science Environment
# Learning Plan
### Lesson 2-1: IPython
In this lesson, you learn how to use IPython.
### Lesson 2-2: Jupyter
In this lesson, you learn how to use Jupyter.
### Lesson 2-3: Conda
In this lesson, you learn how to use Conda.
# Lesson 2-1: IPython
Interactive Python
- A powerful interactive shell.
- A kernel for [Jupyter](https://jupyter.org).
- Support for interactive data visualization and use of [GUI toolkits](http://ipython.org/ipython-doc/stable/interactive/reference.html#gui-event-loop-support).
- Flexible, [embeddable interpreters](http://ipython.org/ipython-doc/stable/interactive/reference.html#embedding-ipython)
- Easy to use, high performance tools for [parallel computing](https://ipyparallel.readthedocs.io/en/latest/).
## 2-1-1 : Magic commands
%로 유용한 기능들을 쓸 수 있다.
### 실행 시간 재기
```
%timeit [i**2 for i in range(1000)]
```
timeit은 주어진 라인을 여러번 실행하고 실행 시간을 잰다. 코드의 결과는 출력하지 않는다.
%%는 cell magics라고 불리며 셀 전체에 적용된다. 반드시 셀 첫줄에 써야 한다.
```
%%timeit
[i**2 for i in range(1000)]
```
- % : line magic
- %% : cell magic
### 히스토리
```
%history
```
### 셀의 내용을 파일에 쓰기.
%%writefile [filename]
```
%%writefile hello.py
def hello():
print('Hello world')
hello()
```
### 파일 실행하기
```
%run hello.py
```
### 다시 로드하기
파이썬은 한번 로드된 모듈은 import 문을 실행해도 다시 로드하지 않는다.
하지만 자신이 만든 모듈을 계속 수정하고 불러와야 할 때 이 점은 매우 불편할 수 있다.
이 작동 방식을 바꾸는 방법을 magic command가 제공한다. built-in은 아니고 extension으로 존재한다.
```
from hello import hello
hello()
%%writefile hello.py
def hello():
print('Bye world')
hello()
from hello import hello
hello()
%load_ext autoreload
%autoreload 2
from hello import hello
hello()
```
%autoreload : Reload all modules (except those excluded by %aimport) automatically now.
%autoreload 0 : Disable automatic reloading.
%autoreload 1 : Reload all modules imported with %aimport every time before executing the Python code typed.
%autoreload 2 : Reload all modules (except those excluded by %aimport) every time before executing the Python code typed.
ref : https://ipython.org/ipython-doc/3/config/extensions/autoreload.html
경험 상
%autoreload 2가 가장 편리하다.
### 노트북 상에서 그래프 표시하기
Python에서 가장 전통적인 그래프 그리는 라이브러리는 matplotlib이다.
matplotlib은 직접적으로 노트북 위에서 그래프를 보여주는 기능을 제공하지는 않는다.
따라서 그냥 matplotlib을 쓰면 노트북 상에서는 아무것도 보이지 않는다.
하지만 magic command로 이를 가능케 할 수 있다.
```
%matplotlib inline
from matplotlib import pyplot as plt
plt.plot([1,2,3,4,5,6,7,8,9,10], [4,6,3,6,12,3,8,4,2,9])
```
### 모든 magic commands 보기
```
%magic
```
## 2-1-2 : Shell Commands
Command Line Interface(CLI)를 Python 안에서 쓸 수 있다
```
!pip --version
!date
```
자주 쓰이는 명령어는 느낌표(!) 없이도 사용 가능하다.
(사실은 magic command에 해당한다)
```
cd ..
pwd
ls
```
## 2-1-3 : Help & Tab completion
```
ran
range()
open('02_')
from random import
from random import randint
range?
```
### 구현 코드를 직접 확인하기
```
randint??
```
## 2-1-4 : 이전 명령어 & 결과 보기
### 직전 결과
```
79 * 94
_
```
### 전전 결과
```
92 * 21
13 * 93
__
```
### 이전 명령어 & 결과
```
In[30]
Out[30]
```
## 2-1-5 : pdb
Python Debugger
```
def buggy_function(numbers):
length = len(numbers)
for k, i in enumerate(range(length)):
print(k, numbers[i+1] - numbers[i])
buggy_function([1,4,9,20,30])
%debug
```
**PDB 명령어 실행내용 **
- help 도움말
- next 다음 문장으로 이동
- print 변수값 화면에 표시
- list 소스코드 리스트 출력. 현재 위치 화살표로 표시됨
- where 콜스택 출력
- continue 계속 실행. 다음 중단점에 멈추거나 중단점 없으면 끝까지 실행
- step Step Into 하여 함수 내부로 들어감
- return 현재 함수의 리턴 직전까지 실행
- !변수명 = 값 변수에 값 재설정
- up : 한 프레임 위로
- down : 한 프레임 아래로
- quit : pdb 종료
### 예제
```
buggy_function([1,3,4,5])
def exception_function(numbers):
length = len(numbers)
assert False
for i in range(length):
print(numbers[i+1] - numbers[i])
```
### pdb 자동 실행
```
%pdb on
%pdb off
%pdb
```
# Lesson 2-2: Jupyter Notebook
## Why
그래프 하나, 숫자 하나로는 사람들을 설득하기 쉽지 않다.

https://www.buzzfeed.com/jsvine/the-ferguson-area-is-even-more-segregated-than-you-thought?utm_term=.la9LbenExx#.yh7QWLg2rr
### Literate computing
computational reproducibility
http://blog.fperez.org/2013/04/literate-computing-and-computational.html
### Interesting Jupyter Notebooks
https://github.com/jupyter/jupyter/wiki/A-gallery-of-interesting-Jupyter-Notebooks
## Terminology
### Notebook Document or "notebook"
Notebook documents (or “notebooks”, all lower case) are documents produced by the Jupyter Notebook App, which contain both computer code (e.g. python) and rich text elements (paragraph, equations, figures, links, etc...). Notebook documents are both human-readable documents containing the analysis description and the results (figures, tables, etc..) as well as executable documents which can be run to perform data analysis.
References: Notebook documents [in the project homepage](http://ipython.org/notebook.html#notebook-documents) and [in the official docs](http://jupyter-notebook.readthedocs.io/en/latest/notebook.html#notebook-documents).
### Jupyter Notebook App
#### Server-client application for notebooks
The Jupyter Notebook App is a server-client application that allows editing and running notebook documents via a web browser. The Jupyter Notebook App can be executed on a local desktop requiring no internet access (as described in this document) or can be installed on a remote server and accessed through the internet.
In addition to displaying/editing/running notebook documents, the Jupyter Notebook App has a “Dashboard” (Notebook Dashboard), a “control panel” showing local files and allowing to open notebook documents or shutting down their kernels.
### Kernel
** Computational engine for notebooks**
The Jupyter Notebook App is a server-client application that allows editing and running notebook documents via a web browser. The Jupyter Notebook App can be executed on a local desktop requiring no internet access (as described in this document) or can be installed on a remote server and accessed through the internet.
In addition to displaying/editing/running notebook documents, the Jupyter Notebook App has a “Dashboard” (Notebook Dashboard), a “control panel” showing local files and allowing to open notebook documents or shutting down their kernels.
### Notebook Dashboard
**Manager of notebooks**
The Notebook Dashboard is the component which is shown first when you launch Jupyter Notebook App. The Notebook Dashboard is mainly used to open notebook documents, and to manage the running kernels (visualize and shutdown).
The Notebook Dashboard has other features similar to a file manager, namely navigating folders and renaming/deleting files.
## Why the name
#### IPython Notebook -> Jupyter Notebook
- 2001 : IPython
- NumPy, SciPy, Matplotlib, pandas, etc.
- Around 2010 : IPython Notebook
- 2014 : Jupyter
### Language agnostic : 언어에 상관 없는
IPython은 Jupyter의 커널 중 하나일 뿐.

https://www.oreilly.com/ideas/the-state-of-jupyter
## Display
```
from IPython.display import YouTubeVideo
YouTubeVideo('xuNj5paMuow')
from IPython.display import Image
Image(url='https://d1jnx9ba8s6j9r.cloudfront.net/blog/wp-content/uploads/2017/05/Deep-Neural-Network-What-is-Deep-Learning-Edureka.png')
from IPython.display import Audio, IFrame, HTML
```
## Markdown
https://gist.github.com/ihoneymon/652be052a0727ad59601
## HTML
<table>
<tr>
<th>Month</th>
<th>Savings</th>
</tr>
<tr>
<td>January</td>
<td>100</td>
</tr>
<tr>
<td>February</td>
<td>80</td>
</tr>
<tr>
<td colspan="2">Sum: 180</td>
</tr>
</table>
## Latex
Inline
sigmoid : $ f(t) = \frac{1}{1+e^{−t}} $
Block
$$ f(t) = \frac{1}{1+e^{−t}} $$
## kernel control
- kernel interrupt : i i
- kernel restart : 0 0
## Widget
`conda install -y -c conda-forge ipywidgets`
```
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
```
### interact
인터렉티브!
```
def f(x):
return x
interact(f, x=10);
interact(f, x=True);
interact(f, x='Hi there!');
```
### interact as a decorator
```
@interact(x=True, y=1.0)
def g(x, y):
return (x, y)
```
### fixed
인자 고정시키기
```
def h(p, q):
return (p, q)
interact(h, p=5, q=fixed(20));
```
### 더 자유롭게 컨트롤하기
```
interact(f, x=widgets.IntSlider(min=-10,max=30,step=1,value=10));
```
### interactive
바로 보여주는 대신 객체로 리턴하기
```
from IPython.display import display
def f(a, b):
display(a + b)
return a+b
w = interactive(f, a=10, b=20)
type(w)
w.children
display(w);
w.kwargs
w.result
```
### 두 위젯 간에 상호작용하기
```
x_widget = widgets.FloatSlider(min=0.0, max=10.0, step=0.05)
y_widget = widgets.FloatSlider(min=0.5, max=10.0, step=0.05, value=5.0)
def update_x_range(*args):
x_widget.max = 2.0 * y_widget.value
y_widget.observe(update_x_range, 'value')
def printer(x, y):
print(x, y)
interact(printer,x=x_widget, y=y_widget);
```
### 작동 방식

### Multiple widgets
```
from IPython.display import display
w = widgets.IntSlider()
display(w)
display(w)
w.value
w.value = 100
```
# Lesson 2-3: Conda
패키지, 디펜던시, 가상 환경 관리의 끝판왕 - Python부터 R, Ruby, Lua, Scala, Java, JavaScript, C/ C++, FORTRAN 등등
## pip vs. conda
- pip : 파이썬 패키지 관리자. 파이썬만 관리한다.
- 파이썬 너머에 의존성이 있는 경우는 관리하지 못함
- conda : 패키지 관리자이자 가상 환경 관리자
- 언어 상관 없이 모두 관리한다. 파이썬도 패키지 중 하나일 뿐.
- 패키지 관리 뿐 아니라 가상 환경 생성 및 관리도 가능하다.
- 파이썬으로 쓰여짐
## 가상 환경 관리
### 새 가상 환경 만들기
`conda create --name tensorflow`
파이썬만 있는 깨끗한 환경을 원할 때
`conda create --name tensorflow python`
파이썬 버전을 지정하고 싶을 때
`conda create --name tensorflow python=2.7`
### 가상 환경 안으로 들어가기
`source activate tensorflow`
### Jupyter에 새 kernel 등록하기
`pip install ipykernel`
`python -m ipykernel install --user --name tensorflow --display-name "Python (TensorFlow)"`
### 가상 환경 빠져나오기
`source deactivate`
### 가상 환경 목록 보기
`conda env list`
### 설치된 패키지 목록 보기
`conda list`
## Miniconda
- Anaconda : 수학, 과학 패키지가 모두 함꼐 들어 있다.
- Miniconda : 파이썬과 최소한의 패키지만 들어있다. 필요한 패키지만 conda로 직접 설치할 수 있다.
https://conda.io/miniconda.html
| true |
code
| 0.212559 | null | null | null | null |
|
# Alternative Models
In order to ensure the model used to make predictions for the analysis, I also tried training & testing various other models that were good candidates (based on the characteristics of our data).
Specifically, we also tested the following regression models:
1. Linear (Lasso Regularization)
2. Linear (Ridge Regularization)
3. SGD
4. Decision Tree
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
from sklearn.linear_model import SGDRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score, mean_squared_error
import seaborn as sns
%matplotlib inline
# Import & preview input variables
X = pd.read_csv('./output/model_X.csv')
X.head()
# Input & preview output variables
y = pd.read_csv('./output/model_y.csv', header=None, squeeze=True)
y.head()
# Split data into training & testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
```
## Linear (Lasso Regularization)
We're going to first try the simplest of the list by adding _Lasso regularization_ to the Linear Regression. The hope is that with the corrective properties (by penalizing complexity), we will be able to get substantially higher training & testing scores.
We're going to test the Lasso model with various alpha values to spot the config with optimal scores.
```
# Function to run Lasso model
def runLasso(alpha=1.0):
"""
Compute the training & testing scores of the Linear Regression (with Lasso regularization)
along with the SUM of coefficients used.
Input:
alpha: the degree of penalization for model complexity
Output:
alpha: the degree of penalization for model complexity
train_scoreL: Training score
test_scoreL: Testing score
coeff_used: SUM of all coefficients used in model
"""
# Instantiate & train
lasso_reg = Lasso(alpha=alpha)
lasso_reg.fit(X_train, y_train)
# Predict testing data
pred_train = lasso_reg.predict(X_train)
pred_test = lasso_reg.predict(X_test)
# Score
train_scoreL = lasso_reg.score(X_train,y_train)
test_scoreL = lasso_reg.score(X_test,y_test)
coeff_used = np.sum(lasso_reg.coef_!=0)
print("Lasso Score (" + str(alpha) + "):")
print(train_scoreL)
print(test_scoreL)
print(' ')
print("Coefficients Used:")
print(coeff_used)
print('-------')
return (alpha, train_scoreL, test_scoreL, coeff_used)
runLasso()
# Test the Lasso regularization for a range of alpha variables
alpha_lasso = [1e-15, 1e-10, 1e-8, 1e-4, 1e-3,1e-2, 1, 5, 10, 20]
for i in range(10):
runLasso(alpha_lasso[i])
```
### Linear Regression (Lasso) Conclusion
The Lasso linear model does not seem to surpass the simple Linear Regression model trained (see "Airbnb NYC Data Exploration" notebook for details), which had scored 25.6% (training) and 20.2% (testing).
**Therefore, we will discount this as a superior modelling assumption**
## Linear (Ridge Regularization)
Similarly, we're going to test a Linear Regression with _Ridge regularization_. Since the dataset is non-sparse, the hypothesis is that we should get more from the L2 regularization's corrective properties for complexity (more than Lasso's L1 reg.)
We're going to test the Ridge model with various alpha values to spot the config with optimal scores.
```
# Function to run Ridge model
def runRidge(alpha=1.0):
"""
Compute the training & testing scores of the Linear Regression (with Ridge regularization)
along with the SUM of coefficients used.
Input:
alpha: the degree of penalization for model complexity
Output:
alpha: the degree of penalization for model complexity
train_scoreL: Training score
test_scoreL: Testing score
coeff_used: SUM of all coefficients used in model
"""
# Instantiate & train
rid_reg = Ridge(alpha=alpha, normalize=True)
rid_reg.fit(X_train, y_train)
# Predict testing data
pred_train = rid_reg.predict(X_train)
pred_test = rid_reg.predict(X_test)
# Score
train_score = rid_reg.score(X_train,y_train)
test_score = rid_reg.score(X_test,y_test)
coeff_used = np.sum(rid_reg.coef_!=0)
print("Ridge Score (" + str(alpha) + "):")
print(train_score)
print(test_score)
print('-------')
print("Coefficients Used:")
print(coeff_used)
return (alpha, train_score, test_score, coeff_used)
runRidge()
alpha_ridge = [1e-15, 1e-10, 1e-8, 1e-4, 1e-3,1e-2, 1, 5, 10, 20]
for i in range(10):
runRidge(alpha_ridge[i])
```
### Linear Regression (Ridge) Conclusion
The Ridge linear model also does not seem to surpass the simple Linear Regression model (see "Airbnb NYC Data Exploration" notebook for details), which had scored 25.6% (training) and 20.2% (testing).
**Therefore, we will discount Ridge regularization as a superior modelling assumption**
## Stochastic Gradient Descent (SGD) Regression
The SGD regression is different from the former two (Lasso, Ridge) that were based on a Linear Regression model. Since SGD basically applies the squared trick at every point in our data at same time (vs Batch, which looks at points one-by-one), I don't expect scores to differ too much when compared to the previous 2.
```
# Function to run SGD model
def runSGD():
"""
Compute the training & testing scores of the SGD
along with the SUM of coefficients used.
Output:
train_score: Training score
test_score: Testing score
coeff_used: SUM of all coefficients used in model
"""
# Instantiate & train
sgd_reg = SGDRegressor(loss="squared_loss", penalty=None)
sgd_reg.fit(X_train, y_train)
# Predict testing data
pred_train = sgd_reg.predict(X_train)
pred_test = sgd_reg.predict(X_test)
# Score
train_score = sgd_reg.score(X_train,y_train)
test_score = sgd_reg.score(X_test,y_test)
coeff_used = np.sum(sgd_reg.coef_!=0)
print("SGD Score:")
print(train_score)
print(test_score)
print('-------')
print("Coefficients Used:")
print(coeff_used)
return (train_score, test_score, coeff_used)
runSGD()
```
### Stochastic Gradient Descent (SGD) Conclusion
The SGD model also does not seem to surpass the simple Linear Regression model (see "Airbnb NYC Data Exploration" notebook for details), which had scored 25.6% (training) and 20.2% (testing). In fact, the output training & testing scores are negative, indicative of terrible fit to the data.
**Therefore, we will discount SGD as a superior modelling assumption**
## Decision Trees
Unlike the former models, Decision Trees have a very different model structure. That is, it generates a series of nodes & branches that maximize informtion gain. Thus, it naturally is also the model most prone to overfitting
To remedy the overfitting challenge, we'll run the Decision Trees model with the below parameters:
- max_depth
- min_samples_leaf
- min_samples_split
To isolate the effect of these parameters on scores, we'll change one at a time (i.e. keeping other parameters constant)
```
# Function to run Decision Trees
def runTree(max_depth=None, min_samples_leaf=1, min_samples_split=2):
"""
Compute the training & testing scores of the Linear Regression (with Lasso regularization)
along with the SUM of coefficients used.
Input:
max_depth: maximum allowed depth of trees ("distance" between root & leaf)
min_samples_leaf: minimum samples to contain per leaf
min_samples_split: minimum samples to split a node
Output:
max_depth: maximum allowed depth of trees ("distance" between root & leaf)
min_samples_leaf: minimum samples to contain per leaf
min_samples_split: minimum samples to split a node
train_score: Training score
test_score: Testing score
"""
# Instantiate & train
tree_reg = DecisionTreeRegressor(criterion='mse', max_depth=max_depth, min_samples_leaf=min_samples_leaf, min_samples_split=min_samples_split)
tree_reg.fit(X_train, y_train)
# Predict testing data
pred_train = tree_reg.predict(X_train)
pred_test = tree_reg.predict(X_test)
# Score
train_score = tree_reg.score(X_train,y_train)
test_score = tree_reg.score(X_test,y_test)
print("Tree Score (" + str(max_depth) + ', ' + str(min_samples_leaf) + ', ' + str(min_samples_split) + "):")
print(train_score)
print(test_score)
print('-------')
runTree()
depths = [2, 5, 6, 7, 8]
for dep in depths:
runTree(dep)
min_leafs = [2, 4, 6, 8, 10, 12, 14, 16]
for lfs in min_leafs:
runTree(7, lfs)
min_splits = [2, 4, 6, 8, 10]
for splt in min_splits:
runTree(7, 14, splt)
for dep in depths:
for lfs in min_leafs:
runTree(dep, lfs)
```
### Decision Tree Conclusion
Unlike the rest, the Decision Tree model does seem to surpass the simple Linear Regression model (see "Airbnb NYC Data Exploration" notebook for details), which had scored 25.6% (training) and 20.2% (testing).
Based on the tests, seems there is a maximum point where testing error is minimized. Also notable is the fact that the training & testing score seem to be inversely correlated.
```
tree_reg = DecisionTreeRegressor(criterion='mse', max_depth=8, min_samples_leaf=16, min_samples_split=2)
tree_reg.fit(X_train, y_train)
# Predict testing data
pred_train = tree_reg.predict(X_train)
pred_test = tree_reg.predict(X_test)
# Import prediction input
df_nei_Manhattan_EV = pd.read_csv('./data/input/pred_input_Manhattan_EV.csv')
df_nei_Manhattan_HA = pd.read_csv('./data/input/pred_input_Manhattan_HA.csv')
df_nei_Manhattan_HK = pd.read_csv('./data/input/pred_input_Manhattan_HK.csv')
df_nei_Manhattan_UWS = pd.read_csv('./data/input/pred_input_Manhattan_UWS.csv')
df_nei_Brooklyn_BS = pd.read_csv('./data/input/pred_input_Brooklyn_BS.csv')
df_nei_Brooklyn_BU = pd.read_csv('./data/input/pred_input_Brooklyn_BU.csv')
df_nei_Brooklyn_WI = pd.read_csv('./data/input/pred_input_Brooklyn_WI.csv')
df_nei_Queens_AS = pd.read_csv('./data/input/pred_input_Queens_AS.csv')
df_nei_Queens_LI = pd.read_csv('./data/input/pred_input_Queens_LI.csv')
avgRev_Manhattan_EV = round(tree_reg.predict(df_nei_Manhattan_EV)[0],2)
avgRev_Manhattan_HA = round(tree_reg.predict(df_nei_Manhattan_HA)[0],2)
avgRev_Manhattan_HK = round(tree_reg.predict(df_nei_Manhattan_HK)[0],2)
avgRev_Manhattan_UWS = round(tree_reg.predict(df_nei_Manhattan_UWS)[0],2)
avgRev_Brooklyn_BS = round(tree_reg.predict(df_nei_Brooklyn_BS)[0],2)
avgRev_Brooklyn_BU = round(tree_reg.predict(df_nei_Brooklyn_BU)[0],2)
avgRev_Brooklyn_WI = round(tree_reg.predict(df_nei_Brooklyn_WI)[0],2)
avgRev_Queens_AS = round(tree_reg.predict(df_nei_Queens_AS)[0],2)
avgRev_Queens_LI = round(tree_reg.predict(df_nei_Queens_LI)[0],2)
print("--------Manhattan---------")
print(avgRev_Manhattan_EV)
print(avgRev_Manhattan_HA)
print(avgRev_Manhattan_HK)
print(avgRev_Manhattan_UWS)
print("")
print("--------Brooklyn---------")
print(avgRev_Brooklyn_BS)
print(avgRev_Brooklyn_BU)
print(avgRev_Brooklyn_WI)
print("")
print("--------Queens---------")
print(avgRev_Queens_AS)
print(avgRev_Queens_LI)
# Import prediction input
df_nei_1_1 = pd.read_csv('./data/input/pred_input_Manhattan_EV.csv')
df_nei_2_2 = pd.read_csv('./data/input/pred_input_Manhattan_EV_2bed_2_bath.csv')
df_nei_2_1 = pd.read_csv('./data/input/pred_input_Manhattan_EV_2bed_1_bath.csv')
avgRev_1_1 = tree_reg.predict(df_nei_1_1)[0]
avgRev_2_2 = tree_reg.predict(df_nei_2_2)[0]
avgRev_2_1 = tree_reg.predict(df_nei_2_1)[0]
print(round(avgRev_1_1,2))
print(round(avgRev_2_2,2))
print(round(avgRev_2_1,2))
```
# Conclusion
Based on these parameters, seems like the best scoring model (Decision Trees) was a bit too generalized, making the same prediction for variations (e.g. 1 bedroom vs 2 bedroom).
| true |
code
| 0.643497 | null | null | null | null |
|
## Setup
```
%matplotlib qt
from tensorflow.keras.datasets import mnist
import matplotlib.pyplot as plt
import numpy as np
from pathlib import Path
import os
Path('mnist_distribution').mkdir(exist_ok=True)
os.chdir('mnist_distribution')
#load MNIST and concatenates train and test data
(x_train, _), (x_test, _) = mnist.load_data()
data = np.concatenate((x_train, x_test))
```
## 1 Mean pixel value
```
mean = np.mean(data, axis=0)
var = np.sqrt(np.var(data, axis=0))
fig, axs = plt.subplots(1, 2)
ax = axs[0]
ax.imshow(mean, cmap='gray', vmin=0, vmax=255, interpolation='nearest')
ax.axis(False)
ax.set_title('Mean')
ax = axs[1]
pcm = ax.imshow(var, cmap='gray', vmin=0, vmax=255, interpolation='nearest')
ax.axis(False)
ax.set_title('Variance')
plt.colorbar(pcm, ax=axs, shrink=0.5)
fig.savefig('mnist_mean_var.pdf', bbox_inches='tight', pad_inches=0)
```
## 2 Pixel value probability distribution
### 2.1 Plot single pixel distribution
```
px = 14
py = 14
pixels = data[:, px, py]
values = np.arange(256)
probs = np.zeros(256)
unique, count = np.unique(pixels, return_counts=True)
for px_value, n_ocurrences in zip(unique, count):
probs[px_value] = 100 * n_ocurrences / data.shape[0]
fig = plt.figure()
plt.plot(values, probs, linewidth=1)
plt.xlabel('Pixel Value')
plt.ylabel('Probability (%)')
plt.grid()
fig.savefig('mnist_dist_pixel_%dx%d.pdf' % (px, py), bbox_inches='tight')
```
### 2.1 Plotting only column distribution
```
def get_column_distribution(data, column_index):
columns = data[:, :, column_index]
total = columns.shape[0]
n_lines = columns.shape[1]
x = np.arange(n_lines)
y = np.arange(256)
z = np.zeros((256, n_lines))
#Iterates through each pixel calculating it's probability distribution
for i in range(n_lines):
unique, count = np.unique(columns[:, i], return_counts=True)
for px_value, n_ocurrences in zip(unique, count):
z[px_value][i] = n_ocurrences / total
return x, y, z
def plot_column_distribution(x, y, z):
n_lines = x.shape[0]
X, Y = np.meshgrid(x, y)
Z = 100 * z
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.view_init(10, 35)
ax.contour3D(X, Y, Z, n_lines, cmap='viridis', zdir = 'x')
ax.set_xlabel('Line')
ax.set_ylabel('Pixel Value')
ax.set_zlabel('Probability (%)')
ax.set_zlim((0, 100))
return fig
for column_index in [0, 12, 15]:
x, y, z = get_column_distribution(data, column_index)
fig = plot_column_distribution(x, y, z)
fig.savefig('mnist_dist_column_%d.pdf' % column_index, bbox_inches='tight', pad_inches=0)
```
### 2.2 Plotting distribution with image reference
```
def high_light_mnist_column(image, column_index):
alpha = np.full_like(image, 50)[..., np.newaxis]
alpha[:, column_index, :] = 255
image = np.repeat(image[:, :, np.newaxis], 3, axis=2)
return np.append(image, alpha, axis=2)
def plot_column_distribution_and_highlight(x, y, z, highlight):
n_lines = x.shape[0]
X, Y = np.meshgrid(x, y)
Z = 100 * z
fig = plt.figure(figsize=(10, 10))
fig.tight_layout()
plt.subplot(323)
plt.imshow(highlight, cmap='gray', vmin=0, vmax=255, interpolation='nearest')
plt.axis('off')
ax = plt.subplot(122, projection='3d')
ax.view_init(10, 35)
ax.contour3D(X, Y, Z, n_lines, cmap='viridis', zdir = 'x')
ax.set_xlabel('Line')
ax.set_ylabel('Pixel Value')
ax.set_zlabel('Probability (%)')
ax.set_zlim((0, 100))
return fig
plt.ioff()
image = data[0]
for column_index in range(28):
x, y, z = get_column_distribution(data, column_index)
highlight = high_light_mnist_column(image, column_index)
fig = plot_column_distribution_and_highlight(x, y, z, highlight)
# Save as pdf to get the nicest quality
fig.savefig('mnist_highlight_dist_column_%d.pdf' % column_index, bbox_inches='tight', pad_inches=0)
# Save as png to convert images to video or gif
fig.savefig('mnist_highlight_dist_column_%d.png' % column_index, bbox_inches='tight', pad_inches=0, dpi=196)
plt.close(fig)
```
## 3 Sampling from pixel distributions
```
def get_cumulative_distribution(data):
total, n_lines, n_columns = data.shape
dist = np.zeros((n_lines, n_columns, 256))
#Iterates through each pixel calculating it's cumulative probability distribution
for i in range(n_lines):
for j in range(n_columns):
values = dist[i, j, :]
unique, count = np.unique(data[:, i, j], return_counts=True)
for px_value, n_ocurrences in zip(unique, count):
values[px_value] = n_ocurrences
for px_value in range(1, 256):
values[px_value] += values[px_value - 1]
values /= total
return dist
def sample_dist(dist):
p = np.random.uniform()
return np.searchsorted(dist, p)
dist = get_cumulative_distribution(data)
SEED = 279923 # https://youtu.be/nWSFlqBOgl8?t=86 - I love this song
np.random.seed(SEED)
images = np.zeros((3, 28, 28))
for img in images:
for i in range(28):
for j in range(28):
img[i, j] = sample_dist(dist[i,j])
fig = plt.figure()
for i, img in enumerate(images):
plt.subplot(1, 3, i + 1)
plt.imshow(img, cmap='gray', vmin=0, vmax=255, interpolation='nearest')
plt.axis(False)
fig.savefig('mnist_simple_samples.pdf', bbox_inches='tight', pad_inches=0)
```
| true |
code
| 0.732196 | null | null | null | null |
|
# EOS 1 image analysis Python code walk-through
- This is to explain how the image analysis works for the EOS 1. Python version 2.7.15 (Anaconda 64-bit)
- If you are using EOS 1, you can use this code for image analysis after reading through this notebook and understand how it works.
- Alternatively, you can also use the ImgAna_minimum.py script.
- Needless to say, this Python code is not optimized for speed.
- Feel free to share and modify.
## - 00 - import libraries: matplolib for handling images; numpy for matrix manipulation
```
import matplotlib.pyplot as pp
import numpy as np
import warnings
```
## - 01 - function for displaying images and making figures
```
# Input: x_img=numpy_array_of_image, marker=marker_of_1D_plot, x_max=max_value
def fig_out( x_img, fig_dpi=120, marker="k.-", x_max=510 ):
pp.figure( dpi=fig_dpi )
pp.style.use( "seaborn-dark" )
if x_img.ndim == 1:
pp.style.use( "seaborn-darkgrid" )
pp.plot( x_img, marker )
elif x_img.ndim == 2:
if len( x_img[0] ) == 3:
pp.style.use( "seaborn-darkgrid" )
pp.plot( x_img[:,0], 'r-' )
pp.plot( x_img[:,1], 'g-' )
pp.plot( x_img[:,2], 'b-' )
else:
pp.imshow( x_img, cmap="gray", vmin=0, vmax=x_max )
pp.colorbar()
elif x_img.ndim == 3:
x_img = x_img.astype( int )
pp.imshow( x_img )
else:
print "Input not recognized."
## Not raise an error because no other functions not depend on output of this function.
```
In Python, an image is represented by a 3D-numpy array.
For example, a simple image of:
red, green, blue, black
cyan, purple, yellow, white
can be written as the following:
```
x = np.array([[[255,0,0], [0,255,0], [0,0,255], [0,0,0]],
[[0,255,255], [255,0,255], [255,255,0], [255,255,255]]])
fig_out( x, fig_dpi=100 )
# example of an image from EOS 1
img_file = "EOS_imgs/example_spec.jpg"
xi = pp.imread( img_file )
fig_out( xi )
```
## - 02 - function for read in image and then calculating the color_diff_sum heat map
```
# Input: x_img=input_image_as_numpy_array, fo=full_output
def cal_heatmap( x_img, fo=False ):
xf = x_img.astype( float )
if xf.ndim == 2:
cds = abs(xf[:,0]-xf[:,1])
cds += abs(xf[:,0]-xf[:,2])
cds += abs(xf[:,1]-xf[:,2])
elif xf.ndim == 3:
cds = abs(xf[:,:,0]-xf[:,:,1])
cds += abs(xf[:,:,0]-xf[:,:,2])
cds += abs(xf[:,:,1]-xf[:,:,2])
else:
raise ValueError( "Image array not recoginzed." )
if fo == True:
fig_out( cds )
else:
pass
return cds
```
This color_diff_sum metric is used to rank the colorfulness of the pixels.
It highlights bright colors while suppresses white and black, as demonstrated below:
```
cal_heatmap( x )
# try out the heat map function on the example image
hm = cal_heatmap( xi, True )
```
## - 03 - function for finding the reference spectrum
```
# Input: x_hm=heat_map_as_numpy_array, fo=full_output, n=threshold_as_ratio_of_peak
# Input: pf_check=profile_check, rt_check=rotation_check
def find_ref( x_hm, fo=False, n=0.25, pf_check=True, rt_check=False ):
n = float( n )
if n<0.1 or n>0.9:
n = 0.25 # n should be between 0.1 and 0.9, otherwise set to 0.25
else:
pass
h, w = x_hm.shape
if h<w and pf_check==True:
warnings.warn( "Input spectra image appears to be landscape." )
proceed = raw_input( "Continue? (y/N): " )
if proceed=='y' or proceed=='Y':
pass
else:
raise RuntimeError( "Program terminated by user." )
else:
pass
x0 = x_hm.mean( axis=0 )
x0thres = np.argwhere( x0 > x0.max()*n ).flatten()
x0diff = x0thres[1:] - x0thres[:-1]
x0gap = np.where( x0diff > 2. )[0].flatten()
if len( x0gap )==0:
if rt_check==True:
fig_out( x_hm )
rotate = raw_input( "Rotate image? (y/N): " )
if rotate=='y' or rotate=='Y':
raise RuntimeError( "Rotate image then restart program." )
else:
pass
else:
pass
l_edge, r_edge = x0thres[0], x0thres[-1]
else:
d_to_center = []
for i in x0gap:
d_to_center.append( abs( w/2. - x0thres[i:i+2].mean() ) )
d_min = np.argmin( d_to_center )
if d_min==0:
l_edge, r_edge = x0thres[0], x0thres[ x0gap[0] ]
else:
l_edge, r_edge = x0thres[ x0gap[d_min-1]+1 ], x0thres[ x0gap[d_min] ]
x_hm_ref = x_hm[ :, l_edge:r_edge+1 ]
x1 = x_hm_ref.mean( axis=1 )
x1thres = np.argwhere( x1 > x1.max()*n ).flatten()
t_edge, b_edge = x1thres[0], x1thres[-1]
tblr_edge = ( t_edge, b_edge, l_edge, r_edge )
if fo==True:
fig_out( x0, fig_dpi=120 )
fig_out( x1, fig_dpi=120 )
else:
pass
return tblr_edge
# try out the reference spectrum function
top, btm, lft, rgt = find_ref( hm, True )
# check the reference spectrum found
fig_out( xi[top:btm+1, lft:rgt+1, :] )
```
## - 04 - function for checking the alignment (omitted)
```
def align_check():
return 0
```
## - 05 - function for normalizing the sample spectrum
```
# Input: x_img=input_image_as_numpy_array, fo=full_output
# Input: bpeak_chl=channel_used_to_find_blue_peak
# Input: trim_edge=trim_edge_of_image, trim_margin=trim_margin_of_spectra
# Input: gapcal=method_for_calculating_gap_between_reference_and_sample
def norm_sam( x_img, fo=False, bpeak_chl='r', trim_edge=False, trim_margin=True, gapcal='p' ):
h, w, d = x_img.shape
if trim_edge == True:
x_img = x_img[h/4:h*3/4, w/4:w*3/4, :]
else:
pass
x_img = x_img.astype( float )
hm = cal_heatmap( x_img )
t_edge, b_edge, l_edge, r_edge = find_ref( hm )
ref_wid = r_edge - l_edge
if trim_margin == True:
mrg = int( ref_wid/10. )
else:
mrg = 0
half_hgt = int( (b_edge - t_edge)/2. )
x_ref = x_img[ t_edge:b_edge, l_edge+mrg:r_edge-mrg, : ]
y_ref = x_ref.mean( axis=1 )
if bpeak_chl == 'r':
peak_r = y_ref[:half_hgt,0].argmax()
peak_b = y_ref[half_hgt:,0].argmax()+half_hgt
else:
peak_rgb = y_ref.argmax( axis=0 )
peak_r, peak_b = peak_rgb[[0,2]]
if gapcal == 'w':
gap = int( ref_wid*0.901 )
else:
gap = int( ( peak_b-peak_r )*0.368 )
x_sam = x_img[ t_edge:b_edge, r_edge+gap+mrg:r_edge+gap+ref_wid-mrg, : ]
y_sam = x_sam.mean( axis=1 )
max_rgb = y_ref.max( axis=0 )
peak_px = np.array([peak_r, peak_b]).flatten()
peak_nm = np.array([610.65, 449.1])
f = np.polyfit( peak_px, peak_nm, 1 )
wavelength = np.arange(b_edge-t_edge)*f[0]+f[1]
if trim_edge == True:
t_edge, b_edge = t_edge+h/4, b_edge+h/4
l_edge, r_edge = l_edge+w/4, r_edge+w/4
peak_r, peak_b = peak_r+t_edge, peak_b+t_edge
else:
pass
y_sam_norm_r = y_sam[:, 0]/max_rgb[0]
y_sam_norm_g = y_sam[:, 1]/max_rgb[1]
y_sam_norm_b = y_sam[:, 2]/max_rgb[2]
y_sam_norm = np.dstack((y_sam_norm_r, y_sam_norm_g, y_sam_norm_b))[0]
if fo == True:
return ((wavelength, y_sam_norm), (y_ref, y_sam),
(t_edge, b_edge, l_edge, r_edge, peak_r, peak_b, gapcal))
else:
return (wavelength, y_sam_norm)
# try out the sample spectrum function
full_result = norm_sam( xi, True )
wv, sam_norm = full_result[0]
ref_raw, sam_raw = full_result[1]
other_result = full_result[2]
# check the reference spectrum (averaged)
fig_out( ref_raw, fig_dpi=120 )
# check the sample spectrum (averaged) before normalization
fig_out( sam_raw, fig_dpi=120 )
# check the normalized sample spectrum (averaged)
pp.figure( dpi=120 )
pp.style.use( "seaborn-darkgrid" )
pp.plot( wv, sam_norm[:,0], 'r-' )
pp.plot( wv, sam_norm[:,1], 'g-' )
pp.plot( wv, sam_norm[:,2], 'b-' )
pp.xlabel( "wavelength (nm)", size=12 )
pp.ylabel( "normalized intensity", size=12 )
```
## - 06 - function for calculating average intensity over a narrow band
```
# Input: ifn=image_file_name, ch=color_channel
# Input: wlc=wavelength_range_center, wlhs=wavelength_range_half_span
# Input: tm=trim_edge, gp=method_for_gap_calculation, fo=full_output
def cal_I( ifn, ch='g', wlc=535., wlhs=5., te=False, gp='p', fo=False ):
wl_low, wl_high = wlc-wlhs, wlc+wlhs
xi = pp.imread( ifn )
wl_arr, sam_norm = norm_sam( xi, trim_edge=te, gapcal=gp )
if ch=='r' or ch=='R':
y_arr = sam_norm[:,0]
elif ch=='g' or ch=='G':
y_arr = sam_norm[:,1]
elif ch=='b' or ch=='B':
y_arr = sam_norm[:,2]
else:
raise ValueError( "Color channel should be 'r', 'g', or 'b'." )
arg_low = np.where( wl_arr < wl_high )[0][0]
arg_high = np.where( wl_arr > wl_low )[0][-1]
I_sum = y_arr[arg_low:arg_high+1].sum()
I_ave = I_sum/(arg_high-arg_low+1)
if fo == True:
print y_arr[arg_low:arg_high+1]
pp.figure( dpi=120 )
pp.style.use( "seaborn-darkgrid" )
pp.plot( wl_arr, y_arr, 'k.-' )
pp.xlabel( "wavelength (nm)", size=12 )
pp.ylabel( "normalized intensity", size=12 )
else:
pass
return I_ave
# try out the average intensity function
cal_I( img_file, fo=True )
```
## - 07 - function for calculating nitrate concentration
```
# Input: image_file=path_and_name_of_image_file, wl=center_wavelength
def test_N( image_file, wl=530., k=-7.8279, b=-0.14917 ):
I = cal_I( img_file, wlc=wl )
lgI = np.log10(I)
nc = lgI*k + b
print "Nitrate Concentration: "+str(round(nc, 2))+" mg/L"
return nc
# try out the nitrate concentration function
test_N( img_file )
```
The k and b values varies a little bit with each individual EOS 1 device, so to ensure accuracy, a three-point calibration is highly recommended.
## - 08 - function for calibrating nitrate tests
```
def cali_N( img_arr, nc_arr, wl, fo=True ):
if len(img_arr) != len(nc_arr):
raise ValueError( "img_arr and nc_arr should have the same length." )
else:
pass
nc = np.array(nc_arr)
I_arr = []
for img in img_arr:
I_arr.append( cal_I( img, wlc=wl ) )
I_arr = np.array( I_arr )
lgI = np.log10( I_arr )
if fo == True:
Ab = (-1.)*lgI
kf, bf = np.polyfit( nc, Ab, 1 )
print kf, bf
pp.style.use( "seaborn-darkgrid" )
pp.figure( dpi=120 )
pp.plot( nc, Ab, 'k.', label="Calibration Data" )
pp.plot( nc, nc*kf+bf, 'k-', label="Linear Fit" )
pp.xlabel( "Nitrate Concentration (mg/L)", size=12)
pp.ylabel( "Absorbance ("+str(wl-5)+"nm $-$ "+str(wl+5)+"nm)", size=12 )
pp.legend( loc="upper left" )
else:
pass
k, b = np.polyfit( lgI, nc_arr, 1 )
return ((k,b), nc, lgI)
imgs = ["EOS_imgs//0mg.jpg", "EOS_imgs//5mg.jpg", "EOS_imgs//10mg.jpg"]
ncs = [0.0, 5.0, 10.0]
cali_N( imgs, ncs, 530. )
k, b = cali_N( imgs, ncs, 530., fo=False )[0]
```
After you run the cali_N, you will feed the k & b back into test_N as inputs.
Now you've understood how the image analysis code works.
You can keep using this Jupyter Notebook, or go back to:
https://github.com/jianshengfeng/EOS1
and find the Python code ImgAna_minimum.py
ImgAna_minimum.py can either be run as a Python script (i.e., python ImgAna_minimum.py) or used as a Python module (i.e., import ImgAna_minimum).
| true |
code
| 0.336488 | null | null | null | null |
|
# Development Notebook for extracting icebergs from DEMs
by Jessica Scheick
Workflow based on previous methods and code developed by JScheick for Scheick et al 2019 *Remote Sensing*.
***Important note about CRS handling*** This code was developed while also learning about Xarray, rioxarray, rasterio, and other Python geospatial libraries. Since projections are not yet fully handled [smoothly] in any of those resources, and especially not integrated, there's little to no built in checking or handling of CRS. Instead, handling is done manually throughout the code and external to this notebook. This is critical to know because the CRS displayed by a rioxarray dataset may be from one variable added to the dataset, but is not necessarily the original (or read in) CRS for each variable in the dataset (hence the manual, external handling). The `get_mask` and `get_new_var_from_file` methods should reproject new data sources before adding them to the dataset.
```
import numpy as np
import pandas as pd
import xarray as xr
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib.gridspec as gridspec
%matplotlib inline
import hvplot.xarray
# import hvplot.pandas
import holoviews as hv
hv.extension('bokeh','matplotlib')
from holoviews import dim, opts
import datetime as dt
import os
import panel as pn
pn.extension()
import pyproj
import rioxarray
%load_ext autoreload
import icebath as icebath
from icebath.core import build_xrds
from icebath.utils import raster_ops as raster_ops
from icebath.utils import vector_ops as vector_ops
from icebath.core import fl_ice_calcs as icalcs
from icebath.core import build_gdf
%autoreload 2
# laptop dask setup
import dask
from dask.distributed import Client, LocalCluster, performance_report
# cluster=LocalCluster()
# client = Client(cluster) #, processes=False) this flag only works if you're not using a LocalCluster, in which case don't use `cluster` either
client = Client(processes=True, n_workers=2, threads_per_worker=2, memory_limit='7GB', dashboard_address=':8787')
client
# Dask docs of interest
# includes notes and tips on threads vs processes: https://docs.dask.org/en/latest/best-practices.html#best-practices
# Pangeo dask setup
from dask_gateway import GatewayCluster
cluster = GatewayCluster()
# options = cluster.gateway.cluster_options()
# options
# cluster.adapt(minimum=2, maximum=10) # or cluster.scale(n) to a fixed size.
client = cluster.get_client()
client
# reconnect to existing cluster
from dask_gateway import Gateway
g = Gateway()
g.list_clusters()
cluster = g.connect(g.list_clusters()[0].name)
cluster
cluster.scale(0)
client = cluster.get_client()
client
cluster.scale(5)
client.get_versions(check=True)
cluster.close()
def debug_mem():
from pympler import summary, muppy
all_objects = muppy.get_objects()
s = summary.summarize(all_objects)
return s
s = client.run(debug_mem)
from pympler import summary, muppy
summary.print_(list(s.values())[0])
```
## Read in DEMs and apply corrections (tidal, geoid)
```
#Ilulissat Isfjord Mouth, resampled to 50m using CHANGES
# ds = build_xrds.xrds_from_dir('/home/jovyan/icebath/notebooks/supporting_docs/Elevation/ArcticDEM/Regridded_50m_tiles/n69w052/', fjord="JI")
# Ilulissat Isfjord Mouth, original 2m (the files from CHANGES seem much smaller than those from Kane/Pennell.
# data = xr.open_rasterio('/home/jovyan/icebath/notebooks/supporting_docs/Elevation/ArcticDEM/2m_tiles/n69w052/SETSM_W1W1_20100813_102001000E959700_102001000ECB6B00_seg1_2m_v3.0_dem.tif')
ds = build_xrds.xrds_from_dir('/Users/jessica/projects/bathymetry_from_bergs/DEMs/2m/', fjord="JI")
# ds = build_xrds.xrds_from_dir('/Users/jessica/projects/bathymetry_from_bergs/DEMs/KaneW2W2/', fjord="KB", metastr="_meta", bitmask=True)
# ds = build_xrds.xrds_from_dir('/home/jovyan/icebath/notebooks/supporting_docs/Elevation/ArcticDEM/2m_tiles/', fjord="JI")
scrolldem = ds['elevation'].hvplot.image(x='x', y='y',datashade=False, rasterize=True, aspect='equal', cmap='magma', dynamic=True,
xlabel="x (km)", ylabel="y (km)", colorbar=True) #turn off datashade to see hover values + colorbar
scrolldem
```
### Get and Apply Land Mask
**Note: requires a shapefile of the land areas in the ROI**
The default is to use a shapefile of Greenland: `shpfile='/home/jovyan/icebath/notebooks/supporting_docs/Land_region.shp'`, but an alternative file can be specified.
Underlying code is based on: https://gis.stackexchange.com/questions/357490/mask-xarray-dataset-using-a-shapefile
Other results used rioxarray (which isn't on my current working environment), and my previous work did it all manually with gdal.
```
ds.bergxr.get_mask(req_dim=['x','y'], req_vars=None, name='land_mask',
# shpfile='/home/jovyan/icebath/notebooks/supporting_docs/Land_region.shp')
shpfile='/Users/jessica/mapping/shpfiles/Greenland/Land_region/Land_region.shp')
# ds.land_mask.plot()
ds['elevation'] = ds['elevation'].where(ds.land_mask == True)
```
### Apply Geoid Correction
ArcticDEMs come as ellipsoidal height. They are corrected to geoidal height according to geoid_ht = ellipsoid - geoid_offset where geoid_offset is taken from BedMachine v3 and resampled in Xarray (using default "linear" interpolation for multidimensional arrays) to the resolution and extent of the region's dataset.
BedMachine is now available on Pangeo via intake thanks to the Lahmont-Doherty Glaciology group.
- Basic info: https://github.com/ldeo-glaciology/pangeo-bedmachine
- Pangeo gallery glaciology examples: http://gallery.pangeo.io/repos/ldeo-glaciology/pangeo-glaciology-examples/index.html
```
ds = ds.bergxr.to_geoid(source='/Users/jessica/mapping/datasets/160281892/BedMachineGreenland-2017-09-20_3413_'+ds.attrs['fjord']+'.nc')
# ds = ds.bergxr.to_geoid(source='/home/jovyan/icebath/notebooks/supporting_docs/160281892/BedMachineGreenland-2017-09-20_'+ds.attrs['fjord']+'.nc')
ds
```
### Apply Tidal Correction
Uses Tyler Sutterly's pyTMD library
```
# model_path='/home/jovyan/pyTMD/models'
model_path='/Users/jessica/computing/tidal_model_files'
ds=ds.bergxr.tidal_corr(loc=[ds.attrs["fjord"]], model_path=model_path)
# # test to make sure that if you already have a tidal correction it won't reapply it, and test that it will return the tides if you don't have an elevation entered
# ds=ds.bergxr.tidal_corr(loc=["JI"])
# ds=ds.bergxr.tidal_corr(loc=["JI"]) # results in assertion error
# ds.attrs['offset_names'] = ('random')
# ds=ds.bergxr.tidal_corr(loc=["JI"]) # results in longer attribute list
# # go directly to icalcs function, called under the hood above, if you want to see plots
# tides = icalcs.predict_tides(loc='JI',img_time=ds.dtime.values[0], model_path='/home/jovyan/pyTMD/models',
# model='AOTIM-5-2018', epsg=3413, plot=True)
# tides[2]
```
## Extract Icebergs from DEM and put into Geodataframe
Completely automated iceberg delineation in the presence of clouds and/or data gaps (as is common in a DEM) is not yet easily implemented with existing methods. Many techniques have been refined for specific fjords or types of situations. Here, we tailor our iceberg detection towards icebergs that will provide reliable water depth estimates. The following filters are applied during the iceberg extraction process:
- a minimum iceberg horizontal area is specified on a per-fjord basis. These minima are based on icebergs used to infer bathymetry in previous work (Scheick et al 2019).
- a maximum allowed height for the median freeboard is specified on a per-fjord basis. These maxima are determined as 10% of the [largest] grounded ice thickness for the source glaciers. While the freeboard values from the DEM are later filtered to remove outliers in determining water depth, this filtering step during the delineation process removes "icebergs" where low clouds, rather than icebergs, are the surface represented in the DEM.
- a maximum iceberg horizontal area of 1000000 m2 (1km2) is assumed to eliminate large clusters of icebergs, melange, and/or cloud picked up by the delineation algorithm.
- the median freeboard must be greater than 15 m relative to [adjusted] sea level. If not, we can assume the iceberg is either a false positive (e.g. cloud or sea ice) or too small to provide a meaningful water depth estimate.
```
import geopandas as gpd
gdf = gpd.read_file('/Users/jessica/projects/bathymetry_from_bergs/prelim_results/JIicebergs.gpkg', ignore_index=True)
%%prun
# %%timeit -n 1 -r 1
# 3min 17s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
# gdf=None
gdf = build_gdf.xarray_to_gdf(ds)
# gdf.loc[((gdf['sl_adjust']>4.27) & (gdf['sl_adjust']<4.36))].groupby('date').berg_poly.plot()
gdf.groupby('date').berg_poly.plot()
# This requires geoviews[http://geoviews.org/] be installed, and their install pages have warning if your environment uses [non] conda-forge
# libraries and it won't resolve the environment with a conda install, so I'll need to create a new test env to try this
# bergs = gdf.hvplot()
# bergs
# xarray-leaflet may be another good option to try: https://github.com/davidbrochart/xarray_leaflet
# scrolldems*bergs
gdf
```
## Compute Water Depths on Icebergs
```
gdf.berggdf.calc_filt_draft()
gdf.berggdf.calc_rowwise_medmaxmad('filtered_draft')
gdf.berggdf.wat_depth_uncert('filtered_draft')
# def mmm(vals): # mmm = min, med, max
# print(np.nanmin(vals))
# print(np.nanmedian(vals))
# print(np.nanmax(vals))
```
## Extract measured values from BedMachine v3 and IBCAOv4 (where available)
All bathymetry values from these gridded products are included, then later parsed into bathymetric observations and inferred (from e.g. gravimetry, modeling) for comparing with iceberg-inferred water depths.
Note that the datasets are subset to the region of the fjord outside this script to reduce memory requirements during processing.
***Improvement: add CRS handling/checks to catch when a measurement dataset is incompatible and needs to be reprojected***
#### BedMachine Greenland
```
fjord = "JI"
# measfile='/Users/jessica/mapping/datasets/160281892/BedMachineGreenland-2017-09-20.nc'
measfile='/Users/jessica/mapping/datasets/160281892/BedMachineGreenland-2017-09-20_3413_'+fjord+'.nc'
# measfile='/home/jovyan/icebath/notebooks/supporting_docs/160281892/BedMachineGreenland-2017-09-20.nc'
# measfile='/home/jovyan/icebath/notebooks/supporting_docs/160281892/BedMachineGreenland-2017-09-20_'+ds.attrs['fjord']+'.nc'
```
#### IBCAOv4
https://www.gebco.net/data_and_products/gridded_bathymetry_data/arctic_ocean/
Source keys: https://www.gebco.net/data_and_products/gridded_bathymetry_data/gebco_2020/
Downloaded Feb 2021
**NOTE** IBCAO has it's own Polar Stereo projection (EPSG:3996: WGS 84/IBCAO Polar Stereographic) so it needs to be reprojected before being applied to these datasets.
See: https://spatialreference.org/ref/?search=Polar+Stereographic
```
measfile2a='/Users/jessica/mapping/datasets/IBCAO_v4_200m_ice_3413.nc'
# measfile2a='/Users/jessica/mapping/datasets/IBCAO_v4_200m_ice_3413_'+fjord+'.nc'
# measfile2a='/home/jovyan/icebath/notebooks/supporting_docs/IBCAO_v4_200m_ice_3413.nc'
# measfile2a='/home/jovyan/icebath/notebooks/supporting_docs/IBCAO_v4_200m_ice_3413_'+ds.attrs['fjord']+'.nc'
measfile2b='/Users/jessica/mapping/datasets/IBCAO_v4_200m_TID_3413.nc'
# measfile2b='/home/jovyan/icebath/notebooks/supporting_docs/IBCAO_v4_200m_TID_3413.nc'
gdf.berggdf.get_meas_wat_depth([measfile, measfile2a, measfile2b],
vardict={"bed":"bmach_bed", "errbed":"bmach_errbed", "source":"bmach_source",
"ibcao_bathy":"ibcao_bed", "z":"ibcao_source"},
nanval=-9999)
gdf #[gdf['date'].dt.year.astype(int)==2016]
```
### Plot the measured and inferred values
Plots the gridded versus iceberg-freeboard-inferred values for all icebergs relative to the values in BedMachine and IBCAO.
Left plot shows measured values within the gridded datasets; right plot show the modeled/inferred values within the gridded data products (hence the larger error bars).
```
from icebath.utils import plot as ibplot
ibplot.meas_vs_infer_fig(gdf, save=False)
```
## Export the iceberg outlines and data to a geopackage
```
shpgdf = gdf.copy(deep=True)
del shpgdf['DEMarray']
del shpgdf['filtered_draft']
shpgdf.to_file("/Users/jessica/projects/bathymetry_from_bergs/prelim_results/JIbergs_faster.gpkg", driver="GPKG")
```
## Export the iceberg outlines and data to a shapefile
```
shpgdf = gdf.copy(deep=True)
shpgdf['year'] = shpgdf['date'].dt.year.astype(int)
del shpgdf['date']
del shpgdf['DEMarray']
del shpgdf['filtered_draft']
# NOTE: need to rename columns due to name length limits for shapefile; otherwise,
# all ended up as "filtered_#"
shpgdf.to_file("/Users/jessica/projects/bathymetry_from_bergs/prelim_results/icebergs_JI.shp")
```
## Visualizing Iceberg Outlines for a Single DEM
Some attempts at doing this with Holoviews, including to try and have it with a slider bar, are in the misc_dev_notes_notebook. As it stands currently, this implementation should work but is quite slow.
```
timei=1
print(ds['dtime'].isel({'dtime':timei}))
dem = ds.isel({'dtime':timei})
im = dem.elevation.values
# Plot objectives: show DEM, land mask, iceberg outlines. 2nd plot with just orig DEM?
fig = plt.figure(figsize=(12,12)) # width, height in inches
# gs = gridspec.GridSpec(ncols=1, nrows=2, figure=fig)
gs=fig.add_gridspec(3,1, hspace=0.3) # nrows, ncols
# DEM plot
axDEM = plt.subplot(gs[0:2,0])
dem.elevation.plot.pcolormesh(ax=axDEM,
vmin=-10, vmax=75, cmap='magma', # vmin and vmax set the colorbar limits here
xscale='linear', yscale='linear',
cbar_kwargs={'label':"Elevation (m amsl)"})
# land mask
landcm = mpl.colors.ListedColormap([(0.5, 0.35, 0.35, 1.), (0.5, 0., 0.6, 0)])
dem.land_mask.plot(ax=axDEM, cmap=landcm, add_colorbar=False)
# iceberg contours - ultimately add this from geodataframe
# dem.elevation.plot.contour(ax=axDEM, levels=[threshold], colors=['gray'])
# Note: dem.elevation.plot.contour(levels=[threshold], colors=['gray']) will show the plot, but you can't
# add it to these axes and then show it inline from a second cell
# I'm not entirely sure this is plotting what I think; it's also not actually plotting the contoured data
gdf.loc[gdf['date']==ds.dtime.isel({'dtime':timei}).values].berg_poly.plot(ax=axDEM,
linestyle='-',
linewidth=2,
edgecolor='gray',
facecolor=(0,0,0,0))
xmin = -250000
xmax = -232750
ymin = -2268250
ymax = -2251000
# xmin = -235000 #zoom in to figure out empty iceberg DEM during gdf generation
# xmax = -233000
# ymin = -2257500
# ymax = -2255000
while (xmin-xmax) != (ymin-ymax):
print("modify your x and y min/max to make the areas equal")
break
axDEM.set_aspect('equal')
axDEM.set_xlim(xmin, xmax)
axDEM.set_ylim(ymin, ymax)
axDEM.set_xlabel("x (km)")
axDEM.set_ylabel("y (km)")
plt.show()
# Note: gdf['date']==timei is returning all false, so the datetimes will need to be dealt with to get the areas from the geometry column
# areas = gdf.loc[:, gdf['date']==timei].geometry.area()
```
| true |
code
| 0.458894 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/rudyhendrawn/traditional-dance-video-classification/blob/main/tari_vgg16_lstm_224.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import os
import glob
from keras_video import VideoFrameGenerator
import numpy as np
import pandas as pd
```
## Data Loading and Preprocessing
```
# Use sub directories names as classes
classes = [i.split(os.path.sep)[1] for i in glob.glob('Dataset/*')]
classes.sort()
# Some global params
SIZE = (224, 224) # Image size
CHANNELS = 3 # Color channel
NBFRAME = 30 # Frames per video
BS = 2 # Batch size
# Pattern to get videos and classes
glob_pattern = 'Dataset/{classname}/*.mp4'
# Create video frame generator
train = VideoFrameGenerator(
classes=classes,
glob_pattern=glob_pattern,
nb_frames=NBFRAME,
split_val=.20,
split_test=.20,
shuffle=True,
batch_size=BS,
target_shape=SIZE,
nb_channel=CHANNELS,
transformation=None, # Data Augmentation
use_frame_cache=False,
seed=42)
valid = train.get_validation_generator()
test = train.get_test_generator()
from tensorflow.keras.layers import GlobalAveragePooling2D, LSTM, Dense, Dropout, TimeDistributed
from tensorflow.keras.models import Sequential
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
from tensorflow.keras.applications.vgg16 import VGG16
input_shape = (NBFRAME,) + SIZE + (CHANNELS,)
# Define VGG16 model
model_vgg16 = VGG16(weights='imagenet', include_top=False, input_shape=input_shape[1:])
model_vgg16.trainable = False
model = Sequential()
model.add(TimeDistributed(model_vgg16, input_shape=input_shape))
model.add(TimeDistributed(GlobalAveragePooling2D()))
# Define LSTM model
model.add(LSTM(256))
# Dense layer
model.add(Dense(1024, activation='relu'))
model.add(Dropout(.2))
model.add(Dense(int(len(classes)), activation='softmax'))
model.summary()
epochs = 100
earlystop = EarlyStopping(monitor='loss', patience=10)
checkpoint = ModelCheckpoint('Checkpoint/vgg16-lstm-224.h5', monitor='val_acc', save_best_only=True, mode='max', verbose=1)
callbacks = [earlystop, checkpoint]
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['acc'])
history = model.fit(train,
validation_data=valid,
epochs=epochs,
callbacks=callbacks)
model.save('Model/tari/vgg16-lstm-224-100e-0.86.h5')
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# Summarize history for accuracy
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# Summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# Save history to csv
hist_df = pd.DataFrame(history.history)
hist_csv_file = 'history_vgg16_lstm_224.csv'
with open(hist_csv_file, mode='w') as f:
hist_df.to_csv(f)
```
## Testing
```
model.evaluate(test)
y_test = []
y_predict = []
for step in range(test.files_count//BS):
X, y = test.next()
prediction = model.predict(X)
y_test.extend(y)
y_predict.extend(prediction)
y_true = np.argmax(y_test, axis=1)
prediction = np.argmax(y_predict, axis=1)
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, confusion_matrix, classification_report, \
roc_curve, auc
# accuracy: (tp + tn) / (p + n)
accuracy = accuracy_score(y_true, prediction)
print(f'Accuracy: {np.round(accuracy, 3)}')
# precision tp / (tp + fp)
precision = precision_score(y_true, prediction, average='macro')
print(f'Precision: {np.round(precision, 3)}')
# recall: tp / (tp + fn)
recall = recall_score(y_true, prediction, average='macro')
print(f'Recall: {np.round(recall, 3)}')
# f1: 2 tp / (2 tp + fp + fn)
f1 = f1_score(y_true, prediction, average='macro')
print(f'F1 score: {np.round(f1, 3)}')
```
## Discussion
```
target_names = test.classes
print(classification_report(y_true, prediction, target_names=target_names))
matrix = confusion_matrix(y_true, prediction)
sns.heatmap(matrix, annot=True, cmap='Blues')
fpr, tpr, _ = roc_curve(y_true, prediction, pos_label=6)
auc_score = auc(fpr, tpr)
print(f'AUC Score : {np.round(auc_score, 3)}')
plt.plot(fpr, tpr, marker='.')
plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()
```
## Model from checkpoint
```
from tensorflow.keras.models import load_model
ckp_model = load_model('Checkpoint/vgg16-lstm-224.h5')
ckp_model.evaluate(test)
y_test = []
y_predict = []
for step in range(test.files_count//BS):
X, y = test.next()
prediction = ckp_model.predict(X)
y_test.extend(y)
y_predict.extend(prediction)
y_true = np.argmax(y_test, axis=1)
prediction = np.argmax(y_predict, axis=1)
target_names = test.classes
print(classification_report(y_true, prediction, target_names=target_names))
matrix = confusion_matrix(y_true, prediction)
sns.heatmap(matrix, annot=True, cmap='Blues')
# accuracy: (tp + tn) / (p + n)
accuracy = accuracy_score(y_true, prediction)
print(f'Accuracy: {np.round(accuracy, 3)}')
# precision tp / (tp + fp)
precision = precision_score(y_true, prediction, average='macro')
print(f'Precision: {np.round(precision, 3)}')
# recall: tp / (tp + fn)
recall = recall_score(y_true, prediction, average='macro')
print(f'Recall: {np.round(recall, 3)}')
# f1: 2 tp / (2 tp + fp + fn)
f1 = f1_score(y_true, prediction, average='macro')
print(f'F1 score: {np.round(f1, 3)}')
fpr, tpr, _ = roc_curve(y_true, prediction, pos_label=6)
auc_score = auc(fpr, tpr)
print(f'AUC Score : {np.round(auc_score, 3)}')
plt.plot(fpr, tpr, marker='.')
plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()
```
| true |
code
| 0.645064 | null | null | null | null |
|
# Shingling with Jaccard
Comparing document similarities where the set of objects is word or character ngrams taken over a sliding window from the document (shingles). The set of shingles is used to determine the document similarity, Jaccard similarity, between a pair of documents.
```
from tabulate import tabulate
shingle_size = 5
def shingler(doc, size):
return [doc[i:i+size] for i in range(len(doc))][:-size]
def jaccard_dist(shingle1, shingle2):
return len(set(shingle1) & set(shingle2)) / len(set(shingle1) | set(shingle2))
document1 = """An elephant slept in his bunk
And in slumber his chest rose and sunk
But he snored how he snored
All the other beasts roared
So his wife tied a knot in his trunk"""
document2 = """A large red cow
Tried to make a bow
But did not know how
They say
For her legs got mixed
And her horns got fixed
And her tail would get
In her way"""
document3 = """An walrus slept in his bunk
And in slumber his chest rose and sunk
But he snored how he snored
All the other beasts roared
So his wife tied a knot in his whiskers"""
# shingle and discard the last x as these are just the last n<x characters from the document
shingle1 = shingler(document1, shingle_size)
shingle1[0:10]
# shingle and discard the last x as these are just the last n<x characters from the document
shingle2 = shingler(document2, shingle_size)
shingles[0:10]
# shingle and discard the last x as these are just the last n<x characters from the document
shingle3 = shingler(document3, shingle_size)
shingles[0:10]
# Jaccard distance is the size of set intersection divided by the size of set union
print(f"Document 1 and Document 2 Jaccard Distance: {jaccard_dist(shingle1, shingle2)}")
# Jaccard distance is the size of set intersection divided by the size of set union
print(f"Document 1 and Document 3 Jaccard Distance: {jaccard_dist(shingle1, shingle3)}")
# Jaccard distance is the size of set intersection divided by the size of set union
print(f"Document 2 and Document 3 Jaccard Distance: {jaccard_dist(shingle2, shingle3)}")
shingle_sizes = [1,2,3,4,5,6,7,8,9,10,11,12,13,15]
jaccard_list = []
for s in shingle_sizes:
temp_shingle_1 = shingler(document1, s)
temp_shingle_2 = shingler(document2, s)
temp_shingle_3 = shingler(document3, s)
j1 = jaccard_dist(temp_shingle_1, temp_shingle_2)
j2 = jaccard_dist(temp_shingle_2, temp_shingle_3)
j3 = jaccard_dist(temp_shingle_1, temp_shingle_3)
temp_list = []
temp_list.append(j1)
temp_list.append(j2)
temp_list.append(j3)
temp_list.append(s)
jaccard_list.append(temp_list)
print("1:2\t\t2:3\t1:3\tShingle Size")
print(tabulate(jaccard_list))
```
| true |
code
| 0.259755 | null | null | null | null |
|
# 4 - Convolutional Sentiment Analysis
In the previous notebooks, we managed to achieve a test accuracy of ~85% using RNNs and an implementation of the [Bag of Tricks for Efficient Text Classification](https://arxiv.org/abs/1607.01759) model. In this notebook, we will be using a *convolutional neural network* (CNN) to conduct sentiment analysis, implementing the model from [Convolutional Neural Networks for Sentence Classification](https://arxiv.org/abs/1408.5882).
**Note**: This tutorial is not aiming to give a comprehensive introduction and explanation of CNNs. For a better and more in-depth explanation check out [here](https://ujjwalkarn.me/2016/08/11/intuitive-explanation-convnets/) and [here](https://cs231n.github.io/convolutional-networks/).
Traditionally, CNNs are used to analyse images and are made up of one or more *convolutional* layers, followed by one or more linear layers. The convolutional layers use filters (also called *kernels* or *receptive fields*) which scan across an image and produce a processed version of the image. This processed version of the image can be fed into another convolutional layer or a linear layer. Each filter has a shape, e.g. a 3x3 filter covers a 3 pixel wide and 3 pixel high area of the image, and each element of the filter has a weight associated with it, the 3x3 filter would have 9 weights. In traditional image processing these weights were specified by hand by engineers, however the main advantage of the convolutional layers in neural networks is that these weights are learned via backpropagation.
The intuitive idea behind learning the weights is that your convolutional layers act like *feature extractors*, extracting parts of the image that are most important for your CNN's goal, e.g. if using a CNN to detect faces in an image, the CNN may be looking for features such as the existance of a nose, mouth or a pair of eyes in the image.
So why use CNNs on text? In the same way that a 3x3 filter can look over a patch of an image, a 1x2 filter can look over a 2 sequential words in a piece of text, i.e. a bi-gram. In the previous tutorial we looked at the FastText model which used bi-grams by explicitly adding them to the end of a text, in this CNN model we will instead use multiple filters of different sizes which will look at the bi-grams (a 1x2 filter), tri-grams (a 1x3 filter) and/or n-grams (a 1x$n$ filter) within the text.
The intuition here is that the appearance of certain bi-grams, tri-grams and n-grams within the review will be a good indication of the final sentiment.
## Preparing Data
As in the previous notebooks, we'll prepare the data.
Unlike the previous notebook with the FastText model, we no longer explicitly need to create the bi-grams and append them to the end of the sentence.
As convolutional layers expect the batch dimension to be first we can tell TorchText to return the data already permuted using the `batch_first = True` argument on the field.
```
import torch
from torchtext import data
from torchtext import datasets
import random
import numpy as np
SEED = 1234
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.backends.cudnn.deterministic = True
TEXT = data.Field(tokenize = 'spacy', batch_first = True)
LABEL = data.LabelField(dtype = torch.float)
train_data, test_data = datasets.IMDB.splits(TEXT, LABEL)
train_data, valid_data = train_data.split(random_state = random.seed(SEED))
```
Build the vocab and load the pre-trained word embeddings.
```
MAX_VOCAB_SIZE = 25_000
TEXT.build_vocab(train_data,
max_size = MAX_VOCAB_SIZE,
vectors = "glove.6B.100d",
unk_init = torch.Tensor.normal_)
LABEL.build_vocab(train_data)
```
As before, we create the iterators.
```
BATCH_SIZE = 64
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits(
(train_data, valid_data, test_data),
batch_size = BATCH_SIZE,
device = device)
```
## Build the Model
Now to build our model.
The first major hurdle is visualizing how CNNs are used for text. Images are typically 2 dimensional (we'll ignore the fact that there is a third "colour" dimension for now) whereas text is 1 dimensional. However, we know that the first step in almost all of our previous tutorials (and pretty much all NLP pipelines) is converting the words into word embeddings. This is how we can visualize our words in 2 dimensions, each word along one axis and the elements of vectors aross the other dimension. Consider the 2 dimensional representation of the embedded sentence below:

We can then use a filter that is **[n x emb_dim]**. This will cover $n$ sequential words entirely, as their width will be `emb_dim` dimensions. Consider the image below, with our word vectors are represented in green. Here we have 4 words with 5 dimensional embeddings, creating a [4x5] "image" tensor. A filter that covers two words at a time (i.e. bi-grams) will be **[2x5]** filter, shown in yellow, and each element of the filter with have a _weight_ associated with it. The output of this filter (shown in red) will be a single real number that is the weighted sum of all elements covered by the filter.

The filter then moves "down" the image (or across the sentence) to cover the next bi-gram and another output (weighted sum) is calculated.

Finally, the filter moves down again and the final output for this filter is calculated.

In our case (and in the general case where the width of the filter equals the width of the "image"), our output will be a vector with number of elements equal to the height of the image (or lenth of the word) minus the height of the filter plus one, $4-2+1=3$ in this case.
This example showed how to calculate the output of one filter. Our model (and pretty much all CNNs) will have lots of these filters. The idea is that each filter will learn a different feature to extract. In the above example, we are hoping each of the **[2 x emb_dim]** filters will be looking for the occurence of different bi-grams.
In our model, we will also have different sizes of filters, heights of 3, 4 and 5, with 100 of each of them. The intuition is that we will be looking for the occurence of different tri-grams, 4-grams and 5-grams that are relevant for analysing sentiment of movie reviews.
The next step in our model is to use *pooling* (specifically *max pooling*) on the output of the convolutional layers. This is similar to the FastText model where we performed the average over each of the word vectors, implemented by the `F.avg_pool2d` function, however instead of taking the average over a dimension, we are taking the maximum value over a dimension. Below an example of taking the maximum value (0.9) from the output of the convolutional layer on the example sentence (not shown is the activation function applied to the output of the convolutions).

The idea here is that the maximum value is the "most important" feature for determining the sentiment of the review, which corresponds to the "most important" n-gram within the review. How do we know what the "most important" n-gram is? Luckily, we don't have to! Through backpropagation, the weights of the filters are changed so that whenever certain n-grams that are highly indicative of the sentiment are seen, the output of the filter is a "high" value. This "high" value then passes through the max pooling layer if it is the maximum value in the output.
As our model has 100 filters of 3 different sizes, that means we have 300 different n-grams the model thinks are important. We concatenate these together into a single vector and pass them through a linear layer to predict the sentiment. We can think of the weights of this linear layer as "weighting up the evidence" from each of the 300 n-grams and making a final decision.
### Implementation Details
We implement the convolutional layers with `nn.Conv2d`. The `in_channels` argument is the number of "channels" in your image going into the convolutional layer. In actual images this is usually 3 (one channel for each of the red, blue and green channels), however when using text we only have a single channel, the text itself. The `out_channels` is the number of filters and the `kernel_size` is the size of the filters. Each of our `kernel_size`s is going to be **[n x emb_dim]** where $n$ is the size of the n-grams.
In PyTorch, RNNs want the input with the batch dimension second, whereas CNNs want the batch dimension first - we do not have to permute the data here as we have already set `batch_first = True` in our `TEXT` field. We then pass the sentence through an embedding layer to get our embeddings. The second dimension of the input into a `nn.Conv2d` layer must be the channel dimension. As text technically does not have a channel dimension, we `unsqueeze` our tensor to create one. This matches with our `in_channels=1` in the initialization of our convolutional layers.
We then pass the tensors through the convolutional and pooling layers, using the `ReLU` activation function after the convolutional layers. Another nice feature of the pooling layers is that they handle sentences of different lengths. The size of the output of the convolutional layer is dependent on the size of the input to it, and different batches contain sentences of different lengths. Without the max pooling layer the input to our linear layer would depend on the size of the input sentence (not what we want). One option to rectify this would be to trim/pad all sentences to the same length, however with the max pooling layer we always know the input to the linear layer will be the total number of filters. **Note**: there an exception to this if your sentence(s) are shorter than the largest filter used. You will then have to pad your sentences to the length of the largest filter. In the IMDb data there are no reviews only 5 words long so we don't have to worry about that, but you will if you are using your own data.
Finally, we perform dropout on the concatenated filter outputs and then pass them through a linear layer to make our predictions.
```
import torch.nn as nn
import torch.nn.functional as F
class CNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, n_filters, filter_sizes, output_dim,
dropout, pad_idx):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx = pad_idx)
self.conv_0 = nn.Conv2d(in_channels = 1,
out_channels = n_filters,
kernel_size = (filter_sizes[0], embedding_dim))
self.conv_1 = nn.Conv2d(in_channels = 1,
out_channels = n_filters,
kernel_size = (filter_sizes[1], embedding_dim))
self.conv_2 = nn.Conv2d(in_channels = 1,
out_channels = n_filters,
kernel_size = (filter_sizes[2], embedding_dim))
self.fc = nn.Linear(len(filter_sizes) * n_filters, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, text):
#text = [batch size, sent len]
embedded = self.embedding(text)
#embedded = [batch size, sent len, emb dim]
embedded = embedded.unsqueeze(1)
#embedded = [batch size, 1, sent len, emb dim]
conved_0 = F.relu(self.conv_0(embedded).squeeze(3))
conved_1 = F.relu(self.conv_1(embedded).squeeze(3))
conved_2 = F.relu(self.conv_2(embedded).squeeze(3))
#conved_n = [batch size, n_filters, sent len - filter_sizes[n] + 1]
pooled_0 = F.max_pool1d(conved_0, conved_0.shape[2]).squeeze(2)
pooled_1 = F.max_pool1d(conved_1, conved_1.shape[2]).squeeze(2)
pooled_2 = F.max_pool1d(conved_2, conved_2.shape[2]).squeeze(2)
#pooled_n = [batch size, n_filters]
cat = self.dropout(torch.cat((pooled_0, pooled_1, pooled_2), dim = 1))
#cat = [batch size, n_filters * len(filter_sizes)]
return self.fc(cat)
```
Currently the `CNN` model can only use 3 different sized filters, but we can actually improve the code of our model to make it more generic and take any number of filters.
We do this by placing all of our convolutional layers in a `nn.ModuleList`, a function used to hold a list of PyTorch `nn.Module`s. If we simply used a standard Python list, the modules within the list cannot be "seen" by any modules outside the list which will cause us some errors.
We can now pass an arbitrary sized list of filter sizes and the list comprehension will create a convolutional layer for each of them. Then, in the `forward` method we iterate through the list applying each convolutional layer to get a list of convolutional outputs, which we also feed through the max pooling in a list comprehension before concatenating together and passing through the dropout and linear layers.
```
class CNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, n_filters, filter_sizes, output_dim,
dropout, pad_idx):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx = pad_idx)
self.convs = nn.ModuleList([
nn.Conv2d(in_channels = 1,
out_channels = n_filters,
kernel_size = (fs, embedding_dim))
for fs in filter_sizes
])
self.fc = nn.Linear(len(filter_sizes) * n_filters, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, text):
#text = [batch size, sent len]
embedded = self.embedding(text)
#embedded = [batch size, sent len, emb dim]
embedded = embedded.unsqueeze(1)
#embedded = [batch size, 1, sent len, emb dim]
conved = [F.relu(conv(embedded)).squeeze(3) for conv in self.convs]
#conved_n = [batch size, n_filters, sent len - filter_sizes[n] + 1]
pooled = [F.max_pool1d(conv, conv.shape[2]).squeeze(2) for conv in conved]
#pooled_n = [batch size, n_filters]
cat = self.dropout(torch.cat(pooled, dim = 1))
#cat = [batch size, n_filters * len(filter_sizes)]
return self.fc(cat)
```
We can also implement the above model using 1-dimensional convolutional layers, where the embedding dimension is the "depth" of the filter and the number of tokens in the sentence is the width.
We'll run our tests in this notebook using the 2-dimensional convolutional model, but leave the implementation for the 1-dimensional model below for anyone interested.
```
class CNN1d(nn.Module):
def __init__(self, vocab_size, embedding_dim, n_filters, filter_sizes, output_dim,
dropout, pad_idx):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx = pad_idx)
self.convs = nn.ModuleList([
nn.Conv1d(in_channels = embedding_dim,
out_channels = n_filters,
kernel_size = fs)
for fs in filter_sizes
])
self.fc = nn.Linear(len(filter_sizes) * n_filters, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, text):
#text = [batch size, sent len]
embedded = self.embedding(text)
#embedded = [batch size, sent len, emb dim]
embedded = embedded.permute(0, 2, 1)
#embedded = [batch size, emb dim, sent len]
conved = [F.relu(conv(embedded)) for conv in self.convs]
#conved_n = [batch size, n_filters, sent len - filter_sizes[n] + 1]
pooled = [F.max_pool1d(conv, conv.shape[2]).squeeze(2) for conv in conved]
#pooled_n = [batch size, n_filters]
cat = self.dropout(torch.cat(pooled, dim = 1))
#cat = [batch size, n_filters * len(filter_sizes)]
return self.fc(cat)
```
We create an instance of our `CNN` class.
We can change `CNN` to `CNN1d` if we want to run the 1-dimensional convolutional model, noting that both models give almost identical results.
```
INPUT_DIM = len(TEXT.vocab)
EMBEDDING_DIM = 100
N_FILTERS = 100
FILTER_SIZES = [3,4,5]
OUTPUT_DIM = 1
DROPOUT = 0.5
PAD_IDX = TEXT.vocab.stoi[TEXT.pad_token]
model = CNN(INPUT_DIM, EMBEDDING_DIM, N_FILTERS, FILTER_SIZES, OUTPUT_DIM, DROPOUT, PAD_IDX)
```
Checking the number of parameters in our model we can see it has about the same as the FastText model.
Both the `CNN` and the `CNN1d` models have the exact same number of parameters.
```
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f'The model has {count_parameters(model):,} trainable parameters')
```
Next, we'll load the pre-trained embeddings
```
pretrained_embeddings = TEXT.vocab.vectors
model.embedding.weight.data.copy_(pretrained_embeddings)
```
Then zero the initial weights of the unknown and padding tokens.
```
UNK_IDX = TEXT.vocab.stoi[TEXT.unk_token]
model.embedding.weight.data[UNK_IDX] = torch.zeros(EMBEDDING_DIM)
model.embedding.weight.data[PAD_IDX] = torch.zeros(EMBEDDING_DIM)
```
## Train the Model
Training is the same as before. We initialize the optimizer, loss function (criterion) and place the model and criterion on the GPU (if available)
```
import torch.optim as optim
optimizer = optim.Adam(model.parameters())
criterion = nn.BCEWithLogitsLoss()
model = model.to(device)
criterion = criterion.to(device)
```
We implement the function to calculate accuracy...
```
def binary_accuracy(preds, y):
"""
Returns accuracy per batch, i.e. if you get 8/10 right, this returns 0.8, NOT 8
"""
#round predictions to the closest integer
rounded_preds = torch.round(torch.sigmoid(preds))
correct = (rounded_preds == y).float() #convert into float for division
acc = correct.sum() / len(correct)
return acc
```
We define a function for training our model...
**Note**: as we are using dropout again, we must remember to use `model.train()` to ensure the dropout is "turned on" while training.
```
def train(model, iterator, optimizer, criterion):
epoch_loss = 0
epoch_acc = 0
model.train()
for batch in iterator:
optimizer.zero_grad()
predictions = model(batch.text).squeeze(1)
loss = criterion(predictions, batch.label)
acc = binary_accuracy(predictions, batch.label)
loss.backward()
optimizer.step()
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
```
We define a function for testing our model...
**Note**: again, as we are now using dropout, we must remember to use `model.eval()` to ensure the dropout is "turned off" while evaluating.
```
def evaluate(model, iterator, criterion):
epoch_loss = 0
epoch_acc = 0
model.eval()
with torch.no_grad():
for batch in iterator:
predictions = model(batch.text).squeeze(1)
loss = criterion(predictions, batch.label)
acc = binary_accuracy(predictions, batch.label)
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
```
Let's define our function to tell us how long epochs take.
```
import time
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
```
Finally, we train our model...
```
N_EPOCHS = 5
best_valid_loss = float('inf')
for epoch in range(N_EPOCHS):
start_time = time.time()
train_loss, train_acc = train(model, train_iterator, optimizer, criterion)
valid_loss, valid_acc = evaluate(model, valid_iterator, criterion)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'tut4-model.pt')
print(f'Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s')
print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
print(f'\t Val. Loss: {valid_loss:.3f} | Val. Acc: {valid_acc*100:.2f}%')
```
We get test results comparable to the previous 2 models!
```
model.load_state_dict(torch.load('tut4-model.pt'))
test_loss, test_acc = evaluate(model, test_iterator, criterion)
print(f'Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}%')
```
## User Input
And again, as a sanity check we can check some input sentences
**Note**: As mentioned in the implementation details, the input sentence has to be at least as long as the largest filter height used. We modify our `predict_sentiment` function to also accept a minimum length argument. If the tokenized input sentence is less than `min_len` tokens, we append padding tokens (`<pad>`) to make it `min_len` tokens.
```
import spacy
nlp = spacy.load('en')
def predict_sentiment(model, sentence, min_len = 5):
model.eval()
tokenized = [tok.text for tok in nlp.tokenizer(sentence)]
if len(tokenized) < min_len:
tokenized += ['<pad>'] * (min_len - len(tokenized))
indexed = [TEXT.vocab.stoi[t] for t in tokenized]
tensor = torch.LongTensor(indexed).to(device)
tensor = tensor.unsqueeze(0)
prediction = torch.sigmoid(model(tensor))
return prediction.item()
```
An example negative review...
```
predict_sentiment(model, "This film is terrible")
```
An example positive review...
```
predict_sentiment(model, "This film is great")
```
| true |
code
| 0.87456 | null | null | null | null |
|
# Simulators
## Introduction
This notebook shows how to import *Qiskit Aer* simulator backends and use them to execute ideal (noise free) Qiskit Terra circuits.
```
import numpy as np
# Import Qiskit
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit import Aer, execute
from qiskit.tools.visualization import plot_histogram, plot_state_city
```
## Qiskit Aer simulator backends
Qiskit Aer currently includes three high performance simulator backends:
* `QasmSimulator`: Allows ideal and noisy multi-shot execution of qiskit circuits and returns counts or memory
* `StatevectorSimulator`: Allows ideal single-shot execution of qiskit circuits and returns the final statevector of the simulator after application
* `UnitarySimulator`: Allows ideal single-shot execution of qiskit circuits and returns the final unitary matrix of the circuit itself. Note that the circuit cannot contain measure or reset operations for this backend
These backends are found in the `Aer` provider with the names `qasm_simulator`, `statevector_simulator` and `unitary_simulator`, respectively.
```
# List Aer backends
Aer.backends()
```
The simulator backends can also be directly imported from `qiskit.providers.aer`
```
from qiskit.providers.aer import QasmSimulator, StatevectorSimulator, UnitarySimulator
```
## QasmSimulator
The `QasmSimulator` backend is designed to mimic an actual device. It executes a Qiskit `QuantumCircuit` and returns a count dictionary containing the final values of any classical registers in the circuit. The circuit may contain *gates*,
*measurements*, *resets*, *conditionals*, and other advanced simulator options that will be discussed in another notebook.
### Simulating a quantum circuit
The basic operation executes a quantum circuit and returns a counts dictionary of measurement outcomes. Here we execute a simple circuit that prepares a 2-qubit Bell-state $|\psi\rangle = \frac{1}{2}(|0,0\rangle + |1,1 \rangle)$ and measures both qubits.
```
# Construct quantum circuit
circ = QuantumCircuit(2, 2)
circ.h(0)
circ.cx(0, 1)
circ.measure([0,1], [0,1])
# Select the QasmSimulator from the Aer provider
simulator = Aer.get_backend('qasm_simulator')
# Execute and get counts
result = execute(circ, simulator).result()
counts = result.get_counts(circ)
plot_histogram(counts, title='Bell-State counts')
```
### Returning measurement outcomes for each shot
The `QasmSimulator` also supports returning a list of measurement outcomes for each individual shot. This is enabled by setting the keyword argument `memory=True` in the `assemble` or `execute` function.
```
# Construct quantum circuit
circ = QuantumCircuit(2, 2)
circ.h(0)
circ.cx(0, 1)
circ.measure([0,1], [0,1])
# Select the QasmSimulator from the Aer provider
simulator = Aer.get_backend('qasm_simulator')
# Execute and get memory
result = execute(circ, simulator, shots=10, memory=True).result()
memory = result.get_memory(circ)
print(memory)
```
### Starting simulation with a custom initial state
The `QasmSimulator` allows setting a custom initial statevector for the simulation. This means that all experiments in a Qobj will be executed starting in a state $|\psi\rangle$ rather than the all zero state $|0,0,..0\rangle$. The custom state may be set in the circuit using the `initialize` method.
**Note:**
* The initial statevector must be a valid quantum state $|\langle\psi|\psi\rangle|=1$. If not, an exception will be raised.
* The simulator supports this option directly for efficiency, but it can also be unrolled to standard gates for execution on actual devices.
We now demonstrate this functionality by setting the simulator to be initialized in the final Bell-state of the previous example:
```
# Construct a quantum circuit that initialises qubits to a custom state
circ = QuantumCircuit(2, 2)
circ.initialize([1, 0, 0, 1] / np.sqrt(2), [0, 1])
circ.measure([0,1], [0,1])
# Select the QasmSimulator from the Aer provider
simulator = Aer.get_backend('qasm_simulator')
# Execute and get counts
result = execute(circ, simulator).result()
counts = result.get_counts(circ)
plot_histogram(counts, title="Bell initial statevector")
```
## StatevectorSimulator
The `StatevectorSimulator` executes a single shot of a Qiskit `QuantumCircuit` and returns the final quantum statevector of the simulation. The circuit may contain *gates*, and also *measurements*, *resets*, and *conditional* operations.
### Simulating a quantum circuit
The basic operation executes a quantum circuit and returns a counts dictionary of measurement outcomes. Here we execute a simple circuit that prepares a 2-qubit Bell-state $|\psi\rangle = \frac{1}{2}(|0,0\rangle + |1,1 \rangle)$ and measures both qubits.
```
# Construct quantum circuit without measure
circ = QuantumCircuit(2)
circ.h(0)
circ.cx(0, 1)
# Select the StatevectorSimulator from the Aer provider
simulator = Aer.get_backend('statevector_simulator')
# Execute and get counts
result = execute(circ, simulator).result()
statevector = result.get_statevector(circ)
plot_state_city(statevector, title='Bell state')
```
### Simulating a quantum circuit with measurement
Note that if a circuit contains *measure* or *reset* the final statevector will be a conditional statevector *after* simulating wave-function collapse to the outcome of a measure or reset. For the Bell-state circuit this means the final statevector will be *either* $|0,0\rangle$ *or* $|1, 1\rangle$.
```
# Construct quantum circuit with measure
circ = QuantumCircuit(2, 2)
circ.h(0)
circ.cx(0, 1)
circ.measure([0,1], [0,1])
# Select the StatevectorSimulator from the Aer provider
simulator = Aer.get_backend('statevector_simulator')
# Execute and get counts
result = execute(circ, simulator).result()
statevector = result.get_statevector(circ)
plot_state_city(statevector, title='Bell state post-measurement')
```
### Starting simulation with a custom initial state
Like the `QasmSimulator`, the `StatevectorSimulator` also allows setting a custom initial statevector for the simulation. Here we run the previous initial statevector example on the `StatevectorSimulator` and initialize it to the Bell state.
```
# Construct a quantum circuit that initialises qubits to a custom state
circ = QuantumCircuit(2)
circ.initialize([1, 0, 0, 1] / np.sqrt(2), [0, 1])
# Select the StatevectorSimulator from the Aer provider
simulator = Aer.get_backend('statevector_simulator')
# Execute and get counts
result = execute(circ, simulator).result()
statevector = result.get_statevector(circ)
plot_state_city(statevector, title="Bell initial statevector")
```
## Unitary Simulator
The `UnitarySimulator` constructs the unitary matrix for a Qiskit `QuantumCircuit` by applying each gate matrix to an identity matrix. The circuit may only contain *gates*, if it contains *resets* or *measure* operations an exception will be raised.
### Simulating a quantum circuit unitary
For this example we will return the unitary matrix corresponding to the previous examples circuit which prepares a bell state.
```
# Construct an empty quantum circuit
circ = QuantumCircuit(2)
circ.h(0)
circ.cx(0, 1)
# Select the UnitarySimulator from the Aer provider
simulator = Aer.get_backend('unitary_simulator')
# Execute and get counts
result = execute(circ, simulator).result()
unitary = result.get_unitary(circ)
print("Circuit unitary:\n", unitary)
```
### Setting a custom initial unitary
We may also set an initial state for the `UnitarySimulator`, however this state is an initial *unitary matrix* $U_i$, not a statevector. In this case the returned unitary will be $U.U_i$ given by applying the circuit unitary to the initial unitary matrix.
**Note:**
* The initial unitary must be a valid unitary matrix $U^\dagger.U =\mathbb{1}$. If not, an exception will be raised.
* If a `Qobj` contains multiple experiments, the initial unitary must be the correct size for *all* experiments in the `Qobj`, otherwise an exception will be raised.
Let us consider preparing the output unitary of the previous circuit as the initial state for the simulator:
```
# Construct an empty quantum circuit
circ = QuantumCircuit(2)
circ.id([0,1])
# Set the initial unitary
opts = {"initial_unitary": np.array([[ 1, 1, 0, 0],
[ 0, 0, 1, -1],
[ 0, 0, 1, 1],
[ 1, -1, 0, 0]] / np.sqrt(2))}
# Select the UnitarySimulator from the Aer provider
simulator = Aer.get_backend('unitary_simulator')
# Execute and get counts
result = execute(circ, simulator, backend_options=opts).result()
unitary = result.get_unitary(circ)
print("Initial Unitary:\n", unitary)
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
```
| true |
code
| 0.609815 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.