prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# MNIST - Lightning ⚡️ Syft Duet - Data Scientist 🥁
## PART 1: Connect to a Remote Duet Server
As the Data Scientist, you want to perform data science on data that is sitting in the Data Owner's Duet server in their Notebook.
In order to do this, we must run the code that the Data Owner sends us, which importantly includes their Duet Session ID. The code will look like this, importantly with their real Server ID.
```
import syft as sy
duet = sy.duet('xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx')
```
This will create a direct connection from my notebook to the remote Duet server. Once the connection is established all traffic is sent directly between the two nodes.
Paste the code or Server ID that the Data Owner gives you and run it in the cell below. It will return your Client ID which you must send to the Data Owner to enter into Duet so it can pair your notebooks.
```
import torch
import torchvision
import syft as sy
from torch import nn
from pytorch_lightning import Trainer
from pytorch_lightning.experimental.plugins.secure.pysyft import SyLightningModule
from pytorch_lightning.utilities.imports import is_syft_initialized
from pytorch_lightning.metrics import Accuracy
from syft.util import get_root_data_path
duet = sy.join_duet(loopback=True)
sy.client_cache["duet"] = duet
assert is_syft_initialized()
```
## PART 2: Setting up a Model and our Data
The majority of the code below has been adapted closely from the original PyTorch MNIST example which is available in the `original` directory with these notebooks.
The `duet` variable is now your reference to a whole world of remote operations including supported libraries like torch.
Lets take a look at the duet.torch attribute.
```
duet.torch
```
Lets create a model just like the one in the MNIST example. We do this in almost the exact same way as in PyTorch. The main difference is we inherit from sy.Module instead of nn.Module and we need to pass in a variable called torch_ref which we will use internally for any calls that would normally be to torch.
```
class SyNet(sy.Module):
def __init__(self, torch_ref) -> None:
super(SyNet, self).__init__(torch_ref=torch_ref)
self.conv1 = self.torch_ref.nn.Conv2d(1, 32, 3, 1)
self.conv2 = self.torch_ref.nn.Conv2d(32, 64, 3, 1)
self.dropout1 = self.torch_ref.nn.Dropout2d(0.25)
self.dropout2 = self.torch_ref.nn.Dropout2d(0.5)
self.fc1 = self.torch_ref.nn.Linear(9216, 128)
self.fc2 = self.torch_ref.nn.Linear(128, 10)
self.train_acc = Accuracy()
self.test_acc = Accuracy()
def forward(self, x):
x = self.conv1(x)
x = self.torch_ref.nn.functional.relu(x)
x = self.conv2(x)
x = self.torch_ref.nn.functional.relu(x)
x = self.torch_ref.nn.functional.max_pool2d(x, 2)
x = self.dropout1(x)
x = self.torch_ref.flatten(x, 1)
x = self.fc1(x)
x = self.torch_ref.nn.functional.relu(x)
x = self.dropout2(x)
x = self.fc2(x)
output = self.torch_ref.nn.functional.log_softmax(x, dim=1)
return output
class LiftSyLightningModule(SyLightningModule):
def __init__(self, module, duet):
super().__init__(module, duet)
def train(self, mode: bool = True):
if self.is_remote:
return self.remote_model.train(mode)
else:
return self.module.train(mode)
def eval(self):
return self.train(False)
def training_step(self, batch, batch_idx):
data_ptr, target_ptr = batch[0], batch[1] # batch is list so no destructuring
output = self.forward(data_ptr)
loss = self.torch.nn.functional.nll_loss(output, target_ptr)
target = target_ptr.get(delete_obj=False)
real_output = output.get(delete_obj=False)
self.log("train_acc", self.module.train_acc(real_output.argmax(-1), target), on_epoch=True, prog_bar=True)
return loss
def test_step(self, batch, batch_idx):
data, target = batch[0], batch[1] # batch is list so no destructuring
output = self.forward(data)
loss = self.torch.nn.functional.nll_loss(output, target)
self.log("test_loss", loss, on_step=True, on_epoch=True, prog_bar=True)
def configure_optimizers(self):
optimizer = self.torch.optim.SGD(self.model.parameters(), lr=0.1)
return optimizer
@property
def torchvision(self):
tv = duet.torchvision if self.is_remote() else torchvision
return tv
def get_transforms(self):
current_list = duet.python.List if self.is_remote() else list
transforms = current_list()
transforms.append(self.torchvision.transforms.ToTensor())
transforms.append(self.torchvision.transforms.Normalize(0.1307, 0.3081))
transforms_compose = self.torchvision.transforms.Compose(transforms)
return transforms_compose
def train_dataloader(self):
transforms_ptr = self.get_transforms()
train_dataset_ptr = self.torchvision.datasets.MNIST(
str(get_root_data_path()),
train=True,
download=True,
transform=transforms_ptr,
)
train_loader_ptr = self.torch.utils.data.DataLoader(
train_dataset_ptr, batch_size=500
)
return train_loader_ptr
def test_dataloader(self):
transforms = self.get_transforms()
test_dataset = self.torchvision.datasets.MNIST(
str(get_root_data_path()),
train=False,
download=True,
transform=transforms,
)
test_loader = self.torch.utils.data.DataLoader(test_dataset, batch_size=1)
return test_loader
module = SyNet(torch)
model = LiftSyLightningModule(module=module, duet=duet)
limit_train_batches = 1.0 # 1.0 is 100% of data
trainer = Trainer(
default_root_dir="./",
max_epochs=1,
limit_train_batches=limit_train_batches
)
trainer.fit(model)
model = LiftSyLightningModule.load_from_checkpoint(
trainer.checkpoint_callback.best_model_path, module=module, duet=duet
)
if not model.module.is_local:
local_model = model.module.get(
request_block=True,
reason="test evaluation",
timeout_secs=5
)
else:
local_model = model
torch.save(local_model.state_dict(), "weights.pt")
from torch import nn
class NormalModel(nn.Module):
def __init__(self) -> None:
super(NormalModel, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, 1)
self.conv2 = nn.Conv2d(32, 64, 3, 1)
self.dropout1 = nn.Dropout2d(0.25)
self.dropout2 = nn.Dropout2d(0.5)
self.fc1 = nn.Linear(9216, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.conv1(x)
x = nn.functional.relu(x)
x = self.conv2(x)
x = nn.functional.relu(x)
x = nn.functional.max_pool2d(x, 2)
x = self.dropout1(x)
x = torch.flatten(x, 1)
x = self.fc1(x)
x = nn.functional.relu(x)
x = self.dropout2(x)
x = self.fc2(x)
output = nn.functional.log_softmax(x, dim=1)
return output
torch_model = NormalModel()
saved_state_dict = torch.load("weights.pt")
torch_model.load_state_dict(saved_state_dict)
# TorchVision hotfix https://github.com/pytorch/vision/issues/3549
from syft.util import get_root_data_path
from torchvision import datasets
import torch.nn.functional as F
datasets.MNIST.resources = [
(
"https://ossci-datasets.s3.amazonaws.com/mnist/train-images-idx3-ubyte.gz",
"f68b3c2dcbeaaa9fbdd348bbdeb94873",
),
(
"https://ossci-datasets.s3.amazonaws.com/mnist/train-labels-idx1-ubyte.gz",
"d53e105ee54ea40749a09fcbcd1e9432",
),
(
"https://ossci-datasets.s3.amazonaws.com/mnist/t10k-images-idx3-ubyte.gz",
"9fb629c4189551a2d022fa330f9573f3",
),
(
"https://ossci-datasets.s3.amazonaws.com/mnist/t10k-labels-idx1-ubyte.gz",
"ec29112dd5afa0611ce80d1b7f02629c",
),
]
batch_size_test = 100
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST(
get_root_data_path(),
train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize((0.1307,), (0.3081,))
])
),
batch_size=batch_size_test, shuffle=True
)
def test(network, test_loader):
network.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
output = network(data)
test_loss += F.nll_loss(output, target, size_average=False).item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
accuracy = 100. * correct / len(test_loader.dataset)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(test_loss, correct, len(test_loader.dataset), accuracy))
return accuracy.item()
result = test(torch_model, test_loader)
expected_accuracy = 93.0
assert result > expected_accuracy
```
| true |
code
| 0.790267 | null | null | null | null |
|
# Logistic Regression
---
- Author: Diego Inácio
- GitHub: [github.com/diegoinacio](https://github.com/diegoinacio)
- Notebook: [regression_logistic.ipynb](https://github.com/diegoinacio/machine-learning-notebooks/blob/master/Machine-Learning-Fundamentals/regression_logistic.ipynb)
---
Overview and implementation of *Logistic Regression* analysis.
```
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from regression__utils import *
```
$$ \large
h_{\theta}(x)=g(\theta^Tx)=\frac{e^{\theta^Tx}}{1+e^{\theta^Tx}}=\frac{1}{1+e^{-\theta^Tx}}
$$
where:
$$ \large
\theta^Tx=
\begin{bmatrix}
\theta_0 \\
\theta_1 \\
\vdots \\
\theta_i
\end{bmatrix}
\begin{bmatrix}
1 & x_{11} & \cdots & x_{1i} \\
1 & x_{21} & \cdots & x_{2i} \\
\vdots & \vdots & \ddots & \vdots \\
1 & x_{n1} & \cdots & x_{ni}
\end{bmatrix}
$$
where:
- $\large h_\theta(x)$ is the hypothesis;
- $\large g(z)$ is the logistic function or <em>sigmoid</em>;
- $\large \theta_i$ is the parameters (or <em>weights</em>).
```
def arraycast(f):
'''
Decorator for vectors and matrices cast
'''
def wrap(self, *X, y=[]):
X = np.array(X)
X = np.insert(X.T, 0, 1, 1)
if list(y):
y = np.array(y)[np.newaxis]
return f(self, X, y)
return f(self, X)
return wrap
class logisticRegression(object):
def __init__(self, rate=0.001, iters=1024):
self._rate = rate
self._iters = iters
self._theta = None
@property
def theta(self):
return self._theta
def _sigmoid(self, Z):
return 1/(1 + np.exp(-Z))
def _dsigmoid(self, Z):
return self._sigmoid(Z)*(1 - self._sigmoid(Z))
@arraycast
def fit(self, X, y=[]):
self._theta = np.ones((1, X.shape[-1]))
for i in range(self._iters):
thetaTx = np.dot(X, self._theta.T)
h = self._sigmoid(thetaTx)
delta = h - y.T
grad = np.dot(X.T, delta).T
self._theta -= grad*self._rate
@arraycast
def pred(self, x):
return self._sigmoid(np.dot(x, self._theta.T)) > 0.5
# Synthetic data 5
x1, x2, y = synthData5()
```

```
%%time
# Training
rlogb = logisticRegression(rate=0.001, iters=512)
rlogb.fit(x1, x2, y=y)
rlogb.pred(x1, x2)
```

To find the boundary line components:
$$ \large
\theta_0+\theta_1 x_1+\theta_2 x_2=0
$$
Considering $\large x_2$ as the dependent variable:
$$ \large
x_2=-\frac{\theta_0+\theta_1 x_1}{\theta_2}
$$
```
# Prediction
w0, w1, w2 = rlogb.theta[0]
f = lambda x: - (w0 + w1*x)/w2
```

| true |
code
| 0.682441 | null | null | null | null |
|
Deep neural networks have produced large accuracy gains in applications such as computer vision, speech recognition and natural language processing. Rapid advancements in this area have been supported by excellent libraries for developing neural networks. These libraries allow users to express neural networks in terms of a computation graph, i.e., a sequence of mathematical operations, that maps vector inputs to outputs. Given this graph, these libraries support learning network parameters from data and furthermore can optimize computation, for example, by using GPUs. The ease of developing neural networks with these libraries is a significant factor in the proliferation of these models.
Unfortunately, structured prediction problems cannot be easily expressed in neural network libraries. These problems require making a set of interrelated predictions and occur frequently in natural language processing. For example, part-of-speech tagging requires assigning a part-of-speech tag to each word in a sentence, where tags for nearby words may depend on each other. Another example is dependency parsing, which requires predicting a directed tree spanning the words of a sentence. These problems can be posed as predicting a sequence of actions, such as shifts and reduces for parsing. Neural networks can be applied to these problems using locally-normalized models, which produce a probability distribution over each action given all prior actions. However, this approach is known to be suboptimal as it suffers from the *label bias* problem, which is that the scores of future actions cannot affect the scores of previous actions. *Globally-normalized models*, such as conditional random fields, solve this problem by defining a joint distribution over all sequences of actions. These models express a larger class of distributions and provide better predictions than locally-normalized models. Unfortunately, these models cannot be easily expressed or trained using existing neural network libraries.
Our goal is to design a neural network library that supports structured prediction with globally-normalized models. Our observation is that *nondeterministic computation* is a natural formalism for expressing the decision space of a structured prediction problem. For example, we can express a parser as a function that nondeterministically selects a shift or reduce action, applies it to its current state, then recurses to parse the remainder of the sentence. Our library has a nondeterministic choice operator similar to McCarthy's `amb` for this purpose. We combine nondeterministic choice with a computation graph, which, as demonstrated by neural network libraries, is a powerful way for users to express models. Importantly, *the computation graph interacts with nondeterministic computation*: the scores produced by the neural network determine the probabilities of nondeterministic choices, and the nondeterministic choices determine the network's architecture. The combination of these operations results in a powerful formalism for structured prediction where users specify the decision space using nondeterminism and the prediction models using computation graphs.
We implement our library as a Scala monad to leverage Scala's powerful type system, library support, and streamlined syntax for monadic operations. A instance `Pp[X]` of the monad represents a function from neural network parameters to a probability distribution over values of type `X`. The monad supports inference operations that take neural network parameters and return (an approximation of) this distribution. Running inference also generates a neural network and performs a forward pass in this network to compute its outputs, which may influence the probability distribution. The library also supports a variety of optimization algorithms for training parameters from data. These training algorithms use the approximate inference algorithms and also run backpropagation in the generated networks.
```
val path = "/Users/jayantk/github/pnp/"
classpath.addPath(path + "target/scala-2.11/pnp_2.11-0.1.jar")
classpath.addPath(path + "lib/jklol.jar")
classpath.add("com.google.guava" % "guava" % "17.0")
```
To use the `Pp` monad, we statically import its functions. Nondeterministic choices are expressed using the `choose` function, which has several forms. The simplest takes an explicit list of values and their corresponding probabilities:
```
import org.allenai.pnp.Pp
import org.allenai.pnp.Pp._
val flip = choose(Seq(true, false), Seq(0.75, 0.25))
```
This code represents a weighted coin flip that comes up `true` with probability 0.75 and `false` with probability 0.25. `flip` has type `Pp[Boolean]`, representing a distribution over values of type `Boolean`. The `Pp` object represents this distribution *lazily*, so we need to perform inference on this object to get the probability of each value. Many different inference algorithms could be used for this purpose, such as sampling. Here we perform inference using beam search to estimate the k=10 most probable outcomes:
```
val dist = flip.beamSearch(10)
```
We get back the original distribution, which, while expected, is not that interesting. To construct interesting models, we need to combine multiple nondeterministic choices, which we can do conveniently using Scala's for/yield construction:
```
val threeFlips = for {
flip1 <- choose(Seq(true, false), Seq(0.75, 0.25))
flip2 <- choose(Seq(true, false), Seq(0.75, 0.25))
flip3 <- choose(Seq(true, false), Seq(0.75, 0.25))
} yield {
flip1 && flip2 && flip3
}
val threeFlipsDist = threeFlips.beamSearch(10)
```
This code flips three weighted coins and returns true if they all come up true. Inference again returns the expected distribution, which we can verify by computing 0.75 \* 0.75 \* 0.75 = 0.421. There are 8 entries in the returned distribution because each entry represents a way the program can execute, that is, a particular sequence of choices. Executions have additional state (specifically a computation graph) besides the return value, which is why the "duplicate" entries are not collapsed by inference. We'll see how to use the computation graph later on.
The for/yield construction above essentially means "make these choices sequentially and lazily". This construction is mapped by Scala into calls to `flatMap` on the `Pp` monad, which construct a lazy representation of the probability distribution.
Basically, the for/yield translates into a
We can also define functions with nondeterministic choices. The `flipMany` function flips `num` coins and returns a list of the results:
```
def flipMany(num: Int): Pp[List[Boolean]] = {
if (num == 0) {
value(List())
} else {
for {
flip <- choose(Seq(true, false), Seq(0.75, 0.25))
rest <- flipMany(num - 1)
} yield {
flip :: rest
}
}
}
val flips = flipMany(1000)
val flipsDist = flips.beamSearch(10)
```
Recursive functions such as `flipMany` are a natural way to express many structured prediction models. We will see later how to define a sequence tagger using a function very similar to flipMany.
At this point, it is worthwhile noting that inference does **not** explicitly enumerate all of the possible executions of the program, even though the for/yield syntax suggests this interpretation. We can verify that explicit enumeration does not occur by changing the argument 4 above to something large, such as 10000, that would make enumeration computationally infeasible. Inference still completes quickly because `beamSearch` only approximately searches the space of executions.
The examples above demonstrate how to use `Pp` to express a distribution over values in terms of probabilistic choices and perform inference over the results. The monad also allows us to define computation graphs for neural networks. Here's a function implementing a multilayer perceptron:
```
import scala.collection.JavaConverters._
import org.allenai.pnp.{ Env, CompGraph, CompGraphNode }
import com.jayantkrish.jklol.tensor.{ Tensor, DenseTensor }
import com.jayantkrish.jklol.util.IndexedList
import com.google.common.base.Preconditions
def multilayerPerceptron(featureVector: Tensor): Pp[CompGraphNode] = for {
params <- param("params")
bias <- param("bias")
hidden = ((params * featureVector) + bias).tanh
params2 <- param("params2")
bias2 <- param("bias2")
dist = (params2 * hidden) + bias2
} yield {
dist
}
```
This function applies a two-layer neural network to an input feature vector. The feature vector is represented as a ```Tensor``` from the jklol library. Neural network parameters are retrieved by name using the ```param``` function and are instances of ```CompGraphNode```. The function builds a neural network out of these nodes by applying standard operations such as matrix/vector multiplication, addition, and the hyperbolic tangent. These operations are overloaded to create new nodes in the computation graph.
Something that may seem odd is that the return type for this method is `Pp[CompGraphNode]`, that is, a distribution over computation graph nodes. The reason for this type is that operations on `CompGraphNode` are **stateful** and manipulate an underlying computation graph. However, this graph is tracked by the `Pp` monad so it doesn't need to be explicitly referenced. This type also enables the computation graph to interact with nondeterministic choices, as we will see later.
Let's evaluate our neural network with a feature vector and some random parameters:
```
val features = new DenseTensor(
// Dimension specification for the tensor
Array[Int](2), Array[Int](2),
// The tensor's values
Array(1, 1))
// Evaluate the network with the feature
val nnPp = multilayerPerceptron(features)
// Randomly initialize the network parameters
val compGraph = new CompGraph(
IndexedList.create(List("params", "bias", "params2", "bias2").asJava),
Array(DenseTensor.random(Array(2, 1), Array(2, 8), 0.0, 1.0),
DenseTensor.random(Array(1), Array(8), 0.0, 1.0),
DenseTensor.random(Array(0, 1), Array(2, 8), 0.0, 1.0),
DenseTensor.random(Array(0), Array(2), 0.0, 1.0)))
val dist = nnPp.beamSearch(10, Env.init, compGraph).executions
val nnOutput = dist(0).value.value
```
To evaluate the network we define values for the feature vector as well as the named network parameters. These parameters are declared by creating a computation graph containing them. This graph is then passed to the `beamSearch` method which performs the forward pass of inference in the neural network. Inference returns a distribution with a single `CompGraphNode` that contains the network's output as its `value`. The output is a tensor with two values, which is all we can expect given the random inputs.
Again, it may seem odd that `beamSearch` computes the network's forward pass in addition to performing probabilistic inference. This overloading is intentional, as it allows us to combine neural networks with nondeterministic choices to create probability distributions. Let's use our multilayer perceptron to define a probability distribution:
```
def booleanFunction(left: Boolean, right: Boolean): Pp[Boolean] = {
// Build a feature vector from the inputs
val values = Array.ofDim[Double](2)
values(0) = if (left) { 1 } else { 0 }
values(1) = if (right) { 1 } else { 0 }
val featureVector = new DenseTensor(
Array[Int](2), Array[Int](2), values)
for {
dist <- multilayerPerceptron(featureVector)
output <- choose(Array(false, true), dist)
} yield {
output
}
}
val output = booleanFunction(true, true)
val dist = output.beamSearch(10, Env.init, compGraph)
for (d <- dist.executions) {
println(d.value + " " + (d.prob / dist.partitionFunction))
}
```
This function computes a distribution over boolean outputs given two boolean inputs. It encodes the inputs as a feature vector, passes this vector to the multilayer perceptron, then uses the output of the perceptron to choose the output. Note that the input '(true, true)' is encoded as the same feature vector used in the above code block, and that the network has the same parameters. If you look closely at the output of the two above cells, you'll notice that 113.15 = e^4.72 and 12.73 = e^2.54. That's because the values computed by the neural network are logspace weights for each execution. Normalizing these weights gives us a probability distribution over executions.
Next, let's train the network parameters to learn the xor function. First, let's create some training examples:
```
import org.allenai.pnp.PpExample
// Create training data.
val data = List(
(true, true, false),
(true, false, true),
(false, true, true),
(false, false, false)
)
val examples = data.map(x => {
val unconditional = booleanFunction(x._1, x._2)
val conditional = for {
y <- unconditional;
x <- Pp.require(y == x._3)
} yield {
y
}
PpExample.fromDistributions(unconditional, conditional)
})
```
A training example consists of a tuple of an unconditional and a conditional probability distribution. The unconditional distribution is generated by calling `booleanFunction`, and the conditional distribution is generated by constraining the unconditional distribution to have the correct label using ``require``. Using these examples, we can train the network:
```
import com.jayantkrish.jklol.models.DiscreteVariable
import com.jayantkrish.jklol.models.VariableNumMap
import com.jayantkrish.jklol.training.{ StochasticGradientTrainer, Lbfgs }
import com.jayantkrish.jklol.training.NullLogFunction
import org.allenai.pnp.ParametricPpModel
import org.allenai.pnp.PpLoglikelihoodOracle
// Initialize neural net parameters and their dimensionalities.
// TODO(jayantk): This is more verbose than necessary
val v = DiscreteVariable.sequence("boolean", 2);
val h = DiscreteVariable.sequence("hidden", 8);
val inputVar = VariableNumMap.singleton(2, "input", v)
val hiddenVar = VariableNumMap.singleton(1, "hidden", h)
val outputVar = VariableNumMap.singleton(0, "output", v)
val paramNames = IndexedList.create(
List("params", "bias", "params2", "bias2").asJava
)
val family = new ParametricPpModel(
paramNames,
List(inputVar.union(hiddenVar), hiddenVar,
hiddenVar.union(outputVar), outputVar)
);
// Train model
val oracle = new PpLoglikelihoodOracle[Boolean](100, family)
val trainer = StochasticGradientTrainer.createWithL2Regularization(
1000, 1, 1.0, false, false, 10.0, 0.0, new NullLogFunction()
)
val params = family.getNewSufficientStatistics
params.perturb(1.0)
val trainedParams = trainer.train(oracle, params, examples.asJava)
val model = family.getModelFromParameters(trainedParams)
```
TODO (jayantk): The syntax for declaring parameter dimensionalities is overcomplicated at the moment.
The first part of the above code declares the dimensionalities for each parameter of the network, and the second part trains these parameters using 1000 iterations of stochastic gradient descent. Let's evaluate our function with the trained parameters:
```
val marginals = booleanFunction(false, true).beamSearch(
100, Env.init, model.getInitialComputationGraph)
val dist = marginals.executions
```
For the input `(true, true)`, the predicted output is overwhelmingly likely to be `false`. You can change the arguments above to convince yourself that we have indeed learned the xor function.
Of course, any neural network library can be used to learn xor. The power of the interaction between neural networks and nondeterministic choices only appears when we start doing structured prediction. Let's build a shift-reduce parser for a context free grammar. First, let's create some data structures to represent parse trees:
```
abstract class Parse(val pos: String) {
def getTokens: List[String]
}
case class Terminal(word: String, override val pos: String) extends Parse(pos) {
override def getTokens: List[String] = {
List(word)
}
override def toString: String = {
pos + " -> " + word
}
}
case class Nonterminal(left: Parse, right: Parse, override val pos: String) extends Parse(pos) {
override def getTokens: List[String] = {
left.getTokens ++ right.getTokens
}
override def toString: String = {
pos + " -> (" + left.toString + ", " + right.toString + ")"
}
}
```
Let's also create some data structures to represent the parser's state and actions:
```
import scala.collection.mutable.ListBuffer
import scala.collection.mutable.MultiMap
import scala.collection.mutable.{ HashMap, Set }
// The state of a shift-reduce parser consists of a buffer
// of tokens that haven't been consumed yet and a stack
// of parse trees spanning the consumed tokens.
case class ShiftReduceState(tokens: List[String], stack: List[Parse])
// Classes for representing actions of a shift/reduce
// parser.
abstract class Action {
def apply(state: ShiftReduceState): ShiftReduceState
// An action is responsible for generating the computation graph
// that scores it.
def score(state: ShiftReduceState): Pp[CompGraphNode]
def addParams(names: IndexedList[String], vars: ListBuffer[VariableNumMap]): Unit
}
// The shift action consumes the first token on the buffer
// and pushes a parse tree on to the stack.
class Shift(val word: String, val pos: String) extends Action {
val terminal = Terminal(word, pos)
val paramName = "shift_" + word + "_" + pos
override def apply(state: ShiftReduceState): ShiftReduceState = {
ShiftReduceState(state.tokens.tail, (terminal :: state.stack))
}
override def score(state: ShiftReduceState): Pp[CompGraphNode] = {
Pp.param(paramName)
}
override def addParams(names: IndexedList[String], vars: ListBuffer[VariableNumMap]): Unit = {
names.add(paramName)
vars += VariableNumMap.EMPTY
}
}
// The reduce action combines the top two parses on the stack
// into a single parse.
class Reduce(val leftPos: String, val rightPos: String, val rootPos: String) extends Action {
val paramName = "reduce_" + leftPos + "_" + rightPos + "_" + rootPos
override def apply(state: ShiftReduceState): ShiftReduceState = {
val left = state.stack(1)
val right = state.stack(0)
val nonterminal = Nonterminal(left, right, rootPos)
ShiftReduceState(state.tokens, (nonterminal :: state.stack.drop(2)))
}
override def score(state: ShiftReduceState): Pp[CompGraphNode] = {
Pp.param(paramName)
}
override def addParams(names: IndexedList[String], vars: ListBuffer[VariableNumMap]): Unit = {
names.add(paramName)
vars += VariableNumMap.EMPTY
}
}
```
Using these data structures, we can define the parser as follows:
```
class PpParser(
lexActions: MultiMap[String, Action],
grammarActions: MultiMap[(String, String), Action]
) {
def parse(sent: List[String]): Pp[Parse] = {
parse(ShiftReduceState(sent, List()))
}
def parse(state: ShiftReduceState): Pp[Parse] = {
val tokens = state.tokens
val stack = state.stack
if (tokens.size == 0 && stack.size == 1) {
// All tokens consumed and all possible
// reduces performed.
value(stack.head)
} else {
// Queue for each possible action
val actions = ListBuffer[Action]()
// Queue shift actions
if (tokens.size > 0) {
val shifts = lexActions.getOrElse(tokens.head, Set())
actions ++= shifts
}
// Queue reduce actions
if (stack.size >= 2) {
val left = stack(1)
val right = stack(0)
val reduces = grammarActions.getOrElse((left.pos, right.pos), Set())
actions ++= reduces
}
for {
// Score each possible action, nondeterministically
// select one to apply, then recurse on the next
// parser state.
scores <- scoreActions(state, actions);
action <- choose(actions.toArray, scores)
p <- parse(action.apply(state))
} yield {
p
}
}
}
def scoreActions(state: ShiftReduceState, actions: ListBuffer[Action]): Pp[Array[CompGraphNode]] = {
val scoreList = actions.foldRight(Pp.value(List[CompGraphNode]()))((action, list) =>
for {
x <- action.score(state);
l <- list
} yield {
x :: l
})
scoreList.flatMap { x => Pp.value(x.toArray) }
}
// Generate the parameters used in the neural network
// of this parser.
def getParams: ParametricPpModel = {
val paramNames = IndexedList.create[String]()
val paramVars = ListBuffer[VariableNumMap]()
lexActions.values.foreach(_.foreach(_.addParams(paramNames, paramVars)))
grammarActions.values.foreach(_.foreach(_.addParams(paramNames, paramVars)))
new ParametricPpModel(paramNames, paramVars.toList)
}
}
object PpParser {
// Initialize parser actions from maps of string -> part of speech
// for shift actions and (pos, pos) -> pos for reduce actions
def fromMaps(
lexicon: List[(String, String)],
grammar: List[((String, String), String)]
): PpParser = {
val lexActions = new HashMap[String, Set[Action]] with MultiMap[String, Action]
for ((k, v) <- lexicon) {
lexActions.addBinding(k, new Shift(k, v))
}
val grammarActions = new HashMap[(String, String), Set[Action]] with MultiMap[(String, String), Action]
for ((k, v) <- grammar) {
grammarActions.addBinding(k, new Reduce(k._1, k._2, v))
}
new PpParser(lexActions, grammarActions)
}
}
```
All said and done, we've built a globally-normalized shift-reduce parser with neural network factors in less than 200 lines of code, much of which is simple data structures. The scoring function for actions is overly simple, but this is easy to improve using the computation graph operations as we saw in the xor example. Let's use the parser to parse some sentences:
```
// The set of shift actions
val lexicon = List(
("the", "DT"),
("the", "NN"),
("blue", "NN"),
("man", "NN")
)
// The set of reduce actions
val grammar = List(
(("DT", "NN"), "NP"),
(("NN", "NN"), "NN")
)
val parser = PpParser.fromMaps(lexicon, grammar)
// Get the neural network parameters needed to score
// parses in dist
val family = parser.getParams
val model = family.getModelFromParameters(
family.getNewSufficientStatistics)
val cg = model.getInitialComputationGraph
// Run inference
val dist = parser.parse(List("the", "blue", "man"))
val marginals = dist.beamSearch(100, Env.init, cg)
val parses = marginals.executions
```
Parsing seems to work. We initialized the parameters to 0, so we get a uniform distribution over parse trees for the sentence. Now let's train the parser:
```
val trainingData = List[Parse](
Nonterminal(Terminal("the", "DT"), Terminal("man", "NN"), "NP"),
Nonterminal(Terminal("blue", "NN"), Terminal("man", "NN"), "NN")
)
// Convert the trees to unconditional / conditional distributions
// that are used for training.
val examples = trainingData.map(tree => {
val unconditional = parser.parse(tree.getTokens)
val conditional = for {
parse <- unconditional;
_ <- Pp.require(parse == tree)
} yield {
parse
}
PpExample.fromDistributions(unconditional, conditional)
})
val oracle = new PpLoglikelihoodOracle[Parse](100, family)
val trainer = StochasticGradientTrainer.createWithL2Regularization(
1000, 1, 1.0, false, false, 10.0, 0.0, new NullLogFunction())
val params = family.getNewSufficientStatistics
val trainedParams = trainer.train(oracle, params, examples.asJava)
val model = family.getModelFromParameters(trainedParams)
val dist = parser.parse(List("the", "blue", "man"))
val marginals = dist.beamSearch(100, Env.init, model.getInitialComputationGraph)
val parses = marginals.executions
```
The code above is nearly identical to the code for the xor example. We generate unconditional/conditional distributions over parse trees, then maximize loglikelihood with stochastic gradient descent. Parsing the same sentence now gives us a highly peaked distribution on the tree present in the training data.
```
def answerQ(question: String): Pp[String] = {
for {
sentence <- chooseSentence(question)
answer <- chooseAnswer(sentence)
} yield {
answer
}
}
def chooseSentence(question: String): Pp[String] = {
sentences = retrieveSentences(question)
for {
scores <- map(sentences, sentenceNN _)
sent <- choose(sentences, scores)
} yield {
sent
}
}
def sentenceNn(sentence: String): Pp[Expression] = {
// Build a neural net to score the sentence
}
val data = List((answerQ("The thermometer ..."), "temperature"),
(answerQ("What season occurs when ..."), "summer"))
```
| true |
code
| 0.49884 | null | null | null | null |
|
```
#hide
from neos.models import *
from neos.makers import *
from neos.transforms import *
from neos.fit import *
from neos.infer import *
from neos.smooth import *
```
# neos
> ~neural~ nice end-to-end optimized statistics
[](https://zenodo.org/badge/latestdoi/235776682)  [](https://mybinder.org/v2/gh/pyhf/neos/master?filepath=demo_training.ipynb)
<img src="assets/neos_logo.png" alt="neos logo" width="250"/>

## About
Leverages the shoulders of giants ([`jax`](https://github.com/google/jax/), [`fax`](https://github.com/gehring/fax), and [`pyhf`](https://github.com/scikit-hep/pyhf)) to differentiate through a high-energy physics analysis workflow, including the construction of the frequentist profile likelihood.
Documentation can be found at [gradhep.github.io/neos](gradhep.github.io/neos)!
To see examples of `neos` in action, look for the notebooks in the nbs folder with the `demo_` prefix.
If you're more of a video person, see [this talk](https://www.youtube.com/watch?v=3P4ZDkbleKs) given by [Nathan](https://github.com/phinate) on the broader topic of differentiable programming in high-energy physics, which also covers `neos`.
## Install
Just run
```
python -m pip install neos
```
## Contributing
**Please read** [`CONTRIBUTING.md`](https://github.com/pyhf/neos/blob/master/CONTRIBUTING.md) **before making a PR**, as this project is maintained using [`nbdev`](https://github.com/fastai/nbdev), which operates completely using Jupyter notebooks. One should make their changes in the corresponding notebooks in the [`nbs`](nbs) folder (including `README` changes -- see `nbs/index.ipynb`), and not in the library code, which is automatically generated.
## Example usage -- train a neural network to optimize an expected p-value
```
# bunch of imports:
import time
import jax
import jax.experimental.optimizers as optimizers
import jax.experimental.stax as stax
import jax.random
from jax.random import PRNGKey
import numpy as np
from functools import partial
import pyhf
pyhf.set_backend('jax')
pyhf.default_backend = pyhf.tensor.jax_backend(precision='64b')
from neos import data, infer, makers
rng = PRNGKey(22)
```
Let's start by making a basic neural network for regression with the `stax` module found in `jax`:
```
init_random_params, predict = stax.serial(
stax.Dense(1024),
stax.Relu,
stax.Dense(1024),
stax.Relu,
stax.Dense(1),
stax.Sigmoid,
)
```
Now, let's compose a workflow that can make use of this network in a typical high-energy physics statistical analysis.
Our workflow is as follows:
- From a set of normal distributions with different means, we'll generate four blobs of `(x,y)` points, corresponding to a signal process, a nominal background process, and two variations of the background from varying the background distribution's mean up and down.
- We'll then feed these points into the previously defined neural network for each blob, and construct a histogram of the output using kernel density estimation. The difference between the two background variations is used as a systematic uncertainty on the nominal background.
- We can then leverage the magic of `pyhf` to construct an [event-counting statistical model](https://scikit-hep.org/pyhf/intro.html#histfactory) from the histogram yields.
- Finally, we calculate the p-value of a test between the nominal signal and background-only hypotheses. This uses a [profile likelihood-based test statistic](https://arxiv.org/abs/1007.1727).
In code, `neos` can specify this workflow through function composition:
```
# data generator
data_gen = data.generate_blobs(rng,blobs=4)
# histogram maker
hist_maker = makers.hists_from_nn(data_gen, predict, method='kde')
# statistical model maker
model_maker = makers.histosys_model_from_hists(hist_maker)
# CLs value getter
get_cls = infer.expected_CLs(model_maker, solver_kwargs=dict(pdf_transform=True))
```
A peculiarity to note is that each of the functions used in this step actually return functions themselves. The reason we do this is that we need a skeleton of the workflow with all of the fixed parameters to be in place before calculating the loss function, as the only 'moving parts' here are the weights of the neural network.
`neos` also lets you specify hyperparameters for the histograms (e.g. binning, bandwidth) to allow these to be tuned throughout the learning process if neccesary (we don't do that here).
```
bins = np.linspace(0,1,4) # three bins in the range [0,1]
bandwidth = 0.27 # smoothing parameter
get_loss = partial(get_cls, hyperparams=dict(bins=bins,bandwidth=bandwidth))
```
Our loss currently returns a list of metrics -- let's just index into the first one (the CLs value).
```
def loss(params, test_mu):
return get_loss(params, test_mu)[0]
```
Now we just need to initialize the network's weights, and construct a training loop & optimizer:
```
# init weights
_, network = init_random_params(jax.random.PRNGKey(2), (-1, 2))
# init optimizer
opt_init, opt_update, opt_params = optimizers.adam(1e-3)
# define train loop
def train_network(N):
cls_vals = []
_, network = init_random_params(jax.random.PRNGKey(1), (-1, 2))
state = opt_init(network)
losses = []
# parameter update function
def update_and_value(i, opt_state, mu):
net = opt_params(opt_state)
value, grad = jax.value_and_grad(loss)(net, mu)
return opt_update(i, grad, state), value, net
for i in range(N):
start_time = time.time()
state, value, network = update_and_value(i, state, 1.0)
epoch_time = time.time() - start_time
losses.append(value)
metrics = {"loss": losses}
yield network, metrics, epoch_time
```
It's time to train!
```
maxN = 10 # make me bigger for better results (*nearly* true ;])
for i, (network, metrics, epoch_time) in enumerate(train_network(maxN)):
print(f"epoch {i}:", f'CLs = {metrics["loss"][-1]:.5f}, took {epoch_time:.4f}s')
```
And there we go!
You'll notice the first epoch seems to have a much larger training time. This is because `jax` is being used to just-in-time compile some of the code, which is an overhead that only needs to happen once.
If you want to reproduce the full animation from the top of this README, a version of this code with plotting helpers can be found in [`demo_kde_pyhf.ipynb`](https://github.com/pyhf/neos/blob/master/demo_kde_pyhf.ipynb)! :D
## Thanks
A big thanks to the teams behind [`jax`](https://github.com/google/jax/), [`fax`](https://github.com/gehring/fax), and [`pyhf`](https://github.com/scikit-hep/pyhf) for their software and support.
| true |
code
| 0.552781 | null | null | null | null |
|
# Torch Core
This module contains all the basic functions we need in other modules of the fastai library (split with [`core`](/core.html#core) that contains the ones not requiring pytorch). Its documentation can easily be skipped at a first read, unless you want to know what a given fuction does.
```
from fastai.imports import *
from fastai.gen_doc.nbdoc import *
from fastai.layers import *
from fastai.torch_core import *
```
## Global constants
`AdamW = partial(optim.Adam, betas=(0.9,0.99))` <div style="text-align: right"><a href="https://github.com/fastai/fastai/blob/master/fastai/torch_core.py#L43">[source]</a></div>
`bn_types = (nn.BatchNorm1d, nn.BatchNorm2d, nn.BatchNorm3d)` <div style="text-align: right"><a href="https://github.com/fastai/fastai/blob/master/fastai/torch_core.py#L41">[source]</a></div>
`defaults.device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')` <div style="text-align: right"><a href="https://github.com/fastai/fastai/blob/master/fastai/torch_core.py#L62">[source]</a></div>
If you are trying to make fastai run on the CPU, simply change the default device: `defaults.device = 'cpu'`.
Alternatively, if not using wildcard imports: `fastai.torch_core.defaults.device = 'cpu'`.
## Functions that operate conversions
```
show_doc(batch_to_half)
show_doc(flatten_model, full_name='flatten_model')
```
Flattens all the layers of `m` into an array. This allows for easy access to the layers of the model and allows you to manipulate the model as if it was an array.
```
m = simple_cnn([3,6,12])
m
flatten_model(m)
show_doc(model2half)
```
Converting model parameters to half precision allows us to leverage fast `FP16` arithmatic which can speed up the computations by 2-8 times. It also reduces memory consumption allowing us to train deeper models.
**Note**: Batchnorm layers are not converted to half precision as that may lead to instability in training.
```
m = simple_cnn([3,6,12], bn=True)
def show_params_dtype(state_dict):
"""Simple function to pretty print the dtype of the model params"""
for wt_name, param in state_dict.items():
print("{:<30}: {}".format(wt_name, str(param.dtype)))
print()
print("dtypes of model parameters before model2half: ")
show_params_dtype(m.state_dict())
# Converting model to half precision
m_half = model2half(m)
print("dtypes of model parameters after model2half: ")
show_params_dtype(m_half.state_dict())
show_doc(np2model_tensor)
```
It is a wrapper on top of Pytorch's `torch.as_tensor` which converts numpy array to torch tensor, and additionally attempts to map all floats to `torch.float32` and all integers to `torch.int64` for consistencies in model data. Below is an example demonstrating it's functionality for floating number, similar functionality applies to integer as well.
```
a1 = np.ones((2, 3)).astype(np.float16)
a2 = np.ones((2, 3)).astype(np.float32)
a3 = np.ones((2, 3)).astype(np.float64)
b1 = np2model_tensor(a1) # Maps to torch.float32
b2 = np2model_tensor(a2) # Maps to torch.float32
b3 = np2model_tensor(a3) # Maps to torch.float32
print(f"Datatype of as': {a1.dtype}, {a2.dtype}, {a3.dtype}")
print(f"Datatype of bs': {b1.dtype}, {b2.dtype}, {b3.dtype}")
show_doc(requires_grad)
```
Performs both getting and setting of [`requires_grad`](/torch_core.html#requires_grad) parameter of the tensors, which decided whether to accumulate gradients or not.
* If `b` is `None`: The function **gets** the [`requires_grad`](/torch_core.html#requires_grad) for the model parameter, to be more specific it returns the [`requires_grad`](/torch_core.html#requires_grad) of the first element in the model.
* Else if `b` is passed (a boolean value), [`requires_grad`](/torch_core.html#requires_grad) of all parameters of the model is **set** to `b`.
```
# Any Pytorch model
m = simple_cnn([3, 6, 12], bn=True)
# Get the requires_grad of model
print("requires_grad of model: {}".format(requires_grad(m)))
# Set requires_grad of all params in model to false
requires_grad(m, False)
# Get the requires_grad of model
print("requires_grad of model: {}".format(requires_grad(m)))
show_doc(tensor)
```
Handy function when you want to convert any list type object to tensor, initialize your weights manually, and other similar cases.
**NB**: When passing multiple vectors, all vectors must be of same dimensions. (Obvious but can be forgotten sometimes)
```
# Conversion from any numpy array
b = tensor(np.array([1, 2, 3]))
print(b, type(b))
# Passing as multiple parameters
b = tensor(1, 2, 3)
print(b, type(b))
# Passing a single list
b = tensor([1, 2, 3])
print(b, type(b))
# Can work with multiple vectors / lists
b = tensor([1, 2], [3, 4])
print(b, type(b))
show_doc(to_cpu)
```
A wrapper on top of Pytorch's `torch.Tensor.cpu()` function, which creates and returns a copy of a tensor or even a **list** of tensors in the CPU. As described in Pytorch's docs, if the tensor or list of tensor is already on the CPU, the exact data is returned and no copy is made.
Usefult to convert all the list of parameters of the model to CPU in a single call.
```
if torch.cuda.is_available():
a = [torch.randn((1, 1)).cuda() for i in range(3)]
print(a)
print("Id of tensors in a: ")
for i in a: print(id(i))
# Getting a CPU version of the tensors in GPU
b = to_cpu(a)
print(b)
print("Id of tensors in b:")
for i in b: print(id(i))
# Trying to perform to_cpu on a list of tensor already in CPU
c = to_cpu(b)
print(c)
# The tensors in c has exact id as that of b. No copy performed.
print("Id of tensors in c:")
for i in c: print(id(i))
show_doc(to_data)
```
Returns the data attribute from the object or collection of objects that inherits from [`ItemBase`](/core.html#ItemBase) class. Useful to examine the exact values of the data, could be used to work with the data outside of `fastai` classes.
```
# Default example examined
from fastai import *
from fastai.vision import *
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
# Examin the labels
ys = list(data.y)
print("Category display names: ", [ys[0], ys[-1]])
print("Unique classes internally represented as: ", to_data([ys[0], ys[-1]]))
show_doc(to_detach)
show_doc(to_device)
show_doc(to_half)
```
Converts the tensor or list of `FP16`, resulting in less memory consumption and faster computations with the tensor. It does not convert `torch.int` types to half precision.
```
a1 = torch.tensor([1, 2], dtype=torch.int64)
a2 = torch.tensor([1, 2], dtype=torch.int32)
a3 = torch.tensor([1, 2], dtype=torch.int16)
a4 = torch.tensor([1, 2], dtype=torch.float64)
a5 = torch.tensor([1, 2], dtype=torch.float32)
a6 = torch.tensor([1, 2], dtype=torch.float16)
print("dtype of as: ", a1.dtype, a2.dtype, a3.dtype, a4.dtype, a5.dtype, a6.dtype, sep="\t")
b1, b2, b3, b4, b5, b6 = to_half([a1, a2, a3, a4, a5, a6])
print("dtype of bs: ", b1.dtype, b2.dtype, b3.dtype, b4.dtype, b5.dtype, b6.dtype, sep="\t")
show_doc(to_np)
```
Internally puts the data to CPU, and converts to `numpy.ndarray` equivalent of `torch.tensor` by calling `torch.Tensor.numpy()`.
```
a = torch.tensor([1, 2], dtype=torch.float64)
if torch.cuda.is_available():
a = a.cuda()
print(a, type(a), a.device)
b = to_np(a)
print(b, type(b))
show_doc(try_int)
# Converts floating point numbers to integer
print(try_int(12.5), type(try_int(12.5)))
# This is a Rank-1 ndarray, which ideally should not be converted to int
print(try_int(np.array([1.5])), try_int(np.array([1.5])).dtype)
# Numpy array with a single elements are converted to int
print(try_int(np.array(1.5)), type(try_int(np.array(1.5))))
print(try_int(torch.tensor(2.5)), type(try_int(torch.tensor(2.5))))
# Strings are not converted to int (of course)
print(try_int("12.5"), type(try_int("12.5")))
```
## Functions to deal with model initialization
```
show_doc(apply_init)
show_doc(apply_leaf)
show_doc(cond_init)
show_doc(in_channels)
show_doc(init_default)
```
## Functions to get information of a model
```
show_doc(children)
show_doc(children_and_parameters)
show_doc(first_layer)
show_doc(last_layer)
show_doc(num_children)
show_doc(one_param)
show_doc(range_children)
show_doc(trainable_params)
```
## Functions to deal with BatchNorm layers
```
show_doc(bn2float)
show_doc(set_bn_eval)
show_doc(split_bn_bias)
```
## Functions to get random tensors
```
show_doc(log_uniform)
log_uniform(0.5,2,(8,))
show_doc(rand_bool)
rand_bool(0.5, 8)
show_doc(uniform)
uniform(0,1,(8,))
show_doc(uniform_int)
uniform_int(0,2,(8,))
```
## Other functions
```
show_doc(ParameterModule, title_level=3)
show_doc(calc_loss)
show_doc(data_collate)
show_doc(get_model)
show_doc(grab_idx)
show_doc(logit)
show_doc(logit_)
show_doc(model_type)
show_doc(np_address)
show_doc(split_model)
```
If `splits` are layers, the model is split at those (not included) sequentially. If `want_idxs` is True, the corresponding indexes are returned. If `splits` are lists of layers, the model is split according to those.
```
show_doc(split_model_idx)
show_doc(trange_of)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(tensor__array__)
show_doc(ParameterModule.forward)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.647826 | null | null | null | null |
|
```
# default_exp data.metadatasets
```
# Metadatasets: a dataset of datasets
> This functionality will allow you to create a dataset from data stores in multiple, smaller datasets.
* I'd like to thank both Thomas Capelle (https://github.com/tcapelle) and Xander Dunn (https://github.com/xanderdunn) for their contributions to make this code possible.
* This functionality allows you to use multiple numpy arrays instead of a single one, which may be very useful in many practical settings. I've tested it with 10k+ datasets and it works well.
```
#export
from tsai.imports import *
from tsai.utils import *
from tsai.data.validation import *
from tsai.data.core import *
#export
class TSMetaDataset():
" A dataset capable of indexing mutiple datasets at the same time"
def __init__(self, dataset_list, **kwargs):
if not is_listy(dataset_list): dataset_list = [dataset_list]
self.datasets = dataset_list
self.split = kwargs['split'] if 'split' in kwargs else None
self.mapping = self._mapping()
if hasattr(dataset_list[0], 'loss_func'):
self.loss_func = dataset_list[0].loss_func
else:
self.loss_func = None
def __len__(self):
if self.split is not None:
return len(self.split)
else:
return sum([len(ds) for ds in self.datasets])
def __getitem__(self, idx):
if self.split is not None: idx = self.split[idx]
idx = listify(idx)
idxs = self.mapping[idx]
idxs = idxs[idxs[:, 0].argsort()]
self.mapping_idxs = idxs
ds = np.unique(idxs[:, 0])
b = [self.datasets[d][idxs[idxs[:, 0] == d, 1]] for d in ds]
output = tuple(map(torch.cat, zip(*b)))
return output
def _mapping(self):
lengths = [len(ds) for ds in self.datasets]
idx_pairs = np.zeros((np.sum(lengths), 2)).astype(np.int32)
start = 0
for i,length in enumerate(lengths):
if i > 0:
idx_pairs[start:start+length, 0] = i
idx_pairs[start:start+length, 1] = np.arange(length)
start += length
return idx_pairs
@property
def vars(self):
s = self.datasets[0][0][0] if not isinstance(self.datasets[0][0][0], tuple) else self.datasets[0][0][0][0]
return s.shape[-2]
@property
def len(self):
s = self.datasets[0][0][0] if not isinstance(self.datasets[0][0][0], tuple) else self.datasets[0][0][0][0]
return s.shape[-1]
class TSMetaDatasets(FilteredBase):
def __init__(self, metadataset, splits):
store_attr()
self.mapping = metadataset.mapping
def subset(self, i):
return type(self.metadataset)(self.metadataset.datasets, split=self.splits[i])
@property
def train(self):
return self.subset(0)
@property
def valid(self):
return self.subset(1)
```
Let's create 3 datasets. In this case they will have different sizes.
```
vocab = L(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j'])
dsets = []
for i in range(3):
size = np.random.randint(50, 150)
X = torch.rand(size, 5, 50)
y = vocab[torch.randint(0, 10, (size,))]
tfms = [None, TSClassification()]
dset = TSDatasets(X, y, tfms=tfms)
dsets.append(dset)
dsets
metadataset = TSMetaDataset(dsets)
metadataset, metadataset.vars, metadataset.len
```
We'll apply splits now to create train and valid metadatasets:
```
splits = TimeSplitter()(metadataset)
splits
metadatasets = TSMetaDatasets(metadataset, splits=splits)
metadatasets.train, metadatasets.valid
dls = TSDataLoaders.from_dsets(metadatasets.train, metadatasets.valid)
xb, yb = first(dls.train)
xb, yb
```
There also en easy way to map any particular sample in a batch to the original dataset and id:
```
dls = TSDataLoaders.from_dsets(metadatasets.train, metadatasets.valid)
xb, yb = first(dls.train)
mappings = dls.train.dataset.mapping_idxs
for i, (xbi, ybi) in enumerate(zip(xb, yb)):
ds, idx = mappings[i]
test_close(dsets[ds][idx][0].data.cpu(), xbi.cpu())
test_close(dsets[ds][idx][1].data.cpu(), ybi.cpu())
```
For example the 3rd sample in this batch would be:
```
dls.train.dataset.mapping_idxs[2]
#hide
out = create_scripts(); beep(out)
```
| true |
code
| 0.680295 | null | null | null | null |
|
```
import tensorflow as tf
```
## 참고 자료
- [이찬우님 유튜브](https://www.youtube.com/watch?v=4vJ_2NtsTVg&list=PL1H8jIvbSo1piZJRnp9bIww8Fp2ddIpeR&index=2)
### (1) 보편적 Case
- Generator를 사용
- python api를 의존하기 때문에 병목이 있을 수 있음
```
def gen():
for i in range(10):
yield i
dataset = tf.data.Dataset.from_generator(gen, tf.float32)\
.make_one_shot_iterator()\
.get_next()
with tf.Session() as sess:
_data = sess.run(dataset)
print(_data)
with tf.Session() as sess:
for _ in range(10):
_data = sess.run(dataset)
print(_data)
# End of sequence Error 발생
with tf.Session() as sess:
for _ in range(12):
_data = sess.run(dataset)
print(_data)
```
- generator로 label, feature까지 출력하고 싶다면
```
def gen():
for i, j in zip(range(10, 20), range(10)):
yield (i, j)
dataset = tf.data.Dataset.from_generator(gen, (tf.float32, tf.float32))\
.make_one_shot_iterator()\
.get_next()
with tf.Session() as sess:
for _ in range(10):
_label, _feature = sess.run(dataset)
print(_label, _feature)
```
### Minibatch를 하고 싶다면
- shuffle한 후, batch 설정
```
def gen():
for i, j in zip(range(10, 1010), range(1000)):
yield (i, j)
dataset = tf.data.Dataset.from_generator(gen, (tf.float32, tf.float32))\
.shuffle(7777)\
.batch(20)\
.make_one_shot_iterator()\
.get_next()
with tf.Session() as sess:
for _ in range(10):
_label, _feature = sess.run(dataset)
print(_label, _feature)
```
### (2) TextLineDataset
- 병목을 해결 가능
```
dataset = tf.data.TextLineDataset("./test_data.csv")\
.make_one_shot_iterator()\
.get_next()
with tf.Session() as sess:
_data = sess.run(dataset)
print(_data)
```
- b'1,1,2,3,4,5,6,7,8,9' : decoding 필요
```
dataset = tf.data.TextLineDataset("./test_data.csv")\
.make_one_shot_iterator()\
.get_next()
lines = tf.decode_csv(dataset, record_defaults=[[0]]*10)
feature = tf.stack(lines[1:]) #, axis=1)
label = lines[0]
with tf.Session() as sess:
_fea, _lab = sess.run([feature, label])
print(_lab, _fea)
dataset = tf.data.TextLineDataset("./test_data.csv")\
.batch(2)\
.repeat(999999)\
.make_one_shot_iterator()\
.get_next()
lines = tf.decode_csv(dataset, record_defaults=[[0]]*10)
feature = tf.stack(lines[1:], axis=1)
label = tf.expand_dims(lines[0], axis=-1)
feature = tf.cast(feature, tf.float32)
label = tf.cast(label, tf.float32)
# float형으로 정의해야 이상없이 연산이 됨
with tf.Session() as sess:
_fea, _lab = sess.run([feature, label])
for f, l in zip(_fea, _lab):
print(f, l)
```
### Modeling
```
layer1 = tf.layers.dense(feature, units=9, activation=tf.nn.relu)
layer2 = tf.layers.dense(layer1, units=9, activation=tf.nn.relu)
layer3 = tf.layers.dense(layer2, units=9, activation=tf.nn.relu)
layer4 = tf.layers.dense(layer3, units=9, activation=tf.nn.relu)
out = tf.layers.dense(layer4, units=1)
print("label's shape {}".format(label))
# label's shape (?,) : [1, 2, 3, 4, 5, 6]
# int면 계산이 안됨
print("out's shape {}".format(out))
# [[1], [2], [3], [4], [5], [6]]
```
### loss, Optimizer 정의
```
loss = tf.losses.sigmoid_cross_entropy(label, out)
```
- Shapes (?, 1) and (?,) are incompatible error
- shape를 맞춰주기 : ```tf.expand_dims``` 사용
- Value passed to parameter 'x' has DataType int32 not in list of allowed values error
- value의 type을 float32로 바꾸기 : ```tf.cast``` 사용
- Attempting to use uninitialized value accuracy/total error
- accuracy 관련 ```tf.local_variables_initializer()``` 실행
```
train_op = tf.train.GradientDescentOptimizer(1e-2).minimize(loss)
pred = tf.nn.sigmoid(out)
accuracy = tf.metrics.accuracy(label, tf.round(pred))
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
sess.run(tf.local_variables_initializer())
for i in range(30):
_, _loss, _acc = sess.run([train_op, loss, accuracy])
print("step: {}, loss: {}, accuracy: {}".format(i, _loss, _acc))
```
### Accuracy
### TFRecord
- read, write 속도가 빠르게!
| true |
code
| 0.461381 | null | null | null | null |
|
# Dealing with spectrum data
This tutorial demonstrates how to use Spectrum class to do various arithmetic operations of Spectrum. This demo uses the Jsc calculation as an example, namely
\begin{equation}
J_{sc}=\int \phi(E)QE(E) dE
\end{equation}
where $\phi$ is the illumination spectrum in photon flux, $E$ is the photon energy and $QE$ is the quantum efficiency.
```
%matplotlib inline
import numpy as np
import scipy.constants as sc
import matplotlib.pyplot as plt
from pypvcell.spectrum import Spectrum
from pypvcell.illumination import Illumination
from pypvcell.photocurrent import gen_step_qe_array
```
## Quantum efficiency
We first use a function ```gen_step_qe_array``` to generate a quantum efficiency spectrum. This spectrum is a step function with a cut-off at the band gap of 1.42 eV.
```
qe=gen_step_qe_array(1.42,0.9)
plt.plot(qe[:,0],qe[:,1])
plt.xlabel('photon energy (eV)')
plt.ylabel('QE')
```
```qe``` is a numpy array. The recommeneded way to handle it is converting it to ```Spectrum``` class:
```
qe_sp=Spectrum(x_data=qe[:,0],y_data=qe[:,1],x_unit='eV')
```
### Unit conversion
When we want to retrieve the value of ```qe_sp``` we have to specicify the unit of the wavelength. For example, say, converting the wavelength to nanometer:
```
qe=qe_sp.get_spectrum(to_x_unit='nm')
plt.plot(qe[0,:],qe[1,:])
plt.xlabel('wavelength (nm)')
plt.ylabel('QE')
plt.xlim([300,1100])
```
### Arithmetic operation
We can do arithmetic operation directly with Spectrum class such as
```
# Calulate the portion of "non-absorbed" photons, assuming QE is equivalent to absorptivity
tr_sp=1-qe_sp
tr=tr_sp.get_spectrum(to_x_unit='nm')
plt.plot(tr[0,:],tr[1,:])
plt.xlabel('wavelength (nm)')
plt.ylabel('QE')
plt.xlim([300,1100])
```
## Illumination spectrum
pypvcell has a class Illumination that is inherited from ```Spectrum``` to handle the illumination. It inherits all the capability of ```Spectrum``` but has several methods specifically for sun illumination.
Some default standard spectrum is embedded in the ```pypvcell```:
```
std_ill=Illumination("AM1.5g")
```
Show the values of the data
```
ill=std_ill.get_spectrum('nm')
plt.plot(*ill)
plt.xlabel("wavelength (nm)")
plt.ylabel("intensity (W/m^2-nm)")
fig, ax1= plt.subplots()
ax1.plot(*ill)
ax2 = ax1.twinx()
ax2.plot(*qe)
ax1.set_xlim([400,1600])
ax2.set_ylabel('sin', color='r')
ax2.tick_params('y', colors='r')
ill[:,-1]
qe[:,-1]
```
Calcuate the total intensity in W/m^2
```
std_ill.total_power()
```
### Unit conversion of illumination spectrum
It requires a bit of attention of converting spectrum that is in the form of $\phi(E)dE$, i.e., the value of integration is a meaningful quantitfy such as total power. This has been also handled by ```Illumination``` class. In the following case, we convert the wavelength to eV. Please note that the units of intensity is also changed to W/m^2-eV.
```
ill=std_ill.get_spectrum('eV')
plt.plot(*ill)
plt.xlabel("wavelength (eV)")
plt.ylabel("intensity (W/m^2-eV)")
```
## Spectrum multiplication
To calcualte the overall photocurrent, we have to calculate $\phi(E)QE(E) dE$ first. This would involves some unit conversion and interpolation between two spectrum. However, this is easily dealt by ```Spectrum``` class:
```
# calculate \phi(E)QE(E) dE.
# Spectrum class automatically convert the units and align the x-data by interpolating std_ill
jsc_e=std_ill*qe_sp
```
Here's a more delicate point. We should convert the unit to photon flux in order to calculate Jsc.
```
jsc_e_a=jsc_e.get_spectrum('nm',to_photon_flux=True)
plt.plot(*jsc_e_a)
plt.xlim([300,1100])
```
Integrate it yields the total photocurrent density in A/m^2
```
sc.e*np.trapz(y=jsc_e_a[1,:],x=jsc_e_a[0,:])
```
In fact, ```pypvcell``` already provides a function ```calc_jsc()``` for calculating Jsc from given spectrum and QE:
```
from pypvcell.photocurrent import calc_jsc
calc_jsc(std_ill,qe_sp)
```
| true |
code
| 0.637652 | null | null | null | null |
|
# Machine learning methods for sequential data
There are some very robust methods for learning sequential data such as for time-series or language processing tasks. We'll look at recurrent neural networks which leverage the autocorrelated nature of the training data sets.
# Sequential learning
We will utilize two popular frameworks for learning data which are distinctly _non i.i.d_
<img src="imgs/RNN_Apps.png" width="800">
## Recurrent neural networks (RNNs)
<img src="imgs/RNN_Maths.png" width="600">
## Long short-term memory networks (LSTMs)
<img src="imgs/LSTM_Maths.png" width="800">
### Import python packages
```
import sys
import os
import keras
from keras.models import Model
from keras.callbacks import EarlyStopping
import math
import warnings
import numpy as np
import pandas as pd
from keras.layers import Dense, Dropout, Activation
from keras.layers.recurrent import SimpleRNN, LSTM, GRU
from keras.models import Sequential
from keras.models import load_model
from keras.utils.vis_utils import plot_model
import sklearn.metrics as metrics
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, MinMaxScaler
warnings.filterwarnings("ignore")
# Download the data - google colab issue
!git clone https://github.com/argonne-lcf/AI4ScienceTutorial
```
# Data preprocessing
```
def process_data(train, test, lags):
"""Process data
Reshape and split train\test data.
# Arguments
train: String, name of .csv train file.
test: String, name of .csv test file.
lags: integer, time lag.
# Returns
X_train: ndarray.
y_train: ndarray.
X_test: ndarray.
y_test: ndarray.
scaler: StandardScaler.
"""
attr = 'Lane 1 Flow (Veh/5 Minutes)'
df1 = pd.read_csv(train, encoding='utf-8').fillna(0)
df2 = pd.read_csv(test, encoding='utf-8').fillna(0)
# scaler = StandardScaler().fit(df1[attr].values)
scaler = MinMaxScaler(feature_range=(0, 1)).fit(df1[attr].values.reshape(-1, 1))
flow1 = scaler.transform(df1[attr].values.reshape(-1, 1)).reshape(1, -1)[0]
flow2 = scaler.transform(df2[attr].values.reshape(-1, 1)).reshape(1, -1)[0]
train, test = [], []
for i in range(lags, len(flow1)):
train.append(flow1[i - lags: i + 1])
for i in range(lags, len(flow2)):
test.append(flow2[i - lags: i + 1])
train = np.array(train)
test = np.array(test)
np.random.shuffle(train)
X_train = train[:, :-1]
y_train = train[:, -1]
X_test = test[:, :-1]
y_test = test[:, -1]
return X_train, y_train, X_test, y_test, scaler
```
# Model building
```
"""
Define model architecture
"""
def get_rnn(units):
"""RNN(Recurrent Neural Network)
Build RNN Model.
# Arguments
units: List(int), number of input, hidden unit in cell 1, hidden units in cell 2, number of outputs
# Returns
model: Model, nn model.
"""
model = Sequential()
model.add(SimpleRNN(units[1], input_shape=(units[0], 1), return_sequences=True)) # Cell 1
model.add(SimpleRNN(units[2])) # Cell 2 stacked on hidden-layer outputs of Cell 1
model.add(Dropout(0.2)) # Dropout - for regularization
model.add(Dense(units[3], activation='sigmoid')) # Map hidden-states to output
return model
def get_lstm(units):
"""LSTM(Long Short-Term Memory)
Build LSTM Model.
# Arguments
units: List(int), number of input, hidden unit in cell 1, hidden units in cell 2, number of outputs
# Returns
model: Model, nn model.
"""
model = Sequential()
model.add(LSTM(units[1], input_shape=(units[0], 1), return_sequences=True)) # Cell 1
model.add(LSTM(units[2])) # Cell 2 stacked on hidden-layer outputs of Cell 1
model.add(Dropout(0.2)) # Dropout - for regularization
model.add(Dense(units[3], activation='sigmoid')) # Map hidden-states to output
return model
```
# Model training
```
def train_model(model, X_train, y_train, name, config):
"""train
train a single model.
# Arguments
model: Model, NN model to train.
X_train: ndarray(number, lags), Input data for train.
y_train: ndarray(number, ), result data for train.
name: String, name of model.
config: Dict, parameter for train.
"""
model.compile(loss="mse", optimizer="rmsprop", metrics=['mse'])
model.summary()
# early = EarlyStopping(monitor='val_loss', patience=30, verbose=0, mode='auto')
hist = model.fit(
X_train, y_train,
batch_size=config["batch"],
epochs=config["epochs"],
validation_split=0.05)
folder = 'model/'
if not os.path.exists(folder):
os.makedirs(folder)
model.save('model/' + name + '.h5')
df = pd.DataFrame.from_dict(hist.history)
df.to_csv('model/' + name + ' loss.csv', encoding='utf-8', index=False)
return hist
lag = 12
config = {"batch": 256, "epochs": 10}
file1 = 'AI4ScienceTutorial/sess5_timeseries/data/train.csv'
file2 = 'AI4ScienceTutorial/sess5_timeseries/data/test.csv'
X_train, y_train, _, _, _ = process_data(file1, file2, lag)
X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1))
# Check the shapes of our training data
print(X_train.shape)
print(y_train.shape)
m = get_rnn([12, 64, 64, 1])
history = train_model(m, X_train, y_train, 'rnn', config)
plt.figure(figsize=(21, 11))
plt.plot(history.history['loss'], linewidth=4)
plt.plot(history.history['val_loss'], linewidth=4)
plt.title('model loss', fontsize=40)
plt.yticks(fontsize=40)
plt.xticks(fontsize=40)
plt.ylabel('loss', fontsize=40)
plt.xlabel('epoch', fontsize=40)
plt.legend(['train', 'val'], loc='upper left', fontsize=40)
plt.show()
m = get_lstm([12, 64, 64, 1])
history = train_model(m, X_train, y_train, 'lstm', config)
plt.figure(figsize=(21, 11))
plt.plot(history.history['loss'], linewidth=4)
plt.plot(history.history['val_loss'], linewidth=4)
plt.title('model loss', fontsize=40)
plt.yticks(fontsize=40)
plt.xticks(fontsize=40)
plt.ylabel('loss', fontsize=40)
plt.xlabel('epoch', fontsize=40)
plt.legend(['train', 'val'], loc='upper left', fontsize=40)
plt.show()
```
# Prediction
```
"""
Traffic Flow Prediction with Neural Networks(SAEs、LSTM、GRU).
"""
def MAPE(y_true, y_pred):
"""Mean Absolute Percentage Error
Calculate the mape.
# Arguments
y_true: List/ndarray, ture data.
y_pred: List/ndarray, predicted data.
# Returns
mape: Double, result data for train.
"""
y = [x for x in y_true if x > 0]
y_pred = [y_pred[i] for i in range(len(y_true)) if y_true[i] > 0]
num = len(y_pred)
sums = 0
for i in range(num):
tmp = abs(y[i] - y_pred[i]) / y[i]
sums += tmp
mape = sums * (100 / num)
return mape
def eva_regress(y_true, y_pred):
"""Evaluation
evaluate the predicted result.
# Arguments
y_true: List/ndarray, ture data.
y_pred: List/ndarray, predicted data.
"""
mape = MAPE(y_true, y_pred)
vs = metrics.explained_variance_score(y_true, y_pred)
mae = metrics.mean_absolute_error(y_true, y_pred)
mse = metrics.mean_squared_error(y_true, y_pred)
r2 = metrics.r2_score(y_true, y_pred)
print('explained_variance_score:%f' % vs)
print('mape:%f%%' % mape)
print('mae:%f' % mae)
print('mse:%f' % mse)
print('rmse:%f' % math.sqrt(mse))
print('r2:%f' % r2)
def plot_results(y_true, y_preds, names):
"""Plot
Plot the true data and predicted data.
# Arguments
y_true: List/ndarray, ture data.
y_pred: List/ndarray, predicted data.
names: List, Method names.
"""
d = '2016-3-4 00:00'
x = pd.date_range(d, periods=288, freq='5min')
fig = plt.figure(figsize=(21, 11))
ax = fig.add_subplot(111)
ax.plot(x, y_true, label='True Data', linewidth=4)
for name, y_pred in zip(names, y_preds):
ax.plot(x, y_pred, label=name, linewidth=4)
plt.legend(prop={'size': 40})
plt.yticks(fontsize=40)
plt.xticks(fontsize=40)
plt.grid(True)
plt.xlabel('Time of Day', fontsize=50)
plt.ylabel('Flow', fontsize=50)
date_format = mpl.dates.DateFormatter("%H:%M")
ax.xaxis.set_major_formatter(date_format)
fig.autofmt_xdate()
plt.show()
rnn = load_model('model/rnn.h5')
lstm = load_model('model/lstm.h5')
models = [rnn,lstm]
names = ['RNN','LSTM']
lag = 12
file1 = 'AI4ScienceTutorial/sess5_timeseries/data/train.csv'
file2 = 'AI4ScienceTutorial/sess5_timeseries/data/test.csv'
_, _, X_test, y_test, scaler = process_data(file1, file2, lag)
y_test = scaler.inverse_transform(y_test.reshape(-1, 1)).reshape(1, -1)[0]
y_preds = []
for name, model in zip(names, models):
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
predicted = model.predict(X_test)
predicted = scaler.inverse_transform(predicted.reshape(-1, 1)).reshape(1, -1)[0]
y_preds.append(predicted[:288])
eva_regress(y_test, predicted)
plot_results(y_test[: 288], y_preds, names)
```
| true |
code
| 0.716504 | null | null | null | null |
|
# 8.3 PCA
PCA首先识别最靠近数据的超平面,然后将数据投影到该平面上。
## 8.3.1 保留差异性
将训练集投影到低维超平面之前需要选择正确的超平面。
## 8.3.2 主要成分
**主成分分析可以在训练集中识别出哪条轴对差异性的贡献度最高。** 轴的数量与数据集维度数量相同。
第i个轴称为数据的第i个主要成分(PC)
对于每个主要成分,PCA都找到一个指向PC方向的零中心单位向量。由于两个相对的单位向量位于同一轴上,因此PCA返回的单位向量的方向不稳定:如果稍微扰动训练集并再次运行PCA,则单位向量可能会指向原始向量的相反方向。但是,它们通常仍位于相同的轴上。在某些情况下,一对单位向量甚至可以旋转或交换(如果沿这两个轴的方差接近),但是它们定义的平面通常保持不变。
异值分解(SVD)的标准矩阵分解技术,可以将训练集矩阵X分解为三个矩阵$U\sum V^T$的矩阵乘法,其中V包含定义所有主要成分的单位向量。如公式8-1所示:
$$
V = \begin{bmatrix}
| & | & \cdots & | \\
c_1 & c_2 & \cdots & c_n \\
| & | & \cdots & |
\end{bmatrix} \tag{8-1}
$$
```
%matplotlib inline
import matplotlib as mlp
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('ggplot')
np.random.seed(42)
m = 60
w1, w2 = 0.1, 0.3
noise = 0.1
angles = np.random.rand(m) * 3 * np.pi / 2 - 0.5
X = np.empty((m, 3))
X[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * np.random.randn(m) / 2
X[:, 1] = np.sin(angles) * 0.7 + noise * np.random.randn(m) / 2
X[:, 2] = X[:, 0] * w1 + X[:, 1] * w2 + noise * np.random.randn(m)
X
# 使用Numpy的svd()函数来获取训练集的所有主成分
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]
m, n = X.shape
m, n
S = np.zeros(X_centered.shape)
S[:n, :n] = np.diag(s)
np.allclose(X_centered, U.dot(S).dot(Vt))
W2 = Vt.T[:, :2]
X2D = X_centered.dot(W2)
X2D_using_svd = X2D
```
PCA假定数据集以原点为中心。正如我们将看到的,Scikit-Learn的PCA类负责为你居中数据。如果你自己实现PCA(如上例所示),或者使用其他库,请不要忘记首先将数据居中。
## 8.3.3 向下投影到d维度
一旦确定了所有主要成分,你就可以将数据集投影到前d个主要成分定义的超平面上,从而将数据集的维度降低到d维。选择这个超平面可确保投影将保留尽可能多的差异性。
要将训练集投影到超平面上并得到维度为d的简化数据集$X_{d-proj}$,计算训练集矩阵X与矩阵$W_d$的矩阵相乘,矩阵$W_d$定义为包含V的前$d$列的矩阵。如公式8-2所示:
$$
X_{d-proj} = X W_d \tag{8-2}
$$
## 8.3.4 Scikit-Learn PCA
```
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X2D = pca.fit_transform(X)
X2D[:5]
X2D_using_svd[:5]
```
注意在数据集上执行PCA多次可能结果会有轻微的不同,这是由于一些投影轴的方向有可能翻转了。
## 8.3.5 可解释方差比
另一个有用的信息是每个主成分的可解释方差比,可以通过explained_variance_ratio_变量来获得。该比率表示沿每个成分的数据集方差的比率。
```
pca.explained_variance_ratio_
```
此输出告诉你,数据集方差的84.2%位于第一个PC上,而14.6%位于第二个PC上。对于第三个PC,这还不到1.2%,因此可以合理地假设第三个PC携带的信息很少。
## 8.3.6 选择正确的维度
与其任意选择要减小到的维度,不如选择相加足够大的方差部分(例如95%)的维度。当然,如果你是为了数据可视化而降低维度,这种情况下,需要将维度降低到2或3。
以下代码在不降低维度的情况下执行PCA,然后计算保留95%训练集方差所需的最小维度:
```
# 以下代码在不降低维度的情况下执行PCA,然后计算保留95%训练集所需的最小维度
X_train = np.copy(X)
pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
cumsum
d = np.argmax(cumsum >= 0.95) + 1
d
```
然后,你可以设置`n_components=d`并再次运行PCA。但是还有一个更好的选择:将`n_components`设置为0.0到1.0之间的浮点数来表示要保留的方差率,而不是指定要保留的主成分数:
```
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)
X_reduced
```
另一个选择是将可解释方差绘制成维度的函数(简单地用cumsum绘制)。曲线上通常会出现一个拐点,其中可解释方差会停止快速增大。在这种情况下,你可以看到将维度降低到大约100而不会损失太多的可解释方差。

## 8.3.7 PCA压缩
降维后,训练集占用的空间要少得多。例如,将PCA应用于MNIST数据集,同时保留其95%的方差。你会发现每个实例将具有150多个特征,而不是原始的784个特征。因此,尽管保留了大多数方差,但数据集现在不到其原始大小的20%!这是一个合理的压缩率,你可以看到这种维度减小极大地加速了分类算法(例如SVM分类器)。通过应用PCA投影的逆变换,还可以将缩减后的数据集解压缩回784维。由于投影会丢失一些信息(在5%的方差被丢弃),因此这不会给你原始的数据,但可能会接近原始数据。
**原始数据与重构数据(压缩后再解压缩)之间的均方距离称为重构误差**。
```
from sklearn.datasets import fetch_openml
X, y = fetch_openml('mnist_784', version=1, return_X_y=True, as_frame=False)
X.shape
pca = PCA(n_components=154)
X_reduced = pca.fit_transform(X)
X_recovered = pca.inverse_transform(X_reduced)
X_reduced.shape, X_recovered.shape
fig, axes = plt.subplots(ncols=2, figsize=(14, 6))
plt.sca(axes[0])
image = X[:1,]
# image = np.reshape(image, (-1, 1))
image=np.reshape(image, (28, -1))
plt.imshow(image, cmap="gray")
plt.sca(axes[1])
image = X_recovered[:1,]
# image = np.reshape(image, (-1, 1))
image=np.reshape(image, (28, -1))
plt.imshow(image, cmap="gray")
```
PCA逆变换,回到原始数量的维度
$$
X_{recovered} = X_{d-proj}W_d^T \tag{8-3}
$$
## 8.3.8 随机PCA
如果将超参数svd_solver设置为"randomized",则Scikit-Learn将使用一种称为Randomized PCA的随机算法,该算法可以快速找到前d个主成分的近似值。它的计算复杂度为$O(m\times d^2)+O(d^3)$,而不是完全SVD方法的$O(m \times n^2)+O(n^3)$,因此,当d远远小于n时,它比完全的SVD快得多:
```python
rnd_pca = PCA(n_components=154, svd_solver="randomized")
X_reduced = rnd_pca.fit_transform(X)
```
默认情况下,svd_solver实际上设置为"auto":如果m或n大于500并且d小于m或n的80%,则Scikit-Learn自动使用随机PCA算法,否则它将使用完全的SVD方法。如果要强制Scikit-Learn使用完全的SVD,可以将svd_solver超参数设置为"full"。
## 8.3.9 增量PCA
前面的PCA实现的一个问题是,它们要求整个训练集都放入内存才能运行算法。幸运的是已经开发了**增量PCA(IPCA)算法**,它们可以使你把训练集划分为多个小批量,并一次将一个小批量送入IPCA算法。这对于大型训练集和在线(即在新实例到来时动态运行)应用PCA很有用。
以下代码将MNIST数据集拆分为100个小批量(使用NumPy的`array_split()`函数),并将其馈送到Scikit-Learn的`IncrementalPCA`类,来把MNIST数据集的维度降低到154(就像之前做的那样)。请注意,你必须在每个小批量中调用`partial_fit()`方法,而不是在整个训练集中调用`fit()`方法:
```
from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X, n_batches):
inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.transform(X)
```
另外,你可以使用NumPy的`memmap`类,该类使你可以将存储在磁盘上的二进制文件中的大型数组当作完全是在内存中一样来操作,该类仅在需要时才将数据加载到内存中。由于`IncrementalPCA`类在任何给定时间仅使用数组的一小部分,因此内存使用情况处于受控状态。如以下代码所示,这使得调用通常的`fit()`方法成为可能:
```python
X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n))
batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm)
```
| true |
code
| 0.628151 | null | null | null | null |
|
# Social Network Analysis
## Introduction to graph theory
```
%matplotlib inline
import matplotlib.pyplot as mpl
mpl.style.use('_classic_test')
mpl.rcParams['figure.figsize'] = [6.5, 4.5]
mpl.rcParams['figure.dpi'] = 80
mpl.rcParams['savefig.dpi'] = 100
mpl.rcParams['font.size'] = 10
mpl.rcParams['legend.fontsize'] = 'medium'
mpl.rcParams['figure.titlesize'] = 'medium'
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
import matplotlib.cbook
warnings.filterwarnings("ignore",category=matplotlib.cbook.mplDeprecation)
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
G.add_edge(1,2)
nx.draw_networkx(G)
plt.show()
G.add_nodes_from([3, 4])
G.add_edge(3,4)
G.add_edges_from([(2, 3), (4, 1)])
nx.draw_networkx(G)
plt.show()
G.nodes()
G.edges()
G.adjacency_list()
nx.to_dict_of_lists(G)
nx.to_edgelist(G)
nx.to_numpy_matrix(G)
print (nx.to_scipy_sparse_matrix(G))
nx.to_pandas_dataframe(G)
G.add_edge(1,3)
nx.draw_networkx(G)
plt.show()
G.degree()
k = nx.fast_gnp_random_graph(10000, 0.01).degree()
plt.hist(list(k.values()))
```
## Graph algorithms
```
G = nx.krackhardt_kite_graph()
nx.draw_networkx(G)
plt.show()
print (nx.has_path(G, source=1, target=9))
print (nx.shortest_path(G, source=1, target=9))
print (nx.shortest_path_length(G, source=1, target=9))
print (list(nx.shortest_simple_paths(G, source=1, target=9)))
paths = nx.all_pairs_shortest_path(G)
paths[5]
## paths[a][b]
```
### $ Types\ of\ centrality\: $
* #### $ Betweenness$
* #### $ Degree$
* #### $ Closeness$
* #### $ Harmonic$
* #### $ Eigenvector$
```
nx.betweenness_centrality(G)
nx.degree_centrality(G)
nx.closeness_centrality(G)
nx.harmonic_centrality(G)
nx.eigenvector_centrality(G)
nx.clustering(G)
import community # Community module for community detection and clustering
from community import community_louvain
G = nx.powerlaw_cluster_graph(100, 1, .4, seed=101)
partition = community_louvain.best_partition(G)
for i in set(partition.values()):
print("Community", i)
members = list_nodes = [nodes for nodes in partition.keys() if partition[nodes] == i]
print(members)
values = [partition.get(node) for node in G.nodes()]
nx.draw_spring(G, cmap = plt.get_cmap('jet'), node_color = values, node_size=30, with_labels=False)
plt.show()
print ("Modularity score:", community_louvain.modularity(partition, G))
d = nx.coloring.greedy_color(G)
print(d)
nx.draw_networkx(G, node_color=[d[n] for n in sorted(d.keys())])
plt.show()
```
## Graph loading, dumping, and sampling
```
import networkx as nx
dump_file_base = "dumped_graph"
# Be sure the dump_file file doesn't exist
def remove_file(filename):
import os
if os.path.exists(filename):
os.remove(filename)
G = nx.krackhardt_kite_graph()
# GML format write and read
GML_file = dump_file_base + '.gml'
remove_file(GML_file)
nx.write_gml(G, GML_file)
G2 = nx.read_gml(GML_file)
assert sorted(list(G.edges())) == sorted(list(G2.edges()))
```
#### Similar to write_gml and read_gml are the following ones:
- Aadjacency list (read_adjlist and write_adjlist)
- Multiline adjacency list (read_multiline_adjlist and write_multiline_adjlist)
- Edge list (read_edgelist and write_edgelist)
- GEXF (read_gexf and write_gexf)
- Pickle (read_gpickle and write_gpickle)
- GraphML (read_graphml and write_graphml)
- LEDA (read_leda and parse_leda)
- YAML (read_yaml and write_yaml)
- Pajek (read_pajek and write_pajek)
- GIS Shapefile (read_shp and write_shp)
- JSON (load/loads and dump/dumps provides JSON serialization)
### $ Sampling\ Techniques: $
* #### $ Node $
* #### $ Link $
* #### $ Snowball $
```
import snowball_sampling
my_social_network = nx.Graph()
snowball_sampling.snowball_sampling(my_social_network, 2, 'alberto')
nx.draw(my_social_network)
plt.show()
my_sampled_social_network = nx.Graph()
snowball_sampling.snowball_sampling(my_sampled_social_network, 3, 'alberto', sampling_rate=0.2)
nx.draw(my_sampled_social_network)
plt.show()
```
| true |
code
| 0.531088 | null | null | null | null |
|
# 使用序列到序列模型完成数字加法
**作者:** [jm12138](https://github.com/jm12138) <br>
**日期:** 2021.05 <br>
**摘要:** 本示例介绍如何使用飞桨完成一个数字加法任务,将会使用飞桨提供的`LSTM`,组建一个序列到序列模型,并在随机生成的数据集上完成数字加法任务的模型训练与预测。
## 一、环境配置
本教程基于Paddle 2.1 编写,如果你的环境不是本版本,请先参考官网[安装](https://www.paddlepaddle.org.cn/install/quick) Paddle 2.1 。
```
# 导入项目运行所需的包
import paddle
import paddle.nn as nn
import random
import numpy as np
from visualdl import LogWriter
# 打印Paddle版本
print('paddle version: %s' % paddle.__version__)
```
## 二、构建数据集
* 随机生成数据,并使用生成的数据构造数据集
* 通过继承 ``paddle.io.Dataset`` 来完成数据集的构造
```
# 编码函数
def encoder(text, LEN, label_dict):
# 文本转ID
ids = [label_dict[word] for word in text]
# 对长度进行补齐
ids += [label_dict[' ']]*(LEN-len(ids))
return ids
# 单个数据生成函数
def make_data(inputs, labels, DIGITS, label_dict):
MAXLEN = DIGITS + 1 + DIGITS
# 对输入输出文本进行ID编码
inputs = encoder(inputs, MAXLEN, label_dict)
labels = encoder(labels, DIGITS + 1, label_dict)
return inputs, labels
# 批量数据生成函数
def gen_datas(DATA_NUM, MAX_NUM, DIGITS, label_dict):
datas = []
while len(datas)<DATA_NUM:
# 随机取两个数
a = random.randint(0,MAX_NUM)
b = random.randint(0,MAX_NUM)
# 生成输入文本
inputs = '%d+%d' % (a, b)
# 生成输出文本
labels = str(eval(inputs))
# 生成单个数据
inputs, labels = [np.array(_).astype('int64') for _ in make_data(inputs, labels, DIGITS, label_dict)]
datas.append([inputs, labels])
return datas
# 继承paddle.io.Dataset来构造数据集
class Addition_Dataset(paddle.io.Dataset):
# 重写数据集初始化函数
def __init__(self, datas):
super(Addition_Dataset, self).__init__()
self.datas = datas
# 重写生成样本的函数
def __getitem__(self, index):
data, label = [paddle.to_tensor(_) for _ in self.datas[index]]
return data, label
# 重写返回数据集大小的函数
def __len__(self):
return len(self.datas)
print('generating datas..')
# 定义字符表
label_dict = {
'0': 0, '1': 1, '2': 2, '3': 3,
'4': 4, '5': 5, '6': 6, '7': 7,
'8': 8, '9': 9, '+': 10, ' ': 11
}
# 输入数字最大位数
DIGITS = 2
# 数据数量
train_num = 5000
dev_num = 500
# 数据批大小
batch_size = 32
# 读取线程数
num_workers = 8
# 定义一些所需变量
MAXLEN = DIGITS + 1 + DIGITS
MAX_NUM = 10**(DIGITS)-1
# 生成数据
train_datas = gen_datas(
train_num,
MAX_NUM,
DIGITS,
label_dict
)
dev_datas = gen_datas(
dev_num,
MAX_NUM,
DIGITS,
label_dict
)
# 实例化数据集
train_dataset = Addition_Dataset(train_datas)
dev_dataset = Addition_Dataset(dev_datas)
print('making the dataset...')
# 实例化数据读取器
train_reader = paddle.io.DataLoader(
train_dataset,
batch_size=batch_size,
shuffle=True,
drop_last=True
)
dev_reader = paddle.io.DataLoader(
dev_dataset,
batch_size=batch_size,
shuffle=False,
drop_last=True
)
print('finish')
```
## 三、模型组网
* 通过继承 ``paddle.nn.Layer`` 类来搭建模型
* 本次介绍的模型是一个简单的基于 ``LSTM`` 的 ``Seq2Seq`` 模型
* 一共有如下四个主要的网络层:
1. 嵌入层(``Embedding``):将输入的文本序列转为嵌入向量
2. 编码层(``LSTM``):将嵌入向量进行编码
3. 解码层(``LSTM``):将编码向量进行解码
4. 全连接层(``Linear``):对解码完成的向量进行线性映射
* 损失函数为交叉熵损失函数
```
# 继承paddle.nn.Layer类
class Addition_Model(nn.Layer):
# 重写初始化函数
# 参数:字符表长度、嵌入层大小、隐藏层大小、解码器层数、处理数字的最大位数
def __init__(self, char_len=12, embedding_size=128, hidden_size=128, num_layers=1, DIGITS=2):
super(Addition_Model, self).__init__()
# 初始化变量
self.DIGITS = DIGITS
self.MAXLEN = DIGITS + 1 + DIGITS
self.hidden_size = hidden_size
self.char_len = char_len
# 嵌入层
self.emb = nn.Embedding(
char_len,
embedding_size
)
# 编码器
self.encoder = nn.LSTM(
input_size=embedding_size,
hidden_size=hidden_size,
num_layers=1
)
# 解码器
self.decoder = nn.LSTM(
input_size=hidden_size,
hidden_size=hidden_size,
num_layers=num_layers
)
# 全连接层
self.fc = nn.Linear(
hidden_size,
char_len
)
# 重写模型前向计算函数
# 参数:输入[None, MAXLEN]、标签[None, DIGITS + 1]
def forward(self, inputs, labels=None):
# 嵌入层
out = self.emb(inputs)
# 编码器
out, (_, _) = self.encoder(out)
# 按时间步切分编码器输出
out = paddle.split(out, self.MAXLEN, axis=1)
# 取最后一个时间步的输出并复制 DIGITS + 1 次
out = paddle.expand(out[-1], [out[-1].shape[0], self.DIGITS + 1, self.hidden_size])
# 解码器
out, (_, _) = self.decoder(out)
# 全连接
out = self.fc(out)
# 如果标签存在,则计算其损失和准确率
if labels is not None:
# 转置解码器输出
tmp = paddle.transpose(out, [0, 2, 1])
# 计算交叉熵损失
loss = nn.functional.cross_entropy(tmp, labels, axis=1)
# 计算准确率
acc = paddle.metric.accuracy(paddle.reshape(out, [-1, self.char_len]), paddle.reshape(labels, [-1, 1]))
# 返回损失和准确率
return loss, acc
# 返回输出
return out
```
## 四、模型训练与评估
* 使用 ``Adam`` 作为优化器进行模型训练
* 以模型准确率作为评价指标
* 使用 ``VisualDL`` 对训练数据进行可视化
* 训练过程中会同时进行模型评估和最佳模型的保存
```
# 初始化log写入器
log_writer = LogWriter(logdir="./log")
# 模型参数设置
embedding_size = 128
hidden_size=128
num_layers=1
# 训练参数设置
epoch_num = 50
learning_rate = 0.001
log_iter = 2000
eval_iter = 500
# 定义一些所需变量
global_step = 0
log_step = 0
max_acc = 0
# 实例化模型
model = Addition_Model(
char_len=len(label_dict),
embedding_size=embedding_size,
hidden_size=hidden_size,
num_layers=num_layers,
DIGITS=DIGITS)
# 将模型设置为训练模式
model.train()
# 设置优化器,学习率,并且把模型参数给优化器
opt = paddle.optimizer.Adam(
learning_rate=learning_rate,
parameters=model.parameters()
)
# 启动训练,循环epoch_num个轮次
for epoch in range(epoch_num):
# 遍历数据集读取数据
for batch_id, data in enumerate(train_reader()):
# 读取数据
inputs, labels = data
# 模型前向计算
loss, acc = model(inputs, labels=labels)
# 打印训练数据
if global_step%log_iter==0:
print('train epoch:%d step: %d loss:%f acc:%f' % (epoch, global_step, loss.numpy(), acc.numpy()))
log_writer.add_scalar(tag="train/loss", step=log_step, value=loss.numpy())
log_writer.add_scalar(tag="train/acc", step=log_step, value=acc.numpy())
log_step+=1
# 模型验证
if global_step%eval_iter==0:
model.eval()
losses = []
accs = []
for data in dev_reader():
loss_eval, acc_eval = model(inputs, labels=labels)
losses.append(loss_eval.numpy())
accs.append(acc_eval.numpy())
avg_loss = np.concatenate(losses).mean()
avg_acc = np.concatenate(accs).mean()
print('eval epoch:%d step: %d loss:%f acc:%f' % (epoch, global_step, avg_loss, avg_acc))
log_writer.add_scalar(tag="dev/loss", step=log_step, value=avg_loss)
log_writer.add_scalar(tag="dev/acc", step=log_step, value=avg_acc)
# 保存最佳模型
if avg_acc>max_acc:
max_acc = avg_acc
print('saving the best_model...')
paddle.save(model.state_dict(), 'best_model')
model.train()
# 反向传播
loss.backward()
# 使用优化器进行参数优化
opt.step()
# 清除梯度
opt.clear_grad()
# 全局步数加一
global_step += 1
# 保存最终模型
paddle.save(model.state_dict(),'final_model')
```
## 五、模型测试
* 使用保存的最佳模型进行测试
```
# 反转字符表
label_dict_adv = {v: k for k, v in label_dict.items()}
# 输入计算题目
input_text = '12+40'
# 编码输入为ID
inputs = encoder(input_text, MAXLEN, label_dict)
# 转换输入为向量形式
inputs = np.array(inputs).reshape(-1, MAXLEN)
inputs = paddle.to_tensor(inputs)
# 加载模型
params_dict= paddle.load('best_model')
model.set_dict(params_dict)
# 设置为评估模式
model.eval()
# 模型推理
out = model(inputs)
# 结果转换
result = ''.join([label_dict_adv[_] for _ in np.argmax(out.numpy(), -1).reshape(-1)])
# 打印结果
print('the model answer: %s=%s' % (input_text, result))
print('the true answer: %s=%s' % (input_text, eval(input_text)))
```
## 六、总结
* 你还可以通过变换网络结构,调整数据集,尝试不同的参数的方式来进一步提升本示例当中的数字加法的效果
* 同时,也可以尝试在其他的类似的任务中用飞桨来完成实际的实践
| true |
code
| 0.538983 | null | null | null | null |
|
# This file contains code of the paper 'Rejecting Novel Motions in High-Density Myoelectric Pattern Recognition using Hybrid Neural Networks'
```
import scipy.io as sio
import numpy as np
from keras.layers import Conv2D, MaxPool2D, Flatten, Dense,Dropout, Input, BatchNormalization
from keras.models import Model
from keras.losses import categorical_crossentropy
from keras.optimizers import Adadelta
import keras
# load data
path = './data/data'
data=sio.loadmat(path)
wristPronation = data['wristPronation']
wristSupination = data['wristSupination']
wristExtension = data['wristExtension']
wristFlexion = data['wristFlexion']
handOpen = data['handOpen']
handClose = data['handClose']
shoot = data['shoot']
pinch = data['pinch']
typing = data['typing']
writing = data['writing']
mouseManipulating = data['mouseManipulating']
radialDeviation = data['radialDeviation']
ulnarDeviation = data['ulnarDeviation']
```
## part1: CNN
```
def Spatial_Model(input_shape):
input_layer = Input(input_shape)
x = Conv2D(filters=32, kernel_size=(3, 3),activation='relu',name = 'conv_layer1')(input_layer)
x = Conv2D(filters=32, kernel_size=(3, 3), activation='relu',name = 'conv_layer2')(x)
x = Flatten()(x)
x = Dense(units=1024, activation='relu',name = 'dense_layer1')(x)
x = Dropout(0.4)(x)
x = Dense(units=512, activation='relu',name = 'dense_layer2')(x)
x = Dropout(0.4)(x)
output_layer = Dense(units=7, activation='softmax',name = 'output_layer')(x)
model = Model(inputs=input_layer, outputs=output_layer)
return model
def getIntermediate(layer_name,X,model):
intermediate_layer_model = Model(inputs=model.input,
outputs=model.get_layer(layer_name).output)
intermediate_output = intermediate_layer_model.predict(X)
return intermediate_output
def getPointedGesture(X,y,flag):
index = np.where(y==flag)
temp = X[index]
return temp
classNum = 7
X_inliers = np.concatenate((wristPronation,wristSupination,wristExtension,wristFlexion,handOpen,handClose,shoot),axis=0)
print('X_inliers.shape: ',X_inliers.shape)
y_inliers = np.concatenate((np.ones(wristPronation.shape[0])*0,np.ones(wristSupination.shape[0])*1,
np.ones(wristExtension.shape[0])*2,np.ones(wristFlexion.shape[0])*3,
np.ones(handOpen.shape[0])*4,np.ones(handClose.shape[0])*5,
np.ones(shoot.shape[0])*6),axis=0)
print('y_inliers.shape: ',y_inliers.shape)
X_outliers = np.concatenate((typing,writing,mouseManipulating,pinch),axis=0)
print('X_outliers.shape: ',X_outliers.shape)
y_outliers = np.concatenate((np.ones(typing.shape[0])*7,np.ones(writing.shape[0])*8, np.ones(mouseManipulating.shape[0])*9,np.ones(pinch.shape[0])*10),axis=0)
print('y_outliers.shape: ',y_outliers.shape)
model = Spatial_Model((12, 8, 3))
model.summary()
trainModel = False
from sklearn.model_selection import train_test_split
X_train, X_test_norm, y_train, y_test_norm = train_test_split(X_inliers, y_inliers, test_size=0.20, random_state=42)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.2, random_state=1)
y_train_onehot = keras.utils.to_categorical(y_train, classNum)
y_test_onehot = keras.utils.to_categorical(y_test_norm, classNum)
model.compile(loss=categorical_crossentropy, optimizer=Adadelta(lr=0.1), metrics=['acc'])
if trainModel:
model.fit(x=X_train, y=y_train_onehot, batch_size=16, epochs=50, shuffle=True, validation_split=0.05)
model.compile(loss=categorical_crossentropy, optimizer=Adadelta(lr=0.01), metrics=['acc'])
model.fit(x=X_train, y=y_train_onehot, batch_size=16, epochs=50, shuffle=True, validation_split=0.05)
model.save_weights('./model/modelCNN.h5')
else:
model.load_weights('./model/modelCNN.h5')
model_evaluate = []
model_evaluate.append(model.evaluate(X_test_norm,y_test_onehot))
print('model_evaluate',model_evaluate)
layer_name = 'dense_layer2'
X_train_intermediate = getIntermediate(layer_name,X_train,model)
X_test_intermediate_norm = getIntermediate(layer_name,X_test_norm,model)
typing_intermediate = getIntermediate(layer_name,typing,model)
writing_intermediate = getIntermediate(layer_name,writing,model)
mouseManipulating_intermediate = getIntermediate(layer_name,mouseManipulating,model)
pinch_intermediate = getIntermediate(layer_name,pinch,model)
radialDeviation_intermediate = getIntermediate(layer_name,radialDeviation,model)
ulnarDeviation_intermediate = getIntermediate(layer_name,ulnarDeviation,model)
## train Data
wristPronation_intermediate_train = getPointedGesture(X_train_intermediate,y_train,0)
wristSupination_intermediate_train = getPointedGesture(X_train_intermediate,y_train,1)
wristExtension_intermediate_train = getPointedGesture(X_train_intermediate,y_train,2)
wristFlexion_intermediate_train = getPointedGesture(X_train_intermediate,y_train,3)
handOpen_intermediate_train = getPointedGesture(X_train_intermediate,y_train,4)
handClose_intermediate_train = getPointedGesture(X_train_intermediate,y_train,5)
shoot_intermediate_train = getPointedGesture(X_train_intermediate,y_train,6)
## test data
wristPronation_intermediate_test = getPointedGesture(X_test_intermediate_norm,y_test_norm,0)
wristSupination_intermediate_test = getPointedGesture(X_test_intermediate_norm,y_test_norm,1)
wristExtension_intermediate_test = getPointedGesture(X_test_intermediate_norm,y_test_norm,2)
wristFlexion_intermediate_test = getPointedGesture(X_test_intermediate_norm,y_test_norm,3)
handOpen_intermediate_test = getPointedGesture(X_test_intermediate_norm,y_test_norm,4)
handClose_intermediate_test = getPointedGesture(X_test_intermediate_norm,y_test_norm,5)
shoot_intermediate_test = getPointedGesture(X_test_intermediate_norm,y_test_norm,6)
typing_intermediate_test = typing_intermediate
writing_intermediate_test = writing_intermediate
mouseManipulating_intermediate_test = mouseManipulating_intermediate
pinch_intermediate_test = pinch_intermediate
radialDeviation_intermediate_test = radialDeviation_intermediate
ulnarDeviation_intermediate_test = ulnarDeviation_intermediate
outlierData = {'typing_intermediate_test':typing_intermediate_test,
'writing_intermediate_test':writing_intermediate_test,
'mouseManipulating_intermediate_test':mouseManipulating_intermediate_test,
'pinch_intermediate_test':pinch_intermediate_test}
motionNameList = ['wristPronation','wristSupination','wristExtension','wristFlexion','handOpen','handClose','shoot']
trainDataDict = {motionNameList[0]:wristPronation_intermediate_train,motionNameList[1]:wristSupination_intermediate_train,
motionNameList[2]:wristExtension_intermediate_train,motionNameList[3]:wristFlexion_intermediate_train,
motionNameList[4]:handOpen_intermediate_train,motionNameList[5]:handClose_intermediate_train,
motionNameList[6]:shoot_intermediate_train}
testDataNameList = ['wristPronation','wristSupination','wristExtension','wristFlexion','handOpen','handClose','shoot',
'typing','writing','mouseManipulating','pinch','radialDeviation','ulnarDeviation']
testDataDict = {testDataNameList[0]:wristPronation_intermediate_test,testDataNameList[1]:wristSupination_intermediate_test,
testDataNameList[2]:wristExtension_intermediate_test,testDataNameList[3]:wristFlexion_intermediate_test,
testDataNameList[4]:handOpen_intermediate_test,testDataNameList[5]:handClose_intermediate_test,
testDataNameList[6]:shoot_intermediate_test,testDataNameList[7]:typing_intermediate_test[0:150],
testDataNameList[8]:writing_intermediate_test[0:150],testDataNameList[9]:mouseManipulating_intermediate_test[0:150],
testDataNameList[10]:pinch_intermediate_test[0:150],testDataNameList[11]:radialDeviation_intermediate_test[0:150],
testDataNameList[12]:ulnarDeviation_intermediate_test[0:150]}
X_val_intermediate = getIntermediate(layer_name,X_val,model)
wristPronation_intermediate_val = getPointedGesture(X_val_intermediate,y_val,0)
wristSupination_intermediate_val = getPointedGesture(X_val_intermediate,y_val,1)
wristExtension_intermediate_val = getPointedGesture(X_val_intermediate,y_val,2)
wristFlexion_intermediate_val = getPointedGesture(X_val_intermediate,y_val,3)
handOpen_intermediate_val = getPointedGesture(X_val_intermediate,y_val,4)
handClose_intermediate_val = getPointedGesture(X_val_intermediate,y_val,5)
shoot_intermediate_val = getPointedGesture(X_val_intermediate,y_val,6)
valDataDict = {motionNameList[0]:wristPronation_intermediate_val,motionNameList[1]:wristSupination_intermediate_val,
motionNameList[2]:wristExtension_intermediate_val,motionNameList[3]:wristFlexion_intermediate_val,
motionNameList[4]:handOpen_intermediate_val,motionNameList[5]:handClose_intermediate_val,
motionNameList[6]:shoot_intermediate_val}
```
## part2: autoEncoder
```
from keras import regularizers
from keras.losses import mean_squared_error
from keras.optimizers import SGD
def autoModel(input_shape):
input_img = Input(input_shape)
encoded = Dense(256, activation='relu',kernel_regularizer=regularizers.l2(0.002))(input_img)
encoded = BatchNormalization()(encoded)
encoded = Dense(64, activation='relu',kernel_regularizer=regularizers.l2(0.002))(encoded)
encoded = BatchNormalization()(encoded)
decoded = Dense(256, activation='relu',kernel_regularizer=regularizers.l2(0.002))(encoded)
decoded = BatchNormalization()(decoded)
decoded = Dense(512, activation='relu',kernel_regularizer=regularizers.l2(0.002))(decoded)
model = Model(input_img, decoded)
return model
trainAutoFlag = False
if trainAutoFlag:
for motionId in range(len(motionNameList)):
motionName = motionNameList[motionId]
x_train = trainDataDict[motionName]
x_val = valDataDict[motionName]
autoencoder = autoModel((512,))
autoencoder.compile(loss=mean_squared_error, optimizer=SGD(lr=0.1))
autoencoder.fit(x_train, x_train,
epochs=600,
batch_size=16,
shuffle=True,
validation_data=(x_val, x_val))
autoencoder.compile(loss=mean_squared_error, optimizer=SGD(lr=0.01))
autoencoder.fit(x_train, x_train,
epochs=300,
batch_size=16,
shuffle=True,
validation_data=(x_val, x_val))
autoencoder.save_weights('./model/autoencoder/Autoencoder_'+motionName+'.h5')
```
### Calculate ROC curve
```
import matplotlib
import matplotlib.pyplot as plt
from scipy.spatial.distance import pdist
from sklearn.metrics import roc_curve, auc
targetDict = {}
for motionId in range(len(motionNameList)):
targetList = []
motionName = motionNameList[motionId]
print('motionName: ', motionName)
# load models
autoencoder = autoModel((512,))
autoencoder.compile(loss=mean_squared_error, optimizer=Adadelta(lr=0.5))
autoencoder.load_weights('./model/autoencoder/Autoencoder_'+motionName+'.h5')
original = valDataDict[motionName]
decoded_imgs = autoencoder.predict(original)
num = decoded_imgs.shape[0]
for i in range(num):
X = np.vstack([original[i,:],decoded_imgs[i,:]])
lose = pdist(X,'braycurtis')
targetList.append(lose[0])
targetDict[motionName] = targetList
mdDict = {}
for motionId in range(len(motionNameList)):
motionName = motionNameList[motionId]
print('motionName: ', motionName)
# load models
autoencoder = autoModel((512,))
autoencoder.compile(loss=mean_squared_error, optimizer=Adadelta(lr=0.5))
autoencoder.load_weights('./model/autoencoder/AutoEncoder_'+motionName+'.h5')
originalDict = {}
decodedDict = {}
for gestureId in range(len(testDataNameList)):
originalDict[testDataNameList[gestureId]] = testDataDict[testDataNameList[gestureId]]
decodedDict[testDataNameList[gestureId]] = autoencoder.predict(originalDict[testDataNameList[gestureId]])
reconstruction_error = []
for gestureID in range(len(testDataNameList)):
original = originalDict[testDataNameList[gestureID]]
decoded_imgs = decodedDict[testDataNameList[gestureID]]
num = decoded_imgs.shape[0]
for i in range(num):
X = np.vstack([original[i,:],decoded_imgs[i,:]])
lose = pdist(X,'braycurtis')
reconstruction_error.append(lose[0])
mdDict[motionName] = reconstruction_error
outlierAllNum = 150 * 6 #six novel motions, 150 samples for each motion
y_label = []
for motionId in range(len(motionNameList)):
motionName = motionNameList[motionId]
y_label.extend(np.ones(len(testDataDict[motionName])))
y_label.extend(np.zeros(len(testDataDict['typing'])))
y_label.extend(np.zeros(len(testDataDict['writing'])))
y_label.extend(np.zeros(len(testDataDict['mouseManipulating'])))
y_label.extend(np.zeros(len(testDataDict['pinch'])))
y_label.extend(np.zeros(len(testDataDict['radialDeviation'])))
y_label.extend(np.zeros(len(testDataDict['radialDeviation'])))
outliers_fraction_List = []
P_List = []
R_List = []
F1_List = []
TPR_List = []
FPR_List = []
#outliers_fraction = 0.02
for outliers_i in range(-1,101):
outliers_fraction = outliers_i/100
outliers_fraction_List.append(outliers_fraction)
y_pred = np.zeros(len(y_label))
thresholdDict = {}
for motionId in range(len(motionNameList)):
# motionId = 0
motionName = motionNameList[motionId]
distances = targetDict[motionName]
distances = np.sort(distances)
num = len(distances)
# print('outliers_fraction:',outliers_fraction)
if outliers_fraction >= 0:
threshold = distances[num-1-int(outliers_fraction*num)]# get threshold
if outliers_fraction < 0:
threshold = 10000.0
if outliers_fraction == 1.0:
threshold = 0
thresholdDict[motionName] = threshold
mdDistances = mdDict[motionName]
y_pred_temp = (np.array(mdDistances)<=threshold)*1
y_pred = y_pred + y_pred_temp
y_pred = (y_pred>0)*1
TP = np.sum(y_pred[0:-outlierAllNum])
FN = len(y_pred[0:-outlierAllNum])-TP
FP = np.sum(y_pred[-outlierAllNum:])
TN = outlierAllNum - FP
t = 0.00001
P = TP/(TP+FP+t)
R = TP/(TP+FN+t)
F1 = 2*P*R/(P+R+t)
TPR = TP/(TP+FN+t)
FPR = FP/(TN+FP+t)
P_List.append(P)
R_List.append(R)
F1_List.append(F1)
TPR_List.append(TPR)
FPR_List.append(FPR)
roc_auc = auc(FPR_List, TPR_List)
fig, ax = plt.subplots(figsize=(5, 5))
plt.plot(FPR_List, TPR_List, lw=2,label='AUC = %0.2f' % ( roc_auc))
plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r',label='Chance', alpha=.8)
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic(ROC)')
plt.legend(loc="lower right")
plt.show()
```
### calculate classification accuracies
```
resultDict = {}
for motionId in range(len(motionNameList)):
motionName = motionNameList[motionId]
# load models
autoencoder = autoModel((512,))
autoencoder.compile(loss=mean_squared_error, optimizer=Adadelta(lr=0.5))
autoencoder.load_weights('./model/autoencoder/AutoEncoder_'+motionName+'.h5')
# refactore data
originalDict = {}
decodedDict = {}
for gestureId in range(len(testDataNameList)):
originalDict[testDataNameList[gestureId]] = testDataDict[testDataNameList[gestureId]]
decodedDict[testDataNameList[gestureId]] = autoencoder.predict(originalDict[testDataNameList[gestureId]])
loseDict = {}
for gestureID in range(len(testDataNameList)):
loseList= []
original = originalDict[testDataNameList[gestureID]]
decoded_imgs = decodedDict[testDataNameList[gestureID]]
num = decoded_imgs.shape[0]
for i in range(num):
X = np.vstack([original[i,:],decoded_imgs[i,:]])
lose = pdist(X,'braycurtis')
loseList.append(lose[0])
loseDict[testDataNameList[gestureID]] = loseList
resultDict[motionName] = loseDict
outliers_fraction = 0.15
thresholdDict = {}
for motionId in range(len(motionNameList)):
motionName = motionNameList[motionId]
# load model
autoencoder = autoModel((512,))
autoencoder.compile(loss=mean_squared_error, optimizer=Adadelta(lr=0.5))
autoencoder.load_weights('./model/autoencoder/AutoEncoder_'+motionName+'.h5')
# val data
original_val = valDataDict[motionName]
decoded_val = autoencoder.predict(original_val)
loseList= []
original = original_val
decoded_imgs = decoded_val
num = decoded_imgs.shape[0]
for i in range(num):
X = np.vstack([original[i,:],decoded_imgs[i,:]])
lose = pdist(X,'braycurtis')
loseList.append(lose[0])
## calculate threshold for each task
loseArray = np.array(loseList)
loseArraySort = np.sort(loseArray)
anomaly_threshold = loseArraySort[-(int((outliers_fraction*len(loseArray)))+1)]
thresholdDict[motionName] = anomaly_threshold
# plot lose and threshold
fig, ax = plt.subplots(figsize=(5, 5))
t = np.arange(num)
s = loseArray
ax.scatter(t,s,label=motionName)
ax.hlines(anomaly_threshold,0,150,colors = "r")
ax.set(xlabel='sample (n)', ylabel='MSE',
title='MSEs of '+ motionName + ', threshold:' + str(anomaly_threshold))
ax.grid()
plt.legend(loc="lower right")
plt.xlim(xmin = -3)
plt.xlim(xmax = 70)
plt.show()
errorSum = 0
testSum = 0
barDict = {}
outlierClass = 6
rejectMotion = {}
for motionId in range(len(testDataNameList)):
recogList = []
motionName = testDataNameList[motionId]
for recogId in range(len(testDataNameList)-outlierClass):
identyResult = resultDict[testDataNameList[recogId]]
targetResult = np.array(identyResult[motionName])
recogList.append((targetResult<=thresholdDict[testDataNameList[recogId]])*1) # 每一个类别有自己的threshold用于拒判
recogArray = np.array(recogList)
recogArray = np.sum(recogArray,axis=0)
recogArray = (recogArray>0)*1
rejectMotion[testDataNameList[motionId]] = recogArray
if motionId<(len(testDataNameList)-outlierClass):
numError = np.sum(1-recogArray)
else:
numError = np.sum(recogArray)
numTarget = len(recogArray)
if motionId<(len(testDataNameList)-outlierClass):
errorSum = errorSum + numError
testSum = testSum + numTarget
barDict[testDataNameList[motionId]] = (numError/numTarget)
barDict['target overall'] = errorSum/testSum
print(barDict)
import matplotlib.pyplot as plt; plt.rcdefaults()
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
figure(num=None, figsize=(15, 6))
objects = ('wristPronation','wristSupination','wristExtension','wristFlexion','handOpen','handClose','shoot','target overall',
'typing','writing','mouseManipulating','pinch','radialDeviation','ulnarDeviation')
y_pos = np.arange(len(objects))
proposed = []
for i in range(len(objects)):
proposed.append(barDict[objects[i]])
bar_width = 0.35
opacity = 0.8
rects2 = plt.bar(y_pos + bar_width, proposed, bar_width,
alpha=opacity,
label='Proposed')
plt.xticks(y_pos + bar_width, objects)
plt.ylabel('Error Rates of Novelty Detection (%)')
plt.legend()
plt.tight_layout()
plt.show()
```
| true |
code
| 0.670285 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/JSJeong-me/KOSA-Big-Data_Vision/blob/main/Model/0_rf-PCA_All_to_csv.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#!pip install -U pandas-profiling
import pandas as pd
#import pandas_profiling
df = pd.read_csv('credit_cards_dataset.csv')
df.head(3)
#df.profile_report()
#df.corr(method='spearman')
df.columns
```
PCA for Pay_Score Bill_Amount Pay_Amount
```
from sklearn.decomposition import PCA
df_Pay_Score = df[['PAY_0','PAY_2', 'PAY_3', 'PAY_4', 'PAY_5', 'PAY_6']]
df_Bill_Amount = df[[ 'BILL_AMT1', 'BILL_AMT2','BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6']]
df_Pay_Amount = df[['PAY_AMT1','PAY_AMT2', 'PAY_AMT3', 'PAY_AMT4', 'PAY_AMT5', 'PAY_AMT6']]
df_Pay_Score.head(3)
df_Bill_Amount.head(3)
df_Pay_Amount.head(3)
```
PCA instance 생성
```
trans = PCA(n_components=1)
X_Pay_Score = df_Pay_Score.values
X_Bill_Amount = df_Bill_Amount.values
X_Pay_Amount = df_Pay_Amount.values
# transform the data
X_dim = trans.fit_transform(X_Pay_Score)
X_dim.shape
df_X_dim_Pay_Score = pd.DataFrame(X_dim, columns=['Pay_AVR'])
# transform the data
X_dim = trans.fit_transform(X_Bill_Amount)
df_X_dim_Bill_Amount = pd.DataFrame(X_dim, columns=['Bill_AVR'])
# transform the data
X_dim = trans.fit_transform(X_Pay_Amount)
df_X_dim_Pay_Amount = pd.DataFrame(X_dim, columns=['P_AMT_AVR'])
```
목표변수 : default.payment.next.month Input 데이터 셋: X
```
df = pd.concat([df, df_X_dim_Pay_Score, df_X_dim_Bill_Amount, df_X_dim_Pay_Amount], axis=1)
df_pca = df.drop(['PAY_0','PAY_2', 'PAY_3', 'PAY_4', 'PAY_5', 'PAY_6','BILL_AMT1', 'BILL_AMT2','BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6', 'PAY_AMT1','PAY_AMT2', 'PAY_AMT3', 'PAY_AMT4', 'PAY_AMT5', 'PAY_AMT6'], axis =1)
df_pca.columns
columns = list(df_pca.columns)
columns = ['ID','LIMIT_BAL', 'SEX', 'EDUCATION', 'MARRIAGE', 'AGE','Pay_AVR', 'Bill_AVR', 'P_AMT_AVR', 'default.payment.next.month']
df_pca = df_pca[columns]
df_pca.head(3)
df_pca.to_csv('credit_cards_pca.csv',header=True, index=False, encoding='UTF-8')
X = df.drop(['ID','PAY_0','PAY_2', 'PAY_3', 'PAY_4', 'PAY_5', 'PAY_6','BILL_AMT1', 'BILL_AMT2','BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6', 'PAY_AMT1','PAY_AMT2', 'PAY_AMT3', 'PAY_AMT4', 'PAY_AMT5', 'PAY_AMT6', 'default.payment.next.month'], axis =1).values
X.shape
y = df['default.payment.next.month'].values
```
Train Test Data Set 분리
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, random_state=42, shuffle=True)
```
RandomForest 모델 생성 및 학습
```
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=200, criterion='entropy', max_features='log2', max_depth=15)
rf.fit(X_train, y_train)
y_predict = rf.predict(X_test)
```
모델 성능 평가
```
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import numpy as np
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
cnf_matrix = confusion_matrix(y_test, y_predict)
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=['Non_Default','Default'], normalize=False,
title='Non Normalized confusion matrix')
from sklearn.metrics import recall_score
print("Recall score:"+ str(recall_score(y_test, y_predict)))
```
| true |
code
| 0.467757 | null | null | null | null |
|
<h1><font size=12>
Weather Derivatites </h1>
<h1> Rainfall Simulator <br></h1>
Developed by [Jesus Solano](mailto:ja.solano588@uniandes.edu.co) <br>
16 September 2018
```
# Import needed libraries.
import numpy as np
import pandas as pd
import random as rand
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
from scipy.stats import gamma
import time
```
## Simulation Function Core
```
### Build the simulation core.
# Updates the state of the day based on yesterday state.
def updateState(yesterdayDate, yesterdayState, monthTransitions):
yesterdayMonth = yesterdayDate.month
successProbability = monthTransitions['p'+str(yesterdayState)+'1'][yesterdayMonth]
todayState = bernoulli.rvs(successProbability)
return todayState
# Simulates one run of simulation.
def oneRun(daysNumber, startDate, initialState, monthTransitions,fittedGamma):
# Create a variable to store the last day state.
yesterdayState = initialState
# Generate a timestamp with all days in simulation.
dates = pd.date_range(startDate, periods=daysNumber, freq='D')
# Define the total rainfall amount over the simulation.
rainfall = 0
# Loop over days in simulation to calculate rainfall ammount.
for day in dates:
# Update today state based on the yesterday state.
todayState = updateState(day-1, yesterdayState, monthTransitions)
# Computes total accumulated rainfall.
if todayState == 1:
todayRainfall = gamma.rvs(fittedGamma['Shape'][0],fittedGamma['Loc'][0],fittedGamma['Scale'][0])
# Updates rainfall amount.
rainfall += todayRainfall
yesterdayState = todayState
return rainfall
# Run only one iteration(Print structure of results)
# Simulations iterations.
iterations = 10000
# Transitions probabilites.
monthTransitionsProb = pd.read_csv('../results/visibleMarkov/monthTransitions.csv', index_col=0)
# Rainfall amount parameters( Gamma parameters)
fittedGamma = pd.read_csv('../results/visibleMarkov/fittedGamma.csv', index_col=0)
# Number of simulation days(i.e 30, 60)
daysNumber = 30
# Simulation start date ('1995-04-22')
startDate = '2018-08-18'
# State of rainfall last day before start date --> Remember 0 means dry and 1 means wet.
initialState = 0
oneRun(daysNumber,startDate,initialState, monthTransitionsProb,fittedGamma)
```
## Complete Simulation
```
# Run total iterations.
def totalRun(daysNumber,startDate,initialState, monthTransitionsProb,fittedGamma,iterations):
# Array to store all precipitations.
rainfallPerIteration = [None]*iterations
# Loop over each iteration(simulation)
for i in range(iterations):
iterationRainfall = oneRun(daysNumber,startDate,initialState, monthTransitionsProb,fittedGamma)
rainfallPerIteration[i] = iterationRainfall
return rainfallPerIteration
#### Define parameters simulation.
# Simulations iterations.
iterations = 10000
# Transitions probabilites.
monthTransitionsProb = pd.read_csv('../results/visibleMarkov/monthTransitions.csv', index_col=0)
# Rainfall amount parameters( Gamma parameters)
fittedGamma = pd.read_csv('../results/visibleMarkov/fittedGamma.csv', index_col=0)
# Number of simulation days(i.e 30, 60)
daysNumber = 30
# Simulation start date ('1995-04-22')
startDate = '2018-08-18'
# State of rainfall last day before start date --> Remember 0 means dry and 1 means wet.
initialState = 0
```
## Final Results
```
# Final Analysis.
finalSimulation = totalRun(daysNumber,startDate,initialState, monthTransitionsProb,fittedGamma,iterations)
fig = plt.figure(figsize=(20, 10))
plt.hist(finalSimulation,facecolor='steelblue',bins=100, density=True,
histtype='stepfilled', edgecolor = 'black' , hatch = '+')
plt.title('Rainfall Simulation')
plt.xlabel('Rainfall Amount [mm]')
plt.ylabel('Probability ')
plt.grid()
plt.show()
```
| true |
code
| 0.562537 | null | null | null | null |
|
#Importing and Unzipping the dataset
```
!unzip "/content/gdrive/My Drive/P14-Convolutional-Neural-Networks.zip"
!ls
```
#Building the neural network
Importing the libraries
```
from tensorflow.python.keras.models import Sequential
from tensorflow.python.keras.layers import Convolution2D
from tensorflow.python.keras.layers import MaxPooling2D
from tensorflow.python.keras.layers import Flatten
from tensorflow.python.keras.layers import Dense
```
Initialising the neural network
```
classifier=Sequential()
```
Building the CNN and adding the layers
Layer 1 : Convolution Layer
```
classifier.add(Convolution2D(32,3,3,input_shape=(64,64,3),activation='relu'))
```
Layer 2: Max Pooling Layer
```
classifier.add(MaxPooling2D(pool_size=(2,2)))
```
Layer 3,4: Adding additional layers to improve accuracy
```
#Here we do not need to add the input shape ,since the input is not images but feature maps ,
#so Keras will know the size of the input feature maps
classifier.add(Convolution2D(32,3,3,activation='relu'))
classifier.add(MaxPooling2D(pool_size=(2,2)))
```
Layer 5: Flattening Layer
```
classifier.add(Flatten())
```
Layer 6: Classic ANN Layer(Full Connection)
```
classifier.add(Dense(128,activation='relu'))
classifier.add(Dense(1,activation='sigmoid'))
#the output layer has only one node , since the output is binary (there are only 2 categories)
```
Compiling the CNN
```
classifier.compile(optimizer='adam',loss='binary_crossentropy',metrics=['accuracy'])
```
#Image Pre-processing
###Data Augmentation for generalisation and preventing over-fitting
Data augmentation is a strategy that enables practitioners to significantly increase the diversity of data available for training models, without actually collecting new data. Data augmentation techniques such as cropping, padding, and horizontal flipping are commonly used to train large neural networks.
```
#We create two seperate objects of the ImageDataGenerator class one for the training set and one for the test set
from tensorflow.python.keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(
rescale=1./255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
#feature scaling
test_datagen = ImageDataGenerator(rescale=1./255)
```
Augmenting and creating training set
```
training_set = train_datagen.flow_from_directory(
'dataset/training_set',
target_size=(64, 64),
batch_size=32,
class_mode='binary')
```
Augmenting and creating test set
```
test_set = test_datagen.flow_from_directory(
'dataset/test_set',
target_size=(64, 64),
batch_size=32,
class_mode='binary')
```
####Notes:
1. Since the data augmentation is random ,it reduces the chances for overfitting ,since no two images are the same.
2.Data augmentation happens in batches, so a certain kind of data augmentation is applied to a batch of images.
3. The setup of the dataset directory is very important . Making a folder for each category proves to be extremely useful and can be directly used for data augmentation and model fitting.
#Fitting the model on the training set and also testing performance on test set simultaneously.
```
classifier.fit_generator(
training_set,
steps_per_epoch=8000,
epochs=25,
validation_data=test_set,
validation_steps=2000)
```
###Notes:
1.To increase the accuracy of the CNN , we can add more number of convolutional layes to the network ,or tweek the parameters of these layers.
2.Also increasing the target size of the images allows the network to capture the features more effectively and efficiently.
3.Data augmentation can be modified and more complex data augmentation operations can be applied on the dataset to increase the accuracy of the network.
| true |
code
| 0.697184 | null | null | null | null |
|
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
#export
from exp.nb_02_callbacks import *
```
# Initial Setup
```
x_train, y_train, x_valid, y_valid = get_data(url=MNIST_URL)
train_ds = Dataset(x=x_train, y=y_train)
valid_ds = Dataset(x=x_valid, y=y_valid)
nh = 50
bs = 16
c = y_train.max().item() + 1
loss_func = F.cross_entropy
data = DataBunch(*get_dls(train_ds, valid_ds, bs=bs), c=c)
#export
def create_learner(model_func, loss_func, data):
return Learner(*model_func(data), loss_func, data)
learner = create_learner(get_model, loss_func, data)
run = Runner(cbs=[AvgStatsCallback(metrics=[accuracy])])
run.fit(epochs=3, learner=learner)
learner = create_learner(partial(get_model, lr=0.3), loss_func, data)
run = Runner(cbs=[AvgStatsCallback(metrics=[accuracy])])
run.fit(epochs=3, learner=learner)
#export
def get_model_func(lr=0.5):
return partial(get_model, lr=lr)
```
# Annealing
```
We define two new callbacks:
1. a Recorder: to save track of the loss and our scheduled learning rate
2. a ParamScheduler: that can schedule any hyperparameter as long as it's registered in the state_dict of the optimizer
```
```
#export
class Recorder(Callback):
def begin_fit(self):
self.lrs = []
self.losses = []
def after_batch(self):
if not self.in_train:
return
self.lrs.append(self.opt.param_groups[-1]["lr"])
self.losses.append(self.loss.detach().cpu())
def plot_lr(self):
plt.plot(self.lrs)
def plot_loss(self):
plt.plot(self.losses)
class ParamScheduler(Callback):
_order = 1
def __init__(self, pname, sched_func):
self.pname = pname
self.sched_func = sched_func
def set_param(self):
for pg in self.opt.param_groups:
### print(self.sched_func, self.n_epochs, self.epochs)
pg[self.pname] = self.sched_func(self.n_epochs/self.epochs)
def begin_batch(self):
if self.in_train:
self.set_param()
```
```
Let's start with a simple linear schedule going from start to end.
It returns a function that takes a "pos" argument (going from 0 to 1) such that this function goes from "start" (at pos=0) to "end" (at pos=1) in a linear fashion.
```
```
def sched_linear(start, end, pos):
def _inner(start, end, pos):
return start + (end-start)*pos
return partial(_inner, start, end)
```
```
We can refator the above sched_linear function using decorators so that we donot need to create a separate instance of sched_linear for every pos value
```
```
#export
def annealer(f):
def _inner(start, end):
return partial(f, start, end)
return _inner
@annealer
def sched_linear(start, end, pos):
return start + (end-start)*pos
f = sched_linear(1,2)
f
f(pos=0.3)
f(0.3)
f(0.5)
```
```
Some more important acheduler functions
```
```
#export
@annealer
def sched_cos(start, end, pos):
return start + (end-start) * (1 + math.cos(math.pi*(1-pos))) / 2.
@annealer
def sched_no(start, end, pos):
return start
@annealer
def sched_exp(start, end, pos):
return start * ((end/start) ** pos)
annealings = "NO LINEAR COS EXP".split(" ")
a = torch.arange(start=0, end=100)
p = torch.linspace(start=0.01, end=1, steps=100)
fns = [sched_no, sched_linear, sched_cos, sched_exp]
for fn, t in zip(fns, annealings):
f = fn(start=2, end=1e-2)
plt.plot(a, [f(i) for i in p], label=t)
plt.legend();
### in earlier version of Pytorch, a Tensor object did not had "ndim" attribute
### we can add any attribute to any Python object using property() function.
### here we are adding "ndim" attribute to Tensor object using the below monkey-patching
# torch.Tensor.ndim = property(lambda x: len(x.shape))
```
```
In practice we will want to use multiple schedulers and the below function helps us do that
```
```
#export
def combine_scheds(pcts, scheds):
"""
pcts : list of %ages of each scheduler
scheds: list of all schedulers
"""
assert sum(pcts) == 1
pcts = torch.tensor([0] + listify(pcts))
assert torch.all(pcts >= 0)
pcts = torch.cumsum(input=pcts, dim=0)
def _inner(pos):
"""pos is a value b/w (0,1)"""
idx = (pos >= pcts).nonzero().max()
actual_pos = (pos-pcts[idx]) / (pcts[idx+1]-pcts[idx])
return scheds[idx](pos=actual_pos)
return _inner
### Example of a learning rate scheduler annealing:
### using 30% of training budget to go from 0.3 to 0.6 using cosine scheduler
### using the rest 70% of the trainign budget to go from 0.6 to 0.2 using another cosine scheduler
sched = combine_scheds(pcts=[0.3, 0.7], scheds=[sched_cos(start=0.3, end=0.6), sched_cos(start=0.6, end=0.2)])
plt.plot(a, [sched(i) for i in p])
```
```
We can use it for trainign quite easily.
```
```
cbfs = [Recorder,
partial(AvgStatsCallback, metrics=accuracy),
partial(ParamScheduler, pname="lr", sched_func=sched)]
cbfs
bs=512
data = DataBunch(*get_dls(train_ds, valid_ds, bs), c=c)
learner = create_learner(model_func=get_model_func(lr=0.3), loss_func=loss_func, data=data)
run = Runner(cb_funcs=cbfs)
run.fit(epochs=2, learner=learner)
run.recorder.plot_lr()
run.recorder.plot_loss()
```
# Export
```
!python notebook_to_script.py imflash217__02_anneal.ipynb
pct = [0.3, 0.7]
pct = torch.tensor([0] + listify(pct))
pct = torch.cumsum(pct, 0)
pos = 2
(pos >= pct).nonzero().max()
```
| true |
code
| 0.754186 | null | null | null | null |
|
# Non-Gaussian Likelihoods
## Introduction
This example is the simplest form of using an RBF kernel in an `ApproximateGP` module for classification. This basic model is usable when there is not much training data and no advanced techniques are required.
In this example, we’re modeling a unit wave with period 1/2 centered with positive values @ x=0. We are going to classify the points as either +1 or -1.
Variational inference uses the assumption that the posterior distribution factors multiplicatively over the input variables. This makes approximating the distribution via the KL divergence possible to obtain a fast approximation to the posterior. For a good explanation of variational techniques, sections 4-6 of the following may be useful: https://www.cs.princeton.edu/courses/archive/fall11/cos597C/lectures/variational-inference-i.pdf
```
import math
import torch
import gpytorch
from matplotlib import pyplot as plt
%matplotlib inline
```
### Set up training data
In the next cell, we set up the training data for this example. We'll be using 10 regularly spaced points on [0,1] which we evaluate the function on and add Gaussian noise to get the training labels. Labels are unit wave with period 1/2 centered with positive values @ x=0.
```
train_x = torch.linspace(0, 1, 10)
train_y = torch.sign(torch.cos(train_x * (4 * math.pi))).add(1).div(2)
```
## Setting up the classification model
The next cell demonstrates the simplest way to define a classification Gaussian process model in GPyTorch. If you have already done the [GP regression tutorial](../01_Exact_GPs/Simple_GP_Regression.ipynb), you have already seen how GPyTorch model construction differs from other GP packages. In particular, the GP model expects a user to write out a `forward` method in a way analogous to PyTorch models. This gives the user the most possible flexibility.
Since exact inference is intractable for GP classification, GPyTorch approximates the classification posterior using **variational inference.** We believe that variational inference is ideal for a number of reasons. Firstly, variational inference commonly relies on gradient descent techniques, which take full advantage of PyTorch's autograd. This reduces the amount of code needed to develop complex variational models. Additionally, variational inference can be performed with stochastic gradient decent, which can be extremely scalable for large datasets.
If you are unfamiliar with variational inference, we recommend the following resources:
- [Variational Inference: A Review for Statisticians](https://arxiv.org/abs/1601.00670) by David M. Blei, Alp Kucukelbir, Jon D. McAuliffe.
- [Scalable Variational Gaussian Process Classification](https://arxiv.org/abs/1411.2005) by James Hensman, Alex Matthews, Zoubin Ghahramani.
In this example, we're using an `UnwhitenedVariationalStrategy` because we are using the training data as inducing points. In general, you'll probably want to use the standard `VariationalStrategy` class for improved optimization.
```
from gpytorch.models import ApproximateGP
from gpytorch.variational import CholeskyVariationalDistribution
from gpytorch.variational import UnwhitenedVariationalStrategy
class GPClassificationModel(ApproximateGP):
def __init__(self, train_x):
variational_distribution = CholeskyVariationalDistribution(train_x.size(0))
variational_strategy = UnwhitenedVariationalStrategy(
self, train_x, variational_distribution, learn_inducing_locations=False
)
super(GPClassificationModel, self).__init__(variational_strategy)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
latent_pred = gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
return latent_pred
# Initialize model and likelihood
model = GPClassificationModel(train_x)
likelihood = gpytorch.likelihoods.BernoulliLikelihood()
```
### Model modes
Like most PyTorch modules, the `ExactGP` has a `.train()` and `.eval()` mode.
- `.train()` mode is for optimizing variational parameters model hyperameters.
- `.eval()` mode is for computing predictions through the model posterior.
## Learn the variational parameters (and other hyperparameters)
In the next cell, we optimize the variational parameters of our Gaussian process.
In addition, this optimization loop also performs Type-II MLE to train the hyperparameters of the Gaussian process.
```
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
training_iterations = 2 if smoke_test else 50
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.1)
# "Loss" for GPs - the marginal log likelihood
# num_data refers to the number of training datapoints
mll = gpytorch.mlls.VariationalELBO(likelihood, model, train_y.numel())
for i in range(training_iterations):
# Zero backpropped gradients from previous iteration
optimizer.zero_grad()
# Get predictive output
output = model(train_x)
# Calc loss and backprop gradients
loss = -mll(output, train_y)
loss.backward()
print('Iter %d/%d - Loss: %.3f' % (i + 1, training_iterations, loss.item()))
optimizer.step()
```
## Make predictions with the model
In the next cell, we make predictions with the model. To do this, we simply put the model and likelihood in eval mode, and call both modules on the test data.
In `.eval()` mode, when we call `model()` - we get GP's latent posterior predictions. These will be MultivariateNormal distributions. But since we are performing binary classification, we want to transform these outputs to classification probabilities using our likelihood.
When we call `likelihood(model())`, we get a `torch.distributions.Bernoulli` distribution, which represents our posterior probability that the data points belong to the positive class.
```python
f_preds = model(test_x)
y_preds = likelihood(model(test_x))
f_mean = f_preds.mean
f_samples = f_preds.sample(sample_shape=torch.Size((1000,))
```
```
# Go into eval mode
model.eval()
likelihood.eval()
with torch.no_grad():
# Test x are regularly spaced by 0.01 0,1 inclusive
test_x = torch.linspace(0, 1, 101)
# Get classification predictions
observed_pred = likelihood(model(test_x))
# Initialize fig and axes for plot
f, ax = plt.subplots(1, 1, figsize=(4, 3))
ax.plot(train_x.numpy(), train_y.numpy(), 'k*')
# Get the predicted labels (probabilites of belonging to the positive class)
# Transform these probabilities to be 0/1 labels
pred_labels = observed_pred.mean.ge(0.5).float()
ax.plot(test_x.numpy(), pred_labels.numpy(), 'b')
ax.set_ylim([-1, 2])
ax.legend(['Observed Data', 'Mean'])
```
| true |
code
| 0.811657 | null | null | null | null |
|
# 3 - Faster Sentiment Analysis
In the previous notebook we managed to achieve a decent test accuracy of ~85% using all of the common techniques used for sentiment analysis. In this notebook, we'll implement a model that gets comparable results whilst training significantly faster. More specifically, we'll be implementing the "FastText" model from the paper [Bag of Tricks for Efficient Text Classification](https://arxiv.org/abs/1607.01759).
## Preparing Data
One of the key concepts in the FastText paper is that they calculate the n-grams of an input sentence and append them to the end of a sentence. Here, we'll use bi-grams. Briefly, a bi-gram is a pair of words/tokens that appear consecutively within a sentence.
For example, in the sentence "how are you ?", the bi-grams are: "how are", "are you" and "you ?".
The `generate_bigrams` function takes a sentence that has already been tokenized, calculates the bi-grams and appends them to the end of the tokenized list.
```
def generate_bigrams(x):
n_grams = set(zip(*[x[i:] for i in range(2)]))
for n_gram in n_grams:
x.append(' '.join(n_gram))
return x
```
As an example:
```
generate_bigrams(['This', 'film', 'is', 'terrible'])
```
TorchText `Field`s have a `preprocessing` argument. A function passed here will be applied to a sentence after it has been tokenized (transformed from a string into a list of tokens), but before it has been numericalized (transformed from a list of tokens to a list of indexes). This is where we'll pass our `generate_bigrams` function.
```
import torch
from torchtext import data
from torchtext import datasets
SEED = 1234
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.deterministic = True
TEXT = data.Field(tokenize='spacy', preprocessing=generate_bigrams)
LABEL = data.LabelField(dtype=torch.float)
```
As before, we load the IMDb dataset and create the splits.
```
import random
train_data, test_data = datasets.IMDB.splits(TEXT, LABEL)
train_data, valid_data = train_data.split(random_state=random.seed(SEED))
```
Build the vocab and load the pre-trained word embeddings.
```
TEXT.build_vocab(train_data, max_size=25000, vectors="glove.6B.100d")
LABEL.build_vocab(train_data)
```
And create the iterators.
```
BATCH_SIZE = 64
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits(
(train_data, valid_data, test_data),
batch_size=BATCH_SIZE,
device=device)
```
## Build the Model
This model has far fewer parameters than the previous model as it only has 2 layers that have any parameters, the embedding layer and the linear layer. There is no RNN component in sight!
Instead, it first calculates the word embedding for each word using the `Embedding` layer (blue), then calculates the average of all of the word embeddings (pink) and feeds this through the `Linear` layer (silver), and that's it!

We implement the averaging with the `avg_pool2d` (average pool 2-dimensions) function. Initially, you may think using a 2-dimensional pooling seems strange, surely our sentences are 1-dimensional, not 2-dimensional? However, you can think of the word embeddings as a 2-dimensional grid, where the words are along one axis and the dimensions of the word embeddings are along the other. The image below is an example sentence after being converted into 5-dimensional word embeddings, with the words along the vertical axis and the embeddings along the horizontal axis. Each element in this [4x5] tensor is represented by a green block.

The `avg_pool2d` uses a filter of size `embedded.shape[1]` (i.e. the length of the sentence) by 1. This is shown in pink in the image below.

We calculate the average value of all elements covered by the filter, then the filter then slides to the right, calculating the average over the next column of embedding values for each word in the sentence.

Each filter position gives us a single value, the average of all covered elements. After the filter has covered all embedding dimensions we get a [1x5] tensor. This tensor is then passed through the linear layer to produce our prediction.
```
import torch.nn as nn
import torch.nn.functional as F
class FastText(nn.Module):
def __init__(self, vocab_size, embedding_dim, output_dim):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.fc = nn.Linear(embedding_dim, output_dim)
def forward(self, text):
#text = [sent len, batch size]
embedded = self.embedding(text)
#embedded = [sent len, batch size, emb dim]
embedded = embedded.permute(1, 0, 2)
#embedded = [batch size, sent len, emb dim]
pooled = F.avg_pool2d(embedded, (embedded.shape[1], 1)).squeeze(1)
#pooled = [batch size, embedding_dim]
return self.fc(pooled)
```
As previously, we'll create an instance of our `FastText` class.
```
INPUT_DIM = len(TEXT.vocab)
EMBEDDING_DIM = 100
OUTPUT_DIM = 1
model = FastText(INPUT_DIM, EMBEDDING_DIM, OUTPUT_DIM)
```
And copy the pre-trained vectors to our embedding layer.
```
pretrained_embeddings = TEXT.vocab.vectors
model.embedding.weight.data.copy_(pretrained_embeddings)
```
## Train the Model
Training the model is the exact same as last time.
We initialize our optimizer...
```
import torch.optim as optim
optimizer = optim.Adam(model.parameters())
```
We define the criterion and place the model and criterion on the GPU (if available)...
```
criterion = nn.BCEWithLogitsLoss()
model = model.to(device)
criterion = criterion.to(device)
```
We implement the function to calculate accuracy...
```
def binary_accuracy(preds, y):
"""
Returns accuracy per batch, i.e. if you get 8/10 right, this returns 0.8, NOT 8
"""
#round predictions to the closest integer
rounded_preds = torch.round(torch.sigmoid(preds))
correct = (rounded_preds == y).float() #convert into float for division
acc = correct.sum()/len(correct)
return acc
```
We define a function for training our model...
**Note**: we are no longer using dropout so we do not need to use `model.train()`, but as mentioned in the 1st notebook, it is good practice to use it.
```
def train(model, iterator, optimizer, criterion):
epoch_loss = 0
epoch_acc = 0
model.train()
for batch in iterator:
optimizer.zero_grad()
predictions = model(batch.text).squeeze(1)
loss = criterion(predictions, batch.label)
acc = binary_accuracy(predictions, batch.label)
loss.backward()
optimizer.step()
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
```
We define a function for testing our model...
**Note**: again, we leave `model.eval()` even though we do not use dropout.
```
def evaluate(model, iterator, criterion):
epoch_loss = 0
epoch_acc = 0
model.eval()
with torch.no_grad():
for batch in iterator:
predictions = model(batch.text).squeeze(1)
loss = criterion(predictions, batch.label)
acc = binary_accuracy(predictions, batch.label)
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
```
Finally, we train our model...
```
N_EPOCHS = 5
for epoch in range(N_EPOCHS):
train_loss, train_acc = train(model, train_iterator, optimizer, criterion)
valid_loss, valid_acc = evaluate(model, valid_iterator, criterion)
print(f'| Epoch: {epoch+1:02} | Train Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}% | Val. Loss: {valid_loss:.3f} | Val. Acc: {valid_acc*100:.2f}% |')
```
...and get the test accuracy!
The results are comparable to the results in the last notebook, but training takes considerably less time.
```
test_loss, test_acc = evaluate(model, test_iterator, criterion)
print(f'| Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}% |')
```
## User Input
And as before, we can test on any input the user provides.
```
import spacy
nlp = spacy.load('en')
def predict_sentiment(sentence):
tokenized = [tok.text for tok in nlp.tokenizer(sentence)]
indexed = [TEXT.vocab.stoi[t] for t in tokenized]
tensor = torch.LongTensor(indexed).to(device)
tensor = tensor.unsqueeze(1)
prediction = torch.sigmoid(model(tensor))
return prediction.item()
```
An example negative review...
```
predict_sentiment("This film is terrible")
```
An example positive review...
```
predict_sentiment("This film is great")
```
## Next Steps
In the next notebook we'll use convolutional neural networks (CNNs) to perform sentiment analysis, and get our best accuracy yet!
| true |
code
| 0.77712 | null | null | null | null |
|
# Automatic differentiation with JAX
## Main features
- Numpy wrapper
- Auto-vectorization
- Auto-parallelization (SPMD paradigm)
- Auto-differentiation
- XLA backend and JIT support
## How to compute gradient of your objective?
- Define it as a standard Python function
- Call ```jax.grad``` and voila!
- Do not forget to wrap these functions with ```jax.jit``` to speed up
```
import jax
import jax.numpy as jnp
```
- By default, JAX exploits single-precision numbers ```float32```
- You can enable double precision (```float64```) by hands.
```
from jax.config import config
config.update("jax_enable_x64", True)
@jax.jit
def f(x, A, b):
res = A @ x - b
return res @ res
gradf = jax.grad(f, argnums=0, has_aux=False)
```
## Random numbers in JAX
- JAX focuses on the reproducibility of the runs
- Analogue of random seed is **the necessary argument** of all functions that generate something random
- More details and references on the design of ```random``` submodule are [here](https://github.com/google/jax/blob/master/design_notes/prng.md)
```
n = 1000
x = jax.random.normal(jax.random.PRNGKey(0), (n, ))
A = jax.random.normal(jax.random.PRNGKey(0), (n, n))
b = jax.random.normal(jax.random.PRNGKey(0), (n, ))
print("Check correctness", jnp.linalg.norm(gradf(x, A, b) - 2 * A.T @ (A @ x - b)))
print("Compare speed")
print("Analytical gradient")
%timeit 2 * A.T @ (A @ x - b)
print("Grad function")
%timeit gradf(x, A, b).block_until_ready()
jit_gradf = jax.jit(gradf)
print("Jitted grad function")
%timeit jit_gradf(x, A, b).block_until_ready()
hess_func = jax.jit(jax.hessian(f))
print("Check correctness", jnp.linalg.norm(2 * A.T @ A - hess_func(x, A, b)))
print("Time for hessian")
%timeit hess_func(x, A, b).block_until_ready()
print("Emulate hessian and check correctness",
jnp.linalg.norm(jax.jit(hess_func)(x, A, b) - jax.jacfwd(jax.jacrev(f))(x, A, b)))
print("Time of emulating hessian")
hess_umul_func = jax.jit(jax.jacfwd(jax.jacrev(f)))
%timeit hess_umul_func(x, A, b).block_until_ready()
```
## Forward mode vs. backward mode: $m \ll n$
```
fmode_f = jax.jit(jax.jacfwd(f))
bmode_f = jax.jit(jax.jacrev(f))
print("Check correctness", jnp.linalg.norm(fmode_f(x, A, b) - bmode_f(x, A, b)))
print("Forward mode")
%timeit fmode_f(x, A, b).block_until_ready()
print("Backward mode")
%timeit bmode_f(x, A, b).block_until_ready()
```
## Forward mode vs. backward mode: $m \geq n$
```
def fvec(x, A, b):
y = A @ x + b
return jnp.exp(y - jnp.max(y)) / jnp.sum(jnp.exp(y - jnp.max(y)))
grad_fvec = jax.jit(jax.grad(fvec))
jac_fvec = jax.jacobian(fvec)
fmode_fvec = jax.jit(jax.jacfwd(fvec))
bmode_fvec = jax.jit(jax.jacrev(fvec))
n = 1000
m = 1000
x = jax.random.normal(jax.random.PRNGKey(0), (n, ))
A = jax.random.normal(jax.random.PRNGKey(0), (m, n))
b = jax.random.normal(jax.random.PRNGKey(0), (m, ))
J = jac_fvec(x, A, b)
print(J.shape)
grad_fvec(x, A, b)
print("Check correctness", jnp.linalg.norm(fmode_fvec(x, A, b) - bmode_fvec(x, A, b)))
print("Check shape", fmode_fvec(x, A, b).shape, bmode_fvec(x, A, b).shape)
print("Time forward mode")
%timeit fmode_fvec(x, A, b).block_until_ready()
print("Time backward mode")
%timeit bmode_fvec(x, A, b).block_until_ready()
n = 10
m = 1000
x = jax.random.normal(jax.random.PRNGKey(0), (n, ))
A = jax.random.normal(jax.random.PRNGKey(0), (m, n))
b = jax.random.normal(jax.random.PRNGKey(0), (m, ))
print("Check correctness", jnp.linalg.norm(fmode_fvec(x, A, b) - bmode_fvec(x, A, b)))
print("Check shape", fmode_fvec(x, A, b).shape, bmode_fvec(x, A, b).shape)
print("Time forward mode")
%timeit fmode_fvec(x, A, b).block_until_ready()
print("Time backward mode")
%timeit bmode_fvec(x, A, b).block_until_ready()
```
## Hessian-by-vector product
```
def hvp(f, x, z, *args):
def g(x):
return f(x, *args)
return jax.jvp(jax.grad(g), (x,), (z,))[1]
n = 3000
x = jax.random.normal(jax.random.PRNGKey(0), (n, ))
A = jax.random.normal(jax.random.PRNGKey(0), (n, n))
b = jax.random.normal(jax.random.PRNGKey(0), (n, ))
z = jax.random.normal(jax.random.PRNGKey(0), (n, ))
print("Check correctness", jnp.linalg.norm(2 * A.T @ (A @ z) - hvp(f, x, z, A, b)))
print("Time for hvp by hands")
%timeit (2 * A.T @ (A @ z)).block_until_ready()
print("Time for hvp via jvp, NO jit")
%timeit hvp(f, x, z, A, b).block_until_ready()
print("Time for hvp via jvp, WITH jit")
%timeit jax.jit(hvp, static_argnums=0)(f, x, z, A, b).block_until_ready()
```
## Summary
- JAX is a simple and extensible tool in the problem where autodiff is crucial
- JIT is a key to fast Python code
- Input/output dimensions are important
- Hessian matvec is faster than explicit hessian matrix by vector product
| true |
code
| 0.651244 | null | null | null | null |
|
# The biharmonic equation on the Torus
The biharmonic equation is given as
$$
\nabla^4 u = f,
$$
where $u$ is the solution and $f$ is a function. In this notebook we will solve this equation inside a torus with homogeneous boundary conditions $u(r=1)=u'(r=1)=0$ on the outer surface. We solve the equation with the spectral Galerkin method in curvilinear coordinates.
<img src="https://cdn.jsdelivr.net/gh/spectralDNS/spectralutilities@master/figures/torus2.png">
The torus is parametrized by
\begin{align*}
x(r, \theta, \phi) &= (R + r \cos \theta) \cos \phi \\
y(r, \theta, \phi) &= (R + r \cos \theta) \sin \phi \\
z(r, \theta, \phi) &= r \sin \theta
\end{align*}
where the Cartesian domain is $\Omega = \{(x, y, z): \left(\sqrt{x^2+y^2} - R^2\right)^2 + z^2 < 1\}$ and the computational domain is $(r, \theta, \phi) \in D = [0, 1] \times [0, 2\pi] \times [0, 2\pi]$. Hence $\theta$ and $\phi$ are angles which make a full circle, so that their values start and end at the same point, $R$ is the distance from the center of the tube to the center of the torus,
$r$ is the radius of the tube. Note that $\theta$ is the angle in the small circle (around its center), whereas $\phi$ is the angle of the large circle, around origo.
We start the implementation by importing necessary functionality from shenfun and sympy and then defining the coordinates of the surface of the torus.
```
from shenfun import *
from shenfun.la import SolverGeneric2ND
import sympy as sp
from IPython.display import Math
N = 24
R = 3
r, theta, phi = psi = sp.symbols('x,y,z', real=True, positive=True)
rv = ((R + r*sp.cos(theta))*sp.cos(phi), (R + r*sp.cos(theta))*sp.sin(phi), r*sp.sin(theta))
def discourage_powers(expr):
POW = sp.Symbol('POW')
count = sp.count_ops(expr, visual=True)
count = count.replace(POW, 100)
count = count.replace(sp.Symbol, type(sp.S.One))
return count
B0 = FunctionSpace(N, 'L', basis='UpperDirichletNeumann', domain=(0, 1))
B1 = FunctionSpace(N, 'F', dtype='D', domain=(0, 2*np.pi))
B2 = FunctionSpace(N, 'F', dtype='d', domain=(0, 2*np.pi))
T = TensorProductSpace(comm, (B0, B1, B2), coordinates=(psi, rv, sp.Q.positive(r*sp.cos(theta)+R), (), discourage_powers))
T.coors.sg
```
We use Fourier basis functions for the two periodic directions, and a Legendre basis that satisfies the homogeneous boundary conditions for the radial direction.
Note that `rv` represents the position vector $\vec{r}=x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ and that `T.hi` now contains the 3 scaling factors for the torus coordinates:
\begin{align*}
h_r &= \left|\frac{\partial \vec{r}}{\partial r}\right| = 1\\
h_{\theta} &= \left|\frac{\partial \vec{r}}{\partial \theta}\right| = r\\
h_{\phi} &= \left|\frac{\partial \vec{r}}{\partial \phi}\right| = r\cos \theta + R\\
\end{align*}
The covariant basis vectors used by shenfun are
```
T.coors.sg
Math(T.coors.latex_basis_vectors(covariant=True, symbol_names={r: 'r', theta: '\\theta', phi: '\\phi'}))
```
Now check what the biharmonic operator looks like for the torus. Simplify equation using the integral measure $\sqrt{g}$, found as `T.coors.sg`
$$
\sqrt{g} = r (r \cos \theta + R)
$$
```
u = TrialFunction(T)
v = TestFunction(T)
du = div(grad(div(grad(u))))
g = sp.Symbol('g', real=True, positive=True)
replace = [(r*sp.cos(theta)+R, sp.sqrt(g)/r), (2*r*sp.cos(theta)+R, 2*sp.sqrt(g)/r-R)] # to simplify the look
Math((du*T.coors.sg**4).tolatex(symbol_names={r: 'r', theta: '\\theta', phi: '\\phi'}, replace=replace))
```
Glad you're not doing this by hand?
To solve this equation we need to get a variational form that is separable. To get a variational form we multiply the equation by a weight $\omega$ and the complex conjugate of a test function $\overline{v}$, and integrate over the domain by switching to computational coordinates
\begin{align*}
\int_{\Omega} \nabla^4 u\, \overline{v} \omega dV &= \int_{\Omega} f \, \overline{v} \omega dV \\
\int_{D} \nabla^4 u \, \overline{v} \omega \sqrt{g} dr d\theta d\phi &= \int_{D} f \, \overline{v} \omega \sqrt{g} dr d\theta d\phi
\end{align*}
<div class="alert alert-warning">
Note that the functions in the last equation now actually are transformed to computational space, i.e., $u=u(\mathbf{x}(r, \theta, \phi))$ and the same for the rest. We should probably use a new name for the transformed functions, but we keep the same here to keep it simple. Whether the function is transformed or not should be evident from context. If the integral is in computational space, then the functions are transformed.
</div>
For Legendre and Fourier test functions the weight $\omega$ is normally a constant. However, we see that the denominator in some terms above contains $g^2=r^4(r\cos \theta +R)^4$. The term in parenthesis $(r\cos \theta +R)$ makes the variational form above unseparable. If, on the other hand, we change the weight $\omega$ to $g^{3/2}$, then the misbehaving denominator disappears and the variational form becomes separable.
$$
\int_{D} \nabla^4 u \, \overline{v} \, g^2 dr d\theta d\phi = \int_{D} f \, \overline{v} \, g^2 dr d\theta d\phi
$$
Alternatively, we can aim at only removing the $(r\cos \theta +R)$ term from the denominator by using weight $(r\cos \theta +R)^3$
$$
\int_{D} \nabla^4 u \, \overline{v} \, r (r\cos \theta +R)^4 dr d\theta d\phi = \int_{D} f \, \overline{v} \, r \,(r\cos \theta + R)^4 dr d\theta d\phi.
$$
The first actually leads to a coefficient matrix of fewer bands than the second. However, the condition number is larger and round-off errors more severe. In the code below we use the first approach by default, but it can be easily changed with the commented out code.
We verify the implementation by using a manufactured solution that satisfies the boundary conditions. Note that the Legendre basis `ShenBiPolar0Basis`, chosen using `bc='BiPolar0'` with the `Basis`, currently is the only function space in shenfun that can satisfy $u(r=1, \theta, \phi)=u'(r=1, \theta, \phi)=u'(0, \theta, \phi)=0$, where the latter is a pole condition inherited from [Shen's paper on cylindrical coordinates](https://epubs.siam.org/doi/abs/10.1137/S1064827595295301). With the current weights the pole condition is probably not needed.
```
#ue = sp.sin(theta*2)*sp.cos(4*phi)*((1-r))**2 #+B0.sympy_basis(4, x=r)
#ue = (1-sp.exp(-(1-r)**2))**2*sp.cos(4*phi)
xx = r*sp.cos(theta); yy = r*sp.sin(theta)
ue = ((1-r)*sp.exp(-(xx-0.4)**2-(yy-0.3)**2))**2*sp.cos(2*phi)
f = div(grad(div(grad(u)))).tosympy(basis=ue, psi=psi)
fj = Array(T, buffer=f*T.coors.sg**3)
#fj = Array(T, buffer=f*T.hi[2]**3)
f_hat = Function(T)
f_hat = inner(v, fj, output_array=f_hat)
#M = inner(v*T.hi[2]**3, div(grad(div(grad(u)))))
#M = inner(v*T.coors.sg**3, div(grad(div(grad(u)))))
M = inner(div(grad(v*T.coors.sg**3)), div(grad(u)))
u_hat = Function(T)
sol = la.SolverGeneric2ND(M)
u_hat = sol(f_hat, u_hat)
uj = u_hat.backward()
uq = Array(T, buffer=ue)
print('Error =', np.sqrt(inner(1, (uj-uq)**2)))
```
Note that the variational form contains
```
len(M)
```
tensorproduct matrices, but some differ only in the scales. The solver `SolverGeneric2ND` loops over and solves for one Fourier coefficient in the $\phi$-direction at the time, because all submatrices in the $\phi$-direction are diagonal. The matrices in the $\theta$-direction are not necessarily diagonal because of the weight $(r\cos \theta + 3)$. The sparsity pattern of the matrix can be inspected as follows
```
import matplotlib.pyplot as plt
%matplotlib notebook
B = sol.diags(4)
#print(np.linalg.cond(B.toarray()))
plt.spy(B, markersize=0.1)
plt.show()
```
A baded matrix in deed, but quite a large number of bands.
A slice of the solution can be visualized. Here we use $\phi=0$, because that lies in the Cartesian $x-z$-plane.
```
u_hat2 = u_hat.refine([N*3, N*3, N])
ur = u_hat2.backward()
us = ur.get((slice(None), slice(None), 0))
xx, yy, zz = u_hat2.function_space().local_cartesian_mesh(uniform=True)
# Wrap periodic plot around since it looks nicer
xp = np.hstack([xx[:, :, 0], xx[:, 0, 0][:, None]])
zp = np.hstack([zz[:, :, 0], zz[:, 0, 0][:, None]])
up = np.hstack([us, us[:, 0][:, None]])
# plot
plt.figure()
plt.contourf(xp, zp, up)
plt.colorbar()
```
Now print the solution at approximately half the radius
```
from mayavi import mlab
u_hat3 = u_hat.refine([N, N*3, N*3])
ux = u_hat3.backward()
X = u_hat3.function_space().local_mesh(broadcast=True, uniform=True)
print('radius =',X[0][N//2,0,0])
```
Get the $\theta-\phi$ mesh for given radius
```
xj = []
for rv in T.coors.coordinates[1]:
xj.append(sp.lambdify(psi, rv)(X[0][N//2], X[1][N//2], X[2][N//2]))
xx, yy, zz = xj
us = ux[N//2]
```
Wrap around periodic direction to make it nicer
```
xx = np.hstack([xx, xx[:, 0][:, None]])
yy = np.hstack([yy, yy[:, 0][:, None]])
zz = np.hstack([zz, zz[:, 0][:, None]])
us = np.hstack([us, us[:, 0][:, None]])
xx = np.vstack([xx, xx[0]])
yy = np.vstack([yy, yy[0]])
zz = np.vstack([zz, zz[0]])
us = np.vstack([us, us[0]])
mlab.figure(bgcolor=(1, 1, 1))
mlab.mesh(xx, yy, zz, scalars=us, colormap='jet')
mlab.show()
```
## Vector Laplacian
Finally, we look at the vector Laplacian and verify the following
$$
\nabla^2 \vec{u} = \nabla \nabla \cdot \vec{u} - \nabla \times \nabla \times \vec{u}
$$
The vector Laplace $\nabla^2 \vec{u}$ looks like:
```
V = VectorSpace(T)
p = TrialFunction(V)
du = div(grad(p))
replace = [(r*sp.cos(theta)+R, sp.sqrt(g)/r), (2*r*sp.cos(theta)+R, 2*sp.sqrt(g)/r-R)] # to simplify the look
Math(du.tolatex(symbol_names={r: 'r', theta: '\\theta', phi: '\\phi'}, replace=replace))
```
And if we subtract $\nabla \nabla \cdot \vec{u} - \nabla \times \nabla \times \vec{u}$ we should get the zero vector.
```
dv = grad(div(p)) - curl(curl(p))
dw = du-dv
dw.simplify()
Math(dw.tolatex(symbol_names={r: 'r', theta: '\\theta', phi: '\\phi'}))
```
| true |
code
| 0.415847 | null | null | null | null |
|
# Changepoint Detection
Think Bayes, Second Edition
Copyright 2020 Allen B. Downey
License: [Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/)
```
# If we're running on Colab, install empiricaldist
# https://pypi.org/project/empiricaldist/
import sys
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
!pip install empiricaldist
# Get utils.py
from os.path import basename, exists
def download(url):
filename = basename(url)
if not exists(filename):
from urllib.request import urlretrieve
local, _ = urlretrieve(url, filename)
print('Downloaded ' + local)
download('https://github.com/AllenDowney/ThinkBayes2/raw/master/soln/utils.py')
import numpy as np
import pandas as pd
n = 60
t1 = 30
t2 = n-t1
lam1 = 4
lam2 = 2
from scipy.stats import poisson
before = poisson(lam1).rvs(t1)
before
after = poisson(lam2).rvs(t2)
after
data = np.concatenate([before, after])
n = len(data)
lam = 2
lams = np.linspace(0, 10, 51)
D, L = np.meshgrid(data, lams)
like1 = poisson.pmf(D, L).prod(axis=1)
like1 /= like1.sum()
like2 = poisson.pmf(np.sum(data), n*lams)
like2 /= like2.sum()
import matplotlib.pyplot as plt
plt.plot(lams, like1)
plt.plot(lams, like2)
np.sum(lams * like1), np.sum(lams * like2)
poisson.pmf(before, 4)
poisson.pmf(after, 2)
t = 7
def likelihood1(data, t, lam1, lam2):
before = data[:t]
after = data[t:]
like1 = poisson.pmf(before, lam1).prod()
like2 = poisson.pmf(after, lam2).prod()
return like1
like1 = likelihood1(data, t, 4, 2)
like1
from scipy.special import binom
def combos(data):
data = np.asarray(data)
n = data.sum()
k = len(data)
print(n, k)
ns = n - np.cumsum(data) + data
print(ns)
print(data)
cs = binom(ns, data)
print(cs)
return cs.prod() / k**n
combos(data[:t])
from scipy.special import binom
def likelihood2(data, t, lam1, lam2):
before = data[:t].sum()
like1 = poisson.pmf(before, lam1*t) * combos(data[:t])
after = data[t:].sum()
t2 = len(data) - t
n, k = after, t2
like2 = poisson.pmf(after, lam2*t2)
return like1
like2 = likelihood2(data, t, 4, 2)
like2
like2 / like1
from empiricaldist import Pmf
ts = range(1, len(data))
prior_t = Pmf(1, ts)
lams1 = np.linspace(0, 10, 51)
prior_lam1 = Pmf(1, lams1)
lams2 = np.linspace(0, 10, 41)
prior_lam2 = Pmf(1, lams2)
from utils import make_joint
def make_joint3(pmf1, pmf2, pmf3):
"""Make a joint distribution with three parameters."""
joint2 = make_joint(pmf2, pmf1).stack()
joint3 = make_joint(pmf3, joint2).stack()
return Pmf(joint3)
joint_prior = make_joint3(prior_t, prior_lam1, prior_lam2)
joint_prior.head()
```
## Likelihood
```
ts
lams1
T, L = np.meshgrid(ts, lams1)
M = T * L
M.shape
C = np.cumsum(data)[:-1]
C.shape
from scipy.special import binom
like1 = poisson.pmf(C, M) / binom(C+T-1, T-1)
like1.shape
ts2 = len(data) - np.array(ts)
ts2
T2, L2 = np.meshgrid(ts2, lams2)
M2 = T2 * L2
M2.shape
C2 = sum(data) - C
C2.shape
like2 = poisson.pmf(C2, M2) / binom(C2+T2-1, T2-1)
like2.shape
like = like1.T[:, :, None] * like2.T[:, None, :]
like.shape
like.flatten().shape
from utils import normalize
joint_posterior = joint_prior * like.reshape(-1)
normalize(joint_posterior)
from utils import pmf_marginal
posterior_t = pmf_marginal(joint_posterior, 0)
posterior_t.head(3)
posterior_t.plot()
posterior_lam1 = pmf_marginal(joint_posterior, 1)
posterior_lam2 = pmf_marginal(joint_posterior, 2)
posterior_lam1.plot()
posterior_lam2.plot()
```
## Doing it the long way
```
likelihood = joint_prior.copy().unstack().unstack()
likelihood.head()
t = 30
row = likelihood.loc[t].unstack()
row.head()
lams = row.columns
lams.shape
lam_mesh, data_mesh = np.meshgrid(lams, data[:t])
probs = poisson.pmf(data_mesh, lam_mesh)
probs.shape
likelihood1 = probs.prod(axis=0)
likelihood1.shape
lams = row.index
lams.shape
lam_mesh, data_mesh = np.meshgrid(lams, data[t:])
probs = poisson.pmf(data_mesh, lam_mesh)
probs.shape
likelihood2 = probs.prod(axis=0)
likelihood2.shape
likelihood_row = np.multiply.outer(likelihood2, likelihood1)
likelihood_row.shape
likelihood.loc[t] = likelihood_row.flatten()
likelihood.loc[t]
likelihood = joint_prior.copy().unstack().unstack()
likelihood.head()
for t in likelihood.index:
row = likelihood.loc[t].unstack()
lams = row.columns
lam_mesh, data_mesh = np.meshgrid(lams, data[:t])
probs = poisson.pmf(data_mesh, lam_mesh)
likelihood1 = probs.prod(axis=0)
lams = row.index
lam_mesh, data_mesh = np.meshgrid(lams, data[t:])
probs = poisson.pmf(data_mesh, lam_mesh)
likelihood2 = probs.prod(axis=0)
likelihood_row = np.multiply.outer(likelihood2, likelihood1)
likelihood.loc[t] = likelihood_row.flatten()
from utils import normalize
def update(prior, data):
"""
prior: Pmf representing the joint prior
data: sequence f counts
returns: Pmf representing the joint posterior
"""
likelihood = joint_prior.copy().unstack().unstack()
for t in likelihood.index:
row = likelihood.loc[t].unstack()
lams = row.columns
lam_mesh, data_mesh = np.meshgrid(lams, data[:t])
probs = poisson.pmf(data_mesh, lam_mesh)
likelihood1 = probs.prod(axis=0)
lams = row.index
lam_mesh, data_mesh = np.meshgrid(lams, data[t:])
probs = poisson.pmf(data_mesh, lam_mesh)
likelihood2 = probs.prod(axis=0)
likelihood_row = np.multiply.outer(likelihood2, likelihood1)
likelihood.loc[t] = likelihood_row.flatten()
posterior = prior * likelihood.stack().stack()
normalize(posterior)
return posterior
posterior = update(joint_prior, data)
from utils import pmf_marginal
posterior_t = pmf_marginal(posterior, 0)
posterior_t.head(3)
posterior_t.plot()
posterior_lam1 = pmf_marginal(posterior, 1)
posterior_lam2 = pmf_marginal(posterior, 2)
posterior_lam1.plot()
posterior_lam2.plot()
```
## Using emcee
```
try:
import emcee
except:
!pip install emcee
import emcee
print(emcee.__version__)
try:
import corner
except ImportError:
!pip install corner
try:
import tdqm
except ImportError:
!pip install tdqm
from scipy.stats import poisson
from scipy.stats import gamma
alpha, beta = 3, 1
def log_prior(theta):
t, lam1, lam2 = theta
return gamma.logpdf([lam1, lam2], alpha, beta).sum()
def log_likelihood(theta, data):
t, lam1, lam2 = theta
t = int(t)
k1 = data[:t]
k2 = data[t:]
like1 = poisson.logpmf(k1, lam1).sum()
like2 = poisson.logpmf(k2, lam2).sum()
return like1 + like2
def log_posterior(theta, data):
t, lam1, lam2 = theta
if t < 1 or t >= len(data):
return -np.inf
if lam1 < 0 or lam2 < 0:
return -np.inf
return log_likelihood(theta, data)
ndim = 3 # number of parameters in the model
nwalkers = 50 # number of MCMC walkers
nburn = 500 # "burn-in" period to let chains stabilize
nsteps = 2500 # number of MCMC steps to take
np.random.seed(0)
com = 30, 3, 3
starting_guesses = com + np.random.random((nwalkers, ndim))
sampler = emcee.EnsembleSampler(nwalkers, ndim, log_posterior, args=[data])
state = sampler.run_mcmc(starting_guesses, nsteps, progress=True)
flat_samples = sampler.get_chain(discard=100, thin=15, flat=True)
flat_samples.shape
import corner
truths = [30, 4, 2]
labels = ['t', 'lam1', 'lam2']
fig = corner.corner(flat_samples, labels=labels, truths=truths);
stop
```
Based on an example from Chapter 1 of [Bayesian Methods for Hackers](http://nbviewer.jupyter.org/github/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/blob/master/Chapter1_Introduction/Ch1_Introduction_PyMC2.ipynb)
and this example from [Computational Statistics in Python](http://people.duke.edu/~ccc14/sta-663-2016/16C_PyMC3.html#Changepoint-detection)
```
import pymc3 as pm
n = len(data)
t = range(n)
alpha = 1.0 / np.mean(data)
import theano.tensor as T
with pm.Model() as model:
tau = pm.DiscreteUniform('tau', lower=0, upper=n)
lam1 = pm.Exponential('lam1', alpha)
lam2 = pm.Exponential('lam2', alpha)
lam = T.switch(t < tau, lam1, lam2)
Y_obs = pm.Poisson('Y_obs', lam, observed=data)
trace = pm.sample(10000, tune=2000)
pm.traceplot(trace);
tau_sample = trace['tau']
cdf_tau = Cdf(tau_sample)
thinkplot.Cdf(cdf_tau)
lam1_sample = trace['lam1']
cdf_lam1 = Cdf(lam1_sample)
thinkplot.Cdf(cdf_lam1)
lam2_sample = trace['lam2']
cdf_lam2 = Cdf(lam2_sample)
thinkplot.Cdf(cdf_lam2)
stop
# !wget https://raw.githubusercontent.com/baltimore-sun-data/2018-shootings-analysis/master/BPD_Part_1_Victim_Based_Crime_Data.csv
df = pd.read_csv('BPD_Part_1_Victim_Based_Crime_Data.csv', parse_dates=[0])
df.head()
df.shape
shootings = df[df.Description.isin(['HOMICIDE', 'SHOOTING']) & (df.Weapon == 'FIREARM')]
shootings.shape
grouped = shootings.groupby('CrimeDate')
counts = grouped['Total Incidents'].sum()
counts.head()
index = pd.date_range(counts.index[0], counts.index[-1])
counts = counts.reindex(index, fill_value=0)
counts.head()
counts.plot()
thinkplot.decorate(xlabel='Date',
ylabel='Number of shootings')
```
| true |
code
| 0.683789 | null | null | null | null |
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plotly.com/python/getting-started/) by downloading the client and [reading the primer](https://plotly.com/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plotly.com/python/getting-started/#initialization-for-online-plotting) or [offline](https://plotly.com/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plotly.com/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Populate a Table Using a Plotly Mouse Selection Event
Create a table FigureWidget that is updated by a selection event in another FigureWidget. The rows in the table correspond to points selected in the selection event.
```
import plotly.graph_objs as go
import plotly.offline as py
import pandas as pd
import numpy as np
from ipywidgets import interactive, HBox, VBox
py.init_notebook_mode()
df = pd.read_csv('https://raw.githubusercontent.com/jonmmease/plotly_ipywidget_notebooks/master/notebooks/data/cars/cars.csv')
f = go.FigureWidget([go.Scatter(y = df['City mpg'], x = df['City mpg'], mode = 'markers')])
scatter = f.data[0]
N = len(df)
scatter.x = scatter.x + np.random.rand(N)/10 *(df['City mpg'].max() - df['City mpg'].min())
scatter.y = scatter.y + np.random.rand(N)/10 *(df['City mpg'].max() - df['City mpg'].min())
scatter.marker.opacity = 0.5
def update_axes(xaxis, yaxis):
scatter = f.data[0]
scatter.x = df[xaxis]
scatter.y = df[yaxis]
with f.batch_update():
f.layout.xaxis.title = xaxis
f.layout.yaxis.title = yaxis
scatter.x = scatter.x + np.random.rand(N)/10 *(df[xaxis].max() - df[xaxis].min())
scatter.y = scatter.y + np.random.rand(N)/10 *(df[yaxis].max() - df[yaxis].min())
axis_dropdowns = interactive(update_axes, yaxis = df.select_dtypes('int64').columns, xaxis = df.select_dtypes('int64').columns)
# Create a table FigureWidget that updates on selection from points in the scatter plot of f
t = go.FigureWidget([go.Table(
header=dict(values=['ID','Classification','Driveline','Hybrid'],
fill = dict(color='#C2D4FF'),
align = ['left'] * 5),
cells=dict(values=[df[col] for col in ['ID','Classification','Driveline','Hybrid']],
fill = dict(color='#F5F8FF'),
align = ['left'] * 5))])
def selection_fn(trace,points,selector):
t.data[0].cells.values = [df.loc[points.point_inds][col] for col in ['ID','Classification','Driveline','Hybrid']]
scatter.on_selection(selection_fn)
# Put everything together
VBox((HBox(axis_dropdowns.children),f,t))
```
<img src='https://raw.githubusercontent.com/michaelbabyn/plot_data/master/mouse-event-figurewidget.gif'>
#### Reference
See [these Jupyter notebooks](https://github.com/jonmmease/plotly_ipywidget_notebooks) for even more FigureWidget examples.
```
help(go.FigureWidget)
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'selection-events-figure-widget.ipynb', 'python/selection-events/', 'Selection Events with go.FigureWidget',
'Selection Events With FigureWidget',
title = 'Selection Events',
name = 'Selection Events',
has_thumbnail='true', thumbnail='thumbnail/figurewidget-selection-events.gif',
language='python',
display_as='chart_events', order=24,
ipynb= '~notebook_demo/229')
```
| true |
code
| 0.505188 | null | null | null | null |
|
# the Monte Carlo experiment
```
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
```
A handy routines to store and recover python objects, in particular, the experiment resutls dictionaires.
```
import time, gzip
import os, pickle
def save(obj, path, prefix=None):
prefix_ = "" if prefix is None else "%s_"%(prefix,)
filename_ = os.path.join(path, "%s%s.gz"%(prefix_, time.strftime("%Y%m%d-%H%M%S"),))
with gzip.open(filename_, "wb+", 9) as fout_:
pickle.dump(obj, fout_)
return filename_
def load(filename):
with gzip.open(filename, "rb") as f:
return pickle.load(f)
```
The path analyzer
```
from crossing_tree import structural_statistics
```
Collect a list of results returned by path_analyze into aligned data tensors.
```
from crossing_tree import collect_structural_statistics
```
A function implementing various delta choices.
```
import warnings
def get_delta_method(delta=1.0):
if isinstance(delta, str):
if delta == "std":
# the standard deviation of increments
delta_ = lambda X: np.diff(X).std()
elif delta == "med":
# Use the median absolute difference [Jones, Rolls; 2009] p. 11 (arxiv:0911.5204v2)
delta_ = lambda X: np.median(np.abs(np.diff(X)))
elif delta == "mean":
# Use the mean absolute difference
delta_ = lambda X: np.mean(np.abs(np.diff(X)))
elif delta == "iqr":
# Interquartile range
delta_ = lambda X: np.subtract(*np.percentile(np.diff(X), [75, 25]))
elif delta == "rng":
# Use the range estimate as suggested by Geoffrey on 2015-05-28
warnings.warn("""Use of `range`-based grid resolution """
"""is discouraged since it may cause misaligned """
"""crossing trees.""", RuntimeWarning)
delta_ = lambda X: (X.max() - X.min()) / (2**12)
else:
raise ValueError("""Invalid `delta` setting. Accepted values """
"""are: [`iqr`, `std`, `med`, `rng`, `mean`].""")
elif isinstance(delta, float) and delta > 0:
delta_ = lambda X: delta
else:
raise TypeError("""`delta` must be either a float, or a method """
"""identifier.""")
return delta_
```
An MC experiment kernel.
```
from sklearn.base import clone
def experiment(experiment_id, n_replications, methods, generator):
generator = clone(generator)
generator.start()
deltas = [get_delta_method(method_) for method_ in methods]
results = {method_: list() for method_ in methods}
for j in xrange(n_replications):
T, X = generator.draw()
# Apply all methods to the same sample path.
for delta, method in zip(deltas, methods):
result_ = structural_statistics(X, T, scale=delta(X), origin=X[0])
results[method].append(result_)
generator.finish()
return experiment_id, results
```
## Experiments
```
from joblib import Parallel, delayed
```
A couple of random seeds from [here](https://www.random.org/bytes/).
```
# Extra random seeds should be prepended to the array.
master_seeds = [0xD5F60A17, 0x26F9935C, 0x0E4C1E75, 0xDA7C4291, 0x7ABE722E,
0x126F3E10, 0x045300B1, 0xB0A9AD11, 0xEED05353, 0x824736C7,
0x7AA17C9C, 0xB695D6B1, 0x7E214411, 0x538CDEEF, 0xFD55FF46,
0xE14E1801, 0x872F687C, 0xA58440D9, 0xB8A273FD, 0x0BD1DD28,
0xAB6A6AE6, 0x7180E905, 0x870E7BAB, 0x846D0C7A, 0xAEF0422D,
0x16C53C83, 0xE32EA61D, 0xE0AD0A26, 0xCC90CA9A, 0x7D4020D2,]
```
the Monte Carlo experiemnt is run in parallel batches, with each
initialized to a randomly picked seed.
```
MAX_RAND_SEED = np.iinfo(np.int32).max
```
The folder to store the results in
```
OUTPUT_PATH = "../results/"
```
## fBM experiment
```
from crossing_tree.processes import FractionalBrownianMotion
seed = master_seeds.pop()
print("Using seed %X"%(seed,))
random_state = np.random.RandomState(seed)
skip = False
```
Setup
```
n_samples, methods = 1 << 23, ["med", "std", "iqr", "mean",]
hurst_exponents = [0.500, 0.550, 0.600, 0.650, 0.700, 0.750, 0.800, 0.850, 0.900,
0.910, 0.915, 0.920, 0.925, 0.930, 0.935, 0.940, 0.945, 0.950,
0.990,]
n_per_batch, n_batches = 125, 8
```
Run the experiment for the Fractional Brownian Motion.
```
if not skip:
par_ = Parallel(n_jobs=-1, verbose=0)
for hurst_ in hurst_exponents:
name_ = "FBM-%d-%0.3f-%dx%d"%(n_samples, hurst_, n_per_batch, n_batches)
print(name_,)
# Schedule the experiments
seeds = random_state.randint(MAX_RAND_SEED, size=(n_batches,))
schedule_ = (delayed(experiment)(seed_, n_per_batch, methods,
FractionalBrownianMotion(N=n_samples,
hurst=hurst_,
random_state=seed_))
for seed_ in seeds)
# Run the experiment and collect the results
tick_ = time.time()
experiment_ids = list()
results_ = {method: list() for method in methods}
for id_, dict_ in par_(schedule_):
experiment_ids.append(id_)
for method in methods:
results_[method].extend(dict_[method])
results = {key_: collect_structural_statistics(list_)
for key_, list_ in results_.iteritems()}
tock_ = time.time()
# Save the results and log
filename_ = save((tick_, tock_, experiment_ids, results), OUTPUT_PATH, name_)
print("%0.3fsec."%(tock_ - tick_,), filename_)
```
## Hermite process experiment
```
from crossing_tree.processes import HermiteProcess
seed = master_seeds.pop()
print("Using seed %X"%(seed,))
random_state = np.random.RandomState(seed)
skip = False
```
Setup: use no downsampling.
```
n_samples, n_downsample = 1 << 23, 1
degrees, methods = [2, 3, 4], ["med", "std", "iqr", "mean",]
hurst_exponents = [ 0.550, 0.600, 0.650, 0.700, 0.750, 0.800, 0.850, 0.900,
0.910, 0.915, 0.920, 0.925, 0.930, 0.935, 0.940, 0.945, 0.950,
0.990,]
n_per_batch, n_batches = 125, 8
```
Run the experiment for the Hermite process.
```
if not skip:
par_ = Parallel(n_jobs=-1, verbose=0)
for degree_ in degrees:
for hurst_ in hurst_exponents:
name_ = "HRP%d_%d-%d-%0.3f-%dx%d"%(degree_, n_downsample, n_samples, hurst_, n_per_batch, n_batches)
print(name_,)
# Schedule the experiments
seeds = random_state.randint(MAX_RAND_SEED, size=(n_batches,))
schedule_ = (delayed(experiment)(seed_, n_per_batch, methods,
HermiteProcess(N=n_samples,
degree=degree_,
n_downsample=n_downsample,
hurst=hurst_,
random_state=seed_))
for seed_ in seeds)
# Run the experiment and collect the results
tick_ = time.time()
experiment_ids = list()
results_ = {method: list() for method in methods}
for id_, dict_ in par_(schedule_):
experiment_ids.append(id_)
for method in methods:
results_[method].extend(dict_[method])
results = {key_: collect_structural_statistics(list_)
for key_, list_ in results_.iteritems()}
tock_ = time.time()
# Save the results and log
filename_ = save((tick_, tock_, experiment_ids, results), OUTPUT_PATH, name_)
print("%0.3fsec."%(tock_ - tick_,), filename_)
```
## Weierstrass experiment -- $\lambda_0 = 1.2$
```
from crossing_tree.processes import WeierstrassFunction
seed = master_seeds.pop()
print("Using seed %X"%(seed,))
random_state = np.random.RandomState(seed)
skip = False
```
Setup
```
n_samples, lambda_0 = 1 << 23, 1.2
methods = ["med", "std", "iqr", "mean",]
holder_exponents = [0.500, 0.550, 0.600, 0.650, 0.700, 0.750, 0.800, 0.850, 0.900,
0.910, 0.915, 0.920, 0.925, 0.930, 0.935, 0.940, 0.945, 0.950,
0.990,]
n_per_batch, n_batches = 125, 8
```
Run the experimnet for the random Weierstrass function $[0, 1]\mapsto \mathbb{R}$:
$$ W_H(t) = \sum_{k\geq 0} \lambda_0^{-k H} \bigl(\cos(2 \pi \lambda_0^k t + \phi_k) - \cos \phi_k\bigr)\,, $$
with $(\phi_k)_{k\geq0} \sim \mathbb{U}[0, 2\pi]$, and $\lambda_0 > 1$ -- the fundamental harmonic.
```
if not skip:
par_ = Parallel(n_jobs=-1, verbose=0)
for holder_ in holder_exponents:
name_ = "WEI_%g-%d-%0.3f-%dx%d"%(lambda_0, n_samples, holder_, n_per_batch, n_batches)
print(name_,)
# Schedule the experiments
seeds = random_state.randint(MAX_RAND_SEED, size=(n_batches,))
schedule_ = (delayed(experiment)(seed_, n_per_batch, methods,
WeierstrassFunction(N=n_samples,
lambda_0=lambda_0,
holder=holder_,
random_state=seed_,
one_sided=False))
for seed_ in seeds)
# Run the experiment and collect the results
tick_ = time.time()
experiment_ids = list()
results_ = {method: list() for method in methods}
for id_, dict_ in par_(schedule_):
experiment_ids.append(id_)
for method in methods:
results_[method].extend(dict_[method])
results = {key_: collect_structural_statistics(list_)
for key_, list_ in results_.iteritems()}
tock_ = time.time()
# Save the results and log
filename_ = save((tick_, tock_, experiment_ids, results), OUTPUT_PATH, name_)
print("%0.3fsec."%(tock_ - tick_,), filename_)
```
## Additional experiments
### Hermite process experiment: with downsampling
```
from crossing_tree.processes import HermiteProcess
seed = master_seeds.pop()
print("Using seed %X"%(seed,))
random_state = np.random.RandomState(seed)
skip = False
```
Setup
```
n_samples, n_downsample = 1 << 19, 1 << 4
degrees, methods = [2, 3, 4], ["med", "std", "iqr", "mean",]
hurst_exponents = [ 0.550, 0.600, 0.650, 0.700, 0.750, 0.800, 0.850, 0.900,
0.910, 0.915, 0.920, 0.925, 0.930, 0.935, 0.940, 0.945, 0.950,
0.990,]
n_per_batch, n_batches = 125, 8
```
Run the experiment for the Hermite process.
```
if not skip:
par_ = Parallel(n_jobs=-1, verbose=0)
for degree_ in degrees:
for hurst_ in hurst_exponents:
name_ = "HRP%d_%d-%d-%0.3f-%dx%d"%(degree_, n_downsample, n_samples, hurst_, n_per_batch, n_batches)
print(name_,)
# Schedule the experiments
seeds = random_state.randint(MAX_RAND_SEED, size=(n_batches,))
schedule_ = (delayed(experiment)(seed_, n_per_batch, methods,
HermiteProcess(N=n_samples,
degree=degree_,
n_downsample=n_downsample,
hurst=hurst_,
random_state=seed_))
for seed_ in seeds)
# Run the experiment and collect the results
tick_ = time.time()
experiment_ids = list()
results_ = {method: list() for method in methods}
for id_, dict_ in par_(schedule_):
experiment_ids.append(id_)
for method in methods:
results_[method].extend(dict_[method])
results = {key_: collect_structural_statistics(list_)
for key_, list_ in results_.iteritems()}
tock_ = time.time()
# Save the results and log
filename_ = save((tick_, tock_, experiment_ids, results), OUTPUT_PATH, name_)
print("%0.3fsec."%(tock_ - tick_,), filename_)
```
### Weierstrass experiment -- $\lambda_0 = 3$
```
from crossing_tree.processes import WeierstrassFunction
seed = master_seeds.pop()
print("Using seed %X"%(seed,))
random_state = np.random.RandomState(seed)
skip = True
```
Setup
```
n_samples, lambda_0 = 1 << 23, 3.0
methods = ["med", "std", "iqr", "mean",]
holder_exponents = [0.500, 0.550, 0.600, 0.650, 0.700, 0.750, 0.800, 0.850, 0.900,
0.910, 0.915, 0.920, 0.925, 0.930, 0.935, 0.940, 0.945, 0.950,
0.990,]
n_per_batch, n_batches = 125, 8
```
Run the experimnet for the random Weierstrass function $[0, 1]\mapsto \mathbb{R}$:
$$ W_H(t) = \sum_{k\geq 0} \lambda_0^{-k H} \bigl(\cos(2 \pi \lambda_0^k t + \phi_k) - \cos \phi_k\bigr)\,, $$
with $(\phi_k)_{k\geq0} \sim \mathbb{U}[0, 2\pi]$, and $\lambda_0 > 1$ -- the fundamental harmonic.
```
if not skip:
par_ = Parallel(n_jobs=-1, verbose=0)
for holder_ in holder_exponents:
name_ = "WEI_%g-%d-%0.3f-%dx%d"%(lambda_0, n_samples, holder_, n_per_batch, n_batches)
print(name_,)
# Schedule the experiments
seeds = random_state.randint(MAX_RAND_SEED, size=(n_batches,))
schedule_ = (delayed(experiment)(seed_, n_per_batch, methods,
WeierstrassFunction(N=n_samples,
lambda_0=lambda_0,
holder=holder_,
random_state=seed_,
one_sided=False))
for seed_ in seeds)
# Run the experiment and collect the results
tick_ = time.time()
experiment_ids = list()
results_ = {method: list() for method in methods}
for id_, dict_ in par_(schedule_):
experiment_ids.append(id_)
for method in methods:
results_[method].extend(dict_[method])
results = {key_: collect_structural_statistics(list_)
for key_, list_ in results_.iteritems()}
tock_ = time.time()
# Save the results and log
filename_ = save((tick_, tock_, experiment_ids, results), OUTPUT_PATH, name_)
print("%0.3fsec."%(tock_ - tick_,), filename_)
```
### Weierstrass experiment -- $\lambda_0 = 1.7$
```
from crossing_tree.processes import WeierstrassFunction
seed = master_seeds.pop()
print("Using seed %X"%(seed,))
random_state = np.random.RandomState(seed)
skip = True
```
Setup
```
n_samples, lambda_0 = 1 << 23, 1.7
methods = ["med", "std", "iqr", "mean",]
holder_exponents = [0.500, 0.550, 0.600, 0.650, 0.700, 0.750, 0.800, 0.850, 0.900,
0.910, 0.915, 0.920, 0.925, 0.930, 0.935, 0.940, 0.945, 0.950,
0.990,]
n_per_batch, n_batches = 125, 8
```
Run the experimnet for the random Weierstrass function $[0, 1]\mapsto \mathbb{R}$:
$$ W_H(t) = \sum_{k\geq 0} \lambda_0^{-k H} \bigl(\cos(2 \pi \lambda_0^k t + \phi_k) - \cos \phi_k\bigr)\,, $$
with $(\phi_k)_{k\geq0} \sim \mathbb{U}[0, 2\pi]$, and $\lambda_0 > 1$ -- the fundamental harmonic.
```
if not skip:
par_ = Parallel(n_jobs=-1, verbose=0)
for holder_ in holder_exponents:
name_ = "WEI_%g-%d-%0.3f-%dx%d"%(lambda_0, n_samples, holder_, n_per_batch, n_batches)
print(name_,)
# Schedule the experiments
seeds = random_state.randint(MAX_RAND_SEED, size=(n_batches,))
schedule_ = (delayed(experiment)(seed_, n_per_batch, methods,
WeierstrassFunction(N=n_samples,
lambda_0=lambda_0,
holder=holder_,
random_state=seed_,
one_sided=False))
for seed_ in seeds)
# Run the experiment and collect the results
tick_ = time.time()
experiment_ids = list()
results_ = {method: list() for method in methods}
for id_, dict_ in par_(schedule_):
experiment_ids.append(id_)
for method in methods:
results_[method].extend(dict_[method])
results = {key_: collect_structural_statistics(list_)
for key_, list_ in results_.iteritems()}
tock_ = time.time()
# Save the results and log
filename_ = save((tick_, tock_, experiment_ids, results), OUTPUT_PATH, name_)
print("%0.3fsec."%(tock_ - tick_,), filename_)
```
### fBM experiment: super long
```
from crossing_tree.processes import FractionalBrownianMotion
seed = master_seeds.pop()
print("Using seed %X"%(seed,))
random_state = np.random.RandomState(seed)
skip = True
```
Setup
```
n_samples, methods = 1 << 25, ["med", "std", "iqr", "mean",]
hurst_exponents = [0.500, 0.550, 0.600, 0.650, 0.700, 0.750, 0.800, 0.850, 0.900,
0.910, 0.915, 0.920, 0.925, 0.930, 0.935, 0.940, 0.945, 0.950,
0.990,]
n_per_batch, n_batches, n_threads = 334, 3, 4
```
Run the experiment for the Fractional Brownian Motion.
```
if not skip:
par_ = Parallel(n_jobs=-1, verbose=0)
for hurst_ in hurst_exponents:
name_ = "FBM-%d-%0.3f-%dx%d"%(n_samples, hurst_, n_per_batch, n_batches)
print(name_,)
# Schedule the experiments
seeds = random_state.randint(MAX_RAND_SEED, size=(n_batches,))
schedule_ = (delayed(experiment)(seed_, n_per_batch, methods,
FractionalBrownianMotion(N=n_samples,
hurst=hurst_,
random_state=seed_,
n_threads=n_threads))
for seed_ in seeds)
# Run the experiment and collect the results
tick_ = time.time()
experiment_ids = list()
results_ = {method: list() for method in methods}
for id_, dict_ in par_(schedule_):
experiment_ids.append(id_)
for method in methods:
results_[method].extend(dict_[method])
results = {key_: collect_structural_statistics(list_)
for key_, list_ in results_.iteritems()}
tock_ = time.time()
# Save the results and log
filename_ = save((tick_, tock_, experiment_ids, results), OUTPUT_PATH, name_)
print("%0.3fsec."%(tock_ - tick_,), filename_)
```
| true |
code
| 0.550064 | null | null | null | null |
|

<font size=3 color="midnightblue" face="arial">
<h1 align="center">Escuela de Ciencias Básicas, Tecnología e Ingeniería</h1>
</font>
<font size=3 color="navy" face="arial">
<h1 align="center">ECBTI</h1>
</font>
<font size=2 color="darkorange" face="arial">
<h1 align="center">Curso:</h1>
</font>
<font size=2 color="navy" face="arial">
<h1 align="center">Introducción al lenguaje de programación Python</h1>
</font>
<font size=1 color="darkorange" face="arial">
<h1 align="center">Febrero de 2020</h1>
</font>
<h2 align="center">Sesión 04 - Funciones</h2>
## Funciones
<img src="Funcion.png" alt="Drawing" style="width: 200px;"/>
### Matemáticas
$$f(x) = x^2-3$$
- ***Entrada:*** el valor de $x$ (por ejemplo $2$)
- ***Función:*** transforma la entrada $x$ ($2^2-3$)
- ***Salida:*** devuelve el resultado de efectuar dicha transformación del valor de entrada ($f(2)=1$)
### Programación
***Función:*** Fragmento de código con un nombre asociado que realiza una serie de tareas y devuelve un valor.
***Procedimientos:*** Fragmento de código que tienen un nombre asociado y no devuelven valores (scripts).
- En `Python` no existen los procedimientos, ya que cuando el programador no especifica un valor de retorno la función devuelve el valor `None` (nada), equivalente al `null` de Java.
- Además de ayudarnos a programar y depurar dividiendo el programa en partes las funciones también permiten reutilizar código.
- En otros lenguajes las funciones son conocidas con otros nombres, como por ejemplo: subrutinas, rutinas, procedimientos, métodos, subprogramas, etc.
- En `Python` las funciones se declaran de la siguiente forma:
- La lista de parámetros consiste en uno o más parámetros, o incluso, ninguno. A estos parámetros se les llama *argumentos*.
- El cuerpoo de la función consiste de una secuencia de sentencias indentadas, que serán ejecutadas cada vez que la función es llamada.
### Función sin parámetro y sin retorno
Una función puede no tener parámetros de entrada y no contener la sentencia de retorno `return`:
```
def fbienvenida():
print("Hola Mundo")
```
Para llamar la función se escribe el nombre de la función seguida de paréntesis `nombre_Funcion()`
```
fbienvenida()
```
Se observa que lo único que hace esta función es imprimir un mensaje preestablecido como cuerpo de función.
### Función con uno o más parámetros y sin retorno
A una función también se le pueden pasar como argumentos uno o más parámetros
- También podemos encontrarnos con una cadena de texto como primera línea del cuerpo de la función. Estas cadenas se conocen con el nombre de `docstring` (cadena de documentación) y sirven, como su nombre indica, a modo de documentación de la función.
```
def mi_funcion1(param1, param2):
"""Esta función también imprime únicamente los valores de los parámetros
requiere de dos parámetros
Inputs:
param1: puede ser cualquier vaina
param2: también
Outputs:
"""
print('{0} {1}'.format(param1,param2))
mi_funcion1?
```
Para llamar a la función (ejecutar su código) se escribiría:
```
mi_funcion1(1,2)
```
También es posible modificar el orden de los parámetros si indicamos el nombre del parámetro al qué asociar el valor a la hora de llamar a la función:
```
mi_funcion1(param2 = 1, param1 = 2)
```
### Retorno de Valores
- El cuerpo de la función puede contener una o más sentencias de retorno de valores, `return`. Una sentencia de retorno finaliza la ejecución de la función. Si la sentencia de retorno no es una expresión, o no se usa, se retornará el valor especial `None`.
Revisemos el siguiente ejemplo
```
def no_return(x,y):
c = x + y
return c
res = no_return(4,5)
print(res)
```
Ahora incluyamos la palabra reservada `return` para devolver el resultado de lo realizado dentro de la función
```
def sumar(x, y):
c = x + y
return c
```
Llamemos la función `sumar`con los parámetros indicados, `1` y `2`. El valor de la suma `x+y` se almacena en la variable `c` y éste valor se retorna mediante la palabra `return` para ser usada en el cuerpo del programa principal.
```
sumaxy = sumar(1,2)
print(sumaxy)
sumacuadrado = sumaxy ** 2
print(sumacuadrado)
```
Obsérvese que la variable `sumaxy` recibe lo que ha sido regresado de la función `sumar`. El resultado de la evaluación de dicha función se almacena en esa variable que es usada a lo largo del cuerpo del programa principal para efectuar otros cálculos.
El valor especial `None` también se retornará si la palabra `return` no está acompañada de una expresión (situación demasiada frecuente como para ser considerado "error").
```
def sumar(x, y):
c = x + y
return
sumaxy = sumar(1,2)
print(sumaxy)
```
Una función puede ser llamada casi desde cualquier parte del código, por ejemplo, al interior de otra función (`print`) y no necesariamente tiene qué almacenarse el resultado en una variable antes de retornar el valor de su ejecución
```
def dolorosos(t):
""" Devuelve un valor dado en pesos a dólares"""
return t / 3443.63
for valorpesos in (2260, 2580, 27300, 29869):
print('{0} pesos son {1:.2f} dólares'.format(valorpesos,dolorosos(valorpesos)))
```
Obsérvese que en este caso no hubo necesidad de llamar la función aparte, sino que su llamado está incluída dentro de la estructura de la función `print`.
### Retorno de valores múltiples
Una función puede retornar un valor (o mejor, un "objeto", para los amantes de POO). Un objeto puede ser un valor numérico como un entero o un float, pero también puede ser una estructura de datos, como un diccionario o una tupla, por ejemplo.
Si necesitamos retonrar tres valores enteros, se puede hacer a través de una lista o tupla que contiene esos tres valores. Lo que significa que podemos retornar múltiples valores.
Veamos el siguiente ejemplo: Dado un número $x$ determine cuáles serían los valores inmediatamente menor y mayor a este número en la serie de *Fibonacci*.
```
def fib_intervalo(x):
""" Retorna los números de Fibonacci
mayor que x y menor que x"""
if x < 0:
return -1
(ant,post, lub) = (0,1,0)
while True:
if post < x:
lub = post
(ant,post) = (post,ant+post)
else:
return (ant, post)
while True:
x = int(input("Ingrese un número entero >0 (<0 para interrumpir): "))
if x <= 0:
break #interrumpe el programa si x<0
lub, sup = fib_intervalo(x)
print("Mayor número de Fibonacci menor que x: " + str(lub))
print("Menor número de Fibonacci mayor que x: " + str(sup))
```
Obsérves que los valores retornados, y la variable que los recibe, están "empaquetados" en una estrucutra llamada "Tupla" (se verá en una siguiente sesión del curso).
### Número Arbitrario de Parámetros
- Existen situaciones en las que el número exacto de parámetros no puede determinarse a-priori.
- Para definir funciones con un número variable de argumentos colocamos un último parámetro para la función cuyo nombre debe precederse de un signo `*` (asterisco):
```
def varios(param1, param2, *opcionales):
print(type(opcionales))
print(param1)
print(param2)
n = len(opcionales)
for i in range(n):
print(opcionales[i])
varios(1,2)
varios(1,2,3)
varios(1,2,3,4)
varios(1,2,3,4,5,6,7,8,9)
```
Miremos el siguiente ejemplo:
```
def media_aritmetica(*valores):
""" Esta función calcula la media aritmética de un número arbitrario de valores numéricos """
print(float(sum(valores)) / len(valores))
media_aritmetica(5,5,5,5,5,5,5,5)
media_aritmetica(8989.8,78787.78,3453,78778.73)
media_aritmetica(45,55)
media_aritmetica(45)
```
Ahora veamos la situación en la que los datos vienen "empaquetados" en alguna estructura, como por ejemplo, una Lista
```
x = [3, 5, 9, 13, 12, 5, 67, 98]
print(x)
```
Si colocamos el valor de la variable `x` como parámetro en la función se obtendrá el siguiente resultado:
```
media_aritmetica(x)
```
Una primera idea de resolver esta situación sería ingresar los parámetros elemento por elemento mediante su indice...
```
media_aritmetica(x[0], x[1], x[2],x[3], x[4], x[5],x[6],x[7])
```
pero obviamente es completamente impráctico. La solución es recurrir al esquema de una cantidad de parámetros arbitrarios, así estén encapsulados, mediante la inclusión del operador `*`:
```
media_aritmetica(*x)
```
### Variables Locales y Globales
Las variables dentro de las funciones son Locales por defecto. Veamos la siguiente secuencia de ejemplos:
```
def f():
print(s)
s = "Python"
f()
def f():
s = "Perl"
print(s)
f()
s = "Python"
print(s)
def f(ls):
print(ls)
ls = "Perl"
return ls
s = "Python"
print(s)
print(f(s))
def f():
print(s1)
s = "Perl"
print(s)
s1 = "Python"
f()
print(s1)
```
Como se observa, al ejecutar el anterior código se obtuvo el mensaje de errror: `boundLocalError: local variable 's' referenced before assignment`. Esto sucede porque la variable `s` es ambigua en `f()`, es decir, la primera impresión en `f()` la variable global `s` podría ser usada con el valor `Python`. Después de esto, hemos definido la variable local `s` con la asignación `s=Perl`.
En el siguiente código se ha definido la variable `s` como `global` dentro del script. Por lo tanto, todo lo realizado a la variable global `s` dentro del cuerpo de la función `f` es hecho a la variable global `s` afuera de `f`
```
def f():
global s
print(s)
s = "dog"
print(s)
s = "cat"
f()
print(s)
```
### Número arbitrarios de palabras clave como parámetros
En el capítulo anterior se vio cómo pasar un número arbitrario de parámetros posicionales a una función. También es posible pasar un número arbitrario de parámetros de palabras clave (`keywords`) a una función. Para este propósito, tenemos que usar el doble asterisco `**`
```
def f(**kwargs):
print(kwargs)
f()
f(de="German",en="English",fr="French")
```
Un posible caso de uso podría ser
```
def f(a,b,x,y):
print(a,b,x,y)
d = {'a':'append', 'b':'block','x':'extract','y':'yes'}
f(**d)
```
Veamos este último ejemplo:
```
def foo(*posicional, **keywords):
print("Posicional:", posicional)
print("Keywords:", keywords)
```
El argumento `*posicional` almacenará todos los argumentos posicionales pasados a `foo ()`, sin límite de cuántos puede proporcionar.
```
foo('one', 'two', 'three')
```
El argumento `**keywords` almacenará cualquier argumento de palabra clave:
```
foo(a='one', b='two', c='three')
```
Y por supuesto, usar los dos al mismo tiempo
```
foo('one','two',c='three',d='four')
```
## Paso por referencia
Quiénes usan otros lenguaje de programación, se preguntarán por los parámetros por referencia.
En otros lenguajes de programación existe el paso de parámetros por valor y por referencia. En los pasos por valor, una función no puede modificar el valor de las variables que recibe por fuera de su ejecución: un intento por hacerlo simplemente altera las copias locales de dichas variables. Por el contrario, al pasar por referencia, una función obtiene acceso directo a las variables originales, permitiendo así su edición.
En `Python`, en cambio, no se concibe la dialéctica paso por valor/referencia, porque el lenguaje no trabaja con el concepto de variables sino objetos y referencias. Al realizar la asignación `a = 1` no se dice que *a contiene el valor 1* sino que *a referencia a 1*. Así, en comparación con otros lenguajes, podría decirse que ***en `Python` los parámetros siempre se pasan por referencia***.
Ahora bien podríamos preguntar, ¿por qué el siguiente código no modifica los valores originales?
```
def f(a, b, c):
# No altera los objetos originales.
a, b, c = 4, 5, 6
return a,b,c
a, b, c = 1, 2, 3
a,b,c = f(a, b, c)
print(a, b, c) # Imprime 1, 2, 3.
```
La respuesta es que los números enteros (como también los de coma flotante, las cadenas y otros objetos) son inmutables. Es decir, una vez creados, su valor no puede ser modificado. ¿Cómo, no puedo acaso hacer `a = 1` y luego `a = 2`? Claro, pero desde la perspectiva del lenguaje, *no estás cambiando el valor de `a` de `1` a `2` sino quitando la referencia a `1` y poniéndosela a `2`*. En términos más simples, no «cambias» el valor de un objeto sino que le asignas una nueva referencia.
En el código anterior, al ejecutar `a, b, c = 4, 5, 6` estás creando nuevas referencias para los números `4`, `5` y `6` dentro de la función `f` con los nombres `a`, `b` y `c`.
Sin embargo otros objetos, como las listas o diccionarios, son mutables. Veamos un ejemplo:
```
def f(a):
a[0] = "CPython"
a[1] = "PyPy"
a.append("Stackless")
items = ["Perro", "Gato"]
f(items)
items
```
Basta con saber si un objeto es mutable o inmutable para determinar si es posible editarlo dentro de una función y que tenga efecto por fuera de ésta. Aunque no hay necesidad alguna para que se haga así. Por qué?: el paso por referencia es la manera en que los lenguajes que trabajan con variables proveen al programador para retornar más de un valor en una misma función. En cambio, `Python` permite devolver varios objetos utilizando *tuplas* o *listas*. Por ejemplo:
```
a = 1
b = 2
c = 3
def f():
return 4, 5, 6
a, b, c = f()
# Ahora "a" es 4, "b" es 5 y "c" es 6.
```
## Funciones Recursivas
- La Recursión es asociada al concepto de $infinito$.
- El adjetivo "*recursivo*" se origina del verbo latino "*recurrere*", que significa "*volver atrás*". Y esto es lo que una definición recursiva o una función recursiva hace: Es "*volver a funcionar*" o "*volver a sí mismo*".
El factorial es un ejemplo de recursividad:
### Definición de Funciones Recursivas
- La recursividad es un método de programación o codificación de un problema, en el que una función se llama a sí misma una o más veces en su cuerpo.
- Normalmente, está devolviendo el valor devuelto de esta llamada de función.
- Si una definición de función satisface la condición de recursión, llamamos a esta función una *función recursiva*.
### Condición de Finalización
- Una función recursiva tiene que cumplir una condición importante para ser utilizada en un programa: *tiene que terminar*.
- Una función recursiva termina, si con cada llamada recursiva la solución del problema es reducida y se mueve hacia un caso base.
- Un caso base es un caso, donde el problema se puede resolver sin más recursividad.
- Una recursividad puede terminar en un bucle infinito, si el caso base no se cumple en las llamadas.
***Ejemplo:***
Reemplazando los valores calculados dados resulta la siguiente expresión:
### Funciones Recursivas en Python
Una primero implementación del algoritmo del factorial de forma iterativa:
```
def factorial_iterativo(n):
resultado = 1
for i in range(2,n+1):
resultado *= i
return resultado
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
a = 5000
print(factorial_iterativo(a))
print(factorial(a))
def factorial(n):
# print("factorial has been called with n = " + str(n))
if n == 1:
return 1
else:
res = n * factorial(n-1)
print "intermediate result for ", n, " * factorial(" ,n-1, "): ",res
return res
print(factorial(5))
```
- Es una práctica común extender la función factorial para $0$ como argumento.
- Tiene sentido definir $0!$ Para ser $1$, porque hay exactamente una permutación de objetos cero, es decir, si nada es permutar, "*todo*" se deja en su lugar.
- Otra razón es que el número de formas de elegir $n$ elementos entre un conjunto de $n$ se calcula como $\frac{n!}{n! \times 0!}$.
- Todo lo que tenemos que hacer para implementar esto es cambiar la condición de la instrucción `if`:
### Las trampas de la recursión
***Sucesión de Fibonacci:*** La $Sucesión$ de $Fibonacci$ es la secuencia de números: $0 , 1, 1, 2, 3, 5, 8, 13, 21, ...$
- Se define por: $F_n = F_{n-1} + F_{n-2} $ , con $F_0 = 0$ y $F_1 = 1$
- La solución iterativa es fácil de implementar:
```
def fib_iter(n):
lfib = [0,1]
if n == 0:
return 0
for i in range(n-1):
lfib = lfib[i] + lfib[i+1]
return lfib
fib_iter(10)
```
La solución recursiva se acerca más a la definición:
```
def fib_recur(n):
if n == 0:
# print n
return 0
elif n == 1:
# print n
return 1
else:
# i = n - 1
# print i
return fib_recur(n-1) + fib_recur(n-2)
fib_recur(27)
```
***Comentario*:*** Observe que la solución recursiva, `fib_rec`, es **MUCHO MÁS RÁPIDA** que la función iterativa, `fib_iter`.
```
%time fib_iter(10)
%time fib_recur(100)
```
Qué sucede de "malo" en los algoritmos presentados?

ref: https://www.python-course.eu/python3_recursive_functions.php
Obsérvese que en esta secuencia, el cálculo de `f(2)` aparece tres veces en esta secuencia. El de `f(3)`, dos veces, etc. A medida que subimos de nivel, es decir, aumentamos la cantidad de datos de la serie, esos mismos cálculos se repetirán mucha más veces.
- Este algoritmo de recursión no "recuerda" que esos valores ya fueron previamente calculados.
- Podemos implementar ahora un algoritmo que "recuerde":
```
memo = {0:0, 1:1}
def fib_memo(n):
if not n in memo:
memo[n] = fib_memo(n-1) + fib_memo(n-2)
return memo[n]
%time fib_memo(10)
```
### COMENTARIOS FINALES IMPORTANTES!!!
- Aunque la recursión se presenta como una solución muy eficiente, lamentablemente (o quizás no...) en *Python* solo lo es para una cantidad de recursiones relativamente pequeña (del órden de 1000).
- En otros lenguajes, la recursión no presenta esta restricción (peligroso!).
- Cuando tenga la necesidad de realizar este tipo de operaciones, lo más recomendable es regresar a la implementación iterativa.
- Para una mayor información al respecto, los invito a visitar [este Blog](http://blog.moertel.com/posts/2013-05-11-recursive-to-iterative.html "Recursive to iterative")
## Programación Modular y Módulos
> <strong>Programación Modular:</strong> Técnica de diseño de software, que se basa en el principio general del *diseño modular*.
> El *Diseño Modular* es un enfoque que se ha demostrado como indispensable en la ingeniería incluso mucho antes de las primeras computadoras.
> El *Diseño Modular* significa que un sistema complejo se descompone en partes o componentes más pequeños, es decir módulos. Estos componentes pueden crearse y probarse independientemente. En muchos casos, pueden incluso utilizarse en otros sistemas.
> Si desea desarrollar programas que sean legibles, fiables y mantenibles sin demasiado esfuerzo, debe utilizar algún tipo de diseño de software modular. Especialmente si su aplicación tiene un cierto tamaño.
> Existe una variedad de conceptos para diseñar software en forma modular.
> La programación modular es una técnica de diseño de software para dividir su código en partes separadas. Estas piezas se denominan módulos.
> El enfoque para esta separación debe ser tener módulos con no o sólo algunas dependencias sobre otros módulos. En otras palabras: La minimización de las dependencias es la meta.
> Al crear un sistema modular, varios módulos se construyen por separado y más o menos independientemente. La aplicación ejecutable se creará reuniéndolos.
### Importando Módulos
> Cada archivo, que tiene la extensión de archivo `.py` y consta de código `Python` adecuado, se puede ver o es un módulo!
> No hay ninguna sintaxis especial requerida para hacer que un archivo de este tipo sea un módulo.
> Un módulo puede contener objetos arbitrarios, por ejemplo archivos, clases o atributos. Todos estos objetos se pueden acceder después de una importación.
> Hay diferentes maneras de importar módulos. Demostramos esto con el módulo de matemáticas:
Si quisiéramos obtener la raíz cudrada de un número, o el valor de pi, o alguna función trigonométrica simple...
```
x = sin(2*pi)
V = 4/3*pi*r**3
x = sqrt(4)
```
> Para poder usar estas funciones es necesario importar el módulo correspondiente que las contiene. En este caso sería:
```
import numpy as np
import math as mt
```
> El módulo matemático proporciona constantes y funciones matemáticas, `pi (math.pi)`, la función seno (`math.sin()`) y la función coseno (`math.cos()`). Cada atributo o función sólo se puede acceder poniendo "`math`" delante del nombre:
```
mt.sqrt(4)
mt.sin(mt.pi)
mt.
np.
mathraiz = mt.sqrt(4)
print(mathraiz)
numpyraiz = np.sqrt(4)
print(numpyraiz)
```
> Se puede importar más de un módulo en una misma sentencia de importación. En este caso, los nombres de los módulos se deben separar por comas:
```
import math, random
random.random()
```
> Las sentencias de importación pueden colocarse en cualquier parte del programa, pero es un buen estilo colocarlas directamente al principio de un programa.
> Si sólo se necesitan ciertos objetos de un módulo, se pueden importar únicamente esos:
```
from math import sin, pi, sqrt
```
> Los otros objetos, p.ej. `cos`, no estarán disponibles después de esta importación. Será posible acceder a las funciones `sin` y `pi` directamente, es decir, sin prefijarlos con `math`.
> En lugar de importar explícitamente ciertos objetos de un módulo, también es posible importar todo en el espacio de nombres del módulo de importación. Esto se puede lograr usando un asterisco en la importación:
```
from math import *
e
pi
```
> - No se recomienda utilizar la notación de asterisco en una instrucción de importación, excepto cuando se trabaja en el intérprete interactivo de `Python`.
> - Una de las razones es que el origen de un nombre puede ser bastante oscuro, porque no se puede ver desde qué módulo podría haber sido importado. Demostramos otra complicación seria en el siguiente ejemplo:
```
from numpy import *
sin(3)
from math import *
sin(3)
sin(3)
```
> Es usual la notación de asterisco, porque es muy conveniente. Significa evitar una gran cantidad de mecanografía tediosa.
> Otra forma de reducir el esfuerzo de mecanografía consiste en usar alias.
```
import numpy as np
import matplotlib.pyplot as plt
np.
```
> Ahora se pueden prefijar todos los objetos de `numpy` con `np`, en lugar de `numpy`
```
np.diag([3, 11, 7, 9])
```
### Diseñando y Escribiendo Módulos
> Un módulo en `Python` es simplemente un archivo que contiene definiciones y declaraciones de `Python`.
> El nombre del módulo se obtiene del nombre de archivo eliminando el sufijo `.py`.
> - Por ejemplo, si el nombre del archivo es `fibonacci.py`, el nombre del módulo es `fibonacci`.
> Para convertir las funciones `Fibonacci` en un módulo casi no hay nada que hacer, sólo guardar el siguiente código en un archivo `*.py`.
> - El recién creado módulo `fibonacci` está listo para ser usado ahora.
> - Podemos importar este módulo como cualquier otro módulo en un programa o script.
```
import fibonacci
fibonacci.fib(7)
fibonacci.ifib(7)
```
> - Como podrá ver, es inconveniente si tiene que usar esas funciones a menudo en su programa y siempre hay que escribir el nombre completo, es decir, `fibonacci.fib(7)`.
> - Una solución consiste en asignar un alias para obtener un nombre más corto:
```
fib = fibonacci.ifib
fib(10)
```
## Laboratorio
- Escriba un programa para el cálculo de $f(n) = 3 \times n $ (es decir, los múltiplos de $3$).
- Escriba un programa que genere el [Triángulo de Pascal](https://es.wikipedia.org/wiki/Triángulo_de_Pascal) para una cierta cantidad de números, $n$.
- Escriba un programa que extraiga del Triángulo de Pascal los primeros 10 números de la $Sucesión$ de $Fibonacci$.
- Escriba una función *find_index*(), que retorna el índice de un número en la $Sucesión$ de $Fibonacci$ si el número es un elemento de dicha $Sucesión$ y $-1$ si el número no está en la $Sucesión$.
- La suma de los cuadrados de dos números consecutivos de la $Sucesión$ de $Fibonacci$ también es un número de $Fibonacci$. Por ejemplo $2$ y $3$ son números de la Sucesión y $2^2 + 3^2 = 13$ que corresponde al número $F_7$. Use la función del ejercicio anterior para encontrar la posición de la suma de los cuadrados de dos números consecutivos en la $Secuencia$ de $Fibonacci$.
- $Tamiz$ $de$ $Erastótenes$: es un algoritmo simple para encontrar todos los números primos hasta un entero especificado, $n$:
1. Crear una lista de enteros desde $2$ hasta $n$: $2, 3, 4, \ldots, n$.
2. Comience con un contador en $2$, es decir, el primer número primo.
3. A partir de $i+i$, cuente hasta $i$ y elimine esos números de la lista, es decir, $2*i$, $3*i$,$4*i$, $\ldots$
4. Encuentra el número siguiente de la lista, $i$. Este es el siguiente número primo.
5. Establezca $i$ en el número encontrado en el paso anterior.
6. Repita los pasos $3$ y $4$ hasta que $i$ sea mayor que $n$. (Como una mejora: Es suficiente determinar la raíz cuadrada de $n$)
7. Todos los números, que todavía están en la lista, son números primos.
| true |
code
| 0.236032 | null | null | null | null |
|
# Exercise 3 - Quantum error correction
## Historical background
Shor's algorithm gave quantum computers a worthwhile use case—but the inherent noisiness of quantum mechanics meant that building hardware capable of running such an algorithm would be a huge struggle. In 1995, Shor released another landmark paper: a scheme that shared quantum information over multiple qubits in order to reduce errors.[1]
A great deal of progress has been made over the decades since. New forms of error correcting codes have been discovered, and a large theoretical framework has been built around them. The surface codes proposed by Kitaev in 1997 have emerged as the leading candidate, and many variations on the original design have emerged since then. But there is still a lot of progress to make in tailoring codes to the specific details of quantum hardware.[2]
In this exercise we'll consider a case in which artificial 'errors' are inserted into a circuit. Your task is to design the circuit such that these additional gates can be identified.
You'll then need to think about how to implement your circuit on a real device. This means you'll need to tailor your solution to the layout of the qubits. Your solution will be scored on how few entangling gates (the noisiest type of gate) that you use.
### References
1. Shor, Peter W. "Scheme for reducing decoherence in quantum computer memory." Physical review A 52.4 (1995): R2493.
1. Dennis, Eric, et al. "Topological quantum memory." Journal of Mathematical Physics 43.9 (2002): 4452-4505.
## The problem of errors
Errors occur when some spurious operation acts on our qubits. Their effects cause things to go wrong in our circuits. The strange results you may have seen when running on real devices is all due to these errors.
There are many spurious operations that can occur, but it turns out that we can pretend that there are only two types of error: bit flips and phase flips.
Bit flips have the same effect as the `x` gate. They flip the $|0\rangle$ state of a single qubit to $|1\rangle$ and vice-versa. Phase flips have the same effect as the `z` gate, introducing a phase of $-1$ into superpositions. Put simply, they flip the $|+\rangle$ state of a single qubit to $|-\rangle$ and vice-versa.
The reason we can think of any error in terms of just these two is because any error can be represented by some matrix, and any matrix can be written in terms of the matrices $X$ and $Z$. Specifically, for any single qubit matrix $M$,
$$
M = \alpha I + \beta X + \gamma XZ + \delta Z,
$$
for some suitably chosen values $\alpha$, $\beta$, $\gamma$ and $\delta$.
So whenever we apply this matrix to some single qubit state $|\psi\rangle$ we get
$$
M |\psi\rangle = \alpha |\psi\rangle + \beta X |\psi\rangle + \gamma XZ |\psi\rangle + \delta Z |\psi\rangle.
$$
The resulting superposition is composed of the original state, the state we'd have if the error was just a bit flip, the state for just a phase flip and the state for both. If we had some way to measure whether a bit or phase flip happened, the state would then collapse to just one possibility. And our complex error would become just a simple bit or phase flip.
So how do we detect whether we have a bit flip or a phase flip (or both). And what do we do about it once we know? Answering these questions is what quantum error correction is all about.
## An overly simple example
One of the first quantum circuits that most people ever write is to create a pair of entangled qubits. In this journey into quantum error correction, we'll start the same way.
```
from qiskit import QuantumCircuit, Aer
# Make an entangled pair
qc_init = QuantumCircuit(2)
qc_init.h(0)
qc_init.cx(0,1)
# Draw the circuit
display(qc_init.draw('mpl'))
# Get an output
qc = qc_init.copy()
qc.measure_all()
job = Aer.get_backend('qasm_simulator').run(qc)
job.result().get_counts()
```
Here we see the expected result when we run the circuit: the results `00` and `11` occurring with equal probability.
But what happens when we have the same circuit, but with a bit flip 'error' inserted manually.
```
# Make bit flip error
qc_insert = QuantumCircuit(2)
qc_insert.x(0)
# Add it to our original circuit
qc = qc_init.copy()
qc = qc.compose(qc_insert)
# Draw the circuit
display(qc.draw('mpl'))
# Get an output
qc.measure_all()
job = Aer.get_backend('qasm_simulator').run(qc)
job.result().get_counts()
```
Now the results are different: `01` and `10`. The two bit values have gone from always agreeing to always disagreeing. In this way, we detect the effect of the error.
Another way we can detect it is to undo the entanglement with a few more gates. If there are no errors, we return to the initial $|00\rangle$ state.
```
# Undo entanglement
qc_syn = QuantumCircuit(2)
qc_syn.cx(0,1)
qc_syn.h(0)
# Add this after the error
qc = qc_init.copy()
qc = qc.compose(qc_syn)
# Draw the circuit
display(qc.draw('mpl'))
# Get an output
qc.measure_all()
job = Aer.get_backend('qasm_simulator').run(qc)
job.result().get_counts()
```
But what happens if there are errors one of the qubits? Try inserting different errors to find out.
Here's a circuit with all the components we've introduced so far: the initialization `qc_init`, the inserted error in `qc_insert` and the final `qc_syn` which ensures that the final measurement gives a nice definite answer.
```
# Define an error
qc_insert = QuantumCircuit(2)
qc_insert.x(0)
# Undo entanglement
qc_syn = QuantumCircuit(2)
qc_syn.cx(0,1)
qc_syn.h(0)
# Add this after the error
qc = qc_init.copy()
qc = qc.compose(qc_insert)
qc = qc.compose(qc_syn)
# Draw the circuit
display(qc.draw('mpl'))
# Get an output
qc.measure_all()
job = Aer.get_backend('qasm_simulator').run(qc)
job.result().get_counts()
```
You'll find that the output tells us exactly what is going on with the errors. Both the bit and phase flips can be detected. The bit value on the left is `1` only if there is a bit flip (and so if we have inserted an `x(0)` or `x(1)`). The bit on the right similarly tells us there is a phase flip (an inserted `z(0)` or `z(1)`).
This ability to detect and distinguish bit and phase flips is very useful. But it is not quite useful enough. We can only tell *what type* of errors are happening, but not *where*. Without more detail, it is not possible to figure out how to remove the effects of these operations from our computations. For quantum error correction we therefore need something bigger and better.
It's your task to do just that! Here's a list of what you need to submit. Everything here is then explained by the example that follows.
<div class="alert alert-block alert-success">
<b>Goal</b>
Create circuits which can detect `x` and `z` errors on two qubits.
You can come up with a solution of your own. Or just tweak the almost valid solution given below.
</div>
<div class="alert alert-block alert-danger">
<b>What to submit</b>
* You need to supply two circuits:
* `qc_init`: Prepares the qubits (of which there are at least two) in a desired initial state;
* `qc_syn`: Measures a subset of the qubits.
* The artificial errors to be inserted are `x` and `z` gates on two particular qubits. You need to pick the two qubits to be used for this (supplied as the list `error_qubits`).
* There are 16 possible sets of errors to be inserted (including the trivial case of no errors). The measurement result of `qc_syn` should output a unique bit string for each. The grader will return the error message *'Please make sure the circuit is created to the initial layout.'* if this is not satisfied.
* The grader will compile the complete circuit for the backend `ibmq_tokyo` (a retired device). To show that your solution is tailor made for the device, this transpilation should not change the number of `cx` gates. If it does, you will get the error message *'Please make sure the circuit is created to the initial layout.'*
* To guide the transpilation, you'll need to tell the transpiler which qubits on the device should be used as which qubits in your circuit. This is done with an `initial_layout` list.
* You may start with the example given below, which can become a valid answer with a few tweaks.
</div>
## A better example: the surface code
```
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, Aer, transpile
import qiskit.tools.jupyter
from qiskit.test.mock import FakeTokyo
```
In this example we'll use 5 qubits that we'll call code qubits. To keep track of them, we'll define a special quantum register.
```
code = QuantumRegister(5,'code')
```
We'll also have an additional four qubits we'll call syndrome qubits.
```
syn = QuantumRegister(4,'syn')
```
Similarly we define a register for the four output bits, used when measuring the syndrome qubits.
```
out = ClassicalRegister(4,'output')
```
We consider the qubits to be laid out as follows, with the code qubits forming the corners of four triangles, and the syndrome qubits living inside each triangle.
```
c0----------c1
| \ s0 / |
| \ / |
| s1 c2 s2 |
| / \ |
| / s3 \ |
c3----------c4
```
For each triangle we associate a stabilizer operation on its three qubits. For the qubits on the sides, the stabilizers are ZZZ. For the top and bottom ones, they are XXX.
The syndrome measurement circuit corresponds to a measurement of these observables. This is done in a similar way to surface code stabilizers (in fact, this code is a small version of a surface code).
<div class="alert alert-block alert-danger">
<b>Warning</b>
You should remove the barriers before submitting the code as it might interfere with transpilation. It is given here for visualization only.
</div>
```
qc_syn = QuantumCircuit(code,syn,out)
# Left ZZZ
qc_syn.cx(code[0],syn[1])
qc_syn.cx(code[2],syn[1])
qc_syn.cx(code[3],syn[1])
qc_syn.barrier()
# Right ZZZ
#qc_syn.cx(code[1],syn[2])
qc_syn.cx(code[2],syn[2])
qc_syn.cx(code[4],syn[2])
qc_syn.barrier()
# Top XXX
qc_syn.h(syn[0])
qc_syn.cx(syn[0],code[0])
qc_syn.cx(syn[0],code[1])
qc_syn.cx(syn[0],code[2])
qc_syn.h(syn[0])
qc_syn.barrier()
# Bottom XXX
qc_syn.h(syn[3])
qc_syn.cx(syn[3],code[2])
qc_syn.cx(syn[3],code[3])
qc_syn.cx(syn[3],code[4])
qc_syn.h(syn[3])
qc_syn.barrier()
# Measure the auxilliary qubits
qc_syn.measure(syn,out)
qc_syn.draw('mpl')
```
The initialization circuit prepares an eigenstate of these observables, such that the output of the syndrome measurement will be `0000` with certainty.
```
qc_init = QuantumCircuit(code,syn,out)
qc_init.h(syn[0])
qc_init.cx(syn[0],code[0])
qc_init.cx(syn[0],code[1])
qc_init.cx(syn[0],code[2])
qc_init.cx(syn[0],syn[2])
qc_init.cx(code[2],syn[0])
qc_init.h(syn[3])
qc_init.cx(syn[3],code[2])
qc_init.cx(syn[3],code[3])
qc_init.cx(syn[3],code[4])
qc_init.cx(code[4],syn[3])
qc_init.barrier()
qc_init.draw('mpl')
```
Let's check that is true.
```
qc = qc_init.compose(qc_syn)
display(qc.draw('mpl'))
job = Aer.get_backend('qasm_simulator').run(qc)
job.result().get_counts()
```
Now let's make a circuit with which we can insert `x` and `z` gates on our two code qubits. For this we'll need to choose which of the 5 code qubits we have will correspond to the two required for the validity condition.
For this code we need to choose opposite corners.
```
error_qubits = [0,4]
```
Here 0 and 4 refer to the positions of the qubits in the following list, and hence are qubits `code[0]` and `code[4]`.
```
qc.qubits
```
To check that the code does as we require, we can use the following function to create circuits for inserting artificial errors. Here the errors we want to add are listed in `errors` as a simple text string, such as `x0` for an `x` on `error_qubits[0]`.
```
def insert(errors,error_qubits,code,syn,out):
qc_insert = QuantumCircuit(code,syn,out)
if 'x0' in errors:
qc_insert.x(error_qubits[0])
if 'x1' in errors:
qc_insert.x(error_qubits[1])
if 'z0' in errors:
qc_insert.z(error_qubits[0])
if 'z1' in errors:
qc_insert.z(error_qubits[1])
return qc_insert
```
Rather than all 16 possibilities, let's just look at the four cases where a single error is inserted.
```
for error in ['x0','x1','z0','z1']:
qc = qc_init.compose(insert([error],error_qubits,code,syn,out)).compose(qc_syn)
job = Aer.get_backend('qasm_simulator').run(qc)
print('\nFor error '+error+':')
counts = job.result().get_counts()
for output in counts:
print('Output was',output,'for',counts[output],'shots.')
```
Here we see that each bit in the output is `1` when a particular error occurs: the leftmost detects `z` on `error_qubits[1]`, then the next detects `x` on `error_qubits[1]`, and so on.
<div class="alert alert-block alert-danger">
<b>Attention</b>
The correct ordering of the output is important for this exercise. Please follow the order as given below:
1. The leftmost output represents `z` on `code[1]`.
2. The second output from left represents `x` on `code[1]`.
3. The third output from left represents `x` on `code[0]`.
4. The rightmost output represents `z` on `code[0]`.
</div>
When more errors affect the circuit, it becomes hard to unambiguously tell which errors occurred. However, by continuously repeating the syndrome readout to get more results and analysing the data through the process of decoding, it is still possible to determine enough about the errors to correct their effects.
These kinds of considerations are beyond what we will look at in this challenge. Instead we'll focus on something simpler, but just as important: the fewer errors you have, and the simpler they are, the better your error correction will be. To ensure this, your error correction procedure should be tailor-made to the device you are using.
In this challenge we'll be considering the device `ibmq_tokyo`. Though the real version of this was retired some time ago, it still lives on as one of the mock backends.
```
# Please use the backend given here
backend = FakeTokyo()
backend
```
As a simple idea of how our original circuit is laid out, let's see how many two-qubit gates it contains.
```
qc = qc_init.compose(qc_syn)
qc = transpile(qc, basis_gates=['u','cx'])
qc.num_nonlocal_gates()
```
If we were to transpile it to the `ibmq_tokyo` backend, remapping would need to occur at the cost of adding for two-qubit gates.
```
qc1 = transpile(qc,backend,basis_gates=['u','cx'], optimization_level=3)
qc1.num_nonlocal_gates()
```
We can control this to an extent by looking at which qubits on the device would be best to use as the qubits in the code. If we look at what qubits in the code need to be connected by two-qubit gates in `qc_syn`, we find the following required connectivity graph.
```
c0....s0....c1
: : :
: : :
s1....c2....s2
: : :
: : :
c3....s3....c4
```
No set of qubits on `ibmq_tokyo` can provide this, but certain sets like 0,1,2,5,6,7,10,11,12 come close. So we can set an `initial_layout` to tell the transpiler to use these.
```
initial_layout = [0,2,6,10,12,1,5,7,11]
```
These tell the transpiler which qubits on the device to use for the qubits in the circuit (for the order they are listed in `qc.qubits`). So the first five entries in this list tell the circuit which qubits to use as the code qubits and the next four entries in this list are similarly for the syndrome qubits. So we use qubit 0 on the device as `code[0]`, qubit 2 as `code[1]` and so on.
Now let's use this for the transpilation.
```
qc2 = transpile(qc,backend,initial_layout=initial_layout, basis_gates=['u','cx'], optimization_level=3)
qc2.num_nonlocal_gates()
```
Though transpilation is a random process, you should typically find that this uses less two-qubit gates than when no initial layout is provided (you might need to re-run both transpilation code multiple times to see it as transpilation is a random process).
Nevertheless, a properly designed error correction scheme should not need any remapping at all. It should be written for the exact device used, and the number of two-qubit gates should remain constant with certainty. This is a condition for a solution to be valid. So you'll not just need to provide an `initial_layout`, but also design your circuits specifically for that layout.
But that part we leave up to you!
```
code = QuantumRegister(5,'code')
syn = QuantumRegister(4,'syn')
out = ClassicalRegister(4,'output')
initial_layout = [0,2,6,10,12,1,5,7,11]
qc_syn = QuantumCircuit(code,syn,out)
# Left ZZZ
qc_syn.cx(code[0],syn[1])
qc_syn.cx(code[2],syn[1])
qc_syn.cx(code[3],syn[1])
qc_syn.barrier()
# Right ZZZ
#qc_syn.cx(code[1],syn[2])
qc_syn.cx(code[2],syn[2])
qc_syn.cx(code[4],syn[2])
qc_syn.barrier()
# Top XXX
qc_syn.h(syn[0])
qc_syn.cx(syn[0],code[0])
qc_syn.cx(syn[0],code[1])
qc_syn.cx(syn[0],code[2])
qc_syn.h(syn[0])
qc_syn.barrier()
# Bottom XXX
qc_syn.h(syn[3])
qc_syn.cx(syn[3],code[2])
qc_syn.cx(syn[3],code[3])
qc_syn.cx(syn[3],code[4])
qc_syn.h(syn[3])
qc_syn.barrier()
# Measure the auxilliary qubits
qc_syn.measure(syn,out)
qc_syn.draw('mpl')
qc_init = QuantumCircuit(code,syn,out)
qc_init.h(syn[0])
qc_init.cx(syn[0],code[0])
qc_init.cx(syn[0],code[1])
qc_init.cx(syn[0],code[2])
qc_init.cx(syn[0],syn[2])
qc_init.cx(code[2],syn[0])
qc_init.h(syn[3])
qc_init.cx(syn[3],code[2])
qc_init.cx(syn[3],code[3])
qc_init.cx(syn[3],code[4])
qc_init.cx(code[4],syn[3])
qc_init.barrier()
qc_init.draw('mpl')
qc = qc_init.compose(qc_syn)
display(qc.draw('mpl'))
job = Aer.get_backend('qasm_simulator').run(qc)
job.result().get_counts()
print(job.result().get_counts())
error_qubits = [0,4]
for error in ['x0','x1','z0','z1']:
qc = qc_init.compose(insert([error],error_qubits,code,syn,out)).compose(qc_syn)
job = Aer.get_backend('qasm_simulator').run(qc)
print('\nFor error '+error+':')
counts = job.result().get_counts()
for output in counts:
print('Output was',output,'for',counts[output],'shots.')
# Check your answer using following code
from qc_grader import grade_ex3
grade_ex3(qc_init,qc_syn,error_qubits,initial_layout)
# Submit your answer. You can re-submit at any time.
from qc_grader import submit_ex3
submit_ex3(qc_init,qc_syn,error_qubits,initial_layout)
```
## Additional information
**Created by:** James Wootton, Rahul Pratap Singh
**Version:** 1.0.0
| true |
code
| 0.371821 | null | null | null | null |
|
For this problem set, we'll be using the Jupyter notebook:

---
## Part A (2 points)
Write a function that returns a list of numbers, such that $x_i=i^2$, for $1\leq i \leq n$. Make sure it handles the case where $n<1$ by raising a `ValueError`.
```
def squares(n):
"""Compute the squares of numbers from 1 to n, such that the
ith element of the returned list equals i^2.
"""
### BEGIN SOLUTION
if n < 1:
raise ValueError("n must be greater than or equal to 1")
return [i ** 2 for i in range(1, n + 1)]
### END SOLUTION
```
Your function should print `[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]` for $n=10$. Check that it does:
```
squares(10)
"""Check that squares returns the correct output for several inputs"""
from nose.tools import assert_equal
assert_equal(squares(1), [1])
assert_equal(squares(2), [1, 4])
assert_equal(squares(10), [1, 4, 9, 16, 25, 36, 49, 64, 81, 100])
assert_equal(squares(11), [1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121])
"""Check that squares raises an error for invalid inputs"""
from nose.tools import assert_raises
assert_raises(ValueError, squares, 0)
assert_raises(ValueError, squares, -4)
```
---
## Part B (1 point)
Using your `squares` function, write a function that computes the sum of the squares of the numbers from 1 to $n$. Your function should call the `squares` function -- it should NOT reimplement its functionality.
```
def sum_of_squares(n):
"""Compute the sum of the squares of numbers from 1 to n."""
### BEGIN SOLUTION
return sum(squares(n))
### END SOLUTION
```
The sum of squares from 1 to 10 should be 385. Verify that this is the answer you get:
```
sum_of_squares(10)
"""Check that sum_of_squares returns the correct answer for various inputs."""
assert_equal(sum_of_squares(1), 1)
assert_equal(sum_of_squares(2), 5)
assert_equal(sum_of_squares(10), 385)
assert_equal(sum_of_squares(11), 506)
"""Check that sum_of_squares relies on squares."""
orig_squares = squares
del squares
try:
assert_raises(NameError, sum_of_squares, 1)
except AssertionError:
raise AssertionError("sum_of_squares does not use squares")
finally:
squares = orig_squares
```
---
## Part C (1 point)
Using LaTeX math notation, write out the equation that is implemented by your `sum_of_squares` function.
$\sum_{i=1}^n i^2$
---
## Part D (2 points)
Find a usecase for your `sum_of_squares` function and implement that usecase in the cell below.
```
def pyramidal_number(n):
"""Returns the n^th pyramidal number"""
return sum_of_squares(n)
```
| true |
code
| 0.896976 | null | null | null | null |
|
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
from scipy import stats
from compton import setup_rc_params
setup_rc_params()
```
In GMP 2016 they use
\begin{align}
\xi^{(s)} & = c_0^{(s)} + c_2^{(s)} \delta^2 + \Delta_2^{(s)} \\
\xi^{(v)} & = c_0^{(v)} + \Delta_0^{(v)}
\end{align}
and find a posterior for $\Delta$ given the convergence pattern as in Furnstahl (2015).
So the first omitted term for the scalar pieces goes as $\delta^3$ and the first omitted term for the vector piece goes as $\delta^1$.
```
# e^2 delta^2, e^2 delta^3, e^2 delta^4-fitted
gamma_e1e1_proton = np.array([-5.68562, -5.45127, -1.1])
gamma_e1e1_neutron = np.array([-5.68562, -5.45127, -4.0227])
# gamma_m1m1_proton = np.array([-1.13712, 1.95882, 2.2])
# gamma_m1m1_neutron = np.array([-1.13712, 1.95882, 1.26474])
# Use a fitted value for NLO...?
gamma_m1m1_proton = np.array([-1.13712, 1.63, 2.2])
gamma_m1m1_neutron = np.array([-1.13712, 1.63, 1.26474])
gamma_e1m2_proton = np.array([1.13712, 0.55244, -0.4])
gamma_e1m2_neutron = np.array([1.13712, 0.55244, -0.1343])
gamma_m1e2_proton = np.array([1.13712, 1.2701, 1.9])
gamma_m1e2_neutron = np.array([1.13712, 1.2701, 2.36763])
gamma_0_proton = - (gamma_e1e1_proton + gamma_m1m1_proton + gamma_e1m2_proton + gamma_m1e2_proton)
gamma_pi_proton = - gamma_e1e1_proton + gamma_m1m1_proton - gamma_e1m2_proton + gamma_m1e2_proton
gamma_0_neutron = - (gamma_e1e1_neutron + gamma_m1m1_neutron + gamma_e1m2_neutron + gamma_m1e2_neutron)
gamma_pi_neutron = - gamma_e1e1_neutron + gamma_m1m1_neutron - gamma_e1m2_neutron + gamma_m1e2_neutron
gamma_0_proton
gamma_pi_proton
gamma_0_neutron
gamma_pi_neutron
# Table 2
# gamma_e1e1_scalar = [-5.7, -2.6]
# gamma_e1e1_vector = [+1.5]
# gamma_m1m1_scalar = [-1.1, +1.8]
# gamma_m1m1_vector = [+0.5]
# gamma_e1m2_scalar = [+1.1, -0.3]
# gamma_e1m2_vector = [-0.1]
# gamma_m1e2_scalar = [+1.1, +2.2]
# gamma_m1e2_vector = [-0.2]
scalar_idxs = [0, -1]
scalar_idxs_m1m1 = [0, 1, 2]
vector_idxs = [-1]
gamma_e1e1_scalar = (gamma_e1e1_proton + gamma_e1e1_neutron)[scalar_idxs] / 2
gamma_e1e1_vector = (gamma_e1e1_proton - gamma_e1e1_neutron)[vector_idxs] / 2
gamma_m1m1_scalar = (gamma_m1m1_proton + gamma_m1m1_neutron)[scalar_idxs_m1m1] / 2
gamma_m1m1_vector = (gamma_m1m1_proton - gamma_m1m1_neutron)[vector_idxs] / 2
gamma_e1m2_scalar = (gamma_e1m2_proton + gamma_e1m2_neutron)[scalar_idxs] / 2
gamma_e1m2_vector = (gamma_e1m2_proton - gamma_e1m2_neutron)[vector_idxs] / 2
gamma_m1e2_scalar = (gamma_m1e2_proton + gamma_m1e2_neutron)[scalar_idxs] / 2
gamma_m1e2_vector = (gamma_m1e2_proton - gamma_m1e2_neutron)[vector_idxs] / 2
gamma_0_scalar = (gamma_0_proton + gamma_0_neutron)[scalar_idxs_m1m1] / 2
gamma_0_vector = (gamma_0_proton - gamma_0_neutron)[vector_idxs] / 2
gamma_pi_scalar = (gamma_pi_proton + gamma_pi_neutron)[scalar_idxs_m1m1] / 2
gamma_pi_vector = (gamma_pi_proton - gamma_pi_neutron)[vector_idxs] / 2
print('gamma E1E1 Scalar:', gamma_e1e1_scalar)
print('gamma E1E1 Vector:', gamma_e1e1_vector)
print('gamma M1M1 Scalar:', gamma_m1m1_scalar)
print('gamma M1M1 Vector:', gamma_m1m1_vector)
print('gamma E1M2 Scalar:', gamma_e1m2_scalar)
print('gamma E1M2 Vector:', gamma_e1m2_vector)
print('gamma M1E2 Scalar:', gamma_m1e2_scalar)
print('gamma M1E2 Vector:', gamma_m1e2_vector)
print('gamma 0 Scalar:', gamma_0_scalar)
print('gamma 0 Vector:', gamma_0_vector)
print('gamma pi Scalar:', gamma_pi_scalar)
print('gamma pi Vector:', gamma_pi_vector)
def compute_coefficients(y, Q, orders=None):
if orders is None:
orders = np.arange(len(y))
y = np.atleast_1d(y)
diffs = np.diff(y)
diffs = np.insert(diffs, 0, y[0])
return diffs / Q ** orders
delta = 0.4 # Eq. (2)
```
Extract coefficients
```
orders_isoscl = np.array([0, 2])
orders_isoscl_m1m1 = np.array([0, 1, 2])
orders_isovec = np.array([0])
coefs_e1e1_scalar = compute_coefficients(gamma_e1e1_scalar, delta, orders=orders_isoscl)
coefs_e1e1_vector = compute_coefficients(gamma_e1e1_vector, delta, orders=orders_isovec)
coefs_m1m1_scalar = compute_coefficients(gamma_m1m1_scalar, delta, orders=orders_isoscl_m1m1)
coefs_m1m1_vector = compute_coefficients(gamma_m1m1_vector, delta, orders=orders_isovec)
coefs_e1m2_scalar = compute_coefficients(gamma_e1m2_scalar, delta, orders=orders_isoscl)
coefs_e1m2_vector = compute_coefficients(gamma_e1m2_vector, delta, orders=orders_isovec)
coefs_m1e2_scalar = compute_coefficients(gamma_m1e2_scalar, delta, orders=orders_isoscl)
coefs_m1e2_vector = compute_coefficients(gamma_m1e2_vector, delta, orders=orders_isovec)
coefs_0_scalar = compute_coefficients(gamma_0_scalar, delta, orders=orders_isoscl_m1m1)
coefs_0_vector = compute_coefficients(gamma_0_vector, delta, orders=orders_isovec)
coefs_pi_scalar = compute_coefficients(gamma_pi_scalar, delta, orders=orders_isoscl_m1m1)
coefs_pi_vector = compute_coefficients(gamma_pi_vector, delta, orders=orders_isovec)
print('Scalar E1E1 c_n:', coefs_e1e1_scalar)
print('Vector E1E1 c_n:', coefs_e1e1_vector)
print('Scalar M1M1 c_n:', coefs_m1m1_scalar)
print('Vector M1M1 c_n:', coefs_m1m1_vector)
print('Scalar E1M2 c_n:', coefs_e1m2_scalar)
print('Vector E1M2 c_n:', coefs_e1m2_vector)
print('Scalar M1E2 c_n:', coefs_m1e2_scalar)
print('Vector M1E2 c_n:', coefs_m1e2_vector)
print('Scalar 0 c_n:', coefs_0_scalar)
print('Vector 0 c_n:', coefs_0_vector)
print('Scalar pi c_n:', coefs_pi_scalar)
print('Vector pi c_n:', coefs_pi_vector)
```
## 2016 Analysis (Set A Epsilon Priors)
```
def compute_A_eps1_posterior(x, c, Q, first_omitted_order=None, verbose=False):
if first_omitted_order is None:
first_omitted_order = len(c)
n_c = len(c)
# n_c = first_omitted_order
max_c = np.max(np.abs(c))
R = max_c * Q**first_omitted_order
if verbose:
print('R', R)
factor = n_c / (n_c + 1.) / (2. * R)
with np.errstate(divide='ignore'):
return factor * np.where(np.abs(x) <= R, 1., (R / np.abs(x)) ** (n_c + 1))
def plot_scalar_and_vector(x, c_s, c_v, Q, first_omitted_order_s, first_omitted_order_v, num_x_minor=5, num_y_minor=5, ax=None):
"""A convenience function to make the same plot easily"""
from matplotlib.ticker import MultipleLocator, AutoMinorLocator
if ax is None:
fig, ax = plt.subplots()
ax.plot(x, compute_A_eps1_posterior(x, c_s, Q, first_omitted_order=first_omitted_order_s, verbose=True), c='b', ls='--')
ax.plot(x, compute_A_eps1_posterior(x, c_v, Q, first_omitted_order=first_omitted_order_v, verbose=True), c='g', ls=':')
# Grid that work well enough for these densities
dense_x = np.linspace(-50, 50, 5000)
post_s = compute_A_eps1_posterior(dense_x, c_s, Q, first_omitted_order=first_omitted_order_s)
post_v = compute_A_eps1_posterior(dense_x, c_v, Q, first_omitted_order=first_omitted_order_v)
conv = np.convolve(post_s, post_v, mode='same')
conv /= np.trapz(conv, dense_x)
conv_interp = np.interp(x, dense_x, conv)
ax.plot(x, conv_interp, c='r')
ax.margins(x=0)
ax.xaxis.set_minor_locator(AutoMinorLocator(num_x_minor))
ax.yaxis.set_minor_locator(AutoMinorLocator(num_y_minor))
ax.tick_params(which='both', top=True, right=True)
ax.set_ylim(0, None)
return ax
N = 500
d_e1e1 = np.linspace(0, 10, N)
d_m1m1 = np.linspace(0, 3, N)
d_e1m2 = np.linspace(0, 3, N)
d_m1e2 = np.linspace(0, 3, N)
d_0 = np.linspace(0, 8, N)
d_pi = np.linspace(0, 8, N)
first_omitted_s = 3
first_omitted_v = 1
fig, axes = plt.subplots(3, 2, figsize=(7, 5))
print('E1E1')
ax_e1e1 = plot_scalar_and_vector(
d_e1e1, coefs_e1e1_scalar, coefs_e1e1_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
ax=axes[0, 0]
)
ax_e1e1.yaxis.set_major_locator(MultipleLocator(0.1))
ax_e1e1.set_ylabel(r'pr$_{\gamma_{E1E1}}(\Delta)$')
print('M1M1')
ax_m1m1 = plot_scalar_and_vector(
d_m1m1, coefs_m1m1_scalar, coefs_m1m1_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
num_y_minor=4, ax=axes[0, 1]
)
ax_m1m1.yaxis.set_major_locator(MultipleLocator(0.2))
ax_m1m1.set_ylabel(r'pr$_{\gamma_{M1M1}}(\Delta)$')
print('E1M2')
ax_e1m2 = plot_scalar_and_vector(
d_e1m2, coefs_e1m2_scalar, coefs_e1m2_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
ax=axes[1, 0]
)
ax_e1m2.set_ylabel(r'pr$_{\gamma_{E1M2}}(\Delta)$')
print('M1E2')
ax_m1e2 = plot_scalar_and_vector(
d_m1e2, coefs_m1e2_scalar, coefs_m1e2_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
ax=axes[1, 1]
)
ax_m1e2.set_ylabel(r'pr$_{\gamma_{M1E2}}(\Delta)$')
print('0')
ax_0 = plot_scalar_and_vector(
d_0, coefs_0_scalar, coefs_0_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
ax=axes[2, 0]
)
ax_0.yaxis.set_major_locator(MultipleLocator(0.1))
ax_0.set_ylabel(r'pr$_{\gamma_0}(\Delta)$')
print('pi')
ax_pi = plot_scalar_and_vector(
d_pi, coefs_pi_scalar, coefs_pi_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
ax=axes[2, 1]
)
ax_pi.yaxis.set_major_locator(MultipleLocator(0.1))
ax_pi.set_ylabel(r'pr$_{\gamma_{\pi}}(\Delta)$')
fig.tight_layout()
fig.savefig('pol_priors_set_Aeps')
```
Not bad! The $\gamma_0$ and $\gamma_\pi$ are still not exactly right. I'm not sure if I got the NLO corrections right.
## Updated Analysis
Here $\nu_0 = 0$ means that the prior is completely uninformative. To mirror the previous results, use that.
```
def compute_nu_and_tau(c, nu0=0, tau0=1):
c = np.atleast_1d(c)
nu = nu0 + len(c)
tau_sq = (nu0 * tau0**2 + c @ c) / nu
return nu, np.sqrt(tau_sq)
def compute_cbar_estimate(c, nu0=0, tau0=1):
nu, tau = compute_nu_and_tau(c, nu0=nu0, tau0=tau0)
# Either get the MAP value or the mean value...
# return tau * np.sqrt(nu / (nu - 2))
return tau * np.sqrt(nu / (nu + 2))
nu_0 = 0
tau_0 = 1
def plot_scalar_and_vector_gaussian(x, c_s, c_v, Q, first_omitted_order_s, first_omitted_order_v, num_x_minor=5, num_y_minor=5, nu0=0, tau0=1, ax=None, full_sum=True):
"""A convenience function to make the same plot easily"""
from matplotlib.ticker import MultipleLocator, AutoMinorLocator
# nu_s, tau_s = compute_nu_and_tau(c_s, nu0=nu0, tau0=tau0)
# nu_v, tau_v = compute_nu_and_tau(c_v, nu0=nu0, tau0=tau0)
cbar_s = compute_cbar_estimate(c_s, nu0=nu0, tau0=tau0)
cbar_v = compute_cbar_estimate(c_v, nu0=nu0, tau0=tau0)
# print('cbar_s:', cbar_s)
# print('cbar_v:', cbar_v)
if full_sum:
Q_sum_s = Q**first_omitted_order_s / np.sqrt(1 - Q**2)
Q_sum_v = Q**first_omitted_order_v / np.sqrt(1 - Q**2)
else:
Q_sum_s = Q**first_omitted_order_s
Q_sum_v = Q**first_omitted_order_v
std_s = cbar_s * Q_sum_s
std_v = cbar_v * Q_sum_v
if ax is None:
fig, ax = plt.subplots()
norm_s = stats.norm(scale=std_s)
norm_v = stats.norm(scale=std_v)
ax.plot(x, norm_s.pdf(x), c='b', ls='--')
ax.plot(x, norm_v.pdf(x), c='g', ls=':')
norm_tot = stats.norm(scale=np.sqrt(std_s**2 + std_v**2))
ax.plot(x, norm_tot.pdf(x), c='r')
ax.margins(x=0)
ax.xaxis.set_minor_locator(AutoMinorLocator(num_x_minor))
ax.yaxis.set_minor_locator(AutoMinorLocator(num_y_minor))
ax.tick_params(which='both', top=True, right=True)
ax.set_ylim(0, None)
return ax
def plot_scalar_and_vector_student(x, c_s, c_v, Q, first_omitted_order_s, first_omitted_order_v, num_x_minor=5, num_y_minor=5, nu0=0, tau0=1, ax=None, full_sum=True):
"""A convenience function to make the same plot easily"""
from matplotlib.ticker import MultipleLocator, AutoMinorLocator
nu_s, tau_s = compute_nu_and_tau(c_s, nu0=nu0, tau0=tau0)
nu_v, tau_v = compute_nu_and_tau(c_v, nu0=nu0, tau0=tau0)
if full_sum:
Q_sum_s = Q**first_omitted_order_s / np.sqrt(1 - Q**2)
Q_sum_v = Q**first_omitted_order_v / np.sqrt(1 - Q**2)
else:
Q_sum_s = Q**first_omitted_order_s
Q_sum_v = Q**first_omitted_order_v
scale_s = tau_s * Q_sum_s
scale_v = tau_v * Q_sum_v
if ax is None:
fig, ax = plt.subplots()
t_s = stats.t(df=nu_s, scale=scale_s)
t_v = stats.t(df=nu_v, scale=scale_v)
ax.plot(x, t_s.pdf(x), c='b', ls='--')
ax.plot(x, t_v.pdf(x), c='g', ls=':')
# Grid that work well enough for these densities
dense_x = np.linspace(-50, 50, 5000)
post_s = t_s.pdf(dense_x)
post_v = t_v.pdf(dense_x)
conv = np.convolve(post_s, post_v, mode='same')
conv /= np.trapz(conv, dense_x)
conv_interp = np.interp(x, dense_x, conv)
ax.plot(x, conv_interp, c='r')
ax.margins(x=0)
ax.xaxis.set_minor_locator(AutoMinorLocator(num_x_minor))
ax.yaxis.set_minor_locator(AutoMinorLocator(num_y_minor))
ax.tick_params(which='both', top=True, right=True)
ax.set_ylim(0, None)
return ax
```
The Gaussian plots below show the problem with using MAP values when you actually have quite long tails! Point estimates are not always representative of the full distribution.
```
for sum_to_inf in [False, True]:
fig, axes = plt.subplots(3, 2, figsize=(7, 5))
ax_e1e1 = plot_scalar_and_vector_gaussian(
d_e1e1, coefs_e1e1_scalar, coefs_e1e1_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[0, 0], full_sum=sum_to_inf
)
ax_e1e1.yaxis.set_major_locator(MultipleLocator(0.1))
ax_e1e1.set_ylabel(r'pr$_{\gamma_{E1E1}}(\Delta)$')
ax_m1m1 = plot_scalar_and_vector_gaussian(
d_m1m1, coefs_m1m1_scalar, coefs_m1m1_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
num_y_minor=4, nu0=nu_0, tau0=tau_0, ax=axes[0, 1], full_sum=sum_to_inf
)
ax_m1m1.yaxis.set_major_locator(MultipleLocator(0.2))
ax_m1m1.set_ylabel(r'pr$_{\gamma_{M1M1}}(\Delta)$')
ax_e1m2 = plot_scalar_and_vector_gaussian(
d_e1m2, coefs_e1m2_scalar, coefs_e1m2_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[1, 0], full_sum=sum_to_inf
)
ax_e1m2.set_ylabel(r'pr$_{\gamma_{E1M2}}(\Delta)$')
ax_m1e2 = plot_scalar_and_vector_gaussian(
d_m1e2, coefs_m1e2_scalar, coefs_m1e2_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[1, 1], full_sum=sum_to_inf
)
ax_m1e2.set_ylabel(r'pr$_{\gamma_{M1E2}}(\Delta)$')
ax_0 = plot_scalar_and_vector_gaussian(
d_0, coefs_0_scalar, coefs_0_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[2, 0], full_sum=sum_to_inf
)
ax_0.yaxis.set_major_locator(MultipleLocator(0.1))
ax_0.set_ylabel(r'pr$_{\gamma_0}(\Delta)$')
ax_pi = plot_scalar_and_vector_gaussian(
d_pi, coefs_pi_scalar, coefs_pi_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[2, 1], full_sum=sum_to_inf
)
ax_pi.yaxis.set_major_locator(MultipleLocator(0.1))
ax_pi.set_ylabel(r'pr$_{\gamma_{\pi}}(\Delta)$')
if sum_to_inf:
fig.suptitle('Gaussian Distribution, Sum to $Q^\infty$', y=1)
else:
fig.suptitle('Gaussian Distribution, First-Omitted Term Approximation', y=1)
fig.tight_layout()
plt.show()
fig.savefig(f'pol_priors_conjugate_gaussian_sum-inf-{sum_to_inf}')
```
The integrated distributions below look much better.
```
for sum_to_inf in [False, True]:
fig, axes = plt.subplots(3, 2, figsize=(7, 5))
ax_e1e1 = plot_scalar_and_vector_student(
d_e1e1, coefs_e1e1_scalar, coefs_e1e1_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[0, 0], full_sum=sum_to_inf
)
ax_e1e1.yaxis.set_major_locator(MultipleLocator(0.1))
ax_e1e1.set_ylabel(r'pr$_{\gamma_{E1E1}}(\Delta)$')
ax_m1m1 = plot_scalar_and_vector_student(
d_m1m1, coefs_m1m1_scalar, coefs_m1m1_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
num_y_minor=4, nu0=nu_0, tau0=tau_0, ax=axes[0, 1], full_sum=sum_to_inf
)
ax_m1m1.yaxis.set_major_locator(MultipleLocator(0.2))
ax_m1m1.set_ylabel(r'pr$_{\gamma_{M1M1}}(\Delta)$')
ax_e1m2 = plot_scalar_and_vector_student(
d_e1m2, coefs_e1m2_scalar, coefs_e1m2_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[1, 0], full_sum=sum_to_inf
)
ax_e1m2.set_ylabel(r'pr$_{\gamma_{E1M2}}(\Delta)$')
ax_m1e2 = plot_scalar_and_vector_student(
d_m1e2, coefs_m1e2_scalar, coefs_m1e2_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[1, 1], full_sum=sum_to_inf
)
ax_m1e2.set_ylabel(r'pr$_{\gamma_{M1E2}}(\Delta)$')
ax_0 = plot_scalar_and_vector_student(
d_0, coefs_0_scalar, coefs_0_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[2, 0], full_sum=sum_to_inf
)
ax_0.yaxis.set_major_locator(MultipleLocator(0.1))
ax_0.set_ylabel(r'pr$_{\gamma_0}(\Delta)$')
ax_pi = plot_scalar_and_vector_student(
d_pi, coefs_pi_scalar, coefs_pi_vector, delta,
first_omitted_order_s=first_omitted_s, first_omitted_order_v=first_omitted_v,
nu0=nu_0, tau0=tau_0, ax=axes[2, 1], full_sum=sum_to_inf
)
ax_pi.yaxis.set_major_locator(MultipleLocator(0.1))
ax_pi.set_ylabel(r'pr$_{\gamma_{\pi}}(\Delta)$')
if sum_to_inf:
fig.suptitle('Student $t$ Distribution, Sum to $Q^\infty$', y=1)
else:
fig.suptitle('Student $t$ Distribution, First-Omitted Term Approximation', y=1)
fig.tight_layout()
plt.show()
fig.savefig(f'pol_priors_conjugate_student_sum-inf-{sum_to_inf}')
```
| true |
code
| 0.542924 | null | null | null | null |
|
```
from IPython.core.display import HTML
HTML('''<style>
.container { width:100% !important; }
</style>
''')
```
# Refutational Completeness of the Cut Rule
This notebook implements a number of procedures that are needed in our proof of the <em style="color:blue">refutational completeness</em> of the cut rule.
The function $\texttt{complement}(l)$ computes the <em style="color:blue">complement</em> of a literal $l$.
If $p$ is a propositional variable, we have the following:
<ol>
<li>$\texttt{complement}(p) = \neg p$,
</li>
<li>$\texttt{complement}(\neg p) = p$.
</li>
</ol>
```
def complement(l):
"Compute the complement of the literal l."
if isinstance(l, str): # l is a propositional variable
return ('¬', l)
else: # l = ('¬', 'p')
return l[1] # l[1] = p
complement('p')
complement(('¬', 'p'))
```
The function $\texttt{extractVariable}(l)$ extracts the propositional variable from the literal $l$.
If $p$ is a propositional variable, we have the following:
<ol>
<li>$\texttt{extractVariable}(p) = p$,
</li>
<li>$\texttt{extractVariable}(\neg p) = p$.
</li>
</ol>
```
def extractVariable(l):
"Extract the variable of the literal l."
if isinstance(l, str): # l is a propositional variable
return l
else: # l = ('¬', 'p')
return l[1]
extractVariable('p')
extractVariable(('¬', 'p'))
```
The function $\texttt{collectsVariables}(M)$ takes a set of clauses $M$ as its input and computes the set of all propositional variables occurring in $M$. The clauses in $M$ are represented as sets of literals.
```
def collectVariables(M):
"Return the set of all variables occurring in M."
return { extractVariable(l) for C in M
for l in C
}
C1 = frozenset({ 'p', 'q', 'r' })
C2 = frozenset({ ('¬', 'p'), ('¬', 'q'), ('¬', 's') })
collectVariables({C1, C2})
```
Given two clauses $C_1$ and $C_2$ that are represented as sets of literals, the function $\texttt{cutRule}(C_1, C_2)$ computes all clauses that can be derived from $C_1$ and $C_2$ using the *cut rule*. In set notation, the cut rule is the following rule of inference:
$$
\frac{\displaystyle \;C_1\cup \{l\} \quad C_2 \cup \bigl\{\overline{\,l\,}\;\bigr\}}{\displaystyle C_1 \cup C_2}
$$
```
def cutRule(C1, C2):
"Return the set of all clauses that can be deduced by the cut rule from c1 and c2."
return { C1 - {l} | C2 - {complement(l) } for l in C1
if complement(l) in C2
}
C1 = frozenset({ 'p', 'q' })
C2 = frozenset({ ('¬', 'p'), ('¬', 'q') })
cutRule(C1, C2)
```
In the expression $\texttt{saturate}(\texttt{Clauses})$ below, $\texttt{Clauses}$ is a set of clauses represented as sets of literals. The call $\texttt{saturate}(\texttt{Clauses})$ computes all clauses that can be derived from clauses in the set $\texttt{Clauses}$ using the cut rule. The function keeps applying the cut rule until either no new clauses can be derived, or the empty clause $\{\}$ is derived. The resulting set of Clauses is <em style="color:blue">saturated</em> in the following sense: If $C_1$ and $C_2$ are clauses from the set $\texttt{Clauses}$ and the clause $D$ can be derived from $C_1$ and $C_2$ via the cut rule, then $D \in \texttt{Clauses}$.
```
def saturate(Clauses):
while True:
Derived = { C for C1 in Clauses
for C2 in Clauses
for C in cutRule(C1, C2)
}
if frozenset() in Derived:
return { frozenset() } # This is the set notation of ⊥.
Derived -= Clauses # remove clauses that were present before
if Derived == set(): # no new clauses have been found
return Clauses
Clauses |= Derived
C1 = frozenset({ 'p', 'q' })
C2 = frozenset({ ('¬', 'p') })
C3 = frozenset({ ('¬', 'p'), ('¬', 'q') })
saturate({C1, C2, C3})
```
The function $\texttt{findValuation}(\texttt{Clauses})$ takes a set of clauses as input. The function tries to compute a variable interpretation that makes all of the clauses true. If this is successful, a set of literals is returned. This set of literals does not contain any complementary literals and therefore corresponds to a variable assignment satisfying all clauses. If $\texttt{Clauses}$ is unsatisfiable, <tt>False</tt> is returned.
```
def findValuation(Clauses):
"Given a set of Clauses, find a propositional valuation satisfying all of these clauses."
Variables = collectVariables(Clauses)
Clauses = saturate(Clauses)
if frozenset() in Clauses: # The set Clauses is inconsistent.
return False
Literals = set()
for p in Variables:
if any(C for C in Clauses
if p in C and C - {p} <= { complement(l) for l in Literals }
):
Literals |= { p }
else:
Literals |= { ('¬', p) }
return Literals
```
The function $\texttt{toString}(S)$ takes a set $S$ as input. The set $S$ is a set of frozensets and the function converts $S$ into a string that looks like a set of sets.
```
C1 = frozenset({ 'r', 'p', 's' })
C2 = frozenset({ 'r', 's' })
C3 = frozenset({ 'p', 'q', 's' })
C4 = frozenset({ ('¬', 'p'), ('¬', 'q') })
C5 = frozenset({ ('¬', 'p'), 's', ('¬', 'r') })
C6 = frozenset({ 'p', ('¬', 'q'), 'r'})
C7 = frozenset({ ('¬', 'r'), ('¬', 's'), 'q' })
C8 = frozenset({ ('¬', 'p'), ('¬', 's')})
C9 = frozenset({ 'p', ('¬', 'r'), ('¬', 'q') })
C0 = frozenset({ ('¬', 'p'), 'r', 'q', ('¬', 's') })
Clauses = { C0, C1, C2, C3, C4, C5, C6, C7, C8, C9 }
findValuation(Clauses)
```
| true |
code
| 0.412027 | null | null | null | null |
|
# Parameters in QCoDeS
```
import qcodes as qc
import numpy as np
```
QCoDeS provides 3 classes of parameter built in:
- `Parameter` represents a single value at a time
- Example: voltage
- `ArrayParameter` represents an array of values of all the same type that are returned all at once
- Example: voltage vs time waveform
- `MultiParameter` represents a collection of values with different meaning and possibly different dimension
- Example: I and Q, or I vs time and Q vs time
which are described in the "Creating Instrument Drivers" tutorial.
## Parameter
Most of the time you can use `Parameter` directly; even if you have custom `get`/`set` functions, but sometimes it's useful to subclass `Parameter`. Note that since the superclass `Parameter` actually wraps these functions (to include some extra nice-to-have functionality), your subclass should define `get_raw` and `set_raw` rather than `get` and `set`.
```
class MyCounter(qc.Parameter):
def __init__(self, name):
# only name is required
super().__init__(name, label='Times this has been read',
vals=qc.validators.Ints(min_value=0),
docstring='counts how many times get has been called '
'but can be reset to any integer >= 0 by set')
self._count = 0
# you must provide a get method, a set method, or both.
def get_raw(self):
self._count += 1
return self._count
def set_raw(self, val):
self._count = val
c = MyCounter('c')
c2 = MyCounter('c2')
# c() is equivalent to c.get()
print('first call:', c())
print('second call:', c())
# c2(val) is equivalent to c2.set(val)
c2(22)
```
## ArrayParameter
For actions that create a whole array of values at once. When you use it in a `Loop`, it makes a single `DataArray` with the array returned by `get` nested inside extra dimension(s) for the loop.
`ArrayParameter` is, for now, only gettable.
```
class ArrayCounter(qc.ArrayParameter):
def __init__(self):
# only name and shape are required
# the setpoints I'm giving here are identical to the defaults
# this param would get but I'll give them anyway for
# demonstration purposes
super().__init__('array_counter', shape=(3, 2),
label='Total number of values provided',
unit='',
# first setpoint array is 1D, second is 2D, etc...
setpoints=((0, 1, 2), ((0, 1), (0, 1), (0, 1))),
setpoint_names=('index0', 'index1'),
setpoint_labels=('Outer param index', 'Inner param index'),
docstring='fills a 3x2 array with increasing integers')
self._val = 0
def get_raw(self):
# here I'm returning a nested list, but any sequence type will do.
# tuple, np.array, DataArray...
out = [[self._val + 2 * i + j for j in range(2)] for i in range(3)]
self._val += 6
return out
array_counter = ArrayCounter()
# simple get
print('first call:', array_counter())
```
## MultiParameter
Return multiple items at once, where each item can be a single value or an array.
NOTE: Most of the kwarg names here are the plural of those used in `Parameter` and `ArrayParameter`. In particular, `MultiParameter` is the ONLY one that uses `units`, all the others use `unit`.
`MultiParameter` is, for now, only gettable.
```
class SingleIQPair(qc.MultiParameter):
def __init__(self, scale_param):
# only name, names, and shapes are required
# this version returns two scalars (shape = `()`)
super().__init__('single_iq', names=('I', 'Q'), shapes=((), ()),
labels=('In phase amplitude', 'Quadrature amplitude'),
units=('V', 'V'),
# including these setpoints is unnecessary here, but
# if you have a parameter that returns a scalar alongside
# an array you can represent the scalar as an empty sequence.
setpoints=((), ()),
docstring='param that returns two single values, I and Q')
self._scale_param = scale_param
def get_raw(self):
scale_val = self._scale_param()
return (scale_val, scale_val / 2)
scale = qc.ManualParameter('scale', initial_value=2)
iq = SingleIQPair(scale_param=scale)
# simple get
print('simple get:', iq())
class IQArray(qc.MultiParameter):
def __init__(self, scale_param):
# names, labels, and units are the same
super().__init__('iq_array', names=('I', 'Q'), shapes=((5,), (5,)),
labels=('In phase amplitude', 'Quadrature amplitude'),
units=('V', 'V'),
# note that EACH item needs a sequence of setpoint arrays
# so a 1D item has its setpoints wrapped in a length-1 tuple
setpoints=(((0, 1, 2, 3, 4),), ((0, 1, 2, 3, 4),)),
docstring='param that returns two single values, I and Q')
self._scale_param = scale_param
self._indices = np.array([0, 1, 2, 3, 4])
def get_raw(self):
scale_val = self._scale_param()
return (self._indices * scale_val, self._indices * scale_val / 2)
iq_array = IQArray(scale_param=scale)
scale(1)
# simple get
print('simple get', iq_array())
```
| true |
code
| 0.62778 | null | null | null | null |
|
Some notes on downsampling data for display
=======================
The smaller the time step of a simulation, the more accurate it is. Empirically, for the Euler method, it looks like 0.001 JD per step (or about a minute) is decent for our purposes. This means that we now have 365.25 / 0.001 = {{365.25 / 0.001}} points per simulation object, or {{12 * 365.25 / 0.001}} bytes. However, we don't really need such dense points for display. On the other hand, 4MB is not that much and we could probably let it go, but just for fun let's explore some different downsampling schemes.
_Note: We can do both adaptive time steps for the simulation as well as use a better intergrator/gravity model to get by with larger time steps, but I haven't explored this yet as it requires a deeper understanding of such models and my intuition is that it still won't downsample the points to the extent that we want, not to mention being more complicated to program. We'll leave that for version 2.0 of the simulator._
We'll set up a simple simulation with the aim of generating some interesting trajectories. The main property we are looking for are paths that have different curvatures as we expect in simulations we will do - since spacecraft will engage/disengage engines and change attitude.
```
import numpy as np
import numpy.linalg as ln
import matplotlib.pyplot as plt
%matplotlib inline
class Body:
def __init__(self, _mass, _pos, _vel):
self.mass = _mass
self.pos = _pos
self.vel = _vel
self.acc = np.zeros(3)
def setup_sim(self, steps=1000):
self.trace = np.empty((steps, 3), dtype=float)
def update(self, dt, n):
self.pos += self.vel * dt
self.vel += self.acc * dt
self.acc = np.zeros(3)
self.trace[n, :] = self.pos
def plot_xy(self, ax):
ax.plot(self.trace[:, 0], self.trace[:, 1])
def acc_ab(a, b):
r = a.pos - b.pos
r2 = np.dot(r, r)
d = r / ln.norm(r)
Fb = d * (a.mass * b.mass) / r2
Fa = -Fb
a.acc += Fa / a.mass
b.acc += Fb / b.mass
def sim_step(bodies, dt, n):
for n1, b1 in enumerate(bodies):
for b2 in bodies[n1 + 1:]:
acc_ab(b1, b2)
for b1 in bodies:
b1.update(dt, n)
def run_sim(bodies, steps, dt):
for b in bodies:
b.setup_sim(steps)
for n in range(steps):
sim_step(bodies, dt, n)
bodyA = Body(100, np.array([0.0, 1.0, 0.0]), np.array([0.0, -10.0, 0.0]))
bodyB = Body(100, np.array([0.0, -1.0, 0.0]), np.array([10.0, 0.0, 0.0]))
bodyC = Body(100, np.array([1.0, 0.0, 0.0]), np.array([0.0, 10.0, 0.0]))
N = 100000
dt = 1e-5
run_sim([bodyA, bodyB, bodyC], N, dt)
plt.figure(figsize=(20,10))
ax = plt.gca()
#bodyA.plot_xy(ax)
bodyB.plot_xy(ax)
#bodyC.plot_xy(ax)
_ = plt.axis('scaled')
```
Simple decimation
----------------
Let us try a simple decimation type downsampler, taking every Nth point of the simulation
```
def downsample_decimate(body, every=20):
return body.trace[::every, :]
decimated_trace = downsample_decimate(bodyB, every=2000)
def plot_compare(body, downsampled_trace):
ds = downsampled_trace
plt.figure(figsize=(20,10))
plt.plot(ds[:, 0], ds[:, 1], 'ko:')
ax = plt.gca()
body.plot_xy(ax)
plt.title('{} -> {}'.format(body.trace.shape[0], ds.shape[0]))
_ = plt.axis('scaled')
plot_compare(bodyB, decimated_trace)
```
This is unsatisfactory because we are doing **poorly on the loop the loops.** It does not adapt itself to different curvatures. So we either have to have a lot of points when we don't need it - on the straight stretches, or have too few points on the tight curves. Can we do better?
Saturating maximum deviation
--------------------------
This scheme looks at the maximum deviation between the actual trace and the linear-interpolation between the points and adaptively downsamples to keep that deviation under a given threashold.
```
def perp_dist(x, y, z):
"""x, z are endpoints, y is a point on the curve"""
a = y - x
a2 = np.dot(a, a)
b = y - z
b2 = np.dot(b, b)
l = z - x
l2 = np.dot(l, l)
l = l2**0.5
return (a2 - ((l2 + a2 - b2)/(2*l))**2)**0.5
# # Here we'll compute the value for each point, but using just the mid point is probably
# # a pretty good heurstic
# def max_dist(pos, n0, n1):
# return np.array([perp_dist(pos[n0, :], pos[n2, :], pos[n1, :]) for n2 in range(n0, n1)]).max()
# Here we'll just use the midpoint for speed
def mid_dist(pos, n0, n1):
return perp_dist(pos[n0, :], pos[int((n1 + n0)/2), :], pos[n1, :])
def max_deviation_downsampler(pos, thresh=0.1):
adaptive_pos = [pos[0, :]]
last_n = 0
for n in range(1, pos.shape[0]):
#print(pos[last_n,:])
if n == last_n: continue
#print(pos[n, :])
if mid_dist(pos, last_n, n) > thresh:
adaptive_pos.append(pos[n - 1, :])
last_n = n - 1
return np.vstack(adaptive_pos)
max_dev_trace = max_deviation_downsampler(bodyB.trace, thresh=0.005)
plot_compare(bodyB, max_dev_trace)
```
Hey, this is pretty good! One thing that bothers me about this scheme is that it requires memory. It's hidden in how I did the simulation here in the prototype, but we have to keep storing every point during the simulation in a temporary buffer until we can select a point for the ouput trace. **Can we come up with a scheme that is memory less?**
Fractal downsampling
-------------------
Ok, I call this frcatal downsampling because I was inspired by the notion of fractals where the length of a line depends on the scale of measurement. It's possibly more accurately described as length difference threshold downsampling, and that's no fun to say.
In this scheme I keep a running to total of the length of the original trace since the last sampled point and compare it to the length of the straight line segment if we use the current point as the next sampled point. If the ratio between the original length and the downsampled length goes above a given threshold, we use that as the next sampled point.
This discards the requirement for a (potentially very large) scratch buffer, but is it any good?
```
def fractal_downsampler(pos, ratio_thresh=2.0):
d = np.diff(pos, axis=0)
adaptive_pos = [pos[0, :]]
last_n = 0
for n in range(1, pos.shape[0]):
if n == last_n: continue
line_d = ln.norm(pos[n, :] - pos[last_n, :])
curve_d = ln.norm(d[last_n:n,:], axis=1).sum()
if curve_d / line_d > ratio_thresh:
adaptive_pos.append(pos[n - 1, :])
last_n = n - 1
adaptive_pos.append(pos[-1, :])
return np.vstack(adaptive_pos)
fractal_trace = fractal_downsampler(bodyB.trace, ratio_thresh=1.001)
plot_compare(bodyB, fractal_trace)
```
Darn it, not as good as the max deviation downsampler. We do well in the high curvature regions, but are insensitive on the long stretches. This is because we are using a ratio, and the longer the stretch, the more we can drift. I think the soluton to this may be to have an absolute distance difference threshold in addition to the ratio threshold and make this an OR operation - if the ratio OR the absolute distance threshold are exceeded, take a sample.
The ratio threshold takes care of the tight curves and the absolute threshold takes care of the gentle curves.
So ...
```
def fractal_downsampler2(pos, ratio_thresh=1.001, abs_thresh=0.1):
d = np.diff(pos, axis=0)
adaptive_pos = [pos[0, :]]
last_n = 0
for n in range(1, pos.shape[0]):
if n == last_n: continue
line_d = ln.norm(pos[n, :] - pos[last_n, :])
curve_d = ln.norm(d[last_n:n,:], axis=1).sum()
if curve_d / line_d > ratio_thresh or abs(curve_d - line_d) > abs_thresh:
adaptive_pos.append(pos[n - 1, :])
last_n = n - 1
adaptive_pos.append(pos[-1, :])
return np.vstack(adaptive_pos)
fractal_trace2 = fractal_downsampler2(bodyB.trace, ratio_thresh=1.005, abs_thresh=0.0001)
plot_compare(bodyB, fractal_trace2)
```
This looks like a good downsampling scheme. It's nice to have two knobs to control: one for the tight curves and one for the less curvy stretches. This allows us to get close to the max deviation downsampler without needing a ton of memory
| true |
code
| 0.613381 | null | null | null | null |
|
```
import os
os.environ['CUDA_VISIBLE_DEVICES'] = "-1"
import numpy as np
import torch
import pandas as pd
from tqdm.auto import tqdm
from matplotlib import pyplot as plt
import seaborn as sns
```
# Problem setup
We solve the simpler problem where we search for a sparse set of dictionary items $d_i$ that sum up to a given signal $s$ as
$$
s=\sum\limits_i\alpha_id_i,\,\|\alpha\|_0\to\min
$$
We use model data with a random signal from sine waves, and we want to decompose it into a Fourier basis. We try two methods:
1. $l_1$ regularization. Here we just relax the problem to $\|\alpha\|_1\to\min$ and solve a regularized equation $\|s-\alpha_id_i\|_2^2+q\|\alpha\|_1\to\min$. This is lasso linear regression
2. Matching pursuit. Here we use the algorithm that greedely calculates the best matching dictionary element using the scalar product, and then adds it to the decomposition.
We compare the resulting $l_0$-sparsity of the two solutions and their efficiency
```
x = np.linspace(0, 1, 100)
frequencies = np.arange(0, 30)
args = np.repeat(frequencies[:, np.newaxis], len(x), axis=1)
args = np.multiply(x, args)
# the dictionary
D = np.vstack((np.cos(args), np.sin(args)))
print("Dictionary shape", D.shape)
# the signal
n_sig = 3
sig_coeff = np.random.randn(n_sig) + 1
sig_item = np.random.choice(len(D), n_sig, replace=False)
signal = np.dot(sig_coeff, D[sig_item, :])
plt.figure()
plt.plot(x, signal, label="Signal")
for _ in range(2):
idx = np.random.choice(len(D))
plt.plot(x, D[idx, :], label=f"Dictionary item {idx}")
plt.legend()
plt.show()
# converting to pytorch
Dt = torch.tensor(D, dtype=torch.float32)
st = torch.tensor(signal, dtype=torch.float32)
```
# $l_1$-regularization
```
# the coefficient
alpha = torch.nn.Linear(in_features=len(D), out_features=1, bias=False)
aw = list(alpha.parameters())[0]
opt = torch.optim.Adam(alpha.parameters())
q = 1e-3
for _ in tqdm(range(50000)):
opt.zero_grad()
loss = torch.nn.MSELoss()(alpha(Dt.T).flatten(), st) + q * torch.norm(aw.flatten(), p=1)
loss.backward()
opt.step()
loss
awnp = aw.detach().numpy()
sns.heatmap(awnp)
plt.hist(awnp.flatten())
print("l1 gives indices", np.where(np.abs(awnp.flatten()) > 0.1)[0])
print("ground truth indices", sig_item)
```
# Matching pursuit
```
def scalar_product(D, idx, signal):
"""Find the scalar product between a dictionary item and a signal."""
return np.dot(D[idx, :], signal)
def cos_angle(D, idx, signal):
"""Cos of the angle between dictionary item and the signal."""
return scalar_product(D, idx, signal) / (1e-10 + np.linalg.norm(signal) * np.linalg.norm(D[idx, :]))
def max_scalar_product(D, signal):
"""Find index with maximal scalar product between a dictionary item and the signal."""
products = [cos_angle(D, idx, signal) for idx in range(len(D))]
# print(products, np.max(np.abs(products)))
return np.argmax(np.abs(products))
# current signal
signal_c = np.array(signal)
for _ in range(10):
idx_max = max_scalar_product(D, signal_c)
prod_max = scalar_product(D, idx_max, signal_c)
d_max = D[idx_max, :]
signal_c -= d_max * prod_max / np.linalg.norm(d_max) ** 2
print(np.linalg.norm(signal_c), prod_max, idx_max)
```
| true |
code
| 0.71423 | null | null | null | null |
|
# Compute Word Vectors using TruncatedSVD in Amazon Food Reviews.
Data Source: https://www.kaggle.com/snap/amazon-fine-food-reviews
The Amazon Fine Food Reviews dataset consists of reviews of fine foods from Amazon.
Number of reviews: 568,454 Number of users: 256,059 Number of products: 74,258 Timespan: Oct 1999 - Oct 2012 Number of Attributes/Columns in data: 10
Attribute Information:
1. index
2. Id
3. ProductId - unique identifier for the product
4. UserId - unqiue identifier for the user
5. ProfileName
6. HelpfulnessNumerator - number of users who found the review helpful
7. HelpfulnessDenominator - number of users who indicated whether they found the review helpful or not
8. Score - rating between 1 and 5
9. Time - timestamp for the review
10. Summary - brief summary of the review
11. Text - text of the review
12. ProcessedText - Cleaned & Preprocessed Text of the review
**Objective: Perform following tasks on Amazon Food reviews:**<br>
**Task 1. Sample 25000 reviews then find top 10000 words corresponding to top 10000 Inverse Document Frequency(IDF) values.**<br>
**Task 2. Compute co-occurrence matrix on those 10000 words.** <br>
**Task 3. Find optimal value of number of components(reduced dimensions) using maximum variance.**<br>
**Task 4. Apply TruncatedSVD using optimal value of number of components.**<br>
**Task 5. Cluster words using K-Means.**<br>
[Q] How to determine if a review is positive or negative?
[Ans] We could use the Score/Rating. A rating of 4 or 5 could be cosnidered a positive review. A review of 1 or 2 could be considered negative. A review of 3 is nuetral and ignored. This is an approximate and proxy way of determining the polarity (positivity/negativity) of a review.
Loading the data
SQLite Database
In order to load the data, We have used the SQLITE dataset as it easier to query the data and visualise the data efficiently. Here as we only want to get the global sentiment of the recommendations (positive or negative), we will purposefully ignore all Scores equal to 3. If the score id above 3, then the recommendation wil be set to "positive". Otherwise, it will be set to "negative".
```
import sqlite3
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import re
import string
import nltk
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from sklearn.preprocessing import StandardScaler
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import TruncatedSVD
from sklearn.cluster import KMeans
from sklearn.utils.extmath import randomized_svd
connection = sqlite3.connect('FinalAmazonFoodReviewsDataset.sqlite')
data = pd.read_sql_query("SELECT * FROM Reviews", connection)
data.head()
print(data.shape)
print(data["Score"].value_counts())
stop = set(stopwords.words("english")) #set of stopwords
sno = nltk.stem.SnowballStemmer("english")
print(stop)
def cleanhtml(sentence): #function to clean htmltags
cleanr = re.compile("<.*?>")
cleantext = re.sub(cleanr, " ", sentence)
return cleantext
def cleanpunc(sentence): #function to clean the word of any punctuation or special characters
cleaned = re.sub(r'[?|!|\'|"|#]',r'',sentence)
cleaned = re.sub(r'[.|,|)|(|\|/]',r' ',cleaned)
return cleaned
#Code for removing stop-words from 'Text' column
i = 0
final_string = []
s = ""
for sentence in data["Text"].values:
filteredSentence = []
EachReviewText = ""
sentenceHTMLCleaned = cleanhtml(sentence)
for eachWord in sentenceHTMLCleaned.split():
for sentencePunctCleaned in cleanpunc(eachWord).split():
if (sentencePunctCleaned.isalpha()) & (len(sentencePunctCleaned)>2):
if sentencePunctCleaned.lower() not in stop:
sentenceLower = sentencePunctCleaned.lower()
s = (sno.stem(sentenceLower))
filteredSentence.append(s)
EachReviewText = ' '.join(filteredSentence)
final_string.append(EachReviewText)
data["CleanedText"] = final_string
data.head()
```
## Task 1. Sample 25000 reviews then find top 10000 words corresponding to top 10000 Inverse Document Frequency(IDF) values.
```
#taking 25000 random samples
Data = data.sample(n = 25000)
Data.head()
print(Data.shape)
print(Data["Score"].value_counts())
TFIDF_Vec= TfidfVectorizer(ngram_range=(1,1), stop_words = "english")
TFIDF_Count = TFIDF_Vec.fit_transform(Data["CleanedText"].values)
TFIDF_Count.shape
features = TFIDF_Vec.get_feature_names()
idfValues = TFIDF_Vec.idf_
d = dict(zip(features, 11 - idfValues))
sortedDict = sorted(d.items(), key = lambda d: d[1], reverse = True)
#here we are sorting a dictionary where first value(keys) are words and second value(values) are IDF values. There is a 'key'
#argument in sorted function takes a function which will be used to determine according to what values to sort by. Here, we have
#given an anonymous function which takes the data followed by colon then d[1] means in our data second value is idf values so we
#are telling the sorted function to sort the dictionary according to idf values.
sortedDict = sortedDict[0:10000]
#taking top 10000 words corresponding to top 10000 Inverse Document Frequency(IDF) values.
len(sortedDict)
for i in range(10):
print(sortedDict[i])
for i in range(10):
print(sortedDict[i][0])
wordList_idf = []
for i in range(len(sortedDict)):
wordList_idf.append(sortedDict[i][0])
len(wordList_idf)
```
## Task 2. Compute co-occurrence matrix on those 5000 words.
```
Data["CleanedText"].head()
sent = Data["CleanedText"].iloc[3]
sent
len(sent.split())
#checking for any empty text
cnt = 0
for i in Data["CleanedText"]:
cnt += 1
if len(i.split()) == 0:
print(cnt)
def co_occurrence(sentence_array, window_size, word_list):
co_occ = np.zeros((len(word_list), len(word_list)), dtype = int)
for i in sentence_array:
for word in i.split():
if word in word_list:
row = word_list.index(word) #this will give index of a word in word_list array
wordIndexInSentence = i.split().index(word) #this will give index of a word in sentence 'i'
window_left = wordIndexInSentence - window_size
if window_left < 0:
window_left = 0
window_right = wordIndexInSentence + window_size
if window_right > len(i.split()):
window_right = len(i.split())
for context_word in i.split()[window_left:window_right]:
if context_word in word_list:
column = word_list.index(context_word)
co_occ[row][column] += 1
return co_occ
#this is a function to create co-occurrence matrix of all the words which will be passed into "word_list" argument.
#basically this function takes three arguments:
#First: "sentence_series"(numpy ndarray) which is an array which should contain all the reviews/sentences.
#Second: "window_size"(integer) this determines the context size upto which you may want to find the co-occurring words.
#Third: "word_list"(list) this should contain list of words which you may want to find as co-occurring.
#it returns co-occurrence matrix which is a square matrix and each row and column corresponds to a word as defined in
#"word_list"
sent_series = Data["CleanedText"].values
print(type(sent_series))
print(sent_series.shape)
print(len(wordList_idf))
co_occur_matrix = co_occurrence(sent_series, 5, wordList_idf)
print(co_occur_matrix)
print(co_occur_matrix.shape)
```
## Task 3. Find optimal value of number of components(reduced dimensions) using maximum variance.
```
k = [i for i in range(20,241,20)]
components = []
total_var = []
for j in k:
svd = TruncatedSVD(n_components=j, n_iter=10)
svd.fit(co_occur_matrix)
var_perc = sum(svd.explained_variance_ratio_)
components.append(j)
total_var.append(var_perc)
xy = list(zip(components, total_var))
xy
plt.figure(figsize = (14, 12))
plt.plot(components, total_var)
plt.title("Number of Components VS Total Explained Variance", fontsize=25)
plt.xlabel("Number of Components", fontsize=25)
plt.ylabel("Total Explained Variance", fontsize=25)
plt.grid(linestyle='-', linewidth=0.5)
```
**We can see from the graph that we are getting approximately 91% variance at number of components equal to 140. It further means that we are preserving 91% of data even by reducing our dimension from 5000 to 140. Therefore, we are considering our number of components to be 140**
## Task 4. Apply TruncatedSVD using optimal value of number of components.
```
svd = TruncatedSVD(n_components = 140, n_iter = 10)
svd.fit(co_occur_matrix)
var_perc = sum(svd.explained_variance_ratio_)
print("Percentage of variance explained = "+str(var_perc * 100)+"%")
U, Sigma, VT = randomized_svd(co_occur_matrix, n_components = 140, n_iter = 10)
U.shape
```
## Task 5. Cluster words using K-Means.
```
Data_Std = StandardScaler(with_mean = False).fit_transform(U)
print(Data_Std.shape)
print(type(Data_Std))
#taking number of cluster = 1000
KMeans_Apply = KMeans(n_clusters=1000, init = "k-means++", max_iter = 100, n_jobs = -1).fit(Data_Std)
Cluster_indices = {i: np.where(KMeans_Apply.labels_ == i) for i in range(KMeans_Apply.n_clusters)}
```
### Checking for similarity of words in clusters manually
```
#checking for review 981
for i in Cluster_indices[981][0]:
print(wordList_idf[i])
```
**Now in cluster number 981, the above words are related like: understand, sorri, hesit, disagre, error, edit, written, convinc etc**
```
#checking for review 954
for i in Cluster_indices[954][0]:
print(wordList_idf[i])
```
**Now in cluster number 954, the above words are related like: parent, childhood, cute, sister, memori, cigarett, nausea, butterscotch,peppermint etc**
```
#checking for review 925
for i in Cluster_indices[925][0]:
print(wordList_idf[i])
```
**Now in cluster number 925, the above words are related like: upset, relax, stress, diseas, symptom, antibiot, heal, thyroid, immun etc**
```
#checking for review 904
for i in Cluster_indices[904][0]:
print(wordList_idf[i])
```
**Now in cluster number 904, the above words are related like: disgust, gross, spoil, yuck, crap, pungent, harsh, stink, fragranc, lavend etc**
| true |
code
| 0.361883 | null | null | null | null |
|
Results:
- we subsetted Ag1000g P2 (1142 samples) zarr to the positions of the amplicon inserts
- a total of 1417 biallelic SNPs were observed in all samples, only one amplicon (29) did not have variation
- we performed PCA directly on those SNPs without LD pruning
- PCA readily splits Angolan samples `AOcol` and general gambiae vs coluzzii
- populations `GW`, `GAgam`, `FRgam` and some outliers of `CMgam` can be separated
- overall, resolution of clusters is less complete than in whole-genome dataset: https://github.com/malariagen/ag1000g-phase2-data-paper/blob/master/notebooks/figure_PCA.ipynb
- impacts of individual amplicons are different. Highest impact amplicons are 28, 60, 7.
```
%run common.ipynb
# long population names
samples['population'] = samples.population.replace(pop_labels)
# concatenate biallelic site nalts into single array
ampl_flt = dict()
for ampl in callset:
flt = callset[ampl]['biallelic'][:]
nalt = callset[ampl]['NALT'][:]
ampl_flt[ampl] = nalt[flt]
ampl_flt_nalts = np.concatenate([ampl_flt[ampl] for ampl in callset])
ampl_flt_nalts.shape
```
## Alternative PCA for Kenya
```
# country_filter = samples.population.isin(['KE','GW'])
# country_filter.value_counts()
# samples = samples[country_filter]
# read all SNPs
# ampl_snps = dict()
# for ampl in callset:
# ampl_snps[ampl] = callset[ampl]['genotype']
# cat_snps = allel.GenotypeChunkedArray(np.concatenate(list(ampl_snps.values())))
# subset to countries
# cat_snps = cat_snps[:, country_filter]
# recalculate biallelic nalts
# ac = cat_snps.count_alleles()
# flt = (ac.max_allele() == 1) & (ac[:, :2].min(axis=1) > 1)
# ampl_flt_nalts = cat_snps[flt].to_n_alt()
```
## PCA
```
# skip ld_prune, straight to PCA
coords, model = allel.pca(ampl_flt_nalts, n_components=20, scaler='patterson')
fig, ax = plt.subplots()
ax.plot(model.explained_variance_ratio_, 'go')
ax.set_xlabel("principal component")
ax.set_ylabel("variance explained")
plt.xticks(np.arange(0,20, 1));
# add first 12 pc values to samples table
for component in range(12):
samples['pc{}'.format(component + 1)] = coords[:, component]
samples.head()
fig, axs = plt.subplots(2, 2, figsize=(12, 12))
for i, ax in enumerate(axs.flatten()):
comp1 = i*2 + 1
comp2 = i*2 + 2
pc_var1 = model.explained_variance_ratio_[comp1] * 100
pc_var2 = model.explained_variance_ratio_[comp2] * 100
legend = ('full' if i==3 else False)
g = sns.scatterplot(data=samples,
x='pc{}'.format(comp1),
y='pc{}'.format(comp2),
hue='population',
style='m_s',
palette=pop_colors,
legend=legend,
ax=ax);
# attempt to place legend outside
# g.legend(loc='center left', bbox_to_anchor=(1.25, 0.5), ncol=1)
ax.set_xlabel('PC{} ({:.2f}%)'.format(comp1, pc_var1))
ax.set_ylabel('PC{} ({:.2f}%)'.format(comp2, pc_var2));
plt.tight_layout()
```
## Impact of individual amplicons on PCA
```
# extract PCA component coefficients
components = pd.DataFrame(model.components_.T,
columns=range(1,21)) #.abs()
components.head()
# match variants to amplicons
var_ampl = list()
for ampl in callset:
nvar = ampl_flt[ampl].shape[0]
var_ampl.extend([ampl] * nvar)
len(var_ampl)
components['ampl'] = var_ampl
fig, axs = plt.subplots(1, 2, figsize=(10, 12))
sns.heatmap(components.groupby('ampl').mean().iloc[:, :12],
center=0, cmap='coolwarm', cbar=False, ax=axs[0])
sns.heatmap(components.groupby('ampl').std().iloc[:, :12],
center=0, cmap='coolwarm', cbar=False, ax=axs[1])
for i in range(2):
axs[i].set_xlabel('PC');
axs[0].set_title('Component mean')
axs[1].set_title('Component std');
```
| true |
code
| 0.617397 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Serbeld/RX-COVID-19/blob/master/Detection5C_Norm_v2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!pip install lime
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.applications import inception_v3
from tensorflow.keras.layers import Dense,Dropout,Flatten,Input,AveragePooling2D,BatchNormalization
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.utils import to_categorical
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from imutils import paths
import matplotlib.pyplot as plt
import numpy as np
import cv2
import os
import lime
from lime import lime_image
from skimage.segmentation import mark_boundaries
import pandas as pd
plt.rcParams["figure.figsize"] = (10,5)
#Loading the dataset
!pip install h5py
import h5py
from google.colab import drive,files
drive.mount('/content/drive')
hdf5_path = '/content/drive/My Drive/Dataset5C/Dataset5C.hdf5'
dataset = h5py.File(hdf5_path, "r")
import numpy as np
import matplotlib.pylab as plt
#train
train_img = dataset["train_img"]
xt = np.array(train_img)
yt = np.array(dataset["train_labels"])
#test
testX = np.array(dataset["test_img"])
testY = np.array(dataset["test_labels"])
#Validation
xval = np.array(dataset["val_img"])
yval = np.array(dataset["val_labels"])
print("Training Shape: "+ str(xt.shape))
print("Validation Shape: "+ str(xval.shape))
print("Testing Shape: "+ str(testX.shape))
#Categorical values or OneHot
import keras
num_classes = 5
yt = keras.utils.to_categorical(yt,num_classes)
testY = keras.utils.to_categorical(testY,num_classes)
yval = keras.utils.to_categorical(yval,num_classes)
#Image
num_image = 15
print()
print('Healthy: [1 0 0 0 0]')
print('Pneumonia & Covid-19: [0 1 0 0 0]')
print('Cardiomegaly: [0 0 1 0 0]')
print('Other respiratory disease: [0 0 0 1 0]')
print('Pleural Effusion: [0 0 0 0 1]')
print()
print("Output: "+ str(yt[num_image]))
imagen = train_img[num_image]
plt.imshow(imagen)
plt.show()
## global params
INIT_LR = 1e-5 # learning rate
EPOCHS = 10 # training epochs
BS = 4 # batch size
## build network
from tensorflow.keras.models import load_model
#Inputs
inputs = Input(shape=(512, 512, 3), name='images')
inputs2 = BatchNormalization()(inputs)
#Inception Model
output1 = inception_v3.InceptionV3(include_top=False,weights= "imagenet",
input_shape=(512, 512, 3),
classes = 5)(inputs2)
#AveragePooling2D
output = AveragePooling2D(pool_size=(4, 4), strides=None,
padding='valid',name='AvgPooling')(output1)
#Flattened
output = Flatten(name='Flatten')(output)
#ReLU layer
output = Dense(1000, activation = 'relu',name='ReLU')(output)
#Dropout
output = Dropout(0.35,name='Dropout')(output)
#Dense layer
output = Dense(5, activation='softmax',name='softmax')(output)
# the actual model train)
model = Model(inputs=inputs, outputs=output)
print("[INFO] compiling model...")
opt = Adam(lr=INIT_LR, decay=INIT_LR / EPOCHS)
model.compile(loss="categorical_crossentropy", optimizer=opt,
metrics=["accuracy"])
model.summary()
from tensorflow.keras.callbacks import ModelCheckpoint
model_checkpoint = ModelCheckpoint(filepath="/content/drive/My Drive/Dataset5C/Model",
monitor='val_loss', save_best_only=True)
## train
print("[INFO] training head...")
H = model.fit({'images': xt},
{'softmax': yt},
batch_size = BS,
epochs = EPOCHS,
validation_data=(xval, yval),
callbacks=[model_checkpoint],
shuffle=True)
#Load the best model trained
model = load_model("/content/drive/My Drive/Dataset5C/Model")
## eval
print("[INFO] evaluating network...")
print()
print("Loss: "+ str(round(model.evaluate(testX,testY,verbose=0)[0],2))+ " Acc: "+ str(round(model.evaluate(testX,testY,verbose=1)[1],2)))
print()
predIdxs = model.predict(testX)
predIdxs = np.argmax(predIdxs, axis=1) # argmax for the predicted probability
#print(classification_report(testY.argmax(axis=1), predIdxs,target_names=lb.classes_))
cm = confusion_matrix(testY.argmax(axis=1), predIdxs)
total = sum(sum(cm))
#print(total) #60
acc = (cm[0, 0] + cm[1, 1] + cm[2, 2] + cm[3,3]+ cm[4,4]) / total
#sensitivity = cm[0, 0] / (cm[0, 0] + cm[0, 1])
#specificity = cm[1, 1] / (cm[1, 0] + cm[1, 1])
# show the confusion matrix, accuracy, sensitivity, and specificity
print(cm)
print("acc: {:.4f}".format(acc))
#print("sensitivity: {:.4f}".format(sensitivity))
#print("specificity: {:.4f}".format(specificity))
## explain
N = EPOCHS
plt.style.use("ggplot")
plt.figure(1)
plt.plot(np.arange(0, N), H.history["loss"], label="train_loss")
plt.plot(np.arange(0, N), H.history["val_loss"], label="val_loss")
plt.plot(np.arange(0, N), H.history["accuracy"], label="train_acc")
plt.plot(np.arange(0, N), H.history["val_accuracy"], label="val_acc")
plt.title("Precision of COVID-19 detection.")
plt.xlabel("Epoch #")
plt.ylabel("Loss/Accuracy")
plt.legend(loc="lower left")
#plt.axis([0, EPOCHS, 0.3, 0.9])
plt.savefig("/content/drive/My Drive/Dataset5C/Model/trained_cero_plot_Inception_2nd_time.png")
plt.show()
import cv2
plt.figure(2)
for ind in range(1):
explainer = lime_image.LimeImageExplainer()
explanation = explainer.explain_instance(testX[-ind], model.predict,
hide_color=0, num_samples=42)
print("> label:", testY[ind].argmax(), "- predicted:", predIdxs[ind])
temp, mask = explanation.get_image_and_mask(
explanation.top_labels[0], positive_only=True, num_features=5, hide_rest=True)
mask = np.array(mark_boundaries(temp/2 +1, mask))
#print(mask.shape)
imagen = testX[ind]
imagen[:,:,0] = imagen[:,:,2]
imagen[:,:,1] = imagen[:,:,2]
mask[:,:,0] = mask[:,:,2]
mask[:,:,1] = mask[:,:,2]
plt.imshow((mask +imagen)/255)
plt.savefig("/content/drive/My Drive/Dataset5C/Model/trained_pulmons_inception_Normal"+str(ind)+".png")
plt.show()
plt.figure(3)
for ind in range(1):
explainer = lime_image.LimeImageExplainer()
explanation = explainer.explain_instance(testX[-ind], model.predict,
hide_color=0, num_samples=42)
print("> label:", testY[ind].argmax(), "- predicted:", predIdxs[ind])
temp, mask = explanation.get_image_and_mask(
explanation.top_labels[0], positive_only=True, num_features=5, hide_rest=True)
mask = np.array(mark_boundaries(temp/2 +1, mask))
#print(mask.shape)
imagen = testX[ind]
imagen[:,:,0] = imagen[:,:,2]
imagen[:,:,1] = imagen[:,:,2]
mask[:,:,0] = mask[:,:,2]
mask[:,:,1] = mask[:,:,2]
kernel = np.ones((50,50),np.uint8)
mask = cv2.dilate(mask,kernel,iterations = 1)
mask = cv2.blur(mask,(30,30))
plt.imshow((mask +imagen)/255)
plt.savefig("/content/drive/My Drive/Dataset5C/Model/trained_pulmons_inception_Light"+str(ind)+".png")
plt.show()
plt.figure(4)
for ind in range(1):
explainer = lime_image.LimeImageExplainer()
explanation = explainer.explain_instance(testX[-ind], model.predict,
hide_color=0, num_samples=42)
print("> label:", testY[ind].argmax(), "- predicted:", predIdxs[ind])
temp, mask = explanation.get_image_and_mask(
explanation.top_labels[0], positive_only=True, num_features=3, hide_rest=True)
mask = np.array(mark_boundaries(temp/2 +1, mask))
#print(mask.shape)
imagen = testX[ind]
imagen[:,:,0] = imagen[:,:,2]
imagen[:,:,1] = imagen[:,:,2]
mask[:,:,0] = mask[:,:,2]
mask[:,:,1] = mask[:,:,2]
kernel = np.ones((50,50),np.uint8)
mask = cv2.dilate(mask,kernel,iterations = 1)
mask = cv2.blur(mask,(30,30))
mask = np.array(mask, dtype=np.uint8)
mask = cv2.medianBlur(mask,5)
mask = cv2.cvtColor(mask, cv2.COLOR_BGR2GRAY)
mask = cv2.applyColorMap(mask, cv2.COLORMAP_HOT) #heatmap
end = cv2.addWeighted((imagen/255), 0.7, mask/255, 0.3, 0)
plt.imshow((end))
plt.savefig("/content/drive/My Drive/Dataset5C/Model/trained_pulmons_inception_Heat_map_purple"+str(ind)+".png")
plt.show()
plt.figure(4)
for ind in range(1):
explainer = lime_image.LimeImageExplainer()
explanation = explainer.explain_instance(testX[-ind], model.predict,
hide_color=0, num_samples=42)
print("> label:", testY[ind].argmax(), "- predicted:", predIdxs[ind])
temp, mask = explanation.get_image_and_mask(
explanation.top_labels[0], positive_only=True, num_features=2, hide_rest=True)
mask = np.array(mark_boundaries(temp/2 +1, mask))
#print(mask.shape)
imagen = testX[ind]
imagen[:,:,0] = imagen[:,:,2]
imagen[:,:,1] = imagen[:,:,2]
mask[:,:,0] = mask[:,:,2]
mask[:,:,1] = mask[:,:,2]
kernel = np.ones((30,30),np.uint8)
mask = cv2.dilate(mask,kernel,iterations = 2)
mask = cv2.blur(mask,(30,30))
mask = cv2.blur(mask,(30,30))
mask = np.array(mask, dtype=np.uint8)
mask = cv2.medianBlur(mask,5)
mask = cv2.cvtColor(mask, cv2.COLOR_BGR2GRAY)
mask2 = cv2.applyColorMap((mask), cv2.COLORMAP_JET) #heatmap
mask = cv2.blur(mask,(60,60))
mask = cv2.applyColorMap(mask, cv2.COLORMAP_HOT) #heatmap
mask = ((mask*1.1 + mask2*0.7)/255)*(3/2)
end = cv2.addWeighted(imagen/255, 0.8, mask2/255, 0.3, 0)
#end = cv2.addWeighted(end, 0.8, mask/255, 0.2, 0)
plt.imshow((end))
cv2.imwrite("/content/drive/My Drive/Maps/Heat_map"+str(ind)+".png",end*255)
plt.savefig("/content/drive/My Drive/Dataset5C/Model/trained_pulmons_inception_Heat_map"+str(ind)+".png")
plt.show()
plt.figure(5)
for ind in range(1):
explainer = lime_image.LimeImageExplainer()
explanation = explainer.explain_instance(testX[-ind], model.predict,
hide_color=0, num_samples=42)
print("> label:", testY[ind].argmax(), "- predicted:", predIdxs[ind])
temp, mask = explanation.get_image_and_mask(
explanation.top_labels[0], positive_only=True, num_features=1, hide_rest=True)
mask = np.array(mark_boundaries(temp/2 +1, mask))
#print(mask.shape)
imagen = testX[ind]
imagen[:,:,0] = imagen[:,:,2]
imagen[:,:,1] = imagen[:,:,2]
mask[:,:,0] = mask[:,:,2]
mask[:,:,1] = mask[:,:,2]
kernel = np.ones((30,30),np.uint8)
mask = cv2.dilate(mask,kernel,iterations = 2)
mask = cv2.blur(mask,(30,30))
mask = cv2.blur(mask,(30,30))
mask = np.array(mask, dtype=np.uint8)
mask = cv2.medianBlur(mask,5)
mask = cv2.cvtColor(mask, cv2.COLOR_BGR2GRAY)
mask2 = cv2.applyColorMap((mask), cv2.COLORMAP_JET) #heatmap
mask = cv2.blur(mask,(60,60))
mask = cv2.applyColorMap(mask, cv2.COLORMAP_HOT) #heatmap
mask = ((mask*1.1 + mask2*0.7)/255)*(3/2)
end = cv2.addWeighted(imagen/255, 0.8, mask2/255, 0.3, 0)
#end = cv2.addWeighted(end, 0.8, mask/255, 0.2, 0)
deep = np.reshape(end,newshape=(512,512,3),order='C')
CHANNEL1=deep[:,:,2]
CHANNEL2=deep[:,:,0]
deep[:,:,0] = CHANNEL1
#deep[:,:,2] = CHANNEL2
plt.imshow((deep))
plt.savefig("/content/drive/My Drive/Dataset5C/Model/trained_pulmons_inception_Heat_map_ma"+str(ind)+".png")
plt.show()
```
| true |
code
| 0.721584 | null | null | null | null |
|
# Chaotic systems prediction using NN
## This notebook is developed to show how well Neural Networks perform when presented with the task of predicting the trajectories of **Chaotic Systems**, this notebook is part of the work presented in *New results for prediction of chaotic systems using Deep Recurrent Neural Networks* in the journal of **Neural Processing Letters**
### In this experiment RNN-LSTM, RNN-GRU and MLP neural networks are trained and tested to predict the trajectories of the chaotic systems of Lorenz, Rabinovich-Fabrikant and Rossler.
## Description of this Notebook
* The initial conditions of the chaotic systems are defined in the *Chaos_Attractors* class
* The *NN_Identifier* class is where the neural test and training takes place, the outputs are graphs that show the performance obtained by the trained model as well as the trajectories identified by the neural network
* In the last cells the global parameters such as the number of epochs, layers, neurons and batch size are defined to train and predict the chaotic systems as well as the time series size.
#Libraries
```
import tensorflow as tf
from keras.models import Sequential
from keras.layers import LSTM, GRU, Dense, Dropout, Masking, Embedding, Flatten
from sklearn.preprocessing import MinMaxScaler
from scipy.integrate import odeint
from google.colab import drive
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math
from mpl_toolkits.mplot3d import Axes3D
fig_size = plt.rcParams["figure.figsize"]
#Save images to you Google Drive Path
drive.mount('/content/gdrive')
images_dir = '/content/gdrive/My Drive/Colab_Images'
```
#Lorenz, Rabinovich–Fabrikant and Rossler Chaotic Systems
```
class ChaosAttractors():
"""
Initial conditions for the systems to display chaotic behaviour are
defined as follows:
Lorenz 63 -> s = 10, r = 8/3, b = 28 and dt = 0.01
Fabrikant-Rabinovich -> a = 0.14, g = 0.1 and dt = 0.01
Rossler -> a = 0.2, b = 0.2, c = 6.3 and dt = 0.01
"""
def __init__(self, steps, lrz_s=10, lrz_r=28, lrz_b=8/3, lrz_dt = 0.01,
rab_fab_a = 0.14, rab_fab_g = 0.1, rab_fab_dt = 0.01,
ros_a=0.2, ros_b=0.2, ros_c=6.3, ros_dt = 0.01):
self.lrz_s = lrz_s
self.lrz_b = lrz_b
self.lrz_r = lrz_r
self.lrz_dt = lrz_dt
self.rab_fab_a = rab_fab_a
self.rab_fab_g = rab_fab_g
self.rab_fab_dt = rab_fab_dt
self.ros_a = ros_a
self.ros_b = ros_b
self.ros_c = ros_c
self.ros_dt = ros_dt
self.steps = steps
"""Lorenz 63 System"""
def lorenz63(self):
xs = np.empty((self.steps + 1,))
ys = np.empty((self.steps + 1,))
zs = np.empty((self.steps + 1,))
xs[0], ys[0], zs[0] = (1.0, 1.0, 1.0)
for i in range(self.steps):
x_dot = self.lrz_s*(ys[i] - xs[i])
y_dot = self.lrz_r*xs[i] - ys[i] - xs[i]*zs[i]
z_dot = xs[i]*ys[i] - self.lrz_b*zs[i]
xs[i + 1] = xs[i] + (x_dot * self.lrz_dt)
ys[i + 1] = ys[i] + (y_dot * self.lrz_dt)
zs[i + 1] = zs[i] + (z_dot * self.lrz_dt)
return xs, ys, zs
"""Rabinovich–Fabrikant equations"""
def rabinovich_fabrikant(self):
xs = np.zeros((self.steps))
ys = np.zeros((self.steps))
zs = np.zeros((self.steps))
xs[0] ,ys[0] ,zs[0] = (-1,0,0.5)
for i in range(1,self.steps):
x = xs[i-1]
y = ys[i-1]
z = zs[i-1]
dx = y*(z - 1 + x*x) + self.rab_fab_g*x
dy = x*(3*z + 1 - x*x) + self.rab_fab_g *y
dz = -2*z*(self.rab_fab_a + x*y)
xs[i] = x+self.rab_fab_dt*dx
ys[i] = y+self.rab_fab_dt*dy
zs[i] = z+self.rab_fab_dt*dz
return xs, ys, zs
"""Rossler Hyperchaotic System"""
def rossler(self):
xs = np.empty([self.steps + 1])
ys = np.empty([self.steps + 1])
zs = np.empty([self.steps + 1])
xs[0], ys[0], zs[0] = (1.0, 1.0, 1.0)
for i in range(self.steps):
x_dot = -ys[i] - zs[i]
y_dot = xs[i] + self.ros_a*ys[i]
z_dot = self.ros_b + xs[i]*zs[i] - self.ros_c*zs[i]
xs[i+1] = xs[i] + (x_dot * self.ros_dt)
ys[i+1] = ys[i] + (y_dot * self.ros_dt)
zs[i+1] = zs[i] + (z_dot * self.ros_dt)
return xs, ys, zs
```
# Neural characterization models
```
class NNIdentifier():
"""
Neural network models to predict chaotic systems
The neural network models used are the RNN-LSTM, RNN-GRU and MLP
...
Attributes
----------
num_neurons : int
Number of neurons used in each layer of the NN
num_neurons : int
Number of layers in the NN
dataset : array[x ,y ,z]
Dataset used to train and test the NN model
training_epochs : int
Number of epochs for training the NN
batch_size: int
Size of the batch passed to the NN
attractor_name: string
Name of the chaotic system (Used for title of the trajectory graph)
chaos_x_series: array[x]
Time series of the chaotic system in the X variable
chaos_y_series: array[x]
Time series of the chaotic system in the Y variable
chaos_z_series: array[x]
Time series of the chaotic system in the Z variable
"""
def __init__(self, num_neurons, num_layers, dataset, training_epochs, batch_size, attractor_name, chaos_x_series, chaos_y_series, chaos_z_series):
self.num_neurons = num_neurons
self.num_layers = num_layers
self.dataset = dataset
self.training_epochs = training_epochs
self.batch_size = batch_size
self.trainX = []
self.trainY = []
self.testX = []
self.testY = []
self.attractor_name = attractor_name
self.look_back = 1
self.chaos_x_series = chaos_x_series
self.chaos_y_series = chaos_y_series
self.chaos_z_series = chaos_z_series
def predict_attractor(self):
self.normalize_datase()
self.train_eval_models()
def create_dataset(self, dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back)]
dataX.append(a)
dataY.append(dataset[i + look_back])
return np.array(dataX), np.array(dataY)
def normalize_datase(self):
# Normalize Uk
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(self.dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.6)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 1
self.trainX, self.trainY = self.create_dataset(train, look_back)
self.testX, self.testY = self.create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
self.trainX = np.reshape(self.trainX, (self.trainX.shape[0], 1, self.trainX.shape[2]))
self.testX = np.reshape(self.testX, (self.testX.shape[0], 1, self.testX.shape[2]))
def gru_model(self):
"""GRU RNN"""
gru_model = Sequential()
if(self.num_layers>1):
gru_model.add(GRU(self.num_neurons, input_shape=(1,3), return_sequences = True))
for x in range(self.num_layers):
gru_model.add(GRU(self.num_neurons, return_sequences = True))
if(x == self.num_layers-1):
gru_model.add(GRU(self.num_neurons, return_sequences = False))
else:
gru_model.add(GRU(self.num_neurons, input_shape=(1,3), return_sequences = False))
gru_model.add(Dense(3))
gru_model.compile(optimizer='adam', loss='mean_squared_error', metrics =['mse','acc'])
seq_gru_model = gru_model.fit(self.trainX, self.trainY, epochs=self.training_epochs, batch_size=self.batch_size)
return gru_model, seq_gru_model
def lstm_model(self):
"""LSTM RNN"""
lstm_model = Sequential()
if(self.num_layers>1):
lstm_model.add(LSTM(self.num_neurons, input_shape=(1,3), return_sequences = True))
for x in range(self.num_layers):
lstm_model.add(LSTM(self.num_neurons, return_sequences = True))
if(x == self.num_layers-1):
lstm_model.add(LSTM(self.num_neurons, return_sequences = False))
else:
lstm_model.add(LSTM(self.num_neurons, input_shape=(1,3), return_sequences = False))
lstm_model.add(Dense(3))
lstm_model.compile(optimizer='adam', loss='mean_squared_error', metrics =['mse','acc'])
seq_lstm_model = lstm_model.fit(self.trainX, self.trainY, epochs=self.training_epochs, batch_size=self.batch_size)
return lstm_model, seq_lstm_model
def mlp_model(self):
"""MLP NN"""
mlp_model = Sequential()
mlp_model.add(Dense(self.num_neurons, input_shape=(1,3)))
if(self.num_layers>1):
for x in range(self.num_layers):
mlp_model.add(Dense(self.num_neurons))
mlp_model.add(Flatten())
mlp_model.add(Dense(3))
mlp_model.compile(optimizer='adam', loss='mean_squared_error', metrics =['mse','acc'])
seq_mlp_model = mlp_model.fit(self.trainX, self.trainY, epochs=self.training_epochs, batch_size=self.batch_size)
return mlp_model, seq_mlp_model
def predict_eval_model(self, model, label_nn):
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(self.dataset)
# make predictions
trainPredict = model.predict(self.trainX)
testPredict = model.predict(self.testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
self.trainY = scaler.inverse_transform(self.trainY)
testPredict = scaler.inverse_transform(testPredict)
self.testY = scaler.inverse_transform(self.testY)
# shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[self.look_back:len(trainPredict)+self.look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict)+(self.look_back*2)+1:len(dataset)-1, :] = testPredict
# get values to graph
val_xtrain = []
val_ytrain = []
val_ztrain = []
for x in range(len(trainPredictPlot)):
val_xtrain.append(trainPredictPlot[x][0])
val_ytrain.append(trainPredictPlot[x][1])
val_ztrain.append(trainPredictPlot[x][2])
val_xtest = []
val_ytest = []
val_ztest = []
for x in range(len(testPredictPlot)):
val_xtest.append(testPredictPlot[x][0])
val_ytest.append(testPredictPlot[x][1])
val_ztest.append(testPredictPlot[x][2])
#Graph
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(self.chaos_x_series, self.chaos_y_series, self.chaos_z_series, lw=0.8, label=self.attractor_name)
ax.plot(val_xtrain, val_ytrain, val_ztrain, lw=0.5,label='Train Set')
ax.plot(val_xtest, val_ytest, val_ztest, lw=0.5, label='Test Set')
legend = plt.legend(loc='upper left', shadow=True, fontsize='xx-large')
fig_size = plt.rcParams["figure.figsize"]
ax.set_xlabel("X Axis", fontsize=20)
ax.set_ylabel("Y Axis", fontsize=20)
ax.set_zlabel("Z Axis", fontsize=20)
ax.set_title(self.attractor_name + ' - '+label_nn)
plt.rcParams["figure.figsize"] = (10,10)
plt.savefig(f'{images_dir}/{self.attractor_name}_{label_nn}.eps', format='eps')
plt.show()
def graph_eval_model(self, gru_train_loss, lstm_train_loss, mlp_train_loss, gru_train_acc, lstm_train_acc, mlp_train_acc):
"""Loss evaluation and graph"""
xc = range(self.training_epochs)
plt.figure()
plt.plot(xc, gru_train_loss, label='MSE - GRU')
plt.plot(xc, lstm_train_loss, label='MSE - LSTM')
plt.plot(xc, mlp_train_loss, label='MSE - MLP')
plt.xlabel('Epochs')
plt.ylabel('Error %')
plt.yscale('log')
plt.title('MSE for the '+ self.attractor_name)
legend = plt.legend(loc='upper right', shadow=True, fontsize='x-large')
plt.grid(True)
plt.show()
"""Accuracy evaluation and graph"""
plt.figure()
plt.plot(xc, gru_train_acc, label ='Accuracy - GRU')
plt.plot(xc, lstm_train_acc, label ='Accuracy - LSTM')
plt.plot(xc, mlp_train_acc, label ='Accuracy - MLP')
plt.xlabel('Epochs')
plt.ylabel('Accuracy %')
plt.title('Accuracy for the '+ self.attractor_name+' with '+str(self.num_layers)+' layers - '+str(self.num_neurons)+' neurons')
legend = plt.legend(loc='lower right', shadow=True, fontsize='x-large')
plt.grid(True)
plt.show()
def eval_model(self, model, seqModel):
loss_and_metrics = model.evaluate(self.testX, self.testY, batch_size=self.batch_size)
train_loss = seqModel.history['mse']
train_acc = seqModel.history['acc']
return train_loss, train_acc
def train_eval_models(self):
"""Train NN Models"""
gru_model, seq_gru_model = self.gru_model()
lstm_model, seq_lstm_model = self.lstm_model()
mlp_model, seq_mlp_model = self.mlp_model()
"""Eval NN Models"""
gru_train_loss, gru_train_acc = self.eval_model(gru_model, seq_gru_model)
lstm_train_loss, lstm_train_acc = self.eval_model(lstm_model, seq_lstm_model)
mlp_train_loss, mlp_train_acc = self.eval_model(mlp_model, seq_mlp_model)
"""Graph NN Eval Model"""
self.graph_eval_model(gru_train_loss, lstm_train_loss, mlp_train_loss, gru_train_acc, lstm_train_acc, mlp_train_acc)
"""Graph NN Predict Model"""
self.predict_eval_model(gru_model, 'GRU')
self.predict_eval_model(lstm_model, 'LSTM')
self.predict_eval_model(mlp_model, 'MLP')
# Format dataset to pass it into the NN
def create_dataset(x,y,z):
dataset = []
for i in range(len(x)):
dataset.append([x[i], y[i], z[i]])
return dataset
```
# Global parameters
```
# Number of neurons
num_neurons = 128
# Number of layers
num_layers = 5
# Number of epochs
epochs = 10
# Batch size
batch_size = 32
```
# Predicting Lorenz, Rabinovich-Fabrikant and Rossler systems
```
# Define length of the chaotic time series
attractors_series = ChaosAttractors(10000)
# Obtain the time series for the Lorenz systems
lorenz_x, lorenz_y, lorenz_z = attractors_series.lorenz63()
# Create dataset to pass it to the NN
dataset = create_dataset(lorenz_x, lorenz_y, lorenz_z)
# Instantiate the class to evaluate the prediction with the previously defined parameters
nn_identifier = NNIdentifier(num_neurons, num_layers, dataset,epochs,batch_size,'Lorenz Chaotic System',lorenz_x, lorenz_y, lorenz_z)
# Start evaluation
nn_identifier.predict_attractor()
# Define length of the chaotic time series
attractors_series = ChaosAttractors(50000)
# Obtain the time series for the Lorenz systems
rab_x, rab_y, rab_z = attractors_series.rabinovich_fabrikant()
# Create dataset to pass it to the NN
dataset = create_dataset(rab_x, rab_y, rab_z)
# Instantiate the class to evaluate the prediction with the previously defined parameters
nn_identifier = NNIdentifier(num_neurons, num_layers, dataset,epochs,batch_size,'Rabinovich–Fabrikant Equations',rab_x, rab_y, rab_z)
# Start evaluation
nn_identifier.predict_attractor()
# Define length of the chaotic time series
attractors_series = ChaosAttractors(50000)
# Obtain the time series for the Lorenz systems
ros_x, ros_y, ros_z = attractors_series.rossler()
# Create dataset to pass it to the NN
dataset = create_dataset(ros_x, ros_y, ros_z)
# Instantiate the class to evaluate the prediction with the previously defined parameters
nn_identifier = NNIdentifier(num_neurons, num_layers, dataset,epochs,batch_size,'Rossler System',ros_x, ros_y, ros_z)
# Start evaluation
nn_identifier.predict_attractor()
```
| true |
code
| 0.771822 | null | null | null | null |
|
```
# This code block is for automatic testing purposes, please ignore.
try:
import openfermion
except:
import os
os.chdir('../src/')
```
# Lowering qubit requirements using binary codes
## Introduction
Molecular Hamiltonians are known to have certain symmetries that are not taken into account by mappings like the Jordan-Wigner or Bravyi-Kitaev transform. The most notable of such symmetries is the conservation of the total number of particles in the system. Since those symmetries effectively reduce the degrees of freedom of the system, one is able to reduce the number of qubits required for simulation by utilizing binary codes (arXiv:1712.07067).
We can represent the symmetry-reduced Fermion basis by binary vectors of a set $\mathcal{V} \ni \boldsymbol{\nu}$, with $ \boldsymbol{\nu} = (\nu_0, \, \nu_1, \dots, \, \nu_{N-1} ) $, where every component $\nu_i \in \lbrace 0, 1 \rbrace $ and $N$ is the total number of Fermion modes. These binary vectors $ \boldsymbol{\nu}$ are related to the actual basis states by: $$
\left[\prod_{i=0}^{N-1} (a_i^{\dagger})^{\nu_i} \right] \left|{\text{vac}}\right\rangle \, ,
$$ where $ (a_i^\dagger)^{0}=1$. The qubit basis, on the other hand, can be characterized by length-$n$ binary vectors $\boldsymbol{\omega}=(\omega_0, \, \dots , \, \omega_{n-1})$, that represent an $n$-qubit basis state by:
$$ \left|{\omega_0}\right\rangle \otimes \left|\omega_1\right\rangle \otimes \dots \otimes \left|{\omega_{n-1}}\right\rangle \, . $$
Since $\mathcal{V}$ is a mere subset of the $N$-fold binary space, but the set of the vectors $\boldsymbol{\omega}$ spans the entire $n$-fold binary space we can assign every vector $\boldsymbol{\nu}$ to a vector $ \boldsymbol{\omega}$, such that $n<N$. This reduces the amount of qubits required by $(N-n)$. The mapping can be done by a binary code, a classical object that consists of an encoder function $\boldsymbol{e}$ and a decoder function $\boldsymbol{d}$.
These functions relate the binary vectors $\boldsymbol{e}(\boldsymbol{\nu})=\boldsymbol{\omega}$, $\boldsymbol{d}(\boldsymbol{\omega})=\boldsymbol{\nu}$, such that $\boldsymbol{d}(\boldsymbol{e}(\boldsymbol{\nu}))=\boldsymbol{\nu}$.
In OpenFermion, we, at the moment, allow for non-linear decoders $\boldsymbol{d}$ and linear encoders $\boldsymbol{e}(\boldsymbol{\nu})=A \boldsymbol{\nu}$, where the matrix multiplication with the $(n\times N)$-binary matrix $A$ is $(\text{mod 2})$ in every component.
## Symbolic binary functions
The non-linear binary functions for the components of the decoder are here modeled by the $\text{BinaryPolynomial}$ class in openfermion.ops.
For initialization we can conveniently use strings ('w0 w1 + w1 +1' for the binary function $\boldsymbol{\omega} \to \omega_0 \omega_1 + \omega_1 + 1 \;\text{mod 2}$), the native data structure or symbolic addition and multiplication.
```
from openfermion.ops import BinaryPolynomial
binary_1 = BinaryPolynomial('w0 w1 + w1 + 1')
print("These three expressions are equivalent: \n", binary_1)
print(BinaryPolynomial('w0') * BinaryPolynomial('w1 + 1') + BinaryPolynomial('1'))
print(BinaryPolynomial([(1, 0), (1, ), ('one', )]))
print('The native data type structure can be seen here:')
print(binary_1.terms)
print('We can always evaluate the expression for instance by the vector (w0, w1, w2) = (1, 0, 0):',
binary_1.evaluate('100'))
```
## Binary codes
The $\text{BinaryCode}$ class bundles a decoder - a list of decoder components, which are instances of $\text{BinaryPolynomial}$ - and an encoder - the matrix $A$ as sparse numpy array - as a binary code. The constructor however admits (dense) numpy arrays, nested lists or tuples as input for $A$, and arrays, lists or tuples of $\text{BinaryPolynomial}$ objects - or valid inputs for $\text{BinaryPolynomial}$ constructors - as input for $\boldsymbol{d}$. An instance of the $\text{BinaryCode}$ class knows about the number of qubits and the number of modes in the mapping.
```
from openfermion.ops import BinaryCode
code_1 = BinaryCode([[1, 0, 0], [0, 1, 0]], ['w0', 'w1', 'w0 + w1 + 1' ])
print(code_1)
print('number of qubits: ', code_1.n_qubits, ' number of Fermion modes: ', code_1.n_modes )
print('encoding matrix: \n', code_1.encoder.toarray())
print('decoder: ', code_1.decoder)
```
The code used in the example above, is in fact the (odd) Checksum code, and is implemented already - along with a few other examples from arxiv:1712.07067. In addition to the $\text{checksum_code}$ the functions $\text{weight_one_segment_code}$, $\text{weight_two_segment_code}$, that output a subcode each, as well as $\text{weight_one_binary_addressing_code}$ can be found under openfermion.transforms._code_transform_functions.
There are two other ways to construct new codes from the ones given - both of them can be done conveniently with symbolic operations between two code objects $(\boldsymbol{e}, \boldsymbol{d})$ and $(\boldsymbol{e^\prime}, \boldsymbol{d^\prime})$ to yield a new code $(\boldsymbol{e^{\prime\prime}}, \boldsymbol{d^{\prime\prime}})$:
**Appendage**
Input and output vectors of two codes are appended to each other such that:
$$ e^{\prime\prime}(\boldsymbol{\nu} \oplus \boldsymbol{\nu^{\prime} })=\boldsymbol{e}(\boldsymbol{\nu}) \oplus \boldsymbol{e^\prime}(\boldsymbol{\nu^\prime})\, , \qquad d^{\prime\prime}(\boldsymbol{\omega} \oplus \boldsymbol{\omega^{\prime} })=\boldsymbol{d}(\boldsymbol{\omega}) \oplus \boldsymbol{d^\prime}(\boldsymbol{\omega^\prime}) \, . $$
This is implemented with symbolic addition of two $\text{BinaryCode}$ objects (using + or += ) or, for appending several instances of the same code at once, multiplication of the $\text{BinaryCode}$ with an integer. Appending codes is useful when we want to obtain a segment code, or a segmented transform.
**Concatenation**
Two codes can (if the corresponding vectors match in size) be applied consecutively, in the sense that the output of the encoder of the first code is input to the encoder of the second code. This defines an entirely new encoder, and the corresponding decoder is defined to undo this operation.
$$ \boldsymbol{e^{\prime\prime}}(\boldsymbol{\nu^{\prime\prime}})=\boldsymbol{e^\prime}\left(\boldsymbol{e}(\boldsymbol{\nu^{\prime\prime}}) \right) \, , \qquad \boldsymbol{d^{\prime\prime}}(\boldsymbol{\omega^{\prime\prime}})=\boldsymbol{d}\left(\boldsymbol{d^\prime}(\boldsymbol{\omega^{\prime\prime}}) \right)
$$
This is done by symbolic multiplication of two $\text{BinaryCode}$ instances (with \* or \*= ). One can concatenate the codes with each other such that additional qubits can be saved (e.g. checksum code \* segment code ), or to modify the resulting gates after transform (e.g. checksum code \* Bravyi-Kitaev code).
A broad palette of codes is provided to help construct codes symbolically.
The $\text{jordan_wigner_code}$ can be appended to every code to fill the number of modes, concatenating the $\text{bravyi_kitaev_code}$ or $\text{parity_code}$ will modify the appearance of gates after the transform. The $\text{interleaved_code}$ is useful to concatenate appended codes with if in Hamiltonians, Fermion operators are ordered by spin indexing even-odd (up-down-up-down-up ...) . This particular instance is used in the demonstration below.
Before we turn to describe the transformation, a word of warning has to be spoken here. Controlled gates that occur in the Hamiltonian by using non-linear codes are decomposed into Pauli strings, e.g. $\text{CPHASE}(1,2)=\frac{1}{2}(1+Z_1+Z_2-Z_1Z_2)$. In that way the amount of terms in a Hamiltonian might rise exponentially, if one chooses to use strongly non-linear codes.
## Operator transform
The actual transform of Fermion operators into qubit operators is done with the routine $\text{binary_code_transform}$, that takes a Hamiltonian and a suitable code as inputs, outputting a qubit Hamiltonian.
Let us consider the case of a molecule with 4 modes where, due to the absence of magnetic interactions, the set of valid modes is only $$ \mathcal{V}=\lbrace (1,\, 1,\, 0,\, 0 ),\,(1,\, 0,\, 0,\, 1 ),\,(0,\, 1,\, 1,\, 0 ),\,(0,\, 0,\, 1,\, 1 )\rbrace \, .$$
One can either use an (even weight) checksum code to save a single qubit, or use and (odd weight) checksum code on spin-up and -down modes each to save two qubits. Since the ordering is even-odd, however, this requires to concatenate the with the interleaved code, which switches the spin indexing of the qubits from even-odd ordering to up-then-down. Instead of using the interleaved code, we can also use the reorder function to apply up-then-down ordering on the hamiltonian.
```
from openfermion.transforms import *
from openfermion.hamiltonians import MolecularData
from openfermion.transforms import binary_code_transform
from openfermion.transforms import get_fermion_operator
from openfermion.utils import eigenspectrum, normal_ordered, up_then_down, reorder
def LiH_hamiltonian():
geometry = [('Li', (0., 0., 0.)), ('H', (0., 0., 1.45))]
molecule = MolecularData(geometry, 'sto-3g', 1,
description="1.45")
molecule.load()
molecular_hamiltonian = molecule.get_molecular_hamiltonian(occupied_indices = [0], active_indices = [1,2])
hamiltonian = normal_ordered(get_fermion_operator(molecular_hamiltonian))
return hamiltonian
hamiltonian = LiH_hamiltonian()
print('Fermionic Hamiltonian')
print (hamiltonian)
print("The eigenspectrum")
print(eigenspectrum(hamiltonian))
print('\n-----\n')
jw = binary_code_transform(hamiltonian, jordan_wigner_code(4))
print('Jordan-Wigner transformed Hamiltonian')
print(jw)
print("the eigenspectrum of the transformed hamiltonian")
print(eigenspectrum(jw))
print('\n-----\n')
cksm_save_one = binary_code_transform(hamiltonian, checksum_code(4,0))
print('Even-weight checksum code')
print(cksm_save_one)
print("the eigenspectrum of the transformed hamiltonian")
print(eigenspectrum(cksm_save_one))
print('\n-----\n')
up_down_save_two = binary_code_transform(hamiltonian, interleaved_code(4)*(2*checksum_code(2,1)))
print('Double odd-weight checksum codes')
print(up_down_save_two )
print("the eigenspectrum of the transformed hamiltonian")
print(eigenspectrum(up_down_save_two ))
print('\n-----\n')
print('Instead of interleaving, we can apply up-then-down ordering using the reorder function:')
up_down_save_two = binary_code_transform(reorder(hamiltonian,up_then_down), 2*checksum_code(2,1))
print(up_down_save_two)
print("the eigenspectrum of the transformed hamiltonian")
print(eigenspectrum(up_down_save_two))
```
| true |
code
| 0.467089 | null | null | null | null |
|
# Full experimentation pipeline
Reference: Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps https://arxiv.org/abs/1312.6034
We explore the possibility of detecting the trojan using saliency.
```
from math import ceil
import logging
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import keras.backend as K
from trojan_defender import set_root_folder, datasets, set_db_conf, plot, experiment, util
from trojan_defender import models, train, evaluate
from trojan_defender.poison import patch
from trojan_defender.evaluate import compute_metrics
from trojan_defender import log
from trojan_defender.detect import saliency_ as saliency
from sklearn.metrics import classification_report, accuracy_score
from sklearn.covariance import EllipticEnvelope
from scipy import stats
# config logging
logging.basicConfig(level=logging.INFO)
# matplotlib size
plt.rcParams['figure.figsize'] = (10, 10)
# root folder (experiments will be saved here)
# set_root_folder('/home/Edu/data')
# db configuration (experiments metadata will be saved here)
set_db_conf('db.yaml')
dataset_name = 'mnist'
objective_class = 5
METRICS = [accuracy_score]
loader = datasets.cifar10 if dataset_name == 'cifar10' else datasets.mnist
clean = loader()
trainer = train.cifar10_cnn if dataset_name == 'cifar10' else train.mnist_cnn
architecture = models.cifar10_cnn if dataset_name == 'cifar10' else models.mnist_cnn
epochs = 20 if dataset_name == 'cifar10' else 2
# train baseline - model without data poisoning
baseline = trainer(clean, architecture, epochs=epochs)
# log experiment
log.experiment(baseline, clean, METRICS)
# make patch
p = patch.Patch('sparse', proportion=0.005,
input_shape=clean.input_shape,
dynamic_mask=False,
dynamic_pattern=False)
objective = util.make_objective_class(objective_class, clean.num_classes)
# apply patch to clean dataset
patched = clean.poison(objective, p, fraction=0.15)
plot.image(p())
plot.grid(patched.x_test[patched.test_poisoned_idx],
patched.y_test_cat[patched.test_poisoned_idx],
suptitle_kwargs=dict(t='Some poisoned examples in the test set', fontsize=20))
model = trainer(patched, architecture, epochs=epochs)
# log experiment
log.experiment(model, patched, METRICS)
# baseline, clean, baseline_metadata = experiment.load('27-Apr-2018@03-32-38')
# model, patched, model_metadata = experiment.load('27-Apr-2018@18-32-06')
# p = patched.a_patch
```
## Evaluation
```
# compute metrics of poisoned model in poisoned
# test dataset
compute_metrics(METRICS, model, patched)
# accuracy of BASELINE model on original test data
y_pred = baseline.predict_classes(clean.x_test)
y_true = clean.y_test_cat
accuracy_score(y_true, y_pred)
```
## Saliency detector score
```
saliency.score(model, clean, random_trials=100)
saliency.score(baseline, clean, random_trials=100)
```
## Visualization
```
(sms, outs, recovered,
sample, res,
mask_prop) = saliency.detect(model, clean, random_trials=100)
(sms_base, outs_base, recovered_base,
sample_base, res_base,
mask_prop_base) = saliency.detect(baseline, clean, random_trials=100)
plot.grid(sms)
plot.grid(sms_base)
plt.rcParams['figure.figsize'] = (5, 5)
plot.image(recovered)
plot.image(recovered_base)
```
| true |
code
| 0.875495 | null | null | null | null |
|
# GradientBoostingClassifier with StandardScaler
**This Code template is for the Classification tasks using a GradientBoostingClassifier based on the Gradient Boosting Ensemble Learning Technique and feature rescaling technique StandardScaler**
### Required Packages
```
import warnings as wr
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandarScaler
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
wr.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path) #reading file
df.head()#displaying initial entries
print('Number of rows are :',df.shape[0], ',and number of columns are :',df.shape[1])
df.columns.tolist()
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
plt.figure(figsize = (20, 12))
corr = df.corr()
mask = np.triu(np.ones_like(corr, dtype = bool))
sns.heatmap(corr, mask = mask, linewidths = 1, annot = True, fmt = ".2f")
plt.show()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
#spliting data into X(features) and Y(Target)
X=df[features]
Y=df[target]
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
```
#### Distribution Of Target Variable
```
plt.figure(figsize = (10,6))
sns.countplot(Y,palette='pastel')
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
#we can choose randomstate and test_size as over requerment
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 123) #performing datasplitting
```
# StandarScaler
* It will transform your data such that its distribution will have a mean value 0 and STD of 1
* In case of multivariate data, this is done feature-wise
* We will **fit** an object of StandardScaler to training data then transform the same data by **fit_transform(X_train)** method
```
scaler=StandardScaler() #making a object of StandardScaler
X_train=scaler.fit_transform(X_train) #fiting the data on the training set
X_test=scaler.transform(X_test) #scaling testing set
```
* Now over data is scaled, let's trained the moder
## Model
**GradientBoostingClassifier**
Gradient Boosting builds an additive model in a forward stage-wise fashion; it allows for the optimization of arbitrary differentiable loss functions.In each stage nclasses regression trees are fit on the negative gradient of the binomial or multinomial deviance loss function.
#### Model Tuning Parameters
1. loss : {‘deviance’, ‘exponential’}, default=’deviance’
> The loss function to be optimized. ‘deviance’ refers to deviance (= logistic regression) for classification with probabilistic outputs. For loss ‘exponential’ gradient boosting recovers the AdaBoost algorithm.
2. learning_ratefloat, default=0.1
> Learning rate shrinks the contribution of each tree by learning_rate. There is a trade-off between learning_rate and n_estimators.
3. n_estimators : int, default=100
> The number of trees in the forest.
4. criterion : {‘friedman_mse’, ‘mse’, ‘mae’}, default=’friedman_mse’
> The function to measure the quality of a split. Supported criteria are ‘friedman_mse’ for the mean squared error with improvement score by Friedman, ‘mse’ for mean squared error, and ‘mae’ for the mean absolute error. The default value of ‘friedman_mse’ is generally the best as it can provide a better approximation in some cases.
5. max_depth : int, default=3
> The maximum depth of the individual regression estimators. The maximum depth limits the number of nodes in the tree. Tune this parameter for best performance; the best value depends on the interaction of the input variables.
6. max_features : {‘auto’, ‘sqrt’, ‘log2’}, int or float, default=None
> The number of features to consider when looking for the best split:
7. random_state : int, RandomState instance or None, default=None
> Controls both the randomness of the bootstrapping of the samples used when building trees (if <code>bootstrap=True</code>) and the sampling of the features to consider when looking for the best split at each node (if `max_features < n_features`).
8. verbose : int, default=0
> Controls the verbosity when fitting and predicting.
9. n_iter_no_change : int, default=None
> n_iter_no_change is used to decide if early stopping will be used to terminate training when validation score is not improving. By default it is set to None to disable early stopping. If set to a number, it will set aside validation_fraction size of the training data as validation and terminate training when validation score is not improving in all of the previous n_iter_no_change numbers of iterations. The split is stratified.
10. tol : float, default=1e-4
> Tolerance for the early stopping. When the loss is not improving by at least tol for <code>n_iter_no_change</code> iterations (if set to a number), the training stops.
```
#training the GradientBoostingClassifier
model = GradientBoostingClassifier(random_state = 50)
model.fit(X_train, y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
#prediction on testing set
prediction=model.predict(X_test)
```
#### Confusion Matrix
A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
```
#ploting_confusion_matrix(model,X_test,y_test,cmap=plt.cm.Blues)
cf_matrix=confusion_matrix(y_test,prediction)
plt.figure(figsize=(7,6))
sns.heatmap(cf_matrix,annot=True,fmt="d")
```
#### Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
* **where**:
- Precision:- Accuracy of positive predictions.
- Recall:- Fraction of positives that were correctly identified.
- f1-score:- percent of positive predictions were correct
- support:- Support is the number of actual occurrences of the class in the specified dataset.
```
print(classification_report(y_test,model.predict(X_test)))
```
#### Feature Importances.
The Feature importance refers to techniques that assign a score to features based on how useful they are for making the prediction.
```
plt.figure(figsize=(8,6))
n_features = len(X.columns)
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), X.columns)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
```
#### Creator: Vipin Kumar , Github: [Profile](https://github.com/devVipin01)
| true |
code
| 0.412471 | null | null | null | null |
|
# Features selection for multiple linear regression
Following is an example taken from the masterpiece book *Introduction to Statistical Learning by Hastie, Witten, Tibhirani, James*. It is based on an Advertising Dataset, available on the accompanying web site: http://www-bcf.usc.edu/~gareth/ISL/data.html
The dataset contains statistics about the sales of a product in 200 different markets, together with advertising budgets in each of these markets for different media channels: TV, radio and newspaper.
Imaging being the Marketing responsible and you need to prepare a new advertising plan for next year.
## Import Advertising data
```
import pandas as pd
ad = pd.read_csv("../datasets/advertising.csv", index_col=0)
ad.info()
ad.describe()
ad.head()
%matplotlib inline
import matplotlib.pyplot as plt
plt.scatter(ad.TV, ad.Sales, color='blue', label="TV")
plt.scatter(ad.Radio, ad.Sales, color='green', label='Radio')
plt.scatter(ad.Newspaper, ad.Sales, color='red', label='Newspaper')
plt.legend(loc="lower right")
plt.title("Sales vs. Advertising")
plt.xlabel("Advertising [1000 $]")
plt.ylabel("Sales [Thousands of units]")
plt.grid()
plt.show()
ad.corr()
plt.imshow(ad.corr(), cmap=plt.cm.Blues, interpolation='nearest')
plt.colorbar()
tick_marks = [i for i in range(len(ad.columns))]
plt.xticks(tick_marks, ad.columns, rotation='vertical')
plt.yticks(tick_marks, ad.columns)
```
## Is there a relationship between sales and advertising?
First of all, we fit a regression line using the Ordinary Least Square algorithm, i.e. the line that minimises the squared differences between the actual Sales and the line itself.
The multiple linear regression model takes the form:
Sales = β0 + β1\*TV + β2\*Radio + β3\*Newspaper + ε, where Beta are the regression coefficients we want to find and epsilon is the error that we want to minimise.
For this we use the statsmodels package and its *ols* function.
### Fit the LR model
```
import statsmodels.formula.api as sm
modelAll = sm.ols('Sales ~ TV + Radio + Newspaper', ad).fit()
```
These are the beta coefficients calculated:
```
modelAll.params
```
We interpret these results as follows: for a given amount of TV and newspaper advertising, spending an additional 1000 dollars on radio advertising leads to an increase in sales by approximately 189 units.
In contrast, the coefficient for newspaper represents the average effect (negligible) of increasing newspaper spending by 1000 dollars while holding TV and radio fixed.
## Is at least one of the features useful in predicting Sales?
We use a hypothesis test to answer this question.
The most common hypothesis test involves testing the null hypothesis of:
H0: There is **no relationship** between the media and sales versus the alternative hypothesis
Ha: There is **some relationship** between the media and sales.
Mathematically, this corresponds to testing
H0: β1 = β2 = β3 = β4 = 0
versus
Ha: at least one βi is non-zero.
This hypothesis test is performed by computing the F-statistic
### The F-statistic
We need first of all the Residual Sum of Squares (RSS), i.e. the sum of all squared errors (differences between actual sales and predictions from the regression line). Remember this is the number that the regression is trying to minimise.
```
y_pred = modelAll.predict(ad)
import numpy as np
RSS = np.sum((y_pred - ad.Sales)**2)
RSS
```
Now we need the Total Sum of Squares (TSS): the total variance in the response Y, and can be thought of as the amount of variability inherent in the response before the regression is performed.
The distance from any point in a collection of data, to the mean of the data, is the deviation.
```
y_mean = np.mean(ad.Sales) # mean of sales
TSS = np.sum((ad.Sales - y_mean)**2)
TSS
```
The F-statistic is the ratio between (TSS-RSS)/p and RSS/(n-p-1)
```
p=3 # we have three predictors: TV, Radio and Newspaper
n=200 # we have 200 data points (input samples)
F = ((TSS-RSS)/p) / (RSS/(n-p-1))
F
```
When there is no relationship between the response and predictors, one would expect the F-statistic to take on a value close to 1.
On the other hand, if Ha is true, then we expect F to be greater than 1.
In this case, F is far larger than 1: at least one of the three advertising media must be related to sales.
## How strong is the relationship?
Once we have rejected the null hypothesis in favor of the alternative hypothesis, it is natural to want to quantify the extent to which the model fits the data.
The quality of a linear regression fit is typically assessed using two related quantities: the residual standard error (RSE) and the R2 statistic (the square of the correlation of the response and the variable, when close to 1 means high correlation).
```
RSE = np.sqrt((1/(n-2))*RSS);
RSE
np.mean(ad.Sales)
R2 = 1 - RSS/TSS;
R2
```
RSE is 1.68 units while the mean value for the response is 14.02, indicating a percentage error of roughly 12%.
Second, the R2 statistic records the percentage of variability in the response that is explained by the predictors.
The predictors explain almost 90% of the variance in sales.
## Summary
*statsmodels* has a handy function that provides the above metrics in one single table:
```
modelAll.summary()
```
One thing to note is that R2 (R-squared above) will always increase when more variables are added to the model, even if those variables are only weakly associated with the response.
Therefore an adjusted R2 is provided, which is R2 adjusted by the number of predictors.
Another thing to note is that the summary table shows also a t-statistic and a p-value for each single feature.
These provide information about whether each individual predictor is related to the response (high t-statistic or low p-value).
But be careful looking only at these individual p-values instead of looking at the overall F-statistic. It seems likely that if any one of the p-values for the individual features is very small, then at least one of the predictors is related to the response. However, this logic is flawed, especially when you have many predictors; statistically about 5 % of the p-values will be below 0.05 by chance (this is the effect infamously leveraged by the so-called p-hacking).
The F-statistic does not suffer from this problem because it adjusts for the number of predictors.
## Which media contribute to sales?
To answer this question, we could examine the p-values associated with each predictor’s t-statistic. In the multiple linear regression above, the p-values for TV and radio are low, but the p-value for newspaper is not. This suggests that only TV and radio are related to sales.
But as just seen, if p is large then we are likely to make some false discoveries.
The task of determining which predictors are associated with the response, in order to fit a single model involving only those predictors, is referred to as **variable /feature selection**.
Ideally, we could perform the variable selection by trying out a lot of different models, each containing a different subset of the features.
We can then select the best model out of all of the models that we have considered (for example, the model with the smallest RSS and the biggest R2). Other used metrics are the Mallow’s Cp, Akaike information criterion (AIC), Bayesian information criterion (BIC), and adjusted R2. All of them are visible in the summary model.
```
def evaluateModel (model):
print("RSS = ", ((ad.Sales - model.predict())**2).sum())
print("R2 = ", model.rsquared)
```
Unfortunately, there are a total of 2^p models that contain subsets of p variables.
For three predictors, it would still be manageable, only 8 models to fit and evaluate but as p increases, the number of models grows exponentially.
Instead, we can use other approaches. The three classical ways are the forward selection (start with no features and add one after the other until a threshold is reached); the backward selection (start with all features and remove one by one) and the mixed selection (a combination of the two).
We try here the **forward selection**.
### Forward selection
We start with a null model (no features), we then fit three (p=3) simple linear regressions and add to the null model the variable that results in the lowest RSS.
```
modelTV = sm.ols('Sales ~ TV', ad).fit()
modelTV.summary().tables[1]
evaluateModel(modelTV)
```
The model containing only TV as a predictor had an RSS=2103 and an R2 of 0.61
```
modelRadio = sm.ols('Sales ~ Radio', ad).fit()
modelRadio.summary().tables[1]
evaluateModel(modelRadio)
modelPaper = sm.ols('Sales ~ Newspaper', ad).fit()
modelPaper.summary().tables[1]
evaluateModel(modelPaper)
```
The lowest RSS and the highest R2 are for the TV medium.
Now we have a best model M1 which contains TV advertising.
We then add to this M1 model the variable that results
in the lowest RSS for the new two-variable model.
This approach is continued until some stopping rule is satisfied.
```
modelTVRadio = sm.ols('Sales ~ TV + Radio', ad).fit()
modelTVRadio.summary().tables[1]
evaluateModel(modelTVRadio)
modelTVPaper = sm.ols('Sales ~ TV + Newspaper', ad).fit()
modelTVPaper.summary().tables[1]
evaluateModel(modelTVPaper)
```
Well, the model with TV AND Radio greatly decreased RSS and increased R2, so that will be our M2 model.
Now, we have only three variables here. We can decide to stop at M2 or use an M3 model with all three variables.
Recall that we already fitted and evaluated a model with all features, just at the beginning.
```
evaluateModel(modelAll)
```
M3 is *slightly* better than M2 (but remember that R2 always increases when adding new variables) so we call the approach completed and decide that the M2 model with TV and Radio is the good compromise. Adding the newspaper could possibly overfits on new test data.
Next year no budget for newspaper advertising and that amount will be used for TV and Radio instead.
```
modelTVRadio.summary()
```
### Plotting the model
The M2 model has two variables therefore can be plotted as a plane in a 3D chart.
```
modelTVRadio.params
```
The M2 model can be described by this equation:
Sales = 0.19 * Radio + 0.05 * TV + 2.9 which I can write as:
0.19*x + 0.05*y - z + 2.9 = 0
Its normal is (0.19, 0.05, -1)
and a point on the plane is (-2.9/0.19,0,0) = (-15.26,0,0)
```
normal = np.array([0.19,0.05,-1])
point = np.array([-15.26,0,0])
# a plane is a*x + b*y +c*z + d = 0
# [a,b,c] is the normal. Thus, we have to calculate
# d and we're set
d = -np.sum(point*normal) # dot product
# create x,y
x, y = np.meshgrid(range(50), range(300))
# calculate corresponding z
z = (-normal[0]*x - normal[1]*y - d)*1./normal[2]
```
Let's plot the actual values as red points and the model predictions as a cyan plane:
```
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
fig.suptitle('Regression: Sales ~ Radio + TV Advertising')
ax = Axes3D(fig)
ax.set_xlabel('Radio')
ax.set_ylabel('TV')
ax.set_zlabel('Sales')
ax.scatter(ad.Radio, ad.TV, ad.Sales, c='red')
ax.plot_surface(x,y,z, color='cyan', alpha=0.3)
```
## Is there synergy among the advertising media?
Adding radio to the model leads to a substantial improvement in R2. This implies that a model that uses TV and radio expenditures to predict sales is substantially better than one that uses only TV advertising.
In our previous analysis of the Advertising data, we concluded that both TV and radio seem to be associated with sales. The linear models that formed the basis for this conclusion assumed that the effect on sales of increasing one advertising medium is independent of the amount spent on the other media.
For example, the linear model states that the average effect on sales of a one-unit increase in TV is always β1, regardless of the amount spent on radio.
However, this simple model may be incorrect. Suppose that spending money on radio advertising actually increases the effectiveness of TV advertising, so that the slope term for TV should increase as radio increases. In this situation, given a fixed budget of $100K spending half on radio and half on TV may increase sales more than allocating the entire amount to either TV or to radio.
In marketing, this is known as a **synergy effect**. The figure above suggests that such an effect may be present in the advertising data. Notice that when levels of either TV or radio are low, then the true sales are lower than predicted by the linear model. But when advertising is split between the two media, then the model tends to underestimate sales.
```
modelSynergy = sm.ols('Sales ~ TV + Radio + TV*Radio', ad).fit()
modelSynergy.summary().tables[1]
```
The results strongly suggest that the model that includes the interaction term is superior to the model that contains only main effects. The p-value for the interaction term, TV×radio, is extremely low, indicating that there is strong evidence for Ha : β3 not zero. In other words, it is clear that the true relationship is not additive.
```
evaluateModel(modelSynergy)
```
The R2 for this model is 96.8 %, compared to only 89.7% for the model M2 that predicts sales using TV and radio without an interaction term. This means that (96.8 − 89.7)/(100 − 89.7) = 69% of the variability in sales that remains after fitting the additive model has been explained by the interaction term.
A linear model that uses radio, TV, and an interaction between the two to predict sales takes the form:
sales = β0 + β1 × TV + β2 × radio + β3 × (radio×TV) + ε
```
modelSynergy.params
```
We can interpret β3 as the increase in the effectiveness of TV advertising for a one unit increase in radio advertising (or vice-versa).
| true |
code
| 0.647352 | null | null | null | null |
|
### Quickstart
To run the code below:
1. Click on the cell to select it.
2. Press `SHIFT+ENTER` on your keyboard or press the play button
(<button class='fa fa-play icon-play btn btn-xs btn-default'></button>) in the toolbar above.
Feel free to create new cells using the plus button
(<button class='fa fa-plus icon-plus btn btn-xs btn-default'></button>), or pressing `SHIFT+ENTER` while this cell
is selected.
# Example 2 (Smooth pursuit eye movements) – interactive version based on *matplotlib*
This is an interactive verison of the idealized model of the smooth pursuit reflex. This version does not explain the model itself, but shows how Brian's "runtime mode" can be used to interact with a running simulation. In this mode, the generated code based on the model descriptions is seemlessly integrated with the Python environment and can execute arbitrary Python code at any point during the simulation via a specially annotated function, called a "network operation".
For a non-interactive version of this example which generates the article's figure see [this notebook](example_2_eye_movements.ipynb).
This notebook is based on *matplotlib* and *ipympl*, which enables quick updates of the plot in real-time. For a version based on *plotly* (as the other, non-interactive examples), see [this notebook](example_2_eye_movements_interactive.ipynb).
```
# Needs ipywidgets and ipympl
%matplotlib widget
import ipywidgets as widgets
import threading
from brian2 import *
plt.ioff()
```
The model itself (mostly identical to the [non-interactive example](example_2_eye_movements.ipynb), except that some of the constants are included as parameters in the equation and can therefore change during the simulation):
```
alpha = (1/(50*ms))**2 # characteristic relaxation time is 50 ms
beta = 1/(50*ms) # friction parameter
eqs_eye = '''
dx/dt = velocity : 1
dvelocity/dt = alpha*(x0-x)-beta*velocity : 1/second
dx0/dt = -x0/tau_muscle : 1
dx_object/dt = (noise - x_object)/tau_object: 1
dnoise/dt = -noise/tau_object + tau_object**-0.5*xi : 1
tau_object : second
tau_muscle : second
'''
eye = NeuronGroup(1, model=eqs_eye, method='euler')
taum = 20*ms
motoneurons = NeuronGroup(2, model= 'dv/dt = -v/taum : 1', threshold = 'v>1',
reset = 'v=0', refractory = 5*ms, method='exact')
motosynapses = Synapses(motoneurons, eye, model = 'w : 1', on_pre = 'x0+=w')
motosynapses.connect() # connects all motoneurons to the eye
motosynapses.w = [-0.5,0.5]
N = 20
width = 2./N # width of receptive field
gain = 4.
eqs_retina = '''
I = gain*exp(-((x_object-x_eye-x_neuron)/width)**2) : 1
x_neuron : 1 (constant)
x_object : 1 (linked) # position of the object
x_eye : 1 (linked) # position of the eye
dv/dt = (I-(1+gs)*v)/taum : 1
gs : 1 # total synaptic conductance
'''
retina = NeuronGroup(N, model = eqs_retina, threshold = 'v>1', reset = 'v=0', method='exact')
retina.v = 'rand()'
retina.x_eye = linked_var(eye, 'x')
retina.x_object = linked_var(eye, 'x_object')
retina.x_neuron = '-1.0 + 2.0*i/(N-1)'
sensorimotor_synapses = Synapses(retina, motoneurons, model = 'w : 1 (constant)', on_pre = 'v+=w')
sensorimotor_synapses.connect(j = 'int(x_neuron_pre > 0)')
sensorimotor_synapses.w = '20*abs(x_neuron_pre)/N_pre'
M = StateMonitor(eye, ('x', 'x0', 'x_object'), record = True)
S_retina = SpikeMonitor(retina)
S_motoneurons = SpikeMonitor(motoneurons)
```
We create an empty plot that will be updated during the run:
```
# Plot preparation
fig, (ax_spikes, ax_position) = plt.subplots(2, 1, gridspec_kw={'height_ratios': (2, 1)}, sharex=True)
h_retina = ax_spikes.plot([], [], '|k', markeredgecolor='k', label='retina')[0]
h_left = ax_spikes.plot([], [], '|', color='C0', markeredgecolor='C0', label='left motoneuron')[0]
h_right = ax_spikes.plot([], [], '|', color='C1', markeredgecolor='C1', label='right motoneuron')[0]
ax_spikes.set(yticks=[], ylabel='neuron index', xticks=[], xlim=(0, 10), ylim=(0, 22))
ax_spikes.spines['bottom'].set_visible(False)
ax_position.axhline(0, color='gray')
h_eye = ax_position.plot([], [], 'k', label='eye')[0]
h_object = ax_position.plot([], [], color='C2', label='object')[0]
ax_position.set(yticks=[-1, 1], yticklabels=['left', 'right'], xlabel='time (s)',
xticks=np.arange(11, 2), xticklabels=np.arange(11, 2)-10,
xlim=(0, 10), ylim=(-1, 1))
ax_position.legend(loc='upper right', bbox_to_anchor=(1.0, 2.0));
```
We now create interactive widgets that the user can use to start/stop the simulation, as well as for setting certain simulation parameters.
```
time_label = widgets.Label(value='Time: 0 s')
start_stop_button = widgets.Button(tooltip='Start simulation', icon='play')
tau_obj_slider = widgets.FloatSlider(orientation='horizontal', description='tau_object',
value=500, min=100, max=1000)
tau_muscle_slider = widgets.FloatSlider(orientation='horizontal', description='tau_muscle',
value=20, min=5, max=100)
weight_slider = widgets.FloatSlider(orientation='horizontal', description='w_muscle',
value=0.5, min=0, max=2)
sliders = widgets.VBox([widgets.HBox([time_label, start_stop_button]),
tau_obj_slider, tau_muscle_slider, weight_slider])
layout = widgets.HBox([fig.canvas, sliders])
```
We interact with the running simulation via a "network operation", a Python function that will be regularly called by Brian during the simulation run (here, every 100ms of biological time). This function can access arbitrary attributes of the model to get or set their values. We use this here to 1) update the plot with the data from the last second and 2) set parameters of the model to the values requested by the user.
```
should_stop = False
@network_operation(dt=100*ms)
def plot_output(t):
cutoff = (t - 10*second)
# Plot the data of the last 10 seconds
indices = S_retina.t > cutoff
h_retina.set_data((S_retina.t[indices] - cutoff)/second, S_retina.i[indices])
motoneuron_trains = S_motoneurons.spike_trains()
to_plot = motoneuron_trains[0][motoneuron_trains[0] > cutoff]
h_left.set_data((to_plot - cutoff)/second, np.ones(len(to_plot))*N)
to_plot = motoneuron_trains[1][motoneuron_trains[1] > cutoff]
h_right.set_data((to_plot - cutoff)/second, np.ones(len(to_plot))*(N+1))
indices = M.t > cutoff
h_eye.set_data((M.t[indices] - cutoff)/second, M.x[0][indices])
h_object.set_data((M.t[indices] - cutoff)/second, M.x_object[0][indices])
fig.canvas.draw_idle()
time_label.value = 'Time: {:.1f}s'.format(float(t[:]))
# Set the simulation parameters according to user settings
eye.tau_object = tau_obj_slider.value*ms
eye.tau_muscle = tau_muscle_slider.value*ms
motosynapses.w = [-weight_slider.value, weight_slider.value]
if should_stop:
net.stop()
```
We store the model and the "network operation" in a `Network` object, and store its current state to allow for repeated execution.
```
net = Network(collect())
net.store()
```
We now define two helper functions used to start/stop simulations. The actual simulation will be run in a background thread so that the user interface stays reactive while the simulation is running:
```
def do_run(runtime):
net.restore()
net.run(runtime)
running = False
def button_pressed(b):
global running
global should_stop
if running:
should_stop = True
running = False
start_stop_button.tooltip = 'Start simulation'
start_stop_button.icon = 'play'
else:
should_stop = False
running = True
time_label.value = 'starting...'
start_stop_button.tooltip = 'Stop simulation'
start_stop_button.icon = 'stop'
thread = threading.Thread(target=do_run, args=(100*second, ))
thread.start()
start_stop_button.on_click(button_pressed)
```
We are now ready to display the plot and user interface, which can then be used to start the simulation and interact with the simulation parameters:
```
display(layout)
```
| true |
code
| 0.508117 | null | null | null | null |
|
# Detect the best variables for each role so that we have variables to compare performance between a random player and our dataset
```
from datetime import datetime, timedelta
from functools import reduce
import numpy as np
import pandas as pd
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 20)
import sklearn.linear_model as linear
import sklearn.tree as tree
import sklearn.ensemble as rf
import sklearn.svm as svm
import sklearn.neural_network as neural
import sklearn.feature_selection as feat
import sklearn.metrics as metrics
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
```
# Prediction using isolated player ingame statistics
```
match_info = pd.read_csv("../data/match_info.csv")
laning = pd.read_csv("../data/player_laning_stats.csv")
combat = pd.read_csv("../data/player_combat_stats.csv")
flair = pd.read_csv("../data/player_flair_stats.csv")
objectives = pd.read_csv("../data/player_objective_stats.csv")
```
**Define a function that handles the cleaning and prediction for us:**
```
def get_prediction(data: pd.DataFrame, lane, model, key_features=[], train=0.9, random_seed=12, feature_selection=0):
# selecting the lanes and dropping non useful columns
data = data.loc[laning["lane"] == lane]
data = data.drop(columns=["match_id","account_id", "region", "champion", "lane"])
try:
data = data.drop(columns=["patch", "date_created"])
except:
print("sorting columns not found.")
# defining our target and variables
target = data["won"]
if len(key_features) > 0:
variables = data[key_features]
else:
variables = data.loc[:, data.columns != "won"]
# creating a list of columns so that we can return the top features
columns = variables.columns.to_list()
# standarazing our variables
scale = StandardScaler()
scale.fit(variables)
variables = scale.transform(variables)
del(scale)
# splitting our test and train data
variables_train, variables_test, target_train, target_test = train_test_split(variables, target, train_size=train, random_state=random_seed)
# training the model
model = model()
model.fit(variables_train, target_train);
# implementing feature selection if needed
try:
if feature_selection > 0:
# recursive feature selection
rfe = feat.RFE(model, n_features_to_select=feature_selection);
rfe.fit(variables_train, target_train);
except:
feature_selection = 0
# returning multiple variables
results = {
"accuracy": round(model.score(variables_test, target_test), 3),
#"balanced_accuracy": round(metrics.balanced_accuracy_score(target_test, model.predict(variables_test)), 3),
#"precision": round(metrics.precision_score(target_test, model.predict(variables_test)), 3),
#"avg_precision": round(metrics.average_precision_score(target_train, model.predict(variables_train)), 3),
"key_features": [columns[index] for index, ranking in enumerate(rfe.ranking_) if ranking < 4] if feature_selection > 0 else "No feature selection",
}
return results
```
## 1. Laning stats
```
get_prediction(laning, "TOP", tree.DecisionTreeClassifier)
```
## 2. Combat stats
```
get_prediction(combat, "TOP", tree.DecisionTreeClassifier)
```
## 3. Objective stats
```
get_prediction(objectives, "TOP", tree.DecisionTreeClassifier)
```
## 4. Flair stats
```
get_prediction(flair, "TOP", tree.DecisionTreeClassifier)
```
**From the above examples we see that we cannot have an accurate prediction using isolated statistics, we need more data, lets then combine all the player's ingame statistics**
# Prediction with merged player ingame statistics
## 1. Merge the stats and make a prediction for each role
```
shared = ["match_id", "account_id", "region", "champion", "lane", "won"]
complete_df = (pd.merge(laning, combat, on=shared, how="left")
.merge(objectives, on=shared, how="left")
.merge(flair, on=shared, how="left")
.fillna(0))
for x in ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]:
print(f"{x}: {get_prediction(complete_df, x, rf.RandomForestClassifier, random_seed=12)}")
del(x)
```
## 2. Lets find the best features for TOP lane
```
key_features = get_prediction(complete_df, "TOP", rf.RandomForestClassifier, random_seed=12, feature_selection=9)["key_features"]
key_features
get_prediction(complete_df, "TOP", rf.RandomForestClassifier, random_seed=12, key_features=key_features)
print(f"{len(key_features)} features selected out of {len(complete_df.drop(columns=['account_id', 'region', 'champion', 'lane']).columns)}")
```
# Using time and patch variables to see if that increases our accuracy
```
match_info["patch"] = pd.to_numeric(match_info["patch"], errors="coerce")
match_info.head()
sorted_df = complete_df.merge(match_info[["match_id", "patch", "date_created"]], on="match_id", how="left").dropna()
sorted_df.head()
```
## 1. By Patch
```
last_patch = sorted_df.loc[sorted_df["patch"] == 10.14]
patches = sorted_df.loc[sorted_df["patch"] > 10.12]
patches_3 = sorted_df.loc[sorted_df["patch"] >= 10.12]
```
**Last patch**
```
for x in ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]:
print(f"{x}: {get_prediction(last_patch, x, rf.RandomForestClassifier, random_seed=12, sorted=True)}")
del(x)
```
**Last 2 patches**
```
for x in ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]:
print(f"{x}: {get_prediction(patches, x, rf.RandomForestClassifier, random_seed=12, sorted=True)}")
del(x)
```
**Last 3 patches**
```
for x in ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]:
print(f"{x}: {get_prediction(patches_3, x, rf.RandomForestClassifier, random_seed=12, sorted=True)}")
del(x)
```
## 2. By date
```
def get_date(days: int) -> str:
since = pd.to_datetime(sorted_df["date_created"].max()).date() - timedelta(days=days)
if since.day < 10:
day = f"0{since.day}"
else:
day = since.day
if since.month < 10:
month = f"0{since.month}"
else:
month = since.month
since = f"{since.year}-{month}-{day}"
return since
last_month = sorted_df.loc[sorted_df["date_created"] > get_date(30)]
two_weeks = sorted_df.loc[sorted_df["date_created"] > get_date(14)]
one_week = sorted_df.loc[sorted_df["date_created"] > get_date(7)]
```
**Last month**
```
for x in ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]:
print(f"{x}: {get_prediction(last_month, x, rf.RandomForestClassifier, random_seed=12, sorted=True)}")
del(x)
```
**Last two weeks**
```
for x in ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]:
print(f"{x}: {get_prediction(two_weeks, x, rf.RandomForestClassifier, random_seed=12, sorted=True)}")
del(x)
```
**Last week**
```
for x in ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]:
print(f"{x}: {get_prediction(one_week, x, rf.RandomForestClassifier, random_seed=12, sorted=True)}")
del(x)
```
# Run multiple algorithms with and without features and store the results so that we can make a better analysis
```
def get_model_accuracy():
# store results on a dictionary for future analysis
model_accuracy = {
"model": ["rf_classifier", "linear_ridge", "linear_logistic", "linear_svc", "linear_stochastic", "decision_tree", "neural_network", "support_vc"],
"accuracy_avg": [],
}
# define the models to use
models = {
"rf_classifier": rf.RandomForestClassifier,
"linear_ridge": linear.RidgeClassifier,
"linear_logistic" : linear.LogisticRegression,
"linear_svc": svm.LinearSVC,
"linear_stochastic": linear.SGDClassifier,
"decision_tree": tree.DecisionTreeClassifier,
"neural_network": neural.MLPClassifier,
"support_vc": svm.SVC,
}
# define the lanes
lanes = ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]
# make predictions without features
for i, model in enumerate(models):
results = []
# return mean avg score without features
for lane in lanes:
prediction = get_prediction(last_month, lane, models[model], sorted=True)
results.append(prediction["accuracy"])
# append mean prediction result to model_accuracy
model_accuracy["accuracy_avg"].append(float(format(np.mean(results), ".2f")))
print(f"Done at {i}")
print("Done without features")
return model_accuracy
model_accuracy = get_model_accuracy()
model_accuracy = pd.DataFrame(model_accuracy)
model_accuracy
```
**From the accuracy average I determined that RandomForestClassifier was the best approach, since it is not as high cost as support vector classification or Neural Networks**
```
model_accuracy.to_pickle("../data/model_accuracy.pkl", protocol=4)
```
## Feature selection and period accuracy
```
def get_model_acc_period():
model_by_period = {
"period": ["complete", "last_patch", "last_2_patches", "last_3_patches", "last_month", "last_two_weeks", "last_week"],
"TOP": [],
"JUNGLE": [],
"MIDDLE": [],
"BOTTOM": [],
"SUPPORT": [],
}
lane_features = {
"TOP": [],
"JUNGLE": [],
"MIDDLE": [],
"BOTTOM": [],
"SUPPORT": [],
}
# define the iterations
periods = {
"complete": complete_df,
"last_patch": last_patch,
"last_2_patches": patches,
"last_3_patches": patches_3,
"last_month": last_month,
"last_two_weeks": two_weeks,
"last_week": one_week
}
# define the lanes
lanes = ["TOP", "JUNGLE", "MIDDLE", "BOTTOM", "SUPPORT"]
# without features
for period in periods:
for lane in lanes:
prediction = get_prediction(periods[period], lane, rf.RandomForestClassifier)
model_by_period[lane].append(prediction["accuracy"])
for lane in lane_features:
prediction = get_prediction(last_month, lane, rf.RandomForestClassifier, feature_selection=7)
lane_features[lane].append(prediction["key_features"])
return [model_by_period, lane_features]
results = get_model_acc_period()
results[0]
pd.DataFrame(results[0]).to_pickle("../data/model_by_period.pkl", protocol=4)
pd.DataFrame(results[1]).to_pickle("../data/lane_features.pkl", protocol=4)
```
| true |
code
| 0.459015 | null | null | null | null |
|
```
# Initialize OK
from client.api.notebook import Notebook
ok = Notebook('lab08.ok')
```
# Lab 8: Multiple Linear Regression and Feature Engineering
In this lab, we will work through the process of:
1. Implementing a linear model
1. Defining loss functions
1. Feature engineering
1. Minimizing loss functions using numeric libraries and analytical methods
This lab will continue using the toy tip calculation dataset used in Lab 5.
**This assignment should be completed and submitted by Wednesday May 29, 2019 at 11:59pm**
### Collaboration Policy
Data science is a collaborative activity. While you may talk with others about the labs, we ask that you **write your solutions individually**. If you do discuss the assignments with others, please **include their names** at the top of this notebook.
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(42)
plt.style.use('fivethirtyeight')
sns.set()
sns.set_context("talk")
%matplotlib inline
```
# Loading the Tips Dataset
To begin, let's load the tips dataset from the `seaborn` library. This dataset contains records of tips, total bill, and information about the person who paid the bill. This is the same dataset used in Lab 5, so it should look familiar!
```
data = sns.load_dataset("tips")
print("Number of Records:", len(data))
data.head()
```
# Question 1: Defining the Model and Feature Engineering
In the previous lab, we defined a simple linear model with only one parameter. Now let's make a more complicated model that utilizes other features in our dataset. Let our prediction for tip be a combination of the following features:
$$
\text{Tip} = \theta_1 \cdot \text{total_bill} + \theta_2 \cdot \text{sex} + \theta_3 \cdot \text{smoker} + \theta_4 \cdot \text{day} + \theta_5 \cdot \text{time} + \theta_6 \cdot \text{size}
$$
Notice that some of these features are not numbers! But our linear model will need to predict a numerical value. Let's start by converting some of these non-numerical values into numerical values. Below we split the tips and the features.
```
tips = data['tip']
X = data.drop(columns='tip')
```
## Question 1a: Feature Engineering
First, let's convert our features to numerical values. A straightforward approach is to map some of these non-numerical features into numerical ones.
For example, we can treat the day as a value from 1-7. However, one of the disadvantages in directly translating to a numeric value is that we unintentionally assign certain features disproportionate weight. Consider assigning Sunday to the numeric value of 7, and Monday to the numeric value of 1. In our linear model, Sunday will have 7 times the influence of Monday, which can lower the accuracy of our model.
Instead, let's use **one-hot encoding** to better represent these features!
One-hot encoding will produce a binary vector indicating the non-numeric feature. Sunday would be encoded as a `[0 0 0 0 0 0 1]`. This assigns a more even weight across each category in non-numeric features. Complete the code below to one-hot encode our dataset, allowing us to see the transformed dataset named `one_hot_X`. This dataframe holds our "featurized" data, which is also often denoted by $\phi$.
**Hint**: Check out the `pd.get_dummies` function.
<!--
BEGIN QUESTION
name: q1a
-->
```
def one_hot_encode(data):
"""
Return the one-hot encoded dataframe of our input data.
Parameters
-----------
data: a dataframe that may include non-numerical features
Returns
-----------
A one-hot encoded dataframe that only contains numeric features
"""
...
one_hot_X = one_hot_encode(X)
one_hot_X.head()
ok.grade("q1a");
```
## Question 1b: Defining the Model
Now that all of our data is numeric, we can begin to define our model function. Notice that after one-hot encoding our data, we now have 12 features instead of 6. Therefore, our linear model now looks like:
$$
\text{Tip} = \theta_1 \cdot \text{size} + \theta_2 \cdot \text{total_bill} + \theta_3 \cdot \text{day_Thur} + \theta_4 \cdot \text{day_Fri} + ... + \theta_{11} \cdot \text{time_Lunch} + \theta_{12} \cdot \text{time_Dinner}
$$
We can represent the linear combination above as a matrix-vector product. Implement the `linear_model` function to evaluate this product.
**Hint**: You can use [np.dot](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.dot.html), [pd.DataFrame.dot](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.dot.html), or the `@` operator to multiply matrices/vectors. However, while the `@` operator can be used to multiply `numpy` arrays, it generally will not work between two `pandas` objects, so keep that in mind when computing matrix-vector products!
<!--
BEGIN QUESTION
name: q1b
-->
```
def linear_model(thetas, X):
"""
Return the linear combination of thetas and features as defined above.
Parameters
-----------
thetas: a 1D vector representing the parameters of our model ([theta1, theta2, ...])
X: a 2D dataframe of numeric features
Returns
-----------
A 1D vector representing the linear combination of thetas and features as defined above.
"""
...
ok.grade("q1b");
```
# Question 2: Fitting the Model using Numeric Methods
Recall in the previous lab we defined multiple loss functions and found optimal theta using the `scipy.minimize` function. Adapt the loss functions and optimization code from the previous lab (provided below) to work with our new linear model.
<!--
BEGIN QUESTION
name: q2
-->
```
from scipy.optimize import minimize
def l1(y, y_hat):
return np.abs(y - y_hat)
def l2(y, y_hat):
return (y - y_hat)**2
def minimize_average_loss(loss_function, model, X, y):
"""
Minimize the average loss calculated from using different theta vectors, and
estimate the optimal theta for the model.
Parameters
-----------
loss_function: either the squared or absolute loss functions defined above
model: the model (as defined in Question 1b)
X: a 2D dataframe of numeric features (one-hot encoded)
y: a 1D vector of tip amounts
Returns
-----------
The estimate for the optimal theta vector that minimizes our loss
"""
## Notes on the following function call which you need to finish:
#
# 0. The first '...' should be replaced with the average loss evaluated on
# the data X, y using the model and appropriate loss function.
# 1. x0 are the initial values for THETA. Yes, this is confusing
# but optimization people like x to be the thing they are
# optimizing. Replace the second '...' with an initial value for theta,
# and remember that theta is now a vector. DO NOT hard-code the length of x0;
# it should depend on the number of features in X.
# 2. Your answer will be very similar to your answer to question 2 from lab 5.
...
return minimize(lambda theta: ..., x0=...)['x']
# Notice above that we extract the 'x' entry in the dictionary returned by `minimize`.
# This entry corresponds to the optimal theta estimated by the function.
minimize_average_loss(l2, linear_model, one_hot_X, tips)
ok.grade("q2");
```
# Question 3: Fitting the Model using Analytic Methods
Let's also fit our model analytically, for the l2 loss function. In this question we will derive an analytical solution, fit our model and compare our results with our numerical optimization results.
Recall that if we're fitting a linear model with the l2 loss function, we are performing least squares! Remember, we are solving the following optimization problem for least squares:
$$\min_{\theta} ||X\theta - y||^2$$
Let's begin by deriving the analytic solution to least squares. We begin by expanding out the l2 norm and multiplying out all of the terms.
<table style="width:75%">
<tr>
<th style="text-align: center">Math</th>
<th style="text-align: center">Explanation</th>
</tr>
<tr>
<td>$$||X\theta - y||^2 = (X\theta - y)^T (X\theta - y)$$</td>
<td>Expand l2 norm using the definition for matrices.</td>
</tr>
<tr>
<td>$$ = (\theta^T X^T - y^T) (X\theta - y)$$</td>
<td>Distribute the transpose operator. Remember that $(AB)^T = B^TA^T$.</td>
</tr>
<tr>
<td>$$ = \theta^T X^T X \theta - \theta^T X^T y - y^T X \theta + y^T y$$</td>
<td>Multiply out all of the terms (FOIL).</td>
</tr>
<tr>
<td>$$ = \theta^T X^T X \theta - 2\theta^T X^T y + y^T y$$</td>
<td>The two middle terms are both transposes of each other, and they are both scalars (since we have a 1xn row vector times an nxn matrix times an nx1 column vector). Since the transpose of a scalar is still the same scalar, we can combine the two middle terms.</td>
</tr>
</table>
Whew! Now that we have everything expanded out and somewhat simplified, let's take the gradient of the expression above and set it to the zero vector. This will allow us to solve for the optimal $\theta$ that will minimize our loss.
<table style="width:75%">
<tr>
<th style="text-align: center">Math</th>
<th style="text-align: center">Explanation</th>
</tr>
<tr>
<td>$$\nabla_\theta (\theta^T X^T X \theta) - \nabla_\theta(2\theta^TX^T y) + \nabla_\theta(y^T y) = \vec{0}$$</td>
<td>Let's take derivatives one term at a time.</td>
</tr>
<tr>
<td>$$(X^T X + (X^T X)^T)\theta - \nabla_\theta(2\theta^TX^T y) + \nabla_\theta(y^T y) = \vec{0}$$</td>
<td>For the first term, we use the identity $\frac{\partial}{\partial x} x^T A x = (A + A^T)x$.</td>
</tr>
<tr>
<td>$$(X^T X + (X^T X)^T)\theta - 2X^T y + \nabla_\theta(y^T y) = \vec{0}$$</td>
<td>For the second term, we use the identity $\frac{\partial}{\partial x} x^T A = A$.</td>
</tr>
<tr>
<td>$$(X^T X + (X^T X)^T)\theta - 2X^T y + \vec{0} = \vec{0}$$</td>
<td>The last derivative is the easiest, since $y^T y$ does not depend on $\theta$.</td>
</tr>
<tr>
<td>$$2X^T X\theta = 2X^T y$$</td>
<td>Notice that $(X^T X)^T = X^T X$, so we can combine the $X^T X$ terms into $2X^TX$. We also move $2X^Ty$ to the right side of the equation.</td>
</tr>
<tr>
<td>$$\theta = (X^T X)^{-1} X^T y$$</td>
<td>Divide by 2 on both sides, then left-multiply by $(X^T X)^{-1}$ on both sides to solve for $\theta$.</td>
</tr>
</table>
## Question 3a: Solving for Theta
Now that we have the analytic solution for $\theta$, let's find the optimal numerical thetas for our tips dataset. Fill out the function below.
Hints:
1. Use the `np.linalg.inv` function to compute matrix inverses
1. To compute the transpose of a matrix, you can use `X.T` or `X.transpose()`
<!--
BEGIN QUESTION
name: q3a
-->
```
def get_analytical_sol(X, y):
"""
Computes the analytical solution to our least squares problem
Parameters
-----------
X: a 2D dataframe of numeric features (one-hot encoded)
y: a 1D vector of tip amounts
Returns
-----------
The estimate for theta computed using the equation mentioned above
"""
...
analytical_thetas = get_analytical_sol(one_hot_X, tips)
print("Our analytical loss is: ", l2(linear_model(analytical_thetas, one_hot_X), tips).mean())
print("Our numerical loss is: ", l2(linear_model(minimize_average_loss(l2, linear_model, one_hot_X, tips), one_hot_X), tips).mean())
ok.grade("q3a");
```
## Question 3b: Fixing our analytical loss
Our analytical loss is surprisingly much worse than our numerical loss. Why is this?
Here is a relevant Stack Overflow post: https://stackoverflow.com/questions/31256252/why-does-numpy-linalg-solve-offer-more-precise-matrix-inversions-than-numpy-li
In summary, `np.linalg.inv` loses precision, which propogates error throughout the calculation. If you're not convinced, try `np.linalg.solve` instead of `np.linalg.inv`, you'll find that our loss is much closer to the expected numerical loss. These results are meant to demonstrate that even if our math is correct, limits of our computational precision and machinery can lead us to poor results.
You might also notice that `one_hot_X` has a rank of 9 while it has 12 columns. This means that $X^TX$ will also have a rank of 9 and 12 columns; thus, $X^TX$ will not be invertible because it does not have full column rank.
Complete the code below to one-hot-encode our dataset such that `one_hot_X_revised` has no redundant features. After this, you should see that the analytical loss and the numerical loss are similar as expected.
**Hint**: Check out the `drop_first` parameter of the `pd.get_dummies` function.
<!--
BEGIN QUESTION
name: q3b
-->
```
def one_hot_encode_revised(data):
"""
Return the one-hot encoded dataframe of our input data, removing redundancies.
Parameters
-----------
data: a dataframe that may include non-numerical features
Returns
-----------
A one-hot encoded dataframe that only contains numeric features without any redundancies.
"""
...
one_hot_X_revised = one_hot_encode_revised(X)
revised_analytical_thetas = get_analytical_sol(one_hot_X_revised, tips)
print("Our analytical loss is: ", l2(linear_model(revised_analytical_thetas, one_hot_X_revised), tips).mean())
print("Our numerical loss is: ", l2(linear_model(minimize_average_loss(l2, linear_model, one_hot_X_revised, tips), one_hot_X_revised), tips).mean())
ok.grade("q3b");
```
## Question 4: Diabetes data
### Let's take a look at the diabetes data we used from Lab 4
```
from sklearn.datasets import load_diabetes
from sklearn import linear_model
from scipy import stats
import statsmodels.api as sm
```
#### Look at a small description of the data to remind you what the data contains, and also load it.
```
diabetes_data = load_diabetes()
print(diabetes_data.DESCR)
```
#### Again, we'll divide the data into portions: the features (X) and the target (Y).
```
# Unpacking the data into new variables
diabetes_features = diabetes_data['data']
diabetes_target = diabetes_data['target']
```
#### And we will fit the model in a more traditional way.
```
model = sm.OLS(diabetes_target, diabetes_features).fit()
model.summary()
```
Using your PSTAT 126 knowledge, which of the variables below are important? Can you think of any interactions that might be worth exploring?
<!--
BEGIN QUESTION
name: q4a
-->
*Write your answer here, replacing this text.*
### Interaction term
Make a new variable named `newvar` to contain an interaction term of columns 5 and 6 in `diabetes_features`.
Create a new variable called `diabetes_features2` that appends this new variable to `diabetes_features`.
One method to this is to use `np.insert` to do this, specifying that `axis = 1`.
<!--
BEGIN QUESTION
name: q4b
-->
```
newvar = ...
diabetes_features2 = ...
ok.grade("q4b");
```
### Regression model with the interaction term
Now, run a regression model with your interaction term added. Name this model `model2.`
<!--
BEGIN QUESTION
name: q4c
-->
```
model2 = ...
model2.summary()
ok.grade("q4c");
```
Is `model2` with the interaction term better or worse than `model`? Explain below.
<!--
BEGIN QUESTION
name: q4d
-->
*Write your answer here, replacing this text.*
# Submit
Make sure you have run all cells in your notebook in order before running the cell below, so that all images/graphs appear in the output.
**Please save before submitting!**
```
# Save your notebook first, then run this cell to submit.
ok.submit()
```
| true |
code
| 0.707569 | null | null | null | null |
|
# camera_calib_python
This is a python based camera calibration "library". Some things:
* Uses [nbdev](https://github.com/fastai/nbdev), which is an awesome and fun way to develop and tinker.
* Uses pytorch for optimization of intrinsic and extrinsic parameters. Each step in the model is modularized as its own pytorch `nn.module` in the `modules.ipynb` notebook.
* Optimization is carried out via the built in `LBFGS` optimizer. The `LBFGS` optimizer uses only the gradient to do a quasi second order optimization. However, I've noticed it's imperfect and can a take long time to converge in some cases.
* The use of pytorch allows the forward pass to be easily modified. It also allows the use of any differentiable loss function although I've noticed that sum of squared errors seems to give the best results of the losses I've tried.
* The fiducial point detector for my calibration board uses a pytorch neural net under the hood (more info [here](https://github.com/justinblaber/fiducial_detect)), which is easily integrated into this library since its python based.
# Tutorial
```
import camera_calib.api as api
```
Before calibration can be done, we need the following information:
1. Images and their respective camera and pose indices
2. Calibration board geometry
3. Fiducial point detector
4. Control point refiner
### 1) Images
```
import re
from pathlib import Path
files_img = list(Path('data/dot_vision_checker').glob('*.png'))
files_img
def _parse_name(name_img):
match = re.match(r'''SERIAL_(?P<serial>.*)_
DATETIME_(?P<date>.*)_
CAM_(?P<cam>.*)_
FRAMEID_(?P<frameid>.*)_
COUNTER_(?P<counter>.*).png''',
name_img,
re.VERBOSE)
return match.groupdict()
imgs = []
for file_img in files_img:
dict_group = _parse_name(file_img.name)
img = api.File16bitImg(file_img)
img.idx_cam = int(dict_group['cam'])-1
img.idx_cb = int(dict_group['counter'])-1
imgs.append(img)
for img in imgs: print(f'{img.name} - cam: {img.idx_cam} - cb: {img.idx_cb}')
```
### 2) Calibration board geometry
The calibration board geometry specifies where fiducial markers and control points are located. For this example, my dot vision checker board is used.
```
h_cb = 50.8
w_cb = 50.8
h_f = 42.672
w_f = 42.672
num_c_h = 16
num_c_w = 16
spacing_c = 2.032
cb_geom = api.CbGeom(h_cb, w_cb,
api.CpCSRGrid(num_c_h, num_c_w, spacing_c),
api.FmCFPGrid(h_f, w_f))
cb_geom.plot()
```
### 3) Fiducial detector
```
from pathlib import Path
```
This fiducial detector will take in an image and return the locations of the fiducial markers. The detector in this example is a neural net trained specifically on my calibration board. More info available at:
* https://github.com/justinblaber/fiducial_detect
```
file_model = Path('models/dot_vision_checker.pth')
detector = api.DotVisionCheckerDLDetector(file_model)
```
### 4) Control Point Refiner
The refiner will take in an image, initial guesses for control points, and the boundaries around the control points, and return a refined point. The boundaries help determine how much neighboring info can be used to refine the control point.
```
refiner = api.OpenCVCheckerRefiner(hw_min=5, hw_max=15, cutoff_it=20, cutoff_norm=1e-3)
```
## Calibrate
Now, we can calibrate
```
calib = api.multi_calib(imgs, cb_geom, detector, refiner)
```
From Bo Li's calibration paper, we know the coordinate graph of calibration board poses and cameras forms a bipartite graph. For debugging purposes this is displayed below.
```
api.plot_bipartite(calib)
```
Plot residuals
```
api.plot_residuals(calib);
```
Plot extrinsics; note that `%matplotlib notebook` can be used to make the plot interactive
```
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(20,20))
ax = fig.add_subplot(2, 2, 1, projection='3d')
api.plot_extrinsics(calib, ax=ax)
ax.view_init(elev=90, azim=-90)
ax = fig.add_subplot(2, 2, 2, projection='3d')
api.plot_extrinsics(calib, ax=ax)
ax.view_init(elev=45, azim=-45)
ax = fig.add_subplot(2, 2, 3, projection='3d')
api.plot_extrinsics(calib, ax=ax)
ax.view_init(elev=0, azim=-90)
ax = fig.add_subplot(2, 2, 4, projection='3d')
api.plot_extrinsics(calib, ax=ax)
ax.view_init(elev=0, azim=0)
plt.subplots_adjust(wspace=0, hspace=0)
```
This matches pretty closely to my camera rig
## Save/Load
Save
```
api.save(calib, '/tmp/calib.pth')
```
Load
```
del calib
calib = api.load('/tmp/calib.pth')
```
# Build
```
from camera_calib.utils import convert_notebook
convert_notebook()
```
| true |
code
| 0.407098 | null | null | null | null |
|
# Highlighting Task - Event Extraction from Text
In this tutorial, we will show how *dimensionality reduction* can be applied over *both the media units and the annotations* of a crowdsourcing task, and how this impacts the results of the CrowdTruth quality metrics. We start with an *open-ended extraction task*, where the crowd was asked to highlight words or phrases in a text that refer to events or actions. The task was executed on [FigureEight](https://www.figure-eight.com/). For more crowdsourcing annotation task examples, click [here](https://raw.githubusercontent.com/CrowdTruth-core/tutorial/getting_started.md).
To replicate this experiment, the code used to design and implement this crowdsourcing annotation template is available here: [template](https://raw.githubusercontent.com/CrowdTruth/CrowdTruth-core/master/tutorial/templates/Event-Text-Highlight/template.html), [css](https://raw.githubusercontent.com/CrowdTruth/CrowdTruth-core/master/tutorial/templates/Event-Text-Highlight/template.css), [javascript](https://raw.githubusercontent.com/CrowdTruth/CrowdTruth-core/master/tutorial/templates/Event-Text-Highlight/template.js).
This is how the task looked like to the workers:

A sample dataset for this task is available in [this file](https://raw.githubusercontent.com/CrowdTruth/CrowdTruth-core/master/tutorial/data/event-text-highlight.csv), containing raw output from the crowd on FigureEight. Download the file and place it in a folder named `data` that has the same root as this notebook. The answers from the crowd are stored in the `tagged_events` column.
```
import pandas as pd
test_data = pd.read_csv("../data/event-text-highlight.csv")
test_data["tagged_events"][0:30]
```
Notice the diverse behavior of the crowd workers. While most annotated each word individually, the worker on *row 2* annotated a chunk of the sentence together in one word phrase. Also, when no answer was picked by the worker, the value in the cell is `[NONE]`.
## A basic pre-processing configuration
Our basic pre-processing configuration attempts to normalize the different ways of performing the crowd annotations.
We set `remove_empty_rows = False` to keep the empty rows from the crowd. This configuration option will set all empty cell values to correspond to a *NONE* token in the annotation vector.
We build the annotation vector to have one component for each word in the sentence. To do this, we break up multiple-word annotations into a list of single words in the `processJudgments` call:
```
judgments[self.outputColumns[0]] = judgments[self.outputColumns[0]].apply(
lambda x: str(x).replace(' ',self.annotation_separator))
```
The final configuration class `Config` is this:
```
import crowdtruth
from crowdtruth.configuration import DefaultConfig
class Config(DefaultConfig):
inputColumns = ["doc_id", "sentence_id", "events", "events_count", "original_sententce", "processed_sentence", "tokens"]
outputColumns = ["tagged_events"]
open_ended_task = True
annotation_separator = ","
remove_empty_rows = False
def processJudgments(self, judgments):
# build annotation vector just from words
judgments[self.outputColumns[0]] = judgments[self.outputColumns[0]].apply(
lambda x: str(x).replace(' ',self.annotation_separator))
# normalize vector elements
judgments[self.outputColumns[0]] = judgments[self.outputColumns[0]].apply(
lambda x: str(x).replace('[',''))
judgments[self.outputColumns[0]] = judgments[self.outputColumns[0]].apply(
lambda x: str(x).replace(']',''))
judgments[self.outputColumns[0]] = judgments[self.outputColumns[0]].apply(
lambda x: str(x).replace('"',''))
judgments[self.outputColumns[0]] = judgments[self.outputColumns[0]].apply(
lambda x: str(x).replace(',,,',','))
judgments[self.outputColumns[0]] = judgments[self.outputColumns[0]].apply(
lambda x: str(x).replace(',,',','))
return judgments
```
Now we can pre-process the data and run the CrowdTruth metrics:
```
data_with_stopwords, config_with_stopwords = crowdtruth.load(
file = "../data/event-text-highlight.csv",
config = Config()
)
processed_results_with_stopwords = crowdtruth.run(
data_with_stopwords,
config_with_stopwords
)
```
## Removing stopwords from Media Units and Annotations
A more complex dimensionality reduction technique involves removing the stopwords from both the *media units* and the crowd *annotations*. Stopwords (i.e. words that are very common in the English language) do not usually contain much useful information. Also, the behavior of the crowds w.r.t them is inconsistent - some workers omit them, some annotate them.
The first step is to build a function that removes stopwords from strings. We will use the `stopwords` corpus in the `nltk` package to get the list of words. We want to build a function that can be reused for both the text in the media units and in the annotations column. Also, we need to be careful about omitting punctuation.
The function `remove_stop_words` does all of these things:
```
import nltk
from nltk.corpus import stopwords
import string
stopword_set = set(stopwords.words('english'))
stopword_set.update(['s'])
def remove_stop_words(words_string, sep):
'''
words_string: string containing all words
sep: separator character for the words in words_string
'''
words_list = words_string.split(sep)
corrected_words_list = ""
for word in words_list:
if word not in stopword_set:
if corrected_words_list != "":
corrected_words_list += sep
corrected_words_list += word
return corrected_words_list
```
In the new configuration class `ConfigDimRed`, we apply the function we just built to both the column that contains the media unit text (`inputColumns[2]`), and the column containing the crowd annotations (`outputColumns[0]`):
```
import pandas as pd
class ConfigDimRed(Config):
def processJudgments(self, judgments):
judgments = Config.processJudgments(self, judgments)
# remove stopwords from input sentence
for idx in range(len(judgments[self.inputColumns[2]])):
judgments.at[idx, self.inputColumns[2]] = remove_stop_words(
judgments[self.inputColumns[2]][idx], " ")
for idx in range(len(judgments[self.outputColumns[0]])):
judgments.at[idx, self.outputColumns[0]] = remove_stop_words(
judgments[self.outputColumns[0]][idx], self.annotation_separator)
if judgments[self.outputColumns[0]][idx] == "":
judgments.at[idx, self.outputColumns[0]] = self.none_token
return judgments
```
Now we can pre-process the data and run the CrowdTruth metrics:
```
data_without_stopwords, config_without_stopwords = crowdtruth.load(
file = "../data/event-text-highlight.csv",
config = ConfigDimRed()
)
processed_results_without_stopwords = crowdtruth.run(
data_without_stopwords,
config_without_stopwords
)
```
## Effect on CrowdTruth metrics
Finally, we can compare the effect of the stopword removal on the CrowdTruth *sentence quality score*.
```
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.scatter(
processed_results_with_stopwords["units"]["uqs"],
processed_results_without_stopwords["units"]["uqs"],
)
plt.plot([0, 1], [0, 1], 'red', linewidth=1)
plt.title("Sentence Quality Score")
plt.xlabel("with stopwords")
plt.ylabel("without stopwords")
```
The red line in the plot runs through the diagonal. All sentences above the line have a higher *sentence quality score* when the stopwords were removed.
The plot shows that removing the stopwords improved the quality for a majority of the sentences. Surprisingly though, some sentences decreased in quality. This effect can be understood when plotting the *worker quality scores*.
```
plt.scatter(
processed_results_with_stopwords["workers"]["wqs"],
processed_results_without_stopwords["workers"]["wqs"],
)
plt.plot([0, 0.8], [0, 0.8], 'red', linewidth=1)
plt.title("Worker Quality Score")
plt.xlabel("with stopwords")
plt.ylabel("without stopwords")
```
The quality of the majority of workers also has increased in the configuration where we removed the stopwords. However, because of the inter-linked nature of the CrowdTruth quality metrics, the annotations of these workers now has a greater weight when calculating the *sentence quality score*. So the stopword removal process had the effect of removing some of the noise in the annotations and therefore increasing the quality scores, but also of *amplifying the true ambiguity in the sentences*.
```
data_with_stopwords["units"]
```
| true |
code
| 0.371479 | null | null | null | null |
|

# terrainbento model Basic with variable $m$ steady-state solution
This model shows example usage of the Basic model from the TerrainBento package with a variable drainage-area exponent, $m$:
$\frac{\partial \eta}{\partial t} = - KQ^m S + D\nabla^2 \eta$
where $K$ and $D$ are constants, $Q$ is discharge, $S$ is local slope, $m$ is the drainage area exponent, and $\eta$ is the topography.
Note that the units of $K$ depend on $m$, so that the value of $K$ used in Basic cannot be meaningfully compared to other values of $K$ unless the valuess of $m$ are the same.
Refer to [Barnhart et al. (2019)](https://www.geosci-model-dev.net/12/1267/2019/) for further explaination. For detailed information about creating a Basic model, see [the detailed documentation](https://terrainbento.readthedocs.io/en/latest/source/terrainbento.derived_models.model_basic.html).
This notebook (a) shows the initialization and running of this model, (b) saves a NetCDF file of the topography, which we will use to make an oblique Paraview image of the landscape, and (c) creates a slope-area plot at steady state.
```
# import required modules
import os
import numpy as np
from terrainbento import Basic
from landlab import imshow_grid
from landlab.io.netcdf import write_netcdf
import matplotlib.pyplot as plt
import matplotlib
np.random.seed(42)
#Ignore warnings
import warnings
warnings.filterwarnings('ignore')
# create the parameter dictionary needed to instantiate the model
params = {
# create the Clock.
"clock": {
"start": 0,
"step": 10,
"stop": 1e7
},
# Create the Grid
"grid": {
"RasterModelGrid": [
(25, 40),
{
"xy_spacing": 40
},
{
"fields": {
"node": {
"topographic__elevation": {
"random": [{
"where": "CORE_NODE"
}]
}
}
}
},
]
},
# Set up Boundary Handlers
"boundary_handlers": {
"NotCoreNodeBaselevelHandler": {
"modify_core_nodes": True,
"lowering_rate": -0.001
}
},
# Parameters that control output.
"output_interval": 1e4,
"save_first_timestep": True,
"output_prefix": "output/basicVm",
"fields": ["topographic__elevation"],
# Parameters that control process and rates.
"water_erodibility": 0.001,
"m_sp": 0.25,
"n_sp": 1.0,
"regolith_transport_parameter": 0.01,
}
# the tolerance here is high, so that this can run on binder and for tests. (recommended value = 0.001 or lower).
tolerance = .001
# we can use an output writer to run until the model reaches steady state.
class run_to_steady(object):
def __init__(self, model):
self.model = model
self.last_z = self.model.z.copy()
self.tolerance = tolerance
def run_one_step(self):
if model.model_time > 0:
diff = (self.model.z[model.grid.core_nodes] -
self.last_z[model.grid.core_nodes])
if max(abs(diff)) <= self.tolerance:
self.model.clock.stop = model._model_time
print("Model reached steady state in " +
str(model._model_time) + " time units\n")
else:
self.last_z = self.model.z.copy()
if model._model_time <= self.model.clock.stop - self.model.output_interval:
self.model.clock.stop += self.model.output_interval
# initialize the model using the Model.from_dict() constructor.
# We also pass the output writer here.
model = Basic.from_dict(params, output_writers={"class": [run_to_steady]})
# to run the model as specified, we execute the following line:
model.run()
#MAKE SLOPE-AREA PLOT
# plot nodes that are not on the boundary or adjacent to it
core_not_boundary = np.array(
model.grid.node_has_boundary_neighbor(model.grid.core_nodes)) == False
plotting_nodes = model.grid.core_nodes[core_not_boundary]
# assign area_array and slope_array
area_array = model.grid.at_node["drainage_area"][plotting_nodes]
slope_array = model.grid.at_node["topographic__steepest_slope"][plotting_nodes]
# instantiate figure and plot
fig = plt.figure(figsize=(6, 3.75))
slope_area = plt.subplot()
slope_area.scatter(area_array,
slope_array,
marker="o",
c="k",
label="Model Basic (m=0.25)")
# make axes log and set limits
slope_area.set_xscale("log")
slope_area.set_yscale("log")
slope_area.set_xlim(9 * 10**1, 3 * 10**5)
slope_area.set_ylim(1e-2, 1e0)
# set x and y labels
slope_area.set_xlabel(r"Drainage area [m$^2$]")
slope_area.set_ylabel("Channel slope [-]")
slope_area.legend(scatterpoints=1, prop={"size": 12})
slope_area.tick_params(axis="x", which="major", pad=7)
plt.show()
# Save stack of all netcdfs for Paraview to use.
# model.save_to_xarray_dataset(filename="basicVm.nc",
# time_unit='years',
# reference_time='model start',
# space_unit='meters')
# remove temporary netcdfs
model.remove_output_netcdfs()
# make a plot of the final steady state topography
plt.figure()
imshow_grid(model.grid, "topographic__elevation",cmap ='terrain',
grid_units=("m", "m"),var_name="Elevation (m)")
plt.show()
```
## Next Steps
- [Welcome page](../Welcome_to_TerrainBento.ipynb)
- There are three additional introductory tutorials:
1) [Introduction terrainbento](../example_usage/Introduction_to_terrainbento.ipynb)
2) [Introduction to boundary conditions in terrainbento](../example_usage/introduction_to_boundary_conditions.ipynb)
3) [Introduction to output writers in terrainbento](../example_usage/introduction_to_output_writers.ipynb).
- Five examples of steady state behavior in coupled process models can be found in the following notebooks:
1) [Basic](model_basic_steady_solution.ipynb) the simplest landscape evolution model in the terrainbento package.
2) **This Notebook**: [BasicVm](model_basic_var_m_steady_solution.ipynb) which permits the drainage area exponent to change
3) [BasicCh](model_basicCh_steady_solution.ipynb) which uses a non-linear hillslope erosion and transport law
4) [BasicVs](model_basicVs_steady_solution.ipynb) which uses variable source area hydrology
5) [BasisRt](model_basicRt_steady_solution.ipynb) which allows for two lithologies with different K values
6) [RealDEM](model_basic_realDEM.ipynb) Run the basic terrainbento model with a real DEM as initial condition.
| true |
code
| 0.743194 | null | null | null | null |
|
# Collecting VerbNet Terms
This notebook parses all the VerbNet .XML definitions - extracting all the possible PREDicates in the FRAME SEMANTICS and the ARG type-value tuples. This will allow DNA to understand/account for all the semantics that can be expressed.
An example XML structure is:
```
<VNCLASS xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" ID="dedicate-79" ...>
<MEMBERS>
<MEMBER name="dedicate" wn="dedicate%2:32:00" grouping="dedicate.01"/>
<MEMBER name="devote" wn="devote%2:32:00" grouping="devote.01"/>
<MEMBER name="commit" wn="commit%2:32:01 commit%2:40:00" grouping="commit.02"/>
</MEMBERS>
<THEMROLES>
...
</THEMROLES>
<FRAMES>
<FRAME>
<DESCRIPTION descriptionNumber="8.1" primary="NP V NP S_ING" secondary="NP-P-ING-SC; to-PP" .../>
<EXAMPLES>
<EXAMPLE>I dedicated myself to the cause.</EXAMPLE>
</EXAMPLES>
<SYNTAX>
<NP value="Agent">
<SYNRESTRS/>
</NP>
<VERB/>
<NP value="Theme">
<SYNRESTRS/>
</NP>
<PREP value="to">
<SYNRESTRS/>
</PREP>
<NP value="Goal">
<SYNRESTRS/>
</NP>
</SYNTAX>
<SEMANTICS>
<PRED value="dedicate">
<ARGS>
<ARG type="Event" value="during(E)"/>
<ARG type="ThemRole" value="Agent"/>
<ARG type="ThemRole" value="Theme"/>
<ARG type="ThemRole" value="Goal"/>
</ARGS>
</PRED>
</SEMANTICS>
</FRAME>
<FRAME>
<DESCRIPTION descriptionNumber="0.2" primary="NP V NP PP.goal" secondary="NP-PP; to-PP" .../>
<EXAMPLES>
<EXAMPLE>I dedicated myself to the cause.</EXAMPLE>
</EXAMPLES>
<SYNTAX>
<NP value="Agent">
<SYNRESTRS/>
</NP>
<VERB/>
<NP value="Theme">
<SYNRESTRS/>
</NP>
<PREP value="to">
<SELRESTRS/>
</PREP>
<NP value="Goal">
<SYNRESTRS>
<SYNRESTR Value="-" type="sentential"/>
</SYNRESTRS>
</NP>
</SYNTAX>
<SEMANTICS>
<PRED value="dedicate">
<ARGS>
<ARG type="Event" value="during(E)"/>
<ARG type="ThemRole" value="Agent"/>
<ARG type="ThemRole" value="Theme"/>
<ARG type="ThemRole" value="Goal"/>
</ARGS>
</PRED>
</SEMANTICS>
</FRAME>
</FRAMES>
<SUBCLASSES/>
</VNCLASS>
```
The above results in capturing the following detail:
* The possible PREDicates in the FRAME SEMANTICS => 'dedicate'
* The ARG type-value tuples =>
* 'Event', 'during(E)'
* 'ThemRole', 'Agent'
* 'ThemRole', 'Theme'
* 'ThemRole', 'Goal'
```
# Imports
from pathlib import Path
import xml.etree.ElementTree as ET
# Constants
verbnet_dir = '/Users/andreaw/Documents/VerbNet3.3'
preds = set()
args = set()
def get_arg_details(etree):
for arg in etree.findall('./FRAMES/FRAME/SEMANTICS/PRED/ARGS/ARG'):
args.add((arg.attrib["type"], arg.attrib["value"]))
# Recursively process the subclasses
for subclass in etree.findall('./SUBCLASSES/VNSUBCLASS'):
get_arg_details(subclass)
def get_pred_details(etree):
for pred in etree.findall('./FRAMES/FRAME/SEMANTICS/PRED'):
preds.add(pred.attrib["value"])
# Recursively process the subclasses
for subclass in etree.findall('./SUBCLASSES/VNSUBCLASS'):
get_pred_details(subclass)
# Process each of the VerbNet files
file_list = Path(verbnet_dir).glob('**/*.xml')
for file_path in file_list:
file_str = str(file_path)
with open(file_str, 'r') as xml_file:
xml_in = xml_file.read()
# Create the tree
vn_class = ET.fromstring(xml_in)
# Process from the top down, recursively
get_pred_details(vn_class)
get_arg_details(vn_class)
print(sorted(preds))
print()
print(sorted(args))
# Process again for VerbNet 3.4
verbnet_dir = '/Users/andreaw/Documents/VerbNet3.4'
# Process each of the VerbNet files
file_list = Path(verbnet_dir).glob('**/*.xml')
for file_path in file_list:
file_str = str(file_path)
with open(file_str, 'r') as xml_file:
xml_in = xml_file.read()
# Create the tree
vn_class = ET.fromstring(xml_in)
# Process from the top down, recursively
get_pred_details(vn_class)
get_arg_details(vn_class)
print(sorted(preds))
print()
print(sorted(args))
```
| true |
code
| 0.356517 | null | null | null | null |
|
# Homework 3
## 1. Implement L1 norm regularization as a custom loss function
```
import torch
def lasso_reg(params, l1_lambda):
l1_penalty = torch.nn.L1Loss(size_average=False)
reg_loss = 0
for param in params:
reg_loss += l1_penalty(param)
loss += l1_lambda * reg_loss
return loss
```
## 2. The third-to-last paragraph in the notebook is concerning early stopping, an "old" regularization technique which involves the stopping of training earlier than the number of epochs would suggest. Read the paragraph and download the paper from Prechelt et al.
### a. Implement early stopping in the $E_{opt}$ specification
In the paper, the value $E_{opt}$ is defned to be the lowest validation set error obtained in epochs up to $t$: $$E_{opt}(t) = \min_{t \le t'} E_{va}(t')$$ where $E_{va}$ is the validation error, i.e. the corresponding error on the validation set. As per instructions, I'm going to use the test data as validation.
```
# import in Colab
import sys
sys.path.append('/content/mnist.py')
sys.path.append('/content/train_utils.py')
import mnist
from train_utils import accuracy, AverageMeter
from torch import nn
class MLP(nn.Module):
def __init__(self):
super().__init__()
self.flat = nn.Flatten()
self.h1 = nn.Linear(28*28, 16)
self.h2 = nn.Linear(16, 32)
self.h3 = nn.Linear(32, 24)
self.out = nn.Linear(24, 10)
def forward(self, X, activ_hidden=nn.functional.relu):
out = self.flat(X)
out = activ_hidden(self.h1(out))
out = activ_hidden(self.h2(out))
out = activ_hidden(self.h3(out))
out = self.out(out)
return out
def train_epoch(model, dataloader, loss_fn, optimizer, loss_meter, performance_meter, performance):
for X, y in dataloader:
optimizer.zero_grad()
y_hat = model(X)
loss = loss_fn(y_hat, y)
loss.backward()
optimizer.step()
acc = performance(y_hat, y)
loss_meter.update(val=loss.item(), n=X.shape[0])
performance_meter.update(val=acc, n=X.shape[0])
def train_model(model, dataloader1, dataloader2, loss_fn, optimizer, num_epochs, performance=accuracy):
model.train()
E = {
"epoch": [],"training perf": [], "validation perf": [], "parameters": [], "optimizer": []
}
for epoch in range(num_epochs):
loss_meter = AverageMeter()
performance_meter = AverageMeter()
train_epoch(model, dataloader1, loss_fn, optimizer, loss_meter, performance_meter, performance)
fin_loss, fin_perf = test_model(model, dataloader2, loss_fn=loss_fn)
E["epoch"].append(epoch)
E["training perf"].append(performance_meter)
E["validation perf"].append(fin_perf)
E["parameters"].append(model.state_dict())
E["optimizer"].append(optimizer.state_dict())
return loss_meter.sum, performance_meter.avg, E
def test_model(model, dataloader, performance=accuracy, loss_fn=None):
# create an AverageMeter for the loss if passed
if loss_fn is not None:
loss_meter = AverageMeter()
performance_meter = AverageMeter()
model.eval()
with torch.no_grad():
for X, y in dataloader:
y_hat = model(X)
loss = loss_fn(y_hat, y) if loss_fn is not None else None
acc = performance(y_hat, y)
if loss_fn is not None:
loss_meter.update(loss.item(), X.shape[0])
performance_meter.update(acc, X.shape[0])
# get final performances
fin_loss = loss_meter.sum if loss_fn is not None else None
fin_perf = performance_meter.avg
return fin_loss, fin_perf
minibatch_size_train = 256
minibatch_size_test = 512
trainloader, testloader, trainset, testset = mnist.get_data(batch_size_train=minibatch_size_test, batch_size_test=minibatch_size_test)
learn_rate = 0.1
num_epochs = 30
model = MLP()
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learn_rate)
train_loss, train_acc, E = train_model(model, trainloader, testloader, loss_fn, optimizer, num_epochs)
```
Since `Validation_error = 1 - Validation_performance`, minimizing the error is equivalent to maximizing the performance.
```
from matplotlib import pyplot as plt
val_list = list(E["validation perf"])
maxval = max(E["validation perf"])
index = val_list.index(max(val_list)) + 1
plt.plot(E["epoch"], E["validation perf"] )
print(f"The best validation performance is {maxval}, obtained at epoch no. {index} out of {num_epochs}.")
```
### b$^*$. Implement early stopping in one of the additional specifications
A stopping criterion described in the paper is based on the *generalization loss*: $$ GL (t) = 100 * \big( \frac{E_{va}(t)}{E_{opt}(t)} -1 \big)$$ that is, the validation error over the minimum so far in percent. We should stop as soon as this value exceeds a certain threshold $\alpha$.
As reported in the paper, this criterion is used to maximize the probability to find a good solution, as opposed to maximizing the average quality of the solutions.
```
alpha = 1
E_opt = 1 - val_list[0]
for i in range(num_epochs):
E_va = 1 - val_list[i]
if E_va < E_opt:
E_opt = E_va
GL = 100 * (E_va/E_opt - 1)
if GL > alpha:
print(f"This stopping criterion halts the computation at epoch {i+1}")
break
```
As we can see, this criterion stops very early, at the first epoch with lower performance. A solution is to add momentum to SGD to minimize oscillations:
```
optimizer = torch.optim.SGD(model.parameters(), lr=learn_rate, momentum=0.9)
num_epochs = 15
train_loss_m, train_acc_m, E_m = train_model(model, trainloader, testloader, loss_fn, optimizer, num_epochs)
from matplotlib import pyplot as plt
val_list = list(E_m["validation perf"])
maxval = max(E_m["validation perf"])
index = val_list.index(max(val_list)) + 1
plt.plot(E_m["epoch"], E_m["validation perf"] )
print(f"The best validation performance is {maxval}, obtained at epoch no. {index} out of {num_epochs}.")
alpha = 2
E_opt = 1 - val_list[0]
for i in range(num_epochs):
E_va = 1 - val_list[i]
if E_va < E_opt:
E_opt = E_va
GL = 100 * (E_va/E_opt - 1)
if GL > alpha:
print(f"This stopping criterion halts the computation at epoch {i+1}")
break
```
From the plot we can see that SGD with momentum performs a lot better than without, reducing oscillations. Nevertheless, this criterion stops very early anyways.
| true |
code
| 0.823896 | null | null | null | null |
|
# Barren Plateaus
<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>
## Overview
In the training of classical neural networks, gradient-based optimization methods encounter the problem of local minimum and saddle points. Correspondingly, the Barren plateau phenomenon could potentially block us from efficiently training quantum neural networks. This peculiar phenomenon was first discovered by McClean et al. in 2018 [[arXiv:1803.11173]](https://arxiv.org/abs/1803.11173). In few words, when we randomly initialize the parameters in random circuit structure meets a certain degree of complexity, the optimization landscape will become very flat, which makes it difficult for the optimization method based on gradient descent to find the global minimum. For most variational quantum algorithms (VQE, etc.), this phenomenon means that when the number of qubits increases, randomly choose a circuit ansatz and randomly initialize the parameters of it may not be a good idea. This will make the optimization landscape corresponding to the loss function into a huge plateau, which makes the quantum neural network's training much more difficult. The initial random value for the optimization process is very likely to stay inside this plateau, and the convergence time of gradient descent will be prolonged.

The figure is generated through [Gradient Descent Viz](https://github.com/lilipads/gradient_descent_viz)
This tutorial mainly discusses how to show the barren plateau phenomenon with Paddle Quantum. Although it does not involve any algorithm innovation, it can improve readers' understanding about gradient-based training for quantum neural network. We first introduce the necessary libraries and packages:
```
import time
import numpy as np
from matplotlib import pyplot as plt
import paddle
from paddle import matmul
from paddle_quantum.circuit import UAnsatz
from paddle_quantum.utils import dagger
from paddle_quantum.state import density_op
```
## Random network structure
Here we follow the original method mentioned in the paper by McClean (2018) and build the following random circuit (currently we do not support the built-in control-Z gate, use CNOT instead):

First, we rotate all the qubits around the $y$-axis of the Bloch sphere with rotation gates $R_y(\pi/4)$.
The remaining structure forms a block, each block can be further divided into two layers:
- Build a layer of random rotation gates on all the qubits, where $R_{\ell,n} \in \{R_x, R_y, R_z\}$. The subscript $\ell$ means the gate is in the $\ell$-th repeated block. In the figure above, $\ell =1$. The second subscript $n$ indicates which qubit it acts on.
- The second layer is composed of CNOT gates, which act on adjacent qubits.
In Paddle Quantum, we can build this circuit with the following code:
```
def rand_circuit(theta, target, num_qubits):
# We need to convert Numpy array to Tensor in PaddlePaddle
const = paddle.to_tensor(np.array([np.pi/4]))
# Initialize the quantum circuit
cir = UAnsatz(num_qubits)
# ============== First layer ==============
# Fixed-angle Ry rotation gates
for i in range(num_qubits):
cir.ry(const, i)
# ============== Second layer ==============
# Target is a random array help determine rotation gates
for i in range(num_qubits):
if target[i] == 0:
cir.rz(theta[i], i)
elif target[i] == 1:
cir.ry(theta[i], i)
else:
cir.rx(theta[i], i)
# ============== Third layer ==============
# Build adjacent CNOT gates
for i in range(num_qubits - 1):
cir.cnot([i, i + 1])
return cir.U
```
## Loss function and optimization landscape
After determining the circuit structure, we also need to define a loss function to determine the optimization landscape. Following the same set up with McClean (2018), we take the loss function from VQE:
$$
\mathcal{L}(\boldsymbol{\theta})= \langle0| U^{\dagger}(\boldsymbol{\theta})H U(\boldsymbol{\theta}) |0\rangle,
\tag{1}
$$
The unitary matrix $U(\boldsymbol{\theta})$ is the quantum neural network with the random structure we built from the last section. For Hamiltonian $H$, we also take the simplest form $H = |00\cdots 0\rangle\langle00\cdots 0|$. After that, we can start sampling gradients with the two-qubit case - generate 300 sets of random network structures and different random initial parameters $\{\theta_{\ell,n}^{( i)}\}_{i=1}^{300}$. Each time the partial derivative with respect to the **first parameter $\theta_{1,1}$** is calculated according to the analytical gradient formula from VQE. Then analyze the mean and variance of these 300 sampled partial gradients. The formula for the analytical gradient is:
$$
\partial \theta_{j}
\equiv \frac{\partial \mathcal{L}}{\partial \theta_j}
= \frac{1}{2} \big[\mathcal{L}(\theta_j + \frac{\pi}{2}) - \mathcal{L}(\theta_j - \frac{\pi}{2})\big].
\tag{2}
$$
For a detailed derivation, see [arXiv:1803.00745](https://arxiv.org/abs/1803.00745).
```
# Hyper parameter settings
np.random.seed(42) # Fixed Numpy random seed
N = 2 # Set the number of qubits
samples = 300 # Set the number of sampled random network structures
THETA_SIZE = N # Set the size of the parameter theta
ITR = 1 # Set the number of iterations
LR = 0.2 # Set the learning rate
SEED = 1 # Fixed the randomly initialized seed in the optimizer
# Initialize the register for the gradient value
grad_info = []
paddle.seed(SEED)
class manual_gradient(paddle.nn.Layer):
# Initialize a list of learnable parameters and fill the initial value with a uniform distribution of [0, 2*pi]
def __init__(self, shape, param_attr= paddle.nn.initializer.Uniform(
low=0.0, high=2 * np.pi),dtype='float64'):
super(manual_gradient, self).__init__()
# Convert Numpy array to Tensor in PaddlePaddle
self.H = paddle.to_tensor(density_op(N))
# Define loss function and forward propagation mechanism
def forward(self):
# Initialize three theta parameter lists
theta_np = np.random.uniform(low=0., high= 2 * np.pi, size=(THETA_SIZE))
theta_plus_np = np.copy(theta_np)
theta_minus_np = np.copy(theta_np)
# Modified to calculate analytical gradient
theta_plus_np[0] += np.pi/2
theta_minus_np[0] -= np.pi/2
# Convert Numpy array to Tensor in PaddlePaddle
theta = paddle.to_tensor(theta_np)
theta_plus = paddle.to_tensor(theta_plus_np)
theta_minus = paddle.to_tensor(theta_minus_np)
# Generate random targets, randomly select circuit gates in rand_circuit
target = np.random.choice(3, N)
U = rand_circuit(theta, target, N)
U_dagger = dagger(U)
U_plus = rand_circuit(theta_plus, target, N)
U_plus_dagger = dagger(U_plus)
U_minus = rand_circuit(theta_minus, target, N)
U_minus_dagger = dagger(U_minus)
# Calculate the analytical gradient
grad = (paddle.real(matmul(matmul(U_plus_dagger, self.H), U_plus))[0][0]
- paddle.real(matmul(matmul(U_minus_dagger, self.H), U_minus))[0][0])/2
return grad
# Define the main block
def main():
# Set the dimension of QNN
sampling = manual_gradient(shape=[THETA_SIZE])
# Sampling to obtain gradient information
grad = sampling()
return grad.numpy()
# Record running time
time_start = time.time()
# Start sampling
for i in range(samples):
if __name__ == '__main__':
grad = main()
grad_info.append(grad)
time_span = time.time() - time_start
print('The main program segment has run in total ', time_span, ' seconds')
print("Use ", samples, " samples to get the mean value of the gradient of the random network's first parameter, and we have:", np.mean(grad_info))
print("Use ", samples, "samples to get the variance of the gradient of the random network's first parameter, and we have:", np.var(grad_info))
```
## Visualization of the Optimization landscape
Next, we use Matplotlib to visualize the optimization landscape. In the case of **two qubits**, we only have two parameters $\theta_1$ and $\theta_2$, and there are 9 possibilities for the random circuit structure in the second layer.

The plain structure shown in the $R_z$-$R_z$ layer from the last figure is something we should avoid. In this case, it's nearly impossible to converge to the theoretical minimum. If you want to try to draw some optimization landscapes yourself, please refer to the following code:
```
# Introduce the necessary packages
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import LinearLocator, FormatStrFormatter
time_start = time.time()
N = 2
# Set the image ratio Vertical: Horizontal = 0.3
fig = plt.figure(figsize=plt.figaspect(0.3))
# Generate points on the x, y axis
X = np.linspace(0, 2 * np.pi, 80)
Y = np.linspace(0, 2 * np.pi, 80)
# Generate 2D mesh
xx, yy = np.meshgrid(X, Y)
# Define the necessary logic gates
def rx(theta):
mat = np.array([[np.cos(theta/2), -1j * np.sin(theta/2)],
[-1j * np.sin(theta/2), np.cos(theta/2)]])
return mat
def ry(theta):
mat = np.array([[np.cos(theta/2), -1 * np.sin(theta/2)],
[np.sin(theta/2), np.cos(theta/2)]])
return mat
def rz(theta):
mat = np.array([[np.exp(-1j * theta/2), 0],
[0, np.exp(1j * theta/2)]])
return mat
def CNOT():
mat = np.array([[1,0,0,0],[0,1,0,0],[0,0,0,1],[0,0,1,0]])
return mat
# ============= The first figure =============
# We visualize the case where the second layer is kron(Ry, Ry)
ax = fig.add_subplot(1, 2, 1, projection='3d')
# Forward propagation to calculate loss function:
def cost_yy(para):
L1 = np.kron(ry(np.pi/4), ry(np.pi/4))
L2 = np.kron(ry(para[0]), ry(para[1]))
U = np.matmul(np.matmul(L1, L2), CNOT())
H = np.zeros((2 ** N, 2 ** N))
H[0, 0] = 1
val = (U.conj().T @ H@ U).real[0][0]
return val
# Draw an image
Z = np.array([[cost_yy([x, y]) for x in X] for y in Y]).reshape(len(Y), len(X))
surf = ax.plot_surface(xx, yy, Z, cmap='plasma')
ax.set_xlabel(r"$\theta_1$")
ax.set_ylabel(r"$\theta_2$")
ax.set_title("Optimization Landscape for Ry-Ry Layer")
# ============= The second figure =============
# We visualize the case where the second layer is kron(Rx, Rz)
ax = fig.add_subplot(1, 2, 2, projection='3d')
def cost_xz(para):
L1 = np.kron(ry(np.pi/4), ry(np.pi/4))
L2 = np.kron(rx(para[0]), rz(para[1]))
U = np.matmul(np.matmul(L1, L2), CNOT())
H = np.zeros((2 ** N, 2 ** N))
H[0, 0] = 1
val = (U.conj().T @ H @ U).real[0][0]
return val
Z = np.array([[cost_xz([x, y]) for x in X] for y in Y]).reshape(len(Y), len(X))
surf = ax.plot_surface(xx, yy, Z, cmap='viridis')
ax.set_xlabel(r"$\theta_1$")
ax.set_ylabel(r"$\theta_2$")
ax.set_title("Optimization Landscape for Rx-Rz Layer")
plt.show()
time_span = time.time() - time_start
print('The main program segment has run in total ', time_span, ' seconds')
```
## More qubits
Then, we will see what happens to the sampled gradients when we increase the number of qubits
```
# Hyper parameter settings
selected_qubit = [2, 4, 6, 8]
samples = 300
grad_val = []
means, variances = [], []
# Record operation time
time_start = time.time()
# Keep increasing the number of qubits
for N in selected_qubit:
grad_info = []
THETA_SIZE = N
for i in range(samples):
class manual_gradient(paddle.nn.Layer):
# Initialize a list of learnable parameters of length THETA_SIZE
def __init__(self, shape, param_attr=paddle.nn.initializer.Uniform(low=0.0, high=2 * np.pi),dtype='float64'):
super(manual_gradient, self).__init__()
# Convert to Tensor in PaddlePaddle
self.H = paddle.to_tensor(density_op(N))
# Define loss function and forward propagation mechanism
def forward(self):
# Initialize three theta parameter lists
theta_np = np.random.uniform(low=0., high= 2 * np.pi, size=(THETA_SIZE))
theta_plus_np = np.copy(theta_np)
theta_minus_np = np.copy(theta_np)
# Modify to calculate analytical gradient
theta_plus_np[0] += np.pi/2
theta_minus_np[0] -= np.pi/2
# Convert to Tensor in PaddlePaddle
theta = paddle.to_tensor(theta_np)
theta_plus = paddle.to_tensor(theta_plus_np)
theta_minus = paddle.to_tensor(theta_minus_np)
# Generate random targets, randomly select circuit gates in rand_circuit
target = np.random.choice(3, N)
U = rand_circuit(theta, target, N)
U_dagger = dagger(U)
U_plus = rand_circuit(theta_plus, target, N)
U_plus_dagger = dagger(U_plus)
U_minus = rand_circuit(theta_minus, target, N)
U_minus_dagger = dagger(U_minus)
# Calculate analytical gradient
grad = (paddle.real(matmul(matmul(U_plus_dagger, self.H), U_plus))[0][0]
- paddle.real(matmul(matmul(U_minus_dagger, self.H), U_minus))[0][0])/2
return grad
# Define the main program segment
def main():
# Set the dimension of QNN
sampling = manual_gradient(shape=[THETA_SIZE])
# Sampling to obtain gradient information
grad = sampling()
return grad.numpy()
if __name__ == '__main__':
grad = main()
grad_info.append(grad)
# Record sampling information
grad_val.append(grad_info)
means.append(np.mean(grad_info))
variances.append(np.var(grad_info))
time_span = time.time() - time_start
print('The main program segment has run in total ', time_span, ' seconds')
grad = np.array(grad_val)
means = np.array(means)
variances = np.array(variances)
n = np.array(selected_qubit)
print("We then draw the statistical results of this sampled gradient:")
fig = plt.figure(figsize=plt.figaspect(0.3))
# ============= The first figure =============
# Calculate the relationship between the average gradient of random sampling and the number of qubits
plt.subplot(1, 2, 1)
plt.plot(n, means, "o-.")
plt.xlabel(r"Qubit #")
plt.ylabel(r"$ \partial \theta_{i} \langle 0|H |0\rangle$ Mean")
plt.title("Mean of {} sampled gradient".format(samples))
plt.xlim([1,9])
plt.ylim([-0.06, 0.06])
plt.grid()
# ============= The second figure =============
# Calculate the relationship between the variance of the randomly sampled gradient and the number of qubits
plt.subplot(1, 2, 2)
plt.semilogy(n, variances, "v")
# Polynomial fitting
fit = np.polyfit(n, np.log(variances), 1)
slope = fit[0]
intercept = fit[1]
plt.semilogy(n, np.exp(n * slope + intercept), "r--", label="Slope {:03.4f}".format(slope))
plt.xlabel(r"Qubit #")
plt.ylabel(r"$ \partial \theta_{i} \langle 0|H |0\rangle$ Variance")
plt.title("Variance of {} sampled gradient".format(samples))
plt.legend()
plt.xlim([1,9])
plt.ylim([0.0001, 0.1])
plt.grid()
plt.show()
```
It should be noted that, in theory, only when the network structure and loss function we choose meet certain conditions (unitary 2-design), see paper [[1]](https://arxiv.org/abs/1803.11173), this effect will appear. Then we might as well visualize the influence of choosing different qubits on the optimization landscape:
 Optimization landscape sampled for 2,4,and 6 qubits from left to right in different z-axis scale. (b) Same landscape in a fixed z-axis scale.")
<div style="text-align:center">(a) Optimization landscape sampled for 2,4,and 6 qubits from left to right in different z-axis scale. (b) Same landscape in a fixed z-axis scale. </div>
$\theta_1$ and $\theta_2$ are the first two circuit parameters, and the remaining parameters are all fixed to $\pi$. This way, it helps us visualize the shape of this high-dimensional manifold. Unsurprisingly, the landscape becomes more flat as $n$ increases. **Notice the rapidly decreasing scale in the $z$-axis**. Compared with the 2-qubit case, the optimized landscape of 6 qubits is very flat.
_______
## References
[1] McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. [Nat. Commun. 9, 4812 (2018).](https://www.nature.com/articles/s41467-018-07090-4)
[2] Cerezo, M., Sone, A., Volkoff, T., Cincio, L. & Coles, P. J. Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks. [arXiv:2001.00550 (2020).](https://arxiv.org/abs/2001.00550)
| true |
code
| 0.724493 | null | null | null | null |
|
# Variational Autoencoders (Toy dataset)
Skeleton code from https://github.com/tudor-berariu/ann2018
## 1. Miscellaneous
```
import torch
from torch import Tensor
assert torch.cuda.is_available()
import matplotlib.pyplot as plt
from math import ceil
def show_images(X: torch.Tensor, nrows=3):
ncols = int(ceil(len(X) / nrows))
ratio = nrows / ncols
fig, axs = plt.subplots(nrows=nrows, ncols=ncols, figsize=(10, 10 * ratio))
for idx, img in enumerate(X):
r, c = idx // ncols, idx % ncols
axs[r][c].imshow(img[0].numpy(), aspect='equal', vmin=0, vmax=1, cmap='binary')
for row_axs in axs:
for ax in row_axs:
ax.set_aspect('equal', 'box')
ax.set_yticklabels([])
ax.set_xticklabels([])
fig.tight_layout()
```
## 2. Our dataset
```
def get_dataset(n, idxs):
X = torch.randn(n * 16) * .1
X[idxs] += 1
X = (X - X.min()) / (X.max() - X.min())
X.clamp_(0, 1)
X = X.reshape(n, 1, 4, 4)
return X
n = 15
idxs = [2, 6, 8, 9, 10, 11, 14, 17, 21, 24, 25, 26, 27, 29, 35, 39, 43, 44, 45,
46, 47, 48, 49, 50, 51, 52, 56, 60, 64, 68, 69, 70, 71, 72, 76, 80, 81,
82, 83, 84, 88, 92, 98, 102, 104, 105, 106, 107, 110, 112, 113, 114,
115, 116, 120, 124, 131, 135, 139, 140, 141, 142, 143, 147, 151, 155,
156, 157, 158, 159, 162, 166, 168, 169, 170, 171, 174, 178, 182, 186,
188, 189, 190, 191, 193, 196, 197, 198, 199, 201, 205, 209, 212, 213,
214, 215, 217, 221, 225, 228, 229, 230, 231, 233, 237]
X = get_dataset(n, idxs)
show_images(X)
print(X.shape)
```
## 3. The Variational Auto-encoder
The encoder computes $q_{\phi}\left(z \mid x\right)$ predicting:
- $\mu_{\phi}\left(x\right)$ and
- $\log \sigma_{\phi}^2\left(x\right)$.
The decoder computes $p_{\theta}\left(x \mid z\right)$.
```
import torch.nn as nn
import torch.nn.functional as F
class VAE(nn.Module):
def __init__(self, nz: int = 1) -> None:
super(VAE, self).__init__()
self.nz = nz # The number of dimensions in the latent space
self.encoder = nn.Sequential(nn.Linear(16, 64), nn.ReLU())
self.mean = nn.Linear(64, nz) # predicts the mean of p(z|x)
self.log_var = nn.Linear(64, nz) # predicts the log-variance of p(z|x)
self.decoder = nn.Sequential(nn.Linear(nz, 64), nn.ReLU(),
nn.Linear(64, 16))
def forward(self, x):
x = x.view(-1, 16) # Drop this if you use convolutional encoders
# Encoding x into mu, and log-var of p(z|x)
x = self.encoder(x)
mean = self.mean(x)
log_var = self.log_var(x)
# ----------------------------------------------------------------
# TODO 1: compute z = (eps * std) + mean (reparametrization trick)
std = torch.exp(log_var / 2)
eps = torch.randn_like(std)
noise = eps * std + mean
# ----------------------------------------------------------------
# Decoding z into p(x|z)
x = self.decoder(noise)
x = torch.sigmoid(x)
return x.view(-1, 1, 4, 4), mean, log_var
def generate(self, nsamples: int = None, noise: Tensor = None) -> Tensor:
# Generate some data
with torch.no_grad():
if noise is None:
noise = torch.randn(nsamples, self.nz)
x = self.decoder(noise)
x = torch.sigmoid(x)
return x.view(-1, 1, 4, 4)
```
## 4. Training the model
The optimization criterion has two components.
- the KL divergence between $q_{\phi}\left(z \mid x\right)$ and $p\left(z\right)$
* both are diagonal gaussians, therefore we have a simple formula for the KL divergence: [wiki](https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence#Examples)
- the reconstruction loss computed using the [binary cross entropy](https://pytorch.org/docs/stable/nn.html#binary-cross-entropy)
```
import torch.optim as optim
import numpy as np
def train(vae: VAE, X: torch.Tensor, nsteps: int = 200000):
bce_trace, kl_trace = [], []
optimizer = optim.Adam(vae.parameters(), lr=.001)
for step in range(nsteps):
optimizer.zero_grad()
rec, mean, log_var = vae(X + torch.randn_like(X) * .05)
# -----------------------------------------------
# TODO 2: compute the two losses (do not average)
std = torch.exp(log_var / 2)
bce = F.binary_cross_entropy(rec, X, reduction='sum')
kl = 0.5 * torch.sum(std ** 2 + mean ** 2 - log_var - 1)
# -----------------------------------------------
(bce + kl).backward()
optimizer.step()
# Chestiuni pentru afișare
bce_trace.append(bce.item())
kl_trace.append(kl.item())
if (step + 1) % 100 == 0:
print(f"\rStep {step + 1:d}: BCE={np.mean(bce_trace):7.5f} "
f"KL={np.mean(kl_trace):7.5f}", end="")
bce_trace.clear()
kl_trace.clear()
if (step + 1) % 2500 == 0:
print("")
%%time
vae = VAE()
train(vae, X)
```
## 5. Evaluating the model
### 5.1 Reconstructions
```
with torch.no_grad():
recon, _, _ = vae(X)
show_images(recon)
```
### 5.2 Samples from the model
```
X_gen = vae.generate(nsamples=15)
show_images(X_gen)
```
### 5.3 Walk the latent space :)
```
N = 36
noise = torch.linspace(-2, 2, N).unsqueeze(1)
X_gen = vae.generate(noise=noise)
show_images(X_gen, nrows=6)
```
| true |
code
| 0.797024 | null | null | null | null |
|
# Datasets - Reduced data, IRFs, models
## Introduction
`gammapy.datasets` are a crucial part of the gammapy API. `datasets` constitute `DL4` data - binned counts, IRFs, models and the associated likelihoods. `Datasets` from the end product of the `makers` stage, see [makers notebook](makers.ipynb), and are passed on to the `Fit` or estimator classes for modelling and fitting purposes.
To find the different types of `Dataset` that are supported see [Datasets home](../../datasets/index.rst#Types-of-supported-datasets)
## Setup
```
import numpy as np
import astropy.units as u
from astropy.time import Time
from regions import CircleSkyRegion
from astropy.coordinates import SkyCoord
from gammapy.datasets import (
MapDataset,
SpectrumDataset,
SpectrumDatasetOnOff,
Datasets,
FluxPointsDataset,
)
from gammapy.data import DataStore, GTI
from gammapy.maps import WcsGeom, RegionGeom, MapAxes, MapAxis, Map
from gammapy.modeling.models import (
SkyModel,
PowerLawSpectralModel,
FoVBackgroundModel,
)
from gammapy.estimators import FluxPoints
from gammapy.utils.scripts import make_path
%matplotlib inline
```
## MapDataset
The counts, exposure, background, masks, and IRF maps are bundled together in a data structure named `MapDataset`. While the `counts`, and `background` maps are binned in reconstructed energy and must have the same geometry, the IRF maps can have a different spatial (coarsely binned and larger) geometry and spectral range (binned in true energies). It is usually recommended that the true energy bin should be larger and more finely sampled and the reco energy bin.
### Creating an empty dataset
An empty `MapDataset` can be directly instantiated from any `WcsGeom` object:
```
energy_axis = MapAxis.from_energy_bounds(
1, 10, nbin=11, name="energy", unit="TeV"
)
geom = WcsGeom.create(
skydir=(83.63, 22.01),
axes=[energy_axis],
width=5 * u.deg,
binsz=0.05 * u.deg,
frame="icrs",
)
dataset_empty = MapDataset.create(geom=geom, name="my-dataset")
```
It is good practice to define a name for the dataset, such that you can identify it later by name. However if you define a name it **must** be unique. Now we can already print the dataset:
```
print(dataset_empty)
```
The printout shows the key summary information of the dataset, such as total counts, fit statistics, model information etc.
`MapDataset.from_geom` has additional keywords, that can be used to define the binning of the IRF related maps:
```
# choose a different true energy binning for the exposure, psf and edisp
energy_axis_true = MapAxis.from_energy_bounds(
0.1, 100, nbin=11, name="energy_true", unit="TeV", per_decade=True
)
# choose a different rad axis binning for the psf
rad_axis = MapAxis.from_bounds(0, 5, nbin=50, unit="deg", name="rad")
gti = GTI.create(0 * u.s, 1000 * u.s)
dataset_empty = MapDataset.create(
geom=geom,
energy_axis_true=energy_axis_true,
rad_axis=rad_axis,
binsz_irf=0.1,
gti=gti,
name="dataset-empty",
)
```
To see the geometry of each map, we can use:
```
dataset_empty.geoms
```
Another way to create a `MapDataset` is to just read an existing one from a FITS file:
```
dataset_cta = MapDataset.read(
"$GAMMAPY_DATA/cta-1dc-gc/cta-1dc-gc.fits.gz", name="dataset-cta"
)
print(dataset_cta)
```
## Accessing contents of a dataset
To further explore the contents of a `Dataset`, you can use e.g. `.info_dict()`
```
# For a quick info, use
dataset_cta.info_dict()
# For a quick view, use
dataset_cta.peek()
```
And access individual maps like:
```
counts_image = dataset_cta.counts.sum_over_axes()
counts_image.smooth("0.1 deg").plot()
```
Of course you can also access IRF related maps, e.g. the psf as `PSFMap`:
```
dataset_cta.psf
```
And use any method on the `PSFMap` object:
```
dataset_cta.psf.plot_containment_radius_vs_energy()
edisp_kernel = dataset_cta.edisp.get_edisp_kernel()
edisp_kernel.plot_matrix()
```
The `MapDataset` typically also contains the information on the residual hadronic background, stored in `MapDataset.background` as a map:
```
dataset_cta.background
```
As a next step we define a minimal model on the dataset using the `.models` setter:
```
model = SkyModel.create("pl", "point", name="gc")
model.spatial_model.position = SkyCoord("0d", "0d", frame="galactic")
model_bkg = FoVBackgroundModel(dataset_name="dataset-cta")
dataset_cta.models = [model, model_bkg]
```
Assigning models to datasets is covered in more detail in the [Modeling notebook](model_management.ipynb). Printing the dataset will now show the mode components:
```
print(dataset_cta)
```
Now we can use `.npred()` to get a map of the total predicted counts of the model:
```
npred = dataset_cta.npred()
npred.sum_over_axes().plot()
```
To get the predicted counts from an individual model component we can use:
```
npred_source = dataset_cta.npred_signal(model_name="gc")
npred_source.sum_over_axes().plot()
```
`MapDataset.background` contains the background map computed from the IRF. Internally it will be combined with a `FoVBackgroundModel`, to allow for adjusting the backgroun model during a fit. To get the model corrected background, one can use `dataset.npred_background()`.
```
npred_background = dataset_cta.npred_background()
npred_background.sum_over_axes().plot()
```
### Using masks
There are two masks that can be set on a `Dataset`, `mask_safe` and `mask_fit`.
- The `mask_safe` is computed during the data reduction process according to the specified selection cuts, and should not be changed by the user.
- During modelling and fitting, the user might want to additionally ignore some parts of a reduced dataset, e.g. to restrict the fit to a specific energy range or to ignore parts of the region of interest. This should be done by applying the `mask_fit`. To see details of applying masks, please refer to [Masks-for-fitting](mask_maps.ipynb#Masks-for-fitting:-mask_fit)
Both the `mask_fit` and `mask_safe` must have the safe `geom` as the `counts` and `background` maps.
```
# eg: to see the safe data range
dataset_cta.mask_safe.plot_grid();
```
In addition it is possible to define a custom `mask_fit`:
```
# To apply a mask fit - in enegy and space
region = CircleSkyRegion(SkyCoord("0d", "0d", frame="galactic"), 1.5 * u.deg)
geom = dataset_cta.counts.geom
mask_space = geom.region_mask([region])
mask_energy = geom.energy_mask(0.3 * u.TeV, 8 * u.TeV)
dataset_cta.mask_fit = mask_space & mask_energy
dataset_cta.mask_fit.plot_grid(vmin=0, vmax=1, add_cbar=True);
```
To access the energy range defined by the mask you can use:
- `dataset.energy_range_safe` : energy range definedby the `mask_safe`
- `dataset.energy_range_fit` : energy range defined by the `mask_fit`
- `dataset.energy_range` : the final energy range used in likelihood computation
These methods return two maps, with the `min` and `max` energy values at each spatial pixel
```
e_min, e_max = dataset_cta.energy_range
# To see the lower energy threshold at each point
e_min.plot(add_cbar=True)
# To see the lower energy threshold at each point
e_max.plot(add_cbar=True)
```
Just as for `Map` objects it is possible to cutout a whole `MapDataset`, which will perform the cutout for all maps in parallel.Optionally one can provide a new name to the resulting dataset:
```
cutout = dataset_cta.cutout(
position=SkyCoord("0d", "0d", frame="galactic"),
width=2 * u.deg,
name="cta-cutout",
)
cutout.counts.sum_over_axes().plot()
```
It is also possible to slice a `MapDataset` in energy:
```
sliced = dataset_cta.slice_by_energy(
energy_min=1 * u.TeV, energy_max=5 * u.TeV, name="slice-energy"
)
sliced.counts.plot_grid();
```
The same operation will be applied to all other maps contained in the datasets such as `mask_fit`:
```
sliced.mask_fit.plot_grid();
```
### Resampling datasets
It can often be useful to coarsely rebin an initially computed datasets by a specified factor. This can be done in either spatial or energy axes:
```
downsampled = dataset_cta.downsample(factor=8)
downsampled.counts.sum_over_axes().plot()
```
And the same downsampling process is possible along the energy axis:
```
downsampled_energy = dataset_cta.downsample(
factor=5, axis_name="energy", name="downsampled-energy"
)
downsampled_energy.counts.plot_grid();
```
In the printout one can see that the actual number of counts is preserved during the downsampling:
```
print(downsampled_energy, dataset_cta)
```
We can also resample the finer binned datasets to an arbitrary coarser energy binning using:
```
energy_axis_new = MapAxis.from_energy_edges([0.1, 0.3, 1, 3, 10] * u.TeV)
resampled = dataset_cta.resample_energy_axis(energy_axis=energy_axis_new)
resampled.counts.plot_grid(ncols=2);
```
To squash the whole dataset into a single energy bin there is the `.to_image()` convenience method:
```
dataset_image = dataset_cta.to_image()
dataset_image.counts.plot()
```
## SpectrumDataset
`SpectrumDataset` inherits from a `MapDataset`, and is specially adapted for 1D spectral analysis, and uses a `RegionGeom` instead of a `WcsGeom`.
A `MapDatset` can be converted to a `SpectrumDataset`, by summing the `counts` and `background` inside the `on_region`, which can then be used for classical spectral analysis. Containment correction is feasible only for circular regions.
```
region = CircleSkyRegion(
SkyCoord(0, 0, unit="deg", frame="galactic"), 0.5 * u.deg
)
spectrum_dataset = dataset_cta.to_spectrum_dataset(
region, containment_correction=True, name="spectrum-dataset"
)
# For a quick look
spectrum_dataset.peek();
```
A `MapDataset` can also be integrated over the `on_region` to create a `MapDataset` with a `RegionGeom`. Complex regions can be handled and since the full IRFs are used, containment correction is not required.
```
reg_dataset = dataset_cta.to_region_map_dataset(
region, name="region-map-dataset"
)
print(reg_dataset)
```
## FluxPointsDataset
`FluxPointsDataset` is a `Dataset` container for precomputed flux points, which can be then used in fitting.
`FluxPointsDataset` cannot be read directly, but should be read through `FluxPoints`, with an additional `SkyModel`. Similarly, `FluxPointsDataset.write` only saves the `data` component to disk.
```
flux_points = FluxPoints.read(
"$GAMMAPY_DATA/tests/spectrum/flux_points/diff_flux_points.fits"
)
model = SkyModel(spectral_model=PowerLawSpectralModel(index=2.3))
fp_dataset = FluxPointsDataset(data=flux_points, models=model)
fp_dataset.plot_spectrum()
```
The masks on `FluxPointsDataset` are `np.array` and the data is a `FluxPoints` object. The `mask_safe`, by default, masks the upper limit points
```
fp_dataset.mask_safe # Note: the mask here is simply a numpy array
fp_dataset.data # is a `FluxPoints` object
fp_dataset.data_shape() # number of data points
```
For an example of fitting `FluxPoints`, see [flux point fitting](../analysis/1D/sed_fitting.ipynb), and can be used for catalog objects, eg see [catalog notebook](catalog.ipynb)
## Datasets
`Datasets` are a collection of `Dataset` objects. They can be of the same type, or of different types, eg: mix of `FluxPointDataset`, `MapDataset` and `SpectrumDataset`.
For modelling and fitting of a list of `Dataset` objects, you can either
- Do a joint fitting of all the datasets together
- Stack the datasets together, and then fit them.
`Datasets` is a convenient tool to handle joint fitting of simultaneous datasets. As an example, please see the [joint fitting tutorial](../analysis/3D/analysis_mwl.ipynb)
To see how stacking is performed, please see [Implementation of stacking](../../datasets/index.html#stacking-multiple-datasets)
To create a `Datasets` object, pass a list of `Dataset` on init, eg
```
datasets = Datasets([dataset_empty, dataset_cta])
print(datasets)
```
If all the datasets have the same type we can also print an info table, collectiong all the information from the individual casll to `Dataset.info_dict()`:
```
datasets.info_table() # quick info of all datasets
datasets.names # unique name of each dataset
```
We can access individual datasets in `Datasets` object by name:
```
datasets["dataset-empty"] # extracts the first dataset
```
Or by index:
```
datasets[0]
```
Other list type operations work as well such as:
```
# Use python list convention to remove/add datasets, eg:
datasets.remove("dataset-empty")
datasets.names
```
Or
```
datasets.append(spectrum_dataset)
datasets.names
```
Let's create a list of spectrum datasets to illustrate some more functionality:
```
datasets = Datasets()
path = make_path("$GAMMAPY_DATA/joint-crab/spectra/hess")
for filename in path.glob("pha_*.fits"):
dataset = SpectrumDatasetOnOff.read(filename)
datasets.append(dataset)
print(datasets)
```
Now we can stack all datasets using `.stack_reduce()`:
```
stacked = datasets.stack_reduce(name="stacked")
print(stacked)
```
Or slice all datasets by a given energy range:
```
datasets_sliced = datasets.slice_by_energy(
energy_min="1 TeV", energy_max="10 TeV"
)
print(datasets_sliced.energy_ranges)
```
| true |
code
| 0.629661 | null | null | null | null |
|
# 使用dask.delayed并行化代码
使用Dask.delayed并行化简单的for循环代码。通常,这是需要转换用于Dask的函数的惟一函数。
这是一种使用dask并行化现有代码库或构建复杂系统的简单方法。
**Related Documentation**
* [Delayed documentation](https://docs.dask.org/en/latest/delayed.html)
* [Delayed screencast](https://www.youtube.com/watch?v=SHqFmynRxVU)
* [Delayed API](https://docs.dask.org/en/latest/delayed-api.html)
* [Delayed examples](https://examples.dask.org/delayed.html)
* [Delayed best practices](https://docs.dask.org/en/latest/delayed-best-practices.html)
Dask有几种并行执行代码的方法。接下来将通过创建dask.distributed.Client来使用分布式调度器。这能为我们提供一些很好的诊断。后续再详细讨论调度器。
```
from dask.distributed import Client
client = Client()
client
print(client)
```
因为本repo environment下面已经安装了Bokeh,所以可以打开上面Dashboard给出的网址,查看 diagnostic dashboard
diagnostic dashboard 的说明可以参考这里: https://docs.dask.org/en/latest/diagnostics-distributed.html
## 基础
一个简单例子,inc和add函数,sleep一会以模拟工作。
```
from time import sleep
def inc(x):
sleep(1)
return x + 1
def add(x, y):
sleep(1)
return x + y
```
使用 %%time 计时代码的执行时间
```
%%time
# This takes three seconds to run because we call each
# function sequentially, one after the other
x = inc(1)
y = inc(2)
z = add(x, y)
```
### 使用dask.delayed装饰器并行化
这两个inc调用可以并行,因为它们彼此完全独立。
使用dask.delayed函数转换inc和add函数。当我们传递参数调用delayed版本时,函数实际上还没有被调用-这就是为什么单元格执行完成得非常快的原因。相反,创建一个delayed对象,来跟踪要调用的函数和要传递给它的参数。
```
from dask import delayed
%%time
# This runs immediately, all it does is build a graph
x = delayed(inc)(1)
y = delayed(inc)(2)
z = delayed(add)(x, y)
```
这很快就结束了,因为还没有真正执行什么。
要获得结果,需要调用compute。注意,这比原始代码运行得快。
```
%%time
# This actually runs our computation using a local thread pool
z.compute()
```
## 刚才发生了什么?
z对象是一个delayed对象。该对象包含计算最终结果所需的所有内容,包括对所有所需函数的引用、它们的输入以及彼此之间的关系。可以像上面那样使用.compute()计算结果,也可以使用.visualize()可视化该值的任务图。
```
z
# Look at the task graph for `z`
z.visualize()
```
注意,这包括前面提到的函数名,以及inc函数输出到add输入的逻辑流。
在 diagnostic dashboard 上每行对应一个thread,,可以看到,两个inc分布在两行,执行完之后,执行了add,总共花费1+1.01 s
### 需要考虑的一些问题
- 为什么从3s到2s?为什么不能并行化到1s呢?
- 如果inc和add函数没有包含sleep(1)会发生什么?dask还能加速这段代码吗?
- 如果有多个输出,或者也想访问x或y呢?
## 并行化for循环
For循环是最常见的想要并行化的东西之一。使用dask.delayed on inc和sum来并行化下面的计算:
```
data = [1, 2, 3, 4, 5, 6, 7, 8]
%%time
# Sequential code
results = []
for x in data:
y = inc(x)
results.append(y)
total = sum(results)
total
%%time
results = []
for x in data:
y = delayed(inc)(x)
results.append(y)
total = delayed(sum)(results)
print("Before computing:", total) # Let's see what type of thing total is
result = total.compute()
print("After computing :", result) # After it's computed
```
## Exercise: 将for循环代码与控制流并行化
通常我们只想delay一部分函数,立即运行另一些函数。当这些函数速度很快时,这一点特别有用,可以帮助我们确定应该调用哪些其他速度较慢的函数。在使用dask.delayed时,通常需要考虑延迟或不延迟的决定。
在下面的例子中,遍历一个输入列表。如果输入是偶数,则调用inc。如果输入是奇数,那么要调用double。为了继续我们的图形构建Python代码,必须立即(而不是延迟)做出调用inc或double的is_even决定。
```
def double(x):
sleep(1)
return 2 * x
def is_even(x):
return not x % 2
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
%%time
# Sequential code
results = []
for x in data:
if is_even(x):
y = double(x)
else:
y = inc(x)
results.append(y)
total = sum(results)
print(total)
results = []
for x in data:
# 判断的语句是需要立即做出决定的
if is_even(x): # even
y = delayed(double)(x)
else: # odd
y = delayed(inc)(x)
results.append(y)
total = delayed(sum)(results)
%time total.compute()
total.visualize()
```
如果不求和,也是可以直接对list执行delayed计算的,一样的。
```
results = []
for x in data:
# 判断的语句是需要立即做出决定的
if is_even(x): # even
y = delayed(double)(x)
else: # odd
y = delayed(inc)(x)
results.append(y)
%time delayed(results).compute()
```
## 复杂函数能delay么?
假如有一个函数是别人写的,通过pip或者conda安装的,函数本身还有很多其他调用,且没有delay包装的,那能不能至少在最外层加delay?
```
def funcs(a, b):
c = func1(a)
d = func2(b)
e = c * func3(d)
f = func4(c) * e
return f
def func1(v1):
sleep(0.5)
return v1**2
def func2(v2):
sleep(0.5)
return v2/2
def func3(v3):
sleep(0.5)
return v3*3+1
def func4(v4):
sleep(0.5)
return v4*2
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
%%time
# Sequential code
results = []
for x,y in zip(data[1:],data[:-1]):
z = funcs(x,y)
results.append(z)
total = sum(results)
print(total)
# Sequential code
results = []
for x,y in zip(data[1:],data[:-1]):
z = delayed(funcs)(x,y)
results.append(z)
total = delayed(sum)(results)
print(total)
%time total.compute()
```
可以看到还是会加速的,通过 查看 diagnostic dashboard,可以进一步查看并行的执行情况。
```
client.close()
```
离开前,关闭之前打开的client。
| true |
code
| 0.299925 | null | null | null | null |
|
⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠
# Disclaimer
👮🚨This notebook is sort of like my personal notes on this subject. It will be changed and updated whenever I have time to work on it. This is not meant to replace a thorough fluid substitution workflow. The intent here is make the major assumptions underlying the process of evaluating the affect of fluid fill on seismic response a little more clear, as well as provide references and background in literature for further study.🚨
At some point I will probably generalize this better so it can be used with real curves. For now it creates some fake blocked logs you can edit just to get a feel for how fluid sub works and how the different fluid fills might look in seismic. Also, currently the rocks are monomineralic.
#### Important Note:
The proper conditioning of logs, calibration of water saturations, reservoir selection for substituion, and rock and mineral parameter selection and calibration are extremely important to the reliability of a fluid substitution's output. These are good candidates for additional tutorials.
This tutorial is focused on the basic workflow from the geophysical perspective and therefore assumes the labor intensive petrophysical work mentioned above is both completed and reliable.
##### Notes for future:
* Incorporate a tuning section
* Put the whole thing in a function and see if I can get interact working so I can just use sliders to change parameters
* Generalize so real .las files can be loaded
* Complete the implementation of the B&W fluid property equations
* Fix a few of the hard-coded parts
* ~~Figure out why fill_betweenx isn't working~~
##### Come up and ask me questions on 7 if anything appears to be amiss! -Thomas
⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠ ⚠
[](https://mybinder.org/v2/gh/tccw/geotools/master?filepath=tutorials%2FFluidSubstitution.ipynb)
```
from collections import namedtuple
from scipy.stats import linregress
from matplotlib.gridspec import GridSpec
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import bruges as b
from IPython.display import HTML
%matplotlib inline
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
<font size="6" color="red">The raw code for this IPython notebook is by default hidden for easier reading.
To toggle on/off the raw code, click <a href="javascript:code_toggle()">here</a>.</font>''')
```
# Porosity and Saturation effects on AVO
### Gassmann's Equations
Gassmann's equations (seen below) describes how the bulk modulus (ratio of pressure change to volume change) of a saturated rock changes as the saturating fluid changes. It provides a useful means for modeling how the seismic response of a formation may change for different filling fluids.
For a discussion of the origin and derivation of Gassmann's equations, see Berryman, 2000 (https://doi.org/10.1190/1.1444667)
$$\textbf{Gassmann Equations}$$
$$\frac{K_{sat}}{K_{mineral} - K_{sat}} = \frac{K_{dry}}{K_{mineral} - K_{dry}} + \frac{K_{fluid}}{\phi(K_{mineral} - K_{fluid})}$$
$$\mu_{sat} = \mu_{dry}$$
$K_{dry} = \text{Dry rock bulk modulus}$
$K_{mineral} = \text{Mineral bulk modulus}$
$K_{sat} = \text{Saturated rock bulk modulus}$
$K_{fluid} = \text{Fluid bulk modulus}$
$\mu_{sat} = \text{Shear modulus of the saturated rock}$
$\mu_{dry} = \text{Shear modulus of the dry rock}$
### Assumptions
1. Porous material is isotropic, elastic, monomineralic, and homogeneous
2. Pore sapce is well connected and in pressure equilibrium
3. Medium is a closed system with no pore fluid movement across boundaries
4. No checmical interaction between fluids and rock frame (i.e. no diagenetic processes)
5. Frequency effects are negligible when considering the measurements. Gassmann's equations are valid only for seismic frequencies (<100 Hz from Mavko, 1998).
These assumptions are often violated in real reservoirs. However, Gassmann's model is still generally the preferred model as it can be easily parameterized. A number of publications exist which suggest ways to modify inputs or assumptions to make these relationships more applicable to more variable rocks. A good general discussion of this can be found in Rob Simm's 2007 article "Practical Gassmann fluid substitution in sand/shale sequences [DOI: 10.3997//1365-2387.2007030](http://dreamcell-dev.co.uk/rpa/papers_downloads/RPA_simm_2007.pdf).
Below we will look at the Avseth et. al, 2006 fluid substitution workflow, which is used in this notebook.
#### Gassmann fluid substitution recipe from Avseth, 2006$^{[1]}$
$\textbf{Step 1:}$ Extract the dynamic bulk and shear moduli from $V_{p}^{(1)}$, $V_{s}^{(1)}$ , and $\rho^{(1)}$:
$K^{(1)}\ =\ \rho((V_{p}^{(1)})^2 - \frac{4}{3}(V_{s}^{(1)})^2)\\ \mu^{(1)}\ =\ \rho(V_{s}^{(1)})^2$
$\textbf{Step 2:}$ Apply Hassmann's relation to transform the bulk modulus:
$\frac{K_{sat}^{(2)}}{K_{mineral}\ -\ K_{sat}^{(2)}}\ -\ \frac{K_{fluid}^{(2)}}{\phi(K_{mineral}\ -\ K_{fluid}^{(2)})}\ =\ \frac{K_{sat}^{(1)}}{K_{mineral}\ -\ K_{sat}^{(1)}}\ -\ \frac{K_{fluid}^{(1)}}{\phi(K_{mineral}\ -\ K_{fluid}^{(1)})}$
$\textbf{Step 3:}$ Leave the shear modulus unchanged:
$\mu_{sat}^{(1)} = \mu_{sat}^{(2)}$
$\textbf{Step 4:}$ Remember to correct the bulk density for the fluid change:
$\rho^{(2)} = \rho^{(1)} + \phi(\rho_{fluid}^{(2)} - \rho_{fluid}^{(1)})$
$\textbf{Step 5:}$ Reassemble the velocities:
$V_p^{(2)} = \sqrt{\frac{K_{sat}^{(2)} + \frac{4}{3} \mu_{sat}^{(2)}}{\rho^{(2)}}}$
$V_s^{(2)} = \sqrt{\frac{\mu_{sat}^{(2)}}{\rho^{(2)}}}$
Below is a basic, blocked log example of Gassmann fluid substitution to help explore the affects of different fluids on the seismic response.
$^{[1]}$Avseth, Per; Mukerji, Tapan; Mavko, Gary. Quantitative Seismic Interpretation: Applying Rock Physics Tools to Reduce Interpretation Risk (Kindle Locations 582-584). Cambridge University Press. Kindle Edition.
```
HTML('<font color="red">The B&W implementation is incomplete and needs more testing for verification</font>')
```
### Batzle and Wang fluid calculations
The most common, and likely most useful, method for calcualting the properties of fluids of varying composition, temperature, and pressure are emperical fluid equations from Batzle & Wang 1992.
These functions take pressure in MPa and temperature in Centigrade. It outputs density in g/cc, velocity in m/s, and bulk modulus (K) in GPa.
$\textbf{Equations for dead oil:}$
$API = \frac{141.5}{\rho_0} - 131.5$
$\rho_P = \rho_0 + (0.00277P - 1.71 \times 10^{-7}P^3)(\rho_0 - 1.15)^2 + 3.49 \times 10^{-4}P$
$\rho = \rho_P / [0.972 + 3.81 \times 10^{-4}(T + 17.78)^{1.175}]$
$V = 15450(77.1 + API)^{-1/2} - 3.7T + 4.64P + 0.0115(0.36API^{1/2} - 1)TP$
```
def bwOil(temp,pressure,API, gasGravity,live = False):
# Pressue in MPa, Temp in C
P = pressure
T = temp
G = gasGravity
rho0 = 141.5 / (API + 131.5)
rhoP = rho0 + (0.00277*P - 1.71e-7 * P**3)*(rho0 - 1.15)**2 + 3.49e-4 * P
#Rg = 0.02123*G*(P*np.exp(4.072/rho0 - 0.00377*T))**1.205 # Eqtn 21a
Rg = 2.03*G*(P*np.exp(0.02878*API - 0.00377*T))**1.205 # Eqtn 21b
Bo = 0.972 + 0.00038*(2.4 * Rg * np.sqrt(G/rho0) + T + 17.8)**1.175 # Eqtn 23
rhoPprime = (rho0/Bo) * (1 + 0.001*Rg)**(-1) # Eqtn 22
if live == False:
rho = rhoP / (0.972 + 3.81e-4 * (T + 17.78)**1.175) #etqn 20
vp = 15450*(77.1 + API)**(-1/2) - 3.7*T + 4.64*P + 0.0115*(0.36*API**(1/2) - 1)*T*P
elif live == True:
rho = (rho0 + 0.0012*G*Rg)/Bo
vp = 2096 * np.sqrt(rhoPprime/(2.6 - rhoPprime)
) - 3.7*T + 4.64*P + 0.0115*(4.12 * (1.08 * rhoPprime**-1 - 1) - 1)*T*P
K = (rho * vp**2)/1e6
return K, rho * 1000
def bwBrine(temp,pressure,salinity):
'''
Pressue in MPa, Temp in C, salinity is weight fraction (i.e. ppm/1e6)
The velocity is not agreeing with the FPE from CREWES but I can't figure out why
'''
S = salinity
P = pressure
T = temp
#eqtn 27 - 29
rhow = 1 + 1e-6 * (-80*T - 3.3*T**2 + 0.00175*T**3 + 489*P -
2*T*P + 0.016*T**2 * P - 1.3e-5 * T**3 * P -
0.333*P**2 - 0.002*T*P**2)
rhobr = rhow + S*(0.668 + 0.44*S + 1e-6 * (300*P - 2400*P*S +
T*(80 + 3*T - 3300*S - 13*P + 47*P*S)))
w = np.array([[1402.85, 1.524, 3.437e-3, -1.197e-5],
[4.871, -0.0111, 1.739e-4, -1.628e-6],
[-0.04783, 2.747e-4, -2.135e-6, 1.237e-8],
[1.487e-4, -6.503e-7, -1.455e-8, 1.327e-10],
[-2.197e-7, 7.987e-10, 5.230e-11, -4.614e-13]], dtype = float)
vpW = np.sum(w[i][j]*np.power(P,[i])*np.power(T,[j]) for i in range(0,4) for j in range(0,3))
vpB = vpW + S*(1170 - 9.6*T + 0.055*T**2 - 8.5e-5 * T**3 + 2.6*P
- 0.0029*T*P - 0.0476*P**2)+ S**1.5 * (780 -10*P + 0.16*P**2) - 820*S**2
K = (rhobr * vpB**2)/1e6
rhobr = np.array(rhobr)
vpB = np.array(vpB)
K = np.array(K)
return K, rhobr * 1000
```
## Input data
```
# Pressure (P), Temperature (T), API, Gas Gravity (G), Salinity weight fraction (S)
# Deepwater GOM pressures and temperatures
P = 100 # MPa
T = 85.5 # degrees C
API = 35
G = 0.6
S = 0.088 # ppm/1e6
# In situ parameters are GOM clean sand 100% brine saturated values
vpInSitu = 3550. # m/s
vsInSitu = 1900. # m/s
rhobInSitu = 2240. # kg/m^3
top_depth = 400
base_depth = 500
resThickness = 100. # thickness in meters
KflInitial, rhoflInitial = bwBrine(P,T,0.025) # Inital brine (this was taken from some GOM well data)
KflBrine, rhoflBrine = bwBrine(P,T,S)
KflOil, rhoflOil = bwOil(P,T,API,G,live = False)
KflGas, rhoflGas = 0.374 * 1e9, 338 # gas Gpa (convert to pascals)
Kmineral = 37.0 * 1e9 # Gpa Quartz from tables (convert to pascals 1e9)
# Convert bulk Modluii to pascals from GPa
KflInitial = KflInitial * 1e9 # convert to pascals
KflBrine = KflBrine * 1e9
KflOil = KflOil * 1e9
# encasing rock properties
vpEncase, vsEncase, rhobEncase = 3300.,1500.,2400.
phi = np.round((2650 - rhobInSitu)/(2650 - rhoflInitial),2) # SS density porosity
bwOil(P,T,API,G,live = False)
bwBrine(P,T,0.025)
```
#### Make the wavelet (currently only supports Ricker and Ormsby wavelets)
* Here I am making the sample 1 ms even though most seismic is 2 ms
* This allows me to make a smooth synthetic without having to interpolate later
```
# wavelet parameters
f = 35 #frequency of ricker wavelet
f_arr = [8,12,50,65]
duration = 0.128 # length of wavelet in seconds
dt = 0.001 # size of time sample for
dz = 1 # for later (should probably be located somewhere else)
wvlt, t_basis = b.filters.ricker(duration, dt, f, return_t=True)
wvlt_orm, t_basis_orm = b.filters.ormsby(duration, dt, f_arr,return_t=True)
sns.set_style(style="ticks")
plt.figure(figsize=(10,7))
plt.plot(t_basis * 1e3, wvlt_orm, label = f'Ormsby $f$: {f_arr}', linewidth=4)
plt.plot(t_basis * 1e3, wvlt, label = f'Ricker peak $f$: {f}', linewidth=4)
plt.xlabel('Time (ms)', size=13)
plt.ylabel('Amplitude', size=13)
plt.title('Two possible wavelets we can use for the synthetic angle gathers', size=17)
plt.xlim(t_basis.min() * 1e3,t_basis.max() * 1e3)
plt.grid(alpha=0.3)
plt.legend()
```
#### Create in situ block curves
```
shape = (1000,)
block_vp, block_vs, block_rhob = np.zeros(shape), np.zeros(shape), np.zeros(shape)
block_vp[:], block_vs[:], block_rhob[:] = vpEncase, vsEncase, rhobEncase
block_vp[top_depth:base_depth], block_vs[top_depth:base_depth], block_rhob[top_depth:base_depth] = vpInSitu, vsInSitu, rhobInSitu
```
#### Naive fluid sub from Avseth, 2006
```
rhofl = np.array([rhoflInitial,rhoflBrine, rhoflOil, rhoflGas])
Kfls = np.array([KflInitial,KflBrine, KflOil, KflGas])
names = ['Initial', 'Brine', 'Oil', 'Gas']
# Order is initial fluid, user defined brine, user defined oil, user defined gas
subs_depth = [b.rockphysics.avseth_fluidsub(
block_vp,block_vs,block_rhob,phi,rhofl[0], rhofl[i],
Kmineral,Kfls[0], Kfls[i]) for i in range(len(Kfls))]
subs_depth = {k:v for k,v in zip(names,subs_depth)}
# Resubbing in the old velocities for the encasing rock.
# There must be a better way to approach this. Will have to think about it more later.
for key in names:
getattr(subs_depth[key],'Vp')[:top_depth] = vpEncase
getattr(subs_depth[key],'Vp')[base_depth:] = vpEncase
getattr(subs_depth[key],'Vs')[:top_depth] = vsEncase
getattr(subs_depth[key],'Vs')[base_depth:] = vsEncase
getattr(subs_depth[key],'rho')[:top_depth] = rhobEncase
getattr(subs_depth[key],'rho')[base_depth:] = rhobEncase
```
### Convert all the curves from depth to time
```
curves=['Vp', 'Vs', 'rho']
twt_tmp = [b.transform.time_to_depth(
getattr(subs_depth[n],c),getattr(subs_depth[n],'Vp'), dt, dz) for n in names for c in curves]
```
### Do some organization to make it easier to plot
* Make sure to use the updated Vp curve for each fluid subbed case for correct timing
* Create the different TWT arrays for plotting
```
twt_tmp_composite = [twt_tmp[x:x+3] for x in range(0, len(twt_tmp),3)]
twt_curves = namedtuple('TWTResults',('Vp','Vs','rho'))
subs_twt = [twt_curves(*twt_tmp_composite[i]) for i in range(len(names))]
subs_twt = {k:v for k,v in zip(names,subs_twt)}
twts = {key:np.linspace(0,len(getattr(subs_twt[key],'Vp')) * dt,
len(getattr(subs_twt[key],'Vp'))) for key in names}
```
### Make the pre-stack synthetics
```
theta = np.arange(0,51,1)
reflectivity = {key:b.reflection.reflectivity(getattr(subs_twt[key],'Vp'),
getattr(subs_twt[key],'Vs'),
getattr(subs_twt[key],'rho'),theta=theta) for key in names}
prstk_gaths = {key:np.apply_along_axis(lambda x: np.convolve(wvlt, x, mode='same'),axis=1,arr=reflectivity[key]) for key in names}
# Get the index of the top of the reservoir in time
top_twt_index = np.argmax(reflectivity['Initial']!=0)
```
#### Calc intercept and gradient
* I am only going to use the first 30 degrees of the reflectivity series as beyond ~30 degrees reflectivity stops behaving linearly in reflectivity vs. $sin^2(\theta)$ space, therefore a linear approximation (like the one used for gradient / intercept) is not a hepful regression.
```
theta_grad = 30
refl = {k:reflectivity[k][:theta_grad,top_twt_index] for k in names}
sintheta = np.sin(np.radians(np.arange(0, theta_grad)))**2
int_grad = {k:linregress(sintheta,refl[k][:]) for k in names}
```
### Plot everything up (the hardest part!)
```
sns.set_style('ticks')
# Some useful stuff to initialize
depth = np.linspace(0,1000,1000)
gain = 45
colors=['k','b','g','r']
titles = [r'Vp $\frac{km}{s^2}$', r'Vs $\frac{km}{s^2}$', r'Density $\frac{kg}{m^3}$',
'Angle Gather (Initial)', 'Angle Gather (100% Brine)', 'Angle Gather (100% Oil)', 'Angle Gather (100% Gas)']
curve_buffer_twt = 0.1
def format_axes(fig):
titles = [r'Vp $\frac{km}{s^2}$', r'Vs $\frac{km}{s^2}$', r'Density $\frac{kg}{m^3}$',
'Angle Gather (Initial)', 'Angle Gather (100% Brine)', 'Angle Gather (100% Oil)',
'Angle Gather (100% Gas)', 'Zoeppritz Reflectivity vs Angle (Upper Interface)', 'Intercept vs. Gradient Crossplot (Upper Interface)']
axes_label_size=12
for i, ax in enumerate(fig.axes):
ax.set_title(titles[i],y = 1.01)
ax.tick_params(labelbottom=True, labelleft=True)
ax.grid(alpha=0.5, linestyle='--')
# labels
for ax in (ax4,ax5,ax6,ax7):
ax.set_xlabel(r'Angle $(\theta)$', size = axes_label_size)
ax1.set_ylabel('TWT (s)', size=axes_label_size)
ax8.set_ylabel('Reflectivity', size=axes_label_size)
ax8.set_xlabel(r'Angle $(\theta)$', size=axes_label_size)
ax9.set_ylabel('Gradient $(G)$', size=axes_label_size)
ax9.set_xlabel('Intercept $(R0)$', size=axes_label_size)
# limits
ax1.set_ylim(0.6,0.9)
ax3.set_xlim(1.65,2.65)
ax8.set_xlim(0,theta.max())
ax9.set_xlim(np.real(getattr(int_grad['Initial'],'intercept')) - 0.2, np.real(getattr(int_grad['Initial'],'intercept')) + 0.2)
ax9.set_ylim(np.real(getattr(int_grad['Initial'],'slope')) - 0.2, np.real(getattr(int_grad['Initial'],'slope')) + 0.2)
ax1.invert_yaxis()
fig = plt.figure(constrained_layout=True, figsize=(17,14))
gs = GridSpec(nrows=4, ncols=7, figure=fig)
ax1 = fig.add_subplot(gs[:2, 0])
ax2 = fig.add_subplot(gs[:2, 1], sharey=ax1)
ax3 = fig.add_subplot(gs[:2, 2], sharey=ax1)
ax4 = fig.add_subplot(gs[:2, 3], sharey=ax1)
ax5 = fig.add_subplot(gs[:2, 4], sharey=ax1, sharex=ax4)
ax6 = fig.add_subplot(gs[:2, 5], sharey=ax1, sharex=ax4)
ax7 = fig.add_subplot(gs[:2, 6], sharey=ax1, sharex=ax4)
ax8 = fig.add_subplot(gs[2:,:4])
ax9 = fig.add_subplot(gs[2:,4:])
for key,c in zip(names, colors):
ax1.plot(getattr(subs_twt[key],'Vp') / 1e3,twts[key], label=f'100% {key}', color=c)
ax2.plot(getattr(subs_twt[key],'Vs') / 1e3,twts[key], label=f'100% {key}', color=c)
ax3.plot(getattr(subs_twt[key],'rho') / 1e3,twts[key], label=f'100% {key}', color=c)
for key,ax in zip(names,(ax4,ax5,ax6,ax7)):
for i in range(0,theta.max(),3):
ax.plot(np.real(prstk_gaths[key][i,:] * gain + i), twts[key][:-1],color='k')
ax.fill_betweenx(twts[key][:-1], i, np.real(prstk_gaths[key][i,:]) * gain + i, color='k',alpha=0.5,
where=np.real(prstk_gaths[key][i,:]) * gain + i > i, interpolate=True)
ax.fill_betweenx(twts[key][:-1], i, np.real(prstk_gaths[key][i,:]) * gain + i, color='r',alpha=0.5,
where=np.real(prstk_gaths[key][i,:]) * gain + i < i, interpolate=True)
# np.argmax(reflectivity['Initial']!=0)
for k,c in zip(names,colors):
ax8.plot(np.real(reflectivity[k][:,top_twt_index]), color=c, label=f'100% {k}')
ax9.scatter(np.real(getattr(int_grad[k],'intercept')),np.real(getattr(int_grad[k],'slope')), color=c,label=f'100% {k}')
ax8.axhline(0, color='k', alpha=0.5)
ax9.axhline(color='k')
ax9.axvline(color='k')
ax1.legend()
ax8.legend()
ax9.legend()
fig.suptitle('Gassmann Fluid Substitution Overview', size = 20, y = 1)
format_axes(fig)
# Uncomment the line below to save the figure. You may need to change the filepath.
# plt.savefig('GassmannFluidSubOverview.png', dpi=350,bbox_inches='tight')
plt.show()
```
| true |
code
| 0.433981 | null | null | null | null |
|
### Converting a `Functional` model to `Sequential` model during `Transfare` Learning.
* This notebook will walk through on how to convert to `Sequential` from `Functional` API using Transfare leaning.
```
import tensorflow as tf
```
### Data Argumentation using `keras api`
```
from tensorflow.keras.preprocessing.image import img_to_array, load_img, ImageDataGenerator
train_path = "bees_v_ant/train"
validation_path = "bees_v_ant/validation"
test_path = '.'
test_gen = ImageDataGenerator(rescale=1./255)
valid_gen = ImageDataGenerator(rescale=1./255)
train_gen = ImageDataGenerator(rescale=1./255)
test_data = test_gen.flow_from_directory(
test_path,
target_size=(224, 224),
classes=["test"]
)
train_data = train_gen.flow_from_directory(
train_path,
target_size=(224, 224),
classes=["ant", 'bee'],
class_mode='categorical',
batch_size=8,
)
valid_data = valid_gen.flow_from_directory(
validation_path,
target_size=(224, 224),
classes=["ant", 'bee'],
class_mode='categorical',
batch_size=8,
)
test_data[0]
```
> Select the `base` model. `VGG16` with 1000 [class names](https://image-net.org/challenges/LSVRC/2014/browse-synsets)
```
vgg_model = tf.keras.applications.vgg16.VGG16()
print(type(vgg_model)) # Functional Model
vgg_model.summary()
```
### `VGG16` model achitecture
<p align="center">
<img src="https://miro.medium.com/max/237/1*Z5jNPTu8Xexp9rRs7RNKbA.png"/>
</p>
It can be ploted using the `plot_model` function from keras as follows:
```python
from keras.applications.vgg16 import VGG16
from keras.utils import plot_model
model = VGG16()
plot_model(model)
```
> Create a ``sequential`` model instance
```
model = tf.keras.Sequential()
```
> Loop through all the `base` model layers and add them to the created `model` model except the output layer.
```
for layer in vgg_model.layers[0:-1]:
model.add(layer)
model.summary()
```
> Set `trainable=False` for all the model layers, this is because we don't want to train them again.
```
for layer in model.layers:
layer.trainable = False
model.summary()
```
> Add the `last` layers for classification with the number of `classes` that we have.
```
output_layer = tf.keras.layers.Dense(2, activation='softmax')
model.add(output_layer)
model.summary()
```
> Compile the ``model``.
```
model.compile(
loss = tf.keras.losses.categorical_crossentropy,
optimizer = tf.keras.optimizers.Adam(),
metrics = ['acc']
)
```
> Train the model with your own data by calling `model.fit()`
```
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_loss',
patience=2,
verbose=0,
)
history = model.fit(
train_data,
epochs = 10,
batch_size = 8,
validation_data = valid_data,
verbose = 1,
callbacks=[early_stopping]
)
```
> Plotting the model `history`.
```
import pandas as pd
from matplotlib import pyplot as plt
import numpy as np
pd.DataFrame(history.history).plot(title="Model History", xlabel="epochs")
plt.show()
```
> Evaluating the `model`.
```
model.evaluate(test_data, verbose=1)
```
> Making ``predictions``.
```
predictions = tf.argmax(model.predict(test_data), axis=1).numpy()
predictions
class_names = np.array(["bee", "ant"])
images = [image for image in test_data[0][0]]
def plot_predictions_images(images_and_classes, labels_pred, cols=5):
rows = 3
fig = plt.figure()
fig.set_size_inches(cols * 2, rows * 2)
for i, (image, label_pred) in enumerate(zip(images_and_classes, labels_pred)):
plt.subplot(rows, cols, i + 1)
plt.axis('off')
plt.imshow(image)
plt.title(class_names[label_pred], color ='g', fontsize=16 )
plot_predictions_images(images[:], predictions[:])
```
| true |
code
| 0.827462 | null | null | null | null |
|
# Word2Vec
**Learning Objectives**
1. Learn how to build a Word2Vec model
2. Prepare training data for Word2Vec
3. Train a Word2Vec model. In this lab we will build a Skip Gram Model
4. Learn how to visualize embeddings and analyze them using the Embedding Projector
## Introduction
Word2Vec is not a singular algorithm, rather, it is a family of model architectures and optimizations that can be used to learn word embeddings from large datasets. Embeddings learned through Word2Vec have proven to be successful on a variety of downstream natural language processing tasks.
Note: This notebook is based on [Efficient Estimation of Word Representations in Vector Space](https://arxiv.org/pdf/1301.3781.pdf) and
[Distributed
Representations of Words and Phrases and their Compositionality](https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf). It is not an exact implementation of the papers. Rather, it is intended to illustrate the key ideas.
These papers proposed two methods for learning representations of words:
* **Continuous Bag-of-Words Model** which predicts the middle word based on surrounding context words. The context consists of a few words before and after the current (middle) word. This architecture is called a bag-of-words model as the order of words in the context is not important.
* **Continuous Skip-gram Model** which predict words within a certain range before and after the current word in the same sentence.
You'll use the skip-gram approach in this notebook. First, you'll explore skip-grams and other concepts using a single sentence for illustration. Next, you'll train your own Word2Vec model on a small dataset. This notebook also contains code to export the trained embeddings and visualize them in the [TensorFlow Embedding Projector](http://projector.tensorflow.org/).
## Skip-gram and Negative Sampling
While a bag-of-words model predicts a word given the neighboring context, a skip-gram model predicts the context (or neighbors) of a word, given the word itself. The model is trained on skip-grams, which are n-grams that allow tokens to be skipped (see the diagram below for an example). The context of a word can be represented through a set of skip-gram pairs of `(target_word, context_word)` where `context_word` appears in the neighboring context of `target_word`.
Consider the following sentence of 8 words.
> The wide road shimmered in the hot sun.
The context words for each of the 8 words of this sentence are defined by a window size. The window size determines the span of words on either side of a `target_word` that can be considered `context word`. Take a look at this table of skip-grams for target words based on different window sizes.
Note: For this lab, a window size of *n* implies n words on each side with a total window span of 2*n+1 words across a word.

The training objective of the skip-gram model is to maximize the probability of predicting context words given the target word. For a sequence of words *w<sub>1</sub>, w<sub>2</sub>, ... w<sub>T</sub>*, the objective can be written as the average log probability

where `c` is the size of the training context. The basic skip-gram formulation defines this probability using the softmax function.

where *v* and *v<sup>'<sup>* are target and context vector representations of words and *W* is vocabulary size. Here *v<sub>0* and *v<sub>1* are model parameters which are updated by gradient descent.
Computing the denominator of this formulation involves performing a full softmax over the entire vocabulary words which is often large (10<sup>5</sup>-10<sup>7</sup>) terms.
The [Noise Contrastive Estimation](https://www.tensorflow.org/api_docs/python/tf/nn/nce_loss) loss function is an efficient approximation for a full softmax. With an objective to learn word embeddings instead of modelling the word distribution, NCE loss can be [simplified](https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf) to use negative sampling.
The simplified negative sampling objective for a target word is to distinguish the context word from *num_ns* negative samples drawn from noise distribution *P<sub>n</sub>(w)* of words. More precisely, an efficient approximation of full softmax over the vocabulary is, for a skip-gram pair, to pose the loss for a target word as a classification problem between the context word and *num_ns* negative samples.
A negative sample is defined as a (target_word, context_word) pair such that the context_word does not appear in the `window_size` neighborhood of the target_word. For the example sentence, these are few potential negative samples (when `window_size` is 2).
```
(hot, shimmered)
(wide, hot)
(wide, sun)
```
In the next section, you'll generate skip-grams and negative samples for a single sentence. You'll also learn about subsampling techniques and train a classification model for positive and negative training examples later in the tutorial.
## Setup
```
import io
import itertools
import os
import re
import string
import numpy as np
import tensorflow as tf
import tqdm
from tensorflow.keras import Model, Sequential
from tensorflow.keras.layers import (
Activation,
Dense,
Dot,
Embedding,
Flatten,
GlobalAveragePooling1D,
Reshape,
)
from tensorflow.keras.layers.experimental.preprocessing import TextVectorization
```
Please check your tensorflow version using the cell below.
```
# Show the currently installed version of TensorFlow you should be using TF 2.6
print("TensorFlow version: ", tf.version.VERSION)
# Change below if necessary
PROJECT = !gcloud config get-value project # noqa: E999
PROJECT = PROJECT[0]
BUCKET = PROJECT
REGION = "us-central1"
OUTDIR = f"gs://{BUCKET}/text_models"
%env PROJECT=$PROJECT
%env BUCKET=$BUCKET
%env REGION=$REGION
%env OUTDIR=$OUTDIR
SEED = 42
AUTOTUNE = tf.data.experimental.AUTOTUNE
```
### Vectorize an example sentence
Consider the following sentence:
`The wide road shimmered in the hot sun.`
Tokenize the sentence:
```
sentence = "The wide road shimmered in the hot sun"
tokens = list(sentence.lower().split())
print(len(tokens))
```
Create a vocabulary to save mappings from tokens to integer indices.
```
vocab, index = {}, 1 # start indexing from 1
vocab["<pad>"] = 0 # add a padding token
for token in tokens:
if token not in vocab:
vocab[token] = index
index += 1
vocab_size = len(vocab)
print(vocab)
```
Create an inverse vocabulary to save mappings from integer indices to tokens.
```
inverse_vocab = {index: token for token, index in vocab.items()}
print(inverse_vocab)
```
Vectorize your sentence.
```
example_sequence = [vocab[word] for word in tokens]
print(example_sequence)
```
### Generate skip-grams from one sentence
The `tf.keras.preprocessing.sequence` module provides useful functions that simplify data preparation for Word2Vec. You can use the `tf.keras.preprocessing.sequence.skipgrams` to generate skip-gram pairs from the `example_sequence` with a given `window_size` from tokens in the range `[0, vocab_size)`.
Note: `negative_samples` is set to `0` here as batching negative samples generated by this function requires a bit of code. You will use another function to perform negative sampling in the next section.
```
window_size = 2
positive_skip_grams, _ = tf.keras.preprocessing.sequence.skipgrams(
example_sequence,
vocabulary_size=vocab_size,
window_size=window_size,
negative_samples=0,
)
print(len(positive_skip_grams))
```
Take a look at few positive skip-grams.
```
for target, context in positive_skip_grams[:5]:
print(
f"({target}, {context}): ({inverse_vocab[target]}, {inverse_vocab[context]})"
)
```
### Negative sampling for one skip-gram
The `skipgrams` function returns all positive skip-gram pairs by sliding over a given window span. To produce additional skip-gram pairs that would serve as negative samples for training, you need to sample random words from the vocabulary. Use the `tf.random.log_uniform_candidate_sampler` function to sample `num_ns` number of negative samples for a given target word in a window. You can call the funtion on one skip-grams's target word and pass the context word as true class to exclude it from being sampled.
Key point: *num_ns* (number of negative samples per positive context word) between [5, 20] is [shown to work](https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf) best for smaller datasets, while *num_ns* between [2,5] suffices for larger datasets.
```
# Get target and context words for one positive skip-gram.
target_word, context_word = positive_skip_grams[0]
# Set the number of negative samples per positive context.
num_ns = 4
context_class = tf.reshape(tf.constant(context_word, dtype="int64"), (1, 1))
negative_sampling_candidates, _, _ = tf.random.log_uniform_candidate_sampler(
true_classes=context_class, # class that should be sampled as 'positive'
num_true=1, # each positive skip-gram has 1 positive context class
num_sampled=num_ns, # number of negative context words to sample
unique=True, # all the negative samples should be unique
range_max=vocab_size, # pick index of the samples from [0, vocab_size]
seed=SEED, # seed for reproducibility
name="negative_sampling", # name of this operation
)
print(negative_sampling_candidates)
print([inverse_vocab[index.numpy()] for index in negative_sampling_candidates])
```
### Construct one training example
For a given positive `(target_word, context_word)` skip-gram, you now also have `num_ns` negative sampled context words that do not appear in the window size neighborhood of `target_word`. Batch the `1` positive `context_word` and `num_ns` negative context words into one tensor. This produces a set of positive skip-grams (labelled as `1`) and negative samples (labelled as `0`) for each target word.
```
# Add a dimension so you can use concatenation (on the next step).
negative_sampling_candidates = tf.expand_dims(negative_sampling_candidates, 1)
# Concat positive context word with negative sampled words.
context = tf.concat([context_class, negative_sampling_candidates], 0)
# Label first context word as 1 (positive) followed by num_ns 0s (negative).
label = tf.constant([1] + [0] * num_ns, dtype="int64")
# Reshape target to shape (1,) and context and label to (num_ns+1,).
target = tf.squeeze(target_word)
context = tf.squeeze(context)
label = tf.squeeze(label)
```
Take a look at the context and the corresponding labels for the target word from the skip-gram example above.
```
print(f"target_index : {target}")
print(f"target_word : {inverse_vocab[target_word]}")
print(f"context_indices : {context}")
print(f"context_words : {[inverse_vocab[c.numpy()] for c in context]}")
print(f"label : {label}")
```
A tuple of `(target, context, label)` tensors constitutes one training example for training your skip-gram negative sampling Word2Vec model. Notice that the target is of shape `(1,)` while the context and label are of shape `(1+num_ns,)`
```
print(f"target :", target)
print(f"context :", context)
print(f"label :", label)
```
### Summary
This picture summarizes the procedure of generating training example from a sentence.

## Lab Task 1
### Skip-gram Sampling table
A large dataset means larger vocabulary with higher number of more frequent words such as stopwords. Training examples obtained from sampling commonly occuring words (such as `the`, `is`, `on`) don't add much useful information for the model to learn from. [Mikolov et al.](https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf) suggest subsampling of frequent words as a helpful practice to improve embedding quality.
The `tf.keras.preprocessing.sequence.skipgrams` function accepts a sampling table argument to encode probabilities of sampling any token. You can use the `tf.keras.preprocessing.sequence.make_sampling_table` to generate a word-frequency rank based probabilistic sampling table and pass it to `skipgrams` function. Take a look at the sampling probabilities for a `vocab_size` of 10.
```
sampling_table = tf.keras.preprocessing.sequence.make_sampling_table(size=10)
print(sampling_table)
```
`sampling_table[i]` denotes the probability of sampling the i-th most common word in a dataset. The function assumes a [Zipf's distribution](https://en.wikipedia.org/wiki/Zipf%27s_law) of the word frequencies for sampling.
Key point: The `tf.random.log_uniform_candidate_sampler` already assumes that the vocabulary frequency follows a log-uniform (Zipf's) distribution. Using these distribution weighted sampling also helps approximate the Noise Contrastive Estimation (NCE) loss with simpler loss functions for training a negative sampling objective.
### Generate training data
Compile all the steps described above into a function that can be called on a list of vectorized sentences obtained from any text dataset. Notice that the sampling table is built before sampling skip-gram word pairs. You will use this function in the later sections.
```
"""
Generates skip-gram pairs with negative sampling for a list of sequences
(int-encoded sentences) based on window size, number of negative samples
and vocabulary size.
"""
def generate_training_data(sequences, window_size, num_ns, vocab_size, seed):
# Elements of each training example are appended to these lists.
targets, contexts, labels = [], [], []
# Build the sampling table for vocab_size tokens.
# TODO 1a
sampling_table = tf.keras.preprocessing.sequence.make_sampling_table(
vocab_size
)
# Iterate over all sequences (sentences) in dataset.
for sequence in tqdm.tqdm(sequences):
# Generate positive skip-gram pairs for a sequence (sentence).
positive_skip_grams, _ = tf.keras.preprocessing.sequence.skipgrams(
sequence,
vocabulary_size=vocab_size,
sampling_table=sampling_table,
window_size=window_size,
negative_samples=0,
)
# Iterate over each positive skip-gram pair to produce training examples
# with positive context word and negative samples.
# TODO 1b
for target_word, context_word in positive_skip_grams:
context_class = tf.expand_dims(
tf.constant([context_word], dtype="int64"), 1
)
(
negative_sampling_candidates,
_,
_,
) = tf.random.log_uniform_candidate_sampler(
true_classes=context_class,
num_true=1,
num_sampled=num_ns,
unique=True,
range_max=vocab_size,
seed=SEED,
name="negative_sampling",
)
# Build context and label vectors (for one target word)
negative_sampling_candidates = tf.expand_dims(
negative_sampling_candidates, 1
)
context = tf.concat(
[context_class, negative_sampling_candidates], 0
)
label = tf.constant([1] + [0] * num_ns, dtype="int64")
# Append each element from the training example to global lists.
targets.append(target_word)
contexts.append(context)
labels.append(label)
return targets, contexts, labels
```
## Lab Task 2: Prepare training data for Word2Vec
With an understanding of how to work with one sentence for a skip-gram negative sampling based Word2Vec model, you can proceed to generate training examples from a larger list of sentences!
### Download text corpus
You will use a text file of Shakespeare's writing for this tutorial. Change the following line to run this code on your own data.
```
path_to_file = tf.keras.utils.get_file(
"shakespeare.txt",
"https://storage.googleapis.com/download.tensorflow.org/data/shakespeare.txt",
)
```
Read text from the file and take a look at the first few lines.
```
with open(path_to_file) as f:
lines = f.read().splitlines()
for line in lines[:20]:
print(line)
```
Use the non empty lines to construct a `tf.data.TextLineDataset` object for next steps.
```
# TODO 2a
text_ds = tf.data.TextLineDataset(path_to_file).filter(
lambda x: tf.cast(tf.strings.length(x), bool)
)
```
### Vectorize sentences from the corpus
You can use the `TextVectorization` layer to vectorize sentences from the corpus. Learn more about using this layer in this [Text Classification](https://www.tensorflow.org/tutorials/keras/text_classification) tutorial. Notice from the first few sentences above that the text needs to be in one case and punctuation needs to be removed. To do this, define a `custom_standardization function` that can be used in the TextVectorization layer.
```
"""
We create a custom standardization function to lowercase the text and
remove punctuation.
"""
def custom_standardization(input_data):
lowercase = tf.strings.lower(input_data)
return tf.strings.regex_replace(
lowercase, "[%s]" % re.escape(string.punctuation), ""
)
"""
Define the vocabulary size and number of words in a sequence.
"""
vocab_size = 4096
sequence_length = 10
"""
Use the text vectorization layer to normalize, split, and map strings to
integers. Set output_sequence_length length to pad all samples to same length.
"""
vectorize_layer = TextVectorization(
standardize=custom_standardization,
max_tokens=vocab_size,
output_mode="int",
output_sequence_length=sequence_length,
)
```
Call `adapt` on the text dataset to create vocabulary.
```
vectorize_layer.adapt(text_ds.batch(1024))
```
Once the state of the layer has been adapted to represent the text corpus, the vocabulary can be accessed with `get_vocabulary()`. This function returns a list of all vocabulary tokens sorted (descending) by their frequency.
```
# Save the created vocabulary for reference.
inverse_vocab = vectorize_layer.get_vocabulary()
print(inverse_vocab[:20])
```
The vectorize_layer can now be used to generate vectors for each element in the `text_ds`.
```
def vectorize_text(text):
text = tf.expand_dims(text, -1)
return tf.squeeze(vectorize_layer(text))
# Vectorize the data in text_ds.
text_vector_ds = (
text_ds.batch(1024).prefetch(AUTOTUNE).map(vectorize_layer).unbatch()
)
```
### Obtain sequences from the dataset
You now have a `tf.data.Dataset` of integer encoded sentences. To prepare the dataset for training a Word2Vec model, flatten the dataset into a list of sentence vector sequences. This step is required as you would iterate over each sentence in the dataset to produce positive and negative examples.
Note: Since the `generate_training_data()` defined earlier uses non-TF python/numpy functions, you could also use a `tf.py_function` or `tf.numpy_function` with `tf.data.Dataset.map()`.
```
sequences = list(text_vector_ds.as_numpy_iterator())
print(len(sequences))
```
Take a look at few examples from `sequences`.
```
for seq in sequences[:5]:
print(f"{seq} => {[inverse_vocab[i] for i in seq]}")
```
### Generate training examples from sequences
`sequences` is now a list of int encoded sentences. Just call the `generate_training_data()` function defined earlier to generate training examples for the Word2Vec model. To recap, the function iterates over each word from each sequence to collect positive and negative context words. Length of target, contexts and labels should be same, representing the total number of training examples.
```
targets, contexts, labels = generate_training_data(
sequences=sequences,
window_size=2,
num_ns=4,
vocab_size=vocab_size,
seed=SEED,
)
print(len(targets), len(contexts), len(labels))
```
### Configure the dataset for performance
To perform efficient batching for the potentially large number of training examples, use the `tf.data.Dataset` API. After this step, you would have a `tf.data.Dataset` object of `(target_word, context_word), (label)` elements to train your Word2Vec model!
```
BATCH_SIZE = 1024
BUFFER_SIZE = 10000
dataset = tf.data.Dataset.from_tensor_slices(((targets, contexts), labels))
dataset = dataset.shuffle(BUFFER_SIZE).batch(BATCH_SIZE, drop_remainder=True)
print(dataset)
```
Add `cache()` and `prefetch()` to improve performance.
```
dataset = dataset.cache().prefetch(buffer_size=AUTOTUNE)
print(dataset)
```
## Lab Task 3: Model and Training
The Word2Vec model can be implemented as a classifier to distinguish between true context words from skip-grams and false context words obtained through negative sampling. You can perform a dot product between the embeddings of target and context words to obtain predictions for labels and compute loss against true labels in the dataset.
### Subclassed Word2Vec Model
Use the [Keras Subclassing API](https://www.tensorflow.org/guide/keras/custom_layers_and_models) to define your Word2Vec model with the following layers:
* `target_embedding`: A `tf.keras.layers.Embedding` layer which looks up the embedding of a word when it appears as a target word. The number of parameters in this layer are `(vocab_size * embedding_dim)`.
* `context_embedding`: Another `tf.keras.layers.Embedding` layer which looks up the embedding of a word when it appears as a context word. The number of parameters in this layer are the same as those in `target_embedding`, i.e. `(vocab_size * embedding_dim)`.
* `dots`: A `tf.keras.layers.Dot` layer that computes the dot product of target and context embeddings from a training pair.
* `flatten`: A `tf.keras.layers.Flatten` layer to flatten the results of `dots` layer into logits.
With the sublassed model, you can define the `call()` function that accepts `(target, context)` pairs which can then be passed into their corresponding embedding layer. Reshape the `context_embedding` to perform a dot product with `target_embedding` and return the flattened result.
Key point: The `target_embedding` and `context_embedding` layers can be shared as well. You could also use a concatenation of both embeddings as the final Word2Vec embedding.
```
class Word2Vec(Model):
def __init__(self, vocab_size, embedding_dim):
super().__init__()
self.target_embedding = Embedding(
vocab_size,
embedding_dim,
input_length=1,
name="w2v_embedding",
)
self.context_embedding = Embedding(
vocab_size, embedding_dim, input_length=num_ns + 1
)
self.dots = Dot(axes=(3, 2))
self.flatten = Flatten()
def call(self, pair):
target, context = pair
we = self.target_embedding(target)
ce = self.context_embedding(context)
dots = self.dots([ce, we])
return self.flatten(dots)
```
### Define loss function and compile model
For simplicity, you can use `tf.keras.losses.CategoricalCrossEntropy` as an alternative to the negative sampling loss. If you would like to write your own custom loss function, you can also do so as follows:
``` python
def custom_loss(x_logit, y_true):
return tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=y_true)
```
It's time to build your model! Instantiate your Word2Vec class with an embedding dimension of 128 (you could experiment with different values). Compile the model with the `tf.keras.optimizers.Adam` optimizer.
```
# TODO 3a
embedding_dim = 128
word2vec = Word2Vec(vocab_size, embedding_dim)
word2vec.compile(
optimizer="adam",
loss=tf.keras.losses.CategoricalCrossentropy(from_logits=True),
metrics=["accuracy"],
)
```
Also define a callback to log training statistics for tensorboard.
```
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir="logs")
```
Train the model with `dataset` prepared above for some number of epochs.
```
dataset
word2vec.fit(dataset, epochs=20, callbacks=[tensorboard_callback])
```
### Visualize training on Tensorboard
In order to visualize how the model has trained we can use tensorboard to show the Word2Vec model's accuracy and loss. To do that, we first have to copy the logs from local to a GCS (Cloud Storage) folder.
```
def copy_tensorboard_logs(local_path: str, gcs_path: str):
"""Copies Tensorboard logs from a local dir to a GCS location.
After training, batch copy Tensorboard logs locally to a GCS location.
Args:
local_path: local filesystem directory uri.
gcs_path: cloud filesystem directory uri.
Returns:
None.
"""
pattern = f"{local_path}/*/events.out.tfevents.*"
local_files = tf.io.gfile.glob(pattern)
gcs_log_files = [
local_file.replace(local_path, gcs_path) for local_file in local_files
]
for local_file, gcs_file in zip(local_files, gcs_log_files):
tf.io.gfile.copy(local_file, gcs_file)
copy_tensorboard_logs("./logs", OUTDIR + "/word2vec_logs")
```
To visualize the embeddings, open Cloud Shell and use the following command:
`tensorboard --port=8081 --logdir OUTDIR/word2vec_logs`
In Cloud Shell, click Web Preview > Change Port and insert port number 8081. Click Change and Preview to open the TensorBoard.

## Lab Task 4: Embedding lookup and analysis
Obtain the weights from the model using `get_layer()` and `get_weights()`. The `get_vocabulary()` function provides the vocabulary to build a metadata file with one token per line.
```
# TODO 4a
weights = word2vec.get_layer("w2v_embedding").get_weights()[0]
vocab = vectorize_layer.get_vocabulary()
```
Create and save the vectors and metadata file.
```
out_v = open("text_models/vectors.tsv", "w", encoding="utf-8")
out_m = open("text_models/metadata.tsv", "w", encoding="utf-8")
for index, word in enumerate(vocab):
if index == 0:
continue # skip 0, it's padding.
vec = weights[index]
out_v.write("\t".join([str(x) for x in vec]) + "\n")
out_m.write(word + "\n")
out_v.close()
out_m.close()
```
Download the `vectors.tsv` and `metadata.tsv` to your local machine and then open [Embedding Projector](https://projector.tensorflow.org/). Here you will have the option to upload the two files you have downloaded and visualize the embeddings.
| true |
code
| 0.527438 | null | null | null | null |
|
# JAX Quickstart
[](https://colab.research.google.com/github/google/jax/blob/main/docs/notebooks/quickstart.ipynb)
**JAX is NumPy on the CPU, GPU, and TPU, with great automatic differentiation for high-performance machine learning research.**
With its updated version of [Autograd](https://github.com/hips/autograd), JAX
can automatically differentiate native Python and NumPy code. It can
differentiate through a large subset of Python’s features, including loops, ifs,
recursion, and closures, and it can even take derivatives of derivatives of
derivatives. It supports reverse-mode as well as forward-mode differentiation, and the two can be composed arbitrarily
to any order.
What’s new is that JAX uses
[XLA](https://www.tensorflow.org/xla)
to compile and run your NumPy code on accelerators, like GPUs and TPUs.
Compilation happens under the hood by default, with library calls getting
just-in-time compiled and executed. But JAX even lets you just-in-time compile
your own Python functions into XLA-optimized kernels using a one-function API.
Compilation and automatic differentiation can be composed arbitrarily, so you
can express sophisticated algorithms and get maximal performance without having
to leave Python.
```
import jax.numpy as jnp
from jax import grad, jit, vmap
from jax import random
# Prevent GPU/TPU warning.
import jax; jax.config.update('jax_platform_name', 'cpu')
```
## Multiplying Matrices
We'll be generating random data in the following examples. One big difference between NumPy and JAX is how you generate random numbers. For more details, see [Common Gotchas in JAX].
[Common Gotchas in JAX]: https://jax.readthedocs.io/en/latest/notebooks/Common_Gotchas_in_JAX.html#%F0%9F%94%AA-Random-Numbers
```
key = random.PRNGKey(0)
x = random.normal(key, (10,))
print(x)
```
Let's dive right in and multiply two big matrices.
```
size = 3000
x = random.normal(key, (size, size), dtype=jnp.float32)
%timeit jnp.dot(x, x.T).block_until_ready() # runs on the GPU
```
We added that `block_until_ready` because JAX uses asynchronous execution by default (see {ref}`async-dispatch`).
JAX NumPy functions work on regular NumPy arrays.
```
import numpy as np
x = np.random.normal(size=(size, size)).astype(np.float32)
%timeit jnp.dot(x, x.T).block_until_ready()
```
That's slower because it has to transfer data to the GPU every time. You can ensure that an NDArray is backed by device memory using {func}`~jax.device_put`.
```
from jax import device_put
x = np.random.normal(size=(size, size)).astype(np.float32)
x = device_put(x)
%timeit jnp.dot(x, x.T).block_until_ready()
```
The output of {func}`~jax.device_put` still acts like an NDArray, but it only copies values back to the CPU when they're needed for printing, plotting, saving to disk, branching, etc. The behavior of {func}`~jax.device_put` is equivalent to the function `jit(lambda x: x)`, but it's faster.
If you have a GPU (or TPU!) these calls run on the accelerator and have the potential to be much faster than on CPU.
```
x = np.random.normal(size=(size, size)).astype(np.float32)
%timeit np.dot(x, x.T)
```
JAX is much more than just a GPU-backed NumPy. It also comes with a few program transformations that are useful when writing numerical code. For now, there are three main ones:
- {func}`~jax.jit`, for speeding up your code
- {func}`~jax.grad`, for taking derivatives
- {func}`~jax.vmap`, for automatic vectorization or batching.
Let's go over these, one-by-one. We'll also end up composing these in interesting ways.
## Using {func}`~jax.jit` to speed up functions
JAX runs transparently on the GPU (or CPU, if you don't have one, and TPU coming soon!). However, in the above example, JAX is dispatching kernels to the GPU one operation at a time. If we have a sequence of operations, we can use the `@jit` decorator to compile multiple operations together using [XLA](https://www.tensorflow.org/xla). Let's try that.
```
def selu(x, alpha=1.67, lmbda=1.05):
return lmbda * jnp.where(x > 0, x, alpha * jnp.exp(x) - alpha)
x = random.normal(key, (1000000,))
%timeit selu(x).block_until_ready()
```
We can speed it up with `@jit`, which will jit-compile the first time `selu` is called and will be cached thereafter.
```
selu_jit = jit(selu)
%timeit selu_jit(x).block_until_ready()
```
## Taking derivatives with {func}`~jax.grad`
In addition to evaluating numerical functions, we also want to transform them. One transformation is [automatic differentiation](https://en.wikipedia.org/wiki/Automatic_differentiation). In JAX, just like in [Autograd](https://github.com/HIPS/autograd), you can compute gradients with the {func}`~jax.grad` function.
```
def sum_logistic(x):
return jnp.sum(1.0 / (1.0 + jnp.exp(-x)))
x_small = jnp.arange(3.)
derivative_fn = grad(sum_logistic)
print(derivative_fn(x_small))
```
Let's verify with finite differences that our result is correct.
```
def first_finite_differences(f, x):
eps = 1e-3
return jnp.array([(f(x + eps * v) - f(x - eps * v)) / (2 * eps)
for v in jnp.eye(len(x))])
print(first_finite_differences(sum_logistic, x_small))
```
Taking derivatives is as easy as calling {func}`~jax.grad`. {func}`~jax.grad` and {func}`~jax.jit` compose and can be mixed arbitrarily. In the above example we jitted `sum_logistic` and then took its derivative. We can go further:
```
print(grad(jit(grad(jit(grad(sum_logistic)))))(1.0))
```
For more advanced autodiff, you can use {func}`jax.vjp` for reverse-mode vector-Jacobian products and {func}`jax.jvp` for forward-mode Jacobian-vector products. The two can be composed arbitrarily with one another, and with other JAX transformations. Here's one way to compose them to make a function that efficiently computes full Hessian matrices:
```
from jax import jacfwd, jacrev
def hessian(fun):
return jit(jacfwd(jacrev(fun)))
```
## Auto-vectorization with {func}`~jax.vmap`
JAX has one more transformation in its API that you might find useful: {func}`~jax.vmap`, the vectorizing map. It has the familiar semantics of mapping a function along array axes, but instead of keeping the loop on the outside, it pushes the loop down into a function’s primitive operations for better performance. When composed with {func}`~jax.jit`, it can be just as fast as adding the batch dimensions by hand.
We're going to work with a simple example, and promote matrix-vector products into matrix-matrix products using {func}`~jax.vmap`. Although this is easy to do by hand in this specific case, the same technique can apply to more complicated functions.
```
mat = random.normal(key, (150, 100))
batched_x = random.normal(key, (10, 100))
def apply_matrix(v):
return jnp.dot(mat, v)
```
Given a function such as `apply_matrix`, we can loop over a batch dimension in Python, but usually the performance of doing so is poor.
```
def naively_batched_apply_matrix(v_batched):
return jnp.stack([apply_matrix(v) for v in v_batched])
print('Naively batched')
%timeit naively_batched_apply_matrix(batched_x).block_until_ready()
```
We know how to batch this operation manually. In this case, `jnp.dot` handles extra batch dimensions transparently.
```
@jit
def batched_apply_matrix(v_batched):
return jnp.dot(v_batched, mat.T)
print('Manually batched')
%timeit batched_apply_matrix(batched_x).block_until_ready()
```
However, suppose we had a more complicated function without batching support. We can use {func}`~jax.vmap` to add batching support automatically.
```
@jit
def vmap_batched_apply_matrix(v_batched):
return vmap(apply_matrix)(v_batched)
print('Auto-vectorized with vmap')
%timeit vmap_batched_apply_matrix(batched_x).block_until_ready()
```
Of course, {func}`~jax.vmap` can be arbitrarily composed with {func}`~jax.jit`, {func}`~jax.grad`, and any other JAX transformation.
This is just a taste of what JAX can do. We're really excited to see what you do with it!
| true |
code
| 0.371336 | null | null | null | null |
|
# A Demo on Backtesting M3 with Various Models
This notebook aims to
1. provide a simple demo how to backtest models with orbit provided functions.
2. add transperancy how our accuracy metrics are derived in https://arxiv.org/abs/2004.08492.
Due to versioning and random seed, there could be subtle difference for the final numbers. This notebook should also be available in colab.
```
!pip install orbit-ml==1.0.13
!pip install fbprophet==0.7.1
import numpy as np
import tqdm
import pandas as pd
import statsmodels.api as sm
import inspect
import random
from fbprophet import Prophet
from statsmodels.tsa.statespace.sarimax import SARIMAX
import orbit
from orbit.models.dlt import DLTMAP
from orbit.utils.dataset import load_m3monthly
from orbit.diagnostics.backtest import BackTester
from orbit.diagnostics.metrics import smape
seed=2021
n_sample=10
random.seed(seed)
```
We can load the m3 dataset from orbit repository. For demo purpose, i set `n_sample` to be `10`. Feel free to adjust it or simply run the entire dataset.
```
data = load_m3monthly()
unique_keys = data['key'].unique().tolist()
if n_sample > 0:
sample_keys = random.sample(unique_keys, 10)
# just get the first 5 series for demo
data = data[data['key'].isin(sample_keys)].reset_index(drop=True)
else:
sample_keys = unique_keys
print(sample_keys)
data.columns
```
We need to provide some meta data such as date column, response column etc.
```
key_col='key'
response_col='value'
date_col='date'
seasonality=12
```
We also provide some setting mimic M3 (see https://forecasters.org/resources/time-series-data/m3-competition/) criteria.
```
backtest_args = {
'min_train_len': 1, # not useful; a placeholder
'incremental_len': 18, # not useful; a placeholder
'forecast_len': 18,
'n_splits': 1,
'window_type': "expanding",
}
```
We are using `DLT` here. To use a multiplicative form, we need a natural log transformation of response. Hence, we need to a wrapper for `DLT`. We also need to build wrapper for signature prupose for `prophet` and `sarima`.
Note that prophet comes with its own multiplicative form.
```
class DLTMAPWrapper(object):
def __init__(self, response_col, date_col, **kwargs):
kw_params = locals()['kwargs']
for key, value in kw_params.items():
setattr(self, key, value)
self.response_col = response_col
self.date_col = date_col
self.model = DLTMAP(
response_col=response_col,
date_col=date_col,
**kwargs)
def fit(self, df):
df = df.copy()
df[[self.response_col]] = df[[self.response_col]].apply(np.log1p)
self.model.fit(df)
def predict(self, df):
df = df.copy()
pred_df = self.model.predict(df)
pred_df['prediction'] = np.clip(np.expm1(pred_df['prediction']).values, 0, None)
return pred_df
class SARIMAXWrapper(object):
def __init__(self, response_col, date_col, **kwargs):
kw_params = locals()['kwargs']
for key, value in kw_params.items():
setattr(self, key, value)
self.response_col = response_col
self.date_col = date_col
self.model = None
self.df = None
def fit(self, df):
df_copy = df.copy()
infer_freq = pd.infer_freq(df_copy[self.date_col])
df_copy = df_copy.set_index(self.date_col)
df_copy = df_copy.asfreq(infer_freq)
endog = df_copy[self.response_col]
sig = inspect.signature(SARIMAX)
all_params = dict()
for key in sig.parameters.keys():
if hasattr(self, key):
all_params[key] = getattr(self, key)
self.df = df_copy
self.model = SARIMAX(endog=endog, **all_params).fit(disp=False)
def predict(self, df, **kwargs):
df_copy = df.copy()
infer_freq = pd.infer_freq(df_copy[self.date_col])
df_copy = df_copy.set_index(self.date_col)
df_copy = df_copy.asfreq(infer_freq)
pred_array = np.array(self.model.predict(start=df_copy.index[0],
end=df_copy.index[-1],
**kwargs))
out = pd.DataFrame({
self.date_col: df[self.date_col],
'prediction': pred_array
})
return out
class ProphetWrapper(object):
def __init__(self, response_col, date_col, **kwargs):
kw_params = locals()['kwargs']
for key, value in kw_params.items():
setattr(self, key, value)
self.response_col = response_col
self.date_col = date_col
self.model = Prophet(**kwargs)
def fit(self, df):
sig = inspect.signature(Prophet)
all_params = dict()
for key in sig.parameters.keys():
if hasattr(self, key):
all_params[key] = getattr(self, key)
object_type = type(self.model)
self.model = object_type(**all_params)
train_df = df.copy()
train_df = train_df.rename(columns={self.date_col: "ds", self.response_col: "y"})
self.model.fit(train_df)
def predict(self, df):
df = df.copy()
df = df.rename(columns={self.date_col: "ds"})
pred_df = self.model.predict(df)
pred_df = pred_df.rename(columns={'yhat': 'prediction', 'ds': self.date_col})
pred_df = pred_df[[self.date_col, 'prediction']]
return pred_df
```
Declare model objects and run backtest. Score shows in the end.
```
dlt = DLTMAPWrapper(
response_col=response_col,
date_col=date_col,
seasonality=seasonality,
seed=seed,
)
sarima = SARIMAXWrapper(
response_col=response_col,
date_col=date_col,
seasonality=seasonality,
seed=seed,
)
prophet = ProphetWrapper(
response_col=response_col,
date_col=date_col,
)
all_scores = []
for key in tqdm.tqdm(sample_keys):
# dlt
df = data[data[key_col] == key]
bt = BackTester(
model=dlt,
df=df,
**backtest_args,
)
bt.fit_predict()
scores_df = bt.score(metrics=[smape])
scores_df[key_col] = key
scores_df['model'] = 'dlt'
all_scores.append(scores_df)
# sarima
df = data[data[key_col] == key]
bt = BackTester(
model=sarima,
df=df,
**backtest_args,
)
bt.fit_predict()
scores_df = bt.score(metrics=[smape])
scores_df[key_col] = key
scores_df['model'] = 'sarima'
all_scores.append(scores_df)
# prophet
df = data[data[key_col] == key]
bt = BackTester(
model=prophet,
df=df,
**backtest_args,
)
bt.fit_predict()
scores_df = bt.score(metrics=[smape])
scores_df[key_col] = key
scores_df['model'] = 'prophet'
all_scores.append(scores_df)
all_scores = pd.concat(all_scores, axis=0, ignore_index=True)
all_scores.groupby('model')['metric_values'].apply(np.mean).reset_index()
```
| true |
code
| 0.507446 | null | null | null | null |
|
# Part 9 - Intro to Encrypted Programs
You believe or you no believe, he dey possible to compute with encrypted data. Make I talk am another way sey he dey possible to run program where **ALL of the variables** in the program dey **encrypted**!
For this tutoria we go learn basic tools of encrypted computation. In particular, we go focus on one popular approach called Secure Multi-Party Computation. We go build encrypted calculator wey fit perform calculations on encrypted numbers for this lesson.
Person wey write am:
- Andrew Trask - Twitter: [@iamtrask](https://twitter.com/iamtrask)
- Théo Ryffel - GitHub: [@LaRiffle](https://github.com/LaRiffle)
Reference wey you fit use:
- Morten Dahl - [Blog](https://mortendahl.github.io) - Twitter: [@mortendahlcs](https://twitter.com/mortendahlcs)
Person wey translate am:
- Temitọpẹ Ọladokun - Twitter: [@techie991](https://twitter.com/techie991)
# Step 1: Encryption Using Secure Multi-Party Computation
SMPC na strange form of "encryptioon". Instead make we use public/private key to encrypt a variable, we go split each value into multiple `shares`, each of dem operates like a private key. Typically, we go distribute these `shares` amongst 2 or more _owners_. Thus, to decrypt the variable, all owners must agree sey make we decryt am. In essence, everyone go get private key.
### Encrypt()
So, let's say we wan "encrypt" a variable `x`, we fit do am in the following way.
So, let's say we wanted to "encrypt" a variable `x`, we could do so in the following way.
> Encryption no dey use floats or real numbers but he dey happen in a mathematical space called [integer quotient ring](http://mathworld.wolfram.com/QuotientRing.html) wey be the integer wey dey between `0` and `Q-1`, where `Q` na prime and "big enough" so that the space can contain all the numbers that we use in our experiments. In practice, given a value `x` integer, we do `x % Q` to fit in the ring. (That's why we dey avoid to use number `x' > Q`).
```
Q = 1234567891011
x = 25
import random
def encrypt(x):
share_a = random.randint(-Q,Q)
share_b = random.randint(-Q,Q)
share_c = (x - share_a - share_b) % Q
return (share_a, share_b, share_c)
encrypt(x)
```
As you dey see am, we don split our variable `x` into 3 different shares, wey we go send to 3 different owners.
### Decrypt()
If you wan decrypt these 3 shares, we go just sum them togeda and then we go take the modulus of the result (mod Q)
```
def decrypt(*shares):
return sum(shares) % Q
a,b,c = encrypt(25)
decrypt(a, b, c)
```
Importantly, notice sey if we try to decrypt with only two shares, the decryption no dey work!
```
decrypt(a, b)
```
We go need all of the owners to participate if we wan decrypt value. Na like this `shares` dey act like private keys, everytin must to dey before we go fit decrypt a value.
# Step 2: Basic Arithmetic Using SMPC
The extraordinary property of Secure Multi-Party Computation na him ability to perform computation **while the variables are still encrypted**. Make we demonstrate simple addition as he dey below.
```
x = encrypt(25)
y = encrypt(5)
def add(x, y):
z = list()
# the first worker adds their shares together
z.append((x[0] + y[0]) % Q)
# the second worker adds their shares together
z.append((x[1] + y[1]) % Q)
# the third worker adds their shares together
z.append((x[2] + y[2]) % Q)
return z
decrypt(*add(x,y))
```
### Success!!!
And there you get am! If each worker (separately) add their shares togeda, the resulting shares go decrypt to the correct vallues (25 + 5 == 30).
As he dey so, SMPC protocols exist go allow make this encrypted computation fit do the following operations:
- addition (which we've just seen)
- multiplication
- comparison
If we use these basic underlying primitives, we go fit perform arbitrary computation!!!
In the next section, we go learn how we fit use PySyft library to perform these operations!
# Step 3: SMPC Using PySyft
In the previous sections, we talk about some intuition wey dey around SMPC if he go work. However, we no wan use hand write everi primitive operations ourselves when we fit write our encrypted programs. So, for this section we go studi the basics of how we go do encrypted computation using PySyft. Particularly, we go focus on how to do 3 primitives wey we mention before: addition, multiplication, and comparison.
First, we go first create few Virtual Worker (wey you don dey familiar as you don study our previous tutorials).
```
import torch
import syft as sy
hook = sy.TorchHook(torch)
bob = sy.VirtualWorker(hook, id="bob")
alice = sy.VirtualWorker(hook, id="alice")
bill = sy.VirtualWorker(hook, id="bill")
```
### Basic Encryption/Decryption
Encryption na simple way of taking PySyft tensor and calling .share(). Decryption na simple way of calling .get() on shared variable.
```
x = torch.tensor([25])
x
encrypted_x = x.share(bob, alice, bill)
encrypted_x.get()
```
### Introspecting the Encrypted Values
If you look Bob, Alice and Bill's workers wella, we go see the shares we done create!
```
bob._objects
x = torch.tensor([25]).share(bob, alice, bill)
# Bob's share
bobs_share = list(bob._objects.values())[0]
bobs_share
# Alice's share
alices_share = list(alice._objects.values())[0]
alices_share
# Bill's share
bills_share = list(bill._objects.values())[0]
bills_share
```
If we want, we fit decrypt these values if we use the SAME approach we don talk about before now!!!
```
Q = x.child.field
(bobs_share + alices_share + bills_share) % Q
```
Look am wella, as we call `.share()` he just split value into 3 shares ans he come send one share go each parties!
# Encrypted Arithmetic
We fit perform arithmetic on the underlying values! API dey constructed on to sey make we perform arithmetic liek the one wey we do with normal PyTorch tensors.
```
x = torch.tensor([25]).share(bob,alice)
y = torch.tensor([5]).share(bob,alice)
z = x + y
z.get()
z = x - y
z.get()
```
# Encrypted Multiplication
For multiplication we go need an additional party who go dey responsible to dey consistently generate random numbers (he no go collude with any other parties). We dey call this person "crypto provider". For all intensive purposes, the crypto provider na just additional VirtualWorker, but he go dey important to acknowledge sey crypto provider no be "owner" onto sey he/she no get him own shares but na someone wey we need to trust make he no go collude with ani existing shareholders.
```
crypto_provider = sy.VirtualWorker(hook, id="crypto_provider")
x = torch.tensor([25]).share(bob,alice, crypto_provider=crypto_provider)
y = torch.tensor([5]).share(bob,alice, crypto_provider=crypto_provider)
# multiplication
z = x * y
z.get()
```
You fit do matrix multiplication
```
x = torch.tensor([[1, 2],[3,4]]).share(bob,alice, crypto_provider=crypto_provider)
y = torch.tensor([[2, 0],[0,2]]).share(bob,alice, crypto_provider=crypto_provider)
# matrix multiplication
z = x.mm(y)
z.get()
```
# Encrypted comparison
He dey possible to private compare private values. We go rely on SecureNN protocol, we fit find the details [here](https://eprint.iacr.org/2018/442.pdf). The result of the comparison na private shared tensor.
```
x = torch.tensor([25]).share(bob,alice, crypto_provider=crypto_provider)
y = torch.tensor([5]).share(bob,alice, crypto_provider=crypto_provider)
z = x > y
z.get()
z = x <= y
z.get()
z = x == y
z.get()
z = x == y + 20
z.get()
```
You fit perform max operations
```
x = torch.tensor([2, 3, 4, 1]).share(bob,alice, crypto_provider=crypto_provider)
x.max().get()
x = torch.tensor([[2, 3], [4, 1]]).share(bob,alice, crypto_provider=crypto_provider)
max_values, max_ids = x.max(dim=0)
max_values.get()
```
# Congratulations!!! - Oya Join the Community!
Clap for una sef as you don finish this notebook tutorial! If you enjoy am and you wan join the movement towards privacy preserving, decentralized ownership of AI and the AI supply chain (data), follow the steps wey dey below.
### Star PySyft on GitHub
The easiset way to helep our community na to star the GitHub repos! This go helep raise awareness of the tools we dey build.
- [Star PySyft](https://github.com/OpenMined/PySyft)
### Join our Slack!
To follow up bumper to bumper on how latest advancements, join our community! You can do so by filling out the form at [http://slack.openmined.org](http://slack.openmined.org)
### Join a Code Project!
The best way to contribute to our community na to become code contributor! You fit go to PySyft GitHub Issues page and filter for "Projects". E go show you all the top level Tickets giving an overview of what projects you fit join! If you no wan join any project, but you wan code small, you fit look for more "one off" mini-projects by searching for GitHub issues marked "good first issue"
- [PySyft Projects](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3AProject)
- [Good First Issue Tickets](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
### Donate
If you no get time to contribute to our codebase, but still like to lend support, you fit be a Backer on our Open Collective. All donations wey we get na for our web hosting and other community expenses such as hackathons and meetups! meetups!
[OpenMined's Open Collective Page](https://opencollective.com/openmined)
| true |
code
| 0.374934 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/mancinimassimiliano/DeepLearningLab/blob/master/Lab4/solution/char_rnn_classification_solution.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Tutorial on Recurrent Neural Networks
Recurrent Neural Networks (RNN) are models which are useful anytime we want to model sequences of data (e.g. video, text). In this tutorial (adapted from [here](https://pytorch.org/tutorials/intermediate/char_rnn_classification_tutorial.html)), we will see how we can predict the language of a name using an RNN model taking single word characters as input.
Specifically, we will train the network on a list of surnames from 18 languages of origin, and predict which language a name is from based on the spelling:
```
$ python predict.py Hinton
(0.63) Scottish
(0.22) English
(0.02) Irish
$ python predict.py Schmidhuber
(0.83) German
(0.08) Czech
(0.07) Dutch
```
# Preparing the Data
The [link](https://download.pytorch.org/tutorial/data.zip) to download the needed data is provided within the official pytorch tutorial. The data must be downloaded and extracted in your virtual machine. We can do this through:
```
!wget https://download.pytorch.org/tutorial/data.zip
!unzip data.zip
```
Under the downloaded directory there are 18 text files named as "[Language].txt". Each file contains a bunch of names, one name per line. In the following, we will take care of data preprocessing by :
* Extracting all the names and numbers of categories from the files.
* Converting from Unicode to ASCII each name.
* Instantiating a dictionary containing all names (values) of a given language (key)
```
import glob
import unicodedata
import string
all_filenames = glob.glob('data/names/*.txt')
all_letters = string.ascii_letters + " .,;'"
n_letters = len(all_letters)
# Turn a Unicode string to plain ASCII, thanks to http://stackoverflow.com/a/518232/2809427
def unicode_to_ascii(s):
return ''.join(
c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn'
and c in all_letters
)
print(unicode_to_ascii('Ślusàrski'))
# Build the category_lines dictionary, a list of names per language
category_lines = {}
all_categories = []
# Read a file and split into lines
def readLines(filename):
lines = open(filename).read().strip().split('\n')
return [unicode_to_ascii(line) for line in lines]
for filename in all_filenames:
category = filename.split('/')[-1].split('.')[0]
all_categories.append(category)
lines = readLines(filename)
category_lines[category] = lines
n_categories = len(all_categories)
print('n_categories =', n_categories)
```
# Turning Names into Tensors
A crucial point in this problem is how to define the input to the network. Since the network threats numbers and not plain text, we must convert text to numerical representation. To this extent we represent each letter as a one-hot vector of size `<1 x n_letters>`. A one-hot vector is filled with 0s except for a 1 at index of the current letter, e.g. `"b" = <0 1 0 0 0 ...>`.
To make a word we join a bunch of those into a 2D matrix `<line_length x 1 x n_letters>`.
That extra 1 dimension is because PyTorch assumes everything is in batches - we're just using a batch size of 1 here.
```
import torch
# Just for demonstration, turn a letter into a <1 x n_letters> Tensor
def letter_to_tensor(letter):
tensor = torch.zeros(1, n_letters)
letter_index = all_letters.find(letter)
tensor[0][letter_index] = 1
return tensor
# Turn a line into a <line_length x n_letters>,
# (or <line_length x 1 x n_letters> if the batch dimension is added)
# of one-hot letter vectors
def line_to_tensor(line,add_batch_dimension=True):
tensor = torch.zeros(len(line), n_letters)
for li, letter in enumerate(line):
letter_index = all_letters.find(letter)
tensor[li][letter_index] = 1
if add_batch_dimension:
return tensor.unsqueeze(1)
else:
return tensor
# Create a batch of samples given a list of lines
def create_batch(lines):
tensors = []
for l in lines:
tensors.append(line_to_tensor(l,add_batch_dimension=False))
padded_tensor = torch.nn.utils.rnn.pad_sequence(tensors, batch_first = False, padding_value=0)
return padded_tensor
```
# Creating the Network
Instantiate a simple recurrent neural network. The newtork should have a recurrent layer followed by a fully connected layer mapping the features of the recurrent unit to the output space (i.e. number of categories).
To run a step of this network we need to pass an input (in our case, the Tensor for the current sequence/s) and a previous hidden state (which we initialize as zeros at first). We'll get back the logits (i.e. network activation before the softmax) for each each language.
```
# Create a simple recurrent network
class SimpleRNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleRNN, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.i2h = nn.RNN(input_size, hidden_size)
self.i2o = nn.Linear(hidden_size, output_size)
# Forward the whole sequence at once
def forward(self, input, hidden=None):
if hidden==None:
hidden = self.init_hidden(input.shape[1])
output, _ = self.i2h(input, hidden)
output = self.i2o(output[-1])
return output
# Instantiate the hidden state of the first element of the sequence dim: 1 x batch_size x hidden_size)
def init_hidden(self,shape=1):
return torch.zeros(1, shape, self.hidden_size)
class SimpleLSTM(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleLSTM, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.i2h = nn.LSTM(input_size, hidden_size)
self.i2o = nn.Linear(hidden_size, output_size)
def forward(self, input, hidden=None, cell=None):
if hidden==None:
hidden = self.init_hidden(input.shape[1])
if cell==None:
cell = self.init_hidden(input.shape[1])
output, (_,_)= self.i2h(input, (hidden,cell))
output = self.i2o(output[-1])
return output
def init_hidden(self,shape=1):
return torch.zeros(1, shape, self.hidden_size)
def init_cell(self,shape=1):
return torch.zeros(1, shape, self.hidden_size)
class SimpleRNNwithCell(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleRNNwithCell, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.i2h = nn.RNNCell(input_size, hidden_size)
self.i2o = nn.Linear(hidden_size, output_size)
def forward(self, input, hidden=None):
if hidden==None:
hidden = self.init_hidden(input.shape[1])
for i in range(input.shape[0]):
hidden = self.i2h(input[i],hidden)
output = self.i2o(hidden)
return output
def init_hidden(self,shape=1):
return torch.zeros(shape, self.hidden_size)
```
# Preparing for Training
Before going into training we should make a few helper functions. The first is to interpret the output of the network, which we know to be a logits of each category. We can use `Tensor.topk` to get the index of the greatest value:
```
def category_from_output(output):
top_n, top_i = output.data.topk(1)
category_i = top_i[0][0]
return all_categories[category_i], category_i
```
We will also want a quick way to get a training example (a name and its language):
```
import random
def random_training_pair(bs=1):
lines = []
categories = []
for b in range(bs):
category = random.choice(all_categories)
line = random.choice(category_lines[category])
lines.append(line)
categories.append(category)
categories_tensor = torch.LongTensor([all_categories.index(c) for c in categories])
lines_tensor = create_batch(lines)
return categories_tensor, lines_tensor
```
# Training the Network
Now all it takes to train this network is show it a bunch of examples, have it make guesses, and tell it if it's wrong.
Since the output of the networks are logits and the task is classification, we can use a standard cross-entropy loss.
```
criterion = nn.CrossEntropyLoss()
```
Now we instantiate a standard training loop where we will:
* Forward the inpu to the network
* Compute the loss
* Backpropagate it
* Do a step of the optimizer
* Reset the optimizer/network's grad
```
def train(rnn, optimizer, categories_tensor, lines_tensor):
optimizer.zero_grad()
output = rnn(lines_tensor)
loss = criterion(output, categories_tensor)
loss.backward()
optimizer.step()
return output, loss.item()
```
Now we just have to:
* Instantiate the network
* Instantiate the optimizer
* Run the training steps for a given number of iterations
```
# Initialize the network:
n_hidden = 128
rnn = SimpleRNN(n_letters, n_hidden, n_categories)
# Initialize the optimizer
learning_rate = 0.005 # Example: different LR could work better
optimizer = torch.optim.SGD(rnn.parameters(), lr=learning_rate)
# Initialize the training loop
batch_size = 2
n_iterations = 100000
print_every = 5000
# Keep track of losses
current_loss = 0
for iter in range(1, n_iterations + 1):
# Get a random training input and target
category_tensor, line_tensor = random_training_pair(bs=batch_size)
# Process it through the train function
output, loss = train(rnn, optimizer, category_tensor, line_tensor)
# Accumulate loss for printing
current_loss += loss
# Print iteration number and loss
if iter % print_every == 0:
print('%d %d%% %.4f ' % (iter, iter / n_iterations * 100, current_loss/print_every))
current_loss = 0
```
# Running on User Input
Finally, followith the original tutorial [in the Practical PyTorch repo](https://github.com/spro/practical-pytorch/tree/master/char-rnn-classification) we instantiate a prediction function and test on some user defined inputs.
```
normalizer = torch.nn.Softmax(dim=-1)
def predict(input_line, n_predictions=3):
print('\n> %s' % input_line)
output = rnn(line_to_tensor(input_line))
output = normalizer(output)
# Get top N categories
topv, topi = output.data.topk(n_predictions, 1, True)
predictions = []
for i in range(n_predictions):
value = topv[0][i]
category_index = topi[0][i]
print('(%.2f) %s' % (value, all_categories[category_index]))
predictions.append([value, all_categories[category_index]])
predict('Dovesky')
predict('Jackson')
predict('Satoshi')
```
| true |
code
| 0.693265 | null | null | null | null |
|
### REGRESSION - KERAS
### The Auto MPG dataset
> The dataset is available from [UCI Machine Learning Repository.](https://archive.ics.uci.edu/ml/index.php)
### Imports
```
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
column_names = ['MPG', 'Cylinders', 'Displacement', 'Horsepower', 'Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(url, names=column_names, na_values='?'
, comment='\t', sep=' ', skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.head()
```
### Data Cleaning
> Removing `NaN` values
```
dataset.isna().sum()
dataset = dataset.dropna()
```
> The ``"Origin"`` column is really categorical, not numeric. So convert that to a one-hot with ``pd.get_dummies``:
```
dataset
dataset["Origin"] = dataset["Origin"].map({1: 'USA', 2: 'Europe', 3: 'Japan'})
dataset = pd.get_dummies(dataset, columns=['Origin'], prefix='', prefix_sep='')
dataset
```
### Splitting datasets
```
train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)
sns.pairplot(train_dataset[['MPG', 'Cylinders', 'Displacement', 'Weight']], diag_kind='kde')
train_dataset.describe()
```
### Split features from labels
```
train_features = train_dataset.copy()
test_features = test_dataset.copy()
train_labels = train_features.pop('MPG')
test_labels = test_features.pop('MPG')
```
### Normalization
* It is good practice to normalize features that use different scales and ranges.
* One reason this is important is because the features are multiplied by the model weights. So the scale of the outputs and the scale of the gradients are affected by the scale of the inputs.
* Although a model might converge without feature normalization, normalization makes training much more stable.
### The Normalization layer
The ``preprocessing.Normalization`` layer is a clean and simple way to build that preprocessing into your model.
The first step is to create the layer:
````
normalizer = preprocessing.Normalization()
````
Then ``.adapt()`` it to the data:
````
normalizer.adapt(np.array(train_features))
````
This calculates the mean and variance, and stores them in the layer.
> [Docs](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing/Normalization)
### Linear regression
### 1. One variable
* Start with a single-variable linear regression, to predict MPG from Horsepower.
* In this case there are two steps:
* Normalize the input horsepower.
* Apply a linear transformation ``(y = mx + b)`` to produce 1 output using layers.Dense.
```
from tensorflow.keras.layers.experimental.preprocessing import Normalization
from tensorflow import keras
train_features
horsepower =train_features['Horsepower'].values
horsepower.ndim
horsepower_normalizer = Normalization(input_shape=[1, ])
horsepower_normalizer.adapt(horsepower)
```
### Creating a model
```
horsepower_model = keras.Sequential([
horsepower_normalizer,
keras.layers.Dense(1)
])
horsepower_model.summary()
horsepower_model.compile(
optimizer = keras.optimizers.Adam(lr=.1),
loss = 'mean_absolute_error' ## 'mean_squared_error'
)
# No need to track the accuracy since it is a Regression task
%%time
history = horsepower_model.fit(
train_features['Horsepower'], train_labels,
epochs=100,
verbose=1,
validation_split = 0.2
)
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_loss(history):
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.ylim([0, 10])
plt.xlabel('Epoch')
plt.ylabel('Error [MPG]')
plt.legend()
plt.grid(True)
plot_loss(history)
```
### Making predictions
```
train_labels[:3].values.astype('float32'), horsepower_model.predict(train_labels[:3])
```
### 2. Multiple inputs
> You can use an almost identical setup to make predictions based on multiple inputs. This model still does the same except that is a matrix and is a vector.
> This time use the Normalization layer that was adapted to the whole dataset.
```
normalizer = Normalization()
normalizer.adapt(train_features.values.astype('float32'))
linear_model = keras.Sequential([
normalizer,
keras.layers.Dense(units=1)
])
linear_model.compile(
optimizer=keras.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error'
)
history = linear_model.fit(
train_features, train_labels,
epochs=100,
verbose=1,
validation_split = 0.2
)
plot_loss(history)
```
## A Deep Neural Net (DNN) regression
> The DNN will be the same as from the previous models exept that this will have some hidden layers
```
horsepower_model = keras.Sequential([
horsepower_normalizer,
keras.layers.Dense(64, activation='relu'),
keras.layers.Dense(64, activation='relu'),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dense(1)
])
horsepower_model.summary()
horsepower_model.compile(
optimizer = keras.optimizers.Adam(lr=.001),
loss = 'mean_absolute_error' ## 'mean_squared_error'
)
horsepower_model.fit(
train_features['Horsepower'], train_labels,
epochs=100,
verbose=1,
validation_split = 0.2
)
train_labels[:3].values.astype('float32'), horsepower_model.predict(train_labels[:3])
```
> The same applies to the full model.
| true |
code
| 0.6563 | null | null | null | null |
|
# Sonic The Hedgehog 1 with dqn
## Step 1: Import the libraries
```
import time
import retro
import random
import torch
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
from IPython.display import clear_output
import math
%matplotlib inline
import sys
sys.path.append('../../')
from algos.agents.dqn_agent import DQNAgent
from algos.models.dqn_cnn import DQNCnn
from algos.preprocessing.stack_frame import preprocess_frame, stack_frame
```
## Step 2: Create our environment
Initialize the environment in the code cell below.
```
env = retro.make(game='SonicTheHedgehog-Genesis', state='GreenHillZone.Act1', scenario='contest')
env.seed(0)
# if gpu is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print("Device: ", device)
```
## Step 3: Viewing our Enviroment
```
print("The size of frame is: ", env.observation_space.shape)
print("No. of Actions: ", env.action_space.n)
env.reset()
plt.figure()
plt.imshow(env.reset())
plt.title('Original Frame')
plt.show()
possible_actions = {
# No Operation
0: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# Left
1: [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
# Right
2: [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
# Left, Down
3: [0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
# Right, Down
4: [0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0],
# Down
5: [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
# Down, B
6: [1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
# B
7: [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
}
```
### Execute the code cell below to play Pong with a random policy.
```
def random_play():
score = 0
env.reset()
for i in range(200):
env.render()
action = possible_actions[np.random.randint(len(possible_actions))]
state, reward, done, _ = env.step(action)
score += reward
if done:
print("Your Score at end of game is: ", score)
break
env.reset()
env.render(close=True)
random_play()
```
## Step 4:Preprocessing Frame
```
plt.figure()
plt.imshow(preprocess_frame(env.reset(), (1, -1, -1, 1), 84), cmap="gray")
plt.title('Pre Processed image')
plt.show()
```
## Step 5: Stacking Frame
```
def stack_frames(frames, state, is_new=False):
frame = preprocess_frame(state, (1, -1, -1, 1), 84)
frames = stack_frame(frames, frame, is_new)
return frames
```
## Step 6: Creating our Agent
```
INPUT_SHAPE = (4, 84, 84)
ACTION_SIZE = len(possible_actions)
SEED = 0
GAMMA = 0.99 # discount factor
BUFFER_SIZE = 100000 # replay buffer size
BATCH_SIZE = 32 # Update batch size
LR = 0.0001 # learning rate
TAU = 1e-3 # for soft update of target parameters
UPDATE_EVERY = 100 # how often to update the network
UPDATE_TARGET = 10000 # After which thershold replay to be started
EPS_START = 0.99 # starting value of epsilon
EPS_END = 0.01 # Ending value of epsilon
EPS_DECAY = 100 # Rate by which epsilon to be decayed
agent = DQNAgent(INPUT_SHAPE, ACTION_SIZE, SEED, device, BUFFER_SIZE, BATCH_SIZE, GAMMA, LR, TAU, UPDATE_EVERY, UPDATE_TARGET, DQNCnn)
```
## Step 7: Watching untrained agent play
```
env.viewer = None
# watch an untrained agent
state = stack_frames(None, env.reset(), True)
for j in range(200):
env.render(close=False)
action = agent.act(state, eps=0.01)
next_state, reward, done, _ = env.step(possible_actions[action])
state = stack_frames(state, next_state, False)
if done:
env.reset()
break
env.render(close=True)
```
## Step 8: Loading Agent
Uncomment line to load a pretrained agent
```
start_epoch = 0
scores = []
scores_window = deque(maxlen=20)
```
## Step 9: Train the Agent with DQN
```
epsilon_by_epsiode = lambda frame_idx: EPS_END + (EPS_START - EPS_END) * math.exp(-1. * frame_idx /EPS_DECAY)
plt.plot([epsilon_by_epsiode(i) for i in range(1000)])
def train(n_episodes=1000):
"""
Params
======
n_episodes (int): maximum number of training episodes
"""
for i_episode in range(start_epoch + 1, n_episodes+1):
state = stack_frames(None, env.reset(), True)
score = 0
eps = epsilon_by_epsiode(i_episode)
# Punish the agent for not moving forward
prev_state = {}
steps_stuck = 0
timestamp = 0
while timestamp < 10000:
action = agent.act(state, eps)
next_state, reward, done, info = env.step(possible_actions[action])
score += reward
timestamp += 1
# Punish the agent for standing still for too long.
if (prev_state == info):
steps_stuck += 1
else:
steps_stuck = 0
prev_state = info
if (steps_stuck > 20):
reward -= 1
next_state = stack_frames(state, next_state, False)
agent.step(state, action, reward, next_state, done)
state = next_state
if done:
break
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
clear_output(True)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
print('\rEpisode {}\tAverage Score: {:.2f}\tEpsilon: {:.2f}'.format(i_episode, np.mean(scores_window), eps), end="")
return scores
scores = train(1000)
```
## Step 10: Watch a Smart Agent!
```
env.viewer = None
# watch an untrained agent
state = stack_frames(None, env.reset(), True)
for j in range(10000):
env.render(close=False)
action = agent.act(state, eps=0.91)
next_state, reward, done, _ = env.step(possible_actions[action])
state = stack_frames(state, next_state, False)
if done:
env.reset()
break
env.render(close=True)
```
| true |
code
| 0.516474 | null | null | null | null |
|
# Star Unpacking
Any object that is an iterable, whether built-in (string, list, tuple, etc) or a custom class will work for unpacking.
<div class="alert alert-block alert-success">
<b>Try This!</b><br>
```python
s = "Hello World!"
s1, s2, s3, s4, s5, s6, s7, s8, s9, s10, s11, s12 = s
print(s7)
```
</div>
<div class="alert alert-block alert-warning">
<b>Food For Thought:</b><br>
What would happen if you didn't have the correct number of items on the left that correlates to the number of items to be unpacked on the right?
</div>
## What If I Don't Need All Of The Unpacked Data?
Sometimes when unpacking, you may not require certain values. There is no special syntax for this, so you can use a throw-away variable.
<div class="alert alert-block alert-danger">
<b>WARNING!</b><br>If you have data you do not need from unpacking, remember to use your <b>del</b> option to clear up your memory!
</div>
**Example:**
```python
data = ['Susie Q', 22, (1986, 7, 15)]
_, age, birthdate = data
del _
```
<div class="alert alert-block alert-info">
<b>Remember:</b><br>Whatever variable(s) you choose, be mindful that they are not used elsewhere. Otherwise, you will overwrite the data!
</div>
## What If I Don't Know The Number Of Items To Unpack?
This is what is referred to as "iterables of arbitrary length" - and if not dealt with properly can cause you a lot of headache.
To address this, you would use "star expressions".
### Example 1
<div class="alert alert-block alert-success">
<b>Try This!</b><br>
Let's say you had a dataset where you wanted to drop the lowest and highest items and return the average.
```python
def drop_first_last(data):
"""
This function takes in an arbitrary dataset and returns the average of what's left.
"""
first, *middle, last = data
return avg(middle)
```
</div>
When you use this particular technique, it is worth noting that regardless of what variables are stored into the one with the asterisk that this new variable is **always** a `list`.
<div class="alert alert-block alert-warning">
<b>Food For Thought:</b><br>
What does the data now look like for each variable that information was unpacked into?
</div>
### Example 2
Let's say you have a "Record" of data consisting of a customer name, phone, email, and contract or order numbers.
```python
record = ('Sam', '972-867-5309', 'samIam@someemail.com', 42, 201, 874)
```
<div class="alert alert-block alert-info">
How would you unpack these? What would each variable's data look like?
</div>
As you've probably been able to determine, it doesn't matter where in your unpacking you have the starred variable. It can be the first, in the middle, or even the last unpacked variable.
Star unpacking allows a developer to leverage known patterns instead of doing a ton of extra coding and checking.
### Example 3 - Strings
Let's say you have a string - let's take a [MongoURL connection string](https://docs.mongodb.com/manual/reference/connection-string/) for example.
Example replica set:
`mongodb://mongodb0.example.com:27017,mongodb1.example.com:27017,mongodb2.example.com:27017/admin?replicaSet=myRepl`
Example with access control enforced:
`mongodb://myDBReader:D1fficultP%40ssw0rd@mongodb0.example.com:27017,mongodb1.example.com:27017,mongodb2.example.com:27017/admin?replicaSet=myRepl`
NOTE: If the username or password includes the at sign @, colon :, slash /, or the percent sign % character, use [percent encoding](https://tools.ietf.org/html/rfc3986#section-2.1).
You can leverage star unpacking to split the data pieces into what you need. Using the [components information](https://docs.mongodb.com/manual/reference/connection-string/#components), how could we get the information we needed?
<div class="alert alert-block alert-success">
<b>Try this!</b>
```python
replica_set = 'mongodb://myDBReader:D1fficultP%40ssw0rd@mongodb0.example.com:27017,mongodb1.example.com:27017,mongodb2.example.com:27017/admin?replicaSet=myRepl'
_, uri_str = replica_set.split(r'//')
user_pw, uri_str = uri_str.split('@')
user, pw = user_pw.split(':')
del user_pw
host_ports, uri_str_2 = uri_str.split('/')
del uri_str
db, *options = uri_str_2.split('?')
del uri_str_2
*host_ports = host_ports.split(',')
```
<div class="alert alert-block alert-danger">
<b>WARNING!</b><br>If you try to use multiple stars in your unpacking, python will not be able to intuitively determine where to stop/end. Be sure there is only 1 variable that has the star for unpacking.
</div>
<hr>
# Keeping Last N Items
Often times it happens that you only need the last N items of some data set, such as but not limited to:
- logs
- grades
- last N quarters of sales
One of the little known features of python is in it's **collections** module: `collections.dequeue`
The `dequeue(maxlen=N)` function will keep a rolling "queue" of fixed size **N**. As new items are added, older items are automatically removed.
Obviously you could do this manually, but why cause yourself the grief of extra code and possible troubleshooting needs? Not only that, but the deque solution is more elegant, pythonic, and _**runs a lot faster**_.
<div class="alert alert-block alert-success">
<b>Try This!</b><br>
```python
from collections import deque
q = deque(maxlen=3)
for item in range(1,6):
q.append(item)
print(q)
```
</div>
Best practices utilize a generator function to decouple the process of searching from the code and getting the results.
## What If We Don't Use maxlen?
This will simply create an unbound queue that you can append or pop items on either end.
<div class="alert alert-block alert-success">
<b>Try This!</b><br>
```python
from collections import deque # this is only needed once in a Jupyter notebook or python script
q = deque()
for item in range(1,5):
if item == 4: # append left
q.appendleft(item)
else:
q.append(item)
if item >= 3:
print(q)
print(q.pop())
print(q)
print(q.popleft())
print(q)
```
</div>
| true |
code
| 0.322744 | null | null | null | null |
|
# Creating a System
## Conventional methods
Systems are defined by a recycle stream (i.e. a tear stream; if any), and a path of unit operations and nested systems. A System object takes care of solving recycle streams by iteratively running its path of units and subsystems until the recycle converges to steady state. Systems can be manually created or automatically generated via the flowsheet or by context management.
### Manually generated
Manually creating a system is **not recommended** as it requires an exponential amount of time and effort for an individual to layout an accurate path. Here we create a trivial system manually as a simple exercise:
```
import biosteam as bst
bst.settings.set_thermo(['Water'])
feed = bst.Stream('feed', Water=100)
recycle = bst.Stream('recycle')
effluent = bst.Stream('effluent')
T1 = bst.MixTank('T1', ins=[feed, recycle])
P1 = bst.Pump('P1', T1-0)
S1 = bst.Splitter('S1', P1-0, [effluent, recycle], split=0.5)
manual_sys = bst.System('manual_sys', path=[T1, P1, S1], recycle=recycle)
manual_sys.simulate()
manual_sys.diagram(
kind='cluster', # Cluster diagrams highlight recycle streams and nested systems.
number=True, # This numbers each unit according to their path order
)
manual_sys.show()
```
Note that the inlets and outlets to a system are inherently connected to the unit operations within the system, but we can still connect systems just like unit operations, as depicted future examples.
### Autogenerated from the flowsheet
The **recommended** way of creating systems is to use the flowsheet. Here we expand on the existing process and create a new system using the flowsheet:
```
water = bst.Stream('water', Water=10)
P2 = bst.Pump('P2', manual_sys-0) # -pipe- notation equivalent to manual_sys.outs[0]
M2 = bst.Mixer('M2', [P2-0, water])
flowsheet_sys = bst.main_flowsheet.create_system('flowsheet_sys')
flowsheet_sys.simulate()
flowsheet_sys.diagram(kind='cluster', number=True)
flowsheet_sys.show()
```
### Autogenerated by context management
System objects' context management feature allows for creating systems of only the units created within the given context:
```
downstream_recycle = bst.Stream('downstream_recycle')
product = bst.Stream('product')
with bst.System('context_sys') as context_sys:
T2 = bst.MixTank('T2', ins=['', downstream_recycle])
P3 = bst.Pump('P3', T2-0)
S2 = bst.Splitter('S2', P3-0, [product, downstream_recycle], split=0.5)
# The feed is empty, no need to run system (yet)
context_sys.diagram('cluster')
context_sys.show()
```
Let's connect two systems together and create a new system from the flowsheet:
```
# -pipe- notation equivalent to context_sys.ins[:] = [flowsheet_sys.outs[0]]
flowsheet_sys-0-context_sys
complete_sys = bst.main_flowsheet.create_system('complete_sys')
complete_sys.simulate()
complete_sys.diagram('cluster')
complete_sys.show()
```
## Drop-in systems
### A simple example
When a system is created by a function, it's called a drop-in system. Here, we create a sugarcane to ethanol production system without facilities (e.g., cooling tower, boiler) by using drop-in systems:
```
from biorefineries.sugarcane import chemicals
from biosteam import Stream, System, settings, main_flowsheet
from biorefineries.sugarcane import (
create_juicing_system_with_fiber_screener as create_juicing_system,
create_sucrose_to_ethanol_system
)
main_flowsheet.clear() # Remove previous unit operations to prevent ID-conflict warnings
settings.set_thermo(chemicals)
denaturant = Stream('denaturant',
Octane=230.69,
units='kg/hr',
price=0.756)
sucrose_solution = Stream('sucrose_solution')
juicing_sys = create_juicing_system(
ID='juicing_sys', # ID of system
outs=[sucrose_solution], # Place sucrose_solution at the 0th outlet (all other streams are defaulted)
)
sucrose_to_ethanol_sys = create_sucrose_to_ethanol_system(ins=[sucrose_solution, denaturant])
# Here are a couple of other ways to connect systems:
# Manually:
# >>> sucrose_to_ethanol_sys.ins[0] = juicing_sys.outs[0]
# With -pipe- notation:
# >>> juicing_sys-0-0-sucrose_to_ethanol_sys
# Manually create a new system and simulate
sugarcane_to_ethanol_sys = System('sugarcane_to_ethanol_sys',
path=[juicing_sys, sucrose_to_ethanol_sys])
sugarcane_to_ethanol_sys.simulate()
sugarcane_to_ethanol_sys.diagram(kind='surface')
sugarcane_to_ethanol_sys.show(data=False)
```
The number of inlets and outlets are rather large. It may be helpful to specify what inlets and outlets do we want to expose:
```
s = main_flowsheet.stream
sugarcane_to_ethanol_sys.load_inlet_ports([s.sugarcane])
sugarcane_to_ethanol_sys.load_outlet_ports([s.ethanol, s.bagasse])
sugarcane_to_ethanol_sys.show(data=False)
```
The ethanol product is now the 0th stream
```
sucrose_to_ethanol_sys.outs[0].show()
```
### System factories
Both `create_juicing_system` and `create_sucrose_to_ethanol_system` are [SystemFactory](../process_tools/SystemFactory.txt) objects, which accept the system `ID`, `ins`, and `outs` (similar to unit operations) and return a new system. Let's first have a look at some of the system factories in the [biorefineries.sugarcane](https://github.com/BioSTEAMDevelopmentGroup/Bioindustrial-Park/tree/master/BioSTEAM%202.x.x/biorefineries/sugarcane) library:
```
create_juicing_system.show()
print()
create_sucrose_to_ethanol_system.show()
```
[SystemFactory](../process_tools/SystemFactory.txt) objects are composed of a function `f` which creates the unit operations, a predefined system `ID`, and `ins` and `outs` dictionaries that serve as keyword arguments to initialize the system's default inlets and outlets.
The signature of a SystemFactory is `f(ID=None, ins=None, outs=None, mockup=False, area=None, udct=None, ...)`. The additional parameters (i.e. mockup, area, and udct) will be discussed in the next section.
### Saving time with mock systems
When creating a biorefinery, we may not be interested in all the subsystems we created with SystemFactory objects. We can save a few milliseconds in computational time (per system) by using mock systems:
```
main_flowsheet.clear() # Remove previous unit operations to prevent ID-conflict warnings
juicing_sys = create_juicing_system(
outs=[sucrose_solution],
mockup=True
)
sucrose_to_ethanol_sys = create_sucrose_to_ethanol_system(
ins=[sucrose_solution, denaturant],
mockup=True
)
# Note that mock systems don't have anything other than `ins`, `outs`, and `units`
juicing_sys.show()
sucrose_to_ethanol_sys.show()
# We can create the system using the flowsheet
sugarcane_to_ethanol_sys = main_flowsheet.create_system('sugarcane_to_ethanol_sys')
sugarcane_to_ethanol_sys.simulate()
sugarcane_to_ethanol_sys.diagram()
sucrose_to_ethanol_sys.outs[0].show()
```
### Using the area naming convention
The area naming convention follows {letter}{area + number} where the letter depends on
the unit operation as follows:
* C: Centrifuge
* D: Distillation column
* E: Evaporator
* F: Flash tank
* H: Heat exchange
* M: Mixer
* P: Pump (including conveying belt)
* R: Reactor
* S: Splitter (including solid/liquid separator)
* T: Tank or bin for storage
* U: Other units
* J: Junction, not a physical unit (serves to adjust streams)
* PS: Process specificiation, not a physical unit (serves to adjust streams)
For example, the first mixer in area 100 would be named M101. When calling a SystemFactory object, we can pass the `area` to name unit operations according to the area convention. In the following example, we name all unit operations in the juicing system under area 300:
```
main_flowsheet.clear() # Remove previous unit operations
juicing_sys = create_juicing_system(area=300, mockup=True)
juicing_sys.show()
```
To access unit operations by their default ID (as originally defined in SystemFactory code), you can request a unit dictionary by passing `udct`=True:
```
main_flowsheet.clear() # Remove previous unit operations
# When udct is True, both the system and the unit dictionary are returned
juicing_sys, udct = create_juicing_system(mockup=True, area=300, udct=True)
unit = udct['U201']
print(repr(unit)) # Originally, this unit was named U201
```
### Creating system factories
Create a SystemFactory object for creating sugarcane to ethanol systems:
```
from biosteam import System, SystemFactory
@SystemFactory(
ID='sugarcane_to_ethanol_sys',
ins=[create_juicing_system.ins[0], # Reuse default from juicing system factory
dict(ID='denaturant',
price=0.756)],
outs=[dict(ID='ethanol',
price=0.789),
dict(ID='bagasse')]
)
def create_sugarcane_to_ethanol_system(ins, outs):
# ins and outs will be stream objects
sugarcane, denaturant = ins
ethanol, bagasse = outs
juicing_sys = create_juicing_system(
ins=sugarcane,
outs=[None, bagasse], # None will default to a stream
mockup=True
)
sucrose_to_ethanol_sys = create_sucrose_to_ethanol_system(
ins=(juicing_sys-0, denaturant),
outs=ethanol,
mockup=True,
)
# The system factory builds a system from units created by the function
create_sugarcane_to_ethanol_system.show()
```
Create the sugarcane to ethanol system and simulate:
```
main_flowsheet.clear() # Remove previous unit operations
sugarcane_to_ethanol_sys = create_sugarcane_to_ethanol_system()
sugarcane_to_ethanol_sys.simulate()
sugarcane_to_ethanol_sys.show()
```
Biorefinery systems can be created by connecting smaller systems, allowing us to create alternative configurations with ease. The [biorefineries](https://github.com/BioSTEAMDevelopmentGroup/Bioindustrial-Park) library has yet to fully implement SystemFactory objects across all functions that create systems, but that is the goal.
| true |
code
| 0.415492 | null | null | null | null |
|
## Imports
```
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from minepy import MINE
from scipy.stats import pearsonr,spearmanr,describe
from scipy.spatial.distance import pdist, squareform
import numpy as np
import copy
import dcor
sns.set()
```
## Pearson’s Correlation Coefficient


#### Generate Data
```
np.random.seed(1077939816)
sample_size = 100
noise_mean = 0
noise_std = 1
theta = np.random.randn(2)
x_1 = np.random.randn(sample_size)*10
y_1 = theta[0]*x_1+theta[1]
y_1_noise = y_1 + np.random.normal(noise_mean,noise_std,size = sample_size).T
ro_1, p_1 = pearsonr(x_1,y_1)
ro_2, p_2 = pearsonr(x_1,y_1_noise)
fig, axs = plt.subplots(nrows=1, ncols=2,figsize = (10,5))
axs.flat[0].scatter(x_1,y_1)
axs.flat[0].set_title("pearsonr:{0},p-value:{1}".format(np.round(ro_1,4),np.round(p_1,4)))
axs.flat[1].scatter(x_1,y_1_noise)
axs.flat[1].set_title("pearsonr:{0},p-value:{1}".format(np.round(ro_2,4),np.round(p_2,4)));
np.random.seed(15)
x_2 = np.random.rand(sample_size)*5
y_2_cuadr = x_2**2 + np.random.normal(noise_mean,noise_std,size = sample_size)
y_2_sin = np.sin(x_2) + np.random.normal(noise_mean,noise_std,size = sample_size)
y_2_log = np.log(x_2) + np.random.normal(noise_mean,noise_std-0.5,size = sample_size)
```
#### Calculate pearsonr and plot
```
ro_0, p_0 = pearsonr(x_2,y_2_cuadr)
ro_1, p_1 = pearsonr(x_2,y_2_log)
ro_2, p_2 = pearsonr(x_2,y_2_sin)
fig, axs = plt.subplots(nrows=1, ncols=3,figsize = (12,4))
axs.flat[0].scatter(x_2,y_2_cuadr)
axs.flat[0].set_title("quadr-ro:{0},p-value:{1}".format(np.round(ro_0,4),np.round(p_0,4)))
axs.flat[1].scatter(x_2,y_2_log)
axs.flat[1].set_title("log-ro:{0},p-value:{1}".format(np.round(ro_1,4),np.round(p_1,4)))
axs.flat[2].scatter(x_2,y_2_sin);
axs.flat[2].set_title("sin-ro:{0},p-value:{1}".format(np.round(ro_2,4),np.round(p_2,4)));
```
### Spearman correlation

```
ro_0, p_0 = spearmanr(x_2,y_2_log)
ro_1, p_1 = spearmanr(x_2,y_2_log)
ro_2, p_2 = spearmanr(x_2,y_2_sin)
fig, axs = plt.subplots(nrows=1, ncols=3,figsize = (12,4))
axs.flat[0].scatter(x_2,y_2_cuadr)
axs.flat[0].set_title("quadr-ro:{0},p-value:{1}".format(np.round(ro_0,4),np.round(p_0,4)))
axs.flat[1].scatter(x_2,y_2_log)
axs.flat[1].set_title("log-ro:{0},p-value:{1}".format(np.round(ro_1,4),np.round(p_1,4)))
axs.flat[2].scatter(x_2,y_2_sin);
axs.flat[2].set_title("sin-ro:{0},p-value:{1}".format(np.round(ro_2,4),np.round(p_2,4)));
x = np.linspace(0,10)
y = np.sin(x) + np.random.normal(0,0.1,50)
r, p = spearmanr(x,y)
plt.scatter(x,y)
plt.title("spearmanr:{0},p-value:{1}".format(np.round(r,3),np.round(p,3)));
plt.show()
x = np.linspace(-10,10)
y = x**2 + np.random.normal(0,5,50)
r, p = spearmanr(x,y)
plt.scatter(x,y)
plt.title("spearmanr:{0},p-value:{1}".format(np.round(r,3),np.round(p,3)));
```
### Distance Correlation

```
def distcorr(Xval, Yval, pval=True, nruns=2000):
""" Compute the distance correlation function, returning the p-value.
Based on Satra/distcorr.py (gist aa3d19a12b74e9ab7941)
>>> a = [1,2,3,4,5]
>>> b = np.array([1,2,9,4,4])
>>> distcorr(a, b)
(0.76267624241686671, 0.404)
"""
X = np.atleast_1d(Xval)
Y = np.atleast_1d(Yval)
if np.prod(X.shape) == len(X):
X = X[:, None]
if np.prod(Y.shape) == len(Y):
Y = Y[:, None]
X = np.atleast_2d(X)
Y = np.atleast_2d(Y)
n = X.shape[0]
if Y.shape[0] != X.shape[0]:
raise ValueError('Number of samples must match')
a = squareform(pdist(X))
b = squareform(pdist(Y))
A = a - a.mean(axis=0)[None, :] - a.mean(axis=1)[:, None] + a.mean()
B = b - b.mean(axis=0)[None, :] - b.mean(axis=1)[:, None] + b.mean()
dcov2_xy = (A * B).sum() / float(n * n)
dcov2_xx = (A * A).sum() / float(n * n)
dcov2_yy = (B * B).sum() / float(n * n)
dcor = np.sqrt(dcov2_xy) / np.sqrt(np.sqrt(dcov2_xx) * np.sqrt(dcov2_yy))
if pval:
greater = 0
for i in range(nruns):
Y_r = copy.copy(Yval)
np.random.shuffle(Y_r)
if distcorr(Xval, Y_r, pval=False) >= dcor:
greater += 1
return (dcor, greater / float(nruns))
else:
return dcor
def dist_corr(X, Y, pval=True, nruns=2000):
""" Distance correlation with p-value from bootstrapping
"""
dc = dcor.distance_correlation(X, Y)
pv = dcor.independence.distance_covariance_test(X, Y, exponent=1.0, num_resamples=nruns)[0]
if pval:
return (dc, pv)
else:
return dc
ro_0, p_0 = dist_corr(x_2,y_2_log)
ro_1, p_1 = dist_corr(x_2,y_2_log)
ro_2, p_2 = dist_corr(x_2,y_2_sin)
fig, axs = plt.subplots(nrows=1, ncols=3,figsize = (12,4))
axs.flat[0].scatter(x_2,y_2_cuadr)
axs.flat[0].set_title("quadr-ro:{0},p-value:{1}".format(np.round(ro_0,4),np.round(p_0,4)))
axs.flat[1].scatter(x_2,y_2_log)
axs.flat[1].set_title("log-ro:{0},p-value:{1}".format(np.round(ro_1,4),np.round(p_1,4)))
axs.flat[2].scatter(x_2,y_2_sin);
axs.flat[2].set_title("sin-ro:{0},p-value:{1}".format(np.round(ro_2,4),np.round(p_2,4)))
plt.show()
x = np.linspace(0,10)
y = np.sin(x) + np.random.normal(0,0.1,50)
r, p = dist_corr(x,y)
plt.scatter(x,y)
plt.title("distcorr:{0},p-value:{1}".format(np.round(r,3),np.round(p,3)));
plt.show()
x = np.linspace(-10,10)
y = x**2 + np.random.normal(0,5,50)
r, p = dist_corr(x,y)
plt.scatter(x,y)
plt.title("distcorr:{0},p-value:{1}".format(np.round(r,3),np.round(p,3)));
from sklearn.datasets import make_classification
X1, Y1 = make_classification(n_features=2, n_redundant=0, n_informative=1,
n_clusters_per_class=1)
d,p = dist_corr(X1[:,0],X1[:,1])
plt.scatter(X1[:,0],X1[:,1])
plt.title("distcorr:{0},p-value:{1}".format(np.round(d,3),np.round(p,3)));
```
### Maximum Information Coefficient


```
def mic(X,Y,pval=True,nruns=100):
mine = MINE(alpha=0.6, c=15, est="mic_approx")
mine.compute_score(X,Y)
mic = mine.mic()
if pval:
greater = 0
for i in range(nruns):
Y_r = copy.copy(Y)
np.random.shuffle(Y_r)
mine.compute_score(X,Y_r)
cur_mine = mine.mic()
if cur_mine >= mic:
greater += 1
return (mic, greater / float(nruns))
else:
return mic
ro_0, p_0 = mic(x_2,y_2_log)
ro_1, p_1 = mic(x_2,y_2_log)
ro_2, p_2 = mic(x_2,y_2_sin)
fig, axs = plt.subplots(nrows=1, ncols=3,figsize = (12,4))
axs.flat[0].scatter(x_2,y_2_cuadr)
axs.flat[0].set_title("MIC-ro:{0},p-value:{1}".format(np.round(ro_0,4),np.round(p_0,4)))
axs.flat[1].scatter(x_2,y_2_log)
axs.flat[1].set_title("MIC-ro:{0},p-value:{1}".format(np.round(ro_1,4),np.round(p_1,4)))
axs.flat[2].scatter(x_2,y_2_sin);
axs.flat[2].set_title("MIC-ro:{0},p-value:{1}".format(np.round(ro_2,4),np.round(p_2,4)))
plt.show()
x = np.linspace(0,10)
y = np.sin(x) + np.random.normal(0,0.1,50)
r, p = mic(x,y)
plt.scatter(x,y)
plt.title("MIC:{0},p-value:{1}".format(np.round(r,3),np.round(p,3)));
plt.show()
x = np.linspace(-10,10)
y = x**2 + np.random.normal(0,5,50)
r, p = mic(x,y)
plt.scatter(x,y)
plt.title("MIC:{0},p-value:{1}".format(np.round(r,3),np.round(p,3)));
X1, Y1 = make_classification(n_features=2, n_redundant=0, n_informative=1,
n_clusters_per_class=1)
d,p = mic(X1[:,0],X1[:,1])
plt.scatter(X1[:,0],X1[:,1])
plt.title("mic:{0},p-value:{1}".format(np.round(d,3),np.round(p,3)));
```
| true |
code
| 0.663042 | null | null | null | null |
|
## Additional training functions
[`train`](/train.html#train) provides a number of extension methods that are added to [`Learner`](/basic_train.html#Learner) (see below for a list and details), along with three simple callbacks:
- [`ShowGraph`](/train.html#ShowGraph)
- [`GradientClipping`](/train.html#GradientClipping)
- [`BnFreeze`](/train.html#BnFreeze)
- [`AccumulateScheduler`](/train.html#AccumulateScheduler)
```
from fastai.gen_doc.nbdoc import *
from fastai.train import *
from fastai.vision import *
```
## [`Learner`](/basic_train.html#Learner) extension methods
These methods are automatically added to all [`Learner`](/basic_train.html#Learner) objects created after importing this module. They provide convenient access to a number of callbacks, without requiring them to be manually created.
```
show_doc(fit_one_cycle)
show_doc(one_cycle_scheduler)
```
See [`OneCycleScheduler`](/callbacks.one_cycle.html#OneCycleScheduler) for details.
```
show_doc(lr_find)
```
See [`LRFinder`](/callbacks.lr_finder.html#LRFinder) for details.
```
show_doc(to_fp16)
```
See [`MixedPrecision`](/callbacks.fp16.html#MixedPrecision) for details.
```
show_doc(to_fp32)
show_doc(mixup)
```
See [`MixUpCallback`](/callbacks.mixup.html#MixUpCallback) for more details.
```
show_doc(Interpretation)
show_doc(Interpretation.from_learner)
show_doc(Interpretation.top_losses)
```
For example in [`ClassificationInterpretation`](/train.html#ClassificationInterpretation) is implemented using argmax on preds to set `self.pred_class` whereas an optional sigmoid is used for `MultilabelClassificationInterpretation`
```
show_doc(ClassificationInterpretation)
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = cnn_learner(data, models.resnet18)
learn.fit(1)
preds,y,losses = learn.get_preds(with_loss=True)
interp = ClassificationInterpretation(learn, preds, y, losses)
show_doc(ClassificationInterpretation.top_losses)
```
Returns tuple of *(losses,indices)*.
```
interp.top_losses(9)
show_doc(ClassificationInterpretation.plot_confusion_matrix)
```
If [`normalize`](/vision.data.html#normalize), plots the percentages with `norm_dec` digits. `slice_size` can be used to avoid out of memory error if your set is too big. `kwargs` are passed to `plt.figure`.
```
interp.plot_confusion_matrix()
show_doc(ClassificationInterpretation.confusion_matrix)
interp.confusion_matrix()
show_doc(ClassificationInterpretation.most_confused)
show_doc(MultiLabelClassificationInterpretation)
jekyll_warn("MultiLabelClassificationInterpretation is not implemented yet. Feel free to implement it :)")
```
#### Working with large datasets
When working with large datasets, memory problems can arise when computing the confusion matrix. For example, an error can look like this:
RuntimeError: $ Torch: not enough memory: you tried to allocate 64GB. Buy new RAM!
In this case it is possible to force [`ClassificationInterpretation`](/train.html#ClassificationInterpretation) to compute the confusion matrix for data slices and then aggregate the result by specifying slice_size parameter.
```
interp.confusion_matrix(slice_size=10)
interp.plot_confusion_matrix(slice_size=10)
interp.most_confused(slice_size=10)
```
## Additional callbacks
We'll show examples below using our MNIST sample. As usual the `on_something` methods are directly called by the fastai library, no need to call them yourself.
```
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
show_doc(ShowGraph, title_level=3)
```
```python
learn = cnn_learner(data, models.resnet18, metrics=accuracy, callback_fns=ShowGraph)
learn.fit(3)
```

```
show_doc(ShowGraph.on_epoch_end)
show_doc(GradientClipping)
learn = cnn_learner(data, models.resnet18, metrics=accuracy,
callback_fns=partial(GradientClipping, clip=0.1))
learn.fit(1)
show_doc(GradientClipping.on_backward_end)
show_doc(BnFreeze)
```
For batchnorm layers where `requires_grad==False`, you generally don't want to update their moving average statistics, in order to avoid the model's statistics getting out of sync with its pre-trained weights. You can add this callback to automate this freezing of statistics (internally, it calls `eval` on these layers).
```
learn = cnn_learner(data, models.resnet18, metrics=accuracy, callback_fns=BnFreeze)
learn.fit(1)
show_doc(BnFreeze.on_epoch_begin)
show_doc(AccumulateScheduler)
```
Let's force `batch_size=2` to mimic a scenario where we can't fit enough batch samples to our memory. We can then set `n_step` as desired to have an effective batch_size of `effective_batch_size=batch_size*n_step`.
It is also important to use loss func with `reduce='sum'` in order to calculate exact average accumulated gradients.
Another important note for users is that `batchnorm` is not yet adapted to accumulated gradients. So you should use this callback at your own risk until a hero fixes it :)
Here we demonstrate this callback with a model without `batchnorm` layers, alternatively you can use `nn.InstanceNorm` or [`nn.GroupNorm`](https://pytorch.org/docs/stable/nn.html#torch.nn.GroupNorm).
```
from torchvision.models import vgg11
data = ImageDataBunch.from_folder(path, bs=2)
learn = cnn_learner(data, resnet18, metrics=accuracy, loss_func=CrossEntropyFlat(reduction='sum'),
callback_fns=partial(AccumulateScheduler, n_step=16))
learn.fit(1)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
```
show_doc(ClassificationInterpretation.plot_top_losses)
show_doc(ClassificationInterpretation.from_learner)
show_doc(ClassificationInterpretation.top_losses)
show_doc(ClassificationInterpretation.confusion_matrix)
show_doc(ClassificationInterpretation.most_confused)
show_doc(ClassificationInterpretation.plot_confusion_matrix)
show_doc(ClassificationInterpretation.plot_multi_top_losses)
```
## Open This Notebook
<button style="display: flex; align-item: center; padding: 4px 8px; font-size: 14px; font-weight: 700; color: #1976d2; cursor: pointer;" onclick="window.location.href = 'https://console.cloud.google.com/mlengine/notebooks/deploy-notebook?q=download_url%3Dhttps%253A%252F%252Fraw.githubusercontent.com%252Ffastai%252Ffastai%252Fmaster%252Fdocs_src%252Ftrain.ipynb';"><img src="https://www.gstatic.com/images/branding/product/1x/cloud_24dp.png" /><span style="line-height: 24px; margin-left: 10px;">Open in GCP Notebooks</span></button>
| true |
code
| 0.84556 | null | null | null | null |
|
# Databolt Flow
For data scientists and data engineers, d6tflow is a python library which makes building complex data science workflows easy, fast and intuitive.
https://github.com/d6t/d6tflow
## Benefits of using d6tflow
[4 Reasons Why Your Machine Learning Code is Probably Bad](https://medium.com/@citynorman/4-reasons-why-your-machine-learning-code-is-probably-bad-c291752e4953)
# Example Usage For a Machine Learning Workflow
Below is an example of a typical machine learning workflow: you retreive data, preprocess it, train a model and evaluate the model output.
In this example you will:
* Build a machine learning workflow made up of individual tasks
* Check task dependencies and their execution status
* Execute the model training task including dependencies
* Save intermediary task output to Parquet, pickle and in-memory
* Load task output to pandas dataframe and model object for model evaluation
* Intelligently rerun workflow after changing a preprocessing parameter
```
import d6tflow
import luigi
import sklearn, sklearn.datasets, sklearn.svm
import pandas as pd
# define workflow
class TaskGetData(d6tflow.tasks.TaskPqPandas): # save dataframe as parquet
def run(self):
iris = sklearn.datasets.load_iris()
df_train = pd.DataFrame(iris.data,columns=['feature{}'.format(i) for i in range(4)])
df_train['y'] = iris.target
self.save(df_train) # quickly save dataframe
class TaskPreprocess(d6tflow.tasks.TaskPqPandas):
do_preprocess = luigi.BoolParameter(default=True) # parameter for preprocessing yes/no
def requires(self):
return TaskGetData() # define dependency
def run(self):
df_train = self.input().load() # quickly load required data
if self.do_preprocess:
df_train.iloc[:,:-1] = sklearn.preprocessing.scale(df_train.iloc[:,:-1])
self.save(df_train)
class TaskTrain(d6tflow.tasks.TaskPickle): # save output as pickle
do_preprocess = luigi.BoolParameter(default=True)
def requires(self):
return TaskPreprocess(do_preprocess=self.do_preprocess)
def run(self):
df_train = self.input().load()
model = sklearn.svm.SVC()
model.fit(df_train.iloc[:,:-1], df_train['y'])
self.save(model)
# Check task dependencies and their execution status
d6tflow.preview(TaskTrain())
# Execute the model training task including dependencies
d6tflow.run(TaskTrain())
# Load task output to pandas dataframe and model object for model evaluation
model = TaskTrain().output().load()
df_train = TaskPreprocess().output().load()
print(sklearn.metrics.accuracy_score(df_train['y'],model.predict(df_train.iloc[:,:-1])))
# Intelligently rerun workflow after changing a preprocessing parameter
d6tflow.preview(TaskTrain(do_preprocess=False))
d6tflow.run(TaskTrain(do_preprocess=False)) # execute with new parameter
```
# Next steps: Transition code to d6tflow
See https://d6tflow.readthedocs.io/en/latest/transition.html
| true |
code
| 0.472805 | null | null | null | null |
|
## Generating partial coherence phase screens for modeling rotating diffusers
```
%pylab
%matplotlib inline
import SimMLA.fftpack as simfft
import SimMLA.grids as grids
import SimMLA.fields as fields
from numpy.fft import fft, ifft, fftshift, ifftshift
from scipy.integrate import simps
from scipy.interpolate import interp1d
```
I am simulating a partially spatially coherent laser beam using a technique described in [Xiao and Voelz, "Wave optics simulation approach for partial spatially coherent beams," Opt. Express 14, 6986-6992 (2006)](https://www.osapublishing.org/oe/abstract.cfm?uri=oe-14-16-6986) and Chapter 9 of [Computational Fourier Optics: A MATLAB Tutorial](http://spie.org/Publications/Book/858456), which is also by Voelz. This workbook demonstrates how to generate the partially coherent beam and propagate it through the dual-MLA system.
Here I am breaking from Xiao and Voelz's implementation by decoupling the phase screen parameters \\( \sigma\_f \\) and \\( \sigma\_r \\).
**Note: This notebook contains LaTeX that may not be visible when viewed from GitHub. Try downloading it and opening it with the Jupyter Notebook application.**
## Build the coordinate system and dual-MLA's
```
numLenslets = 21 # Must be odd; corresponds to the number of lenslets in one dimension
lensletSize = 500 # microns
focalLength = 13700 # microns, lenslet focal lengths
fc = 50000 # microns, collimating lens focal length
dR = -10000 # microns, distance of diffuser from telescope focus
L1 = 500000 # microns, distance between collimating lens and first MLA
L2 = 200000 # microns, distance between second MLA and objective BFP
wavelength = 0.642 # microns
subgridSize = 10001 # Number of grid (or lattice) sites for a single lenslet
physicalSize = numLenslets * lensletSize # The full extent of the MLA
# dim = 1 makes the grid 1D
collGrid = grids.Grid(20001, 5000, wavelength, fc, dim = 1)
grid = grids.GridArray(numLenslets, subgridSize, physicalSize, wavelength, focalLength, dim = 1, zeroPad = 3)
```
Now, the output from the telescope + diffuser may be generated by multiplying the focused Gaussian beam with a random phase mask from the Voelz code.
The input beam has a 4 mm waist (radius), but is focused by a telescope whose first lens has a focal length of 100 mm = 1e5 microns. [Using a Gaussian beam calculator](http://www.calctool.org/CALC/phys/optics/f_NA), this means that the focused beam has a waist diameter of \\( 2w = 10.2 \, \mu m \\) and a beam standard deviation of \\( \frac{5.1 \mu m}{\sqrt{2}} = 3.6 \mu m \\). The measured beam standard deviation in the setup is in reality about \\( 6.0 \, \mu m \\) due to a slight astigmatism in the beam beam and spherical aberration. (The telescope lenses are simple plano-convex lenses.)
After multiplying the beam by the phase screen, the field is Fourier transformed by the second telescope lens with \\( f = 50 \, mm \\) to produce the field in the focal plane of the collimating lens. The following steps are then taken to get the field on the sample:
1. The field from the collimating lens is propagated a distance \\( L_1 \\) to the first MLA.
2. The field immediately after the second MLA is computed via a spatially-parallel Fourier transform operation.
3. This field is propagated a distance \\( L_2 \\) to the back focal plane of the objective.
4. The field is Fourier transformed to produce the field on the sample.
```
Z0 = 376.73 # Impedance of free space, Ohms
power = 100 # mW
beamStd = 6 # microns
sigma_f = 10 # microns, diffuser correlation length
sigma_r = 1 # variance of the random phase
fieldAmp = np.sqrt(power / 1000 * Z0 / beamStd / np.sqrt(np.pi)) # Factor of 1000 converts from mW to W
# The diffuser sits 'dR' microns from the focus
beam = lambda x: fields.GaussianBeamDefocused(fieldAmp, beamStd, wavelength, dR)(x) \
* fields.diffuserMask(sigma_f, sigma_r, collGrid)(x)
# Sample the beam at the diffuser
beamSample = beam(collGrid.px)
# Propagate the sample back to the focal plane of the telescope
beamSample = simfft.fftPropagate(beamSample, collGrid, -dR)
plt.plot(collGrid.px, np.abs(beamSample), linewidth = 2)
plt.xlim((-1000,1000))
plt.xlabel(r'x-position')
plt.ylabel(r'Field amplitude')
plt.grid(True)
plt.show()
plt.plot(collGrid.px, np.angle(beamSample), linewidth = 2, label ='Phase')
plt.plot(collGrid.px, np.abs(beamSample) / np.max(np.abs(beamSample)) * np.angle(beamSample), label = 'Phase with Gaussian envelope')
plt.xlim((-1000,1000))
plt.ylim((-4, 4))
plt.xlabel(r'x-position')
plt.ylabel(r'Field phase, rad')
plt.grid(True)
plt.legend()
plt.show()
```
## Create the input field to the MLA's
The MLA inputs are the Fourier transform of this field when the diffuser is in the focal plane of the collimating lens.
```
scalingFactor = collGrid.physicalSize / (collGrid.gridSize - 1) / np.sqrt(collGrid.wavelength * collGrid.focalLength)
inputField = scalingFactor * np.fft.fftshift(np.fft.fft(np.fft.ifftshift(beamSample)))
plt.plot(collGrid.pX, np.abs(inputField))
plt.xlim((-20000, 20000))
plt.grid(True)
plt.show()
# Interpolate this field onto the MLA grid
mag = np.abs(inputField)
ang = np.angle(inputField)
inputMag = interp1d(collGrid.pX,
mag,
kind = 'nearest',
bounds_error = False,
fill_value = 0.0)
inputAng = interp1d(collGrid.pX,
ang,
kind = 'nearest',
bounds_error = False,
fill_value = 0.0)
plt.plot(grid.px, np.abs(inputMag(grid.px) * np.exp(1j * inputAng(grid.px))))
plt.xlim((-5000, 5000))
plt.grid(True)
plt.show()
field2 = lambda x: inputMag(x) * np.exp(1j * inputAng(x))
interpMag, interpAng = simfft.fftSubgrid(field2, grid)
# Plot the field behind the second MLA center lenslet
plt.plot(grid.pX, np.abs(interpMag[10](grid.pX) * np.exp(1j * interpAng[10](grid.pX))))
plt.xlim((-500, 500))
plt.xlabel('x-position')
plt.ylabel('Field amplitude')
plt.grid(True)
plt.show()
```
## Propagate this field through the dual MLA illuminator
The rest of this code is exactly the same as before: propagate the partially coherent beam through the illuminator and observe the irradiance pattern on the sample.
## Compute many realizations of the diffuser
```
fObj = 3300 # microns
bfpDiam = 2 * 1.4 * fObj # microns, BFP diameter, 2 * NA * f_OBJ
# Grid for interpolating the field after the second MLA
newGridSize = subgridSize * numLenslets # microns
newGrid = grids.Grid(5*newGridSize, 5*physicalSize, wavelength, fObj, dim = 1)
%%time
nIter = 100
#sigma_r = np.array([0.1, 0.3, 1, 3])
sigma_r = np.array([1])
# Create multiple sample irradiance patterns for various values of sigma_r
for sigR in sigma_r:
# New phase mask; the diffuser sits 'dR' microns from the focus
beam = lambda x: fields.GaussianBeamDefocused(fieldAmp, beamStd, wavelength, dR)(x) \
* fields.diffuserMask(sigma_f, sigR, collGrid)(x)
avgIrrad = np.zeros(newGrid.px.size, dtype=np.float128)
for realization in range(nIter):
print('sigma_r: {0:.2f}'.format(sigR))
print('Realization number: {0:d}'.format(realization))
# Propagate the field from the diffuser to the telescope focus
beamSample = beam(collGrid.px)
beamSample = simfft.fftPropagate(beamSample, collGrid, -dR)
# Compute the field in the focal plane of the collimating lens
scalingFactor = collGrid.physicalSize / (collGrid.gridSize - 1) / np.sqrt(collGrid.wavelength * collGrid.focalLength)
afterColl = scalingFactor * np.fft.fftshift(np.fft.fft(np.fft.ifftshift(beamSample)))
# Interpolate the input onto the new grid;
# Propagate it to the first MLA at distance L1 away from the focal plane of the collimating lens
inputMag = interp1d(collGrid.pX,
np.abs(afterColl),
kind = 'nearest',
bounds_error = False,
fill_value = 0.0)
inputAng = interp1d(collGrid.pX,
np.angle(afterColl),
kind = 'nearest',
bounds_error = False,
fill_value = 0.0)
inputField = lambda x: simfft.fftPropagate(inputMag(x) * np.exp(1j * inputAng(x)), grid, L1)
# Compute the field magnitude and phase for each individual lenslet just beyond the second MLA
interpMag, interpPhase = simfft.fftSubgrid(inputField, grid)
# For each interpolated magnitude and phase corresponding to a lenslet
# 1) Compute the full complex field
# 2) Sum it with the other complex fields
field = np.zeros(newGrid.gridSize)
for currMag, currPhase in zip(interpMag, interpPhase):
fieldMag = currMag(newGrid.px)
fieldPhase = currPhase(newGrid.px)
currField = fieldMag * np.exp(1j * fieldPhase)
field = field + currField
# Propagate the field to the objective's BFP and truncate the region outside the aperture
field = simfft.fftPropagate(field, newGrid, L2)
field[np.logical_or(newGrid.px < -bfpDiam / 2, newGrid.px > bfpDiam / 2)] = 0.0
# Propagate the truncated field in the BFP to the sample
scalingFactor = newGrid.physicalSize / (newGrid.gridSize - 1) / np.sqrt(newGrid.wavelength * newGrid.focalLength)
F = scalingFactor * np.fft.fftshift(np.fft.fft(np.fft.ifftshift(field)))
# Compute the irradiance on the sample
Irrad = np.abs(F)**2 / Z0 * 1000
# Save the results for this realization
avgIrrad = avgIrrad + Irrad
# Average irradiance
avgIrrad = avgIrrad / nIter
# Save the results
# The folder 'Rotating Diffuser Calibration' should already exist.
#np.save('Rotating Diffuser Calibration/x-coords_sigR_{0:.3f}.npy'.format(sigR), newGrid.pX)
#np.save('Rotating Diffuser Calibration/avgIrrad_sigR_{0:.3f}.npy'.format(sigR), avgIrrad)
plt.plot(newGrid.pX, avgIrrad)
plt.xlim((-100,100))
plt.xlabel(r'Sample plane x-position, $\mu m$')
plt.ylabel(r'Irradiance, $mW / \mu m$')
plt.grid(True)
plt.show()
# Check the output power
powerOut = simps(avgIrrad, newGrid.pX)
print('The output power is {0:.2f} mW'.format(powerOut))
```
| true |
code
| 0.637031 | null | null | null | null |
|
Note: It is recommended to run this notebook from an [Azure DSVM](https://docs.microsoft.com/en-us/azure/machine-learning/data-science-virtual-machine/overview) instance.
```
# Useful for being able to dump images into the Notebook
import IPython.display as D
```
# Big Picture
In the previous notebooks, we tried together [Custom Vision service](https://github.com/CatalystCode/CVWorkshop/blob/master/%232%20Policy%20Classfication%20With%20Custom%20Vision%20Service.ipynb) in addition to [Transfer Learning](https://github.com/CatalystCode/CVWorkshop/blob/master/%233%20Policy%20Recognition%20with%20Resnet%20and%20Transfer%20Learning.ipynb) which is one of the popular approaches in deep learning where pre-trained models are used as the starting point on computer vision.
So if we look on the big picture, we will realize that the previous notebooks are focusing on preparing/loading training data set, building models, training models then evaluating the output.
In this tutorial, we will move the focus to operationalizing models by deploying trained models as web services so that you can consume it later from any client application via REST API call. For that purporse, we are using Azure Machine Learning Model Management Service.
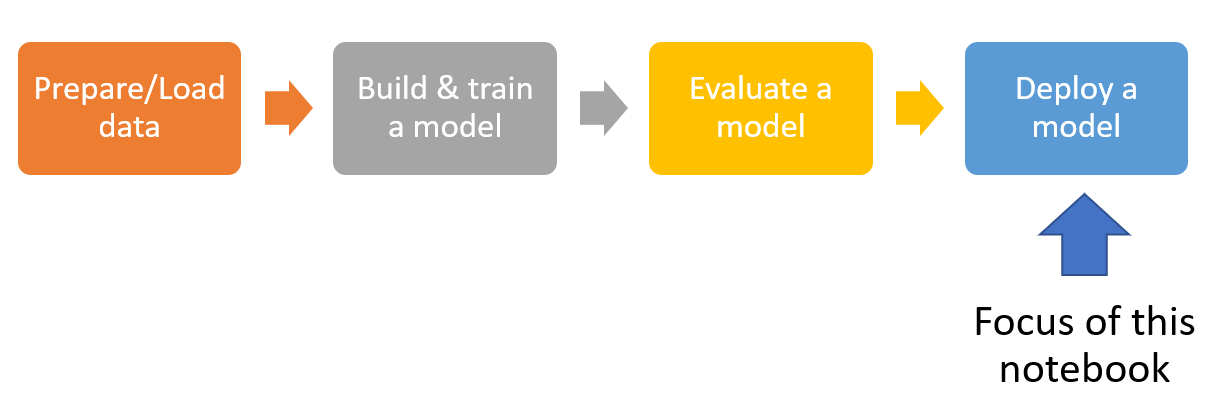
# Azure Model Management Service
Azure Machine Learning Model Management enables you to manage and deploy machine-learning models. It provides different services like creating Docker containers with models for local testing, deploying models to production through Azure ML Compute Environment with [Azure Container Service](https://azure.microsoft.com/en-us/services/container-service/) and versioning & tracking models. Learn more here: [Conceptual Overview of Azure Model Management Service](https://docs.microsoft.com/en-us/azure/machine-learning/preview/model-management-overview)
### What's needed to deploy my model?
* Your Model File or Directory of Model Files
* You need to create a score.py that loads your model and returns the prediction result(s) using the model and also used to generates a schema JSON file
* Schema JSON file for API parameters (validates API input and output)
* Runtime Environment Choice e.g. python or spark-py
* Conda dependency file listing runtime dependencies
### How it works:

Learn more here: [Conceptual Overview of Azure Model Management Service](https://docs.microsoft.com/en-us/azure/machine-learning/preview/model-management-overview)
### Deployment Steps:
* Use your saved, trained, Machine Learning model
* Create a schema for your web service's input and output data
* Create a Docker-based container image
* Create and deploy the web service
### Deployment Target Environments:
1. Local Environment: You can set up a local environment to deploy and test your web service on your local machine or DSVM. (Requires you to install Docker on the machine)
2. Production Environment: You can use Cluster deployment for high-scale production scenarios. It sets up an ACS cluster with Kubernetes as the orchestrator. The ACS cluster can be scaled out to handle larger throughput for your web service calls. (Kubernetes deployment on an Azure Container Service (ACS) cluster)
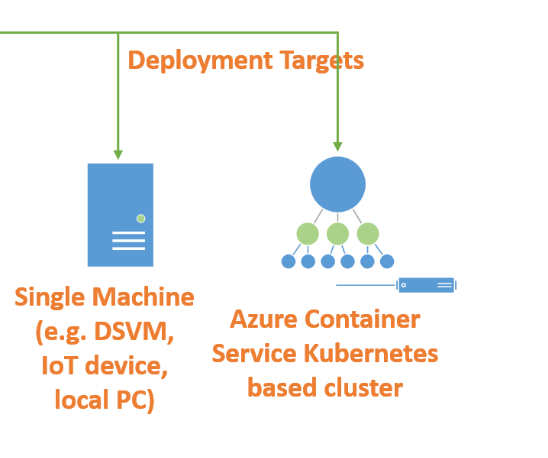
# Challenge
```
# Run the following train.py from the notebook to generate a classifier model
from sklearn.svm import SVC
from cvworkshop_utils import ensure_exists
import pickle
# indicator1, NF1, cellprofiling
X = [[362, 160, 88], [354, 140, 86], [320, 120, 76], [308, 108, 47], [332, 130, 80], [380, 180, 94], [350, 128, 78],
[354, 140, 80], [318, 110, 74], [342, 150, 84], [362, 170, 86]]
Y = ['positive', 'positive', 'negative', 'negative', 'positive', 'positive', 'negative', 'negative', 'negative', 'positive', 'positive']
clf = SVC()
clf = clf.fit(X, Y)
print('Predicted value:', clf.predict([[380, 140, 86]]))
print('Accuracy', clf.score(X,Y))
print('Export the model to output/trainedModel.pkl')
ensure_exists('output')
f = open('output/trainedModel.pkl', 'wb')
pickle.dump(clf, f)
f.close()
print('Import the model from output/trainedModel.pkl')
f2 = open('output/trainedModel.pkl', 'rb')
clf2 = pickle.load(f2)
X_new = [[308, 108, 70]]
print('New Sample:', X_new)
print('Predicted class:', clf2.predict(X_new))
```
Now navigate to the repository root directory then **open "output" folder** and you should be able to see the **created trained model file "trainedModel.pkl"**
```
# Run the following score.py from the notebook to generate the web serivce schema JSON file
# Learn more about creating score file from here: https://docs.microsoft.com/en-us/azure/machine-learning/preview/model-management-service-deploy
def init():
from sklearn.externals import joblib
global model
model = joblib.load('output/trainedModel.pkl')
def run(input_df):
import json
pred = model.predict(input_df)
return json.dumps(str(pred[0]))
def main():
from azureml.api.schema.dataTypes import DataTypes
from azureml.api.schema.sampleDefinition import SampleDefinition
from azureml.api.realtime.services import generate_schema
import pandas
df = pandas.DataFrame(data=[[380, 120, 76]], columns=['indicator1', 'NF1', 'cellprofiling'])
# Check the output of the function
init()
input1 = pandas.DataFrame([[380, 120, 76]])
print("Result: " + run(input1))
inputs = {"input_df": SampleDefinition(DataTypes.PANDAS, df)}
# Generate the service_schema.json
generate_schema(run_func=run, inputs=inputs, filepath='output/service_schema.json')
print("Schema generated")
if __name__ == "__main__":
main()
```
Navigate again to the repository root directory then **open "output" folder** and you should be able to see the **created JSON schema file "service_schema.json"**
By reaching this point, we now have what's needed (Score.py file, trained model and JSON schema file) to start deploying our trained model using Azure Model Management Service. Now it's the time to think which deployment environoment are you going to consider as deployment target (Local Deployment or Cluster Deploymment). In this tutorial, we will walk through both scenarios so feel free to either walk through **scenario A** or **scenario B** or even **both**.
Before deploying, first login to you Azure subscription using your command prompt and register few environment providers.
Once you execute this command, the command prompt will show you a message asking you to open your web browser then navigate to https://aka.ms/devicelogin to enter a specific code given in the terminal to login to your Azure subscription.
```
#Return to your command prompt and execute the following commands
!az login
# Once you are logged in, now let's execute the following commands to register our environment providers
!az provider register -n Microsoft.MachineLearningCompute
!az provider register -n Microsoft.ContainerRegistry
!az provider register -n Microsoft.ContainerService
```
Registering the environments takes some time so you can monitor the status using the following command:
```
az provider show -n {Envrionment Provider Name}
```
Before you complete this tutorial, make sure that all the registration status for all the providers are **"Registered"**.
```
!az provider show -n Microsoft.MachineLearningCompute
!az provider show -n Microsoft.ContainerRegistry
!az provider show -n Microsoft.ContainerService
```
While waiting the enviroment providers to be registered, you can create a resource group to include all the resources that we are going to provision through this tutorial.
```
# command format az group create --name {group name} --location {azure region}
!az group create --name capetownrg --location westus
```
Also create a Model Management account to be used for our deployment whether the local deployment or the custer deployment.
```
# command format az ml account modelmanagement create -l {resource targeted region} -n {model management name} -g {name of created resource group}
!az ml account modelmanagement create -l eastus2 -n capetownmodelmgmt -g capetownrg
```
Once your model management account is create, set the model management you created to be used in our deployment.
```
# command format az ml account modelmanagement set -n {your model management account name} -g {name of created resource group}
!az ml account modelmanagement set -n capetownmodelmgmt -g capetownrg
```
### Cluster Deployment - Enviroment Setup:
If you want to deploy from a cluster you need to setup a cluster deployment environment using the following command first to be able to deploy our trained model as a web service
***Creating the environment may take 10-20 minutes. ***
```
# command format az ml env setup -c --name {your environment name} --location {azure region} -g {name of created resource group}
!az ml env setup -c --name capetownenv --location eastus2 -g capetownrg -y --debug
```
You can use the following command to monitor the status:
```
# command format az ml env show -g {name of created resource group} -n {your environment name}
!az ml env show -g capetownrg -n capetownenv
```
Once your provisioning status is "Succeeded", open your web browser and login to your Azure subscription through the portal and you should be able to see the following resources created in your resource group:
* A storage account
* An Azure Container Registry (ACR)
* A Kubernetes deployment on an Azure Container Service (ACS) cluster
* An Application insights account
Now set set your environment as your deployment enviroment using the following command:
```
# command format az ml env set -n {your environment name} -g {name of created resource group}
!az ml env set -n capetownenv -g capetownrg --debug
```
Now feel free to choose one of the following deployment environments as your targeted environment.
### Local Deployment - Enviroment Setup:
You need to set up a local environment using the following command first to be able to deploy our trained model as a web service
```
# command format az ml env setup -l {azure region} -n {your environment name} -g {name of created resource group}
# !az ml env setup -l eastus2 -n capetownlocalenv -g capetownrg -y
```
Creating the enviroment may take some time so you can use the following command to monitor the status:
```
# command format az ml env show -g {name of created resource group} -n {your environment name}
# !az ml env show -g capetownrg -n capetownlocalenv
```
Once your provisioning status is "Succeeded", open your web browser and login to your Azure subscription through the portal and you should be able to see the following resources created in your resource group:
* A storage account
* An Azure Container Registry (ACR)
* An Application insights account
Now set set your environment as your deployment enviroment using the following command:
```
# command format az ml env set -n {your environment name} -g {name of created resource group}
!az ml env set -n capetownenv -g capetownrg --debug
```
**Whether you finish your enviroment setup by following Scenario A or Scenario B. Now you are ready to deploy our trained model as a web service to cosnume later from any application.**
### Create your Web Service:
As a reminder, here's what's needed to create your webservice:
* Your trained model file -> in our case it's "output/trainedModel.pkl"
* Your score.py file which loads your model and returns the prediction result(s) using the model -> in our case it's "modelmanagement/score.py"
* Your JSON schema file that automatically validate the input and output of your web service -> in our case it's "output/service_schema.json"
* You runtime environment for the Docker container -> in our case it's "python"
* conda dependencies file for additional python packages. (We don't have it in our case)
Use the following command to create your web service:
```
# command format az ml service create realtime --model-file {model file/folder path} -f {scoring file} -n {your web service name} -s {json schema file} -r {runtime choice} -c {conda dependencies file}
!az ml service create realtime -m output/trainedModel.pkl -f score.py -n classifierservice -s output/service_schema.json -r python --debug
```
### Test your Web Service:
Once the web service is successfully created, open your web browser and login to your Azure subscription through the portal then jump into your resource group and open your model management account.
**Open** your model management account
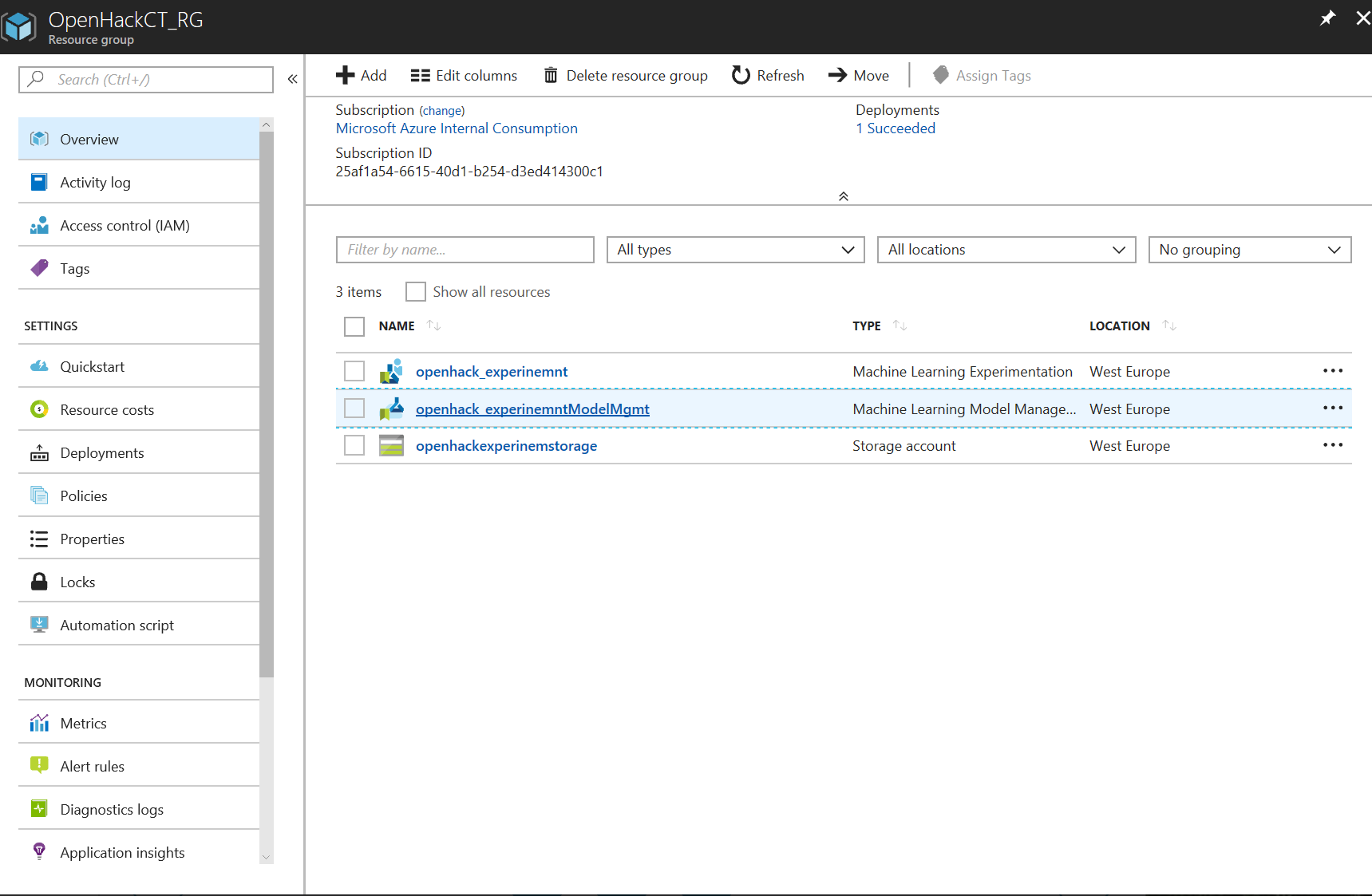
**Click** on "Model Management" under Application Settings
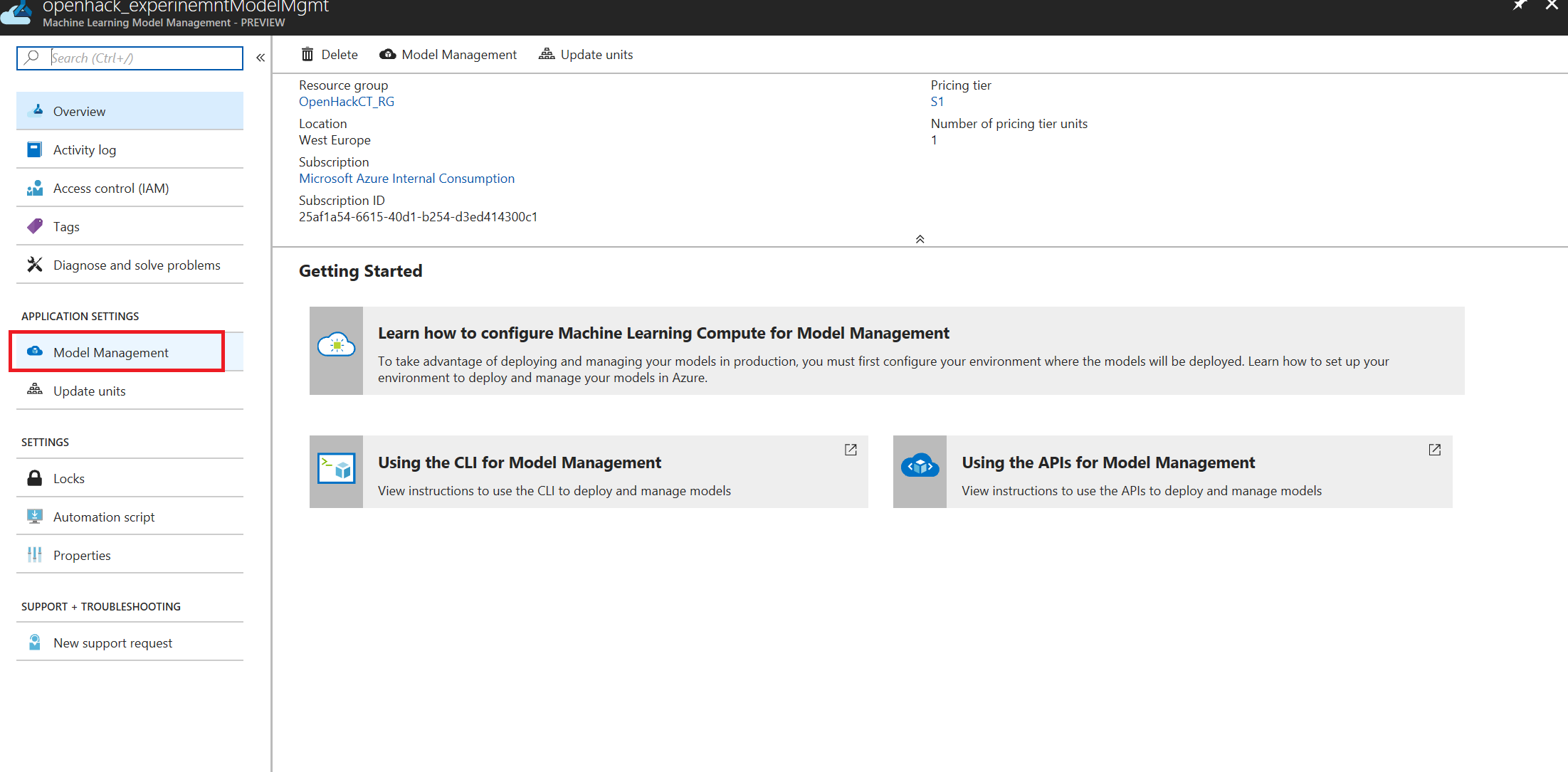
**Click** on "Services" and you select your created "classifier" service from the righ hand side panel

**Copy** your "Service id", "URL" and "Primary key"
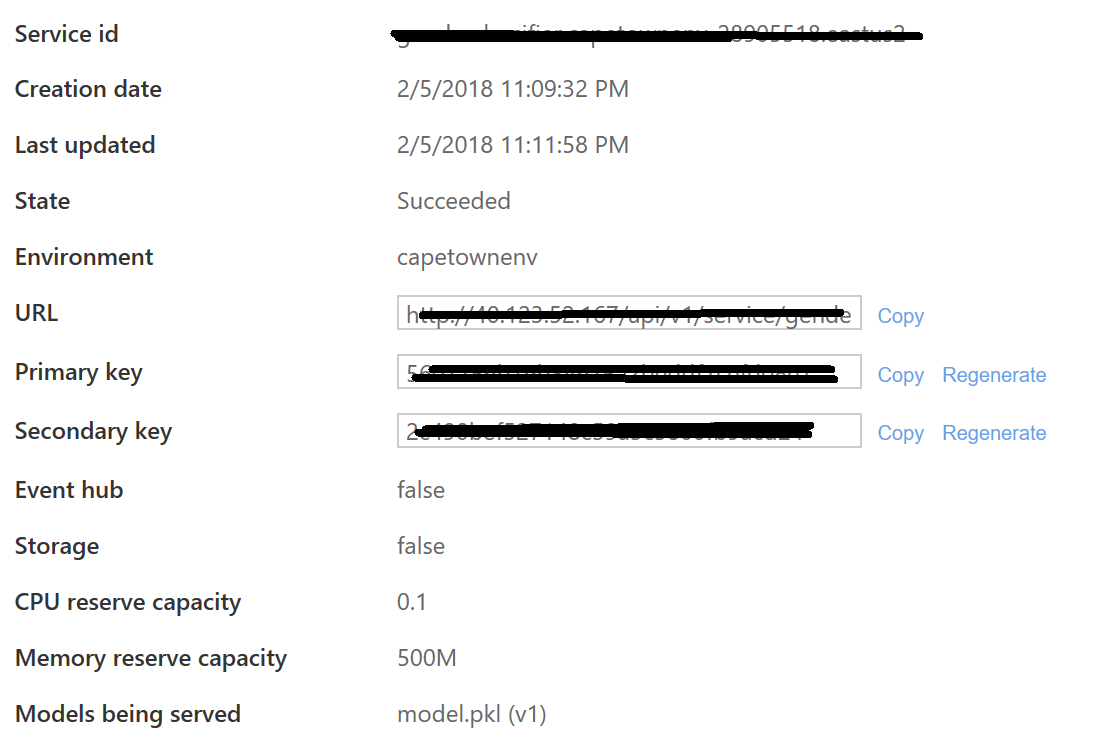
**Call your web service from your terminal:**
```
# command format az ml service run realtime -i {your service id} -d {json input for your web service}
# usage example
!az ml service run realtime -i YOUR_SERVICE_ID -d "{\"input_df\": [{\"NF1\": 120, \"cellprofiling\": 76, \"indicator1\": 380}]}"
```
**Call your web service from [Postman](https://www.getpostman.com/):**
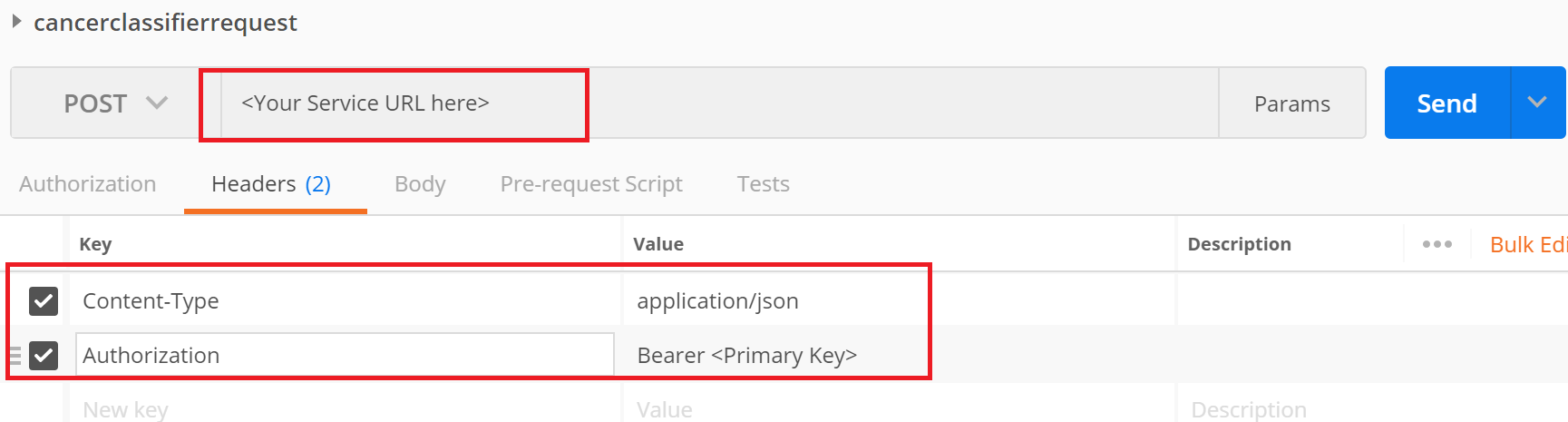
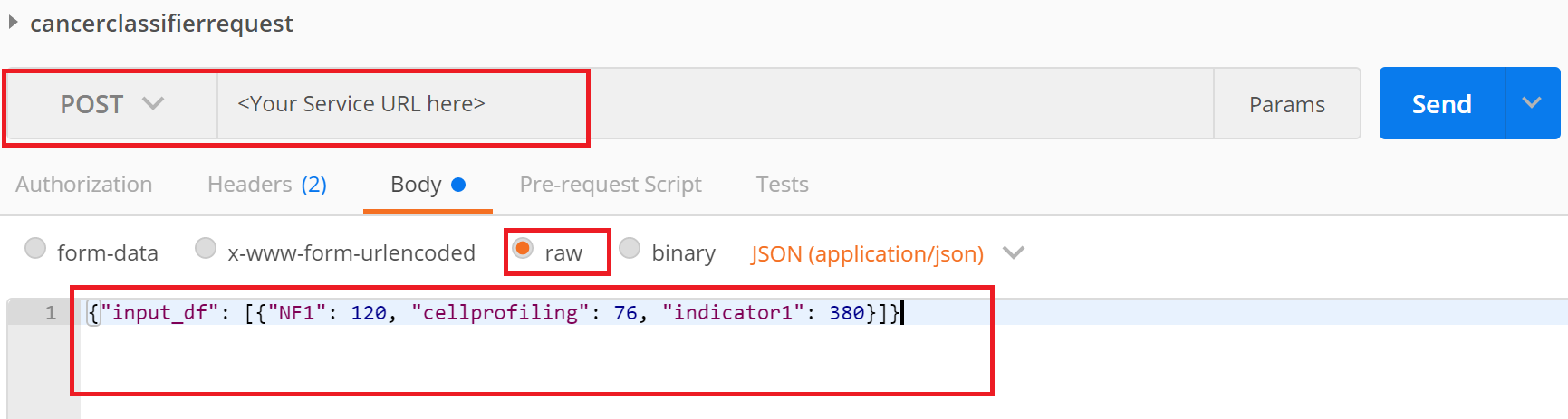
| true |
code
| 0.45042 | null | null | null | null |
|
# Intro to profiling
Python's dirty little secret is that it can be made to run pretty fast.
The bare-metal HPC people will be angrily tweeting at me now, or rather, they would be if they could get their wireless drivers working.
Still, there are some things you *really* don't want to do in Python. Nested loops are usually a bad idea. But often you won't know where your code is slowing down just by looking at it and trying to accelerate everything can be a waste of time. (Developer time, that is, both now and in the future: you incur technical debt if you unintentionally obfuscate code to make it faster when it doesn't need to be).
The first step is always to find the bottlenecks in your code, via _profiling_: analyzing your code by measuring the execution time of its parts.
Tools
-----
2. `cProfile`
1. [`line_profiler`](https://github.com/rkern/line_profiler)
3. `timeit`
**Note**:
If you haven't already installed it, you can do
```console
conda install line_profiler
```
or
```console
pip install line_profiler
```
## Some bad code
Here's a bit of code guaranteed to perform poorly: it sleeps for 1.5 seconds after doing any work! We will profile it and see where we might be able to help.
```
import numpy
from time import sleep
def bad_call(dude):
sleep(.5)
def worse_call(dude):
sleep(1)
def sumulate(foo):
if not isinstance(foo, int):
return
a = numpy.random.random((1000, 1000))
numpy.dot(a,a)
ans = 0
for i in range(foo):
ans += i
bad_call(ans)
worse_call(ans)
return ans
sumulate(150)
```
## using `cProfile`
[`cProfile`](https://docs.python.org/3.4/library/profile.html#module-cProfile) is the built-in profiler in Python (available since Python 2.5). It provides a function-by-function report of execution time. First import the module, then usage is simply a call to `cProfile.run()` with your code as argument. It will print out a list of all the functions that were called, with the number of calls and the time spent in each.
```
import cProfile
cProfile.run('sumulate(150)')
```
You can see here that when our code `sumulate()` executes, it spends almost all its time in the method `time.sleep` (a bit over 1.5 seconds).
If your program is more complicated that this cute demo, you'll have a hard time parsing the long output of `cProfile`. In that case, you may want a profiling visualization tool, like [SnakeViz](https://jiffyclub.github.io/snakeviz/). But that is outside the scope of this tutorial.
## using `line_profiler`
`line_profiler` offers more granular information thatn `cProfile`: it will give timing information about each line of code in a profiled function.
Load the `line_profiler` extension
```
%load_ext line_profiler
```
### For a pop-up window with results in notebook:
IPython has an `%lprun` magic to profile specific functions within an executed statement. Usage:
`%lprun -f func_to_profile <statement>` (get more help by running `%lprun?` in IPython).
### Profiling two functions
```
%lprun -f sumulate sumulate(13)
%lprun -f bad_call -f worse_call sumulate(13)
```
### Write results to a text file
```
%lprun -T timings.txt -f sumulate sumulate(12)
%ls -l
%load timings.txt
```
## Profiling on the command line
Open file, add `@profile` decorator to any function you want to profile, then run
```console
kernprof -l script_to_profile.py
```
which will generate `script_to_profile.py.lprof` (pickled result). To view the results, run
```console
python -m line_profiler script_to_profile.py.lprof
```
```
from IPython.display import IFrame
IFrame('http://localhost:7000/terminals/1', width=800, height=700)
```
## `timeit`
`timeit` is not perfect, but it is helpful.
Potential concerns re: `timeit`
* Returns minimum time of run
* Only runs benchmark 3 times
* It disables garbage collection
```python
python -m timeit -v "print(42)"
```
```python
python -m timeit -r 25 "print(42)"
```
```python
python -m timeit -s "gc.enable()" "print(42)"
```
### Line magic
```
%timeit x = 5
```
### Cell magic
```
%%timeit
x = 5
y = 6
x + y
```
The `-q` flag quiets output. The `-o` flag allows outputting results to a variable. The `-q` flag sometimes disagrees with OSX so please remove it if you're having issues.
```
a = %timeit -qo x = 5
print a
a.all_runs
a.best
a.worst
```
| true |
code
| 0.248625 | null | null | null | null |
|
# Scheduling a Doubles Pickleball Tournament
My friend Steve asked for help in creating a schedule for a round-robin doubles pickleball tournament with 8 or 9 players on 2 courts. ([Pickleball](https://en.wikipedia.org/wiki/Pickleball) is a paddle/ball/net game played on a court that is smaller than tennis but larger than ping-pong.)
To generalize: given *P* players and *C* available courts, we would like to create a **schedule**: a table where each row is a time period (a round of play), each column is a court, and each cell contains a game, which consists of two players partnered together and pitted against two other players. The preferences for the schedule are:
- Each player should partner with each other player exactly once (or as close to that as possible).
- Fewer rounds are better (in other words, try to fill all the courts each round).
- Each player should play against each other player twice, or as close to that as possible.
- A player should not be scheduled to play two games at the same time.
For example, here's a perfect schedule for *P*=8 players on *C*=2 courts:
[([[1, 6], [2, 4]], [[3, 5], [7, 0]]),
([[1, 5], [3, 6]], [[2, 0], [4, 7]]),
([[2, 3], [6, 0]], [[4, 5], [1, 7]]),
([[4, 6], [3, 7]], [[1, 2], [5, 0]]),
([[1, 0], [6, 7]], [[3, 4], [2, 5]]),
([[2, 6], [5, 7]], [[1, 4], [3, 0]]),
([[2, 7], [1, 3]], [[4, 0], [5, 6]])]
This means that in the first round, players 1 and 6 partner against 2 and 4 on one court, while 3 and 5 partner against 7 and 0 on the other. There are 7 rounds.
My strategy for finding a good schedule is to use **hillclimbing**: start with an initial schedule, then repeatedly alter the schedule by swapping partners in one game with partners in another. If the altered schedule is better, keep it; if not, discard it. Repeat.
## Coding it up
The strategy in more detail:
- First form all pairs of players, using `all_pairs(P)`.
- Put pairs together to form a list of games using `initial_games`.
- Use `Schedule` to create a schedule; it calls `one_round` to create each round and `scorer` to evaluate the schedule.
- Use `hillclimb` to improve the initial schedule: call `alter` to randomly alter a schedule, `Schedule` to re-allocate the games to rounds and courts, and `scorer` to check if the altered schedule's score is better.
(Note: with *P* players there are *P × (P - 1) / 2* pairs of partners; this is an even number when either *P* or *P - 1* is divisible by 4, so everything works out when, say, *P*=4 or *P*=9, but for, say, *P*=10 there are 45 pairs, and so `initial_games` chooses to create 22 games, meaning that one pair of players never play together, and thus play one fewer game than everyone else.)
```
import random
from itertools import combinations
from collections import Counter
#### Types
Player = int # A player is an int: `1`
Pair = list # A pair is a list of two players who are partners: `[1, 2]`
Game = list # A game is a list of two pairs: `[[1, 2], [3, 4]]`
Round = tuple # A round is a tuple of games: `([[1, 2], [3, 4]], [[5, 6], [7, 8]])`
class Schedule(list):
"""A Schedule is a list of rounds (augmented with a score and court count)."""
def __init__(self, games, courts=2):
games = list(games)
while games: # Allocate games to courts, one round at a time
self.append(one_round(games, courts))
self.score = scorer(self)
self.courts = courts
#### Functions
def hillclimb(P, C=2, N=100000):
"Schedule games for P players on C courts by randomly altering schedule N times."
sched = Schedule(initial_games(all_pairs(P)), C)
for _ in range(N):
sched = max(alter(sched), sched, key=lambda s: s.score)
return sched
def all_pairs(P): return list(combinations(range(P), 2))
def initial_games(pairs):
"""An initial list of games: [[[1, 2], [3, 4]], ...].
We try to have every pair play every other pair once, and
have each game have 4 different players, but that isn't always true."""
random.shuffle(pairs)
games = []
while len(pairs) >= 2:
A = pairs.pop()
B = first(pair for pair in pairs if disjoint(pair, A)) or pairs[0]
games.append([A, B])
pairs.remove(B)
return games
def disjoint(A, B):
"Do A and B have disjoint players in them?"
return not (players(A) & players(B))
def one_round(games, courts):
"""Place up to `courts` games into `round`, all with disjoint players."""
round = []
while True:
G = first(g for g in games if disjoint(round, g))
if not G or not games or len(round) == courts:
return Round(round)
round.append(G)
games.remove(G)
def players(x):
"All distinct players in a pair, game, or sequence of games."
return {x} if isinstance(x, Player) else set().union(*map(players, x))
def first(items): return next(items, None)
def pairing(p1, p2): return tuple(sorted([p1, p2]))
def scorer(sched):
"Score has penalties for a non-perfect schedule."
penalty = 50 * len(sched) # More rounds are worse (avoid empty courts)
penalty += 1000 * sum(len(players(game)) != 4 # A game should have 4 players!
for round in sched for game in round)
penalty += 1 * sum(abs(c - 2) ** 3 + 8 * (c == 0) # Try to play everyone twice
for c in opponents(sched).values())
return -penalty
def opponents(sched):
"A Counter of {(player, opponent): times_played}."
return Counter(pairing(p1, p2)
for round in sched for A, B in round for p1 in A for p2 in B)
def alter(sched):
"Modify a schedule by swapping two pairs."
games = [Game(game) for round in sched for game in round]
G = len(games)
i, j = random.sample(range(G), 2) # index into games
a, b = random.choice((0, 1)), random.choice((0, 1)) # index into each game
games[i][a], games[j][b] = games[j][b], games[i][a]
return Schedule(games, sched.courts)
def report(sched):
"Print information about this schedule."
for i, round in enumerate(sched, 1):
print('Round {}: {}'.format(i, '; '.join('{} vs {}'.format(*g) for g in round)))
games = sum(sched, ())
P = len(players(sched))
print('\n{} games in {} rounds for {} players'.format(len(games), len(sched), P))
opp = opponents(sched)
fmt = ('{:2X}|' + P * ' {}' + ' {}').format
print('Number of times each player plays against each opponent:\n')
print(' |', *map('{:X}'.format, range(P)), ' Total')
print('--+' + '--' * P + ' -----')
for row in range(P):
counts = [opp[pairing(row, col)] for col in range(P)]
print(fmt(row, *[c or '-' for c in counts], sum(counts) // 2))
```
# 8 Player Tournament
I achieved (in a previous run) a perfect schedule for 8 players: the 14 games fit into 7 rounds, each player partners with each other once, and plays each individual opponent twice:
```
report([
([[1, 6], [2, 4]], [[3, 5], [7, 0]]),
([[1, 5], [3, 6]], [[2, 0], [4, 7]]),
([[2, 3], [6, 0]], [[4, 5], [1, 7]]),
([[4, 6], [3, 7]], [[1, 2], [5, 0]]),
([[1, 0], [6, 7]], [[3, 4], [2, 5]]),
([[2, 6], [5, 7]], [[1, 4], [3, 0]]),
([[2, 7], [1, 3]], [[4, 0], [5, 6]]) ])
```
# 9 Player Tournament
For 9 players, I can fit the 18 games into 9 rounds, but some players play each other 1 or 3 times:
```
report([
([[1, 7], [4, 0]], [[3, 5], [2, 6]]),
([[2, 7], [1, 3]], [[4, 8], [6, 0]]),
([[5, 0], [1, 6]], [[7, 8], [3, 4]]),
([[7, 0], [5, 8]], [[1, 2], [4, 6]]),
([[3, 8], [1, 5]], [[2, 0], [6, 7]]),
([[1, 4], [2, 5]], [[3, 6], [8, 0]]),
([[5, 6], [4, 7]], [[1, 8], [2, 3]]),
([[1, 0], [3, 7]], [[2, 8], [4, 5]]),
([[3, 0], [2, 4]], [[6, 8], [5, 7]]) ])
```
# 10 Player Tournament
With *P*=10 there is an odd number of pairings (45), so two players necessarily play one game less than the other players. Let's see what kind of schedule we can come up with:
```
%time report(hillclimb(P=10))
```
In this schedule several players never play each other; it may be possible to improve on that (in another run that has better luck with random numbers).
# 16 Player Tournament
Let's jump to 16 players on 4 courts (this will take a while):
```
%time report(hillclimb(P=16, C=4))
```
We get a pretty good schedule, although it takes 19 rounds rather than the 15 it would take if every court was filled, and again there are some players who never face each other.
| true |
code
| 0.38393 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/JSJeong-me/KOSA-Big-Data_Vision/blob/main/Roboflow_CLIP_Zero_Shot_Cake.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# How to use CLIP Zero-Shot on your own classificaiton dataset
This notebook provides an example of how to benchmark CLIP's zero shot classification performance on your own classification dataset.
[CLIP](https://openai.com/blog/clip/) is a new zero shot image classifier relased by OpenAI that has been trained on 400 million text/image pairs across the web. CLIP uses these learnings to make predicts based on a flexible span of possible classification categories.
CLIP is zero shot, that means **no training is required**.
Try it out on your own task here!
Be sure to experiment with various text prompts to unlock the richness of CLIP's pretraining procedure.

# Download and Install CLIP Dependencies
```
#installing some dependencies, CLIP was release in PyTorch
import subprocess
CUDA_version = [s for s in subprocess.check_output(["nvcc", "--version"]).decode("UTF-8").split(", ") if s.startswith("release")][0].split(" ")[-1]
print("CUDA version:", CUDA_version)
if CUDA_version == "10.0":
torch_version_suffix = "+cu100"
elif CUDA_version == "10.1":
torch_version_suffix = "+cu101"
elif CUDA_version == "10.2":
torch_version_suffix = ""
else:
torch_version_suffix = "+cu110"
!pip install torch==1.7.1{torch_version_suffix} torchvision==0.8.2{torch_version_suffix} -f https://download.pytorch.org/whl/torch_stable.html ftfy regex
import numpy as np
import torch
print("Torch version:", torch.__version__)
!ls -l
#clone the CLIP repository
!git clone https://github.com/openai/CLIP.git
%cd CLIP
```
# Download Classification Data or Object Detection Data
We will download the [public flowers classificaiton dataset](https://public.roboflow.com/classification/flowers_classification) from Roboflow. The data will come out as folders broken into train/valid/test splits and seperate folders for each class label.
You can easily download your own dataset from Roboflow in this format, too.
We made a conversion from object detection to CLIP text prompts in Roboflow, too, if you want to try that out.
To get your data into Roboflow, follow the [Getting Started Guide](https://blog.roboflow.ai/getting-started-with-roboflow/).
```
!mkdir cake
from google.colab import drive
drive.mount('/content/drive')
%cd ..
!cp /content/drive/MyDrive/Flowers_Classification.v3-augmented.clip.zip .
!pwd
#download classification data
#replace with your link
!curl -L "https://public.roboflow.com/ds/vPLCmk4Knv?key=tCrKLQNpTi" > roboflow.zip; unzip roboflow.zip; rm roboflow.zip
!unzip ./Flowers.zip
import os
#our the classes and images we want to test are stored in folders in the test set
class_names = os.listdir('./test/')
class_names.remove('_tokenization.txt')
class_names
class_names
!pwd
#we auto generate some example tokenizations in Roboflow but you should edit this file to try out your own prompts
#CLIP gets a lot better with the right prompting!
#be sure the tokenizations are in the same order as your class_names above!
%cat ./test/_tokenization.txt
#edit your prompts as you see fit here
%%writefile ./test/_tokenization.txt
daisy
dandelion
cake
candidate_captions = []
with open('./test/_tokenization.txt') as f:
candidate_captions = f.read().splitlines()
!pwd
%cd ./CLIP/
```
# Run CLIP inference on your classification dataset
```
import torch
import clip
from PIL import Image
import glob
def argmax(iterable):
return max(enumerate(iterable), key=lambda x: x[1])[0]
device = "cuda" if torch.cuda.is_available() else "cpu"
model, transform = clip.load("ViT-B/32", device=device)
correct = []
#define our target classificaitons, you can should experiment with these strings of text as you see fit, though, make sure they are in the same order as your class names above
text = clip.tokenize(candidate_captions).to(device)
for cls in class_names:
class_correct = []
test_imgs = glob.glob('./test/' + cls + '/*.jpg')
for img in test_imgs:
print(img)
image = transform(Image.open(img)).unsqueeze(0).to(device)
with torch.no_grad():
image_features = model.encode_image(image)
text_features = model.encode_text(text)
logits_per_image, logits_per_text = model(image, text)
probs = logits_per_image.softmax(dim=-1).cpu().numpy()
pred = class_names[argmax(list(probs)[0])]
print(pred)
if pred == cls:
correct.append(1)
class_correct.append(1)
else:
correct.append(0)
class_correct.append(0)
print('accuracy on class ' + cls + ' is :' + str(sum(class_correct)/len(class_correct)))
print('accuracy on all is : ' + str(sum(correct)/len(correct)))
#Hope you enjoyed!
#As always, happy inferencing
#Roboflow
```
| true |
code
| 0.284092 | null | null | null | null |
|
# Retail Demo Store Experimentation Workshop - A/B Testing Exercise
In this exercise we will define, launch, and evaluate the results of an A/B experiment using the experimentation framework implemented in the Retail Demo Store project. If you have not already stepped through the **[3.1-Overview](./3.1-Overview.ipynb)** workshop notebook, please do so now as it provides the foundation built upon in this exercise.
Recommended Time: 30 minutes
## Prerequisites
Since this module uses the Retail Demo Store's Recommendation service to run experiments across variations that depend on the personalization features of the Retail Demo Store, it is assumed that you have either completed the [Personalization](../1-Personalization/1.1-Personalize.ipynb) workshop or those resources have been pre-provisioned in your AWS environment. If you are unsure and attending an AWS managed event such as a workshop, check with your event lead.
## Exercise 1: A/B Experiment
For the first exercise we will demonstrate how to use the A/B testing technique to implement an experiment over two implementations, or variations, of product recommendations. The first variation will represent our current implementation using the **Default Product Resolver** and the second variation will use the **Personalize Resolver**. The scenario we are simulating is adding product recommendations powered by Amazon Personalize to home page and measuring the impact/uplift in click-throughs for products as a result of deploying a personalization strategy.
### What is A/B Testing?
A/B testing, also known as bucket or split testing, is used to compare the performance of two variations (A and B) of a single variable/experience by exposing separate groups of users to each variation and measuring user responses. An A/B experiment is run for a period of time, typically dictated by the number of users necessary to reach a statistically significant result, followed by statistical analysis of the results to determine if a conclustion can be reached as to the best performing variation.
### Our Experiment Hypothesis
**Sample scenario:**
Website analytics have shown that user sessions frequently end on the home page for our e-commerce site, the Retail Demo Store. Furthermore, when users do make a purchase, most purchases are for a single product. Currently on our home page we are using a basic approach of recommending featured products. We hypothesize that adding personalized recommendations to the home page will result in increasing the click-through rate of products by 25%. The current click-through rate is 15%.
### ABExperiment Class
Before stepping through creating and executing our A/B test, let's look at the relevant source code for the **ABExperiment** class that implements A/B experiments in the Retail Demo Store project.
As noted in the **3.1-Overview** notebook, all experiment types are subclasses of the abstract **Experiment** class. See **[3.1-Overview](./3.1-Overview.ipynb)** for more details on the experimentation framework.
The `ABExperiment.get_items()` method is where item recommendations are retrieved for the experiment. The `ABExperiment.calculate_variation_index()` method is where users are assigned to a variation/group using a consistent hashing algorithm. This ensures that each user is assigned to the same variation across multiple requests for recommended items for the duration of the experiment. Once the variation is determined, the variation's **Resolver** is used to retrieve recommendations. Details on the experiment are added to item list to support conversion/outcome tracking and UI annotation.
```python
# from src/recommendations/src/recommendations-service/experimentation/experiment_ab.py
class ABExperiment(Experiment):
...
def get_items(self, user_id, current_item_id = None, item_list = None, num_results = 10, tracker = None):
...
# Determine which variation to use for the user.
variation_idx = self.calculate_variation_index(user_id)
# Increment exposure counter for variation for this experiment.
self._increment_exposure_count(variation_idx)
# Get item recommendations from the variation's resolver.
variation = self.variations[variation_idx]
resolve_params = {
'user_id': user_id,
'product_id': current_item_id,
'num_results': num_results
}
items = variation.resolver.get_items(**resolve_params)
# Inject experiment details into recommended item list.
rank = 1
for item in items:
correlation_id = self._create_correlation_id(user_id, variation_idx, rank)
item_experiment = {
'id': self.id,
'feature': self.feature,
'name': self.name,
'type': self.type,
'variationIndex': variation_idx,
'resultRank': rank,
'correlationId': correlation_id
}
item.update({
'experiment': item_experiment
})
rank += 1
...
return items
def calculate_variation_index(self, user_id):
""" Given a user_id and this experiment's configuration, return the variation
The same variation will be returned for given user for this experiment no
matter how many times this method is called.
"""
if len(self.variations) == 0:
return -1
hash_str = f'experiments.{self.feature}.{self.name}.{user_id}'.encode('ascii')
hash_int = int(hashlib.sha1(hash_str).hexdigest()[:15], 16)
index = hash_int % len(self.variations)
return index
```
### Setup - Import Dependencies
Throughout this workshop we will need access to some common libraries and clients for connecting to AWS services. Let's set those up now.
```
import boto3
import json
import uuid
import numpy as np
import requests
import pandas as pd
import random
import scipy.stats as scs
import time
import decimal
import matplotlib.pyplot as plt
from boto3.dynamodb.conditions import Key
from random import randint
# import custom scripts used for plotting
from src.plot import *
from src.stats import *
%matplotlib inline
plt.style.use('ggplot')
# We will be using a DynamoDB table to store configuration info for our experiments.
dynamodb = boto3.resource('dynamodb')
# Service discovery will allow us to dynamically discover Retail Demo Store resources
servicediscovery = boto3.client('servicediscovery')
# Retail Demo Store config parameters are stored in SSM
ssm = boto3.client('ssm')
# Utility class to convert types for printing as JSON.
class CompatEncoder(json.JSONEncoder):
def default(self, obj):
if isinstance(obj, decimal.Decimal):
if obj % 1 > 0:
return float(obj)
else:
return int(obj)
else:
return super(CompatEncoder, self).default(obj)
```
### Sample Size Calculation
The first step is to determine the sample size necessary to reach a statistically significant result given a target of 25% gain in click-through rate from the home page. There are several sample size calculators available online including calculators from [Optimizely](https://www.optimizely.com/sample-size-calculator/?conversion=15&effect=20&significance=95), [AB Tasty](https://www.abtasty.com/sample-size-calculator/), and [Evan Miller](https://www.evanmiller.org/ab-testing/sample-size.html#!15;80;5;25;1). For this exercise, we will use the following function to calculate the minimal sample size for each variation.
```
def min_sample_size(bcr, mde, power=0.8, sig_level=0.05):
"""Returns the minimum sample size to set up a split test
Arguments:
bcr (float): probability of success for control, sometimes
referred to as baseline conversion rate
mde (float): minimum change in measurement between control
group and test group if alternative hypothesis is true, sometimes
referred to as minimum detectable effect
power (float): probability of rejecting the null hypothesis when the
null hypothesis is false, typically 0.8
sig_level (float): significance level often denoted as alpha,
typically 0.05
Returns:
min_N: minimum sample size (float)
References:
Stanford lecture on sample sizes
http://statweb.stanford.edu/~susan/courses/s141/hopower.pdf
"""
# standard normal distribution to determine z-values
standard_norm = scs.norm(0, 1)
# find Z_beta from desired power
Z_beta = standard_norm.ppf(power)
# find Z_alpha
Z_alpha = standard_norm.ppf(1-sig_level/2)
# average of probabilities from both groups
pooled_prob = (bcr + bcr+mde) / 2
min_N = (2 * pooled_prob * (1 - pooled_prob) * (Z_beta + Z_alpha)**2
/ mde**2)
return min_N
# This is the conversion rate using the current implementation
baseline_conversion_rate = 0.15
# This is the lift expected by adding personalization
absolute_percent_lift = baseline_conversion_rate * .25
# Calculate the sample size needed to reach a statistically significant result
sample_size = int(min_sample_size(baseline_conversion_rate, absolute_percent_lift))
print('Sample size for each variation: ' + str(sample_size))
```
### Experiment Strategy Datastore
With our sample size defined, let's create an experiment strategy for our A/B experiment. Walk through each of the following steps to configure your environment.
A DynamoDB table was created by the Retail Demo Store CloudFormation template that we will use to store the configuration information for our experiments. The table name can be found in a system parameter.
```
response = ssm.get_parameter(Name='retaildemostore-experiment-strategy-table-name')
table_name = response['Parameter']['Value'] # Do Not Change
print('Experiments DDB table: ' + table_name)
table = dynamodb.Table(table_name)
```
Next we need to lookup the Amazon Personalize campaign ARN for product recommendations. This is the campaign that was created in the [Personalization workshop](../1-Personalization/personalize.ipynb) (or was pre-built for you depending on your workshop event).
```
response = ssm.get_parameter(Name = 'retaildemostore-product-recommendation-campaign-arn')
campaign_arn = response['Parameter']['Value'] # Do Not Change
print('Personalize product recommendations ARN: ' + campaign_arn)
```
### Create A/B Experiment
The Retail Demo Store supports running multiple experiments concurrently. For this workshop we will create a single A/B test/experiment that uniformly splits users between a control group that receives recommendations from the default behavior and a variance group that receives recommendations from Amazon Personalize. The Recommendations service already has logic that supports A/B tests once an active experiment is detected our Experiment Strategy DynamoDB table.
Experiment configurations are stored in a DynamoDB table where each item in the table represents an experiment and has the following fields.
- **id** - Uniquely identified this experience (UUID).
- **feature** - Identifies the Retail Demo Store feature where the experiment should be applied. The name for the home page product recommendations feature is `home_product_recs`.
- **name** - The name of the experiment. Keep the name short but descriptive. It will be used in the UI for demo purposes and when logging events for experiment result tracking.
- **status** - The status of the experiment (`ACTIVE`, `EXPIRED`, or `PENDING`).
- **type** - The type of test (`ab` for an A/B test, `interleaving` for interleaved recommendations, or `mab` for multi-armed bandit test)
- **variations** - List of configurations representing variations for the experiment. For example, for A/B tests of the `home_product_recs` feature, the `variations` can be two Amazon Personalize campaign ARNs (variation type `personalize-recommendations`) or a single Personalize campaign ARN and the default product behavior.
```
feature = 'home_product_recs'
experiment_name = 'home_personalize_ab'
# First, make sure there are no other active experiments so we can isolate
# this experiment for the exercise (to keep things clean/simple).
response = table.scan(
ProjectionExpression='#k',
ExpressionAttributeNames={'#k' : 'id'},
FilterExpression=Key('status').eq('ACTIVE')
)
for item in response['Items']:
response = table.update_item(
Key=item,
UpdateExpression='SET #s = :inactive',
ExpressionAttributeNames={
'#s' : 'status'
},
ExpressionAttributeValues={
':inactive' : 'INACTIVE'
}
)
# Query the experiment strategy table to see if our experiment already exists
response = table.query(
IndexName='feature-name-index',
KeyConditionExpression=Key('feature').eq(feature) & Key('name').eq(experiment_name),
FilterExpression=Key('status').eq('ACTIVE')
)
if response.get('Items') and len(response.get('Items')) > 0:
print('Experiment already exists')
home_page_experiment = response['Items'][0]
else:
print('Creating experiment')
# Default product resolver
variation_0 = {
'type': 'product'
}
# Amazon Personalize resolver
variation_1 = {
'type': 'personalize-recommendations',
'campaign_arn': campaign_arn
}
home_page_experiment = {
'id': uuid.uuid4().hex,
'feature': feature,
'name': experiment_name,
'status': 'ACTIVE',
'type': 'ab',
'variations': [ variation_0, variation_1 ]
}
response = table.put_item(
Item=home_page_experiment
)
print(json.dumps(response, indent=4))
print('Experiment item:')
print(json.dumps(home_page_experiment, indent=4, cls=CompatEncoder))
```
## Load Users
For our experiment simulation, we will load all Retail Demo Store users and run the experiment until the sample size for both variations has been met.
First, let's discover the IP address for the Retail Demo Store's Users service.
```
response = servicediscovery.discover_instances(
NamespaceName='retaildemostore.local',
ServiceName='users',
MaxResults=1,
HealthStatus='HEALTHY'
)
users_service_instance = response['Instances'][0]['Attributes']['AWS_INSTANCE_IPV4']
print('Users Service Instance IP: {}'.format(users_service_instance))
```
Next, let's fetch all users, randomize their order, and load them into a local data frame.
```
# Load all 5K users so we have enough to satisfy our sample size requirements.
response = requests.get('http://{}/users/all?count=5000'.format(users_service_instance))
users = response.json()
random.shuffle(users)
users_df = pd.DataFrame(users)
pd.set_option('display.max_rows', 5)
users_df
```
## Discover Recommendations Service
Next, let's discover the IP address for the Retail Demo Store's Recommendation service. This is the service where the Experimentation framework is implemented and the `/recommendations` endpoint is what we call to simulate our A/B experiment.
```
response = servicediscovery.discover_instances(
NamespaceName='retaildemostore.local',
ServiceName='recommendations',
MaxResults=1,
HealthStatus='HEALTHY'
)
recommendations_service_instance = response['Instances'][0]['Attributes']['AWS_INSTANCE_IPV4']
print('Recommendation Service Instance IP: {}'.format(recommendations_service_instance))
```
## Simulate Experiment
Next we will define a function to simulate our A/B experiment by making calls to the Recommendations service across the users we just loaded. Then we will run our simulation.
### Simulation Function
The following `simulate_experiment` function is supplied with the sample size for each group (A and B) and the probability of conversion for each group that we want to use for our simulation. It runs the simulation long enough to satisfy the sample size requirements and calls the Recommendations service for each user in the experiment.
```
def simulate_experiment(N_A, N_B, p_A, p_B):
"""Returns a pandas dataframe with simulated CTR data
Parameters:
N_A (int): sample size for control group
N_B (int): sample size for test group
Note: final sample size may not match N_A & N_B provided because the
group at each row is chosen at random by the ABExperiment class.
p_A (float): conversion rate; conversion rate of control group
p_B (float): conversion rate; conversion rate of test group
Returns:
df (df)
"""
# will hold exposure/outcome data
data = []
# total number of users to sample for both variations
N = N_A + N_B
if N > len(users):
raise ValueError('Sample size is greater than number of users')
print('Generating data for {} users... this may take a few minutes'.format(N))
# initiate bernoulli distributions to randomly sample from based on simulated probabilities
A_bern = scs.bernoulli(p_A)
B_bern = scs.bernoulli(p_B)
for idx in range(N):
if idx > 0 and idx % 500 == 0:
print('Generated data for {} users so far'.format(idx))
# initite empty row
row = {}
# Get next user from shuffled list
user = users[idx]
# Call Recommendations web service to get recommendations for the user
response = requests.get('http://{}/recommendations?userID={}&feature={}'.format(recommendations_service_instance, user['id'], feature))
recommendations = response.json()
recommendation = recommendations[randint(0, len(recommendations)-1)]
variation = recommendation['experiment']['variationIndex']
row['variation'] = variation
# Determine if variation converts based on probabilities provided
if variation == 0:
row['converted'] = A_bern.rvs()
else:
row['converted'] = B_bern.rvs()
if row['converted'] == 1:
# Update experiment with outcome/conversion
correlation_id = recommendation['experiment']['correlationId']
requests.post('http://{}/experiment/outcome'.format(recommendations_service_instance), data={'correlationId':correlation_id})
data.append(row)
# convert data into dataframe
df = pd.DataFrame(data)
print('Done')
return df
```
### Run Simulation
Next we run the simulation by defining our simulation parameters for sample sizes and probabilities and then call `simulate_experiment`. This will take several minutes depending on the sample sizes.
```
%%time
# Set size of both groups to calculated sample size
N_A = N_B = sample_size
# Use probabilities from our hypothesis
# bcr: baseline conversion rate
p_A = 0.15
# d_hat: difference in a metric between the two groups, sometimes referred to as minimal detectable effect or lift depending on the context
p_B = 0.1875
# Run simulation
ab_data = simulate_experiment(N_A, N_B, p_A, p_B)
ab_data
```
### Inspect Experiment Summary Statistics
Since the **Experiment** class updates statistics for the experiment in the experiment strategy DynamoDB table when a user is exposed to an experiment ("exposure") and when a user converts ("outcome"), we should see updated counts on our experiment. Let's reload our experiment and inspect the exposure and conversion counts for our simulation.
```
# Query DDB table for experiment item.
response = table.get_item(Key={'id': home_page_experiment['id']})
print(json.dumps(response['Item'], indent=4, cls=CompatEncoder))
```
You should now see counters for `conversions` and `exposures` for each variation. These represent how many times a user has been exposed to a variation and how many times a user has converted for a variation (i.e. clicked on a recommended item/product).
### Analyze Simulation Results
Next, let's take a closer look at the results of our simulation. We'll start by calculating some summary statistics.
```
ab_summary = ab_data.pivot_table(values='converted', index='variation', aggfunc=np.sum)
# add additional columns to the pivot table
ab_summary['total'] = ab_data.pivot_table(values='converted', index='variation', aggfunc=lambda x: len(x))
ab_summary['rate'] = ab_data.pivot_table(values='converted', index='variation')
ab_summary
```
The output above tells us how many users converted for each variation, the actual sample size for each variation in the simulation, and the conversion rate for each variation.
Next let's isolate the data and conversion counts for each variation.
```
A_group = ab_data[ab_data['variation'] == 0]
B_group = ab_data[ab_data['variation'] == 1]
A_converted, B_converted = A_group['converted'].sum(), B_group['converted'].sum()
A_converted, B_converted
```
Isolate the actual sample size for each variation.
```
A_total, B_total = len(A_group), len(B_group)
A_total, B_total
```
Calculate the actual conversion rates and uplift for our simulation.
```
p_A, p_B = A_converted / A_total, B_converted / B_total
p_A, p_B
p_B - p_A
```
### Determining Statistical Significance
In statistical hypothesis testing there are two types of errors that can occur. These are referred to as type 1 and type 2 errors.
Type 1 errors occur when the null hypothesis is true but is rejected. In other words, a "false positive" conclusion. Put in A/B testing terms, a type 1 error is when we conclude a statistically significant result when there isn't one.
Type 2 errors occur when we conclude that there is not a winner between two variations when in fact there is an actual winner. In other words, the null hypothesis is false yet we fail to reject it. Therefore, type 2 errors are a "false negative" conclusion.
If the probability of making a type 1 error is determined by "α" (alpha), the probability of a type 2 error is "β" (beta). Beta depends on the power of the test (i.e the probability of not committing a type 2 error, which is equal to 1-β).
Let's inspect the results of our simulation more closely to verify that it is statistically significant.
#### Calculate p-value
Formally, the p-value is the probability of seeing a particular result (or greater) from zero, assuming that the null hypothesis is TRUE. In other words, the p-value is the expected fluctuation in a given sample, similar to the variance. As an example, imagine we ran an A/A test where displayed the same variation to two groups of users. After such an experiment we would expect the conversion rates of both groups to be very similar but not dramatically different.
What we are hoping to see is a p-value that is less than our significance level. The significance level we used when calculating our sample size was 5%, which means we are seeking results with 95% accuracy. 5% is considered the industry standard.
```
p_value = scs.binom(A_total, p_A).pmf(p_B * B_total)
print('p-value = {0:0.9f}'.format(p_value))
```
Is the p-value less than the signficance level of 5%? This tells us the probability of a type 1 error.
Let's plot the data from both groups as binomial distributions.
```
fig, ax = plt.subplots(figsize=(12,6))
xA = np.linspace(A_converted-49, A_converted+50, 100)
yA = scs.binom(A_total, p_A).pmf(xA)
ax.scatter(xA, yA, s=10)
xB = np.linspace(B_converted-49, B_converted+50, 100)
yB = scs.binom(B_total, p_B).pmf(xB)
ax.scatter(xB, yB, s=10)
plt.xlabel('converted')
plt.ylabel('probability')
```
Based the probabilities from our hypothesis, we should see that the test group in blue (B) converted more users than the control group in red (A). However, the plot above is not a plot of the null and alternate hypothesis. The null hypothesis is a plot of the difference between the probability of the two groups.
> Given the randomness of our user selection, group hashing, and probabilities, your simulation results should be different for each simulation run and therefore may or may not be statistically significant.
In order to calculate the difference between the two groups, we need to standardize the data. Because the number of samples can be different between the two groups, we should compare the probability of successes, p.
According to the central limit theorem, by calculating many sample means we can approximate the true mean of the population from which the data for the control group was taken. The distribution of the sample means will be normally distributed around the true mean with a standard deviation equal to the standard error of the mean.
```
SE_A = np.sqrt(p_A * (1-p_A)) / np.sqrt(A_total)
SE_B = np.sqrt(p_B * (1-p_B)) / np.sqrt(B_total)
SE_A, SE_B
fig, ax = plt.subplots(figsize=(12,6))
xA = np.linspace(0, .3, A_total)
yA = scs.norm(p_A, SE_A).pdf(xA)
ax.plot(xA, yA)
ax.axvline(x=p_A, c='red', alpha=0.5, linestyle='--')
xB = np.linspace(0, .3, B_total)
yB = scs.norm(p_B, SE_B).pdf(xB)
ax.plot(xB, yB)
ax.axvline(x=p_B, c='blue', alpha=0.5, linestyle='--')
plt.xlabel('Converted Proportion')
plt.ylabel('PDF')
```
The dashed lines represent the mean conversion rate for each group. The distance between the red dashed line and the blue dashed line is equal to d_hat, or the minimum detectable effect.
```
p_A_actual = ab_summary.loc[0, 'rate']
p_B_actual = ab_summary.loc[1, 'rate']
bcr = p_A_actual
d_hat = p_B_actual - p_A_actual
A_total, B_total, bcr, d_hat
```
Finally, let's calculate the power, alpha, and beta from our simulation.
```
abplot(A_total, B_total, bcr, d_hat, show_power=True)
```
The power value we used when determining out sample size for our experiment was 80%. This is considered the industry standard. Is the power value calculated in the plot above greater than 80%?
```
abplot(A_total, B_total, bcr, d_hat, show_beta=True)
abplot(A_total, B_total, bcr, d_hat, show_alpha=True)
```
Are the alpha and beta values plotted in the graphs above less than our significance level of 5%? If so, we have a statistically significant result.
## Next Steps
You have completed the exercise for implementing an A/B test using the experimentation framework in the Retail Demo Store. Close this notebook and open the notebook for the next exercise, **[3.3-Interleaving-Experiment](./3.3-Interleaving-Experiment.ipynb)**.
### References and Further Reading
- [A/B testing](https://en.wikipedia.org/wiki/A/B_testing), Wikipedia
- [A/B testing](https://www.optimizely.com/optimization-glossary/ab-testing/), Optimizely
- [Evan's Awesome A/B Tools](https://www.evanmiller.org/ab-testing/), Evan Miller
| true |
code
| 0.664622 | null | null | null | null |
|
# SPARTA QuickStart
-----------------------------------
## 1. Extracting Radial Velocities
### 1.1 Reading and handling spectra
#### `Observations` (class)
`Observations` class enables one to load data from a given folder
and place it into a TimeSeries object.
```
from sparta import Observations
```
The `ob.Observations` module can be used to load a batch of spectra from a given folder into an `Observations` class. In the
exmample below we load data measured by the NRES spectrograph. If no folder was specified, a selection box will be toggled.
```
obs_list = Observations(survey='NRES', target_visits_lib='data/TOI677/')
```
<br />
The Resulting object contains the following methods and attributes:
*Methods*:
`calc_PDC, convert_times_to_relative_float_values`
*Speacial attributes*:
`spec_list, observation_TimeSeries`
*Auxiliary attributes*: `time_list, rad_list, file_list, bcv, data_type, first_time`
<br />
### 1.2 Preparing the spectra for analysis
#### `Spectrum` (class)
Once initialized, the Observations module loads all the spectra found in the given folder. The loaded spectra are shifted according to the Barycentric velocity provided in the fits file header, and stored in a list of `Spectrum` objects under `spec_list`.
<br/>
*Attributes:* The two main attributes of this class are `wv`, a list of wavelength vectors, and `sp` the corresponding list of intensities. When loaded as part of the `Observations` class the spectra are shifted to a barycentric frame.
<br/>
*methods:*
`InterpolateSpectrum`: resamples the spectrum on a linear or logarithmic scale.
`TrimSpec`: Cuts the edges of the spectrum, removes zero and NaN paddding.
`FilterSpectrum`: A Butterworth bandpass filter.
`ApplyCosineBell`: Applies a Tuckey window on the data.
`RemoveCosmics`: Removes outliers that deviate above the measured spectrum.
`BarycentricCorrection`: Preforms a barycentric correction.
There is also an 'overall' procedure, that calls all the routines with
some default values, `SpecPreProccess`.
<br/>
### Let's demonstrate the work with Spectrum objects:
```
import copy as cp
import matplotlib.pyplot as plt
# Choose a specifiec observation
spec = cp.deepcopy(obs_list.spec_list[5])
# Remove cosmics, NaNs and zero paddings:
spec.SpecPreProccess(Ntrim=100, CleanMargins=True, RemoveNaNs=True,
delta=0.5, RemCosmicNum=3, FilterLC=4, FilterHC=0.15, alpha=0.3)
# Plot the resulting spectrum
plt.rcParams.update({'font.size': 14})
# plot order 27
plt.figure(figsize=(13, 4), dpi= 80, facecolor='w', edgecolor='k')
plt.plot(spec.wv[20], spec.sp[20], 'k')
plt.xlabel(r'Wavelength [${\rm \AA}$]')
plt.ylabel(r'Normazlied Intensity')
plt.grid()
```
###### <br/>
### Preprocess the measured spectra
Now, assuming that we are pleased by the preproccessing parameters, we will run the procedure on all the measured spectra.
```
import numpy as np
# Keep only the required orders
selected_ords = [10+I for I in np.arange(40)]
obs_list.SelectOrders(
selected_ords,
remove=False)
# Remove NaNs, trim edges, remove cosmics:
# ---------------------------------------
RemoveNaNs = True # Remove NaN values.
CleanMargins = True # Cut the edges of the observed spectra. Remove zero padding.
Ntrim = 100 # Number of pixels to cut from each side of the spectrum.
RemCosmicNum = 3 # Number of sigma of outlier rejection. Only points that deviate upwards are rejected.
# Interpolate the spectrum to evenly sampled bins:
# ------------------------------------------------
delta = 0.5 # 0.5 is equivalent to oversampling of fator 2.
# Interpolate the spectrum to evenly sampled bins:
# ------------------------------------------------
FilterLC = 4 # Stopband freq for low-pass filter. In units of the minimal frequency (max(w)-min(w))**(-1)
FilterHC = 0.15 # Stopband freq for the high-pass filter. In units of the Nyquist frequency.
order = 1 # The order of the Butterworth filter (integer)
# Apply cosine-bell:
# ------------------
alpha = 0.3 # Shape parameter of the Tukey window
obs_list.PreProccessSpectra(Ntrim=Ntrim, CleanMargins=CleanMargins, RemoveNaNs=RemoveNaNs,
delta=delta, RemCosmicNum=RemCosmicNum, FilterLC=FilterLC, FilterHC=FilterHC,
alpha=alpha, verbose=True)
```
<br/>
### 1.3 Preparing the model spectrum
#### `Template` (class)
In order to derive the velocities, we may want to obtain a synthetic template. The next step will therefore be to obtain a PHONIEX template, set it's parameters and make it analysis-ready. The `Template`, at its core, is a `Spectrum` object (stored under the `.model` attribute) with several additional routines.
A synthetic spectrum can be easily downloaded from the PHOENIX ftp, as demonstrated below. Once downloaded, it can be downsampled with integration, broadened, and arranged to match the shape of the obserbed spectrum.
```
from sparta.UNICOR.Template import Template
# Retrieve the template.
# If the template is not located in a local directory
# it will be downloaded from the PHOENIX FTP:
template = Template(temp=5800,
log_g=3.5,
metal=0.5,
alpha=0.0,
min_val=4650,
max_val=7500,
air=False)
# Bin the template, to reduce computational strain:
print('Integrating.', end=' ')
template.integrate_spec(integration_ratio=3)
# Make sure that the data are evenly sampled.
# No over sampling required, so the delta=1 (because when delta<1 sp is oversampled)
print('Interpolating.', end=' ')
template.model.InterpolateSpectrum(delta=1)
# Apply rotational broadening of 6 km/s:
print('Rotating.', end=' ')
template.RotationalBroadening(vsini=6, epsilon=0.5)
# Instrumental broadening for R=53,000
print('Broadening.', end=' ')
template.GaussianBroadening(resolution=53000)
# Cut the template like the observed spectrum
print('Cutting to fit spectra.', end=' ')
template.cut_multiorder_like(obs_list.spec_list[0], margins=150)
# Filter the spectrum Just like the observations were filtered:
template.model.SpecPreProccess(Ntrim=10, CleanMargins=False, RemoveNaNs=False,
delta=1, RemCosmicNum=3, FilterLC=4, FilterHC=0.15, alpha=0.3)
print('Done.')
```
##### Let's see how the model looks against the data
```
# Plot the resulting spectrum
plt.rcParams.update({'font.size': 14})
# plot order 27
plt.figure(figsize=(13, 4), dpi= 80, facecolor='w', edgecolor='k')
ax1 = plt.plot(obs_list.spec_list[0].wv[10], obs_list.spec_list[0].sp[10], 'k', label='Data')
ax2 = plt.plot(template.model.wv[10], template.model.sp[10], 'r', label='Model')
plt.xlabel(r'Wavelength [${\rm \AA}$]')
plt.ylabel(r'Normazlied Intensity')
plt.legend()
plt.grid()
```
If we are pleased with the template, we can now move on to calculate CCF and derive the velocities
<br/>
### Cross-correlating the spectra against the template
The CCF1d class holds the toolds for the cross correlation, and is called by a wrapper in the `Observations` class.
```
# Set the correlation velocity resolution and bounds.
# ---------------------------------------------------
dv = 0.05 # Assumed to be in km/s unless provided as an Astropy Unit.
# Set the velocity range for analysis:
# -----------------------------------
VelBound = [-50, 100] # Boundaries for the cross correlation.
obs_list.calc_rv_against_template(template, dv=dv, VelBound=VelBound, err_per_ord=False, combine_ccfs=True, fastccf=True)
plt.figure(figsize=(13, 4), dpi= 80, facecolor='w', edgecolor='k')
plt.errorbar(obs_list.time_list,
obs_list.vels,
yerr=obs_list.evels,
fmt='.k')
plt.title('RVs!')
plt.xlabel(r'JD $-$ ${\rm JD}_0$')
plt.ylabel(r'RV [km/s]')
plt.grid()
```
#### Plot the CCF
Here's a CCF of observation #4.
The thin gray lines mark the CCFs of each order, and the thick dark line is the combined CCF.
A red stripe is centered around the derived velocity. Its thicknes shows the velocity uncertainty.
```
# %matplotlib inline
_ = obs_list.ccf_list[3].plotCCFs()
```
| true |
code
| 0.677794 | null | null | null | null |
|
# Machine Learning Exercise 7 - K-Means Clustering & PCA
This notebook covers a Python-based solution for the seventh programming exercise of the machine learning class on Coursera. Please refer to the [exercise text](https://github.com/jdwittenauer/ipython-notebooks/blob/master/exercises/ML/ex7.pdf) for detailed descriptions and equations.
In this exercise we'll implement K-means clustering and use it to compress an image. We'll start with a simple 2D data set to see how K-means works, then we'll apply it to image compression. We'll also experiment with principal component analysis and see how it can be used to find a low-dimensional representation of images of faces.
## K-means clustering
To start out we're going to implement and apply K-means to a simple 2-dimensional data set to gain some intuition about how it works. K-means is an iterative, unsupervised clustering algorithm that groups similar instances together into clusters. The algorithm starts by guessing the initial centroids for each cluster, and then repeatedly assigns instances to the nearest cluster and re-computes the centroid of that cluster. The first piece that we're going to implement is a function that finds the closest centroid for each instance in the data.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
%matplotlib inline
def find_closest_centroids(X, centroids):
m = X.shape[0]
k = centroids.shape[0]
idx = np.zeros(m)
for i in range(m):
min_dist = 1000000
for j in range(k):
dist = np.sum((X[i,:] - centroids[j,:]) ** 2)
if dist < min_dist:
min_dist = dist
idx[i] = j
return idx
```
Let's test the function to make sure it's working as expected. We'll use the test case provided in the exercise.
```
data = loadmat('data/ex7data2.mat')
X = data['X']
initial_centroids = initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])
idx = find_closest_centroids(X, initial_centroids)
idx[0:3]
```
The output matches the expected values in the text (remember our arrays are zero-indexed instead of one-indexed so the values are one lower than in the exercise). Next we need a function to compute the centroid of a cluster. The centroid is simply the mean of all of the examples currently assigned to the cluster.
```
def compute_centroids(X, idx, k):
m, n = X.shape
centroids = np.zeros((k, n))
for i in range(k):
indices = np.where(idx == i)
centroids[i,:] = (np.sum(X[indices,:], axis=1) / len(indices[0])).ravel()
return centroids
compute_centroids(X, idx, 3)
```
This output also matches the expected values from the exercise. So far so good. The next part involves actually running the algorithm for some number of iterations and visualizing the result. This step was implmented for us in the exercise, but since it's not that complicated I'll build it here from scratch. In order to run the algorithm we just need to alternate between assigning examples to the nearest cluster and re-computing the cluster centroids.
```
def run_k_means(X, initial_centroids, max_iters):
m, n = X.shape
k = initial_centroids.shape[0]
idx = np.zeros(m)
centroids = initial_centroids
for i in range(max_iters):
idx = find_closest_centroids(X, centroids)
centroids = compute_centroids(X, idx, k)
return idx, centroids
idx, centroids = run_k_means(X, initial_centroids, 10)
cluster1 = X[np.where(idx == 0)[0],:]
cluster2 = X[np.where(idx == 1)[0],:]
cluster3 = X[np.where(idx == 2)[0],:]
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(cluster1[:,0], cluster1[:,1], s=30, color='r', label='Cluster 1')
ax.scatter(cluster2[:,0], cluster2[:,1], s=30, color='g', label='Cluster 2')
ax.scatter(cluster3[:,0], cluster3[:,1], s=30, color='b', label='Cluster 3')
ax.legend()
```
One step we skipped over is a process for initializing the centroids. This can affect the convergence of the algorithm. We're tasked with creating a function that selects random examples and uses them as the initial centroids.
```
def init_centroids(X, k):
m, n = X.shape
centroids = np.zeros((k, n))
idx = np.random.randint(0, m, k)
for i in range(k):
centroids[i,:] = X[idx[i],:]
return centroids
init_centroids(X, 3)
```
Our next task is to apply K-means to image compression. The intuition here is that we can use clustering to find a small number of colors that are most representative of the image, and map the original 24-bit colors to a lower-dimensional color space using the cluster assignments. Here's the image we're going to compress.
```
from IPython.display import Image
Image(filename='data/bird_small.png')
```
The raw pixel data has been pre-loaded for us so let's pull it in.
```
image_data = loadmat('data/bird_small.mat')
image_data
A = image_data['A']
A.shape
```
Now we need to apply some pre-processing to the data and feed it into the K-means algorithm.
```
# normalize value ranges
A = A / 255.
# reshape the array
X = np.reshape(A, (A.shape[0] * A.shape[1], A.shape[2]))
X.shape
# randomly initialize the centroids
initial_centroids = init_centroids(X, 16)
# run the algorithm
idx, centroids = run_k_means(X, initial_centroids, 10)
# get the closest centroids one last time
idx = find_closest_centroids(X, centroids)
# map each pixel to the centroid value
X_recovered = centroids[idx.astype(int),:]
X_recovered.shape
# reshape to the original dimensions
X_recovered = np.reshape(X_recovered, (A.shape[0], A.shape[1], A.shape[2]))
X_recovered.shape
plt.imshow(X_recovered)
```
Cool! You can see that we created some artifacts in the compression but the main features of the image are still there. That's it for K-means. We'll now move on to principal component analysis.
## Principal component analysis
PCA is a linear transformation that finds the "principal components", or directions of greatest variance, in a data set. It can be used for dimension reduction among other things. In this exercise we're first tasked with implementing PCA and applying it to a simple 2-dimensional data set to see how it works. Let's start off by loading and visualizing the data set.
```
data = loadmat('data/ex7data1.mat')
data
X = data['X']
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:, 0], X[:, 1])
```
The algorithm for PCA is fairly simple. After ensuring that the data is normalized, the output is simply the singular value decomposition of the covariance matrix of the original data.
```
def pca(X):
# normalize the features
X = (X - X.mean()) / X.std()
# compute the covariance matrix
X = np.matrix(X)
cov = (X.T * X) / X.shape[0]
# perform SVD
U, S, V = np.linalg.svd(cov)
return U, S, V
U, S, V = pca(X)
U, S, V
```
Now that we have the principal components (matrix U), we can use these to project the original data into a lower-dimensional space. For this task we'll implement a function that computes the projection and selects only the top K components, effectively reducing the number of dimensions.
```
def project_data(X, U, k):
U_reduced = U[:,:k]
return np.dot(X, U_reduced)
Z = project_data(X, U, 1)
Z
```
We can also attempt to recover the original data by reversing the steps we took to project it.
```
def recover_data(Z, U, k):
U_reduced = U[:,:k]
return np.dot(Z, U_reduced.T)
X_recovered = recover_data(Z, U, 1)
X_recovered
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X_recovered[:, 0], X_recovered[:, 1])
```
Notice that the projection axis for the first principal component was basically a diagonal line through the data set. When we reduced the data to one dimension, we lost the variations around that diagonal line, so in our reproduction everything falls along that diagonal.
Our last task in this exercise is to apply PCA to images of faces. By using the same dimension reduction techniques we can capture the "essence" of the images using much less data than the original images.
```
faces = loadmat('data/ex7faces.mat')
X = faces['X']
X.shape
```
The exercise code includes a function that will render the first 100 faces in the data set in a grid. Rather than try to re-produce that here, you can look in the exercise text for an example of what they look like. We can at least render one image fairly easily though.
```
face = np.reshape(X[3,:], (32, 32))
plt.imshow(face)
```
Yikes, that looks awful. These are only 32 x 32 grayscale images though (it's also rendering sideways, but we can ignore that for now). Anyway's let's proceed. Our next step is to run PCA on the faces data set and take the top 100 principal components.
```
U, S, V = pca(X)
Z = project_data(X, U, 100)
```
Now we can attempt to recover the original structure and render it again.
```
X_recovered = recover_data(Z, U, 100)
face = np.reshape(X_recovered[3,:], (32, 32))
plt.imshow(face)
```
Observe that we lost some detail, though not as much as you might expect for a 10x reduction in the number of dimensions.
That concludes exercise 7. In the final exercise we'll implement algorithms for anomaly detection and build a recommendation system using collaborative filtering.
| true |
code
| 0.646153 | null | null | null | null |
|
```
# testing installation
import pandas as pd
import matplotlib.pyplot as plt
conf = pd.read_csv('sensingbee.conf', index_col='param')
import sys, os
sys.path.append(conf.loc['GEOHUNTER_PATH','val'])
sys.path.append(conf.loc['SOURCE_PATH','val'])
import geohunter
import sensingbee
conf
```
# Data preparation
```
import geopandas as gpd
city_shape = gpd.read_file(os.path.join(conf.loc['DATA_PATH','val'],'newcastle.geojson'))
fig, ax = plt.subplots(figsize=(7,5))
city_shape.plot(ax=ax)
```
Get open sensors data of Newcastle upon Tyne from [Urban Observatory data portal](http://newcastle.urbanobservatory.ac.uk/) or from the API.
```
data = pd.read_csv('http://newcastle.urbanobservatory.ac.uk/api/v1.1/sensors/data/csv/?starttime=20180117100000&endtime=20180117120000&data_variable=Temperature')
data.head()
```
Separate data in *samples* and *metadata*
```
# To resampĺe data by median values on regular intervals
samples = data[['Variable','Sensor Name','Timestamp','Value']].loc[data['Flagged as Suspect Reading']==False]
samples['Timestamp'] = pd.to_datetime(samples['Timestamp'])
samples = samples.set_index(['Variable','Sensor Name','Timestamp'])['Value']
level_values = samples.index.get_level_values
samples = (samples.groupby([level_values(i) for i in [0,1]]
+[pd.Grouper(freq=conf.loc['SAMPLE_FREQ','val'], level=-1)]).median())
samples
import shapely
metadata = data[['Sensor Name', 'Ground Height Above Sea Level', 'Broker Name', 'Sensor Centroid Longitude', 'Sensor Centroid Latitude']]
metadata = metadata.set_index('Sensor Name').drop_duplicates()
# Transform into a GeoDataFrame
metadata['geometry'] = metadata.apply(lambda x: shapely.geometry.Point([(x['Sensor Centroid Longitude']), x['Sensor Centroid Latitude']]), axis=1)
metadata = gpd.GeoDataFrame(metadata, geometry=metadata['geometry'], crs={'init':'epsg:4326'})
fig, ax = plt.subplots(figsize=(7,5))
city_shape.plot(ax=ax)
metadata.plot(ax=ax, color='black')
# To get sensors only within city_shape
metadata = gpd.sjoin(metadata, city_shape, op='within')[metadata.columns]
idx = pd.IndexSlice
samples = samples.loc[idx[:,metadata.index,:]]
fig, ax = plt.subplots(figsize=(7,5))
city_shape.plot(ax=ax)
metadata.plot(ax=ax, color='black')
```
Set the regions where predictions have be made. We call this set of regions as "grid"
```
bbox = {'north':city_shape.bounds.max().values[3],
'east':city_shape.bounds.max().values[2],
'south':city_shape.bounds.min().values[1],
'west':city_shape.bounds.min().values[0]}
grid = geohunter.features.Grid(resolution=0.5).fit(city_shape).data
fig, ax = plt.subplots(figsize=(7,5))
city_shape.plot(ax=ax)
grid.plot(ax=ax, color='orange')
class Data(object):
def __init__(self, samples, metadata, grid):
self.samples = samples
self.metadata = metadata
self.metadata['lon'] = self.metadata.geometry.x
self.metadata['lat'] = self.metadata.geometry.y
self.grid = grid
data = Data(samples, metadata, grid)
```
# Feature Engineering
_____
In order to predict spatial variables, one have to translate samples into explanatory variables, also called features. Each spatial variable must be analysed separately and described in terms of spatial features.
One of the ways sensingbee extracts features is from Inverse Distance Weighting (IDW) estimations.
For now, let's extract primary features (Temperature features to predict Temperature, for instance). One can extract IDW from all places in grid, as below.
```
method = sensingbee.feature_engineering.inverse_distance_weighting
idx = pd.IndexSlice
params = {'p': 2, 'threshold': 10/110}
y = samples.loc['Temperature']
if False:
X = pd.DataFrame(index=pd.MultiIndex.from_product([grid.index, samples.index.get_level_values('Timestamp')], names=['Sensor Name', 'Timestamp']))
X = X.loc[~X.index.duplicated(keep='first')]
else:
X = pd.DataFrame(index=y.index)
for var in samples.index.get_level_values('Variable').unique():
for time in samples.index.get_level_values('Timestamp').unique():
v_samples = samples.loc[idx[var, :, time]].reset_index()
v_sensors = metadata.loc[v_samples['Sensor Name']]
v_sensors = v_sensors.dropna()
mask = y.loc[idx[:, time],:]
if grid is not None:
_ = grid.apply(lambda x: method(x,
v_sensors, v_samples.set_index('Sensor Name'), **params), axis=1)
_.index = X.loc[idx[:, time],:].index
X.loc[idx[:, time],var] = _.values
else:
_ = y.loc[idx[:, time],:].reset_index()['Sensor Name']\
.apply(lambda x: method(metadata.loc[x],
v_sensors, v_samples.set_index('Sensor Name'), **params))
_.index = y.loc[idx[:, time],:].index
X.loc[idx[:, time],var] = _.values
fig, ax = plt.subplots(figsize=(7,5))
t = '2018-01-17 10:00:00'
x = X.loc[idx[:,t],:].join(grid, on='Sensor Name')
gpd.GeoDataFrame(x).plot(column='Temperature', ax=ax)
distance_threshold = 10/69 # limit of 10 miles
X_idw, y = sensingbee.feature_engineering.Features(variable='Temperature',
method='idw', p=2, threshold=distance_threshold).transform(samples, metadata)
```
| true |
code
| 0.559711 | null | null | null | null |
|
# Dingocar Demo
This Notebook will take allow you to train a Dingocar (_Donkeycar, down-under_). The model will be trained using data uploaded to your Google Drive. The trained model will be saved in your nominated Google Drive Folder .
## Requirements
A zip file of training data. I recomend a zip file because you'll be transfering the data from drive to the virtual machine this notebook is running on and I found this to be orders of magnitude faster if you zip things up first. If you dont have data but you want to have a play I have a public folder [here](https://drive.google.com/file/d/1gv5k5vK90QOSgenwT42DMm-jmBdB9yEX/view?usp=sharing). Make a folder in your google drive called `dingocar` and add this folder.
Some knowledge of python, and a high level understanding of Machine Learning, not too much, just.
If anyone want an introduction to CNNs.
- [Convolutional Neural Networks (CNNs) explained](https://www.youtube.com/watch?v=YRhxdVk_sIs) Length = 8m:36s
- [A friendly introduction to Convolutional Neural Networks and Image Recognition](https://www.youtube.com/watch?v=2-Ol7ZB0MmU) Length = 32min:07min
```
Training Time:
--------------
Input data --> ML Magic --> Prediction
^ |
| ERROR |
(Prediction - Label)^2
Prediction Time:
----------------
Input data --> ML Magic --> Prediction
```
---
## Setup
First we need to:
- Clone the git repo
- Change to the requied directory
- Install the python modules
- Make a directory on the Google Colab virtual mahine to copy your training data into
```
!git clone https://github.com/tall-josh/dingocar.git
%cd dingocar
!python setup.py develop
%mkdir data
```
## Connect to Google Drive
This piece of code will mount the your google drive to this Google Colab virtual machine. It will prompt you to follow a link to get a verification code. Once you get it, copy and paste it in the box provided and hit enter.
You can nevigate the file system by clicking the "Files" tab in the <-- left side bar. All your google drive files should be in `/content/drive/My\ Drive`
```
from google.colab import drive
drive.mount('/content/drive')
```
Here we copy the contents of '`your/data/directory`' to the '`data`' directory we created earlier.
```
# Gotch'a:
# 1. 'My Drive' has a space so you'll need to delimit it with a '\' or put the
# path in 'single quotes'. ie:
# '/content/drive/My Drive' or /content/drive/My\ Drive
# 2. You can right click on the file system to the right to get the path of the
# file or folder. It ommits the leading '/' before the 'content'. So don't
# forget to add it. ie:
# 'content/' = :-(
# '/content/' = :-)
!rm -r ./data/*
!rsync -r --info=progress2 '/content/drive/My Drive/dingocar/data/tub.zip' ./data
!cd data && unzip tub.zip > _ && cd ..
!echo "Number of examples: `ls data/tub/*.jpg | wc -l`"
```
## Import some required modules
```
%matplotlib inline
import matplotlib
from matplotlib.pyplot import imshow
import os
from PIL import Image
from glob import glob
import numpy as np
import json
from tqdm import tqdm
```
## Load and visualise the data
Donkeycar calls the directory(s) where your training data is stored a "_tub_". The Dingocar follows the same convention.
`Tubs` contain 3 types of files:
- images: in the form of `.jpg`
- records: in the form `.json`
- `meta` which contains some aditional information, also `.json`
Below we set the `tub` location and visualize an image and record
```
from dingocar.parts.datastore import Tub
tub_path = 'data/tub'
tub = Tub(tub_path)
# Tubs provide a simple way to access the training.
# Each entry is a dict record which contains the
# a camera image plus the steering and throttle commands
# that were recorded when driving the car manually.
# The dict keys are as follows.
IMAGE_KEY = "cam/image_array"
STEERING_KEY = "user/angle"
THROTTLE_KEY = "user/throttle"
# Read a single record from the tub
idx = 123
record = tub.get_record(idx)
print(f"Steering: {record[STEERING_KEY]}")
print(f"Throttle: {record[THROTTLE_KEY]}")
imshow(record[IMAGE_KEY])
```
## Data Augmentation
Data augmentation allows us to add a bit more variety to the training data. One very handy augmentation transformation is to randomly mirror the input image and the steering label. This ensurse the data contains the same number or left and right turns so the neural network does not become bias to a specifc direction of turn.
There are also some other augmentation transformations you can apply below. These will hopefully make the network a bit more robust to canging lighting and help prevent overfitting.
```
import config
from functools import partial
from dingocar.parts.augmentation import apply_aug_config
# Play with the data augmentation settings if you like
# In all cases 'aug_prob' is the probability the given
# augmentation will occure. All the other parameters are
# explained below.
aug_config = {
# Mirror the image horizontally
"mirror_y" : {"aug_prob" : 0.5},
# Randomly turn pixels black of white.
# "noise" : The probability a pixel is affected.
# 0.0 : No pixels will be effected
# 1.0 : All pixels will be effected
"salt_and_pepper" : {"aug_prob" : 0.3,
"noise" : 0.2},
# Randomly turn pixels a random color
# "noise" : The probability a pixel is affected.
# 0.0 : No pixels will be effected
# 1.0 : All pixels will be effected
"100s_and_1000s" : {"aug_prob" : 0.3,
"noise" : 0.2},
# Randomly increase or decrease the pixel values by an
# value between 'min_val' and 'max_val'. The resulting
# value will be clipped between 0 and 255
"pixel_saturation" : {"aug_prob" : 0.3,
"min_val" :-20,
"max_val" : 20},
# Randomly shuffle the RGB channel order
"shuffle_channels" : {"aug_prob" : 0.3},
# Randomly set a rectangular setction of the image to 0
# the rectangle height and width is randomly generated
# to be between dimention*min_frac and dimention*max_frac.
# So min_frac = 0.0 and max_frac = 1.0 would result
# in a random rectangel that could cover the entire image,
# or none of the image or anywhere inbetween.
"blockout" : {"aug_prob" : 0.3,
"min_frac" : 0.07,
"max_frac" : 0.3}
}
# If you're unfamiliar with the 'partial' function. It allows you to
# call a function with some of the arguments pre-filled.
# In this case we made a function that is like 'apply_aug_config', but
# has the `aug_config` parameter pre-filled.
record_transform=partial(apply_aug_config, aug_config=aug_config)
record = tub.get_record(idx, record_transform=record_transform)
print(f"Steering: {record[STEERING_KEY]}")
print(f"Throttle: {record[THROTTLE_KEY]}")
imshow(record[IMAGE_KEY])
```
## Define the CNN
```
from tensorflow.python.keras.layers import Convolution2D
from tensorflow.python.keras.layers import Dropout, Flatten, Dense
from dingocar.parts.keras import KerasLinear
from tensorflow.python.keras.layers import Input
from tensorflow.python.keras.models import Model, load_model
# Tub objects maintain a dictionary of data. You can access the data via 'keys'.
# Traditionally x stands for inputs and y stands for outputs.
# In our case, for every input image (x) there are 2 output labels,
# steering angle and throttle (y).
X_KEYS = [IMAGE_KEY]
Y_KEYS = [STEERING_KEY, THROTTLE_KEY]
# If you'd like you can play with this neural network as much as you like. See
# if you can get the network to be more accurate!
# The only things you need to watch out for are:
# 1. 'img_in' cannot change.
# 2. 'angle_out' must always haev 'units=1'
# 3. 'throttle_out' must always have 'units=1'
def convolutional_neural_network():
img_in = Input(shape=(120, 160, 3), name='img_in')
x = img_in
# Convolution2D class name is an alias for Conv2D
x = Convolution2D(filters=24, kernel_size=(5, 5), strides=(2, 2), activation='relu')(x)
x = Convolution2D(filters=32, kernel_size=(5, 5), strides=(2, 2), activation='relu')(x)
x = Convolution2D(filters=64, kernel_size=(5, 5), strides=(2, 2), activation='relu')(x)
x = Convolution2D(filters=64, kernel_size=(3, 3), strides=(2, 2), activation='relu')(x)
x = Convolution2D(filters=64, kernel_size=(3, 3), strides=(1, 1), activation='relu')(x)
x = Flatten(name='flattened')(x)
x = Dense(units=100, activation='linear')(x)
x = Dropout(rate=.2)(x)
x = Dense(units=50, activation='linear')(x)
x = Dropout(rate=.2)(x)
# categorical output of the angle
angle_out = Dense(units=1, activation='linear', name='angle_out')(x)
# continous output of throttle
throttle_out = Dense(units=1, activation='linear', name='throttle_out')(x)
model = Model(inputs=[img_in], outputs=[angle_out, throttle_out])
model.compile(optimizer='adam',
loss={'angle_out': 'mean_squared_error',
'throttle_out': 'mean_squared_error'},
loss_weights={'angle_out': 0.5, 'throttle_out': 0.5})
return model
# KerasLinear is a class the contains some functions we can use to train
# our model and to get predictions out if it later.
model = KerasLinear(model=convolutional_neural_network())
```
## Train the model
```
from manage import train
import config
# Load 16 image at a time into the model
BATCH_SIZE = 32
# 70% of the data is used for training. 30% for validation
TRAIN_TEST_SPLIT = 0.7
# Number of time to look over all the training data
EPOCHS = 100
# Stop training if the validation loss has not improved for the last 'PATIENTS'
# Epochs.
USE_EARLY_STOP = True
PATIENCE = 5
# Where to save the trained model
new_model_path = "/content/drive/My Drive/dingocar/no_mirror1.hdf5"
# If you want to start from a pre-trained model you can add the path here
base_model_path = None
# These are generators that will be used to feed data into the model
# when training. The generator uses a constant random seed so the train/val
# split is the same every time.
train_gen, val_gen = tub.get_train_val_gen(X_KEYS, Y_KEYS,
batch_size=BATCH_SIZE,
train_frac=TRAIN_TEST_SPLIT,
train_record_transform=record_transform,
val_record_transform=None)
training_history = model.train(train_gen,
val_gen,
new_model_path,
epochs=EPOCHS,
patience=PATIENCE,
use_early_stop=USE_EARLY_STOP)
```
# Visualize Predictions
```
from dingocar.parts.keras import KerasLinear
new_model_path = "/content/drive/My Drive/dingocar/no_mirror1.hdf5"
trained_model = new_model_path
# Load a pre-trained model
model = KerasLinear()
model.load(trained_model)
from dingocar.parts.datastore import Tub
_, val_gen = tub.get_train_val_gen(X_KEYS, Y_KEYS,
batch_size=1,
train_frac=TRAIN_TEST_SPLIT,
train_record_transform=None,
val_record_transform=None)
preds = []
truth = []
val_count = int(tub.get_num_records() * (1-TRAIN_TEST_SPLIT))
for _ in tqdm(range(val_count)):
sample = next(val_gen)
pred = model.run(sample[0][0][0])
preds.append(pred)
truth.append((sample[1][0][0], sample[1][1][0]))
preds = np.array(preds)
truth = np.array(truth)
print(preds.shape)
print(truth.shape)
import matplotlib.pyplot as plt
def mean_squared_error(preds, true):
squared_error = (true - preds)**2
return np.mean(squared_error)
def xy_scatter(preds, truth):
fig = plt.figure(figsize=(14,14))
steering_p = preds[...,0]
throttle_p = preds[...,1]
steering_t = truth[...,0]
throttle_t = truth[...,1]
steering_mse = mean_squared_error(steering_p, steering_t)
throttle_mse = mean_squared_error(throttle_p, throttle_t)
plt.plot(steering_p, steering_t, 'b.')
plt.title(f"MSE: {steering_mse:.3f}")
plt.xlabel("predictions")
plt.ylabel("ground truth")
plt.gca().set_xlim(-1, 1)
plt.show()
# fig = plt.gcf()
# fig.savefig(path + "/pred_vs_anno.png", dpi=100)
# Only display the validation set
xy_scatter(preds, truth)
preds = []
truth = []
for idx in tqdm(range(tub.get_num_records())):
sample = tub.get_record(idx)
pred = model.run(sample[IMAGE_KEY])
preds.append(pred)
truth.append((sample[STEERING_KEY], sample[THROTTLE_KEY]))
preds = np.array(preds)
truth = np.array(truth)
print(preds.shape)
from ipywidgets import interact, fixed
import ipywidgets as widgets
def plt_image(ax, image, title):
ax.imshow(image)
ax.set_xticks([])
ax.set_yticks([])
ax.set_title(title)
def plt_samples(idxs, axs, tub):
records = [tub.get_record(i) for i in idxs]
images = [r[IMAGE_KEY] for r in records]
titles = [f"frame: {i}" for i in idxs]
for a,i,t in zip(axs, images, titles):
plt_image(a,i,t)
def time_series(x=300):#, axs=axs, tub=tub):
fig = plt.figure(figsize=(21,12))
plt.tight_layout()
ax1 = plt.subplot2grid((2, 5), (0, 0), colspan=5)
ax2 = plt.subplot2grid((2, 5), (1, 0))
ax3 = plt.subplot2grid((2, 5), (1, 1))
ax4 = plt.subplot2grid((2, 5), (1, 2))
ax5 = plt.subplot2grid((2, 5), (1, 3))
ax6 = plt.subplot2grid((2, 5), (1, 4))
axs = [ax2, ax3, ax4, ax5, ax6]
steering_p = preds[...,0]
throttle_p = preds[...,1]
steering_t = truth[...,0]
throttle_t = truth[...,1]
idxs = np.arange(x-2,x+3)
plt_samples(idxs, axs, tub)
start = x-300
end = x + 300
ax1.plot(steering_p, label="predictions")
ax1.plot(steering_t, label="ground truth")
#ax1.axvline(x=x, linewidth=4, color='r')
ax1.legend(bbox_to_anchor=(0.91, 0.96), loc=2, borderaxespad=0.)
ax1.set_title("Time Series Throttle Predictions vs Ground Truth")
ax1.set_xlabel("time (frames)")
ax1.set_ylabel("steering command")
ax1.set_xlim(start, end)
#time_series(x=600)
interact(time_series, x=(300, len(truth-300)))#, axs=fixed(axs), tub=fixed(tub))
import numpy as np
import matplotlib.pyplot as plt
testData = np.array([[0,0], [0.1, 0], [0, 0.3], [-0.4, 0], [0, -0.5]])
fig, ax = plt.subplots()
sctPlot, = ax.plot(testData[:,0], testData[:,1], "o", picker = 5)
plt.grid(True)
plt.axis([-0.5, 0.5, -0.5, 0.5])
def on_pick(event):
artist = event.artist
artist.set_color(np.random.random(3))
print("click!")
fig.canvas.draw()
fig.canvas.mpl_connect('pick_event', on_pick)
```
| true |
code
| 0.69451 | null | null | null | null |
|
```
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
#default_exp vision.data
#export
from fastai.torch_basics import *
from fastai.data.all import *
from fastai.vision.core import *
#hide
from nbdev.showdoc import *
# from fastai.vision.augment import *
```
# Vision data
> Helper functions to get data in a `DataLoaders` in the vision application and higher class `ImageDataLoaders`
The main classes defined in this module are `ImageDataLoaders` and `SegmentationDataLoaders`, so you probably want to jump to their definitions. They provide factory methods that are a great way to quickly get your data ready for training, see the [vision tutorial](http://docs.fast.ai/tutorial.vision) for examples.
## Helper functions
```
#export
@delegates(subplots)
def get_grid(n, nrows=None, ncols=None, add_vert=0, figsize=None, double=False, title=None, return_fig=False, **kwargs):
"Return a grid of `n` axes, `rows` by `cols`"
nrows = nrows or int(math.sqrt(n))
ncols = ncols or int(np.ceil(n/nrows))
if double: ncols*=2 ; n*=2
fig,axs = subplots(nrows, ncols, figsize=figsize, **kwargs)
axs = [ax if i<n else ax.set_axis_off() for i, ax in enumerate(axs.flatten())][:n]
if title is not None: fig.suptitle(title, weight='bold', size=14)
return (fig,axs) if return_fig else axs
```
This is used by the type-dispatched versions of `show_batch` and `show_results` for the vision application. By default, there will be `int(math.sqrt(n))` rows and `ceil(n/rows)` columns. `double` will double the number of columns and `n`. The default `figsize` is `(cols*imsize, rows*imsize+add_vert)`. If a `title` is passed it is set to the figure. `sharex`, `sharey`, `squeeze`, `subplot_kw` and `gridspec_kw` are all passed down to `plt.subplots`. If `return_fig` is `True`, returns `fig,axs`, otherwise just `axs`.
```
# export
def clip_remove_empty(bbox, label):
"Clip bounding boxes with image border and label background the empty ones"
bbox = torch.clamp(bbox, -1, 1)
empty = ((bbox[...,2] - bbox[...,0])*(bbox[...,3] - bbox[...,1]) <= 0.)
return (bbox[~empty], label[~empty])
bb = tensor([[-2,-0.5,0.5,1.5], [-0.5,-0.5,0.5,0.5], [1,0.5,0.5,0.75], [-0.5,-0.5,0.5,0.5], [-2, -0.5, -1.5, 0.5]])
bb,lbl = clip_remove_empty(bb, tensor([1,2,3,2,5]))
test_eq(bb, tensor([[-1,-0.5,0.5,1.], [-0.5,-0.5,0.5,0.5], [-0.5,-0.5,0.5,0.5]]))
test_eq(lbl, tensor([1,2,2]))
#export
def bb_pad(samples, pad_idx=0):
"Function that collect `samples` of labelled bboxes and adds padding with `pad_idx`."
samples = [(s[0], *clip_remove_empty(*s[1:])) for s in samples]
max_len = max([len(s[2]) for s in samples])
def _f(img,bbox,lbl):
bbox = torch.cat([bbox,bbox.new_zeros(max_len-bbox.shape[0], 4)])
lbl = torch.cat([lbl, lbl .new_zeros(max_len-lbl .shape[0])+pad_idx])
return img,bbox,lbl
return [_f(*s) for s in samples]
img1,img2 = TensorImage(torch.randn(16,16,3)),TensorImage(torch.randn(16,16,3))
bb1 = tensor([[-2,-0.5,0.5,1.5], [-0.5,-0.5,0.5,0.5], [1,0.5,0.5,0.75], [-0.5,-0.5,0.5,0.5]])
lbl1 = tensor([1, 2, 3, 2])
bb2 = tensor([[-0.5,-0.5,0.5,0.5], [-0.5,-0.5,0.5,0.5]])
lbl2 = tensor([2, 2])
samples = [(img1, bb1, lbl1), (img2, bb2, lbl2)]
res = bb_pad(samples)
non_empty = tensor([True,True,False,True])
test_eq(res[0][0], img1)
test_eq(res[0][1], tensor([[-1,-0.5,0.5,1.], [-0.5,-0.5,0.5,0.5], [-0.5,-0.5,0.5,0.5]]))
test_eq(res[0][2], tensor([1,2,2]))
test_eq(res[1][0], img2)
test_eq(res[1][1], tensor([[-0.5,-0.5,0.5,0.5], [-0.5,-0.5,0.5,0.5], [0,0,0,0]]))
test_eq(res[1][2], tensor([2,2,0]))
```
## Show methods -
```
#export
@typedispatch
def show_batch(x:TensorImage, y, samples, ctxs=None, max_n=10, nrows=None, ncols=None, figsize=None, **kwargs):
if ctxs is None: ctxs = get_grid(min(len(samples), max_n), nrows=nrows, ncols=ncols, figsize=figsize)
ctxs = show_batch[object](x, y, samples, ctxs=ctxs, max_n=max_n, **kwargs)
return ctxs
#export
@typedispatch
def show_batch(x:TensorImage, y:TensorImage, samples, ctxs=None, max_n=10, nrows=None, ncols=None, figsize=None, **kwargs):
if ctxs is None: ctxs = get_grid(min(len(samples), max_n), nrows=nrows, ncols=ncols, add_vert=1, figsize=figsize, double=True)
for i in range(2):
ctxs[i::2] = [b.show(ctx=c, **kwargs) for b,c,_ in zip(samples.itemgot(i),ctxs[i::2],range(max_n))]
return ctxs
```
## `TransformBlock`s for vision
These are the blocks the vision application provide for the [data block API](http://docs.fast.ai/data.block).
```
#export
def ImageBlock(cls=PILImage):
"A `TransformBlock` for images of `cls`"
return TransformBlock(type_tfms=cls.create, batch_tfms=IntToFloatTensor)
#export
def MaskBlock(codes=None):
"A `TransformBlock` for segmentation masks, potentially with `codes`"
return TransformBlock(type_tfms=PILMask.create, item_tfms=AddMaskCodes(codes=codes), batch_tfms=IntToFloatTensor)
#export
PointBlock = TransformBlock(type_tfms=TensorPoint.create, item_tfms=PointScaler)
BBoxBlock = TransformBlock(type_tfms=TensorBBox.create, item_tfms=PointScaler, dls_kwargs = {'before_batch': bb_pad})
PointBlock.__doc__ = "A `TransformBlock` for points in an image"
BBoxBlock.__doc__ = "A `TransformBlock` for bounding boxes in an image"
show_doc(PointBlock, name='PointBlock')
show_doc(BBoxBlock, name='BBoxBlock')
#export
def BBoxLblBlock(vocab=None, add_na=True):
"A `TransformBlock` for labeled bounding boxes, potentially with `vocab`"
return TransformBlock(type_tfms=MultiCategorize(vocab=vocab, add_na=add_na), item_tfms=BBoxLabeler)
```
If `add_na` is `True`, a new category is added for NaN (that will represent the background class).
## ImageDataLoaders -
```
#export
class ImageDataLoaders(DataLoaders):
"Basic wrapper around several `DataLoader`s with factory methods for computer vision problems"
@classmethod
@delegates(DataLoaders.from_dblock)
def from_folder(cls, path, train='train', valid='valid', valid_pct=None, seed=None, vocab=None, item_tfms=None,
batch_tfms=None, **kwargs):
"Create from imagenet style dataset in `path` with `train` and `valid` subfolders (or provide `valid_pct`)"
splitter = GrandparentSplitter(train_name=train, valid_name=valid) if valid_pct is None else RandomSplitter(valid_pct, seed=seed)
get_items = get_image_files if valid_pct else partial(get_image_files, folders=[train, valid])
dblock = DataBlock(blocks=(ImageBlock, CategoryBlock(vocab=vocab)),
get_items=get_items,
splitter=splitter,
get_y=parent_label,
item_tfms=item_tfms,
batch_tfms=batch_tfms)
return cls.from_dblock(dblock, path, path=path, **kwargs)
@classmethod
@delegates(DataLoaders.from_dblock)
def from_path_func(cls, path, fnames, label_func, valid_pct=0.2, seed=None, item_tfms=None, batch_tfms=None, **kwargs):
"Create from list of `fnames` in `path`s with `label_func`"
dblock = DataBlock(blocks=(ImageBlock, CategoryBlock),
splitter=RandomSplitter(valid_pct, seed=seed),
get_y=label_func,
item_tfms=item_tfms,
batch_tfms=batch_tfms)
return cls.from_dblock(dblock, fnames, path=path, **kwargs)
@classmethod
def from_name_func(cls, path, fnames, label_func, **kwargs):
"Create from the name attrs of `fnames` in `path`s with `label_func`"
f = using_attr(label_func, 'name')
return cls.from_path_func(path, fnames, f, **kwargs)
@classmethod
def from_path_re(cls, path, fnames, pat, **kwargs):
"Create from list of `fnames` in `path`s with re expression `pat`"
return cls.from_path_func(path, fnames, RegexLabeller(pat), **kwargs)
@classmethod
@delegates(DataLoaders.from_dblock)
def from_name_re(cls, path, fnames, pat, **kwargs):
"Create from the name attrs of `fnames` in `path`s with re expression `pat`"
return cls.from_name_func(path, fnames, RegexLabeller(pat), **kwargs)
@classmethod
@delegates(DataLoaders.from_dblock)
def from_df(cls, df, path='.', valid_pct=0.2, seed=None, fn_col=0, folder=None, suff='', label_col=1, label_delim=None,
y_block=None, valid_col=None, item_tfms=None, batch_tfms=None, **kwargs):
"Create from `df` using `fn_col` and `label_col`"
pref = f'{Path(path) if folder is None else Path(path)/folder}{os.path.sep}'
if y_block is None:
is_multi = (is_listy(label_col) and len(label_col) > 1) or label_delim is not None
y_block = MultiCategoryBlock if is_multi else CategoryBlock
splitter = RandomSplitter(valid_pct, seed=seed) if valid_col is None else ColSplitter(valid_col)
dblock = DataBlock(blocks=(ImageBlock, y_block),
get_x=ColReader(fn_col, pref=pref, suff=suff),
get_y=ColReader(label_col, label_delim=label_delim),
splitter=splitter,
item_tfms=item_tfms,
batch_tfms=batch_tfms)
return cls.from_dblock(dblock, df, path=path, **kwargs)
@classmethod
def from_csv(cls, path, csv_fname='labels.csv', header='infer', delimiter=None, **kwargs):
"Create from `path/csv_fname` using `fn_col` and `label_col`"
df = pd.read_csv(Path(path)/csv_fname, header=header, delimiter=delimiter)
return cls.from_df(df, path=path, **kwargs)
@classmethod
@delegates(DataLoaders.from_dblock)
def from_lists(cls, path, fnames, labels, valid_pct=0.2, seed:int=None, y_block=None, item_tfms=None, batch_tfms=None,
**kwargs):
"Create from list of `fnames` and `labels` in `path`"
if y_block is None:
y_block = MultiCategoryBlock if is_listy(labels[0]) and len(labels[0]) > 1 else (
RegressionBlock if isinstance(labels[0], float) else CategoryBlock)
dblock = DataBlock.from_columns(blocks=(ImageBlock, y_block),
splitter=RandomSplitter(valid_pct, seed=seed),
item_tfms=item_tfms,
batch_tfms=batch_tfms)
return cls.from_dblock(dblock, (fnames, labels), path=path, **kwargs)
ImageDataLoaders.from_csv = delegates(to=ImageDataLoaders.from_df)(ImageDataLoaders.from_csv)
ImageDataLoaders.from_name_func = delegates(to=ImageDataLoaders.from_path_func)(ImageDataLoaders.from_name_func)
ImageDataLoaders.from_path_re = delegates(to=ImageDataLoaders.from_path_func)(ImageDataLoaders.from_path_re)
ImageDataLoaders.from_name_re = delegates(to=ImageDataLoaders.from_name_func)(ImageDataLoaders.from_name_re)
```
This class should not be used directly, one of the factory methods should be preferred instead. All those factory methods accept as arguments:
- `item_tfms`: one or several transforms applied to the items before batching them
- `batch_tfms`: one or several transforms applied to the batches once they are formed
- `bs`: the batch size
- `val_bs`: the batch size for the validation `DataLoader` (defaults to `bs`)
- `shuffle_train`: if we shuffle the training `DataLoader` or not
- `device`: the PyTorch device to use (defaults to `default_device()`)
```
show_doc(ImageDataLoaders.from_folder)
```
If `valid_pct` is provided, a random split is performed (with an optional `seed`) by setting aside that percentage of the data for the validation set (instead of looking at the grandparents folder). If a `vocab` is passed, only the folders with names in `vocab` are kept.
Here is an example loading a subsample of MNIST:
```
path = untar_data(URLs.MNIST_TINY)
dls = ImageDataLoaders.from_folder(path)
```
Passing `valid_pct` will ignore the valid/train folders and do a new random split:
```
dls = ImageDataLoaders.from_folder(path, valid_pct=0.2)
dls.valid_ds.items[:3]
show_doc(ImageDataLoaders.from_path_func)
```
The validation set is a random `subset` of `valid_pct`, optionally created with `seed` for reproducibility.
Here is how to create the same `DataLoaders` on the MNIST dataset as the previous example with a `label_func`:
```
fnames = get_image_files(path)
def label_func(x): return x.parent.name
dls = ImageDataLoaders.from_path_func(path, fnames, label_func)
```
Here is another example on the pets dataset. Here filenames are all in an "images" folder and their names have the form `class_name_123.jpg`. One way to properly label them is thus to throw away everything after the last `_`:
```
show_doc(ImageDataLoaders.from_path_re)
```
The validation set is a random subset of `valid_pct`, optionally created with `seed` for reproducibility.
Here is how to create the same `DataLoaders` on the MNIST dataset as the previous example (you will need to change the initial two / by a \ on Windows):
```
pat = r'/([^/]*)/\d+.png$'
dls = ImageDataLoaders.from_path_re(path, fnames, pat)
show_doc(ImageDataLoaders.from_name_func)
```
The validation set is a random subset of `valid_pct`, optionally created with `seed` for reproducibility. This method does the same as `ImageDataLoaders.from_path_func` except `label_func` is applied to the name of each filenames, and not the full path.
```
show_doc(ImageDataLoaders.from_name_re)
```
The validation set is a random subset of `valid_pct`, optionally created with `seed` for reproducibility. This method does the same as `ImageDataLoaders.from_path_re` except `pat` is applied to the name of each filenames, and not the full path.
```
show_doc(ImageDataLoaders.from_df)
```
The validation set is a random subset of `valid_pct`, optionally created with `seed` for reproducibility. Alternatively, if your `df` contains a `valid_col`, give its name or its index to that argument (the column should have `True` for the elements going to the validation set).
You can add an additional `folder` to the filenames in `df` if they should not be concatenated directly to `path`. If they do not contain the proper extensions, you can add `suff`. If your label column contains multiple labels on each row, you can use `label_delim` to warn the library you have a multi-label problem.
`y_block` should be passed when the task automatically picked by the library is wrong, you should then give `CategoryBlock`, `MultiCategoryBlock` or `RegressionBlock`. For more advanced uses, you should use the data block API.
The tiny mnist example from before also contains a version in a dataframe:
```
path = untar_data(URLs.MNIST_TINY)
df = pd.read_csv(path/'labels.csv')
df.head()
```
Here is how to load it using `ImageDataLoaders.from_df`:
```
dls = ImageDataLoaders.from_df(df, path)
```
Here is another example with a multi-label problem:
```
path = untar_data(URLs.PASCAL_2007)
df = pd.read_csv(path/'train.csv')
df.head()
dls = ImageDataLoaders.from_df(df, path, folder='train', valid_col='is_valid')
```
Note that can also pass `2` to valid_col (the index, starting with 0).
```
show_doc(ImageDataLoaders.from_csv)
```
Same as `ImageDataLoaders.from_df` after loading the file with `header` and `delimiter`.
Here is how to load the same dataset as before with this method:
```
dls = ImageDataLoaders.from_csv(path, 'train.csv', folder='train', valid_col='is_valid')
show_doc(ImageDataLoaders.from_lists)
```
The validation set is a random subset of `valid_pct`, optionally created with `seed` for reproducibility. `y_block` can be passed to specify the type of the targets.
```
path = untar_data(URLs.PETS)
fnames = get_image_files(path/"images")
labels = ['_'.join(x.name.split('_')[:-1]) for x in fnames]
dls = ImageDataLoaders.from_lists(path, fnames, labels)
#export
class SegmentationDataLoaders(DataLoaders):
"Basic wrapper around several `DataLoader`s with factory methods for segmentation problems"
@classmethod
@delegates(DataLoaders.from_dblock)
def from_label_func(cls, path, fnames, label_func, valid_pct=0.2, seed=None, codes=None, item_tfms=None, batch_tfms=None, **kwargs):
"Create from list of `fnames` in `path`s with `label_func`."
dblock = DataBlock(blocks=(ImageBlock, MaskBlock(codes=codes)),
splitter=RandomSplitter(valid_pct, seed=seed),
get_y=label_func,
item_tfms=item_tfms,
batch_tfms=batch_tfms)
res = cls.from_dblock(dblock, fnames, path=path, **kwargs)
return res
show_doc(SegmentationDataLoaders.from_label_func)
```
The validation set is a random subset of `valid_pct`, optionally created with `seed` for reproducibility. `codes` contain the mapping index to label.
```
path = untar_data(URLs.CAMVID_TINY)
fnames = get_image_files(path/'images')
def label_func(x): return path/'labels'/f'{x.stem}_P{x.suffix}'
codes = np.loadtxt(path/'codes.txt', dtype=str)
dls = SegmentationDataLoaders.from_label_func(path, fnames, label_func, codes=codes)
```
# Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| true |
code
| 0.77867 | null | null | null | null |
|
### Plotting the ADCP spectra
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
Little tweaks in the matplotlib configuration to make nicer plots
```
plt.rcParams.update({'font.size': 25, 'legend.handlelength' : 2.0
, 'legend.markerscale': 1., 'legend.fontsize' : 20, 'axes.titlesize' : 35, 'axes.labelsize' : 30})
plt.rc('xtick', labelsize=35)
plt.rc('ytick', labelsize=35)
#plt.rcParams['lines.width'] = 2.
#plt.rcParams['alpha'] = 0.5
#plt.rcParams?
```
Define nice colors
```
color2 = '#6495ed'
color1 = '#ff6347'
color5 = '#8470ff'
color3 = '#3cb371'
color4 = '#ffd700'
color6 = '#ba55d3'
lw1=3
aph=.7
```
### Load data
```
data_path = './outputs/'
slab1=np.load(data_path+'adcp_spec_slab1.npz')
slab2=np.load(data_path+'adcp_spec_slab2.npz')
slab3=np.load(data_path+'adcp_spec_slab3.npz')
slab2ns=np.load(data_path+'adcp_spec_slab2ns.npz')
kK = slab1['kK1']
# scaling factor to account for the variance reduced by hanning window
k1 = slab1['k']
w = np.hanning(k1.size)
Nw = k1.size/w.sum()
Nw
## -2 and -3 slopes in the loglog space
ks = np.array([1.e-3,1])
Es2 = .2e-4*(ks**(-2))
Es3 = .5e-6*(ks**(-3))
rd1 = 22.64 # [km]
Enoise = np.ones(2)*2.*1.e-4
def add_second_axis(ax1):
""" Add a x-axis at the top of the spectra figures """
ax2 = ax1.twiny()
ax2.set_xscale('log')
ax2.set_xlim(ax1.axis()[0], ax1.axis()[1])
kp = 1./np.array([500.,200.,100.,40.,20.,10.,5.])
lp=np.array([500,200,100,40,20,10,5])
ax2.set_xticks(kp)
ax2.set_xticklabels(lp)
plt.xlabel('Wavelength [km]')
def plt_adcp_spectrum(slab,vlevel=1,lw=3):
""" Plots ADCP spectrum in the given vertical level
slab is a dictionary contaning the spectra """
if vlevel==1:
ltit = r'26-50 m, 232 DOF'
fig_num = 'a'
elif vlevel==2:
ltit=r'58-98 m, 238 DOF'
fig_num = 'b'
elif vlevel==3:
ltit=r'106-202 m, 110 DOF'
fig_num = 'c'
fig = plt.figure(facecolor='w', figsize=(12.,10.))
ax1 = fig.add_subplot(111)
ax1.set_rasterization_zorder(1)
ax1.fill_between(slab['k'],slab['Eul']/2.,slab['Euu']/2., color=color1,\
alpha=0.35, zorder=0)
ax1.fill_between(slab['k'],slab['Evl']/2.,slab['Evu']/2.,\
color=color2, alpha=0.35,zorder=0)
ax1.set_xscale('log'); ax1.set_yscale('log')
ax1.loglog(slab['k'],slab['Eu']/2.,color=color1,\
linewidth=lw,label=r'$\hat{C}^u$: across-track',zorder=0)
ax1.loglog(slab['k'],slab['Ev']/2.,color=color2,\
linewidth=lw,label=r'$\hat{C}^v$: along-track',zorder=0)
ax1.loglog(kK,slab['Kpsi']/2,color=color3,linewidth=lw,\
label='$\hat{C}^\psi$: rotational',zorder=0)
ax1.loglog(kK,slab['Kphi']/2,color=color4,linewidth=lw,\
label='$\hat{C}^\phi$: divergent',zorder=0)
ax1.loglog(slab['ks'],slab['Enoise']/2., color='.5',alpha=.7,\
linewidth=lw1,label='instrumental error',zorder=0)
ax1.loglog(ks,Es2,'--', color='k',linewidth=2.,alpha=.5,zorder=0)
ax1.loglog(ks,Es3,'--', color='k',linewidth=2.,alpha=.5,zorder=0)
ax1.axis((1./(1000),1./4,.4e-5,10))
plt.text(0.0011, 5.41,u'k$^{-2}$')
plt.text(0.0047, 5.51,u'k$^{-3}$')
plt.xlabel('Along-track wavenumber [cpkm]')
plt.ylabel(u'KE spectral density [ m$^{2}$ s$^{-2}$/ cpkm]')
lg = plt.legend(loc=(.01,.075),title=ltit, numpoints=1,ncol=2)
lg.draw_frame(False)
plt.axis((1./1.e3,1./5.,.5/1.e4,1.e1))
plt.text(1/20., 5., "ADCP", size=25, rotation=0.,
ha="center", va="center",
bbox = dict(boxstyle="round",ec='k',fc='w'))
plt.text(1/6.5, 4.5, fig_num, size=35, rotation=0.)
add_second_axis(ax1)
plt.savefig('figs/spec_adcp_slab'+str(vlevel)+'_bcf_decomp_ke',bbox_inches='tight')
plt.savefig('figs/spec_adcp_slab'+str(vlevel)+'_bcf_decomp_ke.eps'\
, rasterized=True, dpi=300)
```
### Call the function to plot the spectra
```
## 26-50 m
plt_adcp_spectrum(slab1,vlevel=1)
## 58-98 m
plt_adcp_spectrum(slab2,vlevel=2)
## 106-202 m
plt_adcp_spectrum(slab3,vlevel=3)
```
### Now plot the spectra for sub-transects to the north and south of the polar front
```
fig = plt.figure(figsize=(12.,10.))
ax1 = fig.add_subplot(111)
ax1.fill_between(slab2ns['kns'],slab2ns['Euln']/2,slab2ns['Euun']/2, color=color1, alpha=0.25)
ax1.fill_between(slab2ns['kns'],slab2ns['Evln']/2,slab2ns['Evun']/2, color=color2, alpha=0.25)
ax1.fill_between(slab2ns['kns'],slab2ns['Euls']/2,slab2ns['Euus']/2, color=color1, alpha=0.25)
ax1.fill_between(slab2ns['kns'],slab2ns['Evls']/2,slab2ns['Evus']/2, color=color2, alpha=0.25)
ax1.set_xscale('log'); ax1.set_yscale('log')
ax1.loglog(slab2ns['kns'],slab2ns['Eun']/2,color=color1,linewidth=lw1,label='$\hat{C}^u$: across-track')
ax1.loglog(slab2ns['kns'],slab2ns['Evn']/2,color=color2,linewidth=lw1,label='$\hat{C}^v$: along-track')
ax1.loglog(slab2ns['kns'],slab2ns['Eus']/2,'--',color=color1,linewidth=lw1)
ax1.loglog(slab2ns['kns'],slab2ns['Evs']/2,'--',color=color2,linewidth=lw1)
#ax1.loglog(slab2ns['kKn'],slab2ns['Kpsin']/2,color=color3,linewidth=2.,
# label='$\hat{C}^\psi$: rotational')
#ax1.loglog(slab2ns['kKn'],slab2ns['Kphin']/2,color=color4,linewidth=2.,
# label='$\hat{C}^\phi$: divergent')
#ax1.loglog(slab2ns['kKs'],slab2ns['Kpsis']/2,'--',color=color3,linewidth=2.)
#ax1.loglog(slab2ns['kKs'],slab2ns['Kphis']/2,'--',color=color4,linewidth=2.)
ax1.loglog(slab2ns['ks'],slab2ns['Enoise']/2., color='.5',alpha=.7, linewidth=lw1,label='instrumental error')
ax1.loglog(slab2ns['ks'],slab2ns['Es2'],'--', color='k',linewidth=2.,alpha=.7)
ax1.loglog(slab2ns['ks'],slab2ns['Es3'],'--', color='k',linewidth=2.,alpha=.7)
ax1.axis((1./(1000),1./4,.4e-5,10))
plt.text(0.0011, 5.41,u'k$^{-2}$')
plt.text(0.0047, 5.51,u'k$^{-3}$',fontsize=30)
plt.xlabel('Along-track wavenumber [cpkm]')
plt.ylabel(u'KE spectral density [ m$^{2}$ s$^{-2}$/ cpkm]')
lg = plt.legend(loc=(.01,.05),title=r"58-98 m, 388 (328) DOF North (South) of PF", numpoints=1,ncol=2)
lg.draw_frame(False)
plt.axis((1./1.e3,1./4.,.5/1.e4,1.e1))
plt.text(1/20., 5., "ADCP", size=25, rotation=0.,
ha="center", va="center",
bbox = dict(boxstyle="round",ec='k',fc='w'))
#plt.text(0.7, 4.5, 'd', size=35, rotation=0.)
add_second_axis(ax1)
plt.savefig('figs/spec_adcp_slab2ns_decomp_ke_bw',bbox_inches='tight')
from pyspec import spectrum as spec
ki, Eui = spec.avg_per_decade(slab1['k'],slab1['Eu'].real,nbins = 1000)
ki, Evi = spec.avg_per_decade(slab1['k'],slab1['Ev'].real,nbins = 1000)
plt.loglog(ki,Eui)
plt.loglog(ki,Evi)
plt.loglog(slab1['k'],slab1['Eu'])
plt.loglog(slab1['k'],slab1['Ev'])
from pyspec import helmholtz as helm
E = 1./ki**3/1e10
helm_slab1 = helm.BCFDecomposition(ki,3*E,E)
#helm_slab1 = helm.BCFDecomposition(slab1['k'],3*slab1['Ev'],slab1['Ev'])
plt.loglog(ki,helm_slab1.Cpsi,'r')
plt.loglog(ki,helm_slab1.Cphi,'y')
plt.loglog(ki,3*E/2,'b')
plt.loglog(ki,E/2,'g')
#plt.loglog(slab1['k'],helm_slab1.Cpsi,'r')
#plt.loglog(slab1['k'],helm_slab1.Cphi,'y')
#plt.loglog(slab1['k'],3*slab1['Ev']/2,'m')
#plt.loglog(slab1['k'],slab1['Ev']/2,'g')
slab1['k'].size
dk = 1./(800.)
k = np.arange(0,160/2.)*dk
)
plt.loglog(k[1:79],slab2['Eu'],'m')
```
| true |
code
| 0.57684 | null | null | null | null |
|
<img src="interactive_image.png"/>
# Interactive image
The following interactive widget is intended to allow the developer to explore
images drawn with different parameter settings.
```
# preliminaries
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from jp_doodle import dual_canvas
from IPython.display import display
# Display a canvas with an image which can be adjusted interactively
# Below we configure the canvas using the Python interface.
# This method is terser than using Javascript, but the redraw operations create a jerky effect
# because the canvas displays intermediate states due to roundtrip messages
# between the Python kernal and the Javascript interpreter.
image_canvas = dual_canvas.SnapshotCanvas("interactive_image.png", width=320, height=220)
image_canvas.display_all()
def change_image(x=0, y=0, w=250, h=50, dx=-50, dy=-25,
degrees=0, sx=30, sy=15, sWidth=140, sHeight=20, whole=False
): #sx:30, sy:15, sWidth:140, sHeight:20
if whole:
sx = sy = sWidth = sHeight = None
canvas = image_canvas
with canvas.delay_redraw():
# This local image reference works in "classic" notebook, but not in Jupyter Lab.
canvas.reset_canvas()
mandrill_url = "../mandrill.png"
image_canvas.name_image_url("mandrill", mandrill_url)
canvas.named_image("mandrill",
x, y, w, h, degrees, sx, sy, sWidth, sHeight, dx=dx, dy=dy, name=True)
canvas.fit()
canvas.lower_left_axes(
max_tick_count=4
)
canvas.circle(x=x, y=y, r=10, color="#999")
canvas.fit(None, 30)
#canvas.element.invisible_canvas.show()
change_image()
w = interactive(
change_image,
x=(-100, 100),
y=(-100,100),
dx=(-300, 300),
dy=(-300,300),
w=(-300,300),
h=(-300,300),
degrees=(-360,360),
sx=(0,600),
sy=(0,600),
sWidth=(0,600),
sHeight=(0,600),
)
display(w)
# Display a canvas with an image which can be adjusted interactively
# Using the Javascript interface:
# This approach requires more typing because Python values must
# be explicitly mapped to Javascript variables.
# However the canvas configuration is smooth because no intermediate
# results are shown.
image_canvas2 = dual_canvas.SnapshotCanvas("interactive_image.png", width=320, height=220)
image_canvas2.display_all()
def change_rect_js(x=0, y=0, w=250, h=50, dx=-50, dy=-25,
degrees=0, sx=30, sy=15, sWidth=140, sHeight=20, whole=False
): #sx:30, sy:15, sWidth:140, sHeight:20
if whole:
sx = sy = sWidth = sHeight = None
canvas = image_canvas2
canvas.js_init("""
element.reset_canvas();
var mandrill_url = "../mandrill.png";
element.name_image_url("mandrill", mandrill_url);
element.named_image({image_name: "mandrill",
x:x, y:y, dx:dx, dy:dy, w:w, h:h, degrees:degrees,
sx:sx, sy:sy, sWidth:sWidth, sHeight:sHeight});
element.fit();
element.lower_left_axes({max_tick_count: 4});
element.circle({x:x, y:y, r:5, color:"#999"});
element.fit(null, 30);
""",
x=x, y=y, dx=dx, dy=dy, w=w, h=h, degrees=degrees,
sx=sx, sy=sy, sWidth=sWidth, sHeight=sHeight)
w = interactive(
change_rect_js,
x=(-100, 100),
y=(-100,100),
dx=(-300, 300),
dy=(-300, 300),
w=(-300,300),
h=(-300,300),
fill=True,
lineWidth=(0,20),
degrees=(-360,360),
red=(0,255),
green=(0,255),
blue=(0,255),
alpha=(0.0,1.0,0.1)
)
display(w)
```
| true |
code
| 0.526404 | null | null | null | null |
|
Before running this notebook, it's helpful to
`conda install -c conda-forge nb_conda_kernels`
`conda install -c conda-forge ipywidgets`
and set the kernel to the conda environment in which you installed glmtools (typically, `glmval`)
```
import os
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from glmtools.io.glm import GLMDataset
```
## Use a sample data file included in glmtools
```
from glmtools.test.common import get_sample_data_path
sample_path = get_sample_data_path()
samples = [
"OR_GLM-L2-LCFA_G16_s20181830433000_e20181830433200_c20181830433231.nc",
"OR_GLM-L2-LCFA_G16_s20181830433200_e20181830433400_c20181830433424.nc",
"OR_GLM-L2-LCFA_G16_s20181830433400_e20181830434000_c20181830434029.nc",
]
samples = [os.path.join(sample_path, s) for s in samples]
filename = samples[0]
```
## Use data from the most recent minute or two
Requires siphon.
To load data via siphon from opendap, you must
`conda install -c conda-forge siphon`
```
# Load data from the most recent minute or two!
if False:
from siphon.catalog import TDSCatalog
g16url = "http://thredds-test.unidata.ucar.edu/thredds/catalog/satellite/goes16/GRB16/GLM/LCFA/current/catalog.xml"
satcat = TDSCatalog(g16url)
filename = satcat.datasets[-1].access_urls['OPENDAP']
```
## Load the data
```
glm = GLMDataset(filename)
print(glm.dataset)
```
## Flip through each flash, plotting each.
Event centroids are small black squares.
Group centroids are white circles, colored by group energy.
Flash centroids are red 'x's
```
from glmtools.plot.locations import plot_flash
import ipywidgets as widgets
# print(widgets.Widget.widget_types.values())
fl_id_vals = list(glm.dataset.flash_id.data)
fl_id_vals.sort()
flash_slider = widgets.SelectionSlider(
description='Flash',
options=fl_id_vals,
)
def do_plot(flash_id):
fig = plot_flash(glm, flash_id)
widgets.interact(do_plot, flash_id=flash_slider)
```
# Find flashes in some location
There are hundreds of flashes to browse above, and they are randomly scattered across the full disk. Storms near Lubbock, TX at the time of sample data file had relatively low flash rates, so let's find those.
```
flashes_subset = glm.subset_flashes(lon_range = (-102.5, -100.5), lat_range = (32.5, 34.5))
print(flashes_subset)
from glmtools.plot.locations import plot_flash
import ipywidgets as widgets
# print(widgets.Widget.widget_types.values())
fl_id_vals = list(flashes_subset.flash_id.data)
fl_id_vals.sort()
flash_slider = widgets.SelectionSlider(
description='Flash',
options=fl_id_vals,
)
# from functools import partial
# glm_plotter = partial(plot_flash, glm) # fails with a __name__ attr not found
def do_plot(flash_id):
fig = plot_flash(glm, flash_id)
widgets.interact(do_plot, flash_id=flash_slider)
```
| true |
code
| 0.57081 | null | null | null | null |
|
```
from PIL import Image
import glob
from keras.applications.inception_v3 import InceptionV3
from keras.applications.inception_v3 import preprocess_input, decode_predictions
from keras.preprocessing import image
import numpy as np
import json
```
## Define data path
#### You can add multiple file extensions by extending the glob as shown below
```
images_paths = glob.glob("./data/rit/Harsh2/*.jpg")
images_paths.extend(glob.glob("./data/rit/Harsh2/*.JPG"))
images_paths.extend(glob.glob("./data/rit/Harsh2/*.png"))
def images_to_sprite(data):
"""
Creates the sprite image along with any necessary padding
Source : https://github.com/tensorflow/tensorflow/issues/6322
Args:
data: NxHxW[x3] tensor containing the images.
Returns:
data: Properly shaped HxWx3 image with any necessary padding.
"""
if len(data.shape) == 3:
data = np.tile(data[...,np.newaxis], (1,1,1,3))
data = data.astype(np.float32)
min = np.min(data.reshape((data.shape[0], -1)), axis=1)
data = (data.transpose(1,2,3,0) - min).transpose(3,0,1,2)
max = np.max(data.reshape((data.shape[0], -1)), axis=1)
data = (data.transpose(1,2,3,0) / max).transpose(3,0,1,2)
n = int(np.ceil(np.sqrt(data.shape[0])))
padding = ((0, n ** 2 - data.shape[0]), (0, 0),
(0, 0)) + ((0, 0),) * (data.ndim - 3)
data = np.pad(data, padding, mode='constant',
constant_values=0)
# Tile the individual thumbnails into an image.
data = data.reshape((n, n) + data.shape[1:]).transpose((0, 2, 1, 3)
+ tuple(range(4, data.ndim + 1)))
data = data.reshape((n * data.shape[1], n * data.shape[3]) + data.shape[4:])
data = (data * 255).astype(np.uint8)
return data
def populate_img_arr(images_paths, size=(100,100),should_preprocess= False):
"""
Get an array of images for a list of image paths
Args:
size: the size of image , in pixels
should_preprocess: if the images should be processed (according to InceptionV3 requirements)
Returns:
arr: An array of the loaded images
"""
arr = []
for i,img_path in enumerate(images_paths):
img = image.load_img(img_path, target_size=size)
x = image.img_to_array(img)
arr.append(x)
arr = np.array(arr)
if should_preprocess:
arr = preprocess_input(arr)
return arr
```
## Model Definition
### If you want to use another model, you can change it here
```
model = InceptionV3(include_top=False,pooling='avg')
model.summary()
img_arr = populate_img_arr(images_paths,size=(299,299),should_preprocess=True)
preds = model.predict(img_arr,batch_size=64)
preds.tofile("./oss_data/tensor.bytes")
del img_arr,preds
raw_imgs = populate_img_arr(images_paths ,size=(100,100),should_preprocess=False)
sprite = Image.fromarray(images_to_sprite(raw_imgs).astype(np.uint8))
sprite.save('./oss_data/sprites.png')
del raw_imgs
```
| true |
code
| 0.624608 | null | null | null | null |
|
# Exorad 2.0
This Notebook will show you how to use exorad library to build your own pipeline.
Before we start, let's silent the exorad logger.
```
import warnings
warnings.filterwarnings("ignore")
from exorad.log import disableLogging
disableLogging()
```
## Preparing the instrument
### Load the instrument descrition
The first step is to load the instrument description.
We use here the payload described in `examples/payload_example.xml`.
We call the `LoadOptions` task that parses the xml file into a Python dictionary.
```
from exorad.tasks import LoadOptions
payload_file = 'payload_example.xml'
loadOptions = LoadOptions()
payload = loadOptions(filename=payload_file)
```
## build the channels
Once we have the payload description we can build the channels using the `BuildChannels` taks, this will iterate over the channel and build each of the instruments listed in the payload config. To give it a closer look, let's do it step by step.
Inside `example_payload.xml` are described two channels: "Phot" that is a photometer and "Spec" that is a spectrometer. We want to build them and store them into a dictionary
```
channels = {}
from exorad.tasks import BuildInstrument
buildInstrument = BuildInstrument()
channels['Phot'] = buildInstrument(type="photometer",
name = "Phot",
description=payload['channel']['Phot'],
payload=payload,
write=False, output=None)
channels['Spec'] = buildInstrument(type="spectrometer",
name = "Spec",
description=payload['channel']['Spec'],
payload=payload,
write=False, output=None)
```
## Plot instrument photo-conversion efficiency
Thanks to exorad plotter you can easily plot the channels photon-conversion efficiency. To do so, we need to merge the channel output table to a cumulative table.
```
from exorad.tasks import MergeChannelsOutput
mergeChannelsOutput = MergeChannelsOutput()
table = mergeChannelsOutput(channels=channels)
from exorad.utils.plotter import Plotter
plotter = Plotter(channels=channels, input_table=table)
efficiency_fig = plotter.plot_efficiency()
```
## Acess the payload data
Assume you want to edit one of the payload parameters, for example you quant to move the Quatum Efficiency for the photometer from 0.55 to 0.65.
Then you will need to build the channels again and produce an updated efficiency figure.
```
payload['channel']['Phot']['detector']['qe']['value'] = 0.65
from exorad.tasks import BuildChannels
buildChannels = BuildChannels()
channels = buildChannels(payload=payload, write=False, output=None)
table = mergeChannelsOutput(channels=channels)
plotter = Plotter(channels=channels, input_table=table)
efficiency_fig = plotter.plot_efficiency()
```
## Explore the telescope self emission
Even withot a target, we still have signal in our telescope coming from self emission. This can be expored with exorad.
We can make a plot of the signals using the previous plotter. We have to manually set the lower limit for y-axes because exorad assumes 1e-3 ct/s as lower limit, but for the instrument we built the self emission is far lower because of the low temperature assumed (~60K for optics).
The self emission is stored in the channel output table in a column named `instrument_signal`. Information on the signal produced by each optical element can be retrieved in the channel dictionary under `['built_instr']['optical_path']['signal_table']`
```
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax = plotter.plot_signal(ax, ylim=1e-32, scale='log', channel_edges=False)
```
## Observing a target list
### Load a Target list
To observe a list of targets we first need to define them. Exorad can load target list from file, as the one you can find in `examples/test_target.csv`, or directly from Python. Because the first case is covered by the documentation, let's focus here on the latter. To describe a target in python, you need to use Astropy QTable and to follow the same notation used in the file and described in the documentation. Here we produce an example considering a single target called "test" that has mass 1 solar masses, effective temperature 5000 K, radius 1 solar radius and 10 pc away from us. Obviously, you can add more element to the list if you have more than one target.
```
from astropy.table import QTable, Column
import astropy.units as u
names = Column(['test'], name='star name')
masses = Column([1]*u.M_sun, name='star M')
temperatures = Column([5000]*u.K, name='star Teff')
radii = Column([1] * u.R_sun, name='star R')
distances = Column([10] * u.pc, name='star D')
magK = Column([0]* u.Unit(""), name='star magK')
raw_targetlist = QTable([names, masses,temperatures, radii, distances, magK])
from exorad.tasks import LoadTargetList
loadTargetList = LoadTargetList()
targets = loadTargetList(target_list=raw_targetlist)
# "targets" is now a list of Target classes.
# To read the content of the loaded element we need to convert the Target class into a dictionary
print(targets.target[0].to_dict())
```
### Foregrounds
Before you can observe a target you first need to prepare the table to fill. For that you need to call `PrepareTarget`. This populates the target attribute `table` that contains the merged channel tables and will be populated with the successive steps.
Then we can think about the foregrounds. These are defined in the payload configuration file. In out case we have indicated a zodiacal foreground and a custom one described by a csv file. These are listed now in `payload['common']['foreground']`. The Task `EstimateForegrounds` builds both of them in one shot, but for the sake of learning, let's produce them one per time with their specific classes. The task mentioned requires the target as input and returns it as output because adds foreground information to the class.
Remember that the order is important when you list your contributions in your payload configuration file, because foregrounds can have both emission and transmission. In this optic, an element locate before another, has its light passed through the second one and so its total signal contribution is reduced.
```
from exorad.tasks import PrepareTarget, EstimateForeground, EstimateZodi
target = targets.target[0]
wl_min, wl_max = payload['common']['wl_min']['value'], payload['common']['wl_max']['value']
prepareTarget = PrepareTarget()
target = prepareTarget(target=target, channels=channels)
estimateZodi = EstimateZodi()
target = estimateZodi(zodi=payload['common']['foreground']['zodiacal'],
target=target,
wl_range=(wl_min, wl_max))
estimateForeground = EstimateForeground()
target = estimateForeground(foreground=payload['common']['foreground']['skyFilter'],
target=target,
wl_range=(wl_min, wl_max))
# We plot now the foreground radiances
fig_zodi, ax = target.foreground['zodi'].plot()
fig_zodi.suptitle('zodi')
fig_sky, ax = target.foreground['skyFilter'].plot()
fig_sky.suptitle('skyFilter')
```
Once the contributions has been estimated, we can propagate them. Here we propagate and plot the foregrounds signal. The `PropagateForegroundLight` task also populates the target table with the computed foreground signal.
```
from exorad.tasks import PropagateForegroundLight
propagateForegroundLight = PropagateForegroundLight()
target = propagateForegroundLight(channels=channels, target=target)
plotter = Plotter(channels=channels, input_table=target.table)
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax = plotter.plot_signal(ax, scale='log', channel_edges=False)
# We show here the information content of the target table, that now contains also the foreground signal
print(target.table.keys())
```
### Target source
We can now load the light source we are gonna use for the target. As described in the documentation, we can use a black body, or a phoenix star or a custom sed described in a csv file. Here we use a black body, as indicated in the payload configuration file `<sourceSpectrum> planck </sourceSpectrum>`, and now in the dic `payload['common']['sourceSpectrum']`.
```
from exorad.tasks import LoadSource
loadSource = LoadSource()
target, sed = loadSource(target=target,
source=payload['common']['sourceSpectrum'],
wl_range=(wl_min, wl_max))
fig_source, ax=sed.plot()
fig_source.suptitle(target.name)
```
We can now propagate the source light. The light signal information will be added also to the target table
```
from exorad.tasks import PropagateTargetLight
propagateTargetLight = PropagateTargetLight()
target = propagateTargetLight(channels=channels, target=target)
plotter = Plotter(channels=channels, input_table=target.table)
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax = plotter.plot_signal(ax, scale='log', channel_edges=False)
# We show here the information content of the target table, that now contains also the source signal
print(target.table.keys())
```
## Estimate the noise
The noise estimation is the last step. Exorad computes the photon noise from every signal considered so far, but aldo dark current noise and read noise from the detector. It also takes into account for custom noise source that can be added at channel level or at common level in the payload description.
Finally, all these information will be adedd to the target table, that is now our final product.
```
from exorad.tasks import EstimateNoise
estimateNoise = EstimateNoise()
target = estimateNoise(target=target, channels=channels)
plotter = Plotter(channels=channels, input_table=target.table)
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax = plotter.plot_noise(ax, scale='log', channel_edges=False)
# We show here the information content of the target table, that now contains also all the noise contributions
print(target.table.keys())
```
| true |
code
| 0.662223 | null | null | null | null |
|
# Eurostat bioenergy balance 2018
Extract bioenergy related data from an archive containing XLSB files, one for each EU country which contain multiple sheets for each year (1990-2018).
Walk through excel files (country spreadsheets) and parse selected variables and fuels for each year (sheet in country's spreadsheet).
Somewhere on Eurostat there might be a better source for this data, but I did not find it.
```
import os
import zipfile
import requests
import pandas as pd
import numpy as np
import pyxlsb
def parse_values_for_country(file, country, variables, fuels):
"""Reads fuel variable in multiple sheets 2002-2018.
Sums the values across multiple columns if relevant.
Returns: dict
"""
country_data = {}
for year in range(2002,2019):
df = pd.read_excel(
file,
engine='pyxlsb',
sheet_name=str(year),
skiprows=[0,1,2,3],
index_col=1,
na_values=':',
)
for variable in variables:
for fuel, start, end in fuels:
try:
country_data[(country, year, fuel, variable.lower().replace(' ', '_'))] = df.loc[variable, start:end].sum()
except TypeError:
country_data[(country, year, fuel, variable.lower().replace(' ', '_'))] = pd.to_numeric(df.loc[variable, start:end], errors='coerce').sum()
return country_data
def walk_through_excel_files(directory, variables, fuels):
d = {}
for filename in os.listdir(directory):
if '!' not in filename: # skip readme files
country = filename.split('-')[0]
excel_path = os.path.join(directory, filename)
data = parse_values_for_country(excel_path, country, variables, fuels)
d.update(data)
return d
# Selected variables for bioenergy and some other for context
variables = [
'Primary production',
'Imports',
'Exports',
'Gross inland consumption',
]
fuels = [
('total', 'Total', 'Total'),
('renewables', 'Renewables and biofuels', 'Renewables and biofuels'),
('bioenergy', 'Bioenergy', 'Bioenergy',),
('solid_biomass', 'Primary solid biofuels', 'Primary solid biofuels'),
('biofuels', 'Pure biogasoline', 'Other liquid biofuels'),
('biogas', 'Biogases', 'Biogases'),
('ren_mun_waste', 'Renewable municipal waste', 'Renewable municipal waste'),
]
url = 'https://ec.europa.eu/eurostat/documents/38154/4956218/Energy-Balances-April-2020-edition.zip/69da6e9f-bf8f-cd8e-f4ad-50b52f8ce616'
r = requests.get(url)
with open('eurostat_balances_2020.zip', 'wb') as f:
f.write(r.content)
with zipfile.ZipFile('eurostat_balances_2020.zip', 'r') as zip_archive:
zip_archive.extractall(path='balances/')
# This is quite slow, opening many files, one time for each sheet
# There must be a better way
%time data_dict = walk_through_excel_files('balances/', variables, fuels)
# https://stackoverflow.com/questions/44012099/creating-a-dataframe-from-a-dict-where-keys-are-tuples
df1 = pd.Series(data_dict).reset_index()
df1.columns = ['country', 'year', 'fuel', 'variable', 'value']
df1.head(3)
df2 = df1.set_index(['country', 'year', 'fuel', 'variable']).unstack(level=3)
df2.head(3)
df2.columns = df2.columns.droplevel(0).values
df2.info()
df2.sort_index(ascending=True, inplace=True)
df2['dependency'] = (df2['imports'] - df2['exports']) / df2['gross_inland_consumption']
df2
df2.to_csv(
'balances_bioenergy_2002_2018_ktoe.csv',
decimal=',',
)
df3 = df2.copy()
tj_ktoe = 41.868
df3 = df3.loc[:, 'exports': 'primary_production'] * tj_ktoe
# Keep the share based on the original data in ktoe
df3['dependency'] = df2['dependency']
df3
df3.to_csv(
'balances_bioenergy_2002_2018_tj.csv',
decimal=',',
)
# Some minimal testing
idx = pd.IndexSlice
df2.loc[idx['CZ', 2018, 'bioenergy'], ['exports']]
assert df2.loc[idx['CZ', 2018, 'bioenergy'], ['exports']].item() == 549.453
df2.loc[idx['CZ', 2009, 'bioenergy'], ['primary_production']]
assert df2.loc[idx['CZ', 2009, 'bioenergy'], ['primary_production']].item() == 2761.8
result_cz_2009_bioenergy = df2.loc[idx['CZ', 2009, 'bioenergy']]
result_cz_2009_bioenergy
cz_2009_bioenergy = pd.Series(
{'exports': 318.821,
'gross_inland_consumption': 2568.609,
'imports': 123.617,
'primary_production': 2761.8,
'dependency': -0.075996,
})
cz_2009_bioenergy
cz_2009_bioenergy.name = ('CZ', 2009, 'bioenergy')
pd.testing.assert_series_equal(cz_2009_bioenergy, result_cz_2009_bioenergy)
```
| true |
code
| 0.542803 | null | null | null | null |
|
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Discrete Bayes Filter
```
#format the book
%matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
```
The Kalman filter belongs to a family of filters called *Bayesian filters*. Most textbook treatments of the Kalman filter present the Bayesian formula, perhaps shows how it factors into the Kalman filter equations, but mostly keeps the discussion at a very abstract level.
That approach requires a fairly sophisticated understanding of several fields of mathematics, and it still leaves much of the work of understanding and forming an intuitive grasp of the situation in the hands of the reader.
I will use a different way to develop the topic, to which I owe the work of Dieter Fox and Sebastian Thrun a great debt. It depends on building an intuition on how Bayesian statistics work by tracking an object through a hallway - they use a robot, I use a dog. I like dogs, and they are less predictable than robots which imposes interesting difficulties for filtering. The first published example of this that I can find seems to be Fox 1999 [1], with a fuller example in Fox 2003 [2]. Sebastian Thrun also uses this formulation in his excellent Udacity course Artificial Intelligence for Robotics [3]. In fact, if you like watching videos, I highly recommend pausing reading this book in favor of first few lessons of that course, and then come back to this book for a deeper dive into the topic.
Let's now use a simple thought experiment, much like we did with the g-h filter, to see how we might reason about the use of probabilities for filtering and tracking.
## Tracking a Dog
Let's begin with a simple problem. We have a dog friendly workspace, and so people bring their dogs to work. Occasionally the dogs wander out of offices and down the halls. We want to be able to track them. So during a hackathon somebody invented a sonar sensor to attach to the dog's collar. It emits a signal, listens for the echo, and based on how quickly an echo comes back we can tell whether the dog is in front of an open doorway or not. It also senses when the dog walks, and reports in which direction the dog has moved. It connects to the network via wifi and sends an update once a second.
I want to track my dog Simon, so I attach the device to his collar and then fire up Python, ready to write code to track him through the building. At first blush this may appear impossible. If I start listening to the sensor of Simon's collar I might read **door**, **hall**, **hall**, and so on. How can I use that information to determine where Simon is?
To keep the problem small enough to plot easily we will assume that there are only 10 positions in the hallway, which we will number 0 to 9, where 1 is to the right of 0. For reasons that will be clear later, we will also assume that the hallway is circular or rectangular. If you move right from position 9, you will be at position 0.
When I begin listening to the sensor I have no reason to believe that Simon is at any particular position in the hallway. From my perspective he is equally likely to be in any position. There are 10 positions, so the probability that he is in any given position is 1/10.
Let's represent our belief of his position in a NumPy array. I could use a Python list, but NumPy arrays offer functionality that we will be using soon.
```
import numpy as np
belief = np.array([1./10]*10)
print(belief)
```
In [Bayesian statistics](https://en.wikipedia.org/wiki/Bayesian_probability) this is called a [*prior*](https://en.wikipedia.org/wiki/Prior_probability). It is the probability prior to incorporating measurements or other information. More completely, this is called the *prior probability distribution*. A [*probability distribution*](https://en.wikipedia.org/wiki/Probability_distribution) is a collection of all possible probabilities for an event. Probability distributions always sum to 1 because something had to happen; the distribution lists all possible events and the probability of each.
I'm sure you've used probabilities before - as in "the probability of rain today is 30%". The last paragraph sounds like more of that. But Bayesian statistics was a revolution in probability because it treats probability as a belief about a single event. Let's take an example. I know that if I flip a fair coin infinitely many times I will get 50% heads and 50% tails. This is called [*frequentist statistics*](https://en.wikipedia.org/wiki/Frequentist_inference) to distinguish it from Bayesian statistics. Computations are based on the frequency in which events occur.
I flip the coin one more time and let it land. Which way do I believe it landed? Frequentist probability has nothing to say about that; it will merely state that 50% of coin flips land as heads. In some ways it is meaningless to assign a probability to the current state of the coin. It is either heads or tails, we just don't know which. Bayes treats this as a belief about a single event - the strength of my belief or knowledge that this specific coin flip is heads is 50%. Some object to the term "belief"; belief can imply holding something to be true without evidence. In this book it always is a measure of the strength of our knowledge. We'll learn more about this as we go.
Bayesian statistics takes past information (the prior) into account. We observe that it rains 4 times every 100 days. From this I could state that the chance of rain tomorrow is 1/25. This is not how weather prediction is done. If I know it is raining today and the storm front is stalled, it is likely to rain tomorrow. Weather prediction is Bayesian.
In practice statisticians use a mix of frequentist and Bayesian techniques. Sometimes finding the prior is difficult or impossible, and frequentist techniques rule. In this book we can find the prior. When I talk about the probability of something I am referring to the probability that some specific thing is true given past events. When I do that I'm taking the Bayesian approach.
Now let's create a map of the hallway. We'll place the first two doors close together, and then another door further away. We will use 1 for doors, and 0 for walls:
```
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
```
I start listening to Simon's transmissions on the network, and the first data I get from the sensor is **door**. For the moment assume the sensor always returns the correct answer. From this I conclude that he is in front of a door, but which one? I have no reason to believe he is in front of the first, second, or third door. What I can do is assign a probability to each door. All doors are equally likely, and there are three of them, so I assign a probability of 1/3 to each door.
```
from kf_book.book_plots import figsize, set_figsize
import kf_book.book_plots as book_plots
import matplotlib.pyplot as plt
belief = np.array([1./3, 1./3, 0, 0, 0, 0, 0, 0, 1/3, 0])
plt.figure()
set_figsize(y=2)
book_plots.bar_plot(belief)
```
This distribution is called a [*categorical distribution*](https://en.wikipedia.org/wiki/Categorical_distribution), which is a discrete distribution describing the probability of observing $n$ outcomes. It is a [*multimodal distribution*](https://en.wikipedia.org/wiki/Multimodal_distribution) because we have multiple beliefs about the position of our dog. Of course we are not saying that we think he is simultaneously in three different locations, merely that we have narrowed down our knowledge to one of these three locations. My (Bayesian) belief is that there is a 33.3% chance of being at door 0, 33.3% at door 1, and a 33.3% chance of being at door 8.
This is an improvement in two ways. I've rejected a number of hallway positions as impossible, and the strength of my belief in the remaining positions has increased from 10% to 33%. This will always happen. As our knowledge improves the probabilities will get closer to 100%.
A few words about the [*mode*](https://en.wikipedia.org/wiki/Mode_(statistics))
of a distribution. Given a set of numbers, such as {1, 2, 2, 2, 3, 3, 4}, the *mode* is the number that occurs most often. For this set the mode is 2. A set can contain more than one mode. The set {1, 2, 2, 2, 3, 3, 4, 4, 4} contains the modes 2 and 4, because both occur three times. We say the former set is [*unimodal*](https://en.wikipedia.org/wiki/Unimodality), and the latter is *multimodal*.
Another term used for this distribution is a [*histogram*](https://en.wikipedia.org/wiki/Histogram). Histograms graphically depict the distribution of a set of numbers. The bar chart above is a histogram.
I hand coded the `belief` array in the code above. How would we implement this in code? We represent doors with 1, and walls as 0, so we will multiply the hallway variable by the percentage, like so;
```
belief = hallway * (1./3)
print(belief)
```
## Extracting Information from Sensor Readings
Let's put Python aside and think about the problem a bit. Suppose we were to read the following from Simon's sensor:
* door
* move right
* door
Can we deduce Simon's location? Of course! Given the hallway's layout there is only one place from which you can get this sequence, and that is at the left end. Therefore we can confidently state that Simon is in front of the second doorway. If this is not clear, suppose Simon had started at the second or third door. After moving to the right, his sensor would have returned 'wall'. That doesn't match the sensor readings, so we know he didn't start there. We can continue with that logic for all the remaining starting positions. The only possibility is that he is now in front of the second door. Our belief is:
```
belief = np.array([0., 1., 0., 0., 0., 0., 0., 0., 0., 0.])
```
I designed the hallway layout and sensor readings to give us an exact answer quickly. Real problems are not so clear cut. But this should trigger your intuition - the first sensor reading only gave us low probabilities (0.333) for Simon's location, but after a position update and another sensor reading we know more about where he is. You might suspect, correctly, that if you had a very long hallway with a large number of doors that after several sensor readings and positions updates we would either be able to know where Simon was, or have the possibilities narrowed down to a small number of possibilities. This is possible when a set of sensor readings only matches one to a few starting locations.
We could implement this solution now, but instead let's consider a real world complication to the problem.
## Noisy Sensors
Perfect sensors are rare. Perhaps the sensor would not detect a door if Simon sat in front of it while scratching himself, or misread if he is not facing down the hallway. Thus when I get **door** I cannot use 1/3 as the probability. I have to assign less than 1/3 to each door, and assign a small probability to each blank wall position. Something like
```Python
[.31, .31, .01, .01, .01, .01, .01, .01, .31, .01]
```
At first this may seem insurmountable. If the sensor is noisy it casts doubt on every piece of data. How can we conclude anything if we are always unsure?
The answer, as for the problem above, is with probabilities. We are already comfortable assigning a probabilistic belief to the location of the dog; now we have to incorporate the additional uncertainty caused by the sensor noise.
Say we get a reading of **door**, and suppose that testing shows that the sensor is 3 times more likely to be right than wrong. We should scale the probability distribution by 3 where there is a door. If we do that the result will no longer be a probability distribution, but we will learn how to fix that in a moment.
Let's look at that in Python code. Here I use the variable `z` to denote the measurement. `z` or `y` are customary choices in the literature for the measurement. As a programmer I prefer meaningful variable names, but I want you to be able to read the literature and/or other filtering code, so I will start introducing these abbreviated names now.
```
def update_belief(hall, belief, z, correct_scale):
for i, val in enumerate(hall):
if val == z:
belief[i] *= correct_scale
belief = np.array([0.1] * 10)
reading = 1 # 1 is 'door'
update_belief(hallway, belief, z=reading, correct_scale=3.)
print('belief:', belief)
print('sum =', sum(belief))
plt.figure()
book_plots.bar_plot(belief)
```
This is not a probability distribution because it does not sum to 1.0. But the code is doing mostly the right thing - the doors are assigned a number (0.3) that is 3 times higher than the walls (0.1). All we need to do is normalize the result so that the probabilities correctly sum to 1.0. Normalization is done by dividing each element by the sum of all elements in the list. That is easy with NumPy:
```
belief / sum(belief)
```
FilterPy implements this with the `normalize` function:
```Python
from filterpy.discrete_bayes import normalize
normalize(belief)
```
It is a bit odd to say "3 times as likely to be right as wrong". We are working in probabilities, so let's specify the probability of the sensor being correct, and compute the scale factor from that. The equation for that is
$$scale = \frac{prob_{correct}}{prob_{incorrect}} = \frac{prob_{correct}} {1-prob_{correct}}$$
Also, the `for` loop is cumbersome. As a general rule you will want to avoid using `for` loops in NumPy code. NumPy is implemented in C and Fortran, so if you avoid for loops the result often runs 100x faster than the equivalent loop.
How do we get rid of this `for` loop? NumPy lets you index arrays with boolean arrays. You create a boolean array with logical operators. We can find all the doors in the hallway with:
```
hallway == 1
```
When you use the boolean array as an index to another array it returns only the elements where the index is `True`. Thus we can replace the `for` loop with
```python
belief[hall==z] *= scale
```
and only the elements which equal `z` will be multiplied by `scale`.
Teaching you NumPy is beyond the scope of this book. I will use idiomatic NumPy constructs and explain them the first time I present them. If you are new to NumPy there are many blog posts and videos on how to use NumPy efficiently and idiomatically. For example, this video by Jake Vanderplas is often recommended: https://vimeo.com/79820956.
Here is our improved version:
```
from filterpy.discrete_bayes import normalize
def scaled_update(hall, belief, z, z_prob):
scale = z_prob / (1. - z_prob)
belief[hall==z] *= scale
normalize(belief)
belief = np.array([0.1] * 10)
scaled_update(hallway, belief, z=1, z_prob=.75)
print('sum =', sum(belief))
print('probability of door =', belief[0])
print('probability of wall =', belief[2])
book_plots.bar_plot(belief, ylim=(0, .3))
```
We can see from the output that the sum is now 1.0, and that the probability of a door vs wall is still three times larger. The result also fits our intuition that the probability of a door must be less than 0.333, and that the probability of a wall must be greater than 0.0. Finally, it should fit our intuition that we have not yet been given any information that would allow us to distinguish between any given door or wall position, so all door positions should have the same value, and the same should be true for wall positions.
This result is called the [*posterior*](https://en.wikipedia.org/wiki/Posterior_probability), which is short for *posterior probability distribution*. All this means is a probability distribution *after* incorporating the measurement information (posterior means 'after' in this context). To review, the *prior* is the probability distribution before including the measurement's information.
Another term is the [*likelihood*](https://en.wikipedia.org/wiki/Likelihood_function). When we computed `belief[hall==z] *= scale` we were computing how *likely* each position was given the measurement. The likelihood is not a probability distribution because it does not sum to one.
The combination of these gives the equation
$$\mathtt{posterior} = \frac{\mathtt{likelihood} \times \mathtt{prior}}{\mathtt{normalization}}$$
It is very important to learn and internalize these terms as most of the literature uses them extensively.
Does `scaled_update()` perform this computation? It does. Let me recast it into this form:
```
def scaled_update(hall, belief, z, z_prob):
scale = z_prob / (1. - z_prob)
likelihood = np.ones(len(hall))
likelihood[hall==z] *= scale
return normalize(likelihood * belief)
```
This function is not fully general. It contains knowledge about the hallway, and how we match measurements to it. We always strive to write general functions. Here we will remove the computation of the likelihood from the function, and require the caller to compute the likelihood themselves.
Here is a full implementation of the algorithm:
```python
def update(likelihood, prior):
return normalize(likelihood * prior)
```
Computation of the likelihood varies per problem. For example, the sensor might not return just 1 or 0, but a `float` between 0 and 1 indicating the probability of being in front of a door. It might use computer vision and report a blob shape that you then probabilistically match to a door. It might use sonar and return a distance reading. In each case the computation of the likelihood will be different. We will see many examples of this throughout the book, and learn how to perform these calculations.
FilterPy implements `update`. Here is the previous example in a fully general form:
```
from filterpy.discrete_bayes import update
def lh_hallway(hall, z, z_prob):
""" compute likelihood that a measurement matches
positions in the hallway."""
try:
scale = z_prob / (1. - z_prob)
except ZeroDivisionError:
scale = 1e8
likelihood = np.ones(len(hall))
likelihood[hall==z] *= scale
return likelihood
belief = np.array([0.1] * 10)
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
update(likelihood, belief)
```
## Incorporating Movement
Recall how quickly we were able to find an exact solution when we incorporated a series of measurements and movement updates. However, that occurred in a fictional world of perfect sensors. Might we be able to find an exact solution with noisy sensors?
Unfortunately, the answer is no. Even if the sensor readings perfectly match an extremely complicated hallway map, we cannot be 100% certain that the dog is in a specific position - there is, after all, a tiny possibility that every sensor reading was wrong! Naturally, in a more typical situation most sensor readings will be correct, and we might be close to 100% sure of our answer, but never 100% sure. This may seem complicated, but let's go ahead and program the math.
First let's deal with the simple case - assume the movement sensor is perfect, and it reports that the dog has moved one space to the right. How would we alter our `belief` array?
I hope that after a moment's thought it is clear that we should shift all the values one space to the right. If we previously thought there was a 50% chance of Simon being at position 3, then after he moved one position to the right we should believe that there is a 50% chance he is at position 4. The hallway is circular, so we will use modulo arithmetic to perform the shift.
```
def perfect_predict(belief, move):
""" move the position by `move` spaces, where positive is
to the right, and negative is to the left
"""
n = len(belief)
result = np.zeros(n)
for i in range(n):
result[i] = belief[(i-move) % n]
return result
belief = np.array([.35, .1, .2, .3, 0, 0, 0, 0, 0, .05])
plt.subplot(121)
book_plots.bar_plot(belief, title='Before prediction', ylim=(0, .4))
belief = perfect_predict(belief, 1)
plt.subplot(122)
book_plots.bar_plot(belief, title='After prediction', ylim=(0, .4))
```
We can see that we correctly shifted all values one position to the right, wrapping from the end of the array back to the beginning.
If you execute the next cell by pressing CTRL-Enter in it you can see this in action. This simulates Simon walking around and around the hallway. It does not (yet) incorporate new measurements so the probability distribution does not change.
```
import time
%matplotlib notebook
set_figsize(y=2)
fig = plt.figure()
for _ in range(50):
# Simon takes one step to the right
belief = perfect_predict(belief, 1)
plt.cla()
book_plots.bar_plot(belief, ylim=(0, .4))
fig.canvas.draw()
time.sleep(0.05)
# reset to noninteractive plot settings
%matplotlib inline
set_figsize(y=2);
```
## Terminology
Let's pause a moment to review terminology. I introduced this terminology in the last chapter, but let's take a second to help solidify your knowledge.
The *system* is what we are trying to model or filter. Here the system is our dog. The *state* is its current configuration or value. In this chapter the state is our dog's position. We rarely know the actual state, so we say our filters produce the *estimated state* of the system. In practice this often gets called the state, so be careful to understand the context.
One cycle of prediction and updating with a measurement is called the state or system *evolution*, which is short for *time evolution* [7]. Another term is *system propogation*. It refers to how the state of the system changes over time. For filters, time is usually a discrete step, such as 1 second. For our dog tracker the system state is the position of the dog, and the state evolution is the position after a discrete amount of time has passed.
We model the system behavior with the *process model*. Here, our process model is that the dog moves one or more positions at each time step. This is not a particularly accurate model of how dogs behave. The error in the model is called the *system error* or *process error*.
The prediction is our new *prior*. Time has moved forward and we made a prediction without benefit of knowing the measurements.
Let's work an example. The current position of the dog is 17 m. Our epoch is 2 seconds long, and the dog is traveling at 15 m/s. Where do we predict he will be in two seconds?
Clearly,
$$ \begin{aligned}
\bar x &= 17 + (15*2) \\
&= 47
\end{aligned}$$
I use bars over variables to indicate that they are priors (predictions). We can write the equation for the process model like this:
$$ \bar x_{k+1} = f_x(\bullet) + x_k$$
$x_k$ is the current position or state. If the dog is at 17 m then $x_k = 17$.
$f_x(\bullet)$ is the state propagation function for x. It describes how much the $x_k$ changes over one time step. For our example it performs the computation $15 \cdot 2$ so we would define it as
$$f_x(v_x, t) = v_k t$$.
## Adding Uncertainty to the Prediction
`perfect_sensor()` assumes perfect measurements, but all sensors have noise. What if the sensor reported that our dog moved one space, but he actually moved two spaces, or zero? This may sound like an insurmountable problem, but let's model it and see what happens.
Assume that the sensor's movement measurement is 80% likely to be correct, 10% likely to overshoot one position to the right, and 10% likely to undershoot to the left. That is, if the movement measurement is 4 (meaning 4 spaces to the right), the dog is 80% likely to have moved 4 spaces to the right, 10% to have moved 3 spaces, and 10% to have moved 5 spaces.
Each result in the array now needs to incorporate probabilities for 3 different situations. For example, consider the reported movement of 2. If we are 100% certain the dog started from position 3, then there is an 80% chance he is at 5, and a 10% chance for either 4 or 6. Let's try coding that:
```
def predict_move(belief, move, p_under, p_correct, p_over):
n = len(belief)
prior = np.zeros(n)
for i in range(n):
prior[i] = (
belief[(i-move) % n] * p_correct +
belief[(i-move-1) % n] * p_over +
belief[(i-move+1) % n] * p_under)
return prior
belief = [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]
prior = predict_move(belief, 2, .1, .8, .1)
book_plots.plot_belief_vs_prior(belief, prior)
```
It appears to work correctly. Now what happens when our belief is not 100% certain?
```
belief = [0, 0, .4, .6, 0, 0, 0, 0, 0, 0]
prior = predict_move(belief, 2, .1, .8, .1)
book_plots.plot_belief_vs_prior(belief, prior)
prior
```
Here the results are more complicated, but you should still be able to work it out in your head. The 0.04 is due to the possibility that the 0.4 belief undershot by 1. The 0.38 is due to the following: the 80% chance that we moved 2 positions (0.4 $\times$ 0.8) and the 10% chance that we undershot (0.6 $\times$ 0.1). Overshooting plays no role here because if we overshot both 0.4 and 0.6 would be past this position. **I strongly suggest working some examples until all of this is very clear, as so much of what follows depends on understanding this step.**
If you look at the probabilities after performing the update you might be dismayed. In the example above we started with probabilities of 0.4 and 0.6 in two positions; after performing the update the probabilities are not only lowered, but they are strewn out across the map.
This is not a coincidence, or the result of a carefully chosen example - it is always true of the prediction. If the sensor is noisy we lose some information on every prediction. Suppose we were to perform the prediction an infinite number of times - what would the result be? If we lose information on every step, we must eventually end up with no information at all, and our probabilities will be equally distributed across the `belief` array. Let's try this with 100 iterations. The plot is animated; recall that you put the cursor in the cell and press Ctrl-Enter to execute the code and see the animation.
```
%matplotlib notebook
set_figsize(y=2)
belief = np.array([1.0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
plt.figure()
for i in range(100):
plt.cla()
belief = predict_move(belief, 1, .1, .8, .1)
book_plots.bar_plot(belief)
plt.title('Step {}'.format(i+1))
plt.gcf().canvas.draw()
print('Final Belief:', belief)
# reset to noninteractive plot settings
%matplotlib inline
set_figsize(y=2)
```
After 100 iterations we have lost almost all information, even though we were 100% sure that we started in position 0. Feel free to play with the numbers to see the effect of differing number of updates. For example, after 100 updates a small amount of information is left, after 50 a lot is left, but by 200 iterations essentially all information is lost.
And, if you are viewing this online here is an animation of that output.
<img src="animations/02_no_info.gif">
I will not generate these standalone animations through the rest of the book. Please see the preface for instructions to run this book on the web, for free, or install IPython on your computer. This will allow you to run all of the cells and see the animations. It's very important that you practice with this code, not just read passively.
## Generalizing with Convolution
We made the assumption that the movement error is at most one position. But it is possible for the error to be two, three, or more positions. As programmers we always want to generalize our code so that it works for all cases.
This is easily solved with [*convolution*](https://en.wikipedia.org/wiki/Convolution). Convolution modifies one function with another function. In our case we are modifying a probability distribution with the error function of the sensor. The implementation of `predict_move()` is a convolution, though we did not call it that. Formally, convolution is defined as
$$ (f \ast g) (t) = \int_0^t \!f(\tau) \, g(t-\tau) \, \mathrm{d}\tau$$
where $f\ast g$ is the notation for convolving f by g. It does not mean multiply.
Integrals are for continuous functions, but we are using discrete functions. We replace the integral with a summation, and the parenthesis with array brackets.
$$ (f \ast g) [t] = \sum\limits_{\tau=0}^t \!f[\tau] \, g[t-\tau]$$
Comparison shows that `predict_move()` is computing this equation - it computes the sum of a series of multiplications.
[Khan Academy](https://www.khanacademy.org/math/differential-equations/laplace-transform/convolution-integral/v/introduction-to-the-convolution) [4] has a good introduction to convolution, and Wikipedia has some excellent animations of convolutions [5]. But the general idea is already clear. You slide an array called the *kernel* across another array, multiplying the neighbors of the current cell with the values of the second array. In our example above we used 0.8 for the probability of moving to the correct location, 0.1 for undershooting, and 0.1 for overshooting. We make a kernel of this with the array `[0.1, 0.8, 0.1]`. All we need to do is write a loop that goes over each element of our array, multiplying by the kernel, and summing the results. To emphasize that the belief is a probability distribution I have named it `pdf`.
```
def predict_move_convolution(pdf, offset, kernel):
N = len(pdf)
kN = len(kernel)
width = int((kN - 1) / 2)
prior = np.zeros(N)
for i in range(N):
for k in range (kN):
index = (i + (width-k) - offset) % N
prior[i] += pdf[index] * kernel[k]
return prior
```
This illustrates the algorithm, but it runs very slow. SciPy provides a convolution routine `convolve()` in the `ndimage.filters` module. We need to shift the pdf by `offset` before convolution; `np.roll()` does that. The move and predict algorithm can be implemented with one line:
```python
convolve(np.roll(pdf, offset), kernel, mode='wrap')
```
FilterPy implements this with `discrete_bayes`' `predict()` function.
```
from filterpy.discrete_bayes import predict
belief = [.05, .05, .05, .05, .55, .05, .05, .05, .05, .05]
prior = predict(belief, offset=1, kernel=[.1, .8, .1])
book_plots.plot_belief_vs_prior(belief, prior, ylim=(0,0.6))
```
All of the elements are unchanged except the middle ones. The values in position 4 and 6 should be
$$(0.1 \times 0.05)+ (0.8 \times 0.05) + (0.1 \times 0.55) = 0.1$$
Position 5 should be $$(0.1 \times 0.05) + (0.8 \times 0.55)+ (0.1 \times 0.05) = 0.45$$
Let's ensure that it shifts the positions correctly for movements greater than one and for asymmetric kernels.
```
prior = predict(belief, offset=3, kernel=[.05, .05, .6, .2, .1])
book_plots.plot_belief_vs_prior(belief, prior, ylim=(0,0.6))
```
The position was correctly shifted by 3 positions and we give more weight to the likelihood of an overshoot vs an undershoot, so this looks correct.
Make sure you understand what we are doing. We are making a prediction of where the dog is moving, and convolving the probabilities to get the prior.
If we weren't using probabilities we would use this equation that I gave earlier:
$$ \bar x_{k+1} = x_k + f_{\mathbf x}(\bullet)$$
The prior, our prediction of where the dog will be, is the amount the dog moved plus his current position. The dog was at 10, he moved 5 meters, so he is now at 15 m. It couldn't be simpler. But we are using probabilities to model this, so our equation is:
$$ \bar{ \mathbf x}_{k+1} = \mathbf x_k \ast f_{\mathbf x}(\bullet)$$
We are *convolving* the current probabilistic position estimate with a probabilistic estimate of how much we think the dog moved. It's the same concept, but the math is slightly different. $\mathbf x$ is bold to denote that it is an array of numbers.
## Integrating Measurements and Movement Updates
The problem of losing information during a prediction may make it seem as if our system would quickly devolve into having no knowledge. However, each prediction is followed by an update where we incorporate the measurement into the estimate. The update improves our knowledge. The output of the update step is fed into the next prediction. The prediction degrades our certainty. That is passed into another update, where certainty is again increased.
Let's think about this intuitively. Consider a simple case - you are tracking a dog while he sits still. During each prediction you predict he doesn't move. Your filter quickly *converges* on an accurate estimate of his position. Then the microwave in the kitchen turns on, and he goes streaking off. You don't know this, so at the next prediction you predict he is in the same spot. But the measurements tell a different story. As you incorporate the measurements your belief will be smeared along the hallway, leading towards the kitchen. On every epoch (cycle) your belief that he is sitting still will get smaller, and your belief that he is inbound towards the kitchen at a startling rate of speed increases.
That is what intuition tells us. What does the math tell us?
We have already programmed the update and predict steps. All we need to do is feed the result of one into the other, and we will have implemented a dog tracker!!! Let's see how it performs. We will input measurements as if the dog started at position 0 and moved right one position each epoch. As in a real world application, we will start with no knowledge of his position by assigning equal probability to all positions.
```
from filterpy.discrete_bayes import update
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
prior = np.array([.1] * 10)
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))
```
After the first update we have assigned a high probability to each door position, and a low probability to each wall position.
```
kernel = (.1, .8, .1)
prior = predict(posterior, 1, kernel)
book_plots.plot_prior_vs_posterior(prior, posterior, True, ylim=(0,.5))
```
The predict step shifted these probabilities to the right, smearing them about a bit. Now let's look at what happens at the next sense.
```
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))
```
Notice the tall bar at position 1. This corresponds with the (correct) case of starting at position 0, sensing a door, shifting 1 to the right, and sensing another door. No other positions make this set of observations as likely. Now we will add an update and then sense the wall.
```
prior = predict(posterior, 1, kernel)
likelihood = lh_hallway(hallway, z=0, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))
```
This is exciting! We have a very prominent bar at position 2 with a value of around 35%. It is over twice the value of any other bar in the plot, and is about 4% larger than our last plot, where the tallest bar was around 31%. Let's see one more cycle.
```
prior = predict(posterior, 1, kernel)
likelihood = lh_hallway(hallway, z=0, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))
```
I ignored an important issue. Earlier I assumed that we had a motion sensor for the predict step; then, when talking about the dog and the microwave I assumed that you had no knowledge that he suddenly began running. I mentioned that your belief that the dog is running would increase over time, but I did not provide any code for this. In short, how do we detect and/or estimate changes in the process model if aren't directly measuring it?
For now I want to ignore this problem. In later chapters we will learn the mathematics behind this estimation; for now it is a large enough task just to learn this algorithm. It is profoundly important to solve this problem, but we haven't yet built enough of the mathematical apparatus that is required, and so for the remainder of the chapter we will ignore the problem by assuming we have a sensor that senses movement.
## The Discrete Bayes Algorithm
This chart illustrates the algorithm:
```
book_plots.create_predict_update_chart()
```
This filter is a form of the g-h filter. Here we are using the percentages for the errors to implicitly compute the $g$ and $h$ parameters. We could express the discrete Bayes algorithm as a g-h filter, but that would obscure the logic of this filter.
The filter equations are:
$$\begin{aligned} \bar {\mathbf x} &= \mathbf x \ast f_{\mathbf x}(\bullet)\, \, &\text{Predict Step} \\
\mathbf x &= \|\mathcal L \cdot \bar{\mathbf x}\|\, \, &\text{Update Step}\end{aligned}$$
$\mathcal L$ is the usual way to write the likelihood function, so I use that. The $\|\|$ notation denotes taking the norm. We need to normalize the product of the likelihood with the prior to ensure $x$ is a probability distribution that sums to one.
We can express this in pseudocode.
**Initialization**
1. Initialize our belief in the state
**Predict**
1. Based on the system behavior, predict state at the next time step
2. Adjust belief to account for the uncertainty in prediction
**Update**
1. Get a measurement and associated belief about its accuracy
2. Compute residual between estimated state and measurement
3. Determine whether the measurement matches each state
4. Update state belief if it matches the measurement
When we cover the Kalman filter we will use this exact same algorithm; only the details of the computation will differ.
Algorithms in this form are sometimes called *predictor correctors*. We make a prediction, then correct them.
Let's animate this. I've plotted the position of the doorways in black. Prior are drawn in orange, and the posterior in blue. You can see how the prior shifts the position and reduces certainty, and the posterior stays in the same position and increases certainty as it incorporates the information from the measurement. I've made the measurement perfect with the line `z_prob = 1.0`; we will explore the effect of imperfect measurements in the next section. finally, I draw a thick vertical line to indicate where Simon really is. This is not an output of the filter - we know where Simon really is only because we are simulating his movement.
```
def discrete_bayes_sim(pos, kernel, zs, z_prob_correct, sleep=0.25):
%matplotlib notebook
N = len(hallway)
fig = plt.figure()
for i, z in enumerate(zs):
plt.cla()
prior = predict(pos, 1, kernel)
book_plots.bar_plot(hallway, c='k')
book_plots.bar_plot(prior, ylim=(0,1.0), c='#ff8015')
plt.axvline(i % N + 0.4, lw=5)
fig.canvas.draw()
time.sleep(sleep)
plt.cla()
likelihood = lh_hallway(hallway, z=z, z_prob=z_prob_correct)
pos = update(likelihood, prior)
book_plots.bar_plot(hallway, c='k')
book_plots.bar_plot(pos, ylim=(0,1.0))
plt.axvline(i % 10 + 0.4, lw=5)
fig.canvas.draw()
time.sleep(sleep)
plt.show()
%matplotlib inline
set_figsize(y=2)
print('Final posterior:', pos)
# change these numbers to alter the simulation
kernel = (.1, .8, .1)
z_prob = 1.0
# list of perfect measurements
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
measurements = [hallway[i % len(hallway)] for i in range(25)]
pos = np.array([.1]*10)
discrete_bayes_sim(pos, kernel, measurements, z_prob)
```
## The Effect of Bad Sensor Data
You may be suspicious of the results above because I always passed correct sensor data into the functions. However, we are claiming that this code implements a *filter* - it should filter out bad sensor measurements. Does it do that?
To make this easy to program and visualize I will change the layout of the hallway to mostly alternating doors and hallways, and run the algorithm on 15 correct measurements:
```
hallway = np.array([1, 0, 1, 0, 0]*2)
kernel = (.1, .8, .1)
prior = np.array([.1] * 10)
measurements = [1, 0, 1, 0, 0]
z_prob = 0.75
discrete_bayes_sim(prior, kernel, measurements, z_prob)
```
We have identified the likely cases of having started at position 0 or 5, because we saw this sequence of doors and walls: 1,0,1,0,0. Now I inject a bad measurement. The next measurement should be 1, but instead we get a 0:
```
measurements = [1, 0, 1, 0, 0, 0]
discrete_bayes_sim(prior, kernel, measurements, z_prob)
```
That one bad measurement has significantly eroded our knowledge. Now let's continue with a series of correct measurements.
```
with figsize(y=5.5):
measurements = [0, 1, 0, 1, 0, 0]
for i, m in enumerate(measurements):
likelihood = lh_hallway(hallway, z=m, z_prob=.75)
posterior = update(likelihood, prior)
prior = predict(posterior, 1, kernel)
plt.subplot(3, 2, i+1)
book_plots.bar_plot(posterior, ylim=(0, .4), title='step {}'.format(i+1))
plt.tight_layout()
```
We quickly filtered out the bad sensor reading and converged on the most likely positions for our dog.
## Drawbacks and Limitations
Do not be mislead by the simplicity of the examples I chose. This is a robust and complete filter, and you may use the code in real world solutions. If you need a multimodal, discrete filter, this filter works.
With that said, this filter it is not used often because it has several limitations. Getting around those limitations is the motivation behind the chapters in the rest of this book.
The first problem is scaling. Our dog tracking problem used only one variable, $pos$, to denote the dog's position. Most interesting problems will want to track several things in a large space. Realistically, at a minimum we would want to track our dog's $(x,y)$ coordinate, and probably his velocity $(\dot{x},\dot{y})$ as well. We have not covered the multidimensional case, but instead of an array we use a multidimensional grid to store the probabilities at each discrete location. Each `update()` and `predict()` step requires updating all values in the grid, so a simple four variable problem would require $O(n^4)$ running time *per time step*. Realistic filters can have 10 or more variables to track, leading to exorbitant computation requirements.
The second problem is that the filter is discrete, but we live in a continuous world. The histogram requires that you model the output of your filter as a set of discrete points. A 100 meter hallway requires 10,000 positions to model the hallway to 1cm accuracy. So each update and predict operation would entail performing calculations for 10,000 different probabilities. It gets exponentially worse as we add dimensions. A 100x100 m$^2$ courtyard requires 100,000,000 bins to get 1cm accuracy.
A third problem is that the filter is multimodal. In the last example we ended up with strong beliefs that the dog was in position 4 or 9. This is not always a problem. Particle filters, which we will study later, are multimodal and are often used because of this property. But imagine if the GPS in your car reported to you that it is 40% sure that you are on D street, and 30% sure you are on Willow Avenue.
A forth problem is that it requires a measurement of the change in state. We need a motion sensor to detect how much the dog moves. There are ways to work around this problem, but it would complicate the exposition of this chapter, so, given the aforementioned problems, I will not discuss it further.
With that said, if I had a small problem that this technique could handle I would choose to use it; it is trivial to implement, debug, and understand, all virtues.
## Tracking and Control
We have been passively tracking an autonomously moving object. But consider this very similar problem. I am automating a warehouse and want to use robots to collect all of the items for a customer's order. Perhaps the easiest way to do this is to have the robots travel on a train track. I want to be able to send the robot a destination and have it go there. But train tracks and robot motors are imperfect. Wheel slippage and imperfect motors means that the robot is unlikely to travel to exactly the position you command. There is more than one robot, and we need to know where they all are so we do not cause them to crash.
So we add sensors. Perhaps we mount magnets on the track every few feet, and use a Hall sensor to count how many magnets are passed. If we count 10 magnets then the robot should be at the 10th magnet. Of course it is possible to either miss a magnet or to count it twice, so we have to accommodate some degree of error. We can use the code from the previous section to track our robot since magnet counting is very similar to doorway sensing.
But we are not done. We've learned to never throw information away. If you have information you should use it to improve your estimate. What information are we leaving out? We know what control inputs we are feeding to the wheels of the robot at each moment in time. For example, let's say that once a second we send a movement command to the robot - move left 1 unit, move right 1 unit, or stand still. If I send the command 'move left 1 unit' I expect that in one second from now the robot will be 1 unit to the left of where it is now. This is a simplification because I am not taking acceleration into account, but I am not trying to teach control theory. Wheels and motors are imperfect. The robot might end up 0.9 units away, or maybe 1.2 units.
Now the entire solution is clear. We assumed that the dog kept moving in whatever direction he was previously moving. That is a dubious assumption for my dog! Robots are far more predictable. Instead of making a dubious prediction based on assumption of behavior we will feed in the command that we sent to the robot! In other words, when we call `predict()` we will pass in the commanded movement that we gave the robot along with a kernel that describes the likelihood of that movement.
### Simulating the Train Behavior
We need to simulate an imperfect train. When we command it to move it will sometimes make a small mistake, and its sensor will sometimes return the incorrect value.
```
class Train(object):
def __init__(self, track_len, kernel=[1.], sensor_accuracy=.9):
self.track_len = track_len
self.pos = 0
self.kernel = kernel
self.sensor_accuracy = sensor_accuracy
def move(self, distance=1):
""" move in the specified direction
with some small chance of error"""
self.pos += distance
# insert random movement error according to kernel
r = random.random()
s = 0
offset = -(len(self.kernel) - 1) / 2
for k in self.kernel:
s += k
if r <= s:
break
offset += 1
self.pos = int((self.pos + offset) % self.track_len)
return self.pos
def sense(self):
pos = self.pos
# insert random sensor error
if random.random() > self.sensor_accuracy:
if random.random() > 0.5:
pos += 1
else:
pos -= 1
return pos
```
With that we are ready to write the filter. We will put it in a function so that we can run it with different assumptions. I will assume that the robot always starts at the beginning of the track. The track is implemented as being 10 units long, but think of it as a track of length, say 10,000, with the magnet pattern repeated every 10 units. A length of 10 makes it easier to plot and inspect.
```
def train_filter(iterations, kernel, sensor_accuracy,
move_distance, do_print=True):
track = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
prior = np.array([.9] + [0.01]*9)
normalize(prior)
robot = Train(len(track), kernel, sensor_accuracy)
for i in range(iterations):
robot.move(distance=move_distance)
m = robot.sense()
if do_print:
print('''time {}: pos {}, sensed {}, '''
'''at position {}'''.format(
i, robot.pos, m, track[robot.pos]))
likelihood = lh_hallway(track, m, sensor_accuracy)
posterior = update(likelihood, prior)
index = np.argmax(posterior)
if i < iterations - 1:
prior = predict(posterior, move_distance, kernel)
if do_print:
print(''' predicted position is {}'''
''' with confidence {:.4f}%:'''.format(
index, posterior[index]*100))
book_plots.bar_plot(posterior)
if do_print:
print()
print('final position is', robot.pos)
index = np.argmax(posterior)
print('''predicted position is {} with '''
'''confidence {:.4f}%:'''.format(
index, posterior[index]*100))
```
Read the code and make sure you understand it. Now let's do a run with no sensor or movement error. If the code is correct it should be able to locate the robot with no error. The output is a bit tedious to read, but if you are at all unsure of how the update/predict cycle works make sure you read through it carefully to solidify your understanding.
```
import random
random.seed(3)
np.set_printoptions(precision=2, suppress=True, linewidth=60)
train_filter(4, kernel=[1.], sensor_accuracy=.999,
move_distance=4, do_print=True)
```
We can see that the code was able to perfectly track the robot so we should feel reasonably confident that the code is working. Now let's see how it fairs with some errors.
```
random.seed(5)
train_filter(4, kernel=[.1, .8, .1], sensor_accuracy=.9,
move_distance=4, do_print=True)
```
There was a sensing error at time 1, but we are still quite confident in our position.
Now let's run a very long simulation and see how the filter responds to errors.
```
with figsize(y=5.5):
for i in range (4):
random.seed(3)
plt.subplot(221+i)
train_filter(148+i, kernel=[.1, .8, .1],
sensor_accuracy=.8,
move_distance=4, do_print=False)
plt.title ('iteration {}'.format(148+i))
```
We can see that there was a problem on iteration 149 as the confidence degrades. But within a few iterations the filter is able to correct itself and regain confidence in the estimated position.
## Bayes Theorem
We developed the math in this chapter merely by reasoning about the information we have at each moment. In the process we discovered [*Bayes Theorem*](https://en.wikipedia.org/wiki/Bayes%27_theorem). Bayes theorem tells us how to compute the probability of an event given previous information. That is exactly what we have been doing in this chapter. With luck our code should match the Bayes Theorem equation!
We implemented the `update()` function with this probability calculation:
$$ \mathtt{posterior} = \frac{\mathtt{likelihood}\times \mathtt{prior}}{\mathtt{normalization}}$$
To review, the *prior* is the probability of something happening before we include the probability of the measurement (the *likelihood*) and the *posterior* is the probability we compute after incorporating the information from the measurement.
Bayes theorem is
$$P(A \mid B) = \frac{P(B \mid A)\, P(A)}{P(B)}$$
If you are not familiar with this notation, let's review. $P(A)$ means the probability of event $A$. If $A$ is the event of a fair coin landing heads, then $P(A) = 0.5$.
$P(A \mid B)$ is called a [*conditional probability*](https://en.wikipedia.org/wiki/Conditional_probability). That is, it represents the probability of $A$ happening *if* $B$ happened. For example, it is more likely to rain today if it also rained yesterday because rain systems usually last more than one day. We'd write the probability of it raining today given that it rained yesterday as $P(\mathtt{rain\_today} \mid \mathtt{rain\_yesterday})$.
In the Bayes theorem equation above $B$ is the *evidence*, $P(A)$ is the *prior*, $P(B \mid A)$ is the *likelihood*, and $P(A \mid B)$ is the *posterior*. By substituting the mathematical terms with the corresponding words you can see that Bayes theorem matches out update equation. Let's rewrite the equation in terms of our problem. We will use $x_i$ for the position at *i*, and $Z$ for the measurement. Hence, we want to know $P(x_i \mid Z)$, that is, the probability of the dog being at $x_i$ given the measurement $Z$.
So, let's plug that into the equation and solve it.
$$P(x_i \mid Z) = \frac{P(Z \mid x_i) P(x_i)}{P(Z)}$$
That looks ugly, but it is actually quite simple. Let's figure out what each term on the right means. First is $P(Z \mid x_i)$. This is the the likelihood, or the probability for the measurement at every cell $x_i$. $P(x_i)$ is the *prior* - our belief before incorporating the measurements. We multiply those together. This is just the unnormalized multiplication in the `update()` function:
```python
def update(likelihood, prior):
posterior = prior * likelihood # P(Z|x)*P(x)
return normalize(posterior)
```
The last term to consider is the denominator $P(Z)$. This is the probability of getting the measurement $Z$ without taking the location into account. It is often called the *evidence*. We compute that by taking the sum of $x$, or `sum(belief)` in the code. That is how we compute the normalization! So, the `update()` function is doing nothing more than computing Bayes theorem.
The literature often gives you these equations in the form of integrals. After all, an integral is just a sum over a continuous function. So, you might see Bayes' theorem written as
$$P(A \mid B) = \frac{P(B \mid A)\, P(A)}{\int P(B \mid A_j) P(A_j) \mathtt{d}A_j}\cdot$$
In practice the denominator can be fiendishly difficult to solve analytically (a recent opinion piece for the Royal Statistical Society [called it](http://www.statslife.org.uk/opinion/2405-we-need-to-rethink-how-we-teach-statistics-from-the-ground-up) a "dog's breakfast" [8]. Filtering textbooks are filled with integral laden equations which you cannot be expected to solve. We will learn more techniques to handle this in the **Particle Filters** chapter. Until then, recognize that in practice it is just a normalization term over which we can sum. What I'm trying to say is that when you are faced with a page of integrals, just think of them as sums, and relate them back to this chapter, and often the difficulties will fade. Ask yourself "why are we summing these values", and "why am I dividing by this term". Surprisingly often the answer is readily apparent.
## Total Probability Theorem
We now know the formal mathematics behind the `update()` function; what about the `predict()` function? `predict()` implements the [*total probability theorem*](https://en.wikipedia.org/wiki/Law_of_total_probability). Let's recall what `predict()` computed. It computed the probability of being at any given position given the probability of all the possible movement events. Let's express that as an equation. The probability of being at any position $i$ at time $t$ can be written as $P(X_i^t)$. We computed that as the sum of the prior at time $t-1$ $P(X_j^{t-1})$ multiplied by the probability of moving from cell $x_j$ to $x_i$. That is
$$P(X_i^t) = \sum_j P(X_j^{t-1}) P(x_i | x_j)$$
That equation is called the *total probability theorem*. Quoting from Wikipedia [6] "It expresses the total probability of an outcome which can be realized via several distinct events". I could have given you that equation and implemented `predict()`, but your chances of understanding why the equation works would be slim. As a reminder, here is the code that computes this equation
```python
for i in range(N):
for k in range (kN):
index = (i + (width-k) - offset) % N
result[i] += prob_dist[index] * kernel[k]
```
## Summary
The code is very short, but the result is impressive! We have implemented a form of a Bayesian filter. We have learned how to start with no information and derive information from noisy sensors. Even though the sensors in this chapter are very noisy (most sensors are more than 80% accurate, for example) we quickly converge on the most likely position for our dog. We have learned how the predict step always degrades our knowledge, but the addition of another measurement, even when it might have noise in it, improves our knowledge, allowing us to converge on the most likely result.
This book is mostly about the Kalman filter. The math it uses is different, but the logic is exactly the same as used in this chapter. It uses Bayesian reasoning to form estimates from a combination of measurements and process models.
**If you can understand this chapter you will be able to understand and implement Kalman filters.** I cannot stress this enough. If anything is murky, go back and reread this chapter and play with the code. The rest of this book will build on the algorithms that we use here. If you don't understand why this filter works you will have little success with the rest of the material. However, if you grasp the fundamental insight - multiplying probabilities when we measure, and shifting probabilities when we update leads to a converging solution - then after learning a bit of math you are ready to implement a Kalman filter.
## References
* [1] D. Fox, W. Burgard, and S. Thrun. "Monte carlo localization: Efficient position estimation for mobile robots." In *Journal of Artifical Intelligence Research*, 1999.
http://www.cs.cmu.edu/afs/cs/project/jair/pub/volume11/fox99a-html/jair-localize.html
* [2] Dieter Fox, et. al. "Bayesian Filters for Location Estimation". In *IEEE Pervasive Computing*, September 2003.
http://swarmlab.unimaas.nl/wp-content/uploads/2012/07/fox2003bayesian.pdf
* [3] Sebastian Thrun. "Artificial Intelligence for Robotics".
https://www.udacity.com/course/cs373
* [4] Khan Acadamy. "Introduction to the Convolution"
https://www.khanacademy.org/math/differential-equations/laplace-transform/convolution-integral/v/introduction-to-the-convolution
* [5] Wikipedia. "Convolution"
http://en.wikipedia.org/wiki/Convolution
* [6] Wikipedia. "Law of total probability"
http://en.wikipedia.org/wiki/Law_of_total_probability
* [7] Wikipedia. "Time Evolution"
https://en.wikipedia.org/wiki/Time_evolution
* [8] We need to rethink how we teach statistics from the ground up
http://www.statslife.org.uk/opinion/2405-we-need-to-rethink-how-we-teach-statistics-from-the-ground-up
| true |
code
| 0.794903 | null | null | null | null |
|
# Wasserstein GAN
<img src="https://miro.medium.com/max/3200/1*M_YipQF_oC6owsU1VVrfhg.jpeg" width="800" height="400">
##### Importing libraries
```
import numpy as np
import matplotlib.pyplot as plt
from glob import glob
from PIL import Image
from time import time
import pandas as pd
import argparse
import math
import sys
import re
import itertools
from sklearn.model_selection import train_test_split
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch
import os
os.chdir('C:/Users/Nicolas/Documents/Data/Faces')
```
##### Function to sort files
```
def sorted_alphanumeric(data):
convert = lambda text: int(text) if text.isdigit() else text.lower()
alphanum_key = lambda key: [ convert(c) for c in re.split('([0-9]+)', key) ]
return sorted(data, key=alphanum_key)
```
##### Loading the 800 women
```
def load_women():
faces = pd.read_csv('800_women.csv', header=None).values
faces = faces.ravel().tolist()
return faces
faces = load_women()
y = np.repeat(1, len(faces))
```
##### Removing problematic target names
```
# faces = [i for i in files if (i[-34] == '1') and len(i[-37:-35].strip('\\').strip('d')) == 2 ] # MEN
# y = [i[-34] for i in files if (i[-34] == '1') and len(i[-37:-35].strip('\\').strip('d')) > 1 ] # MEN
assert len(y) == len(faces), 'The X and Y are not of the same length!'
```
#### This is the shape width/height
```
dim = 60
```
#### Cropping function
```
def crop(img):
if img.shape[0]<img.shape[1]:
x = img.shape[0]
y = img.shape[1]
crop_img = img[: , int(y/2-x/2):int(y/2+x/2)]
else:
x = img.shape[1]
y = img.shape[0]
crop_img = img[int(y/2-x/2):int(y/2+x/2) , :]
return crop_img
```
##### Loading and cropping images
```
print('Scaling...', end='')
start = time()
x = []
num_to_load = len(faces) # int(len(faces)/5)
for ix, file in enumerate(faces[:num_to_load]):
image = plt.imread(file, 'jpg')
image = Image.fromarray(image).resize((dim, dim)).convert('L')
image = crop(np.array(image))
x.append(image)
print(f'\rDone. {int(time() - start)} seconds')
```
##### Turning the pictures into arrays
```
x = np.array(x, dtype=np.float32).reshape(-1, 1, 60, 60)
y = np.array(y, dtype=np.float32)
labels = y.copy()
```
##### Turning the targets into a 2D matrix
```
assert x.ndim == 4, 'The input is the wrong shape!'
yy, xx = y.nbytes, x.nbytes
print(f'The size of X is {xx:,} bytes and the size of Y is {yy:,} bytes.')
files, faces = None, None
```
##### Displaying the pictures
```
fig = plt.figure(figsize=(12, 12))
for i in range(1, 5):
plt.subplot(1, 5, i)
rand = np.random.randint(0, x.shape[0])
ax = plt.imshow(x[rand][0, :, :], cmap='gray')
plt.title('<Women>')
yticks = plt.xticks([])
yticks = plt.yticks([])
print('Scaling...', end='')
image_size = x.shape[1] * x.shape[1]
x = (x.astype('float32') - 127.5) / 127.5
print('\rDone. ')
if torch.cuda.is_available():
x = torch.from_numpy(x)
y = torch.from_numpy(y)
print('Tensors successfully flushed to CUDA.')
else:
print('CUDA not available!')
```
##### Making a dataset class
```
class Face():
def __init__(self):
self.len = x.shape[0]
self.x = x
self.y = y
def __getitem__(self, index):
return x[index], y[index].unsqueeze(0)
def __len__(self):
return self.len
```
##### Instantiating the class
```
faces = Face()
```
##### Parsing the args
```
parser = argparse.ArgumentParser()
parser.add_argument("--n_epochs", type=int, default=1_000, help="number of epochs of training")
parser.add_argument("--batch_size", type=int, default=128, help="size of the batches")
parser.add_argument("--lr", type=float, default=0.00005, help="learning rate")
parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation")
parser.add_argument("--latent_dim", type=int, default=32, help="dimensionality of the latent space")
parser.add_argument("--img_size", type=int, default=60, help="size of each image dimension")
parser.add_argument("--channels", type=int, default=1, help="number of image channels")
parser.add_argument("--n_critic", type=int, default=5, help="number of training steps for discriminator per iter")
parser.add_argument("--clip_value", type=float, default=0.005, help="lower and upper clip value for disc. weights")
parser.add_argument("--sample_interval", type=int, default=1, help="interval betwen image samples")
opt, unknown = parser.parse_known_args()
print(opt)
```
#### Making the generator
```
img_shape = (opt.channels, opt.img_size, opt.img_size)
cuda = True if torch.cuda.is_available() else False
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
def block(in_feat, out_feat, normalize=True):
layers = [nn.Linear(in_feat, out_feat)]
if normalize:
layers.append(nn.BatchNorm1d(out_feat, 0.8))
layers.append(nn.LeakyReLU(0.2, inplace=True))
return layers
self.model = nn.Sequential(
*block(opt.latent_dim, 128, normalize=False),
*block(128, 256),
*block(256, 512),
*block(512, 1024),
nn.Linear(1024, int(np.prod(img_shape))),
nn.Tanh()
)
def forward(self, z):
img = self.model(z)
img = img.view(img.shape[0], *img_shape)
return img
```
#### Making the discriminator
```
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(int(np.prod(img_shape)), 512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 1),
)
def forward(self, img):
img_flat = img.view(img.shape[0], -1)
validity = self.model(img_flat)
return validity
# Initialize generator and discriminator
generator = Generator()
discriminator = Discriminator()
if cuda:
generator.cuda()
discriminator.cuda()
```
#### Loading the trained models
```
generator.load_state_dict(torch.load('deep_conv_gan_generator'))
discriminator.load_state_dict(torch.load('deep_conv_gan_discriminator'))
```
#### Setting up the dataloader
```
# Configure data loader
dataloader = torch.utils.data.DataLoader(faces,
batch_size=opt.batch_size,
shuffle=True,
)
```
#### Making the optimizers
```
# Optimizers
optimizer_G = torch.optim.RMSprop(generator.parameters(), lr=opt.lr)
optimizer_D = torch.optim.RMSprop(discriminator.parameters(), lr=opt.lr)
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
```
#### Training the model
```
batches_done = 0
if not os.path.isdir('wsgan'):
os.mkdir('wsgan')
for epoch in range(1, opt.n_epochs + 1):
break # model is already trained!
for i, (imgs, _) in enumerate(dataloader):
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# ---------------------
# Train Discriminator
# ---------------------
optimizer_D.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
fake_imgs = generator(z).detach()
# Adversarial loss
loss_D = -torch.mean(discriminator(real_imgs)) + torch.mean(discriminator(fake_imgs))
loss_D.backward()
optimizer_D.step()
# Clip weights of discriminator
for p in discriminator.parameters():
p.data.clamp_(-opt.clip_value, opt.clip_value)
# Train the generator every n_critic iterations
if i % opt.n_critic == 0:
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad()
# Generate a batch of images
gen_imgs = generator(z)
# Adversarial loss
loss_G = -torch.mean(discriminator(gen_imgs))
loss_G.backward()
optimizer_G.step()
batches_done = epoch * len(dataloader) + i + 1
if epoch >= 500 and epoch % 100 == 0:
val = input("\nContinue training? [y/n]: ")
print()
if val in ('y', 'yes'):
val = True
pass
elif val in ('n', 'no'):
break
else:
pass
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], "wsgan/%d.png" % batches_done, nrow=5, normalize=True)
if epoch % 50 == 0:
print(
"[Epoch %d/%d] [D loss: %f] [G loss: %f]"
% (epoch, opt.n_epochs, loss_G.item(), loss_G.item())
)
```
##### Saving the models
```
torch.save(generator.state_dict(), 'wasserstein_gan_generator')
torch.save(discriminator.state_dict(), 'wasserstein_gan_discriminator')
```
##### Function to save images
```
def sample_image(directory, n_row, batches_done):
"""Saves a grid of generated digits"""
# Sample noise
z = Variable(Tensor(np.random.normal(0, 1, (n_row ** 2, opt.latent_dim))))
gen_imgs = generator(z)
save_image(gen_imgs.data, "%s/%d.png" % (directory, batches_done), nrow=n_row, normalize=True)
```
##### Generating 25,000 pictures
```
if not os.path.isdir('wsgan_800_women'):
os.mkdir('wsgan_800_women')
images = 0
for epoch in range(1, 2_00 + 1): # make it 200!
for i, (imgs, _) in enumerate(dataloader):
with torch.no_grad():
# Adversarial ground truths
valid = Variable(Tensor(imgs.shape[0], 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.shape[0], 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
batches_done = epoch * len(dataloader) + i
sample_image('wsgan_800_women', n_row=5, batches_done=batches_done)
images += 25
if images % 5_000 == 0:
print(f'Pictures created: {images:,}')
if len(os.listdir(os.path.join(os.getcwd(), 'wsgan_800_women'))) >= 1_000:
print('\n25,000 images successfully generated.')
break
```
##### Visualizing the generated images
```
images = []
for file_name in sorted_alphanumeric(glob('wsgan_800_women/*.png')):
if file_name.endswith('.png'):
file_path = os.path.join(file_name)
images.append(file_path)
picture = plt.imread(images[-1])
plt.figure(figsize=(6, 6))
plt.imshow(picture)
plt.xticks([]), plt.yticks([])
plt.title('Generated Faces')
plt.show()
```
| true |
code
| 0.696849 | null | null | null | null |
|
👇 (Press on the three dots to expand the code)
```
# Code preamble: we'll need some packages to display the information in the notebook.
# Feel free to ignore this cell unless you're running the code.
import folium # Map visualizations
import requests # Basic http requests
import json # For handling API return data
import pandas as pd # Pandas is a data manipulation and analysis library
api_base = "https://api.resourcewatch.org/v1"
def show_layer(layer_id, year, provider):
tiles_url = f"{api_base}/layer/{layer_id}/tile/{provider}/{{z}}/{{x}}/{{y}}?year={str(year)}"
attribution = "ResourceWatch & Vizzuality, 2018",
map_object = folium.Map(tiles = tiles_url, attr=attribution, max_zoom = 18, min_zoom= 2)
return map_object
```
# NEX-GDDP & LOCA indicators calculations
As part of the development of PREP we processed data from two climate downscaling datasets: [NEX-GDDP](https://nex.nasa.gov/nex/projects/1356/) (NASA Earth eXchange Global Daily Downscaled Projections) and [LOCA](http://loca.ucsd.edu/) (LOcalized Constructed Analogs). Both these models are *downscaled climate scenarios*, where coarse-resolution climate models are applied to a finer spatial resolution grid. GDDP data is offered at the global scale, while LOCA data covers the contiguous United States. Data access is offered through their homepages (linked above) and through several additional data cloud repositories --[Amazon AWS](https://registry.opendata.aws/nasanex/) and the [OpenNEX initiative](https://nex.nasa.gov/nex/static/htdocs/site/extra/opennex/) among them. For ease of use, we'll illustrate any examples with the GDDP data available in [Google Earth Engine](https://earthengine.google.com/).
The general data structure is similar for both datasets: daily measures of three forecasted variables (minimum and maximum daily temperatures, daily precipitation) are available for two of the scenarios of the Representative Concentration Pathways (RCPs), the RCP 4.5 and RCP 8.5. Roughly, these correspond to different levels of radiative forcing due to greenhouse emissions. The former scenario's level of emissions would peak at 2040 and then decline, while the latter would countinue to rise throughtout the 21st century. Each of these scenarios is comprised of forecasts for a set of models (21 for GDDP, 31 for LOCA), daily, from 2006 to 2100. A historical series is also included, where these models are applied to the historical forcing conditions, from 1950 to 2006. This results in a massive amount of data: about 12 terabytes of compressed netcdf files are available just for GDDP data. This amount of data is unwieldy, so some processing is needed to reduce it into a smaller, simpler dataset. We have applied two processes on the data: first, we are calculating several climate indicators on the data, in addition to the base variables. These indicators are then used to create an ensemble measure (an average of the different models) and their 25th and 75th percentiles. These are presented at two different temporal resolutions: decadal averages and three 30-year period averages.
## The indicators
This information is present in the [PREP website](https://prepdata.org). We'll query the RW API (which powers PREP) to obtain the datasets and their layers. You can check out the actual code we've ran [here](https://github.com/resource-watch/nexgddp-dataprep/tree/develop).
```
nex_datasets = json.loads(requests.get(f"{api_base}/dataset?provider=nexgddp&page[size]=1000&includes=layer").text)['data']
loca_datasets = json.loads(requests.get(f"{api_base}/dataset?provider=loca&page[size]=1000&includes=layer").text)['data']
get_data = lambda dset: (
dset['attributes']['name'],
dset['attributes']['tableName'],
next(iter(dset['attributes']['layer']), {"id": None})['id']
)
df = pd.DataFrame([
*[get_data(dset) for dset in nex_datasets],
*[get_data(dset) for dset in loca_datasets]
])
df.columns = ['description', 'tableName', 'layerId']
df
```
### Calculating an indicator
Given that the data is expressed in several dimensions, the data has to be reduced across these dimensions. This is done in a certain order. Consider the format of the 'raw data': daily maps from 1951 to 2100 for each model. The first step is to extract a single year of the raw data, for a single model. It's from this data from which we calculate the indicator --in this case, the average maximum temperature.

The output we are interested in is still at a lower temporal resolution than the data we have now. If we were to calculate an indicator for the decadal temporal resolution dataset, we would take a whole decade of the indicator, as calculated above, and average it again.

It's from these averaged indicators from where we can calculate the average and the 25th and 75th percentiles. The final measure --the one that can be seen on the web-- is the average of the indicators *across models*. This is known as an ensemble measure.

### Temperature indicators
#### Maximum daily temperature (tasmax)
The maximum daily temperature is already present in the 'raw' datasets. These values are averaged per temporal unit (decadal, 30y) and model, as described above.
```
tasmax_layer = show_layer("964d1388-4490-487d-b9cc-cd282e4d3d28", 1971, "nexgddp")
tasmax_layer
```
#### Minimum daily temperature
Similarly to the indicator above, no processing is needed in this indicator other than the averaging.
```
tasmin_layer = show_layer("c3bb62e8-2d50-4ad2-9ca5-8ce02bed1de5", 1971, "nexgddp")
tasmin_layer
```
#### Average daily temperature
We construct the 'average daily temperature' from the average maximum and minimun daily temperatures. This would be the first step in the processing --we would first construct a 'tasavg' variable, and then procesed with the rest of the analysis as usual.
```
tasavg_layer = show_layer("02e9f747-7c20-4fc8-a773-a5135f24cc91", 1971, "nexgddp")
tasavg_layer
```
#### Heating degree days
[Heating Degree Days (HDDs)](https://en.wikipedia.org/wiki/Heating_degree_day) is a measure of the demand for energy for heating. It's defined in terms of a fixed baseline, which in our case is 65F. The measure is the accumulated difference in *average* temperatures (Kelvin degrees) to this baseline for days where this temperature does not reach the baseline (i.e. in a day hotter than 65F, 0 heating degree days would be accumulated).
```
hdd_layer = show_layer("8bc10da3-e610-4105-9f4e-8ebfb1725874", 1971, "nexgddp")
hdd_layer
```
#### Cooling degree days
In the same vein than HDDs, Cooling Degree Days (CDDs) are the accumulated degrees in excess of the baseline (again, 65F) of the average temperature for a year. It's a measure of energy consumption for cooling in hot days.
```
cdd_layer = show_layer("a632a688-a181-48b5-93bc-d230e24550d9", 1971, "nexgddp")
cdd_layer
```
#### Extreme heat days
The number of extreme heat days in a year is defined as the count of days with a maximum temperature higher than the 99th percentile of the baseline. This baseline is calculated per model and per raster pixel, and is the temperature for which 99% of measures from 1971 to 2000 fall below --any temperature higher than this is considered extreme.

```
xh_layer = show_layer("2266fa97-e19c-4056-a1a9-4d4f29dd178e", 1971, "nexgddp")
xh_layer
# Notice the large difference
xh_layer_2 = show_layer("2266fa97-e19c-4056-a1a9-4d4f29dd178e", 2051, "nexgddp")
xh_layer_2
```
#### Frost free season
The frost free season is the longest streak of days (measured in *number of days*) above 0C per year.
```
ffs_layer = show_layer("83ec85e4-997b-4613-bf9e-2301ba6d7b63", 1971, "nexgddp")
ffs_layer
```
### Precipitation indicators
#### Cummulative precipitation
Precipitation is given in kg m^⁻2 s^-1, both in solid and liquid phases and from all types of clouds. The calculated measure is given as the accumulated yearly precipitation mass per square meter -- it's transformed to mm in the front-end.
```
cummpr_layer = show_layer("56e19aef-3194-4aad-8df0-9bb9064ac8e6", 1971, "nexgddp")
cummpr_layer
```
#### Extreme precipitation days
Calculated with the same method as the extreme temperatures indicator, but the baseline is constructed with the precipitations indicator.
```
xpr_layer = show_layer("7e76e90f-4c35-48fb-9604-3c187a28723b", 1971, "nexgddp")
xpr_layer
```
#### Dry spells
Average count of 5-day perdios without precipitation per year. In this case, we count longer periods as consecutive dry spells. Any excess on a multiple of 5 days is added as a 'fractional' dry spell.
```
dry_layer = show_layer("72996b8f-1f59-4d1d-b48b-490d72677473", 1971, "nexgddp")
dry_layer
```
| true |
code
| 0.42662 | null | null | null | null |
|
### LSTM Model v2
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from utils import split_sequence, get_apple_close_price, plot_series
from utils import plot_residual_forecast_error, print_performance_metrics
from utils import get_range, difference, inverse_difference
from utils import train_test_split, NN_walk_forward_validation
apple_close_price = get_apple_close_price()
short_series = get_range(apple_close_price, '2003-01-01')
# Model parameters
look_back = 5 # days window look back
n_features = 1 # our only feature will be Close price
n_outputs = 5 # days forecast
batch_size = 32 # for NN, batch size before updating weights
n_epochs = 1000 # for NN, number of training epochs
```
We need to first train/test split, then transform and scale our data
```
from scipy.stats import boxcox
from scipy.special import inv_boxcox
train, test= train_test_split(apple_close_price,'2018-05-31')
boxcox_series, lmbda = boxcox(train.values)
transformed_train = boxcox_series
transformed_test = boxcox(test, lmbda=lmbda)
# transformed_train = train.values
# transformed_test = test.values
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaled_train = scaler.fit_transform(transformed_train.reshape(-1, 1))
scaled_test = scaler.transform(transformed_test.reshape(-1, 1))
X_train, y_train = split_sequence(scaled_train, look_back, n_outputs)
y_train = y_train.reshape(-1, n_outputs)
from keras.models import Sequential
from keras.layers import LSTM, Dense, Flatten, LeakyReLU
from keras.optimizers import Adam
import warnings
warnings.simplefilter('ignore')
def build_LSTM(look_back, n_features, n_outputs, optimizer='adam'):
model = Sequential()
model.add(LSTM(50, input_shape=(look_back, n_features)))
model.add(LeakyReLU(alpha=0.2))
model.add(Dense(n_outputs))
model.compile(optimizer=optimizer, loss='mean_squared_error')
return model
model = build_LSTM(look_back, n_features, n_outputs, optimizer=Adam(0.0001))
model.summary()
history = model.fit(X_train, y_train, epochs=n_epochs, batch_size=batch_size, shuffle=False)
plot_series(history.history['loss'], title='MLP model - Loss over time')
model.save_weights('lstm-model_weights.h5')
size = 252 # approx. one year
predictions = NN_walk_forward_validation(model,
scaled_train, scaled_test[:252],
size=size,
look_back=look_back,
n_outputs=n_outputs)
from utils import plot_walk_forward_validation
from utils import plot_residual_forecast_error, print_performance_metrics
```
We need to revert the scaling and transformation:
```
descaled_preds = scaler.inverse_transform(predictions.reshape(-1, 1))
descaled_test = scaler.inverse_transform(scaled_test.reshape(-1, 1))
descaled_preds = inv_boxcox(descaled_preds, lmbda)
descaled_test = inv_boxcox(descaled_test, lmbda)
fig, ax = plt.subplots(figsize=(15, 6))
plt.plot(descaled_test[:size])
plt.plot(descaled_preds)
ax.set_title('Walk forward validation - 5 days prediction')
ax.legend(['Expected', 'Predicted'])
plot_residual_forecast_error(descaled_preds, descaled_test[:size])
print_performance_metrics(descaled_preds,
descaled_test[:size],
model_name='LSTM',
total_days=size, steps=n_outputs)
model.load_weights('cnn-model_weights.h5')
```
| true |
code
| 0.764326 | null | null | null | null |
|
# Summary:
This notebook contains the soft smoothing figures for Swarthmore (Figure 2(a)).
## Load libraries
```
# import packages
from __future__ import division
import networkx as nx
import os
import numpy as np
from sklearn import metrics
from sklearn.preprocessing import label_binarize
from sklearn.metrics import confusion_matrix
from sklearn.metrics import f1_score
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import StratifiedShuffleSplit
import matplotlib.pyplot as plt
## function to create + save dictionary of features
def create_dict(key, obj):
return(dict([(key[i], obj[i]) for i in range(len(key))]))
```
## load helper functions and datasets
```
# set the working directory and import helper functions
#get the current working directory and then redirect into the functions under code
cwd = os.getcwd()
# parents working directory of the current directory: which is the code folder
parent_cwd = os.path.dirname(cwd)
# get into the functions folder
functions_cwd = parent_cwd + '/functions'
# change the working directory to be .../functions
os.chdir(functions_cwd)
# import all helper functions
exec(open('parsing.py').read())
exec(open('ZGL.py').read())
exec(open('create_graph.py').read())
exec(open('ZGL_softing_new_new.py').read())
# import the data from the data folder
data_cwd = os.path.dirname(parent_cwd)+ '/data'
# change the working directory and import the fb dataset
fb100_file = data_cwd +'/Swarthmore42'
A, metadata = parse_fb100_mat_file(fb100_file)
# change A(scipy csc matrix) into a numpy matrix
adj_matrix_tmp = A.todense()
#get the gender for each node(1/2,0 for missing)
gender_y_tmp = metadata[:,1]
# get the corresponding gender for each node in a disctionary form
gender_dict = create_dict(range(len(gender_y_tmp)), gender_y_tmp)
(graph, gender_y) = create_graph(adj_matrix_tmp,gender_dict,'gender',0,None,'yes')
```
## general setup
```
percent_initially_unlabelled = [0.99,0.95,0.9,0.8,0.7,0.6,0.5,0.4,0.3,0.2,0.1,0.05]
percent_initially_labelled = np.subtract(1, percent_initially_unlabelled)
n_iter = 10
cv_setup = 'stratified'
w = [0.001,1,10,100,1000,10000000]
```
## hard smoothing (ZGL)
```
adj_matrix_tmp_ZGL = adj_matrix_tmp
(graph, gender_y) = create_graph(adj_matrix_tmp_ZGL,gender_dict,'gender',0,None,'yes')
# ZGL Setup
adj_matrix_gender = np.array(nx.adjacency_matrix(graph).todense())
# run ZGL
exec(open("/Users/yatong_chen/Google Drive/research/DSG_empirical/code/functions/ZGL.py").read())
(mean_accuracy_zgl_Swarthmore, se_accuracy_zgl_Swarthmore,
mean_micro_auc_zgl_Swarthmore,se_micro_auc_zgl_Swarthmore,
mean_wt_auc_zgl_Swarthmore,se_wt_auc_zgl_Swarthmore) =ZGL(np.array(adj_matrix_gender),
np.array(gender_y),percent_initially_unlabelled,
n_iter,cv_setup)
```
## Soft smoothing (with different parameters w)
```
# ZGL soft smoothing Setup
(graph_new, gender_y_new) = create_graph(adj_matrix_tmp,gender_dict,'gender',0,None,'yes')
adj_matrix_gender = np.array(nx.adjacency_matrix(graph_new).todense())
gender_dict_new = create_dict(range(len(gender_y_new)), gender_y_new)
(mean_accuracy_zgl_softing_new_new_Swarthmore01, se_accuracy_zgl_softing_new_new_Swarthmore01,
mean_micro_auc_zgl_softing_new_new_Swarthmore01,se_micro_auc_zgl_softing_new_new_Swarthmore01,
mean_wt_auc_zgl_softing_new_new_Swarthmore01,se_wt_auc_zgl_softing_new_new_Swarthmore01) = ZGL_softing_new_new(w[0], adj_matrix_gender,
gender_dict_new,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_Swarthmore1, se_accuracy_zgl_softing_new_new_Swarthmore1,
mean_micro_auc_zgl_softing_new_new_Swarthmore1,se_micro_auc_zgl_softing_new_new_Swarthmore1,
mean_wt_auc_zgl_softing_new_new_Swarthmore1,se_wt_auc_zgl_softing_new_new_Swarthmore1) = ZGL_softing_new_new(w[1], adj_matrix_gender,
gender_dict_new,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_Swarthmore10, se_accuracy_zgl_softing_new_new_Swarthmore10,
mean_micro_auc_zgl_softing_new_new_Swarthmore10,se_micro_auc_zgl_softing_new_new_Swarthmore10,
mean_wt_auc_zgl_softing_new_new_Swarthmore10,se_wt_auc_zgl_softing_new_new_Swarthmore10) = ZGL_softing_new_new(w[2], adj_matrix_gender,
gender_dict_new,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_Swarthmore100, se_accuracy_zgl_softing_new_new_Swarthmore100,
mean_micro_auc_zgl_softing_new_new_Swarthmore100,se_micro_auc_zgl_softing_new_new_Swarthmore100,
mean_wt_auc_zgl_softing_new_new_Swarthmore100,se_wt_auc_zgl_softing_new_new_Swarthmore100) = ZGL_softing_new_new(w[3], adj_matrix_gender,
gender_dict_new,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_Swarthmore1000, se_accuracy_zgl_softing_new_new_Swarthmore1000,
mean_micro_auc_zgl_softing_new_new_Swarthmore1000,se_micro_auc_zgl_softing_new_new_Swarthmore1000,
mean_wt_auc_zgl_softing_new_new_Swarthmore1000,se_wt_auc_zgl_softing_new_new_Swarthmore1000) = ZGL_softing_new_new(w[4], adj_matrix_gender,
gender_dict_new,'gender', percent_initially_unlabelled, n_iter,cv_setup)
(mean_accuracy_zgl_softing_new_new_Swarthmore10000, se_accuracy_zgl_softing_new_new_Swarthmore10000,
mean_micro_auc_zgl_softing_new_new_Swarthmore10000,se_micro_auc_zgl_softing_new_new_Swarthmore10000,
mean_wt_auc_zgl_softing_new_new_Swarthmore10000,se_wt_auc_zgl_softing_new_new_Swarthmore10000) = ZGL_softing_new_new(w[5], adj_matrix_gender,
gender_dict_new,'gender', percent_initially_unlabelled, n_iter,cv_setup)
```
## plot
```
%matplotlib inline
from matplotlib.ticker import FixedLocator,LinearLocator,MultipleLocator, FormatStrFormatter
fig = plt.figure()
#seaborn.set_style(style='white')
from mpl_toolkits.axes_grid1 import Grid
grid = Grid(fig, rect=111, nrows_ncols=(1,1),
axes_pad=0.1, label_mode='L')
for i in range(4):
if i == 0:
# set the x and y axis
grid[i].xaxis.set_major_locator(FixedLocator([0,25,50,75,100]))
grid[i].yaxis.set_major_locator(FixedLocator([0.4, 0.5,0.6,0.7,0.8,0.9,1]))
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_Swarthmore,
yerr=se_wt_auc_zgl_Swarthmore, fmt='--o', capthick=2,
alpha=1, elinewidth=8, color='black')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_Swarthmore01,
yerr=se_wt_auc_zgl_softing_new_new_Swarthmore01, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='gold')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_Swarthmore1,
yerr=se_wt_auc_zgl_softing_new_new_Swarthmore1, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='darkorange')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_Swarthmore10,
yerr=se_wt_auc_zgl_softing_new_new_Swarthmore10, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='crimson')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_Swarthmore100,
yerr=se_wt_auc_zgl_softing_new_new_Swarthmore100, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='red')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_Swarthmore1000,
yerr=se_wt_auc_zgl_softing_new_new_Swarthmore1000, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='maroon')
grid[i].errorbar(percent_initially_labelled*100, mean_wt_auc_zgl_softing_new_new_Swarthmore10000,
yerr=se_wt_auc_zgl_softing_new_new_Swarthmore10000, fmt='--o', capthick=2,
alpha=1, elinewidth=3, color='darkred')
grid[i].set_ylim(0.45,1)
grid[i].set_xlim(0,101)
grid[i].annotate('soft: a = 0.001', xy=(3, 0.96),
color='gold', alpha=1, size=12)
grid[i].annotate('soft: a = 1', xy=(3, 0.92),
color='darkorange', alpha=1, size=12)
grid[i].annotate('soft: a = 10', xy=(3, 0.88),
color='red', alpha=1, size=12)
grid[i].annotate('soft: a = 100', xy=(3, 0.84),
color='crimson', alpha=1, size=12)
grid[i].annotate('soft: a = 1000', xy=(3, 0.80),
color='maroon', alpha=1, size=12)
grid[i].annotate('soft: a = 1000000', xy=(3, 0.76),
color='darkred', alpha=1, size=12)
grid[i].annotate('hard smoothing', xy=(3, 0.72),
color='black', alpha=1, size=12)
grid[i].set_ylim(0.4,0.8)
grid[i].set_xlim(0,100)
grid[i].spines['right'].set_visible(False)
grid[i].spines['top'].set_visible(False)
grid[i].tick_params(axis='both', which='major', labelsize=13)
grid[i].tick_params(axis='both', which='minor', labelsize=13)
grid[i].set_xlabel('Percent of Nodes Initially Labeled').set_fontsize(15)
grid[i].set_ylabel('AUC').set_fontsize(15)
grid[0].set_xticks([0,25, 50, 75, 100])
grid[0].set_yticks([0.4,0.6,0.8,1])
grid[0].minorticks_on()
grid[0].tick_params('both', length=4, width=1, which='major', left=1, bottom=1, top=0, right=0)
```
| true |
code
| 0.498047 | null | null | null | null |
|
## Introduction to Exploratory Data Analysis and Visualization
In this lab, we will cover some basic EDAV tools and provide an example using _presidential speeches_.
## Table of Contents
[ -Step 0: Import modules](#step0)
[-Step 1: Read in the speeches](#step1)
[-Step 2: Text processing](#step2)
-Step 3: Visualization
* [ Step 3.1: Word cloud](#step3-1)
* [ Step 3.2: Joy plot](#step3-3)
[-Step 4: Sentence analysis](#step4)
[-Step 5: NRC emotion analysis](#step5)
<a id="Example"></a>
## Part 2: Example using _presidential speeches_.
In this section, we will go over an example using a collection of presidential speeches. The data were scraped from the [Presidential Documents Archive](http://www.presidency.ucsb.edu/index_docs.php) of the [American Presidency Project](http://www.presidency.ucsb.edu/index.php) using the `Rvest` package from `R`. The scraped text files can be found in the `data` folder.
For the lab, we use a handful of basic Natural language processing (NLP) building blocks provided by NLTK (and a few additional libraries), including text processing (tokenization, stemming etc.), frequency analysis, and NRC emotion analysis. It also provides various data visualizations -- an important field of data science.
<a id="step0"></a>
## Step 0: Import modules
**Initial Setup** you need Python installed on your system to run the code examples used in this tutorial. This tutorial is constructed using Python 2.7, which is slightly different from Python 3.5.
We recommend that you use Anaconda for your python installation. For more installation recommendations, please use our [check_env.ipynb](https://github.com/DS-BootCamp-Collaboratory-Columbia/AY2017-2018-Winter/blob/master/Bootcamp-materials/notebooks/Pre-assignment/check_env.ipynb).
The main modules we will use in this notebook are:
* *nltk*:
* *nltk* (Natural Language ToolKit) is the most popular Python framework for working with human language.
* *nltk* doesn’t come with super powerful pre-trained models, but contains useful functions for doing a quick exploratory data analysis.
* [Reference webpage](https://nlpforhackers.io/introduction-nltk/#more-4627)
* [NLTK book](http://www.nltk.org/book/)
* *re* and *string*:
* For text processing.
* *scikit-learn*:
* For text feature extraction.
* *wordcloud*:
* Word cloud visualization.
* Pip installation:
```
pip install wordcloud
```
* Conda installation (not come with Anaconda built-in packages):
```
conda install -c conda-forge wordcloud=1.2.1
```
* *ipywidgets*:
* *ipywidgets* can render interactive controls on the Jupyter notebook. By using the elements in *ipywidgets*, e.g., `IntSlider`, `Checkbox`, `Dropdown`, we could produce fun interactive visualizations.
* Pip installation:
If you use pip, you also have to enable the ipywidget extension in your notebook to render it next time you start the notebook. Type in following command on your terminal:
```
pip install ipywidgets
jupyter nbextension enable --py widgetsnbextension
```
* Conda installation:
If you use conda, the extension will be enabled automatically. There might be version imcompatible issue happened, following command is to install the modules in the specific compatible versions.
```
conda install --yes jupyter_core notebook nbconvert ipykernel ipywidgets=6.0 widgetsnbextension=2.0
```
* [Reference webpage](https://towardsdatascience.com/a-very-simple-demo-of-interactive-controls-on-jupyter-notebook-4429cf46aabd)
* *seaborn*:
* *seaborn* provides a high-level interface to draw statistical graphics.
* A comprehensive [tutorial](https://www.datacamp.com/community/tutorials/seaborn-python-tutorial) on it.
```
# Basic
from random import randint
import pandas as pd
import csv
import numpy as np
from collections import OrderedDict, defaultdict, Counter
# Text
import nltk, re, string
from nltk.corpus.reader.plaintext import PlaintextCorpusReader #Read in text files
from nltk import word_tokenize, sent_tokenize
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
nltk.download('punkt')
# Plot
import ipywidgets as widgets
import seaborn as sns
from ipywidgets import interactive, Layout, HBox, VBox
from wordcloud import WordCloud
from matplotlib import pyplot as plt
from matplotlib import gridspec, cm
# Source code
import sys
sys.path.append("../lib/")
import joypy
```
<a id="step1"></a>
## Step 1: Read in the speeches
```
inaug_corpus = PlaintextCorpusReader("../data/inaugurals", ".*\.txt")
#Accessing the name of the files of the corpus
inaug_files = inaug_corpus.fileids()
for f in inaug_files[:5]:
print(f)
len(inaug_files)
#Accessing all the text of the corpus
inaug_all_text = inaug_corpus.raw()
print("First 100 words in all the text of the corpus: \n >>" + inaug_all_text[:100])
#Accessing all the text for one of the files
inaug_ZacharyTaylor1_text=inaug_corpus.raw('inaugZacharyTaylor-1.txt')
print("First 100 words in one file: \n >>" + inaug_ZacharyTaylor1_text[:100])
```
<a id="step2"></a>
## Step 2: Text processing
For the speeches, we do the text processing as follows and define a function `tokenize_and_stem`:
1. convert all letters to lower cases
2. split text into sentences and then words
3. remove [stop words](https://github.com/arc12/Text-Mining-Weak-Signals/wiki/Standard-set-of-english-stopwords), remove empty words due to formatting errors, and remove punctuation.
4. [stemming words](https://en.wikipedia.org/wiki/Stemming) use NLTK porter stemmer. There are [many other stemmers](http://www.nltk.org/howto/stem.html) built in NLTK. You can play around and see the difference.
Then we compute the [Document-Term Matrix (DTM)](https://en.wikipedia.org/wiki/Document-term_matrix) and [TF-IDF](https://en.wikipedia.org/wiki/Tf%E2%80%93idf).
See [Natural Language Processing with Python](http://www.nltk.org/book/) for a more comprehensive discussion about NLTK.
There are many more interesting topics in NLP, which we will not cover in this lab. In you are interested, here are some online resources.
1. [Named Entity Recognition](https://github.com/charlieg/A-Smattering-of-NLP-in-Python)
2. [Topic modeling](https://medium.com/mlreview/topic-modeling-with-scikit-learn-e80d33668730)
3. [sentiment analysis](https://pythonspot.com/python-sentiment-analysis/) (positive v.s. negative)
3. [Supervised model](https://www.dataquest.io/blog/natural-language-processing-with-python/)
```
stemmer = PorterStemmer()
def tokenize_and_stem(text):
lowers = text.lower()
tokens = [word for sent in nltk.sent_tokenize(lowers) for word in nltk.word_tokenize(sent)]
filtered_tokens = []
# filter out any tokens not containing letters (e.g., numeric tokens, raw punctuation)
for token in tokens:
if re.search('[a-zA-Z]', token) and not token in stopwords.words('english'):
filtered_tokens.append(re.sub(r'[^\w\s]','',token))
stems = [stemmer.stem(t) for t in filtered_tokens]
return stems
#return filtered_tokens
token_dict = {}
for fileid in inaug_corpus.fileids():
token_dict[fileid] = inaug_corpus.raw(fileid)
# Construct a bag of words matrix.
# This will lowercase everything, and ignore all punctuation by default.
# It will also remove stop words.
vectorizer = CountVectorizer(lowercase=True,
tokenizer=tokenize_and_stem,
stop_words='english')
dtm = vectorizer.fit_transform(token_dict.values()).toarray()
```
**TF - IDF**
TF-IDF (term frequency-inverse document frequency) is a numerical statistics that is intended to reflect how important a word is to a document in a collection or corpus. It is often used as a weighting factor in information retrieval, text mining, and user modeling. The TF-IDF value increases proportionally to the number of times a word appears in the document, but is offset by the frequency of the word in the corpus, which helps to adjust for the fact that some words appear more frequently in general.
$$
\begin{aligned}
\mbox{TF}(t) &=\frac{\mbox{Number of times term $t$ appears in a document}}{\mbox{Total number of terms in the document}}\\
\mbox{IDF}(t) &=\log{\frac{\mbox{Total number of documents}}{\mbox{Number of documents with term $t$ in it}}}\\
\mbox{TF-IDF}(t) &=\mbox{TF}(t)\times\mbox{IDF}(t)
\end{aligned}
$$
```
vectorizer = TfidfVectorizer(tokenizer=tokenize_and_stem,
stop_words='english',
decode_error='ignore')
tfidf_matrix = vectorizer.fit_transform(token_dict.values())
# The above line can take some time (about < 60 seconds)
feature_names = vectorizer.get_feature_names()
num_samples, num_features=tfidf_matrix.shape
print "num_samples: %d, num_features: %d" %(num_samples,num_features)
num_clusters=10
## Checking
print('first term: ' + feature_names[0])
print('last term: ' + feature_names[len(feature_names) - 1])
for i in range(0, 4):
print('random term: ' +
feature_names[randint(1,len(feature_names) - 2)] )
def top_tfidf_feats(row, features, top_n=20):
topn_ids = np.argsort(row)[::-1][:top_n]
top_feats = [(features[i], row[i]) for i in topn_ids]
df = pd.DataFrame(top_feats, columns=['features', 'score'])
return df
def top_feats_in_doc(X, features, row_id, top_n=25):
row = np.squeeze(X[row_id].toarray())
return top_tfidf_feats(row, features, top_n)
print inaug_files[2:3]
print top_feats_in_doc(tfidf_matrix, feature_names, 3, 10)
d =3
top_tfidf = top_feats_in_doc(tfidf_matrix, feature_names, d, 10)
def plot_tfidf_classfeats_h(df, doc):
''' Plot the data frames returned by the function tfidf_feats_in_doc. '''
x = np.arange(len(df))
fig = plt.figure(figsize=(6, 9), facecolor="w")
ax = fig.add_subplot(1, 1, 1)
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.set_frame_on(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
ax.set_xlabel("Tf-Idf Score", labelpad=16, fontsize=14)
ax.set_title(doc, fontsize=16)
ax.ticklabel_format(axis='x', style='sci', scilimits=(-2,2))
ax.barh(x, df.score, align='center', color='#3F5D7D')
ax.set_yticks(x)
ax.set_ylim([-1, x[-1]+1])
yticks = ax.set_yticklabels(df.features)
plt.subplots_adjust(bottom=0.09, right=0.97, left=0.15, top=0.95, wspace=0.52)
plt.show()
plot_tfidf_classfeats_h(top_tfidf, inaug_files[(d-1):d])
```
<a id="step3-1"></a>
## Step 3: Visualization
Data visualization is an integral part of the data science workflow. In the following, we use simple data visualizations to reveal some interesting patterns in our data.
### 1 . Word cloud
```
array_for_word_cloud = []
word_count_array = dtm.sum(0)
for idx, word in enumerate(feature_names):
array_for_word_cloud.append((word,word_count_array[idx]))
def random_color_func(word=None, font_size=None,
position=None, orientation=None, font_path=None, random_state=None):
h = int(360.0 * 45.0 / 255.0)
s = int(100.0 * 255.0 / 255.0)
l = int(100.0 * float(random_state.randint(60, 120)) / 255.0)
return "hsl({}, {}%, {}%)".format(h, s, l)
array_for_word_cloud = dict(array_for_word_cloud)
wordcloud = WordCloud(background_color='white',
width=1600,
height=1000,
color_func=random_color_func).generate_from_frequencies(array_for_word_cloud)
%matplotlib inline
plt.imshow(wordcloud)
plt.axis('off')
plt.show()
```
Let us try making it interactive.
```
word_cloud_dict = {}
counter = 0
for fileid in inaug_corpus.fileids():
row = dtm[counter,:]
word_cloud_dict[fileid] = []
for idx, word in enumerate(feature_names):
word_cloud_dict[fileid].append((word,row[idx]))
counter += 1
def f_wordclouds(t):
df_dict = dict(word_cloud_dict[t])
wordcloud = WordCloud(background_color='white',
color_func=random_color_func).generate_from_frequencies(df_dict)
plt.figure(figsize=(3, 3), dpi=100)
plt.imshow(wordcloud)
plt.axis('off')
plt.show()
interactive_plot_1 = interactive(f_wordclouds, t=widgets.Dropdown(options=inaug_corpus.fileids(),description='text1'))
interactive_plot_2 = interactive(f_wordclouds, t=widgets.Dropdown(options=inaug_corpus.fileids(),description='text2'))
# Define the layout here.
hbox_layout = Layout(display='flex', flex_flow='row', justify_content='space-between', align_items='center')
vbox_layout = Layout(display='flex', flex_flow='column', justify_content='space-between', align_items='center')
%matplotlib inline
HBox([interactive_plot_1,interactive_plot_2])
```
<a id="step3-3"></a>
### 2. Joy plot
The following joy plot allows us to compare the frequencies of the top 10 most frequent words in individual speeches.
```
joy_df = pd.DataFrame(dtm, columns=feature_names)
selected_words = joy_df.sum(0).sort_values(ascending=False).head(10).index
print(selected_words)
%matplotlib inline
plt.rcParams['axes.facecolor'] = 'white'
fig, axes = joypy.joyplot(joy_df.loc[:,selected_words],
range_style='own', grid="y",
colormap=cm.YlGn_r,
title="Top 10 word distribution")
```
<a id="step4"></a>
## Step 4: Sentence analysis
In the previous sections, we focused on word-level distributions in inaugural speeches. Next, we will use sentences as our units of analysis, since they are natural languge units for organizing thoughts and ideas.
For simpler visualization, we chose a subset of better known presidents or presidential candidates on whom to focus our analysis.
```
filter_comparison=["DonaldJTrump","JohnMcCain", "GeorgeBush", "MittRomney", "GeorgeWBush",
"RonaldReagan","AlbertGore,Jr", "HillaryClinton","JohnFKerry",
"WilliamJClinton","HarrySTruman", "BarackObama", "LyndonBJohnson",
"GeraldRFord", "JimmyCarter", "DwightDEisenhower", "FranklinDRoosevelt",
"HerbertHoover","JohnFKennedy","RichardNixon","WoodrowWilson",
"AbrahamLincoln", "TheodoreRoosevelt", "JamesGarfield",
"JohnQuincyAdams", "UlyssesSGrant", "ThomasJefferson",
"GeorgeWashington", "WilliamHowardTaft", "AndrewJackson",
"WilliamHenryHarrison", "JohnAdams"]
```
### Nomination speeches
Next, we first look at the *nomination acceptance speeches* at major parties' national conventions.
Following the same procedure in [step 1](#step1), we will use `pandas` dataframe to store the nomination speech sentences. For each sentence in a speech (`fileid`), we find out the name of the president (`president`) and the term (`term`), and also calculated the number of words in each sentence as *sentence length* (`word_count`) by using a self-defined function `word_count`.
```
def word_count(string):
tokens = [word for word in nltk.word_tokenize(string)]
counter = 0
for token in tokens:
if re.search('[a-zA-Z]', token):
counter += 1
return counter
nomin_corpus = PlaintextCorpusReader("../data/nomimations", ".*\.txt")
nomin_files = nomin_corpus.fileids()
nomin_file_df = pd.DataFrame(columns=["file_id","president","term","raw_text"])
for fileid in nomin_corpus.fileids():
nomin_file_df = nomin_file_df.append({"file_id": fileid,
"president": fileid[0:fileid.find("-")][5:],
"term": fileid.split("-")[-1][0],
"raw_text": nomin_corpus.raw(fileid)}, ignore_index=True)
sentences = []
for row in nomin_file_df.itertuples():
for sentence in sent_tokenize(row[4]):
sentences.append({"file_id": row[1],
"president": row[2],
"term": row[3],
"sentence": sentence})
nomin_sen_df = pd.DataFrame(sentences, columns=["file_id","president","term","sentence"])
nomin_sen_df["word_count"] = [word_count(sentence) for sentence in nomin_sen_df["sentence"]]
```
#### First term
For comparison between presidents, we first limit our attention to speeches for the first terms of former U.S. presidents. We noticed that a number of presidents have very short sentences in their nomination acceptance speeches.
```
filtered_nomin_sen_df = nomin_sen_df.loc[(nomin_sen_df["president"].isin(filter_comparison))&(nomin_sen_df["term"]=='1')]
filtered_nomin_sen_df = filtered_nomin_sen_df.reset_index()
filtered_nomin_sen_df['group_mean'] = filtered_nomin_sen_df.groupby('president')['word_count'].transform('mean')
filtered_nomin_sen_df = filtered_nomin_sen_df.sort_values('group_mean', ascending=False)
%matplotlib inline
plt.figure(figsize=(20, 10))
gs = gridspec.GridSpec(1, 2, width_ratios=[1, 1])
plt.subplot(gs[0])
sns.set(font_scale=1.5)
sns.set_style('whitegrid')
sns.swarmplot(y='president', x='word_count',
data=filtered_nomin_sen_df,
palette = "Set3",
size=2.5,
orient='h'). set(xlabel='Number of words in a sentence')
plt.title("Swarm plot")
plt.subplot(gs[1])
sns.set(font_scale=1.5)
sns.set_style('whitegrid')
sns.violinplot(y='president', x='word_count',
data=filtered_nomin_sen_df,
palette = "Set3", cut = 3,
width=1.5, saturation=0.8, linewidth= 0.3, scale="count",
orient='h').set(xlabel='Number of words in a sentence')
plt.title("Violin plot")
plt.xlim(-3, 350)
plt.tight_layout()
```
#### Second term
```
filtered_nomin_sen_df = nomin_sen_df.loc[(nomin_sen_df["president"].isin(filter_comparison))&(nomin_sen_df["term"]=='2')]
filtered_nomin_sen_df = filtered_nomin_sen_df.reset_index()
filtered_nomin_sen_df['group_mean'] = filtered_nomin_sen_df.groupby('president')['word_count'].transform('mean')
filtered_nomin_sen_df = filtered_nomin_sen_df.sort_values('group_mean', ascending=False)
%matplotlib inline
plt.figure(figsize=(20, 10))
gs = gridspec.GridSpec(1, 2, width_ratios=[1, 1])
plt.subplot(gs[0])
sns.set(font_scale=1.5)
sns.set_style('whitegrid')
sns.swarmplot(y='president', x='word_count',
data=filtered_nomin_sen_df,
palette = "Set3",
size=2.5,
orient='h'). set(xlabel='Number of words in a sentence')
plt.title("Swarm plot")
plt.subplot(gs[1])
sns.violinplot(y='president', x='word_count',
data=filtered_nomin_sen_df,
palette = "Set3", cut = 3,
width=1.5, saturation=0.8, linewidth= 0.3, scale="count",
orient='h').set(xlabel='Number of words in a sentence')
plt.title("Violin plot")
plt.xlim(-3, 350)
plt.tight_layout()
```
### Inaugural speeches
We notice that the sentences in inaugural speeches are longer than those in nomination acceptance speeches.
```
inaug_file_df = pd.DataFrame(columns=["file_id","president","term","raw_text"])
for fileid in inaug_corpus.fileids():
inaug_file_df = inaug_file_df.append({"file_id": fileid,
"president": fileid[0:fileid.find("-")][5:],
"term": fileid.split("-")[-1][0],
"raw_text": inaug_corpus.raw(fileid)}, ignore_index=True)
sentences = []
for row in inaug_file_df.itertuples():
for sentence in sent_tokenize(row[4]):
sentences.append({"file_id": row[1],
"president": row[2],
"term": row[3],
"sentence": sentence})
inaug_sen_df = pd.DataFrame(sentences, columns=["file_id","president","term","sentence"])
wordCounts = [word_count(sentence) for sentence in inaug_sen_df["sentence"]]
inaug_sen_df["word_count"] = wordCounts
filtered_inaug_sen_df = inaug_sen_df.loc[(inaug_sen_df["president"].isin(filter_comparison))&(inaug_sen_df["term"]=='1')]
filtered_inaug_sen_df = filtered_inaug_sen_df.reset_index()
filtered_inaug_sen_df['group_mean'] = filtered_inaug_sen_df.groupby('president')['word_count'].transform('mean')
filtered_inaug_sen_df = filtered_inaug_sen_df.sort_values('group_mean', ascending=False)
%matplotlib inline
plt.figure(figsize=(20, 10))
gs = gridspec.GridSpec(1, 2, width_ratios=[1, 1])
plt.subplot(gs[0])
sns.set(font_scale=1.5)
sns.set_style('whitegrid')
sns.swarmplot(y='president', x='word_count',
data=filtered_inaug_sen_df,
palette = "Set3",
size=2.5,
orient='h'). set(xlabel='Number of words in a sentence')
plt.title("Swarm plot")
plt.subplot(gs[1])
sns.set(font_scale=1.5)
sns.set_style('whitegrid')
sns.violinplot(y='president', x='word_count',
data=filtered_inaug_sen_df,
palette = "Set3", cut = 3,
width=1.5, saturation=0.8, linewidth= 0.3, scale="count",
orient='h').set(xlabel='Number of words in a sentence')
plt.title("Violin plot")
plt.xlim(-3, 350)
plt.tight_layout()
```
<a id="step5"></a>
## Step 5: NRC emotion analsis
For each extracted sentence, we apply sentiment analysis using [NRC sentiment lexion](http://saifmohammad.com/WebPages/NRC-Emotion-Lexicon.htm). "The NRC Emotion Lexicon is a list of English words and their associations with eight basic emotions (anger, fear, anticipation, trust, surprise, sadness, joy, and disgust) and two sentiments (negative and positive). The annotations were manually done by crowdsourcing."
```
wordList = defaultdict(list)
emotionList = defaultdict(list)
with open('../data/NRC-emotion-lexicon-wordlevel-alphabetized-v0.92.txt', 'r') as f:
reader = csv.reader(f, delimiter='\t')
headerRows = [i for i in range(0, 46)]
for row in headerRows:
next(reader)
for word, emotion, present in reader:
if int(present) == 1:
#print(word)
wordList[word].append(emotion)
emotionList[emotion].append(word)
from __future__ import division # for Python 2.7 only
def generate_emotion_count(string):
emoCount = Counter()
tokens = [word for word in nltk.word_tokenize(string)]
counter = 0
for token in tokens:
token = token.lower()
if re.search('[a-zA-Z]', token):
counter += 1
emoCount += Counter(wordList[token])
for emo in emoCount:
emoCount[emo]/=counter
return emoCount
emotionCounts = [generate_emotion_count(sentence) for sentence in nomin_sen_df["sentence"]]
nomin_sen_df_with_emotion = pd.concat([nomin_sen_df, pd.DataFrame(emotionCounts).fillna(0)], axis=1)
emotionCounts = [generate_emotion_count(sentence) for sentence in inaug_sen_df["sentence"]]
inaug_sen_df_with_emotion = pd.concat([inaug_sen_df, pd.DataFrame(emotionCounts).fillna(0)], axis=1)
inaug_sen_df_with_emotion.sample(n=3)
```
### Sentence length variation over the course of the speech, with emotions.
How our presidents (or candidates) alternate between long and short sentences and how they shift between different sentiments in their speeches. It is interesting to note that some presidential candidates' speech are more colorful than others. Here we used the same color theme as in the movie "Inside Out."
```
def make_rgb_transparent(color_name, bg_color_name, alpha):
from matplotlib import colors
rgb = colors.colorConverter.to_rgb(color_name)
bg_rgb = colors.colorConverter.to_rgb(bg_color_name)
return [alpha * c1 + (1 - alpha) * c2
for (c1, c2) in zip(rgb, bg_rgb)]
def f_plotsent_len(InDf, InTerm, InPresident):
import numpy as np
import pylab as pl
from matplotlib import colors
from math import sqrt
from matplotlib import collections as mc
col_use={"zero":"lightgray",
"anger":"#ee0000",
"anticipation":"#ffb90f",
"disgust":"#66cd00",
"fear":"blueviolet",
"joy":"#eead0e",
"sadness":"#1874cd",
"surprise":"#ffb90f",
"trust":"#ffb90f",
"negative":"black",
"positive":"#eead0e"}
InDf["top_emotion"] = InDf.loc[:,'anger':'trust'].idxmax(axis=1)
InDf["top_emotion_value"] = InDf.loc[:,'anger':'trust'].max(axis=1)
InDf.loc[InDf["top_emotion_value"] < 0.05, "top_emotion"] = "zero"
InDf.loc[InDf["top_emotion_value"] < 0.05, "top_emotion_value"] = 1
tempDf = InDf.loc[(InDf["president"]==InPresident)&(InDf["term"]==InTerm)]
pt_col_use = []
lines = []
for i in tempDf.index:
pt_col_use.append(make_rgb_transparent(col_use[tempDf.at[i,"top_emotion"]],
"white",
sqrt(sqrt(tempDf.at[i,"top_emotion_value"]))))
lines.append([(i,0),(i,tempDf.at[i,"word_count"])])
%matplotlib inline
lc = mc.LineCollection(lines, colors=pt_col_use, linewidths=min(5,300/len(tempDf.index)))
fig, ax = pl.subplots() #figsize=(15, 6)
ax.add_collection(lc)
ax.autoscale()
ax.axis('off')
plt.title(InPresident, fontsize=30)
plt.tight_layout()
plt.show()
f_plotsent_len(nomin_sen_df_with_emotion, '1', 'HillaryClinton')
f_plotsent_len(nomin_sen_df_with_emotion, '1', 'DonaldJTrump')
f_plotsent_len(nomin_sen_df_with_emotion, '1', 'BarackObama')
f_plotsent_len(nomin_sen_df_with_emotion, '1', 'GeorgeWBush')
```
### Clustering of emotions
```
sns.set(font_scale=1.3)
sns.clustermap(inaug_sen_df_with_emotion.loc[:,'anger':'trust'].corr(),
figsize=(6,7))
```
| true |
code
| 0.748893 | null | null | null | null |
|
# Intro to Python!
Stuart Geiger and Yu Feng for The Hacker Within
# Contents
## 1. Installing Python
## 2. The Language
- Expressions
- List, Tuple and Dictionary
- Strings
- Functions
## 3. Example: Word Frequency Analysis with Python
- Reading text files
- Geting and using python packages : wordcloud
- Histograms
- Exporting data as text files
## 1. Installing Python:
- Easy way : with a Python distribution, anaconda: https://www.continuum.io/downloads
- Hard way : install python and all dependencies yourself
- Super hard way : compile everything from scratch
### Three Python user interfaces
#### Python Shell `python`
```
[yfeng1@waterfall ~]$ python
Python 2.7.12 (default, Sep 29 2016, 13:30:34)
[GCC 6.2.1 20160916 (Red Hat 6.2.1-2)] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>>
```
#### Jupyter Notebook (in a browser, like this)
#### IDEs: PyCharm, Spyder, etc.
We use Jupyter Notebook here.
Jupyter Notebook is included in the Anaconda distribution.
# Expressions
```
2 + 3
2 / 3
2 * 3
2 ** 3
```
# Variables
```
num = 2 ** 3
print(num)
num
type(num)
name = "The Hacker Within"
type(name)
name + 8
name + str(8)
```
# Lists
```
num_list = [0,1,2,3,4,5,6,7,8]
print(num_list)
type(num_list)
num_list[3]
num_list[3] = 10
print(num_list)
```
Appending new items to a list
```
num_list.append(3)
print(num_list)
```
# Loops and iteration
```
for num in num_list:
print(num)
for num in num_list:
print(num, num * num)
num_list.append("LOL")
print(num_list)
```
## If / else conditionals
```
for num in num_list:
if type(num) is int or type(num) is float:
print(num, num * num)
else:
print("ERROR!", num, "is not an int")
```
## Functions
```
def process_list(input_list):
for num in input_list:
if type(num) is int or type(num) is float:
print(num, num * num)
else:
print("ERROR!", num, "is not an int")
process_list(num_list)
process_list([1,3,4,14,1,9])
```
## Dictionaries
Store a key : value relationship
```
yearly_value = {2001: 10, 2002: 14, 2003: 18, 2004: 20}
print(yearly_value)
yearly_value = {}
yearly_value[2001] = 10
yearly_value[2002] = 14
yearly_value[2003] = 18
yearly_value[2004] = 20
print(yearly_value)
yearly_value.pop(2001)
yearly_value
yearly_value[2001] = 10213
```
You can iterate through dictionaries too:
```
for key, value in yearly_value.items():
print(key, value)
for key, value in yearly_value.items():
print(key, value * 1.05)
```
# Strings
We have seen strings a few times.
String literals can be defined with single or double quotation marks. Triple quotes allow multi-line strings.
```
name = "the hacker within"
name_long = """
~*~*~*~*~*~*~*~*~*~*~
THE HACKER WITHIN
~*~*~*~*~*~*~*~*~*~*~
"""
print(name)
print(name_long)
```
Strings have many built in methods:
```
print(name.upper())
print(name.split())
print(name.upper().split())
```
Strings are also a kind of list, and substrings can be accessed with string[start,end]
```
print(name[4:10])
print(name[4:])
print(name[:4])
count = 0
for character in name:
print(count, character)
count = count + 1
print(name.find('hacker'))
print(name[name.find('hacker'):])
```
# Functions
```
def square_num(num):
return num * num
print(square_num(10))
print(square_num(9.1))
print(square_num(square_num(10)))
def yearly_adjustment(yearly_dict, adjustment):
for key, value in yearly_dict.items():
print(key, value * adjustment)
yearly_adjustment(yearly_value, 1.05)
```
We can expand on this a bit, adding some features:
```
def yearly_adjustment(yearly_dict, adjustment, print_values = False):
adjusted_dict = {}
for key, value in yearly_value.items():
if print_values is True:
print(key, value * adjustment)
adjusted_dict[key] = value * adjustment
return adjusted_dict
adjusted_yearly = yearly_adjustment(yearly_value, 1.05)
adjusted_yearly = yearly_adjustment(yearly_value, 1.05, print_values = True)
adjusted_yearly
```
# Example: word counts
If you begin a line in a notebook cell with ```!```, it will execute a bash command as if you typed it in the terminal. We will use this to download a list of previous THW topics with the curl program.
```
!curl -o thw.txt http://stuartgeiger.com/thw.txt
# and that's how it works, that's how you get to curl
with open('thw.txt') as f:
text = f.read()
text
words = text.split()
lines = text.split("\n")
lines[0:5]
```
But there is an error! R always appears as "RR" -- so we will replace "RR" with "R"
```
text.replace("RR", "R")
text = text.replace("RR", "R")
words = text.split()
lines = text.split("\n")
lines[0:5]
```
### Wordcloud library
```
!pip install wordcloud
from wordcloud import WordCloud
wordcloud = WordCloud()
wordcloud.generate(text)
wordcloud.to_image()
wordcloud = WordCloud(width=800, height=300, prefer_horizontal=1, stopwords=None)
wordcloud.generate(text)
wordcloud.to_image()
```
## Freqency counts
```
freq_dict = {}
for word in words:
if word in freq_dict:
freq_dict[word] = freq_dict[word] + 1
else:
freq_dict[word] = 1
print(freq_dict)
```
A better way to do this is:
```
freq_dict = {}
for word in words:
freq_dict[word] = freq_dict.get(word, 0) + 1
print(freq_dict)
```
# Outputting to files
Let's start from a loop that prints the values to the screen
```
for word, freq in sorted(freq_dict.items()):
line = word + "\t" + str(freq)
print(line)
```
Then expand this to writing a file object:
```
with open("freq_dict_thw.csv", 'w') as f:
for word, freq in sorted(freq_dict.items()):
line = word + ", " + str(freq) + "\n"
f.write(line)
!head -10 freq_dict_thw.csv
```
| true |
code
| 0.512571 | null | null | null | null |
|
# Vanilla Recurrent Neural Network
<br>
Character level implementation of vanilla recurrent neural network
## Import dependencies
```
import numpy as np
import matplotlib.pyplot as plt
```
## Parameters Initialization
```
def initialize_parameters(hidden_size, vocab_size):
'''
Returns:
parameters -- a tuple of network parameters
adagrad_mem_vars -- a tuple of mem variables required for adagrad update
'''
Wxh = np.random.randn(hidden_size, vocab_size) * 0.01
Whh = np.random.randn(hidden_size, hidden_size) * 0.01
Why = np.random.randn(vocab_size, hidden_size) * 0.01
bh = np.zeros([hidden_size, 1])
by = np.zeros([vocab_size, 1])
mWxh, mWhh, mWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
mbh, mby = np.zeros_like(bh), np.zeros_like(by) # memory variables for Adagrad
parameter = (Wxh, Whh, Why, bh, by)
adagrad_mem_vars = (mWxh, mWhh, mWhy, mbh, mby)
return (parameter, adagrad_mem_vars)
```
## Forward Propogation
```
def softmax(X):
t = np.exp(X)
return t / np.sum(t, axis=0)
def forward_propogation(X, parameters, seq_length, hprev):
'''
Implement the forward propogation in the network
Arguments:
X -- input to the network
parameters -- a tuple containing weights and biases of the network
seq_length -- length of sequence of input
hprev -- previous hidden state
Returns:
caches -- tuple of activations and hidden states for each step of forward prop
'''
caches = {}
caches['h0'] = np.copy(hprev)
Wxh, Whh, Why, bh, by = parameters
for i in range(seq_length):
x = X[i].reshape(vocab_size, 1)
ht = np.tanh(np.dot(Whh, caches['h' + str(i)]) + np.dot(Wxh, x) + bh)
Z = np.dot(Why, ht) + by
A = softmax(Z)
caches['A' + str(i+1)] = A
caches['h' + str(i+1)] = ht
return caches
```
## Cost Computation
```
def compute_cost(Y, caches):
"""
Implement the cost function for the network
Arguments:
Y -- true "label" vector, shape (vocab_size, number of examples)
caches -- tuple of activations and hidden states for each step of forward prop
Returns:
cost -- cross-entropy cost
"""
seq_length = len(caches) // 2
cost = 0
for i in range(seq_length):
y = Y[i].reshape(vocab_size, 1)
cost += - np.sum(y * np.log(caches['A' + str(i+1)]))
return np.squeeze(cost)
```
## Backward Propogation
```
def backward_propogation(X, Y, caches, parameters):
'''
Implement Backpropogation
Arguments:
Al -- Activations of last layer
Y -- True labels of data
caches -- tuple containing values of `A` and `h` for each char in forward prop
parameters -- tuple containing parameters of the network
Returns
grads -- tuple containing gradients of the network parameters
'''
Wxh, Whh, Why, bh, by = parameters
dWhh, dWxh, dWhy = np.zeros_like(Whh), np.zeros_like(Wxh), np.zeros_like(Why)
dbh, dby = np.zeros_like(bh), np.zeros_like(by)
dhnext = np.zeros_like(caches['h0'])
seq_length = len(caches) // 2
for i in reversed(range(seq_length)):
y = Y[i].reshape(vocab_size, 1)
x = X[i].reshape(vocab_size, 1)
dZ = np.copy(caches['A' + str(i+1)]) - y
dWhy += np.dot(dZ, caches['h' + str(i+1)].T)
dby += dZ
dht = np.dot(Why.T, dZ) + dhnext
dhraw = dht * (1 - caches['h' + str(i+1)] * caches['h' + str(i+1)])
dbh += dhraw
dWhh += np.dot(dhraw, caches['h' + str(i)].T)
dWxh += np.dot(dhraw, x.T)
dhnext = np.dot(Whh.T, dhraw)
for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients
grads = (dWxh, dWhh, dWhy, dbh, dby)
return grads
```
## Parameters Update
```
def update_parameters(parameters, grads, adagrad_mem_vars, learning_rate):
'''
Update parameters of the network using Adagrad update
Arguments:
paramters -- tuple containing weights and biases of the network
grads -- tuple containing the gradients of the parameters
learning_rate -- rate of adagrad update
Returns
parameters -- tuple containing updated parameters
'''
a = np.copy(parameters[0])
for param, dparam, mem in zip(parameters, grads, adagrad_mem_vars):
mem += dparam * dparam
param -= learning_rate * dparam / np.sqrt(mem + 1e-8) # adagrad update
return (parameters, adagrad_mem_vars)
```
## Sample text from model
```
def print_sample(ht, seed_ix, n, parameters):
"""
Samples a sequence of integers from the model.
Arguments
ht -- memory state
seed_ix --seed letter for first time step
n -- number of chars to extract
parameters -- tuple containing network weights and biases
"""
Wxh, Whh, Why, bh, by = parameters
x = np.eye(vocab_size)[seed_ix].reshape(vocab_size, 1)
ixes = []
for t in range(n):
ht = np.tanh(np.dot(Wxh, x) + np.dot(Whh, ht) + bh)
y = np.dot(Why, ht) + by
p = np.exp(y) / np.sum(np.exp(y))
ix = np.random.choice(range(vocab_size), p=p.ravel()) ### why not argmax of p??
x = np.eye(vocab_size)[ix].reshape(vocab_size, 1)
ixes.append(ix)
txt = ''.join(ix_to_char[ix] for ix in ixes)
print('----\n %s \n----' % txt)
def get_one_hot(p, char_to_ix, data, vocab_size):
'''
Gets indexes of chars of `seq_length` from `data`, returns them in one hot representation
'''
inputs = [char_to_ix[ch] for ch in data[p:p+seq_length]]
targets = [char_to_ix[ch] for ch in data[p+1:p+seq_length+1]]
X = np.eye(vocab_size)[inputs]
Y = np.eye(vocab_size)[targets]
return X, Y
```
## Model
```
def Model(data, seq_length, lr, char_to_ix, ix_to_char, num_of_iterations):
'''
Train RNN model and return trained parameters
'''
parameters, adagrad_mem_vars = initialize_parameters(hidden_size, vocab_size)
costs = []
n, p = 0, 0
smooth_loss = -np.log(1.0 / vocab_size) * seq_length
while n < num_of_iterations:
if p + seq_length + 1 >= len(data) or n == 0:
hprev = np.zeros((hidden_size, 1)) # reset RNN memory
p = 0 # go from start of data
X, Y = get_one_hot(p, char_to_ix, data, vocab_size)
caches = forward_propogation(X, parameters, seq_length, hprev)
cost = compute_cost(Y, caches)
grads = backward_propogation(X, Y, caches, parameters)
parameters, adagrad_mem_vars = update_parameters(parameters, grads, adagrad_mem_vars, lr)
smooth_loss = smooth_loss * 0.999 + cost * 0.001
if n % 1000 == 0:
print_sample(hprev, char_to_ix['a'], 200, parameters)
print('Iteration: %d -- Cost: %0.3f' % (n, smooth_loss))
costs.append(cost)
hprev = caches['h' + str(seq_length)]
n+=1
p+=seq_length
plt.plot(costs)
return parameters
```
## Implementing the model on a text
```
data = open('data/text-data.txt', 'r').read() # read a text file
chars = list(set(data)) # vocabulary
data_size, vocab_size = len(data), len(chars)
print ('data has %d characters, %d unique.' % (data_size, vocab_size))
char_to_ix = { ch:i for i,ch in enumerate(chars) } # maps char to it's index in vocabulary
ix_to_char = { i:ch for i,ch in enumerate(chars) } # maps index in vocabular to corresponding character
# hyper-parameters
learning_rate = 0.1
hidden_size = 100
seq_length = 25
num_of_iterations = 20000
parameters = Model(data, seq_length, learning_rate, char_to_ix, ix_to_char, num_of_iterations)
```
| true |
code
| 0.725509 | null | null | null | null |
|
# Sonar - Decentralized Model Training Simulation (local)
DISCLAIMER: This is a proof-of-concept implementation. It does not represent a remotely product ready implementation or follow proper conventions for security, convenience, or scalability. It is part of a broader proof-of-concept demonstrating the vision of the OpenMined project, its major moving parts, and how they might work together.
# Getting Started: Installation
##### Step 1: install IPFS
- https://ipfs.io/docs/install/
##### Step 2: Turn on IPFS Daemon
Execute on command line:
> ipfs daemon
##### Step 3: Install Ethereum testrpc
- https://github.com/ethereumjs/testrpc
##### Step 4: Turn on testrpc with 1000 initialized accounts (each with some money)
Execute on command line:
> testrpc -a 1000
##### Step 5: install openmined/sonar and all dependencies (truffle)
##### Step 6: Locally Deploy Smart Contracts in openmined/sonar
From the OpenMined/Sonar repository root run
> truffle compile
> truffle migrate
you should see something like this when you run migrate:
```
Using network 'development'.
Running migration: 1_initial_migration.js
Deploying Migrations...
Migrations: 0xf06039885460a42dcc8db5b285bb925c55fbaeae
Saving successful migration to network...
Saving artifacts...
Running migration: 2_deploy_contracts.js
Deploying ConvertLib...
ConvertLib: 0x6cc86f0a80180a491f66687243376fde45459436
Deploying ModelRepository...
ModelRepository: 0xe26d32efe1c573c9f81d68aa823dcf5ff3356946
Linking ConvertLib to MetaCoin
Deploying MetaCoin...
MetaCoin: 0x6d3692bb28afa0eb37d364c4a5278807801a95c5
```
The address after 'ModelRepository' is something you'll need to copy paste into the code
below when you initialize the "ModelRepository" object. In this case the address to be
copy pasted is `0xe26d32efe1c573c9f81d68aa823dcf5ff3356946`.
##### Step 7: execute the following code
# The Simulation: Diabetes Prediction
In this example, a diabetes research center (Cure Diabetes Inc) wants to train a model to try to predict the progression of diabetes based on several indicators. They have collected a small sample (42 patients) of data but it's not enough to train a model. So, they intend to offer up a bounty of $5,000 to the OpenMined commmunity to train a high quality model.
As it turns out, there are 400 diabetics in the network who are candidates for the model (are collecting the relevant fields). In this simulation, we're going to faciliate the training of Cure Diabetes Inc incentivizing these 400 anonymous contributors to train the model using the Ethereum blockchain.
Note, in this simulation we're only going to use the sonar and syft packages (and everything is going to be deployed locally on a test blockchain). Future simulations will incorporate mine and capsule for greater anonymity and automation.
### Imports and Convenience Functions
```
import warnings
import numpy as np
import phe as paillier
from sonar.contracts import ModelRepository,Model
from syft.he.Paillier import KeyPair
from syft.nn.linear import LinearClassifier
import numpy as np
from sklearn.datasets import load_diabetes
def get_balance(account):
return repo.web3.fromWei(repo.web3.eth.getBalance(account),'ether')
warnings.filterwarnings('ignore')
```
### Setting up the Experiment
```
# for the purpose of the simulation, we're going to split our dataset up amongst
# the relevant simulated users
diabetes = load_diabetes()
y = diabetes.target
X = diabetes.data
validation = (X[0:5],y[0:5])
anonymous_diabetes_users = (X[6:],y[6:])
# we're also going to initialize the model trainer smart contract, which in the
# real world would already be on the blockchain (managing other contracts) before
# the simulation begins
# ATTENTION: copy paste the correct address (NOT THE DEFAULT SEEN HERE) from truffle migrate output.
repo = ModelRepository('0xb0f99be3d5c858efaabe19bcc54405f3858d48bc', ipfs_host='localhost', web3_host='localhost') # blockchain hosted model repository
# we're going to set aside 10 accounts for our 42 patients
# Let's go ahead and pair each data point with each patient's
# address so that we know we don't get them confused
patient_addresses = repo.web3.eth.accounts[1:10]
anonymous_diabetics = list(zip(patient_addresses,
anonymous_diabetes_users[0],
anonymous_diabetes_users[1]))
# we're going to set aside 1 account for Cure Diabetes Inc
cure_diabetes_inc = repo.web3.eth.accounts[1]
```
## Step 1: Cure Diabetes Inc Initializes a Model and Provides a Bounty
```
pubkey,prikey = KeyPair().generate(n_length=1024)
diabetes_classifier = LinearClassifier(desc="DiabetesClassifier",n_inputs=10,n_labels=1)
initial_error = diabetes_classifier.evaluate(validation[0],validation[1])
diabetes_classifier.encrypt(pubkey)
diabetes_model = Model(owner=cure_diabetes_inc,
syft_obj = diabetes_classifier,
bounty = 1,
initial_error = initial_error,
target_error = 10000
)
model_id = repo.submit_model(diabetes_model)
```
## Step 2: An Anonymous Patient Downloads the Model and Improves It
```
model_id
model = repo[model_id]
diabetic_address,input_data,target_data = anonymous_diabetics[0]
repo[model_id].submit_gradient(diabetic_address,input_data,target_data)
```
## Step 3: Cure Diabetes Inc. Evaluates the Gradient
```
repo[model_id]
old_balance = get_balance(diabetic_address)
print(old_balance)
new_error = repo[model_id].evaluate_gradient(cure_diabetes_inc,repo[model_id][0],prikey,pubkey,validation[0],validation[1])
new_error
new_balance = get_balance(diabetic_address)
incentive = new_balance - old_balance
print(incentive)
```
## Step 4: Rinse and Repeat
```
model
for i,(addr, input, target) in enumerate(anonymous_diabetics):
try:
model = repo[model_id]
# patient is doing this
model.submit_gradient(addr,input,target)
# Cure Diabetes Inc does this
old_balance = get_balance(addr)
new_error = model.evaluate_gradient(cure_diabetes_inc,model[i+1],prikey,pubkey,validation[0],validation[1],alpha=2)
print("new error = "+str(new_error))
incentive = round(get_balance(addr) - old_balance,5)
print("incentive = "+str(incentive))
except:
"Connection Reset"
```
| true |
code
| 0.542682 | null | null | null | null |
|
```
!pip install neural-tangents
```
## Imports
```
import time
import itertools
import numpy.random as npr
import jax.numpy as np
from jax.config import config
from jax import jit, grad, random
from jax.nn import log_softmax
from jax.experimental import optimizers
import jax.experimental.stax as jax_stax
import neural_tangents.stax as nt_stax
import neural_tangents
from PIL import Image
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torchvision import transforms, datasets
from torchvision.datasets import FashionMNIST
def data_to_numpy(dataloader):
X = []
y = []
for batch_id, (cur_X, cur_y) in enumerate(dataloader):
X.extend(cur_X.numpy())
y.extend(cur_y.numpy())
X = np.asarray(X)
y = np.asarray(y)
return X, y
def _one_hot(x, k, dtype=np.float32):
"""Create a one-hot encoding of x of size k."""
return np.array(x[:, None] == np.arange(k), dtype)
def cifar_10():
torch.manual_seed(0)
D = 32
num_classes = 10
torch.manual_seed(0)
if torch.cuda.is_available():
device = torch.device('cuda:0')
else:
device = torch.device('cpu')
cifar10_stats = {
"mean" : (0.4914, 0.4822, 0.4465),
"std" : (0.24705882352941178, 0.24352941176470588, 0.2615686274509804),
}
simple_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(cifar10_stats['mean'], cifar10_stats['std']),
])
train_loader = torch.utils.data.DataLoader(
datasets.CIFAR10(root='./data', train=True, download=True, transform=simple_transform),
batch_size=2048, shuffle=True, pin_memory=True)
test_loader = torch.utils.data.DataLoader(
datasets.CIFAR10(root='./data', train=False, download=True, transform=simple_transform),
batch_size=2048, shuffle=True, pin_memory=True)
train_images, train_labels = data_to_numpy(train_loader)
test_images, test_labels = data_to_numpy(test_loader)
train_images = np.transpose(train_images, (0, 2, 3, 1))
test_images = np.transpose(test_images , (0, 2, 3, 1))
train_labels = _one_hot(train_labels, num_classes)
test_labels = _one_hot(test_labels, num_classes)
return train_images, train_labels, test_images, test_labels
%%time
train_images, train_labels, test_images, test_labels = cifar_10()
train_images.shape, train_labels.shape, test_images.shape, test_labels.shape
train_images.shape, train_labels.shape, test_images.shape, test_labels.shape
```
## Define training primitives
Note: The training code is based on the following example: https://github.com/google/jax/blob/master/examples/mnist_classifier.py.
```
def loss(params, batch):
inputs, targets = batch
preds = predict(params, inputs)
return -np.mean(np.sum(log_softmax(preds, axis=1) * targets, axis=1))
def accuracy(params, batch):
inputs, targets = batch
target_class = np.argmax(targets, axis=1)
predicted_class = np.argmax(predict(params, inputs), axis=1)
return np.mean(predicted_class == target_class)
@jit
def update(i, opt_state, batch):
params = get_params(opt_state)
return opt_update(i, grad(loss)(params, batch), opt_state)
rng_state = npr.RandomState(0)
def data_stream_of(images, labels, batch_size=500, batch_limit=None):
assert len(images) == len(labels)
rng = npr.RandomState(0)
n = len(images)
perm = rng.permutation(n)
for i in range(n // batch_size):
if (batch_limit is not None) and i >= batch_limit:
break
batch_idx = perm[i * batch_size:(i + 1) * batch_size]
yield images[batch_idx], labels[batch_idx]
```
## Train a small CNN in JAX with NTK parameterization
Here I do a few epochs to make sure that my training code works.
I do mix `jax.stax` with `neural_tangents.stax` because I want to use both BatchNorm and NTK parameterizaton.
```
channels = 32
num_classes = 10
init_random_params, predict = jax_stax.serial(
nt_stax.Conv(channels, (3, 3), padding='SAME'), jax_stax.BatchNorm(), nt_stax.Relu(),
nt_stax.Conv(channels, (3, 3), strides=(2,2), padding='SAME'), jax_stax.BatchNorm(), nt_stax.Relu(),
nt_stax.Conv(channels, (3, 3), strides=(2,2), padding='SAME'), jax_stax.BatchNorm(), nt_stax.Relu(),
nt_stax.Conv(channels, (3, 3), strides=(2,2), padding='SAME'), jax_stax.BatchNorm(), nt_stax.Relu(),
nt_stax.AvgPool((1, 1)), nt_stax.Flatten(),
nt_stax.Dense(num_classes), jax_stax.Identity,
)
rng = random.PRNGKey(0)
step_size = 10.
num_epochs = 10
batch_size = 500
momentum_mass = 0.9
opt_init, opt_update, get_params = optimizers.momentum(step_size, mass=momentum_mass)
_, init_params = init_random_params(rng, (batch_size, 32, 32, 3))
opt_state = opt_init(init_params)
itercount = itertools.count()
print("\nStarting training...")
for epoch in range(num_epochs):
start_time = time.time()
for batch in data_stream_of(train_images, train_labels):
opt_state = update(next(itercount), opt_state, batch)
params = get_params(opt_state)
train_accs = [accuracy(params, batch) for batch in data_stream_of(train_images, train_labels)]
train_acc = np.average(train_accs)
test_accs = [accuracy(params, batch) for batch in data_stream_of(test_images, test_labels)]
test_acc = np.average(test_accs)
epoch_time = time.time() - start_time
print(f"Epoch {epoch} in {epoch_time:0.2f} sec")
print(f"Training set accuracy {train_acc}")
print(f"Test set accuracy {test_acc}")
```
## Train a ResNet
```
num_classes = 10
def WideResnetBlock(channels, strides=(1, 1), channel_mismatch=False):
Main = jax_stax.serial(
nt_stax.Conv(channels, (3, 3), strides, padding='SAME'), jax_stax.BatchNorm(), nt_stax.Relu(),
nt_stax.Conv(channels, (3, 3), padding='SAME'), jax_stax.BatchNorm(), nt_stax.Relu(),
jax_stax.Identity
)
Shortcut = nt_stax.Identity() if not channel_mismatch else nt_stax.Conv(channels, (3, 3), strides, padding='SAME')
return jax_stax.serial(jax_stax.FanOut(2),
jax_stax.parallel(Main, Shortcut),
jax_stax.FanInSum,
jax_stax.Identity)
def WideResnetGroup(n, channels, strides=(1, 1)):
blocks = []
blocks += [WideResnetBlock(channels, strides, channel_mismatch=True)]
for _ in range(n - 1):
blocks += [WideResnetBlock(channels, (1, 1))]
return jax_stax.serial(*blocks)
def WideResnet(num_classes, num_channels=32, block_size=1):
return jax_stax.serial(
nt_stax.Conv(num_channels, (3, 3), padding='SAME'), jax_stax.BatchNorm(), nt_stax.Relu(),
WideResnetGroup(block_size, num_channels),
WideResnetGroup(block_size, num_channels, (2, 2)),
WideResnetGroup(block_size, num_channels, (2, 2)),
nt_stax.AvgPool((1, 1)),
nt_stax.Flatten(),
nt_stax.Dense(num_classes),
jax_stax.Identity
)
init_random_params, predict = WideResnet(num_classes)
rng = random.PRNGKey(0)
step_size = 10.
num_epochs = 10
momentum_mass = 0.9
opt_init, opt_update, get_params = optimizers.momentum(step_size, mass=momentum_mass)
_, init_params = init_random_params(rng, (batch_size, 32, 32, 3))
opt_state = opt_init(init_params)
itercount = itertools.count()
print("\nStarting training...")
for epoch in range(num_epochs):
start_time = time.time()
for batch in data_stream_of(train_images, train_labels):
opt_state = update(next(itercount), opt_state, batch)
params = get_params(opt_state)
train_accs = [accuracy(params, batch) for batch in data_stream_of(train_images, train_labels, batch_limit=4)]
train_acc = np.average(train_accs)
test_accs = [accuracy(params, batch) for batch in data_stream_of(test_images, test_labels, batch_limit=4)]
test_acc = np.average(test_accs)
epoch_time = time.time() - start_time
print(f"Epoch {epoch} in {epoch_time:0.2f} sec")
print(f"Training set accuracy {train_acc}")
print(f"Test set accuracy {test_acc}")
```
## Train a linearization of ResNet
Note: I have removed BatchNorm layers because with them training didn't work.
```
from jax.tree_util import tree_multimap
from jax.api import jvp
from jax.api import vjp
# copied from
def linearize(f, params):
"""Returns a function `f_lin`, the first order taylor approximation to `f`.
Example:
>>> # Compute the MSE of the first order Taylor series of a function.
>>> f_lin = linearize(f, params)
>>> mse = np.mean((f(new_params, x) - f_lin(new_params, x)) ** 2)
"""
@jit
def f_lin(p, *args, **kwargs):
dparams = tree_multimap(lambda x, y: x - y, p, params)
f_params_x, proj = jvp(lambda param: f(param, *args, **kwargs),
(params,), (dparams,))
return f_params_x + proj
return f_lin
def WideResnetBlock(channels, strides=(1, 1), channel_mismatch=False):
Main = jax_stax.serial(
nt_stax.Conv(channels, (3, 3), strides, padding='SAME'), nt_stax.Relu(),
nt_stax.Conv(channels, (3, 3), padding='SAME'), nt_stax.Relu(),
jax_stax.Identity
)
Shortcut = nt_stax.Identity() if not channel_mismatch else nt_stax.Conv(channels, (3, 3), strides, padding='SAME')
return jax_stax.serial(jax_stax.FanOut(2),
jax_stax.parallel(Main, Shortcut),
jax_stax.FanInSum,
jax_stax.Identity)
def WideResnetGroup(n, channels, strides=(1, 1)):
blocks = []
blocks += [WideResnetBlock(channels, strides, channel_mismatch=True)]
for _ in range(n - 1):
blocks += [WideResnetBlock(channels, (1, 1))]
return jax_stax.serial(*blocks)
def WideResnet(num_classes, num_channels=32, block_size=1):
return jax_stax.serial(
nt_stax.Conv(num_channels, (3, 3), padding='SAME'), nt_stax.Relu(),
WideResnetGroup(block_size, num_channels),
WideResnetGroup(block_size, num_channels, (2, 2)),
WideResnetGroup(block_size, num_channels, (2, 2)),
nt_stax.AvgPool((1, 1)),
nt_stax.Flatten(),
nt_stax.Dense(num_classes),
jax_stax.Identity
)
num_classes = 10
init_random_params, predict = WideResnet(num_classes, num_channels=512)
rng = random.PRNGKey(0)
step_size = 1.
num_epochs = 100
momentum_mass = 0.9
opt_init, opt_update, get_params = optimizers.momentum(step_size, mass=momentum_mass)
_, init_params = init_random_params(rng, (batch_size, 32, 32, 3))
opt_state = opt_init(init_params)
itercount = itertools.count()
predict = linearize(predict, init_params) # !important: linearization
print("\nStarting training...")
for epoch in range(num_epochs):
start_time = time.time()
for batch in data_stream_of(train_images, train_labels, batch_size=100):
opt_state = update(next(itercount), opt_state, batch)
params = get_params(opt_state)
train_accs = [accuracy(params, batch) for batch in data_stream_of(train_images, train_labels, batch_size=100, batch_limit=20)]
train_acc = np.average(train_accs)
test_accs = [accuracy(params, batch) for batch in data_stream_of(test_images, test_labels, batch_size=100, batch_limit=20)]
test_acc = np.average(test_accs)
epoch_time = time.time() - start_time
print(f"Epoch {epoch} in {epoch_time:0.2f} sec")
print(f"Training set accuracy {train_acc}")
print(f"Test set accuracy {test_acc}")
```
| true |
code
| 0.804214 | null | null | null | null |
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
eth = pd.read_csv("ETH.csv").set_index("Date")
rai = pd.read_csv("RAI.csv").set_index('Date')
rai.index = pd.to_datetime(rai.index)
rai.index = pd.to_datetime(rai.index.date)
eth.index = pd.to_datetime(eth.index)
prices = pd.concat([eth, rai], axis=1).dropna()
prices.columns = ['ETH', 'RAI']
prices['RAI'] = prices['RAI'].astype(float)
prices['ETH'] = prices['ETH'].astype(float)
prices['Ratio'] = prices['ETH'] / prices['RAI']
prices['Ratio'].plot(kind='line')
plt.show()
prices["Log Ratio"] = np.log(prices['Ratio']+1)
prices['Log Ratio'].plot(kind='line')
plt.show()
prices['Log Ratio Diff'] = prices['Log Ratio'].diff()
prices['Log Ratio Diff'].plot.hist(bins=10)
plt.show()
import seaborn as sns
sns.kdeplot(prices['Log Ratio Diff'])
initial_ratio = prices['Log Ratio'].iloc[-1]
from scipy.stats import norm
mu, std = norm.fit(prices['Log Ratio Diff'].dropna())
mu = mu/24
std = std / (24**.5)
mu*100
mu, std
run = 0
timesteps = 100
np.random.seed(seed=run)
deltas = np.random.normal(mu, std, 100)
ratios = np.exp(initial_ratio + deltas.cumsum()) - 1
initial_ratio
np.exp(0)
rai_res = 4953661
eth_res = 7785
rai_res/eth_res
```
$$ A \cdot B = C$$
$$ (A+\Delta A) \cdot (B + \Delta B) = C$$
$$ A \Delta B + B \Delta A + \Delta B \Delta A = 0$$
$$ \frac{A}{B} = R_{1}$$
$$ \frac{A+\Delta A}{B + \Delta B} = R_{2}$$
$$ A = B R_{1}$$
$$ A+\Delta A = R_{2} [B + \Delta B]$$
$$ B R_{1}+\Delta A = R_{2} [B + \Delta B]$$
$$ \Delta A = B R_{2} + \Delta B R_{2} - B R_{1}$$
$$ A \Delta B + [B + \Delta B] \cdot [B R_{2} + \Delta B R_{2} - B R_{1}] - B R_{1}] = 0$$
```
rai_res / eth_res
true = 600
def agent_action(signal, s):
#Find current ratio
current_ratio = s['RAI_balance'] / s['ETH_balance']
eth_res = s['ETH_balance']
rai_res = s['RAI_balance']
#Find the side of the trade
if signal < current_ratio:
action_key = "eth_sold"
else:
action_key = "tokens_sold"
#Constant for equations
C = rai_res * eth_res
#Find the maximum shift that the trade should be able to sap up all arbitrage opportunities
max_shift = abs(rai_res / eth_res - true)
#Start with a constant choice of 10 eth trade
eth_size = 10
#Decide on sign of eth
if action == "eth_sold":
eth_delta = eth_size
else:
eth_delta = -eth_size
#Compute the RAI delta to hold C constant
rai_delta = C / (eth_res + eth_delta) - rai_res
#Caclulate the implied shift in ratio
implied_shift = abs((rai_res + rai_delta)/ (eth_res + eth_delta) - rai_res / eth_res)
#While the trade is too large, cut trade size in half
while implied_shift > max_shift:
#Cut trade in half
eth_size = eth_size/2
rai_delta = C / (eth_res + eth_delta) - rai_res
implied_shift = abs((rai_res + rai_delta)/ (eth_res + eth_delta) - rai_res / eth_res)
if action_key == "eth_sold":
I_t = s['ETH_balance']
O_t = s['RAI_balance']
I_t1 = s['ETH_balance']
O_t1 = s['RAI_balance']
delta_I = eth_delta
delta_O = rai_delta
else:
I_t = s['RAI_balance']
O_t = s['ETH_balance']
I_t1 = s['RAI_balance']
O_t1 = s['ETH_balance']
delta_I = rai_delta
delta_O = eth_delta
return I_t, O_t, I_t1, O_t1, delta_I, delta_O, action_key
s = {"RAI_balance": 4960695.994,
"ETH_balance": 7740.958682}
signal = 651.4802496080162
agent_action(signal, s)
eth_size
delta_I = uniswap_events['eth_delta'][t]
delta_O = uniswap_events['token_delta'][t]
action_key = 'eth_sold'
implied_shift
max_shift
(rai_res + rai_delta)/ (eth_res + eth_delta)
I_t, O_t, I_t1, O_t1, delta_I, delta_O, action_key
```
| true |
code
| 0.39458 | null | null | null | null |
|
# Dropout
Dropout [1] is a technique for regularizing neural networks by randomly setting some features to zero during the forward pass. In this exercise you will implement a dropout layer and modify your fully-connected network to optionally use dropout.
[1] [Geoffrey E. Hinton et al, "Improving neural networks by preventing co-adaptation of feature detectors", arXiv 2012](https://arxiv.org/abs/1207.0580)
```
# As usual, a bit of setup
from __future__ import print_function
import time
import numpy as np
import matplotlib.pyplot as plt
from cs682.classifiers.fc_net import *
from cs682.data_utils import get_CIFAR10_data
from cs682.gradient_check import eval_numerical_gradient, eval_numerical_gradient_array
from cs682.solver import Solver
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# for auto-reloading external modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
def rel_error(x, y):
""" returns relative error """
return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))
# Load the (preprocessed) CIFAR10 data.
data = get_CIFAR10_data()
for k, v in data.items():
print('%s: ' % k, v.shape)
```
# Dropout forward pass
In the file `cs682/layers.py`, implement the forward pass for dropout. Since dropout behaves differently during training and testing, make sure to implement the operation for both modes.
Once you have done so, run the cell below to test your implementation.
```
np.random.seed(231)
x = np.random.randn(500, 500) + 10
for p in [0.25, 0.4, 0.7]:
out, _ = dropout_forward(x, {'mode': 'train', 'p': p})
out_test, _ = dropout_forward(x, {'mode': 'test', 'p': p})
print('Running tests with p = ', p)
print('Mean of input: ', x.mean())
print('Mean of train-time output: ', out.mean())
print('Mean of test-time output: ', out_test.mean())
print('Fraction of train-time output set to zero: ', (out == 0).mean())
print('Fraction of test-time output set to zero: ', (out_test == 0).mean())
print()
```
# Dropout backward pass
In the file `cs682/layers.py`, implement the backward pass for dropout. After doing so, run the following cell to numerically gradient-check your implementation.
```
np.random.seed(231)
x = np.random.randn(10, 10) + 10
dout = np.random.randn(*x.shape)
dropout_param = {'mode': 'train', 'p': 0.2, 'seed': 123}
out, cache = dropout_forward(x, dropout_param)
dx = dropout_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda xx: dropout_forward(xx, dropout_param)[0], x, dout)
# Error should be around e-10 or less
print('dx relative error: ', rel_error(dx, dx_num))
```
## Inline Question 1:
What happens if we do not divide the values being passed through inverse dropout by `p` in the dropout layer? Why does that happen?
## Answer:
The model would be train with a small portion of the input than it would get in test time.
# Fully-connected nets with Dropout
In the file `cs682/classifiers/fc_net.py`, modify your implementation to use dropout. Specifically, if the constructor of the net receives a value that is not 1 for the `dropout` parameter, then the net should add dropout immediately after every ReLU nonlinearity. After doing so, run the following to numerically gradient-check your implementation.
```
np.random.seed(231)
N, D, H1, H2, C = 2, 15, 20, 30, 10
X = np.random.randn(N, D)
y = np.random.randint(C, size=(N,))
for dropout in [1, 0.75, 0.5]:
print('Running check with dropout = ', dropout)
model = FullyConnectedNet([H1, H2], input_dim=D, num_classes=C,
weight_scale=5e-2, dtype=np.float64,
dropout=dropout, seed=123)
loss, grads = model.loss(X, y)
print('Initial loss: ', loss)
# Relative errors should be around e-6 or less; Note that it's fine
# if for dropout=1 you have W2 error be on the order of e-5.
for name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
grad_num = eval_numerical_gradient(f, model.params[name], verbose=False, h=1e-5)
print('%s relative error: %.2e' % (name, rel_error(grad_num, grads[name])))
print()
```
## Regularization experiment
As an experiment, we will train a pair of two-layer networks on 500 training examples: one will use no dropout, and one will use a keep probability of 0.25. We will then visualize the training and validation accuracies of the two networks over time.
```
# Train two identical nets, one with dropout and one without
np.random.seed(231)
num_train = 500
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
solvers = {}
dropout_choices = [1, 0.25]
for dropout in dropout_choices:
model = FullyConnectedNet([500], dropout=dropout)
print(dropout)
solver = Solver(model, small_data,
num_epochs=25, batch_size=100,
update_rule='adam',
optim_config={
'learning_rate': 5e-4,
},
verbose=True, print_every=100)
solver.train()
solvers[dropout] = solver
# Plot train and validation accuracies of the two models
train_accs = []
val_accs = []
for dropout in dropout_choices:
solver = solvers[dropout]
train_accs.append(solver.train_acc_history[-1])
val_accs.append(solver.val_acc_history[-1])
plt.subplot(3, 1, 1)
for dropout in dropout_choices:
plt.plot(solvers[dropout].train_acc_history, 'o', label='%.2f dropout' % dropout)
plt.title('Train accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(ncol=2, loc='lower right')
plt.subplot(3, 1, 2)
for dropout in dropout_choices:
plt.plot(solvers[dropout].val_acc_history, 'o', label='%.2f dropout' % dropout)
plt.title('Val accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(ncol=2, loc='lower right')
plt.gcf().set_size_inches(15, 15)
plt.show()
```
## Inline Question 2:
Compare the validation and training accuracies with and without dropout -- what do your results suggest about dropout as a regularizer?
## Answer:
Our experiment shows that although the train accuracy for having dropouts is lower, it actually has a higher accuracy in validation.
## Inline Question 3:
Suppose we are training a deep fully-connected network for image classification, with dropout after hidden layers (parameterized by keep probability p). How should we modify p, if at all, if we decide to decrease the size of the hidden layers (that is, the number of nodes in each layer)?
## Answer:
We should have a larger p, because when decreasing the size of the hidden layers, we would need to keep more nodes in order to not lose the representation of the original data.
| true |
code
| 0.706292 | null | null | null | null |
|
## Visualizing-Food-Insecurity-with-Pixie-Dust-and-Watson-Analytics
_IBM Journey showing how to visualize US Food Insecurity with Pixie Dust and Watson Analytics._
Often in data science we do a great deal of work to glean insights that have an impact on society or a subset of it and yet, often, we end up not communicating our findings or communicating them ineffectively to non data science audiences. That's where visualizations become the most powerful. By visualizing our insights and predictions, we, as data scientists and data lovers, can make a real impact and educate those around us that might not have had the same opportunity to work on a project of the same subject. By visualizing our findings and those insights that have the most power to do social good, we can bring awareness and maybe even change. This Code Pattern walks you through how to do just that, with IBM's Data Science Experience (DSX), Pandas, Pixie Dust and Watson Analytics.
For this particular Code Pattern, food insecurity throughout the US is focused on. Low access, diet-related diseases, race, poverty, geography and other factors are considered by using open government data. For some context, this problem is a more and more relevant problem for the United States as obesity and diabetes rise and two out of three adult Americans are considered obese, one third of American minors are considered obsese, nearly ten percent of Americans have diabetes and nearly fifty percent of the African American population have heart disease. Even more, cardiovascular disease is the leading global cause of death, accounting for 17.3 million deaths per year, and rising. Native American populations more often than not do not have grocery stores on their reservation... and all of these trends are on the rise. The problem lies not only in low access to fresh produce, but food culture, low education on healthy eating as well as racial and income inequality.
The government data that I use in this journey has been conveniently combined into a dataset for our use, which you can find in this repo under combined_data.csv. You can find the original, government data from the US Bureau of Labor Statistics https://www.bls.gov/cex/ and The United States Department of Agriculture https://www.ers.usda.gov/data-products/food-environment-atlas/data-access-and-documentation-downloads/.
### What is DSX, Pixie Dust and Watson Analytics and why should I care enough about them to use them for my visualizations?
IBM's Data Science Experience, or DSX, is an online browser platform where you can use notebooks or R Studio for your data science projects. DSX is unique in that it automatically starts up a Spark instance for you, allowing you to work in the cloud without any extra work. DSX also has open data available to you, which you can connect to your notebook. There are also other projects available, in the form of notebooks, which you can follow along with and apply to your own use case. DSX also lets you save your work, share it and collaborate with others, much like I'm doing now!
Pixie Dust is a visualization library you can use on DSX. It is already installed into DSX and once it's imported, it only requires one line of code (two words) to use. With that same line of code, you can pick and choose different values to showcase and visualize in whichever way you want from matplotlib, seaborn and bokeh. If you have geographic data, you can also connect to google maps and Mapbox, depending on your preference. Check out a tutorial on Pixie Dust here: https://ibm-watson-data-lab.github.io/pixiedust/displayapi.html#introduction
IBM's Watson Analytics is another browser platform which allows you to input your data, conduct analysis on it and then visualize your findings. If you're new to data science, Watson recommends connections and visualizations with the data it has been given. These visualizations range from bar and scatter plots to predictive spirals, decision trees, heatmaps, trend lines and more. The Watson platform then allows you to share your findings and visualizations with others, completing your pipeline. Check out my visualizations with the link further down in the notebook, or in the images in this repo.
### Let's start with DSX.
Here's a tutorial on getting started with DSX: https://datascience.ibm.com/docs/content/analyze-data/creating-notebooks.html.
To summarize the introduction, you must first make an account and log in. Then, you can create a project (I titled mine: "Diet-Related Disease"). From there, you'll be able to add data and start a notebook. To begin, I used the combined_data.csv as my data asset. You'll want to upload it as a data asset and once that is complete, go into your notebook in the edit mode (click on the pencil icon next to your notebook on the dashboard). To load your data in your notebook, you'll click on the "1001" data icon in the top right. The combined_data.csv should show up. Click on it and select "Insert Pandas Data Frame". Once you do that, a whole bunch of code will show up in your first cell. Once you see that, run the cell and follow along with my tutorial!
_Quick Note: In Github you can view all of the visualizations by selecting the circle with the dash in the middle at the top right of the notebook!_
```
from io import StringIO
import requests
import json
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#Insert Pandas Data Frame
import sys
import types
import pandas as pd
from botocore.client import Config
import ibm_boto3
def __iter__(self): return 0
# @hidden_cell
# The following code accesses a file in your IBM Cloud Object Storage. It includes your credentials.
# You might want to remove those credentials before you share your notebook.
client_3ebc7942f56c4334ae3dfda7d1f19d40 = ibm_boto3.client(service_name='s3',
ibm_api_key_id='-9FQb_5uaEltHpWcqXkeVsFIShUoUOJht768ihN-VgYq',
ibm_auth_endpoint="https://iam.ng.bluemix.net/oidc/token",
config=Config(signature_version='oauth'),
endpoint_url='https://s3-api.us-geo.objectstorage.service.networklayer.com')
body = client_3ebc7942f56c4334ae3dfda7d1f19d40.get_object(Bucket='testpixiestorage302e1eb2addc4a09a8e6c82f7f1ae0e3',Key='combined_data.csv')['Body']
# add missing __iter__ method, so pandas accepts body as file-like object
if not hasattr(body, "__iter__"): body.__iter__ = types.MethodType( __iter__, body )
df_data_1 = pd.read_csv(body)
df_data_1.head()
```
### Cleaning data and Exploring
This notebook starts out as a typical data science pipeline: exploring what our data looks like and cleaning the data. Though this is often considered the boring part of the job, it is extremely important. Without clean data, our insights and visualizations could be inaccurate or unclear.
To initially explore, I used matplotlib to see a correlation matrix of our original data. I also looked at some basic statistics to get a feel for what kind of data we are looking at. I also went ahead and plotted using pandas and seaborn to make bar plots, scatterplots and regression plots. You can also find the meanings of the values at the following link in my repo: https://github.com/IBM/visualize-food-insecurity/blob/mjmyers/data/Variable%20list.xlsx.
```
df_data_1.columns
df_data_1.describe()
#to see columns distinctly and evaluate their state
df_data_1['PCT_LACCESS_POP10'].unique()
df_data_1['PCT_REDUCED_LUNCH10'].unique()
df_data_1['PCT_DIABETES_ADULTS10'].unique()
df_data_1['FOODINSEC_10_12'].unique()
#looking at correlation in a table format
df_data_1.corr()
#checking out a correlation matrix with matplotlib
plt.matshow(df_data_1.corr())
#we notice that there is a great deal of variables which makes it hard to read!
#other stats
df_data_1.max()
df_data_1.min()
df_data_1.std()
# Plot counts of a specified column using Pandas
df_data_1.FOODINSEC_10_12.value_counts().plot(kind='barh')
# Bar plot example
sns.factorplot("PCT_SNAP09", "PCT_OBESE_ADULTS10", data=df_data_1,size=3,aspect=2)
# Regression plot
sns.regplot("FOODINSEC_10_12", "PCT_OBESE_ADULTS10", data=df_data_1, robust=True, ci=95, color="seagreen")
sns.despine();
```
After looking at the data I realize that I'm only interested in seeing the connection between certain values and because the dataset is so large it's bringing in irrelevant information and creating noise. To change this, I created a smaller data frame, making sure to remove NaN and 0 values (0s in this dataset generally mean that a number was not recorded).
```
#create a dataframe of values that are most interesting to food insecurity
df_focusedvalues = df_data_1[["State", "County","PCT_REDUCED_LUNCH10", "PCT_DIABETES_ADULTS10", "PCT_OBESE_ADULTS10", "FOODINSEC_10_12", "PCT_OBESE_CHILD11", "PCT_LACCESS_POP10", "PCT_LACCESS_CHILD10", "PCT_LACCESS_SENIORS10", "SNAP_PART_RATE10", "PCT_LOCLFARM07", "FMRKT13", "PCT_FMRKT_SNAP13", "PCT_FMRKT_WIC13", "FMRKT_FRVEG13", "PCT_FRMKT_FRVEG13", "PCT_FRMKT_ANMLPROD13", "FOODHUB12", "FARM_TO_SCHOOL", "SODATAX_STORES11", "State_y", "GROC12", "SNAPS12", "WICS12", "PCT_NHWHITE10", "PCT_NHBLACK10", "PCT_HISP10", "PCT_NHASIAN10", "PCT_65OLDER10", "PCT_18YOUNGER10", "POVRATE10", "CHILDPOVRATE10"]]
#remove NaNs and 0s
df_focusedvalues = df_focusedvalues[(df_focusedvalues != 0).all(1)]
df_focusedvalues = df_focusedvalues.dropna(how='any')
```
Before visualizing, a quick heatmap is created so that we can see what correlations we may want to visualize. I visualized a few of these relationships using seaborn, but I ultimately want to try out other visualizations. The quickest way to explore these is through Pixie Dust.
```
#look at heatmap of correlations with the dataframe to see what we should visualize
corr = df_focusedvalues.corr()
sns.heatmap(corr,
xticklabels=corr.columns.values,
yticklabels=corr.columns.values)
```
We can immediately see that a fair amount of strong correlations and relationships exist. Some of these include 18 and younger and Hispanic, an inverse relationship between Asian and obese, a correlation between sodatax and Hispanic, African American and obesity as well as food insecurity, sodatax and obese minors, farmers markets and aid such as WIC and SNAP, obese minors and reduced lunches and a few more.
Let's try and plot some of these relationships with seaborn.
```
#Percent of the population that is white vs SNAP aid participation (positive relationship)
sns.regplot("PCT_NHWHITE10", "SNAP_PART_RATE10", data=df_focusedvalues, robust=True, ci=95, color="seagreen")
sns.despine();
#Percent of the population that is Hispanic vs SNAP aid participation (negative relationship)
sns.regplot("SNAP_PART_RATE10", "PCT_HISP10", data=df_focusedvalues, robust=True, ci=95, color="seagreen")
sns.despine();
#Eligibility and use of reduced lunches in schools vs percent of the population that is Hispanic (positive relationship)
sns.regplot("PCT_REDUCED_LUNCH10", "PCT_HISP10", data=df_focusedvalues, robust=True, ci=95, color="seagreen")
sns.despine();
#Percent of the population that is black vs percent of the population with diabetes (positive relationship)
sns.regplot("PCT_NHBLACK10", "PCT_DIABETES_ADULTS10", data=df_focusedvalues, robust=True, ci=95, color="seagreen")
sns.despine();
#Percent of population with diabetes vs percent of population with obesity (positive relationship)
sns.regplot("PCT_DIABETES_ADULTS10", "PCT_OBESE_ADULTS10", data=df_focusedvalues, robust=True, ci=95, color="seagreen")
sns.despine();
```
### Now, let's visualize with Pixie Dust.
Now that we've gained some initial insights, let's try out a different tool: Pixie Dust!
As you can see in the notebook below, to activate Pixie Dust, we just import it and then write:
```display(your_dataframe_name)```
After doing this your dataframe will show up in a column-row table format. To visualize your data, you can click the chart icon at the top left (looks like an arrow going up). From there you can choose from a variety of visuals. Once you select the type of chart you want, you can then select the variables you want to showcase. It's worth playing around with this to see how you can create the most effective visualizations for your audience. The notebook below showcases a couple options such as scatterplots, bar charts, line charts, and histograms.
```
import pixiedust
#looking at the dataframe table. Pixie Dust does this automatically, but to find it again you can click the table icon.
display(df_focusedvalues)
#using seaborn in Pixie Dust to look at Food Insecurity and the Percent of the population that is black in a scatter plot
display(df_focusedvalues)
#using matplotlib in Pixie Dust to view Food Insecurity by state in a bar chart
display(df_focusedvalues)
#using bokeh in Pixie Dust to view the percent of the population that is black vs the percent of the population that is obese in a line chart
display(df_focusedvalues)
#using seaborn in Pixie Dust to view obesity vs diabetes in a scatterplot
display(df_focusedvalues)
#using matplotlib in Pixie Dust to view the percent of the population that is white vs SNAP participation rates in a histogram
display(df_focusedvalues)
#using bokeh in Pixie Dust to view the trends in obesity, diabetes, food insecurity and the percent of the population that is black in a line graph
display(df_focusedvalues)
#using matplotlib in Pixie Dust to view childhood obesity vs reduced school lunches in a scatterplot
display(df_focusedvalues)
```
### Let's download our dataframe and work with it on Watson Analytics.
Once you follow along, you can take the new .csv (found under "Data Services" --> "Object Storage" from the top button) and upload it to Watson Analytics. Again, if you do not have an account, you'll want to set one up. Once you are logged in and ready to go, you can upload the data (saved in this repo as df_focusedvalues.csv) to your Watson platform.
```
#First get your credentials by going to the "1001" button again and under your csv file selecting "Insert Credentials".
#The cell below will be hidden because it has my personal credentials so go ahead and insert your own.
# @hidden_cell
# The following code contains the credentials for a file in your IBM Cloud Object Storage.
# You might want to remove those credentials before you share your notebook.
credentials_1 = {
'IBM_API_KEY_ID': '-9FQb_5uaEltHpWcqXkeVsFIShUoUOJht768ihN-VgYq',
'IAM_SERVICE_ID': 'iam-ServiceId-c8681118-cbee-4807-9adf-ac48dfd1cfdd',
'ENDPOINT': 'https://s3-api.us-geo.objectstorage.service.networklayer.com',
'IBM_AUTH_ENDPOINT': 'https://iam.ng.bluemix.net/oidc/token',
'BUCKET': 'testpixiestorage302e1eb2addc4a09a8e6c82f7f1ae0e3',
'FILE': 'combined_data.csv'
}
df_focusedvalues.to_csv('df_focusedvalues.csv',index=False)
import ibm_boto3
from ibm_botocore.client import Config
cos = ibm_boto3.client(service_name='s3',
ibm_api_key_id=credentials_1['IBM_API_KEY_ID'],
ibm_service_instance_id=credentials_1['IAM_SERVICE_ID'],
ibm_auth_endpoint=credentials_1['IBM_AUTH_ENDPOINT'],
config=Config(signature_version='oauth'),
endpoint_url=credentials_1['ENDPOINT'])
cos.upload_file(Filename='df_focusedvalues.csv',Bucket=credentials_1['BUCKET'],Key='df_focusedvalues.csv')
```
Once this is complete, go get your csv file from Data Services, Object Storage! (Find this above! ^)
### Using Watson to visualize our insights.
Once you've set up your account, you can see that the Watson plaform has three sections: data, discover and display. You uploaded your data to the "data" section, but now you'll want to go to the "discover" section. Under "discover" you can select your dataframe dataset for use. Once you've selected it, the Watson platform will suggest different insights to visualize. You can move forward with its selections or your own, or both. You can take a look at mine here (you'll need an account to view): https://ibm.co/2xAlAkq or see the screen shots attached to this repo. You can also go into the "display" section and create a shareable layout like mine (again you'll need an account): https://ibm.co/2A38Kg6.
You can see that with these visualizations the user can see the impact of food insecurity by state, geographically distributed and used aid such as reduced school lunches, a map of diabetes by state, a predictive model for food insecurity and diabetes (showcasing the factors that, in combination, suggest a likelihood of food insecurity), drivers of adult diabetes, drivers of food insecurity, the relationship with the frequency of farmers market locations, food insecurity and adult obesity, as well as the relationship between farmers markets, the percent of the population that is Asian, food insecurity and poverty rates.
By reviewing our visualizations both in DSX and Watson, we learn that obesity and diabetes almost go hand in hand, along with food insecurity. We can also learn that this seems to be an inequality issue, both in income and race, with Black and Hispanic populations being more heavily impacted by food insecurity and diet-related diseases than those of the White and Asian populations. We can also see that school-aged children who qualify for reduced lunch are more likely obese than not whereas those that have a farm-to-school program are more unlikely to be obese.
Like many data science investigations, this analysis could have a big impact on policy and people's approach to food insecurity in the U.S. What's best is that we can create many projects much like this in a quick time period and share them with others by using Pandas, Pixie Dust as well as Watson's predictive and recommended visualizations.
| true |
code
| 0.434221 | null | null | null | null |
|
# 0. Import
```
import torch
```
# 1. Data
เราจะสร้างข้อมูลขึ้นมาเป็น Tensor ขนาด 10 Row, 3 Column [เรื่อง Tensor จะอธิบายต่อไป](https://www.bualabs.com/archives/1629/what-is-tensor-element-wise-broadcasting-operations-high-order-tensor-numpy-array-matrix-vector-tensor-ep-1/)
```
z = torch.tensor([
[ 1, 2, 3 ],
[ 11, 12, 13 ],
[ 0.1, 0.2, 0.3 ],
[ -1, -2, -3 ],
[ 10, 20, 30 ],
[ -5, 0, 5 ],
[ -11, 1/12, 13 ],
[ -0.1, -0.2, -0.3 ],
[ -11, -12, -13 ],
[ -10, -20, -30 ],
]).float()
z.shape
z
```
# 2. สูตรของ Softmax คือดังนี้
$$\sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \text{ for } i = 1, \dotsc , K \text{ and } \mathbf z=(z_1,\dotsc,z_K) \in R^K$$
# 2.1 ตัวตั้ง (Dividen)
เราจะมาหาตัวตั้ง เอา a มา exp ให้หมด แล้วเก็บไว้ก่อน
```
exp_z = torch.exp(z)
exp_z
```
## 2.2 ตัวหาร (Divisor)
ตัวหารคือผลรวมของ exp_a เราจะ sum ตามมิติที่ 1 Column ให้เหลือแต่ Row โดย keepdim=True จะได้ดูง่าย
```
sum_exp_z = torch.sum(exp_z, 1, keepdim=True)
sum_exp_z
```
# 3. หา Softmax ของ a
นำตัวตั้ง Dividen หารด้วยตัวหาร Divisor จะได้ค่า Softmax
```
softmax_z = exp_z / sum_exp_z
softmax_z
```
# 4. Softmax Function
ได้เป็น ฟังก์ชันดังนี้
```
def softmax(z):
exp_z = torch.exp(z)
sum_exp_z = torch.sum(exp_z, 1, keepdim=True)
return exp_z / sum_exp_z
```
# 5. การใช้งาน Softmax
Softmax มีคุณสมบัติพิเศษ คือ จะรวมกันได้เท่ากับ 1 จึงถูกนำมาใช้เป็นความน่าจะเป็น Probability / Likelihood
ดูตัวอย่างแถวแรก
```
z[0]
softmax_z[0]
```
บวกกันได้ 1
```
softmax_z[0].sum()
```
แถวสอง
```
z[1]
softmax_z[1]
```
ก็บวกกันแล้วได้ 1
```
softmax_z[1].sum()
```
# 6. Numerical Stability
ถ้า Input มีขนาดใหญ่มาก เมื่อ exp จะ Error ได้ เราสามารถปรับ x โดย x = x - max(x) ก่อนเข้า Softmax Function เรียกว่า Numerical Stability
```
n = torch.tensor([
[ 10, 20, 30 ],
[ -100, -200, -300 ],
[ 0.001, 0.0001, 0.0001 ],
[ 70, 80, 90 ],
[ 100, 1000, 10000 ],
]).float()
```
เมื่อเลขใหญ่เกินกว่าระบบจะรับได้ จะมีค่าเป็น Not a Number (nan)
```
m = softmax(n)
m
```
เราจะปรับฟังก์ชัน Softmax ให้ Numerical Stability รับเลขใหญ่ ๆ ได้
```
def softmax2(z):
z = z - z.max(1, keepdim=True)[0]
exp_z = torch.exp(z)
sum_exp_z = torch.sum(exp_z, 1, keepdim=True)
return exp_z / sum_exp_z
m = softmax2(n)
m
```
# 5. สรุป
1. เราสามารถคำนวน Softmax Function ได้ไม่ยาก
1. Softmax ทำให้อะไรที่มีค่าน้อยก็จะยิ่งถูกกดให้น้อย อะไรที่มากก็จะยิ่งดันให้ใกล้ 1 ใกล้เคียงกับ Max Function ที่ใช้หาค่ามากที่สุด
1. Softmax มักถูกนำมาใช้เป็นความน่าจะเป็น Probability / Likelihood ใช้เป็นส่วนประกอบของ Cross Entropy Loss ใน Neural Network
# Credit
* https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/
* https://en.wikipedia.org/wiki/Softmax_function
* https://medium.com/data-science-bootcamp/understand-the-softmax-function-in-minutes-f3a59641e86d
| true |
code
| 0.525125 | null | null | null | null |
|
# PerfForesightConsumerType: Perfect foresight consumption-saving
```
# Initial imports and notebook setup, click arrow to show
from copy import copy
import matplotlib.pyplot as plt
import numpy as np
from HARK.ConsumptionSaving.ConsIndShockModel import PerfForesightConsumerType
from HARK.utilities import plot_funcs
mystr = lambda number: "{:.4f}".format(number)
```
The module `HARK.ConsumptionSaving.ConsIndShockModel` concerns consumption-saving models with idiosyncratic shocks to (non-capital) income. All of the models assume CRRA utility with geometric discounting, no bequest motive, and income shocks are fully transitory or fully permanent.
`ConsIndShockModel` currently includes three models:
1. A very basic "perfect foresight" model with no uncertainty.
2. A model with risk over transitory and permanent income shocks.
3. The model described in (2), with an interest rate for debt that differs from the interest rate for savings.
This notebook provides documentation for the first of these three models.
$\newcommand{\CRRA}{\rho}$
$\newcommand{\DiePrb}{\mathsf{D}}$
$\newcommand{\PermGroFac}{\Gamma}$
$\newcommand{\Rfree}{\mathsf{R}}$
$\newcommand{\DiscFac}{\beta}$
## Statement of perfect foresight consumption-saving model
The `PerfForesightConsumerType` class the problem of a consumer with Constant Relative Risk Aversion utility
${\CRRA}$
\begin{equation}
U(C) = \frac{C^{1-\CRRA}}{1-\rho},
\end{equation}
has perfect foresight about everything except whether he will die between the end of period $t$ and the beginning of period $t+1$, which occurs with probability $\DiePrb_{t+1}$. Permanent labor income $P_t$ grows from period $t$ to period $t+1$ by factor $\PermGroFac_{t+1}$.
At the beginning of period $t$, the consumer has an amount of market resources $M_t$ (which includes both market wealth and currrent income) and must choose how much of those resources to consume $C_t$ and how much to retain in a riskless asset $A_t$, which will earn return factor $\Rfree$. The consumer cannot necessarily borrow arbitarily; instead, he might be constrained to have a wealth-to-income ratio at least as great as some "artificial borrowing constraint" $\underline{a} \leq 0$.
The agent's flow of future utility $U(C_{t+n})$ from consumption is geometrically discounted by factor $\DiscFac$ per period. If the consumer dies, he receives zero utility flow for the rest of time.
The agent's problem can be written in Bellman form as:
\begin{eqnarray*}
V_t(M_t,P_t) &=& \max_{C_t}~U(C_t) ~+ \DiscFac (1 - \DiePrb_{t+1}) V_{t+1}(M_{t+1},P_{t+1}), \\
& s.t. & \\
A_t &=& M_t - C_t, \\
A_t/P_t &\geq& \underline{a}, \\
M_{t+1} &=& \Rfree A_t + Y_{t+1}, \\
Y_{t+1} &=& P_{t+1}, \\
P_{t+1} &=& \PermGroFac_{t+1} P_t.
\end{eqnarray*}
The consumer's problem is characterized by a coefficient of relative risk aversion $\CRRA$, an intertemporal discount factor $\DiscFac$, an interest factor $\Rfree$, and age-varying sequences of the permanent income growth factor $\PermGroFac_t$ and survival probability $(1 - \DiePrb_t)$.
While it does not reduce the computational complexity of the problem (as permanent income is deterministic, given its initial condition $P_0$), HARK represents this problem with *normalized* variables (represented in lower case), dividing all real variables by permanent income $P_t$ and utility levels by $P_t^{1-\CRRA}$. The Bellman form of the model thus reduces to:
\begin{eqnarray*}
v_t(m_t) &=& \max_{c_t}~U(c_t) ~+ \DiscFac (1 - \DiePrb_{t+1}) \PermGroFac_{t+1}^{1-\CRRA} v_{t+1}(m_{t+1}), \\
& s.t. & \\
a_t &=& m_t - c_t, \\
a_t &\geq& \underline{a}, \\
m_{t+1} &=& \Rfree/\PermGroFac_{t+1} a_t + 1.
\end{eqnarray*}
## Solution method for PerfForesightConsumerType
Because of the assumptions of CRRA utility, no risk other than mortality, and no artificial borrowing constraint, the problem has a closed form solution. In fact, the consumption function is perfectly linear, and the value function composed with the inverse utility function is also linear. The mathematical solution of this model is described in detail in the lecture notes [PerfForesightCRRA](https://www.econ2.jhu.edu/people/ccarroll/public/lecturenotes/consumption/PerfForesightCRRA).
The one period problem for this model is solved by the function `solveConsPerfForesight`, which creates an instance of the class `ConsPerfForesightSolver`. To construct an instance of the class `PerfForesightConsumerType`, several parameters must be passed to its constructor as shown in the table below.
## Example parameter values to construct an instance of PerfForesightConsumerType
| Parameter | Description | Code | Example value | Time-varying? |
| :---: | --- | --- | --- | --- |
| $\DiscFac$ |Intertemporal discount factor | $\texttt{DiscFac}$ | $0.96$ | |
| $\CRRA $ |Coefficient of relative risk aversion | $\texttt{CRRA}$ | $2.0$ | |
| $\Rfree$ | Risk free interest factor | $\texttt{Rfree}$ | $1.03$ | |
| $1 - \DiePrb_{t+1}$ |Survival probability | $\texttt{LivPrb}$ | $[0.98]$ | $\surd$ |
|$\PermGroFac_{t+1}$|Permanent income growth factor|$\texttt{PermGroFac}$| $[1.01]$ | $\surd$ |
|$\underline{a}$|Artificial borrowing constraint|$\texttt{BoroCnstArt}$| $None$ | |
|$(none)$|Maximum number of gridpoints in consumption function |$\texttt{aXtraCount}$| $200$ | |
|$T$| Number of periods in this type's "cycle" |$\texttt{T_cycle}$| $1$ | |
|(none)| Number of times the "cycle" occurs |$\texttt{cycles}$| $0$ | |
Note that the survival probability and income growth factor have time subscripts; likewise, the example values for these parameters are *lists* rather than simply single floats. This is because those parameters are *time-varying*: their values can depend on which period of the problem the agent is in. All time-varying parameters *must* be specified as lists, even if the same value occurs in each period for this type.
The artificial borrowing constraint can be any non-positive `float`, or it can be `None` to indicate no artificial borrowing constraint. The maximum number of gridpoints in the consumption function is only relevant if the borrowing constraint is not `None`; without an upper bound on the number of gridpoints, kinks in the consumption function will propagate indefinitely in an infinite horizon model if there is a borrowing constraint, eventually resulting in an overflow error. If there is no artificial borrowing constraint, then the number of gridpoints used to represent the consumption function is always exactly two.
The last two parameters in the table specify the "nature of time" for this type: the number of (non-terminal) periods in this type's "cycle", and the number of times that the "cycle" occurs. *Every* subclass of `AgentType` uses these two code parameters to define the nature of time. Here, `T_cycle` has the value $1$, indicating that there is exactly one period in the cycle, while `cycles` is $0$, indicating that the cycle is repeated in *infinite* number of times-- it is an infinite horizon model, with the same "kind" of period repeated over and over.
In contrast, we could instead specify a life-cycle model by setting `T_cycle` to $1$, and specifying age-varying sequences of income growth and survival probability. In all cases, the number of elements in each time-varying parameter should exactly equal $\texttt{T_cycle}$.
The parameter $\texttt{AgentCount}$ specifies how many consumers there are of this *type*-- how many individuals have these exact parameter values and are *ex ante* homogeneous. This information is not relevant for solving the model, but is needed in order to simulate a population of agents, introducing *ex post* heterogeneity through idiosyncratic shocks. Of course, simulating a perfect foresight model is quite boring, as there are *no* idiosyncratic shocks other than death!
The cell below defines a dictionary that can be passed to the constructor method for `PerfForesightConsumerType`, with the values from the table here.
```
PerfForesightDict = {
# Parameters actually used in the solution method
"CRRA": 2.0, # Coefficient of relative risk aversion
"Rfree": 1.03, # Interest factor on assets
"DiscFac": 0.96, # Default intertemporal discount factor
"LivPrb": [0.98], # Survival probability
"PermGroFac": [1.01], # Permanent income growth factor
"BoroCnstArt": None, # Artificial borrowing constraint
"aXtraCount": 200, # Maximum number of gridpoints in consumption function
# Parameters that characterize the nature of time
"T_cycle": 1, # Number of periods in the cycle for this agent type
"cycles": 0, # Number of times the cycle occurs (0 --> infinitely repeated)
}
```
## Solving and examining the solution of the perfect foresight model
With the dictionary we have just defined, we can create an instance of `PerfForesightConsumerType` by passing the dictionary to the class (as if the class were a function). This instance can then be solved by invoking its `solve` method.
```
PFexample = PerfForesightConsumerType(**PerfForesightDict)
PFexample.cycles = 0
PFexample.solve()
```
The $\texttt{solve}$ method fills in the instance's attribute `solution` as a time-varying list of solutions to each period of the consumer's problem. In this case, `solution` will be a list with exactly one instance of the class `ConsumerSolution`, representing the solution to the infinite horizon model we specified.
```
print(PFexample.solution)
```
Each element of `solution` has a few attributes. To see all of them, we can use the \texttt{vars} built in function:
the consumption functions reside in the attribute $\texttt{cFunc}$ of each element of `ConsumerType.solution`. This method creates a (time varying) attribute $\texttt{cFunc}$ that contains a list of consumption functions.
```
print(vars(PFexample.solution[0]))
```
The two most important attributes of a single period solution of this model are the (normalized) consumption function $\texttt{cFunc}$ and the (normalized) value function $\texttt{vFunc}$. Let's plot those functions near the lower bound of the permissible state space (the attribute $\texttt{mNrmMin}$ tells us the lower bound of $m_t$ where the consumption function is defined).
```
print("Linear perfect foresight consumption function:")
mMin = PFexample.solution[0].mNrmMin
plot_funcs(PFexample.solution[0].cFunc, mMin, mMin + 10.0)
print("Perfect foresight value function:")
plot_funcs(PFexample.solution[0].vFunc, mMin + 0.1, mMin + 10.1)
```
An element of `solution` also includes the (normalized) marginal value function $\texttt{vPfunc}$, and the lower and upper bounds of the marginal propensity to consume (MPC) $\texttt{MPCmin}$ and $\texttt{MPCmax}$. Note that with a linear consumption function, the MPC is constant, so its lower and upper bound are identical.
### Liquidity constrained perfect foresight example
Without an artificial borrowing constraint, a perfect foresight consumer is free to borrow against the PDV of his entire future stream of labor income-- his "human wealth" $\texttt{hNrm}$-- and he will consume a constant proportion of his total wealth (market resources plus human wealth). If we introduce an artificial borrowing constraint, both of these features vanish. In the cell below, we define a parameter dictionary that prevents the consumer from borrowing *at all*, create and solve a new instance of `PerfForesightConsumerType` with it, and then plot its consumption function.
```
LiqConstrDict = copy(PerfForesightDict)
LiqConstrDict["BoroCnstArt"] = 0.0 # Set the artificial borrowing constraint to zero
LiqConstrExample = PerfForesightConsumerType(**LiqConstrDict)
LiqConstrExample.cycles = 0 # Make this type be infinite horizon
LiqConstrExample.solve()
print("Liquidity constrained perfect foresight consumption function:")
plot_funcs(LiqConstrExample.solution[0].cFunc, 0.0, 10.0)
# At this time, the value function for a perfect foresight consumer with an artificial borrowing constraint is not computed nor included as part of its $\texttt{solution}$.
```
## Simulating the perfect foresight consumer model
Suppose we wanted to simulate many consumers who share the parameter values that we passed to `PerfForesightConsumerType`-- an *ex ante* homogeneous *type* of consumers. To do this, our instance would have to know *how many* agents there are of this type, as well as their initial levels of assets $a_t$ and permanent income $P_t$.
### Setting simulation parameters
Let's fill in this information by passing another dictionary to `PFexample` with simulation parameters. The table below lists the parameters that an instance of `PerfForesightConsumerType` needs in order to successfully simulate its model using the `simulate` method.
| Description | Code | Example value |
| :---: | --- | --- |
| Number of consumers of this type | $\texttt{AgentCount}$ | $10000$ |
| Number of periods to simulate | $\texttt{T_sim}$ | $120$ |
| Mean of initial log (normalized) assets | $\texttt{aNrmInitMean}$ | $-6.0$ |
| Stdev of initial log (normalized) assets | $\texttt{aNrmInitStd}$ | $1.0$ |
| Mean of initial log permanent income | $\texttt{pLvlInitMean}$ | $0.0$ |
| Stdev of initial log permanent income | $\texttt{pLvlInitStd}$ | $0.0$ |
| Aggregrate productivity growth factor | $\texttt{PermGroFacAgg}$ | $1.0$ |
| Age after which consumers are automatically killed | $\texttt{T_age}$ | $None$ |
We have specified the model so that initial assets and permanent income are both distributed lognormally, with mean and standard deviation of the underlying normal distributions provided by the user.
The parameter $\texttt{PermGroFacAgg}$ exists for compatibility with more advanced models that employ aggregate productivity shocks; it can simply be set to 1.
In infinite horizon models, it might be useful to prevent agents from living extraordinarily long lives through a fortuitous sequence of mortality shocks. We have thus provided the option of setting $\texttt{T_age}$ to specify the maximum number of periods that a consumer can live before they are automatically killed (and replaced with a new consumer with initial state drawn from the specified distributions). This can be turned off by setting it to `None`.
The cell below puts these parameters into a dictionary, then gives them to `PFexample`. Note that all of these parameters *could* have been passed as part of the original dictionary; we omitted them above for simplicity.
```
SimulationParams = {
"AgentCount": 10000, # Number of agents of this type
"T_sim": 120, # Number of periods to simulate
"aNrmInitMean": -6.0, # Mean of log initial assets
"aNrmInitStd": 1.0, # Standard deviation of log initial assets
"pLvlInitMean": 0.0, # Mean of log initial permanent income
"pLvlInitStd": 0.0, # Standard deviation of log initial permanent income
"PermGroFacAgg": 1.0, # Aggregate permanent income growth factor
"T_age": None, # Age after which simulated agents are automatically killed
}
PFexample.assign_parameters(**SimulationParams)
```
To generate simulated data, we need to specify which variables we want to track the "history" of for this instance. To do so, we set the `track_vars` attribute of our `PerfForesightConsumerType` instance to be a list of strings with the simulation variables we want to track.
In this model, valid arguments to `track_vars` include $\texttt{mNrm}$, $\texttt{cNrm}$, $\texttt{aNrm}$, and $\texttt{pLvl}$. Because this model has no idiosyncratic shocks, our simulated data will be quite boring.
### Generating simulated data
Before simulating, the `initialize_sim` method must be invoked. This resets our instance back to its initial state, drawing a set of initial $\texttt{aNrm}$ and $\texttt{pLvl}$ values from the specified distributions and storing them in the attributes $\texttt{aNrmNow_init}$ and $\texttt{pLvlNow_init}$. It also resets this instance's internal random number generator, so that the same initial states will be set every time `initialize_sim` is called. In models with non-trivial shocks, this also ensures that the same sequence of shocks will be generated on every simulation run.
Finally, the `simulate` method can be called.
```
PFexample.track_vars = ['mNrm']
PFexample.initialize_sim()
PFexample.simulate()
# Each simulation variable $\texttt{X}$ named in $\texttt{track_vars}$ will have the *history* of that variable for each agent stored in the attribute $\texttt{X_hist}$ as an array of shape $(\texttt{T_sim},\texttt{AgentCount})$. To see that the simulation worked as intended, we can plot the mean of $m_t$ in each simulated period:
plt.plot(np.mean(PFexample.history['mNrm'], axis=1))
plt.xlabel("Time")
plt.ylabel("Mean normalized market resources")
plt.show()
```
A perfect foresight consumer can borrow against the PDV of his future income-- his human wealth-- and thus as time goes on, our simulated agents approach the (very negative) steady state level of $m_t$ while being steadily replaced with consumers with roughly $m_t=1$.
The slight wiggles in the plotted curve are due to consumers randomly dying and being replaced; their replacement will have an initial state drawn from the distributions specified by the user. To see the current distribution of ages, we can look at the attribute $\texttt{t_age}$.
```
N = PFexample.AgentCount
F = np.linspace(0.0, 1.0, N)
plt.plot(np.sort(PFexample.t_age), F)
plt.xlabel("Current age of consumers")
plt.ylabel("Cumulative distribution")
plt.show()
```
The distribution is (discretely) exponential, with a point mass at 120 with consumers who have survived since the beginning of the simulation.
One might wonder why HARK requires users to call `initialize_sim` before calling `simulate`: Why doesn't `simulate` just call `initialize_sim` as its first step? We have broken up these two steps so that users can simulate some number of periods, change something in the environment, and then resume the simulation.
When called with no argument, `simulate` will simulate the model for $\texttt{T_sim}$ periods. The user can optionally pass an integer specifying the number of periods to simulate (which should not exceed $\texttt{T_sim}$).
In the cell below, we simulate our perfect foresight consumers for 80 periods, then seize a bunch of their assets (dragging their wealth even more negative), then simulate for the remaining 40 periods.
The `state_prev` attribute of an AgenType stores the values of the model's state variables in the _previous_ period of the simulation.
```
PFexample.initialize_sim()
PFexample.simulate(80)
PFexample.state_prev['aNrm'] += -5.0 # Adjust all simulated consumers' assets downward by 5
PFexample.simulate(40)
plt.plot(np.mean(PFexample.history['mNrm'], axis=1))
plt.xlabel("Time")
plt.ylabel("Mean normalized market resources")
plt.show()
```
| true |
code
| 0.801198 | null | null | null | null |
|
# Likelihood based models
This notebook will outline the likelihood based approach to training on Bandit feedback.
Although before proceeding we will study the output of the simmulator in a little more detail.
```
from numpy.random.mtrand import RandomState
from recogym import Configuration
from recogym.agents import Agent
from sklearn.linear_model import LogisticRegression
from recogym import verify_agents
from recogym.agents import OrganicUserEventCounterAgent, organic_user_count_args
from recogym.evaluate_agent import verify_agents, plot_verify_agents
import gym, recogym
from copy import deepcopy
from recogym import env_1_args
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
plt.rcParams['figure.figsize'] = [6, 3]
ABTestNumberOfUsers=1000
NumberOfProducts=10
NumberOfSamples = 20
env_1_args['phi_var']=0.0
env_1_args['number_of_flips']=0
env_1_args['sigma_mu_organic'] = 0.0
env_1_args['sigma_omega']=1
env_1_args['random_seed'] = 42
env_1_args['num_products'] = NumberOfProducts
env_1_args['K'] = 5
env_1_args['number_of_flips'] = 5
env = gym.make('reco-gym-v1')
env.init_gym(env_1_args)
data = deepcopy(env).generate_logs(ABTestNumberOfUsers)
```
# Logistic Regression Model
## Turn Data into Features
Now we are going to build a _Logistic Regression_ model.
The model will predict _the probability of the click_ for the following data:
* _`Views`_ is a total amount of views of a particular _`Product`_ shown during _Organic_ _`Events`_ **before** a _Bandit_ _`Event`_.
* _`Action`_ is a proposed _`Product`_ at a _Bandit_ _`Event`_.
For example, assume that we have _`10`_ products. In _Organic_ _`Events`_, these products were shown to a user as follows:
<table>
<tr>
<th>Product ID</th>
<th>Views</th>
</tr>
<tr>
<td>0</td>
<td>0</td>
</tr>
<tr>
<td>1</td>
<td>0</td>
</tr>
<tr>
<td>2</td>
<td>0</td>
</tr>
<tr>
<td>3</td>
<td>7</td>
</tr>
<tr>
<td>4</td>
<td>0</td>
</tr>
<tr>
<td>5</td>
<td>0</td>
</tr>
<tr>
<td>6</td>
<td>0</td>
</tr>
<tr>
<td>7</td>
<td>8</td>
</tr>
<tr>
<td>8</td>
<td>11</td>
</tr>
<tr>
<td>9</td>
<td>0</td>
</tr>
</table>
When we want to know the probability of the click for _`Product`_ = _`8`_ with available amounts of _`Views`_, the input data for the model will be:
_`0 0 0 7 0 0 0 0 8 11 0`_ _**`8`**_
The first 10 numbers are _`Views`_ of _`Products`_ (see above), the latest one is the _`Action`_.
The output will be two numbers:
* $0^{th}$ index: $1 - \mathbb{P}_c(P=p|V)$.
* $1^{st}$ index: $\mathbb{P}_c(P=p|V)$.
Here, $\mathbb{P}_c(P=p|V)$ is the probability of the click for a _`Product`_ $p$, provided that we have _`Views`_ $V$.
In all following models, an _`Action`_ will not be used as a number, but it will be decoded as a _vector_.
In our current example, the _`Action`_ is _`8`_. Thus, it is encoded as:
_`0 0 0 0 0 0 0 0`_ _**`1`**_ _`0`_
Here,
* Vector of _`Actions`_ has a size that is equal to the _*number of `Products`*_ i.e. _`10`_.
* _`Action`_ _`8`_ is marked as _`1`_ (_`Action`_ starts with _`0`_).
```
import math
import numpy as np
def build_train_data(data):
"""
Build Train Data
Parameters:
data: offline experiment logs
the data contains both Organic and Bandit Events
Returns:
:(outs, history, actions)
"""
num_products = int(data.v.max() + 1)
number_of_users = int(data.u.max()) + 1
history = []
actions = []
outs = []
for user_id in range(number_of_users):
views = np.zeros((0, num_products))
for _, user_datum in data[data['u'] == user_id].iterrows():
if user_datum['z'] == 'organic':
assert (math.isnan(user_datum['a']))
assert (math.isnan(user_datum['c']))
assert (not math.isnan(user_datum['v']))
view = int(user_datum['v'])
tmp_view = np.zeros(num_products)
tmp_view[view] = 1
# Append the latest view at the beginning of all views.
views = np.append(tmp_view[np.newaxis, :], views, axis = 0)
else:
assert (user_datum['z'] == 'bandit')
assert (not math.isnan(user_datum['a']))
assert (not math.isnan(user_datum['c']))
assert (math.isnan(user_datum['v']))
action = int(user_datum['a'])
action_flags = np.zeros(num_products, dtype = np.int8)
action_flags[int(action)] = 1
click = int(user_datum['c'])
history.append(views.sum(0))
actions.append(action_flags)
outs.append(click)
return np.array(outs), history, actions
clicks, history, actions = build_train_data(data)
data[0:27]
history[0:8]
actions[0:8]
```
Look at the data and see how it maps into the features - which is the combination of the history and the actions and the label which is clicks. Note that only the bandit events correspond to records in the training data.
In order to do personalisation it is necessary to cross the action and history features. _Why_? We do the simplest possible cross an element wise kronecker product.
```
from recogym.agents import FeatureProvider
class CrossFeatureProvider(FeatureProvider):
"""Feature provider as an abstract class that defined interface of setting/getting features"""
def __init__(self, config):
super(CrossFeatureProvider, self).__init__(config)
self.feature_data = None
def observe(self, observation):
"""Consider an Organic Event for a particular user"""
for session in observation.sessions():
self.feature_data[session['v']] += 1
def features(self, observation):
"""Provide feature values adjusted to a particular feature set"""
return self.feature_data
def reset(self):
self.feature_data = np.zeros((self.config.num_products))
class ModelBasedAgent(Agent):
def __init__(self, env, feature_provider, model):
# Set environment as an attribute of Agent.
self.env = env
self.feature_provider = feature_provider
self.model = model
self.reset()
def act(self, observation, reward, done):
"""Act method returns an action based on current observation and past history"""
self.feature_provider.observe(observation)
cross_features = np.kron(np.eye(env.config.num_products),self.feature_provider.features(observation))
prob = self.model.predict_proba(cross_features)[:, 1]
action = np.argmax(prob)
prob = np.zeros_like(prob)
prob[action] = 1.0
return {
**super().act(observation, reward, done),
**{
'a': action,
'ps': 1.,
'ps-a': prob,
}
}
def reset(self):
self.feature_provider.reset()
def build_history_agent(env_args, data):
outs, history, actions = build_train_data(data)
features = np.vstack([np.kron(aa,hh) for hh, aa in zip(history, actions)])
config = Configuration(env_args)
logreg = LogisticRegression(
solver = 'lbfgs',
max_iter = 5000,
random_state = config.random_seed
)
log_reg_fit = logreg.fit(features, outs)
return ModelBasedAgent(
config,
CrossFeatureProvider(config),
log_reg_fit
)
likelihood_logreg = build_history_agent(env_1_args, data)
organic_counter_agent = OrganicUserEventCounterAgent(Configuration({
**organic_user_count_args,
**env_1_args,
'select_randomly': True,
}))
result = verify_agents(env, 5000, {'likelihood logreg': likelihood_logreg, 'organic count': organic_counter_agent})
fig = plot_verify_agents(result)
plt.show()
```
| true |
code
| 0.769286 | null | null | null | null |
|
# Bayesian Probabilistic Matrix Factorization
**Published**: November 6, 2020
**Author**: Xinyu Chen [[**GitHub homepage**](https://github.com/xinychen)]
**Download**: This Jupyter notebook is at our GitHub repository. If you want to evaluate the code, please download the notebook from the [**transdim**](https://github.com/xinychen/transdim/blob/master/imputer/BPMF.ipynb) repository.
This notebook shows how to implement the Bayesian Probabilistic Matrix Factorization (BPMF), a fully Bayesian matrix factorization model, on some real-world data sets. For an in-depth discussion of BPMF, please see [1].
<div class="alert alert-block alert-info">
<font color="black">
<b>[1]</b> Ruslan Salakhutdinov, Andriy Mnih (2008). <b>Bayesian probabilistic matrix factorization using Markov chain Monte Carlo</b>. ICML 2008. <a href="https://www.cs.toronto.edu/~amnih/papers/bpmf.pdf" title="PDF"><b>[PDF]</b></a> <a href="https://www.cs.toronto.edu/~rsalakhu/BPMF.html" title="Matlab code"><b>[Matlab code]</b></a>
</font>
</div>
#### Import some necessary packages
```
import numpy as np
from numpy.linalg import inv as inv
from numpy.random import normal as normrnd
from scipy.linalg import khatri_rao as kr_prod
from scipy.stats import wishart
from numpy.linalg import solve as solve
from scipy.linalg import cholesky as cholesky_upper
from scipy.linalg import solve_triangular as solve_ut
import matplotlib.pyplot as plt
%matplotlib inline
```
#### Define some functions
```
def mvnrnd_pre(mu, Lambda):
src = normrnd(size = (mu.shape[0],))
return solve_ut(cholesky_upper(Lambda, overwrite_a = True, check_finite = False),
src, lower = False, check_finite = False, overwrite_b = True) + mu
def cov_mat(mat, mat_bar):
mat = mat - mat_bar
return mat.T @ mat
```
#### Sample factor $\boldsymbol{W}$
```
def sample_factor_w(tau_sparse_mat, tau_ind, W, X, tau, beta0 = 1, vargin = 0):
"""Sampling N-by-R factor matrix W and its hyperparameters (mu_w, Lambda_w)."""
dim1, rank = W.shape
W_bar = np.mean(W, axis = 0)
temp = dim1 / (dim1 + beta0)
var_mu_hyper = temp * W_bar
var_W_hyper = inv(np.eye(rank) + cov_mat(W, W_bar) + temp * beta0 * np.outer(W_bar, W_bar))
var_Lambda_hyper = wishart.rvs(df = dim1 + rank, scale = var_W_hyper)
var_mu_hyper = mvnrnd_pre(var_mu_hyper, (dim1 + beta0) * var_Lambda_hyper)
if dim1 * rank ** 2 > 1e+8:
vargin = 1
if vargin == 0:
var1 = X.T
var2 = kr_prod(var1, var1)
var3 = (var2 @ tau_ind.T).reshape([rank, rank, dim1]) + var_Lambda_hyper[:, :, np.newaxis]
var4 = var1 @ tau_sparse_mat.T + (var_Lambda_hyper @ var_mu_hyper)[:, np.newaxis]
for i in range(dim1):
W[i, :] = mvnrnd_pre(solve(var3[:, :, i], var4[:, i]), var3[:, :, i])
elif vargin == 1:
for i in range(dim1):
pos0 = np.where(sparse_mat[i, :] != 0)
Xt = X[pos0[0], :]
var_mu = tau * Xt.T @ sparse_mat[i, pos0[0]] + var_Lambda_hyper @ var_mu_hyper
var_Lambda = tau * Xt.T @ Xt + var_Lambda_hyper
W[i, :] = mvnrnd_pre(solve(var_Lambda, var_mu), var_Lambda)
return W
```
#### Sample factor $\boldsymbol{X}$
```
def sample_factor_x(tau_sparse_mat, tau_ind, W, X, beta0 = 1):
"""Sampling T-by-R factor matrix X and its hyperparameters (mu_x, Lambda_x)."""
dim2, rank = X.shape
X_bar = np.mean(X, axis = 0)
temp = dim2 / (dim2 + beta0)
var_mu_hyper = temp * X_bar
var_X_hyper = inv(np.eye(rank) + cov_mat(X, X_bar) + temp * beta0 * np.outer(X_bar, X_bar))
var_Lambda_hyper = wishart.rvs(df = dim2 + rank, scale = var_X_hyper)
var_mu_hyper = mvnrnd_pre(var_mu_hyper, (dim2 + beta0) * var_Lambda_hyper)
var1 = W.T
var2 = kr_prod(var1, var1)
var3 = (var2 @ tau_ind).reshape([rank, rank, dim2]) + var_Lambda_hyper[:, :, np.newaxis]
var4 = var1 @ tau_sparse_mat + (var_Lambda_hyper @ var_mu_hyper)[:, np.newaxis]
for t in range(dim2):
X[t, :] = mvnrnd_pre(solve(var3[:, :, t], var4[:, t]), var3[:, :, t])
return X
```
#### Sampling Precision $\tau$
```
def sample_precision_tau(sparse_mat, mat_hat, ind):
var_alpha = 1e-6 + 0.5 * np.sum(ind)
var_beta = 1e-6 + 0.5 * np.sum(((sparse_mat - mat_hat) ** 2) * ind)
return np.random.gamma(var_alpha, 1 / var_beta)
def compute_mape(var, var_hat):
return np.sum(np.abs(var - var_hat) / var) / var.shape[0]
def compute_rmse(var, var_hat):
return np.sqrt(np.sum((var - var_hat) ** 2) / var.shape[0])
```
#### BPMF Implementation
```
def BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter):
"""Bayesian Probabilistic Matrix Factorization, BPMF."""
dim1, dim2 = sparse_mat.shape
W = init["W"]
X = init["X"]
if np.isnan(sparse_mat).any() == False:
ind = sparse_mat != 0
pos_obs = np.where(ind)
pos_test = np.where((dense_mat != 0) & (sparse_mat == 0))
elif np.isnan(sparse_mat).any() == True:
pos_test = np.where((dense_mat != 0) & (np.isnan(sparse_mat)))
ind = ~np.isnan(sparse_mat)
pos_obs = np.where(ind)
sparse_mat[np.isnan(sparse_mat)] = 0
dense_test = dense_mat[pos_test]
del dense_mat
tau = 1
W_plus = np.zeros((dim1, rank))
X_plus = np.zeros((dim2, rank))
temp_hat = np.zeros(sparse_mat.shape)
show_iter = 200
mat_hat_plus = np.zeros(sparse_mat.shape)
for it in range(burn_iter + gibbs_iter):
tau_ind = tau * ind
tau_sparse_mat = tau * sparse_mat
W = sample_factor_w(tau_sparse_mat, tau_ind, W, X, tau)
X = sample_factor_x(tau_sparse_mat, tau_ind, W, X)
mat_hat = W @ X.T
tau = sample_precision_tau(sparse_mat, mat_hat, ind)
temp_hat += mat_hat
if (it + 1) % show_iter == 0 and it < burn_iter:
temp_hat = temp_hat / show_iter
print('Iter: {}'.format(it + 1))
print('MAPE: {:.6}'.format(compute_mape(dense_test, temp_hat[pos_test])))
print('RMSE: {:.6}'.format(compute_rmse(dense_test, temp_hat[pos_test])))
temp_hat = np.zeros(sparse_mat.shape)
print()
if it + 1 > burn_iter:
W_plus += W
X_plus += X
mat_hat_plus += mat_hat
mat_hat = mat_hat_plus / gibbs_iter
W = W_plus / gibbs_iter
X = X_plus / gibbs_iter
print('Imputation MAPE: {:.6}'.format(compute_mape(dense_test, mat_hat[pos_test])))
print('Imputation RMSE: {:.6}'.format(compute_rmse(dense_test, mat_hat[pos_test])))
print()
return mat_hat, W, X
```
## Evaluation on Guangzhou Speed Data
**Scenario setting**:
- Tensor size: $214\times 61\times 144$ (road segment, day, time of day)
- Non-random missing (NM)
- 40% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('./data/tensor.mat')['tensor']
random_matrix = scipy.io.loadmat('./data/random_matrix.mat')['random_matrix']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.4
## Non-random missing (NM)
binary_tensor = np.zeros(tensor.shape)
for i1 in range(tensor.shape[0]):
for i2 in range(tensor.shape[1]):
binary_tensor[i1, i2, :] = np.round(random_matrix[i1, i2] + 0.5 - missing_rate)
binary_mat = binary_tensor.reshape([binary_tensor.shape[0], binary_tensor.shape[1] * binary_tensor.shape[2]])
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 10
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 10
init = {"W": 0.01 * np.random.randn(dim1, rank), "X": 0.01 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $214\times 61\times 144$ (road segment, day, time of day)
- Random missing (RM)
- 40% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Guangzhou-data-set/tensor.mat')['tensor']
random_tensor = scipy.io.loadmat('../datasets/Guangzhou-data-set/random_tensor.mat')['random_tensor']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.4
## Random missing (RM)
binary_mat = (np.round(random_tensor + 0.5 - missing_rate)
.reshape([random_tensor.shape[0], random_tensor.shape[1] * random_tensor.shape[2]]))
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 80
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 80
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $214\times 61\times 144$ (road segment, day, time of day)
- Random missing (RM)
- 60% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Guangzhou-data-set/tensor.mat')['tensor']
random_tensor = scipy.io.loadmat('../datasets/Guangzhou-data-set/random_tensor.mat')['random_tensor']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.6
## Random missing (RM)
binary_mat = (np.round(random_tensor + 0.5 - missing_rate)
.reshape([random_tensor.shape[0], random_tensor.shape[1] * random_tensor.shape[2]]))
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 80
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 80
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
## Evaluation on Birmingham Parking Data
**Scenario setting**:
- Tensor size: $30\times 77\times 18$ (parking slot, day, time of day)
- Non-random missing (NM)
- 40% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Birmingham-data-set/tensor.mat')['tensor']
random_matrix = scipy.io.loadmat('../datasets/Birmingham-data-set/random_matrix.mat')['random_matrix']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.4
## Non-random missing (NM)
binary_tensor = np.zeros(tensor.shape)
for i1 in range(tensor.shape[0]):
for i2 in range(tensor.shape[1]):
binary_tensor[i1, i2, :] = np.round(random_matrix[i1, i2] + 0.5 - missing_rate)
binary_mat = binary_tensor.reshape([binary_tensor.shape[0], binary_tensor.shape[1] * binary_tensor.shape[2]])
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 20
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 20
init = {"W": 0.01 * np.random.randn(dim1, rank), "X": 0.01 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $30\times 77\times 18$ (parking slot, day, time of day)
- Random missing (RM)
- 40% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Birmingham-data-set/tensor.mat')
tensor = tensor['tensor']
random_tensor = scipy.io.loadmat('../datasets/Birmingham-data-set/random_tensor.mat')
random_tensor = random_tensor['random_tensor']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.4
## Random missing (RM)
binary_mat = (np.round(random_tensor + 0.5 - missing_rate)
.reshape([random_tensor.shape[0], random_tensor.shape[1] * random_tensor.shape[2]]))
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 20
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 20
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $30\times 77\times 18$ (parking slot, day, time of day)
- Random missing (RM)
- 60% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Birmingham-data-set/tensor.mat')
tensor = tensor['tensor']
random_tensor = scipy.io.loadmat('../datasets/Birmingham-data-set/random_tensor.mat')
random_tensor = random_tensor['random_tensor']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.6
## Random missing (RM)
binary_mat = (np.round(random_tensor + 0.5 - missing_rate)
.reshape([random_tensor.shape[0], random_tensor.shape[1] * random_tensor.shape[2]]))
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 20
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 20
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
## Evaluation on Hangzhou Flow Data
**Scenario setting**:
- Tensor size: $80\times 25\times 108$ (metro station, day, time of day)
- Non-random missing (NM)
- 40% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Hangzhou-data-set/tensor.mat')['tensor']
random_matrix = scipy.io.loadmat('../datasets/Hangzhou-data-set/random_matrix.mat')['random_matrix']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.4
## Non-random missing (NM)
binary_tensor = np.zeros(tensor.shape)
for i1 in range(tensor.shape[0]):
for i2 in range(tensor.shape[1]):
binary_tensor[i1, i2, :] = np.round(random_matrix[i1, i2] + 0.5 - missing_rate)
binary_mat = binary_tensor.reshape([binary_tensor.shape[0], binary_tensor.shape[1] * binary_tensor.shape[2]])
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.01 * np.random.randn(dim1, rank), "X": 0.01 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $80\times 25\times 108$ (metro station, day, time of day)
- Random missing (RM)
- 40% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Hangzhou-data-set/tensor.mat')['tensor']
random_tensor = scipy.io.loadmat('../datasets/Hangzhou-data-set/random_tensor.mat')['random_tensor']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.4
## Random missing (RM)
binary_mat = (np.round(random_tensor + 0.5 - missing_rate)
.reshape([random_tensor.shape[0], random_tensor.shape[1] * random_tensor.shape[2]]))
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $80\times 25\times 108$ (metro station, day, time of day)
- Random missing (RM)
- 60% missing rate
```
import scipy.io
tensor = scipy.io.loadmat('../datasets/Hangzhou-data-set/tensor.mat')['tensor']
random_tensor = scipy.io.loadmat('../datasets/Hangzhou-data-set/random_tensor.mat')['random_tensor']
dense_mat = tensor.reshape([tensor.shape[0], tensor.shape[1] * tensor.shape[2]])
missing_rate = 0.6
## Random missing (RM)
binary_mat = (np.round(random_tensor + 0.5 - missing_rate)
.reshape([random_tensor.shape[0], random_tensor.shape[1] * random_tensor.shape[2]]))
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
## Evaluation on Seattle Speed Data
**Scenario setting**:
- Tensor size: $323\times 28\times 288$ (road segment, day, time of day)
- Non-random missing (NM)
- 40% missing rate
```
import pandas as pd
dense_mat = pd.read_csv('../datasets/Seattle-data-set/mat.csv', index_col = 0)
NM_mat = pd.read_csv('../datasets/Seattle-data-set/NM_mat.csv', index_col = 0)
dense_mat = dense_mat.values
NM_mat = NM_mat.values
missing_rate = 0.4
## Non-random missing (NM)
binary_tensor = np.zeros((dense_mat.shape[0], 28, 288))
for i1 in range(binary_tensor.shape[0]):
for i2 in range(binary_tensor.shape[1]):
binary_tensor[i1, i2, :] = np.round(NM_mat[i1, i2] + 0.5 - missing_rate)
sparse_mat = np.multiply(dense_mat, binary_tensor.reshape([dense_mat.shape[0], dense_mat.shape[1]]))
```
**Model setting**:
- Low rank: 10
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 10
init = {"W": 0.01 * np.random.randn(dim1, rank), "X": 0.01 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $323\times 28\times 288$ (road segment, day, time of day)
- Random missing (RM)
- 40% missing rate
```
import pandas as pd
dense_mat = pd.read_csv('../datasets/Seattle-data-set/mat.csv', index_col = 0)
RM_mat = pd.read_csv('../datasets/Seattle-data-set/RM_mat.csv', index_col = 0)
dense_mat = dense_mat.values
RM_mat = RM_mat.values
missing_rate = 0.4
## Random missing (RM)
binary_mat = np.round(RM_mat + 0.5 - missing_rate)
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 50
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 50
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $323\times 28\times 288$ (road segment, day, time of day)
- Random missing (RM)
- 60% missing rate
```
import pandas as pd
dense_mat = pd.read_csv('../datasets/Seattle-data-set/mat.csv', index_col = 0)
RM_mat = pd.read_csv('../datasets/Seattle-data-set/RM_mat.csv', index_col = 0)
dense_mat = dense_mat.values
RM_mat = RM_mat.values
missing_rate = 0.6
## Random missing (RM)
binary_mat = np.round(RM_mat + 0.5 - missing_rate)
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 50
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 50
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
## Evaluation on London Movement Speed Data
London movement speed data set is is a city-wide hourly traffic speeddataset collected in London.
- Collected from 200,000+ road segments.
- 720 time points in April 2019.
- 73% missing values in the original data.
| Observation rate | $>90\%$ | $>80\%$ | $>70\%$ | $>60\%$ | $>50\%$ |
|:------------------|--------:|--------:|--------:|--------:|--------:|
|**Number of roads**| 17,666 | 27,148 | 35,912 | 44,352 | 52,727 |
If want to test on the full dataset, you could consider the following setting for masking observations as missing values.
```python
import numpy as np
np.random.seed(1000)
mask_rate = 0.20
dense_mat = np.load('../datasets/London-data-set/hourly_speed_mat.npy')
pos_obs = np.where(dense_mat != 0)
num = len(pos_obs[0])
sample_ind = np.random.choice(num, size = int(mask_rate * num), replace = False)
sparse_mat = dense_mat.copy()
sparse_mat[pos_obs[0][sample_ind], pos_obs[1][sample_ind]] = 0
```
Notably, you could also consider to evaluate the model on a subset of the data with the following setting.
```
import numpy as np
np.random.seed(1000)
missing_rate = 0.4
dense_mat = np.load('../datasets/London-data-set/hourly_speed_mat.npy')
binary_mat = dense_mat.copy()
binary_mat[binary_mat != 0] = 1
pos = np.where(np.sum(binary_mat, axis = 1) > 0.7 * binary_mat.shape[1])
dense_mat = dense_mat[pos[0], :]
## Non-random missing (NM)
binary_mat = np.zeros(dense_mat.shape)
random_mat = np.random.rand(dense_mat.shape[0], 30)
for i1 in range(dense_mat.shape[0]):
for i2 in range(30):
binary_mat[i1, i2 * 24 : (i2 + 1) * 24] = np.round(random_mat[i1, i2] + 0.5 - missing_rate)
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 20
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 20
init = {"W": 0.01 * np.random.randn(dim1, rank), "X": 0.01 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
import numpy as np
np.random.seed(1000)
missing_rate = 0.4
dense_mat = np.load('../datasets/London-data-set/hourly_speed_mat.npy')
binary_mat = dense_mat.copy()
binary_mat[binary_mat != 0] = 1
pos = np.where(np.sum(binary_mat, axis = 1) > 0.7 * binary_mat.shape[1])
dense_mat = dense_mat[pos[0], :]
## Random missing (RM)
random_mat = np.random.rand(dense_mat.shape[0], dense_mat.shape[1])
binary_mat = np.round(random_mat + 0.5 - missing_rate)
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 20
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 20
init = {"W": 0.01 * np.random.randn(dim1, rank), "X": 0.01 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
import numpy as np
np.random.seed(1000)
missing_rate = 0.6
dense_mat = np.load('../datasets/London-data-set/hourly_speed_mat.npy')
binary_mat = dense_mat.copy()
binary_mat[binary_mat != 0] = 1
pos = np.where(np.sum(binary_mat, axis = 1) > 0.7 * binary_mat.shape[1])
dense_mat = dense_mat[pos[0], :]
## Random missing (RM)
random_mat = np.random.rand(dense_mat.shape[0], dense_mat.shape[1])
binary_mat = np.round(random_mat + 0.5 - missing_rate)
sparse_mat = np.multiply(dense_mat, binary_mat)
```
**Model setting**:
- Low rank: 20
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 20
init = {"W": 0.01 * np.random.randn(dim1, rank), "X": 0.01 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
## Eavluation on NYC Taxi Flow Data
**Scenario setting**:
- Tensor size: $30\times 30\times 1461$ (origin, destination, time)
- Random missing (RM)
- 40% missing rate
```
import scipy.io
dense_tensor = scipy.io.loadmat('../datasets/NYC-data-set/tensor.mat')['tensor'].astype(np.float32)
rm_tensor = scipy.io.loadmat('../datasets/NYC-data-set/rm_tensor.mat')['rm_tensor']
missing_rate = 0.4
## Random missing (RM)
binary_tensor = np.round(rm_tensor + 0.5 - missing_rate)
sparse_tensor = dense_tensor.copy()
sparse_tensor[binary_tensor == 0] = np.nan
dim1, dim2, dim3 = dense_tensor.shape
dense_mat = np.zeros((dim1 * dim2, dim3))
sparse_mat = np.zeros((dim1 * dim2, dim3))
for i in range(dim1):
dense_mat[i * dim2 : (i + 1) * dim2, :] = dense_tensor[i, :, :]
sparse_mat[i * dim2 : (i + 1) * dim2, :] = sparse_tensor[i, :, :]
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $30\times 30\times 1461$ (origin, destination, time)
- Random missing (RM)
- 60% missing rate
```
import scipy.io
dense_tensor = scipy.io.loadmat('../datasets/NYC-data-set/tensor.mat')['tensor'].astype(np.float32)
rm_tensor = scipy.io.loadmat('../datasets/NYC-data-set/rm_tensor.mat')['rm_tensor']
missing_rate = 0.6
## Random missing (RM)
binary_tensor = np.round(rm_tensor + 0.5 - missing_rate)
sparse_tensor = dense_tensor.copy()
sparse_tensor[binary_tensor == 0] = np.nan
dim1, dim2, dim3 = dense_tensor.shape
dense_mat = np.zeros((dim1 * dim2, dim3))
sparse_mat = np.zeros((dim1 * dim2, dim3))
for i in range(dim1):
dense_mat[i * dim2 : (i + 1) * dim2, :] = dense_tensor[i, :, :]
sparse_mat[i * dim2 : (i + 1) * dim2, :] = sparse_tensor[i, :, :]
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $30\times 30\times 1461$ (origin, destination, time)
- Non-random missing (NM)
- 40% missing rate
```
import scipy.io
dense_tensor = scipy.io.loadmat('../datasets/NYC-data-set/tensor.mat')['tensor'].astype(np.float32)
nm_tensor = scipy.io.loadmat('../datasets/NYC-data-set/nm_tensor.mat')['nm_tensor']
missing_rate = 0.4
## Non-random missing (NM)
binary_tensor = np.zeros(dense_tensor.shape)
for i1 in range(dense_tensor.shape[0]):
for i2 in range(dense_tensor.shape[1]):
for i3 in range(61):
binary_tensor[i1, i2, i3 * 24 : (i3 + 1) * 24] = np.round(nm_tensor[i1, i2, i3] + 0.5 - missing_rate)
sparse_tensor = dense_tensor.copy()
sparse_tensor[binary_tensor == 0] = np.nan
dim1, dim2, dim3 = dense_tensor.shape
dense_mat = np.zeros((dim1 * dim2, dim3))
sparse_mat = np.zeros((dim1 * dim2, dim3))
for i in range(dim1):
dense_mat[i * dim2 : (i + 1) * dim2, :] = dense_tensor[i, :, :]
sparse_mat[i * dim2 : (i + 1) * dim2, :] = sparse_tensor[i, :, :]
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
## Evaluation on Pacific Surface Temperature Data
**Scenario setting**:
- Tensor size: $30\times 84\times 396$ (location x, location y, month)
- Random missing (RM)
- 40% missing rate
```
import numpy as np
np.random.seed(1000)
dense_tensor = np.load('../datasets/Temperature-data-set/tensor.npy').astype(np.float32)
pos = np.where(dense_tensor[:, 0, :] > 50)
dense_tensor[pos[0], :, pos[1]] = 0
random_tensor = np.random.rand(dense_tensor.shape[0], dense_tensor.shape[1], dense_tensor.shape[2])
missing_rate = 0.4
## Random missing (RM)
binary_tensor = np.round(random_tensor + 0.5 - missing_rate)
sparse_tensor = dense_tensor.copy()
sparse_tensor[binary_tensor == 0] = np.nan
sparse_tensor[sparse_tensor == 0] = np.nan
dim1, dim2, dim3 = dense_tensor.shape
dense_mat = np.zeros((dim1 * dim2, dim3))
sparse_mat = np.zeros((dim1 * dim2, dim3))
for i in range(dim1):
dense_mat[i * dim2 : (i + 1) * dim2, :] = dense_tensor[i, :, :]
sparse_mat[i * dim2 : (i + 1) * dim2, :] = sparse_tensor[i, :, :]
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $30\times 84\times 396$ (location x, location y, month)
- Random missing (RM)
- 60% missing rate
```
import numpy as np
np.random.seed(1000)
dense_tensor = np.load('../datasets/Temperature-data-set/tensor.npy').astype(np.float32)
pos = np.where(dense_tensor[:, 0, :] > 50)
dense_tensor[pos[0], :, pos[1]] = 0
random_tensor = np.random.rand(dense_tensor.shape[0], dense_tensor.shape[1], dense_tensor.shape[2])
missing_rate = 0.6
## Random missing (RM)
binary_tensor = np.round(random_tensor + 0.5 - missing_rate)
sparse_tensor = dense_tensor.copy()
sparse_tensor[binary_tensor == 0] = np.nan
sparse_tensor[sparse_tensor == 0] = np.nan
dim1, dim2, dim3 = dense_tensor.shape
dense_mat = np.zeros((dim1 * dim2, dim3))
sparse_mat = np.zeros((dim1 * dim2, dim3))
for i in range(dim1):
dense_mat[i * dim2 : (i + 1) * dim2, :] = dense_tensor[i, :, :]
sparse_mat[i * dim2 : (i + 1) * dim2, :] = sparse_tensor[i, :, :]
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
**Scenario setting**:
- Tensor size: $30\times 84\times 396$ (location x, location y, month)
- Non-random missing (NM)
- 40% missing rate
```
import numpy as np
np.random.seed(1000)
dense_tensor = np.load('../datasets/Temperature-data-set/tensor.npy').astype(np.float32)
pos = np.where(dense_tensor[:, 0, :] > 50)
dense_tensor[pos[0], :, pos[1]] = 0
random_tensor = np.random.rand(dense_tensor.shape[0], dense_tensor.shape[1], int(dense_tensor.shape[2] / 3))
missing_rate = 0.4
## Non-random missing (NM)
binary_tensor = np.zeros(dense_tensor.shape)
for i1 in range(dense_tensor.shape[0]):
for i2 in range(dense_tensor.shape[1]):
for i3 in range(int(dense_tensor.shape[2] / 3)):
binary_tensor[i1, i2, i3 * 3 : (i3 + 1) * 3] = np.round(random_tensor[i1, i2, i3] + 0.5 - missing_rate)
sparse_tensor = dense_tensor.copy()
sparse_tensor[binary_tensor == 0] = np.nan
sparse_tensor[sparse_tensor == 0] = np.nan
dim1, dim2, dim3 = dense_tensor.shape
dense_mat = np.zeros((dim1 * dim2, dim3))
sparse_mat = np.zeros((dim1 * dim2, dim3))
for i in range(dim1):
dense_mat[i * dim2 : (i + 1) * dim2, :] = dense_tensor[i, :, :]
sparse_mat[i * dim2 : (i + 1) * dim2, :] = sparse_tensor[i, :, :]
```
**Model setting**:
- Low rank: 30
- The number of burn-in iterations: 1000
- The number of Gibbs iterations: 200
```
import time
start = time.time()
dim1, dim2 = sparse_mat.shape
rank = 30
init = {"W": 0.1 * np.random.randn(dim1, rank), "X": 0.1 * np.random.randn(dim2, rank)}
burn_iter = 1000
gibbs_iter = 200
mat_hat, W, X = BPMF(dense_mat, sparse_mat, init, rank, burn_iter, gibbs_iter)
end = time.time()
print('Running time: %d seconds'%(end - start))
```
### License
<div class="alert alert-block alert-danger">
<b>This work is released under the MIT license.</b>
</div>
| true |
code
| 0.519948 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.