prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Chapter 4
## 4.2.1 均方誤差 (Mean Squared Error)
```
# 均方根函數
import numpy as np
# y為預測輸出,t為正確答案
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
# 假設正確答案為"2"
t = [0,0,1,0,0,0,0,0,0,0]
# 例一:"2"的機率為最高時(0.6)
y = [0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0]
print('Example 1 - MSE: ', mean_squared_error(np.array(y), np.array(t)))
# 例二:"7"的機率為最高時(0.6)
y = [0.1,0.05,0.1,0.0,0.05,0.1,0.0,0.6,0.0,0.0]
print('Example 2 - MSE: ', mean_squared_error(np.array(y), np.array(t)))
print('As you could imagine, MSE of example 2 is higher than the one of example 1.')
```
## 4.2.2 交叉熵誤差 (Cross Entropy Error)
```
# 建立交叉熵函數
import numpy as np
def cross_entropy_error(y,t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
t = [0,0,1,0,0,0,0,0,0,0]
# 例一:"2"的機率為最高時(0.6)
y = [0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0]
print('Example 1 - Cross Entropy Error: ', cross_entropy_error(np.array(y), np.array(t)))
# 例二:"7"的機率為最高時(0.6)
y = [0.1,0.05,0.1,0.0,0.05,0.1,0.0,0.6,0.0,0.0]
print('Example 2 - Cross Entropy Error: ', cross_entropy_error(np.array(y), np.array(t)))
```
## 4.2.3 小批次學習
```
import sys, os, numpy as np,
from TextbookProgram.mnist import load_mnist
sys.path.append(os.pardir)
(x_train, t_train), (x_test, t_test) = load_mnist(normalize = True, one_hot_label = True)
print(x_train.shape)
print(t_train.shape)
# Numpy 的 random choice 方法
import numpy as np
random_choice_demo = np.random.choice(60000, 10)
print(random_choice_demo)
# 以Numpy隨機取出10張訓練資料,建立小樣本
train.size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
```
## 4.2.4 以"批次對應版"執行交叉熵誤差
## (待完成)
```
# 建立新的交叉熵函數
import numpy as np
def cross_entropy_error(y,t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
```
## 4.2.5 為什麼要設定損失函數?
展開神經網路的學習時,不可以把辨識準確度當作"指標"的理由,是因為當辨識度變成指標時,在任何位置,參數微分後幾乎都會變成0
## 4.3.2 數值微分的範例
```
# 建立數值微分函數
def numerical_diff(f,x):
h = 1e-4 # 10^(-4) = 0.0001
return (f(x+h) - f(x-h)) / (2*h)
def function_1(x):
return 0.01 * x ** 2 + 0.1 * x
import numpy as np
import matplotlib.pylab as plt
x = np.arange(0.0, 20.0, 0.1) # 建立從0到10間隔為0.1的x陣列
y = function_1(x)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x, y, 'r')
plt.show()
# 在x=5及x=10時,分別計算此函數的微分
print('X=5時的數值微分', numerical_diff(function_1, 5))
print('X=10時的數值微分', numerical_diff(function_1, 10))
```
## 4.3.3 偏微分
```
# 建立有兩個變數的函式
def function_2(x):
return x[0]**2 + x[1]**2
# 或 return np.sum(x**2)
# 建立偏微分的函式 - x[0]=3, x[1]=4
# 偏微分x[0]時的改寫
def function_tmp1(x0):
return x0*x0 + 4.0**2.0
print('對x[0]進行偏微分時', numerical_diff(function_tmp1, 3))
# 偏微分x[1]時的改寫
def function_tmp2(x1):
return 3**2 + x1*x1
print('對x[1]進行偏微分時', numerical_diff(function_tmp2, 4))
```
## 4.4 梯度
```
# 一次進行所有變數的偏微分
import numpy as np
def numerical_gradient(f,x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 產生和x同形狀的陣列
for idx in range(x.size):
tmp_val = x[idx]
# 計算f(x+h)
x[idx] = tmp_val + h
fxh1 = f(x)
# 計算f(x-h)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 恢復原值
return grad
# 使用Numerical Gradient進行多變數的微分
print(numerical_gradient(function_2, np.array([3.0, 4.0])))
print(numerical_gradient(function_2, np.array([0.0, 2.0])))
print(numerical_gradient(function_2, np.array([3.0, 0.0])))
# 使用官網提供的python程式繪製2D梯度圖:f(x[0],x[1]) = x[0]**2 + x[1]**2
# coding: utf-8
# cf.http://d.hatena.ne.jp/white_wheels/20100327/p3
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D
def _numerical_gradient_no_batch(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 値を元に戻す
return grad
def numerical_gradient(f, X):
if X.ndim == 1:
return _numerical_gradient_no_batch(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_no_batch(f, x)
return grad
def function_2(x):
if x.ndim == 1:
return np.sum(x**2)
else:
return np.sum(x**2, axis=1)
def tangent_line(f, x):
d = numerical_gradient(f, x)
print(d)
y = f(x) - d*x
return lambda t: d*t + y
if __name__ == '__main__':
x0 = np.arange(-2, 2.5, 0.25)
x1 = np.arange(-2, 2.5, 0.25)
X, Y = np.meshgrid(x0, x1)
X = X.flatten()
Y = Y.flatten()
grad = numerical_gradient(function_2, np.array([X, Y]).T).T
plt.figure()
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666")
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid()
plt.draw()
plt.show()
```
## 4.4.1 梯度法
```
# 建立梯度下降法函式
# f:需最佳化的函數;init_x:預設值;lr:learning rate;step_num:使用梯度法重復的步鄹
import numpy as np
def numerical_gradient(f,x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 產生和x同形狀的陣列
for idx in range(x.size):
tmp_val = x[idx]
# 計算f(x+h)
x[idx] = tmp_val + h
fxh1 = f(x)
# 計算f(x-h)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 恢復原值
return grad
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x = x - lr * grad
return x
# 利用梯度法求出f(x[0],x[1]) = x[0]**2 + x[1]**2的最小值
def function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0,4.0])
print(gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100))
# 使用官網提供的python程式繪製梯度下降法的過程
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
from TextbookProgram.gradient_2d import numerical_gradient
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append( x.copy() )
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
def function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])
lr = 0.1
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()
# 學習率太大的範例
init_x = np.array([-3.0, 4.0])
lr_too_large = gradient_descent(function_2, init_x=init_x, lr=10.0, step_num=100)
print(lr_too_large)
# 學習率太小的範例
init_x = np.array([-3.0, 4.0])
lr_too_small = gradient_descent(function_2, init_x=init_x, lr=1e-10, step_num=100)
print(lr_too_small)
```
## 4.4.2 神經網路的梯度
```
# 建立簡單神經網路模型:Simple Net
import sys, os
sys.path.append(os.pardir) # Set import location
import numpy as np
from TextbookProgram.functions import softmax, cross_entropy_error
from TextbookProgram.gradient import numerical_gradient
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3) # 以常態初始化
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y,t)
return loss
net = simpleNet()
print(net.W) # 權重參數
# 測試神經網路模型
x = np.array([0.6,0.9])
p = net.predict(x)
print('Predicted value od p: ', p)
print('最大值的索引值:', np.argmax(p))
t = np.array([0,0,1]) # 正確答案標簽
print('Loss: ', net.loss(x,t))
# 計算梯度
def f(w):
return net.loss(x,t)
dW = numerical_gradient(f, net.W)
print('列印各權重的梯度:', dW)
# 使用lambda來設定簡單的函數
f = lambda w: net.loss(x,t)
dW = numerical_gradient(f, net.W)
print('dW: ', dW)
```
## 4.5.1 雙層神經網路的類別
```
import sys, os
import numpy as np
from TextbookProgram.functions import *
from TextbookProgram.gradient import numerical_gradient
class TwoLayerNet:
# __init__進行初始化,引數:輸入層的神經元數量、隱藏層的神經元數量、輸出層的神經元數量
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 權重初始化
# params:維持神經網路參數字典變數(實例變數)
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 預測函數,x市屬
def predict(self,x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
y = softmax(a2)
return y
# 計算損失函數
# x:輸入資料,t:訓練資料(正確資料)
def loss(self,x,t):
y = self.predict(x)
return cross_entropy_error(y,t)
# 計算辨識準確度
def accuracy(self,x,t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 計算權重參數的梯度
# x:輸入資料,t:訓練資料(正確資料)
# grads:維持梯度的字典變數(numerical_gradient的回傳值)
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x,t)
grads={}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
# 範例一
net = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)
print('Shape of W1 is',net.params['W1'].shape)
print('Shape of b1 is',net.params['b1'].shape)
print('Shape of W2 is',net.params['W2'].shape)
print('Shape of b2 is',net.params['b2'].shape)
# 範例一的推論
x = np.random.rand(100, 784)
y = net.predict(x)
# 範例二
x = np.random.rand(100,784) # 虛擬輸入資料
t = np.random.rand(100,10) # 虛擬正確答案標簽
grads = net.numerical_gradient(x,t) # 計算梯度
print('Shape of gradient of W1 is ', grads['W1'].shape)
print('Shape of gradient of b1 is ', grads['b1'].shape)
print('Shape of gradient of W2 is ', grads['W2'].shape)
print('Shape of gradient of b2 is ', grads['b2'].shape)
```
## 4.5.2 執行小批次學習
### (需要更新實測)
```
import numpy as np
from TextbookProgram.mnist import load_mnist
from TextbookProgram.two_layer_net import TwoLayerNet
(x_train,t_train), (x_test,t_test) = load_mnist(normalize=True, one_hot_label=True)
train_loss_list = []
# 設定超參數
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
network = TwoLayerNet(input_size=784, hidden_sizee=50, output_size=10)
for i in range(iters_num):
# 取得小批次
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 計算梯度
grad = network.numerical_gradient(x_batch, t_batch)
# grad = network.gradient(x_batch, t_batch) # 高速版
# 更新參數
for ley in ('W1', 'b1', 'W2', 'b2'):
network.params[key] = network.params[key] - learning_rate * grad[key]
# 記錄學習過程
loss = network.loss(x_batch, t_batch)
train_loss_list.appned(loss)
```
## 4.5.3 利用測試資料評估
```
import numpy as np
from TextbookProgram.mnist import load_mnist
from TextbookProgram.two_layer_net import TwoLayerNet
(x_train,t_train), (x_test,t_test) = load_mnist(normalize=True, one_hot_label=True)
train_loss_list = []
# 新增加的部分
train_acc_list = []
test_acc_list = []
# 每 1 epoch 的重復次數
iter_per_epoch = max(train/batch_size, 1)
# 設定超參數
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
network = TwoLayerNet(input_size=784, hidden_sizee=50, output_size=10)
for i in range(iters_num):
# 取得小批次
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 計算梯度
grad = network.numerical_gradient(x_batch, t_batch)
# grad = network.gradient(x_batch, t_batch) # 高速版
# 更新參數
for ley in ('W1', 'b1', 'W2', 'b2'):
network.params[key] = network.params[key] - learning_rate * grad[key]
# 記錄學習過程
loss = network.loss(x_batch, t_batch)
train_loss_list.appned(loss)
# 新增加的部分:計算 1 epoch 的便是準確度
if 1 % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print('train acc, test acc | ' + str(train_acc) + ',' + str(test_acc))
```
| true |
code
| 0.408719 | null | null | null | null |
|
# Train faster, more flexible models with Amazon SageMaker Linear Learner
Today Amazon SageMaker is launching several additional features to the built-in linear learner algorithm. Amazon SageMaker algorithms are designed to scale effortlessly to massive datasets and take advantage of the latest hardware optimizations for unparalleled speed. The Amazon SageMaker linear learner algorithm encompasses both linear regression and binary classification algorithms. These algorithms are used extensively in banking, fraud/risk management, insurance, and healthcare. The new features of linear learner are designed to speed up training and help you customize models for different use cases. Examples include classification with unbalanced classes, where one of your outcomes happens far less frequently than another. Or specialized loss functions for regression, where it’s more important to penalize certain model errors more than others.
In this blog post we'll cover three things:
1. Early stopping and saving the best model
1. New ways to customize linear learner models, including:
* Hinge loss (support vector machines)
* Quantile loss
* Huber loss
* Epsilon-insensitive loss
* Class weights options
1. Then we'll walk you through a hands-on example of using class weights to boost performance in binary classification
## Early Stopping
Linear learner trains models using Stochastic Gradient Descent (SGD) or variants of SGD like Adam. Training requires multiple passes over the data, called *epochs*, in which the data are loaded into memory in chunks called *batches*, sometimes called *minibatches*. How do we know how many epochs to run? Ideally, we'd like to continue training until convergence - that is, until we no longer see any additional benefits. Running additional epochs after the model has converged is a waste of time and money, but guessing the right number of epochs is difficult to do before submitting a training job. If we train for too few epochs, our model will be less accurate than it should be, but if we train for too many epochs, we'll waste resources and potentially harm model accuracy by overfitting. To remove the guesswork and optimize model training, linear learner has added two new features: automatic early stopping and saving the best model.
Early stopping works in two basic regimes: with or without a validation set. Often we split our data into training, validation, and testing data sets. Training is for optimizing the loss, validation is for tuning hyperparameters, and testing is for producing an honest estimate of how the model will perform on unseen data in the future. If you provide linear learner with a validation data set, training will stop early when validation loss stops improving. If no validation set is available, training will stop early when training loss stops improving.
#### Early Stopping with a validation data set
One big benefit of having a validation data set is that we can tell if and when we start overfitting to the training data. Overfitting is when the model gives predictions that are too closely tailored to the training data, so that generalization performance (performance on future unseen data) will be poor. The following plot on the right shows a typical progression during training with a validation data set. Until epoch 5, the model has been learning from the training set and doing better and better on the validation set. But in epochs 7-10, we see that the model has begun to overfit on the training set, which shows up as worse performance on the validation set. Regardless of whether the model continues to improve (overfit) on the training data, we want to stop training after the model starts to overfit. And we want to restore the best model from just before the overfitting started. These two features are now turned on by default in linear learner.
The default parameter values for early stopping are shown in the following code. To tweak the behavior of early stopping, try changing the values. To turn off early stopping entirely, choose a patience value larger than the number of epochs you want to run.
early_stopping_patience=3,
early_stopping_tolerance=0.001,
The parameter early_stoping_patience defines how many epochs to wait before ending training if no improvement is made. It's useful to have a little patience when deciding to stop early, since the training curve can be bumpy. Performance may get worse for one or two epochs before continuing to improve. By default, linear learner will stop early if performance has degraded for three epochs in a row.
The parameter early_stopping_tolerance defines the size of an improvement that's considered significant. If the ratio of the improvement in loss divided by the previous best loss is smaller than this value, early stopping will consider the improvement to be zero.
#### Early stopping without a validation data set
When training with a training set only, we have no way to detect overfitting. But we still want to stop training once the model has converged and improvement has levelled off. In the left panel of the following figure, that happens around epoch 25.
<img src="images/early_stop.png">
#### Early stopping and calibration
You may already be familiar with the linear learner automated threshold tuning for binary classification models. Threshold tuning and early stopping work together seamlessly by default in linear learner.
When a binary classification model outputs a probability (e.g., logistic regression) or a raw score (SVM), we convert that to a binary prediction by applying a threshold, for example:
predicted_label = 1 if raw_prediction > 0.5 else 0
We might want to tune the threshold (0.5 in the example) based on the metric we care about most, such as accuracy or recall. Linear learner does this tuning automatically using the 'binary_classifier_model_selection_criteria' parameter. When threshold tuning and early stopping are both turned on (the default), then training stops early based on the metric you request. For example, if you provide a validation data set and request a logistic regression model with threshold tuning based on accuracy, then training will stop when the model with auto-thresholding reaches optimal performance on the validation data. If there is no validation set and auto-thresholding is turned off, then training will stop when the best value of the loss function on the training data is reached.
## New loss functions
The loss function is our definition of the cost of making an error in prediction. When we train a model, we push the model weights in the direction that minimizes loss, given the known labels in the training set. The most common and well-known loss function is squared loss, which is minimized when we train a standard linear regression model. Another common loss function is the one used in logistic regression, variously known as logistic loss, cross-entropy loss, or binomial likelihood. Ideally, the loss function we train on should be a close match to the business problem we're trying to solve. Having the flexibility to choose different loss functions at training time allows us to customize models to different use cases. In this section, we'll discuss when to use which loss function, and introduce several new loss functions that have been added to linear learner.
<img src="images/loss_functions.png">
### Squared loss
predictor_type='regressor',
loss='squared_loss',
$$\text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^{N} (w_0 + \mathbf{x_i}^\intercal \mathbf{w} - y_i)^2$$
We'll use the following notation in all of the loss functions we discuss:
$w_0$ is the bias that the model learns
$\mathbf{w}$ is the vector of feature weights that the model learns
$y_i$ and $\mathbf{x_i}$ are the label and feature vector, respectively, from example $i$ of the training data
$N$ is the total number of training examples
Squared loss is a first choice for most regression problems. It has the nice property of producing an estimate of the mean of the label given the features. As seen in the plot above, squared loss implies that we pay a very high cost for very wrong predictions. This can cause problems if our training data include some extreme outliers. A model trained on squared loss will be very sensitive to outliers. Squared loss is sometimes known as mean squared error (MSE), ordinary least squares (OLS), or $\text{L}_2$ loss. Read more about [squared loss](https://en.wikipedia.org/wiki/Least_squares) on wikipedia.
### Absolute loss
predictor_type='regressor',
loss='absolute_loss',
$$\text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^{N} |w_0 + \mathbf{x_i}^\intercal \mathbf{w} - y_i|$$
Absolute loss is less common than squared loss, but can be very useful. The main difference between the two is that training a model on absolute loss will produces estimates of the median of the label given the features. Squared loss estimates the mean, and absolute loss estimates the median. Whether you want to estimate the mean or median will depend on your use case. Let's look at a few examples:
* If an error of -2 costs you \$2 and an error of +50 costs you \$50, then absolute loss models your costs better than squared loss.
* If an error of -2 costs you \$2, while an error of +50 is simply unacceptably large, then it's important that your errors are generally small, and so squared loss is probably the right fit.
* If it's important that your predictions are too high as often as they're too low, then you want to estimate the median with absolute loss.
* If outliers in your training data are having too much influence on the model, try switching from squared to absolute loss. Large errors get a large amount of attention from absolute loss, but with squared loss, large errors get squared and become huge errors attracting a huge amount of attention. If the error is due to an outlier, it might not deserve a huge amount of attention.
Absolute loss is sometimes also known as $\text{L}_1$ loss or least absolute error. Read more about [absolute loss](https://en.wikipedia.org/wiki/Least_absolute_deviations) on wikipedia.
### Quantile loss
predictor_type='regressor',
loss='quantile_loss',
quantile=0.9,
$$ \text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^N q(y_i - w_o - \mathbf{x_i}^\intercal \mathbf{w})^\text{+} + (1-q)(w_0 + \mathbf{x_i}^\intercal \mathbf{w} - y_i)^\text{+} $$
$$ \text{where the parameter } q \text{ is the quantile you want to predict}$$
Quantile loss lets us predict an upper or lower bound for the label, given the features. To make predictions that are larger than the true label 90% of the time, train quantile loss with the 0.9 quantile. An example would be predicting electricity demand where we want to build near peak demand since building to the average would result in brown-outs and upset customers. Read more about [quantile loss](https://en.wikipedia.org/wiki/Quantile_regression) on wikipedia.
### Huber loss
predictor_type='regressor',
loss='huber_loss',
huber_delta=0.5,
$$ \text{Let the error be } e_i = w_0 + \mathbf{x_i}^\intercal \mathbf{w} - y_i \text{. Then Huber loss solves:}$$
$$ \text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^N I(|e_i| < \delta) \frac{e_i^2}{2} + I(|e_i| >= \delta) |e_i|\delta - \frac{\delta^2}{2} $$
$$ \text{where } I(a) = 1 \text{ if } a \text{ is true, else } 0 $$
Huber loss is an interesting hybrid of $\text{L}_1$ and $\text{L}_2$ losses. Huber loss counts small errors on a squared scale and large errors on an absolute scale. In the plot above, we see that Huber loss looks like squared loss when the error is near 0 and absolute loss beyond that. Huber loss is useful when we want to train with squared loss, but want to avoid squared loss's sensitivity to outliers. Huber loss gives less importance to outliers by not squaring the larger errors. Read more about [Huber loss](https://en.wikipedia.org/wiki/Huber_loss) on wikipedia.
### Epsilon-insensitive loss
predictor_type='regressor',
loss='eps_insensitive_squared_loss',
loss_insensitivity=0.25,
For epsilon-insensitive squared loss, we minimize
$$ \text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^N max(0, (w_0 + \mathbf{x_i}^\intercal \mathbf{w} - y_i)^2 - \epsilon^2) $$
And for epsilon-insensitive absolute loss, we minimize
$$ \text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^N max(0, |w_0 + \mathbf{x_i}^\intercal \mathbf{w} - y_i| - \epsilon) $$
Epsilon-insensitive loss is useful when errors don't matter to you as long as they're below some threshold. Set the threshold that makes sense for your use case as epsilon. Epsilon-insensitive loss will allow the model to pay no cost for making errors smaller than epsilon.
### Logistic regression
predictor_type='binary_classifier',
loss='logistic',
binary_classifier_model_selection_criteria='recall_at_target_precision',
target_precision=0.9,
Each of the losses we've discussed is for regression problems, where the labels are floating point numbers. The last two losses we'll cover, logistic regression and support vector machines, are for binary classification problems where the labels are one of two classes. Linear learner expects the class labels to be 0 or 1. This may require some preprocessing, for example if your labels are coded as -1 and +1, or as blue and yellow. Logistic regression produces a predicted probability for each data point:
$$ p_i = \sigma(w_0 + \mathbf{x_i}^\intercal \mathbf{w}) $$
The loss function minimized in training a logistic regression model is the log likelihood of a binomial distribution. It assigns the highest cost to predictions that are confident and wrong, for example a prediction of 0.99 when the true label was 0, or a prediction of 0.002 when the true label was positive. The loss function is:
$$ \text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^N y_i \text{log}(p) - (1 - y_i) \text{log}(1 - p) $$
$$ \text{where } \sigma(x) = \frac{\text{exp}(x)}{1 + \text{exp}(x)} $$
Read more about [logistic regression](https://en.wikipedia.org/wiki/Logistic_regression) on wikipedia.
### Hinge loss (support vector machine)
predictor_type='binary_classifier',
loss='hinge_loss',
margin=1.0,
binary_classifier_model_selection_criteria='recall_at_target_precision',
target_precision=0.9,
Another popular option for binary classification problems is the hinge loss, also known as a Support Vector Machine (SVM) or Support Vector Classifier (SVC) with a linear kernel. It places a high cost on any points that are misclassified or nearly misclassified. To tune the meaning of "nearly", adjust the margin parameter:
It's difficult to say in advance whether logistic regression or SVM will be the right model for a binary classification problem, though logistic regression is generally a more popular choice then SVM. If it's important to provide probabilities of the predicted class labels, then logistic regression will be the right choice. If all that matters is better accuracy, precision, or recall, then either model may be appropriate. One advantage of logistic regression is that it produces the probability of an example having a positive label. That can be useful, for example in an ad serving system where the predicted click probability is used as an input to a bidding mechanism. Hinge loss does not produce class probabilities.
Whichever model you choose, you're likely to benefit from linear learner's options for tuning the threshold that separates positive from negative predictions
$$\text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^{N} y_i(\frac{m+1}{2} - w_0 - \mathbf{x_i}^\text{T}\mathbf{w})^\text{+} + (1-y_i)\frac{m-1}{2} + w_o + \mathbf{x_i}^\text{T}\mathbf{w})^\text{+}$$
$$\text{where } a^\text{+} = \text{max}(0, a)$$
Note that the hinge loss we use is a reparameterization of the usual hinge loss: typically hinge loss expects the binary label to be in {-1, 1}, whereas ours expects the binary labels to be in {0, 1}. This reparameterization allows LinearLearner to accept the same data format for binary classification regardless of the training loss. Read more about [hinge loss](https://en.wikipedia.org/wiki/Hinge_loss) on wikipedia.
## Class weights
In some binary classification problems, we may find that our training data is highly unbalanced. For example, in credit card fraud detection, we're likely to have many more examples of non-fraudulent transactions than fraudulent. In these cases, balancing the class weights may improve model performance.
Suppose we have 98% negative and 2% positive examples. To balance the total weight of each class, we can set the positive class weight to be 49. Now the average weight from the positive class is 0.98 $\cdot$ 1 = 0.98, and the average weight from the negative class is 0.02 $\cdot$ 49 = 0.98. The negative class weight multiplier is always 1.
To incorporate the positive class weight in training, we multiply the loss by the positive weight whenever we see a positive class label. For logistic regression, the weighted loss is:
Weighted logistic regression:
$$ \text{argmin}_{w_0, \mathbf{w}} \sum_{i=1}^N p y_i \text{log}(\sigma(w_0 + \mathbf{x_i}^\intercal \mathbf{w})) - (1 - y_i) \text{log}(1 - \sigma(w_0 + \mathbf{x_i}^\intercal \mathbf{w})) $$
$$ \text{where } p \text{ is the weight for the positive class.} $$
The only difference between the weighted and unweighted logistic regression loss functions is the presense of the class weight, $p$ on the left-hand term in the loss. Class weights in the hinge loss (SVM) classifier are applied in the same way.
To apply class weights when training a model with linear learner, supply the weight for the positive class as a training parameter:
positive_example_weight_mult=200,
Or to ask linear learner to calculate the positive class weight for you:
positive_example_weight_mult='balanced',
## Hands-on example: Detecting credit card fraud
In this section, we'll look at a credit card fraud detection dataset. The data set (Dal Pozzolo et al. 2015) was downloaded from [Kaggle](https://www.kaggle.com/mlg-ulb/creditcardfraud/data). We have features and labels for over a quarter million credit card transactions, each of which is labeled as fraudulent or not fraudulent. We'd like to train a model based on the features of these transactions so that we can predict risky or fraudulent transactions in the future. This is a binary classification problem.
We'll walk through training linear learner with various settings and deploying an inference endpoint. We'll evaluate the quality of our models by hitting that endpoint with observations from the test set. We can take the real-time predictions returned by the endpoint and evaluate them against the ground-truth labels in our test set.
Next, we'll apply the linear learner threshold tuning functionality to get better precision without sacrificing recall. Then, we'll push the precision even higher using the linear learner new class weights feature. Because fraud can be extremely costly, we would prefer to have high recall, even if this means more false positives. This is especially true if we are building a first line of defense, flagging potentially fraudulent transactions for further review before taking actions that affect customers.
First we'll do some preprocessing on this data set: we'll shuffle the examples and split them into train and test sets. To run this under notebook under your own AWS account, you'll need to change the Amazon S3 locations. First download the raw data from [Kaggle](https://www.kaggle.com/mlg-ulb/creditcardfraud/data) and upload to your SageMaker notebook instance (or wherever you're running this notebook). Only 0.17% of the data have positive labels, making this a challenging classification problem.
```
import boto3
import io
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import sagemaker
import sagemaker.amazon.common as smac
from sagemaker import get_execution_role
from sagemaker.predictor import csv_serializer, json_deserializer
# Set data locations
bucket = '<your_s3_bucket_here>' # replace this with your own bucket
prefix = 'sagemaker/DEMO-linear-learner-loss-weights' # replace this with your own prefix
s3_train_key = '{}/train/recordio-pb-data'.format(prefix)
s3_train_path = os.path.join('s3://', bucket, s3_train_key)
local_raw_data = 'creditcard.csv.zip'
role = get_execution_role()
# Confirm access to s3 bucket
for obj in boto3.resource('s3').Bucket(bucket).objects.all():
print(obj.key)
# Read the data, shuffle, and split into train and test sets, separating the labels (last column) from the features
raw_data = pd.read_csv(local_raw_data).as_matrix()
np.random.seed(0)
np.random.shuffle(raw_data)
train_size = int(raw_data.shape[0] * 0.7)
train_features = raw_data[:train_size, :-1]
train_labels = raw_data[:train_size, -1]
test_features = raw_data[train_size:, :-1]
test_labels = raw_data[train_size:, -1]
# Convert the processed training data to protobuf and write to S3 for linear learner
vectors = np.array([t.tolist() for t in train_features]).astype('float32')
labels = np.array([t.tolist() for t in train_labels]).astype('float32')
buf = io.BytesIO()
smac.write_numpy_to_dense_tensor(buf, vectors, labels)
buf.seek(0)
boto3.resource('s3').Bucket(bucket).Object(s3_train_key).upload_fileobj(buf)
```
We'll wrap the model training setup in a convenience function that takes in the S3 location of the training data, the model hyperparameters that define our training job, and the S3 output path for model artifacts. Inside the function, we'll hardcode the algorithm container, the number and type of EC2 instances to train on, and the input and output data formats.
```
from sagemaker.amazon.amazon_estimator import get_image_uri
def predictor_from_hyperparams(s3_train_data, hyperparams, output_path):
"""
Create an Estimator from the given hyperparams, fit to training data, and return a deployed predictor
"""
# specify algorithm containers and instantiate an Estimator with given hyperparams
container = get_image_uri(boto3.Session().region_name, 'linear-learner')
linear = sagemaker.estimator.Estimator(container,
role,
train_instance_count=1,
train_instance_type='ml.m4.xlarge',
output_path=output_path,
sagemaker_session=sagemaker.Session())
linear.set_hyperparameters(**hyperparams)
# train model
linear.fit({'train': s3_train_data})
# deploy a predictor
linear_predictor = linear.deploy(initial_instance_count=1, instance_type='ml.m4.xlarge')
linear_predictor.content_type = 'text/csv'
linear_predictor.serializer = csv_serializer
linear_predictor.deserializer = json_deserializer
return linear_predictor
```
And add another convenience function for setting up a hosting endpoint, making predictions, and evaluating the model. To make predictions, we need to set up a model hosting endpoint. Then we feed test features to the endpoint and receive predicted test labels. To evaluate the models we create in this exercise, we'll capture predicted test labels and compare them to actuals using some common binary classification metrics.
```
def evaluate(linear_predictor, test_features, test_labels, model_name, verbose=True):
"""
Evaluate a model on a test set given the prediction endpoint. Return binary classification metrics.
"""
# split the test data set into 100 batches and evaluate using prediction endpoint
prediction_batches = [linear_predictor.predict(batch)['predictions'] for batch in np.array_split(test_features, 100)]
# parse raw predictions json to exctract predicted label
test_preds = np.concatenate([np.array([x['predicted_label'] for x in batch]) for batch in prediction_batches])
# calculate true positives, false positives, true negatives, false negatives
tp = np.logical_and(test_labels, test_preds).sum()
fp = np.logical_and(1-test_labels, test_preds).sum()
tn = np.logical_and(1-test_labels, 1-test_preds).sum()
fn = np.logical_and(test_labels, 1-test_preds).sum()
# calculate binary classification metrics
recall = tp / (tp + fn)
precision = tp / (tp + fp)
accuracy = (tp + tn) / (tp + fp + tn + fn)
f1 = 2 * precision * recall / (precision + recall)
if verbose:
print(pd.crosstab(test_labels, test_preds, rownames=['actuals'], colnames=['predictions']))
print("\n{:<11} {:.3f}".format('Recall:', recall))
print("{:<11} {:.3f}".format('Precision:', precision))
print("{:<11} {:.3f}".format('Accuracy:', accuracy))
print("{:<11} {:.3f}".format('F1:', f1))
return {'TP': tp, 'FP': fp, 'FN': fn, 'TN': tn, 'Precision': precision, 'Recall': recall, 'Accuracy': accuracy,
'F1': f1, 'Model': model_name}
```
And finally we'll add a convenience function to delete prediction endpoints after we're done with them:
```
def delete_endpoint(predictor):
try:
boto3.client('sagemaker').delete_endpoint(EndpointName=predictor.endpoint)
print('Deleted {}'.format(predictor.endpoint))
except:
print('Already deleted: {}'.format(predictor.endpoint))
```
Let's begin by training a binary classifier model with the linear learner default settings. Note that we're setting the number of epochs to 40, which is much higher than the default of 10 epochs. With early stopping, we don't have to worry about setting the number of epochs too high. Linear learner will stop training automatically after the model has converged.
```
# Training a binary classifier with default settings: logistic regression
defaults_hyperparams = {
'feature_dim': 30,
'predictor_type': 'binary_classifier',
'epochs': 40
}
defaults_output_path = 's3://{}/{}/defaults/output'.format(bucket, prefix)
defaults_predictor = predictor_from_hyperparams(s3_train_path, defaults_hyperparams, defaults_output_path)
```
And now we'll produce a model with a threshold tuned for the best possible precision with recall fixed at 90%:
```
# Training a binary classifier with automated threshold tuning
autothresh_hyperparams = {
'feature_dim': 30,
'predictor_type': 'binary_classifier',
'binary_classifier_model_selection_criteria': 'precision_at_target_recall',
'target_recall': 0.9,
'epochs': 40
}
autothresh_output_path = 's3://{}/{}/autothresh/output'.format(bucket, prefix)
autothresh_predictor = predictor_from_hyperparams(s3_train_path, autothresh_hyperparams, autothresh_output_path)
```
### Improving recall with class weights
Now we'll improve on these results using a new feature added to linear learner: class weights for binary classification. We introduced this feature in the *Class Weights* section, and now we'll look into its application to the credit card fraud dataset by training a new model with balanced class weights:
```
# Training a binary classifier with class weights and automated threshold tuning
class_weights_hyperparams = {
'feature_dim': 30,
'predictor_type': 'binary_classifier',
'binary_classifier_model_selection_criteria': 'precision_at_target_recall',
'target_recall': 0.9,
'positive_example_weight_mult': 'balanced',
'epochs': 40
}
class_weights_output_path = 's3://{}/{}/class_weights/output'.format(bucket, prefix)
class_weights_predictor = predictor_from_hyperparams(s3_train_path, class_weights_hyperparams, class_weights_output_path)
```
The first training examples used the default loss function for binary classification, logistic loss. Now let's train a model with hinge loss. This is also called a support vector machine (SVM) classifier with a linear kernel. Threshold tuning is supported for all binary classifier models in linear learner.
```
# Training a binary classifier with hinge loss and automated threshold tuning
svm_hyperparams = {
'feature_dim': 30,
'predictor_type': 'binary_classifier',
'loss': 'hinge_loss',
'binary_classifier_model_selection_criteria': 'precision_at_target_recall',
'target_recall': 0.9,
'epochs': 40
}
svm_output_path = 's3://{}/{}/svm/output'.format(bucket, prefix)
svm_predictor = predictor_from_hyperparams(s3_train_path, svm_hyperparams, svm_output_path)
```
And finally, let's see what happens with balancing the class weights for the SVM model:
```
# Training a binary classifier with hinge loss, balanced class weights, and automated threshold tuning
svm_balanced_hyperparams = {
'feature_dim': 30,
'predictor_type': 'binary_classifier',
'loss': 'hinge_loss',
'binary_classifier_model_selection_criteria': 'precision_at_target_recall',
'target_recall': 0.9,
'positive_example_weight_mult': 'balanced',
'epochs': 40
}
svm_balanced_output_path = 's3://{}/{}/svm_balanced/output'.format(bucket, prefix)
svm_balanced_predictor = predictor_from_hyperparams(s3_train_path, svm_balanced_hyperparams, svm_balanced_output_path)
```
Now we'll make use of the prediction endpoint we've set up for each model by sending them features from the test set and evaluating their predictions with standard binary classification metrics.
```
# Evaluate the trained models
predictors = {'Logistic': defaults_predictor, 'Logistic with auto threshold': autothresh_predictor,
'Logistic with class weights': class_weights_predictor, 'Hinge with auto threshold': svm_predictor,
'Hinge with class weights': svm_balanced_predictor}
metrics = {key: evaluate(predictor, test_features, test_labels, key, False) for key, predictor in predictors.items()}
pd.set_option('display.float_format', lambda x: '%.3f' % x)
display(pd.DataFrame(list(metrics.values())).loc[:, ['Model', 'Recall', 'Precision', 'Accuracy', 'F1']])
```
The results are in! With threshold tuning, we can accurately predict 85-90% of the fraudulent transactions in the test set (due to randomness in training, recall will vary between 0.85-0.9 across multiple runs). But in addition to those true positives, we'll have a high number of false positives: 90-95% of the transactions we predict to be fraudulent are in fact not fraudulent (precision varies between 0.05-0.1). This model would work well as a first line of defense, flagging potentially fraudulent transactions for further review. If we instead want a model that gives very few false alarms, at the cost of catching far fewer of the fraudulent transactions, then we should optimize for higher precision:
binary_classifier_model_selection_criteria='recall_at_target_precision',
target_precision=0.9,
And what about the results of using our new feature, class weights for binary classification? Training with class weights has made a huge improvement to this model's performance! The precision is roughly doubled, while recall is still held constant at 85-90%.
Balancing class weights improved the performance of our SVM predictor, but it still does not match the corresponding logistic regression model for this dataset. Comparing all of the models we've fit so far, logistic regression with class weights and tuned thresholds did the best.
#### Note on target vs. observed recall
It's worth taking some time to look more closely at these results. If we asked linear learner for a model calibrated to a target recall of 0.9, then why didn't we get exactly 90% recall on the test set? The reason is the difference between training, validation, and testing. Linear learner calibrates thresholds for binary classification on the validation data set when one is provided, or else on the training set. Since we did not provide a validation data set, the threshold were calculated on the training data. Since the training, validation, and test data sets don't match exactly, the target recall we request is only an approximation. In this case, the threshold that produced 90% recall on the training data happened to produce only 85-90% recall on the test data (due to some randomness in training, the results will vary from one run to the next). The variation of recall in the test set versus the training set is dependent on the number of positive points. In this example, although we have over 280,000 examples in the entire dataset, we only have 337 positive examples, hence the large difference. The accuracy of this approximation can be improved by providing a large validation data set to get a more accurate threshold, and then evaluating on a large test set to get a more accurate benchmark of the model and its threshold. For even more fine-grained control, we can set the number of calibration samples to a higher number. It's default value is already quite high at 10 million samples:
num_calibration_samples=10000000,
#### Clean Up
Finally we'll clean up by deleting the prediction endpoints we set up:
```
for predictor in [defaults_predictor, autothresh_predictor, class_weights_predictor,
svm_predictor, svm_balanced_predictor]:
delete_endpoint(predictor)
```
We've just shown how to use the linear learner new early stopping feature, new loss functions, and new class weights feature to improve credit card fraud prediction. Class weights can help you optimize recall or precision for all types of fraud detection, as well as other classification problems with rare events, like ad click prediction or mechanical failure prediction. Try using class weights in your binary classification problem, or try one of the new loss functions for your regression problems: use quantile prediction to put confidence intervals around your predictions by learning 5% and 95% quantiles. For more information about new loss functions and class weights, see the linear learner [documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/linear-learner.html).
##### References
Andrea Dal Pozzolo, Olivier Caelen, Reid A. Johnson and Gianluca Bontempi. Calibrating Probability with Undersampling for Unbalanced Classification. In Symposium on Computational Intelligence and Data Mining (CIDM), IEEE, 2015. See link to full license text on [Kaggle](https://www.kaggle.com/mlg-ulb/creditcardfraud).
| true |
code
| 0.573738 | null | null | null | null |
|
# Getting Started with SYMPAIS
[](https://colab.research.google.com/github/ethanluoyc/sympais/blob/master/notebooks/getting_started.ipynb)
## Setup
```
try:
import google.colab
IN_COLAB = True
except:
IN_COLAB = False
```
### Install SYMPAIS
```
# (TODO(yl): Simplify when we make this public)
GIT_TOKEN = ""
if IN_COLAB:
!pip install -U pip setuptools wheel
if GIT_TOKEN:
!pip install git+https://{GIT_TOKEN}@github.com/ethanluoyc/sympais.git#egg=sympais
else:
!pip install git+https://github.com/ethanluoyc/sympais.git#egg=sympais
```
### Download and install pre-built RealPaver v0.4
```
if IN_COLAB:
!curl -L "https://drive.google.com/uc?export=download&id=1_Im0Ot5TjkzaWfid657AV_gyMpnPuVRa" -o realpaver
!chmod u+x realpaver
!cp realpaver /usr/local/bin
import jax
import jax.numpy as jnp
from sympais import tasks
from sympais import methods
from sympais.methods import run_sympais, run_dmc
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib
import numpy as onp
import math
%load_ext autoreload
%autoreload 2
%matplotlib inline
```
## Load a task
```
task = tasks.Sphere(nd=3)
task.profile
task.constraints
task.domains
```
## Run DMC baseline
```
dmc_output = run_dmc(task, seed=0, num_samples=int(1e8))
print(dmc_output)
```
## Run SYMPAIS
```
sympais_output = run_sympais(
task,
key=jax.random.PRNGKey(0),
num_samples=int(1e6),
num_proposals=100,
tune=False,
init='realpaver',
num_warmup_steps=500,
window_size=100
)
print(sympais_output)
```
## Create your own problem
In this section, we will show how to implement a new probabilistic analysis
task similar to the sphere task above.
A probabilistic ananlysis `Task` consists of an input `Profile` $p(\mathbf{x})$ and a list of constraints `cs`. A user create a new `Task` either by calling the super class constructor or subclassing the base class.
Consider a two-dimensional problems where we would like to know the probablity that the
the inputs $x \in [-10, 10]$ and $y \in [-10, 10]$ are jointly in the interior of a two-dimensional _cube_. The set of constraints is
$$
\begin{align}
x + y &\leq 1.0, \\
x + y &\geq -1.0, \\
y - x &\geq -1.0, \\
y - x &\leq 1.0.
\end{align}
$$
First, let's import the related modules used for defining the tasks
```
import sympy
from sympais import tasks
from sympais import profiles
from sympais import distributions as dist
```
### Independent profile
We will first show how to define a task when the input variables are _independent_.
We use `Profile` for defining the input distribution and SymPy expressions for defining the constraints.
The `Profile` uses the following iterface. To create a customized profile, the user needs to implement
`profile.log_prob` and `profile.sample` functions. Note that unlike numpyro distributions, the samples
are represented as a dictionary from variable names to their values. This is so that it is easier to integrate
with a symbolic execution engine.
```
help(profiles.Profile)
```
When the input random variables are independent, we provide a convenience `IndependentProfile` class which allows you to specify the per-component distribution. `IndependentProfile` implements `sample` and `log_prob` by dispatching to the individual components and then aggretating the results.
We are now ready to define a task for the `cube` problem. The code is shown below.
```
class IndependentCubeTask(tasks.Task):
def __init__(self):
profile = profiles.IndependentProfile({
"x": dist.Normal(loc=-2, scale=1),
"y": dist.Normal(loc=-2, scale=1)
})
domains = {"x": (-10., 10.), "y": (-10., 10.)}
b = 1.0
x = sympy.Symbol("x")
y = sympy.Symbol("y")
c1 = x + y <= b # type: sympy.Expr
c2 = x + y >= -b # type: sympy.Expr
c3 = y - x >= -b # type: sympy.Expr
c4 = y - x <= b # type: sympy.Expr
super().__init__(profile, [c1, c2, c3, c4], domains)
```
Let us create some helper functions for visualizing the profile and the constraints.
```
b = 1.
def f1(x):
return b - x
def f2(x):
return -b - x
def f3(x):
return -b + x
def f4(x):
return b + x
x = sympy.Symbol('x')
x1, = sympy.solve(f1(x)-f3(x))
x2, = sympy.solve(f1(x)-f4(x))
x3, = sympy.solve(f2(x)-f3(x))
x4, = sympy.solve(f2(x)-f4(x))
y1 = f1(x1)
y2 = f1(x2)
y3 = f2(x3)
y4 = f2(x4)
N = 200
X, Y = jnp.meshgrid(jnp.linspace(-4,4,N), jnp.linspace(-4, 4, N))
xr = jnp.linspace(-3, 3, 100)
def plot_constraints(ax):
ax.plot(x1, y1, 'k', markersize=5)
ax.plot(x2, y2, 'k', markersize=5)
ax.plot(x3, y3, 'k', markersize=5)
ax.plot(x4, y4, 'k', markersize=5)
ax.fill([x1,x2,x4,x3],[y1,y2,y4,y3],'gray', alpha=0.5);
y1r = f1(xr)
y2r = f2(xr)
y3r = f3(xr)
y4r = f4(xr)
ax.plot(xr, y1r, 'w--')
ax.plot(xr, y2r, 'w--')
ax.plot(xr, y3r, 'w--')
ax.plot(xr, y4r, 'w--')
cube_task = IndependentCubeTask()
logp = cube_task.profile.log_prob(
{'x': X.reshape(-1), "y": Y.reshape(-1)}).reshape((N, N))
fig, ax = plt.subplots(1, 1, figsize=(3,3))
ax.contourf(X, Y, logp, levels=20, cmap='Blues_r')
plot_constraints(ax)
ax.set(xlim=(-3,2), ylim=(-3,2), xlabel='$x$', ylabel='$y$');
```
### Correlated profile
In the general case, the inputs may be correlated. In this case, the user needs to provide a custom implementation
of `Profile`. We will show how to do this for the case where $x$ and $y$ are jointly Gaussian.
```
from numpyro import distributions as numpyro_dist
class CorrelatedProfile(profiles.Profile):
def __init__(self):
self._dist = numpyro_dist.MultivariateNormal(
loc=jnp.array([-2, -2]), covariance_matrix=jnp.array([[1.0, 0.8], [0.8, 1.5]])
)
def sample(self, rng, sample_shape=()):
samples = self._dist.sample(rng, sample_shape=sample_shape)
# We needs the [..., ] to maintain batch dimensions.
return {'x': samples[..., 0], 'y': samples[..., 1]}
def log_prob(self, samples):
samples = jnp.stack([samples['x'], samples['y']], -1)
return self._dist.log_prob(samples)
class CorrelatedCubeTask(tasks.Task):
def __init__(self):
b = 1.0
x = sympy.Symbol("x")
y = sympy.Symbol("y")
c1 = x + y <= b # type: sympy.Expr
c2 = x + y >= -b # type: sympy.Expr
c3 = y - x >= -b # type: sympy.Expr
c4 = y - x <= b # type: sympy.Expr
profile = CorrelatedProfile()
domains = {"x": (-10., 10.), "y": (-10., 10.)}
super().__init__(profile, [c1, c2, c3, c4], domains)
```
All of the benchmarks are define similarly to the examples shown above.
If you are interested, check our the source code in src/sympais/tasks for more examples.
```
correlated_cube_task = CorrelatedCubeTask()
logp = correlated_cube_task.profile.log_prob(
{'x': X.reshape(-1), "y": Y.reshape(-1)}).reshape((N, N))
fig, ax = plt.subplots(1, 1, figsize=(3,3))
ax.contourf(X, Y, logp, levels=20, cmap='Blues_r')
plot_constraints(ax)
ax.set(xlim=(-3,2), ylim=(-3,2), xlabel='$x$', ylabel='$y$');
```
### Run samplers
Now we have our new task definitions, let's run DMC and SYMPAIS on these tasks.
```
dmc_output = run_dmc(correlated_cube_task, seed=0, num_samples=int(1e8), batch_size=int(1e6))
print(dmc_output)
sympais_output = run_sympais(
correlated_cube_task,
key=jax.random.PRNGKey(0),
num_samples=int(1e6),
num_proposals=100,
tune=False,
init='realpaver',
num_warmup_steps=500,
window_size=100
)
print(sympais_output)
```
| true |
code
| 0.500549 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
### Agent Testing - Single Job Set
In this notebook we test the performance of the agent trained with a single job set.
We can then compare its performance to the random and shortest-job-first agents in the exploration notebook. Notice that in this case we are using the same job set for all agents.
Then we show the performance of the agent for an unseen job set and notice that it performs poorly, almost like a random agent.
This lab was tested with Ray version 0.8.5. Please make sure you have this version installed in your Compute Instance.
```
!pip install ray[rllib]==0.8.5
```
Import the necessary packages.
```
import sys, os
sys.path.insert(0, os.path.join(os.getcwd(), '../agent_training/training_scripts/environment'))
os.environ.setdefault('PYTHONPATH', os.path.join(os.getcwd(), '../agent_training/training_scripts/environment'))
import ray
import ray.rllib.agents.pg as pg
from ray.rllib.models.torch.torch_modelv2 import TorchModelV2
from ray.rllib.models import ModelCatalog
from ray.rllib.utils.annotations import override
from ray.tune.registry import register_env
import gym
from gym import spaces
from environment import Parameters, Env
import torch
import torch.nn as nn
import numpy as np
```
Here we define the RL environment class according to the Gym specification in the same way that was done in the agent training script. The difference is that here we add two new methods, *observe* and *plot_state_img*, allowing us to visualize the states of the environment as the agent acts.
Details about how to work with custom environment in RLLib can be found [here](https://docs.ray.io/en/master/rllib-env.html#configuring-environments).
We also introduce a new parameter to the environment constructor, *unseen*, which is a flag telling the environment to use unseen job sets, meaning job sets different than the ones used for training.
```
class CustomEnv(gym.Env):
def __init__(self, env_config):
simu_len = env_config['simu_len']
num_ex = env_config['num_ex']
unseen = env_config['unseen']
pa = Parameters()
pa.simu_len = simu_len
pa.num_ex = num_ex
pa.unseen = unseen
pa.compute_dependent_parameters()
self.env = Env(pa, render=False, repre='image')
self.action_space = spaces.Discrete(n=pa.num_nw + 1)
self.observation_space = spaces.Box(low=0, high=1, shape=self.env.observe().shape, dtype=np.float)
def reset(self):
self.env.reset()
obs = self.env.observe()
return obs
def step(self, action):
next_obs, reward, done, info = self.env.step(action)
info = {}
return next_obs, reward, done, info
def observe(self):
return self.env.observe()
def plot_state_img(self):
return self.env.plot_state_img()
```
Define the RL environment constructor and register it for use in RLLib.
```
def env_creator(env_config):
return CustomEnv(env_config)
register_env('CustomEnv', env_creator)
```
Here we define the custom model for the agent policy. RLLib supports both TensorFlow and PyTorch and here we are using the PyTorch interfaces.
The policy model is a simple 2-layer feedforward neural network that maps the environment observation array into one of possible 6 actions. It also defines a value function network as a branch of the policy network, to output a single scalar value representing the expected sum of rewards. This value can be used as the baseline for the policy gradient algorithm.
More details about how to work with custom policy models with PyTorch in RLLib can be found [here](https://docs.ray.io/en/master/rllib-models.html#pytorch-models).
```
class CustomModel(TorchModelV2, nn.Module):
def __init__(self, obs_space, action_space, num_outputs, model_config, name):
TorchModelV2.__init__(self, obs_space, action_space, num_outputs, model_config, name)
nn.Module.__init__(self)
self.hidden_layers = nn.Sequential(nn.Linear(20*124, 32), nn.ReLU(),
nn.Linear(32, 16), nn.ReLU())
self.logits = nn.Sequential(nn.Linear(16, 6))
self.value_branch = nn.Sequential(nn.Linear(16, 1))
@override(TorchModelV2)
def forward(self, input_dict, state, seq_lens):
obs = input_dict['obs'].float()
obs = obs.view(obs.shape[0], 1, obs.shape[1], obs.shape[2])
obs = obs.view(obs.shape[0], obs.shape[1] * obs.shape[2] * obs.shape[3])
self.features = self.hidden_layers(obs)
actions = self.logits(self.features)
return actions, state
@override(TorchModelV2)
def value_function(self):
return self.value_branch(self.features).squeeze(1)
```
Now we register the custom policy model for use in RLLib.
```
ModelCatalog.register_custom_model('CustomModel', CustomModel)
```
Here we create a copy of the default Policy Gradient configuration in RLLib and set the relevant parameters for testing a trained agent. In this case we only need the parameters related to the custom model and to our environment.
```
config = pg.DEFAULT_CONFIG
my_config = config.copy()
my_params = {
'use_pytorch' : True,
'model': {'custom_model': 'CustomModel'},
'env': 'CustomEnv',
'env_config': {'simu_len': 50, 'num_ex': 1, 'unseen': False}
}
for key, value in my_params.items():
my_config[key] = value
```
Initialize the Ray backend. Here we run Ray locally.
```
ray.init()
```
Instantiate the policy gradient trainer object from RLLib.
```
trainer = pg.PGTrainer(config=my_config)
```
We can verify the policy model architecture by getting a reference to the policy object from the trainer and a reference to the model object from the policy.
```
policy = trainer.get_policy()
model = policy.model
print(model.parameters)
```
Here we load the model checkpoint, corresponding to the single job set training, into the trainer.
```
checkpoint_path = '../model_checkpoints/single_jobset/checkpoint-300'
trainer.restore(checkpoint_path=checkpoint_path)
```
We then perform a rollout of the trained policy into the RL environment, using the same single job set used for training.
```
import numpy as np
from IPython import display
import matplotlib.pyplot as plt
import time
from random import randint
env = CustomEnv(env_config = my_params['env_config'])
img = env.plot_state_img()
plt.figure(figsize = (16,16))
plt.grid(color='w', linestyle='-', linewidth=0.5)
plt.text(2, -2, "RESOURCES")
plt.text(-4, 10, "CPU")
plt.text(-4, 30, "MEM")
plt.text(14, -2, "JOB QUEUE #1")
plt.text(26, -2, "JOB QUEUE #2")
plt.text(38, -2, "JOB QUEUE #3")
plt.text(50, -2, "JOB QUEUE #4")
plt.text(62, -2, "JOB QUEUE #5")
plt.text(76, 20, "BACKLOG")
plt.imshow(img, vmax=1, cmap='CMRmap')
ax = plt.gca()
ax.set_xticks(np.arange(-.5, 100, 1))
ax.set_xticklabels([])
ax.set_yticks(np.arange(-.5, 100, 1))
ax.set_yticklabels([])
ax.tick_params(axis=u'both', which=u'both',length=0)
image = plt.imshow(img, vmax=1, cmap='CMRmap')
display.display(plt.gcf())
actions = []
rewards = []
done = False
s = 0
txt1 = plt.text(0, 45, '')
txt2 = plt.text(0, 47, '')
obs = env.observe()
while not done:
a = trainer.compute_action(obs)
actions.append(a)
obs, reward, done, info = env.step(a)
rewards.append(reward)
s += 1
txt1.remove()
txt2.remove()
txt1 = plt.text(0, 44, 'STEPS: ' + str(s), fontsize=14)
txt2 = plt.text(0, 46, 'TOTAL AVERAGE JOB SLOWDOWN: ' + str(round(-sum(rewards))), fontsize=14)
img = env.plot_state_img()
image.set_data(img)
display.display(plt.gcf())
display.clear_output(wait=True)
```
And finally we perform another rollout of the trained policy, but now using an unseen job set, meaning a job set different from the one used for training. We notice here that the agent is not able to generalize well and its performance is similar to the performance of a random policy.
This will be mitigated by training the agent with multiple distinct job sets.
```
import numpy as np
from IPython import display
import matplotlib.pyplot as plt
import time
from random import randint
env_config = my_params['env_config']
env_config['unseen'] = True
env = CustomEnv(env_config=env_config)
img = env.plot_state_img()
plt.figure(figsize = (16,16))
plt.grid(color='w', linestyle='-', linewidth=0.5)
plt.text(2, -2, "RESOURCES")
plt.text(-4, 10, "CPU")
plt.text(-4, 30, "MEM")
plt.text(14, -2, "JOB QUEUE #1")
plt.text(26, -2, "JOB QUEUE #2")
plt.text(38, -2, "JOB QUEUE #3")
plt.text(50, -2, "JOB QUEUE #4")
plt.text(62, -2, "JOB QUEUE #5")
plt.text(76, 20, "BACKLOG")
plt.imshow(img, vmax=1, cmap='CMRmap')
ax = plt.gca()
ax.set_xticks(np.arange(-.5, 100, 1))
ax.set_xticklabels([])
ax.set_yticks(np.arange(-.5, 100, 1))
ax.set_yticklabels([])
ax.tick_params(axis=u'both', which=u'both',length=0)
image = plt.imshow(img, vmax=1, cmap='CMRmap')
display.display(plt.gcf())
actions = []
rewards = []
done = False
s = 0
txt1 = plt.text(0, 45, '')
txt2 = plt.text(0, 47, '')
obs = env.observe()
while not done:
a = trainer.compute_action(obs)
actions.append(a)
obs, reward, done, info = env.step(a)
rewards.append(reward)
s += 1
txt1.remove()
txt2.remove()
txt1 = plt.text(0, 44, 'STEPS: ' + str(s), fontsize=14)
txt2 = plt.text(0, 46, 'TOTAL AVERAGE JOB SLOWDOWN: ' + str(round(-sum(rewards))), fontsize=14)
img = env.plot_state_img()
image.set_data(img)
display.display(plt.gcf())
display.clear_output(wait=True)
```
Shutdown the Ray backend.
```
ray.shutdown()
```
| true |
code
| 0.716039 | null | null | null | null |
|
# Create a Learner for inference
```
from fastai.gen_doc.nbdoc import *
```
In this tutorial, we'll see how the same API allows you to create an empty [`DataBunch`](/basic_data.html#DataBunch) for a [`Learner`](/basic_train.html#Learner) at inference time (once you have trained your model) and how to call the `predict` method to get the predictions on a single item.
```
jekyll_note("""As usual, this page is generated from a notebook that you can find in the <code>docs_src</code> folder of the
<a href="https://github.com/fastai/fastai">fastai repo</a>. We use the saved models from <a href="/tutorial.data.html">this tutorial</a> to
have this notebook run quickly.""")
```
## Vision
To quickly get acces to all the vision functionality inside fastai, we use the usual import statements.
```
from fastai.vision import *
```
### A classification problem
Let's begin with our sample of the MNIST dataset.
```
mnist = untar_data(URLs.MNIST_TINY)
tfms = get_transforms(do_flip=False)
```
It's set up with an imagenet structure so we use it to split our training and validation set, then labelling.
```
data = (ImageItemList.from_folder(mnist)
.split_by_folder()
.label_from_folder()
.add_test_folder('test')
.transform(tfms, size=32)
.databunch()
.normalize(imagenet_stats))
```
Now that our data has been properly set up, we can train a model. We already did in the [look at your data tutorial](/tutorial.data.html) so we'll just load our saved results here.
```
learn = create_cnn(data, models.resnet18).load('mini_train')
```
Once everything is ready for inference, we just have to call `learn.export` to save all the information of our [`Learner`](/basic_train.html#Learner) object for inference: the stuff we need in the [`DataBunch`](/basic_data.html#DataBunch) (transforms, classes, normalization...), the model with its weights and all the callbacks our [`Learner`](/basic_train.html#Learner) was using. Everything will be in a file named `export.pkl` in the folder `learn.path`. If you deploy your model on a different machine, this is the file you'll need to copy.
```
learn.export()
```
To create the [`Learner`](/basic_train.html#Learner) for inference, you'll need to use the [`load_learner`](/basic_train.html#load_learner) function. Note that you don't have to specify anything: it remembers the classes, the transforms you used or the normalization in the data, the model, its weigths... The only argument needed is the folder where the 'export.pkl' file is.
```
learn = load_learner(mnist)
```
You can now get the predictions on any image via `learn.predict`.
```
img = data.train_ds[0][0]
learn.predict(img)
```
It returns a tuple of three things: the object predicted (with the class in this instance), the underlying data (here the corresponding index) and the raw probabilities. You can also do inference on a larger set of data by adding a *test set*. This is done by passing an [`ItemList`](/data_block.html#ItemList) to [`load_learner`](/basic_train.html#load_learner).
```
learn = load_learner(mnist, test=ImageItemList.from_folder(mnist/'test'))
preds,y = learn.get_preds(ds_type=DatasetType.Test)
preds[:5]
```
### A multi-label problem
Now let's try these on the planet dataset, which is a little bit different in the sense that each image can have multiple tags (and not just one label).
```
planet = untar_data(URLs.PLANET_TINY)
planet_tfms = get_transforms(flip_vert=True, max_lighting=0.1, max_zoom=1.05, max_warp=0.)
```
Here each images is labelled in a file named `labels.csv`. We have to add [`train`](/train.html#train) as a prefix to the filenames, `.jpg` as a suffix and indicate that the labels are separated by spaces.
```
data = (ImageItemList.from_csv(planet, 'labels.csv', folder='train', suffix='.jpg')
.random_split_by_pct()
.label_from_df(label_delim=' ')
.transform(planet_tfms, size=128)
.databunch()
.normalize(imagenet_stats))
```
Again, we load the model we saved in [look at your data tutorial](/tutorial.data.html).
```
learn = create_cnn(data, models.resnet18).load('mini_train')
```
Then we can export it before loading it for inference.
```
learn.export()
learn = load_learner(planet)
```
And we get the predictions on any image via `learn.predict`.
```
img = data.train_ds[0][0]
learn.predict(img)
```
Here we can specify a particular threshold to consider the predictions to be correct or not. The default is `0.5`, but we can change it.
```
learn.predict(img, thresh=0.3)
```
### A regression example
For the next example, we are going to use the [BIWI head pose](https://data.vision.ee.ethz.ch/cvl/gfanelli/head_pose/head_forest.html#db) dataset. On pictures of persons, we have to find the center of their face. For the fastai docs, we have built a small subsample of the dataset (200 images) and prepared a dictionary for the correspondance fielname to center.
```
biwi = untar_data(URLs.BIWI_SAMPLE)
fn2ctr = pickle.load(open(biwi/'centers.pkl', 'rb'))
```
To grab our data, we use this dictionary to label our items. We also use the [`PointsItemList`](/vision.data.html#PointsItemList) class to have the targets be of type [`ImagePoints`](/vision.image.html#ImagePoints) (which will make sure the data augmentation is properly applied to them). When calling [`transform`](/tabular.transform.html#tabular.transform) we make sure to set `tfm_y=True`.
```
data = (PointsItemList.from_folder(biwi)
.random_split_by_pct(seed=42)
.label_from_func(lambda o:fn2ctr[o.name])
.transform(get_transforms(), tfm_y=True, size=(120,160))
.databunch()
.normalize(imagenet_stats))
```
As before, the road to inference is pretty straightforward: load the model we trained before, export the [`Learner`](/basic_train.html#Learner) then load it for production.
```
learn = create_cnn(data, models.resnet18, lin_ftrs=[100], ps=0.05).load('mini_train');
learn.export()
learn = load_learner(biwi)
```
And now we can a prediction on an image.
```
img = data.valid_ds[0][0]
learn.predict(img)
```
To visualize the predictions, we can use the [`Image.show`](/vision.image.html#Image.show) method.
```
img.show(y=learn.predict(img)[0])
```
### A segmentation example
Now we are going to look at the [camvid dataset](http://mi.eng.cam.ac.uk/research/projects/VideoRec/CamVid/) (at least a small sample of it), where we have to predict the class of each pixel in an image. Each image in the 'images' subfolder as an equivalent in 'labels' that is its segmentations mask.
```
camvid = untar_data(URLs.CAMVID_TINY)
path_lbl = camvid/'labels'
path_img = camvid/'images'
```
We read the classes in 'codes.txt' and the function maps each image filename with its corresponding mask filename.
```
codes = np.loadtxt(camvid/'codes.txt', dtype=str)
get_y_fn = lambda x: path_lbl/f'{x.stem}_P{x.suffix}'
```
The data block API allows us to uickly get everything in a [`DataBunch`](/basic_data.html#DataBunch) and then we can have a look with `show_batch`.
```
data = (SegmentationItemList.from_folder(path_img)
.random_split_by_pct()
.label_from_func(get_y_fn, classes=codes)
.transform(get_transforms(), tfm_y=True, size=128)
.databunch(bs=16, path=camvid)
.normalize(imagenet_stats))
```
As before, we load our model, export the [`Learner`](/basic_train.html#Learner) then create a new one with [`load_learner`](/basic_train.html#load_learner).
```
learn = unet_learner(data, models.resnet18).load('mini_train');
learn.export()
learn = load_learner(camvid)
```
And now we can a prediction on an image.
```
img = data.train_ds[0][0]
learn.predict(img);
```
To visualize the predictions, we can use the [`Image.show`](/vision.image.html#Image.show) method.
```
img.show(y=learn.predict(img)[0])
```
## Text
Next application is text, so let's start by importing everything we'll need.
```
from fastai.text import *
```
### Language modelling
First let's look a how to get a language model ready for inference. Since we'll load the model trained in the [visualize data tutorial](/tutorial.data.html), we load the vocabulary used there.
```
imdb = untar_data(URLs.IMDB_SAMPLE)
vocab = Vocab(pickle.load(open(imdb/'tmp'/'itos.pkl', 'rb')))
data_lm = (TextList.from_csv(imdb, 'texts.csv', cols='text', vocab=vocab)
.random_split_by_pct()
.label_for_lm()
.databunch())
```
Like in vision, we just have to type `learn.export()` after loading our pretrained model to save all the information inside the [`Learner`](/basic_train.html#Learner) we'll need. In this case, this includes all the vocabulary we created. The only difference is that we will specify a filename, since we have several model in the same path (language model and classifier).
```
learn = language_model_learner(data_lm, AWD_LSTM, pretrained=False).load('mini_train_lm', with_opt=False);
learn.export(fname = 'export_lm.pkl')
```
Now let's define our inference learner.
```
learn = load_learner(imdb, fname = 'export_lm.pkl')
```
Then we can predict with the usual method, here we can specify how many words we want the model to predict.
```
learn.predict('This is a simple test of', n_words=20)
```
You can also use beam search to generate text.
```
learn.beam_search('This is a simple test of', n_words=20, beam_sz=200)
```
### Classification
Now let's see a classification example. We have to use the same vocabulary as for the language model if we want to be able to use the encoder we saved.
```
data_clas = (TextList.from_csv(imdb, 'texts.csv', cols='text', vocab=vocab)
.split_from_df(col='is_valid')
.label_from_df(cols='label')
.databunch(bs=42))
```
Again we export the [`Learner`](/basic_train.html#Learner) where we load our pretrained model.
```
learn = text_classifier_learner(data_clas, AWD_LSTM, pretrained=False).load('mini_train_clas', with_opt=False);
learn.export(fname = 'export_clas.pkl')
```
Now let's use [`load_learner`](/basic_train.html#load_learner).
```
learn = load_learner(imdb, fname = 'export_clas.pkl')
```
Then we can predict with the usual method.
```
learn.predict('I really loved that movie!')
```
## Tabular
Last application brings us to tabular data. First let's import everything we'll need.
```
from fastai.tabular import *
```
We'll use a sample of the [adult dataset](https://archive.ics.uci.edu/ml/datasets/adult) here. Once we read the csv file, we'll need to specify the dependant variable, the categorical variables, the continuous variables and the processors we want to use.
```
adult = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(adult/'adult.csv')
dep_var = 'salary'
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
cont_names = ['education-num', 'hours-per-week', 'age', 'capital-loss', 'fnlwgt', 'capital-gain']
procs = [FillMissing, Categorify, Normalize]
```
Then we can use the data block API to grab everything together.
```
data = (TabularList.from_df(df, path=adult, cat_names=cat_names, cont_names=cont_names, procs=procs)
.split_by_idx(valid_idx=range(800,1000))
.label_from_df(cols=dep_var)
.databunch())
```
We define a [`Learner`](/basic_train.html#Learner) object that we fit and then save the model.
```
learn = tabular_learner(data, layers=[200,100], metrics=accuracy)
learn.fit(1, 1e-2)
learn.save('mini_train')
```
As in the other applications, we just have to type `learn.export()` to save everything we'll need for inference (here it includes the inner state of each processor).
```
learn.export()
```
Then we create a [`Learner`](/basic_train.html#Learner) for inference like before.
```
learn = load_learner(adult)
```
And we can predict on a row of dataframe that has the right `cat_names` and `cont_names`.
```
learn.predict(df.iloc[0])
```
| true |
code
| 0.611614 | null | null | null | null |
|
```
import numpy as np
import numpy.random as npr
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.decomposition import PCA
import statsmodels.api as sm
from numpy.linalg import cond
N=2000
D=5 # number of features
mean = np.zeros(D)
corr = 0.9
y_noise = 0.1
# designate the core feature
num_corefea = np.int(D/2)
true_cause = np.arange(num_corefea).astype(int)
```
## generate simulated datasets with core and spurious features
The outcome model is the same in training and testing; the outcome only depends on the core feature.
In the training set, the covariates have high correlation. In the test set, the covariates have low correlation.
```
# simulate strongly correlated features for training
train_cov = np.ones((D, D)) * corr + np.eye(D) * (1 - corr)
train_x_true = npr.multivariate_normal(mean, train_cov, size=N)
train_x_true = train_x_true * np.concatenate([-1 * np.ones(D//2), np.ones(D - D//2)]) # create both positive and negatively correlated covariates
# train_x_true = np.exp(npr.multivariate_normal(mean, train_cov, size=N)) # exponential of gaussian; no need to be gaussian
# simulate weakly correlated features for testing
test_cov = np.ones((D, D)) * (1 - corr) + np.eye(D) * corr
test_x_true = npr.multivariate_normal(mean, test_cov, size=N)
# test_x_true = np.exp(npr.multivariate_normal(mean, test_cov, size=N)) # exponential of gaussian; no need to be gaussian
# add observation noise to the x
# spurious correlation more often occurs when the signal to noise ratio is lower
x_noise = np.array(list(np.ones(num_corefea)*0.4) + list(np.ones(D-num_corefea)*0.3))
train_x = train_x_true + x_noise * npr.normal(size=[N,D])
test_x = test_x_true + x_noise * npr.normal(size=[N,D])
print("\ntrain X correlation\n", np.corrcoef(train_x.T))
print("\ntest X correlation\n",np.corrcoef(test_x.T))
# generate outcome
# toy model y = x + noise
truecoeff = npr.uniform(size=num_corefea) * 10
train_y = train_x_true[:,true_cause].dot(truecoeff) + y_noise * npr.normal(size=N)
test_y = test_x_true[:,true_cause].dot(truecoeff) + y_noise * npr.normal(size=N)
```
# baseline naive regression on all features
```
# regularization parameter for ridge regression
alpha = 10
def fitcoef(cov_train, train_y, cov_test=None, test_y=None):
# linearReg
print("linearReg")
reg = LinearRegression()
reg.fit(cov_train, train_y)
print("coef", reg.coef_, "intercept", reg.intercept_)
print("train accuracy", reg.score(cov_train, train_y))
if cov_test is not None:
print("test accuracy", reg.score(cov_test, test_y))
# # linearReg with statsmodels
# print("linearReg with statsmodels")
# model = sm.OLS(train_y,sm.add_constant(cov_train, prepend=False))
# result = model.fit()
# print(result.summary())
# ridgeReg
print("ridgeReg")
reg = Ridge(alpha=alpha)
reg.fit(cov_train, train_y)
print("coef", reg.coef_, "intercept", reg.intercept_)
print("train accuracy", reg.score(cov_train, train_y))
if cov_test is not None:
print("test accuracy", reg.score(cov_test, test_y))
```
all three features have coefficient different from zeuo
test accuracy degrades much from training accuracy.
```
print("\n###########################\nall features")
cov_train = np.column_stack([train_x])
cov_test = np.column_stack([test_x])
fitcoef(cov_train, train_y, cov_test, test_y)
```
next consider oracle, regression only on the core feature
```
print("\n###########################\nall features")
cov_train = np.column_stack([train_x[:,true_cause]])
cov_test = np.column_stack([test_x[:,true_cause]])
fitcoef(cov_train, train_y, cov_test, test_y)
```
## causal-rep
now try adjust for pca factor, then learn feature coefficient, construct a prediction function using the learned feature mapping, predict on the test set
```
# fit pca to high correlated training dataset
pca = PCA(n_components=1)
pca.fit(train_x)
pca.transform(train_x)
# consider features 0,1 (have to consider a subset of features;
# alternatively one can consider features 0,2
# cannot consider all three due to colinearity issues
# (a.k.a. violation of overlap))
print("\n###########################\ncore + spurious 1 + pca")
candidate_trainfea = train_x[:,:-1]
candidate_testfea = test_x[:,:-1]
adjust_trainC = pca.transform(train_x)
cov_train = np.column_stack([candidate_trainfea, adjust_trainC])
print("linearReg")
feareg = LinearRegression()
feareg.fit(cov_train, train_y)
print("coef", feareg.coef_, "intercept", feareg.intercept_)
print("train accuracy", feareg.score(cov_train, train_y))
# cond(candidate_trainfea.dot(candidate_trainfea.T))
```
above, after adjusting for pca factor, the spurious feature 1 returns close to zero coefficient
```
# construct a prediction model using the learned
# feature combination of "core + spurious 1"
learned_fea_train = candidate_trainfea.dot(feareg.coef_[:candidate_trainfea.shape[1]])[:,np.newaxis]
predreg = LinearRegression()
predreg.fit(learned_fea_train, train_y)
print("trainfea_coef", predreg.coef_, "intercept", predreg.intercept_)
print("trainfea accuracy", predreg.score(learned_fea_train, train_y))
# apply the prediction model on the test data
learned_fea_test = candidate_testfea.dot(feareg.coef_[:candidate_trainfea.shape[1]])[:,np.newaxis]
print("testfea accuracy", predreg.score(learned_fea_test, test_y))
```
above, the test accuracy no longer degrades much from the training accuracy.
also note that the test accuracy is very close to the oracle accuracy.
| true |
code
| 0.582254 | null | null | null | null |
|
# Deep $Q$-learning
In this notebook, we'll build a neural network that can learn to play games through reinforcement learning. More specifically, we'll use $Q$-learning to train an agent to play a game called [Cart-Pole](https://gym.openai.com/envs/CartPole-v0). In this game, a freely swinging pole is attached to a cart. The cart can move to the left and right, and the goal is to keep the pole upright as long as possible.

We can simulate this game using [OpenAI Gym](https://github.com/openai/gym). First, let's check out how OpenAI Gym works. Then, we'll get into training an agent to play the Cart-Pole game.
```
import gym
import numpy as np
# Create the Cart-Pole game environment
env = gym.make('CartPole-v1')
# Number of possible actions
print('Number of possible actions:', env.action_space.n)
```
We interact with the simulation through `env`. You can see how many actions are possible from `env.action_space.n`, and to get a random action you can use `env.action_space.sample()`. Passing in an action as an integer to `env.step` will generate the next step in the simulation. This is general to all Gym games.
In the Cart-Pole game, there are two possible actions, moving the cart left or right. So there are two actions we can take, encoded as 0 and 1.
Run the code below to interact with the environment.
```
actions = [] # actions that the agent selects
rewards = [] # obtained rewards
state = env.reset()
while True:
action = env.action_space.sample() # choose a random action
state, reward, done, _ = env.step(action)
rewards.append(reward)
actions.append(action)
if done:
break
```
We can look at the actions and rewards:
```
print('Actions:', actions)
print('Rewards:', rewards)
```
The game resets after the pole has fallen past a certain angle. For each step while the game is running, it returns a reward of 1.0. The longer the game runs, the more reward we get. Then, our network's goal is to maximize the reward by keeping the pole vertical. It will do this by moving the cart to the left and the right.
## $Q$-Network
To keep track of the action values, we'll use a neural network that accepts a state $s$ as input. The output will be $Q$-values for each available action $a$ (i.e., the output is **all** action values $Q(s,a)$ _corresponding to the input state $s$_).
<img src="assets/q-network.png" width=550px>
For this Cart-Pole game, the state has four values: **the position and velocity of the cart, and the angle and velocity of the pole**. Thus, the neural network has **four inputs**, one for each value in the state, and **two outputs**, one for each possible action.
As explored in the lesson, to get the training target, we'll first use the context provided by the state $s$ to choose an action $a$, then simulate the game using that action. This will get us the next state, $s'$, and the reward $r$. With that, we can calculate $\hat{Q}(s,a) = r + \gamma \max_{a'}{Q(s', a')}$. Then we update the weights by minimizing $(\hat{Q}(s,a) - Q(s,a))^2$.
Below is one implementation of the $Q$-network. It uses two fully connected layers with ReLU activations. Two seems to be good enough, three might be better. Feel free to try it out.
```
import tensorflow as tf
class QNetwork:
def __init__(self, learning_rate=0.01, state_size=4,
action_size=2, hidden_size=10,
name='QNetwork'):
# state inputs to the Q-network
with tf.variable_scope(name):
self.inputs_ = tf.placeholder(tf.float32, [None, state_size], name='inputs')
# ReLU hidden layers
self.fc1 = tf.contrib.layers.fully_connected(self.inputs_, hidden_size)
self.fc2 = tf.contrib.layers.fully_connected(self.fc1, hidden_size)
# Linear output layer
self.output = tf.contrib.layers.fully_connected(self.fc2, action_size,
activation_fn=None)
# One hot encode the actions to later choose the Q-value for the action
# ???: How to choose action for the calculation?
self.actions_ = tf.placeholder(tf.int32, [None], name='actions')
one_hot_actions = tf.one_hot(self.actions_, action_size)
# Target Q values for training
self.targetQs_ = tf.placeholder(tf.float32, [None], name='target')
### Train with loss (targetQ - Q)^2
# output has length 2, for two actions. This next line chooses
# one value from output (per row) according to the one-hot encoded actions.
self.Q = tf.reduce_sum(tf.multiply(self.output, one_hot_actions), axis=1)
print(self.Q)
self.loss = tf.reduce_mean(tf.square(self.targetQs_ - self.Q))
self.opt = tf.train.AdamOptimizer(learning_rate).minimize(self.loss)
```
## Experience replay
Reinforcement learning algorithms can have stability issues due to correlations between states. To reduce correlations when training, we can store the agent's experiences and later draw a random mini-batch of those experiences to train on.
Here, we'll create a `Memory` object that will store our experiences, our transitions $<s, a, r, s'>$. This memory will have a maximum capacity, so we can keep newer experiences in memory while getting rid of older experiences. Then, we'll sample a random mini-batch of transitions $<s, a, r, s'>$ and train on those.
Below, I've implemented a `Memory` object. If you're unfamiliar with `deque`, this is a double-ended queue. You can think of it like a tube open on both sides. You can put objects in either side of the tube. But if it's full, adding anything more will push an object out the other side. This is a great data structure to use for the memory buffer.
```
from collections import deque
class Memory():
def __init__(self, max_size=1000):
self.buffer = deque(maxlen=max_size)
def add(self, experience):
self.buffer.append(experience)
def sample(self, batch_size):
idx = np.random.choice(np.arange(len(self.buffer)),
size=batch_size,
replace=False)
return [self.buffer[ii] for ii in idx]
```
## $Q$-Learning training algorithm
We will use the below algorithm to train the network. For this game, the goal is to keep the pole upright for 195 frames. So we can start a new episode once meeting that goal. The game ends if the pole tilts over too far, or if the cart moves too far the left or right. When a game ends, we'll start a new episode. Now, to train the agent:
* Initialize the memory $D$
* Initialize the action-value network $Q$ with random weights
* **For** episode $\leftarrow 1$ **to** $M$ **do**
* Observe $s_0$
* **For** $t \leftarrow 0$ **to** $T-1$ **do**
* With probability $\epsilon$ select a random action $a_t$, otherwise select $a_t = \mathrm{argmax}_a Q(s_t,a)$
* Execute action $a_t$ in simulator and observe reward $r_{t+1}$ and new state $s_{t+1}$
* Store transition $<s_t, a_t, r_{t+1}, s_{t+1}>$ in memory $D$
* Sample random mini-batch from $D$: $<s_j, a_j, r_j, s'_j>$
* Set $\hat{Q}_j = r_j$ if the episode ends at $j+1$, otherwise set $\hat{Q}_j = r_j + \gamma \max_{a'}{Q(s'_j, a')}$
* Make a gradient descent step with loss $(\hat{Q}_j - Q(s_j, a_j))^2$
* **endfor**
* **endfor**
You are welcome (and encouraged!) to take the time to extend this code to implement some of the improvements that we discussed in the lesson, to include fixed $Q$ targets, double DQNs, prioritized replay, and/or dueling networks.
## Hyperparameters
One of the more difficult aspects of reinforcement learning is the large number of hyperparameters. Not only are we tuning the network, but we're tuning the simulation.
```
train_episodes = 1000 # max number of episodes to learn from
max_steps = 200 # max steps in an episode
gamma = 0.99 # future reward discount
# Exploration parameters
explore_start = 1.0 # exploration probability at start
explore_stop = 0.01 # minimum exploration probability
decay_rate = 0.0001 # exponential decay rate for exploration prob
# Network parameters
hidden_size = 64 # number of units in each Q-network hidden layer
learning_rate = 0.0001 # Q-network learning rate
# Memory parameters
memory_size = 10000 # memory capacity
batch_size = 20 # experience mini-batch size
pretrain_length = batch_size # number experiences to pretrain the memory
tf.reset_default_graph()
mainQN = QNetwork(name='main', hidden_size=hidden_size, learning_rate=learning_rate)
```
## Populate the experience memory
Here we re-initialize the simulation and pre-populate the memory. The agent is taking random actions and storing the transitions in memory. This will help the agent with exploring the game.
```
env.step(0)
# Initialize the simulation
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
memory = Memory(max_size=memory_size)
# Make a bunch of random actions and store the experiences
for ii in range(pretrain_length):
# Make a random action
action = env.action_space.sample()
next_state, reward, done, _ = env.step(action)
if done:
# The simulation fails so no next state
next_state = np.zeros(state.shape)
# Add experience to memory
memory.add((state, action, reward, next_state))
# Start new episode
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
else:
# Add experience to memory
memory.add((state, action, reward, next_state))
state = next_state
```
## Training
Below we'll train our agent.
```
state
# Now train with experiences
saver = tf.train.Saver()
rewards_list = []
rewards_list2 = []
loss = 0
with tf.Session() as sess:
# Initialize variables
sess.run(tf.global_variables_initializer())
step = 0
for ep in range(1, train_episodes):
total_reward = 0
t = 0
while t < max_steps:
step += 1
# Uncomment this next line to watch the training
env.render()
# Explore or Exploit
explore_p = explore_stop + (explore_start - explore_stop)*np.exp(-decay_rate*step)
if explore_p > np.random.rand():
# Make a random action
action = env.action_space.sample()
else:
# Get action from Q-network
feed = {mainQN.inputs_: state.reshape((1, *state.shape))}
Qs = sess.run(mainQN.output, feed_dict=feed)
action = np.argmax(Qs)
# Take action, get new state and reward
next_state, reward, done, _ = env.step(action)
total_reward += reward
if done:
# the episode ends so no next state
next_state = np.zeros(state.shape)
t = max_steps
if (ep % 50) == 0:
print('Episode: {}'.format(ep),
'Total reward: {}'.format(total_reward),
'Average reward of last 10 ep: {}'.format(sum(rewards_list2[-10:]) / 10),
'Training loss: {:.4f}'.format(loss),
'Explore P: {:.4f}'.format(explore_p))
rewards_list.append((ep, total_reward))
rewards_list2.append(total_reward)
# Add experience to memory
memory.add((state, action, reward, next_state))
# Start new episode
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
else:
# Add experience to memory
memory.add((state, action, reward, next_state))
state = next_state
t += 1
# Sample mini-batch from memory
batch = memory.sample(batch_size)
states = np.array([each[0] for each in batch])
actions = np.array([each[1] for each in batch])
rewards = np.array([each[2] for each in batch])
next_states = np.array([each[3] for each in batch])
# Create target Q
target_Qs = sess.run(mainQN.output, feed_dict={mainQN.inputs_: next_states})
# Set target_Qs to 0 for states where episode ends
episode_ends = (next_states == np.zeros(states[0].shape)).all(axis=1)
target_Qs[episode_ends] = (0, 0)
targets = rewards + gamma * np.max(target_Qs, axis=1)
# Train network
loss, _ = sess.run([mainQN.loss, mainQN.opt],
feed_dict={mainQN.inputs_: states,
mainQN.targetQs_: targets,
mainQN.actions_: actions})
saver.save(sess, "checkpoints/cartpole.ckpt")
```
## Training with Fixed Q Target
```
# Now train with experiences
saver = tf.train.Saver()
rewards_list = []
rewards_list2 = []
loss = 0
with tf.Session() as sess:
# Initialize variables
sess.run(tf.global_variables_initializer())
step = 0
for ep in range(1, train_episodes):
total_reward = 0
t = 0
# Fixed Q Traget implementation version 2
# target_Qs = sess.run(mainQN.output, feed_dict={mainQN.inputs_: next_states})
while t < max_steps:
step += 1
# Uncomment this next line to watch the training
env.render()
# Explore or Exploit
explore_p = explore_stop + (explore_start - explore_stop)*np.exp(-decay_rate*step)
if explore_p > np.random.rand():
# Make a random action
action = env.action_space.sample()
else:
# Get action from Q-network
feed = {mainQN.inputs_: state.reshape((1, *state.shape))}
Qs = sess.run(mainQN.output, feed_dict=feed)
action = np.argmax(Qs)
# Take action, get new state and reward
next_state, reward, done, _ = env.step(action)
total_reward += reward
if done:
# the episode ends so no next state
next_state = np.zeros(state.shape)
t = max_steps
if (ep % 50) == 0:
print('Episode: {}'.format(ep),
'Total reward: {}'.format(total_reward),
'Average reward of last 10 ep: {}'.format(sum(rewards_list2[-10:]) / 10),
'Training loss: {:.4f}'.format(loss),
'Explore P: {:.4f}'.format(explore_p))
rewards_list.append((ep, total_reward))
rewards_list2.append(total_reward)
# Add experience to memory
memory.add((state, action, reward, next_state))
# Start new episode
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
else:
# Add experience to memory
memory.add((state, action, reward, next_state))
state = next_state
t += 1
# Sample mini-batch from memory
batch = memory.sample(batch_size)
states = np.array([each[0] for each in batch])
actions = np.array([each[1] for each in batch])
rewards = np.array([each[2] for each in batch])
next_states = np.array([each[3] for each in batch])
# Fixed Q Traget implementation version 1
if (step - 1) % 100 == 0:
target_Qs = sess.run(mainQN.output, feed_dict={mainQN.inputs_: next_states})
# Set target_Qs to 0 for states where episode ends
episode_ends = (next_states == np.zeros(states[0].shape)).all(axis=1)
target_Qs[episode_ends] = (0, 0)
# Fixed Q Traget implementation version 2
# if step == 1:
# target_Qs = sess.run(mainQN.output, feed_dict={mainQN.inputs_: next_states})
# # Set target_Qs to 0 for states where episode ends
# episode_ends = (next_states == np.zeros(states[0].shape)).all(axis=1)
# target_Qs[episode_ends] = (0, 0)
targets = rewards + gamma * np.max(target_Qs, axis=1)
# Train network
loss, _ = sess.run([mainQN.loss, mainQN.opt],
feed_dict={mainQN.inputs_: states,
mainQN.targetQs_: targets,
mainQN.actions_: actions})
saver.save(sess, "checkpoints/cartpole_fixedqtarget.ckpt")
```
## Training with Double DQN
```
# Now train with experiences
saver = tf.train.Saver()
rewards_list = []
rewards_list2 = []
loss = 0
with tf.Session() as sess:
# Initialize variables
sess.run(tf.global_variables_initializer())
step = 0
for ep in range(1, train_episodes):
total_reward = 0
t = 0
# Fixed Q Traget implementation version 2
# target_Qs = sess.run(mainQN.output, feed_dict={mainQN.inputs_: next_states})
while t < max_steps:
step += 1
# Uncomment this next line to watch the training
env.render()
# Explore or Exploit
explore_p = explore_stop + (explore_start - explore_stop)*np.exp(-decay_rate*step)
if explore_p > np.random.rand():
# Make a random action
action = env.action_space.sample()
else:
# Get action from Q-network
feed = {mainQN.inputs_: state.reshape((1, *state.shape))}
Qs = sess.run(mainQN.output, feed_dict=feed)
action = np.argmax(Qs)
# Take action, get new state and reward
next_state, reward, done, _ = env.step(action)
total_reward += reward
if done:
# the episode ends so no next state
next_state = np.zeros(state.shape)
t = max_steps
if (ep % 50) == 0:
print('Episode: {}'.format(ep),
'Total reward: {}'.format(total_reward),
'Average reward of last 10 ep: {}'.format(sum(rewards_list2[-10:]) / 10),
'Training loss: {:.4f}'.format(loss),
'Explore P: {:.4f}'.format(explore_p))
rewards_list.append((ep, total_reward))
rewards_list2.append(total_reward)
# Add experience to memory
memory.add((state, action, reward, next_state))
# Start new episode
env.reset()
# Take one random step to get the pole and cart moving
state, reward, done, _ = env.step(env.action_space.sample())
else:
# Add experience to memory
memory.add((state, action, reward, next_state))
state = next_state
t += 1
# Sample mini-batch from memory
batch = memory.sample(batch_size)
states = np.array([each[0] for each in batch])
actions = np.array([each[1] for each in batch])
rewards = np.array([each[2] for each in batch])
next_states = np.array([each[3] for each in batch])
# Fixed Q Traget implementation version 1
if (step - 1) % 100 == 0:
target_Qs = sess.run(mainQN.output, feed_dict={mainQN.inputs_: next_states})
# Set target_Qs to 0 for states where episode ends
episode_ends = (next_states == np.zeros(states[0].shape)).all(axis=1)
target_Qs[episode_ends] = (0, 0)
# Fixed Q Traget implementation version 2
# if step == 1:
# target_Qs = sess.run(mainQN.output, feed_dict={mainQN.inputs_: next_states})
# # Set target_Qs to 0 for states where episode ends
# episode_ends = (next_states == np.zeros(states[0].shape)).all(axis=1)
# target_Qs[episode_ends] = (0, 0)
targets = rewards + gamma * target_Qs[states][action]
# Train network
loss, _ = sess.run([mainQN.loss, mainQN.opt],
feed_dict={mainQN.inputs_: states,
mainQN.targetQs_: targets,
mainQN.actions_: actions})
saver.save(sess, "checkpoints/cartpole_fixedqtarget.ckpt")
```
## Visualizing training
Below we plot the total rewards for each episode. The rolling average is plotted in blue.
```
%matplotlib inline
import matplotlib.pyplot as plt
def running_mean(x, N):
cumsum = np.cumsum(np.insert(x, 0, 0))
return (cumsum[N:] - cumsum[:-N]) / N
eps, rews = np.array(rewards_list).T
smoothed_rews = running_mean(rews, 10)
plt.plot(eps[-len(smoothed_rews):], smoothed_rews)
plt.plot(eps, rews, color='grey', alpha=0.3)
plt.xlabel('Episode')
plt.ylabel('Total Reward')
```
## Playing Atari Games
So, Cart-Pole is a pretty simple game. However, the same model can be used to train an agent to play something much more complicated like Pong or Space Invaders. Instead of a state like we're using here though, you'd want to use convolutional layers to get the state from the screen images.

I'll leave it as a challenge for you to use deep Q-learning to train an agent to play Atari games. Here's the original paper which will get you started: http://www.davidqiu.com:8888/research/nature14236.pdf.
| true |
code
| 0.622316 | null | null | null | null |
|
# Model Optimization with an Image Classification Example
1. [Introduction](#Introduction)
2. [Prerequisites and Preprocessing](#Prequisites-and-Preprocessing)
3. [Train the model](#Train-the-model)
4. [Optimize trained model using SageMaker Neo and Deploy](#Optimize-trained-model-using-SageMaker-Neo-and-Deploy)
5. [Request Inference](#Request-Inference)
6. [Delete the Endpoints](#Delete-the-Endpoints)
## Introduction
***
Welcome to our model optimization example for image classification. In this demo, we will use the Amazon SageMaker Image Classification algorithm to train on the [caltech-256 dataset](http://www.vision.caltech.edu/Image_Datasets/Caltech256/) and then we will demonstrate Amazon SageMaker Neo's ability to optimize models.
## Prequisites and Preprocessing
***
### Setup
To get started, we need to define a few variables and obtain certain permissions that will be needed later in the example. These are:
* A SageMaker session
* IAM role to give learning, storage & hosting access to your data
* An S3 bucket, a folder & sub folders that will be used to store data and artifacts
* SageMaker's specific Image Classification training image which should not be changed
We also need to upgrade the [SageMaker SDK for Python](https://sagemaker.readthedocs.io/en/stable/v2.html) to v2.33.0 or greater and restart the kernel.
```
!~/anaconda3/envs/mxnet_p36/bin/pip install --upgrade sagemaker>=2.33.0
import sagemaker
from sagemaker import session, get_execution_role
role = get_execution_role()
sagemaker_session = session.Session()
# S3 bucket and folders for saving code and model artifacts.
# Feel free to specify different bucket/folders here if you wish.
bucket = sagemaker_session.default_bucket()
folder = 'DEMO-ImageClassification'
model_with_custom_code_sub_folder = folder + '/model-with-custom-code'
validation_data_sub_folder = folder + '/validation-data'
training_data_sub_folder = folder + '/training-data'
training_output_sub_folder = folder + '/training-output'
compilation_output_sub_folder = folder + '/compilation-output'
from sagemaker import session, get_execution_role
from sagemaker.amazon.amazon_estimator import get_image_uri
# S3 Location to save the model artifact after training
s3_training_output_location = 's3://{}/{}'.format(bucket, training_output_sub_folder)
# S3 Location to save the model artifact after compilation
s3_compilation_output_location = 's3://{}/{}'.format(bucket, compilation_output_sub_folder)
# S3 Location to save your custom code in tar.gz format
s3_model_with_custom_code_location = 's3://{}/{}'.format(bucket, model_with_custom_code_sub_folder)
from sagemaker.image_uris import retrieve
aws_region = sagemaker_session.boto_region_name
training_image = retrieve(framework='image-classification', region=aws_region, image_scope='training')
```
### Data preparation
In this demo, we are using [Caltech-256](http://www.vision.caltech.edu/Image_Datasets/Caltech256/) dataset, pre-converted into `RecordIO` format using MXNet's [im2rec](https://mxnet.apache.org/versions/1.7/api/faq/recordio) tool. Caltech-256 dataset contains 30608 images of 256 objects. For the training and validation data, the splitting scheme followed is governed by this [MXNet example](https://github.com/apache/incubator-mxnet/blob/8ecdc49cf99ccec40b1e342db1ac6791aa97865d/example/image-classification/data/caltech256.sh). The example randomly selects 60 images per class for training, and uses the remaining data for validation. It takes around 50 seconds to convert the entire Caltech-256 dataset (~1.2GB) into `RecordIO` format on a p2.xlarge instance. SageMaker's training algorithm takes `RecordIO` files as input. For this demo, we will download the `RecordIO` files and upload it to S3. We then initialize the 256 object categories as well to a variable.
```
import os
import urllib.request
def download(url):
filename = url.split("/")[-1]
if not os.path.exists(filename):
urllib.request.urlretrieve(url, filename)
# Dowload caltech-256 data files from MXNet's website
download('http://data.mxnet.io/data/caltech-256/caltech-256-60-train.rec')
download('http://data.mxnet.io/data/caltech-256/caltech-256-60-val.rec')
# Upload the file to S3
s3_training_data_location = sagemaker_session.upload_data('caltech-256-60-train.rec', bucket, training_data_sub_folder)
s3_validation_data_location = sagemaker_session.upload_data('caltech-256-60-val.rec', bucket, validation_data_sub_folder)
class_labels = ['ak47', 'american-flag', 'backpack', 'baseball-bat', 'baseball-glove', 'basketball-hoop', 'bat',
'bathtub', 'bear', 'beer-mug', 'billiards', 'binoculars', 'birdbath', 'blimp', 'bonsai-101',
'boom-box', 'bowling-ball', 'bowling-pin', 'boxing-glove', 'brain-101', 'breadmaker', 'buddha-101',
'bulldozer', 'butterfly', 'cactus', 'cake', 'calculator', 'camel', 'cannon', 'canoe', 'car-tire',
'cartman', 'cd', 'centipede', 'cereal-box', 'chandelier-101', 'chess-board', 'chimp', 'chopsticks',
'cockroach', 'coffee-mug', 'coffin', 'coin', 'comet', 'computer-keyboard', 'computer-monitor',
'computer-mouse', 'conch', 'cormorant', 'covered-wagon', 'cowboy-hat', 'crab-101', 'desk-globe',
'diamond-ring', 'dice', 'dog', 'dolphin-101', 'doorknob', 'drinking-straw', 'duck', 'dumb-bell',
'eiffel-tower', 'electric-guitar-101', 'elephant-101', 'elk', 'ewer-101', 'eyeglasses', 'fern',
'fighter-jet', 'fire-extinguisher', 'fire-hydrant', 'fire-truck', 'fireworks', 'flashlight',
'floppy-disk', 'football-helmet', 'french-horn', 'fried-egg', 'frisbee', 'frog', 'frying-pan',
'galaxy', 'gas-pump', 'giraffe', 'goat', 'golden-gate-bridge', 'goldfish', 'golf-ball', 'goose',
'gorilla', 'grand-piano-101', 'grapes', 'grasshopper', 'guitar-pick', 'hamburger', 'hammock',
'harmonica', 'harp', 'harpsichord', 'hawksbill-101', 'head-phones', 'helicopter-101', 'hibiscus',
'homer-simpson', 'horse', 'horseshoe-crab', 'hot-air-balloon', 'hot-dog', 'hot-tub', 'hourglass',
'house-fly', 'human-skeleton', 'hummingbird', 'ibis-101', 'ice-cream-cone', 'iguana', 'ipod', 'iris',
'jesus-christ', 'joy-stick', 'kangaroo-101', 'kayak', 'ketch-101', 'killer-whale', 'knife', 'ladder',
'laptop-101', 'lathe', 'leopards-101', 'license-plate', 'lightbulb', 'light-house', 'lightning',
'llama-101', 'mailbox', 'mandolin', 'mars', 'mattress', 'megaphone', 'menorah-101', 'microscope',
'microwave', 'minaret', 'minotaur', 'motorbikes-101', 'mountain-bike', 'mushroom', 'mussels',
'necktie', 'octopus', 'ostrich', 'owl', 'palm-pilot', 'palm-tree', 'paperclip', 'paper-shredder',
'pci-card', 'penguin', 'people', 'pez-dispenser', 'photocopier', 'picnic-table', 'playing-card',
'porcupine', 'pram', 'praying-mantis', 'pyramid', 'raccoon', 'radio-telescope', 'rainbow', 'refrigerator',
'revolver-101', 'rifle', 'rotary-phone', 'roulette-wheel', 'saddle', 'saturn', 'school-bus',
'scorpion-101', 'screwdriver', 'segway', 'self-propelled-lawn-mower', 'sextant', 'sheet-music',
'skateboard', 'skunk', 'skyscraper', 'smokestack', 'snail', 'snake', 'sneaker', 'snowmobile',
'soccer-ball', 'socks', 'soda-can', 'spaghetti', 'speed-boat', 'spider', 'spoon', 'stained-glass',
'starfish-101', 'steering-wheel', 'stirrups', 'sunflower-101', 'superman', 'sushi', 'swan',
'swiss-army-knife', 'sword', 'syringe', 'tambourine', 'teapot', 'teddy-bear', 'teepee',
'telephone-box', 'tennis-ball', 'tennis-court', 'tennis-racket', 'theodolite', 'toaster', 'tomato',
'tombstone', 'top-hat', 'touring-bike', 'tower-pisa', 'traffic-light', 'treadmill', 'triceratops',
'tricycle', 'trilobite-101', 'tripod', 't-shirt', 'tuning-fork', 'tweezer', 'umbrella-101', 'unicorn',
'vcr', 'video-projector', 'washing-machine', 'watch-101', 'waterfall', 'watermelon', 'welding-mask',
'wheelbarrow', 'windmill', 'wine-bottle', 'xylophone', 'yarmulke', 'yo-yo', 'zebra', 'airplanes-101',
'car-side-101', 'faces-easy-101', 'greyhound', 'tennis-shoes', 'toad', 'clutter']
```
## Train the model
***
Now that we are done with all the setup that is needed, we are ready to train our object detector. To begin, let us create a ``sagemaker.estimator.Estimator`` object. This estimator is required to launch the training job.
We specify the following parameters while creating the estimator:
* ``image_uri``: This is set to the training_image uri we defined previously. Once set, this image will be used later while running the training job.
* ``role``: This is the IAM role which we defined previously.
* ``instance_count``: This is the number of instances on which to run the training. When the number of instances is greater than one, then the image classification algorithm will run in distributed settings.
* ``instance_type``: This indicates the type of machine on which to run the training. For this example we will use `ml.p3.8xlarge`.
* ``volume_size``: This is the size in GB of the EBS volume to use for storing input data during training. Must be large enough to store training data as File Mode is used.
* ``max_run``: This is the timeout value in seconds for training. After this amount of time SageMaker terminates the job regardless of its current status.
* ``input_mode``: This is set to `File` in this example. SageMaker copies the training dataset from the S3 location to a local directory.
* ``output_path``: This is the S3 path in which the training output is stored. We are assigning it to `s3_training_output_location` defined previously.
```
ic_estimator = sagemaker.estimator.Estimator(image_uri=training_image,
role=role,
instance_count=1,
instance_type='ml.p3.8xlarge',
volume_size = 50,
max_run = 360000,
input_mode= 'File',
output_path=s3_training_output_location,
base_job_name='img-classification-training'
)
```
Following are certain hyperparameters that are specific to the algorithm which are also set:
* ``num_layers``: The number of layers (depth) for the network. We use 18 in this samples but other values such as 50, 152 can be used.
* ``image_shape``: The input image dimensions,'num_channels, height, width', for the network. It should be no larger than the actual image size. The number of channels should be same as the actual image.
* ``num_classes``: This is the number of output classes for the new dataset. Imagenet was trained with 1000 output classes but the number of output classes can be changed for fine-tuning. For caltech, we use 257 because it has 256 object categories + 1 clutter class.
* ``num_training_samples``: This is the total number of training samples. It is set to 15240 for caltech dataset with the current split.
* ``mini_batch_size``: The number of training samples used for each mini batch. In distributed training, the number of training samples used per batch will be N * mini_batch_size where N is the number of hosts on which training is run.
* ``epochs``: Number of training epochs.
* ``learning_rate``: Learning rate for training.
* ``top_k``: Report the top-k accuracy during training.
* ``precision_dtype``: Training datatype precision (default: float32). If set to 'float16', the training will be done in mixed_precision mode and will be faster than float32 mode.
```
ic_estimator.set_hyperparameters(num_layers=18,
image_shape = "3,224,224",
num_classes=257,
num_training_samples=15420,
mini_batch_size=128,
epochs=5,
learning_rate=0.01,
top_k=2,
use_pretrained_model=1,
precision_dtype='float32')
```
Next we setup the input ``data_channels`` to be used later for training.
```
train_data = sagemaker.inputs.TrainingInput(s3_training_data_location,
content_type='application/x-recordio',
s3_data_type='S3Prefix')
validation_data = sagemaker.inputs.TrainingInput(s3_validation_data_location,
content_type='application/x-recordio',
s3_data_type='S3Prefix')
data_channels = {'train': train_data, 'validation': validation_data}
```
After we've created the estimator object, we can train the model using ``fit()`` API
```
ic_estimator.fit(inputs=data_channels, logs=True)
```
## Optimize trained model using SageMaker Neo and Deploy
***
We will use SageMaker Neo's ``compile_model()`` API while specifying ``MXNet`` as the framework and the version to optimize the model. When calling this API, we also specify the target instance family, correct input shapes for the model and the S3 location to which the compiled model artifacts would be stored. For this example, we will choose ``ml_c5`` as the target instance family.
```
optimized_ic = ic_estimator.compile_model(target_instance_family='ml_c5',
input_shape={'data':[1, 3, 224, 224]},
output_path=s3_compilation_output_location,
framework='mxnet',
framework_version='1.8')
```
After compiled artifacts are generated and we have a ``sagemaker.model.Model`` object, we then create a ``sagemaker.mxnet.model.MXNetModel`` object while specifying the following parameters:
* ``model_data``: s3 location where compiled model artifact is stored
* ``image_uri``: Neo's Inference Image URI for MXNet
* ``framework_version``: set to MXNet's v1.8.0
* ``role`` & ``sagemaker_session`` : IAM role and sagemaker session which we defined in the setup
* ``entry_point``: points to the entry_point script. In our example the script has SageMaker's hosting functions implementation
* ``py_version``: We are required to set to python version 3
* ``env``: A dict to specify the environment variables. We are required to set MMS_DEFAULT_RESPONSE_TIMEOUT to 500
* ``code_location``: s3 location where repacked model.tar.gz is stored. Repacked tar file consists of compiled model artifacts and entry_point script
```
from sagemaker.mxnet.model import MXNetModel
optimized_ic_model = MXNetModel(model_data=optimized_ic.model_data,
image_uri=optimized_ic.image_uri,
framework_version='1.8.0',
role=role,
sagemaker_session=sagemaker_session,
entry_point='inference.py',
py_version='py37',
env={'MMS_DEFAULT_RESPONSE_TIMEOUT': '500'},
code_location=s3_model_with_custom_code_location
)
```
We can now deploy this ``sagemaker.mxnet.model.MXNetModel`` using the ``deploy()`` API, for which we need to use an instance_type belonging to the target_instance_family we used for compilation. For this example, we will choose ``ml.c5.4xlarge`` instance as we compiled for ``ml_c5``. The API also allow us to set the number of initial_instance_count that will be used for the Endpoint. By default the API will use ``JSONSerializer()`` and ``JSONDeserializer()`` for ``sagemaker.mxnet.model.MXNetModel`` whose ``CONTENT_TYPE`` is ``application/json``. The API creates a SageMaker endpoint that we can use to perform inference.
**Note**: If you compiled the model for a GPU `target_instance_family` then please make sure to deploy to one of the same target `instance_type` below and also make necessary changes in the entry point script `inference.py`
```
optimized_ic_classifier = optimized_ic_model.deploy(initial_instance_count = 1, instance_type = 'ml.c5.4xlarge')
```
## Request Inference
***
Once the endpoint is in ``InService`` we can then send a test image ``test.jpg`` and get the prediction result from the endpoint using SageMaker's ``predict()`` API. Instead of sending the raw image to the endpoint for prediction we will prepare and send the payload which is in a form acceptable by the API. Upon receiving the prediction result we will print the class label and probability.
```
import PIL.Image
import numpy as np
from IPython.display import Image
test_file = 'test.jpg'
test_image = PIL.Image.open(test_file)
payload = np.asarray(test_image.resize((224, 224)))
Image(test_file)
%%time
result = optimized_ic_classifier.predict(payload)
index = np.argmax(result)
print("Result: label - " + class_labels[index] + ", probability - " + str(result[index]))
```
## Delete the Endpoint
***
Having an endpoint running will incur some costs. Therefore as an optional clean-up job, you can delete it.
```
print("Endpoint name: " + optimized_ic_classifier.endpoint_name)
optimized_ic_classifier.delete_endpoint()
```
| true |
code
| 0.281504 | null | null | null | null |
|
#### 여기서는 Tutorial에서 배운 개념을 이용하여 간단하게 ReplayBuffer를 분산 환경에서 활용해보겠습니다. <br> 아래와 같은 작업을 수행합니다. <br>
1. 여럿의 agent(혹은 actor)가 공유 Replay Buffer에 경험데이터를 넣는다.
2. Learner는 batch만큼 그 공유 ReplayBuffer에서 load한 후 원하는 작업을 수행한다.
#### 질문 <br>
1. Class의 method는 공유가 잘 되는데, class 안에 있는 __init__ 에서 선언된 variable은 불러올 수가 없었다. 어떻게 해야하는 걸까?
: 현재로써는 class 안에 변수를 전달하는 method를 따로 만들어서 ray.get으로 접근하는 방법을 쓰고있음..
```
import sys
IN_COLAB = "google.colab" in sys.modules
if IN_COLAB:
!pip install ray
import ray
import time
import numpy as np
ray.init()
# 간단한 env를 정의하겠습니다. environment의 일반적인 메소드만 넣고 어떤 의미가 있는 행동이나 상태를 정의한 것은 아닙니다.
class Env:
def reset(self):
return np.ones((2,2))
def step(self, action):
# state, reward, done 모두 random하게 지정. state의 크기는 2x2 차원을 가지는 2차원 matrix.
state = action*np.random.randn(2, 2)
reward = np.sum(state)
# done은 numpy의 random.randn 이 0.06 보다 작을 때만 1을 주었습니다. 더 자주 done이 발생하도록 하고 싶다면, 0.06을 더 키우면 됩니다.
done = 1 if abs(np.random.randn())<0.06 else 0
return state, reward, done
# Buffer를 정의합니다.
@ray.remote
class Buffer:
def __init__(self, buffer_size):
self.buffer_size = buffer_size
self.state_buffer = np.zeros((buffer_size, 2 ,2))
self.action_buffer = np.zeros(buffer_size)
self.reward_buffer = np.zeros(buffer_size)
self.next_state_buffer = np.zeros((buffer_size, 2 ,2))
self.done_buffer = np.zeros(buffer_size)
self.act_idx_buffer = np.zeros(buffer_size)
self.store_idx = 0
self.current_size = 0
self.total_store_count = 0
def store(self, state, action, next_state, reward, done, actor_idx):
self.state_buffer[self.store_idx] = state
self.action_buffer[self.store_idx] = action
self.reward_buffer[self.store_idx] = reward
self.next_state_buffer[self.store_idx] = next_state
self.done_buffer[self.store_idx] = done
self.act_idx_buffer[self.store_idx] = actor_idx
self.store_idx = (self.store_idx + 1) % self.buffer_size
self.current_size = min(self.current_size+1, self.buffer_size)
self.total_store_count += 1
def batch_load(self, batch_size):
indices = np.random.randint(self.current_size, size=batch_size)
return dict(
states=self.state_buffer[indices],
actions=self.action_buffer[indices],
rewards=self.reward_buffer[indices],
next_states=self.next_state_buffer[indices],
dones=self.done_buffer[indices],
actindices=self.act_idx_buffer[indices])
def return_current_size(self):
return self.total_store_count
# actor의 역할은 각각 env에서 경험한 것을 buffer에 넘겨주는 역할을 합니다.
@ray.remote
class Actor:
def __init__(self, memory, actor_idx):
self.env = Env()
self.memory = memory # ray를 통해 공유하는 learner class입니다.
self.actor_idx = actor_idx # 어떤 actor에서 온 데이터인지 보기 위한 변수입니다.
def explore(self):
state = self.env.reset()
# actor는 멈추지 않아도 되기 때문에, 다음과 같이 무한 loop로 exploration하도록 설정
while 1:
action = np.random.randint(3)
next_state, reward, done = self.env.step(action)
# 공유 메모리에 데이터를 저장합니다.
self.memory.store.remote(state, action, next_state, reward, done, self.actor_idx)
time.sleep(0.005) # 쥬피터 노트북의 출력이 불안정할 때 time.sleep으로 조절을 하면 수월합니다. Colab의 경우는 없어도 잘 출력이 됩니다.
state = next_state
if done: state = self.env.reset()
# 공유 Buffer를 통해 학습을 진행하는 Learner를 정의합니다.
class Learner:
def __init__(self, memory, buffer_size, batch_size):
self.memory = memory
self.batch_size = batch_size
def update_network(self):
# 저장된 buffer에서 데이터를 로딩합니다.
batch = ray.get(self.memory.batch_load.remote(self.batch_size))
print("batch is loaded.")
''' update를 하는 부분 '''
loss = np.random.randn()
buffer_store_count = ray.get(self.memory.return_current_size.remote())
return loss, batch['states'].shape, batch['actindices'], buffer_store_count # 결과를 확인하기 위해서, loss 이외에 몇 가지를 추가
buffer_size = 5000 # Replay Buffer 사이즈
batch_size = 16 # Replay Buffer에서 가지고 올 샘플 개수
memory = Buffer.remote(batch_size)
learner = Learner(memory, buffer_size, batch_size)
num_actors = 5 # actor의 개수
# num_actors 개수만큼 선언하고, explore 실행. actor라는 변수가 계속 중복이 되지만 실행은 잘 된다.
for idx in range(num_actors):
actor = Actor.remote(memory, idx)
actor.explore.remote()
time.sleep(1) # 잠시 actor가 어느정도 쌓을 때까지 대기
n_updates = 100 # learner가 update_network 메소드를 실행하는 횟수
for update_idx in range(n_updates):
loss, batch_stat_shape, act_indices, buf_size = learner.update_network()
print(f'Number of updates: {update_idx}')
print(f'Loss: {loss}')
print(f'State shape in Batch: {batch_stat_shape}')
print(f'Actor index: {act_indices}')
print(f'Buffer store index: {buf_size}\n')
time.sleep(0.5)
```
- Loss: random한 실수값 <br>
- State shape: (batch, state[0], state[1])의 자원을 가지는 출력 <br>
- Actor index: batch 안의 각 sample이 어느 actor에게 나온 것인지 출력 <br>
- Buffer store index: Buffer에 저장되는 현재 store index(각 update 사이에 얼마나 저장되었는지)를 출력 <br><br>
#### 대략 아래와 같은 결과가 나오면 의도대로 나온 것입니다.
Number of updates: 9
Loss: -1.7283143861676746
State shape in Batch: (16, 2, 2)
Actor index: [ 4. 12. 1. 3. 4. 4. 1. 14. 2. 15. 11. 0. 1. 15. 15. 9.]
Buffer store index: 1863
Number of updates: 10
Loss: -1.3466382853532786
State shape in Batch: (16, 2, 2)
Actor index: [ 9. 8. 13. 15. 14. 9. 0. 4. 2. 8. 13. 7. 2. 2. 0. 11.]
Buffer store index: 2023
Number of updates: 11
Loss: -0.8023523911669711
State shape in Batch: (16, 2, 2)
Actor index: [ 3. 9. 9. 7. 12. 3. 12. 6. 12. 5. 10. 7. 0. 11. 3. 6.]
Buffer store index: 2181
| true |
code
| 0.622144 | null | null | null | null |
|
# IMDB Movie Reviews Sentiment Classification
\* This project was inspired by a book 'Deep Learning with Python' by François Chollet.
- Internet Movie Database로부터 가져온 양극단의 리뷰 5만개로 이루어진 IMDB dataset을 사용. 이 dataset은 training data 25,000개와 test data 25,000개로 나뉘어 있고, 각각 50%는 부정, 50%는 긍정리뷰로 구성되어 있음
- 리뷰 텍스트를 기반으로 영화 리뷰를 긍정과 부정으로 분류하기 - **Binary classification**
## Loading the data
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense
```
`num_words=10000` = 훈련데이터에서 가장 자주 나타나는 단어 10,000개만 사용
```
(X_train, y_train), (X_test, y_test) = imdb.load_data(num_words=10000)
X_train[0]
```
labels : 0 = 부정 / 1 = 긍정
```
y_train[0]
```
## Preparing the data
신경망에 숫자리스트를 주입할 수 없으므로, 리스트를 텐서로 바꿔주기
#### 리스트를 텐서로 바꾸는 방법
1. Embedding
2. One-hot encoding
이 프로젝트에서는 one-hot encoding방법을 사용
### One-hot encoding
0과 1의 벡터로 변환하기
ex) 시퀀스 [2, 4]를 인덱스 2와 4의 위치는 1이고 나머지는 모두 0인 10,000차원의 벡터로 각각 변환
#### enumerate(sequences)
index와 그 index에 해당하는 값을 짝지어줌
a = [2, 4, 6, 8]
list(enumerate(a)) = [(0, 2), (1, 4), (2, 6), (3, 8)]
```
def vectorize_sequences(sequences, dimension=10000):
result = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
result[i, sequence] = 1 # sequence의 인덱스 해당하는 자리에만 1로 채워주기
return result
X_train = vectorize_sequences(X_train)
X_test = vectorize_sequences(X_test)
X_train[0]
y_train = np.asarray(y_train).astype('float32')
y_test = np.asarray(y_test).astype('float32')
y_train[:10]
model = Sequential([
Dense(16, activation='relu', input_shape=(10000,)),
Dense(16, activation='relu'),
Dense(1, activation='sigmoid')
])
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
X_val = X_train[:10000]
partial_X_train = X_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]
history = model.fit(partial_X_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(X_val, y_val))
result = model.evaluate(X_test, y_test)
result
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc)+1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
```
We can see that val_loss is the lowest at epoch 4.
```
model = Sequential([
Dense(16, activation='relu', input_shape=(10000,)),
Dense(16, activation='relu'),
Dense(1, activation='sigmoid')
])
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
history = model.fit(partial_X_train,
partial_y_train,
epochs=4,
batch_size=512,
validation_data=(X_val, y_val))
result = model.evaluate(X_test, y_test)
print(result)
```
| true |
code
| 0.753143 | null | null | null | null |
|
# How to create STAC Catalogs
## STAC Community Sprint, Arlington, November 7th 2019
This notebook runs through some of the basics of using PySTAC to create a static STAC. It was part of a 30 minute presentation at the [community STAC sprint](https://github.com/radiantearth/community-sprints/tree/master/11052019-arlignton-va) in Arlington, VA in November 2019.
This tutorial will require the `boto3`, `rasterio`, and `shapely` libraries:
```
!pip install boto3
!pip install rasterio
!pip install shapely
```
We can import pystac with the alias `stac` to access all of the API we need (saving a glorious 2 characters):
```
import pystac as stac
```
## Creating a catalog from a local file
To give us some material to work with, lets download a single image from the [Spacenet 5 challenge](https://www.topcoder.com/challenges/30099956). We'll use a temporary directory to save off our single-item STAC.
```
import os
import urllib.request
from tempfile import TemporaryDirectory
tmp_dir = TemporaryDirectory()
img_path = os.path.join(tmp_dir.name, 'image.tif')
url = ('http://spacenet-dataset.s3.amazonaws.com/'
'spacenet/SN5_roads/train/AOI_7_Moscow/MS/'
'SN5_roads_train_AOI_7_Moscow_MS_chip996.tif')
urllib.request.urlretrieve(url, img_path)
```
We want to create a Catalog. Let's check the pydocs for `Catalog` to see what information we'll need. (We use `__doc__` instead of `help()` here to avoid printing out all the docs for the class.)
```
print(stac.Catalog.__doc__)
```
Let's just give an ID and a description. We don't have to worry about the HREF right now; that will be set later.
```
catalog = stac.Catalog(id='test-catalog', description='Tutorial catalog.')
```
There are no children or items in the catalog, since we haven't added anything yet.
```
print(list(catalog.get_children()))
print(list(catalog.get_items()))
```
We'll now create an Item to represent the image. Check the pydocs to see what you need to supply:
```
print(stac.Item.__doc__)
```
Using [rasterio](https://rasterio.readthedocs.io/en/stable/), we can pull out the bounding box of the image to use for the image metadata. If the image contained a NoData border, we would ideally pull out the footprint and save it as the geometry; in this case, we're working with a small chip the most likely has no NoData values.
```
import rasterio
from shapely.geometry import Polygon, mapping
def get_bbox_and_footprint(raster_uri):
with rasterio.open(raster_uri) as ds:
bounds = ds.bounds
bbox = [bounds.left, bounds.bottom, bounds.right, bounds.top]
footprint = Polygon([
[bounds.left, bounds.bottom],
[bounds.left, bounds.top],
[bounds.right, bounds.top],
[bounds.right, bounds.bottom]
])
return (bbox, mapping(footprint))
bbox, footprint = get_bbox_and_footprint(img_path)
print(bbox)
print(footprint)
```
We're also using `datetime.utcnow()` to supply the required datetime property for our Item. Since this is a required property, you might often find yourself making up a time to fill in if you don't know the exact capture time.
```
from datetime import datetime
item = stac.Item(id='local-image',
geometry=footprint,
bbox=bbox,
datetime=datetime.utcnow(),
properties={})
```
We haven't added it to a catalog yet, so it's parent isn't set. Once we add it to the catalog, we can see it correctly links to it's parent.
```
item.get_parent() is None
catalog.add_item(item)
item.get_parent()
```
`describe()` is a useful method on `Catalog` - but be careful when using it on large catalogs, as it will walk the entire tree of the STAC.
```
catalog.describe()
```
### Adding Assets
We've created an Item, but there aren't any assets associated with it. Let's create one:
```
print(stac.Asset.__doc__)
item.add_asset(key='image', asset=stac.Asset(href=img_path, media_type=stac.MediaType.GEOTIFF))
```
At any time we can call `to_dict()` on STAC objects to see how the STAC JSON is shaping up. Notice the asset is now set:
```
import json
print(json.dumps(item.to_dict(), indent=4))
```
Note that the link `href` properties are `null`. This is OK, as we're working with the STAC in memory. Next, we'll talk about writing the catalog out, and how to set those HREFs.
### Saving the catalog
As the JSON above indicates, there's no HREFs set on these in-memory items. PySTAC uses the `self` link on STAC objects to track where the file lives. Because we haven't set them, they evaluate to `None`:
```
print(catalog.get_self_href() is None)
print(item.get_self_href() is None)
```
In order to set them, we can use `normalize_hrefs`. This method will create a normalized set of HREFs for each STAC object in the catalog, according to the [best practices document](https://github.com/radiantearth/stac-spec/blob/v0.8.1/best-practices.md#catalog-layout)'s recommendations on how to lay out a catalog.
```
catalog.normalize_hrefs(os.path.join(tmp_dir.name, 'stac'))
```
Now that we've normalized to a root directory (the temporary directory), we see that the `self` links are set:
```
print(catalog.get_self_href())
print(item.get_self_href())
```
We can now call `save` on the catalog, which will recursively save all the STAC objects to their respective self HREFs.
Save requires a `CatalogType` to be set. You can review the [API docs](https://pystac.readthedocs.io/en/stable/api.html#catalogtype) on `CatalogType` to see what each type means (unfortunately `help` doesn't show docstrings for attributes).
```
catalog.save(catalog_type=stac.CatalogType.SELF_CONTAINED)
!ls {tmp_dir.name}/stac/*
with open(catalog.get_self_href()) as f:
print(f.read())
with open(item.get_self_href()) as f:
print(f.read())
```
As you can see, all links are saved with relative paths. That's because we used `catalog_type=CatalogType.SELF_CONTAINED`. If we save an Absolute Published catalog, we'll see absolute paths:
```
catalog.save(catalog_type=stac.CatalogType.ABSOLUTE_PUBLISHED)
```
Now the links included in the STAC item are all absolute:
```
with open(item.get_self_href()) as f:
print(f.read())
```
Notice that the Asset HREF is absolute in both cases. We can make the Asset HREF relative to the STAC Item by using `.make_all_asset_hrefs_relative()`:
```
catalog.make_all_asset_hrefs_relative()
catalog.save(catalog_type=stac.CatalogType.SELF_CONTAINED)
with open(item.get_self_href()) as f:
print(f.read())
```
### Creating an EO Item
In the code above, we encapsulated our imagery as a core STAC item. However, there's more information that we can encapsulate, given that we know this is a World View 3 image. We can do this by creating an `EOItem`, which is an Item that is extended via the [eo extension](https://github.com/radiantearth/stac-spec/tree/v0.8.1/extensions/eo):
```
print(stac.EOItem.__doc__)
```
To create the EOItem, we'll need to encode some more information. First, let's define the bands of World View 3:
```
# From: https://www.spaceimagingme.com/downloads/sensors/datasheets/DG_WorldView3_DS_2014.pdf
wv3_bands = [stac.Band(name='Coastal', description='Coastal: 400 - 450 nm', common_name='coastal'),
stac.Band(name='Blue', description='Blue: 450 - 510 nm', common_name='blue'),
stac.Band(name='Green', description='Green: 510 - 580 nm', common_name='green'),
stac.Band(name='Yellow', description='Yellow: 585 - 625 nm', common_name='yellow'),
stac.Band(name='Red', description='Red: 630 - 690 nm', common_name='red'),
stac.Band(name='Red Edge', description='Red Edge: 705 - 745 nm', common_name='rededge'),
stac.Band(name='Near-IR1', description='Near-IR1: 770 - 895 nm', common_name='nir08'),
stac.Band(name='Near-IR2', description='Near-IR2: 860 - 1040 nm', common_name='nir09')]
```
We can now create an EO Item, and add it to our catalog:
```
eo_item = stac.EOItem(id='local-image-eo',
geometry=footprint,
bbox=bbox,
datetime=datetime.utcnow(),
properties={},
gsd=0.3,
platform="Maxar",
instrument="WorldView3",
bands=wv3_bands)
eo_item
eo_item.add_asset(key='image', asset=stac.EOAsset(href=img_path,
media_type=stac.MediaType.GEOTIFF,
bands=list(range(0,8))))
```
Let's clear the in-memory catalog, add the EO item, and save to a new STAC:
```
catalog.clear_items()
list(catalog.get_items())
catalog.add_item(eo_item)
list(catalog.get_items())
catalog.normalize_and_save(root_href=os.path.join(tmp_dir.name, 'stac-eo'),
catalog_type=stac.CatalogType.SELF_CONTAINED)
```
Now, if we read the catalog from the filesystem, PySTAC recognizes the EOItem and loads it in with the correct type:
```
catalog2 = stac.Catalog.from_file(os.path.join(tmp_dir.name, 'stac-eo', 'catalog.json'))
list(catalog2.get_items())
next(catalog2.get_all_items()).assets
import json
print(json.dumps(eo_item.to_dict(), indent=4))
```
### Collections
Collections are a subtype of Catalog that have some additional properties to make them more searchable. They also can define common properties so that items in the collection don't have to duplicate common data for each item. Let's create a collection to hold common properties between two images from the Spacenet 5 challenge.
First we'll get another image, and it's bbox and footprint:
```
url2 = ('http://spacenet-dataset.s3.amazonaws.com/'
'spacenet/SN5_roads/train/AOI_7_Moscow/MS/'
'SN5_roads_train_AOI_7_Moscow_MS_chip997.tif')
img_path2 = os.path.join(tmp_dir.name, 'image.tif')
urllib.request.urlretrieve(url2, img_path2)
bbox2, footprint2 = get_bbox_and_footprint(img_path2)
```
We can take a look at the pydocs for Collection to see what information we need to supply in order to satisfy the spec.
```
print(stac.Collection.__doc__)
```
Beyond what a Catalog reqiures, a Collection requires a license, and an `Extent` that describes the range of space and time that the items it hold occupy.
```
print(stac.Extent.__doc__)
```
An Extent is comprised of a SpatialExtent and a TemporalExtent. These hold one or more bounding boxes and time intervals, respectively, that completely cover the items contained in the collections.
Let's start with creating two new items - these will be core Items, not `EOItems`, although they will be imparted with `eo` information by the collection. This is why we add `eo` to the `stac_extensions`. We are also adding `EOAssets` to the Items, so that the assets have the proper `eo:bands` metadata associated with them:
```
collection_item1 = stac.Item(id='local-image-col-1',
geometry=footprint,
bbox=bbox,
datetime=datetime.utcnow(),
properties={},
stac_extensions=['eo'])
collection_item1.add_asset('image', stac.EOAsset(href=img_path,
media_type=stac.MediaType.GEOTIFF,
bands=list(range(0,8))))
collection_item2 = stac.Item(id='local-image-col-2',
geometry=footprint2,
bbox=bbox2,
datetime=datetime.utcnow(),
properties={},
stac_extensions=['eo'])
collection_item2.add_asset('image', stac.EOAsset(href=img_path,
media_type=stac.MediaType.GEOTIFF,
bands=list(range(0,8))))
```
We can use our two items' metadata to find out what the proper bounds are:
```
from shapely.geometry import shape
unioned_footprint = shape(footprint).union(shape(footprint2))
collection_bbox = list(unioned_footprint.bounds)
spatial_extent = stac.SpatialExtent(bboxes=[collection_bbox])
collection_interval = sorted([collection_item1.datetime, collection_item2.datetime])
temporal_extent = stac.TemporalExtent(intervals=[collection_interval])
collection_extent = stac.Extent(spatial=spatial_extent, temporal=temporal_extent)
```
We can list the common properties for the items, with their proper extension names, and use it in the Collection properties:
```
common_properties = { 'eo:bands': [b.to_dict() for b in wv3_bands],
'eo:gsd': 0.3,
'eo:platform': 'Maxar',
'eo:instrument': 'WorldView3'
}
collection = stac.Collection(id='wv3-images',
description='Spacenet 5 images over Moscow',
extent=collection_extent,
properties=common_properties,
license='CC-BY-SA-4.0')
```
Now if we add our items to our Collection, and our Collection to our Catalog, we get the following STAC that can be saved:
```
collection.add_items([collection_item1, collection_item2])
catalog.clear_items()
catalog.clear_children()
catalog.add_child(collection)
catalog.describe()
catalog.normalize_and_save(root_href=os.path.join(tmp_dir.name, 'stac-collection'),
catalog_type=stac.CatalogType.SELF_CONTAINED)
```
Notice our collection item does not have any of the `eo` metadata in it's properties:
```
collection_item1.to_dict()
```
However, when we read the catalog in, the collection information is merged with the item metadata, and we get `EOItem`s in our STAC:
```
catalog3 = stac.Catalog.from_file(os.path.join(tmp_dir.name, 'stac-collection', 'catalog.json'))
catalog3.describe()
col_items = list(catalog3.get_all_items())
col_items[0].bands
```
### Cleanup
Don't forget to clean up the temporary directory!
```
tmp_dir.cleanup()
```
## Creating a STAC of imagery from Spacenet 5 data
Now, let's take what we've learned and create a Catalog with more data in it.
### Allowing PySTAC to read from AWS S3
PySTAC aims to be virtually zero-dependency (notwithstanding the why-isn't-this-in-stdlib datetime-util), so it doesn't have the ability to read from or write to anything but the local file system. However, we can hook into PySTAC's IO in the following way. Learn more about how to use STAC_IO in the [documentation on the topic](https://pystac.readthedocs.io/en/latest/concepts.html#using-stac-io):
```
from urllib.parse import urlparse
import boto3
from pystac import STAC_IO
def my_read_method(uri):
parsed = urlparse(uri)
if parsed.scheme == 's3':
bucket = parsed.netloc
key = parsed.path[1:]
s3 = boto3.resource('s3')
obj = s3.Object(bucket, key)
return obj.get()['Body'].read().decode('utf-8')
else:
return STAC_IO.default_read_text_method(uri)
def my_write_method(uri, txt):
parsed = urlparse(uri)
if parsed.scheme == 's3':
bucket = parsed.netloc
key = parsed.path[1:]
s3 = boto3.resource("s3")
s3.Object(bucket, key).put(Body=txt)
else:
STAC_IO.default_write_text_method(uri, txt)
STAC_IO.read_text_method = my_read_method
STAC_IO.write_text_method = my_write_method
```
We'll need a utility to list keys for reading the lists of files from S3:
```
# From https://alexwlchan.net/2017/07/listing-s3-keys/
def get_s3_keys(bucket, prefix):
"""Generate all the keys in an S3 bucket."""
s3 = boto3.client('s3')
kwargs = {'Bucket': bucket, 'Prefix': prefix}
while True:
resp = s3.list_objects_v2(**kwargs)
for obj in resp['Contents']:
yield obj['Key']
try:
kwargs['ContinuationToken'] = resp['NextContinuationToken']
except KeyError:
break
```
Let's make a STAC of imagery over Moscow as part of the Spacenet 5 challenge. As a first step, we can list out the imagery and extract IDs from each of the chips.
```
moscow_training_chip_uris = list(get_s3_keys(bucket='spacenet-dataset',
prefix='spacenet/SN5_roads/train/AOI_7_Moscow/PS-MS'))
import re
chip_id_to_data = {}
def get_chip_id(uri):
return re.search(r'.*\_chip(\d+)\.', uri).group(1)
for uri in moscow_training_chip_uris:
chip_id = get_chip_id(uri)
chip_id_to_data[chip_id] = { 'img': 's3://spacenet-dataset/{}'.format(uri) }
```
For this tutorial, we'll only take a subset of the data.
```
chip_id_to_data = dict(list(chip_id_to_data.items())[:10])
chip_id_to_data
```
Let's turn each of those chips into a STAC Item that represents the image.
```
chip_id_to_items = {}
```
We'll create core `Item`s for our imagery, but mark them with the `eo` extension as we did above, and store the `eo` data in a `Collection`.
Note that the image CRS is in WGS:84 (Lat/Lng). If it wasn't, we'd have to reproject the footprint to WGS:84 in order to be compliant with the spec (which can easily be done with [pyproj](https://github.com/pyproj4/pyproj)).
Here we're taking advantage of `rasterio`'s ability to read S3 URIs, which only grabs the GeoTIFF metadata and does not pull the whole file down.
```
for chip_id in chip_id_to_data:
img_uri = chip_id_to_data[chip_id]['img']
print('Processing {}'.format(img_uri))
bbox, footprint = get_bbox_and_footprint(img_uri)
item = stac.Item(id='img_{}'.format(chip_id),
geometry=footprint,
bbox=bbox,
datetime=datetime.utcnow(),
properties={},
stac_extensions=['eo'])
item.add_asset(key='ps-ms',
asset=stac.EOAsset(href=img_uri,
media_type=stac.MediaType.COG,
bands=list(range(0, 8))))
chip_id_to_items[chip_id] = item
```
### Creating the Collection
All of these images are over Moscow. In Spacenet 5, we have a couple cities that have imagery; a good way to separate these collections of imagery. We can store all of the common `eo` metadata in the collection.
```
from shapely.geometry import (shape, MultiPolygon)
footprints = list(map(lambda i: shape(i.geometry).envelope,
chip_id_to_items.values()))
collection_bbox = MultiPolygon(footprints).bounds
spatial_extent = stac.SpatialExtent(bboxes=[collection_bbox])
datetimes = sorted(list(map(lambda i: i.datetime,
chip_id_to_items.values())))
temporal_extent = stac.TemporalExtent(intervals=[[datetimes[0], datetimes[-1]]])
collection_extent = stac.Extent(spatial=spatial_extent, temporal=temporal_extent)
common_properties = { 'eo:bands': [b.to_dict() for b in wv3_bands],
'eo:gsd': 0.3,
'eo:platform': 'Maxar',
'eo:instrument': 'WorldView3'
}
collection = stac.Collection(id='wv3-images',
description='Spacenet 5 images over Moscow',
extent=collection_extent,
properties=common_properties,
license='CC-BY-SA-4.0')
collection.add_items(chip_id_to_items.values())
collection.describe()
```
Now, we can create a Catalog and add the collection.
```
catalog = stac.Catalog(id='spacenet5', description='Spacenet 5 Data (Test)')
catalog.add_child(collection)
catalog.describe()
```
## Adding label items to the Spacenet 5 catalog
We can use the [label extension](https://github.com/radiantearth/stac-spec/tree/v0.8.1/extensions/label) of the STAC spec to represent the training data in our STAC. For this, we need to grab the URIs of the GeoJSON of roads:
```
moscow_training_geojson_uris = list(get_s3_keys(bucket='spacenet-dataset',
prefix='spacenet/SN5_roads/train/AOI_7_Moscow/geojson_roads_speed/'))
for uri in moscow_training_geojson_uris:
chip_id = get_chip_id(uri)
if chip_id in chip_id_to_data:
chip_id_to_data[chip_id]['label'] = 's3://spacenet-dataset/{}'.format(uri)
```
We'll add the LabelItems to their own subcatalog; since they don't inherit the Collection's `eo` properties, they shouldn't go in the Collection.
```
label_catalog = stac.Catalog(id='spacenet-data-labels', description='Labels for Spacenet 5')
catalog.add_child(label_catalog)
```
We can check the pydocs to see what a LabelItem needs in order to fit the spec:
```
print(stac.LabelItem.__doc__)
```
This loop creates our LabelItems and associates each to the appropriate source image Item.
```
for chip_id in chip_id_to_data:
img_item = collection.get_item('img_{}'.format(chip_id))
label_uri = chip_id_to_data[chip_id]['label']
label_item = stac.LabelItem(id='label_{}'.format(chip_id),
geometry=img_item.geometry,
bbox=img_item.bbox,
datetime=datetime.utcnow(),
properties={},
label_description="SpaceNet 5 Road labels",
label_type=stac.LabelType.VECTOR,
label_tasks=['segmentation', 'regression'])
label_item.add_source(img_item)
label_item.add_geojson_labels(label_uri)
label_catalog.add_item(label_item)
```
Now we have a STAC of training data!
```
catalog.describe()
label_item = catalog.get_child('spacenet-data-labels').get_item('label_1')
label_item.to_dict()
```
| true |
code
| 0.388067 | null | null | null | null |
|
# Safari Challenge
In this challenge, you must use what you've learned to train a convolutional neural network model that classifies images of animals you might find on a safari adventure.
## Explore the data
The training images you must use are in the **/safari/training** folder. Run the cell below to see an example of each image class, and note the shape of the images (which indicates the dimensions of the image and its color channels).
```
import numpy as np
import os
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
%matplotlib inline
# The images are in the data/shapes folder
data_path = 'data/safari/training'
# Get the class names
classes = os.listdir(data_path)
classes.sort()
print(len(classes), 'classes:')
print(classes)
# Show the first image in each folder
fig = plt.figure(figsize=(12, 12))
i = 0
for sub_dir in os.listdir(data_path):
i+=1
img_file = os.listdir(os.path.join(data_path,sub_dir))[0]
img_path = os.path.join(data_path, sub_dir, img_file)
img = mpimg.imread(img_path)
img_shape = np.array(img).shape
a=fig.add_subplot(1, len(classes),i)
a.axis('off')
imgplot = plt.imshow(img)
a.set_title(img_file + ' : ' + str(img_shape))
plt.show()
```
Now that you've seen the images, use your preferred framework (PyTorch or TensorFlow) to train a CNN classifier for them. Your goal is to train a classifier with a validation accuracy of 95% or higher.
Add cells as needed to create your solution.
> **Note**: There is no single "correct" solution. Sample solutions are provided in [05 - Safari CNN Solution (PyTorch).ipynb](05%20-%20Safari%20CNN%20Solution%20(PyTorch).ipynb) and [05 - Safari CNN Solution (TensorFlow).ipynb](05%20-%20Safari%20CNN%20Solution%20(TensorFlow).ipynb).
# Prepare the data
```
from tensorflow.keras.preprocessing.image import ImageDataGenerator
img_size = (200, 200)
batch_size = 20
print("Getting Data...")
datagen = ImageDataGenerator(rescale=1./255, # normalize pixel values
validation_split=0.3) # hold back 30% of the images for validation
print("Preparing training dataset...")
train_generator = datagen.flow_from_directory(
data_path,
target_size=img_size,
batch_size=batch_size,
class_mode='categorical',
subset='training') # set as training data
print("Preparing validation dataset...")
validation_generator = datagen.flow_from_directory(
data_path,
target_size=img_size,
batch_size=batch_size,
class_mode='categorical',
subset='validation') # set as validation data
classnames = list(train_generator.class_indices.keys())
print('Data generators ready')
```
# Define the CNN
```
# Define a CNN classifier network
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Dropout, Flatten, Dense
# Define the model as a sequence of layers
model = Sequential()
# The input layer accepts an image and applies a convolution that uses 32 6x6 filters and a rectified linear unit activation function
model.add(Conv2D(32, (6, 6), input_shape=train_generator.image_shape, activation='relu'))
# Next we'll add a max pooling layer with a 2x2 patch
model.add(MaxPooling2D(pool_size=(2,2)))
# We can add as many layers as we think necessary - here we'll add another convolution and max pooling layer
model.add(Conv2D(32, (6, 6), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
# And another set
model.add(Conv2D(32, (6, 6), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
# A dropout layer randomly drops some nodes to reduce inter-dependencies (which can cause over-fitting)
model.add(Dropout(0.2))
# Flatten the feature maps
model.add(Flatten())
# Generate a fully-cpnnected output layer with a predicted probability for each class
# (softmax ensures all probabilities sum to 1)
model.add(Dense(train_generator.num_classes, activation='softmax'))
# With the layers defined, we can now compile the model for categorical (multi-class) classification
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
print(model.summary())
```
# Train the model
```
# Train the model over 5 epochs using 30-image batches and using the validation holdout dataset for validation
num_epochs = 15
history = model.fit(
train_generator,
steps_per_epoch = train_generator.samples // batch_size,
validation_data = validation_generator,
validation_steps = validation_generator.samples // batch_size,
epochs = num_epochs)
```
# View the loss history
```
%matplotlib inline
from matplotlib import pyplot as plt
epoch_nums = range(1,num_epochs+1)
training_loss = history.history["loss"]
validation_loss = history.history["val_loss"]
plt.plot(epoch_nums, training_loss)
plt.plot(epoch_nums, validation_loss)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['training', 'validation'], loc='upper right')
plt.show()
```
## Evaluate model performance
```
# Tensorflow doesn't have a built-in confusion matrix metric, so we'll use SciKit-Learn
import numpy as np
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
%matplotlib inline
print("Generating predictions from validation data...")
# Get the image and label arrays for the first batch of validation data
x_test = validation_generator[0][0]
y_test = validation_generator[0][1]
# Use the model to predict the class
class_probabilities = model.predict(x_test)
# The model returns a probability value for each class
# The one with the highest probability is the predicted class
predictions = np.argmax(class_probabilities, axis=1)
# The actual labels are hot encoded (e.g. [0 1 0], so get the one with the value 1
true_labels = np.argmax(y_test, axis=1)
# Plot the confusion matrix
cm = confusion_matrix(true_labels, predictions)
plt.imshow(cm, interpolation="nearest", cmap=plt.cm.Blues)
plt.colorbar()
tick_marks = np.arange(len(classnames))
plt.xticks(tick_marks, classnames, rotation=85)
plt.yticks(tick_marks, classnames)
plt.xlabel("Predicted Shape")
plt.ylabel("Actual Shape")
plt.show()
```
## Save your model
Add code below to save your model's trained weights.
```
# Code to save your model
modelFileName = 'models/saffari_classifier.h5'
model.save(modelFileName)
del model # deletes the existing model variable
print('model saved as', modelFileName)
```
## Use the trained model
Now that we've trained your model, modify the following code as necessary to use it to predict the classes of the provided test images.
```
from tensorflow.keras import models
import numpy as np
from random import randint
import os
%matplotlib inline
# Function to predict the class of an image
def predict_image(classifier, image):
import numpy
# Default value
index = 0
from tensorflow import convert_to_tensor
# The model expects a batch of images as input, so we'll create an array of 1 image
imgfeatures = img.reshape(1, img.shape[0], img.shape[1], img.shape[2])
# We need to format the input to match the training data
# The generator loaded the values as floating point numbers
# and normalized the pixel values, so...
imgfeatures = imgfeatures.astype('float32')
imgfeatures /= 255
# Use the model to predict the image class
class_probabilities = classifier.predict(imgfeatures)
# Find the class predictions with the highest predicted probability
index = int(np.argmax(class_probabilities, axis=1)[0])
# Return the predicted index
return index
# Load your model
model = models.load_model(modelFileName)
# The images are in the data/shapes folder
test_data_path = 'data/safari/test'
# Show the test images with predictions
fig = plt.figure(figsize=(8, 12))
i = 0
for img_file in os.listdir(test_data_path):
i+=1
img_path = os.path.join(test_data_path, img_file)
img = mpimg.imread(img_path)
# Get the image class prediction
index = predict_image(model, np.array(img))
a=fig.add_subplot(1, len(classes),i)
a.axis('off')
imgplot = plt.imshow(img)
a.set_title(classes[index])
plt.show()
```
Hopefully, your model predicted all four of the image classes correctly!
| true |
code
| 0.596316 | null | null | null | null |
|
```
import numpy as np
timesteps = 100
input_features = 32
output——feature = 64
import keras
keras.__version__
```
# Understanding recurrent neural networks
This notebook contains the code samples found in Chapter 6, Section 2 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
---
[...]
## A first recurrent layer in Keras
The process we just naively implemented in Numpy corresponds to an actual Keras layer: the `SimpleRNN` layer:
```
from keras.layers import SimpleRNN
```
There is just one minor difference: `SimpleRNN` processes batches of sequences, like all other Keras layers, not just a single sequence like
in our Numpy example. This means that it takes inputs of shape `(batch_size, timesteps, input_features)`, rather than `(timesteps,
input_features)`.
Like all recurrent layers in Keras, `SimpleRNN` can be run in two different modes: it can return either the full sequences of successive
outputs for each timestep (a 3D tensor of shape `(batch_size, timesteps, output_features)`), or it can return only the last output for each
input sequence (a 2D tensor of shape `(batch_size, output_features)`). These two modes are controlled by the `return_sequences` constructor
argument. Let's take a look at an example:
```
from keras.models import Sequential
from keras.layers import Embedding, SimpleRNN
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32))
model.summary()
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.summary()
```
It is sometimes useful to stack several recurrent layers one after the other in order to increase the representational power of a network.
In such a setup, you have to get all intermediate layers to return full sequences:
```
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32)) # This last layer only returns the last outputs.
model.summary()
```
Now let's try to use such a model on the IMDB movie review classification problem. First, let's preprocess the data:
```
from keras.datasets import imdb
from keras.preprocessing import sequence
max_features = 10000 # number of words to consider as features
maxlen = 500 # cut texts after this number of words (among top max_features most common words)
batch_size = 32
print('Loading data...')
(input_train, y_train), (input_test, y_test) = imdb.load_data(num_words=max_features)
print(len(input_train), 'train sequences')
print(len(input_test), 'test sequences')
print('Pad sequences (samples x time)')
input_train = sequence.pad_sequences(input_train, maxlen=maxlen)
input_test = sequence.pad_sequences(input_test, maxlen=maxlen)
print('input_train shape:', input_train.shape)
print('input_test shape:', input_test.shape)
```
Let's train a simple recurrent network using an `Embedding` layer and a `SimpleRNN` layer:
```
from keras.layers import Dense
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
```
Let's display the training and validation loss and accuracy:
```
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
As a reminder, in chapter 3, our very first naive approach to this very dataset got us to 88% test accuracy. Unfortunately, our small
recurrent network doesn't perform very well at all compared to this baseline (only up to 85% validation accuracy). Part of the problem is
that our inputs only consider the first 500 words rather the full sequences --
hence our RNN has access to less information than our earlier baseline model. The remainder of the problem is simply that `SimpleRNN` isn't very good at processing long sequences, like text. Other types of recurrent layers perform much better. Let's take a look at some
more advanced layers.
[...]
## A concrete LSTM example in Keras
Now let's switch to more practical concerns: we will set up a model using a LSTM layer and train it on the IMDB data. Here's the network,
similar to the one with `SimpleRNN` that we just presented. We only specify the output dimensionality of the LSTM layer, and leave every
other argument (there are lots) to the Keras defaults. Keras has good defaults, and things will almost always "just work" without you
having to spend time tuning parameters by hand.
```
from keras.layers import LSTM
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(LSTM(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
| true |
code
| 0.786654 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/kalz2q/mycolabnotebooks/blob/master/chainer16trainer.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# トレーナとエクステンション
[前章](https://tutorials.chainer.org/ja/15_Advanced_Usage_of_Chainer.html)までは、訓練ループを Python の `while` 文を使って記述してきました。
訓練ループは、以下のような定型的な処理を繰り返し行うものでした。
**訓練ループで行われること**
1. イテレータがデータセットからデータを取り出し、ミニバッチを作成する
2. ミニバッチをネットワークに入力し、順伝播の計算を行う
3. ネットワークの出力と目標値を使って目的関数の値(損失)を計算する
4. 逆伝播によって各パラメータについての目的関数の勾配を計算する
5. 求まった勾配を使ってパラメータを更新する
このような定型的な処理を段階ごとに別々のオブジェクトにまとめ、さらにそれらのオブジェクトをまとめたものが**トレーナ (trainer)** です。
トレーナには**エクステンション (extension)** が用意されており、訓練曲線の可視化、訓練の途中状態やログの保存など、訓練ループ中に付加的な処理を追加することが容易になっています。
## トレーナの使用方法
### トレーナの概要
下図はトレーナを構成するオブジェクトの関係図です。

それぞれの役割は以下のようになっています。
- **データセット (dataset)** : 訓練や検証に使用するためのデータの集合です。
- **イテレータ (iterator)** : データセットの一部をミニバッチとして切り出し、訓練中繰り返しデータセット内のデータを利用しやすくする機能を持ちます。
- **ネットワーク** (network) : 訓練を行いたいネットワークです。パラメータを保持し、ミニバッチを入力として損失を計算します。
- **オプティマイザ (optimizer)** : 選択された最適化の手法を用いて、ネットワークのパラメータの更新を行います。
- **アップデータ (updater)** : イテレータ・オプティマイザを統括し、順伝播・損失・逆伝播の計算、そしてパラメータの更新(オプティマイザの呼び出し)という、訓練ループ内の定型的な処理を実行します。
- **トレーナ (trainer)** : アップデータを受け取り、訓練全体の管理を行います。イテレータを用いてミニバッチを繰り返し作成し、オプティマイザを使ってネットワークのパラメータを更新します。訓練の終了タイミングの決定や、設定されたエクステンションの呼び出しも担います。
- **エクステンション (extension)** : トレーナに設定することができる付加的な機能です。エクステンションは複数設定することができます。よく利用されるエクステンションには、訓練の途中結果の保存や、検証用データセットによる訓練途中での性能の検証、訓練進捗の可視化などがあります。
次節より、トレーナを構成する各オブジェクトを順番に準備していきます。
まず、本章で利用するパッケージを予めいくつかインポートしておきます。
```
import numpy as np
import matplotlib.pyplot as plt
import chainer
import chainer.links as L
import chainer.functions as F
```
### データセットの準備
ここでは scikit-learn の標準機能で用意されているデータセットのうち、[Chainer の基礎](https://tutorials.chainer.org/ja/14_Basics_of_Chainer.html)の章でも利用した Iris というデータセットを使用します。これは、アヤメ科の植物のうち 3 種(Setosa、Versicolour、Virginica)のいずれかであるサンプル 150 個について、
- 花弁の長さ
- 花弁の幅
- がく片([注釈1](#note1))の長さ
- がく片の幅
の 4 つを測って集めたものです。
ここでは、各サンプルを見てそれが 3 種類の植物のうちどれに属するのかを予測します。
まず、[Step 1 : データセットの準備(応用編)](https://tutorials.chainer.org/ja/15_Advanced_Usage_of_Chainer.html#Step-1-:-データセットの準備(応用編))と同様に、scikit-learn の機能を使ってデータセットを読み込み、これを使って Chainer の `TupleDataset` クラスを利用してデータセットオブジェクトを作成します。
```
from sklearn.datasets import load_iris
# Iris データセットの読み込み
dataset = load_iris()
# 入力値と目標値を別々の変数へ格納
x = dataset.data
t = dataset.target
# Chainer がデフォルトで用いる float32 型へ変換
x = np.array(x, np.float32)
t = np.array(t, np.int32)
from chainer.datasets import TupleDataset
# 入力値と目標値を引数に与え、`TupleDataset` オブジェクトを作成
dataset = TupleDataset(x, t)
```
ここで、データセット全体を 7 : 1 : 2 の比率で分割し、それぞれを訓練用、検証用、テスト用のデータセットとします。
```
from chainer.datasets import split_dataset_random
n_train = int(len(dataset) * 0.7)
n_valid = int(len(dataset) * 0.1)
train, valid_test = split_dataset_random(dataset, n_train, seed=0)
valid, test = split_dataset_random(valid_test, n_valid, seed=0)
print('Training dataset size:', len(train))
print('Validation dataset size:', len(valid))
print('Test dataset size:', len(test))
```
Iris のデータセット 150 件のうち、105 件が訓練用データセットとして取り出されました。
残りの 45 件のうち 15 件が検証用データセットに、30 件がテスト用データセットとなります。
### イテレータの準備
[SerialIterator](https://tutorials.chainer.org/ja/15_Advanced_Usage_of_Chainer.html#SerialIterator) と同様に、訓練用データと検証用データそれぞれに対してイテレータを作成します。
```
from chainer import iterators
batchsize = 32
train_iter = iterators.SerialIterator(train, batchsize)
valid_iter = iterators.SerialIterator(valid, batchsize, shuffle=False, repeat=False)
```
### ネットワークの準備
[Step 2 : ネットワークを決める(応用編)](https://tutorials.chainer.org/ja/15_Advanced_Usage_of_Chainer.html#Step-2-:-ネットワークを決める(応用編))と同じように `Chain` を使って 3 層の多層パーセプトロン (multilayer perceptron、以後 MLP) を定義します。
```
class MLP(chainer.Chain):
def __init__(self, n_mid_units=100, n_out=3):
super().__init__()
with self.init_scope():
self.fc1 = L.Linear(None, n_mid_units)
self.fc2 = L.Linear(n_mid_units, n_mid_units)
self.fc3 = L.Linear(n_mid_units, n_out)
def forward(self, x):
h = F.relu(self.fc1(x))
h = F.relu(self.fc2(h))
h = self.fc3(h)
return h
```
ここで、`self.fc1` に格納された `L.Linear` 層は、インスタンス化の際に第 1 引数に `None` をとっている点に注意してください。
これは、初めてデータがこのネットワークに渡された際に、自動的にこの層の入力側のノード数を決定するということを意味しています。
このような書き方をすることで、同じコードを今回用いるデータセットのように各データの次元数が 4 の場合にも、10 や 100 などその他の次元数の場合でも、使い回せるようになります。
### アップデータの準備
訓練ループを自分で書く場合には、ループの各イテレーションにおいて行われる以下の 5 つのステップを明示的に記述する必要がありました。
1. データセットからミニバッチを作成
2. 順伝播(forward)の計算
3. 損失(loss)の計算
4. 逆伝播(backward)の計算
5. オプティマイザによってパラメータを更新
具体的には、これらのステップは以下のように記述してきました。
```python
# 1. データセットからミニバッチを作成
train_batch = train_iter.next()
x, t = concat_examples(train_batch)
# 2. 順伝播(forward)の計算
y = net(x)
# 3. 損失(loss)の計算
loss = F.softmax_cross_entropy(y, t)
# 4. 逆伝播(backward)の計算
net.cleargrads()
loss.backward()
# 5. オプティマイザによってパラメータを更新
optimizer.update()
```
アップデータを用いることで、これらの一連の処理を隠蔽し、簡潔に記述することができます。
アップデータには、イテレータとオプティマイザを渡す必要があります。
イテレータはデータセットを持っており、上記のステップ 1. を行います。
オプティマイザはネットワークを持っており、上記のステップ 2. 〜 5. を行います。
それでは、イテレータはすでに準備したため、ネットワークとオプティマイザを定義し、アップデータオブジェクトを作成してみましょう。
```
from chainer import optimizers
from chainer import training
# ネットワークを作成
predictor = MLP()
# L.Classifier でラップし、損失の計算などをモデルに含める
net = L.Classifier(predictor)
# 最適化手法を選択してオプティマイザを作成し、最適化対象のネットワークを持たせる
optimizer = optimizers.MomentumSGD(lr=0.1).setup(net)
# アップデータにイテレータとオプティマイザを渡す
updater = training.StandardUpdater(train_iter, optimizer, device=-1) # device=-1でCPUでの計算実行を指定
```
`MLP` は、データを入力して予測値を計算するネットワークでした。
これに損失計算を追加するために、`L.Classifier` を使います。
`L.Classifier` は、ネットワークへ渡される入力値 `x` に加えて、分類問題においては正解ラベルとなる目標値 `t` も引数にとり、指定された目的関数の計算を行って、損失を返すようネットワークをラップします。
デフォルトの目的関数はソフトマックス交差エントロピー(`F.softmax_cross_entropy`)に設定されています。
また、`L.Classifier` はインスタンス化を行う際にネットワークを引数にとり、これを `predictor` という属性に格納します。
つまり、上記コードにおける初めの `predictor` は、`net.predictor` という属性に格納されています。
最後の行で作成している `StandardUpdater` は、複数あるアップデータの実装のうち、最もシンプルなものです。
他にも、複数 GPU を用いてネットワークの訓練を行うための `MultiprocessParallelUpdater` などがあります。
1 つの GPU を用いたネットワークの訓練については、[Step 5 : ネットワークを訓練する(応用編)](https://tutorials.chainer.org/ja/15_Advanced_Usage_of_Chainer.html#Step-5-:-ネットワークを訓練する(応用編))を参照してください。
### トレーナの作成と終了タイミングの指定
訓練を開始するために、トレーナを作成しましょう。
トレーナは、`Trainer` クラスをインスタンス化して作成します。
トレーナは、アップデータを用いて訓練のイテレーションを回します。
その繰り返しの終了タイミングは、`Trainer` のコンストラクタの第 2 引数 `stop_trigger` に `(整数, 単位)` というタプルを渡して指定します。
`単位` には `'iteration'` もしくは `'epoch'` のいずれかの文字列を指定します。
1 **イテレーション (iteration)** とはミニバッチ 1 個分を処理することを表し、1 **エポック (epoch)** とはイテレーションを繰り返してデータセット全体を 1 周することを表します。
例えば、 `(100, 'epoch')` と指定すると、トレーナは 100 エポックで訓練を終了します。
`(100, 'iteration')` と指定すると、100 イテレーション後に訓練を終了します。
トレーナを作るときにこの引数 (`stop_trigger`) を指定しないと、**訓練は自動的には止まらず、永久にループが回り続ける**ことになります。
ここでは 30 エポック分ループを実行した時点で停止するトレーナオブジェクトを作成します。
1 つ目の引数にループ処理を担当するアップデータオブジェクトを渡し、2 つ目に停止条件を表すタプルを指定します。
```
trainer = training.Trainer(updater, (30, 'epoch'), out='results/iris_result1')
```
`out` 引数は、ログや訓練途中のパラメータの値など、次節で解説するエクステンションを用いて行われる訓練ループに加わる付加的な処理の結果を保存する場所を指定します。
指定されたパスにディレクトリがない場合は、自動的に作成されます。
### エクステンション
エクステンションを使うと、トレーナが統括する訓練ループの途中に付加的な処理を追加することができます。
たとえば、大きなネットワークを大量のデータを用いて訓練する場合、損失の値が十分に小さくなり、収束するまでに数日から数週間かかる場合もあります。
このような場合は、もし何らかの理由によって訓練が中断された場合でも、途中から再開できるように訓練途中のネットワークのパラメータなどを**スナップショット (snapshot)** として保存しておく、といったことがよく行われます。
その他にも、便利なエクステンションが多く用意されています。
エクステンションは必要に応じて自分で作成することもできますが、ここでは予め用意されているエクステンションをトレーナに追加してみましょう。
エクステンションをトレーナに追加するには、 `trainer.extend()` というメソッドを使います。
```
from chainer.training import extensions
trainer.extend(extensions.LogReport(trigger=(1, 'epoch'), log_name='log'))
trainer.extend(extensions.snapshot(filename='snapshot_epoch-{.updater.epoch}'))
trainer.extend(extensions.dump_graph('main/loss'))
trainer.extend(extensions.Evaluator(valid_iter, net, device=-1), name='val')
trainer.extend(extensions.PrintReport(['epoch', 'iteration', 'main/loss', 'main/accuracy', 'val/main/loss', 'val/main/accuracy', 'fc1/W/data/mean', 'elapsed_time']))
trainer.extend(extensions.PlotReport(['fc1/W/grad/mean'], x_key='epoch', file_name='mean.png'))
trainer.extend(extensions.PlotReport(['main/loss', 'val/main/loss'], x_key='epoch', file_name='loss.png'))
trainer.extend(extensions.PlotReport(['main/accuracy', 'val/main/accuracy'], x_key='epoch', file_name='accuracy.png'))
trainer.extend(extensions.ParameterStatistics(net.predictor.fc1, {'mean': np.mean}, report_grads=True))
```
ここで追加されたエクステンションを 1 つずつ解説します。
#### LogReport
指定された周期で、損失の値や正解率など、後述する**レポータ (reporter)** がレポートした値を自動的に集計し、`Trainer` オブジェクト作成時に `out` 引数で指定したディレクトリに、`log_name` 引数に指定されたファイル名でそれらの集計された情報を JSON 形式で保存します。
レポートされた値の集計を行う周期は、`trigger` という引数に `(数, 単位)` を表すタプルを与えて指定します。
`単位` には `'epoch' `または `'iteration'` が指定できます。
上記のコード中では `(1, 'epoch')` となっているため、1 エポックが終わる度に毎回レポートされた値を集計し、ログファイルに記録します。
#### snapshot
トレーナオブジェクトを指定されたタイミング(デフォルトでは 1 エポックごと)で保存します。
トレーナオブジェクトは前述のようにアップデータを持っており、アップデータはさらにオプティマイザとネットワークを保持しています。
そのため、トレーナオブジェクトのスナップショットを保存しておけば、その時点から訓練を再開することが可能になります。
訓練プログラムが異常終了した場合などに役立ちます。
また、スナップショットから訓練済みモデルをとりだして推論だけを行いたい場合にもスナップショットを取っておく必要があります。
`filename` という引数に保存時のファイル名を指定することができます。
この引数に渡された文字列は、内部で `filename.format(trainer)` とトレーナオブジェクトを使ってフォーマットされるため、保存時のイテレーション数などの情報をファイル名に使用することができます。
イテレーション数は `trainer.updater.iteration` に格納されており、エポック数は `trainer.updater.epoch` に格納されているため、上記コード中のように `filename` に渡す文字列中の `{.updater.iteration}` はイテレーション数を表す数値に、`{.updater.epoch}` はエポック数を表す数値に置き換えられます。
#### dump_graph
指定された `Variable` オブジェクトからたどることができる計算グラフを Graphviz で描画可能な DOT 形式で保存します。
起点となる `Variable` は名前で指定することもできます。
この例では、`'main/loss'` という文字列を指定しています。
これは後述するレポータという機能を用いて、`L.Classifier` 内でレポートされている損失につけられた名前です。
#### Evaluator
検証用データセットのイテレータと、訓練を行うネットワークのオブジェクトを渡しておくことで、訓練中に指定されたタイミングで検証用データセットを用いたネットワークの評価を行います。
#### PrintReport
`LogReport` で集計した値を標準出力に出力します。
どの値を出力するかをリストの形で与えます。
#### PlotReport
第 1 引数に与えられるリストで指定された値の時間変化をグラフに描画し、出力ディレクトリに `file_name` 引数に指定されたファイル名で画像として保存します。
グラフの作成には Matplotlib が使用されるため、Matplotlib がインストールされている必要があります。
`PlotReport` エクステンションは、複数個追加することができます。
今回は、3 つの `PlotReport` を追加しています。
1 つ目は、1 層目の全結合層のパラメータが持つ勾配の平均値の変遷を描画したグラフを `mean.png` に保存します。
2 つ目は、訓練用データセットと検証用データセットのそれぞれで計算した損失の値の変遷を 1 つのグラフにまとめ、`loss.png` という画像ファイルに保存します。
3 つ目は、訓練用・検証用データセットのそれぞれで計算した正解率の値の変遷を 1 つのグラフにまとめ、`accuracy.png` に保存します。
#### ParameterStatistics
指定した `Link` が持つパラメータの平均・分散・最小値・最大値などの統計値を計算し、レポートします。
パラメータが発散していないかなどをチェックするのに便利です。
パラメータの勾配を統計値の計算の対象にしたい場合は、`report_grads` を `True` にする必要があります。
### その他の代表的な拡張
ここで紹介したエクステンションは、上で紹介した以外にも様々なオプションを持っており、柔軟に組み合わせることができます。
詳しくは公式ドキュメントの [Extensions](https://docs.chainer.org/en/stable/reference/training.html#extensions) の項を御覧ください。
### 訓練の開始
エクステンションの追加まで完了したため、訓練を開始します。
訓練の開始は、`trainer.run()` メソッドを呼び出すことで行います。
```
trainer.run()
```
訓練が停止しました。
まず、`trainer` の `out` 引数に指定した結果出力のためのディレクトリ `results/iris_result1` の中身を確認してみましょう。
```
!ls results/iris_result1/
```
色々なファイルが作成されています。
これらに今回の訓練の結果や、途中経過などが記録されています。
#### ログファイルの確認
まず、保存されたログファイルを読み込んで、内容を 10 だけ表示してみます。
ログファイルは JSON 形式で保存されているため、Pandas を使って読み込むと、ノートブック上で見やすく表示することができます。
```
import json
import pandas as pd
log = json.load(open('results/iris_result1/log'))
df_result = pd.DataFrame(log)
df_result.tail(10)
```
#### PlotReport で作成されたグラフを確認する
次に、損失の変遷を記録したグラフを確認します。
グラフの描画結果は、先程内容を確認した `results/iris_result1/` ディレクトリの中に `loss.png` というファイル名で画像として保存されています。
Jupyter Notebook からは `IPython` モジュールを使うことで、ディスクに保存されている画像を読み込んで表示することができます。
`loss.png` を表示してみましょう。
```
from IPython.display import Image
Image('results/iris_result1/loss.png')
```
また、正解率のグラフは `acccuracy.png` という名前で保存されています。
こちらも確認してみましょう。
```
Image('results/iris_result1/accuracy.png')
```
#### 計算グラフの可視化
`MLP` というネットワークが、どのような構造になっているのかを、視覚的に確認する方法が、`dump_graph` エクステンションによって出力された DOT ファイルを、`pydot` パッケージを使って画像に変換する方法です。
DOT ファイルは、`cg.dot` というファイル名で結果ディレクトリに保存されています。
これを読み込んで、`pydot` を使って画像に変換し、それを表示してみましょう。
```
import pydot
file = pydot.graph_from_dot_file('results/iris_result1/cg.dot')
file[0].write_png('graph.png')
Image('graph.png', width=600, height=600)
```
ここまでで、トレーナの基本的な使い方の解説は終了です。
次節からは、より高度な使い方について説明します。
## レポータで様々な値を記録する
`PrintReport` エクステンションを使うと、現在のエポック、イテレーション、また損失の値や正解率などを標準出力に表示することができました。
これらの値は特にユーザが明示的に指示しなくともデフォルトで `LogReport` が集計できるようにレポートされているため、このようなことが可能になっています。
集計したい値を明示的に指定し、`LogReport` に集計させるようにすることも可能です。
本節では、その方法について説明します。
ネットワークの中で行われる計算の途中結果などを毎イテレーション集計しておき、値の変化を確認したい場合は、**レポータ (reporter)** という機能を用います。
レポータは、`chainer.reporter` モジュールにある `report` 関数を使って、観測対象としたい変数を指定することで、その値を集計することができる機能です。
まずは、レポータの観測対象に `MLP` 内の計算の途中結果を追加してみます。
今回は、ネットワークの定義自体を修正し、`forward` メソッドの中で途中結果を `chainer.reporter.report()` 関数に渡します。
```
from chainer import reporter
class MLP2(chainer.Chain):
def __init__(self, n_mid_units=100, n_out=3):
super().__init__()
with self.init_scope():
self.fc1 = L.Linear(None, n_mid_units)
self.fc2 = L.Linear(n_mid_units, n_mid_units)
self.fc3 = L.Linear(n_mid_units, n_out)
def forward(self, x):
h = F.relu(self.fc1(x))
h = F.relu(self.fc2(h))
reporter.report({'avg_y': F.average(h), 'var_y':F.cross_covariance(h, h)}, self)
h = self.fc3(h)
return h
```
この `MLP2` では、2 層目の `fc2` の出力値に ReLU を適用したあとの値について平均と分散を計算し、 `avg_y` と `var_y` という名前でレポータに登録しています。
こうすると、`forward` が呼び出される度にこれらの値がレポートされるようになるため、`LogReport` はその変遷を集計することができます。
このネットワークを訓練して、新しくレポートされる値を `PrintReport` を用いて確認してみましょう。
まずは、新しいネットワークの訓練のための `trainer` オブジェクトを作成します。
```
# ネットワーク (+ Classifier)
net = L.Classifier(MLP2())
# オプティマイザ
optimizer = optimizers.MomentumSGD(lr=0.1).setup(net)
# イテレータ
train_iter = iterators.SerialIterator(train, 32)
# アップデータ
updater = training.StandardUpdater(train_iter, optimizer, device=-1) # device=-1でCPUでの計算実行を指定
# トレーナ
trainer = training.Trainer(updater, (30, 'epoch'))
```
次に、 `LogReport` と `PrintReport` を設定します。
このとき他のエクステンションも `LogReport` が集計した値を用いるため、`LogReport` の追加は必須です。
`PrintReport` には、表示したい値の名前を設定します。
- `epoch`、`iteration`、`elapsed_time`: トレーナオブジェクトがデフォルトでレポートする値で、それぞれエポック数、イテレーション数、経過時間を表します。
- `main` は、オプティマイザが保持するモデル(今回は `L.Classifier`)を表します。
- `main/accuracy` は、`L.Classifier` がデフォルトでレポートする正解率です。
- `main/loss` は、`L.Classifier` がデフォルトでレポートする損失の値です。
- `main/predictor` は、`L.Classifier` に渡されたネットワーク(今回は `MLP2`)を表します。
- `main/predictor/avg_y` は、`net` が保持している ` predictor` の中でレポートされている `avg_y` の値を指します。
- `main/predictor/var_y` は、同様に、`net` が保持している `predictor` の中でレポートされている `var_y` の値を指します。
```
trainer.extend(extensions.LogReport())
trainer.extend(extensions.PrintReport([
'epoch', 'iteration',
'main/accuracy',
'main/predictor/avg_y',
'main/predictor/var_y',
]))
```
訓練を開始します。
```
trainer.run()
```
新しくレポートした `avg_y`、`var_y` の集計結果が出力されています。
これらの新しい観測値は、`PlotReport` でグラフを描画する対象に指定すれば、訓練過程での値の変化を描画したグラフを作成させることもできます。
## 訓練の早期終了
**早期終了 (early stopping)** とは、過学習を避けるために行う正則化の一種で、訓練用データセットにフィットしすぎてしまい、途中からテスト用データセットでのエラーが大きくなっていってしまう前に、訓練を途中で打ち切る方法をいいます。
Chainer では `EarlyStoppingTrigger` オブジェクトを作成し、これを訓練終了タイミングを指示するタプルの代わりにトレーナに渡すことで行えます。
`EarlyStoppingTrigger` には、どの指標を用いて早期終了の判断を行うかと、最大の訓練の長さなどを指定します。
以下に使用例を示します。
```
net = L.Classifier(MLP())
train_iter = iterators.SerialIterator(train, batchsize)
valid_iter = iterators.SerialIterator(valid, batchsize, False, False)
```
今回は、早期終了が発生するよう、学習率をわざと大きめに設定します。
```
optimizer = optimizers.MomentumSGD(lr=0.1).setup(net)
updater = training.StandardUpdater(train_iter, optimizer, device=-1)
```
早期終了は、`EarlyStoppingTrigger` のインスタンスを `Trainer` のコンストラクタの `stop_trigger` 引数に渡すことで設定します。
`EarlyStoppingTrigger` のコンストラクタに渡す引数で、挙動を定義します。
- `monitor` には、早期終了の判断に使われる指標を指定します。これには、`PrintReport` 等で用いられるのと同じ、レポータによって報告される値を参照する際の形式で指定します。次の `check_trigger` で指定するタイミングで繰り返し行われる値のチェックの際に、これまでの `monitor` の値の平均値が、これまでの最良のものよりも悪化していれば、訓練を停止します。今回は、`Evaluator` によってレポートされる検証用データセットに対する損失をチェック対象に指定します。
- `check_trigger` は、レポートされている変数の値をチェックするタイミングを指定します。今回は、毎エポックチェックを行います。
- `max_trigger` は、トレーナでのループの最大イテレーション数または最大エポック数を指定します。早期終了が行われなかった場合に、ループが永久に続くことを防止します。この例では、最大 30 エポック実行する設定にしています。
- `patients` は、早期終了のしやすさを指定します。たとえば 3 を指定すると、チェック時にそれまでの最良の値を更新できないことが 3 回連続で続いた場合に限って、早期終了するという動作になります。
それでは、`EarlyStoppingTrigger` を作成し、トリガーとトレーナに渡します。
```
from chainer.training.triggers import EarlyStoppingTrigger
trigger = EarlyStoppingTrigger(monitor='val/main/loss', check_trigger=(1, 'epoch'),
patients=5, max_trigger=(30, 'epoch'))
trainer = training.Trainer(updater, trigger, out='results/iris_result5')
```
早期終了の様子が確認しやすいようにエクステンションを設定します。
また、検証用データセットに対する正解率を `monitor` に使用するため、`Evaluator` を使って検証用データセットに対する正解率を毎エポック計算します。
```
from chainer.training import extensions
trainer.extend(extensions.LogReport(trigger=(1, 'epoch'), log_name='log'))
trainer.extend(extensions.Evaluator(valid_iter, net, device=-1), name='val')
trainer.extend(extensions.PlotReport(['main/loss', 'val/main/loss'], x_key='epoch', file_name='loss.png'))
trainer.extend(extensions.PlotReport(['main/accuracy', 'val/main/accuracy'], x_key='epoch', file_name='accuracy.png'))
trainer.extend(extensions.PrintReport([
'epoch', 'main/loss', 'main/accuracy',
'val/main/loss', 'val/main/accuracy', 'elapsed_time']))
```
訓練を実行します。
```
trainer.run()
!ls results/iris_result5/
Image('results/iris_result5/loss.png')
Image('results/iris_result5/accuracy.png')
```
最大エポック数には 30 を指定していましたが、それよりも早く訓練が終了しました。
早期終了を使用すると、特定の指標での改善が見られなくなった時点で訓練を停止させることができるため、効果の薄い計算が続くことを防ぐことにもなり、計算資源の節約にもなります。
本章では、[前章](https://tutorials.chainer.org/ja/15_Advanced_Usage_of_Chainer.html#Step-5-:-ネットワークを訓練する(応用編))まで行っていたような訓練ループを明示的に書く方法ではなく、トレーナを使って訓練ループを設定し、エクステンションを使って様々な訓練時の情報を集計したり、可視化したり、活用したりする方法を紹介しました。
次章では画像処理の基礎について解説します。
<hr />
<div class="alert alert-info">
**注釈 1**
がく片とは、花弁の付け根にある緑の葉のようなもののことです。
[▲上へ戻る](#ref_note1)
</div>
| true |
code
| 0.659789 | null | null | null | null |
|
```
%load_ext autoreload
%autoreload 2
# default_exp indexers.facerecognition.photo
```
# Photo
This file contains many convenience functions and classes to work with photos in the context of importing data from external sources and machine learning. It contains functions for reading, plotting, resizing, etc.
```
# export
from pyintegrators.data.schema import *
from pyintegrators.data.basic import *
from insightface.utils import face_align
from matplotlib.pyplot import imshow
from matplotlib import patches
from matplotlib.collections import PatchCollection
from numpy.linalg import norm
from hashlib import sha256
import cv2
import matplotlib.pyplot as plt
import math
import numpy as np
# export
def show_images(images, cols = 3, titles = None):
image_list = [x.data for x in images] if isinstance(images[0], Photo) else images
assert((titles is None) or (len(image_list) == len(titles)))
n_images = len(image_list)
if titles is None: titles = ["" for i in range(1,n_images + 1)]
fig = plt.figure()
for n, (image, title) in enumerate(zip(image_list, titles)):
a = fig.add_subplot(int(np.ceil(n_images/float(cols))), cols , n + 1)
a.axis('off')
if image.ndim == 2:
plt.gray()
plt.imshow(image[:,:,::-1])
a.set_title(title)
fig.set_size_inches(np.array(fig.get_size_inches()) * n_images)
plt.show()
def get_size(img, maxsize):
s = img.shape
assert len(s) > 1
div = max(s) / maxsize
return (int(s[1]//div), int(s[0]//div))
def resize(img, maxsize):
size = get_size(img, maxsize)
return cv2.resize(img, dsize=size, interpolation=cv2.INTER_CUBIC)
def get_height_width_channels(img):
s = img.shape
if len(s) == 2: return s[0], s[1], 1
else: return img.shape
# export
class IPhoto(Photo):
def __init__(self, data=None, embedding=None,path=None, *args, **kwargs):
self.private = ["data", "embedding", "path"]
super().__init__(*args, **kwargs)
self.data=data
self.embedding=embedding
self.path=path
def show(self):
fig,ax = plt.subplots(1)
fig.set_figheight(15)
fig.set_figwidth(15)
ax.axis('off')
imshow(self.data[:,:,::-1])
fig.set_size_inches((6,6))
plt.show()
def draw_boxes(self, boxes):
print(f"Plotting {len(boxes)} face boundingboxes")
fig,ax = plt.subplots(1)
fig.set_figheight(15)
fig.set_figwidth(15)
ax.axis('off')
# Display the image
ax.imshow(self.data[:,:,::-1])
ps = []
# Create a Rectangle patch
for b in boxes:
rect = self.box_to_rect(b)
ax.add_patch(rect)
ps.append(rect)
fig.set_size_inches((6,6))
plt.show()
def get_crop(self, box, landmark=None):
b = [max(0, int(x)) for x in box]
if landmark is not None:
return face_align.norm_crop(self.data, landmark=landmark)
else:
return self.data[b[1]:b[3], b[0]:b[2], :]
def get_crops(self, boxes, landmarks=None):
crops = []
if landmarks is None:
print("you are getting unnormalized crops, which are lower quality for recognition")
for i, b in enumerate(boxes):
crop = self.get_crop(b, landmarks[i] if landmarks is not None else None)
crops.append(crop)
return crops
def plot_crops(self, boxes, landmarks=None):
crops = self.get_crops(boxes, landmarks)
show_images(crops, cols=3)
@classmethod
def from_data(cls,*args, **kwargs):
res = super().from_data(*args, **kwargs)
if res.file:
res.file[0]
return res
@classmethod
def from_path(cls, path, size=None):
data = cv2.imread(str(path))
res = cls.from_np(data, size)
return res
@classmethod
def from_np(cls, data, size=None, *args, **kwargs):
if size is not None: data = resize(data, size)
h,w,c = get_height_width_channels(data)
res = cls(data=data, height=h, width=w, channels=c, *args, **kwargs)
file = File.from_data(sha256=sha256(data.tobytes()).hexdigest())
res.add_edge("file", file)
return res
@staticmethod
def box_to_rect(box):
x = box[0]
y = box[1]
w = box[2]-box[0]
h = box[3]-box[1]
return patches.Rectangle((x,y),w,h, linewidth=2,edgecolor='r',facecolor='none')
p = IPhoto.from_path(PYI_TESTDATA / "photos" / "faceclustering" / "modern_family1.jpg")
p.show()
box = [240,240,400,400]
crop = p.get_crop(box)
crop = IPhoto.from_np(crop)
crop.show()
p.draw_boxes([box])
# hide
from nbdev.export import *
notebook2script()
```
| true |
code
| 0.681714 | null | null | null | null |
|
# Trigonometric time series model
```
%pylab inline
import pymc3 as pm
import theano.tensor as tt
t = np.linspace(0., 10., 1000)
# 3.5Hz sine wave
func = lambda a, b, omega: a*np.sin(2*np.pi*omega*t)+b*np.cos(2*np.pi*omega*t)
y = func(1., 0., 3.5)
data = y + np.random.normal(size = t.shape[0])
_, ax = plt.subplots(1, 1, figsize=(15, 3))
ax.plot(t, data)
ax.plot(t, y);
with pm.Model() as model:
a = pm.Normal("a", mu=1, sd=2)
b = pm.Normal("b", mu=1, sd=2)
omega = pm.Gamma("omega", 1., 1.)
regression = a * tt.sin(2 * np.pi * omega * t) +\
b * tt.cos(2 * np.pi * omega * t)
sd = pm.HalfCauchy("sd", 0.5)
observed = pm.Normal("observed",
mu=regression,
sd=sd,
observed=data)
with model:
step1 = pm.Metropolis([omega])
trace = pm.sample(10000, tune=5000, step=step1)
pm.traceplot(trace);
omegapost = trace.get_values(varname='omega', combine=False)
apost = trace.get_values(varname='a', combine=False)
bpost = trace.get_values(varname='b', combine=False)
_, ax = plt.subplots(1, 1, figsize=(15, 3))
ax.plot(t, data, alpha=.5)
ax.plot(t, y, color='k', alpha=.5)
for ia, ib, io in zip(apost, bpost, omegapost):
y_ = func(ia.mean(), ib.mean(), io.mean())
ax.plot(t, y_, alpha=.5);
with model:
trace2 = pm.sample(1000, tune=1000)
pm.traceplot(trace2);
pm.pairplot(trace2, alpha=.05);
model.free_RVs
logp_dlogp_cond = model.logp_dlogp_function([model.free_RVs[0],
model.free_RVs[2]])
pt = model.test_point
pt
pt['b'] = np.array(0.)
pt['sd_log__'] = np.log(0.5)
logp_dlogp_cond.set_extra_values(pt)
pt['a'] = np.array(2.)
pt
logp_dlogp_cond.dict_to_array(pt)
pt['b'] = np.array(0.)
pt['sd_log__'] = np.log(1.)
logp_dlogp_cond.set_extra_values(pt)
# grid search
omega_ = np.linspace(0, 4, 200)
a_ = np.linspace(-4, 4, 200)
ov_, av_ = np.meshgrid(omega_, a_)
logvec = np.asarray([logp_dlogp_cond(np.asarray([a__, np.log(o__)]))[0]
for o__, a__ in zip(ov_.flatten(), av_.flatten())])
ll = logvec.reshape(av_.shape)
_, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.imshow(ll.T, cmap='viridis',
extent=[a_[0], a_[-1], omega_[0], omega_[-1]], origin='lower'
)
ax.set_xlabel('a')
ax.set_ylabel('omega');
pt['b'] = np.array(0.)
pt['sd_log__'] = np.log(1.)
logp_dlogp_cond.set_extra_values(pt)
# grid search
omega_ = np.linspace(3, 4, 200)
a_ = np.linspace(-4, 4, 200)
ov_, av_ = np.meshgrid(omega_, a_)
logvec = np.asarray([logp_dlogp_cond(np.asarray([a__, np.log(o__)]))[0]
for o__, a__ in zip(ov_.flatten(), av_.flatten())])
ll = logvec.reshape(av_.shape)
_, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.imshow(ll.T, cmap='viridis',
extent=[a_[0], a_[-1], omega_[0], omega_[-1]], aspect=4, origin='lower'
)
ax.set_xlabel('a')
ax.set_ylabel('omega');
pt['b'] = np.array(0.)
pt['sd_log__'] = np.log(1.)
logp_dlogp_cond.set_extra_values(pt)
# grid search
omega_ = np.linspace(0, .25, 200)
a_ = np.linspace(-4, 4, 200)
ov_, av_ = np.meshgrid(omega_, a_)
logvec = np.asarray([logp_dlogp_cond(np.asarray([a__, np.log(o__)]))[0]
for o__, a__ in zip(ov_.flatten(), av_.flatten())])
ll = logvec.reshape(av_.shape)
_, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.imshow(ll.T, cmap='viridis',
extent=[a_[0], a_[-1], omega_[0], omega_[-1]], aspect=16, origin='lower'
)
ax.set_xlabel('a')
ax.set_ylabel('omega');
pt['b'] = np.array(0.)
pt['sd_log__'] = np.log(1.)
logp_dlogp_cond.set_extra_values(pt)
# grid search
omega_ = np.linspace(0, .25, 200)
a_ = np.linspace(-10, 10, 200)
ov_, av_ = np.meshgrid(omega_, a_)
logvec = np.asarray([logp_dlogp_cond(np.asarray([a__, np.log(o__)]))[0]
for o__, a__ in zip(ov_.flatten(), av_.flatten())])
ll = logvec.reshape(av_.shape)
_, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.imshow(ll.T, cmap='viridis',
extent=[a_[0], a_[-1], omega_[0], omega_[-1]], aspect=16*2, origin='lower'
)
ax.set_xlabel('a')
ax.set_ylabel('omega');
```
GP
```
with pm.Model() as model:
η_per = pm.HalfCauchy("η_per", beta=2, testval=1.0)
period = pm.Normal("period", mu=1 / 3.5, sd=1.)
periodic = η_per**2 * pm.gp.cov.Cosine(1, period)
gp_periodic = pm.gp.Marginal(cov_func=periodic)
noise = pm.HalfCauchy("noise", beta=2, testval=1.0)
y_ = gp_periodic.marginal_likelihood(
"y", X=t[:, np.newaxis], y=data, noise=noise)
mp = model.test_point
mp
with model:
mp = pm.find_MAP()
mp
mp2 = mp
# mp2['noise_log__'] = np.log(1)
# mp2['η_per_log__'] = np.log(1)
# mp2['period'] = np.array(1/3.5)
mu_pred, cov_pred = gp_periodic.predict(t[:, np.newaxis], point=mp2)
_, ax = plt.subplots(1, 1, figsize=(15, 3))
ax.plot(t, data, alpha=.5)
ax.plot(t, y, color='k', alpha=.5)
ax.plot(t, mu_pred)
model.free_RVs
logp_dlogp_cond = model.logp_dlogp_function([model.free_RVs[0], model.free_RVs[1]])
pt = model.test_point
pt
logp_dlogp_cond.set_extra_values(mp)
logp_dlogp_cond.dict_to_array(pt)
# grid search
omega_ = np.linspace(0, 4, 100)
a_ = np.linspace(0, 1, 100)
ov_, av_ = np.meshgrid(omega_, a_)
logvec = np.asarray([logp_dlogp_cond(np.asarray([np.log(a__), 1/o__]))[0]
for o__, a__ in zip(ov_.flatten(), av_.flatten())])
ll = logvec.reshape(av_.shape)
_, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.imshow(ll.T, cmap='viridis',
extent=[a_[0], a_[-1], omega_[0], omega_[-1]], aspect=1/16*2, origin='lower'
)
ax.set_xlabel('a')
ax.set_ylabel('omega');
```
| true |
code
| 0.619356 | null | null | null | null |
|
<p style="z-index: 101;background: #fde073;text-align: center;line-height: 2.5;overflow: hidden;font-size:22px;">Please <a href="https://www.pycm.ir/doc/#Cite" target="_blank">cite us</a> if you use the software</p>
# Example-8 (Confidence interval)
## Install matplotlib
```
import sys
!{sys.executable} -m pip -q -q install matplotlib;
```
## Plot function
```
import numpy as np
import matplotlib.pyplot as plt
import pycm
def plot_ci(cm,param,alpha=0.05,method="normal-approx"):
"""
Plot two-sided confidence interval.
:param cm: ConfusionMatrix
:type cm : pycm.ConfusionMatrix object
:param param: input parameter
:type param: str
:param alpha: type I error
:type alpha: float
:param method: binomial confidence intervals method
:type method: str
:return: None
"""
conf_str = str(round(100*(1-alpha)))
print(conf_str+"%CI :")
if param in cm.class_stat.keys():
mean = []
error = [[],[]]
data = cm.CI(param,alpha=alpha,binom_method=method)
class_names_str = list(map(str,(cm.classes)))
for class_index, class_name in enumerate(cm.classes):
print(str(class_name)+" : "+str(data[class_name][1]))
mean.append(cm.class_stat[param][class_name])
error[0].append(cm.class_stat[param][class_name]-data[class_name][1][0])
error[1].append(data[class_name][1][1]-cm.class_stat[param][class_name])
fig = plt.figure()
plt.errorbar(mean,class_names_str,xerr = error,fmt='o',capsize=5,linestyle="dotted")
plt.ylabel('Class')
fig.suptitle("Param :"+param + ", Alpha:"+str(alpha), fontsize=16)
for index,value in enumerate(mean):
down_point = data[cm.classes[index]][1][0]
up_point = data[cm.classes[index]][1][1]
plt.text(value, class_names_str[index], "%f" %value, ha="center",va="top",color="red")
plt.text(down_point, class_names_str[index], "%f" %down_point, ha="right",va="bottom",color="red")
plt.text(up_point , class_names_str[index], "%f" %up_point, ha="left",va="bottom",color="red")
else:
mean = cm.overall_stat[param]
data = cm.CI(param,alpha=alpha,binom_method=method)
print(data[1])
error = [[],[]]
up_point = data[1][1]
down_point = data[1][0]
error[0] = [cm.overall_stat[param] - down_point]
error[1] = [up_point - cm.overall_stat[param]]
fig = plt.figure()
plt.errorbar(mean,[param],xerr = error,fmt='o',capsize=5,linestyle="dotted")
fig.suptitle("Alpha:"+str(alpha), fontsize=16)
plt.text(mean, param, "%f" %mean, ha="center",va="top",color="red")
plt.text(down_point, param, "%f" %down_point, ha="right",va="bottom",color="red")
plt.text(up_point, param, "%f" %up_point, ha="left",va="bottom",color="red")
plt.show()
cm = pycm.ConfusionMatrix(matrix={0:{0:13,1:2,2:5},1:{0:1,1:10,2:6},2:{0:2,1:0,2:9}})
```
## TPR
```
plot_ci(cm,param="TPR",method="normal-approx")
plot_ci(cm,param="TPR",method="wilson")
plot_ci(cm,param="TPR",method="agresti-coull")
```
## FPR
```
plot_ci(cm,param="FPR",method="normal-approx")
plot_ci(cm,param="FPR",method="wilson")
plot_ci(cm,param="FPR",method="agresti-coull")
```
## AUC
```
plot_ci(cm,param="AUC")
```
## PLR
```
plot_ci(cm,param="PLR")
```
## Overall ACC
```
plot_ci(cm,param="Overall ACC")
```
## Kappa
```
plot_ci(cm,param="Kappa")
```
| true |
code
| 0.516595 | null | null | null | null |
|
# Driving a skyrmion with spin-polarised current
**Author:** Weiwei Wang (2014)
**Edited:** Marijan Beg (2016)
The implemented equation in finmag with STT is [1,2],
\begin{equation}
\frac{\partial \mathbf{m}}{\partial t} = - \gamma \mathbf{m} \times \mathbf{H} + \alpha \mathbf{m} \times \frac{\partial \mathbf{m}}{\partial t} + u (\mathbf{j}_s \cdot \nabla) \mathbf{m} - \beta u [\mathbf{m}\times (\mathbf{j}_s \cdot \nabla)\mathbf{m}]
\end{equation}
where $\mathbf{j}_s$ is the current density. $u$ is the material parameter, and by default,
$$u=u_{ZL}=\frac{u_0}{1+\beta^2}$$
There is an option "using_u0" in sim.set_zhangli method, u=u0 if "using_u0 = True" and
$$u_0=\frac{g \mu_B P}{2 |e| M_s}=\frac{g \mu_B P a^3}{2 |e| \mu_s}$$
where $\mu_B=|e|\hbar/(2m)$ is the Bohr magneton, $P$ is the polarization rate, $e$ is the electron charge.
The implemented Landau-Lifshitz-Gilbert equation with Slonczewski spin-transfer torque is [3],
\begin{equation}
\frac{\partial \mathbf{m}}{\partial t} = - \gamma \mathbf{m} \times \mathbf{H} + \alpha \mathbf{m} \times \frac{\partial \mathbf{m}}{\partial t}
+ \gamma \beta \epsilon (\mathbf{m} \times \mathbf{m}_p \times \mathbf{m})
\end{equation}
where
\begin{align*}
\beta&=\left|\frac{\hbar}{\mu_0 e}\right|\frac{J}{tM_\mathrm{s}}\,\,\, \mathrm{and}\\
\epsilon&=\frac{P\Lambda^2}{(\Lambda^2+1)+(\Lambda^2-1)(\mathbf{m}\cdot\mathbf{m}_p)}
\end{align*}
[1] S. Zhang and Z. Li, Roles of nonequilibrium conduction electrons on the magnetization dynamics of ferromagnets, Phys. Rev. Lett. 93, 127204 (2004).
[2] A. Thiaville, Y. Nakatani, J. Miltat and Y. Suzuki, Micromagnetic understanding of current-driven domain wall motion in patterned nanowires, Europhys. Lett. 69, 990 (2005).
[3] J. Xiao, A. Zangwill, and M. D. Stiles, “Boltzmann test of Slonczewski’s theory of spin-transfer torque,” Phys. Rev. B, 70, 172405 (2004).
## Skyrmion nucleation
Import the related modules and create a two-dimensional rectangular mesh:
```
%matplotlib inline
import os
import matplotlib.pyplot as plt
import dolfin as df
import numpy as np
from finmag import Simulation as Sim
from finmag.energies import Exchange, DMI, UniaxialAnisotropy, Zeeman
from finmag.util.dmi_helper import find_skyrmion_center_2d
from finmag.util.helpers import set_logging_level
import finmag
mesh = df.RectangleMesh(df.Point(0, 0), df.Point(200, 40), 200, 40)
```
We define a function to generate a skyrmion in the track,
```
def m_init_one(pos):
x, y = pos
x0 = 50
y0 = 20
if (x-x0)**2 + (y-y0)**2 < 10**2:
return (0, 0, -1)
else:
return (0, 0, 1)
```
Create function that can plot scalar field of one magnetisation component:
```
def plot_2d_comp(sim, comp='z', title=None):
"""expects a simulation object sim and a component to plot. Component can be
'x' or 'y' or 'z'
Not optimised for speed.
"""
finmag.logger.info("plot_2d_comp: at t = {:g}".format(sim.t))
comps = {'x': 0, 'y': 1, 'z': 2}
assert comp in comps, "print unknown component {}, we know: {}".format(comp, comp.keys())
m = sim.get_field_as_dolfin_function('m')
# get mesh coordinates for plotting
coords = mesh.coordinates()
mym = []
for coord in coords:
mym.append(m(coord))
import matplotlib.pyplot as plt
import matplotlib.tri as tri
import numpy as np
x = [ r[0] for r in coords]
y = [ r[1] for r in coords]
# extract i-ith component of magnetisation
mi = [ m[comps[comp]] for m in mym]
# Create the Triangulation; no triangles so Delaunay triangulation created.
triang = tri.Triangulation(x, y)
# tripcolor plot.
plt.figure()
plt.gca().set_aspect('equal')
plt.tripcolor(triang, mi, shading='flat', cmap=plt.cm.rainbow)
if title:
plt.title(title)
else:
plt.title('Plot of {} component of m at t={:.3f}ns'.format(comp, sim.t * 1e9))
sim = Sim(mesh, Ms=5.8e5, unit_length=1e-9, pbc=None)
sim.add(UniaxialAnisotropy(K1=6e5, axis=[0, 0, 1]))
sim.add(Exchange(A=1.5e-11))
sim.add(DMI(D=3e-3))
sim.add(Zeeman((0, 0, 1e5)))
sim.alpha = 0.5
sim.set_m(m_init_one)
sim.relax()
plot_2d_comp(sim, comp='z', title='relaxed magnetisation (z-comp)')
```
## Moving a skyrmion with Zhang-Li term
We apply a spin-polarised current in the $x$ direction.
```
Jx = (-2e12, 0, 0)
```
Now, we can add a Zhang-Li term to the LLG equation.
```
#We use the zhang-li spin-transfer torque with parameters that polarisation=0.5 and beta=0.01
sim.set_zhangli(Jx, P=0.5, beta=0.01, using_u0=False)
# every 0.1ns save vtk data
sim.schedule('save_vtk', every=1e-10, filename='vtks/m.pvd', overwrite=True)
# every 0.1ns save raw data
sim.schedule('save_m', every=1e-10, filename='npys/m.pvd', overwrite=True)
# every 0.1ns create plot for notebook
sim.schedule(plot_2d_comp, every=1e-10)
# now do the calculation (events scheduled above will be done automatically)
sim.run_until(0.5e-9)
```
## Slonczewski spin-transfer torque
If we want to move a skyrmion with perpendicular current (Slonczewski STT term), the following line should be used instead of `set_zhangli` method.
```
#sim.set_stt(current_density=1e10, polarisation=0.5, thickness=0.4e-9, direction=(0,1,0))
```
| true |
code
| 0.553143 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/chavgova/My-AI/blob/master/emotion_recognition_02.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
IMPORT
```
#this is the copy of another projecct and ill make changes to see how i can make it better
import librosa
import librosa.display
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from matplotlib.pyplot import specgram
import keras
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding
from keras.layers import LSTM
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.utils import to_categorical
from keras.layers import Input, Flatten, Dropout, Activation
from keras.layers import Conv1D, MaxPooling1D, AveragePooling1D
from keras.models import Model
from keras.callbacks import ModelCheckpoint
from sklearn.metrics import confusion_matrix
from keras import regularizers
import os
from google.colab import drive
import os
path = '/content/drive/My Drive/My_AI/RawData'
mylist = []
#for root, directories, files in os.walk(path, topdown=False):
# for name in files:
# #print(os.path.join(root, name))
# mylist.append(name)
mylist = os.listdir(path)
print(mylist)
print(mylist[50])
print(mylist[18][6:-16])
```
LABLES
```
feeling_list=[]
for item in mylist:
if int(item[18:-4])%2==0: #female
if item[6:-16]=='01':
feeling_list.append('female_neutral')
elif item[6:-16]=='02':
feeling_list.append('female_calm')
elif item[6:-16]=='03':
feeling_list.append('female_happy')
elif item[6:-16]=='04':
feeling_list.append('female_sad')
elif item[6:-16]=='05':
feeling_list.append('female_angry')
elif item[6:-16]=='06':
feeling_list.append('female_fearful')
elif item[6:-16]=='07':
feeling_list.append('female_disgust')
elif item[6:-16]=='08':
feeling_list.append('female_surprised')
else:
if item[6:-16]=='01':
feeling_list.append('male_neutral')
elif item[6:-16]=='02':
feeling_list.append('male_calm')
elif item[6:-16]=='03':
feeling_list.append('male_happy')
elif item[6:-16]=='04':
feeling_list.append('male_sad')
elif item[6:-16]=='05':
feeling_list.append('male_angry')
elif item[6:-16]=='06':
feeling_list.append('male_fearful')
elif item[6:-16]=='07':
feeling_list.append('male_disgust')
elif item[6:-16]=='08':
feeling_list.append('male_surprised')
import pandas as pd
labels = pd.DataFrame(feeling_list)
labels[:10] #print
```
Getting the features of audio files using librosa
```
import librosa
import numpy as np
def extract_feature(my_file, **kwargs):
mfcc = kwargs.get("mfcc")
chroma = kwargs.get("chroma")
mel = kwargs.get("mel")
contrast = kwargs.get("contrast")
tonnetz = kwargs.get("tonnetz")
X, sample_rate = librosa.core.load(my_file)
if chroma or contrast:
stft = np.abs(librosa.stft(X))
result = np.array([])
if mfcc:
mfccs = np.mean(librosa.feature.mfcc(y=X, sr=sample_rate, n_mfcc=40).T, axis=0)
result = np.hstack((result, mfccs))
if chroma:
chroma = np.mean(librosa.feature.chroma_stft(S=stft, sr=sample_rate).T,axis=0)
result = np.hstack((result, chroma))
if mel:
mel = np.mean(librosa.feature.melspectrogram(X, sr=sample_rate).T,axis=0)
result = np.hstack((result, mel))
if contrast:
contrast = np.mean(librosa.feature.spectral_contrast(S=stft, sr=sample_rate).T,axis=0)
result = np.hstack((result, contrast))
if tonnetz:
tonnetz = np.mean(librosa.feature.tonnetz(y=librosa.effects.harmonic(X), sr=sample_rate).T,axis=0)
result = np.hstack((result, tonnetz))
return result
f = os.fspath('/content/drive/My Drive/My_AI/RawData/03-01-08-01-01-02-01.wav')
a = extract_feature(f, mel=True, mfcc=True, contrast=True, chroma=True, tonnetz=True)
#print(a, a.shape)
df = pd.DataFrame(columns=['all_features'])
bookmark=0
#mylist = mylist[:100]
for index,y in enumerate(mylist):
#sample_rate = np.array(sample_rate)
all_features_ndarray = extract_feature('/content/drive/My Drive/My_AI/RawData/'+y, mel=True, mfcc=True, contrast=True, chroma=True, tonnetz=True)
df.loc[bookmark] = [all_features_ndarray]
bookmark=bookmark+1
#df[:5] #print
df3 = pd.DataFrame(df['all_features'].values.tolist())
newdf = pd.concat([df3,labels], axis=1)
rnewdf = newdf.rename(index=str, columns={"0": "label"})
rnewdf[:10] #print
from sklearn.utils import shuffle
rnewdf = shuffle(newdf)
rnewdf[:10] #print
rnewdf=rnewdf.fillna(0)
```
Dividing the data into test and train
```
newdf1 = np.random.rand(len(rnewdf)) < 0.8
train = rnewdf[newdf1]
test = rnewdf[~newdf1]
train[250:260]
trainfeatures = train.iloc[:, :-1]
trainlabel = train.iloc[:, -1:]
testfeatures = test.iloc[:, :-1]
testlabel = test.iloc[:, -1:]
from keras.utils import np_utils
from sklearn.preprocessing import LabelEncoder
X_train = np.array(trainfeatures)
y_train = np.array(trainlabel)
X_test = np.array(testfeatures)
y_test = np.array(testlabel)
lb = LabelEncoder()
y_train = np_utils.to_categorical(lb.fit_transform(y_train))
y_test = np_utils.to_categorical(lb.fit_transform(y_test))
y_train
X_train.shape
```
Changing dimension for CNN model
```
x_traincnn =np.expand_dims(X_train, axis=2)
x_testcnn= np.expand_dims(X_test, axis=2)
print(x_testcnn)
model = Sequential()
model.add(Conv1D(256, 5,padding='same',
input_shape=(193,1)))
model.add(Activation('relu'))
model.add(Conv1D(128, 5,padding='same'))
model.add(Activation('relu'))
model.add(Dropout(0.1))
model.add(MaxPooling1D(pool_size=(8)))
model.add(Conv1D(128, 5,padding='same',))
model.add(Activation('relu'))
#model.add(Conv1D(128, 5,padding='same',))
#model.add(Activation('relu'))
#model.add(Conv1D(128, 5,padding='same',))
#model.add(Activation('relu'))
#model.add(Dropout(0.2))
model.add(Conv1D(128, 5,padding='same',))
model.add(Activation('relu'))
model.add(Flatten())
model.add(Dense(16))
model.add(Activation('softmax'))
opt = keras.optimizers.RMSprop(lr=0.00001, decay=1e-6)
model.summary()
model.compile(loss='categorical_crossentropy', optimizer=opt,metrics=['accuracy'])
```
Removed the whole training part for avoiding unnecessary long epochs list
```
cnnhistory=model.fit(x_traincnn, y_train, batch_size=32, epochs=200, validation_data=(x_testcnn, y_test))
plt.plot(cnnhistory.history['loss'])
plt.plot(cnnhistory.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
| true |
code
| 0.483405 | null | null | null | null |
|
# PyTorch (Lightning) integration
This package includes an integration with PyTorch that allows you to convert an `ImageSequence` into a PyTorch `Dataset` in a single line of code. This can then be used to train models using PyTorch and derived frameworks, such als [PyTorch Lightning](https://github.com/PyTorchLightning/pytorch-lightning). This notebook showcases the use and walks you through the whole process from loading data to training the model.
```
import pvinspect as pv
from pvinspect.integration.pytorch import ClassificationDataset
import pytorch_lightning as pl
import torch as t
import torchvision as tv
from typing import List
from sklearn import model_selection
import numpy as np
```
## Step 1: Set up `LightningModule`
We set up a very basic `LightningModule` for classification of defects on solar cells. We omit the dataloaders, since we pass them in dynamically lateron. For more information, please refer to the [docs](https://pytorch-lightning.readthedocs.io/en/stable/).
```
class DefectModel(pl.LightningModule):
def __init__(
self,
pos_weight: List[float],
learning_rate: float,
):
super().__init__()
# let's use a very small resnet
self.model = tv.models.ResNet(tv.models.resnet.BasicBlock, layers=[1, 1, 1, 1], num_classes=2)
self.pos_weight = t.tensor(pos_weight)
self.learning_rate = learning_rate
def forward(self, x):
return self.model.forward(x)
def training_step(self, batch, batch_idx):
x, y = batch
y_hat = self(x)
return {'loss': t.nn.functional.binary_cross_entropy_with_logits(y_hat, y, pos_weight=self.pos_weight.to(x))}
def validation_step(self, batch, batch_idx):
x, y = batch
y_hat = self(x)
return {'loss': t.nn.functional.binary_cross_entropy_with_logits(y_hat, y, pos_weight=self.pos_weight.to(x))}
def configure_optimizers(self):
return t.optim.Adam(self.parameters(), lr=self.learning_rate)
```
## Step 2: Load data
Here, we'll use the cell images provided with the [ELPV dataset](https://github.com/zae-bayern/elpv-dataset) [[1](http://dx.doi.org/10.1016/j.solener.2019.02.067)]. This toolbox provides a convenience method for loading this data as well as additional defect annotations. In addition, a split in training and test data is provided by the meta property `testset`. Here, we'll only use the training data.
```
all_data = pv.data.datasets.elpv().pandas.query('testset == False')
all_data.meta_to_pandas()
all_data.pandas.query('crack == True').head(N=8, cols=4)
```
## Step 3: Train/validation split
We'll train for two of the defect classes (`crack` and `inactive`). To this end, we map labels into the label powerset and use this to perform a stratified 80/20 split.
```
# generate label powerset
is_crack = np.array(all_data.meta_to_pandas()['crack'].to_list())*1
is_inactive = np.array(all_data.meta_to_pandas()['inactive'].to_list())*2
labels = is_crack+is_inactive
# perform stratified split of sample ids
idx_train, idx_val = model_selection.train_test_split(list(range(len(all_data))), test_size=0.8, stratify=labels)
# get subsets using sample ids
train_data = all_data.pandas.iloc[idx_train]
val_data = all_data.pandas.iloc[idx_val]
```
## Step 4: Generate class weights
The dataset is highly imbalanced. To this end, we compute weights for the two classes as follows:
```
n_samples = len(train_data)
n_crack = len(train_data.pandas.query('crack == True'))
n_inactive = len(train_data.pandas.query('inactive == True'))
pos_weight = [n_crack / (n_samples-n_crack), n_inactive / (n_samples-n_inactive)]
```
## Step 5: Compute statistics for normalization
Here, we compute the mean and standard deviation using the first 50 images, since we do (not yet) support auto calibration, like you might know it from FastAI. However, we plan to [implement this](https://github.com/ma0ho/pvinspect/issues/6).
```
mean = np.mean([x.data for x in train_data.pandas.iloc[:50]])
std = np.std([x.data for x in train_data.pandas.iloc[:50]])
(mean, std)
```
## Step 6: Set up data augmentation pipeline
This is as usual using PyTorch transforms. However, we support any data augmentation library that results in callable transform-objects.
```
train_tfms = tv.transforms.Compose([
tv.transforms.ToPILImage(),
tv.transforms.Resize((150, 150)),
tv.transforms.RandomVerticalFlip(),
tv.transforms.RandomHorizontalFlip(),
tv.transforms.RandomAffine(degrees=10),
tv.transforms.ToTensor(),
tv.transforms.Normalize([mean/255], [std/255]), # statistics are computed on original images (uint8)
tv.transforms.Lambda(lambda x: x.repeat(3,1,1))
])
val_tfms = tv.transforms.Compose([
tv.transforms.ToPILImage(),
tv.transforms.Resize((150, 150)),
tv.transforms.ToTensor(),
tv.transforms.Normalize([mean/255], [std/255]),
tv.transforms.Lambda(lambda x: x.repeat(3,1,1))
])
```
## Step 7: Convert `ImageSequence`s into `Dataset`s and create `DataLoader`s
This is the main part of the PyTorch integration. Here, `pv.integration.pytorch.ClassificationDataset` extends `pv.integration.pytorch.Dataset`, which itself extends the PyTorch `Dataset`. Note that we are not restricted to classification tasks, since we can use the more general purpose `pv.integration.pytorch.Dataset` instead. However, `ClassificationDataset` conveniently converts meta attributes listet in the `meta_classes` attribute into one-hot tensors. Furthermore, it allows to convert classification results back into meta attributes of the `ImageSequence` using the [`result_sequence`](https://ma0ho.github.io/pvinspect/integration/pytorch/dataset.html#pvinspect.integration.pytorch.dataset.ClassificationDataset.result_sequence) method (not shown here).
```
train_ds = ClassificationDataset(train_data, meta_classes=['crack', 'inactive'], data_transform=train_tfms)
val_ds = ClassificationDataset(train_data, meta_classes=['crack', 'inactive'], data_transform=val_tfms)
train_dl = t.utils.data.DataLoader(train_ds, batch_size=16, shuffle=True)
val_dl = t.utils.data.DataLoader(val_ds, batch_size=16, shuffle=False)
```
## Step 8: Set up `Trainer` and train model
Now, set up a PyTorch Lightning `Trainer` and train the model using `train_dl` and `val_dl`.
```
model = DefectModel(pos_weight, 1e-4)
trainer = pl.Trainer(gpus=1, logger=None, progress_bar_refresh_rate=20, max_epochs=2)
trainer.fit(model, train_dl, val_dl)
```
## References
[[1](http://dx.doi.org/10.1016/j.solener.2019.02.067)] Deitsch, S.; Christlein, V.; Berger, S.; Buerhop-Lutz, C.; Maier, A.; Gallwitz, F. & Riess, C. Automatic classification of defective photovoltaic module cells in electroluminescence images. Solar Energy, Elsevier BV, 2019, 185, 455-468.
| true |
code
| 0.723627 | null | null | null | null |
|
# TRAVELING SALESMAN PROBLEM
The traveling salesman problem (also called the traveling salesperson problem or TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?"
In this project, I am going to solve different TSPs with different approaches. I have three different problem sets with 51 cities, 101 cities, and 130 cities.
I am going to use following approaches to solve the TSPs:
* Nearest Neighbor
* 2-OPT
* Nearest Neighbor + 2-OPT (Hybrid)
* Particle Swarm Optimization
* COTS Solution (Google OR Tools)
In this report, I am going to provide solutions, results, and their comparisons according to their accuracy and complexity. Also, I am going to include my comments & improvements for each algorithm.
I am going to start with modeling and reading the data. For this purpose, I am going to read the data and create a City object with city number, X, and Y values in the each row.
Let's start with City class then:
```
class City:
"""Class for City object. Attributes:
-City ID
-X coordinate
-Y coordinate
-Z value for Particle Swarm Optimization
"""
def __init__(self, city_id, x, y):
self.__city_id = city_id
self.__x = x
self.__y = y
self.z = city_id # particle swarm optimization parameter
def __str__(self):
return self.__city_id
def __repr__(self):
return self.__city_id
def __eq__(self, other):
return self.__city_id == other.__city_id
def __lt__(self, other):
return self.z < other.z
def __sub__(self, other):
self.z -= other.z
return self
def __add__(self, other):
self.z += other.z
return self
def scale(self, scalar):
"""Scales the City's z parameter with the given scalar value."""
self.z = self.z * scalar
return self
def get_city_id(self):
return self.__city_id
def get_x(self):
return self.__x
def get_y(self):
return self.__y
def distance(self, other):
"""Calculates the Euclidean distance between two cities."""
return round(((self.__x - other.__x) ** 2 + (self.__y - other.__y) ** 2) ** (1/2))
```
After that, I am going to the read the data, create the City objects, and store them in a list. For this purpose, I am going to use a helper function, txt_reader.
```
def txt_reader(file_name):
"""Reads the given input files and store the cities."""
city_list = []
txt_file = open(file_name, "r")
txt_file.readline() # skip the header line
for line in txt_file:
temp_list = line.rstrip().split(" ")
temp_city = City(temp_list[0], int(float(temp_list[1])), int(float(temp_list[2])))
city_list.append(temp_city)
return city_list
```
Now, I can read the data and model it.
Before focusing on the solutions, I am going to implement other helper functions, calc_path_distance & visualize_route. I am going to use these functions to calculate the distance of the route and visualize the route.
```
def calc_path_distance(city_list):
"""Calculates the distance of the TSP route."""
path_distance = 0
for i in range(len(city_list) - 1):
path_distance += city_list[i].distance(city_list[i + 1])
path_distance += city_list[-1].distance(city_list[0]) # adds the arc between starting city & ending city.
return path_distance
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
def visualize_route(title, route):
"""Visualizes the route for the TSP."""
fig = plt.figure()
fig.suptitle(title)
x = []
y = []
for city in route:
x.append(city.get_x())
y.append(city.get_y())
x.append(route[0].get_x())
y.append(route[0].get_y())
graph, = plt.plot(x, y, 'ko')
graph, = plt.plot(x, y, 'darkorange')
# Since I can not use animation on Jupyter Notebook, this part is commented.
#def animate(i):
# graph.set_data(x[:i + 1], y[:i + 1])
# return graph
#ani = FuncAnimation(fig, animate, frames=len(route) + 10, interval=500)
plt.show()
plt.show(block=True)
```
Here, all the helper functions are implemented. I am going to start with the first solution, which is Nearest Neighbor.
## Nearest Neighbor
The nearest neighbour algorithm was one of the first algorithms used to solve the travelling salesman problem approximately. In that problem, the salesman starts at a random city and repeatedly visits the nearest city until all have been visited. The algorithm quickly yields a short tour, but usually not the optimal one.
The algorithm can be summed up with the following steps:
1. Initialize all vertices as unvisited.
2. Select an arbitrary vertex, set it as the current vertex u. Mark u as visited.
3. Find out the shortest edge connecting the current vertex u and an unvisited vertex v.
4. Set v as the current vertex u. Mark v as visited.
5. If all the vertices in the domain are visited, then terminate. Else, go to step 3.
I am going to implement this algorithm in three parts.
Firstly, I am going to implement a function which takes a city and a city list as input; and returns the nearest city to the given city in the given city list.
```
from sys import maxsize
def nearest_neighbor(city, city_list):
"""Finds the nearest neighbor of a given city."""
min_distance = maxsize
nearest_city = None
for c in city_list:
temp_distance = city.distance(c)
if temp_distance < min_distance:
min_distance = temp_distance
nearest_city = c
return nearest_city, min_distance
```
Secondly, I am going to implement a function, which takes a starting city and city list as input; and returns a route (with the nearest neighbor principle) and its distance.
```
def nearest_neighbor_algorithm(next_city, city_list):
"""Creates a route by starting with the given city & following the nearest neighbors."""
copy_city_list = city_list[:]
path = [next_city]
copy_city_list.remove(next_city)
while copy_city_list:
next_step = nearest_neighbor(next_city, copy_city_list)
next_city = next_step[0]
path.append(next_city)
copy_city_list.remove(next_city)
path_distance = calc_path_distance(path)
path.append(path[0]) # add starting city to route, to create a cycle.
return path, path_distance
```
Thirdly and lastly, I am going to implement a function to try all starting city alternatives for the previous function. Simply, it makes an iteration for each starting city. This function takes a city list, and returns the best route and its distance among all alternatives.
```
def nna_iteration(city_list):
"""Finds the best route by changing the starting city."""
best_path = []
best_distance = maxsize
for city in city_list:
result = nearest_neighbor_algorithm(city, city_list)
if best_distance > result[1]:
best_path = result[0]
best_distance = result[1]
return best_path, best_distance
```
Now, I can try the Nearest Neighbor Algorithm with 51 cities.
```
import time
city_list = txt_reader("data/51_Cities.txt")
t0 = time.time()
nna_result = nna_iteration(city_list)
t1 = time.time()
print("Nearest Neighbor Path: " + str(nna_result[0]) + "\nNearest Neighbor Solution: " + str(nna_result[1]) + "\nNearest Neighbor Elapsed Time: " + str(round((t1 - t0), 3)) + " seconds")
# visualize_route("Nearest Neighbor --- Solution: " + str(nna_result[1]), nna_result[0])
```
*Since, I cannot use animation on Jupyter Notebook, I am going to add a .gif for the animated result (51 Cities) for this and other solutions.
You can run the shared source code on any IDE to see the live animated result or uncomment the visualize_route function to see the final result.*
### Nearest Neighbor Result
Result of the Nearest Neighbor can be seen below:
<img align="left" width="640" height="480" src="media/nna.gif">
**Nearest Neighbor Path:** [8, 26, 31, 28, 3, 20, 35, 36, 29, 21, 50, 9, 49, 5, 38, 11, 32, 1, 22, 2, 16, 34, 30, 10, 39, 33, 45, 15, 44, 37, 17, 4, 18, 47, 12, 46, 51, 27, 6, 48, 23, 7, 43, 24, 14, 25, 13, 41, 19, 42, 40, 8]
**Nearest Neighbor Solution:** 482
**Nearest Neighbor Elapsed Time:** 0.101 seconds
So, there is 13.1% error compared the optimal solution; but for 51 cities, running time of this algorithm is 0.101 seconds.
As it seen on the .gif, the algorithm creates the route in a greedy way, and there are multiple knots. The algorithm can be improved with following approaches:
1. Untangling these knots. (Later on I am going to fuse another algorithm (2-OPT) with Nearest Neighbor to accomplish this.)
2. Being less greedy with considering the consequences.
## 2-OPT
In optimization, 2-OPT is a simple local search algorithm for solving the traveling salesman problem. The main idea behind it is to take a route that crosses over itself and reorder it so that it does not.
The algorithm can be summed up with the following steps:
Let's say i & j are indexes.
1. Take route[0] to route[i-1] and add them in order to new_route
2. Take route[i] to route[j] and add them in reverse order to new_route
3. Take route[j+1] to end and add them in order to new_route
A complete 2-OPT local search will compare every possible valid combination of the swapping mechanism. This technique can be applied to the travelling salesman problem as well as many related problems.
I am going to implement this algorithm in two parts.
Firstly, I am going to implement a function which takes a route, i & j; and returns the new_route.
```
def two_opt_swap(route, i, j):
"""Finds an alternative route of the given route with 2-OPT."""
new_list1 = route[0:i]
new_list2 = route[i:j]
new_list2.reverse()
new_list3 = route[j:]
return new_list1 + new_list2 + new_list3
```
Secondly and lastly, I am going to implement a function to compare every possible valid combination of the swapping mechanism. This function takes a route; and returns the best route and its distance among all alternatives.
```
from itertools import combinations
def two_opt(route):
"""Tries all alternative 2-OPT routes of the given route."""
copy_route = route[:]
index_list = []
best = calc_path_distance(copy_route)
for i in range(len(copy_route)):
index_list.append(i)
comb_index = list(combinations(index_list, 2)) # all alternative 2-OPTs
i = 0
while i < len(comb_index):
temp_list = (two_opt_swap(copy_route, comb_index[i][0], comb_index[i][1]))
if calc_path_distance(temp_list) < best:
copy_route = temp_list
best = calc_path_distance(temp_list)
i = 0
i = i + 1
copy_route.append(copy_route[0]) # add starting city to route, to create a cycle.
return copy_route, best
```
Now, I can try the 2-OPT Algorithm with 51 cities.
```
t2 = time.time()
two_opt_result = two_opt(city_list)
t3 = time.time()
print("2-OPT Path: " + str(two_opt_result[0]) + "\n2-OPT Solution: " + str(two_opt_result[1]) + "\n2-OPT Elapsed Time: " + str(round((t3 - t2), 3)) + " seconds")
#visualize_route("2-OPT --- Solution: " + str(two_opt_result[1]), two_opt_result[0])
```
### 2-OPT Result
Result of the 2-OPT can be seen below:
<img align="left" width="640" height="480" src="media/2-opt.gif">
**2-OPT Path:** [46, 32, 1, 22, 28, 3, 36, 35, 20, 2, 11, 38, 5, 49, 9, 50, 16, 29, 21, 34, 30, 10, 39, 33, 45, 15, 44, 37, 17, 42, 40, 19, 41, 13, 4, 12, 47, 18, 25, 14, 6, 24, 43, 7, 23, 48, 8, 26, 31, 27, 51, 46]
**2-OPT Solution:** 461
**2-OPT Elapsed Time:** 2.416 seconds
So, there is 8.2% error compared the optimal solution and running time of this algorithm is 2.416 seconds for 51 cities. Note that, initial route affects the running time, and same route given to the both algorithm.
It can be said that, it is better than the Nearest Neighbor, but it is much slower.
As it seen on the .gif, there are no knots in this algorithm; but it creates the route without considering any nearest path. So the algorithm can be improved with the following approaches:
1. Feeding it with the Nearest Neighbor output, so it can also be greedy.
2. Increasing the number of deleted edges, such as **3-OPT**, but it will be slower.
## Nearest Neighbor + 2-OPT (Hybrid)
Since I have these two algorithms, and they cover up each others weak parts; now I am going to use Nearest Neighbor's output as an input to 2-OPT.
```
t4 = time.time()
nna_result2 = nna_iteration(city_list)
hybrid_result = two_opt(nna_result2[0])
hybrid_result[0].pop()
t5 = time.time()
print("Nearest Neighbor + 2-OPT (Hybrid) Path: " + str(hybrid_result[0]) + "\nHybrid Solution: " + str(hybrid_result[1]) + "\nHybrid Elapsed Time: " + str(round((t5 - t4), 3)) + " seconds")
#visualize_route("Nearest Neighbor + 2-OPT (Hybrid) --- Solution: " + str(hybrid_result[1]), hybrid_result[0])
```
### Nearest Neighbor + 2-OPT (Hybrid) Result
Result of the Hybrid can be seen below:
<img align="left" width="640" height="480" src="media/hybrid.gif">
**Hybrid Path:** [8, 26, 31, 28, 3, 36, 35, 20, 29, 2, 16, 50, 21, 34, 30, 10, 39, 33, 45, 15, 44, 42, 40, 19, 41, 13, 25, 14, 24, 43, 7, 23, 48, 6, 27, 51, 46, 12, 47, 18, 4, 17, 37, 5, 49, 9, 38, 11, 32, 1, 22, 8]
**Hybrid Solution:** 428
**Hybrid Elapsed Time:** 0.817 seconds
So, there is 0.4% error compared the optimal solution and running time of this algorithm is 0.817 seconds for 51 cities.
Since 2-OPT is feeded with an already good solution, it ran in a much shorter time compared the previous execution.
## Particle Swarm Optimization
In computational science, particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality.
It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formula over the particle's position and velocity.
Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.
Equation for the Particle Swarm Optimization can be seen below:
<img align="left" src="media/pso_eq.png">
And a visual representation (a particle swarm searching for the global minimum of a function) of the algorithm can be seen below:
<img align="left" src="media/pso_vis.gif">
To understand better, an analogy between the algorithm and bird swarms can be used. Bird swarms look for the food randomly, and when one of the birds find food, other birds will look for the food around it.
To implement this algorithm, I have added a Z value to the City object, which represents the index of a city in a route. Each particle will have their own route, and they are going to minimize the distance by sharing their best personal routes in each iteration.
I have implemented components of the equation and decided on the parameters with trying different parameters of different PSO variations.
```
import random
t0 = time.time()
# Constants
c1 = 1.494 # self confidence
c2 = 1.494 # swarm confidence
w = 0.729 # inertia weight
# Iteration number and swarm size
maxIter = 1000
swarmSize = 500
# lists for particles, their positions, and their velocities.
p = [] # particles
x = [] # positions of the particles
v = [] # velocities of the particles
best = [maxsize for i in range(swarmSize)] # best values for each particle, maxsize at inital
g = 0 # index of the global best
org_city_list = txt_reader('data/51_Cities.txt')
num_city = len(org_city_list)
for i in range(swarmSize):
route1 = []
route2 = []
route3 = []
for c in range(num_city):
org_city = org_city_list[c]
city1 = City(org_city.get_city_id(), org_city.get_x(), org_city.get_y())
city2 = City(org_city.get_city_id(), org_city.get_x(), org_city.get_y())
city3 = City(org_city.get_city_id(), org_city.get_x(), org_city.get_y())
rand = random.random() * 50
# added a random value to create variation between initial routes of particles
city1.z = rand + i
city2.z = rand + i
city3.z = 0 # velocity is zero at the beginning.
route1.append(city1)
route2.append(city2)
route3.append(city3)
p.append(route1)
x.append(route2)
v.append(route3)
for n in range(maxIter):
# algorithm can be improved by using a dynamic inertia weight
# if n < maxIter/2:
# w = (0.85 - 0.55) * (maxIter/2 - n) / (maxIter/2) + 0.55
# else:
# w = (0.85 - 0.55) * (maxIter - n) / (maxIter/2) + 0.55
# w = min(max(w + 0.0004,0.69),0.8)
for i in range(swarmSize):
res = calc_path_distance(sorted(x[i]))
if res < min(best): # finds the global best
for c in range(num_city):
p[g][c].z = x[i][c].z
g = i
print('New cost: ', str(res))
if res < best[i]: # finds the personal best
best[i] = res
for c in range(num_city):
p[i][c].z = x[i][c].z
for c in range(num_city): # finds the next velocity and position of the particles
rand1 = random.random()
rand2 = random.random()
v[i][c].z = w * v[i][c].z + c1 * rand1 * (p[i][c].z - x[i][c].z) + c2 * rand2 * (p[g][c].z - x[i][c].z) #next velocities
x[i][c].z = x[i][c].z + v[i][c].z # next positions
p[g].sort() # sort the particles by their z value.
p[g].append(p[g][0]) # add starting city to route, to create a cycle.
t1 = time.time()
print("Particle Swarm Optimization Path: " + str(p[g]) + "\nParticle Swarm Optimization Solution: " + str(calc_path_distance(p[g])) + "\nParticle Swarm Optimization Elapsed Time: " + str(round((t1 - t0), 3)) + " seconds")
#visualize_route("Particle Swarm Optimization --- Solution: " + str(calc_path_distance(p[g])), p[g])
```
### Particle Swarm Optimization Result
Result of the Particle Swarm Optimization can be seen below:
<img align="left" width="640" height="480" src="media/pso_best.gif">
**Particle Swarm Optimization Path:** [31, 26, 7, 23, 48, 1, 32, 11, 38, 51, 12, 4, 18, 25, 13, 41, 19, 40, 42, 44, 17, 37, 15, 45, 33, 39, 10, 30, 9, 49, 5, 47, 46, 27, 6, 14, 24, 43, 8, 22, 2, 16, 50, 34, 21, 29, 20, 35, 36, 3, 28, 31]
**Particle Swarm Optimization Solution:** 489
**Particle Swarm Optimization Elapsed Time:** 138.369 seconds
Max. iteration is 1000, swarm size is 500 for this execution.
*Note that; path, solution, and running time can change in other execution since particles are starting and moving randomly.*
For this execution, there is 14.7% error compared the optimal solution and running time of this algorithm is 138.369 seconds for 51 cities. It can be said that, this algorithm did not performed as good as the previous ones.
The algorithm can be improved with the following approaches:
1. A dynamic (according to iteration) inertia weight can be used. (Please check the commented inertia weight part in the code.)
2. Max. iteration number and swarm size can be fine tuned.
3. Algorithm can be fed with another algorithms output, so particles can have their starting routes with good ones, instead of random ones.
## COTS Solution (Google OR Tools)
These are the Commercial-of-the-shelf solutions provided by Google OR Tools. I am not going to include codes on here, I only coded a function to fit our data to the solution, you can see it on the shared source code, google_or.py.
In this part, I have explored the results with different parameters; such as First Solution Strategy parameters and Local Search options parameters, etc.
Almost all the parameters in the shared link are explored: https://developers.google.com/optimization/routing/routing_options
I am going to include some of the results to the report.
### COTS Solution (Google OR Tools) Result
#### Guided Local Search Result (Meta-Heuristic)
<img align="left" width="640" height="480" src="media/gls.gif">
**Google OR (GUIDED LOCAL SEARCH) Path:** [1, 32, 11, 38, 5, 37, 17, 4, 18, 47, 12, 46, 51, 27, 6, 48, 23, 7, 43, 24, 14, 25, 13, 41, 40, 19, 42, 44, 15, 45, 33, 39, 10, 49, 9, 30, 34, 50, 16, 21, 29, 2, 20, 35, 36, 3, 28, 31, 26, 8, 22, 1]
**Google OR (GUIDED LOCAL SEARCH) Solution:** 426
**Time Limit:** 30 seconds
It gives the best solution, which is 426 and there is no error for 51 cities
#### Savings Result (Heuristic)
<img align="left" width="640" height="480" src="media/savings.gif">
**Google OR (SAVINGS) Path:** [1, 27, 6, 48, 23, 24, 43, 7, 26, 8, 31, 28, 3, 36, 35, 20, 29, 21, 16, 38, 5, 49, 9, 50, 34, 30, 10, 39, 33, 45, 15, 44, 42, 19, 40, 41, 13, 25, 14, 18, 4, 17, 37, 12, 47, 51, 46, 32, 11, 2, 22, 1]
**Google OR (SAVINGS) Solution:** 436
For 51 cities, there is 2.3% error compared to optimal solution.
## Conclusion
In this project, I have solved different TSPs with different approaches. I had three different problem sets with 51 cities, 101 cities, and 130 cities. For each different problem sets, I have used following approaches and tried to deeply understand each one of them.
* Nearest Neighbor
* 2-OPT
* Nearest Neighbor + 2-OPT (Hybrid)
* Particle Swarm Optimization
* COTS Solution (Google OR Tools)
For each approaches, I have reported the results and added my comments to how to improve them.
For the final part of this report, I am going to include a table which includes the comparisons of these approaches.
*Note that, bold ones are the algorithms I have implemented, others are COTS solutions provided by Google. Algorithms are tested with 51 cities.*
You can see the final comparison below:
| Algorithm | Solution | Error |
| --- | --- | --- |
| Guided Local Search | 426 | 0 |
| **Nearest Neighbor + 2-OPT (Hybrid)** | 428 | .46 |
| Path Most Constrained Arc | 430 | .93 |
| Tabu Search | 430 | .93 |
| Global Cheapest Arc | 432 | 1.40 |
| First Unbound Min. Value | 433 | 1.64 |
| Local Cheapest Arc | 435 | 2.11 |
| Savings | 436 | 2.34 |
| Simulated Annealing | 438 | 2.81 |
| Generic Tabu Search | 438 | 2.81 |
| Path Cheapest Arc | 439 | 3.05 |
| Greedy Descent | 439 | 3.05 |
| Local Cheapest Insertion | 442 | 3.75 |
| Christofides | 449 | 5.39 |
| Parallel Cheapest Insertion | 450 | 5.63 |
| **2-OPT** | 461 | 8.21 |
| **Nearest Neighbor** | 482 | 13.14 |
| **Particle Swarm Optimization** | 489 | 14.78 |
| true |
code
| 0.725844 | null | null | null | null |
|
# Nozzles (part I)
```
# Necessary modules to solve problems
import numpy as np
from scipy.optimize import root_scalar
# Pint gives us some helpful unit conversion
from pint import UnitRegistry
ureg = UnitRegistry()
Q_ = ureg.Quantity # We will use this to construct quantities (value + unit)
%matplotlib inline
from matplotlib import pyplot as plt
# these lines are only for helping improve the display
import matplotlib_inline.backend_inline
matplotlib_inline.backend_inline.set_matplotlib_formats('pdf', 'png')
plt.rcParams['figure.dpi']= 300
plt.rcParams['savefig.dpi'] = 300
```
## Converging nozzles
Let's now take our understanding of isentropic flows in varying-area ducts and apply them to converging nozzles.
```
from matplotlib.patches import Arc
fig, ax = plt.subplots(figsize=(1.5,1.5),subplot_kw={'aspect': 'equal'})
arc = Arc([1,1.1], 1, 1, theta1=190, theta2=270)
ax.add_patch(arc)
arc = Arc([1,-0.1], 1, 1, theta1=90, theta2=170)
ax.add_patch(arc)
ax.set_xlim(0.25, 1.25)
ax.set_ylim(0, 1)
ax.axis('off')
cc = plt.Circle((1.0, 0.3), 0.075, alpha=0.2)
ax.add_artist(cc)
cc = plt.Circle((0.4, 0.1), 0.075, alpha=0.2)
ax.add_artist(cc)
ax.text(1.0, 0.3, '2', horizontalalignment='center', verticalalignment='center')
ax.text(0.4, 0.1, '1', horizontalalignment='center', verticalalignment='center')
ax.arrow(0.6, 0.5, 0.5, 0, head_width=0.025, color='k')
fig.tight_layout()
plt.show()
```
Consider a converging-only nozzle, from a large supply of air at 300 K and 10 bar to a receiver with variable pressure $p_{\text{rec}}$ that we can control.
Since the supply tank has such a large cross-sectional area compared to the nozzle, we can assume that the velocity is approximately zero, and so that is the stagnation state:
$$
\begin{gather*}
T_1 = T_{t1} \\
p_1 = p_{t1} \;.
\end{gather*}
$$
From the energy equation, stagnation enthalpy and temperature are constant:
$$
\begin{gather*}
h_{t1} + q = h_{t2} + w_s \\
h_{t1} = h_{t2} \\
\rightarrow T_{t1} = T_{t2} \;.
\end{gather*}
$$
Clearly, the receiver pressure $p_{\text{rec}}$ controls the flow.
```
gamma = 1.4
pt1 = Q_(10.0, 'bar')
Tt1 = Q_(300, 'K')
gas_constant_air = Q_(287, 'J/(kg*K)')
def stagnation_pressure(mach, gamma):
'''Calculate ratio of static to stagnation pressure'''
return (1 + 0.5*(gamma - 1)*mach**2)**(-gamma/(gamma - 1))
def stagnation_temperature(mach, gamma):
'''Calculate ratio of static to stagnation temperature'''
return 1.0 / (1.0 + 0.5*(gamma - 1)*mach**2)
def find_mach_pressure(mach, pressure_ratio, gamma):
'''Used to find Mach number for given stagnation pressure and gamme'''
return (pressure_ratio - stagnation_pressure(mach, gamma))
def find_mach_temperature(mach, temperature_ratio, gamma):
'''Used to find Mach number for given stagnation temperature and gamme'''
return (temperature_ratio - stagnation_temperature(mach, gamma))
```
### 1. No flow
If $p_{\text{rec}} = 10$ bar, then there is no flow through the nozzle.
### 2. Isentropic expansion
If $p_{\text{rec}} < 10$ bar, then the gas will accelerate through the nozzle as it expands isentropically and the pressure drops until $p = p_{\text{rec}}$ at the exit.
We can use the pressure ratio to find the exit Mach number and temperature.
For example, if $p_{\text{rec}} = 8.02$ bar:
$$
\begin{align*}
\frac{p_2}{p_{t2}} &= \frac{p_2}{p_{t1}} \frac{p_{t1}}{p_{t2}} = f(\gamma, M_2) \\
&= \frac{8.02}{10} \left( 1 \right) = 0.802 \;,
\end{align*}
$$
where $\frac{p_{t1}}{p_{t2}} = 1$ since the flow is isentropic.
```
p2 = Q_(8.02, 'bar')
pt2 = pt1
Tt2 = Tt1
p2_pt2 = (p2 / pt1) * (pt1 / pt2)
root = root_scalar(find_mach_pressure, x0=0.1, x1=0.2, args=(p2_pt2, gamma))
M2 = root.root
print(f'M2 = {M2:.3f}')
T2_Tt2 = stagnation_temperature(M2, gamma)
T2 = T2_Tt2 * Tt2
print(f'T2 = {T2: .1f}')
a2 = np.sqrt(gamma * gas_constant_air * T2)
V2 = a2 * M2
print(f'V2 = {V2.to("m/s"): .1f}')
```
### 3. Critical pressure
Let's examine when we lower the receiver pressure to $p_{\text{rec}} = 5.283$ bar:
$$
\begin{align*}
\frac{p_2}{p_{t2}} &= \frac{p_2}{p_{t1}} \frac{p_{t1}}{p_{t2}} = f(\gamma, M_2) \\
&= \frac{5.283}{10} \left( 1 \right) = 0.5283 \;.
\end{align*}
$$
```
p2 = Q_(5.283, 'bar')
pt2 = pt1
Tt2 = Tt1
p2_pt2 = (p2 / pt1) * (pt1 / pt2)
root = root_scalar(find_mach_pressure, x0=0.1, x1=0.2, args=(p2_pt2, gamma))
M2 = root.root
print(f'M2 = {M2:.3f}')
```
For this nozzle, $p_{\text{rec}} = 5.283$ bar is the **critical pressure**,
where the velocity leaving the nozzle is sonic.
Now, what if we tried to reduce the receiver pressure below this critical pressure?
Mathematically this corresponds to a supersonic velocity, but we know that a converging-only nozzle *cannot* increase the velocity past the sonic point. So, that means that further reducing the receiver pressure has *no effect* on the flow inside the nozzle.
Thus, once the critical pressure is reached, the flow is **choked**.
We can find the critical pressure ratio:
$$
\frac{p_{\text{crit}}}{p_t} = \left(\frac{1}{1+\frac{\gamma-1}{2}}\right)^{\gamma/(\gamma-1)} = \left(\frac{2}{\gamma+1}\right)^{\gamma/(\gamma-1)} \;.
$$
If the receiver pressure is below the critical pressure ($p_{\text{rec}} < p_{\text{crit}}$), then the flow is choked.
## Example: mass flow in converging nozzle
Air flows from a large reservoir through a converging nozzle with an exit area of 50 cm$^2$.
The reservoir is large enough that the supply temperature and pressure remain approximately constant at 500 kPa and 400 K as the flow exhausts through the nozzle. Assuming isentropic flow of air as an ideal gas with a constant ratio of specific heats ($\gamma = 1.4$).
Plot the mass flow rate for a range of back pressures from 0 to 500 kPa.
First, find the critical pressure for this nozzle, and the temperature associated with that pressure:
```
gamma = 1.4
gas_constant_air = Q_(287, 'J/(kg*K)')
exit_area = Q_(50, 'cm^2')
pt = Q_(500, 'kPa')
Tt = Q_(400, 'K')
back_pressures = Q_(np.linspace(0, 500, 15, endpoint=True), 'kPa')
p_crit = pt * (2 / (gamma+1))**(gamma/(gamma-1))
print(f'Critical pressure = {p_crit: .2f}')
T_crit = Tt * stagnation_temperature(1.0, gamma)
print(f'Exit temperature = {T_crit: .2f}')
```
We can find the mass flow rate with
$$
\begin{align*}
\dot{m} &= \rho_e A_e V_e \\
&= \left(\frac{p_e}{R T_e} \right) A_e \left( M_e \sqrt{\gamma R T_e} \right) \;.
\end{align*}
$$
For back pressures that are higher than the critical pressure, we can use the stagnation pressure ratio to find the corresponding exit Mach number, and then the other properties.
For back pressures that are lower than the critical pressure, the exit conditions are locked at the critical conditions and the Mach number is one.
```
mass_flow_rates = Q_(np.zeros_like(back_pressures), 'kg/s')
for idx, p in enumerate(back_pressures):
if p > p_crit:
root = root_scalar(find_mach_pressure, x0=0.1, x1=0.2, args=(p/pt, gamma))
Me = root.root
pe = pt * stagnation_pressure(Me, gamma)
Te = Tt * stagnation_temperature(Me, gamma)
mass_flow_rates[idx] = (
pe * exit_area * Me * np.sqrt(gamma * gas_constant_air * Te) /
(gas_constant_air * Te)
).to('kg/s')
else:
mass_flow_rates[idx] = (
p_crit * exit_area * np.sqrt(gamma * gas_constant_air * T_crit) /
(gas_constant_air * T_crit)
).to('kg/s')
plt.plot(back_pressures.to('kPa').magnitude, mass_flow_rates.magnitude, 'o-')
plt.xlabel('Back pressure (kPa)')
plt.ylabel('Mass flow rate (kg/s)')
plt.grid()
plt.show()
print(f'Max flow rate: {np.max(mass_flow_rates): .3f}')
```
## Converging-diverging nozzles
Converging-diverging nozzles, also known as de Laval nozzles, are designed to obtain a supersonic flow. The "correct" or design operation is for subsonic flow between points 1 and 2, reaching sonic flow at location 2 (the throat), and then isentropic supersonic flow in the diverging section from points 2 to 3.
Consider a converging-diverging nozzle, exhausting air from a supply tank at 300 K and 10 bar to a receiver with variable pressure $p_{\text{rec}}$ that we can control.
The **area ratio**, or the ratio of the exit area to the throat area ($\frac{A_3}{A_2}$), is 2.494.
```
# plot a converging-diverging nozzle with a conical diverging section
# formulas based on http://seitzman.gatech.edu/classes/ae6450/nozzle_geometries.pdf
from matplotlib.patches import Arc
from matplotlib.lines import Line2D
fig, ax = plt.subplots(figsize=(3,3),subplot_kw={'aspect': 'equal'})
arc = Arc([1,1.1], 1, 1, theta1=190, theta2=270)
ax.add_patch(arc)
arc = Arc([1,-0.1], 1, 1, theta1=90, theta2=170)
ax.add_patch(arc)
cc = plt.Circle((1.0, 0.29), 0.1, alpha=0.2)
ax.add_artist(cc)
cc = plt.Circle((0.4, 0.1), 0.1, alpha=0.2)
ax.add_artist(cc)
ax.text(1.0, 0.29, '2', horizontalalignment='center', verticalalignment='center')
ax.text(0.4, 0.1, '1', horizontalalignment='center', verticalalignment='center')
R1 = 0.5
Rt = 0.1
alpha = 10 # degrees
epsilon = 20
L1 = R1 * np.sin(alpha * np.pi/180)
Re = np.sqrt(epsilon) * Rt
RN = Rt + R1 * (1 - np.cos(alpha*np.pi/180))
LN = (Re - RN) / np.tan(alpha * np.pi/180)
arc = Arc([1,1.1], 1, 1, theta1=270, theta2=(270+alpha), linewidth=0.8)
ax.add_patch(arc)
arc = Arc([1,-0.1], 1, 1, theta1=(90-alpha), theta2=90, linewidth=0.8)
ax.add_patch(arc)
# lines start at x=1, y=0.5
plt.plot([1+L1, 1+L1+LN], [0.5+RN, 0.5+Re], '-', color='k', linewidth=0.8)
plt.plot([1+L1, 1+L1+LN], [0.5-RN, 0.5-Re], '-', color='k', linewidth=0.8)
cc = plt.Circle((1+L1+LN, 0.2), 0.1, alpha=0.2)
ax.add_artist(cc)
ax.text(1+L1+LN, 0.2, '3', horizontalalignment='center', verticalalignment='center')
ax.arrow(0.75, 0.5, 0.5, 0, head_width=0.025, color='k')
ax.set_xlim(0.25, 3.15)
ax.set_ylim(0, 1)
ax.axis('off')
fig.tight_layout()
plt.show()
```
### Design operation: third critical
The design operation of a converging-diverging nozzle is supersonic flow at the exit, and fully isentropic throughout.
We can use the sonic reference area to find the supersonic Mach number associated with this condition:
$$
\begin{align*}
\frac{A_3}{A_3^*} &= \frac{A_3}{A_2} \frac{A_2}{A_2^*} \frac{A_2^*}{A_3^*} \\
&= (2.494) \left(1 \right) \left( 1 \right) = 2.494 \;,
\end{align*}
$$
which is a function of $M_3$. $\frac{A_2}{A_2^*} = 1$ because the velocity is sonic at the throat, and $\frac{A_2^*}{A_3^*} = 1$ because the flow is isentropic in the diverging section.
With $M_3$ we can obtain the stagnation pressure ratio at the exit:
$$
p_3 = \frac{p_3}{p_{t3}} \frac{p_{t3}}{p_{t1}} p_{t1} \;.
$$
```
def reference_area(mach, gamma):
'''Calculate reference area ratio'''
return ((1.0/mach) * ((1 + 0.5*(gamma-1)*mach**2) /
((gamma + 1)/2))**((gamma+1) / (2*(gamma-1)))
)
def find_mach_area(mach, area_ratio, gamma):
'''Used to find Mach number for given reference area ratio and gamma'''
return (area_ratio - reference_area(mach, gamma))
A3_A2 = 2.494
pt3 = pt1
root = root_scalar(find_mach_area, x0=2, x1=2.5, args=(A3_A2, gamma))
M_third = root.root
print(f'M3 = {M_third: .2f}')
p3_pt3 = stagnation_pressure(M_third, gamma)
p_third = p3_pt3 * (pt3/pt1) * pt1
print(f'p3 = {p_third: .3f}')
```
This is the **third critical** operating point of the nozzle, which is the design operation.
### First critical
The **first critical** operating point is associated with subsonic exhaust, but choked flow, so the velocity is sonic at the throat.
```
root = root_scalar(find_mach_area, x0=0.1, x1=0.2, args=(A3_A2, gamma))
M_first = root.root
print(f'M3 = {M_first: .2f}')
p3_pt3 = stagnation_pressure(M_first, gamma)
p_first = p3_pt3 * (pt3/pt1) * pt1
print(f'p3 = {p_first: .3f}')
```
Above the first critical point, the nozzle acts like a Venturi tube, which can be used to relate the pressure drop to flow rate.
Below the first critical point, the nozzle is choked and the conditions from the inlet to the throat do not change.
```
area_ratios_converging = np.logspace(2, 0, 100, endpoint=True)
area_ratios_diverging = np.linspace(1.0, A3_A2, 100, endpoint=True)
pressures_converging = np.zeros_like(area_ratios_converging)
machs_converging = np.zeros_like(area_ratios)
for idx, area_ratio in enumerate(area_ratios_converging):
root = root_scalar(
find_mach_area, x0=0.1, x1=0.15, bracket=(0.001,1.0), args=(area_ratio, gamma)
)
machs_converging[idx] = root.root
pressures_converging[idx] = stagnation_pressure(machs_first[idx], gamma)
pressures_first = np.zeros_like(area_ratios_diverging)
pressures_third = np.zeros_like(area_ratios_diverging)
for idx, area_ratio in enumerate(area_ratios_diverging):
root = root_scalar(
find_mach_area, x0=0.1, x1=0.2, bracket=(0.001,1.0), args=(area_ratio, gamma)
)
pressures_first[idx] = stagnation_pressure(root.root, gamma)
root = root_scalar(
find_mach_area, x0=2.5, x1=3.0, bracket=(1.0,10.0), args=(area_ratio, gamma)
)
pressures_third[idx] = stagnation_pressure(root.root, gamma)
pressures_first = np.concatenate((pressures_converging, pressures_first))
pressures_third = np.concatenate((pressures_converging, pressures_third))
fig, ax = plt.subplots()
ax.plot(pressures_first, '-')
ax.plot(pressures_third, '--')
ax.set_ylabel(r'$p/p_t$')
ax.set_xlabel('Distance in nozzle')
fig.tight_layout()
plt.show()
```
## Nozzle performance
The efficiency of a nozzle is described by the actual increase in kinetic energy normalized by the ideal increase in kinetic energy:
$$
\eta_n \equiv \frac{\text{actual } \Delta \text{KE}}{\text{ideal } \Delta \text{KE}} \;.
$$
We can express this using more convenient quantities by examining the energy equation:
$$
\begin{gather*}
h_{t1} + q = h_{t2} + w_s \\
h_{t1} = h_{t2} \\
h_1 + \frac{V_1^2}{2} = h_2 + \frac{V_2^2}{2} \\
h_1 - h_2 = \frac{V_2^2 - V_1^2}{2} = \Delta \text{KE}
\end{gather*}
$$
so
$$
\eta_n = \frac{\Delta h_{\text{actual}}}{\Delta h_{\text{ideal}}} = \frac{h_1 - h_2}{h_1 - h_{2s}} \;,
$$
where subscripts 1 and 2 indicate the inlet and outlet, and subscript $s$ indicates the ideal (i.e., isentropic) outlet condition.
The performance of nozzles is also sometimes described using a **velocity coefficient**, which relates the actual outlet velocity to the ideal outlet velocity:
$$
C_v \equiv \frac{V_2}{V_{2s}} \;,
$$
and a **discharge coefficient**, which relates the actual mass flow rate to the ideal mass flow rate:
$$
C_d \equiv \frac{\dot{m}}{\dot{m}_s} \;.
$$
## Diffuser performance
Although most of our analysis has focused on nozzles, diffusers behave the same—just opposite!
The purpose of a diffuser is to convert kinetic energy into pressure energy.
One common performance metric is the **total-pressure recovery factor**, which is the ratio of the outlet stagnation pressure to the inlet stagnation pressure:
$$
\eta_r \equiv \frac{p_{t2}}{p_{t1}} = e^{-\Delta s / R} = \frac{A_1^*}{A_2^*} \;.
$$
The diffuser efficiency is represented by the ratio of the actual pressure rise to the ideal pressure rise:
$$
\eta_d \equiv \frac{p_2 - p_1}{p_{2s} - p_1} \;.
$$
| true |
code
| 0.657648 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/mlvlab/COSE474/blob/master/2_MNIST_Tutorial%20(CNN).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## MNIST_Tutorial (CNN) in PyTorch
### Reference
* [PyTorch Tutorial MNIST](https://github.com/GunhoChoi/PyTorch-FastCampus/tree/master/03_CNN_Basics/0_MNIST)
* [VISUALIZING MODELS, DATA, AND TRAINING WITH TENSORBOARD](https://tutorials.pytorch.kr/intermediate/tensorboard_tutorial.html?highlight=mnist)
### GOALS
1. We will make a simple convolutional neural network(CNN).
2. Then, we will train the network with MNIST.
3. We will learn how to use Tensorboard as well to monitor training.
### Settings
Import required libraries
Set hyperparameters
```
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torch.nn.init as init
import torchvision.datasets as dset
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
# Writer will output to ./runs/ directory by default
writer = SummaryWriter()
# Setting hyperparameters
batch_size = 256
learning_rate = 0.0002
num_epoch = 10
```
### Data Generation
Download Data
Set DataLoader
```
# Loading MNIST dataset
mnist_train = dset.MNIST("./", train=True, transform=transforms.ToTensor(),
target_transform=None, download=True)
mnist_test = dset.MNIST("./", train=False, transform=transforms.ToTensor(),
target_transform=None, download=True)
train_loader = torch.utils.data.DataLoader(mnist_train, batch_size = batch_size,
shuffle = True, num_workers = 2, drop_last = True)
test_loader = torch.utils.data.DataLoader(mnist_test, batch_size = batch_size,
shuffle = False, num_workers = 2, drop_last = True)
```
### Define Convolutional Neural Network
1. MNIST data
2. 3 convolutional layers
3. 2 fully connected layers
```
# Creating CNN model
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.layer = nn.Sequential(
nn.Conv2d(1,16,5),
nn.ReLU(),
nn.Conv2d(16,32,5),
nn.ReLU(),
nn.MaxPool2d(2,2),
nn.Conv2d(32,64,5),
nn.ReLU(),
nn.MaxPool2d(2,2)
)
self.fc_layer = nn.Sequential(
nn.Linear(64*3*3,100),
nn.ReLU(),
nn.Linear(100,10)
)
def forward(self, x):
out = self.layer(x)
out = out.view(batch_size, -1)
out = self.fc_layer(out)
return out
```
### Train & Test
```
# Declare device(GPU/CPU), declare Loss func and optimizer
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model = CNN().to(device)
loss_func = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
loss_arr = []
train_iter = 0
test_iter = 0
test_acc_iter = 0
# Training
for i in range(num_epoch):
for j, [image, label] in enumerate(train_loader):
x = image.to(device)
y_ = label.to(device)
optimizer.zero_grad()
output = model.forward(x)
loss = loss_func(output, y_)
loss.backward()
optimizer.step()
if j % 1000 == 0:
print(loss)
loss_arr.append(loss.cpu().detach().numpy())
# Tensorboard : train_loss
writer.add_scalar('Loss/train', loss.item(), train_iter)
train_iter += 1
correct = 0
total = 0
# Testing
with torch.no_grad():
for k, [image, label] in enumerate(test_loader):
x = image.to(device)
y_ = label.to(device)
output = model.forward(x)
_, output_index = torch.max(output, 1)
test_loss = loss_func(output, y_)
total += label.size(0)
correct += (output_index == y_).sum().float()
accuracy = 100*correct/total
# Tensorboard : test_loss
writer.add_scalar('Loss/test', test_loss.item(), test_iter)
test_iter += 1
# Tensorboard : test_Accuracy
writer.add_scalar('Accuracy/test', accuracy.item(), test_acc_iter)
test_acc_iter += 1
print("Accuracy of Test Data : {}".format(100*correct/total))
# Tensorboard : image (1 batch)
images, labels = next(iter(train_loader))
grid = torchvision.utils.make_grid(images)
writer.add_image('images', grid, 0)
# Tensorboard : model graph
grp = images.to(device)
writer.add_graph(model, grp)
writer.close()
```
### Using Tensorboard to monitor training & testing
```
# Install tf-nightly package
!pip install -q tf-nightly-2.0-preview
%load_ext tensorboard
# Run tensorboard
# if you cannot see anything, just try running one more time
%tensorboard --logdir=runs
# you can use linux command like 'ls, cd, cd.., pip, rm'.
# (option) remove 'runs' directory
!rm -rf runs
# (option) list files to check 'runs' directory
ls
```
| true |
code
| 0.757032 | null | null | null | null |
|


```
import tensorflow as tf
import os
import time
import numpy as np
import pathlib
from matplotlib import pyplot as plt
from IPython import display
BUFFER_SIZE = 400
EPOCHS = 100
LAMBDA = 100
dataset_name = 'cityscapes'
BATCH_SIZE = 1
IMG_WIDTH = 256
IMG_HEIGHT = 256
patch_size = 8
num_patches = (IMG_HEIGHT // patch_size) ** 2
projection_dim = 64
embed_dim = 64
num_heads = 2
ff_dim = 32
assert IMG_WIDTH == IMG_HEIGHT, "image width and image height must have same dims"
_URL = f'http://efrosgans.eecs.berkeley.edu/pix2pix/datasets/{dataset_name}.tar.gz'
path_to_zip = tf.keras.utils.get_file(f'{dataset_name}.tar.gz',
origin=_URL,
extract=True)
PATH = os.path.join(os.path.dirname(path_to_zip), f'{dataset_name}/')
def load(image_file):
image = tf.io.read_file(image_file)
image = tf.image.decode_jpeg(image)
w = tf.shape(image)[1]
w = w // 2
real_image = image[:, :w, :]
input_image = image[:, w:, :]
input_image = tf.cast(input_image, tf.float32)
real_image = tf.cast(real_image, tf.float32)
return input_image, real_image
inp, re = load(PATH+'train/100.jpg')
# casting to int for matplotlib to show the image
plt.figure()
plt.imshow(inp/255.0)
plt.figure()
plt.imshow(re/255.0)
def resize(input_image, real_image, height, width):
input_image = tf.image.resize(input_image, [height, width],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
real_image = tf.image.resize(real_image, [height, width],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
return input_image, real_image
def random_crop(input_image, real_image):
stacked_image = tf.stack([input_image, real_image], axis=0)
cropped_image = tf.image.random_crop(
stacked_image, size=[2, IMG_HEIGHT, IMG_WIDTH, 3])
return cropped_image[0], cropped_image[1]
# normalizing the images to [-1, 1]
def normalize(input_image, real_image):
input_image = (input_image / 127.5) - 1
real_image = (real_image / 127.5) - 1
return real_image, input_image
@tf.function()
def random_jitter(input_image, real_image):
# resizing to 286 x 286 x 3
input_image, real_image = resize(input_image, real_image, 286, 286)
# randomly cropping to 256 x 256 x 3
input_image, real_image = random_crop(input_image, real_image)
if tf.random.uniform(()) > 0.5:
# random mirroring
input_image = tf.image.flip_left_right(input_image)
real_image = tf.image.flip_left_right(real_image)
return input_image, real_image
plt.figure(figsize=(6, 6))
for i in range(4):
rj_inp, rj_re = random_jitter(inp, re)
plt.subplot(2, 2, i+1)
plt.imshow(rj_inp/255.0)
plt.axis('off')
plt.show()
def load_image_train(image_file):
input_image, real_image = load(image_file)
input_image, real_image = random_jitter(input_image, real_image)
input_image, real_image = normalize(input_image, real_image)
return input_image, real_image
def load_image_test(image_file):
input_image, real_image = load(image_file)
input_image, real_image = resize(input_image, real_image,
IMG_HEIGHT, IMG_WIDTH)
input_image, real_image = normalize(input_image, real_image)
return input_image, real_image
```
## Input Pipeline
```
train_dataset = tf.data.Dataset.list_files(PATH+'train/*.jpg')
train_dataset = train_dataset.map(load_image_train,
num_parallel_calls=tf.data.AUTOTUNE)
train_dataset = train_dataset.shuffle(BUFFER_SIZE)
train_dataset = train_dataset.batch(BATCH_SIZE)
# load, split and scale the maps dataset ready for training
from os import listdir
from numpy import asarray
from numpy import vstack
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.preprocessing.image import load_img
# example of pix2pix gan for satellite to map image-to-image translation
from numpy import load
from numpy import zeros
from numpy import ones
from numpy.random import randint
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.initializers import RandomNormal
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input
from tensorflow.keras.layers import Conv2D
from tensorflow.keras.layers import Conv2DTranspose
from tensorflow.keras.layers import LeakyReLU
from tensorflow.keras.layers import Activation
from tensorflow.keras.layers import Concatenate
from tensorflow.keras.layers import Dropout
from tensorflow.keras.layers import BatchNormalization
from tensorflow.keras.layers import LeakyReLU
from matplotlib import pyplot
# define an encoder block
def define_encoder_block(layer_in, n_filters, batchnorm=True):
# weight initialization
init = RandomNormal(stddev=0.02)
# add downsampling layer
g = Conv2D(n_filters, (4,4), strides=(2,2), padding='same', kernel_initializer=init)(layer_in)
# conditionally add batch normalization
if batchnorm:
g = BatchNormalization()(g, training=True)
# leaky relu activation
g = LeakyReLU(alpha=0.2)(g)
return g
# define a decoder block
def decoder_block(layer_in, skip_in, n_filters, dropout=True):
# weight initia\lization
init = RandomNormal(stddev=0.02)
# add upsampling layer
g = Conv2DTranspose(n_filters, (4,4), strides=(2,2), padding='same', kernel_initializer=init)(layer_in)
# add batch normalization
g = BatchNormalization()(g, training=True)
# conditionally add dropout
if dropout:
g = Dropout(0.5)(g, training=True)
# merge with skip connection
g = Concatenate()([g, skip_in])
# relu activation
g = Activation('relu')(g)
return g
# define the standalone generator model
def define_generator_unet(image_shape=(256,256,3)):
# weight initialization
init = RandomNormal(stddev=0.02)
# image input
in_image = Input(shape=image_shape)
# encoder model
e1 = define_encoder_block(in_image, 64, batchnorm=False)
e2 = define_encoder_block(e1, 128)
e3 = define_encoder_block(e2, 256)
e4 = define_encoder_block(e3, 512)
e5 = define_encoder_block(e4, 512)
e6 = define_encoder_block(e5, 512)
e7 = define_encoder_block(e6, 512)
# bottleneck, no batch norm and relu
b = Conv2D(512, (4,4), strides=(2,2), padding='same', kernel_initializer=init)(e7)
b = Activation('relu')(b)
# decoder model
d1 = decoder_block(b, e7, 512)
d2 = decoder_block(d1, e6, 512)
d3 = decoder_block(d2, e5, 512)
d4 = decoder_block(d3, e4, 512, dropout=False)
d5 = decoder_block(d4, e3, 256, dropout=False)
d6 = decoder_block(d5, e2, 128, dropout=False)
d7 = decoder_block(d6, e1, 64, dropout=False)
# output
g = Conv2DTranspose(3, (4,4), strides=(2,2), padding='same', kernel_initializer=init)(d7)
out_image = Activation('tanh')(g)
# define model
model = Model(in_image, out_image)
return model
unet = define_generator_unet()
unet.summary()
# load, split and scale the maps dataset ready for training
from os import listdir
from numpy import asarray
from numpy import vstack
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.preprocessing.image import load_img
# example of pix2pix gan for satellite to map image-to-image translation
from numpy import load
from numpy import zeros
from numpy import ones
from numpy.random import randint
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.initializers import RandomNormal
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input
from tensorflow.keras.layers import Conv2D
from tensorflow.keras.layers import Conv2DTranspose
from tensorflow.keras.layers import LeakyReLU
from tensorflow.keras.layers import Activation
from tensorflow.keras.layers import Concatenate
from tensorflow.keras.layers import Dropout
from tensorflow.keras.layers import BatchNormalization
from tensorflow.keras.layers import LeakyReLU
from matplotlib import pyplot
# define an encoder block
def define_encoder_block(layer_in, n_filters, batchnorm=True):
# weight initialization
g = Conv2D(n_filters, (4,4), strides=(2,2), padding='same')(layer_in)
# conditionally add batch normalization
if batchnorm:
g = BatchNormalization()(g, training=True)
# leaky relu activation
g = LeakyReLU(alpha=0.2)(g)
return g
# define a decoder block
def decoder_block(layer_in, n_filters, dropout=True):
# weight initialization
# add upsampling layer
g = Conv2DTranspose(n_filters, (4,4), strides=(2,2), padding='same')(layer_in)
# add batch normalization
g = BatchNormalization()(g, training=True)
# conditionally add dropout
if dropout:
g = Dropout(0.5)(g, training=True)
# merge with skip connection
#g = Concatenate()([g, skip_in])
# relu activation
g = Activation('relu')(g)
return g
# define the standalone generator model
def define_generator_ae(image_shape=(256,256,3)):
# weight initialization
# image input
in_image = Input(shape=image_shape)
# encoder model
e1 = define_encoder_block(in_image, 64, batchnorm=False)
e2 = define_encoder_block(e1, 128)
e3 = define_encoder_block(e2, 256)
e4 = define_encoder_block(e3, 512)
e5 = define_encoder_block(e4, 512)
e6 = define_encoder_block(e5, 512)
e7 = define_encoder_block(e6, 512)
# bottleneck, no batch norm and relu
b = Conv2D(512, (4,4), strides=(2,2), padding='same')(e7)
b = Activation('relu')(b)
# decoder model
d1 = decoder_block(b, 512)
d2 = decoder_block(d1, 512)
d3 = decoder_block(d2, 512)
d4 = decoder_block(d3, 512, dropout=False)
d5 = decoder_block(d4, 256, dropout=False)
d6 = decoder_block(d5, 128, dropout=False)
d7 = decoder_block(d6, 64, dropout=False)
# output
g = Conv2DTranspose(3, (4,4), strides=(2,2), padding='same')(d7)
out_image = Activation('tanh')(g)
# define model
model = Model(in_image, out_image)
return model
ae = define_generator_ae()
class Patches(tf.keras.layers.Layer):
def __init__(self, patch_size):
super(Patches, self).__init__()
self.patch_size = patch_size
def call(self, images):
batch_size = tf.shape(images)[0]
patches = tf.image.extract_patches(
images=images,
sizes=[1, self.patch_size, self.patch_size, 1],
strides=[1, self.patch_size, self.patch_size, 1],
rates=[1, 1, 1, 1],
padding="SAME",
)
patch_dims = patches.shape[-1]
patches = tf.reshape(patches, [batch_size, -1, patch_dims])
return patches
class PatchEncoder(tf.keras.layers.Layer):
def __init__(self, num_patches, projection_dim):
super(PatchEncoder, self).__init__()
self.num_patches = num_patches
self.projection = layers.Dense(units=projection_dim)
self.position_embedding = layers.Embedding(
input_dim=num_patches, output_dim=projection_dim
)
def call(self, patch):
positions = tf.range(start=0, limit=self.num_patches, delta=1)
encoded = self.projection(patch) + self.position_embedding(positions)
return encoded
class TransformerBlock(tf.keras.layers.Layer):
def __init__(self, embed_dim, num_heads, ff_dim, rate=0.1):
super(TransformerBlock, self).__init__()
self.att = layers.MultiHeadAttention(num_heads=num_heads, key_dim=embed_dim)
self.ffn = tf.keras.Sequential(
[layers.Dense(ff_dim, activation="relu"), layers.Dense(embed_dim),]
)
self.layernorm1 = layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = layers.Dropout(rate)
self.dropout2 = layers.Dropout(rate)
def call(self, inputs, training):
attn_output = self.att(inputs, inputs)
attn_output = self.dropout1(attn_output, training=training)
out1 = self.layernorm1(inputs + attn_output)
ffn_output = self.ffn(out1)
ffn_output = self.dropout2(ffn_output, training=training)
return self.layernorm2(out1 + ffn_output)
from tensorflow import Tensor
from tensorflow.keras.layers import Input, Conv2D, ReLU, BatchNormalization,\
Add, AveragePooling2D, Flatten, Dense
from tensorflow.keras.models import Model
def relu_bn(inputs: Tensor) -> Tensor:
relu = ReLU()(inputs)
bn = BatchNormalization()(relu)
return bn
def residual_block(x: Tensor, downsample: bool, filters: int, kernel_size: int = 3) -> Tensor:
y = Conv2D(kernel_size=kernel_size,
strides= (1 if not downsample else 2),
filters=filters,
padding="same")(x)
y = relu_bn(y)
y = Conv2D(kernel_size=kernel_size,
strides=1,
filters=filters,
padding="same")(y)
if downsample:
x = Conv2D(kernel_size=1,
strides=2,
filters=filters,
padding="same")(x)
out = Add()([x, y])
out = relu_bn(out)
return out
from tensorflow.keras import layers
def Generator():
inputs = layers.Input(shape=(256, 256, 3))
patches = Patches(patch_size)(inputs)
encoded_patches = PatchEncoder(num_patches, projection_dim)(patches)
x = TransformerBlock(64, num_heads, ff_dim)(encoded_patches)
x = TransformerBlock(64, num_heads, ff_dim)(x)
x = TransformerBlock(64, num_heads, ff_dim)(x)
x = TransformerBlock(64, num_heads, ff_dim)(x)
x = layers.Reshape((8, 8, 1024))(x)
x = layers.Conv2DTranspose(512, (5, 5), strides=(2, 2), padding='same', use_bias=False)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = residual_block(x, downsample=False, filters=512)
x = layers.Conv2DTranspose(256, (5, 5), strides=(2, 2), padding='same', use_bias=False)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = residual_block(x, downsample=False, filters=256)
x = layers.Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', use_bias=False)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = residual_block(x, downsample=False, filters=64)
x = layers.Conv2DTranspose(32, (5, 5), strides=(4, 4), padding='same', use_bias=False)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = residual_block(x, downsample=False, filters=32)
x = layers.Conv2D(3, (3, 3), strides=(1, 1), padding='same', use_bias=False, activation='tanh')(x)
return tf.keras.Model(inputs=inputs, outputs=x)
vit = Generator()
def generate_images(model, test_input, tar):
prediction = model(test_input, training=True)
plt.figure(figsize=(15, 15))
display_list = [test_input[0], tar[0], prediction[0]]
title = ['Input Image', 'Ground Truth', 'Predicted Image']
for i in range(3):
plt.subplot(1, 3, i+1)
plt.title(title[i])
# getting the pixel values between [0, 1] to plot it.
plt.imshow(display_list[i] * 0.5 + 0.5)
plt.axis('off')
plt.show()
def generate_all(inp, ae, unet, vit):
return ae(inp), unet(inp), vit(inp)
for inp, tar in train_dataset.take(1):
generate_images(vit, inp, tar)
vit.load_weights('weights/gen-nocgan-weights.h5')
unet.load_weights('weights/unet-cityscapes-weights.h5')
ae.load_weights('weights/autoencoder-cityscapes-weights.h5')
def display_image(images:list, display=True, save=False, name=None) -> np.ndarray:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img1, img2, img3, img4, img5 = images
img1 = np.array(img1).astype(np.float32) * 0.5 + 0.5
img2 = np.array(img2).astype(np.float32) * 0.5 + 0.5
img3 = np.array(img3).astype(np.float32) * 0.5 + 0.5
img4 = np.array(img4).astype(np.float32) * 0.5 + 0.5
img5 = np.array(img5).astype(np.float32) * 0.5 + 0.5
im_h = cv2.hconcat([img1, img2, img3, img4, img5])
plt.xticks([])
plt.yticks([])
if display:
plt.imshow(im_h)
if save:
if name is not None:
plt.imsave(name, im_h.astype(np.float32))
else:
raise AttributeError('plt.imsave expected to have a name to save the image')
return im_h
ae_out, unet_out, vit_out = generate_all(inp, ae, unet, vit)
imgs = display_image([inp[0], tar[0], ae_out[0], unet_out[0], vit_out[0]], save=True, name='comp3.png')
def gens(ae, unet, vit, dataset):
with tf.device('/device:GPU:0'):
ae_outs, unet_outs, vit_outs = list(), list(), list()
targets = list()
for n, (input_image, target) in dataset.enumerate():
target = np.array(target)
targets.append(target)
input_image = np.array(input_image)
a = np.squeeze(np.array(ae(input_image, training=False)).reshape((-1, 256, 256, 3)))
u = np.squeeze(np.array(unet(input_image, training=False)).reshape((-1, 256, 256, 3)))
v = np.squeeze(np.array(vit(input_image, training=False)).reshape((-1, 256, 256, 3)))
ae_outs.append(a)
unet_outs.append(u)
vit_outs.append(v)
print(n)
if (n + 1) % 500 == 0:
break
return ae_outs, unet_outs, vit_outs, targets
a, u, v, targets = gens(ae, unet, vit, train_dataset)
a = np.array(a)
u = np.array(u)
v = np.array(v)
targets = np.array(targets)
v = v.reshape((-1, 3, 256, 256))
u = u.reshape((-1, 3, 256, 256))
a = a.reshape((-1, 3, 256, 256))
targets = targets.reshape(-1, 3, 256, 256)
v = v * 0.5 + 0.5
u = u * 0.5 + 0.5
a = a * 0.5 + 0.5
targets = targets * 0.5 + 0.5
v = v * 255
u = u * 255
a = a * 255
targets = targets * 255
'''
From https://github.com/tsc2017/Inception-Score
Code derived from https://github.com/openai/improved-gan/blob/master/inception_score/model.py and https://github.com/tensorflow/tensorflow/blob/master/tensorflow/contrib/gan/python/eval/python/classifier_metrics_impl.py
Usage:
Call get_inception_score(images, splits=10)
Args:
images: A numpy array with values ranging from 0 to 255 and shape in the form [N, 3, HEIGHT, WIDTH] where N, HEIGHT and WIDTH can be arbitrary. A dtype of np.uint8 is recommended to save CPU memory.
splits: The number of splits of the images, default is 10.
Returns:
Mean and standard deviation of the Inception Score across the splits.
'''
!pip3 install tensorflow_gan
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import tensorflow_gan as tfgan
import os
import functools
import numpy as np
import time
from tensorflow.python.ops import array_ops
# pip install tensorflow-gan
import tensorflow_gan as tfgan
session=tf.compat.v1.InteractiveSession()
# A smaller BATCH_SIZE reduces GPU memory usage, but at the cost of a slight slowdown
BATCH_SIZE = 64
INCEPTION_TFHUB = 'https://tfhub.dev/tensorflow/tfgan/eval/inception/1'
INCEPTION_OUTPUT = 'logits'
# Run images through Inception.
inception_images = tf.compat.v1.placeholder(tf.float32, [None, 3, None, None], name = 'inception_images')
def inception_logits(images = inception_images, num_splits = 1):
images = tf.transpose(images, [0, 2, 3, 1])
size = 299
images = tf.compat.v1.image.resize_bilinear(images, [size, size])
generated_images_list = array_ops.split(images, num_or_size_splits = num_splits)
logits = tf.map_fn(
fn = tfgan.eval.classifier_fn_from_tfhub(INCEPTION_TFHUB, INCEPTION_OUTPUT, True),
elems = array_ops.stack(generated_images_list),
parallel_iterations = 8,
back_prop = False,
swap_memory = True,
name = 'RunClassifier')
logits = array_ops.concat(array_ops.unstack(logits), 0)
return logits
logits=inception_logits()
def get_inception_probs(inps):
session=tf.get_default_session()
n_batches = int(np.ceil(float(inps.shape[0]) / BATCH_SIZE))
preds = np.zeros([inps.shape[0], 1000], dtype = np.float32)
for i in range(n_batches):
inp = inps[i * BATCH_SIZE:(i + 1) * BATCH_SIZE] / 255. * 2 - 1
preds[i * BATCH_SIZE : i * BATCH_SIZE + min(BATCH_SIZE, inp.shape[0])] = session.run(logits,{inception_images: inp})[:, :1000]
preds = np.exp(preds) / np.sum(np.exp(preds), 1, keepdims=True)
return preds
def preds2score(preds, splits=10):
scores = []
for i in range(splits):
part = preds[(i * preds.shape[0] // splits):((i + 1) * preds.shape[0] // splits), :]
kl = part * (np.log(part) - np.log(np.expand_dims(np.mean(part, 0), 0)))
kl = np.mean(np.sum(kl, 1))
scores.append(np.exp(kl))
return np.mean(scores), np.std(scores)
def get_inception_score(images, splits=10):
assert(type(images) == np.ndarray)
assert(len(images.shape) == 4)
assert(images.shape[1] == 3)
assert(np.min(images[0]) >= 0 and np.max(images[0]) > 10), 'Image values should be in the range [0, 255]'
print('Calculating Inception Score with %i images in %i splits' % (images.shape[0], splits))
start_time=time.time()
preds = get_inception_probs(images)
mean, std = preds2score(preds, splits)
print('Inception Score calculation time: %f s' % (time.time() - start_time))
return mean, std # Reference values: 11.38 for 50000 CIFAR-10 training set images, or mean=11.31, std=0.10 if in 10 splits.
from math import floor
from numpy import ones
from numpy import expand_dims
from numpy import log
from numpy import mean
from numpy import std
from numpy import exp
from numpy.random import shuffle
from tensorflow.keras.applications.inception_v3 import InceptionV3
from tensorflow.keras.applications.inception_v3 import preprocess_input
from tensorflow.keras.datasets import cifar10
from skimage.transform import resize
from numpy import asarray
# scale an array of images to a new size
def scale_images(images, new_shape):
images_list = list()
for image in images:
# resize with nearest neighbor interpolation
new_image = resize(image, new_shape, 0)
# store
images_list.append(new_image)
return asarray(images_list)
# assumes images have any shape and pixels in [0,255]
def calculate_inception_score(images, n_split=10, eps=1E-16):
# load inception v3 model
model = InceptionV3()
# enumerate splits of images/predictions
scores = list()
n_part = floor(images.shape[0] / n_split)
for i in range(n_split):
# retrieve images
ix_start, ix_end = i * n_part, (i+1) * n_part
subset = images[ix_start:ix_end]
# convert from uint8 to float32
subset = subset.astype('float32')
# scale images to the required size
subset = scale_images(subset, (299,299,3))
# pre-process images, scale to [-1,1]
subset = preprocess_input(subset)
# predict p(y|x)
p_yx = model.predict(subset)
# calculate p(y)
p_y = expand_dims(p_yx.mean(axis=0), 0)
# calculate KL divergence using log probabilities
kl_d = p_yx * (log(p_yx + eps) - log(p_y + eps))
# sum over classes
sum_kl_d = kl_d.sum(axis=1)
# average over images
avg_kl_d = mean(sum_kl_d)
# undo the log
is_score = exp(avg_kl_d)
# store
scores.append(is_score)
# average across images
is_avg, is_std = mean(scores), std(scores)
return is_avg, is_std
import numpy
from numpy import cov
from numpy import trace
from numpy import iscomplexobj
from numpy import asarray
from numpy.random import randint
from scipy.linalg import sqrtm
from tensorflow.keras.applications.inception_v3 import InceptionV3
from tensorflow.keras.applications.inception_v3 import preprocess_input
from tensorflow.keras.datasets.mnist import load_data
from skimage.transform import resize
# scale an array of images to a new size
def scale_images(images, new_shape):
images_list = list()
for image in images:
# resize with nearest neighbor interpolation
new_image = resize(image, new_shape, 0)
# store
images_list.append(new_image)
return asarray(images_list)
# calculate frechet inception distance
def calculate_fid(model, images1, images2):
# calculate activations
act1 = model.predict(images1)
act2 = model.predict(images2)
# calculate mean and covariance statistics
mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False)
mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False)
# calculate sum squared difference between means
ssdiff = numpy.sum((mu1 - mu2)**2.0)
# calculate sqrt of product between cov
covmean = sqrtm(sigma1.dot(sigma2))
# check and correct imaginary numbers from sqrt
if iscomplexobj(covmean):
covmean = covmean.real
# calculate score
fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean)
return fid
model = InceptionV3(include_top=False, pooling='avg', input_shape=(299, 299, 3))
targets1 = scale_images(targets, (299,299,3))
v1 = scale_images(v, (299,299,3))
u1 = scale_images(u, (299,299,3))
a1 = scale_images(a, (299,299,3))
fid = calculate_fid(model, targets1, v1)
print('FID (vit): %.3f' % fid)
fid = calculate_fid(model, u1, targets1)
print('FID (unet): %.3f' % fid)
fid = calculate_fid(model, a1, targets1)
print('FID (autoencoder): %.3f' % fid)
vs = calculate_inception_score(v)
us = calculate_inception_score(u)
as1 = calculate_inception_score(a)
print('vit', vs)
print('us', us)
print('as', as1)
for inp, tar in train_dataset.take(1):
plt.imshow(np.array(unet(inp)).reshape(256, 256, 3) * 0.5 + 0.5)
get_inception_score(a)
np.max(v[0])
import numpy as np
import matplotlib.pyplot as plt
from skimage import data, img_as_float
from skimage.metrics import structural_similarity as ssim
from skimage.metrics import mean_squared_error
ssim_v = ssim(targets.reshape(-1, 256, 256, 3), v.reshape(-1, 256, 256, 3), data_range=targets.max() - targets.min(), multichannel=True)
ssim_u = ssim(targets.reshape(-1, 256, 256, 3), u.reshape(-1, 256, 256, 3), data_range=targets.max() - targets.min(), multichannel=True)
ssim_a = ssim(targets.reshape(-1, 256, 256, 3), a.reshape(-1, 256, 256, 3), data_range=targets.max() - targets.min(), multichannel=True)
print(ssim_v)
print(ssim_u)
print(ssim_a)
v: (1.4361017, 0.014119227)
a: (1.4175382, 0.011378809)
u: (1.3666638, 0.01198301)
=============================
v: (1.2742561, 0.014417181)
a: (1.3371006, 0.008001634)
u: (1.3666638, 0.01198301)
===========================
np.array(targets).shape
plt.imshow(p[1].reshape(256, 256, 3))
\begin{table}[h!]
\centering
\begin{tabular}{||c c c c||}
\hline
Model & FID & IS & SSIM \\ [0.5ex]
\hline\hline
Tensor-to-image(Ours) & 834 & 1.267 & 0.70 \\
U-net & 3946 & 1.163 & 0.52 \\
Autoencoder & 21182 & 1.203 & 0.26 \\ [1ex]
\hline
\end{tabular}
\end{table}
```
| true |
code
| 0.713419 | null | null | null | null |
|
**Srayan Gangopadhyay**
*17th May 2020*
# Testing Runge-Kutta method for 2nd-order ODEs
## Introducing the code
**1. Docstring, importing required modules, and info about correct form of ODE**
To solve a second-order differential equation using the Runge-Kutta method, we first need to rewrite it as two first-order ODEs as explained in the comment below.
```
"""
Upgrading Euler method to 4th-order Runge-Kutta
for 2nd-order ODEs
Srayan Gangopadhyay
2020-05-17
"""
import numpy as np
import matplotlib.pyplot as plt
# y' = dy/dx
# For a function of form y'' = f(x, y, y')
# Define y' = v so y'' = v'
```
**2. Function definition and parameters**
For the function $y'' = f(x, y, y')$ with initial conditions $y(x=0) = y_0$ and $y'(x=0) = y'_0$, the code takes as its input the right hand side of the equation $v' = f(x, y, v)$ where $v = y'$, as well as the initial conditions.
We also define the step size $h$, which determines the precision, and the $x$-value up to which we will integrate. From these parameters, the number of steps is calculated and empty arrays are initialised to hold the values for $y$ and $y'$, which will be determined by integration.
For the tests in this notebook, the problems and solutions are taken from Paul's Online Notes \[1].
```
def func(x, y, v): # RHS of v' = in terms of x, y, v
return 9*y
# PARAMETERS
y0 = 2 # y(x=0) =
v0 = -1 # y'(x=0) =
h = 0.01 # step size
end = 3 # x-value to stop integration
steps = int(end/h) # number of steps
x = np.linspace(0, end, steps) # array of x-values (discrete time)
y = np.zeros(steps) # empty array for solution
v = np.zeros(steps)
y[0] = y0 # inserting initial value
v[0] = v0
```
**3. Integrating using RK4 algorithm**
There are a few different definitions of the 4th-order Runge-Kutta algorithm, we chose to use the Wolfram Mathworld definition \[2].
```
# INTEGRATING
# using https://mathworld.wolfram.com/Runge-KuttaMethod.html
for i in range(0, steps-1):
k1y = h * v[i]
k1v = h * func(x[i], y[i], v[i])
k2y = h * (v[i] + 0.5*k1v)
k2v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k1v), (v[i] + 0.5*k1v))
k3y = h * (v[i] + 0.5*k2v)
k3v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k2v), (v[i] + 0.5*k2v))
k4y = h * (v[i] + k3v)
k4v = h * func(x[i+1], (y[i] + k3v), (v[i] + k3v))
y[i+1] = y[i] + (k1y + 2*k2y + 2*k3y + k4y) / 6
v[i+1] = v[i] + (k1v + 2*k2v + 2*k3v + k4v) / 6
```
**4. Plotting**
We then plot the calculated solution as well as, for these test cases, the known analytical solution.
```
plt.plot(x, y)
plt.plot(x, y, 'o', label='Approx. soln (RK4)')
plt.plot(x, (7/6)*np.exp(-3*x) + (5/6)*np.exp(3*x), label='True soln')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
```
We can see that the RK4 algorithm gives a solution which closely approximates the true solution, although the error grows with increasing $x$ (as expected for this type of numerical method.)
## More test cases
```
def func(x, y, v): # RHS of v' = in terms of x, y, v
return -3*v + 10*y
# PARAMETERS
y0 = 4 # y(x=0) =
v0 = -2 # y'(x=0) =
h = 0.01 # step size
end = 3 # x-value to stop integration
steps = int(end/h) # number of steps
x = np.linspace(0, end, steps) # array of x-values (discrete time)
y = np.zeros(steps) # empty array for solution
v = np.zeros(steps)
y[0] = y0 # inserting initial value
v[0] = v0
# INTEGRATING
# using https://mathworld.wolfram.com/Runge-KuttaMethod.html
for i in range(0, steps-1):
k1y = h * v[i]
k1v = h * func(x[i], y[i], v[i])
k2y = h * (v[i] + 0.5*k1v)
k2v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k1v), (v[i] + 0.5*k1v))
k3y = h * (v[i] + 0.5*k2v)
k3v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k2v), (v[i] + 0.5*k2v))
k4y = h * (v[i] + k3v)
k4v = h * func(x[i+1], (y[i] + k3v), (v[i] + k3v))
y[i+1] = y[i] + (k1y + 2*k2y + 2*k3y + k4y) / 6
v[i+1] = v[i] + (k1v + 2*k2v + 2*k3v + k4v) / 6
plt.plot(x, y)
plt.plot(x, y, 'o', label='Approx. soln (RK4)')
plt.plot(x, (10/7)*np.exp(-5*x) + (18/7)*np.exp(2*x), label='True soln')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
def func(x, y, v): # RHS of v' = in terms of x, y, v
return (-2/3)*v + (8/3)*y
# PARAMETERS
y0 = -6 # y(x=0) =
v0 = -18 # y'(x=0) =
h = 0.01 # step size
end = 3 # x-value to stop integration
steps = int(end/h) # number of steps
x = np.linspace(0, end, steps) # array of x-values (discrete time)
y = np.zeros(steps) # empty array for solution
v = np.zeros(steps)
y[0] = y0 # inserting initial value
v[0] = v0
# INTEGRATING
# using https://mathworld.wolfram.com/Runge-KuttaMethod.html
for i in range(0, steps-1):
k1y = h * v[i]
k1v = h * func(x[i], y[i], v[i])
k2y = h * (v[i] + 0.5*k1v)
k2v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k1v), (v[i] + 0.5*k1v))
k3y = h * (v[i] + 0.5*k2v)
k3v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k2v), (v[i] + 0.5*k2v))
k4y = h * (v[i] + k3v)
k4v = h * func(x[i+1], (y[i] + k3v), (v[i] + k3v))
y[i+1] = y[i] + (k1y + 2*k2y + 2*k3y + k4y) / 6
v[i+1] = v[i] + (k1v + 2*k2v + 2*k3v + k4v) / 6
plt.plot(x, y)
plt.plot(x, y, 'o', label='Approx. soln (RK4)')
plt.plot(x, (-9)*np.exp((4/3)*x) + (3)*np.exp(-2*x), label='True soln')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
def func(x, y, v): # RHS of v' = in terms of x, y, v
return 4*v - 9*y
# PARAMETERS
y0 = 0 # y(x=0) =
v0 = -8 # y'(x=0) =
h = 0.01 # step size
end = 3 # x-value to stop integration
steps = int(end/h) # number of steps
x = np.linspace(0, end, steps) # array of x-values (discrete time)
y = np.zeros(steps) # empty array for solution
v = np.zeros(steps)
y[0] = y0 # inserting initial value
v[0] = v0
# INTEGRATING
# using https://mathworld.wolfram.com/Runge-KuttaMethod.html
for i in range(0, steps-1):
k1y = h * v[i]
k1v = h * func(x[i], y[i], v[i])
k2y = h * (v[i] + 0.5*k1v)
k2v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k1v), (v[i] + 0.5*k1v))
k3y = h * (v[i] + 0.5*k2v)
k3v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k2v), (v[i] + 0.5*k2v))
k4y = h * (v[i] + k3v)
k4v = h * func(x[i+1], (y[i] + k3v), (v[i] + k3v))
y[i+1] = y[i] + (k1y + 2*k2y + 2*k3y + k4y) / 6
v[i+1] = v[i] + (k1v + 2*k2v + 2*k3v + k4v) / 6
plt.plot(x, y)
plt.plot(x, y, 'o', label='Approx. soln (RK4)')
plt.plot(x, (-8/np.sqrt(5))*np.exp(2*x)*np.sin(x*np.sqrt(5)), label='True soln')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
def func(x, y, v): # RHS of v' = in terms of x, y, v
return 8*v - 17*y
# PARAMETERS
y0 = -4 # y(x=0) =
v0 = -1 # y'(x=0) =
h = 0.001 # step size
end = 5 # x-value to stop integration
steps = int(end/h) # number of steps
x = np.linspace(0, end, steps) # array of x-values (discrete time)
y = np.zeros(steps) # empty array for solution
v = np.zeros(steps)
y[0] = y0 # inserting initial value
v[0] = v0
# INTEGRATING
# using https://mathworld.wolfram.com/Runge-KuttaMethod.html
for i in range(0, steps-1):
k1y = h * v[i]
k1v = h * func(x[i], y[i], v[i])
k2y = h * (v[i] + 0.5*k1v)
k2v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k1v), (v[i] + 0.5*k1v))
k3y = h * (v[i] + 0.5*k2v)
k3v = h * func((x[i] + 0.5*h), (y[i] + 0.5*k2v), (v[i] + 0.5*k2v))
k4y = h * (v[i] + k3v)
k4v = h * func(x[i+1], (y[i] + k3v), (v[i] + k3v))
y[i+1] = y[i] + (k1y + 2*k2y + 2*k3y + k4y) / 6
v[i+1] = v[i] + (k1v + 2*k2v + 2*k3v + k4v) / 6
plt.plot(x, y)
plt.plot(x, y, 'o', label='Approx. soln (RK4)')
plt.plot(x, -4*np.exp(4*x)*np.cos(x)+15*np.exp(4*x)*np.sin(x), label='True soln')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
```
## Sources
\[1]: P. Dawkins, Differential Equations - Real & Distinct Roots, 06-Mar-2018. \[Online]. Available: https://tutorial.math.lamar.edu/Classes/DE/RealRoots.aspx. \[Accessed: 17-May-2020].
\[2]: E. W. Weisstein, “Runge-Kutta Method,” Wolfram MathWorld. \[Online]. Available: https://mathworld.wolfram.com/Runge-KuttaMethod.html. \[Accessed: 17-May-2020].
| true |
code
| 0.680905 | null | null | null | null |
|
# Developing an AI application
Going forward, AI algorithms will be incorporated into more and more everyday applications. For example, you might want to include an image classifier in a smart phone app. To do this, you'd use a deep learning model trained on hundreds of thousands of images as part of the overall application architecture. A large part of software development in the future will be using these types of models as common parts of applications.
In this project, you'll train an image classifier to recognize different species of flowers. You can imagine using something like this in a phone app that tells you the name of the flower your camera is looking at. In practice you'd train this classifier, then export it for use in your application. We'll be using [this dataset](http://www.robots.ox.ac.uk/~vgg/data/flowers/102/index.html) of 102 flower categories, you can see a few examples below.
<img src='assets/Flowers.png' width=500px>
The project is broken down into multiple steps:
* Load and preprocess the image dataset
* Train the image classifier on your dataset
* Use the trained classifier to predict image content
We'll lead you through each part which you'll implement in Python.
When you've completed this project, you'll have an application that can be trained on any set of labeled images. Here your network will be learning about flowers and end up as a command line application. But, what you do with your new skills depends on your imagination and effort in building a dataset. For example, imagine an app where you take a picture of a car, it tells you what the make and model is, then looks up information about it. Go build your own dataset and make something new.
First up is importing the packages you'll need. It's good practice to keep all the imports at the beginning of your code. As you work through this notebook and find you need to import a package, make sure to add the import up here.
```
# Import packages
import torch
from torch import nn, optim
import torch.nn.functional as F
from torchvision import datasets, transforms, models
import matplotlib.pyplot as plt
import numpy as np
from workspace_utils import active_session
from PIL import Image
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
```
## Load the data
Here you'll use `torchvision` to load the data ([documentation](http://pytorch.org/docs/0.3.0/torchvision/index.html)). The data should be included alongside this notebook, otherwise you can [download it here](https://s3.amazonaws.com/content.udacity-data.com/nd089/flower_data.tar.gz). The dataset is split into three parts, training, validation, and testing. For the training, you'll want to apply transformations such as random scaling, cropping, and flipping. This will help the network generalize leading to better performance. You'll also need to make sure the input data is resized to 224x224 pixels as required by the pre-trained networks.
The validation and testing sets are used to measure the model's performance on data it hasn't seen yet. For this you don't want any scaling or rotation transformations, but you'll need to resize then crop the images to the appropriate size.
The pre-trained networks you'll use were trained on the ImageNet dataset where each color channel was normalized separately. For all three sets you'll need to normalize the means and standard deviations of the images to what the network expects. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`, calculated from the ImageNet images. These values will shift each color channel to be centered at 0 and range from -1 to 1.
```
data_dir = 'flowers'
train_dir = data_dir + '/train'
valid_dir = data_dir + '/valid'
test_dir = data_dir + '/test'
# Define transforms for the training, validation, and testing sets
# For the training set, randomly rotate, flip, and crop prior to normalizing to improve training
train_transforms = transforms.Compose([transforms.RandomHorizontalFlip(),
transforms.RandomResizedCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
# For the validation and testing sets, just crop and normalize the images
validate_transforms = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
test_transforms = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
# Load the datasets with ImageFolder
train_dataset = datasets.ImageFolder(train_dir, transform=train_transforms)
validate_dataset = datasets.ImageFolder(valid_dir, transform=validate_transforms)
test_dataset = datasets.ImageFolder(test_dir, transform=test_transforms)
# Using the image datasets and the transforms, define the dataloaders
trainloader = torch.utils.data.DataLoader(train_dataset, batch_size = 32, shuffle=True)
validloader = torch.utils.data.DataLoader(validate_dataset, batch_size = 32, shuffle=True)
testloader = torch.utils.data.DataLoader(test_dataset, batch_size = 32, shuffle=True)
```
### Label mapping
You'll also need to load in a mapping from category label to category name. You can find this in the file `cat_to_name.json`. It's a JSON object which you can read in with the [`json` module](https://docs.python.org/2/library/json.html). This will give you a dictionary mapping the integer encoded categories to the actual names of the flowers.
```
import json
with open('cat_to_name.json', 'r') as f:
cat_to_name = json.load(f)
```
# Building and training the classifier
Now that the data is ready, it's time to build and train the classifier. As usual, you should use one of the pretrained models from `torchvision.models` to get the image features. Build and train a new feed-forward classifier using those features.
We're going to leave this part up to you. Refer to [the rubric](https://review.udacity.com/#!/rubrics/1663/view) for guidance on successfully completing this section. Things you'll need to do:
* Load a [pre-trained network](http://pytorch.org/docs/master/torchvision/models.html) (If you need a starting point, the VGG networks work great and are straightforward to use)
* Define a new, untrained feed-forward network as a classifier, using ReLU activations and dropout
* Train the classifier layers using backpropagation using the pre-trained network to get the features
* Track the loss and accuracy on the validation set to determine the best hyperparameters
We've left a cell open for you below, but use as many as you need. Our advice is to break the problem up into smaller parts you can run separately. Check that each part is doing what you expect, then move on to the next. You'll likely find that as you work through each part, you'll need to go back and modify your previous code. This is totally normal!
When training make sure you're updating only the weights of the feed-forward network. You should be able to get the validation accuracy above 70% if you build everything right. Make sure to try different hyperparameters (learning rate, units in the classifier, epochs, etc) to find the best model. Save those hyperparameters to use as default values in the next part of the project.
One last important tip if you're using the workspace to run your code: To avoid having your workspace disconnect during the long-running tasks in this notebook, please read in the earlier page in this lesson called Intro to
GPU Workspaces about Keeping Your Session Active. You'll want to include code from the workspace_utils.py module.
**Note for Workspace users:** If your network is over 1 GB when saved as a checkpoint, there might be issues with saving backups in your workspace. Typically this happens with wide dense layers after the convolutional layers. If your saved checkpoint is larger than 1 GB (you can open a terminal and check with `ls -lh`), you should reduce the size of your hidden layers and train again.
```
# Build and train network
# Use a pretrained VGG 19 layer network with batch normalization
model = models.vgg19_bn(pretrained=True)
model
```
The VGG-19 layer model with batch normalization uses a classifier with 25088 inputs and 1000 outputs. To adapt this model to the flower data, it needs to have 102 outputs (the number of flower species in the dataset).
```
class DeepNetworkClassifier(nn.Module):
def __init__(self, input_units, output_units, hidden_units,p_drop=0.2):
'''
Builds a classifier for a pretrained deep neural network for the flower dataset
Inputs
------
input_units: int, the number of inputs to the model (needs to match ImageNet model)
output_units: int, the number of outputs from the model (needs to match the number of flower classes)
hidden_units: int, the number of hidden units in the hidden layer
'''
super().__init__()
# Create input layer with input units based on model architecture
self.input = nn.Linear(input_units,hidden_units)
# Create output layer with 102 outputs (for 102 flower classes)
self.output = nn.Linear(hidden_units,output_units)
# Define level of dropout
self.dropout = nn.Dropout(p=p_drop)
def forward(self, x):
'''
Performs a forward pass through the network and returns the log probabilities
x: layer in model
'''
# Apply ReLU activation function and dropout to the input layer
x = F.relu(self.input(x))
x = self.dropout(x)
# Apply Log Softmax function to output layer
x = self.output(x)
x = F.log_softmax(x,dim=1)
return x
# Use GPU if it's available
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Turn off gradient calculations for model parameters
for param in model.parameters():
param.requires_grad = False
# Replace the classifier with one designed for the flower dataset
classifier = DeepNetworkClassifier(25088, 102, 1000)
model.classifier = classifier
# Add the NLLLoss criterion (since LogSoftmax is called in the classifier)
criterion = nn.NLLLoss()
# Define the optimizer
optimizer = optim.Adam(model.classifier.parameters(), lr = 0.001)
# Send the model to the GPU
model.to(device);
# Keep the workspace active
with active_session():
# Train the network
# Define the number of epochs
epochs = 3
# Initialize some counters
steps = 0
running_loss = 0
print_every = 10
for epoch in range(epochs):
for images, labels in trainloader:
steps += 1
# Send the images and labels to the GPU
images, labels = images.to(device), labels.to(device)
# Zero gradients for this step
optimizer.zero_grad()
# Perform a forward pass on the models
log_ps = model(images)
# Calculate loss
loss = criterion(log_ps, labels)
# Backpropagate error
loss.backward()
# Take next step
optimizer.step()
# Aggregate loss
running_loss += loss.item()
# Display results
if steps % print_every == 0:
# Set model to evaluate mode
model.eval()
# Initialize the validation loss and accuracy
valid_loss = 0
valid_acc = 0
# Run validation dataset through the network
with torch.no_grad():
for images, labels in validloader:
# Send the images and labels to the GPU
images_v, labels_v = images.to(device), labels.to(device)
# Perform forward pass with validation images
log_ps_valid = model.forward(images_v)
# Calculate validation loss and aggregate
loss = criterion(log_ps_valid, labels_v)
valid_loss += loss
# Calculate validation accuracy
# Calculate the probabilities from the log_probabilities
ps = torch.exp(log_ps_valid)
# Determine the top probability
top_p, top_class = ps.topk(1, dim=1)
# Compare top_class to label
valid_equality = top_class == labels_v.view(*top_class.shape)
# Calculate accuracy by aggregating the equalities
valid_acc += torch.mean(valid_equality.type(torch.FloatTensor)).item()
# Print Results
print(f"Epoch {epoch+1}/{epochs}.. "
f"Training Loss: {running_loss/print_every:.3f}.. "
f"Validation Loss: {valid_loss/len(validloader):.3f}.. "
f"Validation Accuracy: {valid_acc/len(validloader):.3f}")
running_loss = 0
model.train()
```
## Testing your network
It's good practice to test your trained network on test data, images the network has never seen either in training or validation. This will give you a good estimate for the model's performance on completely new images. Run the test images through the network and measure the accuracy, the same way you did validation. You should be able to reach around 70% accuracy on the test set if the model has been trained well.
```
# Run the test dataset through the model
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Set model to evaluate mode
model.eval()
# Initialize the testing accuracy
test_acc = 0
# Run test dataset through the network
with torch.no_grad():
for images, labels in testloader:
# Send the images and labels to the GPU
images_t, labels_t = images.to(device), labels.to(device)
# Perform forward pass with validation images
log_ps_test = model.forward(images_t)
# Calculate test accuracy
# Calculate the probabilities from the log_probabilities
ps_test = torch.exp(log_ps_test)
# Determine the top probability
top_p, top_class = ps_test.topk(1, dim=1)
# Compare top_class to label
test_equality = top_class == labels_t.view(*top_class.shape)
# Calculate accuracy by aggregating the equalities
test_acc += torch.mean(test_equality.type(torch.FloatTensor)).item()
# Print Results
print("Test Accuracy: {:.3f}".format(test_acc/len(testloader)))
model.train();
```
## Save the checkpoint
Now that your network is trained, save the model so you can load it later for making predictions. You probably want to save other things such as the mapping of classes to indices which you get from one of the image datasets: `image_datasets['train'].class_to_idx`. You can attach this to the model as an attribute which makes inference easier later on.
```model.class_to_idx = image_datasets['train'].class_to_idx```
Remember that you'll want to completely rebuild the model later so you can use it for inference. Make sure to include any information you need in the checkpoint. If you want to load the model and keep training, you'll want to save the number of epochs as well as the optimizer state, `optimizer.state_dict`. You'll likely want to use this trained model in the next part of the project, so best to save it now.
```
# Save the checkpoint
checkpoint = {'input_size': 25088,
'output_size': 102,
'hidden_units': 1000,
'state_dict': model.state_dict(),
'epochs': epochs,
'optimizer_state_dict': optimizer.state_dict(),
'class_to_idx':train_dataset.class_to_idx,
'arch':'vgg19_bn'}
torch.save(checkpoint, 'checkpoint.pth')
```
## Loading the checkpoint
At this point it's good to write a function that can load a checkpoint and rebuild the model. That way you can come back to this project and keep working on it without having to retrain the network.
```
# Write a function that loads a checkpoint and rebuilds the model
def load_checkpoint(filepath):
'''
Rebuilds a VGG 19 layer model with batch normalization from a trained model
filepath: string, contains filepath where the trained model parameters are saved in a dictionary
returns: a pytorch model, the optimizer, and the number of epochs
'''
model_dict = torch.load(filepath, map_location='cpu')
model = models.vgg19_bn(pretrained=True)
for param in model.parameters():
param.requires_grad = False
model.classifier = DeepNetworkClassifier(model_dict['input_size'], model_dict['output_size'], model_dict['hidden_units'])
model.load_state_dict(model_dict['state_dict'])
model.class_to_idx = model_dict['class_to_idx']
optimizer = optim.Adam(model.classifier.parameters())
optimizer.load_state_dict(model_dict['optimizer_state_dict'])
epochs = model_dict['epochs']
return model, optimizer, epochs
model, optimizer, epochs = load_checkpoint('checkpoint.pth')
```
# Inference for classification
Now you'll write a function to use a trained network for inference. That is, you'll pass an image into the network and predict the class of the flower in the image. Write a function called `predict` that takes an image and a model, then returns the top $K$ most likely classes along with the probabilities. It should look like
```python
probs, classes = predict(image_path, model)
print(probs)
print(classes)
> [ 0.01558163 0.01541934 0.01452626 0.01443549 0.01407339]
> ['70', '3', '45', '62', '55']
```
First you'll need to handle processing the input image such that it can be used in your network.
## Image Preprocessing
You'll want to use `PIL` to load the image ([documentation](https://pillow.readthedocs.io/en/latest/reference/Image.html)). It's best to write a function that preprocesses the image so it can be used as input for the model. This function should process the images in the same manner used for training.
First, resize the images where the shortest side is 256 pixels, keeping the aspect ratio. This can be done with the [`thumbnail`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) or [`resize`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) methods. Then you'll need to crop out the center 224x224 portion of the image.
Color channels of images are typically encoded as integers 0-255, but the model expected floats 0-1. You'll need to convert the values. It's easiest with a Numpy array, which you can get from a PIL image like so `np_image = np.array(pil_image)`.
As before, the network expects the images to be normalized in a specific way. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`. You'll want to subtract the means from each color channel, then divide by the standard deviation.
And finally, PyTorch expects the color channel to be the first dimension but it's the third dimension in the PIL image and Numpy array. You can reorder dimensions using [`ndarray.transpose`](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ndarray.transpose.html). The color channel needs to be first and retain the order of the other two dimensions.
```
def process_image(image):
''' Scales, crops, and normalizes a PIL image for a PyTorch model,
returns an Numpy array
'''
# Process a PIL image for use in a PyTorch model
# Open the image
im = Image.open(image)
# Obtain the dimensions of the image
(w,h) = im.size
# Resize the image to 256 pixels on the shortest side
if w < h:
aspect_ratio = h/w
im.thumbnail((256, 256*aspect_ratio))
else:
aspect_ratio = w/h
im.thumbnail((256*aspect_ratio, 256))
# Obtain the new dimensions of the image
(w_new,h_new) = im.size
# Center crop the image to 224 x 224
cropped_image = im.crop((w_new//2 - 112, h_new//2 - 112, w_new//2 + 112, h_new//2 + 112))
# Convert image to numpy array
np_im = np.array(cropped_image)
# Scale from 0-255 to 0-1
np_im = np_im / 255
# Normalize
means = np.array([0.485, 0.456, 0.406])
stds = np.array([0.229, 0.224, 0.225])
image = (np_im - means) / stds
# Rearrange dimensions to match expected input into PyTorch (color channel in 1st dim instead of 3rd dim)
image = image.transpose((2,0,1))
return image
```
To check your work, the function below converts a PyTorch tensor and displays it in the notebook. If your `process_image` function works, running the output through this function should return the original image (except for the cropped out portions).
```
def imshow(image, ax=None, title=None):
"""Imshow for Tensor."""
if ax is None:
fig, ax = plt.subplots()
# PyTorch tensors assume the color channel is the first dimension
# but matplotlib assumes is the third dimension
image = image.numpy().transpose((1, 2, 0))
# Undo preprocessing
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
image = std * image + mean
# Image needs to be clipped between 0 and 1 or it looks like noise when displayed
image = np.clip(image, 0, 1)
# Turn off axes labels for cleaner image
ax.tick_params(axis='both', length=0)
ax.set_xticklabels('')
ax.set_yticklabels('')
ax.imshow(image)
plt.show()
# Grab an image from one of the datasets
test_image = 'flowers/train/1/image_06735.jpg'
# Display the original image
print('Original Image')
display(Image.open(test_image))
# Convert it from a numpy array (output of process_image function) to a tensor (input of imshow function)
test_image_tensor = torch.from_numpy(process_image(test_image))
# Display cropped image
print('Processed Image')
imshow(test_image_tensor)
```
## Class Prediction
Once you can get images in the correct format, it's time to write a function for making predictions with your model. A common practice is to predict the top 5 or so (usually called top-$K$) most probable classes. You'll want to calculate the class probabilities then find the $K$ largest values.
To get the top $K$ largest values in a tensor use [`x.topk(k)`](http://pytorch.org/docs/master/torch.html#torch.topk). This method returns both the highest `k` probabilities and the indices of those probabilities corresponding to the classes. You need to convert from these indices to the actual class labels using `class_to_idx` which hopefully you added to the model or from an `ImageFolder` you used to load the data ([see here](#Save-the-checkpoint)). Make sure to invert the dictionary so you get a mapping from index to class as well.
Again, this method should take a path to an image and a model checkpoint, then return the probabilities and classes.
```python
probs, classes = predict(image_path, model)
print(probs)
print(classes)
> [ 0.01558163 0.01541934 0.01452626 0.01443549 0.01407339]
> ['70', '3', '45', '62', '55']
```
```
def predict(image_path, model, topk=5):
''' Predict the class (or classes) of an image using a trained deep learning model.
'''
# Call the process_image function on the image
image = process_image(image_path)
# Convert to a tensor
image_tensor = torch.from_numpy(image)
image_tensor = image_tensor.unsqueeze(0)
# Run the test dataset through the model
# Set model to evaluate mode
model.to(torch.double)
model.eval()
# Run the image through the network
with torch.no_grad():
#for images, labels in testloader
#for image, label in image_loader:
# Perform a forward pass with the image
log_ps = model(image_tensor)
# Calculate the probabilities from the log_probabilities
ps = torch.exp(log_ps)
# Determine the top k probabilities
top_p, top_class = ps.topk(topk, dim=1)
labels = []
for i in top_class.tolist()[0]:
for cls, idx in model.class_to_idx.items():
if idx == i:
labels.append(cls)
# Return model to train mode
model.train()
return top_p.tolist()[0], labels
probs, classes = predict(test_image, model)
print(probs)
print(classes)
labels = []
for cls in classes:
labels.append(cat_to_name[cls])
print(labels)
```
## Sanity Checking
Now that you can use a trained model for predictions, check to make sure it makes sense. Even if the testing accuracy is high, it's always good to check that there aren't obvious bugs. Use `matplotlib` to plot the probabilities for the top 5 classes as a bar graph, along with the input image. It should look like this:
<img src='assets/inference_example.png' width=300px>
You can convert from the class integer encoding to actual flower names with the `cat_to_name.json` file (should have been loaded earlier in the notebook). To show a PyTorch tensor as an image, use the `imshow` function defined above.
```
fig, (ax1,ax2) = plt.subplots(2,1,figsize=(4,8))
## NOTE: The imshow function creates an instance of subplots, so a second subplot could not be created.
## To display both in the same plot, I copied the imshow function but removed the lines creating the subplots
image = test_image_tensor.numpy().transpose((1, 2, 0))
# Undo preprocessing
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
image = std * image + mean
# Image needs to be clipped between 0 and 1 or it looks like noise when displayed
image = np.clip(image, 0, 1)
# Turn off axes labels for cleaner image
ax1.set_title(cat_to_name['1'])
ax1.tick_params(axis='both', length=0)
ax1.set_xticklabels('')
ax1.set_yticklabels('')
ax1.imshow(image)
ax2.barh(np.arange(len(probs)),probs)
ax2.invert_yaxis()
ax2.set_yticks(np.arange(len(probs)))
ax2.set_yticklabels(labels)
plt.show()
```
| true |
code
| 0.854854 | null | null | null | null |
|
# Machine Learning Exercise 3 - Multi-Class Classification
This notebook covers a Python-based solution for the third programming exercise of the machine learning class on Coursera. Please refer to the [exercise text](https://github.com/jdwittenauer/ipython-notebooks/blob/master/exercises/ML/ex3.pdf) for detailed descriptions and equations.
For this exercise we'll use logistic regression to recognize hand-written digits (0 to 9). We'll be extending the implementation of logistic regression we wrote in exercise 2 and apply it to one-vs-all classification. Let's get started by loading the data set. It's in MATLAB's native format, so to load it in Python we need to use a SciPy utility.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
%matplotlib inline
data = loadmat('data/ex3data1.mat')
data
data['X'].shape, data['y'].shape
```
Great, we've got our data loaded. The images are represented in martix X as a 400-dimensional vector (of which there are 5,000 of them). The 400 "features" are grayscale intensities of each pixel in the original 20 x 20 image. The class labels are in the vector y as a numeric class representing the digit that's in the image.
The exercise code in MATLAB has a function provided to visualize the hand-written digits. I'm not going to reproduce that in Python, but there's an illustration in the exercise PDF if one is interested in seeing what the images look like. We're going to move on to our logistic regression implementation.
The first task is to modify our logistic regression implementation to be completely vectorized (i.e. no "for" loops). This is because vectorized code, in addition to being short and concise, is able to take advantage of linear algebra optimizations and is typically much faster than iterative code. However if you look at our cost function implementation from exercise 2, it's already vectorized! So we can re-use the same implementation here. Note we're skipping straight to the final, regularized version.
```
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def cost(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
reg = (learningRate / 2 * len(X)) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
return np.sum(first - second) / (len(X)) + reg
```
Next we need the function that computes the gradient. Again, we already defined this in the previous exercise, only in this case we do have a "for" loop in the update step that we need to get rid of. Here's the original code for reference:
```
def gradient_with_loop(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y
for i in range(parameters):
term = np.multiply(error, X[:,i])
if (i == 0):
grad[i] = np.sum(term) / len(X)
else:
grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
return grad
```
In our new version we're going to pull out the "for" loop and compute the gradient for each parameter at once using linear algebra (except for the intercept parameter, which is not regularized so it's computed separately). To follow the math behind the transformation, refer to the exercise 3 text.
Also note that we're converting the data structures to NumPy matrices (which I've used for the most part throughout these exercises). This is done in an attempt to make the code look more similar to Octave than it would using arrays because matrices automatically follow matrix operation rules vs. element-wise operations, which is the default for arrays. There is some debate in the community over wether or not the matrix class should be used at all, but it's there so we're using it in these examples.
```
def gradient(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1])
error = sigmoid(X * theta.T) - y
grad = ((X.T * error) / len(X)).T + ((learningRate / len(X)) * theta)
# intercept gradient is not regularized
grad[0, 0] = np.sum(np.multiply(error, X[:,0])) / len(X)
return np.array(grad).ravel()
```
Now that we've defined our cost and gradient functions, it's time to build a classifier. For this task we've got 10 possible classes, and since logistic regression is only able to distiguish between 2 classes at a time, we need a strategy to deal with the multi-class scenario. In this exercise we're tasked with implementing a one-vs-all classification approach, where a label with k different classes results in k classifiers, each one deciding between "class i" and "not class i" (i.e. any class other than i). We're going to wrap the classifier training up in one function that computes the final weights for each of the 10 classifiers and returns the weights as a k X (n + 1) array, where n is the number of parameters.
```
from scipy.optimize import minimize
def one_vs_all(X, y, num_labels, learning_rate):
rows = X.shape[0]
params = X.shape[1]
# k X (n + 1) array for the parameters of each of the k classifiers
all_theta = np.zeros((num_labels, params + 1))
# insert a column of ones at the beginning for the intercept term
X = np.insert(X, 0, values=np.ones(rows), axis=1)
# labels are 1-indexed instead of 0-indexed
for i in range(1, num_labels + 1):
theta = np.zeros(params + 1)
y_i = np.array([1 if label == i else 0 for label in y])
y_i = np.reshape(y_i, (rows, 1))
# minimize the objective function
fmin = minimize(fun=cost, x0=theta, args=(X, y_i, learning_rate), method='TNC', jac=gradient)
all_theta[i-1,:] = fmin.x
return all_theta
```
A few things to note here...first, we're adding an extra parameter to theta (along with a column of ones to the training data) to account for the intercept term. Second, we're transforming y from a class label to a binary value for each classifier (either is class i or is not class i). Finally, we're using SciPy's newer optimization API to minimize the cost function for each classifier. The API takes an objective function, an initial set of parameters, an optimization method, and a jacobian (gradient) function if specified. The parameters found by the optimization routine are then assigned to the parameter array.
One of the more challenging parts of implementing vectorized code is getting all of the matrix interactions written correctly, so I find it useful to do some sanity checks by looking at the shapes of the arrays/matrices I'm working with and convincing myself that they're sensible. Let's look at some of the data structures used in the above function.
```
rows = data['X'].shape[0]
params = data['X'].shape[1]
all_theta = np.zeros((10, params + 1))
X = np.insert(data['X'], 0, values=np.ones(rows), axis=1)
theta = np.zeros(params + 1)
y_0 = np.array([1 if label == 0 else 0 for label in data['y']])
y_0 = np.reshape(y_0, (rows, 1))
X.shape, y_0.shape, theta.shape, all_theta.shape
```
These all appear to make sense. Note that theta is a one-dimensional array, so when it gets converted to a matrix in the code that computes the gradient, it turns into a (1 X 401) matrix. Let's also check the class labels in y to make sure they look like what we're expecting.
```
np.unique(data['y'])
```
Let's make sure that our training function actually runs, and we get some sensible outputs, before going any further.
```
all_theta = one_vs_all(data['X'], data['y'], 10, 1)
all_theta
```
We're now ready for the final step - using the trained classifiers to predict a label for each image. For this step we're going to compute the class probability for each class, for each training instance (using vectorized code of course!) and assign the output class label as the class with the highest probability.
```
def predict_all(X, all_theta):
rows = X.shape[0]
params = X.shape[1]
num_labels = all_theta.shape[0]
# same as before, insert ones to match the shape
X = np.insert(X, 0, values=np.ones(rows), axis=1)
# convert to matrices
X = np.matrix(X)
all_theta = np.matrix(all_theta)
# compute the class probability for each class on each training instance
h = sigmoid(X * all_theta.T)
# create array of the index with the maximum probability
h_argmax = np.argmax(h, axis=1)
# because our array was zero-indexed we need to add one for the true label prediction
h_argmax = h_argmax + 1
return h_argmax
```
Now we can use the predict_all function to generate class predictions for each instance and see how well our classifier works.
```
y_pred = predict_all(data['X'], all_theta)
correct = [1 if a == b else 0 for (a, b) in zip(y_pred, data['y'])]
accuracy = (sum(map(int, correct)) / float(len(correct)))
print 'accuracy = {0}%'.format(accuracy * 100)
```
Almost 98% isn't too bad! That's all for exercise 3. In the next exercise, we'll look at how to implement a feed-forward neural network from scratch.
| true |
code
| 0.479138 | null | null | null | null |
|
# <u>Spotify Hit Predictor Model for 60's Dataset</u>
### Importing Libraries
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import tensorflow as tf
from tensorflow import keras
%matplotlib inline
import matplotlib as mpl #add'l plotting functionality
```
### Loading Dataset
```
df=pd.read_csv("dataset-of-60s.csv")
df.head()
df.info()
df.shape
```
### Shuffling of Data
```
df=df.sample(frac=1)
df.head()
```
### Balancing of Data
```
#Dropping Categorical features
X=df.drop(['target',"track","artist","uri"],axis=1)
X.shape #modified dataframe for X
Y=df["target"]
hit_flop_count=Y.value_counts()
hit_flop_count
Y=Y.values
```
### Standardizing the Inputs
```
scaler=StandardScaler()
scaled_X=scaler.fit_transform(X)
```
### Split the dataset into Train, Test, Validation set
```
#train-test split in 90%-10%
x_train, x_test, y_train, y_test = train_test_split(scaled_X, Y,
test_size=0.1, random_state=1)
#Train-Validation split 90%-10%
x_train, x_val, y_train, y_val = train_test_split(x_train,y_train,
test_size=(1/9), random_state=1)
#1/9 of 90% is 10% as we are using train if we use Scaled X then we use test size as 0.1
x_train.shape,x_test.shape,x_val.shape
```
### Creating Deep Learning Algorithm
```
nn = 200 #number of neurons in hidden layers
target_count = 2 #ouput i.e. 1 and 0
model_60 = keras.Sequential([
keras.layers.Flatten(), #to flaten our data for better results
keras.layers.Dense(nn, activation=tf.nn.relu),# first hidden layer
keras.layers.Dense(nn, activation=tf.nn.relu),# second hidden layer
keras.layers.Dense(nn, activation=tf.nn.relu),# third hidden layer
keras.layers.Dense(target_count, activation=tf.nn.softmax)# output layer
])
model_60.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
#fitting the model
model_fit = model_60.fit(x_train, y_train, epochs=20,
validation_data=(x_val, y_val), batch_size=100)
#Storing the predictions
predictions = model_60.predict(x_test)
```
### Visualize Neural Network Loss History
#### Loss Variation Plot
```
training_loss = model_fit.history['loss']
validation_loss = model_fit.history['val_loss']
epoch_count1 = range(1, len(training_loss) + 1)
#-------------plotting--------------------------
mpl.rcParams['figure.dpi'] = 400 #high res figures
plt.subplot(2,1,2)
plt.title('Loss Variation Plot')
plt.plot(epoch_count1, training_loss, color='violet', label='Training Loss')
plt.plot(epoch_count1, validation_loss, color='indigo', label='Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
```
#### Accuracy Variation Plot
```
training_acc = model_fit.history['accuracy']
validation_acc = model_fit.history['val_accuracy']
epoch_count2 = range(1, len(training_acc) + 1)
#plotting
plt.subplot(2,1,2)
plt.title('Accuracy Variation Plot')
plt.plot(epoch_count2, training_acc, color='red', label='Training Accuracy')
plt.plot(epoch_count2, validation_acc, color='green', label='Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
```
### Testing Model
```
print(predictions[215])
print('Predicted:', np.argmax(predictions[215]))
print('Original:', y_test[215])
```
### Saving model and Verifying
```
model_60.save('Trained_model_60') #saved as protobuf (.pb)
model_60.summary()
model = tf.keras.models.load_model('Trained_model_60')
print(x_test[1])
print(x_test[1].reshape( 1,-1))
v = model.predict(x_test[1].reshape( 1,-1))
print(v)
```
| true |
code
| 0.712582 | null | null | null | null |
|
<table>
<tr align=left><td><img align=left src="./images/CC-BY.png">
<td>Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license. (c) Kyle T. Mandli</td>
</table>
```
from __future__ import print_function
%matplotlib inline
import os
import numpy
import matplotlib.pyplot as plt
import matplotlib.animation
from IPython.display import HTML
from clawpack import pyclaw
from clawpack import riemann
```
# Nonlinear Scalar Conservation Laws
Up until now we have mostly assumed that our PDE
$$
q_t + f(q)_x = 0
$$
has been linear, i.e. $f(q) = A q$. Part of this was to establish the basic theory while we know what the true solution should look like. We now will investigate how nonlinear problems do not simply translate but can deform the solution in interesting ways. Note that we will assume that $f(q)$ is convex/concave, i.e. $f''(q)$ does not change sign.
As a test problem we will consider basic traffic flow as our PDE of choice. For this we assume that we can model traffic, or the density of cars, as a continuum as we do for fluids. This leads us to the conservation law
$$
q_t + (U(q) q)_x = 0
$$
where $q$ represents the density of cars and $U(q)$ the speed of those cars. We then need to specify the relationship between the speed at which the cars travel and the local density of cars.
The Lighthill, Whitham, and Richards (LWR) equation uses a simple function for the speed that is
$$
U(q) = u_{\text{max}}(1 - q) \text{ for } 0 \leq q \leq 1
$$
where $u_{\text{max}}$ is the speed limit and assumed constant. Adding this to our previous equation leads us to a flux defined as
$$
f(q) = u_{\text{max}}(1 - q) q
$$
that is concave with respect to $q$.
```
def traffic_animation(init_condition="gaussian"):
solver = pyclaw.ClawSolver1D(riemann.traffic_1D)
solver.bc_lower[0] = pyclaw.BC.extrap
solver.bc_upper[0] = pyclaw.BC.extrap
x = pyclaw.Dimension(-30.0,30.0,500,name='x')
domain = pyclaw.Domain(x)
num_eqn = 1
state = pyclaw.State(domain,num_eqn)
grid = state.grid
xc=grid.p_centers[0]
if init_condition.lower() == "shock":
state.q[0, :] = 0.75 * (xc > 0)
elif init_condition.lower() == "rarefaction":
state.q[0, :] = 0.75 * (xc < 0)
elif init_condition.lower() == "gaussian":
state.q[0, :] = 1.0 * numpy.exp(-xc**2 / 10.0**2)
else:
raise ValueError("Unknown initial condition requested.")
state.problem_data['efix']=True
state.problem_data['umax']=1.
claw = pyclaw.Controller()
claw.tfinal = 25.0
claw.num_output_times = 20
claw.solution = pyclaw.Solution(state,domain)
claw.solver = solver
claw.keep_copy = True
claw.run()
x = claw.frames[0].grid.dimensions[0].centers
fig = plt.figure()
axes = plt.subplot(1, 1, 1)
axes.set_xlim((x[0], x[-1]))
axes.set_ylim((-0.1, 1.1))
axes.set_title("Traffic Flow")
def init():
axes.set_xlim((x[0], x[-1]))
axes.set_ylim((-0.1, 1.1))
computed_line, = axes.plot(x[0], claw.frames[0].q[0, :][0], 'bo-')
return (computed_line, )
computed_line, = init()
def fplot(n):
computed_line.set_data([x,], [claw.frames[n].q[0, :]])
return (computed_line, )
frames_to_plot = range(0, len(claw.frames))
plt.close(fig)
return matplotlib.animation.FuncAnimation(fig, fplot, frames=frames_to_plot, interval=100,
blit=True, init_func=init, repeat=False)
HTML(traffic_animation().to_jshtml())
```
Let us first examine how the characteristics behave in this simple case where the initial condition is smooth but leads to a discontinuous solution. If we think of the $k$th car whose trajectory is $X_k(t)$. If we assume that the $k$th car makes a decision on how fast she goes $U_(q_k(t))$ then we have
$$
X'_k(t) = U_k(q_k(t)) = U([X_{k+1}(t) - X_k(t)]^{-1}) \quad \text{for} ~ k=1,\ldots,m
$$
with the boundaries appropriately specified.
Note that for these test cases that the characteristic speed agrees with the speed at which the particles are moving. This is a general property of nonlinear hyperbolic PDEs and arises as $f'(q) \neq u$ as it is in the linear case.
## Quasilinear Forms and Characteristics
One useful way we can analyze what may go on given a nonlinear flux is to study the quasilinear form of the PDE defined as
$$
q_t + f'(q)q_x = 0.
$$
If $q(x,t)$ is smooth then we would have
$$
X'(t) = f'(q(X(t), t))
$$
and
$$
\frac{\text{d}}{\text{d}t} q(X(t), t) = X'(t) q_x + q_t = 0
$$
and therefore $q(x,t)$ is constant on the characteristic curves defined by $X(t)$.
As we know once we have the characteristics and know that $q$ needs to be constant on them that we need to simply trace back the characteristics to the initial condition (or boundary condition) to find out what the solution is. Often times we represent this as
$$
q(x,t) = q_0(\xi)
$$
where
$$
x = \xi + f'(q_0(\xi)) t.
$$
## Burgers Equation
Another of the often used basic equations that are solved when considering nonlinear conservation laws is Burgers equation, defined as
$$
u_t + \left( \frac{1}{2} u^2 \right)_x = 0.
$$
Sometimes this is also referred to as the inviscid Burgers equation as the Burgers equation is meant to be a simplified model of fluid flow which usually also includes viscosity in
$$
u_t + \left( \frac{1}{2} u^2 \right)_x = \epsilon u_{xx}.
$$
We will use this eventually to define the set of solutions that are "physical".
The Burgers equation also can be written in non-conservative form as
$$
u_t + u u_x = 0
$$
but as we will see for discontinuous solutions that we will come to different answers than the conservative form. We will discuss this later again in relation to entropy conditions.
```
path = os.path.join(os.environ.get("CLAW", os.getcwd()), "pyclaw", "fvmbook", "chap11", "burgers")
os.chdir(path)
import burgers1D
def burgers_animation():
# compute the solution with the method define above:
claw = burgers1D.burgers()
claw.keep_copy = True
claw.run()
x = claw.frames[0].grid.dimensions[0].centers
fig = plt.figure()
axes = plt.subplot(1, 1, 1)
axes.set_xlim((x[0], x[-1]))
axes.set_ylim((-3.5, 6))
axes.set_title("Burgers Equation")
def init():
axes.set_xlim((x[0], x[-1]))
axes.set_ylim((-3.5, 6))
computed_line, = axes.plot(x[0], claw.frames[0].q[0, :][0], 'bo-')
return (computed_line, )
computed_line, = init()
def fplot(n):
computed_line.set_data([x,], [claw.frames[n].q[0, :]])
return (computed_line, )
frames_to_plot = range(0, len(claw.frames))
plt.close(fig)
return matplotlib.animation.FuncAnimation(fig, fplot, frames=frames_to_plot, interval=100,
blit=True, init_func=init, repeat=False)
HTML(burgers_animation().to_jshtml())
```
## Rarefaction Waves
The first type of nonlinaer wave we will consider is ararefaction wave. In traffic flow this occurs if $q_x(x,0) < 0$. The characteristic speed is
$$
f'(q) = U(q) + q U'(q) = u_{\text{max}} ( 1- 2q).
$$
```
HTML(traffic_animation(init_condition="rarefaction").to_jshtml())
```
From this example we see that the cars are being "rarefied", spreading out, or becoming less dense and that the solution is smooth. In this case as well we sometimes call this a **centered rarefaction wave** as it is centered at zero and moving in both directions.
## Compression Waves
The original solution of traffic flow is an example of a **compression wave**. These types of waves usually are composed of a shock and then a rarefaction wave and are called compression waves as they represent a compression of density of cars.
```
HTML(traffic_animation(init_condition="gaussian").to_jshtml())
```
## Vanishing Viscosity Limit
As we know, once a shock form the strong form of the PDE breaks down and only the integral form, or **weak form**, is valid.
One way to avoid this situation is to add a vanishingly small amount of viscosity to the solution such as
$$
q_t + f(q)_x = \epsilon q_{xx}.
$$
This keeps the shock from completely forming and is also motivated by fluid mechanics where often times the viscosity is small with respect to the other terms in the equation.
Unfortunately this formulation is now a parabolic equation so often we look at this as a means for picking a limiting solution as we will see later. As $\epsilon \rightarrow 0$ we recover the **vanishing viscosity limit** and re-obtain the original hyperbolic formulation.
## Equal-Area Rule
The equal-area rule concerns how to take a solution that is no longer a function, similar to a breaking wave, and placing a shock such that the triple-valued function divides the overlap into equal areas under the curve. This in reality is a consequence of conservation, we do not want to loose the value of the integral of $q(x,t)$ and so place the shock accordingly.
## Shock Speed
Although the equal-area rule works we often desire a m ore fundamental way to know the location and speed of a shock. Say that we have a shock traveling at a speed $s(t)$. The integral conservation law provides us a way to find this speed by integrating over the rectangle $[x_0, x_0 + \Delta x] \times [t_0, t_0 + \Delta t]$ that the shock will exactly split from corner to corner. If we set up this integral we then have
$$
\int^{x_0 + \Delta x}_{x_0} q(x, t_0 + \Delta t) dx - \int^{x_0 + \Delta x}_{x_0} q(x, t_0) dx = \int^{t_0 + \Delta t}_{t_0} f(q(x_0, t)) dt - \int^{t_0 + \Delta t}_{t_0} f(q(x_0 + \Delta x, t)) dt.
$$
By design the values along the rectangle are constant and the integral conservation law can be rewritten as
$$\begin{aligned}
\int^{x_0 + \Delta x}_{x_0} q(x, t_0 + \Delta t) dx - \int^{x_0 + \Delta x}_{x_0} q(x, t_0) dx &= \int^{t_0 + \Delta t}_{t_0} f(q(x_0, t)) dt - \int^{t_0 + \Delta t}_{t_0} f(q(x_0 + \Delta x, t)) dt \\
\Delta x q_r - \Delta x q_\ell &= \Delta t f(q_\ell) - \Delta t f(q_r) + \mathcal{O}(\Delta t^2).
\end{aligned}$$
Noting that the speed of the shock should approximately be
$$
s(t) = \frac{\Delta x}{\Delta t} + \mathcal{O}(\Delta t^2)
$$
as this rectangle shrinks we have
$$
s(t) (q_r - q_\ell) = f(q_r) - f(q_\ell).
$$
This expression is often called the **Rankine-Hugoniot jump condition**.
If we have a scalar conservation law then this condition is often rewritten as
$$
s = \frac{f(q_r) - f(q_\ell)}{q_r - q_\ell}.
$$
Note that we have written the jump condition in terms of $q_r$ and $q_\ell$. In general these values are changing in time and could cause the shock speed to change in time.
In the case where $q_r \approx q_\ell$ we see that this is starting to approach a derivative of $f(q)$ with respect to $q$ and the problem starts to become linear. We often call this type of shock a **weak shock**.
For traffic flow we have
$$
s = u_{\text{max}} [1 - (q_\ell + q_r)] = \frac{1}{2} [ f'(q_\ell) + f'(q_r)].
$$ and for Burgers equation we have
$$
s = \frac{1}{2} (u_\ell + u_r).
$$
This averaging is not coincidental. For quadratic flux functions the shock speed is the average of the characteristic speeds on either side of the shock. This is also indicative of the equal-area rule.
## Rankine-Hugoniot Conditions for Systems
In the case of systems we can of course not divide through by the difference in states to isolate the shock speed. Instead we must in general solve a nonlinear system to find the shock speed.
In the case of a linear hyperbolic PDE we can start to see though how we may accomplish this. If $f(q) = A q$ then we would have
$$
A (q_r - q_\ell) = s(q_r - q_\ell).
$$
This is of course a eigenproblem where the shock speed $s$ corresponds to the eigenvalues and the jump in $q$ the eigenvectors.
## Similarity Solutions and Centered Rarefactions
So far we have not specifically cared about Riemann problem data. In this case a conservation law in general will be a similarity solution. In the case of our form of equation then the solution is a function
$$
q(x,t) = \widetilde{q}(\xi) \quad \text{where} \quad \xi = x/t.
$$
Using this fact in combination with our Riemann problem initial condition we can compute
$$
q_t(x,t) = -\frac{x}{t^2} \widetilde{q}'(\xi) \quad \text{and} \quad f(q)_x = \frac{1}{t} f'(\widetilde{q}(\xi)) \widetilde{q}'(\xi)
$$
leading to
$$\begin{aligned}
f(q)_x &= -q_t \\
\frac{1}{t} f'(\widetilde{q}(\xi)) \widetilde{q}'(\xi) &= \frac{x}{t^2} \widetilde{q}'(\xi) \\
f'(\widetilde{q}(\xi)) \widetilde{q}'(\xi) &= \xi \widetilde{q}'(\xi)
\end{aligned}$$
For the scalar case either $\widetilde{q}(\xi) = 0$ or
$$
f'(\widetilde{q}(\xi)) = \xi
$$
allowing us to calculate the solution of the centered rarefaction directly.
### Example: Traffic Flow
We know that if $q_\ell > q_r$ that we have a rarefaction. This implies that
$$
\widetilde{q}(\xi) = \left \{ \begin{aligned}
q_\ell && \text{for } \xi \leq f'(q_\ell) \\
q_r && \text{for } \xi \geq f'(q_r)
\end{aligned} \right .$$
This leaves a wedge, the rarefaction wave to still compute. From our statement before we know
$$\begin{aligned}
f'(\widetilde{q}(\xi)) &= \xi \\
u_\text{max} [ 1 - 2 \widetilde{q}(\xi)] &= \xi \\
\widetilde{q}(\xi) &= \frac{1}{2} \left[1 - \frac{\xi}{u_\text{max}} \right] \quad \text{for} \quad f'(q_\ell) \leq \xi \leq f'(q_r)
\end{aligned}$$
Note that this satisfies the condition that the solution is continuous.
## Weak Solutions
We will now derive a different from of the conservation law, more similar to the weak form of PDEs that are common in finite element analysis. If we instead start from the strong form and integrate over space-time arbitrarily we have
$$
\int^{t_1}_{t_0} \int^{x_1}_{x_0} [q_t + f(q)_x] dx dt = 0.
$$
Introduce a **test function** $\phi(x,t)$ and rewrite the above integral as
$$
\int^{\infty}_{0} \int^{\infty}_{-\infty} [q_t + f(q)_x] \phi(x, t) dx dt = 0.
$$
where we require that $\phi(x,t)$ has compact support. In particular we would get back our original integral if
$$
\phi(x,t) = \left \{ \begin{aligned}
1 &\quad\text{if} ~ (x, t) \in [x_0, x_1] \times [t_0, t_1] \\
0 &\quad \text{otherwise}
\end{aligned} \right .
$$
Integrating by parts then gives us
$$
\int^{\infty}_{0} \int^{\infty}_{-\infty} [q \phi_t + f(q) \phi_x] dx dt = - \int^\infty_0 q(x, 0) \phi(x, 0) dx.
$$
Note that now the derivatives are no longer on $q$ or $f(q)$ but on the test functions.
The function $q(x,t)$ is called a **weak solution** of the conservation law with given initial data $q(x,0)$ if
$$
\int^{\infty}_{0} \int^{\infty}_{-\infty} [q \phi_t + f(q) \phi_x] dx dt = - \int^\infty_0 q(x, 0) \phi(x, 0) dx
$$
holds for all function $\phi \in C^1_0$.
## Why Should You Be Careful When Manipulating Conservation Laws?
Transforming a conservation law into different differential forms has a consequence that the weak solutions one might find may not be equivalent. This is best shown by an example.
### Example: Burgers' Equation
The canonical form of Burgers' equation is
$$
u_t + \left( \frac{1}{2} u^2 \right )_x = 0
$$
with a quasilinear form defined by
$$
u_t + u u_x = 0.
$$
If we multiply this latter form by $2u$ we get
$$\begin{aligned}
2 u u_t + 2 u^2 u_x &= 0 \\
(u^2)_t + \left(\frac{2}{3} u^3 \right)_x &= 0.
\end{aligned}$$
This form again is now a conservation law for $u^2$. For smooth solutions, i.e. strong solutions, the first form and last form have equivalent solutions. However for weak solutions we find differences. If we have shocks in our solution, i.e. $u_\ell > u_r$, then we have shock speeds
$$
s_1 = \frac{1}{2} (u_\ell + u_r)
$$
as before and
$$
s_2 = \frac{2}{3} \left(\frac{u_r^3 - u_\ell^3}{u^2_r - u_\ell^2} \right).
$$
Clearly $s_1 \neq s_2$ in this case. What we have done requires that the solution $u$ must be smooth and therefore leads to a different set of weak solutions.
## Nonuniqueness, Admissibility , and Entropy Conditions
Unfortunately when we are computing weak solutions to a PDE we often find that nonuniqueness can be an issue. In this last section we consider ways to pick out the relevant solution.
**Basic Problem:** is that if we consider the weak form of the equation for a Riemann problem (or others for that matter) that both a rarefaction and a shock are solutions. We know that there really is only one solution but the weak form allows both so we need a means of picking the solution that is correct.
One idea we have already mentioned, the vanishing viscosity limit, can be used to pick out a solution. We know that in the case where we have added the elliptic term $\epsilon u_{xx}$ that the equation now has a unique, smooth solution.
Often these types of conditions are called **admissibility conditions** or **entropy conditions**. The latter often includes a function $\eta(q)$ called an **entropy function** that helps to determine the solution that we want.
The first entropy condition we will define is used only for scalar conservation laws but is useful none the less.
**Entropy Condition - Lax:** For a convex scalar conservation law, a discontinuity propagating with speed $s$ given by the Rankine-Hugoniot condition satisfies the Lax entropy condition if
$$
f'(q_\ell) > s > f'(q_r).
$$
In this condition $f'(q)$ is the characteristic speed so this condition suggests that the characteristics on either side should be *impinging* on the shock.
If the flux function is non-convex we do have a more general entropy condition as well.
**Entropy Condition - Oleinik:** $q(x,t)$ is the entropy solution to a scalar conservation law $q_t + f(q)_x = 0$ with $f''(q) > 0$ if there exists a constant $E > 0$ s.t. $\forall a > 0, t > 0$, and $x \in \mathbb R$,
$$
\frac{q(x + a, t) - q(x,t)}{a} < \frac{E}{t}.
$$
### Entropy Functions
As mentioned an alternative approach to admissibility conditions is defining an entropy function. Usually these are derived from some physical principle as the namesake suggests.
In general an entropy should be conserved when $q(x,t)$ is smooth and decrease or increase at a shock.
One example is the entropy of gas. By the laws of thermodynamics we know that entropy must be produced at an admissible shock but is reduced across an inadmissible shock.
Turning to the mathematical definitions we need an entropy function $\eta(q)$ and an entropy flux $\psi(q)$ that satisfies a new integral conservation law defined by
$$
\int_{x_1}^{x_2} \eta(q(x,t_2)) dx = \int^{x_2}_{x_1} \eta(q(x,t_1)) dx + \int^{t_2}_{t_1} \psi(q(x_1, t)) dt - \int^{t_2}_{t_1} \psi(q(x_2, t)) dt.
$$
This holds whenever $q(x,t)$ is smooth. When $q(x,t)$ is not smooth we expect this equation not to hold but instead turns into an inequality statement
$$
\int_{x_1}^{x_2} \eta(q(x,t_2)) dx \leq \int^{x_2}_{x_1} \eta(q(x,t_1)) dx + \int^{t_2}_{t_1} \psi(q(x_1, t)) dt - \int^{t_2}_{t_1} \psi(q(x_2, t)) dt.
$$
As perhaps expected if $q(x,t)$ is indeed smooth it can be manipulated as we have done before to derive
$$
\eta(q)_t + \psi(q)_x = 0.
$$
Note also that if $\eta$ and $\psi$ are smooth functions we can write
$$
\eta'(q) q_t + \psi'(q) q_x = 0,
$$
which comparing this to the original quasilinear form
$$
q_t + f'(q) q_x = 0
$$
from before allows us to identify
$$
\psi'(q) = \eta'(q) f'(q)
$$
that should hold.
Interestingly for systems of equations we still require only scalar functions for $\eta$ and $\psi$. This makes sense physically as entropy is only a scalar function. Now however when we take a derivative of $\eta$ for instance we have
$$
\eta'(q) = \begin{bmatrix} \frac{\partial \eta}{\partial q_1} & \frac{\partial \eta}{\partial q_2} & \cdots & \frac{\partial \eta}{\partial q_1} \end{bmatrix}.
$$
We can also relate the idea of vanishing viscosity solution to the idea of entropy functions. Define the related viscous equation as
$$
q^\epsilon_t + f(q^\epsilon)_x = \epsilon q^\epsilon_{xx}
$$
and the associated entropy equation as
$$
\eta(q^\epsilon)_t + \psi(q^\epsilon)_x = \epsilon \eta'(q^\epsilon) q^\epsilon_{xx}
$$
we can write (for smooth solutions) the expression derived before as
$$
\eta(q^\epsilon)_t + \psi(q^\epsilon)_x = \epsilon(\eta'(q^\epsilon) q^\epsilon_x)_x - \epsilon \eta''(q^\epsilon) (q^\epsilon_x)^2.
$$
Integrating this equation over our usual rectangle leads to
$$\begin{aligned}
\int^{x_2}_{x_1} \eta(q^\epsilon(x, t_2)) dx &= \int^{x_2}_{x_1} \eta(q^\epsilon(x,t_1) dx - \left ( \int^{t_2}_{t_1} \psi(q^\epsilon(x_2, t)) dt - \int^{t_2}_{t_1} \psi(q^\epsilon(x_1, t)) dt \right) \\
&+ \epsilon \int^{t_2}_{t_1} [\eta'(q^\epsilon(x_2,t)) q^\epsilon_x(x_2, t) - \eta'(q^\epsilon(x_1,t)) q^\epsilon_x(x_1, t)] dt \\
&- \epsilon \int^{t_2}_{t_1} \int^{x_2}_{x_1} \eta''(q^\epsilon) (q^\epsilon_x)^2 dx dt
\end{aligned}$$
The usual flux differences are here but there are two additional terms that are multiplied by $\epsilon$. As $\epsilon \rightarrow 0$ one can show that an entropy integral relation results.
We can also derive a true weak form of the entropy condition as was done before. A weak solution $q$ satisfied the **weak form of the entropy inequality** if
$$
\int^\infty_0 \int^\infty_{-\infty} [\phi_t \eta(q) + \phi_x \psi(q)] dx dt + \int^\infty_{-\infty} \phi(x, 0) \eta(q(x,0)) dx \geq 0
$$
for all $\phi in C^1_0(\mathbb R \times \mathbb R)$ with $\phi(x,t) \geq 0$ $\forall x,t$.
Another useful form of the entropy conditions can be defined similar to the Rankine-Hugoniot conditions and are derived similar to as before where now they take the form
$$
s(\eta(q_r) - \eta(q_\ell)) \leq \psi(q_r) - \psi(q_\ell).
$$
#### Example: Burgers' Equation
As was discussed previously we can use
$$
\eta(u) = u^2
$$
with
$$
\psi(u) = \frac{2}{3} u^3.
$$
If we have a shock propagating at speed
$$
s = \frac{1}{2} (u_\ell + u_r)
$$
then the entropy condition requires
$$
\frac{1}{2} (u_\ell + u_r) (u^2_r - u^2_\ell) \geq \frac{2}{3} (u^3_r - u^3_\ell).
$$
This then leads to the expression
$$
\frac{1}{6} (u_\ell - u_r)^3 \geq 0
$$
implying that the entropy condition is only satisfied if $u_\ell > u_r$ we have already noticed due to the Lax entropy condition.
### The Kruzkov Entropies
The previous analysis assumes that the entropy function should be strictly convex with $\eta'' > 0$ at all $q$. We can relax this condition by utilizing an idea due to Kruzkov who suggested a family of entropy functions rather than just one. This is generalized to
$$
\eta_k(q) = |q - k|, \quad \psi_k(q) = \text{sign}(q-k)[f(q) - f(k)]
$$
where $k \in \mathbb R$. Note that ever $\eta_k$ is a piecewise defined, linear function of $q$ but that the higher derivatives are not neccesarily continuous. We also see that $\eta''(q) = \delta(q - k)$ because of this.
### Long-Term Behavior and N-Wave Decay
We have seen before that for longer term behavior of solutions to both Burgers' equation and traffic-flow that we see an N-wave like solution that appears to be decaying. This is indicative of the idea that entropy increases over a shock and information is "lost".
| true |
code
| 0.68763 | null | null | null | null |
|
# Predict a car's market price using its attributes
Using fundamental machine learning k nearest neighbor regression technique.
Date May 15, 2018
Reference --> http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsRegressor.html
About the Data --> http://archive.ics.uci.edu/ml/datasets/Automobile
```
import pandas as pd
#df = pd.read_csv('imports-85.csv')
df = pd.read_table('imports-85.data', sep=",")
df.info()
df.columns = ['symboling', 'normalized-losses', 'make', 'fuel-type', 'aspiration', 'num-of-doors', 'body-style', 'drive-wheels', 'engine-location', 'wheel-base', 'length', 'width', 'height', 'curb-weight', 'engine-type', 'num-of-cylinders', 'engine-size', 'fuel-system', 'bore', 'stroke', 'compression-ratio', 'horsepower', 'peak-rpm', 'city-mpg', 'highway-mpg', 'price']
df.info()
df.shape
#replace cells with ? with Nan
import numpy
df.replace('?',numpy.nan,inplace=True)
```
# Convert and clean up
convert numbered columns to numeric
```
df['symboling'] = df['symboling'].astype(int)
df['symboling_n'] = (max(df['symboling']) - df['symboling'])/max(df['symboling'])
df['symboling_n']
df['wheel-base'] = df['wheel-base'].astype(float)
df['wheel-base_n'] = (max(df['wheel-base']) - df['wheel-base'])/max(df['wheel-base'])
df['length'] = df['length'].astype(float)
df['length_n'] = (max(df['length']) - df['length'])/max(df['length'])
df['width'] = df['width'].astype(float)
def normit(col):
newcol = col+'_n'
df[newcol] = (max(df[col]) - df[col])/max(df[col])
return
df['height'] = df['height'].astype(float)
normit('height')
df['curb-weight'] = df['curb-weight'].astype(int)
normit('curb-weight')
df['engine-size'] = df['engine-size'].astype(int)
normit('engine-size')
# 3.21 factor for this size engine
df['bore'].fillna(3.21,inplace=True)
df['bore'] = df['bore'].astype(float)
normit('bore')
df['stroke'] = df['stroke'].astype(float)
normit('stroke')
df['compression-ratio'] = df['compression-ratio'].astype(int)
normit('compression-ratio')
# 111 factor for this size engine
df['horsepower'].fillna(111,inplace=True)
df['horsepower'] = df['horsepower'].astype(int)
normit('horsepower')
df['highway-mpg'] = df['highway-mpg'].astype(int)
normit('highway-mpg')
# 25000 factor for this size car
df['price'].fillna(25000,inplace=True)
df['price'] = df['price'].astype(int)
normit('price')
```
# Normalize loss column
Using rough ratio wheel base to loss = 1.24 based on data
```
# fill in Nans in normalized losses with wheel-base ratio 1.24 factor
df['normalized-losses'].fillna(1.24*df['wheel-base'],inplace=True)
df.info()
```
# Train
Using K Nearest Neighbor Regressor
```
numcolumns = ['symboling_n','wheel-base_n',
'length_n',
'height_n',
'curb-weight_n',
'engine-size_n',
'bore_n',
'stroke_n',
'compression-ratio_n',
'horsepower_n',
'highway-mpg_n']
numcolumns
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
%matplotlib inline
hyper_params = [x for x in (1,3,5,7,9)]
cols = numcolumns
target = 'price'
def knn_train_test(thecols,targ,dfn,k1):
# nearest neighbors regression loop through hyper_params
# setting the iterator as the hyper_param
train_df = dfn.iloc[0:180]
test_df = dfn.iloc[180:]
knn = KNeighborsRegressor(n_neighbors=k1, algorithm='brute', metric='euclidean')
knn.fit(train_df[thecols], train_df[targ])
predictions = knn.predict(test_df[thecols])
# performance using MSE and RMSE
# RMSE is aka residual sum of squares
y_true = test_df[targ].as_matrix()
y_pred = predictions
return mean_squared_error(y_true,y_pred)
rmse_values = []
for h in hyper_params:
mse = knn_train_test(['symboling_n'],target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title('Symboling')
plt.show()
rmse_values = []
col = ['wheel-base_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['length_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['height_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['curb-weight_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['engine-size_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['bore_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
# 3.15 factor for this size engine
df['stroke'].fillna(3.15,inplace=True)
normit('stroke')
rmse_values = []
col = ['stroke_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['compression-ratio_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['horsepower_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['highway-mpg_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['curb-weight_n','compression-ratio_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
print(rmse_values)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['curb-weight_n','compression-ratio_n','engine-size_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['curb-weight_n','compression-ratio_n','height_n','engine-size_n']
for h in hyper_params:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
plt.scatter(hyper_params,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
```
# Top 3 models
In the last step, vary the hyperparameter value from 1 to 25 and plot the resulting RMSE values.
```
rmse_values = []
col = ['curb-weight_n','compression-ratio_n']
hyper_param2 = [x for x in (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25)]
for h in hyper_param2:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
print(rmse_values)
plt.scatter(hyper_param2,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['curb-weight_n','compression-ratio_n','engine-size_n']
hyper_param2 = [x for x in (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25)]
for h in hyper_param2:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
print(rmse_values)
plt.scatter(hyper_param2,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
rmse_values = []
col = ['curb-weight_n','height_n','compression-ratio_n','engine-size_n']
hyper_param2 = [x for x in (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25)]
for h in hyper_param2:
mse = knn_train_test(col,target,df,h)
rmse_values.append(mse**0.5)
print(rmse_values)
plt.scatter(hyper_param2,rmse_values)
plt.xlabel('k neighbor value')
plt.ylabel('R-MSE')
plt.title(col)
plt.show()
```
# Conclusion
This analysis suggests that a car's curb weight, engine size and compression ratio - these 3 features - are most predictive of a car's price.
| true |
code
| 0.54952 | null | null | null | null |
|
# Linear models for regression problems

## Ordinary least squares
Linear regression models the **output**, or **target** variable $y \in \mathrm{R}$ as a linear combination of the $P$-dimensional input $\mathbf{x} \in \mathbb{R}^{P}$. Let $\mathbf{X}$ be the $N \times P$ matrix with each row an input vector (with a 1 in the first position), and similarly let $\mathbf{y}$ be the $N$-dimensional vector of outputs in the **training set**, the linear model will predict the $\mathbf{y}$ given $\mathbf{x}$ using the **parameter vector**, or **weight vector** $\mathbf{w} \in \mathbb{R}^P$ according to
$$
\mathbf{y} = \mathbf{X} \mathbf{w} + \boldsymbol{\varepsilon},
$$
where $\boldsymbol{\varepsilon} \in \mathrm{R}^N$ are the **residuals**, or the errors of the prediction. The $\mathbf{w}$ is found by minimizing an **objective function**, which is the **loss function**, $L(\mathbf{w})$, i.e. the error measured on the data. This error is the **sum of squared errors (SSE) loss**.
\begin{align}
L(\mathbf{w}) &= \text{SSE}(\mathbf{w})\\
&= \sum_i^N (y_i - \mathbf{x}_i^T\mathbf{w})^2\\
&= (\mathbf{y} - \mathbf{X}^T\mathbf{w})^T (\mathbf{y} - \mathbf{X}^T\mathbf{w})\\
&= \|\mathbf{y} - \mathbf{X}^T\mathbf{w}\|_2^2,
\end{align}
Minimizing the SSE is the Ordinary Least Square **OLS** regression as objective function.
which is a simple **ordinary least squares (OLS)** minimization whose analytic solution is:
$$
\mathbf{w}_{\text{OLS}} = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}
$$
The gradient of the loss:
$$
\partial\frac{L(\mathbf{w}, \mathbf{X}, \mathbf{y})}{\partial\mathbf{w}} = 2 \sum_i \mathbf{x}_i (\mathbf{x}_i \cdot \mathbf{w} - y_i)
$$
## Linear regression with scikit-learn
Scikit learn offer many models for supervised learning, and they all follow the same application programming interface (API), namely:
```
model = Estimator()
model.fit(X, y)
predictions = model.predict(X)
```
```
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
import sklearn.linear_model as lm
import sklearn.metrics as metrics
np.set_printoptions(precision=2)
pd.set_option('precision', 2)
```
Linear regression of `Advertising.csv` dataset with TV and Radio advertising as input features and Sales as target. The linear model that minimizes the MSE is a plan (2 input features) defined as: Sales = 0.05 TV + .19 Radio + 3:

## Overfitting
In statistics and machine learning, overfitting occurs when a statistical model describes random errors or noise instead of the underlying relationships. Overfitting generally occurs when a model is **excessively complex**, such as having **too many parameters relative to the number of observations**. A model that has been overfit will generally have poor predictive performance, as it can exaggerate minor fluctuations in the data.
A learning algorithm is trained using some set of training samples. If the learning algorithm has the capacity to overfit the training samples the performance on the **training sample set** will improve while the performance on unseen **test sample set** will decline.
The overfitting phenomenon has three main explanations:
- excessively complex models,
- multicollinearity, and
- high dimensionality.
### Model complexity
Complex learners with too many parameters relative to the number of observations may overfit the training dataset.
### Multicollinearity
Predictors are highly correlated, meaning that one can be linearly predicted from the others. In this situation the coefficient estimates of the multiple regression may change erratically in response to small changes in the model or the data. Multicollinearity does not reduce the predictive power or reliability of the model as a whole, at least not within the sample data set; it only affects computations regarding individual predictors. That is, a multiple regression model with correlated predictors can indicate how well the entire bundle of predictors predicts the outcome variable, but it may not give valid results about any individual predictor, or about which predictors are redundant with respect to others. In case of perfect multicollinearity the predictor matrix is singular and therefore cannot be inverted. Under these circumstances, for a general linear model $\mathbf{y} = \mathbf{X} \mathbf{w} + \boldsymbol{\varepsilon}$, the ordinary least-squares estimator, $\mathbf{w}_{OLS} = (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T \mathbf{y}$, does not exist.
An example where correlated predictor may produce an unstable model follows:
We want to predict the business potential (pb) of some companies given their business volume (bv) and the taxes (tx) they are paying. Here pb ~ 10% of bv.
However, taxes = 20% of bv (tax and bv are highly collinear), therefore there is an infinite number of linear combinations of tax and bv that lead to the same prediction. Solutions with very large coefficients will produce excessively large predictions.
```
bv = np.array([10, 20, 30, 40, 50]) # business volume
tax = .2 * bv # Tax
bp = .1 * bv + np.array([-.1, .2, .1, -.2, .1]) # business potential
X = np.column_stack([bv, tax])
beta_star = np.array([.1, 0]) # true solution
'''
Since tax and bv are correlated, there is an infinite number of linear combinations
leading to the same prediction.
'''
# 10 times the bv then subtract it 9 times using the tax variable:
beta_medium = np.array([.1 * 10, -.1 * 9 * (1/.2)])
# 100 times the bv then subtract it 99 times using the tax variable:
beta_large = np.array([.1 * 100, -.1 * 99 * (1/.2)])
print("L2 norm of coefficients: small:%.2f, medium:%.2f, large:%.2f." %
(np.sum(beta_star ** 2), np.sum(beta_medium ** 2), np.sum(beta_large ** 2)))
print("However all models provide the exact same predictions.")
assert np.all(np.dot(X, beta_star) == np.dot(X, beta_medium))
assert np.all(np.dot(X, beta_star) == np.dot(X, beta_large))
```
Multicollinearity between the predictors: business volumes and tax produces unstable models with arbitrary large coefficients.

Dealing with multicollinearity:
- Regularisation by e.g. $\ell_2$ shrinkage: Introduce a bias in the solution by making $(X^T X)^{-1}$ non-singular. See $\ell_2$ shrinkage.
- Feature selection: select a small number of features. See: Isabelle Guyon and André Elisseeff *An introduction to variable and feature selection* The Journal of Machine Learning Research, 2003.
- Feature selection: select a small number of features using $\ell_1$ shrinkage.
- Extract few independent (uncorrelated) features using e.g. principal components analysis (PCA), partial least squares regression (PLS-R) or regression methods that cut the number of predictors to a smaller set of uncorrelated components.
### High dimensionality
High dimensions means a large number of input features. Linear predictor associate one parameter to each input feature, so a high-dimensional situation ($P$, number of features, is large) with a relatively small number of samples $N$ (so-called large $P$ small $N$ situation) generally lead to an overfit of the training data. Thus it is generally a bad idea to add many input features into the learner. This phenomenon is called the **curse of dimensionality**.
One of the most important criteria to use when choosing a learning algorithm is based on the relative size of $P$ and $N$.
- Remenber that the "covariance" matrix $\mathbf{X}^T\mathbf{X}$ used in the linear model is a $P \times P$ matrix of rank $\min(N, P)$. Thus if $P > N$ the equation system is overparameterized and admit an infinity of solutions that might be specific to the learning dataset. See also ill-conditioned or singular matrices.
- The sampling density of $N$ samples in an $P$-dimensional space is proportional to $N^{1/P}$. Thus a high-dimensional space becomes very sparse, leading to poor estimations of samples densities. To preserve a constant density, an exponential growth in the number of observations is required. 50 points in 1D, would require 2 500 points in 2D and 125 000 in 3D!
- Another consequence of the sparse sampling in high dimensions is that all sample points are close to an edge of the sample. Consider $N$ data points uniformly distributed in a $P$-dimensional unit ball centered at the origin. Suppose we consider a nearest-neighbor estimate at the origin. The median distance from the origin to the closest data point is given by the expression: $d(P, N) = \left(1 - \frac{1}{2}^{1/N}\right)^{1/P}.$
A more complicated expression exists for the mean distance to the closest point. For N = 500, P = 10 , $d(P, N ) \approx 0.52$, more than halfway to the boundary. Hence most data points are closer to the boundary of the sample space than to any other data point. The reason that this presents a problem is that prediction is much more difficult near the edges of the training sample. One must extrapolate from neighboring sample points rather than interpolate between them.
*(Source: T Hastie, R Tibshirani, J Friedman. *The Elements of Statistical Learning: Data Mining, Inference, and Prediction.* Second Edition, 2009.)*
- Structural risk minimization provides a theoretical background of this phenomenon. (See VC dimension.)
- See also bias–variance trade-off.
## Regularization using penalization of coefficients
Regarding linear models, overfitting generally leads to excessively complex solutions (coefficient vectors), accounting for noise or spurious correlations within predictors. **Regularization** aims to alleviate this phenomenon by constraining (biasing or reducing) the capacity of the learning algorithm in order to promote simple solutions. Regularization penalizes "large" solutions forcing the coefficients to be small, i.e. to shrink them toward zeros.
The objective function $J(\mathbf{w})$ to minimize with respect to $\mathbf{w}$ is composed of a loss function $L(\mathbf{w})$ for goodness-of-fit and a penalty term $\Omega(\mathbf{w})$ (regularization to avoid overfitting). This is a trade-off where the respective contribution of the loss and the penalty terms is controlled by the regularization parameter $\lambda$.
Therefore the **loss function** $L(\mathbf{w})$ is combined with a **penalty function** $\Omega(\mathbf{w})$ leading to the general form:
$$
J(\mathbf{w}) = L(\mathbf{w}) + \lambda \Omega(\mathbf{w}).
$$
The respective contribution of the loss and the penalty is controlled by the **regularization parameter** $\lambda$.
For regression problems the loss is the SSE given by:
\begin{align*}
L(\mathbf{w}) = SSE(\mathbf{w}) &= \sum_i^N (y_i - \mathbf{x}_i^T\mathbf{w})^2\\
&= \|\mathbf{y} - \mathbf{x}\mathbf{w}\|_2^2
\end{align*}
Popular penalties are:
- Ridge (also called $\ell_2$) penalty: $\|\mathbf{w}\|_2^2$. It shrinks coefficients toward 0.
- Lasso (also called $\ell_1$) penalty: $\|\mathbf{w}\|_1$. It performs feature selection by setting some coefficients to 0.
- ElasticNet (also called $\ell_1\ell_2$) penalty: $\alpha \left(\rho~\|\mathbf{w}\|_1 + (1-\rho)~\|\mathbf{w}\|_2^2 \right)$. It performs selection of group of correlated features by setting some coefficients to 0.
The next figure shows the predicted performance (r-squared) on train and test sets with an increasing number of input features. The number of predictive features is always 10% of the total number of input features. Therefore, the signal to noise ratio (SNR) increases by increasing the number of input features. The performances on the training set rapidly reach 100% (R2=1). However, the performance on the test set decreases with the increase of the input dimensionality. The difference between the train and test performances (blue shaded region) depicts the overfitting phenomena. Regularisation using penalties of the coefficient vector norm greatly limits the overfitting phenomena.

With scikit-learn:
```
# Dataset with some correlation
X, y, coef = datasets.make_regression(n_samples=100, n_features=10, n_informative=5, random_state=0,
effective_rank=3, coef=True)
lr = lm.LinearRegression().fit(X, y)
l2 = lm.Ridge(alpha=10).fit(X, y) # lambda is alpha!
l1 = lm.Lasso(alpha=.1).fit(X, y) # lambda is alpha !
l1l2 = lm.ElasticNet(alpha=.1, l1_ratio=.9).fit(X, y)
pd.DataFrame(np.vstack((coef, lr.coef_, l2.coef_, l1.coef_, l1l2.coef_)),
index=['True', 'lr', 'l2', 'l1', 'l1l2'])
```
## Ridge regression ($\ell_2$-regularization)
Ridge regression impose a $\ell_2$ penalty on the coefficients, i.e. it penalizes with the Euclidean norm of the coefficients while minimizing SSE. The objective function becomes:
\begin{align}
\text{Ridge}(\mathbf{w}) &= \sum_i^N (y_i - \mathbf{x}_i^T\mathbf{w})^2 + \lambda \|\mathbf{w}\|_2^2\\
&= \|\mathbf{y} - \mathbf{x}\mathbf{w}\|_2^2 + \lambda \|\mathbf{w}\|_2^2.
\end{align}
The $\mathbf{w}$ that minimises $F_{Ridge}(\mathbf{w})$ can be found by the following derivation:
\begin{align}
\nabla_{\mathbf{w}}\text{Ridge}(\mathbf{w}) &= 0\\
\nabla_{\mathbf{w}}\big((\mathbf{y} - \mathbf{X}\mathbf{w})^T (\mathbf{y} - \mathbf{X}\mathbf{w}) + \lambda \mathbf{w}^T\mathbf{w}\big) &= 0\\
\nabla_{\mathbf{w}}\big((\mathbf{y}^T\mathbf{y} - 2 \mathbf{w}^T\mathbf{X}^T\mathbf{y} + \mathbf{w}^T\mathbf{X}^T\mathbf{X}\mathbf{w} + \lambda \mathbf{w}^T\mathbf{w})\big) &= 0\\
-2\mathbf{X}^T\mathbf{y} + 2 \mathbf{X}^T\mathbf{X}\mathbf{w} + 2 \lambda \mathbf{w} &= 0\\
-\mathbf{X}^T\mathbf{y} + (\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I}) \mathbf{w} &= 0\\
(\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I}) \mathbf{w} &= \mathbf{x}^T\mathbf{y}\\
\mathbf{w} &= (\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I})^{-1} \mathbf{x}^T\mathbf{y}
\end{align}
- The solution adds a positive constant to the diagonal of $\mathbf{X}^T\mathbf{X}$ before inversion. This makes the problem nonsingular, even if $\mathbf{X}^T\mathbf{X}$ is not of full rank, and was the main motivation behind ridge regression.
- Increasing $\lambda$ shrinks the $\mathbf{w}$ coefficients toward 0.
- This approach **penalizes** the objective function by the **Euclidian ($\ell_2$) norm** of the coefficients such that solutions with large coefficients become unattractive.
The gradient of the loss:
$$
\partial\frac{L(\mathbf{w}, \mathbf{X}, \mathbf{y})}{\partial\mathbf{w}} = 2 (\sum_i \mathbf{x}_i (\mathbf{x}_i \cdot \mathbf{w} - y_i) + \lambda \mathbf{w})
$$
## Lasso regression ($\ell_1$-regularization)
Lasso regression penalizes the coefficients by the $\ell_1$ norm. This constraint will reduce (bias) the capacity of the learning algorithm. To add such a penalty forces the coefficients to be small, i.e. it shrinks them toward zero. The objective function to minimize becomes:
\begin{align}
\text{Lasso}(\mathbf{w}) &= \sum_i^N (y_i - \mathbf{x}_i^T\mathbf{w})^2 + \lambda\|\mathbf{w}\|_1.
\end{align}
This penalty forces some coefficients to be exactly zero, providing a feature selection property.
### Sparsity of the $\ell_1$ norm
#### Occam's razor
Occam's razor (also written as Ockham's razor, and **lex parsimoniae** in Latin, which means law of parsimony) is a problem solving principle attributed to William of Ockham (1287-1347), who was an English Franciscan friar and scholastic philosopher and theologian. The principle can be interpreted as stating that **among competing hypotheses, the one with the fewest assumptions should be selected**.
#### Principle of parsimony
The simplest of two competing theories is to be preferred. Definition of parsimony: Economy of explanation in conformity with Occam's razor.
Among possible models with similar loss, choose the simplest one:
- Choose the model with the smallest coefficient vector, i.e. smallest $\ell_2$ ($\|\mathbf{w}\|_2$) or $\ell_1$ ($\|\mathbf{w}\|_1$) norm of $\mathbf{w}$, i.e. $\ell_2$ or $\ell_1$ penalty. See also bias-variance tradeoff.
- Choose the model that uses the smallest number of predictors. In other words, choose the model that has many predictors with zero weights. Two approaches are available to obtain this: (i) Perform a feature selection as a preprocessing prior to applying the learning algorithm, or (ii) embed the feature selection procedure within the learning process.
#### Sparsity-induced penalty or embedded feature selection with the $\ell_1$ penalty
The penalty based on the $\ell_1$ norm promotes **sparsity** (scattered, or not dense): it forces many coefficients to be exactly zero. This also makes the coefficient vector scattered.
The figure bellow illustrates the OLS loss under a constraint acting on the $\ell_1$ norm of the coefficient vector. I.e., it illustrates the following optimization problem:
$$
\begin{aligned}
\underset{\mathbf{w}}{\text{minimize}} ~& \|\mathbf{y} - \mathbf{X}\mathbf{w}\|_2^2 \\
\text{subject to} ~& \|\mathbf{w}\|_1 \leq 1.
\end{aligned}
$$

### Optimization issues
*Section to be completed*
- No more closed-form solution.
- Convex but not differentiable.
- Requires specific optimization algorithms, such as the fast iterative shrinkage-thresholding algorithm (FISTA): Amir Beck and Marc Teboulle, *A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems* SIAM J. Imaging Sci., 2009.
The ridge penalty shrinks the coefficients toward zero. The figure illustrates: the OLS solution on the left. The $\ell_1$ and $\ell_2$ penalties in the middle pane. The penalized OLS in the right pane. The right pane shows how the penalties shrink the coefficients toward zero. The black points are the minimum found in each case, and the white points represents the true solution used to generate the data.

## Elastic-net regression ($\ell_1$-$\ell_2$-regularization)
The Elastic-net estimator combines the $\ell_1$ and $\ell_2$ penalties, and results in the problem to
\begin{align}
\text{Enet}(\mathbf{w}) &= \sum_i^N (y_i - \mathbf{x}_i^T\mathbf{w})^2 + \alpha \left(\rho~\|\mathbf{w}\|_1 + (1-\rho)~\|\mathbf{w}\|_2^2 \right),
\end{align}
where $\alpha$ acts as a global penalty and $\rho$ as an $\ell_1 / \ell_2$ ratio.
### Rational
- If there are groups of highly correlated variables, Lasso tends to arbitrarily select only one from each group. These models are difficult to interpret because covariates that are strongly associated with the outcome are not included in the predictive model. Conversely, the elastic net encourages a grouping effect, where strongly correlated predictors tend to be in or out of the model together.
- Studies on real world data and simulation studies show that the elastic net often outperforms the lasso, while enjoying a similar sparsity of representation.
## Regression performance evaluation metrics: R-squared, MSE and MAE
Common regression [metrics](https://scikit-learn.org/stable/modules/model_evaluation.html) are:
- $R^2$ : R-squared
- MSE: Mean Squared Error
- MAE: Mean Absolute Error
### R-squared
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. We will consider the **explained variance** also known as the coefficient of determination, denoted $R^2$ pronounced **R-squared**.
The total sum of squares, $SS_\text{tot}$ is the sum of the sum of squares explained by the regression, $SS_\text{reg}$, plus the sum of squares of residuals unexplained by the regression, $SS_\text{res}$, also called the SSE, i.e. such that
$$
SS_\text{tot} = SS_\text{reg} + SS_\text{res}
$$

The mean of $y$ is
$$
\bar{y} = \frac{1}{n}\sum_i y_i.
$$
The total sum of squares is the total squared sum of deviations from the mean of $y$, i.e.
$$
SS_\text{tot}=\sum_i (y_i-\bar{y})^2
$$
The regression sum of squares, also called the explained sum of squares:
$$
SS_\text{reg} = \sum_i (\hat{y}_i -\bar{y})^2,
$$
where $\hat{y}_i = \beta x_i + \beta_0$ is the estimated value of salary $\hat{y}_i$ given a value of experience $x_i$.
The sum of squares of the residuals (**SSE, Sum Squared Error**), also called the residual sum of squares (RSS) is:
$$
SS_\text{res}=\sum_i (y_i - \hat{y_i})^2.
$$
$R^2$ is the explained sum of squares of errors. It is the variance explain by the regression divided by the total variance, i.e.
$$
R^2 = \frac{\text{explained SS}}{\text{total SS}}
= \frac{SS_\text{reg}}{SS_{tot}}
= 1 - {SS_{res}\over SS_{tot}}.
$$
_Test_
Let $\hat{\sigma}^2 = SS_\text{res} / (n-2)$ be an estimator of the variance of $\epsilon$. The $2$ in the denominator stems from the 2 estimated parameters: intercept and coefficient.
- **Unexplained variance**: $\frac{SS_\text{res}}{\hat{\sigma}^2} \sim \chi_{n-2}^2$
- **Explained variance**: $\frac{SS_\text{reg}}{\hat{\sigma}^2} \sim \chi_{1}^2$. The single degree of freedom comes from the difference between $\frac{SS_\text{tot}}{\hat{\sigma}^2} (\sim \chi^2_{n-1})$ and $\frac{SS_\text{res}}{\hat{\sigma}^2} (\sim \chi_{n-2}^2)$, i.e. $(n-1) - (n-2)$ degree of freedom.
The Fisher statistics of the ratio of two variances:
$$
F = \frac{\text{Explained variance}}{\text{Unexplained variance}} = \frac{SS_\text{reg} / 1}{ SS_\text{res} / (n - 2)} \sim F(1, n-2)
$$
Using the $F$-distribution, compute the probability of observing a value greater than $F$ under $H_0$, i.e.: $P(x > F|H_0)$, i.e. the survival function $(1 - \text{Cumulative Distribution Function})$ at $x$ of the given $F$-distribution.
```
import sklearn.metrics as metrics
from sklearn.model_selection import train_test_split
X, y = datasets.make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=1)
lr = lm.LinearRegression()
lr.fit(X_train, y_train)
yhat = lr.predict(X_test)
r2 = metrics.r2_score(y_test, yhat)
mse = metrics.mean_squared_error(y_test, yhat)
mae = metrics.mean_absolute_error(y_test, yhat)
print("r2: %.3f, mae: %.3f, mse: %.3f" % (r2, mae, mse))
```
In pure numpy:
```
res = y_test - lr.predict(X_test)
y_mu = np.mean(y_test)
ss_tot = np.sum((y_test - y_mu) ** 2)
ss_res = np.sum(res ** 2)
r2 = (1 - ss_res / ss_tot)
mse = np.mean(res ** 2)
mae = np.mean(np.abs(res))
print("r2: %.3f, mae: %.3f, mse: %.3f" % (r2, mae, mse))
```
| true |
code
| 0.650883 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/RoseSarlake/Computer-Vision/blob/main/CV_Assignment0.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 1.OpenCV_basic.txt
Reading, displaying and writing an image
```
from google.colab import drive
drive.mount('/content/drive')
import numpy as np
import cv2
from google.colab.patches import cv2_imshow
from matplotlib import pyplot as plt
# Load an color image in grayscale
img = cv2.imread("/content/drive/MyDrive/Colab/CV/images/messi.jpg",0)
#print(type(img))
# Write an image
cv2.imwrite("/content/drive/MyDrive/Colab/CV/images/messigray.png",img)
# Display an image
#cv2.namedWindow('image',cv2.WINDOW_NORMAL)
cv2_imshow(img)
# for PC, if not waitkey, it will only show in very short time
cv2.waitKey(0)
cv2.destroyAllWindows()
```
Use of keys to manage program execution
```
img = cv2.imread("/content/drive/MyDrive/Colab/CV/images/messi.jpg",0)
cv2_imshow(img)
# not works for colab
k = cv2.waitKey(0)
if k == 27: # wait for ESC key to exit
cv2.destroyAllWindows()
elif k == ord('s'): # wait for 's' key to save and exit
cv2.imwrite('messigray.png',img)
cv2.destroyAllWindows()
```
Matplotlib (Graphics Library)
```
img = cv2.imread("/content/drive/MyDrive/Colab/CV/images/messi.jpg",0)
plt.imshow(img, cmap = 'gray', interpolation = 'bicubic')
plt.xticks([]), plt.yticks([]) # to hide tick values on X and Y axis
plt.show()
```
Drawing on images
```
# create a black image
img = np.zeros((512,512,3), np.uint8)
# blue diagonal line with 5 px thickness
img = cv2.line(img,(0,0),(511,511),(255,0,0),5)
# a green rectangle (3 px thickness)
img = cv2.rectangle(img,(384,0),(510,128),(0,255,0),3)
# an ellipse
img = cv2.ellipse(img,(256,256),(100,50),0,0,180,255,-1)
# a yellow polygon
pts = np.array([[10,5],[20,30],[70,20],[50,10]], np.int32)
pts = pts.reshape((-1,1,2))
img = cv2.polylines(img,[pts],True,(0,255,255))
# add text to the image
font = cv2.FONT_HERSHEY_SIMPLEX
cv2.putText(img,'OpenCV',(10,500), font, 4,(255,255,255),2,cv2.LINE_AA)
cv2_imshow(img)
```
# 2.matrix simulation
1)Monoband
```
def mat_mono():
# create a 256*256 matrix with all 0,and set the data type as unit8
gray = np.zeros((256,256),dtype="uint8")
# increase the value in both x and y axis to the 255
# based on the coordinates, the top-left is black(0), the bottom-right is white(255)
for i in range(256):
for j in range(256):
gray[i,j]= (i*0.5 + j*0.5)
cv2_imshow(gray)
# show the matrix
print ("image shape:"+str(img.shape))
print(gray)
```
2)Triband
```
def mat_tri():
# create a 256*256 matrix with all 0 in three channels, and define the data type as unit8
r = np.zeros((256,256),dtype="uint8")
g = np.zeros((256,256),dtype="uint8")
b = np.zeros((256,256),dtype="uint8")
for i in range(256):
for j in range(256):
r[i,j]= (i*0.3 + j*0.7)
g[i,j]= 255-j
b[i,j]= i
#merge the three layer in BGR color order
img = cv2.merge((b,g,r))
cv2_imshow(img)
print ("image shape:"+str(img.shape))
print(img)
```
# 3.display several images simultaneosly
1)display two 3 channels images simultaneosly
```
def displayMI(img1,img2):
#Resize the first image to 1/4 of original image size
re_img1 = cv2.resize(img1, (0, 0), None, .25, .25)
#Resize the second image to have the same size with the first one
re_img2 = cv2.resize(img2, (re_img1.shape[1], re_img1.shape[0]), None, .25, .25)
# Two ways to display:
#Stack arrays in sequence horizontally
dis_hstack = np.hstack((re_img1, re_img2))
#Join a sequence of arrays along an existing axis.
#axis = 0 vertically, axis = 1 horizontally
dis_concat = np.concatenate((re_img1, re_img2),axis=0)
# Display image1, image2, and show two images simutaneosly
print("first image:")
cv2_imshow(re_img1)
print("second image:")
cv2_imshow(re_img2)
print("two images (hstack method):")
cv2_imshow(dis_hstack)
print("two images (concatenate method):")
cv2_imshow(dis_concat)
```
2)display monoband and triband image at same time
```
def displayMIChan(inimg):
# from the 3 channel color image to grayscale image
grey = cv2.cvtColor(inimg, cv2.COLOR_RGB2GRAY)
# In order to show different channel images simutaneosly, make the grey scale image have three channels
grey_3_channel = cv2.cvtColor(grey, cv2.COLOR_GRAY2BGR)
# Two ways to display:
#Stack arrays in sequence horizontally
dis_hstack = np.hstack((inimg, grey_3_channel))
#Join a sequence of arrays along an existing axis.
#axis = 0 vertically, axis = 1 horizontally
dis_concat = np.concatenate((inimg, grey_3_channel),axis=1)
# Display original image, greyscale image, and show two images simutaneosly
print("original image:")
cv2_imshow(inimg)
print("greyscale image:")
cv2_imshow(grey)
print("two images (hstack method):")
cv2_imshow(dis_hstack)
print("two images (concatenate method):")
cv2_imshow(dis_concat)
```
# 4.display several images with their titles
Using Matplotlib to create the subplot, the images size can be different.
```
def displayYtitle(img_1, img_2, title1, title2):
# change the channals order (see IMPORTANT NOTE)
b, g, r = cv2.split(img_1)
img_1 = cv2.merge([r, g, b])
b, g, r = cv2.split(img_2)
img_2 = cv2.merge([r, g, b])
# 1 rows, 2 cols, index 1
plt.subplot(121)
plt.imshow(img_1)
# give the subplot a title1
plt.title(title1)
# Get or set the current tick locations and labels of the x-axis.
# No need in this case,hide it
plt.xticks([]), plt.yticks([])
# 1 rows, 2 cols, index 2
plt.subplot(122), plt.imshow(img_2), plt.title(title2)
plt.xticks([]), plt.yticks([])
# Display the figure
plt.show()
```
IMPORTANT NOTE: Due to matplotlib uses RGB color order (not BGR in openCV), colors in our displayed image will be reversed.
cv2.COLOR_BGR2RGB also can be used
# 5.modifies the color of pixels in a list of pixel coordinates
```
def color_pi(img,x,y,r,g,b):
# check if the location is out of the image
if x <= img.shape[0] and y <= image.shape[1]:
# check if it has the correct rgb value
if r in range(0,256) and g in range(0,256) and b in range(0,256):
# change the order from rgb to bgr for opencv display
img[x,y] = (b,g,r)
else:
print("input valid values from 0 to 255")
else:
print("out of the image range")
cv2_imshow(img)
# save the changed image
cv2.imwrite("/content/drive/MyDrive/Colab/CV/images/changed.png",img)
```
# 6.examples
1)displays a matrix of simulated real numbers
```
mat_mono()
mat_tri()
```
2) Display images simultaneosly
```
# 3 channals
my_image_1 = cv2.imread("/content/drive/MyDrive/Colab/CV/images/dinog.jpg")
my_image_2 = cv2.imread("/content/drive/MyDrive/Colab/CV/images/dinob.jpg")
displayMI(my_image_1,my_image_2)
# different channals
my_image_3 = cv2.imread("/content/drive/MyDrive/Colab/CV/images/dinor.jpg")
displayMIChan(my_image_3)
```
3) Display images with their titles simultaneously
```
displayYtitle(my_image_1, my_image_2,"Image 1","Image 2")
```
4)Modifies the color of pixels
```
color_pi(my_image_3,4,6,255,0,0)
```
| true |
code
| 0.390156 | null | null | null | null |
|
# 字典和集合
> 字典这个数据结构活跃在所有 Python 程序的背后,即便你的源码里并没有直接用到它。
> ——A. M. Kuchling
`dict` 是 Python 语言的基石。
可散列对象需要实现 `__hash__` 和 `__eq__` 函数。
如果两个可散列对象是相等的,那么它们的散列值一定是一样的。
## 范映射类型
collections.abc 模块中有 Mapping 和 MutableMapping 两个抽象基类,起作用是为 dict 和其他类似的类型定义形式接口。
//pic
但非抽象映射类型一般不会直接继承这些抽象基类,而是直接对 dict 或 collections.User.Dict 进行扩展。
这些抽象基类的主要作用是作为形式化的文档,以及跟 isinstance 一起被用来判定某个数据是否为广义上的映射类型。
```
my_dict = {}
isinstance(my_dict, collections.abc.Mapping)
```
> 用 instance 而不是用 type 是用来避免参数可能不是 dict 而是其他的映射类型
标准库的所有映射类型都是利用 dict 实现。
什么是可散列的数据类型?
字典的提供了多种构造方法
link
```
# 字典提供了很多种构造方法
a = dict(one=1, two=2, three=3)
b = {'one': 1, 'two': 2, 'three': 3}
c = dict(zip(['one', 'two', 'three'], [1, 2, 3]))
d = dict([('two', 2), ('one', 1), ('three', 3)])
e = dict({'three': 3, 'one': 1, 'two': 2})
a == b == c == d == e
```
## 字典推导
字典推导(dictcomp)可以从任何以键值对为元素的可迭代对象构建出字典
```
DIAL_CODES = [
(86, 'China'),
(91, 'India'),
(1, 'United States')
]
country_code = {country: code for code, country in DIAL_CODES}
country_code
```
## 常见的映射方法
dict、defaultdict、OrderedDict 的常见方法,后两个数据类型是 dict 的变种,位于 collections 模块内。
- setdefault 处理找不到的键
d[k] 无法找到正确的键时,会抛出异常。
用 d.get(k, default) 来代替 d[k], 可以对找不到的键设置默认返回值。
```
"""
03-dict-set/index0.py
创建一个从单词到其出现频率的映射
"""
import sys
import re
WORD_RE = re.compile(r'\w+')
index = {}
with open(sys.argv[1], encoding='uft-8') as fp:
for line_no, line in enumerate(fp, 1):
for match in WORD_RE.finditer(line):
word = match.group()
column_no = match.start() + 1
location = (line_no, column_no)
# 提取单词出现情况,如果没有出现过返回 []
occurences = index.get(word, [])
occurences.append(location)
index[word] = occurences
# 以字符顺序打印结果
for word in sorted(index, key=str.upper):
print(word, index[word])
```
```sh
$ python index0.py zen.txt
a [(19, 48), (20, 53)]
Although [(11, 1), (16, 1), (18, 1)]
ambiguity [(14, 16)]
and [(15, 23)]
are [(21, 12)]
aren [(10, 15)]
at [(16, 38)]
bad [(19, 50)]
be [(15, 14), (16, 27), (20, 50)]
beats [(11, 23)]
Beautiful [(3, 1)]
better [(3, 14), (4, 13), (5, 11), (6, 12), (7, 9), (8, 11), (17, 8), (18, 25)]
break [(10, 40)]
by [(1, 20)]
cases [(10, 9)]
complex [(5, 23)]
...
```
使用 dict.setdefault
```
"""
03-dict-set/index.py
创建一个从单词到其出现频率的映射
"""
import sys
import re
WORD_RE = re.compile(r'\w+')
index = {}
with open(sys.argv[1], encoding='uft-8') as fp:
for line_no, line in enumerate(fp, 1):
for match in WORD_RE.finditer(line):
word = match.group()
column_no = match.start() + 1
location = (line_no, column_no)
# 注意这行与上面的区别
index.setdefault(word, []).append(location)
# 效果等同于:
# if key not in my_dict:
# my_dict[key] = []
# my_dict[key].append(new_value)
# 以字符顺序打印结果
for word in sorted(index, key=str.upper):
print(word, index[word])
```
## 映射的弹性键查询
某个键不存在时,希望读取时能得到一个默认值,有两个方式:
- 通过 defaultdict 类型
- 自定义 dict 子类
### defaultdict 处理找不到的键
```
"""
03-dict-set/index_default.py
创建一个从单词到其出现频率的映射
"""
import sys
import re
import collections
WORD_RE = re.compile(r'\w+')
index = collections.defaultdict(list)
with open(sys.argv[1], encoding='utf-8') as fp:
for line_no, line in enumerate(fp, 1):
for match in WORD_RE.finditer(line):
word = match.group()
column_no = match.start()+1
location = (line_no, column_no)
# index 如何没有 word 的记录, default_factory 会被调用,这里是创建一个空列表返回
index[word].append(location)
# print in alphabetical order
for word in sorted(index, key=str.upper):
print(word, index[word])
```
defaultdict 里的 default_factory 只在 __getitem__ 里调用。
实际上,上面的机制是通过特殊方法 __missing__ 支持的。
### __missing__
如果 dict 继承类提供了 __missing__ 方法,且 __getitem__ 遇到找不到键的情况是会自动调用它,而不是抛出异常
```
class StrKeyDict0(dict): # <1>
def __missing__(self, key):
if isinstance(key, str): # <2>
raise KeyError(key)
return self[str(key)] # <3>
def get(self, key, default=None):
try:
return self[key] # <4>
except KeyError:
return default # <5>
def __contains__(self, key):
return key in self.keys() or str(key) in self.keys() # <6>
d = StrKeyDict0([('2', 'Two'), ('4', 'Four')])
print(d['2'])
print(d['4'])
# d[1] error
print(d.get('2'))
print(d.get('4'))
print(d.get(1, 'N/A'))
# defaultdcit & __missing__
class mydefaultdict(dict):
def __init__(self, value, value_factory):
super().__init__(value)
self._value_factory = value_factory
def __missing__(self, key):
# 要避免循环调用
# return self[key]
self[key] = self._value_factory()
return self[key]
d = mydefaultdict({1:1}, list)
print(d[1])
print(d[2])
d[3].append(1)
print(d)
```
## 字典的变种
> 此节总结了标准库 collections 模块中,除了 defaultdict 之外的不同映射类型
- collections.OrderedDict
- collections.ChainMap
容纳多个不同的映射对象,然后在进行键查找操作时会从前到后逐一查找,直到被找到为止
- collections.Counter
- collections.UserDict
dict 的纯 Python 实现,让用户集成写子类的
```
# UserDict
# 定制化字典时,尽量继承 UserDict 而不是 dict
from collections import UserDict
class mydict(UserDict):
def __getitem__(self, key):
print('Getting key', key)
return super().__getitem__(key)
d = mydict({1:1})
print(d[1], d[2])
# MyppingProxyType 用于构建 Mapping 的只读实例
from types import MappingProxyType
d = {1: 1}
d_proxy = MappingProxyType(d)
print(d_proxy[1])
try:
d_proxy[1] = 1
except Exception as e:
print(repr(e))
d[1] = 2
print(d_proxy[1])
# set 的操作
# 子集 & 真子集
a, b = {1, 2}, {1, 2}
print(a <= b, a < b)
# discard
a = {1, 2, 3}
a.discard(3)
print(a)
# pop
print(a.pop(), a.pop())
try:
a.pop()
except Exception as e:
print(repr(e))
```
### 集合字面量
除空集之外,集合的字面量——`{1}`、`{1, 2}`,等等——看起来跟它的数学形式一模一样。**如果是空集,那么必须写成 `set()` 的形式**,否则它会变成一个 `dict`.
跟 `list` 一样,字面量句法会比 `set` 构造方法要更快且更易读。
### 集合和字典的实现
集合和字典采用散列表来实现:
1. 先计算 key 的 `hash`, 根据 hash 的某几位(取决于散列表的大小)找到元素后,将该元素与 key 进行比较
2. 若两元素相等,则命中
3. 若两元素不等,则发生散列冲突,使用线性探测再散列法进行下一次查询。
这样导致的后果:
1. 可散列对象必须支持 `hash` 函数;
2. 必须支持 `__eq__` 判断相等性;
3. 若 `a == b`, 则必须有 `hash(a) == hash(b)`。
注:所有由用户自定义的对象都是可散列的,因为他们的散列值由 id() 来获取,而且它们都是不相等的。
### 字典的空间开销
由于字典使用散列表实现,所以字典的空间效率低下。使用 `tuple` 代替 `dict` 可以有效降低空间消费。
不过:内存太便宜了,不到万不得已也不要开始考虑这种优化方式,**因为优化往往是可维护性的对立面**。
往字典中添加键时,如果有散列表扩张的情况发生,则已有键的顺序也会发生改变。所以,**不应该在迭代字典的过程各种对字典进行更改**。
```
# 字典中就键的顺序取决于添加顺序
keys = [1, 2, 3]
dict_ = {}
for key in keys:
dict_[key] = None
for key, dict_key in zip(keys, dict_):
print(key, dict_key)
assert key == dict_key
# 字典中键的顺序不会影响字典比较
```
| true |
code
| 0.252407 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Find-correlation-between-params" data-toc-modified-id="Find-correlation-between-params-1"><span class="toc-item-num">1 </span>Find correlation between params</a></span></li></ul></div>
```
%cd ..
%load_ext autoreload
%autoreload 2
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
import pipeline
data_dir = os.getcwd() + "/experiments/batch_DA/3/"
df_AE = pd.read_csv(data_dir + "AE.csv")
df_SVD = pd.read_csv(data_dir + "SVD.csv")
df_AE.tail()
df_SVD["percent_improvement"].mean()
df_SVD["percent_improvement"].std()
#Plot L2 on left axis and percent improvement on y axis against time
# Create some mock data
t = df_SVD.index
fig, ax1 = plt.subplots()
color = 'tab:red'
ax1.set_xlabel('time (s)')
ax1.set_ylabel('MSE', color=color)
# multiple line plot
ax1.plot( t, 'l2_loss', data=df_SVD, marker='+', color=color, )
ax1.plot(t, 'l2_loss', data=df_AE, marker='o', color=color)
ax1.set_ylim(0, 5000)
ax1.tick_params(axis='y', labelcolor=color)
ax1.set_xlim(100, 150)
ax2 = ax1.twinx() # instantiate a second axes that shares the same x-axis
color = 'tab:blue'
ax2.set_ylabel('DA percentage Improvement %', color=color) # we already handled the x-label with ax1
ax2.plot( t, 'percent_improvement', data=df_SVD, marker='+', color=color, )
ax2.plot(t, 'percent_improvement', data=df_AE, marker='o', color=color)
ax2.set_ylim(30, 100)
ax2.tick_params(axis='y', labelcolor=color)
fig.tight_layout() # otherwise the right y-label is slightly clipped
fig.legend(["SVD-MSE", "AE-MSE"] + ["SVD-% improve", "AE-% improve"])
fig.set_size_inches(15, 9)
plt.show()
fig.savefig("all_values.png")
#Now look at values for all AE
#data_dir = os.getcwd() + "/experiments/batch_DA/2/"
df_AE = pd.read_csv(data_dir + "AE.csv")
df_AE.head()
#and plot
#Plot L2 on left axis and percent improvement on y axis against time
# Create some mock data
t = df_AE.index
fig, ax1 = plt.subplots()
color = 'tab:red'
ax1.set_xlabel('time (s)')
ax1.set_ylabel('MSE', color=color)
# multiple line plot
#ax1.plot( t, 'l2_loss', data=df_SVD, marker='+', color=color, )
ax1.plot(t, 'l2_loss', data=df_AE, marker='o', color=color)
ax1.plot(t, 'l1_loss', data=df_AE, marker='+', color=color)
ax1.tick_params(axis='y', labelcolor=color)
ax2 = ax1.twinx() # instantiate a second axes that shares the same x-axis
color = 'tab:blue'
ax2.set_ylabel('DA percentage Improvement %', color=color) # we already handled the x-label with ax1
#ax2.plot( t, 'percent_improvement', data=df_SVD, marker='+', color=color, )
ax2.plot(t, 'percent_improvement', data=df_AE, marker='o', color=color)
ax2.set_ylim((-30, 100))
ax2.tick_params(axis='y', labelcolor=color)
ax2.set_xlim((0, 200))
fig.tight_layout() # otherwise the right y-label is slightly clipped
fig.legend(["AE-MSE", "AE-L1"] + ["AE-% improve"])
fig.set_size_inches(15, 9)
plt.show()
```
## Find correlation between params
```
#copied from here: https://towardsdatascience.com/feature-selection-with-pandas-e3690ad8504b
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
#import statsmodels.api as sm
%matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import RFE
from sklearn.linear_model import RidgeCV, LassoCV, Ridge, Lasso
#ADD column to df
df_AE["da_ratio"] = df_AE["da_MAE_mean"] / df_AE["ref_MAE_mean"]
#Using Pearson Correlation
plt.figure(figsize=(12,10))
cor = df_AE.corr()
sns.heatmap(cor, annot=True, cmap=plt.cm.Reds)
plt.savefig("correlation_AE_data.png")
plt.show()
#plt.savefig("correlation_AE_data.png")
```
NOTE: there is NO correlation between percentage improvement and the reconstruction error. In fact the correlation coefficients are positive for this case (0.068 and 0.071) for L1 and L2 losses respectively when we would expect them to be negative (i.e. better reconstruction gives lower losses and higher percentage improvement).
```
#Plot for SVD
df_SVD["da_ratio"] = df_SVD["da_MAE_mean"] / df_SVD["ref_MAE_mean"]
plt.figure(figsize=(12,10))
cor = df_SVD.corr()
sns.heatmap(cor, annot=True, cmap=plt.cm.Reds)
plt.savefig("correlation_SVD_data.png")
plt.show()
```
| true |
code
| 0.696539 | null | null | null | null |
|
This notebook was prepared by [Donne Martin](https://github.com/donnemartin). Source and license info is on [GitHub](https://github.com/donnemartin/interactive-coding-challenges).
# Challenge Notebook
## Problem: Implement a binary search tree with an insert method.
* [Constraints](#Constraints)
* [Test Cases](#Test-Cases)
* [Algorithm](#Algorithm)
* [Code](#Code)
* [Unit Test](#Unit-Test)
## Constraints
* Can we insert None values?
* No
* Can we assume we are working with valid integers?
* Yes
* Can we assume all left descendents <= n < all right descendents?
* Yes
* Do we have to keep track of the parent nodes?
* This is optional
* Can we assume this fits in memory?
* Yes
## Test Cases
### Insert
Insert will be tested through the following traversal:
### In-Order Traversal
* 5, 2, 8, 1, 3 -> 1, 2, 3, 5, 8
* 1, 2, 3, 4, 5 -> 1, 2, 3, 4, 5
If the `root` input is `None`, return a tree with the only element being the new root node.
You do not have to code the in-order traversal, it is part of the unit test.
## Algorithm
Refer to the [Solution Notebook](http://nbviewer.ipython.org/github/donnemartin/interactive-coding-challenges/blob/master/graphs_trees/bst/bst_solution.ipynb). If you are stuck and need a hint, the solution notebook's algorithm discussion might be a good place to start.
## Code
```
class Node(object):
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Bst(object):
def __init__(self):
self.root = None
def insert(self, data):
def _insert(curr, data):
if curr.data > data:
if curr.left is None:
curr.left = Node(data)
else:
_insert(curr.left, data)
else:
if curr.right is None:
curr.right = Node(data)
else:
_insert(curr.right, data)
if self.root is None:
self.root = Node(data)
else:
_insert(self.root, data)
```
## Unit Test
**The following unit test is expected to fail until you solve the challenge.**
```
%run dfs.py
%run ../utils/results.py
# %load test_bst.py
import unittest
class TestTree(unittest.TestCase):
def __init__(self, *args, **kwargs):
super(TestTree, self).__init__()
self.results = Results()
def test_tree_one(self):
bst = Bst()
bst.insert(5)
bst.insert(2)
bst.insert(8)
bst.insert(1)
bst.insert(3)
in_order_traversal(bst.root, self.results.add_result)
self.assertEqual(str(self.results), '[1, 2, 3, 5, 8]')
self.results.clear_results()
def test_tree_two(self):
bst = Bst()
bst.insert(1)
bst.insert(2)
bst.insert(3)
bst.insert(4)
bst.insert(5)
in_order_traversal(bst.root, self.results.add_result)
self.assertEqual(str(self.results), '[1, 2, 3, 4, 5]')
print('Success: test_tree')
def main():
test = TestTree()
test.test_tree_one()
test.test_tree_two()
if __name__ == '__main__':
main()
```
## Solution Notebook
Review the [Solution Notebook](http://nbviewer.ipython.org/github/donnemartin/interactive-coding-challenges/blob/master/graphs_trees/bst/bst_solution.ipynb) for a discussion on algorithms and code solutions.
| true |
code
| 0.65946 | null | null | null | null |
|
Notes:
- Uppercase count good distinction
- Count of bad words good distinction (rises sharply only after a certain point, probably too sensitive for badness)
- Count of length seems to have a small difference with shorter texts more likely to be toxic
- Count of typos looks like a good distinction, but surprisingly inversely correlated with text with less typos more likely to be toxic - is length the underlying cause?
## Load Data
```
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
dir_path = os.path.realpath('..')
path = 'data/raw/train.csv'
full_path = os.path.join(dir_path, path)
df = pd.read_csv(full_path, header=0, index_col=0)
print("Dataset has {} rows, {} columns.".format(*df.shape))
target = ['toxic', 'severe_toxic', 'obscene', 'threat', 'insult', 'identity_hate']
df['none'] = 1-df[target].max(axis=1)
df['total'] = df[target].sum(axis=1)
df.head()
df.describe()
```
## Summary statistics
```
# Calculate means
mean = df[target].mean().sort_values(ascending=False)
# Barplot
sns.barplot(x=mean.index, y=mean.values)
print(mean)
```
## Correlations between labels
```
# Calculate correlations
corr = df[target].corr()
# Heatmap
sns.heatmap(corr, annot=True, fmt='.2f')
```
## Count of uppercase words (proxy for 'shouting')
```
df['processed'] = df['comment_text'].str.split()
df['uppercase_count'] = df['processed'].apply(lambda x: sum(1 for t in x if t.isupper() and len(t)>2))
fig, ax = plt.subplots(figsize=(16,4))
x= df[df['none']==0]['uppercase_count']
sns.distplot(x, ax=ax, hist=False, label='Any-toxic')
x= df[df['none']==1]['uppercase_count']
sns.distplot(x, ax=ax, hist=False, label='Non-toxic')
# x= df[df['toxic']==1]['uppercase_count']
# sns.distplot(x, ax=ax, hist=False, label='Toxic')
# x= df[df['severe_toxic']==1]['uppercase_count']
# sns.distplot(x, ax=ax, hist=False, label='Severe Toxic')
# x= df[df['threat']==1]['uppercase_count']
# sns.distplot(x, ax=ax, hist=False, label='Threat')
ax.set_xlim([0, 200])
```
## Count of bad words
```
path = 'data/external/badwords.txt'
bad_words = []
f = open(os.path.join(dir_path, path), mode='rt', encoding='utf-8')
for line in f:
words = line.split(', ')
for word in words:
word = word.replace('\n', '')
bad_words.append(word)
# bad_words = f.read().splitlines()
f.close()
bad_words[:10]
def bad_words_count(corpus):
"Count the number of bad words"
count = []
for row in corpus:
i = 0
for err in chkr:
i += 1
count.append(i)
return count
df['bad_words'] = df['processed'].apply(lambda x: sum(1 for t in x if t in bad_words))
import collections
import re
import operator
# Looking at what bad words appear
count = collections.defaultdict(int)
for word in bad_words:
word = re.sub('[*()]', '', word)
count[word] += df['comment_text'].str.count(word).sum()
sorted(count.items(), key=operator.itemgetter(1), reverse=True)
fig, ax = plt.subplots(figsize=(16,4))
x= df[df['none']==0]['bad_words']
sns.distplot(x, ax=ax, hist=False, label='Any-toxic')
x= df[df['none']==1]['bad_words']
sns.distplot(x, ax=ax, hist=False, label='Non-toxic')
ax.set_xlim([0, 50])
```
## Count of typos
```
from enchant.checker import SpellChecker
def typo_count(corpus):
"Count the number of errors found by pyenchant"
count = []
for row in corpus:
chkr = SpellChecker("en_US")
chkr.set_text(row)
i = 0
for err in chkr:
i += 1
count.append(i)
return count
df['typos'] = typo_count(df.comment_text)
fig, ax = plt.subplots(figsize=(16,4))
x= df[df['none']==0]['typos']
sns.distplot(x, ax=ax, hist=False, label='Any-toxic')
x= df[df['none']==1]['typos']
sns.distplot(x, ax=ax, hist=False, label='Non-toxic')
# x= df[df['toxic']==1]['typos']
# sns.distplot(x, ax=ax, hist=False, label='Toxic')
x= df[df['severe_toxic']==1]['typos']
sns.distplot(x, ax=ax, hist=False, label='Severe Toxic')
ax.set_xlim([0, 200])
```
## Doc length
```
df['length'] = [len(t) for t in df['processed']]
df.head()
fig, ax = plt.subplots(figsize=(16,4))
x= df[df['none']==0]['length']
sns.distplot(x, ax=ax, hist=False, label='Any-toxic')
x= df[df['none']==1]['length']
sns.distplot(x, ax=ax, hist=False, label='Non-toxic')
# x= df[df['toxic']==1]['typos']
# sns.distplot(x, ax=ax, hist=False, label='Toxic')
# x= df[df['severe_toxic']==1]['typos']
# sns.distplot(x, ax=ax, hist=False, label='Severe Toxic')
ax.set_xlim([0, 500])
```
## Pairplot
```
import seaborn as sns
datas = df[['typos', 'length', 'uppercase_count', 'bad_words', 'none', 'total']]
sns.pairplot(datas, plot_kws={'alpha':0.25},)
```
## Output
```
features = df.drop(['none', 'total', 'processed'], axis=1)
features.head()
path = 'data/processed/features.csv'
full_path = os.path.join(dir_path, path)
features.to_csv(full_path, header=True, index=True)
```
## Misc
```
print(df[df['total'] == 1])
```
| true |
code
| 0.327208 | null | null | null | null |
|
# 12. Analysing proteins using python
In previous sections we have primarily focused on showing you the basic components of python. We have primarily looked at small example cases where we process some type of input data to generate some kind of text or numerical output.
In this section we want to show you how you can go beyond this and use python to do everything from loading complex structure files to generating graphs and interactive objects. We don't necessarily expect you to learn exactly how all of this works, instead we want to show you what can be done should you wish to look further into these tools and libaries.
The particular use case we are looking at, is some basic analysis of crystallographic coordinates for a protein (HIV-1 protease) in complex with the ligand indinavir. It assumes that you have a certain amount of prior knowledge about the type of data that can be collected and deposited to the RSCB PDB from crystallographic experiments. For more information please see the [RSCB PDB website](https://www.rcsb.org/).
It is worth noting that we are only providing a very minimal overview of some of the things you could do. If you want to chat about how you could be using these tools to do you own work, please do get in contact with one of the course instructors.
### Python libraries
In this tutorial we will be using three main non-standard python libraries:
1. [MDAnalysis](https://www.mdanalysis.org/):
MDAnalysis is a python library primarily developed to help with the anlysis of Molecular Dynamics (MD) trajectories. Beyond just MD, it offers many different tools and functions that can be useful when trying to explore atomistic models.
2. [NGLView](https://github.com/nglviewer/nglview)
NGLView is a powerful widget that allows you to visualise molecular models within jupyter notebooks.
3. [Matplotlib](https://matplotlib.org/)
One of the main plotting tools for python, matplotlib offers a wide range of functionality to generate graphs of everything from a simple scatter plot to [complex animated 3D plots](https://matplotlib.org/gallery/animation/random_walk.html#sphx-glr-gallery-animation-random-walk-py).
## Using MDAnalysis to load a PDB structure
Here we will look at how we can use MDAnalysis to load a PDB file (stored under `datafiles/1HSG.pdb`) and look at its basic properties (e.g. number of atoms, residues, chains, non-protein atoms).
We will only be giving a very superficial overview of MDAnalysis, if you want to know more, please have a look at the [MDAnalysis user guide](https://userguide.mdanalysis.org/1.0.0/index.html).
One of the core components of MDAnalysis is the `Universe` class. You can consider this as the container where we store all the information about the structure file. In a PDB structure, this includes (amongst many other things): 3D coordinates for all the heavy atoms, atom names (i.e. pseudo-arbitrary labels about the types of atoms in the structure), elements, residue names, chain identifiers, and temperature factors.
First, let us create a `Universe` class and call it `pdb` by passing it a string with the path to our PDB file:
```
import MDAnalysis
pdb = MDAnalysis.Universe('datafiles/1HSG.pdb')
```
The `Universe` object has plenty of different attributes and methods, most of which we will not cover here.
The main one that you will work with in the MD tutorial is `trajectory`, which allows you to traverse through a simulation trajectory. However since we only have a single PDB structure, we don't have to deal with this here.
Let's use the `Universe` to gather some basic information about the 1HSG structure. Take some time to look at its [PDB entry](https://www.rcsb.org/structure/1hsg). From the page, we can see that the structure has a total of 1686 atoms, 198 residues, and two chains (called `A` and `B`). We can use MDAnalysis to recover this data.
```
# We can get the number of atoms using the "atoms" sub-class
# "atoms" handles all the information about the atoms in a structure
# here it has a `n_atoms` attribute which tells you how many atoms there are
print("number of atoms: ", pdb.atoms.n_atoms)
# We can also use `n_residues` to get the number of residues
print("number of residues: ", pdb.atoms.n_residues)
# And `n_segments` for chains (MDAnalysis calls chains "segments")
print("number of chains", pdb.atoms.n_segments)
```
As you probably noticed, the number of residues returned as 326, not 198. Why do you think this is?
> Answer: the PDB page states the number of protein residues, so there are 128 non-protein residues
Let's use MDAnalysis to get a little bit more information about these residues.
Here we use one of the `Universe` methods `select_atoms`. Similar to what you may get a chance to do with VMD (MD tutorial), and Pymol (docking/homology modelling tutorial), this allows you to use a text based selection to capture a specific portion of your `Universe`.
For example, if we wanted to get all the protein residues:
```
protein_residues = pdb.select_atoms('protein')
print("number of protein residues: ", protein_residues.atoms.n_residues)
```
Similarly, we can do the same to get the number of non-protein residues:
```
non_protein_residues = pdb.select_atoms('not protein')
print("number of non-protein residues:", non_protein_residues.atoms.n_residues)
```
We can keep using `select_atoms` on these newly created subsampled objects to go deeper into the details.
How many of them are waters?
```
# Create a selection from non_protein_residues that only includes waters
# In the PDB waters are named HOH, so we can make a selection from this
# Here we use the "resname" selection to select by residue name
waters = non_protein_residues.select_atoms('resname HOH')
print("number of waters: ", waters.atoms.n_residues)
# What about non-water non-protein residues?
not_water = non_protein_residues.select_atoms('not resname HOH')
print("number of non-water, non-protein residues: ", not_water.atoms.n_residues)
```
As we can see, there is 1 non-protein non-water residue.
Let's find out more information about it.
First let's see what this residue is called. Here we will be using the `residues` object, which is like `atoms`, but rather than containing atomic information it contains information about the residues. Specifically here we are looking at `resnames` that tells us what the residue name is:
```
print("residue name: ", not_water.residues.resnames)
```
MK1 is the PDB name for the drug indinavir. You can look at the PDB entry for it [here](https://www.rcsb.org/ligand/MK1).
Since the PDB file contains per-atom information (in `atoms`), we can use MDAnalysis to list the atoms that make indinavir:
```
print(not_water.atoms.types)
```
We can also use the coordinates from the PDB file to obtain more information about MK1. Since MDAnalysis takes the coordinate information from the PDB file, we could use the MK1 coordinates (accessible under `not_water.atoms.positions`) to calculate the center of geometry. MDAnalysis provides a simple method for doing this called `center_of_geometry()`:
```
print(not_water.center_of_geometry())
```
#### Exercise 1 - Protein center of geometry
What about the center of the geometry of the protein? Using the `protein_residues` subselection we made earlier, apply the same thing to work out what the center of geometry of the protein atoms is.
```
# Exercise 1:
print(protein_residues.center_of_geometry())
```
## Visualising a PDB using NGLView
Having access to all the information contained in a PDB file is great, however looking at a text or numerical outputs can be quite a lot to digest. Here we can use NGLView to have a look at the visual representation of our protein.
Handily, nglview offers a direct interface to read in MDAnalysis objects through the `show_mdanalysis` method. To facilitate things, we will be doing so here to look at the `Universe` named `pdb` that we created earlier. There are plenty of other ways to feed information to and customise NGLView, but we will leave it to you to look into it more, if it is something you are interested in.
### NGLView controls
After executing the code below, you should see a widget pop up with the representation of a protein in cartoon form.
NGLView widgets can be directly interacted with, here are some basic things you can do:
1. Rotating the structure
This can be done by left-clicking within the protein viewer and dragging a given direction.
2. Zooming into the structure
This can be done by scrolling with your mouse wheel.
3. Translating the structure
This can be done by right-clicking and dragging with your mouse.
4. Going full screen
This can be done by going to "view" in the toolbar and clicking on "Full screen".
Once entered, you can exit full screen by pressing the "Esc" button on your keyboard.
```
import nglview
# Use the `show_mdanalysis` method to parse an MDAnalysis Universe class
pdbview = nglview.show_mdanalysis(pdb)
# Here we set this gui_style attribute so we get a nice interface to interact with
pdbview.gui_style = 'ngl'
# The defaults for NGLView are great, but let's customise a little bit
pdbview.clear_representations()
# We make the protein residues show up as cartoons coloured by their secondary structure
pdbview.add_representation('cartoon', selection='protein', color='sstruc')
# We make the ligand show up in a licorice representation
pdbview.add_representation('licorice', selection='MK1')
# We make the waters show up as red spheres
pdbview.add_representation('ball+stick', selection='water', color='red')
# Finally we call the NGLView object to get an output
pdbview
```
## Looking at temperature factors
Up until now, we've done things that could mostly be done by looking at the [PDB entry for 1HSG](https://www.rcsb.org/structure/1hsg). Let's apply these things to look at something that could be useful on a day to day basis.
Here we will analyse the protein's temperature factors (also known as bfactors) to know which parts of the protein are moving the most. If you want to know more about temperature factors, see [this useful guide by the PDB](https://pdb101.rcsb.org/learn/guide-to-understanding-pdb-data/dealing-with-coordinates).
Temperature factors are recorded in PDB files and are read by MDAnalysis when available. These can be found as an attribute of the `atoms` class.
```
# Temperature factors of the protein residues
print(protein_residues.atoms.tempfactors)
```
Just printing the raw numbers isn't very informative.
What we can do here is plot the temperature factors of the alpha carbons in our protein.
Do to this, let us first create a selection of the alpha carbon atoms (named "CA") for each chain:
```
# Alpha carbons for chain A (also known as segid A)
chainA_alphaC = protein_residues.select_atoms('name CA and segid A')
# Alpha carbons for chain B (also known as segid B)
chainB_alphaC = protein_residues.select_atoms('name CA and segid B')
```
Now let's use the plotting library matplotlib to create a plot of the alpha carbon temperature factors for each residue in each chain.
```
# We import pyplot from matplotlib
# Note the "inline" call is some jupyter magic to be able to show the plot
%matplotlib inline
from matplotlib import pyplot as plt
# We pass the residue ids and alpha carbon temperature factors to pyplot's plot function
plt.plot(chainA_alphaC.resids, chainA_alphaC.atoms.tempfactors, label='chain A')
plt.plot(chainB_alphaC.resids, chainB_alphaC.atoms.tempfactors, label='chain B')
# Let's add some titles and legends
plt.title('Plot of alpha carbon temperature factors')
plt.xlabel('residue number')
plt.ylabel('temperature factor')
plt.legend()
# We call show() to show the plot
plt.show()
```
Here we have a plot with the blue line showing the alpha carbon temperature factors for chain A, and the yellow line for chain B. As we can see, the two chains don't completely agree, but there are particular patterns to observe. Specifically, we see very low temperature factors in the regions around residues 25 and 80. We also see defined peaks near residues 15 and 70.
Knowing this information can be quite useful when trying to work out what parts of your protein are moving and what might be influencing this motion.
That being said, looking purely at a plot does not help. What we can also do, is use NGLView to directly plot the temperature factors unto the cartoon representation of our protein. We do this in the following way:
```
# Create an NGL view based on our protein_residues selection
pdbview = nglview.show_mdanalysis(pdb)
# Set the interaction session interface type
pdbview.gui_style = 'ngl'
# Clear the representations and add a cartoon representation coloured by "beta factor"
pdbview.clear_representations()
pdbview.add_representation('cartoon', color='bfactor')
# We'll also show the ligand atoms as licorice
pdbview.add_representation('licorice', selection='MK1')
# Show the widget
pdbview
```
Using the plot we created, can you work out what the colouring scheme of NGLView shows?
> Answer: Here we go from red being low beta factor regions, to blue being high ones. That is to say that bluer regions are more mobile.
Using these the plot and the NGLView representation, can you explain why there happens to be more mobile regions?
> Answer: think about which areas are more solvent exposed and therefore more likely to be in motion.
Looking at where the ligand is situated, are there any mobile residues that may influence binding?
> Answer: the loops composed of residues 49-52 are quite mobile and close to the ligand. In fact previous [work by Hornak et al.](https://www.pnas.org/content/103/4/915) shows that these can spontaneously open and close. Doing a molecular dynamics simulation (as you will in the MD tutorial), might be helpful in elucidating how these loops move.
| true |
code
| 0.647352 | null | null | null | null |
|
# Example: CanvasXpress correlation Chart No. 3
This example page demonstrates how to, using the Python package, create a chart that matches the CanvasXpress online example located at:
https://www.canvasxpress.org/examples/correlation-3.html
This example is generated using the reproducible JSON obtained from the above page and the `canvasxpress.util.generator.generate_canvasxpress_code_from_json_file()` function.
Everything required for the chart to render is included in the code below. Simply run the code block.
```
from canvasxpress.canvas import CanvasXpress
from canvasxpress.js.collection import CXEvents
from canvasxpress.render.jupyter import CXNoteBook
cx = CanvasXpress(
render_to="correlation3",
data={
"z": {
"Annt1": [
"Desc:1",
"Desc:2",
"Desc:3",
"Desc:4"
],
"Annt2": [
"Desc:A",
"Desc:B",
"Desc:A",
"Desc:B"
],
"Annt3": [
"Desc:X",
"Desc:X",
"Desc:Y",
"Desc:Y"
],
"Annt4": [
5,
10,
15,
20
],
"Annt5": [
8,
16,
24,
32
],
"Annt6": [
10,
20,
30,
40
]
},
"x": {
"Factor1": [
"Lev:1",
"Lev:2",
"Lev:3",
"Lev:1",
"Lev:2",
"Lev:3"
],
"Factor2": [
"Lev:A",
"Lev:B",
"Lev:A",
"Lev:B",
"Lev:A",
"Lev:B"
],
"Factor3": [
"Lev:X",
"Lev:X",
"Lev:Y",
"Lev:Y",
"Lev:Z",
"Lev:Z"
],
"Factor4": [
5,
10,
15,
20,
25,
30
],
"Factor5": [
8,
16,
24,
32,
40,
48
],
"Factor6": [
10,
20,
30,
40,
50,
60
]
},
"y": {
"vars": [
"V1",
"V2",
"V3",
"V4"
],
"smps": [
"S1",
"S2",
"S3",
"S4",
"S5",
"S6"
],
"data": [
[
5,
10,
25,
40,
45,
50
],
[
95,
80,
75,
70,
55,
40
],
[
25,
30,
45,
60,
65,
70
],
[
55,
40,
35,
30,
15,
1
]
]
}
},
config={
"correlationAnchorLegend": True,
"correlationAnchorLegendAlignWidth": 20,
"correlationAxis": "variables",
"graphType": "Correlation",
"title": "Correlation Plot",
"yAxisTitle": "Correlation Title"
},
width=613,
height=713,
events=CXEvents(),
after_render=[],
other_init_params={
"version": 35,
"events": False,
"info": False,
"afterRenderInit": False,
"noValidate": True
}
)
display = CXNoteBook(cx)
display.render(output_file="correlation_3.html")
```
| true |
code
| 0.708641 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/PGM-Lab/probai-2021-pyro/blob/main/Day1/notebooks/students_PPLs_Intro.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
# Setup
Let's begin by installing and importing the modules we'll need.
```
!pip install -q --upgrade pyro-ppl torch
import pyro
import torch
import pyro.distributions as dist
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
# 1. **Pyro’s distributions** (http://docs.pyro.ai/en/stable/distributions.html) :
---
* Pyro provides a wide range of distributions: **Normal, Beta, Cauchy, Dirichlet, Gumbel, Poisson, Pareto, etc.**
---
```
normal = dist.Normal(0,1)
normal
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* Samples from the distributions are [Pytorch’s Tensor objects](https://pytorch.org/cppdocs/notes/tensor_creation.html) (i.e. multidimensional arrays).
---
```
sample = normal.sample()
sample
sample = normal.sample(sample_shape=[3,4,5])
sample
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* We can query the **dimensionlity** of a tensor with the ``shape`` property
---
```
sample = normal.sample(sample_shape=[3,4,5])
sample.shape
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* Operations, like **log-likelihood**, are defined over tensors.
---
```
normal.log_prob(sample)
torch.sum(normal.log_prob(sample))
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* **Multiple distributions** can be embedded in single object.
* Below we define **three Normal distributions with different means but the same scale** in a single object.
---
```
normal = dist.Normal(torch.tensor([1.,2.,3.]),1.)
normal
normal.sample()
normal.log_prob(normal.sample())
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
### **<span style="color:red">Exercise: Open the notebook and play around</span>**
* Test that everything works.
* Play a bit with the code in Section 1 of the notebook.
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
# 2. **Pyro’s models** (http://pyro.ai/examples/intro_part_i.html) :
---
* In Pyro, a probabilistic model is defined as a **stochastic function** (i.e. every time it is run, it returns a new sample).
* Each random variable is associated with a **primitive stochastic function** using the construct ``pyro.sample(...)``.
---
### 2.1 A Temperature Model
As initial running example, we consider the problem of **modelling the temperature**. We first start with a simple model where temperture is modeled using a random Normal variable.
```
def model():
temp = pyro.sample('temp', dist.Normal(15.0, 2.0))
return temp
print(model())
print(model())
```
See how the model is a stochastic function which **returns a different value everytime it is invoked**.
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
### 2.2 A Temperature-Sensor Model
---
* In Pyro, a stochastic method is defined as a **composition of primitive stochastic functions**.
* The temperature Model: we consider the presence of a **temperature sensor**.
* The temperature sensor gives **noisy observations** about the real temperature.
* The **error** of the sensor's measurements **is known**.
* A graphical representation of this model:
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/PGM-Tem-Sensor.png?raw=1" alt="Drawing" width="150">
</center>
---
```
def model():
temp = pyro.sample('temp', dist.Normal(15.0, 2.0))
sensor = pyro.sample('sensor', dist.Normal(temp, 1.0))
return (temp, sensor)
out1 = model()
out1
```
---
* The above method defines a joint probability distribution:
$$p(sensor, temp) = p(sensor|temp)p(temp)$$
* In this case, we have a simple dependency between the variables. But, as we are in a PPL, dependencies can be expressed in terms of complex deterministic functions (more examples later).
---
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
# 3. **Pyro’s inference** (http://pyro.ai/examples/intro_part_ii.html) :
### Auxiliary inference functions (more details on Day 3)
To make inference on Pyro, we will use a variational inference method, which performs gradient-based optimization to solve the inference problem. More details will be given on Day 3.
```
from torch.distributions import constraints
from pyro.optim import SGD
from pyro.infer import Trace_ELBO
import matplotlib.pyplot as plt
from pyro.contrib.autoguide import AutoDiagonalNormal
def svi(temperature_model, guide, obs, num_steps = 5000, plot = False):
pyro.clear_param_store()
svi = pyro.infer.SVI(model=temperature_model,
guide=guide,
optim=SGD({"lr": 0.001, "momentum":0.1}),
loss=Trace_ELBO())
losses, a,b = [], [], []
for t in range(num_steps):
losses.append(svi.step(obs))
if t%250==0:
print('Step: '+str(t)+'. Loss: ' +str(losses[-1]))
if (plot):
plt.plot(losses)
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
plt.show()
```
---
* To make inference in Pyro over a given model we need to define a *guide*, this *guide* has the same signature than its counterpart model.
* The guide must provide samples for those variables of the model which are not observed using again the ``pyro.sample`` construct.
* Guides are also parametrized using Pyro's parameters (``pyro.param``), so the variational inference algorithm will optimize these parameters.
* All of that will be explained in detail on Day 3.
---
```
#The guide
def guide(obs):
a = pyro.param("mean", torch.tensor(0.0))
b = pyro.param("scale", torch.tensor(1.), constraint=constraints.positive)
temp = pyro.sample('temp', dist.Normal(a, b))
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
### 3.1 Conditioning on a single observation
Now, we continue with the last model defined in section 2.2, and assume we have a sensor reading and we want to compute the posterior distribution over the real temperature.
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/PGM-Tem-Sensor.png?raw=1" alt="Drawing" width="150">
</center>
---
* This can be achived by introducing **observations in the random variable** with the keyword ``obs=``.
---
```
#The observatons
obs = {'sensor': torch.tensor(18.0)}
def model(obs):
temp = pyro.sample('temp', dist.Normal(15.0, 2.0))
sensor = pyro.sample('sensor', dist.Normal(temp, 1.0), obs=obs['sensor'])
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* Inference is made using the previously defined auxiliary functions, ``svi`` and ``guide``.
* We can query the **posterior probability distribution**:
$$p(temp | sensor=18)=\frac{p(sensor=18|temp)p(temp)}{\int p(sensor=18|temp)p(temp) dtemp}$$
---
```
#Run inference
svi(model,guide,obs, plot=True)
#Print results
print("P(Temperature|Sensor=18.0) = ")
print(dist.Normal(pyro.param("mean").item(), pyro.param("scale").item()))
print("")
```
---
* Inference is an **optimization procedure**.
* The **ELBO function is minimized** during the variational inference process.
---
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
### 3.2 Learning from a bunch of observations
---
* Let us assume we have a **set of observations** about the temperature at different time steps.
* In this case, and following a probabilistic modelling approach, we define a **set of random variables**.
* One random variable for each **observation**, using a standard ``for-loop``.
---
```
#The observatons
obs = {'sensor': torch.tensor([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1])}
def model(obs):
for i in range(obs['sensor'].shape[0]):
temp = pyro.sample(f'temp_{i}', dist.Normal(15.0, 2.0))
sensor = pyro.sample(f'sensor_{i}', dist.Normal(temp, 1.0), obs=obs['sensor'][i])
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* What if we do **not know the mean temperature**.
* We can **infer it from the data** by, e.g., using a **maximum likelihood** approach,
$$ \mu_{t} = \arg\max_\mu \ln p(s_1,\ldots,s_n|\mu) = \arg\max_\mu \prod_i \int_{t_i} p(s_i|t_i)p(t_i|\mu) dt_i $$
where $s_i$ and $t_i$ denote the sensor reading and the real temperature at time $i$.
* The graphical model:
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/PGM-Tem_sensor4.png?raw=1" alt="Drawing" width="150">
</center>
* With PPLs, we do not have to care about the **underlying inference problem** We just define the model and let the **PPL's engine** make the work for us.
* We use Pyro's parameters (defined as ``pyro.param``), which are free variables we can optimize.
---
```
#The observatons
obs = {'sensor': torch.tensor([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1])}
def model(obs):
mean_temp = pyro.param('mean_temp', torch.tensor(15.0))
for i in range(obs['sensor'].shape[0]):
temp = pyro.sample(f'temp_{i}', dist.Normal(mean_temp, 2.0))
sensor = pyro.sample(f'sensor_{i}', dist.Normal(temp, 1.0), obs=obs['sensor'][i])
#@title
#Define the guide
def guide(obs):
for i in range(obs['sensor'].shape[0]):
mean_i = pyro.param(f'mean_{i}', obs['sensor'][i])
scale_i = pyro.param(f'scale_{i}', torch.tensor(1.), constraint=constraints.positive)
temp = pyro.sample(f'temp_{i}', dist.Normal(mean_i, scale_i))
#@title
#Run inference
svi(model, guide, obs, num_steps=1000)
#Print results
print("Estimated Mean Temperature")
print(pyro.param("mean_temp").item())
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* Instead of performing *maximum likelihood* learning, we can perform **Bayesian learning**.
* We treat the unknown quantity as a **random variable**.
* This model can be graphically represented as follows:
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/PGM-Tem-Sensor2.png?raw=1" alt="Drawing" width="150">
</center>
---
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
```
#The observatons
obs = {'sensor': torch.tensor([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1])}
def model(obs):
mean_temp = pyro.sample('mean_temp', dist.Normal(15.0, 2.0))
for i in range(obs['sensor'].shape[0]):
temp = pyro.sample(f'temp_{i}', dist.Normal(mean_temp, 2.0))
sensor = pyro.sample(f'sensor_{i}', dist.Normal(temp, 1.0), obs=obs['sensor'][i])
```
---
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* We perform inference over this model:
$$ p(\mu_t | s_1,\ldots, s_n)=\frac{p(\mu_t)\prod_{i=1}^n \int p(s_i|t_i)p(t_i|\mu_t)dt_i }{\int \prod_{i=1}^n p(s_i|\mu_t)p(\mu_t) d\mu} $$
---
```
#@title
#Define the guide
def guide(obs):
mean = pyro.param("mean", torch.mean(obs['sensor']))
scale = pyro.param("scale", torch.tensor(1.), constraint=constraints.positive)
mean_temp = pyro.sample('mean_temp', dist.Normal(mean, scale))
for i in range(obs['sensor'].shape[0]):
mean_i = pyro.param(f'mean_{i}', obs['sensor'][i])
scale_i = pyro.param(f'scale_{i}', torch.tensor(1.), constraint=constraints.positive)
temp = pyro.sample(f'temp_{i}', dist.Normal(mean_i, scale_i))
import time
#Run inference
start = time.time()
svi(model, guide, obs, num_steps=1000)
#Print results
print("P(mean_temp|Sensor=[18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1]) =")
print(dist.Normal(pyro.param("mean").item(), pyro.param("scale").item()))
print("")
end = time.time()
print(f"{(end - start)} seconds")
```
---
* The result of the learning is **not a point estimate**.
* We have a **posterior distribution** which captures **uncertainty** about the estimation.
---
```
import numpy as np
import scipy.stats as stats
mu = 19.312837600708008
scale = 0.6332376003265381
x = np.linspace(mu - 3*scale, mu + 3*scale, 100)
plt.plot(x, stats.norm.pdf(x, mu, scale), label='Posterior')
point = 19.123859405517578
plt.plot([point, point],[0., 1.], label='Point Estimate')
plt.legend()
plt.show()
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
### 3.3 The use of ``plate`` construct
---
* Pyro can exploit **conditional independencies and vectorization** to make inference much faster.
* This can be done with the construct **``plate``**.
* With this construct, we can indicate that the variables $s_i$ and $t_i$ are **conditionally indepdendent** from another variables $s_j$ and $t_j$ given $\mu_t$.
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/PGM-Tem-Sensor2.png?raw=1" alt="Drawing" width="150">
</center>
---
```
#The observatons
obs = {'sensor': torch.tensor([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1])}
def model(obs):
mean_temp = pyro.sample('mean_temp', dist.Normal(15.0, 2.0))
with pyro.plate('a', obs['sensor'].shape[0]):
temp = pyro.sample('temp', dist.Normal(mean_temp, 2.0))
sensor = pyro.sample('sensor', dist.Normal(temp, 1.0), obs=obs['sensor'])
```
---
* The ``plate`` construct reflects the standard notational use in graphical models denoting the **repetition of some parts of of the graph**.
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/PGM-Tem-Sensor3.png?raw=1" alt="Drawing" width="250">
</center>
* We can here make a distinction between **local** and **global** random variables:
>* **Local random variables** caputure **specific information** about the $i$-th data sample (i.e. the real temperature at this moment in time).
>* **Global random variables** capture **common information** about all the data samples (i.e. the average temperature of all data samples).
---
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
Observe how inference in this model is much **faster**.
```
#@title
#Define the guide
def guide(obs_sensor):
mean = pyro.param("mean", torch.mean(obs['sensor']))
scale = pyro.param("scale", torch.tensor(1.), constraint=constraints.positive)
mean_temp = pyro.sample('mean_temp', dist.Normal(mean, scale))
with pyro.plate('a', obs['sensor'].shape[0]) as i:
mean_i = pyro.param('mean_i', obs['sensor'][i])
scale_i = pyro.param('scale_i', torch.tensor(1.), constraint=constraints.positive)
temp = pyro.sample('temp', dist.Normal(mean_i, scale_i))
#Run inference
start = time.time()
svi(model, guide, obs, num_steps=1000)
#Print results
print("P(mean_temp|Sensor=[18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1]) =")
print(dist.Normal(pyro.param("mean").item(), pyro.param("scale").item()))
print("")
end = time.time()
print(f"{(end - start)} seconds")
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
### **<span style="color:red">Exercise 1: </span>The role of *prior distributions* in learning**
In this case we just want to llustrate how the output of learning depends of the particular prior we introduce in the model. Play with different options and extract conclusions:
1. What happens if we change the mean of the prior?
2. What happens if we change the scale of the prior?
3. What happens to the posterior if the number of data samples deacreases and increases?
```
#The observatons
sample_size = 10
obs = {'sensor': torch.tensor(np.random.normal(18,2,sample_size))}
def model(obs):
mean_temp = pyro.sample('mean_temp', dist.Normal(15.0, 2.0))
with pyro.plate('a', obs['sensor'].shape[0]):
temp = pyro.sample('temp', dist.Normal(mean_temp, 2.0))
sensor = pyro.sample('sensor', dist.Normal(temp, 1.0), obs=obs['sensor'])
#Run inference
svi(model, guide, obs, num_steps=1000)
#Print results
print("P(Temperature|Sensor=18.0) = ")
print(dist.Normal(pyro.param("mean").item(), pyro.param("scale").item()))
x = np.linspace(16, 20, 100)
plt.plot(x, stats.norm.pdf(x, pyro.param("mean").item(), pyro.param("scale").item()), label='Posterior')
point = 18
plt.plot([point, point],[0., 1.], label='Point Estimate')
plt.xlim(16,20)
plt.legend()
plt.show()
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
# **4. Icecream Shop**
* We have an ice-cream shop and we **record the ice-cream sales and the average temperature of the day** (using a temperature sensor).
* We know **temperature affects the sales** of ice-creams.
* We want to **precisely model** how temperature affects ice-cream sales.
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/raw/main/Day1/Figures/Ice-cream_shop_-_Florida.jpg" alt="Drawing" width=300 >
</center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* We have **observations** from temperature and sales.
* Sales are modeled with a **Poisson** distribution:
>- The rate of the Poisson **linearly depends of the real temperature**.
---
Next figure provides a graphical and a probabilistic description of the model:
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/Ice-Cream-Shop-Model.png?raw=1" alt="Drawing" width=700>
</center>
```
#The observatons
obs = {'sensor': torch.tensor([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1]),
'sales': torch.tensor([46., 47., 49., 44., 50., 54., 51., 52., 49., 53.])}
def model(obs):
mean_temp = pyro.sample('mean_temp', dist.Normal(15.0, 2.0))
alpha = pyro.sample('alpha', dist.Normal(0.0, 100.0))
beta = pyro.sample('beta', dist.Normal(0.0, 100.0))
with pyro.plate('a', obs['sensor'].shape[0]):
temp = pyro.sample('temp', dist.Normal(mean_temp, 2.0))
sensor = pyro.sample('sensor', dist.Normal(temp, 1.0), obs=obs['sensor'])
rate = torch.max(torch.tensor(0.001), alpha + beta*temp)
sales = pyro.sample('sales', dist.Poisson(rate), obs=obs['sales'])
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
```
#@title
#Define the guide
def guide(obs):
mean = pyro.param("mean", torch.mean(obs['sensor']))
scale = pyro.param("scale", torch.tensor(1.), constraint=constraints.positive)
mean_temp = pyro.sample('mean_temp', dist.Normal(mean, scale))
alpha_mean = pyro.param("alpha_mean", torch.mean(obs['sensor']))
alpha_scale = pyro.param("alpha_scale", torch.tensor(1.), constraint=constraints.positive)
alpha = pyro.sample('alpha', dist.Normal(alpha_mean, alpha_scale))
beta_mean = pyro.param("beta_mean", torch.tensor(1.0))
beta_scale = pyro.param("beta_scale", torch.tensor(1.), constraint=constraints.positive)
beta = pyro.sample('beta', dist.Normal(beta_mean, beta_scale))
with pyro.plate('a', obs['sensor'].shape[0]) as i:
mean_i = pyro.param('mean_i', obs['sensor'][i])
scale_i = pyro.param('scale_i', torch.tensor(1.), constraint=constraints.positive)
temp = pyro.sample('temp', dist.Normal(mean_i, scale_i))
```
---
* We run the **(variational) inference engine** and get the results.
* With PPLs, we only care about modeling, **not about the low-level details** of the machine-learning solver.
---
```
#Run inference
svi(model, guide, obs, num_steps=1000)
#Print results
print("Posterior temperature mean")
print(dist.Normal(pyro.param("mean").item(), pyro.param("scale").item()))
print("")
print("Posterior alpha")
print(dist.Normal(pyro.param("alpha_mean").item(), pyro.param("alpha_scale").item()))
print("")
print("Posterior aeta")
print(dist.Normal(pyro.param("beta_mean").item(), pyro.param("beta_scale").item()))
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
### <span style="color:red">Exercise 2: Introduce Humidity in the Icecream shop model </span>
---
* Assume we also have a bunch of **humidity sensor measurements**.
* Assume the **sales are also linearly influenced by the humidity**.
* **Extend the above model** in order to integrate all of that.
---
Next figure provides a graphical and a probabilistic description of the model:
<center>
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/Ice-Cream-Shop-Model-Humidity.png?raw=1" alt="Drawing" width=700>
</center>
```
#The observatons
obs = {'sensor': torch.tensor([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1]),
'sales': torch.tensor([46., 47., 49., 44., 50., 54., 51., 52., 49., 53.]),
'sensor_humidity': torch.tensor([82.8, 87.6, 69.1, 74.2, 80.3, 94.2, 91.2, 92.2, 99.1, 93.2])}
def model(obs):
mean_temp = pyro.sample('mean_temp', dist.Normal(15.0, 2.0))
## Introduce a random variable "mean_humidity"
alpha = pyro.sample('alpha', dist.Normal(0.0, 100.0))
beta = pyro.sample('beta', dist.Normal(0.0, 100.0))
## Introduce a coefficient for the humidity "gamma"
with pyro.plate('a', obs['sensor'].shape[0]):
temp = pyro.sample('temp', dist.Normal(mean_temp, 2.0))
sensor = pyro.sample('sensor', dist.Normal(temp, 1.0), obs=obs['sensor'])
#Add the 'humidity' variable and the 'sensor_humidity' variable
#Add the linear dependency for the rate with respect to temp and humidity (keep torch.max to avoid numerical stability issues)
rate = torch.max(torch.tensor(0.001), ????)
sales = pyro.sample('sales', dist.Poisson(rate), obs=obs['sales'])
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* We run the **(variational) inference engine** and get the results.
* With PPLs, we only care about modeling, **not about the low-level details** of the machine-learning solver.
---
```
#@title
#Auxiliary Guide Code
def guide(obs):
mean = pyro.param("mean", torch.mean(obs['sensor']))
scale = pyro.param("scale", torch.tensor(1.), constraint=constraints.positive)
mean_temp = pyro.sample('mean_temp', dist.Normal(mean, scale))
meanH = pyro.param("meanH", torch.mean(obs['sensor_humidity']))
scaleH = pyro.param("scaleH", torch.tensor(1.), constraint=constraints.positive)
mean_humidity = pyro.sample('mean_humidity', dist.Normal(meanH, scaleH))
alpha_mean = pyro.param("alpha_mean", torch.mean(obs['sensor']), constraint=constraints.positive)
alpha_scale = pyro.param("alpha_scale", torch.tensor(1.), constraint=constraints.positive)
alpha = pyro.sample('alpha', dist.Normal(alpha_mean, alpha_scale))
beta_mean = pyro.param("beta_mean", torch.tensor(1.0), constraint=constraints.positive)
beta_scale = pyro.param("beta_scale", torch.tensor(1.), constraint=constraints.positive)
beta = pyro.sample('beta', dist.Normal(beta_mean, beta_scale))
gamma_mean = pyro.param("gamma_mean", torch.tensor(1.0), constraint=constraints.positive)
gamma_scale = pyro.param("gamma_scale", torch.tensor(1.), constraint=constraints.positive)
gamma = pyro.sample('gamma', dist.Normal(gamma_mean, gamma_scale))
with pyro.plate('a', obs['sensor'].shape[0]) as i:
mean_i = pyro.param('mean_i', obs['sensor'][i])
scale_i = pyro.param('scale_i', torch.tensor(1.), constraint=constraints.positive)
temp = pyro.sample('temp', dist.Normal(mean_i, scale_i))
meanH_i = pyro.param('meanH_i', obs['sensor_humidity'][i])
scaleH_i = pyro.param('scaleH_i', torch.tensor(1.), constraint=constraints.positive)
humidity = pyro.sample('humidity', dist.Normal(meanH_i, scaleH_i))
#Run inference
svi(model, guide, obs, num_steps=1000)
#Print results
print("Posterior Temperature Mean")
print(dist.Normal(pyro.param("mean").item(), pyro.param("scale").item()))
print("")
print("Posterior Humidity Mean")
print(dist.Normal(pyro.param("meanH").item(), pyro.param("scaleH").item()))
print("")
print("Posterior Alpha")
print(dist.Normal(pyro.param("alpha_mean").item(), pyro.param("alpha_scale").item()))
print("")
print("Posterior Beta")
print(dist.Normal(pyro.param("beta_mean").item(), pyro.param("beta_scale").item()))
print("")
print("Posterior Gamma")
print(dist.Normal(pyro.param("gamma_mean").item(), pyro.param("gamma_scale").item()))
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
# 5. **Temporal Models**
If we think there is a temporal dependency between the variables, we can easily encode that with PPLs.
---
* Let us assume that there is a **temporal dependency** between the variables.
* E.g. the current **real temperature must be similar to the real temperature in the previous time step**.
* This temporal dependency can **be modeled** using a **for-loop** in Pyro
* Consider the **graphical representation**.
---
<img src="https://github.com/PGM-Lab/probai-2021-pyro/raw/main/Day1/Figures/tempmodel-temporal-III.png" alt="Drawing" style="width: 350px;" >
```
#The observatons
obs = {'sensor': torch.tensor([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1])}
def model(obs):
mean_temp = pyro.sample('mean_temp', dist.Normal(15.0, 2.0))
for i in range(obs['sensor'].shape[0]):
if i==0:
temp = pyro.sample(f'temp_{i}', dist.Normal(mean_temp, 2.0))
else:
temp = pyro.sample(f'temp_{i}', dist.Normal(prev_temp, 2.0))
sensor = pyro.sample(f'sensor_{i}', dist.Normal(temp, 1.0), obs=obs['sensor'][i])
prev_temp = temp
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* We run the **(variational) inference engine** and get the results.
* With PPLs, we only care about modeling, **not about the low-level details** of the machine-learning solver.
---
```
#@title
#Define the guide
def guide(obs):
mean = pyro.param("mean", torch.mean(obs['sensor']))
scale = pyro.param("scale", torch.tensor(1.), constraint=constraints.positive)
mean_temp = pyro.sample('mean_temp', dist.Normal(mean, scale))
for i in range(obs['sensor'].shape[0]):
mean_i = pyro.param(f'mean_{i}', obs['sensor'][i])
scale_i = pyro.param(f'scale_{i}', torch.tensor(1.), constraint=constraints.positive)
temp = pyro.sample(f'temp_{i}', dist.Normal(mean_i, scale_i))
import time
#Run inference
svi(model, guide, obs, num_steps=2000)
smooth_temp=[]
for i in range(obs['sensor'].shape[0]):
smooth_temp.append(pyro.param(f'mean_{i}').item())
print('Finished')
```
---
* Plot the **observered measurements** of the temperature **against** the inferred **real temperature**.
* By querying the **local hidden** we can **smooth** the temperature.
* The **recovered temperature** is much less noisy than the measured one.
---
```
import matplotlib.pyplot as plt
plt.plot([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1], label='Sensor Temp')
plt.plot(smooth_temp, label='Smooth Temp')
plt.legend()
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
### <span style="color:red">Exercise 3: Temporal Extension of the Iceacream shop model </span>
---
* **Extends** Excersise 2.
* Assume temperature depends of the **temperature in the previous day**.
* Assume humidity depends of the **humidity in the previous day**.
* Assume sales depends on the **current temperature and humidity**.
* Use the following **graphical representation for reference**.
* Consider here that the plate representation has to be coded in Pyro using a **``for-loop``**.
---
<img src="https://github.com/PGM-Lab/probai-2021-pyro/raw/main/Day1/Figures/icecream-model-temporal.png" alt="Drawing" width=500 >
```
#The observatons
obs = {'sensor': torch.tensor([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1]),
'sales': torch.tensor([46., 47., 49., 44., 50., 54., 51., 52., 49., 53.]),
'sensor_humidity': torch.tensor([82.8, 87.6, 69.1, 74.2, 80.3, 94.2, 91.2, 92.2, 99.1, 93.2])}
def model(obs):
mean_temp = pyro.sample('mean_temp', dist.Normal(15.0, 2.0))
## Introduce a random variable "mean_humidity"
alpha = pyro.sample('alpha', dist.Normal(0.0, 100.0))
beta = pyro.sample('beta', dist.Normal(0.0, 100.0))
## Introduce a coefficient for the humidity "gamma"
for i in range(obs['sensor'].shape[0]):
if i==0:
temp = pyro.sample(f'temp_{i}', dist.Normal(mean_temp, 2.0))
#Introduce the 'humidity' variable at time 0.
else:
temp = pyro.sample(f'temp_{i}', dist.Normal(prev_temp, 2.0))
#Introduce the f'humidity_{i}' variable defining the transition
sensor = pyro.sample(f'sensor_{i}', dist.Normal(temp, 1.0), obs=obs['sensor'][i])
#Introduce the f'sensor_humidity_{i}' variable.
#Add the linear dependency for the rate with respect to temp and humidity (keep torch.max to avoid numerical stability issues)
rate = torch.max(torch.tensor(0.01),????)
sales = pyro.sample(f'sales_{i}', dist.Poisson(rate), obs=obs['sales'][i])
prev_temp = temp
#Keep humidity for the next time step.
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* We run the **(variational) inference engine** and get the results.
* With PPLs, we only care about modeling, **not about the low-level details** of the machine-learning solver.
---
```
#@title
#Define the guide
def guide(obs):
mean = pyro.param("mean", torch.mean(obs['sensor']))
scale = pyro.param("scale", torch.tensor(1.), constraint=constraints.greater_than(0.01))
mean_temp = pyro.sample('mean_temp', dist.Normal(mean, scale))
meanH = pyro.param("meanH", torch.mean(obs['sensor_humidity']), constraint=constraints.positive)
scaleH = pyro.param("scaleH", torch.tensor(1.), constraint=constraints.greater_than(0.01))
humidity_mean = pyro.sample('mean_humidity', dist.Normal(meanH, scaleH))
alpha_mean = pyro.param("alpha_mean", torch.mean(obs['sensor']))
alpha_scale = pyro.param("alpha_scale", torch.tensor(1.), constraint=constraints.greater_than(0.01))
alpha = pyro.sample('alpha', dist.Normal(alpha_mean, alpha_scale))
beta_mean = pyro.param("beta_mean", torch.tensor(0.0))
beta_scale = pyro.param("beta_scale", torch.tensor(1.), constraint=constraints.greater_than(0.01))
beta = pyro.sample('beta', dist.Normal(beta_mean, beta_scale))
gamma_mean = pyro.param("gamma_mean", torch.tensor(0.0))
gamma_scale = pyro.param("gamma_scale", torch.tensor(1.), constraint=constraints.greater_than(0.01))
gamma = pyro.sample('gamma', dist.Normal(gamma_mean, gamma_scale))
for i in range(obs['sensor'].shape[0]):
mean_i = pyro.param(f'mean_{i}', obs['sensor'][i])
scale_i = pyro.param(f'scale_{i}', torch.tensor(1.), constraint=constraints.greater_than(0.01))
temp = pyro.sample(f'temp_{i}', dist.Normal(mean_i, scale_i))
meanH_i = pyro.param(f'meanH_{i}', obs['sensor_humidity'][i])
scaleH_i = pyro.param(f'scaleH_{i}', torch.tensor(1.), constraint=constraints.greater_than(0.01))
humidity_i = pyro.sample(f'humidity_{i}', dist.Normal(meanH_i, scaleH_i))
import time
#Run inference
svi(model, guide, obs, num_steps=2000)
smooth_temp=[]
smooth_humidity=[]
for i in range(obs['sensor'].shape[0]):
smooth_temp.append(pyro.param(f'mean_{i}').item())
smooth_humidity.append(pyro.param(f'meanH_{i}').item())
print('Finished')
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
---
* We can plot the observered measurements of the temperature against the **inferred real temperature** by our model.
* The **recovered temperature** is much less noisy than the real one.
---
```
plt.plot([18., 18.7, 19.2, 17.8, 20.3, 22.4, 20.3, 21.2, 19.5, 20.1], label='Sensor Temp')
plt.plot(smooth_temp, label='Smooth Temp')
plt.legend()
```
---
* We can plot the observered measurements of the humidity against the **inferred real humidity** by our model.
* The **recovered humidity** is much less noisy than the real one.
---
```
humidity = torch.tensor([82.8, 87.6, 69.1, 74.2, 80.3, 94.2, 91.2, 92.2, 99.1, 93.2])
plt.plot(humidity.detach().numpy(), label='Sensor Humidity')
plt.plot(smooth_humidity, label='Smooth Humidity')
plt.legend()
```
<img src="https://github.com/PGM-Lab/probai-2021-pyro/blob/main/Day1/Figures/blue.png?raw=1" alt="Drawing" width=2000 height=20>
| true |
code
| 0.601594 | null | null | null | null |
|
# 5.9 含并行连结的网络(GoogLeNet)
```
import time
import torch
from torch import nn, optim
import torch.nn.functional as F
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(torch.__version__)
print(device)
```
## 5.9.1 Inception 块
```
class Inception(nn.Module):
# c1 - c4为每条线路里的层的输出通道数
def __init__(self, in_c, c1, c2, c3, c4):
super(Inception, self).__init__()
# 线路1,单1 x 1卷积层
self.p1_1 = nn.Conv2d(in_c, c1, kernel_size=1)
# 线路2,1 x 1卷积层后接3 x 3卷积层
self.p2_1 = nn.Conv2d(in_c, c2[0], kernel_size=1)
self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
# 线路3,1 x 1卷积层后接5 x 5卷积层
self.p3_1 = nn.Conv2d(in_c, c3[0], kernel_size=1)
self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
# 线路4,3 x 3最大池化层后接1 x 1卷积层
self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
self.p4_2 = nn.Conv2d(in_c, c4, kernel_size=1)
def forward(self, x):
p1 = F.relu(self.p1_1(x))
p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
p4 = F.relu(self.p4_2(self.p4_1(x)))
return torch.cat((p1, p2, p3, p4), dim=1) # 在通道维上连结输出
```
## 5.9.2 GoogLeNet模型
```
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
nn.Conv2d(64, 192, kernel_size=3, padding=1),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
Inception(256, 128, (128, 192), (32, 96), 64),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
Inception(512, 160, (112, 224), (24, 64), 64),
Inception(512, 128, (128, 256), (24, 64), 64),
Inception(512, 112, (144, 288), (32, 64), 64),
Inception(528, 256, (160, 320), (32, 128), 128),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
Inception(832, 384, (192, 384), (48, 128), 128),
d2l.GlobalAvgPool2d())
net = nn.Sequential(b1, b2, b3, b4, b5, d2l.FlattenLayer(), nn.Linear(1024, 10))
X = torch.rand(1, 1, 96, 96)
for blk in net.children():
X = blk(X)
print('output shape: ', X.shape)
```
## 5.9.3 获取数据和训练模型
```
batch_size = 128
# 如出现“out of memory”的报错信息,可减小batch_size或resize
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
```
| true |
code
| 0.797852 | null | null | null | null |
|
# Modeling and Simulation in Python
Chapter 23
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import functions from the modsim.py module
from modsim import *
```
### Code from the previous chapter
```
m = UNITS.meter
s = UNITS.second
kg = UNITS.kilogram
degree = UNITS.degree
params = Params(x = 0 * m,
y = 1 * m,
g = 9.8 * m/s**2,
mass = 145e-3 * kg,
diameter = 73e-3 * m,
rho = 1.2 * kg/m**3,
C_d = 0.3,
angle = 45 * degree,
velocity = 40 * m / s,
t_end = 20 * s)
def make_system(params):
"""Make a system object.
params: Params object with angle, velocity, x, y,
diameter, duration, g, mass, rho, and C_d
returns: System object
"""
unpack(params)
# convert angle to degrees
theta = np.deg2rad(angle)
# compute x and y components of velocity
vx, vy = pol2cart(theta, velocity)
# make the initial state
init = State(x=x, y=y, vx=vx, vy=vy)
# compute area from diameter
area = np.pi * (diameter/2)**2
return System(params, init=init, area=area)
def drag_force(V, system):
"""Computes drag force in the opposite direction of `V`.
V: velocity
system: System object with rho, C_d, area
returns: Vector drag force
"""
unpack(system)
mag = -rho * V.mag**2 * C_d * area / 2
direction = V.hat()
f_drag = mag * direction
return f_drag
def slope_func(state, t, system):
"""Computes derivatives of the state variables.
state: State (x, y, x velocity, y velocity)
t: time
system: System object with g, rho, C_d, area, mass
returns: sequence (vx, vy, ax, ay)
"""
x, y, vx, vy = state
unpack(system)
V = Vector(vx, vy)
a_drag = drag_force(V, system) / mass
a_grav = Vector(0, -g)
a = a_grav + a_drag
return vx, vy, a.x, a.y
def event_func(state, t, system):
"""Stop when the y coordinate is 0.
state: State object
t: time
system: System object
returns: y coordinate
"""
x, y, vx, vy = state
return y
```
### Optimal launch angle
To find the launch angle that maximizes distance from home plate, we need a function that takes launch angle and returns range.
```
def range_func(angle, params):
"""Computes range for a given launch angle.
angle: launch angle in degrees
params: Params object
returns: distance in meters
"""
params = Params(params, angle=angle)
system = make_system(params)
results, details = run_ode_solver(system, slope_func, events=event_func)
x_dist = get_last_value(results.x) * m
return x_dist
```
Let's test `range_func`.
```
%time range_func(45, params)
```
And sweep through a range of angles.
```
angles = linspace(20, 80, 21)
sweep = SweepSeries()
for angle in angles:
x_dist = range_func(angle, params)
print(angle, x_dist)
sweep[angle] = x_dist
```
Plotting the `Sweep` object, it looks like the peak is between 40 and 45 degrees.
```
plot(sweep, color='C2')
decorate(xlabel='Launch angle (degree)',
ylabel='Range (m)',
title='Range as a function of launch angle',
legend=False)
savefig('figs/chap10-fig03.pdf')
```
We can use `max_bounded` to search for the peak efficiently.
```
%time res = max_bounded(range_func, [0, 90], params)
```
`res` is an `ModSimSeries` object with detailed results:
```
res
```
`x` is the optimal angle and `fun` the optional range.
```
optimal_angle = res.x * degree
max_x_dist = res.fun
```
### Under the hood
Read the source code for `max_bounded` and `min_bounded`, below.
Add a print statement to `range_func` that prints `angle`. Then run `max_bounded` again so you can see how many times it calls `range_func` and what the arguments are.
```
%psource max_bounded
%psource min_bounded
```
### The Manny Ramirez problem
Finally, let's solve the Manny Ramirez problem:
*What is the minimum effort required to hit a home run in Fenway Park?*
Fenway Park is a baseball stadium in Boston, Massachusetts. One of its most famous features is the "Green Monster", which is a wall in left field that is unusually close to home plate, only 310 feet along the left field line. To compensate for the short distance, the wall is unusually high, at 37 feet.
Although the problem asks for a minimum, it is not an optimization problem. Rather, we want to solve for the initial velocity that just barely gets the ball to the top of the wall, given that it is launched at the optimal angle.
And we have to be careful about what we mean by "optimal". For this problem, we don't want the longest range, we want the maximum height at the point where it reaches the wall.
If you are ready to solve the problem on your own, go ahead. Otherwise I will walk you through the process with an outline and some starter code.
As a first step, write a function called `height_func` that takes a launch angle and a params as parameters, simulates the flights of a baseball, and returns the height of the baseball when it reaches a point 94.5 meters (310 feet) from home plate.
```
# Solution goes here
```
Always test the slope function with the initial conditions.
```
# Solution goes here
# Solution goes here
```
Test your function with a launch angle of 45 degrees:
```
# Solution goes here
```
Now use `max_bounded` to find the optimal angle. Is it higher or lower than the angle that maximizes range?
```
# Solution goes here
# Solution goes here
# Solution goes here
```
With initial velocity 40 m/s and an optimal launch angle, the ball clears the Green Monster with a little room to spare.
Which means we can get over the wall with a lower initial velocity.
### Finding the minimum velocity
Even though we are finding the "minimum" velocity, we are not really solving a minimization problem. Rather, we want to find the velocity that makes the height at the wall exactly 11 m, given given that it's launched at the optimal angle. And that's a job for `fsolve`.
Write an error function that takes a velocity and a `Params` object as parameters. It should use `max_bounded` to find the highest possible height of the ball at the wall, for the given velocity. Then it should return the difference between that optimal height and 11 meters.
```
# Solution goes here
```
Test your error function before you call `fsolve`.
```
# Solution goes here
```
Then use `fsolve` to find the answer to the problem, the minimum velocity that gets the ball out of the park.
```
# Solution goes here
# Solution goes here
```
And just to check, run `error_func` with the value you found.
```
# Solution goes here
```
| true |
code
| 0.772198 | null | null | null | null |
|
# Model Fitting - XGBoost
Fit the XGBoost model using the training dataset. XGBoost is faster and has potentially better accuracy. This allow me to use more features and test changes faster.
```
%load_ext autoreload
%autoreload 2
%matplotlib notebook
import numpy as np
from numpy import mean
from numpy import std
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import GradientBoostingClassifier
from matplotlib.lines import Line2D
import joblib
from src.data.labels_util import load_labels, LabelCol, get_labels_file, load_clean_labels, get_workouts
from src.data.imu_util import (
get_sensor_file, ImuCol, load_imu_data, Sensor, fix_epoch, resample_uniformly, time_to_row_range, get_data_chunk,
normalize_with_bounds, data_to_features, list_imu_abspaths, clean_imu_data
)
from src.data.util import find_nearest, find_nearest_index, shift, low_pass_filter, add_col
from src.data.workout import Activity, Workout
from src.data.data import DataState
from src.data.build_features import main as build_features
from src.data.features_util import list_test_files
from src.model.train import evaluate_model_accuracy, train_model, create_xgboost
from src.model.predict import evaluate_on_test_data, evaluate_on_test_data_plot
from src.visualization.visualize import multiplot
from src.config import (
TRAIN_BOOT_DIR, TRAIN_POLE_DIR, TRAIN_FEATURES_FILENAME, TRAIN_LABELS_FILENAME, BOOT_MODEL_FILE,
POLE_MODEL_FILE
)
# import data types
from pandas import DataFrame
from numpy import ndarray
from typing import List, Tuple, Optional
```
### Evaluate quality of model and training data
Use k-fold cross-validation to evaluate the performance of the model.
```
# UNCOMMENT to use. It's very slow.
# print('Boot model:')
# features: ndarray = np.load(TRAIN_BOOT_DIR / TRAIN_FEATURES_FILENAME)
# labels: ndarray = np.load(TRAIN_BOOT_DIR / TRAIN_LABELS_FILENAME)
# evaluate_model_accuracy(features, labels, create_xgboost())
# print('Pole model:')
# features: ndarray = np.load(TRAIN_POLE_DIR / TRAIN_FEATURES_FILENAME)
# labels: ndarray = np.load(TRAIN_POLE_DIR / TRAIN_LABELS_FILENAME)
# evaluate_model_accuracy(features, labels)
```
### Train model
```
print('Train boot model:')
# train_model(Activity.Boot, create_xgboost())
print('Train pole model:')
# train_model(Activity.Pole, create_xgboost())
```
### Test model
**NOTE**: Move the trained model (the pickle files) to the ```models``` directory and edit the paths in ```config.py``` to point to the latest model.
```
print('Test boot model:')
evaluate_on_test_data_plot(Activity.Boot, False, test_idx=0)
print('Test pole model:')
evaluate_on_test_data_plot(Activity.Pole, False, test_idx=0)
```
| true |
code
| 0.633949 | null | null | null | null |
|
### Generating `publications.json` partitions
This is a template notebook for generating metadata on publications - most importantly, the linkage between the publication and dataset (datasets are enumerated in `datasets.json`)
Process goes as follows:
1. Import CSV with publication-dataset linkages. Your csv should have at the minimum, fields (spelled like the below):
* `dataset` to hold the dataset_ids, and
* `title` for the publication title.
Update the csv with these field names to ensure this code will run. We read in, dedupe and format the title
2. Match to `datasets.json` -- alert if given dataset doesn't exist yet
3. Generate list of dicts with publication metadata
4. Write to a publications.json file
#### Import CSV containing publication-dataset linkages
Set `linkages_path` to the location of the csv containg dataset-publication linkages and read in csv
```
import pandas as pd
import datetime
import os
file_name = 'foodaps_usda_linkages.csv'
rcm_subfolder = '20190619_usda_foodaps'
linkages_path = os.path.join('/Users/andrewnorris/RichContextMetadata/metadata',rcm_subfolder,file_name)
# linkages_path = os.path.join(os.getcwd(),'SNAP_DATA_DIMENSIONS_SEARCH_DEMO.csv')
linkages_csv = pd.read_csv(linkages_path)
linkages_path
```
Format/clean linkage data - apply `scrub_unicode` to `title` field.
```
import unicodedata
def scrub_unicode (text):
"""
try to handle the unicode edge cases encountered in source text,
as best as possible
"""
x = " ".join(map(lambda s: s.strip(), text.split("\n"))).strip()
x = x.replace('“', '"').replace('”', '"')
x = x.replace("‘", "'").replace("’", "'").replace("`", "'")
x = x.replace("`` ", '"').replace("''", '"')
x = x.replace('…', '...').replace("\\u2026", "...")
x = x.replace("\\u00ae", "").replace("\\u2122", "")
x = x.replace("\\u00a0", " ").replace("\\u2022", "*").replace("\\u00b7", "*")
x = x.replace("\\u2018", "'").replace("\\u2019", "'").replace("\\u201a", "'")
x = x.replace("\\u201c", '"').replace("\\u201d", '"')
x = x.replace("\\u20ac", "€")
x = x.replace("\\u2212", " - ") # minus sign
x = x.replace("\\u00e9", "é")
x = x.replace("\\u017c", "ż").replace("\\u015b", "ś").replace("\\u0142", "ł")
x = x.replace("\\u0105", "ą").replace("\\u0119", "ę").replace("\\u017a", "ź").replace("\\u00f3", "ó")
x = x.replace("\\u2014", " - ").replace('–', '-').replace('—', ' - ')
x = x.replace("\\u2013", " - ").replace("\\u00ad", " - ")
x = str(unicodedata.normalize("NFKD", x).encode("ascii", "ignore").decode("utf-8"))
# some content returns text in bytes rather than as a str ?
try:
assert type(x).__name__ == "str"
except AssertionError:
print("not a string?", type(x), x)
return x
```
Scrub titles of problematic characters, drop nulls and dedupe
```
linkages_csv.head()
linkages_csv['title'] = linkages_csv['title'].apply(scrub_unicode)
linkages_csv = linkages_csv.loc[pd.notnull(linkages_csv.dataset)].drop_duplicates()
linkages_csv = linkages_csv.loc[pd.notnull(linkages_csv.title)].drop_duplicates()
pub_metadata_fields = ['title']
original_metadata_cols = list(set(linkages_csv.columns.values.tolist()) - set(pub_metadata_fields)-set(['dataset']))
```
#### Generate list of dicts of metadata
Read in `datasets.json`. Update `datasets_path` to your local.
```
import json
datasets_path = '/Users/andrewnorris/RCDatasets/datasets.json'
with open(datasets_path) as json_file:
datasets = json.load(json_file)
```
Create list of dictionaries of publication metadata. `format_metadata` iterrates through `linkages_csv` dataframe, splits the `dataset` field (for when multiple datasets are listed); throws an error if the dataset doesn't exist and needs to be added to `datasets.json`.
```
def create_pub_dict(linkages_dataframe,datasets):
pub_dict_list = []
for i, r in linkages_dataframe.iterrows():
r['title'] = scrub_unicode(r['title'])
ds_id_list = [f for f in [d.strip() for d in r['dataset'].split(",")] if f not in [""," "]]
for ds in ds_id_list:
check_ds = [b for b in datasets if b['id'] == ds]
if len(check_ds) == 0:
print('dataset {} isnt listed in datasets.json. Please add to file'.format(ds))
required_metadata = r[pub_metadata_fields].to_dict()
required_metadata.update({'datasets':ds_id_list})
pub_dict = required_metadata
if len(original_metadata_cols) > 0:
original_metadata = r[original_metadata_cols].to_dict()
original_metadata.update({'date_added':datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')})
pub_dict.update({'original':original_metadata})
pub_dict_list.append(pub_dict)
return pub_dict_list
```
Generate publication metadata and export to json
```
linkage_list = create_pub_dict(linkages_csv,datasets)
```
Update `pub_path` to be:
`<name_of_subfolder>_publications.json`
```
json_pub_path = os.path.join('/Users/andrewnorris/RCPublications/partitions/',rcm_subfolder+'_publications.json')
with open(json_pub_path, 'w') as outfile:
json.dump(linkage_list, outfile, indent=2)
```
| true |
code
| 0.358971 | null | null | null | null |
|
# Bootstrap distances to the future
Estimate uncertainty of distance to the future values per sample and model using the bootstrap of observed distances across time.
## Define inputs, outputs, and parameters
```
# Define inputs.
model_distances = snakemake.input.model_distances
# Define outputs.
output_table = snakemake.output.output_table
bootstrap_figure_for_simulated_sample_validation = snakemake.output.bootstrap_figure_for_simulated_sample_validation
bootstrap_figure_for_simulated_sample_test = snakemake.output.bootstrap_figure_for_simulated_sample_test
bootstrap_figure_for_natural_sample_validation = snakemake.output.bootstrap_figure_for_natural_sample_validation
bootstrap_figure_for_natural_sample_test = snakemake.output.bootstrap_figure_for_natural_sample_test
# Define parameters.
n_bootstraps = snakemake.params.n_bootstraps
error_types = ["validation", "test"]
```
## Import dependencies
```
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import numpy as np
import pandas as pd
import seaborn as sns
%matplotlib inline
```
## Configure plots and analyses
```
sns.set_style("white")
# Display figures at a reasonable default size.
mpl.rcParams['figure.figsize'] = (6, 4)
# Disable top and right spines.
mpl.rcParams['axes.spines.top'] = False
mpl.rcParams['axes.spines.right'] = False
# Display and save figures at higher resolution for presentations and manuscripts.
mpl.rcParams['savefig.dpi'] = 200
mpl.rcParams['figure.dpi'] = 120
# Display text at sizes large enough for presentations and manuscripts.
mpl.rcParams['font.weight'] = "normal"
mpl.rcParams['axes.labelweight'] = "normal"
mpl.rcParams['font.size'] = 14
mpl.rcParams['axes.labelsize'] = 14
mpl.rcParams['legend.fontsize'] = 12
mpl.rcParams['xtick.labelsize'] = 12
mpl.rcParams['ytick.labelsize'] = 12
mpl.rc('text', usetex=False)
color_by_predictor = {
'naive': '#cccccc',
'offspring': '#000000',
'normalized_fitness': '#999999',
'fitness': '#000000',
'ep': '#4575b4',
'ep_wolf': '#4575b4',
'ep_star': '#4575b4',
'ep_x': '#4575b4',
'ep_x_koel': '#4575b4',
'ep_x_wolf': '#4575b4',
'oracle_x': '#4575b4',
'rb': '#4575b4',
'cTiter': '#91bfdb',
'cTiter_x': '#91bfdb',
'cTiterSub': '#91bfdb',
'cTiterSub_star': '#91bfdb',
'cTiterSub_x': '#91bfdb',
'fra_cTiter_x': '#91bfdb',
'ne_star': '#2ca25f',
'dms_star': '#99d8c9',
"dms_nonepitope": "#99d8c9",
"dms_entropy": "#99d8c9",
'unnormalized_lbi': '#fc8d59',
'lbi': '#fc8d59',
'delta_frequency': '#d73027',
'ep_x-ne_star': "#ffffff",
'ep_star-ne_star': "#ffffff",
'lbi-ne_star': "#ffffff",
'ne_star-lbi': "#ffffff",
'cTiter_x-ne_star': "#ffffff",
'cTiter_x-ne_star-lbi': "#ffffff",
'fra_cTiter_x-ne_star': "#ffffff"
}
histogram_color_by_predictor = {
'naive': '#cccccc',
'offspring': '#000000',
'normalized_fitness': '#000000',
'fitness': '#000000',
'ep': '#4575b4',
'ep_wolf': '#4575b4',
'ep_star': '#4575b4',
'ep_x': '#4575b4',
'ep_x_koel': '#4575b4',
'ep_x_wolf': '#4575b4',
'oracle_x': '#4575b4',
'rb': '#4575b4',
'cTiter': '#91bfdb',
'cTiter_x': '#91bfdb',
'cTiterSub': '#91bfdb',
'cTiterSub_star': '#91bfdb',
'cTiterSub_x': '#91bfdb',
'fra_cTiter_x': '#91bfdb',
'ne_star': '#2ca25f',
'dms_star': '#99d8c9',
"dms_nonepitope": "#99d8c9",
"dms_entropy": "#99d8c9",
'unnormalized_lbi': '#fc8d59',
'lbi': '#fc8d59',
'delta_frequency': '#d73027',
'ep_x-ne_star': "#999999",
'ep_star-ne_star': "#999999",
'lbi-ne_star': "#999999",
'ne_star-lbi': "#999999",
'cTiter_x-ne_star': "#999999",
'cTiter_x-ne_star-lbi': "#999999",
'fra_cTiter_x-ne_star': "#999999"
}
name_by_predictor = {
"naive": "naive",
"offspring": "observed fitness",
"normalized_fitness": "true fitness",
"fitness": "estimated fitness",
"ep": "epitope mutations",
"ep_wolf": "Wolf epitope mutations",
"ep_star": "epitope ancestor",
"ep_x": "epitope antigenic\nnovelty",
"ep_x_koel": "Koel epitope antigenic novelty",
"ep_x_wolf": "Wolf epitope antigenic novelty",
"oracle_x": "oracle antigenic novelty",
"rb": "Koel epitope mutations",
"cTiter": "antigenic advance",
"cTiter_x": "HI antigenic novelty",
"cTiterSub": "linear HI mut phenotypes",
"cTiterSub_star": "ancestral HI mut phenotypes",
"cTiterSub_x": "HI sub cross-immunity",
"fra_cTiter_x": "FRA antigenic novelty",
"ne_star": "mutational load",
"dms_star": "DMS mutational\neffects",
"dms_nonepitope": "DMS mutational load",
"dms_entropy": "DMS entropy",
"unnormalized_lbi": "unnormalized LBI",
"lbi": "LBI",
"delta_frequency": "delta frequency",
'ep_x-ne_star': "mutational load +\nepitope antigenic\nnovelty",
'ep_star-ne_star': "mutational load +\nepitope ancestor",
'lbi-ne_star': "mutational load +\n LBI",
'ne_star-lbi': "mutational load +\n LBI",
'cTiter_x-ne_star': "mutational load +\nHI antigenic novelty",
'cTiter_x-ne_star-lbi': "mutational load +\nHI antigenic novelty +\nLBI",
'fra_cTiter_x-ne_star': "mutational load +\nFRA antigenic novelty"
}
name_by_sample = {
"simulated_sample_3": "simulated populations",
"natural_sample_1_with_90_vpm_sliding": "natural populations"
}
color_by_model = {name_by_predictor[predictor]: color for predictor, color in color_by_predictor.items()}
predictors_by_sample = {
"simulated_sample_3": [
"naive",
"normalized_fitness",
"ep_x",
"ne_star",
"lbi",
"delta_frequency",
"ep_star-ne_star",
"ep_x-ne_star",
"lbi-ne_star"
],
"natural_sample_1_with_90_vpm_sliding": [
"naive",
"ep_x",
"cTiter_x",
"ne_star",
"dms_star",
"lbi",
"delta_frequency",
"ep_star-ne_star",
"ep_x-ne_star",
"cTiter_x-ne_star",
"ne_star-lbi",
"cTiter_x-ne_star-lbi"
]
}
df = pd.read_table(model_distances)
```
## Bootstrap hypothesis tests
Perform [bootstrap hypothesis tests](https://en.wikipedia.org/wiki/Bootstrapping_(statistics)#Bootstrap_hypothesis_testing) (Efron and Tibshirani 1993) between biologically-informed models and the naive model for each dataset.
The following logic is copied from the article linked above to support the logic of the functions defined below.
Calculate test statistic _t_:
$$
t = \frac{\bar{x}-\bar{y}}{\sqrt{\sigma_x^2/n + \sigma_y^2/m}}
$$
Create two new data sets whose values are $x_i^{'} = x_i - \bar{x} + \bar{z}$ and $y_i^{'} = y_i - \bar{y} + \bar{z}$, where $\bar{z}$ is the mean of the combined sample.
Draw a random sample ($x_i^*$) of size $n$ with replacement from $x_i^{'}$ and another random sample ($y_i^*$) of size $m$ with replacement from $y_i^{'}$.
Calculate the test statistic $t^* = \frac{\bar{x^*}-\bar{y^*}}{\sqrt{\sigma_x^{*2}/n + \sigma_y^{*2}/m}}$
Repeat 3 and 4 $B$ times (e.g. $B=1000$) to collect $B$ values of the test statistic.
Estimate the p-value as $p = \frac{\sum_{i=1}^B I\{t_i^* \geq t\}}{B}$ where $I(\text{condition}) = 1$ when ''condition'' is true and 0 otherwise.
```
def get_model_distances_by_build(df, sample, error_type, predictors):
return df.query(
f"(sample == '{sample}') & (error_type == '{error_type}') & (predictors == '{predictors}')"
)["validation_error"].values
def calculate_t_statistic(x_dist, y_dist):
"""Calculate the t statistic between two given distributions.
"""
# Calculate mean and variance for the two input distributions.
x_mean = x_dist.mean()
x_var = np.var(x_dist)
x_length = x_dist.shape[0]
y_mean = y_dist.mean()
y_var = np.var(y_dist)
y_length = y_dist.shape[0]
# Calculate the test statistic t.
t = (x_mean - y_mean) / np.sqrt((x_var / x_length) + (y_var / y_length))
return t
def bootstrap_t(x_dist_adjusted, y_dist_adjusted):
"""For a given pair of distributions that have been recentered on the mean of the union of their original distributions,
create a single bootstrap sample from each distribution and calculate the corresponding t statistic for that sample.
"""
x_dist_adjusted_sample = np.random.choice(x_dist_adjusted, size=x_dist_adjusted.shape[0], replace=True)
y_dist_adjusted_sample = np.random.choice(y_dist_adjusted, size=y_dist_adjusted.shape[0], replace=True)
return calculate_t_statistic(x_dist_adjusted_sample, y_dist_adjusted_sample)
def compare_distributions_by_bootstrap(x_dist, y_dist, n_bootstraps):
"""Compare the means of two given distributions by a bootstrap hypothesis test.
Returns the p-value, t statistic, and the bootstrap distribution of t values.
"""
# Calculate means of input distributions.
x_mean = x_dist.mean()
y_mean = y_dist.mean()
# Calculate the test statistic t.
t = calculate_t_statistic(x_dist, y_dist)
# Calculate mean of joint distribution.
z_dist = np.concatenate([x_dist, y_dist])
z_mean = z_dist.mean()
# Create new distributions centered on the mean of the joint distribution.
x_dist_adjusted = x_dist - x_mean + z_mean
y_dist_adjusted = y_dist - y_mean + z_mean
bootstrapped_t_dist = np.array([
bootstrap_t(x_dist_adjusted, y_dist_adjusted)
for i in range(n_bootstraps)
])
p_value = (bootstrapped_t_dist >= t).sum() / n_bootstraps
return (p_value, t, bootstrapped_t_dist)
example_model_dist = get_model_distances_by_build(
df,
"simulated_sample_3",
"validation",
"normalized_fitness"
)
example_naive_dist = get_model_distances_by_build(
df,
"simulated_sample_3",
"validation",
"naive"
)
example_model_difference = example_model_dist - example_naive_dist
example_null_difference = example_model_difference - example_model_difference.mean()
example_model_dist
example_naive_dist
fig, ax = plt.subplots(1, 1, figsize=(6, 4))
bins = np.arange(
min(example_model_difference.min(), example_null_difference.min()),
max(example_model_difference.max(), example_null_difference.max()),
0.5
)
ax.hist(example_model_difference, bins=bins, label="true fitness", alpha=0.5)
ax.hist(example_null_difference, bins=bins, label="null model", alpha=0.5)
ax.axvline(x=example_model_difference.mean(), label="model mean", color="blue")
ax.axvline(x=example_null_difference.mean(), label="null model mean", color="orange")
ax.set_xlim(-6, 6)
ax.set_xlabel("Model - naive distance to future (AAs)")
ax.set_ylabel("Number of timepoints")
ax.set_title(
"Example model and null distributions\nfor differences between distances to the future",
fontsize=12
)
ax.legend(frameon=False)
# Compare all model distributions to the corresponding naive model distribution for
# all samples and error types. Store the resulting p-values and metadata in a new
# data frame.
p_values = []
bootstrapped_t_distributions = []
for sample, predictors in predictors_by_sample.items():
sample_df = df.query(f"sample == '{sample}'")
for error_type in error_types:
error_type_df = sample_df.query(f"error_type == '{error_type}'")
naive_dist = error_type_df.query("predictors == 'naive'")["validation_error"].values
for predictor in predictors:
if predictor == "naive":
continue
predictor_dist = error_type_df.query(f"predictors == '{predictor}'")["validation_error"].values
# Calculate the difference between the model's distance to the future
# and the naive model's at the same timepoint. This difference should
# account for timepoint-to-timepoint variation observed across all models.
difference_dist = predictor_dist - naive_dist
# Center the observed distribution by its mean to produce a null distribution
# with the same variance and a mean of zero. We want to test whether the
# observed differences between this model and the naive model are different
# from zero.
null_difference_dist = difference_dist - difference_dist.mean()
# Perform the bootstrap hypothesis test between the differences distributions.
p_value, t, bootstrapped_t_dist = compare_distributions_by_bootstrap(
null_difference_dist,
difference_dist,
n_bootstraps
)
p_values.append({
"sample": sample,
"error_type": error_type,
"predictors": predictor,
"t": t,
"p_value": p_value
})
bootstrapped_t_distributions.append(
pd.DataFrame({
"sample": sample,
"error_type": error_type,
"predictors": predictor,
"empirical_t": t,
"p_value": p_value,
"bootstrap_t": bootstrapped_t_dist
})
)
bootstrapped_t_distributions_df = pd.concat(bootstrapped_t_distributions)
bootstrapped_t_distributions_df.head()
bootstrapped_t_distributions_df.shape
def plot_histogram_by_sample_and_type(df, sample, error_type):
example_df = df.query(f"(sample == '{sample}') & (error_type == '{error_type}')")
example_df = example_df.sort_values("empirical_t", ascending=False).copy()
grouped_df = example_df.groupby("predictors", sort=False)
predictors = grouped_df["predictors"].first().values
empirical_t_values = grouped_df["empirical_t"].first().values
sample_p_values = grouped_df["p_value"].first().values
n_rows = int(np.ceil(sample_p_values.shape[0] / 2.0))
n_cells = 2 * n_rows
fig, all_axes = plt.subplots(
n_rows,
2,
figsize=(8, n_rows),
sharex=True,
sharey=True
)
axes = all_axes.flatten()
bins = np.arange(-5, 5, 0.25)
for i, predictor in enumerate(predictors):
ax = axes[i]
if sample_p_values[i] < 1.0 / n_bootstraps:
p_value = f"$p$ < {1.0 / n_bootstraps}"
else:
p_value = f"$p$ = {sample_p_values[i]}"
ax.hist(
example_df.query(f"predictors == '{predictor}'")["bootstrap_t"].values,
bins=bins,
color=histogram_color_by_predictor[predictor]
)
ax.axvline(
empirical_t_values[i],
color="orange"
)
ax.text(
0.01,
0.9,
f"$t$ = {empirical_t_values[i]:.2f}, {p_value}",
horizontalalignment="left",
verticalalignment="center",
transform=ax.transAxes,
fontsize=10
)
ax.set_title(
name_by_predictor[predictor].replace("\n", " "),
fontsize=10
)
if (i >= n_cells - 2) or (n_cells > len(predictors) and i == n_cells - 3):
ax.set_xlabel("$t$ statistic")
ax.xaxis.set_ticks_position('bottom')
ax.tick_params(which='major', width=1.00, length=5)
ax.xaxis.set_major_locator(ticker.AutoLocator())
else:
ax.xaxis.set_ticks([])
ax.xaxis.set_visible(False)
# Clear subplots that do not have any data.
for i in range(len(predictors), n_cells):
axes[i].axis("off")
fig.text(
0.0,
0.5,
"bootstrap samples",
rotation="vertical",
horizontalalignment="center",
verticalalignment="center"
)
fig.text(
0.5,
0.99,
f"{name_by_sample[sample]}, {error_type} period",
horizontalalignment="center",
verticalalignment="center",
fontsize=12
)
fig.tight_layout(pad=0.75, w_pad=1.0, h_pad=0.1)
return fig, axes
sample = "simulated_sample_3"
error_type = "validation"
fig, axes = plot_histogram_by_sample_and_type(
bootstrapped_t_distributions_df,
sample,
error_type
)
plt.savefig(bootstrap_figure_for_simulated_sample_validation, bbox_inches="tight")
sample = "simulated_sample_3"
error_type = "test"
fig, axes = plot_histogram_by_sample_and_type(
bootstrapped_t_distributions_df,
sample,
error_type
)
plt.savefig(bootstrap_figure_for_simulated_sample_test, bbox_inches="tight")
sample = "natural_sample_1_with_90_vpm_sliding"
error_type = "validation"
fig, axes = plot_histogram_by_sample_and_type(
bootstrapped_t_distributions_df,
sample,
error_type
)
plt.savefig(bootstrap_figure_for_natural_sample_validation, bbox_inches="tight")
sample = "natural_sample_1_with_90_vpm_sliding"
error_type = "test"
fig, axes = plot_histogram_by_sample_and_type(
bootstrapped_t_distributions_df,
sample,
error_type
)
plt.savefig(bootstrap_figure_for_natural_sample_test, bbox_inches="tight")
p_value_df = pd.DataFrame(p_values)
p_value_df
```
Identify models whose mean distances are significantly closer to future populations than the naive model ($\alpha=0.05$).
```
p_value_df[p_value_df["p_value"] < 0.05]
p_value_df.to_csv(output_table, sep="\t", index=False)
```
## Compare distributions of composite and individual models
Perform bootstrap hypothesis tests between composite models and their respective individual models to determine whether any composite models are significantly more accurate. We only perform these for natural populations.
```
composite_models = {
"simulated_sample_3": [
{
"individual": ["ne_star", "lbi"],
"composite": "lbi-ne_star"
},
{
"individual": ["ep_x", "ne_star"],
"composite": "ep_x-ne_star"
},
{
"individual": ["ep_star", "ne_star"],
"composite": "ep_star-ne_star"
}
],
"natural_sample_1_with_90_vpm_sliding": [
{
"individual": ["cTiter_x", "ne_star"],
"composite": "cTiter_x-ne_star"
},
{
"individual": ["ne_star", "lbi"],
"composite": "ne_star-lbi"
},
{
"individual": ["ep_x", "ne_star"],
"composite": "ep_x-ne_star"
},
{
"individual": ["ep_star", "ne_star"],
"composite": "ep_star-ne_star"
}
]
}
composite_vs_individual_p_values = []
for error_type in error_types:
for sample, models in composite_models.items():
for model in models:
composite_dist = get_model_distances_by_build(df, sample, error_type, model["composite"])
for individual_model in model["individual"]:
individual_dist = get_model_distances_by_build(df, sample, error_type, individual_model)
# Calculate the difference between the composite model's distance to the future
# and the individual model's at the same timepoint. This difference should
# account for timepoint-to-timepoint variation observed across all models.
difference_dist = composite_dist - individual_dist
# Center the observed distribution by its mean to produce a null distribution
# with the same variance and a mean of zero. We want to test whether the
# observed differences between the composite and individual models are different
# from zero.
null_difference_dist = difference_dist - difference_dist.mean()
p_value, t, bootstrapped_t_dist = compare_distributions_by_bootstrap(
null_difference_dist,
difference_dist,
n_bootstraps
)
composite_vs_individual_p_values.append({
"sample": sample,
"error_type": error_type,
"individual_model": individual_model,
"composite_model": model["composite"],
"t": t,
"p_value": p_value
})
composite_vs_individual_p_values_df = pd.DataFrame(composite_vs_individual_p_values)
composite_vs_individual_p_values_df.query("p_value < 0.05")
```
## Calculate bootstraps for all models and samples
```
df["error_difference"] = df["validation_error"] - df["null_validation_error"]
bootstrap_distances = []
for (sample, error_type, predictors), group_df in df.groupby(["sample", "error_type", "predictors"]):
if sample not in predictors_by_sample:
continue
if predictors not in predictors_by_sample[sample]:
continue
print(f"Processing: {sample}, {error_type}, {predictors}")
# Calculate difference between validation error
bootstrap_distribution = [
group_df["error_difference"].sample(frac=1.0, replace=True).mean()
for i in range(n_bootstraps)
]
bootstrap_distances.append(pd.DataFrame({
"sample": sample,
"error_type": error_type,
"predictors": predictors,
"bootstrap_distance": bootstrap_distribution
}))
bootstraps_df = pd.concat(bootstrap_distances)
bootstraps_df["model"] = bootstraps_df["predictors"].map(name_by_predictor)
bootstraps_df.head()
def plot_bootstrap_distances(bootstraps_df, predictors, title, width=16, height=8):
fig, axes = plt.subplots(2, 1, figsize=(width, height), gridspec_kw={"hspace": 0.5})
sample_name = bootstraps_df["sample"].drop_duplicates().values[0]
bootstrap_df = bootstraps_df.query("error_type == 'validation'")
bootstrap_df = bootstrap_df[bootstrap_df["predictors"].isin(predictors)].copy()
# Use this order for both validation and test facets as in Tables 1 and 2.
models_order = bootstrap_df.groupby("model")["bootstrap_distance"].mean().sort_values().reset_index()["model"].values
predictors_order = bootstrap_df.groupby("predictors")["bootstrap_distance"].mean().sort_values().reset_index()["predictors"].values
median_naive_distance = bootstrap_df.query("predictors == 'naive'")["bootstrap_distance"].median()
validation_ax = axes[0]
validation_ax = sns.violinplot(
x="model",
y="bootstrap_distance",
data=bootstrap_df,
order=models_order,
ax=validation_ax,
palette=color_by_model,
cut=0
)
max_distance = bootstrap_df["bootstrap_distance"].max() + 0.3
validation_ax.set_ylim(top=max_distance + 0.6)
for index, predictor in enumerate(predictors_order):
if predictor == "naive":
continue
p_value = p_value_df.query(f"(sample == '{sample_name}') & (error_type == 'validation') & (predictors == '{predictor}')")["p_value"].values[0]
if p_value < (1.0 / n_bootstraps):
p_value_string = f"p < {1.0 / n_bootstraps}"
else:
p_value_string = f"p = {p_value:.4f}"
validation_ax.text(
index,
max_distance,
p_value_string,
fontsize=12,
horizontalalignment="center",
verticalalignment="center"
)
validation_ax.axhline(y=median_naive_distance, label="naive", color="#999999", zorder=-10)
validation_ax.title.set_text(f"Validation of {name_by_sample[sample]}")
validation_ax.set_xlabel("Model")
validation_ax.set_ylabel("Bootstrapped model - naive\ndistance to future (AAs)")
bootstrap_df = bootstraps_df.query("error_type == 'test'")
bootstrap_df = bootstrap_df[bootstrap_df["predictors"].isin(predictors)].copy()
median_naive_distance = bootstrap_df.query("predictors == 'naive'")["bootstrap_distance"].median()
test_ax = axes[1]
test_ax = sns.violinplot(
x="model",
y="bootstrap_distance",
data=bootstrap_df,
order=models_order,
ax=test_ax,
palette=color_by_model,
cut=0
)
max_distance = bootstrap_df["bootstrap_distance"].max() + 0.3
test_ax.set_ylim(top=max_distance + 0.6)
for index, predictor in enumerate(predictors_order):
if predictor == "naive":
continue
p_value = p_value_df.query(f"(sample == '{sample_name}') & (error_type == 'test') & (predictors == '{predictor}')")["p_value"].values[0]
if p_value < (1.0 / n_bootstraps):
p_value_string = f"p < {1.0 / n_bootstraps}"
else:
p_value_string = f"p = {p_value:.4f}"
test_ax.text(
index,
max_distance,
p_value_string,
fontsize=12,
horizontalalignment="center",
verticalalignment="center"
)
test_ax.set_xlabel("Model")
test_ax.set_ylabel("Bootstrapped model - naive\ndistance to future (AAs)")
test_ax.axhline(y=median_naive_distance, label="naive", color="#999999", zorder=-10)
test_ax.title.set_text(f"Test of {name_by_sample[sample]}")
sns.despine()
return fig, axes
sample = "simulated_sample_3"
fig, axes = plot_bootstrap_distances(
bootstraps_df.query(f"sample == '{sample}'"),
predictors_by_sample[sample],
name_by_sample[sample],
width=16
)
plt.tight_layout()
#plt.savefig(bootstrap_figure_for_simulated_sample, bbox_inches="tight")
sample = "natural_sample_1_with_90_vpm_sliding"
fig, axes = plot_bootstrap_distances(
bootstraps_df.query(f"sample == '{sample}'"),
predictors_by_sample[sample],
name_by_sample[sample],
width=24
)
plt.tight_layout()
#plt.savefig(bootstrap_figure_for_natural_sample, bbox_inches="tight")
```
| true |
code
| 0.64131 | null | null | null | null |
|
# AR6 WG1 - SPM.4
This notebook reproduces the panel a) of **Figure SPM.4** of the IPCC's *Working Group I contribution to the Sixth Assessment Report* ([AR6 WG1](https://www.ipcc.ch/assessment-report/ar6/)).
The data supporting the SPM figure is published under a Creative Commons CC-BY license at
the [Centre for Environmental Data Analyis (CEDA)](https://catalogue.ceda.ac.uk/uuid/ae4f1eb6fce24adcb92ddca1a7838a5c).
This notebook uses a version of that data which was processed for interoperability with the format used by IPCC WG3, the so-called IAMC format.
The notebook is available under an open-source [BSD-3 License](https://github.com/openscm/AR6-WG1-Data-Compilation/blob/main/LICENSE) in the [openscm/AR6-WG1-Data-Compilation](https://github.com/openscm/AR6-WG1-Data-Compilation) GitHub repository.
The notebook uses the Python package [pyam](https://pyam-iamc.readthedocs.io), which provides a suite of features and methods for the analysis, validation and visualization of reference data and scenario results
generated by integrated assessment models, macro-energy tools and other frameworks
in the domain of energy transition, climate change mitigation and sustainable development.
```
import matplotlib.pyplot as plt
import pyam
import utils
rc = pyam.run_control()
rc.update("plotting.yaml")
```
## Import and inspect the scenario data
Import the scenario data as a [pyam.IamDataFrame](https://pyam-iamc.readthedocs.io/en/stable/api/iamdataframe.html)
and display the timeseries data in wide, IAMC-style format
using [timeseries()](https://pyam-iamc.readthedocs.io/en/stable/api/iamdataframe.html#pyam.IamDataFrame.timeseries)...
```
df = pyam.IamDataFrame(utils.DATA_DIR / "processed" / "fig-spm4" / "fig-spm4-timeseries.csv")
df
df.timeseries()
```
## Create a simple plot for each species
Use [matplotlib](https://matplotlib.org) and
the [pyam plotting module](https://pyam-iamc.readthedocs.io/en/stable/gallery/index.html)
to create a multi-panel figure.
```
species = ["CO2", "CH4", "N2O", "Sulfur"]
# We first create a matplotlib figure with several "axes" objects (i.e., individual plots)
fig, ax = plt.subplots(1, len(species), figsize=(15, 5))
# Then, we iterate over the axes, plotting the graph for each species as we go along
for i, s in enumerate(species):
# Show legend only for the left-most figure
show_legend = True if i==len(species) - 1 else False
(
df.filter(variable=f"Emissions|{s}")
.plot(ax=ax[i], color="scenario", legend=dict(loc="outside right") if show_legend else False)
)
# We can also modify the axes objects directly to produce a better figure
ax[i].set_title(s)
# Clean and show the plot
plt.tight_layout()
fig
```
| true |
code
| 0.624379 | null | null | null | null |
|
# Linear Regression
Example from [Introduction to Computation and Programming Using Python](https://mitpress.mit.edu/books/introduction-computation-and-programming-using-python-revised-and-expanded-edition)
```
import matplotlib.pyplot as plot
from numpy import (
array,
asarray,
correlate,
cov,
genfromtxt,
mean,
median,
polyfit,
std,
var,
)
from scipy.stats import linregress
```
## Calculate regression line using linear fit _y = ax + b_
```
def linear_fit_byhand(x_vals, y_vals):
x_sum = sum(x_vals)
y_sum = sum(y_vals)
xy_sum = sum(x_vals * y_vals)
xsquare_sum = sum(x_vals ** 2)
count = len(x_vals)
# y = ax + b
# a = (NΣXY - (ΣX)(ΣY)) / (NΣX^2 - (ΣX)^2)
a_value = ((count * xy_sum) - (x_sum * y_sum)) / (
(count * xsquare_sum) - x_sum ** 2
)
# b = (ΣY - b(ΣX)) / N
b_value = (y_sum - a_value * x_sum) / count
est_yvals = a_value * x_vals + b_value
# calculate spring constant
k = 1 / a_value
# plot regression line
plot.plot(
x_vals,
est_yvals,
label="Linear fit by hand, k = "
+ str(round(k))
+ ", RSquare = "
+ str(r_square(y_vals, est_yvals)),
)
```
## Least-squares regression of scipy
```
def linear_regression(x_vals, y_vals):
a_value, b_value, r_value, p_value, std_err = linregress(x_vals, y_vals)
est_yvals = a_value * x_vals + b_value
k = 1 / a_value
plot.plot(
x_vals,
est_yvals,
label="Least-squares fit, k = "
+ str(round(k))
+ ", RSquare = "
+ str(r_value ** 2),
)
```
## Calculate regression line using linear fit _y = ax + b_
```
def linear_fit(x_vals, y_vals):
a_value, b_value = polyfit(x_vals, y_vals, 1)
est_yvals = a_value * array(x_vals) + b_value
# calculate spring constant
k = 1 / a_value
# plot regression line
plot.plot(
x_vals,
est_yvals,
label="Linear fit, k = "
+ str(round(k))
+ ", RSquare = "
+ str(r_square(y_vals, est_yvals)),
)
```
## Calculate quadratic fit _ax^2+bx+c_
```
def quadratic_fit(x_vals, y_vals):
a_value, b_value, c_value = polyfit(x_vals, y_vals, 2)
est_yvals = a_value * (x_vals ** 2) + b_value * (x_vals) + c_value
plot.plot(
x_vals,
est_yvals,
label="Quadratic fit, RSquare = " + str(r_square(y_vals, est_yvals)),
)
```
## Calculate cubic fit _ax^3+bx^2+cx+d_
```
def cubic_fit(x_vals, y_vals):
a_value, b_value, c_value, d_value = polyfit(x_vals, y_vals, 3)
est_yvals = a_value * (x_vals ** 3) + b_value * (x_vals ** 2)
est_yvals += c_value * x_vals + d_value
plot.plot(
x_vals,
est_yvals,
label="Cubic fit, RSquare = " + str(r_square(y_vals, est_yvals)),
)
```
## Method to display summary statistics
```
def display_statistics(x_vals, y_vals):
print("Mean(x)=%s Mean(Y)=%s" % (mean(x_vals), mean(y_vals)))
print("Median(x)=%s Median(Y)=%s" % (median(x_vals), median(y_vals)))
print("StdDev(x)=%s StdDev(Y)=%s" % (std(x_vals), std(y_vals)))
print("Var(x)=%s Var(Y)=%s" % (var(x_vals), var(y_vals)))
print("Cov(x,y)=%s" % cov(x_vals, y_vals))
print("Cor(x,y)=%s" % correlate(x_vals, y_vals))
```
## Plot data (x and y values) together with regression lines
```
def plot_data(vals):
x_vals = asarray([i[0] * 9.81 for i in vals])
y_vals = asarray([i[1] for i in vals])
# plot measurement values
plot.plot(x_vals, y_vals, "bo", label="Measured displacements")
plot.title("Measurement Displacement of Spring", fontsize="x-large")
plot.xlabel("|Force| (Newtons)")
plot.ylabel("Distance (meters)")
linear_fit_byhand(x_vals, y_vals)
linear_fit(x_vals, y_vals)
linear_regression(x_vals, y_vals)
quadratic_fit(x_vals, y_vals)
cubic_fit(x_vals, y_vals)
display_statistics(x_vals, y_vals)
```
## Calculate Coefficient of Determination (R^2)
Takes `measured` and `estimated` one dimensional arrays:
- `measured` is the one dimensional array of measured values
- `estimated` is the one dimensional array of predicted values
and calculates
$$R^2$$
where
$$R^2=1-\frac{EE}{MV}$$
and
$$0 \leq R^2 \leq 1$$.
- `EE` is the estimated error
- `MV` is the variance of the actual data
|Result |Interpretation|
|---------|--------------|
|$$R^2=1$$| the model explains all of the variability in the data |
|$$R^2=0$$| there is no linear relationship |
```
def r_square(measured, estimated):
estimated_error = ((estimated - measured) ** 2).sum()
m_mean = measured.sum() / float(len(measured))
m_variance = ((m_mean - measured) ** 2).sum()
return 1 - (estimated_error / m_variance)
```
## Test the equations
```
plot_data(genfromtxt("data/spring.csv", delimiter=","))
plot.legend(loc="best")
plot.tight_layout()
plot.show()
```
| true |
code
| 0.713874 | null | null | null | null |
|
# Heterogeneous Effects
> **Author**
- [Paul Schrimpf *UBC*](https://economics.ubc.ca/faculty-and-staff/paul-schrimpf/)
**Prerequisites**
- [Regression](regression.ipynb)
- [Machine Learning in Economics](ml_in_economics.ipynb)
**Outcomes**
- Understand potential outcomes and treatment effects
- Apply generic machine learning inference to data from a randomized experiment
```
# Uncomment following line to install on colab
#! pip install qeds fiona geopandas xgboost gensim folium pyLDAvis descartes
import pandas as pd
import numpy as np
import patsy
from sklearn import linear_model, ensemble, base, neural_network
import statsmodels.formula.api as smf
import statsmodels.api as sm
from sklearn.utils.testing import ignore_warnings
from sklearn.exceptions import ConvergenceWarning
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
```
In this notebook, we will learn how to apply machine learning methods to analyze
results of a randomized experiment. We typically begin analyzing
experimental results by calculating the difference in mean
outcomes between the treated and control groups. This difference estimates well
the average treatment effect. We can obtain more
nuanced results by recognizing that the effect of most experiments
might be heterogeneous. That is, different people could be affected by
the experiment differently. We will use machine learning methods to
explore this heterogeneity in treatment effects.
## Outline
- [Heterogeneous Effects](#Heterogeneous-Effects)
- [Background and Data](#Background-and-Data)
- [Potential Outcomes and Treatment Effects](#Potential-Outcomes-and-Treatment-Effects)
- [Generic Machine Learning Inference](#Generic-Machine-Learning-Inference)
- [Causal Trees and Forests](#Causal-Trees-and-Forests)
- [References](#References)
## Background and Data
We are going to use data from a randomized experiment in Indonesia
called Program Keluarga Harapan (PKH). PKH was a conditional cash
transfer program designed to improve child health. Eligible pregnant
women would receive a cash transfer if they attended at least 4
pre-natal and 2 post-natal visits, received iron supplements, and had
their baby delivered by a doctor or midwife. The cash transfers were
given quarterly and were about 60-220 dollars or 15-20 percent of
quarterly consumption. PKH eligibility was randomly assigned at the
kecamatan (district) level. All pregnant women living in a treated
kecamatan could choose to participate in the experiment. For more
information see [[hetACE+11]](#het-alatas2011) or [[hetTri16]](#het-triyana2016).
We are using the data provided with [[hetTri16]](#het-triyana2016).
```
url = "https://datascience.quantecon.org/assets/data/Triyana_2016_price_women_clean.csv.gz"
df = pd.read_csv(url)
df.describe()
```
## Potential Outcomes and Treatment Effects
Since program eligibility was randomly assigned (and what
policymakers could choose to change), we will focus on estimating
the effect of eligibility. We will let
$ d_i $ be a 1 if person $ i $ was eligible and be 0 if not.
Let $ y_i $ be an outcome of interest. Below, we
will look at midwife usage and birth weight as outcomes.
It is
useful to think about potential outcomes of the treatment. The potential treated
outcome is $ y_i(1) $. For subjects who actually were treated,
$ y_i(1) = y_i $ is the observed outcome. For untreated subjects,
$ y_i(1) $ is what mother i ‘s baby’s birth weight would have
been if she had been eligible for the program. Similarly, we can
define the potential untreated outcome $ y_i(0) $ .
The individual treatment effect for subject i is $ y_i(1) - y_i(0) $.
Individual treatment effects are impossible to know since we always
only observe $ y_i(1) $ or $ y_i(0) $, but never both.
When treatment is randomly assigned, we can estimate average treatment
effects because
$$
\begin{align*}
E[y_i(1) - y_i(0) ] = & E[y_i(1)] - E[y_i(0)] \\
& \text{random assignment } \\
= & E[y_i(1) | d_i = 1] - E[y_i(0) | d_i = 0] \\
= & E[y_i | d_i = 1] - E[y_i | d_i = 0 ]
\end{align*}
$$
### Average Treatment Effects
Let’s estimate the average treatment effect.
```
# some data prep for later
formula = """
bw ~ pkh_kec_ever +
C(edu)*C(agecat) + log_xp_percap + hh_land + hh_home + C(dist) +
hh_phone + hh_rf_tile + hh_rf_shingle + hh_rf_fiber +
hh_wall_plaster + hh_wall_brick + hh_wall_wood + hh_wall_fiber +
hh_fl_tile + hh_fl_plaster + hh_fl_wood + hh_fl_dirt +
hh_water_pam + hh_water_mechwell + hh_water_well + hh_water_spring + hh_water_river +
hh_waterhome +
hh_toilet_own + hh_toilet_pub + hh_toilet_none +
hh_waste_tank + hh_waste_hole + hh_waste_river + hh_waste_field +
hh_kitchen +
hh_cook_wood + hh_cook_kerosene + hh_cook_gas +
tv + fridge + motorbike + car + goat + cow + horse
"""
bw, X = patsy.dmatrices(formula, df, return_type="dataframe")
# some categories are empty after dropping rows will Null, drop now
X = X.loc[:, X.sum() > 0]
bw = bw.iloc[:, 0]
treatment_variable = "pkh_kec_ever"
treatment = X["pkh_kec_ever"]
Xl = X.drop(["Intercept", "pkh_kec_ever", "C(dist)[T.313175]"], axis=1)
#scale = bw.std()
#center = bw.mean()
loc_id = df.loc[X.index, "Location_ID"].astype("category")
import re
# remove [ ] from names for compatibility with xgboost
Xl = Xl.rename(columns=lambda x: re.sub('\[|\]','_',x))
# Estimate average treatment effects
from statsmodels.iolib.summary2 import summary_col
tmp = pd.DataFrame(dict(birthweight=bw,treatment=treatment,assisted_delivery=df.loc[X.index, "good_assisted_delivery"]))
usage = smf.ols("assisted_delivery ~ treatment", data=tmp).fit(cov_type="cluster", cov_kwds={'groups':loc_id})
health= smf.ols("bw ~ treatment", data=tmp).fit(cov_type="cluster", cov_kwds={'groups':loc_id})
summary_col([usage, health])
```
The program did increase the percent of births assisted by a medical
professional, but on average, did not affect birth weight.
### Conditional Average Treatment Effects
Although we can never estimate individual treatment effects, the
logic that lets us estimate unconditional average treatment effects
also suggests that we can estimate conditional average treatment effects.
$$
\begin{align*}
E[y_i(1) - y_i(0) |X_i=x] = & E[y_i(1)|X_i = x] - E[y_i(0)|X_i=x] \\
& \text{random assignment } \\
= & E[y_i(1) | d_i = 1, X_i=x] - E[y_i(0) | d_i = 0, X_i=x] \\
= & E[y_i | d_i = 1, X_i = x] - E[y_i | d_i = 0, X_i=x ]
\end{align*}
$$
Conditional average treatment effects tell us whether there are
identifiable (by X) groups of people for with varying treatment effects vary.
Since conditional average treatment effects involve conditional
expectations, machine learning methods might be useful.
However, if we want to be able to perform statistical inference, we
must use machine learning methods carefully. We will detail one
approach below. [[hetAI16]](#het-athey2016b) and [[hetWA18]](#het-wager2018) are
alternative approaches.
## Generic Machine Learning Inference
In this section, we will describe the “generic machine learning
inference” method of [[hetCDDFV18]](#het-cddf2018) to explore heterogeneity in
conditional average treatment effects.
This approach allows any
machine learning method to be used to estimate $ E[y_i(1) -
y_i(0) |X_i=x] $.
Inference for functions estimated by machine learning methods is
typically either impossible or requires very restrictive assumptions.
[[hetCDDFV18]](#het-cddf2018) gets around this problem by focusing on inference for
certain summary statistics of the machine learning prediction for
$ E[y_i(1) - y_i(0) |X_i=x] $ rather than
$ E[y_i(1) - y_i(0) |X_i=x] $ itself.
### Best Linear Projection of CATE
Let $ s_0(x) = E[y_i(1) - y_i(0) |X_i=x] $ denote the true
conditional average treatment effect. Let $ S(x) $ be an estimate
or noisy proxy for $ s_0(x) $. One way to summarize how well
$ S(x) $ approximates $ s_0(x) $ is to look at the best linear
projection of $ s_0(x) $ on $ S(x) $.
$$
\DeclareMathOperator*{\argmin}{arg\,min}
\beta_0, \beta_1 = \argmin_{b_0,b_1} E[(s_0(x) -
b_0 - b_1 (S(x)-E[S(x)]))^2]
$$
Showing that $ \beta_0 = E[y_i(1) - y_i(0)] $
is the unconditional average treatment effect is not difficult. More interestingly,
$ \beta_1 $ is related to how well $ S(x) $ approximates
$ s_0(x) $. If $ S(x) = s_0(x) $, then $ \beta_1=1 $. If
$ S(x) $ is completely uncorrelated with $ s_0(x) $, then
$ \beta_1 = 0 $.
The best linear projection of the conditional average treatment
effect tells us something about how well $ S(x) $ approximates
$ s_0(x) $, but does not directly quantify how much the conditional
average treatment effect varies with $ x $. We could try looking
at $ S(x) $ directly, but if $ x $ is high dimensional, reporting or visualizing
$ S(x) $ will be difficult. Moreover, most
machine learning methods have no satisfactory method to determine inferences
on $ S(x) $. This is very problematic if we want to use
$ S(x) $ to shape future policy decisions. For example, we might
want to use $ S(x) $ to target the treatment to people with
different $ x $. If we do this, we need to know whether the
estimated differences across $ x $ in $ S(x) $ are precise or
caused by noise.
### Grouped Average Treatment Effects
To deal with both these issues, [[hetCDDFV18]](#het-cddf2018) focuses on
grouped average treatment effects (GATE) with groups defined by
$ S(x) $. Partition the data into a fixed, finite number of groups
based on $ S(x) $ . Let
$ G_{k}(x) = 1\{\ell_{k-1} \leq S(x) \leq \ell_k \} $ where
$ \ell_k $ could be a constant chosen by the researcher or evenly
spaced quantiles of $ S(x) $. The $ k $ th grouped average
treatment effect is then $ \gamma_k = E[y(1) - y(0) | G_k(x)] $.
If the true $ s_0(x) $ is not constant, and $ S(x) $
approximates $ s_0(x) $ well, then the grouped average treatment
effects will increase with $ k $. If the conditional average treatment effect
has no heterogeneity (i.e. $ s_0(x) $ is constant) and/or
$ S(x) $ is a poor approximation to $ s_0(x) $,
then the grouped average treatment effect will tend to
be constant with $ k $ and may even be non-monotonic due to
estimation error.
### Estimation
We can estimate both the best linear projection of the conditional average treatment
effect and the grouped treatment effects by using
particular regressions. Let $ B(x) $ be an estimate of the outcome
conditional on no treatment, i.e. $ B(x) = \widehat{E[y(0)|x]} $
. Then the estimates of $ \beta $ from the regression
$$
y_i = \alpha_0 + \alpha_1 B(x_i) + \beta_0 (d_i-P(d=1)) + \beta_1
(d_i-P(d=1))(S(x_i) - E[S(x_i)]) + \epsilon_i
$$
are consistent estimates of the best linear projection of the
conditional average treatment effect if $ B(x_i) $ and
$ S(x_i) $ are uncorrelated with $ y_i $ . We can ensure that
$ B(x_i) $ and $ S(x_i) $ are uncorrelated with $ y_i $ by
using the familiar idea of sample-splitting and cross-validation. The
usual regression standard errors will also be valid.
Similarly, we can estimate grouped average treatment effects from the
following regression.
$$
y_i = \alpha_0 + \alpha_1 B(x_i) + \sum_k \gamma_k (d_i-P(d=1)) 1(G_k(x_i)) +
u_i
$$
The resulting estimates of $ \gamma_k $ will be consistent and
asymptotically normal with the usual regression standard errors.
```
# for clustering standard errors
def get_treatment_se(fit, cluster_id, rows=None):
if cluster_id is not None:
if rows is None:
rows = [True] * len(cluster_id)
vcov = sm.stats.sandwich_covariance.cov_cluster(fit, cluster_id.loc[rows])
return np.sqrt(np.diag(vcov))
return fit.HC0_se
def generic_ml_model(x, y, treatment, model, n_split=10, n_group=5, cluster_id=None):
nobs = x.shape[0]
blp = np.zeros((n_split, 2))
blp_se = blp.copy()
gate = np.zeros((n_split, n_group))
gate_se = gate.copy()
baseline = np.zeros((nobs, n_split))
cate = baseline.copy()
lamb = np.zeros((n_split, 2))
for i in range(n_split):
main = np.random.rand(nobs) > 0.5
rows1 = ~main & (treatment == 1)
rows0 = ~main & (treatment == 0)
mod1 = base.clone(model).fit(x.loc[rows1, :], (y.loc[rows1]))
mod0 = base.clone(model).fit(x.loc[rows0, :], (y.loc[rows0]))
B = mod0.predict(x)
S = mod1.predict(x) - B
baseline[:, i] = B
cate[:, i] = S
ES = S.mean()
## BLP
# assume P(treat|x) = P(treat) = mean(treat)
p = treatment.mean()
reg_df = pd.DataFrame(dict(
y=y, B=B, treatment=treatment, S=S, main=main, excess_S=S-ES
))
reg = smf.ols("y ~ B + I(treatment-p) + I((treatment-p)*(S-ES))", data=reg_df.loc[main, :])
reg_fit = reg.fit()
blp[i, :] = reg_fit.params.iloc[2:4]
blp_se[i, :] = get_treatment_se(reg_fit, cluster_id, main)[2:]
lamb[i, 0] = reg_fit.params.iloc[-1]**2 * S.var()
## GATEs
cutoffs = np.quantile(S, np.linspace(0,1, n_group + 1))
cutoffs[-1] += 1
for k in range(n_group):
reg_df[f"G{k}"] = (cutoffs[k] <= S) & (S < cutoffs[k+1])
g_form = "y ~ B + " + " + ".join([f"I((treatment-p)*G{k})" for k in range(n_group)])
g_reg = smf.ols(g_form, data=reg_df.loc[main, :])
g_fit = g_reg.fit()
gate[i, :] = g_fit.params.values[2:] #g_fit.params.filter(regex="G").values
gate_se[i, :] = get_treatment_se(g_fit, cluster_id, main)[2:]
lamb[i, 1] = (gate[i,:]**2).sum()/n_group
out = dict(
gate=gate, gate_se=gate_se,
blp=blp, blp_se=blp_se,
Lambda=lamb, baseline=baseline, cate=cate,
name=type(model).__name__
)
return out
def generic_ml_summary(generic_ml_output):
out = {
x: np.nanmedian(generic_ml_output[x], axis=0)
for x in ["blp", "blp_se", "gate", "gate_se", "Lambda"]
}
out["name"] = generic_ml_output["name"]
return out
kw = dict(x=Xl, treatment=treatment, n_split=11, n_group=5, cluster_id=loc_id)
@ignore_warnings(category=ConvergenceWarning)
def evaluate_models(models, y, **other_kw):
all_kw = kw.copy()
all_kw["y"] = y
all_kw.update(other_kw)
return list(map(lambda x: generic_ml_model(model=x, **all_kw), models))
def generate_report(results):
summaries = list(map(generic_ml_summary, results))
df_plot = pd.DataFrame({
mod["name"]: np.median(mod["cate"], axis=1)
for mod in results
})
print("Correlation in median CATE:")
display(df_plot.corr())
sns.pairplot(df_plot, diag_kind="kde", kind="reg")
print("\n\nBest linear projection of CATE")
df_cate = pd.concat({
s["name"]: pd.DataFrame(dict(blp=s["blp"], se=s["blp_se"]))
for s in summaries
}).T.stack()
display(df_cate)
print("\n\nGroup average treatment effects:")
df_groups = pd.concat({
s["name"]: pd.DataFrame(dict(gate=s["gate"], se=s["gate_se"]))
for s in summaries
}).T.stack()
display(df_groups)
import xgboost as xgb
models = [
linear_model.LassoCV(cv=10, n_alphas=25, max_iter=500, tol=1e-4, n_jobs=1),
ensemble.RandomForestRegressor(n_estimators=200, min_samples_leaf=20),
xgb.XGBRegressor(n_estimators=200, max_depth=3, reg_lambda=2.0, reg_alpha=0.0, objective="reg:squarederror"),
neural_network.MLPRegressor(hidden_layer_sizes=(20, 10), max_iter=500, activation="logistic",
solver="adam", tol=1e-3, early_stopping=True, alpha=0.0001)
]
results = evaluate_models(models, y=bw)
generate_report(results)
```
From the second table above, we see that regardless of the machine
learning method, the estimated intercept (the first row of the table)
is near 0 and statistically insignificant. Given our results for the unconditional
ATE above, we should expect this. The estimate of the
slopes are also either near 0, very imprecise, or both. This means
that either the conditional average treatment effect is near 0 or that all
four machine learning methods are very poor proxies for the true
conditional average treatment effect.
### Assisted Delivery
Let’s see what we get when we look at assisted delivery.
```
ad = df.loc[X.index, "good_assisted_delivery"]#"midwife_birth"]
results_ad = evaluate_models(models, y=ad)
generate_report(results_ad)
```
Now, the results are more encouraging. For all four machine learning
methods, the slope estimate is positive and statistically
significant. From this, we can conclude that the true conditional
average treatment effect must vary with at least some covariates, and
the machine learning proxies are at least somewhat correlated with the
true conditional average treatment effect.
### Covariate Means by Group
Once we’ve detected heterogeneity in the grouped average treatment effects
of using medical professionals for assisted delivery, it’s interesting to see
how effects vary across groups. This could help
us understand why the treatment effect varies or how to
develop simple rules for targeting future treatments.
```
df2 = df.loc[X.index, :]
df2["edu99"] = df2.edu == 99
df2["educ"] = df2["edu"]
df2.loc[df2["edu99"], "educ"] = np.nan
variables = [
"log_xp_percap","agecat","educ","tv","goat",
"cow","motorbike","hh_cook_wood","pkh_ever"
]
def cov_mean_by_group(y, res, cluster_id):
n_group = res["gate"].shape[1]
gate = res["gate"].copy()
gate_se = gate.copy()
dat = y.to_frame()
for i in range(res["cate"].shape[1]):
S = res["cate"][:, i]
cutoffs = np.quantile(S, np.linspace(0, 1, n_group+1))
cutoffs[-1] += 1
for k in range(n_group):
dat[f"G{k}"] = ((cutoffs[k] <= S) & (S < cutoffs[k+1])) * 1.0
g_form = "y ~ -1 + " + " + ".join([f"G{k}" for k in range(n_group)])
g_reg = smf.ols(g_form, data=dat.astype(float))
g_fit = g_reg.fit()
gate[i, :] = g_fit.params.filter(regex="G").values
rows = ~y.isna()
gate_se[i, :] = get_treatment_se(g_fit, cluster_id, rows)
out = pd.DataFrame(dict(
mean=np.nanmedian(gate, axis=0),
se=np.nanmedian(gate_se, axis=0),
group=list(range(n_group))
))
return out
def compute_group_means_for_results(results):
to_cat = []
for res in results:
for v in variables:
to_cat.append(
cov_mean_by_group(df2[v], res, loc_id)
.assign(method=res["name"], variable=v)
)
group_means = pd.concat(to_cat, ignore_index=True)
group_means["plus2sd"] = group_means.eval("mean + 1.96*se")
group_means["minus2sd"] = group_means.eval("mean - 1.96*se")
return group_means
group_means_ad = compute_group_means_for_results(results_ad)
g = sns.FacetGrid(group_means_ad, col="variable", col_wrap=3, hue="method", sharey=False)
g.map(plt.plot, "group", "mean")
g.map(plt.plot, "group", "plus2sd", ls="--")
g.map(plt.plot, "group", "minus2sd", ls="--")
g.add_legend();
```
From this, we see that the group predicted to be most affected by treatment
are less educated, less likely to own a TV or
motorbike, and more likely to participate in the program.
If we wanted to maximize the program impact with a limited budget, targeting the program towards
less educated and less wealthy mothers could be a good idea. The existing financial incentive
already does this to some extent. As one might expect, a fixed-size
cash incentive has a bigger behavioral impact on less wealthy
individuals. If we want to further target these individuals, we
could alter eligibility rules and/or increase the cash transfer
for those with lower wealth.
### Caution
When exploring treatment heterogeneity like above, we need to
interpret our results carefully. In particular, looking at grouped
treatment effects and covariate means conditional on group leads to
many hypothesis tests (although we never stated null hypotheses or
reported p-values, the inevitable eye-balling of differences in the
above graphs compared to their confidence intervals has the same
issues as formal hypothesis tests). When we perform many hypothesis
tests, we will likely stumble upon some statistically
significant differences by chance. Therefore, writing about a single large difference found in the
above analysis as though it is our main
finding would be misleading (and perhaps unethical). The correct thing to do is to present all
results that we have looked at. See [this excellent news article](https://slate.com/technology/2013/07/statistics-and-psychology-multiple-comparisons-give-spurious-results.html)
by statistician Andrew Gelman for more information.
## Causal Trees and Forests
[[hetAI16]](#het-athey2016b) develop the idea of “causal trees.” The purpose and
method are qualitatively similar to the grouped average treatment
effects. The main difference is that the groups in [[hetAI16]](#het-athey2016b)
are determined by a low-depth regression tree instead of by quantiles
of a noisy estimate of the conditional average treatment effect. As
above, sample-splitting is used to facilitate inference.
Causal trees share many downsides of regression trees. In
particular, the branches of the tree and subsequent results can be
sensitive to small changes in the data. [[hetWA18]](#het-wager2018) develop a
causal forest estimator to address this concern. This causal forest
estimates $ E[y_i(1) - y_i(0) |X_i=x] $ directly. Unlike most
machine learning estimators, [[hetWA18]](#het-wager2018) prove that causal
forests are consistent and pointwise asymptotically normal, albeit
with a slower than $ \sqrt{n} $ rate of convergence. In practice,
this means that either the sample size must be very large (and/or $ x $
relatively low dimension) to get precise estimates.
## References
<a id='het-alatas2011'></a>
\[hetACE+11\] Vivi Alatas, Nur Cahyadi, Elisabeth Ekasari, Sarah Harmoun, Budi Hidayat, Edgar Janz, Jon Jellema, H Tuhiman, and M Wai-Poi. Program keluarga harapan : impact evaluation of indonesia’s pilot household conditional cash transfer program. Technical Report, World Bank, 2011. URL: [http://documents.worldbank.org/curated/en/589171468266179965/Program-Keluarga-Harapan-impact-evaluation-of-Indonesias-Pilot-Household-Conditional-Cash-Transfer-Program](http://documents.worldbank.org/curated/en/589171468266179965/Program-Keluarga-Harapan-impact-evaluation-of-Indonesias-Pilot-Household-Conditional-Cash-Transfer-Program).
<a id='het-athey2016b'></a>
\[hetAI16\] Susan Athey and Guido Imbens. Recursive partitioning for heterogeneous causal effects. *Proceedings of the National Academy of Sciences*, 113(27):7353–7360, 2016. URL: [http://www.pnas.org/content/113/27/7353](http://www.pnas.org/content/113/27/7353), [arXiv:http://www.pnas.org/content/113/27/7353.full.pdf](https://arxiv.org/abs/http://www.pnas.org/content/113/27/7353.full.pdf), [doi:10.1073/pnas.1510489113](https://doi.org/10.1073/pnas.1510489113).
<a id='het-cddf2018'></a>
\[hetCDDFV18\] Victor Chernozhukov, Mert Demirer, Esther Duflo, and Iván Fernández-Val. Generic machine learning inference on heterogenous treatment effects in randomized experimentsxo. Working Paper 24678, National Bureau of Economic Research, June 2018. URL: [http://www.nber.org/papers/w24678](http://www.nber.org/papers/w24678), [doi:10.3386/w24678](https://doi.org/10.3386/w24678).
<a id='het-triyana2016'></a>
\[hetTri16\] Margaret Triyana. Do health care providers respond to demand-side incentives? evidence from indonesia. *American Economic Journal: Economic Policy*, 8(4):255–88, November 2016. URL: [http://www.aeaweb.org/articles?id=10.1257/pol.20140048](http://www.aeaweb.org/articles?id=10.1257/pol.20140048), [doi:10.1257/pol.20140048](https://doi.org/10.1257/pol.20140048).
<a id='het-wager2018'></a>
\[hetWA18\] Stefan Wager and Susan Athey. Estimation and inference of heterogeneous treatment effects using random forests. *Journal of the American Statistical Association*, 0(0):1–15, 2018. URL: [https://doi.org/10.1080/01621459.2017.1319839](https://doi.org/10.1080/01621459.2017.1319839), [arXiv:https://doi.org/10.1080/01621459.2017.1319839](https://arxiv.org/abs/https://doi.org/10.1080/01621459.2017.1319839), [doi:10.1080/01621459.2017.1319839](https://doi.org/10.1080/01621459.2017.1319839).
| true |
code
| 0.54462 | null | null | null | null |
|
# Construction of Regression Models using Data
Author: Jerónimo Arenas García (jarenas@tsc.uc3m.es)
Jesús Cid Sueiro (jcid@tsc.uc3m.es)
Notebook version: 2.1 (Sep 27, 2019)
Changes: v.1.0 - First version. Extracted from regression_intro_knn v.1.0.
v.1.1 - Compatibility with python 2 and python 3
v.2.0 - New notebook generated. Fuses code from Notebooks R1, R2, and R3
v.2.1 - Updated index notation
```
# Import some libraries that will be necessary for working with data and displaying plots
# To visualize plots in the notebook
%matplotlib inline
import numpy as np
import scipy.io # To read matlab files
import pandas as pd # To read data tables from csv files
# For plots and graphical results
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import pylab
# For the student tests (only for python 2)
import sys
if sys.version_info.major==2:
from test_helper import Test
# That's default image size for this interactive session
pylab.rcParams['figure.figsize'] = 9, 6
```
## 1. The regression problem
The goal of regression methods is to predict the value of some *target* variable $S$ from the observation of one or more *input* variables $X_0, X_1, \ldots, X_{K-1}$ (that we will collect in a single vector $\bf X$).
Regression problems arise in situations where the value of the target variable is not easily accessible, but we can measure other dependent variables, from which we can try to predict $S$.
<img src="figs/block_diagram.png" width=600>
The only information available to estimate the relation between the inputs and the target is a *dataset* $\mathcal D$ containing several observations of all variables.
$$\mathcal{D} = \{{\bf x}_k, s_k\}_{k=0}^{K-1}$$
The dataset $\mathcal{D}$ must be used to find a function $f$ that, for any observation vector ${\bf x}$, computes an output $\hat{s} = f({\bf x})$ that is a good predition of the true value of the target, $s$.
<img src="figs/predictor.png" width=300>
Note that for the generation of the regression model, we exploit the statistical dependence between random variable $S$ and random vector ${\bf X}$. In this respect, we can assume that the available dataset $\mathcal{D}$ consists of i.i.d. points from the joint distribution $p_{S,{\bf X}}(s,{\bf x})$. If we had access to the true distribution, a statistical approach would be more accurate; however, in many situations such knowledge is not available, but using training data to do the design is feasible (e.g., relying on historic data, or by manual labelling of a set of patterns).
## 2. Examples of regression problems.
The <a href=http://scikit-learn.org/>scikit-learn</a> package contains several <a href=http://scikit-learn.org/stable/datasets/> datasets</a> related to regression problems.
* <a href=http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_boston.html#sklearn.datasets.load_boston > Boston dataset</a>: the target variable contains housing values in different suburbs of Boston. The goal is to predict these values based on several social, economic and demographic variables taken frome theses suburbs (you can get more details in the <a href = https://archive.ics.uci.edu/ml/datasets/Housing > UCI repository </a>).
* <a href=http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_diabetes.html#sklearn.datasets.load_diabetes /> Diabetes dataset</a>.
We can load these datasets as follows:
```
from sklearn import datasets
# Load the dataset. Select it by uncommenting the appropriate line
D_all = datasets.load_boston()
#D_all = datasets.load_diabetes()
# Extract data and data parameters.
X = D_all.data # Complete data matrix (including input and target variables)
S = D_all.target # Target variables
n_samples = X.shape[0] # Number of observations
n_vars = X.shape[1] # Number of variables (including input and target)
```
This dataset contains
```
print(n_samples)
```
observations of the target variable and
```
print(n_vars)
```
input variables.
## 3. Scatter plots
### 3.1. 2D scatter plots
When the instances of the dataset are multidimensional, they cannot be visualized directly, but we can get a first rough idea about the regression task if we plot the target variable versus one of the input variables. These representations are known as <i>scatter plots</i>
Python methods `plot` and `scatter` from the `matplotlib` package can be used for these graphical representations.
```
# Select a dataset
nrows = 4
ncols = 1 + (X.shape[1]-1)/nrows
# Some adjustment for the subplot.
pylab.subplots_adjust(hspace=0.2)
# Plot all variables
for idx in range(X.shape[1]):
ax = plt.subplot(nrows,ncols,idx+1)
ax.scatter(X[:,idx], S) # <-- This is the key command
ax.get_xaxis().set_ticks([])
ax.get_yaxis().set_ticks([])
plt.ylabel('Target')
```
## 4. Evaluating a regression task
In order to evaluate the performance of a given predictor, we need to quantify the quality of predictions. This is usually done by means of a loss function $l(s,\hat{s})$. Two common losses are
- Square error: $l(s, \hat{s}) = (s - \hat{s})^2$
- Absolute error: $l(s, \hat{s}) = |s - \hat{s}|$
Note that both the square and absolute errors are functions of the estimation error $e = s-{\hat s}$. However, this is not necessarily the case. As an example, imagine a situation in which we would like to introduce a penalty which increases with the magnitude of the estimated variable. For such case, the following cost would better fit our needs: $l(s,{\hat s}) = s^2 \left(s-{\hat s}\right)^2$.
```
# In this section we will plot together the square and absolute errors
grid = np.linspace(-3,3,num=100)
plt.plot(grid, grid**2, 'b-', label='Square error')
plt.plot(grid, np.absolute(grid), 'r--', label='Absolute error')
plt.xlabel('Error')
plt.ylabel('Cost')
plt.legend(loc='best')
plt.show()
```
In general, we do not care much about an isolated application of the regression model, but instead, we are looking for a generally good behavior, for which we need to average the loss function over a set of samples. In this notebook, we will use the average of the square loss, to which we will refer as the `mean-square error` (MSE).
$$\text{MSE} = \frac{1}{K}\sum_{k=0}^{K-1} \left(s^{(k)}- {\hat s}^{(k)}\right)^2$$
The following code fragment defines a function to compute the MSE based on the availability of two vectors, one of them containing the predictions of the model, and the other the true target values.
```
# We start by defining a function that calculates the average square error
def square_error(s, s_est):
# Squeeze is used to make sure that s and s_est have the appropriate dimensions.
y = np.mean(np.power((np.squeeze(s) - np.squeeze(s_est)), 2))
return y
```
### 4.1. Training and test data
The major goal of the regression problem is that the predictor should make good predictions for arbitrary new inputs, not taken from the dataset used by the regression algorithm.
Thus, in order to evaluate the prediction accuracy of some regression algorithm, we need some data, not used during the predictor design, to *test* the performance of the predictor under new data. To do so, the original dataset is usually divided in (at least) two disjoint sets:
* **Training set**, $\cal{D}_{\text{train}}$: Used by the regression algorithm to determine predictor $f$.
* **Test set**, $\cal{D}_{\text{test}}$: Used to evaluate the performance of the regression algorithm.
A good regression algorithm uses $\cal{D}_{\text{train}}$ to obtain a predictor with small average loss based on $\cal{D}_{\text{test}}$
$$
{\bar R}_{\text{test}} = \frac{1}{K_{\text{test}}}
\sum_{ ({\bf x},s) \in \mathcal{D}_{\text{test}}} l(s, f({\bf x}))
$$
where $K_{\text{test}}$ is the size of the test set.
As a designer, you only have access to training data. However, for illustration purposes, you may be given a test dataset for many examples in this course. Note that in such a case, using the test data to adjust the regression model is completely forbidden. You should work as if such test data set were not available at all, and recur to it just to assess the performance of the model after the design is complete.
To model the availability of a train/test partition, we split next the boston dataset into a training and test partitions, using 60% and 40% of the data, respectively.
```
from sklearn.model_selection import train_test_split
X_train, X_test, s_train, s_test = train_test_split(X, S, test_size=0.4, random_state=0)
```
### 4.2. A first example: A baseline regression model
A first very simple method to build the regression model is to use the average of all the target values in the training set as the output of the model, discarding the value of the observation input vector.
This approach can be considered as a baseline, given that any other method making an effective use of the observation variables, statistically related to $s$, should improve the performance of this method.
The following code fragment uses the train data to compute the baseline regression model, and it shows the MSE calculated over the test partitions.
```
S_baseline = np.mean(s_train)
print('The baseline estimator is:', S_baseline)
#Compute MSE for the train data
#MSE_train = square_error(s_train, S_baseline)
#Compute MSE for the test data. IMPORTANT: Note that we still use
#S_baseline as the prediction.
MSE_test = square_error(s_test, S_baseline)
#print('The MSE for the training data is:', MSE_train)
print('The MSE for the test data is:', MSE_test)
```
## 5. Parametric and non-parametric regression models
Generally speaking, we can distinguish two approaches when designing a regression model:
- Parametric approach: In this case, the estimation function is given <i>a priori</i> a parametric form, and the goal of the design is to find the most appropriate values of the parameters according to a certain goal
For instance, we could assume a linear expression
$${\hat s} = f({\bf x}) = {\bf w}^\top {\bf x}$$
and adjust the parameter vector in order to minimize the average of the quadratic error over the training data. This is known as least-squares regression, and we will study it in Section 8 of this notebook.
- Non-parametric approach: In this case, the analytical shape of the regression model is not assumed <i>a priori</i>.
## 6. Non parametric method: Regression with the $k$-nn method
The principles of the $k$-nn method are the following:
- For each point where a prediction is to be made, find the $k$ closest neighbors to that point (in the training set)
- Obtain the estimation averaging the labels corresponding to the selected neighbors
The number of neighbors is a hyperparameter that plays an important role in the performance of the method. You can test its influence by changing $k$ in the following piece of code.
```
from sklearn import neighbors
n_neighbors = 1
knn = neighbors.KNeighborsRegressor(n_neighbors)
knn.fit(X_train, s_train)
s_hat_train = knn.predict(X_train)
s_hat_test = knn.predict(X_test)
print('The MSE for the training data is:', square_error(s_train, s_hat_train))
print('The MSE for the test data is:', square_error(s_test, s_hat_test))
max_k = 25
n_neighbors_list = np.arange(max_k)+1
MSE_train = []
MSE_test = []
for n_neighbors in n_neighbors_list:
knn = neighbors.KNeighborsRegressor(n_neighbors)
knn.fit(X_train, s_train)
s_hat_train = knn.predict(X_train)
s_hat_test = knn.predict(X_test)
MSE_train.append(square_error(s_train, s_hat_train))
MSE_test.append(square_error(s_test, s_hat_test))
plt.plot(n_neighbors_list, MSE_train,'bo', label='Training square error')
plt.plot(n_neighbors_list, MSE_test,'ro', label='Test square error')
plt.xlabel('$k$')
plt.axis('tight')
plt.legend(loc='best')
plt.show()
```
Although the above figures illustrate evolution of the training and test MSE for different selections of the number of neighbors, it is important to note that **this figure, and in particular the red points, cannot be used to select the value of such parameter**. Remember that it is only legal to use the test data to assess the final performance of the method, what includes also that any parameters inherent to the method should be adjusted using the train data only.
## 7. Hyperparameter selection via cross-validation
An inconvenient of the application of the $k$-nn method is that the selection of $k$ influences the final error of the algorithm. In the previous experiments, we kept the value of $k$ that minimized the square error on the training set. However, we also noticed that the location of the minimum is not necessarily the same from the perspective of the test data. Ideally, we would like that the designed regression model works as well as possible on future unlabeled patterns that are not available during the training phase. This property is known as <i>generalization</i>. Fitting the training data is only pursued in the hope that we are also indirectly obtaining a model that generalizes well. In order to achieve this goal, there are some strategies that try to guarantee a correct generalization of the model. One of such approaches is known as <b>cross-validation</b>
Since using the test labels during the training phase is not allowed (they should be kept aside to simultate the future application of the regression model on unseen patterns), we need to figure out some way to improve our estimation of the hyperparameter that requires only training data. Cross-validation allows us to do so by following the following steps:
- Split the training data into several (generally non-overlapping) subsets. If we use $M$ subsets, the method is referred to as $M$-fold cross-validation. If we consider each pattern a different subset, the method is usually referred to as leave-one-out (LOO) cross-validation.
- Carry out the training of the system $M$ times. For each run, use a different partition as a <i>validation</i> set, and use the restating partitions as the training set. Evaluate the performance for different choices of the hyperparameter (i.e., for different values of $k$ for the $k$-NN method).
- Average the validation error over all partitions, and pick the hyperparameter that provided the minimum validation error.
- Rerun the algorithm using all the training data, keeping the value of the parameter that came out of the cross-validation process.
<img src="https://chrisjmccormick.files.wordpress.com/2013/07/10_fold_cv.png">
**Exercise**: Use `Kfold` function from the `sklearn` library to validate parameter `k`. Use a 10-fold validation strategy. What is the best number of neighbors according to this strategy? What is the corresponding MSE averaged over the test data?
```
from sklearn.model_selection import KFold
max_k = 25
n_neighbors_list = np.arange(max_k)+1
MSE_val = np.zeros((max_k,))
nfolds = 10
kf = KFold(n_splits=nfolds)
for train, val in kf.split(X_train):
for idx,n_neighbors in enumerate(n_neighbors_list):
knn = neighbors.KNeighborsRegressor(n_neighbors)
knn.fit(X_train[train,:], s_train[train])
s_hat_val = knn.predict(X_train[val,:])
MSE_val[idx] += square_error(s_train[val], s_hat_val)
MSE_val = [el/10 for el in MSE_val]
selected_k = np.argmin(MSE_val) + 1
plt.plot(n_neighbors_list, MSE_train,'bo', label='Training square error')
plt.plot(n_neighbors_list, MSE_val,'ro', label='Validation square error')
plt.plot(selected_k, MSE_test[selected_k-1],'gs', label='Test square error')
plt.xlabel('$k$')
plt.axis('tight')
plt.legend(loc='best')
plt.show()
print('Cross-validation selected the following value for the number of neighbors:', selected_k)
print('Test MSE:', MSE_test[selected_k-1])
```
## 8. A parametric regression method: Least squares regression
### 8.1. Problem definition
- The goal is to learn a (possibly non-linear) regression model from a set of $L$ labeled points, $\{{\bf x}_k,s_k\}_{k=0}^{K-1}$.
- We assume a parametric function of the form:
$${\hat s}({\bf x}) = f({\bf x}) = w_0 z_0({\bf x}) + w_1 z_1({\bf x}) + \dots w_{m-1} z_{m-1}({\bf x})$$
where $z_i({\bf x})$ are particular transformations of the input vector variables.
Some examples are:
- If ${\bf z} = {\bf x}$, the model is just a linear combination of the input variables
- If ${\bf z} = \left[\begin{array}{c}1\\{\bf x}\end{array}\right]$, we have again a linear combination with the inclusion of a constant term.
- For unidimensional input $x$, ${\bf z} = [1, x, x^2, \dots,x^{M}]^\top$ would implement a polynomia of degree $m-1$.
- Note that the variables of ${\bf z}$ could also be computed combining different variables of ${\bf x}$. E.g., if ${\bf x} = [x_1,x_2]^\top$, a degree-two polynomia would be implemented with
$${\bf z} = \left[\begin{array}{c}1\\x_1\\x_2\\x_1^2\\x_2^2\\x_1 x_2\end{array}\right]$$
- The above expression does not assume a polynomial model. For instance, we could consider ${\bf z} = [\log(x_1),\log(x_2)]$
Least squares (LS) regression finds the coefficients of the model with the aim of minimizing the square of the residuals. If we define ${\bf w} = [w_0,w_1,\dots,w_M]^\top$, the LS solution would be defined as
\begin{equation}{\bf w}_{LS} = \arg \min_{\bf w} \sum_{k=0}^{K-1} e_k^2 = \arg \min_{\bf w} \sum_{k=0}^{K-1} \left[s_k - {\hat s}_k \right]^2 \end{equation}
### 8.2. Vector Notation
In order to solve the LS problem it is convenient to define the following vectors and matrices:
- We can group together all available target values to form the following vector
$${\bf s} = \left[s_0, s_1, \dots, s_{K-1} \right]^\top$$
- The estimation of the model for a single input vector ${\bf z}_k$ (which would be computed from ${\bf x}_k$), can be expressed as the following inner product
$${\hat s}_k = {\bf z}_k^\top {\bf w}$$
- If we now group all input vectors into a matrix ${\bf Z}$, so that each row of ${\bf Z}$ contains the transpose of the corresponding ${\bf z}_k$, we can express
$$
\hat{{\bf s}}
= \left[{\hat s}_0, {\hat s}_1, \dots, {\hat s}_{K-1} \right]^\top
= {\bf Z} {\bf w}, \;\;\;\; \text{with} \;\;
{\bf Z} = \left[\begin{array}{c} {\bf z}_0^\top \\
{\bf z}_1^\top \\
\vdots \\
{\bf z}_{K-1}^\top \\
\end{array}\right]$$
### 8.3. Least-squares solution
- Using the previous notation, the cost minimized by the LS model can be expressed as
$$C({\bf w}) = \sum_{k=0}^{K-1} \left[s_k - {\hat s}_k \right]^2 = \|{\bf s} - {\hat{\bf s}}\|^2 = \|{\bf s} - {\bf Z}{\bf w}\|^2$$
- Since the above expression depends quadratically on ${\bf w}$ and is non-negative, we know that there is only one point where the derivative of $C({\bf w})$ becomes zero, and that point is necessarily a minimum of the cost
$$\nabla_{\bf w} \|{\bf s} - {\bf Z}{\bf w}\|^2\Bigg|_{{\bf w} = {\bf w}_{LS}} = {\bf 0}$$
<b>Exercise:</b>
Solve the previous problem to show that
$${\bf w}_{LS} = \left( {\bf Z}^\top{\bf Z} \right)^{-1} {\bf Z}^\top{\bf s}$$
The next fragment of code adjusts polynomia of increasing order to randomly generated training data.
```
n_points = 20
n_grid = 200
frec = 3
std_n = 0.2
max_degree = 20
colors = 'brgcmyk'
#Location of the training points
X_tr = (3 * np.random.random((n_points,1)) - 0.5)
#Labels are obtained from a sinusoidal function, and contaminated by noise
S_tr = np.cos(frec*X_tr) + std_n * np.random.randn(n_points,1)
#Equally spaced points in the X-axis
X_grid = np.linspace(np.min(X_tr),np.max(X_tr),n_grid)
#We start by building the Z matrix
Z = []
for el in X_tr.tolist():
Z.append([el[0]**k for k in range(max_degree+1)])
Z = np.matrix(Z)
Z_grid = []
for el in X_grid.tolist():
Z_grid.append([el**k for k in range(max_degree+1)])
Z_grid = np.matrix(Z_grid)
plt.plot(X_tr,S_tr,'b.')
for k in [1, 2, n_points]: # range(max_degree+1):
Z_iter = Z[:,:k+1]
# Least square solution
#w_LS = (np.linalg.inv(Z_iter.T.dot(Z_iter))).dot(Z_iter.T).dot(S_tr)
# Least squares solution, with leass numerical errors
w_LS, resid, rank, s = np.linalg.lstsq(Z_iter, S_tr)
#estimates at all grid points
fout = Z_grid[:,:k+1].dot(w_LS)
fout = np.array(fout).flatten()
plt.plot(X_grid,fout,colors[k%len(colors)]+'-',label='Degree '+str(k))
plt.legend(loc='best')
plt.ylim(1.2*np.min(S_tr), 1.2*np.max(S_tr))
plt.show()
```
It may seem that increasing the degree of the polynomia is always beneficial, as we can implement a more expressive function. A polynomia of degree $M$ would include all polynomia of lower degrees as particular cases. However, if we increase the number of parameters without control, the polynomia would eventually get expressive enough to adjust any given set of training points to arbitrary precision, what does not necessarily mean that the solution is obtaining a model that can be extrapolated to new data.
The conclusions is that, when adjusting a parametric model using least squares, we need to validate the model, for which we can use the cross-validation techniques we introudece in Section 7. In this contexts, validating the model implies:
- Validating the kind of model that will be used, e.g., linear, polynomial, logarithmic, etc ...
- Validating any additional parameters that the nodel may have, e.g., if selecting a polynomial model, the degree of the polynomia.
The code below shows the performance of different models. However, no validation process is considered, so the reported test MSEs could not be used as criteria to select the best model.
```
# Linear model with no bias
w_LS, resid, rank, s = np.linalg.lstsq(X_train, s_train)
s_hat_test = X_test.dot(w_LS)
print('Test MSE for linear model without bias:', square_error(s_test, s_hat_test))
# Linear model with no bias
Z_train = np.hstack((np.ones((X_train.shape[0],1)), X_train))
Z_test = np.hstack((np.ones((X_test.shape[0],1)), X_test))
w_LS, resid, rank, s = np.linalg.lstsq(Z_train, s_train)
s_hat_test = Z_test.dot(w_LS)
print('Test MSE for linear model with bias:', square_error(s_test, s_hat_test))
# Polynomial model degree 2
Z_train = np.hstack((np.ones((X_train.shape[0],1)), X_train, X_train**2))
Z_test = np.hstack((np.ones((X_test.shape[0],1)), X_test, X_test**2))
w_LS, resid, rank, s = np.linalg.lstsq(Z_train, s_train)
s_hat_test = Z_test.dot(w_LS)
print('Test MSE for polynomial model (order 2):', square_error(s_test, s_hat_test))
```
| true |
code
| 0.591074 | null | null | null | null |
|
# Sentiment Analysis with TreeLSTMs in TensorFlow Fold
The [Stanford Sentiment Treebank](http://nlp.stanford.edu/sentiment/treebank.html) is a corpus of ~10K one-sentence movie reviews from Rotten Tomatoes. The sentences have been parsed into binary trees with words at the leaves; every sub-tree has a label ranging from 0 (highly negative) to 4 (highly positive); 2 means neutral.
For example, `(4 (2 Spiderman) (3 ROCKS))` is sentence with two words, corresponding a binary tree with three nodes. The label at the root, for the entire sentence, is `4` (highly positive). The label for the left child, a leaf corresponding to the word `Spiderman`, is `2` (neutral). The label for the right child, a leaf corresponding to the word `ROCKS` is `3` (moderately positive).
This notebook shows how to use TensorFlow Fold train a model on the treebank using binary TreeLSTMs and [GloVe](http://nlp.stanford.edu/projects/glove/) word embedding vectors, as described in the paper [Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks](http://arxiv.org/pdf/1503.00075.pdf) by Tai et al. The original [Torch](http://torch.ch) source code for the model, provided by the authors, is available [here](https://github.com/stanfordnlp/treelstm).
The model illustrates three of the more advanced features of Fold, namely:
1. [Compositions](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/blocks.md#wiring-things-together-in-more-complicated-ways) to wire up blocks to form arbitrary directed acyclic graphs
2. [Forward Declarations](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/blocks.md#recursion-and-forward-declarations) to create recursive blocks
3. [Metrics](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#class-tdmetric) to create models where the size of the output is not fixed, but varies as a function of the input data.
```
# boilerplate
import codecs
import functools
import os
import tempfile
import zipfile
from nltk.tokenize import sexpr
import numpy as np
from six.moves import urllib
import tensorflow as tf
sess = tf.InteractiveSession()
import tensorflow_fold as td
```
## Get the data
Begin by fetching the word embedding vectors and treebank sentences.
```
data_dir = tempfile.mkdtemp()
print('saving files to %s' % data_dir)
def download_and_unzip(url_base, zip_name, *file_names):
zip_path = os.path.join(data_dir, zip_name)
url = url_base + zip_name
print('downloading %s to %s' % (url, zip_path))
urllib.request.urlretrieve(url, zip_path)
out_paths = []
with zipfile.ZipFile(zip_path, 'r') as f:
for file_name in file_names:
print('extracting %s' % file_name)
out_paths.append(f.extract(file_name, path=data_dir))
return out_paths
full_glove_path, = download_and_unzip(
'http://nlp.stanford.edu/data/', 'glove.840B.300d.zip',
'glove.840B.300d.txt')
train_path, dev_path, test_path = download_and_unzip(
'http://nlp.stanford.edu/sentiment/', 'trainDevTestTrees_PTB.zip',
'trees/train.txt', 'trees/dev.txt', 'trees/test.txt')
```
Filter out words that don't appear in the dataset, since the full dataset is a bit large (5GB). This is purely a performance optimization and has no effect on the final results.
```
filtered_glove_path = os.path.join(data_dir, 'filtered_glove.txt')
def filter_glove():
vocab = set()
# Download the full set of unlabeled sentences separated by '|'.
sentence_path, = download_and_unzip(
'http://nlp.stanford.edu/~socherr/', 'stanfordSentimentTreebank.zip',
'stanfordSentimentTreebank/SOStr.txt')
with codecs.open(sentence_path, encoding='utf-8') as f:
for line in f:
# Drop the trailing newline and strip backslashes. Split into words.
vocab.update(line.strip().replace('\\', '').split('|'))
nread = 0
nwrote = 0
with codecs.open(full_glove_path, encoding='utf-8') as f:
with codecs.open(filtered_glove_path, 'w', encoding='utf-8') as out:
for line in f:
nread += 1
line = line.strip()
if not line: continue
if line.split(u' ', 1)[0] in vocab:
out.write(line + '\n')
nwrote += 1
print('read %s lines, wrote %s' % (nread, nwrote))
filter_glove()
```
Load the filtered word embeddings into a matrix and build an dict from words to indices into the matrix. Add a random embedding vector for out-of-vocabulary words.
```
def load_embeddings(embedding_path):
"""Loads embedings, returns weight matrix and dict from words to indices."""
print('loading word embeddings from %s' % embedding_path)
weight_vectors = []
word_idx = {}
with codecs.open(embedding_path, encoding='utf-8') as f:
for line in f:
word, vec = line.split(u' ', 1)
word_idx[word] = len(weight_vectors)
weight_vectors.append(np.array(vec.split(), dtype=np.float32))
# Annoying implementation detail; '(' and ')' are replaced by '-LRB-' and
# '-RRB-' respectively in the parse-trees.
word_idx[u'-LRB-'] = word_idx.pop(u'(')
word_idx[u'-RRB-'] = word_idx.pop(u')')
# Random embedding vector for unknown words.
weight_vectors.append(np.random.uniform(
-0.05, 0.05, weight_vectors[0].shape).astype(np.float32))
return np.stack(weight_vectors), word_idx
weight_matrix, word_idx = load_embeddings(filtered_glove_path)
```
Finally, load the treebank data.
```
def load_trees(filename):
with codecs.open(filename, encoding='utf-8') as f:
# Drop the trailing newline and strip \s.
trees = [line.strip().replace('\\', '') for line in f]
print('loaded %s trees from %s' % (len(trees), filename))
return trees
train_trees = load_trees(train_path)
dev_trees = load_trees(dev_path)
test_trees = load_trees(test_path)
```
## Build the model
We want to compute a hidden state vector $h$ for every node in the tree. The hidden state is the input to a linear layer with softmax output for predicting the sentiment label.
At the leaves of the tree, words are mapped to word-embedding vectors which serve as the input to a binary tree-LSTM with $0$ for the previous states. At the internal nodes, the LSTM takes $0$ as input, and previous states from its two children. More formally,
\begin{align}
h_{word} &= TreeLSTM(Embedding(word), 0, 0) \\
h_{left, right} &= TreeLSTM(0, h_{left}, h_{right})
\end{align}
where $TreeLSTM(x, h_{left}, h_{right})$ is a special kind of LSTM cell that takes two hidden states as inputs, and has a separate forget gate for each of them. Specifically, it is [Tai et al.](http://arxiv.org/pdf/1503.00075.pdf) eqs. 9-14 with $N=2$. One modification here from Tai et al. is that instead of L2 weight regularization, we use recurrent droupout as described in the paper [Recurrent Dropout without Memory Loss](http://arxiv.org/pdf/1603.05118.pdf).
We can implement $TreeLSTM$ by subclassing the TensorFlow [`BasicLSTMCell`](https://www.tensorflow.org/versions/r1.0/api_docs/python/contrib.rnn/rnn_cells_for_use_with_tensorflow_s_core_rnn_methods#BasicLSTMCell).
```
class BinaryTreeLSTMCell(tf.contrib.rnn.BasicLSTMCell):
"""LSTM with two state inputs.
This is the model described in section 3.2 of 'Improved Semantic
Representations From Tree-Structured Long Short-Term Memory
Networks' <http://arxiv.org/pdf/1503.00075.pdf>, with recurrent
dropout as described in 'Recurrent Dropout without Memory Loss'
<http://arxiv.org/pdf/1603.05118.pdf>.
"""
def __init__(self, num_units, keep_prob=1.0):
"""Initialize the cell.
Args:
num_units: int, The number of units in the LSTM cell.
keep_prob: Keep probability for recurrent dropout.
"""
super(BinaryTreeLSTMCell, self).__init__(num_units)
self._keep_prob = keep_prob
def __call__(self, inputs, state, scope=None):
with tf.variable_scope(scope or type(self).__name__):
lhs, rhs = state
c0, h0 = lhs
c1, h1 = rhs
concat = tf.contrib.layers.linear(
tf.concat([inputs, h0, h1], 1), 5 * self._num_units)
# i = input_gate, j = new_input, f = forget_gate, o = output_gate
i, j, f0, f1, o = tf.split(value=concat, num_or_size_splits=5, axis=1)
j = self._activation(j)
if not isinstance(self._keep_prob, float) or self._keep_prob < 1:
j = tf.nn.dropout(j, self._keep_prob)
new_c = (c0 * tf.sigmoid(f0 + self._forget_bias) +
c1 * tf.sigmoid(f1 + self._forget_bias) +
tf.sigmoid(i) * j)
new_h = self._activation(new_c) * tf.sigmoid(o)
new_state = tf.contrib.rnn.LSTMStateTuple(new_c, new_h)
return new_h, new_state
```
Use a placeholder for the dropout keep probability, with a default of 1 (for eval).
```
keep_prob_ph = tf.placeholder_with_default(1.0, [])
```
Create the LSTM cell for our model. In addition to recurrent dropout, apply dropout to inputs and outputs, using TF's build-in dropout wrapper. Put the LSTM cell inside of a [`td.ScopedLayer`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#class-tdscopedlayer) in order to manage variable scoping. This ensures that our LSTM's variables are encapsulated from the rest of the graph and get created exactly once.
```
lstm_num_units = 300 # Tai et al. used 150, but our regularization strategy is more effective
tree_lstm = td.ScopedLayer(
tf.contrib.rnn.DropoutWrapper(
BinaryTreeLSTMCell(lstm_num_units, keep_prob=keep_prob_ph),
input_keep_prob=keep_prob_ph, output_keep_prob=keep_prob_ph),
name_or_scope='tree_lstm')
```
Create the output layer using [`td.FC`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#class-tdfc).
```
NUM_CLASSES = 5 # number of distinct sentiment labels
output_layer = td.FC(NUM_CLASSES, activation=None, name='output_layer')
```
Create the word embedding using [`td.Embedding`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#class-tdembedding). Note that the built-in Fold layers like `Embedding` and `FC` manage variable scoping automatically, so there is no need to put them inside scoped layers.
```
word_embedding = td.Embedding(
*weight_matrix.shape, initializer=weight_matrix, name='word_embedding')
```
We now have layers that encapsulate all of the trainable variables for our model. The next step is to create the Fold blocks that define how inputs (s-expressions encoded as strings) get processed and used to make predictions. Naturally this requires a recursive model, which we handle in Fold using a [forward declaration](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/blocks.md#recursion-and-forward-declarations). The recursive step is to take a subtree (represented as a string) and convert it into a hidden state vector (the LSTM state), thus embedding it in a $n$-dimensional space (where here $n=300$).
```
embed_subtree = td.ForwardDeclaration(name='embed_subtree')
```
The core the model is a block that takes as input a list of tokens. The tokens will be either:
* `[word]` - a leaf with a single word, the base-case for the recursion, or
* `[lhs, rhs]` - an internal node consisting of a pair of sub-expressions
The outputs of the block will be a pair consisting of logits (the prediction) and the LSTM state.
```
def logits_and_state():
"""Creates a block that goes from tokens to (logits, state) tuples."""
unknown_idx = len(word_idx)
lookup_word = lambda word: word_idx.get(word, unknown_idx)
word2vec = (td.GetItem(0) >> td.InputTransform(lookup_word) >>
td.Scalar('int32') >> word_embedding)
pair2vec = (embed_subtree(), embed_subtree())
# Trees are binary, so the tree layer takes two states as its input_state.
zero_state = td.Zeros((tree_lstm.state_size,) * 2)
# Input is a word vector.
zero_inp = td.Zeros(word_embedding.output_type.shape[0])
word_case = td.AllOf(word2vec, zero_state)
pair_case = td.AllOf(zero_inp, pair2vec)
tree2vec = td.OneOf(len, [(1, word_case), (2, pair_case)])
return tree2vec >> tree_lstm >> (output_layer, td.Identity())
```
Note that we use the call operator `()` to create blocks that reference the `embed_subtree` forward declaration, for the recursive case.
Define a per-node loss function for training.
```
def tf_node_loss(logits, labels):
return tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=labels)
```
Additionally calculate fine-grained and binary hits (i.e. un-normalized accuracy) for evals. Fine-grained accuracy is defined over all five class labels and will be calculated for all labels, whereas binary accuracy is defined of negative vs. positive classification and will not be calcluated for neutral labels.
```
def tf_fine_grained_hits(logits, labels):
predictions = tf.cast(tf.argmax(logits, 1), tf.int32)
return tf.cast(tf.equal(predictions, labels), tf.float64)
def tf_binary_hits(logits, labels):
softmax = tf.nn.softmax(logits)
binary_predictions = (softmax[:, 3] + softmax[:, 4]) > (softmax[:, 0] + softmax[:, 1])
binary_labels = labels > 2
return tf.cast(tf.equal(binary_predictions, binary_labels), tf.float64)
```
The [`td.Metric`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#class-tdmetric) block provides a mechaism for accumulating results across sequential and recursive computations without having the thread them through explictly as return values. Metrics are wired up here inside of a [`td.Composition`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/blocks.md#wiring-things-together-in-more-complicated-ways) block, which allows us to explicitly specify the inputs of sub-blocks with calls to `Block.reads()` inside of a [`Composition.scope()`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#tdcompositionscope) context manager.
For training, we will sum the loss over all nodes. But for evals, we would like to separately calcluate accuracies for the root (i.e. entire sentences) to match the numbers presented in the literature. We also need to distinguish between neutral and non-neutral sentiment labels, because binary sentiment doesn't get calculated for neutral nodes.
This is easy to do by putting our block creation code for calculating metrics inside of a function and passing it indicators. Note that this needs to be done in Python-land, because we can't inspect the contents of a tensor inside of Fold (since it hasn't been run yet).
```
def add_metrics(is_root, is_neutral):
"""A block that adds metrics for loss and hits; output is the LSTM state."""
c = td.Composition(
name='predict(is_root=%s, is_neutral=%s)' % (is_root, is_neutral))
with c.scope():
# destructure the input; (labels, (logits, state))
labels = c.input[0]
logits = td.GetItem(0).reads(c.input[1])
state = td.GetItem(1).reads(c.input[1])
# calculate loss
loss = td.Function(tf_node_loss)
td.Metric('all_loss').reads(loss.reads(logits, labels))
if is_root: td.Metric('root_loss').reads(loss)
# calculate fine-grained hits
hits = td.Function(tf_fine_grained_hits)
td.Metric('all_hits').reads(hits.reads(logits, labels))
if is_root: td.Metric('root_hits').reads(hits)
# calculate binary hits, if the label is not neutral
if not is_neutral:
binary_hits = td.Function(tf_binary_hits).reads(logits, labels)
td.Metric('all_binary_hits').reads(binary_hits)
if is_root: td.Metric('root_binary_hits').reads(binary_hits)
# output the state, which will be read by our by parent's LSTM cell
c.output.reads(state)
return c
```
Use [NLTK](http://www.nltk.org/) to define a `tokenize` function to split S-exprs into left and right parts. We need this to run our `logits_and_state()` block since it expects to be passed a list of tokens and our raw input is strings.
```
def tokenize(s):
label, phrase = s[1:-1].split(None, 1)
return label, sexpr.sexpr_tokenize(phrase)
```
Try it out.
```
tokenize('(X Y)')
tokenize('(X Y Z)')
```
Embed trees (represented as strings) by tokenizing and piping (`>>`) to `label_and_logits`, distinguishing between neutral and non-neutral labels. We don't know here whether or not we are the root node (since this is a recursive computation), so that gets threaded through as an indicator.
```
def embed_tree(logits_and_state, is_root):
"""Creates a block that embeds trees; output is tree LSTM state."""
return td.InputTransform(tokenize) >> td.OneOf(
key_fn=lambda pair: pair[0] == '2', # label 2 means neutral
case_blocks=(add_metrics(is_root, is_neutral=False),
add_metrics(is_root, is_neutral=True)),
pre_block=(td.Scalar('int32'), logits_and_state))
```
Put everything together and create our top-level (i.e. root) model. It is rather simple.
```
model = embed_tree(logits_and_state(), is_root=True)
```
Resolve the forward declaration for embedding subtrees (the non-root case) with a second call to `embed_tree`.
```
embed_subtree.resolve_to(embed_tree(logits_and_state(), is_root=False))
```
[Compile](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/running.md#batching-inputs) the model.
```
compiler = td.Compiler.create(model)
print('input type: %s' % model.input_type)
print('output type: %s' % model.output_type)
```
## Setup for training
Calculate means by summing the raw metrics.
```
metrics = {k: tf.reduce_mean(v) for k, v in compiler.metric_tensors.items()}
```
Magic numbers.
```
LEARNING_RATE = 0.05
KEEP_PROB = 0.75
BATCH_SIZE = 100
EPOCHS = 20
EMBEDDING_LEARNING_RATE_FACTOR = 0.1
```
Training with [Adagrad](https://www.tensorflow.org/versions/master/api_docs/python/train/optimizers#AdagradOptimizer).
```
train_feed_dict = {keep_prob_ph: KEEP_PROB}
loss = tf.reduce_sum(compiler.metric_tensors['all_loss'])
opt = tf.train.AdagradOptimizer(LEARNING_RATE)
```
Important detail from section 5.3 of [Tai et al.]((http://arxiv.org/pdf/1503.00075.pdf); downscale the gradients for the word embedding vectors 10x otherwise we overfit horribly.
```
grads_and_vars = opt.compute_gradients(loss)
found = 0
for i, (grad, var) in enumerate(grads_and_vars):
if var == word_embedding.weights:
found += 1
grad = tf.scalar_mul(EMBEDDING_LEARNING_RATE_FACTOR, grad)
grads_and_vars[i] = (grad, var)
assert found == 1 # internal consistency check
train = opt.apply_gradients(grads_and_vars)
saver = tf.train.Saver()
```
The TF graph is now complete; initialize the variables.
```
sess.run(tf.global_variables_initializer())
```
## Train the model
Start by defining a function that does a single step of training on a batch and returns the loss.
```
def train_step(batch):
train_feed_dict[compiler.loom_input_tensor] = batch
_, batch_loss = sess.run([train, loss], train_feed_dict)
return batch_loss
```
Now similarly for an entire epoch of training.
```
def train_epoch(train_set):
return sum(train_step(batch) for batch in td.group_by_batches(train_set, BATCH_SIZE))
```
Use [`Compiler.build_loom_inputs()`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#tdcompilerbuild_loom_inputsexamples-metric_labelsfalse-chunk_size100-orderedfalse) to transform `train_trees` into individual loom inputs (i.e. wiring diagrams) that we can use to actually run the model.
```
train_set = compiler.build_loom_inputs(train_trees)
```
Use [`Compiler.build_feed_dict()`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#tdcompilerbuild_feed_dictexamples-batch_sizenone-metric_labelsfalse-orderedfalse) to build a feed dictionary for validation on the dev set. This is marginally faster and more convenient than calling `build_loom_inputs`. We used `build_loom_inputs` on the train set so that we can shuffle the individual wiring diagrams into different batches for each epoch.
```
dev_feed_dict = compiler.build_feed_dict(dev_trees)
```
Define a function to do an eval on the dev set and pretty-print some stats, returning accuracy on the dev set.
```
def dev_eval(epoch, train_loss):
dev_metrics = sess.run(metrics, dev_feed_dict)
dev_loss = dev_metrics['all_loss']
dev_accuracy = ['%s: %.2f' % (k, v * 100) for k, v in
sorted(dev_metrics.items()) if k.endswith('hits')]
print('epoch:%4d, train_loss: %.3e, dev_loss_avg: %.3e, dev_accuracy:\n [%s]'
% (epoch, train_loss, dev_loss, ' '.join(dev_accuracy)))
return dev_metrics['root_hits']
```
Run the main training loop, saving the model after each epoch if it has the best accuracy on the dev set. Use the [`td.epochs`](https://github.com/tensorflow/fold/blob/master/tensorflow_fold/g3doc/py/td.md#tdepochsitems-nnone-shuffletrue-prngnone) utility function to memoize the loom inputs and shuffle them after every epoch of training.
```
best_accuracy = 0.0
save_path = os.path.join(data_dir, 'sentiment_model')
for epoch, shuffled in enumerate(td.epochs(train_set, EPOCHS), 1):
train_loss = train_epoch(shuffled)
accuracy = dev_eval(epoch, train_loss)
if accuracy > best_accuracy:
best_accuracy = accuracy
checkpoint_path = saver.save(sess, save_path, global_step=epoch)
print('model saved in file: %s' % checkpoint_path)
```
The model starts to overfit pretty quickly even with dropout, as the LSTM begins to memorize the training set (which is rather small).
## Evaluate the model
Restore the model from the last checkpoint, where we saw the best accuracy on the dev set.
```
saver.restore(sess, checkpoint_path)
```
See how we did.
```
test_results = sorted(sess.run(metrics, compiler.build_feed_dict(test_trees)).items())
print(' loss: [%s]' % ' '.join(
'%s: %.3e' % (name.rsplit('_', 1)[0], v)
for name, v in test_results if name.endswith('_loss')))
print('accuracy: [%s]' % ' '.join(
'%s: %.2f' % (name.rsplit('_', 1)[0], v * 100)
for name, v in test_results if name.endswith('_hits')))
```
Not bad! See section 3.5.1 of [our paper](https://arxiv.org/abs/1702.02181) for discussion and a comparison of these results to the state of the art.
| true |
code
| 0.614278 | null | null | null | null |
|
# Name
Deploying a trained model to Cloud Machine Learning Engine
# Label
Cloud Storage, Cloud ML Engine, Kubeflow, Pipeline
# Summary
A Kubeflow Pipeline component to deploy a trained model from a Cloud Storage location to Cloud ML Engine.
# Details
## Intended use
Use the component to deploy a trained model to Cloud ML Engine. The deployed model can serve online or batch predictions in a Kubeflow Pipeline.
## Runtime arguments
| Argument | Description | Optional | Data type | Accepted values | Default |
|--------------------------|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|----------|--------------|-----------------|---------|
| model_uri | The URI of a Cloud Storage directory that contains a trained model file.<br/> Or <br/> An [Estimator export base directory](https://www.tensorflow.org/guide/saved_model#perform_the_export) that contains a list of subdirectories named by timestamp. The directory with the latest timestamp is used to load the trained model file. | No | GCSPath | | |
| project_id | The ID of the Google Cloud Platform (GCP) project of the serving model. | No | GCPProjectID | | |
| model_id | The name of the trained model. | Yes | String | | None |
| version_id | The name of the version of the model. If it is not provided, the operation uses a random name. | Yes | String | | None |
| runtime_version | The Cloud ML Engine runtime version to use for this deployment. If it is not provided, the default stable version, 1.0, is used. | Yes | String | | None |
| python_version | The version of Python used in the prediction. If it is not provided, version 2.7 is used. You can use Python 3.5 if runtime_version is set to 1.4 or above. Python 2.7 works with all supported runtime versions. | Yes | String | | 2.7 |
| model | The JSON payload of the new [model](https://cloud.google.com/ml-engine/reference/rest/v1/projects.models). | Yes | Dict | | None |
| version | The new [version](https://cloud.google.com/ml-engine/reference/rest/v1/projects.models.versions) of the trained model. | Yes | Dict | | None |
| replace_existing_version | Indicates whether to replace the existing version in case of a conflict (if the same version number is found.) | Yes | Boolean | | FALSE |
| set_default | Indicates whether to set the new version as the default version in the model. | Yes | Boolean | | FALSE |
| wait_interval | The number of seconds to wait in case the operation has a long run time. | Yes | Integer | | 30 |
## Input data schema
The component looks for a trained model in the location specified by the `model_uri` runtime argument. The accepted trained models are:
* [Tensorflow SavedModel](https://cloud.google.com/ml-engine/docs/tensorflow/exporting-for-prediction)
* [Scikit-learn & XGBoost model](https://cloud.google.com/ml-engine/docs/scikit/exporting-for-prediction)
The accepted file formats are:
* *.pb
* *.pbtext
* model.bst
* model.joblib
* model.pkl
`model_uri` can also be an [Estimator export base directory, ](https://www.tensorflow.org/guide/saved_model#perform_the_export)which contains a list of subdirectories named by timestamp. The directory with the latest timestamp is used to load the trained model file.
## Output
| Name | Description | Type |
|:------- |:---- | :--- |
| job_id | The ID of the created job. | String |
| job_dir | The Cloud Storage path that contains the trained model output files. | GCSPath |
## Cautions & requirements
To use the component, you must:
* [Set up the cloud environment](https://cloud.google.com/ml-engine/docs/tensorflow/getting-started-training-prediction#setup).
* Run the component under a secret [Kubeflow user service account](https://www.kubeflow.org/docs/started/getting-started-gke/#gcp-service-accounts) in a Kubeflow cluster. For example:
```
```python
mlengine_deploy_op(...).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
* Grant read access to the Cloud Storage bucket that contains the trained model to the Kubeflow user service account.
## Detailed description
Use the component to:
* Locate the trained model at the Cloud Storage location you specify.
* Create a new model if a model provided by you doesn’t exist.
* Delete the existing model version if `replace_existing_version` is enabled.
* Create a new version of the model from the trained model.
* Set the new version as the default version of the model if `set_default` is enabled.
Follow these steps to use the component in a pipeline:
1. Install the Kubeflow Pipeline SDK:
```
%%capture --no-stderr
KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.14/kfp.tar.gz'
!pip3 install $KFP_PACKAGE --upgrade
```
2. Load the component using KFP SDK
```
import kfp.components as comp
mlengine_deploy_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/a97f1d0ad0e7b92203f35c5b0b9af3a314952e05/components/gcp/ml_engine/deploy/component.yaml')
help(mlengine_deploy_op)
```
### Sample
Note: The following sample code works in IPython notebook or directly in Python code.
In this sample, you deploy a pre-built trained model from `gs://ml-pipeline-playground/samples/ml_engine/census/trained_model/` to Cloud ML Engine. The deployed model is `kfp_sample_model`. A new version is created every time the sample is run, and the latest version is set as the default version of the deployed model.
#### Set sample parameters
```
# Required Parameters
PROJECT_ID = '<Please put your project ID here>'
# Optional Parameters
EXPERIMENT_NAME = 'CLOUDML - Deploy'
TRAINED_MODEL_PATH = 'gs://ml-pipeline-playground/samples/ml_engine/census/trained_model/'
```
#### Example pipeline that uses the component
```
import kfp.dsl as dsl
import kfp.gcp as gcp
import json
@dsl.pipeline(
name='CloudML deploy pipeline',
description='CloudML deploy pipeline'
)
def pipeline(
model_uri = 'gs://ml-pipeline-playground/samples/ml_engine/census/trained_model/',
project_id = PROJECT_ID,
model_id = 'kfp_sample_model',
version_id = '',
runtime_version = '1.10',
python_version = '',
version = '',
replace_existing_version = 'False',
set_default = 'True',
wait_interval = '30'):
task = mlengine_deploy_op(
model_uri=model_uri,
project_id=project_id,
model_id=model_id,
version_id=version_id,
runtime_version=runtime_version,
python_version=python_version,
version=version,
replace_existing_version=replace_existing_version,
set_default=set_default,
wait_interval=wait_interval).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
#### Compile the pipeline
```
pipeline_func = pipeline
pipeline_filename = pipeline_func.__name__ + '.zip'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
```
#### Submit the pipeline for execution
```
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
```
## References
* [Component python code](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/component_sdk/python/kfp_component/google/ml_engine/_deploy.py)
* [Component docker file](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/Dockerfile)
* [Sample notebook](https://github.com/kubeflow/pipelines/blob/master/components/gcp/ml_engine/deploy/sample.ipynb)
* [Cloud Machine Learning Engine Model REST API](https://cloud.google.com/ml-engine/reference/rest/v1/projects.models)
* [Cloud Machine Learning Engine Version REST API](https://cloud.google.com/ml-engine/reference/rest/v1/projects.versions)
## License
By deploying or using this software you agree to comply with the [AI Hub Terms of Service](https://aihub.cloud.google.com/u/0/aihub-tos) and the [Google APIs Terms of Service](https://developers.google.com/terms/). To the extent of a direct conflict of terms, the AI Hub Terms of Service will control.
| true |
code
| 0.834474 | null | null | null | null |
|
```
import tensorflow as tf
```
tf.train.Coordinator: help multiple thread stop together and report exceptions to a program that waits for them to stop.
tf.train.QueueRunner: create a number of threads cooperatiing to **enqueue** tensors in the **same** queue.
## Coordinator
### Key method
tf.train.Coordinator.should_stop
return `True` if the threads should stop. This is called from threads, so the thread know if it should stop.
tf.train.Coordinator.request_stop
request that the threads should stop. when this is called, calls to `should_top` will return `True`.
tf.train.Coordinator.join
This call blocks until a set of threads have terminated.
note: there is a message about **exc_info**, check it, I think this a oppotunity to study how to hanle exception in thread.
### Simple example
```
import time
import threading
import random
def worker(coord):
while not coord.should_stop():
time.sleep(10)
thread_id = threading.current_thread().name
print("worker %s running" % (thread_id,))
rand_int = random.randint(0,10)
if rand_int > 5:
print("worker %s requst stop" % (thread_id,))
coord.request_stop()
print("worker %s stopped" % (thread_id,))
coord = tf.train.Coordinator()
threads = [threading.Thread(target=worker, args=(coord,),name=str(i)) for i in range(3)]
for t in threads:
t.start()
coord.join(threads)
```
## Queue
### RandomShuffleQueue
A queue is a TensorFlow data structure that stores tensors across multiple steps, and expose operations that enqueue and dequeue tensors.
classic usage of Queue is:
* Multiple threads prepare training examples and enqueue them.
* A training thread executes a training op that dequeues mini-batches from the queue
## QueueRunner
The `QueueRunner` class creates a number of threads that repeatly run an `enqueue` op. These threads can use a coordinator to stop together. In addition a queue runner runs a closer thread that automatically closes the queue if an exception is reported to the coordinator.
## Put it together
```
def simple_shuffle_batch(source, capacity, batch_size=10):
queue = tf.RandomShuffleQueue(capacity=capacity, min_after_dequeue=int(0.9*capacity),
shapes=source.shape, dtypes=source.dtype)
enqueue = queue.enqueue(source)
num_threads = 4
qr = tf.train.QueueRunner(queue,[enqueue]*num_threads)
tf.train.add_queue_runner(qr)
return queue.dequeue_many(batch_size)
```
The `simple_shuffle_batch` use a `QueueRunner` to execute the `enqueue` ops. but the queue runner don't start yet. Now we need start the queue runner and start a main thread to dequeue elements from queue.
```
input = tf.constant(list(range(1, 100)))
input = tf.data.Dataset.from_tensor_slices(input)
input = input.make_one_shot_iterator().get_next()
get_batch = simple_shuffle_batch(input, capacity=20)
# start queue runner directly
sess = tf.Session()
with sess.as_default() as sess:
tf.train.start_queue_runners()
while True:
try:
print(sess.run(get_batch))
except tf.errors.OutOfRangeError:
print("queue is empty")
break
input.dtype
```
Or, we can start queue runners indirectly with `tf.train.MonitorSession`
```
input = tf.constant(list(range(1, 100)))
input = tf.data.Dataset.from_tensor_slices(input)
input = input.make_one_shot_iterator().get_next()
get_batch = simple_shuffle_batch(input, capacity=20)
# start queue runner directly
with tf.train.MonitoredSession() as sess:
while not sess.should_stop():
print(sess.run(get_batch))
```
## To-Do list
`tf.train.shuffle_batch`.
| true |
code
| 0.325433 | null | null | null | null |
|
## Section 7.1: A First Plotly Streaming Plot
Welcome to Plotly's Python API User Guide.
> Links to the other sections can be found on the User Guide's [homepage](https://plot.ly/python/user-guide#Table-of-Contents:)
Section 7 is divided, into separate notebooks, as follows:
* [7.0 Streaming API introduction](https://plot.ly/python/intro_streaming)
* [7.1 A First Plotly Streaming Plot](https://plot.ly/python/streaming_part1)
<hr>
Check which version is installed on your machine and please upgrade if needed.
```
# (*) Import plotly package
import plotly
# Check plolty version (if not latest, please upgrade)
plotly.__version__
```
<hr>
Import a few modules and sign in to Plotly using our credentials file:
```
# (*) To communicate with Plotly's server, sign in with credentials file
import plotly.plotly as py
# (*) Useful Python/Plotly tools
import plotly.tools as tls
# (*) Graph objects to piece together plots
from plotly.graph_objs import *
import numpy as np # (*) numpy for math functions and arrays
```
Finally, retrieve the stream ids in our credentials file as set up in <a href="https://plot.ly/python/streaming-tutorial#Get-your-stream-tokens" target="_blank">subsection 7.1</a>:
```
stream_ids = tls.get_credentials_file()['stream_ids']
```
### 7.1 A first Plotly streaming plot
Making Plotly streaming plots sums up to working with two objects:
* A stream id object (`Stream` in the `plotly.graph_objs` module),
* A stream link object (`py.Stream`).
The stream id object is a graph object that embeds a particular stream id to each of your plot's traces. As all graph objects, the stream id object is equipped with extensive `help()` documentation, key validation and a nested update method. In brief, the stream id object initializes the connection between a trace in your Plotly graph and a data stream(for that trace).
Meanwhile, the stream link object, like all objects in the `plotly.plotly` module, links content in your Python/IPython session to Plotly's servers. More precisely, it is the interface that updates the data in the plotted traces in real-time(as identified with the unique stream id used in the corresponding stream id object).
If you find the `Stream`/`py.Stream` terminalogy too confusing --- and you do not mind not having access to the methods associated with Plotly graph objects' --- you can forgo the use of the stream id object and substitute it by a python `dict()` in the following examples.
So, we start by making an instance of the stream id object:
```
help(Stream) # call help() to see the specifications of the Stream object!
# Get stream id from stream id list
stream_id = stream_ids[0]
# Make instance of stream id object
stream = Stream(
token=stream_id, # (!) link stream id to 'token' key
maxpoints=80 # (!) keep a max of 80 pts on screen
)
```
The `'maxpoints'` key set the maxiumum number of points to keep on the plot from an incoming stream.
Streaming Plotly plots are initialized with a standard (i.e. REST API) call to `py.plot()` or `py.iplot()` that embeds your unique stream ids in each of the plot's traces.
Each Plotly trace object (e.g. `Scatter`, `Bar`, `Histogram`, etc. More in <a href="https://plot.ly/python/overview#0.4-Plotly's-graph-objects" target="_blank">Section 0</a>) has a `'stream'` key made available to link the trace object in question to a corresponding stream object.
In our first example, we link a scatter trace object to the stream:
```
# Initialize trace of streaming plot by embedding the unique stream_id
trace1 = Scatter(
x=[],
y=[],
mode='lines+markers',
stream=stream # (!) embed stream id, 1 per trace
)
data = Data([trace1])
```
Then, add a title to the layout object and initialize your Plotly streaming plot:
```
# Add title to layout object
layout = Layout(title='Time Series')
# Make a figure object
fig = Figure(data=data, layout=layout)
# (@) Send fig to Plotly, initialize streaming plot, open new tab
unique_url = py.plot(fig, filename='s7_first-stream')
```
Great! Your Plotly streaming plot is intialized. Here's a screenshot:
<img src="http://i.imgur.com/Lx7ICLI.png" />
<br>
Now, let's add data on top of it, or more precisely, send a *stream* of data to it.
So, first
```
help(py.Stream) # run help() of the Stream link object
# (@) Make instance of the `Stream link` object
# with the same stream id as the `Stream Id` object
s = py.Stream(stream_id)
# (@) Open the stream
s.open()
```
We can now use the Stream Link object `s` in order to `stream` data to our plot.
As an example, we will send a time stream and some random numbers(for 200 iterations):
```
# (*) Import module keep track and format current time
import datetime
import time
i = 0 # a counter
k = 5 # some shape parameter
N = 200 # number of points to be plotted
# Delay start of stream by 5 sec (time to switch tabs)
time.sleep(5)
while i<N:
i += 1 # add to counter
# Current time on x-axis, random numbers on y-axis
x = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S.%f')
y = (np.cos(k*i/50.)*np.cos(i/50.)+np.random.randn(1))[0]
# (-) Both x and y are numbers (i.e. not lists nor arrays)
# (@) write to Plotly stream!
s.write(dict(x=x, y=y))
# (!) Write numbers to stream to append current data on plot,
# write lists to overwrite existing data on plot (more in 7.2).
time.sleep(0.08) # (!) plot a point every 80 ms, for smoother plotting
# (@) Close the stream when done plotting
s.close()
```
A stream of data totalling 200 points is sent to Plotly's servers in real-time.
Watching this unfold in an opened plot.ly tab looks something like (in the old UI):
```
from IPython.display import YouTubeVideo
YouTubeVideo('OVQ2Guypp_M', width='100%', height='350')
```
It took Plotly around 15 seconds to plot the 200 data points sent in the data stream. After that, the generated plot looks like any other Plotly plot.
With that said, if you have enough computer resources to let a server run indefinitely, why not have
>>> while True:
as the while-loop expression and never close the stream.
Luckily, it turns out that Plotly has access to such computer resources; a simulation generated using the same code as the above has been running since March 2014.
This plot is embedded below:
```
# Embed never-ending time series streaming plot
tls.embed('streaming-demos','12')
# Note that the time point correspond to internal clock of the servers,
# that is UTC time.
```
Anyone can view your streaming graph in real-time. All viewers will see the same data simultaneously (try it! Open up this notebook up in two different browser windows and observer
that the graphs are plotting identical data!).
Simply put, Plotly's streaming API is awesome!
In brief: to make a Plotly streaming plot:
1. Make a `stream id object` (`Stream` in the `plotly.graph_objs` module) containing the `stream id`(which is found in the **settings** of your Plotly account) and the maximum number of points to be keep on screen (which is optional).
2. Provide the `stream id object` as the key value for the `stream` attribute in your trace object.
3. Make a `stream link object` (`py.Stream`) containing the same stream id as the `stream id object` and open the stream with the `.open()` method.
4. Write data to the `stream link object` with the `.write()` method. When done, close the stream with the `.close()` method.
Here are the links to the subsections' notebooks:
* [7.0 Streaming API introduction](https://plot.ly/python/intro_streaming)
* [7.1 A first Plotly streaming plot](https://plot.ly/python/streaming_part1)
<div style="float:right; \">
<img src="http://i.imgur.com/4vwuxdJ.png"
align=right style="float:right; margin-left: 5px; margin-top: -10px" />
</div>
<h4>Got Questions or Feedback? </h4>
Reach us here at: <a href="https://community.plot.ly" target="_blank">Plotly Community</a>
<h4> What's going on at Plotly? </h4>
Check out our twitter:
<a href="https://twitter.com/plotlygraphs" target="_blank">@plotlygraphs</a>
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install publisher --upgrade
import publisher
publisher.publish(
's7_streaming_p1-first-stream', 'python/streaming_part1//', 'Getting Started with Plotly Streaming',
'Getting Started with Plotly Streaming',
title = 'Getting Started with Plotly Streaming',
thumbnail='', language='python',
layout='user-guide', has_thumbnail='false')
```
| true |
code
| 0.607721 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/maragraziani/interpretAI_DigiPath/blob/main/hands-on-session-2/hands-on-session-2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# <center> Hands-on Session 2</center>
## <center> Explainable Graph Representations in Digital Pathology</center>
**Presented by:**
- Guillaume Jaume
- Pre-doc researcher with EPFL & IBM Research
- gja@zurich.ibm.com
<br/>
- Pushpak Pati
- Pre-doc researcher with ETH & IBM Research
- pus@zurich.ibm.com
#### Content
* [Introduction & Motivation](#Intro)
* [Installation & Data](#Section0)
* [(1) Cell Graph construction](#Section1)
* [(2) Cell Graph classification](#Section2)
* [(3) Cell Graph explanation](#Section3)
* [(4) Nuclei concept analysis](#Section4)
#### Take-away
* Motivation of entity-graph modeling for model explainability
* Getting familiar with the histocartography library and BRACS dataset
* Tools to construct and analyze cell-graphs
* Understand and use post-hoc graph explainability techniques
## Introduction & Motivation:
The first part of this tutorial will guide you to build **interpretable entity-based representations** of tissue regions.
The motivation for shifting from pixel- to entity-based analysis is as follows:
- Cancer diagnosis and prognosis from tissue specimens highly depend on the phenotype and topological distribution of constituting histological entities, *e.g.,* cells, nuclei, tissue regions. To adequately characterize the tissue composition and utilize the tissue structure-to-function relationship, an entity-paradigm is imperative.
### <center> "*Tissue composition matters for analyzing tissue functionality.*" </center>
<figure class="image">
<img src="Figures/fig1_1.png" width="750">
<img src="Figures/fig1_2.png" width="750">
</figure>
- The entity-based processing enables to delineate the diagnostically relevant and irrelevant histopathological entities. The set of entities and corresponding inter- and intra-entity interactions can be customized by using task-specific prior pathological knowledge.
### <center> "*Entity-paradigm enables to incorporate pathological prior during diagnosis.*" </center>
<figure class="image">
<img src="Figures/fig2.png" width="750">
</figure>
- Unlike most of the deep learning techniques operating at pixel-level, the entity-based analysis preserves the notion of histopathological entities, which the pathologists can relate to and reason with. Thus, explainability of the entity-graph based methodologies can be interpreted by pathologists, which can potentially lead to build trust and adoption of AI in clinical practice. Notably, the produced explanations in the entity-space are better localized, and therefore better discernible.
### <center> "*Pathologically comprehensible and localized explanations in the entity-space.*" </center>
<figure class="image">
<img src="Figures/fig3.png" width="750">
</figure>
- Further, the light-weight and flexible graph representation allows to scale to large and arbitrary tissue regions by including arbitrary number of nodes and edges.
### <center> "*Context vs Resolution trade-off.*" </center>
<figure class="image">
<img src="Figures/context.png" width="550">
</figure>
In this tutorial, we will focus on nuclei as entities to build **Cell-graphs**. A similar approach can naturally be extended to other histopathological entities, such as tissue regions, glands.
**References:**
- [Hierarchical Graph Representations in Digital Pathology.](https://arxiv.org/pdf/2102.11057.pdf) Pati et al., arXiv:2102.11057, 2021.
- [CGC-Net: Cell Graph Convolutional Network for Grading of Colorectal Cancer Histology Images.](https://arxiv.org/pdf/1909.01068.pdf) Zhou et al., IEEE CVPR Workshops, 2019.
<div id="Section0"></div>
## Installation and Data
- Running on **Colab**: this tutorial requires a GPU. Colab allows you to use a K80 GPU for 12h. Please do the following steps:
- Open the tab *Runtime*
- Click on *Change Runtime Type*
- Set the hardware to *GPU* and *Save*
- Installation of the **histocartography** library, a Python-based library to facilitate entity-graph analysis and explainability in Computational Pathology. Documentation and examples can be checked [here](https://github.com/histocartography/histocartography).
<figure class="image">
<img src="Figures/hcg_logo.png" width="450">
</figure>
- Downloading samples from the **BRACS** dataset, a large cohort of H&E stained breast carcinoma tissue regions. More information and download link to the dataset can be found [here](https://www.bracs.icar.cnr.it/).
<figure class="image">
<img src="Figures/bracs_logo.png" width="450">
</figure>
```
# installing missing packages
!pip install histocartography
!pip install mpld3
# Required only if you run this code on Colab:
# Get dependent files
!wget https://raw.githubusercontent.com/maragraziani/interpretAI_DigiPath/main/hands-on-session-2/cg_bracs_cggnn_3_classes_gin.yml
!wget https://raw.githubusercontent.com/maragraziani/interpretAI_DigiPath/main/hands-on-session-2/utils.py
# Get images
import os
!mkdir images
os.chdir('images')
!wget --content-disposition https://ibm.box.com/shared/static/6320wnhxsjte9tjlqb02zn0jaxlca5vb.png
!wget --content-disposition https://ibm.box.com/shared/static/d8rdupnzbo9ufcnc4qaluh0s2w7jt8mh.png
!wget --content-disposition https://ibm.box.com/shared/static/yj6kho8j5ovypafnheoju7y18bvtk32h.png
os.chdir('..')
import os
from glob import glob
from PIL import Image
# 1. set up inline show
import matplotlib.pyplot as plt
%matplotlib inline
import mpld3
mpld3.enable_notebook()
# 2. visualize the images: We will work with these 3 samples throughout the tutorial
images = [(Image.open(path), os.path.basename(path).split('.')[0])
for path in glob(os.path.join('images', '*.png'))]
for image, image_name in images:
print('Image:', image_name)
display(image)
```
<div id="Section1"></div>
## 1) Image-to-Graph: Cell-Graph construction
This code enables to build a cell-graph for an input H&E image. The step-by-step procedure to define a cell-graph is as follows,
- **Nodes**: Detecting nuclei using HoverNet
- **Node features**: Extracting features to characterize the nuclei
- **Edges**: Constructing k-NN graph to denote the intter-nuclei interactions
**References:**
- [Hierarchical Graph Representations in Digital Pathology.](https://arxiv.org/pdf/2102.11057.pdf) Pati et al., arXiv:2102.11057, 2021.
- [Hover-Net: Simultaneous segmentation and classification of nuclei in multi-tissue histology images.](https://arxiv.org/pdf/1812.06499.pdf) Graham et al., Medical Image Analysis, 2019.
- [PanNuke Dataset Extension, Insights and Baselines.](https://arxiv.org/abs/2003.10778) Gamper et al., arXiv:2003.10778, 2020.
```
import os
from glob import glob
from PIL import Image
import numpy as np
import torch
from tqdm import tqdm
from dgl.data.utils import save_graphs
from histocartography.preprocessing import NucleiExtractor, DeepFeatureExtractor, KNNGraphBuilder, NucleiConceptExtractor
import warnings
warnings.filterwarnings("ignore")
# Define nuclei extractor: HoverNet pre-trained on the PanNuke dataset.
nuclei_detector = NucleiExtractor()
# Define a deep feature extractor with ResNet34 and patches 72 resized to 224 to match ResNet input
feature_extractor = DeepFeatureExtractor(architecture='resnet34', patch_size=72, resize_size=224)
# Define a graph builder to build a DGLGraph object
graph_builder = KNNGraphBuilder(k=5, thresh=50, add_loc_feats=True)
# Define nuclei concept extractor: extract nuclei-level attributes - will be useful later for understanding the model
nuclei_concept_extractor = NucleiConceptExtractor(
concept_names='area,eccentricity,roundness,roughness,shape_factor,mean_crowdedness,glcm_entropy,glcm_contrast'
)
# Load image fnames to process
image_fnames = glob(os.path.join('images', '*.png'))
# Create output directories
os.makedirs('cell_graphs', exist_ok=True)
os.makedirs('nuclei_concepts', exist_ok=True)
for image_name in tqdm(image_fnames):
print('Processing...', image_name)
# 1. load image
image = np.array(Image.open(image_name))
# 2. nuclei detection
nuclei_map, nuclei_centroids = nuclei_detector.process(image)
# 3. nuclei feature extraction
features = feature_extractor.process(image, nuclei_map)
# 4. build the cell graph
cell_graph = graph_builder.process(
instance_map=nuclei_map,
features=features
)
# 5. extract the nuclei-level concept, i.e., properties: shape, size, etc.
concepts = nuclei_concept_extractor.process(image, nuclei_map)
# 6. print graph properties
print('Number of nodes:', cell_graph.number_of_nodes())
print('Number of edges:', cell_graph.number_of_edges())
print('Number of features per node:', cell_graph.ndata['feat'].shape[1])
# 7. save graph with DGL library and concepts
image_id = os.path.basename(image_name).split('.')[0]
save_graphs(os.path.join('cell_graphs', image_id + '.bin'), [cell_graph])
with open(os.path.join('nuclei_concepts', image_id + '.npy'), 'wb') as f:
np.save(f, concepts)
from histocartography.visualization import OverlayGraphVisualization, InstanceImageVisualization
from utils import *
# Visualize the nuclei detection
visualizer = InstanceImageVisualization()
viz_nuclei = visualizer.process(image, instance_map=nuclei_map)
show_inline(viz_nuclei)
# Visualize the resulting cell graph
visualizer = OverlayGraphVisualization(
instance_visualizer=InstanceImageVisualization(
instance_style="filled+outline"
)
)
viz_cg = visualizer.process(
canvas=image,
graph=cell_graph,
instance_map=nuclei_map
)
show_inline(viz_cg)
```
<div id="Section2"></div>
## 2) Cell-graph classification
Given the set of cell graphs generated for the 4000 H&E images in the BRACS dataset, a Graph Neural Network (GNN) is trained to classify each sample as either *Benign*, *Atypical* or *Malignant*.
A GNN is an artifical neural network designed to operate on graph-structured data. They work in an analogous way as Convolutional Neural Networks (CNNs). For each node, a GNN layer is aggregating and updating information from its neighbors to contextualize the node feature representation. More information about GNNs can be found [here](https://github.com/guillaumejaume/graph-neural-networks-roadmap).
<figure class="image">
<img src="Figures/gnn.png" width="650">
</figure>
**References:**
- [Hierarchical Graph Representations in Digital Pathology.](https://arxiv.org/pdf/2102.11057.pdf) Pati et al., arXiv:2102.11057, 2021.
- [Benchmarking Graph Neural Networks.](https://arxiv.org/pdf/2003.00982.pdf) Dwivedi et al., NeurIPS, 2020.
```
import os
import yaml
from histocartography.ml import CellGraphModel
# 1. load CG-GNN config
config_fname = 'cg_bracs_cggnn_3_classes_gin.yml'
with open(config_fname, 'r') as file:
config = yaml.load(file)
# 2. declare cell graph model: A pytorch model for predicting the tumor type given an input cell-graph
model = CellGraphModel(
gnn_params=config['gnn_params'],
classification_params=config['classification_params'],
node_dim=514,
num_classes=3,
pretrained=True
)
# 3. print model
print('PyTorch Model is defined as:', model)
```
<div id="Section3"></div>
### 3) Cell Graph explanation: Apply GraphGradCAM to CG-GNN
As presented in the first hands-on session, GradCAM is a popular (post-hoc) feature attribution method that allows to highlight regions of the input that are activated by the neural network, *i.e.,* elements of the input that *explain* the prediction. As the input is now a set of *interpretable* biologically-defined nuclei, the explanation is also biologically *interpretable*.
We use a modified version of GradCAM that can work with GNNs: GraphGradCAM. Specifically, GraphGradCAM follows 2 steps:
- Computation of channel-wise importance score:
<figure class="image">
<img src="Figures/eq1.png" width="180">
</figure>
where, $w_k^{(l)}$ is the importance score of channel $k$ in layer $l$. $|V|$ is the number of nodes in the graph, $H^{(l)}_{n, k}$ are the node embeddings in channel $k$ at layer $l$ and, $y_{\max}$ is the logit value of the predicted class.
- Node-wise importance score computation:
<figure class="image">
<img src="Figures/eq2.png" width="250">
</figure>
where, $L(l, v)$ denotes the importance of node $v \in V$ in layer $l$, and $d(l)$ denotes the number of node attributes at layer $l$.
**Note:** GraphGradCAM is one of the feature attribution methods to determine input-level importance scores. There exists a rich literature proposing other approaches. For instance, the GNNExplainer, GraphGradCAM++, GraphLRP etc.
**References:**
- [Grad-CAM : Visual Explanations from Deep Networks.](https://arxiv.org/pdf/1610.02391.pdf) Selvaraju et al., ICCV, 2017.
- [Explainability methods for graph convolutional neural networks.](https://openaccess.thecvf.com/content_CVPR_2019/papers/Pope_Explainability_Methods_for_Graph_Convolutional_Neural_Networks_CVPR_2019_paper.pdf) Pope et al., CVPR, 2019.
- [Quantifying Explainers of Graph Neural Networks in Computational Pathology.](https://arxiv.org/pdf/2011.12646.pdf) Jaume et al., CVPR, 2021.
```
import torch
from glob import glob
import tqdm
import numpy as np
from PIL import Image
from dgl.data.utils import load_graphs
from histocartography.interpretability import GraphGradCAMExplainer
from histocartography.utils.graph import set_graph_on_cuda
is_cuda = torch.cuda.is_available()
INDEX_TO_TUMOR_TYPE = {
0: 'Benign',
1: 'Atypical',
2: 'Malignant'
}
# 1. Define a GraphGradCAM explainer
explainer = GraphGradCAMExplainer(model=model)
# 2. Load preprocessed cell graphs, concepts & images
cg_fnames = glob(os.path.join('cell_graphs', '*.bin'))
image_fnames = glob(os.path.join('images', '*.png'))
concept_fnames = glob(os.path.join('nuclei_concepts', '*.npy'))
cg_fnames.sort()
image_fnames.sort()
concept_fnames.sort()
# 3. Explain all our samples
output = []
for cg_name, image_name, concept_name in zip(cg_fnames, image_fnames, concept_fnames):
print('Processing...', image_name)
image = np.array(Image.open(image_name))
concepts = np.load(concept_name)
graph, _ = load_graphs(cg_name)
graph = graph[0]
graph = set_graph_on_cuda(graph) if is_cuda else graph
importance_scores, logits = explainer.process(
graph,
output_name=cg_name.replace('.bin', '')
)
print('logits: ', logits)
print('prediction: ', INDEX_TO_TUMOR_TYPE[np.argmax(logits)], '\n')
output.append({
'image_name': os.path.basename(image_name).split('.')[0],
'image': image,
'graph': graph,
'importance_scores': importance_scores,
'logits': logits,
'concepts': concepts
})
from histocartography.visualization import OverlayGraphVisualization, InstanceImageVisualization
INDEX_TO_TUMOR_TYPE = {
0: 'Benign',
1: 'Atypical',
2: 'Malignant'
}
# Visualize the cell graph along with its relative node importance
visualizer = OverlayGraphVisualization(
instance_visualizer=InstanceImageVisualization(),
colormap='plasma'
)
for i, instance in enumerate(output):
print(instance['image_name'], instance['logits'])
node_attributes = {}
node_attributes["color"] = instance['importance_scores']
node_attributes["thickness"] = 15
node_attributes["radius"] = 10
viz_cg = visualizer.process(
canvas=instance['image'],
graph=instance['graph'],
node_attributes=node_attributes,
)
show_inline(viz_cg, title='Sample: {}'.format(INDEX_TO_TUMOR_TYPE[np.argmax(instance['logits'])]))
```
<div id="Section4"></div>
### 4) Nuclei concept analysis: These nodes are important, but why?
We were able to identify what are the important nuclei, *i.e.,* the discriminative nodes, using GraphGradCAM. We would like to push our analysis one step further to understand if the attributes (shape, size, etc.) of the important nuclei match prior pathological knowledge. For instance, it is known that cancerous nuclei are larger than benign ones or that atypical nuclei are expected to have irregular shapes.
To this end, we extract a set of nuclei-level attributes on the most important nuclei.
**Note**: A *quantitative* analysis can be performed by studying nuclei-concept distributions and how they align with prior pathological knowledge. However, this analysis is beyond the scope of this tutorial. The reader can refer to [this work](https://arxiv.org/pdf/2011.12646.pdf) for more details.
**References:**
- [Quantifying Explainers of Graph Neural Networks in Computational Pathology.](https://arxiv.org/pdf/2011.12646.pdf) Jaume et al., CVPR, 2021.
```
for i, out in enumerate(output):
if 'benign' in out['image_name']:
benign_data = out
elif 'atypical' in out['image_name']:
atypical_data = out
elif 'malignant' in out['image_name']:
malignant_data = out
```
#### Nuclei visualization
- Visualizing the 20 most important nuclei
- Visualizing 20 random nuclei for comparison
```
# Top k nuclei
from utils import get_patches, plot_patches
k = 20
nuclei = get_patches(out=benign_data, k=k)
plot_patches(nuclei, ncol=10)
nuclei = get_patches(out=atypical_data, k=k)
plot_patches(nuclei, ncol=10)
nuclei = get_patches(out=malignant_data, k=k)
plot_patches(nuclei, ncol=10)
# Top k nuclei
from utils import get_patches, plot_patches
k = 20
nuclei = get_patches(out=benign_data, k=k, random=True)
plot_patches(nuclei, ncol=10)
nuclei = get_patches(out=atypical_data, k=k, random=True)
plot_patches(nuclei, ncol=10)
nuclei = get_patches(out=malignant_data, k=k, random=True)
plot_patches(nuclei, ncol=10)
#area,eccentricity,roundness,roughness,shape_factor,mean_crowdedness,glcm_entropy,glcm_contrast
FEATURE_TO_INDEX = {
'area': 0,
'eccentricity': 1,
'roundness': 2,
'roughness': 3,
'shape_factor': 4,
'mean_crowdedness': 5,
'glcm_entropy': 6,
'glcm_contrast': 7,
}
def compute_concept_ratio(data1, data2, feature, k):
index = FEATURE_TO_INDEX[feature]
important_indices = (-data1['importance_scores']).argsort()[:k]
important_data1 = data1['concepts'][important_indices, index]
important_indices = (-data2['importance_scores']).argsort()[:k]
important_data2 = data2['concepts'][important_indices, index]
return sum(important_data1) / sum(important_data2)
```
#### Pathological fact: "Cancerous nuclei are expected to be larger than benign ones": area(Malignant) > area(Benign)
```
k = 20
ratio = compute_concept_ratio(malignant_data, benign_data, 'area', k)
print('Ratio between the area of important malignant and benign nuclei: ', round(ratio, 4))
```
#### Pathological fact: "Atypical nuclei are hyperchromatic (solid) and Malignant are vesicular (porous)": contrast(Malignant) > contrast(Atypical)
```
k = 20
ratio = compute_concept_ratio(malignant_data, atypical_data, 'glcm_contrast', k)
print('Ratio between the contrast of important malignant and atypical nuclei: ', round(ratio, 4))
```
#### Pathological fact: "Benign nuclei are crowded than Atypical": crowdedness(Atypical) > crowdedness(Benign)
```
k = 20
ratio = compute_concept_ratio(atypical_data, benign_data, 'mean_crowdedness', k)
print('Ratio between the crowdeness of important atypical and benign nuclei: ', round(ratio, 4))
```
## Conclusion:
Considering the adoption of Graph Neural Networks in various domains, such as pathology, radiology, computation biology, satellite and natural images, graph interpretability and explainability is imperative. The presented algorithms and tools aim to motivate and instruct in the aforementioned direction. Though the presented technologies are demonstrated for digital pathology, they can be seamlessly transferred to other domains by building domain specific relevant graph representations. Potentially, entity-graph modeling and analysis can identify relevant cues for explainable stratification.
<figure class="image">
<img src="Figures/conclusion.png" width="850">
</figure>
| true |
code
| 0.531331 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/jonkrohn/ML-foundations/blob/master/notebooks/single-point-regression-gradient.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Gradient of a Single-Point Regression
In this notebook, we calculate the gradient of quadratic cost with respect to a straight-line regression model's parameters. We keep the partial derivatives as simple as possible by limiting the model to handling a single data point.
```
import torch
```
Let's use the same data as we did in the [*Regression in PyTorch* notebook](https://github.com/jonkrohn/ML-foundations/blob/master/notebooks/regression-in-pytorch.ipynb) as well as for demonstrating the Moore-Penrose Pseudoinverse in the [*Linear Algebra II* notebook](https://github.com/jonkrohn/ML-foundations/blob/master/notebooks/2-linear-algebra-ii.ipynb):
```
xs = torch.tensor([0, 1, 2, 3, 4, 5, 6, 7.])
ys = torch.tensor([1.86, 1.31, .62, .33, .09, -.67, -1.23, -1.37])
```
The slope of a line is given by $y = mx + b$:
```
def regression(my_x, my_m, my_b):
return my_x*my_m + my_b
```
Let's initialize $m$ and $b$ with the same "random" near-zero values as we did in the *Regression in PyTorch* notebook:
```
m = torch.tensor([0.9]).requires_grad_()
b = torch.tensor([0.1]).requires_grad_()
```
To keep the partial derivatives as simple as possible, let's move forward with a single instance $i$ from the eight possible data points:
```
i = 7
x = xs[i]
y = ys[i]
x
y
```
**Step 1**: Forward pass
We can flow the scalar tensor $x$ through our regression model to produce $\hat{y}$, an estimate of $y$. Prior to any model training, this is an arbitrary estimate:
```
yhat = regression(x, m, b)
yhat
```
**Step 2**: Compare $\hat{y}$ with true $y$ to calculate cost $C$
In the *Regression in PyTorch* notebook, we used mean-squared error, which averages quadratic cost over multiple data points. With a single data point, here we can use quadratic cost alone. It is defined by: $$ C = (\hat{y} - y)^2 $$
```
def squared_error(my_yhat, my_y):
return (my_yhat - my_y)**2
C = squared_error(yhat, y)
C
```
**Step 3**: Use autodiff to calculate gradient of $C$ w.r.t. parameters
```
C.backward()
```
The partial derivative of $C$ with respect to $m$ ($\frac{\partial C}{\partial m}$) is:
```
m.grad
```
And the partial derivative of $C$ with respect to $b$ ($\frac{\partial C}{\partial b}$) is:
```
b.grad
```
**Return to *Calculus II* slides here to derive $\frac{\partial C}{\partial m}$ and $\frac{\partial C}{\partial b}$.**
$$ \frac{\partial C}{\partial m} = 2x(\hat{y} - y) $$
```
2*x*(yhat.item()-y)
```
$$ \frac{\partial C}{\partial b} = 2(\hat{y}-y) $$
```
2*(yhat.item()-y)
```
### The Gradient of Cost, $\nabla C$
The gradient of cost, which is symbolized $\nabla C$ (pronounced "nabla C"), is a vector of all the partial derivatives of $C$ with respect to each of the individual model parameters:
$\nabla C = \nabla_p C = \left[ \frac{\partial{C}}{\partial{p_1}}, \frac{\partial{C}}{\partial{p_2}}, \cdots, \frac{\partial{C}}{\partial{p_n}} \right]^T $
In this case, there are only two parameters, $m$ and $b$:
$\nabla C = \left[ \frac{\partial{C}}{\partial{m}}, \frac{\partial{C}}{\partial{b}} \right]^T $
```
nabla_C = torch.tensor([m.grad.item(), b.grad.item()]).T
nabla_C
```
| true |
code
| 0.553988 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/kevincong95/cs231n-emotiw/blob/master/notebooks/audio/1.0-la-audio-error-analysis.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!git clone 'https://github.com/kevincong95/cs231n-emotiw.git'
```
## Retrieve and Preprocess the Raw Data
```
# Switch to TF 1.x and navigate to the directory
%tensorflow_version 1.x
!pwd
import os
os.chdir('cs231n-emotiw')
!pwd
# Install required packages
!pip install -r 'requirements-predictions.txt'
!wget 'https://storage.googleapis.com/cs231n-emotiw/data/Train_labels.txt'
!wget 'https://storage.googleapis.com/cs231n-emotiw/data/Val_labels.txt'
!wget 'https://storage.googleapis.com/cs231n-emotiw/data/train-full.zip'
!wget 'https://storage.googleapis.com/cs231n-emotiw/data/val-full.zip'
!unzip '/content/val-full.zip'
%tensorflow_version 1.x
import os
os.chdir('/content/cs231n-emotiw')
from src.preprocessors.audio_preprocessor import AudioPreprocessor
audio_preprocessor_val = AudioPreprocessor(video_folder='Val/' , output_folder='val-full-4/' , label_path='./Val_labels.txt')
audio_preprocessor_val.preprocess(batch_size=32)
```
## Retrieve Preprocessed Data
```
!cp '/content/drive/My Drive/Machine-Learning-Projects/cs231n-project/datasets/emotiw/val-final-audio.zip' '/content/'
!unzip val-final-audio.zip
%tensorflow_version 2.x
!wget 'https://storage.googleapis.com/cs231n-emotiw/data/val-final-audio.zip'
!unzip val-final-audio.zip
import numpy as np
import glob
#X_train = np.load('/content/drive/My Drive/Machine-Learning-Projects/cs231n-project/notebooks/audio-final/audio-pickle-all-X-openl3-train.pkl', allow_pickle=True)
#Y_train = np.load('/content/drive/My Drive/Machine-Learning-Projects/cs231n-project/notebooks/audio-final/audio-pickle-all-Y-openl3-train.pkl' , allow_pickle=True)
X_val = np.load('/content/drive/My Drive/Machine-Learning-Projects/cs231n-project/datasets/emotiw/audio-pickle-all-X-openl3.pkl' , allow_pickle=True)
Y_val = np.load('/content/drive/My Drive/Machine-Learning-Projects/cs231n-project/datasets/emotiw/audio-pickle-all-Y-openl3.pkl' , allow_pickle=True)
s = np.arange(X_val.shape[0])
np.random.shuffle(s)
X_val = X_val[s]
Y_val = Y_val[s]
video_path = '/content/Val/'
videos = glob.glob(video_path + '/*.mp4')
videos = np.asarray(videos)
videos = videos[s]
```
## Retrieve Model and Predict/Evaluate
```
import tensorflow as tf
!wget 'https://storage.googleapis.com/cs231n-emotiw/models/openl3-cnn-lstm-tuned-lr.h5'
model = tf.keras.models.load_model('openl3-cnn-lstm-tuned-lr.h5')
model.summary()
print(X_val.shape)
```
## Evaluate Model Performance
```
predictions = model.predict(X_val)
model.evaluate(X_val , Y_val)
```
#### F1 Score
```
from sklearn.metrics import f1_score
y_pred = model.predict(X_val)
Y_class = y_pred.argmax(axis=-1)
f1_score(Y_val, Y_class, average='micro')
from sklearn import metrics
import pandas as pd
import seaborn as sn
import matplotlib.pyplot as plt
classes=['Pos' , 'Neu' , 'Neg']
con_mat = tf.math.confusion_matrix(labels=Y_val, predictions=Y_class).numpy()
con_mat_norm = np.around(con_mat.astype('float') / con_mat.sum(axis=1)[:, np.newaxis], decimals=2)
con_mat_df = pd.DataFrame(con_mat_norm,
index = classes,
columns = classes)
figure = plt.figure(figsize=(11, 9))
plt.title("Audio Model Confusion Matrix")
sn.heatmap(con_mat_df, annot=True,cmap=plt.cm.Blues)
from sklearn.metrics import classification_report
target_names = ["Positive" , "Neutral" , "Negative"]
print(classification_report(Y_val, Y_class, target_names=target_names))
```
## Visualize some of the Embeddings on a per frame basis
```
import matplotlib.pyplot as plt
import cv2
class_names = ["Positive" , "Neutral" , "Negative"]
def plot_embeddings(i, time_point, predictions_array, true_label, embeddings):
predictions_array, true_label = predictions_array, true_label[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
embed_sqr = np.concatenate([embeddings[i][time_point]]*embeddings.shape[2])
embed_sqr = cv2.resize(embed_sqr, (28, 28))
plt.imshow(embed_sqr, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array[i])
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array, true_label[i]
plt.grid(False)
plt.xticks(range(3))
plt.yticks([])
thisplot = plt.bar(range(3), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
i = 0
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_embeddings(i , 1 , predictions, Y_val , X_val)
plt.subplot(1,2,2)
plot_value_array(i, predictions[i], Y_val)
plt.show()
# Plot the first X test images, their predicted labels, and the true labels.
# Color correct predictions in blue and incorrect predictions in red.
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_embeddings(i , 1 , predictions, Y_val , X_val)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions[i], Y_val)
plt.tight_layout()
plt.show()
```
## Visualize the input spectrograms and how they affect predictions
```
# TO DO
import librosa
import librosa.display
from librosa.feature import melspectrogram
import sys
from moviepy.video.io.ffmpeg_tools import ffmpeg_extract_audio
import os
!mkdir '/content/Val/tmp'
files = sorted(glob.glob('/content/cs231n-emotiw/Val/*.mp4'))
def plot_spectrogram(i, video_path, video_name , predictions_array, true_label):
predictions_array, true_label = predictions_array, true_label[i]
output_wav_file = video_name[:-3] + 'extracted_audio.wav'
ffmpeg_extract_audio(video_path + video_name, video_path + "/tmp/" + output_wav_file)
y, sr = librosa.load(video_path + "/tmp/" + output_wav_file)
S = librosa.feature.melspectrogram(y=y, sr=sr, n_mels=128,
fmax=8000)
S_dB = librosa.power_to_db(S, ref=np.max)
librosa.display.specshow(S_dB, x_axis='time',
y_axis='mel', sr=sr,
fmax=8000)
#plt.colorbar(format='%+2.0f dB')
#plt.title('Mel-frequency spectrogram')
plt.tight_layout()
plt.yticks([])
plt.xticks([])
plt.ylabel("")
predicted_label = np.argmax(predictions_array[i])
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
video_name = '/content/Val/100_1.mp4'
video_path = '/content/Val/'
video_name = os.path.basename(video_name)
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_spectrogram(0 , video_path , video_name , predictions, Y_val)
plt.subplot(1,2,2)
plot_value_array(0, predictions[0], Y_val)
plt.show()
# Plot the first X test images, their predicted labels, and the true labels.
# Color correct predictions in blue and incorrect predictions in red.
import glob
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
video_name = os.path.basename(videos[i])
plot_spectrogram(i , video_path , video_name , predictions, Y_val)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions[i], Y_val)
plt.tight_layout()
plt.show()
```
| true |
code
| 0.632815 | null | null | null | null |
|
```
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
%matplotlib inline
```
### Device configuration
```
# device configuration
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
```
### Hyper parameters
```
# hyper parameters
num_epochs = 5
num_classes = 10
batch_size = 128
learning_rate = 0.001
```
### MNIST dataset and loader
```
# MNIST dataset and loader
train_dataset = torchvision.datasets.MNIST(root='./mnist', download=True, train=True, transform=torchvision.transforms.ToTensor())
test_dataset = torchvision.datasets.MNIST(root='./mnist', download=True, train=False, transform=torchvision.transforms.ToTensor())
train_dataloader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_dataloader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)
```
### Convnet definition
```
# cnn definition
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__()
self.layer1 = nn.Sequential(nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5, padding=2),
nn.BatchNorm2d(num_features=16),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
self.layer2 = nn.Sequential(nn.Conv2d(in_channels=16, out_channels=32, kernel_size=5, padding=2),
nn.BatchNorm2d(32),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
self.fc = nn.Linear(in_features=32 * 7 * 7, out_features=num_classes)
#self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
x = x.reshape(x.size(0), -1)
x = self.fc(x)
#x = self.softmax(x) no need to do softmax, which is inside CrossEntropyLoss
return x
model = ConvNet(num_classes).to(device)
```
### Loss and optimizer
```
# loss and optimizer
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(params=model.parameters(), lr=learning_rate)
```
### Train the model
```
# train the model
losses = []
for epoch in range(num_epochs):
print('epoch: ', epoch)
for i, (images, labels) in enumerate(train_dataloader):
images = images.to(device)
labels = labels.to(device)
# forward pass
outputs = model(images)
loss = criterion(outputs, labels)
# backward pass
model.zero_grad()
loss.backward()
optimizer.step()
if (i + 1) % 100 == 0:
print(' step: {}, loss: {}'.format(i, loss.item()))
losses.append(loss)
```
### Train loss curve
```
plt.figure(figsize=(20, 10))
plt.plot(losses)
plt.title('training loss')
plt.xlabel('iteration')
plt.ylabel('training loss')
plt.grid(True)
```
### Test the model
```
# test the model
model.eval()
with torch.no_grad():
total = 0
correct = 0
for images, labels in test_dataloader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
_, prediction = torch.max(outputs.data, 1)
total += batch_size
correct += (prediction == labels).sum().item()
print('test accuracy: {}'.format(correct / total))
```
| true |
code
| 0.871803 | null | null | null | null |
|
(pandas_intro)=
# Introduction
```{index} Pandas: basics
```
[Pandas](https://pandas.pydata.org/docs/) is an open source library for Python that can be used for data manipulation and analysis. If your data can be put into a spreadsheet, Pandas is exactly what you need!
Pandas is a very powerful tool with highly optimised performance. The full documentation can be found [here](https://pandas.pydata.org/docs/index.html).
To start working with pandas you can simply import it. A standard alias used for pandas is "pd":
```
import pandas as pd
```
(pandas_objects)=
## Pandas objects
**DataFrame** is a 2D data structure with columns and rows, much like a table or Excel spreadsheet. To manually create a DataFrame, we can create a dictionary of lists. The keys are used as a table header and values in each list as rows:
```
df = pd.DataFrame({
"Rock_type": ["granite",
"andesite",
"limestone"],
"Density": [2.6, 2.8, 2.3],
"Main_mineral": ["quartz",
"feldspar",
"calcite"]})
# Use df.head() to display
# top rows
df.head()
```
To extract data from specific column, we can call the column name in two ways:
```
# First method
# Similar to calling dictionary keys
# Works for all column names
print(df["Rock_type"])
# Second method
# This will only work if the column name
# has no spaces and is not named like
# any pandas attribute, e.g. T will mean
# transpose and it won't extract a column
print(df.Rock_type)
pd.Series(["granite", "andesite", "limestone"])
```
(reading_files)=
## Reading files
``` {index} Pandas: reading and writing files
```
Most of the time we will want to load data in different file formats, rather than manually creating a dataframe. Pandas have a very easy syntax for reading files:
pd.read_*
where * can be [csv](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_csv.html), [excel](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_excel.html), [html](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_html.html), [sql](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_sql.html) and so on. For .txt file extentions we can use
pd.read_csv(file_name, delimiter=" ") or pd.read_fwf(file_name)
In this example we will look at New Zealand earthquake data in .csv format from [IRIS](https://ds.iris.edu/ieb/). With .head() we can specify how many rows to print, in this case, we want to display first 4 rows (that includes header):
```
nz_eqs = pd.read_csv("../../geosciences/data/nz_largest_eq_since_1970.csv")
nz_eqs.head(4)
```
We can check DataFrame shape by using:
```
nz_eqs.shape
```
We have 25,000 rows and 11 columns, that's a lot of data!
(writing_files)=
## Writing files
Let's say we want to export this data as an excel spreadsheet but we only want to export magnitude, latitude, longitude and depth columns:
```
nz_eqs.to_excel("../../geosciences/data/nz_eqs.xlsx",
sheet_name="Earthquakes",
columns=["mag", "lat", "lon",
"depth_km"])
```
ExcelWriter object allows us to export more than one sheet into the same file:
```
with pd.ExcelWriter("../../geosciences/data/nz_eqs.xlsx") as writer:
nz_eqs.to_excel(writer, sheet_name="Earthquakes",
columns=["mag", "lat", "lon",
"depth_km"])
nz_eqs.to_excel(writer, sheet_name="Extra info",
columns=["region", "iris_id",
"timestamp"])
```
# References
The notebook was compiled based on these tutorials:
* [Pandas official Getting Started tutorials](https://pandas.pydata.org/docs/getting_started/index.html#getting-started)
* [Kaggle tutorial](https://www.kaggle.com/learn/pandas)
| true |
code
| 0.664268 | null | null | null | null |
|
# Introduction to Modeling Libraries
```
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
```
## Interfacing Between pandas and Model Code
```
import pandas as pd
import numpy as np
data = pd.DataFrame({
'x0': [1, 2, 3, 4, 5],
'x1': [0.01, -0.01, 0.25, -4.1, 0.],
'y': [-1.5, 0., 3.6, 1.3, -2.]})
data
data.columns
data.values
df2 = pd.DataFrame(data.values, columns=['one', 'two', 'three'])
df2
model_cols = ['x0', 'x1']
data.loc[:, model_cols].values
data['category'] = pd.Categorical(['a', 'b', 'a', 'a', 'b'],
categories=['a', 'b'])
data
dummies = pd.get_dummies(data.category, prefix='category')
data_with_dummies = data.drop('category', axis=1).join(dummies)
data_with_dummies
```
## Creating Model Descriptions with Patsy
y ~ x0 + x1
```
data = pd.DataFrame({
'x0': [1, 2, 3, 4, 5],
'x1': [0.01, -0.01, 0.25, -4.1, 0.],
'y': [-1.5, 0., 3.6, 1.3, -2.]})
data
import patsy
y, X = patsy.dmatrices('y ~ x0 + x1', data)
y
X
np.asarray(y)
np.asarray(X)
patsy.dmatrices('y ~ x0 + x1 + 0', data)[1]
coef, resid, _, _ = np.linalg.lstsq(X, y)
coef
coef = pd.Series(coef.squeeze(), index=X.design_info.column_names)
coef
```
### Data Transformations in Patsy Formulas
```
y, X = patsy.dmatrices('y ~ x0 + np.log(np.abs(x1) + 1)', data)
X
y, X = patsy.dmatrices('y ~ standardize(x0) + center(x1)', data)
X
new_data = pd.DataFrame({
'x0': [6, 7, 8, 9],
'x1': [3.1, -0.5, 0, 2.3],
'y': [1, 2, 3, 4]})
new_X = patsy.build_design_matrices([X.design_info], new_data)
new_X
y, X = patsy.dmatrices('y ~ I(x0 + x1)', data)
X
```
### Categorical Data and Patsy
```
data = pd.DataFrame({
'key1': ['a', 'a', 'b', 'b', 'a', 'b', 'a', 'b'],
'key2': [0, 1, 0, 1, 0, 1, 0, 0],
'v1': [1, 2, 3, 4, 5, 6, 7, 8],
'v2': [-1, 0, 2.5, -0.5, 4.0, -1.2, 0.2, -1.7]
})
y, X = patsy.dmatrices('v2 ~ key1', data)
X
y, X = patsy.dmatrices('v2 ~ key1 + 0', data)
X
y, X = patsy.dmatrices('v2 ~ C(key2)', data)
X
data['key2'] = data['key2'].map({0: 'zero', 1: 'one'})
data
y, X = patsy.dmatrices('v2 ~ key1 + key2', data)
X
y, X = patsy.dmatrices('v2 ~ key1 + key2 + key1:key2', data)
X
```
## Introduction to statsmodels
### Estimating Linear Models
```
import statsmodels.api as sm
import statsmodels.formula.api as smf
def dnorm(mean, variance, size=1):
if isinstance(size, int):
size = size,
return mean + np.sqrt(variance) * np.random.randn(*size)
# For reproducibility
np.random.seed(12345)
N = 100
X = np.c_[dnorm(0, 0.4, size=N),
dnorm(0, 0.6, size=N),
dnorm(0, 0.2, size=N)]
eps = dnorm(0, 0.1, size=N)
beta = [0.1, 0.3, 0.5]
y = np.dot(X, beta) + eps
X[:5]
y[:5]
X_model = sm.add_constant(X)
X_model[:5]
model = sm.OLS(y, X)
results = model.fit()
results.params
print(results.summary())
data = pd.DataFrame(X, columns=['col0', 'col1', 'col2'])
data['y'] = y
data[:5]
results = smf.ols('y ~ col0 + col1 + col2', data=data).fit()
results.params
results.tvalues
results.predict(data[:5])
```
### Estimating Time Series Processes
```
init_x = 4
import random
values = [init_x, init_x]
N = 1000
b0 = 0.8
b1 = -0.4
noise = dnorm(0, 0.1, N)
for i in range(N):
new_x = values[-1] * b0 + values[-2] * b1 + noise[i]
values.append(new_x)
MAXLAGS = 5
model = sm.tsa.AR(values)
results = model.fit(MAXLAGS)
results.params
```
## Introduction to scikit-learn
```
train = pd.read_csv('datasets/titanic/train.csv')
test = pd.read_csv('datasets/titanic/test.csv')
train[:4]
train.isnull().sum()
test.isnull().sum()
impute_value = train['Age'].median()
train['Age'] = train['Age'].fillna(impute_value)
test['Age'] = test['Age'].fillna(impute_value)
train['IsFemale'] = (train['Sex'] == 'female').astype(int)
test['IsFemale'] = (test['Sex'] == 'female').astype(int)
predictors = ['Pclass', 'IsFemale', 'Age']
X_train = train[predictors].values
X_test = test[predictors].values
y_train = train['Survived'].values
X_train[:5]
y_train[:5]
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
y_predict[:10]
```
(y_true == y_predict).mean()
```
from sklearn.linear_model import LogisticRegressionCV
model_cv = LogisticRegressionCV(10)
model_cv.fit(X_train, y_train)
from sklearn.model_selection import cross_val_score
model = LogisticRegression(C=10)
scores = cross_val_score(model, X_train, y_train, cv=4)
scores
```
## Continuing Your Education
```
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
```
| true |
code
| 0.449272 | null | null | null | null |
|
# End-to-End Machine Leanrning Project
In this chapter you will work through an example project end to end, pretending to be a recently hired data scientist at a real estate company. Here are the main steps you will go through:
1. Look at the big picture
2. Get the data
3. Discover and visualize the data to gain insights.
4. Prepare the data for Machine learning algorithms.
5. Select a model and train it
6. Fine-tune your model.
7. Present your solution
8. Launch, monitor, and maintain your system.
## Working with Real Data
When you are learning about Machine Leaning, it is best to experimentwith real-world data, not artificial datasets.
Fortunately, there are thousands of open datasets to choose from, ranging across all sorts of domains. Here are a few places you can look to get data:
* Popular open data repositories:
- [UC Irvine Machine Learning Repository](http://archive.ics.uci.edu/ml/)
- [Kaggle](https://www.kaggle.com/datasets) datasets
- Amazon's [AWS](https://registry.opendata.aws/) datasets
* Meta Portals:
- [Data Portals](http://dataportals.org/)
- [OpenDataMonitor](http://opendatamonitor.eu/)
- [Quandl](http://quandl.com)
## Frame the Problem
The problem is that your model' output (a prediction of a district's median housing price) will be fed to another ML system along with many other signals*. This downstream will determine whether it is worth investing in a given area or not. Getting this right is critical, as it directly affects revenue.
```
Other Signals
|
Upstream Components --> (District Data) --> [District Pricing prediction model](your component) --> (District prices) --> [Investment Analaysis] --> Investments
```
### Pipelines
A sequence of data processing components is called a **data pipeline**. Pipelines are very common in Machine Learning systems, since a lot of data needs to manipulated to make sure the machine learning model/algorithms understands the data, as algorithms understand only numbers.
## Download the Data:
You could use your web browser and download the data, but it is preferabble to make a function to do the same.
```
import os
import tarfile
import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handsonml-2/master"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
"""
Function to download the housing_data
"""
os.makedirs(housing_path, exist_ok=True)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
import numpy as np
```
| true |
code
| 0.623377 | null | null | null | null |
|
```
import open3d as o3d
import numpy as np
import os
import sys
# monkey patches visualization and provides helpers to load geometries
sys.path.append('..')
import open3d_tutorial as o3dtut
# change to True if you want to interact with the visualization windows
o3dtut.interactive = not "CI" in os.environ
```
# Multiway registration
Multiway registration is the process of aligning multiple pieces of geometry in a global space. Typically, the input is a set of geometries (e.g., point clouds or RGBD images) $\{\mathbf{P}_{i}\}$. The output is a set of rigid transformations $\{\mathbf{T}_{i}\}$, so that the transformed point clouds $\{\mathbf{T}_{i}\mathbf{P}_{i}\}$ are aligned in the global space.
Open3D implements multiway registration via pose graph optimization. The backend implements the technique presented in [\[Choi2015\]](../reference.html#choi2015).
## Input
The first part of the tutorial code reads three point clouds from files. The point clouds are downsampled and visualized together. They are misaligned.
```
def load_point_clouds(voxel_size=0.0):
pcds = []
for i in range(3):
pcd = o3d.io.read_point_cloud("../../test_data/ICP/cloud_bin_%d.pcd" %
i)
pcd_down = pcd.voxel_down_sample(voxel_size=voxel_size)
pcds.append(pcd_down)
return pcds
voxel_size = 0.02
pcds_down = load_point_clouds(voxel_size)
o3d.visualization.draw_geometries(pcds_down,
zoom=0.3412,
front=[0.4257, -0.2125, -0.8795],
lookat=[2.6172, 2.0475, 1.532],
up=[-0.0694, -0.9768, 0.2024])
```
## Pose graph
A pose graph has two key elements: nodes and edges. A node is a piece of geometry $\mathbf{P}_{i}$ associated with a pose matrix $\mathbf{T}_{i}$ which transforms $\mathbf{P}_{i}$ into the global space. The set $\{\mathbf{T}_{i}\}$ are the unknown variables to be optimized. `PoseGraph.nodes` is a list of `PoseGraphNode`. We set the global space to be the space of $\mathbf{P}_{0}$. Thus $\mathbf{T}_{0}$ is the identity matrix. The other pose matrices are initialized by accumulating transformation between neighboring nodes. The neighboring nodes usually have large overlap and can be registered with [Point-to-plane ICP](../Basic/icp_registration.ipynb#point-to-plane-ICP).
A pose graph edge connects two nodes (pieces of geometry) that overlap. Each edge contains a transformation matrix $\mathbf{T}_{i,j}$ that aligns the source geometry $\mathbf{P}_{i}$ to the target geometry $\mathbf{P}_{j}$. This tutorial uses [Point-to-plane ICP](../Basic/icp_registration.ipynb#point-to-plane-ICP) to estimate the transformation. In more complicated cases, this pairwise registration problem should be solved via [Global registration](global_registration.ipynb).
[\[Choi2015\]](../reference.html#choi2015) has observed that pairwise registration is error-prone. False pairwise alignments can outnumber correctly aligned pairs. Thus, they partition pose graph edges into two classes. **Odometry edges** connect temporally close, neighboring nodes. A local registration algorithm such as ICP can reliably align them. **Loop closure edges** connect any non-neighboring nodes. The alignment is found by global registration and is less reliable. In Open3D, these two classes of edges are distinguished by the `uncertain` parameter in the initializer of `PoseGraphEdge`.
In addition to the transformation matrix $\mathbf{T}_{i}$, the user can set an information matrix $\mathbf{\Lambda}_{i}$ for each edge. If $\mathbf{\Lambda}_{i}$ is set using function `get_information_matrix_from_point_clouds`, the loss on this pose graph edge approximates the RMSE of the corresponding sets between the two nodes, with a line process weight. Refer to Eq (3) to (9) in [\[Choi2015\]](../reference.html#choi2015) and [the Redwood registration benchmark](http://redwood-data.org/indoor/registration.html) for details.
The script creates a pose graph with three nodes and three edges. Among the edges, two of them are odometry edges (`uncertain = False`) and one is a loop closure edge (`uncertain = True`).
```
def pairwise_registration(source, target):
print("Apply point-to-plane ICP")
icp_coarse = o3d.pipelines.registration.registration_icp(
source, target, max_correspondence_distance_coarse, np.identity(4),
o3d.pipelines.registration.TransformationEstimationPointToPlane())
icp_fine = o3d.pipelines.registration.registration_icp(
source, target, max_correspondence_distance_fine,
icp_coarse.transformation,
o3d.pipelines.registration.TransformationEstimationPointToPlane())
transformation_icp = icp_fine.transformation
information_icp = o3d.pipelines.registration.get_information_matrix_from_point_clouds(
source, target, max_correspondence_distance_fine,
icp_fine.transformation)
return transformation_icp, information_icp
def full_registration(pcds, max_correspondence_distance_coarse,
max_correspondence_distance_fine):
pose_graph = o3d.pipelines.registration.PoseGraph()
odometry = np.identity(4)
pose_graph.nodes.append(o3d.pipelines.registration.PoseGraphNode(odometry))
n_pcds = len(pcds)
for source_id in range(n_pcds):
for target_id in range(source_id + 1, n_pcds):
transformation_icp, information_icp = pairwise_registration(
pcds[source_id], pcds[target_id])
print("Build o3d.pipelines.registration.PoseGraph")
if target_id == source_id + 1: # odometry case
odometry = np.dot(transformation_icp, odometry)
pose_graph.nodes.append(
o3d.pipelines.registration.PoseGraphNode(
np.linalg.inv(odometry)))
pose_graph.edges.append(
o3d.pipelines.registration.PoseGraphEdge(source_id,
target_id,
transformation_icp,
information_icp,
uncertain=False))
else: # loop closure case
pose_graph.edges.append(
o3d.pipelines.registration.PoseGraphEdge(source_id,
target_id,
transformation_icp,
information_icp,
uncertain=True))
return pose_graph
print("Full registration ...")
max_correspondence_distance_coarse = voxel_size * 15
max_correspondence_distance_fine = voxel_size * 1.5
with o3d.utility.VerbosityContextManager(
o3d.utility.VerbosityLevel.Debug) as cm:
pose_graph = full_registration(pcds_down,
max_correspondence_distance_coarse,
max_correspondence_distance_fine)
```
Open3D uses the function `global_optimization` to perform pose graph optimization. Two types of optimization methods can be chosen: `GlobalOptimizationGaussNewton` or `GlobalOptimizationLevenbergMarquardt`. The latter is recommended since it has better convergence property. Class `GlobalOptimizationConvergenceCriteria` can be used to set the maximum number of iterations and various optimization parameters.
Class `GlobalOptimizationOption` defines a couple of options. `max_correspondence_distance` decides the correspondence threshold. `edge_prune_threshold` is a threshold for pruning outlier edges. `reference_node` is the node id that is considered to be the global space.
```
print("Optimizing PoseGraph ...")
option = o3d.pipelines.registration.GlobalOptimizationOption(
max_correspondence_distance=max_correspondence_distance_fine,
edge_prune_threshold=0.25,
reference_node=0)
with o3d.utility.VerbosityContextManager(
o3d.utility.VerbosityLevel.Debug) as cm:
o3d.pipelines.registration.global_optimization(
pose_graph,
o3d.pipelines.registration.GlobalOptimizationLevenbergMarquardt(),
o3d.pipelines.registration.GlobalOptimizationConvergenceCriteria(),
option)
```
The global optimization performs twice on the pose graph. The first pass optimizes poses for the original pose graph taking all edges into account and does its best to distinguish false alignments among uncertain edges. These false alignments have small line process weights, and they are pruned after the first pass. The second pass runs without them and produces a tight global alignment. In this example, all the edges are considered as true alignments, hence the second pass terminates immediately.
## Visualize optimization
The transformed point clouds are listed and visualized using `draw_geometries`.
```
print("Transform points and display")
for point_id in range(len(pcds_down)):
print(pose_graph.nodes[point_id].pose)
pcds_down[point_id].transform(pose_graph.nodes[point_id].pose)
o3d.visualization.draw_geometries(pcds_down,
zoom=0.3412,
front=[0.4257, -0.2125, -0.8795],
lookat=[2.6172, 2.0475, 1.532],
up=[-0.0694, -0.9768, 0.2024])
```
## Make a combined point cloud
`PointCloud` has a convenience operator `+` that can merge two point clouds into a single one. In the code below, the points are uniformly resampled using `voxel_down_sample` after merging. This is recommended post-processing after merging point clouds since it can relieve duplicated or over-densified points.
```
pcds = load_point_clouds(voxel_size)
pcd_combined = o3d.geometry.PointCloud()
for point_id in range(len(pcds)):
pcds[point_id].transform(pose_graph.nodes[point_id].pose)
pcd_combined += pcds[point_id]
pcd_combined_down = pcd_combined.voxel_down_sample(voxel_size=voxel_size)
o3d.io.write_point_cloud("multiway_registration.pcd", pcd_combined_down)
o3d.visualization.draw_geometries([pcd_combined_down],
zoom=0.3412,
front=[0.4257, -0.2125, -0.8795],
lookat=[2.6172, 2.0475, 1.532],
up=[-0.0694, -0.9768, 0.2024])
```
<div class="alert alert-info">
**Note:**
Although this tutorial demonstrates multiway registration for point clouds, the same procedure can be applied to RGBD images. See [Make fragments](../ReconstructionSystem/make_fragments.rst) for an example.
</div>
| true |
code
| 0.305095 | null | null | null | null |
|
# Coupling a Landlab groundwater with a Mesa agent-based model
This notebook shows a toy example of how one might couple a simple groundwater model (Landlab's `GroundwaterDupuitPercolator`, by [Litwin et al. (2020)](https://joss.theoj.org/papers/10.21105/joss.01935)) with an agent-based model (ABM) written using the [Mesa](https://mesa.readthedocs.io/en/latest/) Agent-Based Modeling (ABM) package.
The purpose of this tutorial is to demonstrate the technical aspects of creating an integrated Landlab-Mesa model. The example is deliberately very simple in terms of the processes and interactions represented, and not meant to be a realistic portrayal of water-resources decision making. But the example does show how one might build a more sophisticated and interesting model using these basic ingredients.
(Greg Tucker, November 2021; created from earlier notebook example used in May 2020
workshop)
## Running the groundwater model
The following section simply illustrates how to create a groundwater model using the `GroundwaterDupuitPercolator` component.
Imports:
```
from landlab import RasterModelGrid, imshow_grid
from landlab.components import GroundwaterDupuitPercolator
import matplotlib.pyplot as plt
```
Set parameters:
```
base_depth = 22.0 # depth of aquifer base below ground level, m
initial_water_table_depth = 2.0 # starting depth to water table, m
dx = 100.0 # cell width, m
pumping_rate = 0.001 # pumping rate, m3/s
well_locations = [800, 1200]
K = 0.001 # hydraulic conductivity, (m/s)
n = 0.2 # porosity, (-)
dt = 3600.0 # time-step duration, s
background_recharge = 0.1 / (3600 * 24 * 365.25) # recharge rate from infiltration, m/s
```
Create a grid and add fields:
```
# Raster grid with closed boundaries
# boundaries = {'top': 'closed','bottom': 'closed','right':'closed','left':'closed'}
grid = RasterModelGrid((41, 41), xy_spacing=dx) # , bc=boundaries)
# Topographic elevation field (meters)
elev = grid.add_zeros("topographic__elevation", at="node")
# Field for the elevation of the top of an impermeable geologic unit that forms
# the base of the aquifer (meters)
base = grid.add_zeros("aquifer_base__elevation", at="node")
base[:] = elev - base_depth
# Field for the elevation of the water table (meters)
wt = grid.add_zeros("water_table__elevation", at="node")
wt[:] = elev - initial_water_table_depth
# Field for the groundwater recharge rate (meters per second)
recharge = grid.add_zeros("recharge__rate", at="node")
recharge[:] = background_recharge
recharge[well_locations] -= pumping_rate / (
dx * dx
) # pumping rate, in terms of recharge
```
Instantiate the component (note use of an array/field instead of a scalar constant for `recharge_rate`):
```
gdp = GroundwaterDupuitPercolator(
grid,
hydraulic_conductivity=K,
porosity=n,
recharge_rate=recharge,
regularization_f=0.01,
)
```
Define a couple of handy functions to run the model for a day or a year:
```
def run_for_one_day(gdp, dt):
num_iter = int(3600.0 * 24 / dt)
for _ in range(num_iter):
gdp.run_one_step(dt)
def run_for_one_year(gdp, dt):
num_iter = int(365.25 * 3600.0 * 24 / dt)
for _ in range(num_iter):
gdp.run_one_step(dt)
```
Run for a year and plot the water table:
```
run_for_one_year(gdp, dt)
imshow_grid(grid, wt, colorbar_label="Water table elevation (m)")
```
### Aside: calculating a pumping rate in terms of recharge
The pumping rate at a particular grid cell (in volume per time, representing pumping from a well at that location) needs to be given in terms of a recharge rate (depth of water equivalent per time) in a given grid cell. Suppose for example you're pumping 16 gallons/minute (horrible units of course). That equates to:
16 gal/min x 0.00378541 m3/gal x (1/60) min/sec =
```
Qp = 16.0 * 0.00378541 / 60.0
print(Qp)
```
...equals about 0.001 m$^3$/s. That's $Q_p$. The corresponding negative recharge in a cell of dimensions $\Delta x$ by $\Delta x$ would be
$R_p = Q_p / \Delta x^2$
```
Rp = Qp / (dx * dx)
print(Rp)
```
## A very simple ABM with farmers who drill wells into the aquifer
For the sake of illustration, our ABM will be extremely simple. There are $N$ farmers, at random locations, who each pump at a rate $Q_p$ as long as the water table lies above the depth of their well, $d_w$. Once the water table drops below their well, the well runs dry and they switch from crops to pasture.
### Check that Mesa is installed
For the next step, we must verify that Mesa is available. If it is not, use one of the installation commands below to install, then re-start the kernel (Kernel => Restart) and continue.
```
try:
from mesa import Model
except ModuleNotFoundError:
print(
"""
Mesa needs to be installed in order to run this notebook.
Normally Mesa should be pre-installed alongside the Landlab notebook collection.
But it appears that Mesa is not already installed on the system on which you are
running this notebook. You can install Mesa from a command prompt using either:
`conda install -c conda-forge mesa`
or
`pip install mesa`
"""
)
raise
```
### Defining the ABM
In Mesa, an ABM is created using a class for each Agent and a class for the Model. Here's the Agent class (a Farmer). Farmers have a grid location and an attribute: whether they are actively pumping their well or not. They also have a well depth: the depth to the bottom of their well. Their action consists of checking whether their well is wet or dry; if wet, they will pump, and if dry, they will not.
```
from mesa import Agent, Model
from mesa.space import MultiGrid
from mesa.time import RandomActivation
class FarmerAgent(Agent):
"""An agent who pumps from a well if it's not dry."""
def __init__(self, unique_id, model, well_depth=5.0):
super().__init__(unique_id, model)
self.pumping = True
self.well_depth = well_depth
def step(self):
x, y = self.pos
print(f"Farmer {self.unique_id}, ({x}, {y})")
print(f" Depth to the water table: {self.model.wt_depth_2d[x,y]}")
print(f" Depth to the bottom of the well: {self.well_depth}")
if self.model.wt_depth_2d[x, y] >= self.well_depth: # well is dry
print(" Well is dry.")
self.pumping = False
else:
print(" Well is pumping.")
self.pumping = True
```
Next, define the model class. The model will take as a parameter a reference to a 2D array (with the same dimensions as the grid) that contains the depth to water table at each grid location. This allows the Farmer agents to check whether their well has run dry.
```
class FarmerModel(Model):
"""A model with several agents on a grid."""
def __init__(self, N, width, height, well_depth, depth_to_water_table):
self.num_agents = N
self.grid = MultiGrid(width, height, True)
self.depth_to_water_table = depth_to_water_table
self.schedule = RandomActivation(self)
# Create agents
for i in range(self.num_agents):
a = FarmerAgent(i, self, well_depth)
self.schedule.add(a)
# Add the agent to a random grid cell (excluding the perimeter)
x = self.random.randrange(self.grid.width - 2) + 1
y = self.random.randrange(self.grid.width - 2) + 1
self.grid.place_agent(a, (x, y))
def step(self):
self.wt_depth_2d = self.depth_to_water_table.reshape(
(self.grid.width, self.grid.height)
)
self.schedule.step()
```
### Setting up the Landlab grid, fields, and groundwater simulator
```
base_depth = 22.0 # depth of aquifer base below ground level, m
initial_water_table_depth = 2.8 # starting depth to water table, m
dx = 100.0 # cell width, m
pumping_rate = 0.004 # pumping rate, m3/s
well_depth = 3 # well depth, m
background_recharge = 0.002 / (365.25 * 24 * 3600) # recharge rate, m/s
K = 0.001 # hydraulic conductivity, (m/s)
n = 0.2 # porosity, (-)
dt = 3600.0 # time-step duration, s
num_agents = 12 # number of farmer agents
run_duration_yrs = 15 # run duration in years
grid = RasterModelGrid((41, 41), xy_spacing=dx)
elev = grid.add_zeros("topographic__elevation", at="node")
base = grid.add_zeros("aquifer_base__elevation", at="node")
base[:] = elev - base_depth
wt = grid.add_zeros("water_table__elevation", at="node")
wt[:] = elev - initial_water_table_depth
depth_to_wt = grid.add_zeros("water_table__depth_below_ground", at="node")
depth_to_wt[:] = elev - wt
recharge = grid.add_zeros("recharge__rate", at="node")
recharge[:] = background_recharge
recharge[well_locations] -= pumping_rate / (
dx * dx
) # pumping rate, in terms of recharge
gdp = GroundwaterDupuitPercolator(
grid,
hydraulic_conductivity=K,
porosity=n,
recharge_rate=recharge,
regularization_f=0.01,
)
```
### Set up the Farmer model
```
nc = grid.number_of_node_columns
nr = grid.number_of_node_rows
farmer_model = FarmerModel(
num_agents, nc, nr, well_depth, depth_to_wt.reshape((nr, nc))
)
```
Check the spatial distribution of wells:
```
import numpy as np
def get_well_count(model):
well_count = np.zeros((nr, nc), dtype=int)
pumping_well_count = np.zeros((nr, nc), dtype=int)
for cell in model.grid.coord_iter():
cell_content, x, y = cell
well_count[x][y] = len(cell_content)
for agent in cell_content:
if agent.pumping:
pumping_well_count[x][y] += 1
return well_count, pumping_well_count
well_count, p_well_count = get_well_count(farmer_model)
imshow_grid(grid, well_count.flatten())
```
#### Set the initial recharge field
```
recharge[:] = -(pumping_rate / (dx * dx)) * p_well_count.flatten()
imshow_grid(grid, -recharge * 3600 * 24, colorbar_label="Pumping rate (m/day)")
```
### Run the model
```
for i in range(run_duration_yrs):
# Run the groundwater simulator for one year
run_for_one_year(gdp, dt)
# Update the depth to water table
depth_to_wt[:] = elev - wt
# Run the farmer model
farmer_model.step()
# Count the number of pumping wells
well_count, pumping_well_count = get_well_count(farmer_model)
total_pumping_wells = np.sum(pumping_well_count)
print(f"In year {i + 1} there are {total_pumping_wells} pumping wells")
print(f" and the greatest depth to water table is {np.amax(depth_to_wt)} meters.")
# Update the recharge field according to current pumping rate
recharge[:] = (
background_recharge - (pumping_rate / (dx * dx)) * pumping_well_count.flatten()
)
print(f"Total recharge: {np.sum(recharge)}")
print("")
plt.figure()
imshow_grid(grid, wt)
imshow_grid(grid, wt)
# Display the area of water table that lies below the well depth
depth_to_wt[:] = elev - wt
too_deep = depth_to_wt > well_depth
imshow_grid(grid, too_deep)
```
This foregoing example is very simple, and leaves out many aspects of the complex problem of water extraction as a "tragedy of the commons". But it does illustrate how one can build a model that integrates agent-based dynamics with continuum dynamics by combining Landlab grid-based model code with Mesa ABM code.
| true |
code
| 0.567817 | null | null | null | null |
|
```
%load_ext autoreload
%autoreload 2
from metrics import CorefEvaluator
from document import Document
import json
import os
from ClEval import ClEval, print_clusters
from datetime import datetime
def get_timestamp():
return str(datetime.timestamp(datetime.now())).split('.')[0]
get_timestamp()
```
# Dummy text
```
txt = """
Microsoft (NASDAQ:MSFT) was once considered a mature tech stock that was owned for stability and income instead of growth. But over the past five years, Microsoft stock rallied roughly 300% as a visionary CEO turned its business upside down.
Satya Nadella, who succeeded Steve Ballmer in 2014, reduced Microsoft's dependence on sales of Windows and Office licenses and expanded its ecosystem with a "mobile first, cloud first" mantra. Nadella ditched the company's Windows Phone and smartphone ambitions, launched mobile versions of its apps on iOS and Android, and aggressively expanded its cloud services.
That transformation initially throttled earnings growth, but it paid off as the commercial cloud business -- which included Office 365, Dynamics 365, and Azure -- became its new growth engine. Microsoft also expanded its Surface and Xbox businesses to maintain a healthy presence in the PC and gaming markets, respectively.
Those strengths buoyed Microsoft's results throughout the COVID-19 crisis, and its stock has risen nearly 11% year to date even as the S&P 500 slipped over 12%. But looking further ahead, will Microsoft continue to outperform the market?
"""
```
# Visualization setup
```
from VISUALIZATION import highlighter as viz
from IPython.core.display import display, HTML
display(HTML(open('VISUALIZATION/highlighter/highlight.css').read()))
display(HTML(open('VISUALIZATION/highlighter/highlight.js').read()))
```
# Model setup
- Stanford CoreNLP Deterministic
- NeuralCoref
- SpanBERT Large
```
from MODEL_WRAPPERS.Corenlp import CoreNLP
corenlp = CoreNLP(ram="8G", viz=viz)
from MODEL_WRAPPERS.Neuralcoref import Coref
params = {
"greed": 0.50,
"max_dist": 100,
"max_dist_match": 500
}
neuralcoref = Coref(params, spacy_size="lg", viz=viz)
from MODEL_WRAPPERS.Spanbert import SpanBert
spanbert = SpanBert(viz=viz)
models = [corenlp, neuralcoref, spanbert]
```
# Batch prediction, testing iterating models
```
import timeit
import json
for model in models:
print("Prediction with {}".format(str(model.__class__)))
start = timeit.default_timer()
clusters = predict(model, txt)
#show(model)
stop = timeit.default_timer()
print('Time: ', stop - start)
print()
```
# Dataset Loader
```
data_path = os.path.join(os.path.dirname(os.getcwd()), "coreference_data")
dev_path = os.path.join(data_path, "dev_data")
datasets = [os.path.join(dev_path, f) for f in os.listdir(dev_path)]
datasets
```
## News datasets
```
news_path = os.path.join(data_path, "news_data")
datasets = [os.path.join(news_path, f) for f in os.listdir(news_path)]
datasets
```
# out of domain
```
outdomain = os.path.join(data_path, "out_of_domain")
datasets = [os.path.join(outdomain, f) for f in os.listdir(outdomain)]
datasets
```
# Preco large
```
preco_large = os.path.join(data_path, "big_files", "preco.coreflite")
```
## Generalized API
### Temp data
```
gum, lit, onto, prec = datasets
#model = corenlp # corenlp, neuralcoref, spanbert
onto_test = os.path.join(data_path, "ontonotes_test.coreflite")
gum_news = os.path.join(data_path, "gum_news.coreflite")
gum_no_news = os.path.join(data_path, "gum_no_news.coreflite")
from tqdm import tqdm
#dataset = onto_test
#model = corenlp
#outliers = []
dataset = preco_large
model = spanbert
#GUM_VERSION_2 = ["GUM_interview_ants.conll", "GUM_interview_brotherhood.conll", "GUM_interview_cocktail.conll", "GUM_interview_cyclone.conll", "GUM_interview_daly.conll", "GUM_interview_dungeon.conll", "GUM_interview_gaming.conll", "GUM_interview_herrick.conll", "GUM_interview_hill.conll", "GUM_interview_libertarian.conll", "GUM_interview_licen.conll", "GUM_interview_mckenzie.conll", "GUM_interview_messina.conll", "GUM_interview_peres.conll", "GUM_news_asylum.conll", "GUM_news_crane.conll", "GUM_news_defector.conll", "GUM_news_flag.conll", "GUM_news_hackers.conll", "GUM_news_ie9.conll", "GUM_news_imprisoned.conll", "GUM_news_korea.conll", "GUM_news_nasa.conll", "GUM_news_sensitive.conll", "GUM_news_stampede.conll", "GUM_news_taxes.conll", "GUM_news_warhol.conll", "GUM_news_warming.conll", "GUM_news_worship.conll", "GUM_voyage_athens.conll", "GUM_voyage_chatham.conll", "GUM_voyage_cleveland.conll", "GUM_voyage_coron.conll", "GUM_voyage_cuba.conll", "GUM_voyage_fortlee.conll", "GUM_voyage_merida.conll", "GUM_voyage_oakland.conll", "GUM_voyage_thailand.conll", "GUM_voyage_vavau.conll", "GUM_voyage_york.conll", "GUM_whow_arrogant.conll", "GUM_whow_basil.conll", "GUM_whow_cactus.conll", "GUM_whow_chicken.conll", "GUM_whow_cupcakes.conll", "GUM_whow_flirt.conll", "GUM_whow_glowstick.conll", "GUM_whow_joke.conll", "GUM_whow_languages.conll", "GUM_whow_overalls.conll", "GUM_whow_packing.conll", "GUM_whow_parachute.conll", "GUM_whow_quidditch.conll", "GUM_whow_skittles.conll"]
with open(dataset, "r", encoding="utf8") as data:
modelstr = str(model.__class__).split(".")[1]
datastr = dataset.split("\\")[-1].split(".")[0]
filename = "{}_{}_{}.txt".format(modelstr, datastr, get_timestamp())
filepath = os.path.join(os.getcwd(), "logs", filename)
all_docs = data.readlines()
#print("Total of {} docs".format(len(all_docs)))
FILES_TO_COUNT = len(all_docs)
dataset_scorer = CorefEvaluator()
#for i, doc in tqdm(enumerate(all_docs)):
for i in tqdm(range(len(all_docs))):
doc = all_docs[i]
doc = json.loads(doc)
docname = doc["doc_key"]
cleval = ClEval(model=model)
cleval.pipeline(doc,
tokens=False,
adjust_wrong_offsets=True,
no_singletons=True)
#cleval.compare()
conll_score, lea_score = cleval.show_score(verbose=False)
print("{} - {}. {}/{}\t\tconll: {}\t lea: {}".format(
datastr, docname, i+1, len(all_docs),
conll_score, lea_score
))
#cleval.show_score(verbose=True)
#print("p/r/f", cleval.scorer.get_prf_conll())
dataset_scorer.update(cleval.doc)
#if i == 19:
# break
dataset_scorer.detailed_score(modelstr, datastr)
print(dataset_scorer.get_conll())
#cleval.write_scores_to_file(modelstr, datastr)
#cleval.show()
g = cleval.gold_clusters
gs = cleval.gold_clusters_no_singletons
viz.raw_render(cleval.tokens, g)
viz.raw_render(cleval.tokens, gs)
from utils import flatten
combined_tokens = zip(cleval.tokens, cleval.pred_tokens())
for c in combined_tokens:
print(c)
pflat = flatten(cleval.pred_clusters)
cl = sorted(pflat, key=lambda x: x[0])
for c in cl:
print(c, cleval.tokens[c[0]-1:c[1]+1])
print(c, cleval.pred_tokens()[c[0]:c[1]+1])
pflat = flatten(cleval.gold_clusters)
cl = sorted(pflat, key=lambda x: x[0])
for c in cl:
print(c, cleval.tokens[c[0]:c[1]+1])
tokens = cleval.tokens
clusters = cleval.pred_clusters
for clust in clusters:
for mention in clust:
print(mention)
viz.raw_render(cleval.tokens, cleval.gold_clusters)
spandoc = cleval.model.doc
spandoc.keys()
len(cleval.tokens)
len(spandoc["document"])
spandoc["document"][0:20]
spandoc["antecedent_indices"][0:20]
```
| true |
code
| 0.351812 | null | null | null | null |
|
# Joint TV for multi-contrast MR
This demonstration shows how to do a synergistic reconstruction of two MR images with different contrast. Both MR images show the same underlying anatomy but of course with different contrast. In order to make use of this similarity a joint total variation (TV) operator is used as a regularisation in an iterative image reconstruction approach.
This demo is a jupyter notebook, i.e. intended to be run step by step.
You could export it as a Python file and run it one go, but that might
make little sense as the figures are not labelled.
Author: Christoph Kolbitsch, Evangelos Papoutsellis, Edoardo Pasca
First version: 16th of June 2021
CCP PETMR Synergistic Image Reconstruction Framework (SIRF).
Copyright 2021 Rutherford Appleton Laboratory STFC.
Copyright 2021 Physikalisch-Technische Bundesanstalt.
This is software developed for the Collaborative Computational
Project in Positron Emission Tomography and Magnetic Resonance imaging
(http://www.ccppetmr.ac.uk/).
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
# Initial set-up
```
# Make sure figures appears inline and animations works
%matplotlib notebook
# Make sure everything is installed that we need
!pip install brainweb nibabel --user
# Initial imports etc
import numpy
from numpy.linalg import norm
import matplotlib.pyplot as plt
import random
import os
import sys
import shutil
import brainweb
from tqdm.auto import tqdm
# Import SIRF functionality
import notebook_setup
import sirf.Gadgetron as mr
from sirf_exercises import exercises_data_path
# Import CIL functionality
from cil.framework import AcquisitionGeometry, BlockDataContainer, BlockGeometry, ImageGeometry
from cil.optimisation.functions import Function, OperatorCompositionFunction, SmoothMixedL21Norm, L1Norm, L2NormSquared, BlockFunction, MixedL21Norm, IndicatorBox, TotalVariation, LeastSquares, ZeroFunction
from cil.optimisation.operators import GradientOperator, BlockOperator, ZeroOperator, CompositionOperator, LinearOperator, FiniteDifferenceOperator
from cil.optimisation.algorithms import PDHG, FISTA, GD
from cil.plugins.ccpi_regularisation.functions import FGP_TV
```
# Utilities
```
# First define some handy function definitions
# To make subsequent code cleaner, we have a few functions here. You can ignore
# ignore them when you first see this demo.
def plot_2d_image(idx,vol,title,clims=None,cmap="viridis"):
"""Customized version of subplot to plot 2D image"""
plt.subplot(*idx)
plt.imshow(vol,cmap=cmap)
if not clims is None:
plt.clim(clims)
plt.colorbar()
plt.title(title)
plt.axis("off")
def crop_and_fill(templ_im, vol):
"""Crop volumetric image data and replace image content in template image object"""
# Get size of template image and crop
idim_orig = templ_im.as_array().shape
idim = (1,)*(3-len(idim_orig)) + idim_orig
offset = (numpy.array(vol.shape) - numpy.array(idim)) // 2
vol = vol[offset[0]:offset[0]+idim[0], offset[1]:offset[1]+idim[1], offset[2]:offset[2]+idim[2]]
# Make a copy of the template to ensure we do not overwrite it
templ_im_out = templ_im.copy()
# Fill image content
templ_im_out.fill(numpy.reshape(vol, idim_orig))
return(templ_im_out)
# This functions creates a regular (pattern='regular') or random (pattern='random') undersampled k-space data
# with an undersampling factor us_factor and num_ctr_lines fully sampled k-space lines in the k-space centre.
# For more information on this function please see the notebook f_create_undersampled_kspace
def create_undersampled_kspace(acq_orig, us_factor, num_ctr_lines, pattern='regular'):
"""Create a regular (pattern='regular') or random (pattern='random') undersampled k-space data"""
# Get ky indices
ky_index = acq_orig.parameter_info('kspace_encode_step_1')
# K-space centre in the middle of ky_index
ky0_index = len(ky_index)//2
# Fully sampled k-space centre
ky_index_subset = numpy.arange(ky0_index-num_ctr_lines//2, ky0_index+num_ctr_lines//2)
if pattern == 'regular':
ky_index_outside = numpy.arange(start=0, stop=len(ky_index), step=us_factor)
elif pattern == 'random':
ky_index_outside = numpy.asarray(random.sample(list(ky_index), len(ky_index)//us_factor))
else:
raise ValueError('pattern should be "random" or "linear"')
# Combine fully sampled centre and outer undersampled region
ky_index_subset = numpy.concatenate((ky_index_subset, ky_index_outside), axis=0)
# Ensure k-space points are note repeated
ky_index_subset = numpy.unique(ky_index_subset)
# Create new k-space data
acq_new = preprocessed_data.new_acquisition_data(empty=True)
# Select raw data
for jnd in range(len(ky_index_subset)):
cacq = preprocessed_data.acquisition(ky_index_subset[jnd])
acq_new.append_acquisition(cacq)
acq_new.sort()
return(acq_new)
```
### Joint TV reconstruction of two MR images
Assume we want to reconstruct two MR images $u$ and $v$ and utilse the similarity between both images using a joint TV ($JTV$) operator we can formulate the reconstruction problem as:
$$
\begin{equation}
(u^{*}, v^{*}) \in \underset{u,v}{\operatorname{argmin}} \frac{1}{2} \| A_{1} u - g\|^{2}_{2} + \frac{1}{2} \| A_{2} v - h\|^{2}_{2} + \alpha\,\mathrm{JTV}_{\eta, \lambda}(u, v)
\end{equation}
$$
* $JTV_{\eta, \lambda}(u, v) = \sum \sqrt{ \lambda|\nabla u|^{2} + (1-\lambda)|\nabla v|^{2} + \eta^{2}}$
* $A_{1}$, $A_{2}$: __MR__ `AcquisitionModel`
* $g_{1}$, $g_{2}$: __MR__ `AcquisitionData`
### Solving this problem
In order to solve the above minimization problem, we will use an alternating minimisation approach, where one variable is fixed and we solve wrt to the other variable:
$$
\begin{align*}
u^{k+1} & = \underset{u}{\operatorname{argmin}} \frac{1}{2} \| A_{1} u - g\|^{2}_{2} + \alpha_{1}\,\mathrm{JTV}_{\eta, \lambda}(u, v^{k}) \quad \text{subproblem 1}\\
v^{k+1} & = \underset{v}{\operatorname{argmin}} \frac{1}{2} \| A_{2} v - h\|^{2}_{2} + \alpha_{2}\,\mathrm{JTV}_{\eta, 1-\lambda}(u^{k+1}, v) \quad \text{subproblem 2}\\
\end{align*}$$
We are going to use a gradient descent approach to solve each of these subproblems alternatingly.
The *regularisation parameter* `alpha` should be different for each subproblem. But not to worry at this stage. Maybe we should use $\alpha_{1}, \alpha_{2}$ in front of the two JTVs and a $\lambda$, $1-\lambda$ for the first JTV and $1-\lambda$, $\lambda$, for the second JTV with $0<\lambda<1$.
This notebook builds on several other notebooks and hence certain steps will be carried out with minimal documentation. If you want more explainations, then we would like to ask you to refer to the corresponding notebooks which are mentioned in the following list. The steps we are going to carry out are
- (A) Get a T1 and T2 map from brainweb which we are going to use as ground truth $u_{gt}$ and $v_{gt}$ for our reconstruction (further information: `introduction` notebook)
- (B) Create __MR__ `AcquisitionModel` $A_{1}$ and $A_{2}$ and simulate undersampled __MR__ `AcquisitionData` $g_{1}$ and $g_{2}$ (further information: `acquisition_model_mr_pet_ct` notebook)
- (C) Set up the joint TV reconstruction problem
- (D) Solve the joint TV reconstruction problem (further information on gradient descent: `gradient_descent_mr_pet_ct` notebook)
# (A) Get brainweb data
We will download and use data from the brainweb.
```
fname, url= sorted(brainweb.utils.LINKS.items())[0]
files = brainweb.get_file(fname, url, ".")
data = brainweb.load_file(fname)
brainweb.seed(1337)
for f in tqdm([fname], desc="mMR ground truths", unit="subject"):
vol = brainweb.get_mmr_fromfile(f, petNoise=1, t1Noise=0.75, t2Noise=0.75, petSigma=1, t1Sigma=1, t2Sigma=1)
T2_arr = vol['T2']
T1_arr = vol['T1']
# Normalise image data
T2_arr /= numpy.max(T2_arr)
T1_arr /= numpy.max(T1_arr)
# Display it
plt.figure();
slice_show = T1_arr.shape[0]//2
plot_2d_image([1,2,1], T1_arr[slice_show, :, :], 'T1', cmap="Greys_r")
plot_2d_image([1,2,2], T2_arr[slice_show, :, :], 'T2', cmap="Greys_r")
```
Ok, we got to two images with T1 and T2 contrast BUT they brain looks a bit small. Spoiler alert: We are going to reconstruct MR images with a FOV 256 x 256 voxels. As the above image covers 344 x 344 voxels, the brain would only cover a small part of our MR FOV. In order to ensure the brain fits well into our MR FOV, we are going to scale the images.
In order to do this we are going to use an image `rescale` from the skimage package and simply rescale the image by a factor 2 and then crop it. To speed things up, we are going to already select a single slice because also our MR scan is going to be 2D.
```
from skimage.transform import rescale
# Select central slice
central_slice = T1_arr.shape[0]//2
T1_arr = T1_arr[central_slice, :, :]
T2_arr = T2_arr[central_slice, :, :]
# Rescale by a factor 2.0
T1_arr = rescale(T1_arr, 2,0)
T2_arr = rescale(T2_arr, 2.0)
# Select a central ROI with 256 x 256
# We could also skip this because it is automaticall done by crop_and_fill()
# but we would like to check if we did the right thing
idim = [256, 256]
offset = (numpy.array(T1_arr.shape) - numpy.array(idim)) // 2
T1_arr = T1_arr[offset[0]:offset[0]+idim[0], offset[1]:offset[1]+idim[1]]
T2_arr = T2_arr[offset[0]:offset[0]+idim[0], offset[1]:offset[1]+idim[1]]
# Now we make sure our image is of shape (1, 256, 256) again because in __SIRF__ even 2D images
# are expected to have 3 dimensions.
T1_arr = T1_arr[numpy.newaxis,...]
T2_arr = T2_arr[numpy.newaxis,...]
# Display it
plt.figure();
slice_show = T1_arr.shape[0]//2
plot_2d_image([1,2,1], T1_arr[slice_show, :, :], 'T1', cmap="Greys_r")
plot_2d_image([1,2,2], T2_arr[slice_show, :, :], 'T2', cmap="Greys_r")
```
Now, that looks better. Now we have got images we can use for our MR simulation.
# (B) Simulate undersampled MR AcquisitionData
```
# Create MR AcquisitionData
mr_acq = mr.AcquisitionData(exercises_data_path('MR', 'PTB_ACRPhantom_GRAPPA')
+ '/ptb_resolutionphantom_fully_ismrmrd.h5' )
# Calculate CSM
preprocessed_data = mr.preprocess_acquisition_data(mr_acq)
csm = mr.CoilSensitivityData()
csm.smoothness = 200
csm.calculate(preprocessed_data)
# Calculate image template
recon = mr.FullySampledReconstructor()
recon.set_input(preprocessed_data)
recon.process()
im_mr = recon.get_output()
# Display the coil maps
plt.figure();
csm_arr = numpy.abs(csm.as_array())
plot_2d_image([1,2,1], csm_arr[0, 0, :, :], 'Coil 0', cmap="Greys_r")
plot_2d_image([1,2,2], csm_arr[2, 0, :, :], 'Coil 2', cmap="Greys_r")
```
We want to use these coilmaps to simulate our MR raw data. Nevertheless, they are obtained from a phantom scan which unfortunately has got some signal voids inside. If we used these coil maps directly, then these signal voids would cause artefacts. We are therefore going to interpolate the coil maps first.
We are going to calculate a mask from the `ImageData` `im_mr`:
```
im_mr_arr = numpy.squeeze(numpy.abs(im_mr.as_array()))
im_mr_arr /= numpy.max(im_mr_arr)
mask = numpy.zeros_like(im_mr_arr)
mask[im_mr_arr > 0.2] = 1
plt.figure();
plot_2d_image([1,1,1], mask, 'Mask', cmap="Greys_r")
```
Now we are going to interpolate between the values defined by the mask:
```
from scipy.interpolate import griddata
# Target grid for a square image
xi = yi = numpy.arange(0, im_mr_arr.shape[0])
xi, yi = numpy.meshgrid(xi, yi)
# Define grid points in mask
idx = numpy.where(mask == 1)
x = xi[idx[0], idx[1]]
y = yi[idx[0], idx[1]]
# Go through each coil and interpolate linearly
csm_arr = csm.as_array()
for cnd in range(csm_arr.shape[0]):
cdat = csm_arr[cnd, 0, idx[0], idx[1]]
cdat_intp = griddata((x,y), cdat, (xi,yi), method='linear')
csm_arr[cnd, 0, :, :] = cdat_intp
# No extrapolation was done by griddate and we will set these values to 0
csm_arr[numpy.isnan(csm_arr)] = 0
# Display the coil maps
plt.figure();
plot_2d_image([1,2,1], numpy.abs(csm_arr[0, 0, :, :]), 'Coil 0', cmap="Greys_r")
plot_2d_image([1,2,2], numpy.abs(csm_arr[2, 0, :, :]), 'Coil 2', cmap="Greys_r")
```
This is not the world's best interpolation but it will do for the moment. Let's replace the data in the coils maps with the new interpolation
```
csm.fill(csm_arr);
```
Next we are going to create the two __MR__ `AcquisitionModel` $A_{1}$ and $A_{2}$
```
# Create undersampled acquisition data
us_factor = 2
num_ctr_lines = 30
pattern = 'random'
acq_us = create_undersampled_kspace(preprocessed_data, us_factor, num_ctr_lines, pattern)
# Create two MR acquisition models
A1 = mr.AcquisitionModel(acq_us, im_mr)
A1.set_coil_sensitivity_maps(csm)
A2 = mr.AcquisitionModel(acq_us, im_mr)
A2.set_coil_sensitivity_maps(csm)
```
and simulate undersampled __MR__ `AcquisitionData` $g_{1}$ and $g_{2}$
```
# MR
u_gt = crop_and_fill(im_mr, T1_arr)
g1 = A1.forward(u_gt)
v_gt = crop_and_fill(im_mr, T2_arr)
g2 = A2.forward(v_gt)
```
Lastly we are going to add some noise
```
g1_arr = g1.as_array()
g1_max = numpy.max(numpy.abs(g1_arr))
g1_arr += (numpy.random.random(g1_arr.shape) - 0.5 + 1j*(numpy.random.random(g1_arr.shape) - 0.5)) * g1_max * 0.01
g1.fill(g1_arr)
g2_arr = g2.as_array()
g2_max = numpy.max(numpy.abs(g2_arr))
g2_arr += (numpy.random.random(g2_arr.shape) - 0.5 + 1j*(numpy.random.random(g2_arr.shape) - 0.5)) * g2_max * 0.01
g2.fill(g2_arr)
```
Just to check we are going to apply the backward/adjoint operation to do a simply image reconstruction.
```
# Simple reconstruction
u_simple = A1.backward(g1)
v_simple = A2.backward(g2)
# Display it
plt.figure();
plot_2d_image([1,2,1], numpy.abs(u_simple.as_array())[0, :, :], '$u_{simple}$', cmap="Greys_r")
plot_2d_image([1,2,2], numpy.abs(v_simple.as_array())[0, :, :], '$v_{simple}$', cmap="Greys_r")
```
These images look quite poor compared to the ground truth input images, because they are reconstructed from an undersampled k-space. In addition, you can see a strange "structure" going through the centre of the brain. This has something to do with the coil maps. As mentioned above, our coil maps have these two "holes" in the centre and this creates this artefacts. Nevertheless, this is not going to be a problem for our reconstruction as we will see later on.
# (C) Set up the joint TV reconstruction problem
So far we have used mainly __SIRF__ functionality, now we are going to use __CIL__ in order to set up the reconstruction problem and then solve it. In order to be able to reconstruct both $u$ and $v$ at the same time, we will make use of `BlockDataContainer`. In the following we will define an operator which allows us to project a $(u,v)$ `BlockDataContainer` object into either $u$ or $v$. In literature, this operator is called **[Projection Map (or Canonical Projection)](https://proofwiki.org/wiki/Definition:Projection_(Mapping_Theory))** and is defined as:
$$ \pi_{i}: X_{1}\times\cdots\times X_{n}\rightarrow X_{i}$$
with
$$\pi_{i}(x_{0},\dots,x_{i},\dots,x_{n}) = x_{i},$$
mapping an element $x$ from a Cartesian Product $X =\prod_{k=1}^{n}X_{k}$ to the corresponding element $x_{i}$ determined by the index $i$.
```
class ProjectionMap(LinearOperator):
def __init__(self, domain_geometry, index, range_geometry=None):
self.index = index
if range_geometry is None:
range_geometry = domain_geometry.geometries[self.index]
super(ProjectionMap, self).__init__(domain_geometry=domain_geometry,
range_geometry=range_geometry)
def direct(self,x,out=None):
if out is None:
return x[self.index]
else:
out.fill(x[self.index])
def adjoint(self,x, out=None):
if out is None:
tmp = self.domain_geometry().allocate()
tmp[self.index].fill(x)
return tmp
else:
out[self.index].fill(x)
```
In the following we define the `SmoothJointTV` class. Our plan is to use the Gradient descent (`GD`) algorithm to solve the above problems. This implements the `__call__` method required to monitor the objective value and the `gradient` method that evaluates the gradient of `JTV`.
For the two subproblems, the first variations with respect to $u$ and $v$ variables are:
$$
\begin{equation}
\begin{aligned}
& A_{1}^{T}*(A_{1}u - g_{1}) - \alpha_{1} \mathrm{div}\bigg( \frac{\nabla u}{|\nabla(u, v)|_{2,\eta,\lambda}}\bigg)\\
& A_{2}^{T}*(A_{2}v - g_{2}) - \alpha_{2} \mathrm{div}\bigg( \frac{\nabla v}{|\nabla(u, v)|_{2,\eta,1-\lambda}}\bigg)
\end{aligned}
\end{equation}
$$
where $$|\nabla(u, v)|_{2,\eta,\lambda} = \sqrt{ \lambda|\nabla u|^{2} + (1-\lambda)|\nabla v|^{2} + \eta^{2}}.$$
```
class SmoothJointTV(Function):
def __init__(self, eta, axis, lambda_par):
r'''
:param eta: smoothing parameter making SmoothJointTV differentiable
'''
super(SmoothJointTV, self).__init__(L=8)
# smoothing parameter
self.eta = eta
# GradientOperator
FDy = FiniteDifferenceOperator(u_simple, direction=1)
FDx = FiniteDifferenceOperator(u_simple, direction=2)
self.grad = BlockOperator(FDy, FDx)
# Which variable to differentiate
self.axis = axis
if self.eta==0:
raise ValueError('Need positive value for eta')
self.lambda_par=lambda_par
def __call__(self, x):
r""" x is BlockDataContainer that contains (u,v). Actually x is a BlockDataContainer that contains 2 BDC.
"""
if not isinstance(x, BlockDataContainer):
raise ValueError('__call__ expected BlockDataContainer, got {}'.format(type(x)))
tmp = numpy.abs((self.lambda_par*self.grad.direct(x[0]).pnorm(2).power(2) + (1-self.lambda_par)*self.grad.direct(x[1]).pnorm(2).power(2)+\
self.eta**2).sqrt().sum())
return tmp
def gradient(self, x, out=None):
denom = (self.lambda_par*self.grad.direct(x[0]).pnorm(2).power(2) + (1-self.lambda_par)*self.grad.direct(x[1]).pnorm(2).power(2)+\
self.eta**2).sqrt()
if self.axis==0:
num = self.lambda_par*self.grad.direct(x[0])
else:
num = (1-self.lambda_par)*self.grad.direct(x[1])
if out is None:
tmp = self.grad.range.allocate()
tmp[self.axis].fill(self.grad.adjoint(num.divide(denom)))
return tmp
else:
self.grad.adjoint(num.divide(denom), out=out[self.axis])
```
Now we are going to put everything together and define our two objective functions which solve the two subproblems which we defined at the beginning
```
alpha1 = 0.05
alpha2 = 0.05
lambda_par = 0.5
eta = 1e-12
# BlockGeometry for the two modalities
bg = BlockGeometry(u_simple, v_simple)
# Projection map, depending on the unkwown variable
L1 = ProjectionMap(bg, index=0)
L2 = ProjectionMap(bg, index=1)
# Fidelity terms based on the acqusition data
f1 = 0.5*L2NormSquared(b=g1)
f2 = 0.5*L2NormSquared(b=g2)
# JTV for each of the subproblems
JTV1 = alpha1*SmoothJointTV(eta=eta, axis=0, lambda_par = lambda_par )
JTV2 = alpha2*SmoothJointTV(eta=eta, axis=1, lambda_par = 1-lambda_par)
# Compose the two objective functions
objective1 = OperatorCompositionFunction(f1, CompositionOperator(A1, L1)) + JTV1
objective2 = OperatorCompositionFunction(f2, CompositionOperator(A2, L2)) + JTV2
```
# (D) Solve the joint TV reconstruction problem
```
# We start with zero-filled images
x0 = bg.allocate(0.0)
# We use a fixed step-size for the gradient descent approach
step_size = 0.1
# We are also going to log the value of the objective functions
obj1_val_it = []
obj2_val_it = []
for i in range(10):
gd1 = GD(x0, objective1, step_size=step_size, \
max_iteration = 4, update_objective_interval = 1)
gd1.run(verbose=1)
# We skip the first one because it gets repeated
obj1_val_it.extend(gd1.objective[1:])
# Here we are going to do a little "trick" in order to better see, when each subproblem is optimised, we
# are going to append NaNs to the objective function which is currently not optimised. The NaNs will not
# show up in the final plot and hence we can nicely see each subproblem.
obj2_val_it.extend(numpy.ones_like(gd1.objective[1:])*numpy.nan)
gd2 = GD(gd1.solution, objective2, step_size=step_size, \
max_iteration = 4, update_objective_interval = 1)
gd2.run(verbose=1)
obj2_val_it.extend(gd2.objective[1:])
obj1_val_it.extend(numpy.ones_like(gd2.objective[1:])*numpy.nan)
x0.fill(gd2.solution)
print('* * * * * * Outer Iteration ', i, ' * * * * * *\n')
```
Finally we can look at the images $u_{jtv}$ and $v_{jtv}$ and compare them to the simple reconstruction $u_{simple}$ and $v_{simple}$ and the original ground truth images.
```
u_jtv = numpy.squeeze(numpy.abs(x0[0].as_array()))
v_jtv = numpy.squeeze(numpy.abs(x0[1].as_array()))
plt.figure()
plot_2d_image([2,3,1], numpy.squeeze(numpy.abs(u_simple.as_array()[0, :, :])), '$u_{simple}$', cmap="Greys_r")
plot_2d_image([2,3,2], u_jtv, '$u_{JTV}$', cmap="Greys_r")
plot_2d_image([2,3,3], numpy.squeeze(numpy.abs(u_gt.as_array()[0, :, :])), '$u_{gt}$', cmap="Greys_r")
plot_2d_image([2,3,4], numpy.squeeze(numpy.abs(v_simple.as_array()[0, :, :])), '$v_{simple}$', cmap="Greys_r")
plot_2d_image([2,3,5], v_jtv, '$v_{JTV}$', cmap="Greys_r")
plot_2d_image([2,3,6], numpy.squeeze(numpy.abs(v_gt.as_array()[0, :, :])), '$v_{gt}$', cmap="Greys_r")
```
And let's look at the objective functions
```
plt.figure()
plt.plot(obj1_val_it, 'o-', label='subproblem 1')
plt.plot(obj2_val_it, '+-', label='subproblem 2')
plt.xlabel('Number of iterations')
plt.ylabel('Value of objective function')
plt.title('Objective functions')
plt.legend()
# Logarithmic y-axis
plt.yscale('log')
```
# Next steps
The above is a good demonstration for a synergistic image reconstruction of two different images. The following gives a few suggestions of what to do next and also how to extend this notebook to other applications.
## Number of iterations
In our problem we have several regularisation parameters such as $\alpha_{1}$, $\alpha_{2}$ and $\lambda$. In addition, the number of inner iterations for each subproblem (currently set to 3) and the number of outer iterations (currently set to 10) also determine the final solution. Of course, for infinite number of total iterations it shouldn't matter but usually we don't have that much time.
__TODO__: Change the number of iterations and see what happens to the objective functions. For a given number of total iterations, do you think it is better to have a high number of inner or high number of outer iterations? Why? Does this also depend on the undersampling factor?
## Spatial misalignment
In the above example we simulated our data such that there is a perfect spatial match between $u$ and $v$. For real world applications this usually cannot be assumed.
__TODO__: Add spatial misalignment between $u$ and $v$. This can be achieved e.g. by calling `numpy.roll` on `T2_arr` before calling `v_gt = crop_and_fill(im_mr, T2_arr)`. What is the effect on the reconstructed images? For a more "advanced" misalignment, have a look at notebook `BrainWeb`.
__TODO__: One way to minimize spatial misalignment is to use image registration to ensure both $u$ and $v$ are well aligned. In the notebook `sirf_registration` you find information about how to register two images and also how to resample one image based on the spatial transformation estimated from the registration. Try to use this to correct for the misalignment you introduced above. For a real world example, at which point in the code would you have to carry out the registration+resampling? (some more information can also be found at the end of notebook `de_Pierro_MAPEM`)
## Pathologies
The images $u$ and $v$ show the same anatomy, just with a different contrast. Clinically more useful are of course images which show complementary image information.
__TODO__: Add a pathology to either $u$ and $v$ and see how this effects the reconstruction. For something more advanced, have a loot at the notebook `BrainWeb`.
## Single anatomical prior
So far we have alternated between two reconstruction problems. Another option is to do a single regularised reconstruction and simply use a previously reconstructed image for regularisation.
__TODO__: Adapt the above code such that $u$ is reconstructed first without regularisation and is then used for a regularised reconstruction of $v$ without any further updates of $u$.
## Complementary k-space trajectories
We used the same k-space trajectory for $u$ and $v$. This is of course not ideal for such an optimisation, because the same k-space trajectory also means the same pattern of undersampling artefacts. Of course the artefacts in each image will be different because of the different image content but it still would be better if $u$ and $v$ were acquired with different k-space trajectories.
__TODO__: Create two different k-space trajectories and compare the results to a reconstruction using the same k-space trajectories.
__TODO__: Try different undersampling factors and compare results for _regular_ and _random_ undersampling patterns.
## Other regularisation options
In this example we used a TV-based regularisation, but of course other regularisers could also be used, such as directional TV.
__TODO__: Have a look at the __CIL__ notebook `02_Dynamic_CT` and adapt the `SmoothJointTV` class above to use directional TV.
| true |
code
| 0.517998 | null | null | null | null |
|
# Malware Classification
**Data taken from**<br>
https://github.com/Te-k/malware-classification
Here is the plan that we will follow :
- Extract as many features as we can from binaries to have a good training data set. The features have to be integers or floats to be usable by the algorithms
- Identify the best features for the algorithm : we should select the information that best allows to differenciate legitimate files from malware.
- Choose a classification algorithm
- Test the efficiency of the algorithm and identify the False Positive/False negative rate
### How was the data generated
- Some features were extracted using Manalyzer. The PE features extracted are almost used directly as they are integers (field size, addresses, parameters…)
The author of data quotes:
```
So I extracted all the PE parameters I could by using pefile, and considered especially the one that are relevant for identifying malware, like the entropy of section for packer detection. As we can only have a fix list of feature (and not one per section), I extracted the Mean, Minimum and Maximum of entropy for sections and resources.
```
For legitimate file, I gathered all the Windows binaries (exe + dll) from Windows 2008, Windows XP and Windows 7 32 and 64 bits, so exactly 41323 binaries. It is not a perfect dataset as there is only Microsoft binaries and not binaries from application which could have different properties, but I did not find any easy way to gather easily a lot of legitimate binaries, so it will be enough for playing.<br>
Regarding malware, I used a part of [Virus Share](https://virusshare.com) collection by downloading one archive (the 134th) and kept only PE files (96724 different files).<br>
I used [pefile](https://github.com/erocarrera/pefile) to extract all these features from the binaries and store them in a csv file (ugly code is here, data are here).
### Services used:
- https://manalyzer.org : Manalyzer is a free service which performs static analysis on PE executables to detect undesirable behavior. Try it online, or check out the underlying software on https://github.com/JusticeRage/Manalyze
- https://virusshare.com : VirusShare.com is a repository of malware samples to provide security researchers, incident responders, forensic analysts, and the morbidly curious access to samples of live malicious code.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
```
## load the dataset
```
df = pd.read_csv("../dataset/malware.csv", sep="|")
df.head(10)
```
### Scripts used to generate above data
- https://github.com/Te-k/malware-classification/blob/master/checkmanalyzer.py
- https://github.com/Te-k/malware-classification/blob/master/checkpe.py
- https://github.com/Te-k/malware-classification/blob/master/generatedata.py
## Analysis
```
df.shape
df.columns
```
## Distribution of legitimate and malwares
```
df["_type"] = "legit"
df.loc[df['legitimate'] == 0, '_type'] = "malware"
df['_type'].value_counts()
df['_type'].value_counts(normalize=True) * 100
pd.crosstab(df['_type'], 'count').plot(kind='bar', color=['green', 'red'])
plt.title("Distribution of legitimite and malware")
## todo add more visualizations
```
## Feature Selection
The idea of feature selection is to reduce the 54 features extracted to a smaller set of feature which are the most relevant for differentiating legitimate binaries from malware.
```
legit_binaries = df[0:41323].drop(['legitimate'], axis=1)
malicious_binaries = df[41323::].drop(['legitimate'], axis=1)
```
## Manual data cleaning & feature selection
So a first way of doing it manually could be to check the different values and see if there is a difference between the two groups. For instance, we can take the parameter FileAlignment (which defines the alignment of sections and is by default 0x200 bytes) and check the values :
```
legit_binaries['FileAlignment'].value_counts(normalize=True) * 100
malicious_binaries['FileAlignment'].value_counts(normalize=True) * 100
```
So if we remove the 20 malware having weird values here, there is not much difference on this value between the two groups, this parameter would not make a good feature for us.
On the other side, some values are clearly interesting like the max entropy of the sections which can be represented with an histogram:
```
plt.figure(figsize=(15,10))
plt.hist([legit_binaries['SectionsMaxEntropy'], malicious_binaries['SectionsMaxEntropy']], range=[0,8], normed=True, color=["green", "red"],label=["legitimate", "malicious"])
plt.legend()
plt.title("distribution of Section Max Entropy for legit vs malaicious binaries")
plt.show()
xlabel = 'Machine'
ylabel = 'ImageBase'
plt.figure(figsize=(10,6))
plt.scatter(_df[xlabel], _df[ylabel], label=_df['legitimate'], color=['green', 'red'])
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.title("Distribution by %s & %s" % (xlabel, ylabel))
def plotDistributionForFeature(colName, figsize=(7,5)):
global legit_binaries
global malicious_binaries
plt.figure(figsize=figsize)
plt.hist(
[legit_binaries[colName], malicious_binaries[colName]],
range=[0,8],
normed=True,
color=["green", "red"],
label=["legitimate", "malicious"])
plt.legend()
plt.title("distribution of %s for legit vs malaicious binaries" % colName)
plt.show()
avoidCols = ['_type', 'Name', 'md5', 'legitimate']
for col in df.columns:
if col not in avoidCols:
plotDistributionForFeature(col)
```
## Automatic Feature Selection
some algorithms have been developed to identify the most interesting features and reduce the dimensionality of the data set (see the Scikit page for Feature Selection).
In our case, we will use the Tree-based feature selection:
```
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.feature_selection import SelectFromModel
X = df.drop(['Name', 'md5', 'legitimate', '_type'], axis=1).values
y = df['legitimate'].values
fsel = ExtraTreesClassifier().fit(X, y)
model = SelectFromModel(fsel, prefit=True)
X_new = model.transform(X)
print ("Shape before feaure selection: ", X.shape)
print ("Shape after feaure selection: ", X_new.shape)
```
So in this case, the algorithm selected 13 important features among the 54, and we can notice that indeed the SectionsMaxEntropy is selected but other features (like the Machine value) are surprisingly also good parameters for this classification :
```
nb_features = X_new.shape[1]
indices = np.argsort(fsel.feature_importances_)[::-1][:nb_features]
for f in range(nb_features):
print("%d. feature %s (%f)" % (f + 1, df.columns[2+indices[f]], fsel.feature_importances_[indices[f]]))
```
## Test train split
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_new, y ,test_size=0.2)
```
# Classification: selecting Models
```
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier, AdaBoostClassifier
from sklearn.linear_model import LogisticRegression
algorithms = {
"DecisionTree": DecisionTreeClassifier(max_depth=10),
"RandomForest": RandomForestClassifier(n_estimators=50),
"GradientBoosting": GradientBoostingClassifier(n_estimators=50),
"AdaBoost": AdaBoostClassifier(n_estimators=100),
"LogisticRegression": LogisticRegression()
}
results = {}
print("\nNow testing algorithms")
for algo in algorithms:
clf = algorithms[algo]
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
print("%s : %f %%" % (algo, score*100))
results[algo] = score
winner = max(results, key=results.get)
print('\nWinner algorithm is %s with a %f %% success' % (winner, results[winner]*100))
```
## Evaluation
```
from sklearn.metrics import confusion_matrix
# Identify false and true positive rates
clf = algorithms[winner]
res = clf.predict(X_test)
mt = confusion_matrix(y_test, res)
print("False positive rate : %f %%" % ((mt[0][1] / float(sum(mt[0])))*100))
print('False negative rate : %f %%' % ( (mt[1][0] / float(sum(mt[1]))*100)))
```
## Results
### 99.38% Accuracy
### False positive rate : 0.383678 %
### False negative rate : 0.937162 %
### Why it’s not enough?
First, a bit of vocabulary for measuring IDS accuracy (taken from Wikipedia):
- *Sensitivity* : the proportion of positives identified as such (or true positive rate)
- *Specificity* : the proportion of negatives correctly identified as such (or true negative)
- *False Positive Rate (FPR)* : the proportion of events badly identified as positive over the total number of negatives
- *False Negative Rate (FNR)* : the proportion of events badly identified as negative over the total number of positives
### So why 99.38% is not enough?
- Because you can’t just consider the sensitivity/specificity of the algorithm, you have to consider the malicious over legitimate traffic ratio to understand how many alerts will be generated by the IDS. And this ratio is extremely low.
- Let’s consider the you have 1 malicious event every 10 000 event (it’s a really high ratio) and 1 000 000 events per day, you will have :
- 100 malicious events, 99 identified by the tool and 1 false negative (0.93% FNR but let’s consider 1% here)
- 999 900 legitimate events, around *3835* identified as malicious (0.38% FPR)
- So in the end, the *analyst would received 3934 alerts per day* with only *99 true positive in it (2.52%)*. Your IDS is useless here.
## Visualization
To be done
| true |
code
| 0.719014 | null | null | null | null |
|
# Welcome to PySyft
The goal of this notebook is to provide step by step explanation of the internal workings of PySyft for developers and have working examples of the API to play with.
**Note:** You should be able to run these without any issues. This notebook will be automatically run by CI and flagged if it fails. If your commit breaks this notebook, either fix the issue or add some information here for others.
```
assert True is True
import sys
import pytest
import syft as sy
from syft.core.node.common.service.auth import AuthorizationException
from syft.util import key_emoji
sy.LOG_FILE = "syft_do.log"
sy.logger.remove()
_ = sy.logger.add(sys.stdout, level="DEBUG")
```
Bob decides has some data he wants to share with Alice using PySyft.
The first thing Bob needs to do is to create a Node to handle all the PySyft services he will need to safely and securely share his data with Alice.
```
somedevice = sy.Device()
```
This is a device, it is a Node and it has a name, id and address.
```
print(somedevice.name, somedevice.id, somedevice.address)
```
The ID is a class called UID which is essentially a uuid. The address is a combination of up to four different locations, identifying the path to resolve the final target of the address.
```
print(somedevice.address.vm, somedevice.address.device, somedevice.address.domain, somedevice.address.network)
print(somedevice.address.target_id)
```
UIDs are hard to read and compare so we have a function which converts them to 2 x emoji.
Just like the "name", Emoji uniqueness is not guaranteed but is very useful during debugging.
```
print(somedevice.address.target_id.pprint)
print(somedevice.address.pprint)
```
Most things that are "pretty printed" include an emoji, a name and a class, additionally with a UID and "visual UID" emoji.
📌 somedevice.address.target_id is a "Location" which is pointing to this specific location with a name and address.
💠 [📱] somedevice.address is the "Address" of somedevice (Think up to 4 x locations) in this case the contents of the List [] show it only has the Location of a device currently.
**note:** Sometimes Emoji's look like this: 🙓. The dynamically generated code point doesnt have an Emoji. A PR fix would be welcome. 🙂
```
print(somedevice.id, somedevice.address.target_id.id)
print(somedevice.id.emoji(), "==", somedevice.address.target_id.id.emoji())
print(somedevice.pprint)
assert somedevice.id == somedevice.address.target_id.id
```
Interaction with a Node like a device is always done through a client. Clients can "send" messages and Nodes can "receive" them. Bob needs to get a client for his device. But first it might be a good idea to name is device so that its easier to follow.
```
bob_device = sy.Device(name="Bob's iPhone")
assert bob_device.name == "Bob's iPhone"
bob_device_client = bob_device.get_client()
```
When you ask a node for a client you get a "Client" which is named after the device and has the same "UID" and "Address" (4 x Locations) as the device it was created from, and it will have a "Route" that connects it to the "Device"
```
assert bob_device_client.name == "Bob's iPhone Client"
print(bob_device_client.pprint, bob_device.pprint)
print(bob_device.id.emoji(), "==", bob_device_client.id.emoji())
assert bob_device.id == bob_device_client.device.id
assert bob_device.address == bob_device_client.address
```
📡 [📱] Bob's iPhone Client is a "DeviceClient" and it has the same UID and "Address" as Bob's Device
Now we have something that can send and receive lets take it for a spin.
Since everything is handled with a layer of abstraction the smallest unit of work is a "SyftMessage". Very little can be done without sending a message from a Client to a Node. There are many types of "SyftMessage" which boil down to whether or not they are Sync or Async, and whether or not they expect a response.
Lets make a ReprMessage which simply gets a message and prints it at its destination Node.
SyftMessage's all have an "address" field, without this they would never get delivered. They also generally have a msg_id which can be used to keep track of them.
```
msg = sy.ReprMessage(address=bob_device_client.address)
print(msg.pprint)
print(bob_device_client.address.pprint)
assert msg.address == bob_device_client.address
```
What type of Message is ReprMessage you ask?
```
print(sy.ReprMessage.mro())
```
Its an "Immediate" "WithoutReply" okay so Sync and no response.
Now lets send it, remember we need a Client not a Node for sending.
```
with pytest.raises(AuthorizationException):
bob_device_client.send_immediate_msg_without_reply(
msg=sy.ReprMessage(address=bob_device_client.address)
)
```
Oh oh! Why did Auth fail? We'll we can see from the debug that the 🔑 (VerifyKey) of the sender was matched to the 🗝 (Root VerifyKey) of the destination and they don't match. This client does not have sufficient permission to send a ReprMessage.
First lets take a look at the keys involved.
```
print(bob_device_client.keys)
print(bob_device.keys)
assert bob_device_client.verify_key != bob_device.root_verify_key
```
Not to worry we have a solution, lets get a client which does have this permission.
```
bob_device_client = bob_device.get_root_client()
```
Lets take a look again.
```
print(bob_device_client.keys)
print(bob_device.keys)
assert bob_device_client.verify_key == bob_device.root_verify_key
```
Lets try sending the message again.
```
bob_device_client.send_immediate_msg_without_reply(
msg=sy.ReprMessage(address=bob_device_client.address)
)
```
Woohoo! 🎉
Okay so theres a lot going on but lets step through it.
The ReprMessage is created by the Client, and then signed with the Client's SigningKey.
The SigningKey and VerifyKey are a pair and the VerifyKey is public and derived from the SigningKey.
When we call get_root_client() we update the Node with the newly generated key on the Client so that the Client will now have permission to execute root actions.
Behind every message type is a service which executes the message on a Node.
To run ReprMessage on our Device Node, we can see that during startup it adds a service to handle these kinds of messages:
```python
# common/node.py
self.immediate_services_without_reply.append(ReprService)
````
Not all actions / services require "root". To enable this a decorator is added like so:
```python
# repr_service.py
class ReprService(ImmediateNodeServiceWithoutReply):
@staticmethod
@service_auth(root_only=True)
```
Okay so Bob has root access to his own device, but he wants to share some data and compute resources of this device to someone else. So to do that he needs to create a "Sub Node" which will be a "VirtualMachine". Think of this as a partition or slice of his device which can be allocated memory, storage and compute.
```
bob_vm = sy.VirtualMachine(name="Bob's VM")
```
Since VirtualMachine is a Node (Server) it will need a Client to issue commands to it.
Lets make one.
**note:** Why do we need a root client? The registration process is two way and the Registeree will need to update its address in response to a successful registration.
```
bob_vm_client = bob_vm.get_root_client()
```
Okay so now Bob has two Nodes and their respective clients, but they know nothing of each other.
They both have addresses that only point to themselves.
```
print(bob_device_client.address.pprint)
print(bob_vm_client.address.pprint)
```
Lets register Bob's vm with its device since the Device is higher up in the level of scope.
```
bob_device_client.register(client=bob_vm_client)
```
Whoa.. Okay lots happening. As you can see there are two messages and two Authentications. The first one is the `RegisterChildNodeMessage` which is dispatched to the address of the Device. Once it is received it stores the address of the registering Node and then dispatches a new `HeritageUpdateMessage` back to the sender of the first message.
**note:** This is not a reply message, this is a completely independent message that happens to be sent back to the sender's address.
```python
issubclass(RegisterChildNodeMessage, SignedImmediateSyftMessageWithoutReply)
issubclass(HeritageUpdateService, SignedImmediateSyftMessageWithoutReply)
```
You will also notice that the Messages turned into Protobufs and then Signed.
Lets see how this works for `ReprMessage`.
1) ✉️ -> Proto 🔢
Every message that is sent requires and the following method signatures:
```python
def _object2proto(self) -> ReprMessage_PB:
def _proto2object(proto: ReprMessage_PB) -> "ReprMessage":
def get_protobuf_schema() -> GeneratedProtocolMessageType:
```
The get_protobuf_schema method will tell the caller what Protobuf class to use, and then the _object2proto method will be called to turn normal python into a protobuf message.
```python
# repr_service.py
def _object2proto(self) -> ReprMessage_PB:
return ReprMessage_PB(
msg_id=self.id.serialize(), address=self.address.serialize(),
)
```
Any type which isnt a normal Protobuf primitive must be converted to a proto or serialized before being stored.
**note:** self.id and self.address also need to be serialized so this will call their `_object2proto` methods.
At this point we are using code auto generated by `protoc` as per the build script:
```bash
$ ./scripts/build_proto.sh
```
Here is the .proto definition for `ReprMessage`
```c++
// repr_service.proto
syntax = "proto3";
package syft.core.node.common.service;
import "proto/core/common/common_object.proto";
import "proto/core/io/address.proto";
message ReprMessage {
syft.core.common.UID msg_id = 1;
syft.core.io.Address address = 2;
}
```
Once the message needs to be Deserialized the `_proto2object` method will be called.
```python
# repr_service.py
return ReprMessage(
msg_id=_deserialize(blob=proto.msg_id),
address=_deserialize(blob=proto.address),
)
```
Two things to pay attention to:
1) `RegisterChildNodeMessage` has caused Bob's Device Store has been updated with an entry representing Bob's VM Address
2) `HeritageUpdateService` has caused Bob's VM to update its address to now include the `SpecificLocation` of Bob's Device.
**note:** The Address for Bob's VM Client inside the Store does not include the "Device" part of the "Address" (4 x Locations) since it isn't updated until after the HeritageUpdateService message is sent.
```
print(bob_device.store.pprint)
assert bob_vm_client.address.target_id.id in bob_device.store
print(bob_vm_client.address.pprint, bob_vm_client.address.target_id.id.emoji())
```
What about `SignedMessage`? If you read `message.py` you will see that all messages inherit from `SignedMessage` and as such contain the following fields.
```c++
message SignedMessage {
syft.core.common.UID msg_id = 1;
string obj_type = 2;
bytes signature = 3;
bytes verify_key = 4;
bytes message = 5;
}
```
The actual message is serialized and stored in the `message` field and a hash of its bytes is calculated using the Client's `SigningKey`.
The contents of `message` are not encrypted and can be read at any time by simply deserializing them.
```
def get_signed_message_bytes() -> bytes:
# return a signed message fixture containing the uid from get_uid
blob = (
b'\n?syft.core.common.message.SignedImmediateSyftMessageWithoutReply\x12\xad\x02\n\x12\n\x10\x8c3\x19,'
+ b'\xcd\xd3\xf3N\xe2\xb0\xc6\tU\xdf\x02u\x126syft.core.node.common.service.repr_service.ReprMessage'
+ b'\x1a@@\x82\x13\xfaC\xfb=\x01H\x853\x1e\xceE+\xc6\xb5\rX\x16Z\xb8l\x02\x10\x8algj\xd6U\x11]\xe9R\x0ei'
+ b'\xd8\xca\xb9\x00=\xa1\xeeoEa\xe2C\xa0\x960\xf7A\xfad<(9\xe1\x8c\x93\xf1\x0b" \x81\xff\xcc\xfc7\xc4U.'
+ b'\x8a*\x1f"=0\x10\xc4\xef\x88\xc80\x01\xf0}3\x0b\xd4\x97\xad/P\x8f\x0f*{\n6'
+ b'syft.core.node.common.service.repr_service.ReprMessage\x12A\n\x12\n\x10\x8c3\x19,'
+ b'\xcd\xd3\xf3N\xe2\xb0\xc6\tU\xdf\x02u\x12+\n\x0bGoofy KirchH\x01R\x1a\n\x12\n\x10\xfb\x1b\xb0g[\xb7LI'
+ b'\xbe\xce\xe7\x00\xab\n\x15\x14\x12\x04Test'
)
return blob
sig_msg = sy.deserialize(blob=get_signed_message_bytes(), from_bytes=True)
```
We can get the nested message with a property called `message`
```
repr_msg = sig_msg.message
print(repr_msg.pprint, sig_msg.pprint)
print(repr_msg.address.pprint, sig_msg.address.pprint)
print(repr_msg.address.target_id.id.emoji(), sig_msg.address.target_id.id.emoji())
assert sig_msg.id == repr_msg.id
assert sig_msg.address == repr_msg.address
```
Notice the UID's of `ReprMessage` and `SignedImmediateSyftMessageWithoutReply` are the same. So are the delivery address's.
But the original bytes are still available and serialization / deserialization or serde (ser/de) is bi-directional and reversible
```
assert repr_msg.serialize(to_bytes=True) == sig_msg.serialized_message
print(repr_msg.pprint, " ⬅️ ", sig_msg.pprint)
from nacl.signing import SigningKey, VerifyKey
def get_signing_key() -> SigningKey:
# return a the signing key used to sign the get_signed_message_bytes fixture
key = "e89ff2e651b42393b6ecb5956419088781309d953d72bd73a0968525a3a6a951"
return SigningKey(bytes.fromhex(key))
```
Lets try re-signing it with the same key it was signed with.
```
sig_msg_comp = repr_msg.sign(signing_key=get_signing_key())
signing_key = get_signing_key()
verify_key = signing_key.verify_key
print(f"SigningKey: {key_emoji(key=signing_key)}")
print(f"VerifyKey: {key_emoji(key=verify_key)}")
print(type(signing_key), type(verify_key))
print(f"🔑 {key_emoji(key=sig_msg.verify_key)} == {key_emoji(key=verify_key)} 🔑")
print(bytes(verify_key))
assert sig_msg_comp == sig_msg
assert sig_msg.verify_key == verify_key
assert VerifyKey(bytes(verify_key)) == verify_key
```
The message is signed with the `SigningKey`, a consistent `VerifyKey` is derived from the `SigningKey`. Both keys can be transformed to bytes and back easily.
Okay now Bob wants to protect his Device(s) and its / their VM(s). To do that he needs to add them to a higher level Node called a `Domain`.
```
bob_domain = sy.Domain(name="Bob's Domain")
bob_domain_client = bob_domain.get_root_client()
```
Okay lets follow the same proceedure and link up these nodes.
```
print(bob_domain.address.pprint)
bob_domain_client.register(client=bob_device_client)
```
Thats interesting, we see theres two `HeritageUpdateMessage` that get sent. The address update is "Flowing" upward to the leaf VM nodes.
```
print(bob_vm.address.pprint)
print(bob_device.address.pprint)
print(bob_domain.address.pprint)
assert bob_domain_client.id == bob_device.address.domain.id
assert bob_device.id == bob_vm.address.device.id
```
Now that the Nodes are aware of each other, we can send a message to any child node by dispatching a message on a parent Client and addressing the Child node.
**note:** We are changing the bob_vm root_verify_key because ReprMessage is a root message. We should change this example.
Note, the repr service has the service_auth decorator.
`@service_auth(root_only=True)`
```python
class ReprService(ImmediateNodeServiceWithoutReply):
@staticmethod
@service_auth(root_only=True)
def process(node: AbstractNode, msg: ReprMessage, verify_key: VerifyKey) -> None:
print(node.__repr__())
@staticmethod
def message_handler_types() -> List[Type[ReprMessage]]:
return [ReprMessage]
```
For the purpose of the demonstration we will override the destination nodes root_verify_key with the one of our new domain client and the secure ReprMessage will be executed. Normally the remote node is not running in the same python REPL as the client.
```
# Just to bypass the auth we will set the root verify key on destination so that it will accept this message
bob_vm.root_verify_key = bob_domain_client.verify_key # inject 📡🔑 as 📍🗝
bob_domain_client.send_immediate_msg_without_reply(
msg=sy.ReprMessage(address=bob_vm.address)
)
```
| true |
code
| 0.485966 | null | null | null | null |
|
# Lesson 1 - FastAI
## New to ML? Don't know where to start?
Machine learning may seem complex at first, given the math, background understanding, and code involved. However, if you truly want to learn, the best place to start is by building and messing around with a model. FastiAI makes it super easy to create and modify models to best solve your problem! Don't worry too much if you don't understand, we will get there.
## Our First Model
As I have said above, the best way to learn is by actually creating your first model
```
from fastai.vision.all import * #IMPORT
path = untar_data(URLs.PETS)/'images' #DATA SET
def is_cat(x): return x[0].isupper() #Labels for the dataset (This dataset cat labels begin w/ uppercase letter)
#Create dataset (Training data, test data) and correctly gets imgs w/ labels
dls = ImageDataLoaders.from_name_func(
path, get_image_files(path), valid_pct=0.2, seed=42,
label_func=is_cat, item_tfms=Resize(224))
learn = cnn_learner(dls, resnet34, metrics=error_rate) #Creating architecture
learn.fine_tune(1) #Training
```
>Look at that, we created our first model and all with a few lines of code.
### Why don't we test our cat classifier?
```
img = PILImage.create(image_cat())
img.to_thumb(192)
uploader = widgets.FileUpload()
uploader
img = PILImage.create(uploader.data[0])
img.to_thumb(192)
is_cat,_,probs = learn.predict(img)
print(f"Is this a cat?: {is_cat}.")
print(f"Probability it's a cat: {probs[1].item():.6f}")
```
>Fantastic, you can now classify cats!
## Deep Learning Is Not Just for Image Classification
Often people think machine learning model are used only for images, this is **not** true at all!
Below you will see numerous other types of models, each with its benifits!
## A segmentation model
```
path = untar_data(URLs.CAMVID_TINY)
dls = SegmentationDataLoaders.from_label_func( #Segmentation
path, bs=8, fnames = get_image_files(path/"images"),
label_func = lambda o: path/'labels'/f'{o.stem}_P{o.suffix}',
codes = np.loadtxt(path/'codes.txt', dtype=str)
)
learn = unet_learner(dls, resnet34)
learn.fine_tune(8)
learn.show_results(max_n=2, figsize=(10,12))
```
### A natural language model
```
from fastai.text.all import *
dls = TextDataLoaders.from_folder(untar_data(URLs.IMDB), valid='test')
learn = text_classifier_learner(dls, AWD_LSTM, drop_mult=0.5, metrics=accuracy)
learn.fine_tune(2, 1e-2)
learn.predict("I really liked that movie!")
```
### A salary prediction model (Regression)
```
from fastai.tabular.all import *
path = untar_data(URLs.ADULT_SAMPLE)
dls = TabularDataLoaders.from_csv(path/'adult.csv', path=path, y_names="salary",
cat_names = ['workclass', 'education', 'marital-status', 'occupation',
'relationship', 'race'],
cont_names = ['age', 'fnlwgt', 'education-num'],
procs = [Categorify, FillMissing, Normalize])
learn = tabular_learner(dls, metrics=accuracy)
learn.fit_one_cycle(3)
```
### The below is a reccomendation model (AKA Regression model)
```
from fastai.collab import *
path = untar_data(URLs.ML_SAMPLE)
dls = CollabDataLoaders.from_csv(path/'ratings.csv')
learn = collab_learner(dls, y_range=(0.5,5.5))
learn.fine_tune(10)
learn.show_results()
```
# Conclusion
I hope you feel more comfortable with machine learning and recognize the many benefits it can serve you :)
## Questionnaire
1. **Do you need these for deep learning?**
- Lots of math T / **F**
- Lots of data T / **F**
- Lots of expensive computers T / **F**
- A PhD T / **F**
1. **Name five areas where deep learning is now the best in the world.**
Vision, Natural language processing, Medicine, Robotics, and Games
1. **What was the name of the first device that was based on the principle of the artificial neuron?**
Mark I Perceptron
1. **Based on the book of the same name, what are the requirements for parallel distributed processing (PDP)?**
Processing units, State of activation, Output function, Pattern of connectivity, Propagation rule, Activation rule, Learning rule, Environment
1. **What were the two theoretical misunderstandings that held back the field of neural networks?**
Single layer network unable to learn simple mathimatical functions.
More layers make network too big and slow to be useful.
1. **What is a GPU?**
A graphics card is a processor that can handle 1000's of tasks at the same time. Particularly great for deep learning.
1. **Open a notebook and execute a cell containing: `1+1`. What happens?**
2
1. **Follow through each cell of the stripped version of the notebook for this chapter. Before executing each cell, guess what will happen.**
1. **Complete the Jupyter Notebook online appendix.**
1. **Why is it hard to use a traditional computer program to recognize images in a photo?**
They are missing the weight assignment needed to recognize patterns within images to accomplish the task.
1. **What did Samuel mean by "weight assignment"?**
The weight is another form of input that has direct influence on the model's performance.
1. **What term do we normally use in deep learning for what Samuel called "weights"?**
Parameters
1. **Draw a picture that summarizes Samuel's view of a machine learning model.**
https://vikramriyer.github.io/assets/images/machine_learning/fastai/model.jpeg
1. **Why is it hard to understand why a deep learning model makes a particular prediction?**
There are many layers, each with numerous neurons. Therefore, it gets complex really fast what each neuron is looking for when viewing an image, and how that impacts the perediction.
1. **What is the name of the theorem that shows that a neural network can solve any mathematical problem to any level of accuracy?**
Universal approximation theorem
1. **What do you need in order to train a model?**
Data with labels
1. **How could a feedback loop impact the rollout of a predictive policing model?**
The more the model is used the more biased the data becomes, and therefore, the more bias the model becomes.
1. **Do we always have to use 224×224-pixel images with the cat recognition model?**
No.
1. **What is the difference between classification and regression?**
Classification is about categorizing/labeling objects.
Regression is about predicting numerical quantities, such as temp.
1. **What is a validation set? What is a test set? Why do we need them?**
The validation set measures the accuracy of the model during training.
The test set is used during the final evaluation to test the accuracy of the model.
We need both of them because the validation set could cause some bias in the model as we would are fitting the model towards it during training. However, the test set removes this and evaluates the model on unseen data, thereby, giving an accurate metric of accuracy.
1. **What will fastai do if you don't provide a validation set?**
Fastai will automatically create a validation dataset for us.
1. **Can we always use a random sample for a validation set? Why or why not?**
It is not reccomended where order is neccessary, example ordered by time.
1. **What is overfitting? Provide an example.**
This is when the model begins to fit to the training data rather than generalizing for similar unseen datasets. For example a model that does amazing on the training data, but performs poorly on test data: Good indication that model may have overfitted.
1. **What is a metric? How does it differ from "loss"?**
The loss is the value calculated by the model to determine the impact each neuron has on the end result: Therefore, the value is used by models to measure its performance. The metric gives us, humans, an overall value of how accurate the model was: Therefore, a value we use to understand the models performance.
1. **How can pretrained models help?**
A pretrained model already has the fundementals. Therefore, it can use this prior knowledge to learn faster and perform better on similer datasets.
1. **What is the "head" of a model?**
The final layers from the pretrained model that have been replaced with new layers (w/ randomized weights) to better align with our dataset. These final layers are often the only thing trained while the rest of the model is frozen.
1. **What kinds of features do the early layers of a CNN find? How about the later layers?**
The early layers often extract simple features like edges.
The later layers are more complex and can identify advanced features like faces.
1. **Are image models only useful for photos?**
No. Lots of other forms of data can be converted into images that can be used to solve such non-photo data problems.
1. **What is an "architecture"?**
This is the structure of the model we use to solve the problem.
1. **What is segmentation?**
Method of labeling all pixels within an image and masking it.
1. **What is `y_range` used for? When do we need it?**
Specifies the range of values that can be perdicted by model. For example, movie rating's 0-5.
1. **What are "hyperparameters"?**
These are the parameters that we can adjust to help the model perform better (Ex: Epochs).
1. **What's the best way to avoid failures when using AI in an organization?**
Begin with the most simplest model and then slowly building up to more complexity. This way you have something working and don't get lost as you add onto the model.
### Further Research
Each chapter also has a "Further Research" section that poses questions that aren't fully answered in the text, or gives more advanced assignments. Answers to these questions aren't on the book's website; you'll need to do your own research!
1. **Why is a GPU useful for deep learning? How is a CPU different, and why is it less effective for deep learning?** </br>
Modern GPUs provide a far superior processing power, memory bandwidth, and efficiency over the CPU.
1. **Try to think of three areas where feedback loops might impact the use of machine learning. See if you can find documented examples of that happening in practice.** </br>
I believe feedback loops are primarly great for recommendation models. This is because the feedback loops create a bias model. For example, if a viewer like a movie, he/she will like similer movies. Being bias here towards particular types of movie is the best way to keep the viewer engaged.
| true |
code
| 0.586523 | null | null | null | null |
|
# 1. Import Library
```
from keras.datasets import cifar10
import numpy as np
np.random.seed(10)
```
# 資料準備
```
(x_img_train,y_label_train),(x_img_test,y_label_test)=cifar10.load_data()
print("train data:",'images:',x_img_train.shape,
" labels:",y_label_train.shape)
print("test data:",'images:',x_img_test.shape ,
" labels:",y_label_test.shape)
x_img_train_normalize = x_img_train.astype('float32') / 255.0
x_img_test_normalize = x_img_test.astype('float32') / 255.0
from keras.utils import np_utils
y_label_train_OneHot = np_utils.to_categorical(y_label_train)
y_label_test_OneHot = np_utils.to_categorical(y_label_test)
y_label_test_OneHot.shape
```
# 建立模型
```
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D, ZeroPadding2D
model = Sequential()
#卷積層1
model.add(Conv2D(filters=32,kernel_size=(3,3),
input_shape=(32, 32,3),
activation='relu',
padding='same'))
model.add(Dropout(rate=0.25))
model.add(MaxPooling2D(pool_size=(2, 2)))
#卷積層2與池化層2
model.add(Conv2D(filters=64, kernel_size=(3, 3),
activation='relu', padding='same'))
model.add(Dropout(0.25))
model.add(MaxPooling2D(pool_size=(2, 2)))
#Step3 建立神經網路(平坦層、隱藏層、輸出層)
model.add(Flatten())
model.add(Dropout(rate=0.25))
model.add(Dense(1024, activation='relu'))
model.add(Dropout(rate=0.25))
model.add(Dense(10, activation='softmax'))
print(model.summary())
```
# 載入之前訓練的模型
```
try:
model.load_weights("SaveModel/CifarModelCnn_v1.h5")
print("載入模型成功!繼續訓練模型")
except :
print("載入模型失敗!開始訓練一個新模型")
```
# 訓練模型
```
model.compile(loss='categorical_crossentropy',
optimizer='adam', metrics=['accuracy'])
train_history=model.fit(x_img_train_normalize, y_label_train_OneHot,
validation_split=0.2,
epochs=10, batch_size=128, verbose=1)
import matplotlib.pyplot as plt
def show_train_history(train_acc,test_acc):
plt.plot(train_history.history[train_acc])
plt.plot(train_history.history[test_acc])
plt.title('Train History')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
show_train_history('acc','val_acc')
show_train_history('loss','val_loss')
```
# 評估模型準確率
```
scores = model.evaluate(x_img_test_normalize,
y_label_test_OneHot, verbose=0)
scores[1]
```
# 進行預測
```
prediction=model.predict_classes(x_img_test_normalize)
prediction[:10]
```
# 查看預測結果
```
label_dict={0:"airplane",1:"automobile",2:"bird",3:"cat",4:"deer",
5:"dog",6:"frog",7:"horse",8:"ship",9:"truck"}
import matplotlib.pyplot as plt
def plot_images_labels_prediction(images,labels,prediction,
idx,num=10):
fig = plt.gcf()
fig.set_size_inches(12, 14)
if num>25: num=25
for i in range(0, num):
ax=plt.subplot(5,5, 1+i)
ax.imshow(images[idx],cmap='binary')
title=str(i)+','+label_dict[labels[i][0]]
if len(prediction)>0:
title+='=>'+label_dict[prediction[i]]
ax.set_title(title,fontsize=10)
ax.set_xticks([]);ax.set_yticks([])
idx+=1
plt.show()
plot_images_labels_prediction(x_img_test,y_label_test,
prediction,0,10)
```
# 查看預測機率
```
Predicted_Probability=model.predict(x_img_test_normalize)
def show_Predicted_Probability(y,prediction,
x_img,Predicted_Probability,i):
print('label:',label_dict[y[i][0]],
'predict:',label_dict[prediction[i]])
plt.figure(figsize=(2,2))
plt.imshow(np.reshape(x_img_test[i],(32, 32,3)))
plt.show()
for j in range(10):
print(label_dict[j]+
' Probability:%1.9f'%(Predicted_Probability[i][j]))
show_Predicted_Probability(y_label_test,prediction,
x_img_test,Predicted_Probability,0)
show_Predicted_Probability(y_label_test,prediction,
x_img_test,Predicted_Probability,3)
```
# confusion matrix
```
prediction.shape
y_label_test.shape
y_label_test
y_label_test.reshape(-1)
import pandas as pd
print(label_dict)
pd.crosstab(y_label_test.reshape(-1),prediction,
rownames=['label'],colnames=['predict'])
print(label_dict)
```
# Save model to JSON
```
model_json = model.to_json()
with open("SaveModel/CifarModelCnn_v1.json", "w") as json_file:
json_file.write(model_json)
```
# Save Model to YAML
```
model_yaml = model.to_yaml()
with open("SaveModel/CifarModelCnn_v1.yaml", "w") as yaml_file:
yaml_file.write(model_yaml)
```
# Save Weight to h5
```
model.save_weights("SaveModel/CifarModelCnn_v1.h5")
print("Saved model to disk")
for layer in model.layers:
lay_config = layer.get_config()
lay_weights = layer.get_weights()
print('*** layer config ***')
print(lay_config)
print('*** layer weights ***')
print(lay_weights)
layer = model.layers[0]
lay_config = layer.get_config()
lay_weights = layer.get_weights()
print('*** cifar-10 layer config ***')
print(lay_config)
print('*** cifar-10 layer weights ***')
print(lay_weights)
layer = model.layers[3]
lay_config = layer.get_config()
lay_weights = layer.get_weights()
print('*** cifar-10 layer-2 config ***')
print(lay_config)
print('*** cifar-10 layer-2 weights ***')
print(lay_weights)
layidx = 0
params_list = model.layers[0].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
images = weights_array.reshape(3, 32, 3, 3)
plotpos = 1
for idx in range(32):
plt.subplot(1, 32, plotpos)
plt.imshow(images[0][idx])
plt.gray()
plt.axis('off')
plotpos += 1
plt.show()
layidx = 3
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
images = weights_array.reshape(32, 64, 3, 3)
plotpos = 1
for idx1 in range(32):
for idx2 in range(64):
# 画像データのイメージを表示
plt.subplot(32, 64, plotpos)
plt.imshow(images[idx1][idx2])
plt.gray()
plt.axis('off')
plotpos += 1
plt.show()
layidx = 8
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
image = weights_array.reshape(1024, 4096)
plt.imshow(image)
plt.gray()
plt.axis('off')
plt.show()
layidx = 10
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
image = weights_array.reshape(10, 1024)
plt.imshow(image)
plt.gray()
plt.axis('off')
plt.show()
import codecs, json
print("output weights as JSON")
filename = "SaveModel/CifarModelCnnParamsCnn_v1_layer%02d.json"
layidx = 0
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
dict = {}
dict['weights'] = weights_array.tolist()
dict['biases'] = biases_array.tolist()
file_path = filename % layidx
json.dump(dict,
codecs.open(file_path, 'w', encoding='utf-8'),
separators=(',', ':'),
sort_keys=False,
indent=4)
layidx = 3
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
dict = {}
dict['weights'] = weights_array.tolist()
dict['biases'] = biases_array.tolist()
file_path = filename % layidx
json.dump(dict,
codecs.open(file_path, 'w', encoding='utf-8'),
separators=(',', ':'),
sort_keys=False,
indent=4)
layidx = 8
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
dict = {}
dict['weights'] = weights_array.tolist()
dict['biases'] = biases_array.tolist()
file_path = filename % layidx
json.dump(dict,
codecs.open(file_path, 'w', encoding='utf-8'),
separators=(',', ':'),
sort_keys=False,
indent=4)
layidx = 10
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
dict = {}
dict['weights'] = weights_array.tolist()
dict['biases'] = biases_array.tolist()
file_path = filename % layidx
json.dump(dict,
codecs.open(file_path, 'w', encoding='utf-8'),
separators=(',', ':'),
sort_keys=False,
indent=4)
print("done")
#from keras.models import load_model
#model2 = load_model('./SaveModel/cifarCnnModelnew.h5')
# 再学習
train_history=model.fit(x_img_train_normalize, y_label_train_OneHot,
validation_split=0.2,
epochs=100, batch_size=128, verbose=1)
show_train_history('acc','val_acc')
scores = model.evaluate(x_img_test_normalize,
y_label_test_OneHot, verbose=0)
scores[1]
Predicted_Probability=model.predict(x_img_test_normalize)
def show_Predicted_Probability(y,prediction,
x_img,Predicted_Probability,i):
print('label:',label_dict[y[i][0]],
'predict:',label_dict[prediction[i]])
plt.figure(figsize=(2,2))
plt.imshow(np.reshape(x_img_test[i],(32, 32,3)))
plt.show()
for j in range(10):
print(label_dict[j]+
' Probability:%1.9f'%(Predicted_Probability[i][j]))
show_Predicted_Probability(y_label_test,prediction,
x_img_test,Predicted_Probability,100)
import pandas as pd
print(label_dict)
pd.crosstab(y_label_test.reshape(-1),prediction,
rownames=['label'],colnames=['predict'])
model_json = model.to_json()
with open("SaveModel/CifarModelCnn_v2.json", "w") as json_file:
json_file.write(model_json)
model_yaml = model.to_yaml()
with open("SaveModel/CifarModelCnn_v2.yaml", "w") as yaml_file:
yaml_file.write(model_yaml)
model.save_weights("SaveModel/CifarModelCnn_v2.h5")
print("Saved model to disk")
for layer in model.layers:
lay_config = layer.get_config()
lay_weights = layer.get_weights()
print('*** layer config ***')
print(lay_config)
print('*** layer weights ***')
print(lay_weights)
import codecs, json
print("output weights as JSON")
filename = "SaveModel/CifarModelCnnParamsCnn_v2_layer%02d.json"
layidx = 0
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
dict = {}
dict['weights'] = weights_array.tolist()
dict['biases'] = biases_array.tolist()
file_path = filename % layidx
json.dump(dict,
codecs.open(file_path, 'w', encoding='utf-8'),
separators=(',', ':'),
sort_keys=False,
indent=4)
layidx = 3
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
dict = {}
dict['weights'] = weights_array.tolist()
dict['biases'] = biases_array.tolist()
file_path = filename % layidx
json.dump(dict,
codecs.open(file_path, 'w', encoding='utf-8'),
separators=(',', ':'),
sort_keys=False,
indent=4)
layidx = 8
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
dict = {}
dict['weights'] = weights_array.tolist()
dict['biases'] = biases_array.tolist()
file_path = filename % layidx
json.dump(dict,
codecs.open(file_path, 'w', encoding='utf-8'),
separators=(',', ':'),
sort_keys=False,
indent=4)
layidx = 10
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
biases_array = params_list[1]
dict = {}
dict['weights'] = weights_array.tolist()
dict['biases'] = biases_array.tolist()
file_path = filename % layidx
json.dump(dict,
codecs.open(file_path, 'w', encoding='utf-8'),
separators=(',', ':'),
sort_keys=False,
indent=4)
print("done")
x_img_train[0]
x_img_train_normalize_test = x_img_train[0].astype('float32') / 255.0
x_img_train_normalize_test.shape
layidx = 0
params_list = model.layers[layidx].get_weights()
weights_array = params_list[0]
weights_array[0].shape
weights_array[0][0].shape
weights_array[0][0][0].shape
layidx = 0
params_list = model.layers[layidx].get_weights()
lay_config = model.layers[layidx].get_config()
weights_array = params_list[0]
biases_array = params_list[1]
print(weights_array)
weights_array.shape
print(lay_config)
layidx = 3
params_list = model.layers[layidx].get_weights()
lay_config = model.layers[layidx].get_config()
weights_array = params_list[0]
biases_array = params_list[1]
weights_array.shape
```
| true |
code
| 0.549943 | null | null | null | null |
|
```
%pylab inline
```
# Генерирование гауссовских случайных процессов
## 1. Генерирование с помощью многомерного нормального вектора
Если вам нужно сгенерировать реализацию гауссовского случайного процесса $X = (X_t)_{t \geqslant 0}$ фиксированной известной (и не слишком большой) длины $n$, можно воспользоваться тем фактом, что конечномерные распределения гауссовского случайного процесса являются нормальными, а его моменты (математическое ожидание $m(t)$ и ковариационная функция $R(t_1, t_2)$ известны. В этом случае достаточно рассмотреть $n$ моментов времени $t_1, \ldots, t_n$ и сгенерировать $n$-мерный случайный гауссовский вектор с нужными математическим ожиданием $m(t_1), \ldots, m(t_n)$ и ковариационной матрицей $\Sigma = R(t_i, t_i)$.
Заметим, что если $Z$ - стандартно нормально распределенная случайная величина, т.е. $Z \sim N(0, 1)$, то ее линейное преобразование $X = \mu + \sigma Z$ имеет также нормальное распределение, причем $X \sim N(\mu, \sigma^2)$.
Аналогичное соотношение существует и для многомерных нормальных векторов. А именно, пусть $\mathbf{Z} = (Z_1, \ldots, Z_n) \sim N(0, \mathbf{I})$, где $\mathbf{I} = \mathrm{diag}(1, \ldots, 1)$ - единичная матрица. Тогда случайный вектор $\mathbf{X} = \mathbf{\mu} + \mathbf{C} \mathbf{Z}$ имеет нормальное $N(\mathbf{\mu}, \mathbf{\Sigma})$ распределение, где $\mathbf{\mu} = (\mu_1, \ldots, \mu_n)$ - желаемый вектор средних, а матрицы $\mathbf{C}$ и $\mathbf{\Sigma}$ связаны соотношениями $\mathbf{\Sigma} = \mathbf{C} \mathbf{C}^T$. Последнее соотношение называется разложением Холецкого положительно полуопределенной $n \times n$ матрицы $\mathbf{\Sigma}$, причем $n \times n$ матрица $\mathbf{C}$ оказывается нижнетреугольной.
Поэтому, чтобы сгенерировать многомерный нормальный вектор, можно поступить следующим способом. Сгенерируем $\mathbf{Z} = (Z_1, \ldots, Z_n) \sim N(0, \mathbf{I})$, вычислим $\mathbf{C}$ и положим $\mathbf{X} = \mathbf{\mu} + \mathbf{C} \mathbf{Z}$.
### 1.1. Винеровский процесс
Рассмотрим этот подход на примере простого броуновского движения $B = (B_t)_{t \geqslant 0}$. Для этого процесса $\mathrm{E} B_t = 0$, $R(s, t) = \mathrm{E} [B_s B_t] = \mathrm{min}(s, t)$.
Вычислим вектор математических ожиданий и ковариационную матрицу для $t_i = \Delta i, i = 0, \ldots, 1000, \Delta = 10^{-2}$.
```
def compute_bm_mean(timestamps):
return np.zeros_like(timestamps)
def compute_bm_cov(timestamps):
n = len(timestamps)
R = np.zeros((n, n))
for i in xrange(n):
for j in xrange(n):
R[i, j] = min(timestamps[i], timestamps[j])
return R
timestamps = timestamps = np.linspace(1e-2, 10, 1000)
cov_bm = compute_bm_cov(timestamps)
mean_bm = compute_bm_mean(timestamps)
figure(figsize=(6, 3))
subplot(1, 2, 1)
imshow(cov_bm, interpolation='nearest')
subplot(1, 2, 2)
plot(timestamps, cov_bm[500, :])
c_bm = np.linalg.cholesky(cov_bm)
Z = np.random.normal(size=1000)
X = mean_bm + np.dot(c_bm, Z)
figure(figsize=(9, 3))
subplot(1, 2, 1)
plot(timestamps, Z)
title('Brownian motion increments')
subplot(1, 2, 2)
plot(timestamps, X)
title('Brownian motion sample path')
```
### 1.2. Фрактальное броуновское движение
Стандартное фрактальное броуновское движение $B^H = (B^H_t)_{t \geqslant 0}$
на $[0,T]$ с параметром Хёрста $H \in (0,1)$ -
это гауссовский процесс с непрерывными траекториями такой, что
$$
B^H_0 = 0,
\qquad
\mathrm{E} B^H_t = 0,
\qquad
\mathrm{E} [B^H_t B^H_s] = \frac{1}{2}
\big(|t|^{2H} + |s|^{2H} - |t - s|^{2H}\big).
$$
В случае, когда $H=\frac{1}{2}$, фрактальное броуновское движение является
обыкновенным броуновским движением, в случае же $H\neq\frac{1}{2}$ процесс $B^H$ является некоторым гауссовским процессом.
```
def compute_fbm_matrix(timestamps, hurst):
ts_begin = timestamps[0]
dt = timestamps[1] - timestamps[0]
time = np.array([ts - ts_begin for ts in timestamps]) + dt
n = len(time)
K = np.zeros(shape=(n, n))
for index, t in enumerate(time):
K[index, :] = np.power(time, 2. * hurst) + \
np.power(t, 2. * hurst) - \
np.power(np.abs(time - t), 2. * hurst)
K *= 0.5
return K
```
Вначале убедимся, что траектория fBm при $H = 1/2$ выглядит похожей на траекторию обыкновенного броуновского движения, а его ковариационная матрица равна ковариационной матрице обыкновенного броуновского движения.
```
timestamps = np.linspace(0.01, 10, 1000)
cov_fbm = compute_fbm_matrix(timestamps, 0.5)
cov_fbm_chol = np.linalg.cholesky(cov_fbm)
figure(figsize=(6, 3))
subplot(1, 2, 1)
imshow(cov_fbm, interpolation='nearest')
subplot(1, 2, 2)
plot(timestamps, cov_fbm[500, :])
c_bm = np.linalg.cholesky(cov_fbm)
Z = np.random.normal(size=1000)
X = mean_bm + np.dot(c_bm, Z)
figure(figsize=(9, 3))
subplot(1, 2, 1)
plot(timestamps, Z)
title('Brownian motion increments')
subplot(1, 2, 2)
plot(timestamps, X)
title('Fractional Brownian motion sample path')
```
Теперь посмотрим, что происходит с процессом fBM при $H < 1/2$.
```
timestamps = np.linspace(0.01, 10, 1000)
cov_fbm = compute_fbm_matrix(timestamps, 0.1)
cov_fbm_chol = np.linalg.cholesky(cov_fbm)
figure(figsize=(6, 3))
subplot(1, 2, 1)
imshow(cov_fbm, interpolation='nearest')
subplot(1, 2, 2)
plot(timestamps, cov_fbm[500, :])
c_bm = np.linalg.cholesky(cov_fbm)
Z = np.random.normal(size=1000)
X = mean_bm + np.dot(c_bm, Z)
figure(figsize=(9, 3))
subplot(1, 2, 1)
plot(timestamps, Z)
title('Brownian motion increments')
subplot(1, 2, 2)
plot(timestamps, X)
title('Fractional Brownian motion sample path')
```
Рассмотрим еще случай $H > 1/2$.
```
timestamps = np.linspace(0.01, 10, 1000)
cov_fbm = compute_fbm_matrix(timestamps, 0.9)
cov_fbm_chol = np.linalg.cholesky(cov_fbm)
figure(figsize=(6, 3))
subplot(1, 2, 1)
imshow(cov_fbm, interpolation='nearest')
subplot(1, 2, 2)
plot(timestamps, cov_fbm[500, :])
c_bm = np.linalg.cholesky(cov_fbm)
Z = np.random.normal(size=1000)
X = mean_bm + np.dot(c_bm, Z)
figure(figsize=(9, 3))
subplot(1, 2, 1)
plot(timestamps, Z)
title('Brownian motion increments')
subplot(1, 2, 2)
plot(timestamps, X)
title('Fractional Brownian motion sample path')
```
Еще раз отобразим траектории fBm при различных увеличивающихся $H$.
```
Z = np.random.normal(size=1000)
for H in [0.1, 0.3, 0.5, 0.7, 0.9]:
cov_fbm = compute_fbm_matrix(timestamps, H)
c_bm = np.linalg.cholesky(cov_fbm)
X = mean_bm + np.dot(c_bm, Z)
plot(timestamps, X)
```
### 1.3. Процесс Орнштейна-Уленбека
Процесс Орнштейна-Уленбека - это гауссовский процесс $X = (X_t)_{t \geqslant 0}$ с непрерывными траекториями такой, что
$$
X_t = e^{-t} B_{e^{2t}},
$$
где $B = (B_t)_{t \geqslant 0}$ - обыкновенное броуновское движение.
Легко показать, что $\mathrm{E} X_t = 0$, $\mathrm{E} [X_s X_t] = e^{-|s - t|}$.
```
def compute_ou_cov(timestamps):
n = len(timestamps)
R = np.zeros((n, n))
for i in xrange(n):
for j in xrange(n):
R[i, j] = np.exp(-np.abs(timestamps[i] - timestamps[j]))
return R
timestamps = np.linspace(0.01, 10, 1000)
cov_ou = compute_ou_cov(timestamps)
cov_ou_chol = np.linalg.cholesky(cov_ou)
figure(figsize=(6, 3))
subplot(1, 2, 1)
imshow(cov_ou, interpolation='nearest')
subplot(1, 2, 2)
plot(timestamps, cov_ou[500, :])
c_ou = np.linalg.cholesky(cov_ou)
Z = np.random.normal(size=1000)
X = mean_bm + np.dot(c_ou, Z)
figure(figsize=(9, 3))
subplot(1, 2, 1)
plot(timestamps, Z)
title('Brownian motion increments')
subplot(1, 2, 2)
plot(timestamps, X)
title('OU process sample path')
```
| true |
code
| 0.682759 | null | null | null | null |
|
# Maximising the utility of an Open Address
Anthony Beck (GeoLytics), John Daniels (UU), Paul Williams (UU), Dave Pearson (UU), Matt Beare (Beare Essentials)

Go down for licence and other metadata about this presentation
\newpage
# The view of addressing from United Utilities
Unless states otherwise all content is under a CC-BY licence. All images are re-used under licence - follow the image URL for the licence conditions.


\newpage
## Using Ipython for presentations
A short video showing how to use Ipython for presentations
```
from IPython.display import YouTubeVideo
YouTubeVideo('F4rFuIb1Ie4')
## PDF output using pandoc
import os
### Export this notebook as markdown
commandLineSyntax = 'ipython nbconvert --to markdown 201609_UtilityAddresses_Presentation.ipynb'
print (commandLineSyntax)
os.system(commandLineSyntax)
### Export this notebook and the document header as PDF using Pandoc
commandLineSyntax = 'pandoc -f markdown -t latex -N -V geometry:margin=1in DocumentHeader.md 201609_UtilityAddresses_Presentation.md --filter pandoc-citeproc --latex-engine=xelatex --toc -o interim.pdf '
os.system(commandLineSyntax)
### Remove cruft from the pdf
commandLineSyntax = 'pdftk interim.pdf cat 1-5 22-end output 201609_UtilityAddresses_Presentation.pdf'
os.system(commandLineSyntax)
### Remove the interim pdf
commandLineSyntax = 'rm interim.pdf'
os.system(commandLineSyntax)
```
## The environment
In order to replicate my environment you need to know what I have installed!
### Set up watermark
This describes the versions of software used during the creation.
Please note that critical libraries can also be watermarked as follows:
```python
%watermark -v -m -p numpy,scipy
```
```
%install_ext https://raw.githubusercontent.com/rasbt/python_reference/master/ipython_magic/watermark.py
%load_ext watermark
%watermark -a "Anthony Beck" -d -v -m -g
#List of installed conda packages
!conda list
#List of installed pip packages
!pip list
```
## Running dynamic presentations
You need to install the [RISE Ipython Library](https://github.com/damianavila/RISE) from [Damián Avila](https://github.com/damianavila) for dynamic presentations
## About me

* Honorary Research Fellow, University of Nottingham: [orcid](http://orcid.org/0000-0002-2991-811X)
* Director, Geolytics Limited - A spatial data analytics consultancy
## About this presentation
* [Available on GitHub](https://github.com/AntArch/Presentations_Github/tree/master/20151008_OpenGeo_Reuse_under_licence) - https://github.com/AntArch/Presentations_Github/
* [Fully referenced PDF](https://github.com/AntArch/Presentations_Github/blob/master/201609_UtilityAddresses_Presentation/201609_UtilityAddresses_Presentation.pdf)
\newpage
To convert and run this as a static presentation run the following command:
```
# Notes don't show in a python3 environment
!jupyter nbconvert 201609_UtilityAddresses_Presentation.ipynb --to slides --post serve
```
To close this instances press *control 'c'* in the *ipython notebook* terminal console
Static presentations allow the presenter to see *speakers notes* (use the 's' key)
If running dynamically run the scripts below
## Pre load some useful libraries
```
#Future proof python 2
from __future__ import print_function #For python3 print syntax
from __future__ import division
# def
import IPython.core.display
# A function to collect user input - ipynb_input(varname='username', prompt='What is your username')
def ipynb_input(varname, prompt=''):
"""Prompt user for input and assign string val to given variable name."""
js_code = ("""
var value = prompt("{prompt}","");
var py_code = "{varname} = '" + value + "'";
IPython.notebook.kernel.execute(py_code);
""").format(prompt=prompt, varname=varname)
return IPython.core.display.Javascript(js_code)
# inline
%pylab inline
```
\newpage
# Addresses

are part of the fabric of everyday life
\newpage
# Addresses

Have economic and commercial impact
\newpage
# Addresses

Support governance and democracy
* Without an address, it is harder for individuals to register as legal residents.
* They are *not citizens* and are excluded from:
* public services
* formal institutions.
* This impacts on democracy.
\newpage
# Addresses

Support Legal and Social integration
* Formal versus Informal
* Barring individuals and businesses from systems:
* financial
* legal
* government
* ....
\newpage
# Addresses
bridge gaps - provide the link between ***people*** and ***place***

\newpage
# Utility Addresses
## In the beginning ...... was the ledger

\newpage
## Bespoke digital addresses
* Digitisation and data entry to create a bespoke Address Database -
* Fit for UU's operational purpose
* Making utilities a key *owner* of address data
* Subject to IP against PAF matching

\newpage
## Policy mandates
Open Water - A shared view of addresses requiring a new addressing paradigm - Address Base Premium?

\newpage
# Utility addressing:
* Postal delivery (Billing)
* Services and Billing to properties within the extent of the UU operational area
* Billing to customers outside the extent of UU operational area
* Asset/Facilities Management (infrastructure)
* Premises
* But utilties manage different assets to Local Authorities
* is an address the best way to manage a geo-located asset?
* Bill calculation
* Cross referencing Vaulation Office and other detals.

\newpage
. . . .
**It's not just postal addressing**
. . . .
**Address credibility is critical**
. . . .
Utilities see the full life-cycle of an address - especially the birth and death
\newpage
## asset management
* UU manage assets and facilities
> According to ABP a Waste Water facility is neither a postal address or a non-postal address.
Really? Is it having an existential crisis?

\newpage
## A connected spatial network

\newpage
## Serving customers who operate **somewhere**

* UU serve customers located in
* Buildings
* Factories
* Houses
* Fields
\newpage
## Serving customers who operate **anywhere**

\newpage
# Utility addressing issues
* Addresses are a pain
* Assets as locations
* Services as locatons
* People at locations

\newpage
# Issues: addresses = postal address.
* Is *Postal* a constraining legacy?
* Is *address* a useful term?

\newpage
# Issues: Do formal *addresses* actually help utilities?
* External addresses (ABP for example) are another product(s) to manage
* which may not fit the real business need
* which may not have full customer or geographic coverage

\newpage
# What is an address?
## Address abstraction
* Address did not spring fully formed into existance.
* They are used globally
* but developed nationally
* and for different reasons

\newpage
## Royal Mail - postal delivery

In a postal system:
* a *Delivery Point* (DP) is a single mailbox or other place at which mail is delivered.
* a single DP may be associated with multiple addresses
* An *Access Point* provides logistical detail.
The postal challenge is to solve the last 100 meters. In such a scenario the *post person* is critical.
DPs were collected by the Royal Mail for their operational activities and sold under licence as the *Postal Address File* (PAF). PAF is built around the 8-character *Unique Delivery Point Reference Number* (UDPRN). The problem with PAF is that the spatial context is not incorporated into the product. Delivery points are decoupled from their spatial context - a delivery point with a spatial context should provide the clear location of the point of delivery (a door in a house, a post-room at an office etc.).
\newpage
## LLPG - asset management
](https://dl.dropboxusercontent.com/u/393477/ImageBank/ForAddresses/LBH-LLPG-System-flow-Diagram.png)
An LLPG (Local Land and Property Gazetteer) is a collection of address and location data created by a local authority.
It is an Asset/Facilities Management tool to support public service delivery:
* Local Authority
* Police
* Fire
* Ambulance
It incorporates:
* Non postal addresses (i.e. something that the Royal Mail wouldn't deliver post to)
* a 12-digit Unique Property Reference Number for every building and plot of land
* National Street Gazetteer
Prior to the initialization of the LLPGs, local authorities would have different address data held across different departments and the purpose of the Local Land and Property Gazetteers was to rationalize the data, so that a property or a particular plot of land is referred to as the same thing, even if they do have different names.
\newpage
## Addresses as assets?
](http://joncruddas.org.uk/sites/joncruddas.org.uk/files/styles/large/public/field/image/post-box.jpg?itok=ECnzLyhZ)
* So what makes the following 'non-postal' *facilities* addresses:
* Chimney
* Post box - which is clearly having a letter delivered ;-)
* Electricity sub-station
* Context is critical
* So why is a waste-water facility not an address in ABP (when an Electricity sub-station is)?
* Because it is not *of interest* to a council and the Royal Mail have never been asked to deliver mail to it.
\newpage
## Korea: The Jibeon system - taxation

* Until recently, the Republic of Korea (Korea) has used land parcel numbers ( jibeon) to identify unique locations.
* These parcel numbers were assigned chronologically according to date of construction and without reference to the street where they were located.
* This meant that adjacent buildings did not necessarily follow a sequential numbering system.
* This system was initially used to identify land for census purposes and to levy taxes.
* In addition, until the launch of the new addressing system, the jibeon was also used to identify locations (i.e. a physical address).
\newpage
## World Bank - social improvement

The World Bank has taken a *street addressing* view-point (@_addressing_2012, p.57). This requires up-to-date mapping and bureacracy (to deliver a street gazetteer and to provide the street infrastructure (furniture)). However, (@_addressing_2012, p.44) demonstrates that this is a cumbersome process with a number of issues, not the least:
* Urban bias
* Cost of infrastucture development
* Lack of community involvment
\newpage
## Denmark: An addressing commons with impact


\newpage
## Denmark: An addressing commons with impact
* Geocoded address infrastructure
* Defined the semantics of purpose
* what is an address
* Open data
* an address commons
* The re-use statistics are staggering:
* 70% of deliveries are to the private sector,
* 20% are to central government
* 10% are to municipalities.
* Benefits:
* Efficiencies
* No duplication
* Improved confidence
* Known quality
A credible service providing a mutlitude of efficiencies (@_addressing_2012, pp.50 - 54)
\newpage
# UK Addressing
## Geoplace - Formal
](https://www.geoplace.co.uk/documents/10181/67776/NAG+infographic/835d83a5-e2d8-4a26-bc95-c857b315490a?t=1434370410424)
* GeoPlace is a limited liability partnership owned equally by the [Local Government Association](http://www.local.gov.uk/) and [Ordnance Survey](http://www.ordnancesurvey.co.uk/).
* It has built a synchronised database containing spatial address data from
* 348 local authorities in England and Wales (the *Local Land and Property Gazetteers* (LLPG) which cumulatively create the *National Land and Property Gazetteer* (NLPG)),
* Royal Mail,
* Valuation Office Agency and
* Ordnance Survey datasets.
* The NAG Hub database is owned by GeoPlace and is the authoritative single source of government-owned national spatial address information, containing over 225 million data records relating to about 34 million address features. GeoPlace is a production organisation with no product sales or supply operations.
* The NAG is made available to public and private sector customers through Ordnance Survey’s [AddressBase](http://www.ordnancesurvey.co.uk/business-and-government/products/addressbase.html) products.
\newpage
## The AddressBase Family

* The National Address Gazetteer Hub database is owned by GeoPlace and is claimed to be *the authoritative single source of government-owned national spatial address information*, containing over 225 million data records relating to about 34 million address features.
* Each address has its own *Unique Property Reference Number* (UPRN). The AddressBase suite have been designed to integrate into the [Ordnance Survey MasterMap suite of products](http://www.ordnancesurvey.co.uk/business-and-government/products/mastermap-products.html).
AddressBase is available at three levels of granularity (lite, plus and premium).
* AB+ merges two address datasets together (PAF and Local Authority) to provide the best available view of addresses currently defined by Local Authorities, giving many advantages over AddressBase.
* AB+ lets you link additional information to a single address, place it on a map, and carry out spatial analysis that enables improved business practices.
* Geoplace argue that further value comes from additional information in the product which includes:
* A more detailed classification – allowing a better understanding of the type (e.g. Domestic, Commercial or Mixed) and function of a property (e.g. Bank or Restaurant)
* Local Authority addresses not contained within PAF – giving a more complete picture of the current addresses and properties (assuming they are in scope (see below))
* Cross reference to OS MasterMap TOIDs – allowing simple matching to OS MasterMap Address Layer 2, Integrated Transport Network or Topography Layer
* Spatial coordinates
* Unique Property Reference Number (UPRN) – which provides the ability to cross reference data with other organisations, and maintain data integrity.
* Premium includes the address lifecycle
AddressBase supports the UK Location Strategy concept of a 'core reference geography', including the key principles of the European Union INSPIRE directive, that data should only be collected once and kept where it can be maintained most effectively (see [AddressBase products user guide](http://www.ordnancesurvey.co.uk/docs/user-guides/addressbase-products-user-guide.pdf)). *It's probably worthwhile mentioning that this is not an open address layer - however, a [2104 feasibility study sponsored by the department of Business, Innovation and Skills](https://www.gov.uk/government/publications/an-open-national-address-gazetteer) included a recommendation that AddressBase lite is made openly available*.
\newpage
## Address lifecycle
](https://dl.dropboxusercontent.com/u/393477/ImageBank/ForAddresses/ABP_Lifecycle.png)
* This ability to maintain an overview of the lifecycle of address and property status means the AddressBase Premium has introduced new potential use cases.
* This has seen companies incorporating AddressBase Premium into their business systems to replace PAF or bespoke addressing frameworks - in theory the ability to authoritatively access the address lifecycle provides greater certainty for a number of business operations.
* At *United Utilites* (UU) AddressBase Premium is replacing a multitude of bespoke and PAF based addressing products.
\newpage
## [Open National Address Gazetteer](https://www.gov.uk/government/publications/an-open-national-address-gazetteer) - *informal?*
The *Department for Business, Innovation & Skills* (BIS) on the need for an [Open National Address Gazetteer](https://www.gov.uk/government/publications/an-open-national-address-gazetteer) commissioned a review of *open addressing* which was published January 2014.
. . . . .
It recommended:
* the UK Government commission an 'open' addressing product based on a variation of the 'freemium' model
* data owners elect to release a basic ('Lite') product as Open Data that leaves higher value products to be licensed
. . . . .
AddressBase Lite was proposed with an annual release cycle. Critically this contains the UPRN which could be be key for product interoperability.
* This would allow the creation of a shared interoperable address spine along the lines of the Denmark model
\newpage
## Open NAG - [*'Responses received'*](https://www.gov.uk/government/publications/an-open-national-address-gazetteer) April 2014
With the exception of the PAF advisory board and Royal Mail there was support for the BIS review across the respondants with some notable calls for the *Totally Open* option (particularly from those organisations who are not part of the Public Sector Mapping Agreement) and that the UPRN should be released under an open data licence (as a core reference data set that encourages product interoperability).
. . . . .
A number of quotes have been selected below:
\newpage
## Addresses as an Open Core Reference
>....Address data and specific locations attached to them **are part of Core Reference data sets recognised by government as a key component of our National Information Infrastructure** (as long argued by APPSI). The report published by BIS gives us **a chance to democratise access to addressing data** and meet many of the Government’s avowed intentions. We urge acceptance of Option 6 *(freemium)* or 7 *(an independent open data product)*.
**David Rhind *Chair of the Advisory Panel on Public Sector Information* **
>....**Freely available data are much more likely to be adopted** by users and embedded in operational systems. **A national register, free at the point of delivery will undoubtedly help in joining up services, increasing efficiency and reducing duplication**.
**Office of National Statistics**
\newpage
## Monopoly rent exploitation
>... we expressed concern that, for almost all other potential customers (non-public sector), **the prices are prohibitive**, and appear designed to protect OS’s existing policy of setting high prices for a small captive market, **extracting monopoly rent**.
**Keith Dugmore *Director, DUG* **
\newpage
## The benefit of current credible addresses
>**The problem of out-of-date addresses is a very significant commercial cost** for the whole of the UK and is also arguably underplayed in the report.
**Individual Respondent 3**
\newpage
## Licences
>Whatever licence the data is available under, **it must permit the data to be combined with other open data and then re-published**. ... The [Open Government Licence](http://www.nationalarchives.gov.uk/doc/open-government-licence/version/2/) fulfils this criteria, but it should be noted that the [OS OpenData Licence](http://www.ordnancesurvey.co.uk/docs/licences/os-opendata-licence.pdf) (enforced by OS on it's OS OpenData products, and via the PSMA) does not. The use of the latter would represent a significant restriction on down-stream data use, and so should be avoided.
**Individual Respondent 6**
\newpage
# Taking Stock
## Addresses are heterogeneous

In terms of:
* What they mean
* What they are used for
* Who uses them
* How they are accessed
\newpage
## Assets can have addresses
So - anything can have an address (the *Internet of Things*)
](http://joncruddas.org.uk/sites/joncruddas.org.uk/files/styles/large/public/field/image/post-box.jpg?itok=ECnzLyhZ)
\newpage
## National data silos

They have been created to solve national issues.
No unifying semantics
\newpage
##

\newpage
## Addresses are bureaucratic and costly

Severely protracted when formal/informal issues are encountered.
\newpage
## Addresses can be opaque

**transparent and reproducible?**
\newpage
## Addresses are of global significance

\newpage
## Addresses are ripe for disruption

\newpage
# Address Disruption
## Formal versus informal

\newpage
## Technology
Streets are so last century.....

* Ubiquitous GPS/GNSS
* Structured crowdsourced geo-enabled content (wikipedia, OSM)
\newpage
## Interoperability

* Will the semantic web provide address interoperabilty?
* between addressing systems
* to incorporate additional data
* VOA
* ETC
\newpage
## Globalisation

* Addressing is a **core reference geography**
* Global brands will demand (or invoke) consistent global addressing
* How will licences impact on this?
\newpage
# A new global address paradigm?
* [Amazon drone delivery in the UK requires](https://www.theguardian.com/technology/2016/jul/25/amazon-to-test-drone-delivery-uk-government)
* A new view over addressing complements streets and buildings but is geo-coded at source
* and supports accurate delivery throughout the delivery chain using a global referencing system.
Is there a universal approach which allows all avenues to be satisfied?

\newpage
## How might this look?
.
.
Requirements for a Global Address Framework
.
.
\newpage
## WGS84 algorithmic address minting

**A global addressing framework needs to be transparent and reproducible.**
**A global addressing framework should be based on a spatial reference system.**
**A global addressing framework needs to be lightweight and cheap so it can be implemented in a timely manner.**
\newpage
## Small footprint

**Ubiquitous access across platforms.**
**No dependency on internet access.**
\newpage
## Short/memorable

\newpage
## Self checking

**Improving validity and credibility of downstream business processes.**
\newpage
## Unlimited spatial recording

* What are the spatial requirements for the range of addressing options?
* [Manila has a population density of 42,857 people per square km](http://en.wikipedia.org/wiki/List_of_cities_proper_by_population_density).
* [Map Kibera](http://mapkibera.org/) and OSM has revolutionised service delivery in Kibera (Kenya).
* Address Kibera could do the same thing for citizenship.
**A global addressing framework should meet the needs of the rural, urban, formal and informal communities equally.**
\newpage
## Open and interoperable

\newpage
## Open and interoperable
> the lack of a consistent and transparent legal and policy framework for sharing spatial data continues to be an additional roadblock.
@pomfret_spatial_2010
**A global addressing framework should be open or available with as few barriers as possible.**
\newpage
## Indoor use and 3D

Incorporating wifi-triangulation - *individual room* addressing and navigation.
Seamless integration with BIM and CityGML.
*Addressing isn't only about buildings - think about the Internet of Things*
\newpage
## Inherent geo-statistical aggregation (spatially scalable)

GIS free multi-scale analysis and reporting during disaster scenarios.
\newpage
# Utility address concepts
* A means of communicating location to third parties in a way **they** understand.
* Delivery
* Contract engineer
* Incident reporting
* Hence, addresses are all about sharing
* We need to *buy into* disambiguating stakeholder semantics
* Democratise the infrastructure
* Democratise re-use
* Everything is mediated by a human in the information exchange
* Everyone has their own semantics
* Formal and vernacular geographies
\newpage
## Addresses mediate space
In business systems addresses are bridge a between technology stacks and social systems.

\newpage
## Addresses mediate space
In business systems addresses are bridge a between technology stacks and social systems.

* Challenges
* find an unambiguous way to encode these different address types across the enterprise (and/or as part of an open initiative)
* find ways to dynamically transform these address so that each end-user community get the most appropriate address be they:
* formal addresses
* vernacular (informal) addresses
* Postal address
* Asset location
\newpage
* Most people in the UK think of an address as a *postal address*
* This is a mindset we should be trying to break
* A delivery address is only one facet to an address
* What do addresses enable
* Services
* Postal services
* Utility services
* etc
* Routing
* Vehicle navigation
* People navigation
* Asset/Infrastructure management
* Information integration
* Lifecycle
* Geodemographics
* Hence, addressing information covers a range of requirements:
* Semantic
* GIS
* Database
* Challenges
* find an unambiguous way to encode these different address types across the enterprise (and/or as part of an open initiative)
* find ways to dynamically transform these address so that each end-user community get the most appropriate address be they:
* formal addresses
* vernacular (informal) addresses
* Postal address
* Asset location
\newpage
In terms of assets two things spring to mind -
1. we no longer need streets and buildings to provide an address.
* GNSS already does this globally.
* The challenge is to translate GNSS into something appropriate for other services
1. The Access point/Delivery point metaphor used by Royal Mail may be important for traction
* solving the last 100m problem (or location of local drone delivery depot)

\newpage
# Current utility addressing?
## A shared view over addressing?

\newpage
## A shared view over addressing?
Not really....
* ABP isn’t a silver bullet
* Subset of required ‘formal - delivery’ addresses
* Mis-match in terms of assets
* Why does a sewage works not have an address when a post-box does?
* Not plug and play
* Lag in the system - the lifecycle feedback does not have credibility for time critical applications.
* The co-ordinating spine is not freely available (under a permissive licence)
* Inset areas - an aglomoration of 'addresses'
* VOA link is a cludge

\newpage
## Addresses should mediate systems
* Bridge the gap between a building focussed 2d view of the world and the 3d world in which we inhabit.
* Harmonise the edge cases relationships between UPRNs and VOAs

\newpage
## Issues about ABP
* Users over a barrel
* Needed to buy ABP as AL2 was being removed
* Data model change
* a hostage to someone else's data model
* Lifecycle benefit not being realised (at least not for utilities)
* Altough utilities have a significant value add
* Update frequency
* Different view of property hierarchy
* 2d and 3d metaphors against VOA
* a better 2.5 view of the world would be appreciated.
* Licences do not encourage re-use and innovation
\newpage
## This begs the question
> Why should utilities replace a functional bespoke address system with an address framework (ABP) that does not meet all their business requirements?
This creates a paradox when products like AddressBase are stipulated in Government policy documents (such as OpenWater)
How can this gap be bridged? Can *open addresses* help?
**Addresses need to be fit-for-purpose for the end user**
\newpage
# Future Addressing
## What do Utilities need from an Open Address infrastructure
> Ant Beck will talk about how addresses are employed within United Utilities: from bespoke addressing, to the current implementation of Geoplace’s Address Base.
>**The current approach to addressing hinders effective market activities so consideration is given to how Open approaches can disrupt the addressing landscape and improve utility services.**
* Should this simply emulate Address Base Premium?
* No
* Like Denmark should it exploit technological developments to be:
* More robust
* Improve use case
* More flexible
# Future Addressing
## What do Utilities need from an Open Address infrastructure
* Should it embrace technological development to make operational activities more efficient
* Use disruptive technologies to facilitate geo-coded addressing of assets in a flexible and credible manner
* How can such an infrastructure interoperate with other formal and informal sources to provide benefits
* What licence would a service be under.
* OS licence? -**No - it is restrictive**
* The point is to encourage:
* adoption
* engagement
* re-use
> We would like to see an *open address infrastructure* in the UK **provide a platform for 21st Century addressing**
> It should **not simply aim to emulate ABP** - there are other use cases
\newpage
## What can Utilities bring to Open Addresses
* A credible publisher of addressing updates under open licences providing:
* additional content
* improved lifecycle information
* expanded use cases
* improving confidence and credibility
* Critical lifecycle data updates
* potentially faster than local government (lag is critical to some users).
\newpage
## What can Open Addresses bring to Utilities
* Fill the gap of formal and informal addresses
* But share a common reference Spine
* UPRN?
* But what about the 3d world
* Add value
* Link to different geoaddressing paradigm
* W3W
* GeoHash
* etc.
* Linked data?
* Property life-cycle?
* Spatially consistent
* Crowd enhanced
* Service innovation
* enhanced business intelligence from shared knowledge
* geo-demographics protecting the disenfranchised
* who are our sensitive customers - what are their needs?
\newpage
# Final thoughts
Utilities have the potential to be:
* Key consumers of open addressing data
* Key providers of open addressing content
**United Utilities would like to help frame this debate and be part of any solution.**
\newpage
# References
| true |
code
| 0.555194 | null | null | null | null |
|
# Which is the fastest axis of an array?
I'd like to know: which axes of a NumPy array are fastest to access?
```
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
```
## A tiny example
```
a = np.arange(9).reshape(3, 3)
a
' '.join(str(i) for i in a.ravel(order='C'))
' '.join(str(i) for i in a.ravel(order='F'))
```
## A seismic volume
```
volume = np.load('data/F3_volume_3x3_16bit.npy')
volume.shape
```
Let's look at how the indices vary:
```
idx = np.indices(volume.shape)
idx.shape
```
We can't easily look at the indices for 190 × 190 × 190 samples (6 859 000 samples). So let's look at a small subset: 5 × 5 × 5 = 125 samples. We can make a plot of how the indices vary in each direction. For C-ordering, the indices on axis 0 vary slowly: they start at 0 and stay at 0 for 25 samples; then they increment by one. So if we ask for all the data for which axis 0 has index 2 (say), the computer just has to retrieve a contiguous chunk of memory and it gets all the samples.
On the other hand, if we ask for all the samples for which axis 2 has index 2, we have to retrieve non-contiguous samples from memory, effectively opening a lot of memory 'drawers' and taking one pair of socks out of each one.
```
from matplotlib.font_manager import FontProperties
annot = ['data[2, :, :]', 'data[:, 2, :]', 'data[:, :, 2]']
mono = FontProperties()
mono.set_family('monospace')
fig, axs = plt.subplots(ncols=3, figsize=(15,3), facecolor='w')
for i, ax in enumerate(axs):
data = idx[i, :5, :5, :5].ravel(order='C')
ax.plot(data, c=f'C{i}')
ax.scatter(np.where(data==2), data[data==2], color='r', s=10, zorder=10)
ax.text(65, 4.3, f'axis {i}', color=f'C{i}', size=15, ha='center')
ax.text(65, -0.7, annot[i], color='red', size=12, ha='center', fontproperties=mono)
ax.set_ylim(-1, 5)
_ = plt.suptitle("C order", size=18)
plt.savefig('/home/matt/Pictures/3d-array-corder.png')
fig, axs = plt.subplots(ncols=3, figsize=(15,3), facecolor='w')
for i, ax in enumerate(axs):
data = idx[i, :5, :5, :5].ravel(order='F')
ax.plot(data, c=f'C{i}')
ax.scatter(np.where(data==2), data[data==2], color='r', s=10, zorder=10)
ax.text(65, 4.3, f'axis {i}', color=f'C{i}', size=15, ha='center')
ax.text(65, -0.7, annot[i], color='red', size=12, ha='center', fontproperties=mono)
ax.set_ylim(-1, 5)
_ = plt.suptitle("Fortran order", size=18)
plt.savefig('/home/matt/Pictures/3d-array-forder.png')
```
At the risk of making it more confusing, it might help to look at the plots together. Shown here is the C ordering:
```
plt.figure(figsize=(15,3))
plt.plot(idx[0, :5, :5, :5].ravel(), zorder=10)
plt.plot(idx[1, :5, :5, :5].ravel(), zorder=9)
plt.plot(idx[2, :5, :5, :5].ravel(), zorder=8)
```
This organization is reflected in `ndarray.strides`, which tells us how many bytes must be traversed to get to the next index in each axis. Each 2-byte step through memory gets me to the next index in axis 2, but I must strude 72200 bytes to get to the next index of axis 0:
```
volume.strides
```
## Aside: figure for blog post
```
fig, axs = plt.subplots(ncols=2, figsize=(10,3), facecolor='w')
for i, ax in enumerate(axs):
data = idx[i, :3, :3, 0].ravel(order='C')
ax.plot(data, 'o-', c='gray')
ax.text(0, 1.8, f'axis {i}', color='gray', size=15, ha='left')
plt.savefig('/home/matt/Pictures/2d-array-corder.png')
```
## Accessing the seismic data
Let's make all the dimensions the same, to avoid having to slice later. I'll make a copy, otherwise we'll have a view of the original array.
Alternatively, change the shape here to see effect of small dimensions, eg try `volume = volume[:10, :290, :290]` with C ordering.
```
volume = volume[:190, :190, :190].copy()
def get_slice_3d(volume, x, axis, n=None):
"""
Naive function... but only works on 3 dimensions.
NB Using ellipses slows down last axis.
"""
# Force cube shape
if n is None and not np.sum(np.diff(volume.shape)):
n = np.min(volume.shape)
if axis == 0:
data = volume[x, :n, :n]
if axis == 1:
data = volume[:n, x, :n]
if axis == 2:
data = volume[:n, :n, x]
return data + 1
%timeit get_slice_3d(volume, 150, axis=0)
%timeit get_slice_3d(volume, 150, axis=1)
%timeit get_slice_3d(volume, 150, axis=2)
```
Let's check that changing the memory layout to Fortran ordering makes the last dimension fastest:
```
volumef = np.asfortranarray(volume)
%timeit get_slice_3d(volumef, 150, axis=0)
%timeit get_slice_3d(volumef, 150, axis=1)
%timeit get_slice_3d(volumef, 150, axis=2)
```
Axes 0 and 1 are > 10 times faster than axis 2.
What about if we do something like take a Fourier transform over the first axis?
```
from scipy.signal import welch
%timeit s = [welch(tr, fs=500) for tr in volume[:, 10]]
%timeit s = [welch(tr, fs=500) for tr in volumef[:, 10]]
```
No practical difference. Hm.
I'm guessing this is because the DFT takes way longer than the data access.
```
del(volume)
del(volumef)
```
## Fake data in _n_ dimensions
Let's make a function to generate random data in any number of dimensions.
Be careful: these volumes get big really quickly!
```
def makend(n, s, equal=True, rev=False, fortran=False):
"""
Make an n-dimensional hypercube of randoms.
"""
if equal:
incr = np.zeros(n, dtype=int)
elif rev:
incr = list(reversed(np.arange(n)))
else:
incr = np.arange(n)
shape = incr + np.ones(n, dtype=int)*s
a = np.random.random(shape)
m = f"Shape: {tuple(shape)} "
m += f"Memory: {a.nbytes/1e6:.0f}MB "
m += f"Order: {'F' if fortran else 'C'}"
print (m)
if fortran:
return np.asfortranarray(a)
else:
return a
```
I tried implementing this as a context manager, so you wouldn't have to delete the volume each time after using it. I tried the `@contextmanager` decorator, and I tried making a class with `__enter__()` and `__exit__()` methods. Each time, I tried putting the `del` command as part of the exit routine. They both worked fine... except they did not delete the volume from memory.
## 2D data
```
def get_slice_2d(volume, x, axis, n=None):
"""
Naive function... but only works on 2 dimensions.
"""
if n is None and not np.sum(np.diff(volume.shape)):
n = np.min(volume.shape)
if axis == 0:
data = volume[x, :n]
if axis == 1:
data = volume[:n, x]
return data + 1
dim = 2
v = makend(dim, 6000, fortran=False)
for n in range(dim):
%timeit get_slice_2d(v, 3001, n)
del v
dim = 2
v = makend(dim, 6000, fortran=True)
for n in range(dim):
%timeit get_slice_2d(v, 3001, n)
del v
```
This has been between 3.3 and 12 times faster.
## 1D convolution on an array
```
def convolve(data, kernel=np.arange(10), axis=0):
func = lambda tr: np.convolve(tr, kernel, mode='same')
return np.apply_along_axis(func, axis=axis, arr=data)
dim = 2
v = makend(dim, 6000, fortran=False)
%timeit convolve(v, axis=0)
%timeit convolve(v, axis=1)
del v
dim = 2
v = makend(dim, 6000, fortran=True)
%timeit convolve(v, axis=0)
%timeit convolve(v, axis=1)
del v
```
Speed is double on fast axis, i.e. second axis on default C order.
## `np.mean()` across axes
Let's try taking averages across different axes. In C order it should be faster to get the `mean` on `axis=1` because that involves getting the rows:
```
a = [[ 2, 4],
[10, 20]]
np.mean(a, axis=0), np.mean(a, axis=1)
```
Let's see how this looks on our data:
```
dim = 2
v = makend(dim, 6000, fortran=False)
%timeit np.mean(v, axis=0)
%timeit np.mean(v, axis=1)
del v
dim = 2
v = makend(dim, 6000, fortran=True)
%timeit np.mean(v, axis=0)
%timeit np.mean(v, axis=1)
del v
```
We'd expect the difference to be even more dramatic with `median` because it has to sort every row or column:
```
v = makend(dim, 6000, fortran=False)
%timeit np.median(v, axis=0)
%timeit np.median(v, axis=1)
del v
v = makend(dim, 6000, fortran=False)
%timeit v.mean(axis=0)
%timeit v.mean(axis=1)
del v
```
## 3D arrays
In a nutshell:
C order: first axis is fastest, last axis is slowest; factor of two between others.
Fortran order: last axis is fastest, first axis is slowest; factor of two between others.
```
dim = 3
v = makend(dim, 600)
for n in range(dim):
%timeit get_slice_3d(v, 201, n)
del v
```
Non-equal axes doesn't matter.
```
dim = 3
v = makend(dim, 600, equal=False, rev=True)
for n in range(dim):
%timeit get_slice_3d(v, 201, n)
del v
```
Fortran order results in a fast last axis, as per. But the middle axis is pretty fast too.
```
dim = 3
v = makend(dim, 600, fortran=True)
for n in range(dim):
%timeit get_slice_3d(v, 201, n)
del v
```
For C ordering, the last dimension is more than 20x slower than the other two.
## 4 dimensions
Axes 0 and 1 are fast (for C ordering), axis 2 is half speed, axis 3 is ca. 15 times slower than fast axis.
```
def get_slice_4d(volume, x, axis, n=None):
"""
Naive function... but only works on 4 dimensions.
"""
if n is None and not np.sum(np.diff(volume.shape)):
n = np.min(volume.shape)
if axis == 0:
data = volume[x, :n, :n, :n]
if axis == 1:
data = volume[:n, x, :n, :n]
if axis == 2:
data = volume[:n, :n, x, :n]
if axis == 3:
data = volume[:n, :n, :n, x]
return data + 1
dim = 4
v = makend(dim, 100, equal=True)
for n in range(dim):
%timeit get_slice_4d(v, 51, n)
del v
dim = 4
v = makend(dim, 100, equal=True, fortran=True)
for n in range(dim):
%timeit get_slice_4d(v, 51, n)
del v
```
## 5 dimensions
We are taking 4-dimensional hyperplanes from a 5-dimensional hypercube.
Axes 0 and 1 are fast, axis 2 is half speed, axis 3 is quarter speed, and the last axis is about 5x slower than that.
```
def get_slice_5d(volume, x, axis, n=None):
"""
Naive function... but only works on 5 dimensions.
"""
if n is None and not np.sum(np.diff(volume.shape)):
n = np.min(volume.shape)
if axis == 0:
data = volume[x, :n, :n, :n, :n]
if axis == 1:
data = volume[:n, x, :n, :n, :n]
if axis == 2:
data = volume[:n, :n, x, :n, :n]
if axis == 3:
data = volume[:n, :n, :n, x, :n]
if axis == 4:
data = volume[:n, :n, :n, :n, x]
return data + 1
dim = 5
v = makend(dim, 40)
for n in range(dim):
%timeit get_slice_5d(v, 21, n)
del v
dim = 5
v = makend(dim, 40, fortran=True)
for n in range(dim):
%timeit get_slice_5d(v, 21, n)
del v
```
What about when we're doing something like getting the mean on an array?
```
dim = 5
v = makend(dim, 40, fortran=True)
for n in range(dim):
%timeit np.mean(v, axis=n)
del v
```
## 6 dimensions and beyond
In general, first _n_/2 dimensions are fast, then gets slower until last dimension is several (5-ish) times slower than the first.
```
def get_slice_6d(volume, x, axis, n=None):
"""
Naive function... but only works on 6 dimensions.
"""
if n is None and not np.sum(np.diff(volume.shape)):
n = np.min(volume.shape)
if axis == 0:
data = volume[x, :n, :n, :n, :n, :n]
if axis == 1:
data = volume[:n, x, :n, :n, :n, :n]
if axis == 2:
data = volume[:n, :n, x, :n, :n, :n]
if axis == 3:
data = volume[:n, :n, :n, x, :n, :n]
if axis == 4:
data = volume[:n, :n, :n, :n, x, :n]
if axis == 5:
data = volume[:n, :n, :n, :n, :n, x]
return data + 1
dim = 6
v = makend(dim, 23)
for n in range(dim):
%timeit get_slice_6d(v, 12, n)
del v
```
| true |
code
| 0.4112 | null | null | null | null |
|
# Demonstration notebook for the Pulse of the City project.
In this notebook, you will find examples of how to run the scripts and obtain results from the pedestrian traffic prediction, as well as the spatial interpolation and visualisation systems.
** Index: **
1. [Part 1: Predicting pedestrian traffic](#Part-1:-Predicting-pedestrian-traffic)
2. [Part 2: Spatial interpolation and visualisation](#Part-2:-Spatial-interpolation-and-visualisation)
---
# Part 1: Predicting pedestrian traffic
An example of getting predictions from the prediction module and making use of them.
Import and initialise the predictor object.
```
# Import the predictor class into your workspace
import Predictor
# Initialise the predictor object
predictor = Predictor.Predictor()
```
Generate predictions for a certain timeframe
- Make sure the date-time string is in `yyyy-mm-ddTHH:MM:SS` format.
- First and second parameters define the start and the end of the requested time frame (start included, end excluded from the interval).
```
# Generate the predictions for a specific time frame
predictions = predictor.predict_timeframe("2020-01-11T12:00:00", "2020-01-11T14:00:00")
print(predictions)
```
##### NOTE: these predictions are stored as a pandas dataframe,
So, you can use all of the included functionality with it, such as saving it to a `.csv` file with `predictions.to_csv("<filename>.csv")`
---
As you can see, not passing the optional `request_ids` parameter results in predictions for all modelled locations.
If you only want to generate predictions for a certain location, you can do the following:
```
# Print the list of modelled locations with their IDs
Predictor.dump_names()
# Find the ID(s) of location(s) you wish to predict for and include a list of them for the `request_ids` parameter.
ids = [0, 11, 17]
predictions_specific = predictor.predict_timeframe("2020-01-11T12:00:00", "2020-01-11T14:00:00", ids)
# NOTE: even if you are predicting for one location, you will need to pass it as an array (e.g. [5]).
print(predictions_specific)
```
---
As you may have noticed, the prediction dataframe contains 3 columns for each location: `low`, `mid` and `high`. These colums represent the prediction **together with the limits of the confidence interval**:
- `low` is the lower bound of the confidence interval,
- `mid` is the prediction itself,
- `high` is the higher bound of the confidence interval.
If you do not need the confidence interval for your purpose, you can also pass an optional parameter `ci` as `False`:
```
predictions_no_ci = predictor.predict_timeframe("2020-01-11T12:00:00", "2020-01-11T14:00:00", [8, 11], ci=False)
print(predictions_no_ci)
```
---
To access the predicted values directly, convert the dataframe into an array, by doing the following:
```
pred_values = predictions_no_ci.values[:, 1:] # the '[:, 1:]' picks all rows with all but the 1st (date-time) column.
```
Then you can use standard python indexing to access any element(s) in the array:
```
print(pred_values[0, 1]) # First row, second column
print(pred_values[0]) # First row, all columns
print(pred_values[:, 1]) # All rows, second column
```
**If you are using the confidence interval**, to parse the predictions, do the following:
```
# (setting up a new prediction dataframe for demonstration)
predictions = predictor.predict_timeframe("2020-01-11T09:00:00", "2020-01-11T21:00:00", [0, 11])
print(predictions)
# Get the IDs of columns that contain the different components of the predictions:
dataframe_ids = Predictor.get_prediction_ids(predictions)
# This matrix contains indices for each type of prediction (low, mid, high).
# First row is lower bound IDs:
low_ids = dataframe_ids[0]
# Second row is the actual prediction IDs:
pred_ids = dataframe_ids[1]
# Third row is the upper bound IDs:
high_ids = dataframe_ids[2]
# Now, to get the actual values, just convert the dataframe into an array:
dataframe_values = predictions.values
# Here, we do not remove the date-time column, as that will be taken care of by the IDs.
# And now you can access whichever values you wish:
# To get only the actual predictions:
prediction_values = dataframe_values[:, pred_ids] # NOTE: 1st index is the time index, ':' takes all rows.
print("Predictions: \n" + str(prediction_values))
# Works the same way with lower or upper bounds:
high_values = dataframe_values[:, high_ids]
low_values = dataframe_values[:, low_ids]
print("Highs: \n" + str(high_values))
print("Lows: \n" + str(low_values))
```
## Now you can use these values for anything you like!
### Example: plotting the curve
```
# import the plotting library
from matplotlib import pyplot as plt
# Create a new figure
plt.figure(figsize = (15, 7))
plt.title("Pedestrian count prediction")
# Plot the prediction curves:
# 1st column in the prediction values stores predictions for location 0 - Plein 1944 primark:West
plt.plot(prediction_values[:, 0], label = "Plein 1944 primark:West")
# 2nd column is for location 11 - Kop Molenstraat:Molenstraat
plt.plot(prediction_values[:, 1], label = "Kop Molenstraat:Molenstraat")
# Add the confidence interval as a coloured area between lows and highs:
# For Plein 1944 primark:West:
plt.fill_between(
range(12), # X axis indices for the area - in this case, we fill the whole range of 12 predictions
list(low_values[:, 0]), # Lower bound of the area to fill
list(high_values[:, 0]), # Higher bound of the area to fill
alpha = 0.1 # Making the area transparent.
)
# For Kop Molenstraat:Molenstraat:
plt.fill_between(
range(12),
list(low_values[:, 1]),
list(high_values[:, 1]),
alpha = 0.1
)
# You can use the date-time column values as x tick labels
plt.xticks(range(12), predictions.values[:, 0], rotation=20)
# Set the name of axes
plt.xlabel("Time")
plt.ylabel("Predicted pedestrian count")
# Add a legend
plt.legend()
# Show the figure
plt.show()
```
---
# Part 2: Spatial interpolation and visualisation
An example of using the spatial interpolation module of the project.
Import and initialise the interpolator object
```
# Import the interpolator class into your workspace
import Interpolator
# Initialise the interpolator object.
# The parameter of the initialisation determines the resolution scale of the interpolation
# 1.0 - 100% - 1600x950
# 0.5 - 50% - 800x475, etc.
interpolator = Interpolator.Interpolator(1.0)
```
Now, you can either:
1. Interpolate a prediction for a certain date and hour:
```
# The resulting image is saved in Images/Interpolation.png by default
# if you would like to change the name of the resulting image, pass an optional parameter 'filename' with the chosen name:
interpolator.interpolate_predict("2020-01-15T13:00:00", filename="Demo1")
```
Or
2. Interpolate your own array of data from the 42 locations (e.g. actual observations, pulled from the Numina API).
```
# For demonstration purposes, array of 42 random values will be interpolated:
# Generate 42 random values with numpy's random library
import numpy as np
values = np.random.uniform(0, 2500, 42)
# Interpolate these values and visualise them on the map:
interpolator.interpolate_data(values, filename="Demo2")
```
## Thank you for using my project and good luck!
**Made by:** *Domantas Giržadas, 2020*
| true |
code
| 0.610076 | null | null | null | null |
|
## Estimating the coefficient of a regression model via scikit-learn
```
'''
loading the dataset
'''
from data import load_data
import numpy as np
from sklearn.preprocessing import StandardScaler
df = load_data()
X = df[['RM']].values
y = df['MEDV'].values
sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()
'''
train the Linear Regressor
'''
from sklearn.linear_model import LinearRegression
slr = LinearRegression()
slr.fit(X, y)
print('Slope: %.3f' % slr.coef_[0])
print('Intercept: %.3f' % slr.intercept_)
import os
import matplotlib.pyplot as plt
def lin_regplot(X, y, model, name=''):
plt.scatter(X, y, c='blue')
plt.plot(X, model.predict(X), color='red')
return plt
# plt.xlabel('Average number of rooms [RM] (standardized)')
# plt.ylabel('Price in $1000\'s [MEDV] (standardized)')
# plt.show()
# if not os.path.exists(os.path.join(os.getcwd(), 'figures')):
# os.mkdir('figures')
# plt.savefig('./figures/%s.png' % (name), dpi=100)
# plt.gcf().clear()
'''
plot a graph to compare with the results of our LinearRegression class
'''
p = lin_regplot(X, y, slr, 'plotting-sklearn-linear-reg')
plt.xlabel('Average number of rooms [RM] (standardized)')
plt.ylabel('Price in $1000\'s [MEDV] (standardized)')
plt.show()
plt.gcf().clear()
```
## Fitting a robust regression model using RANSAC
__RANdom SAmple Consensus (RANSAC)__ algorithm, fits a regression model to a subset of the data, the so-called _inliers_, thus eliminating the impact of _outliers_ on the prediction model.
```
from sklearn.linear_model import RANSACRegressor
ransac = RANSACRegressor(LinearRegression(),
max_trials=100,
min_samples=50,
residual_metric=lambda x: np.sum(np.abs(x), axis=1),
residual_threshold=5.0,
random_state=0)
ransac.fit(X, y)
'''
plot the inliers and outliers obtained from RANSAC
'''
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)
line_X = np.arange(3, 10, 1)
line_y_ransac = ransac.predict(line_X[:, np.newaxis])
plt.scatter(X[inlier_mask], y[inlier_mask],
c='blue', marker='o', label='Inliers')
plt.scatter(X[outlier_mask], y[outlier_mask],
c='lightgreen', marker='s', label='Outliers')
plt.plot(line_X, line_y_ransac, color='red')
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.legend(loc='upper left')
plt.show()
# plt.savefig('./figures/ransac-plot.png', dpi=120)
plt.gcf().clear()
print('Slope: %.3f' % ransac.estimator_.coef_[0])
print('Intercept: %.3f' % ransac.estimator_.intercept_)
```
## Evaluating the performance of linear regression models
We will now use all variables in the dataset and train a multiple regression model
```
'''
load data and train regressor
'''
from sklearn.model_selection import train_test_split
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
'''
Time to plot
------------
Since our model uses multiple explanatory variables, we can't visualize the linear
regression line in a two-dimensional plot, but we can plot the residuals versus the
predicted values to diagnose our regression model.
'''
plt.scatter(y_train_pred, y_train_pred - y_train,
c='blue', marker='o', label='Training Data')
plt.scatter(y_test_pred, y_test_pred - y_test,
c='lightgreen', marker='s', label='Test Data')
plt.xlabel('Predicted values')
plt.ylabel('Residulas')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red')
plt.xlim([-10, 50])
plt.show()
# plt.savefig('./figures/preds-vs-residuals.png', dpi=120)
plt.gcf().clear()
```
## Training a linear regression into a curve - polynomial regression
We will now discuss how to use the PolynomialFeatures transformer class from scikit-learn to add a quadratic term ( d = 2 ) to a simple regression problem with one explanatory variable, and compare the polynomial to the linear fit.
```
'''
testing polynomial regression
on random dummy data.
'''
# 1. Add a second degree polynomial term
from sklearn.preprocessing import PolynomialFeatures
X = np.array([258.0, 270.0, 294.0,
320.0, 342.0, 368.0,
396.0, 446.0, 480.0,
586.0])[:, np.newaxis]
y = np.array([236.4, 234.4, 252.8,
298.6, 314.2, 342.2,
360.8, 368.0, 391.2,
390.8])
lr = LinearRegression()
pr = LinearRegression()
quadratic = PolynomialFeatures(degree=2)
X_quad = quadratic.fit_transform(X)
# 2. Fit a simple linear regression model for compqarison
lr.fit(X, y)
X_fit = np.arange(250, 600, 10)[:, np.newaxis]
y_lin_fit = lr.predict(X_fit)
# 3. Fit a multiple regression model on the transformed features for
# polynomial regression:
pr.fit(X_quad, y)
y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))
# Plot the results
plt.scatter(X, y, label='training points')
plt.plot(X_fit, y_lin_fit,
label='linear fit', linestyle='--')
plt.plot(X_fit, y_quad_fit,
label='quadratic fit')
plt.legend(loc='upper left')
# plt.savefig('./figures/linear-vs-quad.png', dpi=120)
plt.show()
plt.gcf().clear()
'''
Finding MSE and R^2 score.
'''
from sklearn.metrics import mean_squared_error,\
r2_score
y_lin_pred = lr.predict(X)
y_quad_pred = pr.predict(X_quad)
print('Training MSE linear: %.3f, quadratic: %.3f' % (
mean_squared_error(y, y_lin_pred),
mean_squared_error(y, y_quad_pred)))
print('Training R^2 linear: %.3f, quadratic: %.3f' % (
r2_score(y, y_lin_pred),
r2_score(y, y_quad_pred)))
```
## Modeling nonlinear relationships in the Housing Dataset
We will model the relationship between house prices and LSTAT (percent lower status of the population) using second degree (quadratic) and third degree (cubic) polynomials and compare it to a linear fit.
```
X = df[['LSTAT']].values
y = df['MEDV'].values
regr = LinearRegression()
# create polynomial features
quadratic = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
X_quad = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)
# linear fit
X_fit = np.arange(X.min(), X.max(), 1)[:, np.newaxis]
regr = regr.fit(X, y)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y, regr.predict(X))
# quadratic fit
regr = regr.fit(X_quad, y)
y_quad_fit = regr.predict(quadratic.fit_transform(X_fit))
quad_r2 = r2_score(y, regr.predict(X_quad))
# cubic fit
regr = regr.fit(X_cubic, y)
y_cubic_fit = regr.predict(cubic.fit_transform(X_fit))
cubic_r2 = r2_score(y, regr.predict(X_cubic))
# Plotting results
plt.scatter(X, y,
label='training points',
color='lightgray')
plt.plot(X_fit, y_lin_fit,
label='linear (d=1), $R^2=%.2f$'%linear_r2,
color='blue',
lw=2,
linestyle=':')
plt.plot(X_fit, y_quad_fit,
label='linear (d=1), $R^2=%.2f$'%quad_r2,
color='red',
lw=2,
linestyle='-')
plt.plot(X_fit, y_cubic_fit,
label='linear (d=1), $R^2=%.2f$'%cubic_r2,
color='green',
lw=2,
linestyle='--')
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.legend(loc='upper right')
# plt.savefig('./figures/polynomial-reg-plot.png', dpi=120)
plt.show()
plt.gcf().clear()
```
__Note:__ Polynomial features are not always the best choice for modelling nonlinear relationships.<br>
_For example_, just by looking at __MEDV-LSTAT__ scatterplot, we could propose that a log transformation of the __LSTAT__ feature and the square root of __MEDV__ may project the data onto a linear feature space suitable for linear regression fit.
```
"""Let's test the above hypothesis"""
# transform features
X_log = np.log(X)
y_sqrt = np.sqrt(y)
# fit features
X_fit = np.arange(X_log.min() - 1,
X_log.max() + 1,
1)[:, np.newaxis]
regr = regr.fit(X_log, y_sqrt)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y_sqrt, regr.predict(X_log))
# plot results
plt.scatter(X_log, y_sqrt,
label='training points',
color='lightgray')
plt.plot(X_fit, y_lin_fit,
label='linear (d=1), $R^2=%.2f$' % linear_r2,
color='blue',
lw=2)
plt.xlabel('log(% lower status of the population [LSTAT])')
plt.ylabel('$\sqrt{Price \; in \; \$1000\'s [MEDV]}$')
plt.legend(loc='lower left')
plt.show()
# plt.savefig('./figures/log-sqrt-tranform-plot.png', dpi=120)
plt.clf()
plt.close('all')
```
## Decision tree regression
To use a decision tree for regression, we will replace entropy as the impurity measure of a node `t` by the MSE
```
from sklearn.tree import DecisionTreeRegressor
X = df[['LSTAT']].values
y = df['MEDV'].values
tree = DecisionTreeRegressor(max_depth=3)
tree.fit(X, y)
sort_idx = X.flatten().argsort()
lin_regplot(X[sort_idx], y[sort_idx], tree)
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.show()
# plt.savefig('./figures/decision-tree-regression.png', dpi=120)
plt.gcf().clear()
```
## Random forest regression
The random forest algorithm is an ensemble technique that combines multiple decision trees. A random forest usually has a better generalization performance than an individual decision tree due to randomness that helps to
decrease the model variance.
```
"""
let's use all the features in the Housing Dataset to fit a random forest regression model on 60 percent of the samples and evaluate its performance
on the remaining 40 percent.
"""
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = \
train_test_split(X, y,
test_size=0.4,
random_state=1)
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=1000,
criterion='mse',
random_state=1,
n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)
"""evaluating performance via MSE AND R^2 score"""
print('MSE train: %.3f, test: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
plt.scatter(y_train_pred,
y_train_pred - y_train,
c='black',
marker='o',
s=35,
alpha=0.5,
label='Training data')
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='lightgreen',
marker='s',
s=35,
alpha=0.7,
label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red')
plt.xlim([-10, 50])
plt.show()
# plt.savefig('./figures/random-forest-plot.png', dpi=120)
plt.gcf().clear()
```
| true |
code
| 0.786669 | null | null | null | null |
|
## Scaling to Minimum and Maximum values - MinMaxScaling
Minimum and maximum scaling squeezes the values between 0 and 1. It subtracts the minimum value from all the observations, and then divides it by the value range:
X_scaled = (X - X.min / (X.max - X.min)
```
import pandas as pd
# dataset for the demo
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
# the scaler - for min-max scaling
from sklearn.preprocessing import MinMaxScaler
# load the the Boston House price data
# this is how we load the boston dataset from sklearn
boston_dataset = load_boston()
# create a dataframe with the independent variables
data = pd.DataFrame(boston_dataset.data,
columns=boston_dataset.feature_names)
# add target
data['MEDV'] = boston_dataset.target
data.head()
# let's separate the data into training and testing set
X_train, X_test, y_train, y_test = train_test_split(data.drop('MEDV', axis=1),
data['MEDV'],
test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
# set up the scaler
scaler = MinMaxScaler()
# fit the scaler to the train set, it will learn the parameters
scaler.fit(X_train)
# transform train and test sets
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# the scaler stores the maximum values of the features, learned from train set
scaler.data_max_
# tthe scaler stores the minimum values of the features, learned from train set
scaler.min_
# the scaler also stores the value range (max - min)
scaler.data_range_
# let's transform the returned NumPy arrays to dataframes
X_train_scaled = pd.DataFrame(X_train_scaled, columns=X_train.columns)
X_test_scaled = pd.DataFrame(X_test_scaled, columns=X_test.columns)
import matplotlib.pyplot as plt
import seaborn as sns
# let's compare the variable distributions before and after scaling
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 5))
# before scaling
ax1.set_title('Before Scaling')
sns.kdeplot(X_train['RM'], ax=ax1)
sns.kdeplot(X_train['LSTAT'], ax=ax1)
sns.kdeplot(X_train['CRIM'], ax=ax1)
# after scaling
ax2.set_title('After Min-Max Scaling')
sns.kdeplot(X_train_scaled['RM'], ax=ax2)
sns.kdeplot(X_train_scaled['LSTAT'], ax=ax2)
sns.kdeplot(X_train_scaled['CRIM'], ax=ax2)
plt.show()
# let's compare the variable distributions before and after scaling
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 5))
# before scaling
ax1.set_title('Before Scaling')
sns.kdeplot(X_train['AGE'], ax=ax1)
sns.kdeplot(X_train['DIS'], ax=ax1)
sns.kdeplot(X_train['NOX'], ax=ax1)
# after scaling
ax2.set_title('After Min-Max Scaling')
sns.kdeplot(X_train_scaled['AGE'], ax=ax2)
sns.kdeplot(X_train_scaled['DIS'], ax=ax2)
sns.kdeplot(X_train_scaled['NOX'], ax=ax2)
plt.show()
```
| true |
code
| 0.710735 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/ayulockin/Explore-NFNet/blob/main/Train_Basline_Cifar10.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
* This is the baseline notebook to setup training a ResNet20 model on Cifar10 dataset.
* Horizontal Flip and Rotation is used as augmentation policy. Albumentation package is used to do the same.
# 🧰 Setups, Installations and Imports
```
%%capture
!pip install wandb --upgrade
!pip install albumentations
!git clone https://github.com/ayulockin/Explore-NFNet
import tensorflow as tf
print(tf.__version__)
import tensorflow_datasets as tfds
import sys
sys.path.append("Explore-NFNet")
import os
import cv2
import numpy as np
from functools import partial
import matplotlib.pyplot as plt
# Imports from the cloned repository
from models.resnet import resnet_v1
from models.mini_vgg import get_mini_vgg
# Augmentation related imports
import albumentations as A
# Seed everything for reproducibility
def seed_everything():
# Set the random seeds
os.environ['TF_CUDNN_DETERMINISTIC'] = '1'
np.random.seed(hash("improves reproducibility") % 2**32 - 1)
tf.random.set_seed(hash("by removing stochasticity") % 2**32 - 1)
seed_everything()
# Avoid TensorFlow to allocate all the GPU at once.
# Ref: https://www.tensorflow.org/guide/gpu
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
try:
# Currently, memory growth needs to be the same across GPUs
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
logical_gpus = tf.config.experimental.list_logical_devices('GPU')
print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPUs")
except RuntimeError as e:
# Memory growth must be set before GPUs have been initialized
print(e)
import wandb
from wandb.keras import WandbCallback
wandb.login()
DATASET_NAME = 'cifar10'
IMG_HEIGHT = 32
IMG_WIDTH = 32
NUM_CLASSES = 10
SHUFFLE_BUFFER = 1024
BATCH_SIZE = 1024
EPOCHS = 100
AUTOTUNE = tf.data.experimental.AUTOTUNE
print(f'Global batch size is: {BATCH_SIZE}')
```
# ⛄ Download and Prepare Dataset
```
(train_ds, val_ds, test_ds), info = tfds.load(name=DATASET_NAME,
split=["train[:85%]", "train[85%:]", "test"],
with_info=True,
as_supervised=True)
@tf.function
def preprocess(image, label):
# preprocess image
image = tf.cast(image, tf.float32)
image = image/255.0
return image, label
# Define the augmentation policies. Note that they are applied sequentially with some probability p.
transforms = A.Compose([
A.HorizontalFlip(p=0.7),
A.Rotate(limit=30, p=0.7)
])
# Apply augmentation policies.
def aug_fn(image):
data = {"image":image}
aug_data = transforms(**data)
aug_img = aug_data["image"]
return aug_img
@tf.function
def apply_augmentation(image, label):
aug_img = tf.numpy_function(func=aug_fn, inp=[image], Tout=tf.float32)
aug_img.set_shape((IMG_HEIGHT, IMG_WIDTH, 3))
return aug_img, label
train_ds = (
train_ds
.shuffle(SHUFFLE_BUFFER)
.map(preprocess, num_parallel_calls=AUTOTUNE)
.map(apply_augmentation, num_parallel_calls=AUTOTUNE)
.batch(BATCH_SIZE)
.prefetch(AUTOTUNE)
)
val_ds = (
val_ds
.map(preprocess, num_parallel_calls=AUTOTUNE)
.batch(BATCH_SIZE)
.prefetch(AUTOTUNE)
)
test_ds = (
test_ds
.map(preprocess, num_parallel_calls=AUTOTUNE)
.batch(BATCH_SIZE)
.prefetch(AUTOTUNE)
)
def show_batch(image_batch, label_batch):
plt.figure(figsize=(10,10))
for n in range(25):
ax = plt.subplot(5,5,n+1)
plt.imshow(image_batch[n])
# plt.title(f'{np.argmax(label_batch[n].numpy())}')
plt.title(f'{label_batch[n].numpy()}')
plt.axis('off')
image_batch, label_batch = next(iter(train_ds))
show_batch(image_batch, label_batch)
print(image_batch.shape, label_batch.shape)
```
# 🐤 Model
```
def GetModel(use_bn):
return resnet_v1((IMG_HEIGHT, IMG_WIDTH, 3), 20, num_classes=NUM_CLASSES, use_bn=use_bn) ## Returns a ResNet20 model.
tf.keras.backend.clear_session()
test_model = GetModel(use_bn=True)
test_model.summary()
print(f"Total learnable parameters: {test_model.count_params()/1e6} M")
```
# 📲 Callbacks
```
earlystopper = tf.keras.callbacks.EarlyStopping(
monitor='val_loss', patience=10, verbose=0, mode='auto',
restore_best_weights=True
)
reducelronplateau = tf.keras.callbacks.ReduceLROnPlateau(
monitor="val_loss", factor=0.5,
patience=3, verbose=1
)
```
# 🚋 Train with W&B
```
tf.keras.backend.clear_session()
# Intialize model
model = GetModel(use_bn=True)
model.compile('adam', 'sparse_categorical_crossentropy', metrics=['acc'])
# Intialize W&B run
run = wandb.init(entity='ayush-thakur', project='nfnet', job_type='train-baseline')
# Train model
model.fit(train_ds,
epochs=EPOCHS,
validation_data=val_ds,
callbacks=[WandbCallback(),
reducelronplateau,
earlystopper])
# Evaluate model on test set
loss, acc = model.evaluate(test_ds)
wandb.log({'Test Accuracy': round(acc, 3)})
# Close W&B run
run.finish()
```
| true |
code
| 0.675176 | null | null | null | null |
|
# Output part of infinite matter dataframe as LaTeX table
This notebook generates Tables II and III in the Appendix of _Quantifying uncertainties and correlations in the nuclear-matter equation of state_ by [BUQEYE](https://buqeye.github.io/) members Christian Drischler, Jordan Melendez, Dick Furnstahl, and Daniel Phillips (see [[arXiv:2004.07805]](https://arxiv.org/abs/2004.07805)).
Data is read in from nuclear matter calculations (both SNM and PNM) and outputs total energies at each EFT order as a function of both density and Fermi momentum in the form of LaTeX tables. It uses pandas to manipulate the data and dump it to LaTeX. The details are easily modified.
```
%load_ext autoreload
%autoreload 2
import pandas as pd
import numpy as np
```
## Data import and processing
The calculations for infinite matter are stored in a standardized csv file in the data directory. Both symmetric nuclear matter (SNM) and pure neutron matter (PNN) are included. The fields in the file are
| field | units | description |
| :---: | :---: | :---- |
| kf | $$\text{fm}^{-1}$$ | Fermi momentum. |
| n | $$\text{fm}^{-3}$$ | Density. |
| Kin | MeV | Kinetic energy. |
| MBPT_HF | MeV | Hartree-Fock energy (leading order in MBPT). |
| MBPT_2 | MeV | 2nd-order contribution in MBPT (not total). |
| MBPT_3 | MeV | 3rd-order contribution in MBPT (not total). |
| MBPT_4 | MeV | 4th-order contribution in MBPT (not total). |
| total | MeV | Total energy (sum of all contributions). |
| Lambda | MeV | Regulator parameter.
| OrderEFT | | Order of the EFT: LO, NLO, N2LO, N3LO |
| Body | | Two-body only (NN) or two-plus-three (NN+3N)
| x | | Proton fraction: 0.5 is SNM; 0.0 is PNM.
| fit | | Index for the fit.
The following is commented code from another notebook that identifies the indexes for fits from arXiv:1710.08220.
```
# EFT orders LO, NLO, N2LO, N3LO
#orders = np.array([0, 2, 3, 4]) # powers of Q
# body = 'NN-only'
# body = 'NN+3N'
# Lambda = 450
# Specify by index what fits will be used for the 3NF [N2LO, N3LO]
# The indices follow the fits in Fig. 3 of arXiv:1710.08220
# fits = {450: [1, 7], 500: [4, 10]}
# fits_B = {450: [2, 8], 500: [5, 11]}
# fits_C = {450: [3, 9], 500: [6, 12]}
# Replace the following with the path to the desired data file
data_file = '../data/all_matter_data.csv'
# Read infinite matter data from specified csv file into a dataframe df
df = pd.read_csv(data_file)
# Make copies of the dataframe for experiments
df_kin = df.copy()
df_all = df.copy()
# Convert differences to total energy prediction at each MBPT order
#mbpt_orders = ['Kin', 'MBPT_HF', 'MBPT_2', 'MBPT_3', 'MBPT_4']
#df[mbpt_orders] = df[mbpt_orders].apply(np.cumsum, axis=1)
```
### Replacements in column names or values
These are minor fixes to the files that we fix by hand.
```
df = df.replace({'OrderEFT' : 'NLO'}, 'N1LO') # makes columns align correctly
# We notice some truncation problems we fix by hand.
df = df.replace({'kf' : 0.904594}, 0.904590) # fix a truncation difference
df = df.replace({'kf' : 0.961274}, 0.961270) # fix a truncation difference
# For our basic tables we only need the 'total' column, so delete the other energies.
pop_list = ['Kin', 'MBPT_HF', 'MBPT_2', 'MBPT_3', 'MBPT_4']
for col in pop_list:
df.pop(col)
# check it
df
def dump_to_file(df, output_file, kf_column='snm'):
"""
Output adjusted dataframe to a file in LaTeX format for tables.
Modify the format here or generalize for different looks.
"""
with open(output_file, 'w') as of:
of.write('% description\n')
of.write(df.to_latex(
index=False,
formatters={'LO':'${:,.2f}$'.format,
'N1LO':'${:,.2f}$'.format,
'N2LO':'${:,.2f}$'.format,
'N3LO':'${:,.2f}$'.format,
'kf_snm':'${:,.2f}$'.format},
columns=['n', kf_column, 'LO', 'N1LO', 'N2LO', 'N3LO'],
escape=False
))
Lambdas = (450, 500)
for Lambda in Lambdas:
s_Lambda = (df['Lambda']==Lambda)
# s_x = (df['x']==0.5) | (df['x']==0.0)
s_x_SNM = df['x']==0.5 # select SNM (proton fraction 1/2)
s_x_PNM = df['x']==0.0 # select PNM (proton fraction 0)
s_Body = df['Body']=='NN+3N' # 'NN+3N' or 'NN-only'
s_n = True # df['n']==0.5 # could select a subset of densities
# For the 'fit', the LO and NLO values are NaN, so use pd.isna
if Lambda == 450:
s_fit = df['fit'].isin([1.0, 7.0]) | pd.isna(df['fit'])
elif Lambda == 500:
s_fit = df['fit'].isin([4.0, 10.0]) | pd.isna(df['fit'])
# Make a table just for SNM and a specified Lamba
df_SNM = df.loc[s_Lambda & s_x_SNM & s_Body & s_n & s_fit ]
df_SNM.pop('x') # we don't want 'x' anymore
df_SNM = df_SNM.rename(columns={"kf": "kf_snm"})
# Make a table just for PNM and a specified Lamba
df_PNM = df.loc[s_Lambda & s_x_PNM & s_Body & s_n & s_fit ]
df_PNM.pop('x') # we don't want 'x' anymore
df_PNM = df_PNM.rename(columns={"kf": "kf_pnm"})
# Check the tables
df_SNM
# Pivoting here means to take the row entries for OrderEFT and make them columns
df_SNM_pivoted = df_SNM.pivot_table(values='total', columns='OrderEFT',
index=('n','kf_snm')).reset_index()
df_PNM_pivoted = df_PNM.pivot_table(values='total', columns='OrderEFT',
index=('n','kf_pnm')).reset_index()
SNM_output_file = f'SNM_table_Lambda{Lambda}.tex'
dump_to_file(df_SNM_pivoted, SNM_output_file, kf_column='kf_snm')
PNM_output_file = f'PNM_table_Lambda{Lambda}.tex'
dump_to_file(df_PNM_pivoted, PNM_output_file, kf_column='kf_pnm')
```
| true |
code
| 0.364014 | null | null | null | null |
|
Lambda School Data Science
*Unit 2, Sprint 1, Module 4*
---
# Logistic Regression
- do train/validate/test split
- begin with baselines for classification
- express and explain the intuition and interpretation of Logistic Regression
- use sklearn.linear_model.LogisticRegression to fit and interpret Logistic Regression models
Logistic regression is the baseline for classification models, as well as a handy way to predict probabilities (since those too live in the unit interval). While relatively simple, it is also the foundation for more sophisticated classification techniques such as neural networks (many of which can effectively be thought of as networks of logistic models).
### Setup
Run the code cell below. You can work locally (follow the [local setup instructions](https://lambdaschool.github.io/ds/unit2/local/)) or on Colab.
Libraries:
- category_encoders
- numpy
- pandas
- scikit-learn
```
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Linear-Models/master/data/'
!pip install category_encoders==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
```
# Do train/validate/test split
## Overview
### Predict Titanic survival 🚢
Kaggle is a platform for machine learning competitions. [Kaggle has used the Titanic dataset](https://www.kaggle.com/c/titanic/data) for their most popular "getting started" competition.
Kaggle splits the data into train and test sets for participants. Let's load both:
```
import pandas as pd
train = pd.read_csv(DATA_PATH+'titanic/train.csv')
test = pd.read_csv(DATA_PATH+'titanic/test.csv')
```
Notice that the train set has one more column than the test set:
```
train.shape, test.shape
```
Which column is in train but not test? The target!
```
set(train.columns) - set(test.columns)
```
### Why doesn't Kaggle give you the target for the test set?
#### Rachel Thomas, [How (and why) to create a good validation set](https://www.fast.ai/2017/11/13/validation-sets/)
> One great thing about Kaggle competitions is that they force you to think about validation sets more rigorously (in order to do well). For those who are new to Kaggle, it is a platform that hosts machine learning competitions. Kaggle typically breaks the data into two sets you can download:
>
> 1. a **training set**, which includes the _independent variables,_ as well as the _dependent variable_ (what you are trying to predict).
>
> 2. a **test set**, which just has the _independent variables._ You will make predictions for the test set, which you can submit to Kaggle and get back a score of how well you did.
>
> This is the basic idea needed to get started with machine learning, but to do well, there is a bit more complexity to understand. **You will want to create your own training and validation sets (by splitting the Kaggle “training” data). You will just use your smaller training set (a subset of Kaggle’s training data) for building your model, and you can evaluate it on your validation set (also a subset of Kaggle’s training data) before you submit to Kaggle.**
>
> The most important reason for this is that Kaggle has split the test data into two sets: for the public and private leaderboards. The score you see on the public leaderboard is just for a subset of your predictions (and you don’t know which subset!). How your predictions fare on the private leaderboard won’t be revealed until the end of the competition. The reason this is important is that you could end up overfitting to the public leaderboard and you wouldn’t realize it until the very end when you did poorly on the private leaderboard. Using a good validation set can prevent this. You can check if your validation set is any good by seeing if your model has similar scores on it to compared with on the Kaggle test set. ...
>
> Understanding these distinctions is not just useful for Kaggle. In any predictive machine learning project, you want your model to be able to perform well on new data.
### 2-way train/test split is not enough
#### Hastie, Tibshirani, and Friedman, [The Elements of Statistical Learning](http://statweb.stanford.edu/~tibs/ElemStatLearn/), Chapter 7: Model Assessment and Selection
> If we are in a data-rich situation, the best approach is to randomly divide the dataset into three parts: a training set, a validation set, and a test set. The training set is used to fit the models; the validation set is used to estimate prediction error for model selection; the test set is used for assessment of the generalization error of the final chosen model. Ideally, the test set should be kept in a "vault," and be brought out only at the end of the data analysis. Suppose instead that we use the test-set repeatedly, choosing the model with the smallest test-set error. Then the test set error of the final chosen model will underestimate the true test error, sometimes substantially.
#### Andreas Mueller and Sarah Guido, [Introduction to Machine Learning with Python](https://books.google.com/books?id=1-4lDQAAQBAJ&pg=PA270)
> The distinction between the training set, validation set, and test set is fundamentally important to applying machine learning methods in practice. Any choices made based on the test set accuracy "leak" information from the test set into the model. Therefore, it is important to keep a separate test set, which is only used for the final evaluation. It is good practice to do all exploratory analysis and model selection using the combination of a training and a validation set, and reserve the test set for a final evaluation - this is even true for exploratory visualization. Strictly speaking, evaluating more than one model on the test set and choosing the better of the two will result in an overly optimistic estimate of how accurate the model is.
#### Hadley Wickham, [R for Data Science](https://r4ds.had.co.nz/model-intro.html#hypothesis-generation-vs.hypothesis-confirmation)
> There is a pair of ideas that you must understand in order to do inference correctly:
>
> 1. Each observation can either be used for exploration or confirmation, not both.
>
> 2. You can use an observation as many times as you like for exploration, but you can only use it once for confirmation. As soon as you use an observation twice, you’ve switched from confirmation to exploration.
>
> This is necessary because to confirm a hypothesis you must use data independent of the data that you used to generate the hypothesis. Otherwise you will be over optimistic. There is absolutely nothing wrong with exploration, but you should never sell an exploratory analysis as a confirmatory analysis because it is fundamentally misleading.
>
> If you are serious about doing an confirmatory analysis, one approach is to split your data into three pieces before you begin the analysis.
#### Sebastian Raschka, [Model Evaluation](https://sebastianraschka.com/blog/2018/model-evaluation-selection-part4.html)
> Since “a picture is worth a thousand words,” I want to conclude with a figure (shown below) that summarizes my personal recommendations ...
<img src="https://sebastianraschka.com/images/blog/2018/model-evaluation-selection-part4/model-eval-conclusions.jpg" width="600">
Usually, we want to do **"Model selection (hyperparameter optimization) _and_ performance estimation."** (The green box in the diagram.)
Therefore, we usually do **"3-way holdout method (train/validation/test split)"** or **"cross-validation with independent test set."**
### What's the difference between Training, Validation, and Testing sets?
#### Brandon Rohrer, [Training, Validation, and Testing Data Sets](https://end-to-end-machine-learning.teachable.com/blog/146320/training-validation-testing-data-sets)
> The validation set is for adjusting a model's hyperparameters. The testing data set is the ultimate judge of model performance.
>
> Testing data is what you hold out until very last. You only run your model on it once. You don’t make any changes or adjustments to your model after that. ...
## Follow Along
> You will want to create your own training and validation sets (by splitting the Kaggle “training” data).
Do this, using the [sklearn.model_selection.train_test_split](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html) function:
## Challenge
For your assignment, you'll do a 3-way train/validate/test split.
Then next sprint, you'll begin to participate in a private Kaggle challenge, just for your cohort!
You will be provided with data split into 2 sets: training and test. You will create your own training and validation sets, by splitting the Kaggle "training" data, so you'll end up with 3 sets total.
# Begin with baselines for classification
## Overview
We'll begin with the **majority class baseline.**
[Will Koehrsen](https://twitter.com/koehrsen_will/status/1088863527778111488)
> A baseline for classification can be the most common class in the training dataset.
[*Data Science for Business*](https://books.google.com/books?id=4ZctAAAAQBAJ&pg=PT276), Chapter 7.3: Evaluation, Baseline Performance, and Implications for Investments in Data
> For classification tasks, one good baseline is the _majority classifier,_ a naive classifier that always chooses the majority class of the training dataset (see Note: Base rate in Holdout Data and Fitting Graphs). This may seem like advice so obvious it can be passed over quickly, but it is worth spending an extra moment here. There are many cases where smart, analytical people have been tripped up in skipping over this basic comparison. For example, an analyst may see a classification accuracy of 94% from her classifier and conclude that it is doing fairly well—when in fact only 6% of the instances are positive. So, the simple majority prediction classifier also would have an accuracy of 94%.
## Follow Along
Determine majority class
What if we guessed the majority class for every prediction?
#### Use a classification metric: accuracy
[Classification metrics are different from regression metrics!](https://scikit-learn.org/stable/modules/model_evaluation.html)
- Don't use _regression_ metrics to evaluate _classification_ tasks.
- Don't use _classification_ metrics to evaluate _regression_ tasks.
[Accuracy](https://scikit-learn.org/stable/modules/model_evaluation.html#accuracy-score) is a common metric for classification. Accuracy is the ["proportion of correct classifications"](https://en.wikipedia.org/wiki/Confusion_matrix): the number of correct predictions divided by the total number of predictions.
What is the baseline accuracy if we guessed the majority class for every prediction?
## Challenge
In your assignment, your Sprint Challenge, and your upcoming Kaggle challenge, you'll begin with the majority class baseline. How quickly can you beat this baseline?
# Express and explain the intuition and interpretation of Logistic Regression
## Overview
To help us get an intuition for *Logistic* Regression, let's start by trying *Linear* Regression instead, and see what happens...
## Follow Along
### Linear Regression?
```
train.describe()
# 1. Import estimator class
from sklearn.linear_model import LinearRegression
# 2. Instantiate this class
linear_reg = LinearRegression()
# 3. Arrange X feature matrices (already did y target vectors)
features = ['Pclass', 'Age', 'Fare']
X_train = train[features]
X_val = val[features]
# Impute missing values
from sklearn.impute import SimpleImputer
imputer = SimpleImputer()
X_train_imputed = imputer.fit_transform(X_train)
X_val_imputed = imputer.transform(X_val)
# 4. Fit the model
linear_reg.fit(X_train_imputed, y_train)
# 5. Apply the model to new data.
# The predictions look like this ...
linear_reg.predict(X_val_imputed)
# Get coefficients
pd.Series(linear_reg.coef_, features)
test_case = [[1, 5, 500]] # 1st class, 5-year old, Rich
linear_reg.predict(test_case)
```
### Logistic Regression!
```
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver='lbfgs')
log_reg.fit(X_train_imputed, y_train)
print('Validation Accuracy', log_reg.score(X_val_imputed, y_val))
# The predictions look like this
log_reg.predict(X_val_imputed)
log_reg.predict(test_case)
log_reg.predict_proba(test_case)
# What's the math?
log_reg.coef_
log_reg.intercept_
# The logistic sigmoid "squishing" function, implemented to accept numpy arrays
import numpy as np
def sigmoid(x):
return 1 / (1 + np.e**(-x))
sigmoid(log_reg.intercept_ + np.dot(log_reg.coef_, np.transpose(test_case)))
```
So, clearly a more appropriate model in this situation! For more on the math, [see this Wikipedia example](https://en.wikipedia.org/wiki/Logistic_regression#Probability_of_passing_an_exam_versus_hours_of_study).
# Use sklearn.linear_model.LogisticRegression to fit and interpret Logistic Regression models
## Overview
Now that we have more intuition and interpretation of Logistic Regression, let's use it within a realistic, complete scikit-learn workflow, with more features and transformations.
## Follow Along
Select these features: `['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked']`
(Why shouldn't we include the `Name` or `Ticket` features? What would happen here?)
Fit this sequence of transformers & estimator:
- [category_encoders.one_hot.OneHotEncoder](http://contrib.scikit-learn.org/category_encoders/onehot.html)
- [sklearn.impute.SimpleImputer](https://scikit-learn.org/stable/modules/generated/sklearn.impute.SimpleImputer.html)
- [sklearn.preprocessing.StandardScaler](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html)
- [sklearn.linear_model.LogisticRegressionCV](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegressionCV.html)
Get validation accuracy.
Plot coefficients:
Generate [Kaggle](https://www.kaggle.com/c/titanic) submission:
## Challenge
You'll use Logistic Regression for your assignment, your Sprint Challenge, and optionally for your first model in our Kaggle challenge!
# Review
For your assignment, you'll use a [**dataset of 400+ burrito reviews**](https://srcole.github.io/100burritos/). How accurately can you predict whether a burrito is rated 'Great'?
> We have developed a 10-dimensional system for rating the burritos in San Diego. ... Generate models for what makes a burrito great and investigate correlations in its dimensions.
- Do train/validate/test split. Train on reviews from 2016 & earlier. Validate on 2017. Test on 2018 & later.
- Begin with baselines for classification.
- Use scikit-learn for logistic regression.
- Get your model's validation accuracy. (Multiple times if you try multiple iterations.)
- Get your model's test accuracy. (One time, at the end.)
- Commit your notebook to your fork of the GitHub repo.
- Watch Aaron's [video #1](https://www.youtube.com/watch?v=pREaWFli-5I) (12 minutes) & [video #2](https://www.youtube.com/watch?v=bDQgVt4hFgY) (9 minutes) to learn about the mathematics of Logistic Regression.
# Sources
- Brandon Rohrer, [Training, Validation, and Testing Data Sets](https://end-to-end-machine-learning.teachable.com/blog/146320/training-validation-testing-data-sets)
- Hadley Wickham, [R for Data Science](https://r4ds.had.co.nz/model-intro.html#hypothesis-generation-vs.hypothesis-confirmation), Hypothesis generation vs. hypothesis confirmation
- Hastie, Tibshirani, and Friedman, [The Elements of Statistical Learning](http://statweb.stanford.edu/~tibs/ElemStatLearn/), Chapter 7: Model Assessment and Selection
- Mueller and Guido, [Introduction to Machine Learning with Python](https://books.google.com/books?id=1-4lDQAAQBAJ&pg=PA270), Chapter 5.2.2: The Danger of Overfitting the Parameters and the Validation Set
- Provost and Fawcett, [Data Science for Business](https://books.google.com/books?id=4ZctAAAAQBAJ&pg=PT276), Chapter 7.3: Evaluation, Baseline Performance, and Implications for Investments in Data
- Rachel Thomas, [How (and why) to create a good validation set](https://www.fast.ai/2017/11/13/validation-sets/)
- Sebastian Raschka, [Model Evaluation](https://sebastianraschka.com/blog/2018/model-evaluation-selection-part4.html)
- Will Koehrsen, ["A baseline for classification can be the most common class in the training dataset."](https://twitter.com/koehrsen_will/status/1088863527778111488)
| true |
code
| 0.565539 | null | null | null | null |
|
```
from pyspark.conf import SparkConf
from pyspark.sql import SparkSession
from pyspark.sql.functions import *
from pyspark.sql.types import BooleanType, IntegerType
from datetime import *
from settings import obtener_timestamp, obtener_dia_semana
""" Configuramos Spark """
conf = SparkConf()
conf.setAppName("ProcesamientoDatos")
conf.setMaster("local[*]")
spark = SparkSession.builder.config(conf=conf).getOrCreate()
```
Leemos los datos procesados del archivo guardado
```
data = spark.read.format('parquet').load('./../datos/processed/full.parquet/')
data.printSchema()
tiempo_fin = obtener_timestamp("2013-01-01", "01:30")
tiempo_inicio = tiempo_fin - timedelta(minutes=30)
```
### Consulta 1: Rutas frequentes
En esta primera búsqueda lo que vamos a obtener es las 10 rutas más frecuentes durante los 30 minutos anteriores. Estas rutas contarán únicamente si el viaje ha sido completado, es decir, si el usuario se ha bajado del taxi. La salida de la consulta será la siguiente:
hora_subida, hora_bajada, celda_subida_1, celda_bajada_1, ..., celda_subida_10, celda_bajada_10, tiempo_ejecucion
```
mejor = data.filter(data.hora_subida <= tiempo_fin) \
.filter(data.hora_subida >= tiempo_inicio) \
.filter(data.hora_bajada <= tiempo_fin) \
.filter(data.hora_bajada >= tiempo_inicio) \
.groupBy("cuad_longitud_subida", "cuad_latitud_subida", "cuad_longitud_bajada", "cuad_latitud_bajada") \
.count().orderBy(desc("count"))
mejor = mejor.take(10)
mejor
```
### Consulta 1B: Rutas frequentes
En esta primera búsqueda lo que vamos a obtener es las 10 rutas más frecuentes en los dias de una semana durante los 30 minutos anteriores a una fecha dada. Estas rutas contarán únicamente si el viaje ha sido completado, es decir, si el usuario se ha bajado del taxi. La salida de la consulta será la siguiente:
hora_subida, hora_bajada, celda_subida_1, celda_bajada_1, ..., celda_subida_10, celda_bajada_10, tiempo_ejecucion
```
dia_elegido = obtener_dia_semana("Lunes")
```
Debido a diversas limitaciones de spark utilizamos variables globales para hacer las limitaciones de tiempo
```
hora_fin = datetime.strptime("00:30:00", "%H:%M:%S")
hora_inicio = (hora_fin - timedelta(minutes=30))
def comparar_hora(hora):
"""
Metodo que filtra las horas de los registros para que concuerden
con las horas de busqueda deseada
:param hora: Timestamp completo
:return: True si las horas del timestamp estan entre las deseadas
False si lo contrario
"""
if hora.time() <= hora_fin.time() and hora.time() >= hora_inicio.time():
return True
return False
def relevancia(fecha):
"""
Metodo que da mas relevancia a los viajes mas cercanos a la
fecha de busqueda deseada.
Si la diferencia es menor a un mes de la fecha
dada los registros tienen más relevancia
:param fecha: Timestamp completo
:return: 2 si el viaje esta cerca de la fecha deseada, 1 si no
"""
diferencia = fecha - tiempo_fin
if diferencia < timedelta(days=30) and diferencia > timedelta(days=-30):
return 2
else:
return 1
comprobar_hora = udf(comparar_hora, BooleanType())
calcular_relevancia = udf(relevancia, IntegerType())
filtered = data.filter(data.dia_semana == dia_elegido) \
.filter(comprobar_hora(data.hora_subida)) \
.filter(comprobar_hora(data.hora_bajada)) \
.withColumn('relevancia', calcular_relevancia(data.hora_subida))
frequent = filtered.groupBy("cuad_longitud_subida", "cuad_latitud_subida", \
"cuad_longitud_bajada", "cuad_latitud_bajada") \
.sum("relevancia") \
.select(col("cuad_longitud_subida"), col("cuad_latitud_subida"), \
col("cuad_longitud_bajada"), col("cuad_latitud_bajada"), \
col("sum(relevancia)").alias("frecuencia")) \
.orderBy("frecuencia", ascending=False)
filtered.show()
mes = "06"
hora = "15:00"
HORA_FIN = datetime.strptime(mes + " " + hora, "%m %H:%M")
print(HORA_FIN)
```
| true |
code
| 0.407746 | null | null | null | null |
|
# Guide
## Quick-start
Let's import our package and define two small lists that we would like to compare in similarity
```
from polyfuzz import PolyFuzz
from_list = ["apple", "apples", "appl", "recal", "house", "similarity"]
to_list = ["apple", "apples", "mouse"]
```
Then, we instantiate our PolyFuzz model and choose `TF-IDF` as our similarity measure. We matche the two lists and
check the results.
**NOTE**: We can also use `EditDistance` and `Embeddings` as our matchers.
```
model = PolyFuzz("TF-IDF").match(from_list, to_list)
model.get_matches()
```
As expected, we can see high similarity between the `apple` words. Moreover, we could not find a single match for `similarity` which is why it is mapped to `None`.
#### Precision Recall Curve
Next, we would like to see how well our model is doing on our data. Although this method is unsupervised, we can use the similarity score as a proxy for the accuracy of our model (assuming we trust that similarity score).
A minimum similarity score might be used to identify when a match could be considered to be correct. For example, we can assume that if a similarity score pass 0.95 we are quite confident that the matches are correct. This minimum similarity score can be defined as **`Precision`** since it shows you how precise we believe the matches are at a minimum.
**`Recall`** can then be defined as as the percentage of matches found at a certain minimum similarity score. A high recall means that for a certain minimum precision score, we find many matches.
```
model.visualize_precision_recall(kde=True)
```
#### Group Matches
We can group the matches `To` as there might be significant overlap in strings in our `from_list`.
To do this, we calculate the similarity within strings in `from_list` and use single linkage to then group the strings with a high similarity.
```
model.group(link_min_similarity=0.75)
model.get_matches()
```
As can be seen above, we grouped `apple` and `apples` together to `apple` such that when a string is mapped to `apple` it will fall in the cluster of [`apples`, `apple`] and will be mapped to the first instance in the cluster which is `apples`.
For example, `appl` is mapped to `apple` and since `apple` falls into the cluster [`apples`, `apple`], `appl` will be mapped to `apples`.
## Multiple Models
You might be interested in running multiple models with different matchers and different parameters in order to compare the best results.
Fortunately, **`PolyFuzz`** allows you to exactly do this!
Below, you will find all models currently implemented in PolyFuzz and are compared against one another.
```
from polyfuzz.models import EditDistance, TFIDF, Embeddings, RapidFuzz
from polyfuzz import PolyFuzz
from jellyfish import jaro_winkler_similarity
from flair.embeddings import TransformerWordEmbeddings, WordEmbeddings
from_list = ["apple", "apples", "appl", "recal", "house", "similarity"]
to_list = ["apple", "apples", "mouse"]
# BERT
bert = TransformerWordEmbeddings('bert-base-multilingual-cased') # https://huggingface.co/transformers/pretrained_models.html
bert_matcher = Embeddings(bert, model_id="BERT", min_similarity=0)
# FastText
fasttext = WordEmbeddings('en-crawl')
fasttext_matcher = Embeddings(fasttext, min_similarity=0)
# TF-IDF
tfidf_matcher = TFIDF(n_gram_range=(3, 3), min_similarity=0, model_id="TF-IDF")
tfidf_large_matcher = TFIDF(n_gram_range=(3, 6), min_similarity=0)
# Edit Distance models with custom distance function
base_edit_matcher = EditDistance(n_jobs=1)
jellyfish_matcher = EditDistance(n_jobs=1, scorer=jaro_winkler_similarity)
# Edit distance with RapidFuzz --> slightly faster implementation than Edit Distance
rapidfuzz_matcher = RapidFuzz(n_jobs=1)
matchers = [bert_matcher, fasttext_matcher, tfidf_matcher, tfidf_large_matcher,
base_edit_matcher, jellyfish_matcher, rapidfuzz_matcher]
model = PolyFuzz(matchers).match(from_list, to_list)
model.visualize_precision_recall(kde=True)
```
#### Custom Grouper
We can even use one of the `polyfuzz.models` to be used as the grouper in case you would like to use something else than the standard `TF-IDF` matcher:
```
base_edit_grouper = EditDistance(n_jobs=1)
model.group(base_edit_grouper)
model.get_matches("Model 1")
model.get_clusters("Model 1")
```
## Custom Models
Although the options above are a great solution for comparing different models, what if you have developed your own? What if you want a different similarity/distance measure that is not defined in PolyFuzz? That is where custom models come in. If you follow the structure of PolyFuzz's `BaseMatcher` you can quickly implement any model you would like.
Below, we are implementing the `ratio` similarity measure from `RapidFuzz`.
```
import numpy as np
import pandas as pd
from rapidfuzz import fuzz
from polyfuzz.models import EditDistance, TFIDF, Embeddings, BaseMatcher
class MyModel(BaseMatcher):
def match(self, from_list, to_list):
# Calculate distances
matches = [[fuzz.ratio(from_string, to_string) / 100 for to_string in to_list] for from_string in from_list]
# Get best matches
mappings = [to_list[index] for index in np.argmax(matches, axis=1)]
scores = np.max(matches, axis=1)
# Prepare dataframe
matches = pd.DataFrame({'From': from_list,'To': mappings, 'Similarity': scores})
return matches
```
It is important that the `match` function takes in two lists of strings and throws out a pandas dataframe with three columns:
* From
* To
* Similarity
Then, we can simply create an instance of `MyModel` and pass it through `PolyFuzz`:
```
from_list = ["apple", "apples", "appl", "recal", "house", "similarity"]
to_list = ["apple", "apples", "mouse"]
custom_matcher = MyModel()
model = PolyFuzz(custom_matcher).match(from_list, to_list)
model.visualize_precision_recall(kde=True)
```
| true |
code
| 0.538923 | null | null | null | null |
|
```
# hide
# all_tutorial
! [ -e /content ] && pip install -Uqq mrl-pypi # upgrade mrl on colab
```
# Tutorial - RL Train Cycle Overview
>Overview of the RL training cycle
## RL Train Cycle Overview
The goal of this tutorial is to walk through the RL fit cycle to familiarize ourselves with the `Events` cycle and get a better understanding of how `Callback` and `Environment` classes work.
## Performance Notes
The workflow in this notebook is more CPU-constrained than GPU-constrained due to the need to evaluate samples on CPU. If you have a multi-core machine, it is recommended that you uncomment and run the `set_global_pool` cells in the notebook. This will trigger the use of multiprocessing, which will result in 2-4x speedups.
This notebook may run slow on Collab due to CPU limitations.
If running on Collab, remember to change the runtime to GPU
## High Level Overview
### The Environment
At the highest level, we have the `Environment` class. The `Environment` holds together several sub-modules and orchestrates them during the fit loop. The following are contained in the `Environment`:
- `agent` - This is the actual model we're training
- `template_cb` - this holds a `Template` class that we use to define our chemical space
- `samplers` - samplers generate new samples to train on
- `buffer` - the buffer collects and distributes samples from all the `samplers`
- `rewards` - rewards score samples
- `losses` - losses generate values we can backpropagate through
- `log` - the log holds a record of all samples in the training process
### Callbacks and the Event Cycle
Each one of the above items is a `Callback`. A `Callback` is a a general class that can hook into the `Environment` fit cycle at a number of pre-defined `Events`. When the `Environment` calls a specific `Event`, the event name is passed to every callback in the `Environment`. If a given `Callback` has a defined function named after the event, that function is called. This creates a very flexible system for customizing training loops.
We'll be looking more at `Events` later. For now, we'll just list them in brief. These are the events called during the RL training cycle in the order they are executed:
- `setup` - called when the `Environment` is created, used to set up values
- `before_train` - called before training is started
- `build_buffer` - draws samples from `samplers` into the `buffer`
- `filter_buffer` - filters samples in the buffer
- `after_build_buffer` - called after buffer filtering. Used for cleanup, logging, etc
- `before_batch` - called before a batch starts, used to set up the `batch state`
- `sample_batch` - samples are drawn from `sampers` and `buffer` into the `batch state`
- `before_filter_batch` - allows preprocessing of samples before filtering
- `filter_batch` - filters samples in `batch state`
- `after_sample` - used for calculating sampling metrics
- `before_compute_reward` - used to set up any values needed for reward computation
- `compute_reward` - used by `rewards` to compute rewards for all samples in the `batch state`
- `after_compute_reward` - used for logging reward metrics
- `reward_modification` - modify rewards in ways not tracked by the log
- `after_reward_modification` - log reward modification metrics
- `get_model_outputs` - generate necessary tensors from the model
- `after_get_model_outputs` - used for any processing required prior to loss calculation
- `compute_loss` - compute loss values
- `zero_grad` - zero grad
- `before_step` - used for computation before optimizer step (ie gradient clipping)
- `step` - step optimizer
- `after_batch` - compute batch stats
- `after_train` - final event after all training batches
```
import sys
sys.path.append('..')
from mrl.imports import *
from mrl.core import *
from mrl.chem import *
from mrl.templates.all import *
from mrl.torch_imports import *
from mrl.torch_core import *
from mrl.layers import *
from mrl.dataloaders import *
from mrl.g_models.all import *
from mrl.vocab import *
from mrl.policy_gradient import *
from mrl.train.all import *
from mrl.model_zoo import *
from collections import Counter
# set_global_pool(min(10, os.cpu_count()))
```
## Getting Started
We start by creating all the components we need to train a model
### Agent
The `Agent` is the actual model we want to train. For this example, we will use the `LSTM_LM_Small_ZINC` model, which is a `LSTM_LM` model trained on a chunk of the ZINC database.
The agent will actually contain two versions of the model. The main model that we will train with every update iteration, and a baseline model which is updated as an exponentially weighted moving average of the main model. Both models are used in the RL training algorithm we will set up later
```
agent = LSTM_LM_Small_ZINC(drop_scale=0.5,opt_kwargs={'lr':5e-5})
```
### Template
The `Template` class is used to conrol the chemical space. We can set parameters on what molecular properties we want to allow. For this example, we set the following:
- Hard Filters - must have qualities
- `ValidityFilter` - must be a valid chemical structure
- `SingleCompoundFilter` - samples must be single compounds
- `RotBondFilter` - compounds can have at most 8 rotatable bonds
- `ChargeFilter` - compounds must have no net charge
- Soft Filters - nice to have qualities
- `QEDFilter` - Compounds get a score bonus of +1 if their QED value is greater than 0.5
- `SAFilter` - compounds get a score bonus of + if their SA score is less than 5
We then pass the `Template` to the `TemplateCallback` which integrates the template into the fit loop. Note that we pass `prefilter=True` to the `TemplateCallback`, which ensures compounds that don't meet our hard filters are removed from training
```
template = Template([ValidityFilter(),
SingleCompoundFilter(),
RotBondFilter(None, 8),
ChargeFilter(0, 0)],
[QEDFilter(0.5, None, score=1.),
SAFilter(None, 5, score=1.)])
template_cb = TemplateCallback(template, prefilter=True)
```
### Reward
For the reward, we will load a scikit-learn linear regression model. This model was trained to predict affinity against erbB1 using molecular fingerprints as inputs
This score function is extremely simple and likely won't translate well to real affinity. It is used as a lightweight example
```
class FP_Regression_Score():
def __init__(self, fname):
self.model = torch.load(fname)
self.fp_function = partial(failsafe_fp, fp_function=ECFP6)
def __call__(self, samples):
mols = to_mols(samples)
fps = maybe_parallel(self.fp_function, mols)
fps = [fp_to_array(i) for i in fps]
x_vals = np.stack(fps)
preds = self.model.predict(x_vals)
return preds
# if in the repo
reward_function = FP_Regression_Score('../files/erbB1_regression.sklearn')
# if in Collab:
# download_files()
# reward_function = FP_Regression_Score('files/erbB1_regression.sklearn')
reward = Reward(reward_function, weight=1.)
aff_reward = RewardCallback(reward, 'aff')
```
We can think of the score function as a black box that takes in samples (SMILES strings) and returns a single numeric score for each sample. Any score function that follows this paradigm can be integrated into MRL
```
samples = ['Brc1cc2c(NCc3cccs3)ncnc2s1',
'Brc1cc2c(NCc3ccncc3)ncnc2s1']
reward_function(samples)
```
### Loss Function
For our loss, we will use the `PPO` reinforcement learning algorithm. See the [PPO](arxiv.org/pdf/1707.06347.pdf) paper for full details.
The gist of it is the loss function takes a batch of samples and directs he model to increase the probability of above-average samples (relative to the batch mean) and decrease he probability of below-average samples.
```
pg = PPO(0.99,
0.5,
lam=0.95,
v_coef=0.5,
cliprange=0.3,
v_cliprange=0.3,
ent_coef=0.01,
kl_target=0.03,
kl_horizon=3000,
scale_rewards=True)
loss = PolicyLoss(pg, 'PPO',
value_head=ValueHead(256),
v_update_iter=2,
vopt_kwargs={'lr':1e-3})
```
### Samplers
`Samplers` fill the role of generating samples to train on. We will use four samplers for this run:
- `sampler1`: `ModelSampler` - this sampler will draw samples from the main model in the `Agent`. We set `buffer_size=1000`, which means we will generate 1000 samples every time we build the buffer. We set `p_batch=0.5`, which means during training, 50% of each batch will be sampled on the fly from the main model and the rest of the batch will come from the buffer
- `sampler2`: `ModelSampler` - this sampler is the same as `sampler1`, but we draw from the baseline model instead of the main model. We set `p_batch=0.`, so this sampler will only contribute to the buffer
- `sampler3`: `LogSampler` - this sampler looks through the log of previous samples. Based on our input arguments, it grabs the top `95` percentile of samples in the log, and randomly selects `100` samples from that subset
- `sampler4`: `DatasetSampler` - this sampler is seeded wih erbB1 training data used to train the score function. This sampler will randomly select 4 samples from the dataset to add to the buffer
```
gen_bs = 1500
# if in the repo
df = pd.read_csv('../files/erbB1_affinity_data.csv')
# if in Collab
# download_files()
# df = pd.read_csv('files/erbB1_affinity_data.csv')
df = df[df.neg_log_ic50>9.2]
sampler1 = ModelSampler(agent.vocab, agent.model, 'live', 1000, 0.5, gen_bs)
sampler2 = ModelSampler(agent.vocab, agent.base_model, 'base', 1000, 0., gen_bs)
sampler3 = LogSampler('samples', 'rewards', 10, 95, 100)
sampler4 = DatasetSampler(df.smiles.values, 'erbB1_data', buffer_size=4)
samplers = [sampler1, sampler2, sampler3, sampler4]
```
### Other Callbacks
We'll add three more callbacks:
- `MaxCallback`: this will grab the max reward within a batch that came from the source `live`. `live` is the name we gave to `sampler1` above. This means the max callback will grab all outputs from `sampler1` corresponding to samples from the live model and add the largest to the batch metrics
- `PercentileCallback`: this does the same as `MaxCallback` but instead of printing the maximum score, it prints the 90th percentile score
- `NoveltyReward`: this is reward modification that gives a bonus score of `0.05` to new samples (ie samples that haven't appeared before in training)
```
live_max = MaxCallback('rewards', 'live')
live_p90 = PercentileCallback('rewards', 'live', 90)
new_cb = NoveltyReward(weight=0.05)
cbs = [new_cb, live_p90, live_max]
```
## Training Walkthrough
Now we will step through the training cycle looking at how each callback event is used
### Setup
The first event occurs when we create our `Environment` using the callbacks we set up before. Instantiating the `Environment` registers all callbacks and runs the `setup` event. Many callbacks use the `setup` event to add terms to the batch log or the metrics log.
```
env = Environment(agent, template_cb, samplers=samplers, rewards=[aff_reward], losses=[loss],
cbs=cbs)
```
Inside the environment, we just created a `Buffer` and a `Log`.
The `Buffer` holds a list of samples, which is currently empty
```
env.buffer
env.buffer.buffer
```
The `Log` holds a number of containers for tracking training outputs
- `metrics`: dictionary of batch metrics. Each key maps to a list where each value in the list is the metric term for given batch
- `batch_log`: dictionary of batch items. Each key maps to a list. Each element in that list is a list containing the batch values for that key in a given batch
- `unique_samples`: dictionary of unique samples and the rewards for those samples. Useful for looking up if a sample has been seen before
- `df`: dataframe of unique samples and all associated values stored in the `batch_log`
We can see that these log terms have already been populated during the `setup` event
```
env.log.metrics
env.log.batch_log
env.log.df
```
The keys in the above dictionaries were added by the associated callbacks. For example, look at the `setup` method in `ModelSampler`, the type of sampler we used for `sampler1`:
```
def setup(self):
if self.p_batch>0. and self.track:
log = self.environment.log
log.add_metric(f'{self.name}_diversity')
log.add_metric(f'{self.name}_valid')
log.add_metric(f'{self.name}_rewards')
log.add_metric(f'{self.name}_new')
```
We gave `sampler1` the name `live`. As a result, the terms `live_diversity`, `live_valid`, `live_rewards` and `live_new` were added to the metrics.
We can also look at the `setup` method of our loss function `loss`:
```
def setup(self):
if self.track:
log = self.environment.log
log.add_metric(self.name)
log.add_log(self.name)
```
This is responsible for the `PPO` terms in the `batch_log` and the `metrics`. The PPO metrics term will store the average PPO loss value across a batch, while the PPO batch log term will store the PPO value for each item in a batch
### The Fit Cycle
At this point, we could start training using `Environment.fit`. We could call `env.fit(200, 90, 10, 2)` to train for 10 batches with a batch size of 200. For this tutorial, we will step through each part of the fit cycle and observe what is happening
### Before Train
The first stage of the fit cycle is the `before_train` stage. This sets the batch size and sequence length based on the inputs to `Environment.fit` (which we will set manually) and prints the top of the log
```
env.bs = 200 # batch size of 200
env.sl = 90 # max sample length of 90 steps
mb = master_bar(range(1))
env.log.pbar = mb
env.report = 1
env.log.report = 1 # report stats every batch
env('before_train')
```
### Build Buffer
The next stage of the cycle is the `build_buffer` stage. This consists of the following events:
- `build_buffer`: samplers add items to the buffer
- `filter_buffer`: the buffer is filtered
- `after_build_buffer`: use as needed
Going into this stage, our buffer is empty:
```
env.buffer.buffer
```
#### build_buffer
By calling the `build_buffer` event, our samplers will add items to the buffer
```
env('build_buffer')
```
Now we have 2004 items in the buffer.
```
len(env.buffer.buffer)
```
We can use the `buffer_sources` attribute to see where each item came from. We have 1000 items from `live_buffer` which corresponds to `sampler1`, sampling from the main model.
We have 1000 items from `base_buffer` which corresponds to `sampler2`, sampling from the baseline model.
We have 4 items from `erbB1_data_buffer`, our dataset sampler (`sampler4`).
Our log sampler, `sampler3` was set to start sampling after 10 training iterations, so we don't currently have any samples from that sampler
```
Counter(env.buffer.buffer_sources)
```
#### filter_buffer
It's likely some of these samples don't match our compound requirements defined in the `Template` we used, so we want to filter the buffer for passing compounds. This is what the `filter_buffer` does. For this current example, the only callback doing any buffer filtering is the template callback. However, the `filter_buffer` can be used to implement any form of buffer filtering.
Any callback that passes a list of boolean values to `Buffer._filter_buffer` can filter the buffer.
After filtering, we have 1829 remaining samples
```
env('filter_buffer')
len(env.buffer.buffer)
Counter(env.buffer.buffer_sources)
```
#### after_build_buffer
Next is the `after_build_buffer` event. None of our current callbacks make use of this event, but it exists to allow for evaluation/postprocessing/whatever after buffer creation.
### Sample Batch
The next event stage is the `sample_batch` stage. This consists of the following events:
- `before_batch`: set up/refresh any required state prior to batch sampling
- `sample_batch`: draw one batch of samples
- `before_filter_batch`: evaluate unfiltered batch
- `filter_batch`: filter batch
- `after_sample`: compute sample based metrics
#### before_batch
This event is used to create a new `BatchState` for the environment. The batch state is a container designed to hold any values required by the batch
```
env.batch_state = BatchState()
env('before_batch')
```
Currently the batch state only has placeholder values for commonly generated terms
```
env.batch_state
```
#### sample_batch
Now we actually draw samples to form a batch. All of our `Sampler` objects have a `p_batch` value, which designated what percentage of the batch should come from that sampler. Batch sampling is designed such that individual sampler `p_batch` values are respected, and any remaining batch percentage comes from the buffer.
Only `sampler1` has `p_batch>0.`, with a value of `p_batch=0.5`. This means 50% of the batch will be sampled on he fly from `sampler1`, and the remaining 50% of the batch will come from the buffer.
Using a hybrid of live sampling and buffer sampling seems to work best. That said, it is possible to have every batch be 100% buffer samples (like offline RL), or have 100% be live samples (like online RL)
```
env('sample_batch')
```
Now we can see we've populated several terms in the batch state. `BatchState.samples` now has a list of samples. `BatchState.sources` has the source of each sample.
We also added `BatchState.live_raw` and `BatchState.base_raw`. These terms hold the outputs of `sampler1` and `sampler2`. When we filter `BatchState.samples`, we can refer to the `_raw` terms to see what samples were removed.
Note that `BatchState.base_raw` is an empty list since `sampler2.p_batch=0.`
```
env.batch_state.keys()
```
`BatchState.sources` holds the source of each sample. We have 100 samples from `live`, which corresponds to our on the fly samples from `sampler1`. The remaining 100 samples come from `live_buffer` and `base_buffer`. This means they came from either `sampler1` (live) or `sampler2` (base) by way of being sampled from the buffer
```
Counter(env.batch_state['sources'])
env.batch_state['samples'][:5]
env.batch_state['sources'][:5]
env.batch_state['live_raw'][:5]
env.batch_state['base_raw']
```
#### before_filter_batch
This event is not used by any of our current callbacks. It provides a hook to influence the batch state prior to filtering
#### filter_batch
Now the batch will be filtered by our `Template`, as well as any other callbacks with a `filter_batch` method
```
env('filter_batch')
```
We can see that 13 of our 200 samples were removed by filtering
```
len(env.batch_state['samples'])
```
We can compare the values in `BatchState.samples` and `BatchState.live_raw` to see what was filtered
```
raw_samples = env.batch_state['live_raw']
filtered_samples = [env.batch_state['samples'][i] for i in range(len(env.batch_state['samples']))
if env.batch_state.sources[i]=='live']
len(filtered_samples), len(raw_samples)
# filtered compounds
[i for i in raw_samples if not i in filtered_samples]
```
#### after_sample
The `after_sample` event is used to calculate metrics related to sampling
```
env('after_sample')
```
We can see that several values have been added to `Environment.log.metrics`
- `new`: percent of samples that have not been seen before
- `diversity`: number of unique samples relative to the number of total samples
- `bs`: true batch size after filtering
- `valid`: percent of samples that passed filtering
- `live_diversity`: number of unique samples relative to the number of total samples from `sampler1`
- `live_valid`: percent of samples that passed filtering from `sampler1`
- `live_new`: percent of samples that have not been seen before from `sampler1`
```
env.log.metrics
```
### Compute Reward
After we sample a batch, we enter the `compute_reward` stage. This consists of the following events:
- `before_compute_reward` - used to set up any values needed for reward computation
- `compute_reward` - used by `rewards` to compute rewards for all samples in the `batch state`
- `after_compute_reward` - used for logging reward metrics
- `reward_modification` - modify rewards in ways not tracked by the log
- `after_reward_modification` - log reward modification metrics
#### before_compute_reward
This event can be used to set up any values needed for reward computation. Most rewards only need the raw samples as inputs, but rewards can use other inputs if needed. The only requirement for a reward is that it returns a tensor with one value per batch item.
By default, the `Agent` class will tensorize the samples present at this step. Our `PPO` loss will also add placeholder values for the terms needed by that function
```
env('before_compute_reward')
```
A number of new items have populated the batch state
```
env.batch_state.keys()
env.batch_state.x # x tensor
env.batch_state.y # y tensor
env.batch_state.mask # padding mask
```
#### compute_reward
This step actually computes rewards. The `BatchState` has a tensor of 0s as a placeholder for reward values. Rewards will compute a numeric score for each item in the batch and add it to `BatchState.rewards`
```
env.batch_state.rewards
env('compute_reward')
env.batch_state.rewards
```
So where did these rewards come from?
One reward term comes from our `Template`. We specified soft rewards for compounds with `QED>=0.5` and `SA<=5`. Compounds could score a maximum of 2 from the template.
We also have the reward from the erbB1 regression model we set up earlier.
The specific rewards from each of these sources are logged in the `BatchState`
For the `Template`, we have `BatchState.template` and `BatchState.template_passes`
```
env.batch_state.keys()
```
Template scores:
```
env.batch_state.template
```
`BatchState.template_passes` shows which samples passed the hard filters. Since we decided to prefilter with our template earlier, all remaining samples are passing
```
env.batch_state.template_passes
```
And here we have the erbB2 regression scores
```
env.batch_state.aff
```
#### after_compute_reward
This event is used to calculate metrics on the rewards
```
env('after_compute_reward')
env.log.metrics
```
#### reward_modification
The reward modification event can be thought of as a second reward that isn't logged. The reason for including this is to allow for transient, "batch context" rewards that don't affect logged values.
When we set up our callbacks earlier, we had a term
`new_cb = NoveltyReward(weight=0.05)`
Which would add a bonus score of 0.05 to new, never before seen samples. The point of this callback is to give the model a soft incentive to generate novel samples.
We want this score to impact our current batch. However, if we treated it the same as our actual rewards, the samples would be saved into `env.log` with their scores inflated by 0.05. Later, when our `LogSampler` samples from the log, the sampling would be influenced by a score that was only supposed to be given once.
Separating out rewards and reward modifications lets us avoid this
```
env('reward_modification')
env.batch_state.novel
```
#### after_reward_modification
Similar to `after_compute_reward`, this event can be used to compute stats on reward modifications
```
env('after_reward_modification')
env.log.metrics
```
### Get Model Outputs
After computing rewards, we move to set up our loss calculation. The `get_model_outputs` stage is based on generating the values that we will be backpropagating through. This stage consists of the following events:
- `get_model_outputs` - generate necessary tensors from the model
- `after_get_model_outputs` - used for any processing required prior to loss calculation
#### get_model_outputs
This is where we generate tensor values used for loss computation.
The specifics of what happens here depends on the type of model used. For autoregressive models, this step involves taking the `x` and `y` tensors we generated during the `before_compute_reward` event and doing a forward pass.
`x` is a tensor of size `(bs, sl)`. Running `x` through the model will give a set of log probabilities of size `(bs, sl, d_vocab)`. We then use `y` to gather the relevant log probs to get a gathered log prob tensor of size `(bs, sl)`.
We generate these values from both the main model and the baseline model
```
env('get_model_outputs')
env.batch_state.keys()
env.batch_state.model_logprobs.shape, env.batch_state.model_gathered_logprobs.shape
```
#### after_get_model_outputs
This event is not used by any of our current callbacks, but can be used for any sort of post-processing needed before loss computation
### Compute Loss
Now we actually compute a loss value and do an optimizer update. See the `PPO` class for a description of the policy gradient algorithm used.
Loss computation consists of the following steps:
- `compute_loss` - compute loss values
- `zero_grad` - zero grad
- `before_step` - used for computation before optimizer step (ie gradient clipping)
- `step` - step optimizer
#### compute_loss
When we first created our `BatchState`, there was a placehoder value for `loss`. This is the value that will ulimately be backpropagated through. This means we can run any sort of loss configuration, so long as the final values end up in `BatchState.loss`.
For example, the `PPO` policy gradient algorithm we are using involved a `ValueHead` that predicts values at every time step. This model is held in the `PolicyLoss` callback that holds the `PPO` class. During the `compute_loss` event, `PPO` computes an additional loss for the value head that is added to `BatchState.loss`. `PolicyLoss` also holds an optimizer for the `ValueHead` parameters.
```
env.batch_state.loss
env('compute_loss')
env.batch_state.loss
```
#### zero_grad
This is an event to zero gradients of all optimizers in play. We currently have one optimizer in `Agent` for our generative model and one in `PolicyLoss` for the `ValueHead` of our policy gradient algorithm.
```
env('zero_grad')
env.batch_state.loss.backward()
```
#### before_step
This is an event before the actual optimizer step. This is used for things like gradient clipping
```
env('before_step')
```
#### step
This is the actual optimizer step. This will step both the `Agent` and `PolicyLoss` optimizers
```
env('step')
```
### After Batch
The `after_batch` stage consists of a single `after_batch` event. This is used for any updates at the end of the batch.
In particular, the `Log` will update `Log.df` and the `Agent` will update he baseline model
```
env('after_batch')
env.log.df
```
### After Train
The `after_train` event can be used to calculate any final statistics or other values as desired
```
env('after_train')
```
### Conclusions
Hopefully walking through the training process step by step has made he process more understandable. We conclude by simply running `Environment.fit` so we don't have to go through things step by step anymore
```
env.fit(200, 90, 50, 4)
```
| true |
code
| 0.604895 | null | null | null | null |
|
## Chemical kinetics
In chemistry one is often interested in how fast a chemical process proceeds. Chemical reactions (when viewed as single events on a molecular scale) are probabilitic. However, most reactive systems of interest involve very large numbers of molecules (a few grams of a simple substance containts on the order of $10^{23}$ molecules. The sheer number allows us to describe this inherently stochastic process deterministically.
### Law of mass action
In order to describe chemical reactions as as system of ODEs in terms of concentrations ($c_i$) and time ($t$), one can use the [law of mass action](https://en.wikipedia.org/wiki/Law_of_mass_action):
$$
\frac{dc_i}{dt} = \sum_j S_{ij} r_j
$$
where $r_j$ is given by:
$$
r_j = k_j\prod_l c_l^{R_{jl}}
$$
and $S$ is a matrix with the overall net stoichiometric coefficients (positive for net production, negative for net consumption), and $R$ is a matrix with the multiplicities of each reactant for each equation.
### Example: Nitrosylbromide
We will now look at the following (bi-directional) chemical reaction:
$$
\mathrm{2\,NO + Br_2 \leftrightarrow 2\,NOBr}
$$
which describes the equilibrium between nitrogen monoxide (NO) and bromine (Br$_2$) and nitrosyl bromide (NOBr). It can be represented as a set of two uni-directional reactions (**f**orward and **b**ackward):
$$
\mathrm{2\,NO + Br_2 \overset{k_f}{\rightarrow} 2\,NOBr} \\
\mathrm{2\,NOBr \overset{k_b}{\rightarrow} 2\,NO + Br_2}
$$
The law of mass action tells us that the rate of the first process (forward) is proportional to the concentration Br$_2$ and the square of the concentration of NO. The rate of the second reaction (the backward process) is in analogy proportional to the square of the concentration of NOBr. Using the proportionality constants $k_f$ and $k_b$ we can formulate our system of nonlinear ordinary differential equations as follows:
$$
\frac{dc_1}{dt} = 2(k_b c_3^2 - k_f c_2 c_1^2) \\
\frac{dc_2}{dt} = k_b c_3^2 - k_f c_2 c_1^2 \\
\frac{dc_3}{dt} = 2(k_f c_2 c_1^2 - k_b c_3^2)
$$
where we have denoted the concentration of NO, Br$_2$, NOBr with $c_1,\ c_2,\ c_3$ respectively.
This ODE system corresponds to the following two matrices:
$$
S = \begin{bmatrix}
-2 & 2 \\
-1 & 1 \\
2 & -2
\end{bmatrix}
$$
$$
R = \begin{bmatrix}
2 & 1 & 0 \\
0 & 0 & 2
\end{bmatrix}
$$
### Solving the initial value problem numerically
We will now integrate this system of ordinary differential equations numerically as an initial value problem (IVP) using the ``odeint`` solver provided by ``scipy``:
```
import numpy as np
from scipy.integrate import odeint
```
By looking at the [documentation](https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.integrate.odeint.html) of odeint we see that we need to provide a function which computes a vector of derivatives ($\dot{\mathbf{y}} = [\frac{dy_1}{dt}, \frac{dy_2}{dt}, \frac{dy_3}{dt}]$). The expected signature of this function is:
f(y: array[float64], t: float64, *args: arbitrary constants) -> dydt: array[float64]
in our case we can write it as:
```
def rhs(y, t, kf, kb):
rf = kf * y[0]**2 * y[1]
rb = kb * y[2]**2
return [2*(rb - rf), rb - rf, 2*(rf - rb)]
%load_ext scipy2017codegen.exercise
```
Replace **???** by the proper arguments for ``odeint``, you can write ``odeint?`` to read its documentaiton.
```
%exercise exercise_odeint.py
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(tout, yout)
_ = plt.legend(['NO', 'Br$_2$', 'NOBr'])
```
Writing the ``rhs`` function by hand for larger reaction systems quickly becomes tedious. Ideally we would like to construct it from a symbolic representation (having a symbolic representation of the problem opens up many possibilities as we will soon see). But at the same time, we need the ``rhs`` function to be fast. Which means that we want to produce a fast function from our symbolic representation. Generating a function from our symbolic representation is achieved through *code generation*.
In summary we will need to:
1. Construct a symbolic representation from some domain specific representation using SymPy.
2. Have SymPy generate a function with an appropriate signature (or multiple thereof), which we pass on to the solver.
We will achieve (1) by using SymPy symbols (and functions if needed). For (2) we will use a function in SymPy called ``lambdify``―it takes a symbolic expressions and returns a function. In a later notebook, we will look at (1), for now we will just use ``rhs`` which we've already written:
```
import sympy as sym
sym.init_printing()
y, k = sym.symbols('y:3'), sym.symbols('kf kb')
ydot = rhs(y, None, *k)
ydot
```
## Exercise
Now assume that we had constructed ``ydot`` above by applying the more general law of mass action, instead of hard-coding the rate expressions in ``rhs``. Then we could have created a function corresponding to ``rhs`` using ``lambdify``:
```
%exercise exercise_lambdify.py
plt.plot(tout, odeint(f, y0, tout, k_vals))
_ = plt.legend(['NO', 'Br$_2$', 'NOBr'])
```
In this example the gains of using a symbolic representation are arguably limited. However, it is quite common that the numerical solver will need another function which calculates the [Jacobian](https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant) of $\dot{\mathbf{y}}$ (given as Dfun in the case of ``odeint``). Writing that by hand is both tedious and error prone. But SymPy solves both of those issues:
```
sym.Matrix(ydot).jacobian(y)
```
In the next notebook we will look at an example where providing this as a function is beneficial for performance.
| true |
code
| 0.508788 | null | null | null | null |
|
# Combine datasets together
```
# Import libraries
import os #operating system
import glob # for reading multiple files
from glob import glob
import pandas as pd #pandas for dataframe management
import matplotlib.pyplot as plt #matplotlib for plotting
import matplotlib.dates as mdates # alias for date formatting
import numpy as np # for generating synthetic data
# datetime stuff
from datetime import date
import holidays
# Handle date time conversions between pandas and matplotlib
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
# Set some variables
dataPath = '../data' # set data path
year = 2019
# Define a function to read the data
def read_data(file):
# Read in excel
df = (pd.read_excel(
file,
skiprows=range(1,9),
usecols='B:C',
header=0,
))
# remove last rows
df.drop(
df.tail(2).index,
inplace=True
)
# fix index and naming
df.columns = ['date', 'demand']
df['date'] = pd.to_datetime(df['date']) # convert column to datetime
df.set_index('date', inplace=True)
return df
```
# Read all the data
```
# Create a list of files to combine
PATH = dataPath
EXT = "*.xls"
all_files = [file
for path, subdir, files in os.walk(PATH)
for file in glob(os.path.join(path, EXT))]
# Assemble files into a final dataframe
df = pd.DataFrame()
for file in all_files:
tmp = read_data(file)
dfs = [df, tmp]
df = pd.concat(dfs)
```
# Data processing
```
df.sort_index(inplace=True)
df['demand'] = df['demand'].apply(pd.to_numeric, errors='coerce')
ts_daily = df.resample('D').mean()
days = ts_daily.index.strftime("%Y-%m-%d")
ts_monthly = df.resample('M').mean()
months = ts_monthly.index.strftime("%Y-%m")
```
## Daily
```
def create_date_labels(df):
""" Function to create day labels that could be useful for plotting
"""
df['year'] = df.index.year
df['month'] = df.index.month
df['day'] = df.index.day
df['weekday'] = df.index.weekday
df['month_name'] = df.index.month_name()
df['day_name'] = df.index.day_name()
return df
ts_daily = create_date_labels(ts_daily)
```
### Filter by weekends and holidays
```
# Check the holidays resolving
brazil_holidays = holidays.Brazil()
for ptr in holidays.Brazil(years = 2019).items():
print(ptr)
# reset index and convert timestamp to date
ts_daily.reset_index(inplace=True)
ts_daily['date'] = ts_daily['date'].apply(lambda x: x.date())
ts_daily['holiday'] = ts_daily['date'].apply(lambda x: x in brazil_holidays)
ts_daily.set_index('date', inplace=True)
ts_daily.head()
# Check
ts_daily.loc[ts_daily['weekday'] < 5] # Weekday
ts_daily.loc[ts_daily['weekday'] >= 5] # Weekend
ts_daily.loc[ts_daily['holiday'] == True] # Holiday
```
# Plotting
```
import seaborn as sns # plotting library
sns.set(rc={'figure.figsize':(11, 4)})
# Basic quick plot
ts_daily['demand'].plot()
ts_daily.loc[ts_daily['month_name'] == 'January', 'demand'].plot()
# plot with more customization
cols_plot = ['demand']
timerange = '2019'
axes = ts_daily[cols_plot].plot(
marker='o',
alpha=0.5,
linestyle='-',
figsize=(14, 8),
subplots=True)
for ax in axes:
ax.set_ylabel('demand (GWh)')
ax.set_title(f'demand for {timerange}')
def plotBox(df, col='demand', grp='month_name'):
fig, ax = plt.subplots(1, 1, figsize=(14, 8), sharex=True)
sns.boxplot(data=df, x=grp, y=col, ax=ax)
ax.set_label(f'{col}')
ax.set_title(f'boxplot for year {year}')
ax.set_xlabel('')
# all data
plotBox(ts_daily, 'demand')
# Weekend
plotBox(ts_daily.loc[ts_daily['weekday'] >= 5], 'demand')
# holiday
plotBox(ts_daily.loc[ts_daily['holiday'] == True], 'demand')
# weekday
plotBox(ts_daily.loc[ts_daily['weekday'] < 5], 'demand')
plotBox(ts_daily, col='demand', grp='day_name')
```
| true |
code
| 0.492188 | null | null | null | null |
|
# Additional analyses for manuscript revisions
This notebook contains additional analyses performed for a revised version of the manuscript. In particular, two analyses are performed:
1. Determining whether there is a bias in the linear arrangement of motifs in strong enhancers and silencers.
2. Associating differentially expressed genes in Crx-/- vs. wildtype P21 retinas with the activity of nearby library members.
```
import os
import sys
import itertools
import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.axes_divider import make_axes_locatable
from pybedtools import BedTool
from IPython.display import display
sys.path.insert(0, "utils")
import fasta_seq_parse_manip, modeling, plot_utils, predicted_occupancy, sequence_annotation_processing
data_dir = "Data"
downloads_dir = os.path.join(data_dir, "Downloaded")
figures_dir = "Figures"
all_seqs = fasta_seq_parse_manip.read_fasta(os.path.join(data_dir, "library1And2.fasta"))
# Drop scrambled sequences
all_seqs = all_seqs[~(all_seqs.index.str.contains("scr"))]
plot_utils.set_manuscript_params()
```
Load in MPRA data and other metrics.
```
# Mapping activity class to a color
color_mapping = {
"Silencer": "#e31a1c",
"Inactive": "#33a02c",
"Weak enhancer": "#a6cee3",
"Strong enhancer": "#1f78b4",
np.nan: "grey"
}
color_mapping = pd.Series(color_mapping)
# Sort order for the four activity bins
class_sort_order = ["Silencer", "Inactive", "Weak enhancer", "Strong enhancer"]
# MPRA measurements
activity_df = pd.read_csv(os.path.join(data_dir, "wildtypeMutantPolylinkerActivityAnnotated.txt"), sep="\t", index_col=0)
activity_df["group_name_WT"] = sequence_annotation_processing.to_categorical(activity_df["group_name_WT"])
activity_df["group_name_MUT"] = sequence_annotation_processing.to_categorical(activity_df["group_name_MUT"])
# Only keep sequences that were measured in WT form
activity_df = activity_df[activity_df["expression_log2_WT"].notna()]
# TF occupancy metrics, also separate out the WT sequences
occupancy_df = pd.read_csv(os.path.join(data_dir, "predictedOccupancies.txt"), sep="\t", index_col=0)
wt_occupancy_df = occupancy_df[occupancy_df.index.str.contains("WT$")].copy()
wt_occupancy_df = sequence_annotation_processing.remove_mutations_from_seq_id(wt_occupancy_df)
wt_occupancy_df = wt_occupancy_df.loc[activity_df.index]
n_tfs = len(wt_occupancy_df.columns)
# PWMs
pwms = predicted_occupancy.read_pwm_files(os.path.join("Data", "Downloaded", "Pwm", "photoreceptorAndEnrichedMotifs.meme"))
pwms = pwms.rename(lambda x: x.split("_")[0])
motif_len = pwms.apply(len)
mu = 9
ewms = pwms.apply(predicted_occupancy.ewm_from_letter_prob).apply(predicted_occupancy.ewm_to_dict)
# WT sequences measured in the assay
wt_seqs = all_seqs[all_seqs.index.str.contains("WT")].copy()
wt_seqs = sequence_annotation_processing.remove_mutations_from_seq_id(wt_seqs)
wt_seqs = wt_seqs[activity_df.index]
```
## Analysis for linear arrangement bias
For each TF besides CRX, identify strong enhancers with exactly one position occupied by CRX and exactly one position occupied by the other TF. Count the number of times the occupied position is 5' (left) or 3' (right) of the CRX position. Because all sequences are centered on CRX motifs in a forward orientation, we do not need to consider orientation.
```
occupied_cutoff = 0.5
strong_mask = activity_df["group_name_WT"].str.contains("Strong")
strong_mask = strong_mask & strong_mask.notna()
# {tf name: [number of times TF is 5' of central CRX, number of times 3']}
tf_order_counts = {}
for tf in ewms.index.drop("CRX"):
left_counts = right_counts = 0
# Get strong enhancers with a motif for this TF
has_tf_mask = (wt_occupancy_df[tf] > occupied_cutoff) & strong_mask
has_tf_seqs = wt_seqs[has_tf_mask]
# Get the predicted occupancy landscape only for CRX and the other TF
for seq in has_tf_seqs:
occupancy_landscape = predicted_occupancy.total_landscape(seq, ewms[["CRX", tf]], mu) > occupied_cutoff
# Only consider the sequence if there is exactly one CRX and exactly one of the other TF
fwd_counts = occupancy_landscape[tf + "_F"].sum()
rev_counts = occupancy_landscape[tf + "_R"].sum()
if (occupancy_landscape["CRX_F"].sum() == 1) and (occupancy_landscape["CRX_R"].sum() == 0) and (fwd_counts + rev_counts == 1):
# By construction, the motif will only be in the F or R column
if fwd_counts == 1:
col = occupancy_landscape[tf + "_F"]
else:
col = occupancy_landscape[tf + "_R"]
tf_start_pos = col[col].index[0]
# CRX start position should always be the same, but just in case it's not do this
crx_occ = occupancy_landscape["CRX_F"]
crx_start_pos = crx_occ[crx_occ].index[0]
if tf_start_pos < crx_start_pos:
left_counts += 1
elif tf_start_pos > crx_start_pos:
right_counts += 1
# else they start at the same position, ignore it
tf_order_counts[tf] = [left_counts, right_counts]
tf_order_counts = pd.DataFrame.from_dict(tf_order_counts, orient="index", columns=["left", "right"])
tf_order_counts["binom_pval"] = tf_order_counts.apply(stats.binom_test, axis=1)
tf_order_counts["binom_qval"] = modeling.fdr(tf_order_counts["binom_pval"])
display(tf_order_counts)
```
Now do the same analyses as above for silencers with NRL. Then create a contingency table to determine whether the left/right positioning of NRL motifs is independent of whether a sequence is a strong enhancer or silencer.
```
silencer_mask = activity_df["group_name_WT"].str.contains("Silencer")
silencer_mask = silencer_mask & silencer_mask.notna()
has_nrl_mask = (wt_occupancy_df["NRL"] > occupied_cutoff) & silencer_mask
has_nrl_seqs = wt_seqs[has_nrl_mask]
silencer_left_counts = silencer_right_counts = 0
for seq in has_nrl_seqs:
occupancy_landscape = predicted_occupancy.total_landscape(seq, ewms[["CRX", "NRL"]], mu) > occupied_cutoff
# Only consider the sequence if there is exactly one CRX and exactly one of the other TF
fwd_counts = occupancy_landscape["NRL_F"].sum()
rev_counts = occupancy_landscape["NRL_R"].sum()
if (occupancy_landscape["CRX_F"].sum() == 1) & (occupancy_landscape["CRX_R"].sum() == 0) & (fwd_counts + rev_counts == 1):
# Samw as above
if fwd_counts == 1:
col = occupancy_landscape["NRL_F"]
else:
col = occupancy_landscape["NRL_R"]
tf_start_pos = col[col].index[0]
crx_occ = occupancy_landscape["CRX_F"]
crx_start_pos = crx_occ[crx_occ].index[0]
if tf_start_pos < crx_start_pos:
silencer_left_counts += 1
elif tf_start_pos > crx_start_pos:
silencer_right_counts += 1
silencer_order_counts = pd.Series([silencer_left_counts, silencer_right_counts], index=["left", "right"])
# Join with strong enhancer counts
contingency_table = pd.DataFrame.from_dict({"Silencer": silencer_order_counts, "Strong enhancer": tf_order_counts.loc["NRL", ["left", "right"]]}, orient="index").astype(int)
display(contingency_table)
odds, pval = stats.fisher_exact(contingency_table)
print(f"The linear arrangement of CRX-NRL motifs is independent of whether a sequence is a strong enhancer or silencer, Fisher's exact test p={pval:.2f}, odds ratio={odds:.1f}")
```
## Analysis of gene expression changes in Crx-/- retina
First, read in the RNA-seq data, CPM normalize each replicate, compute mean expression across replicates, and then compute the fold changes between Crx-/- and WT.
```
rnaseq_df = pd.read_csv(os.path.join(downloads_dir, "rogerRnaseqRaw2014.txt"), sep="\t", usecols=["Wta", "Wtb", "Crxa", "Crxb"])
# Add a pseudocount too when CPM normalizing
rnaseq_df = (rnaseq_df + 1) / (rnaseq_df.sum() / 1e6)
# Compute averages and then log2 FC
ko_wt_fc_log2 = np.log2(rnaseq_df[["Crxa", "Crxb"]].mean(axis=1) / rnaseq_df[["Wta", "Wtb"]].mean(axis=1))
```
Next, read in a BED file of the library and intersect it with [Supplementary file 4](https://doi.org/10.7554/eLife.48216.022) from Murphy *et al.*, 2019 to associate sequences to genes.
```
bed_columns = ["chrom", "begin", "end", "label", "score", "strand"]
# Load in BED file
library_bed = pd.read_csv(os.path.join(data_dir, "library1And2.bed"), sep="\t", header=None, names=bed_columns)
# Pull out sequences that were measured
library_bed = library_bed.set_index("label").loc[activity_df.index].reset_index()[bed_columns]
library_bed = BedTool.from_dataframe(library_bed).sort()
# Read in ATAC data and intersect with the library
atac_df = pd.read_excel(os.path.join(downloads_dir, "murphyAtac2019.xlsx"), sheet_name="peakUnion_counts", skiprows=1)
atac_bed = BedTool.from_dataframe(atac_df[["Chr", "Start", "End", "PeakID"]]).sort()
atac_bed = atac_bed.intersect(library_bed, wo=True).to_dataframe()
atac_bed = atac_bed[["chrom", "start", "end", "name", "thickEnd"]].rename(columns={"thickEnd": "library_label"})
atac_df = atac_df.set_index("PeakID").loc[atac_bed["name"]].reset_index()
atac_df["library_label"] = atac_bed["library_label"]
```
Get the gene closest to every library member, and then get the fold change.
```
def get_nearest_gene_fc(gene):
if gene in ko_wt_fc_log2.index:
return ko_wt_fc_log2[gene]
else:
return np.nan
library_nearest_gene = atac_df.set_index("library_label")["Nearest Gene"]
library_gene_fc = library_nearest_gene.apply(get_nearest_gene_fc)
library_gene_fc = library_gene_fc[library_gene_fc.notna()]
activity_has_gene_df = activity_df.loc[library_gene_fc.index]
```
Now get genes that have an absolute fold change of 2 (log2 = 1) or more.
```
library_gene_de = library_gene_fc[library_gene_fc.abs() >= 1]
up_mask = (library_gene_de > 0).replace({False: "Down-regulated", True: "Up-regulated"})
de_direction_grouper = library_gene_de.groupby(up_mask)
```
Determine enrichment of silencers being near up-regulated genes and enhancers being near down-regulated genes.
```
# Silencers
silencer_count_contingency = de_direction_grouper.apply(lambda x: activity_has_gene_df.loc[x.index, "group_name_WT"].str.contains("Silencer").value_counts()).unstack()
oddsratio, pval = stats.fisher_exact(silencer_count_contingency)
print(f"Direction of differential expression is independent of having a silencer nearby, Fisher's exact test p={pval:.3f}, OR={oddsratio:.2f}")
silencer_count_contingency = silencer_count_contingency.div(silencer_count_contingency.sum(axis=1), axis=0)
display(silencer_count_contingency)
fig, ax = plt.subplots()
ax.bar([0, 1], silencer_count_contingency[True], tick_label=silencer_count_contingency.index)
ax.set_ylabel("Fraction of genes near a silencer")
# Enhancers
enhancer_count_contingency = de_direction_grouper.apply(lambda x: activity_has_gene_df.loc[x.index, "group_name_WT"].str.contains("enhancer").value_counts()).unstack()
oddsratio, pval = stats.fisher_exact(enhancer_count_contingency)
print(f"Direction of differential expression is independent of having an enhancer nearby, Fisher's exact test p={pval:.3f}, OR={oddsratio:.2f}")
enhancer_count_contingency = enhancer_count_contingency.div(enhancer_count_contingency.sum(axis=1), axis=0)
display(enhancer_count_contingency)
fig, ax = plt.subplots()
ax.bar([0, 1], enhancer_count_contingency[True], tick_label=enhancer_count_contingency.index)
ax.set_ylabel("Fraction of genes near an enhancer")
```
| true |
code
| 0.436742 | null | null | null | null |
|
# Neural Sequence Distance Embeddings
[](https://colab.research.google.com/github/gcorso/NeuroSEED/blob/master/tutorial/NeuroSEED.ipynb)
The improvement of data-dependent heuristics and representation for biological sequences is a critical requirement to fully exploit the recent technological and scientific advancements for human microbiome analysis. This notebook presents Neural Sequence Distance Embeddings (NeuroSEED), a novel framework to embed biological sequences in geometric vector spaces that unifies recently proposed approaches. We demonstrate its capacity by presenting different ways it can be applied to the tasks of edit distance approximation, closest string retrieval, hierarchical clustering and multiple sequence alignment. In particular, the hyperbolic space is shown to be a key component to embed biological sequences and obtain competitive heuristics. Benchmarked with common bioinformatics and machine learning baselines, the proposed approaches display significant accuracy and/or runtime improvements on real-world datasets formed by sequences from samples of the human microbiome.
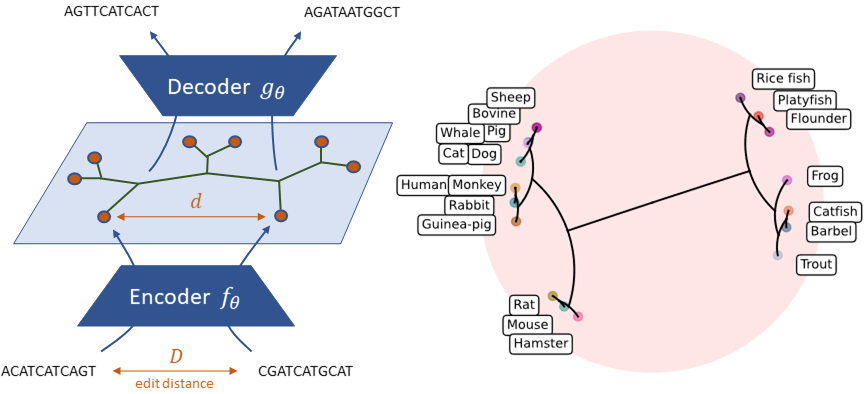
Figure 1: On the left, a diagram of the NeuroSEED underlying idea: embed sequences in vector spaces preserving the edit distance between them and then extract information from the vector space. On the right, an example of the hierarchical clustering produced on the Poincarè disk from the P53 tumour protein from 20 different organisms.
## Introduction and Motivation
### Motivation
Dysfunctions of the human microbiome (Morgan & Huttenhower, 2012) have been linked to many serious diseases ranging from diabetes and antibiotic resistance to inflammatory bowel disease. Its usage as a biomarker for the diagnosis and as a target for interventions is a very active area of research. Thanks to the advances in sequencing technologies, modern analysis relies on sequence reads that can be generated relatively quickly. However, to fully exploit the potential of these advances for personalised medicine, the computational methods used in the analysis have to significantly improve in terms of speed and accuracy.
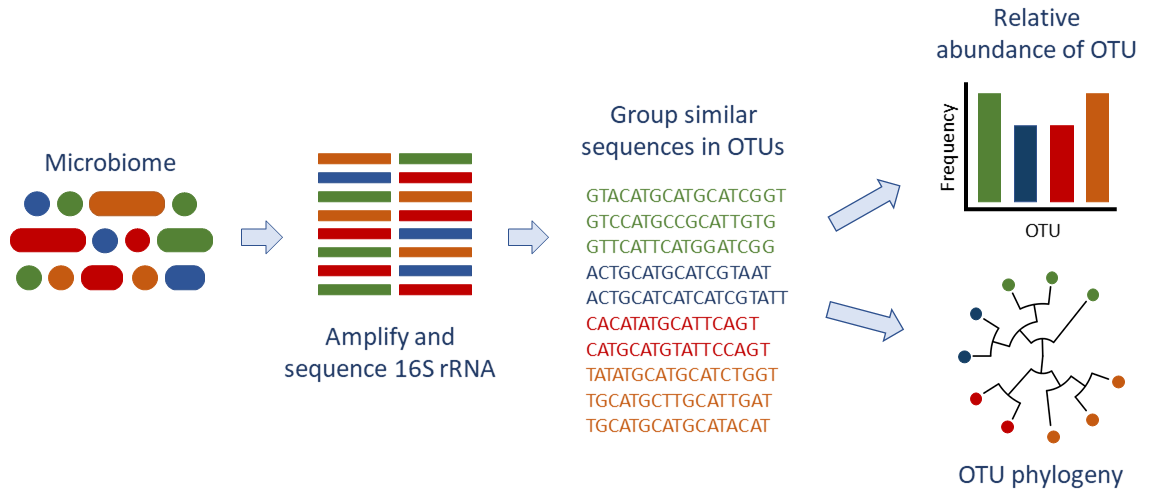
Figure 2: Traditional approach to the analysis of the 16S rRNA sequences from the microbiome.
### Problem
While the number of available biological sequences has been growing exponentially over the past decades, most of the problems related to string matching have not been addressed by the recent advances in machine learning. Classical algorithms are data-independent and, therefore, cannot exploit the low-dimensional manifold assumption that characterises real-world data. Exploiting the available data to produce data-dependent heuristics and representations would greatly accelerate large-scale analyses that are critical to microbiome analysis and other biological research.
Unlike most tasks in computer vision and NLP, string matching problems are typically formulated as combinatorial optimisation problems. These discrete formulations do not fit well with the current deep learning approaches causing these problems to be left mostly unexplored by the community. Current supervised learning methods also suffer from the lack of labels that characterises many downstream applications with biological sequences. On the other hand, common self-supervised learning approaches, very successful in NLP, are less effective in the biological context where relations tend to be per-sequence rather than per-token (McDermott et al. 2021).
### Neural Sequence Distance Embedding
In this notebook, we present Neural Sequence Distance Embeddings (NeuroSEED), a general framework to produce representations for biological sequences where the distance in the embedding space is correlated with the evolutionary distance between sequences. This control over the geometric interpretation of the representation space enables the use of geometrical data processing tools for the analysis of the spectrum of sequences.
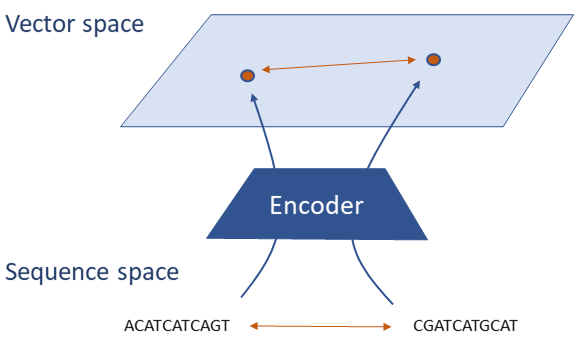
Figure 3: The key idea of NeuroSEED is to learn an encoder function that preserves distances between the sequence and vector space.
Examining the task of embedding sequences to preserve the edit distance reveals the importance of data-dependent approaches and of using a geometry that matches well the underlying distribution in the data analysed. For biological datasets, that have an implicit hierarchical structure given by evolution, the hyperbolic space provides significant improvement.
We show the potential of the framework by analysing three fundamental tasks in bioinformatics: closest string retrieval, hierarchical clustering and multiple sequence alignment. For all tasks, relatively simple unsupervised approaches using NeuroSEED encoders significantly outperform data-independent heuristics in terms of accuracy and/or runtime. In the paper (preprint will be available soon) and the [complete repository](https://github.com/gcorso/NeuroSEED) we also present more complex geometrical approaches to hierarchical clustering and multiple sequence alignment.
## 2. Analysis
To improve readability and limit the size of the notebook we make use of some subroutines in the [official repository](https://github.com/gcorso/NeuroSEED) for the research project. The code in the notebook is our best effort to convey the promising application of hyperbolic geometry to this novel research direction.
Install and import the required packages.
```
!pip3 install geomstats
!apt install clustalw
!pip install biopython
!pip install python-Levenshtein
!pip install Cython
!pip install networkx
!pip install tqdm
!pip install gdown
!pip install torch==1.7.1+cu101 torchvision==0.8.2+cu101 torchaudio==0.7.2 -f https://download.pytorch.org/whl/torch_stable.html
!git clone https://github.com/gcorso/NeuroSEED.git
import os
os.chdir("NeuroSEED")
!cd hierarchical_clustering/relaxed/mst; python setup.py build_ext --inplace; cd ../unionfind; python setup.py build_ext --inplace; cd ..; cd ..; cd ..;
os.environ['GEOMSTATS_BACKEND'] = 'pytorch'
import torch
import os
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import time
from geomstats.geometry.poincare_ball import PoincareBall
from edit_distance.train import load_edit_distance_dataset
from util.data_handling.data_loader import get_dataloaders
from util.ml_and_math.loss_functions import AverageMeter
```
### Dataset description
As microbiome analysis is one of the most critical applications where the methods presented could be applied, we chose to use a dataset containing a portion of the 16S rRNA gene widely used in the biological literature to analyse microbiome diversity. Qiita (Clemente et al. 2015) contains more than 6M sequences of up to 152 bp that cover the V4 hyper-variable region collected from skin, saliva and faeces samples of uncontacted Amerindians. The full dataset can be found on the [European Nucleotide Archive](https://www.ebi.ac.uk/ena/browser/text-search?query=ERP008799), but, in this notebook, we will only use a subset of a few tens of thousands that have been preprocessed and labelled with pairwise distances. We also provide results on the RT988 dataset (Zheng et al. 2019), another dataset of 16S rRNA that contains slightly longer sequences (up to 465 bp).
```
!gdown --id 1yZTOYrnYdW9qRrwHSO5eRc8rYIPEVtY2 # for edit distance approximation
!gdown --id 1hQSHR-oeuS9bDVE6ABHS0SoI4xk3zPnB # for closest string retrieval
!gdown --id 1ukvUI6gUTbcBZEzTVDpskrX8e6EHqVQg # for hierarchical clustering
```
### Edit distance approximation
**Edit distance** The task of finding the distance or similarity between two strings and the related task of global alignment lies at the foundation of bioinformatics. Due to the resemblance with the biological mutation process, the edit distance and its variants are typically used to measure similarity between sequences. Given two string $s_1$ and $s_2$, their edit distance $ED(s_1, s_2)$ is defined as the minimum number of insertions, deletions or substitutions needed to transform $s_1$ in $s_2$. We always deal with the classical edit distance where the same weight is given to every operation, however, all the approaches developed can be applied to any distance function of choice.
**Task and loss function** As represented in Figure 3, the task is to learn an encoding function $f$ such that given any pair of sequences from the domain of interest $s_1$ and $s_2$:
\begin{equation}ED(s_1, s_2) \approx n \; d(f(s_1), f(s_2)) \end{equation}
where $n$ is the maximum sequence length and $d$ is a distance function over the vector space. In practice this is enforced in the model by minimising the mean squared error between the actual and the predicted edit distance. To make the results more interpretable and comparable across different datasets, we report results using \% RMSE defined as:
\begin{equation}
\text{% RMSE}(f, S) = \frac{100}{n} \, \sqrt{L(f, S)} = \frac{100}{n} \, \sqrt{\sum_{s_1, s_2 \in S} (ED(s_1, s_2) - n \; d(f(s_1), f(s_2)))^2}
\end{equation}
which can be interpreted as an approximate average error in the distance prediction as a percentage of the size of the sequences.
In this notebook, we only show the code to run a simple linear layer on the sequence which, in the hyperbolic space, already gives particularly good results. Later we will also report results for more complex models whose implementation can be found in the [NeuroSEED repository](https://github.com/gcorso/NeuroSEED).
```
class LinearEncoder(nn.Module):
""" Linear model which simply flattens the sequence and applies a linear transformation. """
def __init__(self, len_sequence, embedding_size, alphabet_size=4):
super(LinearEncoder, self).__init__()
self.encoder = nn.Linear(in_features=alphabet_size * len_sequence,
out_features=embedding_size)
def forward(self, sequence):
# flatten sequence and apply layer
B = sequence.shape[0]
sequence = sequence.reshape(B, -1)
emb = self.encoder(sequence)
return emb
class PairEmbeddingDistance(nn.Module):
""" Wrapper model for a general encoder, computes pairwise distances and applies projections """
def __init__(self, embedding_model, embedding_size, scaling=False):
super(PairEmbeddingDistance, self).__init__()
self.hyperbolic_metric = PoincareBall(embedding_size).metric.dist
self.embedding_model = embedding_model
self.radius = nn.Parameter(torch.Tensor([1e-2]), requires_grad=True)
self.scaling = nn.Parameter(torch.Tensor([1.]), requires_grad=True)
def normalize_embeddings(self, embeddings):
""" Project embeddings to an hypersphere of a certain radius """
min_scale = 1e-7
max_scale = 1 - 1e-3
return F.normalize(embeddings, p=2, dim=1) * self.radius.clamp_min(min_scale).clamp_max(max_scale)
def encode(self, sequence):
""" Use embedding model and normalization to encode some sequences. """
enc_sequence = self.embedding_model(sequence)
enc_sequence = self.normalize_embeddings(enc_sequence)
return enc_sequence
def forward(self, sequence):
# flatten couples
(B, _, N, _) = sequence.shape
sequence = sequence.reshape(2 * B, N, -1)
# encode sequences
enc_sequence = self.encode(sequence)
# compute distances
enc_sequence = enc_sequence.reshape(B, 2, -1)
distance = self.hyperbolic_metric(enc_sequence[:, 0], enc_sequence[:, 1])
distance = distance * self.scaling
return distance
```
General training and evaluation routines used to train the models:
```
def train(model, loader, optimizer, loss, device):
avg_loss = AverageMeter()
model.train()
for sequences, labels in loader:
# move examples to right device
sequences, labels = sequences.to(device), labels.to(device)
# forward propagation
optimizer.zero_grad()
output = model(sequences)
# loss and backpropagation
loss_train = loss(output, labels)
loss_train.backward()
optimizer.step()
# keep track of average loss
avg_loss.update(loss_train.data.item(), sequences.shape[0])
return avg_loss.avg
def test(model, loader, loss, device):
avg_loss = AverageMeter()
model.eval()
for sequences, labels in loader:
# move examples to right device
sequences, labels = sequences.to(device), labels.to(device)
# forward propagation and loss computation
output = model(sequences)
loss_val = loss(output, labels).data.item()
avg_loss.update(loss_val, sequences.shape[0])
return avg_loss.avg
```
The linear model is trained on 7000 sequences (+700 of validation) and tested on 1500 different sequences:
```
EMBEDDING_SIZE = 128
device = 'cuda' if torch.cuda.is_available() else 'cpu'
torch.manual_seed(2021)
if device == 'cuda':
torch.cuda.manual_seed(2021)
# load data
datasets = load_edit_distance_dataset('./edit_qiita_large.pkl')
loaders = get_dataloaders(datasets, batch_size=128, workers=1)
# model, optimizer and loss
encoder = LinearEncoder(152, EMBEDDING_SIZE)
model = PairEmbeddingDistance(embedding_model=encoder, embedding_size=EMBEDDING_SIZE)
model.to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)
loss = nn.MSELoss()
# training
for epoch in range(0, 21):
t = time.time()
loss_train = train(model, loaders['train'], optimizer, loss, device)
loss_val = test(model, loaders['val'], loss, device)
# print progress
if epoch % 5 == 0:
print('Epoch: {:02d}'.format(epoch),
'loss_train: {:.6f}'.format(loss_train),
'loss_val: {:.6f}'.format(loss_val),
'time: {:.4f}s'.format(time.time() - t))
# testing
for dset in loaders.keys():
avg_loss = test(model, loaders[dset], loss, device)
print('Final results {}: loss = {:.6f}'.format(dset, avg_loss))
```
Therefore, our linear model after only 50 epochs has a $\% RMSE \approx 2.6$ that, as we will see, is significantly better than any data-independent baseline.
### Closest string retrieval
This task consists of finding the sequence that is closest to a given query among a large number of reference sequences and is very commonly used to classify sequences. Given a set of reference strings $R$ and a set of queries $Q$, the task is to identify the string $r_q \in R$ that minimises $ED(r_q, q)$ for each $q \in Q$. This task is performed in an unsupervised setting using models trained for edit distance approximation. Therefore, given a pretrained encoder $f$, its prediction is taken to be the string $r_q \in R$ that minimises $d(f(r_q), f(q))$ for each $q \in Q$. This allows for sublinear retrieval (via locality-sensitive hashing or other data structures) which is critical in real-world applications where databases can have billions of reference sequences. As performance measures, we report the top-1, top-5 and top-10 scores, where top-$k$ indicates the percentage of times the model ranks the closest string within its top-$k$ predictions.
```
from closest_string.test import closest_string_testing
closest_string_testing(encoder_model=model, data_path='./closest_qiita_large.pkl',
batch_size=128, device=device, distance='hyperbolic')
```
Evaluated on a dataset composed of 1000 reference and 1000 query sequences (disjoint from the edit distance training set) the simple model we trained is capable of detecting the closest sequence correctly 44\% of the time and in approximately 3/4 of the cases it places the real closest sequence in its top-10 choices.
### Hierarchical clustering
Hierarchical clustering (HC) consists of constructing a hierarchy over clusters of data by defining a tree with internal points corresponding to clusters and leaves to datapoints. The goodness of the tree can be measured using Dasgupta's cost (Dasgupta 2016).
One simple approach to use NeuroSEED to speed up hierarchical clustering is similar to the one adopted in the previous section: estimate the pairwise distance matrix with a model pretrained for *edit distance approximation* and then use the matrix as the basis for classical agglomerative clustering algorithms (e.g. Single, Average and Complete Linkage). The computational cost to generate the matrix goes from $O(N^2M^2)$ to $O(N(M+N))$ and by using optimisations like locality-sensitive hashing the clustering itself can be accelerated.
The following code computes the pairwise distance matrix and then runs a series of agglomerative clustering heuristics (Single, Average, Complete and Ward Linkage) on it.
```
from hierarchical_clustering.unsupervised.unsupervised import hierarchical_clustering_testing
hierarchical_clustering_testing(encoder_model=model, data_path='./hc_qiita_large_extr.pkl',
batch_size=128, device=device, distance='hyperbolic')
```
An alternative approach to performing hierarchical clustering we propose uses the continuous relaxation of Dasgupta's cost (Chami et al. 2020) to embed sequences in the hyperbolic space. In comparison to Chami et al. (2020), we show that it is possible to significantly decrease the number of pairwise distances required by directly mapping the sequences.
This allows to considerably speed up the construction especially when dealing with a large number of sequences without requiring any pretrained model. Figure 1 shows an example of this approach when applied to a small dataset of proteins and the code for it is in the NeuroSEED repository.
### Multiple Sequence Alignment
Multiple Sequence Alignment is another very common task in bioinformatics and there are several ways of using NeuroSEED to accelerate heuristics. The most commonly used programs such as the Clustal series and MUSCLE are based on a phylogenetic tree estimation phase from the pairwise distances which produces a guide tree, which is then used to guide a progressive alignment phase.
In Clustal algorithm for MSA on a subset of RT988 of 1200 sequences, the construction of the distance matrix and the tree takes 99\% of the total running time (the rest takes 24s out of 35 minutes). Therefore, one obvious improvement that NeuroSEED can bring is to speed up this phase using the hierarchical clustering techniques seen in the previous section.
The following code uses the model pretrained for edit distance to approximate the neighbour joining tree construction and the runs clustalw using that guide tree:
```
from multiple_alignment.guide_tree.guide_tree import approximate_guide_trees
# performs neighbour joining algorithm on the estimate of the pairwise distance matrix
approximate_guide_trees(encoder_model=model, dataset=datasets['test'],
batch_size=128, device=device, distance='hyperbolic')
# Command line clustalw using the tree generated with the previous command.
# The substitution matrix and gap penalties are set to simulate the classical edit distance used to train the model
!clustalw -infile="sequences.fasta" -dnamatrix=multiple_alignment/guide_tree/matrix.txt -transweight=0 -type='DNA' -gapopen=1 -gapext=1 -gapdist=10000 -usetree='njtree.dnd' | grep 'Alignment Score'
```
An alternative method we propose for the MSA uses an autoencoder to convert the Steiner string approximation problem in a continuous optimisation task. More details on this in our paper and repository.
## 3. Benchmark
In this section, we compare the NeuroSEED approach to classical baseline alignment-free approaches such as k-mer and contrast the performance of neural models with different architectures and on different geometric spaces.
### Edit distance approximation
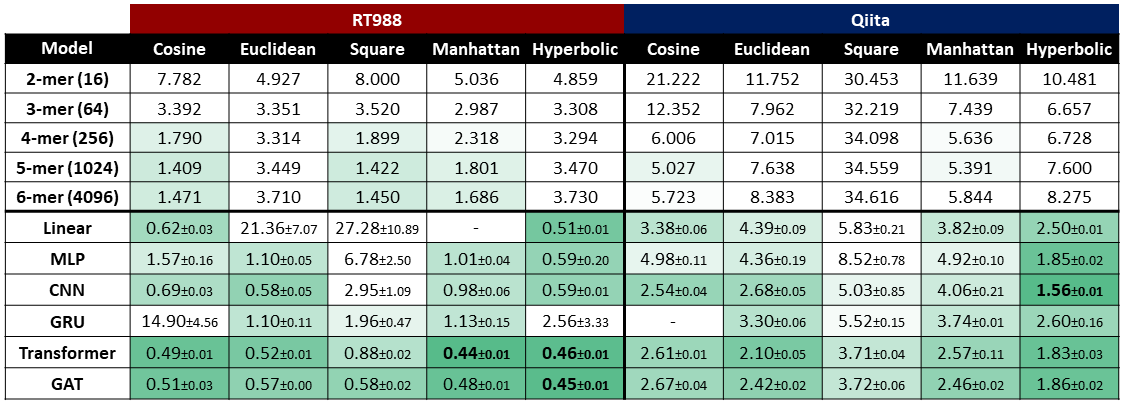
Figure 4: \% RMSE test set results on the Qiita and RT988 datasets. The first five models are the k-mer baselines and, in parentheses, we indicate the dimension of the embedding space. The remaining are encoder models trained with the NeuroSEED framework and they all have an embedding space dimension equal to 128. - indicates that the model did not converge.
Figure 4 highlights the advantage provided by data-dependent methods when compared to the data-independent baseline approaches. Moreover, the results show that it is critical for the geometry of the embedding space to reflect the structure of the low dimensional manifold on which the data lies. In these biological datasets, there is an implicit hierarchical structure given by the evolution process which is well reflected by the *hyperbolic* plane. Thanks to this close correspondence, even relatively simple models like the linear regression and MLP perform very well with this distance function.
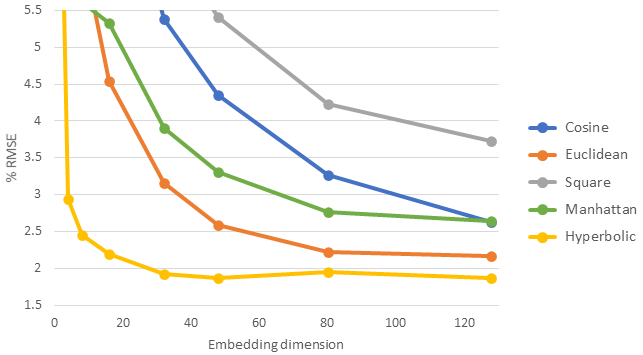
Figure 5: \% RMSE on Qiita dataset for a Transformer with different distance functions.
The clear benefit of using the hyperbolic space is evident when analysing the dimension required for the embedding space (Figure 5). In these experiments, we run the Transformer model tuned on the Qiita dataset with an embedding size of 128 on a range of dimensions. The hyperbolic space provides significantly more efficient embeddings, with the model reaching the 'elbow' at dimension 32 and matching the performance of the other spaces with dimension 128 with only 4 to 16. Given that the space to store the embedding and the time to compute distances between them scale linearly with the size of the space, this would provide a significant improvement in downstream tasks over other NeuroSEED approaches.
**Running time** A critical step behind most of the algorithms analysed in the rest of the paper is the computation of the pairwise distance matrix of a set of sequences. Taking as an example the RT988 dataset (6700 sequences of length up to 465 bases), optimised C code computes on a CPU approximately 2700 pairwise distances per second and takes 2.5 hours for the whole matrix. In comparison, using a trained NeuroSEED model, the same matrix can be approximated in 0.3-3s (similar value for the k-mer baseline) on the same CPU. The computational complexity for $N$ sequences of length $M$ is reduced from $O(N^2\; M^2)$ to $O(N(M + N))$ (assuming the model is linear w.r.t. the length and constant embedding size). The training process takes typically 0.5-3 hours on a GPU. However, in applications such as microbiome analysis, biologists typically analyse data coming from the same distribution (e.g. the 16S rRNA gene) for multiple individuals, therefore the initial cost would be significantly amortised.
### Closest string retrieval
Figure 6 shows that also in this task the data-dependent models outperform the baselines even when these operate on larger spaces. In terms of distance function, the *cosine* distance achieves performances on par with the *hyperbolic*. This can be explained by the fact that for a set of points on the same hypersphere, the ones with the smallest *cosine* or *hyperbolic* distance are the same. So the *cosine* distance is capable of providing good orderings of sequence similarity but inferior approximations of their distance.
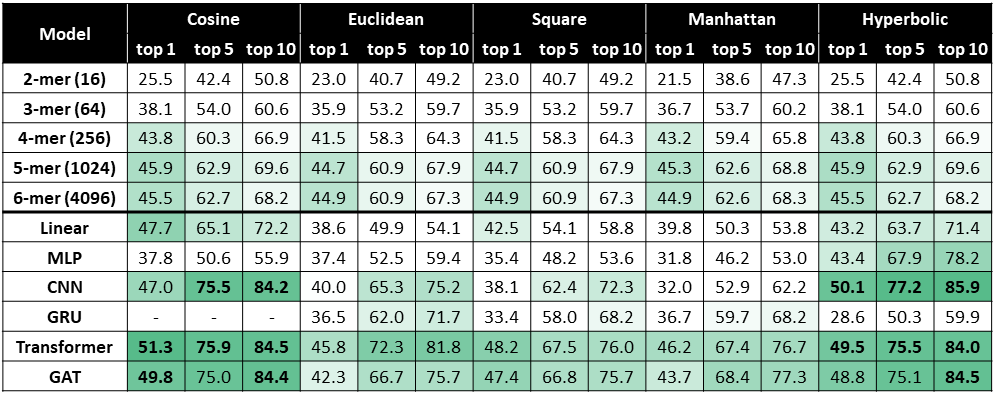
Figure 6: Accuracy of different models in the *closest string retrieval* task on the Qiita dataset.
### Hierarchical clustering
The results (Figure 7) show that the difference in performance between the most expressive models and the round truth distances is not statistically significant. The *hyperbolic* space achieves the best performance and, although the relative difference between the methods is not large in terms of percentage Dasgupta's cost (but still statistically significant), it results in a large performance gap when these trees are used for tasks such as MSA. The total CPU time taken to construct the tree is reduced from more than 30 minutes to less than one in this dataset and the difference is significantly larger when scaling to datasets of more and longer sequences.
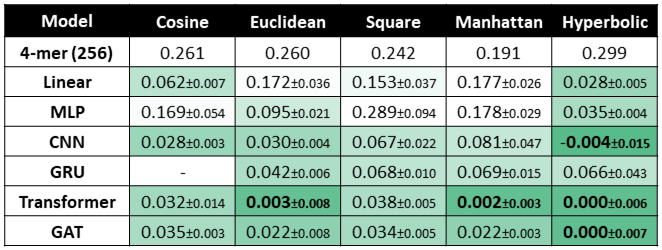
Figure 7: Average Linkage \% increase in Dasgupta's cost of NeuroSEED models compared to the performance of clustering on the ground truth distances. Average Linkage was the best performing clustering heuristic across all models.
### Multiple Sequence Alignment
The results reported in Figure 8 show that the alignment scores obtained when using the NeuroSEED heuristics with models such as GAT are not statistically different from those obtained with the ground truth distances. Most of the models show a relatively large variance in performance across different runs. This has positive and negative consequences: the alignment obtained using a single run may not be very accurate, but, by training an ensemble of models and applying each of them, we are likely to obtain a significantly better alignment than the one from the ground truth matrix while still only taking a fraction of the time.
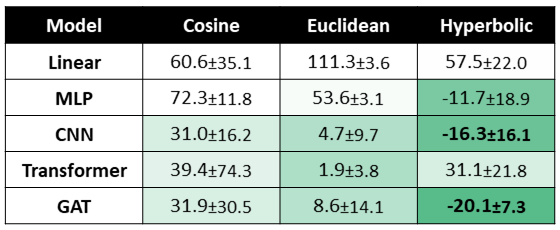
Figure 8: Percentage change in the alignment cost (- alignment score) returned by Clustal when using the heuristics to generate the tree as opposed to using NJ on real distances. The alignment was done on 1.2k unseen sequences from the RT988 dataset.
## 4. Limitations
As mentioned in the introduction, we believe that the NeuroSEED framework has the potential to be applied to numerous problems and, therefore, this project constitutes only an initial analysis of its geometrical properties and applications. Below we list some of the limitations of the current analysis and potential directions of research to cover them.
**Type of sequences** Both the datasets analysed consist of sequence reads of the same part of the genome. This is a very common set-up for sequence analysis (for example for microbiome analysis) and it is enabled by biotechnologies that can amplify and sequence certain parts of the genome selectively, but it is not ubiquitous. Shotgun metagenomics consists of sequencing random parts of the genome. This would, we believe, generate sequences lying on a low-dimensional manifold where the hierarchical relationship of evolution is combined with the relationship based on the specific position in the whole genome. Therefore, more complex geometries such as product spaces might be best suited.
**Type of labels** In this project, we work with edit distances between strings, these are very expensive when large scale analysis is required, but it is feasible to produce several thousand exact pairwise distance values from which the model can learn. For different definitions of distance, however, this might not be the case. If it is only feasible to determine which sequences are closest, then encoders can be trained using triplet loss and then most of the approaches presented would still apply. Future work could explore the robustness of this framework to inexact estimates of the distances as labels and whether NeuroSEED models, once trained, could provide more accurate predictions than its labels.
**Architectures** Throughout the project we used models that have been shown to work well for other types of sequences and tasks. However, the correct inductive biases that models should have to perform SEED are likely to be different to the ones used for other tasks and even dependent on the type of distance it tries to preserve. Moreover, the capacity of the hyperbolic space could be further exploited using models that directly operate in the hyperbolic space (Peng et al. 2021).
**Self-supervised embeddings** One potential application of NeuroSEED that was not explored in this project is the direct use of the embedding produced by NeuroSEED for downstream tasks. This would enable the use of a wide range of geometric data processing tools for the analysis of biological sequences.
## References
(Morgan & Huttenhower, 2012) Xochitl C Morgan and Curtis Huttenhower. Human microbiome analysis. PLoS Comput Biol, 2012.
(McDermott et al. 2021) Matthew McDermott, Brendan Yap, Peter Szolovits, and Marinka Zitnik. Rethinking relational encoding in language model: Pre-training for general sequences. arXiv preprint, 2021.
(Clemente et al. 2015) Jose C Clemente, Erica C Pehrsson, Martin J Blaser, Kuldip Sandhu, Zhan Gao, Bin Wang, Magda Magris, Glida Hidalgo, Monica Contreras, Oscar Noya-Alarcon, et al. ´The microbiome of uncontacted amerindians. Science advances, 2015.
(Zheng et al. 2019)Wei Zheng, Le Yang, Robert J Genco, Jean Wactawski-Wende, Michael Buck, and Yijun Sun. Sense: Siamese neural network for sequence embedding and alignment free comparison. Bioinformatics, 2019.
(Dasgupta 2016) Sanjoy Dasgupta. A cost function for similarity-based hierarchical clustering. In Proceedings of the forty-eighth annual ACM symposium on Theory of Computing, 2016.
(Chami et al. 2020) Ines Chami, Albert Gu, Vaggos Chatziafratis, and Christopher Re. From trees to continuous embeddings and back: Hyperbolic hierarchical clustering. Advances in Neural Information Processing Systems 33, 2020.
| true |
code
| 0.894675 | null | null | null | null |
|
# Training and Serving with TensorFlow on Amazon SageMaker
*(This notebook was tested with the \"Python 3 (Data Science)\" kernel.)*
Amazon SageMaker is a fully-managed service that provides developers and data scientists with the ability to build, train, and deploy machine learning (ML) models quickly. Amazon SageMaker removes the heavy lifting from each step of the machine learning process to make it easier to develop high-quality models. The SageMaker Python SDK makes it easy to train and deploy models in Amazon SageMaker with several different machine learning and deep learning frameworks, including TensorFlow.
In this notebook, we use the SageMaker Python SDK to launch a training job and deploy the trained model. We use a Python script to train a classification model on the [MNIST dataset](http://yann.lecun.com/exdb/mnist), and show how to train with both TensorFlow 1.x and TensorFlow 2.x scripts.
## Set up the environment
Let's start by setting up the environment:
```
import sagemaker
from sagemaker import get_execution_role
sagemaker_session = sagemaker.Session()
role = get_execution_role()
region = sagemaker_session.boto_region_name
```
We also define the TensorFlow version here, and create a quick helper function that lets us toggle between TF 1.x and 2.x in this notebook.
```
tf_version = '2.1.0' # replace with '1.15.2' for TF 1.x
def use_tf2():
return tf_version.startswith('2')
```
## Training Data
The [MNIST dataset](http://yann.lecun.com/exdb/mnist) is a dataset consisting of handwritten digits. There is a training set of 60,000 examples, and a test set of 10,000 examples. The digits have been size-normalized and centered in a fixed-size image.
The dataset has already been uploaded to an Amazon S3 bucket, ``sagemaker-sample-data-<REGION>``, under the prefix ``tensorflow/mnist``. There are four ``.npy`` file under this prefix:
* ``train_data.npy``
* ``eval_data.npy``
* ``train_labels.npy``
* ``eval_labels.npy``
```
training_data_uri = 's3://sagemaker-sample-data-{}/tensorflow/mnist'.format(region)
```
## Construct a script for distributed training
The training code is very similar to a training script we might run outside of Amazon SageMaker. The SageMaker Python SDK handles transferring our script to a SageMaker training instance. On the training instance, SageMaker's native TensorFlow support sets up training-related environment variables and executes the training code.
We can use a Python script, a Python module, or a shell script for the training code. This notebook's training script is a Python script adapted from a TensorFlow example of training a convolutional neural network on the MNIST dataset.
We have modified the training script to handle the `model_dir` parameter passed in by SageMaker. This is an Amazon S3 path which can be used for data sharing during distributed training and checkpointing and/or model persistence. Our script also contains an argument-parsing function to handle processing training-related variables.
At the end of the training job, our script exports the trained model to the path stored in the environment variable `SM_MODEL_DIR`, which always points to `/opt/ml/model`. This is critical because SageMaker uploads all the model artifacts in this folder to S3 at end of training.
For more about writing a TensorFlow training script for SageMaker, see [the SageMaker documentation](https://sagemaker.readthedocs.io/en/stable/using_tf.html#prepare-a-script-mode-training-script).
Here is the entire script:
```
training_script = 'mnist-2.py' if use_tf2() else 'mnist.py'
!pygmentize {training_script}
```
## Create a SageMaker training job
The SageMaker Python SDK's `sagemaker.tensorflow.TensorFlow` estimator class handles creating a SageMaker training job. Let's call out a couple important parameters here:
* `entry_point`: our training script
* `distributions`: configuration for the distributed training setup. It's required only if we want distributed training either across a cluster of instances or across multiple GPUs. Here, we use parameter servers as the distributed training schema. SageMaker training jobs run on homogeneous clusters. To make parameter server more performant in the SageMaker setup, we run a parameter server on every instance in the cluster, so there is no need to specify the number of parameter servers to launch. Script mode also supports distributed training with [Horovod](https://github.com/horovod/horovod). You can find the full documentation on how to configure `distributions` in the [SageMaker Python SDK API documentation](https://sagemaker.readthedocs.io/en/stable/sagemaker.tensorflow.html#sagemaker.tensorflow.estimator.TensorFlow).
```
from sagemaker.tensorflow import TensorFlow
estimator = TensorFlow(entry_point=training_script,
role=role,
instance_count=1,
instance_type='ml.p2.xlarge',
framework_version=tf_version,
py_version='py3')
```
To start a training job, we call `estimator.fit(training_data_uri)`.
An S3 location is used here as the input. `fit` creates a default channel named "training", and the data at the S3 location is downloaded to the "training" channel. In the training script, we can then access the training data from the location stored in `SM_CHANNEL_TRAINING`. `fit` accepts a couple other types of input as well. For details, see the [API documentation](https://sagemaker.readthedocs.io/en/stable/estimators.html#sagemaker.estimator.EstimatorBase.fit).
When training starts, `mnist.py` is executed, with the estimator's `hyperparameters` and `model_dir` passed as script arguments. Because we didn't define either in this example, no hyperparameters are passed, and `model_dir` defaults to `s3://<DEFAULT_BUCKET>/<TRAINING_JOB_NAME>`, so the script execution is as follows:
```bash
python mnist.py --model_dir s3://<DEFAULT_BUCKET>/<TRAINING_JOB_NAME>
```
When training is complete, the training job uploads the saved model to S3 so that we can use it with TensorFlow Serving.
```
estimator.fit(training_data_uri)
```
## Deploy the trained model to an endpoint
After we train our model, we can deploy it to a SageMaker Endpoint, which serves prediction requests in real-time. To do so, we simply call `deploy()` on our estimator, passing in the desired number of instances and instance type for the endpoint. This creates a SageMaker Model, which is then deployed to an endpoint.
The Docker image used for TensorFlow Serving runs an implementation of a web server that is compatible with SageMaker hosting protocol. For more about using TensorFlow Serving with SageMaker, see the [SageMaker documentation](https://sagemaker.readthedocs.io/en/stable/using_tf.html#deploy-tensorflow-serving-models).
```
predictor = estimator.deploy(initial_instance_count=1, instance_type='ml.c5.xlarge')
```
## Invoke the endpoint
We then use the returned predictor object to invoke our endpoint. For demonstration purposes, let's download the training data and use that as input for inference.
```
import numpy as np
!aws --region {region} s3 cp s3://sagemaker-sample-data-{region}/tensorflow/mnist/train_data.npy train_data.npy
!aws --region {region} s3 cp s3://sagemaker-sample-data-{region}/tensorflow/mnist/train_labels.npy train_labels.npy
train_data = np.load('train_data.npy')
train_labels = np.load('train_labels.npy')
```
The formats of the input and the output data correspond directly to the request and response formats of the `Predict` method in the [TensorFlow Serving REST API](https://www.tensorflow.org/serving/api_rest). SageMaker's TensforFlow Serving endpoints can also accept additional input formats that are not part of the TensorFlow REST API, including the simplified JSON format, line-delimited JSON objects ("jsons" or "jsonlines"), and CSV data.
In this example we use a `numpy` array as input, which is serialized into the simplified JSON format. In addtion, TensorFlow serving can also process multiple items at once, which we utilize in the following code. For complete documentation on how to make predictions against a SageMaker Endpoint using TensorFlow Serving, see the [SageMaker documentation](https://sagemaker.readthedocs.io/en/stable/using_tf.html#making-predictions-against-a-sagemaker-endpoint).
```
predictions = predictor.predict(train_data[:50])
for i in range(0, 50):
if use_tf2():
prediction = np.argmax(predictions['predictions'][i])
else:
prediction = predictions['predictions'][i]['classes']
label = train_labels[i]
print('prediction: {}, label: {}, matched: {}'.format(prediction, label, prediction == label))
```
## Delete the endpoint
Let's delete our to prevent incurring any extra costs.
```
predictor.delete_endpoint()
```
| true |
code
| 0.370937 | null | null | null | null |
|
# Saving and Loading Models
<a href="https://colab.research.google.com/github/jwangjie/gpytorch/blob/master/examples/00_Basic_Usage/Saving_and_Loading_Models.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
In this bite-sized notebook, we'll go over how to save and load models. In general, the process is the same as for any PyTorch module.
```
# COMMENT this if not used in colab
!pip install gpytorch
import math
import torch
import gpytorch
from matplotlib import pyplot as plt
```
## Saving a Simple Model
First, we define a GP Model that we'd like to save. The model used below is the same as the model from our
<a href="../01_Exact_GPs/Simple_GP_Regression.ipynb">Simple GP Regression</a> tutorial.
```
train_x = torch.linspace(0, 1, 100)
train_y = torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * 0.2
# We will use the simplest form of GP model, exact inference
class ExactGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
# initialize likelihood and model
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = ExactGPModel(train_x, train_y, likelihood)
```
### Change Model State
To demonstrate model saving, we change the hyperparameters from the default values below. For more information on what is happening here, see our tutorial notebook on <a href="Hyperparameters.ipynb">Initializing Hyperparameters</a>.
```
model.covar_module.outputscale = 1.2
model.covar_module.base_kernel.lengthscale = 2.2
```
### Getting Model State
To get the full state of a GPyTorch model, simply call `state_dict` as you would on any PyTorch model. Note that the state dict contains **raw** parameter values. This is because these are the actual `torch.nn.Parameters` that are learned in GPyTorch. Again see our notebook on hyperparamters for more information on this.
```
model.state_dict()
```
### Saving Model State
The state dictionary above represents all traininable parameters for the model. Therefore, we can save this to a file as follows:
```
torch.save(model.state_dict(), 'model_state.pth')
```
### Loading Model State
Next, we load this state in to a new model and demonstrate that the parameters were updated correctly.
```
state_dict = torch.load('model_state.pth')
model = ExactGPModel(train_x, train_y, likelihood) # Create a new GP model
model.load_state_dict(state_dict)
model.state_dict()
```
## A More Complex Example
Next we demonstrate this same principle on a more complex exact GP where we have a simple feed forward neural network feature extractor as part of the model.
```
class GPWithNNFeatureExtractor(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super(GPWithNNFeatureExtractor, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
self.feature_extractor = torch.nn.Sequential(
torch.nn.Linear(1, 2),
torch.nn.BatchNorm1d(2),
torch.nn.ReLU(),
torch.nn.Linear(2, 2),
torch.nn.BatchNorm1d(2),
torch.nn.ReLU(),
)
def forward(self, x):
x = self.feature_extractor(x)
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
# initialize likelihood and model
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = GPWithNNFeatureExtractor(train_x, train_y, likelihood)
```
### Getting Model State
In the next cell, we once again print the model state via `model.state_dict()`. As you can see, the state is substantially more complex, as the model now includes our neural network parameters. Nevertheless, saving and loading is straight forward.
```
model.state_dict()
torch.save(model.state_dict(), 'my_gp_with_nn_model.pth')
state_dict = torch.load('my_gp_with_nn_model.pth')
model = GPWithNNFeatureExtractor(train_x, train_y, likelihood)
model.load_state_dict(state_dict)
model.state_dict()
```
| true |
code
| 0.763807 | null | null | null | null |
|
# Demonstrate the Sankey class by producing three basic diagrams
Code taken from the [Sankey API](http://matplotlib.org/api/sankey_api.html) at Matplotlib doc
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.sankey import Sankey
```
## Example 1 -- Mostly defaults
This demonstrates how to create a simple diagram by implicitly calling the
Sankey.add() method and by appending finish() to the call to the class.
```
Sankey(flows=[0.25, 0.15, 0.60, -0.20, -0.15, -0.05, -0.50, -0.10],
labels=['', '', '', 'First', 'Second', 'Third', 'Fourth', 'Fifth'],
orientations=[-1, 1, 0, 1, 1, 1, 0, -1]).finish()
plt.title("The default settings produce a diagram like this.");
# Notice:
# 1. Axes weren't provided when Sankey() was instantiated, so they were
# created automatically.
# 2. The scale argument wasn't necessary since the data was already
# normalized.
# 3. By default, the lengths of the paths are justified.
```
## Example 2
This demonstrates:
1. Setting one path longer than the others
2. Placing a label in the middle of the diagram
3. Using the scale argument to normalize the flows
4. Implicitly passing keyword arguments to PathPatch()
5. Changing the angle of the arrow heads
6. Changing the offset between the tips of the paths and their labels
7. Formatting the numbers in the path labels and the associated unit
8. Changing the appearance of the patch and the labels after the figure is created
```
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, xticks=[], yticks=[],
title="Flow Diagram of a Widget")
sankey = Sankey(ax=ax, scale=0.01, offset=0.2, head_angle=180,
format='%.0f', unit='%')
sankey.add(flows=[25, 0, 60, -10, -20, -5, -15, -10, -40],
labels=['', '', '', 'First', 'Second', 'Third', 'Fourth',
'Fifth', 'Hurray!'],
orientations=[-1, 1, 0, 1, 1, 1, -1, -1, 0],
pathlengths=[0.25, 0.25, 0.25, 0.25, 0.25, 0.8, 0.25, 0.25,
0.25],
patchlabel="Widget\nA",
alpha=0.2, lw=2.0) # Arguments to matplotlib.patches.PathPatch()
diagrams = sankey.finish()
diagrams[0].patch.set_facecolor('#37c959')
diagrams[0].texts[-1].set_color('r')
diagrams[0].text.set_fontweight('bold')
# Notice:
# 1. Since the sum of the flows is nonzero, the width of the trunk isn't
# uniform. If verbose.level is helpful (in matplotlibrc), a message is
# given in the terminal window.
# 2. The second flow doesn't appear because its value is zero. Again, if
# verbose.level is helpful, a message is given in the terminal window.
```
## Example 3
This demonstrates:
1. Connecting two systems
2. Turning off the labels of the quantities
3. Adding a legend
```
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, xticks=[], yticks=[], title="Two Systems")
sankey = Sankey(ax=ax, unit=None)
flows = [0.25, 0.15, 0.60, -0.10, -0.05, -0.25, -0.15, -0.10, -0.35]
sankey.add(flows=flows, label='one',
orientations=[-1, 1, 0, 1, 1, 1, -1, -1, 0])
sankey.add(flows=[-0.25, 0.15, 0.1], fc='#37c959', label='two',
orientations=[-1, -1, -1], prior=0, connect=(0, 0))
diagrams = sankey.finish()
diagrams[-1].patch.set_hatch('/')
ax.legend(loc='best');
# Notice that only one connection is specified, but the systems form a
# circuit since: (1) the lengths of the paths are justified and (2) the
# orientation and ordering of the flows is mirrored.
```
| true |
code
| 0.644113 | null | null | null | null |
|
# Effect of the sample size in cross-validation
In the previous notebook, we presented the general cross-validation framework
and how to assess if a predictive model is underfiting, overfitting, or
generalizing. Besides these aspects, it is also important to understand how
the different errors are influenced by the number of samples available.
In this notebook, we will show this aspect by looking a the variability of
the different errors.
Let's first load the data and create the same model as in the previous
notebook.
```
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing(as_frame=True)
data, target = housing.data, housing.target
target *= 100 # rescale the target in k$
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">If you want a deeper overview regarding this dataset, you can refer to the
Appendix - Datasets description section at the end of this MOOC.</p>
</div>
```
from sklearn.tree import DecisionTreeRegressor
regressor = DecisionTreeRegressor()
```
## Learning curve
To understand the impact of the number of samples available for training on
the statistical performance of a predictive model, it is possible to
synthetically reduce the number of samples used to train the predictive model
and check the training and testing errors.
Therefore, we can vary the number of samples in the training set and repeat
the experiment. The training and testing scores can be plotted similarly to
the validation curve, but instead of varying a hyperparameter, we vary the
number of training samples. This curve is called the **learning curve**.
It gives information regarding the benefit of adding new training samples
to improve a model's statistical performance.
Let's compute the learning curve for a decision tree and vary the
proportion of the training set from 10% to 100%.
```
import numpy as np
train_sizes = np.linspace(0.1, 1.0, num=5, endpoint=True)
train_sizes
```
We will use a `ShuffleSplit` cross-validation to assess our predictive model.
```
from sklearn.model_selection import ShuffleSplit
cv = ShuffleSplit(n_splits=30, test_size=0.2)
```
Now, we are all set to carry out the experiment.
```
from sklearn.model_selection import learning_curve
results = learning_curve(
regressor, data, target, train_sizes=train_sizes, cv=cv,
scoring="neg_mean_absolute_error", n_jobs=2)
train_size, train_scores, test_scores = results[:3]
# Convert the scores into errors
train_errors, test_errors = -train_scores, -test_scores
```
Now, we can plot the curve.
```
import matplotlib.pyplot as plt
plt.errorbar(train_size, train_errors.mean(axis=1),
yerr=train_errors.std(axis=1), label="Training error")
plt.errorbar(train_size, test_errors.mean(axis=1),
yerr=test_errors.std(axis=1), label="Testing error")
plt.legend()
plt.xscale("log")
plt.xlabel("Number of samples in the training set")
plt.ylabel("Mean absolute error (k$)")
_ = plt.title("Learning curve for decision tree")
```
Looking at the training error alone, we see that we get an error of 0 k$. It
means that the trained model (i.e. decision tree) is clearly overfitting the
training data.
Looking at the testing error alone, we observe that the more samples are
added into the training set, the lower the testing error becomes. Also, we
are searching for the plateau of the testing error for which there is no
benefit to adding samples anymore or assessing the potential gain of adding
more samples into the training set.
If we achieve a plateau and adding new samples in the training set does not
reduce the testing error, we might have reach the Bayes error rate using the
available model. Using a more complex model might be the only possibility to
reduce the testing error further.
## Summary
In the notebook, we learnt:
* the influence of the number of samples in a dataset, especially on the
variability of the errors reported when running the cross-validation;
* about the learning curve that is a visual representation of the capacity
of a model to improve by adding new samples.
| true |
code
| 0.850531 | null | null | null | null |
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="fig/cover-small.jpg">
*This notebook contains an excerpt from the [Whirlwind Tour of Python](http://www.oreilly.com/programming/free/a-whirlwind-tour-of-python.csp) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/WhirlwindTourOfPython).*
*The text and code are released under the [CC0](https://github.com/jakevdp/WhirlwindTourOfPython/blob/master/LICENSE) license; see also the companion project, the [Python Data Science Handbook](https://github.com/jakevdp/PythonDataScienceHandbook).*
<!--NAVIGATION-->
< [Introduction](00-Introduction.ipynb) | [Contents](Index.ipynb) | [A Quick Tour of Python Language Syntax](02-Basic-Python-Syntax.ipynb) >
# How to Run Python Code
Python is a flexible language, and there are several ways to use it depending on your particular task.
One thing that distinguishes Python from other programming languages is that it is *interpreted* rather than *compiled*.
This means that it is executed line by line, which allows programming to be interactive in a way that is not directly possible with compiled languages like Fortran, C, or Java. This section will describe four primary ways you can run Python code: the *Python interpreter*, the *IPython interpreter*, via *Self-contained Scripts*, or in the *Jupyter notebook*.
### The Python Interpreter
The most basic way to execute Python code is line by line within the *Python interpreter*.
The Python interpreter can be started by installing the Python language (see the previous section) and typing ``python`` at the command prompt (look for the Terminal on Mac OS X and Unix/Linux systems, or the Command Prompt application in Windows):
```
$ python
Python 3.5.1 |Continuum Analytics, Inc.| (default, Dec 7 2015, 11:24:55)
Type "help", "copyright", "credits" or "license" for more information.
>>>
```
With the interpreter running, you can begin to type and execute code snippets.
Here we'll use the interpreter as a simple calculator, performing calculations and assigning values to variables:
``` python
>>> 1 + 1
2
>>> x = 5
>>> x * 3
15
```
The interpreter makes it very convenient to try out small snippets of Python code and to experiment with short sequences of operations.
### The IPython interpreter
If you spend much time with the basic Python interpreter, you'll find that it lacks many of the features of a full-fledged interactive development environment.
An alternative interpreter called *IPython* (for Interactive Python) is bundled with the Anaconda distribution, and includes a host of convenient enhancements to the basic Python interpreter.
It can be started by typing ``ipython`` at the command prompt:
```
$ ipython
Python 3.5.1 |Continuum Analytics, Inc.| (default, Dec 7 2015, 11:24:55)
Type "copyright", "credits" or "license" for more information.
IPython 4.0.0 -- An enhanced Interactive Python.
? -> Introduction and overview of IPython's features.
%quickref -> Quick reference.
help -> Python's own help system.
object? -> Details about 'object', use 'object??' for extra details.
In [1]:
```
The main aesthetic difference between the Python interpreter and the enhanced IPython interpreter lies in the command prompt: Python uses ``>>>`` by default, while IPython uses numbered commands (e.g. ``In [1]:``).
Regardless, we can execute code line by line just as we did before:
``` ipython
In [1]: 1 + 1
Out[1]: 2
In [2]: x = 5
In [3]: x * 3
Out[3]: 15
```
Note that just as the input is numbered, the output of each command is numbered as well.
IPython makes available a wide array of useful features; for some suggestions on where to read more, see [Resources for Further Learning](16-Further-Resources.ipynb).
### Self-contained Python scripts
Running Python snippets line by line is useful in some cases, but for more complicated programs it is more convenient to save code to file, and execute it all at once.
By convention, Python scripts are saved in files with a *.py* extension.
For example, let's create a script called *test.py* which contains the following:
``` python
# file: test.py
print("Running test.py")
x = 5
print("Result is", 3 * x)
```
To run this file, we make sure it is in the current directory and type ``python`` *``filename``* at the command prompt:
```
$ python test.py
Running test.py
Result is 15
```
For more complicated programs, creating self-contained scripts like this one is a must.
### The Jupyter notebook
A useful hybrid of the interactive terminal and the self-contained script is the *Jupyter notebook*, a document format that allows executable code, formatted text, graphics, and even interactive features to be combined into a single document.
Though the notebook began as a Python-only format, it has since been made compatible with a large number of programming languages, and is now an essential part of the [*Jupyter Project*](https://jupyter.org/).
The notebook is useful both as a development environment, and as a means of sharing work via rich computational and data-driven narratives that mix together code, figures, data, and text.
For an introduction to Jupyter, you might consult the [*Jupyter notebook introduction*](https://realpython.com/jupyter-notebook-introduction/).
To get some more knowledge about how a Markdown cell works and how to format text in such a cell, you might want to take a look at the [*Introduction of Markdown*](https://daringfireball.net/projects/markdown/) and copy the text under [*this link*](https://daringfireball.net/projects/markdown/index.text) to a Markdown cell and execute its content.
If the Jupyter notebook is not installed on the computer you are working on, you can use [*Google colab*](https://colab.research.google.com/).
<!--NAVIGATION-->
< [Introduction](00-Introduction.ipynb) | [Contents](Index.ipynb) | [A Quick Tour of Python Language Syntax](02-Basic-Python-Syntax.ipynb) >
| true |
code
| 0.737442 | null | null | null | null |
|
# Riemann Staircase
A notebook to caclulate functions to visualise the prime staircase using Riemann's formula.
```
from mpmath import *
from sympy import mobius
import numpy as np
import matplotlib.pyplot as plt
from tqdm.notebook import trange
mp.dps = 30; mp.pretty = True
def Li(x, rho=1):
return ei(rho * log(x))
def secondary(x, zetazeros):
res = 0
for rho in zetazeros:
a = Li(x, rho) + Li(x, rho.conjugate())
res += a
return res
def Ns(x):
N = 1
y = x
while y >= 2:
if mobius(N) != 0:
yield N, y
N += 1
y = x ** (1/N)
import gzip
with gzip.open("data/zeros6.gz", "rt") as f:
lines = f.readlines()
zetazeros = [mpc(0.5, float(s.strip())) for s in lines]
```
An approximation of $\pi(x)$ using the first $n$ Riemann zeros.
```
def pi_approx(x, n_zeros):
total = 0
for N, y in Ns(x):
row = mobius(N) * (Li(y) - secondary(y, zetazeros[:n_zeros]) - log(2) + quad(lambda t: 1/(t*(t*t-1)*log(t)), [y, inf])) / N
total += row
return total
```
Plot the approximation for a few values of $n$.
```
def plot_funcs(funcs, rng, npoints=200):
points = np.linspace(rng[0], rng[1], npoints)
plt.figure()
for func in funcs:
plt.plot(points, [func(p) for p in points])
plt.plot(points, [0]*npoints, linestyle=':')
plt.rcParams["figure.figsize"]=10,7
plot_funcs([primepi, pi_approx0], [2, 50], 200)
plot_funcs([primepi, pi_approx30], [2, 50], 200)
plot_funcs([primepi, pi_approx60], [2, 50], 200)
plot_funcs([primepi, pi_approx90], [2, 50], 200)
```
## Precompute for multiple zeros
```
%%time
rng = [2, 50]
npoints = 500
n_doublings = 13
points = np.linspace(rng[0], rng[1], npoints)
values = np.zeros((n_doublings, npoints))
n_zeros = 0
for i in range(n_doublings):
print(i, n_zeros)
for j in trange(len(points)):
p = points[j]
values[i, j] = float(pi_approx(p, n_zeros))
if n_zeros == 0:
n_zeros = 1
else:
n_zeros *= 2
```
Export data for use in javascript
```
pi_values = np.zeros(npoints)
for i, p in enumerate(points):
pi_values[i] = float(primepi(p))
data = np.empty((values.shape[0] + 2, values.shape[1]))
data[0] = points
data[1:values.shape[0]+1] = values
data[-1] = pi_values
np.savetxt("staircase.csv", data, delimiter=",")
```
Show an interactive plot using `ipywidgets`
```
def plot_points(n=0):
plt.figure()
plt.plot(points, pi_values)
plt.plot(points, values[n])
plt.ylim(0, 16)
plt.show()
%matplotlib inline
from ipywidgets import interactive
import matplotlib.pyplot as plt
interactive_plot = interactive(plot_points, n=(0, len(values)-1, 1))
output = interactive_plot.children[-1]
plt.rcParams["figure.figsize"]=10,7
interactive_plot
```
| true |
code
| 0.437283 | null | null | null | null |
|
# datasets
```
import h5py
import cupy as cp
#加载数据的function
def load_dataset():
train_dataset = h5py.File('../datasets/train_signs.h5', "r")
train_set_x_orig = cp.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = cp.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('../datasets/test_signs.h5', "r")
test_set_x_orig = cp.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = cp.array(test_dataset["test_set_y"][:]) # your test set labels
classes = cp.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
#加载数据
train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes=load_dataset()
trainX=train_set_x_orig/255 #shape(1080,64,64,3)样本数,高,宽,通道数
trainX=trainX.transpose(0,3,1,2)
testX=test_set_x_orig/255
testX=testX.transpose(0,3,1,2)
trainy=train_set_y_orig
testy=test_set_y_orig
#转为one-hot编码
n_class = cp.max(testy).tolist() + 1
trainy=cp.eye(n_class)[trainy].reshape(-1,6)
testy=cp.eye(n_class)[testy].reshape(-1,6)
print('trainX shape:',trainX.shape)
print('trainy shape:',trainy.shape)
print('testX shape:',testX.shape)
print('testy shape:',testy.shape)
```
# 1.shinnosuke functional model
```
from shinnosuke.layers.Convolution import Conv2D,MaxPooling2D,MeanPooling2D
from shinnosuke.layers.Activation import Activation
from shinnosuke.layers.Normalization import BatchNormalization
from shinnosuke.layers.Dropout import Dropout
from shinnosuke.layers.FC import Flatten,Dense
from shinnosuke.layers.Base import Input
from shinnosuke.models import Model
X_input=Input(shape=(None,3,64,64))
X=Conv2D(8,(5,5),padding='VALID',initializer='normal',activation='relu')(X_input)
X=BatchNormalization(axis=1)(X)
X=MaxPooling2D((4,4))(X)
X=Conv2D(16,(3,3),padding='SAME',initializer='normal',activation='relu')(X)
X=MaxPooling2D((4,4))(X)
X=Flatten()(X)
X=Dense(6,initializer='normal',activation='softmax')(X)
model=Model(inputs=X_input,outputs=X)
model.compile(optimizer='sgd',loss='sparse_categorical_cross_entropy')
model.fit(trainX,trainy,batch_size=256,epochs=100,validation_ratio=0.)
acc,loss=model.evaluate(testX,testy)
print('test acc: %f,test loss: %f'%(acc,loss))
```
# shinnosuke sequential model
```
from shinnosuke.models import Sequential
m=Sequential()
m.add(Conv2D(8,(5,5),input_shape=(None,3,64,64),padding='VALID',initializer='normal'))
m.add(Activation('relu'))
m.add(BatchNormalization(axis=1))
m.add(MaxPooling2D((4,4)))
m.add(Conv2D(16,(3,3),padding='VALID',initializer='normal'))
m.add(Activation('relu'))
m.add(MaxPooling2D((4,4)))
m.add(Flatten())
m.add(Dense(6,initializer='normal',activation='softmax'))
m.compile(optimizer='sgd',loss='sparse_categorical_cross_entropy')
m.fit(trainX,trainy,batch_size=256,epochs=100,validation_ratio=0.)
acc,loss=m.evaluate(testX,testy)
print('test acc: %f,test loss: %f'%(acc,loss))
```
# keras-gpu functional model
```
trainX=cp.asnumpy(trainX)
trainy=cp.asnumpy(trainy)
testX=cp.asnumpy(testX)
testy=cp.asnumpy(testy)
import keras
from keras.models import Sequential,Model
from keras.layers import Dense, Dropout, Flatten,Input,Conv2D, MaxPooling2D,BatchNormalization,Activation
X_input=Input(shape=(3,64,64))
X=Conv2D(8,(5,5),padding='VALID',kernel_initializer='normal',activation='relu',data_format='channels_first')(X_input)
X=BatchNormalization(axis=1)(X)
X=MaxPooling2D((4,4))(X)
X=Conv2D(16,(3,3),padding='SAME',kernel_initializer='normal',activation='relu',data_format='channels_first')(X)
X=MaxPooling2D((4,4))(X)
X=Flatten()(X)
X=Dense(6,kernel_initializer='normal',activation='softmax')(X)
model=Model(inputs=X_input,outputs=X)
model.compile(optimizer='sgd',loss='categorical_crossentropy',metrics=['accuracy'])
model.fit(trainX,trainy,batch_size=256,epochs=100)
loss,acc=model.evaluate(testX,testy)
print('test acc: %f,test loss: %f'%(acc,loss))
```
# keras-gpu sequential model
```
m=Sequential()
m.add(Conv2D(8,(5,5),input_shape=(3,64,64),padding='VALID',kernel_initializer='normal',data_format='channels_first'))
m.add(Activation('relu'))
m.add(BatchNormalization(axis=1))
m.add(MaxPooling2D((4,4)))
m.add(Conv2D(16,(3,3),padding='VALID',kernel_initializer='normal',data_format='channels_first'))
m.add(Activation('relu'))
m.add(MaxPooling2D((4,4)))
m.add(Flatten())
m.add(Dense(6,kernel_initializer='normal',activation='softmax'))
m.compile(optimizer='sgd',loss='categorical_crossentropy',metrics=['accuracy'])
m.fit(trainX,trainy,batch_size=256,epochs=100)
loss,acc=m.evaluate(testX,testy)
print('test acc: %f,test loss: %f'%(acc,loss))
```
| true |
code
| 0.639342 | null | null | null | null |
|
# Improving generalization with regularizers and constraints
Neural networks usually have a very large number of parameters, which may lead to overfitting in many cases (especially when you do not have a large dataset). There's a large number of methods for regularization, and here we cover the most usual ones which are already implemented in Keras.
For more details and theoretical grounds for the regularization methods described here, a good reference is [Chapter 7 of the Deep Learning Book](http://www.deeplearningbook.org/contents/regularization.html).
## Regularizers (`keras.regularizers`)
- `l1(l=0.01)`: L1 weight regularization penalty, also known as LASSO
- `l2(l=0.01)`: L2 weight regularization penalty, also known as weight decay, or Ridge
- `l1l2(l1=0.01, l2=0.01)`: L1-L2 weight regularization penalty, also known as ElasticNet
- `activity_l1(l=0.01)`: L1 activity regularization
- `activity_l2(l=0.01)`: L2 activity regularization
- `activity_l1l2(l1=0.01, l2=0.01)`: L1+L2 activity regularization
```
# Example: Defining a Dense layer with l2 regularization on the weights and activations
from keras.regularizers import l2, activity_l2
model.add(Dense(256, W_regularizer=l2(0.01), activity_regularizer=activity_l2(0.05)))
```
## Constraints (`keras.constraints`)
- `maxnorm(m=2)`: maximum-norm constraint
- `nonneg()`: non-negativity constraint
- `unitnorm()`: unit-norm constraint, enforces the matrix to have unit norm along the last axis
```
# Example: enforce non-negativity on a convolutional layer weights
from keras.constraints import nonneg
model.add(Convolution1D(64, 3, border_mode='same', W_constraint=nonneg()))
```
## Dropout
Dropout is a different regularization technique, based on dropping out random internal features and/or inputs during training. In its usual formulation (which is the one implemented in Keras), dropout will set an input or feature to zero with probability P only during training (or, equivalently, setting a fraction P of the inputs/features to zero).
This is how you use Dropout in Keras:
```
from keras.layers import Dropout
model.add(Dense(128, input_dim=64))
model.add(Dropout(0.5)) # Dropout 50% of the features from the dense layer
```
Note that whenever Dropout is the first layer of a network, you have to specify the `input_shape` as usual. The parameter passed to Dropout should be between zero and one, and 0.5 is the usual value chosen for internal features. For inputs, you usually want to drop out a smaller amount of input features (0.1 or 0.2 are good values to start with).
As an alternative to this sort of "binary" dropout, one can also apply a multiplicative one-centered Gaussian noise to the inputs/features. This is implemented in Keras as the `GaussianDropout` layer:
```
from keras.layers.noise import GaussianDropout
model.add(GaussianDropout(0.1)) # Dropout 50% of the features
```
where the parameter is the $\sigma$ for the Gaussian distribution to be sampled.
## Adding noise to the inputs and/or internal features
Instead of multiplicative Gaussian noise, you can also use good old additive Gaussian noise, too. Usage is similar to the dropout layers described above:
```
from keras.layers.noise import GaussianNoise
model.add(GaussianNoise(0.2))
```
Again, the parameter is the $\sigma$ for the Gaussian distribution, but this time the noise is zero-centered as usual for additive Gaussian noise.
## Early stopping
Early stopping avoids overfitting the training data by monitoring the performance on a validation set and stopping when it stops improving. In Keras, it is implemented as a callback (`keras.callbacks.EarlyStopping`). In order to avoid noise in the performance metric used for the validation set, early stopping is implemented in Keras with a "patience" term: training stops when no improvement is seen for `patience` epochs.
```
early_stop = EarlyStopping(patience=5)
```
Note that the model parameters after training with early stopping will correspond to those from the last epoch, not those for the "best" epoch. So, most of the time, `EarlyStopping` is used in combination with the `ModelCheckpoint` callback with `save_best_only=True` , so you can load the best model after `EarlyStopping` interrupts your model training.
| true |
code
| 0.727746 | null | null | null | null |
|
# Identify DOSTA Sensors with Missing Two-Point Calibrations
During a review of the dissolved oxygen data, it was discovered that there was an error in how the instrument calibration coefficients were being applied. The two-point calibration values, supplied by the vendor if a multipoint calibration was not warranted, were not being passed to the equation used to convert the raw measurements to dissolved oxygen. The resulting calculated dissolved oxygen values were incorrect. The error in the formulation of the equation was identified and corrected, with the correction going into effect on September 10, 2020.
The code below identifies the instruments impacted using the OOI M2M API to access calibration values for the sensors from the Asset Management database and determine which sensors had two-point calibration values. The default values are set to a slope of 1 and offset of 0. If the vendor applied a two-point calibration, those values will be different. The error in the code always assumed the default values for the two-point calibration.
```
import pandas as pd
from datetime import datetime, timedelta
from ooi_data_explorations.common import list_deployments, get_deployment_dates, \
get_calibrations_by_refdes, get_vocabulary
def missing_two_point(sites, node, sensor):
"""
Use the OOI M2M API to locate the DOSTA sensors that had nondefault two-point
calibration values; default is a slope of 1 and offset of 0. These are the
sensors that would have had miscalculated dissolved oxygen data as the
function was always assuming the default values.
:param site: Site name to query
:param node: Node name to query
:param sensor: Sensor name to query
:return: pandas dataframe listing affected sensors
"""
# create an empty pandas dataframe
data = pd.DataFrame(columns=['Array', 'Platform', 'Node', 'Instrument', 'RefDes', 'Asset_ID',
'Serial Number', 'deployment', 'gitHub_changeDate', 'file', 'URL',
'changeType', 'dateRangeStart', 'dateRangeEnd', 'annotation'])
# loop through the sites
for site in sites:
# for each site, loop through the deployments
deployments = list_deployments(site, node, sensor)
for deploy in deployments:
# get the deployment dates and convert to a datetime object
start, stop = get_deployment_dates(site, node, sensor, deploy)
vocab = get_vocabulary(site, node, sensor)
start = datetime.strptime(start, '%Y-%m-%dT%H:%M:%S.000Z')
stop = datetime.strptime(stop, '%Y-%m-%dT%H:%M:%S.000Z')
# advance the start time by 30 days to ensure we only get calibration
# data for the deployment of interest (exclude potentially overlapping)
adj_start = start + timedelta(days=30)
adj_stop = start + timedelta(days=31)
# use the site, node, sensor and advanced start and stop dates to
# access the sensor calibration data (using 1 day in the middle
# of the deployment limits the response to just this deployment)
cal = get_calibrations_by_refdes(site, node, sensor,
adj_start.strftime('%Y-%m-%dT%H:%M:%S.000Z'),
adj_stop.strftime('%Y-%m-%dT%H:%M:%S.000Z'))
# extract the two-point calibration values
two_point = cal[0]['sensor']['calibration'][1]['calData'][0]['value']
# check to see if a two-point calibration was available
if two_point != [0.0, 1.0]:
# if so, add the information to the dataframe
percent_error = abs(100 - (two_point[0] + two_point[1] * 100))
annotation = (('ALGORITHM CORRECTION: During a review of the dissolved oxygen data, it was ' +
'discovered that there was an error in how the instrument calibration ' +
'coefficients were being applied. The two-point calibration values, supplied by ' +
'the vendor if a multipoint calibration was not warranted, were not being passed ' +
'to the equation used to convert the raw measurements to dissolved oxygen. The ' +
'resulting calculated dissolved oxygen values were incorrect. The error in the ' +
'formulation of the equation was identified and corrected, with the correction ' +
'going into effect on 2020-09-10. Users who have requested data for this sensor ' +
'({0}) prior to 2020-09-10 for deployment {1} between {2} and {3} are encouraged ' +
'to re-download the data. The estimated error in the dissolved oxygen ' +
'calculation in this instance is {4:.2f} percent.').format(cal[0]['referenceDesignator'],
deploy, start, stop,
percent_error))
data = data.append({'Array': vocab[0]['tocL1'],
'Platform': vocab[0]['tocL2'] ,
'Node': vocab[0]['tocL3'],
'Instrument': vocab[0]['instrument'],
'RefDes': cal[0]['referenceDesignator'],
'Asset_ID': cal[0]['sensor']['uid'],
'Serial Number': cal[0]['sensor']['serialNumber'],
'deployment': deploy,
'gitHub_changeDate': '2020-09-10',
'file': 'ParameterFunctions.csv',
'URL': 'https://github.com/oceanobservatories/preload-database/commit/c07c9229d01040da16e2cf6270c7180d4ed57f20',
'changeType': 'algorithmCorrection',
'dateRangeStart': start,
'dateRangeEnd': stop,
'annotation': annotation}, ignore_index=True)
# return the results
return data
```
## Coastal Endurance Array
Two sets of DOSTA sensors were potentially impacted by the error in the Coastal Endurance (CE) Array: the sensors mounted on the near-surface instrument frame (NSIF) for the shelf and offshore coastal surface moorings, and the sensors on the coastal surface piercing profiler (CSPP).
```
# find the endurance instruments affected
sites = ['CE02SHSM', 'CE04OSSM', 'CE07SHSM', 'CE09OSSM']
node = 'RID27'
sensor = '04-DOSTAD000'
nsif = missing_two_point(sites, node, sensor)
sites = ['CE01ISSP', 'CE02SHSP', 'CE06ISSP', 'CE07SHSP']
node = 'SP001'
sensor = '01-DOSTAJ000'
cspp = missing_two_point(sites, node, sensor)
endurance = pd.concat([nsif, cspp], ignore_index=True)
endurance
endurance.to_csv('endurance.dosta.changelog.csv')
```
## Coastal Pioneer Array
Three sets of DOSTA sensors were potentially impacted by the error in the Coastal Pioneer (CP) Array: the sensors mounted on the near-surface instrument frame (NSIF) and the multi-function node (MFN) for the coastal surface moorings, and the sensors on the coastal surface piercing profiler (CSPP).
```
# find the pioneer instruments affected
sites = ['CP01CNSM', 'CP03ISSM', 'CP04OSSM']
sensor = '04-DOSTAD000'
nsif = missing_two_point(sites, 'RID27', sensor)
mfn = missing_two_point(sites, 'MFD37', sensor)
sites = ['CP01CNSP', 'CP03ISSP']
node = 'SP001'
sensor = '01-DOSTAJ000'
cspp = missing_two_point(sites, node, sensor)
pioneer = pd.concat([nsif, mfn, cspp], ignore_index=True)
pioneer
pioneer.to_csv('pioneer.dosta.changelog.csv')
```
## Global Arrays (Argentine Basin, Irminger Sea, Southern Ocean and Station Papa)
4 sets of DOSTA sensors were potentially impacted by the error in the Global Arrays: the sensors mounted on the subsurface plate of the buoy and the near-surface instrument frame (NSIF), the sensors connected to the CTDBP on the mooring riser, and the sensors on the flanking mooring subsurface sphere.
```
sites = ['GA01SUMO', 'GI01SUMO', 'GS01SUMO']
buoy = missing_two_point(sites, 'SBD11', '04-DOSTAD000')
nsif = missing_two_point(sites, 'RID16', '06-DOSTAD000')
imm = [missing_two_point(sites, 'RII11', '02-DOSTAD031'),
missing_two_point(sites, 'RII11', '02-DOSTAD032'),
missing_two_point(sites, 'RII11', '02-DOSTAD033')]
sites = ['GA03FLMA', 'GA03FLMB', 'GI03FLMA', 'GI03FLMB', 'GP03FLMA', 'GP03FLMB', 'GS03FLMA', 'GS03FLMB']
sphere = missing_two_point(sites, 'RIS01', '03-DOSTAD000')
garray = pd.concat([buoy, nsif, pd.concat(imm), sphere], ignore_index=True)
garray
garray.to_csv('globals.dosta.changelog.csv')
```
| true |
code
| 0.539772 | null | null | null | null |
|
# Logistic Regression
Here is logistic regression to sats.csv. We have 3 collumns, exam 1 , exam 2 and if it's submitted.
#### Initialize
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
df=pd.read_csv("sats.csv")
X=df.iloc[:,:-1].values
y=df.iloc[:,-1].values
df.head()
df.describe()
```
### Plot
```
pos , neg = (y==1).reshape(100,1) , (y==0).reshape(100,1)
fig = plt.figure(1)
ax = fig.add_subplot(111, facecolor='#FFF5EE')
plt.scatter(X[pos[:,0],0],X[pos[:,0],1],c="#808000",marker="+", s=50)
plt.scatter(X[neg[:,0],0],X[neg[:,0],1],c="#8B0000",marker="o",s=20)
plt.xlabel("Exam1")
plt.ylabel("Exam2")
plt.legend(["Submitted","Not submitted"])
```
### Sigmoid
formula:
$ g(z) = \frac{1}{(1+e^{-z})}$
```
def sigmoid(z):
g=1/ (1 + np.exp(-z))
return g
# testing the sigmoid function
sigmoid(0)
```
### Compute the Cost Function and Gradient
$J(\Theta) = \frac{1}{m} \sum_{i=1}^{m} [ -y^{(i)}log(h_{\Theta}(x^{(i)})) - (1 - y^{(i)})log(1 - (h_{\Theta}(x^{(i)}))]$
$ \frac{\partial J(\Theta)}{\partial \Theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_{\Theta}(x^{(i)}) - y^{(i)})x_j^{(i)}$
```
def costFunction(theta, X, y):
m=len(y)
predictions = sigmoid(np.dot(X,theta))
error = (-y * np.log(predictions)) - ((1-y)*np.log(1-predictions))
# cost func
cost = 1/m * sum(error)
# drad func
grad = 1/m * np.dot(X.transpose(),(predictions - y))
return cost[0] , grad
```
### Feature scaling
```
def featureNormalization(X):
"""
Take in numpy array of X values and return normalize X values,
the mean and standard deviation of each feature
"""
mean=np.mean(X,axis=0)
std=np.std(X,axis=0)
X_norm = (X - mean)/std
return X_norm , mean , std
m , n = X.shape[0], X.shape[1]
X, X_mean, X_std = featureNormalization(X)
X= np.append(np.ones((m,1)),X,axis=1)
y=y.reshape(m,1)
initial_theta = np.zeros((n+1,1))
cost, grad= costFunction(initial_theta,X,y)
print("Cost of initial theta is",cost)
print("Gradient at initial theta (zeros):",grad)
```
### Gradient Descent
```
def gradientDescent(X,y,theta,alpha,num_iters):
"""
Take in numpy array X, y and theta and update theta by taking num_iters gradient steps
with learning rate of alpha
return theta and the list of the cost of theta during each iteration
"""
m=len(y)
J_history =[]
for i in range(num_iters):
cost, grad = costFunction(theta,X,y)
theta = theta - (alpha * grad)
J_history.append(cost)
return theta , J_history
theta , J_history = gradientDescent(X,y,initial_theta,1,400)
print("Theta optimized by gradient descent:",theta)
print("The cost of the optimized theta:",J_history[-1])
```
### Plotting of Cost Function
```
plt.plot(J_history)
plt.xlabel("Iteration")
plt.ylabel("$J(\Theta)$")
plt.title("Cost function using Gradient Descent")
```
### Plotting the decision boundary
From Machine Learning Resources:
$h_\Theta(x) = g(z)$, where g is the sigmoid function and $z = \Theta^Tx$
Since $h_\Theta(x) \geq 0.5$ is interpreted as predicting class "1", $g(\Theta^Tx) \geq 0.5$ or $\Theta^Tx \geq 0$ predict class "1"
$\Theta_1 + \Theta_2x_2 + \Theta_3x_3 = 0$ is the decision boundary
Since, we plot $x_2$ against $x_3$, the boundary line will be the equation $ x_3 = \frac{-(\Theta_1+\Theta_2x_2)}{\Theta_3}$
```
plt.scatter(X[pos[:,0],1],X[pos[:,0],2],c="r",marker="+",label="Admitted")
plt.scatter(X[neg[:,0],1],X[neg[:,0],2],c="b",marker="x",label="Not admitted")
x_value= np.array([np.min(X[:,1]),np.max(X[:,1])])
y_value=-(theta[0] +theta[1]*x_value)/theta[2]
plt.plot(x_value,y_value, "g")
plt.xlabel("Exam 1 score")
plt.ylabel("Exam 2 score")
plt.legend(loc=0)
```
### Prediction
```
def classifierPredict(theta,X):
"""
take in numpy array of theta and X and predict the class
"""
predictions = X.dot(theta)
return predictions>0
x_test = np.array([45,85])
x_test = (x_test - X_mean)/X_std
x_test = np.append(np.ones(1),x_test)
prob = sigmoid(x_test.dot(theta))
print("For a student with scores 45 and 85, we predict an admission probability of",prob[0])
```
### Accuracy on training set
```
p=classifierPredict(theta,X)
print("Train Accuracy:", sum(p==y)[0],"%")
```
| true |
code
| 0.505615 | null | null | null | null |
|
## Adding the required Libraries
```
import numpy as np
import pandas as pd
pd.set_option('display.max_columns',None)
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as colors
import seaborn as sns
import nltk
from nltk.tokenize import sent_tokenize
from nltk.corpus import words
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from nltk.stem import PorterStemmer
from nltk.sentiment.vader import SentimentIntensityAnalyzer
from nltk.sentiment.util import *
from textblob import TextBlob
from sklearn.feature_extraction.text import TfidfVectorizer
from wordcloud import WordCloud
import re
from collections import Counter
import datetime as dt
#Reading the dataset
tweets = pd.read_csv(r'C:\Users\tejas\Desktop\final_kanye.csv')
tweets.head(10)
tweets.shape
```
Our dataset contains <b>27010 rows and 12 columns.
```
tweets.describe()
tweets.info()
```
The <b>info</b> function gives us the description of each columns in our dataset - the datatype and the number of non-null values.
## Data Preparation and Preprocessing
After we extract the raw tweets, the data/tweets contains many <i>unnecessary letters and characters</i> which needs to be removed before we perform the sentiment analysis and build the model.
After carefully analysing the dataset, we find that some of the tweets have been repeated or are a retweet of the original tweet. <u>These duplicate tweets might interfere in our model and sentiment analysis, hence we need to remove it.
```
#Checking the duplicate tweets by converting the tweets into a set.
tweets_set=set(tweets.Text)
print(len(tweets_set))
print("Duplicate Tweet Count:", len(tweets.Text)-len(tweets_set))
```
Our dateset has been reduced from <b>27010 rows</b> to <b>24531 rows</b>. The count of the duplicate tweets is <b>2479.
```
#Removing the dulipacte tweets
kanye_original = tweets.drop_duplicates(subset = 'Text', keep = 'first')
kanye_original.shape
kanye = pd.DataFrame(kanye_original.Text)
```
After removing the duplicate tweets from our dataset, we will be cleaning our data ie.-removing the punctuations, numbers, URLs and emojis using the <b>Regex (Regular expressions).
```
#Removing URLs
kanye.Text = [re.sub(r'http\S+',"", i) for i in kanye.Text]
kanye.Text = [re.sub(r'com',"",i) for i in kanye.Text]
#Removing the retweet text 'RT'.
kanye.Text = [re.sub('^RT[\s]','',i) for i in kanye.Text]
#Removing the hashtag symbol '#'.
kanye.Text = [re.sub('^#[\s]','',i) for i in kanye.Text]
#Removing all punctuations and numbers
kanye.Text = [re.sub('[^a-zA-Z]', ' ',i) for i in kanye.Text]
#Converting into lower case
kanye.Text = [low.lower() for low in kanye.Text]
#Removing Emojis
def preprocess(Text):
emojis = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)',Text)
Text = re.sub('[\W]+',' ', Text.lower()) +\
' '.join(emojis).replace('-','')
return Text
kanye.Text = kanye.Text.apply(preprocess)
kanye.Text.head()
```
After removing the unnecessary characters from our tweets,we now need to remove the redundant words, known as <b>stopwords.</b> <i><u>Stopwords are the words that occur frequently in the text and are not considered informative.</i> These words are removed before the model is built. Lets check the stopwords present in the English language.
```
#Checking the stopwords list
cachedStopWords=set(stopwords.words("english"))
print(cachedStopWords)
#Removing Stop Words
kanye.Text=kanye.Text.apply(lambda tweet: ' '.join([word for word in tweet.split() if word not in cachedStopWords]))
```
After removing the stopwords we will be performing <b>Stemming</b> and <b>Lemmatizations</b>.
<b>Stemming</b> can defined as the <u>process of reducing inflected (derived) words to their word stem, base or root form—generally a written word form.
```
#Stemming
porter = PorterStemmer()
def stemWords(word):
return porter.stem(word)
kanye["Text"] = kanye["Text"].apply(lambda tweet: ' '.join([stemWords(word) for word in tweet.split()]))
```
<b>Lemmatization</b> is defined as <u>the process of grouping together the inflected forms of a word so they can be analysed as a single item, identified by the word's lemma, or dictionary form.
```
#Lemmatization:
lema = WordNetLemmatizer()
def lemmatizeWords(word):
return lema.lemmatize(word)
kanye.Text = kanye.Text.apply(lambda tweet: ' '.join([lemmatizeWords(word) for word in tweet.split()]))
```
Now that our data is cleaned and preprocessed, we can now perform the sentiment analysis and build the model.
## Sentiment Analysis
For performing the sentiment analysis, we will be using the <b>TextBlob</b> package and the <b>VADER Sentiment Analyser.
```
pol = []
for i in kanye.Text:
blob = TextBlob(i) #Using the TextBlob
pol.append(blob.sentiment.polarity)
#Adding polarity to the dataframe
kanye['Polarity']=pol
kanye.head()
```
Lets count the number of tweets as per the polarity of the tweets. We will group the tweets as positive, negative and neutral tweets.
```
#Counting the number of tweets based on the polarity
positive=0
negative=0
neutral=0
sent=[]
for i in pol:
if i>=0.2:
positive+=1
sent.append('Positive')
elif i<=0:
negative+=1
sent.append('Negative')
else:
neutral+=1
sent.append('Neutral')
print("Positive Tweets:",positive)
print("Negative Tweets:",negative)
print("Neutral Tweets:",neutral)
kanye['Sentiment']=sent
kanye.head()
```
After dividing the tweets into the groups mentioned above, we find that the majority of the tweets are off negative sentiment(17123 tweets).
```
#Preparing words by splitting the tweets
words=[]
words=[word for tweet in kanye.Text for word in tweet.split()]
```
Now we will use the <b>VADER Sentiment Analyser</b> to get the polarity of the tweets.
```
import nltk
nltk.download('vader_lexicon')
#Using the VADER Sentiment Analyzer
sid = SentimentIntensityAnalyzer()
sentiment_scores = kanye.Text.apply(lambda x: sid.polarity_scores(x))
sentimental_score = pd.DataFrame(list(sentiment_scores))
sentimental_score.tail()
```
Lets divide the tweets into the following groups and assign the overall sentiment of the tweet.
```
sentimental_score['Sentiment'] = sentimental_score['compound'].apply(lambda x: 'negative' if x <= 0 else ('positive' if x >=0.2 else 'neutral'))
sentimental_score.head()
#Checking the number of tweets per sentiment
sns.set_style(style='darkgrid')
sns.set_context('poster')
fig= plt.figure(figsize=(10,5))
sent_count = pd.DataFrame.from_dict(Counter(sentimental_score['Sentiment']), orient = 'index').reset_index()
sent_count.columns = ['sentiment', 'count']
sns.barplot(y="count", x='sentiment', data=sent_count)
```
### WordCloud
Wordcloud is an image that comprises of words with different sizes and colors. The size of the words gives frequency of the word -<i><u>more frequent the words is, the bigger and bolder it will appear on the WordCloud.
```
wordcloud=WordCloud(background_color='black',max_words=100,max_font_size=50,scale=5,collocations=False,
normalize_plurals=True).generate(' '.join(words))
plt.figure(figsize = (12, 12), facecolor="None")
plt.imshow(wordcloud,interpolation='bilinear')
plt.axis("off")
plt.title("WordCloud",fontsize=18)
plt.show()
```
Now we will count the frequency of the words used in the tweets. For our analysis, we will observe the <u>first 60 most frequent words.
```
sns.set(style="darkgrid")
sns.set_context('notebook')
#Counting the word frequency of the tweets
counts = Counter(words).most_common(60)
counts_df = pd.DataFrame(counts)
counts_df.columns = ['word', 'frequency']
fig = plt.subplots(figsize = (12, 10))
plt.title("Word Frequency",fontsize=18)
sns.barplot(y="word", x='frequency', data=counts_df)
#Finding the frequency of the polarity
sns.set_context('talk')
fig,ax = plt.subplots(figsize = (12, 8))
ax.set(title='Tweet Sentiments distribution', xlabel='polarity', ylabel='frequency')
sns.distplot(kanye['Polarity'], bins=30)
```
This plot gives the distibution of the polarity of the tweets with a majority tweets either of neutral polarity or slightly of positive polarity.
```
#Counting the number of different tweets
sns.set_style(style='darkgrid')
sns.set_context('poster')
fig= plt.figure(figsize=(10,5))
sns.countplot(kanye.Sentiment)
```
As we can see, majority of the tweets are of negative sentiment.
```
#Counting the number of tweets per hour
tweets['date'] = pd.to_datetime(tweets['date'])
hour = list(tweets.date.dt.hour)
count_hours=Counter(hour)
sns.set_context("talk")
fig,ax=plt.subplots(figsize=(12,10))
ax.set(title='Count of Tweets per Hour', xlabel='Hour (24 hour time)', ylabel='count')
sns.barplot(x=list(count_hours.keys()),y=list(count_hours.values()),color='blue')
```
The above tweets gives us the number of tweets per hour.
## Model Prediction
### Required Libraries
```
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.naive_bayes import MultinomialNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
from sklearn.metrics import accuracy_score, precision_score, recall_score,f1_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn import model_selection
```
Before we can build the model, we need to transform the text data into the numerical features as we cannot directly feed the model the raw data.
We can convert the text document into the numerical representation by vectorization.
### TfiDF Vectorizer
<b>TfiDF Vectorizer</b> is a method to transforms text to feature vectors that can be used <u>to evaluate how important a word is to a document in a collection or corpus.</u>
It is termed as the <b>Term Frequency Inverse Document Frequency</b>.<ul>
1.Term Frequency: The number of times the particular word appears in a single document.
2.Inverse Document Frequency:The log ratio of the total number of documents divided by the total documents where that particular word appears.
Hence the TfiDf can be calculated by:<l>
TfiDF = Tf * iDf
```
#Definining the vectorizer
vect = TfidfVectorizer(ngram_range=(1,1), max_features=100,smooth_idf=True,use_idf=True).fit(kanye.Text)
#Transform the vectorizer
X_txt = vect.transform(kanye.Text)
#Transforming to a data frame
X_df=pd.DataFrame(X_txt.toarray(), columns=vect.get_feature_names())
X_df.head(10)
```
The <b>LabelEncoder</b> to convert the categorical features into numerical features. We will use it to the Sentiment column.
```
X_df['Sentiment'] = sent
label = LabelEncoder()
X_df['Label'] = label.fit_transform(X_df['Sentiment'])
X_df.head()
```
After converting the Sentiment column into the numerical values, we find that:<ul>
Negative Sentiment-0
Neutral Setiment-1
Positive Sentiment-2
We have our target variable(Label) and the predictor variables. Now we will split our dataset into training and testing dataset, using the train_test_split method.
```
#Splitting the dataset into training and testing set
X = X_df.drop(['Sentiment','Label'],axis=1)
y = X_df.Label
X_train, X_test, y_train, y_test = train_test_split(X , y, test_size=0.2, random_state=0) #Testing dataset size-20% of the total
```
## Naives Bayes
```
nb = MultinomialNB().fit(X_train, y_train) #Training the model
#Predicting the test set
y_pred_nb= nb.predict(X_test)
#Checking the accuracy,precision,recall,f1 scores
accuracy_score_nb = accuracy_score(y_test, y_pred_nb)
precision_score_nb = precision_score(y_test, y_pred_nb , average = 'micro')
recall_score_nb = recall_score(y_test, y_pred_nb , average = 'micro')
f1_score_nb = f1_score(y_test, y_pred_nb , average = 'micro')
print("Accuracy Score: " , accuracy_score_nb)
print("Precision Score: " , precision_score_nb)
print("Recall Score: " , recall_score_nb)
print("F1 Score: " , f1_score_nb)
print("Classification Report:\n",classification_report(y_test, y_pred_nb))
#Constructing a confusion matrix
cm_nb = confusion_matrix(y_test, y_pred_nb)
df_cm_nb = pd.DataFrame(cm_nb)
categories = ['Negative','Neutral','Positive']
plt.figure(figsize=(10,8))
sns.heatmap(df_cm_nb, cmap='inferno' ,annot=True, annot_kws={"size": 18}, xticklabels = categories,
yticklabels = categories,fmt="d")
```
### Hyperparameter Optimization
```
#Getting the parameters of the particular model
nb.get_params().keys()
NB_opti = MultinomialNB() #Using the MultinomialNB
param_grid = {'alpha':[1,2,3,4], } #Selecting the parameters
model_NB = model_selection.GridSearchCV(estimator=NB_opti, #GridSearch
param_grid=param_grid,
cv=10)
model_NB.fit(X_train,y_train)
print(model_NB.best_score_) #Gives the best score of the model
print(model_NB.best_estimator_.get_params()) #Gives the best parameters of the model
```
## Decision Tree
```
DT = DecisionTreeClassifier().fit(X_train, y_train) #Training the model
#predicting the test set
y_pred_dt= DT.predict(X_test)
#Checking the accuracy,precision,recall and f1 scores
accuracy_score_dt = accuracy_score(y_test, y_pred_dt)
precision_score_dt = precision_score(y_test, y_pred_dt , average = 'micro')
recall_score_dt = recall_score(y_test, y_pred_dt , average = 'micro')
f1_score_dt = f1_score(y_test, y_pred_dt , average = 'micro')
print("Accuracy Score: " , accuracy_score_dt)
print("Precision Score: " , precision_score_dt)
print("Recall Score: " , recall_score_dt)
print("F1 Score: " , f1_score_dt)
print("Classification Report:\n",classification_report(y_test, y_pred_dt))
#Construting the confusion matrix
cm_dt = confusion_matrix(y_test, y_pred_dt)
df_cm_dt = pd.DataFrame(cm_dt)
categories = ['Negative','Neutral','Positive']
plt.figure(figsize=(10,8))
sns.heatmap(df_cm_dt, cmap='inferno' ,annot=True, annot_kws={"size": 20}, xticklabels = categories,
yticklabels = categories,fmt="d")
```
### Hyperparamter Optimization
```
#Getting the parameters of the particular model
DT.get_params().keys()
DT_opti = DecisionTreeClassifier()
param_grid = {"max_depth" : [1,3,5,7], #Setting the parameters for the model
"criterion" : ["gini","entropy"],
"min_samples_split" : [2,3,4],
"max_leaf_nodes" : [7,8,9],
"min_samples_leaf": [2,3,4],
}
model_DT = model_selection.GridSearchCV(estimator=DT_opti, #GridSearch
param_grid=param_grid,
cv=10)
model_DT.fit(X_train,y_train)
print(model_DT.best_score_) #Gives the best score of the model
print(model_DT.best_estimator_.get_params()) #Gives the best parameters
```
## Random Forest
```
RF = RandomForestClassifier(n_jobs=1).fit(X_train, y_train) #Training the model
#Predicting the test set
y_pred_RF = RF.predict(X_test)
#Checking the accuracy,precision,recall and f1 scores
accuracy_score_RF = accuracy_score(y_test, y_pred_RF)
precision_score_RF = precision_score(y_test, y_pred_RF , average = 'micro')
recall_score_RF = recall_score(y_test, y_pred_RF, average = 'micro')
f1_score_RF = f1_score(y_test, y_pred_RF, average = 'micro')
print("Accuracy Score: " , accuracy_score_RF)
print("Precision Score: " , precision_score_RF)
print("Recall Score: " , recall_score_RF)
print("F1 Score:" , f1_score_RF)
print("Classification Report:\n",classification_report(y_test, y_pred_RF))
#Construting the confusion matrix
cm_RF = confusion_matrix(y_test, y_pred_RF)
df_cm_RF = pd.DataFrame(cm_RF)
categories = ['Negative','Neutral','Positive']
plt.figure(figsize=(10,8))
sns.heatmap(df_cm_RF, cmap='inferno' ,annot=True, annot_kws={"size": 18}, xticklabels = categories,
yticklabels = categories,fmt="d")
```
### Hyperparameter Optimization
```
#Getting the parameters of the particular model
RF.get_params().keys()
RF_opti1 = RandomForestClassifier()
param_grid = {"n_estimators": np.arange(100,1500,100), #Selecting the parameters
"max_depth": np.arange(1,20),
"criterion": ["gini","entropy"],
}
model_RF1 = model_selection.RandomizedSearchCV(estimator=RF_opti1, #RandomizedSearch
param_distributions=param_grid,
n_iter=10,
scoring='accuracy',
verbose=10,
n_jobs=1,
cv=5)
model_RF1.fit(X_train,y_train)
print(model_RF1.best_score_) #Gives the best score of the model
print(model_RF1.best_estimator_.get_params()) #Gives the best parameters of the model
```
| true |
code
| 0.408395 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/csaybar/EarthEngineMasterGIS/blob/master/module06/04_RUSLE.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<!--COURSE_INFORMATION-->
<img align="left" style="padding-right:10px;" src="https://user-images.githubusercontent.com/16768318/73986808-75b3ca00-4936-11ea-90f1-3a6c352766ce.png" width=10% >
<img align="right" style="padding-left:10px;" src="https://user-images.githubusercontent.com/16768318/73986811-764c6080-4936-11ea-9653-a3eacc47caed.png" width=10% >
**Bienvenidos!** Este *colab notebook* es parte del curso [**Introduccion a Google Earth Engine con Python**](https://github.com/csaybar/EarthEngineMasterGIS) desarrollado por el equipo [**MasterGIS**](https://www.mastergis.com/). Obten mas informacion del curso en este [**enlace**](https://www.mastergis.com/product/google-earth-engine/). El contenido del curso esta disponible en [**GitHub**](https://github.com/csaybar/EarthEngineMasterGIS) bajo licencia [**MIT**](https://opensource.org/licenses/MIT).
### **Ejercicio N°01: RUSLE a Nivel Mundial**
<img src="https://user-images.githubusercontent.com/16768318/73690808-1604b700-46c9-11ea-8bdd-43e0e490a0a3.gif" align="right" width = 60%/>
Genere una funcion para calcular la Ecuacion Universal de Perdida de Suelo (RUSLE) para cualquier parte del mundo. La funcion debe tener los siguientes parametros.**rusle(roi, prefix, folder, scale)**
http://cybertesis.unmsm.edu.pe/handle/cybertesis/10078
```
#@title Credenciales Google Earth Engine
import os
credential = '{"refresh_token":"PON_AQUI_TU_TOKEN"}'
credential_file_path = os.path.expanduser("~/.config/earthengine/")
os.makedirs(credential_file_path,exist_ok=True)
with open(credential_file_path + 'credentials', 'w') as file:
file.write(credential)
import ee
ee.Initialize()
#@title mapdisplay: Crea mapas interactivos usando folium
import folium
def mapdisplay(center, dicc, Tiles="OpensTreetMap",zoom_start=10):
'''
:param center: Center of the map (Latitude and Longitude).
:param dicc: Earth Engine Geometries or Tiles dictionary
:param Tiles: Mapbox Bright,Mapbox Control Room,Stamen Terrain,Stamen Toner,stamenwatercolor,cartodbpositron.
:zoom_start: Initial zoom level for the map.
:return: A folium.Map object.
'''
center = center[::-1]
mapViz = folium.Map(location=center,tiles=Tiles, zoom_start=zoom_start)
for k,v in dicc.items():
if ee.image.Image in [type(x) for x in v.values()]:
folium.TileLayer(
tiles = v["tile_fetcher"].url_format,
attr = 'Google Earth Engine',
overlay =True,
name = k
).add_to(mapViz)
else:
folium.GeoJson(
data = v,
name = k
).add_to(mapViz)
mapViz.add_child(folium.LayerControl())
return mapViz
```
### **1) Factor R**
El **factor R** es el factor de erosividad de la lluvia. Este factor indica el potencial erosivo de la lluvia que afecta en el proceso de erosion del suelo. Haciendo una analogia, se podria decir que una lluvia fuerte un dia al año puede producir suficiente energia para erosionar el suelo que varias lluvias de mediana intensidad a lo largo de un ano.
El factor erosividad (R) es definido como la sumatoria anual de los promedios de los valores individuales del indice de tormenta de erosion (EI30). Donde E es la energia cinetica por unidad de area e I30 es la maxima intensidad en 30 minutos de precipitacion. Esto se puede definir en la siguiente ecuacion:
<img src="https://user-images.githubusercontent.com/16768318/73694650-67fd0b00-46d0-11ea-87f6-4ed9501cf964.png" width = 60%>
Por tanto, la energia de la tormenta (EI o R) indica el volumen de lluvia y escurrimiento, pero una larga y suave lluvia puede tener el mismo valor de E que una lluvia de corta y mas alta intensidad. (Mannaerts, 1999). La energia se calcula a partir de la formula de Brown y Foster:
<img src="https://user-images.githubusercontent.com/16768318/73694782-b3171e00-46d0-11ea-94fe-94f3f57941c5.png" width = 40%>
A partir de la ecuación anterior, el calculo del factor R es un proceso complejo y requiere datos horarios o diarios de varios anos. Por lo que se han desarrollado diferentes ecuaciones que adaptan la erosividad local mediante una formula que solo requiera una data mensual o anual de precipitacion. A continuacion, se muestran algunas de las formulas adaptadas para una precipitacion media anual.
<img src="https://user-images.githubusercontent.com/16768318/73694993-228d0d80-46d1-11ea-8bc4-9962963850b7.png">
Si bien es cierto, se usa ampliamente una precipitacion media anual para estimar el **factor R** debido a la escasez de informacion, para este ejemplo se ha optado por utilizar la formula desarrollada por **(Wischmeier & Smith, 1978)** debido a que se cuenta con una serie historica de informacion de precipitacion mensual. La formula es:
<img src="https://user-images.githubusercontent.com/16768318/73695488-2b321380-46d2-11ea-8033-0063f27698d8.png" width = 50%>
```
# Monthly precipitation in mm at 1 km resolution:
# https://zenodo.org/record/3256275#.XjibuDJKiM8
clim_rainmap = ee.Image("OpenLandMap/CLM/CLM_PRECIPITATION_SM2RAIN_M/v01")
year = clim_rainmap.reduce(ee.Reducer.sum())
R_monthly = ee.Image(10).pow(ee.Image(1.5).multiply(clim_rainmap.pow(2).divide(year).log10().subtract(-0.08188))).multiply(1.735)
factorR = R_monthly.reduce(ee.Reducer.sum())
center_coordinate = [0,0]
palette_rain = ["#450155", "#3B528C", "#21918D", "#5DCA63","#FFE925"]
mapdisplay(center_coordinate, {'Factor_R':factorR.getMapId({'min':0,'max':6000,'palette':palette_rain})},zoom_start=3)
```
### **2) Factor K**
A diferencia del factor R, el factor K muestra qué tan susceptible es el suelo a la erosion hidrica, esto es determinado por las propiedades fisicas y quimicas del suelo, que dependen de las caracteristicas de estos. Para determinar el factor K, existen una gran cantidad de formulas empiricas, adecuadas para diversos lugares del mundo y donde intervienen caracteristicas del suelo como porcentaje de arena, limo, arcilla; estructura del suelo; contenido de carbono organico o materia orgánica; entre otros.
El factor K puede variar en una escala de 0 a 1, donde 0 indica suelos con la menor susceptibilidad a la erosion y 1 indica suelos altamente susceptibles a la erosion hidrica del suelo; cabe mencionar que esta escala fue hecha para el sistema de unidades americanas, y adaptandose al sistema internacional, la escala varia a normalmente entre 0 y 0.07.
A continuacion, se muestran algunas ecuaciones para la estimación de este factor:
<img src="https://user-images.githubusercontent.com/16768318/73704444-039b7500-46eb-11ea-9ccd-b7850bb17911.png" width = 50%>
<img src="https://user-images.githubusercontent.com/16768318/73704442-039b7500-46eb-11ea-870c-a557ca50b777.png" width = 50%>
<img src="https://user-images.githubusercontent.com/16768318/73704443-039b7500-46eb-11ea-9469-104f04983dfd.png" width = 50%>
Para este ejemplo se ha optado por utilizar la formula desarrollada por **Williams (1975)**.
```
# Cargamos toda la informacion necesaria para estimar el factor K
sand = ee.Image("OpenLandMap/SOL/SOL_CLAY-WFRACTION_USDA-3A1A1A_M/v02").select('b0')
silt = ee.Image('users/aschwantes/SLTPPT_I').divide(100)
clay = ee.Image("OpenLandMap/SOL/SOL_SAND-WFRACTION_USDA-3A1A1A_M/v02").select('b0')
morg = ee.Image("OpenLandMap/SOL/SOL_ORGANIC-CARBON_USDA-6A1C_M/v02").select('b0').multiply(0.58)
sn1 = sand.expression('1 - b0 / 100', {'b0': sand})
orgcar = ee.Image("OpenLandMap/SOL/SOL_ORGANIC-CARBON_USDA-6A1C_M/v02").select('b0')
#Juntando todas las imagenes en una sola
soil = ee.Image([sand, silt, clay, morg, sn1, orgcar]).rename(['sand', 'silt', 'clay', 'morg', 'sn1', 'orgcar'] )
factorK = soil.expression(
'(0.2 + 0.3 * exp(-0.0256 * SAND * (1 - (SILT / 100)))) * (1 - (0.25 * CLAY / (CLAY + exp(3.72 - 2.95 * CLAY)))) * (1 - (0.7 * SN1 / (SN1 + exp(-5.51 + 22.9 * SN1))))',
{
'SAND': soil.select('sand'),
'SILT': soil.select('silt'),
'CLAY': soil.select('clay'),
'MORG': soil.select('morg'),
'SN1': soil.select('sn1'),
'CORG': soil.select('orgcar')
});
center_coordinate = [0,0]
palette_k = palette = [
'FFFFFF', 'CE7E45', 'DF923D', 'F1B555', 'FCD163', '99B718', '74A901',
'66A000', '529400', '3E8601', '207401', '056201', '004C00', '023B01',
'012E01', '011D01', '011301'
]
viz_param_k = {'min': 0.0, 'max': 0.5, 'palette': palette_k};
mapdisplay(center_coordinate, {'Factor_K':factorK.getMapId(viz_param_k)},zoom_start=3)
```
### **3) Factor LS**
El factor LS expresa el efecto de la topografia local sobre la tasa de erosion del suelo, combinando los efectos de la longitud de la pendiente (L) y la inclinación de la pendiente (S). A medida que mayor sea la longitud de la pendiente, mayor sera la cantidad de escorrentia acumulada y de la misma forma, mientras mas pronunciada sea la pendiente de la superficie, mayor sera la velocidad de la escorrentia, que influye directamente en la erosion. Existen diversas metodologias basadas en SIG para calcular estos factores, como se pueden mostrar a continuación:
<img src="https://user-images.githubusercontent.com/16768318/73706484-7ce99680-46f0-11ea-8e0e-5fbb4a00731d.png" width = 50%>
```
facc = ee.Image("WWF/HydroSHEDS/15ACC")
dem = ee.Image("WWF/HydroSHEDS/03CONDEM")
slope = ee.Terrain.slope(dem)
ls_factors = ee.Image([facc, slope]).rename(['facc','slope'])
factorLS = ls_factors.expression(
'(FACC*270/22.13)**0.4*(SLOPE/0.0896)**1.3',
{
'FACC': ls_factors.select('facc'),
'SLOPE': ls_factors.select('slope')
});
center_coordinate = [0,0]
palette_ls = palette = [
'FFFFFF', 'CE7E45', 'DF923D', 'F1B555', 'FCD163', '99B718', '74A901',
'66A000', '529400', '3E8601', '207401', '056201', '004C00', '023B01',
'012E01', '011D01', '011301'
]
viz_param_k = {'min': 0, 'max': 100, 'palette': palette_ls};
mapdisplay(center_coordinate, {'Factor_LS':factorLS.getMapId(viz_param_k)},zoom_start=3)
```
### **4) Factor C**
El factor C se utiliza para determinar la eficacia relativa de los sistemas de manejo del suelo y de los cultivos en terminos de prevencion o reduccion de la perdida de suelo. Este factor indica como la cobertura vegetal y los cultivos afectaran la perdida media anual de suelos y como se distribuira el potencial de perdida de suelos en el tiempo (Rahaman, 2015).
El valor de C depende del tipo de vegetacion, la etapa de crecimiento y el porcentaje de cobertura. Valores mas altos del factor C indican que no hay efecto de cobertura y perdida de suelo, mientras que el menor valor de C significa un efecto de cobertura muy fuerte que no produce erosion.
```
ndvi_median = ee.ImageCollection("MODIS/006/MOD13A2").median().multiply(0.0001).select('NDVI')
geo_ndvi = [
'FFFFFF', 'CE7E45', 'DF923D', 'F1B555', 'FCD163', '99B718', '74A901',
'66A000', '529400', '3E8601', '207401', '056201', '004C00', '023B01',
'012E01', '011D01', '011301'
]
l8_viz_params = {'palette':geo_ndvi,'min':0,'max': 0.8}
mapdisplay([0,0],{'composite_median':ndvi_median.getMapId(l8_viz_params)},zoom_start=3)
```
Otra forma de hallar este factor C, es haciendo una comparación entre el NDVI a partir de las fórmulas Van de Kniff (1999) [C1] y su adaptacion para paises asiaticos, que tambien se adecuan a la realidad de la costa peruana de Lin (2002) [C2]. Por ultimo se tiene la ecuacion formulada por De Jong(1994) [C3] adaptado a estudios de degradacion de suelos en un entorno mediterraneo.
<center>
<img src="https://user-images.githubusercontent.com/16768318/73713048-e6bf6b80-4703-11ea-80b1-1940e6b55707.png" width = 50%>
</center>
```
factorC = ee.Image(0.805).multiply(ndvi_median).multiply(-1).add(0.431)
```
### **5) Calculo de la Erosion**
**A = R\*K\*LS\*C\*1**
<img src="https://user-images.githubusercontent.com/16768318/73690808-1604b700-46c9-11ea-8bdd-43e0e490a0a3.gif">
```
erosion = factorC.multiply(factorR).multiply(factorLS).multiply(factorK)
geo_erosion = ["#00BFBF", "#00FF00", "#FFFF00", "#FF7F00", "#BF7F3F", "#141414"]
l8_viz_params = {'palette':geo_erosion,'min':0,'max': 6000}
mapdisplay([0,0],{'composite_median':erosion.getMapId(l8_viz_params)},zoom_start=3)
```
### **Funcion para descargar RUSLE en cualquier parte del mundo**
[Respuesta aqui](https://gist.github.com/csaybar/19a9db35f8c8044448d885b68e8c9eb8)
```
#Ponga su funcion aqui (cree un snippet!)
# Ambito de estudio aqui
geometry = ee.Geometry.Polygon([[[-81.9580078125,-5.659718554577273],
[-74.99267578125,-5.659718554577273],
[-74.99267578125,2.04302395742204],
[-81.9580078125,2.04302395742204],
[-81.9580078125,-5.659718554577273]]])
ec_erosion = rusle(geometry,'RUSLE_','RUSLE_MASTERGIS', scale = 100)
# Genere una vizualizacion de su ambito de estudio
geo_erosion = ["#00BFBF", "#00FF00", "#FFFF00", "#FF7F00", "#BF7F3F", "#141414"]
l8_viz_params = {'palette':geo_erosion,'min':0,'max': 6000}
center = geometry.centroid().coordinates().getInfo()
mapdisplay(center,{'composite_median':ec_erosion.select('A').getMapId(l8_viz_params)},zoom_start=6)
```
### **¿Dudas con este Jupyer-Notebook?**
Estaremos felices de ayudarte!. Create una cuenta Github si es que no la tienes, luego detalla tu problema ampliamente en: https://github.com/csaybar/EarthEngineMasterGIS/issues
**Tienes que dar clic en el boton verde!**
<center>
<img src="https://user-images.githubusercontent.com/16768318/79680748-d5511000-81d8-11ea-9f89-44bd010adf69.png" width = 70%>
</center>
| true |
code
| 0.498596 | null | null | null | null |
|
# Import Packages
```
import os
import numpy as np
import matplotlib.pyplot as plt
import quantities as pq
import neo
from neurotic._elephant_tools import CausalAlphaKernel, instantaneous_rate
pq.markup.config.use_unicode = True # allow symbols like mu for micro in output
pq.mN = pq.UnitQuantity('millinewton', pq.N/1e3, symbol = 'mN'); # define millinewton
# make figures interactive and open in a separate window
# %matplotlib qt
# make figures interactive and inline
%matplotlib notebook
# make figures non-interactive and inline
# %matplotlib inline
colors = {
'B38': '#EFBF46', # yellow
'I2': '#DC5151', # red
'B8a/b': '#DA8BC3', # pink
'B6/B9': '#64B5CD', # light blue
'B3/B6/B9': '#5A9BC5', # medium blue
'B3': '#4F80BD', # dark blue
'B4/B5': '#00A86B', # jade green
'Force': '0.7', # light gray
'Model': '0.2', # dark gray
}
```
# Load Data
```
directory = 'spikes-firing-rates-and-forces'
# filename = 'JG07 Tape nori 0.mat'
# filename = 'JG08 Tape nori 0.mat'
filename = 'JG08 Tape nori 1.mat'
# filename = 'JG08 Tape nori 1 superset.mat' # this file is missing spikes for several swallows
# filename = 'JG08 Tape nori 2.mat'
# filename = 'JG11 Tape nori 0.mat'
# filename = 'JG12 Tape nori 0.mat'
# filename = 'JG12 Tape nori 1.mat'
# filename = 'JG14 Tape nori 0.mat'
file_basename = '.'.join(os.path.basename(filename).split('.')[:-1])
# read the data file containing force and spike trains
reader = neo.io.NeoMatlabIO(os.path.join(directory, filename))
blk = reader.read_block()
seg = blk.segments[0]
sigs = {sig.name:sig for sig in seg.analogsignals}
spiketrains = {st.name:st for st in seg.spiketrains}
```
# Plot Empirical Force
```
# plot the swallowing force measured by the force transducer
fig, ax = plt.subplots(1, 1, sharex=True, figsize=(8,4))
ax.plot(sigs['Force'].times.rescale('s'), sigs['Force'].rescale('mN'), c=colors['Force'])
ax.set_xlabel('Time (s)')
ax.set_ylabel('Force (mN)')
ax.set_title(file_basename)
plt.tight_layout()
```
# Model Parameters
```
# parameters for constructing the model
# - model force = sum of scaled (weighted) firing rates + offset
# - comment/uncomment an entry in firing_rate_params to exclude/include the unit (I2 muscle or motor neurons)
# - weights can be positive or negative
# - rate constants determine how quickly the effect of a unit builds and decays
# - the model will be plotted below against the empirical force, both normalized by their peak values
offset = 0
# firing_rate_params = {
# # 'I2': {'weight': -0.002, 'rate_constant': 1},
# # 'B8a/b': {'weight': 0.05, 'rate_constant': 1},
# 'B3': {'weight': 0.05, 'rate_constant': 1},
# 'B6/B9': {'weight': 0.05, 'rate_constant': 0.5},
# 'B38': {'weight': 0.025, 'rate_constant': 1},
# # 'B4/B5': {'weight': 0.05, 'rate_constant': 1},
# }
firing_rate_params = {
# 'I2': {'weight': -0.02, 'rate_constant': 1},
# 'B8a/b': {'weight': 0.05, 'rate_constant': 1},
'B3': {'weight': 0.05, 'rate_constant': 1},
'B6/B9': {'weight': 0.1, 'rate_constant': 0.5},
'B38': {'weight': 0.05, 'rate_constant': 1},
# 'B4/B5': {'weight': 0.05, 'rate_constant': 1},
}
```
# Generate Firing Rate Model
```
firing_rates = {}
for name, params in firing_rate_params.items():
weight = params['weight']
rate_constant = params['rate_constant']
# convolve the spike train with the kernel
firing_rates[name] = instantaneous_rate(
spiketrain=spiketrains[name],
sampling_period=0.0002*pq.s, # 5 kHz, same as data acquisition rate
kernel=CausalAlphaKernel(rate_constant*pq.s),
)
firing_rates[name].name = f'{name}\nweight: {weight}\nrate const: {rate_constant} sec'
# scale the firing rate by its weight
firing_rates[name] *= weight
# create the model by summing the firing rates and adding the offset
firing_rates['Model'] = None
for name, params in firing_rate_params.items():
if firing_rates['Model'] is None:
firing_rates['Model'] = firing_rates[name].copy()
else:
firing_rates['Model'] += firing_rates[name]
firing_rates['Model'] += offset*pq.Hz
firing_rates['Model'].name = f'Model = Sum of\nScaled Rates + {offset}'
```
# Plot Model
```
# plot each spike train and the scaled (weighted) firing rate
fig, axes = plt.subplots(len(firing_rates)+1, 1, sharex=True, figsize=(8,2*len(firing_rates)))
for i, name in enumerate(firing_rates):
ax = axes[i]
if name in spiketrains:
ax.eventplot(positions=spiketrains[name], lineoffsets=-1, colors=colors[name])
ax.plot(firing_rates[name].times.rescale('s'), firing_rates[name].rescale('Hz'), c=colors[name])
ax.set_ylabel(firing_rates[name].name)
ax.set_ylim(-2, 3)
# plot force and the model, both normalized by their peaks
axes[-1].plot(sigs['Force'].times.rescale('s'), sigs['Force']/sigs['Force'].max(), c=colors['Force'])
axes[-1].plot(firing_rates['Model'].times.rescale('s'), firing_rates['Model']/firing_rates['Model'].max(), c=colors['Model'])
axes[-1].set_ylabel('Model vs. Force\n(both normalized)')
axes[-1].set_xlabel('Time (s)')
axes[0].set_title(file_basename)
plt.tight_layout()
```
# Plot Model for Grant
```
# use with JG08 Tape nori 1
time_slices = {
'I2': [670.7, 680.83],
'B8a/b': [673.5, 679.59],
'B3': [675.645, 680.83],
'B6/B9': [674.25, 680.83],
'B38': [670.7, 680.83],
'Model': [672.26, 680.2],
'Force': [672.26, 680.2],
}
# plot each spike train and the scaled (weighted) firing rate
fig, axes = plt.subplots(2*len(firing_rate_params)+1, 1, sharex=True, figsize=(6,len(firing_rate_params)*(16/17)+1*(20/17)), gridspec_kw={'height_ratios': [3, 1]*len(firing_rate_params) + [5]})
for i, name in enumerate(firing_rate_params):
ax = axes[2*i]
fr = firing_rates[name]
st = spiketrains[name]
if name in time_slices:
fr = fr.copy().time_slice(time_slices[name][0]*pq.s, time_slices[name][1]*pq.s)
st = st.copy().time_slice(time_slices[name][0]*pq.s, time_slices[name][1]*pq.s)
ax.plot(fr.times.rescale('s'), fr.rescale('Hz'), c=colors[name])
ax.annotate(name, xy=(0, 0.5), xycoords='axes fraction',
ha='right', va='center', fontsize='large', color=colors[name], fontfamily='Serif',
)
# ax.set_ylim(0, 2.2)
ax.axis('off')
ax = axes[2*i+1]
ax.eventplot(positions=st, lineoffsets=-1, colors=colors[name])
ax.axis('off')
# plot force and the model, both normalized by their peaks
force = sigs['Force'].copy().time_slice(time_slices['Force'][0]*pq.s, time_slices['Force'][1]*pq.s)
model = firing_rates['Model'].time_slice(time_slices['Model'][0]*pq.s, time_slices['Model'][1]*pq.s)
axes[-1].plot(force.times.rescale('s'), force/force.max(), c=colors['Force'])
axes[-1].plot(model.times.rescale('s'), model/model.max(), c=colors['Model'])
axes[-1].annotate('Model\nvs.', xy=(-0.04, 0.6), xycoords='axes fraction',
ha='center', va='center', fontsize='large', color=colors['Model'], fontfamily='Serif',
)
axes[-1].annotate('Force', xy=(-0.04, 0.35), xycoords='axes fraction',
ha='center', va='center', fontsize='large', color=colors['Force'], fontfamily='Serif',
)
axes[-1].axis('off')
plt.tight_layout(0)
```
| true |
code
| 0.635138 | null | null | null | null |
|
```
# set tf 1.x for colab
%tensorflow_version 1.x
# setup only for running on google colab
# ! shred -u setup_google_colab.py
! wget https://raw.githubusercontent.com/hse-aml/intro-to-dl/master/setup_google_colab.py -O setup_google_colab.py
import setup_google_colab
# please, uncomment the week you're working on
# setup_google_colab.setup_week1()
# setup_google_colab.setup_week2()
# setup_google_colab.setup_week2_honor()
setup_google_colab.setup_week3()
# setup_google_colab.setup_week4()
# setup_google_colab.setup_week5()
# setup_google_colab.setup_week6()
```
# Fine-tuning InceptionV3 for flowers classification
In this task you will fine-tune InceptionV3 architecture for flowers classification task.
InceptionV3 architecture (https://research.googleblog.com/2016/03/train-your-own-image-classifier-with.html):
<img src="https://github.com/hse-aml/intro-to-dl/blob/master/week3/images/inceptionv3.png?raw=1" style="width:70%">
Flowers classification dataset (http://www.robots.ox.ac.uk/~vgg/data/flowers/102/index.html) consists of 102 flower categories commonly occurring in the United Kingdom. Each class contains between 40 and 258 images:
<img src="https://github.com/hse-aml/intro-to-dl/blob/master/week3/images/flowers.jpg?raw=1" style="width:70%">
# Import stuff
```
import sys
sys.path.append("..")
import grading
import download_utils
# !!! remember to clear session/graph if you rebuild your graph to avoid out-of-memory errors !!!
download_utils.link_all_keras_resources()
import tensorflow as tf
import keras
from keras import backend as K
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
print(tf.__version__)
print(keras.__version__)
import cv2 # for image processing
from sklearn.model_selection import train_test_split
import scipy.io
import os
import tarfile
import keras_utils
from keras_utils import reset_tf_session
import warnings
warnings.filterwarnings('ignore', category=DeprecationWarning)
warnings.filterwarnings('ignore', category=FutureWarning)
```
# Fill in your Coursera token and email
To successfully submit your answers to our grader, please fill in your Coursera submission token and email
```
grader = grading.Grader(assignment_key="2v-uxpD7EeeMxQ6FWsz5LA",
all_parts=["wuwwC", "a4FK1", "qRsZ1"])
# token expires every 30 min
COURSERA_TOKEN = "kbq50loyqKlaw3NK"
COURSERA_EMAIL = "mailid_coursera@whatever.com"
```
# Load dataset
Dataset was downloaded for you, it takes 12 min and 400mb.
Relevant links (just in case):
- http://www.robots.ox.ac.uk/~vgg/data/flowers/102/index.html
- http://www.robots.ox.ac.uk/~vgg/data/flowers/102/102flowers.tgz
- http://www.robots.ox.ac.uk/~vgg/data/flowers/102/imagelabels.mat
```
# we downloaded them for you, just link them here
download_utils.link_week_3_resources()
```
# Prepare images for model
```
# we will crop and resize input images to IMG_SIZE x IMG_SIZE
IMG_SIZE = 250
def decode_image_from_raw_bytes(raw_bytes):
img = cv2.imdecode(np.asarray(bytearray(raw_bytes), dtype=np.uint8), 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
return img
```
We will take a center crop from each image like this:
<img src="https://github.com/hse-aml/intro-to-dl/blob/master/week3/images/center_crop.jpg?raw=1" style="width:50%">
```
def image_center_crop(img):
"""
Makes a square center crop of an img, which is a [h, w, 3] numpy array.
Returns [min(h, w), min(h, w), 3] output with same width and height.
For cropping use numpy slicing.
"""
h, w, c = img.shape
min_dim = int(min(h, w)/2)
center = (int(h/2), int(w/2))
cropped_img = img[center[0] - min_dim: center[0] + min_dim, center[1] - min_dim: center[1] + min_dim]
return cropped_img
def prepare_raw_bytes_for_model(raw_bytes, normalize_for_model=True):
img = decode_image_from_raw_bytes(raw_bytes) # decode image raw bytes to matrix
img = image_center_crop(img) # take squared center crop
img = cv2.resize(img, (IMG_SIZE, IMG_SIZE)) # resize for our model
if normalize_for_model:
img = img.astype("float32") # prepare for normalization
img = keras.applications.inception_v3.preprocess_input(img) # normalize for model
return img
# reads bytes directly from tar by filename (slow, but ok for testing, takes ~6 sec)
def read_raw_from_tar(tar_fn, fn):
with tarfile.open(tar_fn) as f:
m = f.getmember(fn)
return f.extractfile(m).read()
# test cropping
raw_bytes = read_raw_from_tar("102flowers.tgz", "jpg/image_00001.jpg")
img = decode_image_from_raw_bytes(raw_bytes)
print(img.shape)
plt.imshow(img)
plt.show()
img = prepare_raw_bytes_for_model(raw_bytes, normalize_for_model=False)
print(img.shape)
plt.imshow(img)
plt.show()
## GRADED PART, DO NOT CHANGE!
# Test image preparation for model
prepared_img = prepare_raw_bytes_for_model(read_raw_from_tar("102flowers.tgz", "jpg/image_00001.jpg"))
grader.set_answer("qRsZ1", list(prepared_img.shape) + [np.mean(prepared_img), np.std(prepared_img)])
list(prepared_img.shape) + [np.mean(prepared_img), np.std(prepared_img)] # expected by grader
# you can make submission with answers so far to check yourself at this stage
grader.submit(COURSERA_EMAIL, COURSERA_TOKEN)
```
# Prepare for training
```
# read all filenames and labels for them
# read filenames firectly from tar
def get_all_filenames(tar_fn):
with tarfile.open(tar_fn) as f:
return [m.name for m in f.getmembers() if m.isfile()]
all_files = sorted(get_all_filenames("102flowers.tgz")) # list all files in tar sorted by name
all_labels = scipy.io.loadmat('imagelabels.mat')['labels'][0] - 1 # read class labels (0, 1, 2, ...)
# all_files and all_labels are aligned now
N_CLASSES = len(np.unique(all_labels))
print(N_CLASSES)
# split into train/test
tr_files, te_files, tr_labels, te_labels = \
train_test_split(all_files, all_labels, test_size=0.2, random_state=42, stratify=all_labels)
# will yield raw image bytes from tar with corresponding label
def raw_generator_with_label_from_tar(tar_fn, files, labels):
label_by_fn = dict(zip(files, labels))
with tarfile.open(tar_fn) as f:
while True:
m = f.next()
if m is None:
break
if m.name in label_by_fn:
yield f.extractfile(m).read(), label_by_fn[m.name]
# batch generator
BATCH_SIZE = 32
def batch_generator(items, batch_size):
"""
Implement batch generator that yields items in batches of size batch_size.
There's no need to shuffle input items, just chop them into batches.
Remember about the last batch that can be smaller than batch_size!
Input: any iterable (list, generator, ...). You should do `for item in items: ...`
In case of generator you can pass through your items only once!
Output: In output yield each batch as a list of items.
"""
items = list(items)
for i in range(0, len(items), batch_size):
yield items[i: i+batch_size]
## GRADED PART, DO NOT CHANGE!
# Test batch generator
def _test_items_generator():
for i in range(10):
yield i
grader.set_answer("a4FK1", list(map(lambda x: len(x), batch_generator(_test_items_generator(), 3))))
list(map(lambda x: len(x), batch_generator(_test_items_generator(), 3))) # expedcted by grader
# you can make submission with answers so far to check yourself at this stage
grader.submit(COURSERA_EMAIL, COURSERA_TOKEN)
def train_generator(files, labels):
while True: # so that Keras can loop through this as long as it wants
for batch in batch_generator(raw_generator_with_label_from_tar(
"102flowers.tgz", files, labels), BATCH_SIZE):
# prepare batch images
batch_imgs = []
batch_targets = []
for raw, label in batch:
img = prepare_raw_bytes_for_model(raw)
batch_imgs.append(img)
batch_targets.append(label)
# stack images into 4D tensor [batch_size, img_size, img_size, 3]
batch_imgs = np.stack(batch_imgs, axis=0)
# convert targets into 2D tensor [batch_size, num_classes]
batch_targets = keras.utils.np_utils.to_categorical(batch_targets, N_CLASSES)
yield batch_imgs, batch_targets
# test training generator
for _ in train_generator(tr_files, tr_labels):
print(_[0].shape, _[1].shape)
plt.imshow(np.clip(_[0][0] / 2. + 0.5, 0, 1))
break
```
# Training
You cannot train such a huge architecture from scratch with such a small dataset.
But using fine-tuning of last layers of pre-trained network you can get a pretty good classifier very quickly.
```
# remember to clear session if you start building graph from scratch!
s = reset_tf_session()
# don't call K.set_learning_phase() !!! (otherwise will enable dropout in train/test simultaneously)
def inception(use_imagenet=True):
# load pre-trained model graph, don't add final layer
model = keras.applications.InceptionV3(include_top=False, input_shape=(IMG_SIZE, IMG_SIZE, 3),
weights='imagenet' if use_imagenet else None)
# add global pooling just like in InceptionV3
new_output = keras.layers.GlobalAveragePooling2D()(model.output)
# add new dense layer for our labels
new_output = keras.layers.Dense(N_CLASSES, activation='softmax')(new_output)
model = keras.engine.training.Model(model.inputs, new_output)
return model
model = inception()
model.summary()
# how many layers our model has
print(len(model.layers)) # deep model with 313 layers
# set all layers trainable by default
for layer in model.layers:
layer.trainable = True
if isinstance(layer, keras.layers.BatchNormalization):
# we do aggressive exponential smoothing of batch norm
# parameters to faster adjust to our new dataset
layer.momentum = 0.9
# fix deep layers (fine-tuning only last 50)
for layer in model.layers[:-50]:
# fix all but batch norm layers, because we neeed to update moving averages for a new dataset!
if not isinstance(layer, keras.layers.BatchNormalization):
layer.trainable = False
# compile new model
model.compile(
loss='categorical_crossentropy', # we train 102-way classification
optimizer=keras.optimizers.adamax(lr=1e-2), # we can take big lr here because we fixed first layers
metrics=['accuracy'] # report accuracy during training
)
# we will save model checkpoints to continue training in case of kernel death
model_filename = 'flowers.{0:03d}.hdf5'
last_finished_epoch = None
#### uncomment below to continue training from model checkpoint
#### fill `last_finished_epoch` with your latest finished epoch
# from keras.models import load_model
# s = reset_tf_session()
# last_finished_epoch = 10
# model = load_model(model_filename.format(last_finished_epoch))
```
Training takes **2 hours**. You're aiming for ~0.93 validation accuracy.
```
# fine tune for 2 epochs (full passes through all training data)
# we make 2*8 epochs, where epoch is 1/8 of our training data to see progress more often
model.fit_generator(
train_generator(tr_files, tr_labels),
steps_per_epoch=len(tr_files) // BATCH_SIZE // 8,
epochs=2 * 8,
validation_data=train_generator(te_files, te_labels),
validation_steps=len(te_files) // BATCH_SIZE // 4,
callbacks=[keras_utils.TqdmProgressCallback(),
keras_utils.ModelSaveCallback(model_filename)],
verbose=0,
initial_epoch=last_finished_epoch or 0
)
## GRADED PART, DO NOT CHANGE!
# Accuracy on validation set
test_accuracy = model.evaluate_generator(
train_generator(te_files, te_labels),
len(te_files) // BATCH_SIZE // 2
)[1]
grader.set_answer("wuwwC", test_accuracy)
print(test_accuracy)
# you can make submission with answers so far to check yourself at this stage
grader.submit(COURSERA_EMAIL, COURSERA_TOKEN)
```
That's it! Congratulations!
What you've done:
- prepared images for the model
- implemented your own batch generator
- fine-tuned the pre-trained model
| true |
code
| 0.588594 | null | null | null | null |
|
# Dataset Distribution
```
import numpy as np
import math
from torch.utils.data import random_split
```
## Calculating Mean & Std
Calculates mean and std of dataset.
```
def get_norm(dataset):
mean = dataset.data.mean(axis=(0, 1, 2)) / 255.
std = dataset.data.std(axis=(0, 1, 2)) / 255.
return mean, std
```
## Split Dataset
Splits dataset into multiple subsets.
### TODO
- [ ] bias
```
def random_split_by_dist(
dataset,
size: int,
dist: callable = None,
**params
):
"""Split `dataset` into subsets by distribution function.
Parameters
----------
dataset : datasets
See `torchvision.datasets` .
size : int
Number (Length) of subsets.
dist : function
Distribution function which retures np.array.
Sum of returned array SHOULD be 1.
Returns
-------
out : subsets
Of `dataset`.
"""
assert size != 0, "`size` > 0"
dist = dist or uniform # default value
# calculates distribution `dist_val`
dist_val = dist(size, **params) # dist_val: np.array
assert math.isclose(sum(dist_val), 1.), "sum of `dist` SHOULD be 1."
N = len(dataset)
result = np.full(size, N) * dist_val
result = np.around(result).astype('int') # to integers
result = result.clip(1, None) # to positive integers
# adjustment for that summation of `result` SHOULD be `N`
result[-1] = N - sum(result[:-1])
while True:
if result[-1] < 1:
result[result.argmax()] -= 1
result[-1] += 1
else:
break
return random_split(dataset, sorted(result))
def uniform(
size: int,
**params # no longer needed
):
assert len(params) == 0, \
"uniform() got an unexpected keyword argument {}".format(
', '.join(["""\'""" + k + """\'""" for k in params.keys()])
)
return np.ones(size) / size
def normal(
size: int,
loc: float = 0.,
scale: float = 1.,
lower: float = 0.,
upper: float = None
):
"""Calculate normal (Gaussian) distribution.
Uses `abs` to restrict to non-zeros.
In fact, it is not a normal distribution because there are only
positive elements in `result`.
See https://numpy.org/doc/stable/reference/random/generated/numpy.random.normal.html .
Parameters
----------
size : int
Number (Length) of chunks.
Same as length of returned np.array.
loc : float
Mean (“centre”) of the distribution.
scale : float
Standard deviation (spread or “width”) of the distribution.
MUST be non-negative.
lower : float
Lower-bound before applying scaling.
upper : float
Upper-bound before applying scaling.
Returns
-------
out : np.array
Returns normal (Gaussian) distribution.
"""
result = np.random.normal(loc, scale, size)
result = abs(result) # `result` SHOULD be only positive.
result = result.clip(lower, upper)
return result / sum(result)
def pareto(
size: int,
alpha: float = 1.16, # by 80-20 rule, log(5)/log(4)
lower: float = 0.,
upper: float = None
):
"""Calculate Pareto distribution.
See https://numpy.org/doc/stable/reference/random/generated/numpy.random.pareto.html .
Parameters
----------
size : int
Number (Length) of chunks.
Same as length of returned np.array.
alpha : float
Shape of the distribution.
Must be positive.
lower : float
Lower-bound before applying scaling.
upper : float
Upper-bound before applying scaling.
Returns
-------
out : np.array
Returns Pareto distribution.
"""
result = np.random.pareto(alpha, size)
result = result.clip(lower, upper)
return result / sum(result)
```
# main
```
if __name__ == "__main__":
from pprint import pprint
import torchvision.datasets as dset
import torchvision.transforms as transforms
"""Test `get_norm`"""
transform = transforms.Compose([
transforms.ToTensor()
])
trainDataset = dset.CIFAR10(root='cifar', train=True, download=True, transform=transform)
pprint(get_norm(trainDataset))
"""Test `adv_random_split`"""
pprint([len(subset) for subset in random_split_by_dist(
trainDataset,
size=10,
dist=pareto,
alpha=2.
)])
```
| true |
code
| 0.874935 | null | null | null | null |
|
# `nnetsauce` Examples
Examples of:
- Multitask, AdaBoost, Deep, Random Bag, Ridge2, Ridge2 Multitask, Nonlinear GLM __classifiers__
- Nonlinear GLM model for __regression__
```
!pip install git+https://github.com/techtonique/nnetsauce.git@cythonize --upgrade
```
Multitask Classifier
```
import nnetsauce as ns
import numpy as np
from sklearn.datasets import load_breast_cancer, load_wine, load_iris, make_classification
from sklearn.linear_model import ElasticNet, LinearRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics
from time import time
# dataset no. 1 ----------
breast_cancer = load_breast_cancer()
Z = breast_cancer.data
t = breast_cancer.target
np.random.seed(123)
X_train, X_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
# Linear Regression is used
regr = LinearRegression()
fit_obj = ns.MultitaskClassifier(regr, n_hidden_features=5,
n_clusters=2, type_clust="gmm")
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
print(fit_obj.score(X_test, y_test))
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
```
AdaBoost
```
import nnetsauce as ns
import numpy as np
from sklearn.datasets import load_breast_cancer, load_wine, load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics
from time import time
# dataset no. 1 ----------
# logistic reg
breast_cancer = load_breast_cancer()
Z = breast_cancer.data
t = breast_cancer.target
np.random.seed(123)
X_train, X_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
# SAMME
clf = LogisticRegression(solver='liblinear', multi_class = 'ovr',
random_state=123)
fit_obj = ns.AdaBoostClassifier(clf,
n_hidden_features=np.int(56.13806152),
direct_link=True,
n_estimators=1000, learning_rate=0.09393372,
col_sample=0.52887573, row_sample=0.87781372,
dropout=0.10216064, n_clusters=2,
type_clust="gmm",
verbose=1, seed = 123,
method="SAMME")
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
# 29.34
print(fit_obj.score(X_test, y_test))
preds = fit_obj.predict(X_test)
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
print(metrics.classification_report(preds, y_test))
# SAMME.R
clf = LogisticRegression(solver='liblinear', multi_class = 'ovr',
random_state=123)
fit_obj = ns.AdaBoostClassifier(clf,
n_hidden_features=np.int(11.22338867),
direct_link=True,
n_estimators=250, learning_rate=0.01126343,
col_sample=0.72684326, row_sample=0.86429443,
dropout=0.63078613, n_clusters=2,
type_clust="gmm",
verbose=1, seed = 123,
method="SAMME.R")
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
# 6.906151294708252
print(fit_obj.score(X_test, y_test))
preds = fit_obj.predict(X_test)
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
print(metrics.classification_report(preds, y_test))
# dataset no. 2 ----------
wine = load_wine()
Z = wine.data
t = wine.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
# SAMME
clf = LogisticRegression(solver='liblinear', multi_class = 'ovr',
random_state=123)
fit_obj = ns.AdaBoostClassifier(clf,
n_hidden_features=np.int(8.21154785e+01),
direct_link=True,
n_estimators=1000, learning_rate=2.96252441e-02,
col_sample=4.22766113e-01, row_sample=7.87268066e-01,
dropout=1.56909180e-01, n_clusters=3,
type_clust="gmm",
verbose=1, seed = 123,
method="SAMME")
start = time()
fit_obj.fit(Z_train, y_train)
print(time() - start)
# 22.685115098953247
print(fit_obj.score(Z_test, y_test))
preds = fit_obj.predict(Z_test)
print(metrics.classification_report(preds, y_test))
# dataset no. 3 ----------
iris = load_iris()
Z = iris.data
t = iris.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
# SAMME.R
clf = LogisticRegression(solver='liblinear', multi_class = 'ovr',
random_state=123)
fit_obj = ns.AdaBoostClassifier(clf,
n_hidden_features=np.int(19.66918945),
direct_link=True,
n_estimators=250, learning_rate=0.28534302,
col_sample=0.45474854, row_sample=0.87833252,
dropout=0.15603027, n_clusters=0,
verbose=1, seed = 123,
method="SAMME.R")
start = time()
fit_obj.fit(Z_train, y_train)
print(time() - start)
# 1.413327932357788
print(fit_obj.score(Z_test, y_test))
preds = fit_obj.predict(Z_test)
print(metrics.classification_report(preds, y_test))
```
Deep Classifier
```
import nnetsauce as ns
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_digits
digits = load_digits()
X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=123)
# layer 1 (base layer) ----
layer1_regr = RandomForestClassifier(n_estimators=10, random_state=123)
layer1_regr.fit(X_train, y_train)
# Accuracy in layer 1
print(layer1_regr.score(X_test, y_test))
# layer 2 using layer 1 ----
layer2_regr = ns.CustomClassifier(obj = layer1_regr, n_hidden_features=5,
direct_link=True, bias=True,
nodes_sim='uniform', activation_name='relu',
n_clusters=2, seed=123)
layer2_regr.fit(X_train, y_train)
# Accuracy in layer 2
print(layer2_regr.score(X_test, y_test))
# layer 3 using layer 2 ----
layer3_regr = ns.CustomClassifier(obj = layer2_regr, n_hidden_features=10,
direct_link=True, bias=True, dropout=0.7,
nodes_sim='uniform', activation_name='relu',
n_clusters=2, seed=123)
layer3_regr.fit(X_train, y_train)
# Accuracy in layer 3
print(layer3_regr.score(X_test, y_test))
```
Random Bag Classifier
```
import nnetsauce as ns
import numpy as np
from sklearn.datasets import load_breast_cancer, load_wine, load_iris, make_classification
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics
from time import time
# dataset no. 1 ----------
breast_cancer = load_breast_cancer()
Z = breast_cancer.data
t = breast_cancer.target
np.random.seed(123)
X_train, X_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
# decision tree
clf = DecisionTreeClassifier(max_depth=2, random_state=123)
fit_obj = ns.RandomBagClassifier(clf, n_hidden_features=2,
direct_link=True,
n_estimators=100,
col_sample=0.9, row_sample=0.9,
dropout=0.3, n_clusters=0, verbose=0)
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
#0.8955960273742676
print(fit_obj.score(X_test, y_test))
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
start = time()
[fit_obj.fit(X_train, y_train) for _ in range(10)]
print(time() - start)
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
# dataset no. 2 ----------
wine = load_wine()
Z = wine.data
t = wine.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
clf = DecisionTreeClassifier(max_depth=2, random_state=123)
fit_obj = ns.RandomBagClassifier(clf, n_hidden_features=5,
direct_link=True,
n_estimators=100,
col_sample=0.5, row_sample=0.5,
dropout=0.1, n_clusters=3,
type_clust="gmm", verbose=1)
start = time()
fit_obj.fit(Z_train, y_train)
print(time() - start)
# 1.8651049137115479
print(fit_obj.score(Z_test, y_test))
preds = fit_obj.predict(Z_test)
print(metrics.classification_report(preds, y_test))
# dataset no. 3 ----------
iris = load_iris()
Z = iris.data
t = iris.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
clf = LogisticRegression(solver='liblinear', multi_class = 'ovr',
random_state=123)
fit_obj = ns.RandomBagClassifier(clf, n_hidden_features=5,
direct_link=False,
n_estimators=100,
col_sample=0.5, row_sample=0.5,
dropout=0.1, n_clusters=0, verbose=0,
n_jobs=1)
start = time()
fit_obj.fit(Z_train, y_train)
print(time() - start)
# 0.4114112854003906
print(fit_obj.score(Z_test, y_test))
# dataset no. 4 ----------
X, y = make_classification(n_samples=2500, n_features=20,
random_state=783451)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=351452)
clf = DecisionTreeClassifier(max_depth=1, random_state=123)
fit_obj = ns.RandomBagClassifier(clf, n_hidden_features=5,
direct_link=True,
n_estimators=100,
col_sample=0.5, row_sample=0.5,
dropout=0.1, n_clusters=3,
type_clust="gmm", verbose=1)
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
# 5.983736038208008
print(fit_obj.score(X_test, y_test))
preds = fit_obj.predict(X_test)
print(metrics.classification_report(preds, y_test))
```
Ridge2 Classifier
```
import nnetsauce as ns
import numpy as np
from sklearn.datasets import load_digits, load_breast_cancer, load_wine, load_iris
from sklearn.model_selection import train_test_split
from time import time
# dataset no. 1 ----------
breast_cancer = load_breast_cancer()
X = breast_cancer.data
y = breast_cancer.target
# split data into training test and test set
np.random.seed(123)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# create the model with nnetsauce
fit_obj = ns.Ridge2Classifier(lambda1 = 6.90185578e+04,
lambda2 = 3.17392781e+02,
n_hidden_features=95,
n_clusters=2,
row_sample = 4.63427734e-01,
dropout = 3.62817383e-01,
type_clust = "gmm")
# fit the model on training set
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
# get the accuracy on test set
start = time()
print(fit_obj.score(X_test, y_test))
print(time() - start)
# get area under the curve on test set (auc)
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
# dataset no. 2 ----------
wine = load_wine()
Z = wine.data
t = wine.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
# create the model with nnetsauce
fit_obj = ns.Ridge2Classifier(lambda1 = 8.64135756e+04,
lambda2 = 8.27514666e+04,
n_hidden_features=109,
n_clusters=3,
row_sample = 5.54907227e-01,
dropout = 1.84484863e-01,
type_clust = "gmm")
# fit the model on training set
fit_obj.fit(Z_train, y_train)
# get the accuracy on test set
print(fit_obj.score(Z_test, y_test))
# dataset no. 3 ----------
iris = load_iris()
Z = iris.data
t = iris.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
# create the model with nnetsauce
fit_obj = ns.Ridge2Classifier(lambda1 = 1.87500081e+04,
lambda2 = 3.12500069e+04,
n_hidden_features=47,
n_clusters=3,
row_sample = 7.37500000e-01,
dropout = 1.31250000e-01,
type_clust = "gmm")
# fit the model on training set
start = time()
fit_obj.fit(Z_train, y_train)
print(time() - start)
# get the accuracy on test set
start = time()
print(fit_obj.score(Z_test, y_test))
print(time() - start)
# dataset no. 4 ----------
digits = load_digits()
Z = digits.data
t = digits.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
# create the model with nnetsauce
fit_obj = ns.Ridge2Classifier(lambda1 = 7.11914091e+04,
lambda2 = 4.63867241e+04,
n_hidden_features=13,
n_clusters=0,
row_sample = 7.65039063e-01,
dropout = 5.21582031e-01,
type_clust = "gmm")
# fit the model on training set
fit_obj.fit(Z_train, y_train)
# get the accuracy on test set
print(fit_obj.score(Z_test, y_test))
```
Ridge2 Multitask Classifier
```
import nnetsauce as ns
import numpy as np
from sklearn.datasets import load_breast_cancer, load_wine, load_iris, load_digits, make_classification
from sklearn.model_selection import train_test_split
from sklearn import metrics
from time import time
# dataset no. 1 ----------
breast_cancer = load_breast_cancer()
Z = breast_cancer.data
t = breast_cancer.target
np.random.seed(123)
X_train, X_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
print(Z.shape)
fit_obj = ns.Ridge2MultitaskClassifier(n_hidden_features=np.int(9.83730469e+01),
dropout=4.31054687e-01,
n_clusters=np.int(1.71484375e+00),
lambda1=1.24023438e+01, lambda2=7.30263672e+03)
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
print(fit_obj.score(X_test, y_test))
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
# dataset no. 2 ----------
wine = load_wine()
Z = wine.data
t = wine.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
fit_obj = ns.Ridge2MultitaskClassifier(n_hidden_features=15,
dropout=0.1, n_clusters=3,
type_clust="gmm")
start = time()
fit_obj.fit(Z_train, y_train)
print(time() - start)
print(fit_obj.score(Z_test, y_test))
preds = fit_obj.predict(Z_test)
print(metrics.classification_report(preds, y_test))
# dataset no. 3 ----------
iris = load_iris()
Z = iris.data
t = iris.target
np.random.seed(123)
Z_train, Z_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
fit_obj = ns.Ridge2MultitaskClassifier(n_hidden_features=10,
dropout=0.1, n_clusters=2)
start = time()
fit_obj.fit(Z_train, y_train)
print(time() - start)
print(fit_obj.score(Z_test, y_test))
# dataset no. 4 ----------
X, y = make_classification(n_samples=2500, n_features=20,
random_state=783451)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=351452)
fit_obj = ns.Ridge2MultitaskClassifier(n_hidden_features=5,
dropout=0.1, n_clusters=3,
type_clust="gmm")
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
print(fit_obj.score(X_test, y_test))
preds = fit_obj.predict(X_test)
print(metrics.classification_report(preds, y_test))
# dataset no. 5 ----------
digits = load_digits()
X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=123)
fit_obj = ns.Ridge2MultitaskClassifier(n_hidden_features=25,
dropout=0.1, n_clusters=3,
type_clust="gmm")
start = time()
fit_obj.fit(X_train, y_train)
print(time() - start)
print(fit_obj.score(X_test, y_test))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
```
GLM Regressor with __loss function plot__
```
import numpy as np
import nnetsauce as ns
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from time import time
import matplotlib.pyplot as plt
boston = load_boston()
X = boston.data
y = boston.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2020)
print(f"\n Example 1 -----")
obj2 = ns.GLMRegressor(n_hidden_features=3,
lambda1=1e-2, alpha1=0.5,
lambda2=1e-2, alpha2=0.5,
optimizer=ns.optimizers.Optimizer(type_optim="sgd"))
start = time()
obj2.fit(X_train, y_train, learning_rate=0.1, batch_prop=0.25, verbose=1)
print(f"\n Elapsed: {time() - start}")
plt.plot(obj2.optimizer.results[2])
print(obj2.beta)
print("RMSE: ")
print(np.sqrt(obj2.score(X_test, y_test))) # RMSE
print(f"\n Example 2 -----")
obj2.optimizer.type_optim = "scd"
start = time()
obj2.fit(X_train, y_train, learning_rate=0.01, batch_prop=0.8, verbose=1)
print(f"\n Elapsed: {time() - start}")
plt.plot(obj2.optimizer.results[2])
print(obj2.beta)
print("RMSE: ")
print(np.sqrt(obj2.score(X_test, y_test))) # RMSE
print(f"\n Example 3 -----")
obj2.optimizer.type_optim = "sgd"
obj2.set_params(lambda1=1e-2, alpha1=0.1,
lambda2=1e-1, alpha2=0.9)
start = time()
obj2.fit(X_train, y_train, batch_prop=0.25, verbose=1)
print(f"\n Elapsed: {time() - start}")
plt.plot(obj2.optimizer.results[2])
print(obj2.beta)
print("RMSE: ")
print(np.sqrt(obj2.score(X_test, y_test))) # RMSE
print(f"\n Example 4 -----")
obj2.optimizer.type_optim = "scd"
start = time()
obj2.fit(X_train, y_train, learning_rate=0.01, batch_prop=0.8, verbose=1)
print(f"\n Elapsed: {time() - start}")
plt.plot(obj2.optimizer.results[2])
print(obj2.beta)
print("RMSE: ")
print(np.sqrt(obj2.score(X_test, y_test))) # RMSE
print(f"\n Example 5 -----")
obj2.optimizer.type_optim = "sgd"
obj2.set_params(lambda1=1, alpha1=0.5,
lambda2=1e-2, alpha2=0.1)
start = time()
obj2.fit(X_train, y_train, learning_rate=0.1, batch_prop=0.5, verbose=1)
print(f"\n Elapsed: {time() - start}")
plt.plot(obj2.optimizer.results[2])
print(obj2.beta)
print("RMSE: ")
print(np.sqrt(obj2.score(X_test, y_test))) # RMSE
print(f"\n Example 6 -----")
obj2.optimizer.type_optim = "scd"
start = time()
obj2.fit(X_train, y_train, learning_rate=0.1, batch_prop=0.5, verbose=1)
print(f"\n Elapsed: {time() - start}")
plt.plot(obj2.optimizer.results[2])
print(obj2.beta)
print("RMSE: ")
print(np.sqrt(obj2.score(X_test, y_test))) # RMSE
```
GLM Classifier with __loss function plot__
```
import numpy as np
from sklearn.datasets import load_breast_cancer, load_wine, load_iris, make_classification, load_digits
from sklearn.model_selection import train_test_split
from sklearn import metrics
from time import time
import matplotlib.pyplot as plt
print(f"\n method = 'momentum' ----------")
# dataset no. 1 ----------
breast_cancer = load_breast_cancer()
Z = breast_cancer.data
t = breast_cancer.target
np.random.seed(123)
X_train, X_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
print(f"\n 1 - breast_cancer dataset ----------")
fit_obj = ns.GLMClassifier(n_hidden_features=5,
n_clusters=2, type_clust="gmm")
start = time()
fit_obj.fit(X_train, y_train, verbose=1)
print(time() - start)
plt.plot(fit_obj.optimizer.results[2])
print(fit_obj.score(X_test, y_test))
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
# dataset no. 2 ----------
wine = load_wine()
Z = wine.data
t = wine.target
np.random.seed(123575)
X_train, X_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
print(f"\n 2 - wine dataset ----------")
fit_obj = ns.GLMClassifier(n_hidden_features=3,
n_clusters=2, type_clust="gmm")
start = time()
fit_obj.fit(X_train, y_train, verbose=1)
print(time() - start)
plt.plot(fit_obj.optimizer.results[2])
print(fit_obj.score(X_test, y_test))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
# dataset no. 3 ----------
iris = load_iris()
Z = iris.data
t = iris.target
np.random.seed(123575)
X_train, X_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
print(f"\n 3 - iris dataset ----------")
fit_obj = ns.GLMClassifier(n_hidden_features=3,
n_clusters=2, type_clust="gmm")
start = time()
fit_obj.fit(X_train, y_train, verbose=1)
print(time() - start)
plt.plot(fit_obj.optimizer.results[2])
print(fit_obj.score(X_test, y_test))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
# dataset no. 4 ----------
X, y = make_classification(n_samples=2500, n_features=20,
random_state=783451)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=351452)
print(f"\n 4 - make_classification dataset ----------")
fit_obj = ns.GLMClassifier(n_hidden_features=5,
dropout=0.1, n_clusters=3,
type_clust="gmm")
start = time()
fit_obj.fit(X_train, y_train, verbose=1)
print(time() - start)
print(fit_obj.score(X_test, y_test))
preds = fit_obj.predict(X_test)
print(metrics.classification_report(preds, y_test))
# dataset no. 5 ----------
digits = load_digits()
X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=123)
print(f"\n 5 - digits dataset ----------")
fit_obj = ns.GLMClassifier(n_hidden_features=25,
dropout=0.1, n_clusters=3,
type_clust="gmm")
start = time()
fit_obj.fit(X_train, y_train, verbose=1)
print(time() - start)
print(fit_obj.score(X_test, y_test))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
print(f"\n method = 'exp' ----------")
# dataset no. 1 ----------
breast_cancer = load_breast_cancer()
Z = breast_cancer.data
t = breast_cancer.target
np.random.seed(123)
X_train, X_test, y_train, y_test = train_test_split(Z, t, test_size=0.2)
print(f"\n 1 - breast_cancer dataset ----------")
opt = ns.Optimizer()
opt.set_params(learning_method = "exp")
fit_obj = ns.GLMClassifier(optimizer=opt)
fit_obj.set_params(lambda1=1e-5, lambda2=100)
fit_obj.optimizer.type_optim = "scd"
start = time()
fit_obj.fit(X_train, y_train, verbose=1, learning_rate=0.01, batch_prop=0.5)
print(time() - start)
plt.plot(fit_obj.optimizer.results[2])
print(fit_obj.score(X_test, y_test))
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
print(f"\n method = 'poly' ----------")
# dataset no. 1 ----------
print(f"\n 1 - breast_cancer dataset ----------")
opt = ns.Optimizer()
opt.set_params(learning_method = "poly")
fit_obj = ns.GLMClassifier(optimizer=opt)
fit_obj.set_params(lambda1=1, lambda2=1)
fit_obj.optimizer.type_optim = "scd"
start = time()
fit_obj.fit(X_train, y_train, verbose=1, learning_rate=0.001, batch_prop=0.5)
print(time() - start)
plt.plot(fit_obj.optimizer.results[2])
print(fit_obj.score(X_test, y_test))
print(fit_obj.score(X_test, y_test, scoring="roc_auc"))
start = time()
preds = fit_obj.predict(X_test)
print(time() - start)
print(metrics.classification_report(preds, y_test))
```
| true |
code
| 0.651216 | null | null | null | null |
|
## Model Components
The 5 main components of a `WideDeep` model are:
1. `wide`
2. `deeptabular`
3. `deeptext`
4. `deepimage`
5. `deephead`
The first 4 of them will be collected and combined by `WideDeep`, while the 5th one can be optionally added to the `WideDeep` model through its corresponding parameters: `deephead` or alternatively `head_layers`, `head_dropout` and `head_batchnorm`.
Through the development of the package, the `deeptabular` component became one of the core values of the package. Currently `pytorch-widedeep` offers three models that can be passed as the `deeptabular` components. The possibilities are numerous, and therefore, that component will be discussed on its own in a separated notebook.
### 1. `wide`
The `wide` component is a Linear layer "plugged" into the output neuron(s). This can be implemented in `pytorch-widedeep` via the `Wide` model.
The only particularity of our implementation is that we have implemented the linear layer via an Embedding layer plus a bias. While the implementations are equivalent, the latter is faster and far more memory efficient, since we do not need to one hot encode the categorical features.
Let's assume we the following dataset:
```
import torch
import pandas as pd
import numpy as np
from torch import nn
df = pd.DataFrame({"color": ["r", "b", "g"], "size": ["s", "n", "l"]})
df.head()
```
one hot encoded, the first observation would be
```
obs_0_oh = (np.array([1.0, 0.0, 0.0, 1.0, 0.0, 0.0])).astype("float32")
```
if we simply numerically encode (label encode or `le`) the values:
```
obs_0_le = (np.array([0, 3])).astype("int64")
```
Note that in the functioning implementation of the package we start from 1, saving 0 for padding, i.e. unseen values.
Now, let's see if the two implementations are equivalent
```
# we have 6 different values. Let's assume we are performing a regression, so pred_dim = 1
lin = nn.Linear(6, 1)
emb = nn.Embedding(6, 1)
emb.weight = nn.Parameter(lin.weight.reshape_as(emb.weight))
lin(torch.tensor(obs_0_oh))
emb(torch.tensor(obs_0_le)).sum() + lin.bias
```
And this is precisely how the linear model `Wide` is implemented
```
from pytorch_widedeep.models import Wide
# ?Wide
wide = Wide(wide_dim=10, pred_dim=1)
wide
```
Note that even though the input dim is 10, the Embedding layer has 11 weights. Again, this is because we save `0` for padding, which is used for unseen values during the encoding process.
As I mentioned, `deeptabular` has enough complexity on its own and it will be described in a separated notebook. Let's then jump to `deeptext`.
### 3. `deeptext`
`pytorch-widedeep` offers one model that can be passed to `WideDeep` as the `deeptext` component, `DeepText`, which is a standard and simple stack of LSTMs on top of word embeddings. You could also add a FC-Head on top of the LSTMs. The word embeddings can be pre-trained. In the future I aim to include some simple pretrained models so that the combination between text and images is fair.
*While I recommend using the `wide` and `deeptabular` models within this package when building the corresponding wide and deep model components, it is very likely that the user will want to use custom text and image models. That is perfectly possible. Simply, build them and pass them as the corresponding parameters. Note that the custom models MUST return a last layer of activations (i.e. not the final prediction) so that these activations are collected by `WideDeep` and combined accordingly. In addition, the models MUST also contain an attribute `output_dim` with the size of these last layers of activations.*
Let's have a look to the `DeepText` class within `pytorch-widedeep`
```
import torch
from pytorch_widedeep.models import DeepText
# ?DeepText
X_text = torch.cat((torch.zeros([5, 1]), torch.empty(5, 4).random_(1, 4)), axis=1)
deeptext = DeepText(vocab_size=4, hidden_dim=4, n_layers=1, padding_idx=0, embed_dim=4)
deeptext
```
You could, if you wanted, add a Fully Connected Head (FC-Head) on top of it
```
deeptext = DeepText(
vocab_size=4,
hidden_dim=8,
n_layers=1,
padding_idx=0,
embed_dim=4,
head_hidden_dims=[8, 4],
)
deeptext
```
Note that since the FC-Head will receive the activations from the last hidden layer of the stack of RNNs, the corresponding dimensions must be consistent.
### 4. DeepImage
Similarly to `deeptext`, `pytorch-widedeep` offers one model that can be passed to `WideDeep` as the `deepimage` component, `DeepImage`, which iseither a pretrained ResNet (18, 34, or 50. Default is 18) or a stack of CNNs, to which one can add a FC-Head. If is a pretrained ResNet, you can chose how many layers you want to defrost deep into the network with the parameter `freeze_n`
```
from pytorch_widedeep.models import DeepImage
# ?DeepImage
X_img = torch.rand((2, 3, 224, 224))
deepimage = DeepImage(head_hidden_dims=[512, 64, 8], head_activation="leaky_relu")
deepimage
deepimage(X_img)
```
if `pretrained=False` then a stack of 4 CNNs are used
```
deepimage = DeepImage(pretrained=False, head_hidden_dims=[512, 64, 8])
deepimage
```
### 5. deephead
The `deephead` component is not defined outside `WideDeep` as the rest of the components.
When defining the `WideDeep` model there is a parameter called `head_layers_dim` (and the corresponding related parameters. See the package documentation) that define the FC-head on top of `DeeDense`, `DeepText` and `DeepImage`.
Of course, you could also chose to define it yourself externally and pass it using the parameter `deephead`. Have a look
```
from pytorch_widedeep.models import WideDeep
# ?WideDeep
```
| true |
code
| 0.606848 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.