prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
```
import pandas as pd
import numpy as np
import os
from sklearn.model_selection import train_test_split
from matplotlib import pyplot as plt
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Activation, Dropout, Flatten, Dense
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import tensorflow as tf
import cv2
```
Hyper parameters
```
epochs = 20
width = height = 224
```
Prepare dataset
```
!pip install -q kaggle
!mkdir -p ~/.kaggle
!cp kaggle.json ~/.kaggle/
!kaggle datasets download -d jangedoo/utkface-new
!unzip -qq utkface-new.zip
images = [] # x
ages = [] # y
for image_name in os.listdir('crop_part1'):
parts = image_name.split('_')
ages.append(int(parts[0]))
image = cv2.imread(f'crop_part1/{image_name}')
image = cv2.resize(image, (width, height))
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
images.append(image)
images = pd.Series(images, name='Images')
ages = pd.Series(ages, name='Ages')
df = pd.concat([images, ages], axis=1)
df.head()
print(df['Ages'][0])
plt.imshow(df['Images'][0])
print(df['Ages'][1])
plt.imshow(df['Images'][1])
plt.figure(figsize=(18, 6))
plt.hist(df['Ages'], bins=df['Ages'].max())
plt.show()
```
Too many faces of people between 0 and 4 years old. The model would fit too well to these ages and not enough to the other ages. To resolve this I'm only going to include a third of the images between these ages.
```
under_4 = df[df['Ages'] <= 4]
under_4_small = under_4.sample(frac=0.3)
up_4 = df[df['Ages'] > 4]
df = pd.concat([under_4_small, up_4])
plt.figure(figsize=(18, 6))
plt.hist(df['Ages'], bins=df['Ages'].max())
plt.show()
```
This looks much better! The dataframe is more representative of the population now. However, there aren't many images of people over 80, which would cause the model to not train well enough on those ages. It's best to just remove over 80s and only have a model that can predict the ages of people under 80.
```
df = df[df['Ages'] < 80]
plt.figure(figsize=(18, 6))
plt.hist(df['Ages'], bins=df['Ages'].max())
plt.show()
X = np.array(df['Images'].values.tolist())
Y = np.array(df['Ages'].values.tolist())
X.shape
x_train, x_val, y_train, y_val = train_test_split(X, Y, test_size=0.2, stratify=Y)
print(x_train.shape)
print(y_train.shape)
print(x_val.shape)
print(y_val.shape)
data_generator = ImageDataGenerator(rescale=1./225,
horizontal_flip=True)
train_data = data_generator.flow(x_train, y_train, batch_size=32)
val_data = data_generator.flow(x_val, y_val, batch_size=32)
```
Train
```
base_model = tf.keras.applications.MobileNetV2(
input_shape=(width, height, 3),
weights='imagenet',
include_top=False,
pooling='avg'
)
for layer in base_model.layers:
layer.trainable = False
model = tf.keras.Sequential([
base_model,
Dropout(0.5),
Dense(1, activation='relu')
])
model.compile(loss='mean_squared_error',
optimizer=Adam(learning_rate=0.001))
model.fit(train_data,
validation_data=val_data,
epochs=epochs,
shuffle=True)
```
Inference
```
!wget --content-disposition https://github.com/SajjadAemmi/Face-Alignment/blob/main/models/shape_predictor_68_face_landmarks.dat?raw=true
from imutils.face_utils import FaceAligner
import imutils
import dlib
detector = dlib.get_frontal_face_detector()
predictor = dlib.shape_predictor('shape_predictor_68_face_landmarks.dat')
fa = FaceAligner(predictor, desiredFaceWidth=256)
def process_and_predict(image_path):
image = cv2.imread(image_path)
image = imutils.resize(image, width=800)
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
rects = detector(gray, 2)
for i, rect in enumerate(rects):
faceAligned = fa.align(image, gray, rect)
faceAligned = cv2.resize(faceAligned, (width, height))
faceAligned = cv2.cvtColor(faceAligned, cv2.COLOR_BGR2RGB)
plt.imshow(faceAligned)
faceAligned = faceAligned / 255.0
faceAligned = np.expand_dims(faceAligned, axis=0)
age = model.predict(faceAligned)
print('Age:', int(age))
process_and_predict('/content/trump.jpg')
```
| true |
code
| 0.520984 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
datafile = 'data/ex1data1.txt'
cols = np.loadtxt(datafile,delimiter=',',usecols=(0,1),unpack=True) #Read in comma separated data
#Form the usual "X" matrix and "y" vector
X = np.transpose(np.array(cols[:-1]))
y = np.transpose(np.array(cols[-1:]))
m = y.size # number of training examples
#Insert the usual column of 1's into the "X" matrix
X = np.insert(X,0,1,axis=1)
#Plot the data to see what it looks like
plt.figure(figsize=(10,6))
plt.plot(df.A,df.B,'rx',markersize=10)
plt.grid(True) #Always plot.grid true!
plt.ylabel('Profit in $10,000s')
plt.xlabel('Population of City in 10,000s')
#gradient decent
iterations = 1500
alpha = 0.01
def h(theta,X): #Linear hypothesis function
return np.dot(X,theta)
def computeCost(mytheta,X,y): #Cost function
"""
theta_start is an n- dimensional vector of initial theta guess
X is matrix with n- columns and m- rows
y is a matrix with m- rows and 1 column
"""
#note to self: *.shape is (rows, columns)
return float((1./(2*m)) * np.dot((h(mytheta,X)-y).T,(h(mytheta,X)-y)))
#Test that running computeCost with 0's as theta returns 32.07:
initial_theta = np.zeros((X.shape[1],1)) #(theta is a vector with n rows and 1 columns (if X has n features) )
print(computeCost(initial_theta,X,y))
#Actual gradient descent minimizing routine
def descendGradient(X, theta_start = np.zeros(2)):
"""
theta_start is an n- dimensional vector of initial theta guess
X is matrix with n- columns and m- rows
"""
theta = theta_start
jvec = [] #Used to plot cost as function of iteration
thetahistory = [] #Used to visualize the minimization path later on
for meaninglessvariable in range(iterations):
tmptheta = theta
jvec.append(computeCost(theta,X,y))
# Buggy line
#thetahistory.append(list(tmptheta))
# Fixed line
thetahistory.append(list(theta[:,0]))
#Simultaneously updating theta values
for j in range(len(tmptheta)):
tmptheta[j] = theta[j] - (alpha/m)*np.sum((h(theta,X) - y)*np.array(X[:,j]).reshape(m,1))
theta = tmptheta
return theta, thetahistory, jvec
#Actually run gradient descent to get the best-fit theta values
initial_theta = np.zeros((X.shape[1],1))
theta, thetahistory, jvec = descendGradient(X,initial_theta)
#Plot the convergence of the cost function
def plotConvergence(jvec):
plt.figure(figsize=(10,6))
plt.plot(range(len(jvec)),jvec,'bo')
plt.grid(True)
plt.title("Convergence of Cost Function")
plt.xlabel("Iteration number")
plt.ylabel("Cost function")
dummy = plt.xlim([-0.05*iterations,1.05*iterations])
#dummy = plt.ylim([4,8])
plotConvergence(jvec)
dummy = plt.ylim([4,7])
#Plot the line on top of the data to ensure it looks correct
def myfit(xval):
return theta[0] + theta[1]*xval
plt.figure(figsize=(10,6))
plt.plot(X[:,1],y[:,0],'rx',markersize=10,label='Training Data')
plt.plot(X[:,1],myfit(X[:,1]),'b-',label = 'Hypothesis: h(x) = %0.2f + %0.2fx'%(theta[0],theta[1]))
plt.grid(True) #Always plot.grid true!
plt.ylabel('Profit in $10,000s')
plt.xlabel('Population of City in 10,000s')
plt.legend()
#Import necessary matplotlib tools for 3d plots
from mpl_toolkits.mplot3d import axes3d, Axes3D
from matplotlib import cm
import itertools
fig = plt.figure(figsize=(12,12))
ax = fig.gca(projection='3d')
xvals = np.arange(-10,10,.5)
yvals = np.arange(-1,4,.1)
myxs, myys, myzs = [], [], []
for david in xvals:
for kaleko in yvals:
myxs.append(david)
myys.append(kaleko)
myzs.append(computeCost(np.array([[david], [kaleko]]),X,y))
scat = ax.scatter(myxs,myys,myzs,c=np.abs(myzs),cmap=plt.get_cmap('YlOrRd'))
plt.xlabel(r'$\theta_0$',fontsize=30)
plt.ylabel(r'$\theta_1$',fontsize=30)
plt.title('Cost (Minimization Path Shown in Blue)',fontsize=30)
plt.plot([x[0] for x in thetahistory],[x[1] for x in thetahistory],jvec,'bo-')
plt.show()
datafile = 'data/ex1data2.txt'
#Read into the data file
cols = np.loadtxt(datafile,delimiter=',',usecols=(0,1,2),unpack=True) #Read in comma separated data
#Form the usual "X" matrix and "y" vector
X = np.transpose(np.array(cols[:-1]))
y = np.transpose(np.array(cols[-1:]))
m = y.size # number of training examples
#Insert the usual column of 1's into the "X" matrix
X = np.insert(X,0,1,axis=1)
#Quick visualize data
plt.grid(True)
plt.xlim([-100,5000])
dummy = plt.hist(X[:,0],label = 'col1')
dummy = plt.hist(X[:,1],label = 'col2')
dummy = plt.hist(X[:,2],label = 'col3')
plt.title('Clearly we need feature normalization.')
plt.xlabel('Column Value')
plt.ylabel('Counts')
dummy = plt.legend()
#Feature normalizing the columns (subtract mean, divide by standard deviation)
#Store the mean and std for later use
#Note don't modify the original X matrix, use a copy
stored_feature_means, stored_feature_stds = [], []
Xnorm = X.copy()
for icol in range(Xnorm.shape[1]):
stored_feature_means.append(np.mean(Xnorm[:,icol]))
stored_feature_stds.append(np.std(Xnorm[:,icol]))
#Skip the first column
if not icol: continue
#Faster to not recompute the mean and std again, just used stored values
Xnorm[:,icol] = (Xnorm[:,icol] - stored_feature_means[-1])/stored_feature_stds[-1]
#Quick visualize the feature-normalized data
plt.grid(True)
plt.xlim([-5,5])
dummy = plt.hist(Xnorm[:,0],label = 'col1')
dummy = plt.hist(Xnorm[:,1],label = 'col2')
dummy = plt.hist(Xnorm[:,2],label = 'col3')
plt.title('Feature Normalization Accomplished')
plt.xlabel('Column Value')
plt.ylabel('Counts')
dummy = plt.legend()
#Run gradient descent with multiple variables, initial theta still set to zeros
#(Note! This doesn't work unless we feature normalize! "overflow encountered in multiply")
initial_theta = np.zeros((Xnorm.shape[1],1))
theta, thetahistory, jvec = descendGradient(Xnorm,initial_theta)
#Plot convergence of cost function:
plotConvergence(jvec)
#print "Final result theta parameters: \n",theta
print("Check of result: What is price of house with 1650 square feet and 3 bedrooms?")
ytest = np.array([1650.,3.])
#To "undo" feature normalization, we "undo" 1650 and 3, then plug it into our hypothesis
ytestscaled = [(ytest[x]-stored_feature_means[x+1])/stored_feature_stds[x+1] for x in range(len(ytest))]
ytestscaled.insert(0,1)
print("$%0.2f" % float(h(theta,ytestscaled)))
from numpy.linalg import inv
#Implementation of normal equation to find analytic solution to linear regression
def normEqtn(X,y):
#restheta = np.zeros((X.shape[1],1))
return np.dot(np.dot(inv(np.dot(X.T,X)),X.T),y)
print ("Normal equation prediction for price of house with 1650 square feet and 3 bedrooms")
print ("$%0.2f" % float(h(normEqtn(X,y),[1,1650.,3])))
```
| true |
code
| 0.577436 | null | null | null | null |
|
# Welcome to Jupyter!
With Jupyter notebooks you can write and execute code, annotate it with Markdownd and use powerful visualization tools all in one document.
## Running code
Code cells can be executed in sequence by pressing Shift-ENTER. Try it now.
```
import math
from matplotlib import pyplot as plt
a=1
b=2
a+b
```
## Visualisations
Many Python visualization libratries, matplotlib for exampl, intergate seamlessly with Jupyter. Visualiazations will appear directly in the notebook.
```
def display_sinusoid():
X = range(180)
Y = [math.sin(x/10.0) for x in X]
plt.plot(X, Y)
display_sinusoid()
```
## Tensorflow environment and accelerators
On Google's AI Platform notebooks, Tensorflow support is built-in and powerful accelerators are supported out of the box. Run this cell to test if your current notebook instance has Tensorflow and an accelerator (in some codelabs, you will add an accelerator later).
```
import tensorflow as tf
from tensorflow.python.client import device_lib
print("Tensorflow version " + tf.__version__)
try: # detect TPUs
tpu = tf.distribute.cluster_resolver.TPUClusterResolver.connect() # TPU detection
strategy = tf.distribute.TPUStrategy(tpu)
except ValueError: # detect GPUs
strategy = tf.distribute.MirroredStrategy() # for GPU or multi-GPU machines (works on CPU too)
#strategy = tf.distribute.get_strategy() # default strategy that works on CPU and single GPU
#strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy() # for clusters of multi-GPU machines
print("Number of accelerators: ", strategy.num_replicas_in_sync)
```
## Restarting
If you get stuck, the Jupyter environment can be restarted from the menu Kernel > Restart Kernel.
You can also run the entire notebook using Run > Run All Cells. Try it now.
## License
---
author: Martin Gorner<br>
twitter: @martin_gorner
---
Copyright 2021 Google LLC
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
---
This is not an official Google product but sample code provided for an educational purpose
```
```
| true |
code
| 0.476214 | null | null | null | null |
|
# Using Deep Learning for Medical Imaging
In the United States, it takes an average of [1 to 5 days](https://www.ncbi.nlm.nih.gov/pubmed/29132998) to receive a diagnosis after a chest x-ray. This long wait has been shown to increase anxiety in 45% of patients. In addition, impoverished countries usually lack personnel with the technical knowledge to read chest x-rays, assuming an x-ray machine is even available. In such cases, a [short term solution](https://www.theatlantic.com/health/archive/2016/09/radiology-gap/501803/) has been to upload the images online and have volunteers read the images; volunteers diagnose an average of 4000 CT scans per week. This solution works somewhat, but many people travel for days to a clinic and cannot keep traveling back and forth for a diagnosis or treatment, nor can those with more life threatning injuries wait days for a diagnosis.
Clearly, there is a shortage of trained physicians/radiologists for the amount of care needed. To help reduce diagnosis time, we can turn to deep learning. Specifically, I will be using 3 pre-trained models (VGG19, MobileNet, and ResNet50) to apply transfer learning to chest x-rays. The largest database of chest x-ray images are compiled by the NIH Clinical Center and can be found [here](https://www.nih.gov/news-events/news-releases/nih-clinical-center-provides-one-largest-publicly-available-chest-x-ray-datasets-scientific-community). The database has 112,120 X-ray images from over 30,000 patients. There are 14 different pathologies/conditions and a 'no findings' label, for a total of 15 different labels. Due to time constraints, this notebook will go through the steps as I used transfer learning to train two of these labels: pneumonia and effusion.
## 1 - Retrieving the Data
For this project, I used tensorflow and Keras for my deep learning library. Unfortunately, I ran into reproduciblity problems, which seems to be a common problem (see [machinelearningmastery](https://machinelearningmastery.com/reproducible-results-neural-networks-keras/) and this [StackOverflow question](https://stackoverflow.com/questions/48631576/reproducible-results-using-keras-with-tensorflow-backend)) which is why I set random seeds for python hash seed, numpy, and python in my import section.
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import os
import cv2
import random
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import os
import cv2
import random
from PIL import Image
import skimage
from skimage import io
from skimage.transform import resize
from numpy import expand_dims
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_score, recall_score,accuracy_score, f1_score, roc_curve, confusion_matrix, roc_curve,roc_auc_score
import tensorflow as tf
os.environ['PYTHONHASHSEED']='0'
np.random.seed(42)
random.seed(42)
import keras
from keras import backend as K
# import keras.backend.tensorflow_backend as K
tf.random.set_seed(42)
from keras.preprocessing.image import load_img, ImageDataGenerator, img_to_array
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten, Conv2D, GlobalAveragePooling2D, BatchNormalization
from keras.models import Model
from keras.optimizers import RMSprop, Adam
from keras.applications.vgg19 import preprocess_input, decode_predictions, VGG19
from keras.applications.mobilenet import MobileNet
from keras.applications.resnet import ResNet50
dirpath = 'all_images/'
alldata_df = pd.read_csv('./Data_Entry_2017.csv')
```
## 2 - Data Exploration
The master dataframe below shows all the info we know regarding each image, including the image filename, label(s), patient information, and image height and width.
```
alldata_df.head()
```
### 2.1 - Pathologies
One thing to notice is that each image can have multiple labels. To isolate each individual pathology, I will create a column for each pathology and use 0 and 1 to indicate if the image has that pathology or not respectively.
```
alldata_df['Labels List'] = alldata_df['Finding Labels'].apply(lambda x: x.split('|'))
pathology_lst = ['Cardiomegaly', 'No Finding', 'Hernia', 'Infiltration', 'Nodule',
'Emphysema', 'Effusion', 'Atelectasis', 'Pleural_Thickening',
'Pneumothorax', 'Mass', 'Fibrosis', 'Consolidation', 'Edema',
'Pneumonia']
def get_label(col, pathology):
if pathology in col:
return 1
else:
return 0
for pathology in pathology_lst:
alldata_df[pathology] = alldata_df['Labels List'].apply(lambda x: get_label(x, pathology))
```
Below is a table of the percentage of each type of label that makes up the dataset. Not surprisingly, the 'no findings' label makes up the majority of the images, at about 50%. The two pathologies I'd like to train are pneumonia and effusion. Pneumonia, a pathology that most of us has heard of, takes up about 1.2% of the dataset whereas effusion is ~10%. This corresponds to a total of 1431 and 13317 images for pneumonia and effusion respectively. Due to the small amount of images available for pneumonia, I suspect it will be difficult to get good results.
```
alldata_df[pathology_lst].sum()/alldata_df.shape[0]*100
```
### 2.2 - Image Data
There are two things to explore with the image data before diving into creating models. Its useful to know the height and widths of the images, especially since the models I'm using are expecting a dimension of 224 x 224 pixels.
The distribution of the heights and widths are shown in the histograms below. Most of the images have a height of 2000 pixels, although a good number of them hover at 2500 and 3000, with a minimum of ~970 pixels. The width of the images also has 3 distinct peaks, but the max is at 2500, and significant peaks at 2000 and 3000 pixels, with a minimum of ~1140 pixels. All the images have dimensions greater than 224.
```
fig, (axis1, axis2) = plt.subplots(1, 2, figsize=(15, 4))
sns.distplot(alldata_df['Height]'], ax = axis1)
sns.distplot(alldata_df['OriginalImage[Width'], ax = axis2)
axis1.set_title('Distribution of Image Height')
axis2.set_title('Distribution of Image Widths')
for ax in [axis1, axis2]:
ax.set_xlabel('Pixels')
ax.set_ylabel('Density')
plt.tight_layout()
```
Another column is the view position. There are two unique values for this columns: PA and AP. These represent if the X-rays pass from the back to the front or vice versa. Thus, I'd like to find out if there are any stark differences in the images between the two view positions. Most of the images are in the PA viewing position. This is preferred because AP position creates 'shadows', but 'AP' images are taken because the patient is unable to stand up for the 'PA' position and need to lie down on a table.
```
alldata_df['View Position'].value_counts()/alldata_df.shape[0]*100
def get_images(filename_df, target_pathology, num_images = 500, imageSize = 224):
X = []
sample_df = filename_df.sample(n = num_images)
sample_df.reset_index(drop = True, inplace = True)
truncated_image_filename_lst = sample_df['Image Index'].values
full_image_filename_lst = []
for truncated_filename in truncated_image_filename_lst:
full_image_filename_lst.append(find_file(truncated_filename))
for i, file in enumerate(full_image_filename_lst):
img_file = cv2.imread(file)
img_file = cv2.resize(img_file, (imageSize, imageSize), interpolation = cv2.INTER_CUBIC)
img_arr = np.asarray(img_file)
if img_arr.shape == (224, 224, 3):
X.append(img_arr)
else:
sample_df.drop(i, inplace = True)
y = sample_df[target_pathology]
return np.array(X), np.array(y)
# images extractred from 12 files,
image_dir = sorted([dir for dir in os.listdir(dirpath) if 'images' in dir ])
def find_file(filename):
for dirfile in image_dir:
if filename in os.listdir(dirpath + dirfile + '/images'):
return dirpath + dirfile + '/images/' + filename
pa_images, _ = get_images(alldata_df[alldata_df['View Position']=='PA'], 'No Finding', num_images = 9, imageSize = 224)
ap_images, _ = get_images(alldata_df[(alldata_df['View Position']=='AP') & (alldata_df['No Finding']==1)], 'No Finding', num_images = 9, imageSize = 224)
```
Below I've plotted 16 images total. To make sure there aren't any differences due to pathologies, I only took from the 'no findings' label. The first 8 images are X-rays in the PA position (the majority), and the latter 8 images are in the AP position.
The PA images seem to generally have a white mass near the bottom, although how much white varies from image to image. In addition, there is a small protrusion to the left of the spine, and a larger protrusion to the right of the spine.
The AP images are similar, but much blurrier, possibly due to the shadows mentioned before.
```
plt.figure(figsize = (13, 6))
print('Images for PA view')
for i in range(8):
plt.subplot(2, 4, i+1)
tmp1 = pa_images[i].astype(np.uint8)
plt.imshow(tmp1)
plt.tight_layout()
plt.figure(figsize = (13, 6))
print('Images for AP view')
for i in range(8):
plt.subplot(2, 4, i+1)
tmp1 = ap_images[i].astype(np.uint8)
plt.imshow(tmp1)
plt.tight_layout()
```
I looked at the percentages of AP vs PA view positions for 'pneumonia' and 'effusion', and threw in the overall percentage and 'no finding' for comparison. The overall and no findings are pretty close, with 'PA' positions at 60-65%. However, the 'PA' positions for 'pneumonia' and 'effusion' are lower, at 45-50%. Although removing 'AP' images might improve the models, for pneumonia it would leave too little images to train on.
```
pathology_percent_lst = ['No Finding', 'Pneumonia', 'Effusion']
pa_percent_lst = [alldata_df[(alldata_df[path]==1) & (alldata_df['View Position'] == 'PA')].shape[0]/alldata_df[(alldata_df[path]==1)].shape[0]*100 for path in pathology_percent_lst]
ap_percent_lst = [alldata_df[(alldata_df[path]==1) & (alldata_df['View Position'] == 'AP')].shape[0]/alldata_df[(alldata_df[path]==1)].shape[0]*100 for path in pathology_percent_lst]
pathology_percent_lst.insert(0, 'Overall')
pa_percent_lst.insert(0, alldata_df[alldata_df['View Position']=='PA'].shape[0]/alldata_df.shape[0]*100)
ap_percent_lst.insert(0, alldata_df[alldata_df['View Position']=='AP'].shape[0]/alldata_df.shape[0]*100)
ap_pa_percent_df = pd.DataFrame(np.array([pa_percent_lst, ap_percent_lst]),
columns = pathology_percent_lst,
index = ['PA', 'AP'])
ap_pa_percent_df
```
### 2.3 - Splitting into Training, Validation, and Test Sets
Lastly, the original [paper](http://openaccess.thecvf.com/content_cvpr_2017/papers/Wang_ChestX-ray8_Hospital-Scale_Chest_CVPR_2017_paper.pdf) split the images into training/validation and test sets and released that information to the public so we can easily compare our results to theirs. I have split my own data into the same training/validation, and test sets as the original authors.
```
train_val_filenames = pd.read_csv('./train_val_list.txt', sep=" ", header=None)
test_filenames = pd.read_csv('./test_list.txt', sep=" ", header=None)
train_val_filenames.shape[0] + test_filenames.shape[0]
train_val_df = alldata_df[alldata_df['Image Index'].isin(train_val_filenames.values.flatten())]
test_df = alldata_df[alldata_df['Image Index'].isin(test_filenames.values.flatten())]
```
## 3 - Pneumonia
First, I will be performing transfer learning on pneumonia images. In order, the three models I will be using are VGG18, MobileNet, and ResNet50.
### 3.1 - VGG19 Model
First I must preprocess the images. The VGG model is expecting an image size of 224 x 224 pixels
```
imgSize = 224
```
Note: After writing this notebook, I realized my smaller test set should have the same distribution of pathologies as the original test set. This will be corrected the next time I improve upon this project.
```
# Get test images
Xtest_pneu, ytest_pneu = get_images(test_df[test_df['Pneumonia']==1],
'Pneumonia',
num_images = test_df[test_df['Pneumonia']==1].shape[0],
imageSize = imgSize)
Xtest_notpneu, ytest_notpneu = get_images(test_df[test_df['Pneumonia']==0],
'Pneumonia',
num_images = test_df[test_df['Pneumonia']==1].shape[0],
imageSize = imgSize)
X_test_pneu = np.concatenate((Xtest_pneu, Xtest_notpneu), axis = 0)
y_test_pneu = np.concatenate((ytest_pneu, ytest_notpneu))
```
I use sklearn's train_test_split function to shuffle test set. Unfortunately that means I lose 1% of the images, so it leaves me with 1099 images total in the test set.
```
_, X_test_pneu, _, y_test_pneu = train_test_split(X_test_pneu,
y_test_pneu,
test_size=0.99,
random_state=42,
stratify = y_test_pneu)
```
The training and validation sets have a total of 1752 and 351 images respectively.
```
# get training images and split into validation set
Xtrain_pneu, ytrain_pneu = get_images(train_val_df[train_val_df['Pneumonia']==1],
'Pneumonia',
num_images = train_val_df[train_val_df['Pneumonia']==1].shape[0],
imageSize = imgSize)
Xtrain_notpneu, ytrain_notpneu = get_images(train_val_df[train_val_df['Pneumonia']==0],
'Pneumonia',
num_images = train_val_df[train_val_df['Pneumonia']==1].shape[0],
imageSize = imgSize)
Xtrain_pneu = np.concatenate((Xtrain_pneu, Xtrain_notpneu), axis = 0)
ytrain_pneu = np.concatenate((ytrain_pneu, ytrain_notpneu))
X_train_pneu, X_val_pneu, y_train_pneu, y_val_pneu = train_test_split(Xtrain_pneu,
ytrain_pneu,
test_size=0.2,
random_state=42,
stratify = ytrain_pneu)
```
Next, I need to convert the images into a format accepted by the VGG model.
```
def convert_X_data(Xtrain, Xval, Xtest, imageSize = 224, num_classes = 2):
if K.image_data_format() == 'channels_first':
Xtrain_model = Xtrain.reshape(Xtrain.shape[0], 3, imageSize, imageSize)
Xval_model = Xval.reshape(Xval.shape[0], 3, imageSize, imageSize)
Xtest_model = Xtest.reshape(Xtest.shape[0], 3, imageSize, imageSize)
else:
Xtrain_model = Xtrain.reshape(Xtrain.shape[0], imageSize, imageSize, 3)
Xval_model = Xval.reshape(Xval.shape[0], imageSize, imageSize, 3)
Xtest_model = Xtest.reshape(Xtest.shape[0], imageSize, imageSize, 3)
# input_shape = (img_rows, img_cols, 1)
Xtrain_model = Xtrain_model.astype('float32')
Xval_model = Xval_model.astype('float32')
Xtest_model = Xtest_model.astype('float32')
Xtrain_model = preprocess_input(Xtrain_model)
Xval_model = preprocess_input(Xval_model)
Xtest_model = preprocess_input(Xtest_model)
return Xtrain_model, Xval_model, Xtest_model
def convert_y_data(ytrain, yval, ytest, num_classes = 2):
ytrain_model = keras.utils.to_categorical(ytrain, num_classes)
yval_model = keras.utils.to_categorical(yval, num_classes)
ytest_model = keras.utils.to_categorical(ytest, num_classes)
return ytrain_model, yval_model, ytest_model
X_train_pneu_model, X_val_pneu_model, X_test_pneu_model = convert_X_data(X_train_pneu,
X_val_pneu,
X_test_pneu,
imageSize = imgSize,
num_classes = 2)
y_train_pneu_model, y_val_pneu_model, y_test_pneu_model = convert_y_data(y_train_pneu,
y_val_pneu,
y_test_pneu,
num_classes = 2)
```
Lastly, keras only has built in functions for accuracy and loss. I am interested in looking at accuracy, precision, recall, and f1 scores however, so I will write my own function to get these metrics.
The two metrics I'm most concerned about are the recall and f1-score. I am interested in the recall because for a medical related dataset, I believe it is best to reduce false negatives. However, I know there are cases where the model can predict all 0 or all 1, which would skew the precision and recalls. As such, it is important to look at f1-scores as well.
```
def get_metrics(model, xtest, ytrue, verbose = True):
y_pred_probs = model.predict(xtest)
try:
y_pred_classes = model.predict_classes(xtest)
except AttributeError:
y_pred_classes = [np.argmax(i) for i in y_pred_probs]
y_pred_probs = y_pred_probs[:, 0]
try:
y_pred_classes = y_pred_classes[:, 0]
except: #IndexError:
pass
if verbose:
print('Accuracy Score: {}'.format(accuracy_score(ytrue, y_pred_classes)))
print('Precision Score: {}'.format(precision_score(ytrue, y_pred_classes)))
print('Recall: {}'.format(recall_score(ytrue, y_pred_classes)))
print('F1 Score: {}'.format(f1_score(ytrue, y_pred_classes)))
print('Confusion matrix: \n{}'.format(confusion_matrix(ytrue, y_pred_classes)))
return accuracy_score(ytrue, y_pred_classes), precision_score(ytrue, y_pred_classes), recall_score(ytrue, y_pred_classes), f1_score(ytrue, y_pred_classes)
```
#### 3.1.1 - VGG Baseline with Pneumonia Images
The first step is to establish what the baseline metrics will be for the VGG model. To do this, first I import the layers from the VGG model. Since this model was trained on the ImageNet dataset, it expects to predict from 1000 classes. I replace this last layer with a dense layer with 2 classes and softmax activation, and compile the model with keras's categorical cross entropy loss function. Lastly, due to the reproducibility issues mentioned in the beginning, I run the model 3 times and average the metrics and show the standard deviation.
For the baseline metric, the model has an accuracy of ~50% while the precision is ~0.55 and recall and f1 score at ~0.23, so this is just about as good as flipping a coin given that the test set is balanced. In addition, the standard deviation for the recall and precision scores are just about as big as the averaged scores themselves, so the reliability of this baseline model is very poor.
```
num_classes = 2
vgg_model = VGG19()
vgg_baseline_acc_scores = []
vgg_baseline_prec_scores = []
vgg_baseline_recall_scores = []
vgg_baseline_f1_scores = []
for i in range(3):
vgg_model_baseline = Sequential()
for layer in vgg_model.layers[:-1]:
vgg_model_baseline.add(layer)
vgg_model_baseline.add(Dense(num_classes, activation = 'softmax'))
# freeze layers, excluding from future training. weights are not updated.
for layer in vgg_model_baseline.layers:
layer.trainable = False
vgg_model_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
vgg_model_baseline_history = vgg_model_baseline.fit(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model, y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(vgg_model_baseline, X_test_pneu_model, y_test_pneu, verbose = True)
vgg_baseline_acc_scores.append(acc)
vgg_baseline_prec_scores.append(prec)
vgg_baseline_recall_scores.append(recall)
vgg_baseline_f1_scores.append(f1)
print('Accuracy of VGG baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_baseline_acc_scores) * 100, np.std(vgg_baseline_acc_scores)*100))
print('Precision of VGG baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_baseline_prec_scores), np.std(vgg_baseline_prec_scores)))
print('Recall of VGG baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_baseline_recall_scores), np.std(vgg_baseline_recall_scores)))
print('f1 score of VGG baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_baseline_f1_scores), np.std(vgg_baseline_f1_scores)))
```
#### 3.1.2 - Training Layers with VGG19 and Pneumonia Images
A way to fine tune and hopefully improve upon this baseline model is to unfreeze certain layers. That is, the weights imported by the VGG (or any) model is optimized for the ImageNet dataset. Unfreezing layers allows the model to learn the features of your current dataset. Typically, the first layers of the models are kept frozen as they are able to extract big/common features, while the last layers are able to extract features that are more specific to your dataset.
VGG19 has 26 layers, and I found that it is optimal to train the last 4 layers, leaving the first 22 layers frozen. With this model, the accuracy rises slightly to ~53% while the precision stays the same. Recall and f1-score rises to over 0.60. In addition, standard deviations have drastically reduced.
```
vgg_frozen_acc_scores = []
vgg_frozen_prec_scores = []
vgg_frozen_recall_scores = []
vgg_frozen_f1_scores = []
for i in range(3):
vgg_model_frozen = Sequential()
for layer in vgg_model.layers[:-1]:
vgg_model_frozen.add(layer)
vgg_model_frozen.add(Dense(num_classes, activation = 'softmax'))
# freeze layers, excluding from future training. weights are not updated.
for layer in vgg_model_frozen.layers[:-4]:
layer.trainable = False
vgg_model_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
vgg_model_frozen_history = vgg_model_frozen.fit(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model, y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(vgg_model_frozen, X_test_pneu_model, y_test_pneu, verbose = True)
vgg_frozen_acc_scores.append(acc)
vgg_frozen_prec_scores.append(prec)
vgg_frozen_recall_scores.append(recall)
vgg_frozen_f1_scores.append(f1)
print('Accuracy of VGG model with last 4 layers trained: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_frozen_acc_scores) * 100, np.std(vgg_frozen_acc_scores)*100))
print('Precision of VGG model with last 4 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_frozen_prec_scores), np.std(vgg_frozen_prec_scores)))
print('Recall of VGG model with last 4 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_frozen_recall_scores), np.std(vgg_frozen_recall_scores)))
print('f1 score of VGG model with last 4 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_frozen_f1_scores), np.std(vgg_frozen_f1_scores)))
```
#### 3.1.3 - Adding Augmented Images to VGG19 Model with Pneumonia Images
So far, I've been able to get an ok f1 score, but an accuracy of 55% concerns me because that's barely doing beter than randomly guessing if an image shows pneumonia or not. I believe part of that is the low number of images in the training set, with a total of 1752 images. Normally, a deep learning model will want hundreds of thousands of images. To help with this, I can generate images from the ones I already have by altering them. The alterations are defined in the Image Data Generator function below, but to summarize, the image generator can zoom, shift the image horizontally, or shift the image vertically. If the image is shifted, black pixels fill in the empty space.
As usual, I want to get a baseline for this augmented images model. Unfortunately, the metrics seem to be similar to the non-augmented baseline scores.
```
gen = ImageDataGenerator(zoom_range=0.05,
height_shift_range=0.05,
width_shift_range=0.05,
fill_mode = 'constant',
cval = 0)
vgg_aug_baseline_acc_scores = []
vgg_aug_baseline_prec_scores = []
vgg_aug_baseline_recall_scores = []
vgg_aug_baseline_f1_scores = []
for i in range(3):
vgg_model_aug_baseline = Sequential()
for layer in vgg_model.layers[:-1]:
vgg_model_aug_baseline.add(layer)
vgg_model_aug_baseline.add(Dense(num_classes, activation = 'softmax'))
for layer in vgg_model_aug_baseline.layers:
layer.trainable = False
vgg_model_aug_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
vgg_model_aug_baseline_history = vgg_model_aug_baseline.fit_generator(gen.flow(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_pneu_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(vgg_model_aug_baseline, X_test_pneu_model, y_test_pneu, verbose = True)
vgg_aug_baseline_acc_scores.append(acc)
vgg_aug_baseline_prec_scores.append(prec)
vgg_aug_baseline_recall_scores.append(recall)
vgg_aug_baseline_f1_scores.append(f1)
print('Accuracy of VGG augmented baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_aug_baseline_acc_scores) * 100, np.std(vgg_aug_baseline_acc_scores)*100))
print('Precision of VGG augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_aug_baseline_prec_scores), np.std(vgg_aug_baseline_prec_scores)))
print('Recall of VGG augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_aug_baseline_recall_scores), np.std(vgg_aug_baseline_recall_scores)))
print('f1 score of VGG augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_aug_baseline_f1_scores), np.std(vgg_aug_baseline_f1_scores)))
```
Again, I'd like to fine tune the augmented image model by letting some layers be trainable. I found the optimal number of trainable layers to be 5. The accuracy of the augmented model with trainable layers is slightly higher, but the standard deviation is also larger, and the precision, recall, and f1-score are either the same or lower than the baseline model with trainable layers.
```
vgg_aug_frozen_acc_scores = []
vgg_aug_frozen_prec_scores = []
vgg_aug_frozen_recall_scores = []
vgg_aug_frozen_f1_scores = []
for i in range(3):
vgg_model_aug_frozen = Sequential()
for layer in vgg_model.layers[:-1]:
vgg_model_aug_frozen.add(layer)
vgg_model_aug_frozen.add(Dense(num_classes, activation = 'softmax'))
for layer in vgg_model_aug_frozen.layers[:-5]:
layer.trainable = False
vgg_model_aug_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
vgg_model_aug_frozen_history = vgg_model_aug_frozen.fit_generator(gen.flow(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_pneu_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(vgg_model_aug_frozen, X_test_pneu_model, y_test_pneu, verbose = True)
vgg_aug_frozen_acc_scores.append(acc)
vgg_aug_frozen_prec_scores.append(prec)
vgg_aug_frozen_recall_scores.append(recall)
vgg_aug_frozen_f1_scores.append(f1)
print('Accuracy of VGG augmented model with last 5 layers trained: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_aug_frozen_acc_scores) * 100, np.std(vgg_aug_frozen_acc_scores)*100))
print('Precision of VGG augmented model with last 5 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_aug_frozen_prec_scores), np.std(vgg_aug_frozen_prec_scores)))
print('Recall of VGG augmented model with last 5 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_aug_frozen_recall_scores), np.std(vgg_aug_frozen_recall_scores)))
print('f1 score of VGG augmented model with last 5 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(vgg_aug_frozen_f1_scores), np.std(vgg_aug_frozen_f1_scores)))
```
#### 3.1.4 - VGG19 Pnuemonia Summary for Pneumonia Images
A table that summarizes the metrics of the VGG model for pneumonia is below. Overall, it shows that the best VGG model comes from the baseline model while training the last 4 layers, as it has the highest recall and f1-score.
| Model | Accuracy | Precision | Recall | F1-score |
|------|------|------|------|------|
| VGG19 baseline | 49.50 +/- 1.29%| 0.545 +/- 0.055 | 0.236 +/- 0.279| 0.229 +/- 0.226 |
| VGG19 baseline with training | 53.75 +/- 0.43% | 0.525 +/- 0.006 | 0.800 +/- 0.105 | 0.631 +/- 0.031 |
| VGG19 augmented baseline | 51.08 +/- 0.79% | 0.548 +/- 0.022 | 0.245 +/- 0.286 | 0.244 +/- 0.237 |
| VGG19 augmented with training | 54.14 +/- 1.30% | 0.538 +/- 0.004 | 0.573 +/- 0.141 | 0.546 +/- 0.074 |
### 3.2 - MobileNet Model
The next model to try is MobileNet model. This model also expects images of 224 x 224, so the training and test sets are already set up.
#### 3.2.1 - MobileNet Baseline with Pneumonia Images
The rest of the notebook follows the same steps as the VGG model, so here I'll be establishing the baseline metrics for MobileNet. Here I use the argument include_top = False. When compared to the original MobileNet model however, this takes away the last two layers of the model instead of just one. To make up for this, I have to include the GlobalAveragePooling2D layer back in.
For MobileNet's baseline, accuracy is again at ~50% whereas the precision is slightly worse and the recall and f1 score are slightly better than VGG's baseline. All of these metrics are lower than the best VGG model.
```
mobilenet_model = MobileNet(include_top=False, input_shape=(imgSize, imgSize, 3))
mobilenet_baseline_acc_scores = []
mobilenet_baseline_prec_scores = []
mobilenet_baseline_recall_scores = []
mobilenet_baseline_f1_scores = []
for i in range(3):
x=mobilenet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
mobilenet_model_baseline=Model(inputs=mobilenet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in mobilenet_model_baseline.layers:
layer.trainable = False
mobilenet_model_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
mobilenet_model_baseline_history = mobilenet_model_baseline.fit(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(mobilenet_model_baseline,
X_test_pneu_model,
y_test_pneu)
mobilenet_baseline_acc_scores.append(acc)
mobilenet_baseline_prec_scores.append(prec)
mobilenet_baseline_recall_scores.append(recall)
mobilenet_baseline_f1_scores.append(f1)
print('Accuracy of MobileNet baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(mobilenet_baseline_acc_scores) * 100, np.std(mobilenet_baseline_acc_scores)*100))
print('Precision of MobileNet baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_baseline_prec_scores), np.std(mobilenet_baseline_prec_scores)))
print('Recall of MobileNet baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_baseline_recall_scores), np.std(mobilenet_baseline_recall_scores)))
print('f1 score of MobileNet baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_baseline_f1_scores), np.std(mobilenet_baseline_f1_scores)))
```
#### 3.2.2 - MobileNet Training Layers with Pneumonia Images
There are ~85 layers in the MobileNet model, so its more difficult to find the sweet spot of how many layers to train compared to VGG. Due to time, I trained up to the last 25 layers, and found that the optimal number of trainable layers is 21. Accuracy is slightly higher, at 53%, but the precision has stayed the same as MobileNet's baseline. Its recall and f1-scores hwoever, have improved so that they are at least 0.6, and generally the standard deviations are more stable.
```
mobilenet_frozen_acc_scores = []
mobilenet_frozen_prec_scores = []
mobilenet_frozen_recall_scores = []
mobilenet_frozen_f1_scores = []
for i in range(3):
x=mobilenet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
mobilenet_model_baseline=Model(inputs=mobilenet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in mobilenet_model_baseline.layers[:-21]:
layer.trainable = False
mobilenet_model_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
mobilenet_model_baseline_history = mobilenet_model_baseline.fit(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(mobilenet_model_baseline,
X_test_pneu_model,
y_test_pneu)
mobilenet_frozen_acc_scores.append(acc)
mobilenet_frozen_prec_scores.append(prec)
mobilenet_frozen_recall_scores.append(recall)
mobilenet_frozen_f1_scores.append(f1)
print('Accuracy of MobileNet model with last 21 layers trained: {:0.2f} +/- {:0.2f}%'.format(np.mean(mobilenet_frozen_acc_scores) * 100, np.std(mobilenet_frozen_acc_scores)*100))
print('Precision of MobileNet model with last 21 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_frozen_prec_scores), np.std(mobilenet_frozen_prec_scores)))
print('Recall of MobileNet model with last 21 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_frozen_recall_scores), np.std(mobilenet_frozen_recall_scores)))
print('f1 score of MobileNet model with last 21 layers trained: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_frozen_f1_scores), np.std(mobilenet_frozen_f1_scores)))
```
#### 3.2.3 - Adding Augmented Images to MobileNet with Pneumonia Images
The metrics for the baseline augmented model for MobileNet are similar to the metrics for the non-augmented model. One thing to note based on the confusion matrix is that the model seems to heavily class everything as 0 or 1 (not pneumonia vs pneumonia).
```
mobilenet_aug_baseline_acc_scores = []
mobilenet_aug_baseline_prec_scores = []
mobilenet_aug_baseline_recall_scores = []
mobilenet_aug_baseline_f1_scores = []
for i in range(3):
x=mobilenet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
mobilenet_model_aug_baseline=Model(inputs=mobilenet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in mobilenet_model_aug_baseline.layers:
layer.trainable = False
mobilenet_model_aug_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
mobilenet_model_aug_baseline_history = mobilenet_model_aug_baseline.fit_generator(gen.flow(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_pneu_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(mobilenet_model_aug_baseline,
X_test_pneu_model,
y_test_pneu)
mobilenet_aug_baseline_acc_scores.append(acc)
mobilenet_aug_baseline_prec_scores.append(prec)
mobilenet_aug_baseline_recall_scores.append(recall)
mobilenet_aug_baseline_f1_scores.append(f1)
print('Accuracy of MobileNet augmented baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(mobilenet_aug_baseline_acc_scores) * 100, np.std(mobilenet_aug_baseline_acc_scores)*100))
print('Precision of MobileNet augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_aug_baseline_prec_scores), np.std(mobilenet_aug_baseline_prec_scores)))
print('Recall of MobileNet augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_aug_baseline_recall_scores), np.std(mobilenet_aug_baseline_recall_scores)))
print('f1 score of MobileNet augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_aug_baseline_f1_scores), np.std(mobilenet_aug_baseline_f1_scores)))
```
Fine tuning the training of layers and finding a sweet spot was very difficult for the augmented MobileNet model. At the moment, the best model I found was to train the last 11 layers of the model. This gives similar scores with MobileNet's trained layers, but with larger standard deviations.
```
mobilenet_aug_frozen_acc_scores = []
mobilenet_aug_frozen_prec_scores = []
mobilenet_aug_frozen_recall_scores = []
mobilenet_aug_frozen_f1_scores = []
for i in range(3):
x=mobilenet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
mobilenet_model_aug_frozen=Model(inputs=mobilenet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in mobilenet_model_aug_frozen.layers[:-11]:
layer.trainable = False
mobilenet_model_aug_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
mobilenet_model_aug_frozen_history = mobilenet_model_aug_frozen.fit_generator(gen.flow(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_pneu_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(mobilenet_model_aug_frozen,
X_test_pneu_model,
y_test_pneu)
mobilenet_aug_frozen_acc_scores.append(acc)
mobilenet_aug_frozen_prec_scores.append(prec)
mobilenet_aug_frozen_recall_scores.append(recall)
mobilenet_aug_frozen_f1_scores.append(f1)
print('Accuracy of MobileNet augmented model while training last 11 layers: {:0.2f} +/- {:0.2f}%'.format(np.mean(mobilenet_aug_frozen_acc_scores) * 100, np.std(mobilenet_aug_frozen_acc_scores)*100))
print('Precision of MobileNet augmented model while training last 11 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_aug_frozen_prec_scores), np.std(mobilenet_aug_frozen_prec_scores)))
print('Recall of MobileNet augmented model while training last 11 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_aug_frozen_recall_scores), np.std(mobilenet_aug_frozen_recall_scores)))
print('f1 score of MobileNet augmented model while training last 11 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(mobilenet_aug_frozen_f1_scores), np.std(mobilenet_aug_frozen_f1_scores)))
```
#### 3.2.4 - MobileNet Pnuemonia Summary for Pneumonia Images
A table that summarizes the results of each of the MobileNet models is below. The two models with trained layers had similar f1-scores, but the baseline model with trained layers had a much higher recall, leading me to pick that as the better model.
| Model | Accuracy | Precision | Recall | F1-score |
|------|------|------|------|------|
| MobileNet baseline | 50.47 +/- 2.28% | 0.488 +/- 0.079 | 0.344 +/- 0.314 | 0.325 +/- 0.231 |
| MobileNet baseline with training | 53.78 +/- 0.32% | 0.522 +/- 0.003 | 0.876 +/- 0.069 | 0.653 +/- 0.018 |
| MobileNet augmented baseline | 49.65 +/- 0.19% | 0.405 +/- 0.085 | 0.341 +/- 0.461 | 0.240 +/- 0.300 |
| MobileNet augmented with training | 53.05 +/- 1.12% | 0.521 +/- 0.010 | 0.797 +/- 0.123 | 0.626 +/- 0.029 |
### 3.3 - ResNet50 Model
Lastly, we have a ResNet model, specifically the ResNet50 model. I chose this model because it gets good results for most image recognition problems.
#### 3.3.1 - ResNet Baseline with Pneumonia Images
Similarly to MobileNet, I utilize the include_top = False argument and I have to add the GlobalAveragePooling2D and Dense layers. This model also expects an image size of 224 x 224.
I had high hopes that this baseline would be higher than 50%, but it was not to be. The recall is much higher than the other baselines at ~0.86, but I belive this is because the model tends to predict everything to be 1 (has pneumonia). This is a good reminder of why you should check confusion matrices.
```
resnet_model = ResNet50(include_top=False, input_shape=(imgSize, imgSize, 3))
resnet_baseline_acc_scores = []
resnet_baseline_prec_scores = []
resnet_baseline_recall_scores = []
resnet_baseline_f1_scores = []
for i in range(3):
x=resnet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
resnet_model_baseline=Model(inputs=resnet_model.input,outputs=preds)
for layer in resnet_model_baseline.layers:
layer.trainable = False
resnet_model_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
resnet_model_baseline_history = resnet_model_baseline.fit(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(resnet_model_baseline,
X_test_pneu_model,
y_test_pneu)
resnet_baseline_acc_scores.append(acc)
resnet_baseline_prec_scores.append(prec)
resnet_baseline_recall_scores.append(recall)
resnet_baseline_f1_scores.append(f1)
print('Accuracy of ResNet baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(resnet_baseline_acc_scores) * 100, np.std(resnet_baseline_acc_scores)*100))
print('Precision of ResNet baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_baseline_prec_scores), np.std(resnet_baseline_prec_scores)))
print('Recall of ResNet baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_baseline_recall_scores), np.std(resnet_baseline_recall_scores)))
print('f1 score of ResNet baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_baseline_f1_scores), np.std(resnet_baseline_f1_scores)))
```
#### 3.3.2 - ResNet50 Training Layers with Pneumonia Images
I found that the optimal number of layers to train is 22, which has an accuracy that finally breaks past 53%, for an accuracy of ~54%. Not much of an improvement but I was beginning to wonder if any model could break 53%. The precision, recall, and f1-scores all hover at around 0.50.
```
resnet_frozen_acc_scores = []
resnet_frozen_prec_scores = []
resnet_frozen_recall_scores = []
resnet_frozen_f1_scores = []
for i in range(3):
x=resnet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
resnet_model_frozen=Model(inputs=resnet_model.input,outputs=preds)
for layer in resnet_model_frozen.layers[:-22]:
layer.trainable = False
resnet_model_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
resnet_model_frozen_history = resnet_model_frozen.fit(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, prec, recall, f1 = get_metrics(resnet_model_frozen,
X_test_pneu_model,
y_test_pneu)
resnet_frozen_acc_scores.append(acc)
resnet_frozen_prec_scores.append(prec)
resnet_frozen_recall_scores.append(recall)
resnet_frozen_f1_scores.append(f1)
print('Accuracy of ResNet model while training last 22 layers: {:0.2f} +/- {:0.2f}%'.format(np.mean(resnet_frozen_acc_scores) * 100, np.std(resnet_frozen_acc_scores)*100))
print('Precision of ResNet model while training last 22 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_frozen_prec_scores), np.std(resnet_frozen_prec_scores)))
print('Recall of ResNet model while training last 22 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_frozen_recall_scores), np.std(resnet_frozen_recall_scores)))
print('f1 score of ResNet model while training last 22 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_frozen_f1_scores), np.std(resnet_frozen_f1_scores)))
```
#### 3.3.3 - Adding Augmented Images to ResNet Model with Pneumonia Images
Again, not too much improvement here over the ResNet baseline model without augmented images. In fact, all the metrics aside from accuracy has a worse score with larger standard deviations.
```
resnet_aug_baseline_acc_scores = []
resnet_aug_baseline_prec_scores = []
resnet_aug_baseline_recall_scores = []
resnet_aug_baseline_f1_scores = []
for i in range(3):
x=resnet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
resnet_model_aug_baseline=Model(inputs=resnet_model.input,outputs=preds)
for layer in resnet_model_aug_baseline.layers:
layer.trainable = False
resnet_model_aug_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
resnet_model_aug_baseline_history = resnet_model_aug_baseline.fit_generator(gen.flow(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_pneu_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, pres, recall, f1 = get_metrics(resnet_model_aug_baseline,
X_test_pneu_model,
y_test_pneu)
resnet_aug_baseline_acc_scores.append(acc)
resnet_aug_baseline_prec_scores.append(pres)
resnet_aug_baseline_recall_scores.append(recall)
resnet_aug_baseline_f1_scores.append(f1)
print('Accuracy of ResNet augmented baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(resnet_aug_baseline_acc_scores) * 100, np.std(resnet_aug_baseline_acc_scores)*100))
print('Precision of ResNet augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_aug_baseline_prec_scores), np.std(resnet_aug_baseline_prec_scores)))
print('Recall of ResNet augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_aug_baseline_recall_scores), np.std(resnet_aug_baseline_recall_scores)))
print('f1 score of ResNet augmented baseline model: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_aug_baseline_f1_scores), np.std(resnet_aug_baseline_f1_scores)))
```
The optimal number of layers to train for the ResNet augmented model is 14. While the accuracy still hovers at ~55%, the recall is at almost 0.90 with a relatively small standard deviation. However, the one must be careful since the confusion matrices show that the model tends to categorize the images as 1 (has pneumonia).
```
resnet_aug_frozen_acc_scores = []
resnet_aug_frozen_prec_scores = []
resnet_aug_frozen_recall_scores = []
resnet_aug_frozen_f1_scores = []
for i in range(3):
x=resnet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
resnet_model_aug_frozen=Model(inputs=resnet_model.input,outputs=preds)
for layer in resnet_model_aug_frozen.layers[:-14]:
layer.trainable = False
resnet_model_aug_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
resnet_model_aug_frozen_history = resnet_model_aug_frozen.fit_generator(gen.flow(X_train_pneu_model,
y_train_pneu_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_pneu_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_pneu_model,
y_val_pneu_model))
acc, pres, recall, f1 = get_metrics(resnet_model_aug_frozen,
X_test_pneu_model,
y_test_pneu)
resnet_aug_frozen_acc_scores.append(acc)
resnet_aug_frozen_prec_scores.append(pres)
resnet_aug_frozen_recall_scores.append(recall)
resnet_aug_frozen_f1_scores.append(f1)
print('Accuracy of ResNet augmented model while training 14 layers: {:0.2f} +/- {:0.2f}%'.format(np.mean(resnet_aug_frozen_acc_scores) * 100, np.std(resnet_aug_frozen_acc_scores)*100))
print('Precision of ResNet augmented model while training 14 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_aug_frozen_prec_scores), np.std(resnet_aug_frozen_prec_scores)))
print('Recall of ResNet augmented model while training 14 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_aug_frozen_recall_scores), np.std(resnet_aug_frozen_recall_scores)))
print('f1 score of ResNet augmented model while training 14 layers: {:0.3f} +/- {:0.3f}'.format(np.mean(resnet_aug_frozen_f1_scores), np.std(resnet_aug_frozen_f1_scores)))
```
#### 3.3.4 - ResNet50 Pnuemonia Summary for Pneumonia
The table summarizing the ResNet50's metrics is below. Overall, the max f1-score achieved was 0.667 and the max recall was ~0.90. These were attained by the model with augmented images and training layers.
| Model | Accuracy | Precision | Recall | F1-score |
|------|------|------|------|------|
| ResNet50 baseline | 49.56 +/- 0.65% | 0.496 +/- 0.005 | 0.862 +/- 0.189 | 0.622 +/- 0.061 |
| ResNet50 baseline with training | 54.47 +/- 2.17% | 0.549 +/- 0.021 | 0.493 +/- 0.214 | 0.496 +/- 0.120 |
| ResNet50 augmented baseline | 49.71 +/- 1.15% | 0.487 +/- 0.022 | 0.665 +/- 0.347 | 0.517 +/- 0.183 |
| ResNet50 augmented with training | 55.14 +/- 1.34% | 0.530 +/- 0.008 | 0.899 +/- 0.042 | 0.667 +/- 0.013 |
### 3.4 - Summary of Pneumonia Images
As a reminder, a table of the best models from each architecture (VGG, MobileNet, and ResNet) are summarized below. Overall, each model gives similar results, with accuracies between 53-55% and recalls between 0.80 and 0.90. This means that the best model I found (so far...) for identifying images with pneumonia is with ResNet50 with 14 trained layers. However, the other two models aren't too far behind.
The low accuracy is a concern to me because it means none of these models do particularly well. I believe part of the problem stems from the training data only having ~1750 images, which is probably not enough to train on. Augmenting images helped a little for the ResNet model, but not enough.
| Model | Accuracy | Precision | Recall | F1-score |
|------|------|------|------|------|
| VGG19 baseline with training | 53.75 +/- 0.43% | 0.525 +/- 0.006 | 0.800 +/- 0.105 | 0.631 +/- 0.031 |
| MobileNet baseline with training | 53.78 +/- 0.32% | 0.522 +/- 0.003 | 0.876 +/- 0.069 | 0.653 +/- 0.018 |
| ResNet50 augmented with training | 55.14 +/- 1.34% | 0.530 +/- 0.008 | 0.899 +/- 0.042 | 0.667 +/- 0.013 |
## 4 - Effusion
### 4.1 - VGG19 Model for Effusion Images
I suspected that it was difficult to train pneumonia images due to the low number of images in the training set. One way to test this theory is to use find a pathology with more images. However, with more images comes longer computational times, which is why I chose to train effusion images, which had the second most abundant images in the dataset. As a reference, there are ~14000, ~3500, and ~9200 images total for the training, validation, and test sets.
```
# Get test images
Xtest_eff, ytest_eff = get_images(test_df[test_df['Effusion']==1],
'Effusion',
num_images = test_df[test_df['Effusion']==1].shape[0],
imageSize = imgSize)
Xtest_noteff, ytest_noteff = get_images(test_df[test_df['Effusion']==0],
'Effusion',
num_images = test_df[test_df['Effusion']==1].shape[0],
imageSize = imgSize)
X_test_eff = np.concatenate((Xtest_eff, Xtest_noteff), axis = 0)
y_test_eff = np.concatenate((ytest_eff, ytest_noteff))
_, X_test_eff, _, y_test_eff = train_test_split(X_test_eff,
y_test_eff,
test_size=0.99,
random_state=42,
stratify = y_test_eff)
# get training images and split into validation set
Xtrain_eff, ytrain_eff = get_images(train_val_df[train_val_df['Effusion']==1],
'Effusion',
num_images = train_val_df[train_val_df['Effusion']==1].shape[0],
imageSize = imgSize)
Xtrain_noteff, ytrain_noteff = get_images(train_val_df[train_val_df['Effusion']==0],
'Effusion',
num_images = train_val_df[train_val_df['Effusion']==1].shape[0],
imageSize = imgSize)
Xtrain_eff = np.concatenate((Xtrain_eff, Xtrain_noteff), axis = 0)
ytrain_eff = np.concatenate((ytrain_eff, ytrain_noteff))
X_train_eff, X_val_eff, y_train_eff, y_val_eff = train_test_split(Xtrain_eff,
ytrain_eff,
test_size=0.2,
random_state=42,
stratify = ytrain_eff)
X_train_eff_model, X_val_eff_model, X_test_eff_model = convert_X_data(X_train_eff,
X_val_eff,
X_test_eff,
imageSize = imgSize,
num_classes = 2)
y_train_eff_model, y_val_eff_model, y_test_eff_model = convert_y_data(y_train_eff,
y_val_eff,
y_test_eff,
num_classes = 2)
```
#### 4.1.1 - VGG Baseline for Effusion Images
This is the first model for the effusion pathology. Already the metrics are generally higher than that of pneumonia's baselines. Possibly this is just because there are more images the model can train on.
```
vgg_baseline_acc_eff_scores = []
vgg_baseline_pres_eff_scores = []
vgg_baseline_recall_eff_scores = []
vgg_baseline_f1_eff_scores = []
for i in range(3):
vgg_model_baseline = Sequential()
for layer in vgg_model.layers[:-1]:
vgg_model_baseline.add(layer)
vgg_model_baseline.add(Dense(num_classes, activation = 'softmax'))
# freeze layers, excluding from future training. weights are not updated.
for layer in vgg_model_baseline.layers:
layer.trainable = False
vgg_model_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
vgg_model_baseline_history = vgg_model_baseline.fit(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model, y_val_eff_model))
acc, prec, recall, f1 = get_metrics(vgg_model_baseline, X_test_eff_model, y_test_eff, verbose = True)
vgg_baseline_acc_eff_scores.append(acc)
vgg_baseline_pres_eff_scores.append(pres)
vgg_baseline_recall_eff_scores.append(recall)
vgg_baseline_f1_eff_scores.append(f1)
print('Accuracy of VGG baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_baseline_acc_eff_scores) * 100, np.std(vgg_baseline_acc_eff_scores)*100))
print('Precision of VGG baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_baseline_pres_eff_scores) * 100, np.std(vgg_baseline_pres_eff_scores)*100))
print('Recall of VGG baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_baseline_recall_eff_scores) * 100, np.std(vgg_baseline_recall_eff_scores)*100))
print('f1 score of VGG baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_baseline_f1_eff_scores) * 100, np.std(vgg_baseline_f1_eff_scores)*100))
```
#### 4.1.2 - VGG19 Training Layers for Effusion Images
After training the last 2 layers, the accuracy jumps up to 63%, which I'm becoming more convinced is because of the number of images. The precision stays the same but the recall and f1-scores jump to at least 0.67.
```
print('Accuracy of baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_baseline_acc_eff_scores) * 100, np.std(vgg_baseline_acc_eff_scores)*100))
print('Accuracy of baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_baseline_pres_eff_scores) * 100, np.std(vgg_baseline_pres_eff_scores)*100))
print('Accuracy of baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_baseline_recall_eff_scores) * 100, np.std(vgg_baseline_recall_eff_scores)*100))
print('f1 score of baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_baseline_f1_eff_scores) * 100, np.std(vgg_baseline_f1_eff_scores)*100))
vgg_frozen_acc_eff_scores = []
vgg_frozen_pres_eff_scores = []
vgg_frozen_recall_eff_scores = []
vgg_frozen_f1_eff_scores = []
for i in range(3):
vgg_model_frozen = Sequential()
for layer in vgg_model.layers[:-1]:
vgg_model_frozen.add(layer)
vgg_model_frozen.add(Dense(num_classes, activation = 'softmax'))
# freeze layers, excluding from future training. weights are not updated.
for layer in vgg_model_frozen.layers[:-2]:
layer.trainable = False
vgg_model_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
vgg_model_frozen_history = vgg_model_frozen.fit(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model, y_val_eff_model))
acc, prec, recall, f1 = get_metrics(vgg_model_frozen, X_test_eff_model, y_test_eff, verbose = True)
vgg_frozen_acc_eff_scores.append(acc)
vgg_frozen_pres_eff_scores.append(pres)
vgg_frozen_recall_eff_scores.append(recall)
vgg_frozen_f1_eff_scores.append(f1)
print('Accuracy of VGG model while training last 2 layers: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_frozen_acc_eff_scores) * 100, np.std(vgg_frozen_acc_eff_scores)*100))
print('Precision of VGG model while training last 2 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_frozen_pres_eff_scores), np.std(vgg_frozen_pres_eff_scores)))
print('Recall of VGG model while training last 2 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_frozen_recall_eff_scores), np.std(vgg_frozen_recall_eff_scores)))
print('f1 score of VGG model while training last 2 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_frozen_f1_eff_scores), np.std(vgg_frozen_f1_eff_scores)))
```
#### 4.1.3 - Adding Augmented Images to VGG19 Effusion Images
Not much change in accuracy and precision compared to the baseline model. However, recall and f1-scores drop quite a bit, to under 0.15. The confusion matrix shows that the model tends to predict most images as 0 (no effusion), resulting in a mediocre precision and an extremely low recall, which drops the f1-score.
```
vgg_aug_baseline_acc_eff_scores = []
vgg_aug_baseline_pres_eff_scores = []
vgg_aug_baseline_recall_eff_scores = []
vgg_aug_baseline_f1_eff_scores = []
for i in range(3):
vgg_model_aug_baseline = Sequential()
for layer in vgg_model.layers[:-1]:
vgg_model_aug_baseline.add(layer)
vgg_model_aug_baseline.add(Dense(num_classes, activation = 'softmax'))
# freeze layers, excluding from future training. weights are not updated.
for layer in vgg_model_aug_baseline.layers:
layer.trainable = False
vgg_model_aug_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
vgg_model_aug_baseline_history = vgg_model_aug_baseline.fit_generator(gen.flow(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_eff_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model, y_val_eff_model))
acc, prec, recall, f1 = get_metrics(vgg_model_aug_baseline, X_test_eff_model, y_test_eff, verbose = True)
vgg_aug_baseline_acc_eff_scores.append(acc)
vgg_aug_baseline_pres_eff_scores.append(pres)
vgg_aug_baseline_recall_eff_scores.append(recall)
vgg_aug_baseline_f1_eff_scores.append(f1)
print('Accuracy of VGG augmented baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_aug_baseline_acc_eff_scores) * 100, np.std(vgg_aug_baseline_acc_eff_scores)*100))
print('Precision of VGG augmented baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_aug_baseline_pres_eff_scores), np.std(vgg_aug_baseline_pres_eff_scores)))
print('Recall of VGG augmented baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_aug_baseline_recall_eff_scores), np.std(vgg_aug_baseline_recall_eff_scores)))
print('f1 score of VGG augmented baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_aug_baseline_f1_eff_scores), np.std(vgg_aug_baseline_f1_eff_scores)))
```
Training the last layer of the augmented vgg model improves the recall and therefore f1-score, but they are still not as high as the baseline model with trained layers.
```
vgg_aug_frozen_acc_eff_scores = []
vgg_aug_frozen_pres_eff_scores = []
vgg_aug_frozen_recall_eff_scores = []
vgg_aug_frozen_f1_eff_scores = []
for i in range(3):
vgg_model_aug_frozen = Sequential()
for layer in vgg_model.layers[:-1]:
vgg_model_aug_frozen.add(layer)
vgg_model_aug_frozen.add(Dense(num_classes, activation = 'softmax'))
# freeze layers, excluding from future training. weights are not updated.
for layer in vgg_model_aug_frozen.layers[:-1]:
layer.trainable = False
vgg_model_aug_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
vgg_model_aug_frozen_history = vgg_model_aug_frozen.fit_generator(gen.flow(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_eff_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model, y_val_eff_model))
acc, prec, recall, f1 = get_metrics(vgg_model_aug_frozen, X_test_eff_model, y_test_eff, verbose = True)
vgg_aug_frozen_acc_eff_scores.append(acc)
vgg_aug_frozen_pres_eff_scores.append(pres)
vgg_aug_frozen_recall_eff_scores.append(recall)
vgg_aug_frozen_f1_eff_scores.append(f1)
print('Accuracy of VGG augmented model while training last 1 layer: {:0.2f} +/- {:0.2f}%'.format(np.mean(vgg_aug_frozen_acc_eff_scores) * 100, np.std(vgg_aug_frozen_acc_eff_scores)*100))
print('Precision of VGG augmented model while training last 1 layer: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_aug_frozen_pres_eff_scores), np.std(vgg_aug_frozen_pres_eff_scores)))
print('Recall of VGG augmented model while training last 1 layer: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_aug_frozen_recall_eff_scores), np.std(vgg_aug_frozen_recall_eff_scores)))
print('f1 score of VGG augmented model while training last 1 layer: {:0.3f} +/- {:0.3f}%'.format(np.mean(vgg_aug_frozen_f1_eff_scores), np.std(vgg_aug_frozen_f1_eff_scores)))
```
#### 4.1.4 - Summary of VGG19 Model with Effusion Images
Overall, the best VGG19 model for effusion images was the baseline model after training the last 2 layers, with an f1-score of 0.67 and recall of 0.76.
| Model | Accuracy | Precision | Recall | F1-score |
|------|------|------|------|------|
| VGG19 baseline | 53.09 +/- 1.24% | 53.111 +/- 0.000 | 57.413 +/- 5.408 | 54.928 +/- 1.630 |
| VGG19 with training | 63.06 +/- 1.92% | 0.531 +/- 0.000 | 0.764 +/- 0.109 | 0.672 +/- 0.019 |
| VGG19 augmented | 50.05 +/- 0.48% | 0.531 +/- 0.000 | 0.081 +/- 0.040 | 0.135 +/- 0.059 |
| VGG19 augmented with training | 50.02 +/- 1.59% | 0.531 +/- 0.000 | 0.632 +/- 0.297 | 0.522 +/- 0.145 |
### 4.2 - MobileNet Model for Effusion Images
#### 4.2.1 - MobileNet Baseline for Effusion Images
The baseline model for MobileNet has no surprises, with similar accuracy and precisions as other baselines. The recall is slightly higher at 0.65, which increases the f1-score compared to other baselines.
```
mobilenet_baseline_acc_scores = []
mobilenet_baseline_pres_scores = []
mobilenet_baseline_recall_scores = []
mobilenet_baseline_f1_scores = []
for i in range(3):
x=mobilenet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
mobilenet_model_baseline=Model(inputs=mobilenet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in mobilenet_model_baseline.layers:
layer.trainable = False
mobilenet_model_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
mobilenet_model_baseline_history = mobilenet_model_baseline.fit(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model,
y_val_eff_model))
acc, pres, recall, f1 = get_metrics(mobilenet_model_baseline,
X_test_eff_model,
y_test_eff)
mobilenet_baseline_acc_scores.append(acc)
mobilenet_baseline_pres_scores.append(pres)
mobilenet_baseline_recall_scores.append(recall)
mobilenet_baseline_f1_scores.append(f1)
print('Accuracy of MobileNet baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(mobilenet_baseline_acc_scores) * 100, np.std(mobilenet_baseline_acc_scores)*100))
print('Precision of MobileNet baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_baseline_pres_scores), np.std(mobilenet_baseline_pres_scores)))
print('Recall of MobileNet baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_baseline_recall_scores), np.std(mobilenet_baseline_recall_scores)))
print('f1 score of MobileNet baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_baseline_f1_scores), np.std(mobilenet_baseline_f1_scores)))
```
#### 4.2.2. - MobileNet Training Layers for Effusion Images
Unfortunately at the time of writing, I seem to be having trouble reproducing the results I got in my preliminary work, so these metrics will be excluded from the summary table.
```
mobilenet_frozen_acc_scores = []
mobilenet_frozen_pres_scores = []
mobilenet_frozen_recall_scores = []
mobilenet_frozen_f1_scores = []
for i in range(3):
x=mobilenet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
mobilenet_model_frozen=Model(inputs=mobilenet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in mobilenet_model_frozen.layers[:-24]:
layer.trainable = False
mobilenet_model_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
mobilenet_model_frozen_history = mobilenet_model_frozen.fit(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model,
y_val_eff_model))
acc, pres, recall, f1 = get_metrics(mobilenet_model_frozen,
X_test_eff_model,
y_test_eff)
mobilenet_frozen_acc_scores.append(acc)
mobilenet_frozen_pres_scores.append(pres)
mobilenet_frozen_recall_scores.append(recall)
mobilenet_frozen_f1_scores.append(f1)
print('Accuracy of MobileNet model while training last 24 layers: {:0.2f} +/- {:0.2f}%'.format(np.mean(mobilenet_frozen_acc_scores) * 100, np.std(mobilenet_frozen_acc_scores)*100))
print('Precision of MobileNet model while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_frozen_pres_scores), np.std(mobilenet_frozen_pres_scores)))
print('Recall of MobileNet model while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_frozen_recall_scores), np.std(mobilenet_frozen_recall_scores)))
print('f1 score of MobileNet model while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_frozen_f1_scores), np.std(mobilenet_frozen_f1_scores)))
```
#### 4.2.3 - Adding Augmented Images to MobileNet for Effusion Images
```
mobilenet_aug_baseline_acc_scores = []
mobilenet_aug_baseline_pres_scores = []
mobilenet_aug_baseline_recall_scores = []
mobilenet_aug_baseline_f1_scores = []
for i in range(3):
x=mobilenet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
mobilenet_model_aug_baseline=Model(inputs=mobilenet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in mobilenet_model_aug_baseline.layers:
layer.trainable = False
mobilenet_model_aug_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
mobilenet_model_aug_baseline_history = mobilenet_model_aug_baseline.fit_generator(gen.flow(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_eff_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model,
y_val_eff_model))
acc, pres, recall, f1 = get_metrics(mobilenet_model_aug_baseline,
X_test_eff_model,
y_test_eff)
mobilenet_aug_baseline_acc_scores.append(acc)
mobilenet_aug_baseline_pres_scores.append(pres)
mobilenet_aug_baseline_recall_scores.append(recall)
mobilenet_aug_baseline_f1_scores.append(f1)
print('Accuracy of MobileNet augmented baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(mobilenet_aug_baseline_acc_scores) * 100, np.std(mobilenet_aug_baseline_acc_scores)*100))
print('Precision of MobileNet augmetned baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_aug_baseline_pres_scores), np.std(mobilenet_aug_baseline_pres_scores)))
print('Recall of MobileNet augmetned baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_aug_baseline_recall_scores), np.std(mobilenet_aug_baseline_recall_scores)))
print('f1 score of MobileNet augmetned baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_aug_baseline_f1_scores), np.std(mobilenet_aug_baseline_f1_scores)))
```
Again, I was unable to find the optimal number of layers to train, so these metrics will be removed from the summary.
```
mobilenet_aug_frozen_acc_scores = []
mobilenet_aug_frozen_pres_scores = []
mobilenet_aug_frozen_recall_scores = []
mobilenet_aug_frozen_f1_scores = []
for i in range(3):
x=mobilenet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
mobilenet_model_aug_frozen=Model(inputs=mobilenet_model.input,outputs=preds)
for layer in mobilenet_model_aug_frozen.layers[:-24]:
layer.trainable = False
mobilenet_model_aug_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
mobilenet_model_aug_frozen_history = mobilenet_model_aug_frozen.fit_generator(gen.flow(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_eff_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model,
y_val_eff_model))
acc, pres, recall, f1 = get_metrics(mobilenet_model_aug_frozen,
X_test_eff_model,
y_test_eff)
mobilenet_aug_frozen_acc_scores.append(acc)
mobilenet_aug_frozen_pres_scores.append(pres)
mobilenet_aug_frozen_recall_scores.append(recall)
mobilenet_aug_frozen_f1_scores.append(f1)
print('Accuracy of MobileNet augmented model while training last 24 layers: {:0.2f} +/- {:0.2f}%'.format(np.mean(mobilenet_aug_frozen_acc_scores) * 100, np.std(mobilenet_aug_frozen_acc_scores)*100))
print('Precision of MobileNet augmetned model while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_aug_frozen_pres_scores), np.std(mobilenet_aug_frozen_pres_scores)))
print('Recall of MobileNet augmetned model while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_aug_frozen_recall_scores), np.std(mobilenet_aug_frozen_recall_scores)))
print('f1 score of MobileNet augmetned model while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(mobilenet_aug_frozen_f1_scores), np.std(mobilenet_aug_frozen_f1_scores)))
```
#### 4.2.4 - Summary of MobileNet Model with Effusion Images
Since I was unable to optimize the number of trainable layers in this notebook, I only have the baselines of the augmented and non augmented models. This section will have to be revisted at a later date.
| Model | Accuracy | Precision | Recall | F1-score |
|------|------|------|------|------|
| MobileNet baseline | 49.72 +/- 1.53% | 0.488 +/- 0.022 | 0.655 +/- 0.324 | 0.519 +/- 0.172 |
| MobileNet augmented baseline | 49.98 +/- 0.29% | 0.455 +/- 0.065 | 0.552 +/- 0.409 | 0.417 +/- 0.284 |
### 4.3 - ResNet Model for Effusion Images
#### 4.3.1 - ResNet Baseline for Effusion Images
Finally, we reach the last model for effusion images. As expected, accuracy is around 50% and precision is around 0.50. The recall and f1-score however, seem to be higher than normal for a baseline.
```
resnet_baseline_acc_scores = []
resnet_baseline_pres_scores = []
resnet_baseline_recall_scores = []
resnet_baseline_f1_scores = []
for i in range(3):
x=resnet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
resnet_model_baseline=Model(inputs=resnet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in resnet_model_baseline.layers:
layer.trainable = False
resnet_model_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
resnet_model_baseline_history = resnet_model_baseline.fit(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model,
y_val_eff_model))
acc, pres, recall, f1 = get_metrics(resnet_model_baseline,
X_test_eff_model,
y_test_eff)
resnet_baseline_acc_scores.append(acc)
resnet_baseline_pres_scores.append(pres)
resnet_baseline_recall_scores.append(recall)
resnet_baseline_f1_scores.append(f1)
print('Accuracy of ResNet baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(resnet_baseline_acc_scores) * 100, np.std(resnet_baseline_acc_scores)*100))
print('Precision of ResNet baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_baseline_pres_scores), np.std(resnet_baseline_pres_scores)))
print('Recall of ResNet baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_baseline_recall_scores), np.std(resnet_baseline_recall_scores)))
print('f1 score of ResNet baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_baseline_f1_scores), np.std(resnet_baseline_f1_scores)))
```
#### 4.3.2 - ResNet Training Layers for Effusion Images
With the last 26 layers trained on the baseline ResNet model, the accuracy increases to 62%, precision rises slightly to 0.59, and recall and f1-scores rises to 0.70 and above.
```
resnet_frozen_acc_scores = []
resnet_frozen_pres_scores = []
resnet_frozen_recall_scores = []
resnet_frozen_f1_scores = []
for i in range(3):
x=resnet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
resnet_model_frozen=Model(inputs=resnet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in resnet_model_frozen.layers[:-26]:
layer.trainable = False
resnet_model_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
resnet_model_frozen_history = resnet_model_frozen.fit(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model,
y_val_eff_model))
acc, pres, recall, f1 = get_metrics(resnet_model_frozen,
X_test_eff_model,
y_test_eff)
resnet_frozen_acc_scores.append(acc)
resnet_frozen_pres_scores.append(pres)
resnet_frozen_recall_scores.append(recall)
resnet_frozen_f1_scores.append(f1)
print('Accuracy of ResNet model while training last 24 layers: {:0.2f} +/- {:0.2f}%'.format(np.mean(resnet_frozen_acc_scores) * 100, np.std(resnet_frozen_acc_scores)*100))
print('Precision of ResNet model while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_frozen_pres_scores), np.std(resnet_frozen_pres_scores)))
print('Recall of model ResNet while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_frozen_recall_scores), np.std(resnet_frozen_recall_scores)))
print('f1 score of model ResNet while training last 24 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_frozen_f1_scores), np.std(resnet_frozen_f1_scores)))
```
#### 4.3.3 - Adding Augmented Images to ResNet for Effusion Images
The baseline model with augmented images have slightly better metrics than the baseline model without augmentation. The metrics are still lower than those of the baseline layer with fine tuning.
```
resnet_aug_baseline_acc_scores = []
resnet_aug_baseline_pres_scores = []
resnet_aug_baseline_recall_scores = []
resnet_aug_baseline_f1_scores = []
for i in range(3):
x=resnet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
resnet_model_aug_baseline=Model(inputs=resnet_model.input,outputs=preds)
# freeze layers, excluding from future training. weights are not updated.
for layer in resnet_model_aug_baseline.layers:
layer.trainable = False
resnet_model_aug_baseline.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
resnet_model_aug_baseline_history = resnet_model_aug_baseline.fit_generator(gen.flow(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_eff_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model,
y_val_eff_model))
acc, pres, recall, f1 = get_metrics(resnet_model_aug_baseline,
X_test_eff_model,
y_test_eff)
resnet_aug_baseline_acc_scores.append(acc)
resnet_aug_baseline_pres_scores.append(pres)
resnet_aug_baseline_recall_scores.append(recall)
resnet_aug_baseline_f1_scores.append(f1)
print('Accuracy of ResNet augmented baseline model: {:0.2f} +/- {:0.2f}%'.format(np.mean(resnet_aug_basealine_acc_scores) * 100, np.std(resnet_aug_baseline_acc_scores)*100))
print('Precision of ResNet augmented baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_aug_baseline_pres_scores), np.std(resnet_aug_baseline_pres_scores)))
print('Recall of ResNet augmented baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_aug_baseline_recall_scores), np.std(resnet_aug_baseline_recall_scores)))
print('f1 score of ResNet augmented baseline model: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_aug_baseline_f1_scores), np.std(resnet_aug_baseline_f1_scores)))
```
After training the last 27 images for the augmented model, all metrics are quite similar to baseline with fine tuning.
```
resnet_aug_frozen_acc_scores = []
resnet_aug_frozen_pres_scores = []
resnet_aug_frozen_recall_scores = []
resnet_aug_frozen_f1_scores = []
for i in range(3):
x=resnet_model.output
x=GlobalAveragePooling2D()(x)
preds=Dense(2,activation='softmax')(x)
resnet_model_aug_frozen=Model(inputs=resnet_model.input,outputs=preds)
for layer in resnet_model_aug_frozen.layers[:-27]:
layer.trainable = False
resnet_model_aug_frozen.compile(loss = 'categorical_crossentropy',
optimizer = Adam(learning_rate = 0.001),
metrics = ['acc'])
batchsize = 64
resnet_model_aug_frozen_history = resnet_model_aug_frozen.fit_generator(gen.flow(X_train_eff_model,
y_train_eff_model,
batch_size=batchsize),
steps_per_epoch = len(X_train_eff_model)//batchsize,
epochs = 15,
verbose = 0,
validation_data=(X_val_eff_model,
y_val_eff_model))
acc, pres, recall, f1 = get_metrics(resnet_model_aug_frozen,
X_test_eff_model,
y_test_eff)
resnet_aug_frozen_acc_scores.append(acc)
resnet_aug_frozen_pres_scores.append(pres)
resnet_aug_frozen_recall_scores.append(recall)
resnet_aug_frozen_f1_scores.append(f1)
print('Accuracy of ResNet augmented model while training last 27 layers: {:0.2f} +/- {:0.2f}%'.format(np.mean(resnet_aug_frozen_acc_scores) * 100, np.std(resnet_aug_frozen_acc_scores)*100))
print('Precision of ResNet augmented model while training last 27 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_aug_frozen_pres_scores), np.std(resnet_aug_frozen_pres_scores)))
print('Recall of ResNet augmented model while training last 27 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_aug_frozen_recall_scores), np.std(resnet_aug_frozen_recall_scores)))
print('f1 score of ResNet augmented model while training last 27 layers: {:0.3f} +/- {:0.3f}%'.format(np.mean(resnet_aug_frozen_f1_scores), np.std(resnet_aug_frozen_f1_scores)))
```
#### 4.3.4 - Summary of ResNet50 Model with Effusion Images
Overall, the two models with trained layers have similar results. However, the model without augmented images has better recall and f1-scores as well as generally smaller standard deviations.
| Model | Accuracy | Precision | Recall | F1-score |
|------|------|------|------|------|
| ResNet baseline | 47.50 +/- 2.92% | 0.460 +/- 0.047 | 0.519 +/- 0.340 | 0.450 +/- 0.156 |
| ResNet with training | 62.76 +/- 0.11% | 0.585 +/- 0.002 | 0.878 +/- 0.009 | 0.702 +/- 0.002 |
| ResNet augmented | 51.13 +/- 1.25% | 0.518 +/- 0.014 | 0.561 +/- 0.343 | 0.471 +/- 0.202 |
| ResNet augmented with training | 63.88 +/- 0.25% | 0.606 +/- 0.007 | 0.793 +/- 0.050 | 0.686 +/- 0.014 |
### 4.4 - Summary of Effusion Images
In the end, I have two models that produce reasonable results for effusion images. For both the VGG19 and Resnet50 models, the models without augmented images and trained layers did the best. Between VGG and ResNet however, the winner is ResNet.
These results are interesting because even though there are almost 10 times more effusion images compared to pneumonia images, the number of images is still relatively small compared to what these models are generally used to seeing. I would have thought that augmenting image would have helped here. Perhaps one reason it didn't help is because the augmented images are being generated in the fit_generator function, so I cannot pick the images to be augmented. Perhaps in a future iteration of this project, I can
| Model | Accuracy | Precision | Recall | F1-score |
|------|------|------|------|------|
| VGG19 with training | 63.06 +/- 1.92% | 0.531 +/- 0.000 | 0.764 +/- 0.109 | 0.672 +/- 0.019 |
| ResNet with training | 62.76 +/- 0.11% | 0.585 +/- 0.002 | 0.878 +/- 0.009 | 0.702 +/- 0.002 |
## 5 - Future Research
So far, I've only applied this transfer learning technique to two pathologies, but there are 12 more! Future research would definately be to extend this project to the other 12 pathologies. In addition, it would also be interesting to see if building a model from scratch would be more beneficial considering how difficult and time consuming it was to try and find the optimal number of layers to train.
| true |
code
| 0.429609 | null | null | null | null |
|
## Collaborative filtering
```
from fastai.gen_doc.nbdoc import *
```
This package contains all the necessary functions to quickly train a model for a collaborative filtering task. Let's start by importing all we'll need.
```
from fastai.collab import *
```
## Overview
Collaborative filtering is when you're tasked to predict how much a user is going to like a certain item. The fastai library contains a [`CollabFilteringDataset`](/collab.html#CollabFilteringDataset) class that will help you create datasets suitable for training, and a function `get_colab_learner` to build a simple model directly from a ratings table. Let's first see how we can get started before delving into the documentation.
For this example, we'll use a small subset of the [MovieLens](https://grouplens.org/datasets/movielens/) dataset to predict the rating a user would give a particular movie (from 0 to 5). The dataset comes in the form of a csv file where each line is a rating of a movie by a given person.
```
path = untar_data(URLs.ML_SAMPLE)
ratings = pd.read_csv(path/'ratings.csv')
ratings.head()
```
We'll first turn the `userId` and `movieId` columns in category codes, so that we can replace them with their codes when it's time to feed them to an `Embedding` layer. This step would be even more important if our csv had names of users, or names of items in it. To do it, we simply have to call a [`CollabDataBunch`](/collab.html#CollabDataBunch) factory method.
```
data = CollabDataBunch.from_df(ratings)
```
Now that this step is done, we can directly create a [`Learner`](/basic_train.html#Learner) object:
```
learn = collab_learner(data, n_factors=50, y_range=(0.,5.))
```
And then immediately begin training
```
learn.fit_one_cycle(5, 5e-3, wd=0.1)
show_doc(CollabDataBunch)
```
The init function shouldn't be called directly (as it's the one of a basic [`DataBunch`](/basic_data.html#DataBunch)), instead, you'll want to use the following factory method.
```
show_doc(CollabDataBunch.from_df)
```
Take a `ratings` dataframe and splits it randomly for train and test following `pct_val` (unless it's None). `user_name`, `item_name` and `rating_name` give the names of the corresponding columns (defaults to the first, the second and the third column). Optionally a `test` dataframe can be passed an a `seed` for the separation between training and validation set. The `kwargs` will be passed to [`DataBunch.create`](/basic_data.html#DataBunch.create).
## Model and [`Learner`](/basic_train.html#Learner)
```
show_doc(CollabLearner, title_level=3)
```
This is a subclass of [`Learner`](/basic_train.html#Learner) that just introduces helper functions to analyze results, the initialization is the same as a regular [`Learner`](/basic_train.html#Learner).
```
show_doc(CollabLearner.bias)
show_doc(CollabLearner.get_idx)
show_doc(CollabLearner.weight)
show_doc(EmbeddingDotBias, title_level=3)
```
Creates a simple model with `Embedding` weights and biases for `n_users` and `n_items`, with `n_factors` latent factors. Takes the dot product of the embeddings and adds the bias, then if `y_range` is specified, feed the result to a sigmoid rescaled to go from `y_range[0]` to `y_range[1]`.
```
show_doc(EmbeddingNN, title_level=3)
```
`emb_szs` will overwrite the default and `kwargs` are passed to [`TabularModel`](/tabular.models.html#TabularModel).
```
show_doc(collab_learner)
```
More specifically, binds [`data`](/tabular.data.html#tabular.data) with a model that is either an [`EmbeddingDotBias`](/collab.html#EmbeddingDotBias) with `n_factors` if `use_nn=False` or a [`EmbeddingNN`](/collab.html#EmbeddingNN) with `emb_szs` otherwise. In both cases the numbers of users and items will be inferred from the data, `y_range` can be specified in the `kwargs` and you can pass [`metrics`](/metrics.html#metrics) or `wd` to the [`Learner`](/basic_train.html#Learner) constructor.
## Links with the Data Block API
```
show_doc(CollabLine, doc_string=False, title_level=3)
```
Subclass of [`TabularLine`](/tabular.data.html#TabularLine) for collaborative filtering.
```
show_doc(CollabList, title_level=3, doc_string=False)
```
Subclass of [`TabularList`](/tabular.data.html#TabularList) for collaborative filtering.
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(EmbeddingDotBias.forward)
show_doc(CollabList.reconstruct)
show_doc(EmbeddingNN.forward)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.702249 | null | null | null | null |
|
# Aerospike Python Client Tutorial
### Refer to https://www.aerospike.com/docs/client/python/index.html for information on installing the Aerospike Python client.
#### Tested with Python 3.7
```
# IP Address or DNS name for one host in your Aerospike cluster
AS_HOST ="127.0.0.1"
# Please reach out to us if you do not have a feature key
AS_FEATURE_KEY_PATH = "/etc/aerospike/features.conf"
AS_PORT = 3000 # Usually 3000, but change here if not
import aerospike
```
## Create Sample Data and load it into Aerospike
```
# We create age vs salary data, using three different Gaussian distributions
import numpy as np
import pandas as pd
import math
# Create covariance matrix from std devs + correlation
def covariance_matrix(std_dev_1,std_dev_2,correlation):
return [[std_dev_1 ** 2, correlation * std_dev_1 * std_dev_2],
[correlation * std_dev_1 * std_dev_2, std_dev_2 ** 2]]
# Return a bivariate sample given means/std dev/correlation
def age_salary_sample(distribution_params,sample_size):
mean = [distribution_params["age_mean"], distribution_params["salary_mean"]]
cov = covariance_matrix(distribution_params["age_std_dev"],distribution_params["salary_std_dev"],
distribution_params["age_salary_correlation"])
return np.random.multivariate_normal(mean, cov, sample_size).T
# Define the characteristics of our age/salary distribution
age_salary_distribution_1 = {"age_mean":25,"salary_mean":50000,
"age_std_dev":1,"salary_std_dev":5000,"age_salary_correlation":0.3}
age_salary_distribution_2 = {"age_mean":45,"salary_mean":80000,
"age_std_dev":4,"salary_std_dev":10000,"age_salary_correlation":0.7}
age_salary_distribution_3 = {"age_mean":35,"salary_mean":70000,
"age_std_dev":2,"salary_std_dev":9000,"age_salary_correlation":0.1}
distribution_data = [age_salary_distribution_1,age_salary_distribution_2,age_salary_distribution_3]
# Sample age/salary data for each distributions
group_1_ages,group_1_salaries = age_salary_sample(age_salary_distribution_1,sample_size=100)
group_2_ages,group_2_salaries = age_salary_sample(age_salary_distribution_2,sample_size=120)
group_3_ages,group_3_salaries = age_salary_sample(age_salary_distribution_3,sample_size=80)
ages=np.concatenate([group_1_ages,group_2_ages,group_3_ages])
salaries=np.concatenate([group_1_salaries,group_2_salaries,group_3_salaries])
print("Data created")
# Turn the above records into a Data Frame
# First of all, create an array of arrays
inputBuf = []
for i in range(0, len(ages)) :
id = i + 1 # Avoid counting from zero
name = "Individual: {:03d}".format(id)
# Note we need to make sure values are typed correctly
# salary will have type numpy.float64 - if it is not cast as below, an error will be thrown
age = float(ages[i])
salary = int(salaries[i])
inputBuf.append((id, name,age,salary))
for i in inputBuf:
print (i)
```
## Connect to the Aerospike
```
# Configure the client
config = {
'hosts': [ (AS_HOST, AS_PORT) ]
}
# Create a client and connect it to the cluster
try:
client = aerospike.client(config).connect()
except:
import sys
print("failed to connect to the cluster with", config['hosts'])
sys.exit(1)
```
## Write Data
```
# Type 'show namespaces' at the aql prompt if you are not sure about the namespace
namespace= "test"
write_set= "write_set"
for i in inputBuf:
_id, _name, _age, _salary = i
key = (namespace, write_set,_id)
client.put(key, {'id': _id,'name': _name,'age': _age,'salary': _salary})
```
## Read Data
```
for i in inputBuf:
_id, _name, _age, _salary = i
key = (namespace, write_set,_id)
(key, metadata, record) = client.get(key)
print(record)
```
| true |
code
| 0.436802 | null | null | null | null |
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Version Check
Note: Animations are available in version 1.12.10+
Run `pip install plotly --upgrade` to update your Plotly version.
```
import plotly
plotly.__version__
```
#### Import Data
Let us import some apple stock data for this animation.
```
import plotly.plotly as py
from plotly.grid_objs import Grid, Column
from plotly.tools import FigureFactory as FF
import time
from datetime import datetime
import numpy as np
import pandas as pd
appl = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/finance-charts-apple.csv')
appl.columns = [col.replace('AAPL.', '') for col in appl.columns]
apple_data_matrix = appl.head(10).round(2)
table = FF.create_table(apple_data_matrix)
py.iplot(table, filename='apple_data_table')
```
#### Make the Grid
```
def to_unix_time(dt):
epoch = datetime.utcfromtimestamp(0)
return (dt - epoch).total_seconds() * 1000
appl_price = list(appl['Adjusted'])
my_columns = []
for k in range(len(appl.Date) - 1):
my_columns.append(Column(list(appl.Date)[:k + 1], 'x{}'.format(k + 1)))
my_columns.append(Column(appl_price[:k + 1], 'y{}'.format(k + 1)))
grid = Grid(my_columns)
py.grid_ops.upload(grid, 'AAPL-daily-stock-price' + str(time.time()), auto_open=False)
```
#### Make the Figure
```
data=[dict(type='scatter',
xsrc=grid.get_column_reference('x1'),
ysrc= grid.get_column_reference('y1'),
name='AAPL',
mode='lines',
line=dict(color= 'rgb(114, 186, 59)'),
fill='tozeroy',
fillcolor='rgba(114, 186, 59, 0.5)')]
axis=dict(ticklen=4,
mirror=True,
zeroline=False,
showline=True,
autorange=False,
showgrid=False)
layout = dict(title='AAPL Daily Stock Price',
font=dict(family='Balto'),
showlegend=False,
autosize=False,
width=800,
height=400,
xaxis=dict(axis, **{'nticks':12, 'tickangle':-45,
'range': [to_unix_time(datetime(2015, 2, 17)),
to_unix_time(datetime(2016, 11, 30))]}),
yaxis=dict(axis, **{'title': '$', 'range':[0,170]}),
updatemenus=[dict(type='buttons',
showactive=False,
y=1,
x=1.1,
xanchor='right',
yanchor='top',
pad=dict(t=0, r=10),
buttons=[dict(label='Play',
method='animate',
args=[None, dict(frame=dict(duration=50, redraw=False),
transition=dict(duration=0),
fromcurrent=True,
mode='immediate')])])])
frames=[{'data':[{'xsrc': grid.get_column_reference('x{}'.format(k + 1)),
'ysrc': grid.get_column_reference('y{}'.format(k + 1))}],
'traces': [0]
} for k in range(len(appl.Date) - 1)]
fig=dict(data=data, layout=layout, frames=frames)
py.icreate_animations(fig, 'AAPL-stockprice' + str(time.time()))
```
#### Reference
For additional information on filled area plots in Plotly see: https://plot.ly/python/filled-area-plots/.
For more documentation on creating animations with Plotly, see https://plot.ly/python/#animations.
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
!pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'filled-area-animation.ipynb', 'python/filled-area-animation/', 'Filled-Area Animation | plotly',
'How to make an animated filled-area plot with apple stock data in Python.',
title='Filled-Area Animation | plotly',
name='Filled-Area Animation',
language='python',
page_type='example_index', has_thumbnail='true', thumbnail='thumbnail/apple_stock_animation.gif',
display_as='animations', ipynb= '~notebook_demo/128', order=3)
```
| true |
code
| 0.590838 | null | null | null | null |
|
# Time series forecasting with DeepAR - Synthetic data
DeepAR is a supervised learning algorithm for forecasting scalar time series. This notebook demonstrates how to prepare a dataset of time series for training DeepAR and how to use the trained model for inference.
```
import time
import numpy as np
np.random.seed(1)
import pandas as pd
import json
import matplotlib.pyplot as plt
```
We will use the sagemaker client library for easy interface with sagemaker and s3fs for uploading the training data to S3. (Use `pip` to install missing libraries)
```
!conda install -y s3fs
import boto3
import s3fs
import sagemaker
from sagemaker import get_execution_role
```
Let's start by specifying:
- The S3 bucket and prefix that you want to use for training and model data. This should be within the same region as the Notebook Instance, training, and hosting.
- The IAM role arn used to give training and hosting access to your data. See the documentation for how to create these. Here we use the `get_execution_role` function to obtain the role arn which was specified when creating the notebook.
```
bucket = '<your_s3_bucket_name_here>'
prefix = 'sagemaker/DEMO-deepar'
sagemaker_session = sagemaker.Session()
role = get_execution_role()
s3_data_path = "{}/{}/data".format(bucket, prefix)
s3_output_path = "{}/{}/output".format(bucket, prefix)
```
Next, we configure the container image to be used for the region that we are running in.
```
containers = {
'us-east-1': '522234722520.dkr.ecr.us-east-1.amazonaws.com/forecasting-deepar:latest',
'us-east-2': '566113047672.dkr.ecr.us-east-2.amazonaws.com/forecasting-deepar:latest',
'us-west-2': '156387875391.dkr.ecr.us-west-2.amazonaws.com/forecasting-deepar:latest',
'eu-west-1': '224300973850.dkr.ecr.eu-west-1.amazonaws.com/forecasting-deepar:latest'
}
image_name = containers[boto3.Session().region_name]
```
### Generating and uploading data
In this toy example we want to train a model that can predict the next 48 points of syntheticly generated time series.
The time series that we use have hourly granularity.
```
freq = 'H'
prediction_length = 48
```
We also need to configure the so-called `context_length`, which determines how much context of the time series the model should take into account when making the prediction, i.e. how many previous points to look at. A typical value to start with is around the same size as the `prediction_length`. In our example we will use a longer `context_length` of `72`. Note that in addition to the `context_length` the model also takes into account the values of the time series at typical seasonal windows e.g. for hourly data the model will look at the value of the series 24h ago, one week ago one month ago etc. So it is not necessary to make the `context_length` span an entire month if you expect monthly seasonalities in your hourly data.
```
context_length = 72
```
For this notebook, we will generate 200 noisy time series, each consisting of 400 data points and with seasonality of 24 hours. In our dummy example, all time series start at the same time point `t0`. When preparing your data, it is important to use the correct start point for each time series, because the model uses the time-point as a frame of reference, which enables it to learn e.g. that weekdays behave differently from weekends.
```
t0 = '2016-01-01 00:00:00'
data_length = 400
num_ts = 200
period = 24
```
Each time series will be a noisy sine wave with a random level.
```
time_series = []
for k in range(num_ts):
level = 10 * np.random.rand()
seas_amplitude = (0.1 + 0.3*np.random.rand()) * level
sig = 0.05 * level # noise parameter (constant in time)
time_ticks = np.array(range(data_length))
source = level + seas_amplitude*np.sin(time_ticks*(2*np.pi)/period)
noise = sig*np.random.randn(data_length)
data = source + noise
index = pd.DatetimeIndex(start=t0, freq=freq, periods=data_length)
time_series.append(pd.Series(data=data, index=index))
time_series[0].plot()
plt.show()
```
Often one is interested in tuning or evaluating the model by looking at error metrics on a hold-out set. For other machine learning tasks such as classification, one typically does this by randomly separating examples into train/test sets. For forecasting it is important to do this train/test split in time rather than by series.
In this example, we will leave out the last section of each of the time series we just generated and use only the first part as training data. Here we will predict 48 data points, therefore we take out the trailing 48 points from each time series to define the training set. The test set contains the full range of each time series.
```
time_series_training = []
for ts in time_series:
time_series_training.append(ts[:-prediction_length])
time_series[0].plot(label='test')
time_series_training[0].plot(label='train', ls=':')
plt.legend()
plt.show()
```
The following utility functions convert `pandas.Series` objects into the appropriate JSON strings that DeepAR can consume. We will use these to write the data to S3.
```
def series_to_obj(ts, cat=None):
obj = {"start": str(ts.index[0]), "target": list(ts)}
if cat:
obj["cat"] = cat
return obj
def series_to_jsonline(ts, cat=None):
return json.dumps(series_to_obj(ts, cat))
encoding = "utf-8"
s3filesystem = s3fs.S3FileSystem()
with s3filesystem.open(s3_data_path + "/train/train.json", 'wb') as fp:
for ts in time_series_training:
fp.write(series_to_jsonline(ts).encode(encoding))
fp.write('\n'.encode(encoding))
with s3filesystem.open(s3_data_path + "/test/test.json", 'wb') as fp:
for ts in time_series:
fp.write(series_to_jsonline(ts).encode(encoding))
fp.write('\n'.encode(encoding))
```
### Train a model
We can now define the estimator that will launch the training job.
```
estimator = sagemaker.estimator.Estimator(
sagemaker_session=sagemaker_session,
image_name=image_name,
role=role,
train_instance_count=1,
train_instance_type='ml.c4.xlarge',
base_job_name='DEMO-deepar',
output_path="s3://" + s3_output_path
)
```
Next we need to set some hyperparameters: for example, frequency of the time series used, number of data points the model will look at in the past, number of predicted data points. The other hyperparameters concern the model to train (number of layers, number of cells per layer, likelihood function) and the training options such as number of epochs, batch size, and learning rate. Refer to the documentation for a full description of the available parameters.
```
hyperparameters = {
"time_freq": freq,
"context_length": str(context_length),
"prediction_length": str(prediction_length),
"num_cells": "40",
"num_layers": "3",
"likelihood": "gaussian",
"epochs": "20",
"mini_batch_size": "32",
"learning_rate": "0.001",
"dropout_rate": "0.05",
"early_stopping_patience": "10"
}
estimator.set_hyperparameters(**hyperparameters)
```
We are ready to launch the training job. SageMaker will start an EC2 instance, download the data from S3, start training the model and save the trained model.
If you provide the `test` data channel, as we do in this example, DeepAR will also calculate accuracy metrics for the trained model on this test data set. This is done by predicting the last `perdiction_length` points of each time series in the test set and comparing this to the actual value of the time series. The computed error metrics will be included as part of the log output.
**Note:** the next cell may take a few minutes to complete, depending on data size, model complexity, and training options.
```
data_channels = {
"train": "s3://{}/train/".format(s3_data_path),
"test": "s3://{}/test/".format(s3_data_path)
}
estimator.fit(inputs=data_channels)
```
### Create endpoint and predictor
Now that we have trained a model, we can use it to perform predictions by deploying it to an endpoint.
**Note:** remember to delete the enpoint after running this experiment. A cell at the very bottom of this notebook will do that: make sure you run it at the end.
```
job_name = estimator.latest_training_job.name
endpoint_name = sagemaker_session.endpoint_from_job(
job_name=job_name,
initial_instance_count=1,
instance_type='ml.m4.xlarge',
deployment_image=image_name,
role=role
)
```
To query the endpoint and perform predictions, we can define the following utility class: this allows making requests using `pandas.Series` objects rather than raw JSON strings.
```
class DeepARPredictor(sagemaker.predictor.RealTimePredictor):
def set_prediction_parameters(self, freq, prediction_length):
"""Set the time frequency and prediction length parameters. This method **must** be called
before being able to use `predict`.
Parameters:
freq -- string indicating the time frequency
prediction_length -- integer, number of predicted time points
Return value: none.
"""
self.freq = freq
self.prediction_length = prediction_length
def predict(self, ts, cat=None, encoding="utf-8", num_samples=100, quantiles=["0.1", "0.5", "0.9"]):
"""Requests the prediction of for the time series listed in `ts`, each with the (optional)
corresponding category listed in `cat`.
Parameters:
ts -- list of `pandas.Series` objects, the time series to predict
cat -- list of integers (default: None)
encoding -- string, encoding to use for the request (default: "utf-8")
num_samples -- integer, number of samples to compute at prediction time (default: 100)
quantiles -- list of strings specifying the quantiles to compute (default: ["0.1", "0.5", "0.9"])
Return value: list of `pandas.DataFrame` objects, each containing the predictions
"""
prediction_times = [x.index[-1]+1 for x in ts]
req = self.__encode_request(ts, cat, encoding, num_samples, quantiles)
res = super(DeepARPredictor, self).predict(req)
return self.__decode_response(res, prediction_times, encoding)
def __encode_request(self, ts, cat, encoding, num_samples, quantiles):
instances = [series_to_obj(ts[k], cat[k] if cat else None) for k in range(len(ts))]
configuration = {"num_samples": num_samples, "output_types": ["quantiles"], "quantiles": quantiles}
http_request_data = {"instances": instances, "configuration": configuration}
return json.dumps(http_request_data).encode(encoding)
def __decode_response(self, response, prediction_times, encoding):
response_data = json.loads(response.decode(encoding))
list_of_df = []
for k in range(len(prediction_times)):
prediction_index = pd.DatetimeIndex(start=prediction_times[k], freq=self.freq, periods=self.prediction_length)
list_of_df.append(pd.DataFrame(data=response_data['predictions'][k]['quantiles'], index=prediction_index))
return list_of_df
predictor = DeepARPredictor(
endpoint=endpoint_name,
sagemaker_session=sagemaker_session,
content_type="application/json"
)
predictor.set_prediction_parameters(freq, prediction_length)
```
### Make predictions and plot results
Now we can use the previously created `predictor` object. For simplicity, we will predict only the first few time series used for training, and compare the results with the actual data we kept in the test set.
```
list_of_df = predictor.predict(time_series_training[:5])
actual_data = time_series[:5]
for k in range(len(list_of_df)):
plt.figure(figsize=(12,6))
actual_data[k][-prediction_length-context_length:].plot(label='target')
p10 = list_of_df[k]['0.1']
p90 = list_of_df[k]['0.9']
plt.fill_between(p10.index, p10, p90, color='y', alpha=0.5, label='80% confidence interval')
list_of_df[k]['0.5'].plot(label='prediction median')
plt.legend()
plt.show()
```
### Delete endpoint
```
sagemaker_session.delete_endpoint(endpoint_name)
```
| true |
code
| 0.641787 | null | null | null | null |
|

Find this notebook in https://colab.research.google.com/github/ricardokleinklein/NLP_GenMods/blob/main/Tacotron2.ipynb
# Modelos Generativos
## Tacotron2 - Audio
Creado por *Ricardo Kleinlein* para [Saturdays.AI](https://saturdays.ai/).
Disponible bajo una licencia [Creative Commons](https://creativecommons.org/licenses/by/4.0/).
---
## Sobre el uso de Jupyter Notebooks
Este notebook ha sido implementado en Python, pero para su ejecución no es
necesario conocer el lenguaje en profundidad. Solamente se debe ejecutar cada
una de las celdas, teniendo en cuenta que hay que ejecutar una celda a la vez
y secuencialmente, tal y como figuran en orden de aparición.
Para ejecutar cada celda pulse en el botón ▶ en la esquina superior izquierda
de cada celda. Mientras se esté ejecutando ese fragmento de código,
el botón estará girando. En caso de querer detener dicha ejecución, pulse
nuevamente sobre este botón mientras gira y la ejecución se detendrá. En caso
de que la celda tenga alguna salida (texto, gráficos, etc) será mostrada
justo después de esta y antes de mostrar la siguiente celda. El notebook
estará guiado con todas las explicaciones necesarias, además irá acompañado
por comentarios en el código para facilitar su lectura.
En caso de tener alguna duda, anótela. Dedicaremos un tiempo a plantear y
resolver la mayoría delas dudas que puedan aparecer.
## Objetivo del notebook
Implementar, descargar y utilizar un modelo de Estado del Arte (Tacotron2)
de Text-To-Speech Synthesis (TTS).
## Sobre el modelo
A la hora de generar una voz sintética, existen una serie de factores que se
engloban dentro de lo que denominamos "prosodia", que constituyen algunos
factores especialmente peliagudos de modelar por sistemas automáticos: el
ritmo, el énfasis o la entonación. Entre otros atributos físicos, son estos
factores los que hacen una voz más reconocible que otra en muchos casos.
Hemos visto en las diapositivas un poco sobre el modelo Wavenet de
generación de habla natural. En ese caso, el modelo era un modelo
autorregresivo, esto es, que empleaba predicciones anteriores para elaborar
futuros puntos de la muestra.
El modelo Tacotron original [[paper](https://arxiv.org/abs/1703.10135)] empleaba como componente fundamental
Wavenet a la hora de construir habla. Sin embargo, dicho modelo es muy
lento a la hora de generar, puesto que tiene que ver muy atrás en el tiempo
para generar cada punto de la muestra.
Por ello, Tacotron2 [[paper](https://arxiv.org/abs/1712.05884)] construye sobre esta idea, y propone una
solución de compromiso donde sacrifica parte de la "personalidad" de la voz
por eficiencia en la generación. Si bien Wavenet entraba dentro de la
familia de modelos autorregresivos, Tacotron2 se enmarca dentro de las
estrategias "flow-density".
En la imagen inferior se muestra un diagrama de las partes que componen este
sistema de síntesis de voz natural.

El modelo complementario WaveGlow es un modelo que ha aprendido a generar
espectrogramas a partir de texto. Mediante la combinación de Tacotron2 con
WaveGlow, el texto nuevo que escribamos como input podrá ser interpretado
como habla natural, y se generará en formato de audio.
Se podrían modificar aspectos de la voz resultante incorporando información
adicional a diferentes niveles dentro del modelo, pero en este ejercicio nos
vamos a centrar en cargar el modelo y generar nuestros propios audios.
## Instalar las librerías necesarias
```
%%bash
pip install numpy scipy librosa unidecode inflect librosa
apt-get update
apt-get install -y libsndfile1
```
## Importar los modelos pre-entrenados
Estos modelos ocupan mucho espacio en memoria, pero sus tiempos de
entrenamiento son aún peores, y requieren de una infraestructura avanzada
para poder entrenarlos en plazos de tiempo razonables. Desde luego, exceden
en mucho las capacidades de la mayoría de nuestros ordenadores, o del
servidor default que Colab nos proporciona.
Afortunadamente, NVIDIA proporciona un servidor desde el que descargar un
modelo completamente preentrenado.
### Tacotron2
Esta versión de Tacotron2 es casi idéntica en arquitectura al original como
aparece publicado en el paper, con modificaciones mínimas en algunas capas.
Ha sido entrenado en la base de datos [LJSpeech](https://keithito.com/LJ-Speech-Dataset/), la cual constituye una
de las referencias principales a la hora de entrenar modelos de síntesis de
voz. Probablemente la otra mayor base de datos a tal efecto sea [VCTK](https://datashare.ed.ac.uk/handle/10283/2950),
desarrollada por Junichi Yamagishi en Edimburgo, con quién trabajé en Tokyo.
LJSpeech consta de ...
```
from typing import Tuple
from IPython.display import Audio
import torch
TacotronModel = Tuple[torch.nn.Module, torch.nn.Module]
tacotron2 = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub',
'nvidia_tacotron2', model_math='fp16')
tacotron2 = tacotron2.to('cuda')
tacotron2.eval()
```
Podemos repasar las líneas desplegadas para comprobar, junto con el diagrama
mostrado al inicio, que la arquitectura es correcta.
### WaveGlow
En nuestro ejemplo, WaveGlow juega el rol de un *vocoder*, una herramienta
que convierte una codificación numérica del habla en sonidos audibles.
```
waveglow = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub', 'nvidia_waveglow', model_math='fp16')
waveglow = waveglow.remove_weightnorm(waveglow)
waveglow = waveglow.to('cuda')
waveglow.eval()
```
En este momento ya estamos preparados para sintetizar audio. Por comodidad,
vamos a agrupar una serie de operaciones dedicadas a preprocesar el input
con que alimentaremos al modelo:
```
utils = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub',
'nvidia_tts_utils')
def synthesize(text: str, model: TacotronModel):
"""Adjust input text length by padding, and feed to model.
:param text: Uttered speech.
:param model: Tuple with instances of (Tacotron, WaveGlow).
:return:
numpy.ndarray with utterance.
"""
sequences, lengths = utils.prepare_input_sequence([text])
with torch.no_grad():
mel, _, _ = model[0].infer(sequences, lengths)
audio = model[1].infer(mel)
return audio[0].data.cpu().numpy()
```
## Playground
Ahora solo resta escribir una cadena de texto (en inglés para obtener
mejores resultados) y escuchar cuál es el resultado.
```
text = "Isn't Machine Learning something absolutely fabulous?"
signal = synthesize(text, (tacotron2, waveglow))
Audio(signal, rate=22050)
```
| true |
code
| 0.675751 | null | null | null | null |
|
```
from __future__ import division
import numpy as np
from pyspark import SparkConf
from pyspark import SparkContext
conf = SparkConf()
conf.setMaster('spark://ip-172-31-9-200:7077')
conf.setAppName('spark_analytics_chpt_4')
conf.set("spark.executor.memory", "10g")
sc = SparkContext(conf=conf)
```
Data from https://archive.ics.uci.edu/ml/machine-learning-databases/covtype/
```
raw_data = sc.textFile('covtype.data')
raw_data.count()
from pyspark.mllib.linalg import Vectors
from pyspark.mllib.regression import LabeledPoint
def to_float(s):
try:
return float(s)
except:
return float('nan')
def clean(line):
for x in line.split(','):
values = map(to_float, line.split(','))
featureVector = Vectors.dense(values[:-1])
label = values[-1] - 1
return LabeledPoint(label, featureVector)
data = raw_data.map(clean)
data.take(5)
training_data, cv_data, test_data = data.randomSplit([0.8, 0.1, 0.1])
training_data.cache()
cv_data.cache()
test_data.cache()
training_data.count(), cv_data.count(), test_data.count()
```
## Decision Tree
```
from pyspark.mllib.evaluation import MulticlassMetrics
from pyspark.mllib.tree import DecisionTree, DecisionTreeModel
model = DecisionTree.trainClassifier(training_data, 7, {}, 'gini', 4, 100)
predictions = model.predict(data.map(lambda x: x.features))
labels_and_predictions = data.map(lambda lp: lp.label).zip(predictions)
metrics = MulticlassMetrics(labels_and_predictions)
metrics.confusionMatrix()
metrics.precision()
map(lambda cat: (metrics.precision(cat), metrics.recall(cat)), [0, 1, 2, 3, 4, 6])
def classProbabilities(data):
countsByCategory = data.map(lambda x: x.label).countByValue()
counts = np.array(countsByCategory.values()) / sum(countsByCategory.values())
return counts
trainPriorProbabilities = classProbabilities(training_data)
cvPriorProbabilities = classProbabilities(cv_data)
sum([x[0] * x[1] for x in zip(trainPriorProbabilities, cvPriorProbabilities)])
for impurity in ('gini', 'entropy'):
for depth in (1, 20):
for bins in (10, 300):
model = DecisionTree.trainClassifier(training_data, 7, {}, impurity, depth, bins)
predictions = model.predict(cv_data.map(lambda x: x.features))
labels_and_predictions = cv_data.map(lambda lp: lp.label).zip(predictions)
metrics = MulticlassMetrics(labels_and_predictions)
accuracy = metrics.precision()
print (impurity, depth, bins), accuracy
model = DecisionTree.trainClassifier(training_data.union(cv_data), 7, {}, 'entropy', 20, 300)
predictions = model.predict(data.map(lambda x: x.features))
labels_and_predictions = data.map(lambda lp: lp.label).zip(predictions)
metrics = MulticlassMetrics(labels_and_predictions)
accuracy = metrics.precision()
print accuracy
```
## Random Forest
```
from pyspark.mllib.tree import RandomForest
forest = RandomForest.trainClassifier(training_data, 7, {10:4, 11:40}, 20, 'auto', 'entropy', 30, 300)
predictions = model.predict(data.map(lambda x: x.features))
labels_and_predictions = data.map(lambda lp: lp.label).zip(predictions)
metrics = MulticlassMetrics(labels_and_predictions)
accuracy = metrics.precision()
print accuracy
from pyspark.mllib.linalg import Vectors
input = '2709,125,28,67,23,3224,253,207,61,6094,0,29'
vector = Vectors.dense([to_float(x) for x in input.split(',')])
result = forest.predict(vector)
```
| true |
code
| 0.597373 | null | null | null | null |
|
# Brain connectome comparison using geodesic distances
**Authors:** S. Shailja and B.S. Manjunath
**Affiliation:** University of California, Santa Barbara
The goal of this notebook is to study the importance of geodesic distances on manifolds. Towards that end, we propose the following twin study. We utilize the structural connectomes of 412 human subjects in five different resolutions and two edge weights. Data consists of 206 twin pairs (133 Monozygotic (MZ) and 73 Dizygotic (DZ)).
A connectivity graph is computed from neural fiber connections between different anatomically identified Regions of Interest (ROIs) of the brain. For each subject, we have an undirected graph with 83, 129, 234, 463, and 1015 nodes and we consider the following edge weights for our study:
- number_of_fibers: the count of the fibers connecting two ROIs.
- fiber_length_mean: The mean of the fiber lengths connecting two ROIs.
We investigate the performance of geodesic distances on manifolds to assess the network similarity between pairs of twins in structural networks at different network resolutions. We compare these metrics with Euclidean distances.
<!-- <table><tr>
<td> <img src="emg_wristband.png" style="width: 200px;"/> </td>
<td> <img src="paper_rock_scissors.png" style="width: 300px;"/> </td>
</tr></table>
Figure 1. Left: EMG device: Armband with 8 electrodes recording the electrical activity of the arm's muscle tissues. Right: Three out of the four hand gestures classes considered, here "paper", "rock", "scissors". -->
# 1. Introduction and Motivation
Diffusion Tensor Imaging (DTI) is a magnetic resonance imaging technique that discovers the connections between much larger areas of the gray matter of the human brain. In recent years, analysis of fibers in DTI has received wide interest due to its potential applications in computational pathology, surgery, and studies of diseases, such as brain tumors, Alzheimer’s, and schizophrenia. Among them, one way to analyze the fiber tracts is to generate a connectivity matrix that provides a compact description of pairwise connectivity of ROIs derived from anatomical or computational brain atlases. For example, the connectivity matrices can be used to compute multiple graph theory-based metrics to distinguish between the brains. However, such methods analyze the derived network parameters overlooking the actual difference between the networks.
In this research work, we assess the similarity in structural networks by comparing the connectivity matrices. We evaluate the efficacy of distance metrics in different geometrical spaces. We demonstrate the usefulness of geodesic distances that considers the complex geometric nature of the graph. Furthermore, we evaluate the performance and consistency of the results at different graph resolutions. The computed structural connectomes based on the data of the Human Connectome Project (HCP) are publicly available to download from https://braingraph.org/cms/download-pit-group-connectomes/ [[CBB2017]](#References).
## Outline
In this notebook, we will:
- Compute the Euclidean distances on adjacency matrices for each pair of twins (MZ and DZ).
- Regularize the symmetric semi-positive definite graph Laplacians to symmetric positive-definite matrices and evaluate distances on SPD manifold.
- Statistical analysis of similarity metrics with Euclidean distance as baseline using Wilcoxon rank sum non-parametric test [[CJ1985]](#References).
# 2. Analysis
We import required Python packages.
```
import numpy as np
from numpy import linalg as la
import geomstats.backend as gs
import csv
import pandas as pd
import math
import scipy.stats as stats
import geomstats.geometry.spd_matrices as spd
import warnings
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import matplotlib as mpl
gs.random.seed(2021)
import sys
!{sys.executable} -m pip install seaborn
import seaborn as sns
import sys
!pip install networkx
import networkx as nx
import os
path = os.getcwd()
print(path)
```
## 2.1. Dataset description
The connectomes generated by the PIT Bioinformatics Group can be downloaded from https://braingraph.org/cms/download-pit-group-connectomes/.
- 86 nodes set, 1064 brains, 1 000 000 streamlines, 10x repeated & averaged (18 MB)
- 129 nodes set, 1064 brains, 1 000 000 streamlines, 10x repeated & averaged (33 MB)
- 234 nodes set, 1064 brains, 1 000 000 streamlines, 10x repeated & averaged (71 MB)
- 463 nodes set, 1064 brains, 1 000 000 streamlines, 10x repeated & averaged (138 MB)
- 1015 nodes set, 1064 brains, 1 000 000 streamlines, 10x repeated & averaged (265 MB)
The connectomes were generated from MRI scans obtained from the Human Connectome Project. To download the connectomes, you have to agree to the terms and conditions of Human Connectome Project. Please uncompress the data before running the code. A set of sample data is included in the data folder.
The metadata of each subject consists of subject id, family id, twin id and zygosity. It can be downloaded from the publicly available HCP website https://www.humanconnectome.org/study/hcp-young-adult/data-releases. We have uploaded the metadata as a CSV file in the data folder. Please agree to the same data use terms of the Human Connectome Project as above.
Please agree to the HCP open access data use terms and conditions. https://www.humanconnectome.org/storage/app/media/data_use_terms/DataUseTerms-HCP-Open-Access-26Apr2013.pdf
```
# save the metadata file from HCP dataset
with open(path +'/data/HCP_zygocity.csv', newline='') as csvfile:
reader = csv.DictReader(csvfile)
dic = {}
for row in reader:
if(row['ZygosityGT'] == "MZ" or row['ZygosityGT'] == "DZ"):
if not dic.get(row['ZygosityGT'] + "_" + row['FAMILY_ID']):
dic[row['ZygosityGT'] + "_" + row['FAMILY_ID']] = [row['SUBJECT_ID']]
else:
dic[row['ZygosityGT'] + "_" + row['FAMILY_ID']].append(row['SUBJECT_ID'])
print(row)
# print(dic.keys())
```
We explore the dataset by showing illustrative connectivity matrices of MZ and DZ twin pairs with 83 ROIs and fiber_length_mean as edge weight.
```
import matplotlib.pyplot as plt
labels_str = ['MZ twin pairs ', 'DZ twin pairs']
G1 = nx.read_gpickle(path + "/data/repeated_10_scale_33/195445.gpickle")
weight = "fiber_length_mean"
A1 = nx.adjacency_matrix(G1, weight = weight).todense()
G2 = nx.read_gpickle(path + "/data/repeated_10_scale_33/151425.gpickle")
weight = "fiber_length_mean"
A2 = nx.adjacency_matrix(G1, weight = weight).todense()
G1 = nx.read_gpickle(path + "/data/repeated_10_scale_33/898176.gpickle")
weight = "fiber_length_mean"
A_1 = nx.adjacency_matrix(G1, weight = weight).todense()
G2 = nx.read_gpickle(path + "/data/repeated_10_scale_33/109123.gpickle")
weight = "fiber_length_mean"
A_2 = nx.adjacency_matrix(G1, weight = weight).todense()
fig = plt.figure(figsize=(12, 4))
ax = fig.add_subplot(121)
imgplot = ax.imshow(A1)
ax.set_title(labels_str[0])
ax = fig.add_subplot(122)
imgplot = ax.imshow(A_1)
ax.set_title(labels_str[1])
plt.show()
fig = plt.figure(figsize=(12, 4))
ax = fig.add_subplot(121)
imgplot = ax.imshow(A2)
ax = fig.add_subplot(122)
imgplot = ax.imshow(A_2)
plt.show()
```
We can directly compare the connectivity matrices using Euclidean distance. However, the Euclidean space may not fully describe the actual geometry of the data as shown in Figure 1. So, we compute the graph Laplacian which transforms the matrices in the symmetric, semi-positive definite manifold. Finally, we regularize the graph Laplacian with a small parameter to analyze the connectivity data in the symmetric, positive-definite manifold.
We eigen decompose raw correlation matrices and lower-bound small eigenvalues to 0.5, and re-compose them into regularized correlation matrices to ensure that the matrices are SPD.
<table><tr>
<td> <img src="geodesic.jpeg" style="width: 200px;"/> <figcaption>Figure 1 - Euclidean distance in blue and the corresponding geodesic distance in orange along the manifold.</figcaption></td>
</tr></table>
```
def findSPD(L1):
eigval, eigvec = np.linalg.eig(L1)
eigval[eigval < 0.5] = 0.5
return eigvec.dot(np.diag(eigval)).dot(eigvec.T)
```
Using `geomstats`, we check that these matrices belong to the space of Symmetric Positive Definite (SPD) matrices.
```
G1 = nx.read_gpickle(path + "/data/repeated_10_scale_33/715950.gpickle")
weight = "fiber_length_mean"
weight = "number_of_fibers"
D1 = nx.adjacency_matrix(G1, weight = weight).todense()
L1 = nx.normalized_laplacian_matrix(G1, nodelist = G1.nodes(), weight = weight).toarray()
m = L1.shape[0]
manifold = spd.SPDMatrices(m)
print(gs.all(manifold.belongs(findSPD(L1))))
```
## 2.1. Distance functions
Euclidean Distance:
We compute the 2-norm and Frobenius norm between two connectivity matrices using `geomstats` tools.
<!--
The Euclidean norm or ${\displaystyle \ell _{2}}$-norm for vectors, the induced matrix norm. -->
${\displaystyle \|A_1 - A_2\|_{2}={\sqrt {\lambda _{\max }\left((A_1 - A_2) ^{*}(A_1 - A_2)\right)}},}$
${\displaystyle \|A_1 - A_2\|_{\text{F}}={\sqrt {\sum _{i=1}^{m}\sum _{j=1}^{n}|{a_1}_{ij} - {a_2}_{ij}|^{2}}}={\sqrt {\operatorname {trace} \left((A_1 - A_2) ^{*}(A_1 - A_2)\right)}},}$
where $A_1$ and $A_2$ are adjacency matrices of a twin pair.
```
def euclidean(G1, G2, weight):
G1.remove_nodes_from(list(nx.isolates(G1)))
G2.remove_nodes_from(list(nx.isolates(G2)))
G1.remove_nodes_from(np.setdiff1d(G1.nodes,G2.nodes))
G2.remove_nodes_from(np.setdiff1d(G2.nodes,G1.nodes))
A1,A2 = [nx.adjacency_matrix(G, weight = weight).todense() for G in [G1,G2]]
return gs.linalg.norm((A1 - A2), 2)
def frobenius(G1, G2, weight):
G1.remove_nodes_from(list(nx.isolates(G1)))
G2.remove_nodes_from(list(nx.isolates(G2)))
G1.remove_nodes_from(np.setdiff1d(G1.nodes,G2.nodes))
G2.remove_nodes_from(np.setdiff1d(G2.nodes,G1.nodes))
A1,A2 = [nx.adjacency_matrix(G, weight = weight).todense() for G in [G1,G2]]
return gs.linalg.norm(A1 - A2)
```
We compute the Bures-Wasserstein distance $d(A_1, A_2)$ on the manifold of n × n positive definite matrices using `geomstats` tools, where
$d(A_1, A_2)=\left[ trace\, A_1+trace\, A_2-2 \times trace(A_1^{1/2}A_2A_1^{1/2})^{1/2}\right]^{1/2}.$
```
def buresWasserstein(G1, G2, weight):
G1.remove_nodes_from(list(nx.isolates(G1)))
G2.remove_nodes_from(list(nx.isolates(G2)))
G1.remove_nodes_from(np.setdiff1d(G1.nodes,G2.nodes))
G2.remove_nodes_from(np.setdiff1d(G2.nodes,G1.nodes))
L1 = nx.normalized_laplacian_matrix(G1, nodelist = G1.nodes(), weight = weight).toarray()
L2 = nx.normalized_laplacian_matrix(G2, nodelist = G2.nodes(), weight = weight).toarray()
L1 = findSPD(L1)
L2 = findSPD(L2)
m = L2.shape[0]
manifold2 = spd.SPDMetricBuresWasserstein(m)
return manifold2.squared_dist(L1, L2)
```
## 2.2. Statistical Analysis
Euclidean distance and Bures-Wasserstein distance was computed for each pair of twins (MZ and DZ) providing group-wise statistics to investigate the impact of genetics on structural connectivity of brain networks. Our working hypotheses is that connectivity between MZ pairs would be more similar than between DZ pairs. We utilized Wilcoxon rank sum non-parametric test given the small sample size. We compare the p-values for both the metrics to highlight the sensitivity towards manifolds.
The following demonstration is for 45 MZ and 45 DZ pairs with 83 nodes due to data uploading limit. However, the tables show the results of the full dataset (206) analysis and with different nodes count.
```
# For number of nodes = 83:
d_MZ_fiber_length_mean_E = []
d_DZ_fiber_length_mean_E = []
d_MZ_number_of_fibers_E = []
d_DZ_number_of_fibers_E = []
d_MZ_fiber_length_mean_B = []
d_DZ_fiber_length_mean_B = []
d_MZ_number_of_fibers_B = []
d_DZ_number_of_fibers_B = []
countM = 0
countD = 0
for key in dic.keys():
try:
G1 = nx.read_gpickle(path + "/data/repeated_10_scale_33/" + dic[key][0] + ".gpickle")
G2 = nx.read_gpickle(path + "/data/repeated_10_scale_33/" + dic[key][1] + ".gpickle")
if (key.split("_")[0] == "MZ"):
d_m = euclidean(G1, G2, "fiber_length_mean")
d_MZ_fiber_length_mean_E.append(d_m)
d_m = euclidean(G1, G2, "number_of_fibers")
d_MZ_number_of_fibers_E.append(d_m)
d_m = buresWasserstein(G1, G2, "fiber_length_mean")
d_MZ_fiber_length_mean_B.append(d_m)
d_m = buresWasserstein(G1, G2, "number_of_fibers")
d_MZ_number_of_fibers_B.append(d_m)
elif (key.split("_")[0] == "DZ"):
d_d = euclidean(G1, G2, "fiber_length_mean")
d_DZ_fiber_length_mean_E.append(d_d)
d_d = euclidean(G1, G2, "number_of_fibers")
d_DZ_number_of_fibers_E.append(d_d)
d_d = buresWasserstein(G1, G2, "fiber_length_mean")
d_DZ_fiber_length_mean_B.append(d_d)
d_d = buresWasserstein(G1, G2, "number_of_fibers")
d_DZ_number_of_fibers_B.append(d_d)
except:
continue
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import matplotlib as mpl
cmap = sns.color_palette("Set2");
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
mpl.rc('axes', labelsize=14)
fig = plt.figure(figsize=(15, 15))
plt.subplot(2, 2, 1)
d = pd.DataFrame(list(zip(d_MZ_fiber_length_mean_E, d_DZ_fiber_length_mean_E)),
columns =['MZ', 'DZ'])
fvalue, pvalue = stats.wilcoxon(d['MZ'], d['DZ'])
ax = sns.boxplot( data=d, fliersize = 0.01, width = 0.3, linewidth = 2,palette = cmap)
ax.annotate('$nodes = 83, p = $'+ str(round(pvalue,5)), xy=(350, 350), xycoords='axes points',
size=14, ha='right', va='top',
bbox=dict(boxstyle='round', fc='w'))
# plt.figure(figsize=(6,6))
plt.ylabel('Euclidean Distance')
plt.title('weight = "fiber_length_mean"')
plt.subplot(2, 2, 3)
d = pd.DataFrame(list(zip(d_MZ_number_of_fibers_E, d_DZ_number_of_fibers_E)),
columns =['MZ', 'DZ'])
fvalue, pvalue = stats.wilcoxon(d['MZ'], d['DZ'])
ax = sns.boxplot( data=d, fliersize = 0.01, width = 0.3, linewidth = 2,palette = cmap)
ax.annotate('$nodes = 83, p = $'+ str(round(pvalue,5)), xy=(350, 350), xycoords='axes points',
size=14, ha='right', va='top',
bbox=dict(boxstyle='round', fc='w'))
plt.ylabel('Euclidean Distance')
plt.title('weight = "number_of_fibers"')
plt.subplot(2, 2, 2)
d = pd.DataFrame(list(zip(d_MZ_fiber_length_mean_B, d_DZ_fiber_length_mean_B)),
columns =['MZ', 'DZ'])
fvalue, pvalue = stats.wilcoxon(d['MZ'], d['DZ'])
ax = sns.boxplot( data=d, fliersize = 0.01, width = 0.3, linewidth = 2,palette = cmap)
ax.annotate('$nodes = 83, p = $'+ str(round(pvalue,5)), xy=(350, 350), xycoords='axes points',
size=14, ha='right', va='top',
bbox=dict(boxstyle='round', fc='w'))
# plt.figure(figsize=(6,6))
plt.ylabel('Bures-Wasserstein Distance')
plt.title('weight = "fiber_length_mean"')
plt.subplot(2, 2, 4)
d = pd.DataFrame(list(zip(d_MZ_number_of_fibers_B, d_DZ_number_of_fibers_B)),
columns =['MZ', 'DZ'])
fvalue, pvalue = stats.wilcoxon(d['MZ'], d['DZ'])
ax = sns.boxplot( data=d, fliersize = 0.01, width = 0.3, linewidth = 2,palette = cmap)
ax.annotate('$nodes = 83, p = $'+ str(round(pvalue,7)), xy=(350, 350), xycoords='axes points',
size=14, ha='right', va='top',
bbox=dict(boxstyle='round', fc='w'))
plt.ylabel('Bures-Wasserstein Distance')
plt.title('weight = "number_of_fibers"')
plt.show()
```
We compare the Euclidean distance with Bures-Wasserstein distance. Statistical analysis results for comparing structural networks of two groups (MZ & DZ) for number of nodes ranging from 83 to 1015. The following plot summarizes our finding, by directly comparing the accuracy of each method in the classification task.
#### edge weight: fiber_length_mean
| Distance metric/no. of nodes | 83 | 129 | 234 | 463 | 1015 |
| :- | -: |-: |-: |-: | :-: |
| 2-norm (p-value) | 0.0422 | 0.0553 | 0.0619 | 0.0919 | 0.1474 |
| Frobenius norm (p-value) | 0.1257 | 0.16846 | 0.3429 | 0.32643 | 0.3746 |
| Bures-Wasserstein (p-value) | 0.00379 | 0.01346 | 0.00234 | 0.00475 | 0.03645 |
#### edge weight: number_of_fibers
| Distance metric/no. of nodes | 83 | 129 | 234 | 463 | 1015 |
| :- | -: |-: |-: |-: | :-: |
| 2-norm (p-value) | 0.00198 | 0.00354 | 0.02049 | 0.03694 | 0.09631 |
| Frobenius norm (p-value) | 0.2147 | 7.815e-05 | 0.00054 | 0.00152785 | 0.00666 |
| Bures-Wasserstein (p-value)| 4.140e-06 | 3.9664e-05 | 1.05155e-05 |3.2756e-05 | 0.000320488 |
## 2.3. Results
As seen above, the Bures-Wasserstein distance provides greater sensitivity for differentiating MZ from DZ based on the similarity between structural connectivity networks. Further analyzes on a different number of nodes also follow a similar trend. A smaller p-value shows that the distances significantly differ between the MZ and DZ groups.
With the help of `geomstats`, we implemented other common geodesic distances defined on SPD manifold.
- Log Euclidean Distance: ${\displaystyle \|\log(A_1) - \log(A_2)\|_{\text{F}}}$
- Affine Invariant Distance: ${\displaystyle \|\log(A_1^{-1/2}A_2A_1^{-1/2}\|_{\text{F}}}$
```
from geomstats.geometry.matrices import Matrices
def affineInviantDistance(G1, G2, weight):
G1.remove_nodes_from(list(nx.isolates(G1)))
G2.remove_nodes_from(list(nx.isolates(G2)))
G1.remove_nodes_from(np.setdiff1d(G1.nodes,G2.nodes))
G2.remove_nodes_from(np.setdiff1d(G2.nodes,G1.nodes))
L1 = nx.normalized_laplacian_matrix(G1, nodelist = G1.nodes(), weight = weight).toarray()
L2 = nx.normalized_laplacian_matrix(G2, nodelist = G2.nodes(), weight = weight).toarray()
m = L2.shape[0]
manifold = spd.SPDMatrices(m)
L1 = findSPD(L1)
L2 = findSPD(L2)
A = gs.linalg.inv(gs.linalg.sqrtm(L1))
return gs.linalg.norm(manifold.logm(Matrices.mul(A, L2, A)))
def LogEuclideanDistance(G1, G2, weight):
G1.remove_nodes_from(list(nx.isolates(G1)))
G2.remove_nodes_from(list(nx.isolates(G2)))
G1.remove_nodes_from(np.setdiff1d(G1.nodes,G2.nodes))
G2.remove_nodes_from(np.setdiff1d(G2.nodes,G1.nodes))
L1 = nx.normalized_laplacian_matrix(G1, nodelist = G1.nodes(), weight = weight).toarray()
L2 = nx.normalized_laplacian_matrix(G2, nodelist = G2.nodes(), weight = weight).toarray()
m = L2.shape[0]
manifold = spd.SPDMatrices(m)
# print(gs.all(manifold.belongs(L1)), gs.all(manifold.belongs(L2)))
L1 = findSPD(L1)
L2 = findSPD(L2)
return gs.linalg.norm(manifold.logm(L1) - manifold.logm(L2) )
d_MZ_fiber_length_mean_A = []
d_DZ_fiber_length_mean_A = []
d_MZ_fiber_length_mean_L = []
d_DZ_fiber_length_mean_L = []
d_MZ_number_of_fibers_A = []
d_DZ_number_of_fibers_A = []
d_MZ_number_of_fibers_L = []
d_DZ_number_of_fibers_L = []
for key in dic.keys():
try:
G1 = nx.read_gpickle(path + "/data/repeated_10_scale_33/" + dic[key][0] + ".gpickle")
G2 = nx.read_gpickle(path + "/data/repeated_10_scale_33/" + dic[key][1] + ".gpickle")
if (key.split("_")[0] == "MZ"):
d_m = affineInviantDistance(G1, G2, "fiber_length_mean")
d_MZ_fiber_length_mean_A.append(d_m)
d_m = affineInviantDistance(G1, G2, "number_of_fibers")
d_MZ_number_of_fibers_A.append(d_m)
d_m = LogEuclideanDistance(G1, G2, "fiber_length_mean")
d_MZ_fiber_length_mean_L.append(d_m)
d_m = LogEuclideanDistance(G1, G2, "number_of_fibers")
d_MZ_number_of_fibers_L.append(d_m)
elif (key.split("_")[0] == "DZ"):
d_d = affineInviantDistance(G1, G2, "fiber_length_mean")
d_DZ_fiber_length_mean_A.append(d_d)
d_d = affineInviantDistance(G1, G2, "number_of_fibers")
d_DZ_number_of_fibers_A.append(d_d)
d_d = LogEuclideanDistance(G1, G2, "fiber_length_mean")
d_DZ_fiber_length_mean_L.append(d_d)
d_d = LogEuclideanDistance(G1, G2, "number_of_fibers")
d_DZ_number_of_fibers_L.append(d_d)
except:
continue
d = pd.DataFrame(list(zip(d_MZ_number_of_fibers_A, d_DZ_number_of_fibers_L)),
columns =['MZ', 'DZ'])
# d.boxplot(column=['MZ', 'DZ'], grid=False)
fvalue, pvalue = stats.wilcoxon(d['MZ'], d['DZ'])
d = pd.DataFrame(list(zip(d_MZ_fiber_length_mean_A, d_DZ_fiber_length_mean_L)),
columns =['MZ', 'DZ'])
# d.boxplot(column=['MZ', 'DZ'], grid=False)
fvalue, pvalue = stats.wilcoxon(d['MZ'], d['DZ'])
```
#### edge weight: fiber_length_mean
| Distance metric/no. of nodes | 83 | 129 | 234 | 463 | 1015 |
| :- | -: |-: |-: |-: | :-: |
| Affine Invariant (p-value) | 0.00492 | 0.01389 | 0.0018 | 0.0039 | 0.0143 |
| Log Euclidean (p-value) | 0.00492 | 0.01410 | 0.0019 | 0.00393 | 0.0136 |
#### edge weight: number_of_fibers
| Distance metric/no. of nodes | 83 | 129 | 234 | 463 | 1015 |
| :- | -: |-: |-: |-: | :-: |
| Affine Invariant (p-value) | 3.0094e-06 | 3.4367e-05 | 9.9947e-06 | 2.2217e-05 | 0.00029 |
| Log Euclidean (p-value)| 3.0910e-06 | 3.1217e-05 | 9.9947e-06 | 2.2767e-05 | 0.00028 |
## 2.4. Discussion
This research work studies the difference between two graphs on SPD manifold. Applying geodesic distances on SPD manifold accounts for the complex geometric properties of connectivity graphs.
The results of our study show how connectivity analysis discovers genetic influences on brain networks. Through the analysis of connectivity matrices on a manifold instead of a vector space, we demonstrate the sensitivity of geodesic distances as compared to Euclidean distances. Finally, we highlight the consistency of our results with different graph resolutions (node counts) and edge weights.
## 2.5. Role of Geomstats in the analysis
In this study, we exploited the SPD distance metrics implemented in the package `geomstats`. Various manifolds and distance metrics to analyze data on manifolds are easy to understand.
The class `ToTangentSpace` is also convenient to simply transform the data on the SPD manifold into tangent vectors and apply standard learning methods on them.
# 3. Limitations and perspectives
In this analysis, we have focused on SPD manifold and utilized the distance metrics implemented in `geomstats`. It was encouraging to see the improvement in p-value after using geodesic distances on SPD manifolds. In the future, we plan to analyze the transformed tangent vectors and apply learning methods.
Furthermore, we intend to evaluate the reproducibility of our approach on additional datasets. Integrating distance metrics with data-driven learning approaches can greatly improve our understanding of human brain connectivity.
## Limitation of Geomstats
We tried to utilize other geodesic distances defined for positive definite Riemannian metrics, it was not yet implemented in `geomstats`. It would be interesting to compare different distance metrics defined on SPD manifolds and compare their efficiency and performance.
```
import geomstats.geometry.riemannian_metric as rm
def riemannianGD(G1, G2, weight):
G1.remove_nodes_from(list(nx.isolates(G1)))
G2.remove_nodes_from(list(nx.isolates(G2)))
G1.remove_nodes_from(np.setdiff1d(G1.nodes,G2.nodes))
G2.remove_nodes_from(np.setdiff1d(G2.nodes,G1.nodes))
L1 = nx.normalized_laplacian_matrix(G1, nodelist = G1.nodes(), weight = weight).toarray()
L2 = nx.normalized_laplacian_matrix(G2, nodelist = G2.nodes(), weight = weight).toarray()
m = L2.shape[0]
manifold = spd.SPDMatrices(m)
L1 = findSPD(L1)
L2 = findSPD(L2)
manifold2 = rm.RiemannianMetric(m)
return manifold2.dist(L1, L2)
# d_MZ_fiber_length_mean_R = []
# d_DZ_fiber_length_mean_R = []
# for key in dic.keys():
# G1 = nx.read_gpickle(path + "/data/repeated_10_scale_33/" + dic[key][0] + ".gpickle")
# G2 = nx.read_gpickle(path + "/data/repeated_10_scale_33/" + dic[key][1] + ".gpickle")
# if (key.split("_")[0] == "MZ"):
# d_m = riemannianGD(G1, G2, "fiber_length_mean")
# d_MZ_fiber_length_mean_R.append(d_m)
# d_m = riemannianGD(G1, G2, "number_of_fibers")
# d_MZ_number_of_fibers_A.append(d_m)
# elif (key.split("_")[0] == "DZ"):
# d_d = riemannianGD(G1, G2, "fiber_length_mean")
# d_DZ_fiber_length_mean_R.append(d_d)
# d_d = riemannianGD(G1, G2, "number_of_fibers")
# d_DZ_number_of_fibers_R.append(d_d)
```
## Proposed features for Geomstats and Giotto-TDA
A class that can be used to plot points in SPD space would be helpful in visualizing the geodesic distances.
## References
.. [CBB2017] Csaba Kerepesi, Balázs Szalkai, Bálint Varga, Vince Grolmusz: The braingraph.org Database of High Resolution Structural Connectomes and the Brain Graph Tools, Cognitive Neurodynamics Vol. 11 No. 5, pp. 483-486 (2017) http://dx.doi.org/10.1007/s11571-017-9445-1.
.. [CJ1985] Cuzick, J. (1985). A Wilcoxon‐type test for trend. Statistics in medicine, 4(1), 87-90.
| true |
code
| 0.467636 | null | null | null | null |
|
```
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as skl
import torch.linalg as lin
```
## LQR with deterministic dynamics

위에 기술된 최적화 문제는
환경 $f(\textbf{x}_t, \textbf{u}_t)$ 가 선형(Linear)이고, Cost function이 Quadratic 형태입니다. LQR 수업에서 배웠던 수식과 동일하게 구성이 되어 있습니다.
$\textbf{x}_t$는 시점 $t$에서 시스템의 상태를 나타냅니다. $\textbf{u}_t$는 시점 $t$에서의 행동, 혹은 시스템에 넣어주는 저희의 action을 표현하는 벡터입니다. $\textbf{C}_t\ 와\ \textbf{c}_t$ 는 각각 cost fucntion에서 2차항과 1차항의 계수입니다. $\textbf{F}_t \ 와 \ \textbf{f}_t$ 는 Linear Dynamics의 계수들입니다.
위의 수식에서는 시간에 따른 가변성이 있을 수도 있어 다음과 같이 $t$를 첨자로 두었으나, 저희가 구현할 문제에 대해서는 시간에 invariant하다고 가정을 할 것입니다.
다음과 같은 문제를 효율적으로 풀 수 있는 기법 중 하나인 LQR을 구현해볼 것입니다.
## optimization 문제 기본 setting
우선 LQR 알고리즘을 구현하기 이전에 문제의 기본 세팅을 하겠습니다.
state, action의 dimension 그리고 cost function, linear Dynamics의 계수를 세팅하겠습니다.
(각 계수들은 미리 정해두었습니다. 위의 주석은 계수에 대한 기본 설명, 행렬의 크기입니다.)
```
state_dim = 2 # state dimension
action_dim = 2 # action dimension
T = 10
# Cost function's coefficient of second order term
# matrix shape [(state_dim + action_dim) * (state_dim + action_dim)]
C = torch.eye(n=(state_dim + action_dim)) / 10
# Cost function's coefficient of first order term
# matrix shape [(state_dim + action_dim), 1)]
c = torch.rand(size=(state_dim + action_dim, 1))
# Linear Dynamics's coefficient of first order term
# matrix shape [state_dim * (state_dim + action_dim)]
F = torch.rand(size=(state_dim, state_dim + action_dim)) / 10
# Linear Dynamics's coefficient of constant term
# matrix shape[(state_dim, 1)]
f = torch.zeros(size=(state_dim, 1))
# dictionary of K
Large_K = dict()
small_k = dict()
# dictionary of V
Large_V = dict()
small_v = dict()
# dictionary of Q
Large_Q = dict()
small_q = dict()
```
## 시점 T에서 LQR을 통한 최적 행동의 계수 K 구하기

강의에서 보셨던 것처럼 $\textbf{K}_T \ 와 \ \textbf{k}_T$ 를 구하고, 그 값을 바탕으로 시점 $T$에서의 optimal한 action, $\textbf{u}_T$ 를 구할 수 있습니다.
$\textbf{u}_T$의 계산을 위해 필요한 계수를 구하고, 그 값들을 dictionary에 저장하도록 하겠습니다
(추후에 forward 과정을 위해서 필요하기 때문!!!!)
```
K_T = - torch.matmul(torch.linalg.inv(C[:action_dim, :action_dim]), C[state_dim:, :state_dim])
k_T = - torch.matmul(torch.linalg.inv(C[state_dim:, state_dim:]), c[state_dim:, :])
print("K_T: ", K_T)
print("k_T: ", k_T)
Large_K[T] = K_T
small_k[T] = k_T
```
### 함수화
```
def calculate_K(Q, q, state_dim, action_dim):
K_t = - torch.matmul(torch.linalg.inv(Q[:action_dim, :action_dim]), Q[state_dim:, :state_dim])
k_t = - torch.matmul(torch.linalg.inv(Q[state_dim:, state_dim:]), q[state_dim:, :])
return K_t, k_t
```
## 시점 T에서의 최적 행동을 바탕으로 cost 계산

앞서 구한 action $\textbf{u}_T$를 objective의 cost function에 대입하여 $Q((\textbf{x}_t, \textbf{u}_t)$를 $V(\textbf{x}_t)$로 상태변수 $\textbf{x}_t$ 만을 인자로 가지는 함수로 바꿀 수 있습니다.
```
V_T = C[:state_dim, state_dim] + torch.matmul(C[:state_dim, state_dim:], Large_K[T]) + torch.matmul(Large_K[T].T, C[state_dim:, :state_dim]) + torch.matmul(torch.matmul(Large_K[T].T, C[state_dim:, state_dim:]), Large_K[T])
v_T = c[:state_dim, :] + torch.matmul(C[:state_dim, state_dim:], small_k[T]) + torch.matmul(Large_K[T].T, c[state_dim:, :]) + torch.matmul(torch.matmul(Large_K[T].T, C[state_dim:, state_dim:]), small_k[T])
print("V_T: ", V_T)
print("v_T: ", v_T)
Large_V[T] = V_T
small_v[T] = v_T
```
### 함수화
```
def calculate_V(C, c, state_dim, action_dim, K_t, small_k):
V_t = C[:state_dim, :state_dim] + torch.matmul(C[:state_dim, state_dim:], K_t) + torch.matmul(K_t.T, C[state_dim:, :state_dim]) + torch.matmul(torch.matmul(K_t.T, C[state_dim:, state_dim:]), K_t)
v_t = c[:state_dim, :] + torch.matmul(C[:state_dim, state_dim:], small_k) + torch.matmul(K_t.T, c[state_dim:, :]) + torch.matmul(torch.matmul(K_t.T, C[state_dim:, state_dim:]), small_k)
return V_t, v_t
```
## 시점 T-1 에서의 cost를 $\textbf{x}_{t-1}, \ \textbf{u}_{t-1}$ 로 표현

C와 F는 time-invariant 한 coefficient이고, $\textbf{V}_T\ 와 \ \textbf{v}_T $는 이전 셀에서 구했습니다.
```
Q_t = C + torch.matmul(torch.matmul(F.T, Large_V[T]), F)
q_t = c + torch.matmul(torch.matmul(F.T, Large_V[T]), f) + torch.matmul(F.T, small_v[T])
Large_Q[T-1] = Q_t
small_q[T-1] = q_t
```
### 함수화
```
def calculate_Q(C, c, Large_V, small_v, F, f):
Q_t = C + torch.matmul(torch.matmul(F.T, Large_V), F)
q_t = c + torch.matmul(torch.matmul(F.T, Large_V), f) + torch.matmul(F.T, small_v)
return Q_t, q_t
```
## Backword recursion 시점 T=0 까지 진행

위의 3가지 과정을 시점 T-1, T-2, ... , 1 까지 반복하여 coefficient(V, K, Q)를 구하고 저장합니다.
```
T = 10
state_dim = 2
action_dim = 2
C = torch.rand(size=(state_dim + action_dim, state_dim + action_dim))
# invertible check about matrix C
while True:
if (torch.matrix_rank(C) == state_dim + action_dim) and (torch.matrix_rank(C[:state_dim, :state_dim]) == state_dim) and (torch.matrix_rank(C[state_dim:, state_dim:]) == action_dim):
break
else:
C = torch.rand(size=(state_dim + action_dim, state_dim + action_dim))
c = torch.rand(size=(state_dim + action_dim, 1))
F = torch.rand(size=(state_dim, state_dim + action_dim)) / 10
f = torch.rand(size=(state_dim, 1))
K_t, k_t = calculate_K(C, c, state_dim, action_dim)
Large_K[T] = K_t
small_k[T] = k_t
V_t, v_t = calculate_V(C, c, state_dim, action_dim, K_t, k_t)
Large_V[T] = V_t
small_v[T] = v_t
for time in range(T-1, 0, -1):
# calculate Q
Q_t, q_t = calculate_Q(C, c, V_t, v_t, F, f)
Large_Q[time] = Q_t
small_q[time] = q_t
K_t, k_t = calculate_K(Q_t, q_t, state_dim, action_dim)
Large_K[time] = K_t
small_k[time] = k_t
V_t, v_t = calculate_V(C, c, state_dim, action_dim, K_t, k_t)
Large_V[time] = V_t
small_v[time] = v_t
```
### 함수화
```
def backward_recursion(state_dim, action_dim, C, c, F, f, T):
# dictionary of K
Large_K = dict()
small_k = dict()
# dictionary of V
Large_V = dict()
small_v = dict()
# dictionary of Q
Large_Q = dict()
small_q = dict()
K_t, k_t = calculate_K(C, c, state_dim, action_dim)
Large_K[T] = K_t
small_k[T] = k_t
V_t, v_t = calculate_V(C, c, state_dim, action_dim, K_t, k_t)
Large_V[T] = V_t
small_v[T] = v_t
for time in range(T-1, 0, -1):
# calculate Q
Q_t, q_t = calculate_Q(C, c, V_t, v_t, F, f)
Large_Q[time] = Q_t
small_q[time] = q_t
K_t, k_t = calculate_K(Q_t, q_t, state_dim, action_dim)
Large_K[time] = K_t
small_k[time] = k_t
V_t, v_t = calculate_V(C, c, state_dim, action_dim, K_t, k_t)
Large_V[time] = V_t
small_v[time] = v_t
return Large_Q, small_q, Large_K, small_k, Large_V, small_v
backward_recursion(state_dim, action_dim, C, c, F, f, T)
```
## forward recursion 진행


```
x_dict = dict()
u_dict = dict()
x0 = torch.randn(size=(state_dim, 1))
x_dict[1] = x0
for time in range(1, T):
u_t = torch.matmul(Large_K[time], x_dict[time]) + small_k[time]
u_dict[time] = u_t
next_x = torch.matmul(F, torch.cat([x_dict[time], u_t], dim=0)) + f
x_dict[time+1] = next_x
```
### 함수화
```
def forward_recursion(x0, Large_K, small_k, F, f, T):
x_dict = dict()
u_dict = dict()
x_dict[1] = x0
for time in range(1, T):
u_t = torch.matmul(Large_K[time], x_dict[time]) + small_k[time]
u_dict[time] = u_t
next_x = torch.matmul(F, torch.cat([x_dict[time], u_t], dim=0)) + f
x_dict[time+1] = next_x
return x_dict, u_dict
x_dict, u_dict = forward_recursion(x0, Large_K, small_k, F, f, T)
xs = dict()
for state in range(state_dim):
xs[state] = []
us = dict()
for action in range(action_dim):
us[action] = []
for key, item in x_dict.items():
print('x at time ' + str(key) + ': ', item )
for state in range(state_dim):
xs[state].append(float(item[state]))
for key, item in u_dict.items():
print('u at time ' + str(key) + ': ', item )
for action in range(action_dim):
us[action].append(float(item[action]))
```
# Implementation: Data Center temperature control
비즈니스 전체 영역에서의 언택트 환경이 확장됨에 따라 데이터 사용량이 급증하고 전세계적으로 대용량 데이터 관리를 위한 하이퍼스케일 데이터센터 건립이 증가하고 있습니다.
데이터의 용량과 속도가 빠르게 증가함에 따라 서버의 처리량도 증가하고 온도 또한 높아집니다.
서버의 온도 상승은 고장 및 성능 하락의 원인이 돼 이를 냉각시키는 과정이 필요하며 데이터센터 에너지 소비의 35% 이상이 서버 냉각에서 발생합니다.
그래서 데이터 센터의 온도 제어를 LQR을 통해서 최적의 온도 trajectory와 action sequence를 구해보고자 합니다.
편의상 데이터 센터의 온도는 선형적인 시스템에 의해서 가동이 되고 있다고 가정하고,
최적의 온도 또한 0도로 가정을 하겠습니다.
구역의 개수와 에어컨 개수를 각 3개로 예를 들자면 다음과 같이 시스템을 수식으로 나타낼 수 있습니다.
(수식의 계수들은 미리 정해두었습니다)


### coefficent
$F_M $ : 기존 구역의 temperature가 유지(Maintain)되는 정도
$F_r $ : 구역에서 다른 구역으로 temperature가 방출(Release)되는 비율
$E_power $: 에어컨 성능(Power)의 정도
$f_i $: i번째 구역에 외부로 부터 들어오는 열의 정도
$I $: 항등행렬, 밑의 첨자는 항등행렬의 크기
$t_c $: 현재 temperature에 대한 페널티 크기
$e^{1}_{c},$ : 사용한 에너지에 대한 페널티 크기
$ \epsilon_{ij} $: i구역의 에어컨 제어가 j 구역에 미치는 영향 정도(random term)
로 생각하시면 됩니다.
### setting coefficient
```
import random
# number of sector and airconditioner
state_dim = 3
action_dim = 3
T = 20
total_dim = state_dim + action_dim
# matrix shape [(state_dim + action_dim) * (state_dim + action_dim)]
C = torch.eye(n=state_dim + action_dim)
# set t_c and e_c
C[:state_dim, :state_dim] = C[:state_dim, :state_dim] * 10
C[state_dim:, state_dim:] = C[state_dim:, state_dim:] * 5
# matrix shape [(state_dim + action_dim), 1)]
c = torch.zeros(size=(total_dim, 1))
# matrix shape [state_dim * (state_dim + action_dim)]
# set F_M, F_r, E_power, epsilon_ij
F = torch.zeros(size=(state_dim, total_dim))
for i in range(state_dim):
for j in range(state_dim):
if i != j:
F[i, j] = random.uniform(0, 1) / 10
else:
F[i, i] = 0.9
for i in range(state_dim):
for j in range(action_dim):
if i != j:
F[i, state_dim + j] = - random.uniform(0, 1) / 10
else:
F[j, state_dim + j] = - random.uniform(0.5, 1)
# matrix shape[(state_dim, 1)]
# set f_i
f = torch.rand(size=(state_dim, 1))
```
### initial temperature
```
x0 = torch.ones(size=(state_dim, 1)) * 50
```
### check invertible
```
torch.matrix_rank(C) == total_dim
```
# 직접 구현
### def calculate_Q

```
def calculate_Q(C, c, F, f, V_t, v_t, state_dim, action_dim):
"""
C : torch.tensor() with shape(state_dim + action_dim, state_dim + action_dim)
c : torch.tensor() with shape(state_dim + action_dim, 1)
F : torch.tensor() with shape(state_dim, state_dim + action_dim)
f : torch.tensor() with shape(state_dim, 1)
V : torch.tensor() with shape(state_dim, state_dim)
v : torch.tensor() with shape(state_dim, 1)
"""
"""
Q : torch.tensor() with shape(state_dim + action_dim, state_dim + action_dim)
q: torch.tensor() with shape(state_dim + action_dim, 1)
"""
return Q_t, q_t
```
### def calculate_V

```
def calculate_V(C, c, K_t, k_t, state_dim, action_dim):
"""
C : torch.tensor() with shape(state_dim + action_dim, state_dim + action_dim)
c : torch.tensor() with shape(state_dim + action_dim, 1)
K : torch.tensor() with shape(action_dim, state_dim)
k : torch.tensor() with shape(action_dim, 1)
"""
"""
V : torch.tensor() with shape(state_dim, state_dim)
v : torch.tensor() with shape(state_dim, 1)
"""
return V_t, v_t
```
### def calculate_K

```
def calculate_K(Q, q, state_dim, action_dim):
"""
Q : torch.tensor() with shape(state_dim + action_dim, state_dim + action_dim)
q : torch.tensor() with shape(state_dim + action_dim, 1)
"""
"""
K : torch.tensor() with shape(action_dim, state_dim)
k : torch.tensor() with shape(action_dim, 1)
"""
return K_t, k_t
```
### backward recursion

```
def backward_recursion(state_dim, action_dim, C, c, F, f, T):
"""
C : torch.tensor() with shape(state_dim + action_dim, state_dim + action_dim)
c : torch.tensor() with shape(state_dim + action_dim, 1)
F : torch.tensor() with shape(state_dim, state_dim + action_dim)
f : torch.tensor() with shape(state_dim, 1)
"""
# dictionary of K
Large_K = dict()
small_k = dict()
# dictionary of V
Large_V = dict()
small_v = dict()
# dictionary of Q
Large_Q = dict()
small_q = dict()
"""
calculate K, k, V, v at time T and save result at dictionary mentioned above
by using function calcualte V, K
"""
"""
calculate Q, q, K, k, V, v,at time T-1 to 1 and save result at dictionary mentioned above with for loop
by using function calcualte V, K, Q
"""
return Large_Q, small_q, Large_K, small_k, Large_V, small_v
```
### def forward_recursion

```
def forward_recursion(x0, Large_K, small_k, F, f, T):
"""
F : torch.tensor() with shape(state_dim, state_dim + action_dim)
f : torch.tensor() with shape(state_dim, 1)
K : torch.tensor() with shape(action_dim, state_dim)
k : torch.tensor() with shape(action_dim, 1)
"""
x_dict = dict()
u_dict = dict()
x_dict[1] = x0
"""
calculate x, u at time 1 to T-1 and save result at dictionary mentioned above with for loop
"""
return x_dict, u_dict
Large_Q, small_q, Large_K, small_k, Large_V, small_v = backward_recursion(state_dim, action_dim, C, c, F, f, T)
x_dict, u_dict = forward_recursion(x0, Large_K, small_k, F, f, T)
```
### print and plot temperature and energy trajectory
```
xs = dict()
for state in range(state_dim):
xs[state] = []
us = dict()
for action in range(action_dim):
us[action] = []
for key, item in x_dict.items():
for state in range(state_dim):
xs[state].append(float(item[state]))
for key, item in u_dict.items():
for action in range(action_dim):
us[action].append(float(item[action]))
for state in range(state_dim):
plt.plot(xs[state])
plt.legend(["Region" + str(i+1) for i in range(state_dim)])
plt.title("Temperature")
plt.clf()
for action in range(action_dim):
plt.plot(us[action])
plt.legend(["Region" + str(i+1) for i in range(action_dim)])
plt.title("Energy")
```
| true |
code
| 0.567457 | null | null | null | null |
|
### Working with Avro files
Here are some examples of working with ZTF alerts stored as avro files.
```
import os
import io
import gzip
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from avro.datafile import DataFileReader, DataFileWriter
from avro.io import DatumReader, DatumWriter
import fastavro
from astropy.time import Time
from astropy.io import fits
import aplpy
%matplotlib inline
```
A handful of sample alerts are available in the [ztf-avro-alert](https://github.com/ZwickyTransientFacility/ztf-avro-alert) repository, which also [documents](https://zwickytransientfacility.github.io/ztf-avro-alert/schema.html) the packet contents.
```
DATA_DIR = '../../ztf-avro-alert/data/'
```
Let's count packets. Just for fun let's make it a generator--we could have millions of these alerts to look at!
```
def find_files(root_dir):
for dir_name, subdir_list, file_list in os.walk(root_dir, followlinks=True):
for fname in file_list:
if fname.endswith('.avro'):
yield dir_name+'/'+fname
print('{} has {} avro files'.format(DATA_DIR, len(list(find_files(DATA_DIR)))))
```
Let's grab the first file and look at it
```
fname = next(find_files(DATA_DIR))
fname
```
Let's use the python `avro` library to see what's in the file.
```
%%time
with open(fname,'rb') as f:
freader = DataFileReader(f,DatumReader())
for packet in freader:
print(packet.keys())
```
Now let's compare the call syntax of the faster `fastavro` package:
```
%%time
with open(fname,'rb') as f:
freader = fastavro.reader(f)
schema = freader.schema
for packet in freader:
print(packet.keys())
```
Basically the same, and the latter is faster. Here's the schema that was stored in the packet:
```
schema
```
Once we have the packet in python data structures our downstream processing should be independent of how we got the packet (from files or from a Kafka stream).
### Playing with packet contents
Once these are in memory they are just a python dictionary, so the top-level attributes are easy to access.
```
type(packet)
packet
print('JD: {} Filter: {} Mag: {:.2f}+/-{:.2f}'.format(
packet['candidate']['jd'],packet['candidate']['fid'],
packet['candidate']['magpsf'],packet['candidate']['sigmapsf']))
```
**NOTE ESPECIALLY**: the magnitudes here do not include the magnitude of the underlying reference source (if present), so if this is a variable star further adjustment is needed. Example to come...
Record access like this is a little verbose; let's wrap things up in a dataframe for ease of access (and faster loading).
Now let's extract the lightcurves. The alert packet formats are nested, so the historical detections (if present) have the same structure as the candidate triggering the alert (minus a couple fields).
```
def make_dataframe(packet):
df = pd.DataFrame(packet['candidate'], index=[0])
df_prv = pd.DataFrame(packet['prv_candidates'])
return pd.concat([df,df_prv], ignore_index=True)
dflc = make_dataframe(packet)
dflc
dflc.columns
```
We see that some of the historical detections are upper limits, signified by the NaNs. Note that the most recent candidate has a few fields that are not present for the `prv_candidates`.
Let's plot it!
```
def plot_lightcurve(dflc, days_ago=True):
filter_color = {1:'green', 2:'red', 3:'pink'}
if days_ago:
now = Time.now().jd
t = dflc.jd - now
xlabel = 'Days Ago'
else:
t = dflc.jd
xlabel = 'Time (JD)'
plt.figure()
for fid, color in filter_color.items():
# plot detections in this filter:
w = (dflc.fid == fid) & ~dflc.magpsf.isnull()
if np.sum(w):
plt.errorbar(t[w],dflc.loc[w,'magpsf'], dflc.loc[w,'sigmapsf'],fmt='.',color=color)
wnodet = (dflc.fid == fid) & dflc.magpsf.isnull()
if np.sum(wnodet):
plt.scatter(t[w],dflc.loc[w,'diffmaglim'], marker='v',color=color,alpha=0.25)
plt.gca().invert_yaxis()
plt.xlabel(xlabel)
plt.ylabel('Magnitude')
plot_lightcurve(dflc)
```
Now let's figure out how to display the cutout images. These are gzip-compressed fits files stored as bytes:
```
packet['cutoutScience']
stamp = packet['cutoutScience']['stampData']
type(stamp)
with open('tmp.fits.gz', 'wb') as f:
f.write(stamp)
def plot_cutout(stamp, fig=None, subplot=None, **kwargs):
with gzip.open(io.BytesIO(stamp), 'rb') as f:
with fits.open(io.BytesIO(f.read())) as hdul:
if fig is None:
fig = plt.figure(figsize=(4,4))
if subplot is None:
subplot = (1,1,1)
ffig = aplpy.FITSFigure(hdul[0],figure=fig, subplot=subplot, **kwargs)
ffig.show_grayscale(stretch='arcsinh')
return ffig
plot_cutout(stamp)
```
Now let's make a nice helper function:
```
def show_stamps(packet):
#fig, axes = plt.subplots(1,3, figsize=(12,4))
fig = plt.figure(figsize=(12,4))
for i, cutout in enumerate(['Science','Template','Difference']):
stamp = packet['cutout{}'.format(cutout)]['stampData']
ffig = plot_cutout(stamp, fig=fig, subplot = (1,3,i+1))
ffig.set_title(cutout)
show_stamps(packet)
```
| true |
code
| 0.498962 | null | null | null | null |
|
```
%matplotlib inline
import numpy as np
import pylab as plt
import cv2
data_root = '/diskmnt/a/makov/yaivan/2016-02-11_Pin/'
```
Список файлов:
* empty - файл полученный с томографа без коррекций
* corr - то же изображение что и empty, но с коррекцией
* tomo - то же, что и empty, но полученное в ходе проведения эксперимента
* white - пустой пучок используемый для нормировки изображений (получен в тот-же день при калибровке)
* black_1, black_2 - темновые токи, полученные в разное время
```
empty = plt.imread(data_root+'first_projection.tif').astype('float32')
corr = plt.imread(data_root+'first_projection_corr.tif').astype('float32')
tomo = plt.imread(data_root+'Raw/pin_2.24um_0000.tif').astype('float32')
white = np.fromfile(data_root+'white0202_2016-02-11.ffr',dtype='<u2').astype('float32').reshape((2096, 4000))
black_1 = np.fromfile(data_root+'black0101_2016-02-09.ffr',dtype='<u2').astype('float32').reshape((2096, 4000))
black_2 = np.fromfile(data_root+'black0201_2016-02-16.ffr',dtype='<u2').astype('float32').reshape((2096, 4000))
def show_frame(data, label):
data_filtered = cv2.medianBlur(data,5)
plt.figure(figsize=(12,10))
plt.imshow(data_filtered)
plt.title(label+' filtered')
plt.colorbar(orientation='horizontal')
plt.show()
plt.figure(figsize=(12,8))
plt.plot(data[1000])
plt.grid(True)
plt.title(label+' filtered: central cut')
plt.show()
plt.figure(figsize=(12,10))
plt.imshow(data_filtered)
plt.colorbar(orientation='horizontal')
plt.title(label)
plt.show()
plt.figure(figsize=(12,8))
plt.plot(data_filtered[1000])
plt.grid(True)
plt.title(label+': central cut')
plt.show()
```
## Вот пучок без объекта.
По осям - отсчёты детектора.
Здесь и далее первая картинка и центральное сечение - как есть. Вторая картинка - с применениейм медианной фильтрации (чтобы убрать шумы сцинстиллятора).
```
show_frame(white, 'White')
```
## Вот темновой ток 1
по осям - отсчёты детектора
```
show_frame(black_1, 'Black_1')
```
## Вот темновой ток 2
по осям - отсчёты детектора
```
show_frame(black_2, 'Black_2')
```
## Вот разница между темновыми токами
```
show_frame(black_1 - black_2, 'Black_1 - Black_2')
```
## Вот никак не скорректированное изображение
```
show_frame(empty, 'Empty')
```
## Вот отнормированное изображение (силами томографа)
Странно, что на центральном срезе максимум не на 65535 (2^16), а примерно 65535\*__0.8. Это значит что нам при реконструкции нужно нормироваться не на 65535 при взятии логарифма, а на максимум по синограмме?__
```
show_frame(corr, 'Corr')
```
## Вот изображение из томографического зксперимента
```
show_frame(tomo, 'tomo image')
```
## Вот разница изображений отнормированных томографом в ручном режиме и режиме томографа
Они видимо немого сдвинуты
```
show_frame(corr - tomo, 'corr / tomo image')
```
## Вот моя попытка отнормировать изображение
Видны следы от прямого пучка (сетка на заднем фоне), но это видимо связано с тем, что прямой пучок зависит от расстояний детектор-источник (сферичность интенсивности), и прямой пучок был померян для другого рассотояния.
К тому-же интенсивнось прямого пучка видимо была меньше (в 16 раз?), чем при проведениии зксперимента. (__это надо проверить__)
```
white_norm = (white - black_1)
white_norm[white_norm<1] = 1
empty_norm = (empty/16 - black_1)
empty_norm[empty_norm<1] =1
my_corr = empty_norm/white_norm
my_corr[my_corr>1.1] = 1.1
show_frame(my_corr, 'my_corr image')
```
## Скорректированный пучок нами поделеённый на скорреткироваанный скайсканом.
Они вроде совпадают, с точностью до шумов.
Отсюда следует, что нормировка происходит по формуле $$Signal=k\times 2^{16}\frac{I_1-dark}{I_0-dark}, k=0.87$$
```
show_frame(my_corr*65535*0.87/corr, 'my_corr/corr image')
```
| true |
code
| 0.475118 | null | null | null | null |
|
# 1.Loading libraries and Dataset
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import ElasticNet
from sklearn import metrics
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import cross_val_score
from scipy import stats
#Reading Dataset
df = pd.read_csv('../input/nyc-rolling-sales.csv')
# Little peek into the dataset
df.head()
#Dropping column as it is empty
del df['EASE-MENT']
#Dropping as it looks like an iterator
del df['Unnamed: 0']
del df['SALE DATE']
#Checking for duplicated entries
sum(df.duplicated(df.columns))
#Delete the duplicates and check that it worked
df = df.drop_duplicates(df.columns, keep='last')
sum(df.duplicated(df.columns))
```
# 2.Data Inspection & Visualization
```
#shape of dataset
df.shape
#Description of every column
df.info()
#Let's convert some of the columns to appropriate datatype
df['TAX CLASS AT TIME OF SALE'] = df['TAX CLASS AT TIME OF SALE'].astype('category')
df['TAX CLASS AT PRESENT'] = df['TAX CLASS AT PRESENT'].astype('category')
df['LAND SQUARE FEET'] = pd.to_numeric(df['LAND SQUARE FEET'], errors='coerce')
df['GROSS SQUARE FEET']= pd.to_numeric(df['GROSS SQUARE FEET'], errors='coerce')
#df['SALE DATE'] = pd.to_datetime(df['SALE DATE'], errors='coerce')
df['SALE PRICE'] = pd.to_numeric(df['SALE PRICE'], errors='coerce')
df['BOROUGH'] = df['BOROUGH'].astype('category')
#checking missing values
df.columns[df.isnull().any()]
miss=df.isnull().sum()/len(df)
miss=miss[miss>0]
miss.sort_values(inplace=True)
miss
miss=miss.to_frame()
miss.columns=['count']
miss.index.names=['Name']
miss['Name']=miss.index
miss
#plot the missing values
sns.set(style='whitegrid',color_codes=True)
sns.barplot(x='Name', y='count',data=miss)
plt.xticks(rotation=90)
sns
```
There are many missing values in the columns :
* LAND SQUARE FEET
* GROSS SQUARE FEET
* SALE PRICE
We can drop the rows with missing values or we can fill them up with their mean, median or any other relation.
For time being, let's fill these up with mean values.<br>
Further, We will try to predict the value of SALE PRICE as test data.
```
# For time being, let's fill these up with mean values.
df['LAND SQUARE FEET']=df['LAND SQUARE FEET'].fillna(df['LAND SQUARE FEET'].mean())
df['GROSS SQUARE FEET']=df['GROSS SQUARE FEET'].fillna(df['GROSS SQUARE FEET'].mean())
# Splitting dataset
test=df[df['SALE PRICE'].isna()]
data=df[~df['SALE PRICE'].isna()]
test = test.drop(columns='SALE PRICE')
# Print first 5 rows of test
print(test.shape)
test.head()
#Printing first rows of our data
print(data.shape)
data.head(10)
#correlation between the features
corr = data.corr()
sns.heatmap(corr)
```
Last row represents the correlation of different features with SALE PRICE
```
#numeric correlation
corr['SALE PRICE'].sort_values(ascending=False)
numeric_data=data.select_dtypes(include=[np.number])
numeric_data.describe()
```
**SALE PRICE**
```
plt.figure(figsize=(15,6))
sns.boxplot(x='SALE PRICE', data=data)
plt.ticklabel_format(style='plain', axis='x')
plt.title('Boxplot of SALE PRICE in USD')
plt.show()
sns.distplot(data['SALE PRICE'])
# Remove observations that fall outside those caps
data = data[(data['SALE PRICE'] > 100000) & (data['SALE PRICE'] < 5000000)]
```
Let's Check Again
```
sns.distplot(data['SALE PRICE'])
#skewness of SalePrice
data['SALE PRICE'].skew()
```
SALE PRICE is highly right skewed. So, we will log transform it so that it give better results.
```
sales=np.log(data['SALE PRICE'])
print(sales.skew())
sns.distplot(sales)
```
Well now we can see the symmetry and thus it is normalised.
**Let's Visualize Numerical data**
**SQUARE FEET**
```
plt.figure(figsize=(10,6))
sns.boxplot(x='GROSS SQUARE FEET', data=data,showfliers=False)
plt.figure(figsize=(10,6))
sns.boxplot(x='LAND SQUARE FEET', data=data,showfliers=False)
data = data[data['GROSS SQUARE FEET'] < 10000]
data = data[data['LAND SQUARE FEET'] < 10000]
plt.figure(figsize=(10,6))
sns.regplot(x='GROSS SQUARE FEET', y='SALE PRICE', data=data, fit_reg=False, scatter_kws={'alpha':0.3})
plt.figure(figsize=(10,6))
sns.regplot(x='LAND SQUARE FEET', y='SALE PRICE', data=data, fit_reg=False, scatter_kws={'alpha':0.3})
```
**Total Units, Commercial Units, Residential Units**
```
data[["TOTAL UNITS", "SALE PRICE"]].groupby(['TOTAL UNITS'], as_index=False).count().sort_values(by='SALE PRICE', ascending=False)
```
Removing rows with TOTAL UNITS == 0 and one outlier with 2261 units
```
data = data[(data['TOTAL UNITS'] > 0) & (data['TOTAL UNITS'] != 2261)]
plt.figure(figsize=(10,6))
sns.boxplot(x='TOTAL UNITS', y='SALE PRICE', data=data)
plt.title('Total Units vs Sale Price')
plt.show()
plt.figure(figsize=(10,6))
sns.boxplot(x='COMMERCIAL UNITS', y='SALE PRICE', data=data)
plt.title('Commercial Units vs Sale Price')
plt.show()
plt.figure(figsize=(10,6))
sns.boxplot(x='RESIDENTIAL UNITS', y='SALE PRICE', data=data)
plt.title('Residential Units vs Sale Price')
plt.show()
```
**Let's Visualize categorical data**
```
cat_data=data.select_dtypes(exclude=[np.number])
cat_data.describe()
```
**TAX CLASS AT PRESENT**
```
# Starting with TAX CLASS AT PRESENT
data['TAX CLASS AT PRESENT'].unique()
pivot=data.pivot_table(index='TAX CLASS AT PRESENT', values='SALE PRICE', aggfunc=np.median)
pivot
pivot.plot(kind='bar', color='black')
```
**TAX CLASS AT TIME OF SALE**
```
# TAX CLASS AT TIME OF SALE
data['TAX CLASS AT TIME OF SALE'].unique()
pivot=data.pivot_table(index='TAX CLASS AT TIME OF SALE', values='SALE PRICE', aggfunc=np.median)
pivot
pivot.plot(kind='bar', color='red')
```
**BOROUGH**
```
# BOROUGH
data['BOROUGH'].unique()
pivot=data.pivot_table(index='BOROUGH', values='SALE PRICE', aggfunc=np.median)
pivot
pivot.plot(kind='bar', color='blue')
```
***It means max sale price is of BOROUGH==1 that is Manhattan.***
**BUILDING CLASS CATEGORY**
```
# BUILDING CLASS CATEGORY
print(data['BUILDING CLASS CATEGORY'].nunique())
pivot=data.pivot_table(index='BUILDING CLASS CATEGORY', values='SALE PRICE', aggfunc=np.median)
pivot
pivot.plot(kind='bar', color='Green')
```
# 3. Data Pre Processing
**Let's see our dataset again**
```
del data['ADDRESS']
del data['APARTMENT NUMBER']
data.info()
```
**Normalising and Transforming Numerical columns**
```
numeric_data.columns
#transform the numeric features using log(x + 1)
from scipy.stats import skew
skewed = data[numeric_data.columns].apply(lambda x: skew(x.dropna().astype(float)))
skewed = skewed[skewed > 0.75]
skewed = skewed.index
data[skewed] = np.log1p(data[skewed])
scaler = StandardScaler()
scaler.fit(data[numeric_data.columns])
scaled = scaler.transform(data[numeric_data.columns])
for i, col in enumerate(numeric_data.columns):
data[col] = scaled[:,i]
data.head()
#Dropping few columns
del data['BUILDING CLASS AT PRESENT']
del data['BUILDING CLASS AT TIME OF SALE']
del data['NEIGHBORHOOD']
```
**One hot encoding categorical columns**
```
#Select the variables to be one-hot encoded
one_hot_features = ['BOROUGH', 'BUILDING CLASS CATEGORY','TAX CLASS AT PRESENT','TAX CLASS AT TIME OF SALE']
# Convert categorical variables into dummy/indicator variables (i.e. one-hot encoding).
one_hot_encoded = pd.get_dummies(data[one_hot_features])
one_hot_encoded.info(verbose=True, memory_usage=True, null_counts=True)
# Replacing categorical columns with dummies
fdf = data.drop(one_hot_features,axis=1)
fdf = pd.concat([fdf, one_hot_encoded] ,axis=1)
fdf.info()
```
## Train/Test Split
```
Y_fdf = fdf['SALE PRICE']
X_fdf = fdf.drop('SALE PRICE', axis=1)
X_fdf.shape , Y_fdf.shape
X_train ,X_test, Y_train , Y_test = train_test_split(X_fdf , Y_fdf , test_size = 0.3 , random_state =34)
# Training set
X_train.shape , Y_train.shape
#Testing set
X_test.shape , Y_test.shape
```
# 4. Modelling
```
# RMSE
def rmse(y_test,y_pred):
return np.sqrt(mean_squared_error(y_test,y_pred))
```
### 4.1 Linear Regression
```
linreg = LinearRegression()
linreg.fit(X_train, Y_train)
Y_pred_lin = linreg.predict(X_test)
rmse(Y_test,Y_pred_lin)
```
### 4.2. Lasso Regression
```
alpha=0.00099
lasso_regr=Lasso(alpha=alpha,max_iter=50000)
lasso_regr.fit(X_train, Y_train)
Y_pred_lasso=lasso_regr.predict(X_test)
rmse(Y_test,Y_pred_lasso)
```
### 4.3. Ridge Regression
```
ridge = Ridge(alpha=0.01, normalize=True)
ridge.fit(X_train, Y_train)
Y_pred_ridge = ridge.predict(X_test)
rmse(Y_test,Y_pred_ridge)
```
### 4.4. RandomForest Regressor
```
rf_regr = RandomForestRegressor()
rf_regr.fit(X_train, Y_train)
Y_pred_rf = rf_regr.predict(X_test)
rmse(Y_test,Y_pred_rf)
```
# 5. Conclusion
**We can see that Random Forest Regressor works best for this dataset with RSME score of 0.588**
| true |
code
| 0.579817 | null | null | null | null |
|
# Python Comments
Comments are lines that exist in computer programs that are ignored by compilers and interpreters.
Including comments in programs makes code more readable for humans as it provides some information or explanation about what each part of a program is doing.
In general, it is a good idea to write comments while you are writing or updating a program as it is easy to forget your thought process later on, and comments written later may be less useful in the long term.
In Python, we use the hash (#) symbol to start writing a comment.
```
#Print Hello, world to console
print("Hello, world")
```
# Multi Line Comments
If we have comments that extend multiple lines, one way of doing it is to use hash (#) in the beginning of each line.
```
#This is a long comment
#and it extends
#Multiple lines
```
Another way of doing this is to use triple quotes, either ''' or """.
```
"""This is also a
perfect example of
multi-line comments"""
```
# DocString in python
Docstring is short for documentation string.
It is a string that occurs as the first statement in a module, function, class, or method definition.
```
def double(num):
"""
function to double the number
"""
return 2 * num
print (double(10))
print (double.__doc__) #Docstring is available to us as the attribute __doc__ of the function
```
# Python Indentation
1. Most of the programming languages like C, C++, Java use braces { } to define a block of code. Python uses indentation.
2. A code block (body of a function, loop etc.) starts with indentation and ends with the first unindented line. The amount of indentation is up to you, but it must be consistent throughout that block.
3. Generally four whitespaces are used for indentation and is preferred over tabs.
```
for i in range(10):
print (i)
```
Indentation can be ignored in line continuation. But it's a good idea to always indent. It makes the code more readable.
```
if True:
print ("Machine Learning")
c = "AAIC"
if True: print "Machine Learning"; c = "AAIC" #always add parenthesis
```
# Python Statement
Instructions that a Python interpreter can execute are called statements.
Examples:
```
a = 1 #single statement
```
# Multi-Line Statement
In Python, end of a statement is marked by a newline character. But we can make a statement extend over multiple lines with the line continuation character (\).
```
a = 1 + 2 + 3 + \
4 + 5 + 6 + \
7 + 8
print (a)
#another way is
a = (1 + 2 + 3 +
4 + 5 + 6 +
7 + 8)
print (a)
a = 10; b = 20; c = 30 #put multiple statements in a single line using ;
```
| true |
code
| 0.21963 | null | null | null | null |
|
# 基于注意力的神经机器翻译
此笔记本训练一个将缅甸语翻译为英语的序列到序列(sequence to sequence,简写为 seq2seq)模型。此例子难度较高,需要对序列到序列模型的知识有一定了解。
训练完此笔记本中的模型后,你将能够输入一个缅甸语句子,例如 *"ဘာကိစ္စ မဖြစ်ရ မှာ လဲ?"*,并返回其英语翻译 *"Why not?"*
对于一个简单的例子来说,翻译质量令人满意。但是更有趣的可能是生成的注意力图:它显示在翻译过程中,输入句子的哪些部分受到了模型的注意。
<img src="https://tensorflow.google.cn/images/spanish-english.png" alt="spanish-english attention plot">
请注意:运行这个例子用一个 P100 GPU 需要花大约 10 分钟。
```
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.model_selection import train_test_split
import unicodedata
import re
import numpy as np
import os
import io
import time
```
## 下载和准备数据集
我们将使用 http://www.manythings.org/anki/ 提供的一个语言数据集。这个数据集包含如下格式的语言翻译对:
```
May I borrow this book? ¿Puedo tomar prestado este libro?
```
这个数据集中有很多种语言可供选择。我们将使用英语 - 缅甸语数据集。为方便使用,我们在谷歌云上提供了此数据集的一份副本。但是你也可以自己下载副本。下载完数据集后,我们将采取下列步骤准备数据:
1. 给每个句子添加一个 *开始* 和一个 *结束* 标记(token)。
2. 删除特殊字符以清理句子。
3. 创建一个单词索引和一个反向单词索引(即一个从单词映射至 id 的词典和一个从 id 映射至单词的词典)。
4. 将每个句子填充(pad)到最大长度。
```
'''
# 下载文件
path_to_zip = tf.keras.utils.get_file(
'spa-eng.zip', origin='http://storage.googleapis.com/download.tensorflow.org/data/spa-eng.zip',
extract=True)
path_to_file = os.path.dirname(path_to_zip)+"/spa-eng/spa.txt"
'''
path_to_file = "./lan/mya.txt"
# 将 unicode 文件转换为 ascii
def unicode_to_ascii(s):
return ''.join(c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn')
def preprocess_sentence(w):
w = unicode_to_ascii(w.lower().strip())
# 在单词与跟在其后的标点符号之间插入一个空格
# 例如: "he is a boy." => "he is a boy ."
# 参考:https://stackoverflow.com/questions/3645931/python-padding-punctuation-with-white-spaces-keeping-punctuation
w = re.sub(r"([?.!,¿])", r" \1 ", w)
w = re.sub(r'[" "]+', " ", w)
# 除了 (a-z, A-Z, ".", "?", "!", ","),将所有字符替换为空格
w = re.sub(r"[^a-zA-Z?.!,¿]+", " ", w)
w = w.rstrip().strip()
# 给句子加上开始和结束标记
# 以便模型知道何时开始和结束预测
w = '<start> ' + w + ' <end>'
return w
en_sentence = u"May I borrow this book?"
sp_sentence = u"¿Puedo tomar prestado este libro?"
print(preprocess_sentence(en_sentence))
print(preprocess_sentence(sp_sentence).encode('utf-8'))
# 1. 去除重音符号
# 2. 清理句子
# 3. 返回这样格式的单词对:[ENGLISH, SPANISH]
def create_dataset(path, num_examples):
lines = io.open(path, encoding='UTF-8').read().strip().split('\n')
word_pairs = [[preprocess_sentence(w) for w in l.split('\t')] for l in lines[:num_examples]]
return zip(*word_pairs)
en, sp = create_dataset(path_to_file, None)
print(en[-1])
print(sp[-1])
def max_length(tensor):
return max(len(t) for t in tensor)
def tokenize(lang):
lang_tokenizer = tf.keras.preprocessing.text.Tokenizer(
filters='')
lang_tokenizer.fit_on_texts(lang)
tensor = lang_tokenizer.texts_to_sequences(lang)
tensor = tf.keras.preprocessing.sequence.pad_sequences(tensor,
padding='post')
return tensor, lang_tokenizer
def load_dataset(path, num_examples=None):
# 创建清理过的输入输出对
targ_lang, inp_lang = create_dataset(path, num_examples)
input_tensor, inp_lang_tokenizer = tokenize(inp_lang)
target_tensor, targ_lang_tokenizer = tokenize(targ_lang)
return input_tensor, target_tensor, inp_lang_tokenizer, targ_lang_tokenizer
```
### 限制数据集的大小以加快实验速度(可选)
在超过 10 万个句子的完整数据集上训练需要很长时间。为了更快地训练,我们可以将数据集的大小限制为 3 万个句子(当然,翻译质量也会随着数据的减少而降低):
```
# 尝试实验不同大小的数据集
num_examples = 30000
input_tensor, target_tensor, inp_lang, targ_lang = load_dataset(path_to_file, num_examples)
# 计算目标张量的最大长度 (max_length)
max_length_targ, max_length_inp = max_length(target_tensor), max_length(input_tensor)
# 采用 80 - 20 的比例切分训练集和验证集
input_tensor_train, input_tensor_val, target_tensor_train, target_tensor_val = train_test_split(input_tensor, target_tensor, test_size=0.2)
# 显示长度
print(len(input_tensor_train), len(target_tensor_train), len(input_tensor_val), len(target_tensor_val))
def convert(lang, tensor):
for t in tensor:
if t!=0:
print ("%d ----> %s" % (t, lang.index_word[t]))
print ("Input Language; index to word mapping")
convert(inp_lang, input_tensor_train[0])
print ()
print ("Target Language; index to word mapping")
convert(targ_lang, target_tensor_train[0])
```
### 创建一个 tf.data 数据集
```
BUFFER_SIZE = len(input_tensor_train)
BATCH_SIZE = 64
steps_per_epoch = len(input_tensor_train)//BATCH_SIZE
embedding_dim = 256
units = 1024
vocab_inp_size = len(inp_lang.word_index)+1
vocab_tar_size = len(targ_lang.word_index)+1
dataset = tf.data.Dataset.from_tensor_slices((input_tensor_train, target_tensor_train)).shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE, drop_remainder=True)
example_input_batch, example_target_batch = next(iter(dataset))
example_input_batch.shape, example_target_batch.shape
```
## 编写编码器 (encoder) 和解码器 (decoder) 模型
实现一个基于注意力的编码器 - 解码器模型。关于这种模型,你可以阅读 TensorFlow 的 [神经机器翻译 (序列到序列) 教程](https://github.com/tensorflow/nmt)。本示例采用一组更新的 API。此笔记本实现了上述序列到序列教程中的 [注意力方程式](https://github.com/tensorflow/nmt#background-on-the-attention-mechanism)。下图显示了注意力机制为每个输入单词分配一个权重,然后解码器将这个权重用于预测句子中的下一个单词。下图和公式是 [Luong 的论文](https://arxiv.org/abs/1508.04025v5)中注意力机制的一个例子。
<img src="https://tensorflow.google.cn/images/seq2seq/attention_mechanism.jpg" width="500" alt="attention mechanism">
输入经过编码器模型,编码器模型为我们提供形状为 *(批大小,最大长度,隐藏层大小)* 的编码器输出和形状为 *(批大小,隐藏层大小)* 的编码器隐藏层状态。
下面是所实现的方程式:
<img src="https://tensorflow.google.cn/images/seq2seq/attention_equation_0.jpg" alt="attention equation 0" width="800">
<img src="https://tensorflow.google.cn/images/seq2seq/attention_equation_1.jpg" alt="attention equation 1" width="800">
本教程的编码器采用 [Bahdanau 注意力](https://arxiv.org/pdf/1409.0473.pdf)。在用简化形式编写之前,让我们先决定符号:
* FC = 完全连接(密集)层
* EO = 编码器输出
* H = 隐藏层状态
* X = 解码器输入
以及伪代码:
* `score = FC(tanh(FC(EO) + FC(H)))`
* `attention weights = softmax(score, axis = 1)`。 Softmax 默认被应用于最后一个轴,但是这里我们想将它应用于 *第一个轴*, 因为分数 (score) 的形状是 *(批大小,最大长度,隐藏层大小)*。最大长度 (`max_length`) 是我们的输入的长度。因为我们想为每个输入分配一个权重,所以 softmax 应该用在这个轴上。
* `context vector = sum(attention weights * EO, axis = 1)`。选择第一个轴的原因同上。
* `embedding output` = 解码器输入 X 通过一个嵌入层。
* `merged vector = concat(embedding output, context vector)`
* 此合并后的向量随后被传送到 GRU
每个步骤中所有向量的形状已在代码的注释中阐明:
```
class Encoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, enc_units, batch_sz):
super(Encoder, self).__init__()
self.batch_sz = batch_sz
self.enc_units = enc_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.enc_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
def call(self, x, hidden):
x = self.embedding(x)
output, state = self.gru(x, initial_state = hidden)
return output, state
def initialize_hidden_state(self):
return tf.zeros((self.batch_sz, self.enc_units))
encoder = Encoder(vocab_inp_size, embedding_dim, units, BATCH_SIZE)
# 样本输入
sample_hidden = encoder.initialize_hidden_state()
sample_output, sample_hidden = encoder(example_input_batch, sample_hidden)
print ('Encoder output shape: (batch size, sequence length, units) {}'.format(sample_output.shape))
print ('Encoder Hidden state shape: (batch size, units) {}'.format(sample_hidden.shape))
class BahdanauAttention(tf.keras.layers.Layer):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, query, values):
# 隐藏层的形状 == (批大小,隐藏层大小)
# hidden_with_time_axis 的形状 == (批大小,1,隐藏层大小)
# 这样做是为了执行加法以计算分数
hidden_with_time_axis = tf.expand_dims(query, 1)
# 分数的形状 == (批大小,最大长度,1)
# 我们在最后一个轴上得到 1, 因为我们把分数应用于 self.V
# 在应用 self.V 之前,张量的形状是(批大小,最大长度,单位)
score = self.V(tf.nn.tanh(
self.W1(values) + self.W2(hidden_with_time_axis)))
# 注意力权重 (attention_weights) 的形状 == (批大小,最大长度,1)
attention_weights = tf.nn.softmax(score, axis=1)
# 上下文向量 (context_vector) 求和之后的形状 == (批大小,隐藏层大小)
context_vector = attention_weights * values
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weights
attention_layer = BahdanauAttention(10)
attention_result, attention_weights = attention_layer(sample_hidden, sample_output)
print("Attention result shape: (batch size, units) {}".format(attention_result.shape))
print("Attention weights shape: (batch_size, sequence_length, 1) {}".format(attention_weights.shape))
class Decoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, dec_units, batch_sz):
super(Decoder, self).__init__()
self.batch_sz = batch_sz
self.dec_units = dec_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.dec_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc = tf.keras.layers.Dense(vocab_size)
# 用于注意力
self.attention = BahdanauAttention(self.dec_units)
def call(self, x, hidden, enc_output):
# 编码器输出 (enc_output) 的形状 == (批大小,最大长度,隐藏层大小)
context_vector, attention_weights = self.attention(hidden, enc_output)
# x 在通过嵌入层后的形状 == (批大小,1,嵌入维度)
x = self.embedding(x)
# x 在拼接 (concatenation) 后的形状 == (批大小,1,嵌入维度 + 隐藏层大小)
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# 将合并后的向量传送到 GRU
output, state = self.gru(x)
# 输出的形状 == (批大小 * 1,隐藏层大小)
output = tf.reshape(output, (-1, output.shape[2]))
# 输出的形状 == (批大小,vocab)
x = self.fc(output)
return x, state, attention_weights
decoder = Decoder(vocab_tar_size, embedding_dim, units, BATCH_SIZE)
sample_decoder_output, _, _ = decoder(tf.random.uniform((64, 1)),
sample_hidden, sample_output)
print ('Decoder output shape: (batch_size, vocab size) {}'.format(sample_decoder_output.shape))
```
## 定义优化器和损失函数
```
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')
def loss_function(real, pred):
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
```
## 检查点(基于对象保存)
```
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(optimizer=optimizer,
encoder=encoder,
decoder=decoder)
```
## 训练
1. 将 *输入* 传送至 *编码器*,编码器返回 *编码器输出* 和 *编码器隐藏层状态*。
2. 将编码器输出、编码器隐藏层状态和解码器输入(即 *开始标记*)传送至解码器。
3. 解码器返回 *预测* 和 *解码器隐藏层状态*。
4. 解码器隐藏层状态被传送回模型,预测被用于计算损失。
5. 使用 *教师强制 (teacher forcing)* 决定解码器的下一个输入。
6. *教师强制* 是将 *目标词* 作为 *下一个输入* 传送至解码器的技术。
7. 最后一步是计算梯度,并将其应用于优化器和反向传播。
```
@tf.function
def train_step(inp, targ, enc_hidden):
loss = 0
with tf.GradientTape() as tape:
enc_output, enc_hidden = encoder(inp, enc_hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']] * BATCH_SIZE, 1)
# 教师强制 - 将目标词作为下一个输入
for t in range(1, targ.shape[1]):
# 将编码器输出 (enc_output) 传送至解码器
predictions, dec_hidden, _ = decoder(dec_input, dec_hidden, enc_output)
loss += loss_function(targ[:, t], predictions)
# 使用教师强制
dec_input = tf.expand_dims(targ[:, t], 1)
batch_loss = (loss / int(targ.shape[1]))
variables = encoder.trainable_variables + decoder.trainable_variables
gradients = tape.gradient(loss, variables)
optimizer.apply_gradients(zip(gradients, variables))
return batch_loss
EPOCHS = 10
for epoch in range(EPOCHS):
start = time.time()
enc_hidden = encoder.initialize_hidden_state()
total_loss = 0
for (batch, (inp, targ)) in enumerate(dataset.take(steps_per_epoch)):
batch_loss = train_step(inp, targ, enc_hidden)
total_loss += batch_loss
if batch % 100 == 0:
print('Epoch {} Batch {} Loss {:.4f}'.format(epoch + 1,
batch,
batch_loss.numpy()))
# 每 2 个周期(epoch),保存(检查点)一次模型
if (epoch + 1) % 2 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print('Epoch {} Loss {:.4f}'.format(epoch + 1,
total_loss / steps_per_epoch))
print('Time taken for 1 epoch {} sec\n'.format(time.time() - start))
```
## 翻译
* 评估函数类似于训练循环,不同之处在于在这里我们不使用 *教师强制*。每个时间步的解码器输入是其先前的预测、隐藏层状态和编码器输出。
* 当模型预测 *结束标记* 时停止预测。
* 存储 *每个时间步的注意力权重*。
请注意:对于一个输入,编码器输出仅计算一次。
```
def evaluate(sentence):
attention_plot = np.zeros((max_length_targ, max_length_inp))
sentence = preprocess_sentence(sentence)
inputs = [inp_lang.word_index[i] for i in sentence.split(' ')]
inputs = tf.keras.preprocessing.sequence.pad_sequences([inputs],
maxlen=max_length_inp,
padding='post')
inputs = tf.convert_to_tensor(inputs)
result = ''
hidden = [tf.zeros((1, units))]
enc_out, enc_hidden = encoder(inputs, hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']], 0)
for t in range(max_length_targ):
predictions, dec_hidden, attention_weights = decoder(dec_input,
dec_hidden,
enc_out)
# 存储注意力权重以便后面制图
attention_weights = tf.reshape(attention_weights, (-1, ))
attention_plot[t] = attention_weights.numpy()
predicted_id = tf.argmax(predictions[0]).numpy()
result += targ_lang.index_word[predicted_id] + ' '
if targ_lang.index_word[predicted_id] == '<end>':
return result, sentence, attention_plot
# 预测的 ID 被输送回模型
dec_input = tf.expand_dims([predicted_id], 0)
return result, sentence, attention_plot
# 注意力权重制图函数
def plot_attention(attention, sentence, predicted_sentence):
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1)
ax.matshow(attention, cmap='viridis')
fontdict = {'fontsize': 14}
ax.set_xticklabels([''] + sentence, fontdict=fontdict, rotation=90)
ax.set_yticklabels([''] + predicted_sentence, fontdict=fontdict)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
plt.show()
def translate(sentence):
result, sentence, attention_plot = evaluate(sentence)
print('Input: %s' % (sentence))
print('Predicted translation: {}'.format(result))
attention_plot = attention_plot[:len(result.split(' ')), :len(sentence.split(' '))]
plot_attention(attention_plot, sentence.split(' '), result.split(' '))
```
## 恢复最新的检查点并验证
```
# 恢复检查点目录 (checkpoint_dir) 中最新的检查点
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
translate(u'hace mucho frio aqui.')
translate(u'esta es mi vida.')
translate(u'¿todavia estan en casa?')
# 错误的翻译
translate(u'trata de averiguarlo.')
```
| true |
code
| 0.558688 | null | null | null | null |
|
# Python review of concepts
Mainly to point out useful aspects of Python you may have glossed over. Assumes you already know Python fairly well.
## Python as a language
### Why Python?
- Huge community - especially in data science and ML
- Easy to learn
- Batteries included
- Extensive 3rd party libraries
- Widely used in both industry and academia
- Most important “glue” language bridging multiple communities
```
import __hello__
```
### Versions
- Only use Python 3 (current release version is 3.8, container is 3.7)
- Do not use Python 2
```
import sys
sys.version
```
### Multi-paradigm
#### Procedural
```
x = []
for i in range(5):
x.append(i*i)
x
```
#### Functional
```
list(map(lambda x: x*x, range(5)))
```
#### Object-oriented
```
class Robot:
def __init__(self, name, function):
self.name = name
self.function = function
def greet(self):
return f"I am {self.name}, a {self.function} robot!"
fido = Robot('roomba', 'vacuum cleaner')
fido.name
fido.function
fido.greet()
```
### Dynamic typing
#### Complexity of a + b
```
1 + 2.3
type(1), type(2.3)
'hello' + ' world'
[1,2,3] + [4,5,6]
import numpy as np
np.arange(3) + 10
```
### Several Python implementations!
- CPtyhon
- Pypy
- IronPython
- Jython
### Global interpreter lock (GIL)
- Only applies to CPython
- Threads vs processes
- Avoid threads in general
- Performance not predictable
```
from concurrent.futures import ThreadPoolExecutor
def f(n):
x = np.random.uniform(0,1,n)
y = np.random.uniform(0,1,n)
count = 0
for i in range(n):
if x[i]**2 + y[i]**2 < 1:
count += 1
return count*4/n
n = 100000
niter = 4
%%time
[f(n) for i in range(niter)]
%%time
with ThreadPoolExecutor(4) as pool:
xs = list(pool.map(f, [n]*niter))
xs
```
## Coding in Python
```
import this
```
### Coding conventions
- PEP 8
- Avoid magic numbers
- Avoid copy and paste
- extract common functionality into functions
[Style Guide for Python Code](https://www.python.org/dev/peps/pep-0008/)
### Data types
- Integers
- Arbitrary precision
- Integer division operator
- Base conversion
- Check if integer
```
import math
n = math.factorial(100)
n
f'{n:,}'
h = math.sqrt(3**2 + 4**2)
h
h.is_integer()
```
- Floats
- Checking for equality
- Catastrophic cancellation
- Complex
```
x = np.arange(9).reshape(3,3)
x = x / x.sum(axis=0)
λ = np.linalg.eigvals(x)
λ[0]
λ[0] == 1
math.isclose(λ[0], 1)
def var(xs):
"""Returns variance of sample data."""
n = 0
s = 0
ss = 0
for x in xs:
n +=1
s += x
ss += x*x
v = (ss - (s*s)/n)/(n-1)
return v
xs = np.random.normal(1e9, 1, int(1e6))
var(xs)
np.var(xs)
```
- Boolean
- What evaluates as False?
```
stuff = [[], [1], {},'', 'hello', 0, 1, 1==1, 1==2]
for s in stuff:
if s:
print(f'{s} evaluates as True')
else:
print(f'{s} evaluates as False')
```
- String
- Unicode by default
- b, r, f strings
```
u'\u732b'
```
String formatting
- Learn to use the f-string.
```
import string
char = 'e'
pos = string.ascii_lowercase.index(char) + 1
f"The letter {char} has position {pos} in the alphabet"
n = int(1e9)
f"{n:,}"
x = math.pi
f"{x:8.2f}"
import datetime
now = datetime.datetime.now()
now
f"{now:%Y-%m-%d %H:%M}"
```
### Data structures
- Immutable - string, tulle
- Mutable - list, set, dictionary
- Collections module
- heapq
```
import collections
[x for x in dir(collections) if not x.startswith('_')]
```
### Functions
- \*args, \*\*kwargs
- Care with mutable default values
- First class objects
- Anonymous functions
- Decorators
```
def f(*args, **kwargs):
print(f"args = {args}") # in Python 3.8, you can just write f'{args = }'
print(f"kwargs = {kwargs}")
f(1,2,3,a=4,b=5,c=6)
def g(a, xs=[]):
xs.append(a)
return xs
g(1)
g(2)
h = lambda x, y, z: x**2 + y**2 + z**2
h(1,2,3)
from functools import lru_cache
def fib(n):
print(n, end=', ')
if n <= 1:
return n
else:
return fib(n-2) + fib(n-1)
fib(10)
@lru_cache(maxsize=100)
def fib_cache(n):
print(n, end=', ')
if n <= 1:
return n
else:
return fib_cache(n-2) + fib_cache(n-1)
fib_cache(10)
```
### Classes
- Key idea is encapsulation into objects
- Everything in Python is an object
- Attributes and methods
- What is self?
- Special methods - double underscore methods
- Avoid complex inheritance schemes - prefer composition
- Learn “design patterns” if interested in OOP
```
(3.0).is_integer()
'hello world'.title()
class Student:
def __init__(self, first, last):
self.first = first
self.last = last
@property
def name(self):
return f'{self.first} {self.last}'
s = Student('Santa', 'Claus')
s.name
```
### Enums
Use enums readability when you have a discrete set of CONSTANTS.
```
from enum import Enum
class Day(Enum):
MON = 1
TUE = 2
WED = 3
THU = 4
FRI = 5
SAT = 6
SUN = 7
for day in Day:
print(day)
```
### NamedTuple
```
from collections import namedtuple
Student = namedtuple('Student', ['name', 'email', 'age', 'gpa', 'species'])
abe = Student('Abraham Lincoln', 'abe.lincoln@gmail.com', 23, 3.4, 'Human')
abe.species
abe[1:4]
```
### Data Classes
Simplifies creation and use of classes for data records.
Note: NamedTuple serves a similar function but are immutable.
```
from dataclasses import dataclass
@dataclass
class Student:
name: str
email: str
age: int
gpa: float
species: str = 'Human'
abe = Student('Abraham Lincoln', 'abe.lincoln@gmail.com', age=23, gpa=3.4)
abe
abe.email
abe.species
```
**Note**
The type annotations are informative only. Python does *not* enforce them.
```
Student(*'abcde')
```
### Imports, modules and namespaces
- A namespace is basically just a dictionary
- LEGB
- Avoid polluting the global namespace
```
[x for x in dir(__builtin__) if x[0].islower()][:8]
x1 = 23
def f1(x2):
print(locals())
# x1 is global (G), x2 is enclosing (E), x3 is local
def g(x3):
print(locals())
return x3 + x2 + x1
return g
x = 23
def f2(x):
print(locals())
def g(x):
print(locals())
return x
return g
g1 = f1(3)
g1(2)
g2 = f2(3)
g2(2)
```
### Loops
- Prefer vectorization unless using numba
- Difference between continue and break
- Avoid infinite loops
- Comprehensions and generator expressions
```
import string
{char: ord(char) for char in string.ascii_lowercase}
```
### Iterations and generators
- The iterator protocol
- `__iter__` and `__next__`
- iter()
- next()
- What happens in a for loop
- Generators with `yield` and `yield from`
```
class Iterator:
"""A silly class that implements the Iterator protocol and Strategy pattern.
start = start of range to apply func to
stop = end of range to apply func to
"""
def __init__(self, start, stop, func):
self.start = start
self.stop = stop
self.func = func
def __iter__(self):
self.n = self.start
return self
def __next__(self):
if self.n >= self.stop:
raise StopIteration
else:
x = self.func(self.n)
self.n += 1
return x
sq = Iterator(0, 5, lambda x: x*x)
list(sq)
```
### Generators
Like functions, but lazy.
```
def cycle1(xs, n):
"""Cuycles through values in xs n times."""
for i in range(n):
for x in xs:
yield x
list(cycle1([1,2,3], 4))
for x in cycle1(['ann', 'bob', 'stop', 'charles'], 1000):
if x == 'stop':
break
else:
print(x)
def cycle2(xs, n):
"""Cuycles through values in xs n times."""
for i in range(n):
yield from xs
list(cycle2([1,2,3], 4))
```
Because they are lazy, generators can be used for infinite streams.
```
def fib():
a, b = 1, 1
while True:
yield a
a, b = b, a + b
for n in fib():
if n > 100:
break
print(n, end=', ')
```
You can even slice infinite generators. More when we cover functional programming.
```
import itertools as it
list(it.islice(fib(), 5, 10))
```
| true |
code
| 0.454896 | null | null | null | null |
|
# Unlocking the Black Box: How to Visualize Data Science Project Pipeline with Yellowbrick Library
No matter whether you are a novice data scientist or a well-seasoned and established professional working in the field for a long time, you most likely faced a challenge of interpreting results generated at any stage of the data science pipeline, be it data ingestion or wrangling, feature selection or model evaluation. This issue becomes even more prominent when the need arises to present interim findings to a group of stakeholders, clients, etc. How do you deal in that case with the long arrays of numbers, scientific notations and formulas which tell a story of your data set? That's when visualization library like Yellowbrick becomes an essential tool in the arsenal of any data scientist and helps to undertake that endevour by providing interpretable and comprehensive visualization means for any stage of a project pipeline.
### Introduction
In this post we will explain how to integrate visualization step into each stage of your project without a need to create customized and time-consuming charts, while getting the benefit of drawing necessary insights into the data you are working with. Because, let's agree on that, unlike computers, human eye perceives graphical represenation of information way better, than it does with bits and digits. Yellowbrick machine learning visualization library serves just that purpose - to "create publication-ready figures and interactive data explorations while still allowing developers fine-grain control of figures. For users, Yellowbrick can help evaluate the performance, stability, and predictive value of machine learning models and assist in diagnosing problems throughout the machine learning workflow" ( http://www.scikit-yb.org/en/latest/about.html ).
For the purpose of this exercise we will be using a dataset from UCI Machine Learning Repository on Absenteeism at Work ( https://archive.ics.uci.edu/ml/machine-learning-databases/00445/ ). This data set contains a mix of continuous, binary and hierarchical features, along with continuous target representing a number of work hours an employee has been absent for from work. Such a variety in data makes for an interesting wrangling, feature selection and model evaluation task, results of which we will make sure to visualize along the way.
To begin, we will need to pip install and import Yellowbrick Pyhton library. To do that, simply run the following command from your command line:
$ pip install yellowbrick
Once that's done, let's import Yellowbrick along with other essential packages, libraries and user-preference set up into the Jupyter Notebook.
```
import numpy as np
import pandas as pd
%matplotlib inline
from cycler import cycler
import matplotlib.style
import matplotlib as mpl
mpl.style.use('seaborn-white')
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
from sklearn.cluster import KMeans
from sklearn.linear_model import RidgeCV
from sklearn.model_selection import KFold
from sklearn.naive_bayes import MultinomialNB
from sklearn.svm import LinearSVC, NuSVC, SVC
from sklearn.tree import DecisionTreeRegressor
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import StratifiedKFold
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import Ridge, Lasso, ElasticNet
from sklearn.linear_model import LogisticRegressionCV, LogisticRegression, SGDClassifier
from sklearn.ensemble import BaggingClassifier, ExtraTreesClassifier, RandomForestClassifier, RandomTreesEmbedding, GradientBoostingClassifier
import warnings
warnings.filterwarnings("ignore")
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split as tts
from sklearn.metrics import roc_curve
from sklearn.metrics import f1_score
from sklearn.metrics import recall_score
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from yellowbrick.features import Rank1D
from yellowbrick.features import Rank2D
from yellowbrick.classifier import ClassBalance
from yellowbrick.model_selection import LearningCurve
from yellowbrick.model_selection import ValidationCurve
from yellowbrick.classifier import ClassPredictionError
from yellowbrick.classifier import ClassificationReport
from yellowbrick.features.importances import FeatureImportances
```
### Data Ingestion and Wrangling
Now we are ready to proceed with downloading a zipped archive containing the dataset directly from the UCI Machine Learning Repository and extracting the data file. To perform this step, we will be using the urllib.request module which helps with opening URLs (mostly HTTP) in a complex world.
```
import urllib.request
print('Beginning file download...')
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/00445/Absenteeism_at_work_AAA.zip'
urllib.request.urlretrieve( url ## , Specify a path to folder you want the archive to be stored in, e.g. '/Users/Yara/Downloads/Absenteeism_at_work_AAA.zip')
)
```
Unzip the archive and extract a CSV data file which we will be using. Zipfile module does that flawlessly.
```
import zipfile
fantasy_zip = zipfile.ZipFile('C:\\Users\\Yara\\Downloads\\Absenteeism_at_work_AAA.zip')
fantasy_zip.extract('Absenteeism_at_work.csv', 'C:\\Users\\Yara\\Downloads')
fantasy_zip.close()
```
Load the data and place it in the same folder as your Python code.
```
dataset = pd.read_csv('C:\\Users\\Yara\\Downloads\\Absenteeism_at_work.csv', 'Absenteeism_at_work.csv', delimiter=';')
```
Let's take a look at a couple of randomly selected rows from the loaded data set.
```
dataset.sample(10)
dataset.ID.count()
```
As we can see, selected dataset contains 740 instances, each instance representing an employed individual. Features provided in the dataset are those considered to be related to the number of hours an employee was absent from work (target). For the purpose of this exercise, we will subjectively group all instances into 3 categories, thus, converting continuous target into categorical. To identify appropriate bins for the target, let's look at the min, max and mean values.
```
# Getting basic statistical information for the target
print(dataset.loc[:, 'Absenteeism time in hours'].mean())
print(dataset.loc[:, 'Absenteeism time in hours'].min())
print(dataset.loc[:, 'Absenteeism time in hours'].max())
```
If approximately 7 hours of absence is an average value accross our dataset, it makes sense to group records in the following manner:
1) Low rate of absence (Low), if 'Absenteeism time in hours' value is < 6;
2) Medium rate of absence (Medium), if 'Absenteeism time in hours' value is between 6 and 30;
3) High rate of absence (High), if 'Absenteeism time in hours' value is > 30.
Upon grouping, we will be further exploring data and selecting relevant features from the dataset in order to predict an absentee category for the instances in the test portion of the data.
```
dataset['Absenteeism time in hours'] = np.where(dataset['Absenteeism time in hours'] < 6, 1, dataset['Absenteeism time in hours'])
dataset['Absenteeism time in hours'] = np.where(dataset['Absenteeism time in hours'].between(6, 30), 2, dataset['Absenteeism time in hours'])
dataset['Absenteeism time in hours'] = np.where(dataset['Absenteeism time in hours'] > 30, 3, dataset['Absenteeism time in hours'])
#Let's look at the data now!
dataset.head()
```
Once the target is taken care of, time to look at the features. Those of them storing unique identifiers and / or data which might 'leak' information to the model, should be dropped from the data set. For instance, 'Reason for absence' feature stores the information 'from the future' since it will not be available in the real world business scenario when running the model on a new set of data. Therefore, it is highly correlated with the target.
```
dataset = dataset.drop(['ID', 'Reason for absence'], axis=1)
dataset.columns
```
We are now left with the set of features and a target to use in a machine learning model of our choice. So, let's separate features from the target, and split our dataset into a matrix of features (X) and an array of target values (y).
```
features = ['Month of absence', 'Day of the week', 'Seasons',
'Transportation expense', 'Distance from Residence to Work',
'Service time', 'Age', 'Work load Average/day ', 'Hit target',
'Disciplinary failure', 'Education', 'Son', 'Social drinker',
'Social smoker', 'Pet', 'Weight', 'Height', 'Body mass index']
target = ['Absenteeism time in hours']
X = dataset.drop(['Absenteeism time in hours'], axis=1)
y = dataset.loc[:, 'Absenteeism time in hours']
# Setting up some visual preferences prior to visualizing data
class color:
PURPLE = '\033[95m'
CYAN = '\033[96m'
DARKCYAN = '\033[36m'
BLUE = '\033[94m'
GREEN = '\033[92m'
YELLOW = '\033[93m'
RED = '\033[91m'
BOLD = '\033[1m'
UNDERLINE = '\033[4m'
END = '\033[0m'
```
### Exploratory Analysis and Feature Selection
Whenever one deals with a categorical target, it is important to remember to test the data set for class imbalance issue. Machine learning models struggle with performing well on imbalanced data where one class is overrepresented, while the other one is underrepresented. While such data sets are representative of the real life, e.g. no company will have majority or even half of its employees missing work on a massive scale, they need to be adjusted for the machine learning purposes, to improve algorithms' ability to pick up patterns present in that data.
And to check for the potential class imbalance in our data, we will use Class Balance Visualizer from Yellowbrick.
```
# Calculating population breakdown by target category
Target = y.value_counts()
print(color.BOLD, 'Low:', color.END, Target[1])
print(color.BOLD, 'Medium:', color.END, Target[2])
print(color.BOLD, 'High:', color.END, Target[3])
# Creating class labels
classes = ["Low", "Medium", "High"]
# Instantiate the classification model and visualizer
mpl.rcParams['axes.prop_cycle'] = cycler('color', ['red', 'limegreen', 'yellow'])
forest = RandomForestClassifier()
fig, ax = plt.subplots(figsize=(10, 7))
visualizer = ClassBalance(forest, classes=classes, ax=ax)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid(axis='x')
visualizer.fit(X, y) # Fit the training data to the visualizer
visualizer.score(X, y) # Evaluate the model on the test data
g = visualizer.show()
```
There is an obvious class imbalance here, therefore, we can expect the model to have difficulties learning the pattern for Medium and High categories, unless data resampling is performed or class weight parameter applied within selected model if chosen algorithm allows it.
With that being said, let's proceed with assessing feature importance and selecting those which will be used further in a model of our choice. Yellowbrick library provides a number of convenient vizualizers to perform feature analysis, and we will use a couple of them for demonstration purposes, as well as to make sure that consistent results are returned when different methods are applied.
Rank 1D visualizer utilizes Shapiro-Wilk algorithm that takes into account only a single feature at a time and assesses the normality of the distribution of instances with respect to the feature. Let's see how it works!
```
# Creating 1D visualizer with the Sharpiro feature ranking algorithm
fig, ax = plt.subplots(figsize=(10, 7))
visualizer = Rank1D(features=features, ax=ax, algorithm='shapiro')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.show()
```
Rank 2D Visualizer, in its turn, utilizes a ranking algorithm that takes into account pairs of features at a time. It provides an option for a user to select ranking algorithm of their choice. We are going to experiment with covariance and Pearson, and compare the results.
```
# Instantiate visualizer using covariance ranking algorithm
figsize=(10, 7)
fig, ax = plt.subplots(figsize=figsize)
visualizer = Rank2D(features=features, ax=ax, algorithm='covariance', colormap='summer')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.show()
# Instantiate visualizer using Pearson ranking algorithm
figsize=(10, 7)
fig, ax = plt.subplots(figsize=figsize)
visualizer = Rank2D(features=features, algorithm='pearson', colormap='winter')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.show()
```
Visual representation of feature correlation makes it much easier to spot pairs of features, which have high or low correlation coefficients. For instance, lighter colours on both plots indicate strong correlation between such pairs of features as 'Body mass index' and 'Weight'; 'Seasons' and 'Month of absence', etc.
Another way of estimating feature importance relative to the model is to rank them by feature_importances_ attribute when data is fitted to the model. The Yellowbrick Feature Importances visualizer utilizes this attribute to rank and plot features' relative importances. Let's look at how this approach works with Ridge, Lasso and ElasticNet models.
```
# Visualizing Ridge, Lasso and ElasticNet feature selection models side by side for comparison
# Ridge
# Create a new figure
mpl.rcParams['axes.prop_cycle'] = cycler('color', ['red'])
fig = plt.gcf()
fig.set_size_inches(10,10)
ax = plt.subplot(311)
labels = features
viz = FeatureImportances(Ridge(alpha=0.1), ax=ax, labels=labels, relative=False)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid(False)
# Fit and display
viz.fit(X, y)
viz.show()
# ElasticNet
# Create a new figure
mpl.rcParams['axes.prop_cycle'] = cycler('color', ['salmon'])
fig = plt.gcf()
fig.set_size_inches(10,10)
ax = plt.subplot(312)
labels = features
viz = FeatureImportances(ElasticNet(alpha=0.01), ax=ax, labels=labels, relative=False)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid(False)
# Fit and display
viz.fit(X, y)
viz.show()
# Lasso
# Create a new figure
mpl.rcParams['axes.prop_cycle'] = cycler('color', ['purple'])
fig = plt.gcf()
fig.set_size_inches(10,10)
ax = plt.subplot(313)
labels = features
viz = FeatureImportances(Lasso(alpha=0.01), ax=ax, labels=labels, relative=False)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid(False)
# Fit and display
viz.fit(X, y)
viz.show()
```
Having analyzed the output of all utilized visualizations (Shapiro algorithm, Pearson Correlation Ranking, Covariance Ranking, Lasso, Ridge and ElasticNet), we can now select a set of features which have meaningful coefficient values (positive or negative). These are the features to be kept in the model:
- Disciplinary failure
- Day of the week
- Seasons
- Distance from Residence to Work
- Number of children (Son)
- Social drinker
- Social smoker
- Height
- Weight
- BMI
- Pet
- Month of absence
Graphic visualization of the feature coefficients calculated in a number of different ways significantly simplifies feature selection process, making it more obvious, as it provides an easy way to visualy compare multiple values and consider only those which are statistically significant to the model.
Now let's drop features which didn't make it and proceed with creating models.
```
# Dropping features from X based on visual feature importance visualization
X = X.drop(['Transportation expense', 'Age', 'Transportation expense', 'Service time', 'Hit target', 'Education','Work load Average/day '], axis=1)
```
Some of the features which are going to be further utilized in the modeling stage, might be of a hierarchical type and require encoding. Let's look at the top couple of rows to see if we have any of those.
```
X.head()
```
Looks like 'Month of absence', 'Day of week' and 'Seasons' are not binary. Therefore, we'll be using pandas get_dummies function to encode them.
```
# Encoding some categorical features
X = pd.get_dummies(data=X, columns=['Month of absence', 'Day of the week', 'Seasons'])
X.head()
print(X.columns)
```
### Model Evaluation and Selection
Our matrix of features X is now ready to be fitted to a model, but first we need to split the data into train and test portions for further model validation.
```
# Perform 80/20 training/test split
X_train, X_test, y_train, y_test = tts(X, y, test_size=0.20, random_state=42)
```
For the purpose of model evaluation and selection we will be using Yellowbrick's Classification Report Visualizer, which displays the precision, recall, F1, and support scores for the model. In order to support easier interpretation and problem detection, the report integrates numerical scores with a color-coded heatmap. All heatmaps are normalized, i.e. in the range from 0 to 1, to facilitate easy comparison of classification models across different classification reports.
```
# Creating a function to visualize estimators
def visual_model_selection(X, y, estimator):
visualizer = ClassificationReport(estimator, classes=['Low', 'Medium', 'High'], cmap='PRGn')
visualizer.fit(X, y)
visualizer.score(X, y)
visualizer.show()
visual_model_selection(X, y, BaggingClassifier())
visual_model_selection(X, y, LogisticRegression(class_weight='balanced'))
visual_model_selection(X, y, KNeighborsClassifier())
visual_model_selection(X, y, RandomForestClassifier(class_weight='balanced'))
visual_model_selection(X, y, ExtraTreesClassifier(class_weight='balanced'))
```
For the purposes of this exercise we will consider F1 score when estimating models' performance and making a selection. All of the above models visualized through Yellowbrick's Classification Report Visualizer make clear that classifier algorithms performed the best. We need to pay special attention to the F1 score for the underrepresented classes, such as "High" and "Medium", as they contained significantly less instances than "Low" class. Therefore, high F1 score for all three classes indicate a very strong performance of the following models: Bagging Classifier, Random Forest Classifier, Extra Trees Classifier.
We will also use Class Prediction Error visualizer for these models to confirm their strong performance.
```
# Visualizaing class prediction error for Bagging Classifier model
classes = ['Low', 'Medium', 'High']
mpl.rcParams['axes.prop_cycle'] = cycler('color', ['turquoise', 'cyan', 'teal', 'coral', 'blue', 'lime', 'lavender', 'lightblue', 'darkgreen', 'tan', 'salmon', 'gold', 'darkred', 'darkblue'])
fig = plt.gcf()
fig.set_size_inches(10,10)
ax = plt.subplot(311)
visualizer = ClassPredictionError(BaggingClassifier(), classes=classes, ax=ax)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid(False)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
g = visualizer.show()
# Visualizaing class prediction error for Random Forest Classifier model
classes = ['Low', 'Medium', 'High']
mpl.rcParams['axes.prop_cycle'] = cycler('color', ['coral', 'tan', 'darkred'])
fig = plt.gcf()
fig.set_size_inches(10,10)
ax = plt.subplot(312)
visualizer = ClassPredictionError(RandomForestClassifier(class_weight='balanced'), classes=classes, ax=ax)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid(False)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
g = visualizer.show()
# Visualizaing class prediction error for Extra Trees Classifier model
classes = ['Low', 'Medium', 'High']
mpl.rcParams['axes.prop_cycle'] = cycler('color', ['limegreen', 'yellow', 'orange'])
fig = plt.gcf()
fig.set_size_inches(10,10)
ax = plt.subplot(313)
visualizer = ClassPredictionError(ExtraTreesClassifier(class_weight='balanced'), classes=classes, ax=ax)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid(False)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
g = visualizer.show()
```
### Model Optimization
Now we can conclude that ExtraTreesClassifier seems to perform better as it had no instances from "High" class reported under the "Low" class.
However, decision trees become more overfit the deeper they are because at each level of the tree the partitions are dealing with a smaller subset of data. One way to avoid overfitting is by adjusting the depth of the tree. Yellowbrick's Validation Curve visualizer explores the relationship of the "max_depth" parameter to the R2 score with 10 shuffle split cross-validation.
So let's proceed with hyperparameter tuning for our selected ExtraTreesClassifier model using Validation Curve visualizer!
```
# Performing Hyperparameter tuning
# Validation Curve
mpl.rcParams['axes.prop_cycle'] = cycler('color', ['purple', 'darkblue'])
fig = plt.gcf()
fig.set_size_inches(10,10)
ax = plt.subplot(411)
viz = ValidationCurve(ExtraTreesClassifier(class_weight='balanced'), ax=ax, param_name="max_depth", param_range=np.arange(1, 11), cv=3, scoring="accuracy")
# Fit and show the visualizer
viz.fit(X, y)
viz.show()
```
We can observe on the above chart that even though training score keeps rising continuosly, cross validation score drops down at max_depth=7. Therefore, we will chose that parameter for our selected model to optimize its performance.
```
visual_model_selection(X, y, ExtraTreesClassifier(class_weight='balanced', max_depth=7))
```
### Conclusions
As we demonstrated in this article, visualization techniques prove to be a useful tool in the machine learning toolkit, and Yellowbrick provides a wide selection of visualizers to meet the needs at every step and stage of the data science project pipeline. Ranging from feature analysis and selection, to model selection and optimization, Yellowbrick visualizers make it easy to make a decision as to which features to keep in the model, which model performs best, and how to tune model's hyperparameters to achieve its optimal performance for future use. Moreover, visualizing algorithmic output also makes it easy to present insights to the audience and stakeholders, and contribute to the simplified interpretability of the machine learning results.
| true |
code
| 0.632673 | null | null | null | null |
|
### Utilitary Functions
Definition of functions that don't belong to a specific class inside the logic of the problem solution
```
import numpy as np
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import copy
%matplotlib inline
def pseudo_transpose(listt):
'''
Utilitary function used to compute the transpose of a matrix
expressed in the shape of a vector
'''
result = np.empty(9)
for i in range(9):
result[i] = listt[3 * (i % 3) + math.floor(1 / 3)]
return result
def moving_average(a, n=5) :
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
def plot_agents_avg_reward(title, data, styles, labels):
sns.set_style('white')
sns.set_context('talk')
plt.subplot(1, 1, 1)
plt.title(title)
for i in range(len(data)):
plt.plot(range(len(data[i])), data[i], styles[i], label = labels[i])
plt.ylabel('Average Reward')
plt.xlabel('Time Step')
plt.legend(loc=4, bbox_to_anchor=(1.4, 0))
sns.despine()
plt.show()
```
### Game
Definition of the class that represents a game. Important methods for this experiments are the ones related with joint actions. The game class makes sure that agent1 and agent2 get the corresponding feedback of each other so that they can update they shared knowledge and obtain a solution based on it.
```
class Game(object):
'''
Definition of the game values and game actions (play) based on the involved agents
'''
def __init__(self, game_values, iterations, agent1, agent2):
self.game_values = game_values
self.iterations = iterations
self.agent1 = agent1
self.agent2 = agent2
self.history_values_agent1 = []
self.history_values_agent2 = []
def run(self):
for i in range(self.iterations):
self.agent1.compute_action()
self.agent2.compute_action()
self.play(self.agent1.last_action, self.agent2.last_action)
def play(self, action_agent1, action_agent2):
'''
Defines a step in the game. Based on the input actions, the output of the game is
computed for a joint scenario
'''
value = self.get_game_value(action_agent1, action_agent2)
agent1.add_action_value(action_agent1, value[0])
agent2.add_action_value(action_agent2, value[1])
self.agent1.add_extended_action_value(agent1.last_action * 3 + agent2.last_action , value[0])
self.agent2.add_extended_action_value(agent2.last_action * 3 + agent1.last_action, value[1])
return value
def run_joint(self, experiments = 1):
history_values_agent1 = np.empty((experiments, iterations))
history_values_agent2 = np.empty((experiments, iterations))
for e in range(experiments):
self.agent1.reset()
self.agent2.reset()
for i in range(self.iterations):
tmp_agent1_values = copy.copy(self.agent1.extended_values)
tmp_agent1_actions_count = copy.copy(self.agent1.extended_actions_count)
self.agent1.compute_action_joint(self.agent2.extended_values, self.agent2.extended_actions_count, i)
self.agent2.compute_action_joint(tmp_agent1_values, tmp_agent1_actions_count, i)
value = self.play(self.agent1.last_action, self.agent2.last_action)
history_values_agent1[e][i] = value[0]
history_values_agent2[e][i] = value[1]
self.history_values_agent1 = np.mean(history_values_agent1, axis=0)
self.history_values_agent2 = np.mean(history_values_agent2, axis=0)
def get_game_value(self, position_1, position_2):
'''
Obtains a tuple with the values for the players after each of them choose an
action/position to play. Player 1 is the row player and Player 2 the column one
'''
return (np.random.normal(self.game_values[position_1][position_2][0],
self.game_values[position_1][position_2][1]),
np.random.normal(self.game_values[position_1][position_2][0],
self.game_values[position_1][position_2][1]))
```
### Agent
Definition of the agent class which contains the history of the values and the methods to select a position for the game and play it.
```
class Agent(object):
def __init__(self):
self.reset()
def reset(self):
self.actions_count = np.ones(3) # count for the action taken
self.values = np.zeros(3) # values obtained so far -> average
def compute_action(self, iteration = None):
'''
Gets the position/action for the following game based on the policy of the agent.
For this base class the policy follows a random choice
'''
action = np.random.choice(3)
self.last_action = action
self.actions_count[action] += 1
def add_action_value(self, action, value):
self.values[action] = ((self.values[action] * (self.actions_count[action] - 1) + value)
/ (self.actions_count[action]))
class BoltzmannActionLearner(Agent):
def __init__(self, t):
self.t = t
super(BoltzmannActionLearner, self).__init__()
def compute_action(self, iteration = None):
'''
Gets the position/action for the following game based on the policy of the agent.
For this class the decision is taken based on the boltzmann definition
'''
if iteration != None:
t = 3 * ((self.num_iterations - iteration) / self.num_iterations)
numerator = np.exp(self.values / t)
denominator = np.sum(numerator)
pdf = numerator / denominator #probability distribution function
action = np.random.choice(len(self.values), p=pdf)
self.last_action = action
self.actions_count[action] += 1 #increment in the counter of the actions
class BoltzmannJointActionLearner(Agent):
def __init__(self, t, num_iterations):
self.t = t
self.num_iterations = num_iterations
super(BoltzmannJointActionLearner, self).__init__()
def __str__(self):
return 'Boltzamn JAL'
def reset(self):
self.actions_count = np.ones(3) # count for the action taken
self.values = np.zeros(3) # values obtained so far -> average
self.extended_actions_count = np.ones(9)
self.extended_values = np.zeros(9)
def compute_action(self, iteration = None):
'''
Gets the position/action for the following game based on the policy of the agent.
This method works as a simulation of the two agents into a single agent.
Not real practical application. Kept as utilitary for possible further testing
'''
numerator = np.exp(self.values / t)
denominator = np.sum(numerator)
pdf = numerator / denominator #probability distribution function
action = np.random.choice(len(self.values), p=pdf)
self.last_action = action
self.actions_count[action] += 1
def compute_action_joint(self, external_agent_values, external_agent_actions_count, iteration = None):
'''
Gets the position/action for the following game based on the policy of the agent
and the values of the external agent getting an average of the obtained values.'''
if iteration != None:
t = 0.05 * ((self.num_iterations - iteration) / self.num_iterations)
avg_values = ((self.extended_values + pseudo_transpose(external_agent_values))
/ (self.extended_actions_count + pseudo_transpose(external_agent_actions_count)))
numerator = np.exp(avg_values / t)
denominator = np.sum(numerator)
pdf = numerator / denominator #probability distribution function
action = np.random.choice(len(self.extended_values), p=pdf)
self.last_action = math.floor(action / 3)
self.actions_count[self.last_action] += 1
def add_extended_action_value(self, action, value):
self.extended_actions_count[action] += 1
self.extended_values[action] = ((self.extended_values[action] *
(self.extended_actions_count[action] - 1) + value)
/ (self.extended_actions_count[action]))
class OptimisticBoltzmannJointActionLearner(Agent):
def __init__(self, t, num_iterations):
self.t = t
self.num_iterations = num_iterations
super(OptimisticBoltzmannJointActionLearner, self).__init__()
def __str__(self):
return 'Optimistic Boltzamn JAL'
def reset(self):
self.actions_count = np.zeros(3) # count for the action taken
self.values = np.zeros(3) # values obtained so far -> average
self.extended_actions_count = np.ones(9)
self.extended_values = np.zeros(9)
self.max_values = np.zeros(9)
def compute_action_joint(self, ext_agent_max_values, ext_agent_actions_count, iteration = None):
'''
Gets the position/action for the following game based on the policy of the agent
and the values of the external agent getting an average of the obtained values.'''
if iteration != None:
t = 2 * ((self.num_iterations - iteration) / self.num_iterations)
avg_values = (self.max_values + ext_agent_max_values) / 2
numerator = np.exp(avg_values / t)
denominator = np.sum(numerator)
pdf = numerator / denominator #probability distribution function
action = np.random.choice(len(self.extended_values), p=pdf)
self.last_action = math.floor(action / 3)
self.actions_count[self.last_action] += 1
def add_action_value(self, action, value):
'''
Adds a corresponding action value taking into consideration the posibility
of a new max value for the chosen action
'''
# Re-asign max value if required
if value >= self.max_values[action]:
self.max_values[action] = value
self.values[action] = ((self.values[action] * (self.actions_count[action] - 1) + value)
/ (self.actions_count[action]))
def add_extended_action_value(self, action, value):
# Re-asign max value if required
if value >= self.max_values[action]:
self.max_values[action] = value
self.extended_actions_count[action] += 1
self.extended_values[action] = ((self.extended_values[action]
* (self.extended_actions_count[action] - 1) + value)
/ (self.extended_actions_count[action]))
```
### Exercise A
```
sigma = 0.2
sigma0 = 0.2
sigma1 = 0.2
iterations = 5000
experiments = 500 # Used to compute an average of the iterations and smooth the final charts
game_values = [[(11, sigma0), (-30, sigma), (0, sigma)],
[(-30, sigma), (7, sigma1), (6, sigma)],
[(0, sigma), (0, sigma), (5, sigma)]]
agent1 = BoltzmannJointActionLearner(None, iterations)
agent2 = BoltzmannJointActionLearner(None, iterations)
game = Game(game_values, iterations, agent1, agent2)
game.run_joint(experiments)
values_boltzman = moving_average((game.history_values_agent1
+ game.history_values_agent2) / 2, 10)
agent1 = OptimisticBoltzmannJointActionLearner(None, iterations)
agent2 = OptimisticBoltzmannJointActionLearner(None, iterations)
game = Game(game_values, iterations, agent1, agent2)
game.run_joint(experiments)
values_optimistic_boltzman = moving_average((game.history_values_agent1
+ game.history_values_agent2) / 2, 10)
plot_agents_avg_reward('Results - \u03C3 = \u03C3 0 = \u03C3 1 = {}'.format(sigma),
[values_boltzman, values_optimistic_boltzman],
['b-', 'r-'],
['Boltzman', 'OptimisticBoltzman'])
```
### Exercise B
```
sigma = 0.1
sigma0 = 4.0
sigma1 = 0.1
game_values = [[(11, sigma0), (-30, sigma), (0, sigma)],
[(-30, sigma), (7, sigma1), (6, sigma)],
[(0, sigma), (0, sigma), (5, sigma)]]
agent1 = BoltzmannJointActionLearner(None, iterations)
agent2 = BoltzmannJointActionLearner(None, iterations)
game = Game(game_values, iterations, agent1, agent2)
game.run_joint(experiments)
values_boltzman = moving_average((game.history_values_agent1
+ game.history_values_agent2) / 2, 10)
agent1 = OptimisticBoltzmannJointActionLearner(None, iterations)
agent2 = OptimisticBoltzmannJointActionLearner(None, iterations)
game = Game(game_values, iterations, agent1, agent2)
game.run_joint(experiments)
values_optimistic_boltzman = moving_average((game.history_values_agent1
+ game.history_values_agent2) / 2, 10)
plot_agents_avg_reward('Results - \u03C3 = {}, \u03C3 0 = {}, \u03C3 1 = {}'. format(sigma, sigma0, sigma1),
[values_boltzman, values_optimistic_boltzman],
['b-', 'r-'],
['Boltzman', 'OptimisticBoltzman'])
```
### Exercise C
```
sigma = 0.1
sigma0 = 0.1
sigma1 = 4.0
game_values = [[(11, sigma0), (-30, sigma), (0, sigma)],
[(-30, sigma), (7, sigma1), (6, sigma)],
[(0, sigma), (0, sigma), (5, sigma)]]
agent1 = BoltzmannJointActionLearner(None, iterations)
agent2 = BoltzmannJointActionLearner(None, iterations)
game = Game(game_values, iterations, agent1, agent2)
game.run_joint(experiments)
values_boltzman = moving_average((game.history_values_agent1
+ game.history_values_agent2) / 2, 10)
agent1 = OptimisticBoltzmannJointActionLearner(None, iterations)
agent2 = OptimisticBoltzmannJointActionLearner(None, iterations)
game = Game(game_values, iterations, agent1, agent2)
game.run_joint(experiments)
values_optimistic_boltzman = moving_average((game.history_values_agent1
+ game.history_values_agent2) / 2, 10)
plot_agents_avg_reward('Results - \u03C3 = {}, \u03C3 0 = {}, \u03C3 1 = {}'. format(sigma, sigma0, sigma1),
[values_boltzman, values_optimistic_boltzman],
['b-', 'r-'],
['Boltzman', 'OptimisticBoltzman'])
```
| true |
code
| 0.637369 | null | null | null | null |
|
# Artificial Intelligence in Finance
## Data-Driven Finance (a)
## Financial Econometrics and Regression
```
import numpy as np
def f(x):
return 2 + 1 / 2 * x
x = np.arange(-4, 5)
x
y = f(x)
y
x
y
beta = np.cov(x, y, ddof=0)[0, 1] / x.var()
beta
alpha = y.mean() - beta * x.mean()
alpha
y_ = alpha + beta * x
np.allclose(y_, y)
```
## Data Availability
In addition to a (paid) subscribtion to the Eikon Data API (https://developers.refinitiv.com/eikon-apis/eikon-data-apis), the following code requires the `eikon` Python package:
pip install eikon
```
import eikon as ek
import configparser
c = configparser.ConfigParser()
c.read('../aiif.cfg')
ek.set_app_key(c['eikon']['app_id'])
ek.__version__
symbols = ['AAPL.O', 'MSFT.O', 'NFLX.O', 'AMZN.O']
data = ek.get_timeseries(symbols,
fields='CLOSE',
start_date='2019-07-01',
end_date='2020-07-01')
data.info()
data.tail()
data = ek.get_timeseries('AMZN.O',
fields='*',
start_date='2020-09-24',
end_date='2020-09-25',
interval='minute')
data.info()
data.head()
data_grid, err = ek.get_data(['AAPL.O', 'IBM', 'GOOG.O', 'AMZN.O'],
['TR.TotalReturnYTD', 'TR.WACCBeta',
'YRHIGH', 'YRLOW',
'TR.Ebitda', 'TR.GrossProfit'])
data_grid
```
In addition to a (free paper trading) account with Oanda (http://oanda.com), the following code requires the `tpqoa` package:
pip install --upgrade git+https://github.com/yhilpisch/tpqoa.git
```
import tpqoa
oa = tpqoa.tpqoa('../aiif.cfg')
oa.stream_data('BTC_USD', stop=5)
data = ek.get_timeseries('AAPL.O',
fields='*',
start_date='2020-09-25 15:00:00',
end_date='2020-09-25 15:15:00',
interval='tick')
data.info()
data.head(8)
news = ek.get_news_headlines('R:TSLA.O PRODUCTION',
date_from='2020-06-01',
date_to='2020-08-01',
count=7
)
news
storyId = news['storyId'][1]
from IPython.display import HTML
HTML(ek.get_news_story(storyId))
import nlp
import requests
sources = [
'https://nr.apple.com/dE0b1T5G3u', # iPad Pro
'https://nr.apple.com/dE4c7T6g1K', # MacBook Air
'https://nr.apple.com/dE4q4r8A2A', # Mac Mini
]
html = [requests.get(url).text for url in sources]
data = [nlp.clean_up_text(t) for t in html]
data[0][0:1001]
from twitter import Twitter, OAuth
t = Twitter(auth=OAuth(c['twitter']['access_token'],
c['twitter']['access_secret_token'],
c['twitter']['api_key'],
c['twitter']['api_secret_key']),
retry=True)
l = t.statuses.home_timeline(count=15)
for e in l:
print(e['text'])
l = t.statuses.user_timeline(screen_name='dyjh', count=5)
for e in l:
print(e['text'])
d = t.search.tweets(q='#Python', count=7)
for e in d['statuses']:
print(e['text'])
l = t.statuses.user_timeline(screen_name='elonmusk', count=50)
tl = [e['text'] for e in l]
tl[:5]
wc = nlp.generate_word_cloud(' '.join(tl), 35)
```
## Normative Theories Revisited
### Mean-Variance Portfolio Theory
```
import numpy as np
import pandas as pd
from pylab import plt, mpl
from scipy.optimize import minimize
plt.style.use('seaborn')
mpl.rcParams['savefig.dpi'] = 300
mpl.rcParams['font.family'] = 'serif'
np.set_printoptions(precision=5, suppress=True,
formatter={'float': lambda x: f'{x:6.3f}'})
url = 'http://hilpisch.com/aiif_eikon_eod_data.csv'
raw = pd.read_csv(url, index_col=0, parse_dates=True).dropna()
raw.info()
symbols = ['AAPL.O', 'MSFT.O', 'INTC.O', 'AMZN.O', 'GLD']
rets = np.log(raw[symbols] / raw[symbols].shift(1)).dropna()
(raw[symbols[:]] / raw[symbols[:]].iloc[0]).plot(figsize=(10, 6));
weights = len(rets.columns) * [1 / len(rets.columns)]
weights
def port_return(rets, weights):
return np.dot(rets.mean(), weights) * 252 # annualized
port_return(rets, weights)
def port_volatility(rets, weights):
return np.dot(weights, np.dot(rets.cov() * 252 , weights)) ** 0.5 # annualized
port_volatility(rets, weights)
def port_sharpe(rets, weights):
return port_return(rets, weights) / port_volatility(rets, weights)
port_sharpe(rets, weights)
w = np.random.random((1000, len(symbols)))
w = (w.T / w.sum(axis=1)).T
w[:5]
w[:5].sum(axis=1)
pvr = [(port_volatility(rets[symbols], weights),
port_return(rets[symbols], weights))
for weights in w]
pvr = np.array(pvr)
psr = pvr[:, 1] / pvr[:, 0]
plt.figure(figsize=(10, 6))
fig = plt.scatter(pvr[:, 0], pvr[:, 1],
c=psr, cmap='coolwarm')
cb = plt.colorbar(fig)
cb.set_label('Sharpe ratio')
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.title(' | '.join(symbols));
bnds = len(symbols) * [(0, 1),]
bnds
cons = {'type': 'eq', 'fun': lambda weights: weights.sum() - 1}
opt_weights = {}
for year in range(2010, 2019):
rets_ = rets[symbols].loc[f'{year}-01-01':f'{year}-12-31']
ow = minimize(lambda weights: -port_sharpe(rets_, weights),
len(symbols) * [1 / len(symbols)],
bounds=bnds,
constraints=cons)['x']
opt_weights[year] = ow
opt_weights
res = pd.DataFrame()
for year in range(2010, 2019):
rets_ = rets[symbols].loc[f'{year}-01-01':f'{year}-12-31']
epv = port_volatility(rets_, opt_weights[year])
epr = port_return(rets_, opt_weights[year])
esr = epr / epv
rets_ = rets[symbols].loc[f'{year + 1}-01-01':f'{year + 1}-12-31']
rpv = port_volatility(rets_, opt_weights[year])
rpr = port_return(rets_, opt_weights[year])
rsr = rpr / rpv
res = res.append(pd.DataFrame({'epv': epv, 'epr': epr, 'esr': esr,
'rpv': rpv, 'rpr': rpr, 'rsr': rsr},
index=[year + 1]))
res
res.mean()
res[['epv', 'rpv']].corr()
res[['epv', 'rpv']].plot(kind='bar', figsize=(10, 6),
title='Expected vs. Realized Portfolio Volatility');
res[['epr', 'rpr']].corr()
res[['epr', 'rpr']].plot(kind='bar', figsize=(10, 6),
title='Expected vs. Realized Portfolio Return');
res[['esr', 'rsr']].corr()
res[['esr', 'rsr']].plot(kind='bar', figsize=(10, 6),
title='Expected vs. Realized Sharpe Ratio');
```
### Capital Asset Pricing Model
```
r = 0.005
market = '.SPX'
rets = np.log(raw / raw.shift(1)).dropna()
res = pd.DataFrame()
for sym in rets.columns[:4]:
print('\n' + sym)
print(54 * '=')
for year in range(2010, 2019):
rets_ = rets.loc[f'{year}-01-01':f'{year}-12-31']
muM = rets_[market].mean() * 252
cov = rets_.cov().loc[sym, market]
var = rets_[market].var()
beta = cov / var
rets_ = rets.loc[f'{year + 1}-01-01':f'{year + 1}-12-31']
muM = rets_[market].mean() * 252
mu_capm = r + beta * (muM - r)
mu_real = rets_[sym].mean() * 252
res = res.append(pd.DataFrame({'symbol': sym,
'mu_capm': mu_capm,
'mu_real': mu_real},
index=[year + 1]),
sort=True)
print('{} | beta: {:.3f} | mu_capm: {:6.3f} | mu_real: {:6.3f}'
.format(year + 1, beta, mu_capm, mu_real))
sym = 'AMZN.O'
res[res['symbol'] == sym].corr()
res[res['symbol'] == sym].plot(kind='bar',
figsize=(10, 6), title=sym);
grouped = res.groupby('symbol').mean()
grouped
grouped.plot(kind='bar', figsize=(10, 6), title='Average Values');
```
### Arbitrage-Pricing Theory
```
factors = ['.SPX', '.VIX', 'EUR=', 'XAU=']
res = pd.DataFrame()
np.set_printoptions(formatter={'float': lambda x: f'{x:5.2f}'})
for sym in rets.columns[:4]:
print('\n' + sym)
print(71 * '=')
for year in range(2010, 2019):
rets_ = rets.loc[f'{year}-01-01':f'{year}-12-31']
reg = np.linalg.lstsq(rets_[factors],
rets_[sym], rcond=-1)[0]
rets_ = rets.loc[f'{year + 1}-01-01':f'{year + 1}-12-31']
mu_apt = np.dot(rets_[factors].mean() * 252, reg)
mu_real = rets_[sym].mean() * 252
res = res.append(pd.DataFrame({'symbol': sym,
'mu_apt': mu_apt, 'mu_real': mu_real},
index=[year + 1]))
print('{} | fl: {} | mu_apt: {:6.3f} | mu_real: {:6.3f}'
.format(year + 1, reg.round(2), mu_apt, mu_real))
sym = 'AMZN.O'
res[res['symbol'] == sym].corr()
res[res['symbol'] == sym].plot(kind='bar',
figsize=(10, 6), title=sym);
grouped = res.groupby('symbol').mean()
grouped
grouped.plot(kind='bar', figsize=(10, 6), title='Average Values');
factors = pd.read_csv('http://hilpisch.com/aiif_eikon_eod_factors.csv',
index_col=0, parse_dates=True)
factors.info()
(factors / factors.iloc[0]).plot(figsize=(10, 6));
start = '2017-01-01'
end = '2020-01-01'
retsd = rets.loc[start:end].copy()
retsd.dropna(inplace=True)
retsf = np.log(factors / factors.shift(1))
retsf = retsf.loc[start:end]
retsf.dropna(inplace=True)
retsf = retsf.loc[retsd.index].dropna()
retsf.corr()
res = pd.DataFrame()
np.set_printoptions(formatter={'float': lambda x: f'{x:5.2f}'})
split = int(len(retsf) * 0.5)
for sym in rets.columns[:4]:
print('\n' + sym)
print(74 * '=')
retsf_, retsd_ = retsf.iloc[:split], retsd.iloc[:split]
reg = np.linalg.lstsq(retsf_, retsd_[sym], rcond=-1)[0]
retsf_, retsd_ = retsf.iloc[split:], retsd.iloc[split:]
mu_apt = np.dot(retsf_.mean() * 252, reg)
mu_real = retsd_[sym].mean() * 252
res = res.append(pd.DataFrame({'mu_apt': mu_apt,
'mu_real': mu_real}, index=[sym,]),
sort=True)
print('fl: {} | apt: {:.3f} | real: {:.3f}'
.format(reg.round(1), mu_apt, mu_real))
res.plot(kind='bar', figsize=(10, 6));
sym
rets_sym = np.dot(retsf_, reg)
rets_sym = pd.DataFrame(rets_sym,
columns=[sym + '_apt'],
index=retsf_.index)
rets_sym[sym + '_real'] = retsd_[sym]
rets_sym.mean() * 252
rets_sym.std() * 252 ** 0.5
rets_sym.corr()
rets_sym.cumsum().apply(np.exp).plot(figsize=(10, 6));
rets_sym['same'] = (np.sign(rets_sym[sym + '_apt']) ==
np.sign(rets_sym[sym + '_real']))
rets_sym['same'].value_counts()
rets_sym['same'].value_counts()[True] / len(rets_sym)
```
<img src='http://hilpisch.com/taim_logo.png' width="350px" align="right">
<br><br><br><a href="http://tpq.io" target="_blank">http://tpq.io</a> | <a href="http://twitter.com/dyjh" target="_blank">@dyjh</a> | <a href="mailto:ai@tpq.io">ai@tpq.io</a>
| true |
code
| 0.419856 | null | null | null | null |
|
```
name = '2017-06-02-matplotlib-contourf-subplots'
title = 'Filled contour plots and colormap normalization'
tags = 'matplotlib'
author = 'Maria Zamyatina'
from nb_tools import connect_notebook_to_post
from IPython.core.display import HTML, Image
html = connect_notebook_to_post(name, title, tags, author)
```
Today we are going to learn some tricks about plotting two dimensional data with matplotlib contourf function.
```
import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
%matplotlib inline
```
Let us start with creating two sample 2D arrays, Z1 and Z2.
```
# Array 1
delta1 = 0.025
x1 = np.arange(-3.0, 3.0, delta1)
y1 = np.arange(-2.0, 2.0, delta1)
X1, Y1 = np.meshgrid(x1, y1)
Z1_1 = mlab.bivariate_normal(X1, Y1, 1.0, 1.0, 0.0, 0.0)
Z2_1 = mlab.bivariate_normal(X1, Y1, 1.5, 0.5, 1, 1)
Z1 = 10.0 * (Z2_1 - Z1_1)
# Array 2
delta2 = 0.05
x2 = np.arange(-6.0, 6.0, delta2)
y2 = np.arange(-4.0, 4.0, delta2)
X2, Y2 = np.meshgrid(x2, y2)
Z1_2 = mlab.bivariate_normal(X2, Y2, 1.0, 1.0, 0.0, 0.0)
Z2_2 = mlab.bivariate_normal(X2, Y2, 1.5, 0.5, 1, 1)
Z2 = 30.0 * (Z2_2 - Z1_2)
print(Z1.shape, Z2.shape)
```
And now straight to plotting!
Step 0. Plot Z1, Z2 and the difference between them on the three subplots using contourf().
```
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(12, 4))
ax[0].contourf(X1, Y1, Z1)
ax[1].contourf(X2, Y2, Z2)
ax[2].contourf(X2, Y2, Z1 - Z2)
ax[0].set_title('Z1')
ax[1].set_title('Z2')
ax[2].set_title('diff')
plt.ioff()
```
Step 1. Add a colorbar to each of the subplots in order to be able to interpret the data. Alternatively we could have chosen to use contour() to add contours on top of filled contours, but not today.
```
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(14, 4))
p1 = ax[0].contourf(X1, Y1, Z1)
p2 = ax[1].contourf(X2, Y2, Z2)
p3 = ax[2].contourf(X2, Y2, Z1 - Z2)
fig.colorbar(p1, ax=ax[0])
fig.colorbar(p2, ax=ax[1])
fig.colorbar(p3, ax=ax[2])
ax[0].set_title('Z1')
ax[1].set_title('Z2')
ax[2].set_title('diff')
plt.ioff()
```
> Why did we call fig.colobar(...), not ax.colorbar(...)? The reason is that creation of a colorbar requires addition of a new axis to the figure. Think about the following for a moment:
> * By writing ax[0].contourf(..., Z1) you say 'display Z1 using contourf() method of axis [0] on axis [0]'. In other words, you use axis method to reserve axis [0] for displaying Z1, and unless you want to overlay Z1 with some other array, you can't use axis [0] for anything else.
> * Colorbar is exactly 'something else', something extra, that needs to be shown on an additional axis, and in order to create such an axis we use a figure method, fig.colorbar().
> Why fig.colorbar(p1, ...), not fig.colorbar(...)? The reason is that we need to pass an object to the fig.colorbar(), which we want to show the colorbar for. To have a colorbar for one subplot we need to do two things:
> 1. Create the required object (known as mappable in Python terminology) by assigning the output from contourf() to a variable, e.g. p1.
> 2. Pass the object to fig.colorbar().
Step 2. If Z1 and Z2 describe the same variable, it is logical to have the same colorbar for the first two subplots.
> **Tip**. If you want to have **one colorbar for two or more contour plots**, then you need to not only control the colorbar, but also control the levels in these contour plots. That is, to compare the same levels between the plots, the plots should have the same contour levels. One way of doing this is to calculate the levels ahead of time.
Let us create an array of equally spaced values (or levels) that encompasses minima and maxima from both datasets and pass this array to levels keyword of contourf().
```
print(Z1.min(), Z1.max(), Z2.min(), Z2.max())
Z_range = np.arange( round(min(Z1.min(), Z2.min()))-1, round(max(Z1.max(), Z2.max()))+2, 1)
Z_range
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(14, 4))
p1 = ax[0].contourf(X1, Y1, Z1, levels=Z_range)
p2 = ax[1].contourf(X2, Y2, Z2, levels=Z_range)
p3 = ax[2].contourf(X2, Y2, Z1 - Z2)
fig.colorbar(p1, ax=ax[0])
fig.colorbar(p2, ax=ax[1])
fig.colorbar(p3, ax=ax[2])
ax[0].set_title('Z1')
ax[1].set_title('Z2')
ax[2].set_title('diff')
plt.ioff()
```
Note that it has become much easier to see that the gradients on the first subplot are much smaller than on the second one. At the same time, though, having a colorbar for each of the two subplots has become redundant.
Step 3. Create a common colorbar for the first two suplots.
```
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(14, 4))
p1 = ax[0].contourf(X1, Y1, Z1, levels=Z_range)
p2 = ax[1].contourf(X2, Y2, Z2, levels=Z_range)
p3 = ax[2].contourf(X2, Y2, Z1 - Z2)
fig.colorbar(p3, ax=ax[2])
cax = fig.add_axes([0.18, 0., 0.4, 0.03])
fig.colorbar(p1, cax=cax, orientation='horizontal')
ax[0].set_title('Z1')
ax[1].set_title('Z2')
ax[2].set_title('diff')
plt.ioff()
```
Step 4. Use a diverging colormap for plotting the difference between arrays.
```
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(14, 4))
p1 = ax[0].contourf(X1, Y1, Z1, levels=Z_range)
p2 = ax[1].contourf(X2, Y2, Z2, levels=Z_range)
p3 = ax[2].contourf(X2, Y2, Z1 - Z2, cmap='RdBu_r')
fig.colorbar(p3, ax=ax[2])
cax = fig.add_axes([0.18, 0., 0.4, 0.03])
fig.colorbar(p1, cax=cax, orientation='horizontal')
ax[0].set_title('Z1')
ax[1].set_title('Z2')
ax[2].set_title('diff')
plt.ioff()
```
> **Tip**. If the **range of your data is non-symmetrical around zero**, but you want to **set the middle point of a colormap to zero**, you could try to **normalize** your **colormap**.
Step 5. Introduce MidpointNormalize class that would scale data values to colors and add the capability to specify the middle point of a colormap. Use norm keyword of contourf().
```
import matplotlib.colors as colors
class MidpointNormalize(colors.Normalize):
def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
self.midpoint = midpoint
colors.Normalize.__init__(self, vmin, vmax, clip)
def __call__(self, value, clip=None):
# I'm ignoring masked values and all kinds of edge cases to make a
# simple example...
x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
return np.ma.masked_array(np.interp(value, x, y))
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15, 4))
p1 = ax[0].contourf(X1, Y1, Z1, levels=Z_range)
p2 = ax[1].contourf(X2, Y2, Z2, levels=Z_range)
p3 = ax[2].contourf(X2, Y2, Z1 - Z2, norm=MidpointNormalize(midpoint=0.), cmap='RdBu_r')
fig.colorbar(p3, ax=ax[2])
cax = fig.add_axes([0.18, 0., 0.4, 0.03])
fig.colorbar(p1, cax=cax, orientation='horizontal')
ax[0].set_title('Z1')
ax[1].set_title('Z2')
ax[2].set_title('diff')
plt.ioff()
```
## References:
* Anatomy of matplotlib | SciPy 2015 Tutorial | Benjamin Root and Joe Kington (https://www.youtube.com/watch?v=MKucn8NtVeI)
* https://stackoverflow.com/questions/26065811/same-color-bar-range-for-different-plots-matplotlib?answertab=active#tab-top
* https://matplotlib.org/users/colormapnorms.html
* https://stackoverflow.com/questions/7404116/defining-the-midpoint-of-a-colormap-in-matplotlib/7746125#7746125
```
HTML(html)
```
| true |
code
| 0.651022 | null | null | null | null |
|
# Symbulate Documentation
# Random Processes
<a id='contents'></a>
1. [**RandomProcess and TimeIndex**](#time)
1. [**Defining a RandomProcess explicitly as a function of time**](#Xt)
1. [**Process values at particular time points**](#value)
1. [**Mean function**](#mean)
1. [**Defining a RandomProcess incrementally**](#rw)
< [Conditioning](conditioning.html) | [Contents](index.html) | [Markov processes](mc.html) >
Be sure to import Symbulate using the following commands.
```
from symbulate import *
%matplotlib inline
```
<a id='process'></a>
### Random processes
A **random process** (a.k.a. **stochastic process**) is an indexed collection of random variables defined on some probability space. The index often represents "time", which can be either discrete or continuous.
- A **discrete time stochastic process** is a collection of countably many random variables, e.g. $X_n$ for $n=0 ,1, 2,\ldots$. For each outcome in the probability space, the outcome of a discrete time stochastic process is a *sequence* (in $n$). (Remember Python starts indexing at 0. The zero-based-index is often natural in stochastic process contexts in which there is a time 0, i.e. $X_0$ is the initial value of the process.)
- A **continuous time stochastic process** is a collection of uncountably many random variables, e.g. $X_t$ for $t\ge0$. For each outcome in the probability space, the outcome of a discrete time stochastic process is a *function* (a.k.a. *sample path*) (of $t$).
<a id='time'></a>
### RandomProcess and TimeIndex
Much like `RV`, a **RandomProcess** can be defined on a ProbabilitySpace. For a `RandomProcess`, however, the **TimeIndex** must also be specified. TimeIndex takes a single parameter, the **sampling frequency** `fs`. While many values of `fs` are allowed, the two most common inputs for `fs` are
* `TimeIndex(fs=1)`, for a discrete time process $X_n, n = 0, 1, 2, \ldots$.
* `TimeIndex(fs=inf)`, for a continuous time process $X(t), t\ge0$.
<a id='Xt'></a>
### Defining a RandomProcess explicity as a function of time
A random variable is a function $X$ which maps an outcome $\omega$ in a probability space $\Omega$ to a real value $X(\omega)$. Similarly, a random process is a function $X$ which maps an outcome $\omega$ and a time $t$ in the time index set to the process value at that time $X(\omega, t)$. In some situations, the function defining the random process can be specified explicitly.
*Example.* Let $X(t) = A + B t, t\ge0$ where $A$ and $B$ are independent with $A\sim$ Bernoulli(0.9) and $B\sim$ Bernoulli(0.7). In this case, there are only 4 possible sample paths.
* $X(t) = 0$, when $A=0, B=0$, which occurs with probability $0.03$
* $X(t) = 1$, when $A=1, B=0$, which occurs with probability $0.27$
* $X(t) = t$, when $A=0, B=1$, which occurs with probability $0.07$
* $X(t) = 1+t$, when $A=1, B=1$, which occurs with probability $0.63$
The following code defines a RandomProcess `X` by first defining an appropriate function `f`. Note that an outcome in the probability space consists of an $A, B$ pair, represented as $\omega_0$ and $\omega_1$ in the function. A RandomProcess is then defined by specifying: the probability space, the time index set, and the $X(\omega, t)$ function.
```
def f(omega, t):
return omega[0] + omega[1] * t
X = RandomProcess(Bernoulli(0.9) * Bernoulli(0.7), TimeIndex(fs=inf), f)
```
Like RV, RandomProcess only defines the random process. Values of the process can be simulated using the usual [simulation tools](sim.html). Since a stochastic process is a collection of random variables, many of the commands in the previous sections ([Random variables](rv.html), [Multiple random variables](joint.html), [Conditioning](conditioning.html)) are useful when simulating stochastic processes.
For a given outcome in the probability space, a random process outputs a **sample path** which describes how the value of the process evolves over time for that particular outcome. Calling `.plot()` for a RandomProcess will return a plot of sample paths. The parameter `alpha` controls the weight of the line drawn in the plot. The paramaters `tmin` and `tmax` control the range of time values in the display.
```
X.sim(1).plot(alpha = 1)
```
Simulate and plot many sample paths, specifying the range of $t$ values to plot. Note that the darkness of a path represents its relative likelihood.
```
X.sim(100).plot(tmin=0, tmax=2)
```
<a id='value'></a>
### Process values at particular time points
The value $X(t)$ (or $X_n$) of a stochastic process at any particular point in time $t$ (or $n$) is a random variable. These random variables can be accessed using brackets `[]`. Note that the value inside the brackets represents *time* $t$ or $n$. Many of the commands in the previous sections ([Random variables](rv.html), [Multiple random variables](joint.html), [Conditioning](conditioning.html)) are useful when simulating stochastic processes.
*Example.* Let $X(t) = A + B t, t\ge0$ where $A$ and $B$ are independent with $A\sim$ Bernoulli(0.9) and $B\sim$ Bernoulli(0.7).
Find the distribution of $X(1.5)$, the process value at time $t=1.5$.
```
def f(omega, t):
return omega[0] * t + omega[1]
X = RandomProcess(Bernoulli(0.9) * Bernoulli(0.7), TimeIndex(fs=inf), f)
X[1.5].sim(10000).plot()
```
Find the joint distribution of process values at times 1 and 1.5.
```
(X[1] & X[1.5]).sim(1000).plot("tile")
```
Find the conditional distribution of $X(1.5)$ given $X(1) = 1)$.
```
(X[1.5] | (X[1] == 1)).sim(10000).plot()
```
<a id='mean'></a>
### Mean function
The mean function of a stochastic process $X(t)$ is a deterministic function which maps $t$ to $E(X(t))$. The mean function can be estimated and plotted by simulating many sample paths of the process and using `.mean()`.
```
paths = X.sim(1000)
plot(paths)
plot(paths.mean(), 'r')
```
The **variance** function maps $t$ to $Var(X(t))$; similarly for the **standard deviation** function. These functions can be used to give error bands about the mean function.
```
# This illustrates the functionality, but is not an appropriate example for +/- 2SD
plot(paths)
paths.mean().plot('--')
(paths.mean() + 2 * paths.sd()).plot('--')
(paths.mean() - 2 * paths.sd()).plot('--')
```
<a id='rw'></a>
### Defining a RandomProcess incrementally
There are few situations like the linear process in the example above in which the random process can be expressed explicitly as a function of the probability space outcome and the time value. More commonly, random processes are often defined incrementally, by specifying the next value of the process given the previous value.
*Example.* At each point in time $n=0, 1, 2, \ldots$ a certain type of "event" either occurs or not. Suppose the probability that the event occurs at any particular time is $p=0.5$, and occurrences are independent from time to time. Let $Z_n=1$ if an event occurs at time $n$, and $Z_n=0$ otherwise. Then $Z_0, Z_1, Z_2,\ldots$ is a **Bernoulli process**. In a Bernoulli process, let $X_n$ count the number of events that have occurred up to and including time $n$, starting with 0 events at time 0. Since $Z_{n+1}=1$ if an event occurs at time $n+1$ and $Z_{n+1} = 0$ otherwise, $X_{n+1} = X_n + Z_{n+1}$.
The following code defines the random process $X$. The probability space corresponds to the independent Bernoulli random variables; note that `inf` allows for infinitely many values. Also notice how the process is defined incrementally through $X_{n+1} = X_n + Z_{n+1}$.
```
P = Bernoulli(0.5)**inf
Z = RV(P)
X = RandomProcess(P, TimeIndex(fs=1))
X[0] = 0
for n in range(100):
X[n+1] = X[n] + Z[n+1]
```
The above code defines a random process incrementally. Once a RandomProcess is defined, it can be manipulated the same way, regardless of how it is defined.
```
X.sim(1).plot(alpha = 1)
X.sim(100).plot(tmin = 0, tmax = 5)
X[5].sim(10000).plot()
(X[5] & X[10]).sim(10000).plot("tile")
(X[10] | (X[5] == 3)).sim(10000).plot()
(X[5] | (X[10] == 4)).sim(10000).plot()
```
< [Conditioning](conditioning.html) | [Contents](index.html) | [Markov processes](mc.html) >
| true |
code
| 0.646265 | null | null | null | null |
|
# Autoencoders
## Imports
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
```
## Load Dataset
```
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255
x_test = x_test.astype('float32') / 255
print(x_train)
print(x_test)
x_train = x_train[..., tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape)
```
### Adding noise to images
```
noise_factor = 0.2
x_train_noisy = x_train + noise_factor * tf.random.normal(shape=x_train.shape)
x_test_noisy = x_test + noise_factor * tf.random.normal(shape=x_test.shape)
x_train_noisy = tf.clip_by_value(x_train_noisy, clip_value_min=0., clip_value_max=1.)
x_test_noisy = tf.clip_by_value(x_test_noisy, clip_value_min=0., clip_value_max=1.)
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i+1)
plt.title("Original + Noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
plt.show()
```
## Model
```
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3,3), activation='relu', padding='same', strides=2),
layers.Conv2D(8, (3,3), activation='relu', padding='same', strides=2)
])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3,3), activation='sigmoid', padding='same')
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
autoencoder.encoder.summary()
```
## Optimizer
```
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
```
## Train
```
autoencoder.fit(x_train_noisy, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test_noisy, x_test))
autoencoder.decoder.summary()
```
## Testing
```
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
ax = plt.subplot(2, n, i+1)
plt.title('Original + Noise')
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
bx = plt.subplot(2, n, i+n+1)
plt.title("Reconstructed")
plt.imshow(tf.squeeze(decoded_imgs[i]))
plt.gray()
bx.get_xaxis().set_visible(False)
bx.get_yaxis().set_visible(False)
plt.show()
```
credits: [Intro to Autoencoders](https://www.tensorflow.org/tutorials/generative/autoencoder#:~:text=An%20autoencoder%20is%20a%20special,representation%20back%20to%20an%20image.)
| true |
code
| 0.746745 | null | null | null | null |
|
# Semantic Vector Space
Construct a basic semantic vector set for disambiguating coordinate relations.
```
import collections
from datetime import datetime
from tools.langtools import PositionsTF
from tools.significance import apply_fishers, contingency_table
from tools.locations import data_locations
from cxbuilders import wordConstructions
from sklearn.metrics.pairwise import pairwise_distances
from scipy.stats import chi2_contingency
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
from tf.app import use
from tf.fabric import Fabric
# load custom BHSA data + heads
TF = Fabric(locations=data_locations.values())
load_features = ['g_cons_utf8', 'trailer_utf8', 'label', 'lex',
'role', 'rela', 'typ', 'function', 'language',
'pdp', 'gloss', 'vs', 'vt', 'nhead', 'head',
'mother', 'nu', 'prs', 'sem_set', 'ls', 'st',
'kind', 'top_assoc', 'number', 'obj_prep',
'embed', 'freq_lex', 'sp']
api = TF.load(' '.join(load_features))
F, E, T, L = api.F, api.E, api.T, api.L # shortform TF methods
A = use('bhsa', api=api, silent=True)
A.displaySetup(condenseType='phrase', withNodes=True, extraFeatures='lex')
```
## Get Context Counts Around Window (bag of words)
For every lexeme found in a timephrase, count the other lexemes that occur in it's vicinity of 5 words for every occurrence of that word in the Hebrew Bible. This allows us to construct an approximate semantic profile that can be compared between terms.
A "bag of words" model means that we do not consider the position of a context word relative to the target word (i.e. "ngrams").
```
words = wordConstructions(A)
words.findall(2)
def get_window(word, model='bagofwords'):
'''
Build a contextual window, return context words.
'''
window = 5
context = 'sentence'
confeat = 'lex'
P = PositionsTF(word, context, A).get
fore = list(range(-window, 0))
back = list(range(1, window+1))
conwords = []
for pos in (fore + back):
cword = P(pos, confeat)
if cword:
if model == 'bagofwords':
conwords.append(f'{cword}')
elif model == 'ngram':
conwords.append(f'{pos}.{cword}')
return conwords
wordcons = collections.defaultdict(lambda:collections.Counter())
timelexs = set()
for ph in F.otype.s('timephrase'):
for w in L.d(ph,'word'):
cx = words.findall(w)[0]
if cx.name == 'cont':
timelexs.add(L.u(w,'lex')[0])
timewords = set(
w for lex in timelexs
for w in L.d(lex,'word')
)
print(f'{len(timewords)} timewords ready for analysis...')
for w in timewords:
context = get_window(w)
wordcons[F.lex.v(w)].update(context)
wordcons = pd.DataFrame(wordcons).fillna(0)
print(f'{wordcons.shape[1]} words analyzed...')
print(f'\t{wordcons.shape[0]} word contexts analyzed...')
wordcons.head()
wordcons.shape[0] * wordcons.shape[1]
wordcons['CNH/'].sort_values(ascending=False).head(10)
```
## Measure Target Word / Context Associations
```
# contingency table
ct = contingency_table(wordcons)
```
### Apply ΔP
We need an efficient (i.e. simple) normalization method for such a large dataset. ΔP is such a test that includes contingency information [(Gries 2008)](https://www.researchgate.net/publication/233650934_Dispersions_and_adjusted_frequencies_in_corpora_further_explorations).
```
a = wordcons
b = ct['b']
c = ct['c']
d = ct['d']
deltap = (a/(a+b)) - (c/(c+d)).fillna(0)
```
## Calculate Cosine Distance
```
distances_raw = pairwise_distances(np.nan_to_num(deltap.T.values), metric='cosine')
dist = pd.DataFrame(distances_raw, columns=wordcons.columns, index=wordcons.columns)
```
## Testing Efficacy
We want to use semantic vectors to disambiguate coordinate relations when there is more than one candidate to connect a target to.
### Hypothesis: Candidates for coordinate pairs can be distinguished by selecting the candidate with the shortest distance in semantic space from the target word.
```
def show_dist(target, compares):
"""Return candidates in order of distance."""
return sorted(
(dist[target][comp], comp)
for comp in compares
)
```
### K>B: with XLH or JWM?
```
A.pretty(777703)
show_dist('K>B/', ('XLH[', 'JWM/'))
```
Success. The test shows that XLH is more semantically similar.
### <RPL: <NN or JWM?
```
A.pretty(817713)
show_dist('<RPL/', ('JWM/', '<NN/'))
```
Success. <NN/ is correctly selected as more semantically similar.
### >PLH/: LJLH or >JCWN?
```
A.pretty(862564)
show_dist('>PLH/', ('LJLH/', '>JCWN/'))
```
Sucess. LJLH is most similar semantically.
### MRWD: <NJH or JWM?
```
A.pretty(872677)
show_dist('MRWD/', ('<NJ=/', 'JWM/'))
```
Sucess.
### >M: >B or MWT?
```
A.pretty(874237)
show_dist('>M/', ('>B/', 'MWT/'))
```
Sucess.
# Export Vector Resource
```
import pickle
dist_dict = dist.to_dict()
with open('semvector.pickle', 'wb') as outfile:
pickle.dump(dist_dict, outfile)
```
| true |
code
| 0.490297 | null | null | null | null |
|
# TensorFlow实现VGG16
## 导入需要使用的库
```
import inspect
import os
import numpy as np
import tensorflow as tf
```
## 定义卷积层
```
'''Convolution op wrapper, use RELU activation after convolution
Args:
layer_name: e.g. conv1, pool1...
x: input tensor, [batch_size, height, width, channels]
out_channels: number of output channels (or comvolutional kernels)
kernel_size: the size of convolutional kernel, VGG paper used: [3,3]
stride: A list of ints. 1-D of length 4. VGG paper used: [1, 1, 1, 1]
is_pretrain: if load pretrained parameters, freeze all conv layers.
Depending on different situations, you can just set part of conv layers to be freezed.
the parameters of freezed layers will not change when training.
Returns:
4D tensor
'''
def conv_layer(layer_name, x, out_channels, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=True):
in_channels = x.get_shape()[-1]
with tf.variable_scope(layer_name):
w = tf.get_variable(name='weights',
trainable=is_pretrain,
shape=[kernel_size[0], kernel_size[1], in_channels, out_channels],
initializer=tf.contrib.layers.xavier_initializer()) # default is uniform distribution initialization
b = tf.get_variable(name='biases',
trainable=is_pretrain,
shape=[out_channels],
initializer=tf.constant_initializer(0.0))
x = tf.nn.conv2d(x, w, stride, padding='SAME', name='conv')
x = tf.nn.bias_add(x, b, name='bias_add')
x = tf.nn.relu(x, name='relu')
return x
```
## 定义池化层
```
'''Pooling op
Args:
x: input tensor
kernel: pooling kernel, VGG paper used [1,2,2,1], the size of kernel is 2X2
stride: stride size, VGG paper used [1,2,2,1]
padding:
is_max_pool: boolen
if True: use max pooling
else: use avg pooling
'''
def pool(layer_name, x, kernel=[1,2,2,1], stride=[1,2,2,1], is_max_pool=True):
if is_max_pool:
x = tf.nn.max_pool(x, kernel, strides=stride, padding='SAME', name=layer_name)
else:
x = tf.nn.avg_pool(x, kernel, strides=stride, padding='SAME', name=layer_name)
return x
```
## 定义全连接层
```
'''Wrapper for fully connected layers with RELU activation as default
Args:
layer_name: e.g. 'FC1', 'FC2'
x: input feature map
out_nodes: number of neurons for current FC layer
'''
def fc_layer(layer_name, x, out_nodes,keep_prob=0.8):
shape = x.get_shape()
# 处理没有预先做flatten的输入
if len(shape) == 4:
size = shape[1].value * shape[2].value * shape[3].value
else:
size = shape[-1].value
with tf.variable_scope(layer_name):
w = tf.get_variable('weights',
shape=[size, out_nodes],
initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable('biases',
shape=[out_nodes],
initializer=tf.constant_initializer(0.0))
flat_x = tf.reshape(x, [-1, size]) # flatten into 1D
x = tf.nn.bias_add(tf.matmul(flat_x, w), b)
x = tf.nn.relu(x)
x = tf.nn.dropout(x, keep_prob)
return x
```
## 定义VGG16网络
```
def vgg16_net(x, n_classes, is_pretrain=True):
with tf.name_scope('VGG16'):
x = conv_layer('conv1_1', x, 64, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
x = conv_layer('conv1_2', x, 64, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
with tf.name_scope('pool1'):
x = pool('pool1', x, kernel=[1,2,2,1], stride=[1,2,2,1], is_max_pool=True)
x = conv_layer('conv2_1', x, 128, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
x = conv_layer('conv2_2', x, 128, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
with tf.name_scope('pool2'):
x = pool('pool2', x, kernel=[1,2,2,1], stride=[1,2,2,1], is_max_pool=True)
x = conv_layer('conv3_1', x, 256, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
x = conv_layer('conv3_2', x, 256, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
x = conv_layer('conv3_3', x, 256, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
with tf.name_scope('pool3'):
x = pool('pool3', x, kernel=[1,2,2,1], stride=[1,2,2,1], is_max_pool=True)
x = conv_layer('conv4_1', x, 512, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
x = conv_layer('conv4_2', x, 512, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
x = conv_layer('conv4_3', x, 512, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
with tf.name_scope('pool4'):
x = pool('pool4', x, kernel=[1,2,2,1], stride=[1,2,2,1], is_max_pool=True)
x = conv_layer('conv5_1', x, 512, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
x = conv_layer('conv5_2', x, 512, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
x = conv_layer('conv5_3', x, 512, kernel_size=[3,3], stride=[1,1,1,1], is_pretrain=is_pretrain)
with tf.name_scope('pool5'):
x = pool('pool5', x, kernel=[1,2,2,1], stride=[1,2,2,1], is_max_pool=True)
x = fc_layer('fc6', x, out_nodes=4096)
assert x.get_shape().as_list()[1:] == [4096]
x = fc_layer('fc7', x, out_nodes=4096)
fc8 = fc_layer('fc8', x, out_nodes=n_classes)
# softmax = tf.nn.softmax(fc8)
return x
```
# 定义损失函数
采用交叉熵计算损失
```
'''Compute loss
Args:
logits: logits tensor, [batch_size, n_classes]
labels: one-hot labels
'''
def loss(logits, labels):
with tf.name_scope('loss') as scope:
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels,name='cross-entropy')
loss = tf.reduce_mean(cross_entropy, name='loss')
tf.summary.scalar(scope+'/loss', loss)
return loss
```
# 定义准确率
```
'''
Evaluate the quality of the logits at predicting the label.
Args:
logits: Logits tensor, float - [batch_size, NUM_CLASSES].
labels: Labels tensor,
'''
def accuracy(logits, labels):
with tf.name_scope('accuracy') as scope:
correct = tf.equal(tf.arg_max(logits, 1), tf.arg_max(labels, 1))
correct = tf.cast(correct, tf.float32)
accuracy = tf.reduce_mean(correct)*100.0
tf.summary.scalar(scope+'/accuracy', accuracy)
return accuracy
```
# 定义优化函数
```
def optimize(loss, learning_rate, global_step):
'''optimization, use Gradient Descent as default
'''
with tf.name_scope('optimizer'):
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
#optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss, global_step=global_step)
return train_op
```
# 定义加载模型函数
```
def load_with_skip(data_path, session, skip_layer):
data_dict = np.load(data_path, encoding='latin1').item()
for key in data_dict:
if key not in skip_layer:
with tf.variable_scope(key, reuse=True):
for subkey, data in zip(('weights', 'biases'), data_dict[key]):
session.run(tf.get_variable(subkey).assign(data))
```
# 定义训练图片读取函数
```
def read_cifar10(data_dir, is_train, batch_size, shuffle):
"""Read CIFAR10
Args:
data_dir: the directory of CIFAR10
is_train: boolen
batch_size:
shuffle:
Returns:
label: 1D tensor, tf.int32
image: 4D tensor, [batch_size, height, width, 3], tf.float32
"""
img_width = 32
img_height = 32
img_depth = 3
label_bytes = 1
image_bytes = img_width*img_height*img_depth
with tf.name_scope('input'):
if is_train:
filenames = [os.path.join(data_dir, 'data_batch_%d.bin' %ii)
for ii in np.arange(1, 6)]
else:
filenames = [os.path.join(data_dir, 'test_batch.bin')]
filename_queue = tf.train.string_input_producer(filenames)
reader = tf.FixedLengthRecordReader(label_bytes + image_bytes)
key, value = reader.read(filename_queue)
record_bytes = tf.decode_raw(value, tf.uint8)
label = tf.slice(record_bytes, [0], [label_bytes])
label = tf.cast(label, tf.int32)
image_raw = tf.slice(record_bytes, [label_bytes], [image_bytes])
image_raw = tf.reshape(image_raw, [img_depth, img_height, img_width])
image = tf.transpose(image_raw, (1,2,0)) # convert from D/H/W to H/W/D
image = tf.cast(image, tf.float32)
# # data argumentation
# image = tf.random_crop(image, [24, 24, 3])# randomly crop the image size to 24 x 24
# image = tf.image.random_flip_left_right(image)
# image = tf.image.random_brightness(image, max_delta=63)
# image = tf.image.random_contrast(image,lower=0.2,upper=1.8)
image = tf.image.per_image_standardization(image) #substract off the mean and divide by the variance
if shuffle:
images, label_batch = tf.train.shuffle_batch(
[image, label],
batch_size = batch_size,
num_threads= 64,
capacity = 20000,
min_after_dequeue = 3000)
else:
images, label_batch = tf.train.batch(
[image, label],
batch_size = batch_size,
num_threads = 64,
capacity= 2000)
## ONE-HOT
n_classes = 10
label_batch = tf.one_hot(label_batch, depth= n_classes)
label_batch = tf.cast(label_batch, dtype=tf.int32)
label_batch = tf.reshape(label_batch, [batch_size, n_classes])
return images, label_batch
```
# 定义训练函数
```
IMG_W = 32
IMG_H = 32
N_CLASSES = 10
BATCH_SIZE = 32
learning_rate = 0.01
MAX_STEP = 10 # it took me about one hour to complete the training.
IS_PRETRAIN = False
image_size = 32 # 输入图像尺寸
images = tf.Variable(tf.random_normal([batch_size, image_size, image_size, 3], dtype=tf.float32, stddev=1e-1))
vgg16_net(image, N_CLASSES, IS_PRETRAIN)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
def train():
pre_trained_weights = './/vgg16_pretrain//vgg16.npy'
data_dir = './/data//cifar-10-batches-bin//'
train_log_dir = './/logs//train//'
val_log_dir = './/logs//val//'
with tf.name_scope('input'):
tra_image_batch, tra_label_batch = read_cifar10(data_dir=data_dir,
is_train=True,
batch_size= BATCH_SIZE,
shuffle=True)
val_image_batch, val_label_batch = read_cifar10(data_dir=data_dir,
is_train=False,
batch_size= BATCH_SIZE,
shuffle=False)
x = tf.placeholder(tf.float32, shape=[BATCH_SIZE, IMG_W, IMG_H, 3])
y_ = tf.placeholder(tf.int16, shape=[BATCH_SIZE, N_CLASSES])
logits = vgg16_net(x, N_CLASSES, IS_PRETRAIN)
loss_1 = loss(logits, y_)
accuracy = accuracy(logits, y_)
my_global_step = tf.Variable(0, name='global_step', trainable=False)
train_op = optimize(loss_1, learning_rate, my_global_step)
saver = tf.train.Saver(tf.global_variables())
summary_op = tf.summary.merge_all()
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
print(x.shape())
print(y_.shape())
if(IS_PRETRAIN):
load_with_skip(pre_trained_weights, sess, ['fc6','fc7','fc8'])
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(sess=sess, coord=coord)
tra_summary_writer = tf.summary.FileWriter(train_log_dir, sess.graph)
val_summary_writer = tf.summary.FileWriter(val_log_dir, sess.graph)
try:
for step in np.arange(MAX_STEP):
if coord.should_stop():
break
tra_images,tra_labels = sess.run([tra_image_batch, tra_label_batch])
_, tra_loss, tra_acc = sess.run([train_op, loss, accuracy],
feed_dict={x:tra_images, y_:tra_labels})
if step % 50 == 0 or (step + 1) == MAX_STEP:
print ('Step: %d, loss: %.4f, accuracy: %.4f%%' % (step, tra_loss, tra_acc))
summary_str = sess.run(summary_op)
tra_summary_writer.add_summary(summary_str, step)
if step % 200 == 0 or (step + 1) == MAX_STEP:
val_images, val_labels = sess.run([val_image_batch, val_label_batch])
val_loss, val_acc = sess.run([loss, accuracy],
feed_dict={x:val_images,y_:val_labels})
print('** Step %d, val loss = %.2f, val accuracy = %.2f%% **' %(step, val_loss, val_acc))
summary_str = sess.run(summary_op)
val_summary_writer.add_summary(summary_str, step)
if step % 2000 == 0 or (step + 1) == MAX_STEP:
checkpoint_path = os.path.join(train_log_dir, 'model.ckpt')
saver.save(sess, checkpoint_path, global_step=step)
except tf.errors.OutOfRangeError:
print('Done training -- epoch limit reached')
finally:
coord.request_stop()
coord.join(threads)
train()
```
## VGG16使用
```
def time_tensorflow_run(session, target, feed, info_string):
num_steps_burn_in = 10 # 预热轮数
total_duration = 0.0 # 总时间
total_duration_squared = 0.0 # 总时间的平方和用以计算方差
for i in range(num_batches + num_steps_burn_in):
start_time = time.time()
_ = session.run(target,feed_dict=feed)
duration = time.time() - start_time
if i >= num_steps_burn_in: # 只考虑预热轮数之后的时间
if not i % 10:
print('%s:step %d,duration = %.3f' % (datetime.now(), i - num_steps_burn_in, duration))
total_duration += duration
total_duration_squared += duration * duration
mn = total_duration / num_batches # 平均每个batch的时间
vr = total_duration_squared / num_batches - mn * mn # 方差
sd = math.sqrt(vr) # 标准差
print('%s: %s across %d steps, %.3f +/- %.3f sec/batch' % (datetime.now(), info_string, num_batches, mn, sd))
def run_benchmark():
with tf.Graph().as_default():
'''定义图片尺寸224,利用tf.random_normal函数生成标准差为0.1的正态分布的随机数来构建224x224的随机图片'''
image_size = 224 # 输入图像尺寸
images = tf.Variable(tf.random_normal([batch_size, image_size, image_size, 3], dtype=tf.float32, stddev=1e-1))
#构建keep_prob的placeholder
keep_prob = tf.placeholder(tf.float32)
prediction,softmax,fc8,p = vgg16_net(images,keep_prob)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
#设置keep_prob为1.0,运用time_tensorflow_run来评测forward运算随机
time_tensorflow_run(sess, prediction,{keep_prob:1.0}, "Forward")
# 用以模拟训练的过程
objective = tf.nn.l2_loss(fc8) # 给一个loss
grad = tf.gradients(objective, p) # 相对于loss的 所有模型参数的梯度
#评测backward运算时间
time_tensorflow_run(sess, grad, {keep_prob:0.5},"Forward-backward")
batch_size = 32
num_batches = 100
run_benchmark()
```
## 其他参数
```
# Construct model
pred = conv_net(x, weights, biases, keep_prob)
# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# Evaluate model
correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# Initializing the variables
init = tf.global_variables_initializer()
saver=tf.train.Saver()
```
https://blog.csdn.net/roguesir/article/details/77051250
https://blog.csdn.net/zhangwei15hh/article/details/78417789
https://blog.csdn.net/v1_vivian/article/details/77898652
| true |
code
| 0.714217 | null | null | null | null |
|
# Road Following - Data Collection (using Gamepad)
If you've run through the collision avoidance sample, your should be familiar following three steps
1. Data collection
2. Training
3. Deployment
In this notebook, we'll do the same exact thing! Except, instead of classification, you'll learn a different fundamental technique, **regression**, that we'll use to
enable JetBot to follow a road (or really, any path or target point).
1. Place the JetBot in different positions on a path (offset from center, different angles, etc)
> Remember from collision avoidance, data variation is key!
2. Display the live camera feed from the robot
3. Using a gamepad controller, place a 'green dot', which corresponds to the target direction we want the robot to travel, on the image.
4. Store the X, Y values of this green dot along with the image from the robot's camera
Then, in the training notebook, we'll train a neural network to predict the X, Y values of our label. In the live demo, we'll use
the predicted X, Y values to compute an approximate steering value (it's not 'exactly' an angle, as
that would require image calibration, but it's roughly proportional to the angle so our controller will work fine).
So how do you decide exactly where to place the target for this example? Here is a guide we think may help
1. Look at the live video feed from the camera
2. Imagine the path that the robot should follow (try to approximate the distance it needs to avoid running off road etc.)
3. Place the target as far along this path as it can go so that the robot could head straight to the target without 'running off' the road.
> For example, if we're on a very straight road, we could place it at the horizon. If we're on a sharp turn, it may need to be placed closer to the robot so it doesn't run out of boundaries.
Assuming our deep learning model works as intended, these labeling guidelines should ensure the following:
1. The robot can safely travel directly towards the target (without going out of bounds etc.)
2. The target will continuously progress along our imagined path
What we get, is a 'carrot on a stick' that moves along our desired trajectory. Deep learning decides where to place the carrot, and JetBot just follows it :)
### Labeling example video
Execute the block of code to see an example of how to we labeled the images. This model worked after only 123 images :)
```
from IPython.display import HTML
HTML('<iframe width="560" height="315" src="https://www.youtube.com/embed/FW4En6LejhI" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>')
```
### Import Libraries
So lets get started by importing all the required libraries for "data collection" purpose. We will mainly use OpenCV to visualize and save image with labels. Libraries such as uuid, datetime are used for image naming.
```
# IPython Libraries for display and widgets
import traitlets
import ipywidgets.widgets as widgets
from IPython.display import display
# Camera and Motor Interface for JetBot
from jnmouse import Robot, Camera, bgr8_to_jpeg
# Basic Python packages for image annotation
from uuid import uuid1
import os
import json
import glob
import datetime
import numpy as np
import cv2
import time
```
### Display Live Camera Feed
First, let's initialize and display our camera like we did in the teleoperation notebook.
We use Camera Class from jnmouse to enable CSI MIPI camera. Our neural network takes a 224x224 pixel image as input. We'll set our camera to that size to minimize the filesize of our dataset (we've tested that it works for this task). In some scenarios it may be better to collect data in a larger image size and downscale to the desired size later.
```
camera = Camera()
widget_width = camera.width
widget_height = camera.height
image_widget = widgets.Image(format='jpeg', width=widget_width, height=widget_height)
target_widget = widgets.Image(format='jpeg', width=widget_width, height=widget_height)
x_slider = widgets.FloatSlider(min=-1.0, max=1.0, step=0.001, description='x')
y_slider = widgets.FloatSlider(min=-1.0, max=1.0, step=0.001, description='y')
def display_xy(camera_image):
image = np.copy(camera_image)
x = x_slider.value
y = y_slider.value
x = int(x * widget_width / 2 + widget_width / 2)
y = int(y * widget_height / 2 + widget_height / 2)
image = cv2.circle(image, (x, y), 8, (0, 255, 0), 3)
image = cv2.circle(image, (widget_width / 2, widget_height), 8, (0, 0,255), 3)
image = cv2.line(image, (x,y), (widget_width / 2, widget_height), (255,0,0), 3)
jpeg_image = bgr8_to_jpeg(image)
return jpeg_image
time.sleep(1)
traitlets.dlink((camera, 'value'), (image_widget, 'value'), transform=bgr8_to_jpeg)
traitlets.dlink((camera, 'value'), (target_widget, 'value'), transform=display_xy)
display(widgets.HBox([image_widget, target_widget]), x_slider, y_slider)
```
### Create Gamepad Controller
This step is similar to "Teleoperation" task. In this task, we will use gamepad controller to label images.
The first thing we want to do is create an instance of the Controller widget, which we'll use to label images with "x" and "y" values as mentioned in introduction. The Controller widget takes a index parameter, which specifies the number of the controller. This is useful in case you have multiple controllers attached, or some gamepads appear as multiple controllers. To determine the index of the controller you're using,
Visit http://html5gamepad.com.
Press buttons on the gamepad you're using
Remember the index of the gamepad that is responding to the button presses
Next, we'll create and display our controller using that index.
```
controller = widgets.Controller(index=0)
display(controller)
```
### Connect Gamepad Controller to Label Images
Now, even though we've connected our gamepad, we haven't yet attached the controller to label images! We'll connect that to the left and right vertical axes using the dlink function. The dlink function, unlike the link function, allows us to attach a transform between the source and target.
```
widgets.jsdlink((controller.axes[2], 'value'), (x_slider, 'value'))
widgets.jsdlink((controller.axes[3], 'value'), (y_slider, 'value'))
```
### Collect data
The following block of code will display the live image feed, as well as the number of images we've saved. We store
the target X, Y values by
1. Place the green dot on the target
2. Press 'down' on the DPAD to save
This will store a file in the ``dataset_xy`` folder with files named
``xy_<x value>_<y value>_<uuid>.jpg``
where `<x value>` and `<y value>` are the coordinates **in pixel (not in percentage)** (count from the top left corner).
When we train, we load the images and parse the x, y values from the filename
```
DATASET_DIR = 'dataset_xy'
# we have this "try/except" statement because these next functions can throw an error if the directories exist already
try:
os.makedirs(DATASET_DIR)
except FileExistsError:
print('Directories not created because they already exist')
for b in controller.buttons:
b.unobserve_all()
count_widget = widgets.IntText(description='count', value=len(glob.glob(os.path.join(DATASET_DIR, '*.jpg'))))
def xy_uuid(x, y):
return 'xy_%03d_%03d_%s' % (x * widget_width / 2 + widget_width / 2, y * widget_height / 2 + widget_height / 2, uuid1())
def save_snapshot(change):
if change['new']:
uuid = xy_uuid(x_slider.value, y_slider.value)
image_path = os.path.join(DATASET_DIR, uuid + '.jpg')
with open(image_path, 'wb') as f:
f.write(image_widget.value)
count_widget.value = len(glob.glob(os.path.join(DATASET_DIR, '*.jpg')))
controller.buttons[13].observe(save_snapshot, names='value')
display(widgets.VBox([
target_widget,
count_widget
]))
```
Again, let's close the camera conneciton properly so that we can use the camera in other notebooks.
```
camera.stop()
```
### Next
Once you've collected enough data, we'll need to copy that data to our GPU desktop or cloud machine for training. First, we can call the following terminal command to compress our dataset folder into a single zip file.
> If you're training on the JetBot itself, you can skip this step!
The ! prefix indicates that we want to run the cell as a shell (or terminal) command.
The -r flag in the zip command below indicates recursive so that we include all nested files, the -q flag indicates quiet so that the zip command doesn't print any output
```
def timestr():
return str(datetime.datetime.now().strftime('%Y-%m-%d_%H-%M-%S'))
!zip -r -q road_following_{DATASET_DIR}_{timestr()}.zip {DATASET_DIR}
```
You should see a file named road_following_<Date&Time>.zip in the Jupyter Lab file browser. You should download the zip file using the Jupyter Lab file browser by right clicking and selecting Download.
| true |
code
| 0.285496 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/suredream/CNN-Sentinel/blob/master/mnist.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Version Control
```
%%bash
function auth(){
echo $(grep $1 ~/.auth_git | cut -d'"' -f 4 )
}
user=$(auth .user) pwd=$(auth .pwd) token=$(auth .token) email=$(auth .email) name=$(auth .name)
function git_clone(){
clone_url="https://"$user":"$pwd$"@github.com/"$user"/"$1
git clone $clone_url tmp && mv tmp/.git . && rm -rf tmp && git reset --hard
git config --global user.email "$email" && git config --global user.name "$name"
echo "https://github.com/"$user"/"$1
}
function git_push() {
git add -u && git commit -m "$2" && git push "https://"$token"@github.com/"$user"/"$1".git"
}
# git_clone learn_torch
git pull
# git add README.md
# git add ex_main.py
# git add run_dataclass.py
# git_push learn_torch "edit"
# git status
#%%time
#!pip install -qr requirements.txt
```
# Dependency
```
!pip install -qr tfrecord
# import torch, tensorflow as tf
# print('torch({}), tf({})'.format(torch.__version__, tf.__version__))
# import tensorflow_datasets as tfds
# mnist = tfds.load(name='mnist')
mnist['test']
```
# Get Data
The MNIST database of handwritten digits has 60,000 training examples, and 10,000 test examples. Each example included in the MNIST database is a 28x28 grayscale image of handwritten digit and its corresponding label(0-9).
```
import torchvision.datasets as dset
dset.MNIST??
!ls ../data/MNIST/raw
../data/MNIST/raw/t10k-images-idx3-ubyte
../data/MNIST/raw/t10k-labels-idx1-ubyte
import codecs
def get_int(b: bytes) -> int:
return int(codecs.encode(b, 'hex'), 16)
SN3_PASCALVINCENT_TYPEMAP = {
8: (torch.uint8, np.uint8, np.uint8),
9: (torch.int8, np.int8, np.int8),
11: (torch.int16, np.dtype('>i2'), 'i2'),
12: (torch.int32, np.dtype('>i4'), 'i4'),
13: (torch.float32, np.dtype('>f4'), 'f4'),
14: (torch.float64, np.dtype('>f8'), 'f8')
}
def read_sn3_pascalvincent_tensor(path: str, strict: bool = True) -> torch.Tensor:
"""Read a SN3 file in "Pascal Vincent" format (Lush file 'libidx/idx-io.lsh').
Argument may be a filename, compressed filename, or file object.
"""
# read
with open(path, "rb") as f:
data = f.read()
# parse
magic = get_int(data[0:4])
nd = magic % 256
ty = magic // 256
assert 1 <= nd <= 3
assert 8 <= ty <= 14
m = SN3_PASCALVINCENT_TYPEMAP[ty]
s = [get_int(data[4 * (i + 1): 4 * (i + 2)]) for i in range(nd)]
parsed = np.frombuffer(data, dtype=m[1], offset=(4 * (nd + 1)))
assert parsed.shape[0] == np.prod(s) or not strict
return torch.from_numpy(parsed.astype(m[2], copy=False)).view(*s)
def read_label_file(path: str) -> torch.Tensor:
x = read_sn3_pascalvincent_tensor(path, strict=False)
assert(x.dtype == torch.uint8)
assert(x.ndimension() == 1)
return x.long()
def read_image_file(path: str) -> torch.Tensor:
x = read_sn3_pascalvincent_tensor(path, strict=False)
assert(x.dtype == torch.uint8)
assert(x.ndimension() == 3)
return x
data = read_image_file('../data/MNIST/raw/t10k-images-idx3-ubyte')
targets = read_label_file('../data/MNIST/raw/t10k-labels-idx1-ubyte')
train_loader = torch.utils.data.DataLoader(
dataset=(data, targets),
batch_size=batch_size,
shuffle=True)
from torchvision import datasets, transforms
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)),
])
transform(image)
from torchvision import datasets, transforms
transform = transforms.Compose([
transforms.ToPILImage(),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)),
])
# data.shape
image = data[0,:,:]#.ToPILImage()
print(image.shape, type(image))
transform(image)
data[0,:,:].values
# type(data), type(targets)
# data.shape, targets.shape
# from torchvision import datasets, transforms
# dataset1 = datasets.MNIST('../data', train=True, download=True,
# transform=transform)
# dataset2 = datasets.MNIST('../data', train=False,
# transform=transform)
# !aws s3 cp s3://com.climate.production.users/people/jun.xiong/projects/mnist/ . --recursive
# loader
import torch, torchvision
from tfrecord.torch.dataset import TFRecordDataset
import matplotlib.pyplot as plt
batch_size = 64
tfrecord_path = "train/train.tfrecords.gz"
index_path = None
description = {"idx":"int", "image": "byte", "digit": "int"}
dataset = TFRecordDataset(tfrecord_path, index_path, description, compression_type='gzip')
loader = torch.utils.data.DataLoader(dataset, batch_size=batch_size)
row = next(iter(loader))
# print(row)
# viz
data, target = row['image'].reshape(batch_size,1,28,28), row['digit'].reshape(batch_size)
img = torchvision.utils.make_grid(data)
img = img.numpy().transpose(1,2,0)
std = [0.5,0.5,0.5]
mean = [0.5,0.5,0.5]
img = img*std+mean
print([target[i] for i in range(64)])
plt.imshow(img)
# https://github.com/vahidk/tfrecord
import torch
from tfrecord.torch.dataset import TFRecordDataset
from torchvision import transforms
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize(mean=[0.5,0.5,0.5],std=[0.5,0.5,0.5])])
def get_loader(tfrecord_path):
index_path = None
description = {"idx":"int", "image": "byte", "digit": "int"}
dataset = TFRecordDataset(tfrecord_path, index_path, description, compression_type='gzip', transform=transform)
return torch.utils.data.DataLoader(dataset, batch_size=64)
train_loader = get_loader("train/train.tfrecords.gz")
test_loader = get_loader("val/record/test.tfrecords.gz")
row = next(iter(train_loader))
print(row)
from __future__ import print_function
import argparse
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.optim.lr_scheduler import StepLR
if True:
train_kwargs = {'batch_size': 64}
test_kwargs = {'batch_size': 1000}
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
dataset1 = datasets.MNIST('../data', train=True, download=True,
transform=transform)
dataset2 = datasets.MNIST('../data', train=False,
transform=transform)
train_loader = torch.utils.data.DataLoader(dataset1,**train_kwargs)
test_loader = torch.utils.data.DataLoader(dataset2, **test_kwargs)
# for batch_idx, (data, target) in enumerate(train_loader):
# break
data = next(iter(train_loader))
data = next(iter(train_loader))
data, target = next(iter(train_loader))
data.shape, target.shape
data.shape, target.shape
img = torchvision.utils.make_grid(data)
img = img.numpy().transpose(1,2,0)
std = [0.5,0.5,0.5]
mean = [0.5,0.5,0.5]
img = img*std+mean
print([labels[i] for i in range(64)])
plt.imshow(img)
```
# Create Idx
```
# from glob import glob
# for f in glob('train/*.tfrecord'):
# # !echo ${f} ${f}.idx
# !python -m tfrecord.tools.tfrecord2idx train/${f} train/${f}.idx
for f in glob('val/*.tfrecord'):
# !echo ${f} ${f}.idx
!python -m tfrecord.tools.tfrecord2idx val/${f} val/${f}.idx
import torch
from tfrecord.torch.dataset import MultiTFRecordDataset
tfrecord_pattern = "train/{}.tfrecord"
index_pattern = "train/{}.tfrecord.idx"
splits = {
"tfrecord_1": 1,
"tfrecord_2": 1,
}
description = {"idx":"int", "image": "int", "digit": "int"}
dataset = MultiTFRecordDataset(tfrecord_pattern, index_pattern, splits, description)
loader = torch.utils.data.DataLoader(dataset, batch_size=32)
data = next(iter(loader))
print(data)
import itertools
dict(zip([f.split('/')[1].split('.')[0] for f in glob(f'train/tf*.tfrecord')], itertools.repeat(1)))
import torch
from tfrecord.torch.dataset import MultiTFRecordDataset
from glob import glob
import itertools
# transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize(mean=[0.5,0.5,0.5],std=[0.5,0.5,0.5])])
# def get_data_load(folder, batch_size=64):
# tfrecord_pattern = f"{folder}/{{}}.tfrecord.gz"
# # print(tfrecord_pattern)
# index_pattern = f"{folder}/{{}}.tfrecord.idx"
# flist = [f.split('/')[1].split('.')[0] for f in glob(f'{folder}/tf*.tfrecord')]
# splits = dict(zip(flist, itertools.repeat(1)))
# description = {"idx":"int", "image": "int", "digit": "int"}
# dataset = MultiTFRecordDataset(tfrecord_pattern, index_pattern, splits, description, transform=transform)
# return torch.utils.data.DataLoader(dataset, batch_size=batch_size)
tfrecord_path = "/tmp/data.tfrecord.gz"
index_path = None
description = {"idx":"int", "image": "byte", "label": "float"}
dataset = TFRecordDataset(tfrecord_path, index_path, description, )
loader = torch.utils.data.DataLoader(dataset, batch_size=32)
train_loader = get_data_load('train')
test_loader = get_data_load('val')
data = next(iter(train_loader))
print(data)
%run -i run_dataclass.py
train = MY_MNIST(transform=None)
# train[0]
for (cnt,i) in enumerate(train):
image = i['img']
label = i['target']
ax = plt.subplot(4, 4, cnt+1)
ax.axis('off')
ax.imshow(image)
ax.set_title(label)
plt.pause(0.001)
if cnt ==15:
break
import numpy as np
import tensorflow as tf
!ls -l /content/record/train.tfrecords
import torch
from tfrecord.torch.dataset import TFRecordDataset
tfrecord_path = "/content/record/train.tfrecords"
index_path = None
description = {"idx":"int", "image": "byte", "digit": "int"}
dataset = TFRecordDataset(tfrecord_path, index_path, description)
loader = torch.utils.data.DataLoader(dataset, batch_size=32)
data = next(iter(loader))
print(data['image'].shape)
```
# Create TFrecord from numpy
```
%run -i run_numpy_array.py
import tensorflow.keras.datasets.mnist as mnist
# https://www.programcreek.com/python/?code=ddbourgin%2Fnumpy-ml%2Fnumpy-ml-master%2Fnumpy_ml%2Ftests%2Ftest_nn.py
(x_train, y_train), (x_test, y_test) = mnist.load_data()
class DatasetMNIST(torch.utils.data.Dataset):
def __init__(self, X, y, transform=None):
self.X = X
self.y = y
self.transform = transform
def __len__(self):
return self.X.shape[0]
def __getitem__(self, index):
image = torch.from_numpy(self.X[index, :, :]).reshape(1,28,28)
label = self.y[index]
if self.transform is not None:
image = self.transform(image)
return image, label
test_set = DatasetMNIST(x_train, y_train)
a, b = test_set[0]
type(a), type(b)
a.shape
y_train[0]
%run -i run_numpy_array.py
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train.shape, y_train.shape, x_test.shape, y_test.shape
x_train.shape[0]
%%time
def _int64_feature(value):
return tf.train.Feature(int64_list=tf.train.Int64List(value=[value]))
def _bytes_feature(value):
return tf.train.Feature(bytes_list=tf.train.BytesList(value=[value]))
def write_to_tfrecord(X, y, filename):
options = tf.io.TFRecordOptions(compression_type='GZIP')
writer = tf.io.TFRecordWriter(filename, options=options)
for i in range(X.shape[0]):
image_raw = X[i].tobytes()
example = tf.train.Example(features=tf.train.Features(
feature={
'idx': _int64_feature(i),
'digit': _int64_feature(y[i]),
'image': _bytes_feature(image_raw)
}))
writer.write(example.SerializeToString())
writer.close()
write_to_tfrecord(x_train, y_train, 'record/train.tfrecords.gz')
write_to_tfrecord(x_test, y_test, 'record/test.tfrecords.gz')
!aws s3 cp record/test.tfrecords.gz s3://com.climate.production.users/people/jun.xiong/projects/mnist/val/
!aws s3 cp record/train.tfrecords.gz s3://com.climate.production.users/people/jun.xiong/projects/mnist/train/
```
# Insert
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, 1)
self.conv2 = nn.Conv2d(32, 64, 3, 1)
self.dropout1 = nn.Dropout(0.25)
self.dropout2 = nn.Dropout(0.5)
self.fc1 = nn.Linear(9216, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, 2)
x = self.dropout1(x)
x = torch.flatten(x, 1)
x = self.fc1(x)
x = F.relu(x)
x = self.dropout2(x)
x = self.fc2(x)
output = F.log_softmax(x, dim=1)
return output
def train(args, model, device, train_loader, optimizer, epoch):
model.train()
# for batch_idx, (data, target) in enumerate(train_loader):
for batch_idx, row in enumerate(train_loader):
data, target = row['image'].reshape(64,1,28,28), row['digit'].reshape(64)
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % args.log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
if args.dry_run:
break
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
# for data, target in test_loader:
for row in test_loader:
data, target = row['image'].reshape(64,1,28,28), row['digit'].reshape(64)
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
if True:
device = torch.device('cpu')
model = Net().to(device)
optimizer = optim.Adadelta(model.parameters(), lr=args.lr)
scheduler = StepLR(optimizer, step_size=1, gamma=args.gamma)
for epoch in range(1, args.epochs + 1):
train(args, model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
scheduler.step()
if args.save_model:
torch.save(model.state_dict(), "mnist_cnn.pt")
args.epochs
data.reshape?
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize(mean=[0.5,0.5,0.5],std=[0.5,0.5,0.5])])
data_train = datasets.MNIST(root = "./data/",
transform=transform,
train = True,
download = True)
data_test = datasets.MNIST(root="./data/",
transform = transform,
train = False)
data_loader_train = torch.utils.data.DataLoader(dataset=data_train,
batch_size = 64,
shuffle = True,
num_workers=2)
data_loader_test = torch.utils.data.DataLoader(dataset=data_test,
batch_size = 64,
shuffle = True,
num_workers=2)
print(len(data_train))
images, labels = next(iter(data_loader_train))
img = torchvision.utils.make_grid(images)
img = img.numpy().transpose(1,2,0)
std = [0.5,0.5,0.5]
mean = [0.5,0.5,0.5]
img = img*std+mean
print([labels[i] for i in range(64)])
plt.imshow(img)
import torchvision
import matplotlib.pyplot as plt
row = next(iter(train_loader))
images, labels = row['image'], row['digit']
img = torchvision.utils.make_grid(images)
img = img.numpy().transpose(1,2,0)
std = [0.5,0.5,0.5]
mean = [0.5,0.5,0.5]
img = img*std+mean
print([labels[i] for i in range(64)])
plt.imshow(img)
data = next(iter(train_loader))
data
data['image'].shape
MultiTFRecordDataset?
# from torchvision import datasets, transforms
# transform=transforms.Compose([
# transforms.ToTensor(),
# transforms.Normalize((0.1307,), (0.3081,))
# ])
# dataset1 = datasets.MNIST('../data', train=True, download=True, transform=transform)
# dataset2 = datasets.MNIST('../data', train=False,
# transform=transform)
!ls -l ../data/MNIST/raw/
from __future__ import print_function
import argparse
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.optim.lr_scheduler import StepLR
from tfrecord.torch.dataset import MultiTFRecordDataset
class Net1(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, 1)
self.conv2 = nn.Conv2d(32, 64, 3, 1)
self.dropout1 = nn.Dropout(0.25)
self.dropout2 = nn.Dropout(0.5)
self.fc1 = nn.Linear(9216, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, 2)
x = self.dropout1(x)
x = torch.flatten(x, 1)
x = self.fc1(x)
x = F.relu(x)
x = self.dropout2(x)
x = self.fc2(x)
output = F.log_softmax(x, dim=1)
return output
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Sequential(torch.nn.Conv2d(1,64,kernel_size=3,stride=1,padding=1),
torch.nn.ReLU(),
torch.nn.Conv2d(64,128,kernel_size=3,stride=1,padding=1),
torch.nn.ReLU(),
torch.nn.MaxPool2d(stride=2,kernel_size=2))
self.dense = torch.nn.Sequential(torch.nn.Linear(14*14*128,1024),
torch.nn.ReLU(),
torch.nn.Dropout(p=0.5),
torch.nn.Linear(1024, 10))
def forward(self, x):
x = self.conv1(x)
x = x.view(-1, 14*14*128)
x = self.dense(x)
return x
def train(args, model, device, train_loader, optimizer, epoch):
model.train()
# for batch_idx, (data, target) in enumerate(train_loader):
for row in train_loader:
batch_idx, data, target = row['idx'], row['image'], row['digit']
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % args.log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
if args.dry_run:
break
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
# for idx, data, target in test_loader:
for row in test_loader:
batch_idx, data, target = row['idx'], row['image'], row['digit']
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
from collections import namedtuple
d = {'no_cuda':False, 'batch_size':64, 'test_batch_size':1000,'epochs':14, 'lr':1.0, 'gamma':0.7, 'dry_run':False, 'log_interval':10, 'save_model':True}
args = namedtuple('args', d.keys())(*d.values())
def main():
# # Training settings
# parser = argparse.ArgumentParser(description='PyTorch MNIST Example')
# parser.add_argument('--batch-size', type=int, default=64, metavar='N',
# help='input batch size for training (default: 64)')
# parser.add_argument('--test-batch-size', type=int, default=1000, metavar='N',
# help='input batch size for testing (default: 1000)')
# parser.add_argument('--epochs', type=int, default=14, metavar='N',
# help='number of epochs to train (default: 14)')
# parser.add_argument('--lr', type=float, default=1.0, metavar='LR',
# help='learning rate (default: 1.0)')
# parser.add_argument('--gamma', type=float, default=0.7, metavar='M',
# help='Learning rate step gamma (default: 0.7)')
# parser.add_argument('--no-cuda', action='store_true', default=False,
# help='disables CUDA training')
# parser.add_argument('--dry-run', action='store_true', default=False,
# help='quickly check a single pass')
# parser.add_argument('--seed', type=int, default=1, metavar='S',
# help='random seed (default: 1)')
# parser.add_argument('--log-interval', type=int, default=10, metavar='N',
# help='how many batches to wait before logging training status')
# parser.add_argument('--save-model', action='store_true', default=False,
# help='For Saving the current Model')
# args = parser.parse_args()
# args =
use_cuda = not args.no_cuda and torch.cuda.is_available()
# torch.manual_seed(args.seed)
device = torch.device("cuda" if use_cuda else "cpu")
train_kwargs = {'batch_size': args.batch_size}
test_kwargs = {'batch_size': args.test_batch_size}
if use_cuda:
cuda_kwargs = {'num_workers': 1,
'pin_memory': True,
'shuffle': True}
train_kwargs.update(cuda_kwargs)
test_kwargs.update(cuda_kwargs)
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
# dataset1 = datasets.MNIST('../data', train=True, download=True,
# transform=transform)
# dataset2 = datasets.MNIST('../data', train=False,A
# transform=transform)
# # train_loader = torch.utils.data.DataLoader(dataset1,**train_kwargs)
# # test_loader = torch.utils.data.DataLoader(dataset2, **test_kwargs)
print(Net)
model = Net().to(device)
optimizer = optim.Adadelta(model.parameters(), lr=args.lr)
scheduler = StepLR(optimizer, step_size=1, gamma=args.gamma)
for epoch in range(1, args.epochs + 1):
train(args, model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
scheduler.step()
if args.save_model:
torch.save(model.state_dict(), "mnist_cnn.pt")
# if __name__ == '__main__':
main()
# s3://com.climate.production.analytics/dsw/scratch/sagemaker/data/mnist-tfrecords/
# https://zhuanlan.zhihu.com/p/77952356
import tensorflow as tf
print (tf.__version__)
def tfrecord_parser(serialized_example):
"""Parses a single tf.Example into image and label tensors."""
feature = {
"idx": tf.FixedLenFeature([1], tf.int64),
"image": tf.FixedLenFeature([28 * 28], tf.int64),
"digit": tf.FixedLenFeature([1], tf.int64),
}
features = tf.parse_single_example(serialized_example, features=feature)
# 28 x 28 is size of MNIST example
image = tf.cast(tf.reshape(features["image"], [28 * 28]), tf.float32)
digit = tf.reshape(features["digit"], [1])
return {"image": image}, digit
batch_size = 256
num_shards = 1
shard_index = 0
num_epochs = 1
# tfrecord_glob_pattern = f"*.tfrecord"
filenames = ['s3://com.climate.production.analytics/dsw/scratch/sagemaker/data/mnist-tfrecords/train/tfrecord_1.tfrecord']
ds = tf.data.TFRecordDataset(filenames[:])
for x, y in ds.map(read_tfrecord):
image = torch.from_numpy(x.numpy())
digit = torch.from_numpy(y.numpy())
break
image, digit
# volume = torch.from_numpy(x.numpy())
# segmentation = torch.from_numpy(y.numpy())
# return volume, segmentation
# ds = (
# tf.data.Dataset.list_files(tfrecord_glob_pattern, shuffle=True)
# .interleave(tf.data.TFRecordDataset, cycle_length=2)
# .shard(num_shards=num_shards, index=shard_index)
# .repeat(num_epochs)
# .shuffle(buffer_size=100)
# .map(tfrecord_parser, num_parallel_calls=4)
# .batch(batch_size=batch_size)
# )
!aws s3 cp s3://com.climate.production.analytics/dsw/scratch/sagemaker/data/mnist-tfrecords/train/tfrecord_1.tfrecord .
import argparse
import os
import json
import ast
import tensorflow as tf
import logging as _logging
from tensorflow.python.platform import tf_logging
def model_fn(features, labels, mode, params):
# model taken from https://www.kaggle.com/ilufei/mnist-with-tensorflow-dnn-97
layer1 = tf.keras.layers.Dense(
params["nr_neurons_first_layer"],
activation="relu",
input_shape=(params["batch_size"], 784),
kernel_initializer=tf.contrib.layers.xavier_initializer(),
)(features["image"])
dropped_out = tf.layers.dropout(
inputs=layer1, rate=0.4, training=(mode == tf.estimator.ModeKeys.TRAIN)
)
layer2 = tf.keras.layers.Dense(
128,
activation="relu",
kernel_initializer=tf.contrib.layers.xavier_initializer(),
)(dropped_out)
layer3 = tf.keras.layers.Dense(
64, activation="relu", kernel_initializer=tf.contrib.layers.xavier_initializer()
)(layer2)
layer4 = tf.keras.layers.Dense(
32, activation="relu", kernel_initializer=tf.contrib.layers.xavier_initializer()
)(layer3)
layer5 = tf.keras.layers.Dense(
16, activation="relu", kernel_initializer=tf.contrib.layers.xavier_initializer()
)(layer4)
logits = tf.keras.layers.Dense(
10, kernel_initializer=tf.contrib.layers.xavier_initializer()
)(layer5)
predictions = tf.argmax(logits, 1)
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions={"preds": predictions},
export_outputs={
"SIGNATURE_NAME": tf.estimator.export.PredictOutput(
{"preds": predictions}
)
},
)
cross_entropy = tf.losses.sparse_softmax_cross_entropy(labels=labels, logits=logits)
if mode == tf.estimator.ModeKeys.TRAIN:
optimizer = tf.train.AdamOptimizer(learning_rate=1e-3)
train_op = optimizer.minimize(
loss=cross_entropy, global_step=tf.train.get_or_create_global_step()
)
return tf.estimator.EstimatorSpec(
mode=mode, loss=cross_entropy, train_op=train_op
)
accuracy = tf.metrics.accuracy(
labels=tf.cast(labels, tf.int64), predictions=tf.cast(predictions, tf.int64)
)
eval_metric_ops = {"accuracy": accuracy}
# Provide an estimator spec for `ModeKeys.EVAL` mode.
return tf.estimator.EstimatorSpec(
mode=mode, loss=cross_entropy, eval_metric_ops=eval_metric_ops
)
def tfrecord_parser(serialized_example):
"""Parses a single tf.Example into image and label tensors."""
feature = {
"idx": tf.FixedLenFeature([1], tf.int64),
"image": tf.FixedLenFeature([28 * 28], tf.int64),
"digit": tf.FixedLenFeature([1], tf.int64),
}
features = tf.parse_single_example(serialized_example, features=feature)
# 28 x 28 is size of MNIST example
image = tf.cast(tf.reshape(features["image"], [28 * 28]), tf.float32)
digit = tf.reshape(features["digit"], [1])
return {"image": image}, digit
def main():
# tf.logging.set_verbosity(tf.logging.DEBUG)
# TF 1.13 and 1.14 handle logging a bit different, so wrapping the logging setup in a try/except block
try:
tf_logger = tf_logging._get_logger()
handler = tf_logger.handlers[0]
handler.setFormatter(
_logging.Formatter("%(asctime)s - %(name)s - %(levelname)s - %(message)s")
)
except:
pass
main()
from box import Box
!ls ../data/MNIST/raw
!aws s3 cp s3://com.climate.production.analytics/dsw/scratch/sagemaker/data/mnist-tfrecords/val/ val --recursive
MultiTFRecordDataset??
```
| true |
code
| 0.553988 | null | null | null | null |
|
# diverse development using pennlinckit
```
import sys
factor = sys.argv[1]
```
#### pennlinckit contains data, plotting, brain, network science, and math functions common to neuroscience projects
```
import pennlinckit
```
#### standard libraries
```
import numpy as np
import scipy.stats
import seaborn as sns
import matplotlib.pylab as plt
from scipy.stats import pearsonr, spearmanr
data = pennlinckit.data.dataset('pnc')
data.load_matrices('rest')
```
## What is in this object?
#### You will probably be most interested in the matrices:
```
data.matrix.shape
```
#### You can always double check what dataset you called with:
```
data.source
```
#### All data objects will have a "measures" method, which is a pandas dataframe with all the info you need
```
data.measures.head()
data.measures.columns
```
#### Sometimes it's confusing to have all these odd names, which is why we have a data_dict method
```
data.data_dict['overall_psychopathology_4factorv2']
```
#### Let's only look at subjects that have a matrix for resting-state and cognitive scores
```
data.filter('matrix')
data.filter('cognitive')
data.matrix.shape
```
#### Let's only look at people who did not move a lot
```
data.filter('==',value=0,column='restRelMeanRMSMotionExclude')
data.matrix.shape
```
## Let's see what regions predict what mental illness symtom factors best
```
def region_predict(data,region,factor,**model_args):
data.targets = data.measures[factor].values
data.features = data.matrix[:,region]
model_args['self'] = data
pennlinckit.utils.predict(**model_args)
data.matrix[np.isnan(data.matrix)]= 0.0 #the diagonal has np.nan, have to set to zero for sklearn
# factor = 'F1_Exec_Comp_Res_Accuracy_RESIDUALIZED'
prediction = np.zeros((400,len(data.measures.subject)))
for node in range(400):
region_predict(data,node,factor,**{'model':'deep','cv':'KFold','folds':5,'neurons':400,'layers':10,'remove_linear_vars':['restRelMeanRMSMotion','sex']})
prediction[node] = data.prediction
data.features.shape
prediction_acc = np.zeros(400)
for node in range(data.matrix.shape[-1]):
prediction_acc[node] = pearsonr(prediction[node],data.corrected_targets)[0]
np.save('/home/mb3152/diverse_development/data/prediction_{0}.npy'.format(factor),prediction)
np.save('/home/mb3152/diverse_development/data/prediction_acc_{0}.npy'.format(factor),prediction_acc)
np.save('/home/mb3152/diverse_development/data/prediction_regressed_targets_{0}.npy'.format(factor),data.corrected_targets)
1/0
```
## I submitted each factor to the cluster (see submit.py)
#### Now let's look at the outputs
```
factors = ['mood_4factorv2','psychosis_4factorv2', 'externalizing_4factorv2', 'phobias_4factorv2','overall_psychopathology_4factorv2'] #clincal factors
factors = ['F1_Exec_Comp_Res_Accuracy_RESIDUALIZED','F2_Social_Cog_Accuracy_RESIDUALIZED','F3_Memory_Accuracy_RESIDUALIZED'] #cogi factors
all_factor_predictions = np.zeros((5,data.matrix.shape[-1],data.matrix.shape[0]))
prediction_acc = np.zeros((len(factors),data.matrix.shape[-1]))
for fidx, factor in enumerate(factors):
prediction_acc[fidx] = np.load('/home/mb3152/diverse_development/data/prediction_acc_{0}.npy'.format(factor))
all_factor_predictions[fidx] = np.load('/home/mb3152/diverse_development/data/prediction_{0}.npy'.format(factor))
# from the adult HCP
adult_pc = np.load('/home/mb3152/diverse_development/data/hcp_pc.npy').mean(axis=0)
adult_strength = np.load('/home/mb3152/diverse_development/data/hcp_strength.npy').mean(axis=0)
pearsonr(prediction_acc.mean(axis=0),adult_pc)
pearsonr(prediction_acc.mean(axis=0),adult_strength)
high_predict = prediction_acc.mean() + (prediction_acc.std())
flexible_nodes = (prediction_acc>high_predict).sum(axis=0)
print(pearsonr(flexible_nodes,adult_pc))
spincorrs = pennlinckit.brain.spin_test(adult_pc,flexible_nodes)
spin_stat = pennlinckit.brain.spin_stat(adult_pc,flexible_nodes,spincorrs)
import seaborn as sns
import matplotlib.pylab as plt
from pennlinckit import plotting
%matplotlib inline
plt.close()
f,axes = plt.subplots(1,2,figsize=(5.5,3))
sns.regplot(x=flexible_nodes,y=adult_pc,ax=axes[0],truncate=False,x_jitter=.2,scatter_kws={"s": 50,'alpha':0.35})
plt.sca(axes[0])
r,p = pearsonr(adult_pc,flexible_nodes)
plt.text(2.25,.025,'r={0},p={1}'.format(np.around(r,2),np.around(p,4)))
plt.ylabel('participation coef')
plt.xlabel('prediction flex')
sns.histplot(spincorrs,ax=axes[1])
plt.sca(axes[1])
plt.vlines(r,0,100,colors='black')
plt.tight_layout()
sns.despine()
plt.savefig('flex.pdf')
flex_colors = np.zeros((400,4))
flex_colors[flexible_nodes>=2] = np.array([235,93,104,256])/256.
pennlinckit.brain.write_cifti(flex_colors,'flex_nodes')
for factor in factors: print (data.data_dict[factor])
flexible_nodes = np.zeros((400))
for high_predict in [0.05,0.06,0.07,0.08]:
flexible_nodes =flexible_nodes+ (prediction_acc>high_predict).sum(axis=0)
print(pearsonr(flexible_nodes,adult_pc))
flexible_nodes[flexible_nodes>=6] = 6
flex_colors = pennlinckit.brain.make_heatmap(flexible_nodes,cmap=sns.diverging_palette(220, 10,n=1001))
pennlinckit.brain.write_cifti(flex_colors,'flex_nodes_cont')
allen = pennlinckit.data.allen_brain_institute()
allen_ge = np.corrcoef(allen.expression)
diverse_club = adult_pc >= np.percentile(adult_pc,80)
rich_club = adult_strength >= np.percentile(adult_strength,80)
diverse_club[200:] = False
rich_club[200:] = False
diverse_ge = allen_ge[np.ix_(diverse_club,diverse_club)].flatten()
rich_ge = allen_ge[np.ix_(rich_club,rich_club)].flatten()
diverse_ge = diverse_ge[np.isnan(diverse_ge)==False]
diverse_ge = diverse_ge[diverse_ge!=1]
rich_ge = rich_ge[np.isnan(rich_ge)==False]
rich_ge = rich_ge[rich_ge!=1]
scipy.stats.ttest_ind(diverse_ge,rich_ge)
```
| true |
code
| 0.388183 | null | null | null | null |
|
# Slider bar decline curve in python
Created by Thomas Martin, PhD canidate at [CoRE](https://core.mines.edu/) at Colorado School of Mines. Personal website is [here](https://tmartin.carrd.co/), and email is thomasmartin@mines.edu.
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import pylab
import scipy as sp
from scipy.optimize import curve_fit
from matplotlib.widgets import Slider, Button, RadioButtons
cd drive/My Drive/T21_well_bonanza
ls
```
### Wyoming production data, had to change from a .xls to a .csv
```
df = pd.read_csv('RAPI3723253.csv')
df = df.rename(columns={"OIL BBLS":"oilBBLS", "GAS MCF":"gasMCF","WATER BBLS":"waterBBLS", "Month/Year":"Month_Year"})
df.head()
```
Let's make a quick QC plot (no sliders)
```
plt.figure(figsize=(6,3), dpi=150)
plt.plot(df.index, df.oilBBLS, color='g')
plt.xlabel('Months since 1st production', size = 18)
plt.ylabel('BBLs per Month', size =16)
```
# Production Slider
```
#@title String fields
Fluid_type = 'Gas' #@param ["Oil", "Gas", "Water"]
#@title What Months do you want to show { display-mode: "form" }
MinMonth_slider = 1 #@param {type:"slider", min:1, max:323, step:1}
MaxMonth_slider = 152 #@param {type:"slider", min:0, max:323, step:1}
#print(MinMonth_slider)
#print(MaxMonth_slider)
if MinMonth_slider > MaxMonth_slider:
print('Error Error!, check min and max month')
def model_func(x, a, k, b):
return a * np.exp(-k*x) + b
plt.figure(figsize=(10,6), dpi=150)
if Fluid_type == "Oil":
y = df.oilBBLS[MinMonth_slider:MaxMonth_slider]
p0 = (1.,1.e-12,1.) # starting search koefs
plt.semilogy(df.index[MinMonth_slider:MaxMonth_slider], df.oilBBLS[MinMonth_slider:MaxMonth_slider], color='g', linewidth=2, label='Prod data')
elif Fluid_type == "Gas":
y = df.gasMCF[MinMonth_slider:MaxMonth_slider]
p0 = (1.,1.e-12,1.) # starting search koefs
plt.semilogy(df.index[MinMonth_slider:MaxMonth_slider], df.gasMCF[MinMonth_slider:MaxMonth_slider], color='r', linewidth=2, label='Prod data')
elif Fluid_type == "Water":
p0 = (1.,1.e-11,1.) # starting search koefs
y = df.waterBBLS[MinMonth_slider:MaxMonth_slider]
plt.semilogy(df.index[MinMonth_slider:MaxMonth_slider], df.waterBBLS[MinMonth_slider:MaxMonth_slider], color='b', linewidth=2, label='Prod data')
x = df.index[MinMonth_slider:MaxMonth_slider]
opt, pcov = curve_fit(model_func, x, y, p0, maxfev=50000)
a, k, b = opt
x2 = np.linspace(MinMonth_slider, MaxMonth_slider, 20)
y2 = model_func(x2, a, k, b)
plt.plot(x2, y2, linewidth=3, linestyle='--', color='black', label='Fit. func: $f(x) = %.3f e^{%.3f x} %+.3f$' % (a,k,b))
plt.legend()
plt.grid(True)
plt.xlabel('Months since 1st production', size = 18)
if Fluid_type == "Oil":
plt.ylim(2,20000)
plt.ylabel('BBLs per Month', size =16)
elif Fluid_type == "Gas":
plt.ylim(2,200000)
plt.ylabel('MCF per Month', size =16)
elif Fluid_type == "water":
plt.ylim(2,2000)
plt.ylabel('BBL per month', size =16)
print('Number of Months')
print(MaxMonth_slider- MinMonth_slider,)
```
| true |
code
| 0.416114 | null | null | null | null |
|
# Algoritmos de Ordenação
```
from IPython.display import Image
Image("complexity.png")
```
## 1. Selection Sort
```
# Implementação
class SelectionSort(object):
def sort(self, data):
for i in range(0, len(data)-1):
min_index = self.min_index(i + 1, data)
if (data[min_index] < data[i]):
data[i], data[min_index] = data[min_index], data[i]
return data
def min_index(self, index, data):
min_index = index
for i in range(index + 1, len(data)):
if (data[i] < data[min_index]):
min_index = i
return min_index
sorter = SelectionSort()
print(sorter.sort([5, 4, 3, 2, 1]))
```
## 2. Merge Sort
```
# Implementação
class MergeSort(object):
def sort(self, data):
if len(data) <= 1:
return data
else:
max_size = len(data)
mid = int(max_size/2)
data[:mid] = self.sort(data[:mid])
data[mid:] = self.sort(data[mid:])
i = 0
j = mid
while j < max_size:
if data[i] >= data[j]:
les = data[j]
data[i + 1: j + 1] = data[i : j]
data[i] = les
i = i + 1
j = j + 1
else:
i = i + 1
return data
sorter = MergeSort()
print(sorter.sort([5, 2, 3, 2, 1]))
```
## 3. Insertion Sort
```
# Implementação
class InsertSort(object):
def sort(self, data):
max_size = len(data)
key = 0
for i in range(1, max_size):
pivot = key
if (data[i] < data[pivot]):
while (data[i] <= data[pivot]):
if (pivot > 0):
pivot = pivot - 1
else:
break
else:
while (data[i] > data[pivot]):
if (pivot < max_size-1):
pivot = pivot + 1
else:
break
les = data[i]
data[pivot + 1: i + 1] = data[pivot: i]
data[pivot] = les
return data
sorter = InsertSort()
print(sorter.sort([3, 2, 5, 4, 1]))
```
## 4. Quick Sort
```
# Implementação
class QuickSort(object):
def sort(self, data):
max_size = len(data)
if (max_size > 1):
pivot_index = int(max_size / 2) + (max_size % 2)
pivot = data[pivot_index]
i = 0
j = max_size - 1
while (i <= j):
while (data[i] < pivot) and (i < max_size):
i = i + 1
while (data[j] > pivot) and (j > 0):
j = j - 1
if (i <= j):
data[i], data[j] = data[j], data[i]
i = i + 1
j = j - 1
if (j > 0):
data[:j+1] = self.sort(data[:j+1])
if (i < max_size):
data[i:] = self.sort(data[i:])
return data
sorter = QuickSort()
print(sorter.sort([3, 2, 5, 4, 1]))
```
| true |
code
| 0.213705 | null | null | null | null |
|
# Quantum Teleportation
This notebook demonstrates quantum teleportation. We first use Qiskit's built-in simulators to test our quantum circuit, and then try it out on a real quantum computer.
## Contents
1. [Overview](#overview)
2. [The Quantum Teleportation Protocol](#how)
3. [Simulating the Teleportation Protocol](#simulating)
3.1 [How will we Test this Result on a Real Quantum Computer?](#testing)
3.2 [Using the Statevector Simulator](#simulating-sv)
3.3 [Using the QASM Simulator](#simulating-qs)
4. [Teleportation on a Real Quantum Computer](#real_qc)
4.1 [IBM hardware and Deferred Measurement](#deferred-measurement)
4.2 [Executing](#executing)
4. [References](#references)
## 1. Overview <a id='overview'></a>
Alice wants to send quantum information to Bob. Specifically, suppose she wants to send the qubit state
$\vert\psi\rangle = \alpha\vert0\rangle + \beta\vert1\rangle$.
This entails passing on information about $\alpha$ and $\beta$ to Bob.
There exists a theorem in quantum mechanics which states that you cannot simply make an exact copy of an unknown quantum state. This is known as the no-cloning theorem. As a result of this we can see that Alice can't simply generate a copy of $\vert\psi\rangle$ and give the copy to Bob. We can only copy classical states (not superpositions).
However, by taking advantage of two classical bits and an entangled qubit pair, Alice can transfer her state $\vert\psi\rangle$ to Bob. We call this teleportation because, at the end, Bob will have $\vert\psi\rangle$ and Alice won't anymore.
## 2. The Quantum Teleportation Protocol <a id='how'></a>
To transfer a quantum bit, Alice and Bob must use a third party (Telamon) to send them an entangled qubit pair. Alice then performs some operations on her qubit, sends the results to Bob over a classical communication channel, and Bob then performs some operations on his end to receive Alice’s qubit.

We will describe the steps on a quantum circuit below. Here, no qubits are actually ‘sent’, you’ll just have to imagine that part!
First we set up our session:
```
# Do the necessary imports
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, BasicAer, IBMQ
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from qiskit.extensions import Initialize
from qiskit_textbook.tools import random_state, array_to_latex
```
and create our quantum circuit:
```
qr = QuantumRegister(3) # Protocol uses 3 qubits
crz = ClassicalRegister(1) # and 2 classical bits
crx = ClassicalRegister(1) # in 2 different registers
teleportation_circuit = QuantumCircuit(qr, crz, crx)
```
#### Step 1
A third party, Telamon, creates an entangled pair of qubits and gives one to Bob and one to Alice.
The pair Telamon creates is a special pair called a Bell pair. In quantum circuit language, the way to create a Bell pair between two qubits is to first transfer one of them to the X-basis ($|+\rangle$ and $|-\rangle$) using a Hadamard gate, and then to apply a CNOT gate onto the other qubit controlled by the one in the X-basis.
```
def create_bell_pair(qc, a, b):
"""Creates a bell pair in qc using qubits a & b"""
qc.h(a) # Put qubit a into state |+>
qc.cx(a,b) # CNOT with a as control and b as target
## SETUP
# Protocol uses 3 qubits and 2 classical bits in 2 different registers
qr = QuantumRegister(3)
crz, crx = ClassicalRegister(1), ClassicalRegister(1)
teleportation_circuit = QuantumCircuit(qr, crz, crx)
## STEP 1
# In our case, Telamon entangles qubits q1 and q2
# Let's apply this to our circuit:
create_bell_pair(teleportation_circuit, 1, 2)
# And view the circuit so far:
teleportation_circuit.draw()
```
Let's say Alice owns $q_1$ and Bob owns $q_2$ after they part ways.
#### Step 2
Alice applies a CNOT gate to $q_1$, controlled by $\vert\psi\rangle$ (the qubit she is trying to send Bob). Then Alice applies a Hadamard gate to $|\psi\rangle$. In our quantum circuit, the qubit ($|\psi\rangle$) Alice is trying to send is $q_0$:
```
def alice_gates(qc, psi, a):
qc.cx(psi, a)
qc.h(psi)
## SETUP
# Protocol uses 3 qubits and 2 classical bits in 2 different registers
qr = QuantumRegister(3)
crz, crx = ClassicalRegister(1), ClassicalRegister(1)
teleportation_circuit = QuantumCircuit(qr, crz, crx)
## STEP 1
create_bell_pair(teleportation_circuit, 1, 2)
## STEP 2
teleportation_circuit.barrier() # Use barrier to separate steps
alice_gates(teleportation_circuit, 0, 1)
teleportation_circuit.draw()
```
#### Step 3
Next, Alice applies a measurement to both qubits that she owns, $q_1$ and $\vert\psi\rangle$, and stores this result in two classical bits. She then sends these two bits to Bob.
```
def measure_and_send(qc, a, b):
"""Measures qubits a & b and 'sends' the results to Bob"""
qc.barrier()
qc.measure(a,0)
qc.measure(b,1)
## SETUP
# Protocol uses 3 qubits and 2 classical bits in 2 different registers
qr = QuantumRegister(3)
crz, crx = ClassicalRegister(1), ClassicalRegister(1)
teleportation_circuit = QuantumCircuit(qr, crz, crx)
## STEP 1
create_bell_pair(teleportation_circuit, 1, 2)
## STEP 2
teleportation_circuit.barrier() # Use barrier to separate steps
alice_gates(teleportation_circuit, 0, 1)
## STEP 3
measure_and_send(teleportation_circuit, 0 ,1)
teleportation_circuit.draw()
```
#### Step 4
Bob, who already has the qubit $q_2$, then applies the following gates depending on the state of the classical bits:
00 $\rightarrow$ Do nothing
01 $\rightarrow$ Apply $X$ gate
10 $\rightarrow$ Apply $Z$ gate
11 $\rightarrow$ Apply $ZX$ gate
(*Note that this transfer of information is purely classical*.)
```
# This function takes a QuantumCircuit (qc), integer (qubit)
# and ClassicalRegisters (crz & crx) to decide which gates to apply
def bob_gates(qc, qubit, crz, crx):
# Here we use c_if to control our gates with a classical
# bit instead of a qubit
qc.x(qubit).c_if(crx, 1) # Apply gates if the registers
qc.z(qubit).c_if(crz, 1) # are in the state '1'
## SETUP
# Protocol uses 3 qubits and 2 classical bits in 2 different registers
qr = QuantumRegister(3)
crz, crx = ClassicalRegister(1), ClassicalRegister(1)
teleportation_circuit = QuantumCircuit(qr, crz, crx)
## STEP 1
create_bell_pair(teleportation_circuit, 1, 2)
## STEP 2
teleportation_circuit.barrier() # Use barrier to separate steps
alice_gates(teleportation_circuit, 0, 1)
## STEP 3
measure_and_send(teleportation_circuit, 0 ,1)
## STEP 4
teleportation_circuit.barrier() # Use barrier to separate steps
bob_gates(teleportation_circuit, 2, crz, crx)
teleportation_circuit.draw()
```
And voila! At the end of this protocol, Alice's qubit has now teleported to Bob.
## 3. Simulating the Teleportation Protocol <a id='simulating'></a>
### 3.1 How Will We Test the Protocol on a Quantum Computer? <a id='testing'></a>
In this notebook, we will initialise Alice's qubit in a random state $\vert\psi\rangle$ (`psi`). This state will be created using an `Initialize` gate on $|q_0\rangle$. In this chapter we use the function `random_state` to choose `psi` for us, but feel free to set `psi` to any qubit state you want.
```
# Create random 1-qubit state
psi = random_state(1)
# Display it nicely
array_to_latex(psi, pretext="|\\psi\\rangle =")
# Show it on a Bloch sphere
plot_bloch_multivector(psi)
```
Let's create our initialisation gate to create $|\psi\rangle$ from the state $|0\rangle$:
```
init_gate = Initialize(psi)
init_gate.label = "init"
```
If the quantum teleportation circuit works, then at the end of the circuit the qubit $|q_2\rangle$ will be in this state. We will check this using the statevector simulator.
### 3.2 Using the Statevector Simulator <a id='simulating-sv'></a>
We can use the statevector simulator to verify our qubit has been teleported.
```
## SETUP
qr = QuantumRegister(3) # Protocol uses 3 qubits
crz = ClassicalRegister(1) # and 2 classical registers
crx = ClassicalRegister(1)
qc = QuantumCircuit(qr, crz, crx)
## STEP 0
# First, let's initialise Alice's q0
qc.append(init_gate, [0])
qc.barrier()
## STEP 1
# Now begins the teleportation protocol
create_bell_pair(qc, 1, 2)
qc.barrier()
## STEP 2
# Send q1 to Alice and q2 to Bob
alice_gates(qc, 0, 1)
## STEP 3
# Alice then sends her classical bits to Bob
measure_and_send(qc, 0, 1)
## STEP 4
# Bob decodes qubits
bob_gates(qc, 2, crz, crx)
# Display the circuit
qc.draw()
```
At the time of writing, there is a rendering issue with the `Initialise` gate in the image above, but the circuit operates just fine. We can see below, using our statevector simulator, that the state of $|q_2\rangle$ is the same as the state $|\psi\rangle$ we created above, while the states of $|q_0\rangle$ and $|q_1\rangle$ have been collapsed to either $|0\rangle$ or $|1\rangle$. The state $|\psi\rangle$ has been teleported from qubit 0 to qubit 2.
```
backend = BasicAer.get_backend('statevector_simulator')
out_vector = execute(qc, backend).result().get_statevector()
plot_bloch_multivector(out_vector)
```
You can run this cell a few times to make sure. You may notice that the qubits 0 & 1 change states, but qubit 2 is always in the state $|\psi\rangle$.
### 3.3 Using the QASM Simulator <a id='simulating-qs'></a>
Quantum teleportation is designed to send qubits between two parties. We do not have the hardware to demonstrate this, but we can demonstrate that the gates perform the correct transformations on a single quantum chip. Here we use the QASM simulator to simulate how we might test our protocol.
On a real quantum computer, we would not be able to sample the statevector, so if we wanted to check our teleportation circuit is working, we need to do things slightly differently. You will remember that we used `Initialize` to turn our $|0\rangle$ qubit into the state $|\psi\rangle$:
$$ |0\rangle \xrightarrow{\text{Initialise}} |\psi\rangle $$
Since all quantum gates are reversible, we can find the inverse of Initialise using:
```
inverse_init_gate = init_gate.gates_to_uncompute()
```
This operation has the property:
$$ |\psi\rangle \xrightarrow{\text{Inverse Initialise}} |0\rangle $$
To prove the qubit $|q_0\rangle$ has been teleported to $|q_2\rangle$, if we do this inverse initialisation on $|q_2\rangle$, we expect to measure $|0\rangle$ with certainty. We do this in the circuit below:
```
## SETUP
qr = QuantumRegister(3) # Protocol uses 3 qubits
crz = ClassicalRegister(1) # and 2 classical registers
crx = ClassicalRegister(1)
qc = QuantumCircuit(qr, crz, crx)
## STEP 0
# First, let's initialise Alice's q0
qc.append(init_gate, [0])
qc.barrier()
## STEP 1
# Now begins the teleportation protocol
create_bell_pair(qc, 1, 2)
qc.barrier()
## STEP 2
# Send q1 to Alice and q2 to Bob
alice_gates(qc, 0, 1)
## STEP 3
# Alice then sends her classical bits to Bob
measure_and_send(qc, 0, 1)
## STEP 4
# Bob decodes qubits
bob_gates(qc, 2, crz, crx)
## STEP 5
# reverse the initialisation process
qc.append(inverse_init_gate, [2])
# Display the circuit
qc.draw()
```
Again, there is a rendering issue with the `inverse_init_gate` (called 'disentangler' on the circuit diagram), but we can clearly see the gate appearing in the image. Finally, we measure the third qubit and store the result in the third classical bit:
```
# Need to add a new ClassicalRegister
# to see the result
cr_result = ClassicalRegister(1)
qc.add_register(cr_result)
qc.measure(2,2)
qc.draw()
```
and we run our experiment:
```
backend = BasicAer.get_backend('qasm_simulator')
counts = execute(qc, backend, shots=1024).result().get_counts()
plot_histogram(counts)
```
We can see we have a 100% chance of measuring $q_2$ (the leftmost bit in the string) in the state $|0\rangle$. This is the expected result, and indicates the teleportation protocol has worked properly.
## 4. Teleportation on a Real Quantum Computer <a id='real_qc'></a>
### 4.1 IBM hardware and Deferred Measurement <a id='deferred-measurement'></a>
The IBM quantum computers currently do not support instructions after measurements, meaning we cannot run the quantum teleportation in its current form on real hardware. Fortunately, this does not limit our ability to perform any computations due to the _deferred measurement principle_ discussed in chapter 4.4 of [1]. The principle states that any measurement can be postponed until the end of the circuit, i.e. we can move all the measurements to the end, and we should see the same results.

Any benefits of measuring early are hardware related: If we can measure early, we may be able to reuse qubits, or reduce the amount of time our qubits are in their fragile superposition. In this example, the early measurement in quantum teleportation would have allowed us to transmit a qubit state without a direct quantum communication channel.
While moving the gates allows us to demonstrate the "teleportation" circuit on real hardware, it should be noted that the benefit of the teleportation process (transferring quantum states via classical channels) is lost.
Let us re-write the `bob_gates` function to `new_bob_gates`:
```
def new_bob_gates(qc, a, b, c):
qc.cz(a, c)
qc.cx(b, c)
```
And create our new circuit:
```
qc = QuantumCircuit(3,1)
# First, let's initialise Alice's q0
qc.append(init_gate, [0])
qc.barrier()
# Now begins the teleportation protocol
create_bell_pair(qc, 1, 2)
qc.barrier()
# Send q1 to Alice and q2 to Bob
alice_gates(qc, 0, 1)
qc.barrier()
# Alice sends classical bits to Bob
new_bob_gates(qc, 0, 1, 2)
# We undo the initialisation process
qc.append(inverse_init_gate, [2])
# See the results, we only care about the state of qubit 2
qc.measure(2,0)
# View the results:
qc.draw()
```
### 4.2 Executing <a id='executing'></a>
```
# First, see what devices we are allowed to use by loading our saved accounts
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
provider.backends()
# get the least-busy backend at IBM and run the quantum circuit there
from qiskit.providers.ibmq import least_busy
backend = least_busy(provider.backends(filters=lambda b: b.configuration().n_qubits >= 3 and
not b.configuration().simulator and b.status().operational==True))
job_exp = execute(qc, backend=backend, shots=8192)
# Get the results and display them
exp_result = job_exp.result()
exp_measurement_result = exp_result.get_counts(qc)
print(exp_measurement_result)
plot_histogram(exp_measurement_result)
```
As we see here, there are a few results in which we measured $|1\rangle$. These arise due to errors in the gates and the qubits. In contrast, our simulator in the earlier part of the notebook had zero errors in its gates, and allowed error-free teleportation.
```
error_rate_percent = sum([exp_measurement_result[result] for result in exp_measurement_result.keys() if result[0]=='1']) \
* 100./ sum(list(exp_measurement_result.values()))
print("The experimental error rate : ", error_rate_percent, "%")
```
## 5. References <a id='references'></a>
[1] M. Nielsen and I. Chuang, Quantum Computation and Quantum Information, Cambridge Series on Information and the Natural Sciences (Cambridge University Press, Cambridge, 2000).
```
import qiskit
qiskit.__qiskit_version__
```
| true |
code
| 0.613237 | null | null | null | null |
|
# Model viewer
Quickly view results of previously run models in Jupyter Notebook. Results and parameters can also be viewed in the directory itself, but this notebook provides a quick way to either (1) view all data from a single run in one place and (2) compare the same file across multiple runs. It does require some familiarity with how the output files are named.
```
import glob
import json
import os
import pprint as pp
import matplotlib.pyplot as plt
from PIL import Image
from ea_drought_burn.config import DATA_DIR
# Set working directory to the earthpy data directory
os.chdir(os.path.join(DATA_DIR, "woolsey-fire"))
def view_output(val):
"""View output from one or more models
Parameters
----------
val: str
a model id or filename
Returns
-------
None
"""
return view_file(val) if val[-4] == "." else view_model(val)
def view_file(filename):
"""View a single output across all models
Parameters
----------
filename: str
the filename to view
Returns
-------
None
"""
path = os.path.join("outputs", "models", "*")
ext = os.path.splitext(filename)[-1].lower()
for fp in sorted(glob.iglob(os.path.join(path, filename))):
if ext == ".json":
print(f"{fp}\n")
with open(fp) as f:
pp.pprint(json.load(f), sort_dicts=False)
print("-" * 80)
elif ext == ".png":
im = Image.open(fp)
fig, ax = plt.subplots(figsize=(20, 20))
ax.imshow(im, interpolation=None)
plt.axis("off")
elif ext == ".txt":
print(f"{fp}\n")
with open(fp) as f:
print(f.read())
print("-" * 80)
def view_model(model_id):
"""View the results of a saved model
Parameters
----------
model_id: str
the id of the model to view
Returns
-------
None
"""
path = os.path.join("outputs", "models", model_id)
# Show classification report
for fp in sorted(glob.iglob(os.path.join(path, "*.txt"))):
print("Classification report\n")
with open(fp) as f:
print(f.read())
print("-" * 80)
# Show params and results as pretty-printed dicts
for fp in sorted(glob.iglob(os.path.join(path, "*.json"))):
print(f"{os.path.basename(fp)}\n")
with open(fp) as f:
pp.pprint(json.load(f), sort_dicts=False)
print("-" * 80)
# Show all saved images
for fp in sorted(glob.iglob(os.path.join(path, "*.png"))):
im = Image.open(fp)
fig, ax = plt.subplots(figsize=(20, 20))
ax.imshow(im, interpolation=None)
plt.axis("off")
# List completed models
model_dir = os.path.join("outputs", "models")
models = []
for dirname in os.listdir(model_dir):
if os.path.isdir(os.path.join(model_dir, dirname)):
models.append(dirname)
# Sort by run time
models.sort(key=lambda fn: fn.split("_")[-1])
models
# View model output
view_output(models[-1])
```
| true |
code
| 0.536799 | null | null | null | null |
|
# Bayesian Survival Analysis
Copyright 2017 Allen Downey
MIT License: https://opensource.org/licenses/MIT
```
from __future__ import print_function, division
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import thinkbayes2
import thinkplot
```
## Survival analysis
Suppose that you are an auto insurance company interested in the time between collisions for a particular driver. If the probability of a collision is roughly constant over time, the time between collisions will follow an exponential distribution.
Here's an example with parameter $\lambda = 0.5$ collisions / year.
```
from thinkbayes2 import MakeExponentialPmf
pmf = MakeExponentialPmf(lam=0.5, high=30)
thinkplot.Pdf(pmf)
thinkplot.Config(xlabel='Lifetime', ylabel='PMF')
```
For the exponential distribution, the mean and standard deviation are $1/\lambda$.
In this case they are only approximate because we truncated the distribution.
```
pmf.Mean(), pmf.Std()
```
From the PMF, we can compute the CDF.
```
cdf = pmf.MakeCdf()
thinkplot.Cdf(cdf)
thinkplot.Config(xlabel='Lifetime', ylabel='CDF')
```
And from the CDF, we can compute the survival function, which is the complement of the CDF.
$SF(x) = Prob\{X > x\} = 1 - Prob\{X \le x\} = 1 - CDF(x)$
```
from survival import MakeSurvivalFromCdf
sf = MakeSurvivalFromCdf(cdf)
thinkplot.Plot(sf)
thinkplot.Config(xlabel='Lifetime', ylabel='Survival function')
```
From the survival function we can get the hazard function, which is the probability of a collision at $x$, given no collision prior to $x$.
```
hf = sf.MakeHazardFunction()
thinkplot.Plot(hf)
thinkplot.Config(xlabel='Lifetime', ylabel='Hazard function')
```
If the distribution is truly exponential, the hazard function is constant for all $x$.
In this case it goes to 1 at the end, again because we truncated the distribution.
**Exercise:** Go back and increase the value of `high`, and confirm that the hazard function is a constant until we approach the point where we cut off the distribution.
## Remaining lifetime
Given the survival function, we can compute the distribution of remaining lifetime, conditioned on current age. The following function computes the mean remaining lifetime for a range of ages.
```
def RemainingLifetime(sf):
"""Computes remaining lifetime as a function of age.
sf: survival function
returns: Series that maps from age to remaining lifetime
"""
pmf = sf.MakePmf()
d = {}
for t in sorted(pmf.Values()):
pmf[t] = 0
if pmf.Total():
pmf.Normalize()
d[t] = pmf.Mean() - t
return pd.Series(d)
```
And here's what it looks like for the exponential survival function.
```
mean_rem_life = RemainingLifetime(sf)
thinkplot.Plot(mean_rem_life)
thinkplot.Config(xlabel='Lifetime', ylabel='Survival function')
```
The mean time until a collision is pretty much constant, until we approach the point where we truncate the distribution.
## The Weibull distribution
The Weibull distribution is a generalization of the exponential distribution that takes an additional "shape" parameter, `k`.
When `k=1`, the Weibull is an exponential distribution. Other values of `k` yield survival curves with different shapes, and hazard functions that increase, decrease, or both. So the Weibull family can capture a wide range of survival patterns.
```
from thinkbayes2 import MakeWeibullPmf
pmf = MakeWeibullPmf(lam=2.0, k=1.5, high=30)
thinkplot.Pdf(pmf)
thinkplot.Config(xlabel='Lifetime', ylabel='PMF')
```
**Exercise**: In the previous section, replace the exponential distribution with a Weibull distribituion and run the analysis again. What can you infer about the values of the parameters and the behavior of the hazard function and remaining lifetime?
## Bayesian survival analysis
Suppose you are the manager of a large building with many light fixtures. To figure out how often you will need to replace lightbulbs, you install 10 bulbs and measure the time until they fail.
To generate some fake data, I'll choose a Weibull distribution and generate a random sample (let's suppose it's in years):
```
def SampleWeibull(lam, k, n=1):
return np.random.weibull(k, size=n) * lam
data = SampleWeibull(lam=2, k=1.5, n=10)
data
```
**Exercise:** Write a class called `LightBulb` that inherits from `Suite` and provides a `Likelihood` function that takes an observed lifespan as data and a tuple, `(lam, k)`, as a hypothesis. It should return a likelihood proportional to the probability of the observed lifespan in a Weibull distribution with the given parameters.
Test your method by creating a `LightBulb` object with an appropriate prior and update it with the data above.
Plot the posterior distributions of `lam` and `k`. As the sample size increases, does the posterior distribution converge on the values of `lam` and `k` used to generate the sample?
```
# Hint
from thinkbayes2 import Suite, Joint, EvalWeibullPdf
class LightBulb(Suite, Joint):
def Likelihood(self, data, hypo):
lam, k = hypo
x = data
like = 1
return like
# Solution goes here
from itertools import product
lams = np.linspace(0.001, 6, 101)
ks = np.linspace(0.001, 8, 101)
suite = LightBulb(product(lams, ks))
suite.UpdateSet(data)
thinkplot.Contour(suite)
pmf_lam = suite.Marginal(0)
thinkplot.Pdf(pmf_lam)
pmf_lam.Mean()
pmf_k = suite.Marginal(1)
thinkplot.Pdf(pmf_k)
pmf_k.Mean()
```
**Exercise:** Go back and run this analysis again with `n=20` and see if the posterior distributions seem to be converging on the actual parameters.
## Censored data
**Exercise:** Now suppose that instead of observing a complete lifespan, you observe a lightbulb that has operated for 1 year and is still working. Write another version of `LightBulb` that takes data in this form and performs an update.
```
# Hint
from thinkbayes2 import EvalWeibullCdf
class LightBulb2(Suite, Joint):
def Likelihood(self, data, hypo):
lam, k = hypo
x = data
like = 1
return like
# Solution goes here
from itertools import product
lams = np.linspace(0.001, 10, 101)
ks = np.linspace(0.001, 10, 101)
suite = LightBulb2(product(lams, ks))
suite.Update(1)
thinkplot.Contour(suite)
pmf_lam = suite.Marginal(0)
thinkplot.Pdf(pmf_lam)
pmf_lam.Mean()
pmf_k = suite.Marginal(1)
thinkplot.Pdf(pmf_k)
pmf_k.Mean()
```
Note: based on this data alone, we can rule out some small values of `lam` and `k`, but we can't rule out large values. Without more data or a more informative prior, the results are not useful.
To see why, try increasing the upper bounds in the prior distribition.
## Left censored data
**Exercise:** Suppose you install a light bulb and then you don't check on it for a year, but when you come back, you find that it has burned out. Extend `LightBulb` to handle this kind of data, too.
```
# Hint
class LightBulb3(Suite, Joint):
def Likelihood(self, data, hypo):
lam, k = hypo
x = data
like = 1
return like
# Solution goes here
from itertools import product
lams = np.linspace(0.001, 20, 101)
ks = np.linspace(0.001, 20, 101)
suite = LightBulb3(product(lams, ks))
suite.Update(1)
thinkplot.Contour(suite)
pmf_lam = suite.Marginal(0)
thinkplot.Pdf(pmf_lam)
pmf_lam.Mean()
pmf_k = suite.Marginal(1)
thinkplot.Pdf(pmf_k)
pmf_k.Mean()
```
This example has some of the same problems as the previous one. Based on this data alone, we can't pin down the parameters much.
## Pulling it together
**Exercise:** Suppose you have 15 lightbulbs installed at different times over a 10 year period. When you observe them, some have died and some are still working. Write a version of `LightBulb` that takes data in the form of a `(flag, x)` tuple, where:
1. If `flag` is `eq`, it means that `x` is the actual lifespan of a bulb that has died.
2. If `flag` is `gt`, it means that `x` is the current age of a bulb that is still working, so it is a lower bound on the lifespan.
3. If `flag` is `lt`, it means that `x` is the elapsed time between installation and the first time the bulb is seen broken, so it is an upper bound on the lifespan.
To help you test, I will generate some fake data.
First, I'll generate a Pandas DataFrame with random start times and lifespans. The columns are:
* `start`: time when the bulb was installed
* `lifespan`: lifespan of the bulb in years
* `end`: time when bulb died or will die
* `age_t`: age of the bulb at t=10
```
import pandas as pd
lam = 2
k = 1.5
n = 15
t_end = 10
starts = np.random.uniform(0, t_end, n)
lifespans = SampleWeibull(lam, k, n)
df = pd.DataFrame({'start': starts, 'lifespan': lifespans})
df['end'] = df.start + df.lifespan
df['age_t'] = t_end - df.start
df.head()
```
Now I'll process the DataFrame to generate data in the form we want for the update.
```
data = []
for i, row in df.iterrows():
if row.end < t_end:
data.append(('eq', row.lifespan))
else:
data.append(('gt', row.age_t))
for pair in data:
print(pair)
# Hint
class LightBulb4(Suite, Joint):
def Likelihood(self, data, hypo):
lam, k = hypo
flag, x = data
like = 1
return like
# Solution goes here
from itertools import product
lams = np.linspace(0.001, 10, 101)
ks = np.linspace(0.001, 10, 101)
suite = LightBulb4(product(lams, ks))
suite.UpdateSet(data)
thinkplot.Contour(suite)
pmf_lam = suite.Marginal(0)
thinkplot.Pdf(pmf_lam)
pmf_lam.Mean()
pmf_k = suite.Marginal(1)
thinkplot.Pdf(pmf_k)
pmf_k.Mean()
```
## Prediction
Suppose we know that, for a particular kind of lightbulb in a particular location, the distribution of lifespans is well modeled by a Weibull distribution with `lam=2` and `k=1.5`. If we install `n=100` lightbulbs and come back one year later, what is the distribution of `c`, the number of lightbulbs that have burned out?
The probability that any given bulb has burned out comes from the CDF of the distribution.
```
lam = 2
k = 1.5
p = EvalWeibullCdf(1, lam, k)
p
```
The number of bulbs that have burned out is distributed Binom(n, p).
```
from thinkbayes2 import MakeBinomialPmf
n = 100
pmf_c = MakeBinomialPmf(n, p)
thinkplot.Pdf(pmf_c)
```
Or we can approximate the distribution with a random sample.
```
n = 100
sample = np.random.binomial(n, p, 1000)
pdf_c = thinkbayes2.EstimatedPdf(sample)
thinkplot.Pdf(pdf_c)
np.mean(sample), np.std(sample)
```
**Exercise:** Now suppose that `lam` and `k` are not known precisely, but we have a `LightBulb` object that represents the joint posterior distribution of the parameters after seeing some data. Compute the posterior predictive distribution for `c`, the number of bulbs burned out after one year.
```
# Solution goes here
# Solution goes here
# Solution goes here
# Solution goes here
```
| true |
code
| 0.588121 | null | null | null | null |
|
# Imports
```
import numpy as np
import sklearn.metrics
from sklearn import linear_model
from sklearn.datasets import load_breast_cancer
```
# Load Data
"Breast Cancer" is a tiny dataset for binary classification
```
features, targets = load_breast_cancer(return_X_y=True)
print('Features')
print('shape:', features.shape)
print('data:')
print(features)
print('Targets')
print('shape:', targets.shape)
print('data:')
print(targets)
```
# Model
Create super simple logistic classifier
```
model = linear_model.LogisticRegression(solver='liblinear')
model.fit(features, targets)
```
Predicted outputs
```
predictions = model.predict(features)
print(predictions)
```
# Metrics
**Confusion Matrix**
```python
' Confusion matrix layout'
' PREDICTED LABEL'
' 0 1 '
'TRUE 0' [[ TN FP ]
'LABEL 1' [ FN TP ]]
```
Confusion matrix in sklearn
```
cm = sklearn.metrics.confusion_matrix(targets, predictions)
print('Confusion Matrix:')
print(cm)
```
Confusion matrix in pure numpy
```
def confusion_matrix(y_true, y_pred, result=None, nb_classes=None, norm='none'):
"""Compute confusion matrix. Works with NumPy and PyTorch tensors seamlessly"""
assert y_true.shape == y_pred.shape
if nb_classes==None:
nb_classes = int(max(y_true.max(), y_pred.max())) + 1
if result is None:
confusion_matrix = np.zeros((nb_classes, nb_classes), dtype=np.long)
else:
confusion_matrix = result
for true_class_idx in range(nb_classes):
y_pred_for_class = y_pred[y_true==true_class_idx]
for pred_class_idx in range(nb_classes):
tmp = (y_pred_for_class==pred_class_idx).sum()
confusion_matrix[true_class_idx, pred_class_idx] = tmp
if norm == 'none':
return confusion_matrix # return raw
elif norm == 'row':
return confusion_matrix / confusion_matrix.sum(axis=1, keepdims=True) # rows sum to 1
elif norm == 'col':
return confusion_matrix / confusion_matrix.sum(axis=0, keepdims=True) # cols sum to 1
else:
raise ValueError('norm must be "none", "row" or "col"')
cm = confusion_matrix(targets, predictions)
print(cm)
```
Confusion matrix manually for 2-class problem
```
pred_for_neg = predictions[targets==0] # predictions for class #1
pred_for_pos = predictions[targets==1] # predictions for class #2
TN = np.sum(pred_for_neg==0)
FP = np.sum(pred_for_neg==1)
FN = np.sum(pred_for_pos==0)
TP = np.sum(pred_for_pos==1)
cm = np.array([[TN, FP],
[FN, TP]])
print(cm)
```
Per class classification accuracy
```
cm_true = cm / cm.sum(axis=1, keepdims=True)
print(cm_true)
```
Per class accuracy for true classes only
```
cm_true.diagonal()
```
**Precision and Recall**
In sklearn
```
print('Accuracy: ', sklearn.metrics.accuracy_score(targets, predictions))
print('Precision: ', sklearn.metrics.precision_score(targets, predictions))
print('Recall: ', sklearn.metrics.recall_score(targets, predictions))
```
In numpy
```
# each cm row is actual class
assert cm.shape == (2, 2)
(TN, FP) = cm[0]
(FN, TP) = cm[1]
print('Accuracy: ', (TP+TN) / np.sum(cm))
print('Precision:', TP / (TP+FP))
print('Recall: ', TP / (TP+FN))
```
And manually from confusion matrix
```
print('Accuracy: ', cm.trace() / cm.sum() )
```
| true |
code
| 0.546254 | null | null | null | null |
|
```
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
heart_df = pd.read_csv("data/heart-disease.csv")
heart_df.head() # classification dataset - supervised learning
```
## 1. Tuning hyperparameters by hand
so far we've worked with training and test datasets.
You train a model on a training set and evaluate it on a test dataset.
But hyperparameter tuning introduces a thrid set, **a validation set.**
Now the process becomes, **train a model on the training data, (try to) improve its hyperparameters on the validation set and evaluate it on the test set.**
```
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier()
clf.get_params()
```
The parameters we are going to adjust (check documentation for definition)
* **max_depth** - the maximum depth of the tree
* **max_features** - the number of features to consider when looking for the best split
* **min_samples_leaf** - the minimum number of samples required to be at a leaf node
* **min_samples_split**
* **n_estimators** - the number of trees in the forest
```
# From 100 samples
# Train - 70, Validation - 15, Test - 15
```
#### Create an evaluation function for models
```
def evaluate_preds(y_true,y_preds):
"""
Performs evaluation comparison on y_true labels vs. y_pred labels
on a classification model.
"""
accuracy = accuracy_score(y_true,y_preds)
precision = precision_score(y_true,y_preds)
recall = recall_score(y_true,y_preds)
f1 = f1_score(y_true,y_preds)
metric_dict = {
"accuracy":round(accuracy,2),
"precision":round(precision,2),
"recall":round(recall,2),
"f1":round(f1,2)
} # A dictionary that stores the results of the evaluation metrics
print(f"Acc: {accuracy * 100:.2f}%")
print(f"Precision: {precision:.2f}")
print(f"Recall: {recall:.2f}")
print(f"F1 score: {f1:.2f}")
return metric_dict
len(heart_df)
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.ensemble import RandomForestClassifier
np.random.seed(42) # Results are reproducable
# Shuffle the data
heart_df_shuffle = heart_df.sample(frac=1)
# Split into X and y
X = heart_df_shuffle.drop("target",axis=1)
y = heart_df_shuffle["target"]
# Split the data into train, validation and test splits
# train - 70%, validation - 15%, test - 15%
train_split = round(0.7 * len(heart_df_shuffle)) # 70%
valid_split = round(train_split + 0.15 * len(heart_df_shuffle)) # index + next 15% of data
# [from:to]
X_train,y_train = X[:train_split],y[:train_split]
X_valid,y_valid = X[train_split:valid_split],y[train_split:valid_split]
X_test,y_test = X[valid_split:],y[valid_split:]
# len(X_train),len(X_valid),len(X_test)
# Train the model
clf = RandomForestClassifier() # instantiates with base line parameters
clf.fit(X_train, y_train)
# Make baseline predictions (on valid set)
y_preds = clf.predict(X_valid) # tune model on valid set
# Evaluate the classifier on validation set
baseline_metrics = evaluate_preds(y_valid, y_preds)
baseline_metrics
```
Beautiful, now let's try and improve the results.
We'll change 1 of the hyperparameters, n_estimators to 100 and see if it improves on the validation set.
```
np.random.seed(42)
# Create a second classifier with different hyperparameters
clf_2 = RandomForestClassifier(n_estimators=100) # adjusting n_estimators
clf_2.fit(X_train, y_train)
# Make predictions
y_preds_2 = clf_2.predict(X_valid)
# Evaluate the 2nd classifier
clf_2_metrics = evaluate_preds(y_valid, y_preds_2)
clf_2_metrics
# Different models on same data
```
How about we try another parameter?
Wait...
Building new models with new hyperparameters each time (by hand) is taking a lot of time.
Is there a better way?
Ans) **RandomizedSearchCV** provided by Sklearn
| true |
code
| 0.602471 | null | null | null | null |
|
# 6장. 알고리즘 체인과 파이프라인
*아래 링크를 통해 이 노트북을 주피터 노트북 뷰어(nbviewer.org)로 보거나 구글 코랩(colab.research.google.com)에서 실행할 수 있습니다.*
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://nbviewer.org/github/rickiepark/intro_ml_with_python_2nd_revised/blob/main/06-algorithm-chains-and-pipelines.ipynb"><img src="https://jupyter.org/assets/share.png" width="60" />주피터 노트북 뷰어로 보기</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/rickiepark/intro_ml_with_python_2nd_revised/blob/main/06-algorithm-chains-and-pipelines.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩(Colab)에서 실행하기</a>
</td>
</table>
<b><font size=2>이 노트북은 맷플롯립 그래프에 한글을 쓰기 위해 나눔 폰트를 사용합니다. 컴퓨터에 나눔 폰트가 없다면 설치해 주세요.<br><br><font color='red'>주의: 코랩에서 실행하는 경우 아래 셀을 실행하고 ⌘+M . 또는 Ctrl+M . 을 눌러 런타임을 재시작한 다음 처음부터 다시 실행해 주세요.</font></b>
```
# 노트북이 코랩에서 실행 중인지 체크합니다.
import os
import sys
if 'google.colab' in sys.modules and not os.path.isdir('mglearn'):
# 사이킷런 최신 버전을 설치합니다.
!pip install -q --upgrade scikit-learn
# mglearn을 다운받고 압축을 풉니다.
!wget -q -O mglearn.tar.gz https://bit.ly/mglearn-tar-gz
!tar -xzf mglearn.tar.gz
# 나눔 폰트를 설치합니다.
!sudo apt-get -qq -y install fonts-nanum
import matplotlib.font_manager as fm
fm._rebuild()
import sklearn
from preamble import *
import matplotlib
# 나눔 폰트를 사용합니다.
matplotlib.rc('font', family='NanumBarunGothic')
matplotlib.rcParams['axes.unicode_minus'] = False
from sklearn.svm import SVC
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# 데이터 적재와 분할
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
# 훈련 데이터의 최솟값, 최댓값을 계산합니다
scaler = MinMaxScaler().fit(X_train)
# 훈련 데이터의 스케일을 조정합니다
X_train_scaled = scaler.transform(X_train)
svm = SVC()
# 스케일 조정된 훈련데이터에 SVM을 학습시킵니다
svm.fit(X_train_scaled, y_train)
# 테스트 데이터의 스케일을 조정하고 점수를 계산합니다
X_test_scaled = scaler.transform(X_test)
print("테스트 점수: {:.2f}".format(svm.score(X_test_scaled, y_test)))
```
## 6.1 데이터 전처리와 매개변수 선택
```
from sklearn.model_selection import GridSearchCV
# 이 코드는 예를 위한 것입니다. 실제로 사용하지 마세요.
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=5)
grid.fit(X_train_scaled, y_train)
print("최상의 교차 검증 정확도: {:.2f}".format(grid.best_score_))
print("테스트 점수: {:.2f}".format(grid.score(X_test_scaled, y_test)))
print("최적의 매개변수: ", grid.best_params_)
mglearn.plots.plot_improper_processing()
```
## 6.2 파이프라인 구축하기
```
from sklearn.pipeline import Pipeline
pipe = Pipeline([("scaler", MinMaxScaler()), ("svm", SVC())])
pipe.fit(X_train, y_train)
print("테스트 점수: {:.2f}".format(pipe.score(X_test, y_test)))
```
## 6.3 그리드 서치에 파이프라인 적용하기
```
param_grid = {'svm__C': [0.001, 0.01, 0.1, 1, 10, 100],
'svm__gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5)
grid.fit(X_train, y_train)
print("최상의 교차 검증 정확도: {:.2f}".format(grid.best_score_))
print("테스트 세트 점수: {:.2f}".format(grid.score(X_test, y_test)))
print("최적의 매개변수:", grid.best_params_)
mglearn.plots.plot_proper_processing()
rnd = np.random.RandomState(seed=0)
X = rnd.normal(size=(100, 10000))
y = rnd.normal(size=(100,))
from sklearn.feature_selection import SelectPercentile, f_regression
select = SelectPercentile(score_func=f_regression, percentile=5).fit(X, y)
X_selected = select.transform(X)
print("X_selected.shape:", X_selected.shape)
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import Ridge
print("교차 검증 점수 (릿지): {:.2f}".format(
np.mean(cross_val_score(Ridge(), X_selected, y, cv=5))))
pipe = Pipeline([("select", SelectPercentile(score_func=f_regression,
percentile=5)),
("ridge", Ridge())])
print("교차 검증 점수 (파이프라인): {:.2f}".format(
np.mean(cross_val_score(pipe, X, y, cv=5))))
```
## 6.4 파이프라인 인터페이스
```
def fit(self, X, y):
X_transformed = X
for name, estimator in self.steps[:-1]:
# 마지막 단계를 빼고 fit과 transform을 반복합니다
X_transformed = estimator.fit_transform(X_transformed, y)
# 마지막 단계 fit을 호출합니다
self.steps[-1][1].fit(X_transformed, y)
return self
def predict(self, X):
X_transformed = X
for step in self.steps[:-1]:
# 마지막 단계를 빼고 transform을 반복합니다
X_transformed = step[1].transform(X_transformed)
# 마지막 단계 predict을 호출합니다
return self.steps[-1][1].predict(X_transformed)
```
#### 파이프라인 그리기
```
from sklearn import set_config
set_config(display='diagram')
pipe
```
### 6.4.1 `make_pipleline`을 사용한 파이프라인 생성
```
from sklearn.pipeline import make_pipeline
# 표준적인 방법
pipe_long = Pipeline([("scaler", MinMaxScaler()), ("svm", SVC(C=100))])
# 간소화된 방법
pipe_short = make_pipeline(MinMaxScaler(), SVC(C=100))
print("파이프라인 단계:\n", pipe_short.steps)
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
pipe = make_pipeline(StandardScaler(), PCA(n_components=2), StandardScaler())
print("파이프라인 단계:\n", pipe.steps)
```
### 6.4.2 단계 속성에 접근하기
```
# cancer 데이터셋에 앞서 만든 파이프라인을 적용합니다
pipe.fit(cancer.data)
# "pca" 단계의 두 개 주성분을 추출합니다
components = pipe.named_steps["pca"].components_
print("components.shape:", components.shape)
```
### 6.4.3 그리드 서치 안의 파이프라인의 속성에 접근하기
```
from sklearn.linear_model import LogisticRegression
pipe = make_pipeline(StandardScaler(), LogisticRegression(max_iter=1000))
param_grid = {'logisticregression__C': [0.01, 0.1, 1, 10, 100]}
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=4)
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("최상의 모델:\n", grid.best_estimator_)
print("로지스틱 회귀 단계:\n",
grid.best_estimator_.named_steps["logisticregression"])
print("로지스틱 회귀 계수:\n",
grid.best_estimator_.named_steps["logisticregression"].coef_)
```
## 6.5 전처리와 모델의 매개변수를 위한 그리드 서치
```
# 보스턴 주택 데이터셋이 1.0 버전에 deprecated 되었고 1.2 버전에서 삭제됩니다.
# 경고 메시지를 피하기 위해 다음 코드를 추가합니다.
import warnings
warnings.filterwarnings("ignore", category=FutureWarning)
from sklearn.datasets import load_boston
boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target,
random_state=0)
from sklearn.preprocessing import PolynomialFeatures
pipe = make_pipeline(
StandardScaler(),
PolynomialFeatures(),
Ridge())
param_grid = {'polynomialfeatures__degree': [1, 2, 3],
'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5, n_jobs=-1)
grid.fit(X_train, y_train)
mglearn.tools.heatmap(grid.cv_results_['mean_test_score'].reshape(3, -1),
xlabel="ridge__alpha", ylabel="polynomialfeatures__degree",
xticklabels=param_grid['ridge__alpha'],
yticklabels=param_grid['polynomialfeatures__degree'], vmin=0)
plt.show() # 책에는 없음
print("최적의 매개변수:", grid.best_params_)
print("테스트 세트 점수: {:.2f}".format(grid.score(X_test, y_test)))
param_grid = {'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
pipe = make_pipeline(StandardScaler(), Ridge())
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("다항 특성이 없을 때 점수: {:.2f}".format(grid.score(X_test, y_test)))
```
## 6.6 모델 선택을 위한 그리드 서치
```
pipe = Pipeline([('preprocessing', StandardScaler()), ('classifier', SVC())])
from sklearn.ensemble import RandomForestClassifier
param_grid = [
{'classifier': [SVC()], 'preprocessing': [StandardScaler()],
'classifier__gamma': [0.001, 0.01, 0.1, 1, 10, 100],
'classifier__C': [0.001, 0.01, 0.1, 1, 10, 100]},
{'classifier': [RandomForestClassifier(n_estimators=100)],
'preprocessing': [None], 'classifier__max_features': [1, 2, 3]}]
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("최적의 매개변수:\n{}\n".format(grid.best_params_))
print("최상의 교차 검증 점수: {:.2f}".format(grid.best_score_))
print("테스트 세트 점수: {:.2f}".format(grid.score(X_test, y_test)))
```
### 6.6.1 중복 계산 피하기
```
pipe = Pipeline([('preprocessing', StandardScaler()), ('classifier', SVC())],
memory="cache_folder")
```
## 6.7 요약 및 정리
| true |
code
| 0.513363 | null | null | null | null |
|
# Tutorial NlOpt
## Зачем это нужно?
В современных компетенциях инженерных или научных специальностей всё чаще приходится сталкиваться с теми или иными задачами требующими оптимизации функции.
В общем смысле под оптимизацией понимают поиск экстремума исследуемой функции.
$$f(x,y) \rightarrow max(min)$$
Заметим, что в случае простейших школьных функций одной переменной достаточно всего лишь приравнять производную от этой функции к нулю и решить полученное уравнение.
Но в более серьёзных задачах, где функции могут уже зависеть от нескольких переменных, такой метод может стать невозможным. Заметим также, что в зависимости от задачи
и самой функции, требуется применять разный алгоритм оптимизации.
К сожалению, использование внутренних команд питон может быть недостаточно для решения поставленной проблемы. В помощь этому приведем туториал по основам использования
мультиязычной и мультиплатформенной библиотеки NlOpt https://nlopt.readthedocs.io/en/latest/. В ней реализовано большое количество различных алгоритмов оптимизации число которых растёт, благодаря поддержке со стороны разработчиков. В качестве примера разберём несколько алгоритмов для оптимизации функции Химмельблау на языке питон. Будет приведён готовый программный код, который сразу можно будет использовать на практике.
> В туториале опущен вопрос по установке модуля на компьютер. С этим необходимо будет справиться самостоятельно.
## Сам процесс написания кода
Вид функции Химмельблау
$$f(x,y)=(x^2+y-11)^2+(x+y^2-7)^2$$
Вначале введём наши модули
```
import nlopt
from numpy import *
```
Вторым этапом распишем функцию *myfunc*
Для этого в строках *grad[0]* и *grad[1]* записываются частные производные функции от первой и второй переменных соответственно. *myfunc* возвращает саму функцию Химмельблау.
```
def myfunc(x, grad):
if grad.size > 0:
grad[0] = 4.0*x[0]*(x[0]**2+x[1]-11.0)+2.0*(x[0]+x[1]**2-7.0)
grad[1] = 2.0*(x[0]**2+x[1]-11.0)+4.0*x[1]*(x[0]+x[1]**2-7.0)
return ((x[0]**2+x[1]-11.0)**2+(x[0]+x[1]**2-7.0)**2)
```
Затем выбираем сам алгоритм оптимизации. На сайте представлен полный список всех алгоритмов и их описание. Со списком можно ознакомиться по ссылке https://nlopt.readthedocs.io/en/latest/NLopt_Algorithms/ Обращаем внимание, что **2** означает количество переменных от которых зависит исследуемая функция.
```
opt = nlopt.opt(nlopt.LN_BOBYQA, 2)
```
Дальше по пунктам:
- Запускам нашу функцию
- Задаём точность
- Выбираем начальную точку
- Задаём переменную, которая и будет равна оптимальному значению функции
- Вывод полученных результатов
```
opt.set_min_objective(myfunc)
opt.set_xtol_rel(1e-6)
x= opt.optimize([ 12.5, 1.5])
minf = opt.last_optimum_value()
print ("optimum at ", x[0], x[1])
print ("minimum value = ", minf)
```
На этом всё. В дальнейших уроках разберём оптимизацию с ограничением.
| true |
code
| 0.25333 | null | null | null | null |
|
# Stacking LSTM Layers
-----------------
Here we implement an LSTM model on all a data set of Shakespeare works. We will stack multiple LSTM models for a more accurate representation of Shakespearean language. We will also use characters instead of words.
```
import os
import re
import string
import requests
import numpy as np
import collections
import random
import pickle
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()
```
Start a computational graph session.
```
sess = tf.Session()
```
Set RNN Parameters
```
num_layers = 3 # Number of RNN layers stacked
min_word_freq = 5 # Trim the less frequent words off
rnn_size = 128 # RNN Model size, has to equal embedding size
epochs = 10 # Number of epochs to cycle through data
batch_size = 100 # Train on this many examples at once
learning_rate = 0.0005 # Learning rate
training_seq_len = 50 # how long of a word group to consider
save_every = 500 # How often to save model checkpoints
eval_every = 50 # How often to evaluate the test sentences
prime_texts = ['thou art more', 'to be or not to', 'wherefore art thou']
```
Download/store Shakespeare data
```
data_dir = 'temp'
data_file = 'shakespeare.txt'
model_path = 'shakespeare_model'
full_model_dir = os.path.join(data_dir, model_path)
```
Declare the punctuation and then create the model and data directories
```
# Declare punctuation to remove, everything except hyphens and apostrophes
punctuation = string.punctuation
punctuation = ''.join([x for x in punctuation if x not in ['-', "'"]])
# Make Model Directory
if not os.path.exists(full_model_dir):
os.makedirs(full_model_dir)
# Make data directory
if not os.path.exists(data_dir):
os.makedirs(data_dir)
```
Load the Shakespeare Data
```
print('Loading Shakespeare Data')
# Check if file is downloaded.
if not os.path.isfile(os.path.join(data_dir, data_file)):
print('Not found, downloading Shakespeare texts from www.gutenberg.org')
shakespeare_url = 'http://www.gutenberg.org/cache/epub/100/pg100.txt'
# Get Shakespeare text
response = requests.get(shakespeare_url)
shakespeare_file = response.content
# Decode binary into string
s_text = shakespeare_file.decode('utf-8')
# Drop first few descriptive paragraphs.
s_text = s_text[7675:]
# Remove newlines
s_text = s_text.replace('\r\n', '')
s_text = s_text.replace('\n', '')
# Write to file
with open(os.path.join(data_dir, data_file), 'w') as out_conn:
out_conn.write(s_text)
else:
# If file has been saved, load from that file
with open(os.path.join(data_dir, data_file), 'r') as file_conn:
s_text = file_conn.read().replace('\n', '')
print('Done Loading Data.')
```
Clean and split the text data.
```
# Clean text
print('Cleaning Text')
s_text = re.sub(r'[{}]'.format(punctuation), ' ', s_text)
s_text = re.sub('\s+', ' ', s_text ).strip().lower()
# Split up by characters
char_list = list(s_text)
```
Build word vocabulary function and transform the text.
```
def build_vocab(characters):
character_counts = collections.Counter(characters)
# Create vocab --> index mapping
chars = character_counts.keys()
vocab_to_ix_dict = {key:(ix+1) for ix, key in enumerate(chars)}
# Add unknown key --> 0 index
vocab_to_ix_dict['unknown']=0
# Create index --> vocab mapping
ix_to_vocab_dict = {val:key for key,val in vocab_to_ix_dict.items()}
return(ix_to_vocab_dict, vocab_to_ix_dict)
# Build Shakespeare vocabulary
print('Building Shakespeare Vocab by Characters')
ix2vocab, vocab2ix = build_vocab(char_list)
vocab_size = len(ix2vocab)
print('Vocabulary Length = {}'.format(vocab_size))
# Sanity Check
assert(len(ix2vocab) == len(vocab2ix))
```
Convert text to word vectors
```
s_text_ix = []
for x in char_list:
try:
s_text_ix.append(vocab2ix[x])
except:
s_text_ix.append(0)
s_text_ix = np.array(s_text_ix)
```
Define LSTM RNN Model Class
```
class LSTM_Model():
def __init__(self, rnn_size, num_layers, batch_size, learning_rate,
training_seq_len, vocab_size, infer_sample=False):
self.rnn_size = rnn_size
self.num_layers = num_layers
self.vocab_size = vocab_size
self.infer_sample = infer_sample
self.learning_rate = learning_rate
if infer_sample:
self.batch_size = 1
self.training_seq_len = 1
else:
self.batch_size = batch_size
self.training_seq_len = training_seq_len
self.lstm_cell = tf.contrib.rnn.BasicLSTMCell(rnn_size)
self.lstm_cell = tf.contrib.rnn.MultiRNNCell([self.lstm_cell for _ in range(self.num_layers)])
self.initial_state = self.lstm_cell.zero_state(self.batch_size, tf.float32)
self.x_data = tf.placeholder(tf.int32, [self.batch_size, self.training_seq_len])
self.y_output = tf.placeholder(tf.int32, [self.batch_size, self.training_seq_len])
with tf.variable_scope('lstm_vars'):
# Softmax Output Weights
W = tf.get_variable('W', [self.rnn_size, self.vocab_size], tf.float32, tf.random_normal_initializer())
b = tf.get_variable('b', [self.vocab_size], tf.float32, tf.constant_initializer(0.0))
# Define Embedding
embedding_mat = tf.get_variable('embedding_mat', [self.vocab_size, self.rnn_size],
tf.float32, tf.random_normal_initializer())
embedding_output = tf.nn.embedding_lookup(embedding_mat, self.x_data)
rnn_inputs = tf.split(axis=1, num_or_size_splits=self.training_seq_len, value=embedding_output)
rnn_inputs_trimmed = [tf.squeeze(x, [1]) for x in rnn_inputs]
decoder = tf.contrib.legacy_seq2seq.rnn_decoder
outputs, last_state = decoder(rnn_inputs_trimmed,
self.initial_state,
self.lstm_cell)
# RNN outputs
output = tf.reshape(tf.concat(axis=1, values=outputs), [-1, rnn_size])
# Logits and output
self.logit_output = tf.matmul(output, W) + b
self.model_output = tf.nn.softmax(self.logit_output)
loss_fun = tf.contrib.legacy_seq2seq.sequence_loss_by_example
loss = loss_fun([self.logit_output],[tf.reshape(self.y_output, [-1])],
[tf.ones([self.batch_size * self.training_seq_len])],
self.vocab_size)
self.cost = tf.reduce_sum(loss) / (self.batch_size * self.training_seq_len)
self.final_state = last_state
gradients, _ = tf.clip_by_global_norm(tf.gradients(self.cost, tf.trainable_variables()), 4.5)
optimizer = tf.train.AdamOptimizer(self.learning_rate)
self.train_op = optimizer.apply_gradients(zip(gradients, tf.trainable_variables()))
def sample(self, sess, words=ix2vocab, vocab=vocab2ix, num=20, prime_text='thou art'):
state = sess.run(self.lstm_cell.zero_state(1, tf.float32))
char_list = list(prime_text)
for char in char_list[:-1]:
x = np.zeros((1, 1))
x[0, 0] = vocab[char]
feed_dict = {self.x_data: x, self.initial_state:state}
[state] = sess.run([self.final_state], feed_dict=feed_dict)
out_sentence = prime_text
char = char_list[-1]
for n in range(num):
x = np.zeros((1, 1))
x[0, 0] = vocab[char]
feed_dict = {self.x_data: x, self.initial_state:state}
[model_output, state] = sess.run([self.model_output, self.final_state], feed_dict=feed_dict)
sample = np.argmax(model_output[0])
if sample == 0:
break
char = words[sample]
out_sentence = out_sentence + char
return(out_sentence)
```
Initialize the LSTM Model
```
lstm_model = LSTM_Model(rnn_size, num_layers, batch_size, learning_rate,
training_seq_len, vocab_size)
# Tell TensorFlow we are reusing the scope for the testing
with tf.variable_scope(tf.get_variable_scope(), reuse=True):
test_lstm_model = LSTM_Model(rnn_size,num_layers, batch_size, learning_rate,
training_seq_len, vocab_size, infer_sample=True)
```
Create model saver
```
saver = tf.train.Saver(tf.global_variables())
```
Create batches for each epoch
```
num_batches = int(len(s_text_ix)/(batch_size * training_seq_len)) + 1
# Split up text indices into subarrays, of equal size
batches = np.array_split(s_text_ix, num_batches)
# Reshape each split into [batch_size, training_seq_len]
batches = [np.resize(x, [batch_size, training_seq_len]) for x in batches]
```
Initialize all variables and train the model!
```
# Initialize all variables
init = tf.global_variables_initializer()
sess.run(init)
# Train model
train_loss = []
iteration_count = 1
for epoch in range(epochs):
# Shuffle word indices
random.shuffle(batches)
# Create targets from shuffled batches
targets = [np.roll(x, -1, axis=1) for x in batches]
# Run a through one epoch
print('Starting Epoch #{} of {}.'.format(epoch+1, epochs))
# Reset initial LSTM state every epoch
state = sess.run(lstm_model.initial_state)
for ix, batch in enumerate(batches):
training_dict = {lstm_model.x_data: batch, lstm_model.y_output: targets[ix]}
# We need to update initial state for each RNN cell:
for i, (c, h) in enumerate(lstm_model.initial_state):
training_dict[c] = state[i].c
training_dict[h] = state[i].h
temp_loss, state, _ = sess.run([lstm_model.cost, lstm_model.final_state, lstm_model.train_op],
feed_dict=training_dict)
train_loss.append(temp_loss)
# Print status every 10 gens
if iteration_count % 10 == 0:
summary_nums = (iteration_count, epoch+1, ix+1, num_batches+1, temp_loss)
print('Iteration: {}, Epoch: {}, Batch: {} out of {}, Loss: {:.2f}'.format(*summary_nums))
# Save the model and the vocab
if iteration_count % save_every == 0:
# Save model
model_file_name = os.path.join(full_model_dir, 'model')
saver.save(sess, model_file_name, global_step = iteration_count)
print('Model Saved To: {}'.format(model_file_name))
# Save vocabulary
dictionary_file = os.path.join(full_model_dir, 'vocab.pkl')
with open(dictionary_file, 'wb') as dict_file_conn:
pickle.dump([vocab2ix, ix2vocab], dict_file_conn)
if iteration_count % eval_every == 0:
for sample in prime_texts:
print(test_lstm_model.sample(sess, ix2vocab, vocab2ix, num=10, prime_text=sample))
iteration_count += 1
```
Plot loss over time
```
plt.plot(train_loss, 'k-')
plt.title('Sequence to Sequence Loss')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()
```
| true |
code
| 0.507446 | null | null | null | null |
|
#### Verification Alignment
A forecast is verified by comparing a set of initializations at a given lead to
observations over some window of time. However, there are a few ways to decide *which*
initializations or verification window to use in this alignment.
One must pass the keyword ``alignment=...`` to the hindcast `.verify()` method to set the behavior for aligning forecasts with the verification product. Note that the alignment decision only matters for [hindcast experiments](terminology.html#simulation-design). [Perfect-model experiments](terminology.html#simulation-design) are perfectly time-aligned by design, equating to our `same_inits` keyword.
The available keywords for hindcast alignment are:
* `'same_inits'`: Use a common set of initializations that verify
across all leads. This ensures that there is no bias in the result due to the state
of the system for the given initializations.
* `'same_verifs'`: Use a common verification window across all leads. This ensures
that there is no bias in the result due to the observational period being verified
against.
* `'maximize'`: Use all available initializations at each lead that verify against
the observations provided. This changes both the set of initializations and the
verification window used at each lead.
```
# linting
%load_ext nb_black
%load_ext lab_black
from climpred import HindcastEnsemble
from climpred.tutorial import load_dataset
from esmtools.stats import rm_trend
import matplotlib.pyplot as plt
plt.style.use("fivethirtyeight")
%matplotlib inline
import numpy as np
import warnings
# Supress datetime warnings for this page.
warnings.filterwarnings("ignore")
def create_hindcast_object():
"""Loads in example data from CESM-DPLE and ERSST observations and detrends."""
hind = load_dataset("CESM-DP-SST")["SST"]
verif = load_dataset("ERSST")["SST"]
# Bias-correct over same period as CESM-DPLE.
verif = verif - verif.sel(time=slice(1964, 2014)).mean("time")
# Remove linear trend.
hind_dt = rm_trend(hind, dim="init").rename("SST")
verif_dt = rm_trend(verif, dim="time").rename("SST")
# Create `HindcastEnsemble` object from `climpred`.
hindcast = HindcastEnsemble(hind)
hindcast = hindcast.add_observations(verif)
hindcast_dt = HindcastEnsemble(hind_dt)
hindcast_dt = hindcast_dt.add_observations(verif_dt)
return hindcast, hindcast_dt
hindcast, hindcast_dt = create_hindcast_object()
```
The user can simply change the alignment strategy by passing in the keyword `alignment=...`. Note that the choice of alignment strategy changes the lead-dependent metric results.
```
f, axs = plt.subplots(ncols=2, figsize=(12, 4), sharex=True)
for alignment in ["same_inits", "same_verifs", "maximize"]:
hindcast.verify(metric="acc", comparison="e2o", dim="init", alignment=alignment)[
"SST"
].plot(label=alignment, ax=axs[0])
hindcast_dt.verify(metric="acc", comparison="e2o", dim="init", alignment=alignment)[
"SST"
].plot(label=alignment, ax=axs[1])
axs[0].legend()
axs[1].legend()
axs[0].set(
ylabel="anomaly\ncorrelation coefficient",
xlabel="lead year",
xticks=np.arange(1, 11),
title="SST with trend",
)
axs[1].set(
ylabel="anomaly\ncorrelation coefficient", xlabel="lead year", title="detrended SST"
)
f.suptitle("Verification with Different Alignment Methods", fontsize=14, weight="bold")
plt.subplots_adjust(top=0.85)
plt.show()
```
These alignment keywords also extend to reference forecasts (e.g. `reference='persistence'`), which uses the identical set of initializations (and alignment strategy) in its computation. Below, the dashed lines represent the persistence forecast for the given alignment strategy, while the solid lines denote the initialized anomaly correlation coefficient (as in the above plots).
```
COLORS = ["#008FD5", "#FC4F30", "#E5AE38"]
f, axs = plt.subplots()
for alignment, color in zip(["same_inits", "same_verifs", "maximize"], COLORS):
result = hindcast_dt.verify(
metric="acc",
reference="persistence",
comparison="e2o",
dim="init",
alignment=alignment,
)
result.sel(skill="initialized").SST.plot(label=alignment, color=color)
result.sel(skill="persistence").SST.plot(linestyle="--", color=color, lw=3)
axs.set(
ylabel="anomaly\ncorrelation coefficient",
xlabel="lead year",
xticks=np.arange(1, 11),
title="Detrended SST Verification with Persistence",
)
plt.legend()
plt.show()
```
We'll be using the same example data as above. `climpred` will be aligning the following initialization and verification dates:
```
print(f"initialization dates: \n{hindcast.get_initialized().init.to_index()}")
print(f"verification dates: \n{hindcast.get_observations().time.to_index()}")
```
We use the standard python library `logging` to log the initializations and verification dates used in alignment at each lead. The user can check these logs to ensure that the expected initializations and verification dates are being retained. See the logging section on this page for more details.
```
import logging
# Print log to screen with initializations and verification dates.
logger = logging.getLogger()
logger.setLevel(logging.INFO)
```
## Same Verification Dates
`alignment='same_verifs'`
The `same_verifs` alignment finds a set of verification dates that can be verified against over all leads. It also requires that the verification data have an observation at each initialization being retained. This is so that the reference forecast, such as persistence, uses an identical set of initializations in deriving its forecast. Notice in the logger output that a common set of verification dates spanning 1965-2015 are used, while the initialization window slides one year at each lead.
**References**:
1. Boer, George J., et al. "The decadal climate prediction project (DCPP) contribution to CMIP6." Geoscientific Model Development (Online) 9.10 (2016). [https://doi.org/10.5194/gmd-9-3751-2016]
2. Hawkins, Ed, et al. "The interpretation and use of biases in decadal climate predictions." Journal of climate 27.8 (2014): 2931-2947. [https://doi.org/10.1175/JCLI-D-13-00473.1]
3. Smith, Doug M., Rosie Eade, and Holger Pohlmann. "A comparison of full-field and anomaly initialization for seasonal to decadal climate prediction." Climate dynamics 41.11-12 (2013): 3325-3338. [https://doi.org/10.1007/s00382-013-1683-2]
```
skill = hindcast.verify(
metric="acc", comparison="e2o", dim="init", alignment="same_verifs"
)
```
Here, we include a figure of a simpler alignment case with annual initializations from 1990 through 2000 and three lead years. We verify this hypothetical initialized ensemble against a product that spans 1995 through 2002.
Two conditions must be met when selecting the verification window:
1. There must be a union between the initialization dates and verification dates. This
is represented by the black vertical lines in the top panel below, which leave out
1990-1994 initializations since there aren't observations before 1995. This logic
exists so that any reference forecasts
(e.g. a persistence forecast) use an identical set of initializations as the
initialized forecast.
2. A given verification time must exist across all leads. This is to ensure that at each
lead, the entire set of chosen verification dates can be verified against. This is
represented by diagonals in the top panel below (and the dashed black lines).
Without the first stipulation, this would set the verification window at 1995-2001.
This leaves us with a verification window of [1998, 1999, 2000, 2001] which can be verified against across all leads (and have a complimentary persistence forecast with the same set of initializations used at each lead).

## Same Initializations
`alignment='same_inits'`
The `same_inits` alignment finds a set of initializations that can verify over all leads. It also requires that the verification data have an observation at each initialization being retained. This is so that the reference forecast, such as persistence, uses an identical set of initializations in deriving its forecast. Notice in the logger output that a common set of initializations spanning 1955-2005 are used, while the verification window slides one year at each lead.
```
skill = hindcast.verify(
metric="acc", comparison="e2o", dim="init", alignment="same_inits"
)
```
Here, we include a figure of a simpler alignment case with annual initializations from 1990 through 2000 and three lead years. We verify this hypothetical initialized ensemble against a product that spans 1995 through 2002.
Two conditions must be met to retain the initializations for verification:
1. There must be an observation in the verification data for the given initialization.
In combination with (1), initializations 1990 through 1994 are left out. This logic
exists so that any reference forecast (e.g. a persistence forecast) use an identical set of initializations as the
initialized forecast.
2. All forecasted times (i.e., initialization + lead year) for a given initialization
must be contained in the verification data. Schematically, this means that there must
be a union between a column in the top panel and the time series in the bottom panel.
The 2000 initialization below is left out since the verification data does not
contain 2003.
This leaves us with initializations [1995, 1996, ..., 1999] which can verify against the observations at all three lead years.

## Maximize Degrees of Freedom
`alignment='maximize'`
The `maximize` alignment verifies against every available observation at each lead. This means that both the initializations and verification dates could be different at each lead. It also requires that the verification data have an observation at each initialization being retained. This is so that the reference forecast, such as persistence, uses an identical set of initializations in deriving its forecast.
Notice in the logger output that the initialization window shrinks from 1955-2014 (N=60) at lead year 1 to 1955-2005 (N=51) at lead year 10. Similarly, the verification window spans 1956-2015 at lead year 1 and 1965-2015 at lead year 10. However, using the other two alignment strategies (`same_verifs` and `same_inits`), there is a fixed N=51 to ensure constant initializations or verification dates, while the number of samples is extended to as high as 60 with this alignment strategy.
**References**:
1. Yeager, S. G., et al. "Predicting near-term changes in the Earth System: A large ensemble of initialized decadal prediction simulations using the Community Earth System Model." Bulletin of the American Meteorological Society 99.9 (2018): 1867-1886. [https://doi.org/10.1175/BAMS-D-17-0098.1]
```
skill = hindcast.verify(
metric="acc", comparison="e2o", dim="init", alignment="maximize"
)
```
Here, we include a figure of a simpler alignment case with annual initializations from 1990 through 2000 and three lead years. We verify this hypothetical initialized ensemble against a product that spans 1995 through 2002.
Two conditions must be met when selecting initializations/verifications at each lead:
1. There must be a union between the initialization dates and verification dates. This
is represented by the black vertical lines in the top panel below, which leave out
1990-1994 initializations since there aren't observations before 1995. This logic
exists so that any reference forecasts
(e.g. a persistence forecast) use an identical set of initializations as the
initialized forecast.
2. The selected initializations must verify with the provided observations for the given lead.
This is shown by the hatching in the figure below. The 2000 initialization is left out
at lead year 3 since there is no observation for 2003.
This leaves us with the following alignment:
* LY1 initializations: [1995, 1996, 1997, 1998, 1999, 2000]
* LY2 initializations: [1995, 1996, 1997, 1998, 1999, 2000]
* LY3 initializations: [1995, 1996, 1997, 1998, 1999]

## Logging
``climpred`` uses the standard library ``logging`` to store the initializations and verification dates used at each lead for a given computation. This is used internally for testing, but more importantly, can be activated by the user so they can be sure of how computations are being done.
To see the log interactively, e.g. while working in Jupyter notebooks or on the command line use the following:
```
import logging
logger = logging.getLogger()
logger.setLevel(logging.INFO)
skill = hindcast.verify(
metric="acc", comparison="e2o", dim="init", alignment="same_verifs"
)
```
The `INFO` level reports the minimum and maximum bounds for initializations and verification dates. To see every single initialization and verification date used, set the level to `DEBUG`.
```
logger.setLevel(logging.DEBUG)
skill = hindcast.isel(lead=slice(0, 2)).verify(
metric="acc", comparison="e2o", dim="init", alignment="same_verifs"
)
```
One can also save out the log to a file.
```
logger = logging.getLogger()
logger.setLevel(logging.INFO)
fh = logging.FileHandler("hindcast.out")
logger.addHandler(fh)
skill = hindcast.verify(
metric="acc", comparison="e2o", dim="init", alignment="same_verifs"
)
skill = hindcast.verify(
metric="acc", comparison="e2o", dim="init", alignment="same_verifs"
)
!cat hindcast.out
!rm hindcast.out
```
| true |
code
| 0.588534 | null | null | null | null |
|
# DecisionTreeRegressor with Normalize
This Code template is for regression analysis using simple DecisionTreeRegressor based on the Classification and Regression Trees algorithm along with Normalize Feature Scaling technique.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor,plot_tree
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
from sklearn.preprocessing import Normalizer
warnings.filterwarnings('ignore')
```
#### Initialization
Filepath of CSV file
```
file_path=""
```
List of features which are required for model training .
```
features=[]
```
Target feature for prediction.
```
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path);
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)#plotting correlation matrix
plt.show()
```
### Data Rescaling
#### Normalizer:
Normalize samples individually to unit norm.
Each sample (i.e. each row of the data matrix) with at least one non zero component is rescaled independently of other samples so that its norm (l1 or l2) equals one.
This transformer is able to work both with dense numpy arrays and scipy.sparse matrix (use CSR format if you want to avoid the burden of a copy / conversion).
Scaling inputs to unit norms is a common operation for text classification or clustering for instance. For instance the dot product of two l2-normalized TF-IDF vectors is the cosine similarity of the vectors and is the base similarity metric for the Vector Space Model commonly used by the Information Retrieval community.
```
X_scaled=Normalizer().fit_transform(X)
X_scaled=pd.DataFrame(data = X_scaled,columns = X.columns)
X_scaled.head()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X_scaled,Y,test_size=0.2,random_state=123)
```
### Model
Decision tree is the most powerful and popular tool for classification and prediction. A Decision tree is a flowchart like tree structure, where each internal node denotes a test on an attribute, each branch represents an outcome of the test, and each leaf node holds a outcome label.
Decision trees can also be applied to regression problems, using the DecisionTreeRegressor class.
As in the classification setting, the fit method will take as argument arrays X and y, only that in this case y is expected to have floating point values instead of integer values
#### Model Tuning Parameter
> - criterion -> The function to measure the quality of a split. Supported criteria are “mse” for the mean squared error, which is equal to variance reduction as feature selection criterion and minimizes the L2 loss using the mean of each terminal node, “friedman_mse”, which uses mean squared error with Friedman’s improvement score for potential splits, “mae” for the mean absolute error, which minimizes the L1 loss using the median of each terminal node, and “poisson” which uses reduction in Poisson deviance to find splits.
> - max_depth -> The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples.
> - max_leaf -> Grow a tree with max_leaf_nodes in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
> - max_features -> The number of features to consider when looking for the best split: **{auto , sqrt, log2}**
```
model = DecisionTreeRegressor(random_state=123)
model = model.fit(x_train,y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
The model score function computes the accuracy, either the fraction or the count of correct predictions.
> **score**: The **score** function returns the coefficient of determination <code>R<sup>2</sup></code> of the prediction.
```
print("Accuracy on test: {:.2f} %".format(model.score(x_test, y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred = model.predict(x_test)
print("R2 Score: {:.2f}%".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Feature Importances
The Feature importance refers to techniques that assign a score to features based on how useful they are for making the prediction.
```
plt.figure(figsize=(8,6))
n_features = len(X.columns)
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), X.columns)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
n=len(x_test) if len(x_test)<20 else 20
plt.figure(figsize=(14,10))
plt.plot(range(n),y_test[0:n], color = "green")
plt.plot(range(n),model.predict(x_test[0:n]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Prediction Plot
Tree Plot
Plot a decision tree.The visualization is fit automatically to the size of the axis. Use the figsize or dpi arguments of plt.figure to control the size of the rendering.
```
fig, axes = plt.subplots(nrows = 1,ncols = 1,figsize = (3,3), dpi=400)
cls_target = [str(x) for x in pd.unique(y_train)]
cls_target.sort()
plot_tree(model,feature_names = X.columns, class_names=cls_target,filled = True)
fig.savefig('./tree.png')
```
#### Creator:Shreepad Nade , Github: [Profile](https://github.com/shreepad-nade)
| true |
code
| 0.531696 | null | null | null | null |
|
# 1-异常检测
## note:
* [covariance matrix](http://docs.scipy.org/doc/numpy/reference/generated/numpy.cov.html)
* [multivariate_normal](http://docs.scipy.org/doc/numpy/reference/generated/numpy.random.multivariate_normal.html)
* [seaborn bivariate kernel density estimate](https://stanford.edu/~mwaskom/software/seaborn/generated/seaborn.kdeplot.html#seaborn.kdeplot)
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(context='notebook',style='white',palette=sns.color_palette("RdBu"))
import numpy as np
import pandas as pd
import scipy.io as scio
from scipy import stats
from sklearn.model_selection import train_test_split
```
You want to divide data into 3 set.
1. Training set
2. Cross Validation set
3. Test set.
You shouldn't be doing prediction using training data or Validation data as it does in the exercise.
```
mat = scio.loadmat('data/ex8data1.mat')
mat.keys()
X = mat.get('X')
```
divide original validation data into validation and test set
```
Xval, Xtest, yval, ytest = train_test_split(mat.get('Xval'),
mat.get('yval').ravel(),
test_size=0.5)
sns.regplot(x = 'Latency', y = 'Throughput',
data=pd.DataFrame(X, columns=['Latency', 'Throughput']),
fit_reg=False,
scatter_kws={"s":20,
"alpha":0.5})
plt.show()
```
## estimate multivariate Gaussian parameters 𝜇 and 𝜎2
> according to data, X1, and X2 is not independent
```
mu = X.mean(axis=0)
print(mu, '\n')
cov = np.cov(X.T)
print(cov)
# example of creating 2d grid to calculate probability density
np.dstack(np.mgrid[0:3,0:3])
# create multi-var Gaussian model
multi_normal = stats.multivariate_normal(mu, cov)
# create a grid
x, y = np.mgrid[0:30:0.01, 0:30:0.01]
pos = np.dstack((x, y))
fig, ax = plt.subplots()
# plot probability density
ax.contourf(x, y, multi_normal.pdf(pos), cmap='Blues')
# plot original data points
sns.regplot(x = 'Latency', y = 'Throughput',
data=pd.DataFrame(X, columns=['Latency', 'Throughput']),
fit_reg=False,
ax=ax,
scatter_kws={"s":10,
"alpha":0.4})
plt.show()
```
## select threshold 𝜖
```
def select_threshold(X, Xval, yval):
"""use CV data to find the best epsilon
Returns:
e: best epsilon with the highest f-score
f-score: such best f-score
"""
# create multivariate model using training data
mu = X.mean(axis=0)
cov = np.cov(X.T)
multi_normal = stats.multivariate_normal(mu, cov)
# this is key, use CV data for fine tuning hyper parameters
pval = multi_normal.pdf(Xval)
# set up epsilon candidates
epsilon = np.linspace(np.min(pval), np.max(pval), num=10000)
# calculate f-score
fs = []
for e in epsilon:
y_pred = (pval <= e).astype('int')
fs.append(f1_score(yval, y_pred))
# find the best f-score
argmax_fs = np.argmax(fs)
return epsilon[argmax_fs], fs[argmax_fs]
from sklearn.metrics import f1_score, classification_report
e, fs = select_threshold(X, Xval, yval)
print('Best epsilon: {}\nBest F-score on validation data: {}'.format(e, fs))
```
## visualize prediction of Xval using learned 𝜖
```
def select_threshold(X, Xval, yval):
"""use CV data to find the best epsilon
Returns:
e: best epsilon with the highest f-score
f-score: such best f-score
"""
# create multivariate model using training data
mu = X.mean(axis=0)
cov = np.cov(X.T)
multi_normal = stats.multivariate_normal(mu, cov)
# this is key, use CV data for fine tuning hyper parameters
pval = multi_normal.pdf(Xval)
# set up epsilon candidates
epsilon = np.linspace(np.min(pval), np.max(pval), num=10000)
# calculate f-score
fs = []
for e in epsilon:
y_pred = (pval <= e).astype('int')
fs.append(f1_score(yval, y_pred))
# find the best f-score
argmax_fs = np.argmax(fs)
return epsilon[argmax_fs], fs[argmax_fs]
def predict(X, Xval, e, Xtest, ytest):
"""with optimal epsilon, combine X, Xval and predict Xtest
Returns:
multi_normal: multivariate normal model
y_pred: prediction of test data
"""
Xdata = np.concatenate((X, Xval), axis=0)
mu = Xdata.mean(axis=0)
cov = np.cov(Xdata.T)
multi_normal = stats.multivariate_normal(mu, cov)
# calculate probability of test data
pval = multi_normal.pdf(Xtest)
y_pred = (pval <= e).astype('int')
print(classification_report(ytest, y_pred))
return multi_normal, y_pred
multi_normal, y_pred = predict(X, Xval, e, Xtest, ytest)
# construct test DataFrame
data = pd.DataFrame(Xtest, columns=['Latency', 'Throughput'])
data['y_pred'] = y_pred
# create a grid for graphing
x, y = np.mgrid[0:30:0.01, 0:30:0.01]
pos = np.dstack((x, y))
fig, ax = plt.subplots()
# plot probability density
ax.contourf(x, y, multi_normal.pdf(pos), cmap='Blues')
# plot original Xval points
sns.regplot(x = 'Latency', y = 'Throughput',
data=data,
fit_reg=False,
ax=ax,
scatter_kws={"s":10,
"alpha":0.4})
# mark the predicted anamoly of CV data. We should have a test set for this...
anamoly_data = data[data['y_pred']==1]
ax.scatter(anamoly_data['Latency'], anamoly_data['Throughput'], marker='x', s=50)
plt.show()
```
## high dimension data
```
mat = scio.loadmat('data/ex8data2.mat')
X = mat.get('X')
Xval, Xtest, yval, ytest = train_test_split(mat.get('Xval'),
mat.get('yval').ravel(),
test_size=0.5)
e, fs = select_threshold(X, Xval, yval)
print('Best epsilon: {}\nBest F-score on validation data: {}'.format(e, fs))
multi_normal, y_pred = predict(X, Xval, e, Xtest, ytest)
print('find {} anamolies'.format(y_pred.sum()))
```
# 2-推荐系统
```
movies_mat = scio.loadmat('data/ex8_movies.mat')
Y, R = movies_mat.get('Y'), movies_mat.get('R')
Y.shape, R.shape
m, u = Y.shape
# m: how many movies
# u: how many users
n = 10 # how many features for a movie
param_mat = scio.loadmat('./data/ex8_movieParams.mat')
theta, X = param_mat.get('Theta'), param_mat.get('X')
theta.shape, X.shape
def serialize(X, theta):
"""serialize 2 matrix
"""
# X (movie, feature), (1682, 10): movie features
# theta (user, feature), (943, 10): user preference
return np.concatenate((X.ravel(), theta.ravel()))
def deserialize(param, n_movie, n_user, n_features):
"""into ndarray of X(1682, 10), theta(943, 10)"""
return param[:n_movie * n_features].reshape(n_movie, n_features), \
param[n_movie * n_features:].reshape(n_user, n_features)
# recommendation fn
def cost(param, Y, R, n_features):
"""compute cost for every r(i, j)=1
Args:
param: serialized X, theta
Y (movie, user), (1682, 943): (movie, user) rating
R (movie, user), (1682, 943): (movie, user) has rating
"""
# theta (user, feature), (943, 10): user preference
# X (movie, feature), (1682, 10): movie features
n_movie, n_user = Y.shape
X, theta = deserialize(param, n_movie, n_user, n_features)
inner = np.multiply(X @ theta.T - Y, R)
return np.power(inner, 2).sum() / 2
def gradient(param, Y, R, n_features):
# theta (user, feature), (943, 10): user preference
# X (movie, feature), (1682, 10): movie features
n_movies, n_user = Y.shape
X, theta = deserialize(param, n_movies, n_user, n_features)
inner = np.multiply(X @ theta.T - Y, R) # (1682, 943)
# X_grad (1682, 10)
X_grad = inner @ theta
# theta_grad (943, 10)
theta_grad = inner.T @ X
# roll them together and return
return serialize(X_grad, theta_grad)
def regularized_cost(param, Y, R, n_features, l=1):
reg_term = np.power(param, 2).sum() * (l / 2)
return cost(param, Y, R, n_features) + reg_term
def regularized_gradient(param, Y, R, n_features, l=1):
grad = gradient(param, Y, R, n_features)
reg_term = l * param
return grad + reg_term
# use subset of data to calculate the cost as in pdf...
users = 4
movies = 5
features = 3
X_sub = X[:movies, :features]
theta_sub = theta[:users, :features]
Y_sub = Y[:movies, :users]
R_sub = R[:movies, :users]
param_sub = serialize(X_sub, theta_sub)
cost(param_sub, Y_sub, R_sub, features)
param = serialize(X, theta) # total real params
cost(serialize(X, theta), Y, R, 10) # this is real total cost
n_movie, n_user = Y.shape
X_grad, theta_grad = deserialize(gradient(param, Y, R, 10),
n_movie, n_user, 10)
assert X_grad.shape == X.shape
assert theta_grad.shape == theta.shape
```
## regularized cost
```
# in the ex8_confi.m, lambda = 1.5, and it's using sub data set
regularized_cost(param_sub, Y_sub, R_sub, features, l=1.5)
regularized_cost(param, Y, R, 10, l=1) # total regularized cost
```
## regularized gradient
```
n_movie, n_user = Y.shape
X_grad, theta_grad = deserialize(regularized_gradient(param, Y, R, 10),
n_movie, n_user, 10)
assert X_grad.shape == X.shape
assert theta_grad.shape == theta.shape
```
## parse movie_id.txt
```
movie_list = []
with open('./data/movie_ids.txt', encoding='latin-1') as f:
for line in f:
tokens = line.strip().split(' ')
movie_list.append(' '.join(tokens[1:]))
movie_list = np.array(movie_list)
```
## reproduce my ratings
```
ratings = np.zeros(1682)
ratings[0] = 4
ratings[6] = 3
ratings[11] = 5
ratings[53] = 4
ratings[63] = 5
ratings[65] = 3
ratings[68] = 5
ratings[97] = 2
ratings[182] = 4
ratings[225] = 5
ratings[354] = 5
```
## prepare data
```
Y, R = movies_mat.get('Y'), movies_mat.get('R')
Y = np.insert(Y, 0, ratings, axis=1) # now I become user 0
Y.shape
R = np.insert(R, 0, ratings != 0, axis=1)
R.shape
n_features = 50
n_movie, n_user = Y.shape
l = 10
X = np.random.standard_normal((n_movie, n_features))
theta = np.random.standard_normal((n_user, n_features))
X.shape, theta.shape
param = serialize(X, theta)
Y_norm = Y - Y.mean() # 这不对吧? 这难道不是每一行减去每一行的均值?
Y_norm.mean()
```
## training
```
import scipy.optimize as opt
res = opt.minimize(fun=regularized_cost,
x0=param,
args=(Y_norm, R, n_features, l),
method='TNC',
jac=regularized_gradient)
#这里很慢
res
X_trained, theta_trained = deserialize(res.x, n_movie, n_user, n_features)
X_trained.shape, theta_trained.shape
prediction = X_trained @ theta_trained.T
my_preds = prediction[:, 0] + Y.mean()
idx = np.argsort(my_preds)[::-1] # Descending order
idx.shape
# top ten idx
my_preds[idx][:10]
for m in movie_list[idx][:10]:
print(m)
```
| true |
code
| 0.661841 | null | null | null | null |
|
# Logistic Regression
---
Lets first import required libraries:
```
import pandas as pd
import numpy as np
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix, jaccard_score, log_loss
import itertools
import matplotlib.pyplot as plt
%matplotlib inline
```
## Customer churn with Logistic Regression
A telecommunications company is concerned about the number of customers leaving their land-line business for cable competitors. They need to understand who is leaving. Imagine that you are an analyst at this company and you have to find out who is leaving and why.
<h2 id="about_dataset">About the dataset</h2>
We will use a telecommunications dataset for predicting customer churn. This is a historical customer dataset where each row represents one customer. The data is relatively easy to understand, and you may uncover insights you can use immediately. Typically it is less expensive to keep customers than acquire new ones, so the focus of this analysis is to predict the customers who will stay with the company.
This data set provides information to help you predict what behavior will help you to retain customers. You can analyze all relevant customer data and develop focused customer retention programs.
The dataset includes information about:
- Customers who left within the last month – the column is called Churn
- Services that each customer has signed up for – phone, multiple lines, internet, online security, online backup, device protection, tech support, and streaming TV and movies
- Customer account information – how long they had been a customer, contract, payment method, paperless billing, monthly charges, and total charges
- Demographic info about customers – gender, age range, and if they have partners and dependents
Telco Churn is a hypothetical data file that concerns a telecommunications company's efforts to reduce turnover in its customer base. Each case corresponds to a separate customer and it records various demographic and service usage information. Before you can work with the data, you must use the URL to get the ChurnData.csv.
### Load Data From CSV File
```
churn_df = pd.read_csv("ChurnData.csv")
churn_df.head()
```
<h2 id="preprocessing">Data pre-processing and selection</h2>
Lets select some features for the modeling. Also we change the target data type to be integer, as it is a requirement by the skitlearn algorithm:
```
churn_df = churn_df[['tenure', 'age', 'address', 'income', 'ed', 'employ', 'equip', 'callcard', 'wireless','churn']]
churn_df['churn'] = churn_df['churn'].astype('int')
churn_df.head()
```
How many rows and columns are in this dataset in total? What are the name of columns?
```
print(churn_df.shape)
print(churn_df.head(0))
```
Lets define X, and y for our dataset:
```
X = np.asarray(churn_df[['tenure', 'age', 'address', 'income', 'ed', 'employ', 'equip']])
X[0:5]
y = np.asarray(churn_df['churn'])
y [0:5]
```
Also, we normalize the dataset:
```
X = preprocessing.StandardScaler().fit(X).transform(X)
X[0:5]
```
## Train/Test dataset
Okay, we split our dataset into train and test set:
```
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=4)
print ('Train set:', X_train.shape, y_train.shape)
print ('Test set:', X_test.shape, y_test.shape)
```
<h2 id="modeling">Modeling (Logistic Regression with Scikit-learn)</h2>
Lets build our model using __LogisticRegression__ from Scikit-learn package. This function implements logistic regression and can use different numerical optimizers to find parameters, including ‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’ solvers. You can find extensive information about the pros and cons of these optimizers if you search it in internet.
The version of Logistic Regression in Scikit-learn, support regularization. Regularization is a technique used to solve the overfitting problem in machine learning models.
__C__ parameter indicates __inverse of regularization strength__ which must be a positive float. Smaller values specify stronger regularization.
Now lets fit our model with train set:
```
LR = LogisticRegression(C=0.01, solver='liblinear').fit(X_train,y_train)
LR
```
Now we can predict using our test set:
```
yhat = LR.predict(X_test)
print(yhat)
print(y_test)
```
__predict_proba__ returns estimates for all classes, ordered by the label of classes. So, the first column is the probability of class 1, P(Y=1|X), and second column is probability of class 0, P(Y=0|X):
```
yhat_prob = LR.predict_proba(X_test)
```
<h2 id="evaluation">Evaluation</h2>
### jaccard index
Lets try jaccard index for accuracy evaluation. we can define jaccard as the size of the intersection divided by the size of the union of two label sets. If the entire set of predicted labels for a sample strictly match with the true set of labels, then the subset accuracy is 1.0; otherwise it is 0.0.
```
jaccard_score(y_test, yhat)
```
### confusion matrix
Another way of looking at accuracy of classifier is to look at __confusion matrix__.
```
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
print(confusion_matrix(y_test, yhat, labels=[1,0]))
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, yhat, labels=[1,0])
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=['churn=1','churn=0'],normalize= False, title='Confusion matrix')
```
Look at first row. The first row is for customers whose actual churn value in test set is 1.
As you can calculate, out of 40 customers, the churn value of 15 of them is 1.
And out of these 15, the classifier correctly predicted 6 of them as 1, and 9 of them as 0.
It means, for 6 customers, the actual churn value were 1 in test set, and classifier also correctly predicted those as 1. However, while the actual label of 9 customers were 1, the classifier predicted those as 0, which is not very good. We can consider it as error of the model for first row.
What about the customers with churn value 0? Lets look at the second row.
It looks like there were 25 customers whom their churn value were 0.
The classifier correctly predicted 24 of them as 0, and one of them wrongly as 1. So, it has done a good job in predicting the customers with churn value 0. A good thing about confusion matrix is that shows the model’s ability to correctly predict or separate the classes. In specific case of binary classifier, such as this example, we can interpret these numbers as the count of true positives, false positives, true negatives, and false negatives.
```
print (classification_report(y_test, yhat))
```
Based on the count of each section, we can calculate precision and recall of each label:
- __Precision__ is a measure of the accuracy provided that a class label has been predicted. It is defined by: precision = TP / (TP + FP)
- __Recall__ is true positive rate. It is defined as: Recall = TP / (TP + FN)
So, we can calculate precision and recall of each class.
__F1 score:__
Now we are in the position to calculate the F1 scores for each label based on the precision and recall of that label.
The F1 score is the harmonic average of the precision and recall, where an F1 score reaches its best value at 1 (perfect precision and recall) and worst at 0. It is a good way to show that a classifer has a good value for both recall and precision.
And finally, we can tell the average accuracy for this classifier is the average of the F1-score for both labels, which is 0.72 in our case.
### log loss
Now, lets try __log loss__ for evaluation. In logistic regression, the output can be the probability of customer churn is yes (or equals to 1). This probability is a value between 0 and 1.
Log loss( Logarithmic loss) measures the performance of a classifier where the predicted output is a probability value between 0 and 1.
```
log_loss(y_test, yhat_prob)
```
## Thanks for Reading :)
Created by [Saeed Aghabozorgi](https://www.linkedin.com/in/saeedaghabozorgi/) and modified by [Tarun Kamboj](https://www.linkedin.com/in/kambojtarun/).
| true |
code
| 0.641647 | null | null | null | null |
|
# Rigid-body transformations in three-dimensions
> Marcos Duarte
> Laboratory of Biomechanics and Motor Control ([http://demotu.org/](http://demotu.org/))
> Federal University of ABC, Brazil
The kinematics of a rigid body is completely described by its pose, i.e., its position and orientation in space (and the corresponding changes, translation and rotation). In a three-dimensional space, at least three coordinates and three angles are necessary to describe the pose of the rigid body, totalizing six degrees of freedom for a rigid body.
In motion analysis, to describe a translation and rotation of a rigid body with respect to a coordinate system, typically we attach another coordinate system to the rigid body and determine a transformation between these two coordinate systems.
A transformation is any function mapping a set to another set. For the description of the kinematics of rigid bodies, we are interested only in what is called rigid or Euclidean transformations (denoted as SE(3) for the three-dimensional space) because they preserve the distance between every pair of points of the body (which is considered rigid by definition). Translations and rotations are examples of rigid transformations (a reflection is also an example of rigid transformation but this changes the right-hand axis convention to a left hand, which usually is not of interest). In turn, rigid transformations are examples of [affine transformations](https://en.wikipedia.org/wiki/Affine_transformation). Examples of other affine transformations are shear and scaling transformations (which preserves angles but not lengths).
We will follow the same rationale as in the notebook [Rigid-body transformations in a plane (2D)](http://nbviewer.ipython.org/github/BMClab/bmc/blob/master/notebooks/Transformation2D.ipynb) and we will skip the fundamental concepts already covered there. So, you if haven't done yet, you should read that notebook before continuing here.
## Translation
A pure three-dimensional translation of a rigid body (or a coordinate system attached to it) in relation to other rigid body (with other coordinate system) is illustrated in the figure below.
<br>
<figure><img src='./../images/translation3D.png' alt='translation 3D'/> <figcaption><center><i>Figure. A point in three-dimensional space represented in two coordinate systems, with one coordinate system translated.</i></center></figcaption> </figure>
The position of point $\mathbf{P}$ originally described in the $xyz$ (local) coordinate system but now described in the $\mathbf{XYZ}$ (Global) coordinate system in vector form is:
$$ \mathbf{P_G} = \mathbf{L_G} + \mathbf{P_l} $$
Or in terms of its components:
$$ \begin{array}{}
\mathbf{P_X} =& \mathbf{L_X} + \mathbf{P}_x \\
\mathbf{P_Y} =& \mathbf{L_Y} + \mathbf{P}_y \\
\mathbf{P_Z} =& \mathbf{L_Z} + \mathbf{P}_z
\end{array} $$
And in matrix form:
$$
\begin{bmatrix}
\mathbf{P_X} \\
\mathbf{P_Y} \\
\mathbf{P_Z}
\end{bmatrix} =
\begin{bmatrix}
\mathbf{L_X} \\
\mathbf{L_Y} \\
\mathbf{L_Z}
\end{bmatrix} +
\begin{bmatrix}
\mathbf{P}_x \\
\mathbf{P}_y \\
\mathbf{P}_z
\end{bmatrix}
$$
From classical mechanics, this is an example of [Galilean transformation](http://en.wikipedia.org/wiki/Galilean_transformation).
Let's use Python to compute some numeric examples:
```
# Import the necessary libraries
import numpy as np
# suppress scientific notation for small numbers:
np.set_printoptions(precision=4, suppress=True)
```
For example, if the local coordinate system is translated by $\mathbf{L_G}=[1, 2, 3]$ in relation to the Global coordinate system, a point with coordinates $\mathbf{P_l}=[4, 5, 6]$ at the local coordinate system will have the position $\mathbf{P_G}=[5, 7, 9]$ at the Global coordinate system:
```
LG = np.array([1, 2, 3]) # Numpy array
Pl = np.array([4, 5, 6])
PG = LG + Pl
PG
```
This operation also works if we have more than one point (NumPy try to guess how to handle vectors with different dimensions):
```
Pl = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 2D array with 3 rows and 2 columns
PG = LG + Pl
PG
```
## Rotation
A pure three-dimensional rotation of a $xyz$ (local) coordinate system in relation to other $\mathbf{XYZ}$ (Global) coordinate system and the position of a point in these two coordinate systems are illustrated in the next figure (remember that this is equivalent to describing a rotation between two rigid bodies).
<br>
<figure><img src='./../images/rotation3D.png' alt='rotation 3D'/> <figcaption><center><i>A point in three-dimensional space represented in two coordinate systems, with one system rotated.</i></center></figcaption> </figure>
In analogy to the rotation in two dimensions, we can calculate the rotation matrix that describes the rotation of the $xyz$ (local) coordinate system in relation to the $\mathbf{XYZ}$ (Global) coordinate system using the direction cosines between the axes of the two coordinate systems:
$$ \mathbf{R_{Gl}} = \begin{bmatrix}
\cos\mathbf{X}x & \cos\mathbf{X}y & \cos\mathbf{X}z \\
\cos\mathbf{Y}x & \cos\mathbf{Y}y & \cos\mathbf{Y}z \\
\cos\mathbf{Z}x & \cos\mathbf{Z}y & \cos\mathbf{Z}z
\end{bmatrix} $$
Note however that for rotations around more than one axis, these angles will not lie in the main planes ($\mathbf{XY, YZ, ZX}$) of the $\mathbf{XYZ}$ coordinate system, as illustrated in the figure below for the direction angles of the $y$ axis only. Thus, the determination of these angles by simple inspection, as we have done for the two-dimensional case, would not be simple.
<br>
<figure>
<img src='./../images/directioncosine3D.png' width=260 alt='direction angles 3D'/> <figcaption><center><i>Figure. Definition of direction angles for the $y$ axis of the local coordinate system in relation to the $\mathbf{XYZ}$ Global coordinate system.</i></center></figcaption>
</figure>
Note that the nine angles shown in the matrix above for the direction cosines are obviously redundant since only three angles are necessary to describe the orientation of a rigid body in the three-dimensional space.
An important characteristic of angles in the three-dimensional space is that angles cannot be treated as vectors: the result of a sequence of rotations of a rigid body around different axes depends on the order of the rotations, as illustrated in the next figure.
<br>
<figure>
<img src='./../images/rotationsseqs2.png' alt='rotations'/><figcaption><i>Figure. The result of a sequence of rotations around different axes of a coordinate system depends on the order of the rotations. In the first example (first row), the rotations are around a Global (fixed) coordinate system. In the second example (second row), the rotations are around a local (rotating) coordinate system.</i></figcaption>
</figure>
Let's focus now on how to understand rotations in the three-dimensional space, looking at the rotations between coordinate systems (or between rigid bodies). Later we will apply what we have learned to describe the position of a point in these different coordinate systems.
### Euler angles
There are different ways to describe a three-dimensional rotation of a rigid body (or of a coordinate system). The most straightforward solution would probably be to use a [spherical coordinate system](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/ReferenceFrame.ipynb#Spherical-coordinate-system), but spherical coordinates would be difficult to give an anatomical or clinical interpretation. A solution that has been often employed in biomechanics to handle rotations in the three-dimensional space is to use Euler angles. Under certain conditions, Euler angles can have an anatomical interpretation, but this representation also has some caveats. Let's see the Euler angles now.
[Leonhard Euler](https://en.wikipedia.org/wiki/Leonhard_Euler) in the XVIII century showed that two three-dimensional coordinate systems with a common origin can be related by a sequence of up to three elemental rotations about the axes of the local coordinate system, where no two successive rotations may be about the same axis, which now are known as [Euler (or Eulerian) angles](http://en.wikipedia.org/wiki/Euler_angles).
#### Elemental rotations
First, let's see rotations around a fixed Global coordinate system as we did for the two-dimensional case. The next figure illustrates elemental rotations of the local coordinate system around each axis of the fixed Global coordinate system.
<br>
<figure>
<img src='./../images/rotations.png' alt='rotations'/> <figcaption><center><i>Figure. Elemental rotations of the $xyz$ coordinate system around each axis, $\mathbf{X}$, $\mathbf{Y}$, and $\mathbf{Z}$, of the fixed $\mathbf{XYZ}$ coordinate system. Note that for better clarity, the axis around where the rotation occurs is shown perpendicular to this page for each elemental rotation.</i></center></figcaption>
</figure>
#### Rotations around the fixed coordinate system
The rotation matrices for the elemental rotations around each axis of the fixed $\mathbf{XYZ}$ coordinate system (rotations of the local coordinate system in relation to the Global coordinate system) are shown next.
Around $\mathbf{X}$ axis:
<span class="notranslate">
$$ \mathbf{R_{Gl,\,X}} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha \\
0 & \sin\alpha & \cos\alpha
\end{bmatrix} $$
</span>
Around $\mathbf{Y}$ axis:
$$ \mathbf{R_{Gl,\,Y}} =
\begin{bmatrix}
\cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta
\end{bmatrix} $$
Around $\mathbf{Z}$ axis:
$$ \mathbf{R_{Gl,\,Z}} =
\begin{bmatrix}
\cos\gamma & -\sin\gamma & 0\\
\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix} $$
These matrices are the rotation matrices for the case of two-dimensional coordinate systems plus the corresponding terms for the third axes of the local and Global coordinate systems, which are parallel.
To understand why the terms for the third axes are 1's or 0's, for instance, remember they represent the cosine directors. The cosines between $\mathbf{X}x$, $\mathbf{Y}y$, and $\mathbf{Z}z$ for the elemental rotations around respectively the $\mathbf{X}$, $\mathbf{Y}$, and $\mathbf{Z}$ axes are all 1 because $\mathbf{X}x$, $\mathbf{Y}y$, and $\mathbf{Z}z$ are parallel ($\cos 0^o$). The cosines of the other elements are zero because the axis around where each rotation occurs is perpendicular to the other axes of the coordinate systems ($\cos 90^o$).
#### Rotations around the local coordinate system
The rotation matrices for the elemental rotations this time around each axis of the $xyz$ coordinate system (rotations of the Global coordinate system in relation to the local coordinate system), similarly to the two-dimensional case, are simply the transpose of the above matrices as shown next.
Around $x$ axis:
$$ \mathbf{R}_{\mathbf{lG},\,x} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & \sin\alpha \\
0 & -\sin\alpha & \cos\alpha
\end{bmatrix} $$
Around $y$ axis:
$$ \mathbf{R}_{\mathbf{lG},\,y} =
\begin{bmatrix}
\cos\beta & 0 & -\sin\beta \\
0 & 1 & 0 \\
\sin\beta & 0 & \cos\beta
\end{bmatrix} $$
Around $z$ axis:
$$ \mathbf{R}_{\mathbf{lG},\,z} =
\begin{bmatrix}
\cos\gamma & \sin\gamma & 0\\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix} $$
Notice this is equivalent to instead of rotating the local coordinate system by $\alpha, \beta, \gamma$ in relation to axes of the Global coordinate system, to rotate the Global coordinate system by $-\alpha, -\beta, -\gamma$ in relation to the axes of the local coordinate system; remember that $\cos(-\:\cdot)=\cos(\cdot)$ and $\sin(-\:\cdot)=-\sin(\cdot)$.
The fact that we chose to rotate the local coordinate system by a counterclockwise (positive) angle in relation to the Global coordinate system is just a matter of convention.
#### Sequence of elemental rotations
Consider now a sequence of elemental rotations around the $\mathbf{X}$, $\mathbf{Y}$, and $\mathbf{Z}$ axes of the fixed $\mathbf{XYZ}$ coordinate system illustrated in the next figure.
<br>
<figure><img src='./../images/rotations_XYZ.png' alt='rotations'/> <figcaption><center><i>Figure. Sequence of elemental rotations of the $xyz$ coordinate system around each axis, $\mathbf{X}$, $\mathbf{Y}$, $\mathbf{Z}$, of the fixed $\mathbf{XYZ}$ coordinate system.</i></center></figcaption> </figure>
This sequence of elemental rotations (each one of the local coordinate system with respect to the fixed Global coordinate system) is mathematically represented by a multiplication between the rotation matrices:
$$ \begin{array}{l l}
\mathbf{R_{Gl,\;XYZ}} & = \mathbf{R_{Z}} \mathbf{R_{Y}} \mathbf{R_{X}} \\
\\
& = \begin{bmatrix}
\cos\gamma & -\sin\gamma & 0\\
\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & -sin\alpha \\
0 & \sin\alpha & cos\alpha
\end{bmatrix} \\
\\
& =
\begin{bmatrix}
\cos\beta\:\cos\gamma \;&\;
\sin\alpha\:\sin\beta\:cos\gamma-\cos\alpha\:\sin\gamma \;&\;
\cos\alpha\:\sin\beta\:cos\gamma+\sin\alpha\:\sin\gamma \;\;\; \\
\cos\beta\:\sin\gamma \;&\;
\sin\alpha\:\sin\beta\:sin\gamma+\cos\alpha\:\cos\gamma \;&\;
\cos\alpha\:\sin\beta\:sin\gamma-\sin\alpha\:\cos\gamma \;\;\; \\
-\sin\beta \;&\; \sin\alpha\:\cos\beta \;&\; \cos\alpha\:\cos\beta \;\;\;
\end{bmatrix}
\end{array} $$
Note that the order of the matrices.
We can check this matrix multiplication using [Sympy](http://sympy.org/en/index.html):
```
#import the necessary libraries
from IPython.core.display import Math, display
import sympy as sym
cos, sin = sym.cos, sym.sin
a, b, g = sym.symbols('alpha, beta, gamma')
# Elemental rotation matrices of xyz in relation to XYZ:
RX = sym.Matrix([[1, 0, 0], [0, cos(a), -sin(a)], [0, sin(a), cos(a)]])
RY = sym.Matrix([[cos(b), 0, sin(b)], [0, 1, 0], [-sin(b), 0, cos(b)]])
RZ = sym.Matrix([[cos(g), -sin(g), 0], [sin(g), cos(g), 0], [0, 0, 1]])
# Rotation matrix of xyz in relation to XYZ:
RXYZ = RZ*RY*RX
display(Math(sym.latex(r'\mathbf{R_{Gl,\,XYZ}}=') + sym.latex(RXYZ, mat_str='matrix')))
```
For instance, we can calculate the numerical rotation matrix for these sequential elemental rotations by $90^o$ around $\mathbf{X,Y,Z}$:
```
R = sym.lambdify((a, b, g), RXYZ, 'numpy')
R = R(np.pi/2, np.pi/2, np.pi/2)
display(Math(r'\mathbf{R_{Gl,\,XYZ\,}}(90^o, 90^o, 90^o) =' + \
sym.latex(sym.Matrix(R).n(chop=True, prec=3))))
```
Examining the matrix above and the correspondent previous figure, one can see they agree: the rotated $x$ axis (first column of the above matrix) has value -1 in the $\mathbf{Z}$ direction $[0,0,-1]$, the rotated $y$ axis (second column) is at the $\mathbf{Y}$ direction $[0,1,0]$, and the rotated $z$ axis (third column) is at the $\mathbf{X}$ direction $[1,0,0]$.
We also can calculate the sequence of elemental rotations around the $x$, $y$, $z$ axes of the rotating $xyz$ coordinate system illustrated in the next figure.
<br>
<figure>
<img src='./../images/rotations_xyz2.png' alt='rotations'/> <figcaption><center><i>Figure. Sequence of elemental rotations of a second $xyz$ local coordinate system around each axis, $x$, $y$, $z$, of the rotating $xyz$ coordinate system.</i></center></figcaption>
</figure>
Likewise, this sequence of elemental rotations (each one of the local coordinate system with respect to the rotating local coordinate system) is mathematically represented by a multiplication between the rotation matrices (which are the inverse of the matrices for the rotations around $\mathbf{X,Y,Z}$ as we saw earlier):
$$ \begin{array}{l l}
\mathbf{R}_{\mathbf{lG},\,xyz} & = \mathbf{R_{z}} \mathbf{R_{y}} \mathbf{R_{x}} \\
\\
& = \begin{bmatrix}
\cos\gamma & \sin\gamma & 0\\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\beta & 0 & -\sin\beta \\
0 & 1 & 0 \\
sin\beta & 0 & \cos\beta
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & \sin\alpha \\
0 & -\sin\alpha & \cos\alpha
\end{bmatrix} \\
\\
& =
\begin{bmatrix}
\cos\beta\:\cos\gamma \;&\;
\sin\alpha\:\sin\beta\:\cos\gamma+\cos\alpha\:\sin\gamma \;&\;
\cos\alpha\:\sin\beta\:\cos\gamma-\sin\alpha\:\sin\gamma \;\;\; \\
-\cos\beta\:\sin\gamma \;&\;
-\sin\alpha\:\sin\beta\:\sin\gamma+\cos\alpha\:\cos\gamma \;&\;
\cos\alpha\:\sin\beta\:\sin\gamma+\sin\alpha\:\cos\gamma \;\;\; \\
\sin\beta \;&\; -\sin\alpha\:\cos\beta \;&\; \cos\alpha\:\cos\beta \;\;\;
\end{bmatrix}
\end{array} $$
As before, the order of the matrices is from right to left.
Once again, we can check this matrix multiplication using [Sympy](http://sympy.org/en/index.html):
```
a, b, g = sym.symbols('alpha, beta, gamma')
# Elemental rotation matrices of xyz (local):
Rx = sym.Matrix([[1, 0, 0], [0, cos(a), sin(a)], [0, -sin(a), cos(a)]])
Ry = sym.Matrix([[cos(b), 0, -sin(b)], [0, 1, 0], [sin(b), 0, cos(b)]])
Rz = sym.Matrix([[cos(g), sin(g), 0], [-sin(g), cos(g), 0], [0, 0, 1]])
# Rotation matrix of xyz' in relation to xyz:
Rxyz = Rz*Ry*Rx
Math(sym.latex(r'\mathbf{R}_{\mathbf{lG},\,xyz}=') + sym.latex(Rxyz, mat_str='matrix'))
```
For instance, let's calculate the numerical rotation matrix for these sequential elemental rotations by $90^o$ around $x,y,z$:
```
R = sym.lambdify((a, b, g), Rxyz, 'numpy')
R = R(np.pi/2, np.pi/2, np.pi/2)
display(Math(r'\mathbf{R}_{\mathbf{lG},\,xyz\,}(90^o, 90^o, 90^o) =' + \
sym.latex(sym.Matrix(R).n(chop=True, prec=3))))
```
Once again, let's compare the above matrix and the correspondent previous figure to see if it makes sense. But remember that this matrix is the Global-to-local rotation matrix, $\mathbf{R}_{\mathbf{lG},\,xyz}$, where the coordinates of the local basis' versors are rows, not columns, in this matrix. With this detail in mind, one can see that the previous figure and matrix also agree: the rotated $x$ axis (first row of the above matrix) is at the $\mathbf{Z}$ direction $[0,0,1]$, the rotated $y$ axis (second row) is at the $\mathbf{-Y}$ direction $[0,-1,0]$, and the rotated $z$ axis (third row) is at the $\mathbf{X}$ direction $[1,0,0]$.
In fact, this example didn't serve to distinguish versors as rows or columns because the $\mathbf{R}_{\mathbf{lG},\,xyz}$ matrix above is symmetric!
Let's look on the resultant matrix for the example above after only the first two rotations, $\mathbf{R}_{\mathbf{lG},\,xy}$ to understand this difference:
```
Rxy = Ry*Rx
R = sym.lambdify((a, b), Rxy, 'numpy')
R = R(np.pi/2, np.pi/2)
display(Math(r'\mathbf{R}_{\mathbf{lG},\,xy\,}(90^o, 90^o) =' + \
sym.latex(sym.Matrix(R).n(chop=True, prec=3))))
```
Comparing this matrix with the third plot in the figure, we see that the coordinates of versor $x$ in the Global coordinate system are $[0,1,0]$, i.e., local axis $x$ is aligned with Global axis $Y$, and this versor is indeed the first row, not first column, of the matrix above. Confer the other two rows.
What are then in the columns of the local-to-Global rotation matrix?
The columns are the coordinates of Global basis' versors in the local coordinate system! For example, the first column of the matrix above is the coordinates of $X$, which is aligned with $z$: $[0,0,1]$.
#### Rotations in a coordinate system is equivalent to minus rotations in the other coordinate system
Remember that we saw for the elemental rotations that it's equivalent to instead of rotating the local coordinate system, $xyz$, by $\alpha, \beta, \gamma$ in relation to axes of the Global coordinate system, to rotate the Global coordinate system, $\mathbf{XYZ}$, by $-\alpha, -\beta, -\gamma$ in relation to the axes of the local coordinate system. The same property applies to a sequence of rotations: rotations of $xyz$ in relation to $\mathbf{XYZ}$ by $\alpha, \beta, \gamma$ result in the same matrix as rotations of $\mathbf{XYZ}$ in relation to $xyz$ by $-\alpha, -\beta, -\gamma$:
$$ \begin{array}{l l}
\mathbf{R_{Gl,\,XYZ\,}}(\alpha,\beta,\gamma) & = \mathbf{R_{Gl,\,Z}}(\gamma)\, \mathbf{R_{Gl,\,Y}}(\beta)\, \mathbf{R_{Gl,\,X}}(\alpha) \\
& = \mathbf{R}_{\mathbf{lG},\,z\,}(-\gamma)\, \mathbf{R}_{\mathbf{lG},\,y\,}(-\beta)\, \mathbf{R}_{\mathbf{lG},\,x\,}(-\alpha) \\
& = \mathbf{R}_{\mathbf{lG},\,xyz\,}(-\alpha,-\beta,-\gamma)
\end{array}
$$
Confer that by examining the $\mathbf{R_{Gl,\,XYZ}}$ and $\mathbf{R}_{\mathbf{lG},\,xyz}$ matrices above.
Let's verify this property with Sympy:
```
RXYZ = RZ*RY*RX
# Rotation matrix of xyz in relation to XYZ:
display(Math(sym.latex(r'\mathbf{R_{Gl,\,XYZ\,}}(\alpha,\beta,\gamma) =')))
display(Math(sym.latex(RXYZ, mat_str='matrix')))
# Elemental rotation matrices of XYZ in relation to xyz and negate all angles:
Rx_neg = sym.Matrix([[1, 0, 0], [0, cos(-a), -sin(-a)], [0, sin(-a), cos(-a)]]).T
Ry_neg = sym.Matrix([[cos(-b), 0, sin(-b)], [0, 1, 0], [-sin(-b), 0, cos(-b)]]).T
Rz_neg = sym.Matrix([[cos(-g), -sin(-g), 0], [sin(-g), cos(-g), 0], [0, 0, 1]]).T
# Rotation matrix of XYZ in relation to xyz:
Rxyz_neg = Rz_neg*Ry_neg*Rx_neg
display(Math(sym.latex(r'\mathbf{R}_{\mathbf{lG},\,xyz\,}(-\alpha,-\beta,-\gamma) =')))
display(Math(sym.latex(Rxyz_neg, mat_str='matrix')))
# Check that the two matrices are equal:
display(Math(sym.latex(r'\mathbf{R_{Gl,\,XYZ\,}}(\alpha,\beta,\gamma) \;==\;' + \
r'\mathbf{R}_{\mathbf{lG},\,xyz\,}(-\alpha,-\beta,-\gamma)')))
RXYZ == Rxyz_neg
```
#### Rotations in a coordinate system is the transpose of inverse order of rotations in the other coordinate system
There is another property of the rotation matrices for the different coordinate systems: the rotation matrix, for example from the Global to the local coordinate system for the $xyz$ sequence, is just the transpose of the rotation matrix for the inverse operation (from the local to the Global coordinate system) of the inverse sequence ($\mathbf{ZYX}$) and vice-versa:
$$ \begin{array}{l l}
\mathbf{R}_{\mathbf{lG},\,xyz}(\alpha,\beta,\gamma) & = \mathbf{R}_{\mathbf{lG},\,z\,} \mathbf{R}_{\mathbf{lG},\,y\,} \mathbf{R}_{\mathbf{lG},\,x} \\
& = \mathbf{R_{Gl,\,Z\,}^{-1}} \mathbf{R_{Gl,\,Y\,}^{-1}} \mathbf{R_{Gl,\,X\,}^{-1}} \\
& = \mathbf{R_{Gl,\,Z\,}^{T}} \mathbf{R_{Gl,\,Y\,}^{T}} \mathbf{R_{Gl,\,X\,}^{T}} \\
& = (\mathbf{R_{Gl,\,X\,}} \mathbf{R_{Gl,\,Y\,}} \mathbf{R_{Gl,\,Z}})^\mathbf{T} \\
& = \mathbf{R_{Gl,\,ZYX\,}^{T}}(\gamma,\beta,\alpha)
\end{array}
$$
Where we used the properties that the inverse of the rotation matrix (which is orthonormal) is its transpose and that the transpose of a product of matrices is equal to the product of their transposes in reverse order.
Let's verify this property with Sympy:
```
RZYX = RX*RY*RZ
Rxyz = Rz*Ry*Rx
display(Math(sym.latex(r'\mathbf{R_{Gl,\,ZYX\,}^T}=') + sym.latex(RZYX.T, mat_str='matrix')))
display(Math(sym.latex(r'\mathbf{R}_{\mathbf{lG},\,xyz\,}(\alpha,\beta,\gamma) \,==\,' + \
r'\mathbf{R_{Gl,\,ZYX\,}^T}(\gamma,\beta,\alpha)')))
Rxyz == RZYX.T
```
#### Sequence of rotations of a Vector
We saw in the notebook [Rigid-body transformations in a plane (2D)](http://nbviewer.jupyter.org/github/BMClab/bmc/blob/master/notebooks/Transformation2D.ipynb#Rotation-of-a-Vector) that the rotation matrix can also be used to rotate a vector (in fact, a point, image, solid, etc.) by a given angle around an axis of the coordinate system. Let's investigate that for the 3D case using the example earlier where a book was rotated in different orders and around the Global and local coordinate systems.
Before any rotation, the point shown in that figure as a round black dot on the spine of the book has coordinates $\mathbf{P}=[0, 1, 2]$ (the book has thickness 0, width 1, and height 2).
After the first sequence of rotations shown in the figure (rotated around $X$ and $Y$ by $90^0$ each time), $\mathbf{P}$ has coordinates $\mathbf{P}=[1, -2, 0]$ in the global coordinate system. Let's verify that:
```
P = np.array([[0, 1, 2]]).T
RXY = RY*RX
R = sym.lambdify((a, b), RXY, 'numpy')
R = R(np.pi/2, np.pi/2)
P1 = np.dot(R, P)
print('P1 =', P1.T)
```
As expected.
The reader is invited to deduce the position of point $\mathbf{P}$ after the inverse order of rotations, but still around the Global coordinate system.
Although we are performing vector rotation, where we don't need the concept of transformation between coordinate systems, in the example above we used the local-to-Global rotation matrix, $\mathbf{R_{Gl}}$. As we saw in the notebook for the 2D transformation, when we use this matrix, it performs a counter-clockwise (positive) rotation.
If we want to rotate the vector in the clockwise (negative) direction, we can use the very same rotation matrix entering a negative angle or we can use the inverse rotation matrix, the Global-to-local rotation matrix, $\mathbf{R_{lG}}$ and a positive (negative of negative) angle, because $\mathbf{R_{Gl}}(\alpha) = \mathbf{R_{lG}}(-\alpha)$, but bear in mind that even in this latter case we are rotating around the Global coordinate system!
Consider now that we want to deduce algebraically the position of the point $\mathbf{P}$ after the rotations around the local coordinate system as shown in the second set of examples in the figure with the sequence of book rotations. The point has the same initial position, $\mathbf{P}=[0, 1, 2]$, and after the rotations around $x$ and $y$ by $90^0$ each time, what is the position of this point?
It's implicit in this question that the new desired position is in the Global coordinate system because the local coordinate system rotates with the book and the point never changes its position in the local coordinate system. So, by inspection of the figure, the new position of the point is $\mathbf{P1}=[2, 0, 1]$.
Let's naively try to deduce this position by repeating the steps as before:
```
Rxy = Ry*Rx
R = sym.lambdify((a, b), Rxy, 'numpy')
R = R(np.pi/2, np.pi/2)
P1 = np.dot(R, P)
print('P1 =', P1.T)
```
The wrong answer.
The problem is that we defined the rotation of a vector using the local-to-Global rotation matrix. One correction solution for this problem is to continuing using the multiplication of the Global-to-local rotation matrices, $\mathbf{R}_{xy} = \mathbf{R}_y\,\mathbf{R}_x$, transpose $\mathbf{R}_{xy}$ to get the Global-to-local coordinate system, $\mathbf{R_{XY}}=\mathbf{R^T}_{xy}$, and then rotate the vector using this matrix:
```
Rxy = Ry*Rx
RXY = Rxy.T
R = sym.lambdify((a, b), RXY, 'numpy')
R = R(np.pi/2, np.pi/2)
P1 = np.dot(R, P)
print('P1 =', P1.T)
```
The correct answer.
Another solution is to understand that when using the Global-to-local rotation matrix, counter-clockwise rotations (as performed with the book the figure) are negative, not positive, and that when dealing with rotations with the Global-to-local rotation matrix the order of matrix multiplication is inverted, for example, it should be $\mathbf{R\_}_{xyz} = \mathbf{R}_x\,\mathbf{R}_y\,\mathbf{R}_z$ (an added underscore to remind us this is not the convention adopted here).
```
R_xy = Rx*Ry
R = sym.lambdify((a, b), R_xy, 'numpy')
R = R(-np.pi/2, -np.pi/2)
P1 = np.dot(R, P)
print('P1 =', P1.T)
```
The correct answer.
The reader is invited to deduce the position of point $\mathbf{P}$ after the inverse order of rotations, around the local coordinate system.
In fact, you will find elsewhere texts about rotations in 3D adopting this latter convention as the standard, i.e., they introduce the Global-to-local rotation matrix and describe sequence of rotations algebraically as matrix multiplication in the direct order, $\mathbf{R\_}_{xyz} = \mathbf{R}_x\,\mathbf{R}_y\,\mathbf{R}_z$, the inverse we have done in this text. It's all a matter of convention, just that.
#### The 12 different sequences of Euler angles
The Euler angles are defined in terms of rotations around a rotating local coordinate system. As we saw for the sequence of rotations around $x, y, z$, the axes of the local rotated coordinate system are not fixed in space because after the first elemental rotation, the other two axes rotate.
Other sequences of rotations could be produced without combining axes of the two different coordinate systems (Global and local) for the definition of the rotation axes. There is a total of 12 different sequences of three elemental rotations that are valid and may be used for describing the rotation of a coordinate system with respect to another coordinate system:
$$ xyz \quad xzy \quad yzx \quad yxz \quad zxy \quad zyx $$
$$ xyx \quad xzx \quad yzy \quad yxy \quad zxz \quad zyz $$
The first six sequences (first row) are all around different axes, they are usually referred as Cardan or Tait–Bryan angles. The other six sequences (second row) have the first and third rotations around the same axis, but keep in mind that the axis for the third rotation is not at the same place anymore because it changed its orientation after the second rotation. The sequences with repeated axes are known as proper or classic Euler angles.
Which order to use it is a matter of convention, but because the order affects the results, it's fundamental to follow a convention and report it. In Engineering Mechanics (including Biomechanics), the $xyz$ order is more common; in Physics the $zxz$ order is more common (but the letters chosen to refer to the axes are arbitrary, what matters is the directions they represent). In Biomechanics, the order for the Cardan angles is most often based on the angle of most interest or of most reliable measurement. Accordingly, the axis of flexion/extension is typically selected as the first axis, the axis for abduction/adduction is the second, and the axis for internal/external rotation is the last one. We will see about this order later. The $zyx$ order is commonly used to describe the orientation of a ship or aircraft and the rotations are known as the nautical angles: yaw, pitch and roll, respectively (see next figure).
<br>
<figure><img src='https://upload.wikimedia.org/wikipedia/commons/thumb/1/16/Yaw_Axis.svg/319px-Yaw_Axis.svg.png' alt='translation and rotation 3D'/> <figcaption><center><i>Figure. The principal axes of an aircraft and the names for the rotations around these axes (<a href="https://en.wikipedia.org/wiki/Euler_angles">image from Wikipedia</a>).</i></center></figcaption> </figure>
If instead of rotations around the rotating local coordinate system we perform rotations around the fixed Global coordinate system, we will have other 12 different sequences of three elemental rotations, these are called simply rotation angles. So, in total there are 24 possible different sequences of three elemental rotations, but the 24 orders are not independent; with the 12 different sequences of Euler angles at the local coordinate system we can obtain the other 12 sequences at the Global coordinate system.
The Python function `euler_rotmat.py` (code at the end of this text) determines the rotation matrix in algebraic form for any of the 24 different sequences (and sequences with only one or two axes can be inputed). This function also determines the rotation matrix in numeric form if a list of up to three angles are inputed.
For instance, the rotation matrix in algebraic form for the $zxz$ order of Euler angles at the local coordinate system and the correspondent rotation matrix in numeric form after three elemental rotations by $90^o$ each are:
```
import sys
sys.path.insert(1, r'./../functions')
from euler_rotmat import euler_rotmat
Ra, Rn = euler_rotmat(order='zxz', frame='local', angles=[90, 90, 90])
```
#### Line of nodes
The second axis of rotation in the rotating coordinate system is also referred as the nodal axis or line of nodes; this axis coincides with the intersection of two perpendicular planes, one from each Global (fixed) and local (rotating) coordinate systems. The figure below shows an example of rotations and the nodal axis for the $xyz$ sequence of the Cardan angles.
<div class='center-align'><figure><img src='./../images/Node.png' alt='rotations'/> <figcaption><center><i>Figure. First row: example of rotations for the $xyz$ sequence of the Cardan angles. The Global (fixed) $XYZ$ coordinate system is shown in green, the local (rotating) $xyz$ coordinate system is shown in blue. The nodal axis (<b>N</b>, shown in red) is defined by the intersection of the $YZ$ and $xy$ planes and all rotations can be described in relation to this nodal axis or to a perpendicular axis to it. Second row: starting from no rotation, the local coordinate system is rotated by $\alpha$ around the $x$ axis, then by $\beta$ around the rotated $y$ axis, and finally by $\gamma$ around the twice rotated $z$ axis. Note that the line of nodes coincides with the $y$ axis for the second rotation. </i></center></figcaption> </figure></div>
#### Determination of the Euler angles
Once a convention is adopted, the corresponding three Euler angles of rotation can be found.
For example, for the $\mathbf{R}_{xyz}$ rotation matrix:
```
R = euler_rotmat(order='xyz', frame='local')
```
The corresponding Cardan angles for the `xyz` sequence can be given by:
$$ \begin{array}{}
\alpha = \arctan\left(\dfrac{\sin(\alpha)}{\cos(\alpha)}\right) = \arctan\left(\dfrac{-\mathbf{R}_{21}}{\;\;\;\mathbf{R}_{22}}\right) \\
\\
\beta = \arctan\left(\dfrac{\sin(\beta)}{\cos(\beta)}\right) = \arctan\left(\dfrac{\mathbf{R}_{20}}{\sqrt{\mathbf{R}_{00}^2+\mathbf{R}_{10}^2}}\right) \\
\\
\gamma = \arctan\left(\dfrac{\sin(\gamma)}{\cos(\gamma)}\right) = \arctan\left(\dfrac{-\mathbf{R}_{10}}{\;\;\;\mathbf{R}_{00}}\right)
\end{array} $$
Note that we prefer to use the mathematical function `arctan` rather than simply `arcsin` because the latter cannot for example distinguish $45^o$ from $135^o$ and also for better numerical accuracy. See the text [Angular kinematics in a plane (2D)](https://nbviewer.jupyter.org/github/BMClab/bmc/blob/master/notebooks/KinematicsAngular2D.ipynb) for more on these issues.
And here is a Python function to compute the Euler angles of rotations from the Global to the local coordinate system for the $xyz$ Cardan sequence:
```
def euler_angles_from_rot_xyz(rot_matrix, unit='deg'):
""" Compute Euler angles from rotation matrix in the xyz sequence."""
import numpy as np
R = np.array(rot_matrix, copy=False).astype(np.float64)[:3, :3]
angles = np.zeros(3)
angles[0] = np.arctan2(-R[2, 1], R[2, 2])
angles[1] = np.arctan2( R[2, 0], np.sqrt(R[0, 0]**2 + R[1, 0]**2))
angles[2] = np.arctan2(-R[1, 0], R[0, 0])
if unit[:3].lower() == 'deg': # convert from rad to degree
angles = np.rad2deg(angles)
return angles
```
For instance, consider sequential rotations of 45$^o$ around $x,y,z$. The resultant rotation matrix is:
```
Ra, Rn = euler_rotmat(order='xyz', frame='local', angles=[45, 45, 45], showA=False)
```
Let's check that calculating back the Cardan angles from this rotation matrix using the `euler_angles_from_rot_xyz()` function:
```
euler_angles_from_rot_xyz(Rn, unit='deg')
```
We could implement a function to calculate the Euler angles for any of the 12 sequences (in fact, plus another 12 sequences if we consider all the rotations from and to the two coordinate systems), but this is tedious. There is a smarter solution using the concept of [quaternion](http://en.wikipedia.org/wiki/Quaternion), but we wont see that now.
Let's see a problem with using Euler angles known as gimbal lock.
### Gimbal lock
[Gimbal lock](http://en.wikipedia.org/wiki/Gimbal_lock) is the loss of one degree of freedom in a three-dimensional coordinate system that occurs when an axis of rotation is placed parallel with another previous axis of rotation and two of the three rotations will be around the same direction given a certain convention of the Euler angles. This "locks" the system into rotations in a degenerate two-dimensional space. The system is not really locked in the sense it can't be moved or reach the other degree of freedom, but it will need an extra rotation for that.
For instance, let's look at the $zxz$ sequence of rotations by the angles $\alpha, \beta, \gamma$:
$$ \begin{array}{l l}
\mathbf{R}_{zxz} & = \mathbf{R_{z}} \mathbf{R_{x}} \mathbf{R_{z}} \\
\\
& =
\begin{bmatrix}
\cos\gamma & \sin\gamma & 0\\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\beta & \sin\beta \\
0 & -\sin\beta & \cos\beta
\end{bmatrix}
\begin{bmatrix}
\cos\alpha & \sin\alpha & 0\\
-\sin\alpha & \cos\alpha & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{array} $$
Which results in:
```
a, b, g = sym.symbols('alpha, beta, gamma')
# Elemental rotation matrices of xyz (local):
Rz = sym.Matrix([[cos(a), sin(a), 0], [-sin(a), cos(a), 0], [0, 0, 1]])
Rx = sym.Matrix([[1, 0, 0], [0, cos(b), sin(b)], [0, -sin(b), cos(b)]])
Rz2 = sym.Matrix([[cos(g), sin(g), 0], [-sin(g), cos(g), 0], [0, 0, 1]])
# Rotation matrix for the zxz sequence:
Rzxz = Rz2*Rx*Rz
Math(sym.latex(r'\mathbf{R}_{zxz}=') + sym.latex(Rzxz, mat_str='matrix'))
```
Let's examine what happens with this rotation matrix when the rotation around the second axis ($x$) by $\beta$ is zero:
$$ \begin{array}{l l}
\mathbf{R}_{zxz}(\alpha, \beta=0, \gamma) =
\begin{bmatrix}
\cos\gamma & \sin\gamma & 0\\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\alpha & \sin\alpha & 0\\
-\sin\alpha & \cos\alpha & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{array} $$
The second matrix is the identity matrix and has no effect on the product of the matrices, which will be:
```
Rzxz = Rz2*Rz
Math(sym.latex(r'\mathbf{R}_{xyz}(\alpha, \beta=0, \gamma)=') + \
sym.latex(Rzxz, mat_str='matrix'))
```
Which simplifies to:
```
Rzxz = sym.simplify(Rzxz)
Math(sym.latex(r'\mathbf{R}_{xyz}(\alpha, \beta=0, \gamma)=') + \
sym.latex(Rzxz, mat_str='matrix'))
```
Despite different values of $\alpha$ and $\gamma$ the result is a single rotation around the $z$ axis given by the sum $\alpha+\gamma$. In this case, of the three degrees of freedom one was lost (the other degree of freedom was set by $\beta=0$). For movement analysis, this means for example that one angle will be undetermined because everything we know is the sum of the two angles obtained from the rotation matrix. We can set the unknown angle to zero but this is arbitrary.
In fact, we already dealt with another example of gimbal lock when we looked at the $xyz$ sequence with rotations by $90^o$. See the figure representing these rotations again and perceive that the first and third rotations were around the same axis because the second rotation was by $90^o$. Let's do the matrix multiplication replacing only the second angle by $90^o$ (and let's use the `euler_rotmat.py`:
```
Ra, Rn = euler_rotmat(order='xyz', frame='local', angles=[None, 90., None], showA=False)
```
Once again, one degree of freedom was lost and we will not be able to uniquely determine the three angles for the given rotation matrix and sequence.
Possible solutions to avoid the gimbal lock are: choose a different sequence; do not rotate the system by the angle that puts the system in gimbal lock (in the examples above, avoid $\beta=90^o$); or add an extra fourth parameter in the description of the rotation angles.
But if we have a physical system where we measure or specify exactly three Euler angles in a fixed sequence to describe or control it, and we can't avoid the system to assume certain angles, then we might have to say "Houston, we have a problem".
A famous situation where such a problem occurred was during the Apollo 13 mission. This is an actual conversation between crew and mission control during the Apollo 13 mission (Corke, 2011):
>`Mission clock: 02 08 12 47`
**Flight**: *Go, Guidance.*
**Guido**: *He’s getting close to gimbal lock there.*
**Flight**: *Roger. CapCom, recommend he bring up C3, C4, B3, B4, C1 and C2 thrusters, and advise he’s getting close to gimbal lock.*
**CapCom**: *Roger.*
*Of note, it was not a gimbal lock that caused the accident with the the Apollo 13 mission, the problem was an oxygen tank explosion.*
## Determination of the rotation matrix
A typical way to determine the rotation matrix for a rigid body in biomechanics is to use motion analysis to measure the position of at least three non-collinear markers placed on the rigid body, and then calculate a basis with these positions, analogue to what we have described in the notebook [Rigid-body transformations in a plane (2D)](http://nbviewer.ipython.org/github/BMClab/bmc/blob/master/notebooks/Transformation2D.ipynb).
### Basis
If we have the position of three markers: **m1**, **m2**, **m3**, a basis (formed by three orthogonal versors) can be found as:
- First axis, **v1**, the vector **m2-m1**;
- Second axis, **v2**, the cross product between the vectors **v1** and **m3-m1**;
- Third axis, **v3**, the cross product between the vectors **v1** and **v2**.
Then, each of these vectors are normalized resulting in three orthogonal versors.
For example, given the positions m1 = [1,0,0], m2 = [0,1,0], m3 = [0,0,1], a basis can be found:
```
m1 = np.array([1, 0, 0])
m2 = np.array([0, 1, 0])
m3 = np.array([0, 0, 1])
v1 = m2 - m1
v2 = np.cross(v1, m3 - m1)
v3 = np.cross(v1, v2)
print('Versors:')
v1 = v1/np.linalg.norm(v1)
print('v1 =', v1)
v2 = v2/np.linalg.norm(v2)
print('v2 =', v2)
v3 = v3/np.linalg.norm(v3)
print('v3 =', v3)
print('\nNorm of each versor:\n',
np.linalg.norm(np.cross(v1, v2)),
np.linalg.norm(np.cross(v1, v3)),
np.linalg.norm(np.cross(v2, v3)))
```
Remember from the text [Rigid-body transformations in a plane (2D)](http://nbviewer.ipython.org/github/BMClab/bmc/blob/master/notebooks/Transformation2D.ipynb) that the versors of this basis are the columns of the $\mathbf{R_{Gl}}$ and the rows of the $\mathbf{R_{lG}}$ rotation matrices, for instance:
```
RlG = np.array([v1, v2, v3])
print('Rotation matrix from Global to local coordinate system:\n', RlG)
```
And the corresponding angles of rotation using the $xyz$ sequence are:
```
euler_angles_from_rot_xyz(RlG)
```
These angles don't mean anything now because they are angles of the axes of the arbitrary basis we computed. In biomechanics, if we want an anatomical interpretation of the coordinate system orientation, we define the versors of the basis oriented with anatomical axes (e.g., for the shoulder, one versor would be aligned with the long axis of the upper arm).
We will see how to perform this computation later. Now we will combine translation and rotation in a single transformation.
## Translation and Rotation
Consider the case where the local coordinate system is translated and rotated in relation to the Global coordinate system as illustrated in the next figure.
<br>
<figure><img src='./../images/transrot3D.png' alt='translation and rotation 3D'/> <figcaption><center><i>Figure. A point in three-dimensional space represented in two coordinate systems, with one system translated and rotated.</i></center></figcaption> </figure>
The position of point $\mathbf{P}$ originally described in the local coordinate system, but now described in the Global coordinate system in vector form is:
$$ \mathbf{P_G} = \mathbf{L_G} + \mathbf{R_{Gl}}\mathbf{P_l} $$
This means that we first *disrotate* the local coordinate system and then correct for the translation between the two coordinate systems. Note that we can't invert this order: the point position is expressed in the local coordinate system and we can't add this vector to another vector expressed in the Global coordinate system, first we have to convert the vectors to the same coordinate system.
If now we want to find the position of a point at the local coordinate system given its position in the Global coordinate system, the rotation matrix and the translation vector, we have to invert the expression above:
$$ \begin{array}{l l}
\mathbf{P_G} = \mathbf{L_G} + \mathbf{R_{Gl}}\mathbf{P_l} \implies \\
\\
\mathbf{R_{Gl}^{-1}}\cdot\mathbf{P_G} = \mathbf{R_{Gl}^{-1}}\left(\mathbf{L_G} + \mathbf{R_{Gl}}\mathbf{P_l}\right) \implies \\
\\
\mathbf{R_{Gl}^{-1}}\mathbf{P_G} = \mathbf{R_{Gl}^{-1}}\mathbf{L_G} + \mathbf{R_{Gl}^{-1}}\mathbf{R_{Gl}}\mathbf{P_l} \implies \\
\\
\mathbf{P_l} = \mathbf{R_{Gl}^{-1}}\left(\mathbf{P_G}-\mathbf{L_G}\right) = \mathbf{R_{Gl}^T}\left(\mathbf{P_G}-\mathbf{L_G}\right) \;\;\;\;\; \text{or} \;\;\;\;\; \mathbf{P_l} = \mathbf{R_{lG}}\left(\mathbf{P_G}-\mathbf{L_G}\right)
\end{array} $$
The expression above indicates that to perform the inverse operation, to go from the Global to the local coordinate system, we first translate and then rotate the coordinate system.
### Transformation matrix
It is possible to combine the translation and rotation operations in only one matrix, called the transformation matrix:
$$ \begin{bmatrix}
\mathbf{P_X} \\
\mathbf{P_Y} \\
\mathbf{P_Z} \\
1
\end{bmatrix} =
\begin{bmatrix}
. & . & . & \mathbf{L_{X}} \\
. & \mathbf{R_{Gl}} & . & \mathbf{L_{Y}} \\
. & . & . & \mathbf{L_{Z}} \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\mathbf{P}_x \\
\mathbf{P}_y \\
\mathbf{P}_z \\
1
\end{bmatrix} $$
Or simply:
$$ \mathbf{P_G} = \mathbf{T_{Gl}}\mathbf{P_l} $$
Remember that in general the transformation matrix is not orthonormal, i.e., its inverse is not equal to its transpose.
The inverse operation, to express the position at the local coordinate system in terms of the Global reference system, is:
$$ \mathbf{P_l} = \mathbf{T_{Gl}^{-1}}\mathbf{P_G} $$
And in matrix form:
$$ \begin{bmatrix}
\mathbf{P_x} \\
\mathbf{P_y} \\
\mathbf{P_z} \\
1
\end{bmatrix} =
\begin{bmatrix}
\cdot & \cdot & \cdot & \cdot \\
\cdot & \mathbf{R^{-1}_{Gl}} & \cdot & -\mathbf{R^{-1}_{Gl}}\:\mathbf{L_G} \\
\cdot & \cdot & \cdot & \cdot \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\mathbf{P_X} \\
\mathbf{P_Y} \\
\mathbf{P_Z} \\
1
\end{bmatrix} $$
### Example with actual motion analysis data
*The data for this example is taken from page 183 of David Winter's book.*
Consider the following marker positions placed on a leg (described in the laboratory coordinate system with coordinates $x, y, z$ in cm, the $x$ axis points forward and the $y$ axes points upward): lateral malleolus (**lm** = [2.92, 10.10, 18.85]), medial malleolus (**mm** = [2.71, 10.22, 26.52]), fibular head (**fh** = [5.05, 41.90, 15.41]), and medial condyle (**mc** = [8.29, 41.88, 26.52]). Define the ankle joint center as the centroid between the **lm** and **mm** markers and the knee joint center as the centroid between the **fh** and **mc** markers. An anatomical coordinate system for the leg can be defined as: the quasi-vertical axis ($y$) passes through the ankle and knee joint centers; a temporary medio-lateral axis ($z$) passes through the two markers on the malleolus, an anterior-posterior as the cross product between the two former calculated orthogonal axes, and the origin at the ankle joint center.
a) Calculate the anatomical coordinate system for the leg as described above.
b) Calculate the rotation matrix and the translation vector for the transformation from the anatomical to the laboratory coordinate system.
c) Calculate the position of each marker and of each joint center at the anatomical coordinate system.
d) Calculate the Cardan angles using the $zxy$ sequence for the orientation of the leg with respect to the laboratory (but remember that the letters chosen to refer to axes are arbitrary, what matters is the directions they represent).
```
# calculation of the joint centers
mm = np.array([2.71, 10.22, 26.52])
lm = np.array([2.92, 10.10, 18.85])
fh = np.array([5.05, 41.90, 15.41])
mc = np.array([8.29, 41.88, 26.52])
ajc = (mm + lm)/2
kjc = (fh + mc)/2
print('Poition of the ankle joint center:', ajc)
print('Poition of the knee joint center:', kjc)
# calculation of the anatomical coordinate system axes (basis)
y = kjc - ajc
x = np.cross(y, mm - lm)
z = np.cross(x, y)
print('Versors:')
x = x/np.linalg.norm(x)
y = y/np.linalg.norm(y)
z = z/np.linalg.norm(z)
print('x =', x)
print('y =', y)
print('z =', z)
Oleg = ajc
print('\nOrigin =', Oleg)
# Rotation matrices
RGl = np.array([x, y , z]).T
print('Rotation matrix from the anatomical to the laboratory coordinate system:\n', RGl)
RlG = RGl.T
print('\nRotation matrix from the laboratory to the anatomical coordinate system:\n', RlG)
# Translational vector
OG = np.array([0, 0, 0]) # Laboratory coordinate system origin
LG = Oleg - OG
print('Translational vector from the anatomical to the laboratory coordinate system:\n', LG)
```
To get the coordinates from the laboratory (global) coordinate system to the anatomical (local) coordinate system:
$$ \mathbf{P_l} = \mathbf{R_{lG}}\left(\mathbf{P_G}-\mathbf{L_G}\right) $$
```
# position of each marker and of each joint center at the anatomical coordinate system
mml = np.dot(RlG, (mm - LG)) # equivalent to the algebraic expression RlG*(mm - LG).T
lml = np.dot(RlG, (lm - LG))
fhl = np.dot(RlG, (fh - LG))
mcl = np.dot(RlG, (mc - LG))
ajcl = np.dot(RlG, (ajc - LG))
kjcl = np.dot(RlG, (kjc - LG))
print('Coordinates of mm in the anatomical system:\n', mml)
print('Coordinates of lm in the anatomical system:\n', lml)
print('Coordinates of fh in the anatomical system:\n', fhl)
print('Coordinates of mc in the anatomical system:\n', mcl)
print('Coordinates of kjc in the anatomical system:\n', kjcl)
print('Coordinates of ajc in the anatomical system (origin):\n', ajcl)
```
## Problems
1. For the example about how the order of rotations of a rigid body affects the orientation shown in a figure above, deduce the rotation matrices for each of the 4 cases shown in the figure. For the first two cases, deduce the rotation matrices from the global to the local coordinate system and for the other two examples, deduce the rotation matrices from the local to the global coordinate system.
2. Consider the data from problem 7 in the notebook [Frame of reference](http://nbviewer.ipython.org/github/BMClab/bmc/blob/master/notebooks/ReferenceFrame.ipynb) where the following anatomical landmark positions are given (units in meters): RASIS=[0.5,0.8,0.4], LASIS=[0.55,0.78,0.1], RPSIS=[0.3,0.85,0.2], and LPSIS=[0.29,0.78,0.3]. Deduce the rotation matrices for the global to anatomical coordinate system and for the anatomical to global coordinate system.
3. For the data from the last example, calculate the Cardan angles using the $zxy$ sequence for the orientation of the leg with respect to the laboratory (but remember that the letters chosen to refer to axes are arbitrary, what matters is the directions they represent).
## References
- Corke P (2011) [Robotics, Vision and Control: Fundamental Algorithms in MATLAB](http://www.petercorke.com/RVC/). Springer-Verlag Berlin.
- Robertson G, Caldwell G, Hamill J, Kamen G (2013) [Research Methods in Biomechanics](http://books.google.com.br/books?id=gRn8AAAAQBAJ). 2nd Edition. Human Kinetics.
- [Maths - Euler Angles](http://www.euclideanspace.com/maths/geometry/rotations/euler/).
- Murray RM, Li Z, Sastry SS (1994) [A Mathematical Introduction to Robotic Manipulation](http://www.cds.caltech.edu/~murray/mlswiki/index.php/Main_Page). Boca Raton, CRC Press.
- Ruina A, Rudra P (2013) [Introduction to Statics and Dynamics](http://ruina.tam.cornell.edu/Book/index.html). Oxford University Press.
- Siciliano B, Sciavicco L, Villani L, Oriolo G (2009) [Robotics - Modelling, Planning and Control](http://books.google.com.br/books/about/Robotics.html?hl=pt-BR&id=jPCAFmE-logC). Springer-Verlag London.
- Winter DA (2009) [Biomechanics and motor control of human movement](http://books.google.com.br/books?id=_bFHL08IWfwC). 4 ed. Hoboken, USA: Wiley.
- Zatsiorsky VM (1997) [Kinematics of Human Motion](http://books.google.com.br/books/about/Kinematics_of_Human_Motion.html?id=Pql_xXdbrMcC&redir_esc=y). Champaign, Human Kinetics.
## Function `euler_rotmatrix.py`
```
# %load ./../functions/euler_rotmat.py
#!/usr/bin/env python
"""Euler rotation matrix given sequence, frame, and angles."""
from __future__ import division, print_function
__author__ = 'Marcos Duarte, https://github.com/demotu/BMC'
__version__ = 'euler_rotmat.py v.1 2014/03/10'
def euler_rotmat(order='xyz', frame='local', angles=None, unit='deg',
str_symbols=None, showA=True, showN=True):
"""Euler rotation matrix given sequence, frame, and angles.
This function calculates the algebraic rotation matrix (3x3) for a given
sequence ('order' argument) of up to three elemental rotations of a given
coordinate system ('frame' argument) around another coordinate system, the
Euler (or Eulerian) angles [1]_.
This function also calculates the numerical values of the rotation matrix
when numerical values for the angles are inputed for each rotation axis.
Use None as value if the rotation angle for the particular axis is unknown.
The symbols for the angles are: alpha, beta, and gamma for the first,
second, and third rotations, respectively.
The matrix product is calulated from right to left and in the specified
sequence for the Euler angles. The first letter will be the first rotation.
The function will print and return the algebraic rotation matrix and the
numerical rotation matrix if angles were inputed.
Parameters
----------
order : string, optional (default = 'xyz')
Sequence for the Euler angles, any combination of the letters
x, y, and z with 1 to 3 letters is accepted to denote the
elemental rotations. The first letter will be the first rotation.
frame : string, optional (default = 'local')
Coordinate system for which the rotations are calculated.
Valid values are 'local' or 'global'.
angles : list, array, or bool, optional (default = None)
Numeric values of the rotation angles ordered as the 'order'
parameter. Enter None for a rotation whith unknown value.
unit : str, optional (default = 'deg')
Unit of the input angles.
str_symbols : list of strings, optional (default = None)
New symbols for the angles, for instance, ['theta', 'phi', 'psi']
showA : bool, optional (default = True)
True (1) displays the Algebraic rotation matrix in rich format.
False (0) to not display.
showN : bool, optional (default = True)
True (1) displays the Numeric rotation matrix in rich format.
False (0) to not display.
Returns
-------
R : Matrix Sympy object
Rotation matrix (3x3) in algebraic format.
Rn : Numpy array or Matrix Sympy object (only if angles are inputed)
Numeric rotation matrix (if values for all angles were inputed) or
a algebraic matrix with some of the algebraic angles substituted
by the corresponding inputed numeric values.
Notes
-----
This code uses Sympy, the Python library for symbolic mathematics, to
calculate the algebraic rotation matrix and shows this matrix in latex form
possibly for using with the IPython Notebook, see [1]_.
References
----------
.. [1] http://nbviewer.ipython.org/github/duartexyz/BMC/blob/master/Transformation3D.ipynb
Examples
--------
>>> # import function
>>> from euler_rotmat import euler_rotmat
>>> # Default options: xyz sequence, local frame and show matrix
>>> R = euler_rotmat()
>>> # XYZ sequence (around global (fixed) coordinate system)
>>> R = euler_rotmat(frame='global')
>>> # Enter numeric values for all angles and show both matrices
>>> R, Rn = euler_rotmat(angles=[90, 90, 90])
>>> # show what is returned
>>> euler_rotmat(angles=[90, 90, 90])
>>> # show only the rotation matrix for the elemental rotation at x axis
>>> R = euler_rotmat(order='x')
>>> # zxz sequence and numeric value for only one angle
>>> R, Rn = euler_rotmat(order='zxz', angles=[None, 0, None])
>>> # input values in radians:
>>> import numpy as np
>>> R, Rn = euler_rotmat(order='zxz', angles=[None, np.pi, None], unit='rad')
>>> # shows only the numeric matrix
>>> R, Rn = euler_rotmat(order='zxz', angles=[90, 0, None], showA='False')
>>> # Change the angles' symbols
>>> R = euler_rotmat(order='zxz', str_symbols=['theta', 'phi', 'psi'])
>>> # Negativate the angles' symbols
>>> R = euler_rotmat(order='zxz', str_symbols=['-theta', '-phi', '-psi'])
>>> # all algebraic matrices for all possible sequences for the local frame
>>> s=['xyz','xzy','yzx','yxz','zxy','zyx','xyx','xzx','yzy','yxy','zxz','zyz']
>>> for seq in s: R = euler_rotmat(order=seq)
>>> # all algebraic matrices for all possible sequences for the global frame
>>> for seq in s: R = euler_rotmat(order=seq, frame='global')
"""
import numpy as np
import sympy as sym
try:
from IPython.core.display import Math, display
ipython = True
except:
ipython = False
angles = np.asarray(np.atleast_1d(angles), dtype=np.float64)
if ~np.isnan(angles).all():
if len(order) != angles.size:
raise ValueError("Parameters 'order' and 'angles' (when " +
"different from None) must have the same size.")
x, y, z = sym.symbols('x, y, z')
sig = [1, 1, 1]
if str_symbols is None:
a, b, g = sym.symbols('alpha, beta, gamma')
else:
s = str_symbols
if s[0][0] == '-': s[0] = s[0][1:]; sig[0] = -1
if s[1][0] == '-': s[1] = s[1][1:]; sig[1] = -1
if s[2][0] == '-': s[2] = s[2][1:]; sig[2] = -1
a, b, g = sym.symbols(s)
var = {'x': x, 'y': y, 'z': z, 0: a, 1: b, 2: g}
# Elemental rotation matrices for xyz (local)
cos, sin = sym.cos, sym.sin
Rx = sym.Matrix([[1, 0, 0], [0, cos(x), sin(x)], [0, -sin(x), cos(x)]])
Ry = sym.Matrix([[cos(y), 0, -sin(y)], [0, 1, 0], [sin(y), 0, cos(y)]])
Rz = sym.Matrix([[cos(z), sin(z), 0], [-sin(z), cos(z), 0], [0, 0, 1]])
if frame.lower() == 'global':
Rs = {'x': Rx.T, 'y': Ry.T, 'z': Rz.T}
order = order.upper()
else:
Rs = {'x': Rx, 'y': Ry, 'z': Rz}
order = order.lower()
R = Rn = sym.Matrix(sym.Identity(3))
str1 = r'\mathbf{R}_{%s}( ' %frame # last space needed for order=''
#str2 = [r'\%s'%var[0], r'\%s'%var[1], r'\%s'%var[2]]
str2 = [1, 1, 1]
for i in range(len(order)):
Ri = Rs[order[i].lower()].subs(var[order[i].lower()], sig[i] * var[i])
R = Ri * R
if sig[i] > 0:
str2[i] = '%s:%s' %(order[i], sym.latex(var[i]))
else:
str2[i] = '%s:-%s' %(order[i], sym.latex(var[i]))
str1 = str1 + str2[i] + ','
if ~np.isnan(angles).all() and ~np.isnan(angles[i]):
if unit[:3].lower() == 'deg':
angles[i] = np.deg2rad(angles[i])
Rn = Ri.subs(var[i], angles[i]) * Rn
#Rn = sym.lambdify(var[i], Ri, 'numpy')(angles[i]) * Rn
str2[i] = str2[i] + '=%.0f^o' %np.around(np.rad2deg(angles[i]), 0)
else:
Rn = Ri * Rn
Rn = sym.simplify(Rn) # for trigonometric relations
try:
# nsimplify only works if there are symbols
Rn2 = sym.latex(sym.nsimplify(Rn, tolerance=1e-8).n(chop=True, prec=4))
except:
Rn2 = sym.latex(Rn.n(chop=True, prec=4))
# there are no symbols, pass it as Numpy array
Rn = np.asarray(Rn)
if showA and ipython:
display(Math(str1[:-1] + ') =' + sym.latex(R, mat_str='matrix')))
if showN and ~np.isnan(angles).all() and ipython:
str2 = ',\;'.join(str2[:angles.size])
display(Math(r'\mathbf{R}_{%s}(%s)=%s' %(frame, str2, Rn2)))
if np.isnan(angles).all():
return R
else:
return R, Rn
```
| true |
code
| 0.577674 | null | null | null | null |
|
There are two main functions
* decision_function
* predict_proba
Most of classifiers have at least one of them, and many have both
```
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_circles
import numpy as np
import matplotlib.pyplot as plt
import mglearn
%matplotlib inline
X, y = make_circles(noise=0.25, factor=0.5, random_state=1)
# we rename the classes "blue" and "red" for illustration purposes
y_named = np.array(["blue", "red"])[y]
# We can call train_test_split with arbitrarily many arrays;
# all will be split in a consistent manner
X_train, X_test, y_train_named, y_test_named, y_train, y_test = train_test_split(X,
y_named,
y,
random_state=0)
# build the gradient boosting model
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train_named)
```
Uncertaintly in Binary classification case
```
print("Shape of probabilities: ", gbrt.predict_proba(X_test).shape)
# show the first few entries of predict_proba
print("Predicted probabilities:\n", gbrt.predict_proba(X_test[:6]))
fig, axes = plt.subplots(1, 2, figsize=(13, 5))
mglearn.tools.plot_2d_separator(
gbrt, X, ax=axes[0], alpha=.4, fill=True, cm=mglearn.cm2)
scores_image = mglearn.tools.plot_2d_scores(
gbrt, X, ax=axes[1], alpha=.5, cm=mglearn.ReBl, function='predict_proba')
for ax in axes:
# plot training and test points
mglearn.discrete_scatter(X_test[:, 0], X_test[:, 1], y_test,
markers='^', ax=ax)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train,
markers='o', ax=ax)
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
# don't want a transparent colorbar
cbar = plt.colorbar(scores_image, ax=axes.tolist())
cbar.set_alpha(1)
cbar.draw_all()
axes[0].legend(["Test class 0", "Test class 1", "Train class 0",
"Train class 1"], ncol=4, loc=(.1, 1.1))
```
Uncertaintly in Multi class classification
```
from sklearn.datasets import load_iris
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=42)
gbrt = GradientBoostingClassifier(learning_rate=0.01, random_state=0)
gbrt.fit(X_train, y_train)
# show the first few entries of predict_proba
print("Predicted probabilities:\n{}".format(gbrt.predict_proba(X_test)[:6]))
# show that sums across rows are one
print("Sums: {}".format(gbrt.predict_proba(X_test)[:6].sum(axis=1)))
print("Argmax of predicted probabilities:\n{}".format(np.argmax(gbrt.predict_proba(X_test), axis=1)))
print("Predictions:\n{}".format(gbrt.predict(X_test)))
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
# represent each target by its class name in the iris dataset
named_target = iris.target_names[y_train]
logreg.fit(X_train, named_target)
print("unique classes in training data: {}".format(logreg.classes_))
print("predictions: {}".format(logreg.predict(X_test)[:10]))
argmax_dec_func = np.argmax(logreg.decision_function(X_test), axis=1)
print("argmax of decision function: {}".format(argmax_dec_func[:10]))
print("argmax combined with classes_: {}".format(logreg.classes_[argmax_dec_func][:10]))
```
| true |
code
| 0.826764 | null | null | null | null |
|
## Notebook 1:
```
### Notebook 1
### Data set 1 (Viburnum)
### Language: Bash
### Data Location: NCBI SRA PRJNA299402 & PRJNA299407
%%bash
## make a new directory for this analysis
mkdir -p empirical_1/
mkdir -p empirical_1/halfrun
mkdir -p empirical_1/fullrun
## import Python libraries
import pandas as pd
import numpy as np
import ipyparallel
import urllib2
import glob
import os
```
### Download the sequence data
Sequence data for this study is archived on the NCBI sequence read archive (SRA). The data were run in two separate Illumina runs, but are combined under a single project id number.
+ Project SRA: SRP055977
+ Project number: PRJNA277574
+ Biosample numbers: SAMN03394519 -- SAMN03394561
+ Runs: SRR1915524 -- SRR1915566
+ The barcodes file is in the github repository for this [project]().
The library contains 95 samples. We uploaded the two demultiplexed samples for each individual separately, so each sample has 2 files. Below we examine just the first library (the "half" data set) and then both libraries combined (the "full" data set). We analyze on 64 samples since the remaining samples are replicate individuals within species that are part of a separate project.
You can download the data set using the script below:
```
%%bash
## get the data from Dryad
for run in $(seq 24 28);
do
wget -q -r -nH --cut-dirs=9 \
ftp://ftp-trace.ncbi.nlm.nih.gov/\
sra/sra-instant/reads/ByRun/sra/SRR/\
SRR191/SRR19155$run/SRR19155$run".sra";
done
%%bash
## convert sra files to fastq using fastq-dump tool
fastq-dump *.sra
## IPython code
## This reads in a table mapping sample names to SRA numbers
## that is hosted on github
## open table from github url
url = "https://raw.githubusercontent.com/"+\
"dereneaton/virentes/master/SraRunTable.txt"
intable = urllib2.urlopen(url)
## make name xfer dictionary
DF = pd.read_table(intable, sep="\t")
D = {DF.Run_s[i]:DF.Library_Name_s[i] for i in DF.index}
## change file names and move to fastq dir/
for fname in glob.glob("*.fastq"):
os.rename(fname, "analysis_pyrad/fastq/"+\
D[fname.replace(".fastq",".fq")])
```
### Create a set with reads concatenated from both technical replicates of each sample
```
%%bash
mkdir -p fastq_combined
## IPython code that makes a bash call w/ (!)
## get all the data from the two libraries and concatenate it
lib1tax = glob.glob("/home/deren/Documents/Vib_Lib1/fastq_Lib1/*.gz")
lib2tax = glob.glob("/home/deren/Documents/Vib_Lib1/fastq_Lib2/*.gz")
## names had to be modified to match
taxa = [i.split("/")[-1].split("_", 1)[1] for i in lib1tax]
for tax in taxa:
! cat /home/deren/Documents/Vib_Lib1/fastq_Lib1/Lib1_$tax \
/home/deren/Documents/Vib_Lib1/fastq_Lib2/Lib2_$tax \
> /home/deren/Documents/Vib_Lib1/fastq_combined/$tax
```
## Make a params file
```
%%bash
pyrad --version
%%bash
## create a new default params file
rm params.txt
pyrad -n
%%bash
## substitute new parameters into file
sed -i '/## 1. /c\empirical_1/halfrun ## 1. working directory ' params.txt
sed -i '/## 6. /c\TGCAG ## 6. cutters ' params.txt
sed -i '/## 7. /c\30 ## 7. N processors ' params.txt
sed -i '/## 9. /c\6 ## 9. NQual ' params.txt
sed -i '/## 10./c\.85 ## 10. clust threshold ' params.txt
sed -i '/## 12./c\4 ## 12. MinCov ' params.txt
sed -i '/## 13./c\10 ## 13. maxSH ' params.txt
sed -i '/## 14./c\empirical_1_half_m4 ## 14. output name ' params.txt
sed -i '/## 18./c\/home/deren/Documents/Vib_Lib1/fastq_Lib1/*.fastq ## 18. data location ' params.txt
sed -i '/## 29./c\2,2 ## 29. trim overhang ' params.txt
sed -i '/## 30./c\p,n,s,a ## 30. output formats ' params.txt
cat params.txt
%%bash
pyrad -p params.txt -s 234567 >> log.txt 2>&1
%%bash
sed -i '/## 12./c\2 ## 12. MinCov ' params.txt
sed -i '/## 14./c\empirical_1_half_m2 ## 14. output name ' params.txt
%%bash
pyrad -p params.txt -s 7 >> log.txt 2>&1
```
### Assemble the full data set
Added the 'a' option to output formats to build an ".alleles" file which will be used later for mrbayes/bucky analyses.
```
%%bash
## substitute new parameters into file
sed -i '/## 1. /c\empirical_1/fullrun ## 1. working directory ' params.txt
sed -i '/## 6. /c\TGCAG ## 6. cutters ' params.txt
sed -i '/## 7. /c\30 ## 7. N processors ' params.txt
sed -i '/## 9. /c\6 ## 9. NQual ' params.txt
sed -i '/## 10./c\.85 ## 10. clust threshold ' params.txt
sed -i '/## 12./c\4 ## 12. MinCov ' params.txt
sed -i '/## 13./c\10 ## 13. maxSH ' params.txt
sed -i '/## 14./c\empirical_1_full_m4 ## 14. output name ' params.txt
sed -i '/## 18./c\/home/deren/Documents/Vib_Lib1/fastq_combined/*.fastq ## 18. data location ' params.txt
sed -i '/## 29./c\2,2 ## 29. trim overhang ' params.txt
sed -i '/## 30./c\p,n,s,a ## 30. output formats ' params.txt
%%bash
pyrad -p params.txt -s 234567 >> log.txt 2>&1
%%bash
sed -i '/## 12./c\2 ## 12. MinCov ' params.txt
sed -i '/## 14./c\empirical_1_full_m2 ## 14. output name ' params.txt
%%bash
pyrad -p params.txt -s 7 >> log.txt 2>&1
```
## Results
We are interested in the relationship between the amount of input (raw) data between any two samples, the average coverage they recover when clustered together, and the phylogenetic distances separating samples.
### Raw data amounts (1 sequence lane)
The average number of raw reads per sample is 1.37M.
```
## read in the data
s2dat = pd.read_table("empirical_1/halfrun/stats/s2.rawedit.txt", header=0, nrows=66)
## print summary stats
print s2dat["passed.total"].describe()
## find which sample has the most raw data
maxraw = s2dat["passed.total"].max()
print "\nmost raw data in sample:"
print s2dat['sample '][s2dat['passed.total']==maxraw]
```
### Raw data amounts (2 sequence lanes)
The average nreads now is 2.74M
```
## read in the data
s2dat = pd.read_table("empirical_1/fullrun/stats/s2.rawedit.txt", header=0, nrows=66)
## print summary stats
print s2dat["passed.total"].describe()
## find which sample has the most raw data
maxraw = s2dat["passed.total"].max()
print "\nmost raw data in sample:"
print s2dat['sample '][s2dat['passed.total']==maxraw]
```
### Look at distributions of coverage
pyrad v.3.0.63 outputs depth information for each sample which I read in here and plot. First let's ask which sample has the highest depth of coverage. The std here is the std in means across samples. The std of depths within individuals is much higher.
```
## read in the s3 results
s3dat = pd.read_table("empirical_1/halfrun/stats/s3.clusters.txt", header=0, nrows=66)
## print summary stats
print "summary of means\n=================="
print s3dat['dpt.me'].describe()
## print summary stats
print "\nsummary of std\n=================="
print s3dat['dpt.sd'].describe()
## print summary stats
print "\nsummary of proportion lowdepth\n=================="
print pd.Series(1-s3dat['d>5.tot']/s3dat["total"]).describe()
## find which sample has the greatest depth of retained loci
maxdepth = s3dat["d>5.tot"].max()
print "\nhighest coverage in sample:"
print s3dat['taxa'][s3dat['d>5.tot']==maxdepth]
## read in the s3 results
s3dat = pd.read_table("empirical_1/fullrun/stats/s3.clusters.txt", header=0, nrows=66)
## print summary stats
print "summary of means\n=================="
print s3dat['dpt.me'].describe()
## print summary stats
print "\nsummary of std\n=================="
print s3dat['dpt.sd'].describe()
## print summary stats
print "\nsummary of proportion hidepth\n=================="
print pd.Series(1-s3dat['d>5.tot']/s3dat["total"]).describe()
## find which sample has the greatest depth of retained loci
max_hiprop = (s3dat["d>5.tot"]/s3dat["total"]).max()
print "\nhighest coverage in sample:"
print s3dat['taxa'][s3dat['d>5.tot']/s3dat["total"]==max_hiprop]
## print mean and std of coverage for the highest coverage sample
with open("empirical_1/fullrun/clust.85/lantanoides_D15_Beartown_2.depths", 'rb') as indat:
depths = np.array(indat.read().strip().split(","), dtype=int)
print depths.mean(), depths.std()
import toyplot
import toyplot.svg
import numpy as np
## read in the depth information for this sample
with open("empirical_1/fullrun/clust.85/lantanoides_D15_Beartown_2.depths", 'rb') as indat:
depths = np.array(indat.read().strip().split(","), dtype=int)
## make a barplot in Toyplot
canvas = toyplot.Canvas(width=350, height=300)
axes = canvas.axes(xlabel="Depth of coverage (N reads)",
ylabel="N loci",
label="dataset1/sample=sulcatum_D9_MEX_003")
## select the loci with depth > 5 (kept)
keeps = depths[depths>5]
## plot kept and discarded loci
edat = np.histogram(depths, range(30)) # density=True)
kdat = np.histogram(keeps, range(30)) #, density=True)
axes.bars(edat)
axes.bars(kdat)
#toyplot.svg.render(canvas, "empirical_1_full_depthplot.svg")
cat empirical_1/halfrun/stats/empirical_1_half_m4.stats
```
#### get average number of loci per sample
```
import numpy as np
indat = open("empirical_1/halfrun/stats/empirical_1_half_m4.stats").readlines()
counts = [int(i.strip().split("\t")[1]) for i in indat[8:73]]
print np.mean(counts)
print np.std(counts)
```
#### get average number of samples with data for a locus
```
import numpy as np
import itertools
indat = open("empirical_1/halfrun/stats/empirical_1_half_m4.stats").readlines()
counts = [i.strip().split("\t") for i in indat[81:142]]
#print counts
ntax = [int(i[0]) for i in counts]
ncounts = [int(i[1]) for i in counts]
tots = list(itertools.chain(*[[i]*n for i,n in zip(ntax, ncounts)]))
print np.mean(tots)
print np.std(tots)
cat empirical_1/fullrun/stats/empirical_1_full_m4.stats
import numpy as np
indat = open("empirical_1/fullrun/stats/empirical_1_full_m4.stats").readlines()
counts = [int(i.strip().split("\t")[1]) for i in indat[8:73]]
print np.mean(counts)
print np.std(counts)
import numpy as np
import itertools
indat = open("empirical_1/fullrun/stats/empirical_1_full_m4.stats").readlines()
counts = [i.strip().split("\t") for i in indat[81:140]]
#print counts
ntax = [int(i[0]) for i in counts]
ncounts = [int(i[1]) for i in counts]
tots = list(itertools.chain(*[[i]*n for i,n in zip(ntax, ncounts)]))
print np.mean(tots)
print np.std(tots)
```
## Infer an ML phylogeny
```
%%bash
## raxml argumement w/ ...
raxmlHPC-PTHREADS-AVX -f a -m GTRGAMMA -N 100 -x 12345 -p 12345 -T 35 \
-w /home/deren/Documents/RADmissing/empirical_1/halfrun \
-n empirical_1_halfrun -s empirical_1/halfrun/outfiles/empirical_1_half_m4.phy \
-o "Lib1_clemensiae_DRY6_PWS_2135"
%%bash
raxmlHPC-PTHREADS-AVX -f a -m GTRGAMMA -N 100 -x 12345 -p 12345 -T 35 \
-w /home/deren/Documents/RADmissing/empirical_1/fullrun \
-n empirical_1_fullrun -s empirical_1/fullrun/outfiles/empirical_1_full_m4.phy \
-o "clemensiae_DRY6_PWS_2135"
%%bash
head -n 20 empirical_1/halfrun/RAxML_info.empirical_1_half_m4
%%bash
head -n 20 empirical_1/fullrun/RAxML_info.empirical_1_full_m4
```
### Plot the tree in R using `ape`
```
%load_ext rpy2.ipython
%%R -w 600 -h 1000
library(ape)
tre_half <- read.tree("empirical_1/halfrun/RAxML_bipartitions.empirical_1_halfrun")
#rtre <- root(tre, "Lib1_clemensiae_DRY6_PWS_2135", resolve.root=T)
#rtre <- root(rtre, "Lib1_clemensiae_DRY6_PWS_2135", resolve.root=T)
ltre_half <- ladderize(tre_half)
plot(ltre_half, cex=0.8, edge.width=2)
nodelabels(ltre_half$node.label)
%%R -w 600 -h 1000
library(ape)
svg("outtree.svg", height=11, width=8)
tre_full <- read.tree("empirical_1/fullrun/RAxML_bipartitions.empirical_1_fullrun")
#rtre <- root(tre, "Lib1_clemensiae_DRY6_PWS_2135", resolve.root=T)
#rtre <- root(rtre, "Lib1_clemensiae_DRY6_PWS_2135", resolve.root=T)
ltre_full <- ladderize(tre_full)
plot(ltre_full, cex=0.8, edge.width=3)
#nodelabels(ltre_full$node.label)
dev.off()
```
## BUCKY -- write mrbayes nexus blocks for each locus
The functions `nexmake` and `subsample` are used to split the .loci file into individual nexus files for each locus within a new directory. Each nexus file is given a mrbayes command to run. Then we run the bucky tool `mbsum` to summarize the mrbayes output, and finally run `bucky` to infer concordance trees from the posterior distributions of trees across all loci.
Loci are selected on the basis that they have coverage across all tips of the selected subtree and that they contain at least 1 SNP.
```
def nexmake(taxadict, loc, nexdir, trim):
outloc = open(nexdir+"/"+str(loc)+".nex", 'w')
header = """
#NEXUS
begin data;
dimensions ntax={} nchar={};
format datatype=dna interleave=yes missing=N gap=-;
matrix
""".format(len(taxadict), len(taxadict.values()[0]))
outloc.write(header)
for tax, seq in taxadict.items():
outloc.write("{}{}{}\n"\
.format(tax[trim:trim+9],
" "*(10-len(tax[0:9])),
"".join(seq)))
mbstring = """
;
end;
begin mrbayes;
set autoclose=yes nowarn=yes;
lset nst=6 rates=gamma;
mcmc ngen=2200000 samplefreq=2000;
sump burnin=200000;
sumt burnin=200000;
end;
"""
outloc.write(mbstring)
outloc.close()
def unstruct(amb):
" returns bases from ambiguity code"
D = {"R":["G","A"],
"K":["G","T"],
"S":["G","C"],
"Y":["T","C"],
"W":["T","A"],
"M":["C","A"]}
if amb in D:
return D.get(amb)
else:
return [amb,amb]
def resolveambig(subseq):
N = []
for col in subseq:
N.append([unstruct(i)[np.random.binomial(1, 0.5)] for i in col])
return np.array(N)
def newPIS(seqsamp):
counts = [Counter(col) for col in seqsamp.T if not ("-" in col or "N" in col)]
pis = [i.most_common(2)[1][1] > 1 for i in counts if len(i.most_common(2))>1]
if sum(pis) >= 2:
return sum(pis)
else:
return 0
def parseloci(iloci, taxadict, nexdir, trim=0):
nloc = 0
## create subsampled data set
for loc in iloci:
## if all tip samples have data in this locus
names = [line.split()[0] for line in loc.split("\n")[:-1]]
## check that locus has required samples for each subtree
if all([i in names for i in taxadict.values()]):
seqs = np.array([list(line.split()[1]) for line in loc.split("\n")[:-1]])
seqsamp = seqs[[names.index(tax) for tax in taxadict.values()]]
seqsamp = resolveambig(seqsamp)
pis = newPIS(seqsamp)
if pis:
nloc += 1
## remove invariable columns given this subsampling
keep = []
for n, col in enumerate(seqsamp.T):
if all([i not in ["N","-"] for i in col]):
keep.append(n)
subseq = seqsamp.T[keep].T
## write to a nexus file
nexdict = dict(zip(taxadict.keys(), [i.tostring() for i in subseq]))
nexmake(nexdict, nloc, nexdir, trim)
print nloc, 'loci kept'
```
#### Modify line endings of loci string for easier parsing
```
def getloci(locifile):
## parse the loci file by new line characters
locifile = open(locifile)
lines = locifile.readlines()
## add "|" to end of lines that contain "|"
for idx in range(len(lines)):
if "|" in lines[idx]:
lines[idx] = lines[idx].strip()+"|\n"
## join lines back together into one large string
locistr = "".join(lines)
## break string into loci at the "|\n" character
loci = locistr.split("|\n")[:-1]
## how many loci?
print len(loci), "loci"
return loci
## run on both files
loci_full = getloci("empirical_1/fullrun/outfiles/empirical_1_full_m4.loci")
loci_half = getloci("empirical_1/halfrun/outfiles/empirical_1_half_m4.loci")
```
### Make nexus files
```
parseloci(loci_full[:], deep_dict_f, "deep_dict_full", 0)
parseloci(loci_half[:], deep_dict_h, "deep_dict_half", 0)
#parseloci(loci[:], shallow_dict, "shallow_dict", 0)
## create a parallel client
ipclient = ipyparallel.Client()
lview = ipclient.load_balanced_view()
## call function across all engines
def mrbayes(infile):
import subprocess
cmd = "mb %s" % infile
subprocess.check_call(cmd, shell=True)
## submit all nexus files to run mb
allnex = glob.glob("deep_dict_full/*.nex")
for nex in allnex:
lview.apply(mrbayes, nex)
ipclient.wait_interactive()
```
### Summarize posteriors with `mbsum`
```
def mbsum(nexdir, nloci):
import subprocess
## combine trees from the two replicate runs
for n in range(1, nloci+1):
cmd = "mbsum -n 101 -o {}{}.in {}{}.nex.run1.t {}{}.nex.run2.t".\
format(nexdir, n, nexdir, n, nexdir, n)
subprocess.check_call(cmd, shell=True)
```
### Run Bucky to infer concordance factors
```
import os
import numpy as np
from collections import Counter
def subsample(infile, requires, outgroup, nexdir, trim):
""" sample n taxa from infile to create nex file"""
## counter
loc = 0
## create output directory
if not os.path.exists(nexdir):
os.mkdir(nexdir)
## input .alleles file
loci = open(infile, 'r').read().strip().split("//")
## create a dictionary of {names:seqs}
for locus in xrange(len(loci)):
locnex = [""]*len(requires)
for line in loci[locus].strip().split("\n"):
tax = line.split()[0]
seq = line.split()[-1]
if ">" in tax:
if tax in requires:
locnex[requires.index(tax)] = seq
## if all tips
if len([i for i in locnex if i]) == len(requires):
## if locus is variable
## count how many times each char occurs in each site
ccs = [Counter(i) for i in np.array([list(i) for i in locnex]).T]
## remove N and - characters and the first most occurring base
for i in ccs:
del i['-']
del i['N']
if i:
del i[i.most_common()[0][0]]
## is anything left occuring more than once (minor allele=ma)?
ma = max([max(i.values()) if i else 0 for i in ccs])
if ma > 1:
nexmake(requires, locnex, loc, outgroup, nexdir, trim)
loc += 1
return loc
```
### Subtree 1 (Oreinodentinus) (full data set)
```
## inputs
requires = [">triphyllum_D13_PWS_1783_0",
">jamesonii_D12_PWS_1636_0",
">sulcatum_D9_MEX_003_0",
">acutifolium_DRY3_MEX_006_0",
">dentatum_ELS4_0",
">recognitum_AA_1471_83B_0"]
outgroup = ""
infile = "empirical_1/fullrun/outfiles/empirical_1_full_m4.alleles"
nexdir = "nex_files1"
## run function
nloci = subsample(infile, requires, outgroup, nexdir, trim=1)
print nloci
```
### Subtree 1 (Oreinodentinus) (half data set)
```
## inputs
requires = [">Lib1_triphyllum_D13_PWS_1783_0",
">Lib1_jamesonii_D12_PWS_1636_0",
">Lib1_sulcatum_D9_MEX_003_0",
">Lib1_acutifolium_DRY3_MEX_006_0",
">Lib1_dentatum_ELS4_0",
">Lib1_recognitum_AA_1471_83B_0"]
outgroup = ""
infile = "empirical_1/halfrun/outfiles/empirical_1_half_m4.alleles"
nexdir = "nex_files2"
## run function
nloci = subsample(infile, requires, outgroup, nexdir, trim=6)
print nloci
```
### Subtree 2 (Urceolata) (full data set)
```
## inputs
requires = [">clemensiae_DRY6_PWS_2135_0",
">tinus_D33_WC_277_0",
">taiwanianum_TW1_KFC_1952_0",
">lantanoides_D15_Beartown_2_0",
">amplificatum_D3_SAN_156003_0",
">lutescens_D35_PWS_2077_0",
">lentago_ELS85_0",
">dentatum_ELS4_0"]
outgroup = ""
infile = "empirical_1/fullrun/outfiles/empirical_1_full_m4.alleles"
nexdir = "nex_files5"
## run function
nloci = subsample(infile, requires, outgroup, nexdir, trim=1)
print nloci
```
### Subtree 2 (Urceolata) (half data set)
```
## inputs
requires = [">Lib1_clemensiae_DRY6_PWS_2135_0",
">Lib1_tinus_D33_WC_277_0",
">Lib1_taiwanianum_TW1_KFC_1952_0",
">Lib1_lantanoides_D15_Beartown_2_0",
">Lib1_amplificatum_D3_SAN_156003_0",
">Lib1_lutescens_D35_PWS_2077_0",
">Lib1_lentago_ELS85_0",
">Lib1_dentatum_ELS4_0"]
outgroup = ""
infile = "empirical_1/halfrun/outfiles/empirical_1_half_m4.alleles"
nexdir = "nex_files6"
## run function
nloci = subsample(infile, requires, outgroup, nexdir, trim=6)
print nloci
```
### Run mrbayes on all nex files
```
import ipyparallel
import subprocess
import glob
## create a parallel client
ipclient = ipyparallel.Client()
lview = ipclient.load_balanced_view()
## call function across all engines
def mrbayes(infile):
import subprocess
cmd = "mb %s" % infile
subprocess.check_call(cmd, shell=True)
## run on the full data set
res = lview.map_async(mrbayes, glob.glob("nex_files1/*"))
_ = res.get()
## run on the half data set
res = lview.map_async(mrbayes, glob.glob("nex_files2/*"))
_ = res.get()
## run on the half data set
res = lview.map_async(mrbayes, glob.glob("nex_files3/*"))
_ = res.get()
## run on the half data set
res = lview.map_async(mrbayes, glob.glob("nex_files4/*"))
_ = res.get()
## run on the half data set
res = lview.map_async(mrbayes, glob.glob("nex_files5/*"))
_ = res.get()
## run on the half data set
res = lview.map_async(mrbayes, glob.glob("nex_files6/*"))
_ = res.get()
```
### Run mbsum to summarize the results
```
import os
import subprocess
def mbsum(nexdir, nloci):
## create dir for bucky input files
insdir = os.path.join(nexdir, "ins")
if not os.path.exists(insdir):
os.mkdir(insdir)
## combine trees from the two replicate runs
for n in range(nloci):
cmd = "mbsum -n 101 -o {}/{}.in {}{}.nex.run1.t {}{}.nex.run2.t".\
format(insdir, n, nexdir, n, nexdir, n)
subprocess.check_call(cmd, shell=True)
#mbsum("nex_files1/", 3300)
#mbsum("nex_files2/", 364)
#mbsum("nex_files3/", 1692)
#mbsum("nex_files4/", 169)
mbsum("nex_files5/", 1203)
mbsum("nex_files6/", 106)
```
### Run Bucky
```
args = []
for insdir in ["nex_files5/ins", "nex_files6/ins"]:
## independence test
args.append("bucky --use-independence-prior -k 4 -n 500000 \
-o {}/BUCKY.ind {}/*.in".format(insdir, insdir))
## alpha at three levels
for alpha in [0.1, 1, 10]:
args.append("bucky -a {} -k 4 -n 500000 -c 4 -o {}/BUCKY.{} {}/*.in".\
format(alpha, insdir, alpha, insdir))
def bucky(arg):
import subprocess
subprocess.check_call(arg, shell=True)
return arg
res = lview.map_async(bucky, args)
res.get()
```
#### Cleanup
```
del lbview
ipclient.close()
```
### check out the results
```
%%bash
head -n 40 nex_files1/ins/BUCKY.0.1.concordance
%%bash
head -n 40 nex_files1/ins/BUCKY.1.concordance
%%bash
head -n 40 nex_files2/ins/BUCKY.1.concordance
! head -n 45 nex_files3/ins/BUCKY.0.1.concordance
```
### FINAL BUCKY RESULTS (DEEP_SCALE)
```
! head -n 45 nex_files4/ins/BUCKY.0.1.concordance
! head -n 45 nex_files5/ins/BUCKY.0.1.concordance
! head -n 45 nex_files6/ins/BUCKY.0.1.concordance
```
### Get missing data percentatge for m2 data sets
For this I start raxml to get the info and then quit. Kind of lazy but simpler than calculating it myself.
```
%%bash
## raxml argumement w/ ...
raxmlHPC-PTHREADS-AVX -f a -m GTRGAMMA -N 100 -x 12345 -p 12345 -T 20 \
-w /home/deren/Documents/RADmissing/empirical_1/fullrun \
-n empirical_1_full_m2 -s empirical_1/fullrun/outfiles/empirical_1_m2.phy
%%bash
head -n 20 empirical_1/fullrun/RAxML_info.empirical_1_full_m2
```
### Get average phylo dist (GTRgamma dist)
```
%%R
mean(cophenetic.phylo(ltre))
```
| true |
code
| 0.402539 | null | null | null | null |
|
# MNIST SVD Classification
Follows Chapter 11 of Matrix Methods in Data Mining and Pattern Recognition by Lars Elden,
with added dimensionality reduction visualization
#### Author: Daniel Yan
#### Email: daniel.yan@vanderbilt.edu
```
from keras.datasets import mnist
from matplotlib import pyplot as plt
import numpy as np
```
# Load Data
Load in Keras dataset
```
# Load in mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Reshape to each image to a row vector and column vector
x_train_rowvector = np.reshape(x_train, (-1, 28*28))
x_train_colvector = np.copy(x_train_rowvector).T
x_test_rowvector = np.reshape(x_test, (-1, 28*28))
x_test_colvector = np.copy(x_test_rowvector).T
# Take small sample of 2000 training images
x_train_colvector_sample2000 = x_train_colvector[:, :2000]
y_train_sample2000 = y_train[:2000]
# Take small sample of 200 testing images
x_test_colvector_sample200 = x_test_colvector[:, :200]
y_test_sample200 = y_test[:200]
```
# Visualize Examples
```
# Visualize a few samples
for i in range(5):
print("Label: ", y_train[i])
image = x_train_colvector[:, i]
plt.imshow(image.reshape(28, 28), cmap="Greys")
plt.show()
plt.close()
```
# PCA Visualization
Credits: https://towardsdatascience.com/pca-and-svd-explained-with-numpy-5d13b0d2a4d8
```
# Calculate the covariance matrix
covariance = np.cov(x_train_colvector_sample2000)
# Calculate the eigenvalues and the eigenvectors for the covariance matrix
eigenvalues, eigenvectors = np.linalg.eig(covariance)
# Get the real part of the eigenvalues and eigenvectors only
eigenvalues = np.real(eigenvalues)
eigenvectors = np.real(eigenvectors)
# Project original data onto eigenvectors
pca = np.dot(x_train_colvector_sample2000.T, eigenvectors)
# Get only the first two columns for the first two principal components
pca = pca[:, 0:2]
```
Sort by label
```
pca_list= [0] * 10
y_list = [0] * 10
for i in range(10):
pca_list[i] = (pca[y_train_sample2000 == i])
y_list[i] = (y_train_sample2000[y_train_sample2000 == i])
```
Plot each label separately on graph
```
COLORS = ["red", "blue", "green", "yellow", "darkviolet",
"maroon", "greenyellow", "hotpink", "black", "cyan"]
fig, ax = plt.subplots()
for i in range(10):
# Get the pca array corresponding to the current label
pca_current_label = pca_list[i]
ax.scatter(pca_current_label[:, 0], pca_current_label[:, 1],
c=COLORS[i], label=str(i))
ax.legend()
plt.show()
```
Calculate and plot the mean for each digit in PCA coordinates
```
pca_mean_list = [0] * 10
for i in range(10):
pca_mean_list[i] = np.mean(pca_list[i], axis=0)
COLORS = ["red", "blue", "green", "yellow", "darkviolet",
"maroon", "greenyellow", "hotpink", "black", "cyan"]
fig, ax = plt.subplots()
for i in range(10):
# Get the pca array corresponding to the current label
pca_current_label = pca_mean_list[i]
ax.scatter(pca_current_label[0], pca_current_label[1],
c=COLORS[i], label=str(i))
ax.legend()
plt.show()
```
# SVD Visualization
Compare the PCA visualization with SVD dimensionality reduction
Calculate SVD and use dimensionality reduction to get down to 2 coordinates
```
# Calculate u, s, v
u, s, v = np.linalg.svd(x_train_colvector_sample2000, full_matrices=False)
# Set all singular values greater than the first two to 0
for i in range(2, s.shape[0]):
s[i] = 0
# Calculate the reduced dimensions with svd
svd_cords = np.diag(s) @ v
```
Sort by label
```
svd_list= [0] * 10
for i in range(10):
svd_list[i] = (svd_cords.T[y_train_sample2000 == i])
```
Plot the SVD coordinates
```
COLORS = ["red", "blue", "green", "yellow", "darkviolet",
"maroon", "greenyellow", "hotpink", "black", "cyan"]
fig, ax = plt.subplots()
for i in range(10):
# Get the pca array corresponding to the current label
svd_current_label = svd_list[i]
ax.scatter(svd_current_label[:, 0], svd_current_label[:, 1],
c=COLORS[i], label=str(i))
ax.legend()
plt.show()
```
Calculate and plot the mean for each digit in SVD coordinates
```
svd_mean_list = [0] * 10
for i in range(10):
svd_mean_list[i] = np.mean(svd_list[i], axis=0)
COLORS = ["red", "blue", "green", "yellow", "darkviolet",
"maroon", "greenyellow", "hotpink", "black", "cyan"]
fig, ax = plt.subplots()
for i in range(10):
# Get the pca array corresponding to the current label
svd_current_label = svd_mean_list[i]
ax.scatter(svd_current_label[0], svd_current_label[1],
c=COLORS[i], label=str(i))
ax.legend()
plt.show()
```
# Sorting Training Digits By Label
Sort the training images by label
```
x_list= [0] * 10
y_list = [0] * 10
for i in range(10):
# Get x and y values in each label by the coordinate in the list
x_list[i] = (x_train_colvector[:, y_train == i])
y_list[i] = (y_train[y_train == i])
```
# Mean Clustering Classification
Calculate the Mean Image for Each Digit
```
means_list = [0] * 10
for i in range(10):
means_list[i] = np.mean(x_list[i], axis=1)
```
Visualize the Mean Image for Each Digit
```
for i in range(10):
print("Mean Image for Digit", i)
image = means_list[i]
# Show singular image
plt.imshow(image.reshape(28, 28), cmap="Greys")
plt.show()
plt.close()
```
Classify Each Unknown Digit by the Mean Image
```
# Create vector for y predictions
y_pred = np.zeros(len(y_test_sample200))
# Iterate through all the testing images and make a prediction
for i in range(len(y_pred)):
# Get the unknown digit
x = x_test_colvector_sample200[:, i]
# Calculate the residual of the digit to each of the mean digits
residuals = np.zeros(10)
for j in range(10):
# Calculate residual,
residuals[j] = np.linalg.norm(means_list[j] - x, ord=2)
# Find the minimum residual and store as prediction
y_pred[i] = np.argmin(residuals)
```
Calculate the accuracy score
```
correct = np.where(y_pred == y_test_sample200, 1, 0)
print("Accuracy For Mean Digit: ", np.sum(correct) / len(correct))
```
# SVD Singular Images Visualization
Compute Top 3 Singular Images for each digit and visualize
```
# Iterate through all the digits
for i in range(10):
print("#################################################################")
print("#################################################################")
print("Visualizing Singular Images for " + str(i))
print("#################################################################")
print("#################################################################")
# Calculate the SVD for that digit
u, s, v = np.linalg.svd(x_list[i], full_matrices=False)
# Visualize the first three singular images
for j in range(3):
print("Visualizing Singular Image Number " + str(j + 1))
# Get the singular image
image = u[:, j]
# Show singular image
plt.imshow(image.reshape(28, 28), cmap="Greys")
plt.show()
plt.close()
```
# SVD Singular Image Classification
Compute the Singular Value Decomposition for each digit
```
u_list = [0] * 10
s_list = [0] * 10
v_list = [0] * 10
# Iterate through each digit
for i in range(10):
# Calculate the SVD for that digit
u_list[i], s_list[i], v_list[i] = np.linalg.svd(x_list[i], full_matrices=False)
```
Calculate the Accuracy for Different Number of Singular Images
```
# Store predictions and accuracy at different number of singular images used
acc_list = [0] * 5
pred_list = [0] * 5
# Use only the first k basis image for classification
for k in range(5):
# List to store the values of uk @ uk.T to get the singular images sum
uk_ukt_list = [0] * 10
# Iterate through all digits and calculate uk @ uk.T for that digit
for i in range(10):
uk = np.zeros((784, 784))
uk[:,0:k+1] = u_list[i][:, 0:k+1]
uk_ukt_list[i] = uk @ uk.T
# Iterate through the testing images and get the prediction for each image
# Initialize predictions to 0
y_pred = np.zeros(len(y_test_sample200))
# Iterate through all the testing images
for i in range(len(y_pred)):
# Get the unknown digit
x = x_test_colvector_sample200[:, i]
# Calculate the residual of the digit to each of the singular bases
residuals = np.zeros(10)
# Iterate through the 10 singular bases
for j in range(10):
# Calculate residual, which is norm of (I - uk @ uk.T) @ z
residuals[j] = np.linalg.norm((np.identity(28*28) - uk_ukt_list[j]) @ x, ord=2)
# Find the minimum residual and store that as the predicted digit
y_pred[i] = np.argmin(residuals)
# Store all the predictions for this threshold
pred_list[k] = y_pred
# Calculate and store the accuracy for this threshold
correct = np.where(y_pred == y_test_sample200, 1, 0)
accuracy = np.sum(correct) / len(correct)
print("Accuracy with", k + 1, "singular images: ", accuracy)
acc_list[k] = accuracy
```
# Confusion Matrix Visualization at Each Number of Singular Images
Visualize a confusion matrix at each number of singular images
```
import seaborn
from sklearn import metrics
for k in range(5):
print("Confusion Matrix at", k + 1, "singular images")
# Use scikit-learn to calculate confusion matrix
confusion_matrix = metrics.confusion_matrix(y_test_sample200, pred_list[k], normalize="true")
# Use seaborn to plot heatmap
axes = seaborn.heatmap(confusion_matrix, annot=True)
axes.set(xlabel="Predicted Label", ylabel="Actual Label", title="Confusion Matrix")
# Save as image and show plot.
plt.show()
plt.close()
```
| true |
code
| 0.779679 | null | null | null | null |
|
The goal of this notebook is to verify that you can load the checkpointed model from it's github repo and run it on a few test image samples and verify that the whole inference pipeline works.
```
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
```
First, the imports:
```
%matplotlib inline
import sys
import numpy as np
import cv2 as cv
import tensorflow as tf
from models import resnet as resnet
import matplotlib.pyplot as plt
import pandas as pd
import os
```
Helper functions
```
def _load_dictionary(dict_file):
dictionary = dict()
with open(dict_file, 'r') as lines:
for line in lines:
sp = line.rstrip('\n').split('\t')
idx, name = sp[0], sp[1]
dictionary[idx] = name
return dictionary
# Load the labels:
# dictionary = _load_dictionary("ml2020_dictionary.txt")
# I generated these a priori
def preprocess(img):
rawH = float(img.shape[0])
rawW = float(img.shape[1])
newH = 256.0
newW = 256.0
test_crop = 224.0
if rawH <= rawW:
newW = (rawW/rawH) * newH
else:
newH = (rawH/rawW) * newW
img = cv.resize(img, (int(newW), int(newH)))
img = img[int((newH-test_crop)/2):int((newH-test_crop)/2)+int(test_crop),int((newW-test_crop)/2):int((newW-test_crop)/2)+int(test_crop)]
img = ((img/255.0) - 0.5) * 2.0
img = img[...,::-1]
return img
```
Model declaration and weight restoration
```
images = tf.placeholder(dtype=tf.float32, shape=[None, 224, 224, 3])
net = resnet.ResNet(images, is_training=False)
net.build_model()
logit = net.logit
prob = tf.nn.softmax(logit)
prob_topk, pred_topk = tf.nn.top_k(prob, k=20)
# restore model
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
config.log_device_placement=False
sess = tf.Session(config=config)
saver = tf.train.Saver(tf.global_variables())
saver.restore(sess, "./checkpoints/model.ckpt")
print('Architecture details \n')
print(f'N_class:{net.num_classes},Stages: {net.stages}, N_filters: {net.filters}')
```
In case you want generate the dictionary of labels on the spot:
```
url_ml='https://raw.githubusercontent.com/Tencent/tencent-ml-images/master/data/dictionary_and_semantic_hierarchy.txt'
df_ml=pd.read_csv(url_ml,delimiter=' ')
print(df_ml.shape)
df_ml.head()
dictionary_ml = {}
N_class=df_ml.shape[0]
keys = range(N_class)
values = list(df_ml.loc[:,'category name'].values)
from tqdm.notebook import tqdm
for i in keys:
dictionary_ml[i] = values[i]
# print(dictionary_ml)
# Manual selection
test_dir=os.getcwd()+'/ml_test/'
fig=plt.figure(figsize=(15,10))
for im_ind,im in enumerate(os.listdir(test_dir)):
im=test_dir+im
raw_img = cv.imread(im)
img = preprocess(raw_img)
logits, probs_topk, preds_topk = sess.run([logit, prob_topk, pred_topk], {images:np.expand_dims(img, axis=0)})
preds_topk = np.squeeze(preds_topk)
# print(preds_topk)
names_topk = [dictionary_ml[i] for i in preds_topk]
ax = fig.add_subplot(2,4,im_ind+ 1)
ax.imshow(raw_img[...,::-1])
plt.axis('Off')
predictions = []
for i, pred in enumerate(preds_topk[0:10]):
predictions.append('%d %s: %.3f' % (pred, names_topk[i], probs_topk[0][i]))
ax.set_title('\n'.join(predictions),fontsize=8)
file_name=im.split('/')[-1]
ax.text(0.5,-0.1,f'File: {file_name}',ha="center",
transform=ax.transAxes)
# plt.tight_layout()
```
| true |
code
| 0.409457 | null | null | null | null |
|
# Neural Network for Regression
In the previous homework you implemented a linear regression network. In this exercise, we will solve the same problem with a neural network instead, to leverage the power of Deep Learning.
We will implement our neural networks using a modular approach. For each layer we will implement a `forward` and a `backward` function. The `forward` function will receive inputs, weights, and other parameters and will return both an output and a `cache` object storing data needed for the backward pass, like this:
```python
def layer_forward(x, w):
""" Receive inputs x and weights w """
# Do some computations ...
z = # ... some intermediate value
# Do some more computations ...
out = # the output
cache = (x, w, z, out) # Values we need to compute gradients
return out, cache
```
The backward pass will receive upstream derivatives and the `cache` object, and will return gradients with respect to the inputs and weights, like this:
```python
def layer_backward(dout, cache):
"""
Receive derivative of loss with respect to outputs and cache,
and compute derivative with respect to inputs.
"""
# Unpack cache values
x, w, z, out = cache
# Use values in cache to compute derivatives
dx = # Derivative of loss with respect to x
dw = # Derivative of loss with respect to w
return dx, dw
```
After implementing a bunch of layers this way, we will be able to easily combine them to build networks with different architectures.
```
# As usual, a bit of setup
from exercise_code.data.csv_dataset import CSVDataset
from exercise_code.data.csv_dataset import FeatureSelectorAndNormalizationTransform
from exercise_code.data.dataloader import DataLoader
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import seaborn as sns
pd.options.mode.chained_assignment = None # default='warn'
%matplotlib inline
%load_ext autoreload
%autoreload 2
```
# 1. Load your data
We apply the same dataloading and preprocessing steps as in the previous exercise.
```
target_column = 'SalePrice'
i2dl_exercises_path = os.path.dirname(os.path.abspath(os.getcwd()))
root_path = os.path.join(i2dl_exercises_path, "datasets", 'housing')
housing_file_path = os.path.join(root_path, "housing_train.csv")
download_url = 'https://cdn3.vision.in.tum.de/~dl4cv/housing_train.zip'
# Always make sure this line was run at least once before trying to
# access the data manually, as the data is downloaded in the
# constructor of CSVDataset.
train_dataset = CSVDataset(target_column=target_column, root=root_path, download_url=download_url, mode="train")
df = train_dataset.df
target_column = 'SalePrice'
# Select only 2 features to keep plus the target column.
selected_columns = ['GrLivArea','GarageArea', target_column]
mn, mx, mean = df.min(), df.max(), df.mean()
column_stats = {}
for column in selected_columns:
crt_col_stats = {'min' : mn[column],
'max' : mx[column],
'mean': mean[column]}
column_stats[column] = crt_col_stats
transform = FeatureSelectorAndNormalizationTransform(column_stats, target_column)
def rescale(data, key = "SalePrice", column_stats = column_stats):
""" Rescales input series y"""
mx = column_stats[key]["max"]
mn = column_stats[key]["min"]
return data * (mx - mn) + mn
train_dataset = CSVDataset(mode="train", target_column=target_column, root=root_path, download_url=download_url, transform=transform)
val_dataset = CSVDataset(mode="val", target_column=target_column, root=root_path, download_url=download_url, transform=transform)
test_dataset = CSVDataset(mode="test", target_column=target_column, root=root_path, download_url=download_url, transform=transform)
print("Number of training samples:", len(train_dataset))
print("Number of validation samples:", len(val_dataset))
print("Number of test samples:", len(test_dataset))
```
# 2. Build your Model
Now we want to build our model. But let's first construct the building blocks we want to use. We will define the forward and backward pass for an affine layer and a Sigmoid activation function
## 2.1 Affine Layer
Open the file `exercise_code/networks/layer.py` and implement the `affine_forward` and the `affine_backward` function. Remember, and affine layer computes a function of
$$\mathbf{z} = \mathbf{W} \mathbf{x}$$
To check the correctness of your implementation, we will again use numeric gradient checking:
$$ \frac {df(x)}{dx} = \frac{f(x+h) - f(x-h)}{2h} $$
Once you are done you can test your implementaion by running the following:
```
a=np.random.rand(20,20,8,6,4)
a.shape
s=a.shape[:2]
s
if a.ndim>2 : s = s+ (-1,)
a.shape[:2] + (-1,)
s
b=a.reshape(s)
# Test the affine function
from exercise_code.tests.layer_tests import *
print(AffineLayerTest()())
```
## 2.2 Sigmoid layer:
Implement the forward pass for the sigmoid activation function in the `sigmoid_forward` function and the backward pass in `sigmoid_backward`.
$$ y = \sigma(z) = \frac{1}{1+\mathrm{exp}(-z)}, $$
Test your implementation using the following:
```
# Test the sigmoid function
print(SigmoidTest()())
```
## 2.3 Two-layer regression network
Now that you have all the necessary building block, let's build your first neural network.
Open the file `exercise_code/networks/regression_net.py` and complete the implementation of the `RegressionNet` class. Specifically, you again need co complete the `forward` and `backward` functions. You can run the cell below to test your implementation.
```
from exercise_code.tests.regression_net_tests import test_regression_net
from exercise_code.networks.regression_net import RegressionNet
test_regression_net(RegressionNet)
```
# 3. Optimizer & Loss Function
We have now implemented:
- [x] A dataloader
- [x] A loss function
- [x] A model
- [ ] An optimizer
- [ ] A loss function
The only things missing in out Deep Learning pipeline are an optimizer and a loss function. Since you already implemented SGD and MSE in last weeks' exercise, we will give them to you this time. Have a look at their implementations in `exercise_code/networks/optimizer.py` and `exercise_code/networks/loss.py`.
```
from exercise_code.networks.optimizer import SGD
from exercise_code.networks.loss import MSE, L1
```
# 4. Solver
Now that we have everything together, let's update our solver from exercise_04 and finally start training our model.
Open the file `exercise_code/solver.py` and read through it to familiarize yourself with the API. In the `train` and `_step` functions, you can see all of the components you implemented in the last exercises working together. Now, run the solver to train your model.
We provide you with a default set of hyperparameters here as hyperparameter search is not the scope of this exercise. However, you can still play around with those values and see how the training performance changes. Especially the `std` which is the standard deviation of the gaussian distribution used to initialize the weights of your model is very sensitive.
```
from exercise_code.networks.regression_net import RegressionNet
from exercise_code.solver import Solver
batch_size = 4
lr = 1e-3
hidden_size = 100
std = 1.
epochs = 20
model = RegressionNet(input_size=2, hidden_size=hidden_size, std=std)
train_dataloader = DataLoader(train_dataset, batch_size=batch_size)
val_dataloader = DataLoader(val_dataset, batch_size=batch_size)
test_dataloader = DataLoader(test_dataset, batch_size=batch_size)
solver = Solver(model, train_dataloader, val_dataloader, learning_rate=lr, loss_func=MSE(), optimizer=SGD)
# add test data to test before training
X_test = [test_dataset[i]['features'] for i in range((len(test_dataset)))]
X_test = np.stack(X_test, axis=0)
y_test = [test_dataset[i]['target'] for i in range((len(test_dataset)))]
y_test = np.stack(y_test, axis=0)
y_out = solver.get_dataset_prediction(test_dataloader)
l1_loss = L1()
mse_loss = MSE()
print("L1 loss on test set BEFORE training: {:,.0f}".format(l1_loss(rescale(y_out), rescale(y_test))[0].mean() ))
print("MSE loss on test set BEFORE training: {:,.0f}".format(mse_loss(rescale(y_out), rescale(y_test))[0].mean() ))
solver.train(epochs=epochs)
y_out, _ = model(X_test)
l1_loss = L1()
mse_loss = MSE()
print("L1 loss on test set AFTER training: {:,.0f}".format(l1_loss(rescale(y_out), rescale(y_test))[0].mean() ))
print("MSE loss on test set AFTER training: {:,.0f}".format(mse_loss(rescale(y_out), rescale(y_test))[0].mean() ))
# # Run this cell to visualize your training and validation loss and your prediction
y_out = solver.get_dataset_prediction(test_dataloader)
plt.title('Loss curves')
plt.plot(solver.train_loss_history, '-', label='train')
plt.plot(solver.val_loss_history, '-', label='val')
plt.legend(loc='lower right')
plt.xlabel('Iteration')
plt.show()
if np.shape(X_test)[1]==1:
plt.scatter(X_test, y_test, label = "Ground Truth")
inds = X_test.argsort(0).flatten()
plt.plot(X_test[inds], y_out[inds], color='r', label = "Prediction")
plt.legend()
plt.show()
else:
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = plt.axes(projection='3d')
first_feature = X_test[:, 0]
second_feature = X_test[:, 1]
salePrice = y_test[:, 0]
salePricePred = y_out[:, 0]
ax.plot_trisurf(first_feature, second_feature, salePricePred, linewidth=0, antialiased=True,color ="red")
ax.scatter(first_feature, second_feature, salePrice)
ax.set_xlabel(selected_columns[0])
ax.set_ylabel(selected_columns[1])
ax.set_zlabel(selected_columns[2])
plt.tight_layout()
plt.show()
```
## Save the model for submission
Simply save your objects using the following cell. This will save them to a pickle file `models/two_layer_regression.p`.
```
from exercise_code.tests import save_pickle
save_pickle(
data_dict={
"Regression_Net": RegressionNet
},
file_name="two_layer_regression.p"
)
```
# Submission Goals
- Goal: Successfully implement the forward and backward pass of a two layer regression neural network
- Test cases:
1. Does `forward()` and `backward()` of your 2 layer regression neural net return the correct value and data type?
- Reachable points [0, 100]: 0 if not implemented, 100 if all tests passed, 50 per passed test
- Threshold to clear exercise: 100
- Submission start: __May 22, 2020 12.00__
- Submission deadline : __May 27, 2020 23.59__
- You can make multiple submission uptil the deadline. Your __best submission__ will be considered for bonus
| true |
code
| 0.746198 | null | null | null | null |
|
# Transfer Learning
A Convolutional Neural Network (CNN) for image classification is made up of multiple layers that extract features, such as edges, corners, etc; and then use a final fully-connected layer to classify objects based on these features. You can visualize this like this:
<table>
<tr><td rowspan=2 style='border: 1px solid black;'>⇒</td><td style='border: 1px solid black;'>Convolutional Layer</td><td style='border: 1px solid black;'>Pooling Layer</td><td style='border: 1px solid black;'>Convolutional Layer</td><td style='border: 1px solid black;'>Pooling Layer</td><td style='border: 1px solid black;'>Fully Connected Layer</td><td rowspan=2 style='border: 1px solid black;'>⇒</td></tr>
<tr><td colspan=4 style='border: 1px solid black; text-align:center;'>Feature Extraction</td><td style='border: 1px solid black; text-align:center;'>Classification</td></tr>
</table>
*Transfer Learning* is a technique where you can take an existing trained model and re-use its feature extraction layers, replacing its final classification layer with a fully-connected layer trained on your own custom images. With this technique, your model benefits from the feature extraction training that was performed on the base model (which may have been based on a larger training dataset than you have access to) to build a classification model for your own specific set of object classes.
How does this help? Well, think of it this way. Suppose you take a professional tennis player and a complete beginner, and try to teach them both how to play raquetball. It's reasonable to assume that the professional tennis player will be easier to train, because many of the underlying skills involved in raquetball are already learned. Similarly, a pre-trained CNN model may be easier to train to classify specific set of objects because it's already learned how to identify the features of common objects, such as edges and corners. Fundamentally, a pre-trained model can be a great way to produce an effective classifier even when you have limited data with which to train it.
In this notebook, we'll see how to implement transfer learning for a classification model using PyTorch.
## Install and import libraries
First, let's install and import the PyTorch libraries we're going to use.
```
!pip install torch==1.6.0+cpu torchvision==0.7.0+cpu -f https://download.pytorch.org/whl/torch_stable.html
# Import PyTorch libraries
import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import torch.nn.functional as F
# Other libraries we'll use
import numpy as np
import os
import matplotlib.pyplot as plt
%matplotlib inline
print("Libraries imported - ready to use PyTorch", torch.__version__)
```
## Prepare the base model
To use transfer learning, we need a base model from which we can use the trained feature extraction layers. The ***resnet*** model is an CNN-based image classifier that has been pre-trained using a huge dataset containing a large number of images of 1000 classes of object, so let's download it and take a look at its layers.
```
# Load the model (download if not already present)
model = torchvision.models.resnet34(pretrained=True)
print(model)
```
## Prepare the image data
The pretrained model has many layers, starting with a convolutional layer that starts the feature extraction process from image data, and ending with a fully-connected linear layer that maps the extracted features to 1000 class labels.
For feature extraction to work with our own images, we need to ensure that the image data we use the train our prediction layer has the same number of features (pixel values) as the images originally used to train the feaure extraction layers. The model does not explicitly give this size, but the first convolutional layer applies by a 7x7 kernel with a stride of 2x2 and results in 64 feature values, so the original size must be 64 x (7 ÷ 2), which is 224.
PyTorch includes functions for loading and transforming data. We'll use these to create an iterative loader for training data, and a second iterative loader for test data (which we'll use to validate the trained model). The loaders will transform the image data to match the format used to train the original resnet CNN model, convert the image data into *tensors* (which are the core data structure used in PyTorch), and normalize them.
Run the following cell to define the data loaders and list the classes for our images.
```
# Function to ingest data using training and test loaders
def load_dataset(data_path):
# Resize to 256 x 256, then center-crop to 224x224 (to match the resnet image size)
transformation = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])
# Load all of the images, transforming them
full_dataset = torchvision.datasets.ImageFolder(
root=data_path,
transform=transformation
)
# Split into training (70%) and testing (30%) datasets)
train_size = int(0.7 * len(full_dataset))
test_size = len(full_dataset) - train_size
train_dataset, test_dataset = torch.utils.data.random_split(full_dataset, [train_size, test_size])
# define a loader for the training data we can iterate through in 30-image batches
train_loader = torch.utils.data.DataLoader(
train_dataset,
batch_size=30,
num_workers=0,
shuffle=False
)
# define a loader for the testing data we can iterate through in 30-image batches
test_loader = torch.utils.data.DataLoader(
test_dataset,
batch_size=30,
num_workers=0,
shuffle=False
)
return train_loader, test_loader
# Now load the images from the shapes folder
import os
data_path = 'data/shapes/'
# Get the iterative dataloaders for test and training data
train_loader, test_loader = load_dataset(data_path)
# Get the class names
classes = os.listdir(data_path)
classes.sort()
print('class names:', classes)
```
## Create a prediction layer
We downloaded the complete *resnet* model including its final **fc** linear layer. This fully-connected linear layer takes 512 inputs (the extracted features) and produces 1000 outputs (class predictions based on the original training image classes). We need to replace this layer with one that takes the same number of inputs (so we can use the same number of extracted features), but produces a prediction for each of our image classes.
We also need to freeze the feature extraction layers to retain the trained weights. Then when we train the model using our images, only the final prediction layer will learn new weight and bias values - the pre-trained weights already learned for feature extraction will remain the same.
```
# Set the existing feature extraction layers to read-only
for param in model.parameters():
param.requires_grad = False
# Replace the prediction layer
num_ftrs = model.fc.in_features
model.fc = nn.Linear(num_ftrs, len(classes))
# Now print the full model, which will include the feature extraction layers of the base model and our prediction layer
print(model)
```
## Train the model
With the layers of the CNN defined, we're ready to train it using our image data. The weights used in the feature extraction layers from the base resnet model will not be changed by training, only the final linear layer that maps the features to our shape classes will be trained.
```
def train(model, device, train_loader, optimizer, epoch):
# Set the model to training mode
model.train()
train_loss = 0
print("Epoch:", epoch)
# Process the images in batches
for batch_idx, (data, target) in enumerate(train_loader):
# Use the CPU or GPU as appropriate
data, target = data.to(device), target.to(device)
# Reset the optimizer
optimizer.zero_grad()
# Push the data forward through the model layers
output = model(data)
# Get the loss
loss = loss_criteria(output, target)
# Keep a running total
train_loss += loss.item()
# Backpropagate
loss.backward()
optimizer.step()
# Print metrics for every 10 batches so we see some progress
if batch_idx % 10 == 0:
print('Training set [{}/{} ({:.0f}%)] Loss: {:.6f}'.format(
batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
# return average loss for the epoch
avg_loss = train_loss / (batch_idx+1)
print('Training set: Average loss: {:.6f}'.format(avg_loss))
return avg_loss
def test(model, device, test_loader):
# Switch the model to evaluation mode (so we don't backpropagate or drop)
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
batch_count = 0
for data, target in test_loader:
batch_count += 1
data, target = data.to(device), target.to(device)
# Get the predicted classes for this batch
output = model(data)
# Calculate the loss for this batch
test_loss += loss_criteria(output, target).item()
# Calculate the accuracy for this batch
_, predicted = torch.max(output.data, 1)
correct += torch.sum(target==predicted).item()
# Calculate the average loss and total accuracy for this epoch
avg_loss = test_loss/batch_count
print('Validation set: Average loss: {:.6f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
avg_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# return average loss for the epoch
return avg_loss
# Now use the train and test functions to train and test the model
device = "cpu"
if (torch.cuda.is_available()):
# if GPU available, use cuda (on a cpu, training will take a considerable length of time!)
device = "cuda"
print('Training on', device)
# Create an instance of the model class and allocate it to the device
model = model.to(device)
# Use an "Adam" optimizer to adjust weights
# (see https://pytorch.org/docs/stable/optim.html#algorithms for details of supported algorithms)
optimizer = optim.Adam(model.parameters(), lr=0.001)
# Specify the loss criteria
loss_criteria = nn.CrossEntropyLoss()
# Track metrics in these arrays
epoch_nums = []
training_loss = []
validation_loss = []
# Train over 3 epochs (in a real scenario, you'd likely use many more)
epochs = 3
for epoch in range(1, epochs + 1):
train_loss = train(model, device, train_loader, optimizer, epoch)
test_loss = test(model, device, test_loader)
epoch_nums.append(epoch)
training_loss.append(train_loss)
validation_loss.append(test_loss)
```
## View the loss history
We tracked average training and validation loss for each epoch. We can plot these to verify that the loss reduced over the training process and to detect *over-fitting* (which is indicated by a continued drop in training loss after validation loss has levelled out or started to increase).
```
%matplotlib inline
from matplotlib import pyplot as plt
plt.plot(epoch_nums, training_loss)
plt.plot(epoch_nums, validation_loss)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['training', 'validation'], loc='upper right')
plt.show()
```
## Evaluate model performance
We can see the final accuracy based on the test data, but typically we'll want to explore performance metrics in a little more depth. Let's plot a confusion matrix to see how well the model is predicting each class.
```
#Pytorch doesn't have a built-in confusion matrix metric, so we'll use SciKit-Learn
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
%matplotlib inline
# Set the model to evaluate mode
model.eval()
# Get predictions for the test data and convert to numpy arrays for use with SciKit-Learn
print("Getting predictions from test set...")
truelabels = []
predictions = []
for data, target in test_loader:
for label in target.cpu().data.numpy():
truelabels.append(label)
for prediction in model.cpu()(data).data.numpy().argmax(1):
predictions.append(prediction)
# Plot the confusion matrix
cm = confusion_matrix(truelabels, predictions)
plt.imshow(cm, interpolation="nearest", cmap=plt.cm.Blues)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
plt.xlabel("Actual Shape")
plt.ylabel("Predicted Shape")
plt.show()
```
## Use the trained model
Now that we've trained the model, we can use it to predict the class of an image.
```
# Function to create a random image (of a square, circle, or triangle)
def create_image (size, shape):
from random import randint
import numpy as np
from PIL import Image, ImageDraw
xy1 = randint(10,40)
xy2 = randint(60,100)
col = (randint(0,200), randint(0,200), randint(0,200))
img = Image.new("RGB", size, (255, 255, 255))
draw = ImageDraw.Draw(img)
if shape == 'circle':
draw.ellipse([(xy1,xy1), (xy2,xy2)], fill=col)
elif shape == 'triangle':
draw.polygon([(xy1,xy1), (xy2,xy2), (xy2,xy1)], fill=col)
else: # square
draw.rectangle([(xy1,xy1), (xy2,xy2)], fill=col)
del draw
return img
# Function to predict the class of an image
def predict_image(classifier, image):
import numpy
# Set the classifer model to evaluation mode
classifier.eval()
# Apply the same transformations as we did for the training images
transformation = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])
# Preprocess the image
image_tensor = transformation(image).float()
# Add an extra batch dimension since pytorch treats all inputs as batches
image_tensor = image_tensor.unsqueeze_(0)
# Turn the input into a Variable
input_features = Variable(image_tensor)
# Predict the class of the image
output = classifier(input_features)
index = output.data.numpy().argmax()
return index
# Now let's try it with a new image
from random import randint
from PIL import Image
import os, shutil
# Create a random test image
shape = classes[randint(0, len(classes)-1)]
img = create_image ((128,128), shape)
# Display the image
plt.imshow(img)
index = predict_image(model, img)
print(classes[index])
```
## Learn more
* [PyTorch Documentation](https://pytorch.org/tutorials/beginner/transfer_learning_tutorial.html)
| true |
code
| 0.822439 | null | null | null | null |
|
# [Sensor name]
:::{eval-rst}
:opticon:`tag`
:badge:`[Environment],badge-primary`
:badge:`Sensors,badge-secondary`
:::
## Context
### Purpose
*Describe the purpose of the use case.*
### Sensor description
*Describe the main features of the sensor e.g. variables.*
### Highlights
*Provide 3-5 bullet points that convey the use case’s core procedures. Each bullet point must have a maximum of 85 characters, including spaces.*
* Highlight 1
* Highlight 2
### Contributions
#### Notebook
Author (role), Affiliation, GitHub alias
#### Dataset originator/creator
Institution/Community/Individual (affiliation)
#### Dataset authors
Institution/Community/Individual (affiliation)
#### Dataset documentation
```{bibliography}
:style: plain
:list: bullet
:filter: topic % "replace by the `topic` entry linked to the publication(s) in the `_bibliography/references.bib` file"
```
:::{note}
*Optional: add credits or acknowledgements to data providers or authors of code snippets*
:::
## Install and load libraries
*For installation, add only libraries not listed in the [environment.yml](https://github.com/alan-turing-institute/environmental-ds-book/blob/master/environment.yml) file, but required by the notebook. Libraries can be installed in silent mode e.g. `pip -q install <package_name>`*
*For loading libraries, order them according to their role e.g. libraries to manipulate folders i.e. os (first), handle data i.e. numpy, xarray (second), visualisation e.g. holoviews (third), etc. The cell below contains two libraries, `os` and `warning` which are common among the notebooks. Don't remove them.*
```
import os
import warnings
warnings.filterwarnings(action='ignore')
```
## Set project structure
*The cell below creates a separate folder to save the notebook outputs. This facilitates the reader to inspect inputs/outputs stored within a defined destination folder. Change `<replace-by-notebook-filename>` with your notebook identifier.*
```
notebook_folder = '../sensors/<replace-by-notebook-filename>'
if not os.path.exists(notebook_folder):
os.makedirs(notebook_folder)
```
## Load data
*Load full dataset from original or mirror sources. If the license of the dataset permits, we suggest creating sample data (preprocessed) for the notebook stored in a data repository e.g. Zenodo.*
## Visualisation
*Create a visual narrative of the dataset! We suggest exploring libraries suited for interactive plotting e.g. Holoviews, Panel, Bokeh.*
## Summary
*Provide 3-5 bullet points summarising the main aspects of the dataset and tools covered in the notebook.*
* Sentence 1 e.g. `tool-name` to perform...
* Sentence 2 e.g. `tool-name` to perform...
## Additional information
**Dataset**: Type here details of dataset(s) version.
**License**: The code in this notebook is licensed under the MIT License. The Environmental Data Science book is licensed under the Creative Commons by Attribution 4.0 license. See further details [here](https://github.com/alan-turing-institute/environmental-ds-book/blob/master/LICENSE.md).
**Contact**: If you have any suggestion or report an issue with this notebook, feel free to [create an issue](https://github.com/alan-turing-institute/environmental-ds-book/issues/new/choose) or send a direct message to [environmental.ds.book@gmail.com](mailto:environmental.ds.book@gmail.com).
```
from datetime import date
print(f'Last tested: {date.today()}')
```
| true |
code
| 0.823931 | null | null | null | null |
|
# <div align="center">Credit Fraud Detector</div>
---------------------------------------------------------------------
you can find the kernel link below:
> ###### [ Kaggle](https://www.kaggle.com/janiobachmann/credit-fraud-dealing-with-imbalanced-datasets)
## Introduction
In this kernel we will use various predictive models to see how accurate they are in detecting whether a transaction is a normal payment or a fraud. As described in the dataset, the features are scaled and the names of the features are not shown due to privacy reasons. Nevertheless, we can still analyze some important aspects of the dataset. Let's start!
## Our Goals:
* Understand the little distribution of the "little" data that was provided to us.
* Create a 50/50 sub-dataframe ratio of "Fraud" and "Non-Fraud" transactions. (NearMiss Algorithm)
* Determine the Classifiers we are going to use and decide which one has a higher accuracy.
* Create a Neural Network and compare the accuracy to our best classifier.
* Understand common mistaked made with imbalanced datasets.
## Outline:
I. Understanding our data
a) Gather Sense of our data
II. Preprocessing
a) Scaling and Distributing
b) Splitting the Data
III. Random UnderSampling and Oversampling
a) Distributing and Correlating
b) Anomaly Detection
c) Dimensionality Reduction and Clustering (t-SNE)
d) Classifiers
e) A Deeper Look into Logistic Regression
f) Oversampling with SMOTE
IV. Testing
a) Testing with Logistic Regression
b) Neural Networks Testing (Undersampling vs Oversampling)
## Correcting Previous Mistakes from Imbalanced Datasets:
* Never test on the oversampled or undersampled dataset.
* If we want to implement cross validation, remember to oversample or undersample your training data during cross-validation, not before!
* Don't use accuracy score as a metric with imbalanced datasets (will be usually high and misleading), instead use f1-score, precision/recall score or confusion matrix
## References:
* Hands on Machine Learning with Scikit-Learn & TensorFlow by Aurélien Géron (O'Reilly). CopyRight 2017 Aurélien Géron
* Machine Learning - Over-& Undersampling - Python/ Scikit/ Scikit-Imblearn by Coding-Maniac
* auprc, 5-fold c-v, and resampling methods by Jeremy Lane (Kaggle Notebook)
# <div align="center">Gather Sense of Our Data:</div>
---------------------------------------------------------------------
The first thing we must do is gather a basic sense of our data. Remember, except for the transaction and amount we dont know what the other columns are (due to privacy reasons). The only thing we know, is that those columns that are unknown have been scaled already.
## Summary:
* The transaction amount is relatively small. The mean of all the mounts made is approximately USD 88.
* There are no "Null" values, so we don't have to work on ways to replace values.
* Most of the transactions were Non-Fraud (99.83%) of the time, while Fraud transactions occurs (017%) of the time in the dataframe.
## Feature Technicalities:
* PCA Transformation: The description of the data says that all the features went through a PCA transformation (Dimensionality Reduction technique) (Except for time and amount).
* Scaling: Keep in mind that in order to implement a PCA transformation features need to be previously scaled. (In this case, all the V features have been scaled or at least that is what we are assuming the people that develop the dataset did.)
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
# Imported Libraries
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import tensorflow as tf
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA, TruncatedSVD
import matplotlib.patches as mpatches
import time
# Classifier Libraries
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
import collections
# Other Libraries
from imblearn.datasets import fetch_datasets
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from imblearn.pipeline import make_pipeline as imbalanced_make_pipeline
from imblearn.over_sampling import SMOTE
from imblearn.under_sampling import NearMiss
from imblearn.metrics import classification_report_imbalanced
from sklearn.metrics import precision_score, recall_score, f1_score, roc_auc_score, accuracy_score, classification_report
from collections import Counter
from sklearn.model_selection import KFold, StratifiedKFold
import warnings
warnings.filterwarnings("ignore")
df = pd.read_csv('input/creditcard.csv')
df.head()
df.describe()
# Good No Null Values!
df.isnull().sum().max()
df.columns
# The classes are heavily skewed we need to solve this issue later.
print('No Frauds', round(df['Class'].value_counts()[0]/len(df) * 100,2), '% of the dataset')
print('Frauds', round(df['Class'].value_counts()[1]/len(df) * 100,2), '% of the dataset')
```
***Note:*** Notice how imbalanced is our original dataset! Most of the transactions are non-fraud. If we use this dataframe as the base for our predictive models and analysis we might get a lot of errors and our algorithms will probably overfit since it will "assume" that most transactions are not fraud. But we don't want our model to assume, we want our model to detect patterns that give signs of fraud!
```
colors = ["#0101DF", "#DF0101"]
sns.countplot('Class', data=df, palette=colors)
plt.title('Class Distributions \n (0: No Fraud || 1: Fraud)', fontsize=14);
```
***Distributions:*** By seeing the distributions we can have an idea how skewed are these features, we can also see further distributions of the other features. There are techniques that can help the distributions be less skewed which will be implemented in this notebook in the future.
```
fig, ax = plt.subplots(1, 2, figsize=(18,4))
amount_val = df['Amount'].values
time_val = df['Time'].values
sns.distplot(amount_val, ax=ax[0], color='r')
ax[0].set_title('Distribution of Transaction Amount', fontsize=14)
ax[0].set_xlim([min(amount_val), max(amount_val)])
sns.distplot(time_val, ax=ax[1], color='b')
ax[1].set_title('Distribution of Transaction Time', fontsize=14)
ax[1].set_xlim([min(time_val), max(time_val)])
plt.show();
```
## Scaling and Distributing
In this phase of our kernel, we will first ***scale the columns comprise of Time and Amount*** . Time and amount should be scaled as the other columns. On the other hand, we need to also create a sub sample of the dataframe in order to have an equal amount of Fraud and Non-Fraud cases, helping our algorithms better understand patterns that determines whether a transaction is a fraud or not.
## What is a sub-Sample?
In this scenario, our subsample will be a dataframe with a 50/50 ratio of fraud and non-fraud transactions. Meaning our sub-sample will have the same amount of fraud and non fraud transactions.
## Why do we create a sub-Sample?
In the beginning of this notebook we saw that the original dataframe was heavily imbalanced! Using the original dataframe will cause the following issues:
* Overfitting: Our classification models will assume that in most cases there are no frauds! What we want for our model is to be certain when a fraud occurs.
* Wrong Correlations: Although we don't know what the "V" features stand for, it will be useful to understand how each of this features influence the result (Fraud or No Fraud) by having an imbalance dataframe we are not able to see the true correlations between the class and features.
## Summary:
* Scaled amount and scaled time are the columns with scaled values.
* There are 492 cases of fraud in our dataset so we can randomly get 492 cases of non-fraud to create our new sub dataframe.
* We concat the 492 cases of fraud and non fraud, creating a new sub-sample.
```
# Since most of our data has already been scaled we should scale the columns that are left to scale (Amount and Time)
from sklearn.preprocessing import StandardScaler, RobustScaler
# RobustScaler is less prone to outliers.
std_scaler = StandardScaler()
rob_scaler = RobustScaler()
df['scaled_amount'] = rob_scaler.fit_transform(df['Amount'].values.reshape(-1,1))
df['scaled_time'] = rob_scaler.fit_transform(df['Time'].values.reshape(-1,1))
df.drop(['Time','Amount'], axis=1, inplace=True)
scaled_amount = df['scaled_amount']
scaled_time = df['scaled_time']
df.drop(['scaled_amount', 'scaled_time'], axis=1, inplace=True)
df.insert(0, 'scaled_amount', scaled_amount)
df.insert(1, 'scaled_time', scaled_time)
# Amount and Time are Scaled!
df.head()
```
## Splitting the Data (Original DataFrame)
Before proceeding with the Random UnderSampling technique we have to separate the orginal dataframe. Why? for testing purposes, remember although we are splitting the data when implementing Random UnderSampling or OverSampling techniques, we want to test our models on the original testing set not on the testing set created by either of these techniques. The main goal is to fit the model either with the dataframes that were undersample and oversample (in order for our models to detect the patterns), and test it on the original testing set.
```
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedShuffleSplit
print('No Frauds', round(df['Class'].value_counts()[0]/len(df) * 100,2), '% of the dataset')
print('Frauds', round(df['Class'].value_counts()[1]/len(df) * 100,2), '% of the dataset')
X = df.drop('Class', axis=1)
y = df['Class']
sss = StratifiedKFold(n_splits=5, random_state=None, shuffle=False)
for train_index, test_index in sss.split(X, y):
print("Train:", train_index, "Test:", test_index)
original_Xtrain, original_Xtest = X.iloc[train_index], X.iloc[test_index]
original_ytrain, original_ytest = y.iloc[train_index], y.iloc[test_index]
# We already have X_train and y_train for undersample data thats why I am using original to distinguish and to not overwrite these variables.
# original_Xtrain, original_Xtest, original_ytrain, original_ytest = train_test_split(X, y, test_size=0.2, random_state=42)
# Check the Distribution of the labels
# Turn into an array
original_Xtrain = original_Xtrain.values
original_Xtest = original_Xtest.values
original_ytrain = original_ytrain.values
original_ytest = original_ytest.values
# See if both the train and test label distribution are similarly distributed
train_unique_label, train_counts_label = np.unique(original_ytrain, return_counts=True)
test_unique_label, test_counts_label = np.unique(original_ytest, return_counts=True)
print('-' * 100)
print('Label Distributions: \n')
print(train_counts_label/ len(original_ytrain))
print(test_counts_label/ len(original_ytest))
```
## Random Under-Sampling:
In this phase of the project we will implement "Random Under Sampling" which basically consists of removing data in order to have a more balanced dataset and thus avoiding our models to overfitting.
## Steps:
* The first thing we have to do is determine how imbalanced is our class (use "value_counts()" on the class column to determine the amount for each label)
* Once we determine how many instances are considered fraud transactions (Fraud = "1") , we should bring the non-fraud transactions to the same amount as fraud transactions (assuming we want a 50/50 ratio), this will be equivalent to 492 cases of fraud and 492 cases of non-fraud transactions.
* After implementing this technique, we have a sub-sample of our dataframe with a 50/50 ratio with regards to our classes. Then the next step we will implement is to shuffle the data to see if our models can maintain a certain accuracy everytime we run this script.
***Note:*** The main issue with "Random Under-Sampling" is that we run the risk that our classification models will not perform as accurate as we would like to since there is a great deal of information loss (bringing 492 non-fraud transaction from 284,315 non-fraud transaction)
```
# Since our classes are highly skewed we should make them equivalent in order to have a normal distribution of the classes.
# Lets shuffle the data before creating the subsamples
df = df.sample(frac=1)
# amount of fraud classes 492 rows.
fraud_df = df.loc[df['Class'] == 1]
non_fraud_df = df.loc[df['Class'] == 0][:492]
normal_distributed_df = pd.concat([fraud_df, non_fraud_df])
# Shuffle dataframe rows
new_df = normal_distributed_df.sample(frac=1, random_state=42)
new_df.head()
```
## Equally Distributing and Correlating:
Now that we have our dataframe correctly balanced, we can go further with our analysis and data preprocessing.
```
print('Distribution of the Classes in the subsample dataset')
print(new_df['Class'].value_counts()/len(new_df))
sns.countplot('Class', data=new_df, palette=colors)
plt.title('Equally Distributed Classes', fontsize=14)
plt.show()
```
## Correlation Matrices
Correlation matrices are the essence of understanding our data. We want to know if there are features that influence heavily in whether a specific transaction is a fraud. However, it is important that we use the correct dataframe (subsample) in order for us to see which features have a high positive or negative correlation with regards to fraud transactions.
## Summary and Explanation:
* Negative Correlations: V17, V14, V12 and V10 are negatively correlated. Notice how the lower these values are, the more likely the end result will be a fraud transaction.
* Positive Correlations: V2, V4, V11, and V19 are positively correlated. Notice how the higher these values are, the more likely the end result will be a fraud transaction.
* BoxPlots: We will use boxplots to have a better understanding of the distribution of these features in fradulent and non fradulent transactions.
***Note:*** We have to make sure we use the subsample in our correlation matrix or else our correlation matrix will be affected by the high imbalance between our classes. This occurs due to the high class imbalance in the original dataframe.
```
# Make sure we use the subsample in our correlation
f, (ax1, ax2) = plt.subplots(2, 1, figsize=(24,20))
# Entire DataFrame
corr = df.corr()
sns.heatmap(corr, cmap='coolwarm_r', annot_kws={'size':20}, ax=ax1)
ax1.set_title("Imbalanced Correlation Matrix \n (don't use for reference)", fontsize=14)
sub_sample_corr = new_df.corr()
sns.heatmap(sub_sample_corr, cmap='coolwarm_r', annot_kws={'size':20}, ax=ax2)
ax2.set_title('SubSample Correlation Matrix \n (use for reference)', fontsize=14)
plt.show()
f, axes = plt.subplots(ncols=4, figsize=(20,4))
# Negative Correlations with our Class (The lower our feature value the more likely it will be a fraud transaction)
sns.boxplot(x="Class", y="V17", data=new_df, palette=colors, ax=axes[0])
axes[0].set_title('V17 vs Class Negative Correlation')
sns.boxplot(x="Class", y="V14", data=new_df, palette=colors, ax=axes[1])
axes[1].set_title('V14 vs Class Negative Correlation')
sns.boxplot(x="Class", y="V12", data=new_df, palette=colors, ax=axes[2])
axes[2].set_title('V12 vs Class Negative Correlation')
sns.boxplot(x="Class", y="V10", data=new_df, palette=colors, ax=axes[3])
axes[3].set_title('V10 vs Class Negative Correlation')
plt.show()
f, axes = plt.subplots(ncols=4, figsize=(20,4))
# Positive correlations (The higher the feature the probability increases that it will be a fraud transaction)
sns.boxplot(x="Class", y="V11", data=new_df, palette=colors, ax=axes[0])
axes[0].set_title('V11 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V4", data=new_df, palette=colors, ax=axes[1])
axes[1].set_title('V4 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V2", data=new_df, palette=colors, ax=axes[2])
axes[2].set_title('V2 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V19", data=new_df, palette=colors, ax=axes[3])
axes[3].set_title('V19 vs Class Positive Correlation')
plt.show()
```
## Anomaly Detection:
Our main aim in this section is to remove "extreme outliers" from features that have a high correlation with our classes. This will have a positive impact on the accuracy of our models.
## Interquartile Range Method:
* Interquartile Range (IQR): We calculate this by the difference between the 75th percentile and 25th percentile. Our aim is to create a threshold beyond the 75th and 25th percentile that in case some instance pass this threshold the instance will be deleted.
* Boxplots: Besides easily seeing the 25th and 75th percentiles (both end of the squares) it is also easy to see extreme outliers (points beyond the lower and higher extreme).
## Outlier Removal Tradeoff:
* We have to be careful as to how far do we want the threshold for removing outliers. We determine the threshold by multiplying a number (ex: 1.5) by the (Interquartile Range). The higher this threshold is, the less outliers will detect (multiplying by a higher number ex: 3), and the lower this threshold is the more outliers it will detect.
* The Tradeoff: The lower the threshold the more outliers it will remove however, we want to focus more on "extreme outliers" rather than just outliers. Why? because we might run the risk of information loss which will cause our models to have a lower accuracy. You can play with this threshold and see how it affects the accuracy of our classification models.
## Summary:
* Visualize Distributions: We first start by visualizing the distribution of the feature we are going to use to eliminate some of the outliers. V14 is the only feature that has a Gaussian distribution compared to features V12 and V10.
* Determining the threshold: After we decide which number we will use to multiply with the iqr (the lower more outliers removed), we will proceed in determining the upper and lower thresholds by substrating q25 - threshold (lower extreme threshold) and adding q75 + threshold (upper extreme threshold).
* Conditional Dropping: Lastly, we create a conditional dropping stating that if the "threshold" is exceeded in both extremes, the instances will be removed.
* Boxplot Representation: Visualize through the boxplot that the number of "extreme outliers" have been reduced to a considerable amount.
***Note:*** After implementing outlier reduction our accuracy has been improved by over 3%! Some outliers can distort the accuracy of our models but remember, we have to avoid an extreme amount of information loss or else our model runs the risk of underfitting.
```
from scipy.stats import norm
f, (ax1, ax2, ax3) = plt.subplots(1,3, figsize=(20, 6))
v14_fraud_dist = new_df['V14'].loc[new_df['Class'] == 1].values
sns.distplot(v14_fraud_dist,ax=ax1, fit=norm, color='#FB8861')
ax1.set_title('V14 Distribution \n (Fraud Transactions)', fontsize=14)
v12_fraud_dist = new_df['V12'].loc[new_df['Class'] == 1].values
sns.distplot(v12_fraud_dist,ax=ax2, fit=norm, color='#56F9BB')
ax2.set_title('V12 Distribution \n (Fraud Transactions)', fontsize=14)
v10_fraud_dist = new_df['V10'].loc[new_df['Class'] == 1].values
sns.distplot(v10_fraud_dist,ax=ax3, fit=norm, color='#C5B3F9')
ax3.set_title('V10 Distribution \n (Fraud Transactions)', fontsize=14)
plt.show()
# # -----> V14 Removing Outliers (Highest Negative Correlated with Labels)
v14_fraud = new_df['V14'].loc[new_df['Class'] == 1].values
q25, q75 = np.percentile(v14_fraud, 25), np.percentile(v14_fraud, 75)
print('Quartile 25: {} | Quartile 75: {}'.format(q25, q75))
v14_iqr = q75 - q25
print('iqr: {}'.format(v14_iqr))
v14_cut_off = v14_iqr * 1.5
v14_lower, v14_upper = q25 - v14_cut_off, q75 + v14_cut_off
print('Cut Off: {}'.format(v14_cut_off))
print('V14 Lower: {}'.format(v14_lower))
print('V14 Upper: {}'.format(v14_upper))
outliers = [x for x in v14_fraud if x < v14_lower or x > v14_upper]
print('Feature V14 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V10 outliers:{}'.format(outliers))
new_df = new_df.drop(new_df[(new_df['V14'] > v14_upper) | (new_df['V14'] < v14_lower)].index)
print('----' * 44)
# -----> V12 removing outliers from fraud transactions
v12_fraud = new_df['V12'].loc[new_df['Class'] == 1].values
q25, q75 = np.percentile(v12_fraud, 25), np.percentile(v12_fraud, 75)
v12_iqr = q75 - q25
v12_cut_off = v12_iqr * 1.5
v12_lower, v12_upper = q25 - v12_cut_off, q75 + v12_cut_off
print('V12 Lower: {}'.format(v12_lower))
print('V12 Upper: {}'.format(v12_upper))
outliers = [x for x in v12_fraud if x < v12_lower or x > v12_upper]
print('V12 outliers: {}'.format(outliers))
print('Feature V12 Outliers for Fraud Cases: {}'.format(len(outliers)))
new_df = new_df.drop(new_df[(new_df['V12'] > v12_upper) | (new_df['V12'] < v12_lower)].index)
print('Number of Instances after outliers removal: {}'.format(len(new_df)))
print('----' * 44)
# Removing outliers V10 Feature
v10_fraud = new_df['V10'].loc[new_df['Class'] == 1].values
q25, q75 = np.percentile(v10_fraud, 25), np.percentile(v10_fraud, 75)
v10_iqr = q75 - q25
v10_cut_off = v10_iqr * 1.5
v10_lower, v10_upper = q25 - v10_cut_off, q75 + v10_cut_off
print('V10 Lower: {}'.format(v10_lower))
print('V10 Upper: {}'.format(v10_upper))
outliers = [x for x in v10_fraud if x < v10_lower or x > v10_upper]
print('V10 outliers: {}'.format(outliers))
print('Feature V10 Outliers for Fraud Cases: {}'.format(len(outliers)))
new_df = new_df.drop(new_df[(new_df['V10'] > v10_upper) | (new_df['V10'] < v10_lower)].index)
print('Number of Instances after outliers removal: {}'.format(len(new_df)))
f,(ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20,6))
colors = ['#B3F9C5', '#f9c5b3']
# Boxplots with outliers removed
# Feature V14
sns.boxplot(x="Class", y="V14", data=new_df,ax=ax1, palette=colors)
ax1.set_title("V14 Feature \n Reduction of outliers", fontsize=14)
ax1.annotate('Fewer extreme \n outliers', xy=(0.98, -17.5), xytext=(0, -12),
arrowprops=dict(facecolor='black'),
fontsize=14)
# Feature 12
sns.boxplot(x="Class", y="V12", data=new_df, ax=ax2, palette=colors)
ax2.set_title("V12 Feature \n Reduction of outliers", fontsize=14)
ax2.annotate('Fewer extreme \n outliers', xy=(0.98, -17.3), xytext=(0, -12),
arrowprops=dict(facecolor='black'),
fontsize=14)
# Feature V10
sns.boxplot(x="Class", y="V10", data=new_df, ax=ax3, palette=colors)
ax3.set_title("V10 Feature \n Reduction of outliers", fontsize=14)
ax3.annotate('Fewer extreme \n outliers', xy=(0.95, -16.5), xytext=(0, -12),
arrowprops=dict(facecolor='black'),
fontsize=14)
plt.show()
```
# Dimensionality Reduction and Clustering:
## Understanding t-SNE:
In order to understand this algorithm you have to understand the following terms:
* Euclidean Distance
* Conditional Probability
* Normal and T-Distribution Plots
***Note:*** If you want a simple instructive video look at StatQuest: t-SNE, Clearly Explained by Joshua Starmer
## Summary:
* t-SNE algorithm can pretty accurately cluster the cases that were fraud and non-fraud in our dataset.
* Although the subsample is pretty small, the t-SNE algorithm is able to detect clusters pretty accurately in every scenario (I shuffle the dataset before running t-SNE)
* This gives us an indication that further predictive models will perform pretty well in separating fraud cases from non-fraud cases.
```
# New_df is from the random undersample data (fewer instances)
X = new_df.drop('Class', axis=1)
y = new_df['Class']
# T-SNE Implementation
t0 = time.time()
X_reduced_tsne = TSNE(n_components=2, random_state=42).fit_transform(X.values)
t1 = time.time()
print("T-SNE took {:.2} s".format(t1 - t0))
# PCA Implementation
t0 = time.time()
X_reduced_pca = PCA(n_components=2, random_state=42).fit_transform(X.values)
t1 = time.time()
print("PCA took {:.2} s".format(t1 - t0))
# TruncatedSVD
t0 = time.time()
X_reduced_svd = TruncatedSVD(n_components=2, algorithm='randomized', random_state=42).fit_transform(X.values)
t1 = time.time()
print("Truncated SVD took {:.2} s".format(t1 - t0))
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(24,6))
# labels = ['No Fraud', 'Fraud']
f.suptitle('Clusters using Dimensionality Reduction', fontsize=14)
blue_patch = mpatches.Patch(color='#0A0AFF', label='No Fraud')
red_patch = mpatches.Patch(color='#AF0000', label='Fraud')
# t-SNE scatter plot
ax1.scatter(X_reduced_tsne[:,0], X_reduced_tsne[:,1], c=(y == 0), cmap='coolwarm', label='No Fraud', linewidths=2)
ax1.scatter(X_reduced_tsne[:,0], X_reduced_tsne[:,1], c=(y == 1), cmap='coolwarm', label='Fraud', linewidths=2)
ax1.set_title('t-SNE', fontsize=14)
ax1.grid(True)
ax1.legend(handles=[blue_patch, red_patch])
# PCA scatter plot
ax2.scatter(X_reduced_pca[:,0], X_reduced_pca[:,1], c=(y == 0), cmap='coolwarm', label='No Fraud', linewidths=2)
ax2.scatter(X_reduced_pca[:,0], X_reduced_pca[:,1], c=(y == 1), cmap='coolwarm', label='Fraud', linewidths=2)
ax2.set_title('PCA', fontsize=14)
ax2.grid(True)
ax2.legend(handles=[blue_patch, red_patch])
# TruncatedSVD scatter plot
ax3.scatter(X_reduced_svd[:,0], X_reduced_svd[:,1], c=(y == 0), cmap='coolwarm', label='No Fraud', linewidths=2)
ax3.scatter(X_reduced_svd[:,0], X_reduced_svd[:,1], c=(y == 1), cmap='coolwarm', label='Fraud', linewidths=2)
ax3.set_title('Truncated SVD', fontsize=14)
ax3.grid(True)
ax3.legend(handles=[blue_patch, red_patch])
plt.show()
```
# Classifiers (UnderSampling):
In this section we will train four types of classifiers and decide which classifier will be more effective in detecting fraud transactions. Before we have to split our data into training and testing sets and separate the features from the labels.
## Summary:
* Logistic Regression classifier is more accurate than the other three classifiers in most cases. (We will further analyze Logistic Regression)
* GridSearchCV is used to determine the paremeters that gives the best predictive score for the classifiers.
* Logistic Regression has the best Receiving Operating Characteristic score (ROC), meaning that LogisticRegression pretty accurately separates fraud and non-fraud transactions.
## Learning Curves:
* The wider the gap between the training score and the cross validation score, the more likely your model is overfitting (high variance).
* If the score is low in both training and cross-validation sets this is an indication that our model is underfitting (high bias)
* Logistic Regression Classifier shows the best score in both training and cross-validating sets.
```
# Undersampling before cross validating (prone to overfit)
X = new_df.drop('Class', axis=1)
y = new_df['Class']
# Our data is already scaled we should split our training and test sets
from sklearn.model_selection import train_test_split
# This is explicitly used for undersampling.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Turn the values into an array for feeding the classification algorithms.
X_train = X_train.values
X_test = X_test.values
y_train = y_train.values
y_test = y_test.values
# Let's implement simple classifiers
classifiers = {
"LogisiticRegression": LogisticRegression(),
"KNearest": KNeighborsClassifier(),
"Support Vector Classifier": SVC(),
"DecisionTreeClassifier": DecisionTreeClassifier()
}
# Wow our scores are getting even high scores even when applying cross validation.
from sklearn.model_selection import cross_val_score
for key, classifier in classifiers.items():
classifier.fit(X_train, y_train)
training_score = cross_val_score(classifier, X_train, y_train, cv=5)
print("Classifiers: ", classifier.__class__.__name__, "Has a training score of", round(training_score.mean(), 2) * 100, "% accuracy score")
# Use GridSearchCV to find the best parameters.
from sklearn.model_selection import GridSearchCV
# Logistic Regression
log_reg_params = {"penalty": ['l1', 'l2'], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]}
grid_log_reg = GridSearchCV(LogisticRegression(), log_reg_params)
grid_log_reg.fit(X_train, y_train)
# We automatically get the logistic regression with the best parameters.
log_reg = grid_log_reg.best_estimator_
knears_params = {"n_neighbors": list(range(2,5,1)), 'algorithm': ['auto', 'ball_tree', 'kd_tree', 'brute']}
grid_knears = GridSearchCV(KNeighborsClassifier(), knears_params)
grid_knears.fit(X_train, y_train)
# KNears best estimator
knears_neighbors = grid_knears.best_estimator_
# Support Vector Classifier
svc_params = {'C': [0.5, 0.7, 0.9, 1], 'kernel': ['rbf', 'poly', 'sigmoid', 'linear']}
grid_svc = GridSearchCV(SVC(), svc_params)
grid_svc.fit(X_train, y_train)
# SVC best estimator
svc = grid_svc.best_estimator_
# DecisionTree Classifier
tree_params = {"criterion": ["gini", "entropy"], "max_depth": list(range(2,4,1)),
"min_samples_leaf": list(range(5,7,1))}
grid_tree = GridSearchCV(DecisionTreeClassifier(), tree_params)
grid_tree.fit(X_train, y_train)
# tree best estimator
tree_clf = grid_tree.best_estimator_
# Overfitting Case
log_reg_score = cross_val_score(log_reg, X_train, y_train, cv=5)
print('Logistic Regression Cross Validation Score: ', round(log_reg_score.mean() * 100, 2).astype(str) + '%')
knears_score = cross_val_score(knears_neighbors, X_train, y_train, cv=5)
print('Knears Neighbors Cross Validation Score', round(knears_score.mean() * 100, 2).astype(str) + '%')
svc_score = cross_val_score(svc, X_train, y_train, cv=5)
print('Support Vector Classifier Cross Validation Score', round(svc_score.mean() * 100, 2).astype(str) + '%')
tree_score = cross_val_score(tree_clf, X_train, y_train, cv=5)
print('DecisionTree Classifier Cross Validation Score', round(tree_score.mean() * 100, 2).astype(str) + '%')
# We will undersample during cross validating
undersample_X = df.drop('Class', axis=1)
undersample_y = df['Class']
for train_index, test_index in sss.split(undersample_X, undersample_y):
print("Train:", train_index, "Test:", test_index)
undersample_Xtrain, undersample_Xtest = undersample_X.iloc[train_index], undersample_X.iloc[test_index]
undersample_ytrain, undersample_ytest = undersample_y.iloc[train_index], undersample_y.iloc[test_index]
undersample_Xtrain = undersample_Xtrain.values
undersample_Xtest = undersample_Xtest.values
undersample_ytrain = undersample_ytrain.values
undersample_ytest = undersample_ytest.values
undersample_accuracy = []
undersample_precision = []
undersample_recall = []
undersample_f1 = []
undersample_auc = []
# Implementing NearMiss Technique
# Distribution of NearMiss (Just to see how it distributes the labels we won't use these variables)
X_nearmiss, y_nearmiss = NearMiss().fit_sample(undersample_X.values, undersample_y.values)
print('NearMiss Label Distribution: {}'.format(Counter(y_nearmiss)))
# Cross Validating the right way
for train, test in sss.split(undersample_Xtrain, undersample_ytrain):
undersample_pipeline = imbalanced_make_pipeline(NearMiss(sampling_strategy='majority'), log_reg) # SMOTE happens during Cross Validation not before..
undersample_model = undersample_pipeline.fit(undersample_Xtrain[train], undersample_ytrain[train])
undersample_prediction = undersample_model.predict(undersample_Xtrain[test])
undersample_accuracy.append(undersample_pipeline.score(original_Xtrain[test], original_ytrain[test]))
undersample_precision.append(precision_score(original_ytrain[test], undersample_prediction))
undersample_recall.append(recall_score(original_ytrain[test], undersample_prediction))
undersample_f1.append(f1_score(original_ytrain[test], undersample_prediction))
undersample_auc.append(roc_auc_score(original_ytrain[test], undersample_prediction))
# Let's Plot LogisticRegression Learning Curve
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import learning_curve
def plot_learning_curve(estimator1, estimator2, estimator3, estimator4, X, y, ylim=None, cv=None,
n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
f, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2,2, figsize=(20,14), sharey=True)
if ylim is not None:
plt.ylim(*ylim)
# First Estimator
train_sizes, train_scores, test_scores = learning_curve(
estimator1, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
ax1.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="#ff9124")
ax1.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="#2492ff")
ax1.plot(train_sizes, train_scores_mean, 'o-', color="#ff9124",
label="Training score")
ax1.plot(train_sizes, test_scores_mean, 'o-', color="#2492ff",
label="Cross-validation score")
ax1.set_title("Logistic Regression Learning Curve", fontsize=14)
ax1.set_xlabel('Training size (m)')
ax1.set_ylabel('Score')
ax1.grid(True)
ax1.legend(loc="best")
# Second Estimator
train_sizes, train_scores, test_scores = learning_curve(
estimator2, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
ax2.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="#ff9124")
ax2.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="#2492ff")
ax2.plot(train_sizes, train_scores_mean, 'o-', color="#ff9124",
label="Training score")
ax2.plot(train_sizes, test_scores_mean, 'o-', color="#2492ff",
label="Cross-validation score")
ax2.set_title("Knears Neighbors Learning Curve", fontsize=14)
ax2.set_xlabel('Training size (m)')
ax2.set_ylabel('Score')
ax2.grid(True)
ax2.legend(loc="best")
# Third Estimator
train_sizes, train_scores, test_scores = learning_curve(
estimator3, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
ax3.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="#ff9124")
ax3.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="#2492ff")
ax3.plot(train_sizes, train_scores_mean, 'o-', color="#ff9124",
label="Training score")
ax3.plot(train_sizes, test_scores_mean, 'o-', color="#2492ff",
label="Cross-validation score")
ax3.set_title("Support Vector Classifier \n Learning Curve", fontsize=14)
ax3.set_xlabel('Training size (m)')
ax3.set_ylabel('Score')
ax3.grid(True)
ax3.legend(loc="best")
# Fourth Estimator
train_sizes, train_scores, test_scores = learning_curve(
estimator4, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
ax4.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="#ff9124")
ax4.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="#2492ff")
ax4.plot(train_sizes, train_scores_mean, 'o-', color="#ff9124",
label="Training score")
ax4.plot(train_sizes, test_scores_mean, 'o-', color="#2492ff",
label="Cross-validation score")
ax4.set_title("Decision Tree Classifier \n Learning Curve", fontsize=14)
ax4.set_xlabel('Training size (m)')
ax4.set_ylabel('Score')
ax4.grid(True)
ax4.legend(loc="best")
return plt
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=42)
plot_learning_curve(log_reg, knears_neighbors, svc, tree_clf, X_train, y_train, (0.87, 1.01), cv=cv, n_jobs=4)
from sklearn.metrics import roc_curve
from sklearn.model_selection import cross_val_predict
# Create a DataFrame with all the scores and the classifiers names.
log_reg_pred = cross_val_predict(log_reg, X_train, y_train, cv=5,
method="decision_function")
knears_pred = cross_val_predict(knears_neighbors, X_train, y_train, cv=5)
svc_pred = cross_val_predict(svc, X_train, y_train, cv=5,
method="decision_function")
tree_pred = cross_val_predict(tree_clf, X_train, y_train, cv=5)
from sklearn.metrics import roc_auc_score
print('Logistic Regression: ', roc_auc_score(y_train, log_reg_pred))
print('KNears Neighbors: ', roc_auc_score(y_train, knears_pred))
print('Support Vector Classifier: ', roc_auc_score(y_train, svc_pred))
print('Decision Tree Classifier: ', roc_auc_score(y_train, tree_pred))
log_fpr, log_tpr, log_thresold = roc_curve(y_train, log_reg_pred)
knear_fpr, knear_tpr, knear_threshold = roc_curve(y_train, knears_pred)
svc_fpr, svc_tpr, svc_threshold = roc_curve(y_train, svc_pred)
tree_fpr, tree_tpr, tree_threshold = roc_curve(y_train, tree_pred)
def graph_roc_curve_multiple(log_fpr, log_tpr, knear_fpr, knear_tpr, svc_fpr, svc_tpr, tree_fpr, tree_tpr):
plt.figure(figsize=(16,8))
plt.title('ROC Curve \n Top 4 Classifiers', fontsize=18)
plt.plot(log_fpr, log_tpr, label='Logistic Regression Classifier Score: {:.4f}'.format(roc_auc_score(y_train, log_reg_pred)))
plt.plot(knear_fpr, knear_tpr, label='KNears Neighbors Classifier Score: {:.4f}'.format(roc_auc_score(y_train, knears_pred)))
plt.plot(svc_fpr, svc_tpr, label='Support Vector Classifier Score: {:.4f}'.format(roc_auc_score(y_train, svc_pred)))
plt.plot(tree_fpr, tree_tpr, label='Decision Tree Classifier Score: {:.4f}'.format(roc_auc_score(y_train, tree_pred)))
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([-0.01, 1, 0, 1])
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.annotate('Minimum ROC Score of 50% \n (This is the minimum score to get)', xy=(0.5, 0.5), xytext=(0.6, 0.3),
arrowprops=dict(facecolor='#6E726D', shrink=0.05),
)
plt.legend()
graph_roc_curve_multiple(log_fpr, log_tpr, knear_fpr, knear_tpr, svc_fpr, svc_tpr, tree_fpr, tree_tpr)
plt.show()
```
# A Deeper Look into LogisticRegression:
In this section we will dive a deeper look into the logistic regression classifier.
## Terms:
* True Positives: Correctly Classified Fraud Transactions
* False Positives: Incorrectly Classified Fraud Transactions
* True Negative: Correctly Classified Non-Fraud Transactions
* False Negative: Incorrectly Classified Non-Fraud Transactions
* Precision: True Positives/(True Positives + False Positives)
* Recall: True Positives/(True Positives + False Negatives)
* Precision as the name says, says how precise (how sure) is our model in detecting fraud transactions while recall is the amount of fraud cases our model is able to detect.
* Precision/Recall Tradeoff: The more precise (selective) our model is, the less cases it will detect. Example: Assuming that our model has a precision of 95%, Let's say there are only 5 fraud cases in which the model is 95% precise or more that these are fraud cases. Then let's say there are 5 more cases that our model considers 90% to be a fraud case, if we lower the precision there are more cases that our model will be able to detect.
## Summary:
Precision starts to descend between 0.90 and 0.92 nevertheless, our precision score is still pretty high and still we have a descent recall score.
```
def logistic_roc_curve(log_fpr, log_tpr):
plt.figure(figsize=(12,8))
plt.title('Logistic Regression ROC Curve', fontsize=16)
plt.plot(log_fpr, log_tpr, 'b-', linewidth=2)
plt.plot([0, 1], [0, 1], 'r--')
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.axis([-0.01,1,0,1])
logistic_roc_curve(log_fpr, log_tpr)
plt.show()
from sklearn.metrics import precision_recall_curve
precision, recall, threshold = precision_recall_curve(y_train, log_reg_pred)
from sklearn.metrics import recall_score, precision_score, f1_score, accuracy_score
y_pred = log_reg.predict(X_train)
# Overfitting Case
print('---' * 45)
print('Overfitting: \n')
print('Recall Score: {:.2f}'.format(recall_score(y_train, y_pred)))
print('Precision Score: {:.2f}'.format(precision_score(y_train, y_pred)))
print('F1 Score: {:.2f}'.format(f1_score(y_train, y_pred)))
print('Accuracy Score: {:.2f}'.format(accuracy_score(y_train, y_pred)))
print('---' * 45)
# How it should look like
print('---' * 45)
print('How it should be:\n')
print("Accuracy Score: {:.2f}".format(np.mean(undersample_accuracy)))
print("Precision Score: {:.2f}".format(np.mean(undersample_precision)))
print("Recall Score: {:.2f}".format(np.mean(undersample_recall)))
print("F1 Score: {:.2f}".format(np.mean(undersample_f1)))
print('---' * 45)
undersample_y_score = log_reg.decision_function(original_Xtest)
from sklearn.metrics import average_precision_score
undersample_average_precision = average_precision_score(original_ytest, undersample_y_score)
print('Average precision-recall score: {0:0.2f}'.format(
undersample_average_precision))
from sklearn.metrics import precision_recall_curve
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(12,6))
precision, recall, _ = precision_recall_curve(original_ytest, undersample_y_score)
plt.step(recall, precision, color='#004a93', alpha=0.2,
where='post')
plt.fill_between(recall, precision, step='post', alpha=0.2,
color='#48a6ff')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('UnderSampling Precision-Recall curve: \n Average Precision-Recall Score ={0:0.2f}'.format(
undersample_average_precision), fontsize=16)
```
# SMOTE Technique (Over-Sampling):
<img src="https://raw.githubusercontent.com/rikunert/SMOTE_visualisation/master/SMOTE_R_visualisation_3.png", width=800> SMOTE stands for Synthetic Minority Over-sampling Technique. Unlike Random UnderSampling, SMOTE creates new synthetic points in order to have an equal balance of the classes. This is another alternative for solving the "class imbalance problems".
## Understanding SMOTE:
Solving the Class Imbalance: SMOTE creates synthetic points from the minority class in order to reach an equal balance between the minority and majority class.
Location of the synthetic points: SMOTE picks the distance between the closest neighbors of the minority class, in between these distances it creates synthetic points.
Final Effect: More information is retained since we didn't have to delete any rows unlike in random undersampling.
Accuracy || Time Tradeoff: Although it is likely that SMOTE will be more accurate than random under-sampling, it will take more time to train since no rows are eliminated as previously stated.
## Overfitting during Cross Validation:
In our undersample analysis I want to show you a common mistake I made that I want to share with all of you. It is simple, if you want to undersample or oversample your data you should not do it before cross validating. Why because you will be directly influencing the validation set before implementing cross-validation causing a "data leakage" problem. In the following section you will see amazing precision and recall scores but in reality our data is overfitting!
***Wrong Way***
<img src="asset/1.jpg" />
As mentioned previously, if we get the minority class ("Fraud) in our case, and create the synthetic points before cross validating we have a certain influence on the "validation set" of the cross validation process. Remember how cross validation works, let's assume we are splitting the data into 5 batches, 4/5 of the dataset will be the training set while 1/5 will be the validation set. The test set should not be touched! For that reason, we have to do the creation of synthetic datapoints "during" cross-validation and not before, just like below:
***Right Way***
<img src="asset/1.jpg" />
As you see above, SMOTE occurs "during" cross validation and not "prior" to the cross validation process. Synthetic data are created only for the training set without affecting the validation set.
```
from imblearn.over_sampling import SMOTE
from sklearn.model_selection import train_test_split, RandomizedSearchCV
print('Length of X (train): {} | Length of y (train): {}'.format(len(original_Xtrain), len(original_ytrain)))
print('Length of X (test): {} | Length of y (test): {}'.format(len(original_Xtest), len(original_ytest)))
# List to append the score and then find the average
accuracy_lst = []
precision_lst = []
recall_lst = []
f1_lst = []
auc_lst = []
# Classifier with optimal parameters
# log_reg_sm = grid_log_reg.best_estimator_
log_reg_sm = LogisticRegression()
rand_log_reg = RandomizedSearchCV(LogisticRegression(), log_reg_params, n_iter=4)
# Implementing SMOTE Technique
# Cross Validating the right way
# Parameters
log_reg_params = {"penalty": ['l1', 'l2'], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]}
for train, test in sss.split(original_Xtrain, original_ytrain):
pipeline = imbalanced_make_pipeline(SMOTE(sampling_strategy='minority'), rand_log_reg) # SMOTE happens during Cross Validation not before..
model = pipeline.fit(original_Xtrain[train], original_ytrain[train])
best_est = rand_log_reg.best_estimator_
prediction = best_est.predict(original_Xtrain[test])
accuracy_lst.append(pipeline.score(original_Xtrain[test], original_ytrain[test]))
precision_lst.append(precision_score(original_ytrain[test], prediction))
recall_lst.append(recall_score(original_ytrain[test], prediction))
f1_lst.append(f1_score(original_ytrain[test], prediction))
auc_lst.append(roc_auc_score(original_ytrain[test], prediction))
print('---' * 45)
print('')
print("accuracy: {}".format(np.mean(accuracy_lst)))
print("precision: {}".format(np.mean(precision_lst)))
print("recall: {}".format(np.mean(recall_lst)))
print("f1: {}".format(np.mean(f1_lst)))
print('---' * 45)
labels = ['No Fraud', 'Fraud']
smote_prediction = best_est.predict(original_Xtest)
print(classification_report(original_ytest, smote_prediction, target_names=labels))
y_score = best_est.decision_function(original_Xtest)
average_precision = average_precision_score(original_ytest, y_score)
print('Average precision-recall score: {0:0.2f}'.format(
average_precision))
fig = plt.figure(figsize=(12,6))
precision, recall, _ = precision_recall_curve(original_ytest, y_score)
plt.step(recall, precision, color='r', alpha=0.2,
where='post')
plt.fill_between(recall, precision, step='post', alpha=0.2,
color='#F59B00')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('OverSampling Precision-Recall curve: \n Average Precision-Recall Score ={0:0.2f}'.format(
average_precision), fontsize=16)
# SMOTE Technique (OverSampling) After splitting and Cross Validating
sm = SMOTE(ratio='minority', random_state=42)
# Xsm_train, ysm_train = sm.fit_sample(X_train, y_train)
# This will be the data were we are going to
Xsm_train, ysm_train = sm.fit_sample(original_Xtrain, original_ytrain)
# We Improve the score by 2% points approximately
# Implement GridSearchCV and the other models.
# Logistic Regression
t0 = time.time()
log_reg_sm = grid_log_reg.best_estimator_
log_reg_sm.fit(Xsm_train, ysm_train)
t1 = time.time()
print("Fitting oversample data took :{} sec".format(t1 - t0))
```
# Test Data with Logistic Regression:
## Confusion Matrix:
* Positive/Negative: Type of Class (label) ["No", "Yes"] True/False: Correctly or Incorrectly classified by the model.
* True Negatives (Top-Left Square): This is the number of correctly classifications of the "No" (No Fraud Detected) class or potenial clients that are not willing to suscribe a term deposit.
* False Negatives (Top-Right Square): This is the number of incorrectly classifications of the "No"(No Fraud Detected) class or potential clients that are not willing to suscribe a term depositt.
* False Positives (Bottom-Left Square): This is the number of incorrectly classifications of the "Yes" (Fraud Detected) class or potential clients that are willing to suscribe a term deposit.
* True Positives (Bottom-Right Square): This is the number of correctly classifications of the "Yes" (Fraud Detected) class or potenial clients that are willing to suscribe a term deposit.
## Summary:
* Random UnderSampling: We will evaluate the final performance of the classification models in the random undersampling subset. Keep in mind that this is not the data from the original dataframe.
* Classification Models: The models that performed the best were logistic regression and support vector classifier (SVM)
```
from sklearn.metrics import confusion_matrix
# Logistic Regression fitted using SMOTE technique
y_pred_log_reg = log_reg_sm.predict(X_test)
# Other models fitted with UnderSampling
y_pred_knear = knears_neighbors.predict(X_test)
y_pred_svc = svc.predict(X_test)
y_pred_tree = tree_clf.predict(X_test)
log_reg_cf = confusion_matrix(y_test, y_pred_log_reg)
kneighbors_cf = confusion_matrix(y_test, y_pred_knear)
svc_cf = confusion_matrix(y_test, y_pred_svc)
tree_cf = confusion_matrix(y_test, y_pred_tree)
fig, ax = plt.subplots(2, 2,figsize=(22,12))
sns.heatmap(log_reg_cf, ax=ax[0][0], annot=True, cmap=plt.cm.copper)
ax[0, 0].set_title("Logistic Regression \n Confusion Matrix", fontsize=14)
ax[0, 0].set_xticklabels(['', ''], fontsize=14, rotation=90)
ax[0, 0].set_yticklabels(['', ''], fontsize=14, rotation=360)
sns.heatmap(kneighbors_cf, ax=ax[0][1], annot=True, cmap=plt.cm.copper)
ax[0][1].set_title("KNearsNeighbors \n Confusion Matrix", fontsize=14)
ax[0][1].set_xticklabels(['', ''], fontsize=14, rotation=90)
ax[0][1].set_yticklabels(['', ''], fontsize=14, rotation=360)
sns.heatmap(svc_cf, ax=ax[1][0], annot=True, cmap=plt.cm.copper)
ax[1][0].set_title("Suppor Vector Classifier \n Confusion Matrix", fontsize=14)
ax[1][0].set_xticklabels(['', ''], fontsize=14, rotation=90)
ax[1][0].set_yticklabels(['', ''], fontsize=14, rotation=360)
sns.heatmap(tree_cf, ax=ax[1][1], annot=True, cmap=plt.cm.copper)
ax[1][1].set_title("DecisionTree Classifier \n Confusion Matrix", fontsize=14)
ax[1][1].set_xticklabels(['', ''], fontsize=14, rotation=90)
ax[1][1].set_yticklabels(['', ''], fontsize=14, rotation=360)
plt.show()
from sklearn.metrics import classification_report
print('Logistic Regression:')
print(classification_report(y_test, y_pred_log_reg))
print('KNears Neighbors:')
print(classification_report(y_test, y_pred_knear))
print('Support Vector Classifier:')
print(classification_report(y_test, y_pred_svc))
print('Support Vector Classifier:')
print(classification_report(y_test, y_pred_tree))
# Final Score in the test set of logistic regression
from sklearn.metrics import accuracy_score
# Logistic Regression with Under-Sampling
y_pred = log_reg.predict(X_test)
undersample_score = accuracy_score(y_test, y_pred)
# Logistic Regression with SMOTE Technique (Better accuracy with SMOTE t)
y_pred_sm = best_est.predict(original_Xtest)
oversample_score = accuracy_score(original_ytest, y_pred_sm)
d = {'Technique': ['Random UnderSampling', 'Oversampling (SMOTE)'], 'Score': [undersample_score, oversample_score]}
final_df = pd.DataFrame(data=d)
# Move column
score = final_df['Score']
final_df.drop('Score', axis=1, inplace=True)
final_df.insert(1, 'Score', score)
# Note how high is accuracy score it can be misleading!
final_df
```
# Neural Networks Testing Random UnderSampling Data vs OverSampling (SMOTE):
In this section we will implement a simple Neural Network (with one hidden layer) in order to see which of the two logistic regressions models we implemented in the (undersample or oversample(SMOTE)) has a better accuracy for detecting fraud and non-fraud transactions.
## Our Main Goal:
Our main goal is to explore how our simple neural network behaves in both the random undersample and oversample dataframes and see whether they can predict accuractely both non-fraud and fraud cases. Why not only focus on fraud? Imagine you were a cardholder and after you purchased an item your card gets blocked because the bank's algorithm thought your purchase was a fraud. That's why we shouldn't emphasize only in detecting fraud cases but we should also emphasize correctly categorizing non-fraud transactions.
## The Confusion Matrix:
Here is again, how the confusion matrix works:
* Upper Left Square: The amount of correctly classified by our model of no fraud transactions.
* Upper Right Square: The amount of incorrectly classified transactions as fraud cases, but the actual label is no fraud .
* Lower Left Square: The amount of incorrectly classified transactions as no fraud cases, but the actual label is fraud .
* Lower Right Square: The amount of correctly classified by our model of fraud transactions.
## Summary (Keras || Random UnderSampling):
* Dataset: In this final phase of testing we will fit this model in both the random undersampled subset and oversampled dataset (SMOTE) in order to predict the final result using the original dataframe testing data.
* Neural Network Structure: As stated previously, this will be a simple model composed of one input layer (where the number of nodes equals the number of features) plus bias node, one hidden layer with 32 nodes and one output node composed of two possible results 0 or 1 (No fraud or fraud).
* Other characteristics: The learning rate will be 0.001, the optimizer we will use is the AdamOptimizer, the activation function that is used in this scenario is "Relu" and for the final outputs we will use sparse categorical cross entropy, which gives the probability whether an instance case is no fraud or fraud (The prediction will pick the highest probability between the two.)
```
import keras
from keras import backend as K
from keras.models import Sequential
from keras.layers import Activation
from keras.layers.core import Dense
from keras.optimizers import Adam
from keras.metrics import categorical_crossentropy
n_inputs = X_train.shape[1]
undersample_model = Sequential([
Dense(n_inputs, input_shape=(n_inputs, ), activation='relu'),
Dense(32, activation='relu'),
Dense(2, activation='softmax')
])
undersample_model.summary()
undersample_model.compile(Adam(lr=0.001), loss='sparse_categorical_crossentropy', metrics=['accuracy'])
undersample_model.fit(X_train, y_train, validation_split=0.2, batch_size=25, epochs=20, shuffle=True, verbose=2)
undersample_predictions = undersample_model.predict(original_Xtest, batch_size=200, verbose=0)
undersample_fraud_predictions = undersample_model.predict_classes(original_Xtest, batch_size=200, verbose=0)
import itertools
# Create a confusion matrix
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title, fontsize=14)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
undersample_cm = confusion_matrix(original_ytest, undersample_fraud_predictions)
actual_cm = confusion_matrix(original_ytest, original_ytest)
labels = ['No Fraud', 'Fraud']
fig = plt.figure(figsize=(16,8))
fig.add_subplot(221)
plot_confusion_matrix(undersample_cm, labels, title="Random UnderSample \n Confusion Matrix", cmap=plt.cm.Reds)
fig.add_subplot(222)
plot_confusion_matrix(actual_cm, labels, title="Confusion Matrix \n (with 100% accuracy)", cmap=plt.cm.Greens)
```
# Keras || OverSampling (SMOTE):
```
n_inputs = Xsm_train.shape[1]
oversample_model = Sequential([
Dense(n_inputs, input_shape=(n_inputs, ), activation='relu'),
Dense(32, activation='relu'),
Dense(2, activation='softmax')
])
oversample_model.compile(Adam(lr=0.001), loss='sparse_categorical_crossentropy', metrics=['accuracy'])
oversample_model.fit(Xsm_train, ysm_train, validation_split=0.2, batch_size=300, epochs=20, shuffle=True, verbose=2)
oversample_predictions = oversample_model.predict(original_Xtest, batch_size=200, verbose=0)
oversample_fraud_predictions = oversample_model.predict_classes(original_Xtest, batch_size=200, verbose=0)
oversample_smote = confusion_matrix(original_ytest, oversample_fraud_predictions)
actual_cm = confusion_matrix(original_ytest, original_ytest)
labels = ['No Fraud', 'Fraud']
fig = plt.figure(figsize=(16,8))
fig.add_subplot(221)
plot_confusion_matrix(oversample_smote, labels, title="OverSample (SMOTE) \n Confusion Matrix", cmap=plt.cm.Oranges)
fig.add_subplot(222)
plot_confusion_matrix(actual_cm, labels, title="Confusion Matrix \n (with 100% accuracy)", cmap=plt.cm.Greens)
```
# Conclusion:
Implementing SMOTE on our imbalanced dataset helped us with the imbalance of our labels (more no fraud than fraud transactions). Nevertheless, I still have to state that sometimes the neural network on the oversampled dataset predicts less correct fraud transactions than our model using the undersample dataset. However, remember that the removal of outliers was implemented only on the random undersample dataset and not on the oversampled one. Also, in our undersample data our model is unable to detect for a large number of cases non fraud transactions correctly and instead, misclassifies those non fraud transactions as fraud cases. Imagine that people that were making regular purchases got their card blocked due to the reason that our model classified that transaction as a fraud transaction, this will be a huge disadvantage for the financial institution. The number of customer complaints and customer disatisfaction will increase. The next step of this analysis will be to do an outlier removal on our oversample dataset and see if our accuracy in the test set improves.
| true |
code
| 0.647603 | null | null | null | null |
|
This short example show how to get data from FMI Open Data multipointcoverage format. The format is used in INSPIRE specifications and is somewhat complex. Anyway, it's the most efficient way to get large amounts of data.
Here we fetch all observations from Finland during two days.
This example is for "old" format WFS2. You may try to use new WFS3 beta service as well. It's available in: http://beta.fmi.fi/data/3/wfs/sofp/
```
import requests
import datetime as dt
import xml.etree.ElementTree as ET
import numpy as np
import re
```
Required functions to get param names. Param keys are in the response document but longer names along with other metadata need to be fetched separately.
```
def get_param_names(url):
""" Get parameters metadata"""
req = requests.get(url)
params = {}
if req.status_code == 200:
xmlstring = req.content
tree = ET.ElementTree(ET.fromstring(xmlstring))
for p in tree.iter(tag='{http://inspire.ec.europa.eu/schemas/omop/2.9}ObservableProperty'):
params[p.get('{http://www.opengis.net/gml/3.2}id')] = p.find('{http://inspire.ec.europa.eu/schemas/omop/2.9}label').text
return params
def get_params(tree):
""" Get parameters from response xml tree """
retParams = []
for el in tree.iter(tag='{http://www.opengis.net/om/2.0}observedProperty'):
url = el.get('{http://www.w3.org/1999/xlink}href')
params = re.findall(r"(?<=param=).*,.*(?=&)", url)[0].split(',')
param_names = get_param_names(url)
for p in params:
retParams.append('{} ({})'.format(param_names[p], p))
return retParams
```
Positions are in the separate element. Positions are listed as lat, lon, timestamp.
```
def get_positions(tree):
"""
Function to get times and coordinates from multipointcoverage answer
"""
positions = []
for el in tree.iter(tag='{http://www.opengis.net/gmlcov/1.0}positions'):
pos = el.text.split()
i = 0
while len(pos) > 0:
lat = float(pos.pop(0))
lon = float(pos.pop(0))
timestamp = int(pos.pop(0))
positions.append([lat,lon,timestamp])
return np.array(positions)
```
Get data. For longer periods we have to fetch data in the loop
```
url = 'http://opendata.fmi.fi/wfs'
starttime = dt.datetime.strptime('2010-01-01', "%Y-%m-%d")
endtime = dt.datetime.strptime('2010-01-03', "%Y-%m-%d")
daystep = 1
start = starttime
end = start + dt.timedelta(days=daystep)
if end > endtime: end = endtime
while end <= endtime and start < end:
startStr = start.strftime('%Y-%m-%d')
endStr = end.strftime('%Y-%m-%d')
# Get data
payload = {
'request': 'getFeature',
'storedquery_id': 'fmi::observations::weather::multipointcoverage',
'bbox': '19,59,35,75',
'starttime': startStr,
'endtime': endStr,
}
r = requests.get(url, params=payload)
# Construct XML tree
tree = ET.ElementTree(ET.fromstring(r.content))
# Get geospatial and temporal positions of data elements
positions = get_positions(tree)
# Extract data from XML tree
d = []
for el in tree.iter(tag='{http://www.opengis.net/gml/3.2}doubleOrNilReasonTupleList'):
for pos in el.text.strip().split("\n"):
d.append(pos.strip().split(' '))
# Assign data values to positions
junk = np.append(positions, np.array(d), axis=1)
try:
data = np.append(data, junk, axis=0)
except NameError:
data = junk
print('Time interval {} - {} provided {} rows'.format(startStr, endStr, junk.shape[0]))
start = end
end = start + dt.timedelta(days=daystep)
if end > endtime: end = endtime
print('Done fetching data. Final dimensions of the result: {}'.format(data.shape))
```
Get params from the last XML tree element (they don't change over time)
```
params = get_params(tree)
```
Finally you can do whatever you want with the data. Here we just print some example.
```
print('Params: {}'.format(params))
print(data[0:2])
```
| true |
code
| 0.371992 | null | null | null | null |
|
# Cox model
```
import warnings
import arviz as az
import numpy as np
import pymc3 as pm
import scipy as sp
import theano.tensor as tt
from pymc3 import (
NUTS,
Gamma,
Metropolis,
Model,
Normal,
Poisson,
find_MAP,
sample,
starting,
)
from theano import function as fn
from theano import printing
print(f"Running on PyMC3 v{pm.__version__}")
warnings.filterwarnings("ignore")
%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
```
Here is the original model, implemented in BUGS:
```R
model
{
# Set up data
for(i in 1:Nsubj) {
for(j in 1:T) {
# risk set = 1 if obs.t >= t
Y[i,j] <- step(obs.t[i] - t[j] + eps)
# counting process jump = 1 if obs.t in [ t[j], t[j+1] )
# i.e. if t[j] <= obs.t < t[j+1]
dN[i, j] <- Y[i, j] * step(t[j + 1] - obs.t[i] - eps) * FAIL[i]
}
}
# Model
for(j in 1:T) {
for(i in 1:Nsubj) {
dN[i, j] ~ dpois(Idt[i, j]) # Likelihood
Idt[i, j] <- Y[i, j] * exp(beta[1]*pscenter[i] + beta[2]*
hhcenter[i] + beta[3]*ncomact[i] + beta[4]*rleader[i] + beta[5]*dleader[i] + beta[6]*inter1[i] + beta[7]*inter2[i]) * dL0[j] # Intensity
}
dL0[j] ~ dgamma(mu[j], c)
mu[j] <- dL0.star[j] * c # prior mean hazard
}
c ~ dgamma(0.0001, 0.00001)
r ~ dgamma(0.001, 0.0001)
for (j in 1 : T) { dL0.star[j] <- r * (t[j + 1] - t[j]) }
# next line indicates number of covariates and is for the corresponding betas
for(i in 1:7) {beta[i] ~ dnorm(0.0,0.00001)}
}
```
```
# fmt: off
dta = dict(T=73, Nsubj=430, eps=0.0, t=[1, 21, 85, 128, 129, 148, 178, 204,
206, 210, 211, 212, 225, 238, 241,
248, 259, 273, 275, 281, 286, 289,
301, 302, 303, 304, 313, 317, 323,
344, 345, 349, 350, 351, 355, 356,
359, 364, 385, 386, 389, 390, 391,
392, 394, 395, 396, 397, 398, 399,
400, 406, 415, 416, 426, 427, 434,
435, 437, 441, 447, 448, 449, 450,
451, 453, 455, 456, 458, 459, 460,
461, 462, 463],
obs_t = [460, 313, 435, 350, 435, 350, 350, 460, 460, 448, 225, 225, 396, 435, 396, 396, 453, 396, 456, 397, 397, 396, 395, 275, 449, 395, 395, 462, 302, 302, 458, 461, 396, 241, 389, 458, 304, 304, 395, 395, 364, 460, 415, 463, 396, 459, 441, 435, 396, 458, 437, 396, 356, 356, 396, 455, 396, 462, 399, 400, 350, 350, 395, 395, 441, 355, 85, 458, 128, 396, 386, 386, 386, 462, 458, 390, 390, 396, 396, 396, 427, 458, 395, 275, 275, 395, 359, 395, 395, 441, 395, 463, 178, 275, 463, 396, 396, 259, 396, 396, 458, 441, 396, 463, 396, 463, 435, 396, 437, 396, 398, 463, 460, 462, 460, 460, 210, 396, 435, 458, 385, 323, 323, 359, 396, 396, 460, 238, 441, 450, 392, 458, 396, 458, 396, 396, 462, 435, 396, 394, 396, 435, 458, 1, 395, 395, 451, 462, 458, 462, 396, 286, 396, 349, 449, 462, 455, 21, 463, 461, 461, 456, 435, 396, 460, 462, 462, 435, 435, 460, 386, 396, 458, 386, 461, 441, 435, 435, 463, 456, 396, 275, 460, 406, 460, 406, 317, 406, 461, 396, 359, 458, 463, 435, 462, 458, 396, 396, 273, 396, 435, 281, 275, 396, 447, 225, 447, 396, 435, 416, 396, 248, 396, 435, 435, 396, 461, 385, 396, 458, 458, 396, 461, 396, 448, 396, 396, 460, 455, 456, 463, 462, 458, 463, 396, 462, 395, 456, 396, 463, 396, 435, 459, 396, 396, 396, 395, 435, 455, 395, 461, 344, 396, 395, 396, 317, 396, 395, 426, 461, 396, 289, 441, 395, 396, 458, 396, 396, 435, 396, 395, 396, 441, 345, 396, 359, 435, 435, 396, 396, 395, 458, 461, 458, 212, 301, 458, 456, 395, 396, 395, 435, 396, 396, 303, 458, 460, 400, 396, 462, 359, 458, 396, 206, 441, 396, 458, 396, 462, 396, 396, 275, 396, 395, 435, 435, 462, 225, 458, 462, 396, 396, 289, 396, 303, 455, 400, 400, 359, 461, 396, 462, 460, 463, 463, 463, 204, 435, 435, 396, 396, 396, 463, 458, 396, 455, 435, 396, 396, 463, 396, 461, 463, 460, 441, 460, 435, 435, 460, 455, 460, 395, 460, 460, 460, 435, 449, 463, 462, 129, 391, 396, 391, 391, 434, 356, 462, 396, 349, 225, 396, 435, 461, 391, 391, 351, 211, 461, 212, 434, 148, 356, 458, 456, 455, 435, 463, 463, 462, 435, 463, 437, 460, 396, 406, 451, 460, 435, 396, 460, 455, 396, 398, 456, 458, 396, 456, 449, 396, 128, 396, 462, 463, 396, 396, 396, 435, 460, 396, 458],
FAIL= [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
pscenter= [
-.01434325, -.01460965, .01322687, .00971885, -.03223412, -.01113493, -.01359567, -.03357866, -.0387039, -.0553269, -.03238896, -.07464545, -.07325128, -.07062459, -.07464545, -.07032613, -.0703005, .00965232, -.01408955, .00577483, -.00219072, -.00084567, .01643198, .06509522, .06824313, .07300876, .07300876, .01394272, .06824313, .02063087, .00383186, -.02573045, -.02410864, -.02272752, .05120398, -.00997729, -.00550709, -.02062663, -.03077685, -.01688493, .01035959, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .01149963, .0034338, .0376236, .00733331, .01520069, .03832785, .03832785, -.02622275, -.02622275, -.02622275, -.01492678, -.02897806, -.02897806, -.02897806, -.02847666, -.031893, -.03919478, -.04224754, -.04743705, -.0510477, -.031893, -.01129093, .01706207, .00193999, -.01503116, .003101, -.00083466, .02395027, -.07952866, -.08559135, -.07251801, -.06586029, -.08432532, -.0613939, -.081205, -.07540084, -.08488011, -.08488011, -.08488011, -.07492433, -.08907269, -.09451609, -.05301854, -.08980743, -.0771635, -.0771635, -.08650947, -.07856082, -.0771635, -.08204606, -.08178245, -.05263504, -.05355574, -.05109092, -.04696729, -.04696729, -.04696729, -.05257489, -.05303248, -.05348096, -.04983674, -.04699414, .00584956, -.00792241, -.01719816, -.02138029, -.01576016, -.04274812, -.04014061, .0471441, .0471441, .0471441, .0471441, .0471441, .0471441, .0471441, .04233112, .0471441, .04233112, .050568, .07388823, .0493324, .04512087, .03205975, .02913185, .06010427, .05324252, .06973204, .05579907, .01212243, .07962459, .05054695, .06672142, .14026688, .01734403, .06078221, .06543709, .06438115, .20126908, -.03138622, -.02180659, .01637333, -.02415774, .01828684, .03106104, .04268495, .01897239, .01591935, -.02367065, -.0619156, -.06403028, -.06851645, -.04821694, -.03889525, -.05023452, -.05013452, -.01557191, -.01171948, -.01362136, -.01174715, -.02707938, -.02634164, -.02634164, -.02634164, -.00692153, -.02381614, -.00890537, -.00611669, -.00894752, -.03551984, -.0252678, -.01513384, -.01016569, -.03551984, -.03773227, -.01978032, .06803483, .06706496, .10551275, .15091534, .03092981, .06556855, .10781559, .12671031, .0936299, .09362991, .09362991, .08294538, .09362991, .09362991, .09362991, .01177025, .02610553, .03546937, .03546937, .03546937, .034415, -.00305626, .04973665, .05103208, .07546701, .05306436, .00824125, .01961115, .01202359, -.02919447, -.01016712, .01756074, -.04035511, -.04753104, -.04463152, -.04845615, -.05010044, .00031411, -.07911871, -.08799869, -.07980882, -.09393142, -.08000018, -.07666632, -.07817401, -.07444922, -.07226554, -.08216553, -.0777643, -.07752042, -.05767992, -.04727952, -.03774814, -.06870384, -.05999847, -.05947695, .02989959, .04627543, .02772475, .02883079, .03642944, .02871235, .04148949, .04240279, .07747082, .07626323, .04268012, .03225577, .06468724, -.05140995, -.05399637, -.05351515, .07302427, .02432223, .0490674, .0490674, .0490674, .0490674, .09013112, .10476315, .10476315, .10476315, .10476315, .10476315, .10476315, .10476315, .10476315, .10476315, .10476315, .10476315, .10476315, .10476315, .07008056, .08666077, .01546215, .01667466, .03417671, .05253941, .04293926, .01496588, .02692172, -.03827151, .04809769, .08742411, .04533176, .01455173, .01831875, .02710811, .09834951, .09952456, .06993483, .02945534, .038731, .1181948, .04435538, .04435538, -.02357505, .05824019, .05820741, -.02357505, .09324722, .15534712, .07207468, .04692869, -.03490683, -.04404809, -.05054474, -.05325826, -.0474724, -.04905931, .01068221, .02879751, .00852646, .02693032, .01835589, .02989959, .02989959, .02989959, .04976377, .04439012, .03397319, .02989959, .02989959, .05468828, .04463226, .05886378, .06311052, .02989959, .04595331, .04203459, .01231324, -.01399783, .04595331, .00145386, .04601278, .06459354, -.0007196, .00012216, -.07614055, -.08435525, -.07957162, -.10299519, -.08156988, -.08225659, -.07449063, -.00210284, -.00797183, -.025355, -.01258251, -.04372031, -.03985972, -.03545086, -.03384566, -.04025533, -.07523724, -.05947702, -.061286, -.07666647, -.07663169, -.05902354, -.07652324, -.07645561, -.06258684, -.09604834, -.08813326, -.03292062, -.07848112, -.08239502, -.08316891, -.07244316, -.075417, -.07652324, -.07922532, -.08755959, -.08583414, -.07450142, -.08066016, -.06057205, -.07652324, -.06249051, -.08781742, -.086076, -.07652324, -.07696518, -.0618688, -.06073988, -.06524737, -.04419825, -.04489509, -.04390368, -.04358438, -.04489509, -.04520512, -.04187583, -.03653955, -.03973426, -.03753508, -.03569439, -.06789339, .06689456, .05526327, .05139003, .02641841, .04891529, .07078697, .06862645, .06832582, .04104258, -.00120631, .01947345, .04891779, .04891779, .03561932, .02576244, .03158225, .03608047, .08685057, .04632537, .06841581, -.02899643],
hhcenter= [ -.78348798, -.63418788, -.91218799, -.98388809, -.23518796, .11481193, -1.415588, -1.2535881, -.55738801, -.88128799, -1.109488, .05721192, -1.045788, -.30888793, .29651192, -.36688802, -.50058788, .02271203, -.59088796, -.04198809, .50561196, -.07418796, .98481184, .78921205, .09431199, -.06488796, 2.1662121, .08891205, 1.4004121, 1.316112, 1.9362121, 2.0107121, 1.150712, .31951192, -.23918791, -.1562881, -.9575879, -.07728811, .29641202, 1.2273121, 1.7717118, 1.5764117, .14181189, .72131211, 1.279212, .68241197, -.72808808, -.00488802, -.23938794, -1.000788, .55081207, -.52348799, 1.780612, -.35888812, .36481193, 1.5480118, -.03078791, 1.389112, .30211189, .70901209, -.16668792, 1.435812, .47001198, 2.0838118, 1.1673121, .18461208, -.30608794, 1.4470119, .23301201, -.58458799, .44011191, -.61948794, -.41388795, .263212, .66171199, .92451197, .78081208, .90991193, 1.6920118, 1.334012, 1.2101121, .41591194, -.48498794, -.73278803, -1.093588, .09911207, -.93418807, -.46908805, .0205119, .0535119, -.14228792, -.55708808, -.45498797, -.54008788, -.30998799, -.10958811, -.0960879, -.01338812, -.88168806, -.51788801, .36801198, .46621206, .13271193, -.11208793, -.76768798, -.54508799, -1.2773881, .16641192, .95871216, -.48238799, 1.6281118, -.18848796, -.49718806, -.41348812, -.31628796, -.59528798, -.11718794, -.57058805, -.59488791, -.21248789, -.65658802, -.56298798, -.52698797, -.65758795, -.04988809, .55341202, -.76328796, .254612, 1.3500118, -.54958791, 1.665812, .14671211, 1.963912, .29161194, -.56838793, 1.9371119, .90991193, -.39558789, .39521196, -.55208796, -.05268808, -.77368802, -.45428798, .05841212, -.45308802, -.12458798, .01431207, -.28228804, .79281193, -.26358792, -.54738802, -.38158795, -.54118794, -.72828788, -.58128804, .355912, -.24078794, -1.0384881, -.75038809, -.41018793, -.43538806, -1.566388, -.53388804, -.28388807, -1.2348881, -.69028801, -1.620088, -.78128809, -.54648799, -.92738789, .11871199, .26851204, .61571199, .82891208, 1.1985121, 1.012012, 1.0602121, -.02988811, .79301196, .67731196, .43991187, .9404121, .5254119, 1.0365119, 1.6220121, .61671191, -.50318807, 2.6073117, .02361206, -.60438794, -.79278797, -.18108793, -.48178813, -.44038793, -.22628804, -.07398792, .519512, .40211204, .582012, 1.830512, .80441195, .58801204, -.56368798, -1.5451881, .45991209, -.23448797, -.36918804, 1.3247118, .19541197, -.20818801, 1.163012, -.78228801, -.6048879, -.575288, 1.3241119, .0147119, -.76518792, -.37478802, -.35508797, -.90038794, -1.250888, -.46608803, -.98488802, -1.5185881, -.90908808, -1.048188, -.90138787, -.77278799, -1.248988, -.34448811, -.61628789, .38531187, -.51728791, -.00878807, -.60078806, -.45358798, .46301201, -.22048803, -.71518797, -.76478809, -.75028795, -.4952881, .01731209, -.83718795, .57951194, .54291207, .45341209, .16941194, 1.054112, .61721212, 2.2717118, 1.1593118, 2.0280118, .92281204, 1.0100121, -.1866879, 2.6503119, 2.3914118, -.19948788, -.36418793, -.9259879, -.71058792, -.1104879, .16971211, 1.474812, 1.9360118, 2.5344119, 2.0171118, 1.9387121, .55071193, -.03918811, .20681195, .40421203, -.75518793, -.45678803, -1.0271881, .77211195, 1.146812, -1.147788, -1.565588, -.34888789, 1.303812, 1.952312, 1.639112, .07731203, .25901201, -.45608804, -.5028879, .03641204, -.03808804, .38571194, .31831196, -.17648788, -.44528791, -.55918807, -.53108805, .39721206, -.06328794, -.34038803, -.05988808, -.89548796, -.03518792, .045512, -.1859879, -.039288, -.82568806, .01431207, .40091208, -.2531881, .030412, -.31918809, -.54958791, -.79078788, .36691192, -.324388, -1.0082881, -1.232188, -.53248805, -.23678799, -.89188808, .25111201, -.6766879, -.3565881, -.61228794, -.21078797, -1.0343881, -.58358806, -.15588804, -.39238808, -.67818803, -.19498797, 1.099412, 1.2767119, -.64068788, -.50678796, -.64058799, -.86918801, 1.4048119, -.59648794, .23331194, .68371207, .11251191, -.17128797, .17081194, -.44218799, -.48708794, .09591202, .20131211, -.20108791, -.02158805, -.48188803, -.3012881, -.55008787, -1.146188, -.82128805, -.87638801, -.54488796, -.60288805, -1.003088, -.25078794, -.14818807, -.14738794, -.80938786, -.85988802, -.90188807, -.94998807, -.75718802, -.37418792, -.66708797, 1.0981121, 1.1441121, .47381189, -.12958808, -.34358808, -.84328789, -.33498809, -.98088807, -.6903879, -1.284988, -.80838794, -.91838807, -.81848806, -.34488794, -.83438796, .12971191, .99381214, -.91608804, -.31808802, -.01018806, .98171192, -.91638798, -1.043988, -1.0103881, 1.451612, -.01528808, .02441196, -.41458794, .25691202, .18601207, -.815988, -.02908798, -.59088796, -.35608789, .79691201, 1.8123121, -.98588794, 1.548912, 2.3653121, -.09238812, .96741205, .05891208, -.15618797, -.5660879, -.28338811, -.10088798, 1.1663117, .21981196, .07151202, -.009088, -.49578807, .15441208, -.44488809, -.2677879, -.54388803, -.25468799, .68631202, -.88128799, -.84628791, -1.2549881, -.36198804],
ncomact= [ 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1],
rleader= [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
dleader= [ 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
inter1= [ -.01434325, -.01460965, 0, 0, 0, -.01113493, 0, 0, 0, -.0553269, -.03238896, 0, 0, -.07062459, -.07464545, -.07032613, 0, 0, -.01408955, 0, -.00219072, 0, 0, 0, 0, 0, .07300876, .01394272, 0, 0, 0, 0, 0, 0, .05120398, 0, -.00550709, -.02062663, -.03077685, -.01688493, 0, .01149963, 0, .01149963, .01149963, 0, 0, 0, 0, 0, 0, 0, 0, 0, .01149963, .0034338, .0376236, .00733331, 0, .03832785, .03832785, -.02622275, -.02622275, -.02622275, -.01492678, 0, 0, -.02897806, -.02847666, 0, 0, -.04224754, -.04743705, -.0510477, -.031893, 0, 0, 0, -.01503116, .003101, -.00083466, .02395027, -.07952866, 0, 0, -.06586029, 0, -.0613939, -.081205, -.07540084, -.08488011, -.08488011, 0, -.07492433, -.08907269, -.09451609, 0, -.08980743, 0, -.0771635, 0, 0, -.0771635, -.08204606, 0, -.05263504, 0, -.05109092, -.04696729, 0, -.04696729, 0, -.05303248, -.05348096, 0, 0, .00584956, -.00792241, -.01719816, 0, -.01576016, 0, -.04014061, 0, 0, 0, 0, 0, .0471441, 0, .04233112, 0, .04233112, 0, 0, .0493324, .04512087, .03205975, .02913185, 0, .05324252, 0, 0, 0, 0, .05054695, 0, .14026688, .01734403, .06078221, 0, 0, 0, -.03138622, 0, .01637333, 0, 0, 0, 0, .01897239, .01591935, 0, -.0619156, 0, -.06851645, 0, -.03889525, -.05023452, -.05013452, 0, 0, -.01362136, 0, 0, -.02634164, 0, 0, 0, 0, -.00890537, -.00611669, 0, 0, 0, -.01513384, 0, -.03551984, 0, -.01978032, 0, .06706496, .10551275, 0, .03092981, .06556855, 0, 0, 0, .09362991, 0, 0, 0, 0, 0, 0, .02610553, .03546937, 0, 0, .034415, 0, 0, 0, .07546701, 0, 0, 0, 0, -.02919447, -.01016712, 0, 0, 0, 0, -.04845615, -.05010044, 0, 0, 0, 0, 0, 0, -.07666632, 0, 0, -.07226554, -.08216553, -.0777643, 0, 0, -.04727952, 0, -.06870384, -.05999847, 0, 0, 0, .02772475, .02883079, .03642944, 0, .04148949, 0, 0, 0, .04268012, .03225577, 0, -.05140995, -.05399637, 0, 0, .02432223, 0, .0490674, .0490674, .0490674, 0, 0, 0, 0, 0, 0, 0, 0, .10476315, 0, 0, 0, 0, 0, .07008056, 0, 0, .01667466, 0, .05253941, .04293926, 0, .02692172, 0, 0, .08742411, .04533176, 0, .01831875, 0, .09834951, .09952456, 0, .02945534, .038731, 0, .04435538, 0, -.02357505, 0, 0, -.02357505, .09324722, 0, 0, 0, -.03490683, 0, -.05054474, 0, -.0474724, -.04905931, 0, .02879751, 0, 0, 0, 0, 0, 0, 0, .04439012, 0, .02989959, .02989959, .05468828, .04463226, 0, 0, 0, 0, 0, .01231324, -.01399783, .04595331, .00145386, 0, .06459354, -.0007196, 0, -.07614055, -.08435525, 0, -.10299519, 0, 0, 0, -.00210284, -.00797183, 0, 0, 0, 0, -.03545086, 0, 0, 0, 0, -.061286, -.07666647, 0, -.05902354, -.07652324, -.07645561, 0, 0, 0, -.03292062, 0, 0, 0, 0, -.075417, 0, -.07922532, 0, -.08583414, -.07450142, -.08066016, 0, 0, -.06249051, 0, 0, 0, 0, -.0618688, 0, -.06524737, -.04419825, -.04489509, 0, 0, 0, -.04520512, -.04187583, 0, 0, -.03753508, 0, 0, 0, 0, 0, 0, 0, 0, .06862645, 0, 0, -.00120631, .01947345, 0, 0, .03561932, 0, .03158225, .03608047, 0, 0, 0, -.02899643],
inter2= [-.78348798, -.63418788, 0, 0, 0, .11481193, 0, 0, 0, -.88128799, -1.109488, 0, 0, -.30888793, .29651192, -.36688802, 0, 0, -.59088796, 0, .50561196, 0, 0, 0, 0, 0, 2.1662121, .08891205, 0, 0, 0, 0, 0, 0, -.23918791, 0, -.9575879, -.07728811, .29641202, 1.2273121, 0, 1.5764117, 0, .72131211, 1.279212, 0, 0, 0, 0, 0, 0, 0, 0, 0, .36481193, 1.5480118, -.03078791, 1.389112, 0, .70901209, -.16668792, 1.435812, .47001198, 2.0838118, 1.1673121, 0, 0, 1.4470119, .23301201, 0, 0, -.61948794, -.41388795, .263212, .66171199, 0, 0, 0, 1.6920118, 1.334012, 1.2101121, .41591194, -.48498794, 0, 0, .09911207, 0, -.46908805, .0205119, .0535119, -.14228792, -.55708808, 0, -.54008788, -.30998799, -.10958811, 0, -.01338812, 0, -.51788801, 0, 0, .13271193, -.11208793, 0, -.54508799, 0, .16641192, .95871216, 0, 1.6281118, 0, -.49718806, -.41348812, 0, 0, -.11718794, -.57058805, -.59488791, 0, -.65658802, 0, -.52698797, 0, 0, 0, 0, 0, 1.3500118, 0, 1.665812, 0, 1.963912, 0, 0, 1.9371119, .90991193, -.39558789, .39521196, 0, -.05268808, 0, 0, 0, 0, -.12458798, 0, -.28228804, .79281193, -.26358792, 0, 0, 0, -.72828788, 0, .355912, 0, 0, 0, 0, -.43538806, -1.566388, 0, -.28388807, 0, -.69028801, 0, -.78128809, -.54648799, -.92738789, 0, 0, .61571199, 0, 0, 1.012012, 0, 0, 0, 0, .43991187, .9404121, 0, 0, 0, .61671191, 0, 2.6073117, 0, -.60438794, 0, -.18108793, -.48178813, 0, -.22628804, -.07398792, 0, 0, 0, 1.830512, 0, 0, 0, 0, 0, 0, -.36918804, 1.3247118, 0, 0, 1.163012, 0, 0, 0, 1.3241119, 0, 0, 0, 0, -.90038794, -1.250888, 0, 0, 0, 0, -1.048188, -.90138787, 0, 0, 0, 0, 0, 0, -.00878807, 0, 0, .46301201, -.22048803, -.71518797, 0, 0, -.4952881, 0, -.83718795, .57951194, 0, 0, 0, 1.054112, .61721212, 2.2717118, 0, 2.0280118, 0, 0, 0, 2.6503119, 2.3914118, 0, -.36418793, -.9259879, 0, 0, .16971211, 0, 1.9360118, 2.5344119, 2.0171118, 0, 0, 0, 0, 0, 0, 0, 0, .77211195, 0, 0, 0, 0, 0, 1.952312, 0, 0, .25901201, 0, -.5028879, .03641204, 0, .38571194, 0, 0, -.44528791, -.55918807, 0, .39721206, 0, -.34038803, -.05988808, 0, -.03518792, .045512, 0, -.039288, 0, .01431207, 0, 0, .030412, -.31918809, 0, 0, 0, -.324388, 0, -1.232188, 0, -.23678799, -.89188808, 0, -.6766879, 0, 0, 0, 0, 0, 0, 0, -.67818803, 0, 1.099412, 1.2767119, -.64068788, -.50678796, 0, 0, 0, 0, 0, .68371207, .11251191, -.17128797, .17081194, 0, -.48708794, .09591202, 0, -.20108791, -.02158805, 0, -.3012881, 0, 0, 0, -.87638801, -.54488796, 0, 0, 0, 0, -.14738794, 0, 0, 0, 0, -.75718802, -.37418792, 0, 1.0981121, 1.1441121, .47381189, 0, 0, 0, -.33498809, 0, 0, 0, 0, -.91838807, 0, -.34488794, 0, .12971191, .99381214, -.91608804, 0, 0, .98171192, 0, 0, 0, 0, -.01528808, 0, -.41458794, .25691202, .18601207, 0, 0, 0, -.35608789, .79691201, 0, 0, 1.548912, 0, 0, 0, 0, 0, 0, 0, 0, 1.1663117, 0, 0, -.009088, -.49578807, 0, 0, -.2677879, 0, -.25468799, .68631202, 0, 0, 0, -.36198804])
#fmt: off
def load_data_cox(dta):
array = lambda x : np.array(dta[x], dtype=float)
t = array('t')
obs_t = array('obs_t')
pscenter = array('pscenter')
hhcenter = array('hhcenter')
ncomact = array('ncomact')
rleader = array('rleader')
dleader = array('dleader')
inter1 = array('inter1')
inter2 = array('inter2')
fail = array('FAIL')
return (t, obs_t, pscenter, hhcenter, ncomact,
rleader, dleader, inter1, inter2, fail)
(t, obs_t, pscenter, hhcenter, ncomact, rleader,
dleader, inter1, inter2, fail) = load_data_cox(dta)
X = np.array([pscenter, hhcenter, ncomact, rleader, dleader, inter1, inter2])
X.shape
with Model() as model:
T = len(t) - 1
nsubj = len(obs_t)
# risk set equals one if obs_t >= t
Y = np.array([[int(obs >= time) for time in t] for obs in obs_t])
# counting process. jump = 1 if obs_t \in [t[j], t[j+1])
dN = np.array([[Y[i,j]*int(t[j+1] >= obs_t[i])*fail[i] for j in range(T)] for i in
range(nsubj)])
c = Gamma('c', .0001, .00001)
r = Gamma('r', .001, .0001)
dL0_star = r*np.diff(t)
# prior mean hazard
mu = dL0_star * c
dL0 = Gamma('dL0', mu, c, shape=T)
beta = Normal('beta', np.zeros(7),
np.ones(7)*100, shape=7)
linear_model = tt.exp(tt.dot(X.T, beta))
idt = Y[:, :-1] * tt.outer(linear_model, dL0)
dn_like = Poisson('dn_like', idt, observed=dN)
with model:
trace = sample(2000, n_init=10000, init='advi_map')
az.plot_trace(trace, var_names=['c', 'r']);
az.plot_forest(trace, var_names=['beta']);
%load_ext watermark
%watermark -n -u -v -iv -w
```
| true |
code
| 0.25243 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/agemagician/CodeTrans/blob/main/prediction/transfer%20learning%20fine-tuning/source%20code%20summarization/csharp/small_model.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
**<h3>Summarize the csharp source code using codeTrans transfer learning finetuning model</h3>**
<h4>You can make free prediction online through this
<a href="https://huggingface.co/SEBIS/code_trans_t5_small_source_code_summarization_csharp_transfer_learning_finetune">Link</a></h4> (When using the prediction online, you need to parse and tokenize the code first.)
**1. Load necessry libraries including huggingface transformers**
```
!pip install -q transformers sentencepiece
from transformers import AutoTokenizer, AutoModelWithLMHead, SummarizationPipeline
```
**2. Load the token classification pipeline and load it into the GPU if avilabile**
```
pipeline = SummarizationPipeline(
model=AutoModelWithLMHead.from_pretrained("SEBIS/code_trans_t5_small_source_code_summarization_csharp_transfer_learning_finetune"),
tokenizer=AutoTokenizer.from_pretrained("SEBIS/code_trans_t5_small_source_code_summarization_csharp_transfer_learning_finetune", skip_special_tokens=True),
device=0
)
```
**3 Give the code for summarization, parse and tokenize it**
```
code = "public static DateTime ParseUnixDateTime(double unixTime)\n {\n var dt= new DateTime(1970, 1, 1, 0, 0, 0, 0, System.DateTimeKind.Utc);\n dt= dt.AddSeconds(unixTimeStamp).ToLocalTime();\n return dt;\n }" #@param {type:"raw"}
!pip install antlr4-python3-runtime==4.5.2
import antlr4
!wget https://www.dropbox.com/s/o87gk1jxf8645eu/CSharp4Lexer.py?dl=1 -O CSharp4Lexer.py
from CSharp4Lexer import CSharp4Lexer
def csTokenizer(line):
l = line.replace('\\n', '\n')
parsedVersion = []
stream = antlr4.InputStream(l)
lexer = CSharp4Lexer(stream)
toks = antlr4.CommonTokenStream(lexer)
toks.fetch(500)
identifiers = {}
identCount = 0
for token in toks.tokens:
if token.type == 109:
parsedVersion.append("CODE_INTEGER")
elif token.type == 111:
parsedVersion.append("CODE_REAL")
elif token.type == 112:
parsedVersion.append("CODE_CHAR")
elif token.type == 113:
parsedVersion.append("CODE_STRING")
elif token.type == 9 or token.type == 7 or token.type == 6 or token.type == 4 or token.type == 8 or token.type == 5: # whitespace and comments and newline
pass
else:
parsedVersion.append(str(token.text))
parsedVersion.remove('<EOF>')
return ' '.join(parsedVersion)
tokenized_code = csTokenizer(code)
print("code after tokenization: " + tokenized_code)
```
**4. Make Prediction**
```
pipeline([tokenized_code])
```
| true |
code
| 0.532304 | null | null | null | null |
|
# Spam Filter using Naive Bayes Classifier
```
import os
print(os.listdir("../input"))
```
**Import libraries**
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
```
**Read csv file**
```
df = pd.read_csv('../input/spam.csv', encoding='latin-1')[['v1', 'v2']]
```
Viewing after renaming the columns
```
df.columns = ['label', 'message']
df.head()
```
View the lable statistics
```
df.groupby('label').describe()
```
View the counts of ham and spam present in label column
```
sns.countplot(data=df, x='label')
```
**Steps**
1. Clean and Normalize text
2. Convert text into vectors (BoW) we use TfIdf
3. Train and test Classifier
**Cleaning steps**
<br>
It will be done in following steps:
<br>
1. Remove punctuations
2. Remove all stopwords
3. Apply [stemming](https://en.wikipedia.org/wiki/Stemming) (get the stem of the word).
** Write a method to return normailzed text in form of tokens (lemmas)**
```
import string
from nltk.corpus import stopwords
from nltk import PorterStemmer as Stemmer
def pre_process(text):
text = text.lower()
text = ''.join([t for t in text if t not in string.punctuation])
text = [t for t in text.split() if t not in stopwords.words('english')] # All words other tha stopwrods and punctuations in lowercase
st = Stemmer()
text = [st.stem(t) for t in text]
return text
pre_process('It\'s holiday lads :D. Mount is playing very well!!!')
# Test with our dataset
df['message'][:21].apply(pre_process)
```
Refer scikitlearn for details on TfIDf

**Fit and transform SMS corpus**
```
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf= TfidfVectorizer(analyzer=pre_process)
data = tfidf.fit_transform(df['message'])
message=df.iloc[2]
print(tfidf.transform(df.iloc[2]))
```
**Having messages in form of vectors, we are ready to train our classifier. <br>We will use Naive Bayes which is well known classifier while working with text data.
<br>Before that we will use pipeline feature of sklearn to create a pipeline of TfidfVectorizer followed by Classifier.**
<br>Input will be message passed to first stage TfidfVectorizer which will transform it and pass it to Naive Bayes Classifier to get output label
```
from sklearn.base import TransformerMixin
class DenseTransformer(TransformerMixin):
def fit(self, X, y=None, **fit_params):
return self
def transform(self, X, y=None, **fit_params):
return X.todense()
from sklearn.pipeline import Pipeline
from sklearn.naive_bayes import GaussianNB, MultinomialNB
spam_filter = Pipeline([
('vectorizer', TfidfVectorizer(analyzer=pre_process)),
('to_dense', DenseTransformer()),
('classifier', GaussianNB())
])
```
train test split
```
from sklearn.model_selection import train_test_split
x=df['message']
y=df['label']
x=x.values
y=y.values
x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.20, random_state = 21) #Pareto principle
```
**Train spam_filter**
```
spam_filter.fit(x_train, y_train)
```
**Predict for test cases**
```
predictions = spam_filter.predict(x_test)
count = 0
for i in range(len(y_test)):
if y_test[i] != predictions[i]:
count += 1
print('Total number of test cases', len(y_test))
print('Number of wrong of predictions', count)
```
**Check for wrong predictions that were classified as ham**
```
#x_test[y_test != predictions]
```
**Use classification report to get more details**
```
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
print(classification_report(predictions, y_test))
accuracy_score(y_test, predictions)
```
Function to predict whether passed message is ham or spam
```
def detect_spam(s):
return spam_filter.predict([s])[0]
detect_spam('Your cash-balance is currently 500 pounds - to maximize your cash-in now, send COLLECT to 83600.')
from sklearn.metrics import confusion_matrix
confusion_matrix(predictions,y_test)
```
| true |
code
| 0.446495 | null | null | null | null |
|
Note! For a most up to date version of this notebook, make sure you copy from:
[](https://colab.research.google.com/drive/1wTMIrJhYsQdq_u7ROOkf0Lu_fsX5Mu8a)
## Configs and Hyperparameters
Support a variety of models, you can find more pretrained model from [Tensorflow detection model zoo: COCO-trained models](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/detection_model_zoo.md#coco-trained-models), as well as their pipline config files in [object_detection/samples/configs/](https://github.com/tensorflow/models/tree/master/research/object_detection/samples/configs).
```
# If you forked the repo, you can replace the link.
repo_url = 'https://github.com/roboflow-ai/tensorflow-object-detection-faster-rcnn'
# Number of training steps - 1000 will train very quickly, but more steps will increase accuracy.
num_steps = 10000 # 200000 to improve
# Number of evaluation steps.
num_eval_steps = 50
MODELS_CONFIG = {
'ssd_mobilenet_v2': {
'model_name': 'ssd_mobilenet_v2_coco_2018_03_29',
'pipeline_file': 'ssd_mobilenet_v2_coco.config',
'batch_size': 12
},
'faster_rcnn_inception_v2': {
'model_name': 'faster_rcnn_inception_v2_coco_2018_01_28',
'pipeline_file': 'faster_rcnn_inception_v2_pets.config',
'batch_size': 12
},
'rfcn_resnet101': {
'model_name': 'rfcn_resnet101_coco_2018_01_28',
'pipeline_file': 'rfcn_resnet101_pets.config',
'batch_size': 8
},
}
# Pick the model you want to use
# Select a model in `MODELS_CONFIG`.
selected_model = 'ssd_mobilenet_v2'
# Name of the object detection model to use.
MODEL = MODELS_CONFIG[selected_model]['model_name']
# Name of the pipline file in tensorflow object detection API.
pipeline_file = MODELS_CONFIG[selected_model]['pipeline_file']
# Training batch size fits in Colabe's Tesla K80 GPU memory for selected model.
batch_size = MODELS_CONFIG[selected_model]['batch_size']
# use TF 1.x for Object Detection APIs as they are not ported to TF 2.0 yet
%tensorflow_version 1.x
```
## Clone the `tensorflow-object-detection` repository or your fork.
```
import os
%cd /content
repo_dir_path = os.path.abspath(os.path.join('.', os.path.basename(repo_url)))
!git clone {repo_url}
%cd {repo_dir_path}
!git pull
```
## Install required packages
```
%cd /content
!git clone --quiet https://github.com/tensorflow/models.git
!pip install tf_slim
!apt-get install -qq protobuf-compiler python-pil python-lxml python-tk
!pip install -q Cython contextlib2 pillow lxml matplotlib
!pip install -q pycocotools
%cd /content/models/research
!protoc object_detection/protos/*.proto --python_out=.
import os
os.environ['PYTHONPATH'] += ':/content/models/research/:/content/models/research/slim/'
!python object_detection/builders/model_builder_test.py
```
## Prepare `tfrecord` files
Roboflow automatically creates our TFRecord and label_map files that we need!
**Generating your own TFRecords the only step you need to change for your own custom dataset.**
Because we need one TFRecord file for our training data, and one TFRecord file for our test data, we'll create two separate datasets in Roboflow and generate one set of TFRecords for each.
To create a dataset in Roboflow and generate TFRecords, follow [this step-by-step guide](https://blog.roboflow.ai/getting-started-with-roboflow/).
```
%cd /content/tensorflow-object-detection-faster-rcnn/data
!curl -L "https://app.roboflow.com/ds/robins" > roboflow.zip; unzip roboflow.zip; rm roboflow.zip
# training set
%ls train
# test set
%ls test
# NOTE: Update these TFRecord names from "cells" and "cells_label_map" to your files!
test_record_fname = '/content/tensorflow-object-detection-faster-rcnn/data/test/fire.tfrecord'
train_record_fname = '/content/tensorflow-object-detection-faster-rcnn/data/train/fire.tfrecord'
label_map_pbtxt_fname = '/content/tensorflow-object-detection-faster-rcnn/data/train/fire_label_map.pbtxt'
```
## Download base model
```
%cd /content/models/research
import os
import shutil
import glob
import urllib.request
import tarfile
MODEL_FILE = MODEL + '.tar.gz'
DOWNLOAD_BASE = 'http://download.tensorflow.org/models/object_detection/'
DEST_DIR = '/content/models/research/pretrained_model'
if not (os.path.exists(MODEL_FILE)):
urllib.request.urlretrieve(DOWNLOAD_BASE + MODEL_FILE, MODEL_FILE)
tar = tarfile.open(MODEL_FILE)
tar.extractall()
tar.close()
os.remove(MODEL_FILE)
if (os.path.exists(DEST_DIR)):
shutil.rmtree(DEST_DIR)
os.rename(MODEL, DEST_DIR)
!echo {DEST_DIR}
!ls -alh {DEST_DIR}
fine_tune_checkpoint = os.path.join(DEST_DIR, "model.ckpt")
fine_tune_checkpoint
```
## Configuring a Training Pipeline
```
import os
pipeline_fname = os.path.join('/content/models/research/object_detection/samples/configs/', pipeline_file)
assert os.path.isfile(pipeline_fname), '`{}` not exist'.format(pipeline_fname)
def get_num_classes(pbtxt_fname):
from object_detection.utils import label_map_util
label_map = label_map_util.load_labelmap(pbtxt_fname)
categories = label_map_util.convert_label_map_to_categories(
label_map, max_num_classes=90, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
return len(category_index.keys())
import re
num_classes = get_num_classes(label_map_pbtxt_fname)
with open(pipeline_fname) as f:
s = f.read()
with open(pipeline_fname, 'w') as f:
# fine_tune_checkpoint
s = re.sub('fine_tune_checkpoint: ".*?"',
'fine_tune_checkpoint: "{}"'.format(fine_tune_checkpoint), s)
# tfrecord files train and test.
s = re.sub(
'(input_path: ".*?)(train.record)(.*?")', 'input_path: "{}"'.format(train_record_fname), s)
s = re.sub(
'(input_path: ".*?)(val.record)(.*?")', 'input_path: "{}"'.format(test_record_fname), s)
# label_map_path
s = re.sub(
'label_map_path: ".*?"', 'label_map_path: "{}"'.format(label_map_pbtxt_fname), s)
# Set training batch_size.
s = re.sub('batch_size: [0-9]+',
'batch_size: {}'.format(batch_size), s)
# Set training steps, num_steps
s = re.sub('num_steps: [0-9]+',
'num_steps: {}'.format(num_steps), s)
# Set number of classes num_classes.
s = re.sub('num_classes: [0-9]+',
'num_classes: {}'.format(num_classes), s)
f.write(s)
!cat {pipeline_fname}
model_dir = 'training/'
# Optionally remove content in output model directory to fresh start.
!rm -rf {model_dir}
os.makedirs(model_dir, exist_ok=True)
```
## Run Tensorboard(Optional)
```
!wget https://bin.equinox.io/c/4VmDzA7iaHb/ngrok-stable-linux-amd64.zip
!unzip -o ngrok-stable-linux-amd64.zip
LOG_DIR = model_dir
get_ipython().system_raw(
'tensorboard --logdir {} --host 0.0.0.0 --port 6006 &'
.format(LOG_DIR)
)
get_ipython().system_raw('./ngrok http 6006 &')
```
### Get Tensorboard link
```
! curl -s http://localhost:4040/api/tunnels | python3 -c \
"import sys, json; print(json.load(sys.stdin)['tunnels'][0]['public_url'])"
```
## Train the model
```
!python /content/models/research/object_detection/model_main.py \
--pipeline_config_path={pipeline_fname} \
--model_dir={model_dir} \
--alsologtostderr \
--num_train_steps={num_steps} \
--num_eval_steps={num_eval_steps}
!ls {model_dir}
```
## Exporting a Trained Inference Graph
Once your training job is complete, you need to extract the newly trained inference graph, which will be later used to perform the object detection. This can be done as follows:
```
import re
import numpy as np
output_directory = './fine_tuned_model'
lst = os.listdir(model_dir)
lst = [l for l in lst if 'model.ckpt-' in l and '.meta' in l]
steps=np.array([int(re.findall('\d+', l)[0]) for l in lst])
last_model = lst[steps.argmax()].replace('.meta', '')
last_model_path = os.path.join(model_dir, last_model)
print(last_model_path)
!python /content/models/research/object_detection/export_inference_graph.py \
--input_type=image_tensor \
--pipeline_config_path={pipeline_fname} \
--output_directory={output_directory} \
--trained_checkpoint_prefix={last_model_path}
!ls {output_directory}
```
## Download the model `.pb` file
```
import os
pb_fname = os.path.join(os.path.abspath(output_directory), "frozen_inference_graph.pb")
assert os.path.isfile(pb_fname), '`{}` not exist'.format(pb_fname)
!ls -alh {pb_fname}
```
### Option2 : Download the `.pb` file directly to your local file system
This method may not be stable when downloading large files like the model `.pb` file. Try **option 1** instead if not working.
```
from google.colab import files
files.download(pb_fname)
```
### OPTIONAL: Download the `label_map.pbtxt` file
```
from google.colab import files
files.download(label_map_pbtxt_fname)
```
### OPTIONAL: Download the modified pipline file
If you plan to use OpenVINO toolkit to convert the `.pb` file to inference faster on Intel's hardware (CPU/GPU, Movidius, etc.)
```
files.download(pipeline_fname)
# !tar cfz fine_tuned_model.tar.gz fine_tuned_model
# from google.colab import files
# files.download('fine_tuned_model.tar.gz')
%cd /content
ls
```
upload test image via ui
## Run inference test
Test with images in repository `tensorflow-object-detection/test` directory.
**To test with your own images, you need to place your images inside the `test` directory in this Colab notebook!** More on this below.
```
import os
import glob
# Path to frozen detection graph. This is the actual model that is used for the object detection.
PATH_TO_CKPT = pb_fname
# List of the strings that is used to add correct label for each box.
PATH_TO_LABELS = label_map_pbtxt_fname
# If you want to test the code with your images, just add images files to the PATH_TO_TEST_IMAGES_DIR.
PATH_TO_TEST_IMAGES_DIR = os.path.join(repo_dir_path, "test")
assert os.path.isfile(pb_fname)
assert os.path.isfile(PATH_TO_LABELS)
TEST_IMAGE_PATHS = '/content/pan-fire.jpg'
assert len(TEST_IMAGE_PATHS) > 0, 'No image found in `{}`.'.format(PATH_TO_TEST_IMAGES_DIR)
print(TEST_IMAGE_PATHS)
%cd /content/models/research/object_detection
import numpy as np
import os
import six.moves.urllib as urllib
import sys
import tarfile
import tensorflow as tf
import zipfile
from collections import defaultdict
from io import StringIO
from matplotlib import pyplot as plt
from PIL import Image
# This is needed since the notebook is stored in the object_detection folder.
sys.path.append("..")
from object_detection.utils import ops as utils_ops
# This is needed to display the images.
%matplotlib inline
from object_detection.utils import label_map_util
from object_detection.utils import visualization_utils as vis_util
detection_graph = tf.Graph()
with detection_graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(PATH_TO_CKPT, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
label_map = label_map_util.load_labelmap(PATH_TO_LABELS)
categories = label_map_util.convert_label_map_to_categories(
label_map, max_num_classes=num_classes, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
def load_image_into_numpy_array(image):
(im_width, im_height) = image.size
return np.array(image.getdata()).reshape(
(im_height, im_width, 3)).astype(np.uint8)
# Size, in inches, of the output images.
IMAGE_SIZE = (12, 8)
def run_inference_for_single_image(image, graph):
with graph.as_default():
with tf.Session() as sess:
# Get handles to input and output tensors
ops = tf.get_default_graph().get_operations()
all_tensor_names = {
output.name for op in ops for output in op.outputs}
tensor_dict = {}
for key in [
'num_detections', 'detection_boxes', 'detection_scores',
'detection_classes', 'detection_masks'
]:
tensor_name = key + ':0'
if tensor_name in all_tensor_names:
tensor_dict[key] = tf.get_default_graph().get_tensor_by_name(
tensor_name)
if 'detection_masks' in tensor_dict:
# The following processing is only for single image
detection_boxes = tf.squeeze(
tensor_dict['detection_boxes'], [0])
detection_masks = tf.squeeze(
tensor_dict['detection_masks'], [0])
# Reframe is required to translate mask from box coordinates to image coordinates and fit the image size.
real_num_detection = tf.cast(
tensor_dict['num_detections'][0], tf.int32)
detection_boxes = tf.slice(detection_boxes, [0, 0], [
real_num_detection, -1])
detection_masks = tf.slice(detection_masks, [0, 0, 0], [
real_num_detection, -1, -1])
detection_masks_reframed = utils_ops.reframe_box_masks_to_image_masks(
detection_masks, detection_boxes, image.shape[0], image.shape[1])
detection_masks_reframed = tf.cast(
tf.greater(detection_masks_reframed, 0.5), tf.uint8)
# Follow the convention by adding back the batch dimension
tensor_dict['detection_masks'] = tf.expand_dims(
detection_masks_reframed, 0)
image_tensor = tf.get_default_graph().get_tensor_by_name('image_tensor:0')
# Run inference
output_dict = sess.run(tensor_dict,
feed_dict={image_tensor: np.expand_dims(image, 0)})
# all outputs are float32 numpy arrays, so convert types as appropriate
output_dict['num_detections'] = int(
output_dict['num_detections'][0])
output_dict['detection_classes'] = output_dict[
'detection_classes'][0].astype(np.uint8)
output_dict['detection_boxes'] = output_dict['detection_boxes'][0]
output_dict['detection_scores'] = output_dict['detection_scores'][0]
if 'detection_masks' in output_dict:
output_dict['detection_masks'] = output_dict['detection_masks'][0]
return output_dict
# Output images not showing? Run this cell again, and try the cell above
# This is needed to display the images.
%matplotlib inline
image_path = TEST_IMAGE_PATHS
image = Image.open(image_path)
# the array based representation of the image will be used later in order to prepare the
# result image with boxes and labels on it.
image_np = load_image_into_numpy_array(image)
# Expand dimensions since the model expects images to have shape: [1, None, None, 3]
image_np_expanded = np.expand_dims(image_np, axis=0)
# Actual detection.
output_dict = run_inference_for_single_image(image_np, detection_graph)
# Visualization of the results of a detection.
vis_util.visualize_boxes_and_labels_on_image_array(
image_np,
output_dict['detection_boxes'],
output_dict['detection_classes'],
output_dict['detection_scores'],
category_index,
instance_masks=output_dict.get('detection_masks'),
use_normalized_coordinates=True,
line_thickness=8)
plt.figure(figsize=IMAGE_SIZE)
plt.imshow(image_np)
### Adding your own images to tensorflow-object-detection/data
def upload_files():
from google.colab import files
uploaded = files.upload()
for k, v in uploaded.items():
open(k, 'wb').write(v)
return list(uploaded.keys())
# navigate to correct folder
%cd /content/tensorflow-object-detection/test
# call function to upload
upload_files()
```
| true |
code
| 0.61659 | null | null | null | null |
|
###### Content under Creative Commons Attribution license CC-BY 4.0, code under MIT license (c)2014 L.A. Barba, G.F. Forsyth.
# Relax and hold steady
Ready for more relaxing? This is the third lesson of **Module 5** of the course, exploring solutions to elliptic PDEs.
In [Lesson 1](http://nbviewer.ipython.org/github/numerical-mooc/numerical-mooc/blob/master/lessons/05_relax/05_01_2D.Laplace.Equation.ipynb) and [Lesson 2](http://nbviewer.ipython.org/github/numerical-mooc/numerical-mooc/blob/master/lessons/05_relax/05_02_2D.Poisson.Equation.ipynb) of this module we used the Jacobi method (a relaxation scheme) to iteratively find solutions to Laplace and Poisson equations.
And it worked, so why are we still talking about it? Because the Jacobi method is slow, very slow to converge. It might not have seemed that way in the first two notebooks because we were using small grids, but we did need more than 3,000 iterations to reach the exit criterion while solving the Poisson equation on a $41\times 41$ grid.
You can confirm this below: using `nx,ny=` $128$ on the Laplace problem of Lesson 1, the Jacobi method requires nearly *20,000* iterations before we reach $10^{-8}$ for the L2-norm of the difference between two iterates. That's a *lot* of iterations!
Now, consider this application: an incompressible Navier-Stokes solver has to ensure that the velocity field is divergence-free at every timestep. One of the most common ways to ensure this is to solve a Poisson equation for the pressure field. In fact, the pressure Poisson equation is responsible for the majority of the computational expense of an incompressible Navier-Stokes solver. Imagine having to do 20,000 Jacobi iterations for *every* time step in a fluid-flow problem with many thousands or perhaps millions of grid points!
The Jacobi method is the slowest of all relaxation schemes, so let's learn how to improve on it. In this lesson, we'll study the Gauss-Seidel method—twice as fast as Jacobi, in theory—and the successive over-relaxation (SOR) method. We also have some neat Python tricks lined up for you to get to the solution even faster. Let's go!
### Test problem
Let's use the same example problem as in [Lesson 1](./05_01_2D.Laplace.Equation.ipynb): Laplace's equation with boundary conditions
\begin{equation}
\begin{gathered}
p=0 \text{ at } x=0\\
\frac{\partial p}{\partial x} = 0 \text{ at } x = L\\
p = 0 \text{ at }y = 0 \\
p = \sin \left( \frac{\frac{3}{2}\pi x}{L} \right) \text{ at } y = H
\end{gathered}
\end{equation}
We import our favorite Python libraries, and also some custom functions that we wrote in [Lesson 1](./05_01_2D.Laplace.Equation.ipynb), which we have saved in a 'helper' Python file for re-use.
```
import numpy
from matplotlib import pyplot, cm
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 16
from laplace_helper import p_analytical, plot_3D, L2_rel_error
```
We now have the analytical solution in the array `p_analytical`, and we have the functions `plot_3D` and `L2_rel_error` in our namespace. If you can't remember how they work, just use `help()` and take advantage of the docstrings. It's a good habit to always write docstrings in your functions, and now you see why!
In this notebook, we are going to use larger grids than before, to better illustrate the speed increases we achieve with different iterative methods. Let's create a $128\times128$ grid and initialize.
```
nx = 128
ny = 128
L = 5
H = 5
x = numpy.linspace(0,L,nx)
y = numpy.linspace(0,H,ny)
dx = L/(nx-1)
dy = H/(ny-1)
p0 = numpy.zeros((ny, nx))
p0[-1,:] = numpy.sin(1.5*numpy.pi*x/x[-1])
```
We said above that the Jacobi method takes nearly 20,000 iterations before it satisfies our exit criterion of $10^{-8}$ (L2-norm difference between two consecutive iterations). You'll just have to confirm that now. Have a seat!
```
def laplace2d(p, l2_target):
'''Solves the Laplace equation using the Jacobi method
with a 5-point stencil
Parameters:
----------
p: 2D array of float
Initial potential distribution
l2_target: float
Stopping criterion
Returns:
-------
p: 2D array of float
Potential distribution after relaxation
'''
l2norm = 1
pn = numpy.empty_like(p)
iterations = 0
while l2norm > l2_target:
pn = p.copy()
p[1:-1,1:-1] = .25 * (pn[1:-1,2:] + pn[1:-1,:-2] +\
pn[2:,1:-1] + pn[:-2,1:-1])
##Neumann B.C. along x = L
p[1:-1,-1] = .25 * (2*pn[1:-1,-2] + pn[2:,-1] + pn[:-2, -1])
l2norm = numpy.sqrt(numpy.sum((p - pn)**2)/numpy.sum(pn**2))
iterations += 1
return p, iterations
l2_target = 1e-8
p, iterations = laplace2d(p0.copy(), l2_target)
print ("Jacobi method took {} iterations at tolerance {}".\
format(iterations, l2_target))
```
Would we lie to you? 19,993 iterations before we reach the exit criterion of $10^{-8}$. Yikes!
We can also time how long the Jacobi method takes using the `%%timeit` cell-magic. Go make some tea, because this can take a while—the `%%timeit` magic runs the function a few times and then averages their runtimes to give a more accurate result.
- - -
##### Notes
1. When using `%%timeit`, the return values of a function (`p` and `iterations` in this case) *won't* be saved.
2. We document our timings below, but your timings can vary quite a lot, depending on your hardware. In fact, you may not even see the same trends (some recent hardware can play some fancy tricks with optimizations that you have no control over).
- - -
With those caveats, let's give it a shot:
```
%%timeit
laplace2d(p0.copy(), l2_target)
```
The printed result above (and others to come later) is from a mid-2007 Mac Pro, powered by two 3-GHz quad-core Intel Xeon X5364 (Clovertown). We tried also on more modern machines, and get conflicting results—like the Gauss-Seidel method being slightly slower than Jacobi, even though it required fewer iterations. Don't get too hung up on this: the hardware optimizations applied by more modern CPUs are varied and make a big difference sometimes.
Meanwhile, let's check the overall accuracy of the numerical calculation by comparing it to the analytical solution.
```
pan = p_analytical(x,y)
L2_rel_error(p,pan)
```
That's a pretty small error. Let's assume it is good enough and focus on speeding up the process.
## Gauss-Seidel
You will recall from [Lesson 1](./2D_Laplace_Equation.ipynb) that a single Jacobi iteration is written as:
\begin{equation}
p^{k+1}_{i,j} = \frac{1}{4} \left(p^{k}_{i,j-1} + p^k_{i,j+1} + p^{k}_{i-1,j} + p^k_{i+1,j} \right)
\end{equation}
The Gauss-Seidel method is a simple tweak to this idea: use updated values of the solution as soon as they are available, instead of waiting for the values in the whole grid to be updated.
If you imagine that we progress through the grid points in the order shown by the arrow in Figure 1, then you can see that the updated values $p^{k+1}_{i-1,j}$ and $p^{k+1}_{i,j-1}$ can be used to calculate $p^{k+1}_{i,j}$.
<img src="./figures/solvepath.svg" width=350>
#### Figure 1. Assumed order of updates on a grid.
The iteration formula for Gauss-Seidel is thus:
\begin{equation}
p^{k+1}_{i,j} = \frac{1}{4} \left(p^{k+1}_{i,j-1} + p^k_{i,j+1} + p^{k+1}_{i-1,j} + p^k_{i+1,j} \right)
\end{equation}
There's now a problem for the Python implementation. You can no longer use NumPy's array operations to evaluate the solution updates. Since Gauss-Seidel requires using values immediately after they're updated, we have to abandon our beloved array operations and return to nested `for` loops. Ugh.
We don't like it, but if it saves us a bunch of time, then we can manage. But does it?
Here's a function to compute the Gauss-Seidel updates using a double loop.
```
def laplace2d_gauss_seidel(p, nx, ny, l2_target):
iterations = 0
iter_diff = l2_target+1 #init iter_diff to be larger than l2_target
while iter_diff > l2_target:
pn = p.copy()
iter_diff = 0.0
for j in range(1,ny-1):
for i in range(1,nx-1):
p[j,i] = .25 * (p[j,i-1] + p[j,i+1] + p[j-1,i] + p[j+1,i])
iter_diff += (p[j,i] - pn[j,i])**2
#Neumann 2nd-order BC
for j in range(1,ny-1):
p[j,-1] = .25 * (2*p[j,-2] + p[j+1,-1] + p[j-1, -1])
iter_diff = numpy.sqrt(iter_diff/numpy.sum(pn**2))
iterations += 1
return p, iterations
```
We would then run this with the following function call:
```Python
p, iterations = laplace2d_gauss_seidel(p,1e-8)
```
<br>
But **don't do it**. We did it so that you don't have to!
The solution of our test problem with the Gauss-Seidel method required several thousand fewer iterations than the Jacobi method, but it took nearly *10 minutes* to run on our machine.
##### What happened?
If you think back to the far off days when you first learned about array operations, you might recall that we discovered that NumPy array operations could drastically improve code performance compared with nested `for` loops. NumPy operations are written in C and pre-compiled, so they are *much* faster than vanilla Python.
But the Jacobi method is not algorithmically optimal, giving slow convergence. We want to take advantage of the faster-converging iterative methods, yet unpacking the array operations into nested loops destroys performance. *What can we do?*
## Use Numba!
[Numba](http://numba.pydata.org) is an open-source optimizing compiler for Python. It works by reading Python functions that you give it, and generating a compiled version for you—also called Just-In-Time (JIT) compilation. You can then use the function at performance levels that are close to what you can get with compiled languages (like C, C++ and fortran).
It can massively speed up performance, especially when dealing with loops. Plus, it's pretty easy to use. Like we overheard at a conference: [*Numba is a Big Deal.*](http://twitter.com/lorenaabarba/status/625383941453656065)
##### Caveat
We encourage everyone following the course to use the [Anaconda Python](https://www.continuum.io/downloads) distribution because it's well put-together and simple to use. If you *haven't* been using Anaconda, that's fine, but let us **strongly** suggest that you take the plunge now. Numba is great and easy to use, but it is **not** easy to install without help. Those of you using Anaconda can install it by running <br><br>
`conda install numba`<br><br>
If you *really* don't want to use Anaconda, you will have to [compile all of Numba's dependencies](https://pypi.python.org/pypi/numba).
- - -
### Intro to Numba
Let's dive in! Numba is great and easy to use. We're going to first walk you through a simple example to give you a taste of Numba's abilities.
After installing Numba (see above), we can use it by adding a line to `import numba` and another to `import autojit` (more on this in a bit).
```
import numba
from numba import jit
```
You tell Numba which functions you want to accelerate by using a [Python decorator](http://www.learnpython.org/en/Decorators), a special type of command that tells the Python interpreter to modify a callable object (like a function). For example, let's write a quick function to calculate the $n^{\text{th}}$ number in the Fibonacci sequence:
```
def fib_it(n):
a = 1
b = 1
for i in range(n-2):
a, b = b, a+b
return b
```
There are several faster ways to program the Fibonacci sequence, but that's not a concern right now (but if you're curious, [check them out](http://mathworld.wolfram.com/BinetsFibonacciNumberFormula.html)). Let's use `%%timeit` and see how long this simple function takes to find the 500,000-th Fibonacci number.
```
%%timeit
fib_it(500000)
```
Now let's try Numba! Just add the `@jit` decorator above the function name and let's see what happens!
```
@jit
def fib_it(n):
a = 1
b = 1
for i in range(n-2):
a, b = b, a+b
return b
%%timeit
fib_it(500000)
```
*Holy cow!* In our machine, that's more than 8,000 times faster!
That warning from `%%timeit` is due to the compilation overhead for Numba. The very first time that it executes the function, it has to compile it, then it caches that code for reuse without extra compiling. That's the 'Just-In-Time' bit. You'll see it disappear if we run `%%timeit` again.
```
%%timeit
fib_it(500000)
```
We would agree if you think that this is a rather artificial example, but the speed-up is very impressive indeed. Just adding the one-word decorator!
##### Running in `nopython` mode
Numba is very clever, but it can't optimize everything. When it can't, rather than failing to run, it will fall back to the regular Python, resulting in poor performance again. This can be confusing and frustrating, since you might not know ahead of time which bits of code will speed up and which bits won't.
To avoid this particular annoyance, you can tell Numba to use `nopython` mode. In this case, your code will simply fail if the "jitted" function can't be optimized. It's simply an option to give you "fast or nothing."
Use `nopython` mode by adding the following line above the function that you want to JIT-compile:
```Python
@jit(nopython=True)
```
- - -
##### Numba version check
In these examples, we are using the latest (as of publication) version of Numba: 0.22.1. Make sure to upgrade or some of the code examples below may not run.
- - -
```
print(numba.__version__)
```
## Back to Jacobi
We want to compare the performance of different iterative methods under the same conditions. Because the Gauss-Seidel method forces us to unpack the array operations into nested loops (which are very slow in Python), we use Numba to get the code to perform well. Thus, we need to write a new Jacobi method using for-loops and Numba (instead of NumPy), so we can make meaningful comparisons.
Let's write a "jitted" Jacobi with loops.
```
@jit(nopython=True)
def laplace2d_jacobi(p, pn, l2_target):
'''Solves the Laplace equation using the Jacobi method
with a 5-point stencil
Parameters:
----------
p: 2D array of float
Initial potential distribution
pn: 2D array of float
Allocated array for previous potential distribution
l2_target: float
Stopping criterion
Returns:
-------
p: 2D array of float
Potential distribution after relaxation
'''
iterations = 0
iter_diff = l2_target+1 #init iter_diff to be larger than l2_target
denominator = 0.0
ny, nx = p.shape
l2_diff = numpy.zeros(20000)
while iter_diff > l2_target:
for j in range(ny):
for i in range(nx):
pn[j,i] = p[j,i]
iter_diff = 0.0
denominator = 0.0
for j in range(1,ny-1):
for i in range(1,nx-1):
p[j,i] = .25 * (pn[j,i-1] + pn[j,i+1] + pn[j-1,i] + pn[j+1,i])
#Neumann 2nd-order BC
for j in range(1,ny-1):
p[j,-1] = .25 * (2*pn[j,-2] + pn[j+1,-1] + pn[j-1, -1])
for j in range(ny):
for i in range(nx):
iter_diff += (p[j,i] - pn[j,i])**2
denominator += (pn[j,i]*pn[j,i])
iter_diff /= denominator
iter_diff = iter_diff**0.5
l2_diff[iterations] = iter_diff
iterations += 1
return p, iterations, l2_diff
p, iterations, l2_diffJ = laplace2d_jacobi(p0.copy(), p0.copy(), 1e-8)
print("Numba Jacobi method took {} iterations at tolerance {}".format(iterations, l2_target))
%%timeit
laplace2d_jacobi(p0.copy(), p0.copy(), 1e-8)
```
In our old machine, that's faster than the NumPy version of Jacobi, but on some newer machines it might not be. Don't obsess over this: there is much hardware black magic that we cannot control.
Remember that NumPy is a highly optimized library. The fact that we can get competitive execution times with this JIT-compiled code is kind of amazing. Plus(!) now we get to try out those techniques that aren't possible with NumPy array operations.
##### Note
We're also saving the history of the L2-norm of the difference between consecutive iterations. We'll take a look at that once we have a few more methods to compare.
- - -
##### Another Note
Why did we use
```Python
l2_diff = numpy.zeros(20000)
```
Where did the `20000` come from?
We cheated a little bit. Numba doesn't handle _mutable_ objects well in `nopython` mode, which means we can't use a *list* and append each iteration's value of the L2-norm. So we need to define an array big enough to hold all of them and we know from the first run that Jacobi converges in fewer than 20,000 iterations.
- - -
##### Challenge task
It is possible to get a good estimate of the number of iterations needed by the Jacobi method to reduce the initial error by a factor $10^{-m}$, for given $m$. The formula depends on the largest eigenvalue of the coefficient matrix, which is known for the discrete Poisson problem on a square domain. See Parviz Moin, *"Fundamentals of Engineering Numerical Analysis"* (2nd ed., pp.141–143).
* Find the estimated number of iterations to reduce the initial error by $10^{-8}$ when using the grids listed below, in the section on grid convergence, with $11$, $21$, $41$ and $81$ grid points on each coordinate axis.
## Back to Gauss-Seidel
If you recall, the reason we got into this Numba sidetrack was to try out Gauss-Seidel and compare the performance with Jacobi. Recall from above that the formula for Gauss-Seidel is as follows:
\begin{equation}
p^{k+1}_{i,j} = \frac{1}{4} \left(p^{k+1}_{i,j-1} + p^k_{i,j+1} + p^{k+1}_{i-1,j} + p^k_{i+1,j} \right)
\end{equation}
We only need to slightly tweak the Jacobi function to get one for Gauss-Seidel. Instead of updating `p` in terms of `pn`, we just update `p` using `p`!
```
@jit(nopython=True)
def laplace2d_gauss_seidel(p, pn, l2_target):
'''Solves the Laplace equation using Gauss-Seidel method
with a 5-point stencil
Parameters:
----------
p: 2D array of float
Initial potential distribution
pn: 2D array of float
Allocated array for previous potential distribution
l2_target: float
Stopping criterion
Returns:
-------
p: 2D array of float
Potential distribution after relaxation
'''
iterations = 0
iter_diff = l2_target + 1 #initialize iter_diff to be larger than l2_target
denominator = 0.0
ny, nx = p.shape
l2_diff = numpy.zeros(20000)
while iter_diff > l2_target:
for j in range(ny):
for i in range(nx):
pn[j,i] = p[j,i]
iter_diff = 0.0
denominator = 0.0
for j in range(1,ny-1):
for i in range(1,nx-1):
p[j,i] = .25 * (p[j,i-1] + p[j,i+1] + p[j-1,i] + p[j+1,i])
#Neumann 2nd-order BC
for j in range(1,ny-1):
p[j,-1] = .25 * (2*p[j,-2] + p[j+1,-1] + p[j-1, -1])
for j in range(ny):
for i in range(nx):
iter_diff += (p[j,i] - pn[j,i])**2
denominator += (pn[j,i]*pn[j,i])
iter_diff /= denominator
iter_diff = iter_diff**0.5
l2_diff[iterations] = iter_diff
iterations += 1
return p, iterations, l2_diff
p, iterations, l2_diffGS = laplace2d_gauss_seidel(p0.copy(), p0.copy(), 1e-8)
print("Numba Gauss-Seidel method took {} iterations at tolerance {}".format(iterations, l2_target))
```
Cool! Using the most recently updated values of the solution in the Gauss-Seidel method saved 6,000 iterations! Now we can see how much faster than Jacobi this is, because both methods are implemented the same way:
```
%%timeit
laplace2d_gauss_seidel(p0.copy(), p0.copy(), 1e-8)
```
We get some speed-up over the Numba version of Jacobi, but not a lot. And you may see quite different results—on some of the machines we tried, we could still not beat the NumPy version of Jacobi. This can be confusing, and hard to explain without getting into the nitty grity of hardware optimizations.
Don't lose hope! We have another trick up our sleeve!
## Successive Over-Relaxation (SOR)
Successive over-relaxation is able to improve on the Gauss-Seidel method by using in the update a linear combination of the previous and the current solution, as follows:
\begin{equation}
p^{k+1}_{i,j} = (1 - \omega)p^k_{i,j} + \frac{\omega}{4} \left(p^{k+1}_{i,j-1} + p^k_{i,j+1} + p^{k+1}_{i-1,j} + p^k_{i+1,j} \right)
\end{equation}
The relaxation parameter $\omega$ will determine how much faster SOR will be than Gauss-Seidel. SOR iterations are only stable for $0 < \omega < 2$. Note that for $\omega = 1$, SOR reduces to the Gauss-Seidel method.
If $\omega < 1$, that is technically an "under-relaxation" and it will be slower than Gauss-Seidel.
If $\omega > 1$, that's the over-relaxation and it should converge faster than Gauss-Seidel.
Let's write a function for SOR iterations of the Laplace equation, using Numba to get high performance.
```
@jit(nopython=True)
def laplace2d_SOR(p, pn, l2_target, omega):
'''Solves the Laplace equation using SOR with a 5-point stencil
Parameters:
----------
p: 2D array of float
Initial potential distribution
pn: 2D array of float
Allocated array for previous potential distribution
l2_target: float
Stopping criterion
omega: float
Relaxation parameter
Returns:
-------
p: 2D array of float
Potential distribution after relaxation
'''
iterations = 0
iter_diff = l2_target + 1 #initialize iter_diff to be larger than l2_target
denominator = 0.0
ny, nx = p.shape
l2_diff = numpy.zeros(20000)
while iter_diff > l2_target:
for j in range(ny):
for i in range(nx):
pn[j,i] = p[j,i]
iter_diff = 0.0
denominator = 0.0
for j in range(1,ny-1):
for i in range(1,nx-1):
p[j,i] = (1-omega)*p[j,i] + omega*.25 * (p[j,i-1] + p[j,i+1] + p[j-1,i] + p[j+1,i])
#Neumann 2nd-order BC
for j in range(1,ny-1):
p[j,-1] = .25 * (2*p[j,-2] + p[j+1,-1] + p[j-1, -1])
for j in range(ny):
for i in range(nx):
iter_diff += (p[j,i] - pn[j,i])**2
denominator += (pn[j,i]*pn[j,i])
iter_diff /= denominator
iter_diff = iter_diff**0.5
l2_diff[iterations] = iter_diff
iterations += 1
return p, iterations, l2_diff
```
That wasn't too bad at all. Let's try this out first with $\omega = 1$ and check that it matches the Gauss-Seidel results from above.
```
l2_target = 1e-8
omega = 1
p, iterations, l2_diffSOR = laplace2d_SOR(p0.copy(), p0.copy(), l2_target, omega)
print("Numba SOR method took {} iterations\
at tolerance {} with omega = {}".format(iterations, l2_target, omega))
```
We have the exact same number of iterations as Gauss-Seidel. That's a good sign that things are working as expected.
Now let's try to over-relax the solution and see what happens. To start, let's try $\omega = 1.5$.
```
l2_target = 1e-8
omega = 1.5
p, iterations, l2_diffSOR = laplace2d_SOR(p0.copy(), p0.copy(), l2_target, omega)
print("Numba SOR method took {} iterations\
at tolerance {} with omega = {}".format(iterations, l2_target, omega))
```
Wow! That really did the trick! We dropped from 13939 iterations down to 7108. Now we're really cooking! Let's try `%%timeit` on SOR.
```
%%timeit
laplace2d_SOR(p0.copy(), p0.copy(), l2_target, omega)
```
Things continue to speed up. But we can do even better!
### Tuned SOR
Above, we picked $\omega=1.5$ arbitrarily, but we would like to over-relax the solution as much as possible without introducing instability, as that will result in the fewest number of iterations.
For square domains, it turns out that the ideal factor $\omega$ can be computed as a function of the number of nodes in one direction, e.g., `nx`.
\begin{equation}
\omega \approx \frac{2}{1+\frac{\pi}{nx}}
\end{equation}
This is not some arbitrary formula, but its derivation lies outside the scope of this course. (If you're curious and have some serious math chops, you can check out Reference 3 for more information). For now, let's try it out and see how it works.
```
l2_target = 1e-8
omega = 2./(1 + numpy.pi/nx)
p, iterations, l2_diffSORopt = laplace2d_SOR(p0.copy(), p0.copy(), l2_target, omega)
print("Numba SOR method took {} iterations\
at tolerance {} with omega = {:.4f}".format(iterations, l2_target, omega))
```
Wow! That's *very* fast. Also, $\omega$ is very close to the upper limit of 2. SOR tends to work fastest when $\omega$ approaches 2, but don't be tempted to push it. Set $\omega = 2$ and the walls will come crumbling down.
Let's see what `%%timeit` has for us now.
```
%%timeit
laplace2d_SOR(p0.copy(), p0.copy(), l2_target, omega)
```
Regardless of the hardware in which we tried this, the tuned SOR gave *big* speed-ups, compared to the Jacobi method (whether implemented with NumPy or Numba). Now you know why we told you at the end of [Lesson 1](http://nbviewer.ipython.org/github/numerical-mooc/numerical-mooc/blob/master/lessons/05_relax/05_01_2D.Laplace.Equation.ipynb) that the Jacobi method is the *worst* iterative solver and almost never used.
Just to convince ourselves that everything is OK, let's check the error after the 1,110 iterations of tuned SOR:
```
L2_rel_error(p,pan)
```
Looking very good, indeed.
We didn't explain it in any detail, but notice the very interesting implication of Equation $(5)$: the ideal relaxation factor is a function of the grid size.
Also keep in mind that the formula only works for square domains with uniform grids. If your problem has an irregular geometry, you will need to find a good value of $\omega$ by numerical experiments.
## Decay of the difference between iterates
In the [Poisson Equation notebook](./05_02_2D.Poisson.Equation.ipynb), we noticed how the norm of the difference between consecutive iterations first dropped quite fast, then settled for a more moderate decay rate. With Gauss-Seidel, SOR and tuned SOR, we reduced the number of iterations required to reach the stopping criterion. Let's see how that reflects on the time history of the difference between consecutive solutions.
```
pyplot.figure(figsize=(8,8))
pyplot.xlabel(r'iterations', fontsize=18)
pyplot.ylabel(r'$L_2$-norm', fontsize=18)
pyplot.semilogy(numpy.trim_zeros(l2_diffJ,'b'),
'k-', lw=2, label='Jacobi')
pyplot.semilogy(numpy.trim_zeros(l2_diffGS,'b'),
'k--', lw=2, label='Gauss-Seidel')
pyplot.semilogy(numpy.trim_zeros(l2_diffSOR,'b'),
'g-', lw=2, label='SOR')
pyplot.semilogy(numpy.trim_zeros(l2_diffSORopt,'b'),
'g--', lw=2, label='Optimized SOR')
pyplot.legend(fontsize=16);
```
The Jacobi method starts out with very fast convergence, but then it settles into a slower rate. Gauss-Seidel shows a faster rate in the first few thousand iterations, but it seems to be slowing down towards the end. SOR is a lot faster to converge, though, and optimized SOR just plunges down!
## References
1. [Gonsalves, Richard J. Computational Physics I. State University of New York, Buffalo: (2011): Section 3.1 ](http://www.physics.buffalo.edu/phy410-505/2011/index.html)
2. Moin, Parviz, "Fundamentals of Engineering Numerical Analysis," Cambridge University Press, 2nd edition (2010).
3. Young, David M. "A bound for the optimum relaxation factor for the successive overrelaxation method." Numerische Mathematik 16.5 (1971): 408-413.
```
from IPython.core.display import HTML
css_file = '../../styles/numericalmoocstyle.css'
HTML(open(css_file, "r").read())
```
| true |
code
| 0.648383 | null | null | null | null |
|
## pyHail MESH Animation
This code utilizes the pyHAIL package to plot MESH, or the "maximum expected size of hail", grid the plots, and then create an animation with the plots.
```
from __future__ import print_function
import warnings
import warnings
warnings.filterwarnings('ignore')
"""
MESH sub-module of pyhail
Contains the single pol MESH retrieval for gridded radar data.
Required reflectivity and temperature data.
Joshua Soderholm - 15 June 2018
"""
import os
import netCDF4
import numpy as np
import pyart
import pyhail as ph
from pyhail import common
from pyhail import mesh
from pylab import *
import pyart, boto3, tempfile, os, shutil, datetime, matplotlib
import cartopy.crs as ccrs
import cartopy.feature as cfeature
import pyart
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
from time import time
from datetime import datetime
from dateutil import tz
import os
import cartopy.crs as ccrs
import matplotlib.colors as colors
import cartopy.io.shapereader as shpreader
from skewt import SkewT
import glob
from glob import glob
from botocore.handlers import disable_signing
from matplotlib.animation import FuncAnimation
# from cpol_processing import processing as cpol_prc
from pyhail import hsda, hdr, mesh, common
# Obtaining radar scans...
def get_radar_scan(station='KLOT', date=None, key_index=-20):
'''
Function will pull the latest radar scan from any radar site using
Amazon S3.
----------
Station = Four letter NEXRAD identifier
Example: 'KEPZ'
Date = default is none for current date, else enter date in format "YYYY/MM/DD"
Ex: date ='2013/11/17
Key_index = Number of keys you want pulled from most recent scan.
Ex: key_index = -15 would pull ht most recent 15 scans
'''
# Creating a bucket and a client to be able to pull data from AWS and setting it as unsigned
bucket = 'noaa-nexrad-level2'
s3 = boto3.resource('s3')
s3.meta.client.meta.events.register('choose-signer.s3.*', disable_signing)
# Connects the bucket create above with radar data
aws_radar = s3.Bucket(bucket)
# Setting the date and time to current...
# This will allow for allow the current date's radar scands to be pulled
if date == None:
target_string = datetime.datetime.utcnow().strftime('%Y/%m/%d/'+station)
else:
target_string = date+'/'+station
for obj in aws_radar.objects.filter(Prefix= target_string):
'{0}:{1}'.format(aws_radar.name, obj.key)
my_list_of_keys = [this_object.key for this_object in aws_radar.objects.filter(Prefix= target_string)]
keys = my_list_of_keys[key_index:]
for key in keys:
if 'MDM' in key:
keys.remove(key)
print(keys)
return aws_radar, keys
aws_radar, keys = get_radar_scan(station='KLOT', date='2019/05/27', key_index=-400)
out_path_dir = 'home/amedendorp/Desktop/april182013'
nk = keys[175:210] #:210
nk
localfile = tempfile.NamedTemporaryFile()
aws_radar.download_file(keys[0], localfile.name)
radar = pyart.io.read(localfile.name)
radar.fields.keys()
# Turning the data into grid data and saving it to a folder...
# If the grids are already created, there is no need to run this code block again.
def get_grid(aws_radar, nk):
localfile = tempfile.NamedTemporaryFile()
aws_radar.download_file(nk, localfile.name)
radar = pyart.io.read(localfile.name)
# Create rainfall rate field
# Mask out last 10 gates of each ray, this removes the "ring" around the radar.
radar.fields['reflectivity']['data'][:, -10:] = np.ma.masked
gatefilter = pyart.filters.GateFilter(radar)
gatefilter.exclude_transition()
gatefilter.exclude_masked('reflectivity')
grid = pyart.map.grid_from_radars(
(radar, ), grid_shape=(16, 300, 300),
grid_limits=((0, 15000), (-123000.0, 123000.0), (-123000.0, 123000.0)),
fields=['reflectivity'], weighting_function='Barnes2',
gridding_algo='map_gates_to_grid',
h_factor=0., nb=0.6, bsp=1., min_radius=500., gatefilters=(gatefilter, ))
del radar
return grid
for num,key in enumerate(nk):
print('saving grid', num)
grid = get_grid(aws_radar, key)
name = os.path.join('/home/amedendorp/Desktop/MESH/MESH_grid_' + str(num).zfill(3) + '.nc')
pyart.io.write_grid(name, grid)
del grid
# If the code encounters a .tar file or any other unknown file, it will stop running.
# Every grid created before that will be preserved.
from glob import glob
files = glob('/home/amedendorp/Desktop/MESH/MESH_grid_*')
files.sort()
reader = shpreader.Reader('/home/amedendorp/Downloads/countyl010g_shp_nt00964/countyl010g.shp')
counties = list(reader.geometries())
COUNTIES = cfeature.ShapelyFeature(counties, ccrs.PlateCarree())
# This code was created using a modified version of pyART. The only thing that will change versus default
# pyART is the thickness and color of the lat and lon lines, and the county and state outlines.
def rr_animation(nframe):
plt.clf()
nfile = files[nframe]
radar = pyart.io.read_grid(nfile)
# Converting the default UTC time to local time...
# Converts to 24-hour time. No AM or PM.
utc = netCDF4.num2date(radar.time['data'][0],
radar.time['units'])
print(str(utc))
z = datetime.strptime(str(utc), '%Y-%m-%d %H:%M:%S.%f')
from_zone = tz.tzutc()
to_zone = tz.tzlocal()
z = z.replace(tzinfo=from_zone)
central = z.astimezone(to_zone)
t = datetime.strftime(central, '%Y-%m-%dT%H:%M:%S.%f')
title = ('KLOT ' + str(radar.z['data'][0]/1000) + ' km ' + t + ' \n'
+ ' Maximum Expected Size of Hail')
hail = mesh.main(grid=radar, ref_name='reflectivity',
snd_input='/home/amedendorp/Desktop/Sounding.nc',
sonde_temp='temp', sonde_height='height',
out_ffn=nfile)
projection = ccrs.PlateCarree()
ax = plt.axes(projection=projection)
# Plot site locations...
ANL_lon, ANL_lat = -87.981810, 41.713969
NW_lon, NW_lat = -87.675885, 42.057888
Naperville_lon, Naperville_lat = -88.181798, 41.738107
IBP_lon, IBP_lat = -87.687151, 41.606367
plt.plot([ANL_lon], [ANL_lat], color='black', marker= '.')
plt.plot([NW_lon], [NW_lat], color='black', marker= '.')
plt.plot([Naperville_lon], [Naperville_lat], color='black', marker= '.')
plt.plot([IBP_lon], [IBP_lat], color='black', marker= '.')
# Plot names of sites:
plt.text(ANL_lon + 0.01, ANL_lat - 0., 'ANL', horizontalalignment='left')
plt.text(NW_lon - 0.01, NW_lat - 0, 'Northwestern', horizontalalignment='right')
plt.text(Naperville_lon - 0.01, Naperville_lat + 0.01, 'Naperville', horizontalalignment='left')
plt.text(IBP_lon - 0.01, IBP_lat + 0.01, 'IBP', horizontalalignment='left')
display = pyart.graph.GridMapDisplay(hail)
display.plot_grid('MESH', level= 0, lat_lines=np.arange(41, 43, .5),
lon_lines=np.arange(-89, -86.5, .5), cmap='hot_r', vmax=55, vmin=0)
plt.rcParams.update({'axes.titlesize': '18'})
del radar, display
ax.add_feature(COUNTIES, facecolor='none', edgecolor='gray')
ax.add_feature(cfeature.LAKES, zorder=.5)
fig = plt.figure(figsize=[12,7])
# Match the frames to the amount of grids
sat_anim = FuncAnimation(fig, rr_animation, frames=34)
sat_anim.save('/home/amedendorp/Desktop/pyhailanimtest2.gif',
writer='imagemagick', fps=3)
plt.close
```
| true |
code
| 0.583856 | null | null | null | null |
|
```
__depends__=[]
__dest__="../results/f8.eps"
```
# Plot Terms in the Two-fluid EBTEL Equations
As part of our derivation of the two-fluid EBTEL equations, we'll plot the different terms of the two-fluid electron energy equation,
$$
\frac{L}{\gamma - 1}\frac{dp_e}{dt} = \psi_{TR} - (\mathcal{R}_C + \mathcal{R}_{TR}) + \frac{L}{\gamma - 1}k_Bn\nu_{ei}(T_i - T_e) + LQ_e.
$$
We want to plot each term as a function of time to show their relative contributions to the evolution of the electron energy.
```
import sys
import os
import subprocess
import numpy as np
import seaborn.apionly as sns
import astropy.constants as const
from matplotlib import ticker
import matplotlib.pyplot as plt
sys.path.append(os.path.join(os.environ['EXP_DIR'],'ebtelPlusPlus/rsp_toolkit/python'))
from xml_io import InputHandler,OutputHandler
%matplotlib inline
plt.rcParams.update({'figure.figsize' : [8,5]})
```
Configure the EBTEL run. We'll use $\tau=200$ s and $H_0=0.1$ erg cm$^{-3}$ s$^{-1}$, $L=40$ Mm, and Spitzer conduction.
```
ih = InputHandler(os.path.join(os.environ['EXP_DIR'],'ebtelPlusPlus','config','ebtel.example.cfg.xml'))
config_dict = ih.lookup_vars()
config_dict['calculate_dem'] = False
config_dict['save_terms'] = True
config_dict['use_flux_limiting'] = True
config_dict['use_adaptive_solver'] = True
config_dict['heating']['partition'] = 1.0
config_dict['heating']['background'] = 3.5e-5
config_dict['heating']['events'] = [
{'event':{'magnitude':0.1,'rise_start':0.0,'rise_end':100.0,'decay_start':100.0,'decay_end':200.0}}
]
config_dict['total_time'] = 5000.0
config_dict['tau'] = 0.1
config_dict['adaptive_solver_error'] = 1.0e-9
config_dict['saturation_limit'] = 1.0
config_dict['c1_cond0'] = 6.0
config_dict['c1_rad0'] = 0.6
config_dict['use_c1_grav_correction'] = True
config_dict['use_c1_loss_correction'] = True
config_dict['output_filename'] = '../results/_tmp_'
oh = OutputHandler(config_dict['output_filename']+'.xml',config_dict)
oh.print_to_xml()
```
Run the model.
```
subprocess.call([os.path.join(os.environ['EXP_DIR'],'ebtelPlusPlus','bin','ebtel++.run'),'-c',oh.output_filename])
```
Load the data.
```
data = np.loadtxt(oh.output_dict['output_filename'])
t = data[:,0]
Te = data[:,1]
Ti = data[:,2]
n = data[:,3]
q = data[:,-1]
data = np.loadtxt(oh.output_dict['output_filename']+'.terms')
fce = data[:,0]
fci = data[:,1]
r3 = data[:,2]
rad = data[:,3]
```
Define a function to calculate the Coulomb collision frequency according to [Braginskii (1965)](http://adsabs.harvard.edu/abs/1965RvPP....1..205B).
```
def calc_nu_ei(n,Te):
c1 = 16.*np.sqrt(np.pi)/3.
c2 = const.e.gauss.value**4/(const.m_e.cgs.value*const.m_p.cgs.value)
c3 = 2.*const.k_B.cgs.value*Te/const.m_e.cgs.value
colLog = 20.
return c1*c2*c3**(-3./2.)*n*colLog
```
Calculate the terms as given in the equation above.
```
delta_terms = []
delta_terms.append(fce/(config_dict['loop_length'])/(1.+Te/Ti))
delta_terms.append(-fci/(config_dict['loop_length'])*(Te/Ti)/(1.+Te/Ti))
delta_terms.append(-(Te/Ti*(r3+1.) + 1.)/(1.+Te/Ti)*n**2*rad)
#delta_terms.append(q)
tmp = np.zeros(len(Te))
for i in range(len(Te)):
tmp[i] = const.k_B.cgs.value/(5./3. - 1.)*n[i]*calc_nu_ei(n[i],Te[i])*(Ti[i] - Te[i])
delta_terms.append(tmp)
```
Make the figure.
```
labels = [r'$\mathrm{e}^{-}$ $\mathrm{thermal}$ $\mathrm{conduction}$',
r'$\mathrm{ion}$ $\mathrm{thermal}$ $\mathrm{conduction}$',
r'$\mathrm{radiation}$',r'$\mathrm{equilibration}$']
fig = plt.figure()
ax = fig.gca()
for i in range(len(delta_terms)):
ax.plot(t,delta_terms[i],color=sns.color_palette('deep')[i],label=labels[i])
ax.plot(t,1.0/(config_dict['loop_length'])*1./(1.+Te/Ti)*(fce + (r3*(config_dict['loop_length'])*(n**2)*rad)-Te/Ti*fci),
linestyle='dotted',color='k',label=r'$\psi_{TR}$')
ax.set_xscale('log')
ax.yaxis.set_major_locator(ticker.MaxNLocator(nbins=4))
ax.set_xlim([1,config_dict['total_time']])
ax.set_xlabel(r'$t$ $\mathrm{(s)}$')
ax.set_ylabel(r'$\Delta\bar{E}_e$ $(\mathrm{erg}$ $\mathrm{cm}^{-3}$ $\mathrm{s}^{-1})$')
ax.legend(loc='best')
plt.savefig(__dest__)
plt.show()
```
| true |
code
| 0.352153 | null | null | null | null |
|
```
# Allow us to load `open_cp` without installing
import sys, os.path
sys.path.insert(0, os.path.abspath(".."))
```
# Crime prediction from Hawkes processes
Here we continue to explore the EM algorithm for Hawkes processes, but now concentrating upon:
1. Mohler et al. "Randomized Controlled Field Trials of Predictive Policing". Journal of the American Statistical Association (2015) DOI:10.1080/01621459.2015.1077710
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
```
# Simulation of the process in a single cell
```
import open_cp.sources.sepp as source_sepp
process = source_sepp.SelfExcitingPointProcess(
background_sampler = source_sepp.HomogeneousPoissonSampler(rate=0.1),
trigger_sampler = source_sepp.ExponentialDecaySampler(intensity=0.5, exp_rate=10))
events = process.sample(0, 1000)
fig, ax = plt.subplots(figsize=(18,1))
ax.scatter(events, (np.random.random(len(events))-0.5) * 0.03, alpha=.5)
ax.set(xlim=[900, 1000], ylim=[-0.1,0.1])
```
## Model fitting for cells with varying background rate
We'll create 100 cells with varying background rate, but the same $\omega, \theta$. We use our library to perform this simulation.
```
rates = np.random.random(size=100)
simulation = source_sepp.GridHawkesProcess(rates, 0.5, 10)
cells = simulation.sample(0, 1000)
```
To simulate a steady state, we'll discard the first half of time in each cell.
```
for i in range(100):
times = cells[i]
cells[i] = times[times>=500] - 500
```
The number of events in each cell varies quite a lot.
```
min(len(t) for t in cells), max(len(t) for t in cells)
import open_cp.seppexp
def optimise(cells, initial_omega=10, iterations=100, time=500):
omega = initial_omega
theta = .5
mu = np.zeros_like(cells) + 0.5
for _ in range(iterations):
omega, theta, mu = open_cp.seppexp.maximisation(cells, omega, theta, mu, time)
return omega, theta, mu
def optimise_corrected(cells, initial_omega=10, iterations=100, time=500):
omega = initial_omega
theta = .5
mu = np.zeros_like(cells) + 0.5
for _ in range(iterations):
omega, theta, mu = open_cp.seppexp.maximisation_corrected(cells, omega, theta, mu, time)
return omega, theta, mu
omega, theta, mu = optimise(cells)
omega, theta
omegac, thetac, muc = optimise_corrected(cells)
omegac, thetac
def plot(rates, mu, ax, title):
ax.plot([0,1], [0,1], color="red", linewidth=1)
ax.scatter(rates, mu)
ax.set(xlim=[0,1], ylim=[0,np.max(mu)*1.05], xlabel="$\\mu$", ylabel="predicted $\\mu$",
title=title)
fig, ax = plt.subplots(ncols=2, figsize=(16,6))
plot(rates, mu, ax[0], "From EM algorithm")
plot(rates, muc,ax[1], "From EM algorithm with edge corrections")
```
Noting that our initial estimate for every $\mu$ is $0.5$, this is good convergence.
## More extreme parameters
However, if we try a rather smaller value of $\omega$, then the optimisation doesn't find the real parameters, tending to systematically over-estimate the background rate $\mu$ and under-estimate the aftershock rate.
```
rates = np.random.random(size=100)
simulation = source_sepp.GridHawkesProcess(rates, 0.5, .1)
cells = simulation.sample(0, 1000)
for i in range(100):
times = cells[i]
cells[i] = times[times>=500] - 500
omega, theta, mu = optimise(cells, .1, 100)
omega, theta
omegac, thetac, muc = optimise_corrected(cells, .1, 100)
omegac, thetac
fig, ax = plt.subplots(ncols=2, figsize=(16,6))
plot(rates, mu, ax[0], "From EM algorithm")
plot(rates, muc, ax[1], "From EM algorithm with edge corrections")
```
## Sampling the whole process, not just a "steady state"
```
rates = np.random.random(size=100)
simulation = source_sepp.GridHawkesProcess(rates, 0.5, 10)
cells = simulation.sample(0, 1000)
omega, theta, mu = optimise(cells, 1, 100, 1000)
omega, theta
omegac, thetac, muc = optimise_corrected(cells, 1, 100, 1000)
omegac, thetac
fig, ax = plt.subplots(ncols=2, figsize=(16,6))
plot(rates, mu, ax[0], "From EM algorithm")
plot(rates, muc, ax[1], "From EM algorithm with edge corrections")
```
## Taking a smaller sample
```
rates = np.random.random(size=100)
simulation = source_sepp.GridHawkesProcess(rates, 0.5, 10)
cells = simulation.sample(0, 350)
omega, theta, mu = optimise(cells, 1, 100, 350)
omega, theta
omegac, thetac, muc = optimise_corrected(cells, 1, 100, 350)
omegac, thetac
fig, ax = plt.subplots(ncols=2, figsize=(16,6))
plot(rates, mu, ax[0], "From EM algorithm")
plot(rates, muc, ax[1], "From EM algorithm with edge corrections")
```
| true |
code
| 0.684976 | null | null | null | null |
|
# Qiskit Aer: Applying noise to custom unitary gates
The latest version of this notebook is available on https://github.com/Qiskit/qiskit-tutorial.
## Introduction
This notebook shows how to add custom unitary gates to a quantum circuit, and use them for noise simulations in Qiskit Aer.
```
from qiskit import execute, QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit.quantum_info import Operator, average_gate_fidelity
from qiskit.providers.aer import QasmSimulator
from qiskit.providers.aer.noise import NoiseModel, amplitude_damping_error
from qiskit.tools.visualization import plot_histogram
```
## Creating matrix operators
We can use the `Operator` class in `qiskit.quantum_info` to represent arbitrary matrix operators. If the operator is unitary it can then be added to a quantum circuit and used for simulation on Qiskit Aer.
Lets create two operators below for a CNOT gate and an iSWAP gate:
$$\mbox{CNOT} = \left(\begin{array}
& 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}\right), \quad
\mbox{iSWAP} = \left(\begin{array}
& 1 & 0 & 0 & 0 \\
0 & 0 & i & 0 \\
0 & i & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}\right)$$
```
# CNOT matrix operator with qubit-0 as control and qubit-1 as target
cx_op = Operator([[1, 0, 0, 0],
[0, 0, 0, 1],
[0, 0, 1, 0],
[0, 1, 0, 0]])
# iSWAP matrix operator
iswap_op = Operator([[1, 0, 0, 0],
[0, 0, 1j, 0],
[0, 1j, 0, 0],
[0, 0, 0, 1]])
```
**Note:** The matrix is specified with respect to the tensor product $U_{b}\otimes U_{a}$ for qubits specified by list `[a, b]`.
## Using operators in circuits
Let us demonstrate how these can be used in a circuit. We will consider an example of implementing a CNOT gate decomposed in terms of single-qubit gates and the iSWAP gate as follows.
```
# CNOT in terms of iSWAP and single-qubit gates
cx_circ = QuantumCircuit(2)
# Add gates
cx_circ.sdg(1)
cx_circ.h(1)
cx_circ.sdg(0)
cx_circ.unitary(iswap_op, [0, 1], label='iswap')
cx_circ.sdg(0)
cx_circ.h(0)
cx_circ.sdg(0)
cx_circ.unitary(iswap_op, [0, 1], label='iswap')
cx_circ.s(1)
print(cx_circ)
```
Note that we have assigned an optional *label* of `"iswap"` to the unitary when it is inserted. This allows us to identify this unitary in a Qiskit Aer `NoiseModel` so that we can add errors to these custom unitary gates in noisy circuit simulations.
We can confirm this circuit returns the correct output using the `Operator` class as a simulator for the circuit:
```
# Simulate the unitary for the circuit using Operator:
unitary = Operator(cx_circ)
print(unitary)
```
And to confirm the output is correct we can compute the average gate fidelity:
```
f_ave = average_gate_fidelity(cx_op, unitary)
print("Average Gate Fidelity: F = {:f}".format(f_ave))
```
## Creating a custom unitary in a noise model
The Qiskit Aer `QasmSimulator` supports simulation of arbitrary unitary operators directly as specified by the `"unitary"` in the basis gates.
```
'unitary' in QasmSimulator().configuration().basis_gates
```
This allows us to add noise models to arbitrary unitaries in our simulation when we identify them using the optional `label` argument of `QuantumCircuit.unitary`.
We will now do this by creating a `NoiseModel` that includes a quantum error channel on our custom iSWAP gate. For our example we will create a 2-qubit error consisting of two single-qubit amplitude damping channels with different damping parameters. For now we will assume all the other circuit instructions are ideal.
```
# Error parameters
param_q0 = 0.05 # damping parameter for qubit-0
param_q1 = 0.1 # damping parameter for qubit-1
# Construct the error
qerror_q0 = amplitude_damping_error(param_q0)
qerror_q1 = amplitude_damping_error(param_q1)
iswap_error = qerror_q1.tensor(qerror_q0)
# Build the noise model by adding the error to the "iswap" gate
noise_model = NoiseModel()
noise_model.add_all_qubit_quantum_error(iswap_error, 'iswap')
```
Note that when we add an error to a custom label such as `"iswap"` the `NoiseModel` does not know what gate this label is supposed to apply to, so we must manually add the desired gate string to the noise model `basis_gates`. This ensures that the compiler will unroll to the correct basis gates for the noise model simulation. This can done using the `NoiseModel.add_basis_gates` function:
```
noise_model.add_basis_gates(['unitary'])
print(noise_model.basis_gates)
```
By default the basis gates of a noise model are `['cx','id','u3']` plus any standard `QasmSimulator` basis gates that are added to the noise model.
## Simulating a custom unitary noise model
Let us first take our previous CX circuit and add an initial Hadamard gate and final measurement to create a Bell-state preparation circuit that we may simulator on the `QasmSimulator` both for the ideal and noisy case:
```
# Bell state circuit where iSWAPS should be inserted at barrier locations
bell_circ = QuantumCircuit(2, 2, name='bell')
bell_circ.h(0)
bell_circ = bell_circ + cx_circ
bell_circ.measure([0,1], [0,1])
print(bell_circ)
```
### Ideal output
Let's first see the ideal output. Since this generates a Bell-state we expect two peaks for 00 and 11.
```
# Execute on the simulator without noise
job = execute(bell_circ, QasmSimulator(),
basis_gates=noise_model.basis_gates)
ideal_result = job.result()
ideal_counts = ideal_result.get_counts(bell_circ)
plot_histogram(ideal_counts, title='Ideal output for iSWAP bell-state preparation')
```
### Noisy circuit execution
Finally, let's now simulate it with our custom noise model. Since there is a small amplitude damping error on the two-qubit gates we expect small additional peaks for the 01 and 10 outcome probabilities.
```
# Execute on the simulator without noise
job = execute(bell_circ, QasmSimulator(),
basis_gates=noise_model.basis_gates,
noise_model=noise_model)
noise_result = job.result()
noise_counts = noise_result.get_counts(bell_circ)
plot_histogram(noise_counts, title='Noisy output for iSWAP bell-state preparation')
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
```
| true |
code
| 0.761627 | null | null | null | null |
|
# 🔪 JAX - The Sharp Bits 🔪
*levskaya@ mattjj@*
When walking about the countryside of [Italy](https://iaml.it/blog/jax-intro), the people will not hesitate to tell you that __JAX__ has _"una anima di pura programmazione funzionale"_.
__JAX__ is a language for __expressing__ and __composing__ __transformations__ of numerical programs. As such it needs to control the _unwanted proliferation_ of __side-effects__ in its programs so that analysis and transformation of its computations remain tractable!
This requires us to write code in a _functional_ style with _explicit_ descriptions of how the state of a program changes, which results in __several important differences__ to how you might be used to programming in Numpy, Tensorflow or Pytorch.
Herein we try to cover the most frequent points of trouble that users encounter when starting out in __JAX__.
```
import numpy as onp
from jax import grad, jit
from jax import lax
from jax import random
import jax
import jax.numpy as np
import matplotlib as mpl
from matplotlib import pyplot as plt
from matplotlib import rcParams
rcParams['image.interpolation'] = 'nearest'
rcParams['image.cmap'] = 'viridis'
rcParams['axes.grid'] = False
```
## 🔪 In-Place Updates
In Numpy you're used to doing this:
```
numpy_array = onp.zeros((3,3), dtype=np.float32)
print("original array:")
print(numpy_array)
# In place, mutating update
numpy_array[1, :] = 1.0
print("updated array:")
print(numpy_array)
```
If we try to update a JAX device array in-place, however, we get an __error__! (☉_☉)
```
jax_array = np.zeros((3,3), dtype=np.float32)
# In place update of JAX's array will yield an error!
jax_array[1, :] = 1.0
```
__What gives?!__
Allowing mutation of variables in-place makes program analysis and transformation very difficult. JAX requires a pure functional expression of a numerical program.
Instead, JAX offers the _functional_ update functions: [__index_update__](https://jax.readthedocs.io/en/latest/_autosummary/jax.ops.index_update.html#jax.ops.index_update), [__index_add__](https://jax.readthedocs.io/en/latest/_autosummary/jax.ops.index_add.html#jax.ops.index_add), [__index_min__](https://jax.readthedocs.io/en/latest/_autosummary/jax.ops.index_min.html#jax.ops.index_min), [__index_max__](https://jax.readthedocs.io/en/latest/_autosummary/jax.ops.index_max.html#jax.ops.index_max), and the [__index__](https://jax.readthedocs.io/en/latest/_autosummary/jax.ops.index.html#jax.ops.index) helper.
️⚠️ inside `jit`'d code and `lax.while_loop` or `lax.fori_loop` the __size__ of slices can't be functions of argument _values_ but only functions of argument _shapes_ -- the slice start indices have no such restriction. See the below __Control Flow__ Section for more information on this limitation.
```
from jax.ops import index, index_add, index_update
```
### index_update
If the __input values__ of __index_update__ aren't reused, __jit__-compiled code will perform these operations _in-place_.
```
jax_array = np.zeros((3, 3))
print("original array:")
print(jax_array)
new_jax_array = index_update(jax_array, index[1, :], 1.)
print("old array unchanged:")
print(jax_array)
print("new array:")
print(new_jax_array)
```
### index_add
If the __input values__ of __index_update__ aren't reused, __jit__-compiled code will perform these operations _in-place_.
```
print("original array:")
jax_array = np.ones((5, 6))
print(jax_array)
new_jax_array = index_add(jax_array, index[::2, 3:], 7.)
print("new array post-addition:")
print(new_jax_array)
```
## 🔪 Random Numbers
> _If all scientific papers whose results are in doubt because of bad
> `rand()`s were to disappear from library shelves, there would be a
> gap on each shelf about as big as your fist._ - Numerical Recipes
### RNGs and State
You're used to _stateful_ pseudorandom number generators (PRNGs) from numpy and other libraries, which helpfully hide a lot of details under the hood to give you a ready fountain of pseudorandomness:
```
print(onp.random.random())
print(onp.random.random())
print(onp.random.random())
```
Underneath the hood, numpy uses the [Mersenne Twister](https://en.wikipedia.org/wiki/Mersenne_Twister) PRNG to power its pseudorandom functions. The PRNG has a period of $2^{19937-1}$ and at any point can be described by __624 32bit unsigned ints__ and a __position__ indicating how much of this "entropy" has been used up.
```
onp.random.seed(0)
rng_state = onp.random.get_state()
#print(rng_state)
# --> ('MT19937', array([0, 1, 1812433255, 1900727105, 1208447044,
# 2481403966, 4042607538, 337614300, ... 614 more numbers...,
# 3048484911, 1796872496], dtype=uint32), 624, 0, 0.0)
```
This pseudorandom state vector is automagically updated behind the scenes every time a random number is needed, "consuming" 2 of the uint32s in the Mersenne twister state vector:
```
_ = onp.random.uniform()
rng_state = onp.random.get_state()
#print(rng_state)
# --> ('MT19937', array([2443250962, 1093594115, 1878467924,
# ..., 2648828502, 1678096082], dtype=uint32), 2, 0, 0.0)
# Let's exhaust the entropy in this PRNG statevector
for i in range(311):
_ = onp.random.uniform()
rng_state = onp.random.get_state()
#print(rng_state)
# --> ('MT19937', array([2443250962, 1093594115, 1878467924,
# ..., 2648828502, 1678096082], dtype=uint32), 624, 0, 0.0)
# Next call iterates the RNG state for a new batch of fake "entropy".
_ = onp.random.uniform()
rng_state = onp.random.get_state()
# print(rng_state)
# --> ('MT19937', array([1499117434, 2949980591, 2242547484,
# 4162027047, 3277342478], dtype=uint32), 2, 0, 0.0)
```
The problem with magic PRNG state is that it's hard to reason about how it's being used and updated across different threads, processes, and devices, and it's _very easy_ to screw up when the details of entropy production and consumption are hidden from the end user.
The Mersenne Twister PRNG is also known to have a [number](https://cs.stackexchange.com/a/53475) of problems, it has a large 2.5Kb state size, which leads to problematic [initialization issues](https://dl.acm.org/citation.cfm?id=1276928). It [fails](http://www.pcg-random.org/pdf/toms-oneill-pcg-family-v1.02.pdf) modern BigCrush tests, and is generally slow.
### JAX PRNG
JAX instead implements an _explicit_ PRNG where entropy production and consumption are handled by explicitly passing and iterating PRNG state. JAX uses a modern [Three-fry counter-based PRNG](https://github.com/google/jax/blob/master/design_notes/prng.md) that's __splittable__. That is, its design allows us to __fork__ the PRNG state into new PRNGs for use with parallel stochastic generation.
The random state is described by two unsigned-int32s that we call a __key__:
```
from jax import random
key = random.PRNGKey(0)
key
```
JAX's random functions produce pseudorandom numbers from the PRNG state, but __do not__ change the state!
Reusing the same state will cause __sadness__ and __monotony__, depriving the enduser of __lifegiving chaos__:
```
print(random.normal(key, shape=(1,)))
print(key)
# No no no!
print(random.normal(key, shape=(1,)))
print(key)
```
Instead, we __split__ the PRNG to get usable __subkeys__ every time we need a new pseudorandom number:
```
print("old key", key)
key, subkey = random.split(key)
normal_pseudorandom = random.normal(subkey, shape=(1,))
print(" \---SPLIT --> new key ", key)
print(" \--> new subkey", subkey, "--> normal", normal_pseudorandom)
```
We propagate the __key__ and make new __subkeys__ whenever we need a new random number:
```
print("old key", key)
key, subkey = random.split(key)
normal_pseudorandom = random.normal(subkey, shape=(1,))
print(" \---SPLIT --> new key ", key)
print(" \--> new subkey", subkey, "--> normal", normal_pseudorandom)
```
We can generate more than one __subkey__ at a time:
```
key, *subkeys = random.split(key, 4)
for subkey in subkeys:
print(random.normal(subkey, shape=(1,)))
```
## 🔪 Control Flow
### ✔ python control_flow + autodiff ✔
If you just want to apply `grad` to your python functions, you can use regular python control-flow constructs with no problems, as if you were using [Autograd](https://github.com/hips/autograd) (or Pytorch or TF Eager).
```
def f(x):
if x < 3:
return 3. * x ** 2
else:
return -4 * x
print(grad(f)(2.)) # ok!
print(grad(f)(4.)) # ok!
```
### python control flow + JIT
Using control flow with `jit` is more complicated, and by default it has more constraints.
This works:
```
@jit
def f(x):
for i in range(3):
x = 2 * x
return x
print(f(3))
```
So does this:
```
@jit
def g(x):
y = 0.
for i in range(x.shape[0]):
y = y + x[i]
return y
print(g(np.array([1., 2., 3.])))
```
But this doesn't, at least by default:
```
@jit
def f(x):
if x < 3:
return 3. * x ** 2
else:
return -4 * x
# This will fail!
try:
f(2)
except Exception as e:
print("ERROR:", e)
```
__What gives!?__
When we `jit`-compile a function, we usually want to compile a version of the function that works for many different argument values, so that we can cache and reuse the compiled code. That way we don't have to re-compile on each function evaluation.
For example, if we evaluate an `@jit` function on the array `np.array([1., 2., 3.], np.float32)`, we might want to compile code that we can reuse to evaluate the function on `np.array([4., 5., 6.], np.float32)` to save on compile time.
To get a view of your Python code that is valid for many different argument values, JAX traces it on _abstract values_ that represent sets of possible inputs. There are [multiple different levels of abstraction](https://github.com/google/jax/blob/master/jax/abstract_arrays.py), and different transformations use different abstraction levels.
By default, `jit` traces your code on the `ShapedArray` abstraction level, where each abstract value represents the set of all array values with a fixed shape and dtype. For example, if we trace using the abstract value `ShapedArray((3,), np.float32)`, we get a view of the function that can be reused for any concrete value in the corresponding set of arrays. That means we can save on compile time.
But there's a tradeoff here: if we trace a Python function on a `ShapedArray((), np.float32)` that isn't committed to a specific concrete value, when we hit a line like `if x < 3`, the expression `x < 3` evaluates to an abstract `ShapedArray((), np.bool_)` that represents the set `{True, False}`. When Python attempts to coerce that to a concrete `True` or `False`, we get an error: we don't know which branch to take, and can't continue tracing! The tradeoff is that with higher levels of abstraction we gain a more general view of the Python code (and thus save on re-compilations), but we require more constraints on the Python code to complete the trace.
The good news is that you can control this tradeoff yourself. By having `jit` trace on more refined abstract values, you can relax the traceability constraints. For example, using the `static_argnums` argument to `jit`, we can specify to trace on concrete values of some arguments. Here's that example function again:
```
def f(x):
if x < 3:
return 3. * x ** 2
else:
return -4 * x
f = jit(f, static_argnums=(0,))
print(f(2.))
```
Here's another example, this time involving a loop:
```
def f(x, n):
y = 0.
for i in range(n):
y = y + x[i]
return y
f = jit(f, static_argnums=(1,))
f(np.array([2., 3., 4.]), 2)
```
In effect, the loop gets statically unrolled. JAX can also trace at _higher_ levels of abstraction, like `Unshaped`, but that's not currently the default for any transformation
️⚠️ **functions with argument-__value__ dependent shapes**
These control-flow issues also come up in a more subtle way: numerical functions we want to __jit__ can't specialize the shapes of internal arrays on argument _values_ (specializing on argument __shapes__ is ok). As a trivial example, let's make a function whose output happens to depend on the input variable `length`.
```
def example_fun(length, val):
return np.ones((length,)) * val
# un-jit'd works fine
print(example_fun(5, 4))
bad_example_jit = jit(example_fun)
# this will fail:
try:
print(bad_example_jit(10, 4))
except Exception as e:
print("error!", e)
# static_argnums tells JAX to recompile on changes at these argument positions:
good_example_jit = jit(example_fun, static_argnums=(0,))
# first compile
print(good_example_jit(10, 4))
# recompiles
print(good_example_jit(5, 4))
```
`static_argnums` can be handy if `length` in our example rarely changes, but it would be disastrous if it changed a lot!
Lastly, if your function has global side-effects, JAX's tracer can cause weird things to happen. A common gotcha is trying to print arrays inside __jit__'d functions:
```
@jit
def f(x):
print(x)
y = 2 * x
print(y)
return y
f(2)
```
### Structured control flow primitives
There are more options for control flow in JAX. Say you want to avoid re-compilations but still want to use control flow that's traceable, and that avoids un-rolling large loops. Then you can use these 4 structured control flow primitives:
- `lax.cond` _differentiable_
- `lax.while_loop` __fwd-mode-differentiable__
- `lax.fori_loop` __fwd-mode-differentiable__
- `lax.scan` _differentiable_
#### cond
python equivalent:
```
def cond(pred, true_operand, true_fun, false_operand, false_fun):
if pred:
return true_fun(true_operand)
else:
return false_fun(false_operand)
```
```
from jax import lax
operand = np.array([0.])
lax.cond(True, operand, lambda x: x+1, operand, lambda x: x-1)
# --> array([1.], dtype=float32)
lax.cond(False, operand, lambda x: x+1, operand, lambda x: x-1)
# --> array([-1.], dtype=float32)
```
#### while_loop
python equivalent:
```
def while_loop(cond_fun, body_fun, init_val):
val = init_val
while cond_fun(val):
val = body_fun(val)
return val
```
```
init_val = 0
cond_fun = lambda x: x<10
body_fun = lambda x: x+1
lax.while_loop(cond_fun, body_fun, init_val)
# --> array(10, dtype=int32)
```
#### fori_loop
python equivalent:
```
def fori_loop(start, stop, body_fun, init_val):
val = init_val
for i in range(start, stop):
val = body_fun(i, val)
return val
```
```
init_val = 0
start = 0
stop = 10
body_fun = lambda i,x: x+i
lax.fori_loop(start, stop, body_fun, init_val)
# --> array(45, dtype=int32)
```
#### Summary
$$
\begin{array} {r|rr}
\hline \
\textrm{construct}
& \textrm{jit}
& \textrm{grad} \\
\hline \
\textrm{if} & ❌ & ✔ \\
\textrm{for} & ✔* & ✔\\
\textrm{while} & ✔* & ✔\\
\textrm{lax.cond} & ✔ & ✔\\
\textrm{lax.while_loop} & ✔ & \textrm{fwd}\\
\textrm{lax.fori_loop} & ✔ & \textrm{fwd}\\
\textrm{lax.scan} & ✔ & ✔\\
\hline
\end{array}
$$
<center>$\ast$ = argument-__value__-independent loop condition - unrolls the loop </center>
## 🔪 Convolutions
JAX and XLA offer the very general N-dimensional __conv_general_dilated__ function, but it's not very obvious how to use it. We'll give some examples of the common use-cases. There are also the convenience functions `lax.conv` and `lax.conv_general_padding` for the most common kinds of convolutions.
A survey of the family of convolutional operators, [a guide to convolutional arithmetic](https://arxiv.org/abs/1603.07285) is highly recommended reading!
Let's define a simple diagonal edge kernel:
```
# 2D kernel - HWIO layout
kernel = onp.zeros((3, 3, 3, 3), dtype=np.float32)
kernel += onp.array([[1, 1, 0],
[1, 0,-1],
[0,-1,-1]])[:, :, onp.newaxis, onp.newaxis]
print("Edge Conv kernel:")
plt.imshow(kernel[:, :, 0, 0]);
```
And we'll make a simple synthetic image:
```
# NHWC layout
img = onp.zeros((1, 200, 198, 3), dtype=np.float32)
for k in range(3):
x = 30 + 60*k
y = 20 + 60*k
img[0, x:x+10, y:y+10, k] = 1.0
print("Original Image:")
plt.imshow(img[0]);
```
### lax.conv and lax.conv_with_general_padding
These are the simple convenience functions for convolutions
️⚠️ The convenience `lax.conv`, `lax.conv_with_general_padding` helper function assume __NCHW__ images and __IOHW__ kernels.
```
out = lax.conv(np.transpose(img,[0,3,1,2]), # lhs = NCHW image tensor
np.transpose(kernel,[2,3,0,1]), # rhs = IOHW conv kernel tensor
(1, 1), # window strides
'SAME') # padding mode
print("out shape: ", out.shape)
print("First output channel:")
plt.figure(figsize=(10,10))
plt.imshow(onp.array(out)[0,0,:,:]);
out = lax.conv_with_general_padding(
np.transpose(img,[0,3,1,2]), # lhs = NCHW image tensor
np.transpose(kernel,[2,3,0,1]), # rhs = IOHW conv kernel tensor
(1, 1), # window strides
((2,2),(2,2)), # general padding 2x2
(1,1), # lhs/image dilation
(1,1)) # rhs/kernel dilation
print("out shape: ", out.shape)
print("First output channel:")
plt.figure(figsize=(10,10))
plt.imshow(onp.array(out)[0,0,:,:]);
```
### Dimension Numbers define dimensional layout for conv_general_dilated
The important argument is the 3-tuple of axis layout arguments:
(Input Layout, Kernel Layout, Output Layout)
- __N__ - batch dimension
- __H__ - spatial height
- __W__ - spatial height
- __C__ - channel dimension
- __I__ - kernel _input_ channel dimension
- __O__ - kernel _output_ channel dimension
⚠️ To demonstrate the flexibility of dimension numbers we choose a __NHWC__ image and __HWIO__ kernel convention for `lax.conv_general_dilated` below.
```
dn = lax.conv_dimension_numbers(img.shape, # only ndim matters, not shape
kernel.shape, # only ndim matters, not shape
('NHWC', 'HWIO', 'NHWC')) # the important bit
print(dn)
```
#### SAME padding, no stride, no dilation
```
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1), # window strides
'SAME', # padding mode
(1,1), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape)
print("First output channel:")
plt.figure(figsize=(10,10))
plt.imshow(onp.array(out)[0,:,:,0]);
```
#### VALID padding, no stride, no dilation
```
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1), # window strides
'VALID', # padding mode
(1,1), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape, "DIFFERENT from above!")
print("First output channel:")
plt.figure(figsize=(10,10))
plt.imshow(onp.array(out)[0,:,:,0]);
```
#### SAME padding, 2,2 stride, no dilation
```
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(2,2), # window strides
'SAME', # padding mode
(1,1), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape, " <-- half the size of above")
plt.figure(figsize=(10,10))
print("First output channel:")
plt.imshow(onp.array(out)[0,:,:,0]);
```
#### VALID padding, no stride, rhs kernel dilation ~ Atrous convolution (excessive to illustrate)
```
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1), # window strides
'VALID', # padding mode
(1,1), # lhs/image dilation
(12,12), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape)
plt.figure(figsize=(10,10))
print("First output channel:")
plt.imshow(onp.array(out)[0,:,:,0]);
```
#### VALID padding, no stride, lhs=input dilation ~ Transposed Convolution
```
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1), # window strides
((0, 0), (0, 0)), # padding mode
(2,2), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape, "<-- larger than original!")
plt.figure(figsize=(10,10))
print("First output channel:")
plt.imshow(onp.array(out)[0,:,:,0]);
```
We can use the last to, for instance, implement _transposed convolutions_:
```
# The following is equivalent to tensorflow:
# N,H,W,C = img.shape
# out = tf.nn.conv2d_transpose(img, kernel, (N,2*H,2*W,C), (1,2,2,1))
# transposed conv = 180deg kernel roation plus LHS dilation
# rotate kernel 180deg:
kernel_rot = np.rot90(np.rot90(kernel, axes=(0,1)), axes=(0,1))
# need a custom output padding:
padding = ((2, 1), (2, 1))
out = lax.conv_general_dilated(img, # lhs = image tensor
kernel_rot, # rhs = conv kernel tensor
(1,1), # window strides
padding, # padding mode
(2,2), # lhs/image dilation
(1,1), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape, "<-- transposed_conv")
plt.figure(figsize=(10,10))
print("First output channel:")
plt.imshow(onp.array(out)[0,:,:,0]);
```
### 1D Convolutions
You aren't limited to 2D convolutions, a simple 1D demo is below:
```
# 1D kernel - WIO layout
kernel = onp.array([[[1, 0, -1], [-1, 0, 1]],
[[1, 1, 1], [-1, -1, -1]]],
dtype=np.float32).transpose([2,1,0])
# 1D data - NWC layout
data = onp.zeros((1, 200, 2), dtype=np.float32)
for i in range(2):
for k in range(2):
x = 35*i + 30 + 60*k
data[0, x:x+30, k] = 1.0
print("in shapes:", data.shape, kernel.shape)
plt.figure(figsize=(10,5))
plt.plot(data[0]);
dn = lax.conv_dimension_numbers(data.shape, kernel.shape,
('NWC', 'WIO', 'NWC'))
print(dn)
out = lax.conv_general_dilated(data, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,), # window strides
'SAME', # padding mode
(1,), # lhs/image dilation
(1,), # rhs/kernel dilation
dn) # dimension_numbers = lhs, rhs, out dimension permutation
print("out shape: ", out.shape)
plt.figure(figsize=(10,5))
plt.plot(out[0]);
```
### 3D Convolutions
```
# Random 3D kernel - HWDIO layout
kernel = onp.array([
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
[[0, -1, 0], [-1, 0, -1], [0, -1, 0]],
[[0, 0, 0], [0, 1, 0], [0, 0, 0]]],
dtype=np.float32)[:, :, :, onp.newaxis, onp.newaxis]
# 3D data - NHWDC layout
data = onp.zeros((1, 30, 30, 30, 1), dtype=np.float32)
x, y, z = onp.mgrid[0:1:30j, 0:1:30j, 0:1:30j]
data += (onp.sin(2*x*np.pi)*onp.cos(2*y*np.pi)*onp.cos(2*z*np.pi))[None,:,:,:,None]
print("in shapes:", data.shape, kernel.shape)
dn = lax.conv_dimension_numbers(data.shape, kernel.shape,
('NHWDC', 'HWDIO', 'NHWDC'))
print(dn)
out = lax.conv_general_dilated(data, # lhs = image tensor
kernel, # rhs = conv kernel tensor
(1,1,1), # window strides
'SAME', # padding mode
(1,1,1), # lhs/image dilation
(1,1,1), # rhs/kernel dilation
dn) # dimension_numbers
print("out shape: ", out.shape)
# Make some simple 3d density plots:
from mpl_toolkits.mplot3d import Axes3D
def make_alpha(cmap):
my_cmap = cmap(np.arange(cmap.N))
my_cmap[:,-1] = np.linspace(0, 1, cmap.N)**3
return mpl.colors.ListedColormap(my_cmap)
my_cmap = make_alpha(plt.cm.viridis)
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(x.ravel(), y.ravel(), z.ravel(), c=data.ravel(), cmap=my_cmap)
ax.axis('off')
ax.set_title('input')
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(x.ravel(), y.ravel(), z.ravel(), c=out.ravel(), cmap=my_cmap)
ax.axis('off')
ax.set_title('3D conv output');
```
## 🔪 NaNs
### Debugging NaNs
If you want to trace where NaNs are occurring in your functions or gradients, you can turn on the NaN-checker by:
- setting the `JAX_DEBUG_NANS=True` environment variable.
- adding `from jax.config import config` and `config.update("jax_debug_nans", True)` near the top of your main file
- adding `from jax.config import config` and `config.parse_flags_with_absl()` to your main file, then set the option using a command-line flag like `--jax_debug_nans=True`.
This will cause computations to error-out immediately on production of a NaN.
⚠️ You shouldn't have the NaN-checker on if you're not debugging, as it can introduce lots of device-host round-trips and performance regressions!
## Double (64bit) precision
At the moment, JAX by default enforces single-precision numbers to mitigate the Numpy API's tendency to aggressively promote operands to `double`. This is the desired behavior for many machine-learning applications, but it may catch you by surprise!
```
x = random.uniform(random.PRNGKey(0), (1000,), dtype=np.float64)
x.dtype
```
To use double-precision numbers, you need to set the `jax_enable_x64` configuration variable __at startup__.
There are a few ways to do this:
1. You can enable 64bit mode by setting the environment variable `JAX_ENABLE_X64=True`.
2. You can manually set the `jax_enable_x64` configuration flag at startup:
```
# again, this only works on startup!
from jax.config import config
config.update("jax_enable_x64", True)
```
3. You can parse command-line flags with `absl.app.run(main)`
```
from jax.config import config
config.config_with_absl()
```
4. If you want JAX to run absl parsing for you, i.e. you don't want to do `absl.app.run(main)`, you can instead use
```
from jax.config import config
if __name__ == '__main__':
# calls config.config_with_absl() *and* runs absl parsing
config.parse_flags_with_absl()
```
Note that #2-#4 work for _any_ of JAX's configuration options.
We can then confirm that `x64` mode is enabled:
```
from jax import numpy as np, random
x = random.uniform(random.PRNGKey(0), (1000,), dtype=np.float64)
x.dtype # --> dtype('float64')
```
### Caveats
⚠️ XLA doesn't support 64-bit convolutions on all backends!
## Fin.
If something's not covered here that has caused you weeping and gnashing of teeth, please let us know and we'll extend these introductory _advisos_!
| true |
code
| 0.230573 | null | null | null | null |
|
# Comprehensive Guide to Grouping and Aggregating with Pandas
Chris Mofitt. "Comprehensive Guide to Grouping and Aggregating with Pandas". _Practical Business Python_, 9 Nov. 2020, https://pbpython.com/groupby-agg.html.
```
import pandas as pd
import seaborn as sns
df = sns.load_dataset('titanic')
```
## Pandas aggregation options
### List
```
df['fare'].agg(['sum', 'mean'])
```
### Dictionary
```
df.agg({'fare': ['sum', 'mean'],
'sex': ['count']})
```
### Tuple
```
df.agg(fare_sum=('fare', 'sum'),
fare_mean=('fare', 'mean'),
sex_count=('sex', 'count'))
```
## Groupby
### Basic math
```
agg_func_math = {
'fare':
['sum', 'mean', 'median', 'min', 'max', 'std', 'var', 'mad', 'prod']
}
df.groupby(['embark_town']).agg(agg_func_math).round(2)
```
Use describe to run multiple built-in aggregations at once:
```
agg_func_describe = {'fare': ['describe']}
df.groupby(['embark_town']).agg(agg_func_describe).round(2)
```
### Counting
```
agg_func_count = {'embark_town': ['count', 'nunique', 'size']}
df.groupby(['deck']).agg(agg_func_count)
```
### First and last
Select highest and lowest fare by embarked town (need to sort first to have first and last pick max and min values).
```
agg_func_selection = {'fare': ['first', 'last']}
df.sort_values(by=['fare'],
ascending=False).groupby(['embark_town'
]).agg(agg_func_selection)
```
Instead use idxmax and idxmin to select values that correspond to max and min:
```
agg_func_max_min = {'fare': ['idxmax', 'idxmin']}
df.groupby(['embark_town']).agg(agg_func_max_min)
df.loc[[258, 378]]
df.loc[df.groupby('class')['fare'].idxmax()]
```
### Other libraries
```
from scipy.stats import skew, mode
agg_func_stats = {'fare': [skew, mode, pd.Series.mode]}
df.groupby(['embark_town']).agg(agg_func_stats)
```
### Working with text
```
agg_func_text = {'deck': [ 'nunique', mode, set]}
df.groupby(['class']).agg(agg_func_text)
```
### Custom Functions
Calculate the 25th percentile of the data using four approaches.
First, partial function:
```
from functools import partial
# Use partial
q_25 = partial(pd.Series.quantile, q=0.25)
q_25.__name__ = '25%'
# Define a function
def percentile_25(x):
return x.quantile(.25)
# Define a lambda function
lambda_25 = lambda x: x.quantile(.25)
lambda_25.__name__ = 'lambda_25%'
# Use a lambda function inline
agg_func = {
'fare': [q_25, percentile_25, lambda_25, lambda x: x.quantile(.25)]
}
df.groupby(['embark_town']).agg(agg_func).round(2)
```
### Custom function examples
Count number of null values:
```
def count_nulls(s):
return s.size - s.count()
```
Include NaN values in unique counts:
```
def unique_nan(s):
return s.nunique(dropna=False)
```
Summary of all values together:
```
agg_func_custom_count = {
'embark_town': ['count', 'nunique', 'size', unique_nan, count_nulls, set]
}
df.groupby(['deck']).agg(agg_func_custom_count)
```
To calculate the 90th percentile, use quantile:
```
def percentile_90(x):
return x.quantile(.9)
```
For trimmed mean where lowest 10th percent is excluded, use scipy status function:
```
from scipy.stats import trim_mean
def trim_mean_10(x):
return trim_mean(x, 0.1)
```
For largest value, regardless of sort order:
```
def largest(x):
return x.nlargest(1)
```
Incorporate [sparklines](https://pbpython.com/styling-pandas.html):
```
from sparklines import sparklines
import numpy as np
def sparkline_str(x):
bins=np.histogram(x)[0]
sl = ''.join(sparklines(bins))
return sl
```
All put together:
```
agg_func_largest = {
'fare': [percentile_90, trim_mean_10, largest, sparkline_str]
}
df.groupby(['class', 'embark_town']).agg(agg_func_largest)
```
Get total fares for top 10 and bottom 10:
```
def top_10_sum(x):
return x.nlargest(10).sum()
def bottom_10_sum(x):
return x.nsmallest(10).sum()
agg_func_top_bottom_sum = {
'fare': [top_10_sum, bottom_10_sum]
}
df.groupby('class').agg(agg_func_top_bottom_sum)
```
### Custom functions with multiple columns
Use groupby combined with apply:
```
def summary(x):
result = {
'fare_sum': x['fare'].sum(),
'fare_mean': x['fare'].mean(),
'fare_range': x['fare'].max() - x['fare'].min()
}
return pd.Series(result).round(0)
df.groupby(['class']).apply(summary)
```
## Working with group objects
Figure what percentage of total fares sold can be attributed to each embark_town and class combination (using assign and lambda function to add a pct_total column):
```
df.groupby(['embark_town', 'class']).agg({
'fare': 'sum'
}).assign(pct_total=lambda x: x / x.sum())
```
Simpler to use [pd.crosstab](https://pbpython.com/pandas-crosstab.html):
```
pd.crosstab(df['embark_town'],
df['class'],
values=df['fare'],
aggfunc='sum',
normalize=True)
```
Combine agg functions with pivot table:
```
pd.pivot_table(data=df,
index=['embark_town'],
columns=['class'],
aggfunc=agg_func_top_bottom_sum)
```
Show cumulative total of fares by group and aggregate by town and class, then group:
```
fare_group = df.groupby(['embark_town', 'class']).agg({'fare': 'sum'})
fare_group.groupby(level=0).cumsum()
```
Summarize daily sales and convert to cumulative daily and quarterly view (use [pd.Grouper](https://pbpython.com/pandas-grouper-agg.html)).
Here, include total daily sales as well as cumulative quarter amount:
```
sales = pd.read_excel('https://github.com/chris1610/pbpython/blob/master/data/2018_Sales_Total_v2.xlsx?raw=True')
daily_sales = sales.groupby([pd.Grouper(key='date', freq='D')
]).agg(daily_sales=('ext price',
'sum')).reset_index()
daily_sales['quarter_sales'] = daily_sales.groupby(
pd.Grouper(key='date', freq='Q')).agg({'daily_sales': 'cumsum'})
```
Group daily results, then group by quarter and use cumulative sum:
```
sales.groupby([pd.Grouper(key='date', freq='D')
]).agg(daily_sales=('ext price', 'sum')).groupby(
pd.Grouper(freq='Q')).agg({
'daily_sales': 'cumsum'
}).rename(columns={'daily_sales': 'quarterly_sales'})
```
## Flattening Hierarchical Column Indices
```
df.groupby(['embark_town', 'class']).agg({'fare': ['sum', 'mean']}).round(0)
multi_df = df.groupby(['embark_town', 'class'],
as_index=False).agg({'fare': ['sum', 'mean']})
multi_df.columns = [
'_'.join(col).rstrip('_') for col in multi_df.columns.values
]
```
## Subtotals
Add a subtotal using the [sidetable](https://github.com/chris1610/sidetable) package.
```
import sidetable
df.groupby(['class', 'embark_town', 'sex']).agg({'fare': 'sum'}).stb.subtotal()
```
| true |
code
| 0.457621 | null | null | null | null |
|
# Rigid-body transformations in three-dimensions
> Marcos Duarte
> Laboratory of Biomechanics and Motor Control ([http://demotu.org/](http://demotu.org/))
> Federal University of ABC, Brazil
The kinematics of a rigid body is completely described by its pose, i.e., its position and orientation in space (and the corresponding changes, translation and rotation). In a three-dimensional space, at least three coordinates and three angles are necessary to describe the pose of the rigid body, totalizing six degrees of freedom for a rigid body.
In motion analysis, to describe a translation and rotation of a rigid body with respect to a coordinate system, typically we attach another coordinate system to the rigid body and determine a transformation between these two coordinate systems.
A transformation is any function mapping a set to another set. For the description of the kinematics of rigid bodies, we are interested only in what is called rigid or Euclidean transformations (denoted as SE(3) for the three-dimensional space) because they preserve the distance between every pair of points of the body (which is considered rigid by definition). Translations and rotations are examples of rigid transformations (a reflection is also an example of rigid transformation but this changes the right-hand axis convention to a left hand, which usually is not of interest). In turn, rigid transformations are examples of [affine transformations](https://en.wikipedia.org/wiki/Affine_transformation). Examples of other affine transformations are shear and scaling transformations (which preserves angles but not lengths).
We will follow the same rationale as in the notebook [Rigid-body transformations in a plane (2D)](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/Transformation2D.ipynb) and we will skip the fundamental concepts already covered there. So, you if haven't done yet, you should read that notebook before continuing here.
## Translation
A pure three-dimensional translation of a rigid body (or a coordinate system attached to it) in relation to other rigid body (with other coordinate system) is illustrated in the figure below.
<br>
<figure><img src='./../images/translation3D.png' alt='translation 3D'/> <figcaption><center><i>Figure. A point in three-dimensional space represented in two coordinate systems, with one coordinate system translated.</i></center></figcaption> </figure>
The position of point $\mathbf{P}$ originally described in the $xyz$ (local) coordinate system but now described in the $\mathbf{XYZ}$ (Global) coordinate system in vector form is:
$$ \mathbf{P_G} = \mathbf{L_G} + \mathbf{P_l} $$
Or in terms of its components:
$$ \begin{array}{}
\mathbf{P_X} =& \mathbf{L_X} + \mathbf{P}_x \\
\mathbf{P_Y} =& \mathbf{L_Y} + \mathbf{P}_y \\
\mathbf{P_Z} =& \mathbf{L_Z} + \mathbf{P}_z
\end{array} $$
And in matrix form:
$$
\begin{bmatrix}
\mathbf{P_X} \\
\mathbf{P_Y} \\
\mathbf{P_Z}
\end{bmatrix} =
\begin{bmatrix}
\mathbf{L_X} \\
\mathbf{L_Y} \\
\mathbf{L_Z}
\end{bmatrix} +
\begin{bmatrix}
\mathbf{P}_x \\
\mathbf{P}_y \\
\mathbf{P}_z
\end{bmatrix}
$$
From classical mechanics, this is an example of [Galilean transformation](http://en.wikipedia.org/wiki/Galilean_transformation).
Let's use Python to compute some numeric examples:
```
# Import the necessary libraries
import numpy as np
# suppress scientific notation for small numbers:
np.set_printoptions(precision=4, suppress=True)
```
For example, if the local coordinate system is translated by $\mathbf{L_G}=[1, 2, 3]$ in relation to the Global coordinate system, a point with coordinates $\mathbf{P_l}=[4, 5, 6]$ at the local coordinate system will have the position $\mathbf{P_G}=[5, 7, 9]$ at the Global coordinate system:
```
LG = np.array([1, 2, 3]) # Numpy array
Pl = np.array([4, 5, 6])
PG = LG + Pl
PG
```
This operation also works if we have more than one point (NumPy try to guess how to handle vectors with different dimensions):
```
Pl = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 2D array with 3 rows and 2 columns
PG = LG + Pl
PG
```
## Rotation
A pure three-dimensional rotation of a $xyz$ (local) coordinate system in relation to other $\mathbf{XYZ}$ (Global) coordinate system and the position of a point in these two coordinate systems are illustrated in the next figure (remember that this is equivalent to describing a rotation between two rigid bodies).
<br>
<figure><img src='./../images/rotation3D.png' alt='rotation 3D'/> <figcaption><center><i>A point in three-dimensional space represented in two coordinate systems, with one system rotated.</i></center></figcaption> </figure>
In analogy to the rotation in two dimensions, we can calculate the rotation matrix that describes the rotation of the $xyz$ (local) coordinate system in relation to the $\mathbf{XYZ}$ (Global) coordinate system using the direction cosines between the axes of the two coordinate systems:
$$ \mathbf{R_{Gl}} = \begin{bmatrix}
\cos\mathbf{X}x & \cos\mathbf{X}y & \cos\mathbf{X}z \\
\cos\mathbf{Y}x & \cos\mathbf{Y}y & \cos\mathbf{Y}z \\
\cos\mathbf{Z}x & \cos\mathbf{Z}y & \cos\mathbf{Z}z
\end{bmatrix} $$
Note however that for rotations around more than one axis, these angles will not lie in the main planes ($\mathbf{XY, YZ, ZX}$) of the $\mathbf{XYZ}$ coordinate system, as illustrated in the figure below for the direction angles of the $y$ axis only. Thus, the determination of these angles by simple inspection, as we have done for the two-dimensional case, would not be simple.
<br>
<figure>
<img src='./../images/directioncosine3D.png' width=260 alt='direction angles 3D'/> <figcaption><center><i>Figure. Definition of direction angles for the $y$ axis of the local coordinate system in relation to the $\mathbf{XYZ}$ Global coordinate system.</i></center></figcaption>
</figure>
Note that the nine angles shown in the matrix above for the direction cosines are obviously redundant since only three angles are necessary to describe the orientation of a rigid body in the three-dimensional space.
An important characteristic of angles in the three-dimensional space is that angles cannot be treated as vectors: the result of a sequence of rotations of a rigid body around different axes depends on the order of the rotations, as illustrated in the next figure.
<br>
<figure>
<img src='./../images/rotationsseqs2.png' alt='rotations'/><figcaption><i>Figure. The result of a sequence of rotations around different axes of a coordinate system depends on the order of the rotations. In the first example (first row), the rotations are around a Global (fixed) coordinate system. In the second example (second row), the rotations are around a local (rotating) coordinate system.</i></figcaption>
</figure>
Let's focus now on how to understand rotations in the three-dimensional space, looking at the rotations between coordinate systems (or between rigid bodies). Later we will apply what we have learned to describe the position of a point in these different coordinate systems.
### Euler angles
There are different ways to describe a three-dimensional rotation of a rigid body (or of a coordinate system). The most straightforward solution would probably be to use a [spherical coordinate system](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/ReferenceFrame.ipynb#Spherical-coordinate-system), but spherical coordinates would be difficult to give an anatomical or clinical interpretation. A solution that has been often employed in biomechanics to handle rotations in the three-dimensional space is to use Euler angles. Under certain conditions, Euler angles can have an anatomical interpretation, but this representation also has some caveats. Let's see the Euler angles now.
[Leonhard Euler](https://en.wikipedia.org/wiki/Leonhard_Euler) in the XVIII century showed that two three-dimensional coordinate systems with a common origin can be related by a sequence of up to three elemental rotations about the axes of the local coordinate system, where no two successive rotations may be about the same axis, which now are known as [Euler (or Eulerian) angles](http://en.wikipedia.org/wiki/Euler_angles).
#### Elemental rotations
First, let's see rotations around a fixed Global coordinate system as we did for the two-dimensional case. The next figure illustrates elemental rotations of the local coordinate system around each axis of the fixed Global coordinate system.
<br>
<figure>
<img src='./../images/rotations.png' alt='rotations'/> <figcaption><center><i>Figure. Elemental rotations of the $xyz$ coordinate system around each axis, $\mathbf{X}$, $\mathbf{Y}$, and $\mathbf{Z}$, of the fixed $\mathbf{XYZ}$ coordinate system. Note that for better clarity, the axis around where the rotation occurs is shown perpendicular to this page for each elemental rotation.</i></center></figcaption>
</figure>
#### Rotations around the fixed coordinate system
The rotation matrices for the elemental rotations around each axis of the fixed $\mathbf{XYZ}$ coordinate system (rotations of the local coordinate system in relation to the Global coordinate system) are shown next.
Around $\mathbf{X}$ axis:
$$ \mathbf{R_{Gl,\,X}} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha \\
0 & \sin\alpha & \cos\alpha
\end{bmatrix} $$
Around $\mathbf{Y}$ axis:
$$ \mathbf{R_{Gl,\,Y}} =
\begin{bmatrix}
\cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta
\end{bmatrix} $$
Around $\mathbf{Z}$ axis:
$$ \mathbf{R_{Gl,\,Z}} =
\begin{bmatrix}
\cos\gamma & -\sin\gamma & 0\\
\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix} $$
These matrices are the rotation matrices for the case of two-dimensional coordinate systems plus the corresponding terms for the third axes of the local and Global coordinate systems, which are parallel.
To understand why the terms for the third axes are 1's or 0's, for instance, remember they represent the cosine directors. The cosines between $\mathbf{X}x$, $\mathbf{Y}y$, and $\mathbf{Z}z$ for the elemental rotations around respectively the $\mathbf{X}$, $\mathbf{Y}$, and $\mathbf{Z}$ axes are all 1 because $\mathbf{X}x$, $\mathbf{Y}y$, and $\mathbf{Z}z$ are parallel ($\cos 0^o$). The cosines of the other elements are zero because the axis around where each rotation occurs is perpendicular to the other axes of the coordinate systems ($\cos 90^o$).
#### Rotations around the local coordinate system
The rotation matrices for the elemental rotations this time around each axis of the $xyz$ coordinate system (rotations of the Global coordinate system in relation to the local coordinate system), similarly to the two-dimensional case, are simply the transpose of the above matrices as shown next.
Around $x$ axis:
$$ \mathbf{R}_{\mathbf{lG},\,x} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & \sin\alpha \\
0 & -\sin\alpha & \cos\alpha
\end{bmatrix} $$
Around $y$ axis:
$$ \mathbf{R}_{\mathbf{lG},\,y} =
\begin{bmatrix}
\cos\beta & 0 & -\sin\beta \\
0 & 1 & 0 \\
\sin\beta & 0 & \cos\beta
\end{bmatrix} $$
Around $z$ axis:
$$ \mathbf{R}_{\mathbf{lG},\,z} =
\begin{bmatrix}
\cos\gamma & \sin\gamma & 0\\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix} $$
Notice this is equivalent to instead of rotating the local coordinate system by $\alpha, \beta, \gamma$ in relation to axes of the Global coordinate system, to rotate the Global coordinate system by $-\alpha, -\beta, -\gamma$ in relation to the axes of the local coordinate system; remember that $\cos(-\:\cdot)=\cos(\cdot)$ and $\sin(-\:\cdot)=-\sin(\cdot)$.
The fact that we chose to rotate the local coordinate system by a counterclockwise (positive) angle in relation to the Global coordinate system is just a matter of convention.
#### Sequence of elemental rotations
Consider now a sequence of elemental rotations around the $\mathbf{X}$, $\mathbf{Y}$, and $\mathbf{Z}$ axes of the fixed $\mathbf{XYZ}$ coordinate system illustrated in the next figure.
<br>
<figure><img src='./../images/rotations_XYZ.png' alt='rotations'/> <figcaption><center><i>Figure. Sequence of elemental rotations of the $xyz$ coordinate system around each axis, $\mathbf{X}$, $\mathbf{Y}$, $\mathbf{Z}$, of the fixed $\mathbf{XYZ}$ coordinate system.</i></center></figcaption> </figure>
This sequence of elemental rotations (each one of the local coordinate system with respect to the fixed Global coordinate system) is mathematically represented by a multiplication between the rotation matrices:
$$ \begin{array}{l l}
\mathbf{R_{Gl,\;XYZ}} & = \mathbf{R_{Z}} \mathbf{R_{Y}} \mathbf{R_{X}} \\
\\
& = \begin{bmatrix}
\cos\gamma & -\sin\gamma & 0\\
\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & -sin\alpha \\
0 & \sin\alpha & cos\alpha
\end{bmatrix} \\
\\
& =
\begin{bmatrix}
\cos\beta\:\cos\gamma \;&\;
\sin\alpha\:\sin\beta\:cos\gamma-\cos\alpha\:\sin\gamma \;&\;
\cos\alpha\:\sin\beta\:cos\gamma+\sin\alpha\:\sin\gamma \;\;\; \\
\cos\beta\:\sin\gamma \;&\;
\sin\alpha\:\sin\beta\:sin\gamma+\cos\alpha\:\cos\gamma \;&\;
\cos\alpha\:\sin\beta\:sin\gamma-\sin\alpha\:\cos\gamma \;\;\; \\
-\sin\beta \;&\; \sin\alpha\:\cos\beta \;&\; \cos\alpha\:\cos\beta \;\;\;
\end{bmatrix}
\end{array} $$
Note that the order of the matrices.
We can check this matrix multiplication using [Sympy](http://sympy.org/en/index.html):
```
#import the necessary libraries
from IPython.core.display import Math, display
import sympy as sym
cos, sin = sym.cos, sym.sin
a, b, g = sym.symbols('alpha, beta, gamma')
# Elemental rotation matrices of xyz in relation to XYZ:
RX = sym.Matrix([[1, 0, 0], [0, cos(a), -sin(a)], [0, sin(a), cos(a)]])
RY = sym.Matrix([[cos(b), 0, sin(b)], [0, 1, 0], [-sin(b), 0, cos(b)]])
RZ = sym.Matrix([[cos(g), -sin(g), 0], [sin(g), cos(g), 0], [0, 0, 1]])
# Rotation matrix of xyz in relation to XYZ:
RXYZ = RZ*RY*RX
display(Math(sym.latex(r'\mathbf{R_{Gl,\,XYZ}}=') + sym.latex(RXYZ, mat_str='matrix')))
```
For instance, we can calculate the numerical rotation matrix for these sequential elemental rotations by $90^o$ around $\mathbf{X,Y,Z}$:
```
R = sym.lambdify((a, b, g), RXYZ, 'numpy')
R = R(np.pi/2, np.pi/2, np.pi/2)
display(Math(r'\mathbf{R_{Gl,\,XYZ\,}}(90^o, 90^o, 90^o) =' + \
sym.latex(sym.Matrix(R).n(chop=True, prec=3))))
```
Examining the matrix above and the correspondent previous figure, one can see they agree: the rotated $x$ axis (first column of the above matrix) has value -1 in the $\mathbf{Z}$ direction $[0,0,-1]$, the rotated $y$ axis (second column) is at the $\mathbf{Y}$ direction $[0,1,0]$, and the rotated $z$ axis (third column) is at the $\mathbf{X}$ direction $[1,0,0]$.
We also can calculate the sequence of elemental rotations around the $x$, $y$, $z$ axes of the rotating $xyz$ coordinate system illustrated in the next figure.
<br>
<figure>
<img src='./../images/rotations_xyz2.png' alt='rotations'/> <figcaption><center><i>Figure. Sequence of elemental rotations of a second $xyz$ local coordinate system around each axis, $x$, $y$, $z$, of the rotating $xyz$ coordinate system.</i></center></figcaption>
</figure>
Likewise, this sequence of elemental rotations (each one of the local coordinate system with respect to the rotating local coordinate system) is mathematically represented by a multiplication between the rotation matrices (which are the inverse of the matrices for the rotations around $\mathbf{X,Y,Z}$ as we saw earlier):
$$ \begin{array}{l l}
\mathbf{R}_{\mathbf{lG},\,xyz} & = \mathbf{R_{z}} \mathbf{R_{y}} \mathbf{R_{x}} \\
\\
& = \begin{bmatrix}
\cos\gamma & \sin\gamma & 0\\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\beta & 0 & -\sin\beta \\
0 & 1 & 0 \\
sin\beta & 0 & \cos\beta
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & \sin\alpha \\
0 & -\sin\alpha & \cos\alpha
\end{bmatrix} \\
\\
& =
\begin{bmatrix}
\cos\beta\:\cos\gamma \;&\;
\sin\alpha\:\sin\beta\:\cos\gamma+\cos\alpha\:\sin\gamma \;&\;
\cos\alpha\:\sin\beta\:\cos\gamma-\sin\alpha\:\sin\gamma \;\;\; \\
-\cos\beta\:\sin\gamma \;&\;
-\sin\alpha\:\sin\beta\:\sin\gamma+\cos\alpha\:\cos\gamma \;&\;
\cos\alpha\:\sin\beta\:\sin\gamma+\sin\alpha\:\cos\gamma \;\;\; \\
\sin\beta \;&\; -\sin\alpha\:\cos\beta \;&\; \cos\alpha\:\cos\beta \;\;\;
\end{bmatrix}
\end{array} $$
As before, the order of the matrices is from right to left.
Once again, we can check this matrix multiplication using [Sympy](http://sympy.org/en/index.html):
```
a, b, g = sym.symbols('alpha, beta, gamma')
# Elemental rotation matrices of xyz (local):
Rx = sym.Matrix([[1, 0, 0], [0, cos(a), sin(a)], [0, -sin(a), cos(a)]])
Ry = sym.Matrix([[cos(b), 0, -sin(b)], [0, 1, 0], [sin(b), 0, cos(b)]])
Rz = sym.Matrix([[cos(g), sin(g), 0], [-sin(g), cos(g), 0], [0, 0, 1]])
# Rotation matrix of xyz' in relation to xyz:
Rxyz = Rz*Ry*Rx
Math(sym.latex(r'\mathbf{R}_{\mathbf{lG},\,xyz}=') + sym.latex(Rxyz, mat_str='matrix'))
```
For instance, let's calculate the numerical rotation matrix for these sequential elemental rotations by $90^o$ around $x,y,z$:
```
R = sym.lambdify((a, b, g), Rxyz, 'numpy')
R = R(np.pi/2, np.pi/2, np.pi/2)
display(Math(r'\mathbf{R}_{\mathbf{lG},\,xyz\,}(90^o, 90^o, 90^o) =' + \
sym.latex(sym.Matrix(R).n(chop=True, prec=3))))
```
Once again, let's compare the above matrix and the correspondent previous figure to see if it makes sense. But remember that this matrix is the Global-to-local rotation matrix, $\mathbf{R}_{\mathbf{lG},\,xyz}$, where the coordinates of the local basis' versors are rows, not columns, in this matrix. With this detail in mind, one can see that the previous figure and matrix also agree: the rotated $x$ axis (first row of the above matrix) is at the $\mathbf{Z}$ direction $[0,0,1]$, the rotated $y$ axis (second row) is at the $\mathbf{-Y}$ direction $[0,-1,0]$, and the rotated $z$ axis (third row) is at the $\mathbf{X}$ direction $[1,0,0]$.
In fact, this example didn't serve to distinguish versors as rows or columns because the $\mathbf{R}_{\mathbf{lG},\,xyz}$ matrix above is symmetric!
Let's look on the resultant matrix for the example above after only the first two rotations, $\mathbf{R}_{\mathbf{lG},\,xy}$ to understand this difference:
```
Rxy = Ry*Rx
R = sym.lambdify((a, b), Rxy, 'numpy')
R = R(np.pi/2, np.pi/2)
display(Math(r'\mathbf{R}_{\mathbf{lG},\,xy\,}(90^o, 90^o) =' + \
sym.latex(sym.Matrix(R).n(chop=True, prec=3))))
```
Comparing this matrix with the third plot in the figure, we see that the coordinates of versor $x$ in the Global coordinate system are $[0,1,0]$, i.e., local axis $x$ is aligned with Global axis $Y$, and this versor is indeed the first row, not first column, of the matrix above. Confer the other two rows.
What are then in the columns of the local-to-Global rotation matrix?
The columns are the coordinates of Global basis' versors in the local coordinate system! For example, the first column of the matrix above is the coordinates of $X$, which is aligned with $z$: $[0,0,1]$.
#### Rotations in a coordinate system is equivalent to minus rotations in the other coordinate system
Remember that we saw for the elemental rotations that it's equivalent to instead of rotating the local coordinate system, $xyz$, by $\alpha, \beta, \gamma$ in relation to axes of the Global coordinate system, to rotate the Global coordinate system, $\mathbf{XYZ}$, by $-\alpha, -\beta, -\gamma$ in relation to the axes of the local coordinate system. The same property applies to a sequence of rotations: rotations of $xyz$ in relation to $\mathbf{XYZ}$ by $\alpha, \beta, \gamma$ result in the same matrix as rotations of $\mathbf{XYZ}$ in relation to $xyz$ by $-\alpha, -\beta, -\gamma$:
$$ \begin{array}{l l}
\mathbf{R_{Gl,\,XYZ\,}}(\alpha,\beta,\gamma) & = \mathbf{R_{Gl,\,Z}}(\gamma)\, \mathbf{R_{Gl,\,Y}}(\beta)\, \mathbf{R_{Gl,\,X}}(\alpha) \\
& = \mathbf{R}_{\mathbf{lG},\,z\,}(-\gamma)\, \mathbf{R}_{\mathbf{lG},\,y\,}(-\beta)\, \mathbf{R}_{\mathbf{lG},\,x\,}(-\alpha) \\
& = \mathbf{R}_{\mathbf{lG},\,xyz\,}(-\alpha,-\beta,-\gamma)
\end{array}
$$
Confer that by examining the $\mathbf{R_{Gl,\,XYZ}}$ and $\mathbf{R}_{\mathbf{lG},\,xyz}$ matrices above.
Let's verify this property with Sympy:
```
RXYZ = RZ*RY*RX
# Rotation matrix of xyz in relation to XYZ:
display(Math(sym.latex(r'\mathbf{R_{Gl,\,XYZ\,}}(\alpha,\beta,\gamma) =')))
display(Math(sym.latex(RXYZ, mat_str='matrix')))
# Elemental rotation matrices of XYZ in relation to xyz and negate all angles:
Rx_neg = sym.Matrix([[1, 0, 0], [0, cos(-a), -sin(-a)], [0, sin(-a), cos(-a)]]).T
Ry_neg = sym.Matrix([[cos(-b), 0, sin(-b)], [0, 1, 0], [-sin(-b), 0, cos(-b)]]).T
Rz_neg = sym.Matrix([[cos(-g), -sin(-g), 0], [sin(-g), cos(-g), 0], [0, 0, 1]]).T
# Rotation matrix of XYZ in relation to xyz:
Rxyz_neg = Rz_neg*Ry_neg*Rx_neg
display(Math(sym.latex(r'\mathbf{R}_{\mathbf{lG},\,xyz\,}(-\alpha,-\beta,-\gamma) =')))
display(Math(sym.latex(Rxyz_neg, mat_str='matrix')))
# Check that the two matrices are equal:
display(Math(sym.latex(r'\mathbf{R_{Gl,\,XYZ\,}}(\alpha,\beta,\gamma) \;==\;' + \
r'\mathbf{R}_{\mathbf{lG},\,xyz\,}(-\alpha,-\beta,-\gamma)')))
RXYZ == Rxyz_neg
```
#### Rotations in a coordinate system is the transpose of inverse order of rotations in the other coordinate system
There is another property of the rotation matrices for the different coordinate systems: the rotation matrix, for example from the Global to the local coordinate system for the $xyz$ sequence, is just the transpose of the rotation matrix for the inverse operation (from the local to the Global coordinate system) of the inverse sequence ($\mathbf{ZYX}$) and vice-versa:
$$ \begin{array}{l l}
\mathbf{R}_{\mathbf{lG},\,xyz}(\alpha,\beta,\gamma) & = \mathbf{R}_{\mathbf{lG},\,z\,} \mathbf{R}_{\mathbf{lG},\,y\,} \mathbf{R}_{\mathbf{lG},\,x} \\
& = \mathbf{R_{Gl,\,Z\,}^{-1}} \mathbf{R_{Gl,\,Y\,}^{-1}} \mathbf{R_{Gl,\,X\,}^{-1}} \\
& = \mathbf{R_{Gl,\,Z\,}^{T}} \mathbf{R_{Gl,\,Y\,}^{T}} \mathbf{R_{Gl,\,X\,}^{T}} \\
& = (\mathbf{R_{Gl,\,X\,}} \mathbf{R_{Gl,\,Y\,}} \mathbf{R_{Gl,\,Z}})^\mathbf{T} \\
& = \mathbf{R_{Gl,\,ZYX\,}^{T}}(\gamma,\beta,\alpha)
\end{array}
$$
Where we used the properties that the inverse of the rotation matrix (which is orthonormal) is its transpose and that the transpose of a product of matrices is equal to the product of their transposes in reverse order.
Let's verify this property with Sympy:
```
RZYX = RX*RY*RZ
Rxyz = Rz*Ry*Rx
display(Math(sym.latex(r'\mathbf{R_{Gl,\,ZYX\,}^T}=') + sym.latex(RZYX.T, mat_str='matrix')))
display(Math(sym.latex(r'\mathbf{R}_{\mathbf{lG},\,xyz\,}(\alpha,\beta,\gamma) \,==\,' + \
r'\mathbf{R_{Gl,\,ZYX\,}^T}(\gamma,\beta,\alpha)')))
Rxyz == RZYX.T
```
#### Sequence of rotations of a Vector
We saw in the notebook [Rigid-body transformations in a plane (2D)](http://nbviewer.jupyter.org/github/demotu/BMC/blob/master/notebooks/Transformation2D.ipynb#Rotation-of-a-Vector) that the rotation matrix can also be used to rotate a vector (in fact, a point, image, solid, etc.) by a given angle around an axis of the coordinate system. Let's investigate that for the 3D case using the example earlier where a book was rotated in different orders and around the Global and local coordinate systems.
Before any rotation, the point shown in that figure as a round black dot on the spine of the book has coordinates $\mathbf{P}=[0, 1, 2]$ (the book has thickness 0, width 1, and height 2).
After the first sequence of rotations shown in the figure (rotated around $X$ and $Y$ by $90^0$ each time), $\mathbf{P}$ has coordinates $\mathbf{P}=[1, -2, 0]$ in the global coordinate system. Let's verify that:
```
P = np.array([[0, 1, 2]]).T
RXY = RY*RX
R = sym.lambdify((a, b), RXY, 'numpy')
R = R(np.pi/2, np.pi/2)
P1 = np.dot(R, P)
print('P1 =', P1.T)
```
As expected.
The reader is invited to deduce the position of point $\mathbf{P}$ after the inverse order of rotations, but still around the Global coordinate system.
Although we are performing vector rotation, where we don't need the concept of transformation between coordinate systems, in the example above we used the local-to-Global rotation matrix, $\mathbf{R_{Gl}}$. As we saw in the notebook for the 2D transformation, when we use this matrix, it performs a counter-clockwise (positive) rotation.
If we want to rotate the vector in the clockwise (negative) direction, we can use the very same rotation matrix entering a negative angle or we can use the inverse rotation matrix, the Global-to-local rotation matrix, $\mathbf{R_{lG}}$ and a positive (negative of negative) angle, because $\mathbf{R_{Gl}}(\alpha) = \mathbf{R_{lG}}(-\alpha)$, but bear in mind that even in this latter case we are rotating around the Global coordinate system!
Consider now that we want to deduce algebraically the position of the point $\mathbf{P}$ after the rotations around the local coordinate system as shown in the second set of examples in the figure with the sequence of book rotations. The point has the same initial position, $\mathbf{P}=[0, 1, 2]$, and after the rotations around $x$ and $y$ by $90^0$ each time, what is the position of this point?
It's implicit in this question that the new desired position is in the Global coordinate system because the local coordinate system rotates with the book and the point never changes its position in the local coordinate system. So, by inspection of the figure, the new position of the point is $\mathbf{P1}=[2, 0, 1]$.
Let's naively try to deduce this position by repeating the steps as before:
```
Rxy = Ry*Rx
R = sym.lambdify((a, b), Rxy, 'numpy')
R = R(np.pi/2, np.pi/2)
P1 = np.dot(R, P)
print('P1 =', P1.T)
```
The wrong answer.
The problem is that we defined the rotation of a vector using the local-to-Global rotation matrix. One correction solution for this problem is to continuing using the multiplication of the Global-to-local rotation matrices, $\mathbf{R}_{xy} = \mathbf{R}_y\,\mathbf{R}_x$, transpose $\mathbf{R}_{xy}$ to get the Global-to-local coordinate system, $\mathbf{R_{XY}}=\mathbf{R^T}_{xy}$, and then rotate the vector using this matrix:
```
Rxy = Ry*Rx
RXY = Rxy.T
R = sym.lambdify((a, b), RXY, 'numpy')
R = R(np.pi/2, np.pi/2)
P1 = np.dot(R, P)
print('P1 =', P1.T)
```
The correct answer.
Another solution is to understand that when using the Global-to-local rotation matrix, counter-clockwise rotations (as performed with the book the figure) are negative, not positive, and that when dealing with rotations with the Global-to-local rotation matrix the order of matrix multiplication is inverted, for example, it should be $\mathbf{R\_}_{xyz} = \mathbf{R}_x\,\mathbf{R}_y\,\mathbf{R}_z$ (an added underscore to remind us this is not the convention adopted here).
```
R_xy = Rx*Ry
R = sym.lambdify((a, b), R_xy, 'numpy')
R = R(-np.pi/2, -np.pi/2)
P1 = np.dot(R, P)
print('P1 =', P1.T)
```
The correct answer.
The reader is invited to deduce the position of point $\mathbf{P}$ after the inverse order of rotations, around the local coordinate system.
In fact, you will find elsewhere texts about rotations in 3D adopting this latter convention as the standard, i.e., they introduce the Global-to-local rotation matrix and describe sequence of rotations algebraically as matrix multiplication in the direct order, $\mathbf{R\_}_{xyz} = \mathbf{R}_x\,\mathbf{R}_y\,\mathbf{R}_z$, the inverse we have done in this text. It's all a matter of convention, just that.
#### The 12 different sequences of Euler angles
The Euler angles are defined in terms of rotations around a rotating local coordinate system. As we saw for the sequence of rotations around $x, y, z$, the axes of the local rotated coordinate system are not fixed in space because after the first elemental rotation, the other two axes rotate.
Other sequences of rotations could be produced without combining axes of the two different coordinate systems (Global and local) for the definition of the rotation axes. There is a total of 12 different sequences of three elemental rotations that are valid and may be used for describing the rotation of a coordinate system with respect to another coordinate system:
$$ xyz \quad xzy \quad yzx \quad yxz \quad zxy \quad zyx $$
$$ xyx \quad xzx \quad yzy \quad yxy \quad zxz \quad zyz $$
The first six sequences (first row) are all around different axes, they are usually referred as Cardan or Tait–Bryan angles. The other six sequences (second row) have the first and third rotations around the same axis, but keep in mind that the axis for the third rotation is not at the same place anymore because it changed its orientation after the second rotation. The sequences with repeated axes are known as proper or classic Euler angles.
Which order to use it is a matter of convention, but because the order affects the results, it's fundamental to follow a convention and report it. In Engineering Mechanics (including Biomechanics), the $xyz$ order is more common; in Physics the $zxz$ order is more common (but the letters chosen to refer to the axes are arbitrary, what matters is the directions they represent). In Biomechanics, the order for the Cardan angles is most often based on the angle of most interest or of most reliable measurement. Accordingly, the axis of flexion/extension is typically selected as the first axis, the axis for abduction/adduction is the second, and the axis for internal/external rotation is the last one. We will see about this order later. The $zyx$ order is commonly used to describe the orientation of a ship or aircraft and the rotations are known as the nautical angles: yaw, pitch and roll, respectively (see next figure).
<br>
<figure><img src='https://upload.wikimedia.org/wikipedia/commons/thumb/1/16/Yaw_Axis.svg/319px-Yaw_Axis.svg.png' alt='translation and rotation 3D'/> <figcaption><center><i>Figure. The principal axes of an aircraft and the names for the rotations around these axes (<a href="https://en.wikipedia.org/wiki/Euler_angles">image from Wikipedia</a>).</i></center></figcaption> </figure>
If instead of rotations around the rotating local coordinate system we perform rotations around the fixed Global coordinate system, we will have other 12 different sequences of three elemental rotations, these are called simply rotation angles. So, in total there are 24 possible different sequences of three elemental rotations, but the 24 orders are not independent; with the 12 different sequences of Euler angles at the local coordinate system we can obtain the other 12 sequences at the Global coordinate system.
The Python function `euler_rotmat.py` (code at the end of this text) determines the rotation matrix in algebraic form for any of the 24 different sequences (and sequences with only one or two axes can be inputed). This function also determines the rotation matrix in numeric form if a list of up to three angles are inputed.
For instance, the rotation matrix in algebraic form for the $zxz$ order of Euler angles at the local coordinate system and the correspondent rotation matrix in numeric form after three elemental rotations by $90^o$ each are:
```
import sys
sys.path.insert(1, r'./../functions')
from euler_rotmat import euler_rotmat
Ra, Rn = euler_rotmat(order='zxz', frame='local', angles=[90, 90, 90])
```
#### Line of nodes
The second axis of rotation in the rotating coordinate system is also referred as the nodal axis or line of nodes; this axis coincides with the intersection of two perpendicular planes, one from each Global (fixed) and local (rotating) coordinate systems. The figure below shows an example of rotations and the nodal axis for the $xyz$ sequence of the Cardan angles.
<div class='center-align'><figure><img src='./../images/Node.png' alt='rotations'/> <figcaption><center><i>Figure. First row: example of rotations for the $xyz$ sequence of the Cardan angles. The Global (fixed) $XYZ$ coordinate system is shown in green, the local (rotating) $xyz$ coordinate system is shown in blue. The nodal axis (<b>N</b>, shown in red) is defined by the intersection of the $YZ$ and $xy$ planes and all rotations can be described in relation to this nodal axis or to a perpendicular axis to it. Second row: starting from no rotation, the local coordinate system is rotated by $\alpha$ around the $x$ axis, then by $\beta$ around the rotated $y$ axis, and finally by $\gamma$ around the twice rotated $z$ axis. Note that the line of nodes coincides with the $y$ axis for the second rotation. </i></center></figcaption> </figure></div>
#### Determination of the Euler angles
Once a convention is adopted, the corresponding three Euler angles of rotation can be found.
For example, for the $\mathbf{R}_{xyz}$ rotation matrix:
```
R = euler_rotmat(order='xyz', frame='local')
```
The corresponding Cardan angles for the `xyz` sequence can be given by:
$$ \begin{array}{}
\alpha = \arctan\left(\dfrac{\sin(\alpha)}{\cos(\alpha)}\right) = \arctan\left(\dfrac{-\mathbf{R}_{21}}{\;\;\;\mathbf{R}_{22}}\right) \\
\\
\beta = \arctan\left(\dfrac{\sin(\beta)}{\cos(\beta)}\right) = \arctan\left(\dfrac{\mathbf{R}_{20}}{\sqrt{\mathbf{R}_{00}^2+\mathbf{R}_{10}^2}}\right) \\
\\
\gamma = \arctan\left(\dfrac{\sin(\gamma)}{\cos(\gamma)}\right) = \arctan\left(\dfrac{-\mathbf{R}_{10}}{\;\;\;\mathbf{R}_{00}}\right)
\end{array} $$
Note that we prefer to use the mathematical function `arctan` rather than simply `arcsin` because the latter cannot for example distinguish $45^o$ from $135^o$ and also for better numerical accuracy. See the text [Angular kinematics in a plane (2D)](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/AngularKinematics2D.ipynb) for more on these issues.
And here is a Python function to compute the Euler angles of rotations from the Global to the local coordinate system for the $xyz$ Cardan sequence:
```
def euler_angles_from_rot_xyz(rot_matrix, unit='deg'):
""" Compute Euler angles from rotation matrix in the xyz sequence."""
import numpy as np
R = np.array(rot_matrix, copy=False).astype(np.float64)[:3, :3]
angles = np.zeros(3)
angles[0] = np.arctan2(-R[2, 1], R[2, 2])
angles[1] = np.arctan2( R[2, 0], np.sqrt(R[0, 0]**2 + R[1, 0]**2))
angles[2] = np.arctan2(-R[1, 0], R[0, 0])
if unit[:3].lower() == 'deg': # convert from rad to degree
angles = np.rad2deg(angles)
return angles
```
For instance, consider sequential rotations of 45$^o$ around $x,y,z$. The resultant rotation matrix is:
```
Ra, Rn = euler_rotmat(order='xyz', frame='local', angles=[45, 45, 45], showA=False)
```
Let's check that calculating back the Cardan angles from this rotation matrix using the `euler_angles_from_rot_xyz()` function:
```
euler_angles_from_rot_xyz(Rn, unit='deg')
```
We could implement a function to calculate the Euler angles for any of the 12 sequences (in fact, plus another 12 sequences if we consider all the rotations from and to the two coordinate systems), but this is tedious. There is a smarter solution using the concept of [quaternion](http://en.wikipedia.org/wiki/Quaternion), but we wont see that now.
Let's see a problem with using Euler angles known as gimbal lock.
### Gimbal lock
[Gimbal lock](http://en.wikipedia.org/wiki/Gimbal_lock) is the loss of one degree of freedom in a three-dimensional coordinate system that occurs when an axis of rotation is placed parallel with another previous axis of rotation and two of the three rotations will be around the same direction given a certain convention of the Euler angles. This "locks" the system into rotations in a degenerate two-dimensional space. The system is not really locked in the sense it can't be moved or reach the other degree of freedom, but it will need an extra rotation for that.
For instance, let's look at the $zxz$ sequence of rotations by the angles $\alpha, \beta, \gamma$:
$$ \begin{array}{l l}
\mathbf{R}_{zxz} & = \mathbf{R_{z}} \mathbf{R_{x}} \mathbf{R_{z}} \\
\\
& =
\begin{bmatrix}
\cos\gamma & \sin\gamma & 0\\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\beta & \sin\beta \\
0 & -\sin\beta & \cos\beta
\end{bmatrix}
\begin{bmatrix}
\cos\alpha & \sin\alpha & 0\\
-\sin\alpha & \cos\alpha & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{array} $$
Which results in:
```
a, b, g = sym.symbols('alpha, beta, gamma')
# Elemental rotation matrices of xyz (local):
Rz = sym.Matrix([[cos(a), sin(a), 0], [-sin(a), cos(a), 0], [0, 0, 1]])
Rx = sym.Matrix([[1, 0, 0], [0, cos(b), sin(b)], [0, -sin(b), cos(b)]])
Rz2 = sym.Matrix([[cos(g), sin(g), 0], [-sin(g), cos(g), 0], [0, 0, 1]])
# Rotation matrix for the zxz sequence:
Rzxz = Rz2*Rx*Rz
Math(sym.latex(r'\mathbf{R}_{zxz}=') + sym.latex(Rzxz, mat_str='matrix'))
```
Let's examine what happens with this rotation matrix when the rotation around the second axis ($x$) by $\beta$ is zero:
$$ \begin{array}{l l}
\mathbf{R}_{zxz}(\alpha, \beta=0, \gamma) =
\begin{bmatrix}
\cos\gamma & \sin\gamma & 0\\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\alpha & \sin\alpha & 0\\
-\sin\alpha & \cos\alpha & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{array} $$
The second matrix is the identity matrix and has no effect on the product of the matrices, which will be:
```
Rzxz = Rz2*Rz
Math(sym.latex(r'\mathbf{R}_{xyz}(\alpha, \beta=0, \gamma)=') + \
sym.latex(Rzxz, mat_str='matrix'))
```
Which simplifies to:
```
Rzxz = sym.simplify(Rzxz)
Math(sym.latex(r'\mathbf{R}_{xyz}(\alpha, \beta=0, \gamma)=') + \
sym.latex(Rzxz, mat_str='matrix'))
```
Despite different values of $\alpha$ and $\gamma$ the result is a single rotation around the $z$ axis given by the sum $\alpha+\gamma$. In this case, of the three degrees of freedom one was lost (the other degree of freedom was set by $\beta=0$). For movement analysis, this means for example that one angle will be undetermined because everything we know is the sum of the two angles obtained from the rotation matrix. We can set the unknown angle to zero but this is arbitrary.
In fact, we already dealt with another example of gimbal lock when we looked at the $xyz$ sequence with rotations by $90^o$. See the figure representing these rotations again and perceive that the first and third rotations were around the same axis because the second rotation was by $90^o$. Let's do the matrix multiplication replacing only the second angle by $90^o$ (and let's use the `euler_rotmat.py`:
```
Ra, Rn = euler_rotmat(order='xyz', frame='local', angles=[None, 90., None], showA=False)
```
Once again, one degree of freedom was lost and we will not be able to uniquely determine the three angles for the given rotation matrix and sequence.
Possible solutions to avoid the gimbal lock are: choose a different sequence; do not rotate the system by the angle that puts the system in gimbal lock (in the examples above, avoid $\beta=90^o$); or add an extra fourth parameter in the description of the rotation angles.
But if we have a physical system where we measure or specify exactly three Euler angles in a fixed sequence to describe or control it, and we can't avoid the system to assume certain angles, then we might have to say "Houston, we have a problem".
A famous situation where such a problem occurred was during the Apollo 13 mission. This is an actual conversation between crew and mission control during the Apollo 13 mission (Corke, 2011):
>`Mission clock: 02 08 12 47`
**Flight**: *Go, Guidance.*
**Guido**: *He’s getting close to gimbal lock there.*
**Flight**: *Roger. CapCom, recommend he bring up C3, C4, B3, B4, C1 and C2 thrusters, and advise he’s getting close to gimbal lock.*
**CapCom**: *Roger.*
*Of note, it was not a gimbal lock that caused the accident with the the Apollo 13 mission, the problem was an oxygen tank explosion.*
## Determination of the rotation matrix
A typical way to determine the rotation matrix for a rigid body in biomechanics is to use motion analysis to measure the position of at least three non-collinear markers placed on the rigid body, and then calculate a basis with these positions, analogue to what we have described in the notebook [Rigid-body transformations in a plane (2D)](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/Transformation2D.ipynb).
### Basis
If we have the position of three markers: **m1**, **m2**, **m3**, a basis (formed by three orthogonal versors) can be found as:
- First axis, **v1**, the vector **m2-m1**;
- Second axis, **v2**, the cross product between the vectors **v1** and **m3-m1**;
- Third axis, **v3**, the cross product between the vectors **v1** and **v2**.
Then, each of these vectors are normalized resulting in three orthogonal versors.
For example, given the positions m1 = [1,0,0], m2 = [0,1,0], m3 = [0,0,1], a basis can be found:
```
m1 = np.array([1, 0, 0])
m2 = np.array([0, 1, 0])
m3 = np.array([0, 0, 1])
v1 = m2 - m1
v2 = np.cross(v1, m3 - m1)
v3 = np.cross(v1, v2)
print('Versors:')
v1 = v1/np.linalg.norm(v1)
print('v1 =', v1)
v2 = v2/np.linalg.norm(v2)
print('v2 =', v2)
v3 = v3/np.linalg.norm(v3)
print('v3 =', v3)
print('\nNorm of each versor:\n',
np.linalg.norm(np.cross(v1, v2)),
np.linalg.norm(np.cross(v1, v3)),
np.linalg.norm(np.cross(v2, v3)))
```
Remember from the text [Rigid-body transformations in a plane (2D)](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/Transformation2D.ipynb) that the versors of this basis are the columns of the $\mathbf{R_{Gl}}$ and the rows of the $\mathbf{R_{lG}}$ rotation matrices, for instance:
```
RlG = np.array([v1, v2, v3])
print('Rotation matrix from Global to local coordinate system:\n', RlG)
```
And the corresponding angles of rotation using the $xyz$ sequence are:
```
euler_angles_from_rot_xyz(RlG)
```
These angles don't mean anything now because they are angles of the axes of the arbitrary basis we computed. In biomechanics, if we want an anatomical interpretation of the coordinate system orientation, we define the versors of the basis oriented with anatomical axes (e.g., for the shoulder, one versor would be aligned with the long axis of the upper arm).
We will see how to perform this computation later. Now we will combine translation and rotation in a single transformation.
## Translation and Rotation
Consider the case where the local coordinate system is translated and rotated in relation to the Global coordinate system as illustrated in the next figure.
<br>
<figure><img src='./../images/transrot3D.png' alt='translation and rotation 3D'/> <figcaption><center><i>Figure. A point in three-dimensional space represented in two coordinate systems, with one system translated and rotated.</i></center></figcaption> </figure>
The position of point $\mathbf{P}$ originally described in the local coordinate system, but now described in the Global coordinate system in vector form is:
$$ \mathbf{P_G} = \mathbf{L_G} + \mathbf{R_{Gl}}\mathbf{P_l} $$
This means that we first *disrotate* the local coordinate system and then correct for the translation between the two coordinate systems. Note that we can't invert this order: the point position is expressed in the local coordinate system and we can't add this vector to another vector expressed in the Global coordinate system, first we have to convert the vectors to the same coordinate system.
If now we want to find the position of a point at the local coordinate system given its position in the Global coordinate system, the rotation matrix and the translation vector, we have to invert the expression above:
$$ \begin{array}{l l}
\mathbf{P_G} = \mathbf{L_G} + \mathbf{R_{Gl}}\mathbf{P_l} \implies \\
\\
\mathbf{R_{Gl}^{-1}}\cdot\mathbf{P_G} = \mathbf{R_{Gl}^{-1}}\left(\mathbf{L_G} + \mathbf{R_{Gl}}\mathbf{P_l}\right) \implies \\
\\
\mathbf{R_{Gl}^{-1}}\mathbf{P_G} = \mathbf{R_{Gl}^{-1}}\mathbf{L_G} + \mathbf{R_{Gl}^{-1}}\mathbf{R_{Gl}}\mathbf{P_l} \implies \\
\\
\mathbf{P_l} = \mathbf{R_{Gl}^{-1}}\left(\mathbf{P_G}-\mathbf{L_G}\right) = \mathbf{R_{Gl}^T}\left(\mathbf{P_G}-\mathbf{L_G}\right) \;\;\;\;\; \text{or} \;\;\;\;\; \mathbf{P_l} = \mathbf{R_{lG}}\left(\mathbf{P_G}-\mathbf{L_G}\right)
\end{array} $$
The expression above indicates that to perform the inverse operation, to go from the Global to the local coordinate system, we first translate and then rotate the coordinate system.
### Transformation matrix
It is possible to combine the translation and rotation operations in only one matrix, called the transformation matrix:
$$ \begin{bmatrix}
\mathbf{P_X} \\
\mathbf{P_Y} \\
\mathbf{P_Z} \\
1
\end{bmatrix} =
\begin{bmatrix}
. & . & . & \mathbf{L_{X}} \\
. & \mathbf{R_{Gl}} & . & \mathbf{L_{Y}} \\
. & . & . & \mathbf{L_{Z}} \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\mathbf{P}_x \\
\mathbf{P}_y \\
\mathbf{P}_z \\
1
\end{bmatrix} $$
Or simply:
$$ \mathbf{P_G} = \mathbf{T_{Gl}}\mathbf{P_l} $$
Remember that in general the transformation matrix is not orthonormal, i.e., its inverse is not equal to its transpose.
The inverse operation, to express the position at the local coordinate system in terms of the Global reference system, is:
$$ \mathbf{P_l} = \mathbf{T_{Gl}^{-1}}\mathbf{P_G} $$
And in matrix form:
$$ \begin{bmatrix}
\mathbf{P_x} \\
\mathbf{P_y} \\
\mathbf{P_z} \\
1
\end{bmatrix} =
\begin{bmatrix}
\cdot & \cdot & \cdot & \cdot \\
\cdot & \mathbf{R^{-1}_{Gl}} & \cdot & -\mathbf{R^{-1}_{Gl}}\:\mathbf{L_G} \\
\cdot & \cdot & \cdot & \cdot \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\mathbf{P_X} \\
\mathbf{P_Y} \\
\mathbf{P_Z} \\
1
\end{bmatrix} $$
### Example with actual motion analysis data
*The data for this example is taken from page 183 of David Winter's book.*
Consider the following marker positions placed on a leg (described in the laboratory coordinate system with coordinates $x, y, z$ in cm, the $x$ axis points forward and the $y$ axes points upward): lateral malleolus (**lm** = [2.92, 10.10, 18.85]), medial malleolus (**mm** = [2.71, 10.22, 26.52]), fibular head (**fh** = [5.05, 41.90, 15.41]), and medial condyle (**mc** = [8.29, 41.88, 26.52]). Define the ankle joint center as the centroid between the **lm** and **mm** markers and the knee joint center as the centroid between the **fh** and **mc** markers. An anatomical coordinate system for the leg can be defined as: the quasi-vertical axis ($y$) passes through the ankle and knee joint centers; a temporary medio-lateral axis ($z$) passes through the two markers on the malleolus, an anterior-posterior as the cross product between the two former calculated orthogonal axes, and the origin at the ankle joint center.
a) Calculate the anatomical coordinate system for the leg as described above.
b) Calculate the rotation matrix and the translation vector for the transformation from the anatomical to the laboratory coordinate system.
c) Calculate the position of each marker and of each joint center at the anatomical coordinate system.
d) Calculate the Cardan angles using the $zxy$ sequence for the orientation of the leg with respect to the laboratory (but remember that the letters chosen to refer to axes are arbitrary, what matters is the directions they represent).
```
# calculation of the joint centers
mm = np.array([2.71, 10.22, 26.52])
lm = np.array([2.92, 10.10, 18.85])
fh = np.array([5.05, 41.90, 15.41])
mc = np.array([8.29, 41.88, 26.52])
ajc = (mm + lm)/2
kjc = (fh + mc)/2
print('Poition of the ankle joint center:', ajc)
print('Poition of the knee joint center:', kjc)
# calculation of the anatomical coordinate system axes (basis)
y = kjc - ajc
x = np.cross(y, mm - lm)
z = np.cross(x, y)
print('Versors:')
x = x/np.linalg.norm(x)
y = y/np.linalg.norm(y)
z = z/np.linalg.norm(z)
print('x =', x)
print('y =', y)
print('z =', z)
Oleg = ajc
print('\nOrigin =', Oleg)
# Rotation matrices
RGl = np.array([x, y , z]).T
print('Rotation matrix from the anatomical to the laboratory coordinate system:\n', RGl)
RlG = RGl.T
print('\nRotation matrix from the laboratory to the anatomical coordinate system:\n', RlG)
# Translational vector
OG = np.array([0, 0, 0]) # Laboratory coordinate system origin
LG = Oleg - OG
print('Translational vector from the anatomical to the laboratory coordinate system:\n', LG)
```
To get the coordinates from the laboratory (global) coordinate system to the anatomical (local) coordinate system:
$$ \mathbf{P_l} = \mathbf{R_{lG}}\left(\mathbf{P_G}-\mathbf{L_G}\right) $$
```
# position of each marker and of each joint center at the anatomical coordinate system
mml = np.dot(RlG, (mm - LG)) # equivalent to the algebraic expression RlG*(mm - LG).T
lml = np.dot(RlG, (lm - LG))
fhl = np.dot(RlG, (fh - LG))
mcl = np.dot(RlG, (mc - LG))
ajcl = np.dot(RlG, (ajc - LG))
kjcl = np.dot(RlG, (kjc - LG))
print('Coordinates of mm in the anatomical system:\n', mml)
print('Coordinates of lm in the anatomical system:\n', lml)
print('Coordinates of fh in the anatomical system:\n', fhl)
print('Coordinates of mc in the anatomical system:\n', mcl)
print('Coordinates of kjc in the anatomical system:\n', kjcl)
print('Coordinates of ajc in the anatomical system (origin):\n', ajcl)
```
## Problems
1. For the example about how the order of rotations of a rigid body affects the orientation shown in a figure above, deduce the rotation matrices for each of the 4 cases shown in the figure. For the first two cases, deduce the rotation matrices from the global to the local coordinate system and for the other two examples, deduce the rotation matrices from the local to the global coordinate system.
2. Consider the data from problem 7 in the notebook [Frame of reference](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/ReferenceFrame.ipynb) where the following anatomical landmark positions are given (units in meters): RASIS=[0.5,0.8,0.4], LASIS=[0.55,0.78,0.1], RPSIS=[0.3,0.85,0.2], and LPSIS=[0.29,0.78,0.3]. Deduce the rotation matrices for the global to anatomical coordinate system and for the anatomical to global coordinate system.
3. For the data from the last example, calculate the Cardan angles using the $zxy$ sequence for the orientation of the leg with respect to the laboratory (but remember that the letters chosen to refer to axes are arbitrary, what matters is the directions they represent).
## References
- Corke P (2011) [Robotics, Vision and Control: Fundamental Algorithms in MATLAB](http://www.petercorke.com/RVC/). Springer-Verlag Berlin.
- Robertson G, Caldwell G, Hamill J, Kamen G (2013) [Research Methods in Biomechanics](http://books.google.com.br/books?id=gRn8AAAAQBAJ). 2nd Edition. Human Kinetics.
- [Maths - Euler Angles](http://www.euclideanspace.com/maths/geometry/rotations/euler/).
- Murray RM, Li Z, Sastry SS (1994) [A Mathematical Introduction to Robotic Manipulation](http://www.cds.caltech.edu/~murray/mlswiki/index.php/Main_Page). Boca Raton, CRC Press.
- Ruina A, Rudra P (2013) [Introduction to Statics and Dynamics](http://ruina.tam.cornell.edu/Book/index.html). Oxford University Press.
- Siciliano B, Sciavicco L, Villani L, Oriolo G (2009) [Robotics - Modelling, Planning and Control](http://books.google.com.br/books/about/Robotics.html?hl=pt-BR&id=jPCAFmE-logC). Springer-Verlag London.
- Winter DA (2009) [Biomechanics and motor control of human movement](http://books.google.com.br/books?id=_bFHL08IWfwC). 4 ed. Hoboken, USA: Wiley.
- Zatsiorsky VM (1997) [Kinematics of Human Motion](http://books.google.com.br/books/about/Kinematics_of_Human_Motion.html?id=Pql_xXdbrMcC&redir_esc=y). Champaign, Human Kinetics.
## Function `euler_rotmatrix.py`
```
# %load ./../functions/euler_rotmat.py
#!/usr/bin/env python
"""Euler rotation matrix given sequence, frame, and angles."""
from __future__ import division, print_function
__author__ = 'Marcos Duarte, https://github.com/demotu/BMC'
__version__ = 'euler_rotmat.py v.1 2014/03/10'
def euler_rotmat(order='xyz', frame='local', angles=None, unit='deg',
str_symbols=None, showA=True, showN=True):
"""Euler rotation matrix given sequence, frame, and angles.
This function calculates the algebraic rotation matrix (3x3) for a given
sequence ('order' argument) of up to three elemental rotations of a given
coordinate system ('frame' argument) around another coordinate system, the
Euler (or Eulerian) angles [1]_.
This function also calculates the numerical values of the rotation matrix
when numerical values for the angles are inputed for each rotation axis.
Use None as value if the rotation angle for the particular axis is unknown.
The symbols for the angles are: alpha, beta, and gamma for the first,
second, and third rotations, respectively.
The matrix product is calulated from right to left and in the specified
sequence for the Euler angles. The first letter will be the first rotation.
The function will print and return the algebraic rotation matrix and the
numerical rotation matrix if angles were inputed.
Parameters
----------
order : string, optional (default = 'xyz')
Sequence for the Euler angles, any combination of the letters
x, y, and z with 1 to 3 letters is accepted to denote the
elemental rotations. The first letter will be the first rotation.
frame : string, optional (default = 'local')
Coordinate system for which the rotations are calculated.
Valid values are 'local' or 'global'.
angles : list, array, or bool, optional (default = None)
Numeric values of the rotation angles ordered as the 'order'
parameter. Enter None for a rotation whith unknown value.
unit : str, optional (default = 'deg')
Unit of the input angles.
str_symbols : list of strings, optional (default = None)
New symbols for the angles, for instance, ['theta', 'phi', 'psi']
showA : bool, optional (default = True)
True (1) displays the Algebraic rotation matrix in rich format.
False (0) to not display.
showN : bool, optional (default = True)
True (1) displays the Numeric rotation matrix in rich format.
False (0) to not display.
Returns
-------
R : Matrix Sympy object
Rotation matrix (3x3) in algebraic format.
Rn : Numpy array or Matrix Sympy object (only if angles are inputed)
Numeric rotation matrix (if values for all angles were inputed) or
a algebraic matrix with some of the algebraic angles substituted
by the corresponding inputed numeric values.
Notes
-----
This code uses Sympy, the Python library for symbolic mathematics, to
calculate the algebraic rotation matrix and shows this matrix in latex form
possibly for using with the IPython Notebook, see [1]_.
References
----------
.. [1] http://nbviewer.ipython.org/github/duartexyz/BMC/blob/master/Transformation3D.ipynb
Examples
--------
>>> # import function
>>> from euler_rotmat import euler_rotmat
>>> # Default options: xyz sequence, local frame and show matrix
>>> R = euler_rotmat()
>>> # XYZ sequence (around global (fixed) coordinate system)
>>> R = euler_rotmat(frame='global')
>>> # Enter numeric values for all angles and show both matrices
>>> R, Rn = euler_rotmat(angles=[90, 90, 90])
>>> # show what is returned
>>> euler_rotmat(angles=[90, 90, 90])
>>> # show only the rotation matrix for the elemental rotation at x axis
>>> R = euler_rotmat(order='x')
>>> # zxz sequence and numeric value for only one angle
>>> R, Rn = euler_rotmat(order='zxz', angles=[None, 0, None])
>>> # input values in radians:
>>> import numpy as np
>>> R, Rn = euler_rotmat(order='zxz', angles=[None, np.pi, None], unit='rad')
>>> # shows only the numeric matrix
>>> R, Rn = euler_rotmat(order='zxz', angles=[90, 0, None], showA='False')
>>> # Change the angles' symbols
>>> R = euler_rotmat(order='zxz', str_symbols=['theta', 'phi', 'psi'])
>>> # Negativate the angles' symbols
>>> R = euler_rotmat(order='zxz', str_symbols=['-theta', '-phi', '-psi'])
>>> # all algebraic matrices for all possible sequences for the local frame
>>> s=['xyz','xzy','yzx','yxz','zxy','zyx','xyx','xzx','yzy','yxy','zxz','zyz']
>>> for seq in s: R = euler_rotmat(order=seq)
>>> # all algebraic matrices for all possible sequences for the global frame
>>> for seq in s: R = euler_rotmat(order=seq, frame='global')
"""
import numpy as np
import sympy as sym
try:
from IPython.core.display import Math, display
ipython = True
except:
ipython = False
angles = np.asarray(np.atleast_1d(angles), dtype=np.float64)
if ~np.isnan(angles).all():
if len(order) != angles.size:
raise ValueError("Parameters 'order' and 'angles' (when " +
"different from None) must have the same size.")
x, y, z = sym.symbols('x, y, z')
sig = [1, 1, 1]
if str_symbols is None:
a, b, g = sym.symbols('alpha, beta, gamma')
else:
s = str_symbols
if s[0][0] == '-': s[0] = s[0][1:]; sig[0] = -1
if s[1][0] == '-': s[1] = s[1][1:]; sig[1] = -1
if s[2][0] == '-': s[2] = s[2][1:]; sig[2] = -1
a, b, g = sym.symbols(s)
var = {'x': x, 'y': y, 'z': z, 0: a, 1: b, 2: g}
# Elemental rotation matrices for xyz (local)
cos, sin = sym.cos, sym.sin
Rx = sym.Matrix([[1, 0, 0], [0, cos(x), sin(x)], [0, -sin(x), cos(x)]])
Ry = sym.Matrix([[cos(y), 0, -sin(y)], [0, 1, 0], [sin(y), 0, cos(y)]])
Rz = sym.Matrix([[cos(z), sin(z), 0], [-sin(z), cos(z), 0], [0, 0, 1]])
if frame.lower() == 'global':
Rs = {'x': Rx.T, 'y': Ry.T, 'z': Rz.T}
order = order.upper()
else:
Rs = {'x': Rx, 'y': Ry, 'z': Rz}
order = order.lower()
R = Rn = sym.Matrix(sym.Identity(3))
str1 = r'\mathbf{R}_{%s}( ' %frame # last space needed for order=''
#str2 = [r'\%s'%var[0], r'\%s'%var[1], r'\%s'%var[2]]
str2 = [1, 1, 1]
for i in range(len(order)):
Ri = Rs[order[i].lower()].subs(var[order[i].lower()], sig[i] * var[i])
R = Ri * R
if sig[i] > 0:
str2[i] = '%s:%s' %(order[i], sym.latex(var[i]))
else:
str2[i] = '%s:-%s' %(order[i], sym.latex(var[i]))
str1 = str1 + str2[i] + ','
if ~np.isnan(angles).all() and ~np.isnan(angles[i]):
if unit[:3].lower() == 'deg':
angles[i] = np.deg2rad(angles[i])
Rn = Ri.subs(var[i], angles[i]) * Rn
#Rn = sym.lambdify(var[i], Ri, 'numpy')(angles[i]) * Rn
str2[i] = str2[i] + '=%.0f^o' %np.around(np.rad2deg(angles[i]), 0)
else:
Rn = Ri * Rn
Rn = sym.simplify(Rn) # for trigonometric relations
try:
# nsimplify only works if there are symbols
Rn2 = sym.latex(sym.nsimplify(Rn, tolerance=1e-8).n(chop=True, prec=4))
except:
Rn2 = sym.latex(Rn.n(chop=True, prec=4))
# there are no symbols, pass it as Numpy array
Rn = np.asarray(Rn)
if showA and ipython:
display(Math(str1[:-1] + ') =' + sym.latex(R, mat_str='matrix')))
if showN and ~np.isnan(angles).all() and ipython:
str2 = ',\;'.join(str2[:angles.size])
display(Math(r'\mathbf{R}_{%s}(%s)=%s' %(frame, str2, Rn2)))
if np.isnan(angles).all():
return R
else:
return R, Rn
```
| true |
code
| 0.577674 | null | null | null | null |
|
# Design of Digital Filters
*This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing.
## Example: Non-Recursive versus Recursive Filter
In the following example, the characteristics and computational complexity of a non-recursive and a recursive filter are compared for a particular design. Quantization is not considered. In order to design the filters we need to specify the requirements. This is typically done by a *tolerance scheme*. The scheme states the desired frequency response and allowed deviations. This is explained at an example.
We aim at the design of a low-pass filter with
1. unit amplitude with an allowable symmetric deviation of $\delta_\text{p}$ for $|\Omega| < \Omega_\text{p}$
2. an attenuation of $a_\text{s}$ for $|\Omega| > \Omega_\text{s}$
where the indices p and s denote the pass- and stop-band, respectively. The region between the pass-band $\Omega_\text{p}$ and the stop-band $\Omega_\text{s}$ is known as *transition-band*. The phase of the filter is not specified.
The resulting tolerance scheme is illustrated for the design parameters $\Omega_\text{p} = \frac{\pi}{3}$, $\Omega_\text{s} = \frac{\pi}{3} + 0.05$, $\delta_\text{p} = 1.5$ dB and $a_\text{s} = -60$ dB.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import scipy.signal as sig
def plot_tolerance_scheme(Omp, Oms, d_p, a_s):
Omp = Omp * np.pi
Oms = Oms * np.pi
p = [[0, -d_p], [Omp, -d_p], [Omp, -300], [np.pi, -300], [np.pi, a_s], [Oms, a_s], [Oms, d_p], [0, d_p]]
polygon = mpatches.Polygon(p, closed=True, facecolor='r', alpha=0.3)
plt.gca().add_patch(polygon)
Omp = .3 # normalized corner frequency of pass-band
Oms = .3 + 0.05 # normalized corner frequency of stop-band
d_p = 1.5 # one-sided pass-band ripple in dB
a_s = -60 # stop-band attenuation in dB
plt.figure(figsize = (10, 5))
plot_tolerance_scheme(Omp, Oms, d_p, a_s)
plt.title('Tolerance scheme')
plt.xlabel(r'$\Omega$')
plt.ylabel(r'$|H(e^{j \Omega})|$ in dB')
plt.axis([0, np.pi, -70, 3])
plt.grid();
```
**Exercise**
* What corner frequencies $f_\text{p}$ and $f_\text{s}$ result for a sampling frequency of $f_\text{s} = 48$ kHz?
Solution: It follows that $f_\text{p} = \frac{\Omega_\text{p}}{\pi} \cdot \frac{f_\text{s}}{2} = 8$ kHz and $f_\text{s} = \frac{\Omega_\text{s}}{\pi} \cdot \frac{f_\text{s}}{2} \approx 8.4$ kHz, since the normalized frequency $\Omega = \pi$ corresponds to $\frac{f_\text{s}}{2}$.
The comparison of non-recursive and recursive filters depends heavily on the chosen filter design algorithm. For the design of the non-recursive filter a technique is used which bases on numerical optimization of the filter coefficients with respect to the desired response. The [Remez algorithm](https://en.wikipedia.org/wiki/Remez_algorithm), as implemented in `scipy.signal.remez`, is used for this purpose. The parameters for the algorithm are the corner frequencies of the pass- and stop-band, as well as the desired attenuation in the stop-band. For the recursive filter, a [Chebyshev type II](https://en.wikipedia.org/wiki/Chebyshev_filter) design is used. Here the parameters are the corner frequency and attenuation of the stop-band. The order of both filters has been chosen manually to fit the given tolerance scheme.
```
N = 152 # length of non-recursive filter
M = 13 # order of recursive filter
# design of non-recursive filter
h = sig.remez(N, [0, Omp/2, Oms/2, 1/2], [1, 10**((a_s-5)/20)], weight=[1, 1])
# design of recursive filter
b, a = sig.cheby2(M, -a_s, Oms)
# compute frequency response of filter
Om, Hn = sig.freqz(h, worN=8192)
Om, Hr = sig.freqz(b, a, worN=8192)
# plot frequency response
plt.figure(figsize = (10,5))
plt.plot(Om, 20*np.log10(np.abs(Hn)), 'b-', label=r'non-recursive N=%d'%N)
plt.plot(Om, 20*np.log10(np.abs(Hr)), 'g-', label=r'recursive N=%d'%M)
plot_tolerance_scheme(Omp, Oms, d_p, a_s)
plt.title('Magnitude response')
plt.xlabel(r'$\Omega$')
plt.ylabel(r'$|H(e^{j \Omega})|$ in dB')
plt.legend()
plt.axis([0, np.pi, -70, 3])
plt.grid()
# plot phase
plt.figure(figsize = (10,5))
plt.plot(Om, np.unwrap(np.angle(Hn)), label=r'non-recursive N=%d'%N)
plt.plot(Om, np.unwrap(np.angle(Hr)), label=r'recursive N=%d'%M)
plt.title('Phase response')
plt.xlabel(r'$\Omega$')
plt.ylabel(r'$\varphi(\Omega)$ in rad')
plt.legend(loc=3)
plt.xlim([0, np.pi])
plt.grid()
```
**Exercises**
* How do both designs differ in terms of their magnitude and phase responses?
* Calculate the number of multiplications and additions required to realize the non-recursive filter
* Calculate the number of multiplications and additions required to realize the recursive filter in [transposed direct form II](../recursive_filters/direct_forms.ipynb#Transposed-Direct-Form-II)
* Decrease the corner frequencies and adapt the order of the filters to match the tolerance scheme
Solution: Inspection of the magnitude response $|H(e^{j \Omega})|$ for the designed non-recursive and recursive filters reveals that both fulfill the given tolerance scheme. An obvious difference between both filters is the structure of the magnitude response in the stop-band $\Omega > \Omega_\text{s}$. While the magnitude of the non-recursive filter shows a high number of fluctuations below the desired attenuation, these are much less for the recursive filter. This is a consequence of the different orders of the filters and their respective number of zeros. The non-recursive filter requires $N$ multiplications and $N-1$ additions to compute one output sample, hence 152 multiplications and 151 additions. The recursive filter in transposed direct form II is realized by 7 SOS. Each of the SOS requires 5 multiplications and 4 additions per output sample, resulting in a total of 35 multiplications and 28 additions.
In order to evaluate the computational complexity of both filters, the execution time is measured when filtering a signal $x[k]$ of length $L=10^5$ samples. The non-recursive filter is realized by direct convolution, the recursive filter in transposed direct form II using the respective Python functions.
```
import timeit
reps = 1000 # number of repetitions for timeit
# setup environment for timeit
tsetup = 'import numpy as np; import scipy.signal as sig; from __main__ import h, a, b; x=np.random.normal(size=int(1e5))'
# non-recursive filter
tn = timeit.timeit('np.convolve(x, h, mode="full")', setup=tsetup, number=reps)
# recursive filter
tr = timeit.timeit('sig.lfilter(b, a, x)' , setup=tsetup, number=reps)
# show the results
plt.figure(figsize = (5, 3))
plt.bar(1, tn/reps*1000)
plt.bar(2, tr/reps*1000)
plt.title('Execution time')
plt.xticks([1, 2], ('non-recursive', 'recursive'))
plt.ylabel('time in ms')
plt.grid()
```
**Exercises**
* Do the execution times correspond with the number of algorithmic operations calculated in the previous exercise?
* Estimate the computational load for the filtering of a signal with a sampling rate of 48 kHz
* How could the execution time of the non-recursive filter be decreased?
* Finally, would you prefer the non-recursive or the recursive design for a practical implementation? Consider the numerical complexity, as well as numerical aspects in your decision.
Solution: On general purpose processors, the numerical complexity is mainly determined by the number of multiplications. The ratio of multiplications per output sample for the non-recursive and the recursive filter is given as $\frac{152}{35} \approx 4.3$, the ratio of execution times in above example as $\frac{4.8 \mathrm{ ms}}{1.5 \mathrm{ ms}} \approx 3.2$. The difference between both can be related to the implementation of both methods and their execution on the given hardware. Note that the execution times and their ratio may differ for other environments. The number of samples used in the measurement above relates to a signal with $\frac{10^5}{f_s} \approx 2$ seconds length. The computational load for the non-recursive filter can hence be estimated as $\frac{4.8 \mathrm{ ms}}{2000 \mathrm{ ms}} \approx 2.4 \cdot 10^{-6}$. The execution time for the non-recursive filter may be decreased by using a fast convolution algorithm.
| true |
code
| 0.694834 | null | null | null | null |
|
# Visualizing tweets and the Logistic Regression model
**Objectives:** Visualize and interpret the logistic regression model
**Steps:**
* Plot tweets in a scatter plot using their positive and negative sums.
* Plot the output of the logistic regression model in the same plot as a solid line
## Import the required libraries
We will be using [*NLTK*](http://www.nltk.org/howto/twitter.html), an opensource NLP library, for collecting, handling, and processing Twitter data. In this lab, we will use the example dataset that comes alongside with NLTK. This dataset has been manually annotated and serves to establish baselines for models quickly.
So, to start, let's import the required libraries.
```
import nltk # NLP toolbox
from os import getcwd
import pandas as pd # Library for Dataframes
from nltk.corpus import twitter_samples
import matplotlib.pyplot as plt # Library for visualization
import numpy as np # Library for math functions
from utils import process_tweet, build_freqs # Our functions for NLP
```
## Load the NLTK sample dataset
To complete this lab, you need the sample dataset of the previous lab. Here, we assume the files are already available, and we only need to load into Python lists.
```
# select the set of positive and negative tweets
all_positive_tweets = twitter_samples.strings('positive_tweets.json')
all_negative_tweets = twitter_samples.strings('negative_tweets.json')
tweets = all_positive_tweets + all_negative_tweets ## Concatenate the lists.
labels = np.append(np.ones((len(all_positive_tweets),1)), np.zeros((len(all_negative_tweets),1)), axis = 0)
# split the data into two pieces, one for training and one for testing (validation set)
train_pos = all_positive_tweets[:4000]
train_neg = all_negative_tweets[:4000]
train_x = train_pos + train_neg
print("Number of tweets: ", len(train_x))
```
# Load the extracted features
Part of this week's assignment is the creation of the numerical features needed for the Logistic regression model. In order not to interfere with it, we have previously calculated and stored these features in a CSV file for the entire training set.
So, please load these features created for the tweets sample.
```
data = pd.read_csv('logistic_features.csv'); # Load a 3 columns csv file using pandas function
data.head(10) # Print the first 10 data entries
```
Now let us get rid of the data frame to keep only Numpy arrays.
```
# Each feature is labeled as bias, positive and negative
X = data[['bias', 'positive', 'negative']].values # Get only the numerical values of the dataframe
Y = data['sentiment'].values; # Put in Y the corresponding labels or sentiments
print(X.shape) # Print the shape of the X part
print(X) # Print some rows of X
```
## Load a pretrained Logistic Regression model
In the same way, as part of this week's assignment, a Logistic regression model must be trained. The next cell contains the resulting model from such training. Notice that a list of 3 numeric values represents the whole model, that we have called _theta_ $\theta$.
```
theta = [7e-08, 0.0005239, -0.00055517]
```
## Plot the samples in a scatter plot
The vector theta represents a plane that split our feature space into two parts. Samples located over that plane are considered positive, and samples located under that plane are considered negative. Remember that we have a 3D feature space, i.e., each tweet is represented as a vector comprised of three values: `[bias, positive_sum, negative_sum]`, always having `bias = 1`.
If we ignore the bias term, we can plot each tweet in a cartesian plane, using `positive_sum` and `negative_sum`. In the cell below, we do precisely this. Additionally, we color each tweet, depending on its class. Positive tweets will be green and negative tweets will be red.
```
# Plot the samples using columns 1 and 2 of the matrix
fig, ax = plt.subplots(figsize = (8, 8))
colors = ['red', 'green']
# Color based on the sentiment Y
ax.scatter(X[:,1], X[:,2], c=[colors[int(k)] for k in Y], s = 0.1) # Plot a dot for each pair of words
plt.xlabel("Positive")
plt.ylabel("Negative")
```
From the plot, it is evident that the features that we have chosen to represent tweets as numerical vectors allow an almost perfect separation between positive and negative tweets. So you can expect a very high accuracy for this model!
## Plot the model alongside the data
We will draw a gray line to show the cutoff between the positive and negative regions. In other words, the gray line marks the line where $$ z = \theta * x = 0.$$
To draw this line, we have to solve the above equation in terms of one of the independent variables.
$$ z = \theta * x = 0$$
$$ x = [1, pos, neg] $$
$$ z(\theta, x) = \theta_0+ \theta_1 * pos + \theta_2 * neg = 0 $$
$$ neg = (-\theta_0 - \theta_1 * pos) / \theta_2 $$
The red and green lines that point in the direction of the corresponding sentiment are calculated using a perpendicular line to the separation line calculated in the previous equations(neg function). It must point in the same direction as the derivative of the Logit function, but the magnitude may differ. It is only for a visual representation of the model.
$$direction = pos * \theta_2 / \theta_1$$
```
# Equation for the separation plane
# It give a value in the negative axe as a function of a positive value
# f(pos, neg, W) = w0 + w1 * pos + w2 * neg = 0
# s(pos, W) = (w0 - w1 * pos) / w2
def neg(theta, pos):
return (-theta[0] - pos * theta[1]) / theta[2]
# Equation for the direction of the sentiments change
# We don't care about the magnitude of the change. We are only interested
# in the direction. So this direction is just a perpendicular function to the
# separation plane
# df(pos, W) = pos * w2 / w1
def direction(theta, pos):
return pos * theta[2] / theta[1]
```
The green line in the chart points in the direction where z > 0 and the red line points in the direction where z < 0. The direction of these lines are given by the weights $\theta_1$ and $\theta_2$
```
# Plot the samples using columns 1 and 2 of the matrix
fig, ax = plt.subplots(figsize = (8, 8))
colors = ['red', 'green']
# Color base on the sentiment Y
ax.scatter(X[:,1], X[:,2], c=[colors[int(k)] for k in Y], s = 0.1) # Plot a dot for each pair of words
plt.xlabel("Positive")
plt.ylabel("Negative")
# Now lets represent the logistic regression model in this chart.
maxpos = np.max(X[:,1])
print(maxpos)
offset = 5000 # The pos value for the direction vectors origin
# Plot a gray line that divides the 2 areas.
#arrow(x, y, dx, dy, **kwargs): This draws an arrow from (x, y) to (x+dx, y+dy).
ax.plot([0, maxpos], [neg(theta, 0), neg(theta, maxpos)], color = 'gray')
print([0, maxpos], [neg(theta, 0), neg(theta, maxpos)])
# Plot a green line pointing to the positive direction
ax.arrow(offset, neg(theta, offset), offset, direction(theta, offset), head_width=500, head_length=500, fc='g', ec='g')
#fc: 箭头颜色, ec: 线颜色
# Plot a red line pointing to the negative direction
ax.arrow(offset, neg(theta, offset), -offset, -direction(theta, offset), head_width=500, head_length=500, fc='r', ec='r')
print( -offset, -direction(theta, offset))
plt.show()
```
**Note that more critical than the Logistic regression itself, are the features extracted from tweets that allow getting the right results in this exercise.**
That is all, folks. Hopefully, now you understand better what the Logistic regression model represents, and why it works that well for this specific problem.
| true |
code
| 0.67531 | null | null | null | null |
|
# Student-t Process
PyMC3 also includes T-process priors. They are a generalization of a Gaussian process prior to the multivariate Student's T distribution. The usage is identical to that of `gp.Latent`, except they require a degrees of freedom parameter when they are specified in the model. For more information, see chapter 9 of [Rasmussen+Williams](http://www.gaussianprocess.org/gpml/), and [Shah et al.](https://arxiv.org/abs/1402.4306).
Note that T processes aren't additive in the same way as GPs, so addition of `TP` objects are not supported.
## Samples from a TP prior
The following code draws samples from a T process prior with 3 degrees of freedom and a Gaussian process, both with the same covariance matrix.
```
import pymc3 as pm
import theano.tensor as tt
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# set the seed
np.random.seed(1)
n = 100 # The number of data points
X = np.linspace(0, 10, n)[:, None] # The inputs to the GP, they must be arranged as a column vector
# Define the true covariance function and its parameters
ℓ_true = 1.0
η_true = 3.0
cov_func = η_true**2 * pm.gp.cov.Matern52(1, ℓ_true)
# A mean function that is zero everywhere
mean_func = pm.gp.mean.Zero()
# The latent function values are one sample from a multivariate normal
# Note that we have to call `eval()` because PyMC3 built on top of Theano
tp_samples = pm.MvStudentT.dist(mu=mean_func(X).eval(), cov=cov_func(X).eval(), nu=3).random(size=8)
## Plot samples from TP prior
fig = plt.figure(figsize=(12,5)); ax = fig.gca()
ax.plot(X.flatten(), tp_samples.T, lw=3, alpha=0.6);
ax.set_xlabel("X"); ax.set_ylabel("y"); ax.set_title("Samples from TP with DoF=3");
gp_samples = pm.MvNormal.dist(mu=mean_func(X).eval(), cov=cov_func(X).eval()).random(size=8)
fig = plt.figure(figsize=(12,5)); ax = fig.gca()
ax.plot(X.flatten(), gp_samples.T, lw=3, alpha=0.6);
ax.set_xlabel("X"); ax.set_ylabel("y"); ax.set_title("Samples from GP");
```
## Poisson data generated by a T process
For the Poisson rate, we take the square of the function represented by the T process prior.
```
np.random.seed(7)
n = 150 # The number of data points
X = np.linspace(0, 10, n)[:, None] # The inputs to the GP, they must be arranged as a column vector
# Define the true covariance function and its parameters
ℓ_true = 1.0
η_true = 3.0
cov_func = η_true**2 * pm.gp.cov.ExpQuad(1, ℓ_true)
# A mean function that is zero everywhere
mean_func = pm.gp.mean.Zero()
# The latent function values are one sample from a multivariate normal
# Note that we have to call `eval()` because PyMC3 built on top of Theano
f_true = pm.MvStudentT.dist(mu=mean_func(X).eval(), cov=cov_func(X).eval(), nu=3).random(size=1)
y = np.random.poisson(f_true**2)
fig = plt.figure(figsize=(12,5)); ax = fig.gca()
ax.plot(X, f_true**2, "dodgerblue", lw=3, label="True f");
ax.plot(X, y, 'ok', ms=3, label="Data");
ax.set_xlabel("X"); ax.set_ylabel("y"); plt.legend();
with pm.Model() as model:
ℓ = pm.Gamma("ℓ", alpha=2, beta=2)
η = pm.HalfCauchy("η", beta=3)
cov = η**2 * pm.gp.cov.ExpQuad(1, ℓ)
# informative prior on degrees of freedom < 5
ν = pm.Gamma("ν", alpha=2, beta=1)
tp = pm.gp.TP(cov_func=cov, nu=ν)
f = tp.prior("f", X=X)
# adding a small constant seems to help with numerical stability here
y_ = pm.Poisson("y", mu=tt.square(f) + 1e-6, observed=y)
tr = pm.sample(1000)
pm.traceplot(tr, varnames=["ℓ", "ν", "η"], lines={"ℓ": ℓ_true, "η": η_true, "ν": 3});
n_new = 200
X_new = np.linspace(0, 15, n_new)[:,None]
# add the GP conditional to the model, given the new X values
with model:
f_pred = tp.conditional("f_pred", X_new)
# Sample from the GP conditional distribution
with model:
pred_samples = pm.sample_ppc(tr, vars=[f_pred], samples=1000)
fig = plt.figure(figsize=(12,5)); ax = fig.gca()
from pymc3.gp.util import plot_gp_dist
plot_gp_dist(ax, np.square(pred_samples["f_pred"]), X_new);
plt.plot(X, np.square(f_true), "dodgerblue", lw=3, label="True f");
plt.plot(X, y, 'ok', ms=3, alpha=0.5, label="Observed data");
plt.xlabel("X"); plt.ylabel("True f(x)"); plt.ylim([-2, 20])
plt.title("Conditional distribution of f_*, given f"); plt.legend();
```
| true |
code
| 0.795718 | null | null | null | null |
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plotly.com/python/getting-started/) by downloading the client and [reading the primer](https://plotly.com/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plotly.com/python/getting-started/#initialization-for-online-plotting) or [offline](https://plotly.com/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plotly.com/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Version Check
Plotly's python package is updated frequently. Run `pip install plotly --upgrade` to use the latest version.
```
import plotly
plotly.__version__
from plotly.offline import iplot, init_notebook_mode
import plotly.graph_objs as go
import pandas as pd
import numpy as np
import ipywidgets as widgets
```
We'll configure the notebook for use in [offline](https://plotly.com/python/getting-started/#initialization-for-offline-plotting) mode
```
init_notebook_mode(connected=True)
```
#### Parallel Categories Diagram
The parallel categories diagram is a visualization of multi-dimensional categorical data sets. Each variable in the data set is represented by a column of rectangles, where each rectangle corresponds to a discrete value taken on by that variable. The relative heights of the rectangles reflect the relative frequency of occurrence of the corresponding value.
Combinations of category rectangles across dimensions are connected by ribbons, where the height of the ribbon corresponds to the relative frequency of occurrence of the combination of categories in the data set.
#### Basic Parallel Categories Diagram
In this first example, we visualize the hair color, eye color, and sex of a sample of 8 people. Hovering over a category rectangle displays a tooltip with the number of people with that single trait. Hovering over a ribbon in the diagram displays a tooltip with the number of people with a particular combination of the three traits connected by the ribbon.
The dimension labels can be dragged horizontally to reorder the dimensions and the category rectangles can be dragged vertically to reorder the categories within a dimension.
```
parcats = go.Parcats(
dimensions=[
{'label': 'Hair',
'values': ['Black', 'Black', 'Black', 'Brown',
'Brown', 'Brown', 'Red', 'Brown']},
{'label': 'Eye',
'values': ['Brown', 'Brown', 'Brown', 'Brown',
'Brown', 'Blue', 'Blue', 'Blue']},
{'label': 'Sex',
'values': ['Female', 'Female', 'Female', 'Male',
'Female', 'Male', 'Male', 'Male']}]
)
iplot([parcats])
```
#### Basic Parallel Categories Diagram with Counts
If the frequency of occurrence for each combination of attributes is known in advance, this can be specified using the `counts` property
```
parcats = go.Parcats(
dimensions=[
{'label': 'Hair',
'values': ['Black', 'Brown', 'Brown', 'Brown', 'Red']},
{'label': 'Eye',
'values': ['Brown', 'Brown', 'Brown', 'Blue', 'Blue']},
{'label': 'Sex',
'values': ['Female', 'Male', 'Female', 'Male', 'Male']}],
counts=[6, 10, 40, 23, 7]
)
iplot([parcats])
```
#### Mutli-Color Parallel Categories Diagram
The color of the ribbons can be specified with the `line.color` property. Similar to other trace types, this property may be set to an array of numbers, which are then mapped to colors according to the the colorscale specified in the `line.colorscale` property.
Here is an example of visualizing the survival rate of passengers in the titanic dataset, where the ribbons are colored based on survival outcome.
By setting the `hoveron` property to `'color'` and the `hoverinfo` property to `'count+probability'` the tooltips now display count and probability information for each color (survival outcome) per category.
By setting the `arrangement` property to `'freeform'` it is now possible to drag categories horizontally to reorder dimensions as well as vertically to reorder categories within the dimension.
```
titanic_df = pd.read_csv(
"https://raw.githubusercontent.com/plotly/datasets/master/titanic.csv")
# Create dimensions
class_dim = go.parcats.Dimension(
values=titanic_df.Pclass,
categoryorder='category ascending',
label="Class"
)
gender_dim = go.parcats.Dimension(
values=titanic_df.Sex,
label="Gender"
)
survival_dim = go.parcats.Dimension(
values=titanic_df.Survived,
label="Outcome",
categoryarray=[0, 1],
ticktext=['perished', 'survived'],
)
# Create parcats trace
color = titanic_df.Survived;
colorscale = [[0, 'lightsteelblue'], [1, 'mediumseagreen']];
data = [
go.Parcats(
dimensions=[class_dim, gender_dim, survival_dim],
line={'color': color,
'colorscale': colorscale},
hoveron='color',
hoverinfo='count+probability',
labelfont={'size': 18, 'family': 'Times'},
tickfont={'size': 16, 'family': 'Times'},
arrangement='freeform'
)
]
# Display figure
iplot(data)
```
#### Parallel Categories Linked Brushing
This example demonstrates how the `on_selection` and `on_click` callbacks can be used to implement linked brushing between 3 categorical dimensions displayed with a `parcats` trace and 2 continuous dimensions displayed with a `scatter` trace.
This example also sets the `line.shape` property to `hspline` to cause the ribbons to curve between categories.
**Note:** In order for the callback functions to be executed the figure must be a `FigureWidget`, and the figure should display itself. In particular the `plot` and `iplot` functions should not be used.
```
cars_df = pd.read_csv(
'https://raw.githubusercontent.com/plotly/datasets/master/imports-85.csv')
# Build parcats dimensions
categorical_dimensions = [
'body-style',
'drive-wheels',
'fuel-type'
];
dimensions = [
dict(values=cars_df[label], label=label)
for label in categorical_dimensions
]
# Build colorscale
color = np.zeros(len(cars_df), dtype='uint8')
colorscale = [[0, 'gray'], [1, 'firebrick']]
# Build figure as FigureWidget
fig = go.FigureWidget(
data=[
go.Scatter(
x=cars_df.horsepower,
y=cars_df['highway-mpg'],
marker={'color': 'gray'},
mode='markers',
selected={'marker': {'color': 'firebrick'}},
unselected={'marker': {'opacity': 0.3}}),
go.Parcats(
domain={'y': [0, 0.4]},
dimensions=dimensions,
line={
'colorscale': colorscale,
'cmin': 0,
'cmax': 1,
'color': color,
'shape': 'hspline'})
],
layout=go.Layout(
height=800,
xaxis={'title': 'Horsepower'},
yaxis={'title': 'MPG',
'domain': [0.6, 1]},
dragmode='lasso',
hovermode='closest')
)
# Update color callback
def update_color(trace, points, state):
# Update scatter selection
fig.data[0].selectedpoints = points.point_inds
# Update parcats colors
new_color = np.zeros(len(cars_df), dtype='uint8')
new_color[points.point_inds] = 1
fig.data[1].line.color = new_color
# Register callback on scatter selection...
fig.data[0].on_selection(update_color)
# and parcats click
fig.data[1].on_click(update_color)
# Display figure
fig
```
#### Parallel Categories with Multi-Color Linked Brushing
This example extends the previous example to support brushing with multiple colors. The toggle buttons above may be used to select the active color, and this color will be applied when points are selected in the `scatter` trace and when categories or ribbons are clicked in the `parcats` trace.
```
cars_df = pd.read_csv(
'https://raw.githubusercontent.com/plotly/datasets/master/imports-85.csv')
# Build parcats dimensions
categorical_dimensions = [
'body-style',
'drive-wheels',
'fuel-type'
];
dimensions = [
dict(values=cars_df[label], label=label)
for label in categorical_dimensions
]
# Build colorscale
color = np.zeros(len(cars_df), dtype='uint8')
colorscale = [[0, 'gray'], [0.33, 'gray'],
[0.33, 'firebrick'], [0.66, 'firebrick'],
[0.66, 'blue'], [1.0, 'blue']];
cmin = -0.5
cmax = 2.5
# Build figure as FigureWidget
fig = go.FigureWidget(
data=[
go.Scatter(
x=cars_df.horsepower,
y=cars_df['highway-mpg'],
marker={'color': color,
'cmin': cmin,
'cmax': cmax,
'colorscale': colorscale,
'showscale': True,
'colorbar': {'tickvals': [0, 1, 2],
'ticktext': ['None', 'Red', 'Blue']}
},
mode='markers'),
go.Parcats(
domain={'y': [0, 0.4]},
dimensions=dimensions,
line={
'colorscale': colorscale,
'cmin': cmin,
'cmax': cmax,
'color': color,
'shape': 'hspline'})
],
layout=go.Layout(
height=800,
xaxis={'title': 'Horsepower'},
yaxis={'title': 'MPG',
'domain': [0.6, 1]},
dragmode='lasso',
hovermode='closest')
)
# Build color selection widget
color_toggle = widgets.ToggleButtons(
options=['None', 'Red', 'Blue'],
index=1,
description='Brush Color:',
disabled=False,
)
# Update color callback
def update_color(trace, points, state):
# Compute new color array
new_color = np.array(fig.data[0].marker.color)
new_color[points.point_inds] = color_toggle.index
with fig.batch_update():
# Update scatter color
fig.data[0].marker.color = new_color
# Update parcats colors
fig.data[1].line.color = new_color
# Register callback on scatter selection...
fig.data[0].on_selection(update_color)
# and parcats click
fig.data[1].on_click(update_color)
# Display figure
widgets.VBox([color_toggle, fig])
```
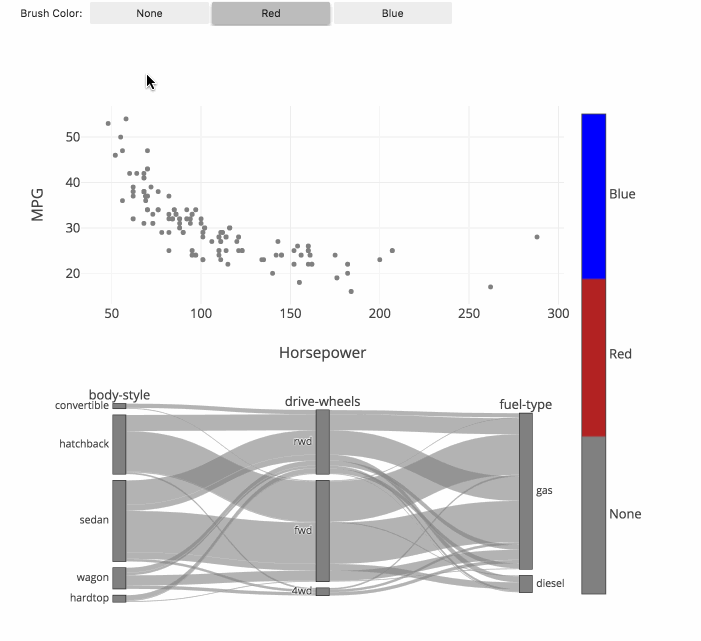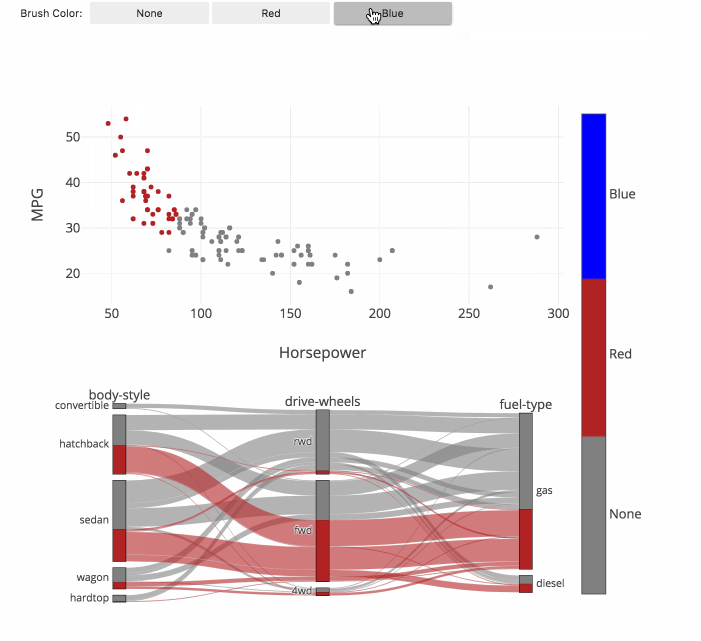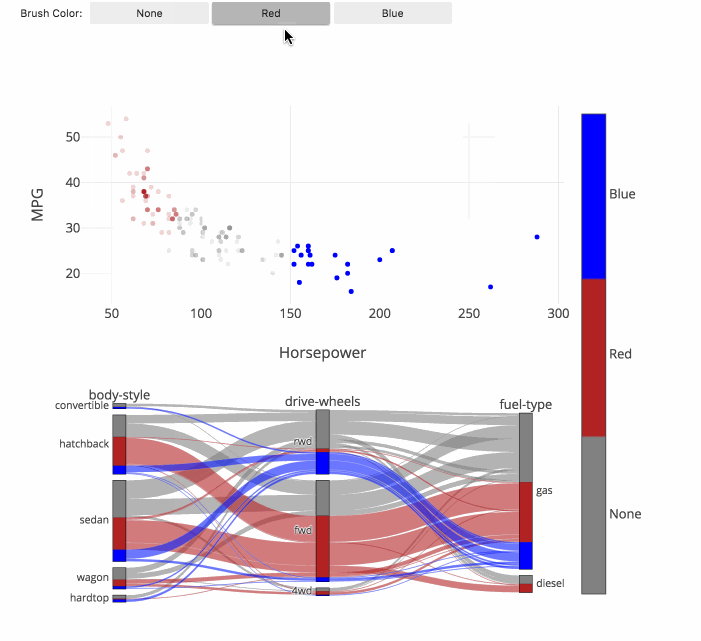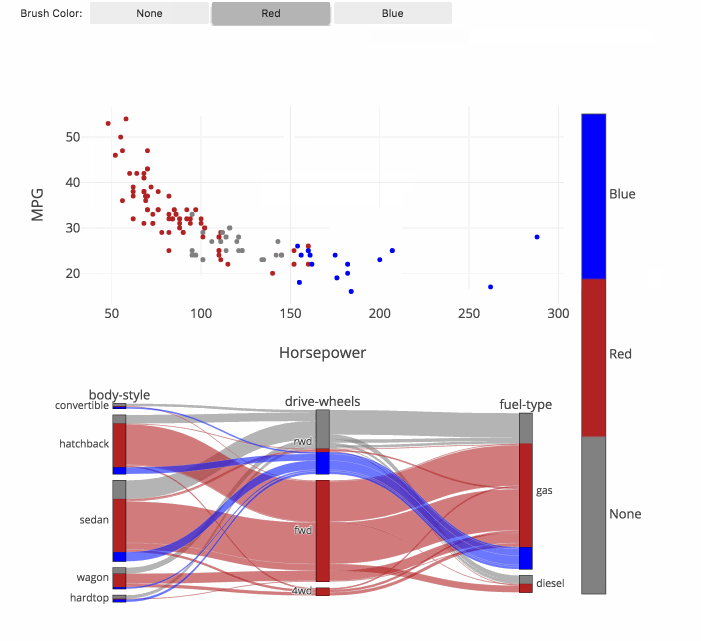
#### Reference
See https://plotly.com/python/reference/#parcats for more information and chart attribute options!
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'parcats.ipynb', 'python/parallel-categories-diagram/', 'Parallel Categories Diagram',
'How to make parallel categories diagrams in Python with Plotly.',
title = 'Python Parallel Categories | Plotly',
has_thumbnail='true', thumbnail='thumbnail/parcats.jpg',
language='python',
display_as='statistical', order=10.3,
uses_plotly_offline=True,
ipynb= '~notebook_demo/258')
```
| true |
code
| 0.611382 | null | null | null | null |
|
<h1><font color='blue'> 8E and 8F: Finding the Probability P(Y==1|X)</font></h1>
<h2><font color='Geen'> 8E: Implementing Decision Function of SVM RBF Kernel</font></h2>
<font face=' Comic Sans MS' size=3>After we train a kernel SVM model, we will be getting support vectors and their corresponsing coefficients $\alpha_{i}$
Check the documentation for better understanding of these attributes:
https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
<img src='https://i.imgur.com/K11msU4.png' width=500>
As a part of this assignment you will be implementing the ```decision_function()``` of kernel SVM, here decision_function() means based on the value return by ```decision_function()``` model will classify the data point either as positive or negative
Ex 1: In logistic regression After traning the models with the optimal weights $w$ we get, we will find the value $\frac{1}{1+\exp(-(wx+b))}$, if this value comes out to be < 0.5 we will mark it as negative class, else its positive class
Ex 2: In Linear SVM After traning the models with the optimal weights $w$ we get, we will find the value of $sign(wx+b)$, if this value comes out to be -ve we will mark it as negative class, else its positive class.
Similarly in Kernel SVM After traning the models with the coefficients $\alpha_{i}$ we get, we will find the value of
$sign(\sum_{i=1}^{n}(y_{i}\alpha_{i}K(x_{i},x_{q})) + intercept)$, here $K(x_{i},x_{q})$ is the RBF kernel. If this value comes out to be -ve we will mark $x_{q}$ as negative class, else its positive class.
RBF kernel is defined as: $K(x_{i},x_{q})$ = $exp(-\gamma ||x_{i} - x_{q}||^2)$
For better understanding check this link: https://scikit-learn.org/stable/modules/svm.html#svm-mathematical-formulation
</font>
## Task E
> 1. Split the data into $X_{train}$(60), $X_{cv}$(20), $X_{test}$(20)
> 2. Train $SVC(gamma=0.001, C=100.)$ on the ($X_{train}$, $y_{train}$)
> 3. Get the decision boundry values $f_{cv}$ on the $X_{cv}$ data i.e. ` `$f_{cv}$ ```= decision_function(```$X_{cv}$```)``` <font color='red'>you need to implement this decision_function()</font>
```
import numpy as np
import pandas as pd
from sklearn.datasets import make_classification
from sklearn.model_selection import GridSearchCV
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import math
X, y = make_classification(n_samples=5000, n_features=5, n_redundant=2,
n_classes=2, weights=[0.7], class_sep=0.7, random_state=15)
xtrain, xtest, ytrain, ytest = train_test_split(X, y, test_size=0.3, random_state=0)
xcv, xtest,ycv, ytest = train_test_split(xtest, ytest, test_size=0.3, random_state=0)
print(xtrain.shape, ytrain.shape, xtest.shape, ytest.shape)
print(xtest.shape, ytest.shape, xcv.shape, ycv.shape)
clf = SVC(random_state=0, decision_function_shape='ovo')
clf = GridSearchCV(clf, {'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma' : [0.001,0.01, 0.1, 1, 10, 100]}, n_jobs=-1, cv=5)
clf = clf.fit(xtrain, ytrain) # set the best parameters
clf.best_estimator_, clf.best_score_
```
### Pseudo code
clf = SVC(gamma=0.001, C=100.)<br>
clf.fit(Xtrain, ytrain)
<font color='green'>def</font> <font color='blue'>decision_function</font>(Xcv, ...): #use appropriate parameters <br>
<font color='green'>for</font> a data point $x_q$ <font color='green'>in</font> Xcv: <br>
<font color='grey'>#write code to implement $(\sum_{i=1}^{\text{all the support vectors}}(y_{i}\alpha_{i}K(x_{i},x_{q})) + intercept)$, here the values $y_i$, $\alpha_{i}$, and $intercept$ can be obtained from the trained model</font><br>
<font color='green'>return</font> <font color='grey'><i># the decision_function output for all the data points in the Xcv</i></font>
fcv = decision_function(Xcv, ...) <i># based on your requirement you can pass any other parameters </i>
<b>Note</b>: Make sure the values you get as fcv, should be equal to outputs of clf.decision_function(Xcv)
```
clf = SVC(random_state=0, gamma=1, C=100, decision_function_shape='ovo')
clf.fit(xtrain, ytrain)
pred = clf.predict(xcv)
clf_dec = clf.decision_function(xcv)
def decision_function(clf, data):
add_intercept = []
for x_q in data:
add_intercept.append(np.sum(clf.dual_coef_ * np.exp(-clf._gamma*np.sum((clf.support_vectors_ - x_q)**2, axis=1))) + clf.intercept_[0])
return add_intercept
fcv = decision_function(clf, xcv)
print(fcv[:5], '\n', clf_dec[:5])
```
<h2><font color='Geen'> 8F: Implementing Platt Scaling to find P(Y==1|X)</font></h2>
Check this <a href='https://drive.google.com/open?id=133odBinMOIVb_rh_GQxxsyMRyW-Zts7a'>PDF</a>
<img src='https://i.imgur.com/CAMnVnh.png'>
```
unique, frequency = np.unique(ytrain, return_counts = True)
count = np.asarray((unique, frequency ))
print(count)
neg, pos = frequency[0], frequency[1]
def target_calib(x):
cal_target = []
for i in x:
if i == 1:
cal_target.append((pos + 1)/(pos + 2))
elif i == 0:
cal_target.append(1 / (neg + 2))
return cal_target
claibrated_target = target_calib(pred.tolist())
```
## TASK F
> 4. Apply SGD algorithm with ($f_{cv}$, $y_{cv}$) and find the weight $W$ intercept $b$ ```Note: here our data is of one dimensional so we will have a one dimensional weight vector i.e W.shape (1,)```
> Note1: Don't forget to change the values of $y_{cv}$ as mentioned in the above image. you will calculate y+, y- based on data points in train data
> Note2: the Sklearn's SGD algorithm doesn't support the real valued outputs, you need to use the code that was done in the `'Logistic Regression with SGD and L2'` Assignment after modifying loss function, and use same parameters that used in that assignment.
<img src='https://i.imgur.com/zKYE9Oc.png'>
if Y[i] is 1, it will be replaced with y+ value else it will replaced with y- value
> 5. For a given data point from $X_{test}$, $P(Y=1|X) = \frac{1}{1+exp(-(W*f_{test}+ b))}$ where ` `$f_{test}$ ```= decision_function(```$X_{test}$```)```, W and b will be learned as metioned in the above step
```
def initialize_weights(dim):
w = np.zeros_like((dim))
b = np.zeros_like((1))
print("Weights-Initialized : ", w.shape)
return w,b
def sigmoid(z):
sigmoid = 1/(1+math.exp(-z))
return sigmoid
def logloss(W, b, X, Y):
N = len(X)
loss=[]
for i in range(N):
z = np.dot(X[i],W) + b
pred = sigmoid(z)
if pred < 0.5:
l = (1-Y[i])*np.log10(1-pred)
loss.append(l)
else:
l = Y[i]*np.log10(pred)
loss.append(l)
loss = (-1 * 1/len(loss) * sum(loss))
return loss
def gradient_dw(x,y,w,b,alpha,N):
dw =x*(y-sigmoid(np.dot(w,x)+b)) - alpha/N * w
return dw
def gradient_db(x,y,w,b):
db =(y-sigmoid(np.dot(w,x)+b))
return db
def pred(w,b, X):
N = len(X.tolist())
predict = []
for i in range(N):
z = np.dot(X[i],w) + b
predict.append(sigmoid(z))
return np.array(predict)
def train(Y_calibrated,fcv,epochs,alpha,eta0):
''' In this function, we will implement logistic regression'''
scale_down_factor = 0.0001
epoch = 1
w, b = initialize_weights(1)
wl = []
bl = []
Lw=np.zeros_like(1)
Lb=0
loss = 0
prev = 0
train_loss = []
test_loss = []
while epoch <= epochs:
y_train_pred = []
y_test_pred = []
np.random.RandomState(seed=2)
for m in range(len(Y_calibrated)):
i = np.random.choice(len(Y_calibrated))
z = np.dot(Y_calibrated[i],w) + b
Lw = gradient_dw(Y_calibrated[i],fcv[i],w,b,alpha,len(Y_calibrated))
Lb = gradient_db(Y_calibrated[i],fcv[i],w,b)
w=(1-(alpha * scale_down_factor/epochs))*w+alpha*Lw
b=b+alpha*Lb
train_loss.append(round(logloss(w,b,Y_calibrated, fcv), 3))
if train_loss[-1] == prev:
break;
else:
prev = train_loss[-1]
print("Epoch: %d, train_Loss: %.3f" %(epoch, train_loss[-1]))
epoch+=1
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(train_loss, label='train_log_loss')
plt.grid()
plt.legend()
plt.title('Log loss vs epoch')
plt.xlabel('Iterations')
plt.ylabel('log loss')
plt.show()
return w,b
alpha=0.0001
eta0=0.0001
N=len(xcv)
epochs=50
w,b = train(claibrated_target,fcv,epochs,alpha,eta0)
w, b
f_test = decision_function(clf, xtest)
def calibrated_test(ftest, weight, bias):
test_prediction = []
for i in ftest:
z = np.dot(i,weight) + bias
test_prediction.append(sigmoid(z))
return np.array(test_prediction)
test_pred = calibrated_test(f_test, w, b)
print(test_pred[:5])
```
__Note: in the above algorithm, the steps 2, 4 might need hyper parameter tuning, To reduce the complexity of the assignment we are excluding the hyerparameter tuning part, but intrested students can try that__
If any one wants to try other calibration algorithm istonic regression also please check these tutorials
1. http://fa.bianp.net/blog/tag/scikit-learn.html#fn:1
2. https://drive.google.com/open?id=1MzmA7QaP58RDzocB0RBmRiWfl7Co_VJ7
3. https://drive.google.com/open?id=133odBinMOIVb_rh_GQxxsyMRyW-Zts7a
4. https://stat.fandom.com/wiki/Isotonic_regression#Pool_Adjacent_Violators_Algorithm
| true |
code
| 0.489259 | null | null | null | null |
|
# COVID-19 exploratory data analysis
ver. A.L. 20200512
**Slightly modified from Greg Rafferty's** https://github.com/raffg/covid-19; <br>see also his
dashboard to monitor the COVID-19 pandemic https://covid-19-raffg.herokuapp.com and his [portfolio](https://github.com/raffg/portfolio/blob/master/README.md)
### Uses data provided by the [Johns Hopkins Center for Systems Science and Engineering](https://github.com/CSSEGISandData/COVID-19)
Requires:
- plotly: https://plotly.com/python (`conda install plotly`)
- cufflinks: https://plotly.com/python/v3/ipython-notebooks/cufflinks (`pip install cufflinks --upgrade`)
## Learning objectives
- How to read (updated) data from the web
- How to organize and analyse data using `pandas`
- How to make interactive graphs using `plotly`
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import glob
import re
from datetime import date, timedelta
import io
import requests
import plotly
print('plotly:', plotly.__version__)
# Standard plotly imports
import plotly.graph_objects as go
from plotly.offline import iplot, init_notebook_mode
# Using plotly + cufflinks in offline mode
import cufflinks
print('cufflinks:', cufflinks.__version__)
cufflinks.go_offline(connected=True)
init_notebook_mode(connected=True)
# # Load files from folder
# path = 'COVID-19/csse_covid_19_data/csse_covid_19_daily_reports'
# all_files = glob.glob(path + "/*.csv")
# files = []
# for filename in all_files:
# file = re.search(r'([0-9]{2}\-[0-9]{2}\-[0-9]{4})', filename)[0]
# df = pd.read_csv(filename, index_col=None, header=0)
# df['date'] = pd.to_datetime(file)
# files.append(df)
# df = pd.concat(files, axis=0, ignore_index=True, sort=False)
```
```
# Load files from web
file_date = date(2020, 1, 22)
dates = []
while file_date <= date.today():
dates.append(file_date)
file_date += timedelta(days=1)
files = []
for file in dates:
file = file.strftime("%m-%d-%Y")
print(file)
url = r'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_daily_reports/{}.csv'.format(file)
raw_string = requests.get(url).content
dff = pd.read_csv(io.StringIO(raw_string.decode('utf-8')))
dff['date'] = pd.to_datetime(file)
dff.rename(columns={'Country_Region': 'Country/Region'}, inplace=True)
files.append(dff)
dff = pd.concat(files, axis=0, ignore_index=True, sort=False)
```
```
dff.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 165400 entries, 0 to 165399
Data columns (total 18 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Province/State 4358 non-null object
1 Country/Region 165400 non-null object
2 Last Update 7617 non-null object
3 Confirmed 165381 non-null float64
4 Deaths 164959 non-null float64
5 Recovered 165012 non-null float64
6 date 165400 non-null datetime64[ns]
7 Latitude 4799 non-null float64
8 Longitude 4799 non-null float64
9 FIPS 143674 non-null float64
10 Admin2 144198 non-null object
11 Province_State 148664 non-null object
12 Last_Update 157783 non-null object
13 Lat 155291 non-null float64
14 Long_ 155291 non-null float64
15 Active 157783 non-null float64
16 Combined_Key 157783 non-null object
17 404: Not Found 0 non-null object
dtypes: datetime64[ns](1), float64(9), object(8)
memory usage: 22.7+ MB
```
```
# Save to disk (overwrite previous version)
#dff.to_csv('./data/csse_covid_19_daily_reports.csv', encoding='utf-8', index=False)
tmp = pd.read_csv('./data/csse_covid_19_daily_reports.csv')
df = tmp
# Rename countries with duplicate naming conventions
df['Country/Region'].replace('Mainland China', 'China', inplace=True)
df['Country/Region'].replace('Hong Kong SAR', 'Hong Kong', inplace=True)
df['Country/Region'].replace(' Azerbaijan', 'Azerbaijan', inplace=True)
df['Country/Region'].replace('Holy See', 'Vatican City', inplace=True)
df['Country/Region'].replace('Iran (Islamic Republic of)', 'Iran', inplace=True)
df['Country/Region'].replace('Taiwan*', 'Taiwan', inplace=True)
df['Country/Region'].replace('Korea, South', 'South Korea', inplace=True)
df['Country/Region'].replace('Viet Nam', 'Vietnam', inplace=True)
df['Country/Region'].replace('Macao SAR', 'Macau', inplace=True)
df['Country/Region'].replace('Russian Federation', 'Russia', inplace=True)
df['Country/Region'].replace('Republic of Moldova', 'Moldova', inplace=True)
df['Country/Region'].replace('Czechia', 'Czech Republic', inplace=True)
df['Country/Region'].replace('Congo (Kinshasa)', 'Congo', inplace=True)
df['Country/Region'].replace('Northern Ireland', 'United Kingdom', inplace=True)
df['Country/Region'].replace('Republic of Korea', 'North Korea', inplace=True)
df['Country/Region'].replace('Congo (Brazzaville)', 'Congo', inplace=True)
df['Country/Region'].replace('Taipei and environs', 'Taiwan', inplace=True)
df['Country/Region'].replace('Others', 'Cruise Ship', inplace=True)
df['Province/State'].replace('Cruise Ship', 'Diamond Princess cruise ship', inplace=True)
df['Province/State'].replace('From Diamond Princess', 'Diamond Princess cruise ship', inplace=True)
# Replace old reporting standards
df['Province/State'].replace('Chicago', 'Illinois', inplace=True)
df['Province/State'].replace('Chicago, IL', 'Illinois', inplace=True)
df['Province/State'].replace('Cook County, IL', 'Illinois', inplace=True)
df['Province/State'].replace('Boston, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace(' Norfolk County, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace('Suffolk County, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace('Middlesex County, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace('Norwell County, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace('Plymouth County, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace('Norfolk County, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace('Berkshire County, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace('Unknown Location, MA', 'Massachusetts', inplace=True)
df['Province/State'].replace('Los Angeles, CA', 'California', inplace=True)
df['Province/State'].replace('Orange, CA', 'California', inplace=True)
df['Province/State'].replace('Santa Clara, CA', 'California', inplace=True)
df['Province/State'].replace('San Benito, CA', 'California', inplace=True)
df['Province/State'].replace('Humboldt County, CA', 'California', inplace=True)
df['Province/State'].replace('Sacramento County, CA', 'California', inplace=True)
df['Province/State'].replace('Travis, CA (From Diamond Princess)', 'California', inplace=True)
df['Province/State'].replace('Placer County, CA', 'California', inplace=True)
df['Province/State'].replace('San Mateo, CA', 'California', inplace=True)
df['Province/State'].replace('Sonoma County, CA', 'California', inplace=True)
df['Province/State'].replace('Berkeley, CA', 'California', inplace=True)
df['Province/State'].replace('Orange County, CA', 'California', inplace=True)
df['Province/State'].replace('Contra Costa County, CA', 'California', inplace=True)
df['Province/State'].replace('San Francisco County, CA', 'California', inplace=True)
df['Province/State'].replace('Yolo County, CA', 'California', inplace=True)
df['Province/State'].replace('Santa Clara County, CA', 'California', inplace=True)
df['Province/State'].replace('San Diego County, CA', 'California', inplace=True)
df['Province/State'].replace('Travis, CA', 'California', inplace=True)
df['Province/State'].replace('Alameda County, CA', 'California', inplace=True)
df['Province/State'].replace('Madera County, CA', 'California', inplace=True)
df['Province/State'].replace('Santa Cruz County, CA', 'California', inplace=True)
df['Province/State'].replace('Fresno County, CA', 'California', inplace=True)
df['Province/State'].replace('Riverside County, CA', 'California', inplace=True)
df['Province/State'].replace('Shasta County, CA', 'California', inplace=True)
df['Province/State'].replace('Seattle, WA', 'Washington', inplace=True)
df['Province/State'].replace('Snohomish County, WA', 'Washington', inplace=True)
df['Province/State'].replace('King County, WA', 'Washington', inplace=True)
df['Province/State'].replace('Unassigned Location, WA', 'Washington', inplace=True)
df['Province/State'].replace('Clark County, WA', 'Washington', inplace=True)
df['Province/State'].replace('Jefferson County, WA', 'Washington', inplace=True)
df['Province/State'].replace('Pierce County, WA', 'Washington', inplace=True)
df['Province/State'].replace('Kittitas County, WA', 'Washington', inplace=True)
df['Province/State'].replace('Grant County, WA', 'Washington', inplace=True)
df['Province/State'].replace('Spokane County, WA', 'Washington', inplace=True)
df['Province/State'].replace('Tempe, AZ', 'Arizona', inplace=True)
df['Province/State'].replace('Maricopa County, AZ', 'Arizona', inplace=True)
df['Province/State'].replace('Pinal County, AZ', 'Arizona', inplace=True)
df['Province/State'].replace('Madison, WI', 'Wisconsin', inplace=True)
df['Province/State'].replace('San Antonio, TX', 'Texas', inplace=True)
df['Province/State'].replace('Lackland, TX', 'Texas', inplace=True)
df['Province/State'].replace('Lackland, TX (From Diamond Princess)', 'Texas', inplace=True)
df['Province/State'].replace('Harris County, TX', 'Texas', inplace=True)
df['Province/State'].replace('Fort Bend County, TX', 'Texas', inplace=True)
df['Province/State'].replace('Montgomery County, TX', 'Texas', inplace=True)
df['Province/State'].replace('Collin County, TX', 'Texas', inplace=True)
df['Province/State'].replace('Ashland, NE', 'Nebraska', inplace=True)
df['Province/State'].replace('Omaha, NE (From Diamond Princess)', 'Nebraska', inplace=True)
df['Province/State'].replace('Douglas County, NE', 'Nebraska', inplace=True)
df['Province/State'].replace('Portland, OR', 'Oregon', inplace=True)
df['Province/State'].replace('Umatilla, OR', 'Oregon', inplace=True)
df['Province/State'].replace('Klamath County, OR', 'Oregon', inplace=True)
df['Province/State'].replace('Douglas County, OR', 'Oregon', inplace=True)
df['Province/State'].replace('Marion County, OR', 'Oregon', inplace=True)
df['Province/State'].replace('Jackson County, OR ', 'Oregon', inplace=True)
df['Province/State'].replace('Washington County, OR', 'Oregon', inplace=True)
df['Province/State'].replace('Providence, RI', 'Rhode Island', inplace=True)
df['Province/State'].replace('Providence County, RI', 'Rhode Island', inplace=True)
df['Province/State'].replace('Grafton County, NH', 'New Hampshire', inplace=True)
df['Province/State'].replace('Rockingham County, NH', 'New Hampshire', inplace=True)
df['Province/State'].replace('Hillsborough, FL', 'Florida', inplace=True)
df['Province/State'].replace('Sarasota, FL', 'Florida', inplace=True)
df['Province/State'].replace('Santa Rosa County, FL', 'Florida', inplace=True)
df['Province/State'].replace('Broward County, FL', 'Florida', inplace=True)
df['Province/State'].replace('Lee County, FL', 'Florida', inplace=True)
df['Province/State'].replace('Volusia County, FL', 'Florida', inplace=True)
df['Province/State'].replace('Manatee County, FL', 'Florida', inplace=True)
df['Province/State'].replace('Okaloosa County, FL', 'Florida', inplace=True)
df['Province/State'].replace('Charlotte County, FL', 'Florida', inplace=True)
df['Province/State'].replace('New York City, NY', 'New York', inplace=True)
df['Province/State'].replace('Westchester County, NY', 'New York', inplace=True)
df['Province/State'].replace('Queens County, NY', 'New York', inplace=True)
df['Province/State'].replace('New York County, NY', 'New York', inplace=True)
df['Province/State'].replace('Nassau, NY', 'New York', inplace=True)
df['Province/State'].replace('Nassau County, NY', 'New York', inplace=True)
df['Province/State'].replace('Rockland County, NY', 'New York', inplace=True)
df['Province/State'].replace('Saratoga County, NY', 'New York', inplace=True)
df['Province/State'].replace('Suffolk County, NY', 'New York', inplace=True)
df['Province/State'].replace('Ulster County, NY', 'New York', inplace=True)
df['Province/State'].replace('Fulton County, GA', 'Georgia', inplace=True)
df['Province/State'].replace('Floyd County, GA', 'Georgia', inplace=True)
df['Province/State'].replace('Polk County, GA', 'Georgia', inplace=True)
df['Province/State'].replace('Cherokee County, GA', 'Georgia', inplace=True)
df['Province/State'].replace('Cobb County, GA', 'Georgia', inplace=True)
df['Province/State'].replace('Wake County, NC', 'North Carolina', inplace=True)
df['Province/State'].replace('Chatham County, NC', 'North Carolina', inplace=True)
df['Province/State'].replace('Bergen County, NJ', 'New Jersey', inplace=True)
df['Province/State'].replace('Hudson County, NJ', 'New Jersey', inplace=True)
df['Province/State'].replace('Clark County, NV', 'Nevada', inplace=True)
df['Province/State'].replace('Washoe County, NV', 'Nevada', inplace=True)
df['Province/State'].replace('Williamson County, TN', 'Tennessee', inplace=True)
df['Province/State'].replace('Davidson County, TN', 'Tennessee', inplace=True)
df['Province/State'].replace('Shelby County, TN', 'Tennessee', inplace=True)
df['Province/State'].replace('Montgomery County, MD', 'Maryland', inplace=True)
df['Province/State'].replace('Harford County, MD', 'Maryland', inplace=True)
df['Province/State'].replace('Denver County, CO', 'Colorado', inplace=True)
df['Province/State'].replace('Summit County, CO', 'Colorado', inplace=True)
df['Province/State'].replace('Douglas County, CO', 'Colorado', inplace=True)
df['Province/State'].replace('El Paso County, CO', 'Colorado', inplace=True)
df['Province/State'].replace('Delaware County, PA', 'Pennsylvania', inplace=True)
df['Province/State'].replace('Wayne County, PA', 'Pennsylvania', inplace=True)
df['Province/State'].replace('Montgomery County, PA', 'Pennsylvania', inplace=True)
df['Province/State'].replace('Fayette County, KY', 'Kentucky', inplace=True)
df['Province/State'].replace('Jefferson County, KY', 'Kentucky', inplace=True)
df['Province/State'].replace('Harrison County, KY', 'Kentucky', inplace=True)
df['Province/State'].replace('Marion County, IN', 'Indiana', inplace=True)
df['Province/State'].replace('Hendricks County, IN', 'Indiana', inplace=True)
df['Province/State'].replace('Ramsey County, MN', 'Minnesota', inplace=True)
df['Province/State'].replace('Carver County, MN', 'Minnesota', inplace=True)
df['Province/State'].replace('Fairfield County, CT', 'Connecticut', inplace=True)
df['Province/State'].replace('Charleston County, SC', 'South Carolina', inplace=True)
df['Province/State'].replace('Spartanburg County, SC', 'South Carolina', inplace=True)
df['Province/State'].replace('Kershaw County, SC', 'South Carolina', inplace=True)
df['Province/State'].replace('Davis County, UT', 'Utah', inplace=True)
df['Province/State'].replace('Honolulu County, HI', 'Hawaii', inplace=True)
df['Province/State'].replace('Tulsa County, OK', 'Oklahoma', inplace=True)
df['Province/State'].replace('Fairfax County, VA', 'Virginia', inplace=True)
df['Province/State'].replace('St. Louis County, MO', 'Missouri', inplace=True)
df['Province/State'].replace('Unassigned Location, VT', 'Vermont', inplace=True)
df['Province/State'].replace('Bennington County, VT', 'Vermont', inplace=True)
df['Province/State'].replace('Johnson County, IA', 'Iowa', inplace=True)
df['Province/State'].replace('Jefferson Parish, LA', 'Louisiana', inplace=True)
df['Province/State'].replace('Johnson County, KS', 'Kansas', inplace=True)
df['Province/State'].replace('Washington, D.C.', 'District of Columbia', inplace=True)
# Interpolate values for missing South Korea data on March 11
# (we skip this, but see the original https://github.com/raffg/covid-19/blob/master/eda.ipynb)
# South Korea data on March 10 seems to be mislabled as North Korea
df.loc[(df['Country/Region'] == 'North Korea') & (df['date'] == '03-10-2020'), 'Country/Region'] = 'South Korea'
df.info()
df
# Re-order the columns for readability
df = df[['date',
'Country/Region',
'Province/State',
'Confirmed',
'Deaths',
'Recovered',
'Latitude',
'Longitude']]
# Fill missing values as 0; create Active cases column
df['Confirmed'] = df['Confirmed'].fillna(0).astype(int)
df['Deaths'] = df['Deaths'].fillna(0).astype(int)
df['Recovered'] = df['Recovered'].fillna(0).astype(int)
df['Active'] = df['Confirmed'] - (df['Deaths'] + df['Recovered'])
# Replace missing values for latitude and longitude
df['Latitude'] = df['Latitude'].fillna(df.groupby('Province/State')['Latitude'].transform('mean'))
df['Longitude'] = df['Longitude'].fillna(df.groupby('Province/State')['Longitude'].transform('mean'))
df.info()
n_reg = len(df['Country/Region'].unique())
print('Number of unique Country/Region:', n_reg)
df[df['Country/Region'] == 'US'].groupby(['date', 'Province/State'])[['Confirmed', 'Deaths', 'Recovered', 'Active']].sum()
df[df['Country/Region'] == 'US'].groupby('date')[['Confirmed', 'Deaths', 'Recovered', 'Active']].sum()
# fatality rate
'{:.2f}%'.format(100 *
df[df['date'] == df['date'].iloc[-1]]['Deaths'].sum() /
df[df['date'] == df['date'].iloc[-1]]['Confirmed'].sum())
fig = go.Figure([go.Scatter(x=df[df['Country/Region'] == 'US'].groupby('date')['date'].first(),
y=df[df['Country/Region'] == 'US'].groupby('date')['Active'].sum())])
fig.update_layout(
title="US: Active COVID-19",
xaxis_title="Date",
yaxis_title="Active infected",
font=dict(
family="Courier New, monospace",
size=16,
color="#7f7f7f"
)
)
fig.show()
geo_us = df[(df['date'] == '2020-03-22') &
(df['Country/Region'] == 'US')].groupby('Province/State',
as_index=False).agg({'Longitude': 'mean',
'Latitude': 'mean'})
temp2 = pd.read_csv('./data/csse_covid_19_daily_reports.csv')
df4 = temp2[temp2['Country/Region'] == 'US'].groupby('Province/State', as_index=False).agg({'Confirmed': 'sum'})
df4 = df4.merge(geo_us, left_on='Province/State', right_on='Province/State')
fig = go.Figure(data=go.Scattergeo(
lon = df4['Longitude'],
lat = df4['Latitude'],
text = df4['Province/State'] + ', ' + ': ' + df4['Confirmed'].astype(str),
mode = 'markers',
marker_size = (200 * df4['Confirmed'] / df4['Confirmed'].max()),
marker = dict(reversescale = False,
autocolorscale = False,
symbol = 'circle',
line = dict(width=1, color='rgba(102, 102, 102)'),
colorscale = 'Reds',
cmin = 0,
color = df4['Confirmed'],
cmax = df4['Confirmed'].max(),
colorbar_title="Confirmed Cases")))
fig.update_layout(title = 'Number of cumulative confirmed cases in the US by state ',
geo=dict(scope='usa',
projection_type='albers usa',
showland = True,
landcolor = "rgb(100, 125, 100)",
showocean = True,
oceancolor = "rgb(150, 150, 250)",
showcountries=True,
showsubunits=True,
showlakes=True,))
fig.show()
eu = ['Albania', 'Andorra', 'Armenia', 'Austria', 'Azerbaijan', 'Belarus', 'Belgium', 'Bosnia and Herzegovina',
'Bulgaria', 'Croatia', 'Cyprus', 'Czech Republic', 'Denmark', 'Estonia', 'Finland', 'France', 'Georgia',
'Germany', 'Greece', 'Hungary', 'Iceland', 'Ireland', 'Italy', 'Kazakhstan', 'Kosovo', 'Latvia', 'Liechtenstein',
'Lithuania', 'Luxembourg', 'Malta', 'Moldova', 'Monaco', 'Montenegro', 'Netherlands', 'North Macedonia', 'Norway',
'Poland', 'Portugal', 'Romania', 'Russia', 'San Marino', 'Serbia', 'Slovakia', 'Slovenia', 'Spain', 'Sweden',
'Switzerland', 'Turkey', 'Ukraine', 'United Kingdom', 'Vatican City']
df3 = df[df['Country/Region'].isin(eu)]
data = df3[df3['date'] == df3['date'].iloc[-1]].groupby('Country/Region').agg({'Active': 'sum',
'Longitude': 'mean',
'Latitude': 'mean',
'Country/Region': 'first',
'Province/State': 'first'})
data.loc[data['Country/Region'] == 'France', 'Latitude'] = 46.2276
data.loc[data['Country/Region'] == 'France', 'Longitude'] = -3.4360
data.loc[data['Country/Region'] == 'United Kingdom', 'Latitude'] = 55.3781
data.loc[data['Country/Region'] == 'United Kingdom', 'Longitude'] = 3.4360
data.loc[data['Country/Region'] == 'Denmark', 'Latitude'] = 56.2639
data.loc[data['Country/Region'] == 'Denmark', 'Longitude'] = 9.5018
data.loc[data['Country/Region'] == 'Netherlands', 'Latitude'] = 52.1326
data.loc[data['Country/Region'] == 'Netherlands', 'Longitude'] = 5.2913
fig = go.Figure(data=go.Scattergeo(
lon = data['Longitude'],
lat = data['Latitude'],
text = data['Country/Region'] + ', ' + data['Country/Region'] + ': ' + data['Active'].astype(str),
mode = 'markers',
marker_size = (100 * data['Active'] / data['Active'].max()),
marker = dict(reversescale = False,
autocolorscale = False,
symbol = 'circle',
line = dict(width=1, color='rgba(102, 102, 102)'),
colorscale = 'Reds',
cmin = 0,
color = data['Active'],
cmax = data['Active'].max(),
colorbar_title="Active Cases")))
fig.update_layout(title = 'Number of active cases by European country ',
geo=dict(scope='europe',
projection_type="natural earth",
showland = True,
landcolor = "rgb(100, 125, 100)",
showocean = True,
oceancolor = "rgb(150, 150, 250)",
showcountries=True,
showsubunits=True,
showlakes=False,))
fig.show()
from IPython.display import Image
Image('./assets/active_cases_eu.png', width=600)
```
## Focus on the epidemiological trajectories in Norway
```
df0 = df[df['Country/Region'] == 'Norway']
df0.head()
df0.tail()
df1 = df[df['Country/Region'] == 'Norway'].groupby('date')[['Confirmed', 'Deaths', 'Recovered', 'Active']].sum()
df1.head()
df1.tail()
```
## Case fatality rate [CFR](https://en.wikipedia.org/wiki/Case_fatality_rate)
```
def fatality_rate_given_country(csse_daily_df, country):
dfc = csse_daily_df[csse_daily_df['Country/Region'] == country]
last = dfc['date'].iloc[-1]
cfr = dfc[dfc['date'] == last]['Deaths'].sum() / dfc[dfc['date'] == last]['Confirmed'].sum()
active = dfc[dfc['date'] == last]['Active'].sum()
confirmed = dfc[dfc['date'] == last]['Confirmed'].sum()
return last, cfr, active, confirmed
countrylist = ['Norway', 'Sweden', 'Denmark', 'Iceland', 'China', 'Italy', 'US']
print('Case fatality rate (accumulated Deaths/accumulated Confirmed) for given country:\n')
for i, c in enumerate(countrylist):
last, cfr, active, confirmed = fatality_rate_given_country(df, c)
print('%s (upto %s) = %.2f%% (confirmed=%d, active=%d)' % (c, last, cfr*100, confirmed, active))
last, cfr, active, confirmed = fatality_rate_given_country(df, 'Norway')
fig = go.Figure([go.Scatter(x=df[df['Country/Region'] == 'Norway'].groupby('date')['date'].first(),
y=df[df['Country/Region'] == 'Norway'].groupby('date')['Active'].sum())])
fig.update_layout(
title="NORWAY: Active COVID-19 (CFR=%.2f%%)" % (cfr*100),
xaxis_title="Date",
yaxis_title="Active infected",
font=dict(
family="Courier New, monospace",
size=16,
color="#7f7f7f"
)
)
fig.show()
from IPython.display import Image
Image('./assets/active_cases_cfr_norway.png', width=600)
region = 'Norway'
fig = go.Figure()
fig.add_trace(go.Scatter(
x=df[df['Country/Region'] == region].groupby('date')['date'].first(),
y=df[df['Country/Region'] == region].groupby('date')['Active'].sum(),
name="Active cases"))
fig.add_trace(go.Scatter(
x=df[df['Country/Region'] == region].groupby('date')['date'].first(),
y=df[df['Country/Region'] == region].groupby('date')['Confirmed'].sum(),
name="Total Confirmed"))
fig.add_trace(go.Scatter(
x=df[df['Country/Region'] == region].groupby('date')['date'].first(),
y=df[df['Country/Region'] == region].groupby('date')['Deaths'].sum(),
name="Deaths"))
fig.add_trace(go.Scatter(
x=df[df['Country/Region'] == region].groupby('date')['date'].first(),
y=df[df['Country/Region'] == region].groupby('date')['Recovered'].sum(),
name="Recovered"))
fig.update_layout(title="COVID-19 infections in {}".format(region),
xaxis_title="Date",
yaxis_title="Number of Individuals")
fig.show()
fig = go.Figure()
countries = ['China', 'Italy', 'South Korea', 'US', 'Spain', 'France', 'Germany', 'Norway']
for country in countries:
fig.add_trace(go.Scatter(
x=df[df['Country/Region'] == country].groupby('date')['date'].first(),
y=df[df['Country/Region'] == country].groupby('date')['Active'].sum(),
name=country,
opacity=0.8))
fig.update_layout(title="Active COVID-19 cases",
xaxis_title="Date",
yaxis_title="Number of Individuals")
fig.show()
from IPython.display import Image
Image('./assets/active_cases_selected_countries.png', width=600)
fig = go.Figure()
for region in ['China', 'Italy', 'US', 'Spain', 'France', 'Germany', 'South Korea', 'Norway']:
fig.add_trace(go.Scatter(
x=df[df['Country/Region'] == region].groupby('date')['date'].first(),
y=df[df['Country/Region'] == region].groupby('date')['Active'].sum(),
name=region,
hoverinfo='x+y+z+text+name',
stackgroup='one'))
fig.update_layout(title="COVID-19 Active Cases Worldwide",
xaxis_title="Date",
yaxis_title="Number of Individuals")
fig.show()
```
| true |
code
| 0.210523 | null | null | null | null |
|
# Maximum Likelihood and Maximum A Posterior
* We looked at the regularization term as a *penalty* term in the objective function. There is another way to interpret the regularization term as well. Specifically, there is a *Bayesian* interpretation.
\begin{eqnarray}
\min E^{\ast}(\mathbf{w}) &=& \max -E^{\ast}(\mathbf{w})\\
& =& \max \exp \left\{ -E^{\ast}(\mathbf{w})\right\}\\
&=& \max \exp \left\{ -\frac{1}{2}\sum_{n=1}^N \left( y(x_n, \mathbf{w}) - t_n \right)^2 - \frac{\lambda}{2}\left\| \mathbf{w} \right\|^2_2 \right\}\\
&=& \max \exp \left\{ -\frac{1}{2}\sum_{n=1}^N \left( y(x_n, \mathbf{w}) - t_n \right)^2 \right\}\exp\left\{-\frac{1}{2}\lambda\left\| \mathbf{w} \right\|^2_2\right\}\\
&=& \max \prod_{n=1}^N \exp \left\{ -\frac{1}{2} \left( y(x_n, \mathbf{w}) - t_n \right)^2 \right\}\exp\left\{-\frac{1}{2}\lambda\left\| \mathbf{w} \right\|^2_2\right\}
\end{eqnarray}
* So, this is a maximization of the *data likelihood* with a *prior*: $p(\mathbf{X}|\mathbf{w})p(\mathbf{w})$
* *Method of Maximum Likelihood:*
* A *data likelihood* is how likely the data is given the parameter set
* So, if we want to maximize how likely the data is to have come from the model we fit, we should find the parameters that maximize the likelihood
* A common trick to maximizing the likelihood is to maximize the log likelihood. Often makes the math much easier. *Why can we maximize the log likelihood instead of the likelihood and still get the same answer?*
* Consider: $\max \ln \exp \left\{ -\frac{1}{2}\left(y(x_n, \mathbf{w}) - t_n\right)^2\right\}$ We go back to our original objective.
* *Method of Maximum A Posteriori (MAP):*
* Bayes Rule: $p(Y|X) = \frac{p(X|Y)p(Y)}{p(X)}$
* Consider: $p(\mathbf{w}|\mathscr{D}) = \frac{p(\mathscr{D}|\mathbf{w})p(\mathbf{w})}{p(\mathscr{D})}$, i.e., posterior $\propto$ likelihood $\times$ prior
## The Gaussian Distribution:
* Consider a univariate Gaussian distribution:
\begin{equation}
\mathscr{N}(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp\left\{ -\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2} \right\}
\end{equation}
* $\sigma^2$ is the variance OR $\frac{1}{\sigma^2}$ is the *precision*
* So, as $\lambda$ gets big, variance gets smaller/tighter. As $\lambda$ gets small, variance gets larger/wider.
* The Gaussian distribution is also called the *Normal* distribution.
* We will often write $N(x|\mu, \sigma^2)$ to refer to a Gaussian with mean $\mu$ and variance $\sigma^2$.
* *What is the multi-variate Gaussian distribution?*
* What is the expected value of $x$ for the Gaussian distribution?
\begin{eqnarray}
E[x] &=& \int x p(x) dx \\
&=& \int x \frac{1}{\sqrt{2\pi \sigma^2}}\exp\left\{ -\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2} \right\} dx
\end{eqnarray}
* *Change of variables:* Let
\begin{eqnarray}
y &=& \frac{x-\mu}{\sigma} \rightarrow x = \sigma y + \mu\\
dy &=& \frac{1}{\sigma} dx \rightarrow dx = \sigma dy
\end{eqnarray}
* Plugging this into the expectation:
\begin{eqnarray}
E[x] &=& \int \left(\sigma y + \mu \right)\frac{1}{\sqrt{2\pi}\sigma} \exp\left\{ - \frac{1}{2} y^2 \right\} \sigma dy \\
&=& \int \frac{\sigma y}{\sqrt{2\pi}} \exp\left\{ - \frac{1}{2} y^2 \right\} dy + \int \frac{\mu}{\sqrt{2\pi}} \exp\left\{ - \frac{1}{2} y^2 \right\} dy
\end{eqnarray}
* The first term is an odd function: $f(-y) = -f(y)$ So, $E[x] = 0 + \mu = \mu$
## Maximum Likelihood vs. Maximum A Posteriori (MAP)
* Lets look at this in terms of binary variables, e.g., Flipping a coin: $X =1$ is heads, $X=0$ is tails
* Let $\mu$ be the probability of heads. If we know $\mu$, then: $P(x = 1 |\mu) = \mu$ and $P(x = 0|\mu) = 1-\mu$
\begin{eqnarray}
P(x|\mu) = \mu^x(1-\mu)^{1-x} = \left\{\begin{array}{c c}\mu & \text{ if } x=1 \\ 1-\mu & \text{ if } x = 0 \end{array}\right.
\end{eqnarray}
* This is called the *Bernoulli* distribution. The mean and variance of a Bernoulli distribution is:
\begin{equation}
E[x] = \mu
\end{equation}
\begin{equation}
E\left[(x-\mu)^2\right] = \mu(1-\mu)
\end{equation}
* So, suppose we conducted many Bernoulli trials (e.g., coin flips) and we want to estimate $\mu$
### Method: Maximum Likelihood
\begin{eqnarray}
p(\mathscr{D}|\mu) &=& \prod_{n=1}^N p(x_n|\mu) \\
&=& \prod_{n=1}^N \mu^{x_n}(1-\mu)^{1-x_n}
\end{eqnarray}
* Maximize : (*What trick should we use?*)
\begin{eqnarray}
\mathscr{L} = \sum_{n=1}^N x_n \ln \mu + (1-x_n)\ln(1-\mu)
\end{eqnarray}
\begin{eqnarray}
\frac{\partial \mathscr{L}}{\partial \mu} = 0 &=& \frac{1}{\mu}\sum_{n=1}^N x_n - \frac{1}{1-\mu }\sum_{n=1}^N (1 - x_n)\\
0 &=& \frac{(1-\mu) \sum_{n=1}^N x_n - \mu \sum_{n=1}^N (1- x_n)}{\mu(1-\mu)}\\
0 &=& \sum_{n=1}^N x_n - \mu \sum_{n=1}^N x_n - \mu \sum_{n=1}^N 1 + \mu \sum_{n=1}^N x_n\\
0 &=& \sum_{n=1}^N x_n - \mu N\\
\mu &=& \frac{1}{N}\sum_{n=1}^N x_n = \frac{m}{N}
\end{eqnarray}
where $m$ is the number of successful trials.
* So, if we flip a coin 1 time and get heads, then $\mu = 1$ and probability of getting tails is 0. *Would you believe that? We need a prior!*
### Method: Maximum A Posteriori:
* Look at several independent trials. Consider N = 3 and m = 2 (N is number of trials, m is number of successes) and look at all ways to get 2 H and 1 T:
* H H T $\rightarrow \mu \mu (1-\mu) = \mu^2(1-\mu)$
* H T H $\rightarrow \mu (1-\mu) \mu = \mu^2(1-\mu)$
* T H H $\rightarrow (1-\mu) \mu \mu = \mu^2(1-\mu)$
* $\left(\begin{array}{c} 3 \\ 2 \end{array}\right) \mu^2(1-\mu) \rightarrow \left(\begin{array}{c} N \\ m \end{array}\right) \mu^m(1-\mu)^{N-m} = \frac{N!}{(N-m)!m!}\mu^m(1-\mu)^{N-m} $
* This is the Binomial Distribution, gives the probability of $m$ observations of $x=1$ out of N independent trails
* So, what we saw is that we need a prior. We want to incorporate our prior belief. Let us place a prior on $\mu$
\begin{equation}
Beta(\mu|a,b) = \frac{\Gamma(a + b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1}
\end{equation}
\begin{equation}
E[\mu] = \frac{a}{a + b}
\end{equation}
\begin{equation}
Var[\mu] = \frac{ab}{(a+b)^2(a+b+1)}
\end{equation}
* Note: $\Gamma(x) = \int_0^\infty u^{x-1}e^{-u} du$ and when $x$ is an integer, then it simplifys to $x!$
* Calculation of the posterior, Take $N = m + l$ observations:
\begin{eqnarray}
p(\mu | m, l, a, b) &\propto& Bin(m,l|\mu)Beta(\mu|a,b) \\
&\propto& \mu^m(1-\mu)^l\mu^{a-1}(1-\mu)^{b-1}\\
&=& \mu^{m+a-1}(1-\mu)^{l+b-1}
\end{eqnarray}
* What does this look like? Beta: $a \leftarrow m+a$, $b \leftarrow l+b$
* So, what's the posterior?
\begin{equation}
p(\mu | m, l, a, b) = \frac{\Gamma(m+a+l+b)}{\Gamma(m+a)\Gamma(l+b)}\mu^{m+a-1}(1-\mu)^{l+b-1}
\end{equation}
* *Conjugate Prior Relationship:* When the posterior is the same form as the prior
* Now we can maximize the (log of the) posterior:
\begin{eqnarray}
\max_\mu ((m+a-1) \ln \mu + (l+b-1) \ln (1-\mu))
\end{eqnarray}
\begin{eqnarray}
\frac{\partial \mathscr{L}}{\partial \mu} = 0&=& \frac{m + a -1}{\mu} - \frac{l + b - 1}{1-\mu}\\
&=& (1-\mu)(m+a-1) - \mu(l+b-1)\\
&=& (m+a-1) - \mu(m+a-1) - \mu(l+b-1)\\
\mu &=& \frac{m+a-1}{m+a+l+b-2}
\end{eqnarray}
* This is the MAP solution. *So, what happens now when you flip one heads, two heads, etc.?*
* Discuss online updating of the prior. Eventually the data takes over the prior.
```
import numpy as np
import matplotlib.pyplot as plt
import math
%matplotlib inline
def plotBeta(a=2,b=2):
'''plotBeta(a=1,b=1): Plot plot beta distribution with parameters a and b'''
xrange = np.arange(0,1,0.001) #get equally spaced points in the xrange
normconst = math.gamma(a+b)/(math.gamma(a)*math.gamma(b))
beta = normconst*xrange**(a-1)*(1-xrange)**(b-1)
fig = plt.figure()
p1 = plt.plot(xrange,beta, 'g')
plt.show()
#Beta Distribution
plotBeta(2,4);
trueMu = 0.5
numFlips = 10
priorA = 2
priorB = 2
flipResult = []
for flip in range(numFlips):
flipResult.append(np.random.binomial(1,trueMu,1)[0])
print(flipResult)
print('Frequentist/Maximum Likelihood Probability of Heads:' + str(sum(flipResult)/len(flipResult)))
print('Bayesian/MAP Probability of Heads:' + str((sum(flipResult)+priorA-1)/(len(flipResult)+priorA+priorB-2)))
input("Hit enter to continue...\n")
```
| true |
code
| 0.568536 | null | null | null | null |
|
# Generative Adversarial Network
In this notebook, we'll be building a generative adversarial network (GAN) trained on the MNIST dataset. From this, we'll be able to generate new handwritten digits!
GANs were [first reported on](https://arxiv.org/abs/1406.2661) in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:
* [Pix2Pix](https://affinelayer.com/pixsrv/)
* [CycleGAN](https://github.com/junyanz/CycleGAN)
* [A whole list](https://github.com/wiseodd/generative-models)
The idea behind GANs is that you have two networks, a generator $G$ and a discriminator $D$, competing against each other. The generator makes fake data to pass to the discriminator. The discriminator also sees real data and predicts if the data it's received is real or fake. The generator is trained to fool the discriminator, it wants to output data that looks _as close as possible_ to real data. And the discriminator is trained to figure out which data is real and which is fake. What ends up happening is that the generator learns to make data that is indistiguishable from real data to the discriminator.

The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector the generator uses to contruct it's fake images. As the generator learns through training, it figures out how to map these random vectors to recognizable images that can foold the discriminator.
The output of the discriminator is a sigmoid function, where 0 indicates a fake image and 1 indicates an real image. If you're interested only in generating new images, you can throw out the discriminator after training. Now, let's see how we build this thing in TensorFlow.
```
%matplotlib inline
import pickle as pkl
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data')
```
## Model Inputs
First we need to create the inputs for our graph. We need two inputs, one for the discriminator and one for the generator. Here we'll call the discriminator input `inputs_real` and the generator input `inputs_z`. We'll assign them the appropriate sizes for each of the networks.
```
def model_inputs(real_dim, z_dim):
inputs_real = tf.placeholder(tf.float32, (None, real_dim), name='input_real')
inputs_z = tf.placeholder(tf.float32, (None, z_dim), name='input_z')
return inputs_real, inputs_z
```
## Generator network

Here we'll build the generator network. To make this network a universal function approximator, we'll need at least one hidden layer. We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.
#### Variable Scope
Here we need to use `tf.variable_scope` for two reasons. Firstly, we're going to make sure all the variable names start with `generator`. Similarly, we'll prepend `discriminator` to the discriminator variables. This will help out later when we're training the separate networks.
We could just use `tf.name_scope` to set the names, but we also want to reuse these networks with different inputs. For the generator, we're going to train it, but also _sample from it_ as we're training and after training. The discriminator will need to share variables between the fake and real input images. So, we can use the `reuse` keyword for `tf.variable_scope` to tell TensorFlow to reuse the variables instead of creating new ones if we build the graph again.
To use `tf.variable_scope`, you use a `with` statement:
```python
with tf.variable_scope('scope_name', reuse=False):
# code here
```
Here's more from [the TensorFlow documentation](https://www.tensorflow.org/programmers_guide/variable_scope#the_problem) to get another look at using `tf.variable_scope`.
#### Leaky ReLU
TensorFlow doesn't provide an operation for leaky ReLUs, so we'll need to make one . For this you can use take the outputs from a linear fully connected layer and pass them to `tf.maximum`. Typically, a parameter `alpha` sets the magnitude of the output for negative values. So, the output for negative input (`x`) values is `alpha*x`, and the output for positive `x` is `x`:
$$
f(x) = max(\alpha * x, x)
$$
#### Tanh Output
The generator has been found to perform the best with $tanh$ for the generator output. This means that we'll have to rescale the MNIST images to be between -1 and 1, instead of 0 and 1.
```
def generator(z, out_dim, n_units=128, reuse=False, alpha=0.01):
with tf.variable_scope('generator', reuse=reuse):
# Hidden layer
h1 = tf.layers.dense(z, n_units, activation=None)
# Leaky ReLU
h1 = tf.maximum(alpha * h1, h1)
# Logits and tanh output
logits = tf.layers.dense(h1, out_dim, activation=None)
out = tf.tanh(logits)
return out
```
## Discriminator
The discriminator network is almost exactly the same as the generator network, except that we're using a sigmoid output layer.
```
def discriminator(x, n_units=128, reuse=False, alpha=0.01):
with tf.variable_scope('discriminator', reuse=reuse):
# Hidden layer
h1 = tf.layers.dense(x, n_units, activation=None)
# Leaky ReLU
h1 = tf.maximum(alpha * h1, h1)
logits = tf.layers.dense(h1, 1, activation=None)
out = tf.sigmoid(logits)
return out, logits
```
## Hyperparameters
```
# Size of input image to discriminator
input_size = 784
# Size of latent vector to generator
z_size = 100
# Sizes of hidden layers in generator and discriminator
g_hidden_size = 128
d_hidden_size = 128
# Leak factor for leaky ReLU
alpha = 0.01
# Smoothing
smooth = 0.1
```
## Build network
Now we're building the network from the functions defined above.
First is to get our inputs, `input_real, input_z` from `model_inputs` using the sizes of the input and z.
Then, we'll create the generator, `generator(input_z, input_size)`. This builds the generator with the appropriate input and output sizes.
Then the discriminators. We'll build two of them, one for real data and one for fake data. Since we want the weights to be the same for both real and fake data, we need to reuse the variables. For the fake data, we're getting it from the generator as `g_model`. So the real data discriminator is `discriminator(input_real)` while the fake discriminator is `discriminator(g_model, reuse=True)`.
```
tf.reset_default_graph()
# Create our input placeholders
input_real, input_z = model_inputs(input_size, z_size)
# Build the model
g_model = generator(input_z, input_size, n_units=g_hidden_size, alpha=alpha)
# g_model is the generator output
d_model_real, d_logits_real = discriminator(input_real, n_units=d_hidden_size, alpha=alpha)
d_model_fake, d_logits_fake = discriminator(g_model, reuse=True, n_units=d_hidden_size, alpha=alpha)
```
## Discriminator and Generator Losses
Now we need to calculate the losses, which is a little tricky. For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_loss_real + d_loss_fake`. The losses will by sigmoid cross-entropys, which we can get with `tf.nn.sigmoid_cross_entropy_with_logits`. We'll also wrap that in `tf.reduce_mean` to get the mean for all the images in the batch. So the losses will look something like
```python
tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))
```
For the real image logits, we'll use `d_logits_real` which we got from the discriminator in the cell above. For the labels, we want them to be all ones, since these are all real images. To help the discriminator generalize better, the labels are reduced a bit from 1.0 to 0.9, for example, using the parameter `smooth`. This is known as label smoothing, typically used with classifiers to improve performance. In TensorFlow, it looks something like `labels = tf.ones_like(tensor) * (1 - smooth)`
The discriminator loss for the fake data is similar. The logits are `d_logits_fake`, which we got from passing the generator output to the discriminator. These fake logits are used with labels of all zeros. Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.
Finally, the generator losses are using `d_logits_fake`, the fake image logits. But, now the labels are all ones. The generator is trying to fool the discriminator, so it wants to discriminator to output ones for fake images.
```
# Calculate losses
d_loss_real = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real,
labels=tf.ones_like(d_logits_real) * (1 - smooth)))
d_loss_fake = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake,
labels=tf.zeros_like(d_logits_real)))
d_loss = d_loss_real + d_loss_fake
g_loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake,
labels=tf.ones_like(d_logits_fake)))
```
## Optimizers
We want to update the generator and discriminator variables separately. So we need to get the variables for each part build optimizers for the two parts. To get all the trainable variables, we use `tf.trainable_variables()`. This creates a list of all the variables we've defined in our graph.
For the generator optimizer, we only want to generator variables. Our past selves were nice and used a variable scope to start all of our generator variable names with `generator`. So, we just need to iterate through the list from `tf.trainable_variables()` and keep variables to start with `generator`. Each variable object has an attribute `name` which holds the name of the variable as a string (`var.name == 'weights_0'` for instance).
We can do something similar with the discriminator. All the variables in the discriminator start with `discriminator`.
Then, in the optimizer we pass the variable lists to `var_list` in the `minimize` method. This tells the optimizer to only update the listed variables. Something like `tf.train.AdamOptimizer().minimize(loss, var_list=var_list)` will only train the variables in `var_list`.
```
# Optimizers
learning_rate = 0.002
# Get the trainable_variables, split into G and D parts
t_vars = tf.trainable_variables()
g_vars = [var for var in t_vars if var.name.startswith('generator')]
d_vars = [var for var in t_vars if var.name.startswith('discriminator')]
d_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(d_loss, var_list=d_vars)
g_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(g_loss, var_list=g_vars)
```
## Training
```
batch_size = 100
epochs = 100
samples = []
losses = []
# Only save generator variables
saver = tf.train.Saver(var_list=g_vars)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
# Get images, reshape and rescale to pass to D
batch_images = batch[0].reshape((batch_size, 784))
batch_images = batch_images*2 - 1
# Sample random noise for G
batch_z = np.random.uniform(-1, 1, size=(batch_size, z_size))
# Run optimizers
_ = sess.run(d_train_opt, feed_dict={input_real: batch_images, input_z: batch_z})
_ = sess.run(g_train_opt, feed_dict={input_z: batch_z})
# At the end of each epoch, get the losses and print them out
train_loss_d = sess.run(d_loss, {input_z: batch_z, input_real: batch_images})
train_loss_g = g_loss.eval({input_z: batch_z})
print("Epoch {}/{}...".format(e+1, epochs),
"Discriminator Loss: {:.4f}...".format(train_loss_d),
"Generator Loss: {:.4f}".format(train_loss_g))
# Save losses to view after training
losses.append((train_loss_d, train_loss_g))
# Sample from generator as we're training for viewing afterwards
sample_z = np.random.uniform(-1, 1, size=(16, z_size))
gen_samples = sess.run(
generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),
feed_dict={input_z: sample_z})
samples.append(gen_samples)
saver.save(sess, './checkpoints/generator.ckpt')
# Save training generator samples
with open('train_samples.pkl', 'wb') as f:
pkl.dump(samples, f)
```
## Training loss
Here we'll check out the training losses for the generator and discriminator.
```
fig, ax = plt.subplots()
losses = np.array(losses)
plt.plot(losses.T[0], label='Discriminator')
plt.plot(losses.T[1], label='Generator')
plt.title("Training Losses")
plt.legend()plt.legend()
```
## Generator samples from training
Here we can view samples of images from the generator. First we'll look at images taken while training.
```
def view_samples(epoch, samples):
fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)
for ax, img in zip(axes.flatten(), samples[epoch]):
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')
return fig, axes
# Load samples from generator taken while training
with open('train_samples.pkl', 'rb') as f:
samples = pkl.load(f)
```
These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 1, 7, 3, 2. Since this is just a sample, it isn't representative of the full range of images this generator can make.
```
_ = view_samples(-1, samples)
```
Below I'm showing the generated images as the network was training, every 10 epochs. With bonus optical illusion!
```
rows, cols = 10, 6
fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)
for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):
for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):
ax.imshow(img.reshape((28,28)), cmap='Greys_r')
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
```
It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise like 1s and 9s.
## Sampling from the generator
We can also get completely new images from the generator by using the checkpoint we saved after training. We just need to pass in a new latent vector $z$ and we'll get new samples!
```
saver = tf.train.Saver(var_list=g_vars)
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))
sample_z = np.random.uniform(-1, 1, size=(16, z_size))
gen_samples = sess.run(
generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),
feed_dict={input_z: sample_z})
_ = view_samples(0, [gen_samples])
```
| true |
code
| 0.786233 | null | null | null | null |
|
### Introduction
This script finds the optimal band gaps of mechanical stack III-V-Si solar cells. I uses a detailed balance approach to calculate the I-V of individual subcells. For calculating efficiency, I add up the maximum power of individual subcell and divide it by the total illumination power.
Details of how the I-V is calculated can be referred to [this paper](http://arxiv.org/abs/1512.02056).
```
%matplotlib inline
import numpy as np
from scipy.interpolate import interp2d
import matplotlib.pyplot as plt
from scipy.io import savemat
from iii_v_si import calc_2j_si_eta, calc_2j_si_eta_direct
from detail_balanced_MJ import calc_1j_eta
def vary_top_eg(top_cell_qe,n_s=1):
topcell_eg = np.linspace(0.9, 3, num=100)
eta = np.zeros(topcell_eg.shape)
for p in range(topcell_eg.shape[0]):
eta[p] = calc_2j_si_eta_direct(top_eg=topcell_eg[p], top_rad_eta=1,
top_qe=top_cell_qe, bot_rad_eta=1,
bot_qe=1, n_s=n_s, mj="MS")
print("At AM1.5g, direct band gap assumption of silicon")
print("max eta %s:" % eta.max())
print("optimal Eg: %s" % topcell_eg[eta.argmax()])
return topcell_eg,eta
```
### Assume that the top cell has 100% EQE
```
eg1,eta1=vary_top_eg(1)
plt.plot(eg1,eta1)
plt.xlabel("top cell's band gap")
plt.ylabel("efficiency")
plt.savefig("mstopeg.pdf")
```
The maximum efficiency is then **42%**, and the optimal band gap is **1.81 eV**. For two-terminal, 2J devices, maximum efficiency is **41%** with a **1.74-eV** top cell on silicon. As we can see, using mechanical stack did not benefit the efficiency fundamentally.
### Try if different EQE values shift the peak
```
qe_range=np.linspace(0.5,1,num=3)
for q in qe_range:
eg,eta = vary_top_eg(q)
plt.plot(eg,eta,hold=True,label="QE=%s"%q)
plt.legend(loc="best")
plt.xlabel("top cell's band gap")
plt.ylabel("efficiency")
```
Different top cell's EQEs do not change the optimal band gap of the top cell, as expected.
### Assume that the top cell has very low EQE
```
eg1,eta1=vary_top_eg(0.001)
plt.plot(eg1,eta1)
plt.xlabel("top cell's band gap")
plt.ylabel("efficiency")
```
The maximum efficiency in this case is around 30%. Which should be very close the limiting efficiency of 1J GaAs. We can check:
```
# calulate the SQ-limit efficiency of silicon
eta = calc_1j_eta(eg=1.12, qe=1, r_eta=1, cell_temperature=300)
print(eta)
```
The SQ-limit efficiency is 30%, which is close to the efficiency of the 2J mechanical stack cell with nearly tranparent top cell.
```
```
| true |
code
| 0.393968 | null | null | null | null |
|
### Please read the 'Model Test' section in `verifyml/DEVELOPMENT.md` before going through this notebook.
Toy example that shows how a new model test can be created and used.
```
"""ListLength test - test passed if the length of a given list is greater than a specified threshold"""
from __future__ import annotations
from dataclasses import dataclass, field
import matplotlib.pyplot as plt
# relative imports can also be used if this is saved as a standalone file
from verifyml.model_tests.ModelTest import ModelTest
from verifyml.model_tests.utils import plot_to_str # converts plots to base64-encoded strings
@dataclass
class ListLength(ModelTest):
""" A test to check that a given list contains more elements than a specified threshold. """
input_list: list[int]
threshold: int
# optional: stores plots to be displayed on the Model Card
plots: dict[str, str] = field(repr=False, default_factory=dict)
# optional
test_name: str = 'A list length test'
test_desc: str = 'A list length test description'
def plot(self, save_plots: bool = True) -> None:
"""Plot the input list with matplotlib and save it as a base64
encoded string if save_plots is True.
"""
fig, ax = plt.subplots()
# show the plot
ax.plot(self.input_list)
# optionally save the plot to the instance
if save_plots:
self.plots['my plot name'] = plot_to_str()
def run(self) -> bool:
"""Runs test by checking if len(input_list) > threshold"""
self.result = len(self.input_list)
self.passed = self.result > self.threshold
return self.passed
```
## Demo Model Card that uses the newly defined test above
### Init 2 ListLength tests - 1 that passes, 1 that fails
```
# set threshold at 4 - tests only pass if list length > 4
threshold = 4
input_list_pass = [1, 2, 3, 4, 5]
input_list_fail = [1, 2, 3, 4]
list_length_test_pass = ListLength(input_list_pass, threshold)
list_length_test_fail = ListLength(input_list_fail, threshold)
# run tests and plot results, saving the plots in the process
list_length_test_pass.run()
list_length_test_fail.run()
list_length_test_pass.plot()
list_length_test_fail.plot()
```
### Create a Model Card and attach the tests to it
```
import verifyml.model_card_toolkit as mctlib
# init model card toolkit and model card
mct = mctlib.ModelCardToolkit()
mc = mct.scaffold_assets()
# init model card test objects that will hold the tests
mc_test_pass, mc_test_fail = mctlib.Test(), mctlib.Test()
# assign the list length tests to them
mc_test_pass.read_model_test(list_length_test_pass)
mc_test_fail.read_model_test(list_length_test_fail)
# create a fairness report with these as fairness tests
fairness_report = mctlib.FairnessReport(
type="Fairness report containing list length tests",
tests=[mc_test_pass, mc_test_fail]
)
# add the report into the model card
mc.fairness_analysis.fairness_reports = [fairness_report]
# update the model card's name
mc.model_details.name = "demo model"
# update the model card assets with this new information
mct.update_model_card(mc)
```
### Export Model Card HTML into a file and also display it
```
from IPython import display
html = mct.export_format(output_file="list_length.html")
display.display(display.HTML(html))
```
| true |
code
| 0.846831 | null | null | null | null |
|
# Water heating
An insulated, rigid tank contains 4 kg of water at 100 kPa, where initially 0.25 of the mass is liquid. An electric heater turns on and operates until all of the liquid has vaporized. (Neglect the heat capacity of the tank and heater.)

**Problem:**
- Determine the final temperature and pressure of the water.
- Determine the electrical work required by this process.
- Determine the total change in entropy associated with this process.
- Plot the state points for the water on a temperature-specific entropy diagram.
First, load the necessary modules and specify the known/initial conditions.
```
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import cantera as ct
import matplotlib_inline.backend_inline
matplotlib_inline.backend_inline.set_matplotlib_formats('pdf', 'png')
plt.rcParams['figure.dpi']= 150
plt.rcParams['savefig.dpi'] = 150
from pint import UnitRegistry
ureg = UnitRegistry()
Q_ = ureg.Quantity
mass = Q_(4, 'kg')
pressure_initial = Q_(100, 'kPa')
quality_initial = 0.25
quality_final = 1.0
# specify the initial state using pressure and quality
state_initial = ct.Water()
state_initial.PQ = pressure_initial.to('Pa').magnitude, quality_initial
state_initial()
```
## Find final temperature and pressure
Due to conservation of mass, since the mass and volume of the system are fixed, the specific volume and density must be constant:
$$
v_2 = v_1 \\
\rho_2 = \rho_1
$$
Therefore the final state is fixed by the density and quality, where $x_2 = 1$:
```
state_final = ct.Water()
state_final.DQ = state_initial.density, quality_final
```
Hmm, what happened here? It looks like Cantera unfortunately does not support specifying the thermodynamic state using density and quality. (With quality as one property, it only supports temperature or pressure as the other property.)
Fortunately, CoolProp *does* support specifying the state the way we need to solve this problem, so let's use that for the final state:
```
from CoolProp.CoolProp import PropsSI
temp_final = PropsSI(
'T', 'D', state_initial.density, 'Q', quality_final, 'water'
) * ureg.kelvin
pres_final = PropsSI(
'P', 'D', state_initial.density, 'Q', quality_final, 'water'
) * ureg.pascal
print(f'Final temperature: {temp_final: .2f}')
print(f'Final pressure: {pres_final: .2f}')
# We can then set the final state using the Cantera object,
# now that we know temperature
state_final = ct.Water()
state_final.TQ = temp_final.magnitude, quality_final
```
## Find electrical work required
To find the work required, we can do an energy balance on the (closed) system:
\begin{equation}
W_{\text{in}} = m (u_2 - u_1)
\end{equation}
```
work = mass * (Q_(state_final.u, 'J/kg') - Q_(state_initial.u, 'J/kg'))
print(f'Electrical work required: {work.to(ureg.megajoule): .2f}')
```
## Find entropy change
The total entropy change is the change in entropy of the system plus that of the surroundings:
$$
\Delta S_{\text{total}} = \Delta S_{\text{system}} + \Delta S_{\text{surr}} \\
\Delta S_{\text{total}} = \Delta S_{\text{system}} = m (s_2 - s_1)
$$
since the entropy change of the surroundings is zero.
```
entropy_change = mass * (Q_(state_final.s, 'J/kg') - Q_(state_initial.s, 'J/kg'))
print(f'Entropy change: {entropy_change: .2f}')
```
This process is irreversible, associated with a positive increase in total entropy.
## Plot the state points for water
We can construct the saturated liquid and saturated vapor lines in a temperature–specific entropy diagram (T–s diagram), and then plot the initial and final states locations along with the process line (of constant density):
```
f = ct.Water()
# Array of temperatures from fluid minimum temperature to critical temperature
temps = np.arange(np.ceil(f.min_temp) + 0.15, f.critical_temperature, 1.0)
def get_sat_entropy_fluid(T):
'''Gets entropy for temperature along saturated liquid line'''
f = ct.Water()
f.TQ = T, 0.0
return f.s
def get_sat_entropy_gas(T):
'''Gets entropy for temperature along saturated vapor line'''
f = ct.Water()
f.TQ = T, 1.0
return f.s
# calculate entropy values associated with temperatures along
# saturation lines
entropies_f = np.array([get_sat_entropy_fluid(T) for T in temps])
entropies_g = np.array([get_sat_entropy_gas(T) for T in temps])
# critical point
f.TP = f.critical_temperature, f.critical_pressure
fig, ax = plt.subplots(figsize=(5, 3))
# Plot the saturated liquid line, critical point,
# and saturated vapor line
ax.plot(entropies_f, temps)
ax.plot(entropies_g, temps)
ax.plot(f.s, f.T, 'o')
plt.xlabel('Specific entropy (J/kg⋅K)')
plt.ylabel('Temperature (K)')
# Plot the initial and final states, and label them
ax.plot(state_initial.s, state_initial.T, 's')
ax.annotate('(1)', xy=(state_initial.s, state_initial.T),
xytext=(0, -20), textcoords='offset points',
ha='right', va='bottom'
)
ax.plot(state_final.s, state_final.T, 's')
ax.annotate('(2)', xy=(state_final.s, state_final.T),
xytext=(20, 0), textcoords='offset points',
ha='right', va='bottom'
)
# show process line of constant density
temps = np.arange(state_initial.T, state_final.T, 1.0)
def get_entrophy(T, density):
f = ct.Water()
f.TD = T, density
return f.s
entropies = np.array([get_entrophy(T, state_initial.density) for T in temps])
ax.plot(entropies, temps, '--')
plt.grid(True)
fig.tight_layout()
plt.show()
```
| true |
code
| 0.693278 | null | null | null | null |
|
# Salary recommandation using a score
Author: Florian Gauthier
The purpose of this Notebook is to find the best score in order to select the optimal salary change in the salary-based recommendation.
The best score will be the one that allows the best compromise between a salary decrease and a raise in job offers, for every job groups & experience buckets.
We first use the 10% sample (~1.2Go) dataset called `sample_10perc.csv` because the full dataset is too big.
```
import numpy as np
import pandas as pd
from pandas.tseries import offsets
from paul_emploi.lib import cleaned_data
from paul_emploi.modeling import salary_recommendation_model, job_offers_optimal_buckets
import matplotlib.pyplot as plt
from matplotlib import gridspec
%matplotlib inline
%load_ext autoreload
%autoreload 2
```
## Import & clean job postings dataset
Let's first `import_clean_job_offers` to import a clean database of job_offers.
```
etalab_path = "/var/data/bayes_impact/"
postings = cleaned_data.job_offers(data_folder=etalab_path, filename_offers="job_offers/sample_10perc.csv")
postings.head(2)
```
## Filter postings
Remove outliers & filter date.
These modules will not be used in production since the filtering will be done before without pandas.
```
# Since our sample has data until early 2016, we use for now SMIC
# 2015 to run some tests. As a maximum salary, we use 50.000€ (which is
# arbitrary.)
# SMIC amounts available here: http://www.salairebrutnet.fr/
SMIC_2015 = 17496
SMIC_2016 = 17604
_MIN_ANNUAL_SALARY = SMIC_2015
# Arbitrary.
_MAX_ANNUAL_SALARY = 50000
def filter_postings(
table_offers,
min_salary=_MIN_ANNUAL_SALARY,
max_salary=_MAX_ANNUAL_SALARY,
nb_months=6):
"""Returns a table containing only job offers that fulfill specific
criteria. It will be used for salary recommendations.
Args :
table_offers: pandas DataFrame containing job postings.
min_salary (int.): exclude all salary under min_salary (ex : SMIC).
max_salary (int.): exclude all salary above max_salary (ex: 50000).
nb_months: number of months to look back to get job offers.
Returns:
a pandas DataFrame containing only job offers that fulfill specific
criteria. It will be used for salary recommendations.
"""
clean_postings = table_offers.copy()
# Exclude outliers.
clean_postings = _filter_outliers(
clean_postings, min_salary, max_salary)
# Grab every offers until nb_months before.
if not clean_postings.empty: # Or it will crash.
clean_postings = _filter_date(clean_postings, nb_months)
# Check if table is not empty.
if clean_postings.empty:
raise ValueError('No job offers match the given criteria.')
interesting_cols = [
'rome_id',
'annual_minimum_salary',
'experience_min_duration']
return clean_postings[interesting_cols]
def _filter_date(table_offers, nb_months):
""" Keep only the latest nb_months of the postings dataset.
Args :
table_offers: pandas DataFrame containing job postings.
nb_months (int.): number of months to look back to get job offers.
Returns:
pandas DataFrame contaning offers of the latest nb_months
of table_offers.
"""
table_offers.set_index(pd.DatetimeIndex(
table_offers.date_debut_imputed), inplace=True)
end_date = table_offers.date_debut_imputed.max()
start_date = (end_date - offsets.DateOffset(months=nb_months)).strftime(
'%Y-%m-%d')
date_mask = (table_offers['date_debut_imputed'] >= start_date)
return table_offers.loc[date_mask].reset_index(drop=True)
def _filter_outliers(
table_offers,
min_salary,
max_salary):
"""Returns a table containing only job offers without outliers.
Args :
table_offers: pandas DataFrame containing job postings.
min_salary (int.): exclude all salary under min_salary (ex : SMIC).
max_salary (int.): exclude all salary above max_salary (ex: 50000).
Returns:
pandas DataFrame containing only job offers with a salary between
[min_salary, max_salary[.
"""
valid_salary_mask = (table_offers.annual_minimum_salary >= min_salary) & (
table_offers.annual_minimum_salary < max_salary)
return table_offers.loc[valid_salary_mask]
clean_postings = filter_postings(postings)
clean_postings.head(2)
```
### Make experience buckets
```
# Select some job groups (some contaning offers, other without so many)
job_groups_examples = [
'G1602',
'K2204',
'K1303',
'K1304',
'G1803',
'A1202',
'B1401']
postings_example = clean_postings.loc[clean_postings.rome_id.isin(job_groups_examples)]
# Bucketize
postings_example_bucketized = postings_example.groupby('rome_id').apply(
job_offers_optimal_buckets.apply_bucketize)
postings_example_bucketized.head(5)
```
### Let's create 2 small subsets
Each of them contains a single `exp_bucket` of a `rome_id`.
```
# Make a dataset contaning only 1 job group & 1 experience bucket
postings_mask_1 = (postings_example_bucketized.rome_id == 'G1602') &\
(postings_example_bucketized.exp_bucket == '[0, 1[')
postings_mask_2 = (postings_example_bucketized.rome_id == 'G1803') &\
(postings_example_bucketized.exp_bucket == '[0, 1[')
postings_1 = postings_example_bucketized.loc[postings_mask_1]
postings_2 = postings_example_bucketized.loc[postings_mask_2]
postings_2.head(2)
```
### Cumulative counts
For each salary, we count the number of offers available.
```
num_offers_with_higher_salary = salary_recommendation_model._compute_job_offers_salary(postings_1)
num_offers_with_higher_salary.head(2)
```
## Chosing the best score
We use the following modules to compute graphs on score.
```
def compute_result_as_df(table_offers, score_label='sqrtO_salary'):
""" Compute every metrics of the score and store them in a pandas Dataframe
"""
num_offers_with_higher_salary = salary_recommendation_model._compute_job_offers_salary(
table_offers)
cumul_offers = num_offers_with_higher_salary.reset_index()
def _scoring(idx):
return _apply_score(num_offers_with_higher_salary, idx, score_label=score_label)
result_as_df = pd.DataFrame(cumul_offers.reset_index()['index'].apply(_scoring).tolist())
result_as_df = pd.concat([cumul_offers, result_as_df], axis=1)
return result_as_df
def _apply_score(
num_offers_with_higher_salary, idx, score_label):
""" Calculate a score to each salaries of table_offers, maximize it and return the amount of
gained offers for the optimal decrease of salary + additional metrics to compute
score comparison.
Args:
num_offers_with_higher_salary: Pandas Series containing the amount of job offers (value)
by salary (index).
idx: the index of the salary on which to compute the score.
score_label: label of the score we decided to compute.
Returns:
a dictionnary containing all the metrics
"""
# Cumulative count.
cumul_offers = num_offers_with_higher_salary.reset_index()
if idx == 0:
return _fill_dict_of_res(0, cumul_offers.annual_minimum_salary.iloc[idx], 0, 0)
delta_salaries = salary_recommendation_model._compute_delta_from_index(
cumul_offers.annual_minimum_salary, idx)
delta_offers = salary_recommendation_model._compute_delta_from_index(
cumul_offers.num_offers_with_higher_salary, idx)
# Compute score.
scores = _compute_scores(delta_offers, delta_salaries, score_label)
# Best score = max(score).
idx_max_score = scores.idxmax()
# Compute results.
final_num_offers = cumul_offers.num_offers_with_higher_salary.iloc[idx_max_score]
final_salary = cumul_offers.annual_minimum_salary.iloc[idx_max_score]
gained_offers = delta_offers.iloc[idx_max_score]
decrease_of_salary = delta_salaries.iloc[idx_max_score]
return _fill_dict_of_res(idx_max_score, final_salary, decrease_of_salary, gained_offers)
def _fill_dict_of_res(idx_max_score, final_salary, decrease_of_salary, gained_offers):
return {
'idx_max_score': idx_max_score,
'final_salary': final_salary,
'decrease_of_salary': decrease_of_salary,
'gained_offers': gained_offers}
def _compute_scores(offers, delta_salaries, score_label):
"""Compute different scores
NOTE: 'O' stands for 'delta(O)' and 'S' stands for 'delta(S)', with 'delta(O)' being the variation
of number of offers and 'delta(S)' the respective variation of salary.
"""
if score_label == 'sqrt(O)_S':
score = np.sqrt(offers) / (delta_salaries)
if score_label == 'sqrt(O)_S²':
score = np.sqrt(offers) / (delta_salaries ** 2)
if score_label == 'log(O)_S':
score = np.log(offers) / (delta_salaries)
if score_label == 'log(O)_S²':
score = np.log(offers) / (delta_salaries ** 2)
if score_label == 'O_S²':
score = offers / (delta_salaries ** 2)
return score
table_offers = postings_1.copy()
#table_offers = postings_2.copy()
# Output example
result_as_df = compute_result_as_df(table_offers=table_offers, score_label='sqrt(O)_S')
result_as_df.head(2)
```
## Score comparaison
We're going to compare scores relatively to 3 metrics :
* Recommended salaries
* Recommended decrease of salary
* Gained offers
### Recommended salaries
* x-axis: salary indexes in ascending values (0: the lowest salary)
* y-axis: recommended salary indexes (also in ascending values).
```
score_label_list = ['sqrt(O)_S', 'sqrt(O)_S²', 'log(O)_S', 'log(O)_S²', 'O_S²']
col_list = ['blue', 'green', 'red', 'darkturquoise', 'purple']
fig = plt.figure(figsize=(15, 15))
gs = gridspec.GridSpec(len(score_label_list), 1)
num_fig = 0
num_col = 0
for score_label in score_label_list:
ax = plt.subplot(gs[num_fig])
result_as_df = compute_result_as_df(table_offers=table_offers, score_label=score_label)
result_as_df.idx_max_score.plot(label=score_label, ax=ax, color=col_list[num_col])
plt.xlabel('Salary indexes (ascending values)')
plt.ylabel('Recommended salary indexes')
plt.legend(loc='upper left')
num_fig += 1
num_col += 1
```
### Recommended decrease of salary
* x-axis: annual_minimul salary in ascending values
* y-axis: recommended decrease of salary
```
fig = plt.figure(figsize=(15, 15))
gs = gridspec.GridSpec(len(score_label_list), 1)
num_fig = 0
num_col = 0
for score_label in score_label_list:
ax = plt.subplot(gs[num_fig])
result_as_df = compute_result_as_df(table_offers=table_offers, score_label=score_label)
result_as_df.set_index('annual_minimum_salary').decrease_of_salary.plot(
label=score_label, ax=ax, color=col_list[num_col])
plt.ylabel('Recommended decrease of salary')
plt.legend(loc='upper left')
num_fig += 1
num_col += 1
```
### Gained offers
* x-axis: annual_minimul salary in ascending values
* y-axis: Gained offers in percent.
```
fig = plt.figure(figsize=(15, 15))
gs = gridspec.GridSpec(len(score_label_list), 1)
num_fig = 0
num_col = 0
for score_label in score_label_list:
ax = plt.subplot(gs[num_fig])
result_as_df = compute_result_as_df(table_offers=table_offers, score_label=score_label)
result_as_df.set_index('annual_minimum_salary').gained_offers.plot(label=score_label, ax=ax, color=col_list[num_col])
plt.ylabel('Gained offers (in %)')
plt.legend(loc='upper left')
num_col += 1
num_fig += 1
```
## And the best score is....
* `sqrt(O)/S` seems to be the best score.
* `ln(O)/S ` and ` sqrt(O)/S` both give too much weight to `salary variation` and we end up always recommending the preceding salary (see first graphs on "Recommended salaries").
* `O/S²` gives too much weight on salary when the latter starts to grow up to a certain point. Then it recommends way too high decrease of salary.
NOTE: `O=delta(O)` being the variation of number of offers and `S=delta(S)` the respective variation of salary.
| true |
code
| 0.726286 | null | null | null | null |
|
### Imports
```
import torch
from tqdm import tqdm
import numpy as np
from rdkit import Chem
from rdkit import RDLogger
RDLogger.DisableLog('rdApp.*')
from rdkit.Chem import Draw
from matplotlib import pyplot as plt
from sklearn.metrics import roc_auc_score as ras
from sklearn.metrics import mean_squared_error
```
### Auglichem imports
```
from auglichem.molecule import Compose, RandomAtomMask, RandomBondDelete, MotifRemoval
from auglichem.molecule.data import MoleculeDatasetWrapper
from auglichem.molecule.models import GCN, AttentiveFP, GINE, DeepGCN
```
### Set up dataset
```
# Create transformation
transform = Compose([
RandomAtomMask([0.1, 0.3]),
RandomBondDelete([0.1, 0.3]),
MotifRemoval()
])
transform = RandomAtomMask(0.1)
# Initialize dataset object
dataset = MoleculeDatasetWrapper("ClinTox", data_path="./data_download", transform=transform, batch_size=128)
# Get train/valid/test splits as loaders
train_loader, valid_loader, test_loader = dataset.get_data_loaders("all")
```
### Initialize model with task from data
```
# Get model
num_outputs = len(dataset.labels.keys())
model = AttentiveFP(task=dataset.task, output_dim=num_outputs)
# Uncomment the following line to use GPU
#model.cuda()
```
### Initialize traning loop
```
if(dataset.task == 'classification'):
criterion = torch.nn.CrossEntropyLoss()
elif(dataset.task == 'regression'):
criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3, weight_decay=1e-5)
```
### Train the model
```
for epoch in range(2):
for bn, data in tqdm(enumerate(train_loader)):
optimizer.zero_grad()
loss = 0.
# Get prediction for all data
_, pred = model(data)
# To use GPU, data must be cast to cuda
#_, pred = model(data.cuda())
for idx, t in enumerate(train_loader.dataset.target):
# Get indices where target has a value
good_idx = np.where(data.y[:,idx]!=-999999999)
# When the data is placed on GPU, target must come back to CPU
#good_idx = np.where(data.y.cpu()[:,idx]!=-999999999)
# Prediction is handled differently for classification and regression
if(train_loader.dataset.task == 'classification'):
current_preds = pred[:,2*(idx):2*(idx+1)][good_idx]
current_labels = data.y[:,idx][good_idx]
elif(train_loader.dataset.task == 'regression'):
current_preds = pred[:,idx][good_idx]
current_labels = data.y[:,idx][good_idx]
loss += criterion(current_preds, current_labels)
loss.backward()
optimizer.step()
```
### Test the model
```
def evaluate(model, test_loader, validation=False):
set_str = "VALIDATION" if validation else "TEST"
with torch.no_grad():
# All targets we're evaluating
target_list = test_loader.dataset.target
# Dictionaries to keep track of predictions and labels for all targets
all_preds = {target: [] for target in target_list}
all_labels = {target: [] for target in target_list}
model.eval()
for data in test_loader:
# Get prediction for all data
_, pred = model(data)
# To use GPU, data must be cast to cuda
#_, pred = model(data.cuda())
for idx, target in enumerate(target_list):
# Get indices where target has a value
good_idx = np.where(data.y[:,idx]!=-999999999)
# When the data is placed on GPU, target must come back to CPU
#good_idx = np.where(data.y.cpu()[:,idx]!=-999999999)
# Prediction is handled differently for classification and regression
if(train_loader.dataset.task == 'classification'):
current_preds = pred[:,2*(idx):2*(idx+1)][good_idx][:,1]
current_labels = data.y[:,idx][good_idx]
elif(train_loader.dataset.task == 'regression'):
current_preds = pred[:,idx][good_idx]
current_labels = data.y[:,idx][good_idx]
# Save predictions and targets
all_preds[target].extend(list(current_preds.detach().cpu().numpy()))
all_labels[target].extend(list(current_labels.detach().cpu().numpy()))
scores = {target: None for target in target_list}
for target in target_list:
if(test_loader.dataset.task == 'classification'):
scores[target] = ras(all_labels[target], all_preds[target])
print("{0} {1} ROC: {2:.5f}".format(target, set_str, scores[target]))
elif(test_loader.dataset.task == 'regression'):
scores[target] = mean_squared_error(all_labels[target], all_preds[target],
squared=False)
print("{0} {1} RMSE: {2:.5f}".format(target, set_str, scores[target]))
evaluate(model, valid_loader, validation=True)
evaluate(model, test_loader)
```
### Model saving/loading example
```
# Save model
torch.save(model.state_dict(), "./saved_models/example_gcn")
# Instantiate new model and evaluate
model = AttentiveFP(task=dataset.task, output_dim=num_outputs)
evaluate(model, test_loader)
# Load saved model and evaluate
model.load_state_dict(torch.load("./saved_models/example_gcn"))
evaluate(model, test_loader)
```
| true |
code
| 0.624294 | null | null | null | null |
|
# SLE-GAN

This example demonstrates [SLE-GAN](https://arxiv.org/abs/2101.04775), which learns to generate images from small datasets.
# Preparation
Let's start by installing nnabla and accessing [nnabla-examples repository](https://github.com/sony/nnabla-examples). If you're running on Colab, make sure that your Runtime setting is set as GPU, which can be set up from the top menu (Runtime → change runtime type), and make sure to click **Connect** on the top right-hand side of the screen before you start.
```
!pip install nnabla-ext-cuda100
!git clone https://github.com/sony/nnabla-examples.git
%cd nnabla-examples/GANs/slegan
```
Now, select a type of object that you want to generate from the drop-down menu.
We have many object categories available ranging from animals to landmark architecutres.
**Make sure to run the cell after making a choice from the drop-down menu.**
```
dataset = "Grumpy_Cat" #@param ["Grumpy_Cat", "Bridge_of_Sighs", "Medici_Fountain", "Obama", "Panda", "Temple_of_Heaven", "Wuzhen", "Dog"]
```
Depending on your choice above, the following cell will download the pre-trained weight parameters.
```
if dataset == "Grumpy_Cat":
url1 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/cat/Gen_iter100000.h5"
url2 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/cat/GenEMA_iter100000.h5"
elif dataset == "Bridge_of_Sighs":
url1 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/bridge/Gen_iter100000.h5"
url2 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/bridge/GenEMA_iter100000.h5"
elif dataset == "Medici_Fountain":
url1 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/fountain/Gen_iter100000.h5"
url2 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/fountain/GenEMA_iter100000.h5"
elif dataset == "Obama":
url1 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/obama/Gen_iter100000.h5"
url2 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/obama/GenEMA_iter100000.h5"
elif dataset == "Panda":
url1 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/panda/Gen_iter100000.h5"
url2 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/panda/GenEMA_iter100000.h5"
elif dataset == "Temple_of_Heaven":
url1 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/temple/Gen_iter100000.h5"
url2 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/temple/GenEMA_iter100000.h5"
elif dataset == "Wuzhen":
url1 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/wuzhen/Gen_iter100000.h5"
url2 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/wuzhen/GenEMA_iter100000.h5"
elif dataset == "Dog":
url1 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/dog/Gen_iter100000.h5"
url2 = "https://nnabla.org/pretrained-models/nnabla-examples/GANs/slegan/dog/GenEMA_iter100000.h5"
!wget $url1 $url2
!mkdir $dataset
!mv *.h5 $dataset
```
# Generation
Now, let's generate the images by simply running the following cell! You can change the number of images to generate and the image size to generate by modifying the numbers after `--batch-size` and `--image-size`.
```
!python generate.py --model-load-path $dataset --batch-size 8 --image-size 256
```
Images have been generated now. Let's see how they look!
```
from IPython.display import Image,display
fname = './result/tmp/Image-Tile/000000.png'
display(Image(fname))
```
Also give it a try with other object categories from the drop-down menu above!
Hope you have fun!
| true |
code
| 0.649606 | null | null | null | null |
|
# Automatic peak finding and calibration tools in Becquerel
`Becquerel` contains tools for obtaining a rough first calibration for an uncalibrated `Spectrum`.
First, some imports:
```
%matplotlib inline
import os
import matplotlib.pyplot as plt
import numpy as np
import becquerel as bq
```
Also some function definitions:
```
def plot_spec(spectrum, xmode='channel'):
if xmode == 'channel':
facecolor = 'green'
else:
facecolor = 'blue'
plt.figure()
spectrum.fill_between(xmode=xmode, facecolor=facecolor, alpha=0.4, ax=plt.gca())
spectrum.plot('k-', lw=0.7, xmode=xmode, ax=plt.gca())
if xmode == 'channel':
plt.xlim(0, spectrum.bin_edges_raw.max())
plt.title('Uncalibrated spectrum')
else:
plt.xlim(0, spectrum.bin_centers_kev[-1])
plt.title('Calibrated spectrum')
plt.yscale('log')
plt.ylim(2e-1)
plt.tight_layout()
def plot_calibrator(cal):
cal.peakfinder.spectrum.apply_calibration(cal.cal)
print('fit gain:', cal.gain, 'keV/channel')
print('fit channels:', cal.fit_channels)
plt.figure()
plt.title('Peaks used in fit')
cal.plot()
plt.tight_layout()
plot_spec(cal.peakfinder.spectrum, xmode='channel')
for x, erg in zip(cal.fit_channels, cal.fit_energies):
chan = cal.peakfinder.spectrum.find_bin_index(x, use_kev=False)
y = cal.peakfinder.spectrum.counts_vals[chan-10:chan+10].max() * 1.5
plt.plot([x, x], [1e-1, y], 'r-', alpha=0.5)
plt.text(x, y, '{:.1f} keV'.format(erg))
plot_spec(cal.peakfinder.spectrum, xmode='energy')
for erg in cal.fit_energies:
x = int(erg / cal.gain)
chan = cal.peakfinder.spectrum.find_bin_index(x, use_kev=False)
y = cal.peakfinder.spectrum.counts_vals[chan-15:chan+15].max() * 1.5
plt.plot([erg, erg], [1e-1, y], 'r-', alpha=0.5)
plt.text(erg, y, '{:.1f} keV'.format(erg))
```
## `PeakFilter` classes
Instances of `PeakFilter` classes generate energy-dependent kernels that can be convolved with a spectrum to extract lines from the background continuum. To instantiate a kernel, the FWHM in channels at a specific channel is required, and the kernel scales the FWHM so that it is proportional to the square root of the channel (approximating the energy resolution of a detector).
Here is what a `GaussianDerivPeakFilter` looks like:
```
# demonstrate energy-dependent kernels
channels = np.arange(1000)
for kernel in [bq.GaussianPeakFilter(1000, 50, 5)]:
plt.figure()
plt.title('{} evaluated at different channels'.format(type(kernel).__name__))
ind = np.arange(1000)
plt.plot([-50, 50], [0, 0], 'k-')
for chan in range(100, 900, 100):
kern = kernel.kernel(chan, np.arange(1001))
plt.plot(ind - chan, kern, '-', lw=1.5, label='Channel {}'.format(chan))
plt.xlim(-50, 50)
plt.xlabel('offset from channel')
plt.ylabel('kernel value')
plt.legend()
plt.tight_layout()
```
We will use the `GaussiaPeakKernel` from now on.
A kernel can create a matrix that can be multiplied with a spectrum to perform the convolution. Here is what such a matrix could look like:
```
# display the kernel matrix
kernel = bq.GaussianPeakFilter(1000, 50, 5)
plt.figure()
plt.title('Matrix of GaussianPeakFilter evaluated across entire spectrum')
kernel.plot_matrix(np.arange(1000))
plt.tight_layout()
```
## `PeakFinder` and `AutoCalibrator` classes
The `PeakFinder` class allows one to automatically select peaks that a `PeakFilter` filters out of the spectrum.
The `AutoCalibrator` class takes the peaks found by a `PeakFinder` and finds the most likely energies associated with those peaks.
It is easiest to explain these classes using examples.
## Example 1: Calibrating a scintillator spectrum
First we read in a raw spectrum from file (this is a simulated background spectrum for a scintillator):
```
counts = []
filename = os.path.join(os.path.dirname(bq.__file__), '../tests/samples/sim_spec.spe')
spec = bq.Spectrum.from_file(filename)
spec = spec.combine_bins(4)
spec.bin_edges_raw *= 4
plot_spec(spec)
plt.figure()
plt.plot(spec.bin_centers_raw, spec.counts_vals)
plt.yscale('log')
plt.show()
```
To filter this spectrum we will use a kernel with a width of 50 channels at 500 channels, to match the strong line in the center (most likely the K-40 line at 1460 keV):
```
kernel = bq.GaussianPeakFilter(500, 50, fwhm_at_0=10)
```
### 1.1 `PeakFinder` class
The `PeakFinder` class uses a `PeakFilter` to filter and calibrate the spectrum.
Under the hood, the kernel estimates the SNR of each peak by separating peaks from the background continuum. We can introspect this process using the `PeakFinder` instance:
```
# show how the kernel estimates the peaks+background and the background
finder = bq.PeakFinder(spec, kernel)
plt.figure()
plt.plot(spec.counts_vals.clip(1e-1), label='Raw spectrum')
plt.plot(finder._peak_plus_bkg.clip(1e-1), label='Peaks+Continuum')
plt.plot(finder._bkg.clip(1e-1), label='Continuum')
plt.plot(finder._signal.clip(1e-1), label='Peaks')
plt.yscale('log')
plt.xlim(0, len(spec))
plt.ylim(3e-1)
plt.xlabel('Channels')
plt.ylabel('Counts')
plt.legend()
plt.tight_layout()
```
The kernel applied directly to the spectral count data produces the estimated signal-to-noise (SNR) of each peak.
```
# plot signal to noise
plt.figure()
plt.title('Kernel applied to spectrum')
finder.plot()
plt.tight_layout()
```
### 1.2 Using `find_peak` to find a specific peak
Use the method `find_peak` to find a specific peak in the spectrum.
Let's try to locate the index of the tallest peak, right in the middle of the spectrum:
```
peak_chan = finder.find_peak(500, min_snr=3.)
print(peak_chan)
plt.figure()
plt.title('find_peak')
finder.plot()
plt.xlim(0,1000)
plt.tight_layout()
finder.centroids
```
Subsequent calls to `find_peak` will store the any new results:
```
peak_chan = finder.find_peak(900, min_snr=3.)
print(peak_chan)
plt.figure()
plt.title('find_peak')
finder.plot()
plt.tight_layout()
```
#### 1.2 Use `reset` to remove all candidate peaks and calibration data
The list of candidate peaks will persist in the `PeakFinder` object, as will any calibration information (will be covered later).
Resetting the current object yields:
```
finder.reset()
plt.figure()
plt.title('after reset')
finder.plot()
plt.tight_layout()
```
### 1.2 Using `find_peaks` to find all peaks above an SNR threshold
Instead of repeatedly calling `find_peak`, one can build up a set of peak candidates using `find_peaks`. The following locates all peaks above channel 50 and an SNR of 2:
```
finder.find_peaks(min_snr=1, xmin=50)
print(finder.centroids)
print(finder.snrs)
plt.figure()
plt.title('find_peaks')
finder.plot()
plt.tight_layout()
```
### 1.4 The `AutoCalibrator.fit` method
The main machinery of auto-calibration is the `fit` method, which matches peak candidates (e.g., the outputs of `find_peaks`) with specific line energies and keeps the best match:
```
cal = bq.AutoCalibrator(finder)
cal.fit(
[351.93, 609.32, 1460.82, 2614.3],
optional=[295.22, 768.36, 1120.294, 1238.122, 1764.49],
gain_range=[2.5e-2, 4e2],
de_max=200.,
)
plot_calibrator(cal)
```
### 1.5 `AutoCalibrator.fit` with only one peak
A special case of the calibrator is when only one peak has been found and only one energy is given. Use this with caution since there is none of the cross-validation that comes with multiple lines.
```
cal.peakfinder.reset()
cal.peakfinder.fwhm_tol=(0.5, 1.2)
cal.peakfinder.find_peak(500, min_snr=3.)
cal.fit([1460.82], gain_range=[2.5e-1, 4e1], de_max=50.)
plot_calibrator(cal)
# looks like there may be an off-by-one or bin center vs edge issue in plotting...
```
## Example 2: Calibrating an HPGe spectrum
Let's perform the same calibration steps using an HPGe spectrum. This spectrum will have many more lines to fit.
```
# read raw HPGe data
filename = os.path.join(os.path.dirname(bq.__file__), '../tests/samples/Mendocino_07-10-13_Acq-10-10-13.Spe')
spec = bq.Spectrum.from_file(filename)
plot_spec(spec)
```
We will again use a `GaussianDerivKernel`, but this one must be much narrower to match the resolution. Not surprisingly, many of the peaks in the spectrum have higher SNR values:
```
# apply the kernel to the data to get SNR
kernel = bq.GaussianPeakFilter(3700, 10, fwhm_at_0=5)
finder = bq.PeakFinder(spec, kernel)
cal = bq.AutoCalibrator(finder)
plt.figure()
plt.title('Kernel applied to spectrum')
cal.peakfinder.plot()
plt.tight_layout()
# find significant peaks
cal.peakfinder.find_peaks(min_snr=15, xmin=400)
print(cal.peakfinder.centroids)
print(cal.peakfinder.snrs)
plt.figure()
plt.title('find_peaks')
cal.peakfinder.plot()
plt.tight_layout()
# perform calibration
cal.fit(
[295.22, 351.93, 511.0, 609.32, 1460.82, 2614.3],
optional=[583.187, 911.20, 1120.294, 1238.122, 1377.67, 1764.49, 2204.06],
gain_range=[0.35, 0.40],
de_max=5.,
)
plot_calibrator(cal)
```
## Example 3: An unusual NaI spectrum
This example shows a real spectrum from a NaI detector with very poor energy resolution and where the dynamic range has cut off the higher energies. Can we still calibrate it?
```
counts = []
filename = os.path.join(os.path.dirname(bq.__file__), '../tests/samples/nai_detector.spe')
spec = bq.Spectrum.from_file(filename)
plot_spec(spec)
kernel = bq.GaussianPeakFilter(700, 50, 10)
finder = bq.PeakFinder(spec, kernel)
cal = bq.AutoCalibrator(finder)
# find significant peaks
cal.peakfinder.find_peaks(min_snr=3, xmin=100)
print(cal.peakfinder.centroids)
print(cal.peakfinder.snrs)
plt.figure()
plt.title('find_peaks')
cal.peakfinder.plot()
plt.tight_layout()
# perform calibration
cal.fit(
[609.32, 1460.82],
optional=[],
gain_range=[0.1, 5.],
de_max=50.,
)
plot_calibrator(cal)
```
That did not work right, the calibrator matched with the wrong lines. To fix this, we could either increase `xmin` to exclude the lower energy lines, increase `min_snr` to exclude the lower significance lines, or add optional energies. Let's try the same fit but with a longer list of prominent background lines:
```
# perform calibration again, but with more optional energies
cal.fit(
[609.32, 1460.82],
optional=[238.63, 338.32, 351.93, 911.20, 1120.294, 1620.50, 1764.49, 2118.514],
gain_range=[0.1, 5.],
de_max=50.,
)
plot_calibrator(cal)
```
Success! The cross-validation used in `AutoCalibrator.fit` was able to find a better match.
## Example 4: CsI detector with Ba-133 and Cs-137 sources
This data is from a small detector with Ba-133 and Cs-137 sources near it. We want to use those sources' lines and any strong backgroud lines to calibrate it.
```
counts = []
filename = os.path.join(os.path.dirname(bq.__file__), '../tests/samples/SGM102432.spe')
spec = bq.Spectrum.from_file(filename)
plot_spec(spec)
kernel = bq.GaussianPeakFilter(2400, 120, 30)
finder = bq.PeakFinder(spec, kernel)
cal = bq.AutoCalibrator(finder)
# find significant peaks
cal.peakfinder.find_peaks(min_snr=3, xmin=200)
print(cal.peakfinder.centroids)
print(cal.peakfinder.snrs)
plt.figure()
plt.title('find_peaks')
cal.peakfinder.plot()
plt.tight_layout()
cal.fit(
[356.0129, 661.657, 1460.82],
optional=[911.20, 1120.294, 1764.49, 2614.3],
gain_range=[0.5, 0.7],
de_max=100.,
)
plot_calibrator(cal)
```
This last plot reveals that the 1460 keV peak does not quite line up with the calibration, so this detector probably exhibits a significant nonlinearity and would have to be calibrated with a more sophisticated method.
| true |
code
| 0.585575 | null | null | null | null |
|
# Adadelta
:label:`sec_adadelta`
Adadelta是AdaGrad的另一种变体( :numref:`sec_adagrad`),
主要区别在于前者减少了学习率适应坐标的数量。
此外,广义上Adadelta被称为没有学习率,因为它使用变化量本身作为未来变化的校准。
Adadelta算法是在 :cite:`Zeiler.2012`中提出的。
## Adadelta算法
简而言之,Adadelta使用两个状态变量,$\mathbf{s}_t$用于存储梯度二阶导数的漏平均值,$\Delta\mathbf{x}_t$用于存储模型本身中参数变化二阶导数的泄露平均值。请注意,为了与其他出版物和实现的兼容性,我们使用作者的原始符号和命名(没有其他真正理由为什么应该使用不同的希腊变量来表示在动量中用于相同用途的参数,即AdaGrad、RMSProp和Adadelta)。
以下是Adadelta的技术细节。鉴于参数du jour是$\rho$,我们获得了与 :numref:`sec_rmsprop`类似的以下泄漏更新:
$$\begin{aligned}
\mathbf{s}_t & = \rho \mathbf{s}_{t-1} + (1 - \rho) \mathbf{g}_t^2.
\end{aligned}$$
与 :numref:`sec_rmsprop`的区别在于,我们使用重新缩放的梯度$\mathbf{g}_t'$执行更新,即
$$\begin{aligned}
\mathbf{x}_t & = \mathbf{x}_{t-1} - \mathbf{g}_t'. \\
\end{aligned}$$
那么,调整后的梯度$\mathbf{g}_t'$是什么?我们可以按如下方式计算它:
$$\begin{aligned}
\mathbf{g}_t' & = \frac{\sqrt{\Delta\mathbf{x}_{t-1} + \epsilon}}{\sqrt{{\mathbf{s}_t + \epsilon}}} \odot \mathbf{g}_t, \\
\end{aligned}$$
其中$\Delta \mathbf{x}_{t-1}$是重新缩放梯度的平方$\mathbf{g}_t'$的泄漏平均值。我们将$\Delta \mathbf{x}_{0}$初始化为$0$,然后在每个步骤中使用$\mathbf{g}_t'$更新它,即
$$\begin{aligned}
\Delta \mathbf{x}_t & = \rho \Delta\mathbf{x}_{t-1} + (1 - \rho) {\mathbf{g}_t'}^2,
\end{aligned}$$
和$\epsilon$(例如$10^{-5}$这样的小值)是为了保持数字稳定性而加入的。
## 代码实现
Adadelta需要为每个变量维护两个状态变量,即$\mathbf{s}_t$和$\Delta\mathbf{x}_t$。这将产生以下实施。
```
%matplotlib inline
from mxnet import np, npx
from d2l import mxnet as d2l
npx.set_np()
def init_adadelta_states(feature_dim):
s_w, s_b = np.zeros((feature_dim, 1)), np.zeros(1)
delta_w, delta_b = np.zeros((feature_dim, 1)), np.zeros(1)
return ((s_w, delta_w), (s_b, delta_b))
def adadelta(params, states, hyperparams):
rho, eps = hyperparams['rho'], 1e-5
for p, (s, delta) in zip(params, states):
# In-placeupdatesvia[:]
s[:] = rho * s + (1 - rho) * np.square(p.grad)
g = (np.sqrt(delta + eps) / np.sqrt(s + eps)) * p.grad
p[:] -= g
delta[:] = rho * delta + (1 - rho) * g * g
```
对于每次参数更新,选择$\rho = 0.9$相当于10个半衰期。由此我们得到:
```
data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
d2l.train_ch11(adadelta, init_adadelta_states(feature_dim),
{'rho': 0.9}, data_iter, feature_dim);
```
为了简洁实现,我们只需使用`Trainer`类中的`adadelta`算法。
```
d2l.train_concise_ch11('adadelta', {'rho': 0.9}, data_iter)
```
## 小结
* Adadelta没有学习率参数。相反,它使用参数本身的变化率来调整学习率。
* Adadelta需要两个状态变量来存储梯度的二阶导数和参数的变化。
* Adadelta使用泄漏的平均值来保持对适当统计数据的运行估计。
## 练习
1. 调整$\rho$的值,会发生什么?
1. 展示如何在不使用$\mathbf{g}_t'$的情况下实现算法。为什么这是个好主意?
1. Adadelta真的是学习率为0吗?你能找到Adadelta无法解决的优化问题吗?
1. 将Adadelta的收敛行为与AdaGrad和RMSProp进行比较。
[Discussions](https://discuss.d2l.ai/t/5771)
| true |
code
| 0.455622 | null | null | null | null |
|
## ISA Create - Sample Assay Plan as a Graph: Mass Spectrometry
Here I am showing how from a JSON-like dictionary describing an MS experiment you can create a full SampleAssayPlan as a graph and visualize how this looks like
```
from isatools.model import *
from isatools.create.models import *
import networkx as nx
import plotly.plotly as py
import plotly.graph_objs as go
import matplotlib.pyplot as plt
import pydot
from graphviz import Digraph
import pygraphviz
%matplotlib inline
# from: https://stackoverflow.com/questions/29586520/can-one-get-hierarchical-graphs-from-networkx-with-python-3/29597209
def hierarchy_pos(G, root=None, width=1., vert_gap = 0.2, vert_loc = 0, xcenter = 0.5):
'''
From Joel's answer at https://stackoverflow.com/a/29597209/2966723.
Licensed under Creative Commons Attribution-Share Alike
If the graph is a tree this will return the positions to plot this in a
hierarchical layout.
G: the graph (must be a tree)
root: the root node of current branch
- if the tree is directed and this is not given,
the root will be found and used
- if the tree is directed and this is given, then
the positions will be just for the descendants of this node.
- if the tree is undirected and not given,
then a random choice will be used.
width: horizontal space allocated for this branch - avoids overlap with other branches
vert_gap: gap between levels of hierarchy
vert_loc: vertical location of root
xcenter: horizontal location of root
'''
# NOTE: This was commented out for testing with ISA-API output (a DiGraph)
# if not nx.is_tree(G):
# raise TypeError('cannot use hierarchy_pos on a graph that is not a tree')
if root is None:
if isinstance(G, nx.DiGraph):
root = next(iter(nx.topological_sort(G))) #allows back compatibility with nx version 1.11
else:
root = random.choice(list(G.nodes))
def _hierarchy_pos(G, root, width=1., vert_gap = 0.2, vert_loc = 0, xcenter = 0.5, pos = None, parent = None):
'''
see hierarchy_pos docstring for most arguments
pos: a dict saying where all nodes go if they have been assigned
parent: parent of this branch. - only affects it if non-directed
'''
if pos is None:
pos = {root:(xcenter,vert_loc)}
else:
pos[root] = (xcenter, vert_loc)
children = list(G.neighbors(root))
if not isinstance(G, nx.DiGraph) and parent is not None:
children.remove(parent)
if len(children)!=0:
dx = width/len(children)
nextx = xcenter - width/2 - dx/2
for child in children:
nextx += dx
pos = _hierarchy_pos(G,child, width = dx, vert_gap = vert_gap,
vert_loc = vert_loc-vert_gap, xcenter=nextx,
pos=pos, parent = root)
return pos
return _hierarchy_pos(G, root, width, vert_gap, vert_loc, xcenter)
```
Here we define the structure of our sampling and assay plan, using a Python dictionary. From it we create a full `isatools.create.models.SampleAssayPlan` object
```
ms_assay_dict = OrderedDict([
('sample', [
{
'node_type': SAMPLE,
'characteristics_category': 'organism part',
'characteristics_value': 'liver',
'size': 1,
'technical_replicates': None,
'is_input_to_next_protocols': True
},
{
'node_type': SAMPLE,
'characteristics_category': 'organism part',
'characteristics_value': 'blood',
'size': 5,
'technical_replicates': None,
'is_input_to_next_protocols': True
},
{
'node_type': SAMPLE,
'characteristics_category': 'organism part',
'characteristics_value': 'heart',
'size': 1,
'technical_replicates': None,
'is_input_to_next_protocols': True
}
]),
('extraction', {}),
('extract', [
{
'node_type': SAMPLE,
'characteristics_category': 'extract type',
'characteristics_value': 'polar fraction',
'size': 1,
'technical_replicates': None,
'is_input_to_next_protocols': True
},
{
'node_type': SAMPLE,
'characteristics_category': 'extract type',
'characteristics_value': 'lipids',
'size': 1,
'technical_replicates': None,
'is_input_to_next_protocols': True
}
]),
('labeling', {}),
('labeled_extract', [
{
'node_type': SAMPLE,
'characteristics_category': 'labeled extract type',
'characteristics_value': '',
'size': 2,
'technical_replicates': None,
'is_input_to_next_protocols': True
}
]),
('mass_spectrometry', {
'instrument': ['Agilent QTQF §'],
'injection_mode': ['FIA', 'LC'],
'acquisition_mode': ['positive mode']
}),
('raw_spectral_data_file', [
{
'node_type': DATA_FILE,
'size': 1,
'technical_replicates': 2,
'is_input_to_next_protocols': False
}
])
])
ms_assay_plan = SampleAndAssayPlan.from_sample_and_assay_plan_dict(ms_assay_dict)
```
The `ms_assay_plan` object is a graph. Let's which are its `nodes`.
```
nx_graph = ms_assay_plan.as_networkx_graph()
# set(nx_graph.nodes)
nx_graph.number_of_nodes()
```
Here we print the `links` or `edges` of the graph
```
# set(nx_graph.edges)
nx_graph.number_of_edges()
nx_graph.size()
```
We output is as a `networkx` graph and we visualize it using `matplotlib`
```
G=nx_graph
# nx.draw(G)
nx.draw(nx_graph,pos=nx.spring_layout(G),node_color=range(G.number_of_nodes()),cmap=plt.cm.Blues, with_labels=False)
SG1 = G.subgraph(['sample_000','extraction_000_000','extract_000_000','extract_001_000','labeling_000_000','labeling_000_003','labeled_extract_000_000','labeled_extract_000_003'])
# print(list(SG.edges))
pos1 = hierarchy_pos(SG1,'sample_000')
nx.draw(SG1, pos=pos1, with_labels=True,node_color = 'b')
plt.savefig('hierarchy1.png')
# SG2 = G.subgraph(['sample_001','extraction_000_001','extract_000_001','extract_001_001','labeling_000_001','labeling_000_004','labeled_extract_000_001','labeled_extract_000_004'])
# # print(list(SG.edges))
# pos2 = hierarchy_pos(SG2,'sample_001')
# nx.draw(SG2, pos=pos2, with_labels=True,node_color = 'pink')
# plt.savefig('hierarchy2.png')
# Generating a graphviz compatible output
dot = Digraph()
for node in nx_graph.nodes:
dot.node(node)
dot.edges(nx_graph.edges)
filename=dot.filename
# print(dot.source)
dot.graph_attr['rankdir'] = 'LR' # to layout from left to right (horizontal), rather than top to bottom (vertical)
dot.render(filename, view=True)
# nx.draw_networkx_edges(nx_graph,pos=nx.spring_layout(nx_graph))
# fig = go.Figure(data=[nx_graph.nodes,nx_graph.edges])
# nx.draw(nx_graph, with_labels=False, font_weight='bold')
nx.drawing.draw_planar(nx_graph,node_color=range(G.number_of_nodes()),cmap=plt.cm.Blues, style='dashed')
nx.nx_agraph.to_agraph(nx_graph).layout()
nx.nx_agraph.to_agraph(nx_graph).write("isa-test.dot")
G=nx.nx_agraph.read_dot("isa-test.dot")
# G = nx.bipartite.gnmk_random_graph(3, 5, 10, seed=123)
# top = nx.bipartite.sets(G)[3]
# pos = nx.bipartite_layout(G, top)
# pos = nx.planar_layout(G)
pos=nx.drawing.layout.planar_layout(G, scale=2, center=None, dim=2)
nx.draw(nx_graph,pos=nx.drawing.layout.planar_layout(G, scale=1, center=None, dim=2),node_color=range(G.number_of_nodes()),cmap=plt.cm.Blues)
NG = nx.karate_club_graph()
res = [0,1,2,3,4,5, 'parrot'] #I've added 'parrot', a node that's not in G
#just to demonstrate that G.subgraph is okay
#with nodes not in G.
k = NG.subgraph(res)
pos = nx.spring_layout(NG) #setting the positions with respect to G, not k.
plt.figure()
nx.draw_networkx(k, pos=pos)
othersubgraph = NG.subgraph(range(6,NG.order()))
nx.draw_networkx(othersubgraph, pos=pos, node_color = 'pink')
plt.show()
```
| true |
code
| 0.492127 | null | null | null | null |
|
### Introduction
An example of implementing the Metapath2Vec representation learning algorithm using components from the `stellargraph` and `gensim` libraries.
**References**
**1.** Metapath2Vec: Scalable Representation Learning for Heterogeneous Networks. Yuxiao Dong, Nitesh V. Chawla, and Ananthram Swami. ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), 135–144, 2017. ([link](https://ericdongyx.github.io/papers/KDD17-dong-chawla-swami-metapath2vec.pdf))
**2.** Distributed representations of words and phrases and their compositionality. T. Mikolov, I. Sutskever, K. Chen, G. S. Corrado, and J. Dean. In Advances in Neural Information Processing Systems (NIPS), pp. 3111-3119, 2013. ([link](https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf))
**3.** Gensim: Topic modelling for humans. ([link](https://radimrehurek.com/gensim/))
**4.** Social Computing Data Repository at ASU [http://socialcomputing.asu.edu]. R. Zafarani and H. Liu. Tempe, AZ: Arizona State University, School of Computing, Informatics and Decision Systems Engineering. 2009.
```
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
import os
import networkx as nx
import numpy as np
import pandas as pd
from stellargraph.data.loader import load_dataset_BlogCatalog3
%matplotlib inline
```
### Load the dataset
The dataset is the BlogCatalog3 network.
It can be downloaded from [here.](http://socialcomputing.asu.edu/datasets/BlogCatalog3)
The following is the description of the dataset from the publisher [4]:
> This is the data set crawled from BlogCatalog ( http://www.blogcatalog.com ). BlogCatalog is a social blog directory website. This contains the friendship network crawled and group memberships. For easier understanding, all the contents are organized in CSV file format.
The statistics of this network are,
- Number of bloggers : 10,312
- Number of friendship pairs: 333,983
- Number of groups: 39
We assume that the dataset file `BlogCatalog-dataset.zip` has been downloaded and unzipped in the directory,
`~/data`
and the data in `csv` format (the files `edges.csv`, `nodes.csv`, `groups.csv`, and `group-edges.csv` can be found in directory,
`~/data/BlogCatalog-dataset/data/`
```
dataset_location = os.path.expanduser("~/data/BlogCatalog-dataset/data")
g_nx = load_dataset_BlogCatalog3(location=dataset_location)
print("Number of nodes {} and number of edges {} in graph.".format(g_nx.number_of_nodes(), g_nx.number_of_edges()))
```
### The Metapath2Vec algorithm
The Metapath2Vec algorithm introduced in [1] is a 2-step representation learning algorithm. The two steps are:
1. Use uniform random walks to generate sentences from a graph. A sentence is a list of node IDs. The set of all sentences makes a corpus. The random walk is driven by a metapath that defines the node type order by which the random walker explores the graph.
2. The corpus is then used to learn an embedding vector for each node in the graph. Each node ID is considered a unique word/token in a dictionary that has size equal to the number of nodes in the graph. The Word2Vec algorithm [2] is used for calculating the embedding vectors.
## Corpus generation using random walks
The `stellargraph` library provides an implementation for uniform, first order, random walks as required by Metapath2Vec. The random walks have fixed maximum length and are controlled by the list of metapath schemas specified in parameter `metapaths`.
A metapath schema defines the type of node that the random walker is allowed to transition to from its current location. In the `stellargraph` implementation of metapath-driven random walks, the metapath schemas are given as a list of node types under the assumption that the input graph is not a multi-graph, i.e., two nodes are only connected by one edge type.
See [1] for a detailed description of metapath schemas and metapth-driven random walks.
For the **BlogCatalog3** dataset we use the following 3 metapaths.
- "user", "group", "user"
- "user", "group", "user", "user"
- "user", "user"
```
from stellargraph.data import UniformRandomMetaPathWalk
from stellargraph import StellarGraph
# Create the random walker
rw = UniformRandomMetaPathWalk(StellarGraph(g_nx))
# specify the metapath schemas as a list of lists of node types.
metapaths = [
["user", "group", "user"],
["user", "group", "user", "user"],
["user", "user"],
]
walks = rw.run(nodes=list(g_nx.nodes()), # root nodes
length=100, # maximum length of a random walk
n=1, # number of random walks per root node
metapaths=metapaths # the metapaths
)
print("Number of random walks: {}".format(len(walks)))
```
### Representation Learning using Word2Vec
We use the Word2Vec [2] implementation in the free Python library gensim [3] to learn representations for each node in the graph.
We set the dimensionality of the learned embedding vectors to 128 as in [1].
```
from gensim.models import Word2Vec
model = Word2Vec(walks, size=128, window=5, min_count=0, sg=1, workers=2, iter=1)
model.wv.vectors.shape # 128-dimensional vector for each node in the graph
```
### Visualise Node Embeddings
We retrieve the Word2Vec node embeddings that are 128-dimensional vectors and then we project them down to 2 dimensions using the [t-SNE](http://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html) algorithm.
```
# Retrieve node embeddings and corresponding subjects
node_ids = model.wv.index2word # list of node IDs
node_embeddings = model.wv.vectors # numpy.ndarray of size number of nodes times embeddings dimensionality
node_targets = [ g_nx.nodes[node_id]['label'] for node_id in node_ids]
```
Transform the embeddings to 2d space for visualisation
```
transform = TSNE #PCA
trans = transform(n_components=2)
node_embeddings_2d = trans.fit_transform(node_embeddings)
# draw the points
label_map = { l: i for i, l in enumerate(np.unique(node_targets))}
node_colours = [ label_map[target] for target in node_targets]
plt.figure(figsize=(20,16))
plt.axes().set(aspect="equal")
plt.scatter(node_embeddings_2d[:,0],
node_embeddings_2d[:,1],
c=node_colours, alpha=0.3)
plt.title('{} visualization of node embeddings'.format(transform.__name__))
plt.show()
```
### Downstream task
The node embeddings calculated using Metapath2Vec can be used as feature vectors in a downstream task such as node attribute inference (e.g., inferring the gender or age attribute of 'user' nodes), community detection (e.g., clustering of 'user' nodes based on the similarity of their embedding vectors), and link prediction (e.g., prediction of friendship relation between 'user' nodes).
| true |
code
| 0.635279 | null | null | null | null |
|
# Using Astropy Quantities and Units for astrophysical calculations
## Authors
Ana Bonaca, Erik Tollerud, Jonathan Foster, Lia Corrales, Kris Stern, Stephanie T. Douglas
## Learning Goals
* Use `Quantity` objects to estimate a hypothetical galaxy's mass
* Take advantage of constants in the `astropy.constants` library
* Print formatted unit strings
* Plot `Quantity` objects with unit labels, using `astropy.visualization.quantity_support`
* Do math with `Quantity` objects
* Convert quantities with `astropy.units`
* Convert between wavelength and energy with `astropy.units.spectral` equivalencies
* Use the small angle approximation with `astropy.units.dimensionless_angles` equivalencies
* Write functions that take `Quantity` objects instead of numpy arrays
* Make synthetic radio observations
* Use `Quantity` objects such as data cubes to facilitate a full derivation of the total mass of a molecular cloud
## Keywords
units, radio astronomy, data cubes, matplotlib
## Companion Content
[Tools for Radio Astronomy](https://www.springer.com/gp/book/9783662053942) by Rohlfs & Wilson
## Summary
In this tutorial we present some examples showing how Astropy's `Quantity` object can make astrophysics calculations easier. The examples include calculating the mass of a galaxy from its velocity dispersion and determining masses of molecular clouds from CO intensity maps. We end with an example of good practices for using quantities in functions you might distribute to other people.
For an in-depth discussion of `Quantity` objects, see the [astropy documentation section](http://docs.astropy.org/en/stable/units/quantity.html).
## Preliminaries
We start by loading standard libraries and set up plotting for ipython notebooks.
```
import numpy as np
import matplotlib.pyplot as plt
# You shouldn't use the `seed` function in real science code, but we use it here for example purposes.
# It makes the "random" number generator always give the same numbers wherever you run it.
np.random.seed(12345)
# Set up matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
```
It's conventional to load the Astropy `units` module as the variable `u`, demonstrated below. This will make working with `Quantity` objects much easier.
Astropy also has a `constants` module where typical physical constants are available. The constants are stored as objects of a subclass of `Quantity`, so they behave just like a `Quantity`. Here, we'll only need the gravitational constant `G`, Planck's constant `h`, and Boltzmann's constant, `k_B`.
```
import astropy.units as u
from astropy.constants import G, h, k_B
```
We will also show an example of plotting while taking advantage of the `astropy.visualization` package, which provides support for `Quantity` units.
```
from astropy.visualization import quantity_support
```
## 1. Galaxy mass
In this first example, we will use `Quantity` objects to estimate a hypothetical galaxy's mass, given its half-light radius and radial velocities of stars in the galaxy.
Let's assume that we measured the half-light radius of the galaxy to be 29 pc projected on the sky at the distance of the galaxy. This radius is often called the "effective radius", so we'll store it as a `Quantity` object with the name `Reff`. The easiest way to create a `Quantity` object is by multiplying the value with its unit. Units are accessed as u."unit", in this case u.pc.
```
Reff = 29 * u.pc
```
A completely equivalent (but more verbose) way of doing the same thing is to use the `Quantity` object's initializer, demonstrated below. In general, the simpler form (above) is preferred, as it is closer to how such a quantity would actually be written in text. The initalizer form has more options, though, which you can learn about from the [astropy reference documentation on Quantity](http://docs.astropy.org/en/stable/api/astropy.units.quantity.Quantity.html).
```
Reff = u.Quantity(29, unit=u.pc)
```
We can access the value and unit of a `Quantity` using the `value` and `unit` attributes.
```
print("""Half light radius
value: {0}
unit: {1}""".format(Reff.value, Reff.unit))
```
The `value` and `unit` attributes can also be accessed within the print function.
```
print("""Half light radius
value: {0.value}
unit: {0.unit}""".format(Reff))
```
Furthermore, we can convert the radius in parsecs to any other unit of length using the ``to()`` method. Here, we convert it to meters.
```
print("{0:.3g}".format(Reff.to(u.m)))
```
Next, we'll first create a synthetic dataset of radial velocity measurements, assuming a normal distribution with a mean velocity of 206 km/s and a velocity dispersion of 4.3 km/s.
```
vmean = 206
sigin = 4.3
v = np.random.normal(vmean, sigin, 500)*u.km/u.s
print("""First 10 radial velocity measurements:
{0}
{1}""".format(v[:10], v.to(u.m/u.s)[:10]))
```
One can ocassionally run into issues when attempting to plot `Quantity` objects with `matplotlib` libraries. It is always possible to fix this by passing the value array (e.g., `v.value`) to `matplotlib` functions. However, calling the `astropy.visualization.quantity_support()` function will change the settings on your `matplotlib` session to better handle astropy `Quantity` objects:
```
quantity_support()
```
Now we can plot a histogram of the velocity dataset. Note that, due to calling `quantity_support`, the x-axis is automatically labeled with the correct units.
```
plt.figure()
plt.hist(v, bins='auto', histtype="step")
plt.ylabel("N")
```
Now we can calculate the velocity dispersion of the galaxy. This demonstrates how you can perform basic operations like subtraction and division with `Quantity` objects, and also use them in standard numpy functions such as `mean()` and `size()`. They retain their units through these operations just as you would expect them to.
```
sigma = np.sqrt(np.sum((v - np.mean(v))**2) / np.size(v))
print("Velocity dispersion: {0:.2f}".format(sigma))
```
Note how we needed to use `numpy` square root function, because the resulting velocity dispersion quantity is a `numpy` array. If we used the python standard `math` library's `sqrt` function instead, we get an error.
```
sigma_scalar = np.sqrt(np.sum((v - np.mean(v))**2) / len(v))
```
In general, you should only use `numpy` functions with `Quantity` objects, *not* the `math` equivalents, unless you are sure you understand the consequences.
Now for the actual mass calculation. If a galaxy is pressure-supported (for example, an elliptical or dwarf spheroidal galaxy), its mass within the stellar extent can be estimated using a straightforward formula: $M_{1/2}=4\sigma^2 R_{eff}/G$. There are caveats to the use of this formula for science -- see Wolf et al. 2010 for details. For demonstrating `Quantity`, you can accept that this is often good enough. For the calculation, we can multiply the quantities together, and `astropy` will keep track of the units.
```
M = 4*sigma**2*Reff/G
M
```
The result is in a composite unit, so it's not really obvious it's a mass. However, it can be decomposed to cancel all of the length units ($km^2 pc/m^3$) using the `decompose()` method.
```
M.decompose()
```
We can also easily express the mass in whatever form you like -- solar masses are common in astronomy, or maybe you want the default SI and CGS units.
```
print("""Galaxy mass
in solar units: {0:.3g}
SI units: {1:.3g}
CGS units: {2:.3g}""".format(M.to(u.Msun), M.si, M.cgs))
```
Or, if you want the log of the mass, you can just use ``np.log10`` as long as the logarithm's argument is dimensionless.
```
np.log10(M.to_value(u.Msun))
```
However, you can't take the log of something with units, as that is not mathematically sensible.
```
np.log10(M)
```
## Exercises
Use `Quantity` and Kepler's law in the form given below to determine the (circular) orbital speed of the Earth around the sun in km/s. No need to look up constants or conversion factors to do this calculation -- it's all in `astropy.units` and `astropy.constants`.
$$v = \sqrt{\frac{G M_{\odot}}{r}}$$
There's a much easier way to figure out the velocity of the Earth using just two units or quantities. Do that and then compare to the Kepler's law answer (the easiest way is probably to compute the percentage difference, if any).
(Completely optional, but a good way to convince yourself of the value of Quantity:) Do the above calculations by hand -- you can use a calculator (or python just for its arithmatic) but look up all the appropriate conversion factors and use paper-and-pencil approaches for keeping track of them all. Which one took longer?
## 2. Molecular cloud mass
In this second example, we will demonstrate how using `Quantity` objects can facilitate a full derivation of the total mass of a molecular cloud using radio observations of isotopes of Carbon Monoxide (CO).
#### Setting up the data cube
Let's assume that we've mapped the inner part of a molecular cloud in the J=1-0 rotational transition of ${\rm C}^{18}{\rm O}$ and are interested in measuring its total mass. The measurement produced a data cube with RA and Dec as spatial coordiates and velocity as the third axis. Each voxel in this data cube represents the brightness temperature of the emission at that position and velocity. Furthermore, we'll assume that we have an independent measurement of distance to the cloud $d=250$ pc and that the excitation temperature is known and constant throughout the cloud: $T_{ex}=25$ K.
```
d = 250 * u.pc
Tex = 25 * u.K
```
We'll generate a synthetic dataset, assuming the cloud follows a Gaussian distribution in each of RA, Dec and velocity. We start by creating a 100x100x300 numpy array, such that the first coordinate is right ascension, the second is declination, and the third is velocity. We use the `numpy.meshgrid` function to create data cubes for each of the three coordinates, and then use them in the formula for a Gaussian to generate an array with the synthetic data cube. In this cube, the cloud is positioned at the center of the cube, with $\sigma$ and the center in each dimension shown below. Note in particular that the $\sigma$ for RA and Dec have different units from the center, but `astropy` automatically does the relevant conversions before computing the exponential.
```
# Cloud's center
cen_ra = 52.25 * u.deg
cen_dec = 0.25 * u.deg
cen_v = 15 * u.km/u.s
# Cloud's size
sig_ra = 3 * u.arcmin
sig_dec = 4 * u.arcmin
sig_v = 3 * u.km/u.s
#1D coordinate quantities
ra = np.linspace(52, 52.5, 100) * u.deg
dec = np.linspace(0, 0.5, 100) * u.deg
v = np.linspace(0, 30, 300) *u.km/u.s
#this creates data cubes of size for each coordinate based on the dimensions of the other coordinates
ra_cube, dec_cube, v_cube = np.meshgrid(ra, dec, v)
data_gauss = np.exp(-0.5*((ra_cube-cen_ra)/sig_ra)**2 +
-0.5*((dec_cube-cen_dec)/sig_dec)**2 +
-0.5*((v_cube-cen_v)/sig_v)**2 )
```
The units of the exponential are dimensionless, so we multiply the data cube by K to get brightness temperature units. Radio astronomers use a rather odd set of units [K km/s] as of integrated intensity (that is, summing all the emission from a line over velocity). As an aside for experts, we're setting up our artificial cube on the main-beam temperature scale (T$_{\rm MB}$) which is the closest we can normally get to the actual brightness temperature of our source.
```
data = data_gauss * u.K
```
We will also need to know the width of each velocity bin and the size of each pixel, so let's calculate that now.
```
# Average pixel size
# This is only right if dec ~ 0, because of the cos(dec) factor.
dra = (ra.max() - ra.min()) / len(ra)
ddec = (dec.max() - dec.min()) / len(dec)
#Average velocity bin width
dv = (v.max() - v.min()) / len(v)
print("""dra = {0}
ddec = {1}
dv = {2}""".format(dra.to(u.arcsec), ddec.to(u.arcsec), dv))
```
We're interested in the integrated intensity over all of the velocity channels, so let's create a 2D quantity array by summing our data cube along the velocity axis (multiplying by the velocity width of a pixel).
```
intcloud = np.sum(data*dv, axis=2)
intcloud.unit
```
We can plot the 2D quantity using matplotlib's imshow function, by passing the quantity's value. Similarly, we can set the correct extent using the values of $x_i$ and $x_f$. Finally, we can set the colorbar label to have proper units.
```
#Note that we display RA in the convential way by going from max to min
plt.imshow(intcloud.value,
origin='lower',
extent=[ra.value.max(), ra.value.min(), dec.value.min(), dec.value.max()],
cmap='hot',
interpolation='nearest',
aspect='equal')
plt.colorbar().set_label("Intensity ({})".format(intcloud.unit))
plt.xlabel("RA (deg)")
plt.ylabel("Dec (deg)");
```
#### Measuring The Column Density of CO
In order to calculate the mass of the molecular cloud, we need to measure its column density. A number of assumptions are required for the following calculation; the most important are that the emission is optically thin (typically true for ${\rm C}^{18}{\rm O}$) and that conditions of local thermodynamic equilibrium hold along the line of sight. In the case where the temperature is large compared to the separation in energy levels for a molecule and the source fills the main beam of the telescope, the total column density for ${\rm C}^{13}{\rm O}$ is
$N=C \frac{\int T_B(V) dV}{1-e^{-B}}$
where the constants $C$ and $B$ are given by:
$C=3.0\times10^{14} \left(\frac{\nu}{\nu_{13}}\right)^2 \frac{A_{13}}{A} {\rm K^{-1} cm^{-2} \, km^{-1} \, s}$
$B=\frac{h\nu}{k_B T}$
(Rohlfs & Wilson [Tools for Radio Astronomy](https://www.springer.com/gp/book/9783662053942)).
Here we have given an expression for $C$ scaled to the values for ${\rm C}^{13}{\rm O}$ ($\nu_{13}$ and $A_{13}$). In order to use this relation for ${\rm C}^{18}{\rm O}$, we need to rescale the frequencies ${\nu}$ and Einstein coefficients $A$. $C$ is in funny mixed units, but that's okay. We'll define it as a `Quantities` object and not have to worry about it.
First, we look up the wavelength for these emission lines and store them as quantities.
```
lambda13 = 2.60076 * u.mm
lambda18 = 2.73079 * u.mm
```
Since the wavelength and frequency of light are related using the speed of light, we can convert between them. However, doing so just using the `to()` method fails, as units of length and frequency are not convertible:
```
nu13 = lambda13.to(u.Hz)
nu18 = lambda18.to(u.Hz)
```
Fortunately, `astropy` comes to the rescue by providing a feature called "unit equivalencies." Equivalencies provide a way to convert between two physically different units that are not normally equivalent, but in a certain context have a one-to-one mapping. For more on equivalencies, see the [equivalencies section of astropy's documentation](http://docs.astropy.org/en/stable/units/equivalencies.html).
In this case, calling the ``astropy.units.spectral()`` function provides the equivalencies necessary to handle conversions between wavelength and frequency. To use it, provide the equivalencies to the `equivalencies` keyword of the ``to()`` call:
```
nu13 = lambda13.to(u.Hz, equivalencies=u.spectral())
nu18 = lambda18.to(u.Hz, equivalencies=u.spectral())
```
Next, we look up Einstein coefficients (in units of s$^{-1}$), and calculate the ratios in constant $C$. Note how the ratios of frequency and Einstein coefficient units are dimensionless, so the unit of $C$ is unchanged.
```
nu13 = 115271096910.13396 * u.Hz
nu18 = 109782318669.689 * u.Hz
A13 = 7.4e-8 / u.s
A18 = 8.8e-8 / u.s
C = 3e14 * (nu18/nu13)**3 * (A13/A18) / (u.K * u.cm**2 * u.km *(1/u.s))
C
```
Now we move on to calculate the constant $B$. This is given by the ratio of $\frac{h\nu}{k_B T}$, where $h$ is Planck's constant, $k_B$ is the Boltzmann's constant, $\nu$ is the emission frequency, and $T$ is the excitation temperature. The constants were imported from `astropy.constants`, and the other two values are already calculated, so here we just take the ratio.
```
B = h * nu18 / (k_B * Tex)
```
The units of $B$ are Hz sec, which can be decomposed to a dimensionless unit if you actually care about its value. Usually this is not necessary, though. Quantities are at their best if you use them without worrying about intermediate units, and only convert at the very end when you want a final answer.
```
print('{0}\n{1}'.format(B, B.decompose()))
```
At this point we have all the ingredients to calculate the number density of $\rm CO$ molecules in this cloud. We already integrated (summed) over the velocity channels above to show the integrated intensity map, but we'll do it again here for clarity. This gives us the column density of CO for each spatial pixel in our map. We can then print out the peak column column density.
```
NCO = C * np.sum(data*dv, axis=2) / (1 - np.exp(-B))
print("Peak CO column density: ")
np.max(NCO)
```
#### CO to Total Mass
We are using CO as a tracer for the much more numerous H$_2$, the quantity we are actually trying to infer. Since most of the mass is in H$_2$, we calculate its column density by multiplying the CO column density with the (known/assumed) H$_2$/CO ratio.
```
H2_CO_ratio = 5.9e6
NH2 = NCO * H2_CO_ratio
print("Peak H2 column density: ")
np.max(NH2)
```
That's a peak column density of roughly 50 magnitudes of visual extinction (assuming the conversion between N$_{\rm H_2}$ and A$_V$ from Bohlin et al. 1978), which seems reasonable for a molecular cloud.
We obtain the mass column density by multiplying the number column density by the mass of an individual H$_2$ molecule.
```
mH2 = 2 * 1.008 * u.Dalton #aka atomic mass unit/amu
rho = NH2 * mH2
```
A final step in going from the column density to mass is summing up over the area area. If we do this in the straightforward way of length x width of a pixel, this area is then in units of ${\rm deg}^2$.
```
dap = dra * ddec
print(dap)
```
Now comes an important subtlety: in the small angle approximation, multiplying the pixel area with the square of distance yields the cross-sectional area of the cloud that the pixel covers, in *physical* units, rather than angular units. So it's tempting to just multiply the area and the square of the distance.
```
da = dap * d**2 # don't actually do it this way - use the version below instead!
print(da)
dap.to(u.steradian).value * d**2
```
But this is **wrong**, because `astropy.units` treats angles (and solid angles) as actual physical units, while the small-angle approximation assumes angles are dimensionless. So if you, e.g., try to convert to a different area unit, it will fail:
```
da.to(u.cm**2)
```
The solution is to use the `dimensionless_angles` equivalency, which allows angles to be treated as dimensionless. This makes it so that they will automatically convert to radians and become dimensionless when a conversion is needed.
```
da = (dap * d**2).to(u.pc**2, equivalencies=u.dimensionless_angles())
da
da.to(u.cm**2)
```
Finally, multiplying the column density with the pixel area and summing over all the pixels gives us the cloud mass.
```
M = np.sum(rho * da)
M.decompose().to(u.solMass)
```
## Exercises
The astro material was pretty heavy on that one, so let's focus on some associated statistics using `Quantity`'s array capabililities. Compute the median and mean of the `data` with the ``np.mean`` and ``np.median`` functions. Why are their values so different?
Similarly, compute the standard deviation and variance (if you don't know the relevant functions, look it up in the numpy docs or just type np.<tab> and a code cell). Do they have the units you expect?
## 3. Using Quantities with Functions
`Quantity` is also a useful tool if you plan to share some of your code, either with collaborators or the wider community. By writing functions that take `Quantity` objects instead of raw numbers or arrays, you can write code that is agnostic to the input unit. In this way, you may even be able to prevent [the destruction of Mars orbiters](http://en.wikipedia.org/wiki/Mars_Climate_Orbiter#Cause_of_failure). Below, we provide a simple example.
Suppose you are working on an instrument, and the person funding it asks for a function to give an analytic estimate of the response function. You determine from some tests it's basically a Lorentzian, but with a different scale along the two axes. Your first thought might be to do this:
```
def response_func(xinarcsec, yinarcsec):
xscale = 0.9
yscale = 0.85
xfactor = 1 / (1 + xinarcsec/xscale)
yfactor = 1 / (1 + yinarcsec/yscale)
return xfactor * yfactor
```
You meant the inputs to be in arcsec, but alas, you send that to your collaborator and they don't look closely and think the inputs are instead supposed to be in arcmin. So they do:
```
response_func(1.0, 1.2)
```
And now they tell all their friends how terrible the instrument is, because it's supposed to have arcsecond resolution, but your function clearly shows it can only resolve an arcmin at best. But you can solve this by requiring they pass in `Quantity` objects. The new function could simply be:
```
def response_func(x, y):
xscale = 0.9 * u.arcsec
yscale = 0.85 * u.arcsec
xfactor = 1 / (1 + x/xscale)
yfactor = 1 / (1 + y/yscale)
return xfactor * yfactor
```
And your collaborator now has to pay attention. If they just blindly put in a number they get an error:
```
response_func(1.0, 1.2)
```
Which is their cue to provide the units explicitly:
```
response_func(1.0*u.arcmin, 1.2*u.arcmin)
```
The funding agency is impressed at the resolution you achieved, and your instrument is saved! You now go on to win the Nobel Prize due to discoveries the instrument makes. And it was all because you used `Quantity` as the input of code you shared.
## Exercise
Write a function that computes the Keplerian velocity you worked out in section 1 (using `Quantity` input and outputs, of course), but allowing for an arbitrary mass and orbital radius. Try it with some reasonable numbers for satellites orbiting the Earth, a moon of Jupiter, or an extrasolar planet. Feel free to use wikipedia or similar for the masses and distances.
| true |
code
| 0.631907 | null | null | null | null |
|
#### Objective
In this notebook I introduce a function to despike logs using rolling statistics to define the what constitutes a spike, and what does not.
I will apply the despiking to the P-wave velocity from one of the wells already used in the [Backusfrom dataframe notebook](https://github.com/mycarta/in-bruges/blob/master/notebooks/Backus_from_dataframe.ipynb).
#### Import libraries
```
import numpy as np
import pandas as pd
from scipy.ndimage.morphology import binary_dilation
from welly import Project, Well
import matplotlib.pyplot as plt
```
#### Import well
```
R39 = Well.from_las('../data/R-39.las')
```
#### Data clean-up and manipulation
- Make dataframe
- Deal with null values
- Select columns of interest
- Convert slowness to velocity
- Add well name column
Make dataframe
```
w39_df = R39.df()
w39_df = w39_df[['DT4P', 'DT4S', 'RHOB']]
w39_df.columns = ['DT', 'DTS', 'RHOB']
w39_df.describe(include = 'all')
```
Checking well R-39 for null values
```
for x in w39_df.columns:
print (x, w39_df[x].isnull().values.any())
print(w39_df.isnull().sum()) # finds how many missing points there are
```
There are no null values.
Convert slowness to velocity (usec/m >> m/s)
```
w39_df['Vp'] = 1.0e6 / w39_df['DT']
w39_df['Vs'] = 1.0e6 / w39_df['DTS']
w39_df.describe(include = 'all')
```
Add well name column
```
w39_df['DEPTH'] = w39_df.index
w39_df['well'] = 'R-39'
w39_df = w39_df.reset_index(drop=True)
w39_df.describe(include = 'all')
```
Drop slownness columns, sort columns
```
w39_df.drop(w39_df.columns[[0, 1]], inplace=True, axis=1)
w39_df = w39_df[['DEPTH', 'Vp', 'Vs', 'RHOB', 'well']]
w39_df.describe(include = 'all')
```
#### Despiking
Get P-wave velocity as an array
```
s=w39_df['Vp'].values
```
Despiking function
```
def despike(s, w, stds):
"""
Despikes a curve using rolling statistics.
First, it calculates the rolling median of the input curve on a long window.
Next, it calculates the difference between the median and the input.
Finally, it replaces the input with the median if their difference exceeds the mean difference
plus a user defined number of standard deviations of the difference.
Args:
s = input curve (ndarray)
w = long window length for the rolling median filter (integer)
std = the number of standard deviations to use to flag spikes (integer)
Returns:
out (ndarray) = despiked curve
"""
m = pd.Series(s).rolling(window=w, center=True).median()
flag = np.where(error_flag(pd.Series(s), m, dev = stds)==1)
out = np.copy(s)
out[flag] = m.values[flag]
return out
def rolling_despike(s, w1=75, w2=9, dev=4, dil=29):
"""
Despikes a curve using rolling statistics.
First, it calculates the rolling median of the input curve on a long window.
Next, it calculates the difference between the median and the input.
Finally, it replaces the input with the median if their difference exceeds the mean difference
plus a user defined number of standard deviations of the difference.
Args:
s = input curve (ndarray)
w = long window length for the rolling median filter (integer)
std = the number of standard deviations to use to flag spikes (integer)
Returns:
out (ndarray) = despiked curve
"""
s = pd.Series(s)
mdn = s.rolling(window=w1, min_periods=1, center=True).apply(lambda x : np.nanmedian(x), 'raw=True')
s_mdn = s.rolling(window=w2, min_periods=1, center=True).apply(lambda x : np.nanmedian(x), 'raw=True')
mdn_mdn = mdn.rolling(window=w2, min_periods=1, center=True).apply(lambda x : np.nanmedian(x), 'raw=True')
flag = np.where(error_flag(s_mdn, mdn_mdn, dev, dil)==1)
out = np.copy(s)
out[flag] = mdn.values[flag]
return out
def error_flag(pred, actual, dev, dil):
"""
Calculate the difference between a predicted and an actual curve
and return a log flagging large differences based on a user-defined distance
(in standard deviation units) from the mean difference
Matteo Niccoli, October 2018
Args:
predicted (ndarray) = predicted log
actual (ndarray) = original log
dev (float) = standard deviations to use, default 1
Returns:
flag (ndarray) = error flag curve
"""
flag = np.zeros(len(pred))
err = np.abs(pred-actual)
err_mean = np.mean(err)
err_std = np.std(err)
flag[np.where(err>(err_mean + (dev*err_std)))] = 1
flag=binary_dilation(flag, np.ones(dil))*1
return flag
plt.figure(figsize=(22,6))
plt.plot(s, 'r', label='Original Vp')
plt.plot(rolling_despike(s), 'k', label='Despiked Vp')
plt.ylim(2800,6200)
plt.xlim(0,4000)
plt.legend();
```
## Compare to Welly despike
```
def rolling_window(s, window_length, func1d, step=1, return_rolled=False):
"""
Private function. Smoother for other smoothing/conditioning functions.
Args:
window_length (int): the window length.
func1d (function): a function that takes a 1D array and returns a
scalar.
step (int): if you want to skip samples in the shifted versions.
Don't use this for smoothing, you will get strange results.
Returns:
ndarray: the resulting array.
"""
# Force odd.
if window_length % 2 == 0:
window_length += 1
shape = s.shape[:-1] + (s.shape[-1], window_length)
strides = s.strides + (step*s.strides[-1],)
data = np.nan_to_num(s)
data = np.pad(data, int(step*window_length//2), mode='edge')
rolled = np.lib.stride_tricks.as_strided(data,
shape=shape,
strides=strides)
result = np.apply_along_axis(func1d, -1, rolled)
result[np.isnan(s)] = np.nan
if return_rolled:
return result, rolled
else:
return result
def despike(s, window_length=45, samples=True, z=2):
"""
Args:
window (int): window length in samples. Default 33 (or 5 m for
most curves sampled at 0.1524 m intervals).
samples (bool): window length is in samples. Use False for a window
length given in metres.
z (float): Z score
Returns:
Curve.
"""
window_length //= 1 if samples else s.step
z *= np.nanstd(s) # Transform to curve's units
curve_sm = rolling_window(s,window_length, np.median)
spikes = np.where(np.nan_to_num(s - curve_sm) > z)[0]
spukes = np.where(np.nan_to_num(curve_sm - s) > z)[0]
out = np.copy(s)
np.copy(s)
out[spikes] = curve_sm[spikes] + z
out[spukes] = curve_sm[spukes] - z
return out
plt.figure(figsize=(22,6))
plt.plot(s, 'r', label='Original Vp')
plt.plot(despike(s), 'k', label='Despiked Vp')
plt.ylim(2800,6200)
plt.xlim(0,3000)
plt.legend();
```
| true |
code
| 0.708843 | null | null | null | null |
|
# Linear regression with Variational Bayes
### Imports
```
import matplotlib.pyplot as plt
%matplotlib notebook
import numpy as np
from scipy.stats import multivariate_normal
```
### Define model and generate data
```
N = 10 # No. data points
w0 = 1. # The offset in the line y = w0 + w1 * x
w1 = .5 # The incline in the same line
gamma = 4. # The *precision* in the observation noise
st_dev = 1. / np.sqrt(gamma) # And corresponding standard deviation
np.random.seed(42)
x = 5 * np.random.rand(N) - 1 # The x-points are sampled uniformly on [-1, 4]
y = np.random.normal(loc=w0 + w1 * x, scale=st_dev) # And the response is sampled from the Normal
```
### Plotting of data (i.e., $x$-axis is the covariate, $y$-axis the response)
```
def data_plotter(x, y=None, true_w0=None, true_w1=None,
approx_w0=None, approx_w1=None):
"""
Use to plot data. If y is not noe it contains responses, and (x,y) will be scatter-plotted
If neither true_w0 nor true_w1 is None, we will plot the line true_w0 + x * true_w1 in red.
If neither approx_w0 nor approx_w1 is None, we plot the line approx_w0 + x * approx_w1 in green.
"""
if y is not None:
plt.plot(x, y, "bo")
# Plot true line if given
if true_w0 is not None and true_w1 is not None:
plt.plot(x, true_w0 + true_w1 * x, "r-")
# Plot approximation if given
if approx_w0 is not None and approx_w1 is not None:
plt.plot(x, approx_w0+ approx_w1* x, "g-", alpha=.2)
```
### ... and of densities ($x$-axis correspond to offset $w_0$, $y$-axis the incline $w_1$)
```
def density_plt(x_range, y_range,
true_loc=None, true_cov=None,
approx_loc=None, approx_cov=None):
"""
Same setup as above: We can choose to plot the "true" solution (in red) and/or the approximation (in green)
"""
x = np.linspace(x_range[0], x_range[1], 100)
y = np.linspace(y_range[0], y_range[1], 100)
x_mesh, y_mesh = np.meshgrid(x, y)
pos = np.empty(x_mesh.shape + (2,))
pos[:, :, 0] = x_mesh
pos[:, :, 1] = y_mesh
if true_loc is not None and true_cov is not None:
rv = multivariate_normal(true_loc, true_cov)
plt.contour(x, y, rv.pdf(pos), colors='r')
if approx_loc is not None and true_cov is not None:
rv = multivariate_normal(approx_loc, approx_cov)
plt.contour(x, y, rv.pdf(pos), colors='g')
```
### Check that it works: Plot the data with the true model on top, and the prior over ($w_0$, $w_1$)
```
# Plot data
data_plotter(x=x, y=y, true_w0=w0, true_w1=w1)
plt.show()
# Plot prior of (w0, w1)
density_plt(x_range=[-2, 2], y_range=[-2, 2],
true_loc=[0, 0], true_cov=[[1, 0], [0, 1]])
plt.show()
```
## Learn the parameters using the variational Bayes formulas
We have **two** variables of interest here, $w_0$ and $w_1$. Both are Gaussian a posteriori, and they are parameterized by their **mean** and **precision** (inverse variance).
The update rules are as follows:
* `q_0_prec` := $1 + \gamma \cdot N$.
* `q_0_mean` := $\gamma \cdot (\sum_i y_i - $ `q_1_mean` $ \cdot \sum_i x_i) /$ `q_0_prec`.
* `q_1_prec` := $1 + \gamma \cdot \sum_i x_i^2$.
* `q_1_mean` := $\gamma \cdot (\sum_i x_i y_i - $ `q_0_mean` $\cdot \sum_i x_i) /$ `q_1_prec`.
```
# Starting-point
q_0_mean = 0.
q_1_mean = 0.
q_0_prec = 1.
q_1_prec = 1.
# Iterate
for iter in range(25):
q_0_prec =
q_0_mean =
q_1_prec =
q_1_mean =
print("Iter {:2d}: W0: {:6.3f} +/- {:6.3f}".format(iter, q_0_mean, 1./np.sqrt(q_0_prec)),
"\tW1: {:6.3f} +/- {:6.3f}".format(q_1_mean, 1./np.sqrt(q_1_prec)) )
```
## Show off
### The variables `q_0_mean`, `q_0_prec`, `q_1_mean`, and `q_1_prec` must be filled for this to work
### First draw some random lines, i.e., values $(w_0, w_1)$, from the Variational Bayes posterior
```
for _ in range(100):
w0_sample = np.random.normal(loc=q_0_mean, scale=1/np.sqrt(q_0_prec))
w1_sample = np.random.normal(loc=q_1_mean, scale=1 / np.sqrt(q_1_prec))
data_plotter(x=x, approx_w0=w0_sample, approx_w1=w1_sample)
data_plotter(x=x, y=y)
plt.show()
```
### And finally, look at the joint pdf of $(w_0, w_1)$ from VB compared to the exact Bayesian solution
```
extended_x = np.ones((N, 2))
extended_x[:, 1] = x
kernel = np.linalg.inv(np.eye(2) / gamma
+ np.matmul(np.transpose(extended_x), extended_x))
bayesian_mean = np.matmul(kernel, np.matmul(np.transpose(extended_x), y))
bayesian_cov = kernel / gamma
density_plt(x_range=[w0 - 2. * st_dev, w0 + 2. * st_dev],
y_range=[w1 - 2. * st_dev, w1 + 2. * st_dev],
true_loc=bayesian_mean,
true_cov=bayesian_cov,
approx_loc=[q_0_mean, q_1_mean],
approx_cov=[[1/q_0_prec, 0], [0, 1/q_1_prec]])
plt.show()
```
| true |
code
| 0.771811 | null | null | null | null |
|
# Chapter 5 - Image Classification
> Deep Learning For Coders with fastai & Pytorch - Image Classification, In this notebook I followed both Jeremy Howard's Lesson on fast.ai and Weigh and Biases reading group videos. Lots of notes added, some cell's order changed some are added to make the topic more understandable for me. (Check Manual calculation `log_softmax` + `nll_loss`). Click `open in colab` button at the right side to view as notebook.
- toc: true
- badges: true
- comments: true
- categories: [fastbook]
- image: images/cyberman.png
***

> I'm a Doctor Who fan and this is my cyberman coffee cup, as I remember got it from Manchester Science Museum.
***
```
#!pip install -Uqq fastbook
import fastbook
fastbook.setup_book()
%config Completer.use_jedi = False
from fastbook import *
```
[[chapter_pet_breeds]]
## PLAYING WITH THE DATASET
```
from fastai.vision.all import *
path = untar_data(URLs.PETS)
```
> Note: __With `untar` we download the data. This data originally come from Oxford University [Visual Geomety Group](https://www.robots.ox.ac.uk/~vgg/data/) and our dataset is [here:](https://www.robots.ox.ac.uk/~vgg/data/pets/)__
```
path
```
> Note: __This is the local download path for my computer.__
```
Path.BASE_PATH = path
```
> Tip: **This is a trick to get the relative path, check above and below**
```
path
```
Now the `path` is looks different.
```
path.ls()
```
> Note: __`#2` is number of item in the list. `annotations` represents target variables of this datasets but we do not use them at this time instead we create our own labels.__
```
(path/"images").ls()
fname = (path/"images").ls()[0]
fname
```
> Note: __The first image in the `path` list.__
```
re.findall(r'(.+)_\d+.jpg$', fname.name)
```
> Note: __Since we don't use the annonations in the Dataset we need to find a way to get breeds form the filename. This is regex `findall` method, Check `geeksforgeeks.org` tutorial [here](https://www.geeksforgeeks.org/python-regex-re-search-vs-re-findall/)__
```
pets = DataBlock(blocks = (ImageBlock, CategoryBlock),
get_items=get_image_files,
splitter=RandomSplitter(seed=42),
get_y=using_attr(RegexLabeller(r'(.+)_\d+.jpg$'), 'name'),
item_tfms=Resize(460),
batch_tfms=aug_transforms(size=224, min_scale=0.75))
dls = pets.dataloaders(path/"images")
```
> Note: __now find all names with RegexLabeller. The `item_tmsf` and `batch_transfdrms` may look a bit meaningless. Check below to find out why.__
***
### PRESIZING
As a summary FastAi gives a chance to augment our images in a smarter way (`presizing`) such that provide much more detail and information for the training. First, we presize images with `item_tfms` then push them to GPU and use augmentation.
[check the original document for the whole idea](https://colab.research.google.com/github/fastai/fastbook/blob/master/05_pet_breeds.ipynb)
```
#id interpolations
#caption A comparison of fastai's data augmentation strategy (left) and the traditional approach (right).
dblock1 = DataBlock(blocks=(ImageBlock(), CategoryBlock()),
get_y=parent_label,
item_tfms=Resize(460))
# Place an image in the 'images/grizzly.jpg' subfolder where this notebook is located before running this
dls1 = dblock1.dataloaders([(Path.cwd()/'images'/'chapter-05'/'grizzly.jpg')]*100, bs=8)
dls1.train.get_idxs = lambda: Inf.ones
x,y = dls1.valid.one_batch()
_,axs = subplots(1, 2)
x1 = TensorImage(x.clone())
x1 = x1.affine_coord(sz=224)
x1 = x1.rotate(draw=30, p=1.)
x1 = x1.zoom(draw=1.2, p=1.)
x1 = x1.warp(draw_x=-0.2, draw_y=0.2, p=1.)
tfms = setup_aug_tfms([Rotate(draw=30, p=1, size=224), Zoom(draw=1.2, p=1., size=224),
Warp(draw_x=-0.2, draw_y=0.2, p=1., size=224)])
x = Pipeline(tfms)(x)
#x.affine_coord(coord_tfm=coord_tfm, sz=size, mode=mode, pad_mode=pad_mode)
TensorImage(x[0]).show(ctx=axs[0])
TensorImage(x1[0]).show(ctx=axs[1]);
dls.show_batch(nrows=3, ncols=3)
pets1 = DataBlock(blocks = (ImageBlock, CategoryBlock),
get_items=get_image_files,
splitter=RandomSplitter(seed=42),
get_y=using_attr(RegexLabeller(r'(.+)_\d+.jpg$'), 'name'))
pets1.summary(path/"images")
```
> Note: __It is alway good to get a quick summary. `pets1.summary(path/"images")` Check the summary above, it has lots of details. It is natural to get an error in this example because we are trying the put diffent size images into the same `DataBlock`.__
***
## BASELINE MODEL
For every project, just start with a Baseline. Baseline is a good point to think about the project/domain/problem at the same time, then start improve and make experiments about architecture, hyperparameters etc.
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(2)
```
> Note: __A basic run is helpful as baseline for the beginning.__
### Defaults for the baseline
```
learn.loss_func
learn.lr
```
> Tip: __Very easy to see default arguments for the learner. Above loss function `loss_func` and learning rate `lr`.__
### One Batch Run
```
first(dls.train)
```
> Note: above and below is same
```
x,y = dls.one_batch()
```
***
### Understanding Labels
```
dls.vocab
dls.vocab[0]
```
> Tip: __`vocab` gives as all labels as text.__
***
### What's inside the tensors?
```
y
```
> Note: __Targets as coded.__
```
x
```
> Note: __Our stacked image tensor.__
***
### Predictions of the baseline model.
```
preds,_ = learn.get_preds(dl=[(x,y)])
preds[0]
```
> Note: __result for first item that adds up to one. There are 37 outputs for 37 image categories and the results are in percentage for probability of each category.__
```
_
```
> Note: __Category codes__
```
len(preds[0]),preds[0].sum()
```
Prediction for 37 categories that adds up to one.
***
## FUNCTION FOR CLASSIFIYING MORE THAN TWO CATEGORY
For classifiying more than two category, we need to employ a new function. It is not totally different than sigmoid, in fact it starts with a sigmoid function.
```
plot_function(torch.sigmoid, min=-4,max=4)
```
> Note: __This is how `torch.sigmoid` squishes values between 0 and 1.__
```
torch.random.manual_seed(42);
acts = torch.randn((6,2))*2
acts
```
> Note: __These are random numbers represent binary results of a hypothetical network. First colums represent 3's the and second is 7's standart deviation of 2. It generally shows how confident the model about the predictions.__
```
acts.sigmoid()
```
> Note: __If we apply the sigmoid, the result become like this(above). Obviously they aren't adds up to one. These are relative confidence over inputs. For example first row says: it's a three. But what is the probability? It is not clear.__
```
(acts[:,0]-acts[:,1]).sigmoid()
```
> Note: __If we take the difference between these relative confidence the results become like this above: Now we can say that for the first item, model is 0.6025 (%60.25) confident.__
this part is a bit different in the lesson video. so check the video. [1:35:20](https://youtu.be/p50s63nPq9I?t=5721)
```
sm_acts = torch.softmax(acts, dim=1)
sm_acts
```
> Note: __`torch.softmax` does that in one step. Now results for each item adds up to one and identical.__
***
### __Log Likelihood__
```
targ = tensor([0,1,0,1,1,0])
```
this is our softmax activations:
```
sm_acts
idx = range(6)
sm_acts[idx, targ]
```
> Note: __Nice trick for getting confidence level for each item.__
lets see everything in a table:
```
from IPython.display import HTML
df = pd.DataFrame(sm_acts, columns=["3","7"])
df['targ'] = targ
df['idx'] = idx
df['loss'] = sm_acts[range(6), targ]
t = df.style.hide_index()
#To have html code compatible with our script
html = t._repr_html_().split('</style>')[1]
html = re.sub(r'<table id="([^"]+)"\s*>', r'<table >', html)
display(HTML(html))
```
> Warning: __I think the last label is wrong here. It must be the confidence instead.__
```
-sm_acts[idx, targ]
```
> Warning: __There is a caveat here. These are neg of our confidence level, not loss.__
Pytorch way of doing the same here:
```
F.nll_loss(sm_acts, targ, reduction='none')
```
> Note: __Anyway, numbers are still not right, that will be addresses in the `Taking the Log` section below. The reason is F.nll_loss (negative log likelihood loss) needs arguments such that log is already applied to make the calculation right.(loss)__
***
### Taking the Log
> Note: Directly from the book:
> Important: __Confusing Name, Beware: The nll in `nll_loss` stands for "negative log likelihood," but it doesn't actually take the log at all! It assumes you have _already_ taken the log. PyTorch has a function called `log_softmax` that combines `log` and `softmax` in a fast and accurate way. `nll_loss` is designed to be used after `log_softmax`.__
When we first take the softmax, and then the log likelihood of that, that combination is called *cross-entropy loss*. In PyTorch, this is available as `nn.CrossEntropyLoss` (which, in practice, actually does `log_softmax` and then `nll_loss`):
pytorch's crossEntropy:
```
loss_func = nn.CrossEntropyLoss()
loss_func(acts, targ)
```
or:
```
F.cross_entropy(acts, targ)
```
> Note: this is the mean of all losses
and this is all results without taking the mean:
```
nn.CrossEntropyLoss(reduction='none')(acts, targ)
```
> Note:Results above are cross entrophy loss for each image in the list (of course our current numbers are fake numbers)
***
### Manual calculation `log_softmax` + `nll_loss`
First log_softmax:
```
log_sm_acts = torch.log_softmax(acts, dim=1)
log_sm_acts
```
Then negative log likelihood:
```
F.nll_loss(log_sm_acts, targ, reduction='none')
```
>Note: __Results are identical__
***
## REVISITING THE BASELINE MODEL (Model Interpretation)
```
#width 600
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix(figsize=(12,12), dpi=60)
interp.most_confused(min_val=5)
```
this is our baseline we can start improveing from this point.
***
## IMPROVING THE MODEL
### Fine Tune
Fine tune the model with default arguments:
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(1, base_lr=0.1)
```
> Note: __This is where we overshot. Our loss just increase over second epoch is there a better way to find a learning rate?__
***
### Learning Rate Finder
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
suggested_lr= learn.lr_find()
```
> Warning: There is a discrepancy between lesson and reading group notebooks. In the book we get two values from the function but in reading group, only one. I thing there was an update for this function that not reflected in the book.
```
suggested_lr
print(f"suggested: {suggested_lr.valley:.2e}")
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(2, base_lr=8.32e-04)
```
At this time it decreases steadily
#### __What's under the hood of `fine_tune`__
When we create a model from a pretrained network fastai automatically freezes all of the pretrained layers for us. When we call the `fine_tune` method fastai does two things:
- Trains the randomly added layers for one epoch, with all other layers frozen
- Unfreezes all of the layers, and trains them all for the number of epochs requested
__Lets do it manually__
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fit_one_cycle(3, 8.32e-04)
learn.unfreeze()
```
Run the `lr_find` again, because having more layers to train, and weights that have already been trained for three epochs, means our previously found learning rate isn't appropriate any more:
```
learn.lr_find()
```
Train again with the new lr.
```
learn.fit_one_cycle(6, lr_max=0.0001)
```
So far so good but there is more way to go
***
### Discriminative Learning Rates
Basically we use variable learning rate for the model. Bigger rate for the later layers and smaller for early layers.
```
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fit_one_cycle(3, 8.32e-04)# first lr
learn.unfreeze()
learn.fit_one_cycle(12, lr_max=slice(0.00005,0.0005))#second lr with a range
```
It is better most of the times.(sometimes I don't get good results, need to arrange the `slice` values more carefully)
```
learn.recorder.plot_loss()
```
> Note: Directly from the book:
As you can see, the training loss keeps getting better and better. But notice that eventually the validation loss improvement slows, and sometimes even gets worse! This is the point at which the model is starting to over fit. In particular, the model is becoming overconfident of its predictions. But this does not mean that it is getting less accurate, necessarily. Take a look at the table of training results per epoch, and you will often see that the accuracy continues improving, even as the validation loss gets worse. In the end what matters is your accuracy, or more generally your chosen metrics, not the loss. The loss is just the function we've given the computer to help us to optimize.
> Important: I need to think about it how loss increase and accuracy stil becoming better.
### Deeper Architectures
In general, a bigger model has the ability to better capture the real underlying relationships in your data, and also to capture and memorize the specific details of your individual images.
However, using a deeper model is going to require more GPU RAM, so you may need to lower the size of your batches to avoid an *out-of-memory error*. This happens when you try to fit too much inside your GPU and looks like:
```
Cuda runtime error: out of memory
```
You may have to restart your notebook when this happens. The way to solve it is to use a smaller batch size, which means passing smaller groups of images at any given time through your model. You can pass the batch size you want to the call creating your `DataLoaders` with `bs=`.
The other downside of deeper architectures is that they take quite a bit longer to train. One technique that can speed things up a lot is *mixed-precision training*. This refers to using less-precise numbers (*half-precision floating point*, also called *fp16*) where possible during training. As we are writing these words in early 2020, nearly all current NVIDIA GPUs support a special feature called *tensor cores* that can dramatically speed up neural network training, by 2-3x. They also require a lot less GPU memory. To enable this feature in fastai, just add `to_fp16()` after your `Learner` creation (you also need to import the module).
You can't really know ahead of time what the best architecture for your particular problem is—you need to try training some. So let's try a ResNet-50 now with mixed precision:
```
from fastai.callback.fp16 import *
learn = cnn_learner(dls, resnet50, metrics=error_rate).to_fp16()
learn.fine_tune(12, freeze_epochs=3)
learn.recorder.plot_loss()
```
As above traing time is not changed much.
| true |
code
| 0.709132 | null | null | null | null |
|
# CNN WITH TF-SLIM
#### ALL CODES ARE FROM [HWALSUKLEE](https://github.com/hwalsuklee/tensorflow-mnist-cnn)
```
import gzip
import os
from scipy import ndimage
from six.moves import urllib
import numpy as np
import tensorflow as tf
import tensorflow.contrib.slim as slim
print ("PACKAGES LOADED")
```
# CNN MODEL WITH TF-SLIM
```
def CNN(inputs, _is_training=True):
x = tf.reshape(inputs, [-1, 28, 28, 1])
batch_norm_params = {'is_training': _is_training, 'decay': 0.9, 'updates_collections': None}
net = slim.conv2d(x, 32, [5, 5], padding='SAME'
, activation_fn = tf.nn.relu
, weights_initializer = tf.truncated_normal_initializer(stddev=0.01)
, normalizer_fn = slim.batch_norm
, normalizer_params = batch_norm_params
, scope='conv1')
net = slim.max_pool2d(net, [2, 2], scope='pool1')
net = slim.conv2d(net, 64, [5, 5], scope='conv2')
net = slim.max_pool2d(net, [2, 2], scope='pool2')
net = slim.flatten(net, scope='flatten3')
net = slim.fully_connected(net, 1024
, activation_fn = tf.nn.relu
, weights_initializer = tf.truncated_normal_initializer(stddev=0.01)
, normalizer_fn = slim.batch_norm
, normalizer_params = batch_norm_params
, scope='fc4')
net = slim.dropout(net, keep_prob=0.7, is_training=_is_training, scope='dropout4')
out = slim.fully_connected(net, 10, activation_fn=None, normalizer_fn=None, scope='fco')
return out
```
# HANDLING MNIST
```
# DATA URL
SOURCE_URL = 'http://yann.lecun.com/exdb/mnist/'
DATA_DIRECTORY = "data"
# PARAMETERS FOR MNIST
IMAGE_SIZE = 28
NUM_CHANNELS = 1
PIXEL_DEPTH = 255
NUM_LABELS = 10
VALIDATION_SIZE = 5000 # Size of the validation set.
# DOWNLOAD MNIST DATA, IF NECESSARY
def maybe_download(filename):
if not tf.gfile.Exists(DATA_DIRECTORY):
tf.gfile.MakeDirs(DATA_DIRECTORY)
filepath = os.path.join(DATA_DIRECTORY, filename)
if not tf.gfile.Exists(filepath):
filepath, _ = urllib.request.urlretrieve(SOURCE_URL + filename, filepath)
with tf.gfile.GFile(filepath) as f:
size = f.size()
print('Successfully downloaded', filename, size, 'bytes.')
return filepath
# EXTRACT IMAGES
def extract_data(filename, num_images):
with gzip.open(filename) as bytestream:
bytestream.read(16)
buf = bytestream.read(IMAGE_SIZE * IMAGE_SIZE * num_images * NUM_CHANNELS)
data = np.frombuffer(buf, dtype=np.uint8).astype(np.float32)
data = (data - (PIXEL_DEPTH / 2.0)) / PIXEL_DEPTH # -0.5~0.5
data = data.reshape(num_images, IMAGE_SIZE, IMAGE_SIZE, NUM_CHANNELS)
data = np.reshape(data, [num_images, -1])
return data # [image index, y, x, channels]
# EXTRACT LABELS
def extract_labels(filename, num_images):
with gzip.open(filename) as bytestream:
bytestream.read(8)
buf = bytestream.read(1 * num_images)
labels = np.frombuffer(buf, dtype=np.uint8).astype(np.int64)
num_labels_data = len(labels)
one_hot_encoding = np.zeros((num_labels_data,NUM_LABELS))
one_hot_encoding[np.arange(num_labels_data),labels] = 1
one_hot_encoding = np.reshape(one_hot_encoding, [-1, NUM_LABELS])
return one_hot_encoding
# AUGMENT TRAINING DATA
def expend_training_data(images, labels):
expanded_images = []
expanded_labels = []
j = 0 # counter
for x, y in zip(images, labels):
j = j+1
# APPEND ORIGINAL DATA
expanded_images.append(x)
expanded_labels.append(y)
# ASSUME MEDIAN COLOR TO BE BACKGROUND COLOR
bg_value = np.median(x) # this is regarded as background's value
image = np.reshape(x, (-1, 28))
for i in range(4):
# ROTATE IMAGE
angle = np.random.randint(-15,15,1)
new_img = ndimage.rotate(image,angle,reshape=False, cval=bg_value)
# SHIFT IAMGE
shift = np.random.randint(-2, 2, 2)
new_img_ = ndimage.shift(new_img,shift, cval=bg_value)
# ADD TO THE LIST
expanded_images.append(np.reshape(new_img_, 784))
expanded_labels.append(y)
expanded_train_total_data = np.concatenate((expanded_images, expanded_labels), axis=1)
np.random.shuffle(expanded_train_total_data)
return expanded_train_total_data
# PREPARE MNIST DATA
def prepare_MNIST_data(use_data_augmentation=True):
# Get the data.
train_data_filename = maybe_download('train-images-idx3-ubyte.gz')
train_labels_filename = maybe_download('train-labels-idx1-ubyte.gz')
test_data_filename = maybe_download('t10k-images-idx3-ubyte.gz')
test_labels_filename = maybe_download('t10k-labels-idx1-ubyte.gz')
train_data = extract_data(train_data_filename, 60000)
train_labels = extract_labels(train_labels_filename, 60000)
test_data = extract_data(test_data_filename, 10000)
test_labels = extract_labels(test_labels_filename, 10000)
validation_data = train_data[:VALIDATION_SIZE, :]
validation_labels = train_labels[:VALIDATION_SIZE,:]
train_data = train_data[VALIDATION_SIZE:, :]
train_labels = train_labels[VALIDATION_SIZE:,:]
if use_data_augmentation:
train_total_data = expend_training_data(train_data, train_labels)
else:
train_total_data = np.concatenate((train_data, train_labels), axis=1)
train_size = train_total_data.shape[0]
return train_total_data, train_size, validation_data, validation_labels, test_data, test_labels
```
# CONFIGURATION
```
MODEL_DIRECTORY = "model/model.ckpt"
LOGS_DIRECTORY = "logs/train"
training_epochs = 10
TRAIN_BATCH_SIZE = 50
display_step = 500
validation_step = 500
TEST_BATCH_SIZE = 5000
```
# PREPARE MNIST DATA
```
batch_size = TRAIN_BATCH_SIZE # BATCH SIZE (50)
num_labels = NUM_LABELS # NUMBER OF LABELS (10)
train_total_data, train_size, validation_data, validation_labels \
, test_data, test_labels = prepare_MNIST_data(True)
# PRINT FUNCTION
def print_np(x, str):
print (" TYPE AND SHAPE OF [%18s ] ARE %s and %14s"
% (str, type(x), x.shape,))
print_np(train_total_data, 'train_total_data')
print_np(validation_data, 'validation_data')
print_np(validation_labels, 'validation_labels')
print_np(test_data, 'test_data')
print_np(test_labels, 'test_labels')
```
# DEFINE MODEL
```
# PLACEHOLDERS
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10]) #answer
is_training = tf.placeholder(tf.bool, name='MODE')
# CONVOLUTIONAL NEURAL NETWORK MODEL
y = CNN(x, is_training)
# DEFINE LOSS
with tf.name_scope("LOSS"):
loss = slim.losses.softmax_cross_entropy(y, y_)
# DEFINE ACCURACY
with tf.name_scope("ACC"):
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# DEFINE OPTIMIZER
with tf.name_scope("ADAM"):
batch = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
1e-4, # LEARNING_RATE
batch * batch_size, # GLOBAL_STEP
train_size, # DECAY_STEP
0.95, # DECAY_RATE
staircase=True) # LR = LEARNING_RATE*DECAY_RATE^(GLOBAL_STEP/DECAY_STEP)
train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss,global_step=batch)
# 'batch' IS AUTOMATICALLY UPDATED AS WE CALL 'train_step'
# SUMMARIES
saver = tf.train.Saver()
tf.summary.scalar('learning_rate', learning_rate)
tf.summary.scalar('loss', loss)
tf.summary.scalar('acc', accuracy)
merged_summary_op = tf.summary.merge_all()
summary_writer = tf.summary.FileWriter(LOGS_DIRECTORY, graph=tf.get_default_graph())
print ("MODEL DEFINED.")
```
# OPEN SESSION
```
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer(), feed_dict={is_training: True})
```
# OPTIMIZE
### FOR TESTING PURPOSES, SKIP THIS SECTION
```
# MAXIMUM ACCURACY
max_acc = 0.
# LOOP
for epoch in range(training_epochs): # training_epochs: 10
# RANDOM SHUFFLE
np.random.shuffle(train_total_data)
train_data_ = train_total_data[:, :-num_labels]
train_labels_ = train_total_data[:, -num_labels:]
# ITERATIONS
total_batch = int(train_size / batch_size)
for iteration in range(total_batch):
# GET CURRENT MINI-BATCH
offset = (iteration * batch_size) % (train_size)
batch_xs = train_data_[offset:(offset + batch_size), :]
batch_ys = train_labels_[offset:(offset + batch_size), :]
# OPTIMIZE
_, train_accuracy, summary = sess.run([train_step, accuracy, merged_summary_op]
, feed_dict={x: batch_xs, y_: batch_ys, is_training: True})
# WRITE LOG
summary_writer.add_summary(summary, epoch*total_batch + iteration)
# DISPLAY
if iteration % display_step == 0:
print("Epoch: [%3d/%3d] Batch: [%04d/%04d] Training Acc: %.5f"
% (epoch + 1, training_epochs, iteration, total_batch, train_accuracy))
# GET ACCURACY FOR THE VALIDATION DATA
if iteration % validation_step == 0:
validation_accuracy = sess.run(accuracy,
feed_dict={x: validation_data, y_: validation_labels, is_training: False})
print("Epoch: [%3d/%3d] Batch: [%04d/%04d] Validation Acc: %.5f"
% (epoch + 1, training_epochs, iteration, total_batch, validation_accuracy))
# SAVE THE MODEL WITH HIGEST VALIDATION ACCURACY
if validation_accuracy > max_acc:
max_acc = validation_accuracy
save_path = saver.save(sess, MODEL_DIRECTORY)
print(" MODEL UPDATED TO [%s] VALIDATION ACC IS %.5f"
% (save_path, validation_accuracy))
print("OPTIMIZATION FINISHED")
```
# COMPUTE TEST ACCURACY
```
# RESTORE SAVED NETWORK
saver.restore(sess, MODEL_DIRECTORY)
# COMPUTE ACCURACY FOR TEST DATA
test_size = test_labels.shape[0]
total_batch = int(test_size / batch_size)
acc_buffer = []
for i in range(total_batch):
offset = (i * batch_size) % (test_size)
batch_xs = test_data[offset:(offset + batch_size), :]
batch_ys = test_labels[offset:(offset + batch_size), :]
y_final = sess.run(y, feed_dict={x: batch_xs, y_: batch_ys, is_training: False})
correct_prediction = np.equal(np.argmax(y_final, 1), np.argmax(batch_ys, 1))
acc_buffer.append(np.sum(correct_prediction.astype(float)) / batch_size)
print("TEST ACCURACY IS: %.4f" % np.mean(acc_buffer))
```
| true |
code
| 0.519826 | null | null | null | null |
|
# Processing Oscilloscope Point Scan
The samples from our oscilloscope connected to our microphone (since our sound card doesn't support going up to 28kHz) will be useful for visualizing the acoustics of our system.
We will have to know beforehand which frequency we want to detect.
This depends on the oscilloscope settings, especially the resolution of the FFT when calculating that on the scope.
```
import os
import pickle
import glob
import skimage
import numpy as np
from collections import Counter
from matplotlib import pyplot as plt
%matplotlib inline
```
## Data Loading
### Format
This function loads in the data.
The data should be in the format
```bash
data_dir/<x_coord>_<y_coord>_<z_coord>.pkl
```
To make the design more modular we pass in the folder name to the function.
Each pickle file should be a numpy array with dimensions $N \times D$, where $N$ is the number of samples collected at the point and $D$ is the dimension of the FFT data.
Therefore, you can also provide a `sample_start` and `sample_end` to filter out the unneeded data.
### Example
For example, a lot of my initial scans had the following parameters.
1. I set the oscilloscope to do a fourier transform with a resolution of $5$ Hz for each frequency bin.
2. The tranducer is outputting $28$ kHz from a sine wave.
3. When measuring with the `OscilloscopeMicrophone` class, I started sampling the FFT data from $0$ Hz to $50000$ Hz.
Therefore, for `sample_start` and `sample_end` I should put $5595$ and $5605$ respectively, so I can look closely at the fourier transform from between $27975$ Hz and $28025$ Hz.
I recommend giving a range of a few Hz even if you are measuring a pure tone because sometimes the FFT may smear.
```
def get_data(data_dir, sample_start=0, sample_end=200, verbose=False):
fnames = list(sorted(glob.glob(os.path.join(data_dir, "*.pkl"))))
print('Found %s records' % len(fnames))
# Load into a list of tuples of xmin, xmax, y, data
data = []
XMIN, XMAX = None, None
for fname in fnames:
with open(fname, 'rb') as f:
fft_data = pickle.load(f)
# Isolate the frequency. In our case, 28kHz is usually around sample 8000 to 10000
try:
amplitudes = fft_data[:, sample_start:sample_end]
except IndexError:
if verbose:
print("indexerror for file %s" % fname)
print('Diagonstics on the length of each sample:')
lengths = [len(arr) for arr in fft_data]
correct_length = min(lengths)
amplitudes = np.array([t[:correct_length] for t in fft_data])
name = os.path.basename(fname).replace('.pkl', '').replace('continuous_', '')
coords = [float(coord) for coord in name.split('_')]
xmin, xmax, y = coords
XMIN = xmin
XMAX = xmax
data.append((xmin, xmax, y, amplitudes))
# Sort by y coordinate (xmin and xmax are expected to be the same for all)
data = list(sorted(data))
if not data:
raise RuntimeError('No Data Found')
return data
```
We also know that the transducer is being fed in a pure sine wave from the signal generator, so we expect a sharp spike at one specific frequency in the fourier transform.
Therefore, we will get the sample have a function that returns the indices and values of the maximum values in each FFT sample.
We also have a function that returns just the maximum amplitude found in your range.
```
def get_maxes_and_freqs(samples):
"""Takes in a N by S array, where N is the number of samples and S is the
dimensions of the FFT sample taken. We will get a list of maxes and the
frequency they correspond to as two np arrays, so we can plot as a scatterplot"""
maxes = samples.max(axis=1)
idxs = samples.argmax(axis=1)
return idxs, maxes
def get_max_amp(samples):
"""Takes in a N by S array, where N is the number of samples and S is the
dimensions of the FFT sample taken. Gets the maximum amplitude of each sample,
and then takes the average of the maximum amplitude over all the samples."""
return samples.max(axis=1).mean()
```
Now we can actually get the data from a scan that I did previously.
```
data = get_data('../data/1551236003')
```
### Data Output Format
Using Python, we've loaded the data as a list of tuples.
We use this format:
```bash
[(x_coord, y_coord, z_coord, ARR)]
```
where `ARR` is the numpy array of `NUM_SAMPLES x REDUCED_FFT_DIM`, where `REDUCED_FFT_DIM` was how much you reduced the FFT bins by supplying `sample_start` and `sample_end`.
```
data
```
Now we can plot the data by processing layers for each XY plane.
If we looked at the numbers from data, we see that this scan is just scanning a box from (0, 0) to (100, 100) with a resolution of 2.
```
# For each frequency bin, we can make an image of what values we have.
# otherwise, make that value -1 or something to show that we don't have info
WIDTH, HEIGHT = 51, 51
image = np.zeros((WIDTH, HEIGHT))
for index, d in enumerate(data):
idx, idy = int(index % WIDTH), int(index / WIDTH)
_, max_amps = get_maxes_and_freqs(d[-1])
image[idx, idy] = max_amps.mean()
plt.figure(figsize=(12, 12))
plt.title("A really old scan of just a transducer at the top at 28 kHz")
plt.xlabel("X Coordinate (mm)")
plt.ylabel("Y Coordinate (mm)")
plt.imshow(image)
plt.show()
```
### Increasing the Resolution
That image was pretty underwhelming, especially noting that the resolution was so poor, I don't even know what's going on.
Here's another example of a completely different scan.
This time let's actually look at what our samples look like.
We'll take everything we have recorded and plot a pickle file.
```
data = get_data('../data/1544186931', sample_start=0, sample_end=100000)
print("Shape of each pickle file.")
print(data[0][-1].shape)
plt.plot(data[0][-1].T)
plt.show()
```
As we can see, the peak we want is probably the ones between bins 3000 and 4000.
I think the peak near 2000 is probably artifacting.
Let's reload our data.
```
data = get_data('../data/1544186931', sample_start=0, sample_end=100000)
# For each frequency bin, we can make an image of what values we have.
# otherwise, make that value -1 or something to show that we don't have info
WIDTH, HEIGHT = 76, 76
image = np.zeros((WIDTH, HEIGHT))
for index, d in enumerate(data):
idx, idy = int(index % WIDTH), int(index / WIDTH)
image[idx, idy] = get_max_amp(d[-1])
plt.figure(figsize=(12, 12))
plt.title("A really old scan of just a transducer at the top at 28 kHz")
plt.xlabel("X Coordinate (mm)")
plt.ylabel("Y Coordinate (mm)")
plt.imshow(image)
plt.show()
```
We see that in this case, we get much better resolution of the transducer and can actually see waves.
We can verify that the wavelengths agree with 28 kHz through an air medium.
| true |
code
| 0.67547 | null | null | null | null |
|
## Concept
The two main structures to work with DQ0 quarantine via the DQ0 SDK are
* Project - the current model environment, a workspace and directory the user can define models in. Project also provides access to trained models.
* Experiment - the DQ0 runtime to execute training runs in the remote quarantine.
Start by importing the core classes
```
%cd ../
# import dq0-sdk api
from dq0.sdk.cli import Project, Experiment
```
## Create a project
Projects act as the working environment for model development.
Each project has a model directory with a .meta file containing the model uuid, attached data sources etc.
Creating a project with `Project.create(name='model_1')` is equivalent to calling the DQ0 Cli command `dq0-cli project create model_1`
# DQ0 SDK Demo
## Prerequistes
* Installed DQ0 SDK. Install with `pip install dq0-sdk`
* Installed DQ0 CLI.
* Proxy running and registered from the DQ0 CLI with `dq0-cli proxy add ...`
* Valid session of DQ0. Log in with `dq0 user login`
* Running instance of DQ0 CLI server: `dq0 server start`
```
# create a project with name 'model_1'. Automatically creates the 'model_1' directory and changes to this directory.
project = Project(name='model_1')
```
## Load a project
Alternatively, you can load an existing project by first cd'ing into this directory and then call Project.load()
This will read in the .meta file of this directory
```
%cd ../dq0-cli/census
# Alternative: load a project from the current model directory
project = Project.load()
project.project_uuid
```
## Create Experiment
To execute DQ0 training commands inside the quarantine you define experiments for your projects.
You can create as many experiments as you like for one project.
```
# Create experiment for project
experiment = Experiment(project=project, name='experiment_1')
```
## Get and attach data source
For new projects you need to attach a data source. Existing (loaded) projects usually already have data sources attached.
```
# first get some info about available data sources
sources = project.get_available_data_sources()
# get info about the first source
info = project.get_data_info(sources[0])
info
```
Get the dataset description:
```
# print data description
info['data_description']
```
Also, inspect the data column types including allowed values for feature generation:
```
# print information about column types and values
info['data_type']
```
Now, attach the dataset to our project
```
# attach the first dataset
project.attach_data_source(sources[0])
```
## Define the model
Working with DQ0 is basically about defining two functions:
* setup_data() - called right before model training to prepare attached data sources
* setup_model() - actual model definition code
The easiest way to define those functions is to write them in the notebook (inline) and pass them to the project before calling deploy. Alternatively, the user can write the complete user_model.py to the project's directory.
### Define fuctions inline
First variant with functions passed to the project instance. Note that you need to define imports inline inside the functions as only those code blocks are replaced in the source files.
```
# define functions
def setup_data():
# load input data
if self.data_source is None:
logger.error('No data source found')
return
data = self.data_source.read()
# read and preprocess the data
dataset_df = self.preprocess()
from sklearn.model_selection import train_test_split
X_train_df, X_test_df, y_train_ts, y_test_ts =\
train_test_split(dataset_df.iloc[:, :-1],
dataset_df.iloc[:, -1],
test_size=0.33,
random_state=42)
self.input_dim = X_train_df.shape[1]
# set data member variables
self.X_train = X_train_df
self.X_test = X_test_df
self.y_train = y_train_ts
self.y_test = y_test_ts
def setup_model():
import tensorflow.compat.v1 as tf
self.optimizer = tf.keras.optimizers.Adam(learning_rate=0.1)
self.loss = tf.keras.losses.SparseCategoricalCrossentropy()
# As an alternative, define the loss function with a string
self.epochs = 10
self.batch_size = 250
# self.optimizer = tf.keras.optimizers.Adam(learning_rate=self.learning_rate)
self.optimizer = 'Adam'
self.num_microbatches = 250
self.metrics = ['accuracy']
self.loss = tf.keras.losses.SparseCategoricalCrossentropy()
self.model = tf.keras.Sequential([
tf.keras.layers.Input(self.input_dim),
tf.keras.layers.Dense(10, activation='tanh'),
tf.keras.layers.Dense(10, activation='tanh'),
tf.keras.layers.Dense(2, activation='softmax')])
def preprocess():
# columns
column_names_list = [
'lastname',
'firstname',
'age',
'workclass',
'fnlwgt',
'education',
'education-num',
'marital-status',
'occupation',
'relationship',
'race',
'sex',
'capital-gain',
'capital-loss',
'hours-per-week',
'native-country',
'income'
]
# columns types list drawn from data source types information above.
columns_types_list = [
{
'name': 'age',
'type': 'int'
},
{
'name': 'workclass',
'type': 'string',
'values': [
'Private',
'Self-emp-not-inc',
'Self-emp-inc',
'Federal-gov',
'Local-gov',
'State-gov',
'Without-pay',
'Never-worked',
'Unknown'
]
},
{
'name': 'fnlwgt',
'type': 'int'
},
{
'name': 'education',
'type': 'string',
'values': [
'Bachelors',
'Some-college',
'11th',
'HS-grad',
'Prof-school',
'Assoc-acdm',
'Assoc-voc',
'9th',
'7th-8th',
'12th',
'Masters',
'1st-4th',
'10th',
'Doctorate',
'5th-6th',
'Preschool'
]
},
{
'name': 'education-num',
'type': 'int'
},
{
'name': 'marital-status',
'type': 'string',
'values': [
'Married-civ-spouse',
'Divorced',
'Never-married',
'Separated',
'Widowed',
'Married-spouse-absent',
'Married-AF-spouse'
]
},
{
'name': 'occupation',
'type': 'string',
'values': [
'Tech-support',
'Craft-repair',
'Other-service',
'Sales',
'Exec-managerial',
'Prof-specialty',
'Handlers-cleaners',
'Machine-op-inspct',
'Adm-clerical',
'Farming-fishing',
'Transport-moving',
'Priv-house-serv',
'Protective-serv',
'Armed-Forces',
'Unknown'
]
},
{
'name': 'relationship',
'type': 'string',
'values': [
'Wife',
'Own-child',
'Husband',
'Not-in-family',
'Other-relative',
'Unmarried'
]
},
{
'name': 'race',
'type': 'string',
'values': [
'White',
'Asian-Pac-Islander',
'Amer-Indian-Eskimo',
'Other',
'Black'
]
},
{
'name': 'sex',
'type': 'string',
'values': [
'Female',
'Male'
]
},
{
'name': 'capital-gain',
'type': 'int'
},
{
'name': 'capital-loss',
'type': 'int'
},
{
'name': 'hours-per-week',
'type': 'int'
},
{
'name': 'native-country',
'type': 'string',
'values': [
'United-States',
'Cambodia',
'England',
'Puerto-Rico',
'Canada',
'Germany',
'Outlying-US(Guam-USVI-etc)',
'India',
'Japan',
'Greece',
'South',
'China',
'Cuba',
'Iran',
'Honduras',
'Philippines',
'Italy',
'Poland',
'Jamaica',
'Vietnam',
'Mexico',
'Portugal',
'Ireland',
'France',
'Dominican-Republic',
'Laos',
'Ecuador',
'Taiwan',
'Haiti',
'Columbia',
'Hungary',
'Guatemala',
'Nicaragua',
'Scotland',
'Thailand',
'Yugoslavia',
'El-Salvador',
'Trinadad&Tobago',
'Peru',
'Hong',
'Holand-Netherlands',
'Unknown'
]
}
]
from dq0.sdk.data.preprocessing import preprocessing
import sklearn.preprocessing
import pandas as pd
if 'dataset' in globals():
# local testing mode
dataset = globals()['dataset']
else:
# get the input dataset
if self.data_source is None:
logger.error('No data source found')
return
# read the data via the attached input data source
dataset = self.data_source.read(
names=column_names_list,
sep=',',
skiprows=1,
index_col=None,
skipinitialspace=True,
na_values={
'capital-gain': 99999,
'capital-loss': 99999,
'hours-per-week': 99,
'workclass': '?',
'native-country': '?',
'occupation': '?'}
)
# drop unused columns
dataset.drop(['lastname', 'firstname'], axis=1, inplace=True)
column_names_list.remove('lastname')
column_names_list.remove('firstname')
# define target feature
target_feature = 'income'
# get categorical features
categorical_features_list = [
col['name'] for col in columns_types_list
if col['type'] == 'string']
# get categorical features
quantitative_features_list = [
col['name'] for col in columns_types_list
if col['type'] == 'int' or col['type'] == 'float']
# get arguments
approach_for_missing_feature = 'imputation'
imputation_method_for_cat_feats = 'unknown'
imputation_method_for_quant_feats = 'median'
features_to_drop_list = None
# handle missing data
dataset = preprocessing.handle_missing_data(
dataset,
mode=approach_for_missing_feature,
imputation_method_for_cat_feats=imputation_method_for_cat_feats,
imputation_method_for_quant_feats=imputation_method_for_quant_feats, # noqa: E501
categorical_features_list=categorical_features_list,
quantitative_features_list=quantitative_features_list)
if features_to_drop_list is not None:
dataset.drop(features_to_drop_list, axis=1, inplace=True)
# get dummy columns
dataset = pd.get_dummies(dataset, columns=categorical_features_list, dummy_na=False)
# unzip categorical features with dummies
categorical_features_list_with_dummies = []
for col in columns_types_list:
if col['type'] == 'string':
for value in col['values']:
categorical_features_list_with_dummies.append('{}_{}'.format(col['name'], value))
# add missing columns
missing_columns = set(categorical_features_list_with_dummies) - set(dataset.columns)
for col in missing_columns:
dataset[col] = 0
# and sort the columns
dataset = dataset.reindex(sorted(dataset.columns), axis=1)
# Scale values to the range from 0 to 1 to be precessed by the neural network
dataset[quantitative_features_list] = sklearn.preprocessing.minmax_scale(dataset[quantitative_features_list])
# label target
y_ts = dataset[target_feature]
le = sklearn.preprocessing.LabelEncoder()
y_bin_nb = le.fit_transform(y_ts)
y_bin = pd.Series(index=y_ts.index, data=y_bin_nb)
dataset.drop([target_feature], axis=1, inplace=True)
dataset[target_feature] = y_bin
return dataset
# set model code in project
project.set_model_code(setup_data=setup_data, setup_model=setup_model, preprocess=preprocess, parent_class_name='NeuralNetworkClassification')
```
### Define functions as source code
Second variant, writing the complete model. Template can be retrieved by `!cat models/user_model.py` which is created by Project create.
```
%%writefile models/user_model.py
import logging
from dq0.sdk.models.tf import NeuralNetworkClassification
logger = logging.getLogger()
class UserModel(NeuralNetworkClassification):
"""Derived from dq0.sdk.models.tf.NeuralNetwork class
Model classes provide a setup method for data and model
definitions.
"""
def __init__(self):
super().__init__()
def setup_data(self):
"""Setup data function. See code above..."""
pass
def preprocess(self):
"""Preprocess the data. See code above..."""
pass
def setup_model(self):
"""Setup model function See code above..."""
pass
```
## Train the model
After testing the model locally directly in this notebook, it's time to train it inside the DQ0 quarantine. This is done by calling experiment.train() which in turn calls the Cli commands `dq0-cli project deploy` and `dq0-cli model train`
```
run = experiment.run()
```
train is executed asynchronously. You can wait for the run to complete or get the state with get_state:
(TBD: in the future there could by a jupyter extension that shows the run progress in a widget.)
```
# wait for completion
run.wait_for_completion(verbose=True)
```
When the run has completed you can retrieve the results:
```
# get training results
print(run.get_results())
```
After train dq0 will run the model checker to evaluate if the trained model is safe and allowed for prediction. Get the state of the checker run together with the other state information with the get_state() function:
```
# get the state whenever you like
print(run.get_state())
# get the model
model = run.get_model()
model.__dict__
# register the model
model.register()
```
## Predict
Finally, it's time to use the trained model to predict something
```
import numpy as np
import pandas as pd
# check DQ0 privacy clearing
if model.predict_allowed:
# create predict set
records = [
{
'lastname': 'some-lastname',
'firstname': 'some-firstname',
'age': 45,
'workclass':'Private',
'fnlwgt': 544091,
'education': 'HS-grad',
'education-num': 9,
'marital-status': 'Married-AF-spouse',
'occupation': 'Exec-managerial',
'relationship': 'Wife',
'race': 'White',
'sex': 'Female',
'capital-gain': 0,
'capital-loss': 0,
'hours-per-week': 25,
'native-country': 'United-States',
'income': '<=50K'
},
{
'lastname': 'some-lastname',
'firstname': 'some-firstname',
'age': 29,
'workclass': 'Federal-gov',
'fnlwgt': 162298,
'education': 'Masters',
'education-num': 14,
'marital-status': 'Married-civ-spouse',
'occupation': 'Exec-managerial',
'relationship': 'Husband',
'race': 'White',
'sex': 'Male',
'capital-gain': 34084,
'capital-loss': 0,
'hours-per-week': 70,
'native-country': 'United-States',
'income': '<=50K'
}
]
dataset = pd.DataFrame.from_records(records)
# drop target (included above only because of compatability with preprocess function)
dataset.drop(['income'], axis=1, inplace=True)
# load or get numpy predict data
# predict_data = np.load(‘X_demo_predict.npy’)
predict_data = dataset.to_numpy()
# call predict
#run = model.predict(predict_data)
run = model.predict(predict_data)
# wait for completion
run.wait_for_completion(verbose=True)
# get predict results
print(run.get_results())
```
| true |
code
| 0.498596 | null | null | null | null |
|
## Author : Syed Arsalan Amin
## Data Science and Business Intelligence Internship - The Sparks Foundation
### Task-2 : Prediction using Unsupervised ML (K-means clustering)
From the given ‘Iris’ dataset, predict the optimum number of clusters
and represent it visually.
#### Github repository : [DataScience-and-Business-Intelligence](https://github.com/SyedArsalanAmin/DataScience-and-Business-Intelligence)
#### Download dataset : [Iris Dataset](https://drive.google.com/file/d/11Iq7YvbWZbt8VXjfm06brx66b10YiwK-/view)
## Importing libraries
```
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()
```
## Loading iris dataset and visualizing the dataframe
```
# importing data
df = pd.read_csv("E:\DataScience & AI\Github_repo\datasets\Iris.csv")
df.head()
df = df.drop(columns=['Species', 'Id']) #dropping the 'Species' and 'Id' columns.
df.head()
def scatter_plot(dataset, col1, col2):
plt.scatter(dataset.iloc[:, col1], dataset.iloc[:, col2])
plt.xlabel("Lenght")
plt.ylabel("Width")
plt.title("Petal/Sepal anaylysis")
scatter_plot(df, 2, 3) # visualizing petal data
scatter_plot(df, 0, 1) # visualizing sepal data
df.describe() # looking into the data for insights
```
#### For a better understading of the data let's take a look at the correlation between different multidimentional features
```
sns.pairplot(df)
```
## Normalizing dataset
```
scaler = MinMaxScaler()
scaled_features = scaler.fit_transform(df) # scaling dataframe
scaled_features.shape
scaled_features[:3] # these are the normalized feature set between 0-1
```
## Predicting suitable no. of cluster using Elbow method
From thr following plot you can see clearly that there is not significant decrease in the cost so we should take 3 as the no. of cluster.
```
# Using Elbow method to predict the no. of clusters
def elbow():
cost = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i)
kmeans.fit_predict(scaled_features)
cost.append(kmeans.inertia_)
plt.plot(np.arange(0, 10), cost, marker='o')
plt.title("Elbow Method")
plt.xlabel("No. of Clusters")
plt.ylabel("Cost Function")
elbow()
# kmeans to preict the category of cluster each iris belong to
kmeans = KMeans(n_clusters=3)
y_pred = kmeans.fit_predict(scaled_features)
y_pred # so thses are the predicted categories of the data we provided to kmeans
```
## Updating dataset with the normalized values
```
# Making normalized dataset
df["SepalLengthCm"] = scaled_features[:, 0]
df["SepalWidthCm"] = scaled_features[:, 1]
df["PetalLengthCm"] = scaled_features[:, 2]
df["PetalWidthCm"] = scaled_features[:, 3]
df["Clusters"] = y_pred
df.head() # Normalized dataset
```
## Storing clusters in variables
```
# Making Petal Clusters
pet_cluster1 = df[df['Clusters'] == 0].reset_index(drop=True)
pet_cluster1.head(3)
pet_cluster2 = df[df['Clusters'] == 1].reset_index(drop=True)
pet_cluster3 = df[df['Clusters'] == 2].reset_index(drop=True)
# Making Sepal Clusters
sep_cluster1 = df[df['Clusters'] == 0].reset_index(drop=True)
sep_cluster2 = df[df['Clusters'] == 1].reset_index(drop=True)
sep_cluster3 = df[df['Clusters'] == 2].reset_index(drop=True)
```
## Visualizing Clusters
```
# Plotting clusters
def plot_sep_cluster():
plt.figure(figsize=(15, 7))
plt.scatter(sep_cluster1.iloc[:, 2], sep_cluster1.iloc[:, 3], c='r',
marker='o', edgecolors='black', label="Cluster-1")
plt.scatter(sep_cluster2.iloc[:, 2], sep_cluster2.iloc[:, 3], c='b',
marker='v', edgecolors='black', label="Cluster-2")
plt.scatter(sep_cluster3.iloc[:, 2], sep_cluster3.iloc[:, 3], c='y',
marker='s', edgecolors='black', label="Cluster-3")
centers = kmeans.cluster_centers_[:, -2:] # cluster center for petals
plt.scatter(centers[:, 0], centers[:, 1], c='black', marker='X', s=200, label="Centroids")
plt.xlabel('Length(cm)')
plt.ylabel('Width(cm)')
plt.legend()
plt.title("Sepal Cluster Anaylysis")
plt.show()
plot_sep_cluster()
def plot_pet_cluster():
plt.figure(figsize=(15, 7))
plt.scatter(pet_cluster1.iloc[:, 0], pet_cluster1.iloc[:, 1], c='r',
marker='o', edgecolors='black', label="Cluster-1")
plt.scatter(pet_cluster2.iloc[:, 0], pet_cluster2.iloc[:, 1], c='b',
marker='v', edgecolors='black', label="Cluster-2")
plt.scatter(pet_cluster3.iloc[:, 0], pet_cluster3.iloc[:, 1], c='y',
marker='s', edgecolors='black', label="Cluster-3")
centers = kmeans.cluster_centers_[:, :-2] # cluster center for petals
centers
plt.scatter(centers[:, 0], centers[:, 1], c='black', marker='X', s=200, label="Centroids")
plt.xlabel('Length(cm)')
plt.ylabel('Width(cm)')
plt.legend()
plt.title("Petal Cluster Analysis")
plt.show()
plot_pet_cluster()
```
| true |
code
| 0.66165 | null | null | null | null |
|
```
from zipline import run_algorithm
from zipline.api import order_target_percent, symbol, order, record
from datetime import datetime
import pytz
import matplotlib.pyplot as plt
from trading_calendars.exchange_calendar_binance import BinanceExchangeCalendar
import pandas as pd
from trading_calendars import get_calendar
import pyfolio as pf
import numpy as np
```
### A few things to note:
#### 1) zipline enters the ordered stock and amount in the order book (order() function). After the handle_data() function has finished, zipline looks for any open orders and tries to fill them. If the trading volume is high enough for this stock, the order is executed after adding the *commission* and applying the *slippage model* which models the influence of your order on the stock price, so your algorithm will be charged more than just the stock price.
#### 2) Order execution - When your algorithm places an order on a given bar, the order begins filling until the next bar regardless of the slippage model used. This way, the backtester guards the algorithm against lookahead bias.
```
def initialize(context):
context.udy = symbol("ETHBTC")
# context.has_ordered = False
context.n_udy_to_buy = 10
def handle_data(context, data):
slowma = data.history(context.udy, fields='price', bar_count=50, frequency='1m').mean()
fastma = data.history(context.udy, fields='price', bar_count=20, frequency='1m').mean()
# trading logic
if fastma > slowma:
# placing buy order
order(context.udy, context.n_udy_to_buy)
buy = True
# order_target_percent(context.udy, 10)
if fastma < slowma:
# placing sell order
order(context.udy, -context.n_udy_to_buy)
sell = True
# order_target_percent(context.udy, -10)
record(ETHBTC=data.current(context.udy, fields='price'),
fastma = fastma,
slowma = slowma)
# standard analysis provided by pyFolio
def analyze_py(context, perf):
# Use PyFolio to generate a performance report
returns, positions, transactions = pf.utils.extract_rets_pos_txn_from_zipline(perf)
print(returns.cumsum())
fig = pf.create_returns_tear_sheet(returns, benchmark_rets=None)
for ax in fig.axes:
ax.tick_params(
axis='x', # changes apply to the x-axis
which='both', # both major and minor ticks are affected
bottom=True,
top=False,
labelbottom=True) # labels along the bottom edge are on
# customized analysis
def analyze(context, perf):
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(511)
ax.set_title('Strategy Results')
ax.semilogy(perf['portfolio_value'], linestyle='-', label='Equity Curve', linewidth=3.0)
ax.legend()
ax.grid(False)
ax = fig.add_subplot(512)
ax.plot(perf['gross_leverage'],
label = 'Exposure', linestyle='-', linewidth=1.0)
ax.legend()
ax.grid(True)
ax = fig.add_subplot(513)
ax.plot(perf['returns'], label='Returns', linestyle='-.', linewidth=1.0)
ax.legend()
ax.grid(True)
ax = fig.add_subplot(514)
ax.plot(perf['max_drawdown'], label='max drawdown', linestyle='-.', linewidth=1.0)
ax.legend()
ax.grid(True)
# calculate 6 months rolling sharp ratio
# risk free rate 2%
# perf['6m_rolling_SR'] = perf['returns'].rolling(180).apply(lambda x: (x.mean() - 0.02))
# perf.fillna(0, inplace = True)
# print(perf['6m_rolling_SR'])
def my_rolling_sharpe(y):
return np.sqrt(126) * (y.mean() / y.std())
ax = fig.add_subplot(515)
perf['6m_rolling_SR'] = perf['returns'].rolling(180).apply(my_rolling_sharpe) # to revisit
# print(perf['6m_rolling_SR'])
ax.plot(perf['6m_rolling_SR'], label='Sharpe', linestyle='-', lw=2, color='orange')
# perf[perf['6m_rolling_SR'] > 0]["6m_rolling_SR"].plot(style='-', lw=2, color='orange',
# label='Sharpe', figsize = (10,7))
ax.legend()
ax.grid(True)
# calculate sharp ratio
# risk_free_rate = 0.02 # 10 year Treasury bond
# daily_rf_return = (1 + risk_free_rate)** 1/252 - 1
# daily_rf_return
%%time
start_date = pd.Timestamp(datetime(2017, 8, 14, tzinfo=pytz.UTC))
end_date = pd.Timestamp(datetime(2018, 2, 15, tzinfo=pytz.UTC))
results = run_algorithm(
start=start_date,
end=end_date,
initialize=initialize,
trading_calendar = get_calendar("Binance"),
analyze=analyze, # customized analysis
handle_data=handle_data,
capital_base=10000,
data_frequency='minute',
bundle='binance_1m',
# benchmark_returns=None
)
# %%time
# start_date = pd.Timestamp(datetime(2017, 7, 14, tzinfo=pytz.UTC))
# end_date = pd.Timestamp(datetime(2019, 12, 31, tzinfo=pytz.UTC))
# results = run_algorithm(
# start=start_date,
# end=end_date,
# initialize=initialize,
# trading_calendar = get_calendar("Binance"),
# analyze=analyze_py, # pyfolio standard analysis
# handle_data=handle_data,
# capital_base=10000,
# data_frequency='minute',
# bundle='binance_1m',
# # benchmark_returns=None
# )
pd.set_option('display.max_columns', None)
results.head(10)
```
#### A moving average strategy , when short-term MA cross above long-term MA, buy 10 ETHBTC and when short-term MA cross below long-term MA, sell 10 ETHBTC.
```
# day 1
results["transactions"][0]
# last day
results["transactions"][-1]
```
| true |
code
| 0.635986 | null | null | null | null |
|
# Simulation to extend Hanna & Olken (2018)
## Universal Basic Incomes versus Targeted Transfers: Anti-Poverty Programs in Developing Countries
Consider different budget levels, and a mix of UBI and targeted transfers.
Simulation notebook.
## Setup
```
def import_or_install(package, pip_install=None):
""" Try to install a package, and pip install if it's unavailable.
Args:
package: Package name.
pip_install: Location to pip install from.
Runs `pip install [package]` if not provided.
"""
import pip
if pip_install is None:
pip_install = package
try:
__import__(package)
except ImportError:
pip.main(['install', package])
import_or_install('pandarallel')
import pandas as pd
import numpy as np
import os
import microdf as mdf
from pandarallel import pandarallel
pandarallel.initialize()
```
## Load data
[This notebook](https://colab.research.google.com/drive/1dxg8kjXHV7Fc-qKlaA0LjNPFrzLD0JVM) downloads this file directly from the Census Bureau.
```
SPM_COLS = ['SPM_ID', 'SPM_NUMPER', 'SPM_RESOURCES', 'SPM_POVTHRESHOLD',
'SPM_WEIGHT']
raw = pd.read_csv(
'https://github.com/MaxGhenis/datarepo/raw/master/pppub19.csv.gz',
usecols=SPM_COLS + ['MARSUPWT'])
```
Source: [World Bank](https://data.worldbank.org/indicator/NY.GDP.MKTP.CD?locations=US) (as of 2018)
```
US_GDP = 20.5e12
```
## Preprocess
```
u = raw.groupby(SPM_COLS).sum()
u.reset_index([i for i in SPM_COLS if i != 'SPM_ID'], inplace=True)
```
Define `y` to be resources per person. Set values below \$1 to \$1 so that CRRA works.
```
u['y0'] = np.maximum(1., u.SPM_RESOURCES / u.SPM_NUMPER)
u['w'] = u.SPM_WEIGHT / 100
```
Assign weighted rank by income.
```
u.sort_values('y0', inplace=True)
u['y0_rank'] = u.w.cumsum()
u['y0_pr'] = u.y0_rank / u.w.sum()
```
### Add noisy income
The actual value of the noisy income isn't important, since it's only used for ranking households. Therefore, random normal noise is sufficient.
Set noise level to match Hanna and Olken's model:
> The typical fit we found of these regressions (the R2) is between 0.53 and 0.66
Their [appendix](https://www.aeaweb.org/content/file?id=8344) shows that they were predicting log income.
Shoot for average: 0.595.
```
np.random.seed(0)
TARGET_R2 = 0.595
def log_noise(y, noise_mean):
return np.exp(np.log(y) + noise_mean * np.random.randn(len(y)))
def r2(noise_mean):
y_noise = log_noise(u.y0, noise_mean)
r = np.corrcoef(np.log(u.y0), np.log(y_noise))[0, 1]
return np.power(r, 2)
NOISE_LEVEL = 1.37
r2(NOISE_LEVEL) # Close to 0.595.
r2(NOISE_LEVEL * 2)
u['y0_l_noise'] = log_noise(u.y0, NOISE_LEVEL)
u['y0_h_noise'] = log_noise(u.y0, NOISE_LEVEL * 2)
```
Re-rank.
```
u.sort_values('y0_l_noise', inplace=True)
u['y0_rank_l_noise'] = u.w.cumsum()
u['y0_pr_l_noise'] = u.y0_rank_l_noise / u.w.sum()
u.sort_values('y0_h_noise', inplace=True)
u['y0_rank_h_noise'] = u.w.cumsum()
u['y0_pr_h_noise'] = u.y0_rank_h_noise / u.w.sum()
```
Check R-squared from noisy to true income rank.
**Low noise**
```
u[['y0_rank', 'y0_rank_l_noise']].corr().iloc[0, 1]
```
**High noise**
```
u[['y0_rank', 'y0_rank_h_noise']].corr().iloc[0, 1]
```
## Analysis
### Define CRRA function
```
def crra(y, w=None, rho=3):
""" Constant relative risk-aversion social welfare function.
Args:
y: Array of after-tax after-transfer income.
w: Optional array of weights. Should be the same length as y.
rho: Coefficient of relative risk-aversion, where higher values of rho
put higher weights on transfers received by the very poor.
Defaults to 3 per Hanna and Olken (2018).
Returns:
CRRA SWF. Also sets any value below 1 to 1.
"""
num = np.power(np.array(y, dtype=float), 1 - rho)
if w is not None:
num *= w
return num.sum() / (1 - rho)
```
Status quo CRRA value.
```
crra0 = crra(u.y0, u.w)
crra0
```
### Define horizontal equity function
From Hanna and Olken (2018):
>At each cutoff c, we calculate, for each household, the percentage of households within ±5 income percentiles (based on actual income) that received the same benefit status—included or excluded—based on the results of proxy-means test prediction. In other words, for households that were included in the program at a given c, we calculate the percentage of similar households that were also included; for households that were excluded, we calculate the percentage of similar households that were also excluded.
**TODO**
### Define simulation function
```
total_hhs = u.w.sum() # Number of SPM units.
def simulate(budget_share_of_gdp, pr_threshold, ubi_share, income_pr_col):
""" Simulate a transfer split between targeted and UBI components.
Args:
budget_share_of_gdp: Total budget to be split between targeted and UBI
components, as a share of US GDP (0 to 100).
pr_threshold: Percentrank below which households get the targeted
transfer. 0 to 100.
ubi_share: Number between 0 and 100 representing the share of the
transfer that goes to a UBI.
income_col: Column indicating the income percent rank (true or noisy).
Returns:
Tuple of (targeted_amount, ubi_amount, crra).
"""
budget = US_GDP * budget_share_of_gdp / 100
ubi_budget = budget * (ubi_share / 100)
targeted_budget = budget * (1 - ubi_share / 100)
ubi_amount = ubi_budget / total_hhs
target_idx = u[income_pr_col] < (pr_threshold / 100)
target_hhs = u[target_idx].w.sum()
targeted_amount = targeted_budget / target_hhs
y1 = u.y0 + ubi_amount + np.where(target_idx, targeted_amount, 0)
return targeted_amount, ubi_amount, crra(y1)
```
## Simulate
Cartesian product function from https://github.com/MaxGhenis/microdf/blob/master/microdf/utils.py
```
SIMX = {
'budget_share_of_gdp': [0.01, 0.1, 0.2, 0.5, 1, 5],
'noise_col': ['y0_pr', 'y0_pr_l_noise', 'y0_pr_h_noise'],
'pr_threshold': np.arange(0, 101, 1),
'ubi_share': np.arange(0, 101, 1)
}
sim = mdf.cartesian_product(SIMX)
```
Usually takes ~25 minutes.
```
%%time
sim[['targeted_amount', 'ubi_amount', 'crra']] = sim.parallel_apply(
lambda row: simulate(row.budget_share_of_gdp, row.pr_threshold,
row.ubi_share, row.noise_col),
axis=1, result_type='expand')
```
## Postprocess
Make the noise column a category.
```
sim['noise'] = pd.Categorical(
np.where(sim.noise_col == 'y0_pr', 'No noise',
np.where(sim.noise_col == 'y0_pr_l_noise', 'Low noise',
'High noise')),
categories = ['No noise', 'Low noise', 'High noise'])
sim.drop(['noise_col'], axis=1, inplace=True)
```
## Export
```
sim.to_csv('sim.csv', index=False)
```
| true |
code
| 0.81231 | null | null | null | null |
|
# Deterministic methods
## Point estimates
If we just want to find the parameter value that maximizes the posterior probability, we can just use numerical optimization over $p(y \mid \theta)p(\theta)$. The value found is known as the Maximum a Posteriori (or MAP), and is the Bayesian counterpart of the Maximum Likelihood Estimate (MLE). However, a point estimate gives relatively little information and may be highly misleading, and hence we are usually interested in estimating the full posterior distribution.
As we have seen, MCMC is one method for estimating the posterior. However, MCMC is relatively slow, and an alternative is to use deterministic Variational Inference (VI) methods which are usually much faster. The trade-off is that VI methods can only find an approximation of the true posterior, and the approximation may not be very good.
## Laplace approximation
The basic idea is to use a Gaussian $N(\mu, \Sigma)$ centered at the mode of the log posterior distribution as an approximation. This can be done by first finding the mode using numerical optimization and using that for $\mu$, then estimating the covariance as the inverse of the Hessian at the mode.
Note that for a Gaussian, the negative log likelihood basically has the form $a + b + \frac{1}{2}x^T A x$ where $A = \Sigma^{-1}$ and $a, b$ are terms that don't depend on $x$. By differentiating, we get that the Hessian is the inverse covariance matrix.
Notes and illustrations in class.
## Entropy
$$
H(p) = -\sum_{i} p_i \log(p_i)
$$
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
def entropy(p):
"""Calculate entropy."""
return -np.sum(p * np.log(p))
for σ in 1, 10, 100:
print('N(1, %3d) entropy = %.2f' % (σ, stats.norm(0, σ).entropy()))
```
## Kullback-Leibler divergence (relative entropy)
$$
D_{\text{KL}}(p \vert\vert q) = \sum_i p_i \log \frac{p_i}{q_i}
$$
In the usual interpretation, $p$ is the true distribution (e.g. posterior probability), and $q$ is an approximation (e.g. prior probability). $D_{\text{KL}}(p \vert\vert q)$ is a measure of how well $q$ approximates $p$, and hence is usually read as the Kullback Leibler divergence from $q$ to $p$.
Properties of $D_{\text{KL}}(p \vert\vert q)$
- non-negative (e.g. use Jensen's inequality)
$$
D_{\text{KL}}(p \vert\vert q) = \sum_i p_i \log \frac{p_i}{q_i} = -\sum_i p_i \log \frac{q_i}{p_i} \ge -\log\sum_i p_i \frac{q_i}{p_i} = 0
$$
- equal to zero only if $p = q$ almost everywhere
- invariant under parameter transforms
- Suppose $p(x) = p_1(x) p_2(x)$ and $q(x) = q_1(x) q_2(x)$, then
$$D_{\text{KL}}(p \vert\vert q) = D_{\text{KL}}(p_1 \vert\vert q_1) + D_{\text{KL}}(p_2 \vert\vert q_2)$$
Note:
- If $p_i = 0$ then $i$ contributes 0 to DKL
- If $q_i = 0$ and $p_i = 0$, then $i$ contributes 0 to DKL
- If $q_i = 0$ and $p_i \ne 0$, then DKL is undefined.
```
xs = np.random.poisson(5, 1000)
ys = np.bincount(xs)
ys = ys/ys.sum()
plt.stem(ys)
pass
r = np.arange(len(ys))
r
fig, axes = plt.subplots(1,3,figsize=(12,3), sharey=True)
for ax, λ in zip(axes, (4, 5,6)):
ax.stem(ys)
ax.stem(r+0.3, stats.poisson(λ).pmf(r), linefmt='C3-', markerfmt='C3o')
ax.set_title('DKL(p, Poisson(%d}) = %.2f' % (λ, stats.entropy(ys, stats.poisson(λ).pmf(r))))
```
## Evidence lower bound (ELBO)
We want to approximate the posterior distribution $p(\theta \mid y)$ with $q(\theta)$. In the usual approach, we want to minimize
\begin{array}
\\
D_{\text{KL}}(q(\theta) \vert\vert p(\theta | y)) &= \int q(\theta) \log \frac{q(\theta)}{p(\theta \mid y)} \ d\theta \\
&= \int q(\theta) \log \frac{q(\theta)}{p(\theta, y)}p(y) \ d\theta \\
&= \int q(\theta) \left( \log \frac{q(\theta)}{p(\theta, y)} + \log p(y) \right) \ d\theta \\
&= \int q(\theta) \log \frac{q(\theta)}{p(\theta, y)} \ d\theta + \int q(\theta) \log p(y) \ d\theta \\
&= - \int q(\theta) \log \frac{p(\theta, y)}{q(\theta)} \ d\theta + \log p(y)
\end{array}
Since the Kullback-Leibler divergence $\ge 0$, the marginal likelihood or evidence $p(y) \ge \int q(\theta) \log \frac{p(\theta, y)}{q(\theta)} \ d\theta$ and $\int q(\theta) \log \frac{p(\theta, y)}{q(\theta)} \ d\theta$ is known as the Evidence Lower Bound (ELBO). The ELBO can also be seen as $E_q[\log p(\theta, y)] - E[\log q(\theta)]$, where the second term is the entropy (or differential entropy).
Hence if $q(\theta)$ is a family of (simple) distributions with tuning parameters $\lambda$, finding the values of $\lambda$ that maximize the ELBO is equivalent to minimizing $D_{\text{KL}}(q(\theta) \vert\vert p(\theta | y))$.
### Variational Inference with a mean field approximation
To estimate $\theta = (\theta_1, \theta_2, \ldots, \theta_n)$, the mean field approximation assumes that
$$
q(\theta) = \prod_{i=1}^{n} q(\theta_i)
$$
The factorization gives a form of the ELBO that can be solved by numerical optimization. Note that the solution found will usually not be the true posterior, since the mean field approximations assume that the variables are independent.
Source: [Variational Inference: A Review for Statisticians](https://arxiv.org/pdf/1601.00670.pdf)
## ADVI
The optimization is usually done with gradient information with derivatives found by automatic differentiation, and hence this family of probabilistic inference engines is known as Automatic Differentiation Variational Inference (ADVI).
For further reading, see [Variational Inference: A Review for Statisticians](https://arxiv.org/pdf/1601.00670.pdf)
| true |
code
| 0.629205 | null | null | null | null |
|
# Comparing drift detectors
We take the image classifier example and use it to compare drift detectors.
We will give an opinionated take here. This is not to take shots at the research that enables TorchDrift, but reflects that the typical application in the wild may be dissimilar to the systematic, controlled experimentation in academic papers. We believe that the purpose of TorchDrift is providing tools to do drift detection as well as presenting good practice for practitioners.
You are encouraged to study the literature, in particular [S. Rabanser et al: Failing Loudly](https://arxiv.org/abs/1810.11953), and also to do your own experimentation and draw your own conclusions.
```
import IPython
import sys
sys.path.insert(0, '../')
import copy
import tqdm
import torchvision
import functools
import torch
from typing import Optional, Any
import torch
import math
import pytorch_lightning as pl
import torchdrift
import sklearn.manifold
%matplotlib inline
from matplotlib import pyplot
torchvision.datasets.utils.download_and_extract_archive('https://download.pytorch.org/tutorial/hymenoptera_data.zip', 'data/')
# these are the standard transforms without the normalization (which we move into the model.step/predict before the forward)
train_transform = torchvision.transforms.Compose([
torchvision.transforms.RandomResizedCrop(size=(224, 224), scale=(0.08, 1.0), ratio=(0.75, 1.3333)),
torchvision.transforms.RandomHorizontalFlip(p=0.5),
torchvision.transforms.ToTensor()])
val_transform = torchvision.transforms.Compose([
torchvision.transforms.Resize(size=256),
torchvision.transforms.CenterCrop(size=(224, 224)),
torchvision.transforms.ToTensor()])
class OurDataModule(pl.LightningDataModule):
def __init__(self, parent: Optional['OurDataModule']=None, additional_transform=None):
if parent is None:
self.train_dataset = torchvision.datasets.ImageFolder('./data/hymenoptera_data/train/',
transform=train_transform)
self.val_dataset = torchvision.datasets.ImageFolder('./data/hymenoptera_data/val/',
transform=val_transform)
self.test_dataset = torchvision.datasets.ImageFolder('./data/hymenoptera_data/test/',
transform=val_transform)
self.train_batch_size = 4
self.val_batch_size = 128
self.additional_transform = None
else:
self.train_dataset = parent.train_dataset
self.val_dataset = parent.val_dataset
self.test_dataset = parent.test_dataset
self.train_batch_size = parent.train_batch_size
self.val_batch_size = parent.val_batch_size
self.additional_transform = additional_transform
if additional_transform is not None:
self.additional_transform = additional_transform
self.prepare_data()
self.setup('fit')
self.setup('test')
def setup(self, typ):
pass
def collate_fn(self, batch):
batch = torch.utils.data._utils.collate.default_collate(batch)
if self.additional_transform:
batch = (self.additional_transform(batch[0]), *batch[1:])
return batch
def train_dataloader(self):
return torch.utils.data.DataLoader(self.train_dataset, batch_size=self.train_batch_size,
num_workers=4, shuffle=True, collate_fn=self.collate_fn)
def val_dataloader(self):
return torch.utils.data.DataLoader(self.val_dataset, batch_size=self.val_batch_size,
shuffle=False, collate_fn=self.collate_fn)
def test_dataloader(self):
return torch.utils.data.DataLoader(self.test_dataset, batch_size=self.val_batch_size,
shuffle=False, collate_fn=self.collate_fn)
def default_dataloader(self, batch_size=None, num_samples=None, shuffle=True):
dataset = self.val_dataset
if batch_size is None:
batch_size = self.val_batch_size
replacement = num_samples is not None
if shuffle:
sampler = torch.utils.data.RandomSampler(dataset, replacement=replacement, num_samples=num_samples)
else:
sampler = None
return torch.utils.data.DataLoader(dataset, batch_size=batch_size, sampler=sampler,
collate_fn=self.collate_fn)
datamodule = OurDataModule()
```
## Feature extractor
We use the TorchVision ResNet18 as the drift detector.
```
feature_extractor = torch.nn.Sequential(
torchvision.transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
torchvision.models.resnet18(pretrained=True)
)
feature_extractor[0].fc = torch.nn.Identity()
```
## Simulating drifted data
For systematic experiments, we want to compare the output of the drift detector on benign (non-drifted) and and drifted, here (partially) out of distribution samples. We simulate out of distribution data by applying a gaussian blur. In reality you might have effects like the camera lense losing focus or dirt impeding the picture quality.
Note that we do not use the drifted data for "training" the drift detector, but just for evaluation!
On the technical side, we take our datamodule as the in-distribution datamodule as is and use a derived datamodule which applies the gaussian blur in addition to the usual transforms as the out of distribution datamodule.
```
def corruption_function(x: torch.Tensor):
return torchdrift.data.functional.gaussian_blur(x, severity=2)
ind_datamodule = datamodule
ood_datamodule = OurDataModule(parent=datamodule, additional_transform=corruption_function)
```
Let us grab a few inputs and show them without and with corruption.
```
inputs, _ = next(iter(datamodule.default_dataloader(shuffle=True)))
inputs_ood = corruption_function(inputs)
N = 6
pyplot.figure(figsize=(15, 5))
for i in range(N):
for j in range(2):
pyplot.subplot(2, N, j * N + i + 1)
if i == 0:
pyplot.ylabel('vanilla' if j == 0 else 'drifted')
pyplot.imshow((inputs if j == 0 else inputs_ood)[i].permute(1, 2, 0))
pyplot.xticks([])
pyplot.yticks([])
```
## Kernel MMD drift detector
Or first detector is the Kernel MMD drift detector. As you may have guessed from the name, it uses a kernel to define a metric on the space of distributions on the feature-space (see our [note on the intuition behind MMD](./note_on_mmd.ipynb)). TorchDrift implements a few kernels in the `detectors.mmd` module, the `GaussianKernel` (also known as squared exponential) is the default, `ExpKernel` (aka Laplacian Kernel) and `RationalQuadraticKernel` are also available.
In our experiments Kernel MMD worked very well, so we suggest it as a default.
```
drift_detector = torchdrift.detectors.KernelMMDDriftDetector()
```
We use the `utils.DriftDetectionExperiment` class to drive our experiment. It lets us set a ratio of OOD samples in the drifted samples and a sample size.
While the statistical tests underpinning the drift detection could also produce p-values, we can also treat the test score as a value that can be thresholded for detection, giving the typical ROC curve. We see that for this setup, the detection power is quite strong.
```
od_model = drift_detector
ind_datamodule = datamodule
ood_datamodule = OurDataModule(parent=datamodule, additional_transform=corruption_function)
ood_ratio = 0.8
sample_size = 10
experiment = torchdrift.utils.DriftDetectionExperiment(od_model, feature_extractor, ood_ratio=ood_ratio, sample_size=sample_size)
experiment.post_training(datamodule.train_dataloader())
auc, (fp, tp) = experiment.evaluate(ind_datamodule, ood_datamodule)
pyplot.plot(fp, tp)
pyplot.title(label=f'{type(od_model).__name__}, $p_{{ood}}$={ood_ratio:.2f}, N={sample_size} AUC={auc:.3f}')
pyplot.show()
```
## Dimension Reduction & Kolmogorov-Smirnov test
Next up is the Kolmogorov-Smirnov two sample test.
We operationalize it by adding a dimension reduction to two PCA components (the PCA reducer estimates the PCA transform on the reference data during fitting and then applies this fixed transform to the test data).
As suggested by _Failing Loudly_, we use the Bonferroni correction and perform the KS test on the marginals.
```
red = torchdrift.reducers.pca.PCAReducer(n_components=2)
detector = torchdrift.detectors.ks.KSDriftDetector()
reducer_detector = torch.nn.Sequential(red, detector)
```
Next we run our experiment just like before. This combination usually gives good results, typically a bit less AUC than the Kernel MMD, but typically between just below 0.8 and 0.75.
```
experiment = torchdrift.utils.DriftDetectionExperiment(reducer_detector, feature_extractor, ood_ratio=ood_ratio, sample_size=sample_size)
experiment.post_training(datamodule.train_dataloader())
auc, (fp, tp) = experiment.evaluate(ind_datamodule, ood_datamodule)
pyplot.plot(fp, tp)
pyplot.title(label=f'{detector}, {red}\n$p_{{ood}}$={ood_ratio:.2f}, N={sample_size} AUC={auc:.3f}')
pyplot.show()
```
## Untrained Autoencoder
Finally we use the Untrained Autoencoder. This is a bit of a funny name because it really half an autoencoder, so we might as well call it a untrained or randomly initialized feature extractor. This performed reasonably well in _Failing Loudly_, so it appears relatively frequently.
In our experiments, this does not work as well as in the ones in _Failing Loudly_. Part of it may be that we have larger images so the feature extractor has "more work to do" and a purely random one does not perform as well. Another part may be that our sample size is lower. We believe that in both of these aspects, our setup is closer to (our) real-world use-cases.
Our conclusion here is that the UAE applied to images directly is not as good a choice as working with a pretrained model. Of course, we would not need to see this as a binary decision but could combine a few layers of our trained model to start off with a randomly initialized top if we think that the topmost layers are too specialized on the classification task to be useful as a drift detector.
```
feature_extractor_red = torch.nn.Sequential(
torchvision.transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
torch.nn.Conv2d(3, 128, kernel_size=5, padding=2, stride=2),
torch.nn.ReLU(),
torch.nn.Conv2d(128, 256, kernel_size=5, padding=2, stride=2),
torch.nn.ReLU(),
torch.nn.Conv2d(256, 1024, kernel_size=5, padding=2, stride=2),
torch.nn.ReLU(),
torch.nn.AdaptiveMaxPool2d(8),
torch.nn.Flatten(),
torch.nn.Linear(1024*8*8, 32)
).cuda().eval()
for m in feature_extractor_red:
if isinstance(m, (torch.nn.Conv2d, torch.nn.Linear)):
torch.nn.init.kaiming_normal_(m.weight, nonlinearity='relu')
torch.nn.init.zeros_(m.bias)
detector = torchdrift.detectors.ks.KSDriftDetector()
experiment = torchdrift.utils.DriftDetectionExperiment(detector, feature_extractor_red, ood_ratio=ood_ratio, sample_size=sample_size)
experiment.post_training(datamodule.train_dataloader())
auc, (fp, tp) = experiment.evaluate(ind_datamodule, ood_datamodule, num_runs=100)
pyplot.plot(fp, tp)
pyplot.title(label=f'{detector}, UAE, $p_{{ood}}$={ood_ratio:.2f}, N={sample_size} AUC={auc:.3f}')
pyplot.show()
```
| true |
code
| 0.800185 | null | null | null | null |
|
# Name
Gather training data by querying BigQuery
# Labels
GCP, BigQuery, Kubeflow, Pipeline
# Summary
A Kubeflow Pipeline component to submit a query to BigQuery and store the result in a Cloud Storage bucket.
# Details
## Intended use
Use this Kubeflow component to:
* Select training data by submitting a query to BigQuery.
* Output the training data into a Cloud Storage bucket as CSV files.
## Runtime arguments:
| Argument | Description | Optional | Data type | Accepted values | Default |
|----------|-------------|----------|-----------|-----------------|---------|
| query | The query used by BigQuery to fetch the results. | No | String | | |
| project_id | The project ID of the Google Cloud Platform (GCP) project to use to execute the query. | No | GCPProjectID | | |
| dataset_id | The ID of the persistent BigQuery dataset to store the results of the query. If the dataset does not exist, the operation will create a new one. | Yes | String | | None |
| table_id | The ID of the BigQuery table to store the results of the query. If the table ID is absent, the operation will generate a random ID for the table. | Yes | String | | None |
| output_gcs_path | The path to the Cloud Storage bucket to store the query output. | Yes | GCSPath | | None |
| dataset_location | The location where the dataset is created. Defaults to US. | Yes | String | | US |
| job_config | The full configuration specification for the query job. See [QueryJobConfig](https://googleapis.github.io/google-cloud-python/latest/bigquery/generated/google.cloud.bigquery.job.QueryJobConfig.html#google.cloud.bigquery.job.QueryJobConfig) for details. | Yes | Dict | A JSONobject which has the same structure as [QueryJobConfig](https://googleapis.github.io/google-cloud-python/latest/bigquery/generated/google.cloud.bigquery.job.QueryJobConfig.html#google.cloud.bigquery.job.QueryJobConfig) | None |
## Input data schema
The input data is a BigQuery job containing a query that pulls data f rom various sources.
## Output:
Name | Description | Type
:--- | :---------- | :---
output_gcs_path | The path to the Cloud Storage bucket containing the query output in CSV format. | GCSPath
## Cautions & requirements
To use the component, the following requirements must be met:
* The BigQuery API is enabled.
* The component is running under a secret [Kubeflow user service account](https://www.kubeflow.org/docs/started/getting-started-gke/#gcp-service-accounts) in a Kubeflow Pipeline cluster. For example:
```
bigquery_query_op(...).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
* The Kubeflow user service account is a member of the `roles/bigquery.admin` role of the project.
* The Kubeflow user service account is a member of the `roles/storage.objectCreator `role of the Cloud Storage output bucket.
## Detailed description
This Kubeflow Pipeline component is used to:
* Submit a query to BigQuery.
* The query results are persisted in a dataset table in BigQuery.
* An extract job is created in BigQuery to extract the data from the dataset table and output it to a Cloud Storage bucket as CSV files.
Use the code below as an example of how to run your BigQuery job.
### Sample
Note: The following sample code works in an IPython notebook or directly in Python code.
#### Set sample parameters
```
%%capture --no-stderr
KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.14/kfp.tar.gz'
!pip3 install $KFP_PACKAGE --upgrade
```
2. Load the component using KFP SDK
```
import kfp.components as comp
bigquery_query_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/2e52e54166795d20e92d287bde7b800b181eda02/components/gcp/bigquery/query/component.yaml')
help(bigquery_query_op)
```
### Sample
Note: The following sample code works in IPython notebook or directly in Python code.
In this sample, we send a query to get the top questions from stackdriver public data and output the data to a Cloud Storage bucket. Here is the query:
```
QUERY = 'SELECT * FROM `bigquery-public-data.stackoverflow.posts_questions` LIMIT 10'
```
#### Set sample parameters
```
# Required Parameters
PROJECT_ID = '<Please put your project ID here>'
GCS_WORKING_DIR = 'gs://<Please put your GCS path here>' # No ending slash
# Optional Parameters
EXPERIMENT_NAME = 'Bigquery -Query'
OUTPUT_PATH = '{}/bigquery/query/questions.csv'.format(GCS_WORKING_DIR)
```
#### Run the component as a single pipeline
```
import kfp.dsl as dsl
import kfp.gcp as gcp
import json
@dsl.pipeline(
name='Bigquery query pipeline',
description='Bigquery query pipeline'
)
def pipeline(
query=QUERY,
project_id = PROJECT_ID,
dataset_id='',
table_id='',
output_gcs_path=OUTPUT_PATH,
dataset_location='US',
job_config=''
):
bigquery_query_op(
query=query,
project_id=project_id,
dataset_id=dataset_id,
table_id=table_id,
output_gcs_path=output_gcs_path,
dataset_location=dataset_location,
job_config=job_config).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
#### Compile the pipeline
```
pipeline_func = pipeline
pipeline_filename = pipeline_func.__name__ + '.zip'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
```
#### Submit the pipeline for execution
```
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
```
#### Inspect the output
```
!gsutil cat OUTPUT_PATH
```
## References
* [Component python code](https://github.com/kubeflow/pipelines/blob/master/component_sdk/python/kfp_component/google/bigquery/_query.py)
* [Component docker file](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/Dockerfile)
* [Sample notebook](https://github.com/kubeflow/pipelines/blob/master/components/gcp/bigquery/query/sample.ipynb)
* [BigQuery query REST API](https://cloud.google.com/bigquery/docs/reference/rest/v2/jobs/query)
## License
By deploying or using this software you agree to comply with the [AI Hub Terms of Service](https://aihub.cloud.google.com/u/0/aihub-tos) and the [Google APIs Terms of Service](https://developers.google.com/terms/). To the extent of a direct conflict of terms, the AI Hub Terms of Service will control.
| true |
code
| 0.746624 | null | null | null | null |
|
## Import
```
# Matplotlib
import matplotlib.pyplot as plt
# Tensorflow
import tensorflow as tf
# Numpy and Pandas
import numpy as np
import pandas as pd
# Ohter import
import sys
from sklearn.preprocessing import StandardScaler
```
## Be sure to used Tensorflow 2.0
```
assert hasattr(tf, "function") # Be sure to use tensorflow 2.0
```
## Load the dataset: Fashion MNIST

```
from sklearn.model_selection import train_test_split
# Fashio MNIST
fashion_mnist = tf.keras.datasets.fashion_mnist
(images, targets), (_, _) = fashion_mnist.load_data()
# Get only a subpart of the dataset
# Get only a subpart
images = images[:10000]
targets = targets [:10000]
images = images.reshape(-1, 784)
images = images.astype(float)
scaler = StandardScaler()
images = scaler.fit_transform(images)
images_train, images_test, targets_train, targets_test = train_test_split(images, targets, test_size=0.2, random_state=1)
print(images_train.shape, targets_train.shape)
print(images_test.shape, targets_test.shape)
```
## Plot one of the data
```
targets_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat", "Sandal",
"Shirt", "Sneaker", "Bag", "Ankle boot"
]
# Plot one image
plt.imshow(images[10].reshape(28, 28), cmap="binary")
#plt.title(targets_names[targets[10]])
plt.title(targets_names[targets[10]])
plt.show()
#print("First line of one image", images[11][0])
print("First line of one image", images[11])
print("Associated target", targets[11])
```
# Create the model

# Add the layers
```
# Flatten
model = tf.keras.models.Sequential()
#model.add(tf.keras.layers.Flatten(input_shape=[28, 28]))
# Add the layers
model.add(tf.keras.layers.Dense(256, activation="relu"))
model.add(tf.keras.layers.Dense(128, activation="relu"))
model.add(tf.keras.layers.Dense(10, activation="softmax"))
model_output = model.predict(images[0:1])
print(model_output, targets[0:1])
```
## Model Summary
```
model.summary()
```
## Compile the model
```
# Compile the model
model.compile(
loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"]
)
```
## Train the model
```
history = model.fit(images_train, targets_train, epochs=50, validation_split=0.2)
loss_curve = history.history["loss"]
acc_curve = history.history["accuracy"]
loss_val_curve = history.history["val_loss"]
acc_val_curve = history.history["val_accuracy"]
plt.plot(loss_curve, label="Train")
plt.plot(loss_val_curve, label="Val")
plt.legend(loc='upper left')
plt.title("Loss")
plt.show()
plt.plot(acc_curve, label="Train")
plt.plot(acc_val_curve, label="Val")
plt.legend(loc='upper left')
plt.title("Accuracy")
plt.show()
loss, acc = model.evaluate(images_test, targets_test)
print("Test loss", loss)
print("Train accuracy", acc)
```
| true |
code
| 0.774328 | null | null | null | null |
|
# Amazon Augmented AI (Amazon A2I) integration with Tabular Data [Example]
1. [Introduction](#Introduction)
2. [Prerequisites](#Prerequisites)
1. [Workteam](#Workteam)
2. [Permissions](#Notebook-Permission)
3. [Client Setup](#Client-Setup)
4. [Create Control Plane Resources](#Create-Control-Plane-Resources)
1. [Create Human Task UI](#Create-Human-Task-UI)
2. [Create Flow Definition](#Create-Flow-Definition)
5. [Starting Human Loops](#Scenario-1-:-When-Activation-Conditions-are-met-,-and-HumanLoop-is-created)
1. [Wait For Workers to Complete Task](#Wait-For-Workers-to-Complete-Task)
2. [Check Status of Human Loop](#Check-Status-of-Human-Loop)
3. [View Task Results](#View-Task-Results)
## Introduction
Amazon Augmented AI (Amazon A2I) makes it easy to build the workflows required for human review of ML predictions. Amazon A2I brings human review to all developers, removing the undifferentiated heavy lifting associated with building human review systems or managing large numbers of human reviewers.
You can create your own workflows for ML models built on Amazon SageMaker or any other tools. Using Amazon A2I, you can allow human reviewers to step in when a model is unable to make a high confidence prediction or to audit its predictions on an on-going basis.
Learn more here: https://aws.amazon.com/augmented-ai/
In this tutorial, we will show how you can use **Amazon A2I with Tabular data.** Tabular data is the most common form of data used by data scientists today for generating models. Use cases include, fraud detection, building customer propensity models, forecasting sales using regression etc. In many cases, data scientists often convert unstructured data such as text or images into structured tables that they then use for training models.
Here we will first train a model and use the outputs of the trained model to build a human loop for review.
For more in depth instructions, visit https://docs.aws.amazon.com/sagemaker/latest/dg/a2i-getting-started.html
To incorporate Amazon A2I into your human review workflows, you need three resources:
* A **worker task template** to create a worker UI. The worker UI displays your input data, such as documents or images, and instructions to workers. It also provides interactive tools that the worker uses to complete your tasks. For more information, see https://docs.aws.amazon.com/sagemaker/latest/dg/a2i-instructions-overview.html
* A **human review workflow**, also referred to as a flow definition. You use the flow definition to configure your human workforce and provide information about how to accomplish the human review task. You can create a flow definition in the Amazon Augmented AI console or with Amazon A2I APIs. To learn more about both of these options, see https://docs.aws.amazon.com/sagemaker/latest/dg/a2i-create-flow-definition.html
* A **human loop** to start your human review workflow. When you use one of the built-in task types, the corresponding AWS service creates and starts a human loop on your behalf when the conditions specified in your flow definition are met or for each object if no conditions were specified. When a human loop is triggered, human review tasks are sent to the workers as specified in the flow definition.
When using a custom task type, as this tutorial will show, you start a human loop using the Amazon Augmented AI Runtime API. When you call `start_human_loop()` in your custom application, a task is sent to human reviewers.
### Install Latest SDK
```
# First, let's get the latest installations of our dependencies
!pip install --upgrade pip
!pip install boto3 --upgrade
!pip install -U botocore
```
## Setup
We need to set up the following data:
* `region` - Region to call A2I.
* `BUCKET` - A S3 bucket accessible by the given role
* Used to store the sample images & output results
* Must be within the same region A2I is called from
* `role` - The IAM role used as part of StartHumanLoop. By default, this notebook will use the execution role
* `workteam` - Group of people to send the work to
### Role and Permissions
The AWS IAM Role used to execute the notebook needs to have the following permissions:
* SagemakerFullAccess
* AmazonSageMakerMechanicalTurkAccess (if using MechanicalTurk as your Workforce)
```
from sagemaker import get_execution_role
import sagemaker
# Setting Role to the default SageMaker Execution Role
role = get_execution_role()
display(role)
import os
import boto3
import botocore
sess = sagemaker.Session()
#bucket
BUCKET = sess.default_bucket() # or use a custom bucket if you created one.
PREFIX = 'a2i-data'
#specify output path for artifacts
OUTPUT_PATH = f's3://{BUCKET}/a2i-results'
# Region
region = boto3.session.Session().region_name
print(region)
```
## Tabular data with Amazon SageMaker
Before creating the template, we will load a tabular dataset, split the data into train and test, store the test data in Amazon S3, and train a machine learning model. The dataset we use is on Breast Cancer prediction and can be found here: [1] Dua, D. and Graff, C. (2019). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science.
Based on the input features, we will first train a model to detect a benign or malignant label.
Once the model is trained, we will create an endpoint, and generate some model predictions. We will then create a WorkerUI to load in our immutable test dataset as a table, and dynamically modify the verify and change predictions if needed.
```
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
def generatedf(split_ratio):
"""Loads the dataset into a dataframe and generates train/test splits"""
data = load_breast_cancer()
df = pd.DataFrame(data.data, columns = data.feature_names)
df['label'] = data.target
cols = list(df.columns)
cols = cols[-1:] + cols[:-1]
df = df[cols]
train, test = train_test_split(df, test_size=split_ratio, random_state=42)
return train, test
train_data, test_data = generatedf(0.2)
train_data.head()
#store the datasets locally
train_data.to_csv('train.csv',index = None, header=None)
test_data.to_csv('test.csv', index = None, header=None)
# load the data into S3
sess.upload_data('train.csv', bucket=BUCKET, key_prefix=os.path.join(PREFIX, 'train'))
sess.upload_data('test.csv', bucket=BUCKET, key_prefix=os.path.join(PREFIX, 'test'))
#load the train and test data filenames from Amazon S3
s3_input_train = sagemaker.s3_input(s3_data='s3://{}/{}/train'.format(BUCKET, PREFIX), content_type='csv')
s3_input_validation = sagemaker.s3_input(s3_data='s3://{}/{}/test/'.format(BUCKET, PREFIX), content_type='csv')
```
### Train and Deploy the model
SageMaker will set up the instance types needed and copy the data over to train the model. This may take about **3** minutes to complete training. Once the model is trained, we will deploy the model as an endpoint. Again, SageMaker will set up the instance required, copy the inference image and the inference code and create a HTTPS endpoint. This may take **4-5** minutes. For more details on how SageMaker creates an endpoint, visit: https://docs.aws.amazon.com/sagemaker/latest/dg/how-it-works-hosting.html
```
from sagemaker.amazon.amazon_estimator import get_image_uri
container = get_image_uri(region, 'xgboost', '0.90-1')
xgb = sagemaker.estimator.Estimator(container,
role,
train_instance_count=1,
train_instance_type='ml.m5.xlarge',
output_path=OUTPUT_PATH,
sagemaker_session=sess)
xgb.set_hyperparameters(max_depth=2,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.8,
silent=0,
objective='binary:logistic',
num_round=100,
eval_metric='auc')
xgb.fit({'train': s3_input_train,
'validation': s3_input_validation})
xgb_predictor = xgb.deploy(initial_instance_count = 1, instance_type = 'ml.m5.xlarge')
from sagemaker.predictor import csv_serializer
xgb_predictor.content_type = 'text/csv'
xgb_predictor.serializer = csv_serializer
xgb_predictor.deserializer = None
## Lets now run predictions on our test set and use it to create a table containing our outputs.
import numpy as np
def predict(data, model, rows=500):
split_array = np.array_split(data, int(data.shape[0] / float(rows) + 1))
predictions = ''
for array in split_array:
predictions = ','.join([predictions, model.predict(array).decode('utf-8')])
return np.round(np.fromstring(predictions[1:], sep=','))
## Generate predictions on the test set for the difference models
predictions = predict(test_data[list(test_data.columns)[1:]].values, xgb_predictor)
predictions
```
### Creating human review Workteam or Workforce
A workforce is the group of workers that you have selected to label your dataset. You can choose either the Amazon Mechanical Turk workforce, a vendor-managed workforce, or you can create your own private workforce for human reviews. Whichever workforce type you choose, Amazon Augmented AI takes care of sending tasks to workers.
When you use a private workforce, you also create work teams, a group of workers from your workforce that are assigned to Amazon Augmented AI human review tasks. You can have multiple work teams and can assign one or more work teams to each job.
To create your Workteam, visit the instructions here: https://docs.aws.amazon.com/sagemaker/latest/dg/sms-workforce-management.html
After you have created your workteam, replace YOUR_WORKTEAM_ARN below
```
WORKTEAM_ARN = 'arn:aws:sagemaker:us-east-2:{account_num}:workteam/private-crowd/stefan-team'#'YOUR_WORKTEAM_ARN'
```
Visit: https://docs.aws.amazon.com/sagemaker/latest/dg/a2i-permissions-security.html to add the necessary permissions to your role
### Client Setup
Here we are going to setup the rest of our clients.
```
import io
import uuid
import time
timestamp = time.strftime("%Y-%m-%d-%H-%M-%S", time.gmtime())
# Amazon SageMaker client
sagemaker_client = boto3.client('sagemaker', region)
# Amazon Augment AI (A2I) client
a2i = boto3.client('sagemaker-a2i-runtime')
# Amazon S3 client
s3 = boto3.client('s3', region)
# Flow definition name - this value is unique per account and region. You can also provide your own value here.
flowDefinitionName = 'fd-sagemaker-tabular-data-demo-' + timestamp
# Task UI name - this value is unique per account and region. You can also provide your own value here.
taskUIName = 'ui-sagemaker-tabular-data-demo-' + timestamp
```
## Create Control Plane Resources
### Create Human Task UI
Create a human task UI resource, giving a UI template in liquid html. This template will be rendered to the human workers whenever human loop is required.
For over 70 pre built UIs, check: https://github.com/aws-samples/amazon-a2i-sample-task-uis.
We will use the following template to render both the test dataset, as well as the model predictions
```
template = r"""
<script src="https://assets.crowd.aws/crowd-html-elements.js"></script>
<style>
table, tr, th, td {
border: 1px solid black;
border-collapse: collapse;
padding: 5px;
}
</style>
<crowd-form>
<div>
<h1>Instructions</h1>
<p>Please review the predictions in the Predictions table based on the input data table below, and make corrections where appropriate. </p>
<p> Here are the labels: </p>
<p> 0: Benign </p>
<p> 1: Malignant </p>
</div>
<div>
<h3> Breast cancer dataset </h3>
<div id="my_table"> {{ task.input.table | skip_autoescape }} </div>
</div>
<br>
<h1> Predictions Table </h1>
<table>
<tr>
<th>ROW NUMBER</th>
<th>MODEL PREDICTION</th>
<th>AGREE/DISAGREE WITH ML RATING?</th>
<th>YOUR PREDICTION</th>
<th>CHANGE REASON </th>
</tr>
{% for pair in task.input.Pairs %}
<tr>
<td>{{ pair.row }}</td>
<td><crowd-text-area name="predicted{{ forloop.index }}" value="{{ pair.prediction }}"></crowd-text-area></td>
<td>
<p>
<input type="radio" id="agree{{ forloop.index }}" name="rating{{ forloop.index }}" value="agree" required>
<label for="agree{{ forloop.index }}">Agree</label>
</p>
<p>
<input type="radio" id="disagree{{ forloop.index }}" name="rating{{ forloop.index }}" value="disagree" required>
<label for="disagree{{ forloop.index }}">Disagree</label>
</p>
</td>
<td>
<p>
<input type="text" name="True Prediction" placeholder="Enter your Prediction" />
</p>
</td>
<td>
<p>
<input type="text" name="Change Reason" placeholder="Explain why you changed the prediction" />
</p>
</td>
</tr>
{% endfor %}
</table>
</crowd-form>
"""
def create_task_ui():
'''
Creates a Human Task UI resource.
Returns:
struct: HumanTaskUiArn
'''
response = sagemaker_client.create_human_task_ui(
HumanTaskUiName=taskUIName,
UiTemplate={'Content': template})
return response
# Create task UI
humanTaskUiResponse = create_task_ui()
humanTaskUiArn = humanTaskUiResponse['HumanTaskUiArn']
print(humanTaskUiArn)
```
### Create the Flow Definition
In this section, we're going to create a flow definition definition. Flow Definitions allow us to specify:
* The workforce that your tasks will be sent to.
* The instructions that your workforce will receive. This is called a worker task template.
* The configuration of your worker tasks, including the number of workers that receive a task and time limits to complete tasks.
* Where your output data will be stored.
This demo is going to use the API, but you can optionally create this workflow definition in the console as well.
For more details and instructions, see: https://docs.aws.amazon.com/sagemaker/latest/dg/a2i-create-flow-definition.html.
```
create_workflow_definition_response = sagemaker_client.create_flow_definition(
FlowDefinitionName= flowDefinitionName,
RoleArn= role,
HumanLoopConfig= {
"WorkteamArn": WORKTEAM_ARN,
"HumanTaskUiArn": humanTaskUiArn,
"TaskCount": 1,
"TaskDescription": "Make sure the labels are correct",
"TaskTitle": "tabular data a2i demo"
},
OutputConfig={
"S3OutputPath" : OUTPUT_PATH
}
)
flowDefinitionArn = create_workflow_definition_response['FlowDefinitionArn'] # let's save this ARN for future use
# Describe flow definition - status should be active
for x in range(60):
describeFlowDefinitionResponse = sagemaker_client.describe_flow_definition(FlowDefinitionName=flowDefinitionName)
print(describeFlowDefinitionResponse['FlowDefinitionStatus'])
if (describeFlowDefinitionResponse['FlowDefinitionStatus'] == 'Active'):
print("Flow Definition is active")
break
time.sleep(2)
```
## Human Loops
Now that we have setup our Flow Definition, we are ready to start the human loop to have the reviewers asynchronously review the outputs generated by our model. First we need to create a dictionary containing our model outputs, so we can load it dynamically
```
item_list = [{'row': "ROW_{}".format(x), 'prediction': predictions[x]} for x in range(5)]
item_list
ip_content = {"table": test_data.reset_index().drop(columns = ['index', 'label']).head().to_html(),
'Pairs': item_list
}
import json
humanLoopName = str(uuid.uuid4())
start_loop_response = a2i.start_human_loop(
HumanLoopName=humanLoopName,
FlowDefinitionArn=flowDefinitionArn,
HumanLoopInput={
"InputContent": json.dumps(ip_content)
}
)
```
### Check Status of Human Loop
```
resp = a2i.describe_human_loop(HumanLoopName=humanLoopName)
print(f'HumanLoop Name: {humanLoopName}')
print(f'HumanLoop Status: {resp["HumanLoopStatus"]}')
print(f'HumanLoop Output Destination: {resp["HumanLoopOutput"]}')
print('\n')
if resp["HumanLoopStatus"] == "Completed":
completed_human_loops.append(resp)
```
### Wait For Workers to Complete Task
Since we are using private workteam, we should go to the labling UI to perform the inspection ourselves.
```
workteamName = WORKTEAM_ARN[WORKTEAM_ARN.rfind('/') + 1:]
print("Navigate to the private worker portal and do the tasks. Make sure you've invited yourself to your workteam!")
print('https://' + sagemaker_client.describe_workteam(WorkteamName=workteamName)['Workteam']['SubDomain'])
```
### Check Status of Human Loop Again
```
resp = a2i.describe_human_loop(HumanLoopName=humanLoopName)
print(f'HumanLoop Name: {humanLoopName}')
print(f'HumanLoop Status: {resp["HumanLoopStatus"]}')
print(f'HumanLoop Output Destination: {resp["HumanLoopOutput"]}')
print('\n')
if resp["HumanLoopStatus"] == "Completed":
completed_human_loops.append(resp)
```
### View Task Results
```
import re
import pprint
pp = pprint.PrettyPrinter(indent=4)
for resp in completed_human_loops:
splitted_string = re.split('s3://' + BUCKET + '/', resp['HumanLoopOutput']['OutputS3Uri'])
output_bucket_key = splitted_string[1]
response = s3.get_object(Bucket=BUCKET, Key=output_bucket_key)
content = response["Body"].read()
json_output = json.loads(content)
pp.pprint(json_output)
print('\n')
```
### Delete Resources
```
a2i.stop_human_loop(HumanLoopName=humanLoopName)
a2i.delete_human_loop(HumanLoopName=humanLoopName)
xgb_predictor.delete_endpoint()
```
| true |
code
| 0.496643 | null | null | null | null |
|
# LassoLars with Quantile Transformer
This Code template is for the regression analysis using a simple LassoLars Regression with Feature Transformation technique QuantileTransformer in a pipeline. It is a lasso model implemented using the LARS algorithm.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import QuantileTransformer
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
from sklearn.linear_model import LassoLars
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
```
### Feature Transformation
Quantile Transformer
This method transforms the features to follow a uniform or a normal distribution. Therefore, for a given feature, this transformation tends to spread out the most frequent values. It also reduces the impact of (marginal) outliers: this is therefore a robust preprocessing scheme.
Transform features using quantiles information.
### Model
LassoLars is a lasso model implemented using the LARS algorithm, and unlike the implementation based on coordinate descent, this yields the exact solution, which is piecewise linear as a function of the norm of its coefficients.
### Tuning parameters
> **fit_intercept** -> whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations
> **alpha** -> Constant that multiplies the penalty term. Defaults to 1.0. alpha = 0 is equivalent to an ordinary least square, solved by LinearRegression. For numerical reasons, using alpha = 0 with the LassoLars object is not advised and you should prefer the LinearRegression object.
> **eps** -> The machine-precision regularization in the computation of the Cholesky diagonal factors. Increase this for very ill-conditioned systems. Unlike the tol parameter in some iterative optimization-based algorithms, this parameter does not control the tolerance of the optimization.
> **max_iter** -> Maximum number of iterations to perform.
> **positive** -> Restrict coefficients to be >= 0. Be aware that you might want to remove fit_intercept which is set True by default. Under the positive restriction the model coefficients will not converge to the ordinary-least-squares solution for small values of alpha. Only coefficients up to the smallest alpha value (alphas_[alphas_ > 0.].min() when fit_path=True) reached by the stepwise Lars-Lasso algorithm are typically in congruence with the solution of the coordinate descent Lasso estimator.
> **precompute** -> Whether to use a precomputed Gram matrix to speed up calculations.
```
model = make_pipeline(QuantileTransformer(),LassoLars())
model.fit(x_train,y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
score: The score function returns the coefficient of determination R2 of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(14,10))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(x_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator: Ageer Harikrishna , Github: [Profile](https://github.com/ageerHarikrishna)
| true |
code
| 0.478955 | null | null | null | null |
|
This notebook contains a short guide on using the solvers w/o backprop or computing gradients. Some issues of interest include:
1. How to define and solve SDEs with this codebase
1. How to run things on a GPU
1. How to gain control over the randomness and enforce deterministic behavior with fixed seeds (e.g. when testing)
1. The subtlety of noise type in SDEs
The other file in the `examples` folder (`latent_sde.py`) contains the use case where gradients need to be taken to fit parameters.
```
import torch
from torch import nn
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
%matplotlib inline
import matplotlib.pyplot as plt
from torchsde import sdeint, BrownianPath, BrownianTree
```
Just like how each ordinary differential equation (ODE) is governed by a vector field, a stochastic differential equation (SDE) is governed by two vector fields, which are called the **drift** and **diffusion** functions:
$$dx(t) = \underbrace{f(x(t), t, \theta_f)}_{\text{drift}} dt + \underbrace{g(x(t), t, \theta_g)}_{\text{diffusion}} dW(t).$$
The output of $f$ is of the same size as the $d$-dimensional state, whereas the output of $g$ may be a matrix of size $(d, m)$.
Here, $W(t)$ is the Brownian motion (aka Wiener process), and it may be $m$ dimensional. It is a stochastic process, and each random draw produces a function of time.
### 1. Solving a simple SDE
To implement an SDE, we create a class with the functions `f` and `g`:
```
class SDE(nn.Module):
def __init__(self):
super().__init__()
self.theta = nn.Parameter(torch.tensor(0.1), requires_grad=False) # Scalar parameter.
self.noise_type = "diagonal"
self.sde_type = "ito"
def f(self, t, y):
return torch.sin(t) + self.theta * y
def g(self, t, y):
return 0.3 * torch.sigmoid(torch.cos(t) * torch.exp(-y))
```
The functions `f` and `g` are arbitrarily chosen for demonstration purposes. The attributes `noise_type` and `sde_type` are used in the solver to determine the particular numerical method being used and must be included. We use `diagonal` here, meaning the output of `g` should be a vector with the same shape as input `y`, and it is an element-wise function.
Note that for any other noise type, we expect the output of `g` to be a matrix, and batch matrix-vector product is performed under the hood.
The requirement of element-wise function is a rather technical condition to ensure the high-order solvers attain their theoretically derived efficiency.
All solvers in the codebase are based on [Itô stochastic integrals](https://en.wikipedia.org/wiki/It%C3%B4_calculus), so we use `ito` for the `sde_type` attribute. The library also has a base class `SDEIto`, which can be inherited from and imported directly, and saves the extra line of setting the `sde_type` attribute. As a side note, our adjoint computation internally computes a Stratonovich correction term and performs the reverse pass with it. We plan to add solvers based on stratonovich SDEs in the future.
Now we instantiate an object of the SDE class and call the function `sdeint` on it.
```
batch_size, d, T = 3, 1, 100
sde = SDE()
ts = torch.linspace(0, 1, T)
y0 = torch.zeros(batch_size, 1).fill_(0.1) # (batch_size, d)
with torch.no_grad():
ys = sdeint(sde, y0, ts, method='srk') # (T, batch_size, d) = (100, 3, 1).
plt.figure()
for i in range(batch_size):
plt.plot(ts, ys[:, i].squeeze(), marker='x', label=f'sample {i}')
plt.xlabel('$t$')
plt.ylabel('$y_t$')
plt.legend()
plt.show()
```
`method='srk'` means the strong order 1.5 Stochastic Runge-Kutta (SRK) method is used. Other possible methods include the strong order 0.5 `euler` and strong order 1.0 `milstein`, both of which are of slightly lower order.
We stress that the drift and diffusion functions don't necessarily need to be defined as the `f` and `g` methods of the class. They can be methods with any name, so long as we provide these names to the solver when they differ from the default `f` and `g`. The following is an example where the function `h` is used as the drift.
```
class SDENewName(nn.Module):
def __init__(self):
super().__init__()
self.theta = nn.Parameter(torch.tensor(0.1), requires_grad=False) # Scalar parameter.
self.noise_type = "diagonal"
self.sde_type = "ito"
def h(self, t, y):
return torch.sin(t) + self.theta * y
def g(self, t, y):
return 0.3 * torch.sigmoid(torch.cos(t) * torch.exp(-y))
sde_new_name = SDENewName()
with torch.no_grad():
ys = sdeint(sde_new_name, y0, ts, method='srk', names={'drift': 'h'}) # Supply a dictionary to the argument `names`.
plt.figure()
for i in range(batch_size):
plt.plot(ts, ys[:, i].squeeze(), marker='x', label=f'sample {i}')
plt.xlabel('$t$')
plt.ylabel('$y_t$')
plt.legend()
plt.show()
```
### 2. Moving to GPUs
Trivially, the previous code may be adapted to run on GPUs, just by moving all tensors to a GPU:
```
if torch.cuda.is_available():
gpu = torch.device('cuda')
sde = SDE().to(gpu)
ts = ts.to(gpu)
y0 = y0.to(gpu)
with torch.no_grad():
ys = sdeint(sde, y0, ts, method='srk') # (100, 3, 1).
plt.figure()
for i in range(batch_size):
plt.plot(ts.cpu(), ys[:, i].squeeze().cpu(), marker='x', label=f'sample {i}')
plt.xlabel('$t$')
plt.ylabel('$y_t$')
plt.legend()
plt.show()
```
A side note is that multi-GPU data parallel is possible with the existing codebase, but the use case has not been tried out extensively and may require defining non-standard SDE classes and methods.
### 3. Explicit control over randomness from the Brownian motion
To gain control over the randomness, we draw Brownian motion samples by instantiating objects of classes `BrownianPath` or `BrownianTree`. `BrownianPath` has fast query, but stores all previous queries, so is costly in memory. `BrownianTree` only stores objects in a fixed size cache, but has slower query, since everything else is reconstructed on the fly based on random seed splitting. Repeated queries on the same Brownian motion object gives deterministic results. Here, we use `BrownianPath` as an example.
```
ts = torch.linspace(0, 1, T)
bm = BrownianPath(t0=0.0, w0=torch.zeros(batch_size, d))
bm_queries = torch.stack([bm(t) for t in ts], dim=0)
plt.figure()
plt.title('Query')
for i in range(batch_size):
plt.plot(ts, bm_queries[:, i].squeeze(), marker='x', label=f'sample {i}')
plt.xlabel('$t$')
plt.ylabel('$W_t$')
plt.legend()
plt.show()
bm_queries2 = torch.stack([bm(t) for t in ts], dim=0)
plt.figure()
plt.title('Query again (samples should be same as before)')
for i in range(batch_size):
plt.plot(ts, bm_queries2[:, i].squeeze(), marker='x', label=f'sample {i}')
plt.xlabel('$t$')
plt.ylabel('$W_t$')
plt.legend()
plt.show()
assert torch.allclose(bm_queries, bm_queries2)
```
In our experience, having the Brownian motion run on CPUs is usually slightly faster than having it run on GPUs (though, generally, this obviously depends on the specific hardware, software, and program). When the latter is necessary, we can achieve this by either putting `w0` on the GPU or using the `to` method of the `bm` object:
```
if torch.cuda.is_available():
# Approach 1:
bm = BrownianPath(t0=0.0, w0=torch.zeros(batch_size, d).to(gpu)) # Runs on GPU.
print(bm(0.5))
# Approach 2:
bm = BrownianPath(t0=0.0, w0=torch.zeros(batch_size, d)) # Runs on CPU.
bm.to(gpu) # Runs on GPU.
print(bm(0.5))
```
We can also feed this fixed Brownian motion sample into the solver to get deterministic behavior:
```
sde = SDE()
ts = torch.linspace(0, 1, T)
y0 = torch.zeros(batch_size, 1).fill_(0.1) # (batch_size, d)
with torch.no_grad():
ys = sdeint(sde, y0, ts, method='srk', bm=bm)
plt.figure()
plt.title('Solve SDE')
for i in range(batch_size):
plt.plot(ts, ys[:, i].squeeze(), marker='x', label=f'sample {i}')
plt.xlabel('$t$')
plt.ylabel('$y_t$')
plt.legend()
plt.show()
with torch.no_grad():
ys = sdeint(sde, y0, ts, method='srk', bm=bm)
plt.figure()
plt.title('Solve SDE again (samples should be same as before)')
for i in range(batch_size):
plt.plot(ts, ys[:, i].squeeze(), marker='x', label=f'sample {i}')
plt.xlabel('$t$')
plt.ylabel('$y_t$')
plt.legend()
plt.show()
# Use a new BM sample, we expect different sample paths.
bm = BrownianPath(t0=0.0, w0=torch.zeros(batch_size, d))
with torch.no_grad():
ys = sdeint(sde, y0, ts, method='srk', bm=bm)
plt.figure()
plt.title('Solve SDE (expect different sample paths)')
for i in range(batch_size):
plt.plot(ts, ys[:, i].squeeze(), marker='x', label=f'sample {i}')
plt.xlabel('$t$')
plt.ylabel('$y_t$')
plt.legend()
plt.show()
```
### 4. Noise type of SDEs affects which solvers can be used and what strong orders can be attained
The supported noise types of this codebase are "diagonal", "additive", "scalar", and "general". The following is a simple summary of each type:
- "diagonal": The diffusion function is an elementwise function, with the output being the same dimension as the state (both $d$-dimensional). There are $d$ independent Brownian motions, each responsible for the noise of only a single state dimension.
- "additive": The diffusion function is a constant w.r.t. the state, i.e. the derivative of the diffusion function w.r.t. the state is 0. The output of the diffusion function is of size $(d, m)$, and the system has $m$ independent Brownian motions. The integral involving the Brownian motion can be loosely interpreted as integrating a sequence of matrix-vector products.
- "scalar": The diffusion function has output shape $(d, 1)$, and a single Brownian motion is shared across all state dimensions.
- "general": The diffusion function has output shape $(d, m)$, and the system has $m$ independent Brownian motions.
It is tempting to use the noise type configuration "general" for all problems. However, since there's little known structure for these SDEs, high-order solvers are not possible, and the current codebase only supports the `euler` method. All three methods (`euler`, `milstein`, and `srk`) are supported for all remaining noise types.
Lastly, for modeling problems, our limited experience have found "diagonal" to be a good setting, where flexibility of models and tractability of numerical integration is rather well-balanced.
| true |
code
| 0.808899 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.